-
PDF
- Split View
-
Views
-
Cite
Cite
Jie Liu, Zhen Yan, Zhi-Qiang Shen, Zhi-Peng Huang, Ru-Shuang Zhao, Ya-Jun Wu, Jian-Ping Yuan, Xin-Ji Wu, New timing measurement results of 16 pulsars, Publications of the Astronomical Society of Japan, Volume 72, Issue 4, August 2020, 70, https://doi.org/10.1093/pasj/psaa058
Close - Share Icon Share
Abstract
A pulsar’s position, proper motion, and parallax are important parameters in timing equations. It is challenging to fit astrometric parameters accurately through pulsar timing, especially for pulsars that show irregular timing properties. With the fast development of related techniques, it is possible to measure astrometric parameters of more and more pulsars in a model-independent manner with very-long-baseline interferometry (VLBI). In this work we select 16 normal pulsars, whose parallax and proper motion have not been successfully fitted with timing observations or show obvious differences from the corresponding latest VLBI solutions, and do further studies on their timing properties. After updating the astrometric parameters in pulsar ephemerides with the latest VLBI measurements, we derive the latest rotation solutions of these pulsars with observation data in the S and C bands obtained from the Shanghai Tian Ma Radio Telescope. Compared with the spin frequency ν inferred from previous rotation solutions, the newly fitted ν show differences larger than 10−9 Hz for most pulsars. The contribution of the Shklovsky effect to the period derivative |$\dot{P}$| can be properly removed by taking advantage of the accurate proper motion and distance of target pulsars measured by VLBI astrometry. This further leads to a precise estimate of the intrinsic characteristic age τc. The differences between the newly measured τc and corresponding previous results are as large as 2% for some pulsars. VLBI astrometric parameter solutions also lead to better measurements of timing irregularities. For PSR B0154+61, the glitch epoch (MJD 58279.5) measured with a previous ephemeris is about 13 d later than the result (MJD 58266.4) obtained with VLBI astrometric parameter solutions.
1 Introduction
It is challenging to obtain accurate pulsar astrometric parameters. Usually, the pulsar distance is roughly estimated based on its dispersion measure (DM) and Galactic electron density distribution models, such as TC93 (Taylor & Cordes 1993), NE2001 (Cordes & Lazio 2002), and YMW16 (Yao et al. 2017). However, the precision of a distance measured by model-dependent methods is limited by the low fidelity of the Galactic electron density distribution models. What is more, the DM-based distance of some individual pulsars may have considerable error (Deller et al. 2009) or systematic bias (Lorimer et al. 2006). The lower or upper limits of the distance can also be estimated by H i absorption measurements for some pulsars (Koribalski et al. 1995). A pulsar’s motion can be estimated by measuring the interstellar scintillation effect (Cordes & Wasserman 1984; Cordes 1986; Gothoskar & Gupta 2000; Ord & Bailes 2005). However, scintillation velocity has a large error and highly depends on measurement of the pulsar’s distance (Gupta 1995).
As well as the optical method for a few pulsars (or their companion stars) with corresponding radiation, there are two common ways to measure the astrometric parameters of pulsars. One is long-term high-accuracy pulsar timing, the other is multi-epoch high-resolution very-long-baseline interferometry (VLBI) observations. As shown in equation (1), pulsar astrometric parameters are not independent of each other. It is difficult to precisely measure pulsar astrometric parameters by pulsar timing, especially for pulsars that show timing irregularities (timing noise or glitches). The position and proper motion of 374 pulsars were measured using extremely long-term timing data obtained from the 76 m Lovell Radio Telescope at Jodrell Bank Observatory (Hobbs et al. 2004). This is the largest sample of pulsar astrometric parameters obtained with pulsar timing so far. Although the “harmonic whitening” method was used in their data analysis process, the fitted astrometric parameters of some pulsars still had large errors. It was almost impossible to obtain relatively reliable proper motion for some of these pulsars.
High-precision VLBI astrometry offers a powerful way to directly measure the parallax and proper motion of a pulsar. Efforts to measure pulsar astrometric parameters by radio interferometry started in the 1970s (Anderson et al. 1975; Brouw & Spoelstra 1976). Initially, it was only possible to perform interferometry observations of several bright nearby pulsars. With the steady progress of VLBI observations and correlation and data processing techniques (Bartel et al. 1985; Deller et al. 2007), astrometry observations of more and more pulsars have been successfully accomplished with VLBI (Gwinn et al. 1986; Sekido et al. 1999; Brisken et al. 2003; Chatterjee et al. 2009; Deller et al. 2009, 2019). The precision of VLBI measurements is getting higher and higher. By now, there are at least 96 pulsars whose astrometric parameters have been accurately measured with VLBI.1 Benefiting from the high accuracy and independence of pulsar astrometric parameters obtained with VLBI, PSR J0337+1715 was successfully identified as a millisecond pulsar stellar triple system by pulsar timing (Ransom et al. 2014).
It is expected that the timing properties of normal pulsars will be better estimated by updating their astrometric parameters using VLBI measurements, as this has proved useful for millisecond pulsars. We select 16 normal pulsars whose parallax and proper motion have not been successfully fitted with timing observations or differ a lot from the corresponding latest VLBI results (Hobbs et al. 2004; Deller et al. 2019). The pulsar name, timing, and VLBI solutions of position (RA, Dec), proper motion (μα, μδ), parallax (PX), and position epoch (Pos. epoch) are listed in table 1 from left to right. These 16 pulsars are frequently observed with the newly built Shanghai Tian Ma Radio Telescope (TMRT). We update the position, proper motion, and parallax in ephemerides (referred to as updated ephemerides) of 16 pulsars using their latest VLBI measurements, and further study their timing properties. This paper is organized as follows. The observations and data reduction are introduced in section 2. Our analysis and detailed results are shown in section 3. A discussion and conclusion are presented in sections 4 and 5, respectively.
| . | . | RA . | Dec . | μα . | μδ . | PX . | Pos. epoch‡ . |
|---|---|---|---|---|---|---|---|
| Name . | Solutions† . | (h m s) . | (° ′ ″) . | (mas yr−1) . | (mas yr−1) . | (mas) . | (MJD) . |
| B0031−07 | Timing | 00:34:08.84(5) | −07:21:53.1(14) | −16(26) | 17(53) | — | 52275 |
| VLBIb | 00:34:08.8703(1) | −07:21:53.409(2) | 10.37(8) | −11.13(16) | 0.93(8) | ||
| B0136+57 | Timing | 01:39:19.744(4) | +58:14:31.73(3) | — | — | — | 52275 |
| VLBIb | 01:39:19.7401(12) | +58:14:31.819(17) | −19.11(7) | −16.60(7) | 0.37(4) | ||
| B0148−06 | Timing | 01:51:22.72(6) | −06:35:03.5(20) | 19(42) | −39(87) | — | 56000 |
| VLBIc | 01:51:22.7179(2) | −06:35:02.987(2) | 10.7(1) | −5.38(7) | 0.23(9) | ||
| B0154+61 | Timing | 01:57:49.80(7) | +62:12:27.3(7) | −51(36) | 81(33) | — | 56000 |
| VLBIc | 01:57:49.9434(1) | +62:12:26.648(1) | 1.57(6) | 44.80(4) | 0.56(3) | ||
| B0450+55 | Timing | 04:54:07.746(6) | +55:43:41.4(1) | 48(6) | −13(12) | — | 52275 |
| VLBIb | 04:54:07.7506(1) | +55:43:41.437(2) | 53.34(6) | −17.56(14) | 0.84(5) | ||
| B0611+22 | Timing | 06:14:17.16(3) | +22:30:36(17) | — | — | — | 56000 |
| VLBIc | 06:14:17.0058(1) | +22:29:56.848(1) | −0.24(4) | −1.25(4) | 0.28(3) | ||
| B0626+24 | Timing | 06:29:05.77(2) | +24:15:50(6) | 32(15) | 400(300) | — | 56000 |
| VLBIc | 06:29:05.7273(1) | +24:15:41.546(1) | 3.56(12) | −4.68(8) | 0.32(5) | ||
| B0727−18 | Timing | 07:29:32.351(3) | −18:36:42.75(7) | — | — | — | 56000 |
| VLBIc | 07:29:32.3369(1) | −18:36:42.244(2) | −13.06(11) | 13.27(44) | 0.50(9) | ||
| B0809+74 | Timing | 08:14:59.49(2) | +74:29:05.8(2) | 18(20) | −49(21) | — | 48382 |
| VLBIa | 08:14:59.5412(10) | +74:29:05.367(15) | 24.02(9) | −44.0(4) | 2.31(4) | ||
| B0820+02 | Timing | 08:23:09.77(1) | +01:59:12.7(5) | −2(8) | 18(24) | — | 56000 |
| VLBIc | 08:23:09.7651(1) | +01:59:12.469(1) | −4.0(2) | 0.15(26) | 0.4(1) | ||
| B1530+27 | Timing | 15:32:10.37(4) | +27:45:49.3(7) | 6(24) | −7(30) | — | 56000 |
| VLBIc | 15:32:10.3646(1) | +27:45:49.623(1) | 1.5(1) | 18.93(11) | 0.59(6) | ||
| B1540−06 | Timing | 15:43:30.136(9) | −06:20:45.5(4) | −18(6) | −14(19) | — | 56000 |
| VLBIc | 15:43:30.1373(1) | −06:20:45.332(2) | −16.79(4) | −0.30(13) | 0.31(4) | ||
| B1541+09 | Timing | 15:43:38.82(4) | +09:29:15(1) | 9(39) | −113(76) | — | 52275 |
| VLBIb | 15:43:38.8250(1) | +09:29:16.339(2) | −7.61(6) | −2.87(7) | 0.13(2) | ||
| B1642−03 | Timing | 16:45:02.0414(6) | −03:17:58.32(3) | — | — | — | 56000 |
| VLBIc | 16:45:02.0406(1) | −03:17:57.819(2) | −1.035(27) | 20.5(2) | 0.26(2) | ||
| B2154+40 | Timing | 21:57:01.84(1) | +40:17:45.9(2) | 0(13) | 7(15) | — | 52275 |
| VLBIb | 21:57:01.8495(1) | +40:17:45.986(2) | 16.13(10) | 4.12(12) | 0.28(6) | ||
| B2351+61 | Timing | 23:54:04.77(1) | +61:55:46.8(1) | 18(8) | −1(6) | — | 56000 |
| VLBIc | 23:54:04.7830(1) | +61:55:46.845(1) | 22.76(5) | 4.897(25) | 0.41(4) |
| . | . | RA . | Dec . | μα . | μδ . | PX . | Pos. epoch‡ . |
|---|---|---|---|---|---|---|---|
| Name . | Solutions† . | (h m s) . | (° ′ ″) . | (mas yr−1) . | (mas yr−1) . | (mas) . | (MJD) . |
| B0031−07 | Timing | 00:34:08.84(5) | −07:21:53.1(14) | −16(26) | 17(53) | — | 52275 |
| VLBIb | 00:34:08.8703(1) | −07:21:53.409(2) | 10.37(8) | −11.13(16) | 0.93(8) | ||
| B0136+57 | Timing | 01:39:19.744(4) | +58:14:31.73(3) | — | — | — | 52275 |
| VLBIb | 01:39:19.7401(12) | +58:14:31.819(17) | −19.11(7) | −16.60(7) | 0.37(4) | ||
| B0148−06 | Timing | 01:51:22.72(6) | −06:35:03.5(20) | 19(42) | −39(87) | — | 56000 |
| VLBIc | 01:51:22.7179(2) | −06:35:02.987(2) | 10.7(1) | −5.38(7) | 0.23(9) | ||
| B0154+61 | Timing | 01:57:49.80(7) | +62:12:27.3(7) | −51(36) | 81(33) | — | 56000 |
| VLBIc | 01:57:49.9434(1) | +62:12:26.648(1) | 1.57(6) | 44.80(4) | 0.56(3) | ||
| B0450+55 | Timing | 04:54:07.746(6) | +55:43:41.4(1) | 48(6) | −13(12) | — | 52275 |
| VLBIb | 04:54:07.7506(1) | +55:43:41.437(2) | 53.34(6) | −17.56(14) | 0.84(5) | ||
| B0611+22 | Timing | 06:14:17.16(3) | +22:30:36(17) | — | — | — | 56000 |
| VLBIc | 06:14:17.0058(1) | +22:29:56.848(1) | −0.24(4) | −1.25(4) | 0.28(3) | ||
| B0626+24 | Timing | 06:29:05.77(2) | +24:15:50(6) | 32(15) | 400(300) | — | 56000 |
| VLBIc | 06:29:05.7273(1) | +24:15:41.546(1) | 3.56(12) | −4.68(8) | 0.32(5) | ||
| B0727−18 | Timing | 07:29:32.351(3) | −18:36:42.75(7) | — | — | — | 56000 |
| VLBIc | 07:29:32.3369(1) | −18:36:42.244(2) | −13.06(11) | 13.27(44) | 0.50(9) | ||
| B0809+74 | Timing | 08:14:59.49(2) | +74:29:05.8(2) | 18(20) | −49(21) | — | 48382 |
| VLBIa | 08:14:59.5412(10) | +74:29:05.367(15) | 24.02(9) | −44.0(4) | 2.31(4) | ||
| B0820+02 | Timing | 08:23:09.77(1) | +01:59:12.7(5) | −2(8) | 18(24) | — | 56000 |
| VLBIc | 08:23:09.7651(1) | +01:59:12.469(1) | −4.0(2) | 0.15(26) | 0.4(1) | ||
| B1530+27 | Timing | 15:32:10.37(4) | +27:45:49.3(7) | 6(24) | −7(30) | — | 56000 |
| VLBIc | 15:32:10.3646(1) | +27:45:49.623(1) | 1.5(1) | 18.93(11) | 0.59(6) | ||
| B1540−06 | Timing | 15:43:30.136(9) | −06:20:45.5(4) | −18(6) | −14(19) | — | 56000 |
| VLBIc | 15:43:30.1373(1) | −06:20:45.332(2) | −16.79(4) | −0.30(13) | 0.31(4) | ||
| B1541+09 | Timing | 15:43:38.82(4) | +09:29:15(1) | 9(39) | −113(76) | — | 52275 |
| VLBIb | 15:43:38.8250(1) | +09:29:16.339(2) | −7.61(6) | −2.87(7) | 0.13(2) | ||
| B1642−03 | Timing | 16:45:02.0414(6) | −03:17:58.32(3) | — | — | — | 56000 |
| VLBIc | 16:45:02.0406(1) | −03:17:57.819(2) | −1.035(27) | 20.5(2) | 0.26(2) | ||
| B2154+40 | Timing | 21:57:01.84(1) | +40:17:45.9(2) | 0(13) | 7(15) | — | 52275 |
| VLBIb | 21:57:01.8495(1) | +40:17:45.986(2) | 16.13(10) | 4.12(12) | 0.28(6) | ||
| B2351+61 | Timing | 23:54:04.77(1) | +61:55:46.8(1) | 18(8) | −1(6) | — | 56000 |
| VLBIc | 23:54:04.7830(1) | +61:55:46.845(1) | 22.76(5) | 4.897(25) | 0.41(4) |
*The symbol — means that parameters are not provided.
†References: a. Brisken et al. (2002); b. Chatterjee et al. (2009); c. Deller et al. (2019). The timing solutions are quoted from Hobbs et al. (2004).
‡The timing positions are inferred to the same epoch as the corresponding VLBI solutions for each pulsar.
| . | . | RA . | Dec . | μα . | μδ . | PX . | Pos. epoch‡ . |
|---|---|---|---|---|---|---|---|
| Name . | Solutions† . | (h m s) . | (° ′ ″) . | (mas yr−1) . | (mas yr−1) . | (mas) . | (MJD) . |
| B0031−07 | Timing | 00:34:08.84(5) | −07:21:53.1(14) | −16(26) | 17(53) | — | 52275 |
| VLBIb | 00:34:08.8703(1) | −07:21:53.409(2) | 10.37(8) | −11.13(16) | 0.93(8) | ||
| B0136+57 | Timing | 01:39:19.744(4) | +58:14:31.73(3) | — | — | — | 52275 |
| VLBIb | 01:39:19.7401(12) | +58:14:31.819(17) | −19.11(7) | −16.60(7) | 0.37(4) | ||
| B0148−06 | Timing | 01:51:22.72(6) | −06:35:03.5(20) | 19(42) | −39(87) | — | 56000 |
| VLBIc | 01:51:22.7179(2) | −06:35:02.987(2) | 10.7(1) | −5.38(7) | 0.23(9) | ||
| B0154+61 | Timing | 01:57:49.80(7) | +62:12:27.3(7) | −51(36) | 81(33) | — | 56000 |
| VLBIc | 01:57:49.9434(1) | +62:12:26.648(1) | 1.57(6) | 44.80(4) | 0.56(3) | ||
| B0450+55 | Timing | 04:54:07.746(6) | +55:43:41.4(1) | 48(6) | −13(12) | — | 52275 |
| VLBIb | 04:54:07.7506(1) | +55:43:41.437(2) | 53.34(6) | −17.56(14) | 0.84(5) | ||
| B0611+22 | Timing | 06:14:17.16(3) | +22:30:36(17) | — | — | — | 56000 |
| VLBIc | 06:14:17.0058(1) | +22:29:56.848(1) | −0.24(4) | −1.25(4) | 0.28(3) | ||
| B0626+24 | Timing | 06:29:05.77(2) | +24:15:50(6) | 32(15) | 400(300) | — | 56000 |
| VLBIc | 06:29:05.7273(1) | +24:15:41.546(1) | 3.56(12) | −4.68(8) | 0.32(5) | ||
| B0727−18 | Timing | 07:29:32.351(3) | −18:36:42.75(7) | — | — | — | 56000 |
| VLBIc | 07:29:32.3369(1) | −18:36:42.244(2) | −13.06(11) | 13.27(44) | 0.50(9) | ||
| B0809+74 | Timing | 08:14:59.49(2) | +74:29:05.8(2) | 18(20) | −49(21) | — | 48382 |
| VLBIa | 08:14:59.5412(10) | +74:29:05.367(15) | 24.02(9) | −44.0(4) | 2.31(4) | ||
| B0820+02 | Timing | 08:23:09.77(1) | +01:59:12.7(5) | −2(8) | 18(24) | — | 56000 |
| VLBIc | 08:23:09.7651(1) | +01:59:12.469(1) | −4.0(2) | 0.15(26) | 0.4(1) | ||
| B1530+27 | Timing | 15:32:10.37(4) | +27:45:49.3(7) | 6(24) | −7(30) | — | 56000 |
| VLBIc | 15:32:10.3646(1) | +27:45:49.623(1) | 1.5(1) | 18.93(11) | 0.59(6) | ||
| B1540−06 | Timing | 15:43:30.136(9) | −06:20:45.5(4) | −18(6) | −14(19) | — | 56000 |
| VLBIc | 15:43:30.1373(1) | −06:20:45.332(2) | −16.79(4) | −0.30(13) | 0.31(4) | ||
| B1541+09 | Timing | 15:43:38.82(4) | +09:29:15(1) | 9(39) | −113(76) | — | 52275 |
| VLBIb | 15:43:38.8250(1) | +09:29:16.339(2) | −7.61(6) | −2.87(7) | 0.13(2) | ||
| B1642−03 | Timing | 16:45:02.0414(6) | −03:17:58.32(3) | — | — | — | 56000 |
| VLBIc | 16:45:02.0406(1) | −03:17:57.819(2) | −1.035(27) | 20.5(2) | 0.26(2) | ||
| B2154+40 | Timing | 21:57:01.84(1) | +40:17:45.9(2) | 0(13) | 7(15) | — | 52275 |
| VLBIb | 21:57:01.8495(1) | +40:17:45.986(2) | 16.13(10) | 4.12(12) | 0.28(6) | ||
| B2351+61 | Timing | 23:54:04.77(1) | +61:55:46.8(1) | 18(8) | −1(6) | — | 56000 |
| VLBIc | 23:54:04.7830(1) | +61:55:46.845(1) | 22.76(5) | 4.897(25) | 0.41(4) |
| . | . | RA . | Dec . | μα . | μδ . | PX . | Pos. epoch‡ . |
|---|---|---|---|---|---|---|---|
| Name . | Solutions† . | (h m s) . | (° ′ ″) . | (mas yr−1) . | (mas yr−1) . | (mas) . | (MJD) . |
| B0031−07 | Timing | 00:34:08.84(5) | −07:21:53.1(14) | −16(26) | 17(53) | — | 52275 |
| VLBIb | 00:34:08.8703(1) | −07:21:53.409(2) | 10.37(8) | −11.13(16) | 0.93(8) | ||
| B0136+57 | Timing | 01:39:19.744(4) | +58:14:31.73(3) | — | — | — | 52275 |
| VLBIb | 01:39:19.7401(12) | +58:14:31.819(17) | −19.11(7) | −16.60(7) | 0.37(4) | ||
| B0148−06 | Timing | 01:51:22.72(6) | −06:35:03.5(20) | 19(42) | −39(87) | — | 56000 |
| VLBIc | 01:51:22.7179(2) | −06:35:02.987(2) | 10.7(1) | −5.38(7) | 0.23(9) | ||
| B0154+61 | Timing | 01:57:49.80(7) | +62:12:27.3(7) | −51(36) | 81(33) | — | 56000 |
| VLBIc | 01:57:49.9434(1) | +62:12:26.648(1) | 1.57(6) | 44.80(4) | 0.56(3) | ||
| B0450+55 | Timing | 04:54:07.746(6) | +55:43:41.4(1) | 48(6) | −13(12) | — | 52275 |
| VLBIb | 04:54:07.7506(1) | +55:43:41.437(2) | 53.34(6) | −17.56(14) | 0.84(5) | ||
| B0611+22 | Timing | 06:14:17.16(3) | +22:30:36(17) | — | — | — | 56000 |
| VLBIc | 06:14:17.0058(1) | +22:29:56.848(1) | −0.24(4) | −1.25(4) | 0.28(3) | ||
| B0626+24 | Timing | 06:29:05.77(2) | +24:15:50(6) | 32(15) | 400(300) | — | 56000 |
| VLBIc | 06:29:05.7273(1) | +24:15:41.546(1) | 3.56(12) | −4.68(8) | 0.32(5) | ||
| B0727−18 | Timing | 07:29:32.351(3) | −18:36:42.75(7) | — | — | — | 56000 |
| VLBIc | 07:29:32.3369(1) | −18:36:42.244(2) | −13.06(11) | 13.27(44) | 0.50(9) | ||
| B0809+74 | Timing | 08:14:59.49(2) | +74:29:05.8(2) | 18(20) | −49(21) | — | 48382 |
| VLBIa | 08:14:59.5412(10) | +74:29:05.367(15) | 24.02(9) | −44.0(4) | 2.31(4) | ||
| B0820+02 | Timing | 08:23:09.77(1) | +01:59:12.7(5) | −2(8) | 18(24) | — | 56000 |
| VLBIc | 08:23:09.7651(1) | +01:59:12.469(1) | −4.0(2) | 0.15(26) | 0.4(1) | ||
| B1530+27 | Timing | 15:32:10.37(4) | +27:45:49.3(7) | 6(24) | −7(30) | — | 56000 |
| VLBIc | 15:32:10.3646(1) | +27:45:49.623(1) | 1.5(1) | 18.93(11) | 0.59(6) | ||
| B1540−06 | Timing | 15:43:30.136(9) | −06:20:45.5(4) | −18(6) | −14(19) | — | 56000 |
| VLBIc | 15:43:30.1373(1) | −06:20:45.332(2) | −16.79(4) | −0.30(13) | 0.31(4) | ||
| B1541+09 | Timing | 15:43:38.82(4) | +09:29:15(1) | 9(39) | −113(76) | — | 52275 |
| VLBIb | 15:43:38.8250(1) | +09:29:16.339(2) | −7.61(6) | −2.87(7) | 0.13(2) | ||
| B1642−03 | Timing | 16:45:02.0414(6) | −03:17:58.32(3) | — | — | — | 56000 |
| VLBIc | 16:45:02.0406(1) | −03:17:57.819(2) | −1.035(27) | 20.5(2) | 0.26(2) | ||
| B2154+40 | Timing | 21:57:01.84(1) | +40:17:45.9(2) | 0(13) | 7(15) | — | 52275 |
| VLBIb | 21:57:01.8495(1) | +40:17:45.986(2) | 16.13(10) | 4.12(12) | 0.28(6) | ||
| B2351+61 | Timing | 23:54:04.77(1) | +61:55:46.8(1) | 18(8) | −1(6) | — | 56000 |
| VLBIc | 23:54:04.7830(1) | +61:55:46.845(1) | 22.76(5) | 4.897(25) | 0.41(4) |
*The symbol — means that parameters are not provided.
†References: a. Brisken et al. (2002); b. Chatterjee et al. (2009); c. Deller et al. (2019). The timing solutions are quoted from Hobbs et al. (2004).
‡The timing positions are inferred to the same epoch as the corresponding VLBI solutions for each pulsar.
2 Observations and data reduction
Pulsar timing observations were carried out in the S and C bands with the 65 m TMRT between MJD 57292 (2015 September 27) and 58866 (2020 January 18). Both S- and C-band receivers are cryogenically cooled dual-polarization receivers with effective frequency coverage of 2200–2300 MHz and 4320–5320 MHz, respectively. For convenience in performing online dedispersion and removing radio frequency interference (RFI), the full bandwidths of the S- and C-band receivers were correspondingly divided into channels with typical widths of 1 and 2 MHz in the Digital Backend System (DIBAS). Data sampling and recording were accomplished with the DIBAS. For both S- and C-band pulsar observations, the time resolution of data sampling was 40.96 μs (Yan et al. 2018). Data were obtained under the incoherent dedispersion online folding observation mode with a subintegration time of 30 s. The observational files were written out as 8-bit psrfits format with 1024 phase bins for each period (Yan et al. 2015). The pulsar parameters used in the online folding observations were obtained from psrcat2 (Manchester et al. 2005). Depending on the flux density of the target pulsars and the observation conditions (weather and RFI), observation durations mostly ranged from 10 to 20 min.
During pulsar observations, time was marked using a local hydrogen atomic clock corrected to GPS. The psrchive (Hotan et al. 2004) and Tempo2 (Hobbs 2012) packages were used for data reduction and analysis. For each pulsar, offline data from all channels and subintegrations were summed to produce a mean pulse profile for each observation. Local ToAs were determined by the cross-correlation of observed pulse profiles with a pulse template and were converted to ToAs at the solar system barycenter with the Jet Propulsion Laboratory’s DE421 ephemeris.
3 Analysis and results
Timing analysis of 16 pulsars was performed using S- and C-band timing data obtained from the TMRT. Pulsar ephemerides were quoted from psrcat (Version 1.59). Astrometric parameters in ephemerides were updated using the VLBI solutions in table 1. The ephemeris after updating of astrometric parameters is referred to as the updated ephemeris. For pulsars that have both S- and C-band data, the timing residuals showed a phase offset between data at different frequencies. The offset was fitted at the first step and kept constant in ephemeris with the measured value. For all pulsars, ν and |$\dot{\nu }$| were fitted based on the updated ephemerides. The epoch of the rotation parameters was set to be the middle date of the data span. According to their different timing properties, these 16 pulsars were classified into three groups: pulsar with glitch, pulsar with loud timing noise, and pulsars without significant timing irregularities. Appropriate methods were used in the data analysis of the pulsars depending on their timing properties.
3.1 Pulsar with glitch
One glitch occurred for PSR B0154+61 around MJD 58266.4. Because of incorrect rotation parameters in the updated ephemeris, the timing residuals of PSR B0154+61 showed an obvious downward trend, in which the glitch was hard to see. The rotation parameters of PSR B0154+61 were first fitted using pre-glitch timing data and kept constant in ephemeris with newly fitted values. Then, the glitch parameters were fitted based on this new ephemeris. The measured glitch parameters were kept constant in ephemeris when obtaining the final rotation solution. In order to study the influence of different ephemerides on the glitch fitting, we also fitted the glitch based on the timing ephemeris with astrometric parameters set to the timing solutions in table 1. The rotation parameters in the timing ephemeris are the same as the rotation parameters in the updated ephemeris. Table 2 shows the glitch parameters measured with the timing and updated ephemerides. The glitch epoch, Δν, and |$\Delta \dot{\nu }$| are MJD 58266.4, 1.45 × 10−9 Hz, and 4.1 × 10−17 s−2, respectively, when measured with the updated ephemeris. They are respectively MJD 58279.5, 1.75 × 10−9 Hz, and 2.6 × 10−17 s−2 when measured with the timing ephemeris. Figure 1 displays the residuals before and after fitting the glitch. The residuals in panel (a) show a sudden downward trend caused by the glitch. In panel (b), the residuals show noticeable fluctuations after fitting the glitch with the timing ephemeris, while no obvious fluctuation is left based on the updated ephemeris in panel (c). The residuals after further fitting ν and |$\dot{\nu }$| in panel (d) show almost no difference from the residuals in panel (c), implying that the final rotation parameters are similar to those derived with the pre-glitch data.
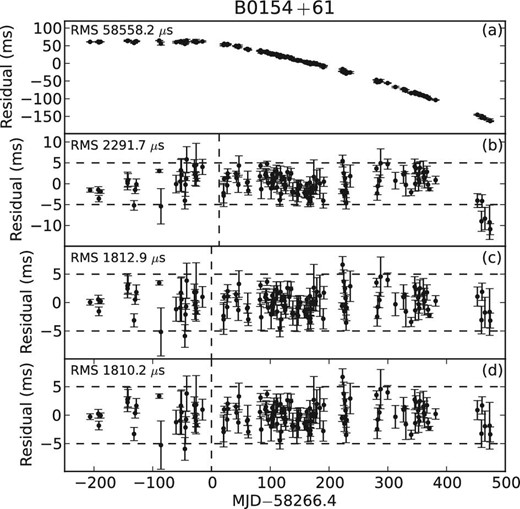
Timing residuals of PSR B0154+61 based on a previous timing ephemeris without fitting the glitch (a) and with the glitch fitted (b). Panel (c) shows the residuals based on the updated ephemeris with the glitch fitted. Panel (d) shows the residuals in (c) with ν and |$\dot{\nu }$| further fitted. The dashed vertical lines indicate the measured epoch of the glitch. The horizontal dashed lines are plotted for comparing residuals and are at ±5 ms.
| . | Timing . | Updated . |
|---|---|---|
| Parameter . | ephemeris . | ephemeris . |
| Glitch epoch (MJD) | 58279.5(7) | 58266.4(5) |
| Δν (10−9 Hz) | 1.75(5) | 1.45(2) |
| Δν/ν (10−9) | 4.11(11) | 3.41(5) |
| |$\Delta \dot{\nu }$| (10−17 s−2) | 2.6(3) | 4.1(1) |
| |$\Delta \dot{\nu } / \dot{\nu }$| (10−3) | −0.75(7) | −1.19(4) |
| RMS residual (μs) | 2291.7 | 1812.9 |
| . | Timing . | Updated . |
|---|---|---|
| Parameter . | ephemeris . | ephemeris . |
| Glitch epoch (MJD) | 58279.5(7) | 58266.4(5) |
| Δν (10−9 Hz) | 1.75(5) | 1.45(2) |
| Δν/ν (10−9) | 4.11(11) | 3.41(5) |
| |$\Delta \dot{\nu }$| (10−17 s−2) | 2.6(3) | 4.1(1) |
| |$\Delta \dot{\nu } / \dot{\nu }$| (10−3) | −0.75(7) | −1.19(4) |
| RMS residual (μs) | 2291.7 | 1812.9 |
| . | Timing . | Updated . |
|---|---|---|
| Parameter . | ephemeris . | ephemeris . |
| Glitch epoch (MJD) | 58279.5(7) | 58266.4(5) |
| Δν (10−9 Hz) | 1.75(5) | 1.45(2) |
| Δν/ν (10−9) | 4.11(11) | 3.41(5) |
| |$\Delta \dot{\nu }$| (10−17 s−2) | 2.6(3) | 4.1(1) |
| |$\Delta \dot{\nu } / \dot{\nu }$| (10−3) | −0.75(7) | −1.19(4) |
| RMS residual (μs) | 2291.7 | 1812.9 |
| . | Timing . | Updated . |
|---|---|---|
| Parameter . | ephemeris . | ephemeris . |
| Glitch epoch (MJD) | 58279.5(7) | 58266.4(5) |
| Δν (10−9 Hz) | 1.75(5) | 1.45(2) |
| Δν/ν (10−9) | 4.11(11) | 3.41(5) |
| |$\Delta \dot{\nu }$| (10−17 s−2) | 2.6(3) | 4.1(1) |
| |$\Delta \dot{\nu } / \dot{\nu }$| (10−3) | −0.75(7) | −1.19(4) |
| RMS residual (μs) | 2291.7 | 1812.9 |
3.2 Pulsar with loud timing noise
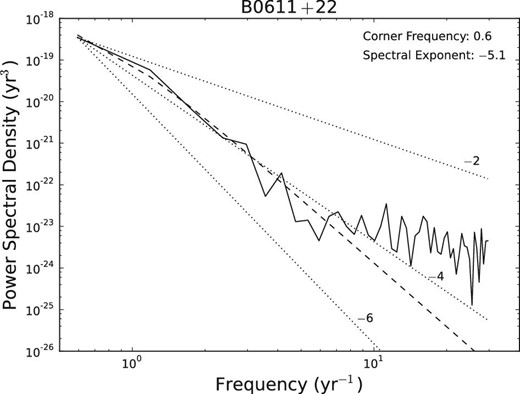
Observed and fitted power spectra of the timing noise for PSR B0611+22. The solid jagged line represents the spectrum of the smoothed and interpolated red noise. The power-law model fitted to the red component is shown as the dashed line. The dotted lines are power spectra with exponents of −2, −4, and −6, respectively.
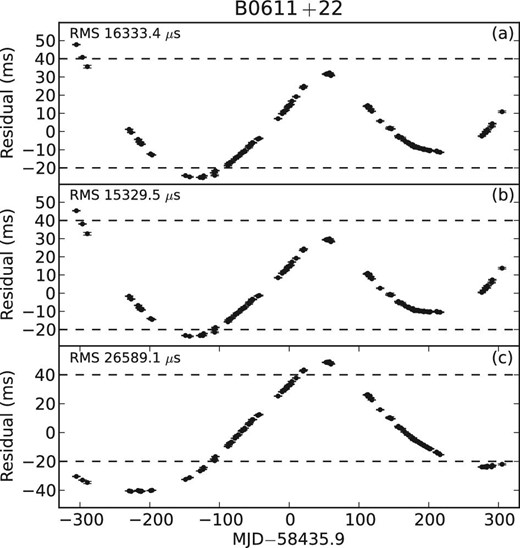
Panels (a) and (b) are the timing residuals based on the previous timing ephemeris and the updated ephemeris without loading the power-law spectrum model, respectively. Panel (c) shows the residuals after fitting ν and |$\dot{\nu }$| with the spectrum model loaded. The horizontal dashed lines are at 40 ms and −20 ms, respectively.
3.3 Pulsars without significant timing irregularities
Although PSRs B0136+57, B0450+55, and B1642−03 have obvious timing noise, the noise is much weaker compared with the timing noise of PSR B0611+22 (Hobbs et al. 2010). They were not fitted with the power-law spectrum model. For pulsars without significant timing irregularities, we only fitted their rotation parameters using the updated ephemerides. The measured rotation parameters were kept constant in both timing and updated ephemerides. We compared the residuals based on the timing ephemeris with corresponding residuals based on the updated ephemeris for each pulsar. They are plotted as panels (a) and (b) in figure 4, respectively.
Timing residuals after fitting ν and |$\dot{\nu }$| based on the timing (a) and updated (b) ephemerides. The data points with dot and square symbols are in the S and C bands, respectively. The axis scales of the two panels are the same for each pulsar.
PSR B0031−07: Both μα and μδ measured by VLBI have opposite directions to the timing solutions. The declination difference between the two solutions is about |${0{^{\prime \prime}_{.}}3}$|. The differences between the residuals shown in panels (a) and (b) for this pulsar are not obvious.
PSR B0136+57: The position difference between the timing and VLBI solutions is not large. As timing proper motion is not provided, the differences in μα and μδ are respectively 19.11 mas yr−1 and 16.6 mas yr−1 between the two solutions. The amplitude of the residual fluctuations in panel (a) are larger than those in panel (b).
PSR B0148−06: For this pulsar, the differences in declination, μα, and μδ are about |${0{^{\prime \prime}_{.}}5}$|, 8.3 mas yr−1, and 33.6 mas yr−1 between the two solutions, respectively. Although the difference between the RMS residuals in panels (a) and (b) is about 0.1 ms, it is hard to discern the differences between the residuals in the two panels.
PSR B0450+55: Both position and proper motion differences between the timing and VLBI solutions are small. There are no obvious differences between the residuals in the two panels.
PSR B0626+24: There are large position and proper motion differences between the two solutions. The differences in declination and μδ are about |${8{^{\prime \prime}_{.}}5}$| and 395 mas yr−1, respectively. However, the timing residuals based on the two kinds of ephemerides only differ a little.
PSR B0727−18: The differences in the declination, μα, and μδ are about |${0{^{\prime \prime}_{.}}5}$|, 13 mas yr−1, and 13.3 mas yr−1 between the two solutions. The differences between the residuals in panels (a) and (b) cannot be discerned clearly.
PSR B0809+74: The differences in position and proper motion between the timing and VLBI solutions are not significant by comparison. The residuals based on the timing ephemeris show small differences compared with those based on the updated ephemeris.
PSR B0820+02: The μδ difference between the two solutions is about 18 mas yr−1, while the differences in position and μα between the two solutions are small. The residuals in panels (a) and (b) show imperceptible differences.
PSR B1530+27: μδ shows opposite directions in the pulsar timing and VLBI solutions. The differences in declination, μα, and μδ are about |${0{^{\prime \prime}_{.}}3}$|, 4.5 mas yr−1, and 12 mas yr−1, respectively. There are no obvious differences between the residuals based on the timing and updated ephemerides.
PSR B1540−06: The differences in position and μα between the timing and VLBI solutions are really small. The difference in μδ between the two solutions is about 14 mas yr−1. We can only find some imperceptible differences between the residuals in the two panels.
PSR B1541+09: The declination and μδ differences between the two solutions for this pulsar are about |${1{^{\prime \prime}_{.}}3}$| and 110 mas yr−1, respectively. There are sinusoidal fluctuations in the residuals based on the timing ephemeris, while the residuals based on the updated ephemeris have no obvious fluctuations.
PSR B1642−03: This pulsar has a declination difference of |${0{^{\prime \prime}_{.}}5}$| and a μδ difference of 20.5 mas yr−1 between the two solutions. The residual fluctuations in panel (a) are obviously different from those that in panel (b).
PSR B2154+40: The differences in the astrometric parameters between the timing and VLBI solutions are small except for μα, for which the difference is 16.13 mas yr−1. It is difficult to see any differences between the residuals in panels (a) and (b).
PSR B2351+61: The timing position and proper motion of this pulsar differ a little from the VLBI solutions. Only small differences can be seen between the residuals in the two panels.
3.4 Comparison with Hobbs et al. (2004)
For convenience in comparing the previous rotation solutions in Hobbs et al. (2004) with the corresponding solutions derived in our work, we also inferred the ν and |$\dot{\nu }$| in Hobbs et al. (2004) to the epoch of our rotation solutions. Table 3 presents the fitted and inferred rotation parameters, the epoch of the solutions, the data span, and the number of ToAs for the 16 pulsars.
| . | . | ν . | |$\dot{\nu }$| . | Epoch . | Epoch|$_{\rm T}^{\,\,\,*}$| . | Data span . | No. of . |
|---|---|---|---|---|---|---|---|
| Name . | Solutions . | (Hz) . | (10−15 s−2) . | (MJD) . | (MJD) . | (MJD) . | ToAs . |
| B0031−07 | Inferred | 1.06050003902(4) | −0.45889(7) | 58227 | 46635 | 57640–58814 | 117 |
| Fitted | 1.060500038930(7) | −0.4578(5) | |||||
| B0136+57 | Inferred | 3.670275200(9) | −144.29(2) | 58476 | 49289 | 58139–58813 | 66 |
| Fitted | 3.67027523674(2) | −144.152(3) | |||||
| B0148−06 | Inferred | 0.6827500310(1) | −0.2021(3) | 58383 | 49347 | 57921–58848 | 81 |
| Fitted | 0.68275002918(1) | −0.2045(8) | |||||
| B0154+61 | Inferred | 0.4251905242(6) | −34.176(2) | 58400 | 49709 | 58058–58742 | 136 |
| Fitted | 0.425190536230(5) | −34.1756(6) | |||||
| B0450+55 | Inferred | 2.934865512(4) | −20.56(1) | 58078 | 49910 | 57292–58866 | 188 |
| Fitted | 2.93486550969(1) | −20.6703(5) | |||||
| B0611+22 | Inferred | 2.98503223(7) | −524.8(2) | 58435 | 49674 | 58130–58741 | 102 |
| Fitted | 2.985032106(5) | −526.2(4) | |||||
| B0626+24 | Inferred | 2.0980882323(8) | −8.791(2) | 58381 | 49438 | 57949–58813 | 131 |
| Fitted | 2.098088239948(10) | −8.7795(9) | |||||
| B0727−18 | Inferred | 1.960113351(5) | −72.56(1) | 58426 | 49720 | 57987–58866 | 75 |
| Fitted | 1.96011325712(3) | −72.868(2) | |||||
| B0809+74 | Inferred | 0.77384911485(4) | −0.1006(1) | 58079 | 49162 | 57349–58810 | 153 |
| Fitted | 0.773849114816(3) | −0.1005(2) | |||||
| B0820+02 | Inferred | 1.15623927397(5) | −0.1404(1) | 58473 | 49281 | 58134–58813 | 71 |
| Fitted | 1.15623927402(1) | −0.136(1) | |||||
| B1530+27 | Inferred | 0.8890182224(3) | −0.6168(6) | 58470 | 49666 | 58076–58866 | 64 |
| Fitted | 0.889018222765(9) | −0.6147(10) | |||||
| B1540−06 | Inferred | 1.4103084243(4) | −1.7391(8) | 58491 | 49423 | 58118–58864 | 60 |
| Fitted | 1.410308423169(3) | −1.7489(3) | |||||
| B1541+09 | Inferred | 1.3360967749(3) | −0.7836(7) | 58356 | 48716 | 58075–58638 | 79 |
| Fitted | 1.33609677905(4) | −0.784(5) | |||||
| B1642−03 | Inferred | 2.5793706170(7) | −11.839(1) | 58072 | 46515 | 57331–58813 | 156 |
| Fitted | 2.57937061296(3) | −11.837(1) | |||||
| B2154+40 | Inferred | 0.6556223737(2) | −1.5075(5) | 58051 | 49277 | 57292–58810 | 88 |
| Fitted | 0.655622382900(5) | −1.4762(3) | |||||
| B2351+61 | Inferred | 1.0584288921(6) | −18.200(1) | 58445 | 49405 | 58077–58813 | 74 |
| Fitted | 1.058428884927(4) | −18.2220(4) |
| . | . | ν . | |$\dot{\nu }$| . | Epoch . | Epoch|$_{\rm T}^{\,\,\,*}$| . | Data span . | No. of . |
|---|---|---|---|---|---|---|---|
| Name . | Solutions . | (Hz) . | (10−15 s−2) . | (MJD) . | (MJD) . | (MJD) . | ToAs . |
| B0031−07 | Inferred | 1.06050003902(4) | −0.45889(7) | 58227 | 46635 | 57640–58814 | 117 |
| Fitted | 1.060500038930(7) | −0.4578(5) | |||||
| B0136+57 | Inferred | 3.670275200(9) | −144.29(2) | 58476 | 49289 | 58139–58813 | 66 |
| Fitted | 3.67027523674(2) | −144.152(3) | |||||
| B0148−06 | Inferred | 0.6827500310(1) | −0.2021(3) | 58383 | 49347 | 57921–58848 | 81 |
| Fitted | 0.68275002918(1) | −0.2045(8) | |||||
| B0154+61 | Inferred | 0.4251905242(6) | −34.176(2) | 58400 | 49709 | 58058–58742 | 136 |
| Fitted | 0.425190536230(5) | −34.1756(6) | |||||
| B0450+55 | Inferred | 2.934865512(4) | −20.56(1) | 58078 | 49910 | 57292–58866 | 188 |
| Fitted | 2.93486550969(1) | −20.6703(5) | |||||
| B0611+22 | Inferred | 2.98503223(7) | −524.8(2) | 58435 | 49674 | 58130–58741 | 102 |
| Fitted | 2.985032106(5) | −526.2(4) | |||||
| B0626+24 | Inferred | 2.0980882323(8) | −8.791(2) | 58381 | 49438 | 57949–58813 | 131 |
| Fitted | 2.098088239948(10) | −8.7795(9) | |||||
| B0727−18 | Inferred | 1.960113351(5) | −72.56(1) | 58426 | 49720 | 57987–58866 | 75 |
| Fitted | 1.96011325712(3) | −72.868(2) | |||||
| B0809+74 | Inferred | 0.77384911485(4) | −0.1006(1) | 58079 | 49162 | 57349–58810 | 153 |
| Fitted | 0.773849114816(3) | −0.1005(2) | |||||
| B0820+02 | Inferred | 1.15623927397(5) | −0.1404(1) | 58473 | 49281 | 58134–58813 | 71 |
| Fitted | 1.15623927402(1) | −0.136(1) | |||||
| B1530+27 | Inferred | 0.8890182224(3) | −0.6168(6) | 58470 | 49666 | 58076–58866 | 64 |
| Fitted | 0.889018222765(9) | −0.6147(10) | |||||
| B1540−06 | Inferred | 1.4103084243(4) | −1.7391(8) | 58491 | 49423 | 58118–58864 | 60 |
| Fitted | 1.410308423169(3) | −1.7489(3) | |||||
| B1541+09 | Inferred | 1.3360967749(3) | −0.7836(7) | 58356 | 48716 | 58075–58638 | 79 |
| Fitted | 1.33609677905(4) | −0.784(5) | |||||
| B1642−03 | Inferred | 2.5793706170(7) | −11.839(1) | 58072 | 46515 | 57331–58813 | 156 |
| Fitted | 2.57937061296(3) | −11.837(1) | |||||
| B2154+40 | Inferred | 0.6556223737(2) | −1.5075(5) | 58051 | 49277 | 57292–58810 | 88 |
| Fitted | 0.655622382900(5) | −1.4762(3) | |||||
| B2351+61 | Inferred | 1.0584288921(6) | −18.200(1) | 58445 | 49405 | 58077–58813 | 74 |
| Fitted | 1.058428884927(4) | −18.2220(4) |
*EpochT is the epoch of the timing rotation solution in Hobbs et al. (2004).
| . | . | ν . | |$\dot{\nu }$| . | Epoch . | Epoch|$_{\rm T}^{\,\,\,*}$| . | Data span . | No. of . |
|---|---|---|---|---|---|---|---|
| Name . | Solutions . | (Hz) . | (10−15 s−2) . | (MJD) . | (MJD) . | (MJD) . | ToAs . |
| B0031−07 | Inferred | 1.06050003902(4) | −0.45889(7) | 58227 | 46635 | 57640–58814 | 117 |
| Fitted | 1.060500038930(7) | −0.4578(5) | |||||
| B0136+57 | Inferred | 3.670275200(9) | −144.29(2) | 58476 | 49289 | 58139–58813 | 66 |
| Fitted | 3.67027523674(2) | −144.152(3) | |||||
| B0148−06 | Inferred | 0.6827500310(1) | −0.2021(3) | 58383 | 49347 | 57921–58848 | 81 |
| Fitted | 0.68275002918(1) | −0.2045(8) | |||||
| B0154+61 | Inferred | 0.4251905242(6) | −34.176(2) | 58400 | 49709 | 58058–58742 | 136 |
| Fitted | 0.425190536230(5) | −34.1756(6) | |||||
| B0450+55 | Inferred | 2.934865512(4) | −20.56(1) | 58078 | 49910 | 57292–58866 | 188 |
| Fitted | 2.93486550969(1) | −20.6703(5) | |||||
| B0611+22 | Inferred | 2.98503223(7) | −524.8(2) | 58435 | 49674 | 58130–58741 | 102 |
| Fitted | 2.985032106(5) | −526.2(4) | |||||
| B0626+24 | Inferred | 2.0980882323(8) | −8.791(2) | 58381 | 49438 | 57949–58813 | 131 |
| Fitted | 2.098088239948(10) | −8.7795(9) | |||||
| B0727−18 | Inferred | 1.960113351(5) | −72.56(1) | 58426 | 49720 | 57987–58866 | 75 |
| Fitted | 1.96011325712(3) | −72.868(2) | |||||
| B0809+74 | Inferred | 0.77384911485(4) | −0.1006(1) | 58079 | 49162 | 57349–58810 | 153 |
| Fitted | 0.773849114816(3) | −0.1005(2) | |||||
| B0820+02 | Inferred | 1.15623927397(5) | −0.1404(1) | 58473 | 49281 | 58134–58813 | 71 |
| Fitted | 1.15623927402(1) | −0.136(1) | |||||
| B1530+27 | Inferred | 0.8890182224(3) | −0.6168(6) | 58470 | 49666 | 58076–58866 | 64 |
| Fitted | 0.889018222765(9) | −0.6147(10) | |||||
| B1540−06 | Inferred | 1.4103084243(4) | −1.7391(8) | 58491 | 49423 | 58118–58864 | 60 |
| Fitted | 1.410308423169(3) | −1.7489(3) | |||||
| B1541+09 | Inferred | 1.3360967749(3) | −0.7836(7) | 58356 | 48716 | 58075–58638 | 79 |
| Fitted | 1.33609677905(4) | −0.784(5) | |||||
| B1642−03 | Inferred | 2.5793706170(7) | −11.839(1) | 58072 | 46515 | 57331–58813 | 156 |
| Fitted | 2.57937061296(3) | −11.837(1) | |||||
| B2154+40 | Inferred | 0.6556223737(2) | −1.5075(5) | 58051 | 49277 | 57292–58810 | 88 |
| Fitted | 0.655622382900(5) | −1.4762(3) | |||||
| B2351+61 | Inferred | 1.0584288921(6) | −18.200(1) | 58445 | 49405 | 58077–58813 | 74 |
| Fitted | 1.058428884927(4) | −18.2220(4) |
| . | . | ν . | |$\dot{\nu }$| . | Epoch . | Epoch|$_{\rm T}^{\,\,\,*}$| . | Data span . | No. of . |
|---|---|---|---|---|---|---|---|
| Name . | Solutions . | (Hz) . | (10−15 s−2) . | (MJD) . | (MJD) . | (MJD) . | ToAs . |
| B0031−07 | Inferred | 1.06050003902(4) | −0.45889(7) | 58227 | 46635 | 57640–58814 | 117 |
| Fitted | 1.060500038930(7) | −0.4578(5) | |||||
| B0136+57 | Inferred | 3.670275200(9) | −144.29(2) | 58476 | 49289 | 58139–58813 | 66 |
| Fitted | 3.67027523674(2) | −144.152(3) | |||||
| B0148−06 | Inferred | 0.6827500310(1) | −0.2021(3) | 58383 | 49347 | 57921–58848 | 81 |
| Fitted | 0.68275002918(1) | −0.2045(8) | |||||
| B0154+61 | Inferred | 0.4251905242(6) | −34.176(2) | 58400 | 49709 | 58058–58742 | 136 |
| Fitted | 0.425190536230(5) | −34.1756(6) | |||||
| B0450+55 | Inferred | 2.934865512(4) | −20.56(1) | 58078 | 49910 | 57292–58866 | 188 |
| Fitted | 2.93486550969(1) | −20.6703(5) | |||||
| B0611+22 | Inferred | 2.98503223(7) | −524.8(2) | 58435 | 49674 | 58130–58741 | 102 |
| Fitted | 2.985032106(5) | −526.2(4) | |||||
| B0626+24 | Inferred | 2.0980882323(8) | −8.791(2) | 58381 | 49438 | 57949–58813 | 131 |
| Fitted | 2.098088239948(10) | −8.7795(9) | |||||
| B0727−18 | Inferred | 1.960113351(5) | −72.56(1) | 58426 | 49720 | 57987–58866 | 75 |
| Fitted | 1.96011325712(3) | −72.868(2) | |||||
| B0809+74 | Inferred | 0.77384911485(4) | −0.1006(1) | 58079 | 49162 | 57349–58810 | 153 |
| Fitted | 0.773849114816(3) | −0.1005(2) | |||||
| B0820+02 | Inferred | 1.15623927397(5) | −0.1404(1) | 58473 | 49281 | 58134–58813 | 71 |
| Fitted | 1.15623927402(1) | −0.136(1) | |||||
| B1530+27 | Inferred | 0.8890182224(3) | −0.6168(6) | 58470 | 49666 | 58076–58866 | 64 |
| Fitted | 0.889018222765(9) | −0.6147(10) | |||||
| B1540−06 | Inferred | 1.4103084243(4) | −1.7391(8) | 58491 | 49423 | 58118–58864 | 60 |
| Fitted | 1.410308423169(3) | −1.7489(3) | |||||
| B1541+09 | Inferred | 1.3360967749(3) | −0.7836(7) | 58356 | 48716 | 58075–58638 | 79 |
| Fitted | 1.33609677905(4) | −0.784(5) | |||||
| B1642−03 | Inferred | 2.5793706170(7) | −11.839(1) | 58072 | 46515 | 57331–58813 | 156 |
| Fitted | 2.57937061296(3) | −11.837(1) | |||||
| B2154+40 | Inferred | 0.6556223737(2) | −1.5075(5) | 58051 | 49277 | 57292–58810 | 88 |
| Fitted | 0.655622382900(5) | −1.4762(3) | |||||
| B2351+61 | Inferred | 1.0584288921(6) | −18.200(1) | 58445 | 49405 | 58077–58813 | 74 |
| Fitted | 1.058428884927(4) | −18.2220(4) |
*EpochT is the epoch of the timing rotation solution in Hobbs et al. (2004).
4 Discussion
With VLBI astrometric parameter solutions, the effects caused by inaccurate astrometric parameters can be properly removed in pulsar timing residuals. Residual variations differ a lot for different pulsars after updating the astrometric parameters using the latest VLBI solutions. For PSR B0611+22, which has loud timing noise, there is a large difference in its declination between the timing and VLBI solutions. However, the differences between the timing residuals based on the two kinds of ephemerides are imperceptible compared with the timing noise (see figure 3). For some pulsars without significant timing irregularities, there are obvious differences between the residuals based on the timing and updated ephemerides (see figure 4). PSR B1541+09 has big differences in declination and μδ between the timing and VLBI solutions, as shown in table 1. Its timing residuals based on the timing ephemeris are apparently different from those based on the updated ephemeris. The differences between timing residuals based on the two kinds of ephemerides are less apparent for pulsars that have small differences in astrometric parameters between the timing and VLBI solutions, like PSR B2351+61. Compared with PSR B1541+09, PSR B0626+24 has larger differences in declination and μδ between the two solutions. However, its timing residuals based on the two kinds of ephemerides have less obvious differences. This is probably because of the large ToA errors for PSR B0626+24. The ToA errors of PSRs B0136+57 and B1642−03 are much smaller than that of PSR B0626+24. For these two pulsars, the declination and proper motion differences between the two solutions are much smaller than for PSR B0626+24, but the differences between the timing residuals based on the two kinds of ephemerides are more obvious than the residual differences for PSR B0626+24.
Timing residual fluctuations caused by inaccurate astrometric parameters influence measurements of timing irregularities. Benefiting from the independence and high accuracy of the astrometric parameters measured by VLBI, it is possible to perform more intrinsic measurements of timing irregularities. PSR B0154+61 suffered one glitch around MJD 58266.4, as shown in panel (a) of figure 1. The proper motion solution of PSR B0154+61 obtained with timing observations has an obvious difference from the VLBI solution: the errors in the timing proper motion are much larger than for the VLBI proper motion solution. Due to inaccurate astrometric parameters, the residuals after fitting the glitch parameters based on the timing ephemeris still have obvious fluctuations, as shown in panel (b). The glitch parameters measured with the timing ephemeris are different from those measured with the updated ephemeris. As shown in table 2, the glitch epoch measured with the timing ephemeris is about 13 d later than that measured with the updated ephemeris. The differences Δν and |$\Delta \dot{\nu }$| between the two solutions are 3 × 10−10 Hz and −1.5 × 10−17 s−2, respectively. In addition, the errors in the parameters measured with the timing ephemeris are larger than those measured with the updated ephemeris.
Pulsar rotation behaviors can be described well by simple spin-down models. However, apparent biases may appear over a long time, especially when timing irregularities exist, so it is necessary to refit the rotation parameters using the latest timing data. Correct rotation solutions are derived on the premise of accurate astrometric parameters. Timing residuals based on timing ephemerides may have obvious fluctuations caused by inaccurate astrometric parameters, like the residuals of PSR B1541+09 shown in panel (a) of figure 4, while none of these fluctuations remain in the timing residuals based on the updated ephemerides. Hence, VLBI astrometric parameter solutions are important for obtaining accurate rotation parameters. Comparing the fitted ν and inferred ν in table 3, they have obvious differences, especially for pulsars with large |$\left|\dot{\nu } \right|$|. Most of the differences between the fitted and the inferred values of ν range from 10−9 to 10−8 Hz. The errors in the fitted ν are much smaller than those for the inferred ν for all pulsars. In most cases, the differences between the fitted and inferred |$\dot{\nu }$| are larger than 10−18 s−2. For pulsars with smaller values of |$\left|\dot{\nu } \right|$|, the differences in |$\dot{\nu }$| between the two solutions are smaller than for the other pulsars. What is more, the errors in the fitted |$\dot{\nu }$| are larger than those for the inferred |$\dot{\nu }$| for these pulsars. This is probably because the time spans of our timing data are relatively not long enough to precisely measure |$\dot{\nu }$|.
Parameters relative to the Shklovsky effect and newly calculated characteristic ages of 16 pulsars.
| . | |$V_{\rm T}{}^{*}$| . | d* . | P . | |$\dot{P}_{\rm m}$| . | |$\dot{P}_{\rm s}$| . | |$\dot{P}_{\rm s}/\dot{P}_{\rm m}$| . | τm . | |$\tau _{\rm i}{}^{\dagger }$| . | |$\tau _{\rm p}{}^{\dagger }$| . |
|---|---|---|---|---|---|---|---|---|---|
| Name . | (km s−1) . | (kpc) . | (s) . | (10−15 s s−1) . | (10−19 s s−1) . | (%) . | (Myr) . | (Myr) . | (Myr) . |
| B0031−07 | 77.00b | 1.26b | 0.942951403386(6) | 0.4070(4) | 4.79323268066(3) | 0.12 | 36.73(4) | 36.78(4) | 36.6243(6) |
| B0136+57 | 319.0b | 2.65b | 0.272459130582(2) | 10.7010(2) | 11.30225636215(7) | 0.01 | 0.40368(1) | 0.40373(1) | 0.403268(5) |
| B0148−06 | 261.0c | 4.60c | 1.46466489529(2) | 0.437(2) | 23.4309420922(4) | 0.53 | 53.1(2) | 53.4(2) | 52.469(6) |
| B0154+61 | 383.7c | 1.80c | 2.35188677732(3) | 189.038(3) | 207.804907222(2) | 0.01 | 0.197256(3) | 0.197278(3) | 0.1973619(5) |
| B0450+55 | 317.0b | 1.19b | 0.340731115855(1) | 2.39977(5) | 31.0821925829(1) | 0.13 | 2.25115(5) | 2.25407(5) | 2.27724(7) |
| B0611+22 | 21.00c | 3.55c | 0.33500477221(4) | 59.05(4) | 0.044956192797(5) | 0 | 0.08995(7) | 0.08995(7) | 0.089332(2) |
| B0626+24 | 84.00c | 3.00c | 0.476624376878(2) | 1.9944(2) | 1.210993642508(6) | 0.01 | 3.7890(4) | 3.7892(4) | 3.78649(6) |
| B0727−18 | 179.9c | 2.04c | 0.510174601578(7) | 18.9659(6) | 8.7433773083(1) | 0 | 0.42649(1) | 0.42651(1) | 0.426675(4) |
| B0809+74 | 102.0a | 0.43a | 1.292241576368(5) | 0.1679(3) | 33.7756638012(1) | 2.01 | 122.1(2) | 124.6(2) | 121.87(1) |
| B0820+02 | 47.80c | 2.66c | 0.864872887877(9) | 0.1014(9) | 0.802517912658(8) | 0.08 | 135.2(12) | 135.3(12) | 131.157(8) |
| B1530+27 | 144.0c | 1.60c | 1.12483633563(1) | 0.778(1) | 15.7478994453(2) | 0.2 | 22.93(4) | 22.98(4) | 22.877(2) |
| B1540−06 | 247.4c | 3.11c | 0.709064757447(1) | 0.8793(1) | 15.07485676089(3) | 0.17 | 12.785(2) | 12.807(2) | 12.7818(6) |
| B1541+09 | 277.0b | 7.20b | 0.74844877682(2) | 0.439(3) | 8.6162327085(2) | 0.2 | 27.02(17) | 27.07(17) | 27.438(3) |
| B1642−03 | 386.4c | 3.97c | 0.387691475966(5) | 1.7791(2) | 15.7506425803(2) | 0.09 | 3.4550(4) | 3.4581(4) | 3.45241(3) |
| B2154+40 | 264.0b | 3.40b | 1.52526824294(1) | 3.4342(7) | 33.7756301241(3) | 0.1 | 7.042(1) | 7.049(1) | 7.0452(1) |
| B2351+61 | 268.0c | 2.42c | 0.944796588832(3) | 16.2657(3) | 30.2915037893(1) | 0.02 | 0.92094(2) | 0.92111(2) | 0.921087(5) |
| . | |$V_{\rm T}{}^{*}$| . | d* . | P . | |$\dot{P}_{\rm m}$| . | |$\dot{P}_{\rm s}$| . | |$\dot{P}_{\rm s}/\dot{P}_{\rm m}$| . | τm . | |$\tau _{\rm i}{}^{\dagger }$| . | |$\tau _{\rm p}{}^{\dagger }$| . |
|---|---|---|---|---|---|---|---|---|---|
| Name . | (km s−1) . | (kpc) . | (s) . | (10−15 s s−1) . | (10−19 s s−1) . | (%) . | (Myr) . | (Myr) . | (Myr) . |
| B0031−07 | 77.00b | 1.26b | 0.942951403386(6) | 0.4070(4) | 4.79323268066(3) | 0.12 | 36.73(4) | 36.78(4) | 36.6243(6) |
| B0136+57 | 319.0b | 2.65b | 0.272459130582(2) | 10.7010(2) | 11.30225636215(7) | 0.01 | 0.40368(1) | 0.40373(1) | 0.403268(5) |
| B0148−06 | 261.0c | 4.60c | 1.46466489529(2) | 0.437(2) | 23.4309420922(4) | 0.53 | 53.1(2) | 53.4(2) | 52.469(6) |
| B0154+61 | 383.7c | 1.80c | 2.35188677732(3) | 189.038(3) | 207.804907222(2) | 0.01 | 0.197256(3) | 0.197278(3) | 0.1973619(5) |
| B0450+55 | 317.0b | 1.19b | 0.340731115855(1) | 2.39977(5) | 31.0821925829(1) | 0.13 | 2.25115(5) | 2.25407(5) | 2.27724(7) |
| B0611+22 | 21.00c | 3.55c | 0.33500477221(4) | 59.05(4) | 0.044956192797(5) | 0 | 0.08995(7) | 0.08995(7) | 0.089332(2) |
| B0626+24 | 84.00c | 3.00c | 0.476624376878(2) | 1.9944(2) | 1.210993642508(6) | 0.01 | 3.7890(4) | 3.7892(4) | 3.78649(6) |
| B0727−18 | 179.9c | 2.04c | 0.510174601578(7) | 18.9659(6) | 8.7433773083(1) | 0 | 0.42649(1) | 0.42651(1) | 0.426675(4) |
| B0809+74 | 102.0a | 0.43a | 1.292241576368(5) | 0.1679(3) | 33.7756638012(1) | 2.01 | 122.1(2) | 124.6(2) | 121.87(1) |
| B0820+02 | 47.80c | 2.66c | 0.864872887877(9) | 0.1014(9) | 0.802517912658(8) | 0.08 | 135.2(12) | 135.3(12) | 131.157(8) |
| B1530+27 | 144.0c | 1.60c | 1.12483633563(1) | 0.778(1) | 15.7478994453(2) | 0.2 | 22.93(4) | 22.98(4) | 22.877(2) |
| B1540−06 | 247.4c | 3.11c | 0.709064757447(1) | 0.8793(1) | 15.07485676089(3) | 0.17 | 12.785(2) | 12.807(2) | 12.7818(6) |
| B1541+09 | 277.0b | 7.20b | 0.74844877682(2) | 0.439(3) | 8.6162327085(2) | 0.2 | 27.02(17) | 27.07(17) | 27.438(3) |
| B1642−03 | 386.4c | 3.97c | 0.387691475966(5) | 1.7791(2) | 15.7506425803(2) | 0.09 | 3.4550(4) | 3.4581(4) | 3.45241(3) |
| B2154+40 | 264.0b | 3.40b | 1.52526824294(1) | 3.4342(7) | 33.7756301241(3) | 0.1 | 7.042(1) | 7.049(1) | 7.0452(1) |
| B2351+61 | 268.0c | 2.42c | 0.944796588832(3) | 16.2657(3) | 30.2915037893(1) | 0.02 | 0.92094(2) | 0.92111(2) | 0.921087(5) |
Parameters relative to the Shklovsky effect and newly calculated characteristic ages of 16 pulsars.
| . | |$V_{\rm T}{}^{*}$| . | d* . | P . | |$\dot{P}_{\rm m}$| . | |$\dot{P}_{\rm s}$| . | |$\dot{P}_{\rm s}/\dot{P}_{\rm m}$| . | τm . | |$\tau _{\rm i}{}^{\dagger }$| . | |$\tau _{\rm p}{}^{\dagger }$| . |
|---|---|---|---|---|---|---|---|---|---|
| Name . | (km s−1) . | (kpc) . | (s) . | (10−15 s s−1) . | (10−19 s s−1) . | (%) . | (Myr) . | (Myr) . | (Myr) . |
| B0031−07 | 77.00b | 1.26b | 0.942951403386(6) | 0.4070(4) | 4.79323268066(3) | 0.12 | 36.73(4) | 36.78(4) | 36.6243(6) |
| B0136+57 | 319.0b | 2.65b | 0.272459130582(2) | 10.7010(2) | 11.30225636215(7) | 0.01 | 0.40368(1) | 0.40373(1) | 0.403268(5) |
| B0148−06 | 261.0c | 4.60c | 1.46466489529(2) | 0.437(2) | 23.4309420922(4) | 0.53 | 53.1(2) | 53.4(2) | 52.469(6) |
| B0154+61 | 383.7c | 1.80c | 2.35188677732(3) | 189.038(3) | 207.804907222(2) | 0.01 | 0.197256(3) | 0.197278(3) | 0.1973619(5) |
| B0450+55 | 317.0b | 1.19b | 0.340731115855(1) | 2.39977(5) | 31.0821925829(1) | 0.13 | 2.25115(5) | 2.25407(5) | 2.27724(7) |
| B0611+22 | 21.00c | 3.55c | 0.33500477221(4) | 59.05(4) | 0.044956192797(5) | 0 | 0.08995(7) | 0.08995(7) | 0.089332(2) |
| B0626+24 | 84.00c | 3.00c | 0.476624376878(2) | 1.9944(2) | 1.210993642508(6) | 0.01 | 3.7890(4) | 3.7892(4) | 3.78649(6) |
| B0727−18 | 179.9c | 2.04c | 0.510174601578(7) | 18.9659(6) | 8.7433773083(1) | 0 | 0.42649(1) | 0.42651(1) | 0.426675(4) |
| B0809+74 | 102.0a | 0.43a | 1.292241576368(5) | 0.1679(3) | 33.7756638012(1) | 2.01 | 122.1(2) | 124.6(2) | 121.87(1) |
| B0820+02 | 47.80c | 2.66c | 0.864872887877(9) | 0.1014(9) | 0.802517912658(8) | 0.08 | 135.2(12) | 135.3(12) | 131.157(8) |
| B1530+27 | 144.0c | 1.60c | 1.12483633563(1) | 0.778(1) | 15.7478994453(2) | 0.2 | 22.93(4) | 22.98(4) | 22.877(2) |
| B1540−06 | 247.4c | 3.11c | 0.709064757447(1) | 0.8793(1) | 15.07485676089(3) | 0.17 | 12.785(2) | 12.807(2) | 12.7818(6) |
| B1541+09 | 277.0b | 7.20b | 0.74844877682(2) | 0.439(3) | 8.6162327085(2) | 0.2 | 27.02(17) | 27.07(17) | 27.438(3) |
| B1642−03 | 386.4c | 3.97c | 0.387691475966(5) | 1.7791(2) | 15.7506425803(2) | 0.09 | 3.4550(4) | 3.4581(4) | 3.45241(3) |
| B2154+40 | 264.0b | 3.40b | 1.52526824294(1) | 3.4342(7) | 33.7756301241(3) | 0.1 | 7.042(1) | 7.049(1) | 7.0452(1) |
| B2351+61 | 268.0c | 2.42c | 0.944796588832(3) | 16.2657(3) | 30.2915037893(1) | 0.02 | 0.92094(2) | 0.92111(2) | 0.921087(5) |
| . | |$V_{\rm T}{}^{*}$| . | d* . | P . | |$\dot{P}_{\rm m}$| . | |$\dot{P}_{\rm s}$| . | |$\dot{P}_{\rm s}/\dot{P}_{\rm m}$| . | τm . | |$\tau _{\rm i}{}^{\dagger }$| . | |$\tau _{\rm p}{}^{\dagger }$| . |
|---|---|---|---|---|---|---|---|---|---|
| Name . | (km s−1) . | (kpc) . | (s) . | (10−15 s s−1) . | (10−19 s s−1) . | (%) . | (Myr) . | (Myr) . | (Myr) . |
| B0031−07 | 77.00b | 1.26b | 0.942951403386(6) | 0.4070(4) | 4.79323268066(3) | 0.12 | 36.73(4) | 36.78(4) | 36.6243(6) |
| B0136+57 | 319.0b | 2.65b | 0.272459130582(2) | 10.7010(2) | 11.30225636215(7) | 0.01 | 0.40368(1) | 0.40373(1) | 0.403268(5) |
| B0148−06 | 261.0c | 4.60c | 1.46466489529(2) | 0.437(2) | 23.4309420922(4) | 0.53 | 53.1(2) | 53.4(2) | 52.469(6) |
| B0154+61 | 383.7c | 1.80c | 2.35188677732(3) | 189.038(3) | 207.804907222(2) | 0.01 | 0.197256(3) | 0.197278(3) | 0.1973619(5) |
| B0450+55 | 317.0b | 1.19b | 0.340731115855(1) | 2.39977(5) | 31.0821925829(1) | 0.13 | 2.25115(5) | 2.25407(5) | 2.27724(7) |
| B0611+22 | 21.00c | 3.55c | 0.33500477221(4) | 59.05(4) | 0.044956192797(5) | 0 | 0.08995(7) | 0.08995(7) | 0.089332(2) |
| B0626+24 | 84.00c | 3.00c | 0.476624376878(2) | 1.9944(2) | 1.210993642508(6) | 0.01 | 3.7890(4) | 3.7892(4) | 3.78649(6) |
| B0727−18 | 179.9c | 2.04c | 0.510174601578(7) | 18.9659(6) | 8.7433773083(1) | 0 | 0.42649(1) | 0.42651(1) | 0.426675(4) |
| B0809+74 | 102.0a | 0.43a | 1.292241576368(5) | 0.1679(3) | 33.7756638012(1) | 2.01 | 122.1(2) | 124.6(2) | 121.87(1) |
| B0820+02 | 47.80c | 2.66c | 0.864872887877(9) | 0.1014(9) | 0.802517912658(8) | 0.08 | 135.2(12) | 135.3(12) | 131.157(8) |
| B1530+27 | 144.0c | 1.60c | 1.12483633563(1) | 0.778(1) | 15.7478994453(2) | 0.2 | 22.93(4) | 22.98(4) | 22.877(2) |
| B1540−06 | 247.4c | 3.11c | 0.709064757447(1) | 0.8793(1) | 15.07485676089(3) | 0.17 | 12.785(2) | 12.807(2) | 12.7818(6) |
| B1541+09 | 277.0b | 7.20b | 0.74844877682(2) | 0.439(3) | 8.6162327085(2) | 0.2 | 27.02(17) | 27.07(17) | 27.438(3) |
| B1642−03 | 386.4c | 3.97c | 0.387691475966(5) | 1.7791(2) | 15.7506425803(2) | 0.09 | 3.4550(4) | 3.4581(4) | 3.45241(3) |
| B2154+40 | 264.0b | 3.40b | 1.52526824294(1) | 3.4342(7) | 33.7756301241(3) | 0.1 | 7.042(1) | 7.049(1) | 7.0452(1) |
| B2351+61 | 268.0c | 2.42c | 0.944796588832(3) | 16.2657(3) | 30.2915037893(1) | 0.02 | 0.92094(2) | 0.92111(2) | 0.921087(5) |
VLBI astrometric parameter solutions are independent and highly accurate. They can bring obvious optimizations for pulsar timing, as discussed above. Hence, it has important meaning to measure pulsar astrometric parameters with VLBI, especially for pulsars with timing irregularities. In addition to the Very Long Baseline Array (VLBA) (Napier et al. 1994), the European VLBI Network (EVN) (Booth 1991), and the Australian Long Baseline Array (LBA) (Norris 1988), the East Asia VLBI Network (EAVN) (Wajima et al. 2016) has great potential to perform pulsar observations. The longest baselines of the VLBA, the European part of the EVN, and the LBA are 8600 km,3 7139 km,4 and 1400 km, respectively. For the EAVN, the maximum of baseline is 5000 km. The EAVN has the ability to conduct observations at frequencies as low as 1.6 GHz; it consists of as many as 21 telescopes. Some of these telescopes are in the Japanese VLBI Network (JVN) (Omodaka & Kameya 1996). Previously, the JVN successfully performed experiments on giant radio pulses of the Crab pulsar (Takefuji et al. 2016). Also, many telescopes in China have the ability to carry out pulsar observations. So, we can expect to obtain accurate pulsar astrometric solutions with the EAVN.
5 Conclusion
Pulsar rotation parameters may have obvious changes over a long time. They are supposed to be measured using the latest timing data. Inaccurate astrometric parameters cause timing residual fluctuations that influence measurements of the rotation parameters. Fluctuations caused by inaccurate timing astrometric parameters can be properly subtracted with independent and accurate astrometric parameters measured by VLBI, leading to more accurate measurements of rotation parameters. Accurate proper motion and distance obtained with VLBI also refine the measurement of pulsar transverse velocity, which further leads to better estimates of the influence of the Shklovsky effect on |$\dot{P}$| and τc; the latter may obviously change after subtracting the Shklovsky effect for some pulsars, like PSR B0809+74 in our sample. Its increment is 2.5 Myr, which amounts to about 2% of the τm. For some pulsars, like PSR B1540−06, the increments of τc are larger than the differences between newly measured τm and previously measured τp. With VLBI astrometric parameter solutions, glitch parameters can also be more accurately measured.
Acknowledgements
We would like to express our appreciation to Professor R. N. Manchester and Dr. M. Sekido for their good suggestions on this work. This work was supported in part by the National Natural Science Foundation of China (Grant Nos. U1631122, 11633007, and 11403073), the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB23010200), the National Key R&D Program of China (2018YFA0404602), and the Knowledge Innovation Program of the Chinese Academy of Sciences (KJCX1-YW-18). The hard work of all members of the TMRT team is vital for the high-quality observational data used in this paper.
Footnotes
References





