-
PDF
- Split View
-
Views
-
Cite
Cite
Michael W Richmond, Masaomi Tanaka, Tomoki Morokuma, Shigeyuki Sako, Ryou Ohsawa, Noriaki Arima, Nozomu Tominaga, Mamoru Doi, Tsutomu Aoki, Ko Arimatsu, Makoto Ichiki, Shiro Ikeda, Yoshifusa Ita, Toshihiro Kasuga, Koji S Kawabata, Hideyo Kawakita, Naoto Kobayashi, Mitsuru Kokubo, Masahiro Konishi, Hiroyuki Maehara, Hiroyuki Mito, Takashi Miyata, Yuki Mori, Mikio Morii, Kentaro Motohara, Yoshikazu Nakada, Shin-Ichiro Okumura, Hiroki Onozato, Yuki Sarugaku, Mikiya Sato, Toshikazu Shigeyama, Takao Soyano, Hidenori Takahashi, Ataru Tanikawa, Ken’ichi Tarusawa, Seitaro Urakawa, Fumihiko Usui, Junichi Watanabe, Takuya Yamashita, Makoto Yoshikawa, An optical search for transients lasting a few seconds, Publications of the Astronomical Society of Japan, Volume 72, Issue 1, February 2020, 3, https://doi.org/10.1093/pasj/psz120
Close - Share Icon Share
Abstract
Using a prototype of the Tomo-e Gozen wide-field CMOS mosaic camera, we acquire wide-field optical images at a cadence of |$2\:$|Hz and search them for transient sources of duration 1.5 to |$11.5\:$|s. Over the course of eight nights, our survey encompasses the equivalent of roughly two days on one square degree, to a fluence equivalent to a limiting magnitude of about |$V = 15.6$| in a 1-s exposure. After examining by-eye the candidates identified by a software pipeline, we find no sources which meet all our criteria. We compute upper limits to the rate of optical transients consistent with our survey, and compare those to the rates expected and observed for representative sources of ephemeral optical light.
1 Introduction
The sky is filled with objects which appear eternal to the average human eye. True, the position and brightness of the planets change from week to week, and that of the Moon from night to night, but every generation of humans has seen the same Moon. To ancient skywatchers, the fixed stars seemed even more constant. On the rare occasions when a comet might appear for a few months, its ephemeral nature was held as a reason that it must be an atmospheric phenomenon and not a true member of the celestial sphere.
Over the past few centuries, astronomers have recognized that some stars do vary appreciably in brightness, and all drift across the sky, albeit slowly. Systematic surveys starting in the nineteenth century found evidence for stellar variation on timescales of years, days, and even hours. In recent decades, improving technology in detectors, telescope control systems, and data analysis has led to the creation of larger and larger catalogs of variable stars. Astronomers have also detected many transient objects: novae, supernovae, gamma-ray bursts (GRBs), fast radio bursts, and tidal disruption events, to name just a few.
Despite these efforts, some regions of parameter space remain largely unexplored. In particular, objects which appear only once for durations of just a few seconds—in a word, “flashes”—have escaped serious study. For example, Berger et al. (2013) presents a compilation of efforts to find optical transients on timescales of less than one hour: the Deep Lens Survey (Becker et al. 2004), ROTSE-III (Rykoff et al. 2005), MASTER (Lipunov et al. 2007), the Fornax Cluster search (Rau et al. 2008), and Pan-STARRS1 (Berger et al. 2013); yet none of these projects is sensitive to flashes shorter than |$20\:$|min. Recent work using the Dark Energy Camera (Andreoni et al. 2019) can detect sources with durations down to |$70\:$|s, but this is still an order of magnitude longer than the timescales of interest to us. There are at least four factors which make it difficult to look for sources which emit for only a few seconds. First, some detectors are not designed to operate at high cadence; large format CCDs require long readout times to produce images with low noise. Secondly, in order to eliminate false positives, it is beneficial to acquire at least two, if not three, measurements of a single event before it disappears; yet it is difficult to accumulate a reasonable signal-to-noise ratio for faint sources in just a few seconds. Thirdly, as we will demonstrate, brief optical flashes do not occur frequently; instruments with high time resolution but small fields of view, such as ULTRASPEC (Dhillon et al. 2014), may fail to find any events even after observing for many nights. Instruments with large fields of view require special optical designs and detectors with large active areas, both of which are expensive. Finally, long stretches of high-cadence measurements will produce a very large dataset, increasing the time and effort required to identify and confirm real transients.
Our effort was inspired by the development of large CMOS detectors which yield low noise even when read out several times per second. Placing a mosaic of such devices on to the focal plane of a Schmidt telescope creates an instrument which can sample large areas of the sky with high cadence, and designing a pipeline to analyze the large volume of data carefully reduces the amount of human oversight required to detect transient sources reliably. In section 2, we describe our equipment and the methods used to acquire images. The processing of those images into calibrated lists of stars is explained in section 3. We discuss the criteria by which transient objects are chosen from the star lists in section 4, and conclude that no objects satisfy all our conditions. In section 5, we use our null result to compute upper limits on the rates of transient sources per square degree. We explain how to convert the rates into volumetric units in section 6, and briefly compare them to observed and expected rates from the literature for two types of source. We compare our survey to three others which sample timescales of a few seconds in section 7.
We assume throughout this work a cosmology with |$H\,_0 = 69.6\:$|km|$\:$|s|$^{-1}\:$|Mpc|$^{-1}$|, |$\Omega _M = 0.286$|, and |$\Omega _{\Lambda } = 0.714$| (Wright 2006).
2 Observations
All images were acquired with the 105-cm Schmidt Telescope at Kiso Observatory, at |$35^\circ {47^{\prime}50{^{\prime \prime }_{.}}0}$| north, |$137^\circ {37^{\prime}31{^{\prime \prime }_{.}}5}$| east in the WGS84 system, and an altitude of |$1132\:$|m. Light was focused on an early version of the Tomo-e Gozen camera (Sako et al. 2016, 2018), referred to hereafter as Tomo-e PM (for “Prototype Model”). This prototype had eight CMOS sensors installed on the focal plane, each with |$2000 \times 1128$| pixels of size |$19\, \mu$|m on a side. The plate scale was approximately |${1{^{\prime \prime}_{.}}19}$| per pixel. Each chip subtended an area of approximately |${39{^{\prime }_{.}}7}\times {22{^{\prime }_{.}}4}$|, and the set of eight covered a total of about |$1.9\:$|deg|$^{2}$|, aligned in a row running east to west. Image frames were obtained by a rolling read operation at two frames per second; since the pixel reset time is only |$0.1\:$|ms, the exposure time of each frame was approximately |$0.5\:$|s. No filters were placed between the sensors and the sky, so the detectors measured light over the range 370 to |$730\:$|nm, with a peak quantum efficiency of 0.68 at |$\lambda = 500\:$|nm.
The data analyzed herein were gathered during eight nights in 2016 March and April; see table 1 for a list of the nights. In order to minimize the number of artificial satellites and space debris in our images, we aimed the telescope in the direction of the the Earth’s shadow. During each night, the pointing of the telescope gradually moved west to follow the shadow; figure 1 shows the area covered during each night. The center of this region is approximately at |${\rm RA} = 190^{\circ }$|, |${\rm Dec} = -8^{\circ }$|, which corresponds to galactic coordinates |${\rm \ell } = 298^{\circ }$|, |${b} = +55^{\circ }$| and ecliptic |${\rm long.} = 192^{\circ }$|, |${\rm lat.} = -3^{\circ }$|. It is far from the plane of the Milky Way, but close to the plane of the ecliptic. As the telescope tracked the field during each night, changes in airmass caused the zero-point of the photometric solution to vary by about |$0.5\:$|mag; in other words, as the field moved towards the horizon and its airmass increased, extinction by the Earth’s atmosphere caused sources to appear about |$0.5\:$|mag fainter at the end of a run than in the middle, when the field was on the meridian. Values larger than |$0.5\:$|mag in the “zp range” column of table 1 indicate that clouds and haze led to more (and more variable) extinction during the night.

Sky coverage during eight nights in 2016 March–April. A different color is used for each night. Each symbol shows the center of a field, but the size of the symbols is not equal to the area of each field. (Color online)
| Date . | Hours . | FWHM (|$^{\prime \prime }$|) . | zp range (mag) . |
|---|---|---|---|
| 2016 March 15 | 8.4 | 4–5 | 0.5 |
| 2016 March 16 | 6.7 | 3–5 | 1.5 |
| 2016 March 17 | 7.9 | 3–4 | 1.5 |
| 2016 March 30 | 5.0 | 4–7 | 0.6 |
| 2016 April 08 | 6.5 | 4–6 | 1.0 |
| 2016 April 09 | 5.3 | 3–4 | 1.0 |
| 2016 April 11 | 6.5 | 5–8 | 0.5 |
| 2016 April 14 | 6.2 | 5–8 | 1.8 |
| Date . | Hours . | FWHM (|$^{\prime \prime }$|) . | zp range (mag) . |
|---|---|---|---|
| 2016 March 15 | 8.4 | 4–5 | 0.5 |
| 2016 March 16 | 6.7 | 3–5 | 1.5 |
| 2016 March 17 | 7.9 | 3–4 | 1.5 |
| 2016 March 30 | 5.0 | 4–7 | 0.6 |
| 2016 April 08 | 6.5 | 4–6 | 1.0 |
| 2016 April 09 | 5.3 | 3–4 | 1.0 |
| 2016 April 11 | 6.5 | 5–8 | 0.5 |
| 2016 April 14 | 6.2 | 5–8 | 1.8 |
| Date . | Hours . | FWHM (|$^{\prime \prime }$|) . | zp range (mag) . |
|---|---|---|---|
| 2016 March 15 | 8.4 | 4–5 | 0.5 |
| 2016 March 16 | 6.7 | 3–5 | 1.5 |
| 2016 March 17 | 7.9 | 3–4 | 1.5 |
| 2016 March 30 | 5.0 | 4–7 | 0.6 |
| 2016 April 08 | 6.5 | 4–6 | 1.0 |
| 2016 April 09 | 5.3 | 3–4 | 1.0 |
| 2016 April 11 | 6.5 | 5–8 | 0.5 |
| 2016 April 14 | 6.2 | 5–8 | 1.8 |
| Date . | Hours . | FWHM (|$^{\prime \prime }$|) . | zp range (mag) . |
|---|---|---|---|
| 2016 March 15 | 8.4 | 4–5 | 0.5 |
| 2016 March 16 | 6.7 | 3–5 | 1.5 |
| 2016 March 17 | 7.9 | 3–4 | 1.5 |
| 2016 March 30 | 5.0 | 4–7 | 0.6 |
| 2016 April 08 | 6.5 | 4–6 | 1.0 |
| 2016 April 09 | 5.3 | 3–4 | 1.0 |
| 2016 April 11 | 6.5 | 5–8 | 0.5 |
| 2016 April 14 | 6.2 | 5–8 | 1.8 |
3 Processing the images
The real-time electronics collect the information from each sensor and package it into units we call “chunks,” which consist of 360 individual images (|$180\:$|s of data at |$2\:$|Hz). As described below, we sometimes treat the information from a single chunk as a unit for calibration.
We list below the steps involved in converting each raw image from a single sensor into a list of astrometrically and photometrically calibrated objects.
Following the method described in Ohsawa et al. (2016), we create a simple model of the bias for each image; it has a structure which repeats every four rows. We subtract this bias from the raw image pixels.
We do not perform any flatfielding. Please see our discussion of this point at the end of this section.
Using the stars and phot routines of the XVista package (Treffers & Richmond 1989),1we identify as stars objects with peaks |$5 \sigma$| above the sky level and FWHM in the range |${1{^{\prime \prime}_{.}}8}$|–|${13{^{\prime \prime}_{.}}0}$|. We perform aperture photometry on each star, measuring the flux within circular apertures of two sizes: one fixed at 10 pixels (|${11{^{\prime \prime}_{.}}8}$|) and one which varied from image to image, equal to 1.5 times the FWHM of the image. The result of this stage is one list of stars per image, with (row, column) positions and instrumental magnitudes on an arbitrary scale.
Objects detected at least twice in the images of a single chunk are combined into an ensemble. These objects are subjected to inhomogeneous ensemble photometry (Honeycutt 1992), bringing them to a single photometric zeropoint. This procedure creates a set of robust statistics, such as the photometric uncertainty as a function of instrumental magnitude.
We calibrate the ensemble averages of each object astrometrically against the UCAC4 (the fourth United States Naval Observatory CCD Astrograph Catalog; Zacharias et al. 2013), and photometrically against the UCAC4’s V-band magnitudes; recall that our measurements are unfiltered. This provides accurate measurements for stars which appear in most of the images of the chunk; in other words, for ordinary stars which do not vary on short timescales.
The objects detected in each individual image are also calibrated against the UCAC4, astrometrically and photometrically, in a similar manner. These results will be less accurate, but provide measurements for transient objects which might not be included in the ensembles.
We create a set of diagnostic graphs and tables, summarizing the properties of objects in each chunk.
We employed a simple first-order model to match the (|$x, y$|) positions of stars on each sensor to the (RA, Dec) positions from the UCAC4. The typical solution involved 30 to 50 stars and yielded residuals of size |$\sim {0{^{\prime \prime}_{.}}5}$|, adequate for our purposes. See figure 2 for details.
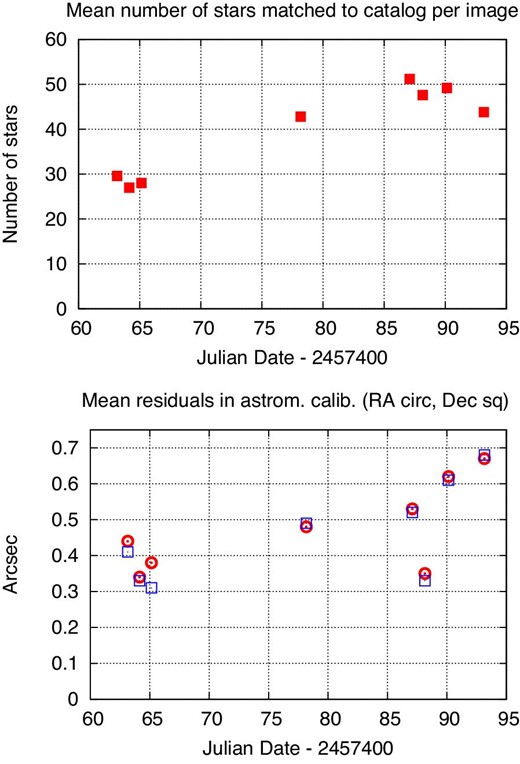
Properties of astrometric solutions in 2016 March and April. In the lower panel, mean residuals in RA are shown as red circles, in Dec by blue squares. (Color online)
We found that using photometric apertures which varied with the seeing produced better results than using fixed apertures, which is not surprising given the considerable variations in FWHM (from |$4{^{\prime \prime }}$| to |$7{^{\prime \prime }}$|, or |$5{^{\prime \prime }}$| to |$8{^{\prime \prime }}$|; see table 1) over the course of some of our nights. Depending on the conditions, bright stars (|$V \sim 11$|) showed scatter of 0.02 to |$0.03\:$|mag, while measurements of faint stars (|$V \sim 16$|) varied by 0.08 to |$0.12\:$|mag from image to image. Figure 3 shows examples under good and adverse conditions. Note that our very short exposures mean that scintillation noise can contribute significantly to the noise floor at moderate airmass.
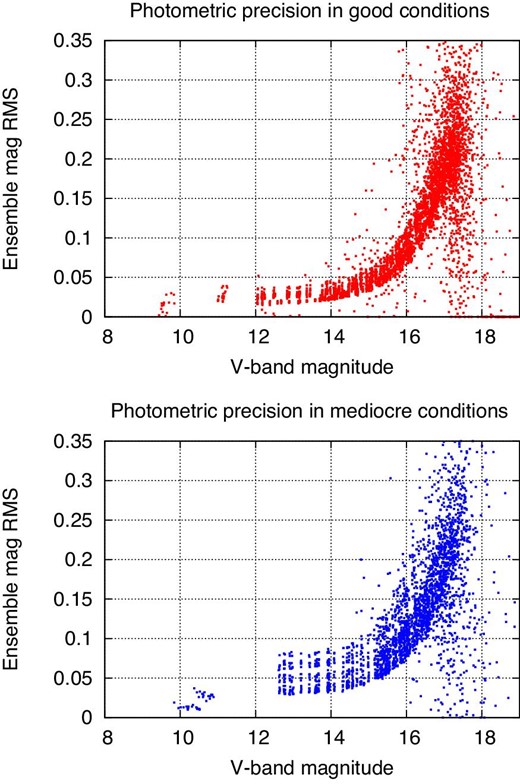
Scatter in repeated measurements as a function of magnitude. Top panel: good conditions, 2016 March 15 around JD 2457463.06; bottom panel: poor conditions, 2016 March 17 around JD 2457465.06. (Color online)
To what extent does the lack of flatfielding degrade our measurements of both brightness and position of each star? Typical stellar images have a FWHM of at least 3 pixels, so that our varying photometric aperture encompasses at least 64 pixels. Our measurements show that the centroid of each object wanders over a range of roughly |$\pm 1$| pixel from image to image, due to fluctuations in the atmosphere. Since we are searching for transient objects, not performing a photometric survey, we may ignore possible large-scale variations in sensitivity across one detector, or between detectors, and consider only the scatter in measurements of brightness of an object from frame to frame. The observed scatter for bright, unsaturated stars (|$V \sim 11$|) is |$0.03\:$|mag, while calculations of the photon, sky, and scintillation noise yield an expected value of |$0.02\:$|mag. Subtracting these in quadrature leaves an amount of |$0.02\:$|mag, which places an upper limit on the effect of uncorrected pixel-to-pixel gain variations on our photometry.
It is more difficult to quantify the effect of our lack of flatfielding on the astrometry of stars in the Tomoe images. The positional accuracy of the UCAC4 is between |${0{^{\prime \prime}_{.}}015}$| and |${0{^{\prime \prime}_{.}}100}$| in each coordinate (Zacharias et al. 2013), while the residuals in our astrometry are roughly an order of magnitude larger (see figure 2). Sub-second fluctuations in the atmosphere change the shape and size of the PSF from one image to the next, but since we measure the mean position of a star as varying by only about |${0{^{\prime \prime}_{.}}100}$| from image to image, it seems unlikely that uncorrected small variations in pixel-to-pixel sensitivity could be responsible for more than this amount. The bulk of the astrometric residuals are likely due to other factors, such as the simple first-order model we employ in our pipeline, or differential chromatic refraction due to our wide passband.
The pipeline produces two lists of stars as its main output. One is based on the ensemble of stars within each chunk of images; the other is a list of every object detected in each individual image. Each list is calibrated in position and magnitude against the UCAC4. The pipeline also produces a set of diagnostic graphs to help us determine the quality of each night.
4 Search for transients
Running the pipeline takes a significant amount of computing power and time. We designed our algorithm which searches for transient objects to operate on the star lists created by the pipeline. Since the data volume is much smaller (by factors of |$\sim 100$|), the time to search, check, and, if necessary, re-search is much smaller. For example, consider the data acquired by one particular chip over a span of six hours and 24 minutes on the night of 2016 April 14. Our pipeline required three hours and 16 minutes to convert the raw images into calibrated lists of stars. Sifting through these lists for transients (a process which we will describe in detail below) took only |$47\:$|s on the same computer. Thus, preparing for the transient search took roughly 250 times longer than the search itself.
Our method is based on measurements made within a single chunk of data: 360 consecutive images spanning |$180\:$|s. As described in the text following the list below, this can cause the method to miss a very small fraction of transients which last for up to two seconds; however, we accept this small drawback in return for a significant simplification in the bookkeeping.
We scan through all objects detected within the chunk and subject them to a series of tests. An object which fails any test is discarded. In order to pass these tests:
An object must be detected between three and 20 times within a single chunk of 360 images.
All detections must appear within a window of |$(N + 3)$| consecutive images, where N is the number of detections. In other words, we look only for objects which brighten once, then fade away; we discard objects which appear repeatedly at regular or irregular intervals. We add 3 extra images to our window of acceptance to accommodate objects close to the limiting magnitude; small random variations in transparency or seeing may cause them to fall just below the detection threshold in, say, one of six images. Figure 4 shows example sequences of detections and non-detections, and our decision in each case. In the terms used by Andreoni et al. (2019), our criteria are min = 3, max = 20, holes = 3, empty = 0.
The magnitude of a candidate must be less than |$(m + 1)$|, where m is the limiting magnitude of the chunk (which we will discuss below). In other words, the object may be slightly fainter, on average, than the limiting magnitude.
The object must be at least 7 pixels (|$8\rlap {.}{^{\prime \prime }}3$|) from its nearest neighbor in the ensemble. This rule rejects many bogus candidates in the outer regions of bright stars.
The object must be at least 10 pixels (|$11\rlap {.}{^{\prime \prime }}8$|) from the edges of the image. Our routines for accurately measuring the properties of an object set this limit.
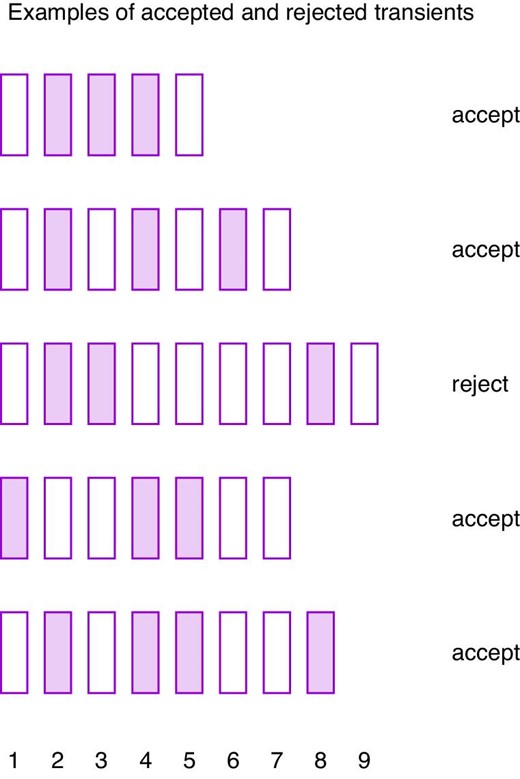
Examples of sequences of images with detections (filled rectangles) and non-detections (empty rectangles), and our algorithm’s decision at the right. (Color online)
Conditions 1 and 2 can cause a real, very brief transient to be missed. If an object appears for exactly three images (|$1.5\:$|s), and those three images span the boundary between two chunks, or if it appears for exactly four images (|$2\:$|s), of which two are the final images of one chunk and the other two are the initial images of the next chunk, then that object will not pass the tests. Since this applies only to a very small fraction of all possible transients (about |$0.6\%$| of those consisting of exactly three or four detections), we accept the losses.
Condition 5 causes us to ignore a thin strip around the edges of each image, amounting to |$2.7\%$| of the area of the survey. We will account for this small inefficiency in our calculations of the control time and transient rates later in this paper.
Describing the “limiting magnitude” for an instrument can be approached in several ways. For example, under optimal conditions, a star of magnitude |$V = 18.5$| produces a signal-to-noise ratio of 5 in a 1-s exposure with Tomo-e (Sako et al. 2018); so one might say that the 0.5-s exposures we studied ought to have a limiting magnitude of |$V = 17.7$|. However, since our search was often conducted in less than optimal conditions, we take a more conservative approach in this paper. In order to calculate the limiting magnitude for a chunk, we begin by counting the number N of “good” images within the chunk. This is normally close to 360, but may be smaller if some frames are rendered unusable by clouds, bad seeing, passing airplanes, or other problems. We then compare the number of images in which each star is detected to N. Bright stars will appear in nearly all of them, but very faint stars may rise above the noise threshold only in a few images. We define the “limiting magnitude” of a chunk to be the magnitude at which the average number of detections falls to |$N/2$|. We record this limiting magnitude for each chunk, and use it not only to test possible transients, but also to compute control times (see section 5).
After running all the star lists through these tests, we found a total of 57 candidate transient objects. We examined each candidate in detail, scrutinizing the images before, during, and after its detections. We discovered that most of these candidates were simply ordinary stars, somewhat fainter than the limiting magnitude of our observations. Due to fortuitous moments of good seeing, they would sometimes pop up above the detection limit for a few consecutive frames before disappearing below the sky noise again. Although our software failed to notice them most of the time, a human eye could often detect them, once their positions were known. We examined 2MASS (Skrutskie et al. 2006) and Digitized Sky Survey (Djorgovski et al. 2003) images at the positions of all candidates to look for faint stars, and rejected all candidates with counterparts in these surveys. One example of this sort of object is shown in figure 5.

Cutouts centered on a candidate of 2016 March 30. The object was detected in the second, fourth, and seventh images in this sequence, but is present in all of them. Each cutout is |$130^{\prime \prime }$| on a side, with north up, east to the left. Time runs from left to right.
A few of the candidates were bright stars, far above the detection limit, which appeared offset from their usual positions due to particularly bad seeing. Short-term atmospheric fluctuations can lead to unusually distorted point spread functions when one integrates for very short durations. An example of this type of candidate is shown in figure 6.

Cutouts centered on a candidate of 2016 April 11, during conditions of poor seeing. The software determined a position for this object in the central 3 images which was sufficiently offset from the usual position that it appeared as a new object. The red circle indicates the size of matching radius. Each cutout is |$130^{\prime \prime }$| on a side, with north up, east to the left. Time runs from left to right. (Color online)
The most promising candidate appeared on the night of 2016 March 17, near RA |$= 169.24$| and Dec |$= 0.97$|. Two of the seven candidates for this night turned out to be the same object, which was moving at a rate of about |$5{^{\prime \prime }}$| per second to the east. It was below the threshold of detection for most of the observations, but rose above the threshold for a few seconds and was detected twice, separated by a few seconds, at an average magnitude of |$V \sim 17.5$|. Figure 7 shows subframes of consecutive images, centered on the candidate. The top row shows the first detection, and the lower row the second detection.

Cutouts centered on the moving candidate from 2016 March 17. Each cutout is |$130^{\prime \prime }$| on a side, with north up, east to the left. Time runs from left to right in each row.
Using tools provided by the Minor Planet Center, we found no known asteroids at this position. The motion is consistent with that of an artificial satellite in high-Earth orbit. When we examined the intervening images, we were able to detect it in most of them—but at a significance level below that required to trigger our star-finding routines.
In summary, we found zero stationary objects which appeared, and then disappeared, over a span of time between 1.5 and |$11.5\:$|s. However, the fact that our procedure did uncover a very faint, moving satellite, at two locations along its orbit, gives us some confidence that it would have flagged a real transient source as well.
What can we learn from this null result?
5 The rate of transient events
Following methods used by supernova researchers starting with Zwicky (1938), we introduce the concept of control time: the time during which a transient event would have been detected by our system, should it have occurred. In the case of supernovae, which remain bright for many weeks, one must take into account the possibility of an explosion happening some time before the start of an observation. Since we are interested in objects which fade only a few seconds after their rise, however, which is an interval much shorter than the duration of our measurements each night, our control time is simply the sum of our exposure times (after removing periods ruined by clouds, bad seeing, and other problems).
In the decades following Zwicky (1938), survey images typically covered the entire extent of some particular galaxy (and of many galaxies, in fact). Any supernova in that galaxy would appear in each survey image, and so the control time for that galaxy would be simply a function of the duration of the survey and the intervals between images. In most modern searches, including ours, which are not confined to some known and finite source, the control time must include a factor in addition to time: the area over which new objects could be detected. Clearly, for example, an eight-hour sequence of images covering 10 square degrees provides more information than an eight-hour sequence of images reaching the same depth, but covering only one square degree. This example makes clear that another variable we must consider is the depth of the survey: an eight-hour sequence of images reaching |$V=15$| provides more information than a similar sequence of images which reaches only |$V=10$|.
In order to characterize our survey for transients, therefore, we must describe
the area of the sky covered; we will use square degrees,
the time span of the observations; we choose seconds,
the depth of the survey; see discussion below.
In most circumstances, astronomers would describe the depth of a survey by its limiting magnitude, or limiting flux; these are appropriate choices to describe sources which are constant in brightness. Since we are searching for objects which might change in brightness considerably from one image to the next, however, or even during the exposure of a single image, it makes more sense to consider the concept of fluence. Fluence is the integral of flux over time; it might be the number of photons collected during one exposure, for example, or summed over several exposures.
As described in the previous section, our pipeline computes a limiting magnitude m for each chunk of images. We apply that value to all the images in a chunk in order to compute control times. Thus, we can not account properly for any changes in sky conditions on timescales shorter than the duration of a chunk (|$180\:$|s).
Even though fluence is a better choice when describing the behavior of very brief transients, most of the literature on surveys for supernova, gamma-ray bursts, and other variable objects characterizes their measurements in terms of a limiting magnitude. In order to compare our results more easily with others, we will convert our results into those terms. Since we are looking for objects with lifetimes of just a few seconds, it is convenient to describe our results in terms of the fluence over a period of one second, or, equivalently, the limiting magnitude in a 1-s exposure. Since the conditions changed significantly within some nights, as well as from night to night, and since the properties of the sources which might appear in our data have very broad ranges, we have chosen to compute control times for a range of observed fluences, rather than a single value. We compute control times for four choices of this parameter, corresponding to limiting magnitudes of |$V = 12.6$|, 13.6, 14.6, and 15.6, in a one-second exposure. The results are presented in table 2. The small value in the final entry for 2016 April 14 is due to a combination of bad seeing and clouds.
| Date . | |$V=12.6$| . | |$V=13.6$| . | |$V=14.6$| . | |$V=15.6$| . |
|---|---|---|---|---|
| 2016 March 15 | 49357 | 49357 | 49357 | 43685 |
| 2016 March 16 | 40520 | 40520 | 38834 | 33083 |
| 2016 March 17 | 43984 | 43741 | 41077 | 32671 |
| 2016 March 30 | 30133 | 29292 | 25108 | 19253 |
| 2016 April 08 | 33068 | 31919 | 28311 | 23028 |
| 2016 April 09 | 30015 | 29298 | 25848 | 10807 |
| 2016 April 11 | 36771 | 34252 | 28888 | 14843 |
| 2016 April 14 | 28216 | 25715 | 20015 | 128 |
| Total | 292069 | 284100 | 257441 | 177502 |
| Date . | |$V=12.6$| . | |$V=13.6$| . | |$V=14.6$| . | |$V=15.6$| . |
|---|---|---|---|---|
| 2016 March 15 | 49357 | 49357 | 49357 | 43685 |
| 2016 March 16 | 40520 | 40520 | 38834 | 33083 |
| 2016 March 17 | 43984 | 43741 | 41077 | 32671 |
| 2016 March 30 | 30133 | 29292 | 25108 | 19253 |
| 2016 April 08 | 33068 | 31919 | 28311 | 23028 |
| 2016 April 09 | 30015 | 29298 | 25848 | 10807 |
| 2016 April 11 | 36771 | 34252 | 28888 | 14843 |
| 2016 April 14 | 28216 | 25715 | 20015 | 128 |
| Total | 292069 | 284100 | 257441 | 177502 |
| Date . | |$V=12.6$| . | |$V=13.6$| . | |$V=14.6$| . | |$V=15.6$| . |
|---|---|---|---|---|
| 2016 March 15 | 49357 | 49357 | 49357 | 43685 |
| 2016 March 16 | 40520 | 40520 | 38834 | 33083 |
| 2016 March 17 | 43984 | 43741 | 41077 | 32671 |
| 2016 March 30 | 30133 | 29292 | 25108 | 19253 |
| 2016 April 08 | 33068 | 31919 | 28311 | 23028 |
| 2016 April 09 | 30015 | 29298 | 25848 | 10807 |
| 2016 April 11 | 36771 | 34252 | 28888 | 14843 |
| 2016 April 14 | 28216 | 25715 | 20015 | 128 |
| Total | 292069 | 284100 | 257441 | 177502 |
| Date . | |$V=12.6$| . | |$V=13.6$| . | |$V=14.6$| . | |$V=15.6$| . |
|---|---|---|---|---|
| 2016 March 15 | 49357 | 49357 | 49357 | 43685 |
| 2016 March 16 | 40520 | 40520 | 38834 | 33083 |
| 2016 March 17 | 43984 | 43741 | 41077 | 32671 |
| 2016 March 30 | 30133 | 29292 | 25108 | 19253 |
| 2016 April 08 | 33068 | 31919 | 28311 | 23028 |
| 2016 April 09 | 30015 | 29298 | 25848 | 10807 |
| 2016 April 11 | 36771 | 34252 | 28888 | 14843 |
| 2016 April 14 | 28216 | 25715 | 20015 | 128 |
| Total | 292069 | 284100 | 257441 | 177502 |
Our goal is to use this information to determine the rate at which transients appear, in units of objects per square degree per second. Since we detected no events, however, we cannot perform this calculation in the simple way. Instead, we will use our measurements to place an upper limit on the rate at which transients appear. We will begin by making two assumptions:
transient events are independent of each other; and
the rate of events, |$\lambda$|, is constant during the course of our survey.
We observed |$N = 0$| events. In order to place limits on the rate |$\lambda$|, we must choose some small probability |$p_0$| that this lack of detections is due purely to chance. We make the arbitrary choice of |$p_0 = 0.05$|, and then reject any rate |$\lambda$| which would yield a probability |$p \lt p_0$| of observing zero events. This technique yields upper limits on the rate of transient events meeting our criteria, which we quote in units of events per square degree per day. These values are listed in table 3 for the four choices of limiting fluence, and are shown in figure 8.
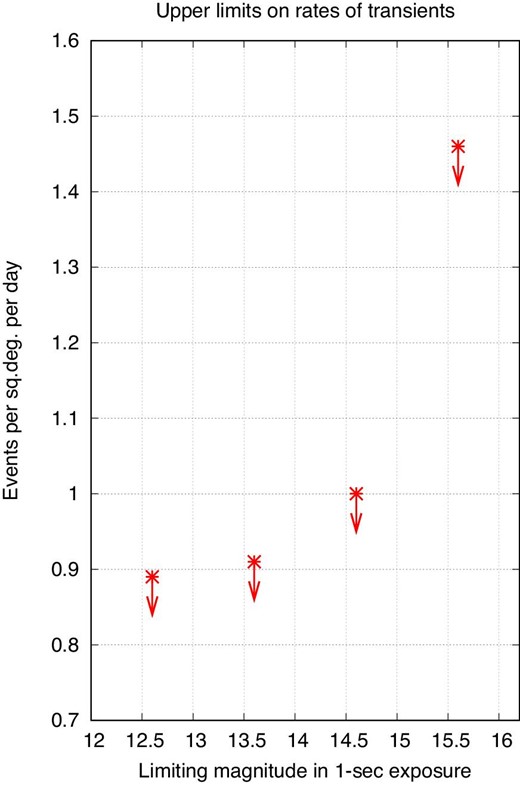
Upper limits to the areal rates of optical flashes. (Color online)
Upper limit (95% confidence level) on rate (events per square degree per day) for several thresholds.
| Fluence|$^{*}$| | |$V=12.6$| | |$V=13.6$| | |$V=14.6$| | |$V=15.6$| |
| Rate | 0.89 | 0.91 | 1.00 | 1.46 |
| Fluence|$^{*}$| | |$V=12.6$| | |$V=13.6$| | |$V=14.6$| | |$V=15.6$| |
| Rate | 0.89 | 0.91 | 1.00 | 1.46 |
|$^{*}$|Equivalent limiting mag in 1-s exposure.
Upper limit (95% confidence level) on rate (events per square degree per day) for several thresholds.
| Fluence|$^{*}$| | |$V=12.6$| | |$V=13.6$| | |$V=14.6$| | |$V=15.6$| |
| Rate | 0.89 | 0.91 | 1.00 | 1.46 |
| Fluence|$^{*}$| | |$V=12.6$| | |$V=13.6$| | |$V=14.6$| | |$V=15.6$| |
| Rate | 0.89 | 0.91 | 1.00 | 1.46 |
|$^{*}$|Equivalent limiting mag in 1-s exposure.
6 The volumetric rate of specific sources
To illustrate the method, we choose two representative sources: a “nearby” type, the impact of a small body on to a white dwarf, and a “distant” variety, the prompt optical flash of a gamma-ray burst. Our goal in the following discussion is to show the steps one can follow to compute volumetric rates from our survey’s data.
6.1 Asteroids and comets falling on to white dwarfs
The collision of small bodies on to the surface of a white dwarf is discussed in Di Stefano et al. (2015), and one sees evidence for it in the abundance of some heavy elements in the spectra of certain white dwarfs. The energy produced in the collision is released over a period which increases with the mass of the impactor. For objects of mass |$m \sim 10^{14}\:$|g, Di Stefano et al. (2015) estimate that the optical flash might last for |$\Delta t \sim 1\:$|s, and contain roughly |$E \sim 10^{31}\:$|erg. Using these values, we compute distances out to which such collisions would be detected, and list them in table 4.
Detection limit |$d_{\rm max}$| and upper limit on volumetric rate for |$10^{31}\:$|erg|$\:$|s|$^{-1}$| comet–WD collision.
| . | |$V=12.6$| . | |$V=13.6$| . | |$V=14.6$| . | |$V=15.6$| . |
|---|---|---|---|---|
| |$d_{\rm max}$| (pc) | 54 | 86 | 136 | 215 |
| Rate (pc|$^{-3}\:$|yr|$^{-1}$|) | 20.4 | 5.2 | 1.4 | 0.53 |
| . | |$V=12.6$| . | |$V=13.6$| . | |$V=14.6$| . | |$V=15.6$| . |
|---|---|---|---|---|
| |$d_{\rm max}$| (pc) | 54 | 86 | 136 | 215 |
| Rate (pc|$^{-3}\:$|yr|$^{-1}$|) | 20.4 | 5.2 | 1.4 | 0.53 |
Detection limit |$d_{\rm max}$| and upper limit on volumetric rate for |$10^{31}\:$|erg|$\:$|s|$^{-1}$| comet–WD collision.
| . | |$V=12.6$| . | |$V=13.6$| . | |$V=14.6$| . | |$V=15.6$| . |
|---|---|---|---|---|
| |$d_{\rm max}$| (pc) | 54 | 86 | 136 | 215 |
| Rate (pc|$^{-3}\:$|yr|$^{-1}$|) | 20.4 | 5.2 | 1.4 | 0.53 |
| . | |$V=12.6$| . | |$V=13.6$| . | |$V=14.6$| . | |$V=15.6$| . |
|---|---|---|---|---|
| |$d_{\rm max}$| (pc) | 54 | 86 | 136 | 215 |
| Rate (pc|$^{-3}\:$|yr|$^{-1}$|) | 20.4 | 5.2 | 1.4 | 0.53 |
Di Stefano et al. (2015) estimate that the number of comet-WD collisions in a typical galaxy is |$8 \times 10^{6}$| per year. If we model the disk of the Milky Way as a thin disk of radius |$10\:$|kpc and height |$1\:$|kpc, its volume is |$3 \times 10^{11}\:$|pc|$^{3}$|; our upper limit to the rate (for a fluence equivalent to |$V = 15.6$| in a 1-s exposure) would imply that no more than |$\sim 1.6 \times 10^{11}$| events should occur within the entire galaxy each year. While this is certainly consistent with the expectations of Di Stefano et al. (2015), it is far from being a strict constraint.
6.2 Prompt optical flashes of gamma-ray bursts
In many cases, optical emission has been detected hours to days after a GRB, as part of the physical process called the afterglow. In a very few cases, optical telescopes have seen flashes at the same time as the initial burst of gamma rays. We will take as models three events in which the optical flash was particularly bright: GRBs 080319B (Racusin et al. 2008; Covino et al. 2008; Woźniak et al. 2009), 130427A (Tanvir et al. 2013; Vestrand et al. 2014), and 160625B (Batsch et al. 2016; Troja et al. 2017; Karpov et al. 2017). All three are classified as “long” GRBs, as instruments detected gamma rays from them for durations longer than two seconds [see Kouveliotou et al. (1993) for the distinction between “short” and “long” GRBs, and Pe’er (2015) for a review of “long” GRB properties]. In each of these cases, the GRB seems to have been caused by the collapse of a massive star.
The calculations of |$d_{\rm max}$| and volumetric rate for these very luminous and distant events are more complicated than those for “nearby” objects for two reasons. First, the relationship between distance and apparent brightness is not the simple Euclidean |$1/r^2$|, due to the curvature of space-time and relativistic effects. Secondly, when determining the observed properties of objects at redshifts |$z \gt 0.5$|, one must account for the difference between the spectral region in which light was emitted in the rest frame, and the spectral region in which the light is detected by the observer; in other words, one must know the shape of the source’s spectral energy distribution.
The amplitude A is proportional to the overall luminosity of prompt emission. We choose to describe it by computing an “overall gamma-ray peak luminosity,” |$L_\gamma$|, for the flash, which we calculate using rest-frame emission in the range 10–|$2000\:$|keV. For a wide range of such luminosities, we then determine the redshifts at which our model’s observed optical brightness would fall below our four limiting magnitudes; the results are shown in figure 9. Note that the intergalactic medium is likely to be ionized at |$z \gtrsim 5.5$| (Songaila 2004), and hence opaque to the (at that time) ultraviolet photons flying toward us. However, it is possible that some windows of low opacity might allow the detection of a small fraction of sources beyond this redshift.
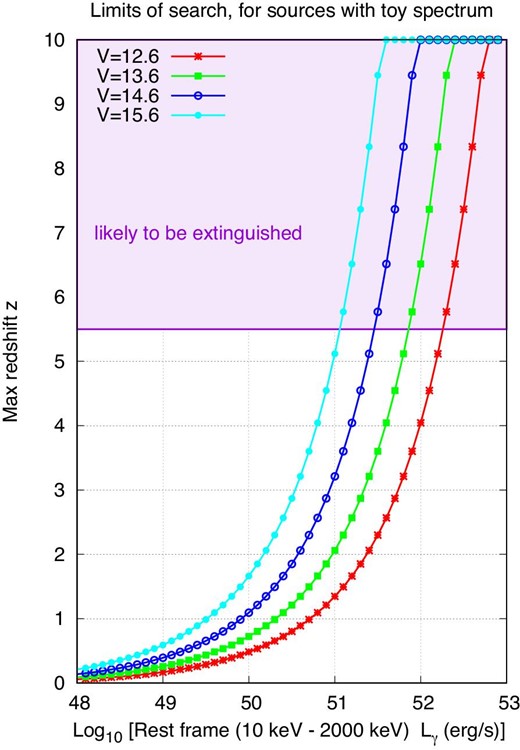
Upper limits to the redshifts at which our survey could detect prompt optical flashes from GRBs. (Color online)
When we set the value of A so that the model optimally matches the gamma-ray and optical observations of the three comparison events (to within an order of magnitude in all cases), we derive a value of |$L_\gamma = 6 \times 10^{52}\:$|erg|$\:$|s|$^{-1}$|. This implies that events similar to those in the comparison set would be detected to redshifts |$z \gt 9$| even for our brightest choice of magnitude limit.
Given a redshift, one can compute the comoving volume within a spherical region and convert the areal rates listed in table 3 into volumetric form. These rates, in units of events per cubic Gpc per year, are displayed in figure 10. We arbitrarily set an upper limit of |$z = 10$| for the explosion of GRBs, causing the rates to reach fixed values at high luminosities, while the flashes can be seen throughout the entire volume. We list those fixed rates in table 5. Note that when the search can detect events anywhere in the volume, the rate for particular limiting magnitude depends solely on the control time; thus, the case of |$V = 15.6$| ceases to provide the most stringent upper limit because its control time was smaller than that of |$V = 14.6$| or |$V = 13.6$|.
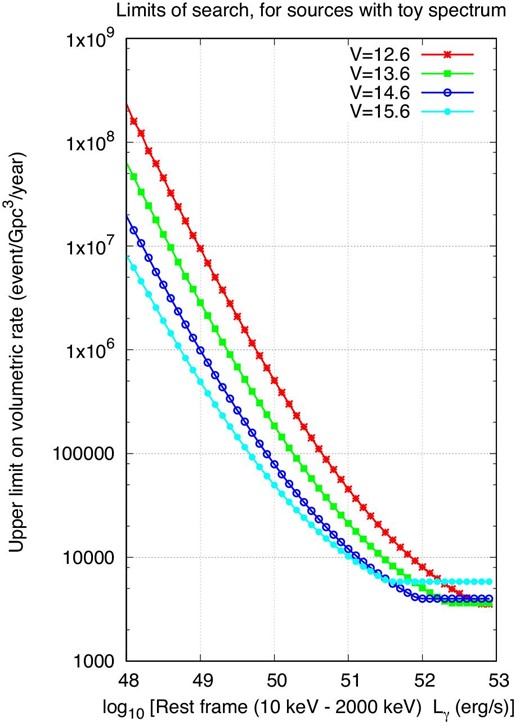
Upper limits to the volumetric rates of GRBs with bright prompt optical flashes.
| . | |$V=12.6$| . | |$V=13.6$| . | |$V=14.6$| . | |$V=15.6$| . |
|---|---|---|---|---|
| If |$L_\gamma$| (erg|$\:$|s|$^{-1}$|) is greater than | |$6.3 \times 10^{52}$| | |$2.5 \times 10^{52}$| | |$1.0 \times 10^{52}$| | |$4.0 \times 10^{51}$| |
| then rate (Gpc|$^{-3}\:$|yr|$^{-1}$|) is less than | |$3600$| | 3700 | 4000 | 5800 |
| . | |$V=12.6$| . | |$V=13.6$| . | |$V=14.6$| . | |$V=15.6$| . |
|---|---|---|---|---|
| If |$L_\gamma$| (erg|$\:$|s|$^{-1}$|) is greater than | |$6.3 \times 10^{52}$| | |$2.5 \times 10^{52}$| | |$1.0 \times 10^{52}$| | |$4.0 \times 10^{51}$| |
| then rate (Gpc|$^{-3}\:$|yr|$^{-1}$|) is less than | |$3600$| | 3700 | 4000 | 5800 |
| . | |$V=12.6$| . | |$V=13.6$| . | |$V=14.6$| . | |$V=15.6$| . |
|---|---|---|---|---|
| If |$L_\gamma$| (erg|$\:$|s|$^{-1}$|) is greater than | |$6.3 \times 10^{52}$| | |$2.5 \times 10^{52}$| | |$1.0 \times 10^{52}$| | |$4.0 \times 10^{51}$| |
| then rate (Gpc|$^{-3}\:$|yr|$^{-1}$|) is less than | |$3600$| | 3700 | 4000 | 5800 |
| . | |$V=12.6$| . | |$V=13.6$| . | |$V=14.6$| . | |$V=15.6$| . |
|---|---|---|---|---|
| If |$L_\gamma$| (erg|$\:$|s|$^{-1}$|) is greater than | |$6.3 \times 10^{52}$| | |$2.5 \times 10^{52}$| | |$1.0 \times 10^{52}$| | |$4.0 \times 10^{51}$| |
| then rate (Gpc|$^{-3}\:$|yr|$^{-1}$|) is less than | |$3600$| | 3700 | 4000 | 5800 |
Let us briefly consider some implications of these calculations. We will begin with a discussion of the rates at which actual GRBs are detected; our conclusions may dishearten the reader. However, a subsequent examination of the properties of one type of GRB progenitor may provide a ray of hope.
The rate at which short GRBs (Berger 2014) occur has been estimated at roughly |$\sim 1\!-\!10$| per Gpc|$^{3}$| per year (Wanderman & Piran 2015), although a few authors suggest higher values of |$\sim 10\!-\!100$| per Gpc|$^{3}$| per year (Nakar et al. 2006; Guetta & Piran 2006). Even the higher end of these estimates would imply that our search would have to continue for years in order to accumulate interesting statistics. However, note that the gamma-rays by which these events are detected are thought to be highly beamed, while one can speculate that the optical emission might be less collimated, and so the rate of optical flashes might be considerably larger. We may also compare our limits to the rate of long GRBs; after all, our toy model is based on observations of such core-collapse events. Even some “long” GRBs have durations less than |$11.5\:$|s, and so fall within our search criteria. The rate of long GRBs is thought to be comparable to that of their short cousins: roughly 1 per Gpc|$^{3}$| per year (Wanderman & Piran 2010). Once again, the conclusion is that our instrument would have to operate for many years to provide meaningful constraints.
If we turn our attention away from observations of gamma-ray bursts, and consider instead properties of the population of objects which give rise to them, our survey becomes somewhat more relevant. The class of short GRBs is thought to be due, in part at least, to the mergers of binary neutron stars (Paczynski 1986; Goodman 1986; Eichler et al. 1989). The rate of mergers between neutron stars (NS) has become a hot topic of late, thanks to the success of LIGO and Virgo. Chruslinska (2019) provides a nice summary of both observational measurements of the rate, and theoretical expectations based on population synthesis and binary evolution. The observations suggest somewhat higher rates than the models, with some estimates reaching a few thousand per Gpc|$^{3}$| per year. Kasliwal et al. (2017) describe a recent search for week-long optical transients with the Palomar Transient Factory which yields limits of the order of 1000 per Gpc|$^{3}$| per year. If (and we stress that this is a big qualification) the NS–NS merger mechanism should produce a prompt spectrum similar to that of the long GRBs in our comparison set, then continuing a search like ours for several months or years could place meaningful constraints on the rates of such mergers.
7 Comparison with other transient searches
Many groups have examined the sky for ephemeral sources over the past century, but the great majority considered timescales much longer than the range of 1.5–|$11.5\:$|s that we explore in this work. For example, the Deep Lens Survey Transient Search (Becker et al. 2004), and efforts using data from ROTSE-III (Rykoff et al. 2005), MASTER (Lipunov et al. 2007), DECam (Andreoni et al. 2019), and PanSTARRS (Berger et al. 2013) all required a source to remain bright for long enough to appear in at least two images of moderate to long exposure time, leading to minimum durations of hundreds or thousands of seconds. Because all these projects could detect sources much fainter than Tomo-e PM, the control volumes they examined were three to five orders of magnitude greater than that described in this work. However, since the transients we seek herein would appear in only a single exposure of all those projects, and so be discarded, there seems little reason to consider them further.
Instead, let us compare our survey briefly with three other projects which are sensitive to transients within our chosen timescale and appear to be ongoing: Pi of the Sky, Mini-Mega-TORTORA, and Gaia.
Pi of the Sky (Sokolowski 2008; Obara et al. 2014) consists of one system in Atacama, Chile, with two cameras, and three systems in INTA, Spain, with four cameras each. Each camera consists of a 85-mm f/1.2 camera lens which focuses light on to a CCD, yielding a field of |$20^{\circ } \times 20^{\circ }$| with pixels subtending |$36{^{\prime \prime }}$| on a side. Exposures of length |$10\:$|s detect objects down to |$V \sim 12$|; this corresponds to a limit of about |$V \sim 9.5$| in a 1-s exposure. The weather at all sites is very good, providing images of very large areas of the sky on many nights per year.
Mini-Mega-TORTORA, hereafter denoted MMT-9 (Karpov et al. 2016), is based at the Special Astrophysical Observatory in the Caucasus, where the sky is somewhat cloudy. Nine independent units, each built around an 85-mm f/1.2 camera lens and Andor Neo CMOS detector, provide images covering |$9^{\circ } \times 11^{\circ }$| with pixels subtending |$16{^{\prime \prime }}$| on a side. Images with exposure times of |$0.128\:$|s are taken 7.5 times per second, providing very high time resolution. The limiting magnitude in a single exposure is |$V \sim 11$|, corresponding to a 1-s limit of |$V \sim 13.3$|.
The Gaia spacecraft rotates on its axis with a period of 108 minutes, causing objects to drift across its focal plane. (Wevers et al. 2018) describe a technique for examining the measurements from individual chips, yielding sets of 11 exposures, each |$4.5\:$|s in length, covering a span of 45–|$50\:$|s. Stars to |$G \sim 20.5$| can be detected in each chip, equivalent to |$V \sim 19.0$| in an 1-s exposure. Over the course of one day, the spacecraft will scan roughly |$1000\:$|deg|$^{2}$| of the sky. Due to the way in which objects are detected and followed across the Gaia focal plane, transients with the very short durations (1.5–|$11.5\:$|s) we consider in this paper will be detected with a low efficiency (|${\sim}0.1$|) and appear in at most two of the nine Astrometric Field chips. Transients of this sort were not included in the analysis of Wevers et al. (2018), nor do they appear in Gaia DR2, but it is possible that researchers might make special efforts to identify them in the low-level data products.
The depth |$d_{\rm max}$| of each survey is measured relative to that of Tomo-e PM, based on the limiting magnitude for an equivalent 1-s exposure. We have estimated an average duration of eight hours per night for the ground-based instruments, and have assumed that both Pi of the Sky and MMT-9 are configured for maximum sky coverage. We have multiplied the “area scanned per hour” entry for Gaia by 0.1 to account for its low efficiency of detecting very brief transients. Table 6 contains the result of these comparisons.
| . | |${\rm Tomo-e PM}$| . | |${\rm Tomo-e}$| . | |${\rm Pi Sky}$| . | |${\rm MMT-9}$| . | |${\rm Gaia}$| . |
|---|---|---|---|---|---|
| Hours per day | 8 | 8 | 8 | 8 | 24 |
| Area per hour (deg|$^{2}$|) | 1.9 | 20.4 | 6400 | 6900 | 3.9 |
| Pixel size (|$^{\prime \prime }$|) | 1.2 | 1.2 | 36 | 16 | 0.18 |
| Lim. mag in image|$^{*}$| | 17.8/14.9 | 17.8/14.9 | 12 | 11 | 20.6 |
| Time resolution (s) | 0.5 | 0.5 | 10 | 0.12 | 4.5 |
| Lim. mag in |$1\:$|s|$^{*}$| | 18.5/15.6 | 18.5/15.6 | 9.5 | 13.3 | 19.0 |
| Normalized |$d_{\rm max}$| | 1.0 | 1.0 | 0.060 | 0.42 | 4.8 |
| RCV | 15.2 | 163 | 11 | 2300 | 10000 |
| . | |${\rm Tomo-e PM}$| . | |${\rm Tomo-e}$| . | |${\rm Pi Sky}$| . | |${\rm MMT-9}$| . | |${\rm Gaia}$| . |
|---|---|---|---|---|---|
| Hours per day | 8 | 8 | 8 | 8 | 24 |
| Area per hour (deg|$^{2}$|) | 1.9 | 20.4 | 6400 | 6900 | 3.9 |
| Pixel size (|$^{\prime \prime }$|) | 1.2 | 1.2 | 36 | 16 | 0.18 |
| Lim. mag in image|$^{*}$| | 17.8/14.9 | 17.8/14.9 | 12 | 11 | 20.6 |
| Time resolution (s) | 0.5 | 0.5 | 10 | 0.12 | 4.5 |
| Lim. mag in |$1\:$|s|$^{*}$| | 18.5/15.6 | 18.5/15.6 | 9.5 | 13.3 | 19.0 |
| Normalized |$d_{\rm max}$| | 1.0 | 1.0 | 0.060 | 0.42 | 4.8 |
| RCV | 15.2 | 163 | 11 | 2300 | 10000 |
|$^{*}$|For Tomo-e, the first value is under optimal conditions; the second value is the faintest limit used in control time calculations.
| . | |${\rm Tomo-e PM}$| . | |${\rm Tomo-e}$| . | |${\rm Pi Sky}$| . | |${\rm MMT-9}$| . | |${\rm Gaia}$| . |
|---|---|---|---|---|---|
| Hours per day | 8 | 8 | 8 | 8 | 24 |
| Area per hour (deg|$^{2}$|) | 1.9 | 20.4 | 6400 | 6900 | 3.9 |
| Pixel size (|$^{\prime \prime }$|) | 1.2 | 1.2 | 36 | 16 | 0.18 |
| Lim. mag in image|$^{*}$| | 17.8/14.9 | 17.8/14.9 | 12 | 11 | 20.6 |
| Time resolution (s) | 0.5 | 0.5 | 10 | 0.12 | 4.5 |
| Lim. mag in |$1\:$|s|$^{*}$| | 18.5/15.6 | 18.5/15.6 | 9.5 | 13.3 | 19.0 |
| Normalized |$d_{\rm max}$| | 1.0 | 1.0 | 0.060 | 0.42 | 4.8 |
| RCV | 15.2 | 163 | 11 | 2300 | 10000 |
| . | |${\rm Tomo-e PM}$| . | |${\rm Tomo-e}$| . | |${\rm Pi Sky}$| . | |${\rm MMT-9}$| . | |${\rm Gaia}$| . |
|---|---|---|---|---|---|
| Hours per day | 8 | 8 | 8 | 8 | 24 |
| Area per hour (deg|$^{2}$|) | 1.9 | 20.4 | 6400 | 6900 | 3.9 |
| Pixel size (|$^{\prime \prime }$|) | 1.2 | 1.2 | 36 | 16 | 0.18 |
| Lim. mag in image|$^{*}$| | 17.8/14.9 | 17.8/14.9 | 12 | 11 | 20.6 |
| Time resolution (s) | 0.5 | 0.5 | 10 | 0.12 | 4.5 |
| Lim. mag in |$1\:$|s|$^{*}$| | 18.5/15.6 | 18.5/15.6 | 9.5 | 13.3 | 19.0 |
| Normalized |$d_{\rm max}$| | 1.0 | 1.0 | 0.060 | 0.42 | 4.8 |
| RCV | 15.2 | 163 | 11 | 2300 | 10000 |
|$^{*}$|For Tomo-e, the first value is under optimal conditions; the second value is the faintest limit used in control time calculations.
The Tomo-e PM system appears comparable to the Pi of the Sky by this metric, and far below the MMT-9 and Gaia instruments. Observations by the full Tomo-e system, which have recently started at the time of writing (2019 June), will increase its RCV by roughly a factor of 10, simply by increasing the number of CMOS sensors from eight to 84; this increase places Tomo-e roughly halfway between Pi of the Sky and MMT-9, in a logarithmic sense.
Of course, this metric is not the only way to evaluate the performance of any of these surveys. Each has its own strengths and weaknesses, and each can and does provide valuable information to those interested in transient events. One of Tomo-e’s strengths is its relatively high angular resolution and uniform PSF across the field of view: it suffers less from crowding and image distortions than Pi of the Sky and MMT-9, which may allow it to make more accurate measurements of some events, or even to detect some marginal events which might appear blended in other systems. On the other hand, its location in the mountains of central Japan, while providing a dark sky, also delivers cloudy weather more frequently than the sites of Pi of the Sky and Gaia.
Acknowledgements
This research has made use of NASA’s Astrophysics Data System. We thank the Minor Planet Center for providing the Minor Planet Checker and NEO Checker services to the community. Ned Wright’s cosmological calculator (Wright 2006) was a great aid in our work.Our studies are supported in part by the Japan Society for the Promotion of Science (JSPS) Grants-in-Aid for Scientific Research (KAKENHI) Grant Numbers JP25103502, JP26247074, JP24103001, JP16H02158, JP16H06341, JP2905, 18H04575, JP18H01272, JP18H01261, and JP18K13599. This research is also supported in part by the Japan Science and Technology (JST) Agency’s Precursory Research for Embryonic Science and Technology (PRESTO), the Research Center for the Early Universe (RESCEU), of the School of Science at the University of Tokyo, and the Optical and Near-infrared Astronomy Inter-University Cooperation Program.
Footnotes
1 |$\langle$| http://spiff.rit.edu/tass/xvista/ |$\rangle$|.
References



