-
PDF
- Split View
-
Views
-
Cite
Cite
Xiao-Hui Fang, Shengbang Qian, Miloslav Zejda, Soonthornthum Boonrucksar, Xiao Zhou, Liying Zhu, Wen Ping Liao, A high-mass-ratio red-dwarf contact binary with an extremely cool close-in red dwarf, Publications of the Astronomical Society of Japan, Volume 71, Issue 6, December 2019, 125, https://doi.org/10.1093/pasj/psz113
Close - Share Icon Share
Abstract
1SWASP J161335.80|$-$|284722.2 (hereafter J161335) is an eclipsing red-dwarf binary with an orbital period of |$0.229778\:$|d, which is around the short-period limit for contact binaries. Three sets of multi-color light curves of J161335 were obtained from different telescopes in 2015 and 2016 and are analyzed using the Wilson–Devinney method. We discovered that the system is a W-type contact system with a contact degree of 19% and a high mass ratio of 0.91. By using all available eclipse times, we found that the observed |$-$| calculated |$(O-C)$| diagram displays a cyclic oscillation with an amplitude of 0.00196(|$\pm 0.00006)\:$|d and a period of 4.79(|$\pm 0.14)\:$|yr while it undergoes a downward parabolic change. This downward variation corresponds to a continuous decrease in the orbital period at a rate of |$dP/dt = -4.26(\pm$|0.01) |$\times$| 10|$^{-7}\:$|d|$\:$|yr|$^{-1}$|. The small-amplitude oscillation is explained as the light travel-time effect from the gravitational influence of a third body with a lowest mass of |$M _{3}$| = 0.15(|$\pm 0.01)M_{\,\odot }$|. In solving the light curves, we found that the third light is increasing, with the wavelength suggesting that the third body may be a cool red dwarf. This is in agreement with the results obtained by analyzing the |$O-C$| diagram. The tertiary red dwarf is orbiting the central red-dwarf binary at an orbital separation of 2.8(|$\pm 0.2$|) au. These results suggest that the J161335 system may be formed through early dynamical interaction where the original low-mass component was replaced by a higher-mass third body and the lower-mass component was kicked out to a wider orbit. In this way, a hierarchical triple system similar to J161335 with a high-mass-ratio binary and a small close-in third body is formed.
1 Introduction
W UMa-type contact binaries consist of two cool components that share a common convective envelope. Both components are usually main-sequence stars with spectral types from A to K. They have nearly the same effective temperature, although their masses are usually quite different. The light variations are continuous and have a small difference between the eclipse depths of the two minima. There are two subtypes of W UMa systems based on whether the more massive component holds a higher temperature than the secondary one (Binnendijk 1970). One is A-type, where the lesser component is cooler than the more massive one, and the primary minimum of the light curves is caused by the more massive component being eclipsed. Another is W-type, where the primary minimum is occultation of the less massive component, which indicates that the small component is the hotter one. The two categories evolve in a similar way but under different circumstances, such as different masses or energy transfer rates, which can lead to the different evolutionary results. The details of the evolutionary relation between A- and W-type were discussed by Gazeas and Stȩpień (2008).
1SWASP J161335.80|$-$|284722.2 (hereafter J161335) is a W UMa-type close binary with a very short orbital period of 0.229778|$\:$|d. The light variability was first reported by Norton et al. (2011), who presented the light curves and periods of 53 candidate short-period eclipsing binaries identified by SuperWASP. The authors also provided further evidence that the period distribution of main-sequence contact binaries shows a sharp cut-off at a low limit of around 0.22|$\:$|d. In fact, this period limit was originally identified by Ruciński (1992). A recent study by Qian et al. (2017) indicated that the short-period limit for EW-type binaries is around 0.20|$\:$|d. Short-period close binaries with a period below 0.23|$\:$|d are important to understand the evolution of low-mass stars and help in investigating the cause of the period cut-off. They are mainly formed from short-period detached systems, though angular momentum loss via magnetic braking and third bodies may play a crucial role during the evolution. The eccentric Kozai–Lidov mechanism can cause dramatic inclination and eccentricity fluctuations, resulting in tidal tightening of inner binaries of triple stars (Naoz & Fabrycky 2014). The orbital period for J161335 was investigated by Lohr et al. (2012), who revised the period as |$19852.817\:$|s and pointed out that the orbital period is decreasing at a rate of |$\dot{P}/P=-3.2\times 10^{-6}\:$|yr|$^{-1}$|. They further updated this period to 19852.821|$\:$|s, albeit to almost the same value as that in the 2012 paper, and gave a revised period change rate of |$-0.158\:$|s|$/$|yr (Lohr et al. 2013). However, J161335 has been ignored for detailed investigation. In this paper we shall present the first observations of multi-color charge-coupled device (CCD) light curves, and derive the photometric parameters by using the Wilson–Devinney (W–D) method (Wilson & Devinney 1971; Wilson 1979, 1990, 1994). Our aim is to study the physical properties as well as its third body, then to understand the formation and the evolutionary state of this triple red dwarf system.
2 Multi-color photometric observations of J161335
CCD photometric observations of J161335 were obtained in two successive years from 2015 to 2016, and three sets of light curves were acquired. It was first monitored in 2015 with the |$2.4\:$|m Thai National Telescope (TNT) of the national Astronomical Research Institute of Thailand. The telescope is a Ritchey–Chretien with two Nasmyth focuses. A research-grade 4|$\:$|K |$\times$| 4|$\:$|K CCD photometer with a BVRI filter system was used at one of the Nasmyth focuses (Qian et al. 2015). Standard Johnson–Bessel BVRI filters were used during the observations. The complete light curves were obtained in 2015 over two consecutive nights of 2015 April 4–5. One year later, a second set of light curves (almost complete) was obtained with the same telescope. The images were reduced with PHOT (measured magnitudes for a list of stars) from the aperture photometry package of IRAF. The third set of light curves was obtained on 2016 April 15, using the |$1.0\:$|m telescope at the South African Astronomical Observatory (SAAO). This telescope is equipped with a back-illuminated 1024 |$\times$| 1024, |$24\:$|micron pixel STE4 CCD camera with a field of view of |${5_{.}^{\prime}3}$||$\times$||${5_{.}^{\prime}3}$|. These images were processed using the C-Munipack software based on the aperture photometry package DAOPHOT.
The same comparison and check stars were used for all the observations. Their coordinates are listed in table 1 and one of the CCD images is shown in figure 1. The resulting curves are shown in figure 2 after all the data was successfully reduced. The typical standard deviations are 0.0175 mag in B, 0.0157 mag in V, 0.0143 mag in R, and 0.0153 mag in I. Based on our CCD photometric data, 29 times of minimum light in different bands were determined with a parabolic fitting method because of the symmetric eclipse profiles. They will be applied to study the period changes in section 3. All of the individual eclipse times are listed in table 2, where I refers to the primary light minimum, II to the secondary. To simplify the descriptions in the following, we use 2016(a), 2016(b), and 2015 to represent the light curves obtained on 2016 April 2, 2016 April 15, and 2015 April 4–5, respectively.

Starfield around J161335 with the comparison and check stars. The target star is shown as “V,” the comparison star as “C,” and the check star as “Ch.”. (Color online)
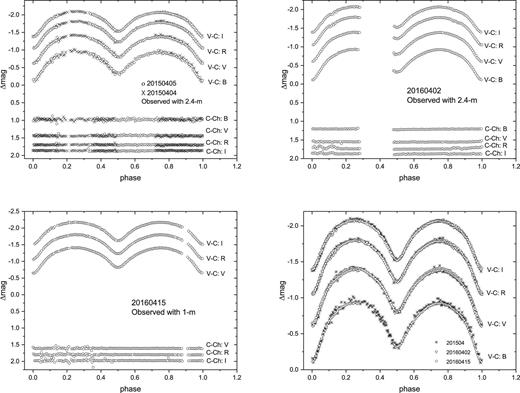
Multi-color light curves of J161335 observed from 2015 to 2016. The last panel is an overlapped image of the three light curves.
| Target . | |$\alpha _{\rm J2000.0}$| . | |$\delta _{\rm J2000.0}$| . |
|---|---|---|
| J161335 | |${16^{\rm h}13^{\rm m}35{^{\rm s}_{.}}80}$| | |$-28^\circ {47^{\prime }22_{.}^{\prime\prime}02}$| |
| Comparison star | |${16^{\rm h}13^{\rm m}34{^{\rm s}_{.}}31}$| | |$-28^\circ {47^{\prime }05_{.}^{\prime\prime}14}$| |
| Check star | |${16^{\rm h}13^{\rm m}25{^{\rm s}_{.}}31}$| | |$-28^\circ {49^{\prime }50_{.}^{\prime\prime}31}$| |
| Target . | |$\alpha _{\rm J2000.0}$| . | |$\delta _{\rm J2000.0}$| . |
|---|---|---|
| J161335 | |${16^{\rm h}13^{\rm m}35{^{\rm s}_{.}}80}$| | |$-28^\circ {47^{\prime }22_{.}^{\prime\prime}02}$| |
| Comparison star | |${16^{\rm h}13^{\rm m}34{^{\rm s}_{.}}31}$| | |$-28^\circ {47^{\prime }05_{.}^{\prime\prime}14}$| |
| Check star | |${16^{\rm h}13^{\rm m}25{^{\rm s}_{.}}31}$| | |$-28^\circ {49^{\prime }50_{.}^{\prime\prime}31}$| |
| Target . | |$\alpha _{\rm J2000.0}$| . | |$\delta _{\rm J2000.0}$| . |
|---|---|---|
| J161335 | |${16^{\rm h}13^{\rm m}35{^{\rm s}_{.}}80}$| | |$-28^\circ {47^{\prime }22_{.}^{\prime\prime}02}$| |
| Comparison star | |${16^{\rm h}13^{\rm m}34{^{\rm s}_{.}}31}$| | |$-28^\circ {47^{\prime }05_{.}^{\prime\prime}14}$| |
| Check star | |${16^{\rm h}13^{\rm m}25{^{\rm s}_{.}}31}$| | |$-28^\circ {49^{\prime }50_{.}^{\prime\prime}31}$| |
| Target . | |$\alpha _{\rm J2000.0}$| . | |$\delta _{\rm J2000.0}$| . |
|---|---|---|
| J161335 | |${16^{\rm h}13^{\rm m}35{^{\rm s}_{.}}80}$| | |$-28^\circ {47^{\prime }22_{.}^{\prime\prime}02}$| |
| Comparison star | |${16^{\rm h}13^{\rm m}34{^{\rm s}_{.}}31}$| | |$-28^\circ {47^{\prime }05_{.}^{\prime\prime}14}$| |
| Check star | |${16^{\rm h}13^{\rm m}25{^{\rm s}_{.}}31}$| | |$-28^\circ {49^{\prime }50_{.}^{\prime\prime}31}$| |
| Date . | HJD (d) . | Filter . | Type . | Mean (d) . | Telescope . |
|---|---|---|---|---|---|
| 2015 Apr 4 | 2457117.42226|$\, \pm \,0.00043$| | B | I | 2457117.42272|$\, \pm \,0.00030$| | |$2.4$| m |
| 2457117.42287|$\, \pm \,0.00023$| | V | I | |||
| 2457117.42311|$\, \pm \,0.00021$| | R | I | |||
| 2457117.42265|$\, \pm \,0.00031$| | I | I | |||
| 2015 Apr 4 | 2457117.30914|$\, \pm \,0.00050$| | B | II | 2457117.30873|$\, \pm \,0.00033$| | |$2.4$| m |
| 2457117.30835|$\, \pm \,0.00025$| | V | II | |||
| 2457117.30841|$\, \pm \,0.00021$| | R | II | |||
| 2457117.30900|$\, \pm \,0.00035$| | I | II | |||
| 2015 Apr 5 | 2457118.34213|$\, \pm \,0.00026$| | B | I | 2457118.34210|$\, \pm \,0.00019$| | |$2.4$| m |
| 2457118.34216|$\, \pm \,0.00016$| | V | I | |||
| 2457118.34199|$\, \pm \,0.00017$| | R | I | |||
| 2457118.34212|$\, \pm \,0.00018$| | I | I | |||
| 2016 Apr 2 | 2457481.38444|$\, \pm \,0.00013$| | B | I | 2457481.38451|$\, \pm \,0.00014$| | |$2.4$| m |
| 2457481.38449|$\, \pm \,0.00014$| | V | I | |||
| 2457481.38455|$\, \pm \,0.00014$| | R | I | |||
| 2457481.38456|$\, \pm \,0.00016$| | I | I | |||
| 2016 Apr 2 | 2457481.26988|$\, \pm \,0.00025$| | B | II | 2457481.26965|$\, \pm \,0.00030$| | |$2.4$| m |
| 2457481.26937|$\, \pm \,0.00062$| | V | II | |||
| 2457481.26950|$\, \pm \,0.00023$| | R | II | |||
| 2457481.26985|$\, \pm \,0.00009$| | I | II | |||
| 2016 Apr 15 | 2457494.48157|$\, \pm \,0.00007$| | V | I | 2457494.48150|$\, \pm \,0.00007$| | |$1.0$| m |
| 2457494.48149|$\, \pm \,0.00008$| | R | I | |||
| 2457494.48144|$\, \pm \,0.00006$| | I | I | |||
| 2016 Apr 15 | 2457494.59641|$\, \pm \,0.00004$| | V | II | 2457494.59645|$\, \pm \,0.00006$| | |$1.0$| m |
| 2457494.59640|$\, \pm \,0.00006$| | R | II | |||
| 2457494.59653|$\, \pm \,0.00007$| | I | II | |||
| 2018 Jul 21 | 2458321.09240|$\, \pm \,0.00029$| | V | II | 2458321.09241|$\, \pm \,0.00026$| | |$1.0$| m (YNOs) |
| 2458321.09187|$\, \pm \,0.00025$| | R | II | |||
| 2458321.09296|$\, \pm \,0.00025$| | I | II |
| Date . | HJD (d) . | Filter . | Type . | Mean (d) . | Telescope . |
|---|---|---|---|---|---|
| 2015 Apr 4 | 2457117.42226|$\, \pm \,0.00043$| | B | I | 2457117.42272|$\, \pm \,0.00030$| | |$2.4$| m |
| 2457117.42287|$\, \pm \,0.00023$| | V | I | |||
| 2457117.42311|$\, \pm \,0.00021$| | R | I | |||
| 2457117.42265|$\, \pm \,0.00031$| | I | I | |||
| 2015 Apr 4 | 2457117.30914|$\, \pm \,0.00050$| | B | II | 2457117.30873|$\, \pm \,0.00033$| | |$2.4$| m |
| 2457117.30835|$\, \pm \,0.00025$| | V | II | |||
| 2457117.30841|$\, \pm \,0.00021$| | R | II | |||
| 2457117.30900|$\, \pm \,0.00035$| | I | II | |||
| 2015 Apr 5 | 2457118.34213|$\, \pm \,0.00026$| | B | I | 2457118.34210|$\, \pm \,0.00019$| | |$2.4$| m |
| 2457118.34216|$\, \pm \,0.00016$| | V | I | |||
| 2457118.34199|$\, \pm \,0.00017$| | R | I | |||
| 2457118.34212|$\, \pm \,0.00018$| | I | I | |||
| 2016 Apr 2 | 2457481.38444|$\, \pm \,0.00013$| | B | I | 2457481.38451|$\, \pm \,0.00014$| | |$2.4$| m |
| 2457481.38449|$\, \pm \,0.00014$| | V | I | |||
| 2457481.38455|$\, \pm \,0.00014$| | R | I | |||
| 2457481.38456|$\, \pm \,0.00016$| | I | I | |||
| 2016 Apr 2 | 2457481.26988|$\, \pm \,0.00025$| | B | II | 2457481.26965|$\, \pm \,0.00030$| | |$2.4$| m |
| 2457481.26937|$\, \pm \,0.00062$| | V | II | |||
| 2457481.26950|$\, \pm \,0.00023$| | R | II | |||
| 2457481.26985|$\, \pm \,0.00009$| | I | II | |||
| 2016 Apr 15 | 2457494.48157|$\, \pm \,0.00007$| | V | I | 2457494.48150|$\, \pm \,0.00007$| | |$1.0$| m |
| 2457494.48149|$\, \pm \,0.00008$| | R | I | |||
| 2457494.48144|$\, \pm \,0.00006$| | I | I | |||
| 2016 Apr 15 | 2457494.59641|$\, \pm \,0.00004$| | V | II | 2457494.59645|$\, \pm \,0.00006$| | |$1.0$| m |
| 2457494.59640|$\, \pm \,0.00006$| | R | II | |||
| 2457494.59653|$\, \pm \,0.00007$| | I | II | |||
| 2018 Jul 21 | 2458321.09240|$\, \pm \,0.00029$| | V | II | 2458321.09241|$\, \pm \,0.00026$| | |$1.0$| m (YNOs) |
| 2458321.09187|$\, \pm \,0.00025$| | R | II | |||
| 2458321.09296|$\, \pm \,0.00025$| | I | II |
| Date . | HJD (d) . | Filter . | Type . | Mean (d) . | Telescope . |
|---|---|---|---|---|---|
| 2015 Apr 4 | 2457117.42226|$\, \pm \,0.00043$| | B | I | 2457117.42272|$\, \pm \,0.00030$| | |$2.4$| m |
| 2457117.42287|$\, \pm \,0.00023$| | V | I | |||
| 2457117.42311|$\, \pm \,0.00021$| | R | I | |||
| 2457117.42265|$\, \pm \,0.00031$| | I | I | |||
| 2015 Apr 4 | 2457117.30914|$\, \pm \,0.00050$| | B | II | 2457117.30873|$\, \pm \,0.00033$| | |$2.4$| m |
| 2457117.30835|$\, \pm \,0.00025$| | V | II | |||
| 2457117.30841|$\, \pm \,0.00021$| | R | II | |||
| 2457117.30900|$\, \pm \,0.00035$| | I | II | |||
| 2015 Apr 5 | 2457118.34213|$\, \pm \,0.00026$| | B | I | 2457118.34210|$\, \pm \,0.00019$| | |$2.4$| m |
| 2457118.34216|$\, \pm \,0.00016$| | V | I | |||
| 2457118.34199|$\, \pm \,0.00017$| | R | I | |||
| 2457118.34212|$\, \pm \,0.00018$| | I | I | |||
| 2016 Apr 2 | 2457481.38444|$\, \pm \,0.00013$| | B | I | 2457481.38451|$\, \pm \,0.00014$| | |$2.4$| m |
| 2457481.38449|$\, \pm \,0.00014$| | V | I | |||
| 2457481.38455|$\, \pm \,0.00014$| | R | I | |||
| 2457481.38456|$\, \pm \,0.00016$| | I | I | |||
| 2016 Apr 2 | 2457481.26988|$\, \pm \,0.00025$| | B | II | 2457481.26965|$\, \pm \,0.00030$| | |$2.4$| m |
| 2457481.26937|$\, \pm \,0.00062$| | V | II | |||
| 2457481.26950|$\, \pm \,0.00023$| | R | II | |||
| 2457481.26985|$\, \pm \,0.00009$| | I | II | |||
| 2016 Apr 15 | 2457494.48157|$\, \pm \,0.00007$| | V | I | 2457494.48150|$\, \pm \,0.00007$| | |$1.0$| m |
| 2457494.48149|$\, \pm \,0.00008$| | R | I | |||
| 2457494.48144|$\, \pm \,0.00006$| | I | I | |||
| 2016 Apr 15 | 2457494.59641|$\, \pm \,0.00004$| | V | II | 2457494.59645|$\, \pm \,0.00006$| | |$1.0$| m |
| 2457494.59640|$\, \pm \,0.00006$| | R | II | |||
| 2457494.59653|$\, \pm \,0.00007$| | I | II | |||
| 2018 Jul 21 | 2458321.09240|$\, \pm \,0.00029$| | V | II | 2458321.09241|$\, \pm \,0.00026$| | |$1.0$| m (YNOs) |
| 2458321.09187|$\, \pm \,0.00025$| | R | II | |||
| 2458321.09296|$\, \pm \,0.00025$| | I | II |
| Date . | HJD (d) . | Filter . | Type . | Mean (d) . | Telescope . |
|---|---|---|---|---|---|
| 2015 Apr 4 | 2457117.42226|$\, \pm \,0.00043$| | B | I | 2457117.42272|$\, \pm \,0.00030$| | |$2.4$| m |
| 2457117.42287|$\, \pm \,0.00023$| | V | I | |||
| 2457117.42311|$\, \pm \,0.00021$| | R | I | |||
| 2457117.42265|$\, \pm \,0.00031$| | I | I | |||
| 2015 Apr 4 | 2457117.30914|$\, \pm \,0.00050$| | B | II | 2457117.30873|$\, \pm \,0.00033$| | |$2.4$| m |
| 2457117.30835|$\, \pm \,0.00025$| | V | II | |||
| 2457117.30841|$\, \pm \,0.00021$| | R | II | |||
| 2457117.30900|$\, \pm \,0.00035$| | I | II | |||
| 2015 Apr 5 | 2457118.34213|$\, \pm \,0.00026$| | B | I | 2457118.34210|$\, \pm \,0.00019$| | |$2.4$| m |
| 2457118.34216|$\, \pm \,0.00016$| | V | I | |||
| 2457118.34199|$\, \pm \,0.00017$| | R | I | |||
| 2457118.34212|$\, \pm \,0.00018$| | I | I | |||
| 2016 Apr 2 | 2457481.38444|$\, \pm \,0.00013$| | B | I | 2457481.38451|$\, \pm \,0.00014$| | |$2.4$| m |
| 2457481.38449|$\, \pm \,0.00014$| | V | I | |||
| 2457481.38455|$\, \pm \,0.00014$| | R | I | |||
| 2457481.38456|$\, \pm \,0.00016$| | I | I | |||
| 2016 Apr 2 | 2457481.26988|$\, \pm \,0.00025$| | B | II | 2457481.26965|$\, \pm \,0.00030$| | |$2.4$| m |
| 2457481.26937|$\, \pm \,0.00062$| | V | II | |||
| 2457481.26950|$\, \pm \,0.00023$| | R | II | |||
| 2457481.26985|$\, \pm \,0.00009$| | I | II | |||
| 2016 Apr 15 | 2457494.48157|$\, \pm \,0.00007$| | V | I | 2457494.48150|$\, \pm \,0.00007$| | |$1.0$| m |
| 2457494.48149|$\, \pm \,0.00008$| | R | I | |||
| 2457494.48144|$\, \pm \,0.00006$| | I | I | |||
| 2016 Apr 15 | 2457494.59641|$\, \pm \,0.00004$| | V | II | 2457494.59645|$\, \pm \,0.00006$| | |$1.0$| m |
| 2457494.59640|$\, \pm \,0.00006$| | R | II | |||
| 2457494.59653|$\, \pm \,0.00007$| | I | II | |||
| 2018 Jul 21 | 2458321.09240|$\, \pm \,0.00029$| | V | II | 2458321.09241|$\, \pm \,0.00026$| | |$1.0$| m (YNOs) |
| 2458321.09187|$\, \pm \,0.00025$| | R | II | |||
| 2458321.09296|$\, \pm \,0.00025$| | I | II |
where the initial epoch is one of the mean eclipse times in table 2, and the orbital period was taken from Lohr et al. (2012). As depicted in figure 2, the light curves show typical EW-type variation. In addition, the depths of the primary minimum decrease with increasing wavelength, i.e., the B-band one is the deepest, while the I-band one is the shallowest. The heights of the two light maxima were unequal in 2015 April, which proves the presence of the positive O’Connell effect (O’Connell 1951); the light maximum after the primary minimum is higher than the other maximum with Max.I |$-$| Max.II = |$-0.025$| mag. However, the other two sets of light curves in 2016 are very symmetrical: Max.I is nearly equal to Max.II. In order to show the variation more clearly, three sets of curves were superposed together, as shown in the last panel of figure 2. All the light curves in 2015 and 2016 mostly match well with each other except for the phase from 0.20 to 0.30 of the curves in 2015. The brightness changes of this part could be evidence for strong magnetic activity on the surface of the components.
3 Orbital period investigations of J161335
Although J161335 was discovered as a variable star (Norton et al. 2011), detailed study of its orbital period changes has been neglected. The period variation is extremely important for investigating the evolutionary states of a binary system and determining its dynamic evolution process (Andronov et al. 2005). More information about the period changes can be obtained directly from the |$O-C$| curves. So, in this part all available times of light minima (about 12 yr) are fully utilized, include 103 eclipse times calculated by Lohr et al. (2013) that were derived using SuperWASP data (Lohr et al. 2014). Eight of our own CCD measurements are also included. In table 2, the last one was acquired using the |$1.0$| m reflecting telescope at Yunnan Observatories (YNOs) on 2018 July 21. We assigned a different weight to these eclipse times because of their different precision. The weight of our observations of the time minima from SuperWASP was set to |$20:1$|. The |$O-C$| diagram is shown in figure 3 along with the epoch number E, where the open circles refer to SuperWASP data and solid dots represent our new observations.
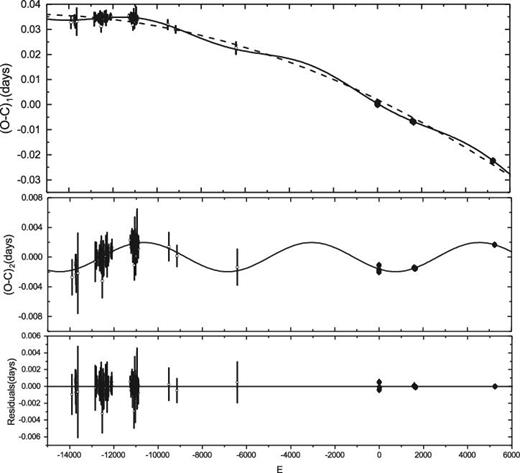
|$(O-C)_1$| values of J161335 from the linear ephemeris of equation (1). In the upper panel, the solid line refers to the combination of a downward parabolic change and a cyclic variation; the dashed line just shows a downward parabolic change corresponding to the long-term decrease of the orbital period. The small open circles represent the eclipse times provided by Lohr, and the solid circles refer to the times from our observations. The |$(O-C)_2$| values are calculated from the new linear ephemeris in equation (2) and are displayed in the middle panel. The solid line refers to a theoretical light travel-time effect caused by a tertiary component. The final residuals are displayed in the bottom panel.
4 Photometric solutions with the W–D method
In this section we will describe the parameter settings for the 2013 version of the W–D program and show the solutions to all the light curves. Koen, Koen, and Gray (2016) proposed the spectral type of this system to be K7, but they also pointed out that this classification may be controversial and uncertain. They listed three kinds of temperatures based on different standards, estimated from infrared color (|$J-K$|) and (|$H-K$|); optical indices (|$B-V$|), (|$V-R$|), and (|$V-I$|); and from the spectroscopic classifications. The also assumed the effective temperature of the primary star T(infrared) = 4450 K, T(optical) = 4450 K, T(spectroscopic) = 4050 K. It seems that an average value |$T_{1}$| = 4317 K applied to the photometric study is reasonable. However, the color index of J161335 is derived to be |$B-V$| = 1.291 from the Simbad database, and the corresponding effective temperature with K8 spectra in the main sequence is determined to be 4100 K (Cox 2000). Therefore, we analyzed both cases with |$T_{1}$| = 4317 K and 4100 K.
We assumed common convective envelopes for the two components (|$T_{\rm eff}$||$\lt $| 7500 K), bolometric albedo coefficients |$A_1=A_2=0.5$|, and gravity-darkening coefficients |$g_1=g_2=0.32$| from Ruciński (1969) and Lucy (1967) respectively. For the limb-darkening, square-root functions were used for both the bolometric and bandpass limb-darkening law, and the coefficients for the different filters were taken from van Hamme’s (1993) table. Mode 3 was chosen to approximate the contact configuration. The adjustable parameters are: the orbital inclination i; the effective temperature of star 2 (|$T_{2}$|); the monochromatic luminosity of star 1 |$L_{1B}$|, |$L_{1V}$|, |$L_{1R}$|, and |$L_{1I}$|; and the dimensionless potential of star 1 (|$\Omega _{1}=\Omega _{2}$| in mode 3 for the contact configuration).
Since no radial velocity observations of J161335 have been obtained yet, the q-search method was used to determine its mass ratio. A series of photometric solutions with different fixed mass ratios were performed. For each q, the differential correction program started from detached mode and rapidly converged to contact mode. Figure 2 shows the unequal heights of the two maxima of the light curves in 2015, while they were equal in 2016. So the 2015 and 2016 light curves were analyzed individually.
Of the three sets of observations [2015, 2016(a), 2016(b)], we chose the light curves of 2016 as the basis for the derivation of the photometric elements because of their symmetry in all bands. The corresponding relationship between the mass ratio and the squared residuals |$\Sigma$| are plotted in figure 4. Note that late-type components exhibit much stronger magnetic activities, because they are in a deep common convective envelope and fast rotating. Therefore, the variation and the asymmetry in the light curves of 2015 are possibly due to dark spots on the surface of the components. Magnetic activity could plausibly mainly explain the light curve changes from 2015 to 2016, but the orbital inclination is not enough to produce the distortion in the light curves within just two years. The inclination was fixed to |$78_{.}^{\circ} 0$|, which is the average value of the four sets of solutions obtained in 2016. Most parameters are nearly the same with no spots or added spots in the model for the 2015 light curves, but the mass ratios are quite different and the minimum sum-of-squared residuals are larger when the spots are removed, so we prefer to put spots on the component surfaces. And one dark spot was introduced on the secondary component during the q-search process. The spot is described by four parameters: spot-center latitude (|$\theta$|), spot-center longitude (|$\psi$|), the angular radius (r), and the temperature factor (|$T_{f}$|). As illustrated in figure 4, there is a minimum at around q = 1.10 for 2016 and q = 1.26 for 2015, irrespective of whether the effective temperature of the primary star is 4100 K or 4317 K. However, it should be mentioned that since no radial velocity observations of J161335 were obtained, the q-search method used to determine its mass ratio is inevitably a less reliable method than the spectroscopic method. So spectroscopic observations are needed to investigate this matter in the future.
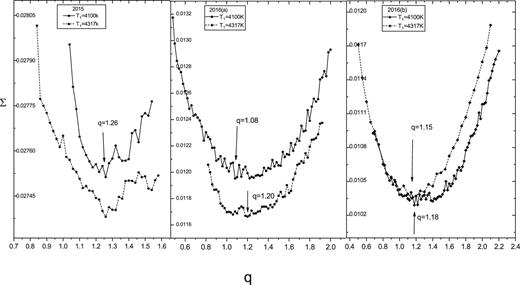
Six sets of photometric solutions are listed in table 3. There is good correlation between the results, so the photometric mass ratio for J161335 is believed to be reliable. In figure 5, the observed data and the theoretical light curves are plotted based on the final solutions. As shown in last panel, the theoretical light curves with one spot on the more massive component fit the data better than the theoretical light curves without spots.
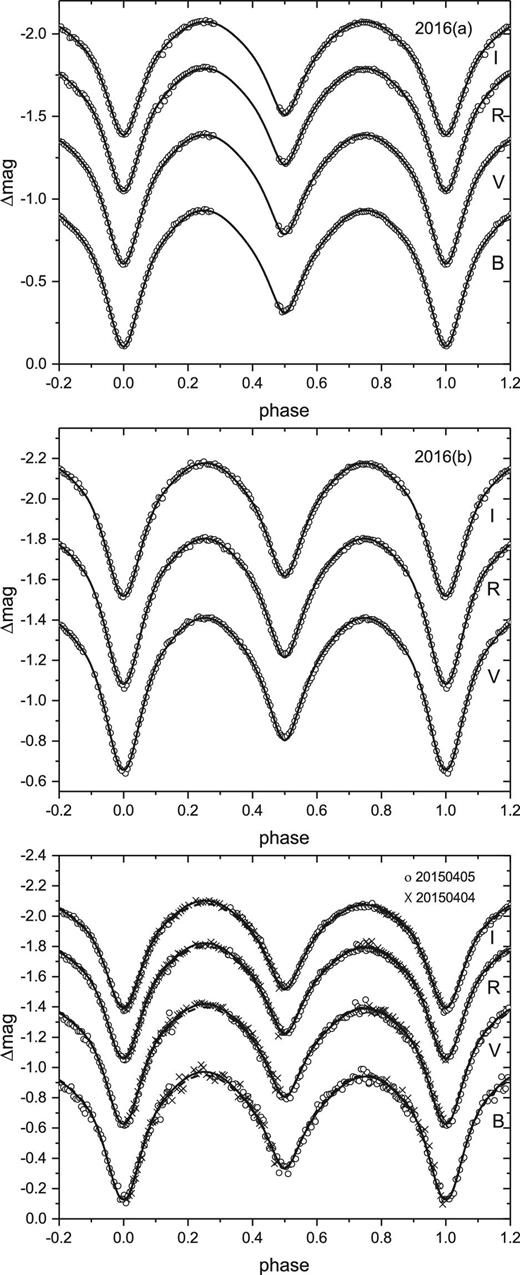
Theoretical light curves calculated using the W–D method. The open circles represent the observations and the solid lines refer to the final theoretical light curves. In the bottom panel the dashed line refers to the theoretical light curve without introducing dark spots and the solid line the case with one spot on the more massive component. Obviously, the fit of the solid line is better than the dashed line.
| Parameter . | 2015 . | 2016(a) . | 2016(b) . | 2015 . | 2016(a) . | 2016(b) . |
|---|---|---|---|---|---|---|
| |$T_{1}(K)$| | 4100(fixed) | 4100(fixed) | 4100(fixed) | 4317(fixed) | 4317(fixed) | 4317(fixed) |
| |$g_{1}$| = |$g_{2}$| | 0.32(fixed) | 0.32(fixed) | 0.32(fixed) | 0.32(fixed) | 0.32(fixed) | 0.32(fixed) |
| |$A_{1}$| = |$A_{2}$| | 0.50(fixed) | 0.50(fixed) | 0.50(fixed) | 0.50(fixed) | 0.50(fixed) | 0.50(fixed) |
| |$x_{1}$| = |$x_{2} (B$|) | 0.828 | 0.828 | ... | 0.831 | 0.830 | ... |
| |$x_{1}$| = |$x_{2} (V$|) | 0.793 | 0.792 | 0.792 | 0.793 | 0.794 | 0.794 |
| |$x_{1}$| = |$x_{2} (R_{\rm c}$|) | 0.760 | 0.760 | 0.760 | 0.760 | 0.759 | 0.759 |
| |$x_{1}$| = |$x_{2} (I_{\rm c}$|) | 0.675 | 0.675 | 0.675 | 0.676 | 0.676 | 0.676 |
| |$y_{1}$| = |$y_{2} (B$|) | 0.089 | 0.087 | ... | |$-$|0.080 | |$-$|0.080 | ... |
| |$y_{1}$| = |$y_{2} (V$|) | 0.188 | 0.187 | 0.184 | 0.080 | 0.080 | 0.080 |
| |$y_{1}$| = |$y_{2} (R_{\rm c}$|) | 0.232 | 0.232 | 0.231 | 0.160 | 0.160 | 0.160 |
| |$y_{1}$| = |$y_{2} (I_{\rm c}$|) | 0.262 | 0.261 | 0.261 | 0.220 | 0.220 | 0.220 |
| q (|$M_2/M_1$|) | 1.26(7) | 1.15(2) | 1.08(4) | 1.26(6) | 1.06(1) | 1.10(1) |
| |$i\ (^{\circ })$| | 78.0(fixed) | 77.9(4) | 78.2(2) | 78.0(fixed) | 77.8(4) | 78.1(3) |
| |$\Omega _{\rm in}$| | 4.1601 | 3.9969 | 3.8681 | 4.1601 | 3.8250 | 3.9108 |
| |$\Omega _{\rm out}$| | 3.5965 | 3.4406 | 3.3185 | 3.5965 | 3.2777 | 3.3588 |
| |$\Omega _{1}=\Omega _{2}$| | 4.0399(59) | 4.0782(66) | 3.7611(575) | 4.0383(131) | 3.7455(218) | 3.8196(116) |
| |$T_{2}\ (K)$| | 3895(5) | 3894(15) | 3917(17) | 4104(6) | 4111(3) | 4126(3) |
| |$L_{1}/(L_{1}+L_{2}+L_{3}$|) (B) | 55.14|$\%$| | 56.68|$\%$| | ... | 54.50|$\%$| | 58.05|$\%$| | ... |
| |$L_{1}/(L_{1}+L_{2}+L_{3}$|) (V) | 53.30|$\%$| | 55.00|$\%$| | 55.72|$\%$| | 52.70|$\%$| | 56.54|$\%$| | 54.98|$\%$| |
| |$L_{1}/(L_{1}+L_{2}+L_{3}$|) (R) | 51.93|$\%$| | 53.39|$\%$| | 54.24|$\%$| | 51.41|$\%$| | 54.91|$\%$| | 53.48|$\%$| |
| |$L_{1}/(L_{1}+L_{2}+L_{3}$|) (I) | 49.75|$\%$| | 50.82|$\%$| | 51.76|$\%$| | 49.40|$\%$| | 52.45|$\%$| | 50.73|$\%$| |
| |$L_{3}/(L_{1}+L_{2}+L_{3}$|) (B) | 1.4(0.6)|$\%$| | 1.8(1.5)|$\%$| | 2.5(1.5)|$\%$| | 2.9(0.5)|$\%$| | ... | |
| |$L_{3}/(L_{1}+L_{2}+L_{3}$|) (V) | 1.9(0.7)|$\%$| | 1.8(1.5)|$\%$| | 2.6(1.9)|$\%$| | 2.7(0.6)|$\%$| | 2.0(1.1)|$\%$| | 2.3(0.5)|$\%$| |
| |$L_{3}/(L_{1}+L_{2}+L_{3}$|) (R) | 2.6(0.6)|$\%$| | 3.1(1.4)|$\%$| | 3.9(1.9)|$\%$| | 3.2(0.5)|$\%$| | 2.5(1.2)|$\%$| | 2.8(0.3)|$\%$| |
| |$L_{3}/(L_{1}+L_{2}+L_{3}$|) (I) | 3.4(0.6)|$\%$| | 4.6(1.4)|$\%$| | 5.6(1.8)|$\%$| | 4.8(0.3)|$\%$| | 4.1(1.1)|$\%$| | 4.2(0.5)|$\%$| |
| |$r_{1}$| (pole) | 0.3509(7) | 0.3569(19) | 0.3636(32) | 0.3510(15) | 0.3637(14) | 0.3591(10) |
| |$r_{1}$| (side) | 0.3700(9) | 0.3765(21) | 0.3841(36) | 0.3702(19) | 0.3839(17) | 0.3786(11) |
| |$r_{1}$| (back) | 0.4101(14) | 0.4153(24) | 0.4329(38) | 0.4103(29) | 0.4220(21) | 0.4154(11) |
| |$r_{2}$| (pole) | 0.3891(7) | 0.3825(64) | 0.3747(111) | 0.3893(15) | 0.3736(41) | 0.3725(35) |
| |$r_{2}$| (side) | 0.4127(8) | 0.4052(82) | 0.3962(142) | 0.4129(19) | 0.3950(53) | 0.3934(44) |
| |$r_{2}$| (back) | 0.4497(13) | 0.4431(13) | 0.4335(227) | 0.4490(28) | 0.4325(83) | 0.4287(69) |
| f | 21.1(1.4)|$\%$| | 21.0(6.3)|$\%$| | 19.5(10.5)|$\%$| | 21.6(2.3)|$\%$| | 18.7(3.9)|$\%$| | 16.5(2.1)|$\%$| |
| |$\Sigma$| res|$^{2}$| | 0.0298 | 0.0116 | 0.0122 | 0.0104 | 0.0010 | 0.0111 |
| Parameter . | 2015 . | 2016(a) . | 2016(b) . | 2015 . | 2016(a) . | 2016(b) . |
|---|---|---|---|---|---|---|
| |$T_{1}(K)$| | 4100(fixed) | 4100(fixed) | 4100(fixed) | 4317(fixed) | 4317(fixed) | 4317(fixed) |
| |$g_{1}$| = |$g_{2}$| | 0.32(fixed) | 0.32(fixed) | 0.32(fixed) | 0.32(fixed) | 0.32(fixed) | 0.32(fixed) |
| |$A_{1}$| = |$A_{2}$| | 0.50(fixed) | 0.50(fixed) | 0.50(fixed) | 0.50(fixed) | 0.50(fixed) | 0.50(fixed) |
| |$x_{1}$| = |$x_{2} (B$|) | 0.828 | 0.828 | ... | 0.831 | 0.830 | ... |
| |$x_{1}$| = |$x_{2} (V$|) | 0.793 | 0.792 | 0.792 | 0.793 | 0.794 | 0.794 |
| |$x_{1}$| = |$x_{2} (R_{\rm c}$|) | 0.760 | 0.760 | 0.760 | 0.760 | 0.759 | 0.759 |
| |$x_{1}$| = |$x_{2} (I_{\rm c}$|) | 0.675 | 0.675 | 0.675 | 0.676 | 0.676 | 0.676 |
| |$y_{1}$| = |$y_{2} (B$|) | 0.089 | 0.087 | ... | |$-$|0.080 | |$-$|0.080 | ... |
| |$y_{1}$| = |$y_{2} (V$|) | 0.188 | 0.187 | 0.184 | 0.080 | 0.080 | 0.080 |
| |$y_{1}$| = |$y_{2} (R_{\rm c}$|) | 0.232 | 0.232 | 0.231 | 0.160 | 0.160 | 0.160 |
| |$y_{1}$| = |$y_{2} (I_{\rm c}$|) | 0.262 | 0.261 | 0.261 | 0.220 | 0.220 | 0.220 |
| q (|$M_2/M_1$|) | 1.26(7) | 1.15(2) | 1.08(4) | 1.26(6) | 1.06(1) | 1.10(1) |
| |$i\ (^{\circ })$| | 78.0(fixed) | 77.9(4) | 78.2(2) | 78.0(fixed) | 77.8(4) | 78.1(3) |
| |$\Omega _{\rm in}$| | 4.1601 | 3.9969 | 3.8681 | 4.1601 | 3.8250 | 3.9108 |
| |$\Omega _{\rm out}$| | 3.5965 | 3.4406 | 3.3185 | 3.5965 | 3.2777 | 3.3588 |
| |$\Omega _{1}=\Omega _{2}$| | 4.0399(59) | 4.0782(66) | 3.7611(575) | 4.0383(131) | 3.7455(218) | 3.8196(116) |
| |$T_{2}\ (K)$| | 3895(5) | 3894(15) | 3917(17) | 4104(6) | 4111(3) | 4126(3) |
| |$L_{1}/(L_{1}+L_{2}+L_{3}$|) (B) | 55.14|$\%$| | 56.68|$\%$| | ... | 54.50|$\%$| | 58.05|$\%$| | ... |
| |$L_{1}/(L_{1}+L_{2}+L_{3}$|) (V) | 53.30|$\%$| | 55.00|$\%$| | 55.72|$\%$| | 52.70|$\%$| | 56.54|$\%$| | 54.98|$\%$| |
| |$L_{1}/(L_{1}+L_{2}+L_{3}$|) (R) | 51.93|$\%$| | 53.39|$\%$| | 54.24|$\%$| | 51.41|$\%$| | 54.91|$\%$| | 53.48|$\%$| |
| |$L_{1}/(L_{1}+L_{2}+L_{3}$|) (I) | 49.75|$\%$| | 50.82|$\%$| | 51.76|$\%$| | 49.40|$\%$| | 52.45|$\%$| | 50.73|$\%$| |
| |$L_{3}/(L_{1}+L_{2}+L_{3}$|) (B) | 1.4(0.6)|$\%$| | 1.8(1.5)|$\%$| | 2.5(1.5)|$\%$| | 2.9(0.5)|$\%$| | ... | |
| |$L_{3}/(L_{1}+L_{2}+L_{3}$|) (V) | 1.9(0.7)|$\%$| | 1.8(1.5)|$\%$| | 2.6(1.9)|$\%$| | 2.7(0.6)|$\%$| | 2.0(1.1)|$\%$| | 2.3(0.5)|$\%$| |
| |$L_{3}/(L_{1}+L_{2}+L_{3}$|) (R) | 2.6(0.6)|$\%$| | 3.1(1.4)|$\%$| | 3.9(1.9)|$\%$| | 3.2(0.5)|$\%$| | 2.5(1.2)|$\%$| | 2.8(0.3)|$\%$| |
| |$L_{3}/(L_{1}+L_{2}+L_{3}$|) (I) | 3.4(0.6)|$\%$| | 4.6(1.4)|$\%$| | 5.6(1.8)|$\%$| | 4.8(0.3)|$\%$| | 4.1(1.1)|$\%$| | 4.2(0.5)|$\%$| |
| |$r_{1}$| (pole) | 0.3509(7) | 0.3569(19) | 0.3636(32) | 0.3510(15) | 0.3637(14) | 0.3591(10) |
| |$r_{1}$| (side) | 0.3700(9) | 0.3765(21) | 0.3841(36) | 0.3702(19) | 0.3839(17) | 0.3786(11) |
| |$r_{1}$| (back) | 0.4101(14) | 0.4153(24) | 0.4329(38) | 0.4103(29) | 0.4220(21) | 0.4154(11) |
| |$r_{2}$| (pole) | 0.3891(7) | 0.3825(64) | 0.3747(111) | 0.3893(15) | 0.3736(41) | 0.3725(35) |
| |$r_{2}$| (side) | 0.4127(8) | 0.4052(82) | 0.3962(142) | 0.4129(19) | 0.3950(53) | 0.3934(44) |
| |$r_{2}$| (back) | 0.4497(13) | 0.4431(13) | 0.4335(227) | 0.4490(28) | 0.4325(83) | 0.4287(69) |
| f | 21.1(1.4)|$\%$| | 21.0(6.3)|$\%$| | 19.5(10.5)|$\%$| | 21.6(2.3)|$\%$| | 18.7(3.9)|$\%$| | 16.5(2.1)|$\%$| |
| |$\Sigma$| res|$^{2}$| | 0.0298 | 0.0116 | 0.0122 | 0.0104 | 0.0010 | 0.0111 |
| Parameter . | 2015 . | 2016(a) . | 2016(b) . | 2015 . | 2016(a) . | 2016(b) . |
|---|---|---|---|---|---|---|
| |$T_{1}(K)$| | 4100(fixed) | 4100(fixed) | 4100(fixed) | 4317(fixed) | 4317(fixed) | 4317(fixed) |
| |$g_{1}$| = |$g_{2}$| | 0.32(fixed) | 0.32(fixed) | 0.32(fixed) | 0.32(fixed) | 0.32(fixed) | 0.32(fixed) |
| |$A_{1}$| = |$A_{2}$| | 0.50(fixed) | 0.50(fixed) | 0.50(fixed) | 0.50(fixed) | 0.50(fixed) | 0.50(fixed) |
| |$x_{1}$| = |$x_{2} (B$|) | 0.828 | 0.828 | ... | 0.831 | 0.830 | ... |
| |$x_{1}$| = |$x_{2} (V$|) | 0.793 | 0.792 | 0.792 | 0.793 | 0.794 | 0.794 |
| |$x_{1}$| = |$x_{2} (R_{\rm c}$|) | 0.760 | 0.760 | 0.760 | 0.760 | 0.759 | 0.759 |
| |$x_{1}$| = |$x_{2} (I_{\rm c}$|) | 0.675 | 0.675 | 0.675 | 0.676 | 0.676 | 0.676 |
| |$y_{1}$| = |$y_{2} (B$|) | 0.089 | 0.087 | ... | |$-$|0.080 | |$-$|0.080 | ... |
| |$y_{1}$| = |$y_{2} (V$|) | 0.188 | 0.187 | 0.184 | 0.080 | 0.080 | 0.080 |
| |$y_{1}$| = |$y_{2} (R_{\rm c}$|) | 0.232 | 0.232 | 0.231 | 0.160 | 0.160 | 0.160 |
| |$y_{1}$| = |$y_{2} (I_{\rm c}$|) | 0.262 | 0.261 | 0.261 | 0.220 | 0.220 | 0.220 |
| q (|$M_2/M_1$|) | 1.26(7) | 1.15(2) | 1.08(4) | 1.26(6) | 1.06(1) | 1.10(1) |
| |$i\ (^{\circ })$| | 78.0(fixed) | 77.9(4) | 78.2(2) | 78.0(fixed) | 77.8(4) | 78.1(3) |
| |$\Omega _{\rm in}$| | 4.1601 | 3.9969 | 3.8681 | 4.1601 | 3.8250 | 3.9108 |
| |$\Omega _{\rm out}$| | 3.5965 | 3.4406 | 3.3185 | 3.5965 | 3.2777 | 3.3588 |
| |$\Omega _{1}=\Omega _{2}$| | 4.0399(59) | 4.0782(66) | 3.7611(575) | 4.0383(131) | 3.7455(218) | 3.8196(116) |
| |$T_{2}\ (K)$| | 3895(5) | 3894(15) | 3917(17) | 4104(6) | 4111(3) | 4126(3) |
| |$L_{1}/(L_{1}+L_{2}+L_{3}$|) (B) | 55.14|$\%$| | 56.68|$\%$| | ... | 54.50|$\%$| | 58.05|$\%$| | ... |
| |$L_{1}/(L_{1}+L_{2}+L_{3}$|) (V) | 53.30|$\%$| | 55.00|$\%$| | 55.72|$\%$| | 52.70|$\%$| | 56.54|$\%$| | 54.98|$\%$| |
| |$L_{1}/(L_{1}+L_{2}+L_{3}$|) (R) | 51.93|$\%$| | 53.39|$\%$| | 54.24|$\%$| | 51.41|$\%$| | 54.91|$\%$| | 53.48|$\%$| |
| |$L_{1}/(L_{1}+L_{2}+L_{3}$|) (I) | 49.75|$\%$| | 50.82|$\%$| | 51.76|$\%$| | 49.40|$\%$| | 52.45|$\%$| | 50.73|$\%$| |
| |$L_{3}/(L_{1}+L_{2}+L_{3}$|) (B) | 1.4(0.6)|$\%$| | 1.8(1.5)|$\%$| | 2.5(1.5)|$\%$| | 2.9(0.5)|$\%$| | ... | |
| |$L_{3}/(L_{1}+L_{2}+L_{3}$|) (V) | 1.9(0.7)|$\%$| | 1.8(1.5)|$\%$| | 2.6(1.9)|$\%$| | 2.7(0.6)|$\%$| | 2.0(1.1)|$\%$| | 2.3(0.5)|$\%$| |
| |$L_{3}/(L_{1}+L_{2}+L_{3}$|) (R) | 2.6(0.6)|$\%$| | 3.1(1.4)|$\%$| | 3.9(1.9)|$\%$| | 3.2(0.5)|$\%$| | 2.5(1.2)|$\%$| | 2.8(0.3)|$\%$| |
| |$L_{3}/(L_{1}+L_{2}+L_{3}$|) (I) | 3.4(0.6)|$\%$| | 4.6(1.4)|$\%$| | 5.6(1.8)|$\%$| | 4.8(0.3)|$\%$| | 4.1(1.1)|$\%$| | 4.2(0.5)|$\%$| |
| |$r_{1}$| (pole) | 0.3509(7) | 0.3569(19) | 0.3636(32) | 0.3510(15) | 0.3637(14) | 0.3591(10) |
| |$r_{1}$| (side) | 0.3700(9) | 0.3765(21) | 0.3841(36) | 0.3702(19) | 0.3839(17) | 0.3786(11) |
| |$r_{1}$| (back) | 0.4101(14) | 0.4153(24) | 0.4329(38) | 0.4103(29) | 0.4220(21) | 0.4154(11) |
| |$r_{2}$| (pole) | 0.3891(7) | 0.3825(64) | 0.3747(111) | 0.3893(15) | 0.3736(41) | 0.3725(35) |
| |$r_{2}$| (side) | 0.4127(8) | 0.4052(82) | 0.3962(142) | 0.4129(19) | 0.3950(53) | 0.3934(44) |
| |$r_{2}$| (back) | 0.4497(13) | 0.4431(13) | 0.4335(227) | 0.4490(28) | 0.4325(83) | 0.4287(69) |
| f | 21.1(1.4)|$\%$| | 21.0(6.3)|$\%$| | 19.5(10.5)|$\%$| | 21.6(2.3)|$\%$| | 18.7(3.9)|$\%$| | 16.5(2.1)|$\%$| |
| |$\Sigma$| res|$^{2}$| | 0.0298 | 0.0116 | 0.0122 | 0.0104 | 0.0010 | 0.0111 |
| Parameter . | 2015 . | 2016(a) . | 2016(b) . | 2015 . | 2016(a) . | 2016(b) . |
|---|---|---|---|---|---|---|
| |$T_{1}(K)$| | 4100(fixed) | 4100(fixed) | 4100(fixed) | 4317(fixed) | 4317(fixed) | 4317(fixed) |
| |$g_{1}$| = |$g_{2}$| | 0.32(fixed) | 0.32(fixed) | 0.32(fixed) | 0.32(fixed) | 0.32(fixed) | 0.32(fixed) |
| |$A_{1}$| = |$A_{2}$| | 0.50(fixed) | 0.50(fixed) | 0.50(fixed) | 0.50(fixed) | 0.50(fixed) | 0.50(fixed) |
| |$x_{1}$| = |$x_{2} (B$|) | 0.828 | 0.828 | ... | 0.831 | 0.830 | ... |
| |$x_{1}$| = |$x_{2} (V$|) | 0.793 | 0.792 | 0.792 | 0.793 | 0.794 | 0.794 |
| |$x_{1}$| = |$x_{2} (R_{\rm c}$|) | 0.760 | 0.760 | 0.760 | 0.760 | 0.759 | 0.759 |
| |$x_{1}$| = |$x_{2} (I_{\rm c}$|) | 0.675 | 0.675 | 0.675 | 0.676 | 0.676 | 0.676 |
| |$y_{1}$| = |$y_{2} (B$|) | 0.089 | 0.087 | ... | |$-$|0.080 | |$-$|0.080 | ... |
| |$y_{1}$| = |$y_{2} (V$|) | 0.188 | 0.187 | 0.184 | 0.080 | 0.080 | 0.080 |
| |$y_{1}$| = |$y_{2} (R_{\rm c}$|) | 0.232 | 0.232 | 0.231 | 0.160 | 0.160 | 0.160 |
| |$y_{1}$| = |$y_{2} (I_{\rm c}$|) | 0.262 | 0.261 | 0.261 | 0.220 | 0.220 | 0.220 |
| q (|$M_2/M_1$|) | 1.26(7) | 1.15(2) | 1.08(4) | 1.26(6) | 1.06(1) | 1.10(1) |
| |$i\ (^{\circ })$| | 78.0(fixed) | 77.9(4) | 78.2(2) | 78.0(fixed) | 77.8(4) | 78.1(3) |
| |$\Omega _{\rm in}$| | 4.1601 | 3.9969 | 3.8681 | 4.1601 | 3.8250 | 3.9108 |
| |$\Omega _{\rm out}$| | 3.5965 | 3.4406 | 3.3185 | 3.5965 | 3.2777 | 3.3588 |
| |$\Omega _{1}=\Omega _{2}$| | 4.0399(59) | 4.0782(66) | 3.7611(575) | 4.0383(131) | 3.7455(218) | 3.8196(116) |
| |$T_{2}\ (K)$| | 3895(5) | 3894(15) | 3917(17) | 4104(6) | 4111(3) | 4126(3) |
| |$L_{1}/(L_{1}+L_{2}+L_{3}$|) (B) | 55.14|$\%$| | 56.68|$\%$| | ... | 54.50|$\%$| | 58.05|$\%$| | ... |
| |$L_{1}/(L_{1}+L_{2}+L_{3}$|) (V) | 53.30|$\%$| | 55.00|$\%$| | 55.72|$\%$| | 52.70|$\%$| | 56.54|$\%$| | 54.98|$\%$| |
| |$L_{1}/(L_{1}+L_{2}+L_{3}$|) (R) | 51.93|$\%$| | 53.39|$\%$| | 54.24|$\%$| | 51.41|$\%$| | 54.91|$\%$| | 53.48|$\%$| |
| |$L_{1}/(L_{1}+L_{2}+L_{3}$|) (I) | 49.75|$\%$| | 50.82|$\%$| | 51.76|$\%$| | 49.40|$\%$| | 52.45|$\%$| | 50.73|$\%$| |
| |$L_{3}/(L_{1}+L_{2}+L_{3}$|) (B) | 1.4(0.6)|$\%$| | 1.8(1.5)|$\%$| | 2.5(1.5)|$\%$| | 2.9(0.5)|$\%$| | ... | |
| |$L_{3}/(L_{1}+L_{2}+L_{3}$|) (V) | 1.9(0.7)|$\%$| | 1.8(1.5)|$\%$| | 2.6(1.9)|$\%$| | 2.7(0.6)|$\%$| | 2.0(1.1)|$\%$| | 2.3(0.5)|$\%$| |
| |$L_{3}/(L_{1}+L_{2}+L_{3}$|) (R) | 2.6(0.6)|$\%$| | 3.1(1.4)|$\%$| | 3.9(1.9)|$\%$| | 3.2(0.5)|$\%$| | 2.5(1.2)|$\%$| | 2.8(0.3)|$\%$| |
| |$L_{3}/(L_{1}+L_{2}+L_{3}$|) (I) | 3.4(0.6)|$\%$| | 4.6(1.4)|$\%$| | 5.6(1.8)|$\%$| | 4.8(0.3)|$\%$| | 4.1(1.1)|$\%$| | 4.2(0.5)|$\%$| |
| |$r_{1}$| (pole) | 0.3509(7) | 0.3569(19) | 0.3636(32) | 0.3510(15) | 0.3637(14) | 0.3591(10) |
| |$r_{1}$| (side) | 0.3700(9) | 0.3765(21) | 0.3841(36) | 0.3702(19) | 0.3839(17) | 0.3786(11) |
| |$r_{1}$| (back) | 0.4101(14) | 0.4153(24) | 0.4329(38) | 0.4103(29) | 0.4220(21) | 0.4154(11) |
| |$r_{2}$| (pole) | 0.3891(7) | 0.3825(64) | 0.3747(111) | 0.3893(15) | 0.3736(41) | 0.3725(35) |
| |$r_{2}$| (side) | 0.4127(8) | 0.4052(82) | 0.3962(142) | 0.4129(19) | 0.3950(53) | 0.3934(44) |
| |$r_{2}$| (back) | 0.4497(13) | 0.4431(13) | 0.4335(227) | 0.4490(28) | 0.4325(83) | 0.4287(69) |
| f | 21.1(1.4)|$\%$| | 21.0(6.3)|$\%$| | 19.5(10.5)|$\%$| | 21.6(2.3)|$\%$| | 18.7(3.9)|$\%$| | 16.5(2.1)|$\%$| |
| |$\Sigma$| res|$^{2}$| | 0.0298 | 0.0116 | 0.0122 | 0.0104 | 0.0010 | 0.0111 |
5 Discussions and conclusions
With the eight new determined times of light minima together with the others kindly provided by Dr. M. E. Lohr, the orbital period changes of the close binary J161335 were analyzed. Meanwhile, six sets of photometric parameters of J161335 were obtained by applying the W–D method (see table 3). We can see that there are some deviations between the 2015 and 2016 results, especially for the mass ratio. This may be influenced by the uncertain activity of dark spots, which prevents us from determining the photometric parameters with high precision (Bradstreet 1985). Short-period contact binaries with these characteristics have been well studied, such as QX And (Qian et al. 2007a), BI CVn (Qian et al. 2008), VW Boo (Liu et al. 2011), and so on. Figure 2 illustrates that the primary minima of 2015 are deeper than those of 2016. This phenomenon is very common in W UMa-type contact binaries, e.g., V1007 Cas (Li et al. 2018), AD Cnc (Qian et al. 2007b), GN Boo (Wang et al. 2015), V523 Cas (Zhang & Zhang 2004); their light curves are variable within a short time interval (a few days, months, or years) due to stellar spot activities on the surface of the components. For our target J161335, introducing a spot provided a good fit to the asymmetric light curves. The spot had survived in 2015, but disappeared in 2016. For the photometric W–D solutions, four dark spot parameters are set to adjustable. The position, size, and temperature of the spot are nearly the same, even though different temperatures (4100 K or 4317 K) are fixed for the more massive component. The average values for the dark spot are |$\theta$| = 2.0037 (0.1251), |$\psi$| = 4.7728 (0.4296), r = 0.2961 (0.0876), T = 0.7244 (0.0738). The geometrical configurations at phases 0 and 0.75 from 2015 to 2016 are plotted in figure 6. The temperature difference between the photospheric surface and the spotted region of the star is about 1100 K. The asymmetric light curves with different heights of Max.I and Min.I can be explained by the O’Connell effect (Zhukov 1985). A spot has its own life cycle which causes the variation in the light curves, e.g., AD Can, where the 17 yr cyclic activity of the dark spot may reveal that the more massive component displays solar-type magnetic activity (Qian et al. 2007b).
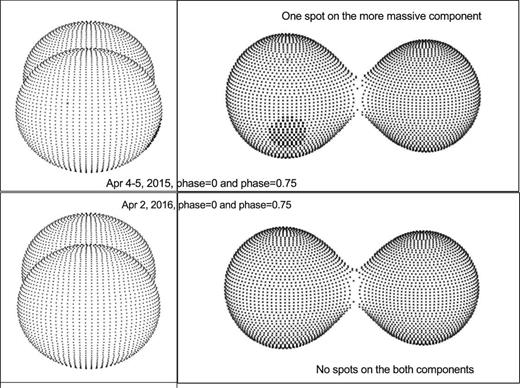
Contact configurations and evolution of the dark spot on the more massive component of the system J161335.
| Star . | Period . | q . | f . | |$dP/dt$| . | Reference . |
|---|---|---|---|---|---|
| . | (d) . | . | . | (10|$^{-7}\:$|d|$\:$|yr|$^{-1}$|) . | . |
| VW Boo | 0.34232 | 0.428 | 6.8|$\%$| | |$-$|1.45 | Liu et al. (2011) |
| AO Cam | 0.32991 | 0.413 | 12.0|$\%$| | |$-$|1.26 | Yang et al. (2010) |
| BI CVn | 0.38421 | 0.410 | 18.0|$\%$| | |$-$|1.51 | Qian et al. (2008) |
| V1007 Cas | 0.33200799 | 0.297 | 8.1|$\%$| | |$-$|1.78 | Li et al. (2018) |
| IK Boo | 0.30311700 | 0.872 | 2.2|$\%$| | |$-$|2.2 | Kriwattanawong, Sanguansak, and Maungkorn (2017) |
| KV Gem | 0.35852240 | 0.357 | 24.6|$\%$| | |$-$|3.9 | Zhang et al. (2014) |
| SS Ari | 0.40599 | 0.308 | 9.4|$\%$| | |$-$|4.03 | Liu et al. (2009) |
| MR Com | 0.41274 | 0.256 | 10.0|$\%$| | |$-$|5.30 | Qian et al. (2013) |
| J161335 | 0.229778 | 0.909 | 18.9|$\%$| | |$-$|4.26 | The present paper |
| Star . | Period . | q . | f . | |$dP/dt$| . | Reference . |
|---|---|---|---|---|---|
| . | (d) . | . | . | (10|$^{-7}\:$|d|$\:$|yr|$^{-1}$|) . | . |
| VW Boo | 0.34232 | 0.428 | 6.8|$\%$| | |$-$|1.45 | Liu et al. (2011) |
| AO Cam | 0.32991 | 0.413 | 12.0|$\%$| | |$-$|1.26 | Yang et al. (2010) |
| BI CVn | 0.38421 | 0.410 | 18.0|$\%$| | |$-$|1.51 | Qian et al. (2008) |
| V1007 Cas | 0.33200799 | 0.297 | 8.1|$\%$| | |$-$|1.78 | Li et al. (2018) |
| IK Boo | 0.30311700 | 0.872 | 2.2|$\%$| | |$-$|2.2 | Kriwattanawong, Sanguansak, and Maungkorn (2017) |
| KV Gem | 0.35852240 | 0.357 | 24.6|$\%$| | |$-$|3.9 | Zhang et al. (2014) |
| SS Ari | 0.40599 | 0.308 | 9.4|$\%$| | |$-$|4.03 | Liu et al. (2009) |
| MR Com | 0.41274 | 0.256 | 10.0|$\%$| | |$-$|5.30 | Qian et al. (2013) |
| J161335 | 0.229778 | 0.909 | 18.9|$\%$| | |$-$|4.26 | The present paper |
| Star . | Period . | q . | f . | |$dP/dt$| . | Reference . |
|---|---|---|---|---|---|
| . | (d) . | . | . | (10|$^{-7}\:$|d|$\:$|yr|$^{-1}$|) . | . |
| VW Boo | 0.34232 | 0.428 | 6.8|$\%$| | |$-$|1.45 | Liu et al. (2011) |
| AO Cam | 0.32991 | 0.413 | 12.0|$\%$| | |$-$|1.26 | Yang et al. (2010) |
| BI CVn | 0.38421 | 0.410 | 18.0|$\%$| | |$-$|1.51 | Qian et al. (2008) |
| V1007 Cas | 0.33200799 | 0.297 | 8.1|$\%$| | |$-$|1.78 | Li et al. (2018) |
| IK Boo | 0.30311700 | 0.872 | 2.2|$\%$| | |$-$|2.2 | Kriwattanawong, Sanguansak, and Maungkorn (2017) |
| KV Gem | 0.35852240 | 0.357 | 24.6|$\%$| | |$-$|3.9 | Zhang et al. (2014) |
| SS Ari | 0.40599 | 0.308 | 9.4|$\%$| | |$-$|4.03 | Liu et al. (2009) |
| MR Com | 0.41274 | 0.256 | 10.0|$\%$| | |$-$|5.30 | Qian et al. (2013) |
| J161335 | 0.229778 | 0.909 | 18.9|$\%$| | |$-$|4.26 | The present paper |
| Star . | Period . | q . | f . | |$dP/dt$| . | Reference . |
|---|---|---|---|---|---|
| . | (d) . | . | . | (10|$^{-7}\:$|d|$\:$|yr|$^{-1}$|) . | . |
| VW Boo | 0.34232 | 0.428 | 6.8|$\%$| | |$-$|1.45 | Liu et al. (2011) |
| AO Cam | 0.32991 | 0.413 | 12.0|$\%$| | |$-$|1.26 | Yang et al. (2010) |
| BI CVn | 0.38421 | 0.410 | 18.0|$\%$| | |$-$|1.51 | Qian et al. (2008) |
| V1007 Cas | 0.33200799 | 0.297 | 8.1|$\%$| | |$-$|1.78 | Li et al. (2018) |
| IK Boo | 0.30311700 | 0.872 | 2.2|$\%$| | |$-$|2.2 | Kriwattanawong, Sanguansak, and Maungkorn (2017) |
| KV Gem | 0.35852240 | 0.357 | 24.6|$\%$| | |$-$|3.9 | Zhang et al. (2014) |
| SS Ari | 0.40599 | 0.308 | 9.4|$\%$| | |$-$|4.03 | Liu et al. (2009) |
| MR Com | 0.41274 | 0.256 | 10.0|$\%$| | |$-$|5.30 | Qian et al. (2013) |
| J161335 | 0.229778 | 0.909 | 18.9|$\%$| | |$-$|4.26 | The present paper |
where G is the gravitational constant and |$P_{3}$| is the period of the |$(O-C)_{2}$| oscillation. When |$i^{\prime }=90^{\circ }$|, the orbital distance between the third body and the central binary is estimated by |$a_{3}$| = |$(M_{1} + M_{2})a{^{\prime }}_{12}/M_{3}$|. All the parameters of the third component are shown in table 5.
| Parameters . | Values and error . |
|---|---|
| Eccentricity (|$e{^{\prime }}$|) | 0.0 |
| Period (|$P_{3}$|) | 4.79(|$\pm 0.16$|) yr |
| Amplitude (|$K_{3}$|) | 0.00196(|$\pm 0.00006$|) d |
| |$a^{\prime }_{12} \sin i{^{\prime }}$| | 0.34(|$\pm 0.01$|) au |
| |$f (m)$| | 1.7(|$\pm 0.1$|) |$\times$| 10|$^{-3}\, M_{\,\odot }$| |
| |$M_{3} \sin i{^{\prime }}$| | 0.15(|$\pm 0.01$|) |$M_{\,\odot }$| |
| |$a_{3}$| | 2.8(|$\pm 0.2$|) au |
| Parameters . | Values and error . |
|---|---|
| Eccentricity (|$e{^{\prime }}$|) | 0.0 |
| Period (|$P_{3}$|) | 4.79(|$\pm 0.16$|) yr |
| Amplitude (|$K_{3}$|) | 0.00196(|$\pm 0.00006$|) d |
| |$a^{\prime }_{12} \sin i{^{\prime }}$| | 0.34(|$\pm 0.01$|) au |
| |$f (m)$| | 1.7(|$\pm 0.1$|) |$\times$| 10|$^{-3}\, M_{\,\odot }$| |
| |$M_{3} \sin i{^{\prime }}$| | 0.15(|$\pm 0.01$|) |$M_{\,\odot }$| |
| |$a_{3}$| | 2.8(|$\pm 0.2$|) au |
| Parameters . | Values and error . |
|---|---|
| Eccentricity (|$e{^{\prime }}$|) | 0.0 |
| Period (|$P_{3}$|) | 4.79(|$\pm 0.16$|) yr |
| Amplitude (|$K_{3}$|) | 0.00196(|$\pm 0.00006$|) d |
| |$a^{\prime }_{12} \sin i{^{\prime }}$| | 0.34(|$\pm 0.01$|) au |
| |$f (m)$| | 1.7(|$\pm 0.1$|) |$\times$| 10|$^{-3}\, M_{\,\odot }$| |
| |$M_{3} \sin i{^{\prime }}$| | 0.15(|$\pm 0.01$|) |$M_{\,\odot }$| |
| |$a_{3}$| | 2.8(|$\pm 0.2$|) au |
| Parameters . | Values and error . |
|---|---|
| Eccentricity (|$e{^{\prime }}$|) | 0.0 |
| Period (|$P_{3}$|) | 4.79(|$\pm 0.16$|) yr |
| Amplitude (|$K_{3}$|) | 0.00196(|$\pm 0.00006$|) d |
| |$a^{\prime }_{12} \sin i{^{\prime }}$| | 0.34(|$\pm 0.01$|) au |
| |$f (m)$| | 1.7(|$\pm 0.1$|) |$\times$| 10|$^{-3}\, M_{\,\odot }$| |
| |$M_{3} \sin i{^{\prime }}$| | 0.15(|$\pm 0.01$|) |$M_{\,\odot }$| |
| |$a_{3}$| | 2.8(|$\pm 0.2$|) au |
The |$B-I$| fitting curve based on the light curves obtained in 2015 (because they are relatively complete compared to the other two sets) is demonstrated in figure 7; this can be used to calculate the phase dependence of the color indices. The amplitude of the variability decreases with increasing wavelength, and the system is reddest during eclipses. This may be potentially relevant evidence of the cool companion in the system (Koen 2014). In order to check whether there is third light in the system, we performed the solutions with third light using the W–D method. The results are listed in table 3. It is found that the contribution of the third light to the total light of the system increases with the wavelength. These results reveal that the third component is a very cool stellar companion and that the radiation is mainly in long-wavelength bands. This is in good agreement with the cyclic variation of the |$O-C$| curves, which supports the presence of an extremely cool third body. It may play an important role in the formation and evolution of J161335 by removing angular momentum from the center of the binary system, which causes the binary’s low angular momentum and a very short initial orbital period (Qian et al. 2015). Binary stars formed through core fragmentation have initial separations in the range from 10 au to 1000 au (e.g., Boss 1986; Bate et al. 1995). Extremely short-period binaries like J161335 may be formed later through dynamical interactions with nearby stars (Bate et al. 2002). The low-mass component in the original binary system is replaced by a higher-mass third body and the lower-mass component is kicked out to a wide orbit. In this way, a hierarchical triple system is formed. The high mass ratio and the small close-in third body of J161335 support such dynamical interaction.
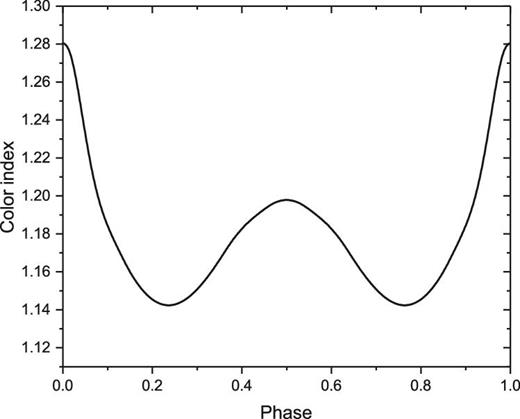
|$B-I$| fitting curve calculated from the data of 2015 April 4–5.
Acknowledgments
This work is partly supported by the National Natural Science Foundation of China (Nos. 11573063, 11611530685) and the Key Science Foundation of Yunnan Province (No. 2017FA001). New CCD photometric observations of J161335 were obtained with the |$2.4$| m Thai National Telescope, the |$1.0$| m telescope at the South African Astronomical Observatory, and the |$1.0$| m telescope at Yunnan Observatories. The authors would like to thank Dr. M. E. Lohr for kindly providing the eclipsing times derived using the SuperWASP data.



