-
PDF
- Split View
-
Views
-
Cite
Cite
Ken Tateuchi, Kentaro Motohara, Masahiro Konishi, Hidenori Takahashi, Yutaro Kitagawa, Natsuko Kato, Soya Todo, Shinya Komugi, Ryou Ohsawa, Mamoru Doi, Yuzuru Yoshii, Ground-based Paα narrow-band imaging of local luminous infrared galaxies. II. Bulge structure and star formation activity, Publications of the Astronomical Society of Japan, Volume 71, Issue 3, June 2019, 64, https://doi.org/10.1093/pasj/psz042
Close - Share Icon Share
Abstract
We present properties of two types of bulges (classical and pseudobulges) in 20 luminous infrared galaxies observed in the near infrared of the H, Ks, and 1.91|$\mu$|m narrow-band targeting of the hydrogen Paα emission line by the University of Tokyo Atacama Observatory 1 m telescope. To classify the two types of bulges, we first perform a two-dimensional bulge–disk decomposition analysis in the Ks-band images. The result shows a tentative bimodal distribution of Sérsic indices with a separation at log (nb) ≈ 0.5, which is consistent with that of classical and normal galaxies. We next measure the extents of the distributions of star-forming regions in Paα emission line images, normalized by the size of the bulges, and find that they decrease with increasing Sérsic indices. These results suggest that star-forming galaxies with classical bulges have compact star-forming regions concentrated within the bulges, while those with pseudobulges have extended star-forming regions beyond the bulges, suggesting that there are different formation scenarios at work in classical and pseudobulges.
1 Introduction
Recent research suggests that there are two types of bulges found at the centers of galaxies, called “classical bulges” and “pseudobulges” (e.g., Kormendy & Kennicutt 2004; Athanassoula 2005; Kormendy & Fisher 2005; Combes 2009; Fisher & Drory 2010). Classical bulges are characterized by a steep increase in density toward their center. They are dynamically hot and supported by stellar velocity dispersion rather than their systemic rotational motion (Fisher & Drory 2008; Guedes et al. 2013). In addition, they are red in color, old in population, and high in metallicity and in α/Fe ratio (Moorthy & Holtzman 2006; Zoccali et al. 2006; Ballero et al. 2007; Lecureur et al. 2007; McWilliam et al. 2008). Also, it is suggested that their positions in the fundamental plane of size versus surface magnitude form a sequence, which is smoothly connected to that of elliptical galaxies (Falcón-Barroso et al. 2002; Thomas & Davies 2006; Jablonka et al. 2007; Driver et al. 2007; Gadotti 2009). On the other hand, pseudobulges are dynamically cold, supported by systemic rotation, and have flat shapes resembling those of exponential disks. Also, they can be identified as outliers in the fundamental plane (Gadotti 2009) and generally have younger stellar populations than those of classical bulges. Kormendy and Kennicutt (2004) classified 75 normal galaxies in the V band by eye, and found that 28.5% of their sample have classical bulges and 71.5% have pseudobulges. Using this sample, Fisher and Drory (2008) showed that the distribution of nb, that is, the Sérsic index of a bulge, is bimodal, where pseudobulges have nb < 2.2 and classical bulges nb ≥ 2.2, and that the types of bulges can be distinguished by the Sérsic index.
Theoretically, classical bulges are thought to be formed by major merger processes (e.g., Kormendy & Kennicutt 2004; Naab & Trujillo 2006; Hopkins et al. 2010), or by the collapse of giant clumps in primordial disks (Elmegreen et al. 2008) to remove their angular momentum. Elliptical galaxies are also expected to be formed by similar processes but through dissipationless (dry) merger, where their progenitors have little gas content (e.g., Kormendy & Kennicutt 2004; Kormendy et al. 2009). On the other hand, pseudobulges are suggested to be built by secular evolution (e.g., Kormendy & Kennicutt 2004). Okamoto (2013) showed by numerical cosmological simulations that some pseudobulges are formed through starburst events even at redshifts of two, which may be an extreme example of the secular evolution.
Furthermore, it is speculated that the formation of the two types of bulges has a deep relationship with the growth of super-massive black holes (SMBHs). Magorrian et al. (1998) found a correlation between the mass of a central SMBH (M•) and the velocity dispersion of the host (σ) in 32 dust-free nearby galaxies, which has been followed up by various observations. This is now known as the “M–σ” relation, suggesting that SMBHs and their hosts co-evolve (e.g., Ferrarese & Merritt 2000; Gebhardt et al. 2000; Kormendy & Gebhardt 2001; Tremaine et al. 2002; Gültekin et al. 2009). Kormendy, Bender, and Cornell (2011) also found that the M–σ relation of classical bulges has a tight correlation, while that of pseudobulges does not. They suggested from this discovery that there are two fundamentally different feeding mechanisms for SMBHs: in a classical bulge, gas is fed to an SMBH through a rapid gas inflow process toward the center of the galaxy, which also results in the stellar mass accumulation of the bulge; in a pseudobulge, gas feeding an SMBH is controlled by a local process working stochastically at a central ∼102 pc region, and is independent of or has a weak connection with the growth of the bulge. Thus, the two types of bulges may have different formation processes, where classical bulges are formed by drastic external factors such as major merger processes similar to those of elliptical galaxies, while pseudobulges evolve more secularly. However, there are few observational studies to verify the formation scenarios.
To understand the formation process of bulges, we focus on LIRGs (luminous infrared galaxies: LIR ≡ 1011–10|$^{12}\, L_{\odot}$|) in the local universe. They are ideal laboratories for studying bulge formation, because half of them are non-irregular galaxies (Wang et al. 2006) whose bulges can be evaluated easily, and might be current formation sites of bulges with ongoing starbursts. Although LIRGs may provide a direct way to understand the detailed mechanism of bulge formation, they are affected by a large amount of dust produced by their active star formations, and optical hydrogen recombination lines such as Hα and Hβ, which are direct probes of star formation activities, are easily attenuated by the dust. We have therefore focused on the hydrogen Paα line (1.8751|$\, \mu$|m), which is relatively insensitive to dust extinction (APaα/AHα = 5.68) and the strongest emission line in the near-infrared (λ = 0.9–2.5|$\, \mu$|m) wavelengths. There are several Paα narrow-band imaging studies of nearby LIRGs by the Near-Infrared Camera and Multi-object Spectrometer (NICMOS) on the Hubble Space Telescope (HST; e.g., Alonso-Herrero et al. 2006; Calzetti et al. 2007; Kennicutt et al. 2007; Rieke et al. 2009). However, some researchers have pointed out that HST/NICMOS may be insensitive to diffuse Paα emission due to its intrinsic high angular resolution (e.g., Alonso-Herrero et al. 2006; Calzetti et al. 2007; Kennicutt et al. 2007; Rieke et al. 2009). On the other hand, due to poor atmospheric transmission around the Paα wavelength, it is difficult to carry out Paα observation from the ground.
We have carried out a Paα narrow-band imaging survey of local LIRGs (Tateuchi et al. 2012, 2013, 2015) with Atacama Near-InfraRed camera (ANIR; Motohara et al. 2008, 2010; Konishi et al. 2015) on the University of Tokyo Atacama Observatory 1 m telescope (miniTAO; Minezaki et al. 2010; Yoshii et al. 2010) installed at the summit of Cerro Chajnantor (5640 m altitude) in northern Chile. Thanks to the high altitude and the extremely low water vapor at the site, we can stably observe Paα emission line even from the ground (Motohara et al. 2010). In this paper, we evaluate the properties of bulges and star-forming regions in LIRGs using the survey data to probe the formation process of classical and pseudobulges.
The paper is organized as follows. We introduce the survey data and describe the selection method of non-irregular galaxies and the method of bulge–disk decomposition in section 2. In section 3, we present the results and discuss the relationship between the types of bulges and the sizes of star-forming regions, and summarize them in section 4.
Throughout this paper, we use a Λ-CDM cosmology with Ωm = 0.3, ΩΛ = 0.7, and H0 = 70 km s−1 Mpc−1.
2 Sample and data analysis
2.1 Sample
We use Ks-band and Paα line images of LIRGs obtained by Tateuchi et al. (2015), consisting of 38 galaxies selected from the Infrared Astronomical Satellite (IRAS) Revised Bright Galaxy Sample (RBGS: Sanders et al. 2003) with bolometric infrared luminosity (LIR) ranging between 4.5 × 1010 and |$6.5\times 10^{11}\, L_{\odot }$|. Their recession velocities are 2800–8100 km s−1, corresponding to distances of 46.6–109.6 Mpc.
2.2 Identification of non-irregular galaxies
We determine whether a galaxy is irregular or not by a combination of the Gini coefficient (G) and the second-order moment (M20) of its surface-brightness distribution, which are non-parametric methods for quantifying galaxy morphology (Lotz et al. 2004). G is a statistic based on the Lorenz curve of fluxes per pixel in a galaxy and represents the relative distribution of pixels covering the galaxy, while M20 is a normalized second-order moment of pixel flux values which is measured to be the brightest 20% of the fluxes of a galaxy. Figure 1 shows an M20–G plot measured in the Ks band. These parameters are affected by the spatial resolution and noise level of the image. Lotz, Primack, and Madau (2004) found that they are reliable if the averaged signal-to-noise ratio (〈S/N〉) per pixel of an image is larger than 2. Also, they found that M20 tends to have a systematic offset greater than ∼15% when the spatial resolution is larger than 500 pc, as the core of a galaxy becomes unresolved, while G is relatively stable with decreasing resolution until the smallest resolved detail is 1000 pc. In our sample the resolution is 180–400 pc, corresponding to a typical seeing size of |${0{^{\prime\prime}_{.}}8}$| and the 〈S/N〉 is over five, which are enough to evaluate the morphology of the galaxies by G and M20. We adopt a criterion defined by Lotz, Primack, and Madau (2004) to distinguish irregular galaxies from the others on the G–M20 diagram, as shown in figure 1. We thus selected 20 non-irregular galaxies out of 38 galaxies for further analysis. The fraction of non-irregular galaxies is consistent with the claim of Wang et al. (2006) that half of LIRGs in the local universe are classified as non-irregular galaxies.
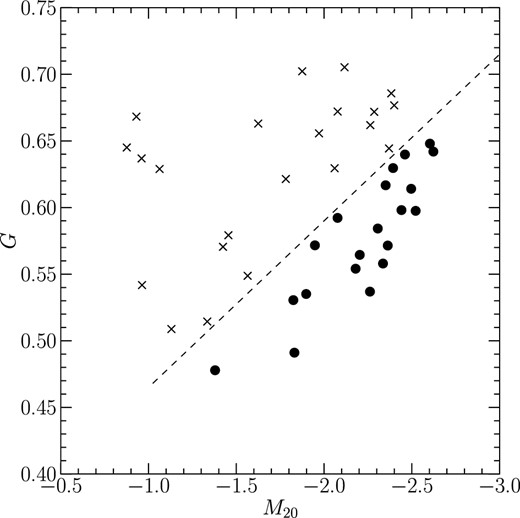
Diagram of Gini coefficients (G) and second-order moments of the brightest 20% of flux of galaxies (M20) measured in the Ks-band images. The dashed line is the threshold between irregulars (crosses) and non-irregulars (circles) defined by Lotz, Primack, and Madau (2004).
2.3 Bulge–disk decomposition
The results of the bulge–disk decomposition are shown in figure 2. For each galaxy, the left panel shows the Ks-band image observed by miniTAO/ANIR, the second from the left a model galaxy composed of the best-fit Sérsic and exponential components, and the third from the left the residual image created by subtracting the model galaxy from the Ks-band image. The residual structure of spiral arms and bars can be seen in the residual image for most of the sample. The right panel shows a radial profile of the surface brightness with model profiles, cut along the major axis of the galaxy.
There is a possibility that the limited spatial resolution (|${0{^{\prime\prime}_{.}}8}$| seeing) in our sample may miss complex structures in a bulge such as double nuclei, thus biasing the results of the bulge–disk decomposition (e.g., Haan et al. 2011; Psychogyios et al. 2016). Therefore, we evaluate the Sérsic indices of the bulges having HST NICMOS F160W data with the same method. These results are almost the same as our results listed in figure 2.
Results of bulge–disk decomposition. For each galaxy, the Ks-band image, a model image with best-fit bulge and disk components, the residual image after subtracting theh best-fit model image from the Ks-band image, and one-dimensional surface brightness profiles with residuals after fitting of the galaxy are shown, from left to right. The filled circles in the right panel are the raw profile measured in the Ks-band image with photometric error bars, the solid lines are the bulge and disk model profiles, and the red solid line is the bulge–disk combined model profile. The red circles in the left and right panels are the effective radius of the bulge and the Paα emission line regions, respectively.
3 Result and discussion
3.1 Properties of bulges
3.1.1 Sérsic indices of bulges
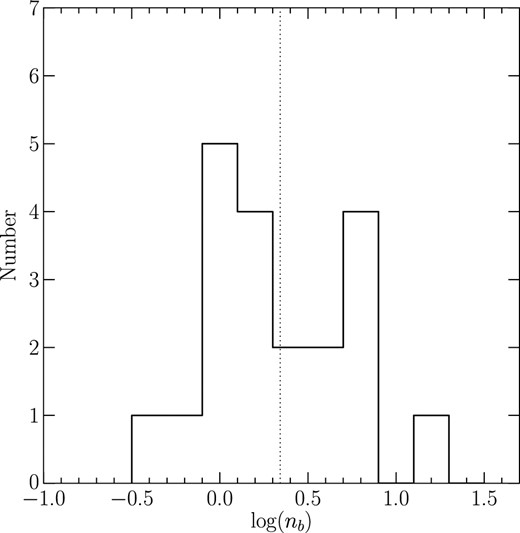
Fisher and Drory (2008) measured the Sérsic indices of normal galaxies in the V band and showed that classical and pseudobulges show a bimodal distribution of Sérsic indices separated at nb = 2.2 [log (nb) = 0.3]. They also claimed that the Sérsic indices measured in the V band and in the H band have almost the same value, suggesting that the criteria can also be used in the Ks band. In figure 3 we show a histogram of the Sérsic indices of the bulges measured in the Ks band. Although it is inconclusive statistically, it shows a bimodal distribution with a separation at log (nb) ≈ 0.5, which is consistent with the result of Fisher and Drory (2008), although the bimodality is statistically tentative. If we follow the criteria of Fisher and Drory (2008) and separate classical and pseudobulges at nb = 2.2 [log (nb) = 0.3], 45% (9/20) of our sample have classical bulges and 55% (11/20) pseudobulges. Although the volume of our sample is not large enough statistically to make a firm conclusion and the difference in the fraction of bulges and pseudobulges is not established at a significant level, this suggests that the fraction of classical bulges in LIRGs is higher than that in normal galaxies of 28.5% (Kormendy & Kennicutt 2004). As classical bulges are expected to be formed through major merger processes (e.g., Kormendy & Kennicutt 2004; Fisher & Drory 2008), this is consistent with the suggestions of previous work that LIRGs may have experienced more major merger events than normal galaxies (e.g., Sanders & Mirabel 1996; Wang et al. 2006).
Distribution of the Sérsic index of the bulges measured in the Ks band. The dotted line represents the border of the classical and pseudobulge classification (classical bulges nb ≥ 2.2, pseudobulges nb < 2.2) shown by a V-band study (Fisher & Drory 2008).
3.1.2 Size and luminosity of bulges
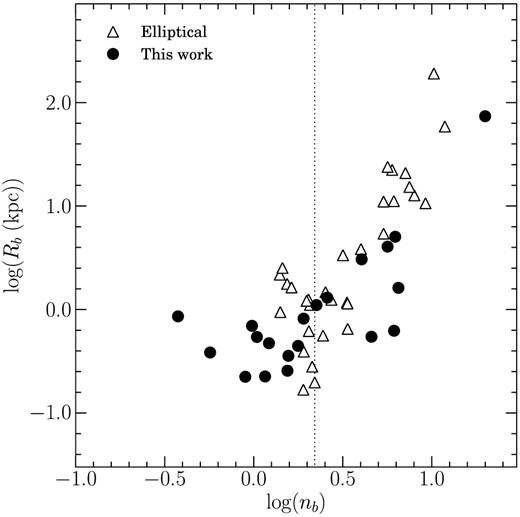
Figure 4 shows the relationship between the Sérsic indices and the effective radii of the bulges. The effective radii of the pseudobulges remain constant, of sub-kiloparsec order, while those of the classical bulges increase with the Sérsic indices, which is consistent with the distribution of normal galaxies (Fisher & Drory 2008).
Figure 5 shows the relationship between the Sérsic indices and B/T ratios, which are obtained from the surface brightness profile fitting in subsection 2.3. It suggests that the B/T ratios increase with the Sérsic indices, again consistent with the properties of normal galaxies (Fisher & Drory 2008).
Relationship between Sérsic indices and bulge-to-total luminosity ratio (B/T) obtained from a model profile from the bulge–disk decomposition in the Ks-band image. The dotted line shows the border of classical and pseudobulges shown in figure 3.
The results presented in this section suggest that the properties of bulges in LIRGs are similar to those in normal galaxies except for the fraction of classical and pseudobulges.
3.2 Distribution of star-forming regions
To understand the relationship between star formation activities and types of bulges, we derive the extent of the distribution of star-forming regions in the Paα narrow-band images. The extents are defined to be a half light radius with ellipticity and position angle the same as those of the bulges in the Ks-band image in a Paα emission line image (Rsf), and are shown in the fourth panels from the left in figure 2 and are listed in table 1. From this sample we remove IRAS F02437+2122, whose Rsf is almost equal to the size of the PSF, and MCG −03–34–064, which is a Seyfert 1 galaxy whose concentrated Paα emission may be strongly contaminated by the active galactic nucleus (AGN). Accordingly, there are 18 galaxies for which we can evaluate Rsf. The effect of AGNs for these galaxies is not so large considering the low effect of AGNs for bolometric luminosities of LIRGs (∼5%; Alonso-Herrero et al. 2012), and Paα flux correlates with far-infrared flux well (Tateuchi et al. 2015).
| Galaxy name . | Hubble type . | Spectral class . | G . | M 20 . | R sf (kpc) . | R b (kpc) . | n b . | |$n_{\rm b}^{\rm HST}$| . | log (B/T) . |
|---|---|---|---|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . |
| NGC 23 | 1 | H ii | 0.63 | −2.39 | 1.59 | 0.82 | 1.9 ± 0.03 | 1.9 | −0.4 |
| NGC 232 | 1 | Sy2 | 0.59 | −2.08 | 0.61 | 1.10 | 2.3 ± 0.03 | — | −0.2 |
| IRAS F02437+2122 | −5 | LINER | 0.61 | −2.50 | 0.23 | 0.55 | 4.6 ± 0.26 | — | −0.4 |
| NGC 1720 | 2 | N | 0.65 | −2.60 | 0.46 | 0.45 | 1.8 ± 0.02 | — | −0.7 |
| ESO 557-G002 | 4 | H ii | 0.54 | −2.26 | 1.34 | 73.82 | 19.9 ± 2.1 | — | −0.2 |
| ESO 320-G030 | 1 | H ii | 0.54 | −1.90 | 0.84 | 0.47 | 1.2 ± 0.02 | — | −0.4 |
| MCG −03–34–064 | −2 | Sy1 | 0.62 | −2.35 | 0.25 | 0.36 | 1.6 ± 0.03 | — | −0.4 |
| NGC 5135 | 2 | Sy2 | 0.60 | −2.52 | 1.63 | 0.70 | 1.0 ± 0.02 | 1.0 | −0.5 |
| NGC 5257 | 3 | H ii | 0.48 | −1.38 | 5.33 | 0.22 | 1.6 ± 0.2 | 2.0 | −1.4 |
| IC 4687 | 3 | H ii | 0.57 | −1.95 | 1.27 | 5.05 | 6.2 ± 0.31 | — | −0.6 |
| ESO 339-G011 | 3 | Sy2 | 0.56 | −2.34 | 3.12 | 0.38 | 0.6 ± 0.02 | — | −0.8 |
| IC 5063 | 0 | Sy2 | 0.58 | −2.31 | 0.44 | 4.05 | 5.7 ± 0.08 | — | −0.2 |
| NGC 7130 | 1 | LINER | 0.53 | −1.82 | 2.22 | 0.62 | 6.1 ± 0.32 | — | −0.5 |
| IC 5179 | 4 | H ii | 0.49 | −1.83 | 4.94 | 1.62 | 6.5 ± 0.43 | — | −0.8 |
| ESO 534-G009 | 2 | LINER | 0.56 | −2.20 | 0.18 | 1.30 | 2.6 ± 0.02 | — | −0.2 |
| CGCG 453-062 | 2 | LINER | 0.55 | −2.18 | 2.49 | 0.23 | 1.2 ± 0.15 | — | −1.0 |
| NGC 7591 | 4 | LINER | 0.64 | −2.46 | 0.62 | 3.06 | 4.0 ± 0.04 | — | −0.2 |
| MCG −01–60–022 | 7 | H ii | 0.60 | −2.44 | 3.19 | 0.26 | 1.5 ± 0.08 | — | −0.7 |
| NGC 7771 | 1 | H ii | 0.57 | −2.36 | 11.76 | 0.86 | 0.4 ± 0.01 | — | −0.9 |
| UGC 12915 | 5 | LINER | 0.64 | −2.62 | 7.86 | 0.54 | 1.0 ± 0.01 | — | −0.6 |
| Galaxy name . | Hubble type . | Spectral class . | G . | M 20 . | R sf (kpc) . | R b (kpc) . | n b . | |$n_{\rm b}^{\rm HST}$| . | log (B/T) . |
|---|---|---|---|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . |
| NGC 23 | 1 | H ii | 0.63 | −2.39 | 1.59 | 0.82 | 1.9 ± 0.03 | 1.9 | −0.4 |
| NGC 232 | 1 | Sy2 | 0.59 | −2.08 | 0.61 | 1.10 | 2.3 ± 0.03 | — | −0.2 |
| IRAS F02437+2122 | −5 | LINER | 0.61 | −2.50 | 0.23 | 0.55 | 4.6 ± 0.26 | — | −0.4 |
| NGC 1720 | 2 | N | 0.65 | −2.60 | 0.46 | 0.45 | 1.8 ± 0.02 | — | −0.7 |
| ESO 557-G002 | 4 | H ii | 0.54 | −2.26 | 1.34 | 73.82 | 19.9 ± 2.1 | — | −0.2 |
| ESO 320-G030 | 1 | H ii | 0.54 | −1.90 | 0.84 | 0.47 | 1.2 ± 0.02 | — | −0.4 |
| MCG −03–34–064 | −2 | Sy1 | 0.62 | −2.35 | 0.25 | 0.36 | 1.6 ± 0.03 | — | −0.4 |
| NGC 5135 | 2 | Sy2 | 0.60 | −2.52 | 1.63 | 0.70 | 1.0 ± 0.02 | 1.0 | −0.5 |
| NGC 5257 | 3 | H ii | 0.48 | −1.38 | 5.33 | 0.22 | 1.6 ± 0.2 | 2.0 | −1.4 |
| IC 4687 | 3 | H ii | 0.57 | −1.95 | 1.27 | 5.05 | 6.2 ± 0.31 | — | −0.6 |
| ESO 339-G011 | 3 | Sy2 | 0.56 | −2.34 | 3.12 | 0.38 | 0.6 ± 0.02 | — | −0.8 |
| IC 5063 | 0 | Sy2 | 0.58 | −2.31 | 0.44 | 4.05 | 5.7 ± 0.08 | — | −0.2 |
| NGC 7130 | 1 | LINER | 0.53 | −1.82 | 2.22 | 0.62 | 6.1 ± 0.32 | — | −0.5 |
| IC 5179 | 4 | H ii | 0.49 | −1.83 | 4.94 | 1.62 | 6.5 ± 0.43 | — | −0.8 |
| ESO 534-G009 | 2 | LINER | 0.56 | −2.20 | 0.18 | 1.30 | 2.6 ± 0.02 | — | −0.2 |
| CGCG 453-062 | 2 | LINER | 0.55 | −2.18 | 2.49 | 0.23 | 1.2 ± 0.15 | — | −1.0 |
| NGC 7591 | 4 | LINER | 0.64 | −2.46 | 0.62 | 3.06 | 4.0 ± 0.04 | — | −0.2 |
| MCG −01–60–022 | 7 | H ii | 0.60 | −2.44 | 3.19 | 0.26 | 1.5 ± 0.08 | — | −0.7 |
| NGC 7771 | 1 | H ii | 0.57 | −2.36 | 11.76 | 0.86 | 0.4 ± 0.01 | — | −0.9 |
| UGC 12915 | 5 | LINER | 0.64 | −2.62 | 7.86 | 0.54 | 1.0 ± 0.01 | — | −0.6 |
*Column (1): Galaxy names. Column (2): Hubble type obtained by HyperLeda database (http://leda.univ-lyon1.fr). Column (3): Classification by optical spectroscopic observation taken from NASA/IPAC Extragalactic Database (NED: https://ned.ipac.caltech.edu/)— Sy1: Seyfert 1; Sy2: Seyfert 2; LINER: LINER; H ii: H ii region; N: unknown. Column (4): Gini coefficient. Column (5): Second-order moment of the brightest 20% of flux of a galaxy. Column (6): Effective radius of distribution of the Paα emission. Column (7): Effective radius of a bulge measured in the Ks band. Column (8): Sérsic index of a bulge measured in the Ks-band image. Column (9): Sérsic index of a bulge measured in HST NICMOS F160W image. Column (10): Ratio of bulge to total (bulge + disk) luminosity.
| Galaxy name . | Hubble type . | Spectral class . | G . | M 20 . | R sf (kpc) . | R b (kpc) . | n b . | |$n_{\rm b}^{\rm HST}$| . | log (B/T) . |
|---|---|---|---|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . |
| NGC 23 | 1 | H ii | 0.63 | −2.39 | 1.59 | 0.82 | 1.9 ± 0.03 | 1.9 | −0.4 |
| NGC 232 | 1 | Sy2 | 0.59 | −2.08 | 0.61 | 1.10 | 2.3 ± 0.03 | — | −0.2 |
| IRAS F02437+2122 | −5 | LINER | 0.61 | −2.50 | 0.23 | 0.55 | 4.6 ± 0.26 | — | −0.4 |
| NGC 1720 | 2 | N | 0.65 | −2.60 | 0.46 | 0.45 | 1.8 ± 0.02 | — | −0.7 |
| ESO 557-G002 | 4 | H ii | 0.54 | −2.26 | 1.34 | 73.82 | 19.9 ± 2.1 | — | −0.2 |
| ESO 320-G030 | 1 | H ii | 0.54 | −1.90 | 0.84 | 0.47 | 1.2 ± 0.02 | — | −0.4 |
| MCG −03–34–064 | −2 | Sy1 | 0.62 | −2.35 | 0.25 | 0.36 | 1.6 ± 0.03 | — | −0.4 |
| NGC 5135 | 2 | Sy2 | 0.60 | −2.52 | 1.63 | 0.70 | 1.0 ± 0.02 | 1.0 | −0.5 |
| NGC 5257 | 3 | H ii | 0.48 | −1.38 | 5.33 | 0.22 | 1.6 ± 0.2 | 2.0 | −1.4 |
| IC 4687 | 3 | H ii | 0.57 | −1.95 | 1.27 | 5.05 | 6.2 ± 0.31 | — | −0.6 |
| ESO 339-G011 | 3 | Sy2 | 0.56 | −2.34 | 3.12 | 0.38 | 0.6 ± 0.02 | — | −0.8 |
| IC 5063 | 0 | Sy2 | 0.58 | −2.31 | 0.44 | 4.05 | 5.7 ± 0.08 | — | −0.2 |
| NGC 7130 | 1 | LINER | 0.53 | −1.82 | 2.22 | 0.62 | 6.1 ± 0.32 | — | −0.5 |
| IC 5179 | 4 | H ii | 0.49 | −1.83 | 4.94 | 1.62 | 6.5 ± 0.43 | — | −0.8 |
| ESO 534-G009 | 2 | LINER | 0.56 | −2.20 | 0.18 | 1.30 | 2.6 ± 0.02 | — | −0.2 |
| CGCG 453-062 | 2 | LINER | 0.55 | −2.18 | 2.49 | 0.23 | 1.2 ± 0.15 | — | −1.0 |
| NGC 7591 | 4 | LINER | 0.64 | −2.46 | 0.62 | 3.06 | 4.0 ± 0.04 | — | −0.2 |
| MCG −01–60–022 | 7 | H ii | 0.60 | −2.44 | 3.19 | 0.26 | 1.5 ± 0.08 | — | −0.7 |
| NGC 7771 | 1 | H ii | 0.57 | −2.36 | 11.76 | 0.86 | 0.4 ± 0.01 | — | −0.9 |
| UGC 12915 | 5 | LINER | 0.64 | −2.62 | 7.86 | 0.54 | 1.0 ± 0.01 | — | −0.6 |
| Galaxy name . | Hubble type . | Spectral class . | G . | M 20 . | R sf (kpc) . | R b (kpc) . | n b . | |$n_{\rm b}^{\rm HST}$| . | log (B/T) . |
|---|---|---|---|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . |
| NGC 23 | 1 | H ii | 0.63 | −2.39 | 1.59 | 0.82 | 1.9 ± 0.03 | 1.9 | −0.4 |
| NGC 232 | 1 | Sy2 | 0.59 | −2.08 | 0.61 | 1.10 | 2.3 ± 0.03 | — | −0.2 |
| IRAS F02437+2122 | −5 | LINER | 0.61 | −2.50 | 0.23 | 0.55 | 4.6 ± 0.26 | — | −0.4 |
| NGC 1720 | 2 | N | 0.65 | −2.60 | 0.46 | 0.45 | 1.8 ± 0.02 | — | −0.7 |
| ESO 557-G002 | 4 | H ii | 0.54 | −2.26 | 1.34 | 73.82 | 19.9 ± 2.1 | — | −0.2 |
| ESO 320-G030 | 1 | H ii | 0.54 | −1.90 | 0.84 | 0.47 | 1.2 ± 0.02 | — | −0.4 |
| MCG −03–34–064 | −2 | Sy1 | 0.62 | −2.35 | 0.25 | 0.36 | 1.6 ± 0.03 | — | −0.4 |
| NGC 5135 | 2 | Sy2 | 0.60 | −2.52 | 1.63 | 0.70 | 1.0 ± 0.02 | 1.0 | −0.5 |
| NGC 5257 | 3 | H ii | 0.48 | −1.38 | 5.33 | 0.22 | 1.6 ± 0.2 | 2.0 | −1.4 |
| IC 4687 | 3 | H ii | 0.57 | −1.95 | 1.27 | 5.05 | 6.2 ± 0.31 | — | −0.6 |
| ESO 339-G011 | 3 | Sy2 | 0.56 | −2.34 | 3.12 | 0.38 | 0.6 ± 0.02 | — | −0.8 |
| IC 5063 | 0 | Sy2 | 0.58 | −2.31 | 0.44 | 4.05 | 5.7 ± 0.08 | — | −0.2 |
| NGC 7130 | 1 | LINER | 0.53 | −1.82 | 2.22 | 0.62 | 6.1 ± 0.32 | — | −0.5 |
| IC 5179 | 4 | H ii | 0.49 | −1.83 | 4.94 | 1.62 | 6.5 ± 0.43 | — | −0.8 |
| ESO 534-G009 | 2 | LINER | 0.56 | −2.20 | 0.18 | 1.30 | 2.6 ± 0.02 | — | −0.2 |
| CGCG 453-062 | 2 | LINER | 0.55 | −2.18 | 2.49 | 0.23 | 1.2 ± 0.15 | — | −1.0 |
| NGC 7591 | 4 | LINER | 0.64 | −2.46 | 0.62 | 3.06 | 4.0 ± 0.04 | — | −0.2 |
| MCG −01–60–022 | 7 | H ii | 0.60 | −2.44 | 3.19 | 0.26 | 1.5 ± 0.08 | — | −0.7 |
| NGC 7771 | 1 | H ii | 0.57 | −2.36 | 11.76 | 0.86 | 0.4 ± 0.01 | — | −0.9 |
| UGC 12915 | 5 | LINER | 0.64 | −2.62 | 7.86 | 0.54 | 1.0 ± 0.01 | — | −0.6 |
*Column (1): Galaxy names. Column (2): Hubble type obtained by HyperLeda database (http://leda.univ-lyon1.fr). Column (3): Classification by optical spectroscopic observation taken from NASA/IPAC Extragalactic Database (NED: https://ned.ipac.caltech.edu/)— Sy1: Seyfert 1; Sy2: Seyfert 2; LINER: LINER; H ii: H ii region; N: unknown. Column (4): Gini coefficient. Column (5): Second-order moment of the brightest 20% of flux of a galaxy. Column (6): Effective radius of distribution of the Paα emission. Column (7): Effective radius of a bulge measured in the Ks band. Column (8): Sérsic index of a bulge measured in the Ks-band image. Column (9): Sérsic index of a bulge measured in HST NICMOS F160W image. Column (10): Ratio of bulge to total (bulge + disk) luminosity.
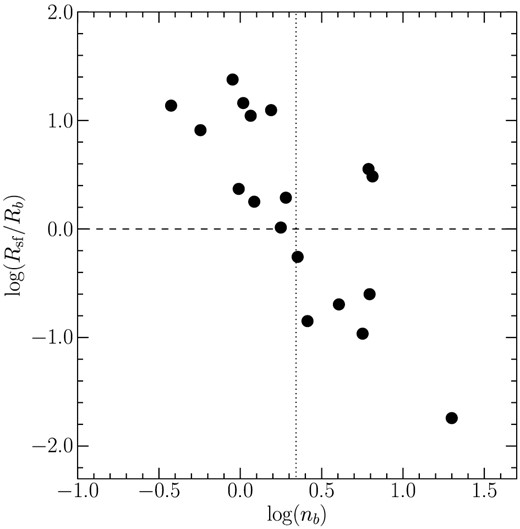
We normalize Rsf by the effective radii of the bulges (Rb) and show the relationship between the Sérsic indices nb and Rsf/Rb in figure 6. It can be seen that Rsf/Rb decreases with increasing nb, and that Rsf becomes equal to Rb at nb ≈ 2.2, which is the separation point for classical and pseudobulges. These results suggest that starburst galaxies with classical bulges have compact star-forming regions concentrated within the bulges, while those with pseudobulges have extended star-forming regions beyond the bulge, possibly along their spiral arms.
Comparison between the Sérsic index of the bulges (nb) and the normalized size of the star-forming regions (Rsf/Rb). The horizontal dashed line represents Rsf = Rb, which means that the size of the star-forming region is the same as that of the bulge. The dotted line shows the border of classical and pseudobulges shown in figure 3. High Sérsic indices of bulges represent compact star-forming regions, while low Sérsic indices of bulges represent extended star-forming regions. (Color online)
Classical bulges are expected to have experienced major merger events to lose angular momentum and have similar properties to elliptical galaxies (Kormendy & Kennicutt 2004). Theoretically, gas tends to be concentrated in the central region of a galaxy after a major merger event (Naab & Trujillo 2006; Hopkins et al. 2013). Also, there is a simulation which forms a classical bulge with inflow of cold gas toward the center of a galaxy (Sales et al. 2012), inducing extreme star formation in the central region. Our result, in which the star formation is concentrated at the centers in the classical bulges, is consistent with such theoretical simulations. On the other hand, pseudobulges are expected to be formed by minor merger events or secular evolution in which galaxies evolve over a long time without any strong interaction (e.g., Kormendy & Kennicutt 2004). In these processes, star-forming activities are expected to occur along their arms and bar-ends and spread beyond the size of the bulge. Our result, where the galaxies with pseudobulges have extended star-forming regions beyond their bulges, is consistent with such pictures.
There is the question whether the observed concentrated star formation in classical bulges is not directly connected with the major merger event that formed the bulge, especially because we have selected non-irregular galaxies, which show little traces of mergers, as the sample. Numerical simulations show that enhanced star formation is expected to peak after the strong morphological disturbances of the first encounter and lasts significantly longer than the merger phase (about 500 Myr after the coalescence phase), during which the star formation is enhanced by more than 10 times (e.g., Lotz et al. 2008; Teyssier et al. 2010). Considering that a typical relaxation timescale for stars in a merger remnant is a few million years after the coalescence phase (Hopkins et al. 2013), our suggestion that classical bulges of LIRGs are formed in recent major merger events which also induced the current star formations does not contradict their non-irregular morphologies.
3.3 Growth of SMBHs and bulges
Our results that classical bulges have compact star-forming regions and pseudobulges have extended star-forming regions suggest that the growth of classical bulges results from a large amount of gas falling into the centers of the galaxies via rapid feeding with major merger processes, which directly affect the growth of SMBHs. On the other hand, pseudobulges are suggested to grow together with disk components via secular evolution, where it is difficult for molecular gas to fall inwards toward the centers of the galaxies, and star formation activities are not always connected with the growth of SMBHs. This picture supports the hypothesis of Kormendy, Bender, and Cornell (2011) that there are two different modes of the black hole feeding mechanism, where the growth of black holes and classical bulges is controlled by the same global process of rapid gas falling with major merging, while that of black holes and pseudobulges is independent of or has a weak connection with the secular evolution.
4 Summary
In this paper we have investigated properties of classical and pseudobulges in local LIRGs, which are considered to be a forming site of bulge structures, using Ks-band and Paα emission line images observed using ANIR on the minTAO 1 m telescope. To classify the types of the bulges, we performed a two-dimensional bulge–disk decomposition analysis in the Ks-band images. The result shows a tentative bimodal distribution of Sérsic indices (nb) with a separation at log (nb) ≈ 0.5, which is consistent with that of local normal galaxies. Also, the extent of the distribution normalized by the sizes of bulges (Rsf/Rb) in Paα emission line images shows a negative correlation against nb. This result means that galaxies with classical bulges have compact star-forming regions concentrated within the bulges, while those with pseudobulges have extended star-forming regions beyond the bulges, suggesting that there are different formation scenarios at work in classical and pseudobulges.
References







