-
PDF
- Split View
-
Views
-
Cite
Cite
Kohji Tsumura, Is the infrared background excess explained by the isotropic zodiacal light from the outer solar system?, Publications of the Astronomical Society of Japan, Volume 70, Issue 5, October 2018, 98, https://doi.org/10.1093/pasj/psy100
Close - Share Icon Share
Abstract
This paper investigates whether an isotropic zodiacal light from the outer solar system can account for the detected background excess in the near-infrared. Assuming that interplanetary dust particles are distributed in a thin spherical shell at the outer solar system (>200 au), thermal emission from such cold (<30 K) dust in the shell has a peak at the far-infrared (∼100 μm). By comparing the calculated thermal emission from the dust shell with the observed background emissions at the far-infrared, the permissible dust amount in the outer solar system is obtained. Even if the maximum dust amount is assumed, the isotropic zodiacal light as the reflected sunlight from the dust shell at the outer solar system cannot explain the detected background excess at the near-infrared.
1 Introduction
The extragalactic background light (EBL) arises from integrated emission from the first star production era to the present day. Thus observation of EBL as the accumulated history of the universe is important in understanding the star formation history. Recent observations show that the measured EBL at optical and near-infrared (NIR) has an excess of ∼30 nW m−2 sr−1 over the cumulative light from galaxies (Tsumura et al. 2013; Matsumoto et al. 2015; Sano et al. 2015, 2016; Matsuura et al. 2017; Mattila et al. 2017), meaning that there are unknown light sources in the universe. As candidate light sources for this NIR background excess, intra-halo light (Cooray et al. 2012; Zemcov et al. 2014), emissions from laser interferometer gravitational-wave observatory (LIGO)-type blackholes (Kashlinsky 2016), and decaying hypothetical particles (Kohri et al. 2017) are proposed.
On the other hand, isolation of the EBL from foreground emissions is difficult due to its diffuse, extended nature. The largest uncertainty comes from the removal of the dominant foreground, the zodiacal light, which is scattered sunlight at optical and NIR, and thermal emission at mid- and far-infrared (FIR) from interplanetary dust (IPD) within the solar system. For this reason, some authors claimed that the NIR background excess is caused by systematic uncertainty in the subtraction of the zodiacal light (Dwek et al. 2005; Kawara et al. 2017). In recent EBL observations, the zodiacal light is subtracted using a model based on morphology and time variation measured by diffuse infrared background experiment (DIRBE) on the cosmic background explorer (COBE) satellite (Kelsall et al. 1998). If there is an isotropic zodiacal light component showing no time variation, it is not included in the zodiacal light model. Thus the isotropic zodiacal light component could be a source of the NIR background excess (Dwek et al. 1998; Chary & Pope 2010).
Such an isotropic zodiacal light component, if it exists, is made by IPD around the Earth or around the outer solar system, because the zodiacal light components made by them show no time variation by the observations from the Earth. Matsumoto et al. (2018) compared the zodiacal light model (Kelsall et al. 1998) with the observational data of the zodiacal light gathered during the journey to Jupiter by Pioneer 10, and no evidence was found that the isotropic zodiacal light component exists around the Earth. For this reason, the other possibility of the existence of IPD around the outer solar system is investigated in this paper.
The zodiacal light is dominated by the thermal emission from the nearby IPD that has a temperature of ∼280 K, and the peak of such thermal emission occurs at the mid-infrared. On the other hand, if the dust exists around the outer solar system and forms the isotropic zodiacal light component, the temperature of such IPD is quite low, and the thermal emission from such low-temperature IPD has its peak at FIR. Thus, the strategy of this paper is to investigate whether the NIR background excess is explained by the isotropic zodiacal light from the IPD around the outer solar system, the amount of which is restricted by the FIR background data.
This paper is organized as follows. In section 2, the acceptable upper limit of IPD amount is obtained from the FIR background data. Using this amount of IPD, the isotropic zodiacal light component at NIR is calculated, and it is compared with the NIR background excess in section 3. The discussion of our results follows in section 4, and the conclusion is in section 5.
2 Far-infrared background excess
2.1 Dust emission formulation
Here the method to calculate the thermal emission from IPD in the outer solar system used in this paper is explained.
![Radial profile of the dust temperature. The solid lines show the Stern case [equation (4)] of a = 10 μm (lower) and 1 μm (upper) cases (Stern et al. 1991), the dashed line shows the Mann case [equation (3)] (Mann et al. 2006), and the dash–dotted line shows the Kelsall case (Kelsall et al. 1998).](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/70/5/10.1093_pasj_psy100/3/m_pasj_70_5_98_f1.jpeg?Expires=1750285457&Signature=nJR7~oxtRcZXMsTLJVHtGVcKDVX629SagdJNgTes~BELXnEaTv~P9jtG9BfKg7VOTKuhIFRaz7bKnJRTaeNee8VvhZhCDIsBb~ThabdSpytSsY04k6e4eMBtInTbXFKNqwa5jNyHZPx3oNdOOyDu1A2H-rFiMWdnFylP0PKpKt8Sx-q1Cgj~4jJgnCnm15ziv-V2YwIe-zCb78wQ5XUgN3qV63WYLNLSkrNjtiEJzRtA8y3KXyi16Ka9ySr7EgYAFHaLYl9tH8el0CbRwk0~kCqcgA4SJ5HCCK8ggDSIQqygXuA00CHg6QKMqEdv0eUpE42iSJTW8cJcDs6UkLwN4w__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
By assuming all IPD particles have the same size a, the temperature of the IPD Tdust is uniquely defined by the distance to the spherical IPD shell, d, from equation (4). Thus the spectral shape of the thermal emission is defined by Tdust (or d), and it is scaled by the IPD amount n [see equation (2)]. The total IPD mass in the spherical shell Mshell can be written as Mshell = 4πa3ρN/3 = 16π2a3ρn/3, where ρ is the average IPD mass density and ρ = 2 g cm−3 is adopted as a typical mass density of IPD.
2.2 Far-infrared data
There are two methods to derive the FIR background brightness. One is to sum up the flux of resolved galaxies and extrapolated fainter unresolved objects, which gives a lower estimate of FIR background brightness because only the identified light sources are taken into account. Open symbols in figure 2 (left-hand panel) denote the values in this method found using photoconductor array camera and spectrometer (PACS) (Berta et al. 2011) and spectral and photometric imaging receiver (SPIRE) (Béthermin et al. 2012) on the Herschel Space Telescope and multiband imaging photometer (MIPS) on the Spitzer Space Telescope (Dole et al. 2006; Odegard et al. 2007), and the solid curve shows a polynomial fitting of these values. Number counts of galaxies obtained by Herschel were fitted by power-law functions, and they were integrated down to 1 μJy at <160 μm using PACS (Berta et al. 2011), and down to zero flux at >250 μm using SPIRE (Béthermin et al. 2012). Although the obtained FIR background value at 70 μm is a lower limit because the curve obtained from the power-law fit is not fully converging at 1 μJy, the other values from PACS are regarded as equivalent to an integration down to zero flux because the fitted curves are converging enough (Berta et al. 2011). The FIR background values from Spitzer were obtained from stacked images of 24 μm sources with >60 μJy at 70 and 160 μm (Dole et al. 2006), and were scaled to 140 and 240 μm using a spectral energy distribution model (Odegard et al. 2007).
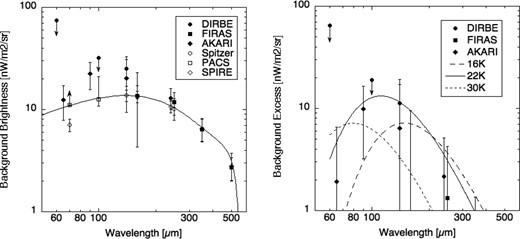
Left: FIR background brightness. Filled symbols are values of direct measurements: filled circles are DIRBE/COBE (Odegard et al. 2007), filled squares are FIRAS/COBE (Lagache et al. 2000), and filled diamonds are FIS/AKARI (Matsuura et al. 2011). Open symbols are values of the integrated light of galaxies: open circles are MIPS/Spitzer (Dole et al. 2006; Odegard et al. 2007), open squares are PACS/Herschel (Berta et al. 2011), and open diamonds are SPIRE/Herschel (Béthermin et al. 2012). The solid line shows a polynomial fitting of the integrated light of galaxies (open symbols). Right: FIR background excess of the directly measured values over the integrated light of galaxies. Thermal emissions from the spherical IPD shell at the outer solar system described in equation (2) are also shown by the dashed curve (16 K, Case A), the solid curves (22 K, Case B), and the dotted curve (30 K, Case C).
The other method is the direct measurements of the sky brightness. This method gives the upper estimate of FIR background brightness because of the big difficulty in subtracting the foreground emissions from our solar system (zodiacal light) and our Galaxy (diffuse Galactic light). Filled symbols in figure 2 (left) denote the values fot this method found using DIRBE (Odegard et al. 2007) and far infrared absolute spectrophotometer (FIRAS) (Lagache et al. 2000) on the COBE satellite and far-infrared surveyor (FIS) on the AKARI satellite (Matsuura et al. 2011). First, the zodiacal light was removed from the directly observed sky brightness based on the zodiacal light model (Kelsall et al. 1998). Then, Galactic foreground emissions were subtracted based on the correlation with the H i 21 cm line data (Snowden et al. 1994; Elvis et al. 1994; Stark et al. 1992), the Hα total intensity data (Reynolds et al. 1998; Haffner et al. 2003), and the 100 μm dust thermal emission data (Schlegel et al. 1998).
As shown in figure 2 (left), the values derived between these two methods are basically consistent with each others, but there is a small excess of FIR background brightness over the integrated light of galaxies at around 100 μm. Figure 2 (right) shows the FIR background excess derived by the difference between the directly measured values and the interoperated values of the integrated light of galaxies. The zodiacal light model uncertainties in the FIR background are 26.7, 6.3, 2.3, and 0.5 nW m−2 sr−1 at 60, 100, 140, and 240 μm, respectively (Kelsall et al. 1998), thus the obtained FIR background excess cannot be explained by the model uncertainty. The origin of this FIR background excess is still unknown, but the contribution of luminous dusty galaxies with hot dust (∼60 K) at z = 2–3 is discussed (Blain et al. 2004).
2.3 Upper limit of IPD amount at the outer solar system
Within this FIR background excess, the isotropic zodiacal light can be acceptable. Assuming that all of the FIR background excess is caused by the isotropic zodiacal light, an upper limit for the amount of IPD in the outer solar system was obtained by fitting this FIR background excess with the thermal emission from the spherical IPD shell at the outer solar system.
Table 1 shows the obtained fitting parameters in the equation (2), and fitted curves are shown in figure 2 (right). The obtained best-fit temperature of IPD is |$T_{\rm dust} \sim 22 >{\rm K}$|, corresponding to |$d \sim 560 >{\rm au}$| in the case of |$a = 10\,\mu{\rm m}$| from figure 1. In this configuration, the upper limit of the total mass of the spherical IPD shell Mshell/MEarth < 8.5 × 10−3 (Case B) is obtained, where MEarth = 5.97 × 1024 kg is the mass of the Earth.
Fitting results of the thermal emissions from the IPD shell to the FIR background excess.
| Case . | IPD size a [μm] . | IPD temperature Tduat [K] . | Distance to the IPD shell d * [au] . | Total IPD mass Mshell/MEarth † . | |$\lambda I_{\lambda }^{\rm NIR}$| at 1 μm [nW/m2/sr] . |
|---|---|---|---|---|---|
| A | 10 | 16 | 1150 | 1.1 × 10−1 | 0.028 |
| B | 10 | 22 | 560 | 8.5 × 10−3 | 0.040 |
| C | 10 | 30 | 240 | 1.1 × 10−4 | 0.016 |
| A’ | 1 | 16 | 4340 | 1.5 × 101 | 0.202 |
| B’ | 1 | 22 | 1840 | 9.1 × 10−1 | 0.378 |
| C’ | 1 | 30 | 760 | 1.1 × 10−2 | 0.158 |
| Case . | IPD size a [μm] . | IPD temperature Tduat [K] . | Distance to the IPD shell d * [au] . | Total IPD mass Mshell/MEarth † . | |$\lambda I_{\lambda }^{\rm NIR}$| at 1 μm [nW/m2/sr] . |
|---|---|---|---|---|---|
| A | 10 | 16 | 1150 | 1.1 × 10−1 | 0.028 |
| B | 10 | 22 | 560 | 8.5 × 10−3 | 0.040 |
| C | 10 | 30 | 240 | 1.1 × 10−4 | 0.016 |
| A’ | 1 | 16 | 4340 | 1.5 × 101 | 0.202 |
| B’ | 1 | 22 | 1840 | 9.1 × 10−1 | 0.378 |
| C’ | 1 | 30 | 760 | 1.1 × 10−2 | 0.158 |
*Distance to the dust shell d is derived from the equation (4) by the dust temperature Tdust.
†Dust mass density ρ = 2 g cm−3 is adapted.
Fitting results of the thermal emissions from the IPD shell to the FIR background excess.
| Case . | IPD size a [μm] . | IPD temperature Tduat [K] . | Distance to the IPD shell d * [au] . | Total IPD mass Mshell/MEarth † . | |$\lambda I_{\lambda }^{\rm NIR}$| at 1 μm [nW/m2/sr] . |
|---|---|---|---|---|---|
| A | 10 | 16 | 1150 | 1.1 × 10−1 | 0.028 |
| B | 10 | 22 | 560 | 8.5 × 10−3 | 0.040 |
| C | 10 | 30 | 240 | 1.1 × 10−4 | 0.016 |
| A’ | 1 | 16 | 4340 | 1.5 × 101 | 0.202 |
| B’ | 1 | 22 | 1840 | 9.1 × 10−1 | 0.378 |
| C’ | 1 | 30 | 760 | 1.1 × 10−2 | 0.158 |
| Case . | IPD size a [μm] . | IPD temperature Tduat [K] . | Distance to the IPD shell d * [au] . | Total IPD mass Mshell/MEarth † . | |$\lambda I_{\lambda }^{\rm NIR}$| at 1 μm [nW/m2/sr] . |
|---|---|---|---|---|---|
| A | 10 | 16 | 1150 | 1.1 × 10−1 | 0.028 |
| B | 10 | 22 | 560 | 8.5 × 10−3 | 0.040 |
| C | 10 | 30 | 240 | 1.1 × 10−4 | 0.016 |
| A’ | 1 | 16 | 4340 | 1.5 × 101 | 0.202 |
| B’ | 1 | 22 | 1840 | 9.1 × 10−1 | 0.378 |
| C’ | 1 | 30 | 760 | 1.1 × 10−2 | 0.158 |
*Distance to the dust shell d is derived from the equation (4) by the dust temperature Tdust.
†Dust mass density ρ = 2 g cm−3 is adapted.
Although an IPD temperature of 22 K is the most likely, a temperature range of between 16 K and 30 K is allowed within the errors of FIR background excess, as shown in figure 2 (right). When a colder IPD temperature is adopted, the required distance from the Sun d becomes larger, thus more masses are allowed within the FIR background excess. For this reason, a more conservative upper limit of the total IPD mass, Mshell/MEarth < 1.1 × 10−1, is obtained (Case A).
3 Near-infrared background excess
Chary and Pope (2010) stated that if they assume the existence of high-albedo IPD (ice mantle grains), with A > 0.8 with ∼50 K at ∼40 au, the NIR background excess can be explained by the isotropic zodiacal light. However, such high-temperature IPD with ∼50 K is not consistent with the FIR background excess obtained in this paper [see figure 2 (right)].
4 Discussion
4.1 Parameter dependence of Mshell
The obtained total mass of the spherical IPD shell Mshell in table 1 depends on the average IPD mass density ρ, and ρ = 2 g cm−3 is adopted in this paper. The mass density range of IPD particles (5–15 μm size) collected at the stratosphere is 0.3–6.0 g cm−3, averaging 2.0 g cm−3 (Love et al. 1994). Grün et al. (1985) also state that the majority of the IPD particles have ρ = 2–3 g cm−3, whereas 20%–40% of the IPD has low density (<1 g cm−3). Such low-density IPD is thought to be of cometary origin (Joswiak et al. 2007; Wiegert et al. 2009). In the outer solar system, contributions of cometary origin IPD may be increased, and thus the average mass density may be smaller than our adopted value of ρ = 2 g cm−3. In such a case of smaller mass density, the required total mass of the spherical IPD shell Mshell becomes low, thus the upper limit obtained in this paper becomes more conservative.
The obtained total IPD mass Mshell also depends on the IPD size a, because smaller IPD is hotter, thus such smaller IPD must be farther away in order for the temperature to be within the allowable range (16–30 K), and then more mass is allowed within the FIR background excess. Results in the case of a = 1 μm are also shown in table 1 for comparison. These results mean that if the IPD in the outer solar system is dominated by small particles (a = 1 μm), about 100 times more IPD masses than the case of a = 10 μm are acceptable in the outer solar system within the FIR background excess, and thus about 10 times more NIR background |$\lambda I_{\lambda }^{\rm NIR}$| is obtained. This result is consistent with the result in Dwek et al. (1998) of 10−3 < Mshell/MEarth < 102 at >700 au for the β = 2 case. On the other hand, the total IPD mass is dominated by large particles (∼100 μm) from the dust size distribution around the Earth (Kral et al. 2017). Although this dust size distribution is valid around the Earth, it is difficult to believe that the small IPD particles (a < 1 μm) are dominated in the outer solar system. Anyway, even in the a = 1 μm case with Mshell ∼ 10 MEarth at ∼4300 au (Case A’), the obtained isotropic zodiacal light at NIR |$\lambda I_{\lambda }^{\rm NIR}$| is still <1/10 of the NIR background excess. Therefore, the NIR background excess cannot be explained even in the small dust size cases.
4.2 Comparison to models and observations
The maximum permissible IPD mass in the outer solar system obtained in this study is much more than the total IPD mass inside Jupiter’s orbit (10−9–10−8 MEarth) (Fixsen & Dwek 2002; Nesvorný et al. 2010). Is it realistic that such an amount of IPD exists in the outer solar system? Outside of the heliosphere (>250 au), IPD are charged in the interstellar environment and ejected by the interstellar magnetic field. According to Belyaev and Rafikov (2010), IPD with a > 15 μm at d > 1000 au and a > 1 μm at d > 100 au are ejected from the solar system. Dwek et al. (1998) stated that only a cloud consisting of IPD larger than ∼1 cm located between ∼5 and 150 au would be stable. Therefore, the IPD shell assumed in this study cannot survive unless there is a continuous supply of IPD. IPD is believed to be supplied from comets (Nesvorný et al. 2010; Yang & Ishiguro 2015) and asteroids (Dermott et al. 1984; Nesvorný et al. 2003; Tsumura et al. 2010), but comets are not active and asteroidal collisions are also less likely to occur in the cold, low-density environment in the outer solar system. Therefore, the large amount of dust assumed in this study cannot be supplied by any of the known mechanisms.
Poppe (2016) constructed a dust-density model based on the in-situ dust counting by Pioneer 10, Galileo, and New Horizons. According to this model, the density of dust of size 20 μm is ∼5 × 10−4 km−3 at 70 au, dominated by dust grains originating from the Edgeworth–Kuiper belt objects and the Oort cloud comets. Even by assuming this dust density is kept up to 1000 au, the mass of a dust shell at 1000 au with 10 au thickness is <3 × 10−7 MEarth, which is much less than the required amount to explain the FIR background excess (see table 1).
In addition, the solar-type star HD 72905 (G1.5V, age ∼0.4 Gyr) has 70 μm excess (Ldust/L⋆ ∼ 10−5) in its spectrum detected by MIPS/Spitzer, and this extra emission is produced by cool (<100 K) dust of <10−2 MEarth (Bryden et al. 2006). Because our solar system has Ldust/L⊙ ∼ 2 × 10−7 (Nesvorný et al. 2010), the amount of IPD in our solar system should be less than that in HD 72905.
For these reasons, it is unlikely that a large amount of dust exists in the outer solar system to explain the FIR background excess, therefore it is even less likely that the NIR background excess can be explained by the isotropic zodiacal light.
5 Summary
This research examined whether the isotropic zodiacal light, if it exists, can explain the observed NIR background excess. The existence of a spherical IPD shell around the outer solar system is assumed to produce the isotropic zodiacal light. From the restriction that thermal emission from the spherical IPD shell must not exceed the observed FIR background excess, the upper limit of the mass of the IPD shell was obtained. Even if the maximum amount of IPD permissible from the FIR background excess is assumed, the isotropic zodiacal light from such an IPD shell cannot explain the detected NIR background excess.
Acknowledgements
The author thanks Ko Arimatsu, Shuji Matsuura, Kei Sano, Masakazu Kobayashi, and Masahiro Nagashima for discussions of the IPD in the outer solar system. This research is supported by JSPS KAKENHI Grant Number 17K18789.
References



