-
PDF
- Split View
-
Views
-
Cite
Cite
Mitsuru Kokubo, Constraints on accretion disk size in the massive type 1 quasar PG 2308+098 from optical continuum reverberation lags, Publications of the Astronomical Society of Japan, Volume 70, Issue 5, October 2018, 97, https://doi.org/10.1093/pasj/psy096
Close - Share Icon Share
Abstract
Two years’ worth of u-, g-, r-, i-, and z-band optical light curves were obtained for the massive type 1 quasar PG 2308+098 at z = 0.433 using the 1.05 m Kiso Schmidt telescope/Kiso Wide Field Camera, and inter-band time lags of the light curves were measured. Wavelength-dependent continuum reverberation lag signals of several tens of days relative to the u-band were detected at g, r, i, and z bands, where the longer wavelength bands showed larger lags. From the wavelength-dependent lags, and assuming the standard disk temperature radial profile |$T \propto R_{\rm disk}^{-3/4}$| and an X-ray/far-ultraviolet reprocessing picture, a constraint on the radius of the accretion disk responsible for the rest-frame 2500 Å disk continuum emission was derived as |$R_{\rm disk} = 9.46^{+0.29}_{-3.12}\:$|light-day. The derived disk size is slightly (1.2–1.8 times) larger than the theoretical disk size of Rdisk = 5.46 light-day predicted from the black hole mass (MBH) and Eddington ratio estimates of PG 2308+098. This result is roughly in accordance with previous studies of lower-mass active galactic nuclei (AGNs), where measured disk sizes have been found to be larger than the standard disk model predictions by a factor of ∼3; however, the disk size discrepancy is more modest in PG 2308+098. By compiling literature values of the disk size constraints from continuum reverberation and gravitational microlensing observations for AGNs/quasars, we show that the MBH dependence of Rdisk is weaker than that expected from the standard disk model. These observations suggest that the standard Shakura–Sunyaev accretion disk theory has limitations in describing AGN/quasar accretion disks.
1 Introduction
Intense radiation from active galactic nuclei (AGNs) at ultraviolet(UV)–optical wavelengths is produced in accretion disks formed around central supermassive black holes (SMBHs). Luminous Seyfert galaxies and quasars are believed to harbor AGN accretion disks with sub-Eddington accretion rates, and the standard thin thermal accretion disk theory of Shakura and Sunyaev (1973) is though to describe such sub-Eddington BH accretion disks reasonably. However, debate has raged regarding the applicability of the standard accretion disk theory to AGNs, with claims of discrepancies between the observed spectral energy distribution of AGNs and the model’s prediction (e.g., Collin et al. 2002; Davis et al. 2007; Kokubo et al. 2014; but see also Kishimoto et al. 2008; Capellupo et al. 2015).
Other than the emission spectrum, the geometry of accretion disks is another predictable property of BH accretion disks. Based on standard accretion disk theory, the radial extent or size of a thin disk can be algebraically expressed as a function of the BH mass and mass accretion rate (e.g., Pooley et al. 2007; Morgan et al. 2010; Fausnaugh et al. 2016); thus, the radial extent can be an essential observational probe to test the standard accretion disk theory in AGNs. However, AGN accretion disks are physically compact, and the current largest optical telescopes are unable to spatially resolve such disks directly, even in the nearest AGNs in the Local Universe.
Nevertheless, two indirect methods are available to measure accretion disk sizes in AGNs: one uses the microlensing phenomena of gravitationally-lensed quasars (e.g., Morgan et al. 2010; Blackburne et al. 2011; Jiménez-Vicente et al. 2012; Chartas et al. 2016), and the other uses inter-band lags of multi-band intrinsic flux variability (e.g., Collier et al. 1999; Sergeev et al. 2005; Cackett et al. 2007; Edelson et al. 2015; Fausnaugh et al. 2016, 2018; Buisson et al. 2017).
The UV–optical microlensing effects observed in lensed high-redshift quasars are caused by the lensing magnification of the quasar accretion disk emission by foreground stars in a lensing galaxy, which enables the accretion disk size to be inferred through modeling of the multi-epoch variability (e.g., Morgan et al. 2010) or single-epoch flux ratio anomalies (e.g., Pooley et al. 2007; Blackburne et al. 2011).
On the other hand, the intrinsic flux variability of normal (unlensed) Seyfert galaxies and quasars can also be used to measure disk sizes under the assumption of the ‘reprocessing’ picture as the variability model. In the reprocessing model, it is assumed that the intrinsic UV–optical continuum variability ubiquitously observed in AGNs is driven by intense, variable X-ray/far-UV (FUV) emission from a compact region in the vicinity of the SMBH (Uttley & Casella 2014; Gardner & Done 2017, and references therein). The variable X-ray/FUV emission irradiates the disk surface, altering the effective temperature of the disk and thus continuously altering the UV–optical flux. It should be noted that the reprocessing diagram unsurprisingly predicts that the variation of the disk’s effective temperature and corresponding disk luminosity at outer radii lags behind the variation at inner radii by light travel times. Although the physical mechanism of the intrinsic UV–optical continuum variability continues to be debated, there is growing evidence that the multi-band light curves of AGNs show strong inter-band correlations with lags between the X-ray and UV–optical bands (e.g., Edelson et al. 2015; Fausnaugh et al. 2016, 2018; Buisson et al. 2017) and the inter-band lags within the UV–optical bands (e.g., Collier et al. 1999; Sergeev et al. 2005; Cackett et al. 2007; Jiang et al. 2017; Mudd et al. 2018; McHardy et al. 2018) in a form consistent with τ ∝ λ4/3, as expected from the reprocessing model based on the standard thin disk model.
Although recent intensive monitoring observations of the simultaneous X-ray, UV, and optical light curves for local Seyfert galaxies (e.g., NGC 4395, NGC 4593, NGC 5548, and NGC4151; see McHardy et al. 2018 and references therein) have confirmed that the wavelength dependence of the continuum reverberation lags at the UV–optical bands is largely consistent with the standard thin disk model (τ ∝ λ4/3), they have also revealed that the absolute disk sizes in these Seyfert galaxies inferred from the lags are generally larger by a factor of ∼3 than those expected from the thin disk model, given the BH mass estimates for these objects (Cackett et al. 2007; Shappee et al. 2014; Edelson et al. 2015; Cackett et al. 2018). Interestingly, the microlensing constraints on the accretion disk sizes for lensed high-redshift quasars are also claimed to be larger than the thin disk predictions by a similar factor, on average (e.g., Morgan et al. 2010; Jiménez-Vicente et al. 2012; Mosquera et al. 2013; Chartas et al. 2016). It has been proposed that local temperature fluctuations on the surface of the standard disk due to thermal instabilities can make the disk sizes measured via the microlensing technique unexpectedly large (Dexter & Agol 2011), but such an inhomogeneous disk picture has difficulty in explaining the observed well-correlated UV–optical light curves (Kokubo 2015). The discrepancies between the observed and model disk sizes, if confirmed, suggest that the standard thin disk model cannot provide an adequate explanation for actual AGN accretion disks.
One way to examine the above-mentioned disk size problem further is to probe disk sizes in AGNs with various BH masses and Eddington ratios by using the continuum reverberation lag method. The X-ray-to-UV/optical simultaneous monitoring observations for the AGN continuum reverberation lag measurements carried out to-date have targeted local Seyfert galaxies, which generally have lower BH masses and in many cases also have lower Eddington ratios compared to the lensed quasar sample (see, e.g., Edelson et al. 2015). It should be noted that continuum reverberation lags can be measured only with multi-band optical observations as inter-band lags at the rest-frame UV–optical bands; thus, optical time-domain wide-field surveys enable the measurement of continuum reverberation lags and, consequently, accretion disk sizes in field quasars with a higher BH mass and/or higher Eddington ratio compared to local Seyfert galaxies. Recently, Jiang et al. (2017) examined the optical inter-band disk continuum reverberation lags for 39 quasars using four years’ worth of g-, r-, i-, and z-band light curves from the Pan-STARRS Medium Deep Survey and reported that the inter-band lags were generally ∼ 2–3 times larger than those predicted by the thin disk model. On the other hand, by examining the continuum lags from weekly sampled g-, r-, i-, and z-band light curves of 15 quasars with BH masses of ∼108–109 M⊙ in the Dark Energy Survey (DES) supernova fields, Mudd et al. (2018) claimed that the disk sizes may be comparable to the standard thin disk model predictions.
In this work, we add a further quasar, PG 2308+098, to the sample of quasars whose continuum reverberation lags have been firmly detected. We observed the u-, g-, r-, i-, and z-band light curves of PG 2308+098 at a redshift of z = 0.433 (Schmidt & Green 1983; Vestergaard & Peterson 2006) for ∼800 d, and detected inter-band continuum reverberation lags in this quasar. To compare our disk size measurement result for PG 2308+098 with those of previous works, we adopt the same analysis method as that used by Mudd et al. (2018). The BH mass of PG 2308+098 is MBH = 109.6 ± 0.1 M⊙, which is more massive compared to the typical BH masses of the quasar samples of Jiang et al. (2017) and Mudd et al. (2018). Therefore, by adding PG 2308+098 to the sample of continuum reverberation mapped quasars, we can examine the BH mass vs. disk size relation over a much wider BH mass range than previous works.
Details of our monitoring observations for PG 2308+098 are described in section 2. Section 3 outlines several analysis methods used to estimate the inter-band lags, and examines the consistency of the estimated lags derived from these analyses. In subsection 4.1, literature values of the disk size constraints from the continuum reverberation and microlensing observations for AGNs/quasars are compiled, and the disk size vs. black hole mass relation for AGNs/quasars is examined; we then demonstrate that the observed AGN/quasar disk sizes are in conflict with the standard accretion disk theory. Implications for the accretion disk structures obtained from an examination of the disk size problem are discussed in subsection 4.2. Section 5 provides a summary and conclusions.
2 Observations
2.1 Observational properties of PG 2308+098
PG 2308+098, also known as 4C 09.72, is a bright (V ∼ 16 mag) type 1 quasar at a redshift of z = 0.433. A BH mass estimate for PG 2308+098 is given by Vestergaard and Peterson (2006) as log (MBH/M⊙) = 9.6 ± 0.1, which is based on a broad Hβ line width taken from Boroson and Green (1992) and a monochromatic luminosity at 5100 Å of log (λLλ [erg s−1]) = 45.8 ± 0.1 taken from Schmidt and Green (1983). Using a bolometric correction factor of BC5100 = 9.26 (Richards et al. 2006), the bolometric luminosity and Eddington ratio of PG 2308+098 are estimated to be log (Lbol [erg s−1]) = 46.8 ± 0.1 and log (Lbol/LEdd) = −0.9 ± 0.1, respectively.
2.2 Five-band optical monitoring observations with the 1.05 m Kiso Schmidt Telescope/KWFC
The u-, g-, r-, i-, and z-band optical light curves of PG 2308+098 were obtained during the period 2015 April to 2017 June using the Kiso Wide Field Camera (KWFC) mounted on the 1.05 m Kiso Schmidt Telescope at the Kiso Observatory, Japan (Sako et al. 2012).1 Part of the data obtained during the period 2015–2016 has already been presented in Kokubo (2016); here, we re-analyze the full dataset, which includes data obtained after the publication of Kokubo (2016). It should be noted that strong broad emission lines, such as Mg ii, Hβ, and Hα, are not strongly contaminated in the five bands at the redshift of PG 2308+098 (see, e.g., Jiang et al. 2017), although the hydrogen Balmer continuum may possibly be a non-negligible contaminant to the g-band light curve (Kokubo et al. 2014; Edelson et al. 2015; Cackett et al. 2018). Possible contamination from the Balmer continuum will be investigated in subsection 3.4.
The KWFC is a mosaic charge-coupled device (CCD) camera composed of four Massachusetts Institute of Technology (MIT) and four Scientific Imaging Technologies, Inc. (SITe) 2 k × 4 k CCD chips, and its full field-of-view is approximately 2° × 2° (see, Sako et al. 2012 for details). During our observations, the KWFC was operated in a fast readout mode, where only the four MIT chips are used and 2 × 2 pixel on-chip binning is applied. In this 28 s fast-readout mode, the pixel scale is |$1{^{\prime\prime}_{.}}89$| pixel−1 and the field of view is limited to 1° × 2°. The four MIT chips are arranged in a 2 × 2 mosaic roughly aligned to the northeast on-sky direction; southwest, southeast, northwest, and northeast are referred to as chip#0, chip#1, chip#2, and chip#3, respectively. Each of the chips has its own particular characteristics. Chip#0, chip#1, chip#2, and chip#3 have gain values of 2.05, 2.30, 2.10, and 2.30 electron ADU−1 and readout noises of 6.8, 6.9, 11.6, and 15.0 electrons, respectively. Kokubo (2016) analyzed only chip#3 images because the pointing of the telescope was always set to introduce the target into chip#3. However, due to telescope pointing errors, the target was sometimes introduced into the other chips instead, in particular into chip#1. Therefore, in this work we also analyzed the images of the other chips to ensure that all the photometry data obtained during the course of our observation runs were included.
During a single visit for each target, the five-band images were obtained quasi-simultaneously in the order g, i, r, u, and z. For each of the five bands, four images with slight spatial offsets (1′ four-point dithering) were obtained. The exposure time for each image was 30 s for every filter during 2015 April–June, and 60 s for the g, r, and i bands and 120 s for the u and z bands during 2015 July–2017 June.
Data reduction was performed by using custom-made python and IRAF/PyRAF scripts,2 which were slightly modified in parts from the scripts used in Kokubo (2016). Each of the CCD chips had a dual amplifier readout, and we treated the two readout areas (corresponding to the two amplifiers) separately, considering slightly different gain factors associated with the different amplifiers. Overscan and bias subtraction, and pixel flat (= dome flat) and illumination flat (= sky flat) corrections were applied in the same way as in Kokubo (2016). Additionally, the L.A.Cosmic algorithm (implemented in an IRAF task lacos_im; van Dokkum 2001) was used to create mask files for pixels affected by cosmic rays. Sky coordinates of the images were calibrated by using the Astrometry.net code and bundled image2xy program (Lang et al. 2010) and index files built from the Two Micron All Sky Survey (2MASS) catalog (Skrutskie et al. 2006).
Aperture photometry was applied using SExtractor (Bertin & Arnouts 1996). SExtractor was applied twice for each image: in the first run, a seeing full-width at half-maximum (FWHM) size was estimated as a median of the FWHM values listed in SExtractor’s output catalog;3 in the second run, the circular aperture diameter was adjusted to twice the seeing FWHM size to maximize the signal-to-noise ratio of the photometric measurements and minimize the effects of systematic centering errors (e.g., Mighell 1999). Photometric measurements affected by cosmic rays identified by lacos_im were excluded from the following analysis.
Zero-point offsets of the images were calibrated for each filter by performing inhomogeneous ensemble photometry (Honeycutt 1992), using the Ensemble software developed by Michael W. Richmond (e.g., Vazquez et al. 2015).4 As comparison stars, field stars within a distance from PG 2308+098 appearing in each frame (8′, 5′, 3′, 3′, and 3′ for u, g, r, i, and z bands) were used to reduce the possible effect of flat-field errors. The same set of comparison stars did not always appear on the images due to the uncertainties of the telescope pointings, and only stars appearing in at least 50% of the frames were used. Inhomogeneous ensemble photometry is a procedure used to find zero-point offsets for each image to minimize the variance of the light curves of the comparison stars. The absolute magnitude scale is arbitrary, and Ensemble sets the magnitude of the brightest star to be zero.
The time stamp of each image was evaluated at mid-exposure, where the reference time frame and the time standard were set to the Barycentric Julian Date (BJD) and Barycentric Dynamical Time (TDB), respectively, using barycorrpy Version 0.2 (Eastman et al. 2010; Kanodia & Wright 2018).5 The time stamp is expressed as the Modified Julian Date (MJD), defined as MJD = BJDTDB − 2400000.5. Multiple exposures obtained during a single visit were binned by taking a weighted average after a 5σ clipping.
Figure 1 and table 1 present the five-band light curves of PG 2308+098. The numbers of observations of the light curves analysed in this work are 24, 28, 25, 29, and 24 for u, g, r, i, and z bands, respectively, and the median cadence is ∼16 d. The light curves of PG 2308+098 show a smooth decline from 2016 July to 2016 August (MJD ∼57200–57600), and then quickly increase until 2016 November (MJD ∼57600–57700). These concave-shaped light curves enable us to constrain the inter-band lags confidently.
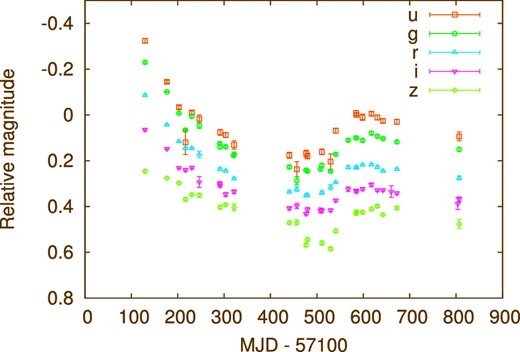
u-, g-, r-, i-, and z-band light curves of PG 2308+098 obtained with the 1.05 m Kiso Schmidt Telescope/Kiso Wide Field Camera. The magnitudes are arbitrarily shifted, for clarity. (Color online)
| MJD . | Magnitude . | Error in magnitude . | Band . |
|---|---|---|---|
| 57229.588 | −0.324 | 0.009 | u |
| 57276.657 | −0.144 | 0.007 | u |
| 57302.468 | −0.034 | 0.008 | u |
| ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ |
| MJD . | Magnitude . | Error in magnitude . | Band . |
|---|---|---|---|
| 57229.588 | −0.324 | 0.009 | u |
| 57276.657 | −0.144 | 0.007 | u |
| 57302.468 | −0.034 | 0.008 | u |
| ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ |
*The light curve in each band is shifted so that the average magnitude is zero. The complete listing of this table is available in the online edition as the supplementary data.
| MJD . | Magnitude . | Error in magnitude . | Band . |
|---|---|---|---|
| 57229.588 | −0.324 | 0.009 | u |
| 57276.657 | −0.144 | 0.007 | u |
| 57302.468 | −0.034 | 0.008 | u |
| ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ |
| MJD . | Magnitude . | Error in magnitude . | Band . |
|---|---|---|---|
| 57229.588 | −0.324 | 0.009 | u |
| 57276.657 | −0.144 | 0.007 | u |
| 57302.468 | −0.034 | 0.008 | u |
| ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ |
*The light curve in each band is shifted so that the average magnitude is zero. The complete listing of this table is available in the online edition as the supplementary data.
3 Continuum reverberation lag measurements
3.1 JAVELIN thin disk reprocessing model
The stochastic behavior of the UV–optical light curves of AGNs/quasars is known to be well modeled by first-order autoregressive Gaussian processes or a damped random walk (DRW) model (MacLeod et al. 2010; Suberlak et al. 2017 and references therein). A DRW time series is defined by an exponential covariance function in the form |$\sigma _{\rm DRW}^2 \exp (-\Delta t/\tau _{\rm DRW})$|, where Δt is the time separating two observations and σDRW and τDRW are the DRW parameters (Zu et al. 2013). DRW modeling of AGN light curves is known to be a powerful tool that interpolates sparsely sampled AGN/quasar light curves, thus enabling the reliable measurement of lags between two light curves (e.g., Zu et al. 2011; Fausnaugh et al. 2016).
JAVELIN (Just Another Vehicle for Estimating Lags In Nuclei)6 is a publicly available python code for estimating reverberation lags for AGN light curves.7 JAVELIN was originally designed to derive the posterior distribution (through MCMC calculations) of the reverberation lags between the continuum and the broad emission line light curves of AGNs/quasars, assuming the DRW model for the continuum light curve and top-hat transfer functions (see Zu et al. 2011 for details). Currently, JAVELIN is widely used not only for broad emission line reverberation lag measurements (e.g., Zu et al. 2011, 2013), but also for inter-band continuum reverberation lag measurements (e.g., Shappee et al. 2014; Fausnaugh et al. 2016, 2018; Starkey et al. 2017; Jiang et al. 2017; Mudd et al. 2018).
First, we tried to constrain β by fitting the five band light curves of PG 2308+098 to the JAVELIN thin disk model without any constraint on β. We adopted the u-band light curve as the driving light curve, and the other four band light curves were taken to be the response light curves. There are six model parameters in the JAVELIN thin disk model: the power-law index β, the DRW parameters for the u-band (i.e., σDRW and τDRW), the lag of the u-band light curve relative to the driving light curve, and the scaling factor and kernel width of the transfer function for each of the g, r, i, and z bands. A hard boundary from 100 to 300 d for the prior distribution of the rest-frame DRW timescale τDRW was imposed, as suggested by Mudd et al. (2018), considering an observational fact that the typical value of τDRW is ∼200 d for luminous quasars (e.g., MacLeod et al. 2010). The allowed observed-frame lags of the g-, r-, i-, and z-band light curves were restricted to a range from −50 to 50 d. MCMC sampling parameters nwalker, nchain, and nburn (numbers of random walkers, sampling iterations, and burn-in iterations for each walker, respectively) were set to 1000, 1000, and 100 (see Foreman-Mackey et al. 2013 for details). Figure 2 shows the posterior distribution of β constrained from the five band light curves of PG 2308+098 with JAVELIN thin disk model fitting. Although the distribution is not inconsistent with the thin disk model value of β = 4/3, the distribution widely spreads from β ∼ 0.2 to 2 with no clear single peak, so it is impossible to derive a point estimate for β from this distribution. This analysis indicates that it is difficult to constrain β from multi-band light curves at rest-frame UV–optical wavelengths alone. Therefore, following Mudd et al. (2018), in the remainder of this study we derive constraints on the continuum reverberation lag (and equivalently the disk size) by fixing β = 4/3. In the case of PG 2308+098, the assumption of β = 4/3 is supported by the fact that the power-law spectral shape of the optical polarized flux spectrum and the variable component spectrum is consistent with the thin disk model prediction of αν = 1/3, as noted in subsection 2.1. The possibility of β ≠ 4/3 will be revisited in subsection 4.2.
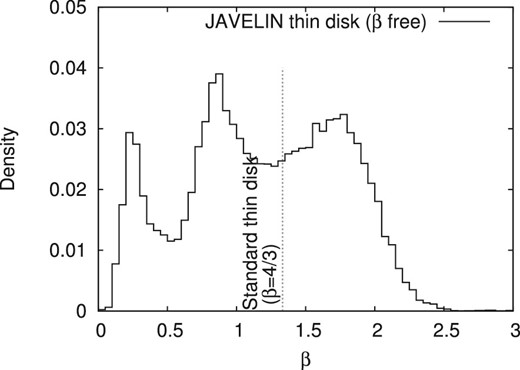
Posterior distribution of β for PG 2308+098, constrained from the JAVELIN thin disk model analysis without fixing β. β = 4/3 corresponds to the standard thin disk model.
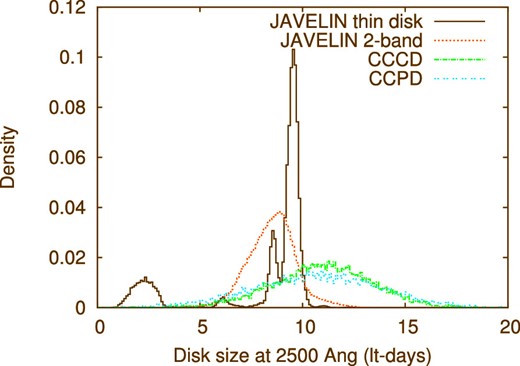
Probability distributions of the disk size at λrest = 2500 Å, Rdisk = cτrest, 2500, on the assumption that the multi-band lag is proportional to λ4/3 (β = 4/3). The distribution of the JAVELIN two-band analysis is calculated from the distributions of the lags of the four bands relative to the u-band (figure 4), and those of cross-correlation centroid distributions (CCCDs) and cross-correlation peak distributions (CCPDs) are calculated from the CCCDs and CCPDs of the four bands (figure 5), respectively. (Color online)
Disk size of PG 2308+098 at λrest = 2500 Å, measured with several analysis methods.
| Method . | R disk(2500 Å) (light-day) . | 1σ range* (light-day) . | 2σ range* (light-day) . | 95th percentile upper limit (light-day) . |
|---|---|---|---|---|
| JAVELIN thin disk | 9.46 | 6.34—9.75 | 1.69—10.09 | 9.91 |
| JAVELIN 2-band lags | 8.57 | 7.37—9.56 | 6.09—11.10 | 10.42 |
| CCCD | 10.99 | 8.47—13.34 | 5.74—15.69 | 14.84 |
| CCPD | 10.72 | 7.53—13.81 | 4.08—16.87 | 15.74 |
| Method . | R disk(2500 Å) (light-day) . | 1σ range* (light-day) . | 2σ range* (light-day) . | 95th percentile upper limit (light-day) . |
|---|---|---|---|---|
| JAVELIN thin disk | 9.46 | 6.34—9.75 | 1.69—10.09 | 9.91 |
| JAVELIN 2-band lags | 8.57 | 7.37—9.56 | 6.09—11.10 | 10.42 |
| CCCD | 10.99 | 8.47—13.34 | 5.74—15.69 | 14.84 |
| CCPD | 10.72 | 7.53—13.81 | 4.08—16.87 | 15.74 |
* ±1σ and ±2σ are defined as 68.2% and 95.4% ranges around a median of a probability distribution.
Disk size of PG 2308+098 at λrest = 2500 Å, measured with several analysis methods.
| Method . | R disk(2500 Å) (light-day) . | 1σ range* (light-day) . | 2σ range* (light-day) . | 95th percentile upper limit (light-day) . |
|---|---|---|---|---|
| JAVELIN thin disk | 9.46 | 6.34—9.75 | 1.69—10.09 | 9.91 |
| JAVELIN 2-band lags | 8.57 | 7.37—9.56 | 6.09—11.10 | 10.42 |
| CCCD | 10.99 | 8.47—13.34 | 5.74—15.69 | 14.84 |
| CCPD | 10.72 | 7.53—13.81 | 4.08—16.87 | 15.74 |
| Method . | R disk(2500 Å) (light-day) . | 1σ range* (light-day) . | 2σ range* (light-day) . | 95th percentile upper limit (light-day) . |
|---|---|---|---|---|
| JAVELIN thin disk | 9.46 | 6.34—9.75 | 1.69—10.09 | 9.91 |
| JAVELIN 2-band lags | 8.57 | 7.37—9.56 | 6.09—11.10 | 10.42 |
| CCCD | 10.99 | 8.47—13.34 | 5.74—15.69 | 14.84 |
| CCPD | 10.72 | 7.53—13.81 | 4.08—16.87 | 15.74 |
* ±1σ and ±2σ are defined as 68.2% and 95.4% ranges around a median of a probability distribution.
3.2 JAVELIN for two-band light curve pairs
JAVELIN was originally designed to derive a reverberation lag between a pair of two-band light curves. Here, we use JAVELIN’s original function to constrain the inter-band lags of the disk continuum of the pairs of two-band light curves of PG 2308+098 to examine the consistency between the result from the JAVELIN thin disk analysis and that derived from the normal JAVELIN two-band analysis.
We again took the shortest wavelength band, i.e., the u band, as the driving light curve of the disk reprocessing. This means that the other four band light curves are assumed to be shifted, scaled, and smoothed versions of the u-band light curve. First, the u-band light curve alone was fitted using the Cont_Model module in JAVELIN to derive constraints on the DRW parameters. Again, the rest-frame DRW timescale τDRW was restricted to 100–300 d when constraining the continuum light curve model, as assumed by Mudd et al. (2018). Then, each of the two-band pairs of light curves, u − g, u − r, u − i, and u − z, was fitted using the Rmap_Model module in JAVELIN to derive the posterior distribution of the observed-frame lag between the two light curves. Again, the observed-frame lags of the four band light curves were restricted to the range from −50 to 50 d.
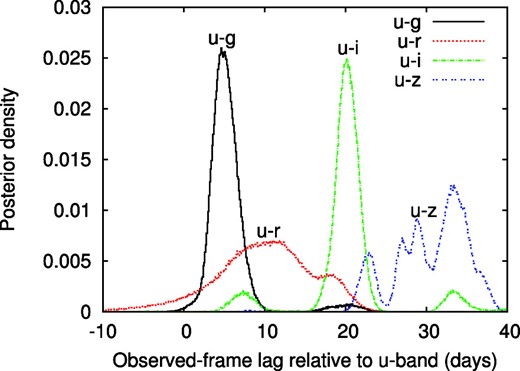
Posterior distributions of the observed-frame lag relative to the u-band light curve, evaluated for u − g, u − r, u − i, and u − z band pair light curves using JAVELIN two-band analysis (subsection 3.2). (Color online)
3.3 Cross-correlation analysis
Cross-correlation analysis is a classical method used to determine a temporal shift between two light curves (Peterson et al. 1998; Welsh 1999). A temporal shift between two light curves can be evaluated by cross-correlating them and finding the lag where the correlation is maximized. Here we explore whether the model-independent cross-correlation method results in lag values consistent with those derived from the DRW-based JAVELIN analyses.
Cross-correlation functions (CCFs) between the two light curves of the four band pairs (u − g, u − r, u − i, and u − z) were evaluated using an interpolation method, where the unevenly sampled light curves are linearly interpolated to calculate correlation coefficients at arbitrary lags (Gaskell & Sparke 1986).8 For each of the band pairs, a CCF was first calculated by interpolating the u-band light curve to the other band light curve sampling. Then, another CCF was calculated by interpolating the latter light curve to the u-band light curve sampling. Finally, a further CCF was calculated as an average of the two CCFs. CCFs were calculated at 0.01-d intervals within the range of −100 ≤ τobs [d] ≤ +100, where a positive lag denotes a positive lag relative to the u-band light curve. An estimate of the lag was evaluated as the centroid of the CCF. The CCF centroid calculation was performed only for CCF points within 80% of the peak value of the CCF. Moreover, another estimate of the lag was evaluated as the peak of the CCF. The uncertainties on the CCFs and their centroids and peaks were estimated using the Flux Randomization and Random Subsample Selection (FR/RSS) method developed by Peterson et al. (2004). A total of 10000 Monte Carlo FR/RSS realizations for each band pair produced a cross-correlation centroid distribution (CCCD) and a cross-correlation peak distribution (CCPD) for the lag relative to the u band, and the distribution widths were used as estimates of the measurement uncertainties of the lags.
Figure 5 presents the CCFs, CCCDs, and CCPDs of the u − g, u − r, u − i, and u − z band pair light curves of PG 2308+098. The CCCDs and CCPDs are generally in agreement with each other, but the CCPDs tend to be more affected by the local peak of the CCFs. Then, as in subsection 3.2, we used equation (4) to calculate probability distributions of τrest, 2500 from the CCCDs and CCPDs of the u − g, u − r, u − i, and u − z band pairs. Figure 3 presents the probability distributions of τrest, 2500 derived from the CCCDs and CCPDs, along with the probability distributions derived from the JAVELIN thin disk and JAVELIN two-band analyses. The median and ±1σ values of the CCCD-based and CCPD-based probability distributions of τrest, 2500 are evaluated to be |$\tau _{{\rm rest,\, 2500}} = 10.99^{+2.35}_{-2.52}\:$|d and |$10.72^{+3.09}_{-3.19}\:$|d, and the 95th percentile upper limits are 14.84 d and 15.74 d, respectively (table 2).
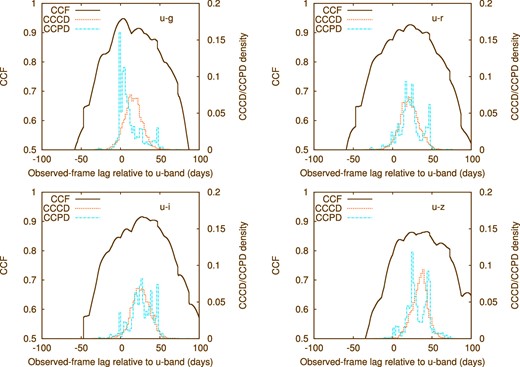
CCFs, CCCDs, and CCPDs of the u − g, u − r, u − i, and u − z band pair light curves of PG 2308+098. A positive lag is defined as a positive observed-frame lag relative to the u-band light curve. (Color online)
3.4 Comparison of JAVELIN thin disk, JAVELIN two-band, and CCCD/CCPD results
It should be noted that the widths of the CCCD/CCPD distributions shown in figure 5 are larger than those of the posterior distributions of the lags derived by JAVELIN shown in figure 4. JAVELIN is known to yield smaller measurement uncertainties on the lag values generally compared to the CCF uncertainties evaluated with the FR/RSS method (e.g., Fausnaugh et al. 2016), and this probably reflects the fact that the cross-correlation analysis does not assume any time-series model for the two light curves. Nevertheless, the trend that the lags become larger at longer wavelength bands, as seen in the results of the JAVELIN two-band analysis, is also seen in the cross-correlation results.
Figure 6 summarizes the lag estimates at g, r, i, and z bands relative to the u band derived from the JAVELIN two-band and the CCF analyses for u − g, u − r, u − i, and u − z-band light curve pairs. The lag spectra as a function of the rest-frame wavelength obtained from these two-band analyses are consistent with each other within the measurement uncertainties. As noted in subsection 2.2, there may be a contribution from the hydrogen Balmer continuum emission to the lag spectra at the g band. However, any clear g-band excess is identified in the observed lag spectra, suggesting that the Balmer continuum contribution, if any, is negligible in the case of PG 2308+098.
![Comparisons of the continuum lags of PG 2308+098 measured with the JAVELIN two-band analysis and the CCF (CCCD and CCPD) analysis. All lags are measured relative to the u-band light curve (λu, rest = 2478 Å.). The observed-frame standard thin disk prediction [equation (5) with MBH = 109.6 M⊙ and $\dot{M}/\dot{M}\,_{\rm Edd} = 10^{-0.9}$], and that inflated by a factor of 3 and 1.82, are also plotted (see subsection 4.1). (Color online)](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/70/5/10.1093_pasj_psy096/3/m_pasj_70_5_97_f6.jpeg?Expires=1749120895&Signature=TWAqi8Tl1z~AbE68Ha8CW8SQfowt3QmCfk9oxlazwF163dZgtXdfNuZYHbsVrJpMDqCuu6gbozd2Xd35O0Gjxz-yW5sTOMCaTVjvVN1k5MRbytcOmwwoNFEY-SQnkbwxvO284zOY12HHTXm4tYxxkBUVl8Zs8R-~W~wmiMKMW7ykuMYgpPYWFNxdUkZB99Ayu6uTg8AoopI6TbB~r0FcxlpNs0bP7s7eVXKoK2zacw6bewGBLdSzpc5ZZp-d1Nlgb~rcFJOZiPpqdpoB43PvUhHrBwdgM0RnM~AgQ-JCY34~ZaKWt9YZ~9FDf6b-RqHN3GDHZJWv1P59vxjVjd1MoQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Comparisons of the continuum lags of PG 2308+098 measured with the JAVELIN two-band analysis and the CCF (CCCD and CCPD) analysis. All lags are measured relative to the u-band light curve (λu, rest = 2478 Å.). The observed-frame standard thin disk prediction [equation (5) with MBH = 109.6 M⊙ and |$\dot{M}/\dot{M}\,_{\rm Edd} = 10^{-0.9}$|], and that inflated by a factor of 3 and 1.82, are also plotted (see subsection 4.1). (Color online)
Figure 7 compares the constraints on the disk sizes at λrest = 2500 Å (i.e., Rdisk = cτrest, 2500) obtained from the results of the JAVELIN thin disk (subsection 3.1), JAVELIN two-band (subsection 3.2), CCPD, and CCCD analyses (subsection 3.3) on the assumption of β = 4/3 (table 2). Again, all disk-size estimates are consistent with each other within the error bars. As shown in figure 7, the 95% upper limits on the disk-size estimates from these analyses strongly suggest that the disk size of PG 2308+098 is not unexpectedly large compared to the standard thin disk prediction. Detailed comparisons among the observed disk size in PG 2308+098, the disk sizes in other reverberation-mapped or microlensing quasars, and the standard thin disk model will be presented in subsection 4.1.

Observational constraints on the disk size at λrest = 2500 Å for PG 2308+098 evaluated with different lag estimation methods (figure 3). Data points denote the point estimates and 1σ ranges, and left-facing arrows denote 95% percentile upper limits on the disk size. The standard thin disk model prediction range in the case of MBH = 109.6 ± 0.1 MBH and |$\dot{M}/\dot{M}\,_{\rm Edd} = 10^{-0.9 \pm 0.1}$|, and that inflated by a factor of 3, are indicated by vertical lines. (Color online)
4 Discussion
4.1 The disk size–BH mass relation
![Flux-weighted disk radius at λrest = 2500 Å vs. the black hole mass relation for AGNs/quasars. Filled and open squares denote, respectively, the ±1σ and ±2σ disk size constraints for PG 2308+098 derived from the JAVELIN thin disk analysis on the assumption of β = 4/3, and the two points are vertically shifted for clarity. The disk size constraints based on the continuum reverberation lags for quasar samples of Jiang et al. (2017) and Mudd et al. (2018), and those based on the microlensing measurements taken from Morgan et al. (2010), are also plotted for comparison (see text in subsection 4.1 for details). The error-bars are ±1σ, except for the data points from Mudd et al. (2018) where the error bars denote ±2σ ranges. Note that MBH (taken from each paper) generally have an uncertainty of 0.4 dex. The standard thin disk model prediction for Eddington ratios of 0.1, 0.3, and 1.0 are denoted by lines [$R_{\rm disk} \propto M_{\rm BH}^{2/3}$; equation (5)], along with an arbitrarily scaled line of $R_{\rm disk} \propto M_{\rm BH}^{1/3}$, and the innermost stable circular orbit (ISCO; RISCO = 6GMBH/c2), for comparison. Note that the black hole mass estimate for the most massive quasar in the sample provided by Jiang et al. (2017), SDSS J083841.70+430519.0 with MBH = 1010 M⊙, may be erroneous (see footnote 11). (Color online)](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/pasj/70/5/10.1093_pasj_psy096/3/m_pasj_70_5_97_f8.jpeg?Expires=1749120895&Signature=e1ksbgbj-8TdOnconM-GYa71FXZ6re~HX8r3nej6Bak7Np-Z8KeYmsMcy9gqdGTaapnIg-3dtKZSA26kJxItgdAT8wE3SPPofNWMwuY7GSQrwMAX4EIuv8Rak-RSPfB1AMVVyp9N0iwC2IuQKhSDbg9AD8GFlNtQ61JZJ9-wHF2MUf4oqvLGDaYYyHRGqH3As2rcqptBFLtpbS1k8wLFWDW6InTXqw4vhtZL5LAAlI5VaSQ0nIu6aR5~y-fjp9HqYIW3DIXMfg9X~wTmxB-zSiSLm5yxrIgNDjW7F5tkKUvrErAZS2fkm4b0sUtRJg3NdffiaxgFf~DBfcEbEihr6g__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Flux-weighted disk radius at λrest = 2500 Å vs. the black hole mass relation for AGNs/quasars. Filled and open squares denote, respectively, the ±1σ and ±2σ disk size constraints for PG 2308+098 derived from the JAVELIN thin disk analysis on the assumption of β = 4/3, and the two points are vertically shifted for clarity. The disk size constraints based on the continuum reverberation lags for quasar samples of Jiang et al. (2017) and Mudd et al. (2018), and those based on the microlensing measurements taken from Morgan et al. (2010), are also plotted for comparison (see text in subsection 4.1 for details). The error-bars are ±1σ, except for the data points from Mudd et al. (2018) where the error bars denote ±2σ ranges. Note that MBH (taken from each paper) generally have an uncertainty of 0.4 dex. The standard thin disk model prediction for Eddington ratios of 0.1, 0.3, and 1.0 are denoted by lines [|$R_{\rm disk} \propto M_{\rm BH}^{2/3}$|; equation (5)], along with an arbitrarily scaled line of |$R_{\rm disk} \propto M_{\rm BH}^{1/3}$|, and the innermost stable circular orbit (ISCO; RISCO = 6GMBH/c2), for comparison. Note that the black hole mass estimate for the most massive quasar in the sample provided by Jiang et al. (2017), SDSS J083841.70+430519.0 with MBH = 1010 M⊙, may be erroneous (see footnote 11). (Color online)
Figure 8 compares the continuum reverberation measurements of the accretion disk sizes at λrest = 2500 Å of PG 2308+098 and those derived by Mudd et al. (2018) for the 15 DES quasars as a function of the BH masses.9 The disk size measurements of Mudd et al. (2018) are taken directly from table 3 in Mudd et al. (2018), where the associated uncertainty ranges are ±2σ (also Mudd 2017). Note that the disk size constraints for the 15 DES quasars by Mudd et al. (2018) and for PG 2308+098 obtained in this work and shown in figure 8 are derived using the same analysis technique (the JAVELIN thin disk model fitting; subsection 3.1); thus, they are directly comparable to each other. Additionally, the g − r, g − i, and g − z two-band lags of the 39 Pan-STARRS quasars (derived using JAVELIN) listed in table 3 of Jiang et al. (2017) were converted into the rest-frame 2500 Å disk size by applying the same procedure described in subsection 3.2 (assuming β = 4/3) and plotted in figure 8. It is important to note that the optical continuum reverberation constraints on the disk sizes at λrest = 2500 Å (Jiang et al. 2016; Mudd et al. 2018, and this work) are directly affected by the choice of β due to the β dependence of the extrapolation of the lag spectrum to driving wavelengths (λ → 0 Å).
Figure 8 also presents the accretion disk sizes at λrest = 2500 Å of gravitationally-lensed quasars reported in Morgan et al. (2010) and derived from microlensing analysis. The analysis in Morgan et al. (2010) is based on time-series observations of microlensing variability and sets constraints on the scale-length Rs of the accretion disks. Note that the disk scale-length Rs is equivalent to the case of X = 1 in equation (5) (see Morgan et al. 2010). Although the reverberation-mapped disk radii are insensitive to disk inclination angles (e.g., Starkey et al. 2017; Hall et al. 2018), the microlensing disk size measurements directly depend on the inclination angle as |$\propto \sqrt{\cos i}$|, and therefore the disk sizes presented in Morgan et al. (2010) were corrected for a mean inclination 〈cos i〉 = 1/2 to obtain face-on estimates. The disk sizes presented in Morgan et al. (2010) were corrected to λrest = 2500 Å assuming β = 4/3. With regard to the measurements made by Morgan et al. (2010), the choice of β had little effect on the disk-size estimates at λrest = 2500 Å because their microlensing observations were carried out at around the rest-frame wavelengths of λrest ≃ 2500 Å (see Morgan et al. 2010 for details). Then, to compare the microlensing-based disk scale-lengths Rs with the reverberation disk sizes, we inflated Rs by a factor of X4/3 = 2.494/3 = 3.37, following equation (5), as in Mudd et al. (2018).
Figure 8 clearly shows that the disk sizes for MBH ≲ 5 × 108 M⊙ quasars derived from continuum reverberation mapping and gravitational microlensing are both generally distributed above the standard thin disk predictions with sub-Eddington accretion rates, requiring super-Eddington accretion rates (Hall et al. 2014). On the other hand, a proportion of quasars with higher BH masses, including PG 2308+070 analyzed in this work, are consistent with sub-Eddington accretion rates.10 Overall, the measured disk sizes appear to have a weaker dependence on MBH than the expectations from the standard thin disk model (|$R_{\rm disk} \propto M_{\rm BH}^{2/3}$| for a given Eddington ratio); this trend has already been noted by Mudd et al. (2018) and Blackburne et al. (2011) in the context of continuum reverberation mapping and microlensing measurements, respectively. Blackburne et al. (2011) pointed out that the mass dependence of the disk size at 2500 Å is about half the expected dependence, i.e., |$\propto M_{\rm BH}^{1/3}$|, and this argument still holds for the combined dataset shown in figure 8.
4.2 Implications for the accretion disk structure in PG 2308+098
Although we show that the discrepancy between the measured disk size of PG 2308+098 and the expected size from the standard disk theory is modest, it remains a general trend that the AGN disk sizes (probed either by microlensing events or continuum reverberation mapping) are generally larger than the standard disk predictions. It should be noted that the presence of non-zero BH spins makes the disk size problem even more significant. The “Soltan argument” (Soltan 1982; Yu & Tremaine 2002; Ueda et al. 2014) suggests that modest radiative efficiencies of η ≳ 0.1 are required for accretion disks in a general population of luminous quasars to account for BH mass density in a low-redshift universe. The radiative efficiency, η, is an increasing function of the BH spin, so the Soltan argument may imply that the quasars generally harbor prograde spinning SMBHs (Yu & Tremaine 2002). If we consider prograde spinning SMBHs (a > 0), the difference between the observations and the model becomes even more significant because a prograde BH accretion disk has a higher radiative efficiency (η > 0.1) which leads to a smaller accretion disk compared to a non-spinning BH disk for a given luminosity or Eddington ratio [see equation (5)]. A maximally prograde SMBH has η ≃ 0.3, and the accretion disk size is expected to be smaller than the non-spinning SMBH accretion disk by a factor of (0.3/0.1)−1/3 = 0.69. On the other hand, a maximally retrograde SMBH has η ≃ 0.04, and the disk size is larger by a factor of (0.04/0.1)−1/3 = 1.36, but there is no physical motivation to consider retrograde SMBHs in actual quasars.
It is important to note that the power-law index for MBH and |$\dot{M}/\dot{M}_{\rm Edd}$| in equation (5) is so small that the disk size discrepancy requires huge modifications of the assumed parameters. For example, to inflate the theoretical disk size by a factor of 3 for a given MBH, a value of the Eddington ratio 33 = 27 times larger is required, which easily violates the basic assumption that normal AGNs/quasars have sub-Eddington accretion rates and can be described by the standard thin disk theory. As for the model parameters, the choice of the factor X in equation (5) potentially has non-negligible effects on the standard disk predictions for Rdisk [see Cackett et al. (2018) for a related discussion]. Interestingly, if we adopt X = 3.89 as suggested by Collier et al. (1999), which is based on detailed calculations of the disk response to continuum emission, the expected disk size increases by a factor of (3.89/2.49)4/3 = 1.81, and therefore the measured disk size of PG 2308+098 is in complete agreement with the standard disk prediction. Nevertheless, the disk sizes in other less-massive AGNs/quasars shown in figure 8 remain larger than the standard disk prediction, even when adopting a value of X = 3.89. Therefore, the larger-than-expected accretion disk sizes, and the shallower slope of the disk size vs. MBH relation compared to the standard thin disk theory confirmed by our disk size measurement for PG 2308+098, may suggest that part of our basic assumption based on the standard thin disk theory is invalid for describing quasar accretion disks.
The power-law index β = 4/3 [equation (1)] assumed throughout this work is taken directly from the standard thin disk model prediction of the disk temperature profile of T(R) ∝ R−3/4. As noted in subsection 2.1, the spectral shape of the polarized flux component and the variable component of PG 2308+098 at the rest-frame UV–optical wavelengths suggests that the assumption of β = 4/3 is not far from reality. Nevertheless, as discussed in subsection 3.1, the multi-band optical continuum reverberation mapping observation alone cannot strongly constrain β (see also Mudd et al. 2018). Therefore, it may still be possible that the wavelength dependence index β can differ from a value of 4/3. Interestingly, Jiang et al. (2017) found tentative evidence of β < 4/3, particularly for the high-luminosity quasars they analyzed. Moreover, Blackburne et al. (2011) noted that microlensing constraints on β for quasars on average imply a value of β < 4/3 (see also Hall et al. 2014). If we adopt a value of β smaller than 4/3, the rest-frame 2500 Å disk-size estimates from the continuum reverberation measurements become generally larger than those shown in figure 8. However, as noted in subsection 4.1, the microlensing constraints on the rest-frame 2500 Å disk sizes are, in principle, largely independent of β (see also Mortonson et al. 2005). Therefore, β < 4/3 makes the disk-size estimates from the continuum reverberation and microlensing measurements inconsistent with each other. Currently, such a discrepancy is not obviously observed in figure 8. Moreover, smaller β results in a steeper temperature radial profile and a bluer UV–optical spectrum, which may contradict with the observed AGN/quasar UV–optical spectra (e.g., Gaskell 2008). Further continuum reverberation/microlensing observations are needed to determine the true value of β.
Another potentially important point of view concerns the metallicity of accretion disks in AGNs. Jiang et al. (2017) claimed that quasars with higher metallicity (probed as the metallicity of broad line regions) appear to have systematically smaller continuum reverberation lags, i.e., smaller disk sizes. The relationship between disk size and metallicity may possibly be explained by large changes in the disk’s opacity as a function of the gas metallicity due to the iron opacity bump, which can significantly modify the thermal properties and structure of AGN accretion disks compared to the standard thin disk model (Jiang et al. 2016, 2017). Because the higher BH masses generally imply a higher broad line region gas metallicity (Matsuoka et al. 2011 and references therein), the above claim may provide another perspective on the weaker MBH dependence of Rdisk than the standard disk model prediction discussed in subsection 4.1. According to this interpretation, the relatively smaller disk size observed in PG 2308+098 implies an intrinsically different disk structure in this high BH mass quasar compared to lower BH mass quasars. As suggested by Jiang et al. (2017), the disk-size problem revealed by the continuum reverberation and microlensing observations may indicate a need for modifications to the standard disk theory so that metallicity-dependent opacity effects are appropriately included.
Finally, it should be noted that the original idea of continuum reverberation mapping is to measure the time lag between the driving X-ray light curve and the responding UV–optical light curves, on the assumption of the reprocessing picture where the X-ray/FUV emission from the central compact X-ray/FUV emission region (“lamppost”) is irradiating the accretion disk surface. Continuum reverberation mapping observations for local well-studied Seyfert galaxies, e.g., NGC 4395 (McHardy et al. 2016), NGC 4593 (Pal & Naik 2018; Cackett et al. 2018), NGC 5548 (Edelson et al. 2015; Fausnaugh et al. 2016), and NGC 4151 (Edelson et al. 2017), were based on this idea and measured the X-ray-to-UV/optical lag as a direct probe of the disk sizes. These X-ray-to-UV/optical continuum reverberation mapping observations revealed that the disk sizes are several times larger than the standard thin disk prediction (see also Buisson et al. 2017). On the other hand, the continuum reverberation disk size constraints discussed in this work (Jiang et al. 2017; Mudd et al. 2018, and this work for PG 2308+098) are based on wavelength-dependent reverberation lag measurements within the rest-frame UV–optical bands. McHardy et al. (2018) pointed out that although X-ray-to-UV/optical reverberation lags are observed to be several times larger in local Seyfert AGNs, the wavelength-dependent continuum lags of these AGNs within the UV–optical bands are generally more consistent with the reprocessing picture utilizing the standard thin disk model (see also Edelson et al. 2017). In other words, the X-ray light curves of AGNs alone appear to show extra offset lags relative to simple disk reprocessing. McHardy et al. (2018) argued that the extra offset lag in the X-ray band might possibly be explained by introducing an additional distant X-ray reflector, probably broad emission line region clouds, which can dilute the X-ray-to-UV/optical disk reprocessing signals. Alternatively, the X-ray emission might first be reprocessed into soft X-ray/FUV photons at around the innermost disk region, and then the FUV photons might be reprocessed into UV–optical disk photons (Gardner & Done 2017; Edelson et al. 2017). Moreover, truncation of the inner accretion disks may produce an additional X-ray-to-UV/optical lag relative to the lamppost disk reprocessing model prediction (Noda et al. 2016). The wavelength-dependent UV–optical inter-band lag measurements are free from such uncertainties regarding the geometry of the X-ray/FUV emitter; nevertheless, as shown in figure 8, the accretion disk sizes inferred from the UV–optical inter-band lag measurements remain larger than the standard thin disk predictions.
The larger disk sizes in each of the AGNs, and the shallower slope of the global Rdisk–MBH relation compared to the standard thin disk model, suggest that this model cannot adequately describe AGN/quasar accretion disks. However, we wish to point out that the compilation of data from the literature and the discussion in section 3 suggest that differences between analysis methods used may introduce systematic biases into the disk size constraints [see also Blackburne et al. (2011) for the case of microlensing measurements]. Homogeneous re-analysis of data from the literature will be useful to investigate the possible systematics of the disk size estimations further. Moreover, future X-ray-to-UV/optical and UV–optical inter-band continuum reverberation mapping observations, as well as microlensing observations, for a statistical sample of AGNs/quasars with high cadence, high-quality light-curve data are needed to obtain conclusive results on the (in)validity of the standard disk theory and to search for a solution to the disk size problem. The Large Synoptic Survey Telescope (LSST) will automatically obtain high-cadence multi-band optical light-curves for millions of quasars, including thousands of gravitationally lensed quasars; thus, LSST will enable optical continuum reverberation measurements and microlensing measurements for a large sample of quasars (e.g., LSST Science Collaboration 2009; Oguri & Marshall 2010).
5 Conclusions
We carried out u-, g-, r-, i-, and z-band monitoring observations for the massive quasar PG 2308+098 using the Kiso Schmidt telescope/KWFC and detected wavelength-dependent continuum reverberation lags at g, r, i, and z bands relative to the u band, where the longer wavelength bands lag behind the shorter wavelength bands. On the assumption of a lamppost X-ray/FUV reprocessing picture and the standard thin disk temperature profile of T(r)∝R−3/4 (i.e., Rdisk = cτrest∝λ4/3), we derived constraints on the flux-weighted radius of the accretion disk at λrest = 2500 Å, as Rdisk = 6.34–9.75 light-day (1σ range from the JAVELIN thin disk analysis). We confirmed that the disk-size estimates from the JAVELIN thin disk, JAVELIN two-band, and two-band CCF (CCCD/CCPD) analyses are consistent with each other within the errors.
The accretion disk sizes of AGNs measured via the continuum reverberation and microlensing techniques are known to be generally ∼ 3 times larger than the standard disk model predictions (e.g., Morgan et al. 2010; Edelson et al. 2015; Fausnaugh et al. 2018). For PG 2308+098, the measured disk size is also larger, although modestly, by a factor of 1.2–1.8 times that of the standard disk model prediction. The compilation of literature data, including the new disk size constraint for PG 2308+098, revealed that the global Rdisk(2500 Å)–MBH relation of AGNs/quasars may have a shallower slope compared to the standard accretion disk model prediction of |$R_{\rm disk} \propto M_{\rm BH}^{2/3}$|. The larger disk sizes and the shallower Rdisk(2500 Å)–MBH slope imply that the standard accretion disk model cannot properly account for AGN/quasar accretion disks. One potentially important factor to be considered is the metallicity of the accretion disks (e.g., Jiang et al. 2016, 2017). Construction of a sophisticated accretion disk theory with appropriate treatment of the opacity effects (including the iron opacity jump), as well as further observations of the continuum reverberation and microlensing events for AGN/quasar accretion disks, will be needed to tackle the disk size problem.
Supplementary data
Complete listing of table 1.
Acknowledgments
We thank Yuki Sarugaku for his support during the KWFC queue mode observations. We are grateful to all the staff of the Kiso Observatory for their efforts to maintain the observation system. This work was supported by JSPS KAKENHI Grant Number 17J01884.
This research has made use of NASA’s Astrophysics Data System Bibliographic Services. This research has made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
This research made use of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration 2013).
Footnotes
Longitude = |${137{^{\circ}_{.}}625406}\,$|E, latitude = |${35{^{\circ}_{.}}797236}\,$|N, and altitude = 1130 m.
IRAF is distributed by the National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation.
The median and the 16% and 84% percentiles of the seeing FWHMs at the u, g, r, i, and z bands evaluated from all the images are |${4{^{\prime\prime}_{.}}8}^{+1.1}_{-0.8}$|, |${4{^{\prime\prime}_{.}}5}^{+1.0}_{-0.8}$|, |${4{^{\prime\prime}_{.}}2}^{+1.5}_{-0.9}$|, |${4{^{\prime\prime}_{.}}0}^{+1.4}_{-0.7}$|, and |${3{^{\prime\prime}_{.}}8}^{+0.8}_{-0.6}$|, respectively.
〈http://spiff.rit.edu/ensemble/〉; accessed 2017 December 12.
JAVELIN internally uses a Markov Chain Monte Carlo (MCMC) Ensemble sampler emcee (Foreman-Mackey et al. 2013).
We used PYCCF V2, Python Cross Correlation Function for reverberation mapping studies, for the cross-correlation analyses (Sun et al. 2018).
Seven quasars have lag detections in multiple years, thus there are 24 data points.
Among the data from Jiang et al. (2017) given in figure 8, we can readily identify one very massive outlier quasar, SDSS J083841.70+430519.0 (MBH = 1010 M⊙ at z = 0.98; Jiang et al. 2017; Kozłowski 2017), which has a disk size a factor of 3 smaller compared to the standard thin disk model. This quasar is ignored in figures 10 and 11 of Mudd et al. (2018). The rest-frame g − r, g − i, and g − z two-band lags of SDSS J083841.70+430519.0 are clearly wavelength-dependent (1.09 ± 0.25, 1.59 ± 0.25, and 5.91 ± 0.25 d, respectively) and the disk size at 2500 Å is robustly determined as 3.93 ± 0.17 light-day on the assumption of a value of β = 4/3. However, the estimated disk radius is unphysically small considering the ISCO of a Schwarzschild BH of MBH = 1010 M⊙, RISCO = 6GMBH/c2 = 3.42 light-day, suggesting that the BH mass estimate for this object is erroneous.
References



