-
PDF
- Split View
-
Views
-
Cite
Cite
Li Teng, Bing He, Peng Gao, Long Gao, Kai Tan, Discover context-specific combinatorial transcription factor interactions by integrating diverse ChIP-Seq data sets, Nucleic Acids Research, Volume 42, Issue 4, 1 February 2014, Page e24, https://doi.org/10.1093/nar/gkt1105
Close - Share Icon Share
Abstract
Combinatorial interactions among transcription factors (TFs) are critical for integrating diverse intrinsic and extrinsic signals, fine-tuning regulatory output and increasing the robustness and plasticity of regulatory systems. Current knowledge about combinatorial regulation is rather limited due to the lack of suitable experimental technologies and bioinformatics tools. The rapid accumulation of ChIP-Seq data has provided genome-wide occupancy maps for a large number of TFs and chromatin modification marks for identifying enhancers without knowing individual TF binding sites. Integration of the two data types has not been researched extensively, resulting in underused data and missed opportunities. We describe a novel method for discovering frequent combinatorial occupancy patterns by multiple TFs at enhancers. Our method is based on probabilistic item set mining and takes into account uncertainty in both types of ChIP-Seq data. By joint analysis of 108 TFs in four human cell types, we found that cell–type-specific interactions among TFs are abundant and that the majority of enhancers have flexible architecture. We show that several families of transposable elements disproportionally overlap with enhancers with combinatorial patterns, suggesting that these transposable element families play an important role in the evolution of combinatorial regulation.
INTRODUCTION
In higher eukaryotes, transcription factors (TFs) rarely operate by themselves, but rather directly or indirectly interact with specific partner TFs or chromatin regulators when binding to enhancers. It has been estimated that roughly 75% of all metazoan TFs heterodimerize with other factors (1). Classical examples of combinatorial TF regulation include the paradigmatic ‘even-skipped stripe 2’ enhancer for body patterning in fly (2) (involving 7 TFs and 34 sites in a 1.7-kb region), the endo16 gene enhancer for endoderm specification in sea urchin (3) (involving 19 TFs and 56 sites in a 2.2-kb region), the Myf5 gene enhancer for muscle development in mouse (4) and the Ifng gene enhancer for the production of interferon gamma in human and mouse (5) (involving 6 TFs and 4 sites in a 55-bp region). Our current knowledge about combinatorial regulation, including rules governing the molecular architecture, evolutionary, spatial and temporal dynamics of enhancers, has relied heavily on studies of these classical enhancers (6,7).
The rapid accumulation of ChIP-Seq data has provided genome-wide occupancy maps for a large number of TFs. By clustering these TF occupancy maps, several recent studies have uncovered hundreds of genomic loci that are co-occupied by multiple TFs in various species and cell types (8–12), suggesting the abundance of combinatorial regulation. However, given the number of TFs in mammalian genomes [∼2,000, (13)], our current knowledge represents only the tip of the iceberg. On the technical side, clustering-based approaches to finding combinatorial TF occupancy patterns have a few shortcomings. First, most analyses use binary presentation of binding peaks, which makes them vulnerable to noise in ChIP-Seq data. Second, because most combinatorial regulatory events occur at enhancers, focusing enhancers will enhance the signal-to-noise ratio. So far most clustering studies have not incorporated such a constraint.
The discovery of unique chromatin signatures associated with enhancers greatly facilitates enhancer mapping without knowledge about the locations of individual TFs (14–16). In addition, such an approach is well suited for finding cell- and developmental-specific enhancers and providing information about enhancer action in the native genomic context. Given the increasing abundance of TF and chromatin modification ChIP-Seq data, a better approach to finding combinatorial patterns would be analyzing multiple TF ChIP-Seq data sets using enhancers defined by chromatin signatures as the genomic location constraint. An advantage of such an approach is the reduction of spurious clusters of TF peaks at non-enhancer sites and presumably non-functional.
We propose a novel probabilistic algorithm to discover frequent combinatorial occupancy patterns (FCOPs) involving multiple TFs at enhancers, taking into account noise in both types of ChIP-Seq data. Our method differs from previous DNA-motif-centered approaches by directly using ChIP-Seq data and thus avoiding complications associated with DNA motif analysis (e.g. motif quality, the need for binding site cutoff). To our best knowledge, this is the first principled approach to integrating TF occupancy and chromatin modification ChIP-Seq data to study combinatorial TF interactions.
By applying our algorithm to a set of 108 TFs in four human cell types, we identify a number of combinatorial TF occupancy patterns that occur frequently in the genome. Additional analyses of identified FCOPs reveal that cell–type-specific TF interactions are abundant and that the majority of enhancers have flexible architecture. In addition, we show that several families of transposable elements (TEs) play an important role in the evolution of complex enhancers occupied by multiple TFs.
MATERIALS AND METHODS
Discover FCOP of multiple TFs by probabilistic frequent itemset mining of uncertain data
Our method borrows idea from frequent itemset mining (FIM) (17). In FIM, customers’ transaction data were collected. Each transaction contains a list of products that are called items. FIM discovers customer buying habits by finding associations between different items that customers place in their ‘shopping baskets’. An itemset is frequent when it occurs in a minimal number of transactions. Here we equate enhancers to transactions and the set of TF binding sites in an enhancer to the itemset. By this analogy, the problem of identifying FCOPs becomes the problem of identifying frequent itemsets. To deal with noise in ChIP-Seq data, we use occurrence probabilities of Transcription Factor Binding Site (TFBSs) and enhancers in our framework. Traditional FIM does not take into account uncertainty associated with transactions and items. Doing so gives rise to an uncertain transaction database, in which the support of an itemset is uncertain and is defined by a discrete probability distribution function. We introduce a novel framework to mine such a probabilistic transaction database.
Problem definition
Given are a set of ‘N’ enhancers predicted by CSI-ANN (18),  , each of which has a probability of being a true enhancer,
, each of which has a probability of being a true enhancer,  , and genome-wide binding peaks of a set of ‘M’ TFs identified by ChIP-Seq,
, and genome-wide binding peaks of a set of ‘M’ TFs identified by ChIP-Seq,  , respectively. For a TF binding peak tj in enhancer ei, we use
, respectively. For a TF binding peak tj in enhancer ei, we use  to denote the binding probability of the TF to the enhancer. For a given set of TFs,
to denote the binding probability of the TF to the enhancer. For a given set of TFs,  , whose peak centers fall within the enhancer, ei, we consider the itemset
, whose peak centers fall within the enhancer, ei, we consider the itemset  as being supported by the enhancer ei. Given a minimum support threshold, minSup, the goal of the algorithm is to exhaustively search for non-redundant frequent combinatorial TF occupancy patterns
as being supported by the enhancer ei. Given a minimum support threshold, minSup, the goal of the algorithm is to exhaustively search for non-redundant frequent combinatorial TF occupancy patterns 
 , whose frequentness probabilities satisfy a given threshold ‘α’.
, whose frequentness probabilities satisfy a given threshold ‘α’.
Probability calculation for enhancers and TF binding peaks
In traditional FIM, it is assumed that both transactions and items of a transaction occur with certainty. However, in our case, the information captured in transactions and items has some degree of uncertainty because the existence of an enhancer and/or a TF binding peak is inferred from ChIP-Seq data. To deal with such uncertainties, we assign a probability to each enhancer predicted by CSI-ANN and each TF binding peak. Because the CSI-ANN algorithm outputs probabilities of predicted enhancers, it is straightforward to use these probabilities directly. For TF ChIP-Seq data, given its better performance compared with other peak callers, we first use MACS with its default parameter setting to call binding peaks (19). To compute the probability of a TF binding peak, we use min-max normalization to transform the MACS fold enrichment score into a range of [0.5, 1]. We choose this range because peaks called using default MACS parameter are relatively strong peaks. We also tested the performance of our algorithm with the normalization ranges of [0.3, 1] and [0.7, 1]. Our result shows that the performance is not sensitive to the choice of normalization range (Supplementary Figure S3). To avoid peaks with extremely high fold enrichment that could skew the normalized probability scores, we truncate the fold enrichment score at 95 percentile and set the probability score of such peaks to 1.
Algorithm to compute the frequentness probability of a combinatorial pattern
Denote X as a combinatorial pattern observed in a set of enhancers.  is the probability of the pattern having support k, k ∈ {0, … , N} and
is the probability of the pattern having support k, k ∈ {0, … , N} and  is the probability of the pattern having a support at least k. X is considered as a frequent pattern when
is the probability of the pattern having a support at least k. X is considered as a frequent pattern when  . We consider two types of uncertainties: those associated with enhancer predictions and those associated with TF binding peak calls. If we only consider the uncertainties of TF binding peaks in an enhancer (i.e. enhancer is certain), the probability of a combinatorial pattern X supported by an enhancer ei can be calculated as follows:
. We consider two types of uncertainties: those associated with enhancer predictions and those associated with TF binding peak calls. If we only consider the uncertainties of TF binding peaks in an enhancer (i.e. enhancer is certain), the probability of a combinatorial pattern X supported by an enhancer ei can be calculated as follows:
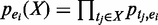 . Considering both types of uncertainties, the overall probability of pattern X having exactly k support can be calculated as
. Considering both types of uncertainties, the overall probability of pattern X having exactly k support can be calculated as 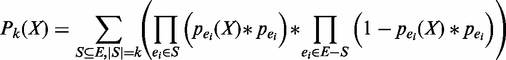
 is the probability of being a true enhancer.
is the probability of being a true enhancer. , which can be computed by the following equation.
, which can be computed by the following equation. 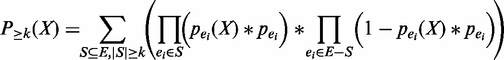
 by brute-force enumeration is inefficient. The time complexity is exponential with respect to the number of transactions. Here we adopt a dynamic programming-based algorithm first proposed by Bernecker et al. (20) to compute the frequentness probability recursively. Briefly, define
by brute-force enumeration is inefficient. The time complexity is exponential with respect to the number of transactions. Here we adopt a dynamic programming-based algorithm first proposed by Bernecker et al. (20) to compute the frequentness probability recursively. Briefly, define 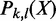 as the probability that k of l enhancers contains pattern X and
as the probability that k of l enhancers contains pattern X and 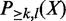 as the probability that at least k of l enhancers contains the pattern. Then,
as the probability that at least k of l enhancers contains the pattern. Then, 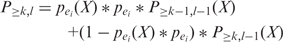
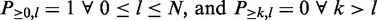
Starting from Equation (4), we can recursively calculate  using Equation (3) till k = minSup, l = N. By definition, the initial values of the dynamic programming matrix are
using Equation (3) till k = minSup, l = N. By definition, the initial values of the dynamic programming matrix are  and
and  . Using this dynamic programming scheme, the computation of the frequentness probability requires at most O(N*minSup) = O(N) time and at most O(N) space.
. Using this dynamic programming scheme, the computation of the frequentness probability requires at most O(N*minSup) = O(N) time and at most O(N) space.
Automatic determination of pattern-specific minimal support threshold
Because different TFs have different numbers of binding sites in the genome, it is expected that patterns involving TFs with more binding sites have more support than patterns involving TFs with fewer binding sites. Therefore, a universal minimal support is not appropriate for computing frequentness probability. Instead, we determine pattern-specific minimal support thresholds that have the same frequentness probability in randomized input data. Such a probability is analogous to a P-value. In this sense, all pattern-specific minimal support thresholds are ‘normalized’ to have a P ≤ 0.01. We generate a set of permutated background transactions based on the binding frequencies of the specific TFs involved in a pattern. We do so by randomly redistributing the peaks of a TF across the set of enhancers. In this way, the number of binding peaks for each TF is unchanged in the permutated data, but the correlation among TFs is destroyed. For a given pattern and a range of minimal support thresholds, we then compute a set of frequentness probabilities in the permutated data as the P-values. We pick the final pattern-specific minimal support threshold as the one that gives a P-value of 0.01. As an example, minimum support thresholds for pairwise patterns calculated this way are shown in Supplementary Figure S4. We also calculated minimum support thresholds for higher-order patterns.
See Supplementary Methods for the rest of method descriptions.
RESULTS
A large fraction of enhancers are occupied by multiple TFs
Using CSI-ANN (18) and cell–type-specific histone modification ChIP-Seq data, we predicted 16 128, 23 731, 23 586 and 3 1327 enhancers in GM12878, K562, HepG2 and H1 cells, respectively. This set of predictions has high quality, as roughly 70% of them overlap with at least one of three other genomic marks for enhancers: distal DHS, sequence conservation and distal p300 site (Supplementary Figure S1).
To assess the extent of combinatorial TF binding at enhancers, we overlapped TF binding peaks with the set of predicted enhancers. We obtained ChIP-Seq data from ENCODE for 62, 65, 44 and 39 TFs for GM12878, K562, HepG2 and H1 cells, respectively (Supplementary Figure S2 andSupplementary Table S1). Figure 1A shows the cumulative distributions of enhancers that contain various number of distinct TF binding peak(s) within the 1 kb enhancer window. As can be seen, 61, 69, 72 and 39% of enhancers are occupied by at least two TFs for GM12878, K562, HepG2 and H1 cells, respectively, suggesting that combinatorial binding is prevalent.

Combinatorial occupancy of enhancers by multiple transcription factors. (A) Cumulative distribution of enhancers overlapping with multiple TF peaks. (B) Overview of our method to identify frequent combinatorial TF occupancy patterns using probabilistic FIM.  , probability of enhancer i.
, probability of enhancer i.  , probability of binding peak of TF
, probability of binding peak of TF  in enhancer
in enhancer  . X, frequent combinatorial occupancy pattern. P ≥ minSup(X), frequentness probability of pattern X with a minimal support minSup. α, frequentness probability threshold.
. X, frequent combinatorial occupancy pattern. P ≥ minSup(X), frequentness probability of pattern X with a minimal support minSup. α, frequentness probability threshold.
Method overview
We introduce a probabilistic algorithm for identifying frequent combinatorial occupancy patterns by multiple TFs at enhancers, termed FCOP in this study (Figure 1B). Our method is motivated by the concept of FIM (21). However, unlike traditional FIM, our method considers the probabilities of both transactions and items as a way to deal with uncertainties in ChIP-Seq data. Our method has the following three components: (i) calculation of probabilities associated with enhancers (transactions) and TF binding peaks (items); (ii) automatic determination of pattern-specific minimum support threshold; and (iii) calculation of frequentness probability of candidate FCOPs using an uncertain transaction database and dynamic programming. The input data consists of genome-wide location information for enhancers and multiple TFs and probability values that are associated with each type of sequence. The only adjustable parameter of our method is the frequentness probability threshold for frequent combinatorial patterns, α. A higher α value will give rise to a set of predictions with higher specificity but lower sensitivity. To pick a default value for the parameter, we ran our method with a range of α values. We found that α value of 0.5 gives a balanced sensitivity and fraction of supported predictions (Supplementary Figure S5). This default value was used for the following analyses. Software implementing our method is freely available to academic use on request.
Performance comparison with alternative algorithms
A couple of groups have used traditional FIM to identify frequent TF combinatorial patterns (22,23). Both approaches used TF binding sites defined by DNA motif scan instead of ChIP-Seq peaks as items. For transactions, Morgan et al. used 100-bp windows across the genome and Sun et al. used a contiguous DNA sequence that contain binding sites of all TFs under consideration for a given pattern. No confidence measure for either TF peaks or enhancers was used in either previous studies. We compared the performance of traditional FIM and our method using Receiver Operating Characteristic (ROC) Curve. To evaluate the performance of the methods, we manually curated a set of gold standard TF interactions identified using experimental protocols. To make the comparison meaningful, we used the same set of transactions and items as the input, i.e. enhancers and TF binding peaks described earlier in the text. As shown in Figure 2A, our method has significantly higher area under the curve values than the traditional FIM [all P < 2.2 × 10−16, statistical test using the method of DeLong et al. (24)]. We note that the area under the curve values in these plots are the lower bounds of the actual values because of the limited coverage of the gold standard set of interactions.
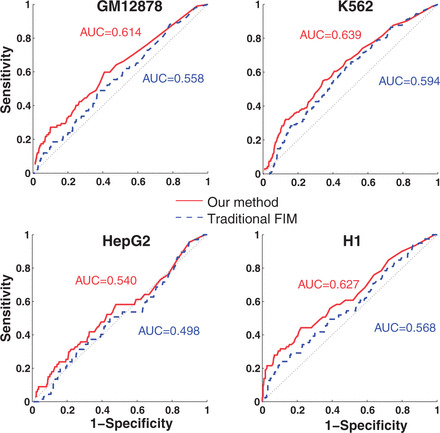
ROCs of our and traditional FIM-based methods. ROC curves are computed using the set of gold standard interactions.
Predicted FCOPs in four cell types
Using the default frequentness probability threshold of 0.5, we discovered 320, 300, 194 and 62 FCOPs in GM12878, K562, HepG2 and H1 cells, respectively. The fraction of TFs involved in FCOPs ranges from 35.5% for GM12878 cell to 70.4% for HepG2 cell. Likewise, the fraction of enhancers that support FCOPs ranges from 30.1% for K562 cell to 67.7% for HepG2 cell (Table 1). On average, each FCOP is supported by 1025, 1086, 1062 and 991 enhancers in GM12878, K562, HepG2, and H1 cells, respectively (Supplementary Table S4). These numbers are much higher than the minimum numbers of support used during the FCOP search, suggesting that the discovered FCOPs are not due to random chance (Supplementary Figure S6).
Summary statistics of predicted combinatorial TF patterns in four cell types
| Statistics . | GM12878 . | H1 . | HepG2 . | K562 . |
|---|---|---|---|---|
| Number of predicted patterns | 320 | 62 | 194 | 300 |
| Number of supported pairwise interactions (%) | 109 (5.8) | 80 (10.8) | 68 (7.2) | 166 (8.0) |
| Number of supported patterns (P-value) | 183 (0) | 21 (5.9E-9) | 35 (4.0E-9) | 100 (8.2E-59) |
| Number of TF pairs, triplets and quadruplets | 38, 210, 72 | 61, 1, 0 | 111, 79, 4 | 137, 154, 9 |
| Number of TFs in patterns (%) | 22 (35.5) | 21 (53.9) | 31 (70.4) | 41 (63.1) |
| Number of enhancers in patterns (%) | 7076 (56) | 13391 (64.6) | 13838 (67.7) | 9073 (30.1) |
| Statistics . | GM12878 . | H1 . | HepG2 . | K562 . |
|---|---|---|---|---|
| Number of predicted patterns | 320 | 62 | 194 | 300 |
| Number of supported pairwise interactions (%) | 109 (5.8) | 80 (10.8) | 68 (7.2) | 166 (8.0) |
| Number of supported patterns (P-value) | 183 (0) | 21 (5.9E-9) | 35 (4.0E-9) | 100 (8.2E-59) |
| Number of TF pairs, triplets and quadruplets | 38, 210, 72 | 61, 1, 0 | 111, 79, 4 | 137, 154, 9 |
| Number of TFs in patterns (%) | 22 (35.5) | 21 (53.9) | 31 (70.4) | 41 (63.1) |
| Number of enhancers in patterns (%) | 7076 (56) | 13391 (64.6) | 13838 (67.7) | 9073 (30.1) |
A TF set is considered to be supported by known TF interactions if any of the pairwise interactions between two TFs in the TF set was supported by known TF interactions. P-values are calculated using binomial distribution.
Summary statistics of predicted combinatorial TF patterns in four cell types
| Statistics . | GM12878 . | H1 . | HepG2 . | K562 . |
|---|---|---|---|---|
| Number of predicted patterns | 320 | 62 | 194 | 300 |
| Number of supported pairwise interactions (%) | 109 (5.8) | 80 (10.8) | 68 (7.2) | 166 (8.0) |
| Number of supported patterns (P-value) | 183 (0) | 21 (5.9E-9) | 35 (4.0E-9) | 100 (8.2E-59) |
| Number of TF pairs, triplets and quadruplets | 38, 210, 72 | 61, 1, 0 | 111, 79, 4 | 137, 154, 9 |
| Number of TFs in patterns (%) | 22 (35.5) | 21 (53.9) | 31 (70.4) | 41 (63.1) |
| Number of enhancers in patterns (%) | 7076 (56) | 13391 (64.6) | 13838 (67.7) | 9073 (30.1) |
| Statistics . | GM12878 . | H1 . | HepG2 . | K562 . |
|---|---|---|---|---|
| Number of predicted patterns | 320 | 62 | 194 | 300 |
| Number of supported pairwise interactions (%) | 109 (5.8) | 80 (10.8) | 68 (7.2) | 166 (8.0) |
| Number of supported patterns (P-value) | 183 (0) | 21 (5.9E-9) | 35 (4.0E-9) | 100 (8.2E-59) |
| Number of TF pairs, triplets and quadruplets | 38, 210, 72 | 61, 1, 0 | 111, 79, 4 | 137, 154, 9 |
| Number of TFs in patterns (%) | 22 (35.5) | 21 (53.9) | 31 (70.4) | 41 (63.1) |
| Number of enhancers in patterns (%) | 7076 (56) | 13391 (64.6) | 13838 (67.7) | 9073 (30.1) |
A TF set is considered to be supported by known TF interactions if any of the pairwise interactions between two TFs in the TF set was supported by known TF interactions. P-values are calculated using binomial distribution.
We further corroborated our predictions using evolutionary conservation and known experimentally derived TF interactions. Interestingly, for all four cell types, a large portion of the frequent TF patterns are supported by enhancers that are significantly more conserved than the full set of enhancers in the genome (P < 0.01, hypergeometric test, Supplementary Figure S7). For instance, 20.4% of enhancers that support FCOPs in GM12878 cell are more conserved than the full set of enhancers in this cell type. These fractions are 34.8%, 35.3% and 50% for K562, HepG2 and H1 cells, respectively. This higher level of conservation is likely due to the requirement of conserving multiple TF binding to the enhancers. Besides a higher conservation level, all four sets of discovered patterns are significantly enriched for known TF protein–protein interactions (P < 0.05, one-sided binomial test) (Table 1), providing additional supporting evidence for the discovered patterns.
Cell–type-specific TF interactions are common
Cell–type-specific interactions among TFs play a critical role in differential gene expression (25). But systematic investigation of this important issue is limited. Taking advantage of our set of predicted FCOPs, we asked to what extent they are cell–type-specific. For simplicity, we focused on pairwise interactions within FCOPs. We first expanded predicted combinatorial patterns into all possible TF pairs. In total we obtained 668 frequent TF pairs in the four cell types. To avoid complication due to missing data, we focused on the set of 54 TFs that are shared by at least two cell types in the ChIP-Seq data. There are 14, 20 and 20 TFs that are shared by 4, 3 and 2 cell types, respectively (Supplementary Figure S2). Among these shared TFs, we predicted 282 interactions that occur in the FCOPs. Only 44 pairs (15.6%) are shared by two cell types and no pair is shared by >2 cell types. For the shared pairs, they are supported by strong evidence of co-occurrence frequencies in the relevant cell types. For instance, the co-occupancy by JunD and REST is observed at 11.9 and 3.8% of enhancers that support the respective FCOPs in K562 and HepG2 cells. In stark contrast, co-occupancy by the same two factors is not frequently observed at enhancers in GM12878 and H1 cells (Figure 3). By the same token, for the unique pairs, they are supported by the lack of co-occupancy in cell types in which no interactions are predicted (Supplementary Figure S8).
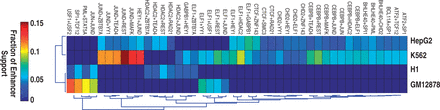
The majority of TF interactions are cell–type-specific. Heat map view of 44 TF interactions that are shared by at least two cell types. Color indicates the fraction of all enhancers in the genome that support a given TF pair.
Even for TF pairs that occur in more than one cell types, the sets of target genes co-regulated by the TF pairs in different cell types may differ for multiple reasons, such as relative arrangement of the two TFs, additional regulators that may be involved and different chromatin context of the involved enhancers. Thus, we asked to what extent genes regulated by the same TF pairs are involved in the same biological process. We performed Gene Ontology enrichment analysis on the target genes of the enhancers supporting 44 TF pairs shared between 2 cell types. We found 21 TF pairs (47%) whose target gene sets do not have any shared GO biological process terms (Supplementary Table S5). In other words, although 47% of the TF pairs are shared by two cell types, genes controlled by them have different functions in the two cell types.
In summary, our result suggests that pairwise TF interactions are fairly dynamic across cell types. Even for TF interactions that occur in multiple cell types, the sets of co-regulated genes could differ substantially in different cell types, leading to diverse regulatory outputs.
The majority of combinatorial patterns have flexible architecture
The spacing and arrangement of TF binding sites in an enhancer affects its regulatory activity, which is known as the cis-regulatory grammar of enhancers. Two models of enhancer architecture have been proposed based on a number of studies. At one extreme, the enhanceosome model postulates that a strict pattern of TF binding site arrangement is required for proper enhancer function (26,27). A well-known example of this model is the interferon beta gene (IFN-β) in which there are fixed binding order and site spacing among the six TFs, ATF-2, c-Jun, IRF-3, IRF-7, p50 and RelA (5). On the other hand, the billboard model states that (28) binding sites in enhancers are flexibly disposed without a strictly defined overall architecture. Many developmental enhancers have such billboard features (29). A well-known example of billboard enhancer is the even-skipped stripe 2 enhancer for body patterning in fly (2).
To better understand the relative abundance of enhancers belonging to each model and the general architectural features of enhancers, we conducted a couple of systematic investigations, taking advantage of our set of predicted FCOPs.
We first asked what fraction of our combinatorial patterns involves TFs with preferred binding site spacing. To this end, we first performed de novo motif finding for each TF using its ChIP-Seq data (see Supplementary Methods). Next, using the set of motifs and the SPAMO tool (30), we identified TF pairs in combinatorial patterns that have a preferred binding site distance that is statistically overrepresented in the set of enhancers supporting the combinatorial patterns. Of the 179 frequent TF pairs in GM12878 cell, 31 of them (17.3%) have preferred binding site distance (SPAMO P < 0.05). These numbers are 101 of 279 (36.2%), 80 of 190 (42.1%) and 26 of 64 (40.6%) for K562, HepG2 and H1 cells, respectively (Figure 4A, Supplementary Table S6). Most TF pairs have only one preferred distance and 95% of the binding site distances are shorter than 126 bp (Supplementary Figure S9). The short distance between TF pairs suggests physical interactions among them. For all TF pairs with preferred binding distances, 23.3% are supported by known TF physical interactions, compared with 16.4% for TF pairs without preferred binding site distance. Taken together, our result suggests that the majority of TFs in combinatorial patterns do not have preferred binding site spacing requirement.
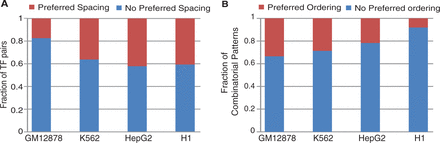
The majority of enhancers do not have strict architectural requirements. (A) Fraction of frequent TF pairs that have preferred binding site spacing in enhancers. Preferred binding site spacing is determined using the SPAMO tool. (B) Fraction of frequent combinatorial patterns in which member TFs have preferred binding order in the enhancers.
Besides preferred binding site distance, we also investigated preferred binding order among TFs in combinatorial patterns. For each pattern, of all possible orderings of the involved TFs, we identified preferred orderings as those that are overrepresented in the set of supporting enhancers (see Supplementary Methods for details). At a P-value cutoff of 0.01, we found that 33.4, 28.7, 21.7 and 8.1% of combinatorial patterns exhibit a preferred binding order for GM12878, K562, HepG2 and H1 cells, respectively (Figure 4B and Supplementary Table S4).
Enhancers belonging to the enhanceosome model have both strict TF binding order and binding site spacing. We next examined what fraction of combinatorial patterns has such stricter architecture. To this end, we considered a pattern belonging to the enhanceosome model if it has a preferred TF binding order and at least one TF pair in the pattern has a preferred binding site distance. In total, we found that 18.4, 17, 15.5 and 3% of the patterns fall into the enhanceosome model in GM12878, K562, HepG2 and H1 cells, respectively (Supplementary Table S4).
In conclusion, our systematic analysis suggests that enhancers with strict architecture only accounts for a small fraction. Both the binding site distance and order of arrangement among the bound TFs are flexible for the majority of complex enhancers that involve multiple bound TFs.
Many combinatorial patterns have significant overlap with TEs
TEs in the human genome are significantly associated with TF binding sites. In several cases their expansion in the genome led to a substantial rewiring of the regulatory network (31–34). However, almost all studies so far focused on binding sites of individual TFs and little is known about the extent of overlap between TEs and combinatorial TF binding sites. To address this issue, we searched for TEs that significantly overlap with FCOPs. We examined 29 families of TEs belonging to four major classes, DNA transposon, long-terminal repeat (LTR) retrotransposon, long interspersed element and short interspersed element. When compared with all enhancers in the genome, we found a remarkable enrichment of a number of TE families among enhancers that support FCOPs (P < 0.01, hypergeometric test, Supplementary Table S4). As an example, we found that the combinatorial pattern [NR2F2, STAT5A, TAL1] significantly overlaps with the ERVL family of LTR retrotransposon (Figure 5A and B). Figure 5C summarizes the fractions of combinatorial patterns that significantly overlap with the four major classes of TEs. For both K562 and H1 cells, LTR retrotransposons overlap with the largest fractions of FCOPs. For HepG2, all four classes of TEs contribute roughly equal fraction of overlap with FCOPs. Besides the most frequently overlapping TEs, it is also worth knowing which TF combinations most frequently overlap with TEs. The top three FCOPs that have most significant overlap with TEs are [JUND, TAL1, TEAD4], [CEBPB, TAL1, TEAD4], [STAT5, TAL1, TEAD4] for K562 cell, [CEBPB, FOXA1, HNF4A], [FOXA1, FOXA2, HNF4A], [HDAC2, HNF4A, HNF4G] for HepG2 cell and [BCL11A, SP1], [NANOG, SP1], [NANOG, TCF12] for H1 cell.
![Overlap between combinatorial patterns and repetitive elements. (A) Three examples of overlap between the TFs NR2F2, STAT5A, TAL1 and the ERVL transposable elements. For TFs, ChIP-Seq peaks are shown. (B) Composite view of 1233 K562 enhancers supporting the combinatorial pattern [NR2F2, STAT5A, TAL1] and their overlap with 111 ERVL family of transposable elements. For each TF, the average fold enrichment values at each position in the 1 kb enhancer window are plotted. For TE, the number of overlapped ERVL sequences at each position in the 1 kb enhancer window is plotted. (C) Fraction of combinatorial patterns that overlap with four major classes of transposable elements. DNA, DNA transposon; LTR, long-terminal repeat retrotransposon; LINE, long interspersed element; SINE, short interspersed element. Inset, breakdown of overlap into TE families.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/nar/42/4/10.1093_nar_gkt1105/6/m_gkt1105f5p.gif?Expires=1750225727&Signature=T10gUu5XGCpd1GbcbYO-2By9DgfVr2xpcKHXd4wO3MgGJ3WOuLco6uaOW-~bMr2dewDnxc1DOU1JZkvCzZCZp7oJ3EOw-e79QTOUE9CSBw8E1oFtff~PyWzNjeFlvVIn6TqteCH9sO6USNImclejp0zg~hExpScBA7btaTEU6UlftDnHkT5XSwuEDHFlDeuDsvOp85ZhGLbqdXbZbKEmGJyE3K5uVPM6q-5LDD4DCbgD67Pu7asApS24ztTQr0j9jnBPPCw36I319LbLiAZMKYvLlXA7xIhv9vn0QZtKIiv5ijL~z9LEbwbm2pXIcNCn21QO2bjnoLXLi2tWv5SUIg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Overlap between combinatorial patterns and repetitive elements. (A) Three examples of overlap between the TFs NR2F2, STAT5A, TAL1 and the ERVL transposable elements. For TFs, ChIP-Seq peaks are shown. (B) Composite view of 1233 K562 enhancers supporting the combinatorial pattern [NR2F2, STAT5A, TAL1] and their overlap with 111 ERVL family of transposable elements. For each TF, the average fold enrichment values at each position in the 1 kb enhancer window are plotted. For TE, the number of overlapped ERVL sequences at each position in the 1 kb enhancer window is plotted. (C) Fraction of combinatorial patterns that overlap with four major classes of transposable elements. DNA, DNA transposon; LTR, long-terminal repeat retrotransposon; LINE, long interspersed element; SINE, short interspersed element. Inset, breakdown of overlap into TE families.
When broken down into individual TE families, for each cell type, the top three TE families that overlap with most FCOPs are ERVL, ERV1, L2 for K562 cell, Alu, ERVL, L1 for HepG2 cell and ERV1, ERVL-MaLR, ERVL for H1 cell (Figure 5C inset). This result suggests that ERV families overlap with a disproportionate fraction of combinatorial binding patterns. ERV (endogenous retrovirus) is a major family of LTR retrotransposons. They are thought to have played an important role in the evolution of mammalian genomes. Among the four cell types, H1 cell stands out in that all TEs that overlap with combinatorial patterns belong to ERV families, suggesting the prominent role of ERVs in shaping the transcriptional regulation network of embryonic stem cells.
DISCCUSSION
Our method integrates both histone modification and TF ChIP-Seq data in a probabilistic framework. The histone modification data are used to generate constraints in the form of enhancers. Furthermore, the histone modification signature used here has been shown to be associated with active enhancers (16,35). Thus, by focusing on combinatorial TF peaks in active enhancer regions, we reduce the chance of finding spurious clusters of TF peaks in the genome. To evaluate the added benefit of the histone modification data, we ran our algorithm by replacing the enhancers with moving windows of the same size across the genome. We found that the performance decreased significantly (Supplementary Figure S10).
An alternative to our FIM-based approach is clustering analysis. It has been used to conduct joint analysis of ChIP-Seq peaks of multiple TFs (8,9,11). The advantage of clustering analysis is its relative simplicity. However, they do not directly address the noise in the underlying ChIP-Seq data. Second, for most clustering algorithms, determining the number of clusters is a difficult problem. Finally, the statistical significance of resulting clusters is typically not assessed in clustering analysis. In comparison, our method addresses all three issues. It treats ChIP-Seq data probabilistically. It is deterministic in terms of number of discovered patterns. Finally, it determines the statistical significance of candidate frequent patterns.
By analyzing a compendium of 108 TF ChIP-Seq data sets in four cell types, we found that the majority of enhancers have flexible architecture in terms of the arrangement and spacing of constituent TF binding sites. Among the four cell types, we found that embryonic stem cell (H1), rather than the terminally differentiated cells, has the largest fraction of enhancers with flexible architecture. This is reminiscent of the observation in fly that many developmental enhancers tend to have a more flexible architecture than enhanceosome (29). In this sense, the architectural difference may reflect different functional requirements of the two classes of enhancers. Enhanceosomes may represent a type of regulatory switches that are mainly responsible for generating gene expression patterns that are relatively simple, whereas enhancers with flexible architecture may be responsible for generating complex patterns of expression such as those during development.
We demonstrate that LTR/ERV retrotransposons overlap with a disproportionate fraction of combinatorial TF binding regions, especially in H1 embryonic stem cells. This is interesting given that ERV elements have been observed to contribute to the rewiring of transcriptional regulatory networks in ESCs and placenta (36–38). The unusual high percentage of ERV-derived combinatorial patterns in H1 cells is likely a consequence of the permissive chromatin state found in ESCs (39,40). It has been suggested that the manipulations that were initially exerted by the ancestral viruses on their hosts to bypass these antiviral control mechanisms have also facilitated their co-option into enhancer elements (41). Along this line, it has been shown that stem cell potency fluctuates with endogenous retrovirus activity in mouse (42).
In summary, we introduce a powerful computational method for uncovering combinatorial interactions among TFs. As the amount of genome-wide localization data continues to accumulate for various regulatory proteins, our method will prove increasingly useful for dissecting combinatorial gene regulation by the action of TFs as well as other types of regulatory proteins.
FUNDING
Funding for open access charge: National Institutes of Health [HG006130 to K.T.].
Conflict of interest statement. None declared.
ACKNOWLEDGEMENT
The authors thank members of the Tan laboratory for helpful discussion. They also thank David Eichmann, Lucas Van Tol and the University of Iowa Institute for Clinical and Translational Science for providing computing support.




Comments