A note on periodicity of long-term variations of optical continuum in active galactic nuclei

Lu, Kai-Xing; Li, Yan-Rong; Bi, Shao-Lan; Wang, Jian-Min

doi:10.1093/mnrasl/slw062

Abstract

Graham et al. found a sample of active galactic nuclei (AGNs) and quasars from the Catalina Real-time Transient Survey (CRTS) that have long-term periodic variations in optical continuum. The nature of the periodicity remains uncertain. We investigate the periodic variability characteristics of the sample by testing the relations of the observed variability periods with AGN optical luminosity, black hole mass and accretion rates, and find no significant correlations. We also test the observed periods in several different aspects related to accretion discs surrounding single black holes, such as the Keplerian rotational periods of 5100 Å photon-emission regions and self-gravity dominated regions and the precessing period of warped discs. These tests shed new lights on understanding AGN variability in general. Under the assumption that the periodic behaviour is associated with supermassive black hole binary systems in particular, we compare the separations (⁠|${\scr {D}}_{\bullet }$|⁠) against characteristic radii of broad-line regions (⁠|$R_{\scriptscriptstyle {\rm BLR}}$|⁠) of the binaries and find |${\scr {D}}_{\bullet }\approx 0.05R_{\scriptscriptstyle {\rm BLR}}$|⁠. This interestingly implies that these binaries have only circumbinary BLRs.

galaxies: active, galaxies: evolution, galaxies: nuclei

INTRODUCTION

The optical and ultraviolet spectra of active galactic nuclei (AGNs) and quasars have been understood profoundly since their discovery. Accretion on to supermassive black holes (SMBHs) located in galactic centres is powering the giant emissions of AGNs and quasars through release of gravitational energy of the infalling gas (Rees 1984). It is well understood that the broad emission lines arise from gas photoionized by accretion discs of SMBHs (Osterbrock & Mathews 1986). According to the hypothesis of supermassive black hole binaries (SMBHBs; Begelman, Blandford & Rees 1980), there should be some AGNs and quasars powered by them at least (Gaskell 1983), manifesting with double-peaked or asymmetric emission lines (Shen & Loeb 2010) and long-term periodic variations (Runnoe et al. 2015). Although there are indeed growing indirect evidence for SMBHBs (see e.g. Yan et al. 2015, based on special characteristic of spectral energy distributions, or Liu, Li & Komossa 2014, based on features of tidal disruption event in galactic centres), identification of them, in particular in sub-parsec scale, is still challenging.

Since long-term monitoring campaigns are extremely time-consuming, only a few AGNs and quasars, such as OJ 287 (Valtonen et al. 2008), PG 1302-102 (Graham et al. 2015a) and PSO J334.2028+01.4075 (Liu et al. 2015), have been found to exhibit long-term periodic (or quasi) variations of a few to ∼10 yr in optical and ultraviolet continuum. A major advance was made recently by Graham et al. (2015b, hereafter G15b), who performed a systematic search for the long-term periodical variations of continuum in quasars covered by the Catalina Real-time Transient Survey (CRTS) and finally identified more than 100 candidates. Periodic variability is generally believed to be a common signature of SMBHBs, but there also exist alternative explanations (Graham et al. 2015a; Li et al. 2016; G15b). The CRTS sample offers an opportunity to test the periodicity and probe the properties of SMBHBs. In this paper, we extend the G15b study to show more statistics of the long-term periodicity. Throughout this work, we assume a standard Λcold dark matter (ΛCDM) cosmology with H₀ = 67 km s⁻¹ Mpc⁻¹, Ω_Λ = 0.68 and Ω_M = 0.32 (Planck Collaboration XXXI 2014).

THE SAMPLE

The CRTS sample consists of 111 quasars with unambiguous observed periods from a few to ∼5 years, as listed in table 1 of G15b. We cross-checked the sample with Sloan Digital Sky Survey (SDSS) data and found available spectra for 90 quasars. Data reduction of the SDSS spectra followed the procedures described in Hu et al. (2008). We measured the 5100 Å luminosity and full width at half-maximum (FWHM) of the broad Hβ and Mg ii lines. We used a relation of L₅₁₀₀ = 0.56L₃₀₀₀ to convert the ultraviolet continuum into 5100 Å (Shen et al. 2008).

Table 1.

Open in new tab

The sample properties. Columns are the objects name, redshifts, optical luminosity, black hole mass, accretion rates, the radii of emitting 5100 Å photons and BLR, and separations of the black hole binaries calculated from Kepler's law, respectively. (The full version is available in a machine-readable form in the online. A portion is shown here for guidance regarding its form and content.)

Object	z	log L₅₁₀₀	log (M_•/M_⊙)	log \|$\dot{\scr {M}}$\|	log (R₅₁₀₀/cm)	log (R_BLR/cm)	log (⁠\|$\scr {D}_{\bullet }/$\|cm)
		(erg s⁻¹)
UM 234	0.729	45.35 ± 0.12	9.19 ± 0.55	−2.28 ± 0.73	15.16 ± 0.54	17.70 ± 0.21	16.54 ± 0.18
SDSS J014350.13+141453.0	1.438	45.65 ± 0.10	9.21 ± 0.53	−1.87 ± 0.71	15.31 ± 0.53	17.87 ± 0.20	16.40 ± 0.17
US 3204	0.954	45.39 ± 0.15	8.95 ± 0.57	−1.74 ± 0.76	15.19 ± 0.57	17.73 ± 0.24	16.40 ± 0.19
SDSS J072908.71+400836.6	0.074	43.53 ± 0.08	7.00 ± 0.52	−0.63 ± 0.68	14.25 ± 0.51	16.72 ± 0.18	15.92 ± 0.17

Object	z	log L₅₁₀₀	log (M_•/M_⊙)	log \|$\dot{\scr {M}}$\|	log (R₅₁₀₀/cm)	log (R_BLR/cm)	log (⁠\|$\scr {D}_{\bullet }/$\|cm)
		(erg s⁻¹)
UM 234	0.729	45.35 ± 0.12	9.19 ± 0.55	−2.28 ± 0.73	15.16 ± 0.54	17.70 ± 0.21	16.54 ± 0.18
SDSS J014350.13+141453.0	1.438	45.65 ± 0.10	9.21 ± 0.53	−1.87 ± 0.71	15.31 ± 0.53	17.87 ± 0.20	16.40 ± 0.17
US 3204	0.954	45.39 ± 0.15	8.95 ± 0.57	−1.74 ± 0.76	15.19 ± 0.57	17.73 ± 0.24	16.40 ± 0.19
SDSS J072908.71+400836.6	0.074	43.53 ± 0.08	7.00 ± 0.52	−0.63 ± 0.68	14.25 ± 0.51	16.72 ± 0.18	15.92 ± 0.17

Table 1.

Open in new tab

The sample properties. Columns are the objects name, redshifts, optical luminosity, black hole mass, accretion rates, the radii of emitting 5100 Å photons and BLR, and separations of the black hole binaries calculated from Kepler's law, respectively. (The full version is available in a machine-readable form in the online. A portion is shown here for guidance regarding its form and content.)

Object	z	log L₅₁₀₀	log (M_•/M_⊙)	log \|$\dot{\scr {M}}$\|	log (R₅₁₀₀/cm)	log (R_BLR/cm)	log (⁠\|$\scr {D}_{\bullet }/$\|cm)
		(erg s⁻¹)
UM 234	0.729	45.35 ± 0.12	9.19 ± 0.55	−2.28 ± 0.73	15.16 ± 0.54	17.70 ± 0.21	16.54 ± 0.18
SDSS J014350.13+141453.0	1.438	45.65 ± 0.10	9.21 ± 0.53	−1.87 ± 0.71	15.31 ± 0.53	17.87 ± 0.20	16.40 ± 0.17
US 3204	0.954	45.39 ± 0.15	8.95 ± 0.57	−1.74 ± 0.76	15.19 ± 0.57	17.73 ± 0.24	16.40 ± 0.19
SDSS J072908.71+400836.6	0.074	43.53 ± 0.08	7.00 ± 0.52	−0.63 ± 0.68	14.25 ± 0.51	16.72 ± 0.18	15.92 ± 0.17

Object	z	log L₅₁₀₀	log (M_•/M_⊙)	log \|$\dot{\scr {M}}$\|	log (R₅₁₀₀/cm)	log (R_BLR/cm)	log (⁠\|$\scr {D}_{\bullet }/$\|cm)
		(erg s⁻¹)
UM 234	0.729	45.35 ± 0.12	9.19 ± 0.55	−2.28 ± 0.73	15.16 ± 0.54	17.70 ± 0.21	16.54 ± 0.18
SDSS J014350.13+141453.0	1.438	45.65 ± 0.10	9.21 ± 0.53	−1.87 ± 0.71	15.31 ± 0.53	17.87 ± 0.20	16.40 ± 0.17
US 3204	0.954	45.39 ± 0.15	8.95 ± 0.57	−1.74 ± 0.76	15.19 ± 0.57	17.73 ± 0.24	16.40 ± 0.19
SDSS J072908.71+400836.6	0.074	43.53 ± 0.08	7.00 ± 0.52	−0.63 ± 0.68	14.25 ± 0.51	16.72 ± 0.18	15.92 ± 0.17

We used the well-established relation between BLR size and AGN 5100 Å luminosity (RL relation; Bentz et al. 2013) to estimate the BLR size

\begin{equation} R_{\scriptscriptstyle {\rm BLR}}\approx 36.3\,\ell _{44}^{0.54}\,{\rm lt\hbox{-}d}, \end{equation}

(1)

where ℓ₄₄ = L₅₁₀₀/10⁴⁴ erg s^{− 1} is the luminosity at 5100 Å. We followed the standard way of estimating BH mass,

\begin{equation} M_{\bullet }=f_{\scriptscriptstyle \rm BLR}\frac{V_{\rm FWHM}^2R_{\scriptscriptstyle {\rm BLR}}}{G}=5.27\times 10^7\,f_{\scriptscriptstyle \rm BLR}V_{3000}^2R_{30}\,\,\mathrm{M}_{\odot }, \end{equation}

(2)

where G is the gravitational constant, |$R_{30}=R_{\scriptscriptstyle {\rm BLR}}/30$| lt-d, V₃₀₀₀ = V_FWHM/3000 km s^{− 1} is the FWHM velocity, and |$f_{\scriptscriptstyle \rm BLR}$| is a constant which includes all the unknown information about the geometry and kinematics of the BLR. The factor |$f_{\scriptscriptstyle \rm BLR}$| is obtained by calibrating equation (2) against SMBH mass obtained from the well known M_• − σ_* relationship in local bulge galaxies. We took |$f_{\scriptscriptstyle \rm BLR}=1.0$| in this paper (Ho & Kim 2014).

Note that equation (2) only applies to local quasars with Hβ emission line (z < 0.7). For high-z quasars, we used the extended relation of equation (2) using Mg ii emission line (Vestergaard & Peterson 2006). We then use the obtained black hole mass to calculate the parameters of accretion discs and extensively explore if the observed long-term periods are related to accretion discs (see Section 3 below).

In Table 1, we list the main properties of the sample. G15b determined the observed periods of the sample by the WWZ–ACF method, which gives a typical uncertainty of 10 per cent for the periods. For the uncertainties of black hole mass estimate, we included the intrinsic scatters of 0.4 dex (Vestergaard & Peterson 2006). For the uncertainties of 5100 Å luminosity L₅₁₀₀, we digitized the light curves from G15b (see their fig. 7) and included the standard deviation of light curves.

Figs 1e–h plot the distributions of the observed periods, 5100 Å luminosities, black hole mass and accretion rates (see Section 3 for a definition). The current sample shows that (1) the period peaks at ∼800 d; (2) the luminosity cover from ∼ 10⁴⁴ erg s^{− 1} to ∼ 10⁴⁷ erg s^{− 1}; (3) the black hole mass at ∼10⁹ M_⊙, but extends to 10¹⁰ M_⊙; and (4) the accretion rate spans from ∼10⁻³ to 10⁻¹. The moderate accretion rates indicate that the objects of the sample are in the regime of standard accretion disc model, which is described by Shakura & Sunyaev (1973).

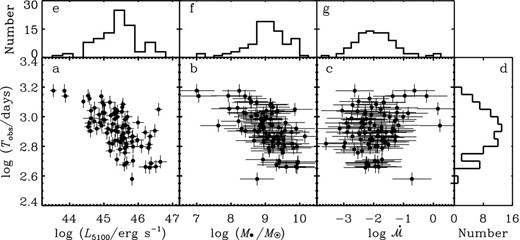
$The observed Tobs in rest-frame versus luminosity (L5100), black hole mass (M•) and accretion rates ($\dot{\scr {M}}$) in panels (a, b, c). The apparent correlations are spurious and caused by the redshift effect (see Section 3.1 for details), panels (d, e, f, g) are the distribution of (Tobs, L5100, M•, $\dot{\scr {M}}$).$

Figure 1.

The observed T_obs in rest-frame versus luminosity (L₅₁₀₀), black hole mass (M_•) and accretion rates (⁠|$\dot{\scr {M}}$|⁠) in panels (a, b, c). The apparent correlations are spurious and caused by the redshift effect (see Section 3.1 for details), panels (d, e, f, g) are the distribution of (T_obs, L₅₁₀₀, M_•, |$\dot{\scr {M}}$|⁠).

Open in new tab Download slide

STATISTICS OF THE PERIODS

As for the accretion discs, we study four characteristic radii and explore if they can account for the long-term periodicity. In the standard accretion disc model, the effective temperature as a function of disc radius is given by

\begin{eqnarray} T_{\rm eff}(R)=\left(\frac{3GM_{\bullet }\dot{M}_{\bullet }}{8\pi R^3\sigma _{_{\rm SB}}}\right)^{1/4} \approx 3.32\times 10^3\,\dot{\scr {M}}^{1/4}M_8^{-1/4}r_3^{-3/4}\,{\rm K},\nonumber\\ \end{eqnarray}

(3)

where |$\sigma _{_{\rm SB}}$| is the Stefan–Boltzman constant, r₃ = R/10³R_g, R_g = 1.5 × 10¹³M₈ cm is the gravitational radius, |$\dot{\scr {M}}=\dot{M}_{\bullet }/L_{\rm Edd}c^{-2}$| is the dimensionless accretion rate, and |$L_{\rm Edd}=1.26\times 10^{38}\left(M_{\bullet }/\,\mathrm{M}_{\odot }\right)\rm erg\,s^{-1}$| is the Eddington luminosity. Here, we neglect the inner boundary condition. The emergent spectra of accretion discs are given by |$L_{\lambda }\propto \int _{R_{\rm in}}^{\infty } B_{\lambda }(T_{\rm eff})R\text{d}R$|⁠, where R_in is the inner radius of the disc and B_λ(T_eff) is the Planck function. This yields the well-known canonic spectra as L_λ ∝ λ^−1/3. It is easy to show that the accretion rate can be expressed by 5100 Å luminosity and black hole mass (Du et al. 2014)

\begin{equation} \dot{\scr {M}}=0.201\left(\frac{\ell _{44}}{\cos i}\right)^{3/2}M_8^{-2}, \end{equation}

(4)

where cos i is the cosine of the inclination angle of the disc. We take cos i = 0.75, which corresponds to the opening angle of the dusty torus.

Correlations with L₅₁₀₀, M_• and |$\dot{\scr {M}}$|

Fig. 1 shows the relation between the rest-frame periods with the 5100 Å luminosities, black hole mass and accretion rates, respectively; apparent correlations can be seen. However, we note that the sample selection is based on both the magnitude limit and the time-span of the monitoring (∼9 years). Since the redshift distribution of the sample spans a wide range of z ∼0–3, the relations of the rest-frame periods with AGN parameters will be significantly distorted by the redshift effect. Specifically, high-z quasars have higher luminosities but smaller rest-frame periods, leading to spurious correlations. We employ partial correlation analysis (see the Appendix) to quantitatively test if the correlations are caused by the redshift effect. The Spearman rank-order coefficients of the correlation between log T_obs and (log L₅₁₀₀, log M_•, |$\log \dot{\scr {M}}$|⁠) are |${\boldsymbol r}=(-0.64, -0.60, 0.14)$|⁠, respectively. The coefficients of the correlation between (log T_obs, log L₅₁₀₀, log M_•, |$\log \dot{\scr {M}}$|⁠) and redshift are |${\boldsymbol r}=(-0.73, 0.81, 0.77, -0.16)$|⁠, respectively. The partial correlation coefficients between log T_obs and (log L₅₁₀₀, log M_•, |$\log \dot{\scr {M}}$|⁠) are |${\boldsymbol r}=(-0.10, -0.09, 0.03)$| with null probabilities of p = (0.08, 0.10, 0.20), respectively. The low values of the partial correlation coefficients confirm that the apparent correlations are spurious. There is no significant correlation between the rest-frame period and optical luminosity, black hole mass and accretion rate.

If the periodicity arises from accretion discs of single black holes, the observed variability period and our correlation analysis provide useful restraints on variability models in accretion discs. For example, Clarke & Shields (1989) proposed a theoretical model based on disc thermal instability and predicted that the continuum variations of AGN obey a relation of P ∝ L^1/2, and the time-scale >100 yr for the high-luminosity AGNs, which is much longer than the observed periods of G15b sample.

On the other hand, under the SMBHB hypothesis, one may expect that the orbital period would depend on the total black hole mass of the system. However, partial correlation analysis shows that there is no correlation between the period (T_obs in rest frame) and measured black hole mass. The intrinsic scatter of black hole mass estimated from the R–L₅₁₀₀ relation is as large as 0.43 dex (e.g. Vestergaard & Peterson 2006). Meanwhile, the possible biases between measured black hole mass and ‘true’ mass may lead to additional scatters (e.g. Shen et al. 2008). It is plausible that the intrinsic correlation between the periods and black hole mass is smeared out due to the large scatter of mass measurements.

Characteristic periods of accretion discs surrounding single black holes

We now turn to calculate the following four characteristic periods of accretion discs surrounding single black holes to test if they can account for the observed periods.

For the standard accretion disc model, the photons with a wavelength λ mainly come from the region with a temperature of T_eff = 2.37 × 10⁸/λ(Å) K (Siemiginowska & Czerny 1989). We thus have the region for 5100 Å photons |$R_{5100}/R_{\rm g}=29.7\dot{\scr {M}}^{1/3}M_8^{-1/3}\lambda _{5100}^{4/3}$| from equation (4), namely,

\begin{equation} \frac{R_{5100}}{R_{\rm g}}=17.4\left(\frac{\ell _{44}}{\cos i}\right)^{1/2}M_8^{-1}\lambda _{5100}^{4/3}, \end{equation}

(5)

where λ₅₁₀₀ = λ/5100Å.

The outer part of accretion discs is optically thick and geometrically thin, dominated by gas pressure. In a pioneering paper, Paczyński (1978) realized that this region is so distant that it is strongly affected by the vertical self-gravity of the disc rather than the central black hole. The self-gravity of the disc is 2πGΣ, while the vertical force of the gravity is given by GM_•R⁻²(H/R). Using the mass density of the outer part of accretion discs (the region C solution in Shakura & Sunyaev 1973)

\begin{equation} \rho =4.38\times 10^{-9}\,\alpha _{0.1}^{-7/10}\dot{\scr {M}}^{11/20}M_8^{-7/10}r_3^{-15/8} {\rm g\,cm^{-3}}, \end{equation}

(6)

we have the Toomre parameter, defined by the ratio of the vertical force of the central black hole to the disc's self-gravity, as

\begin{equation} Q=\frac{M_{\bullet }}{4\pi \rho R^3}=1.10\,\alpha _{0.1}^{7/10}M_8^{-13/10}\dot{\scr {M}}^{-11/20}r_3^{-9/8}, \end{equation}

(7)

where α_0.1 = α/0.1. When Q ≲ 1, the discs become self-gravity dominated. This yields a critical radius of self-gravity as

\begin{equation} \frac{R_{_{\rm SG}}}{R_{\rm g}}=1.09\times 10^3\,\alpha _{0.1}^{28/45}M_8^{-52/45}\dot{\scr {M}}^{-22/45}. \end{equation}

(8)

With two radii of equations (5) and (8), the corresponding Keplerian periods are given by

\begin{equation} T_{5100, {\rm SG}}=2\pi \sqrt{\frac{(R_{5100},R_{\rm SG})^3}{GM_{\bullet }}}, \end{equation}

(9)

where the subscripts refer to the corresponding radii. In addition, to account for the region between R₅₁₀₀ and |$R_{_{\rm SG}}$|⁠, we define an averaged radius as |$\langle R\rangle =\sqrt{R_{5100}R_{_{\rm SG}}}$| and the averaged period as

\begin{equation} \langle T\rangle =2\pi \sqrt{\frac{\langle R\rangle ^3}{GM_{\bullet }}}. \end{equation}

(10)

At last, we can also calculate the characteristic period for warped discs. According to Shakura & Sunyaev (1973), the total mass of the disc within |$R_{_{\rm SG}}$| is

\begin{equation} M_{\rm {disc}}\approx 2\pi R_{_{\rm SG}}^2\Sigma _{_{\rm SG}}\approx 1.42\times 10^5\,\alpha _{0.1}^{-1/45}\ell _{44}^{6/45}M_8^{26/45}\,\,\mathrm{M}_{\odot }, \end{equation}

(11)

where |$\Sigma _{_{\rm SG}}$| is the surface density of the disc at |$R_{_{\rm SG}}$|⁠. The warped discs precess with a typical period

\begin{equation} T_{\rm WD}=2\pi \sqrt{\frac{M_{\bullet }R_{\rm WD}^3}{GM_{\rm {disc}}^2}}, \end{equation}

(12)

where R_WD is typical radius (R_WD = |$R_{_{\rm SG}}$|⁠) of the warped disc (Ulubay-Siddiki, Gerhard & Arnaboldi 2009).

Fig. 2 compares the rest-frame T_obs with T₅₁₀₀, T_SG, T_mean and T_WD in the top panels, and plots their respective ratios in the bottom panels. We find that T_obs is much longer than T₅₁₀₀, but shorter than T_SG, namely T₅₁₀₀ < T_obs < T_SG. This motivates us to compare T_obs with the mean value of rotational periods between R₅₁₀₀ and R_SG. As shown in Fig. 2(g), T_obs is greater than T_mean, implying that T_obs is related to the region between R_SG and 〈R〉 if the observed periodicity arises from an accretion disc surrounding a single black hole. Fig. 2(h) shows that T_obs is much shorter than the period of warped discs driven by the self-gravity torque, so that we can rule out this possibility for the periodicity.

Figure 2.

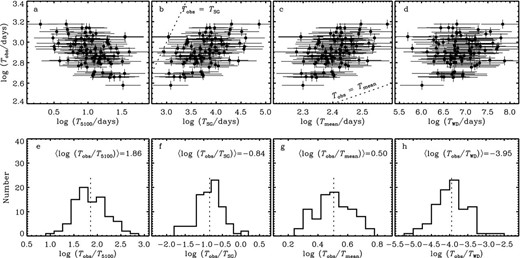
Comparison of observed periods in rest-frame versus the characteristic periods of accretion discs. Panels (a, b, c, d) are the Keplerian periods at the region for 5100 Å photons (T₅₁₀₀), the critical radius of self-gravity (T_SG), averaged radius (T_mean) and the precessing period of warped discs (T_WD) versus observed periods(T_obs), respectively. Their corresponding histograms are shown in panels (e, f, g, h). Vertical dash lines are the average levels.

Open in new tab Download slide

In the next section, under the assumption that the observed periods are associated with SMBHB systems, we discuss several possible processes for the periodicity and calculate the BLR sizes and separations of these SMBHB systems.

SMBHB MODELS

Periodicity explanations

As pointed out by G15b, there exist several plausible processes responsible for the periodicity.

A processing jet. In the sample, by checking the radio band data from the catalogue of VLA-FIRST survey (Chang, Refregier & Helfand 2004), we found that only 13 candidates are radio-loud, indicating that the periodic variations in most candidates are not caused by a precessing jet.
Quasi-periodic oscillation. Abramowicz & Kluźniak (2001) suggested that high-frequency QPOs arise from some type of resonance mechanism. Zhou et al. (2010) showed that the observed time-scales (T) of high-frequency QPOs correlate with black hole mass following T = 6.22 M_•/ (10⁹ M_⊙) d. For G15b sample, the typical value (T ∼ 6.22 d) is much shorter than observed period. On the other hand, as for low-frequency QPOs, Yan et al. (2013) showed that GRS 1915+105 has a mass of ∼12 M_⊙ and exhibits QPO with 1 Hz. If we assume that the period T ∝ M_•, the case of GRS 1915+105 would mean that the period if QPOs of G15b sample, spanning a mass range of 10⁸−10¹⁰M_⊙, lies in a range between ∼100 and 10⁴ d (in observed-frame). This is generally comparable with the range of observed periods in G15b sample.
Periodic accretion. The orbital motion of binaries induces periodic modulation of mass accretion on to each black hole (Farris et al. 2014), which translates into periodic emissions of the accretion discs. The issue about this explanation is that the viscous time of an accretion disc, which reflects the time-scale of its response to a change in mass accretion rate, is generally much longer than the observed periods of the present sample.
Relativistic Doppler boosting. Recently, D'Orazio, Haiman & Schiminovich (2015) proposed an alternative explanation for the periodicity by relativistic Doppler boosting and applied it to the periodic light curve of PG 1302−102. In this model, a large inclination of the binary's orbit is generally required to account for the variation amplitude. This will raise a concern about the obscuration of the outer dusty torus if the dusty torus is coplanar with the binary's orbit.
Warped accretion disc. The accretion discs are warped due to tidal torques if their spin axis is misaligned with the orbital axis of the binaries. The warps precess along with the binary's orbital motion and eclipse some parts of the disc emissions, leading to periodic variations in the disc emissions.

In a nutshell, we can only generally exclude with certainty the possibility of the precessing jet model and high-frequency QPOs for the periodicity. For the other models, we need more observations, in particular spectroscopic data, to test them.

Separations and BLR sizes

Under the assumption that the periodicity arises from a SMBHB system, we now calculate the binary's separation, given with the observed period, and compare it against the BLR size predicted from the R–L relation. Using the Kepler's law of |$\scr {D}_{\bullet }=(GM_{\bullet }T_{\rm obs}^2/4\pi ^2)^{1/3}$| and equation (2), we have the binary's semi-major axis as

\begin{equation} \scr {D}_{\bullet }=\left(\frac{f_{\scriptscriptstyle \rm BLR}}{4\pi ^2}\right)^{1/3}\left(V_{\rm FWHM}^2T_{\rm obs}^{2}R_{\scriptscriptstyle {\rm BLR}}\right)^{1/3}. \end{equation}

(13)

This indicates |$\scr {D}_{\bullet }\propto R_{\scriptscriptstyle {\rm BLR}}^{1/3}$| for given V_FWHM and T_obs (Fig. 3a). We can also rewrite equation (13) into

\begin{equation} \frac{\scr {D}_{\bullet }}{R_{\scriptscriptstyle {\rm BLR}}} =0.07\,f_{\scriptscriptstyle \rm BLR}^{1/3}V_{3000}^{2/3}T_{1}^{2/3}R_{30}^{-2/3}, \end{equation}

(14)

where T₁ = T_obs/year. Fig. 3(b) shows that |$\scr {D}_{\bullet }$| is smaller than |$R_{\scriptscriptstyle {\rm BLR}}$| and, in average, |$\scr {D}_{\bullet }\approx 0.05 R_{\scriptscriptstyle {\rm BLR}}$| in the sample. The FWHM of the |$\log \left(R_{\scriptscriptstyle {\rm BLR}}/\scr {D}_{\bullet }\right)$| distribution is 0.6. This interestingly means that the BLRs of the binary have been merged, but the binary black holes are still corotating.

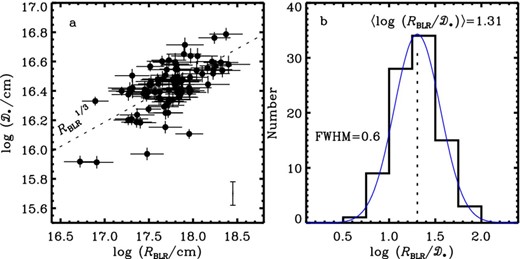
$Comparison of SMBHB separations ($\scr {D}_{\bullet }$) with the sizes of broad-line regions ($R_{\scriptscriptstyle {\rm BLR}}$) in panels (a, b). In panel (a), dotted line is the expected relation. The bar plotted in the right lower corner represents the typical scatters of $\scr {D}_{\bullet }$. In panel (b), blue line is the Gaussian fit to the distribution.$

Figure 3.

Comparison of SMBHB separations (⁠|$\scr {D}_{\bullet }$|⁠) with the sizes of broad-line regions (⁠|$R_{\scriptscriptstyle {\rm BLR}}$|⁠) in panels (a, b). In panel (a), dotted line is the expected relation. The bar plotted in the right lower corner represents the typical scatters of |$\scr {D}_{\bullet }$|⁠. In panel (b), blue line is the Gaussian fit to the distribution.

Open in new tab Download slide

CONCLUSIONS

We have tested the periodicity of long-term optical variations in a sample of AGNs from G15b. The partial correlation analysis shows that the observed periods of G15b sample are uncorrelated with the AGN 5100 Å luminosity, (total) black hole mass and accretion rates. By comparing the observed periods with the characteristic periods of accretion discs surrounding single black holes, we found that the periods generally lie within the Keplerian periods that correspond to the regions between the 5100 Å region and the self-gravity radius. We discussed several existing explanations for the periodicity in the context of SMBHB hypothesis and concluded that further observations (particularly long-term spectroscopic monitoring) are required to test if the periodicity originates from SMBHB systems (e.g. Li et al. 2016). Nevertheless, by assuming that observed periodicity is associated with SMBHB systems, we calculated the SMBHB's separations and found that they are smaller than the sizes of broad-line regions, implying that the binary BLRs have been merged.

We are grateful to the referee for constructive suggestions that significantly improved the manuscript. We thank the IHEP AGN members for useful discussions. This research is supported by NSFC-11173023, −11133006, −11233003, −11273007 and −11573026.

REFERENCES

Abramowicz

M. A.

Kluźniak

W.

2001

A&A

374

L19

Month:	Total Views:
November 2016	1
January 2017	2
February 2017	5
March 2017	3
April 2017	7
May 2017	6
June 2017	8
July 2017	3
August 2017	4
September 2017	2
October 2017	5
November 2017	2
January 2018	2
March 2018	4
April 2018	1
May 2018	2
June 2018	6
July 2018	6
August 2018	1
September 2018	12
November 2018	2
December 2018	4
January 2019	12
February 2019	2
March 2019	12
April 2019	13
May 2019	8
June 2019	11
July 2019	9
August 2019	3
September 2019	16
October 2019	6
November 2019	5
December 2019	7
January 2020	6
February 2020	5
March 2020	3
April 2020	7
June 2020	8
July 2020	2

Article Contents

A note on periodicity of long-term variations of optical continuum in active galactic nuclei

Abstract

INTRODUCTION

THE SAMPLE

STATISTICS OF THE PERIODS

Correlations with L5100, M• and |$\dot{\scr {M}}$|

Characteristic periods of accretion discs surrounding single black holes

SMBHB MODELS

Periodicity explanations

Separations and BLR sizes

CONCLUSIONS

REFERENCES

SUPPORTING INFORMATION

APPENDIX: PARTIAL CORRELATION ANALYSIS

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Correlations with L₅₁₀₀, M_• and |$\dot{\scr {M}}$|