-
PDF
- Split View
-
Views
-
Cite
Cite
J Pelle, C R Argüelles, F L Vieyro, V Crespi, C Millauro, M F Mestre, O Reula, F Carrasco, Imaging fermionic dark matter cores at the centre of galaxies, Monthly Notices of the Royal Astronomical Society, Volume 534, Issue 2, October 2024, Pages 1217–1226, https://doi.org/10.1093/mnras/stae2152
Close - Share Icon Share
ABSTRACT
Current images of the supermassive black hole (SMBH) candidates at the centre of our Galaxy and M87 have opened an unprecedented era for studying strong gravity and the nature of relativistic sources. Very-long-baseline interferometry data show images consistent with a central SMBH within General Relativity (GR). However, it is essential to consider whether other well-motivated dark compact objects within GR could produce similar images. Recent studies have shown that dark matter (DM) haloes modelled as self-gravitating systems of neutral fermions can harbour very dense fermionic cores at their centres, which can mimic the space–time features of a black hole (BH). Such dense, horizonless DM cores can satisfy the observational constraints: they can be supermassive and compact and lack a hard surface. We investigate whether such cores can produce similar observational signatures to those of BHs when illuminated by an accretion disc. We compute images and spectra of the fermion cores with a general-relativistic ray tracing technique, assuming the radiation originates from standard |$\alpha$| discs, which are self-consistently solved within the current DM framework. Our simulated images possess a central brightness depression surrounded by a ring-like feature, resembling what is expected in the BH scenario. For Milky Way-like haloes, the central brightness depressions have diameters down to |${\sim} 35\, \mu \text{as}$| as measured from a distance of approximately |$8\,$| kpc. Finally, we show that the DM cores do not possess photon rings, a key difference from the BH paradigm, which could help discriminate between the models.
1 INTRODUCTION
Three different observational campaigns aimed at the galaxy centre have confirmed that Sgr A* must be a supermassive compact object of roughly |$4\times 10^6 \mathrm{ M}_\odot$|. Two independent campaigns met this conclusion through the study of stellar motions around Sgr A* (Ghez et al. 2005, 2008; Genzel, Eisenhauer & Gillessen 2010; GRAVITY Collaboration 2018, 2020; Do et al. 2019). More recently, a third and independent campaign corroborated the same mass inference for Sgr A* by observing the relativistic images caused by lensed photons on event-horizon scales via Very-long-baseline interferometry (VLBI) techniques (Akiyama et al. 2022b, c, d). These results add up to the first image of the supermassive black hole (SMBH) candidate at the centre of the giant galaxy M87 (Event Horizon Telescope Collaboration 2019) which, unlike Sgr A*, is the source of an active galactic nucleus. Even though the space–time geometry associated with the two objects mentioned above is consistent with that generated by a Kerr black hole (BH; Event Horizon Telescope Collaboration 2019, 2022a; Boero & Moreschi 2021), considerable efforts have been made to provide alternative candidates which may explain the observational signatures (see Cardoso & Pani 2019 for a review). These alternatives include the so-called gravastars (Mazur & Mottola 2004; Visser & Wiltshire 2004; Cattoen, Faber & Visser 2005) motivated within quantum gravity theories; boson stars (Vincent et al. 2016, 2021; Olivares et al. 2020; Rosa, Macedo & Rubiera-Garcia 2023); and compact objects made of dark matter (DM), either self-interacting (Argüelles et al. 2016; Saxton, Younsi & Wu 2016; Yunis et al. 2020) or self-gravitating systems of semidegenerate neutral fermions (Argüelles et al. 2018, 2019a, 2021, 2022b; Becerra-Vergara et al. 2020, 2021), among others.
In this work, we centre our attention on the latter case. We investigate if high-density concentrations of DM fermions, which naturally arise at halo centres, provide gravitational light-bending signatures similar to that of a BH. The motivations for this choice are both theoretical and observational. On the theoretical side, the fermionic DM halo model as defined in Ruffini, Argüelles & Rueda (2015) and Argüelles et al. (2018) incorporates the quantum (fermionic) nature of the particles (not feasible in standard N-body simulations). It self-consistently considers the Pauli exclusion principle, thus yielding a quantum pressure that dominates over the central region of the configurations. As a result, the model predicts novel DM density profiles with a dense core–diluted halo morphology that depends on the fermion mass. On the observational side, distributions with fermion masses in the |${\sim} 50{\!-\!}350$| keV range which naturally account for the large-scale structure of the Universe, can also explain the galaxy rotation curves in different types of galaxies (Argüelles et al. 2018, 2019a; Krut et al. 2023). At the same time, the degenerate fermion core residing at the halo centre can mimic their central BHs (Argüelles et al. 2018, 2019a, 2021, 2022a, 2022b; Becerra-Vergara et al. 2020, 2021), or eventually collapse into one as demonstrated in Chavanis & Alberti (2020), Argüelles et al. (2021, 2023b), and Argüelles, Rueda & Ruffini (2024) from general-relativistic stability criteria.
In the context of active galaxies, Millauro et al. (2024) extends the thin disc solutions of Shakura & Sunyaev (Shakura & Sunyaev 1973) to the case of the above-mentioned core–halo fermionic DM model. This work demonstrates two key results within the fermionic scenario: (i) For a given DM core mass, there exists certain core compactness – i.e. corresponding fermion mass – which produces a luminosity spectrum that is essentially indistinguishable from that of a Schwarzschild BH of the same mass; and (ii) the disc can enter the non-rotating core, achieving accretion efficiencies as high as 28 per cent, comparable to those of rapidly rotating Kerr BHs.
The next step, which is the subject of the present paper, is to study the relativistic images produced by the lensed photons emerging from this extended thin disc solution around fermionic cores. With these two general results – the luminosity spectra of |$\alpha$|–discs and the strong-field images and luminosity patterns around the fermionic cores – we complement the analogous sequence previously shown for boson stars in Guzmán (2006) and Vincent et al. (2016), though in our case applied to typical active-like galaxies.
In this work, we adopt the geometrized unit system where the gravitational constant and the vacuum speed of light are set to unity (|$G=c=1$|).
The article is organized as follows: in Section 2, we briefly describe the fermionic halo model and the accretion disc solutions around the compact fermion cores. In Section 3, we present our numerical methods for producing the images and spectra based on a general-relativistic ray tracing technique adapted to the space–time of our interest. In Section 4, we describe the parameters of the various configurations we explore. In Section 5, we show the results of the different relativistic images cast by the fermion cores for various viewing angles and fermion masses. In Section 6, discuss the results. Finally, in Section 7, we give some conclusions and outline future perspectives.
2 PHYSICAL MODEL
2.1 Fermionic dark matter model for galactic haloes
The fermionic DM halo model under consideration here is commonly referred to as the Ruffini–Argüelles–Rueda (RAR) model (Ruffini et al. 2015). We apply its extended version, which accounts for the effects of particle escape (Argüelles et al. 2018). This model is sometimes called the relativistic fermionic–King model (Chavanis 2022), and it describes a self-gravitating system of massive, neutral fermions (spin 1/2) in hydrostatic equilibrium, incorporating particle escape within the framework of General Relativity (GR). These fermions follow a distribution function of the Fermi–Dirac type with a cut-off given by
where |$\epsilon = \sqrt{p^2 + m^2}-m$| is the particle kinetic energy, |$\epsilon _\mathrm{ c}$| is the cut-off kinetic energy, |$\mu$| is the chemical potential with the rest energy subtracted off, |$T(r)$| is the temperature, and c, |$k_\mathrm{ B}$|, m are the speed of light, the Boltzmann constant, and the fermion mass, respectively. This distribution can be derived from a maximum entropy production principle as first shown in Chavanis (1998), and recently successfully applied to a large set of disc-galaxies rotation curves in Krut et al. (2023).
In this model, the system is regarded as static and spherically symmetric, so the space–time metric is parametrized as
where |$\nu (r)$| and |$\lambda (r)$| are functions to be solved along with the hydrostatic equilibrium equations for the fermionic halo. These equations include the Tolman–Oppenheimer–Volkoff (TOV) equations for a perfect fluid, combined with the Tolman and Klein conditions (representing the zeroth and first laws of thermodynamics in GR) and energy conservation along geodesics. The resulting system of equations (see section 2 of Argüelles et al. 2018) involves a numerical boundary condition problem, for a given DM particle mass.1 There exists a family of RAR profiles that develop a dense core–diluted halo morphology, where fermion-degeneracy pressure supports the core and thermal pressure supports the halo (Argüelles et al. 2018, 2019a, 2021). We adopt the particle mass range from approximately 50 to |$350\,$| keV because, as mentioned in Section 1, the dense fermion cores within this range can mimic the BH candidate in Sgr A* while the outer haloes explain the Galaxy rotation curve (Argüelles et al. 2018, 2019b). Previous works have also used particle masses within this range to model other types of systems ranging from dwarf galaxies to galaxy clusters (see, e.g. Argüelles et al. 2019a, 2023a, 2023b; Krut et al. 2023; for a review). Moreover, larger fermion masses imply more compact cores for a fixed halo boundary condition and a fixed core mass |$M_{\rm c}$|. We show this in Fig. 1 for the cases |$m=48\,$| keV, |$m=155\,$| keV, and |$m=200\,$| keV, with |$M_{\rm c}= 10^7 \mathrm{ M}_\odot$|. It is worth mentioning that these solutions, having a total halo mass of |$10^{12} \mathrm{ M}_\odot$|, are in agreement with the observational relation between halo mass and the masses of their corresponding supermassive central objects (Ferrarese 2002).
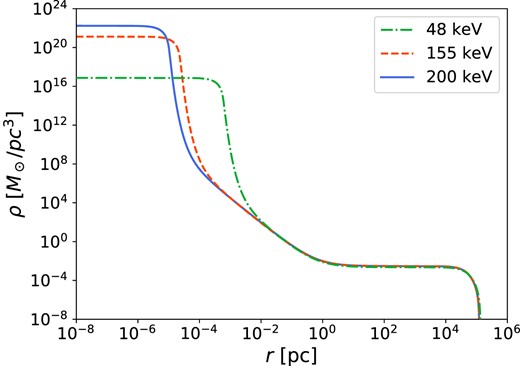
Density core-halo profiles for fermion masses of 48 keV (dashed-dotted), 155 keV (dashed), and 200 keV (solid). All solutions correspond to a core mass of |$M_{\rm c}=1\times 10^7 \mathrm{ M}_\odot$| and a total mass of |$M_\mathrm{ T}=1\times 10^{12} \mathrm{ M}_\odot$| at |$r_\mathrm{ T}=122\,$| kpc, consistent with the Ferrarese relation between the dark central object and the DM halo (Ferrarese 2002).
Since the RAR model is built upon a self-gravitating system of tempered fermions under a perfect fluid ansatz within GR, sufficiently degenerate fermion cores can reach a critical mass of core-collapse into a SMBH (Argüelles et al. 2021, 2023b, 2024). This critical core mass is |$M_{\rm c}^{\mathrm{ cr}}\approx M_{\mathrm{OV}}=0.384 m_{\mathrm{pl}}^3/m^2$|, where |$M_{\mathrm{OV}}$| is the Oppenheimer–Volkoff mass and |$m_{\mathrm{pl}}$| is the Planck mass, as shown in the above references with applications to the problem of SMBH formation in the early Universe. In the specific case of interest for active galaxies with a central object mass of |$M_{\rm c}= 10^7 \mathrm{ M}_\odot$|, a particle mass of |$m=200\,$| keV implies a compact DM core that is very close to its critical value for collapse.
2.2 The thin accretion disc
The solution obtained in Millauro et al. (2024) is the extension of the standard model of a thin disc solution (Shakura & Sunyaev 1973) to the context of regular (i.e. not singular) compact mass distributions. In this solution, the orbital angular velocity is given by the Newtonian expression.2
and a small (highly subsonic) component of radial velocity. The disc is thin, with a height scale |$H \ll r$|, and the viscosity is parametrized with the |$\alpha$|-prescription, where the kinematic viscosity |$\nu$| is given by |$\nu = \alpha c_{\rm s} H$|. Here, |$c_{\rm s}$| is the speed of sound, and |$\alpha$| is a dimensionless parameter smaller than one.
Under these assumptions, the disc is optically thick in the vertical direction, and each disc element is assumed to radiate as a blackbody at a radius-dependent temperature |$T(r)$|. The temperature profile around the DM core solution is given by
where |$\dot{M}$| is the accretion rate, |$r_{\text{in}}$| is the inner radius of the disc, and |$\sigma$| is the Stefan–Boltzmann constant. The last term within brackets on the right-hand side of equation (4) results from the extended central mass distribution and is not present in the standard solution around a BH. For more details on the disc solution, including a plot showing the decreasing |$T(r)$| behaviour inside the DM core, we refer the reader to Millauro et al. (2024).
Additionally, we assume blackbody emission in the local rest frame of the accretion disc at the temperature given in equation (4). The rest-frame four-velocity is
where |$\Omega$| is the angular velocity of equation (3), and the four-velocity vector is subject to the normalization condition |$g_{ab} u^{a}_{\mathrm{d}} u^{b}_{\mathrm{d}} = -1$|.
Given the lack of an innermost stable circular orbit (ISCO) in the RAR space–time, we consider two alternatives for the inner radius of the disc. The first alternative is the radius at which the accretion efficiency saturates to a maximum, |$r_{\text{in}} = r_{\text{sat}}$| (Millauro et al. 2024), with the relative error for the change in efficiency being equal to or lower than 1 per cent. This radius typically corresponds to |$r_{\rm sat} \sim 0.1r_{\rm c}$|, where |$r_{\rm c}$| denotes the radius of the DM core. The second alternative assumes that the disc continues to the centre (e.g. Figs 4 and 5). We have quantitatively analysed the minor differences among the images for these two scenarios in Section 5 to demonstrate that our results are essentially insensitive to the choice of inner radius.
3 RELATIVISTIC RAY TRACING
Strong gravitational fields can significantly influence the observational features of compact objects through various effects, including light bending, gravitational redshift, and, if matter moves at considerable fractions of the speed of light, relativistic beaming. To accurately account for these effects, it is necessary to consider the covariant radiative transfer equation on a curved space–time,
where |$\nu$| represents the radiation frequency, |$I_\nu$| is the specific intensity of the radiation field, |$j_\nu$| and |$\alpha _\nu$| denote the emissivity and absorptivity coefficients of the medium, respectively, and |$\lambda$| is an affine parameter along space–time geodesics. In our model, the accretion disc is infinitesimally thin, with no emission or absorption processes occurring outside. Consequently, both plasma coefficients in the right-hand side of equation (6) are zero, and the radiative transfer is reduced to the connection between the emitting disc and the observation point along geodesics via the conservation of the Lorentz-invariant quantity |$I_\nu /\nu ^3$|.
For our imaging and spectral analysis, we utilize skylight3, an open-source Julia package for general-relativistic ray tracing and radiative transfer in arbitrary space–times (Pelle et al. 2022).skylight is particularly advantageous for its easy extensibility to custom space–times and radiative models, which we leverage to incorporate the RAR space–time and accretion disc model into the code. Specifically, for the space–time, we implement an interpolation scheme to compute the metric coefficients and Christoffel symbols using numerical data from the RAR solutions.
We utilize an updated version of skylight, which includes improvements over the description in Pelle et al. (2022). Most importantly, it calculates observables not by relying on an image-plane approximation for distant observers but directly through the covariant energy-momentum tensor of the radiation field,
where |$k^a = \nu (1, \mathbf {\Omega })$|, |$\nu$| is the frequency, and |$\mathbf {\Omega }$| is the spatial direction in an orthonormal frame. The flux calculation follows as |$F = T^{ab} u_a n_b$|, with |$u^a$| being the four-velocity of the reference frame, and |$n^a$| a vector normal to the flux-measurement surface, such that |$n^a u_a = 0$| and |$n^a n_a = 1$|. This approach enables the precise calculation of fluxes from any position and frame, removing the need for asymptotic flatness of the space–time. Our flux measurements correspond to the static frame along the radial direction. That is, we set |$u^a \propto (\partial _\mathrm{ t})^a$|, and |$n^a \propto (\partial _\mathrm{ r})^a$|, both with adequate normalization.
Finally, the multiscale nature of the model poses a challenge for radiative transfer within the RAR haloes. While the scale of the accretion disc is near that of the central object, the DM halo extends to several kiloparsecs. In principle, this requires integrating the equations across large distances while potentially considering spatial variations in much smaller scales, which can easily lead to numerical instabilities. However, if the influence of the DM halo on radiation is negligible beyond a certain distance, we can mitigate this issue by taking observation points relatively close to the source. Then, we can correct the flux and angle normalization for observations at larger distances according to an inverse-square law as in flat space–time. In Appendix A, we elaborate on the validity of taking our observation points at |$r = 1 \, \text{pc}$| in all scenarios we consider in this work.
4 MODEL PARAMETERS
We use two families of solutions within the RAR DM model. In Table 1, we show various parameters characterizing our chosen solutions. The first family corresponds to haloes typical of active-like galaxies with a supermassive central object of mass |$10^7 \mathrm{ M}_\odot$| and surrounded by a total halo mass of |$10^{12} \mathrm{ M}_\odot$| (see Fig. 1). In this case, we consider fermion masses of |$m =48\, \text{keV}$|, |$155\, \text{keV}$|, and |$200\, \text{keV}$|, in increasing order of core compactness. Thus, as explained in Section 2, for a central object with |$M_{\rm c}=10^7 \mathrm{ M}_\odot$|, the |$200\,$| keV solution implies a fermion core close to its critical value of collapse into a SMBH. For the other solution, we adopt a halo profile with a smaller core mass close to |$4\times 10^6 \mathrm{ M}_\odot$|, surrounded by a Milky Way-like halo, as studied in Becerra-Vergara et al. (2020). In this case, we first adopt a fermion mass of |$200\,$| keV, the same as in the case of the larger active galaxy. However, we also consider more compact cores with |$m=300\, \text{keV}$| and |$m=378\, \text{keV}$|, the latter leading to the critical mass of core-collapse into a SMBH typical of a Milky Way-like galaxy.
Core mass |$M_{\rm c}$|, core gravitational radius |$r_\mathrm{ g}$|, core radius |$r_{\text{c}}$|, saturation radius |$r_{\text{sat}}$|, and corresponding angular radius |$\theta _{\text{sat}}$| for the different RAR solutions considered in this work.
| |$m \,$|(keV) . | |$M_{\rm c}\, ({\rm M}_{\odot }$|) . | |$r_\mathrm{ g}\,$|(cm) . | |$r_{\mathrm{ c}}\, (r_\mathrm{ g}$|) . | |$r_{\text{sat}}\, (r_g$|) . | |$\theta _{\text{sat}}\,$|(as)|$^{4}$| . |
|---|---|---|---|---|---|
| 48 | |$1 \times 10^{7}$| | |$1.48 \times 10^{12}$| | |$947$| | |$78.8$| | 7.71 |
| 155 | |$1 \times 10^{7}$| | |$1.48 \times 10^{12}$| | |$36.7$| | |$3.09$| | 0.30 |
| 200 | |$1 \times 10^{7}$| | |$1.48 \times 10^{12}$| | |$15.5$| | |$1.37$| | 0.13 |
| 200 | |$3.5 \times 10^{6}$| | |$5.17 \times 10^{11}$| | |$81.6$| | |$6.87$| | |$0.23$| |
| 300 | |$3.5 \times 10^{6}$| | |$5.17 \times 10^{11}$| | |$24.4$| | |$2.09$| | 0.07 |
| 378 | |$3.5 \times 10^{6}$| | |$5.17 \times 10^{11}$| | |$7.84$| | |$0.71$| | |$0.02$| |
| |$m \,$|(keV) . | |$M_{\rm c}\, ({\rm M}_{\odot }$|) . | |$r_\mathrm{ g}\,$|(cm) . | |$r_{\mathrm{ c}}\, (r_\mathrm{ g}$|) . | |$r_{\text{sat}}\, (r_g$|) . | |$\theta _{\text{sat}}\,$|(as)|$^{4}$| . |
|---|---|---|---|---|---|
| 48 | |$1 \times 10^{7}$| | |$1.48 \times 10^{12}$| | |$947$| | |$78.8$| | 7.71 |
| 155 | |$1 \times 10^{7}$| | |$1.48 \times 10^{12}$| | |$36.7$| | |$3.09$| | 0.30 |
| 200 | |$1 \times 10^{7}$| | |$1.48 \times 10^{12}$| | |$15.5$| | |$1.37$| | 0.13 |
| 200 | |$3.5 \times 10^{6}$| | |$5.17 \times 10^{11}$| | |$81.6$| | |$6.87$| | |$0.23$| |
| 300 | |$3.5 \times 10^{6}$| | |$5.17 \times 10^{11}$| | |$24.4$| | |$2.09$| | 0.07 |
| 378 | |$3.5 \times 10^{6}$| | |$5.17 \times 10^{11}$| | |$7.84$| | |$0.71$| | |$0.02$| |
Note.|$^{4}$|The angular radius corresponding to |$r_\text{sat}$| is calculated as |$\theta _\text{sat} = r_\text{sat}/1\, \text{pc}$|, where |$1\, \text{pc}$| is the radius of the observation point.
Core mass |$M_{\rm c}$|, core gravitational radius |$r_\mathrm{ g}$|, core radius |$r_{\text{c}}$|, saturation radius |$r_{\text{sat}}$|, and corresponding angular radius |$\theta _{\text{sat}}$| for the different RAR solutions considered in this work.
| |$m \,$|(keV) . | |$M_{\rm c}\, ({\rm M}_{\odot }$|) . | |$r_\mathrm{ g}\,$|(cm) . | |$r_{\mathrm{ c}}\, (r_\mathrm{ g}$|) . | |$r_{\text{sat}}\, (r_g$|) . | |$\theta _{\text{sat}}\,$|(as)|$^{4}$| . |
|---|---|---|---|---|---|
| 48 | |$1 \times 10^{7}$| | |$1.48 \times 10^{12}$| | |$947$| | |$78.8$| | 7.71 |
| 155 | |$1 \times 10^{7}$| | |$1.48 \times 10^{12}$| | |$36.7$| | |$3.09$| | 0.30 |
| 200 | |$1 \times 10^{7}$| | |$1.48 \times 10^{12}$| | |$15.5$| | |$1.37$| | 0.13 |
| 200 | |$3.5 \times 10^{6}$| | |$5.17 \times 10^{11}$| | |$81.6$| | |$6.87$| | |$0.23$| |
| 300 | |$3.5 \times 10^{6}$| | |$5.17 \times 10^{11}$| | |$24.4$| | |$2.09$| | 0.07 |
| 378 | |$3.5 \times 10^{6}$| | |$5.17 \times 10^{11}$| | |$7.84$| | |$0.71$| | |$0.02$| |
| |$m \,$|(keV) . | |$M_{\rm c}\, ({\rm M}_{\odot }$|) . | |$r_\mathrm{ g}\,$|(cm) . | |$r_{\mathrm{ c}}\, (r_\mathrm{ g}$|) . | |$r_{\text{sat}}\, (r_g$|) . | |$\theta _{\text{sat}}\,$|(as)|$^{4}$| . |
|---|---|---|---|---|---|
| 48 | |$1 \times 10^{7}$| | |$1.48 \times 10^{12}$| | |$947$| | |$78.8$| | 7.71 |
| 155 | |$1 \times 10^{7}$| | |$1.48 \times 10^{12}$| | |$36.7$| | |$3.09$| | 0.30 |
| 200 | |$1 \times 10^{7}$| | |$1.48 \times 10^{12}$| | |$15.5$| | |$1.37$| | 0.13 |
| 200 | |$3.5 \times 10^{6}$| | |$5.17 \times 10^{11}$| | |$81.6$| | |$6.87$| | |$0.23$| |
| 300 | |$3.5 \times 10^{6}$| | |$5.17 \times 10^{11}$| | |$24.4$| | |$2.09$| | 0.07 |
| 378 | |$3.5 \times 10^{6}$| | |$5.17 \times 10^{11}$| | |$7.84$| | |$0.71$| | |$0.02$| |
Note.|$^{4}$|The angular radius corresponding to |$r_\text{sat}$| is calculated as |$\theta _\text{sat} = r_\text{sat}/1\, \text{pc}$|, where |$1\, \text{pc}$| is the radius of the observation point.
The parameters of the accretion disc model include an accretion rate fixed at |$10~{{\ \rm per\ cent}}$| of the Eddington accretion rate, with an efficiency of conversion to luminosity of |$10~{{\ \rm per\ cent}}$| as well. As described in Section 2, we consider two alternatives for the inner radius of the disc: |$r_\text{in} = 0$| and |$r_\text{in} = r_\text{sat}$|. We note that |$r_\text{sat}$| depends on the DM distribution and, consequently, the fermion mass. We show the specific values of |$r_\text{sat}$| in Table 1 for each RAR solution considered here. We set the outer radius of the accretion disc to |$10^3 r_\text{sat}$|.
We take our observation points at |$r=1\, \text{pc}$|, for which we provide a detailed justification in Appendix A. We take inclination angles relative to the rotation axis of the accretion disc of |$\xi = 5^\circ$|, |$45^\circ$|, |$85^\circ$|, that is, almost face-on, intermediate, and almost edge-on views, respectively. The cameras have angular apertures of |$80 \theta _\text{sat}$|, where |$\theta _\text{sat} = r_\text{sat}/1\, \text{pc}$| represents the angle subtended by the radius |$r_\text{sat}$| from the observation point. For reference, we show the |$\theta _\text{sat}$| values for each scenario in Table 1. We take camera resolutions of |$1200 \times 1200$| pixels.
For comparison, we also include simulations in a setup where the central object is a Schwarzschild BH with a mass of |$M_{\rm BH} = 10^7 \mathrm{ M}_\odot$|. In this model, we employ the standard Shakura–Sunyaev disc, extending down to the ISCO, with the same accretion rate as in the RAR scenario. The observation points are at the same location as in the RAR scenario. For the scale of the images, we adopt the value of |$\theta _{\text{sat}}$| corresponding to the |$200\, \text{keV}$| RAR solution with |$M_{\rm c} = 10^7 \mathrm{ M}_\odot$|.
5 RESULTS
In the following, we present the results, including images and spectra. In Fig. 2, we show the observed spectra at different inclination angles, comparing the RAR models with |$r_\text{in}=0$| to the BH scenario. From the spectra, we can see that the more compact the DM core (i.e. the larger the fermion mass), the more luminous the solutions are overall, such that there exists a certain core compactness for which the emitted flux resembles that of a BH of the same mass as the DM core. Moreover, accretion onto the most compact RAR solution, which in this case corresponds to a fermion mass of 200 keV, can be more efficient and consequently result in higher fluxes than in the BH scenario (as obtained in Millauro et al. 2024). The fluxes in the RAR cases peak at higher frequencies for larger particle masses, corresponding to the higher temperatures of their discs (see Millauro et al. 2024 for a general discussion of this point).
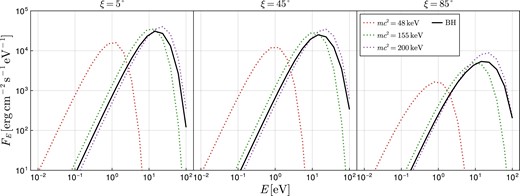
Specific fluxes for an accretion disc extending to the origin around a DM core of |$M_{\rm c} = 1 \times 10^{7} \mathrm{ M}_\odot$|. The columns correspond to observation inclinations relative to the rotation axis of the disc of |$\xi = 5^\circ$|, |$45^\circ$|, |$85^\circ$|. The flux is measured in the static frame along the radial direction.
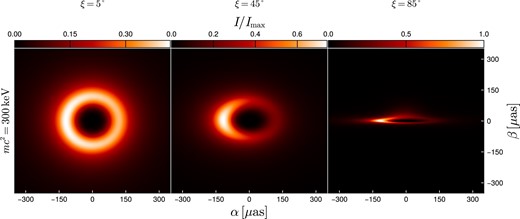
In Fig. 3, we show bolometric images of the RAR solutions for the active galaxies (the first three solutions on Table 1). We show the same for the BH scenario in Fig. 4.
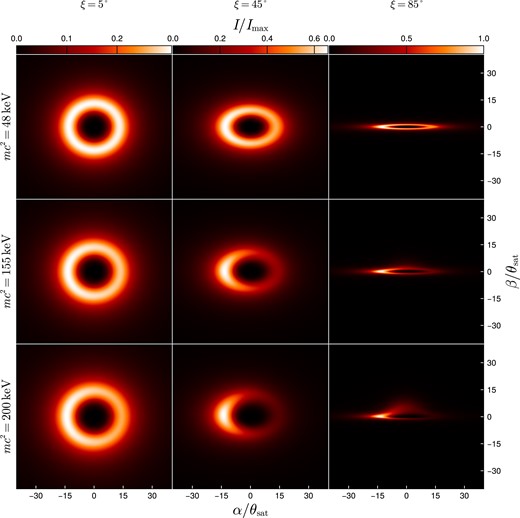
Bolometric intensity for an accretion disc extending to the origin around a DM core of |$M_{\rm c} = 1 \times 10^{7} \mathrm{ M}_\odot$|. The columns correspond to observation inclinations relative to the rotation axis of the disc of |$\xi = 5^\circ$|, |$45^\circ$|, |$85^\circ$|. The intensity is measured in the static frame. Here, |$\alpha$| and |$\beta$| denote the angular coordinates on the sky centred around the radial direction, and |$\theta _\text{sat} = r_\text{sat}/r$|, i.e. the angular radius corresponding to |$r_\text{sat}$|, which we tabulate in Table 1. The intensity has been scaled to |$I_{\text{max}} = 9 \times 10^{15} \, \text{erg} \, \text{cm}^{-2} \, \text{sr}^{-1} \, \text{s}^{-1}$|.
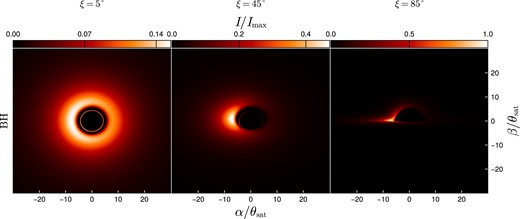
Bolometric intensity for an accretion disc around a BH of |$M_{\rm BH} = 1 \times 10^{7} \mathrm{ M}_\odot$|. The columns correspond to observation inclinations relative to the rotation axis of the disc of |$\xi = 5^\circ$|, |$45^\circ$|, |$85^\circ$|. The intensity is measured in the static frame. Here, |$\alpha$| and |$\beta$| denote the angular coordinates on the sky centred around the radial direction, and |$\theta _\text{sat} = r_\text{sat}/r$|, i.e. the angular radius corresponding to |$r_\text{sat} =$| for the |$200 \, \text{keV}$| configuration. The intensity has been scaled to |$I_{\text{max}}= 1.8 \times 10^{16} \, \text{erg} \, \text{cm}^{-2} \, \text{sr}^{-1} \, \text{s}^{-1}$|.
In Fig. 5, we compare the different sizes of the solutions corresponding to 155 and |$200\,$| keV for an inclination angle of |$\xi =45^{\circ }$|. Given its extension, the |$48\,$| keV solution, which is the least compact, is not included in the comparison.
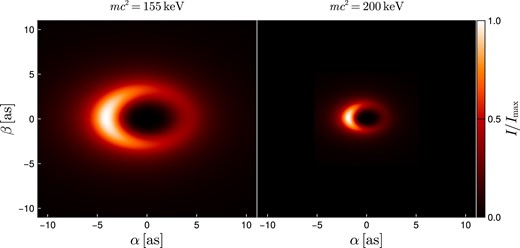
Bolometric intensity for an accretion disc extending to the origin around a DM core of |$M_{\rm c} = 1 \times 10^{7} \mathrm{ M}_\odot$| with an observation inclination relative to the rotation axis of the disc of |$\xi = 45^\circ$|. The intensity is measured in the static frame. Here, |$\alpha$| and |$\beta$| denote the angular coordinates on the celestial sphere centred around the radial direction. The intensity has been scaled to |$I_{\text{max}} = 6 \times 10^{15} \, \text{erg} \, \text{cm}^{-2} \, \text{sr}^{-1} \, \text{s}^{-1}$|.
Fig. 6 shows the image for the Milky Way-like RAR solution for |$m=300\,$| keV with |$r_\text{in}=r_\text{sat}$| (although we also considered other fermion masses of 200 and |$378\,$| keV for this case, we do not include these images to avoid overload). Additionally, although the observation point for the numerical code is at |$r=1\, \text{pc}$| as in every other case, we adopt a reference angular scale for the image corresponding to an observer at |$r=8.277\, \text{kpc}$| (the approximate distance from Earth to Sgr A*), applying an effective decay of solid angles as in flat space–time from the observation point of the code to the reference observer.
The images show differences in the peak brightness at different viewing angles due to enhanced relativistic beaming for more edge-on views. Furthermore, the edge-on BH image has a peak brightness almost twice as high as that in the RAR scenarios due to the higher angular velocities near the ISCO. As expected, the edge-on images exhibit moderate light bending for DM distributions with less compact cores. The effect becomes more pronounced for the more compact cores (as shown in Fig. 7). None the less, even in the latter cases, there are appreciable differences compared to the strong deflection seen in the BH scenario, which is characterized by severe image distortion of the disc portion behind the BH. Additionally, independent of the viewing angle, the BH scenario shows the presence of photon rings, whereas this is not the case for the RAR cores, not even in the critical core mass case, where the light-bending angle is always less than |$\pi$| (see Fig. 7).
Bolometric intensity for an accretion disc with inner radius |$r_{\text{in}}=r_{\text{sat}}$| around a DM core of |$M_{\rm c} = 3.5 \times 10^{6} \mathrm{ M}_\odot$|. The columns correspond to observation inclinations relative to the rotation axis of the disc of |$\xi = 5^\circ$|, |$45^\circ$|, |$85^\circ$|. The intensity is measured in the static frame. Here, |$\alpha$| and |$\beta$| denote the angular coordinates on the sky centred around the radial direction for a fictitious observer at |$r=8.277\, \text{kpc}$|. The intensity has been scaled to |$I_{\text{max}}= 5.7 \times 10^{15} \, \text{erg} \, \text{cm}^{-2} \, \text{sr}^{-1} \, \text{s}^{-1}$|.
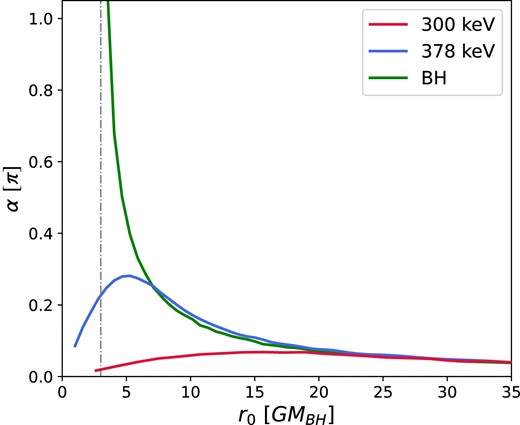
Deflection angle for massless particles in the RAR and Schwarzschild space–times, as a function of closest approach to the centre. |$M_{{\rm BH}}=4\times 10^6 \mathrm{ M}_\odot$|.
Asymmetric brightness patterns are present at intermediate and edge-on views due to relativistic beaming from the high velocities of matter along the line of sight near the core regions. This effect becomes more pronounced with increasing core compactness. Additionally, all the images show a central brightness depression surrounded by a ring-like structure primarily due to the temperature drop toward the centre and, secondarily, to the redshift of photons from that region.
Disc configurations with |$r_\text{in}=0$| and |$r_\text{in}=r_\text{sat}$| are almost visually indistinguishable. This similarity is because the temperatures peak at similar radii and drop abruptly toward the centre in both cases. We confirmed the similarity quantitatively, with relative differences being around |$0.1~{{\ \rm per\ cent}}$| on average at pixels where |$r_0 (\alpha , \beta) \ge r_\text{sat}$|, where |$r_0(\alpha , \beta)$| is the radius of the fluid element observed at angular coordinates |$(\alpha , \beta)$| on the image. Naturally, pixels where |$r_0(\alpha , \beta) \lt r_\text{sat}$| have the highest contrast. However, between the |$r_\text{in}=0$| and |$r_\text{in}=r_\text{sat}$| configurations, the relative differences (under the |$L_2$|-norm) of the observed overall spectra are below |$0.1~{{\ \rm per\ cent}}$| in all scenarios we consider.
6 DISCUSSION
We have calculated the synthetic images produced by accretion discs onto fermionic DM cores at different viewing angles. We have considered a geometrically thin and optically thick disc model with a composite blackbody spectrum given by a radius-dependent temperature profile (Millauro et al. 2024). We applied our model to active-like galaxies with core masses of |$10^7 {\rm M}_{\odot }$|, and using three different DM particle masses: 48, 155, and |$200\,$| keV, which result in different core compactness and consequently different image sizes. Additionally, we studied a hypothetical Milky Way-like galaxy with a lighter DM core of approximately |$4\times 10^6 \mathrm{ M}_\odot$| for different fermion masses of |$200, 300$|, and |$378\,$| keV, implying different core compactness, where, in the latter case, the core is close to its critical mass for gravitational collapse into a BH (Argüelles et al. 2018). We discuss the main results in the following sections.
6.1 Central brightness depression
A notable difference between the DM core and BHs is the absence of an ISCO in the RAR solutions. Spherical fermionic cores admit stable circular orbits at all radii (Crespi 2022). Therefore, in our model, matter can, at least in principle, plunge toward the central region while emitting radiation from the friction between differentially rotating layers.4 The central brightness depression and surrounding ring-like feature in the images for the RAR solutions arise from the temperature drop toward the centre due to the decay of viscous stresses [see also equation (4)], and, secondarily, from the redshift of photons coming from the central region within the core. Thus, we do not expect the inner edge of the central brightness depression in the RAR case to be as sharp as in the BH case with a thin accretion disc truncated at the ISCO.
6.2 Photon rings
As with any static spherically symmetric perfect fluid solution within GR under a fermionic equation of state, the RAR solutions do not have photon rings. The most compact (i.e. critical) solution for self-gravitating neutral massive (spin |$1/2$|) fermions corresponds to full degeneracy, with |$R_{\rm OV}/M_{\rm OV}=8.8$| (e.g. Alberti & Chavanis 2020), where |$R_{\rm OV}$| and |$M_{\rm OV}$| are the Oppenheimer–Volkoff radius and mass, respectively. This lack of photon rings contrasts with the case of BHs, for which photon rings are a universal prediction (Gralla, Holz & Wald 2019; Gralla & Lupsasca 2020; Johnson et al. 2020). The maximum deflection for massless particles in the RAR space–times, we consider is approximately |$3\pi /10$| (Gómez et al. 2016; see Fig. 7 for the specific examples treated in this article), corresponding to the most compact degenerate fermion core with |$r_\mathrm{ c}/M_{\rm c}\approx 9$|. This bound implies that photons do not produce secondary (or higher order) images due to the lack of null geodesics with multiple plane crossings.
The observation of photon rings around the supermassive objects at the centre of our Galaxy and M87 may soon become possible (Johnson et al. 2020; Younsi, Psaltis & Özel 2023; Kocherlakota et al. 2024). Despite the enhanced capabilities of the next-generation Event Horizon Telescope (Ayzenberg et al. 2023; Johnson et al. 2023), measuring photon rings solely with Earth-based interferometry will continue to be challenging even in the ultrahigh resolution regime due to the dynamic nature, changing opacity, and rapid variability of these environments (Tiede et al. 2022). However, future arrays that integrate space-based instruments extending the VLBI baseline are expected to enable these measurements (Gurvits et al. 2022; Johnson et al. 2024). If realized, these would discriminate between the fermionic DM model and the BH paradigm.
6.3 Imaging a |$4\times 10^6 \mathrm{ M}_\odot$| fermion core
In addition, we also calculated the image for a disc in a galaxy with the same core mass as that of Sgr A*. For this, we used core–halo RAR solutions with particle masses of |$200, 300$|, and |$378\,$| keV, such that in the latter case, the highly degenerate fermion core reaches the Oppenheimer–Volkoff critical mass for gravitational collapse into a BH of about |$4\times 10^6 \mathrm{ M}_\odot$|, with the outer halo explaining the Milky Way rotation curve (Argüelles et al. 2018).
We emphasize, however, that our accretion model is not suitable for Sgr A*, as the observed spectral characteristics are consistent with synchrotron radiation from a thick, hot disc with a lower accretion rate rather than thermal blackbody radiation from a thin disc, as shown in Fig. 6. That said, we obtain global features that are at least promising for future work. Specifically, the diameter of the central brightness depression for the |$m=300\,$| keV example shown in Fig. 6, as seen from |$r=8.277\, \text{kpc}$|, is approximately |$100\, \mu \mathrm{as}$| for intermediate viewing angles. In contrast, for the |$m=200\,$| keV case, the diameter is close to three times larger, with a value of approximately |$300\, \mu \mathrm{as}$|. Diameters of the central dark region around that of the EHT image of Sgr A* (|$48.7 \pm 7\, \mu \mathrm{as}$|; Akiyama et al. 2022a) can be obtained for more compact DM core solutions than the |$m=300\,$| keV case, though not as compact as the critical fermion core solution. Indeed, such a critical solution with a fermion mass of |$378\,$| keV and a core mass of |$3.5 \times 10^6 \ \mathrm{ M}_\odot$| has a core radius of |$7.85 r_\mathrm{ g}$|, and a central dark region diameter of approximately |$35\, \mu \mathrm{as}$|, about three times smaller than that of the |$300\,$| keV solution. In future work, we aim to develop a more suitable accretion disc model around RAR fermion cores for low-accretion rates, such as those estimated for the Sgr A*. This development will allow us to compare the resulting images more accurately with those obtained by the EHT.
6.4 Absence of an event horizon
A defining characteristic of BH solutions is the presence of an event horizon. However, only apparent horizons are physically detectable by quasi-local measurements (see Visser 2014 and references therein). Early in the development of the VLBI technology associated with the EHT, it was proposed that detecting a shadow would provide evidence for the existence of an event horizon (Falcke, Melia & Agol 2000). Since then, many works have investigated shadow features for different BH space–times and horizonless compact object alternatives within and beyond GR (see Perlick & Tsupko 2022 for a review).
A broad family of BH mimickers is the so-called ultracompact horizonless objects (Carballo-Rubio et al. 2018), characterized by a physical surface lying just above the would-be event horizon and within the photon surface of the BH candidate. Stimulated by observational results that claimed evidence for the existence of event horizons at galaxy centres (McClintock, Narayan & Rybicki 2004; Narayan & McClintock 2008), many works have put constraints on such BH alternatives from the non-observation of electromagnetic radiation from the putative surface of such objects (see Carballo-Rubio et al. 2022; Event Horizon Telescope Collaboration 2022b for recent results on Sgr A*). However, Visser (2014) argued that the observation of the accretion flows analysed in Narayan & McClintock (2008) only suggests the presence of some sort of horizon (i.e. a one-way membrane of infalling matter), but cannot be interpreted as a claim for the presence of an event horizon.
Such an observable condition of ‘no emitting hard surface’ is fulfilled by specific BH alternatives, such as compact objects made of bosons or fermions. The first case corresponds to the well-studied boson stars (e.g. Vincent et al. 2016 in the context of the present discussion), while the second case, and the subject of this paper, corresponds to highly degenerate DM fermion cores surrounded by a DM halo made of the same particles (Argüelles et al. 2018, 2019a).
7 CONCLUSIONS
We have presented the images cast by an accretion disc around non-singular, horizonless, fermionic DM cores at the centre of active-like galaxies. The neutral (spin |$1/2$|) massive fermions constituting the core are in a dense and degenerate state, followed by a sharp decrease in density ending in a diluted atmosphere that explains the DM haloes in such galaxies. These core–halo DM distributions are known as the RAR profiles and are solutions of the Einstein field equations in spherical symmetry sourced by a perfect fluid ansatz for the finite temperature fermions (Ruffini et al. 2015; Argüelles et al. 2018, 2019a, 2021). For particle masses of the order of |$50{\!-\!}350$| keV, such RAR fermion cores have recently been proven to be an alternative to the BH paradigm in Sgr A* since they explain the orbits of the S-star cluster (Becerra-Vergara et al. 2020, 2021; Argüelles et al. 2022b), while acting as SMBH alternatives in larger galaxies (or eventually collapsing into one; Argüelles et al. 2019a; 2024). We have extended those former results by studying the relativistic images produced by the lensed photons originating from thin discs around the fermionic cores, complementing analogous results already shown for boson stars in Guzmán (2006) and Vincent et al. (2016), though in our case applied to typical active galaxies.
We have obtained image features similar to those expected in the BH case of the same mass as the DM core, with the central brightness depression and surrounding ring-like structure being the most relevant. However, we also find differences, such as the absence of photon rings in the fermionic case. For the case of a Milky Way-like galaxy with a fermion core of about |$4\times 10^6 \mathrm{ M}_\odot$|, we found relativistic images with central brightness depressions consistent with those observed by the EHT. However, we emphasize that our accretion model is unsuitable for Sgr A*. Further work will be devoted to developing an accretion model that applies to Sgr A*, given the improved interferometric capabilities and resolutions that will be possible in the near future (Gurvits et al. 2022; Ayzenberg et al. 2023; Johnson et al. 2023, 2024), especially including space-based instruments.
ACKNOWLEDGEMENTS
JP acknowledges financial support from a Consejo Nacional de Investigaciones Científicas y Técnicas fellowship. CRA acknowledges support from the Argentine agency Consejo Nacional de Investigaciones Científicas y Técnicas (PIP2876), the Agencia Nacional de Promoción Científica y Tecnológica (grant PICT-2020-02990), and the International Center for Relativistic Astrophysics Network. FLV acknowledges support from the Argentine agency Consejo Nacional de Investigaciones Científicas y Técnicas (PIP 2021–0554), and the Agencia Nacional de Promoción Científica y Tecnológica (PICT 2022). MFM acknowledges support from Consejo Nacional de Investigaciones Científicas y Técnicas (PIP2169) and the Universidad Nacional de La Plata (PID G178). This work used computational resources from Centro de Cómputo de Alto Rendimiento–Universidad Nacional de Córdoba (https://ccad.unc.edu.ar/), which is part of Sistema Nacional de Cómputo de Alto Desempeño–Ministerio de Ciencia, Tecnología e Innovación, República Argentina. We would like to acknowledge the collaboration opportunities that arose from the Friends of Friends Meeting in Argentina (https://fof.oac.uncor.edu/2022/), which originated this work. We produced the visualizations of skylight data using makie.jl (Danisch & Krumbiegel 2021), a package for high-performance data visualization in Julia.
DATA AVAILABILITY
The data underlying this article will be shared on reasonable request to the corresponding author.
Footnotes
See also appendix A in Mestre et al. (2024) for details on numerically solving these equations.
The relativistic correction to the angular velocity is around |$0.1~{{\ \rm per\ cent}}$| or below in all scenarios considered in this work.
REFERENCES
APPENDIX A: RADIUS OF THE OBSERVATION POINTS
In the following, we analyse the validity of taking observation points at |$r=1\,$| pc to estimate observable quantities associated with the radiation field at much larger distances. For this, we consider the deviation angles in the Newtonian limit, which we can reasonably apply at radii larger than |$1\,$| pc.
A static metric in the Newtonian limit has the form
where |$\phi$| is identified as the Newtonian gravitational potential, and |$\mathrm{ d}\gamma ^2$| is the three-dimensional flat metric. We can decompose the metric above into a flat background plus a small Newtonian perturbation. In an equal manner, the geodesics of the perturbed space–time decompose as
where the first term of the right-hand side is the background trajectory, and the second term is a small deviation from the background. The background trajectory is a geodesic of the background space–time (a straight line since the background is flat). Besides, we define
where we denote spatial three-vectors in boldface. Since we are interested in null geodesics, |$k^\mu$| must satisfy |$(k^t)^2 = \boldsymbol {k}^2 =: k^2$|, and we can assume |$k=1$| without loss of generality. We can derive the following first-order relation for the deviation vector from the geodesic equations (Carroll 2003):
where evaluation along the background path is implied.
Applying this to our model, in the RAR metric of equation (2), we expand |$e^\nu \approx 1 + \nu$| at large radii, where |$\nu$| is small, identifying |$\phi = \nu /2$| as the Newtonian potential. We can cast the resulting metric into the form of the Newtonian limit by rescaling the radius as
The quotient |$\tilde{r}/r$| remains close to 3 per cent for all |$r \ \gt\ 1\,$| pc.
To test the extent to which the DM distribution can influence light at large distances, we integrated equation (A4) along an ingoing geodesic between |$r = 8\,$| kpc and |$r = 1\,$| pc for each RAR solution considered in this work. We take the initial spatial momentum of the geodesic forming an angle |$\delta = 50 r_\text{sat}/(8\, \text{kpc})$| with the radial direction, while the initial deviation vector is zero. The norms of the final deviation vectors, shown in Table A1, are negligible in all scenarios. This fact means that any significant deflection of light must occur within |$r = 1\,$| pc, and we conclude that it is valid to take the observation points at |$1\,$| pc as we did for our radiative transfer calculations.
Norm of the final deviation vector for an ingoing geodesic in the Newtonian approximation between |$r = 8\,$| kpc and |$r = 1\,$| pc for the RAR solutions we consider in this work.
| |$m \,$|(keV) . | |$M_{\rm c}\, ({\rm M}_{\odot }$|) . | |$\Vert \mathbf {\boldsymbol{ l}}\Vert$| . |
|---|---|---|
| 48 | |$1 \times 10^{7}$| | |$6.2 \times 10^{-12}$| |
| 155 | |$1 \times 10^{7}$| | |$2.5 \times 10^{-13}$| |
| 200 | |$1 \times 10^{7}$| | |$1.1 \times 10^{-13}$| |
| 200 | |$3.5 \times 10^{6}$| | |$6.8 \times 10^{-14}$| |
| 300 | |$3.5 \times 10^{6}$| | |$2 \times 10^{-14}$| |
| 378 | |$3.5 \times 10^{6}$| | |$6.6 \times 10^{-15}$| |
| |$m \,$|(keV) . | |$M_{\rm c}\, ({\rm M}_{\odot }$|) . | |$\Vert \mathbf {\boldsymbol{ l}}\Vert$| . |
|---|---|---|
| 48 | |$1 \times 10^{7}$| | |$6.2 \times 10^{-12}$| |
| 155 | |$1 \times 10^{7}$| | |$2.5 \times 10^{-13}$| |
| 200 | |$1 \times 10^{7}$| | |$1.1 \times 10^{-13}$| |
| 200 | |$3.5 \times 10^{6}$| | |$6.8 \times 10^{-14}$| |
| 300 | |$3.5 \times 10^{6}$| | |$2 \times 10^{-14}$| |
| 378 | |$3.5 \times 10^{6}$| | |$6.6 \times 10^{-15}$| |
Norm of the final deviation vector for an ingoing geodesic in the Newtonian approximation between |$r = 8\,$| kpc and |$r = 1\,$| pc for the RAR solutions we consider in this work.
| |$m \,$|(keV) . | |$M_{\rm c}\, ({\rm M}_{\odot }$|) . | |$\Vert \mathbf {\boldsymbol{ l}}\Vert$| . |
|---|---|---|
| 48 | |$1 \times 10^{7}$| | |$6.2 \times 10^{-12}$| |
| 155 | |$1 \times 10^{7}$| | |$2.5 \times 10^{-13}$| |
| 200 | |$1 \times 10^{7}$| | |$1.1 \times 10^{-13}$| |
| 200 | |$3.5 \times 10^{6}$| | |$6.8 \times 10^{-14}$| |
| 300 | |$3.5 \times 10^{6}$| | |$2 \times 10^{-14}$| |
| 378 | |$3.5 \times 10^{6}$| | |$6.6 \times 10^{-15}$| |
| |$m \,$|(keV) . | |$M_{\rm c}\, ({\rm M}_{\odot }$|) . | |$\Vert \mathbf {\boldsymbol{ l}}\Vert$| . |
|---|---|---|
| 48 | |$1 \times 10^{7}$| | |$6.2 \times 10^{-12}$| |
| 155 | |$1 \times 10^{7}$| | |$2.5 \times 10^{-13}$| |
| 200 | |$1 \times 10^{7}$| | |$1.1 \times 10^{-13}$| |
| 200 | |$3.5 \times 10^{6}$| | |$6.8 \times 10^{-14}$| |
| 300 | |$3.5 \times 10^{6}$| | |$2 \times 10^{-14}$| |
| 378 | |$3.5 \times 10^{6}$| | |$6.6 \times 10^{-15}$| |



