-
PDF
- Split View
-
Views
-
Cite
Cite
Zixian Wang, Sanjib Sharma, Michael R Hayden, Jesse van de Sande, Joss Bland-Hawthorn, Sam Vaughan, Marie Martig, Francesca Pinna, Validating full-spectrum fitting with a synthetic integral-field spectroscopic observation of the Milky Way, Monthly Notices of the Royal Astronomical Society, Volume 534, Issue 2, October 2024, Pages 1175–1204, https://doi.org/10.1093/mnras/stae2148
Close - Share Icon Share
ABSTRACT
Ongoing deep integral-field spectroscopy (IFS) observations of disc galaxies provide opportunities for comparison with the Milky Way (MW) to understand galaxy evolution. However, such comparisons are marred by many challenges such as selection effects, differences in observations and methodology, and proper validation of full-spectrum fitting methods. In this study, we present a novel code GalCraft to address these challenges by generating mock IFS data cubes of the MW using simple stellar population models and a mock MW stellar catalogue derived from E-galaxia. We use the widely adopted full-spectrum fitting code ppxf to investigate the ability to recover kinematics and stellar populations for an edge-on mock MW IFS observation. We confirm that differences in kinematics, mean age, |$[\mathrm{M/H}]$|, and |$[\mathrm{\alpha /Fe}]$| between thin and thick discs can be distinguished. However, the age distribution is overestimated in the ranges between |$2{-}4$| and |$12{-}14$| Gyr compared to the expected values. This is likely due to the age spacing and degeneracy of SSP templates. We find systematic offsets in the recovered kinematics due to insufficient spectral resolution and the variation of line-of-sight velocity distribution with age and |$[\mathrm{M/H}]$|. With future higher resolution and multi-|$[\mathrm{\alpha /Fe}]$| simple stellar population templates, GalCraft will be useful to validate key signatures such as |$[\mathrm{\alpha /Fe}]$|–|$[\mathrm{M/H}]$| distribution at different R and |$|z|$| and potentially infer radial migration and kinematic heating efficiency to study detailed chemodynamical evolution of MW-like galaxies.
1 INTRODUCTION
How galaxies form and evolve with time remains one of the outstanding questions facing astrophysics today. Over the last decade, integral-field spectroscopy (IFS) instruments have enabled us to obtain integrated light observations of galaxies across different regions of the same object, which have much better spatial coverage than single-slit or multislit spectroscopy. Several IFS surveys have already been carried out such as SAMI (Croom et al. 2012), CALIFA (Sánchez et al. 2012), and MaNGA (Bundy et al. 2015) to measure properties of thousands of galaxies to understand their evolution history. In extragalactic analysis, an integrated spectrum is assumed to be a weighted superposition of many simple stellar population (SSP) spectra and the spectral features are reshaped by line-of-sight velocity distributions (LOSVD), dust attenuation and gas emission (Conroy 2013). To decompose these complex components and measure the kinematics and stellar population properties, many stellar population synthesis software have been developed such as ppxf (Cappellari & Emsellem 2004; Cappellari 2017, 2023), starlight (Cid Fernandes et al. 2005), stecmap (Ocvirk et al. 2006), pipe3D (Sánchez et al. 2016), and firefly (Wilkinson et al. 2017) to perform full-spectral fitting to the observational spectra. They have been broadly used to provide spatially resolved galaxy properties in data releases for a wide variety of scientific topics.
Due to our unique vantage point, the Milky Way (MW) is by far the best-studied galaxy in the Universe . It provides an ideal test bed for our understanding of galaxy formation and evolution, and is often used to compare with extragalactic studies. Precise astrometric data from Gaia (Gaia Collaboration et al. 2023) and accurate chemical abundances of individual stars from large spectroscopic surveys such as LAMOST (Zhao et al. 2012), GALAH (Buder et al. 2021) and APOGEE (Majewski et al. 2017) have been analysed in the last decade for Galactic archaeologists to reveal the detailed chemodynamical picture of the MW (Freeman & Bland-Hawthorn 2002; Bland-Hawthorn & Gerhard 2016). This includes the |$[\mathrm{\alpha /Fe}]$|–|$[\mathrm{Fe/H}]$| bimodal distribution (e.g. Nidever et al. 2014; Hayden et al. 2015; Sharma, Hayden & Bland-Hawthorn 2021b), radial migration (e.g. Schönrich & Binney 2009), accretion history and the interplay of chemical and dynamical processes (e.g. Xiang & Rix 2022). In the past decades, many Galactic chemical evolution (GCE) models have been developed to reproduce the |$[\mathrm{\alpha /Fe}]$| bimodality and uncover its origin (e.g. Sanders & Binney 2015; Haywood et al. 2018; Spitoni et al. 2019; Sharma et al. 2021b; Chen et al. 2023). However, because all of these models can reproduce consistent chemodynamical distributions with observations, the origin of |$[\mathrm{\alpha /Fe}]$|-bimodality is still under debate. Moreover, the MW is only one galaxy, whether the formation theories apply to other disc galaxies or whether the MW is unique in the Universe is still an open question. Therefore, it is essential to combine the MW with other Milky Way analogous (MWAs) to address all these questions (van de Sande & Scott 2021).
Several studies compared face-on MWAs from extragalactic IFS surveys with the MW: Boardman et al. (2020) selected 62 MWAs from MaNGA with the criteria of stellar masses and bulge-to-total ratios. They found most of these galaxies have flatter stellar and gas-phase metallicity gradients due to different disc scale lengths. A greater consistency can be found when scaling gradients by these lengths; Zhou et al. (2023) revisited 138 MaNGA galaxies by fitting the spectra with a semi-analytic chemical evolution model (Zhou, Merrifield & Aragón-Salamanca 2022) and measured their star formation and chemical enrichment histories. They detected similar |$[\mathrm{\alpha /Fe}]$| bimodality as the Galactic APOGEE observations (Abdurro’uf et al. 2022) in many of the galaxies. Compared to face-on galaxies, edge-on MWAs are more useful in providing elemental abundance distributions at different R and |$|z|$|. Several studies of nearby edge-on MWAs and lenticular galaxies using MUSE found similar kinematics and |$[\mathrm{\alpha /Fe}]$| differences between the thin and thick discs (e.g. Pinna et al. 2019a, b; Martig et al. 2021; Scott et al. 2021). In particular, Scott et al. (2021) demonstrated that UGC 10 738 has similar |$[\mathrm{\alpha /Fe}]$|–|$[\mathrm{Fe/H}]$| distributions at different projected R and |$|z|$| with the MW observation in Hayden et al. (2015) and model predictions in Sharma et al. (2021b), which supports the commonness of MW’s chemical distributions.
Despite the efforts above, a direct comparison of the MW with its analogues in kinematics and chemistry is still challenging because the observables and methods used for studying the MW are different from those for external galaxies, i.e. utilizing properties of individual stars as opposed to integrated quantities from stellar populations with projection effects. Therefore, the comparisons may be impacted by systematics or biases (Fraser-McKelvie, Merrifield & Aragón-Salamanca 2019; Boardman et al. 2020). In addition, some key processes such as radial migration and kinematic heating have not been extensively explored like the MW on external galaxies, which are also essential to identify whether the MW’s formation and evolution is distinct from the general population. Therefore, to take the MW as an ideal laboratory and test its evolution theories on other MWAs, one needs to remove these observational and methodological biases, transfer the observables of MW and external systems into the same definition, and apply models that consider both chemical enrichment and kinematic processes.
In addition, even though the full-spectrum fitting methods have been useful in providing kinematics and stellar population properties of different components of external galaxies, due to the high degeneracy of all the parameters, it is still difficult to verify how close the measured values are to the ‘actual’ galaxy properties and whether any potential bias is introduced by the measuring methods. This could cause different fitting methods or strategies to obtain different results and lead to different conclusions. Therefore, every individual study has to validate the reliability of their measurements (e.g. Kacharov et al. 2018) and the conclusions are often only made qualitatively. Several studies examined the robustness of different full-spectrum fitting software and investigated effects due to different spectral models (e.g. Ge et al. 2018, 2019; Woo et al. 2024). However, they only tested mock spectra generated using one or two stellar populations, or only tested on global stellar population properties without spatial distribution. Until now, there has not been a comprehensive exploration to perform full-spectrum fitting on a realistic mock galaxy with chemical enrichment and kinematic processes and investigate the recovery ability of spatially resolved properties in detail. All the above considerations lead to the development of tools and studies presented in this work.
In this study, to address the challenges of comparing the MW to other galaxies, we present a novel code GalCraft to generate mock integral-field spectrograph (IFS) data cubes of the MW with integrated spectra using SSP models and mock stellar catalogue from E-galaxia (Sharma et al. in perparation), which is based on the chemodynamical model of Sharma et al. (2021b, hereafter S21) that was verified to be consistent to the current Galactic observations in both kinematics and chemistry across a range of R and |$|z|$|. This mock data cube is in the same format as extragalactic IFS observations. Therefore, extragalactic data analysis methods [e.g. the GIST pipeline (Bittner et al. 2019) with ppxf (Cappellari & Emsellem 2004; Cappellari 2017, 2023)] can be applied to the mock data cube to measure directly comparable parameters in (age, |$[\mathrm{M/H}]$|, |$[\mathrm{\alpha /Fe}]$|, |$V_{\rm LOS}$|, |$\sigma$|, |$h_3$|, |$h_4$|, light/mass fraction distributions). To address the reliability of full-spectrum fitting methods in measuring galaxy properties, we apply ppxf on GalCraft-generated mock edge-on IFS cubes and compare the measured kinematics and stellar population properties to the input values according to the GCE model S21. This paper provides a comprehensive test of full-spectrum fitting methods on a mock galaxy that considers physical chemodynamical processes at different galaxy components. The results will be useful as a reference for future extragalactic data analysis using similar spectrum fitting algorithms.
We describe the ingredients used in GalCraft and detailed procedures of this code in Section 2. In Section 3, we test the ability of broadly used spectral fitting tool ppxf to recover kinematics, stellar population parameters, and light/mass fraction distributions. In Section 4, we discuss the causes of deviations between measured and true (input) values and address potential reasons and future improvements on current algorithms for obtaining better results. We explore the effect of different fitting strategies and provide some suggestions when using such spectral fitting tools for future studies. We also give some caveats about using mock cubes generated from GalCraft code. In Section 5, we talk about future plans on the improvements of GalCraft along with spectral fitting methods and prospect some scientific topics that can be done by using GalCraft. A summary is presented in Section 6.
2 DATA CUBE GENERATION
The purpose of GalCraft is to take the mock stellar catalogue of the MW obtained from E-galaxia (Sharma et al. in preparation), and transform it into a mock data cube in three dimensions (two in spatial and one in spectral) as observed by integral-field spectrographs (IFS) such as PMAS/PPak (Roth et al. 2005; Kelz et al. 2006), AAT/SAMI (Croom et al. 2012), Sloan/MaNGA (Bundy et al. 2015), and VLT/MUSE (Bacon et al. 2010). The GalCraft code takes as input the following set of user-specified input parameters: galaxy distance (d), inclination (i), extinction, SSP templates, instrumental properties, as well as a few additional parameters (see the full list in Table 1). The produced mock data cube can be processed in the same way as real IFS observations data by many methods, particularly codes like Voronoi binning (Cappellari & Copin 2003), Penalized Pixel-Fitting (ppxf, Cappellari & Emsellem 2004; Cappellari 2017, 2023), line-strength indices (e.g. Worthey 1994; Schiavon 2007; Thomas, Maraston & Johansson 2011; Martín-Navarro et al. 2018), or a combination of them (e.g. the GIST pipeline, Bittner et al. 2019). The results can be compared directly with those from IFS observations of MWAs in terms of mass- or light-weighted parameter maps, LOSVD, and mass fraction distributions. The ingredients, flexibility, procedures, and computational expenses of this code are described in detail in the following sub-sections.
| Parameters . | Description . | Unit . |
|---|---|---|
| GALPARAMS: | Observation parameters of the mock galaxy | |
| distance | Distance of the galaxy centre to the observer | kpc |
| |$\theta _{zx}$| | Angles that the galaxy rotates along the Y-axis in the direction from z to x | deg |
| |$\theta _{yz}$| | Angles that the galaxy rotates along the X-axis in the direction from y to z | deg |
| l | Galactic longitude of the centre of the galaxy | deg |
| b | Galactic latitude of the centre of the galaxy | deg |
| SSPPARAMS: | Parameters of the SSP templates | |
| model | The SSP model to be used for the spectrum (MILES or PEGASE-HR) | |
| isochrone | Isochrones used to generate the SSP templates | |
| IMF | Initial-mass function used to generate the SSP templates | |
| single_alpha | If use single |$[\mathrm{\alpha /Fe}]$| or |$\alpha$|-variable templates for the spectrum | bool |
| factor | Oversampling factor of the templates | |
| FWHM_gal | Spectral resolution in FWHM of the output data cube | |$\, {\rm \mathring{\rm A}}$| |
| dlam | Bin width of the wavelength sampling of the output data cube | |$\, {\rm \mathring{\rm A}}$| |
| age_range | Optional age range (inclusive) in for the SSP models | Gyr |
| metal_range | Optional metallicity range (inclusive) in for the SSP models | dex |
| wave_range | Optional wavelength range (inclusive) in for the SSP models | |$\, {\rm \mathring{\rm A}}$| |
| spec_interpolator | Interpolation method to assign the spectrum to the particle given its (age, metallicity, |$[\mathrm{\alpha /Fe}]$|) | |
| INSPARAMS: | Instrument properties | |
| instrument | Instrument name, when using this parameter, the other parameters will be automatically set | |
| spatial_resolution | Spatial resolution of the data cube | arcsec |
| spatial_nbin | Number of spatial bins (spaxels) in two coordinates, in the format of [|$n_x$|, |$n_y$|] | |
| FWHM_spatial | Full width half-maximum of the PSF function to model the atmosphere | arcsec |
| Parameters . | Description . | Unit . |
|---|---|---|
| GALPARAMS: | Observation parameters of the mock galaxy | |
| distance | Distance of the galaxy centre to the observer | kpc |
| |$\theta _{zx}$| | Angles that the galaxy rotates along the Y-axis in the direction from z to x | deg |
| |$\theta _{yz}$| | Angles that the galaxy rotates along the X-axis in the direction from y to z | deg |
| l | Galactic longitude of the centre of the galaxy | deg |
| b | Galactic latitude of the centre of the galaxy | deg |
| SSPPARAMS: | Parameters of the SSP templates | |
| model | The SSP model to be used for the spectrum (MILES or PEGASE-HR) | |
| isochrone | Isochrones used to generate the SSP templates | |
| IMF | Initial-mass function used to generate the SSP templates | |
| single_alpha | If use single |$[\mathrm{\alpha /Fe}]$| or |$\alpha$|-variable templates for the spectrum | bool |
| factor | Oversampling factor of the templates | |
| FWHM_gal | Spectral resolution in FWHM of the output data cube | |$\, {\rm \mathring{\rm A}}$| |
| dlam | Bin width of the wavelength sampling of the output data cube | |$\, {\rm \mathring{\rm A}}$| |
| age_range | Optional age range (inclusive) in for the SSP models | Gyr |
| metal_range | Optional metallicity range (inclusive) in for the SSP models | dex |
| wave_range | Optional wavelength range (inclusive) in for the SSP models | |$\, {\rm \mathring{\rm A}}$| |
| spec_interpolator | Interpolation method to assign the spectrum to the particle given its (age, metallicity, |$[\mathrm{\alpha /Fe}]$|) | |
| INSPARAMS: | Instrument properties | |
| instrument | Instrument name, when using this parameter, the other parameters will be automatically set | |
| spatial_resolution | Spatial resolution of the data cube | arcsec |
| spatial_nbin | Number of spatial bins (spaxels) in two coordinates, in the format of [|$n_x$|, |$n_y$|] | |
| FWHM_spatial | Full width half-maximum of the PSF function to model the atmosphere | arcsec |
| Parameters . | Description . | Unit . |
|---|---|---|
| GALPARAMS: | Observation parameters of the mock galaxy | |
| distance | Distance of the galaxy centre to the observer | kpc |
| |$\theta _{zx}$| | Angles that the galaxy rotates along the Y-axis in the direction from z to x | deg |
| |$\theta _{yz}$| | Angles that the galaxy rotates along the X-axis in the direction from y to z | deg |
| l | Galactic longitude of the centre of the galaxy | deg |
| b | Galactic latitude of the centre of the galaxy | deg |
| SSPPARAMS: | Parameters of the SSP templates | |
| model | The SSP model to be used for the spectrum (MILES or PEGASE-HR) | |
| isochrone | Isochrones used to generate the SSP templates | |
| IMF | Initial-mass function used to generate the SSP templates | |
| single_alpha | If use single |$[\mathrm{\alpha /Fe}]$| or |$\alpha$|-variable templates for the spectrum | bool |
| factor | Oversampling factor of the templates | |
| FWHM_gal | Spectral resolution in FWHM of the output data cube | |$\, {\rm \mathring{\rm A}}$| |
| dlam | Bin width of the wavelength sampling of the output data cube | |$\, {\rm \mathring{\rm A}}$| |
| age_range | Optional age range (inclusive) in for the SSP models | Gyr |
| metal_range | Optional metallicity range (inclusive) in for the SSP models | dex |
| wave_range | Optional wavelength range (inclusive) in for the SSP models | |$\, {\rm \mathring{\rm A}}$| |
| spec_interpolator | Interpolation method to assign the spectrum to the particle given its (age, metallicity, |$[\mathrm{\alpha /Fe}]$|) | |
| INSPARAMS: | Instrument properties | |
| instrument | Instrument name, when using this parameter, the other parameters will be automatically set | |
| spatial_resolution | Spatial resolution of the data cube | arcsec |
| spatial_nbin | Number of spatial bins (spaxels) in two coordinates, in the format of [|$n_x$|, |$n_y$|] | |
| FWHM_spatial | Full width half-maximum of the PSF function to model the atmosphere | arcsec |
| Parameters . | Description . | Unit . |
|---|---|---|
| GALPARAMS: | Observation parameters of the mock galaxy | |
| distance | Distance of the galaxy centre to the observer | kpc |
| |$\theta _{zx}$| | Angles that the galaxy rotates along the Y-axis in the direction from z to x | deg |
| |$\theta _{yz}$| | Angles that the galaxy rotates along the X-axis in the direction from y to z | deg |
| l | Galactic longitude of the centre of the galaxy | deg |
| b | Galactic latitude of the centre of the galaxy | deg |
| SSPPARAMS: | Parameters of the SSP templates | |
| model | The SSP model to be used for the spectrum (MILES or PEGASE-HR) | |
| isochrone | Isochrones used to generate the SSP templates | |
| IMF | Initial-mass function used to generate the SSP templates | |
| single_alpha | If use single |$[\mathrm{\alpha /Fe}]$| or |$\alpha$|-variable templates for the spectrum | bool |
| factor | Oversampling factor of the templates | |
| FWHM_gal | Spectral resolution in FWHM of the output data cube | |$\, {\rm \mathring{\rm A}}$| |
| dlam | Bin width of the wavelength sampling of the output data cube | |$\, {\rm \mathring{\rm A}}$| |
| age_range | Optional age range (inclusive) in for the SSP models | Gyr |
| metal_range | Optional metallicity range (inclusive) in for the SSP models | dex |
| wave_range | Optional wavelength range (inclusive) in for the SSP models | |$\, {\rm \mathring{\rm A}}$| |
| spec_interpolator | Interpolation method to assign the spectrum to the particle given its (age, metallicity, |$[\mathrm{\alpha /Fe}]$|) | |
| INSPARAMS: | Instrument properties | |
| instrument | Instrument name, when using this parameter, the other parameters will be automatically set | |
| spatial_resolution | Spatial resolution of the data cube | arcsec |
| spatial_nbin | Number of spatial bins (spaxels) in two coordinates, in the format of [|$n_x$|, |$n_y$|] | |
| FWHM_spatial | Full width half-maximum of the PSF function to model the atmosphere | arcsec |
2.1 The ingredients
2.1.1 Galactic chemical evolution model
We apply the analytical chemodynamical model of the MW developed by S21 which can predict the joint distribution of position |$(\mathbf {x})$|, velocity |$(\mathbf {v})$|, age |$(\tau)$|, extinction |$E(B-V)$|, photometric magnitude in several bands and chemical abundances (|$[\mathrm{Fe/H}]$|, |$[\mathrm{\alpha /Fe}]$|) of stars in the MW. Compared with previous models (e.g. Chiappini, Matteucci & Gratton 1997; Haywood et al. 2019), this model included a new prescription for the evolution of |$[\mathrm{\alpha /Fe}]$| with age and |$[\mathrm{Fe/H}]$| and a new set of relations describing the velocity dispersion of stars (Sharma et al. 2021a). This model shows for the first time that it can reproduce the |$[\mathrm{\alpha /Fe}]$|-|$[\mathrm{Fe/H}]$| distribution of APOGEE observed stars (Hayden et al. 2015) at different radius R and height |$|z|$| across the Galaxy. In this model, the origin of two |$[\mathrm{\alpha /Fe}]$| sequences is due to two key processes: the delay between the first star formation and sequential occurrence of SN Ia causes the sharp transition from high-|$[\mathrm{\alpha /Fe}]$| to low-|$[\mathrm{\alpha /Fe}]$| at around 10.5 Gyr ago, which is likely to create a valley between the two sequences; the radial migration or so-called churning is responsible for the large spread of the low-|$[\mathrm{\alpha /Fe}]$| sequence along the |$[\mathrm{Fe/H}]$| axis. This model also showed that without churning it is not sufficient to reproduce the two sequences (see their fig. 6). Because this chemical evolution model is purely analytical, it is easy to be inserted into the forward-modelling tool E-galaxia to generate mock stellar catalogues for further analysis. In addition, several free parameters such as radial migration and kinematic heating efficiency are adjustable, which will be useful to implement similar analysis on external galaxies.
2.1.2 E-GALAXIA
To mock the MW IFS data cube, we need a comprehensive stellar catalogue from observations with well-measured parameters such as position |$(\mathbf {x})$|, velocity |$(\mathbf {v})$|, age |$(\tau)$|, and chemical abundances. However, this is impractical as the MW has hundreds of billions of stars being unexplored and the dust in the disc obscures distant light. An alternative way is to employ N-body/hydrodynamical simulations [e.g. EAGLE (Schaye et al. 2015), FIRE-2 (Hopkins et al. 2018)], but most of the simulations only contain |$\sim 10^6$| stellar particles, which is not enough to generate integrated spectra because each spatial bin would only contain less than a hundred particles. This, in turn, would increase the sampling noise of the integrated spectrum and make observables derived from spectra noisy. Even though oversampling can solve this problem, it is still challenging to find a simulation that is observably identical to the MW in all aspects quantitatively, especially the |$[\mathrm{\alpha /Fe}]$| bimodal trends.
Therefore, here we generate a mock catalogue to represent the MW. We use E-galaxia (Sharma et al. in preparation), which is a tool in accordance with the chemical evolution model of S21 and can create a catalogue with the user-defined number of stellar particles (|$N_p$|) containing parameters including position |$({\boldsymbol x, y, z})$|, velocity |$(\mathbf {v_x, v_y, v_z})$|, age |$(\tau)$|, metallicity (|$[\mathrm{M/H}]$|) and |$[\mathrm{\alpha /Fe}]$|, and the parameter distributions are chemodynamically consistent to the MW observations. In E-galaxia, each stellar particle is equivalent to a SSP with an initial birth mass of 1 |$\mathrm{M}_{{\odot }}$|, so one can directly assign spectra using SSP templates under the default unit without transferring from the mass of initial cloud to remaining stars. Other codes like trilegal (Girardi et al. 2005), besancon (Girardi et al. 2005), and Galaxia (Sharma et al. 2011) can also create mock catalogues. However, compared to E-galaxia, the underlying models of these codes lack the information of |$[\mathrm{Fe/H}]$| and |$[\mathrm{\alpha /Fe}]$|, and do not have the processes of radial migration and kinematic heating. Furthermore, the ability of E-galaxia to control the observed properties by regulating the underlying physical process is important for future analysis of external galaxies, whose formation history and dynamical processes are expected to be different from the MW. One caveat is that SSP particles in the current version of E-galaxia are distributed only in the disc and there is no bulge/bar, halo, or nuclear disc structure. This is because the chemical and kinematic distribution functions predicted by S21 are extrapolated from observations in the solar neighbourhood. Nevertheless, particle parameter distributions in E-galaxia are still consistent with APOGEE observations in the range of |$3\lt R_{\rm {gc}}\lt 15$| kpc (S21).
2.1.3 Spectral libraries
To build a mock data cube, one important procedure is to turn particles in E-galaxia into stellar spectra based on their properties, so a spectra library is needed. Given each particle is an SSP in E-galaxia and the integrated spectrum is a sum of many stellar populations We will employ SSP spectral libraries in GalCraft. The SSP spectrum describes the spectral energy distribution (SED) of a stellar population with a single age, metallicity, and chemical abundance patterns. An initial mass function (IMF) is assumed, and the stellar population is evolved using a given isochrone (Conroy 2013). GalCraft currently supports MILES (Vazdekis et al. 2010, 2015) and PEGASE-HR (Le Borgne et al. 2004), both of which will be used in this study.
The MILES SSP library (|$\rm {FWHM}=2.51\, {\rm \mathring{\rm A}}$|, |$3500 \lt \lambda \lt 7500\, {\rm \mathring{\rm A}}$|) is based on the model of Vazdekis (1999). It uses Padova 2000 (Girardi et al. 2000) or BaSTI (Pietrinferni et al. 2004, 2006) isochrones and IMF in unimodal/bimodal (Vazdekis et al. 1996), Kroupa universal/revised (Kroupa 2001) and Chabrier (Chabrier 2003) shapes. For Padova 2000 isochrones, the template grids cover 7 metallicity bins between (–2.32, 0.22) dex, 50 age bins between (0.063, 17.78) Gyr and one scaled-solar |$[\mathrm{\alpha /Fe}]$| bin (Vazdekis et al. 2010). As for BaSTI isochrones, the template grids cover 12 metallicity bins between (–2.27, 0.40) dex, 53 age bins between (0.03, 14.00) Gyr and two |$[\mathrm{\alpha /Fe}]$| bins in 0.0 and 0.4 dex (Vazdekis et al. 2015). Since |$[\mathrm{\alpha /Fe}]$| enhancement is essential in this study, for most of the cases we will use the |$\alpha$|-variable templates.
The PEGASE-HR library (|$\rm {FWHM}=0.55\, {\rm \mathring{\rm A}}$|, |$3900\, {\rm \mathring{\rm A}}\lt \lambda \lt 6800\, {\rm \mathring{\rm A}}$|) is based on the Elodie 3.1 stellar library (Prugniel & Soubiran 2001; Prugniel et al. 2007). The SSP models are computed using Padova 1994 (Bertelli et al. 1994) isochrones with a Salpeter (Salpeter 1955), Kroupa, or top-heavy (Elmegreen & Shadmehri 2003) IMF. The templates grid consists of 7 metallicity bins between (-2.30, 0.70) dex, 68 age bins between (0.001, 20) Gyr, and one scaled-solar |$[\mathrm{\alpha /Fe}]$| bin. In this work, the PEGASE-HR templates are mainly used to explore the effect of spectral resolution on ppxf fitting. Therefore, it is still useful even if it lacks variable |$[\mathrm{\alpha /Fe}]$|. Revised grids interpolated by ulyss (Koleva et al. 2009) in the same way as Kacharov et al. (2018) for PEGASE-HR are also available. The new grids contain 15 steps in metallicity between –2.3 and 0.7 dex and 50 steps in age between 10 Myr and 14 Gyr.
2.2 Configurations of GalCraft
To meet different research purposes, we incorporated a wide range of adjustable parameters in GalCraft. Specifically, the adjustable parameters are divided into three groups: GALPARAMS, SSPPARAMS, and INSPARAMS, as listed with descriptions in Table 1. The user can set up their preferred parameters to obtain the expected data cubes. GALPARAMS is for setting the distance, inclination, and position of the mock MW using coordinates transformation; SSPPARAMS governs the spectral properties, such as the selection of SSP model, single or variable |$[\mathrm{\alpha /Fe}]$|, spectral resolution, age, |$[\mathrm{M/H}]$| and wavelength ranges and interpolation method to be used to assign the spectrum according to particles parameters (see details in Section 2.3). Many interpolation options could be used such as ‘nearest’, ‘linear’, etc. The INSPARAMS controls the instrument spatial sampling, atmospheric effects [point spread function (PSF)], and the number of spatial bins in each coordinate. We also provide an option to derive the data cube in the format of a specified instrument. Alternatively, the user can also design a hypothetical instrument that does not exist by manually setting up these parameters, which will be useful for future instrument designs.
2.3 Procedures of making a mock data-cube
The procedures of generating mock MW data cubes are described in detail as the following steps, along with a flowchart in Fig. 1:
Use E-galaxia to generate a mock stellar catalogue of the MW, with particles containing position |$(\mathbf {x})$|, velocity |$(\mathbf {v})$|, age |$(\tau)$|, extinction |$E(B-V)$|, metallicity (|$[\mathrm{Fe/H}]$|) and |$[\mathrm{\alpha /Fe}]$|, transfer |$[\mathrm{Fe/H}]$| to |$[\mathrm{M/H}]$|.
Load the configurations of Table 1 provided by the user, as well as a list of data cubes to be generated with their centre coordinates in |$(l, b)$| or |$(RA, Dec.)$|.
Apply coordinates transformation based on GALPARAMS parameters to project this mock galaxy on the Celestial sphere with a certain distance and inclination.
Apply the spatial binning based on IFS instrument properties given by INSPARAMS, and find the particles included in each bin, then note the bin index for each particle for later use.
Load the SSP templates with defined age and |$[\mathrm{M/H}]$| ranges by SSPPARAMS, then oversample the spectra by a factor of SSPPARAMS:factor using spline interpolation with the order of three. Next, construct the interpolator to be used to generate integrated spectra in the next step.
Select particles in a spatial bin, assign each particle an SSP spectrum based on its age, |$[\mathrm{M/H}]$|, and |$[\mathrm{\alpha /Fe}]$| by interpolating the templates with the method defined by SSPPARAMS:spec_interpolator. Multiply the spectrum by the particle’s stellar mass because SSP spectral templates are normalized to 1 |$\mathrm{M}_{{\odot }}$|. Shift the spectrum due to its line-of-sight velocity (|$V_{\rm LOS}$|) using the Doppler equation. Then apply a flux calibration due to the particle’s distance and extinction.
Loop the procedure (vi) over all the spatial bins to stack integrated spectra. In the meantime, generate the mass/light-fraction distribution of each spatial bin. The light weights are obtained within the wavelength range given by SSPPARAMS:wave_range.
After generating integrated spectra for all the spatial bins, apply the atmosphere effects by convolving each wavelength slice with a PSF, this can be either a Gaussian or Moffat kernel function with the given INSPARAMS:FWHM_spatial.
Degrade the stacked spectrum to the instrument resolution given by SSPPARAMS:FWHM_gal using convolution with a Gaussian line spread function.
Re-bin the oversampled flux array into the original wave grid or the user-defined wavelength interval and wavelength range, according to SSPPARAMS:dlam and SSPPARAMS:wave_range.
Write the data cube flux array in the format of FITS file with GalCraft configuration parameters in the header.
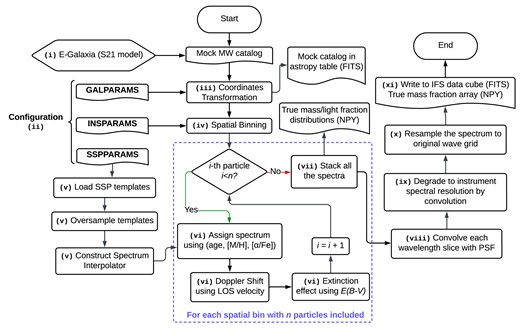
A flowchart demonstrating the workflow of GalCraft code. The numbers on some processes correspond to the steps listed in Section 2.3.
Other than the above procedures, there are a few points that need to be clarified to the users as follows:
The original mock stellar catalogue in step (i) should have two coordinate systems, Cartesian coordinates |$(x, y, z)$| and Galactic coordinates |$(l, b)$|, where |$(l, b)$| are overlapped with |$(y, z)$|, respectively. Therefore, by adjusting |$(\theta _{zx}, \theta _{yz})$|, users can rotate the mock MW into a defined inclination. This is convenient when compared with real observations.
The oversampling in step (v) has two purposes: one is to ensure the validity of degrading – when degrading the SSP templates from the original spectral resolution to instrumental resolution (e.g. from MILES to MUSE), the |$\sigma$| of the Gaussian kernel to be convolved with the templates will be smaller than wavelength interval |$\Delta \lambda$| without oversampling. In this case, the kernel function array becomes invalid with only one element having a value of 1, and the rest having values of 0. Then the degraded spectrum will be still in its original resolution. Another reason is to minimize the particle sampling error when stacking the spectrum with different |$V_{\rm LOS}$|. Fig. 2 shows an example mock integrated spectrum generated by using the non-oversampled (in red and light red) and oversampled (in blue and light blue) MILES SSP templates. The light-colour lines are the spectra convolved with a Gaussian kernel by the given mean velocity and dispersion |$(\mu , \sigma)$|, which is the manner of ppxf during the kinematics measurements. The dark-colour lines are stacked from 2000 spectra shifted by Gaussian distributed |$V_{\rm LOS}$| using the same |$(\mu , \sigma)$|, which is the manner of GalCraft. By calculating the residuals of these two lines (shown in the bottom panel), we find that oversampling can reduce the deviation between the convolved and stacked spectrum significantly by a factor of |$\sim 25$|, which will be helpful to reduce potential issues when ppxf performs Gauss–Hermite convolution to fit on the particle-stacked spectrum.
This package can select a portion of particles within the field of view (FoV) based on the user-defined instrument to generate the data cube, rather than taking a whole catalogue into account. It helps to mimic a more realistic IFS observation and reduce computational expenses.
GalCraft can be executed in the batch mode where users can provide a list of cubes with the central coordinates in |$(l, b)$| or |${\rm (RA, Dec)}$|, and all the cubes can be automatically generated in one execution;
Other than the data cube FITS file, this package also generates some by-products including mass/light-fraction and number of particle distribution arrays for each spatial bin, mass/light-weighted |$[\mathrm{M/H}]$|, |$[\mathrm{\alpha /Fe}]$|, age and kinematic properties. These by-products are obtained from properties of particles in E-galaxia and can be used to calculate the expected true answers that ppxf is expected to recover from full-spectrum fitting. This will be described in detail in Section 3.
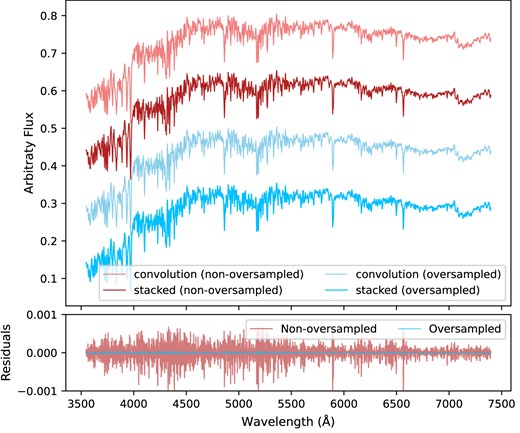
Comparison of the mock integrated spectrum generated by using the non-oversampled (in red and light-red) and the oversampled (in blue and light-blue) MILES templates. The light-colour lines are spectra convolved by a Gaussian kernel with given |$(\mu , \sigma)$|. The dark-colour lines are spectra stacked by 2000 shifted spectrum with different line-of-sight velocities which follow a Gaussian distribution with the same |$(\mu , \sigma)$|. The bottom panel shows residuals of convolved and stacked spectra. We find that oversampling can reduce the deviation between the convolved and stacked spectrum significantly by a factor of |$\sim 25$|.
2.4 Estimate the sampling error
Compared to the real catalogues of the MW (e.g. Gaia), one shortcoming of the E-galaxia mock stellar catalogue is the limited number of particles. Although there are |$10-100$| times more particles |$(10^8)$| in the mock stellar catalogue compared to MWAs in N-body/hydrodynamical simulations, some spatial bins inevitably contain too few particles for robust measurements of their properties. Even for spaxels or Voronoi bins containing more than |$\sim 10^4$| particles, the spectral noise due to finite star particles is still non-negligible. We call this type of spectral noise ‘sampling error’ |$(e_{f, S})$|. One way to reduce sampling error is to generate more particles from E-galaxia. However, this will increase the computational expenses and RAM/memory usage of GalCraft significantly, and exceed most of the HPCs’ limitation (|$\sim 22$| GB for a catalogue containing |$10^8$| particles, hence |$\sim 220$| GB for |$10^9$| particles). Therefore, when mocking IFS observations, one has to ensure that for each integrated spectrum, the sampling error |$(e_{f, S})$| is smaller than the observational flux error (|$e_{f, O}$|) at given instrument conditions and exposure time. In this way, it is safe to apply the data-reduction pipeline on this mock data cube and allow ppxf to derive mathematically reasonable results. This is particularly important in kinematics because the LOSVD effect in GalCraft integrated spectra is implemented by stacking individual spectra of particles with each shifted by its own |$V_{\rm LOS}$|. But ppxf employs the Gauss–Hermite function to convolve with SSP templates and determines the kinematics moments. In Section 3.2, we will provide a detailed example of how to deal with the sampling error for each Voronoi bin.
To estimate the sampling error, the GalCraft code provides an option to apply bootstrapping. First, it randomly re-selects particles from the original E-galaxia catalogue and generates a bootstrapped catalogue with the same particle number (|$N_{\rm p}$|). Then, GalCraft uses this catalogue to generate bootstrapped data cubes by repeating the above procedures a certain number of times, and the sampling error |$(e_{f, S})$| for each spaxel can be represented by the standard deviation of these bootstrapped fluxes. This sampling flux error will be used as the lower limit of the acceptable Gaussian noise when mimicking the real observations and obtaining the final integrated spectra of Voronoi bins. Fig. 3 illustrates how the sampling |$\rm {SNR}$| (flux divided by sampling noise) varies as a function of the number of particles in a spatial bin. The shaded region is the standard deviation of sampling signal-to-noise ratios (SNRs) for spaxels having the same number of particles. We obtain this figure by using the original and bootstrapped mock data cubes later in Section 3.1. It can be seen that a spatial bin with |$\sim 10^3$| particles can generate a spectrum with sampling |$\rm {SNR}\sim 25$||$\text{pix}^{-1}$|, and a spatial bin with |$\sim 10^4$| particles can generate a spectrum with sampling |$\rm {SNR}\sim 80$||$\text{pix}^{-1}$|.

The sampling signal-to-noise ratio (SNR) of an integrated spectrum as a function of the number of particles in a spatial bin. The shaded region is the standard deviation of sampling SNRs for spaxels with the same number of particles. This is calculated by using original and bootstrapped mock data cubes described in Section 3.1. This figure provides an estimation of spectral sampling noise due to the limited number of particles in E-galaxia.
2.5 Computational expenses and multiprocessing strategy
The execution time of GalCraft to generate mock data cubes depends mostly on the number of particles included in the instrument FoV and the spectral interpolation method. In general, the execution time is proportional to the number of particles used, and the ‘nearest’ interpolation is three times faster than the ‘linear’ interpolation. In this code, we apply python-multiprocessing techniques to speed up the computing. For a typical MUSE FoV containing |$6\times 10^6$| particles, the execution time spent with a 24-core CPU (2.50GHz) is |$\sim 1.4$| h. Based on this, the users can roughly estimate the execution time they will spend. If taking into account the bootstrapped cubes, the total execution time will be multiplied by the number of bootstrapping times plus 1. Therefore, it is highly recommended to run it on high-performance computers (HPC) or a Cluster where these 21 jobs can be executed simultaneously.
3 RECOVERY OF THE GALAXY CHEMODYNAMICAL PROPERTIES
In this section, we take ppxf as a representation software to test the ability of full-spectrum fitting methods to recover galaxy properties by applying it to mock cubes generated from GalCraft. We measure kinematics (|$V_{\rm LOS}$|, |$\sigma$|, |$h_3$|, |$h_4$|), stellar population parameters (age, |$[\mathrm{M/H}]$|, |$[\mathrm{\alpha /Fe}]$|) and light/mass fraction distributions of different structural components. The analysis is performed in the same way as extragalactic studies. Then, we compare the results with the input true values that are obtained by properties of SSP particles from E-galaxia catalogue. This test allows us to access the consistency of parameters measured via broadly applied software in other studies (e.g. Pinna et al. 2019a, b; Martig et al. 2021; Scott et al. 2021), which was not possible previously as the true values of external galaxies are unknown. Furthermore, it also provides standard references for the future to better understand extragalactic results (e.g. gradient and flaring) by distinguishing real distributions from artificial effects due to the spectral fitting methods, projected view, and integrated light. We note that our goal is to explore the general performances of the full-spectrum fitting method using template weighting and regularization, i.e. its underlying mathematical framework. We choose to test ppxf because it has been widely used by many previous studies. However, any systematic bias found in this study is not specific to ppxf, but would be equally applicable to other software using the same framework. And we leave testing on other software for future studies.
3.1 Mock cube generation for MUSE instrument
We generate a mock MUSE observation by GalCraft, using the E-galaxia catalogue that contains |$10^8$| particles. We remove particles with stellar age less than 0.25 Gyr because their position and kinematics are erroneous in the current version of E-galaxia, and we confirm that removing these particles does not affect our conclusions. The mock MW catalogue is assumed to have a distance of 26.5 Mpc and inclination of |$86^{\circ }$| to the observer, which is the same as the projection of NGC 5746 observed by MUSE with comprehensive analysis in Martig et al. (2021, hereafter M21). We use MILES |$\alpha$|-variable SSP templates (Vazdekis et al. 2015) with the BaSTI stellar isochrones (Pietrinferni et al. 2004) and Kroupa Universal IMF (Kroupa 2001). The templates have 53 bins in age, 12 bins in |$[\mathrm{M/H}]$|, and 2 bins in |$[\mathrm{\alpha /Fe}]$| and we apply a ‘linear’ interpolation to assign each particle a spectrum based on its age, |$[\mathrm{M/H}]$| and |$[\mathrm{\alpha /Fe}]$|, and then degrade the stacked spectra to MUSE spectral resolution (|$\mathrm{FWHM}\sim 2.65\, {\rm \mathring{\rm A}}$|). Following procedures in Section 2.3, we obtain two mock cubes focusing on the central |$(N_{p}=61575676)$| and the disc |$(N_{p}=7379847)$| regions, as shown in Fig. 4. This observation strategy is also the same as MUSE observations on NGC 5746 in M21. The total execution time spent by GalCraft on a 24-core CPU for these two cubes is |$\sim 14.5$| h. We also generate |$2\times 20$| bootstrapped cubes and use 16th and 84th percentiles to calculate the sampling error of each spaxel. We do not apply extinction in these cubes because here we only focus on full-spectrum fitting validation. Adding extinction would blend all the effects and make it difficult to differentiate their individual impacts. Therefore, we reserve this topic for future studies.
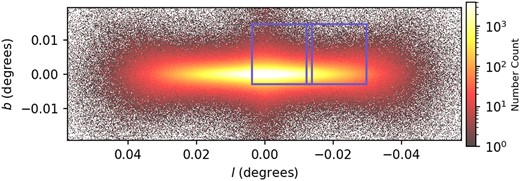
Two mock data cube FoV (in purple) relative to the number distribution of particles in E-galaxia mock stellar catalogue. The model was set with a distance of 26.5 Mpc and inclination of |$86^{\circ }$|. This observation strategy is the same as the MUSE observation on NGC 5746.
The next procedure is to add Gaussian flux error to the spectra. We first derive the observational flux error |$(e_{f, O})$| of the mock cubes. The observational flux error depends on many aspects but can be classified into two main categories: the observation conditions (seeing, air-mass, exposure time, etc.) and the instrumental properties (telescope aperture, system efficiency, dark current, read-out noise, etc.). For simplicity, we ignore the sky conditions, dark current, and read-out noise which only contribute a few per cent to total received photons, and assume the spectral SNR and received photons are defined by
where f is the flux of the target; |$e_{f, O}$| is the observational flux error (by MUSE in this case); N is the received number of photons; t is the exposure time; a is an overall reaction of sky transmission, efficiency, and telescope aperture. Therefore, a should only depend on wavelength for the same instrument. By substituting the above equations, the parameter a can be calculated using f, |$e_{f, O}$| and t from an observation by
In this work, we take all the bulge and disc observations of NGC 5746 from MUSE in M21 and fit equation (3) as a function of wavelength |$(\lambda)$| using a four-degree polynomial, which is described by
where |$a(\lambda)$| is in the unit of |$1/10^{-20}~\rm {erg}~\rm {cm}^{-2}~\, {\rm \mathring{\rm A}}^{-1}$|. Next, we set the bulge and disc mock cubes to have an exposure time of 1729.39 s and 6221.84 s, respectively, and use the equations (2) and 3 to estimate the observational flux error |$e_{f, O}$| of each spaxel. Then we use this error to add Gaussian noise to all the spaxels. Here, the disc exposure time is chosen to satisfy the upper bound of |$e_{f, O} \ge e_{f, S}$|. The bulge exposure time is then determined by assuming the same bulge-to-disc exposure time ratio in MUSE observations of NGC 5746 by M21, and we confirm that |$e_{f, O} \ge e_{f, S}$| also applies. These two values are slightly smaller than those used by M21. Finally, the two mock cubes are stitched together.
3.2 Extracting galaxy properties
We apply the GIST pipeline1 (Bittner et al. 2019) on the stitched mock cube to measure the kinematics and stellar population parameters. The GIST pipeline combines all the tools needed to process the data and users can obtain final results in a single execution. Here, we use a modified version to implement some functionalities that the current public version (v3.1.0) does not have but are needed in this work. A detailed list of added features is given in Appendix A.
We run the GIST pipeline in the following steps: First, we apply the Voronoi tessellation software (Cappellari & Copin 2003) to spatially re-bin the mock cube and increase the spectral SNR to 80 |$\text{pix}^{-1}$|, which results in 1477 Voronoi bins. Most of the Voronoi bins contain |$N_p\gt 10^4$|. For the other Voronoi bins, |$N_p$| is also very close to this number. To ensure the sampling noise |$e_{f, S}$| is less than the MUSE flux error |$e_{f, O}$|, we apply the same Voronoi binning arrangement to all 20 bootstrapped cubes. Then we calculate the sampling noise |$e_{f, S}$| of each Voronoi bin by taking half of the difference between the 16th and 84th percentiles of its 20 bootstrapped integrated spectra. We confirm that on average |$e_{f, O}\gt e_{f, S}$| applies for all the bins.
Next, we apply the full-spectrum fitting method ppxf (Cappellari & Emsellem 2004; Cappellari 2017, 2023) to measure the stellar kinematics of each Voronoi bin. Here, we use the same MILES |$\alpha$|-variable templates (Vazdekis et al. 2015) as when we generated the mock cubes in the same MUSE spectral resolution. In the following analysis, we always use the whole grid of MILES templates in age, |$[\mathrm{M/H}]$|, and |$[\mathrm{\alpha /Fe}]$|. We are aware of some unsafe regions as listed in table 2 of Vazdekis et al. (2015). However, because no particles from the E-galaxia catalogue have ages or |$[\mathrm{M/H}]$| that fall within these regions, it does not affect our conclusions. We also confirm that our conclusions remain the same after removing templates in the unsafe regions. Since there is no emission line or atmosphere effect, we use a wide wavelength range of |$(4750, 6550)\, {\rm \mathring{\rm A}}$| to fit with the Voronoi binned spectra and remove the first and last |$75\, {\rm \mathring{\rm A}}$| to avoid effects caused by spectral oversampling, rebinning and Doppler shift, etc. During the fitting, the MILES templates are convolved with a line-of-sight velocity distribution (LOSVD) described by a Gauss–Hermite equation to match the Voronoi binned spectrum. We parameterize the LOSVD using four moments, which are mean line-of-sight velocity |$V_{\rm LOS}$|, line-of-sight velocity dispersion |$\sigma$|, and the third- and fourth-order moments |$h_3$|, |$h_4$|. No regularization is applied in this process, and we include a fourth-order multiplicative Legendre polynomial during the fitting.
After measuring kinematics, we employ ppxf again to obtain the stellar population parameters for each Voronoi bin. We choose the same templates, spectral resolution, and fitting wavelength range as the previous step. We use the LOSVDs (|$V_{\rm LOS}$|, |$\sigma$|, |$h_3$|, |$h_4$|) measured in the last step as input, and fix them during the fitting to obtain the weight of each template. The best-fitting spectrum is the weighted sum of all the templates. For the initial fitting, we set no regularization to obtain the initial |$\chi ^2$|. To avoid the ill-conditioned inverse problem due to severe degeneracies in mathematics (as discussed in section 3.5 of Cappellari 2017), we then follow the approach in McDermid et al. (2015) and iterate the fitting by increasing regul until |$\chi ^2$| is increased by |$\Delta \chi ^2=\sqrt{2N}$|, where N is the number of wavelength pixels considered for the fit. This iteration process allows us to obtain the smoothest solution that is still compatible with the data within |$1\sigma$| level. At this stage, we note regul reaches the maximum regularization regul|$_{{\rm max}}$|. Next, we choose regul|$=5$| which is between 0 and regul|$_{{\rm max}}$||$(30-100)$| to keep smooth solutions while still allowing for a variation on short time-scales of the star formation, which will disappear if regul is too large (see similar discussions in Pinna et al. 2019a and M21). Here, we only apply the first order of regularization for all the fittings. We employ this fitting strategy using templates normalized to both 1 |$\mathrm{M}_{{\odot }}$| and 1 |$\mathrm{L}_{{\odot }}$| to obtain mass- and light-weighted results, respectively. Fig. 5 is an example of the fitting on one Voronoi binned spectrum. Finally, using the weights, we can calculate light-weighted and mass-weighted age, |$[\mathrm{M/H}]$|, |$[\mathrm{\alpha /Fe}]$|, and light/mass fraction distributions.
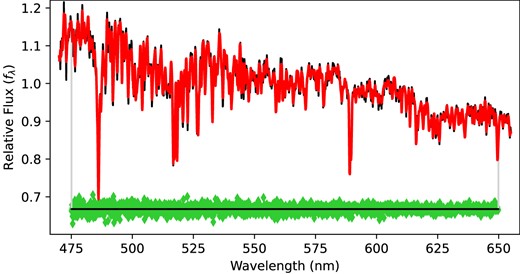
A spectral fit example of a Voronoi bin by ppxf in Section 3.2. The ‘observed’ spectrum is in black while the best-fitting spectrum is in red. Residuals are in green. The fitting area is within the grey lines on both sides.
To estimate uncertainties of template weights and weighted-mean age, |$[\mathrm{M/H}]$|, and |$[\mathrm{\alpha /Fe}]$|, we apply Monte Carlo (MC) realizations similar to the way described in Kacharov et al. (2018), M21, and Cappellari (2023). For each Voronoi-binned spectrum, we first perform a fitting with no regularization and obtain the best-fitting spectrum and residuals compared to the initial input spectrum. Next, we add residuals with signs randomly flipped to the best-fitting spectrum 100 times to obtain resampled spectra. Each resampled spectrum is then fitted by ppxf with regul|$=0.1$| to reduce bias towards smooth solutions. Finally, we calculate uncertainties of template weights and weighted mean properties by taking the half of difference between the 16th and 84th percentiles of 100 MC realizations.
In addition, we also apply the LS module in the GIST pipeline to compute line-strength indices of each Voronoi bin spectrum in the LIS system (Vazdekis et al. 2010) choosing the definitions provided at a spectral resolution of |$8.4 \, {\rm \mathring{\rm A}}$|. This routine was presented by Kuntschner et al. (2006) and Martín-Navarro et al. (2018). Next, given the relationship between templates’ properties (age, |$[\mathrm{M/H}]$|, |$[\mathrm{\alpha /Fe}]$|) and line strengths, the measured line strengths can be matched to SSP-equivalent parameters using the Markov chain Monte Carlo implementation via emcee (Foreman-Mackey et al. 2013). In this work, we follow M21 and use |$\mathrm{H}\beta _{\mathrm{o}}$| as an age indicator and Fe5015, Fe5270, and Fe5335, and |$\mathrm{Mg}b$| to trace metallicity and |$[\mathrm{\alpha /Fe}]$|, respectively. The MC simulation is run 15 times and each one uses 100 walkers and 1000 iterations to obtain uncertainties.
After measuring all the parameters, in the next sub-sections, we compare the kinematics, light- and mass-weighted stellar population parameters, and light/mass fraction distributions of the mock cube with the true values to verify the recovery ability of full-spectrum fitting method ppxf.
3.3 Kinematic maps
Fig. 6 shows the kinematics maps in four moments (|$V_{\rm LOS}$|, |$\sigma$|, |$h_3$|, |$h_4$|) of the mock MUSE cubes. The scale of the colour bar is given in the second line of the upper left corner of each panel. We calculate the true values shown in the first row with the following procedures: First, for each Voronoi bin, we calculate the total flux of each particle in the ppxf fitted wavelength region. Then we plot flux-weighted |$V_{\rm LOS}$| histogram distribution using all the particles included in this bin. Next, we fit this histogram with a Gauss–Hermite equation and obtain four best-fitting moments (|$V_{\rm LOS}$|, |$\sigma$|, |$h_3$|, |$h_4$|). This method is consistent with the definition of light-weighted kinematics which ppxf is expected to recover during the fitting process. The second row is the results from ppxf and the bottom row shows the residuals between ppxf results and the true values.
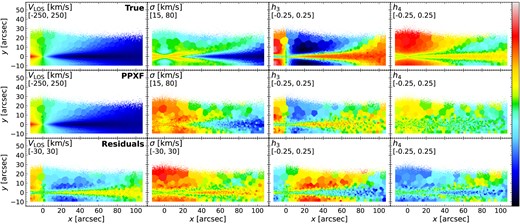
Stellar kinematics maps (|$V_{\rm LOS}$|, |$\sigma$|, |$h_3$|, |$h_4$|) of the mock MUSE cube generated in Section 3.1. The scale of the colour bar is given in the second line of the upper left corner for each panel. Top row: true values calculated by fitting a Gauss–Hermite equation with particles’ velocity distribution weighted by their total flux in ppxf fitted wavelength region for each Voronoi bin. Middle row: results from ppxf. Bottom row: residuals of the ppxf results and the true values. The residual panels indicate results from ppxf have systematic offsets compared to true values.
In this figure, the kinematic moments obtained by ppxf have the same trend compared to the true values. Both show two different structures: one is aligned to |$y\sim 0$| and the thickness increases with x, which has larger absolute |$V_{\rm LOS}$| and |$h_3$|, and smaller |$\sigma$|; the other is in a similar projected radius but vertically higher and thicker, and it has smaller absolute |$V_{\rm LOS}$| and |$h_3$|, but larger |$\sigma$|. An anticorrelation of |$h_3$| with |$V_{\rm LOS}$| which are usually associated with disc-like components (e.g. Krajnović et al. 2008; Guérou et al. 2016; van de Sande et al. 2017) is seen and are similar to MUSE edge-on galaxies studies of Pinna et al. (2019a, b) and M21. These two components are mostly likely to be associated with thin and thick discs. We will explore this in detail in Section 3.6.
However, in the residual panels, all these four moments show systematic offsets. Compared to the true values, |$V_{\rm LOS}$| from ppxf is around 17 km s|$^{-1}$| lower above and below the very thin mid-plane (|$y\sim 0$|) and shows a more significant difference around |$x\sim [10, 30]$| arcsec. Around the galaxy centre, the residual of |$V_{\rm LOS}$| also shows a continuous decrease from negative to positive x; |$\sigma$| is generally overestimated everywhere in the galaxy with few light blue residuals. |$h_3$| is overestimated in regions of |$x\sim [10, 60]$| arcsec and |$y\sim [10, 25]$| arcsec and underestimated in the outer region of |$x\sim [60, 110]$| arcsec; |$h_4$| from ppxf has no significant structures like |$\sigma$| and |$h_3$| maps, which is also seen in real galaxies results (e.g. Pinna et al. 2019a, b and M21), but the true |$h_4$| map clearly shows kinematic differences. The clear structures in these residual panels indicate that it is not because of the fitting uncertainties. We will investigate this in detail in Section 4.1.
3.4 Stellar population property maps
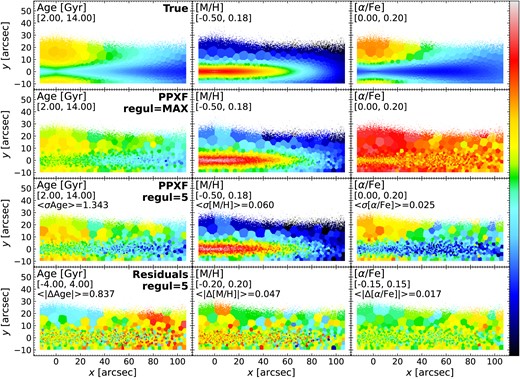
Figs 7 and 8 show the light- and mass-weighted age, |$[\mathrm{M/H}]$| and |$[\mathrm{\alpha /Fe}]$| maps of the mock MUSE cubes, respectively. The first row is the true values by calculating the median age, |$[\mathrm{M/H}]$|, and |$[\mathrm{\alpha /Fe}]$| of E-galaxia particles weighted by luminosity or mass, which are equivalent to light- or mass-weighted values. The second and third rows are results from ppxf with regul|$=$|regul|$_{{\rm max}}$| and regul|$=5$|, respectively. We also write the average uncertainty from MC realizations in the top left corner of the third row. The last row shows the residuals of the ppxf results with regul|$=5$| and the true values, with the average of absolute residual written in the top left corner. For both figures, the overall distributions of these three parameters obtained by ppxf are very close to the true values, and the residuals are within the order of uncertainties on average. This confirms the reliability of spectral fitting methods to measure the weighted age and chemical compositions. Especially, the |$[\mathrm{\alpha /Fe}]$| map from ppxf with regul|$=5$| indicates the capability of ppxf to identify distinct |$[\mathrm{\alpha /Fe}]$|-rich and |$[\mathrm{\alpha /Fe}]$|-poor populations in the thick and thin disc, respectively, even though only two |$[\mathrm{\alpha /Fe}]$| bins are available. The residuals of |$[\mathrm{\alpha /Fe}]$| from ppxf with regul|$=5$| and the true values are flat and no systematic pattern is found.
![Light-weighted stellar population property maps (age, $[\mathrm{M/H}]$ and $[\mathrm{\alpha /Fe}]$) of the mock MUSE cube generated in Section 3.1. The scale of the colour bar is given in the second line of the upper left corner for each panel. First row: true values calculated by the light-weighted average of particles’ age, $[\mathrm{M/H}]$ and $[\mathrm{\alpha /Fe}]$ for each Voronoi bin. Second row: results from ppxf with regul$=$regul$_{{\rm max}}$, calculated using strategies of McDermid et al. 2015. Third row: results from ppxf with regul$=5$ and the average uncertainty of all the Voronoi bins from MC realizations is written in the top left corner. Last row: residuals of ppxf results with regul$=5$ and the true values. The average absolute residual of all the Voronoi bins is written in the top left corner. This figure indicates that ppxf results with proper regularization can identify different galaxy components by their stellar population parameters, which are consistent with true values and the residuals are within the order of uncertainties on average. When applying regul$=$regul$_{{\rm max}}$, the distributions are smoothed and the $[\mathrm{\alpha /Fe}]$ panel becomes inconsistent with the true values.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/534/2/10.1093_mnras_stae2148/1/m_stae2148fig7.jpeg?Expires=1750262358&Signature=z4Jk0~oAm6KLv4q-g1j7RE9P4h5qQCxCug9KSG-Q8uQ8zSKZ1jG~Qv9B9pEApsP3WaAb~AbyIl9Z10a3poqgYtXws7JVLpgJZZ5d3Z9qAgC9JIe~sXI7nJm-XVmcZYYlWB1HuY6y7NJzRnzRN1h1aAC3~6qnKpi2YBwWDWfrpfcD1Yu5IG7OzSNhzEgz9F2fH0oDFJsIZfZ1~~zDC~WjjOOFCJm~qKtnFTUTmgbi0LXzCHgbSZ2fmSm-trJcAhl7tknUB5IYN31jOA0JSM4a-o5y1WAQ~640rDzUW6zhQ5I5QCc2yvwvAyGD99yZn5gyuqodwh3RssQ-MwqdbP~88A__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Light-weighted stellar population property maps (age, |$[\mathrm{M/H}]$| and |$[\mathrm{\alpha /Fe}]$|) of the mock MUSE cube generated in Section 3.1. The scale of the colour bar is given in the second line of the upper left corner for each panel. First row: true values calculated by the light-weighted average of particles’ age, |$[\mathrm{M/H}]$| and |$[\mathrm{\alpha /Fe}]$| for each Voronoi bin. Second row: results from ppxf with regul|$=$|regul|$_{{\rm max}}$|, calculated using strategies of McDermid et al. 2015. Third row: results from ppxf with regul|$=5$| and the average uncertainty of all the Voronoi bins from MC realizations is written in the top left corner. Last row: residuals of ppxf results with regul|$=5$| and the true values. The average absolute residual of all the Voronoi bins is written in the top left corner. This figure indicates that ppxf results with proper regularization can identify different galaxy components by their stellar population parameters, which are consistent with true values and the residuals are within the order of uncertainties on average. When applying regul|$=$|regul|$_{{\rm max}}$|, the distributions are smoothed and the |$[\mathrm{\alpha /Fe}]$| panel becomes inconsistent with the true values.
Same as Fig. 7 but for mass-weighted stellar population properties.
However, mass-weighted age from ppxf is slightly overestimated in the outer regions with more yellow and red Voronoi bins in the residual panel, where the residuals are larger than uncertainties. This overestimation is much more obvious in mass-weighted results. In addition, even though residuals of light-weighted |$[\mathrm{M/H}]$| are mostly close to 0, the mass-weighted |$[\mathrm{M/H}]$| are overestimated in the central regions. This means the age gradient from ppxf is underestimated but |$[\mathrm{M/H}]$| gradient is overestimated, and such effects are more dominant in mass-weighted results. In addition, the |$[\mathrm{\alpha /Fe}]$| distribution from ppxf results with regul|$=$|regul|$_{{\rm max}}$| is almost uniformly high and much larger than the true values for all the Voronoi bins in both light- and mass-weighted results. This is because when regul is very large, the ppxf algorithm forces the result to have very smooth template weights in three-parameter dimensions (age, |$[\mathrm{M/H}]$|, |$[\mathrm{\alpha /Fe}]$|). Since there are only two |$[\mathrm{\alpha /Fe}]$| grids, regularization will force them to have similar weights to achieve smoothness requirements and does not permit large deviations (e.g. more than 2 per cent). Therefore, it will be challenging to identify |$[\mathrm{\alpha /Fe}]$| bimodality. Results from ppxf with regul|$=$|regul|$_{{\rm max}}$| also show much underestimation for age gradients along the x-axis than results with regul|$=5$|. The age and |$[\mathrm{M/H}]$| gradients are essential properties to help understand the star formation and chemical enrichment processes. Therefore, a wrong choice of regularization will then easily lead to wrong conclusions. We will explore the reasons for these offsets in more detail in Section 3.6 using light and mass fraction distributions and the effect of regularization in Sections 4.2 and 4.3.
3.5 SSP-equivalent maps from line-strength indices
Fig. 9 shows the SSP-equivalent age, |$[\mathrm{M/H}]$| and |$[\mathrm{\alpha /Fe}]$| maps of the mock MUSE cubes measured by line-strength indices. This figure shows that the main structures we derived from ppxf are also recovered by the line-strength analysis with consistent trends. In the age panel, young populations are closer to the mid-plane, and old populations are further to the mid-plane or above/below the central region. In the |$[\mathrm{M/H}]$| panel, we see the metallicity gradient from the inner centre to the outer galaxy. In the |$[\mathrm{\alpha /Fe}]$| panel, we could see the |$\alpha$|-rich bins in the centre and |$\alpha$|-poor bins in the outer region, even though the differences are not as obvious as ppxf results in Figs 7 and 8. The main difference compared with ppxf results is that the age panel shows a very low range of |$[1-5]$| Gyr. This is also seen in M21 (Fig. B1) and because of the Balmer line indices being dominated by young stars. Therefore, the SSP-equivalent ages only reflect the fraction of stars formed within the past Gyr (Serra & Trager 2007; Trager & Somerville 2009). The SSP-equivalent |$[\mathrm{M/H}]$| and |$[\mathrm{\alpha /Fe}]$| range are much closer to ppxf results because young populations do not contribute much to the metal lines, which is also indicated in M21. This figure confirms that both line-strength indices and ppxf analysis can identify |$\alpha$|-rich and |$\alpha$|-poor populations.
![SSP-equivalent age, $[\mathrm{M/H}]$ and $[\mathrm{\alpha /Fe}]$ maps of the mock MUSE cube generated in Section 3.1. The parameters are measured by line-strength indices. The scale of the colour bar is given in the second row of the upper left corner for each panel. Similar to Fig. 7, galaxy components with different ages, $[\mathrm{M/H}]$, and $[\mathrm{\alpha /Fe}]$ can be identified. However, the parameter ranges differ from ppxf results and the true values.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/534/2/10.1093_mnras_stae2148/1/m_stae2148fig9.jpeg?Expires=1750262358&Signature=DNWrb0Y7BhQAumn~3v-PHnpAtVnvojDns-P318~D72i8Q22g-7fgC5Cz48gLTpcVVRFBB9924umvLWyhTAqKdB2Xm7LIrN4AcUXBKBLfYX5uJSRYzNLITguzkSJy-IIK7qf3y2RyZscVT8H6YRN7YfUa0750HDy~ZG~HumAe95NCpWtzIXFosVrZ20FVpVrKfEW5D5nq1H06-HdI6nRriUhJ89ZaWXdbVfLZJY7XZLpubqzeRRjLDjtir3EPIBDeAH4mVNfIPdFR86xBiMnIlT2HTt1CH9sEl9I25pxajtTd6JmJx8TQumaE6AnDmLiIoc9OxLjHhpcbrapZdpJ6CA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
SSP-equivalent age, |$[\mathrm{M/H}]$| and |$[\mathrm{\alpha /Fe}]$| maps of the mock MUSE cube generated in Section 3.1. The parameters are measured by line-strength indices. The scale of the colour bar is given in the second row of the upper left corner for each panel. Similar to Fig. 7, galaxy components with different ages, |$[\mathrm{M/H}]$|, and |$[\mathrm{\alpha /Fe}]$| can be identified. However, the parameter ranges differ from ppxf results and the true values.
3.6 Weight fraction distributions of different galaxy components
In addition to calculating the light- and mass-weighted properties, we can also study the light/mass fraction distribution of stellar populations along the age and |$[\mathrm{M/H}]$| dimension. This is done by using weights of templates from ppxf. Because the flux of each template is normalized to either 1 |$\mathrm{L}_{{\odot }}$| or 1 |$\mathrm{M}_{{\odot }}$|, the weights array from ppxf outputs in our tests are equivalent to stellar population light or mass fractions. Therefore, we can study the weight distribution of any component of the mock MW. M21 employed multiple components morphological fitting to a Spitzer 3.6-μm image of NGC 5746 to obtain regions dominated by the boxy/peanut bulge, nuclear disc, and thin and thick discs. In Fig. 10, we artificially select similar regions based on the locations |$(x, y)$| of different components of M21, and name them ‘up per central’, ‘inner central’, ‘thin disc’ and ‘thick disc’, as shown in different colours. We call them ‘up per central’ and ‘inner central’ because there is no boxy/peanut bulge and nuclear disc in the GCE of S21. Note these component definitions are purely following those in M21 to mock their data analysis. In reality, radial scale lengths of the thin disc |$(R^t)$| and thick disc |$(R^T)$| in NGC 5746 and the MW are very different (|$R^t_{\mathrm{MW}}=2.6\pm 0.5$| kpc and |$R^T_{\mathrm{MW}}=2.0\pm 0.2$| kpc from Bland-Hawthorn & Gerhard 2016; |$R^t_{\mathrm{NGC~5746}}=6.1$| kpc and |$R^T_{\mathrm{NGC~5746}}=8.2$| kpc from M21). For each component, the light and mass weights of all the Voronoi bins are combined to represent its light and mass fraction distributions.
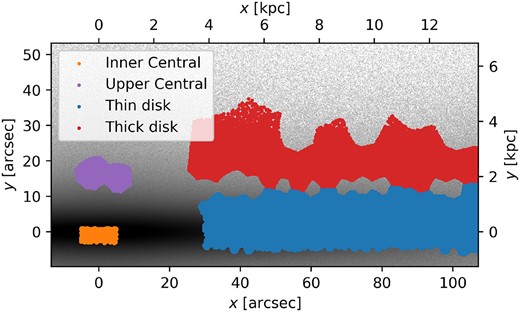
Demonstration of the projected thin disc (blue), thick disc (red), up per central (purple), and inner central (orange) regions on top of a grey-scale image of the mock data cube generated in Section 3.1.
Fig. 11 shows the light and mass fraction distributions of these four components, respectively. The total weights are normalized to one for each panel. The left two columns are light fractions and the right two columns are mass fractions, respectively. The ppxf results (first and third columns) are obtained with regul|$=5$|. The true values (second and last columns) are calculated using particles’ properties in E-galaxia catalogue weighted by luminosity or mass. We only plot the weights above 0.001 |$\text{Gyr}^{-1} \text{dex}^{-1}$|. For the thin disc, true light fractions are dominated by the youngest populations with ages less than 2 Gyr, and ppxf can consistently recover its distribution. True mass fractions indicate a rapid metallicity enrichment history |$\sim 10$| Gyr ago, and it slowly increases later on. However, such a metallicity enrichment trend is indistinguishable in ppxf mass fraction distributions. Moreover, ppxf mass fractions are dominated at relatively young (|$2{-}4$| Gyr) and old (|$12{-}14$| Gyr) stellar populations. The same features are also seen in mass fraction distributions of other galaxy components. We will investigate these findings in detail in Section 4.2–4.5. For the thick disc, both true light and mass fractions show the metallicity enrichment trend which is again not seen in ppxf results. In addition, the thick disc contains populations that are young and more metal poor than the thin disc. One reason is the geometrical definition of the thick disc, which contains young and relatively metal-poor stars that are flared in the outer disc (|$x\sim [60, 100]$| arcsec) due to radial gradients of age and metallicity. Given that NGC 5746 in M21 is analysed to be four times more massive than the MW in total stellar mass, it has a larger scale length and the definition of its thick disc might not apply to the MW. Another reason could be the projection effect, where young stars flared in the outer disc can have large Galactocentric (intrinsic) radius but small projected radius, so they could appear at the front and back of the line of sight in the region of |$x\sim [30, 60]$| arcsec. The up per central mass fractions show a similar metallicity enrichment trend with the thick disc and is more dominant in the old populations, but this domination is smoothed out in the ppxf results. Moreover, light fractions from ppxf are dominated at the age around 8 Gyr, which is inconsistent with the true light fractions. For the inner central, true light and mass fractions are showing a clearer chemical enrichment trend and there is no new population born with |$[\mathrm{M/H}]{}\lt -0.2$| dex in the young region, while the ppxf mass fractions show again two overdensities at |$2{-}4$| and |$12{-}14$| Gyr. Therefore, except for the overestimation in the young and old population regions in mass fraction distributions, and the inconsistency in light fractions of the up per central region, the light and mass fraction distributions of ppxf are generally in agreement with true values.
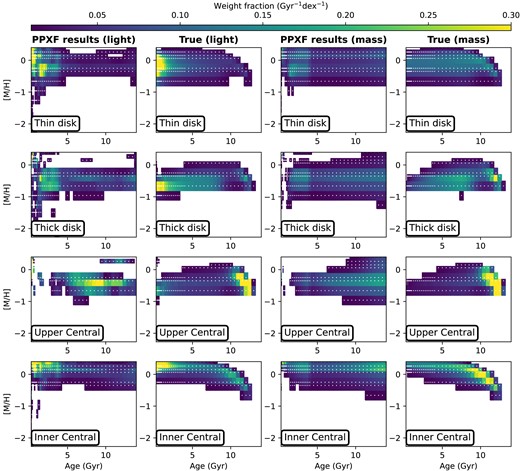
Light and mass fraction distributions of the thin disc, thick disc, inner central, and up per central of the mock data cube generated in Section 3.1. The total template weights are normalized to 1 for each panel. First column: light fraction distributions from ppxf with regul|$=5$|. Second column: True light fraction values calculated using particles’ properties in E-galaxia catalogue. Third column: Mass fraction distributions from ppxf with regul|$=5$|. Last column: true mass fraction values calculated using particles’ properties in E-galaxia catalogue. The colour bar is shown on the top. We only plot the weights with values above 0.001 |$\text{Gyr}^{-1} \text{dex}^{-1}$|. This figure indicates the broad trends of results from ppxf are consistent with the true values for the thin/thick disc and inner central regions. However, both the light and mass fraction distribution from ppxf are different from the true values for the up per central region. In addition, there is an overdensity in |$2{-}4$| Gyr in ppxf mass distributions, and populations around 12 Gyr are smoothed towards older, more metal-rich regions, which are not seen in the true values.
In Fig. 12, we integrate the mass fraction distributions in Fig. 11 along the two axes and derive age and |$[\mathrm{M/H}]$| distributions for each component. The top panels are mass distributions as a function of age which is the definition of star formation history (SFH) or star formation rate (SFR), and the bottom panels are defined as metallicity distribution function (MDF). Results from ppxf are in red lines and the true values are in black lines. For each panel, we calculate the correlation between these two lines to quantify their similarity. For the age distributions, we find the same as in Fig. 11. Compared to the true values, the ppxf results of all the components demonstrate an overestimation of weights in the ranges of |$2{-}4$| Gyr and |$12{-}14$| Gyr and underestimation in the range of |$4-11$| Gyr. The underestimated regions seem to compensate for the overestimated regions. And the thin disc, inner central, and global panels show a peaked feature with age |$\lt 1$| Gyr. For the |$[\mathrm{M/H}]$| distributions, ppxf results are consistent with true values for most regions, as indicated by the correlation coefficients. However, mass fractions in the metal-rich region are overestimated. Other than that, the overall trend of results from ppxf is consistent with true values.
![Age distribution (top row) and $[\mathrm{M/H}]$ distribution (bottom row) of the thin disc, thick disc, inner central, and up per central of the mock data cube generated in Section 3.1. These panels are obtained by integrating the mass fraction distributions in Fig. 11 along $[\mathrm{M/H}]$ and age axis, respectively. Red lines are results from ppxf with regul$=5$. Black lines are the true values calculated using particles’ properties in the mock E-galaxia catalogue. The correlation coefficient of these two lines is written in the top left corner for each panel. The overall trends from ppxf are consistent with the true values for $[\mathrm{M/H}]$. However, same as Fig. 11, the mass fraction is overestimated in $2{-}4$ and $12{-}14$ Gyr and underestimated in $5{-}12$ Gyr for all the components, and the coefficients indicate inconsistency for age distributions. We also find peaked features in regions less than 1 Gyr. The mass weights of the most metal-rich bin are overestimated for all the components.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/534/2/10.1093_mnras_stae2148/1/m_stae2148fig12.jpeg?Expires=1750262358&Signature=vnKd5nWU-LYvaYRmU59bCTZQ1mJU28Evr9E9fUJ1ijWZPnI~kNVmW3dvoNXclAbu7Xi7YYw1u9o7s3OBRpHDD4yzsFQv~DK7IIwlvL6DZukM~Rw8ihxdkBrgVK0sXEhHS-XNpM~baRytwrg2mc~lK8kJtGFdSSZ74~jLHfFyDxdqwItUlKVZ6ZFNspBEhHZsREKt3r5jvOwAz1u5bJr41OaOAz3cxfLqXte2NwEDHcpd9ZSvTXrSRCzpx3U0gY1R~v1uTqT1LtzaF-KgAWr9jToW29WtssIUFz0DkPzwl~nvY1OyiuIlaw-e6pC4ui2PsCDxfh3D9qalp28OOZM~1A__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Age distribution (top row) and |$[\mathrm{M/H}]$| distribution (bottom row) of the thin disc, thick disc, inner central, and up per central of the mock data cube generated in Section 3.1. These panels are obtained by integrating the mass fraction distributions in Fig. 11 along |$[\mathrm{M/H}]$| and age axis, respectively. Red lines are results from ppxf with regul|$=5$|. Black lines are the true values calculated using particles’ properties in the mock E-galaxia catalogue. The correlation coefficient of these two lines is written in the top left corner for each panel. The overall trends from ppxf are consistent with the true values for |$[\mathrm{M/H}]$|. However, same as Fig. 11, the mass fraction is overestimated in |$2{-}4$| and |$12{-}14$| Gyr and underestimated in |$5{-}12$| Gyr for all the components, and the coefficients indicate inconsistency for age distributions. We also find peaked features in regions less than 1 Gyr. The mass weights of the most metal-rich bin are overestimated for all the components.
In conclusion, we find that spectral fitting methods can recover the broad trends of 2D light and mass fraction distributions for different components, but with mass fractions overestimated in |$2{-}4$| Gyr, |$12{-}14$| Gyr, and most metal-rich regions. When integrating into 1D age and metallicity distributions, these inconsistencies are significant. According to correlation coefficients, |$[\mathrm{M/H}]$| distributions are more consistent with the true values than age distributions. We will investigate the reasons for such differences in detail in Sections 4.2–4.5.
3.7 Distributions of |$[\mathrm{\alpha /Fe}]$|-|$[\mathrm{M/H}]$|long different galaxy locations |$(R, z)$|
According to S21, different radial migration and kinematic heating efficiency will cause different fractions of stars in the distinct |$[\mathrm{\alpha /Fe}]$|-rich and |$[\mathrm{\alpha /Fe}]$|-poor sequences. A recent study by Scott et al. (2021) derived this distribution from an external galaxy UGC 10 738 using MILES |$\alpha$|-variable templates (Vazdekis et al. 2015) and concluded it has similar bimodality distributions to the MW. Given we know the true values from the mock stellar catalogue particles, here we explore the recovery ability of spectral fitting methods on measuring the changes of this bimodality at different projected R and |$|z|$|. Different from Scott et al. (2021) where they compared integrated values of UGC 10 738 with individual stellar values of the MW, our integrated-to-integrated value comparison on stellar population level is more direct and there is no systematic bias due to different methodologies. This direct comparison also provides an example for future studies on comparing an integrated version of the MW |$[\mathrm{\alpha /Fe}]$| bimodality with MW-like edge-on galaxies from MUSE observations (e.g. GECKOS survey, van de Sande et al. 2024).
The results are shown in Fig. 13 where we separate different locations in the same way as Hayden et al. (2015). For each panel, the total mass fraction given by true (dotted lines) and ppxf (solid lines) is normalized to 1, respectively. Blue lines are mass fraction distributions for |$[\mathrm{\alpha /Fe}]{}=0.0$| dex while red lines represent |$[\mathrm{\alpha /Fe}]{}=0.4$| dex. The overall trends for |$[\mathrm{\alpha /Fe}]$|-rich and |$[\mathrm{\alpha /Fe}]$|-poor sequences from ppxf are consistent with the true values for most of the panels, which indicates both sequences are well recovered by ppxf, as also shown by correlation coefficients. However, there are some discrepancies such as in the inner regions (|$R\lt 5$| kpc) and thin disc (|$|z|$|<0.5 kpc), where ppxf show smoother metallicity distributions in both the blue and red lines compared to true values. In addition, the mass fraction is underestimated at |$-1\lt [\mathrm{M/H}]\lt 0.0$| dex and overestimated at the most metal-rich regions, which is the same as metallicity distributions in Fig. 12.
![$[\mathrm{M/H}]$ distributions for different $[\mathrm{\alpha /Fe}]$ components distributed along projected R and $|z|$ of the mock cube generated in Section 3.1. For each panel, the total mass fractions of true (dotted lines) and ppxf (solid lines) are normalized to 1, respectively. Blue lines represent mass fraction distributions for $[\mathrm{\alpha /Fe}]$$=0.0$ dex while red lines represent the distributions with $[\mathrm{\alpha /Fe}]$$=0.4$ dex. Solid lines represent the results from ppxf and dotted lines are the true values. This figure is similar to the $[\mathrm{\alpha /Fe}]$-$[\mathrm{Fe/H}]$ distributions in Hayden et al. (2015) and Scott et al. (2021). The correlation coefficient of the dotted and solid lines are written in the same colour in the bottom left corner. For most of the panels, ppxf results are consistent with the true values. The difference appears at the inner central and thin disc, where both lines show a mass fraction underestimation at $[\mathrm{M/H}]$$\sim 0.0$ dex and overestimation at the most metal-rich regions.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/534/2/10.1093_mnras_stae2148/1/m_stae2148fig13.jpeg?Expires=1750262358&Signature=PDd4npZ09c8xlhjtruN6K3wmpl5G4owWgz-gfFAHw3hMUZryVnLjGGQ9rhEZYNFvlFnhuZbXuchvRuFCV4vfY2I~CfpH1hwR2ZLaoOX6m5SP8jexgcJ3UtN4m4UbfbwzmnU2Hlv5MzQYyg70UU2LTMZLJnUzg89jdKwRW59-YVBe7Z6UD7WJT0cTD1zrxjASECm1EtY48zrirHRrXNjlM~GKQu~DU0xLQRX8TRM7uC52teQwwbGhA41jhhPrD~SvFFvhLMtgKMz-PAkOkIA8a14UXorIlTq4oPqNE~Eb0xjG0wlt3oKinTWuKn0Q4NX07o1kVA7wDgGGRcQ-IJt1hg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
|$[\mathrm{M/H}]$| distributions for different |$[\mathrm{\alpha /Fe}]$| components distributed along projected R and |$|z|$| of the mock cube generated in Section 3.1. For each panel, the total mass fractions of true (dotted lines) and ppxf (solid lines) are normalized to 1, respectively. Blue lines represent mass fraction distributions for |$[\mathrm{\alpha /Fe}]$||$=0.0$| dex while red lines represent the distributions with |$[\mathrm{\alpha /Fe}]$||$=0.4$| dex. Solid lines represent the results from ppxf and dotted lines are the true values. This figure is similar to the |$[\mathrm{\alpha /Fe}]$|-|$[\mathrm{Fe/H}]$| distributions in Hayden et al. (2015) and Scott et al. (2021). The correlation coefficient of the dotted and solid lines are written in the same colour in the bottom left corner. For most of the panels, ppxf results are consistent with the true values. The difference appears at the inner central and thin disc, where both lines show a mass fraction underestimation at |$[\mathrm{M/H}]$||$\sim 0.0$| dex and overestimation at the most metal-rich regions.
When comparing different |$[\mathrm{\alpha /Fe}]$| sequences, the peaks of distributions are at the same metallicity position in both ppxf and true results. This differs from our understanding of |$[\mathrm{\alpha /Fe}]$|–|$[\mathrm{M/H}]$| relation of the MW. It is more likely due to the limited number of |$[\mathrm{M/H}]$| and |$[\mathrm{\alpha /Fe}]$| bins in MILES templates that cause the differences of metallicity distribution in different |$[\mathrm{\alpha /Fe}]$| bins to be indistinguishable. Similar findings are also mentioned by Scott et al. (2021) when they analysed the |$[\mathrm{\alpha /Fe}]$|-bimodality of UGC 10 738. Therefore, we emphasize that more |$[\mathrm{M/H}]$| and |$[\mathrm{\alpha /Fe}]$| bins in the spectral templates are necessary to obtain more detailed distributions of this bimodality. It can help to make it more feasible to identify the effect of different radial migration and kinematic heating efficiency from the relative fractions of these two sequences when compared with other IFS observations.
4 DISCUSSION
4.1 Systematic offsets in the kinematics recovery
In Fig. 6, we show the deviations between the kinematics map from ppxf and the true values. To better illustrate the offsets of each moment, we plot their residuals as a function of true velocity dispersion |$\sigma _{\rm {true}}$| in Fig. 14, in which the y-axis is calculated by ppxf fitted value subtracting the true value. Each data point represents one Voronoi bin. The blue-dotted lines represent the instrumental dispersion (|$\sigma _{\rm inst}$|) based on spectral resolution. We also plot the zero-line in red to guide the eyes. The first row demonstrates the results in Fig. 6, and it clearly shows the systematic offsets for each moment: |$\Delta$||$V_{\rm LOS}$| increases with |$\sigma _{\rm {true}}$|, and |$\sigma$| is overestimated for most of the Voronoi bins; as for |$h_3$| and |$h_4$|, the residuals have a slight positive gradient.
![Residuals of four Gauss–Hermite moments $\Delta$($V_{\rm LOS}$, $\sigma$, $h_3$, $h_4$) as a function of true velocity dispersion. Each data point represents a Voronoi bin. The red line at zero is to guide the eyes. The vertical dashed line indicates the instrumental dispersion $\sigma _{\rm inst}$. First row: results from ppxf using MILES templates in MUSE spectral resolution ($\sigma _{\rm inst}$$\sim 62$ km s$^{-1}$), same as the residual panels in Fig. 6. Second row: similar to the first row but results are fitted by ppxf with no penalization on $h_3$ and $h_4$. Third row: results from ppxf on a mock cube similar to Section 3 but generated and fitted using PEGASE-HR (Le Borgne et al. 2004) templates ($\sigma _{\rm inst}$$\sim 15$ km s$^{-1}$). Fourth row: similar to the third row but penalization was turned off during ppxf fitting. Fifth row: similar to the third row but for LOSVD-Convolved mock cubes. Sixth row: similar to the first row but for LOSVD-Convolved mock cubes. Seventh row: similar to the fourth row but all the analysis is in MUSE spectral resolution ($\mathrm{FWHM}\sim 2.65\, {\rm \mathring{\rm A}}$). This figure indicates that both the spectral resolution and the relation between LOSVD and age, $[\mathrm{M/H}]$ create the kinematics systematics.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/534/2/10.1093_mnras_stae2148/1/m_stae2148fig14.jpeg?Expires=1750262358&Signature=rNBIbDc05iWacAkNk2~aAT4Kqk1-xoZu2~Z~wK3e3tZJqQ-IL2ZeIBp3P2F~TFjT6WP8YMuVlizwR0HILlcb7G1gp9Bg3--hUP5KAcBTaTqC0Qs073GCdES0tW2vi2fHDhuqzcQEte0Vft0dbfozCsES7UfIEWOcyATtAxhnpnmU6B6o7d~QP-nRrci1xaY3V1XzclhAmgXtmXCv2tr2MqcSTseroO2OpXI5kHZMSJLO1P8ksArqHjRuGaWGXBIY3bMP0-OtwFPwjvpnEmIgM3bfeOXR3djcu7Hwz2W4M9RyN6aaSE1-21H88vymdvSCgVjwKN3HcMJd7vUTa06TAw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Residuals of four Gauss–Hermite moments |$\Delta$|(|$V_{\rm LOS}$|, |$\sigma$|, |$h_3$|, |$h_4$|) as a function of true velocity dispersion. Each data point represents a Voronoi bin. The red line at zero is to guide the eyes. The vertical dashed line indicates the instrumental dispersion |$\sigma _{\rm inst}$|. First row: results from ppxf using MILES templates in MUSE spectral resolution (|$\sigma _{\rm inst}$||$\sim 62$| km s|$^{-1}$|), same as the residual panels in Fig. 6. Second row: similar to the first row but results are fitted by ppxf with no penalization on |$h_3$| and |$h_4$|. Third row: results from ppxf on a mock cube similar to Section 3 but generated and fitted using PEGASE-HR (Le Borgne et al. 2004) templates (|$\sigma _{\rm inst}$||$\sim 15$| km s|$^{-1}$|). Fourth row: similar to the third row but penalization was turned off during ppxf fitting. Fifth row: similar to the third row but for LOSVD-Convolved mock cubes. Sixth row: similar to the first row but for LOSVD-Convolved mock cubes. Seventh row: similar to the fourth row but all the analysis is in MUSE spectral resolution (|$\mathrm{FWHM}\sim 2.65\, {\rm \mathring{\rm A}}$|). This figure indicates that both the spectral resolution and the relation between LOSVD and age, |$[\mathrm{M/H}]$| create the kinematics systematics.
From Fig. 6, we find that several Voronoi bins have large absolute |$h_3$| and |$h_4$| true values (e.g. central region and the thick disc), which will not be well constrained when SNR is relatively low (Cappellari & Emsellem 2004; Pinna et al. 2021). Therefore, ppxf with keyword bias will penalize them towards lower absolute values during the fitting to make the LOSVD towards a Gaussian shape. However, using different penalizations can result in different kinematic measurements (see full analysis using SAMI galaxies by van de Sande et al. 2017). In our case, when the LOSVD is strongly non-Gaussian, the Gauss-Hermite approximation no longer works well and large |$h3$| and |$h4$| could be obtained. Therefore, we turn off the penalization of these higher order moments and re-measure the kinematics, and show the results in the second row of Fig. 14. A spatially distributed map can also be seen in Fig. B1 of the Appendix B. After turning off penalization, both |$h_3$| and |$h_4$| from ppxf are visually closer to the true values in Fig. B1. However, the second row of Fig. 14 still shows similar trends to the first row, and the four moments are more scattered, which indicates penalization is not the cause of the systematic offsets.
Another possible reason causing the kinematic inconsistency could be the low spectral resolution of the MUSE instrument. As shown in the first row of Fig. 14, |$\sigma _{\rm {true}}$| values for most of the Voronoi bins are smaller than the MUSE instrumental dispersion |$\sigma _{\rm inst}$||$\sim 62$| km s|$^{-1}$|. In this case, the recovery of kinematics will be uncertain. This has been pointed out in fig. 3 of Cappellari (2017), and the only way to avoid it is to increase the instrumental spectral resolution. The explanation is when |$\sigma$||$\lt $||$\sigma _{\rm inst}$|, during ppxf fitting, the broadening of one sharp spectral feature is less than the distance to its nearby wavelength pixels. In this case, the nearby wavelength pixels have minor changes and this brings difficulties for ppxf to measure |$\sigma$| correctly, and |$h_3$| and |$h_4$| will go towards zero because there are also not enough pixels to identify the skewness and kurtosis.
To remove the effect of low spectral resolution, we tested the kinematics recovery again by using PEGASE-HR templates (Le Borgne et al. 2004) generated by Kroupa IMF and PADOVA 1994 isochrones, which has a higher spectral resolution (|$\rm {FWHM}=0.55\, {\rm \mathring{\rm A}}$|) than MUSE (|$\mathrm{FWHM}\sim 2.65\, {\rm \mathring{\rm A}}$|). The instrumental velocity scale of PEGASE-HR is |$\sigma _{\rm inst}$||$\sim 15$| km s|$^{-1}$|, which is smaller than the minimum |$\sigma _{\rm {true}}$| of our Voronoi bins. We repeat all the procedures in Section 3.2 to generate new cubes using PEGASE-HR, and then apply them to the GIST pipeline to measure the kinematics. We keep the original PEGASE-HR spectral resolution throughout the whole process. The third row of Fig. 14 shows the kinematics recovery using PEGASE-HR (also see the kinematics map in Fig. B2). Compared to the first row, the residuals of each panel are slightly better or clearer when using higher spectral resolution templates. However, all these four moments from ppxf still have the same systematic offsets to the true values. Most improvements are for |$h_3$| and |$h_4$|, with less bias to zero values because the higher spectral resolution helps identify skewness and kurtosis. We also show the results by turning off penalization in the fourth row (also see the kinematics map in Fig. B3), and find the |$h_3$| and |$h_4$| residuals are identical to the third row. Therefore, turning off penalization helps on low-spectral-resolution kinematics measurements, but not for higher resolution spectra. The higher spectral resolution improves the kinematics recovery but does not fix the systematics offsets.
Fundamentally, during the spectral fitting process, SSP templates are loaded and convolved with a Gauss–Hermite function by FFT to match the observed spectrum (Cappellari 2017), and the code returns one series of LOSVD moments which are best fitted to the observed spectrum. This means all the templates are assumed to have the same kinematics (|$V_{\rm LOS}$|, |$\sigma$|, |$h_3$|, |$h_4$|) in a line of sight, i.e. stellar populations with different |$[\mathrm{M/H}]$| and ages are assumed to have the same LOSVD. But in real galaxies, due to the joint process of chemical enrichment and dynamical movements of stars, populations with different |$[\mathrm{M/H}]$| and ages are different in LOSVDs. This effect is non-negligible for edge-on projected galaxies because metallicity and age gradients along the disc are the strongest. Therefore, |$V_{\rm LOS}$| should change with |$[\mathrm{M/H}]$| and age, which disagrees with the analysis used in most of the previous studies when employing ppxf, even though ppxf allows such variations. Because of the relation between |$[\mathrm{\alpha /Fe}]$| and |$[\mathrm{M/H}]$|, stars with different |$[\mathrm{\alpha /Fe}]$| should also have different |$V_{\rm LOS}$|.
To investigate it in our mock stellar catalogue, we select one Voronoi bin and split the included particles into three groups using |$[\mathrm{M/H}]$| and age, respectively. We reserve this investigation on |$[\mathrm{\alpha /Fe}]$| for the future due to the limited number of |$[\mathrm{\alpha /Fe}]$| templates. Then, we plot the LOSVDs of these groups of particles, weighted by each particle’s total flux, and show them in the first row of Fig. 15. On the top left panel, particles with |$-0.8\lt [\mathrm{M/H}]{}\lt -0.4$| dex have the sharpest distribution, while particles with |$-0.2\lt [\mathrm{M/H}]{}\lt 0.4$| dex show a nearly normal distribution. In the top-right panel, particles with |$12\lt \rm {age}\lt 14$| Gyr have the broadest distribution, while particles with |$0\lt \rm {age}\lt 8$| Gyr have the narrowest and most peaked distribution. The red line and black line represent ppxf fitted and the true LOSVD for this Voronoi bin, with kinematic parameters written in the top right corner, respectively. Compared to the true LOSVD, the width of ppxf fitted curve in red is close to the youngest populations (|$0\lt \rm {age}\lt 8$| Gyr), which is reasonable because these populations dominate the light. However, the top right panel shows that ppxf tends to also care for the oldest populations by having a more skewed tail of their LOSVD at |$V_{\rm LOS}$| around |$150-300$| km s|$^{-1}$|. Even though the youngest populations dominate the spectral light, the old populations have the most features along the whole fitted wavelength region. Therefore, the differences of the skewness in the region of |$V_{\rm LOS}$| at |$150-300$| km s|$^{-1}$| indicate the effect caused by different spectral features having different LOSVDs. This figure strongly suggests there are limitations on current techniques to obtain unbiased kinematics due to the dependence of |$V_{\rm LOS}$| on age and |$[\mathrm{M/H}]$|.
![LOSVD of particles with different ages and $[\mathrm{M/H}]$ in one Voronoi bin. Particles are divided into three $[\mathrm{M/H}]$ and age groups, then their $V_{\rm LOS}$ histograms are plotted on the left and right panels in different colours, respectively. The grey histograms are the total $V_{\rm LOS}$ distributions of the three groups. The top rows are results using the original mock cubes. while the bottom rows use LOSVD-Convolved mock cubes. The red lines are ppxf results for mock cubes generated and fitted using PEGASE-HR templates in PEGASE-HR spectral resolution ($\rm {FWHM}=0.55\, {\rm \mathring{\rm A}}$). The black lines are the true values calculated by fitting the Gauss–Hermite function with particles’ light-weighted LOSVD in the black histogram. The kinematic parameters for these two lines are written in the top right corner. This figure indicates LOSVD changes with age and $[\mathrm{M/H}]$. After using LOSVD-Convolved cubes, this relationship can be artificially eliminated, and ppxf can measure kinematics consistently.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/534/2/10.1093_mnras_stae2148/1/m_stae2148fig15.jpeg?Expires=1750262358&Signature=F2v3QI-vk5qyEoZJW6VMNYgoKqqmjKSrueG1Eh02uLvi3GoX3UEEjKSsT1lxgCsM4xC3fAYPSo6vP-0TeiD~z8vk7jyOrcRPla4ZPTk7GS3uZDQQqK4FZMHwuslOGoqu6Peq6JN~AdtILf4w19Xuuf3wz3mlKH-E4ll6mKwQnofleEii8WlE3f4uHkBwOUtU1QsEkidENTDRyScmrZ32OB6XhiMlDO0GwTMARqoRoEoicmrXsmSapwlOdiG9-MWKixu146S8uwkCZx~DHPZ3MLNhd8QPlJU21G80HDC2F8QPPFv~Hl4pLs2AVQTXsdBGp2SV3U9ahgMXdszJq87ERw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
LOSVD of particles with different ages and |$[\mathrm{M/H}]$| in one Voronoi bin. Particles are divided into three |$[\mathrm{M/H}]$| and age groups, then their |$V_{\rm LOS}$| histograms are plotted on the left and right panels in different colours, respectively. The grey histograms are the total |$V_{\rm LOS}$| distributions of the three groups. The top rows are results using the original mock cubes. while the bottom rows use LOSVD-Convolved mock cubes. The red lines are ppxf results for mock cubes generated and fitted using PEGASE-HR templates in PEGASE-HR spectral resolution (|$\rm {FWHM}=0.55\, {\rm \mathring{\rm A}}$|). The black lines are the true values calculated by fitting the Gauss–Hermite function with particles’ light-weighted LOSVD in the black histogram. The kinematic parameters for these two lines are written in the top right corner. This figure indicates LOSVD changes with age and |$[\mathrm{M/H}]$|. After using LOSVD-Convolved cubes, this relationship can be artificially eliminated, and ppxf can measure kinematics consistently.
We made a new experiment to verify this effect on spectral fitting results. First, we re-generate mock MUSE cubes following the same procedures as above, but not using each particle’s |$V_{\rm LOS}$| to shift the spectrum. Then we obtain non-kinematic mock data cubes. Next, for each Voronoi bin, we select all the particles included and obtain its |$V_{\rm LOS}$| histogram, which is the true LOSVD as shown in grey in Fig. 15. Then, we directly use this histogram as the LOSVD kernel function and convolve it with all the spectra in this Voronoi bin to add kinematic effect. We do it for all the Voronoi bins and obtain new mock cubes, where spectral templates with different |$[\mathrm{M/H}]$| and age have the same LOSVDs. Therefore, in this way, we eliminated the relation of |$V_{\rm LOS}$| with |$[\mathrm{M/H}]$| and age as mentioned above. Finally, we employ ppxf to the new cubes (hereafter LOSVD-Convolved cubes) and measure the kinematics. The fifth row of Fig. 14 shows the kinematics recovery results. It is clear that all the Gauss–Hermite moments are well recovered with all the data points aligned to the zero line. The red and black lines in the bottom row of Fig. 15 also indicate the correction of ppxf measurements. We also plot the kinematics maps in the same way as Fig. 6 in Appendix (Fig. B4) to better demonstrate the consistency.
We also tested the kinematics recovery on LOSVD-Convolved cubes generated using MILES templates, as shown in the sixth row of Fig. 14 (see also Fig. B5). In this low spectral resolution, even though we make different populations have the same LOSVD for the spectra, there are still systematic offsets appearing in all the panels. We also demonstrate in the last row the results on LOSVD-Convolved cubes generated using PEGASE-HR templates, but in MUSE spectral resolution to remove the effects of different SSP templates (see kinematics maps in Fig. B6). The appearance of offsets indicates the effect purely due to insufficient spectral resolution.
In conclusion, all these results strongly suggest that both the low spectral resolution and variance of LOSVDs in different age and |$[\mathrm{M/H}]$| contribute to the systematic offsets we see in residual panels of Fig. 6. In the future, to remove the systematic offsets of stellar kinematics, one needs to use an instrument with higher spectral resolution than MUSE. This means more exposure time is needed to achieve the same SNR as MUSE observations. As we know |$V_{\rm LOS}$| changes with |$[\mathrm{M/H}]$| and age in the line-of-sight of real galaxy observations, it might be necessary to allow different templates to have different LOSVDs during the spectrum fitting analysis to obtain more accurate results. However, kinematic and stellar population measurements from spectral fitting methods have already been a highly degenerate problem. Allowing variable LOSVDs will increase the degeneracy by a factor of the number of templates. In this case, it is easy for the algorithm to obtain incorrect results. One possible way would be simply assuming a quantitative relation between LOSVD and metallicity and age at different locations of the galaxy and that this relation can be expressed by an analytical equation. This is equivalent to adding a prior to the fitting process to improve the accuracy of kinematics measurement without adding degeneracy. Even though this way has many limitations, it will be still useful for the analysis of MW-like galaxies, and GalCraft can help provide this prior for galaxies in different projections.
Apart from the above analysis on inconsistencies caused by spectral fitting methods, Fig. 15 also shows the deviations between |$V_{\rm LOS}$| histogram (grey line) and the parametrically best-fitted true LOSVD (black line). In the future, we will explore using non-parametric techniques (e.g. BAYES-LOSVD, Falcón-Barroso & Martig 2021) to recover the true kinematic parameters rather than Gauss-Hermite equation, which might result in better fits when the LOSVD is strongly non-Gaussian.
4.2 Inconsistency of mass fraction distributions recovery
In general spectral fitting, measuring mass/light fraction distributions of stellar populations is a highly degenerate problem, especially when one wants to obtain the SFH at different components. In this study, we follow the data analysis procedures in M21 to divide the template’s age and metallicity bin size due to the definition of SFH. However, most of the previous studies did not consider bin size of template grids. Nevertheless, the mass fractions increasing from young to old and metal-poor to metal-rich populations found in Fig. 12 is still seen in some components of the galaxies (e.g. Pinna et al. 2019a, b). In the mock and real data tests of Kacharov et al. (2018), the mass fraction distributions are also smoothed towards old and metal-rich regions (see their fig. 5). The overdense feature of young populations at around |$2{-}4$| and |$12{-}14$| Gyr in our Fig. 12 is also seen in some of the above-mentioned studies. In this section, we re-investigate all these tests more comprehensively and discuss the differences in the mass fraction distribution from ppxf, including whether or not to divide the bin size, effects caused by SNR and different SSP models, and try to address potential reasons causing the inconsistency to the true values. From now on, we refer ‘mass fraction’ as ppxf obtained mass weights of SSP templates normalized by the total weights (for each panel in the figures). And we refer ‘mass fraction (|$\text{Gyr}^{-1}$|)’ and ‘mass fraction (|$\text{dex}^{-1}$|)’ as mass fraction divided by the bin size of age and metallicity grids, respectively, where mass fraction (|$\text{Gyr}^{-1}$|) is also equivalent to SFH.
We first convert the age distribution x-axis of Fig. 12 from linear to log-scale, because MILES templates are closer to being evenly scaled in |$\log \rm {age}$| than linear age, then the width of each step is close to being equal. Next, we re-plot the age distribution recovery in Fig. 16 and calculate the correlation coefficients using the original age grids. The first row shows age distribution in mass fraction (|$\text{Gyr}^{-1}$|), which is the SFH of each component. The thin disc, inner central, and global panels clearly show two overdensity regions, which are pointed out by two green boxes. The thick disc and up per central panels also have peaked features in these boxes, but not significant. The second row shows just the mass fraction without dividing the bin size, and all the panels show relatively smoother distributions than the first row. Therefore, given the differences between the first and second rows are whether or not dividing bin size, we speculate the two overdensity regions are artefacts due to the bin size arrangements of the MILES template grids.
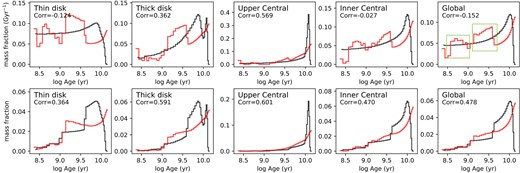
Age distribution recovery of different components of the galaxy from ppxf on the mock MUSE cube generated in Section 3.1. This figure is similar to Fig. 12 but the x-axis is in logarithmic scale. Black lines are the true values and red lines are the results from ppxf. The first row shows mass fraction (|$\text{Gyr}^{-1}$|), which is the representation of SFH, and the two green boxes in the ‘Global’ panel are the two overdensity regions. The second row shows just the mass fraction, which is the direct output from ppxf. The correlation coefficients of the red and black lines are written on the top right corner for each panel.
To verify our speculation, we plot in Fig. 17 a zoom-in of the two overdensity regions pointed out on the top right panel of Fig. 16. The blue and orange lines are mass fraction (|$\text{Gyr}^{-1}$|) and mass fraction distributions, respectively, which are equivalent to the first and second row of Fig. 16, respectively. The mass fraction for each panel is multiplied by a factor for better visualization. We also plot the age bin size of MILES templates as the grey line and the scale in the right y-axis. From these two panels, we find the peaked features of mass fraction (|$\text{Gyr}^{-1}$|) (blue line) appear when the age bin size experiences a decrease from old to young ages, and the mass fraction (orange line) is still relatively smooth. Therefore, we can confirm the peaked features of mass fraction (|$\text{Gyr}^{-1}$|) in our results are due to the non-regularized spacing of MILES age grid. This also explains the better recovery of |$[\mathrm{M/H}]$| distributions (bottom row of Fig. 12) which is due to the almost linearly spaced |$[\mathrm{M/H}]$| grids.

Zoom-in of the two overdensity regions pointed out in Fig. 16. The blue and orange lines are mass fraction (|$\text{Gyr}^{-1}$|) and mass fraction distributions, equivalent to the first and second row of Fig. 16, respectively. The mass fraction for each panel is multiplied by a factor for better visualization. We also plot MILES templates’ age bin size as the grey line and the scale in the right y-axis.
Previous studies applied regularization (McDermid et al. 2015) in ppxf to obtain smooth weight fraction distributions. The regularization works as an extra term in the equation to be minimized during the optimization to damp high-frequency variations in the weight distributions along spectral templates grid (see details in section 3.5 of Cappellari 2017) and leads to smooth weights distributions. However, this smoothness has an effect on weights without dividing the bin size. This explains why mass fraction distributions are smooth in our results, and whether mass fraction (|$\text{Gyr}^{-1}$|) distributions are smooth depends on how the template grids are spaced. For the rest of this section and Section 4.3, we only use the mass fraction without dividing the bin size to justify the recovery consistency (Figs 18 and 20), because this is expected to be achieved by spectral fitting methods with regularization. And we leave investigations on mass fraction (|$\text{Gyr}^{-1}$|) to Sections 4.4 and 4.5.
Although the current ppxf regularization algorithm does not consider the bin size of the template age grid and different regularization strategies (e.g. regul values, order of regularization) can affect the mass fraction recovery (will be discussed in Section 4.3), we still see the inconsistency between spectral fitting results and true mass fraction distributions of the oldest populations in the bottom row of Fig. 16. The main reason is that spectral templates in the oldest and metal-rich regions are very similar and indistinguishable at the current SNR level. Therefore, it is difficult for ppxf to correctly recover the mass distributions in these age-|$[\mathrm{M/H}]$| regions when performing fitting using templates normalized to 1 |$\mathrm{M}_{{\odot }}$|, even though the algorithm has already reached the global minimum. The mass fraction uncertainties in these regions can be much larger (relative uncertainties from 1|$\sigma$| values dividing the mean of MC realizations are |$\sim 20$| per cent for regions less than 8 Gyr and |$50{-}65$| per cent in |$10{-}14$| Gyr). We also confirm in Appendix Fig. B7 that using LOSVD-Convolved cubes do not improve the results significantly, so the effect of systematic offsets in kinematics measurement in Fig. 6 is not the cause of mass fraction distribution inconsistency.
One way to increase the quality of the mass fraction recovery in old- and metal-rich population regions could be to increase the SNR of the spectrum. This can be achieved by requiring a higher target SNR during the process of Voronoi binning but with the cost of reducing the number of Voronoi bins, i.e. details in the spatial distributions. We show in Fig. 18 the age and |$[\mathrm{M/H}]$| distributions at different SNRs (shown in different colours), compared to the true values shown in black lines. This figure is obtained by running the GIST pipeline on the mock MUSE cube generated in Section 3.1 with different target SNRs during Voronoi binning, and then the mass fraction distributions of all the Voronoi bins are added together to represent the global mass distributions of the mock galaxy, and finally integrated through age and |$[\mathrm{M/H}]$| axes, respectively. To make it a fair comparison, we make sure that the spatial pixels used to generate Voronoi bins are the same. According to the correlation coefficients, this figure indicates that with the increase of Voronoi bin SNR, the global mass fraction distributions in both panels are more consistent with the true values. Specifically, the weights of metal-rich and old stellar populations are going lower with higher SNR. Therefore, Fig. 18 indicates that increasing SNR can improve SFH recovery. However, we note that in reality, an integrated spectrum with SNR larger than 1000 is impractical. In addition, even with SNR at 200 |$\text{pix}^{-1}$| is pointless because in this case numerical issues and spectral library uncertainty can become the dominant factor.
![Global age (top panel) and $[\mathrm{M/H}]$ (bottom panel) distributions at different SNRs, which are obtained by running ppxf on the mock MUSE cube generated in Section 3.1 with different target SNRs of Voronoi bins, and then the mass fraction of all the bins are added together to represent the global mass distributions of the galaxy. Black lines are the true values. ‘Corr’ is the correlation coefficient value of the ppxf and true values at each SNR. This figure indicates that increasing SNR can help obtain better mass distributions compared to the true values, especially the issue of metal rich, old stellar population overestimation is alleviated.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/534/2/10.1093_mnras_stae2148/1/m_stae2148fig18.jpeg?Expires=1750262358&Signature=N2lHnL7HxtvEfqOlgKIqwql7nN5sUdg4FVT5~XOQM0zUYLn~CQi03fHiZyqN-6kM8JPDyRJYF1tlEv~s27c07BDLSySbpC64pqhFskpTPOsrFjHQyx92vReRIKB8kv~cJ8DHwIOMBqDaXXdbNt-8NhjPH7MdCPreYIR3De2SSUT29Fincte2Vu2CDWGRKcBAmOzJRPunJKmHijx8dwjrZOT8--0Cd8xBspuTyLQ88GfNXhz~cW8I4hmvDRi0hqftGoFaizpnKPmC8ubekaQGjnmSKKjXDxqew7XzFkRcob3b7EOWXwxKf~wc8sOUvFDkq64-UIFYJ4UN-nghYl87eA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Global age (top panel) and |$[\mathrm{M/H}]$| (bottom panel) distributions at different SNRs, which are obtained by running ppxf on the mock MUSE cube generated in Section 3.1 with different target SNRs of Voronoi bins, and then the mass fraction of all the bins are added together to represent the global mass distributions of the galaxy. Black lines are the true values. ‘Corr’ is the correlation coefficient value of the ppxf and true values at each SNR. This figure indicates that increasing SNR can help obtain better mass distributions compared to the true values, especially the issue of metal rich, old stellar population overestimation is alleviated.
To study the effect of different choice of SSP templates, we re-plot age and |$[\mathrm{M/H}]$| distributions of mock cubes generated by PEGASE-HR templates in Fig. 19. PEGASE-HR templates are evenly spaced in |$\log \rm {age}$|. During the ppxf fitting, we use the same templates and fitting strategies (fitting wavelength region, regularization, etc.) as those in Section 3.2 and also degrade to MUSE spectral resolution to remove the resolution differences (even though we find increasing spectral resolution does not improve the recovery significantly after comparing to Fig. B8 of a PEGASE-HR spectral resolution version). The Voronoi bin allocation is the same as mock cubes generated by MILES templates. According to the correlation coefficients, mass fraction using PEGASE-HR in Fig. 19 are more consistent than those using MILES in Figs 12 and 16 for both age and |$[\mathrm{M/H}]$|. Moreover, the mass fraction – |$\log \rm {age}$| panels (second row) have almost no overdensities than the results using MILES (second row of Fig. 16), and the oldest populations have a more modest increase. Therefore, in our test, PEGASE-HR performs better during the mass fraction recovery and could provide more consistent mass fraction distributions than MILES. We think this is likely due to the templates’ perfectly even spacing in |$\log \rm {age}$|, which leads to smoother input and is preferred by ppxf during regularization. However, the PEGASE-HR templates used in our tests are generated using PADOVA 1994 (Bertelli et al. 1994) isochrones but MILES are generated using BASTI isochrones (Pietrinferni et al. 2004, 2006). Whether isochrones differences can affect mass fraction distribution recovery ability requires further investigations. Moreover, the current limitation of PEGASE-HR templates is they only have one bin in |$[\mathrm{\alpha /Fe}]$|, we emphasize here again the need for multiple-|$[\mathrm{\alpha /Fe}]$| templates.
![Age and $[\mathrm{M/H}]$ distributions of each component for the mock cubes generated using PEGASE-HR templates and degraded to MUSE resolution ($\rm {FWHM}=2.65\, {\rm \mathring{\rm A}}$). The first row demonstrates mass fraction ($\text{Gyr}^{-1}$) changes with age (SFH). The second row shows the mass fraction changes with age (MDF). The third row shows mass fraction changes with $\log \rm {age}$. The fourth row shows cumulative mass fraction distributions and the fifth row shows metallicity distributions.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/534/2/10.1093_mnras_stae2148/1/m_stae2148fig19.jpeg?Expires=1750262358&Signature=G48~ThupX~xnXVviHkVbAaZrsYoJco~BkmmlyB6xSCB10fM~m0nxR586bPpuFpzUwmRrF-p7PtO8U04UWcgmyq1rem67s0Vc5Js9oWFpO~IRQ4yh7lQBfolyVTKykpF3udltnolgJocey-Wd-a3Ra~gNQpa5Ywz8Mw0Xm793HdM2fhqJwlo46mZTUne4b8Ia4YM6z-0DDOQVnOIi1~3Kz~oZisX~5s7663Ss3Lqb92AW-GRuIv54W5SmACQxeNIQtTHveWA5p0Us-8j3nQG1ujP~ZVILa0jEhRxySnHwDcZEZew19N0ViNXQZJUEIlPsiD5Bf5USv19nzz130y5fcw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Age and |$[\mathrm{M/H}]$| distributions of each component for the mock cubes generated using PEGASE-HR templates and degraded to MUSE resolution (|$\rm {FWHM}=2.65\, {\rm \mathring{\rm A}}$|). The first row demonstrates mass fraction (|$\text{Gyr}^{-1}$|) changes with age (SFH). The second row shows the mass fraction changes with age (MDF). The third row shows mass fraction changes with |$\log \rm {age}$|. The fourth row shows cumulative mass fraction distributions and the fifth row shows metallicity distributions.
In the future, non-parametrically, it is worthwhile to test the mass fraction recovery ability using templates with linearly spaced grids (see details in Section 4.4) or modifying regularization to apply smoothness effect in terms of mass weights (|$\text{Gyr}^{-1}$||$\text{dex}^{-1}$|). Another approach is to take the mean of MC realization (e.g. Pessa et al. 2023), which is more consistent with the true values than regularization based on simple tests (see fig. 1 of Cappellari 2023). We can verify whether this is true for a mock MW cube in future studies. Parametrically, one can try to recover both chemical enrichment history and SFH by taking into account chemical evolution theories, which will help remove counterintuitive features in the mass fraction distributions. One approach is to use Bayesian spectral fitting codes, such as Prospector (Leja et al. 2017) or BAGPIPES (Carnall et al. 2018). Another example is the semi-analytic spectral fitting method from Zhou et al. (2022). This method applies spectrum fitting with the predicted best-fitting spectrum from chemical evolution models, which is similar to adding a prior on ppxf during the fitting. Fig. 6 of Zhou et al. (2022) showed that this method has better consistency on mass fraction recovery than ppxf, and the overestimations in metal-rich, |$2{-}4$| and |$12{-}14$| Gyr regions are fixed successfully. Therefore, it provides a way to measure accurate chemical enrichment and SFH for future studies. One important caveat is that their chemical evolution model is a close-box model, which does not apply to galaxies dominated by frequent passive merger events (e.g. NGC 7793 in Kacharov et al. 2018). In addition, this method does not take into account the relation of chemical abundances with velocity, which are important indicators for radial migration and kinematic heating.
4.3 Effect of regularization
In this section, we focus on the effects of different regularization strategies on mass fraction distributions. There are two parameters controlling the regularization process, which are regul and reg_ord, where regul applies linear regularization to the weights during the ppxf fit and reg_ord controls the order of regularization. Kacharov et al. (2018) investigated mass fraction differences of mock data with different order of regularization (see their figs 5 and C2) and concluded that the choice of order of regularization does not affect the results over a significant level. Boecker et al. (2020) tested the mass fraction distributions recovery of the second- and third-order of regularization and compared them to the true values using stellar particles from an EAGLE simulated galaxy. They found results from third-order regularization are more consistent with the true values. Cappellari (2023) compared the mass fraction recovery consistency of non-regularized ppxf fit, an average of 100 ppxf fits to MC realizations, and single regularized ppxf fit (see their fig. 1), and concluded that regularized results are comparable to that of the average of multiple realizations.
The selection of regul value was briefly discussed in Section 3.2. Here, we re-investigate this question in detail by applying different regul and reg_ord strategies on our mock cubes generated in Section 3.1. The results are shown in Fig. 20, where we plot the age distributions on the top panels and |$[\mathrm{M/H}]$| distributions on the bottom panels for different components of the galaxy. We also plot the global mass distributions in the last column. We apply five different strategies during the fitting: the first three cases use first-order regularization with regul|$=5$|, regul|$=10$|, regul|$=20$|, and regul|$=$|regul|$_{{\rm max}}$||$(30-100)$|, respectively; the last uses regul|$=5$| and second-order regularization. Black lines are the true values. When comparing results with the same order of regularization but different regul, we find results with larger regul are smoother, and their weights at old populations are relatively smaller than results with smaller regul. However, in the |$[\mathrm{M/H}]$| distribution panels, weights are going more toward metal-rich populations and the distributions become less consistent with the true values for all the components. For results with the same regul but different orders of regularization, we see results with reg_ord|$=1$| show better consistency with the true values than those with reg_ord|$=2$|. Specifically, results with reg_ord|$=2$| have more mass fractions in the oldest populations.
![Age (top panel) and $[\mathrm{M/H}]$ (bottom panel) distributions for different components by running ppxf on the mock MUSE cube generated in Section 3.1 with different regularization strategies (shown in different colours). Black lines are the true values. The last column shows global age and $[\mathrm{M/H}]$ distributions. This figure indicates that results using the first order of regularization are better than results using the second order of regularization; increasing regul can help obtain smoother results but the mass fractions will go towards metal-rich regions for all the components.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/534/2/10.1093_mnras_stae2148/1/m_stae2148fig20.jpeg?Expires=1750262358&Signature=XOBsntY14D6CyIE9l6LotIcikaW1NLTmyzHdFkaZd0cGTm6iWpPW9~2KPZl6BB5Iu6jJGaf-Vqd2lIFpmxBEy8i2MSG8JU-CJhKqkQVN7f6QHxjA5EvlUX-8Up8UuJu8uTRgyaaYsAFQMfLQMIfi96R7hgszdzQ2yG6PzKIP0sicBva50flduTOlkubizVHECJ3mEqvAyMLe0-wOQIaz17lpXK81~kc5zbOTjeh~xKs2yWDmyJX3pdOe9VPqXC21x~qRp11RrNYZIL-iQ6Ct6IHYepU1cs5PIY--TeJc1EcZVxPqOzQAmzIFXDbqHtKCm-Da9p7z3jQClBO~bfgx7Q__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Age (top panel) and |$[\mathrm{M/H}]$| (bottom panel) distributions for different components by running ppxf on the mock MUSE cube generated in Section 3.1 with different regularization strategies (shown in different colours). Black lines are the true values. The last column shows global age and |$[\mathrm{M/H}]$| distributions. This figure indicates that results using the first order of regularization are better than results using the second order of regularization; increasing regul can help obtain smoother results but the mass fractions will go towards metal-rich regions for all the components.
In conclusion, Fig. 20 indicates that for this mock cube, results using the first order of regularization are better than results using the second order of regularization; increasing regul can help obtain smoother results but the weights will go towards metal-rich regions. Given we do not have the codes to perform third-order regularization, it is hard to say which order is the best. Intuitively, it seems higher order regularization tends to have more mass fraction in the old populations. Therefore, we think the third-order regularization is preferred for EAGLE simulated galaxy test (Boecker et al. 2020) because the particles’ mass weights from the EAGLE simulations are naturally dominated by old and metal-rich populations, then the third-order regularization tends to fit better in this region. Our E-galaxia mocked catalogue has no particle in the metal-rich and oldest regions, so the first-order regularization is better. However, all the above discussions need further verification and we will test the third-order regularization results in the future. For the real galaxy fitting results of Pinna et al. (2019a, b) and M21, they all used second-order regularization and showed an overdensity of mass weights in the oldest, metal-rich populations for different components of the galaxies, which makes it difficult to discuss differences in the formation epoch between these components, and it is not possible to tell if the overdensity is true or instead from full-spectrum fitting artefacts.
4.4 Mass fraction distribution recovery using interpolated MILES templates
According to discussions in Sections 4.2 and 4.3, the overdensity features of age distributions in mass fraction (|$\text{Gyr}^{-1}$|) shown in Fig. 16 are likely due to not considering templates bin size during regularization, and using different regularization strategies can barely alleviate the inconsistencies with the true values. Therefore, we investigate the improvements of age and |$[\mathrm{M/H}]$| distributions using interpolated MILES templates in this section. Fig. 21 shows the age and |$[\mathrm{M/H}]$| distributions of mock cubes generated by GalCraft and fitted by ppxf using MILES templates that are interpolated linearly in age and |$[\mathrm{M/H}]$| grid. The fitting strategies are the same as those in Section 3.2. We can clearly see that the overdensities in age distributions (in |$\text{Gyr}^{-1}$|) at |$2{-}4$| Gyr are alleviated to a large extent in the ‘thick disc’, ‘inner central’, and ‘global’ panels compared to the results using original MILES templates in Fig. 12. In addition, |$[\mathrm{M/H}]$| distributions (in |$\text{dex}^{-1}$|) from ppxf are also more consistent to the true values in terms of correlation coefficients. The increase of old populations still exists, which will be discussed in detail in Section 4.5. We also investigate the results using MILES templates interpolated linearly in |$\log$| age and |$[\mathrm{M/H}]$| (shown in Fig. B9) and find the overdensities still exist with the shape being more similar to the results using PEGASE-HR (Fig. 19). Given PEGASE-HR template grid is also linearly spaced in |$\log$| age, this similarity is expected. In conclusion, we confirm that performing spectral fitting using linearly interpolated templates in age and |$[\mathrm{M/H}]$| can alleviate the overdensities in |$2{-}4$| Gyr. In addition, the new version of ppxf considering bin size during regularization is under development (private communication with Michele Cappellari). Given this is equivalent to interpolating templates as we did in Fig. 21, one can choose this approach in the future to avoid additional template uncertainties due to interpolation.
![Same as Fig. 12 but for the mock cube generated using MILES templates interpolated linearly in age and $[\mathrm{M/H}]$ in MUSE spectral resolution.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/534/2/10.1093_mnras_stae2148/1/m_stae2148fig21.jpeg?Expires=1750262358&Signature=1W2wcb~f5oxUmX1fmAzoxykwtzQnpK4jlsym-ZU0Oj9mvM1Btuvhot1DNJbwE0F9E5OjRDZoMs7El6Im-lX-eio51Z8V9Vm1a00-lFNI4iUykGGnIQSvgZKUu2c4ygkABVXMkwc0B4lInAtRRXWGrOrbvvDQ9R7iNE-OYBLJ6Dkx6kHSttHguUHov1h0iUU~QamNslrJHCBLbPbg1acZQm~eWKpjsCrIv7LOxpRQGE6waSf5-B5R2MS7cmLhQEHFb1OJfrlWq0reNrqVIlyqfYm8vmENOqVbY064KpGw8s4a7-sM92VvVSIDGYuUjAZxcC2QcGcK4-bqm9zPrCKdHw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Same as Fig. 12 but for the mock cube generated using MILES templates interpolated linearly in age and |$[\mathrm{M/H}]$| in MUSE spectral resolution.
4.5 Potential effects of effective age resolution on star formation history recovery
In Section 4.2–4.4, we investigated the effects of template grid spacing and regularization on the recovery of mass fraction distribution. The comparison between Figs 12 and 21 confirms that the overestimation of age distribution (SFH) in the |$2{-}4$| Gyr range is significantly alleviated by using templates with a linearly spaced age grid. However, in Fig. 21, which uses the linearly spaced age grid, narrow peaks at around 1 and 2 Gyr can still be seen prominently in the ‘thin disc’, and moderately in the ‘thick disc’, and ‘inner central’. These peaks differ from the broad |$2{-}4$| Gyr overdensities seen in Fig. 12, but are more similar to peaks seen for the case of the |$\log \rm {age}$| grid (Figs 19 and B9), although they suffer from the additional effect of inconsistent regularization. When using the template grid with linear age spacing, there is an overestimation in |$12{-}14$| Gyr range that is present across all components (Fig. 21). These results suggest that even after fixing the issue of inconsistent regularization with the linearly spaced age grid and trying out different SSP models, the recovery of SFH is far from perfect and a possible reason for this could be the fact that weights of some SSP templates are degenerate with respect to the observed spectra.
To examine the effect of template weight degeneracies on SFH recovery, Zibetti, Rossi & Gallazzi (2024) estimated and explored the age resolution of SSP templates that can be achieved through non-parametric full-spectrum fitting, which we refer to as effective age resolution. The effective age resolution is defined as the smallest width of independent age bins in a reconstructed SFH, and it is limited by the amount of information that is possible to extract from a spectrum. We refer to their Section 2 for a detailed analytical definition. Zibetti et al. (2024) found that the effective age resolution is generally no better than 40 per cent for most age grids older than 100 Myr (see their fig. 4). This fraction is roughly consistent with the mass weights uncertainties in our results. More importantly, Zibetti et al. (2024) found that the age resolution does not vary smoothly but shows some well-defined maxima, for example, at 10 Myr and 1 Gyr. The origin of this could be related to the fact that this is the stage where some unique spectral features develop due to significant changes in stellar evolution. They speculated (their section 5.5) that these maxima in age resolution could be responsible for the peaks seen in SFH of galaxies extracted using non-parametric full-spectrum fitting on IFS data (e.g. CALIFA Cid Fernandes et al. 2013; González Delgado et al. 2017 and MaNGA Sánchez et al. 2019). These peaks in SFH appear across a wide variety of galaxies and span of cosmic time, which lends further support to the idea. Our work where we try to recover the SFH of simulated galaxies further supports this idea – even though the SFH of the simulated galaxy is smooth, the recovered SFH has peaks/overdensities [e.g. see the age distributions in mass fraction (|$\text{Gyr}^{-1}$|) shown in Figs 16, 19, 21, B8, B9]. The overestimation of SFH at |$12{-}14$| Gyr in our results could be due to a combination of a number of factors. Our input SFH as specified in E-galaxia drops sharply to zero at 12.8 Gyr which makes it challenging to recover the SFH. Unfortunately, the spectra of templates at old ages are quite similar to each other (low effective age resolution), this would lead the fitting machinery to assign non-zero weights for old templates. The regularization which favours smoothness will also favour non-zero weights for old populations, even with the input truncating at 12.8 Gyr. Additionally, due to the low luminosity of these old SSPs, to account for a given flux in spectra, a significant mass fraction can be assigned to these old ages as compared to young ages. The linear age grid has more templates at old ages as compared to a |$\log \rm {age}$| grid. This suggests that bias in SFH (which is mass fraction per unit age) due to the above effects is expected to be higher for a grid with linear age as compared to log age. This is evident in our results and can be seen by comparing the SFH at old ages in Figs 21 and B9.
4.6 Caveats when using GalCraft
In this section, we give some caveats when using the GalCraft code. The E-galaxia mock stellar catalogue is generated based on the GCE model of S21. The success of this model is that it can reproduce |$[\mathrm{\alpha /Fe}]$|–|$[\mathrm{Fe/H}]$| bimodality which is quantitatively consistent with the APOGEE observations of the MW (Hayden et al. 2015) by employing radial migration and kinematic heating. However, more complex kinematic and dynamical processes are likely to exist in real galaxies, such as non-asymmetric perturbations due to spiral arms, bars, interlopers, etc. The current model does not have these processes and features, which should be added in the future. In addition, the interpretation of |$[\mathrm{\alpha /Fe}]$| bimodality in S21 due to radial migration and kinematic heating is opposite to findings from simulations which suggest the need of mergers (e.g. Clarke et al. 2019; Buck 2020), and this model lacks stars in the Galactic halo. Therefore, this code is not applicable for comparing the merger features or the halo distributions; This model also lacks descriptions of parameter distributions in the bulge, especially the nuclear disc in the MW centre (e.g. Schultheis et al. 2021) and chemodynamics of the B/P bulge (e.g. Wylie et al. 2021), which could be improved in the future.
5 FUTURE STUDIES
In this study, we did not apply extinction on the mock data cube because this work is purely on testing the kinematics and stellar population recovery via full-spectrum fitting. In real edge-on galaxies, extinction can have an essential effect because it can obscure nearly 50 per cent of the total light from stars in the thin disc, making SNR in this region lower. With the GalCraft code, we can test the kinematics and stellar population recovery of mock cubes with extinction. The extinction model in E-galaxia is assumed as a double exponential distribution mainly in the thin disc, which can be integrated through the line of sight, and each particle will have a |$E(B-V)$| value. Then, we can add the extinction effect to the spectrum by using a specific reddening curve (e.g. Cardelli, Clayton & Mathis 1989; Calzetti et al. 2000), which is also the strategy that ppxf applies to estimate extinction. Ge et al. (2018) has already tested the effect of extinction on full-spectrum fitting results using one stellar population template, we can re-investigate this question with comprehensive mock IFS MW data from the GCE model S21 and also study how different extinction models can affect the projected galaxy properties. In addition, several non-asymmetric features should be added to the chemical evolution model like the spiral arms, bars, mergers, and halo particles to mimic a more realistic MW. It is also necessary to add gas emissions spectral features.
There are several improvements can be made to the choice of SSP models. The current version of GalCraft has embedded MILES and PEGASE-HR templates. In the future, we will add other empirical models such as BC03 (Bruzual & Charlot 2003), X-Shooter (Verro et al. 2022), and theoretical models like starburst99 (Leitherer et al. 1999) and BPASS (Eldridge et al. 2017), which can satisfy different science goals since different models have different advantages. Some interesting tests can also be executed, for example, using one SSP model to generate mock cubes and fit them with another model, which can help study the effect of SSP template uncertainties on full-spectrum fitting results.
In addition, even though we showed in Section 3.4 that the |$[\mathrm{\alpha /Fe}]$|-rich and |$[\mathrm{\alpha /Fe}]$|-poor populations can be well identified using two |$[\mathrm{\alpha /Fe}]$| bins, it is still essential to add more bins to obtain detailed |$[\mathrm{\alpha /Fe}]$| distributions. The MW results in Hayden et al. (2015) have shown that stars in the thin and thick disc have |$[\mathrm{\alpha /Fe}]$| values about 0.0 and 0.2 dex, respectively, and there are some stars with negative |$[\mathrm{\alpha /Fe}]$|, which is also shown in the E-galaxia catalogue. However, it is challenging to use current MILES |$\alpha$|-variable templates to identify these two |$[\mathrm{\alpha /Fe}]$| sequences because most of the weights are in the bin of |$[\mathrm{\alpha /Fe}]$||$=0$|, and it is also difficult to assign a spectrum to particles with negative |$[\mathrm{\alpha /Fe}]$|. Therefore, templates with more |$[\mathrm{\alpha /Fe}]$| bins such as sMILES (Knowles et al. 2023) and FSPS (Conroy, Gunn & White 2009; Conroy & Gunn 2010) will help on the study of |$[\mathrm{\alpha /Fe}]$|–|$[\mathrm{M/H}]$| distributions for external galaxies at different components.
According to Section 4.1, given that spectral resolution is important in stellar kinematics measurements, it is also necessary to increase both the instruments’ and stellar population models’ spectral resolution. Current IFS observations such as MUSE perform well on kinematics measurements of galaxies in the central region. However, to go deeper and obtain distributions of the outer regions, especially the outer thin disc, which normally has lower dispersion, one might need to use instruments and SSP templates with a higher spectral resolution to obtain more accurate kinematics maps.
As discussed in Section 4.1, other than increasing spectral resolution, a prior can be added to the spectral fitting process which assumes the relation between LOSVD and metallicity and age at different locations of the galaxy. Then it can allow templates to have different LOSVDs and the degeneracy is not increased. The other way is to add the evolution of stellar kinematics to the semi-analytic model like the one in Zhou et al. (2022) and make it derive the chemical evolution histories along with kinematic processes directly by fitting with the integrated spectra, where the fitting process is constrained by several model parameters to be more physical. We will test the feasibility of these methods in the future.
As for weight fraction distributions, Section 4.2 demonstrated how the bin size can artificially create peak features in the SFH, and in Section 4.4 we verified that fitting the spectra using templates that are interpolated with grids linearly spaced in age and |$[\mathrm{M/H}]$| can alleviate this effect. Given interpolating semi-empirical spectral libraries is not recommended when fitting with real observational spectra, our tests indicate the need for considering bin size during regularization. In the future, we will also test modifying the regularization algorithm by considering the bin size in age and metallicity. Parametrical methods like Zhou et al. (2022) can also be used to test recovery abilities. Moreover, in this work, we input a smooth SFH for the tests. Whether the mass fraction distribution inconsistencies we found also apply to merger-dominated galaxies with multiple starburst phases can be investigated using GalCraft generated mock cubes of N-body/hydrodynamical simulations.
The aim of GalCraft code is to apply the knowledge we learned from the MW to other MW-like galaxies by mocking the IFS observations as a bridge. Especially, we want to interpret physical processes such as radial migration, kinematic heating, and |$[\mathrm{\alpha /Fe}]$|–|$[\mathrm{M/H}]$| distributions of other galaxies to answer the question of whether all the MWAs have similar processes to the MW, and if not, how much difference can be. However, we have not yet performed any comparison of the mock MW IFS data cube with existing MWA observations due to the lack of extinction and some Galactic components in the current version of E-galaxia, and the artefacts created by full-spectrum fitting methods we found in this work. Therefore, when all these aspects get improved in the future, we will compare our mock MW data cube from GalCraft with real IFS observations from the GECKOS survey (van de Sande et al. 2024), which will observe 35 edge-on MW-like galaxies, and see whether the MW is similar to the so-called MWAs according to their kinematics and stellar population properties.
6 SUMMARY AND CONCLUSIONS
In this work, we present the GalCraft code which uses simple stellar population models and the mock MW catalogue from E-galaxia to generate a mock MW IFS data cube in the same format as extragalactic observations. We aim to eliminate the differences in analysis techniques between the Galactic and extragalactic studies such as the use of individual stars vs. integrated stellar populations, the number density distributions of stellar parameters versus integrated mass- or light-weighted distributions, the results with or without projection effect, etc. The mock data cube can be put into the GIST pipeline to perform data analysis in the same way as extragalactic observations and the results can be compared directly to external galaxies to study the similarities and differences between the MW and its analogues. Therefore, this code is a bridge to link the Galactic and extragalactic studies to understand the formation and evolution of disc galaxies.
The GalCraft code is flexible, allowing users to choose their preferred SSP templates, galaxy distance and inclination, spatial/spectral resolution, and FoV of the instrument. GalCraft is also designed to mock current existing instrumental observations such as MUSE, SAMI, or MaNGA, as well as test the performance of future instrument designs. Moreover, it can also be applied to N-body/hydrodynamical simulations that contain MW-like galaxies and generate mock observations for comparisons.
For the rest of the paper, we applied ppxf (included in the GIST pipeline) as a representation of full-spectrum fitting methods on GalCraft generated mock cubes to test the ability of ppxf to recover kinematics and stellar population properties. The mock MUSE data cubes have a distance of 26.5 Mpc and inclination |$86^{\circ }$|, which is the same as MUSE observations on NGC 5746 from M21.
After comparing the true values calculated from E-galaxia particles’ properties with ppxf results, we found that there are systematic offsets between kinematic moments (|$V_{\rm LOS}$|, |$\sigma$|, |$h_3$|, |$h_4$|) and the true values. We confirm two reasons are causing it:
The velocity dispersion |$\sigma$| of most Voronoi bins are smaller than the instrument velocity dispersion |$\sigma _{\rm inst}$| in MUSE spectral resolution (|$\rm {FWHM}=2.65\, {\rm \mathring{\rm A}}$|).
|$V_{\rm LOS}$| changes with age and |$[\mathrm{M/H}]$| for particles through the line of sight, but most previous studies assumed all stellar population templates have the same LOSVD during the spectral fitting.
By using the higher spectral resolution templates PEGASE-HR (|$\rm {FWHM}=0.55\, {\rm \mathring{\rm A}}$|) and applying the LOSVD-Convolved cubes which eliminate degeneracies of |$V_{\rm LOS}$| with age and |$[\mathrm{M/H}]$|, we can obtain consistent kinematic results with the true values. Therefore, we indicate the need to allow different templates to have different LOSVDs or assume a quantitative relation between LOSVD and metallicity and age at different locations of the galaxy, where the equation coefficients can be measured during spectral fitting. The latter method is equivalent to adding a prior to the fitting process to measure kinematics without adding degeneracy. We will perform tests in the future to verify if kinematics recovery can be improved. In addition, our tests also indicate the need to use non-parametric methods such as BAYES-LOSVD (Falcón-Barroso & Martig 2021) rather than Gauss-Hermite equation for more accurate measurements of |$V_{\rm LOS}$| distributions.
In terms of stellar population properties, we verified that spectral fitting methods can recover light- and mass-weighted age, |$[\mathrm{M/H}]$|, and |$[\mathrm{\alpha /Fe}]$| with good consistency, except the mass-weighed age and |$[\mathrm{M/H}]$| are overestimated in the outer and inner regions of the mock galaxy, respectively. Both the |$[\mathrm{\alpha /Fe}]$|-rich and |$[\mathrm{\alpha /Fe}]$|-poor disc structures can be identified with reasonable regularization values during the fitting. Line-strength indices method can also identify these structures. We found the weight fraction distributions of stellar populations from spectral fitting using MILES templates on MILES-generated mock cubes are mostly consistent with the true values. However, some deviations are shown in mass fraction distributions, where mass fractions normalized by the bin size are overestimated in regions of |$2{-}4$| Gyr, |$12{-}14$| Gyr, the most metal-rich regions, and underestimated in regions of |$5{-}10$| Gyr. This is be due to many reasons including having low SNR that the flux error is larger than templates’ similarities in the region of old- and metal-rich populations, the uneven spacing of age grids in MILES templates, not considering bin size in the current regularization algorithm. We verified that having a regularly spaced age grid (linear or log) resolved the sharp discontinuities originally observed in the SFH with the default MILES library. The |$\log \rm {age}$| grid is still incompatible with the way the regularization is implemented in ppxf, so one should either alter the regularization scheme or use linear age spacing. Even when using the linear age grid, we see narrow peaks at around |$1-2$| Gyr in the SFH. This is most likely due to the fact that the precision of estimating the age of an SSP varies significantly with age as pointed out by Zibetti et al. (2024). In addition, we found that the first-order regularization can obtain better mass fraction distributions than the second-order regularization. Our tests and conclusions are helpful in identifying limitations of extragalactic data analysis using current methods and provide a reference for potential improvements in the future.
Even though GalCraft provides a bridge to link the Galactic and extragalactic studies by transferring MW to mock IFS observations, there remains a need for future improvements to facilitate more accurate measurements of external galaxy properties such as |$[\mathrm{\alpha /Fe}]$|-bimodality and to enable detailed comparisons of the MW with MW-like galaxies. These improvements include more accurate SSP models with higher spectral resolution and more |$[\mathrm{\alpha /Fe}]$| grids, more advanced spectral fitting algorithms, and instruments with deeper observations. Future tests using GalCraft are required including modifying spectral fitting codes to improve the recovery ability of kinematics and stellar population properties, using templates with more |$[\mathrm{\alpha /Fe}]$| grids, and adding extinction, to achieve measurements of known parameters such as radial migration and kinematic heating efficiencies of the MW in external galaxies.
ACKNOWLEDGEMENTS
We thank James Binney, Alina Boecker, Martin Bureau, Andy Casey, Michele Cappellari, Scott Croom, Eric Emsellem, Jesus Falcon-Barroso, Jianhui Lian, Richard McDermid, Martin Roth, Anil Seth, Juntai Shen, Yuan-Sen Ting, Glenn Van de Ven, Gail Zasowski, Ling Zhu and Zhuyun Zhuang for useful discussions. We thank all the attendees who joined the discussions of this work during the conference Linking the Galactic and Extragalactic (Wollongong, Australia) and GECKOS-Oxford conference (Oxford, UK). We also thank the referee for providing useful comments.
ZW acknowledges the HPC service at The University of Sydney for providing HPC resources that have contributed to the research results reported in this paper. Works in this paper were also done using Yoga2, a privately built Linux server for astronomical computing.
ZW is supported by Australian Research Council Centre of Excellence for All Sky Astrophysics in Three Dimensions (ASTRO-3D) through project number CE170100013. MRH acknowledges support from ARC DP grant DP160103747 and ASTRO-3D. SS is funded by ASTRO-3D Research Fellowship and JBH’s Laureate Fellowship from the Australian Research Council. JBH is supported by an ARC Australian Laureate Fellowship (FL140100278) and ASTRO-3D. JvdS acknowledges the support of an Australian Research Council Discovery Early Career Research Award (project number DE200100461) funded by the Australian Government. FP acknowledges support from the Spanish Ministry of Science and Innovation (MICINN) through the project PID2021-128131NB-I00/10.13039/501100011033.
This research has also made use of Astropy,3 a community-developed core python package for Astronomy (Astropy Collaboration 2013, 2018), numpy (Harris et al. 2020), scipy (Virtanen et al. 2020), matplotlib (Hunter 2007), and SpectRes (Carnall 2017).
DATA AVAILABILITY
GalCraft source code is publicly available via https://github.com/purmortal/galcraft. The test data and figures can be shared with reasonable requests.
Footnotes
REFERENCES
APPENDIX A: MODIFICATIONS OF THE GIST PIPELINE
We provide a list of modifications on the GIST pipeline (Bittner et al. 2019) to improve the flexibility of this software: We add more templates such as the original and interpolated PEGASE-HR (Le Borgne et al. 2004) to the software and allow the option to oversample the spectra when degrading to lower spectral resolution, which is for the same reason as we do for the GalCraft code in Section 2.3; we also added the option to select SSP templates with a certain age and |$[\mathrm{M/H}]$| range in some special cases. When measuring stellar kinematics and stellar population properties, we add the options to choose velscale_ratio, reg_ord, and use real spectra noise during the fitting and normalizing the integrated spectrum and noise by the median of the spectrum, which will be important to perform the iteration for estimating regul|$_{{\rm max}}$|; for regularization, we add an option to estimate regul|$_{{\rm max}}$| following the procedures in McDermid et al. (2015) and save the stellar population results with regul|$=$|regul|$_{{\rm max}}$|. We also allow further degrading to lower spectral resolution during the fitting when measuring SFH, which is mainly for the reduction procedures in M21 where they wanted to compare the mass-weighted stellar population parameters from ppxf with the SPP-equivalent parameters from line strength indices in the same spectral resolution; we add the option to change the penalization value bias during ppxf fitting and measure templates weights uncertainties using MC realizations similar to procedures in Kacharov et al. (2018), M21, and Cappellari (2023).
APPENDIX B: COMPLEMENTARY FIGURES
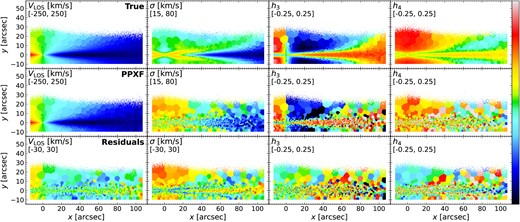
Same as Fig. 6 but turning off the kinematics penalization during ppxf fitting.
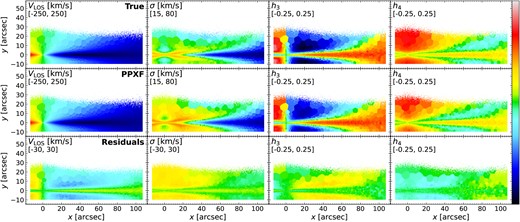
Same as Fig. 6 but for the mock cube generated and fitted by PEGASE-HR templates in PEGASE-HR spectral resolution (|$\rm {FWHM}=0.55\, {\rm \mathring{\rm A}}$|).
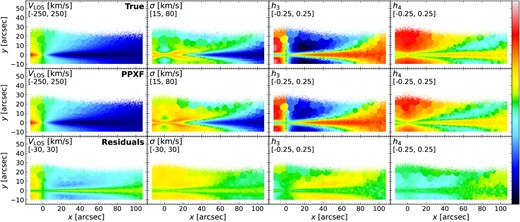
Same as Fig. B2 but turning off the kinematics penalization during ppxf fitting.
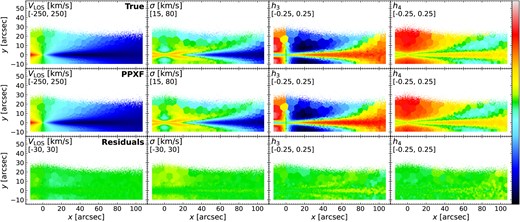
Same as Fig. 6 but for LOSVD-Convolved mock cubes generated and fitted by PEGASE-HR templates in PEGASE-HR spectral resolution (|$\rm {FWHM}=0.55\, {\rm \mathring{\rm A}}$|).
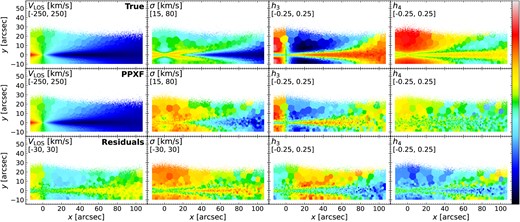
Same as Fig. 6 but for LOSVD-Convolved mock cubes generated and fitted using MILES templates in MUSE spectral resolution (|$\rm {FWHM}=2.65\, {\rm \mathring{\rm A}}$|).
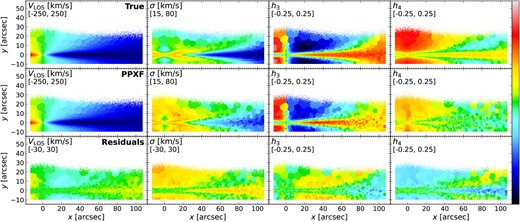
Same as Fig. 6 but for LOSVD-Convolved mock cubes generated and fitted by PEGASE-HR templates in MUSE spectral resolution (|$\rm {FWHM}=2.65\, {\rm \mathring{\rm A}}$|).
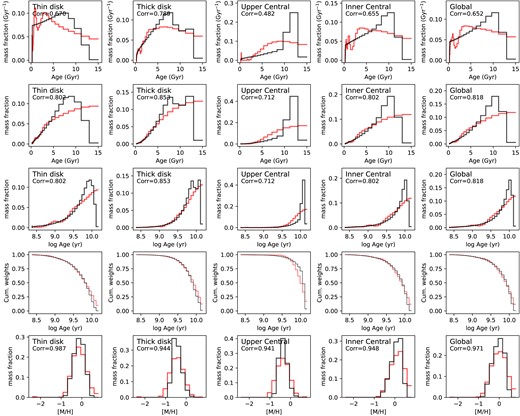
Same as Fig. 19 but for mock cubes generated using PEGASE-HR templates in PEGASE-HR spectral resolution (|$\rm {FWHM}=0.55\, {\rm \mathring{\rm A}}$|).
![Same as Fig. 12 but for mock cubes generated using MILES templates interpolated linearly in $\log$ age and $[\mathrm{M/H}]$ in MUSE spectral resolution.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/534/2/10.1093_mnras_stae2148/1/m_stae2148figb9.jpeg?Expires=1750262358&Signature=euN-hOLLN0TXigoC4QNq3R0G9spdlAJL0aDNBdVSueC-e~1aq6gJBzFup5ysPudyOjEpDBC-WzLH~ZTAB5erEydbtOR~o-zHPDvjGSuwRNuPRiO5JHPpTl-yCtebft3hDogSBtvOPTVlsvfPlvJ8WE3on~tneDWoIBF97LSGYO4jYyMP-998me~-QImu39NDi-4yftvcFJasb--lYZrtsHwWxflGL99fWSFpx6bdUW7rP2XlgMDrffecNNIq1on4jUUb72aJq5HoDz9w~IuEQx-R9A1p~4DnMuj9~3UgpJ~WikfzSAJ8x6WW44qqxppohDJaqUpXPzI9W~8gS~tlUw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Same as Fig. 12 but for mock cubes generated using MILES templates interpolated linearly in |$\log$| age and |$[\mathrm{M/H}]$| in MUSE spectral resolution.
Author notes
These authors contributed equally to this work.




