-
PDF
- Split View
-
Views
-
Cite
Cite
Ata Sarajedini, Metallicities for globular clusters in the fornax, sagittarius, and canis major dwarf spheroidal galaxies and their total luminosities, Monthly Notices of the Royal Astronomical Society, Volume 533, Issue 2, September 2024, Pages 2089–2095, https://doi.org/10.1093/mnras/stae1963
Close - Share Icon Share
ABSTRACT
We present [Fe/H] values for globular clusters associated with the Fornax, Sagittarius, and Canis Major dwarf spheroidal galaxies based on the light curve properties of their ab-type RR Lyrae variables. Fornax is a classical dwarf spheroidal containing five globular clusters and exhibiting a spheroidal shape in the sky. Sagittarius and Canis Major, possess six and four globular clusters, respectively, and have both been tidally disrupted to a significant degree by the gravitational field of the Milky Way galaxy. Based on an analysis of the periods and light curve amplitudes of 76 globular cluster ab-type RR Lyraes in Fornax, 103 in Sagittarius, and 29 in Canis Major, we find mean metallicities of |$\langle$|[Fe/H]|$\rangle$| = –1.67 ± 0.05, –1.76 ± 0.12, and –1.69 ± 0.25 for the globular clusters in Fornax, Sagittarius, and Canis Major, respectively. Given the similarity of these three values, and coupled with the well-established correlation between the mean metal abundance and total luminosity for dwarf spheroidal galaxies, we conclude that the absolute V-band magnitudes of these three galaxies are indistinguishable to within ∼0.8 mag.
1 INTRODUCTION
The determination of metallicities on a uniform scale has been an important development in the study of stellar populations, especially as regards the formation and evolutionary history of globular clusters and their host galaxies. Stellar metal abundance studies generally fall into four broad categories – individual stellar and integrated light photometry and individual stellar and integrated light spectroscopy (see, e.g. Zinn & West 1984; Carretta et al. 2009; Dias et al. 2016, and references therein). In contrast, there is an extensive literature on the use of RR Lyrae (RRL) light curve shapes to calculate their metallicities (e.g. Jurcsik & Kovacs 1995, 1996; Kovacs & Zsoldos 1995; Alcock et al. 2000; Kovacs & Walker 2001; Sarajedini et al. 2006; Mullen et al. 2021, and references therein). For example, Sarajedini & Gokmen (2023) have introduced a new set of mean Galactic globular cluster metallicities based on the periods and V-band amplitudes of the cluster ab-type RRL variable stars – those pulsating in the fundamental mode. They showed that cluster metal abundances determined in this way are statistically indistinguishable from those tabulated in the Harris (1996, 2010 edition) catalogue, which are based on the Carretta et al. (2009) abundance scale and in turn grounded on high-dispersion, high signal-to-noise spectroscopic measurements. Sarajedini & Gokmen (2023) also examined the variation of [Fe/H] differences between their values and those from the Harris (1996) catalogue as a function of various cluster parameters such as metallicity, horizontal branch morphology, the number of ab-type RR Lyraes, and the fraction of first generation and second generation stars in each cluster (Milone et al. 2017); they found no significant correlations between any of these quantities. This suggests that these factors do not significantly influence the determination of the mean cluster [Fe/H] using the periods and/or light curve amplitudes of the ab-type RR Lyraes. This in turn suggests that since RR Lyrae stars are low-mass horizontal branch stars, their metallicity reflects the ‘primordial’ abundance of their host cluster.
Subsequently, Sarajedini (2024a) presented metallicities determined in the same way for 13 of the 14 old globular clusters in the Large Magellanic Cloud. The sole old globular cluster whose metal abundance could not be measured in this way was Hodge 11 since it apparently does not harbour any RRL variables. Sarajedini (2024a) also compared their mean RRL period and amplitude-based metallicities with those from the literature determined using a variety of methods and found little common ground on the metallicity scale of the old LMC globular clusters. They interpreted this to suggest that more work is required to establish a robust metallicity scale for these clusters.
In this work, our goal is to apply the techniques we have used in previous papers in order to determine the mean [Fe/H] values for the globular clusters believed to be members of the Fornax, Sagittarius, and Canis Major dwarf spheroidal (dSph) galaxies using the light curve properties of their ab-type RR Lyrae variables. Two of these dwarf galaxies, Sagittarius (Ibata et al. 1994) and Canis Major (Lewis et al. 2004; Martin et al. 2004), suffer from significant tidal distruption making their total luminosity difficult to measure directly. However, there is a well-known relation between the mean metal abundance and the total absolute V-band magnitude for dwarf galaxies, in the sense that more luminous galaxies tend to enrich themselves in heavy elements to a greater degree (Caldwell et al. 1998 and references therein). As a result, by determining the mean metallicities via their globular clusters, we can infer the total luminosity of each galaxy using this relationship.
In the next section, we begin by describing and examining the metallicity-period-amplitude relations used in previous papers in this series, including an in-depth investigation of a comprehensive analysis presented by Fabrizio et al. (2021). Then, in Section 3, we describe the observational data set to which we apply the metallicity-period-amplitude relations. Section 4 presents our results and the last section summarizes our conclusions.
2 METALLICITY-PERIOD-AMPLITUDE RELATIONS
In our previous papers related to this topic (e.g. Tanakul et al. 2017; Tanakul & Sarajedini 2018; Sarajedini 2021; Sarajedini 2023; Sarajedini & Gokmen 2023; Sarajedini 2024a, 2024b), we have focused on two empirical relations that allow the determination of metal abundance using the periods and V-band amplitudes of ab-type RR Lyrae variables. In the first instance, Alcock et al. (2000, A00) focused on observations of ab-type RRL in the Large Magellanic Cloud (LMC) from the MACHO project. They used the Bailey diagram to derive a relationship between the [Fe/H] of the ab-type RR Lyraes and their periods (Pab) and V-band amplitudes (Amp(V)). Equation (1) shows this relationship as
Similarly, Sarajedini et al. (2006, S06) derived an equation that quantifies the relationship between RRL metallicity and period without needing to know the light curve amplitude. S06 formulated such a relation using observations of 132 Galactic ab-type RRL stars from A. C. Layden (2005, private communication). The result is given in equation (2) as
It should be noted that the set of ab-type RR Lyrae ‘calibrators’ used by S06 exhibits a V-band amplitude range from 0.4 to 1.4 mag (Zinn et al. 2020), which covers the range of amplitudes for the globular cluster RR Lyraes in the present study. As such, any systematic biases due to a mismatch between the amplitudes of the calibrating stars and those in the globular clusters considered herein should be small or negligible.
Sarajedini & Gokmen (2023) showed that both of these equations are able to reproduce the mean metallicity for each of the Galactic globular clusters in their sample as compared with spectroscopic abundance measurements with an accuracy of ±0.28 dex. It is important to note that their sample contains 600 ab-type RRL variables in 33 Galactic globular clusters. This implies that only a period measurement for ab-type RR Lyraes in a globular cluster is sufficient to allow a determination of the mean metallicity of that cluster.
As a follow-up to the analysis presented by Sarajedini & Gokmen (2023), we show in Fig. 1 the field RRL observations from Crestani et al. (2021). This figure illustrates the [Fe/H] values for these stars plotted against their periods. The dashed lines in the upper panel show the Alcock et al. (2000) relation (equation 1) for several distinct V-band amplitudes (top to bottom: Amp(V) = 0.0, 0.5, 1.0, 1.5 mag). The lower panel of Fig. 1 is similar to the top panel except that the dashed line is the S06 relation (equation 2), which simply correlates [Fe/H] with Log(P) without including the V-band amplitude. It is clear from both panels that the illustrated relations faithfully reproduce the observed data from Crestani et al. (2021). This conclusion in turn corroborates the findings of Sarajedini & Gokmen (2023) in this regard.
![The filled circles illustrate the [Fe/H] and Logarithm of the period in days [log(P)] for ab-type RR Lyrae variables from the work of Crestani et al. (2021). The dashed line in the upper panel shows the relation between [Fe/H] and Log(P) for the ab-type RR Lyraes from Sarajedini et al. (2006, equation 2). The dashed lines in the lower panel illustrate the relation from Alcock et al. (2000, equation 1) for four different values of the V-band amplitude as indicated in the panel from the top line to the bottom one.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/533/2/10.1093_mnras_stae1963/1/m_stae1963fig1.jpeg?Expires=1750417976&Signature=lUGQ2R0WaO7Z2ovtqdBoD9shI-vSYZnKRSV3~38Nzk-a2K4KtdJNan8GVQ69-amJFyi-dU9xTiaceZ7dMbSeIr20Syq~GnhyaWPNGk4tJbGtDSMUR5bt9nB7M-jBwsf~5yEnOJK87ZvRFh1D-piwW4SoAvgWXhZ6TeZBrCgmIcKYqNSp6zu3-bfrhTakES7-XGhymvYXFHCldtiC0J8Tq5fdZmmKHchns8bhTSF-dErsAqJRMjhCCLChjKX3k0hEKm0qjysbN8zXRAsPkPQZHO~DM9PU5Ia-PyyKXaH1elWqS21YLFq14SmcaClK5vcfnkfHHcjU5eI59e4RaKQ03Q__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The filled circles illustrate the [Fe/H] and Logarithm of the period in days [log(P)] for ab-type RR Lyrae variables from the work of Crestani et al. (2021). The dashed line in the upper panel shows the relation between [Fe/H] and Log(P) for the ab-type RR Lyraes from Sarajedini et al. (2006, equation 2). The dashed lines in the lower panel illustrate the relation from Alcock et al. (2000, equation 1) for four different values of the V-band amplitude as indicated in the panel from the top line to the bottom one.
More recently, Fabrizio et al. (2021) present the largest and most homogeneous spectroscopic data set of field RRLs to date. Their sample includes iron abundances for a total of 6150 ab-type RRL and 2865 c-type RRL stars. The sample of stars from Crestani et al. (2021), shown earlier, is a subset of the Fabrizio et al. (2021) data set and is on the same abundance scale. Fabrizio et al. (2021) use these data to study the variation of RRL period and amplitude with [Fe/H]. In their Bailey diagram, which plots the amplitudes and periods of RRL variables (their figs 4 and 5), Fabrizio et al. (2021) separate the ‘long period’ and ‘short period’ ab-type RRL with a plane that has the following form
In their table 2, they give the equations that relate [Fe/H], V-band amplitude (Amp(V)), and period (P) for these ‘long period’ and ‘short period’ ab-type RRL stars separately. These equations give Amp(V) as a function of [Fe/H] and Log(P) in days. In principle, they can be inverted to yield [Fe/H] as a function of Amp(V) and period. However, in practice, that is not the case. More specifically, Fig. 2 shows the Bailey diagram of the Crestani et al. (2021) ab-type RRL with the dashed line illustrating the location of the separation line given in equation (3). The blue solid line in Fig. 2 is the predicted location of ‘long period’ ab-type RRL with [Fe/H] = –5.0 while the red solid line is the predicted location of ‘short period’ ab-type RRL with [Fe/H] = +5.0. Clearly, there are no RRL in the Fabrizio et al. (2021) sample possessing these [Fe/H] values. As such, we are left to conclude that the equations in table 2 of Fabrizio et al. (2021) are not valid when inverted to predict [Fe/H] values based on the measured amplitudes and periods of ab-type RRL stars (Fabrizio 2023, private communication).
![The filled circles show the Bailey diagram (i.e. V-band amplitudes and periods) for field ab-type RR Lyrae variables from the work of Crestani et al. (2021). The dashed line shows the long period:short period separation line from footnote 34 of Fabrizio et al. (2021) as given in equation (3). The blue solid line is the ‘long period’ fit for ab-type RR Lyraes with [Fe/H] = –5.0 while the red line is ‘short period’ fit for ab-type RR Lyraes with [Fe/H] = +5.0. See text for details.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/533/2/10.1093_mnras_stae1963/1/m_stae1963fig2.jpeg?Expires=1750417976&Signature=hPhVzmaMprY-w-y5nWiLUspWsyA4FwE5wPg-UVgfsCvOpPFkWsZFb7umRwhevnmD6Na9LnXs00ZmfEeLRjHm-ks4g7SBXbqdB8L070Kf2bNvRqeo~2nlOLFF1HKxz5Dg1MjWmU-kVevUz2lkMlwcoHGb5lHRYYoc1YNv2khmZedX6gFiN9U9tmPEcEjSwUMZIgZ6f624I02hGi3Xd9XKXqEJal1O6a~MndgkszMeTxm8pU8X2swe-P2EeCQ3kWHTpNcZOl8~-xGMfgJFgVuaJyRhox1wjTZQtx9CSWjzCJu8Dw82q2FSK1QIyw99k9MRgGb5N2Aw48W3uuBEtsmgKQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The filled circles show the Bailey diagram (i.e. V-band amplitudes and periods) for field ab-type RR Lyrae variables from the work of Crestani et al. (2021). The dashed line shows the long period:short period separation line from footnote 34 of Fabrizio et al. (2021) as given in equation (3). The blue solid line is the ‘long period’ fit for ab-type RR Lyraes with [Fe/H] = –5.0 while the red line is ‘short period’ fit for ab-type RR Lyraes with [Fe/H] = +5.0. See text for details.
| Cluster name . | N(RRab) . | |$\langle$|Period(RRab)|$\rangle$| . | [Fe/H] . | [Fe/H] . | |$\langle$|[Fe/H]|$\rangle _{ZW}$| . | RR Lyrae reference . |
|---|---|---|---|---|---|---|
| . | . | (d) . | (S06) . | (A00) . | (weighted) . | . |
| Fornax dSph | ||||||
| Cluster 1 | 5 | 0.611 | –1.75 ± 0.11 | –1.74 ± 0.19 | –1.75 ± 0.10 | Mackey & Gilmore (2003) |
| Cluster 2 | 15 | 0.574 | –1.53 ± 0.08 | –1.62 ± 0.18 | –1.54 ± 0.07 | Mackey & Gilmore (2003) |
| Cluster 3 | 32 | 0.613 | –1.76 ± 0.06 | –1.82 ± 0.07 | –1.79 ± 0.05 | Mackey & Gilmore (2003) |
| Cluster 4 | 16 | 0.599 | –1.67 ± 0.08 | –1.67 ± 0.09 | –1.67 ± 0.06 | Greco et al. (2007) |
| Cluster 5 | 8 | 0.577 | –1.54 ± 0.16 | –1.66 ± 0.21 | –1.58 ± 0.13 | Mackey & Gilmore (2003) |
| Sagittarius dSph | ||||||
| M54 | 50 | 0.578 | –1.55 ± 0.05 | –1.51 ± 0.04 | –1.53 ± 0.03 | Layden & Sarajedini (2000) |
| Arp 2 | 8 | 0.583 | –1.52 ± 0.26 | ... | ... | Salinas et al. (2005) |
| Ter 8 | 2 | 0.644 | –1.93 ± 0.28 | ... | ... | Salinas et al. (2005) |
| NGC 2419 | 29 | 0.662 | –2.02 ± 0.05 | –2.19 ± 0.05 | –2.11 ± 0.04 | di Criscienzo et al. (2011) |
| NGC 4147 | 5 | 0.525 | –1.23 ± 0.14 | –1.49 ± 0.11 | –1.39 ± 0.09 | Stetson et al. (2005) |
| NGC 5634 | 9 | 0.672 | –2.06 ± 0.14 | ... | ... | Salinas et al. (2005) |
| Canis Major dSph | ||||||
| NGC 1851 | 15 | 0.589 | –1.61 ± 0.09 | –1.78 ± 0.05 | –1.74 ± 0.04 | Walker (1998) |
| NGC 1904 | 6 | 0.713 | –2.27 ± 0.14 | –2.24 ± 0.13 | –2.25 ± 0.10 | Kains et al. (2012) |
| NGC 2298 | 2 | 0.543 | –1.30 ± 0.77 | –0.93 ± 1.34 | –1.21 ± 0.67 | Clement et al. (1995) |
| NGC 2808 | 6 | 0.579 | –1.57 ± 0.07 | ... | ... | Kunder et al. (2013) |
| Cluster name . | N(RRab) . | |$\langle$|Period(RRab)|$\rangle$| . | [Fe/H] . | [Fe/H] . | |$\langle$|[Fe/H]|$\rangle _{ZW}$| . | RR Lyrae reference . |
|---|---|---|---|---|---|---|
| . | . | (d) . | (S06) . | (A00) . | (weighted) . | . |
| Fornax dSph | ||||||
| Cluster 1 | 5 | 0.611 | –1.75 ± 0.11 | –1.74 ± 0.19 | –1.75 ± 0.10 | Mackey & Gilmore (2003) |
| Cluster 2 | 15 | 0.574 | –1.53 ± 0.08 | –1.62 ± 0.18 | –1.54 ± 0.07 | Mackey & Gilmore (2003) |
| Cluster 3 | 32 | 0.613 | –1.76 ± 0.06 | –1.82 ± 0.07 | –1.79 ± 0.05 | Mackey & Gilmore (2003) |
| Cluster 4 | 16 | 0.599 | –1.67 ± 0.08 | –1.67 ± 0.09 | –1.67 ± 0.06 | Greco et al. (2007) |
| Cluster 5 | 8 | 0.577 | –1.54 ± 0.16 | –1.66 ± 0.21 | –1.58 ± 0.13 | Mackey & Gilmore (2003) |
| Sagittarius dSph | ||||||
| M54 | 50 | 0.578 | –1.55 ± 0.05 | –1.51 ± 0.04 | –1.53 ± 0.03 | Layden & Sarajedini (2000) |
| Arp 2 | 8 | 0.583 | –1.52 ± 0.26 | ... | ... | Salinas et al. (2005) |
| Ter 8 | 2 | 0.644 | –1.93 ± 0.28 | ... | ... | Salinas et al. (2005) |
| NGC 2419 | 29 | 0.662 | –2.02 ± 0.05 | –2.19 ± 0.05 | –2.11 ± 0.04 | di Criscienzo et al. (2011) |
| NGC 4147 | 5 | 0.525 | –1.23 ± 0.14 | –1.49 ± 0.11 | –1.39 ± 0.09 | Stetson et al. (2005) |
| NGC 5634 | 9 | 0.672 | –2.06 ± 0.14 | ... | ... | Salinas et al. (2005) |
| Canis Major dSph | ||||||
| NGC 1851 | 15 | 0.589 | –1.61 ± 0.09 | –1.78 ± 0.05 | –1.74 ± 0.04 | Walker (1998) |
| NGC 1904 | 6 | 0.713 | –2.27 ± 0.14 | –2.24 ± 0.13 | –2.25 ± 0.10 | Kains et al. (2012) |
| NGC 2298 | 2 | 0.543 | –1.30 ± 0.77 | –0.93 ± 1.34 | –1.21 ± 0.67 | Clement et al. (1995) |
| NGC 2808 | 6 | 0.579 | –1.57 ± 0.07 | ... | ... | Kunder et al. (2013) |
| Cluster name . | N(RRab) . | |$\langle$|Period(RRab)|$\rangle$| . | [Fe/H] . | [Fe/H] . | |$\langle$|[Fe/H]|$\rangle _{ZW}$| . | RR Lyrae reference . |
|---|---|---|---|---|---|---|
| . | . | (d) . | (S06) . | (A00) . | (weighted) . | . |
| Fornax dSph | ||||||
| Cluster 1 | 5 | 0.611 | –1.75 ± 0.11 | –1.74 ± 0.19 | –1.75 ± 0.10 | Mackey & Gilmore (2003) |
| Cluster 2 | 15 | 0.574 | –1.53 ± 0.08 | –1.62 ± 0.18 | –1.54 ± 0.07 | Mackey & Gilmore (2003) |
| Cluster 3 | 32 | 0.613 | –1.76 ± 0.06 | –1.82 ± 0.07 | –1.79 ± 0.05 | Mackey & Gilmore (2003) |
| Cluster 4 | 16 | 0.599 | –1.67 ± 0.08 | –1.67 ± 0.09 | –1.67 ± 0.06 | Greco et al. (2007) |
| Cluster 5 | 8 | 0.577 | –1.54 ± 0.16 | –1.66 ± 0.21 | –1.58 ± 0.13 | Mackey & Gilmore (2003) |
| Sagittarius dSph | ||||||
| M54 | 50 | 0.578 | –1.55 ± 0.05 | –1.51 ± 0.04 | –1.53 ± 0.03 | Layden & Sarajedini (2000) |
| Arp 2 | 8 | 0.583 | –1.52 ± 0.26 | ... | ... | Salinas et al. (2005) |
| Ter 8 | 2 | 0.644 | –1.93 ± 0.28 | ... | ... | Salinas et al. (2005) |
| NGC 2419 | 29 | 0.662 | –2.02 ± 0.05 | –2.19 ± 0.05 | –2.11 ± 0.04 | di Criscienzo et al. (2011) |
| NGC 4147 | 5 | 0.525 | –1.23 ± 0.14 | –1.49 ± 0.11 | –1.39 ± 0.09 | Stetson et al. (2005) |
| NGC 5634 | 9 | 0.672 | –2.06 ± 0.14 | ... | ... | Salinas et al. (2005) |
| Canis Major dSph | ||||||
| NGC 1851 | 15 | 0.589 | –1.61 ± 0.09 | –1.78 ± 0.05 | –1.74 ± 0.04 | Walker (1998) |
| NGC 1904 | 6 | 0.713 | –2.27 ± 0.14 | –2.24 ± 0.13 | –2.25 ± 0.10 | Kains et al. (2012) |
| NGC 2298 | 2 | 0.543 | –1.30 ± 0.77 | –0.93 ± 1.34 | –1.21 ± 0.67 | Clement et al. (1995) |
| NGC 2808 | 6 | 0.579 | –1.57 ± 0.07 | ... | ... | Kunder et al. (2013) |
| Cluster name . | N(RRab) . | |$\langle$|Period(RRab)|$\rangle$| . | [Fe/H] . | [Fe/H] . | |$\langle$|[Fe/H]|$\rangle _{ZW}$| . | RR Lyrae reference . |
|---|---|---|---|---|---|---|
| . | . | (d) . | (S06) . | (A00) . | (weighted) . | . |
| Fornax dSph | ||||||
| Cluster 1 | 5 | 0.611 | –1.75 ± 0.11 | –1.74 ± 0.19 | –1.75 ± 0.10 | Mackey & Gilmore (2003) |
| Cluster 2 | 15 | 0.574 | –1.53 ± 0.08 | –1.62 ± 0.18 | –1.54 ± 0.07 | Mackey & Gilmore (2003) |
| Cluster 3 | 32 | 0.613 | –1.76 ± 0.06 | –1.82 ± 0.07 | –1.79 ± 0.05 | Mackey & Gilmore (2003) |
| Cluster 4 | 16 | 0.599 | –1.67 ± 0.08 | –1.67 ± 0.09 | –1.67 ± 0.06 | Greco et al. (2007) |
| Cluster 5 | 8 | 0.577 | –1.54 ± 0.16 | –1.66 ± 0.21 | –1.58 ± 0.13 | Mackey & Gilmore (2003) |
| Sagittarius dSph | ||||||
| M54 | 50 | 0.578 | –1.55 ± 0.05 | –1.51 ± 0.04 | –1.53 ± 0.03 | Layden & Sarajedini (2000) |
| Arp 2 | 8 | 0.583 | –1.52 ± 0.26 | ... | ... | Salinas et al. (2005) |
| Ter 8 | 2 | 0.644 | –1.93 ± 0.28 | ... | ... | Salinas et al. (2005) |
| NGC 2419 | 29 | 0.662 | –2.02 ± 0.05 | –2.19 ± 0.05 | –2.11 ± 0.04 | di Criscienzo et al. (2011) |
| NGC 4147 | 5 | 0.525 | –1.23 ± 0.14 | –1.49 ± 0.11 | –1.39 ± 0.09 | Stetson et al. (2005) |
| NGC 5634 | 9 | 0.672 | –2.06 ± 0.14 | ... | ... | Salinas et al. (2005) |
| Canis Major dSph | ||||||
| NGC 1851 | 15 | 0.589 | –1.61 ± 0.09 | –1.78 ± 0.05 | –1.74 ± 0.04 | Walker (1998) |
| NGC 1904 | 6 | 0.713 | –2.27 ± 0.14 | –2.24 ± 0.13 | –2.25 ± 0.10 | Kains et al. (2012) |
| NGC 2298 | 2 | 0.543 | –1.30 ± 0.77 | –0.93 ± 1.34 | –1.21 ± 0.67 | Clement et al. (1995) |
| NGC 2808 | 6 | 0.579 | –1.57 ± 0.07 | ... | ... | Kunder et al. (2013) |
| Cluster Name . | [Fe/H]|$_{ZW}$| . | Reference . |
|---|---|---|
| Fornax dSph | ||
| Cluster 1 | –2.05 ± 0.10 | Mackey & Gilmore (2003) |
| –2.5 | Letarte et al. (2006) | |
| Cluster 2 | –1.83 ± 0.07 | Mackey & Gilmore (2003) |
| –2.1 | Letarte et al. (2006) | |
| Cluster 3 | –2.04 ± 0.07 | Mackey & Gilmore (2003) |
| –2.4 | Letarte et al. (2006) | |
| –2.3 ± 0.1 | Larsen et al. (2012) | |
| Cluster 4 | –1.56 ± 0.10 | Strader et al. (2003) |
| Cluster 5 | –1.90 ± 0.06 | Mackey & Gilmore (2003) |
| –2.1 ± 0.1 | Larsen et al. (2012) | |
| Sagittarius dSph | ||
| M54 | –1.57 | Harris (1996, 2010 edition) |
| Arp 2 | –1.77 | Harris (1996, 2010 edition) |
| Ter 8 | –2.04 | Harris (1996, 2010 edition) |
| NGC 2419 | –2.03 | Harris (1996, 2010 edition) |
| NGC 4147 | –1.80 | Harris (1996, 2010 edition) |
| NGC 5634 | –1.86 | Harris (1996, 2010 edition) |
| Canis Major dSph | ||
| NGC 1851 | –1.30 | Harris (1996, 2010 edition) |
| NGC 1904 | –1.65 | Harris (1996, 2010 edition) |
| NGC 2298 | –1.88 | Harris (1996, 2010 edition) |
| NGC 2808 | –1.30 | Harris (1996, 2010 edition) |
| Cluster Name . | [Fe/H]|$_{ZW}$| . | Reference . |
|---|---|---|
| Fornax dSph | ||
| Cluster 1 | –2.05 ± 0.10 | Mackey & Gilmore (2003) |
| –2.5 | Letarte et al. (2006) | |
| Cluster 2 | –1.83 ± 0.07 | Mackey & Gilmore (2003) |
| –2.1 | Letarte et al. (2006) | |
| Cluster 3 | –2.04 ± 0.07 | Mackey & Gilmore (2003) |
| –2.4 | Letarte et al. (2006) | |
| –2.3 ± 0.1 | Larsen et al. (2012) | |
| Cluster 4 | –1.56 ± 0.10 | Strader et al. (2003) |
| Cluster 5 | –1.90 ± 0.06 | Mackey & Gilmore (2003) |
| –2.1 ± 0.1 | Larsen et al. (2012) | |
| Sagittarius dSph | ||
| M54 | –1.57 | Harris (1996, 2010 edition) |
| Arp 2 | –1.77 | Harris (1996, 2010 edition) |
| Ter 8 | –2.04 | Harris (1996, 2010 edition) |
| NGC 2419 | –2.03 | Harris (1996, 2010 edition) |
| NGC 4147 | –1.80 | Harris (1996, 2010 edition) |
| NGC 5634 | –1.86 | Harris (1996, 2010 edition) |
| Canis Major dSph | ||
| NGC 1851 | –1.30 | Harris (1996, 2010 edition) |
| NGC 1904 | –1.65 | Harris (1996, 2010 edition) |
| NGC 2298 | –1.88 | Harris (1996, 2010 edition) |
| NGC 2808 | –1.30 | Harris (1996, 2010 edition) |
| Cluster Name . | [Fe/H]|$_{ZW}$| . | Reference . |
|---|---|---|
| Fornax dSph | ||
| Cluster 1 | –2.05 ± 0.10 | Mackey & Gilmore (2003) |
| –2.5 | Letarte et al. (2006) | |
| Cluster 2 | –1.83 ± 0.07 | Mackey & Gilmore (2003) |
| –2.1 | Letarte et al. (2006) | |
| Cluster 3 | –2.04 ± 0.07 | Mackey & Gilmore (2003) |
| –2.4 | Letarte et al. (2006) | |
| –2.3 ± 0.1 | Larsen et al. (2012) | |
| Cluster 4 | –1.56 ± 0.10 | Strader et al. (2003) |
| Cluster 5 | –1.90 ± 0.06 | Mackey & Gilmore (2003) |
| –2.1 ± 0.1 | Larsen et al. (2012) | |
| Sagittarius dSph | ||
| M54 | –1.57 | Harris (1996, 2010 edition) |
| Arp 2 | –1.77 | Harris (1996, 2010 edition) |
| Ter 8 | –2.04 | Harris (1996, 2010 edition) |
| NGC 2419 | –2.03 | Harris (1996, 2010 edition) |
| NGC 4147 | –1.80 | Harris (1996, 2010 edition) |
| NGC 5634 | –1.86 | Harris (1996, 2010 edition) |
| Canis Major dSph | ||
| NGC 1851 | –1.30 | Harris (1996, 2010 edition) |
| NGC 1904 | –1.65 | Harris (1996, 2010 edition) |
| NGC 2298 | –1.88 | Harris (1996, 2010 edition) |
| NGC 2808 | –1.30 | Harris (1996, 2010 edition) |
| Cluster Name . | [Fe/H]|$_{ZW}$| . | Reference . |
|---|---|---|
| Fornax dSph | ||
| Cluster 1 | –2.05 ± 0.10 | Mackey & Gilmore (2003) |
| –2.5 | Letarte et al. (2006) | |
| Cluster 2 | –1.83 ± 0.07 | Mackey & Gilmore (2003) |
| –2.1 | Letarte et al. (2006) | |
| Cluster 3 | –2.04 ± 0.07 | Mackey & Gilmore (2003) |
| –2.4 | Letarte et al. (2006) | |
| –2.3 ± 0.1 | Larsen et al. (2012) | |
| Cluster 4 | –1.56 ± 0.10 | Strader et al. (2003) |
| Cluster 5 | –1.90 ± 0.06 | Mackey & Gilmore (2003) |
| –2.1 ± 0.1 | Larsen et al. (2012) | |
| Sagittarius dSph | ||
| M54 | –1.57 | Harris (1996, 2010 edition) |
| Arp 2 | –1.77 | Harris (1996, 2010 edition) |
| Ter 8 | –2.04 | Harris (1996, 2010 edition) |
| NGC 2419 | –2.03 | Harris (1996, 2010 edition) |
| NGC 4147 | –1.80 | Harris (1996, 2010 edition) |
| NGC 5634 | –1.86 | Harris (1996, 2010 edition) |
| Canis Major dSph | ||
| NGC 1851 | –1.30 | Harris (1996, 2010 edition) |
| NGC 1904 | –1.65 | Harris (1996, 2010 edition) |
| NGC 2298 | –1.88 | Harris (1996, 2010 edition) |
| NGC 2808 | –1.30 | Harris (1996, 2010 edition) |
3 OBSERVATIONAL DATA
Table 1 lists the observational data for the dwarf Spheroidal galaxy RRL samples examined in this work. For each sample of cluster ab-type RRL, we calculate the mean [Fe/H] value based on equations (1) and/or (2) as appropriate and then use the weighted average as our adopted metallicity value. It should be noted that in cases where the number of RR Lyraes in each cluster is less than 10, we used the small-number statistical formulae of Keeping (1962) to calculate the standard errors of each mean metallicity (see Sarajedini & Gokmen 2023 for more information). Table 2 shows the published [Fe/H] values for these same clusters with the references given in the last column. These have all been converted to the Zinn & West (1984) abundance scale ([Fe/H]|$_{ZW}$|), which is the same as the scale used in equations (1) and (2).
3.1 Fornax dSph
Fig. 3 shows the Bailey diagram for the RRL stars in the Fornax globular clusters. The observed properties for these RRL are taken from Mackey & Gilmore (2003; clusters 1, 2, 3, and 5) and Greco et al. (2007; cluster 4). Greco et al. (2009) also publish properties for RRL in cluster 5, but we found the sample from Mackey & Gilmore (2003) to be more comprehensive. In all cases, we omit stars that are likely or suspected to suffer from the Blazhko Effect. Furthermore, in the case of cluster 4, Greco et al. (2007) perform a statistical analysis to estimate how many of the RRLs they identify belong to the Fornax field and how many to the cluster. They conclude that they are all most likely cluster members.
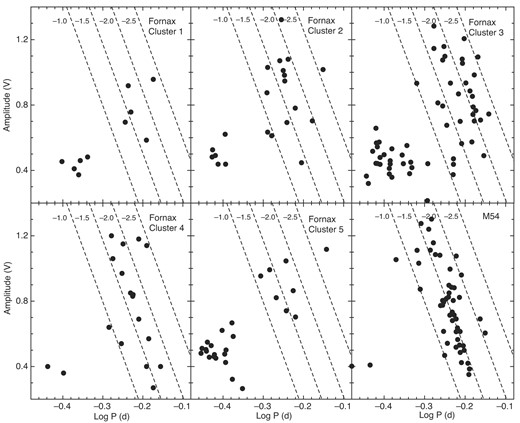
Bailey diagrams for the globular clusters in the Fornax dSph and M54, which is a member of the Sagittarius dSph. For illustrative purposes, the dashed lines represent equation (1) for the specified values of the V-band amplitude.
3.2 Sagittarius dSph
According to Bellazzini et al. (2020), nine globular clusters belong to the Sagittarius (Sgr) dSph. These are NGC 6715 (M54), Terzan 7, Terzan 8, Arp 2, Palomar 12, Whiting 1, NGC 2419, NGC 4147, and NGC 5634. Six of these are believed to harbour RRL variables as listed in Table 1. The Bailey diagram for the RRL stars in M54 is shown in Fig. 3. In addition, NGC 2419 and NGC 4147 were studied in Sarajedini & Gokmen (2023). It should be noted that the study presenting the properties of RRL in Arp 2, Ter 8, and NGC 5634 (i.e. Salinas et al. 2005) does not provide amplitudes for the light curves – only periods. As such, only equation (2) is applicable for the determination of these [Fe/H] values.
3.3 Canis Major dSph
Forbes et al. (2004) list four globular clusters as being members of the Canis Major dSph: NGC 1851, 1904, 2298, and 2808. The first two clusters were studied in Sarajedini & Gokmen (2023). The RRL population of NGC 2298 was investigated by Clement et al. (1995) who found four cluster members – two ab-type and two c-type RRL variables. They provide periods and B-band amplitudes for these stars. We have utilized the relations published by Dorfi & Feuchtinger (1999) to convert these B-band amplitudes to those in the V-band so that we can apply equation (1). However, the resultant mean cluster metal abundance is highly uncertain (see Table 1) because of the small number of RRL identified and characterized in NGC 2298. NGC 2808 was studied by Kunder et al. (2013), who catalogued and characterized eight ab-type RRL in the cluster. Of these stars, four suffer from the Blazhko effect (meaning their amplitudes vary and are uncertain), and three are blended profiles on their CCD images leaving just one genuine ab-type RRL with a reliable period and V-band amplitude. As such, the mean [Fe/H] for NGC 2808 shown in Table 1 results from the application of equation (2) only using the periods of the ab-type RRLs.
4 RESULTS
4.1 Comparison with previous studies
Table 2 lists some of the previously published metallicity values for the globular clusters considered herein. It should be noted that the quoted Fornax cluster [Fe/H]s in Table 2 attributed to Mackey & Gilmore (2003) are actually their averages of values originally listed in table 5 of Strader et al. (2003). For this section, we adopt published [Fe/H] values of –2.3, –2.0, –2.2, –1.6, and –2.0 for Fornax clusters 1, 2, 3, 4, and 5, respectively, from Table 2. Doing so, we find good agreement between our value for Cluster 4 (difference of less than 0.1 dex) but a significant systematic difference of ∼0.5 dex for the other four clusters between our values, and the published ones in the sense that ours are more metal-rich. These differences of ∼0.5 dex in [Fe/H] are primarily between our values and those of Letarte et al. (2006). In that paper, the authors comment that ‘Our abundances appear 0.3–0.5 dex lower than previous estimates. Most of this discrepancy is attributable to different reference calibrators.’
In the case of the Sgr and Canis Major clusters, all of them are included in the Harris (1996, 2010 edition) catalogue of Galactic globular clusters with metallicities on the Carretta et al. (2009) abundance scale. Table 2 lists these [Fe/H] values converted to the Zinn & West (1984) scale for comparison with our RRL based abundances. Taken together, for the 10 globular clusters belonging to the Sgr and Canis Major dSphs, there is a mean difference of +0.014 ± 0.12 dex between the Harris (1996) values and those based on equation (2) in the sense (S06–Harris).
4.2 Dwarf Galaxy luminosities
Table 3 lists the mean metallicities of the globular clusters in each of the dSphs considered herein – Fornax, Sagittarius, and Canis Major. As noted in the Introduction, there is a well-known correlation between the mean metal abundance and the total absolute V-band magnitude for dwarf galaxies (Sarajedini et al. 1997; Caldwell et al. 1998; Sarajedini et al. 2002; Yang et al. 2014). This means that even in cases where the dwarf galaxy has been significantly disrupted by tidal forces (e.g. Sgr and Canis Major), it is possible to estimate its total luminosity by determining the mean metal abundance of its stellar populations, such as its field stars and/or star clusters. Therefore, since the mean metallicities of the three globular cluster systems are essentially identical to within ±0.05 dex, it stands to reason that the total luminosities of Fornax, Sgr, and Canis Major are likely to be very similar as well. Of these three dwarf galaxies, the only one that does not appear to have been significantly tidally disturbed is Fornax.
| Dwarf Galaxy . | N (clusters) . | RRL |$\langle$|[Fe/H]|$\rangle$| . | SEM . |
|---|---|---|---|
| Fornax dSph | 5 | –1.67 | 0.05 |
| Sagittarius dSph | 6 | –1.76 | 0.12 |
| Canis Major dSph | 4 | –1.69 | 0.25 |
| Dwarf Galaxy . | N (clusters) . | RRL |$\langle$|[Fe/H]|$\rangle$| . | SEM . |
|---|---|---|---|
| Fornax dSph | 5 | –1.67 | 0.05 |
| Sagittarius dSph | 6 | –1.76 | 0.12 |
| Canis Major dSph | 4 | –1.69 | 0.25 |
| Dwarf Galaxy . | N (clusters) . | RRL |$\langle$|[Fe/H]|$\rangle$| . | SEM . |
|---|---|---|---|
| Fornax dSph | 5 | –1.67 | 0.05 |
| Sagittarius dSph | 6 | –1.76 | 0.12 |
| Canis Major dSph | 4 | –1.69 | 0.25 |
| Dwarf Galaxy . | N (clusters) . | RRL |$\langle$|[Fe/H]|$\rangle$| . | SEM . |
|---|---|---|---|
| Fornax dSph | 5 | –1.67 | 0.05 |
| Sagittarius dSph | 6 | –1.76 | 0.12 |
| Canis Major dSph | 4 | –1.69 | 0.25 |
Several measurements of Fornax’s total luminosity have been published. van den Bergh (2000) lists MV = –13.1 for Fornax but apparently does not provide a reference source for this Value. This is the number also quoted by Grebel (2000) in her review of star formation in the Local Group (table 2 of Grebel 2000). Lokas (2009) uses the results from Walker et al. (2009) to determine a value of MV = –13.3 ± 0.42, while Wang et al. (2019) give MV = –13.4 ± 0.3. Thus, a value of MV = –13.3 seems most likely for Fornax and by implication for the Sgr and Canis Major dwarf spheroidal galaxies.
Fig. 4 shows the variation of mean [Fe/H] for dwarf galaxies in the Local Group with absolute V-band magnitude (MV) from the compilation of Grebel (2000). The filled circles are the dwarf irregulars, the open circles are the dwarf ellipticals, and the crosses are the dwarf spheroidals. The dashed line is the least squares fit to the dSph galaxies only. The root-mean-square deviation of the MV values around this fitted line is 0.8 mag suggesting that the MV values of Fornax, Sgr, and Canis Major dSph are the same to within ∼0.8 mag. We recognize that the metal abundance of the RRL in these systems likely reflects their primordial [Fe/H] values rather than their mean [Fe/H] values. However, in a relative sense, our analysis to estimate the total V-band luminosity of each galaxy should be sound.
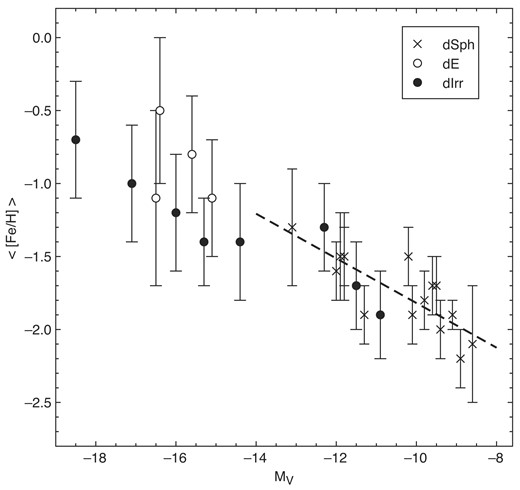
Behaviour of the mean metal abundance for dwarf galaxies in the Local Group with absolute V-band magnitude from Grebel (2000). As indicated in the inset key, the filled circles are the dwarf irregulars, the open circles are the dwarf ellipticals, and the crosses are the dwarf spheroidals. The dashed line is the least squares fit to the dSph galaxies only.
5 CONCLUSIONS
We have gathered data from the literature on the light curve properties (i.e. periods and amplitudes) for ab-type RR Lyrae variables belonging to globular clusters in the Fornax, Sagittarius, and Canis Major dwarf spheroidal galaxies. These stars number 76 among five clusters in Fornax, 103 in six Sagittarius clusters, and 29 RR Lyraes in four globular clusters thought to be members of Canis Major. Application of equations (1) and (2) yield [Fe/H] values for each RR Lyrae star, which then leads to mean values of |$\langle$|[Fe/H]|$\rangle$| = –1.67 ± 0.05, –1.76 ± 0.12, and –1.69 ± 0.25 for the globular clusters in Fornax, Sagittarius, and Canis Major, respectively, on the Zinn & West (1984) abundance. The total absolute V-band magnitude of Fornax, an apparently canonical dwarf spheroidal galaxy with a well-behaved surface brightness profile, has been measured to be |$M_V$| = –13.3. Thus, within the context of the well-known correlation between mean metal abundance and total luminosity for dwarf spheroidal galaxies, and the similarity in the mean [Fe/H] values of these three dwarf galaxies, we infer that the absolute V-band magnitude of the Fornax, Sagittarius, and Canis Major dSph are indistinguishable to within ∼0.8 mag.
ACKNOWLEDGEMENTS
The author is grateful to the Bjorn Lamborn Endowment in Physics for support of this work.
DATA AVAILABILITY
All of the data used in this study are available in the published literature as cited in the text and referenced in the bibliography.



