-
PDF
- Split View
-
Views
-
Cite
Cite
Hiromichi Tagawa, Zoltán Haiman, Flares from stars crossing active galactic nucleus discs on low-inclination orbits, Monthly Notices of the Royal Astronomical Society, Volume 526, Issue 1, November 2023, Pages 69–79, https://doi.org/10.1093/mnras/stad2616
Close - Share Icon Share
ABSTRACT
The origin of the recently discovered new class of transients, X-ray quasi-periodic eruptions (QPEs), remains a puzzle. Due to their periodicity and association with active galactic nuclei (AGNs), it is natural to relate these eruptions to stars or compact objects in tight orbits around supermassive black holes (SMBHs). In this paper, we predict the properties of emission from bow shocks produced by stars crossing AGN discs, and compare them to the observed properties of QPEs. We find that when a star’s orbit is retrograde and has a low inclination (≲40°) with respect to the AGN disc and the star is massive (≳10 M⊙), the breakout emission from the bow shock can explain the observed duration (∼hours) and X-ray luminosity (∼few × 1042 erg s−1) of QPEs. This model can further explain various observed features of QPEs, such as their complex luminosity evolution, the gradual decline of luminosity of the flares over several years, the evolution of the hardness ratio, the modulation of the luminosity during quiescent phases, and the preference of the central SMBHs to have low masses.
1 INTRODUCTION
Recently, a new class of transients, X-ray quasi-periodic eruptions (QPEs), have been discovered. QPEs are characterized by periodic flares with the X-ray luminosity of LX ∼ 1042–|$10^{43}~{\rm erg\, s}^{-1}$| and thermal-like spectra with the temperature of ∼100 eV. The duration of each flare is about an hour followed by a quiescent phase with the luminosity of |$L_{\rm X}\sim 10^{41}~{\rm erg\, s}^{-1}$| and the duration of about 10 h. The period is quite regular and the cycle repeats for at least several years, although some modulations and evolution are also reported (Arcodia et al. 2022; Miniutti et al. 2023a). So far, five QPE events have been reported, whose emission is coming from the central regions of low-mass galaxies harbouring less massive supermassive black holes (SMBHs) with masses of MSMBH ∼ 105–106 M⊙. All of the host galaxies have been classified as active by re-observing them using high-resolution optical spectroscopy (Wevers et al. 2022), although no broad emission lines, common in active galactic nuclei (AGNs), have been detected.
The first QPE source, GSN069, was reported from a type 2 Seyfert galaxy (Miniutti et al. 2019). Thereafter, the second and fifth QPE sources, RX J1301.9+2747 (Giustini, Miniutti & Saxton 2020) and XMMSL1 J024916.6−041244 (Chakraborty et al. 2021), were discovered by XMM–Newton (Jansen et al. 2001), and the third and fourth, eRO-QPE1 and eRO-QPE2 (Arcodia et al. 2021), by the wide-field X-ray telescope eROSITA (extended ROentgen Survey with an Imaging Telescope Array, Predehl et al. 2021). It is remarkable that the QPEs in GSN069 and XMMSL1 J024916.6−041244 followed flares interpreted as tidal disruption events (Miniutti et al. 2019, 2023a; Chakraborty et al. 2021). Among the five QPEs, eRO-QPE1 exhibits a complex evolution of its light curve (Arcodia et al. 2022).
So far, many theoretical models have been proposed. One possibility is disc instability. Various types of instabilities have been considered, such as those related to viscous torques (Pan et al. 2022; Pan, Li & Cao 2023), magnetic pressure (Kaur, Stone & Gilbaum 2023; Śniegowska et al. 2023), and spin–disc misalignment (Raj & Nixon 2021).However, it is not clear why these peculiar AGNs exhibit instability, while other AGNs and X-ray binaries do not (but see Kaur et al. 2023).
Another class of models involves mass transfer (Zalamea, Menou & Beloborodov 2010; Krolik & Linial 2022). To produce the high luminosity of QPEs in these models, high-density objects such as white dwarfs or helium stars are required (King 2020; Zhao et al. 2022). Additionally, in order for the lost mass to be accreted on to the central SMBH during the active phases of about an hour, the eccentricity needs to be as high as ∼0.99 for white dwarfs (King 2020, 2022; Wang et al. 2022). However, these configurations are estimated to be too rare to explain the observed rate of QPEs (Metzger, Stone & Gilbaum 2022; Lu & Quataert 2023). Metzger et al. (2022) proposed that mass transfer between stars counter-rotating with respect to each other around an SMBH can also explain the observed properties. Lu & Quataert (2023) suggested that even without high-density objects and highly eccentric orbits, thermal emission from shocks caused by the collision between the envelope of a star and the disc formed by the mass lost during preceding orbits from the star can account for the observed luminosity. They also explain the pathway to realize this configuration (see also Linial & Sari 2023). However, the duration of emission is typically uncomfortably long due to the slow diffusion of photons in this model. Although advection has been suggested to reduce the time-scale, it is not obvious whether photons can efficiently escape from an optically thick medium without reducing the luminosity and/or temperature.
A third possibility is emission from shocks emerging from collisions between an AGN disc and a star. Suková et al. (2021) and Xian et al. (2021) suggested that the possible modulation of the recurrence time between active phases can be explained by precession of stellar motion due to general relativistic effects in the deep potential well near the central SMBH. Xian et al. (2021) also estimated the luminosity of the flares using formulae in the optically thin limit provided in Nayakshin, Cuadra & Sunyaev (2004). However, in optically thin cases, the luminosity cannot be as high as the observed value; Nayakshin et al. (2004) found an upper limit of |$\sim\!\! 10^{39}~{\rm erg\, s}^{-1}$| (see their equation 37), adopting the stellar position of ∼100rg with the AGN disc temperature of ∼106 K to match the duration and spectrum of the observed QPEs. (Here, rg = GMSMBH/c2 is the gravitational radius, G is the gravitational constant, and c is the speed of light.) Dai, Fuerst & Blandford (2010) predicted the properties of emission from stellar collisions focusing especially on the timing of the flares. On the other hand, previous studies do not take into account emission from shocks breaking out of the AGN disc, which has properties significantly different from their estimates. Additionally, stars on low-inclination orbits with respect to the AGN disc enhance the total heating rate of gas, which helps explain the high observed luminosity of QPEs.
In this paper, we investigate properties of breakout emission from shocks produced by collisions between a star and an AGN disc, by constructing a semi-analytical model. Then, we discuss whether the properties of QPEs can be explained by this collision and shock breakout scenario.
2 METHOD
In this section, we describe procedures to evaluate properties of the shocks and emission associated with the collisions between a star and an AGN disc. Readers not interested in the model details may skip directly to the next section, which describes our results and the comparison to observed QPE properties.
2.1 Model
First, we give a brief overview of the emission model. When a star moves at a supersonic speed within the AGN disc, a bow shock forms along a conical region around and behind the star, if the ram pressure in the star’s envelope or the stellar wind is higher than the pressure of the disc (Fig. 1). We assume that the shape of this shock surface is given by Wilkin (1996). The conical region contains hot post-shock gas, moving along with the star. If the relative velocity of the star to the AGN disc gas is high enough, as expected for stars orbiting around the SMBH with the short orbital time corresponding to the recurrence periods of the QPE events (Table 1), the thermal energy of the shocked gas is dominated by radiation. At any given time, at the intersection of this cone with the surface of the AGN disc, thermal photons from the hot gas break out once the diffusion speed of photons becomes faster than the shock velocity (Fig. 2). To calculate the properties of the emission, we simply sum the emission from each patch along this intersection. Since the duration of the breakout emission from each patch is short, a low-inclination orbit for the star is found to be required to increase the total area from which the breakout emission is released at any given time.
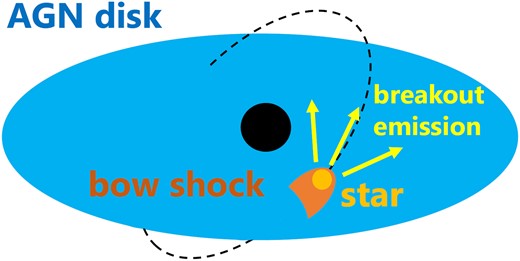
Schematic picture of the breakout emission from the collision between a star and an AGN disc.
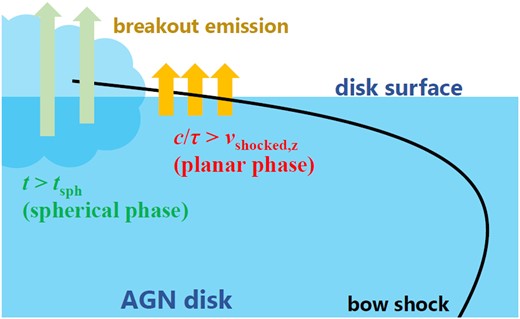
Schematic picture representing the breakout emission from the bow shock in the ‘planar’ and ‘spherical’ phases, corresponding to before and after the hot shocked gas, emerging from the AGN disc surface, doubles its radius.
The properties of the observed QPE events. We refer to Miniutti et al. (2019), Giustini et al. (2020), Arcodia et al. (2021), and Chakraborty et al. (2021) for the properties of GSN069, RXJ1301.9, eRO-QPE1 and eRO-QPE2, and XMMSL1, respectively. For the SMBH masses of eRO-QPE1 and eRO-QPE2, we refer to Chen et al. (2022).
| Name . | SMBH mass (M⊙) . | Period (s) . | Peak luminosity |$~(\rm erg\, s^{-1})$| . | Duration |$~(\rm h)$| . |
|---|---|---|---|---|
| GSN069 | 4 × 105 | 3.16 × 104 | 5 × 1042 | 0.5 |
| RXJ1301.9 | 1.8 × 106 | 1.65 × 104 | 1 × 1042 | ∼0.3 |
| eRO-QPE1 | 9.1 × 105 | 6.66 × 104 | ∼1043 | 7.6 |
| eRO-QPE2 | 2.3 × 105 | 8.6 × 103 | 1 × 1042 | 0.45 |
| XMMSL1 | 8.5 × 104 | 9.0 × 103 | 3 × 1041 | ∼0.3 |
| Name . | SMBH mass (M⊙) . | Period (s) . | Peak luminosity |$~(\rm erg\, s^{-1})$| . | Duration |$~(\rm h)$| . |
|---|---|---|---|---|
| GSN069 | 4 × 105 | 3.16 × 104 | 5 × 1042 | 0.5 |
| RXJ1301.9 | 1.8 × 106 | 1.65 × 104 | 1 × 1042 | ∼0.3 |
| eRO-QPE1 | 9.1 × 105 | 6.66 × 104 | ∼1043 | 7.6 |
| eRO-QPE2 | 2.3 × 105 | 8.6 × 103 | 1 × 1042 | 0.45 |
| XMMSL1 | 8.5 × 104 | 9.0 × 103 | 3 × 1041 | ∼0.3 |
The properties of the observed QPE events. We refer to Miniutti et al. (2019), Giustini et al. (2020), Arcodia et al. (2021), and Chakraborty et al. (2021) for the properties of GSN069, RXJ1301.9, eRO-QPE1 and eRO-QPE2, and XMMSL1, respectively. For the SMBH masses of eRO-QPE1 and eRO-QPE2, we refer to Chen et al. (2022).
| Name . | SMBH mass (M⊙) . | Period (s) . | Peak luminosity |$~(\rm erg\, s^{-1})$| . | Duration |$~(\rm h)$| . |
|---|---|---|---|---|
| GSN069 | 4 × 105 | 3.16 × 104 | 5 × 1042 | 0.5 |
| RXJ1301.9 | 1.8 × 106 | 1.65 × 104 | 1 × 1042 | ∼0.3 |
| eRO-QPE1 | 9.1 × 105 | 6.66 × 104 | ∼1043 | 7.6 |
| eRO-QPE2 | 2.3 × 105 | 8.6 × 103 | 1 × 1042 | 0.45 |
| XMMSL1 | 8.5 × 104 | 9.0 × 103 | 3 × 1041 | ∼0.3 |
| Name . | SMBH mass (M⊙) . | Period (s) . | Peak luminosity |$~(\rm erg\, s^{-1})$| . | Duration |$~(\rm h)$| . |
|---|---|---|---|---|
| GSN069 | 4 × 105 | 3.16 × 104 | 5 × 1042 | 0.5 |
| RXJ1301.9 | 1.8 × 106 | 1.65 × 104 | 1 × 1042 | ∼0.3 |
| eRO-QPE1 | 9.1 × 105 | 6.66 × 104 | ∼1043 | 7.6 |
| eRO-QPE2 | 2.3 × 105 | 8.6 × 103 | 1 × 1042 | 0.45 |
| XMMSL1 | 8.5 × 104 | 9.0 × 103 | 3 × 1041 | ∼0.3 |
In order to compute the emerging luminosity, we need to describe the motion of the star in the AGN disc, and the geometry of the conical bow shock as it intersects the AGN disc surface. We assume that the breakout occurs at the AGN density of ρAGN and the height from the AGN disc mid-plane of z = HAGN. We erect Cartesian coordinates (x, y, z), with the origin at the position of the star in the mid-plane of the AGN disc, the z-axis set to the angular momentum direction of the AGN disc, and the x-axis chosen so that the star moves in the x−z plane. We refer to the components of vectors in these coordinates by the subscripts x, y, or z. The vertical gas density profile around z = HAGN is assumed to be described by ρ = ρAGN(d/d0)n, where d is the distance to the edge of the AGN disc, d0 is d at which photons begin to break out of the AGN disc, and we assume n = 6 in our fiducial model, referring to the density profile of radiation pressure dominated discs (Grishin et al. 2021).
For simplicity, we assume that the star is moving across the AGN disc along a straight trajectory. The stellar velocity is given as v* = v*[sin(θ*), 0, cos(θ*)], and the stellar position is x* = (x*, y*, z*) = v*t[sin(θ*), 0, cos(θ*)], where θ* is the zenith angle between the orbital direction of the star and the angular momentum direction of the AGN disc, t is time, and t = 0 is set to the time at which the star is in the disc mid-plane (z* = 0). The speed of the star is v* = fevKep, where vKep = (GMSMBH/r)1/2 is the Keplerian velocity at the distance r from the SMBH, fe is a factor ranging from (1 − e) to (1 + e) between the apocentre and the pericentre of the orbit, and e is the orbital eccentricity of the star. We set the AGN gas velocity to vrot = vKep(−1, 0, 0), and then, the relative velocity of local gas with respect to the stellar motion is given by vrel = vrot − v*, and the zenith angle of the direction of vrel with respect to the angular momentum direction of the AGN disc is given by θrel = arctan(vrel,x/vrel,z). See Fig. 3 for illustrating these quantities.
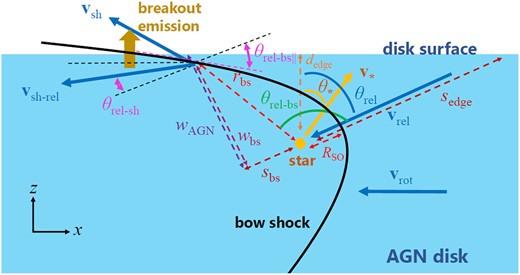
The geometry of the bow shock and the various distances, velocities, and angles as defined in our coordinate systems. The star is moving through the AGN disc in the y = 0 plane. The quantities shown in the figure are defined in the rest frame of the star, except for the velocities v* and vsh, which are depicted in the rest frame of the SMBH.
Next, we consider the geometry of the bow shocks. Referring to previous studies (Wilkin 1996; Mohamed, Mackey & Langer 2012), we assume that the asymptotic shape of a bow shock around the star, with the stand-off radius for the head-on stream RSO in the stellar rest frame, is given by
where rbs is the bow shock distance from the star, and θrel–bs is the angle between vrel and the direction of the bow shock with respect to the star. For a less massive star, the ram pressure of cold gas is equated to the pressure of the envelope of the star, and hence, the distance to the shock in the head-on direction (RSO) is roughly given by the radius of the star. This can be different for a massive star, for which the ram pressure of the stellar wind can be equated to that of the unshocked gas at a much larger radius. Note that the shapes of the bow shocks formed by a solid surface assumed in our model and those produced in the presence of winds considered in Wilkin (1996) are almost identical, as shown by numerical simulations in Yalinewich & Sari (2016).
In the rest of this section, we describe variables in the rest frame of the star unless stated otherwise. The projected distance to the bow shock at rbs (and θrel–bs) from the star along the trajectory of the cold gas motion is sbs = rbscos(π − θrel–bs), and the half-shock width is wbs = rbssin(π − θrel–bs). At each position of the star, the bow shock breaks out of the AGN surface in the direction in which the width of the bow shock wbs is equal to the distance from the trajectory of unshocked gas across the star to the position at which breakout occurs wAGN = (sbs + sedge)/[tan(θrel)cos ϕy], where sedge = dedge/cos(θrel) is the distance of the star to the surface of the AGN disc in the direction of the unshocked gas motion, dedge = HAGN − z* is the distance from the star to the height at which breakout occurs, ϕy ≡ arctan(ybs/wbs), and ybs is the y-coordinate of the bow shock.
The velocities of the unshocked gas parallel and perpendicular to the bow shock surface are, respectively, vc,|| = vrelcos(θrel–bs||) and vc,⊥ = vrelsin(θrel–bs||), where θrel–bs|| = arctan(dwbs/dsbs) is the angle between the bow shock surface at rbs (and θrel–bs) and the unshocked gas motion. Through the bow shock, the velocities of the shocked gas parallel and perpendicular to the shock surface are, respectively, related to the velocity of the cold (unshocked) gas as vsh,|| = vc,|| and vsh,⊥ = vc,⊥(γ − 1/γ + 1), and the sound speed of the shocked gas is given as |$c_{\rm s}=\sqrt{2\gamma /(\gamma -1)} v_{\rm sh,\perp }$| assuming strong shocks. Here, γ is the adiabatic index, which we set to γ = 4/3 as gas is dominated by radiation pressure. The angle between the shocked and unshocked gas motions is
The three-dimensional shocked gas velocity in the stellar rest frame (vsh–rel) can be derived by considering the fact that the shocked gas motion is directed to the −x‴-direction, where x‴ is rotated from x″ around the y″-axis by θrel–sh, x″ is rotated from x′ around the x′-axis by −ϕy, and x′ is rotated from x around the y-axis by θrel − π/2. Since the velocities above are estimated in the rest frame of the star, the velocity of the shocked gas in the rest frame of the central SMBH is given by
To numerically evaluate the properties of the shocks and the emission, both of which depend on the stellar position, the shape and orientation of the bow shock, and the time from the breakout, we discretize the position, the patches along the bow shock, and the time from the breakout by |$i_{\rm max}^{\rm th}$|, |$j_{\rm max}^{\rm th}$|, and |$k_{\rm max}^{\rm th}$| cells, respectively, with imax = jmax = kmax = 500 (Fig. 4). First, we discretize the stellar position as x* = xi = v*ti[sin(θ*), 0, cos(θ*)], where ti = iΔt is the discretized time, i is a positive integer, Δt = tfin/imax is the time-step, and we set the final time tfin to be tmax = 10HAGN/v*,z to ensure that the star’s trajectory is followed until it goes well outside the AGN disc.
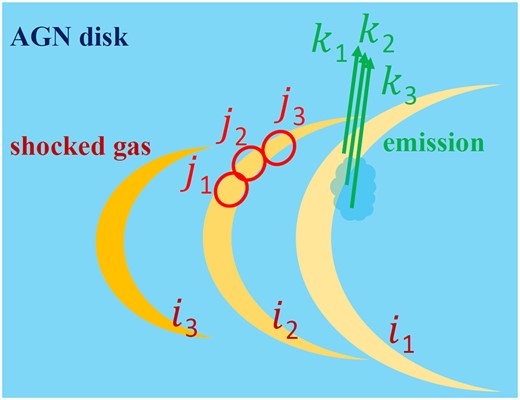
Schematic diagram representing the construction of the light curve from the system. At any given instant (labelled by i), the intersection of the bow shock with the disc surface defines a 1D curve (yellow), trailing the moving star. Each patch along this breakout curve (labelled by j) begins to produce a light curve. At any given time (labelled by k) we observe this system, we sum the contribution from each patch along the breakout curve at each previous position of the star.
At each position of the star, the surface of the bow shock is described by equation (1), and thus, the regions of the shocks breaking out of the AGN disc can be calculated. These regions are defined by the intersection of the two-dimensional parabolic bow shock surface with the flat AGN disc surface – at a given time i, they correspond to a one-dimensional (1D) curve. For the star at the ith position, points along this breakout curve can be enumerated using the angle between the direction from the star towards the breakout point and the star’s velocity vector, θrel–bs,BO,i,j = θrel–bs,BO,i,y0 + (π − θrel–bs,BO,i,y0)(j/jmax), where θrel–bs,BO,i,y0 is θrel–bs for the breakout point in the ybs = 0 plane (see the green angle in Fig. 3) and j is a positive integer. Note that the angle is smallest in the ybs = 0 plane and approaches π at infinite distance from the star.
Below, we designate the physical quantities of the shocks at θrel–bs,BO,i,j with the subscripts i, j. We calculate the surface area of the jth shocked region when the star is at x* = xi as Si,j = ΔxΔyi,j, where Δx = vrel,xΔt is the length that the breakout region moves in the x-direction within Δt due to the motion of the star, and Δyi,j and li,j are the y-direction length and the length of the shock breaking out of the AGN disc between the jth and (j + 1)th cell at t = ti, respectively. Δyi,j = yi,j + 1 − yi,j is derived from the relation
We only consider the emission from shocks for θrel–bs > 0. This is because the breakout emission for θrel–bs < 0 (i.e. when the ‘bottom half’ of the bow shock in Fig. 3, below the star, is breaking out) is likely covered by gas already shocked and expanding. Additionally, we assume that shocks emerge only when |$c_{\mathrm{ s},i,j}\gt c_{\mathrm{ s}, \rm AGN}$| since otherwise strong shocks are not expected. Here, |$c_{\mathrm{ s},\rm AGN}$| is the sound speed in the unshocked AGN disc gas, and we assume |$c_{\mathrm{ s},\rm AGN}=H_{\rm AGN}v_{\rm Kep}/r$|.
After breakout of each patch of the bow shock, we calculate the luminosity and temperature evolution following Nakar & Sari (2010). The emission from the area Si,j is
where tBO,i,j is the breakout time-scale on which the diffusion speed of photons becomes faster than the shock velocity, and tsph,i,j is the time-scale at which the breakout region begins to expand in spherical directions for the shock at the (i, j)th cell. In equation (5), the first, second, and third row correspond to the luminosity in the planar phase, and the fourth row corresponds to that in the spherical phase. Here, ‘planar’ and ‘spherical’ refer to phases before and after the shocked gas doubles its radius through adiabatic expansion caused by the enhancement of its thermal energy, respectively. The evolution of the emission properties is significantly different during these two phases, mainly because the radius of the shocked envelope remains roughly constant during the planar phase, while it increases significantly during the spherically expanding phase.
The time-scales can be calculated as |$t_{{\rm BO},i,j}=c/(\kappa \rho _{\rm AGN} v_{{\rm sh},z,i,j}^2)$| and tsph,i,j = HAGN/vsh,z,i,j, where κ is the opacity of the AGN gas, and we set κ = 0.4 cm2 g−1 for electron scattering (appropriate in the inner, ionized regions of AGN discs; see Section 4.3 for other opacity regimes). We calculated the total luminosity at time tk as
where tk = kΔt is the discretized time, k is a positive integer, and the factor of 2 in equation (6) accounts for the assumption that the shock is symmetric with respect to the y = 0 plane.1 During the transition between the two phases in equation (5), we averaged the luminosities by weighting the duration spent in both phases between tk and tk + 1.
The temperature of the breakout emission is also prescribed following Nakar & Sari (2010). Since the temperature evolution from tsph,i,j to the time at which the colour shell (whose emission characterizes the observed radiation temperature) reaches thermal equilibrium (t1) is not explicitly given, we interpolate this range by a power law.2 After gas in the colour shell becomes thermally coupled with radiation (t2), we adopt the temperature dependence on the time given in the second line of equation (17) in Nakar & Sari (2010).
To compute the typical temperature of emission for the time t = tk, we weigh the temperature at i, j, and k (Ti,j,k) by the luminosity for i, j, and k as
To compute the X-ray luminosity, we assume blackbody spectra with the temperature Ttyp, and the frequency of the X-ray range 0.4–3 keV, considering observations by XMM–Newton. Note that this prescription overestimates the X-ray luminosity when kBTtyp is much higher than that of the X-ray band and the radiation is out of the thermal equilibrium,3 but it is a good approximation in the fiducial model provided in the next section.
2.2 Initial condition
The various parameters of our model are summarized in Table 2. We assume that flares occur twice per orbit around the SMBH as the star collides with the AGN disc (2PQPE = Porb, where Porb is the orbital period of the star). In this case, the semimajor axis of the stellar orbit is estimated as a = (PQPE/π)2/3(GMSMBH)1/3, where PQPE is the period of QPEs. We adopt e = 0 in the fiducial model as the orbital periods of QPEs are observed to be very regular (but see Miniutti et al. 2023a and discussions below), and MSMBH = 106 M⊙ and PQPE = 10 h reflecting the typical properties of QPEs (Table 1). We set the stand-off radius for the bow shock to RSO = 3 × 1011 cm assuming a star with a mass of m* ∼ 10 M⊙ (Torres, Andersen & Giménez 2010). We set the scale height of the AGN disc to HAGN = 1012 cm, corresponding to the aspect ratio of HAGN/a ∼ 0.04(PQPE/10 h)−2/3(MSMBH/106 M⊙)−1/3, and the AGN density to ρAGN = 3 × 10−10 g cm−3. The corresponding bolometric luminosity of the AGN disc is
which is roughly consistent with the luminosity of the quiescent phases in QPEs assuming a standard disc model (Linial & Metzger 2023; Lu & Quataert 2023), and accretion on to the SMBH at ∼0.1 times the Eddington accretion rate, where α is the viscosity parameter, and η is the radiative efficiency. In our fiducial model, we assume that the star’s orbit is retrograde with respect to the AGN disc gas, since otherwise the emission is found to be much dimmer compared to that observed in the QPEs. The zenith angle between the orbital angular momentum directions of the star and the AGN disc (θ*) is set to 80° to roughly reproduce the duration and the luminosity of QPEs.
| Parameter . | Fiducial value . |
|---|---|
| Stand-off radius for the bow shock | |$R_{\rm SO}=3\times 10^{11}\, {\rm cm}$| |
| Zenith angle between the orbital angular momentum direction of the star and the AGN disc | θ* = 80° |
| AGN density | ρAGN = 3 × 10−10 g cm−3 |
| Scale height of the AGN disc | HAGN = 1012 cm |
| Orbital period of the star | |$P_{\rm orb}=20\, {\rm h}$| |
| SMBH mass | |$M_{\rm SMBH}=10^6\, {{\rm M}_\odot }$| |
| Orbital eccentricity of the star | e = 0 |
| Power-law slope for the vertical AGN gas density profile | n = 6 |
| Parameter . | Fiducial value . |
|---|---|
| Stand-off radius for the bow shock | |$R_{\rm SO}=3\times 10^{11}\, {\rm cm}$| |
| Zenith angle between the orbital angular momentum direction of the star and the AGN disc | θ* = 80° |
| AGN density | ρAGN = 3 × 10−10 g cm−3 |
| Scale height of the AGN disc | HAGN = 1012 cm |
| Orbital period of the star | |$P_{\rm orb}=20\, {\rm h}$| |
| SMBH mass | |$M_{\rm SMBH}=10^6\, {{\rm M}_\odot }$| |
| Orbital eccentricity of the star | e = 0 |
| Power-law slope for the vertical AGN gas density profile | n = 6 |
| Parameter . | Fiducial value . |
|---|---|
| Stand-off radius for the bow shock | |$R_{\rm SO}=3\times 10^{11}\, {\rm cm}$| |
| Zenith angle between the orbital angular momentum direction of the star and the AGN disc | θ* = 80° |
| AGN density | ρAGN = 3 × 10−10 g cm−3 |
| Scale height of the AGN disc | HAGN = 1012 cm |
| Orbital period of the star | |$P_{\rm orb}=20\, {\rm h}$| |
| SMBH mass | |$M_{\rm SMBH}=10^6\, {{\rm M}_\odot }$| |
| Orbital eccentricity of the star | e = 0 |
| Power-law slope for the vertical AGN gas density profile | n = 6 |
| Parameter . | Fiducial value . |
|---|---|
| Stand-off radius for the bow shock | |$R_{\rm SO}=3\times 10^{11}\, {\rm cm}$| |
| Zenith angle between the orbital angular momentum direction of the star and the AGN disc | θ* = 80° |
| AGN density | ρAGN = 3 × 10−10 g cm−3 |
| Scale height of the AGN disc | HAGN = 1012 cm |
| Orbital period of the star | |$P_{\rm orb}=20\, {\rm h}$| |
| SMBH mass | |$M_{\rm SMBH}=10^6\, {{\rm M}_\odot }$| |
| Orbital eccentricity of the star | e = 0 |
| Power-law slope for the vertical AGN gas density profile | n = 6 |
3 RESULTS
3.1 Emission properties
We first show the evolution of the bow shock and the corresponding emission. Fig. 5 represents the evolution of several properties. At t = 0, the star is at the mid-plane of the AGN disc, and it passes out of the disc at t = HAGN/v*cos(θ*) = 2.6 × 103 s. At the beginning of the calculation of t = 0, the shocks break out from the AGN disc at the far side, where the angle between the unshocked gas motion and the bow shock direction from the star is θrel–bs = 2.6 rad [black line in panel (a)] and the projected distance to the shock from the star along trajectory of the cold gas motion is sbs ∼ 1.8HAGN [black line in panel (b)]. The direction of unshocked gas flow is almost parallel to the shock surface with θrel–bs|| = 0.20 rad [red line in panel (a)], and the sound velocity of the shocked gas breaking out of the AGN disc at y = 0 is cs = 0.01c. The surface area releasing breakout emission in the planar phase is much larger than the cross-sectional area of the star [panel (c)] due to the low inclination of the orbit.
![The evolution of the properties of the shock and the emission in the fiducial model. (a) The angle between the unshocked gas flow direction and the line connecting the point where the shock is breaking out of the disc and the star θrel–bs (black) and the angle between the bow shock surface and the unshocked gas motion θrel–bs|| (red) on the plane along the stellar orbital motion and the angular momentum direction of the AGN (y = 0) in the stellar rest frame. During the late stages, when the head of the bow shock is exiting the AGN disc, the unshocked gas collides nearly perpendicularly with the surface of the bow shock, which strongly influences the properties (temperature and energy) of the shocked gas. (b) wbs is the half-shock width (red), and sbs (black) and rbs (cyan) are, respectively, the projected distance along the trajectory of unshocked gas and the distance from the star to the bow shock breaking out of the AGN disc for y = 0. These distances from the star to the shock breaking out of the disc all decrease with time. (c) The total area of the shocked gas emitting in the planar phase calculated as ΣjSi,j × tBO,i,j/Δt, in the units of the square of the stand-off radius ($R_{\rm SO}^2$), assumed to be equal to the stellar radius. The total area emitting breakout emission is found to be much larger than the cross-sectional area of the star. (d) The luminosity-weighted temperature [colours are the same as in panel (e)]. (e) The X-ray luminosity between 0.4 keV ≤ hν ≤ 3 KeV (solid black). At any given time, the total luminosity is contributed by a sum of different patches of the bow shock; some of these patches are in the planar phase, before they broke out of the AGN disc and started expanding (ti < tsph,i, blue), and some are afterwards, in a quasi-spherical post-breakout stage (tsph,i < ti,orange). (f) The bolometric luminosity [colours are the same as in panel (e)]. The vertical grey line marks the time at which the star exits the AGN disc surface.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/526/1/10.1093_mnras_stad2616/1/m_stad2616fig5.jpeg?Expires=1749162527&Signature=d6aABFb7mTfclNXlraaGKRcWrRC71KBlxplZiNMCZqcGLlUAp3YCtkF3aUnF13weQd3zj6oje48sZkPSmvjPFHawM~t4qXkgMbPxRu7XeP73f3tAaNCa1A~QgxIJ2YajMN-zPzytCZxymSo6gQnTIGVyL8ordR8CIt9zNvTxC252rZkRrZTQFQVjtCUpilgnB7vPLLfgTCYkFh6XP4lsP6-opVK~qttYrQVzy~XoEG9ne3JbSfGMrmZzAluJAIh32ddqL~KLl3sM8H1WAVJDEWOv70v2YhjoUkyQ6mhI-zYcDeSxpFGOAyt40dKTsgUJjJMYj8W8d1RXF7bjku7aeQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The evolution of the properties of the shock and the emission in the fiducial model. (a) The angle between the unshocked gas flow direction and the line connecting the point where the shock is breaking out of the disc and the star θrel–bs (black) and the angle between the bow shock surface and the unshocked gas motion θrel–bs|| (red) on the plane along the stellar orbital motion and the angular momentum direction of the AGN (y = 0) in the stellar rest frame. During the late stages, when the head of the bow shock is exiting the AGN disc, the unshocked gas collides nearly perpendicularly with the surface of the bow shock, which strongly influences the properties (temperature and energy) of the shocked gas. (b) wbs is the half-shock width (red), and sbs (black) and rbs (cyan) are, respectively, the projected distance along the trajectory of unshocked gas and the distance from the star to the bow shock breaking out of the AGN disc for y = 0. These distances from the star to the shock breaking out of the disc all decrease with time. (c) The total area of the shocked gas emitting in the planar phase calculated as ΣjSi,j × tBO,i,j/Δt, in the units of the square of the stand-off radius (|$R_{\rm SO}^2$|), assumed to be equal to the stellar radius. The total area emitting breakout emission is found to be much larger than the cross-sectional area of the star. (d) The luminosity-weighted temperature [colours are the same as in panel (e)]. (e) The X-ray luminosity between 0.4 keV ≤ hν ≤ 3 KeV (solid black). At any given time, the total luminosity is contributed by a sum of different patches of the bow shock; some of these patches are in the planar phase, before they broke out of the AGN disc and started expanding (ti < tsph,i, blue), and some are afterwards, in a quasi-spherical post-breakout stage (tsph,i < ti,orange). (f) The bolometric luminosity [colours are the same as in panel (e)]. The vertical grey line marks the time at which the star exits the AGN disc surface.
As the star approaches the surface of the AGN disc [rbs decreases, cyan line in panel (b)], θrel–bs|| monotonically increases, and accordingly cs at y = 0 increases to cs = 0.06c since upstream gas flows more vertically on to the shock surface. The surface area of the regions breaking out of the AGN disc also increases [panel (c)], since the condition for shocks (|$c_{\mathrm{ s},i,j}\gt c_{\mathrm{ s},\rm AGN}$|) is satisfied in large areas in the later phases. In t > 2.6 × 103 s, θrel–bs becomes negative, and hence, the emission from the shocks formed after this phase is not considered in this paper as stated in Section 2.1.
After the star passes through the AGN disc surface at t ∼ 2.6 × 103 s [dashed grey lines in panels (d), (e), and (f)], the temperature of the shocked gas decreases with time [black line in panel (d)]. Also, in the planar phase, the radiation is out of thermal equilibrium as photons are deficient and the radiation temperature is higher than the blackbody temperature due to the Comptonization of photons. On the other hand, at the beginning of the spherical phase, the radiation temperature rapidly decreases as the radiation reaches thermal equilibrium. Due to the temperature evolution, the X-ray luminosity also rapidly decreases [black line in panel (e)]. On the other hand, the bolometric luminosity roughly evolves following ∝t−4/3 in the planar phase and ∝t−0.5 in the spherical phase (Nakar & Sari 2010). Note that most of the emission is contributed by patches along the bow shock at distances far beyond the stand-off radius (wbs > RSO). In this model, the contribution from the emission in the spherical phase to the X-ray luminosity is minor compared to that in the planar phase [blue and orange lines in panel (e)]. Cases with more complicated light curves are shown as variations from our fiducial model in the next section.
In this fiducial model, the maximum luminosity in the X-ray band is |$L_{\rm x,max}=1.6\times 10^{42}~{\rm erg\, s}^{-1}$|, the duration for which the X-ray luminosity is above 0.1Lx,max is 3.0 × 103 s, the total radiated bolometric energy is 9.4 × 1046 erg, and that in the X-ray band is 2.8 × 1045 erg. Regions whose half-shock width at breakout is wbs = 0–2RSO, 2–3RSO, and 3–5RSO contribute 10, 82, and 8 per cent of the X-ray luminosity, respectively. Also, 59 and 41 per cent of the X-ray luminosity is contributed by the shocks breaking out of the disc at t < 2500 s and t > 2500 s, respectively. Since the duration for the breakout emission (∼103 s for the planar phase) is not short compared to the dynamical time of the stellar orbit in the AGN disc, the shocked gas keeps emitting until its distance from the star becomes much larger than the size of the stand-off radius (Fig. 6). Hence, the X-ray luminosity is contributed mostly by early shocks formed in the regions with wbs = 2–3RSO, and this emission is released far from the star of sbs ∼ 100RSO. The values of the X-ray luminosity, the duration of the X-ray flare, and the temperature are consistent with those typically observed in QPEs (Table 1). Additionally, the rapid decrease in the temperature is consistent with the trend in the evolution of the hardness ratio found in Miniutti et al. (2023a).
![Contributions to the total X-ray luminosity integrated over the duration of the flare [Ex(sbs,l) = ∫Lx(sbs,l)dt, where Lx(sbs,l) is the X-ray luminosity from shocked regions in the lth cell sbs = sbs,l, whose cell size is 1.8 × 109 cm] from shocked regions at different projected distances from the star, along the unshocked gas trajectory (sbs), shown in units of the stand-off radius (RSO). The black, blue, and orange lines are the total luminosity, the luminosity in the planar phase, and that in the spherical phase, respectively.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/526/1/10.1093_mnras_stad2616/1/m_stad2616fig6.jpeg?Expires=1749162527&Signature=WmrdoLdXm8PtnzeR2cV90IkkfHxAWVmeIY9q0zAUx552VEibLcHw4X05w44B2bUl55UEsbQllXcOlm2Fta2Vkr7m2e6oxLrQCaSI940Ig0LhsBy8eTVfwvflT6A9TDz9MtCIobYqVYJnAtbBLTjGwgK8tNOelgzyhF7sOWkeNM0DRtfyA1hOrCw-POGY2fWkGKKeeQE~3iSNrv0LQctjcIqzZ2LMrJHPbT3l-1qd1JrhTmGU4sRhlinXq5Ie3gQ3ZSO2xvu77QWgrOieH9syAQOqhBUGJbrVr6NA6R6odeKN8dklOQw8eHpb0f-f67f8Tn3GLQ1qmLyfC6jAUQFLyQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Contributions to the total X-ray luminosity integrated over the duration of the flare [Ex(sbs,l) = ∫Lx(sbs,l)dt, where Lx(sbs,l) is the X-ray luminosity from shocked regions in the lth cell sbs = sbs,l, whose cell size is 1.8 × 109 cm] from shocked regions at different projected distances from the star, along the unshocked gas trajectory (sbs), shown in units of the stand-off radius (RSO). The black, blue, and orange lines are the total luminosity, the luminosity in the planar phase, and that in the spherical phase, respectively.
3.2 Parameter dependence
Next, we investigate the parameter dependence of the light curve in the X-ray band. We change the following parameters from the fiducial model (Section 2.2):
In model M2, a smaller bow shock size of RSO = 1 × 1011 cm to investigate the dependence on RSO.
In model M3, a higher AGN gas density of ρAGN = 10−9 g cm−3.
In model M4, a less inclined orbit with θ* = 85°.
In model M5, a thinner disc of HAGN = 5 × 1011 cm, which is still several times thicker than that in the standard α disc model. This is justified as the heating rate by the stellar collisions (|$\sim\!\! 10^{42}~{\rm erg\, s}^{-1}$| on average from the total radiated bolometric energy of 3 × 1046 erg divided by the orbital period in the fiducial model) is higher than the cooling rate of the α disc model at the position of the star.
In model M6, a shorter orbital period of Porb = 5 h.
In model M7, a higher SMBH mass of MSMBH = 107 M⊙.
In model M8, a high orbital eccentricity of e = 0.7.
In model M9, a shallower vertical density profile with n = 3.
In models M10 and M11, highly inclined cases of θ* = 50° and θ* = 0°, respectively.
Also, finally, in model M12, we compare our results specifically to the properties of eRO-QPE1. We set the large bow shock size to RSO = 6 × 1011 cm assuming a star with a mass of ∼30 M⊙ (Torres et al. 2010) and adopt a low-inclination orbit with θ* = 87°. The light curves in the X-ray bands for models M1–M10 are presented in Fig. 7.
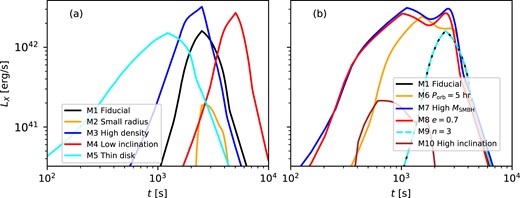
The parameter dependence of the X-ray light curves. (a) The results for the fiducial model (black), for RSO = 1011 cm (orange), ρAGN = 10−9 g cm−3 (blue), θ* = 85° (red), and HAGN = 5 × 1011 cm (cyan). (b) The results for the same fiducial model (black), Porb = 5 h (orange), MSMBH = 107 M⊙ (blue), e = 0.7 (red), n = 3 (cyan), and θ* = 50° (brown).
In model M2, due to the smaller RSO, the amount of gas undergoing shocks with high θrel–bs|| is lower than in the fiducial model. As a result, the X-ray luminosity in this model is lower (orange line in Fig. 7a) by a factor of ∼9 compared to the fiducial model.
In the higher AGN gas density model (M3), the maximum X-ray luminosity is higher [blue line in panel (a)] because the breakout luminosity is proportional to the gas density. On the other hand, the duration is shorter because the breakout time-scale in the planar phase is inversely proportional to the gas density and the luminosity decreases with time as ∝(t/tBO,i,j)−4/3 (equation 5).
In the less inclined model (M4), the total energy of emission and the peak of Lx are both high [red line in panel (a)] because the duration for shocks to emerge is long and the relative velocity between the AGN disc gas and the star is high.
In the thinner disc model (M5), the shocks break out of the disc earlier due to the shorter distance from the disc mid-plane to the AGN surface. Also, the duration of the X-ray emission is slightly shorter than that in the fiducial model (cyan line in Fig. 7a), since tsph is shorter.
In model M6, the high orbital velocity of the star increases both the breakout luminosity and the temperature of shocked gas. The same results are also seen for the high MSMBH and high e cases [models M7 and M8, blue and red lines in panel (b), respectively] in which the orbital velocity is higher at the time of disc-crossing. For the models with the orbital periods of 5 (model M6), 10, 20 (model M1), 40, and 80 h, in which the relative velocities between the star and unshocked AGN gas are 0.24c, 0.19c, 0.15c, 0.095c, and 0.075c, respectively, the peak X-ray luminosities are 2.4 × 1042, 2.0 × 1042, 1.6 × 1042, 8.1 × 1041, and |$1.8\times 10^{41}~{\rm erg\, s}^{-1}$|. The peak X-ray luminosities for Porb = 5, 10, and 20 h are similar, since the maximum peak frequency of the radiation is at around the X-ray band (0.4–3 keV). On the other hand, for Porb ≥ 20 h, the peak X-ray luminosity significantly decreases as Porb increases since the X-ray band is shifted into the Wien tail of the blackbody-like spectra and the temperature of the shocked gas is lower at a lower relative velocity. Thus, in the fiducial settings, the period of QPEs needs to be shorter than 20 h (|$P_{\rm QPE}=\frac{1}{2}P_{\rm orb}$|) to achieve LX ≳ several |$\times 10^{41}~{\rm erg\, s}^{-1}$|. Also, the peak of the multicolour blackbody emission falls in the X-ray band and the X-ray luminosity is largest for PQPE ≲ 10 h.
In these models (M6–M8), multiple components can be found in the X-ray light curve. One is contributed by breakout emission in the early planar phase, which is commonly seen in the other models. Additionally, the emission in the spherical phase contributes a second component, which is relatively bright because the total luminosity and temperature of radiation at the beginning of the spherical phase are high. Such features may have been observed in eRO-QPE1 as discussed in Section 4.2.
In model M9, the properties of the emission are similar to those in the fiducial model [dashed cyan line in panel (b)]. This is because the emission is dominated by the planar phase, and the properties of the emission in the planar phase are not affected by the density profile, n (e.g. equation 5).
In models M10 and M11, the X-ray luminosity is significantly lower (Table 1). This is because of the lower relative velocity of the star and the AGN disc, and because the time for the star to exit the disc is short. Hence, the star needs to orbit in the retrograde direction with respect to the AGN disc to explain the high luminosities of QPEs.
In model M12, the high X-ray luminosity and the long duration as found in eRO-QPE1 are roughly reproduced due to the large values of RSO and θ*. More precise comparisons to eRO-QPE1 would require a detailed modelling of the shock dynamics, which is beyond the scope of this paper.
Overall, we find that the duration of the X-ray emission is significantly influenced by HAGN (model M5) and θ* (model M4), and the X-ray luminosity by R* (model M2) and θ*. To produce the luminosity and the duration observed in QPEs, the star needs to move in the retrograde direction relative to the AGN gas at relatively low inclinations (≲40°) and be massive (≳10 M⊙).
4 DISCUSSION
4.1 Formation process
Here, we discuss the possible origin of the star on a low-inclination orbit relative to the accretion disc. Pathways to form such systems have been proposed by Lu & Quataert (2023). They considered that a tight orbit with a semimajor axis of ∼100 au and a pericentre distance of ∼au can be formed by the Hills mechanism. In this picture, a stellar binary is disrupted by the tidal field of the SMBH, resulting in formation of a star tightly bound to the SMBH and a hypervelocity star. Subsequently, gravitational wave radiation circularizes the stellar orbit and reduces its semimajor axis to ∼au. During the gravitational wave in-spiral, if scatterings by other stars are efficient, the orbital eccentricity tends to be enhanced and the condition for (partial) tidal disruption4 with a large semimajor axis is satisfied. Since scatterings by stars are expected to be inefficient around less massive SMBHs, QPEs are favoured to be associated with less massive SMBHs in this scenario (Lu & Quataert 2023), which is consistent with observations of QPEs. In this process, the star may avoid complete disruption, and the remnant may then form a tight orbit and the stripped envelope may form an accretion disc, which can produce QPEs. If this model is correct, it demonstrates that stars presumably often survive tidal disruption events (especially for low-mass SMBHs), since two QPE events have been observed to follow tidal disruption events (Miniutti et al. 2019; Chakraborty et al. 2021). Note that the lifetime of QPEs in these scenarios is limited by the viscous time-scale (tvis) of the accretion disc, which is typically longer than the observed duration of QPEs as
It is also possible that a star has become tightly bound to the SMBH through the Hills mechanism or other relaxation processes, while an accretion disc forms by unrelated processes such as gas accretion or tidal disruption of another star. In those cases, the accretion disc need not be necessarily reoriented as discussed below.
The model proposed by Lu & Quataert (2023) requires moderate orbital eccentricity in the phases producing QPEs. On the other hand, our model allows all the way down to zero eccentricity, but a low-inclination and retrograde orbit with respect to the accretion disc is required to produce bright emission as seen above. The processes to produce less inclined orbits are discussed in the next section.
4.2 Comparisons to observed events
We next discuss the consistency (or lack thereof) between our model and several observational features.
First, QPEs have been observed with a range of X-ray energies and flare durations. Fig. 8 shows the distribution of LX and the duration for the observed events (filled circles) and models M1–M8, M10, and M12 (crosses). The X-ray luminosity is significantly influenced by θ*, ρAGN, and RSO, and the duration of emission is influenced by θ*, ρAGN, and HAGN (Table 3).
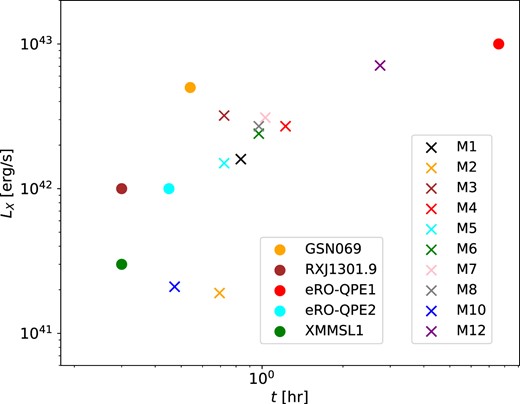
The distribution of the maximum value of LX and the flare duration for the five observed events (filled circles) and models M1–M8, M10, and M12 (crosses).
Results in several different model variants. The first column indicates the model number. In the ‘parameter’ column, we indicate parameters that deviate from the fiducial model.
| Model . | Parameter . | Maximum |$L_{\rm x}~({\rm erg\, s}^{-1})$| . | Duration |$(\rm s)$| . | X-ray energy |$(\rm erg)$| . | Bolometric energy |$(\rm erg)$| . |
|---|---|---|---|---|---|
| M1 | Fiducial | 1.6 × 1042 | 3.0 × 103 | 3 × 1045 | 9 × 1046 |
| M2 | Smaller radius (RSO = 1011) | 1.9 × 1041 | 2.5 × 103 | 3 × 1044 | 1 × 1046 |
| M3 | Higher gas density (ρAGN = 10−9 g cm−3) | 3.2 × 1042 | 2.6 × 103 | 5 × 1045 | 1 × 1047 |
| M4 | Less inclined orbit (θ* = 85°) | 2.7 × 1042 | 4.4 × 103 | 7 × 1045 | 2 × 1047 |
| M5 | A thinner AGN disc (HAGN = 5 × 1011 cm) | 1.5 × 1042 | 2.6 × 103 | 2 × 1045 | 1 × 1047 |
| M6 | Shorter orbital period (Porb = 5 h) | 2.4 × 1042 | 3.5 × 103 | 5 × 1045 | 2 × 1047 |
| M7 | Massive SMBH mass (MSMBH = 107) | 3.1 × 1042 | 3.7 × 103 | 8 × 1045 | 3 × 1047 |
| M8 | High eccentricity (e = 0.7) | 2.7 × 1042 | 3.5 × 103 | 6 × 1045 | 2 × 1047 |
| M9 | Shallower vertical density gradient (n = 3) | 1.6 × 1042 | 3.1 × 103 | 3 × 1045 | 1 × 1047 |
| M10 | Highly inclined orbit (θ* = 50°) | 2.1 × 1041 | 1.7 × 103 | 2 × 1044 | 1 × 1046 |
| M11 | Highly inclined orbit (θ* = 0°) | 1.2 × 1040 | 1.2 × 103 | 9 × 1042 | 1 × 1044 |
| M12 | eRO-QPE1-like (RSO = 6 × 1011, θ* = 87°) | 7.1 × 1042 | 9.9 × 103 | 4 × 1046 | 2 × 1048 |
| Model . | Parameter . | Maximum |$L_{\rm x}~({\rm erg\, s}^{-1})$| . | Duration |$(\rm s)$| . | X-ray energy |$(\rm erg)$| . | Bolometric energy |$(\rm erg)$| . |
|---|---|---|---|---|---|
| M1 | Fiducial | 1.6 × 1042 | 3.0 × 103 | 3 × 1045 | 9 × 1046 |
| M2 | Smaller radius (RSO = 1011) | 1.9 × 1041 | 2.5 × 103 | 3 × 1044 | 1 × 1046 |
| M3 | Higher gas density (ρAGN = 10−9 g cm−3) | 3.2 × 1042 | 2.6 × 103 | 5 × 1045 | 1 × 1047 |
| M4 | Less inclined orbit (θ* = 85°) | 2.7 × 1042 | 4.4 × 103 | 7 × 1045 | 2 × 1047 |
| M5 | A thinner AGN disc (HAGN = 5 × 1011 cm) | 1.5 × 1042 | 2.6 × 103 | 2 × 1045 | 1 × 1047 |
| M6 | Shorter orbital period (Porb = 5 h) | 2.4 × 1042 | 3.5 × 103 | 5 × 1045 | 2 × 1047 |
| M7 | Massive SMBH mass (MSMBH = 107) | 3.1 × 1042 | 3.7 × 103 | 8 × 1045 | 3 × 1047 |
| M8 | High eccentricity (e = 0.7) | 2.7 × 1042 | 3.5 × 103 | 6 × 1045 | 2 × 1047 |
| M9 | Shallower vertical density gradient (n = 3) | 1.6 × 1042 | 3.1 × 103 | 3 × 1045 | 1 × 1047 |
| M10 | Highly inclined orbit (θ* = 50°) | 2.1 × 1041 | 1.7 × 103 | 2 × 1044 | 1 × 1046 |
| M11 | Highly inclined orbit (θ* = 0°) | 1.2 × 1040 | 1.2 × 103 | 9 × 1042 | 1 × 1044 |
| M12 | eRO-QPE1-like (RSO = 6 × 1011, θ* = 87°) | 7.1 × 1042 | 9.9 × 103 | 4 × 1046 | 2 × 1048 |
Results in several different model variants. The first column indicates the model number. In the ‘parameter’ column, we indicate parameters that deviate from the fiducial model.
| Model . | Parameter . | Maximum |$L_{\rm x}~({\rm erg\, s}^{-1})$| . | Duration |$(\rm s)$| . | X-ray energy |$(\rm erg)$| . | Bolometric energy |$(\rm erg)$| . |
|---|---|---|---|---|---|
| M1 | Fiducial | 1.6 × 1042 | 3.0 × 103 | 3 × 1045 | 9 × 1046 |
| M2 | Smaller radius (RSO = 1011) | 1.9 × 1041 | 2.5 × 103 | 3 × 1044 | 1 × 1046 |
| M3 | Higher gas density (ρAGN = 10−9 g cm−3) | 3.2 × 1042 | 2.6 × 103 | 5 × 1045 | 1 × 1047 |
| M4 | Less inclined orbit (θ* = 85°) | 2.7 × 1042 | 4.4 × 103 | 7 × 1045 | 2 × 1047 |
| M5 | A thinner AGN disc (HAGN = 5 × 1011 cm) | 1.5 × 1042 | 2.6 × 103 | 2 × 1045 | 1 × 1047 |
| M6 | Shorter orbital period (Porb = 5 h) | 2.4 × 1042 | 3.5 × 103 | 5 × 1045 | 2 × 1047 |
| M7 | Massive SMBH mass (MSMBH = 107) | 3.1 × 1042 | 3.7 × 103 | 8 × 1045 | 3 × 1047 |
| M8 | High eccentricity (e = 0.7) | 2.7 × 1042 | 3.5 × 103 | 6 × 1045 | 2 × 1047 |
| M9 | Shallower vertical density gradient (n = 3) | 1.6 × 1042 | 3.1 × 103 | 3 × 1045 | 1 × 1047 |
| M10 | Highly inclined orbit (θ* = 50°) | 2.1 × 1041 | 1.7 × 103 | 2 × 1044 | 1 × 1046 |
| M11 | Highly inclined orbit (θ* = 0°) | 1.2 × 1040 | 1.2 × 103 | 9 × 1042 | 1 × 1044 |
| M12 | eRO-QPE1-like (RSO = 6 × 1011, θ* = 87°) | 7.1 × 1042 | 9.9 × 103 | 4 × 1046 | 2 × 1048 |
| Model . | Parameter . | Maximum |$L_{\rm x}~({\rm erg\, s}^{-1})$| . | Duration |$(\rm s)$| . | X-ray energy |$(\rm erg)$| . | Bolometric energy |$(\rm erg)$| . |
|---|---|---|---|---|---|
| M1 | Fiducial | 1.6 × 1042 | 3.0 × 103 | 3 × 1045 | 9 × 1046 |
| M2 | Smaller radius (RSO = 1011) | 1.9 × 1041 | 2.5 × 103 | 3 × 1044 | 1 × 1046 |
| M3 | Higher gas density (ρAGN = 10−9 g cm−3) | 3.2 × 1042 | 2.6 × 103 | 5 × 1045 | 1 × 1047 |
| M4 | Less inclined orbit (θ* = 85°) | 2.7 × 1042 | 4.4 × 103 | 7 × 1045 | 2 × 1047 |
| M5 | A thinner AGN disc (HAGN = 5 × 1011 cm) | 1.5 × 1042 | 2.6 × 103 | 2 × 1045 | 1 × 1047 |
| M6 | Shorter orbital period (Porb = 5 h) | 2.4 × 1042 | 3.5 × 103 | 5 × 1045 | 2 × 1047 |
| M7 | Massive SMBH mass (MSMBH = 107) | 3.1 × 1042 | 3.7 × 103 | 8 × 1045 | 3 × 1047 |
| M8 | High eccentricity (e = 0.7) | 2.7 × 1042 | 3.5 × 103 | 6 × 1045 | 2 × 1047 |
| M9 | Shallower vertical density gradient (n = 3) | 1.6 × 1042 | 3.1 × 103 | 3 × 1045 | 1 × 1047 |
| M10 | Highly inclined orbit (θ* = 50°) | 2.1 × 1041 | 1.7 × 103 | 2 × 1044 | 1 × 1046 |
| M11 | Highly inclined orbit (θ* = 0°) | 1.2 × 1040 | 1.2 × 103 | 9 × 1042 | 1 × 1044 |
| M12 | eRO-QPE1-like (RSO = 6 × 1011, θ* = 87°) | 7.1 × 1042 | 9.9 × 103 | 4 × 1046 | 2 × 1048 |
We expect that θ* is distributed over a wide range. This is because the stellar orbit at ∼100rg is in the plane in which the Hills mechanism occurred, which is presumably randomly oriented. On the other hand, the Bardeen–Petterson effect aligns the accretion disc with the spin direction of the SMBH within the radii (Natarajan & Pringle 1998)
where aSMBH is the dimensionless SMBH spin. In the collision scenario, rw can limit PQPE, and rw in equation (10) is roughly consistent with a ∼ 70–360rg calculated from PQPE and MSMBH for the observed events (Table 1). Although recent general relativistic magneto-hydrodynamic simulations derived smaller radii for alignment by the Bardeen–Petterson effect (Liska et al. 2019, 2021), these values may be underestimated due to the strong magnetic field amplified due to the initially thick disc. Our model requires θ* ≳ 50° to produce QPE flares as bright as ≳a few |$\times 10^{41}~{\rm erg\, s}^{-1}$| (with the fiducial parameters otherwise). This reduces the rate of events by about a factor of several compared to the formation of these systems with all relative orientations.
The finding that the luminous flare in eRO-QPE1 has longer duration (Chakraborty et al. 2021) is consistent with this event having a lower inclination (larger θ*) compared to the other events. The range of the maximum value of LX and the duration in the observed events can also be attributed to variations of the model parameters, θ*, RSO, ρAGN, and HAGN (Fig. 8), since the values of these parameters have not been constrained by observations. Conversely, the QPEs provide novel constraints on these parameters.
Miniutti et al. (2023a) and Chakraborty et al. (2021), respectively, reported that the luminosity for the events GSN069 and XMMSL1 gradually decrease by an order of magnitude in ∼2 and ∼10 yr. Recently, after the disappearance of QPEs in GSN069, their reappearance has been reported (Miniutti et al. 2023b). Prior to this reappearance, the quiescent luminosity is again enhanced, possibly due to additional partial disruption or intense mass-loss from a star. This suggests that QPEs occur when the accretion rate is lower than some critical value. In our scenario, this criterion can arise as follows. The gas additionally lost from the star is initially aligned with the stellar orbit. Due to the vigorous mass-loss, a thicker disc forms as the disc thickness is proportional to the accretion rate (HAGN ∝ LAGN/η). For a thicker disc, the alignment radius by the Bardeen–Petterson effect can become smaller than the distance of the star from the SMBH (|$r_{\rm w}\propto H_{\rm AGN}^{-4/3}$|, equation 10). Then, at the stellar position, the accretion disc is not fully aligned with the SMBH spin, and the QPE brightness is reduced due to the larger inclination angle. In our model, the change in the inclination angle of the accretion disc by ≳30° can explain the inactive and active phases of GSN069, between which the luminosity of QPEs is changed by a factor of ≳10. After the accretion rate decreases below the critical value, the alignment radius exceeds the stellar distance to the SMBH, and the QPEs become brighter again.
Miniutti et al. (2023a) also found that the recurrence time for GSN069 is longer when a stronger QPE is followed by a weaker QPE, and shorter vice versa. On the other hand, Chakraborty et al. (2021) found the opposite trend for XMMSL1. We propose that these modulations can be explained by a low orbital eccentricity. When the stellar orbit is eccentric, the recurrence time between two collisions around the pericentre is shorter than that around the apocentre. Also, emission from shocks around a star moving towards an observer is brighter than that moving away from the observer due to Doppler beaming effects. Hence, slightly eccentric orbits possibly explain the modulation of the recurrence time between QPEs found for GSN069 and XMMSL1.
The luminosity in the quiescent phases of GSN069 also oscillates roughly at the orbital period in GSN069 (Miniutti et al. 2023a). We propose that this can be caused by emission from shocks emerging due to the dissipation of the stellar envelope unbound due to collision with the accretion disc, as proposed by Lu & Quataert (2023). The diffusion time-scale of the shocks within the accretion disc is ∼10 h, being consistent with the observed period of the modulation in the quiescent phases.
Finally, for eRO-QPE1, highly complex evolutions have been found both for the luminosity and the temperature in some phases (Arcodia et al. 2022). We propose that three distinct peaks can arise in the light curve, from emission with high temperature in planar phases, as discussed above for models M6–M8. Other peaks can be contributed by emission from shocks caused by the unbound stellar envelope as presented in Lu & Quataert (2023). To our knowledge, this is the only proposed explanation for the multiple peaks seen in this event.
4.3 Caveats
We have ignored possible absorption and scattering by gas far from the region producing the emission. If the angle between the shock surface and the AGN disc is small, the shocked gas does not go around and intersect the preceding shocks (Linial & Sari 2019). In this case, the optical depth of the shells producing the observed photons is not influenced by the shock on the far sides of the star (the receding shock). Also, the emission from a shock is not obstructed by a preceding shock, as the preceding shock is not expanding fast enough to cover the luminous shell of the receding shock. Even if the shocked gas goes around the preceding shocks in later phases, since the density of the wrapping gas is much lower than the AGN density, we presume that the optical depth of the breakout emission from the preceding shocks is not significantly enhanced by the possible intersection. Thus, our assumption that emission from shocked gas is not obscured by shocked gas elsewhere in the disc appears at least reasonable.
Additionally, we have ignored the acceleration of shocked gas in the direction of the motion of the star (Matzner, Levin & Ro 2013; Irwin et al. 2021). To our knowledge, the impact of this lateral acceleration on the structure of the emerging, expanding cloud, and the corresponding light curve of the breakout emission, has not been investigated in the literature. In near spherically symmetric geometry, the shocked gas that expanded earlier can obscure the breakout emission from gas that shocked later, reducing the overall luminosity. On the other hand, in the planar geometry considered in our model, such obscuration may be avoided since the shocked gas may not cover the later breakout emission (Linial & Sari 2019). Complex light curves in eRO-QPE1 may also be related to absorption and re-emission by expanded shocked gas in some phases. To fully check the validity of neglecting this acceleration, radiative hydrodynamical simulations are desired.
To evaluate the thermalization of the shocked gas, we have considered photons produced by free–free emission, following Nakar & Sari (2010). On the other hand, in high-metallicity environments such as AGNs, bound–free emission dominates the free–free process. Thus, the thermalization process is underestimated in this study, which may somewhat affect the evolution of the temperature in the flares. Also, to calculate the diffusion of photons, the opacity is obtained assuming electron scattering, since we consider emission from inner regions of the AGN disc where gas is ionized. However, flares in outer regions of the AGN disc should be different values of the opacity (Thompson, Quataert & Murray 2005; Jiang & Blaes 2020).
If the alignment of the star with the AGN disc by gaseous interactions is faster than the alignment of the disc to the SMBH spin by the Bardeen–Petterson effect, bright flares due to the stellar collisions are not expected. Here, we consider the evolution of the stellar orbit by the geometric drag (Generozov & Perets 2023). By assuming that the fraction of the velocity change for the star by the drag is the same as the fraction of the mass that the star sweeps within RSO to the stellar mass, the alignment time-scale in the fiducial model is estimated to be |$\sim\!\! P_{\rm orb} m_* {\rm cos}(\theta _*)/(2 \pi R_{\rm SO}^2 H_{\rm AGN} \rho _{\rm AGN}) \sim 50~{\rm kyr}$|. Since the alignment time-scale is much longer than the mass-loss time-scale, the alignment of the star can be ignored in the model.
5 CONCLUSIONS
In this paper, we have evaluated properties of emission from flares caused by bow shocks produced during a collision between a star and an AGN disc. We have included the emission from parts of the bow shock that are about to emerge from the AGN disc’s surface, as well as the parts that have broken out and evolved into an expanding, quasi-spherical cloud. We discussed whether this breakout emission from the bow shocks can explain the properties of the QPE events. Our main results can be summarized as follows:
The two main features – i.e. the duration of about an hour and the peak X-ray luminosity of |$\gtrsim\!\! 10^{41}~{\rm erg\, s}^{-1}$| – observed in the five QPE events can be explained by the breakout emission from the bow shocks.
To produce luminous emission, the star needs to be massive (≳10 M⊙) and on a retrograde and low-inclination (≲40°) orbit with respect to the AGN disc. This is required in order to produce a long bow shock with a large surface area.
Various observed features of QPEs, including the complex luminosity evolution, the gradual decrease of the luminosity of the flares over several years, the evolution of the X-ray hardness ratio, the fluctuations in the luminosity in the quiescent phases, and the relatively low masses of the central SMBHs, can be qualitatively explained in this model.
As we were finalizing this paper for submission, we became aware of two similar studies posted on the arXiv (Franchini et al. 2023; Linial & Metzger 2023). Both investigate the cooling envelope emission from expanding shocked gas formed by the collision between a secondary and an AGN disc, with Linial & Metzger (2023) focusing on a secondary star and Franchini et al. (2023) favouring an ∼100 M⊙ black hole over a star. In our paper, in addition to the cooling, initially optically thick expanding envelope, we also consider the emission from the bow shock as it emerges from the surface of the AGN disc. We find that this bow shock emission can dominate the total X-ray luminosity.
To explain the multiple peaks in eRO-QPE1, we suggest that the breakout emission is required to contribute the initial flares, with secondary contributions from the cooling envelope. Also, in our fiducial model, shocked gas becomes optically thin before it expands by an order of magnitude. On the other hand, in the cooling emission model, since the expanding gas is predicted to remain optically thick until the size of the shocked gas becomes comparable to the semimajor axis of the stellar orbit, the expanding gas may absorb and influence the emission from the AGN disc, which could yield additional observational signatures. Note that in the cooling emission model, the thermal coupling coefficient (η; e.g. Nakar & Sari 2010) and accordingly the X-ray luminosity may be significantly overestimated. In Linial & Metzger (2023), η is estimated after shocked gas adiabatically expands and just before photons deep inside the shocked gas diffuse out. However, η is much lower before the shocked gas adiabatically expands and η does not increase before photons diffuse.5 Meanwhile, in Franchini et al. (2023), the luminosity may be overestimated since the photon diffusion velocity is lower than the expansion velocity of shocked gas in their fiducial model, which needs to be considered as in Linial & Metzger (2023).
Nevertheless, our conclusions are similar to those of Linial & Metzger (2023) and Franchini et al. (2023), namely that collisions between a star and an AGN disc offer a viable explanation for observed QPE flares.
ACKNOWLEDGEMENTS
We thank Shmuel Gilbaum for reproducing our numerical results, which led us to identify and correct two bugs in our code, and Brian Metzger, Itai Linial, and Yuri Levin for useful discussions. This work was financially supported by Japan Society for the Promotion of Science (JSPS) KAKENHI grant number 22KJ0163 (HT), and by NASA grant 80NSSC22K082 and NSF grant AST-2006176 (ZH).
DATA AVAILABILITY
The data underlying this article are available in the article.
Footnotes
In this assumption, we ignore the shear motion of the AGN gas for simplicity.
This prescription negligibly affects the result of this paper, as the temperature evolution in this range is very quick (∼∝t−5).
In this case, the radiation is characterized by a Wien spectrum, Fν ∝ ν3exp(hν/kBT), where h is the Planck constant and ν is the photon frequency.
If part of the stellar envelope lost at pericentre is consumed within an orbital period, it is observed as a partial tidal disruption event.
This is because both the number density of photons required to establish thermal equilibrium (Nakar & Sari 2010) and the number density of photons (whose ratio is the definition of η) during the slow diffusion phases decrease with time with the same power law (as ∝t−3).



