-
PDF
- Split View
-
Views
-
Cite
Cite
Cheng Chen, Rebecca G Martin, C J Nixon, Can a binary star host three giant circumbinary planets?, Monthly Notices of the Royal Astronomical Society, Volume 525, Issue 3, November 2023, Pages 3781–3789, https://doi.org/10.1093/mnras/stad2543
Close - Share Icon Share
ABSTRACT
We investigate the orbital stability of a tilted circumbinary planetary system with three giant planets. The planets are spaced by a constant number (Δ) of mutual Hill radii in the range Δ = 3.4–12.0 such that the period ratio of the inner pair is the same as that of the outer pair. A tilted circumbinary planetary system can be unstable even if the same system around a coplanar binary is stable. For an equal-mass binary, we find that the stability of a three-planet system is qualitatively similar to that of a two-planet system, but the three-planet system is more unstable in mean motion resonance regions. For an unequal-mass binary, there is significantly more instability in the three-planet system as the inner planets can undergo von Zeipel–Kozai–Lidov oscillations. Generally in unstable systems, the inner planets are more likely to be ejected than the outer planets. The most likely unstable outcome for closely spaced systems, with Δ ≲ 8, is a single remaining stable planet. For more widely separated systems, Δ ≳ 8, the most likely unstable outcome is two stable planets, only one being ejected. An observed circumbinary planet with significant eccentricity may suggest that it was formed from an unstable system. Consequently, a binary can host three tilted giant planets if the binary stars are close to equal mass and provided that the planets are well spaced and not close to a mean motion resonance.
1 INTRODUCTION
Although the multiplicity distribution of circumbinary planets (CBPs) has not been confirmed, about half of planets around single stars are known to have siblings in the Kepler data (e.g. Berger et al. 2018; Thompson et al. 2018; Sandford, Kipping & Collins 2019). In the radial velocity planet sample of the California Legacy Survey, 30–40 per cent of Sun-like stars with a massive planet (mass >|$0.3 M_{\rm J}$|, where MJ is the mass of Jupiter) are multiplanet systems (Zhu 2022). Currently, there are only five multiplanet systems that have been found around binaries and all of the CBPs in these systems are nearly coplanar to the binary orbital plane. In the Kepler-47 system, there are three Neptune-sized planets with circular (ep < 0.03) orbits (Orosz et al. 2012a, b; Kostov et al. 2013). In the TOI-1338 system, there are two Saturnian CBPs found by the transit and radial velocity methods (Kostov et al. 2020; Standing et al. 2023). The red dwarf–white dwarf binary system, NN Ser, has two Jupiter-mass CBPs (Mustill et al. 2013). Kepler-451 hosts three Jupiter-mass CBPs (Baran et al. 2015; Esmer et al. 2022). However, the coplanarity of these systems is likely a result of observational bias (e.g. Martin & Triaud 2015; Martin 2017a, b). So, while it has been established from observations that it is possible to generate circumbinary planetary systems with three or more giant planets in the coplanar case, we do not yet know anything about the non-coplanar case, or the more general stability properties of the coplanar case.
Despite the fact that only coplanar CBPs have currently been detected, recent observations have found that there are many misaligned circumbinary discs (e.g. Chiang & Murray-Clay 2004; Winn et al. 2004; Capelo et al. 2012; Kennedy et al. 2012, 2019; Brinch et al. 2016; Kenworthy et al. 2022; Zhu et al. 2022). Polar aligned discs around eccentric binaries may also be common (Aly et al. 2015; Kennedy et al. 2019; Smallwood et al. 2020; Kenworthy et al. 2022). CBPs may form inside these misaligned discs. Theoretically, the formation of misaligned circumbinary discs can result from chaotic accretion (Clarke & Pringle 1993; Bate 2018) and subsequent disc evolution can lead to tilt evolution towards a coplanar alignment (Bate et al. 2000; Lubow & Ogilvie 2000; Nixon et al. 2011) or a polar alignment (Martin & Lubow 2017, 2018; Lubow & Martin 2018; Zanazzi & Lai 2018; Abod et al. 2022). Although about 68 per cent of short-period binaries (period <|$20\ \mathrm{ d}$|) have aligned discs (within 3°), those with longer orbital periods have a larger range of inclinations and binary eccentricities (Czekala et al. 2019). If the alignment time-scale for an extended disc is longer than the disc lifetime, then planetary systems may form in a misaligned disc. Misaligned planetary systems may be expected around binaries with a longer orbital period (Czekala et al. 2019; Martin & Lubow 2019). These planetary systems may be observed in the future with eclipse-timing variations (Martin 2019; Zhang & Fabrycky 2019).
A misaligned CBP has a complicated interaction with the binary. For any inclination around a circular orbit binary, or for low inclination around an eccentric orbit binary, the angular momentum vector of a misaligned CBP precesses around the binary angular momentum vector. The longitude of the ascending node fully circulates over 360° during the nodal precession, these are called circulating orbits. If the binary has a non-zero eccentricity, the angular momentum vector of a misaligned CBP orbit may precess about the binary eccentricity vector. These are called librating orbits (Verrier & Evans 2009; Farago & Laskar 2010; Doolin & Blundell 2011; Naoz et al. 2017; Chen et al. 2019; de Elía et al. 2019). The minimum inclination (critical inclination) for libration decreases with increasing binary eccentricity (eb). Therefore, a CBP orbit with even a small initial inclination can librate around a highly eccentric binary. During nodal libration, a CBP undergoes tilt oscillations while its longitude of ascending node is limited in a range of angles less than 360°.
Close to a binary, even a single planet system can be unstable (e.g. Holman, Touma & Tremaine 1997). Both nodal precession of the orbit and mean motion resonances (MMRs) with the binary play roles in the stability (Doolin & Blundell 2011; Sutherland & Fabrycky 2016). In general, a CBP with a circular orbit is stable if its semimajor axis is greater than about five times separation of the binary, ab for planet masses up to about |$m_{\rm p}=10 M_{\rm J}$| (Doolin & Blundell 2011; Chen, Lubow & Martin 2020). However, stable orbits can exist closer in, down to around 2ab, when the CBP is in a nearly retrograde orbit for small binary eccentricity (Cuello & Giuppone 2019; Giuppone & Cuello 2019; Hong et al. 2019) or in a polar orbit for high eb (Chen et al. 2020).
For a circumbinary planetary system with two massive planets, the dynamics are more complicated because of planet–planet interactions (Chen, Lubow & Martin 2022). These lead to tilt oscillations between the planets, MMRs between the planets, and von Zeipel–Kozai–Lidov (ZKL; von Zeipel 1910; Kozai 1962; Lidov 1962) oscillations of the inner planet that lead to planet eccentricity growth (Chen et al. 2023). The combination of planet–planet and planet–binary interactions can result in a planet being ejected from the system, as several simulations have already shown in coplanar CBP systems (e.g. Smullen, Kratter & Shannon 2016; Sutherland & Fabrycky 2016; Gong 2017; Gong & Ji 2017). The tilt of a circumbinary planetary system with respect to the binary orbit has a large influence on the stability of the system. Planetary systems that are stable around a coplanar binary become unstable for a wide range of parameters in a tilted system (Chen et al. 2023).
On the other hand, around a single star, planet–planet scattering occurs only when the planets form very close to each other. Two planets with masses mp1 and mp2 that form with semimajor axes ap1 and ap2, respectively, around a star with mass mb are unstable if |$\Delta \lesssim 2\sqrt{3}$|, where we define
and the mutual Hill radius between two planets, i and i + 1, is
(Marchal & Bozis 1982; Gladman 1993; Chambers, Wetherill & Boss 1996). However, in observed planetary systems, 93 per cent of planet pairs are greater than 10|$\, R_{\rm Hill}$| apart and 20|$\, R_{\rm Hill}$| apart is the most common separation in the California–Kepler Survey (Weiss et al. 2018).
This stability criterion is not significantly affected if a single star is replaced by a coplanar inner binary, unless the planets are formed very close to the binary (Kratter & Shannon 2014). However, the outcome of an unstable system is more likely to be ejection rather than collision around a binary star (Smullen et al. 2016; Sutherland & Fabrycky 2016; Gong 2017; Gong & Ji 2017; Fleming et al. 2018). This is because of close encounters with the binary. Coplanar planets around a binary must form close to each other to be unstable.
The instability and ejection of CBPs may be a mechanism to produce free-floating planets (FFPs). Gravitational microlensing observations suggest that there are more FFPs than main-sequence stars by a factor of 1–3.5 (e.g. Sumi et al. 2011). There is an excess of planets by a factor of up to seven compared to that predicted by core-collapse models (Padoan & Nordlund 2002; Miret-Roig et al. 2021). There are several mechanisms suggested to form the excess of FFPs. These include planet–planet scattering (Rasio & Ford 1996; Weidenschilling & Marzari 1996; Veras & Raymond 2012), aborted stellar embryo ejection from a stellar nursery (Reipurth & Clarke 2001), and photoerosion of a pre-stellar core by stellar winds from a nearly OB star (Whitworth & Zinnecker 2004). Planet–planet scattering around single stars is one possible mechanism but it cannot explain the large number of FFPs (Veras & Raymond 2012).
In this paper, we model circumbinary systems with three Jupiter-mass CBPs and examine their stability. We consider how many planets can be ejected from a system and the masses of the ejected planets. In Section 2, we first describe the set-up of our simulations and then we show stability maps in Section 2.3 and the final distribution of surviving planets in Section 2.4. Finally, we address our discussion and conclusions in Section 3 and implications for observations of CBPs in Section 4.
2 FIVE-BODY SIMULATIONS
To study the orbital stability of three-planet systems orbiting around a circular or eccentric binary star, we carry out simulations with the N-body simulation package, |$\small{REBOUND}$|, with a |$\small{WHFAST}$| integrator, which is a second-order symplectic Wisdom Holman integrator with 11th order symplectic correctors (Rein & Tamayo 2015).We solve the gravitational equations for the five bodies in the frame of the centre of mass of the five-body system. The central binary has components of masses m1 and m2 with a total mass of mb = m1 + m2 and mass fraction of fb = m2/mb. The binary is in a circular or eccentric orbit with the binary eccentricity eb and their separation ab = 1.0 in simulations.
2.1 Simulation set-up and parameter space explored
The three planets have equal masses |$m_{\rm p1} = m_{\rm p2} = m_{\rm p3} = 0.001m_{\rm b}$|. The planets are initially in circular Keplerian orbits around the centre of mass of the binary. Our simulations do not consider collisions or the formation of S-type planets (planets that orbit around one star of a binary). The planet orbits are defined by six orbital elements: the semimajor axes ap1, ap2, and ap3, inclinations relative to the binary orbital plane ip1, ip2, and ip3, eccentricities ep1, ep2, and ep3, longitude of the ascending nodes measured from the binary semimajor axis ϕp1, ϕp2, and ϕp3, argument of periapsides ωp1, ωp2, and ωp3, and true anomalies νp1, |$\nu _{\rm p2},\ \mathrm{ and} \ \nu _{\rm p3}$|. The initial orbits of the three planets are coplanar to each other and circular, so initially ip1 = ip2 = ip3, ep = 0, ωp = 0, and νp = 0 and we set ϕp = 90° for all planets.
To understand the dynamic interactions between three planets, the inner planet is placed at |$a_{\rm p1}=5 a_{\rm b}$|, where a single CBP is stable for all initial inclinations (Chen et al. 2020). We calculate the semimajor axis of the second and third planets such that they are separated by a fixed number, Δ, of mutual Hill radii. Thus, the semimajor axes of the planets are related by
for i = 1, 2. The planet masses are fixed and ap1 is chosen. For a fixed value for Δ, this equation can first be solved to find ap2 and then with that solution we can then solve it again to find ap3. We consider Δ in the range from 3.4 (≈|$2\sqrt{3}$|) to 12.0. We integrate the simulations for a total time of 14 million binary orbital periods (Tb). The time-step of integration is 0.7 per cent of the initial orbital period of the inner planet. We list the parameters of the four models that we explore in Table 1. We define the orbit of the planet as unstable once at least one of three criteria are met. Instability occurs first, if the eccentricity of the planet becomes large ep ≥ 1.0 so that the planet is not bound to the binary; secondly, if the semimajor axis of the planet increases significantly, |$a_{\rm p} \gt 1000 a_{\rm b}$|; or thirdly, if the semimajor axis of the planet is smaller than the binary separation, ap < ab (see also, for example, Quarles et al. 2020).
Parameters of the simulations. The first column contains the name of the model, and the second, third and fourth columns indicate the binary mass fraction and the binary eccentricity and the semi-major axis of the inner planet, respectively. The fifth and sixth columns are minimum and maximum differences, respectively, of the semimajor axis between two planets, which we consider with an interval of Δ = 0.1.
| Model . | fb . | eb . | ap1 (ab) . | min. Δ . | max. Δ . |
|---|---|---|---|---|---|
| T1 | 0.5 | 0.0 | 5.0 | 3.4 | 12.0 |
| T2 | 0.5 | 0.8 | 5.0 | 3.4 | 12.0 |
| T3 | 0.1 | 0.0 | 5.0 | 3.4 | 12.0 |
| T4 | 0.1 | 0.8 | 5.0 | 3.4 | 12.0 |
| Model . | fb . | eb . | ap1 (ab) . | min. Δ . | max. Δ . |
|---|---|---|---|---|---|
| T1 | 0.5 | 0.0 | 5.0 | 3.4 | 12.0 |
| T2 | 0.5 | 0.8 | 5.0 | 3.4 | 12.0 |
| T3 | 0.1 | 0.0 | 5.0 | 3.4 | 12.0 |
| T4 | 0.1 | 0.8 | 5.0 | 3.4 | 12.0 |
Parameters of the simulations. The first column contains the name of the model, and the second, third and fourth columns indicate the binary mass fraction and the binary eccentricity and the semi-major axis of the inner planet, respectively. The fifth and sixth columns are minimum and maximum differences, respectively, of the semimajor axis between two planets, which we consider with an interval of Δ = 0.1.
| Model . | fb . | eb . | ap1 (ab) . | min. Δ . | max. Δ . |
|---|---|---|---|---|---|
| T1 | 0.5 | 0.0 | 5.0 | 3.4 | 12.0 |
| T2 | 0.5 | 0.8 | 5.0 | 3.4 | 12.0 |
| T3 | 0.1 | 0.0 | 5.0 | 3.4 | 12.0 |
| T4 | 0.1 | 0.8 | 5.0 | 3.4 | 12.0 |
| Model . | fb . | eb . | ap1 (ab) . | min. Δ . | max. Δ . |
|---|---|---|---|---|---|
| T1 | 0.5 | 0.0 | 5.0 | 3.4 | 12.0 |
| T2 | 0.5 | 0.8 | 5.0 | 3.4 | 12.0 |
| T3 | 0.1 | 0.0 | 5.0 | 3.4 | 12.0 |
| T4 | 0.1 | 0.8 | 5.0 | 3.4 | 12.0 |
2.2 Stability maps: two circumbinary planets
To compare with the stability maps for three-planet systems, we first run simulations of two-planet systems by removing the outer planet from the simulation. Fig. 1 shows stability maps for varying planetary system separation, Δ, and initial inclination, ip. The colours of the pixels indicate the stability of the system at the end of each simulation. Blue pixels represent systems in which two CBPs are stable, red pixels represent systems in which only one CBP survived, and white pixels represent systems in which both CBPs are unstable at the end of the simulation. The four horizontal dashed lines indicate the 2:1, 5:2, 3:1, and 4:1 MMRs between the two CBPs. The upper two panels are similar to the maps in fig. 2 of Chen et al. (2023) but extended to larger planet separation. There are two unstable regions around the 3:1 MMR and the 4:1 MMR that were not previously seen. The unstable regions in model T2 (top right) are wider than those in model T1 (top left) due to the larger binary eccentricity eb.
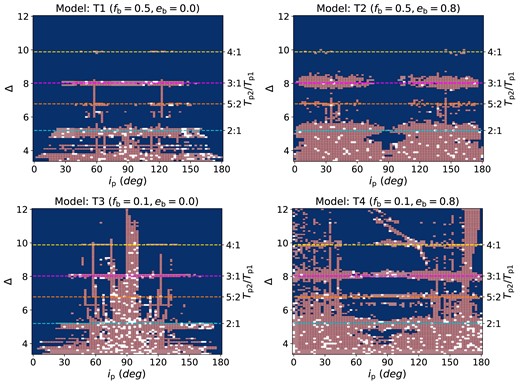
Stability maps for planetary systems with two CBPs around a binary with eb = 0.0 and fb = 0.5 (upper left), eb = 0.8 and fb = 0.5 (upper right), eb = 0.0 and fb = 0.1 (lower left), and eb = 0.8 and fb = 0.1 (lower right). The x-axis is the initial planet inclination ip and the y-axis is the separations of the planets, Δ, in units of their mutual Hill radii. The inner planet has initial semimajor axis |$a_{\rm p1} = 5 a_{\rm b}$|. The four horizontal dashed lines are the 2:1, 5:2, 3:1, and 4:1 MMRs between the inner and middle planets. Blue pixels represent systems in which two planets are stable, red pixels represent systems in which only one planet is stable, and white pixels represent systems in which all the planets are unstable.
The lower left panel shows the stability map for a circular binary system with fb = 0.1. The system is quite unstable between ip = 50° and 130° until the planets are more widely separated than their 2:1 MMR. There are several vertical unstable belts that are similar to the upper left panels in fig. 3 of Chen et al. (2023) in which the inner planet was located farther out, at 10ab. This is because the nodal oscillation time-scale is proportional to 1/(fb(1 − fb)) (Lubow & Martin 2018). A smaller binary mass ratio leads to slower nodal precession. Therefore, the planet–planet interactions become more important compared to the binary–planet interactions. A smaller fb is equivalent to placing the innermost planet at a larger distance to the binary. As a result, the stability map with fb = 0.1 is similar to that with fb = 0.5 and two CBPs at larger ap.
The lower right panel shows the stability map for a binary with eb = 0.8 and fb = 0.1. There are very few stable orbits around the polar region inside of the 2:1 MMR. Outside of the 2:1 MMR, two CBPs are more stable in the region between ip = 50° and 130° except, around MMR regions, compared to the coplanar and retrograde regions. Two CBPs are likely to be unstable even in coplanar orbits, while CBPs in retrograde orbits are relatively stable, although there is a vertical unstable belt around ip = 170°. Further, the region around the 4:1 MMR is more unstable compared to the other three maps.
2.3 Stability maps: three circumbinary planets
Now, we consider planetary systems with three CBPs. Fig. 2 shows the same stability maps as Fig. 1 except there are now three planets in the system. Since the three planets have equal masses, the semimajor axis ratios of ap2/ap1 and ap3/ap2 are equal to each other. Consequently, the inner planet pair and the outer planet pair have the same orbital period ratio because |$T_{\rm p}\propto a_{\rm p}^{1.5}$|. Therefore, if the inner two planets are in an MMR, so are the outer two and therefore the three planets are in a Laplace resonance. The four horizontal dashed lines indicate the 2:1, 5:2, 3:1, and 4:1 MMRs of both the inner pair and the outer pair. For convenience, we just label Tp2/Tp1 on the figures.
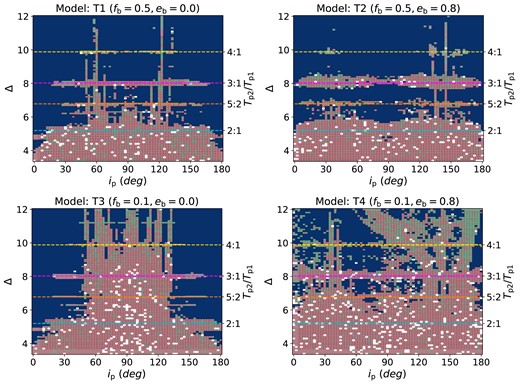
Same as Fig. 1 except these are for three-planet systems. The blue pixels show stable systems. The green pixels show systems with two stable planets. The red pixels show systems with one stable planet and the white pixels have no stable planets.
The stability maps for the three-planet cases are qualitatively quite similar to the two-planet cases, but with additional instability in all models. Unstable MMR locations become wider in their ranges of both separations and inclinations in the three-planet case than in the two-planet case due to the Laplace resonance. Especially around the 2:1 MMR region, three CBPs can only be stable when they are nearly coplanar for model T1. The vertical unstable belts are similar to the two-planet case but extend to larger Δ. The outcomes of most unstable pixels are single planet survival cases for closely spaced planets with Δ ≲ 8, while for Δ ≳ 8, the most likely outcome is two stable planets.
For the equal-mass binary with eb = 0.8 (upper right panel), the regions around the MMRs become more unstable with three planets. Fewer systems can be stable within the 2:1 MMR region. Comparing with model T1, the polar region between the 5:2 and 2:1 MMRs is more stable.
For a circular binary with fb = 0.1 (lower left panel), the region between ip = 50° and 130° is significantly more unstable compared to the two-planet case due to strong ZKL oscillations. In fig. 3 of Chen et al. (2023), we showed that ZKL oscillations between two CBPs may cause the instability of the two-planet system. In Fig. 3, we plot some examples of the evolution of orbital properties of three planets with the time. The four panels show ep (upper left), ap (upper right), ip (lower left), and eb (lower right) with time in units of Tb for model T3 with Δ = 9.0 and ip0 = 30° (left-hand panels) and 60° (right-hand panels). The blue, yellow, and green lines represent the inner, middle, and outer planets, respectively.
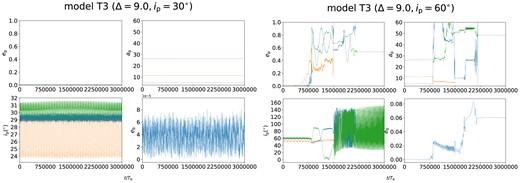
Orbital dynamics in model T3 of Fig. 2 with Δ = 9.0 and the initial ip = 30° (left-hand panels) and 60° (right-hand panels). Each set of four panels shows the planet eccentricity (upper left), planet semimajor axis (upper right), planet inclination (lower left), and binary eccentricity (lower right) and includes the inner planet (blue lines), the middle planet (yellow lines), and the outer planet (green lines).
For the stable case (left) with an initial inclination of ip = 30°, the CBPs undergo tilt oscillations with respect to each other, while the inclinations and semimajor axes are nearly constant with time. For the unstable case (right) with initial inclination ip = 60°, the middle and outer CBPs undergo tilt oscillations initially, but the eccentricity ep of the middle planet gets excited through ZKL-like behaviour. As a result, the system becomes unstable and the inner two planets are ejected, only the outer planet survives.
For an eccentric binary with fb = 0.1 and eb = 0.8 (lower right panel of Fig. 2), there is significantly more instability compared to the two-planet case. There are very few stable cases inside of the 5:2 MMR. Above there, there are more stable cases but the map shows that three-CBP systems are unlikely to be stable in the range ip = 90°–170°. Moreover, unstable cases around this region are heavily dominated by two planets surviving cases (green pixels).
2.4 The number of surviving planets
The complicated orbital interactions of three massive planets and a binary result in different numbers of surviving planets for different binary parameters. At the end of the simulations, the multi-CBP system may be left with three planets, a planet pair, a single CBP, or no planets. Understanding the final distributions of orbital planet properties can help us to predict the multi-CBP system morphology for future discoveries. The abnormal eccentricities of CBPs may be a crucial piece of evidence for planet–planet interactions in the early stages of the system.
The red pixels (single surviving planet cases) in the stability maps dominate most of the unstable outcomes. This suggests that many misaligned CBP systems may only have one surviving massive planet if multiple massive planets form in a compact architecture. In Fig. 4, the dashed bars in each panel show the total number of surviving inner planets, middle planets, and the outer planets in single planet survival cases in the stability maps of models T1–T4. Because the inner planet is the closest planet to the binary, for model T1, the total survival number of inner planets is lower than the middle and outer planets by factors of 1.5 and 2.5, respectively. With the higher eb = 0.8 of model T2, the factors increase to 2.5 and 5.2. With the lower fb = 0.1 of model T3, factors are 1.8 and 3.6, while with fb = 0.1 and eb = 0.8 of model T4, two factors are 2.2 and 5.0. The similar ratios indicate that there could be abundant CBPs with large distances to their host binaries if multicircumbinary planetary systems are common in the Universe.
The green pixels in the stability maps (two surviving planet cases) dominate most of the unstable orbits above the 3:1 MMR region, Δ ≳ 8, in the stability maps. This implies that misaligned CBP systems may have more than one massive CBP if multiple massive planets form in a relatively wide architecture. The solid bars in Fig. 4 represent the number of systems with two surviving planets. The bars represent the total surviving numbers of inner and middle planets survived cases (blue), inner and outer planets survived cases (red), and middle and outer planets survived cases (green). The majority of the unstable cases are those with single surviving planets, which are greater in number than cases in which two planets survived. In model T1, the total number of cases with surviving inner and middle planets is lower than the number of cases in which the inner and outer planets survived, and in which the middle and outer planets survived, by factors of 2.6 and 2.8, respectively. With higher eb = 0.8 of model T2, factors increase to 6.3 and 20.0. With lower fb = 0.1 of model T3, factors are 2.9 and 3.5, while with fb = 0.1 and eb = 0.8 of model T4, two factors are 7.6 and 16.0. The inner planet has the highest chance to become unstable, so therefore we may find more planet pairs with larger separations in binaries.
2.5 The eccentricity of the surviving planets
In this section, we now plot histograms of the eccentricity of the surviving planets. In Fig. 5, each histogram represents the sum of the numbers of inner, middle, and outer planets since the differences between the distributions for different planets are small. The solid histograms are the final eccentricities of planets of models T1–T4 from the blue pixels (three stable planet cases) in the stability maps. The grey empty histograms are those of the green pixels (two stable planet cases) and the cyan empty histograms are those of the red pixels (single stable planet cases). The vertical black, grey, and cyan lines in each panel represent the mean values of the eccentricities of the solid, grey empty, and cyan empty bars, respectively.
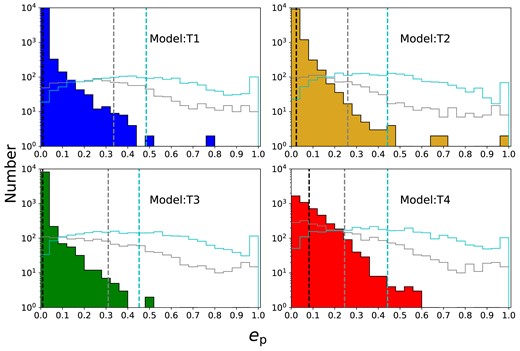
Histograms of the final ep distributions for surviving planets in models T1–T4. The solid histograms show cases in which three planets are stable. The grey histograms show cases in which two planets are stable and the cyan histograms show cases in which only one planet is stable. The three vertical dashed lines indicate the mean values of each histogram.
The vertical black lines show that if all three planets are stable, most of planets gain a little eccentricity, even in the most unstable map (model T4). For the vertical grey lines (two stable planet cases), models T1 and T3 with eb = 0.0 have larger values (>0.3) than those with larger eb of models T2 and T4 since the planets in an eccentric binary system have a higher chance to undergo a close encounter with the binary. Thus, planets get ejected before their eccentricities are excited to larger values. Finally, for the vertical cyan lines (single stable planet cases), they have a similar value of about 0.45 in all four panels and these values are larger than the values of two stable planet cases.
3 CONCLUSIONS
With N-body simulations, we have modelled a circumbinary planetary system consisting of three giant planets around a circular or eccentric binary. The inner planet is at 5ab initially, where a single planet is stable. The outer planets are separated by a constant number of mutual Hill radii in the range 3.4–12.0. With this configuration, the period ratio of the inner pair is the same as that of the outer pair. As a result, if one planet pair is in an MMR, then they are all in a Laplace resonance. With stability maps of varying initial planet inclination and separation, we have shown that the binary mass fraction and the binary eccentricity play important roles in the stability of CBPs. Overall, three-CBP systems around an equal-mass binary (models T1 and T2) are qualitatively similar to maps of two-CBP systems, although there is more instability in three-planet systems. MMRs are wider in the three-planet systems. With a low binary mass fraction fb = 0.1 (model T3), there is significantly more instability in a three-planet system around ip = 50°–130° due to strong ZKL oscillations resulting in excitation of planetary eccentricities and ultimately the ejection of planets.
Our simulations show that the single planet survival cases dominate the unstable outcomes for systems with closely spaced planets with Δ ≲ 8, while two planets survival cases dominate for more widely spaced systems with Δ ≳ 8.0. The surviving planets that were from unstable systems may not be too close to the binary since the inner planet is more likely to be ejected than the other planets. On the other hand, the remaining planets may have significant orbital eccentricities.
If Δ > 10.0 for exoplanetary systems, MMRs do not play a role in the stability of CBPs. Models T1–T2 show that an equal-mass binary can host two or three CBPs with arbitrary inclinations beyond this region. This separation is consistent with the observation that 93 per cent of planet pairs are at least 10|$\, R_{\rm Hill}$| apart (Weiss et al. 2018). A binary system with three compactly spaced massive CBPs is unlikely to remain stable, especially for planets with misaligned orbits to the binary. A system with a relatively wide architecture of three CBPs, separated by more than 8|$\, R_{\rm Hill}$|, is likely to remain stable, especially for a close to equal mass binary system.
4 IMPLICATIONS FOR EXOPLANET OBSERVATIONS
If CBPs are observed to have significant eccentricities, this may imply that the system had additional planets that were ejected after dynamic interactions with the other planets and the binary. The mean value of the planet eccentricities in cases where two planets survived is slightly smaller than cases in which only a single planet survived. The mean value of the eccentricities of single surviving planets is similar to those of two massive planets initially (Chen et al. 2023). Thus, our results suggest that a single massive CBP that has a significant eccentricity might have been a multiplanetary system initially. However, it is hard to distinguish whether this binary system had hosted two or three massive planets before.
Close interactions with the binary result in the inner planet tending to become unstable more easily than the outer planets. The chance of survival of the inner planet is smallest in the single planet survival cases and it decreases with increasing eb and fb. The chance of survival of the inner and middle planets in two planets survival cases is also lowest. Currently, half of confirmed CBPs are located close to the edge of stable radii (Yamanaka & Sasaki 2019). However, our study shows that the inner planet that is located at 5ab has a high chance to get ejected if the system has outer planets (see also Chen et al. 2023). Consequently, it may be hard to find another massive planet beyond a close-in and misaligned massive planet in those systems unless it is far from the binary. On the other hand, we have not considered different ap1 in this study because the outer planet is too far to simulate within reasonable computational time. Chen et al. (2023) showed that different ap1 have different stability maps due to the competition between ZKL oscillations and nodal oscillations. With another distant massive planet outside, we predict that their systems will be more unstable if they are misaligned initially.
Multi-CBP systems could be rare due to the intrinsic distribution of planet pairs. The period ratio distribution of Kepler’s multiplanet systems indicates that the peak of planet pairs has a period ratio near 2.2. Beyond a period ratio of 2.5, it follows a power law with an exponent –1.26 (Steffen & Hwang 2015). Our maps show that the single CBP survival cases dominate around the 5:2 MMR and, thus, the number of giant pairs or triple-giant systems is rare. Nevertheless, this principle may be only valid for the compact multiplanet system. Wide multiplanet single star systems, such as CI Tau, may have two inner Jupiter-mass planets and two outer Saturn-mass planets ranging from 0.1 to 100 au (Clarke et al. 2018) and HR 8799 has four Jupiter-mass planets ranging from 16 to 76 au (Marois et al. 2008).
The ejection of planets from a circumbinary system may generate large number of FFPs. For comparison, the stability of a system with three Jupiter-mass planets around a single star is shown in Fig. 6. There is only instability around regions of the 2:1 MMR and separation Δ < 4.0. Similarly, for a single star with only two Jupiter-mass planets, only the region with separation Δ < 4.0 is unstable (see fig. 1 of Chen et al. 2023). As a result, a single star system hosting three Jupiter-mass planets is very stable compared to those around a binary. Planet–planet interactions around single stars are unlikely to be a significant contributor to FFPs even if there are more than three Jupiter-mass planets unless the system is extremely compact. This conclusion is in agreement with Veras & Raymond (2012). In contrast, a multi-CBP system with three massive planets is more unstable than that with two, especially around the MMR regions. Estimates for the mass of FFPs range from around 0.25 (Mróz et al. 2017) up to about 3.5 (Sumi et al. 2011) Jupiter masses per main-sequence star. Therefore, we suggest that binary systems may contribute most of the FFPs due to planet–planet and binary–planet interactions.
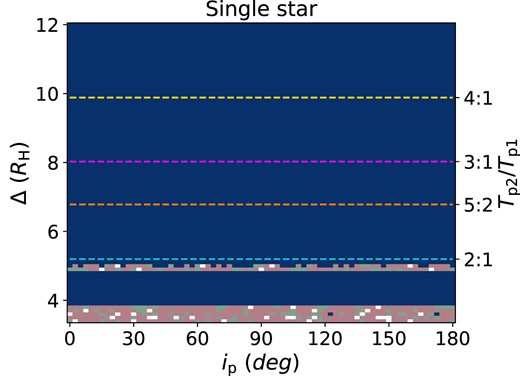
Similar to Fig. 2 except the centre is a single star and the innermost planet is placed at 5 au.
This study could contribute to our understanding of CBP formation and evolution and may help to explain the observational data from the Transiting Exoplanet Survey Satellite and Planetary Transits and Oscillations of stars. These may find many multiple misaligned CBPs around binaries as a result of the well-developed eclipse timing variation (ETV) tools in the near future (Zhang & Fabrycky 2019). While we have only considered one relatively close-in initial location for the innermost planet in the system, current observational methods (except gravitational microlensing and direct image observation) tend to detect more close-in CBPs. Therefore, simulations with close-in CBPs are more important. Nevertheless, the ETV method can also detect planets at far distance to the host star, and, thus, simulations with multi-CBP system with the large separation to the binary may be necessary for future studies.
Although all confirmed CBPs are nearly coplanar to their binary orbital planes, the observational results from Czekala et al. (2019) have shown the wide distribution of disc inclinations. Comparing with our previous study of two CBPs in Chen et al. (2023), hosting three stable Jupiter-mass planets around a binary is more difficult than hosting two stable Jupiter-mass planets initially. Besides, if the inner planet is located at 5ab, we find that there are less planet pairs that can exist with orbital period ratio <2:1 even though they satisfy the minimal separation |$\Delta \approx 2\sqrt{3}$|. A binary with a low mass fraction and a high eccentricity is unlikely to have three Jupiter-mass planets, but it can host at least two planets if they are widely separated enough (Δ > 10.0). An equal-mass binary has a higher chance to host three stable Jupiter-mass planets for all initial inclinations since only MMRs between the planet pair contribute the most to destabilize the system. Moreover, the surviving single planets or planet pairs could have significant eccentricities, which could be confirmed after more CBPs are found in near future.
ACKNOWLEDGEMENTS
Computer support was provided by UNLV’s National Supercomputing Center and DiRAC Data Intensive service at Leicester, operated by the University of Leicester IT Services, which forms part of the STFC DiRAC HPC Facility (www.dirac.ac.uk). CC and CJN acknowledge support from the Science and Technology Facilities Council (grant number ST/Y000544/1). CC thanks for the useful discussion with Dr Wei Zhu on the PPVII conference. CJN acknowledges support from the Leverhulme Trust (grant number RPG-2021-380). RGM acknowledges support from NASA through grant 80NSSC21K0395. We thank Prof. Yan-Xiang Gong for his careful reading of our manuscript and for giving us many insightful comments and suggestions. Simulations in this paper made use of the rebound code, which can be downloaded freely at http://github.com/hannorein/rebound.
DATA AVAILABILITY
The simulations in this paper can be reproduced by using the rebound code (Astrophysics Source Code Library identifier ascl.net/1110.016). The data underlying this article will be shared on reasonable request to the corresponding author.




