-
PDF
- Split View
-
Views
-
Cite
Cite
Rixin Li, Dong Lai, Hydrodynamical evolution of black hole binaries embedded in AGN discs: II. dependence on equation of state, binary mass, and separation scales, Monthly Notices of the Royal Astronomical Society, Volume 522, Issue 2, June 2023, Pages 1881–1894, https://doi.org/10.1093/mnras/stad1117
Close - Share Icon Share
ABSTRACT
Stellar-mass binary black holes (BBHs) embedded in active galactic nucleus (AGN) discs offer a promising dynamical channel to produce black hole mergers that are detectable by LIGO/Virgo. Modelling the interactions between the disc gas and the embedded BBHs is crucial to understand their orbital evolution. Using a suite of 2D high-resolution simulations of prograde equal-mass circular binaries in local disc models, we systematically study how their hydrodynamical evolution depends on the equation of state (EOS; including the γ-law and isothermal EOS) and on the binary mass and separation scales (relative to the supermassive black hole mass and the Hill radius, respectively). We find that binaries accrete slower and contract in orbit if the EOS is far from isothermal such that the surrounding gas is diffuse, hot, and turbulent. The typical orbital decay rate is of the order of a few times the mass doubling rate. For a fixed EOS, the accretion flows are denser, hotter, and more turbulent around more massive or tighter binaries. The torque associated with accretion is often comparable to the gravitational torque, so both torques are essential in determining the long-term binary orbital evolution. We carry out additional simulations with non-accreting binaries and find that their orbital evolution can be stochastic and is sensitive to the gravitational softening length, and the secular orbital evolution can be very different from those of accreting binaries. Our results indicate that stellar-mass BBHs may be hardened efficiently under ideal conditions, namely less massive and wider binaries embedded in discs with a non-isothermal EOS.
1 INTRODUCTION
The detection of gravitational waves from the merging black holes (BHs) by the LIGO/Virgo collaboration (The LIGO Scientific Collaboration 2021) has motivated many theoretical studies of the formation channels of the BH binaries. In addition to the isolated binary evolution channel (e.g. Lipunov, Postnov & Prokhorov 1997; Podsiadlowski, Rappaport & Han 2003; Belczynski et al. 2010, 2016), there are several flavours of dynamical channels, including strong gravitational scatterings in dense star clusters (e.g. Portegies Zwart & McMillan 2000; Miller & Lauburg 2009; Samsing et al. 2014; Rodriguez et al. 2015; Kremer et al. 2019), more gentle ‘tertiary-induced mergers’ (often via Lidov–Kozai mechanism) that take place either in stellar triple/quadrupole systems (e.g. Miller & Hamilton 2002; Silsbee & Tremaine 2017; Liu & Lai 2018, 2019; Fragione & Kocsis 2019; Liu et al. 2019b) or in nuclear clusters dominated by a central supermassive BH (e.g. Antonini & Perets 2012; Petrovich & Antonini 2017; Hamers et al. 2018; Liu, Lai & Wang 2019a; Liu & Lai 2020, 2021), and (hydro)dynamical interactions in active galactic nucleus (AGN) discs (e.g. Bartos et al. 2017; Stone et al. 2017; McKernan et al. 2018; Tagawa et al. 2020; Samsing et al. 2022).
In the AGN disc scenario, an important question concerns how single BHs can be captured into bound binaries and merge. Li et al. (2022a) showed that when the gas effect is negligible, two BHs in tightly packed orbits around a supermassive BH become bound to each other in rare, very close encounters due to gravitational wave emission, leading to highly eccentric BH mergers in the LIGO band. They also showed that weak gas drags do not necessarily enhance the binary capture rate. Whether strong gas drags can facilitate the capture process is still under active study (Li et al., in preparation).
The hydrodynamical evolution of binary black holes (BBHs) in AGN discs is still poorly understood and has only been studied numerically by a handful of previous works. Baruteau et al. (2011, hereafter B11) carried out global simulations in 2D isothermal discs and found that a massive (gap-opening) prograde, equal-mass binary is hardened by dynamical friction from the lagging spiral tails trailing each binary component inside the Hill radius. Li et al. (2021, hereafter L21) used a similar global set-up and found that adequately resolved circum-single disc (CSD) regions in fact lead to expanding binaries. More works from the same group (Dempsey et al. 2022; Li et al. 2022b) further found that the BH feedback on CSDs, binary separation, and the vertical structure of CSDs may play an important role in the evolution of the binary.
In Li & Lai (2022, hereafter Paper I), we performed a suite of 2D hydrodynamical simulations of binaries embedded in AGN discs using a co-rotating local disc (‘shearing-box’) model. We targeted realistic BBH to SMBH mass ratios and surveyed a range of binary eccentricities and mass ratios. We adopted the γ-law equation of state (EOS) with γ = 1.6 (i.e. far from isothermal). We found that circular comparable-mass binaries contract, with an orbital decay rate of a few times the mass doubling rate.
When a simplified EOS (such as the γ-law EOS) is used, the evolution of the binary and the flow dynamics depends only on the dimensionless ratios RH/Hg and RH/ab (where RH is the Hill radius, Hg is the scale height of the AGN disc far from the binary, and ab is the binary semi-major axis), as well as the binary eccentricity eb and mass ratio qb. In this paper, we use the same numerical scheme as in Paper I and conduct a survey of parameter space. We systematically compare the EOS effects on a grid of RH/Hg (which is related to the binary mass with respect to the ‘thermal mass’ of the disc) and RH/ab values. We focus on prograde, equal-mass, and circular binaries throughout this paper. Our goal is to understand how the flow structures around the BBHs and the long-term accretion rate and orbital evolution of BBHs vary in this three-dimensional parameter space.
The paper is organized as follows. In Section 2, we recapitulate our numerical scheme and set-up. Section 3 presents the results of our simulations, compares the accretion flow morphologies for various parameters, and describes how the secular binary orbital evolution varies in the parameter space. We then discuss the relative importance of different torque components on the binary in Section 4 and evolution of non-accreting binaries in Section 5. Section 6 summarizes our findings.
2 METHODS
To study the hydrodynamical evolution of binaries embedded in accretion discs (see the schematic cartoon in fig. 1 in Paper I), we use the code ATHENA (Stone et al. 2008; Stone & Gardiner 2010) with a similar set-up to Paper I. Section 2.1 briefly reiterates our numerical model. Section 2.2 summarizes the parameter choices for our simulations.
2.1 Simulation set-up
We consider a binary (with component masses m1 and m2) centred in a small patch of an accretion disc around a massive object (e.g. a super massive black hole (SMBH) with mass M) using the local shearing box approximation (Goldreich & Lynden-Bell 1965; Hawley, Gammie & Balbus 1995; Stone & Gardiner 2010). The centre of mass of the binary, i.e. the centre of the computational domain – (x, y) = (0, 0) – is located at a fiducial disc radius R from the SMBH. At this location, the Keplerian velocity is |$V_{\rm K}=\sqrt{GM/R}$| and the Keplerian frequency is ΩK = VK/R. Our reference frame rotates at this frequency.
In the rotating frame, we simulate the dynamics of an inviscid compressible flow by solving the following equations of gas dynamics in 2D:
where Σg, |$\boldsymbol {u}$|, P, E, and γ are surface density, velocity, pressure, total energy surface density, and adiabatic index of gas; |$\boldsymbol {I}$| is the identity matrix; |$\boldsymbol {\Omega }_{\rm K}$| aligns with |$\hat{\boldsymbol {z}}$|, |$q_{\rm sh} \equiv \mathbf {-} \text {d}\ln \Omega _{\rm K}/\text {d} \ln R$| is the background shear parameter and is 3/2 for a Keplerian disc; and ϕb is the gravitational potential of the binary
where |$\boldsymbol {r}_1$| and |$\boldsymbol {r}_2$| denote the position vectors of the binary components, |$\boldsymbol {r}_k$| is the centre position of the kth cell in the computational domain, and ξs is the gravitational softening length.
In this work, we consider both the γ-law EOS and the isothermal EOS. For the γ-law EOS, the sound speed of the gas is given by |$c_{\rm s} = \sqrt{\gamma P/\Sigma _{\rm g}}$|. For the isothermal EOS, we do not evolve the energy equation (i.e. equation 3) and adopt |$P = c_{\rm s}^2 \Sigma _{\rm g}$|. Below, we sometimes use γ = 1 to indicate the isothermal EOS for conciseness.
The binary in our models has total mass mb = m1 + m2 and orbits on a prescribed circular orbit with a semi-major axis of ab. The mean orbital frequency, orbital angular momentum, and energy in the inertial frame are thus
where |$\hat{\Omega }_{\rm b}$| is binary normal unit vector, μb = m1m2/mb is the reduced mass, and ℓb and |$\mathcal {E}_{\rm b}$| are the specific angular momentum and specific energy, respectively. Throughout this paper, we consider co-planar, prograde, and equal-mass binaries on prescribed orbits (see Section 2.1 of Paper I for detailed prescriptions).
The binary interacts with the background flow, which, in the shearing box frame, is given by
far from the binary, where |$\boldsymbol {V}_{\rm sh}(x)$| denotes the Keplerian shear, |$\boldsymbol {\Delta V}_{\rm K}$| is the deviation from Keplerian velocity, h ≡ Hg/R is the disc aspect ratio (with Hg the disc scale height), and |$\beta \simeq -\text {d}\ln P/\text {d}\ln R$| is an order unity coefficient determined by the (background) disc pressure profile.
There are several length scales that are relevant to our problem:
Binary semi-major axis ab;
Hill radius RH ≡ R(mb/M)1/3 ≡ Rq1/3 (note that this definition of Hill radius differs from the standard one |$R_{\rm H}^{\prime } = R_{\rm H}/3^{1/3}$|);
Bondi radius |$R_{\rm B} = G m_{\rm b}/c_{\rm s,\infty }^2$|, where cs, ∞ is the sound speed of the background gas (far from the binary); and
Scale height of the background disc Hg = cs, ∞/ΩK.
However, their ratios depend on only two dimensionless parameters:
Similarly, the relevant velocity scales are cs, ∞, vb, the velocity shear across the binary |$V_{\rm s}\equiv |V_{\rm sh}(x=a_{\rm b})| = \frac{3}{2}\Omega _{\rm K} a_{\rm b}$|, and |ΔVK|. The first three are related by the same dimensionless parameters:
For thin discs (h ≪ 1), |ΔVK| is very subsonic (|ΔVK|/cs, ∞ = |β|h ≪ 1) and is typically much smaller than Vs.1
Therefore, we expect our results, when appropriately scaled, depend on various physical quantities only through two dimensionless parameters: q/h3 and λ. The former parameter, q/h3, is also known as the ratio of the binary mass mb to the so-called thermal mass, h3M.
To evaluate the accretion onto the binary components and to calculate the torque, energy transfer rate, and orbital evolution of the binary, we treat each binary component as an absorbing sphere with a sink radius of rs and calculate all quantities along an evaluation radius re immediately outside rs (see Section 2.2 of Paper I for further details; see also Section 5 for our simulation results with non-accreting binaries).
2.2 Numerical parameters
The flow dynamics and results of our simulations depend on the dimensionless parameters (q/h3, λ; see equations 9 and 10) and the EOS (γ). Table 1 summarizes the parameters for all of our runs. For λ = 5 and 7.5 (Run II and Run III series, respectively), we survey a range of γ (1.6, 1.1, 1.001, and isothermal) and a range of q/h3 (1, 3, 9, and 27). For q/h3 = 1 and 3, we further survey a range of λ (5, 7.5, 10, 12.5, and Run II–IV series, respectively) with the same range of γ (1.6, 1.1, 1.001, and isothermal).
| Run . | λ . | q/h3 . | γ . | [c]|$\langle \dot{m}_{\rm b}\rangle$| . | [c]|$\langle \dot{\mathcal {E}}_{\rm b}\rangle$| . | [c]ℓ0 . | [c]|$\displaystyle \frac{\langle \dot{a}_{\rm b}\rangle }{a_{\rm b}}$| . |
|---|---|---|---|---|---|---|---|
| . | . | . | . | [Σ∞vbab] . | |$\displaystyle \left[\frac{\Sigma _\infty v_{\rm b}^3 a_{\rm b}}{m_{\rm b}}\right]$| . | [vbab] . | |$\displaystyle \left[\frac{\langle \dot{m}_{\rm b}\rangle }{m_{\rm b}}\right]$| . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . |
| II† | 5.0 | 1 | 1.6 | 0.17 | −0.48 | −0.23 | −4.81 |
| 1 | 1.1 | 0.66 | −0.99 | 0.13 | −1.99 | ||
| 1 | 1.001 | 0.89 | −0.22 | 0.44 | 0.52 | ||
| 1 | 1.0 | 0.90 | −0.18 | 0.45 | 0.59 | ||
| 3 | 1.6 | 0.19 | −0.43 | −0.08 | −3.63 | ||
| 3 | 1.1 | 1.11 | −0.88 | 0.30 | −0.59 | ||
| 3 | 1.001 | 1.65 | 0.71 | 0.61 | 1.86 | ||
| 3 | 1.0 | 1.66 | 0.64 | 0.60 | 1.77 | ||
| 9 | 1.6 | 0.26 | −0.28 | 0.23 | −1.20 | ||
| 9 | 1.1 | 1.94 | −0.30 | 0.46 | 0.69 | ||
| 9 | 1.001 | 2.86 | 1.55 | 0.64 | 2.09 | ||
| 9 | 1.0 | 2.87 | 1.47 | 0.63 | 2.02 | ||
| 27 | 1.6 | 0.29 | −0.31 | 0.23 | −1.13 | ||
| 27 | 1.1 | 2.30 | −0.16 | 0.48 | 0.86 | ||
| 27 | 1.001 | 3.36 | 0.72 | 0.55 | 1.43 | ||
| 27 | 1.0 | 3.33 | 0.61 | 0.55 | 1.37 | ||
| III | 7.5 | 1 | 1.6 | 0.11 | −0.22 | −0.01 | -3.09 |
| 1 | 1.1 | 0.71 | −0.63 | 0.28 | −0.77 | ||
| 1 | 1.001 | 1.02 | 1.26 | 0.81 | 3.46 | ||
| 1 | 1.0 | 1.01 | 1.22 | 0.80 | 3.40 | ||
| 3 | 1.6 | 0.14 | −0.23 | 0.10 | −2.21 | ||
| 3 | 1.1 | 1.41 | 0.20 | 0.53 | 1.28 | ||
| 3 | 1.001 | 1.69 | 2.03 | 0.80 | 3.40 | ||
| 3 | 1.0 | 1.68 | 2.11 | 0.81 | 3.52 | ||
| 9 | 1.6 | 0.24 | −0.13 | 0.37 | −0.08 | ||
| 9 | 1.1 | 2.18 | 0.71 | 0.58 | 1.65 | ||
| 9 | 1.001 | 3.37 | 3.93 | 0.79 | 3.33 | ||
| 9 | 1.0 | 3.36 | 3.74 | 0.78 | 3.22 | ||
| 27 | 1.6 | 1.16 | −1.81 | 0.11 | −2.12 | ||
| 27 | 1.1 | 2.69 | 1.58 | 0.65 | 2.18 | ||
| 27 | 1.001 | 3.92 | 3.45 | 0.72 | 2.76 | ||
| 27 | 1.0 | 3.99 | 3.18 | 0.70 | 2.59 | ||
| IV | 10 | 1 | 1.6 | 0.08 | −0.14 | 0.07 | −2.47 |
| 1 | 1.1 | 0.89 | −0.11 | 0.47 | 0.76 | ||
| 1 | 1.001 | 0.90 | 0.82 | 0.73 | 2.82 | ||
| 1 | 1.0 | 0.90 | 0.81 | 0.72 | 2.79 | ||
| 3 | 1.6 | 0.14 | −0.18 | 0.18 | −1.58 | ||
| 3 | 1.1 | 1.33 | 0.88 | 0.66 | 2.32 | ||
| 3 | 1.001 | 1.45 | 2.18 | 0.87 | 4.00 | ||
| 3 | 1.0 | 1.43 | 2.22 | 0.89 | 4.10 | ||
| V | 12.5 | 1 | 1.6 | 0.07 | −0.15 | −0.01 | −3.11 |
| 1 | 1.1 | 0.84 | −1.71 | −0.01 | −3.07 | ||
| 1 | 1.001 | 0.87 | −1.93 | −0.05 | −3.42 | ||
| 1 | 1.0 | 0.88 | −2.00 | −0.07 | −3.53 | ||
| 3 | 1.6 | 0.10 | −0.27 | −0.14 | −4.11 | ||
| 3 | 1.1 | 1.24 | −2.74 | −0.05 | −3.42 | ||
| 3 | 1.001 | 1.69 | −3.97 | −0.09 | −3.71 | ||
| 3 | 1.0 | 1.66 | −3.81 | −0.07 | −3.59 |
| Run . | λ . | q/h3 . | γ . | [c]|$\langle \dot{m}_{\rm b}\rangle$| . | [c]|$\langle \dot{\mathcal {E}}_{\rm b}\rangle$| . | [c]ℓ0 . | [c]|$\displaystyle \frac{\langle \dot{a}_{\rm b}\rangle }{a_{\rm b}}$| . |
|---|---|---|---|---|---|---|---|
| . | . | . | . | [Σ∞vbab] . | |$\displaystyle \left[\frac{\Sigma _\infty v_{\rm b}^3 a_{\rm b}}{m_{\rm b}}\right]$| . | [vbab] . | |$\displaystyle \left[\frac{\langle \dot{m}_{\rm b}\rangle }{m_{\rm b}}\right]$| . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . |
| II† | 5.0 | 1 | 1.6 | 0.17 | −0.48 | −0.23 | −4.81 |
| 1 | 1.1 | 0.66 | −0.99 | 0.13 | −1.99 | ||
| 1 | 1.001 | 0.89 | −0.22 | 0.44 | 0.52 | ||
| 1 | 1.0 | 0.90 | −0.18 | 0.45 | 0.59 | ||
| 3 | 1.6 | 0.19 | −0.43 | −0.08 | −3.63 | ||
| 3 | 1.1 | 1.11 | −0.88 | 0.30 | −0.59 | ||
| 3 | 1.001 | 1.65 | 0.71 | 0.61 | 1.86 | ||
| 3 | 1.0 | 1.66 | 0.64 | 0.60 | 1.77 | ||
| 9 | 1.6 | 0.26 | −0.28 | 0.23 | −1.20 | ||
| 9 | 1.1 | 1.94 | −0.30 | 0.46 | 0.69 | ||
| 9 | 1.001 | 2.86 | 1.55 | 0.64 | 2.09 | ||
| 9 | 1.0 | 2.87 | 1.47 | 0.63 | 2.02 | ||
| 27 | 1.6 | 0.29 | −0.31 | 0.23 | −1.13 | ||
| 27 | 1.1 | 2.30 | −0.16 | 0.48 | 0.86 | ||
| 27 | 1.001 | 3.36 | 0.72 | 0.55 | 1.43 | ||
| 27 | 1.0 | 3.33 | 0.61 | 0.55 | 1.37 | ||
| III | 7.5 | 1 | 1.6 | 0.11 | −0.22 | −0.01 | -3.09 |
| 1 | 1.1 | 0.71 | −0.63 | 0.28 | −0.77 | ||
| 1 | 1.001 | 1.02 | 1.26 | 0.81 | 3.46 | ||
| 1 | 1.0 | 1.01 | 1.22 | 0.80 | 3.40 | ||
| 3 | 1.6 | 0.14 | −0.23 | 0.10 | −2.21 | ||
| 3 | 1.1 | 1.41 | 0.20 | 0.53 | 1.28 | ||
| 3 | 1.001 | 1.69 | 2.03 | 0.80 | 3.40 | ||
| 3 | 1.0 | 1.68 | 2.11 | 0.81 | 3.52 | ||
| 9 | 1.6 | 0.24 | −0.13 | 0.37 | −0.08 | ||
| 9 | 1.1 | 2.18 | 0.71 | 0.58 | 1.65 | ||
| 9 | 1.001 | 3.37 | 3.93 | 0.79 | 3.33 | ||
| 9 | 1.0 | 3.36 | 3.74 | 0.78 | 3.22 | ||
| 27 | 1.6 | 1.16 | −1.81 | 0.11 | −2.12 | ||
| 27 | 1.1 | 2.69 | 1.58 | 0.65 | 2.18 | ||
| 27 | 1.001 | 3.92 | 3.45 | 0.72 | 2.76 | ||
| 27 | 1.0 | 3.99 | 3.18 | 0.70 | 2.59 | ||
| IV | 10 | 1 | 1.6 | 0.08 | −0.14 | 0.07 | −2.47 |
| 1 | 1.1 | 0.89 | −0.11 | 0.47 | 0.76 | ||
| 1 | 1.001 | 0.90 | 0.82 | 0.73 | 2.82 | ||
| 1 | 1.0 | 0.90 | 0.81 | 0.72 | 2.79 | ||
| 3 | 1.6 | 0.14 | −0.18 | 0.18 | −1.58 | ||
| 3 | 1.1 | 1.33 | 0.88 | 0.66 | 2.32 | ||
| 3 | 1.001 | 1.45 | 2.18 | 0.87 | 4.00 | ||
| 3 | 1.0 | 1.43 | 2.22 | 0.89 | 4.10 | ||
| V | 12.5 | 1 | 1.6 | 0.07 | −0.15 | −0.01 | −3.11 |
| 1 | 1.1 | 0.84 | −1.71 | −0.01 | −3.07 | ||
| 1 | 1.001 | 0.87 | −1.93 | −0.05 | −3.42 | ||
| 1 | 1.0 | 0.88 | −2.00 | −0.07 | −3.53 | ||
| 3 | 1.6 | 0.10 | −0.27 | −0.14 | −4.11 | ||
| 3 | 1.1 | 1.24 | −2.74 | −0.05 | −3.42 | ||
| 3 | 1.001 | 1.69 | −3.97 | −0.09 | −3.71 | ||
| 3 | 1.0 | 1.66 | −3.81 | −0.07 | −3.59 |
Notes. Columns: (1) run names; (2) ratio between binary semi-major axis ab and RH ≡ Rq−1/3, i.e. λ = RH/ab; (3) q/h3 = (mb/M)(Hg/R)−3 = (RH/Hg)3; (4) γ in the γ-law EOS (the cases with γ = 1 are isothermal runs); (5) time-averaged accretion rate; (6) time-averaged rate of change in binary specific energy; (7) accretion eigenvalue; and (8) binary semimajor axis change rate or migration rate.
†We reserve the name Run I for λ = 2.5, so the run names are consistent with those in Paper I.
| Run . | λ . | q/h3 . | γ . | [c]|$\langle \dot{m}_{\rm b}\rangle$| . | [c]|$\langle \dot{\mathcal {E}}_{\rm b}\rangle$| . | [c]ℓ0 . | [c]|$\displaystyle \frac{\langle \dot{a}_{\rm b}\rangle }{a_{\rm b}}$| . |
|---|---|---|---|---|---|---|---|
| . | . | . | . | [Σ∞vbab] . | |$\displaystyle \left[\frac{\Sigma _\infty v_{\rm b}^3 a_{\rm b}}{m_{\rm b}}\right]$| . | [vbab] . | |$\displaystyle \left[\frac{\langle \dot{m}_{\rm b}\rangle }{m_{\rm b}}\right]$| . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . |
| II† | 5.0 | 1 | 1.6 | 0.17 | −0.48 | −0.23 | −4.81 |
| 1 | 1.1 | 0.66 | −0.99 | 0.13 | −1.99 | ||
| 1 | 1.001 | 0.89 | −0.22 | 0.44 | 0.52 | ||
| 1 | 1.0 | 0.90 | −0.18 | 0.45 | 0.59 | ||
| 3 | 1.6 | 0.19 | −0.43 | −0.08 | −3.63 | ||
| 3 | 1.1 | 1.11 | −0.88 | 0.30 | −0.59 | ||
| 3 | 1.001 | 1.65 | 0.71 | 0.61 | 1.86 | ||
| 3 | 1.0 | 1.66 | 0.64 | 0.60 | 1.77 | ||
| 9 | 1.6 | 0.26 | −0.28 | 0.23 | −1.20 | ||
| 9 | 1.1 | 1.94 | −0.30 | 0.46 | 0.69 | ||
| 9 | 1.001 | 2.86 | 1.55 | 0.64 | 2.09 | ||
| 9 | 1.0 | 2.87 | 1.47 | 0.63 | 2.02 | ||
| 27 | 1.6 | 0.29 | −0.31 | 0.23 | −1.13 | ||
| 27 | 1.1 | 2.30 | −0.16 | 0.48 | 0.86 | ||
| 27 | 1.001 | 3.36 | 0.72 | 0.55 | 1.43 | ||
| 27 | 1.0 | 3.33 | 0.61 | 0.55 | 1.37 | ||
| III | 7.5 | 1 | 1.6 | 0.11 | −0.22 | −0.01 | -3.09 |
| 1 | 1.1 | 0.71 | −0.63 | 0.28 | −0.77 | ||
| 1 | 1.001 | 1.02 | 1.26 | 0.81 | 3.46 | ||
| 1 | 1.0 | 1.01 | 1.22 | 0.80 | 3.40 | ||
| 3 | 1.6 | 0.14 | −0.23 | 0.10 | −2.21 | ||
| 3 | 1.1 | 1.41 | 0.20 | 0.53 | 1.28 | ||
| 3 | 1.001 | 1.69 | 2.03 | 0.80 | 3.40 | ||
| 3 | 1.0 | 1.68 | 2.11 | 0.81 | 3.52 | ||
| 9 | 1.6 | 0.24 | −0.13 | 0.37 | −0.08 | ||
| 9 | 1.1 | 2.18 | 0.71 | 0.58 | 1.65 | ||
| 9 | 1.001 | 3.37 | 3.93 | 0.79 | 3.33 | ||
| 9 | 1.0 | 3.36 | 3.74 | 0.78 | 3.22 | ||
| 27 | 1.6 | 1.16 | −1.81 | 0.11 | −2.12 | ||
| 27 | 1.1 | 2.69 | 1.58 | 0.65 | 2.18 | ||
| 27 | 1.001 | 3.92 | 3.45 | 0.72 | 2.76 | ||
| 27 | 1.0 | 3.99 | 3.18 | 0.70 | 2.59 | ||
| IV | 10 | 1 | 1.6 | 0.08 | −0.14 | 0.07 | −2.47 |
| 1 | 1.1 | 0.89 | −0.11 | 0.47 | 0.76 | ||
| 1 | 1.001 | 0.90 | 0.82 | 0.73 | 2.82 | ||
| 1 | 1.0 | 0.90 | 0.81 | 0.72 | 2.79 | ||
| 3 | 1.6 | 0.14 | −0.18 | 0.18 | −1.58 | ||
| 3 | 1.1 | 1.33 | 0.88 | 0.66 | 2.32 | ||
| 3 | 1.001 | 1.45 | 2.18 | 0.87 | 4.00 | ||
| 3 | 1.0 | 1.43 | 2.22 | 0.89 | 4.10 | ||
| V | 12.5 | 1 | 1.6 | 0.07 | −0.15 | −0.01 | −3.11 |
| 1 | 1.1 | 0.84 | −1.71 | −0.01 | −3.07 | ||
| 1 | 1.001 | 0.87 | −1.93 | −0.05 | −3.42 | ||
| 1 | 1.0 | 0.88 | −2.00 | −0.07 | −3.53 | ||
| 3 | 1.6 | 0.10 | −0.27 | −0.14 | −4.11 | ||
| 3 | 1.1 | 1.24 | −2.74 | −0.05 | −3.42 | ||
| 3 | 1.001 | 1.69 | −3.97 | −0.09 | −3.71 | ||
| 3 | 1.0 | 1.66 | −3.81 | −0.07 | −3.59 |
| Run . | λ . | q/h3 . | γ . | [c]|$\langle \dot{m}_{\rm b}\rangle$| . | [c]|$\langle \dot{\mathcal {E}}_{\rm b}\rangle$| . | [c]ℓ0 . | [c]|$\displaystyle \frac{\langle \dot{a}_{\rm b}\rangle }{a_{\rm b}}$| . |
|---|---|---|---|---|---|---|---|
| . | . | . | . | [Σ∞vbab] . | |$\displaystyle \left[\frac{\Sigma _\infty v_{\rm b}^3 a_{\rm b}}{m_{\rm b}}\right]$| . | [vbab] . | |$\displaystyle \left[\frac{\langle \dot{m}_{\rm b}\rangle }{m_{\rm b}}\right]$| . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . |
| II† | 5.0 | 1 | 1.6 | 0.17 | −0.48 | −0.23 | −4.81 |
| 1 | 1.1 | 0.66 | −0.99 | 0.13 | −1.99 | ||
| 1 | 1.001 | 0.89 | −0.22 | 0.44 | 0.52 | ||
| 1 | 1.0 | 0.90 | −0.18 | 0.45 | 0.59 | ||
| 3 | 1.6 | 0.19 | −0.43 | −0.08 | −3.63 | ||
| 3 | 1.1 | 1.11 | −0.88 | 0.30 | −0.59 | ||
| 3 | 1.001 | 1.65 | 0.71 | 0.61 | 1.86 | ||
| 3 | 1.0 | 1.66 | 0.64 | 0.60 | 1.77 | ||
| 9 | 1.6 | 0.26 | −0.28 | 0.23 | −1.20 | ||
| 9 | 1.1 | 1.94 | −0.30 | 0.46 | 0.69 | ||
| 9 | 1.001 | 2.86 | 1.55 | 0.64 | 2.09 | ||
| 9 | 1.0 | 2.87 | 1.47 | 0.63 | 2.02 | ||
| 27 | 1.6 | 0.29 | −0.31 | 0.23 | −1.13 | ||
| 27 | 1.1 | 2.30 | −0.16 | 0.48 | 0.86 | ||
| 27 | 1.001 | 3.36 | 0.72 | 0.55 | 1.43 | ||
| 27 | 1.0 | 3.33 | 0.61 | 0.55 | 1.37 | ||
| III | 7.5 | 1 | 1.6 | 0.11 | −0.22 | −0.01 | -3.09 |
| 1 | 1.1 | 0.71 | −0.63 | 0.28 | −0.77 | ||
| 1 | 1.001 | 1.02 | 1.26 | 0.81 | 3.46 | ||
| 1 | 1.0 | 1.01 | 1.22 | 0.80 | 3.40 | ||
| 3 | 1.6 | 0.14 | −0.23 | 0.10 | −2.21 | ||
| 3 | 1.1 | 1.41 | 0.20 | 0.53 | 1.28 | ||
| 3 | 1.001 | 1.69 | 2.03 | 0.80 | 3.40 | ||
| 3 | 1.0 | 1.68 | 2.11 | 0.81 | 3.52 | ||
| 9 | 1.6 | 0.24 | −0.13 | 0.37 | −0.08 | ||
| 9 | 1.1 | 2.18 | 0.71 | 0.58 | 1.65 | ||
| 9 | 1.001 | 3.37 | 3.93 | 0.79 | 3.33 | ||
| 9 | 1.0 | 3.36 | 3.74 | 0.78 | 3.22 | ||
| 27 | 1.6 | 1.16 | −1.81 | 0.11 | −2.12 | ||
| 27 | 1.1 | 2.69 | 1.58 | 0.65 | 2.18 | ||
| 27 | 1.001 | 3.92 | 3.45 | 0.72 | 2.76 | ||
| 27 | 1.0 | 3.99 | 3.18 | 0.70 | 2.59 | ||
| IV | 10 | 1 | 1.6 | 0.08 | −0.14 | 0.07 | −2.47 |
| 1 | 1.1 | 0.89 | −0.11 | 0.47 | 0.76 | ||
| 1 | 1.001 | 0.90 | 0.82 | 0.73 | 2.82 | ||
| 1 | 1.0 | 0.90 | 0.81 | 0.72 | 2.79 | ||
| 3 | 1.6 | 0.14 | −0.18 | 0.18 | −1.58 | ||
| 3 | 1.1 | 1.33 | 0.88 | 0.66 | 2.32 | ||
| 3 | 1.001 | 1.45 | 2.18 | 0.87 | 4.00 | ||
| 3 | 1.0 | 1.43 | 2.22 | 0.89 | 4.10 | ||
| V | 12.5 | 1 | 1.6 | 0.07 | −0.15 | −0.01 | −3.11 |
| 1 | 1.1 | 0.84 | −1.71 | −0.01 | −3.07 | ||
| 1 | 1.001 | 0.87 | −1.93 | −0.05 | −3.42 | ||
| 1 | 1.0 | 0.88 | −2.00 | −0.07 | −3.53 | ||
| 3 | 1.6 | 0.10 | −0.27 | −0.14 | −4.11 | ||
| 3 | 1.1 | 1.24 | −2.74 | −0.05 | −3.42 | ||
| 3 | 1.001 | 1.69 | −3.97 | −0.09 | −3.71 | ||
| 3 | 1.0 | 1.66 | −3.81 | −0.07 | −3.59 |
Notes. Columns: (1) run names; (2) ratio between binary semi-major axis ab and RH ≡ Rq−1/3, i.e. λ = RH/ab; (3) q/h3 = (mb/M)(Hg/R)−3 = (RH/Hg)3; (4) γ in the γ-law EOS (the cases with γ = 1 are isothermal runs); (5) time-averaged accretion rate; (6) time-averaged rate of change in binary specific energy; (7) accretion eigenvalue; and (8) binary semimajor axis change rate or migration rate.
†We reserve the name Run I for λ = 2.5, so the run names are consistent with those in Paper I.
Similar to Paper I, the gas in all of our simulations are initialized with Σg = Σ∞ and with the velocity given by the background wind profile |$\boldsymbol {V}_{\rm w}$| (see equation 8). We set the root computational domain size to 10RH in both x and y directions. At all boundaries of the root domain, we adopt a wave-damping open boundary condition (bc) that damps the flow back to its initial state with a wave-damping time-scale |$P_{\rm d} = 0.02\Omega _{\rm b}^{-1}$|. To properly resolve the flow around the binary, we employ multiple levels of static mesh refinement towards the binary, where the resolution at the finest level is ab/δfl = 245.76, where δfl is the cell size at that level. In all simulations, we adopt a sink radius of rs = 0.04ab, an evaluation radius of |$r_{\rm e}=r_{\rm s}+\sqrt{2} \delta _{\rm fl}$|, and a gravitational softening length of 10−8ab.
In each simulation, we prescribe the binary orbital motion and evolve the flow dynamics for |$500\Omega _{\rm b}^{-1}$| for the cases with λ = 5, for |$1000\Omega _{\rm b}^{-1}$| for the cases with λ = 7.5, and for |$2000\Omega _{\rm b}^{-1}$| for the cases with λ = 10 and 12.5. With the accretion rates and torques measured on the fly in each time-step, the long-term binary orbital evolution is determined by the time-averaged long-term measurements in the post-processing analyses (see Section 2.2 in Paper I). The time-averaging is done over the last |$240\Omega _{\rm b}^{-1}$|/|$480\Omega _{\rm b}^{-1}$|/|$960\Omega _{\rm b}^{-1}$| for runs that evolve |$500\Omega _{\rm b}^{-1}$|/|$1000\Omega _{\rm b}^{-1}$|/|$2000\Omega _{\rm b}^{-1}$|. For the particular case with (λ, q/h3, γ) = (7.5, 27, 1.6), the accretion flows around the binary are much more violent since vb is highly supersonic and the CSDs heat up easily. To accommodate this situation, we evolve it for |$2000\Omega _{\rm b}^{-1}$| such that a longer time window is available for analysis.
3 RESULTS
Table 1 summarizes the key parameters and results of our simulation suite in a three-dimensional parameter space, namely λ, q/h3, and γ. We first describe the accretion flow morphologies in Section 3.1 and then present the orbital evolution results in Section 3.2.
3.1 Flow structure
Paper I has demonstrated that the quasi-steady state flow structures outside RH barely change due to binary configuration (e.g. λ, binary eccentricity, and internal mass ratio). Fig. 1 shows that this finding remains valid for different choices of the EOS, where the grand half bow shocks have broadly similar morphologies far away from the binary.
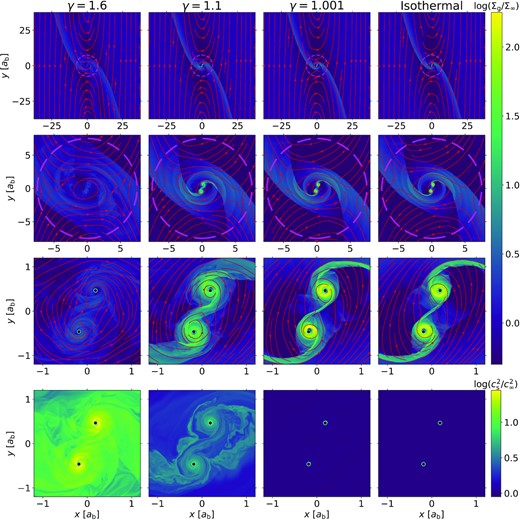
Final snapshots for Run III (λ = 7.5), with q/h3 = 3 and (from left to right) γ = 1.6, 1.1, 1.001, and isothermal, where the mesh is refined progressively towards the binary (zooming in from top to bottom), showing the gas surface density and detailed flow structures (red streamlines) in the first three rows and the thermal structures in the bottom row. The magenta dashed circles in the first two rows with a radius of RH denotes the Hill radius of the binary. The cyan solid circles in the last two rows with a radius of rs = 0.04ab represent the sink radius of each binary component.
For flows inside RH, we find that the CSDs become more massive, more compact, and cooler as γ decreases. When γ = 1.6, the CSDs are hot and puffed up, pushing the circumbinary flows outwards. On the contrary, the CSDs in the isothermal cases and the γ = 1.001 cases are effectively cooled and are able to maintain gas densities that are orders of magnitude higher. The fact that the γ = 1.001 cases exhibit good agreement with the isothermal cases on flow morphologies reassures us of the numerical robustness. In addition, we notice that the small spiral shocks in the CSDs become wider as γ increases. In other words, the spirals wind more tightly with a smaller pitch angle in cases with a smaller γ.
Fig. 2 shows that the circumbinary flows and the CSDs are more turbulent, denser, and hotter as q/h3 increases. The Mach number of the orbital velocity vb/cs, ∞ increases from 2.74 to 8.22 when q/h3 increases from 1 to 27 in Run III series (λ = 7.5), leading to the transition from relatively laminar flows to turbulent flows,2 where each binary component traverses and disrupts the shocks excited by the other component more violently. Moreover, a higher q/h3 represents a deeper potential well around each binary component, which naturally results in a more massive CSD, where more potential energy dissipates into heat. The consequence of the high Mach numbers in fact extends beyond RH, where the cones of the grand half bow shocks become slightly narrower, as expected for Bondi–Hoyle–Lyttleton-like accretion with higher velocities.
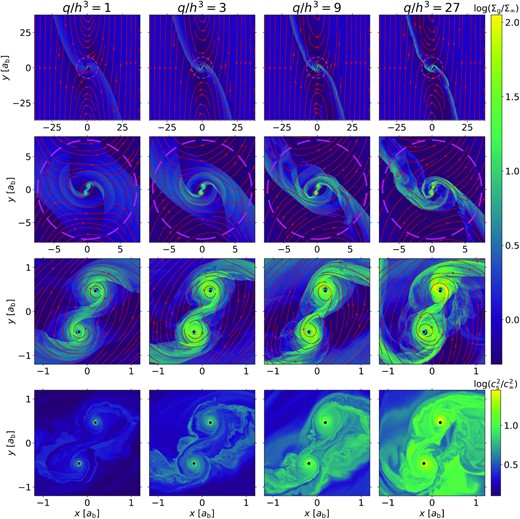
Similar to Fig. 1 but for Run III (λ = 7.5) with γ = 1.1 and (from left to right) q/h3 = 1, 3, 9, and 27.
Figs 3 explores an extended range of λ and once more confirms that the binary separation has little influence on the flow outside RH. Comparing to RH, the binary separation by definition becomes smaller as λ increases, where the circumbinary flow structures resemble more closely with the typical flow pattern around a single object (Tanigawa & Watanabe 2002), i.e. a pair of spiral shock winding from the binary towards RH and forming a pair of shock triple points when joining with the pair of grand half bow shocks. For larger λ, the spiral shocks from the binary as a whole3 are more steady due to less intertwinement with the compact CSDs and their small spiral shocks originated from each binary component.
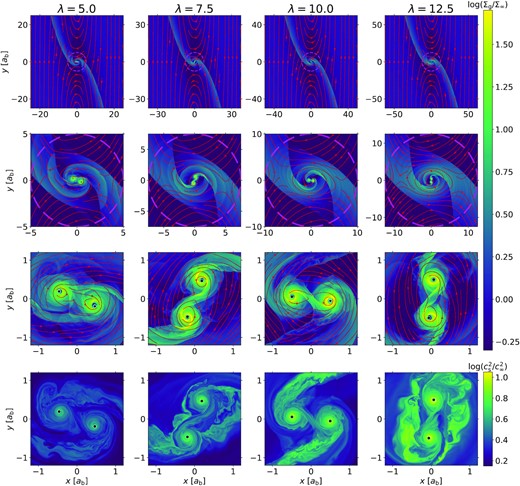
Similar to Fig. 1 but for cases with q/h3 = 3, γ = 1.1, and (from left to right) λ = 5, 7.5, 10, and 12.5. Note that the plotting range varies by column in the first two rows to accommodate different domain sizes and RH.
Furthermore, the CSDs become slightly more massive and hotter as λ increases. Because a smaller binary separation moderately deepens the potential well around each component such that its CSD is able to sustain more gas mass. Moreover, a closer binary has a higher orbital velocity. The corresponding Mach number increases from 3.22 to 5.10 as λ increases from 5 to 12.5 (with q/h3 = 3), again leading to more turbulent CSDs with more heat. We also find that the fast-moving binaries (λ ≳ 10) are able to leave voids (i.e. regions with very low surface density but high temperature) behind along their orbit, whereas such regions are quickly refilled and then cooled by the ambient gas around wider binaries (i.e. smaller λ).
Since the accretion flow morphology strongly depends on γ, q/h3, and λ, similarly strong dependencies of accretion rate and binary orbital evolution on these parameters are expected, which we address in the next section.
3.2 Secular evolution of binary
We employ the same post-processing procedure as described in Paper I to compute the time series of accretion rate and torques onto the binary in each simulation. Fig. 4 shows the secular orbital evolution results as a function of q/h3, grouped by the EOS, for our surveys in Run II series (λ = 5) and Run III series (λ = 7.5). We immediately recognize that all the time-averaged measurements show good agreement between the isothermal cases and the γ = 1.001 cases, which is again reassuring.
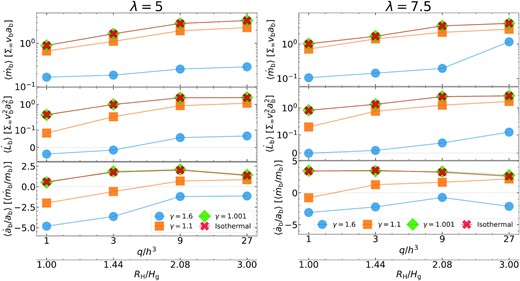
Time-averaged measurements of (from top to bottom) accretion rate |$\langle \dot{m}_{\rm b}\rangle$|, total torque |$\langle \dot{L}_{\rm b}\rangle$|, and binary migration rate |$\langle \dot{a}_{\rm b}\rangle /a_{\rm b}$| as a function of q/h3, colour-coded by the EOS (γ = 1.6: blue circle; 1.1: orange square; 1.001: green diamond; isothermal: red cross), for Run II series (λ = 5, left) and Run III series (λ = 7.5, right). In the middle panels for |$\langle \dot{L}_{\rm b}\rangle$|, the y-axis combines linear (below 10−1) and logarithmic (above 10−1) scales to better show the trends in γ = 1.6 cases.
We find that the time-averaged accretion rate |$\langle \dot{m}_{\rm b}\rangle$|, the total torque |$\langle \dot{L}_{\rm b}\rangle$|, and the binary migration rate |$\langle \dot{a}_{\rm b}\rangle /a_{\rm b}$| generally increase with q/h3 and monotonically decrease with γ, consistent with the findings that the CSDs are more massive and the circumbinary flows are denser in cases with higher q/h3 and/or lower γ (see Figs 1 and 2). It is remarkable that the accretion rates in the isothermal cases are about one order of magnitude higher than those in the cases with γ = 1.6, whereas |$\langle \dot{m}_{\rm b}\rangle$| only increases by a factor of ∼3 when q/h3 increases from 1 to 27. The latter is not surprising since the accretion boost due to the more massive CSDs is attenuated by the much higher binary orbital velocity. One exception is the high |$\langle \dot{m}_{\rm b}\rangle$| in the case of (λ, q/h3, γ) = (7.5, 27, 1.6), where the accretion flow is drastically violent. The CSDs in this case experience severe ram pressure stripping, somewhat similar to the retrograde cases in our Paper I, leading to intermittent disc-less accretion that boosts the accretion rate irregularly. As for |$\langle \dot{L}_{\rm b}\rangle$| and |$\langle \dot{a}_{\rm b}\rangle /a_{\rm b}$|, we observe a similar trend that their changes appear to be more prominent with varying EOS than with varying q/h3.
Furthermore, Fig. 5 shows the binary evolution results as a function of λ, again grouped by the EOS, for our surveys with q/h3 = 1 and 3 across all run series. We find that the accretion rate |$\langle \dot{m}_{\rm b}\rangle$| slightly decreases with λ when γ = 1.6 but varies little with λ when γ ≤ 1.1. For smaller γ, the accretion onto the binary seems to be saturated by the more massive CSDs, whereas for γ = 1.6, |$\langle \dot{m}_{\rm b}\rangle$| is buffered by the diffuse CSDs. Moreover for γ = 1.6, the accretion rate decreases with λ largely because the binary orbits at a higher Mach number and intersects with less streamlines as the binary separation becomes smaller relative to RH.
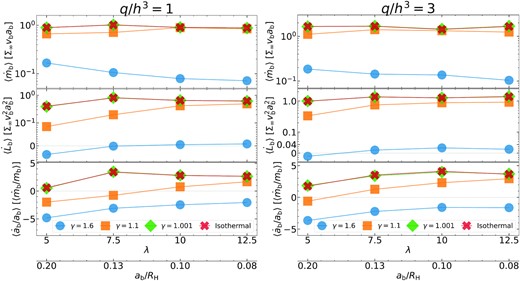
Similar to Fig. 4 but for time-averaged measurements as a function of λ, for q/h3 = 1 (left) and q/h3 = 3 (right). The middle panels again combine linear and logarithmic scales along the y-axis but the transition point is 10−1 for q/h3 = 1 and 0.04 for q/h3 = 3.
On the other hand, we find that both the total torque |$\langle \dot{L}_{\rm b}\rangle$| and the binary migration rate |$\langle \dot{a}_{\rm b}\rangle /a_{\rm b}$| generally slightly increase with λ. In addition, all these measurements tend to flatten out at λ ≳ 10. This trend is understandable since a large region within RH feels the binary as a single object as λ increases, and the hydrodynamical evolution eventually reduces to that around a single object when λ → ∞.
Regarding the direction of binary migration, i.e. the sign of |$\langle \dot{a}_{\rm b}\rangle$|, we find that all runs with γ = 1.6 produce contracting binaries, consistent with the findings in our Paper I. All runs with γ = 1.001 and with the isothermal EOS produce expanding binaries, consistent with previous isothermal studies (e.g. Li et al. 2021, 2022b). In addition, the general trend identified in our results – tighter binaries (λ ≳ 5) with the isothermal EOS expand and wider binaries (λ < 5) may instead contract – is consistent with the recent work of Dempsey et al. (2022, see their fig. 15). The cases with γ = 1.1 produce inspiral binaries at smaller q/h3 and/or λ and outspiral binaries at higher q/h3 and/or λ. We further find that the total angular momentum transferred to the binary is negative for γ = 1.6 and low q/h3 and/or λ. Otherwise, the binary is always fed by positive angular momentum. All these findings indicate that the cases where the binary is able to sustain more massive CSDs yield more positive torques and thus less negative |$\langle \dot{a}_{\rm b}\rangle /a_{\rm b}$|.
4 TORQUES
In this section, we discuss how different torque components contribute to the total torque during the secular binary orbital evolution. The gravitational torque |$\langle \dot{L}_{\rm b,grav}\rangle$| is often perceived as the largest and most important torque. Section 4.1 demystifies such a perception, followed by a detailed comparison of the spatial distribution of |$\langle \dot{L}_{\rm b,grav}\rangle$| in Section 4.2.
4.1 Torque decomposition
Fig. 6 shows the decomposed torque contributions from gravity (i.e. dynamical friction), |$\langle \dot{L}_{\rm b,grav}\rangle$|, and from the hydrodynamical forces associated with gas accretion and pressure, |$\langle \dot{L}_{\rm b,acc}\rangle$| and |$\langle \dot{L}_{\rm b,pres}\rangle$|, for the cases with λ = 5 and q/h3 = 1 (see equations 29–32 of Paper I for the decomposition of |$\dot{L}_{\rm b}$| into various components).
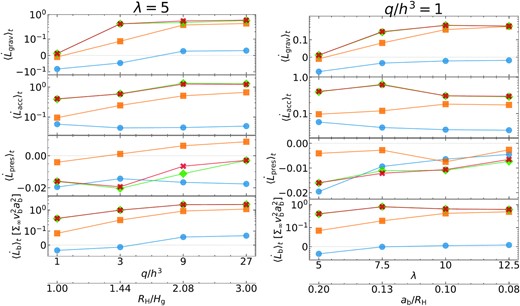
Similar to Figs 4 and 5 but showing the time-averaged (from top to bottom) decomposed and total torques, |$\langle \dot{L}_{\rm grav/acc/pres}\rangle$| and |$\langle \dot{L}_{\rm b}\rangle$|, for Run II series (λ = 5, left) and for runs with q/h3 = 1 (right). All the panels except the third panel combine linear and logarithmic scales along the y-axis with a transition point of 10−1.
We find that |$\langle \dot{L}_{\rm b,acc}\rangle$| is always positive and its magnitude is often comparable to that of |$\langle \dot{L}_{\rm b,grav}\rangle$|. In particular, in the cases with high accretion rates, (i.e. larger q/h3, higher λ, and/or smaller γ), both |$\langle \dot{L}_{\rm b,acc}\rangle$| and |$\langle \dot{L}_{\rm b,grav}\rangle$| are positive and the former is sometimes larger than the latter. This finding indicates that the torque due to the hydrodynamical force from accretion is as essential as the gravitational torque in determining the long-term binary orbital evolution. Neglecting |$\langle \dot{L}_{\rm b,acc}\rangle$| may underestimate the total torque exerted on the binary and in some cases lead to a different binary migration direction (i.e. softening to hardening).
It is not surprising that |$\langle \dot{L}_{\rm b,acc}\rangle$| becomes more important in the cases with high accretion rates. The background gas that enters the binary Hill sphere around the stagnant points at nearly zero velocity in the shearing box frame does carry positive angular momentum in the inertial frame (Tanigawa & Watanabe 2002). As shocks can only transport part of such angular momentum out, the accretion torque becomes important when the accretion rate is high. In our Paper III (Li & Lai, in preparation), we take into account viscosity, which further boosts the accretion rate and enables the accretion torque to dominate the total torque.
Unlike |$\langle \dot{L}_{\rm b,grav}\rangle$| and |$\langle \dot{L}_{\rm b,acc}\rangle$| that monotonically decrease with γ, the torque due to the hydrodynamical force from pressure |$\langle \dot{L}_{\rm b,pres}\rangle$| shows a more complex γ dependency. Such a feature is likely due to the γ dependency of the spiral morphology, i.e. the smaller the γ, the tighter the small spiral shocks are winded in the CSDs. In most cases (except some with γ = 1.1), |$\langle \dot{L}_{\rm b,pres}\rangle$| is negative. The magnitude of |$\langle \dot{L}_{\rm b,pres}\rangle$| is typically small but can be significant when γ = 1.6, where the other two torque components are comparably small, as noted in our Paper I.
4.2 Spatial distribution of gravitational torque
In this section, we follow our Paper I and construct the time-averaged maps (over the last |$36 P_{\rm b}^{\prime }$|; 4 snapshots per |$\Omega _{\rm b}^{-1}$|) for the gas surface density and the gravitational torque surface density in the vicinity of the binary for all the cases shown in Figs 1–3. Fig. 7 shows the 〈Σg〉 maps in the polar coordinates and compares the corresponding cumulative gravitational torque as a function of radius.
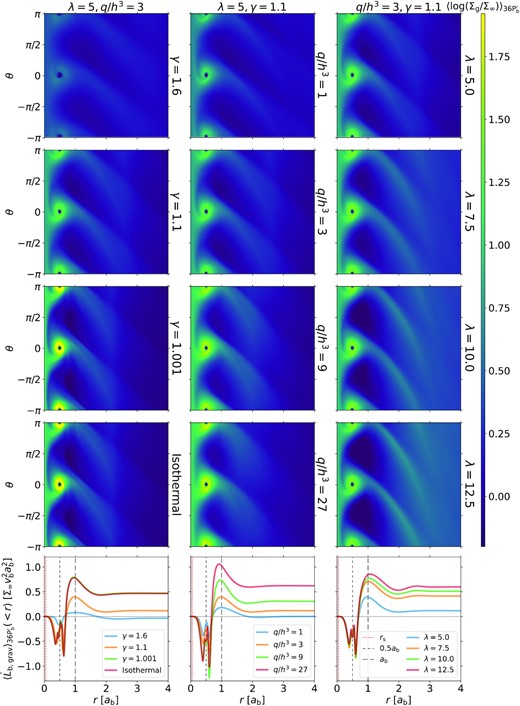
Time-averaged maps of gas density in the polar coordinates (first four rows) and the corresponding cumulative gravitational torque as a function of radius (bottom row) with varying (from left to right) EOS (γ), q/h3, and λ. Several characteristic radial scales are marked by the vertical lines in the bottom row, indicating the sink radius (red short dashed), half binary separation (black medium dashed), and binary separation (black long dashed).
The 〈Σg〉 maps reveal the persistent non-axisymmetric structures that affect the secular binary orbital evolution, including the CSDs and the large spiral shocks extending to a few ab. Any persistent density enhancements within the phase range (0, π/2) and (−π, −π/2) are ‘leading’ with respect to the binary and contribute positive |$\langle \dot{L}_{\rm b,grav}\rangle$|, whereas those in the phase range (π/2, π) and (−π/2, −π) are ‘trailing’ and contribute negative |$\langle \dot{L}_{\rm b,grav}\rangle$|. Generally speaking, we find that the part of the CSDs inside the binary orbit (0.2ab ≲ r < 0.5ab) and the inner part of the large spiral shocks (ab ≲ r ≲ 2ab) provide negative torques, while the remainders of the CSDs (0.5ab < r ≲ 0.8ab) and the large spiral shocks (≳ 2ab) provide positive torques. Also, the net torque of the CSDs is positive and the net torque of the large spiral shocks is negative.
We find that the total gravitational torque |$\langle \dot{L}_{\rm b,grav}\rangle$| decreases with γ and increases with q/h3. When γ is smaller or q/h3 is larger, both the CSDs and the large spiral shocks are more massive/denser, but the positive net torque from the CSDs dominates the total torque. Only in most cases with γ = 1.6 or a few cases with q/h3 = 1 does the negative net torque from the large spiral shocks dominates the total torque. In addition, Fig. 7 shows that the radial profile of the cumulative gravitational torque with γ = 1.001 overlaps well with that of the isothermal case, which reassures us not only the robustness of the code but also our post-processing analyses.
We further find that |$\langle \dot{L}_{\rm b,grav}\rangle$| increases with λ. This increase largely occurs in the region from 0.5ab to ∼ab since the cumulative torque profile inside 0.5ab or outside ∼ab changes little when λ varies. As λ becomes larger, the CSDs are only slightly more massive but the voids within ab are emptier (see also Section 3.1) and clear out more trailing regions, resulting in a more positive net torque. Even for λ ≳ 10, we find that the persistent non-axisymmetric structures only extend out to a few ab (i.e. ∼3ab, a factor of a few smaller than RH), where the cumulative torque profile already becomes flat and roughly equal to the total gravitational torque.
5 COMPARISONS WITH NON-ACCRETING BLACK HOLES
In this section, we perform experiments on the evolution of embedded BBHs where the binary does not accrete at all. Non-accreting binaries are of interest because certain physical processes (e.g. BH feedback) may significantly hamper or even halt the accretion. We thus employ idealized non-accreting binaries as a first attempt to study the effects of these processes, which are challenging to model directly.
Table 2 summarizes the key parameters and results of our experiments (the values are time-averaged over the same time period as specified in Section 2.2). For each case in Run II (λ = 5) with q/h3 = 1, we conduct two simulations with non-accreting binaries with a softening length of ξs = 0.04ab and ξs = 0.08ab, respectively. There is no sink cell in these experiments and all cells in the computational domain contribute to the gravitational torque on the binary via force
where i = 1 or 2 labels a binary component, mk = Σgδ2 is the gas mass in the kth cell, and δ is the cell size of the finest level available at |$\boldsymbol {r}_k$|.
Results for simulations with non-accreting binaries (Run II-NA, λ = 5, q/h3 = 1).
| γ . | ξs . | |$\langle \dot{L}_{\rm b}\rangle$| . | |$\displaystyle \frac{\langle \dot{a}_{\rm b}\rangle }{a_{\rm b}}$| . |
|---|---|---|---|
| . | [ab] . | |$\displaystyle \left[\Sigma _\infty v_{\rm b}^2 a_{\rm b}^2 \right]$| . | |$\displaystyle \left[\frac{\Sigma _\infty a_{\rm b} v_{\rm b}}{m_{\rm b}} \right]$| . |
| (1) . | (2) . | (3) . | (4) . |
| 1.6 | 10−8 | −0.04 | −0.80 |
| 0.04 | −0.89 | −7.15 | |
| 0.08 | −0.67 | −5.37 | |
| 1.1 | 10−8 | 0.08 | −1.32 |
| 0.04 | 7.50 | 59.97 | |
| 0.08 | 0.13 | 1.08 | |
| 1.001 | 10−8 | 0.39 | 0.46 |
| 0.04 | 0.14 | 1.10 | |
| 0.08 | 0.15 | 1.22 | |
| 1 | 10−8 | 0.40 | 0.53 |
| 0.04 | −0.004 | −0.03 | |
| 0.08 | −0.0002 | −0.002 |
| γ . | ξs . | |$\langle \dot{L}_{\rm b}\rangle$| . | |$\displaystyle \frac{\langle \dot{a}_{\rm b}\rangle }{a_{\rm b}}$| . |
|---|---|---|---|
| . | [ab] . | |$\displaystyle \left[\Sigma _\infty v_{\rm b}^2 a_{\rm b}^2 \right]$| . | |$\displaystyle \left[\frac{\Sigma _\infty a_{\rm b} v_{\rm b}}{m_{\rm b}} \right]$| . |
| (1) . | (2) . | (3) . | (4) . |
| 1.6 | 10−8 | −0.04 | −0.80 |
| 0.04 | −0.89 | −7.15 | |
| 0.08 | −0.67 | −5.37 | |
| 1.1 | 10−8 | 0.08 | −1.32 |
| 0.04 | 7.50 | 59.97 | |
| 0.08 | 0.13 | 1.08 | |
| 1.001 | 10−8 | 0.39 | 0.46 |
| 0.04 | 0.14 | 1.10 | |
| 0.08 | 0.15 | 1.22 | |
| 1 | 10−8 | 0.40 | 0.53 |
| 0.04 | −0.004 | −0.03 | |
| 0.08 | −0.0002 | −0.002 |
Note. Columns: (1) γ in the γ-law EOS (the cases with γ = 1 are isothermal runs); (2) gravitational softening length (the rows with ξs = 10−8ab are reference rows from the standard Run-II with accreting binaries); (3) time-averaged rate of change of the binary angular momentum; and (4) binary semimajor axis change rate.
Results for simulations with non-accreting binaries (Run II-NA, λ = 5, q/h3 = 1).
| γ . | ξs . | |$\langle \dot{L}_{\rm b}\rangle$| . | |$\displaystyle \frac{\langle \dot{a}_{\rm b}\rangle }{a_{\rm b}}$| . |
|---|---|---|---|
| . | [ab] . | |$\displaystyle \left[\Sigma _\infty v_{\rm b}^2 a_{\rm b}^2 \right]$| . | |$\displaystyle \left[\frac{\Sigma _\infty a_{\rm b} v_{\rm b}}{m_{\rm b}} \right]$| . |
| (1) . | (2) . | (3) . | (4) . |
| 1.6 | 10−8 | −0.04 | −0.80 |
| 0.04 | −0.89 | −7.15 | |
| 0.08 | −0.67 | −5.37 | |
| 1.1 | 10−8 | 0.08 | −1.32 |
| 0.04 | 7.50 | 59.97 | |
| 0.08 | 0.13 | 1.08 | |
| 1.001 | 10−8 | 0.39 | 0.46 |
| 0.04 | 0.14 | 1.10 | |
| 0.08 | 0.15 | 1.22 | |
| 1 | 10−8 | 0.40 | 0.53 |
| 0.04 | −0.004 | −0.03 | |
| 0.08 | −0.0002 | −0.002 |
| γ . | ξs . | |$\langle \dot{L}_{\rm b}\rangle$| . | |$\displaystyle \frac{\langle \dot{a}_{\rm b}\rangle }{a_{\rm b}}$| . |
|---|---|---|---|
| . | [ab] . | |$\displaystyle \left[\Sigma _\infty v_{\rm b}^2 a_{\rm b}^2 \right]$| . | |$\displaystyle \left[\frac{\Sigma _\infty a_{\rm b} v_{\rm b}}{m_{\rm b}} \right]$| . |
| (1) . | (2) . | (3) . | (4) . |
| 1.6 | 10−8 | −0.04 | −0.80 |
| 0.04 | −0.89 | −7.15 | |
| 0.08 | −0.67 | −5.37 | |
| 1.1 | 10−8 | 0.08 | −1.32 |
| 0.04 | 7.50 | 59.97 | |
| 0.08 | 0.13 | 1.08 | |
| 1.001 | 10−8 | 0.39 | 0.46 |
| 0.04 | 0.14 | 1.10 | |
| 0.08 | 0.15 | 1.22 | |
| 1 | 10−8 | 0.40 | 0.53 |
| 0.04 | −0.004 | −0.03 | |
| 0.08 | −0.0002 | −0.002 |
Note. Columns: (1) γ in the γ-law EOS (the cases with γ = 1 are isothermal runs); (2) gravitational softening length (the rows with ξs = 10−8ab are reference rows from the standard Run-II with accreting binaries); (3) time-averaged rate of change of the binary angular momentum; and (4) binary semimajor axis change rate.
Fig. 8 shows the flow structure in Run II-NA with ξs = 0.04ab. Since there is no sink cells, gas simply accumulates in the potential wells as blobs around the binary components, does not form consistent CSDs, and appears to be largely pressure-supported. The maximum gas density around the binary components is orders of magnitude higher than that in the counterpart simulations with sink cells. Also, we find a similar dependence on γ, where the gas blobs become more massive as γ decreases.
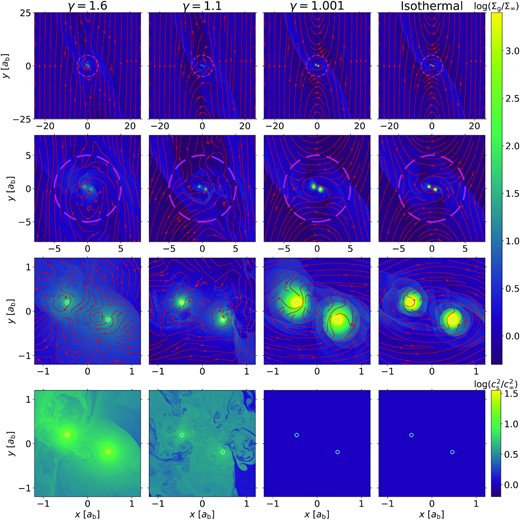
Similar to Fig. 1 but for Run II-NA (λ = 5) with q/h3 = 1, where the binary does not accrete gas and has a softening length ξs = 0.04ab, represented by the cyan solid circles in the bottom two rows.
The circumbinary flow remains prograde in the isothermal case and in the case with γ = 1.001, but the gas may be deflected when getting too close to the dense blobs. For γ ≥ 1.1, the flow around the binary is stochastic since the gas is heated up but no accretion is available to exhaust the excessive energy. In all cases, even the flow outside RH differs from their counterparts with accreting binaries. In particular, the horseshoe flows are heavily disrupted when γ = 1.6. For the cases with ξs = 0.08ab, the flow structure is broadly similar, with smaller but slightly less dense blobs.
The secular orbital evolution of non-accreting binaries depends only on the gravitational torque:
The gravity fgrav, i is largely determined by the dense gas blobs, making |$\boldsymbol {f}_{\rm grav,1}-\boldsymbol {f}_{\rm grav,2}$| almost parallel to |$\boldsymbol {r}_{\rm b}$|. Thus, the value of |$\dot{L}_{\rm grav}$| is sensitive to the deviation of the gas density structure from symmetry, which can easily be stochastic.
The resulting torque on non-accreting binaries is intrinsically stochastic regardless of time-scale. Fig. 9 compares the time series of |$\dot{L}_{\rm b}$| in Run II and Run II-NA with γ = 1.6 and γ = 1.1. Although the running averages of |$\dot{L}_{\rm b}$| in Run II are nearly constant and are in good agreement with the time-averaged results in Table 2 (as also seen in our Paper I), the running averages in Run II-NA show non-negligible irregular variations over hundreds of |$\Omega _{\rm b}^{-1}$|. Moreover, the instantaneous variation amplitudes of |$\dot{L}_{\rm b}$| are very sensitive to the softening length and are much larger in the cases of ξs = 0.04ab, where the gas blobs are denser and more concentrated.
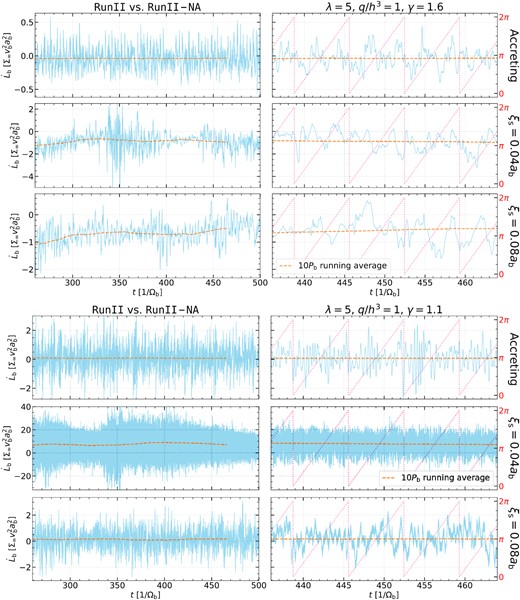
Comparisons of time series of total torques |$\dot{L}_{\rm b}$| (blue solid) on the binary in Run II (with accretion) and Run II-NA (with no accretion, using gravitational softening of 0.04ab or 0.08ab) with q/h3 = 1 and with γ = 1.6 (top) and γ = 1.1 (bottom) for the whole time used for time-averaging (left) and a small slice of time (right). Each time series is accompanied by the |$10P_{\rm b}^{\prime }$| running average (dashed orange) and each slice of time series is accompanied by the binary orbital phase curve with period |$P_{\rm b}^{\prime }$| (pink dotted).
When γ is lower (e.g. ≲ 1.1), the maximum gas surface density in the blobs around non-accreting binaries exceeds 104Σ∞ (as a comparison, max(Σg) ∼ 102Σ∞ when γ = 1.6). Therefore, even slight asymmetries originated from such dense blobs lead to considerable torques, which vary stochastically with frequencies much higher than the binary orbital frequency (see Fig. 9). Also, the relative power on these high frequencies again depends on the softening length (i.e. less power when ξs is larger since the blobs are less concentrated).
The secular orbital evolution of non-accreting binaries thus significantly differ from that of accreting binaries (see also Table 2) and does not present a monotonic trend as a function of γ. Additionally, the secular evolution is affected by the choice of softening length ξs, especially in the cases where the dense gas blobs are highly concentrated within the softening length (e.g. γ = 1.1). That said, for (nearly-)isothermal cases (including γ = 1.001), the gas remains cool such that the dense gas blobs extend far beyond ξs, making the secular evolution less dependent on the softening length.
6 SUMMARY
In this follow-up study to our Paper I, we perform a suite of 2D simulations to study the evolution of prograde equal-mass circular (BBHs) embedded in AGN discs with an extensive coverage of parameter space. As discussed in Section 2.1, the flow dynamics and binary evolution depend on three dimensionless parameters: γ (in the γ-law EOS), q/h3 ≡ (mb/M)(R/Hg)3 ≡ (RH/Hg)3, and λ = RH/ab. As in Paper I, we focus on accreting binaries, resolving the flow down to |$\lesssim 1~{{\ \rm per\ cent}}$| of the Hill radius around each binary component (with finest cells |$\lesssim 0.1~{{\ \rm per\ cent}}$| of Hill radius; Sections 2–4), although we also consider non-accreting binaries (Section 5) in this paper. Our key findings are as follows:
The accretion flow, particularly the morphology and the thermodynamics of the CSDs, considerably depends on γ, q/h3, and λ (see Figs 1–3). The CSDs are generally more massive with decreasing γ and with increasing q/h3 and λ. Also, they are generally hotter and more turbulent with increasing γ, q/h3, and λ, though the λ dependency is somewhat weaker. Moreover, the time-averaged accretion rate |$\langle \dot{m}_{\rm b} \rangle$| (in units of Σ∞abvb) monotonically decreases with γ and increases with q/h3.
For all the accreting binary cases considered in this paper, we find that the binary contracts when γ = 1.6 and expands when γ = 1.001 or when using the isothermal EOS (see Figs 4 and 5 and Table 1). The time-averaged binary migration rate |$\langle \dot{a}_{\rm b} \rangle /a_{\rm b}$| generally decreases with γ and increases with q/h3 and λ. The typical magnitude of |$\langle \dot{a}_{\rm b} \rangle /a_{\rm b}$| is of the order of a few times the mass-doubling rate |$\langle \dot{m}_{\rm b} \rangle /m_{\rm b}$|.
When accretion is allowed, the torque associated with accretion |$\langle \dot{L}_{\rm b,acc}\rangle$| often has a magnitude comparable to the gravitational torque |$\langle \dot{L}_{\rm b,grav}\rangle$| and is thus essential in determining the binary orbital evolution (see Fig. 6). When the CSDs are diffuse and |$\langle \dot{m}_{\rm b} \rangle$| is moderate (i.e. higher γ or smaller q/h3), the torque associated with pressure |$\langle \dot{L}_{\rm b,pres}\rangle$| can also have a comparable contribution to the total torque on the binary.
For prograde equal-mass circular binaries, the gravitational torque |$\langle \dot{L}_{\rm b,grav}\rangle$| is largely determined by the persistent non-axisymmetric flow structures within a few ab, regardless of λ (see Fig. 7). Similar to the parameter dependence of the accretion flow, we find that |$\langle \dot{L}_{\rm b,grav}\rangle$| decreases with γ and increases with q/h3 and with λ.
For non-accreting binaries (see Section 5), the flow structure substantially differs from that around accreting binaries, where a pressure-supported dense blob forms around each binary component instead of a CSD (see Fig. 8). The consequent torque on the binary and its orbital evolution vary stochastically, distinct from those seen for the accreting binaries, and are dependent on the gravitational softening length ξs (see Fig. 9 and Table 2). The torque/evolution is most sensitive to ξs at moderate γ, where the gas blobs are cool enough to be dense but are also hot enough to be highly concentrated within the softening length.
The survey in this work provides a complement to the parameter space covered by our prior work (Paper I), which focused on γ = 1.6, but covers a range of binary mass ratios and eccentricities. These findings are qualitatively consistent with the studies from other groups when they overlap (Li et al. 2021, 2022b; Dempsey et al. 2022). Since the numerical scheme employed in this follow-up paper remains the same as Paper I, our results are still subject to limitations from the 2D local shearing box approximation and from missing physics like viscosity, magnetic field, and so forth. That said, these 2D simulations allow us to explore a large parameter space and evolve the binary for thousands of |$\Omega _{\rm b}^{-1}$| so that we can quantify their secular orbital evolution. Future 3D studies with more realistic physical ingredients, both local and global, are required to better understand the interactions between BBHs and AGN discs.
ACKNOWLEDGEMENTS
This work has been supported in part by the NSF grant AST-2107796 and the NASA grant 80NSSC19K0444. Resources supporting this work were provided by the NASA High-End Computing (HEC) Program through the NASA Center for Climate Simulation (NCCS) at Goddard Space Flight Center.
RL thanks Kaitlin Kratter, Hui Li, Diego Muñoz, Ya-Ping Li, Adam Dempsey, Zoltan Haiman, Yan-Fei Jiang, Paul Duffell, and Barry McKernan for inspiring discussions and useful conversations. This research was supported in part by the National Science Foundation under Grant No. NSF PHY-1748958.
DATA AVAILABILITY
The simulation data underlying this paper will be shared on reasonable request to the corresponding author.
Footnotes
In our calculations, we set h = 0.01, which guarantees that |ΔVK| ≪ Vs for all q/h3 and λ values surveyed in this paper. If the disc has a large thickness, e.g. h = 0.05, then |$|\boldsymbol {\Delta V}_{\rm K}|$| may become comparable to |$\boldsymbol {V}_{\rm s}$|, leading to profoundly asymmetric shear flows in the vicinity of the binary.
Turbulent flows may induce relatively large instantaneous torques on the binary. However, such torques do not undermine the assumption of the binary on a fixed orbit. The duration of these torques is much less than the binary orbital period, therefore the resulting orbital evolution is negligible during the time span of our simulations.
In Paper I, we referred to such large spiral shocks as ‘a small half bow shock’. These two terms are used interchangeably in this paper.



