-
PDF
- Split View
-
Views
-
Cite
Cite
Marcin Wesołowski, Piotr Gronkowski, Konrad J Kossacki, The influence of the porosity of dust particles on the amplitude of the change in the brightness of a comet, Monthly Notices of the Royal Astronomical Society, Volume 517, Issue 4, December 2022, Pages 4950–4958, https://doi.org/10.1093/mnras/stac2967
Close - Share Icon Share
ABSTRACT
The paper presents a new approach to determining the change in the brightness of a comet during an outburst. It was investigated how the porosity of the dust particle translates into an increase in comet brightness during an outburst. It has been shown that the greater the porosity of a given particle, the greater the scattering efficiency, which directly translates into a greater amplitude of the change in the cometary brightness. In the case of dense aggregates with porosity ψ = 0.05, the brightness rate varies from −0.74 to −4.24 mag. In the case of porous agglomerates, the porosity of which is in the range from 0.30 to 0.90, the brightness change ranges from −0.91 to −6.66 mag.
1 INTRODUCTION
Comets are commonly included in the group of celestial bodies whose behaviour is dynamic. This means that we can distinguish two basic phases: quiet sublimation and a rapid change in brightness occurring as a result of a cometary outburst (Wesołowski 2021a, 2022a). The mission Rosetta through the direct observation of the comet 67P/Churyumov–Gerasimenko (hereinafter referred to as 67P) provided a lot of information related to the sublimation activity of the nucleus, as well as the activity associated with numerous outbursts (e.g. Vincent et al. 2016; Rinaldi et al. 2018). A cometary outburst is understood to mean a sudden, unexpected increase in brightness. The change of magnitude during an outburst can be as small as −1, but also higher than −5. The amplitude of the change of brightness during the outburst of comet 17P/Holmes in 2007 was estimated to be over −14 mag. However, such spectacular outbursts are extremely rare. Due to the fact that most cometary outbursts are discovered visually, some of them may be simply overlooked (Gronkowski, Tralle & Wesołowski 2018; Wesołowski 2019). Furthermore, it should be noted that the observations made by Rosetta clearly show that the change in brightness of comet 67P during the outbursts was in most cases less than −1 mag. The consequences of an outburst include the emission of particles of different sizes (Wesołowski, Gronkowski & Tralle 2020a) and an increase in the rate of sublimation from the newly exposed subsurface layers. Additionally, through jets, cometary material from inside the nucleus can be ejected into the coma. The presence of ejected material increases the scattering efficiency of the incident sunlight which in turn translates into the visible amplitude of the outburst. In the light of modern astrophysical research, it seems highly probable that the cometary activity (also during an outburst) is not caused by one specific mechanism, but by several that may occur simultaneously. In the simplest approach, the mechanisms that cause an outburst can be grouped into two groups. The first group consists of external factors such as collisions with other small bodies included in the Solar system or fragments of meteor swarms (Guliev, Poladova & Guliev 2022; Ye & Vaubaillon 2022). In the second group of internal factors, i.e. those related to the nucleus itself, the list of mechanisms causing an outburst may include the sublimation of water ice and more volatile species like CO ice, from the interiors of large porous agglomerates present at the surface, surface erosion under the influence of physico-chemical processes occurring in subsurface layers, and the destruction of cliffs under the influence of thermal and mechanical stresses (Miles et al. 2016; Combi et al. 2019; Kelley et al. 2019; Clements & Fernandez 2021; Saki et al. 2021; Xu et al. 2022). In the context of taking these processes into account, the position of the comet in the Solar system, as well as the shape of the nucleus and the rate of rotation, are of key importance. An additional factor that should be taken into account is the percentage of water ice in relation to the other chemical compounds that make up the nucleus of a given comet. When talking about the other compounds, we mean the mass fraction of dust (silicates and organic matter), also called refractory material in the structure of the nucleus. The rate of emission of material to space, i.e. the activity of a nucleus is unlikely to be uniform. For simplicity, we distinguish active and inactive areas. In the case of cometary particles located in active areas, the possible migration of dust on slopes, hills, or cliffs should be considered. The deposition of material in gravitational lows should be taken into account as well. Note that, the areas of deposition were observed by the Rosetta spacecraft. A review of the chemical composition of cometary particles has recently been discussed in Kührt & Keller (2020). All this makes the cometary activity seem highly individual, and generalizations may be burdened with error.
The aim of this study is to present a new approach to determining the change in brightness of a comet during its outburst. Particularly important in this paper is the assumption that the scattering of the incident sunlight takes place on dense aggregates and porous agglomerates dust. Based on the results obtained during the Rosetta mission, we can distinguish three morphologies of the outburst. We apply the naming convention: A – jet (gas-rich, not necessarily accompanying the increase in the dust production rate), B – broad plume (dust-rich), and C – complex (Vincent et al. 2016). In this paper, type B is considered. Another assumption is two commonly available materials were used in the calculations: astronomical silicate (hereinafter referred to as silicate) and charcoal, which should be treated as typical analogues for cometary dust. It was also determined how the porosity of the particles influences the increase of the change of cometary brightness during the outburst.
2 PHYSICAL MODEL
We assume that the scattering of the incident solar light takes place on aggregates and agglomerates (Fig. 1). For the sake of distinction, let us emphasize that the agglomerates are particles with a larger heterogeneous structure, which are composed of dust aggregates, which in turn consist of submicron dust grains. Dust aggregates have a size range from 10 to 100 μm and are also porous and easily disintegrate, as evidenced by the COSIMA results (Hilchenbach et al. 2016; Hornung et al. 2016). On the other hand, the dimensions of agglomerates reach the size of even cm (Blum et al. 2014, 2017; Gundlach, Fulle & Blum 2020).
The term aggregate denotes a solid particle whose grains are rigidly connected. Such dense particles may appear like irregular grains from the outside but are characterized by complex chemical composition. By contrast, an agglomerate is a porous particle that is composed of grains or aggregates. The cohesive forces in agglomerates are much smaller than the internal cohesive forces of individual grains or aggregates so that the agglomerates are more efficiently fractured (Güttler et al. 2019). We assume that the agglomerates may contain water ice in their structure. This means that the agglomerate can be treated as a model for the ice-dust particle.
The basic element of the agglomerate is a monomer with an average radius value of about 0.1 μm (Kimura, Kolokolova & Mann 2003, 2006). Moreover, individual monomers can form fractal structures (Fulle & Blum 2017). A typical aggregate (as well as the agglomerate) may even contain more than 1000 monomers. The detailed mechanism of the formation of aggregates of different sizes and degrees of porosity and two or three different compositions has been discussed in the papers (Shen, Draine & Johnson 2008, 2009). Moreover, between the components in the agglomerate structure, there are voids (pores) through which the sublimating water ice can reach the surface of the agglomerate. In such a case, the process of sublimation and diffusion of vapour to space is much more complex. Investigation of this scenario is out of the scope of this paper. In the considered model of a nucleus built of single agglomerates, a particular molecule of vapour sublimed within the agglomerate reaches the surface of the agglomerate, and it undergoes multiple collisions with monomers.
3 THE AMPLITUDE OF THE OUTBURST – THEORETICAL APPROACH
3.1 The energy balance
3.2 The amplitude of the outburst
Let us note that the average radius of the dust particle depends on the adopted value of the q coefficient. In equation (10), it was assumed that the integration range meets the following relationship: 10−7 m < r <10−2 m. Moreover, the assumed value of the factor q is close to the observations of the following comets: 1P/Halley (q = 3.5 ± 0.2, Fulle et al. 1995); 22P/Kopff (q = 3.1, Moreno et al. 2012); 26P/Grigg–Skjellerup (q = 3.3, Fulle et al. 1993); 67P/Churyumov–Gerasimenko (coma) (q = 3.7|$^{+0.7}_{-0.1}$|, Marschall et al. 2020); 67P/Churyumov–Gerasimenko (trail) (q = 4.1, Agarwal et al. 2010); 81P/Wild (q = 3.45 ± 0.1, Pozuelos et al. 2014); 103P/Hartley (q = 3.35 ± 0.1, Pozuelos et al. 2014); and 209P/LINEAR (q = 3.25 ± 0.1, Ishiguro et al. 2015).
4 MATERIAL PARAMETERS
Numerical calculations were performed for a comet from the Jupiter family for a wide range of realistic values of individual parameters. In these calculations, it was assumed that the cometary outburst took place at the heliocentric distance, d = 1.5 au. The individual parameters that were used in the numerical calculations are presented in Table 1.
Values of the most important cometary parameters that were used in numerical simulations. They are the same as in the papers of Fanale & Salvail (1984), Davidsson et al. (2002), Prialnik (2006), Gronkowski & Wesołowski (2015), Wesołowski & Gronkowski (2018), Wesołowski, Gronkowski & Tralle (2019), Zubko (2020), Wesołowski (2021b, d), and the literature therein.
| Parameter . | Value(s) . |
|---|---|
| Radius of the comet nucleus (m) | RN = 2000 |
| Density of cometary nucleus (kg m−3) | ρN = 500 |
| Density of dust agglomerate (kg m−3) | ρagg = 600 |
| Albedo of cometary nucleus (−) | AN = 0.05 |
| Emissivity | ϵ = 0.9 |
| Hertz factor | h(ψ) = 0.01 |
| Porosity of the nucleus | ψN = 0.65 |
| Porosity of the agglomerate | 0.5 < ψagl < 0.9 |
| Porosity of the aggregate (rock crumb) | ψagg = 0 |
| Radius of the coma in phase t1 and t2 (m) | Rc(t1) = 108 |
| Solar constant (for d = 1 au) (Wm−2) | S⊙ = 1360.8 ± 0.5 |
| Constant A|$_{\mathrm{H_{2}O}}$| for water ice (Pa) | A|$_{\mathrm{H_{2}O}}$| = 3.56 × 1012 |
| Constant B|$_{\mathrm{H_{2}O}}$| for water ice (K) | B|$_{\mathrm{H_{2}O}}$| = 6141.667 |
| Latent heat of water ice sublimation (J kg−1) | L(T)|$\mathrm{_{H_{2}O}}$| = 2.83 × 106 |
| Constant A|$_{\mathrm{CO_{2}}}$| for carbon dioxide (Pa) | A|$_{\mathrm{CO_{2}}}$| = 107.9 × 1010 |
| Constant B|$_{\mathrm{CO_{2}}}$| for carbon dioxide (K) | B|$_{\mathrm{CO_{2}}}$| = 3148.0 |
| Latent heat of CO2 sublimation (J kg−1) | L(T)|$\mathrm{_{CO_{2}}}$| = 0.594 × 106 |
| The rate of sublimation (molecules kg−2 s−1) | |$\dot{Z}$|(T) = 1.29 × 1019 |
| The average radius of cometary particles (m) | rav = 1.588 × 10−7 |
| The average radius of the dust aggregate (m) | ragg = 14.20 × 10−6 |
| The radius of the dust agglomerate (m) | ragl = 0.25 × 10−3 |
| Refractive index for cometary dust particles | ndust = 1.60 + 0.01i |
| The scattering factor for cometary particles | Q(rav) = 2.38 |
| The scattering factor for dust aggregate | Q|$_{\mathrm{agg}}\, \approx$| 1.17 |
| The scattering factor for dust agglomerate | Q|$_{\mathrm{agl}}\, \approx$| 1.11 |
| Parameter . | Value(s) . |
|---|---|
| Radius of the comet nucleus (m) | RN = 2000 |
| Density of cometary nucleus (kg m−3) | ρN = 500 |
| Density of dust agglomerate (kg m−3) | ρagg = 600 |
| Albedo of cometary nucleus (−) | AN = 0.05 |
| Emissivity | ϵ = 0.9 |
| Hertz factor | h(ψ) = 0.01 |
| Porosity of the nucleus | ψN = 0.65 |
| Porosity of the agglomerate | 0.5 < ψagl < 0.9 |
| Porosity of the aggregate (rock crumb) | ψagg = 0 |
| Radius of the coma in phase t1 and t2 (m) | Rc(t1) = 108 |
| Solar constant (for d = 1 au) (Wm−2) | S⊙ = 1360.8 ± 0.5 |
| Constant A|$_{\mathrm{H_{2}O}}$| for water ice (Pa) | A|$_{\mathrm{H_{2}O}}$| = 3.56 × 1012 |
| Constant B|$_{\mathrm{H_{2}O}}$| for water ice (K) | B|$_{\mathrm{H_{2}O}}$| = 6141.667 |
| Latent heat of water ice sublimation (J kg−1) | L(T)|$\mathrm{_{H_{2}O}}$| = 2.83 × 106 |
| Constant A|$_{\mathrm{CO_{2}}}$| for carbon dioxide (Pa) | A|$_{\mathrm{CO_{2}}}$| = 107.9 × 1010 |
| Constant B|$_{\mathrm{CO_{2}}}$| for carbon dioxide (K) | B|$_{\mathrm{CO_{2}}}$| = 3148.0 |
| Latent heat of CO2 sublimation (J kg−1) | L(T)|$\mathrm{_{CO_{2}}}$| = 0.594 × 106 |
| The rate of sublimation (molecules kg−2 s−1) | |$\dot{Z}$|(T) = 1.29 × 1019 |
| The average radius of cometary particles (m) | rav = 1.588 × 10−7 |
| The average radius of the dust aggregate (m) | ragg = 14.20 × 10−6 |
| The radius of the dust agglomerate (m) | ragl = 0.25 × 10−3 |
| Refractive index for cometary dust particles | ndust = 1.60 + 0.01i |
| The scattering factor for cometary particles | Q(rav) = 2.38 |
| The scattering factor for dust aggregate | Q|$_{\mathrm{agg}}\, \approx$| 1.17 |
| The scattering factor for dust agglomerate | Q|$_{\mathrm{agl}}\, \approx$| 1.11 |
Values of the most important cometary parameters that were used in numerical simulations. They are the same as in the papers of Fanale & Salvail (1984), Davidsson et al. (2002), Prialnik (2006), Gronkowski & Wesołowski (2015), Wesołowski & Gronkowski (2018), Wesołowski, Gronkowski & Tralle (2019), Zubko (2020), Wesołowski (2021b, d), and the literature therein.
| Parameter . | Value(s) . |
|---|---|
| Radius of the comet nucleus (m) | RN = 2000 |
| Density of cometary nucleus (kg m−3) | ρN = 500 |
| Density of dust agglomerate (kg m−3) | ρagg = 600 |
| Albedo of cometary nucleus (−) | AN = 0.05 |
| Emissivity | ϵ = 0.9 |
| Hertz factor | h(ψ) = 0.01 |
| Porosity of the nucleus | ψN = 0.65 |
| Porosity of the agglomerate | 0.5 < ψagl < 0.9 |
| Porosity of the aggregate (rock crumb) | ψagg = 0 |
| Radius of the coma in phase t1 and t2 (m) | Rc(t1) = 108 |
| Solar constant (for d = 1 au) (Wm−2) | S⊙ = 1360.8 ± 0.5 |
| Constant A|$_{\mathrm{H_{2}O}}$| for water ice (Pa) | A|$_{\mathrm{H_{2}O}}$| = 3.56 × 1012 |
| Constant B|$_{\mathrm{H_{2}O}}$| for water ice (K) | B|$_{\mathrm{H_{2}O}}$| = 6141.667 |
| Latent heat of water ice sublimation (J kg−1) | L(T)|$\mathrm{_{H_{2}O}}$| = 2.83 × 106 |
| Constant A|$_{\mathrm{CO_{2}}}$| for carbon dioxide (Pa) | A|$_{\mathrm{CO_{2}}}$| = 107.9 × 1010 |
| Constant B|$_{\mathrm{CO_{2}}}$| for carbon dioxide (K) | B|$_{\mathrm{CO_{2}}}$| = 3148.0 |
| Latent heat of CO2 sublimation (J kg−1) | L(T)|$\mathrm{_{CO_{2}}}$| = 0.594 × 106 |
| The rate of sublimation (molecules kg−2 s−1) | |$\dot{Z}$|(T) = 1.29 × 1019 |
| The average radius of cometary particles (m) | rav = 1.588 × 10−7 |
| The average radius of the dust aggregate (m) | ragg = 14.20 × 10−6 |
| The radius of the dust agglomerate (m) | ragl = 0.25 × 10−3 |
| Refractive index for cometary dust particles | ndust = 1.60 + 0.01i |
| The scattering factor for cometary particles | Q(rav) = 2.38 |
| The scattering factor for dust aggregate | Q|$_{\mathrm{agg}}\, \approx$| 1.17 |
| The scattering factor for dust agglomerate | Q|$_{\mathrm{agl}}\, \approx$| 1.11 |
| Parameter . | Value(s) . |
|---|---|
| Radius of the comet nucleus (m) | RN = 2000 |
| Density of cometary nucleus (kg m−3) | ρN = 500 |
| Density of dust agglomerate (kg m−3) | ρagg = 600 |
| Albedo of cometary nucleus (−) | AN = 0.05 |
| Emissivity | ϵ = 0.9 |
| Hertz factor | h(ψ) = 0.01 |
| Porosity of the nucleus | ψN = 0.65 |
| Porosity of the agglomerate | 0.5 < ψagl < 0.9 |
| Porosity of the aggregate (rock crumb) | ψagg = 0 |
| Radius of the coma in phase t1 and t2 (m) | Rc(t1) = 108 |
| Solar constant (for d = 1 au) (Wm−2) | S⊙ = 1360.8 ± 0.5 |
| Constant A|$_{\mathrm{H_{2}O}}$| for water ice (Pa) | A|$_{\mathrm{H_{2}O}}$| = 3.56 × 1012 |
| Constant B|$_{\mathrm{H_{2}O}}$| for water ice (K) | B|$_{\mathrm{H_{2}O}}$| = 6141.667 |
| Latent heat of water ice sublimation (J kg−1) | L(T)|$\mathrm{_{H_{2}O}}$| = 2.83 × 106 |
| Constant A|$_{\mathrm{CO_{2}}}$| for carbon dioxide (Pa) | A|$_{\mathrm{CO_{2}}}$| = 107.9 × 1010 |
| Constant B|$_{\mathrm{CO_{2}}}$| for carbon dioxide (K) | B|$_{\mathrm{CO_{2}}}$| = 3148.0 |
| Latent heat of CO2 sublimation (J kg−1) | L(T)|$\mathrm{_{CO_{2}}}$| = 0.594 × 106 |
| The rate of sublimation (molecules kg−2 s−1) | |$\dot{Z}$|(T) = 1.29 × 1019 |
| The average radius of cometary particles (m) | rav = 1.588 × 10−7 |
| The average radius of the dust aggregate (m) | ragg = 14.20 × 10−6 |
| The radius of the dust agglomerate (m) | ragl = 0.25 × 10−3 |
| Refractive index for cometary dust particles | ndust = 1.60 + 0.01i |
| The scattering factor for cometary particles | Q(rav) = 2.38 |
| The scattering factor for dust aggregate | Q|$_{\mathrm{agg}}\, \approx$| 1.17 |
| The scattering factor for dust agglomerate | Q|$_{\mathrm{agl}}\, \approx$| 1.11 |
Experimental studies provide us with detailed information on the structure of agglomerates and their physico-chemical properties. For the purpose of laboratory research in terrestrial conditions, cometary dust analogues are mixed with volatile components (Lethuillier et al. 2022). One of the issues is choosing the appropriate equipment and recipe for a specific dust analogue. In the laboratory studies to date, the following have been used as an analogue of cometary dust: a mixture of dust and ice (Grün, Benkhoff & Gebhard 1992), a mixture of silicate minerals and soot (Stoffler et al. 1991), a mixture of liquid water and silicate minerals (Storrs et al. 1988), a mixture of olivine with soot (Grün et al. 1993; Herique et al. 2002), a mixture of silicates containing Mg and Fe, and dust containing carbon (Rotundi et al. 2002). The use of complex analogues can lead to considerable difficulties in the quantitative analysis of the obtained measurement results. Therefore, the latest research suggests the use of simple mixtures (Kaufmann & Hagermann 2018). An example is a mixture of ice and quartz sand (Kossacki 2021; Kossacki et al. 2022a, b). However, the best method to study the properties of comet dust is by performing in situ measurements using a space probe, or by catching the dust in gel patches (sample return space mission). However, both methods are pricey and time-consuming. Thus, the material properties considered in theoretical studies need to be based on uncertain, not representative, or in the worst case just guessed values of parameters. Note that in Levasseur-Regourd et al. (2018), a detailed description of the composition and physical properties of cometary dust particles was presented.
One of the most important parameters that play a key role in our considerations is the porosity of the dust agglomerate. The group of typical dense aggregates contains dust particles with a porosity ψagg < 10 per cent. Whereas, the group of fluffy agglomerates corresponds to dust particles with porosity ψagl > 95 per cent. It should be noted that the assumed range of porosity for these two types of dust is in line with the estimate given by Güttler et al. (2019). The considerations take into account two analogues of comet dust that contain silicates and organic components. In the case of the organic component, charcoal was used due to its availability. Additionally, charcoal also acts as a darkening agent (Lethuillier et al. 2022). For both of these analogs, porosity and density were determined based on the mass method which is the classic method of determining the density of solids (Szydłowski 1999).
The grains used during the measurements were sorted according to their diameter using standardized sieves. In our case, the diameter of these grains ranged from: 0.3 × 10−3 m < dgr < 0.49 × 10−3 m. In the next step, based on the mass method, the necessary measurements and calculations were made, the result of which was the determination of the density and porosity of the selected analogues. In the case of silicate, the mean value of the porosity was ψsilicate = 0.42 ± 0.01, and its density was ρgr,silicate = 2724 ± 10 kg m−3. However, for the charcoal, the analogous parameters were: ψcharcoal = 0.51 ± 0.01 and ρgr,charcoal = 744 ± 10 kg m−3. Moreover, it was assumed that the density of the compact ice is equal to ρgr,ice = 933 kg m−3.
Then the average nucleus density is ρav = 533.4 kg m−3 which is a value similar to that of comet 67P, which is ρ67P = 537.8 ± 0.7 kg m−3 (Preusker et al. 2017).
5 RESULTS OF NUMERICAL SIMULATIONS
5.1 General case
The main aim of this article was to present the effect of the porosity of cometary dust particles on the scattering efficiency of incident sunlight that occurs on aggregates and porous dust agglomerates. In the context of determining the change in the brightness of a comet during its outburst, the key factor is to determine the sublimation rate of given ice. In the case under consideration, for the heliocentric distance, d = 1.5 au, the temperature on the surface of the cometary nucleus was approximately 227 K. Note that the value of this temperature was determined based on the Stefan–Boltzmann law for the grey body for the area that was not active. The simulation results presented later in the article have been divided into two main stages.
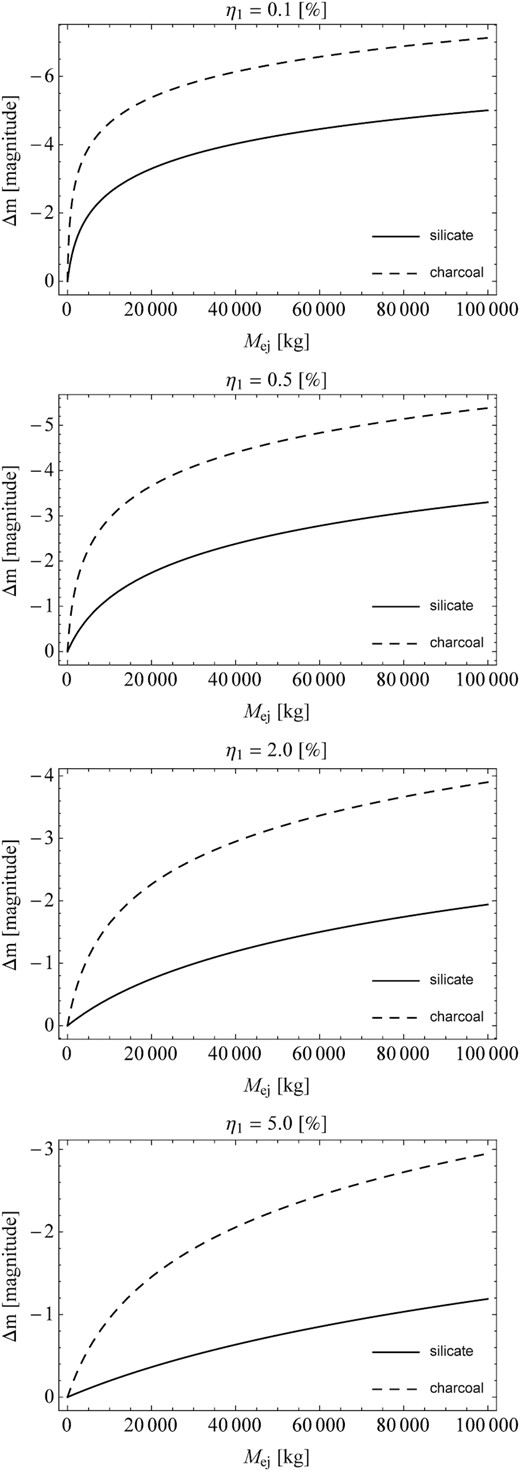
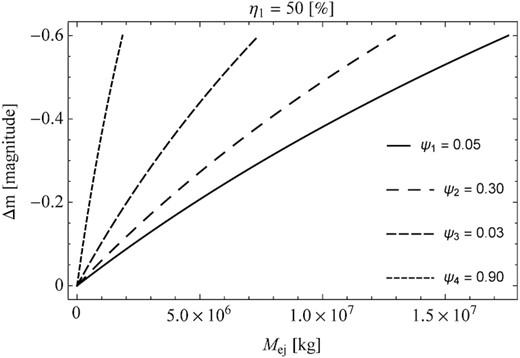
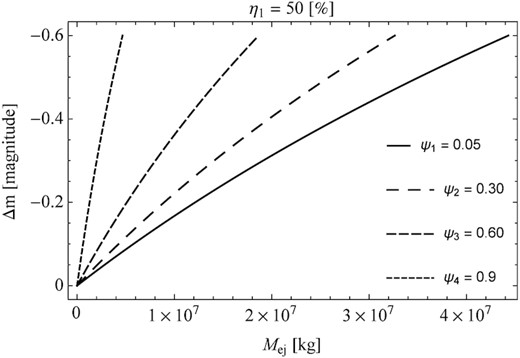
In the first stage, the results of the theoretical considerations of the brightness change as a function of the mass ejected for four exemplary porosities were presented. Note that the solid line refers to dense aggregates with porosity ψ = 0.05. Whereas, the remaining curves are related to the given porous agglomerates. The base particle had a density equal to ρ dust = 3000 kg m−3 (Fulle et al. 2016). Note that this value is consistent with the estimate of the bulk density for dust from comet 67P, which was provided by GIADA measurements (Rotundi et al. 2015). Moreover, in our calculations, the influence of the fraction of the nucleus surface which was active was taken into account. It was also determined for which porosity, with the assumed mass ejected, the start of the cometary brightness increase. The results of these calculations are shown in Figs 2 and 3. From these results, it can be seen that the two basic parameters characterizing the change in comet brightness are the mass ejected and the porosity of the particle on which the incident sunlight scatter.
In the second stage, it was assumed that the scattering of the incident sunlight takes place on two exemplary cometary dust analogues. Using the results of porosity and density measurements of these analogues presented above, the amplitude of the comet outburst was determined. The results of these calculations are shown in Figs 4 and 5. The found differences in the amplitude of the comet brightness change are a consequence of the calculated value of the particle porosity.
A comparison of the scattering efficiency of the incident sunlight between agglomerates of silicate and agglomerates of charcoal is shown in Fig. 6. This figure shows the influence of the particle porosity for a given dust analogue on the amplitude of the change of cometary brightness.
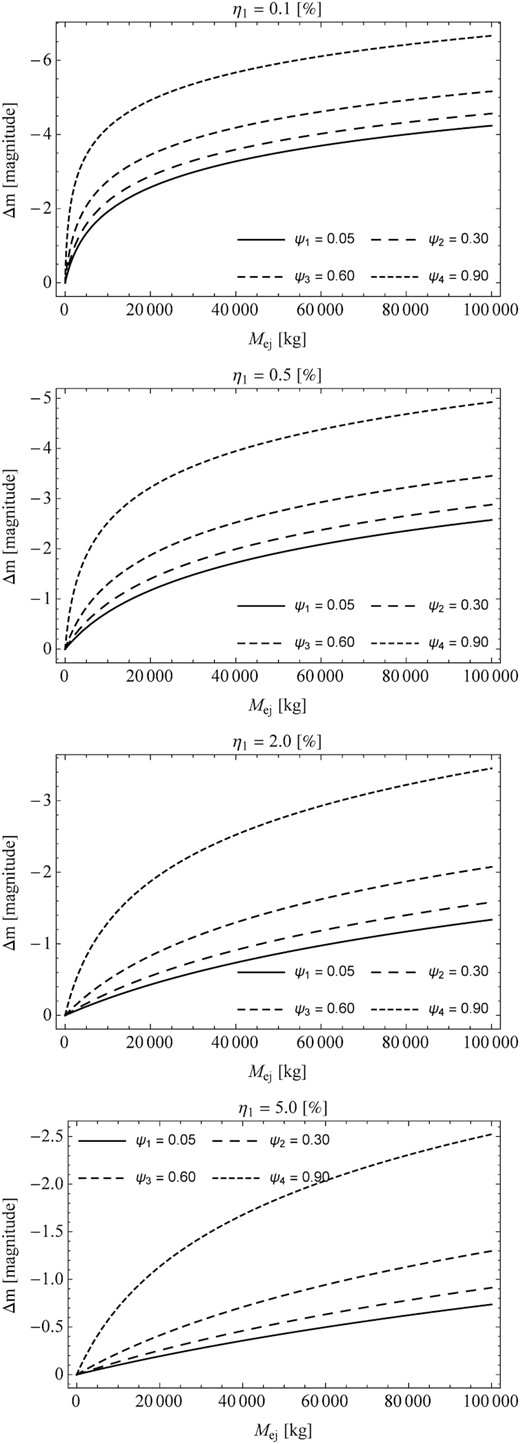
Change in the brightness of a comet Δm as a function of the mass ejected Mej during its outburst. The calculations included three exemplary values of the η1 parameter. It was also assumed that the scattering of the incident light occurs on a dense aggregate (ψ1 = 0.05) or dust agglomerates (ψ2 = 0.30; ψ3 = 0.60; ψ4 = 0.90), and the comet activity is controlled by sublimation of water ice.
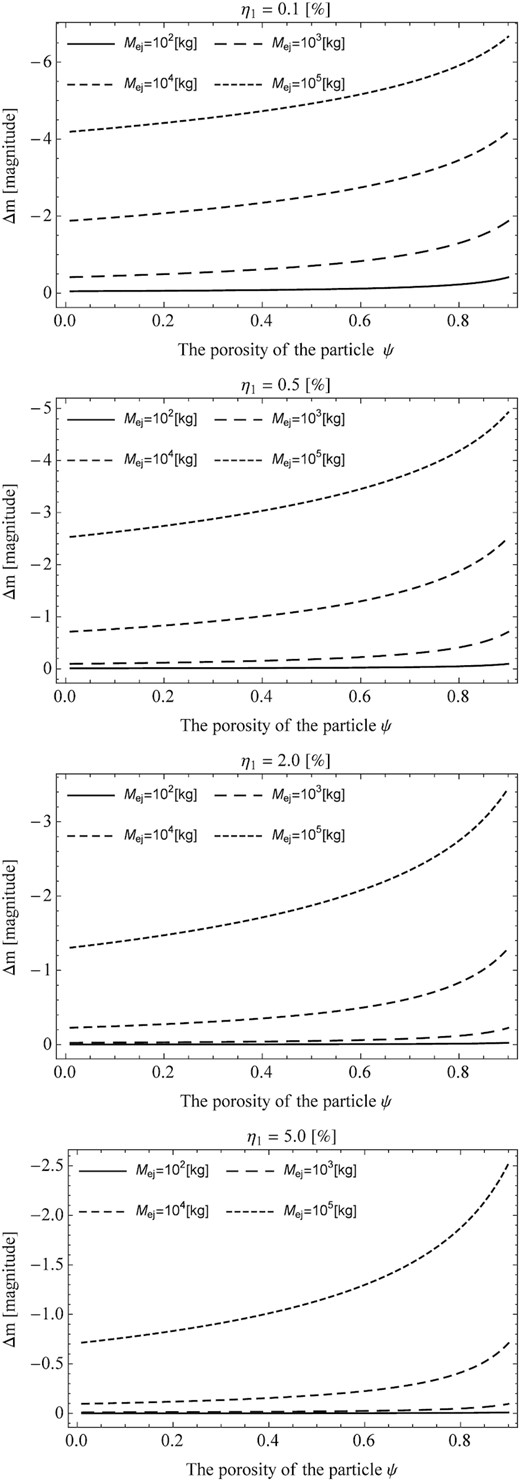
Increase in cometary brightness during an outburst as a function of particle porosity for the determined value of the mass ejected. The same values of the η1 parameter as in Fig. 2 were assumed in the calculations.
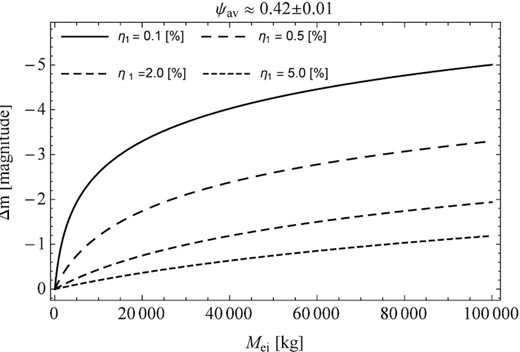
Similar to Fig. 2, but the scattering of the incident sunlight takes place on the dust agglomerates. In these calculations, experimental measurements of the porosity and density of silicate were used, which was used as an analogue of cometary dust due to their comparable density.
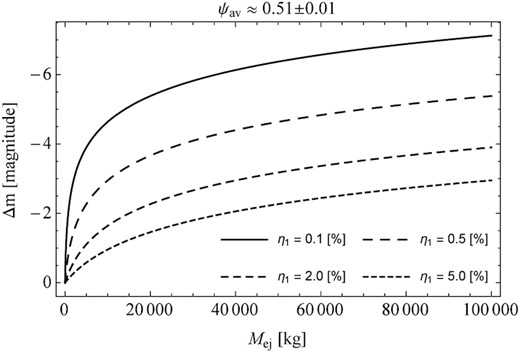
Similar to Fig. 2, but the scattering of the incident sunlight takes place on the dust agglomerates. In these calculations, experimental measurements of the porosity and density of the charcoal, which also act as a darkening agent.
Comparison of the scattering efficiency of incident sunlight that occurs on agglomerates of silicate and agglomerates of charcoal.
5.2 The outburst of comet 67P from 2014 April
Based on the model presented in this paper, the numerical simulation of the outburst of comet 67P, which took place at the end of 2014 April, was carried out. This outburst occurred several months before the comet reached its perihelion. The Rosetta devices recorded a sudden increase in the brightness of the comet from 17.2 to 16.6 mag at a distance of d ≈ 4 au (Tubiana et al. 2015). This corresponds to a change in the cometary brightness by Δm ≈ −0.6 mag. At this point, it should be clearly emphasized that we do not go into detail about the specific mechanism of the outburst. Our considerations, in this case, focus on estimating the mass ejected that caused this outburst. Regardless of the mechanism under consideration, the discarded mass is the basic parameter that determines the brightness of a comet during an outburst. The calculations assume that at a heliocentric distance of about 4 au it is possible to sublimate the CO2 ice or CO ice, which occurs from the deeper layers of the cometary nucleus. As in the case of water ice sublimation, we assume that the scattering of the incident sunlight takes place on both rock crumbs and dust agglomerates. For these particles with a given porosity, the value of the mass ejected was calculated, which determined the amplitude of the outburst. Apart from the mass ejected, the second important parameter is the fraction of the area of the nucleus that was active in the phase of quiet sublimation η1 and during the outburst, respectively. In the case of comets 67P, the value of the η1 parameter could be up to 50 per cent. In other words, the comet nucleus was active wherever the sun was shining (Keller et al. 2017). When analysing the outburst activity of comet 67P, it should be stated that the amplitude of the change in brightness during most of the outbursts oscillated around Δm = −1 mag. There are at least two main reasons for the low value of the outburst amplitude. First, a relatively large percentage of the area that was active during quiet sublimation and outburst in direct comparison with other comets for which the value of the parameter η1 is about a few per cent. Second, the lifetime of a particular jet was in most cases only a few minutes. The result of calculations related to the considered outburst is presented in Figs 7 and 8.
Change in the brightness of comet 67P during its outburst in 2014. In these calculations, it was assumed that the cometary activity corresponded to the sublimation of CO2 ice.
Similar to Fig. 7, but the cometary activity is controlled by the sublimation of CO ice.
6 SUMMARY AND CONCLUSIONS
The paper presents a new approach to calculating the change in the brightness of comets during an outburst. These considerations take into account the fact that the scattering of the incident sunlight takes place on dust aggregates and agglomerates. The main parameter taken into account is the mass ejection that resulted from the destruction of the cometary nucleus fragment. In addition to the mass ejected, the key factor is also the porosity of the particles, which directly translates into the density of the cometary material. These parameters, together with the average particle size, translate into the total cross-section of the nucleus fragment that was destroyed (Cej). In addition, the coma is powered by cometary particles which are emitted into space during the quiet sublimation (C1) and during the outburst (C2). This applies to those particles that rest on the surface or are emitted through the jet. In this case, the rate of outgassing via jet and its duration should be taken into account (Wesołowski 2022a). Taking the above scattering cross-sections into account determines the amplitude of the cometary outburst. The performed calculations were aimed at showing how the degree of porosity of the comet particle translates into the amplitude of the change in the brightness of the comet.
The main results are:
The porosity of the aggregate or agglomerate significantly affects the density of the comet material on which the incident sunlight scatters.
The greater the porosity of a given particle, the greater the scattering efficiency is, which directly translates into a greater amplitude of the change of cometary brightness. In the case of dense aggregates with porosity ψ = 0.05, the brightness rate varies from −0.74 to −4.24 mag. In the case of porous agglomerates, the porosity of which is in the range from 0.30 to 0.90, the brightness change ranges from −0.91 to −6.66 mag for the mass ejected of the order of 105 kg.
In addition to the mass ejected, the key parameter is the area fraction that is active during quiet sublimation η1. The higher the value of this parameter, the smaller the outburst amplitude for the same mass ejected.
The increase of the cometary brightness is more effective in the case of a low value of the η1 parameter but a high degree of porosity of the cometary particle. For example, in the case of a mass ejected of 102 kg, the increase in brightness starts with a porosity of about ψ = 0.80. On the other hand, for the mass ejected of 105 kg, the increase in brightness can be observed at the particle porosity of the order of ψ = 0.30.
The scattering of the incident sunlight for the charcoal analogue is more effective than for the silicate analogue. The obtained differences in the change of the cometary brightness are of the order of about −2.0 mag for the mass ejected of 105 kg. This result is a consequence of the difference in porosity and agglomerate density for these cometary dust analogues.
The greater the porosity of the particle, the smaller the mass ejected determines the given amplitude of the outburst. Confirmation of this fact is the analysis of the outburst of comet 67P, which is presented in Figs 7 and8.
The results of the presented calculations are related to the comet belonging to the Jupiter family. However, this case should be treated as general due to the relevant physical constants that were included in the simulations. In addition, the proposed model of the outburst was used to analyse the change in the brightness of comet 67P. These considerations take into account the outburst that took place at the end of 2014 April. Another problem is the estimate of the maximum mass likely to be ejected during eruption and the corresponding upper estimate for the possible brightening. If the outburst is caused by an increase in gas pressure in the cavity, its depth is important, as well as the size of the area from which the eruption took place. The latter should depend on the insulating properties of the dust mantle. On one hand, in the area covered by the thick dust mantle, the heat wave almost does not penetrate downward and the outburst outgassing of volatile ices is unlikely. On the other hand, in areas covered by thin dust, the underlying material may intensively warm up. This may lead to the intensive sublimation of CO, and CO2 ices. The occurrence of the landslides should prohibit the accumulation of dust on inclined surfaces. According to Kossacki et al. (2022a), the inclination angle of about 25° may be sufficient to cause the sliding of dust down the surface. The area of the gravitational inclination higher than 25° is likely to be active. Therefore, the estimate of the fraction of a nucleus surface, where the surface has a high inclination determines the total area of the possible local outbursts.
Most of the bottom of the basin is flat and covered with smooth sediments, but in one place at the edge, we can see an active pit Fig. 9. The gravitational potential was calculated using the shape model of the nucleus (Preusker et al. 2017). The applied version of the shape model is derived from 1531 images using DLR stereo-photogrammetric technique SPG. Based on this, it can be assumed that it was most likely caused by the outburst. The detailed information on the evolution of pits in the context of the change in the brightness of the comet is presented in Wesołowski (2022c). The pit is located near the shore, where the surface is generally not horizontal, so an outburst at this point may fit the hypothesis about the association of a landslide with local outbursts. Analysing the obtained results of the calculations, we can see that the change of the cometary unity oscillates around −6.0 mag. Comparing the obtained value of the change in brightness, we can conclude that it fits with real cases of outbursts of comets from the Jupiter family, e.g. 15P/Finlay; 63P/Wild 1; 186P/Garradd. Of course, we must remember that each real cometary outburst has a different morphology and usually takes place at a different heliocentric distance. The key factor remains to what extent the results of simulation or observation of a given comet can be generalized to other cases of outbursts.

The gravitational potential distribution on the surface of comet 67P, in the Imhotep region.
ACKNOWLEDGEMENTS
This work has been done due to the support the author received from the Centre for Innovation and Transfer of Natural Sciences and Engineering Knowledge, University of Rzeszów, Poland (RPPK.01.03.00-18-001/10-00). This work was supported by Poland’s National Science Center (Narodowe Centrum Nauki) [decision no. 2018/31/B/ST10/00169]. We thank the reviewers for their helpful comments which significantly contributed to the improvement of our paper.
DATA AVAILABILITY
The data underlying this article will be shared on reasonable request to the corresponding author.




