-
PDF
- Split View
-
Views
-
Cite
Cite
A P Whitworth, F D Priestley, S T Geen, Ionizing feedback from an O star formed in a shock-compressed layer, Monthly Notices of the Royal Astronomical Society, Volume 517, Issue 4, December 2022, Pages 4940–4949, https://doi.org/10.1093/mnras/stac2955
Close - Share Icon Share
ABSTRACT
We develop a simple analytical model for what happens when an O star (or compact cluster of OB stars) forms in a shock-compressed layer and carves out an approximately circular hole in the layer, at the waist of a bipolar H ii region (H iiR). The model is characterized by three parameters: the half-thickness of the undisturbed layer, |$Z_{_{\rm LAYER}}$|, the mean number density of hydrogen molecules in the undisturbed layer, |$n_{_{\rm LAYER}}$|, and the (collective) ionizing output of the star(s), |$\dot{\cal N}_{_{\rm LyC}}$|. The radius of the circular hole is given by |$W_{_{\rm IF}}(t)\sim 3.8\, {\rm pc}\, [Z_{_{\rm LAYER}}/0.1\,{\rm pc}]^{-1/6}[n_{_{\rm LAYER}}/10^4\,{\rm cm^{-3}}]^{-1/3}[\dot{\cal N}_{_{\rm LyC}}/10^{49}\,{\rm s^{-1}}]^{1/6}[t/{\rm Myr}]^{2/3}$|. Similar power-law expressions are obtained for the rate at which ionized gas is fed into the bipolar lobes, the rate at which molecular gas is swept up into a dense ring by the shock front that precedes the ionization front, and the density in this dense ring. We suggest that our model might be a useful zeroth-order representation of many observed H iiRs. From viewing directions close to the mid-plane of the layer, the H iiR will appear bipolar. From viewing directions approximately normal to the layer, it will appear to be a limb-brightened shell but too faint through the centre to be a spherically symmetric bubble. From intermediate viewing angles, more complicated morphologies can be expected.
1 INTRODUCTION
In Whitworth & Priestley (2021), we have derived an approximate analytical solution for the evolution of an H ii region (H iiR) excited by an O star or compact group of OB stars (hereafter, simply ‘the ostar’) that has formed from a filament. This solution is applicable to the situation where the O star has formed at the end of a filament, due to the gravitational focusing that occurs there (e.g. Pon, Johnstone & Heitsch 2011; Pon et al. 2012; Clarke & Whitworth 2015), and also to the situation where the O star has formed at the confluence of a hub-and-spoke system of filaments (e.g. Peretto et al. 2013, 2014; Anderson et al. 2021), since each spoke filament will be eroded by the ionizing radiation from the O star more or less independently of the other spoke filaments.
Here, we consider the situation where the O star (again representing the case of a single O star or a compact cluster of OB stars) has formed near the centre of a shock-compressed molecular layer. For simplicity, we have in mind an approximately plane-parallel layer formed by the collision of two clouds or two converging flows (e.g. Elmegreen & Lada 1977; Elmegreen & Elmegreen 1978; Scoville, Sanders & Clemens 1986; Elmegreen 1994; Whitworth et al. 1994a,b; Tan 2000; Audit & Hennebelle 2005; Heitsch et al. 2006; Hennebelle & Audit 2007; Hennebelle, Audit & Miville-Deschênes 2007; Heitsch, Hartmann & Burkert 2008; Dale et al. 2009, 2011; Wünsch et al. 2010; Inoue & Fukui 2013; Chen & Ostriker 2014; Fukui et al. 2014; Takahira, Tasker & Habe 2014; Balfour et al. 2015; Chen & Ostriker 2015; Balfour, Whitworth & Hubber 2017; Dinnbier et al. 2017; Wu et al. 2017a,b; Inoue et al. 2018; Kohno et al. 2018; Shima et al. 2018; Takahira et al. 2018; Dobashi et al. 2019; Dobbs, Liow & Rieder 2020; Liow & Dobbs 2020; Tanvir & Dale 2020; Dobbs & Wurster 2021; Enokiya et al. 2021; Hayashi et al. 2021; Sakre et al. 2021).
Under this circumstance, the H iiR excited by the O star expands most rapidly in directions approximately normal to the layer. In these directions, the ionization front (IF) may become density bounded, so that ionizing photons escape into the general interstellar medium. In directions close to the plane of the layer, expansion of the H iiR proceeds more slowly, and the IF is preceded by a shock front (SF) that sweeps up the molecular gas in the layer into a dense ring (hereafter, the swept-up ring, SUR); this SUR may become sufficiently dense and massive to spawn a second generation of stars, i.e. a variant on the collect-and-collapse mechanism for propagating star formation (e.g. Whitworth et al. 1994a; Deharveng et al. 2003; Dale, Bonnell & Whitworth 2007; Thompson et al. 2012; Palmeirim et al. 2017). The ionized gas dispersing normal to, and on both sides of, the layer forms a bipolar H iiR. The inside surface of the SUR appears as a bright rim and defines the waist of the bipolar H iiR (e.g. Deharveng et al. 2015; Samal et al. 2018; Whitworth et al. 2018). Similar morphologies can be produced by mechanical feedback from winds and supernovae in layers (e.g. Wareing, Pittard & Falle 2017), and somewhat different configurations have been proposed for more violent cloud/cloud collisions (e.g. Ohama et al. 2018).
Viewed from directions close to the plane of the layer, both lobes of the bipolar H iiR may be visible. Viewed from directions approximately normal to the layer, the bright rim will appear as a ring of enhanced emission. The standard interpretation of such rings of enhanced emission is that they represent the limb-brightened projection of an approximately spherical H iiR (e.g. Deharveng et al. 2010; Anderson et al. 2011; Li et al. 2020). However, there are some cases where the weak emission measure through the centre of the ring, and the low column density of molecular gas, is more compatible with a bipolar H iiR breaking out of a layer (e.g. Beaumont & Williams 2010; Xu et al. 2017; Samal et al. 2018; Kabanovic et al. 2022). One example of an H iiR that can be interpreted in this way is RCW 120 (e.g. Beaumont & Williams 2010; Anderson et al. 2015; Figueira et al. 2017), although alternative physical explanations have been proposed for this source, involving ionizing stars in turbulent clouds (Walch et al. 2015), and stellar-wind bubbles (Mackey et al. 2016) or H ii bubbles (Marsh & Whitworth 2019) due to stars that are moving supersonically relative to the ambient molecular gas. Other examples of partial or total ring-like morphologies include the shell round λ Orionis (Lee, Seon & Jo 2015) and G35.673-00.847 (Dewangan, Devaraj & Ojha 2018).
The plan of the paper is as follows: In Section 2, we define a simple geometric model for the configuration. We introduce the three configuration parameters (|$Z_{_{\rm LAYER}},n_{_{\rm LAYER}},\dot{\cal N}_{_{\rm LyC}}$|) that define a particular realization of the model and the four ansätze that allow us to simplify the dynamical equations. In Section 3, we formulate the equation of ionization balance in the H iiR, between the O star and the IF on the inside of the SUR. In Section 4, we derive approximate expressions for the density and sound speed in the SUR and the bulk velocity of the SUR. In Section 5, we obtain a differential equation for the position of the IF, a numerical solution to this equation, and an approximate analytical solution. In Section 6, we obtain an approximate analytical expression for the rate at which ionized gas boils off the IF and escapes into the bipolar lobes. In Section 7, we obtain a differential equation for the growth of the SUR, a numerical solution to this equation, and an approximate analytical solution. In Section 8, we review the assumptions and approximations made, and attempt to identify those that might alter the results significantly. In Section 9, we discuss the results, and in Section 10 we summarize the main results.
The essential difference between the situation considered here (a ring-shaped IF eroding a circular hole in a plane-parallel layer) and the situation considered in the earlier paper (Whitworth & Priestley 2021; a hemispherical IF eroding the end of a cylindrical filament) is the geometry. Whereas the filament presents a rather small solid angle to the O star, and one that decreases rather fast [as |$L_{_{\rm IF}}^{-2}(t)$|, where |$L_{_{\rm IF}}(t)$| is the distance from the O star to the IF where it eats into the end of the filament], the layer presents a larger solid angle to the O star, and one that decreases more slowly [as |$W_{_{\rm IF}}^{-1}(t)$|, where |$W_{_{\rm IF}}(t)$| is the distance from the O star to the IF where it eats into the layer]. Consequently, at late times the O star releases much more ionized gas from the layer, and sweeps up much more neutral gas into the SUR, in the situation analysed here – than in the situation analysed by Whitworth & Priestley (2021), where much less ionized gas is released from the end of the filament, and much less neutral gas is swept between the IF and the SF.
2 MODEL
In this section, we define the geometry of the model, introduce the three dimensionless parameters that specify a particular configuration (|$Z_{_{0.1}},n_{_4},\dot{\cal N}_{_{49}}$|), and introduce the approximations and assumptions that underlie the subsequent analysis. Most of these approximations and assumptions are evaluated retrospectively in Section 8.
![Cartoon illustrating the geometry of the model on the [w, z] plane. The configuration has cylindrical symmetry about the z-axis and reflection symmetry about the z = 0 plane; w = [x2 + y2]1/2. The O star sits at the origin [w, z] = [0, 0]. The bold outline on the right represents the boundary of the ‘molecular layer’, which is characterized by half-thickness, $Z_{_{\rm LAYER}}$, molecular hydrogen density, $n_{_{\rm LAYER}}$, and effective sound speed, $c_{_{\rm LAYER}}$. In the direction towards the O star, the molecular gas of the layer terminates in a semicircular IF, at distance $W_{_{\rm IF}}(t)$ from the O star. As the IF advances into the layer, it is preceded by an SF, at distance $W_{_{\rm SF}}(t)$ from the O star. Between the IF and the SF is a dense ring of swept-up molecular gas, represented by the thick black meniscus shape, and labelled ‘SWEPT-UP RING’ (SUR), with molecular hydrogen density $n_{_{\rm SUR}}(t)$ and effective sound speed $c_{_{\rm SUR}}$. The H iiR between the O star and the IF is characterized by recombination coefficient, $\alpha _{_{\rm B}}$, adiabatic sound speed, $c_{_{\rm II}}$, and proton density, $n_{_{\rm II}}(r,t)$. Here, r is the distance from the COC of the IF. The ionized gas flowing off the IF disperses as indicated by the curved ‘FLOW-LINES’, to produce a bipolar H iiR, with the SWEPT-UP RING defining its waist.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/517/4/10.1093_mnras_stac2955/1/m_stac2955fig1.jpeg?Expires=1749983167&Signature=JJPuu1YLpvxPkYIW-v3ZraGqBUhpUpjo1R8WDX~wKAxOe1zV5at4jjtVnj~0M~pGVL8TEUI9n48~Kii3VA7XzuzHbDIc4hhfRvaCZjVO07aAgAJwLgH2lwme3Fld1ZN-lCx8914tK8BCy8eQ~XaeftJZbxJBdSmOlEmzBmfRvw6-EBHCTCHlGuOcKJ1SX-3kDsJpKqFm0GpeWJm-eZ8rO6Uxr2s0UuoOGYw7ckc2weVFFyr8tH-h2pEPxlPZhBW2Qx5OhnqfPlCI6KckR4cWTy-eZAApzDvPTez4bUXc2KLq48TE3eBUxO~sOZOteI3~jRnLfNrIzUYs0gfhfNyY6Q__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Cartoon illustrating the geometry of the model on the [w, z] plane. The configuration has cylindrical symmetry about the z-axis and reflection symmetry about the z = 0 plane; w = [x2 + y2]1/2. The O star sits at the origin [w, z] = [0, 0]. The bold outline on the right represents the boundary of the ‘molecular layer’, which is characterized by half-thickness, |$Z_{_{\rm LAYER}}$|, molecular hydrogen density, |$n_{_{\rm LAYER}}$|, and effective sound speed, |$c_{_{\rm LAYER}}$|. In the direction towards the O star, the molecular gas of the layer terminates in a semicircular IF, at distance |$W_{_{\rm IF}}(t)$| from the O star. As the IF advances into the layer, it is preceded by an SF, at distance |$W_{_{\rm SF}}(t)$| from the O star. Between the IF and the SF is a dense ring of swept-up molecular gas, represented by the thick black meniscus shape, and labelled ‘SWEPT-UP RING’ (SUR), with molecular hydrogen density |$n_{_{\rm SUR}}(t)$| and effective sound speed |$c_{_{\rm SUR}}$|. The H iiR between the O star and the IF is characterized by recombination coefficient, |$\alpha _{_{\rm B}}$|, adiabatic sound speed, |$c_{_{\rm II}}$|, and proton density, |$n_{_{\rm II}}(r,t)$|. Here, r is the distance from the COC of the IF. The ionized gas flowing off the IF disperses as indicated by the curved ‘FLOW-LINES’, to produce a bipolar H iiR, with the SWEPT-UP RING defining its waist.
The gas has solar composition [X = 0.70, Y = 0.28, Z = 0.02], and we assume that in the layer all the hydrogen is molecular. The mean mass associated with each hydrogen molecule, when contributions from all other elements, in particular helium, have been taken into account, is therefore |$\bar{m}_{_{\rm H_2}}=2m_{_{\rm H}}/X=4.75\times 10^{-24}\, {\rm g}$|, where |$m_{_{\rm H}}$| is the mass of a hydrogen atom.
In our model, the three dimensionless parameters, |$Z_{_{0.1}}$|, |$n_{_4}$|, and |$\dot{\cal N}_{_{49}}$| (equations 1, 2, and 8), are the only parameters influencing the evolution of the HiiR. They feature in many of the subsequent equations. All the variables used in the analysis, along with the acronyms, are summarized in Table 1.
| Acronyms | ||
| H ii region | H iiR | – |
| Ionization front | IF | – |
| Centre of curvature of IF | COC | – |
| Shock front | SF | – |
| Swept-up ring | SUR | – |
| Configuration parameters and fiducial values | ||
| Half-thickness of layer | |$Z_{_{\rm LAYER}}$| | |$Z_{_{0.1}}\times \left[0.1\, {\rm pc}\right]$| |
| Density of H2 in layer | |$n_{_{\rm LAYER}}$| | |$n_{_4}\times \left[10^4\, \rm {cm}^{-3}\right]$| |
| Output of ionizing photons | |$\dot{\cal N}_{_{\rm LyC}}$| | |$\dot{\cal N}_{_{49}}\, \times \left[10^{49}\, \rm {s}^{-1}\right]$| |
| Effective sound speed in layer | |$c_{_{\rm LAYER}}$| | |$0.31\, {\rm km\, s^{-1}}Z_{_{0.1}}n_{_4}^{1/2}$| |
| Effective sound speed in SUR | |$c_{_{\rm SUR}}$| | |$0.44\, {\rm km\, s^{-1}}Z_{_{0.1}}n_{_4}^{1/2}$| |
| Fixed parameters and values | ||
| Temperature in ionized gas | |$T_{_{\rm II}}$| | |$10^4\, {\rm K}$| |
| Sound speed in ionized gas | |$c_{_{\rm II}}$| | |$15\, {\rm km\, s^{-1}}$| |
| Case B recombination coeff. | |$\alpha _{_{\rm B}}$| | |$2.7\!\times \!10^{-13}\,\rm {cm^3\,s^{-1}}$| |
| Dependent variables | ||
| Distance from O star to IF | |$W_{_{\rm IF}}(t)$| | – |
| Distance from O star to SF | |$W_{_{\rm SF}}(t)$| | – |
| Thickness of SUR | |$\Delta W_{_{\rm SUR}}(t)$| | – |
| Density of protons at IF | |$n_{_{\rm IF}}(t)$| | – |
| Density of protons in H iiR | |$n_{_{\rm II}}(r,t)$| | – |
| Density of H2 in SUR | |$n_{_{\rm SUR}}(t)$| | – |
| Bulk velocity in SUR | |$\upsilon _{_{\rm SUR}}(t)$| | – |
| Mass of SUR | |$M_{_{\rm SUR}}(t)$| | – |
| Independent variables | ||
| Time since O star switch-on | t | – |
| Radial distance from COC | r | – |
| Distance along symmetry axis | z | – |
| Distance from symmetry axis | w | [x2 + y2]1/2 |
| Dimensionless variables | ||
| Dimensionless t | τ | |$c_{_{\rm LAYER}}t/Z_{_{\rm LAYER}}$| |
| Dimensionless |$W_{_{\rm IF}}(t)$| | |$\xi _{_{\rm IF}}(\tau)$| | |$W_{_{\rm IF}}(t)/Z_{_{\rm LAYER}}$| |
| Dimensionless |$W_{_{\rm SF}}(t)$| | |$\xi _{_{\rm SF}}(\tau)$| | |$W_{_{\rm SF}}(t)/Z_{_{\rm LAYER}}$| |
| Dimensionless |$\Delta W_{_{\rm SUR}}(t)$| | |$\delta _{_{\rm SUR}}(\tau)$| | |$\Delta W_{_{\rm SUR}}(t)/Z_{_{\rm LAYER}}$| |
| Acronyms | ||
| H ii region | H iiR | – |
| Ionization front | IF | – |
| Centre of curvature of IF | COC | – |
| Shock front | SF | – |
| Swept-up ring | SUR | – |
| Configuration parameters and fiducial values | ||
| Half-thickness of layer | |$Z_{_{\rm LAYER}}$| | |$Z_{_{0.1}}\times \left[0.1\, {\rm pc}\right]$| |
| Density of H2 in layer | |$n_{_{\rm LAYER}}$| | |$n_{_4}\times \left[10^4\, \rm {cm}^{-3}\right]$| |
| Output of ionizing photons | |$\dot{\cal N}_{_{\rm LyC}}$| | |$\dot{\cal N}_{_{49}}\, \times \left[10^{49}\, \rm {s}^{-1}\right]$| |
| Effective sound speed in layer | |$c_{_{\rm LAYER}}$| | |$0.31\, {\rm km\, s^{-1}}Z_{_{0.1}}n_{_4}^{1/2}$| |
| Effective sound speed in SUR | |$c_{_{\rm SUR}}$| | |$0.44\, {\rm km\, s^{-1}}Z_{_{0.1}}n_{_4}^{1/2}$| |
| Fixed parameters and values | ||
| Temperature in ionized gas | |$T_{_{\rm II}}$| | |$10^4\, {\rm K}$| |
| Sound speed in ionized gas | |$c_{_{\rm II}}$| | |$15\, {\rm km\, s^{-1}}$| |
| Case B recombination coeff. | |$\alpha _{_{\rm B}}$| | |$2.7\!\times \!10^{-13}\,\rm {cm^3\,s^{-1}}$| |
| Dependent variables | ||
| Distance from O star to IF | |$W_{_{\rm IF}}(t)$| | – |
| Distance from O star to SF | |$W_{_{\rm SF}}(t)$| | – |
| Thickness of SUR | |$\Delta W_{_{\rm SUR}}(t)$| | – |
| Density of protons at IF | |$n_{_{\rm IF}}(t)$| | – |
| Density of protons in H iiR | |$n_{_{\rm II}}(r,t)$| | – |
| Density of H2 in SUR | |$n_{_{\rm SUR}}(t)$| | – |
| Bulk velocity in SUR | |$\upsilon _{_{\rm SUR}}(t)$| | – |
| Mass of SUR | |$M_{_{\rm SUR}}(t)$| | – |
| Independent variables | ||
| Time since O star switch-on | t | – |
| Radial distance from COC | r | – |
| Distance along symmetry axis | z | – |
| Distance from symmetry axis | w | [x2 + y2]1/2 |
| Dimensionless variables | ||
| Dimensionless t | τ | |$c_{_{\rm LAYER}}t/Z_{_{\rm LAYER}}$| |
| Dimensionless |$W_{_{\rm IF}}(t)$| | |$\xi _{_{\rm IF}}(\tau)$| | |$W_{_{\rm IF}}(t)/Z_{_{\rm LAYER}}$| |
| Dimensionless |$W_{_{\rm SF}}(t)$| | |$\xi _{_{\rm SF}}(\tau)$| | |$W_{_{\rm SF}}(t)/Z_{_{\rm LAYER}}$| |
| Dimensionless |$\Delta W_{_{\rm SUR}}(t)$| | |$\delta _{_{\rm SUR}}(\tau)$| | |$\Delta W_{_{\rm SUR}}(t)/Z_{_{\rm LAYER}}$| |
| Acronyms | ||
| H ii region | H iiR | – |
| Ionization front | IF | – |
| Centre of curvature of IF | COC | – |
| Shock front | SF | – |
| Swept-up ring | SUR | – |
| Configuration parameters and fiducial values | ||
| Half-thickness of layer | |$Z_{_{\rm LAYER}}$| | |$Z_{_{0.1}}\times \left[0.1\, {\rm pc}\right]$| |
| Density of H2 in layer | |$n_{_{\rm LAYER}}$| | |$n_{_4}\times \left[10^4\, \rm {cm}^{-3}\right]$| |
| Output of ionizing photons | |$\dot{\cal N}_{_{\rm LyC}}$| | |$\dot{\cal N}_{_{49}}\, \times \left[10^{49}\, \rm {s}^{-1}\right]$| |
| Effective sound speed in layer | |$c_{_{\rm LAYER}}$| | |$0.31\, {\rm km\, s^{-1}}Z_{_{0.1}}n_{_4}^{1/2}$| |
| Effective sound speed in SUR | |$c_{_{\rm SUR}}$| | |$0.44\, {\rm km\, s^{-1}}Z_{_{0.1}}n_{_4}^{1/2}$| |
| Fixed parameters and values | ||
| Temperature in ionized gas | |$T_{_{\rm II}}$| | |$10^4\, {\rm K}$| |
| Sound speed in ionized gas | |$c_{_{\rm II}}$| | |$15\, {\rm km\, s^{-1}}$| |
| Case B recombination coeff. | |$\alpha _{_{\rm B}}$| | |$2.7\!\times \!10^{-13}\,\rm {cm^3\,s^{-1}}$| |
| Dependent variables | ||
| Distance from O star to IF | |$W_{_{\rm IF}}(t)$| | – |
| Distance from O star to SF | |$W_{_{\rm SF}}(t)$| | – |
| Thickness of SUR | |$\Delta W_{_{\rm SUR}}(t)$| | – |
| Density of protons at IF | |$n_{_{\rm IF}}(t)$| | – |
| Density of protons in H iiR | |$n_{_{\rm II}}(r,t)$| | – |
| Density of H2 in SUR | |$n_{_{\rm SUR}}(t)$| | – |
| Bulk velocity in SUR | |$\upsilon _{_{\rm SUR}}(t)$| | – |
| Mass of SUR | |$M_{_{\rm SUR}}(t)$| | – |
| Independent variables | ||
| Time since O star switch-on | t | – |
| Radial distance from COC | r | – |
| Distance along symmetry axis | z | – |
| Distance from symmetry axis | w | [x2 + y2]1/2 |
| Dimensionless variables | ||
| Dimensionless t | τ | |$c_{_{\rm LAYER}}t/Z_{_{\rm LAYER}}$| |
| Dimensionless |$W_{_{\rm IF}}(t)$| | |$\xi _{_{\rm IF}}(\tau)$| | |$W_{_{\rm IF}}(t)/Z_{_{\rm LAYER}}$| |
| Dimensionless |$W_{_{\rm SF}}(t)$| | |$\xi _{_{\rm SF}}(\tau)$| | |$W_{_{\rm SF}}(t)/Z_{_{\rm LAYER}}$| |
| Dimensionless |$\Delta W_{_{\rm SUR}}(t)$| | |$\delta _{_{\rm SUR}}(\tau)$| | |$\Delta W_{_{\rm SUR}}(t)/Z_{_{\rm LAYER}}$| |
| Acronyms | ||
| H ii region | H iiR | – |
| Ionization front | IF | – |
| Centre of curvature of IF | COC | – |
| Shock front | SF | – |
| Swept-up ring | SUR | – |
| Configuration parameters and fiducial values | ||
| Half-thickness of layer | |$Z_{_{\rm LAYER}}$| | |$Z_{_{0.1}}\times \left[0.1\, {\rm pc}\right]$| |
| Density of H2 in layer | |$n_{_{\rm LAYER}}$| | |$n_{_4}\times \left[10^4\, \rm {cm}^{-3}\right]$| |
| Output of ionizing photons | |$\dot{\cal N}_{_{\rm LyC}}$| | |$\dot{\cal N}_{_{49}}\, \times \left[10^{49}\, \rm {s}^{-1}\right]$| |
| Effective sound speed in layer | |$c_{_{\rm LAYER}}$| | |$0.31\, {\rm km\, s^{-1}}Z_{_{0.1}}n_{_4}^{1/2}$| |
| Effective sound speed in SUR | |$c_{_{\rm SUR}}$| | |$0.44\, {\rm km\, s^{-1}}Z_{_{0.1}}n_{_4}^{1/2}$| |
| Fixed parameters and values | ||
| Temperature in ionized gas | |$T_{_{\rm II}}$| | |$10^4\, {\rm K}$| |
| Sound speed in ionized gas | |$c_{_{\rm II}}$| | |$15\, {\rm km\, s^{-1}}$| |
| Case B recombination coeff. | |$\alpha _{_{\rm B}}$| | |$2.7\!\times \!10^{-13}\,\rm {cm^3\,s^{-1}}$| |
| Dependent variables | ||
| Distance from O star to IF | |$W_{_{\rm IF}}(t)$| | – |
| Distance from O star to SF | |$W_{_{\rm SF}}(t)$| | – |
| Thickness of SUR | |$\Delta W_{_{\rm SUR}}(t)$| | – |
| Density of protons at IF | |$n_{_{\rm IF}}(t)$| | – |
| Density of protons in H iiR | |$n_{_{\rm II}}(r,t)$| | – |
| Density of H2 in SUR | |$n_{_{\rm SUR}}(t)$| | – |
| Bulk velocity in SUR | |$\upsilon _{_{\rm SUR}}(t)$| | – |
| Mass of SUR | |$M_{_{\rm SUR}}(t)$| | – |
| Independent variables | ||
| Time since O star switch-on | t | – |
| Radial distance from COC | r | – |
| Distance along symmetry axis | z | – |
| Distance from symmetry axis | w | [x2 + y2]1/2 |
| Dimensionless variables | ||
| Dimensionless t | τ | |$c_{_{\rm LAYER}}t/Z_{_{\rm LAYER}}$| |
| Dimensionless |$W_{_{\rm IF}}(t)$| | |$\xi _{_{\rm IF}}(\tau)$| | |$W_{_{\rm IF}}(t)/Z_{_{\rm LAYER}}$| |
| Dimensionless |$W_{_{\rm SF}}(t)$| | |$\xi _{_{\rm SF}}(\tau)$| | |$W_{_{\rm SF}}(t)/Z_{_{\rm LAYER}}$| |
| Dimensionless |$\Delta W_{_{\rm SUR}}(t)$| | |$\delta _{_{\rm SUR}}(\tau)$| | |$\Delta W_{_{\rm SUR}}(t)/Z_{_{\rm LAYER}}$| |
The hot ionized gas in the HiiR disperses due to both the momentum with which this gas boils off the IF and its high thermal pressure. We assume that the ionized gas has uniform and constant gas-kinetic temperature, |$T_{_{\rm II}}=10^4\, {\rm K}$|, hence uniform and constant adiabatic sound speed, |$c_{_{\rm II}}=15\, {\rm km\, s^{-1}}$|, and uniform and constant Case B recombination coefficient, |$\alpha _{_{\rm B}}=2.7\times 10^{-13}\, {\rm cm^3\, s^{-1}}$|.1 We neglect the ionization of helium. The assumption of uniform and constant temperature, and the neglect of helium ionization, is reasonable because we shall be mainly concerned with the ionized gas near the IF. Here, the ionizing radiation is rather hard, and likely to maintain a high gas-kinetic temperature, |$T_{_{\rm II}}\sim 10^4\, {\rm K}$|. Moreover, unless the mean effective temperature of the O star is exceptionally high, no helium-ionizing photons will reach that far; i.e. the helium IFs will be closer to the O star.
As the IF propagates outwards into the layer, it is preceded by an SF, which sweeps up the neutral gas of the layer. The passage of the SF will probably not change the gas-kinetic temperature much, but it is likely to amplify the turbulent motions, so that the effective sound speed in the SUR is increased somewhat. As in Whitworth & Priestley (2021), we assume that |$c_{_{\rm SUR}}\approx 2^{1/2}c_{_{\rm LAYER}}$| (see equations 6 and 28); in other words, the amount of turbulent energy is approximately doubled on passing through the shock. This assumption cannot be justified precisely, but appears to be a good approximation to the amplification of turbulence behind accretion shocks, and does not affect the results significantly.2
The model is concerned with (i) the dynamics of the dispersing ionized gas, (ii) the consequent advance of the IF, and (iii) the sweeping up of neutral gas immediately ahead of the IF. At the heart of the model are the following four ansätze.
Ansatz 1. The HiiR and the SUR have reflection symmetry about the z = 0 plane and cylindrical symmetry about the z-axis (see Fig. 1). Hence, we can switch to cylindrical polar coordinates [w, ϕ, z], so that all quantities only depend on w = [x2 + y2]1/2 and |z|, and are independent of ϕ = tan −1(y/x). For brevity, we will refer to the circle defined by [w, 0 ≤ ϕ < 2π, z] as ‘a point’ with coordinates [w, z].
Ansatz 2. Ionized gas flowing radially off the IF diverges, and so the recombination rate decreases with distance from the IF. This divergence is largely determined by the curvature of the IF, which is of order |$Z_{_{\rm LAYER}}^{-1}$|. We can then compute the position of the IF by integrating the rate of recombination along the w-axis from the O star to the closest point on the IF at |$[w,z]=[W_{_{\rm IF}}(t),0]$| (see equation 17).
Ansatz 3. Ionized gas flows off each point on the IF at the same rate, and this rate can be approximated by the rate at |$[w,z]=[W_{_{\rm IF}}(t),0]$| (computed as described in ansatz2 and Section 3). Evidently, this overestimates the flow rate off all other points on the IF, by a factor that increases with |z|, in particular because ionizing radiation arrives at these points at an increasingly oblique angle to the IF as we move away from the z = 0 plane. We compensate for this by assuming that the area of the IF is only |${\sim} \!4\pi [W_{_{\rm IF}}(t)\!+\!Z_{_{\rm LAYER}}]Z_{_{\rm LAYER}}$| (the projected cross-sectional area of the IF as seen from the O star) rather than the full |${\sim} \!2\pi ^2[W_{_{\rm IF}}(t)\!+\!Z_{_{\rm LAYER}}]Z_{_{\rm LAYER}}$| (the area of the convex inner surface of the SUR).
Ansatz 4. If the gas were to flow radially off the IF to infinity, it would converge on the z-axis to produce a singularity in the volume density. We neglect this convergence, since radiation pressure and/or winds from the O star deflect the ionized gas outwards and away from the O star. We only take account of the divergence in the vicinity of the IF (see Fig. 1), which is where most of the ionizing radiation emitted in these directions is absorbed – as evidenced by the brightness of ‘bright rims’.
Our model does not involve a magnetic field. We speculate on the consequences of including a magnetic field in Section 8.7.
3 IONIZATION BALANCE
In this section, we formulate the condition of ionization balance in the space between the O star and the IF.
4 STRUCTURE OF THE SHOCK-COMPRESSED LAYER
5 ADVANCE OF THE IONIZATION FRONT
In this section, we derive and solve an equation for the advance of the IF.
Accurate numerical solutions for |$\xi _{_{\rm IF}}(\tau)$|, obtained by integrating equations (38) and 39, with initial conditions given by equation (41), are plotted with full lines in Fig. 2, for five representative values of K, distributed about the fiducial value computed in equation (32), viz. |$\, 17.0,\,\,24.0,\,\,34.0,\,\,48.1,\,\,{\rm and}\,\,68.0$|. As expected, the IF advances faster for larger values of K, i.e. if the layer is geometrically thinner and/or less dense, and/or the ionizing output of the O star is larger.
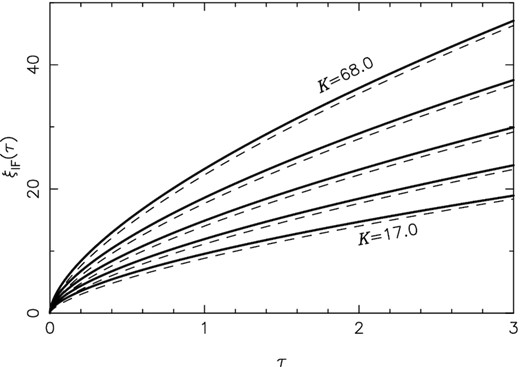
|$\xi _{_{\rm IF}}(\tau)$|, i.e. the distance from the O star to the IF, in dimensionless units, for different values of K = 17.0, 24.0, 34.0, 48.1, and 68.0. The full curves show the run of |$\xi _{_{\rm IF}}(\tau)$| obtained by numerical integration of equations (38) and (39). The dashed curves show the approximate analytical solution of equation (42) for the same K values.
6 DYNAMICS OF THE OVERALL H ii REGION
In this section, we solve for the rate at which ionized gas boils off the IF, and hence for the total mass of H ii released from the filament by the O star.
Strictly speaking, the expressions and estimates derived thus far (equations 16 through 49) pertain only to the gas on the z-axis. The flux of ionizing radiation incident on other parts of the IF decreases with distance from the w-axis, largely because it arrives at increasingly oblique angles. To take account of this, we invoke the third of the ansätze defined in Section 2, i.e. we assume that the expressions and estimates derived thus far obtain everywhere, not just on the w-axis, and to compensate for this we limit the area of the IF to the cross-sectional area of the layer as seen from the O star, |${\approx} 4\pi [W_{_{\rm IF}}(t)\!+\!Z_{_{\rm LAYER}}]Z_{_{\rm LAYER}}\sim 4\pi W_{_{\rm IF}}(t)Z_{_{\rm LAYER}}$|.
7 GROWTH OF THE SHOCK-COMPRESSED RING
In this section, we derive the parameters of the SUR (thickness, mass, and expansion velocity).
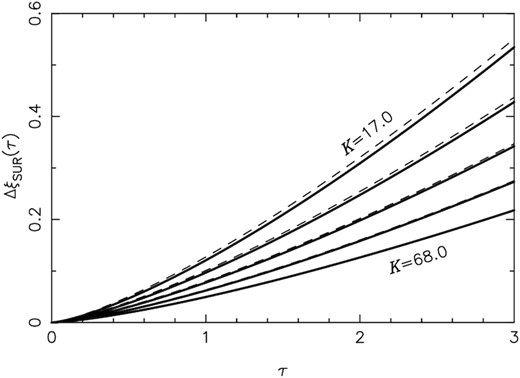
|$\Delta \xi _{_{\rm SUR}}(\tau)$|, i.e. the radial thickness of the SUR, in dimensionless units, for different values of K = 17.0, 24.0, 34.0, 48.1, and 68.0. The full curves show the run of |$\Delta \xi _{_{\rm SUR}}(\tau)$| obtained by numerical integration of equations (53) and (39). The dashed curves show the approximate analytical solution of equation (55) for the same K values.
8 ASSUMPTIONS AND APPROXIMATIONS
In this section, we revisit the approximations and assumptions made in the preceding analysis, and show that they are appropriate.
8.1 Movement of the O star
We have assumed that the O star is stationary. The predictions of the model cannot be applied if the velocity of the O star – in particular the component normal to the layer – is comparable with the speed of advance of the IF (equation 47). Under the circumstance that the O star is actually a compact cluster of OB stars, we must consider both the bulk velocity of the ‘centre of ionizing output’ and the velocities with which the cluster disperses. The model is only applicable to cases where these velocities are relatively small, say |${\lesssim} 1\, {\rm km\, s^{-1}}$|. Since newly formed O stars frequently have velocities exceeding this threshold, and clusters of OB stars may also have velocity dispersions exceeding the threshold, the model will not always be applicable to massive stars formed in a shock-compressed layer, only to those where the massive stars end up with relatively low velocities – that is, excluding the systematic velocities in multiple systems and the random velocities in a tightly bound compact cluster.
8.2 Constancy of the ionizing output, |$\dot{\cal N}_{_{\rm LyC}}$|
We have assumed that the O star switches on instantaneously, and then emits ionizing photons at a constant rate, |$\dot{\cal N}_{_{\rm LyC}}$|. Given the time-scales involved in the evolution of an O star (|${\gtrsim} 3\, {\rm Myr}$|), and in the advance of the IF (equation 46), this is a reasonable assumption for times |$0.1\, {\rm Myr}\lesssim t\lesssim 3\, {\rm Myr}$|, and possibly longer, depending on the precise masses of the stars involved. There will be a short period when the HiiR is small and approximately spherical, and then a short period when it has just broken out of the layer. These two periods together last less than |$0.1\, {\rm Myr}$|, and once they are over, the basic geometry of the model, as sketched in Fig. 1, should be valid.
8.3 Thickness of the SUR
8.4 Fraction of ionizing photons reaching the IF
8.5 Separation of variables
8.6 Speed of SF
Having placed an upper limit on the speed of the SF, we should also check that the SF advances sufficiently fast to compress the gas it sweeps up. Comparing |$\mathrm{ d}W_{_{\rm SF}}/\mathrm{ d}t$| from equation (67), with |$c_{_{\rm SUR}}$| from equation (29), we see that there will only be a shock if the layer is not too thick and not too dense, and the ionizing output is not too small.
8.7 Neglect of magnetic field
Since observations (e.g. Ward-Thompson et al. 2017; Fissel et al. 2019; Soam et al. 2019; Pillai et al. 2020; Doi et al. 2020; Arzoumanian et al. 2021; Kwon et al. 2022; Pattle et al. 2022) and simulations (e.g. Soler et al. 2013; Seifried & Walch 2015; Girichidis et al. 2018; Gómez, Vázquez-Semadeni & Zamora-Avilés 2018) suggest that the gas flows assembling dense star-forming gas structures tend to involve velocities parallel or antiparallel to the large-scale magnetic field, we limit discussion to a large-scale magnetic field parallel to the z-axis. In this situation, there are two effects that should be considered. First, the field will inhibit gravitational fragmentation of the layer (see Section 8.7.1). Secondly, the field will resist the advance of the IF (see Section 8.7.2). We note that large-scale magnetic fields in the interstellar medium are typically |${\lesssim} 10\, \mu {\rm G}$| (e.g. Heiles & Troland 2005).
8.7.1 Stability of the layer against gravitational fragmentation
8.7.2 Magnetic resistance to the advance of the IF
8.8 Star formation in the SUR
It is certainly possible that a second generation of stars will form in the SUR. However, without knowing details of the turbulence there (i.e. how much is in wavelengths that can be rendered unstable against collapse), it is impossible to evaluate this possibility. Such considerations lie outside the scope of the current paper, and would almost certainly have to be addressed with numerical simulations, and a slew of additional parameters regulating the initial and boundary conditions, and the constitutive physics.
9 DISCUSSION
We have explored the possibility that, if an O star, or compact group of OB stars, forms in a shock-compressed layer and stays close to the mid-plane of the layer, then it will carve out an approximately circular hole in the layer. Ionized gas will steam away above and below the layer, producing a bipolar H iiR. At the waist of the bipolar H iiR, an IF will be driven into the layer, producing an approximately circular bright rim, and sweeping up a ring of dense shocked gas, within which a second generation of stars may form.
9.1 Observed morphology
The observed morphology of such a configuration will depend strongly on the viewing angle, relative to the normal to the layer (here the z-axis) and on the wavelength, due to dust extinction.
Observers who are close to the z-axis, and therefore view the layer close to face-on, will see an approximately circular bright rim, which might in the first instance be interpreted with a limb-brightened spherically symmetric model – except that the column densities of ionized and neutral gases through the middle of the ring will be significantly lower than expected. Hence, the model might offer a straightforward explanation for the cylindrical H iiRs observed by Beaumont & Williams (2010).
Observers close to the z = 0 plane will see a bipolar H iiR. Any difference between the size and brightness of the lobes would be attributable to the source (or sources) of ionizing radiation having moved away from the mid-plane of the layer, although the H iiR would cease to be bipolar if this movement were too great. Further asymmetry might also derive from differential extinction due to the dust in the layer.
It follows that there will probably be a range of intermediate angles relative to the z-axis, from which the projected morphology of the H iiR – even if it is intrinsically bipolar, and conforms to our model – will be quite complicated and hard to interpret.
9.2 Overall dynamics and mass budget
The IF advances quite rapidly into the layer, typically at speeds exceeding |$1\, {\rm km\, s^{-1}}$|, sweeping up mass into a dense ring where a second generation of stars may form. Ionized gas flows off the IF and escapes above and below the layer at an approximately constant rate, but most of the mass that is shifted to create the hole in the layer ends up in the dense ring between the IF and the SF.
9.3 Comparison with feedback in a filament
The expressions derived here for the rate at which the IF advances (equation 47), the mass of ionized gas (equation 52), and the mass of gas in the SUR (equation 59) can be compared with those obtained in Whitworth & Priestley (2021) for the case of an O star formed in, or at the end of, a filament.
The rate of advance of the IF has approximately the same dependence on the half-thickness of the undisturbed layer (vice the radius of the undisturbed filament), the density in the undisturbed layer (vice the density in the undisturbed filament), the ionizing output of the O star, and the elapsed time since switch-on. This is because the conditions at the IF are largely dictated by the ionizing output, |$\dot{\cal N}_{_{\rm LyC}}$|, and by physical conditions ahead of the IF (i.e. the density and sound speed in the undisturbed layer (vice filament).
However, the mass of ionized gas flowing off the IF and the mass of neutral gas swept up between the IF and the SF both have different dependences, due to the different geometries. For the layer considered here, the mass of ionized gas increases linearly with time, whereas for the filament the mass of ionized gas only increases as t1/3. Similarly, for the layer, the mass of swept-up neutral gas increases as t4/3, whereas for the filament it only increases as t2/3. This is basically because, as the IF moves further away from the O star, the solid angle presented by the (edge-on) layer decreases much more slowly than the solid angle presented by the (end-on) filament.
We note that the advance of the IF into the layer does not stall, and nor does the advance of the IF into the filament in Whitworth & Priestley (2021). If the O star were to emit ionizing radiation for ever, and the layer were of infinite two-dimensional extent, or the filament were of infinite length, the IF would continue to advance indefinitely, albeit at an ever-decreasing rate. This is because, in these two situations, the ionized gas boiling off the IF diverges and escapes, in principle to infinity; it does not stick around for long on the path taken by ionizing photons from the O star to the IF, and therefore its re-ionization (following recombination) does not use up many of these photons. The advance of the IF slows down because the flux of ionizing radiation reaching the IF decreases due to geometric dilution. This contrasts with the situation where an O star is placed in a uniform medium and ionizes a spherical H iiR. In that case, the resulting H iiR expands until there is pressure balance between the relatively diffuse but hot gas of the H iiR and the relatively dense but cold gas of the surrounding neutral medium, and the advance of the IF then stalls (e.g. Bisbas et al. 2015); thereafter, all the ionizing output of the O star is expended balancing recombination in a static, spherical H iiR.
10 CONCLUSIONS
We have developed a simple model for the feedback from an O star (or equivalently a compact cluster of OB stars), formed in a dense layer such as might result from the collision of two clouds or two colliding streams.
Similarly to the model developed in Whitworth & Priestley (2021) for feedback from an O star formed in, or at the end of, a filament, the model developed here is based on a number of simplifying assumptions, in particular (i) that the O star remains close to the mid-plane of the layer, (ii) that the resulting HiiR is approximately circular when projected on to the mid-plane of the layer, and (iii) that the radius of curvature of the IF, where it eats into the layer, is approximately equal to the half-thickness of the layer.
We derive power-law expressions for the key parameters, in terms of |$Z_{_{0.1}}\!=\!Z_{_{\rm LAYER}}/0.1\,{\rm pc}$| (where |$Z_{_{\rm LAYER}}$| is the half-thickness of the undisturbed layer), |$n_{_4}\!=\!n_{_{\rm LAYER}}/10^4\,{\rm cm^{-3}}$| (where |$n_{_{\rm LAYER}}$| is the volume density of molecular hydrogen in the undisturbed layer), and |$\dot{\cal N}_{_{49}}\!=\!\dot{\cal N}_{_{\rm LyC}}/10^{49}{\rm s^{-1}}$| (where |$\dot{\cal N}_{_{\rm LyC}}$| is the rate at which the O star emits ionizing photons).
The simplifying assumptions made in order to derive these expressions are primarily contained in the ansätze (Section 2). The key approximations made to justify the subsequent analysis, and hence the derivation of the above approximate expressions, are justified retrospectively in Section 8.
ACKNOWLEDGEMENTS
APW and FDP gratefully acknowledge the support of an STFC Consolidated Grant (ST/K00926/1). STG gratefully acknowledges the support of a Spinoza award from the Dutch Science Organization (NWO) for research on the physics and chemistry of the interstellar medium. We thank the referee, Dr. Tom Haworth, for his constructive, encouraging, and prompt report.
DATA AVAILABILITY
All software used will be supplied on request to APW.
Footnotes
Case B invokes the on-the-spot approximation, i.e. recombinations straight into the ground state of hydrogen are ignored on the assumption that such recombinations usually result in the emission of photons just above the Lyman continuum limit. The cross-section presented to such photons by hydrogen atoms is large. Consequently, these photons are unlikely to travel far before they are re-absorbed, producing a compensatory ionization.
Whitworth & Jaffa (2018) show that molecular-line cooling effectively reduces post-shock velocities to transonic values, but the cooling then stalls due to saturation of the cooling lines. If we assume that this factor also applies to the non-thermal velocity dispersion, then the post-shock velocity dispersion should be roughly twice the pre-shock value.



