-
PDF
- Split View
-
Views
-
Cite
Cite
G Lacedelli, T G Wilson, L Malavolta, M J Hooton, A Collier Cameron, Y Alibert, A Mortier, A Bonfanti, R D Haywood, S Hoyer, G Piotto, A Bekkelien, A M Vanderburg, W Benz, X Dumusque, A Deline, M López-Morales, L Borsato, K Rice, L Fossati, D W Latham, A Brandeker, E Poretti, S G Sousa, A Sozzetti, S Salmon, C J Burke, V Van Grootel, M M Fausnaugh, V Adibekyan, C X Huang, H P Osborn, A J Mustill, E Pallé, V Bourrier, V Nascimbeni, R Alonso, G Anglada, T Bárczy, D Barrado y Navascues, S C C Barros, W Baumjohann, M Beck, T Beck, N Billot, X Bonfils, C Broeg, L A Buchhave, J Cabrera, S Charnoz, R Cosentino, Sz Csizmadia, M B Davies, M Deleuil, L Delrez, O Demangeon, B -O Demory, D Ehrenreich, A Erikson, E Esparza-Borges, H G Florén, A Fortier, M Fridlund, D Futyan, D Gandolfi, A Ghedina, M Gillon, M Güdel, P Guterman, A Harutyunyan, K Heng, K G Isaak, J M Jenkins, L Kiss, J Laskar, A Lecavelier des Etangs, M Lendl, C Lovis, D Magrin, L Marafatto, A F Martinez Fiorenzano, P F L Maxted, M Mayor, G Micela, E Molinari, F Murgas, N Narita, G Olofsson, R Ottensamer, I Pagano, A Pasetti, M Pedani, F A Pepe, G Peter, D F Phillips, D Pollacco, D Queloz, R Ragazzoni, N Rando, F Ratti, H Rauer, I Ribas, N C Santos, D Sasselov, G Scandariato, S Seager, D Ségransan, L M Serrano, A E Simon, A M S Smith, M Steinberger, M Steller, Gy Szabó, N Thomas, J D Twicken, S Udry, N Walton, J N Winn, Investigating the architecture and internal structure of the TOI-561 system planets with CHEOPS, HARPS-N, and TESS, Monthly Notices of the Royal Astronomical Society, Volume 511, Issue 3, April 2022, Pages 4551–4571, https://doi.org/10.1093/mnras/stac199
Close - Share Icon Share
ABSTRACT
We present a precise characterization of the TOI-561 planetary system obtained by combining previously published data with TESS and CHEOPS photometry, and a new set of 62 HARPS-N radial velocities (RVs). Our joint analysis confirms the presence of four transiting planets, namely TOI-561 b (P = 0.45 d, R = 1.42 R⊕, M = 2.0 M⊕), c (P = 10.78 d, R = 2.91 R⊕, M = 5.4 M⊕), d (P = 25.7 d, R = 2.82 R⊕, M = 13.2 M⊕), and e (P = 77 d, R = 2.55 R⊕, M = 12.6 R⊕). Moreover, we identify an additional, long-period signal (>450 d) in the RVs, which could be due to either an external planetary companion or to stellar magnetic activity. The precise masses and radii obtained for the four planets allowed us to conduct interior structure and atmospheric escape modelling. TOI-561 b is confirmed to be the lowest density (ρb = 3.8 ± 0.5 g cm−3) ultra-short period (USP) planet known to date, and the low metallicity of the host star makes it consistent with the general bulk density-stellar metallicity trend. According to our interior structure modelling, planet b has basically no gas envelope, and it could host a certain amount of water. In contrast, TOI-561 c, d, and e likely retained an H/He envelope, in addition to a possibly large water layer. The inferred planetary compositions suggest different atmospheric evolutionary paths, with planets b and c having experienced significant gas loss, and planets d and e showing an atmospheric content consistent with the original one. The uniqueness of the USP planet, the presence of the long-period planet TOI-561 e, and the complex architecture make this system an appealing target for follow-up studies.
1 INTRODUCTION
Since the announcement of the first exoplanet orbiting a Sun-like star (Mayor & Queloz 1995), the growing number of discoveries in exoplanetary science have yielded a surprising variety of exoplanets and exoplanetary systems. The field has benefited hugely from dedicated space-based missions, such as CoRoT, Kepler, K2 (Baglin et al. 2006; Borucki et al. 2010; Howell et al. 2014), and recently TESS (Ricker et al. 2014). With more than 170 confirmed planets, and ∼4000 planet candidates, the majority of which will likely turn out to be planets, TESS has increased the census of confirmed exoplanets to more than 4500.1 Alongside the aforementioned missions, which are designed to discover a large number of exoplanets by searching for transit-like signatures around hundreds of thousands of stars, new characterization missions, with a specific focus on the detailed study of known exoplanets, are now starting to operate. Among them, the CHaracterising ExOPlanet Satellite (CHEOPS, Benz et al. 2021), launched on 18 December 2019, is a 30 cm telescope which is collecting ultra-high precision photometry of known exoplanets, aiming at their precise characterization. CHEOPS met its precision requirements both on bright and faint stars, achieving a noise level of ∼15 ppm per 6 h intervals for V ∼ 9 mag stars, and 75 ppm per 3 h for V ∼ 12 mag stars (Benz et al. 2021). The importance of such a high photometric precision is reflected in CHEOPS’ first scientific results, which span a variety of different fields (Lendl et al. 2020; Borsato et al. 2021; Delrez et al. 2021; Leleu et al. 2021; Maxted et al. 2021; Swayne et al. 2021; Szabó et al. 2021; Van Grootel et al. 2021; Morris et al. 2021a; Bonfanti et al. 2021b; Hooton et al. 2022; Barros et al. 2022; Deline et al. 2022; Wilson et al. 2022). As part of its main scientific goals, CHEOPS is refining the radii of known exoplanets to achieve the precision on the bulk density needed for internal structure and atmospheric evolution modelling. To fulfil this aim, radial velocity (RV) follow-ups using high-precision spectrographs are essential to provide the precise planetary masses that can be combined with radii measurements to determine accurate densities. Among the exoplanets having both radius and mass measurements, the ones in well-characterised multiplanetary systems are of particular interest, since they allow for investigation of their formation and evolution processes through comparative planetology, e.g. by comparing their individual inner bulk compositions (e.g. Guenther et al. 2017; Prieto-Arranz et al. 2018), by studying their mutual inclinations and eccentricities (e.g. Fabrycky et al. 2014; Van Eylen et al. 2019; Mills et al. 2019), and by investigating the correlations between their relative sizes, masses and orbital separations (e.g. Lissauer et al. 2011; Ciardi et al. 2013; Millholland, Wang & Laughlin 2017; Weiss et al. 2018; Adams et al. 2020; Jiang, Xie & Zhou 2020).
Within this context, TOI-561, announced simultaneously by Lacedelli et al. (2021) and Weiss et al. (2021) (L21 and W21 hereafter, respectively), is a particularly interesting system, both from the stellar (Section 2.1) and planetary (Section 2.2) perspective. The low stellar metallicity, the presence of an ultra-short period (USP) planet, where USP planets are meant here as planets with periods shorter than one day and radii smaller than 2 R⊕, and the complexity of its planetary configuration make TOI-561 an appealing target for in-depth investigations. In this study, we combine literature data with new TESS observations (Section 3.1), CHEOPS photometry (Section 3.2), and HARPS-N RVs (Section 3.3) to shed light on the planetary architecture and infer the internal structure of the transiting planets. After assessing the planetary configuration using CHEOPS observations (Section 4.1) and performing a thorough analysis of the global RV data set (Section 4.2), we jointly modelled the photometric and spectroscopic data to obtain the planetary parameters (Section 5). We used our derived stellar and planetary properties to model the internal structures of the transiting planets (Section 6) and their atmospheric evolution (Section 7), before discussing our results and presenting our conclusions (Section 8).
2 THE TOI-561 SYSTEM
2.1 The host star
TOI-561 is an old, metal-poor, thick disc star (L21, W21), slightly smaller and cooler than the Sun, located ∼84 pc away from the Solar System. We report the main astrophysical properties of the star in Table 1.
| TOI-561 . | ||
|---|---|---|
| TIC | 377064495 | |
| Gaia EDR3 | 3850421005290172416 | |
| 2MASS | J09524454+0612589 | |
| Parameter | Value | Source |
| RA (J2016; hh:mm:ss.ss) | 09:52:44.43 | A |
| Dec (J2016; dd:mm:ss.ss) | +06:12:57.94 | A |
| μα (mas yr−1) | −108.504 ± 0.022 | A |
| μδ (mas yr−1) | −61.279 ± 0.019 | A |
| γ (km s−1) | 79.54 ± 0.56 | A |
| Parallax (mas) | 11.8342 ± 0.0208 | A |
| Distance (pc) | 84.25 ± 0.12 | B |
| TESS (mag) | 9.527 ± 0.006 | C |
| G (mag) | 10.0181 ± 0.0028 | A |
| GBP (mag) | 10.3945 ± 0.0028 | A |
| GRP (mag) | 9.4692 ± 0.0038 | A |
| V (mag) | 10.252 ± 0.006 | C |
| B (mag) | 10.965 ± 0.082 | C |
| J (mag) | 8.879 ± 0.020 | D |
| H (mag) | 8.504 ± 0.055 | D |
| K (mag) | 8.394 ± 0.019 | D |
| W1 (mag) | 8.337 ± 0.023 | E |
| W2 (mag) | 8.396 ± 0.020 | E |
| Teff (K) | 5372 ± 70 | F |
| log g (cgs) | 4.50 ± 0.12 | F |
| [Fe/H] (dex) | −0.40 ± 0.05 | F |
| [Mg/H] (dex) | −0.17 ± 0.05 | F |
| [Si/H] (dex) | −0.22 ± 0.05 | F |
| [Ti/H] (dex) | −0.12 ± 0.03 | F |
| [α/Fe] (dex) | 0.23 ± 0.04 | F |
| [M/H] (dex) | −0.23 ± 0.06 | G |
| [Y/Mg] (dex) | −0.22 ± 0.07 | Ga |
| |$\log {\rm R}^{\prime }_{\rm HK}$| | −5.003 ± 0.012 | F |
| v sin i (km s−1) | <2 | F |
| R⋆ (R⊙) | 0.843 ± 0.005 | G, IRFM |
| M⋆ (M⊙) | 0.806 ± 0.036 | G, isochrones |
| t⋆ (Gyr) | |$11.0_{-3.5}^{+2.8}$| | G, isochrones |
| ρ⋆ (ρ⊙) | 1.34 ± 0.06 | G, from R⋆ and M⋆ |
| ρ⋆ (g cm−3) | 1.89 ± 0.09 | G, from R⋆ and M⋆ |
| L⋆ (L⊙) | 0.533 ± 0.029 | G, from R⋆ and Teff |
| Spectral type | G9V | F |
| TOI-561 . | ||
|---|---|---|
| TIC | 377064495 | |
| Gaia EDR3 | 3850421005290172416 | |
| 2MASS | J09524454+0612589 | |
| Parameter | Value | Source |
| RA (J2016; hh:mm:ss.ss) | 09:52:44.43 | A |
| Dec (J2016; dd:mm:ss.ss) | +06:12:57.94 | A |
| μα (mas yr−1) | −108.504 ± 0.022 | A |
| μδ (mas yr−1) | −61.279 ± 0.019 | A |
| γ (km s−1) | 79.54 ± 0.56 | A |
| Parallax (mas) | 11.8342 ± 0.0208 | A |
| Distance (pc) | 84.25 ± 0.12 | B |
| TESS (mag) | 9.527 ± 0.006 | C |
| G (mag) | 10.0181 ± 0.0028 | A |
| GBP (mag) | 10.3945 ± 0.0028 | A |
| GRP (mag) | 9.4692 ± 0.0038 | A |
| V (mag) | 10.252 ± 0.006 | C |
| B (mag) | 10.965 ± 0.082 | C |
| J (mag) | 8.879 ± 0.020 | D |
| H (mag) | 8.504 ± 0.055 | D |
| K (mag) | 8.394 ± 0.019 | D |
| W1 (mag) | 8.337 ± 0.023 | E |
| W2 (mag) | 8.396 ± 0.020 | E |
| Teff (K) | 5372 ± 70 | F |
| log g (cgs) | 4.50 ± 0.12 | F |
| [Fe/H] (dex) | −0.40 ± 0.05 | F |
| [Mg/H] (dex) | −0.17 ± 0.05 | F |
| [Si/H] (dex) | −0.22 ± 0.05 | F |
| [Ti/H] (dex) | −0.12 ± 0.03 | F |
| [α/Fe] (dex) | 0.23 ± 0.04 | F |
| [M/H] (dex) | −0.23 ± 0.06 | G |
| [Y/Mg] (dex) | −0.22 ± 0.07 | Ga |
| |$\log {\rm R}^{\prime }_{\rm HK}$| | −5.003 ± 0.012 | F |
| v sin i (km s−1) | <2 | F |
| R⋆ (R⊙) | 0.843 ± 0.005 | G, IRFM |
| M⋆ (M⊙) | 0.806 ± 0.036 | G, isochrones |
| t⋆ (Gyr) | |$11.0_{-3.5}^{+2.8}$| | G, isochrones |
| ρ⋆ (ρ⊙) | 1.34 ± 0.06 | G, from R⋆ and M⋆ |
| ρ⋆ (g cm−3) | 1.89 ± 0.09 | G, from R⋆ and M⋆ |
| L⋆ (L⊙) | 0.533 ± 0.029 | G, from R⋆ and Teff |
| Spectral type | G9V | F |
Notes. (A) Gaia EDR3 (Gaia Collaboration et al. 2021). (B) Bailer-Jones et al. (2021). (C) TESS Input Catalogue Version 8 (TICv8, Stassun et al. 2018). (D) Two Micron All Sky Survey (2MASS; Cutri et al. 2003). (E) Wide-field Infrared Survey Explorer (WISE; Wright et al. 2010). (F) L21. (G) This work.
a Based on W21 abundances.
| TOI-561 . | ||
|---|---|---|
| TIC | 377064495 | |
| Gaia EDR3 | 3850421005290172416 | |
| 2MASS | J09524454+0612589 | |
| Parameter | Value | Source |
| RA (J2016; hh:mm:ss.ss) | 09:52:44.43 | A |
| Dec (J2016; dd:mm:ss.ss) | +06:12:57.94 | A |
| μα (mas yr−1) | −108.504 ± 0.022 | A |
| μδ (mas yr−1) | −61.279 ± 0.019 | A |
| γ (km s−1) | 79.54 ± 0.56 | A |
| Parallax (mas) | 11.8342 ± 0.0208 | A |
| Distance (pc) | 84.25 ± 0.12 | B |
| TESS (mag) | 9.527 ± 0.006 | C |
| G (mag) | 10.0181 ± 0.0028 | A |
| GBP (mag) | 10.3945 ± 0.0028 | A |
| GRP (mag) | 9.4692 ± 0.0038 | A |
| V (mag) | 10.252 ± 0.006 | C |
| B (mag) | 10.965 ± 0.082 | C |
| J (mag) | 8.879 ± 0.020 | D |
| H (mag) | 8.504 ± 0.055 | D |
| K (mag) | 8.394 ± 0.019 | D |
| W1 (mag) | 8.337 ± 0.023 | E |
| W2 (mag) | 8.396 ± 0.020 | E |
| Teff (K) | 5372 ± 70 | F |
| log g (cgs) | 4.50 ± 0.12 | F |
| [Fe/H] (dex) | −0.40 ± 0.05 | F |
| [Mg/H] (dex) | −0.17 ± 0.05 | F |
| [Si/H] (dex) | −0.22 ± 0.05 | F |
| [Ti/H] (dex) | −0.12 ± 0.03 | F |
| [α/Fe] (dex) | 0.23 ± 0.04 | F |
| [M/H] (dex) | −0.23 ± 0.06 | G |
| [Y/Mg] (dex) | −0.22 ± 0.07 | Ga |
| |$\log {\rm R}^{\prime }_{\rm HK}$| | −5.003 ± 0.012 | F |
| v sin i (km s−1) | <2 | F |
| R⋆ (R⊙) | 0.843 ± 0.005 | G, IRFM |
| M⋆ (M⊙) | 0.806 ± 0.036 | G, isochrones |
| t⋆ (Gyr) | |$11.0_{-3.5}^{+2.8}$| | G, isochrones |
| ρ⋆ (ρ⊙) | 1.34 ± 0.06 | G, from R⋆ and M⋆ |
| ρ⋆ (g cm−3) | 1.89 ± 0.09 | G, from R⋆ and M⋆ |
| L⋆ (L⊙) | 0.533 ± 0.029 | G, from R⋆ and Teff |
| Spectral type | G9V | F |
| TOI-561 . | ||
|---|---|---|
| TIC | 377064495 | |
| Gaia EDR3 | 3850421005290172416 | |
| 2MASS | J09524454+0612589 | |
| Parameter | Value | Source |
| RA (J2016; hh:mm:ss.ss) | 09:52:44.43 | A |
| Dec (J2016; dd:mm:ss.ss) | +06:12:57.94 | A |
| μα (mas yr−1) | −108.504 ± 0.022 | A |
| μδ (mas yr−1) | −61.279 ± 0.019 | A |
| γ (km s−1) | 79.54 ± 0.56 | A |
| Parallax (mas) | 11.8342 ± 0.0208 | A |
| Distance (pc) | 84.25 ± 0.12 | B |
| TESS (mag) | 9.527 ± 0.006 | C |
| G (mag) | 10.0181 ± 0.0028 | A |
| GBP (mag) | 10.3945 ± 0.0028 | A |
| GRP (mag) | 9.4692 ± 0.0038 | A |
| V (mag) | 10.252 ± 0.006 | C |
| B (mag) | 10.965 ± 0.082 | C |
| J (mag) | 8.879 ± 0.020 | D |
| H (mag) | 8.504 ± 0.055 | D |
| K (mag) | 8.394 ± 0.019 | D |
| W1 (mag) | 8.337 ± 0.023 | E |
| W2 (mag) | 8.396 ± 0.020 | E |
| Teff (K) | 5372 ± 70 | F |
| log g (cgs) | 4.50 ± 0.12 | F |
| [Fe/H] (dex) | −0.40 ± 0.05 | F |
| [Mg/H] (dex) | −0.17 ± 0.05 | F |
| [Si/H] (dex) | −0.22 ± 0.05 | F |
| [Ti/H] (dex) | −0.12 ± 0.03 | F |
| [α/Fe] (dex) | 0.23 ± 0.04 | F |
| [M/H] (dex) | −0.23 ± 0.06 | G |
| [Y/Mg] (dex) | −0.22 ± 0.07 | Ga |
| |$\log {\rm R}^{\prime }_{\rm HK}$| | −5.003 ± 0.012 | F |
| v sin i (km s−1) | <2 | F |
| R⋆ (R⊙) | 0.843 ± 0.005 | G, IRFM |
| M⋆ (M⊙) | 0.806 ± 0.036 | G, isochrones |
| t⋆ (Gyr) | |$11.0_{-3.5}^{+2.8}$| | G, isochrones |
| ρ⋆ (ρ⊙) | 1.34 ± 0.06 | G, from R⋆ and M⋆ |
| ρ⋆ (g cm−3) | 1.89 ± 0.09 | G, from R⋆ and M⋆ |
| L⋆ (L⊙) | 0.533 ± 0.029 | G, from R⋆ and Teff |
| Spectral type | G9V | F |
Notes. (A) Gaia EDR3 (Gaia Collaboration et al. 2021). (B) Bailer-Jones et al. (2021). (C) TESS Input Catalogue Version 8 (TICv8, Stassun et al. 2018). (D) Two Micron All Sky Survey (2MASS; Cutri et al. 2003). (E) Wide-field Infrared Survey Explorer (WISE; Wright et al. 2010). (F) L21. (G) This work.
a Based on W21 abundances.
We adopted the spectroscopic parameters and stellar abundances from L21 (Table 1), which were derived exploiting the high SNR, high-resolution HARPS-N co-added spectrum (L21, Section 3.1) through an accurate analysis using three independent methods, namely the ares+moog equivalent width method (Sousa 2014; Mortier et al. 2014), the Stellar Parameter Classification (Buchhave et al. 2012, 2014) and the ccfpams method (Malavolta et al. 2017).
Taking advantage of the updated parameters coming from the Gaia EDR3 release (Gaia Collaboration et al. 2021), we then used the L21 spectral parameters as priors on spectral energy distribution selection to infer the stellar radius (R⋆) of TOI-561 using the infrared flux method (IRFM, Blackwell & Shallis 1977). The IRFM compares optical and infrared broad-band fluxes and synthetic photometry of stellar atmospheric models, and uses known relationships between stellar angular diameter, Teff and parallax to derive R⋆, in a MCMC fashion as detailed in Schanche et al. (2020). For this study, we retrieved from the most recent data releases the Gaia G, GBP, GRP (Gaia Collaboration et al. 2021), 2MASS J, H, K (Skrutskie et al. 2006), and WISE W1, W2 (Wright et al. 2010) broad-band photometric magnitudes, and we used the stellar atmospheric models from the atlas Catalogues (Castelli & Kurucz 2003) and the Gaia EDR3 parallax with the offset of Lindegren et al. (2021) applied, to obtain R⋆ =0.843 ± 0.005 R⊙.
We combined two different sets of stellar evolutionary tracks and isochrones, parsec2 (PAdova & TRieste Stellar Evolutionary Code, v1.2S; Marigo et al. 2017) and cles (Code Liègeois d’Évolution Stellaire, Scuflaire et al. 2008), to derive the stellar mass (M⋆) and age (t⋆) of TOI-561. As the star is significantly alpha-enhanced, we avoided using [Fe/H] as a proxy for the stellar metallicity; instead, we inserted both [Fe/H] and [α/Fe] in relation (3) provided by Yi et al. (2001), obtaining an overall scaling of metal abundances [M/H] = −0.23 ± 0.06. Besides [M/H], the main input parameters for computing M⋆ and t⋆ were Teff and R⋆. In addition, we used as inputs |$\log {\rm R}^{\prime }_{\rm HK}$| and the upper limit on v sin i from L21, and the yttrium over magnesium abundance [Y/Mg] = −0.22 ± 0.07, as computed from [Mg/H] and [Y/H] reported by W21. These indices improve the model convergence by discarding unlikely young isochrones, as broadly discussed in section 2.2.3 of Bonfanti & Gillon (2020), and references therein. The parsec results were obtained using the isochrone placement algorithm of Bonfanti et al. (2015), Bonfanti, Ortolani & Nascimbeni (2016), which retrieves the best-fit parameters by interpolating within a pre-computed grid of models, while the cles algorithm models directly the star through a Levenberg–Marquardt minimization (Salmon et al. 2021). The final adopted values (M⋆ = 0.806 ± 0.036 M⊙, |$t_{\star }=11.0_{-3.5}^{+2.8}$| Gyr) are a combination of the outputs from both sets of models, as described in detail in Bonfanti et al. (2021b). The derived mass and radius, listed in Table 1, are consistent within 1σ with the values reported in L21 (R⋆ = 0.849 ± 0.007 R⊙, M⋆ = 0.785 ± 0.018 M⊙).
2.2 The planetary system
The discovery of a multiplanetary system orbiting TOI-561 was announced simultaneously by L21 and W21 in two independent papers. The main planetary parameters from both studies are reported in Table 2.
| TOI-561 b . | Lacedelli et al. (2021) . | Weiss et al. (2021) . |
|---|---|---|
| P (d) | 0.446578 ± 0.000017 | |$0.446573^{+0.000032}_{-0.000021}$| |
| T0 (TBJD) | 1517.498 ± 0.001 | 1517.4973 ± 0.0018 |
| Rp (R⊕) | 1.423 ± 0.066 | 1.45 ± 0.11 |
| K (m s−1) | 1.56 ± 0.35 | 3.1 ± 0.8 |
| Mp (M⊕) | 1.59 ± 0.36 | 3.2 ± 0.8 |
| TOI-561 c | ||
| P (d) | 10.779 ± 0.004 | 10.77892 ± 0.00015 |
| T0 (TBJD) | 1527.060 ± 0.004 | 1527.05825 ± 0.00053 |
| Rp (R⊕) | 2.878 ± 0.096 | 2.90 ± 0.13 |
| K (m s−1) | 1.84 ± 0.33 | 2.4 ± 0.8 |
| Mp (M⊕) | 5.40 ± 0.98 | 7.0 ± 2.3 |
| TOI-561 d | ||
| P (d) | 25.62 ± 0.04 | – |
| T0 (TBJD) | 1521.882 ± 0.004 | – |
| Rp (R⊕) | 2.53 ± 0.13 | – |
| K (m s−1) | 3.06 ± 0.33 | – |
| Mp (M⊕) | 11.95 ± 1.28 | – |
| TOI-561 e | ||
| P (d) | 77.23 ± 0.39 | – |
| T0 (TBJD) | 8538.181 ± 0.004 | – |
| Rp (R⊕) | 2.67 ± 0.11 | – |
| K (m s−1) | 2.84 ± 0.41 | – |
| Mp (M⊕) | 16.0 ± 2.3 | – |
| TOI-561 f|$\, ^a$| | ||
| P (d) | – | 16.287 ± 0.005 |
| T0 (TBJD) | – | 1521.8828 ± 0.0035 |
| Rp (R⊕) | – | 2.32 ± 0.16 |
| K (m s−1) | – | 0.9 ± 0.6 |
| Mp (M⊕) | – | |$3.0^{+2.4}_{-1.9}$| |
| M⋆ (M⊙) | 0.785 ± 0.018 | 0.805 ± 0.030 |
| TOI-561 b . | Lacedelli et al. (2021) . | Weiss et al. (2021) . |
|---|---|---|
| P (d) | 0.446578 ± 0.000017 | |$0.446573^{+0.000032}_{-0.000021}$| |
| T0 (TBJD) | 1517.498 ± 0.001 | 1517.4973 ± 0.0018 |
| Rp (R⊕) | 1.423 ± 0.066 | 1.45 ± 0.11 |
| K (m s−1) | 1.56 ± 0.35 | 3.1 ± 0.8 |
| Mp (M⊕) | 1.59 ± 0.36 | 3.2 ± 0.8 |
| TOI-561 c | ||
| P (d) | 10.779 ± 0.004 | 10.77892 ± 0.00015 |
| T0 (TBJD) | 1527.060 ± 0.004 | 1527.05825 ± 0.00053 |
| Rp (R⊕) | 2.878 ± 0.096 | 2.90 ± 0.13 |
| K (m s−1) | 1.84 ± 0.33 | 2.4 ± 0.8 |
| Mp (M⊕) | 5.40 ± 0.98 | 7.0 ± 2.3 |
| TOI-561 d | ||
| P (d) | 25.62 ± 0.04 | – |
| T0 (TBJD) | 1521.882 ± 0.004 | – |
| Rp (R⊕) | 2.53 ± 0.13 | – |
| K (m s−1) | 3.06 ± 0.33 | – |
| Mp (M⊕) | 11.95 ± 1.28 | – |
| TOI-561 e | ||
| P (d) | 77.23 ± 0.39 | – |
| T0 (TBJD) | 8538.181 ± 0.004 | – |
| Rp (R⊕) | 2.67 ± 0.11 | – |
| K (m s−1) | 2.84 ± 0.41 | – |
| Mp (M⊕) | 16.0 ± 2.3 | – |
| TOI-561 f|$\, ^a$| | ||
| P (d) | – | 16.287 ± 0.005 |
| T0 (TBJD) | – | 1521.8828 ± 0.0035 |
| Rp (R⊕) | – | 2.32 ± 0.16 |
| K (m s−1) | – | 0.9 ± 0.6 |
| Mp (M⊕) | – | |$3.0^{+2.4}_{-1.9}$| |
| M⋆ (M⊙) | 0.785 ± 0.018 | 0.805 ± 0.030 |
aReferred as TOI-561 d in W21.
| TOI-561 b . | Lacedelli et al. (2021) . | Weiss et al. (2021) . |
|---|---|---|
| P (d) | 0.446578 ± 0.000017 | |$0.446573^{+0.000032}_{-0.000021}$| |
| T0 (TBJD) | 1517.498 ± 0.001 | 1517.4973 ± 0.0018 |
| Rp (R⊕) | 1.423 ± 0.066 | 1.45 ± 0.11 |
| K (m s−1) | 1.56 ± 0.35 | 3.1 ± 0.8 |
| Mp (M⊕) | 1.59 ± 0.36 | 3.2 ± 0.8 |
| TOI-561 c | ||
| P (d) | 10.779 ± 0.004 | 10.77892 ± 0.00015 |
| T0 (TBJD) | 1527.060 ± 0.004 | 1527.05825 ± 0.00053 |
| Rp (R⊕) | 2.878 ± 0.096 | 2.90 ± 0.13 |
| K (m s−1) | 1.84 ± 0.33 | 2.4 ± 0.8 |
| Mp (M⊕) | 5.40 ± 0.98 | 7.0 ± 2.3 |
| TOI-561 d | ||
| P (d) | 25.62 ± 0.04 | – |
| T0 (TBJD) | 1521.882 ± 0.004 | – |
| Rp (R⊕) | 2.53 ± 0.13 | – |
| K (m s−1) | 3.06 ± 0.33 | – |
| Mp (M⊕) | 11.95 ± 1.28 | – |
| TOI-561 e | ||
| P (d) | 77.23 ± 0.39 | – |
| T0 (TBJD) | 8538.181 ± 0.004 | – |
| Rp (R⊕) | 2.67 ± 0.11 | – |
| K (m s−1) | 2.84 ± 0.41 | – |
| Mp (M⊕) | 16.0 ± 2.3 | – |
| TOI-561 f|$\, ^a$| | ||
| P (d) | – | 16.287 ± 0.005 |
| T0 (TBJD) | – | 1521.8828 ± 0.0035 |
| Rp (R⊕) | – | 2.32 ± 0.16 |
| K (m s−1) | – | 0.9 ± 0.6 |
| Mp (M⊕) | – | |$3.0^{+2.4}_{-1.9}$| |
| M⋆ (M⊙) | 0.785 ± 0.018 | 0.805 ± 0.030 |
| TOI-561 b . | Lacedelli et al. (2021) . | Weiss et al. (2021) . |
|---|---|---|
| P (d) | 0.446578 ± 0.000017 | |$0.446573^{+0.000032}_{-0.000021}$| |
| T0 (TBJD) | 1517.498 ± 0.001 | 1517.4973 ± 0.0018 |
| Rp (R⊕) | 1.423 ± 0.066 | 1.45 ± 0.11 |
| K (m s−1) | 1.56 ± 0.35 | 3.1 ± 0.8 |
| Mp (M⊕) | 1.59 ± 0.36 | 3.2 ± 0.8 |
| TOI-561 c | ||
| P (d) | 10.779 ± 0.004 | 10.77892 ± 0.00015 |
| T0 (TBJD) | 1527.060 ± 0.004 | 1527.05825 ± 0.00053 |
| Rp (R⊕) | 2.878 ± 0.096 | 2.90 ± 0.13 |
| K (m s−1) | 1.84 ± 0.33 | 2.4 ± 0.8 |
| Mp (M⊕) | 5.40 ± 0.98 | 7.0 ± 2.3 |
| TOI-561 d | ||
| P (d) | 25.62 ± 0.04 | – |
| T0 (TBJD) | 1521.882 ± 0.004 | – |
| Rp (R⊕) | 2.53 ± 0.13 | – |
| K (m s−1) | 3.06 ± 0.33 | – |
| Mp (M⊕) | 11.95 ± 1.28 | – |
| TOI-561 e | ||
| P (d) | 77.23 ± 0.39 | – |
| T0 (TBJD) | 8538.181 ± 0.004 | – |
| Rp (R⊕) | 2.67 ± 0.11 | – |
| K (m s−1) | 2.84 ± 0.41 | – |
| Mp (M⊕) | 16.0 ± 2.3 | – |
| TOI-561 f|$\, ^a$| | ||
| P (d) | – | 16.287 ± 0.005 |
| T0 (TBJD) | – | 1521.8828 ± 0.0035 |
| Rp (R⊕) | – | 2.32 ± 0.16 |
| K (m s−1) | – | 0.9 ± 0.6 |
| Mp (M⊕) | – | |$3.0^{+2.4}_{-1.9}$| |
| M⋆ (M⊙) | 0.785 ± 0.018 | 0.805 ± 0.030 |
aReferred as TOI-561 d in W21.
The two papers presented different RV data sets, collected with HARPS-N and HIRES, respectively, to confirm the planetary nature of three candidates identified by TESS in sector 8, the only available sector at the time of the publications. The TESS-identified signals had periods of ∼0.45, ∼10.8, and ∼16 d. The two inner candidates were confirmed by both L21 and W21, with the names of TOI-561 b (an USP super-Earth, with period Pb ∼ 0.4465 d, and radius Rb ∼ 1.4 R⊕) and TOI-561 c (a warm mini-Neptune, with Pc ∼ 10.779 d, and Rc ∼ 2.9 R⊕). However, two different interpretations for the third TESS signal were proposed by the authors. In the scenario presented in L21, the two transits related to the third TESS signal were interpreted as single transits of two distinct planets, TOI-561 d (Pd ∼ 25.6 d, Rd ∼ 2.5 R⊕), and TOI-561 e (Pe ∼ 77 d, Re ∼ 2.7 R⊕). The periods of these two planets were inferred from the RV analysis, which played an essential role in determining the final planetary architecture. In fact, the ephemeris match between the RV and photometric fits (see fig. 5 of L21) and the non-detection of the 16 d signal in the HARPS-N data set, combined with the different durations of the two TESS transits and results from the long-term stability analysis led the authors to converge on a four-planet configuration, presenting robust mass and radius detection for all the four planets in the system (L21, table 5). In contrast, W21 proposed the presence of a single planet at the period suggested by TESS (TOI-561 f, Pf ∼ 16.29 d, Rf ∼ 2.3 R⊕), based on the analysis of the two available transits. W21 pointed out that the 8.1 d alias of planet f’s orbital period is also consistent with the TESS data, with the even transit falling into the TESS download gap, even though in this case the transit duration would be too long compared to what is expected for a 8 d period planet (Section 4.9, W21). However, the authors could not obtain an accurate mass determination for this planet, with the 60 HIRES RVs being consistent with a non-detection (Section 7.2, W21). An additional discrepancy between the two studies is the mass of the USP planet, differing by almost a factor of 2. According to the W21 analysis, TOI-561 b has a mass of 3.2 ± 0.8 M⊕, making it consistent with a rocky composition and placing it among the population of typical small (<2 R⊕), extremely irradiated USP planets (Sanchis-Ojeda et al. 2015; Dai et al. 2021). Instead, assuming the low mass (Mb = 1.59 ± 0.36 M⊕) inferred from L21 analysis, TOI-561 b is not consistent with a pure rocky composition, and it is the lowest density USP super-Earth known to date, calling for a more complex interpretation (e.g. lighter core composition, deep water reservoirs, presence of a high-metallicity, volatile materials or water steam envelope, etc.).
The complexity of this system and the differences between the two studies demanded further investigations. We therefore decided to collect additional, precise photometric and RV data (Section 3) to shed light on the planetary configuration and on the internal composition of the TOI-561 planets.
3 OBSERVATIONS
3.1 TESS photometry
During its two-year primary mission (Ricker et al. 2014), TESS observed TOI-561 in two-minute cadence mode between 2019 February 2 and February 27 (sector 8). After entering its extended mission, TESS re-observed the star in 2-min cadence mode during sector 35, between 2021 February 9 and March 6. At the beginning of the second orbit, the spacecraft dropped out of Fine Pointing mode for 3.44 d, entering Coarse Pointing mode.3 Data collected during Coarse Pointing mode were flagged and removed from the Pre-search Data Conditioning Simple Aperture Photometry (PDCSAP; Smith et al. 2012; Stumpe et al. 2012, 2014) light curves, leading to a total of 19.86 d of science data. The photometric observations of TOI-561 were reduced by the Science Processing Operations Center (SPOC) pipeline and searched for evidence of transiting planets (Jenkins et al. 2016; Jenkins 2020). For our photometric analysis, we used the light curves based on the PDCSAP, downloading the 2-min cadence data from the Mikulski Archive for Space Telescopes (MAST),4 and removing all the observations encoded as NaN or flagged as bad-quality (DQUALITY>0) points by the SPOC pipeline.5 We performed outlier rejection by doing a cut at 3σ for positive outliers and 5σ (i.e. larger than the deepest transit) for negative outliers. The resulting TESS light curves of sectors 8 and 35 are shown in Fig. 1, and Table 3 summarizes the total number of transits observed by TESS for each planet.
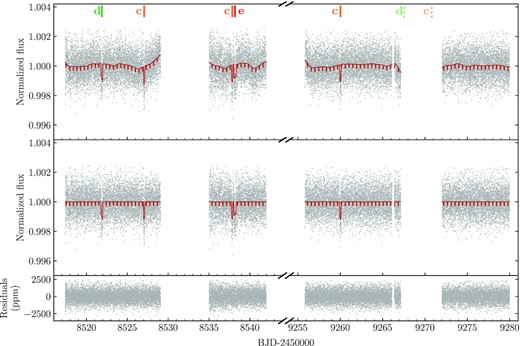
TESS sector 8 (left) and 35 (right) PDCSAP light curves of TOI-561. In the top panel, the dark red solid line shows the best-fitting transit and Matérn-3/2 kernel Gaussian Process (GP) model, as detailed in Section 5. The central panel shows the flattened light curve after the removal of the GP component, with the best-fitting transit model superimposed (dark red solid line). The transits of planets c, d, and e are labelled and highlighted with orange, green, and red vertical lines, respectively. The expected locations of the transits of planets c and d occurring during the data gaps of sector 35 are marked with pale, dashed orange and green lines, respectively. Planet e is not expected to transit in sector 35. The transits of the USP planet are too shallow to be individually visible and are not indicated. Light-curve residuals are shown in the bottom panel.
| . | TOI-561 b . | TOI-561 c . | TOI-561 d . | TOI-561 e . |
|---|---|---|---|---|
| Sector 8 | 41 | 2 | 1 | 1 |
| Sector 35 | 43 | 1 | – | – |
| . | TOI-561 b . | TOI-561 c . | TOI-561 d . | TOI-561 e . |
|---|---|---|---|---|
| Sector 8 | 41 | 2 | 1 | 1 |
| Sector 35 | 43 | 1 | – | – |
| . | TOI-561 b . | TOI-561 c . | TOI-561 d . | TOI-561 e . |
|---|---|---|---|---|
| Sector 8 | 41 | 2 | 1 | 1 |
| Sector 35 | 43 | 1 | – | – |
| . | TOI-561 b . | TOI-561 c . | TOI-561 d . | TOI-561 e . |
|---|---|---|---|---|
| Sector 8 | 41 | 2 | 1 | 1 |
| Sector 35 | 43 | 1 | – | – |
To refine the ephemeris of planet d in time for the scheduling of the CHEOPS observations (Section 4.1), we also extracted the 10-min cadence light curve of sector 35 using the quick-look TESS Full Frame Images (FFIs) calibrated using the TESS Image CAlibrator6 package (tica, Fausnaugh et al. 2020).
3.2 CHEOPS photometry
To confirm the planetary architecture and improve the planetary parameters, we obtained three visits of TOI-561 with CHEOPS, the ESA small class mission dedicated to the characterization of known exoplanets (Benz et al. 2021). The observations, collected within the Guaranteed Time Observing (GTO) programme, were carried out between 2021 January 23 and April 15, for a total of 73.85 h on target. During the three visits, we observed a total of eight transits of TOI-561 b, two transits of TOI-561 c, and one transit of TOI-561 d. The three CHEOPS light curves have an observing efficiency, i.e. the actual time spent observing the target with respect to the total visit duration, of 64 per cent, 75 per cent, and 61 per cent, respectively. The observing efficiency is linked to data gaps, which are intrinsically present in all CHEOPS light curves (see e.g. Bonfanti et al. 2021b; Delrez et al. 2021; Leleu et al. 2021), and are related to CHEOPS’s low-Earth orbit. In fact, during (1) South Atlantic Anomaly (SAA) crossing, (2) target occultation by the Earth, and (3) too high stray light contamination, no data are downlinked. This results in data gaps, whose number and extension depend on the target sky position (Benz et al. 2021). For all the visits, we adopted an exposure time of 60 s. The summary log of the CHEOPS observations is reported in Table 4.
| Visit . | File key . | Starting date . | Duration . | Data points . | Efficiency . | Exposure time . | Planets . |
|---|---|---|---|---|---|---|---|
| (No.) . | . | (UTC) . | (h) . | (No.) . | (Per cent) . | (s) . | . |
| 1 | CH_PR100031_TG037001_V0200 | 2021-01-23T15:29:07 | 15.67 | 604 | 64 | 60 | b,c |
| 2 | CH_PR100008_TG000811_V0200 | 2021-03-29T10:19:08 | 4.42 | 207 | 75 | 60 | b,c |
| 3 | CH_PR100031_TG039301_V0200 | 2021-04-12T23:52:28 | 53.76 | 1978 | 61 | 60 | b,d |
| Visit . | File key . | Starting date . | Duration . | Data points . | Efficiency . | Exposure time . | Planets . |
|---|---|---|---|---|---|---|---|
| (No.) . | . | (UTC) . | (h) . | (No.) . | (Per cent) . | (s) . | . |
| 1 | CH_PR100031_TG037001_V0200 | 2021-01-23T15:29:07 | 15.67 | 604 | 64 | 60 | b,c |
| 2 | CH_PR100008_TG000811_V0200 | 2021-03-29T10:19:08 | 4.42 | 207 | 75 | 60 | b,c |
| 3 | CH_PR100031_TG039301_V0200 | 2021-04-12T23:52:28 | 53.76 | 1978 | 61 | 60 | b,d |
| Visit . | File key . | Starting date . | Duration . | Data points . | Efficiency . | Exposure time . | Planets . |
|---|---|---|---|---|---|---|---|
| (No.) . | . | (UTC) . | (h) . | (No.) . | (Per cent) . | (s) . | . |
| 1 | CH_PR100031_TG037001_V0200 | 2021-01-23T15:29:07 | 15.67 | 604 | 64 | 60 | b,c |
| 2 | CH_PR100008_TG000811_V0200 | 2021-03-29T10:19:08 | 4.42 | 207 | 75 | 60 | b,c |
| 3 | CH_PR100031_TG039301_V0200 | 2021-04-12T23:52:28 | 53.76 | 1978 | 61 | 60 | b,d |
| Visit . | File key . | Starting date . | Duration . | Data points . | Efficiency . | Exposure time . | Planets . |
|---|---|---|---|---|---|---|---|
| (No.) . | . | (UTC) . | (h) . | (No.) . | (Per cent) . | (s) . | . |
| 1 | CH_PR100031_TG037001_V0200 | 2021-01-23T15:29:07 | 15.67 | 604 | 64 | 60 | b,c |
| 2 | CH_PR100008_TG000811_V0200 | 2021-03-29T10:19:08 | 4.42 | 207 | 75 | 60 | b,c |
| 3 | CH_PR100031_TG039301_V0200 | 2021-04-12T23:52:28 | 53.76 | 1978 | 61 | 60 | b,d |
Data were reduced using the latest version of the CHEOPS automatic Data Reduction Pipeline (drp v13; Hoyer et al. 2020), which performs aperture photometry of the target after calibrating the raw images (event flagging, bias, gain, non-linearity, dark current, and flat-field) and correcting them for instrumental and environmental effects (smearing trails, cosmic rays, de-pointing, stray light, and background). The target flux is obtained for a set of three fixed-radius apertures, namely R = 22.5 arcsec (RINF), 25.0 arcsec (DEFAULT), 30.0 arcsec (RSUP), plus an additional one specifically computed to optimize the radius based on the instrumental noise and contamination level of each target (OPTIMAL). Moreover, the drp estimates the contamination in the photometric aperture due to nearby targets using the sources listed in the Gaia DR2 catalogue (Gaia Collaboration et al. 2018) to simulate the CHEOPS Field-of-View (FoV) of the target, as described in detail in Hoyer et al. (2020). No strong contaminants are present in the TOI-561 FoV, and the main contribution to the contamination is due to the smearing trails of a G = 10.20 mag star at a projected sky distance of ∼117.9 arcsec, which rotates around the target inside the CCD window because of the CHEOPS field rotation (Benz et al. 2021). During the third visit three telegraphic pixels (pixels with a non-stable and abnormal behaviour during the visit) appeared within the CHEOPS aperture, one of them inside the CHEOPS PSF (Fig. 2). A careful treatment, described in detail in Appendix A, was applied to correct for their effect. In the subsequent analysis, we adopted for all the visits the RINF photometry (see Fig. A1 in Appendix A), which minimized the light-curve root mean square (RMS) dispersion, and we removed the outliers by applying a 4σ clipping.

Extraction of 60 × 60 arcsec of the CHEOPS FoV during the third visit centred on TOI-561. The dashed black circle represents the RINF photometric aperture surrounding the CHEOPS PSF, whose centroid is marked by the black cross. The positions of the three identified telegraphic pixels, including the one located within the CHEOPS PSF (see Appendix A), are highlighted by the red, circled crosses.
Finally, a variety of non-astrophysical sources, such as varying background, nearby contaminants or others, can produce short-term photometric trends in the CHEOPS light curves on the timescale of one orbit, due to the rotation of the CHEOPS FoV around the target and due to the nature of the spacecraft orbit. To correct for these effects, we detrended the light curves using the basis vectors provided by the drp, as detailed in Section 5. The resulting detrended light curves are shown in Fig. 3.
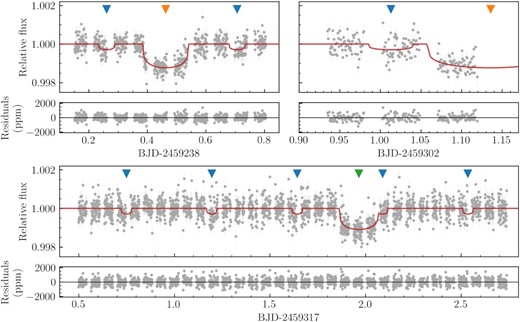
CHEOPS detrended light curves of TOI-561. Visits 1, 2, and 3 are shown in the top left, top right, and bottom panel, respectively. The best-fitting model is over-plotted as a red solid line, and residuals are shown for each visit. The transits of planets b, c, and d are highlighted with blue, orange, and green triangles, respectively.
3.3 HARPS-N spectroscopy
In addition to the 82 RVs published in L21, we collected 62 high-resolution spectra using HARPS-N at the Telescopio Nazionale Galileo (TNG) in La Palma (Cosentino et al. 2012, 2014). These were used to refine the planetary masses and confirm the system configuration. The new observations were collected between 2020 November 15 and 2021 June 1. Following the same strategy of the previous season (L21), in addition to 30 single observations, we collected six points per night on 2021 February 8 and 10, and two points per night on ten additional nights, specifically targeting the USP planet. The exposure time for all the observations was set to 1800 s, resulting in a signal-to-noise ratio (SNR) at 550 nm of 83 ± 20 (median ± standard deviation) and a RV measurement uncertainty of 1.0 ± 0.4 m s−1. All the observations were gathered with the second HARPS-N fibre illuminated by the Fabry-Perot calibration lamp to correct for the instrumental RV drift.
We reduced the global HARPS-N data set (144 RVs in total) using the new version of the HARPS-N Data Reduction Software based on the ESPRESSO pipeline (drs, version 2.3.1; see Dumusque et al. 2021 for more details). We used a G2 flux template to correct for variations in the flux distribution as a function of wavelength, and a G2 binary mask to compute the cross-correlation function (CCF; Baranne et al. 1996; Pepe et al. 2002). We report the RVs and the associated activity indices (see Section 4.2) with their 1σ uncertainties in Table 5. As in L21, we removed from the first season data set five RVs with associated errors >2.5 m s−1 from spectra with SNR <35 (see Appendix B in L21). All the RV uncertainties of the second season data set were below 2.5 m s−1, so no points were removed.
| BJDTDB . | RV . | σRV . | FWHM . | σFWHM . | BIS . | σBIS . | Contrast . | σcontr . | S-index . | σS . | Hα . | σHα . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (d) . | (m s−1) . | (m s−1) . | (km s−1) . | (km s−1) . | (m s−1) . | (m s−1) . | . | . | . | . | (dex) . | (dex) . |
| 2458804.70780 | 79695.97 | 1.13 | 6.415 | 0.002 | −86.82 | 2.26 | 59.879 | 0.021 | 0.1643 | 0.0005 | 0.2101 | 0.0002 |
| 2458805.77552 | 79699.66 | 0.85 | 6.419 | 0.002 | −85.13 | 1.71 | 59.810 | 0.016 | 0.1702 | 0.0003 | 0.2124 | 0.0001 |
| 2458806.76769 | 79697.50 | 0.91 | 6.415 | 0.002 | −83.66 | 1.82 | 59.861 | 0.017 | 0.1689 | 0.0003 | 0.2082 | 0.0001 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| BJDTDB . | RV . | σRV . | FWHM . | σFWHM . | BIS . | σBIS . | Contrast . | σcontr . | S-index . | σS . | Hα . | σHα . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (d) . | (m s−1) . | (m s−1) . | (km s−1) . | (km s−1) . | (m s−1) . | (m s−1) . | . | . | . | . | (dex) . | (dex) . |
| 2458804.70780 | 79695.97 | 1.13 | 6.415 | 0.002 | −86.82 | 2.26 | 59.879 | 0.021 | 0.1643 | 0.0005 | 0.2101 | 0.0002 |
| 2458805.77552 | 79699.66 | 0.85 | 6.419 | 0.002 | −85.13 | 1.71 | 59.810 | 0.016 | 0.1702 | 0.0003 | 0.2124 | 0.0001 |
| 2458806.76769 | 79697.50 | 0.91 | 6.415 | 0.002 | −83.66 | 1.82 | 59.861 | 0.017 | 0.1689 | 0.0003 | 0.2082 | 0.0001 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
Note. This table is available in its entirety in machine-readable form.
| BJDTDB . | RV . | σRV . | FWHM . | σFWHM . | BIS . | σBIS . | Contrast . | σcontr . | S-index . | σS . | Hα . | σHα . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (d) . | (m s−1) . | (m s−1) . | (km s−1) . | (km s−1) . | (m s−1) . | (m s−1) . | . | . | . | . | (dex) . | (dex) . |
| 2458804.70780 | 79695.97 | 1.13 | 6.415 | 0.002 | −86.82 | 2.26 | 59.879 | 0.021 | 0.1643 | 0.0005 | 0.2101 | 0.0002 |
| 2458805.77552 | 79699.66 | 0.85 | 6.419 | 0.002 | −85.13 | 1.71 | 59.810 | 0.016 | 0.1702 | 0.0003 | 0.2124 | 0.0001 |
| 2458806.76769 | 79697.50 | 0.91 | 6.415 | 0.002 | −83.66 | 1.82 | 59.861 | 0.017 | 0.1689 | 0.0003 | 0.2082 | 0.0001 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| BJDTDB . | RV . | σRV . | FWHM . | σFWHM . | BIS . | σBIS . | Contrast . | σcontr . | S-index . | σS . | Hα . | σHα . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (d) . | (m s−1) . | (m s−1) . | (km s−1) . | (km s−1) . | (m s−1) . | (m s−1) . | . | . | . | . | (dex) . | (dex) . |
| 2458804.70780 | 79695.97 | 1.13 | 6.415 | 0.002 | −86.82 | 2.26 | 59.879 | 0.021 | 0.1643 | 0.0005 | 0.2101 | 0.0002 |
| 2458805.77552 | 79699.66 | 0.85 | 6.419 | 0.002 | −85.13 | 1.71 | 59.810 | 0.016 | 0.1702 | 0.0003 | 0.2124 | 0.0001 |
| 2458806.76769 | 79697.50 | 0.91 | 6.415 | 0.002 | −83.66 | 1.82 | 59.861 | 0.017 | 0.1689 | 0.0003 | 0.2082 | 0.0001 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
Note. This table is available in its entirety in machine-readable form.
3.4 HIRES spectroscopy
We included in our analysis 60 high-resolution spectra collected with the W.M. Keck Observatory HIRES instrument on Mauna Kea, Hawaii between 2019 May and 2020 October. The data set was published in W21, and we refer to that paper for details regarding the observing and data reduction procedures. The HIRES data set has an RMS of 5 m s−1, and a median individual RV uncertainty of 1.4 m s−1 (W21).
4 PROBING THE SYSTEM ARCHITECTURE
4.1 CHEOPS confirmation of TOI-561 d
To solve the discrepancy among the planetary architectures proposed by L21 and W21 (Section 2.2), we initially looked for the transits of TOI-561 d (∼25 d) and TOI-561 f (∼16 d) in the TESS sector 35 light curve, whereas TOI-561 e (∼77 d) was not expected to transit during those TESS observations. However, as shown in the top panel of Fig. 4, the transits of planet d and f occurred during the light curve gap (Section 3.1), and so we could not use the new TESS data to conclusively discriminate between the two planetary configurations. None the less, these observations ruled out the planet f alias at ∼8.1 d mentioned in W21, since no transit events were detected at its predicted transit times.
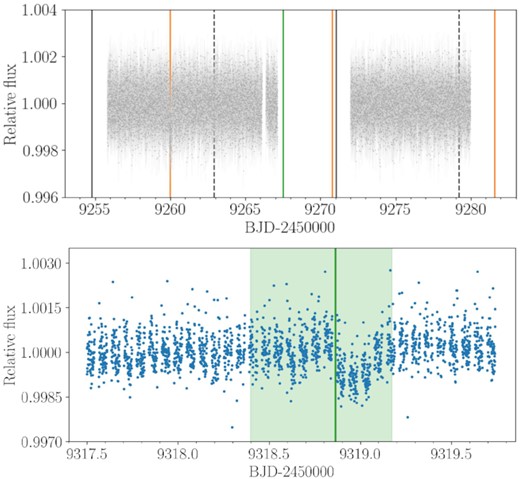
Top: 2-min cadence detrended TESS light curve of sector 35. The predicted transit times of TOI-561 c and d (according to L21 ephemeris), and TOI-561 f (according to W21 ephemeris), are highlighted with orange, green and black vertical solid lines, respectively. The black dashed lines indicate the predicted position of planet f alias at ∼8.1 d. The only transit present in the light curve is the one of TOI-561 c at ∼9260 BJD−2450000, while no transit events occurred at the predicted times of planet f alias. The transits of planet d and f fall into the time-series gap. Bottom: CHEOPS visit scheduled to observe TOI-561 d. The green vertical solid line indicates the predicted transit time used to compute the CHEOPS observing window after the ephemeris update (Section 4.1). The transit occurred within the 68 per cent highest probability density interval, highlighted by the pale green region. We note that this transit is not consistent with the ephemeris propagation of planet f, which would have transited at 9319.94 BJD−2450000, so almost one day after the observed CHEOPS transit.
We therefore decided to probe the L21 scenario collecting a transit of TOI-561 d using CHEOPS. We opted for the scheduling of the last seasonal observing window, in April, in order to take advantage of the most updated ephemeris to optimize the scheduling. For this reason, we performed a global fit adding to the literature data a partial set of the new HARPS-N RVs, as of 2021 March 16, and including the TESS sector 35 light curve extracted from the second data release of the tica FFIs in 2021 March. Even if no transit was detected, the new TESS sector helped to reduce the time window in which to search. In fact, the TESS data partially covered the 3σ-uncertainty transit window, enabling us to exclude some time-spans in the computation of the CHEOPS visit. Thanks to the ephemeris update, the CHEOPS 3σ observing window shrank from ∼7.4 to ∼2.2 d, demonstrating the importance of the early TESS data releases in the scheduling of follow-up observations. The bottom panel of Fig. 4 shows the CHEOPS visit scheduled to observe TOI-561 d, whose transit occurred almost exactly at the predicted time, so confirming the planetary period and giving further credence to the four-planet scenario proposed by L21.
Even updating the ephemeris using the partial new HARPS-N data set, the last possible CHEOPS observing window of TOI-561 e in the 2021 season was still longer than seven days because of ephemeris uncertainties. Even including the full set of RVs would have not helped as the target was no longer observable with CHEOPS when the HARPS-N campaign finished. Given the high pressure on the CHEOPS schedule, we therefore plan the TOI-561 e observations for the 2022 observing season. The ephemeris for the 2022 CHEOPS observations will be updated using the TESS Sectors 45 and 46 observations in November–December 2021, and the results will be presented in a future publication.
4.2 Additional signals in the RV data
Before proceeding with the global modelling, we analysed the RV data sets in order to confirm the robustness of the L21 scenario and search for potential new signals. The ℓ1-periodogram7 (Hara et al. 2017) of the combined HARPS-N and HIRES RVs (Fig. 5) shows four significant peaks corresponding to the planetary periods reported in L21, plus hints of a possible longer period signal with a broad peak around 400–600 d. We investigated the presence of this additional signal in a Bayesian framework using pyorbit8 (Malavolta et al. 2016, 2018), a package for light curve and RVs analysis. We employed the dynesty nested-sampling algorithm (Skilling 2004, 2006; Speagle 2020), assuming 1000 live points, and including offset and jitter terms for each data set. We first performed a four-planet fit of the combined data sets, using the L21 values to impose Gaussian priors on periods and transit times,9 and assuming eccentric orbits with a half-Gaussian zero-mean prior on the eccentricity (with variance 0.098; Van Eylen et al. 2019), except for the circular orbit of the USP planet. We let the semi-amplitude K vary between 0.01 and 100 m s−1. As can be seen in Fig. 6, the RV residuals show an anomalous positive variation at ∼9000 BJD-2450000, and the Generalized Lomb-Scargle (GLS, Zechmeister & Kürster 2009) periodogram of the RV residuals revealed the presence of a significant, broad peak at low frequencies. Moreover, the HARPS-N jitter was 1.84 m s−1, which is unusually high when compared to the value reported in L21 (σHARPS-N = 1.29 ± 0.23 m s−1). We therefore performed a second fit including a fifth Keplerian signal, allowing the period to span between 2 and 900 d. According to the Bayesian Evidence, this model is strongly favoured with respect to the four-planet model, with a difference in the logarithmic evidences |$\Delta \ln \mathcal {Z} = 19.0$| (Kass & Raftery 1995).10 Moreover, the HARPS-N jitter decreased to ∼1.37 m s−1. After this fit, the periodogram of the residuals did not show evidence of additional significant peaks (Fig. 6). This is confirmed also by the comparison with a six-Keplerian model that we tested, with the period of the sixth Keplerian free to span between 2 and 900 d, whose Bayesian Evidence differed by less than two from the five-Keplerian model one, indicating that there was no strong evidence to favour a more complex model (Kass & Raftery 1995).
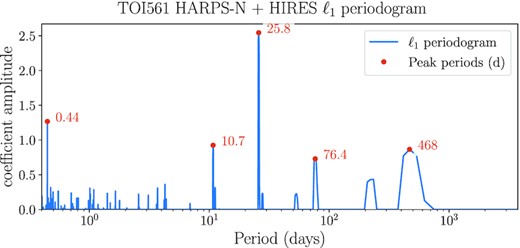
ℓ1-periodogram of the combined HARPS-N and HIRES data sets, computed on a grid of frequencies from 0 to 2.5 cycles per day. The total time-span of the observations is 768 d. The code automatically accounts for the offset between HARPS-N and HIRES data by using the mean value of each data set.
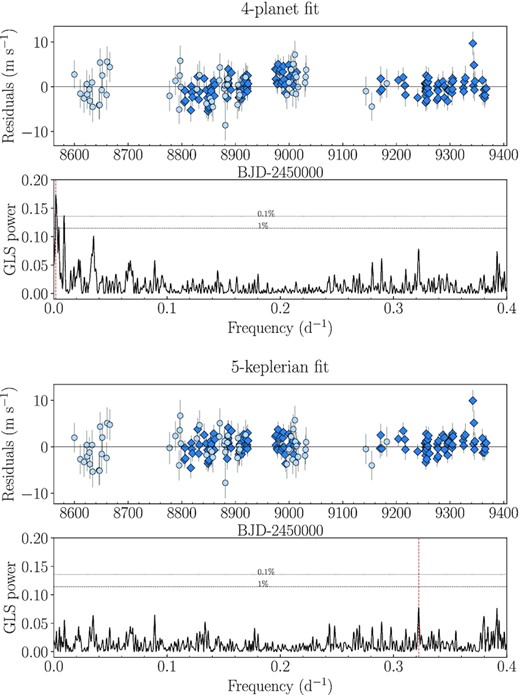
Time-series and GLS periodogram of the RV residuals after the four-planet and five-Keplerian fits as described in Section 4.2. In the residuals plot, the HARPS-N and HIRES RVs are plotted with dark blue diamonds and light blue circles, respectively. In the periodogram plots, the dashed and dotted horizontal lines show the 1 and 0.1 per cent False Alarm Probability (FAP) level, respectively. The red vertical line indicates the main peak of each periodogram. The long-period peak around frequencies 0.0017–0.0025 d−1 (P = 400 − 600 d) in the four-planet residuals periodogram is modelled by the fifth Keplerian, and no more significant peaks are identified in the five-Keplerian residuals periodogram. Moreover, the positive variation at ∼9000 BJD-2450000 in the four-planet fit residuals disappears in the five-Keplerian fit residuals.
The fitted period of the fifth Keplerian was ∼480 d. Such a long-term signal could be induced either by stellar activity, considering that stellar magnetic fields related to magnetic cycles can show variability on timescales of the order of 1–3 yr (e.g. Collier Cameron 2018; Hatzes 2019; Crass et al. 2021), or by an additional long-period planet. We refer here to an eventual long-period planet because, given the inferred semi-amplitude of ∼2 m s−1 (Table 6), an external companion with mass equal to 13 Mj (assuming this value to be the threshold between planetary and sub-stellar objects) would have an inclination of ∼0.03 deg. Such an inclination would imply an almost perpendicular orbit with respect to the orbital plane of the four inner planets, hinting at a very unlikely configuration. Therefore, in the hypothesis of the presence of an external companion, it would most likely be a planetary-mass object.
Parameters of the TOI-561 system, including the fifth Keplerian signal, as determined from the joint photometric and spectroscopic fit described in Section 5.
| . | TOI-561 b . | TOI-561 c . | TOI-561 d . | TOI-561 e . | 5th Keplerian . |
|---|---|---|---|---|---|
| Planetary parameters | |||||
| P (d) | |$0.4465688_{-0.0000008}^{+0.0000007}$| | |$10.778831_{-0.000036}^{+0.000034}$| | |$25.7124_{-0.0002}^{+0.0001}$| | |$77.03_{-0.24}^{+0.25}$| | |$473_{-25}^{+36}$| |
| T0 (TBJD)a | 2317.7498 ± 0.0005 | |$2238.4629_{-0.0009}^{+0.0008}$| | |$2318.966_{-0.004}^{+0.003}$| | |$1538.180_{-0.005}^{+0.004}$| | |$1664_{-33}^{+28}$| |
| a/R⋆ | |$2.685_{-0.025}^{+0.024}$| | |$22.43_{-0.21}^{+0.20}$| | |$40.04_{-0.37}^{+0.36}$| | |$83.22_{-0.79}^{+0.77}$| | |$279_{-10}^{+14}$| |
| a (AU) | 0.0106 ± 0.0001 | 0.0884 ± 0.0009 | 0.158 ± 0.002 | 0.328 ± 0.003 | |$1.1_{-0.4}^{+0.6}$| |
| Rp/R⋆ | 0.0155 ± 0.0004 | 0.0316 ± 0.0004 | 0.0306 ± 0.0008 | |$0.0278_{-0.0014}^{+0.0016}$| | – |
| Rp (R⊕) | 1.425 ± 0.037 | 2.91 ± 0.04 | 2.82 ± 0.07 | |$2.55_{-0.13}^{+0.12}$| | – |
| b | |$0.13_{-0.09}^{+0.10}$| | |$0.12_{-0.08}^{+0.13}$| | |$0.45_{-0.17}^{+0.11}$| | |$0.28_{-0.18}^{+0.15}$| | – |
| i (deg) | |$87.2_{-2.1}^{+1.9}$| | |$89.69_{-0.31}^{+0.21}$| | |$89.40_{-0.11}^{+0.21}$| | |$89.80_{-0.10}^{+0.13}$| | – |
| T14 (h) | 1.31 ± 0.02 | |$3.75_{-0.08}^{+0.05}$| | |$4.54_{-0.29}^{+0.32}$| | |$6.98_{-0.40}^{+0.24}$| | – |
| e | 0 (fixed) | |$0.030_{-0.021}^{+0.035}$| | |$0.122_{-0.048}^{+0.054}$| | |$0.079_{-0.050}^{+0.058}$| | |$0.085_{-0.059}^{+0.083}$| |
| ω (deg) | 90 (fixed) | |$291_{-84}^{+55}$| | |$235_{-26}^{+14}$| | |$143_{-44}^{+42}$| | |$348_{-53}^{+198}$| |
| K (m s−1) | 1.93 ± 0.21 | |$1.81_{-0.22}^{+0.23}$| | |$3.34_{-0.22}^{+0.23}$| | 2.19 ± 0.23 | 1.94 ± 0.27 |
| Mp (M⊕) | 2.00 ± 0.23 | |$5.39_{-0.68}^{+0.69}$| | |$13.2_{-0.9}^{+1.0}$| | 12.6 ± 1.4 | |$20 \pm 3 \, ^b$| |
| ρp (ρ⊕) | 0.69 ± 0.10 | 0.22 ± 0.03 | 0.59 ± 0.06 | 0.76 ± 0.14 | – |
| ρp (g cm−3) | 3.8 ± 0.5 | 1.2 ± 0.2 | 3.2 ± 0.3 | 4.2 ± 0.8 | – |
| Sp (S⊕) | 4745 ± 269 | 68.2 ± 3.9 | 21.4 ± 1.3 | 4.96 ± 0.28 | – |
| |$T_{\rm eq}^c$| (K) | 2310 ± 33 | 800 ± 11 | 598 ± 9 | 415 ± 6 | – |
| |$g_{\rm p}^d$| (m s−2) | 9.7 ± 1.2 | 6.2 ± 0.8 | 16.3 ± 1.5 | 19.0 ± 2.9 | – |
| Common parameters | |||||
| R⋆e (R⊙) | 0.843 ± 0.005 | ||||
| M⋆e (M⊙) | 0.806 ± 0.036 | ||||
| ρ⋆ (ρ⊙) | 1.31 ± 0.05 | ||||
| u1, TESS | 0.33 ± 0.08 | ||||
| u2, TESS | 0.23 ± 0.09 | ||||
| u1, CHEOPS | 0.46 ± 0.07 | ||||
| u2, CHEOPS | 0.22 ± 0.09 | ||||
| |$\sigma _{\rm HARPS-N}^{\rm f}$| (m s−1) | |$1.40_{-0.14}^{+0.15}$| | ||||
| |$\sigma _{\rm HIRES}^{\rm f}$| (m s−1) | |$2.77_{-0.31}^{+0.36}$| | ||||
| |$\gamma ^{\rm g}_{\rm HARPS-N}$| (m s−1) | 79700.41 ± 0.26 | ||||
| |$\gamma ^{\rm g}_{\rm HIRES}$| (m s−1) | −1.20 ± 0.42 | ||||
| . | TOI-561 b . | TOI-561 c . | TOI-561 d . | TOI-561 e . | 5th Keplerian . |
|---|---|---|---|---|---|
| Planetary parameters | |||||
| P (d) | |$0.4465688_{-0.0000008}^{+0.0000007}$| | |$10.778831_{-0.000036}^{+0.000034}$| | |$25.7124_{-0.0002}^{+0.0001}$| | |$77.03_{-0.24}^{+0.25}$| | |$473_{-25}^{+36}$| |
| T0 (TBJD)a | 2317.7498 ± 0.0005 | |$2238.4629_{-0.0009}^{+0.0008}$| | |$2318.966_{-0.004}^{+0.003}$| | |$1538.180_{-0.005}^{+0.004}$| | |$1664_{-33}^{+28}$| |
| a/R⋆ | |$2.685_{-0.025}^{+0.024}$| | |$22.43_{-0.21}^{+0.20}$| | |$40.04_{-0.37}^{+0.36}$| | |$83.22_{-0.79}^{+0.77}$| | |$279_{-10}^{+14}$| |
| a (AU) | 0.0106 ± 0.0001 | 0.0884 ± 0.0009 | 0.158 ± 0.002 | 0.328 ± 0.003 | |$1.1_{-0.4}^{+0.6}$| |
| Rp/R⋆ | 0.0155 ± 0.0004 | 0.0316 ± 0.0004 | 0.0306 ± 0.0008 | |$0.0278_{-0.0014}^{+0.0016}$| | – |
| Rp (R⊕) | 1.425 ± 0.037 | 2.91 ± 0.04 | 2.82 ± 0.07 | |$2.55_{-0.13}^{+0.12}$| | – |
| b | |$0.13_{-0.09}^{+0.10}$| | |$0.12_{-0.08}^{+0.13}$| | |$0.45_{-0.17}^{+0.11}$| | |$0.28_{-0.18}^{+0.15}$| | – |
| i (deg) | |$87.2_{-2.1}^{+1.9}$| | |$89.69_{-0.31}^{+0.21}$| | |$89.40_{-0.11}^{+0.21}$| | |$89.80_{-0.10}^{+0.13}$| | – |
| T14 (h) | 1.31 ± 0.02 | |$3.75_{-0.08}^{+0.05}$| | |$4.54_{-0.29}^{+0.32}$| | |$6.98_{-0.40}^{+0.24}$| | – |
| e | 0 (fixed) | |$0.030_{-0.021}^{+0.035}$| | |$0.122_{-0.048}^{+0.054}$| | |$0.079_{-0.050}^{+0.058}$| | |$0.085_{-0.059}^{+0.083}$| |
| ω (deg) | 90 (fixed) | |$291_{-84}^{+55}$| | |$235_{-26}^{+14}$| | |$143_{-44}^{+42}$| | |$348_{-53}^{+198}$| |
| K (m s−1) | 1.93 ± 0.21 | |$1.81_{-0.22}^{+0.23}$| | |$3.34_{-0.22}^{+0.23}$| | 2.19 ± 0.23 | 1.94 ± 0.27 |
| Mp (M⊕) | 2.00 ± 0.23 | |$5.39_{-0.68}^{+0.69}$| | |$13.2_{-0.9}^{+1.0}$| | 12.6 ± 1.4 | |$20 \pm 3 \, ^b$| |
| ρp (ρ⊕) | 0.69 ± 0.10 | 0.22 ± 0.03 | 0.59 ± 0.06 | 0.76 ± 0.14 | – |
| ρp (g cm−3) | 3.8 ± 0.5 | 1.2 ± 0.2 | 3.2 ± 0.3 | 4.2 ± 0.8 | – |
| Sp (S⊕) | 4745 ± 269 | 68.2 ± 3.9 | 21.4 ± 1.3 | 4.96 ± 0.28 | – |
| |$T_{\rm eq}^c$| (K) | 2310 ± 33 | 800 ± 11 | 598 ± 9 | 415 ± 6 | – |
| |$g_{\rm p}^d$| (m s−2) | 9.7 ± 1.2 | 6.2 ± 0.8 | 16.3 ± 1.5 | 19.0 ± 2.9 | – |
| Common parameters | |||||
| R⋆e (R⊙) | 0.843 ± 0.005 | ||||
| M⋆e (M⊙) | 0.806 ± 0.036 | ||||
| ρ⋆ (ρ⊙) | 1.31 ± 0.05 | ||||
| u1, TESS | 0.33 ± 0.08 | ||||
| u2, TESS | 0.23 ± 0.09 | ||||
| u1, CHEOPS | 0.46 ± 0.07 | ||||
| u2, CHEOPS | 0.22 ± 0.09 | ||||
| |$\sigma _{\rm HARPS-N}^{\rm f}$| (m s−1) | |$1.40_{-0.14}^{+0.15}$| | ||||
| |$\sigma _{\rm HIRES}^{\rm f}$| (m s−1) | |$2.77_{-0.31}^{+0.36}$| | ||||
| |$\gamma ^{\rm g}_{\rm HARPS-N}$| (m s−1) | 79700.41 ± 0.26 | ||||
| |$\gamma ^{\rm g}_{\rm HIRES}$| (m s−1) | −1.20 ± 0.42 | ||||
aTESS Barycentric Julian Date (BJD−2457000). bMinimum mass in the hypothesis of a planetary origin. cComputed as |$T_{\rm eq}~= T_\star \, \biggl (\dfrac{R_\star }{2a}\biggr)^{1/2} \, [f(1-A_{\rm B})]^{1/4}$|, assuming f = 1 and a null Bond albedo (AB = 0). d Planetary surface gravity. e As determined from the stellar analysis in Section 2.1. f RV jitter term. g RV offset.
Parameters of the TOI-561 system, including the fifth Keplerian signal, as determined from the joint photometric and spectroscopic fit described in Section 5.
| . | TOI-561 b . | TOI-561 c . | TOI-561 d . | TOI-561 e . | 5th Keplerian . |
|---|---|---|---|---|---|
| Planetary parameters | |||||
| P (d) | |$0.4465688_{-0.0000008}^{+0.0000007}$| | |$10.778831_{-0.000036}^{+0.000034}$| | |$25.7124_{-0.0002}^{+0.0001}$| | |$77.03_{-0.24}^{+0.25}$| | |$473_{-25}^{+36}$| |
| T0 (TBJD)a | 2317.7498 ± 0.0005 | |$2238.4629_{-0.0009}^{+0.0008}$| | |$2318.966_{-0.004}^{+0.003}$| | |$1538.180_{-0.005}^{+0.004}$| | |$1664_{-33}^{+28}$| |
| a/R⋆ | |$2.685_{-0.025}^{+0.024}$| | |$22.43_{-0.21}^{+0.20}$| | |$40.04_{-0.37}^{+0.36}$| | |$83.22_{-0.79}^{+0.77}$| | |$279_{-10}^{+14}$| |
| a (AU) | 0.0106 ± 0.0001 | 0.0884 ± 0.0009 | 0.158 ± 0.002 | 0.328 ± 0.003 | |$1.1_{-0.4}^{+0.6}$| |
| Rp/R⋆ | 0.0155 ± 0.0004 | 0.0316 ± 0.0004 | 0.0306 ± 0.0008 | |$0.0278_{-0.0014}^{+0.0016}$| | – |
| Rp (R⊕) | 1.425 ± 0.037 | 2.91 ± 0.04 | 2.82 ± 0.07 | |$2.55_{-0.13}^{+0.12}$| | – |
| b | |$0.13_{-0.09}^{+0.10}$| | |$0.12_{-0.08}^{+0.13}$| | |$0.45_{-0.17}^{+0.11}$| | |$0.28_{-0.18}^{+0.15}$| | – |
| i (deg) | |$87.2_{-2.1}^{+1.9}$| | |$89.69_{-0.31}^{+0.21}$| | |$89.40_{-0.11}^{+0.21}$| | |$89.80_{-0.10}^{+0.13}$| | – |
| T14 (h) | 1.31 ± 0.02 | |$3.75_{-0.08}^{+0.05}$| | |$4.54_{-0.29}^{+0.32}$| | |$6.98_{-0.40}^{+0.24}$| | – |
| e | 0 (fixed) | |$0.030_{-0.021}^{+0.035}$| | |$0.122_{-0.048}^{+0.054}$| | |$0.079_{-0.050}^{+0.058}$| | |$0.085_{-0.059}^{+0.083}$| |
| ω (deg) | 90 (fixed) | |$291_{-84}^{+55}$| | |$235_{-26}^{+14}$| | |$143_{-44}^{+42}$| | |$348_{-53}^{+198}$| |
| K (m s−1) | 1.93 ± 0.21 | |$1.81_{-0.22}^{+0.23}$| | |$3.34_{-0.22}^{+0.23}$| | 2.19 ± 0.23 | 1.94 ± 0.27 |
| Mp (M⊕) | 2.00 ± 0.23 | |$5.39_{-0.68}^{+0.69}$| | |$13.2_{-0.9}^{+1.0}$| | 12.6 ± 1.4 | |$20 \pm 3 \, ^b$| |
| ρp (ρ⊕) | 0.69 ± 0.10 | 0.22 ± 0.03 | 0.59 ± 0.06 | 0.76 ± 0.14 | – |
| ρp (g cm−3) | 3.8 ± 0.5 | 1.2 ± 0.2 | 3.2 ± 0.3 | 4.2 ± 0.8 | – |
| Sp (S⊕) | 4745 ± 269 | 68.2 ± 3.9 | 21.4 ± 1.3 | 4.96 ± 0.28 | – |
| |$T_{\rm eq}^c$| (K) | 2310 ± 33 | 800 ± 11 | 598 ± 9 | 415 ± 6 | – |
| |$g_{\rm p}^d$| (m s−2) | 9.7 ± 1.2 | 6.2 ± 0.8 | 16.3 ± 1.5 | 19.0 ± 2.9 | – |
| Common parameters | |||||
| R⋆e (R⊙) | 0.843 ± 0.005 | ||||
| M⋆e (M⊙) | 0.806 ± 0.036 | ||||
| ρ⋆ (ρ⊙) | 1.31 ± 0.05 | ||||
| u1, TESS | 0.33 ± 0.08 | ||||
| u2, TESS | 0.23 ± 0.09 | ||||
| u1, CHEOPS | 0.46 ± 0.07 | ||||
| u2, CHEOPS | 0.22 ± 0.09 | ||||
| |$\sigma _{\rm HARPS-N}^{\rm f}$| (m s−1) | |$1.40_{-0.14}^{+0.15}$| | ||||
| |$\sigma _{\rm HIRES}^{\rm f}$| (m s−1) | |$2.77_{-0.31}^{+0.36}$| | ||||
| |$\gamma ^{\rm g}_{\rm HARPS-N}$| (m s−1) | 79700.41 ± 0.26 | ||||
| |$\gamma ^{\rm g}_{\rm HIRES}$| (m s−1) | −1.20 ± 0.42 | ||||
| . | TOI-561 b . | TOI-561 c . | TOI-561 d . | TOI-561 e . | 5th Keplerian . |
|---|---|---|---|---|---|
| Planetary parameters | |||||
| P (d) | |$0.4465688_{-0.0000008}^{+0.0000007}$| | |$10.778831_{-0.000036}^{+0.000034}$| | |$25.7124_{-0.0002}^{+0.0001}$| | |$77.03_{-0.24}^{+0.25}$| | |$473_{-25}^{+36}$| |
| T0 (TBJD)a | 2317.7498 ± 0.0005 | |$2238.4629_{-0.0009}^{+0.0008}$| | |$2318.966_{-0.004}^{+0.003}$| | |$1538.180_{-0.005}^{+0.004}$| | |$1664_{-33}^{+28}$| |
| a/R⋆ | |$2.685_{-0.025}^{+0.024}$| | |$22.43_{-0.21}^{+0.20}$| | |$40.04_{-0.37}^{+0.36}$| | |$83.22_{-0.79}^{+0.77}$| | |$279_{-10}^{+14}$| |
| a (AU) | 0.0106 ± 0.0001 | 0.0884 ± 0.0009 | 0.158 ± 0.002 | 0.328 ± 0.003 | |$1.1_{-0.4}^{+0.6}$| |
| Rp/R⋆ | 0.0155 ± 0.0004 | 0.0316 ± 0.0004 | 0.0306 ± 0.0008 | |$0.0278_{-0.0014}^{+0.0016}$| | – |
| Rp (R⊕) | 1.425 ± 0.037 | 2.91 ± 0.04 | 2.82 ± 0.07 | |$2.55_{-0.13}^{+0.12}$| | – |
| b | |$0.13_{-0.09}^{+0.10}$| | |$0.12_{-0.08}^{+0.13}$| | |$0.45_{-0.17}^{+0.11}$| | |$0.28_{-0.18}^{+0.15}$| | – |
| i (deg) | |$87.2_{-2.1}^{+1.9}$| | |$89.69_{-0.31}^{+0.21}$| | |$89.40_{-0.11}^{+0.21}$| | |$89.80_{-0.10}^{+0.13}$| | – |
| T14 (h) | 1.31 ± 0.02 | |$3.75_{-0.08}^{+0.05}$| | |$4.54_{-0.29}^{+0.32}$| | |$6.98_{-0.40}^{+0.24}$| | – |
| e | 0 (fixed) | |$0.030_{-0.021}^{+0.035}$| | |$0.122_{-0.048}^{+0.054}$| | |$0.079_{-0.050}^{+0.058}$| | |$0.085_{-0.059}^{+0.083}$| |
| ω (deg) | 90 (fixed) | |$291_{-84}^{+55}$| | |$235_{-26}^{+14}$| | |$143_{-44}^{+42}$| | |$348_{-53}^{+198}$| |
| K (m s−1) | 1.93 ± 0.21 | |$1.81_{-0.22}^{+0.23}$| | |$3.34_{-0.22}^{+0.23}$| | 2.19 ± 0.23 | 1.94 ± 0.27 |
| Mp (M⊕) | 2.00 ± 0.23 | |$5.39_{-0.68}^{+0.69}$| | |$13.2_{-0.9}^{+1.0}$| | 12.6 ± 1.4 | |$20 \pm 3 \, ^b$| |
| ρp (ρ⊕) | 0.69 ± 0.10 | 0.22 ± 0.03 | 0.59 ± 0.06 | 0.76 ± 0.14 | – |
| ρp (g cm−3) | 3.8 ± 0.5 | 1.2 ± 0.2 | 3.2 ± 0.3 | 4.2 ± 0.8 | – |
| Sp (S⊕) | 4745 ± 269 | 68.2 ± 3.9 | 21.4 ± 1.3 | 4.96 ± 0.28 | – |
| |$T_{\rm eq}^c$| (K) | 2310 ± 33 | 800 ± 11 | 598 ± 9 | 415 ± 6 | – |
| |$g_{\rm p}^d$| (m s−2) | 9.7 ± 1.2 | 6.2 ± 0.8 | 16.3 ± 1.5 | 19.0 ± 2.9 | – |
| Common parameters | |||||
| R⋆e (R⊙) | 0.843 ± 0.005 | ||||
| M⋆e (M⊙) | 0.806 ± 0.036 | ||||
| ρ⋆ (ρ⊙) | 1.31 ± 0.05 | ||||
| u1, TESS | 0.33 ± 0.08 | ||||
| u2, TESS | 0.23 ± 0.09 | ||||
| u1, CHEOPS | 0.46 ± 0.07 | ||||
| u2, CHEOPS | 0.22 ± 0.09 | ||||
| |$\sigma _{\rm HARPS-N}^{\rm f}$| (m s−1) | |$1.40_{-0.14}^{+0.15}$| | ||||
| |$\sigma _{\rm HIRES}^{\rm f}$| (m s−1) | |$2.77_{-0.31}^{+0.36}$| | ||||
| |$\gamma ^{\rm g}_{\rm HARPS-N}$| (m s−1) | 79700.41 ± 0.26 | ||||
| |$\gamma ^{\rm g}_{\rm HIRES}$| (m s−1) | −1.20 ± 0.42 | ||||
aTESS Barycentric Julian Date (BJD−2457000). bMinimum mass in the hypothesis of a planetary origin. cComputed as |$T_{\rm eq}~= T_\star \, \biggl (\dfrac{R_\star }{2a}\biggr)^{1/2} \, [f(1-A_{\rm B})]^{1/4}$|, assuming f = 1 and a null Bond albedo (AB = 0). d Planetary surface gravity. e As determined from the stellar analysis in Section 2.1. f RV jitter term. g RV offset.
On one hand, all the five signals, including the long-term one, are recovered in an independent analysis that we performed with the CCF-based scalpels algorithm (Collier Cameron et al. 2021). Concisely, scalpels projects the RV time-series on to the highest variance principal components of the time series of autocorrelation functions of the CCF, with the aim of distinguishing RV variations caused by orbiting planets from activity-induced distortions on each CCF. The absence of the signal in the scalpels shape-driven velocities indicates that the long-term periodicity is not due to shape changes in the line profiles, supporting the idea of a planetary origin. Moreover, TOI-561 is not expected to be a particularly active star given its old age and low |$\log {\rm R}^{\prime }_{\rm HK}$|, as assessed in the L21 and W21 activity analyses. As can be seen in Fig. 7, the GLS periodogram of the majority of the activity indicators extracted with the HARPS-N DRS, i.e. full width at half-maximum (FWHM), bisector span (BIS), contrast and Hα, do not show significant peaks, with none of them exceeding the 0.1 False Alarm Probability (FAP) threshold, which we computed using a bootstrap approach, at the frequency of interest. On the other hand, the periodogram of the S-index, which is particularly sensitive to magnetically induced activity, shows a significant, broad peak at low frequencies, potentially suggesting that the previously identified long-term variability is related to stellar activity. Considering this, we performed an additional dynesty fit assuming a four-planet model and including a Gaussian Process (GP) regression with a quasi-periodic kernel, as formulated in Grunblatt, Howard & Haywood (2015), to account for the long-term signal. We modelled simultaneously the RVs and the S-index time series in order to better inform the GP (Langellier et al. 2021; Osborn et al. 2021), using two independent covariance matrices for each data set with common GP hyper-parameters except for the amplitude of the covariance matrix, assuming uniform, non-informative priors on all of them. The fit suggests a periodicity longer than ∼570 d, but the GP model is too flexible to derive a precise period value, considering also that the global RV baseline (∼768 d) is comparable with the periodicity of the long-term signal. The inferred semi-amplitudes of the four known planets differed by less than 0.07σ from the five-Keplerian model ones, indicating that the different modelling of the long-term signal is not influencing the results for the known, transiting planets. Finally, as in the case of the 5-Keplerian fit, the HARPS-N jitter is significantly improved (σHARPS-N ∼ 1.30 m s−1) when including the GP model. Therefore, since our Bayesian analyses showed that the modelling of the long-term signal is necessary to obtain the best picture of the system, we decided to perform the global fit assuming a five-Keplerian model, but without drawing conclusions on the origin of the fifth signal. We stress that the five-Keplerian fit does not provide absolute evidence of the presence of a fifth planet, since also poorly sampled stellar activity could be well modelled using a Keplerian (Pepe et al. 2013; Mortier & Collier Cameron 2017; Affer et al. 2016), especially in our case where the RV baseline is of the order of the signal periodicity. Since it is not possible to distinguish a true planetary signal from an activity signal that has not been observed long enough to exhibit a loss of coherence in its phase or amplitude, only a follow-up campaign over several years can allow one to better understand the nature of this long-term signal.
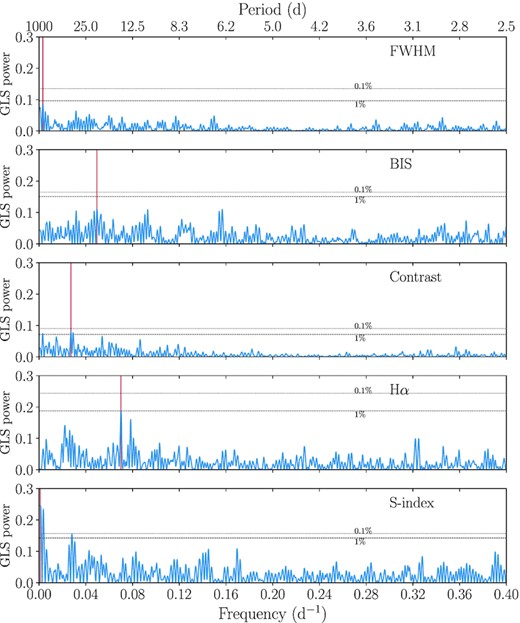
GLS periodogram of the HARPS-N activity indices. The main peak of each periodogram is highlighted with a red vertical line. The dashed and dotted horizontal lines indicate the 1 and 0.1 per cent FAP levels, respectively. The only peak above the 0.1 FAP level is the low-frequency peak in the S-index periodogram, as discussed in Section 4.2.
5 JOINT PHOTOMETRIC AND RV ANALYSIS
To infer the properties of the TOI-561 planets, we jointly modelled all photometric and spectroscopic data with pyorbit, using pyde11 + emcee (Foreman-Mackey et al. 2013) as described in section 5 of L21, and adopting the same convergence criteria. We ran 96 chains (twice the number of the model parameters) for |$250\, 000$| steps, discarding the first |$50\, 000$| as burn-in.
Based on the analysis presented in the previous section, we assumed a five-Keplerian model, including four planets plus a fifth Keplerian with period free to span between 2 and 900 d. We fitted a common value for the stellar density, using the value reported in Table 1 as Gaussian prior. We adopted the quadratic limb-darkening law as parametrized by Kipping (2013), putting Gaussian priors on the u1, u2 coefficients, obtained for the TESS and CHEOPS passband through a bilinear interpolation of limb darkening profiles by Claret (2017) and Claret (2021), respectively, and assuming a 1σ uncertainty of 0.1 for each coefficient. We imposed a half-Gaussian zero-mean prior (Van Eylen et al. 2019) on the planet eccentricities, except for the USP planet, whose eccentricity was fixed to zero. We assumed uniform priors for all the other parameters.
To model the long-term correlated noise in the TESS light curve, we included in the fit a GP regression with a Matérn-3/2 kernel against time, as shown in Fig. 1, and we added a jitter term to account for possible extra white noise. We pre-decorrelated the CHEOPS light curves with the pycheops12 package (Maxted et al. 2021), selecting the detrending parameters according to the Bayes factor to obtain the best correlated noise model for each visit. For all the three CHEOPS visits, a decorrelation for the first three harmonics of the roll angle was necessary, plus first-order polynomials in time, x–y centroid position, and smearing. We then used the detrended light curves (Fig. 3) for the global pyorbit fit. In order to check if the detrending was affecting our results for the planetary parameters, we also performed an independent global analysis with the juliet package (Espinoza, Kossakowski & Brahm 2019), including in the global modelling the basis vectors selected with pycheops to detrend the data simultaneously. All the results were consistent within 1σ, indicating that the pre-detrending did not significantly alter our inferred results. Finally, for both the HARPS-N and HIRES data sets we included jitter and offset terms as free parameters.
We summarize our best-fitting model results in Table 6, and we show the transit model, phase-folded RVs and global RV model in Figs 8, 9, and 10, respectively. We inferred precise masses and radii for all the four planets in the system, whose positions in the mass-radius diagram are shown in Fig. 11. With a radius of Rb = 1.425 ± 0.037 R⊕ and a mass of Mb = 2.00 ± 0.23 M⊕ (from Kb = 1.93 ± 0.21 m s−1), TOI-561 b is located in a region of the mass-radius diagram which is not consistent with a pure rocky composition, as will be also shown in Section 6 by our internal structure modelling. Our analysis confirms TOI-561 b to be the lowest density (ρb = 3.8 ± 0.5 g cm−3) USP planet known to date (Fig. 12). In order to further confirm the planetary density, we also performed a specific RV analysis of TOI-561 b using the Floating Chunk Offset method (FCO; Hatzes 2014). The FCO analysis, detailed in Appendix B, confirms the low mass inferred for TOI-561 b, and consequently its low density. Thanks to the CHEOPS observations, we also improved significantly the radius of TOI-561 c, for which we obtained a value of Rc = 2.91 ± 0.04 R⊕. From the semi-amplitude |$K_{\rm c} = 1.81_{-0.22}^{+0.23}$| m s−1, we inferred a mass of |$M_{\rm c} = 5.39_{-0.68}^{+0.69}$| M⊕, implying a density of ρc = 1.2 ± 0.2 g cm−3. From the combined fit of one TESS and one CHEOPS transit, we inferred a radius of 2.82 ± 0.07 R⊕ for planet d, which has a mass of |$M_{\rm c} = 13.2_{-0.9}^{+1.0}$| M⊕ (from |$K_{\rm d} = 3.34_{-0.22}^{+0.23}$| m s−1) and a resulting density of ρd = 3.2 ± 0.3 g cm−3. Finally, for TOI-561 e, which shows a single transit in TESS sector 8, we derived a radius of |$R_{\rm e} = 2.55_{-0.13}^{+0.12}$| R⊕, a mass of Me = 12.6 ± 1.4 M⊕, and an average density of ρd = 4.2 ± 0.8 g cm−3. Lastly, the period inferred for the fifth Keplerian in the model was |$473_{-25}^{+36}$| d, with a 7.2σ detected semi-amplitude of 1.94 ± 0.27 m s−1. As discussed in Section 4.2, additional data spanning a longer baseline are needed to definitively confirm the planetary nature of this long-term signal.
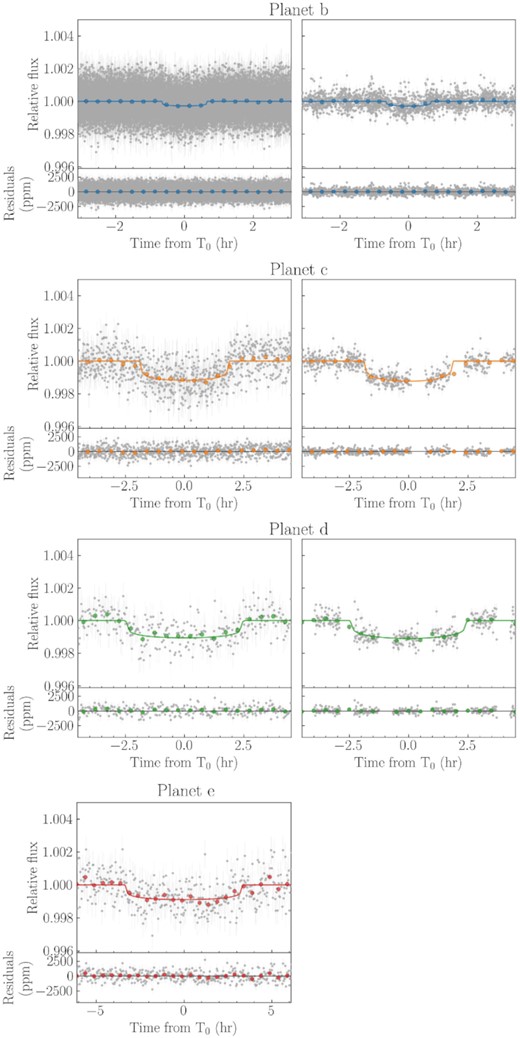
Phase-folded TESS (left) and CHEOPS (right) light curves of TOI-561 b, c, and d. Planet e shows a single transit in the TESS light curve, and it has no CHEOPS observations. For each planet, the coloured line indicates the best-fitting model, and residuals are shown in the bottom panels. Data points binned over 20 min (planet b) and 30 min (planets c, d and e) are shown with coloured dots.
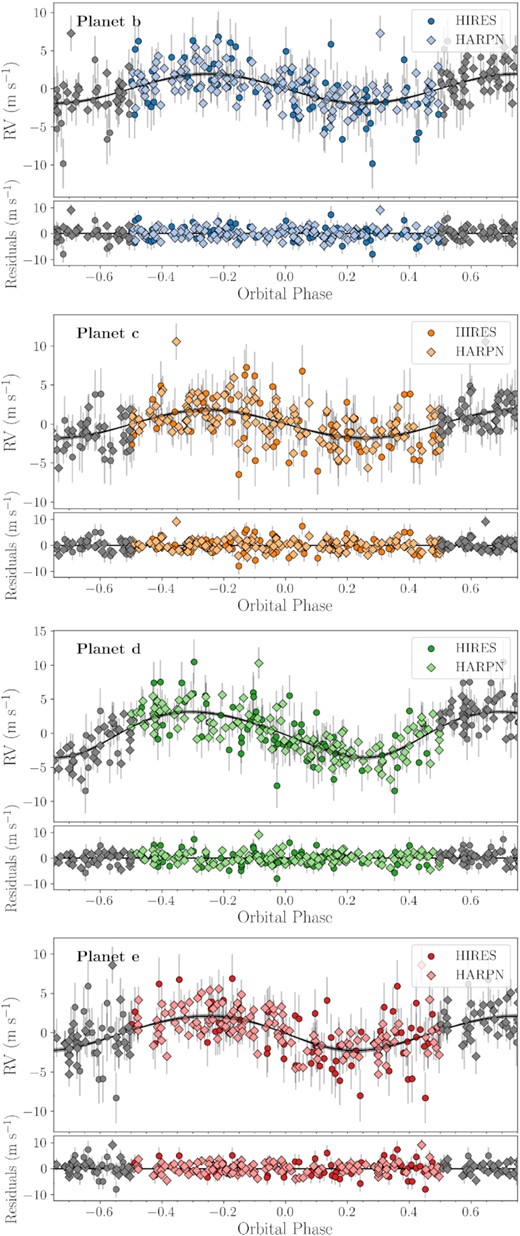
Phase-folded HARPS-N and HIRES RVs with residuals of TOI-561 b, c, d and e, as resulting from the joint photometric and spectroscopic fit. The error bars include the jitter term added in quadrature.
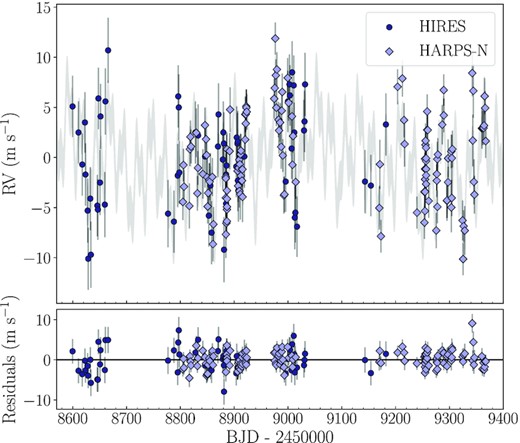
Global model (grey line) with residuals of HARPS-N and HIRES RVs according to the 5-Keplerian photometric and spectroscopic fit. The error bars include the jitter term added in quadrature.
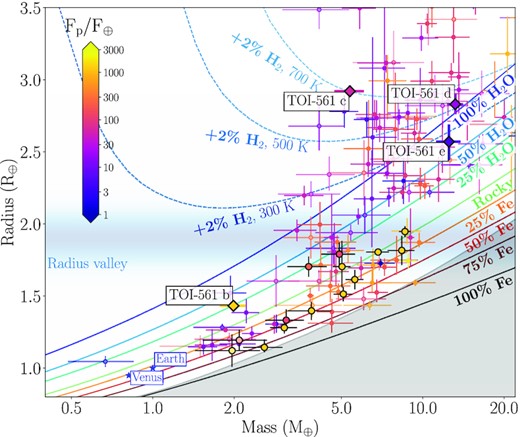
Mass–radius diagram for exoplanets with radii and masses measured with a precision better than 30 per cent, colour coded according to their incidental flux. Data are taken from the Extrasolar Planets Encyclopaedia catalogue (http://exoplanet.eu/catalog/, Schneider et al. 2011) as of 18 October 2021. The TOI-561 planets are labelled, and highlighted with coloured diamonds. The USP planets are emphasized with thick, black-contoured circles. The theoretical mass–radius curves for various chemical compositions (Zeng et al. 2019) are represented by solid coloured lines, while the dashed lines indicate the curves for an Earth-like core surrounded by a H2 envelope (2 per cent mass fraction) at varying equilibrium temperatures. The forbidden region predicted by collisional stripping (Marcus et al. 2010) is marked by the shaded grey region.
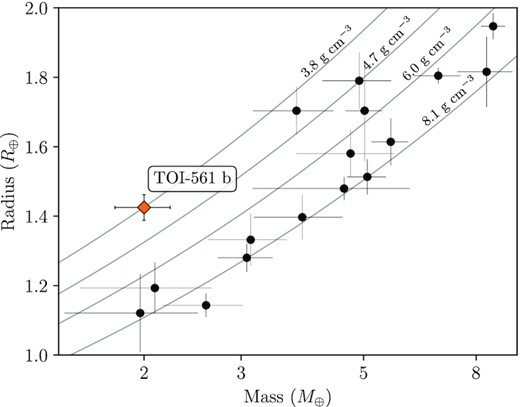
Mass–radius diagram of confirmed USP planets (P < 1 d, Rp< 2 R⊕) as taken from the Extrasolar Planets Encyclopaedia catalogue in date 18 October 2021. Iso-density lines are plotted in grey. TOI-561 b stands out as the lowest density USP planet known to date (ρb = 3.8 ± 0.5 g cm−3).
6 INTERNAL STRUCTURE MODELLING
We modelled the internal planetary structure in a Bayesian framework, following the procedure detailed in Leleu et al. (2021). Our model assumes fully-differentiated planets composed of four layers, comprising an iron and sulfur central core, a silicate mantle which includes Si, Mg, and Fe, a water layer, and a pure H/He gas layer. The inner core is modelled assuming the Hakim et al. (2018) equation of state (EOS), the silicate mantle uses the Sotin, Grasset & Mocquet (2007) EOS, and the water layer uses the Haldemann et al. (2020) EOS. The core, mantle, and water layer compose the ‘solid’ part of the planet. The thickness of the gas envelope is computed as a function of stellar age and irradiation, and mass and radius of the solid part, according to the model presented in Lopez & Fortney (2014). We assumed no compression effects of the gas envelope on the solid part, a hypothesis which is justified a posteriori given the low mass fraction of gas obtained for each planet (see below).
Our Bayesian model fits the planetary system as a whole, rather than performing an independent fit for each planet, in order to account for the correlations between the absolute planetary masses and radii, which depend on the stellar properties. The model fits the stellar (mass, radius, effective temperature, age, chemical abundances of Fe, Mg, Si) and planetary properties (RV semi-amplitudes, transit depths, orbital periods) to derive the posterior distributions of the internal structure parameters. The internal structure parameters modelled for each planet are the mass fractions of the core, mantle and water layer, the mass of the gas envelope, the iron molar fraction in the core, the silicon and magnesium molar fraction in the mantle, the equilibrium temperature, and the age of the planet (equal to the age of the star). For a more extensive discussion on the relation among input data and derived parameters we refer to Leleu et al. (2021). We assumed the mass fraction of the inner core, mantle, and water layer to be uniform on the simplex (the surface on which they add up to one), with the water mass fraction having an upper boundary of 0.5 (Thiabaud et al. 2014; Marboeuf et al. 2014). For the mass of the gas envelope, we assumed a uniform prior in logarithmic space. Finally, we assumed the Si/Mg/Fe molar ratios of each planet to be equal to the stellar atmospheric values (even though Adibekyan et al. (2021a) recently showed that the stellar and planetary abundances may not be always correlated in a one-to-one relation). We emphasize the fact that, as in many Bayesian analyses, the results presented below in terms of planet internal structure depend to some extent on the selection of the priors, which we chose following i.e. Dorn et al. (2017), Dorn et al. (2018), and Leleu et al. (2021). Analysing the same data with very different priors (e.g. non-uniform core/mantle/water mass fraction or gas fraction uniform in linear scale) would lead to different conclusions.
We show the results of the internal structure modelling for the four planets in Fig. 13. As expected from its closeness to the host star, planet b has basically no H/He envelope, while the other three planets show a variable amount of gas mass. Planet c hosts a relatively massive gaseous envelope, with a gas mass of (5 and 95 per cent quantiles) |$M_{\rm gas,c} = 0.07_{-0.02}^{+0.04}$| M⊕ (|$1.3_{-0.4}^{+0.8}$| weight per cent wt per cent). Planet d hosts the most massive envelope (|$M_{\rm gas, d} = 0.10_{-0.07}^{+0.13}$| M⊕), which, considering the total mass of the planet, correspond to a smaller relative mass fraction of |$0.8_{-0.5}^{+1.0}$| wt per cent, while TOI-561 e’s envelope spans a range between −10.7 < log Mgas, e < −1.0, implying an upper limit on the gas mass of 0.11 M⊕ (<0.9 wt per cent). As expected from its low density, TOI-561 b could host a significant amount of water, having a water mass of |$M_{\rm H_2O,b} = 0.62_{-0.44}^{+0.32}$| M⊕ (|$31_{-22}^{+16}$| wt per cent). We stress that this result is highly dependent on the caveat of including only a solid water layer in the model. In fact, a massive water layer, if present on a planet with such a high equilibrium temperature, would imply the presence of a massive steam atmosphere (Turbet et al. 2020). This would in turn considerably change the inferred water mass fraction with respect to a model that includes only a solid water layer. Due to the presence of the gas envelope, the amount of water in both planet c and d is almost unconstrained (|$M_{\rm H_2O,c} = 1.29_{-1.14}^{+1.24}$| M⊕, i.e. |$24_{-21}^{+23}$| wt per cent; |$M_{\rm H_2O,d} = 3.56_{-3.18}^{+2.78}$| M⊕, i.e. |$27_{-24}^{+21}$| wt per cent), while TOI-561 e modelling points toward a massive water layer, with |$M_{\rm H_2O,e} = 4.50_{-3.65}^{+1.69}$| M⊕ (|$36_{-29}^{+13}$| wt per cent).
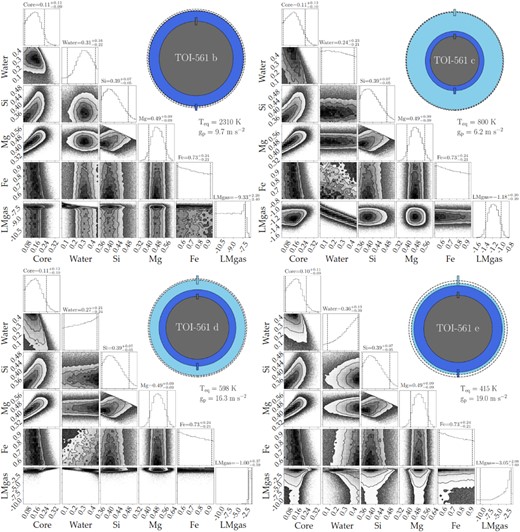
Posterior distributions of the main parameters describing the internal structure of TOI-561 b (top left), c (top right), d (bottom left), and e (bottom right). Each corner plot shows the mass fraction of the inner core and of the water layer, the molar fractions of silicon and magnesium in the mantle, the iron molar fraction in the inner core, and the mass of gas in logarithmic scale. On top of each column are printed the mean and the 5 per cent and 95 per cent quantiles values. For each planet, and we show an illustration of the radius fractions of the inner core+mantle (dark grey), water layer (dark blue), and gas envelope (light blue), corresponding to the medians of the posterior distributions. The coloured rectangles indicate the uncertainty on the corresponding layer thickness, while the black dashed outer rings represent the uncertainty on the total radius. Equilibrium temperature and planetary surface gravity are reported for each planet.
7 ATMOSPHERIC EVOLUTION
We employed the system parameters derived in this work to constrain the evolution of the stellar rotation period, which we use as a proxy for the evolution of the stellar high-energy emission affecting atmospheric escape, and the predicted initial atmospheric mass fraction of the detected transiting planets |$f_{\rm atm}^{\rm start}$|, that is the mass of the planetary atmosphere at the time of the dispersal of the protoplanetary disc. To this end, we used the planetary atmospheric evolution code pasta described by Bonfanti et al. (2021a), which is an updated version of the original code presented by Kubyshkina et al. (2019b), Kubyshkina et al. (2019a). The code models the evolution of the planetary atmospheres combining a model predicting planetary atmospheric escape rates based on hydrodynamic simulations (this has the advantage over other commonly used analytical estimates to account for both XUV-driven and core-powered mass loss; Kubyshkina et al. 2018), a model of the stellar high-energy (X-ray plus extreme ultraviolet; XUV) flux evolution (Bonfanti et al. 2021a), a model relating planetary parameters and atmospheric mass (Johnstone et al. 2015b), and stellar evolutionary tracks (Choi et al. 2016). The main assumptions of the framework are that planet migration did not occur after the dispersal of the protoplanetary disk, and that the planets hosted at some point in the past or still host a hydrogen-dominated atmosphere.
For each planet, the evolution calculations begin at an age of 5 Myr, which is the age assumed in the code for the dispersal of the protoplanetary disc. At each time step, the framework derives the mass-loss rate from the atmospheric escape model employing the stellar flux and the system parameters, and uses it to update the atmospheric mass fraction. This procedure is then repeated until the age of the system is reached or the planetary atmosphere has completely escaped. The free parameters of the algorithm are the initial atmospheric mass fraction at the time of the dispersal of the protoplanetary disc, and the indexes of the power law controlling the stellar rotation period (see Bonfanti et al. 2021a, for a detailed description of the mathematical formulation of the power law), that we use as proxy for the stellar XUV emission.
The free parameters are constrained by implementing the atmospheric evolution algorithm in a Bayesian framework employing the MCMC tool presented by Cubillos et al. (2017). The framework uses the system parameters with their uncertainties as input priors. It then computes millions of forward planetary evolutionary tracks, varying the input parameters according to the shape of the prior distributions, and varying the free parameters within pre-defined ranges, fitting the current planetary atmospheric mass fractions obtained as described in Section 6. The fit is done at the same time for all planets, thus simultaneously constraining the rotational period, and the results are posterior distributions of the free parameters. In particular, we opted for fitting for the planetary atmospheric mass fractions instead of the planetary radii. This enables the code to be more accurate by avoiding the continuous conversion of the atmospheric mass fraction into planetary radius, given the other system parameters (see also Delrez et al. 2021).
Fig. 14 shows the results of the planetary atmospheric evolution simulations. As a proxy for the evolution of the stellar rotation period, in Fig. 14, we show the posterior distribution of the stellar rotation period at an age of 150 Myr, further comparing it to the distribution of stellar rotation periods observed in stars member of young clusters of comparable age and with masses that deviate from M⋆ less than 0.1 M⊙ (from Johnstone et al. 2015a). The inferred posterior distribution for the rotation period is consistent with membership of the slowly rotating period-colours sequence in clusters of this age. However, this comparison should be taken with some caution, since there are no comprehensive studies on the rotation-colour distributions of 150 Myr-old clusters with the same metallicity as TOI-561. The initial atmospheric mass fractions of planets b and c are rather broad and peak at about one planetary mass. This is because both planets are close enough to the host star and have a small enough mass to have been subject to significant atmospheric escape. Therefore, to enable the presence of a thin hydrogen atmosphere, as predicted by the internal structure model, both planets had to host a significant hydrogen envelope after the formation and atmospheric accretion processes. Instead, planets d and e are far from the host star and massive enough not to have been subject to significant atmospheric escape, which is why we obtain an initial atmospheric mass fraction that resembles the current one. We also find that the posterior distributions of all input parameters match well the inserted priors (not shown here). As a whole, the results indicate that the currently observed system parameters are compatible with a scenario in which migration happened (if at all) exclusively inside the protoplanetary disk. Otherwise the code would have led to mismatches between the prior and posterior of the input parameters (particularly for what concerns the planetary masses and/or the stellar mass and age), in addition to showing incoherent results in the posterior distribution of the output parameters. This is for example the case of the TOI-1064 system, which is composed by two transiting planets with comparable masses and irradiation levels, but significantly different radii (Wilson et al. 2022). In our framework in which planets do not migrate after the dispersal of the protoplanetary nebula, reproducing the physical parameters of the planets composing the TOI-1064 system requires different evolutions of the stellar rotation rate, which is not possible, thus calling for a post-nebula migration.
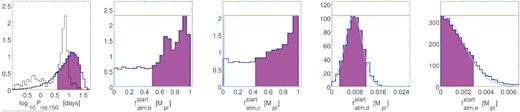
From left to right: Posterior distributions (dark blue lines) of the stellar rotation period at an age of 150 Myr and of the initial atmospheric mass fractions of TOI-561 b, c, d, and e. In each panel, the purple region represents the 68 per cent highest probability density intervals. In the left-hand panel, the black thin line shows the rotation period distribution of stars member of open clusters with ages around 150 Myr. Data are taken from Johnstone et al. (2015a), who report the rotation period of |$\sim \, 2000$| stars belonging to the Pleiades, M50, M35, and NGC 2516, whose ages are between 125 and 150 Myr. To generate the black histogram we selected a sub-sample of 578 stars, which have masses that deviate from M⋆ less than 0.1 M⊙. In the other panels, the horizontal orange lines mark the uniform prior used in the fit, scaled to the highest peak of each posterior distribution for better visualization. The light blue lines indicate the current atmospheric mass fraction of each planet determined as described in Section 6.
8 DISCUSSION AND CONCLUSIONS
In this study, we confirm the presence of four transiting planets around TOI-561, with orbital periods of approximately 0.44, 10.8, 25.7, and 77 d (Table 6). Our analysis disproves the presence of the previously suggested planet TOI-561 f (P ∼ 16.3 d; W21). TOI-561 is one of the few four-planet systems having precise radius and mass measurements for all the planets. Thanks to our global photometric and RV analysis, we refined all masses and radii with respect to the L21 values, and we precisely determined the planetary bulk densities, with uncertainties of 14.4 per cent, 13.6 per cent, 10.2 per cent, and 18.4 per cent for planets b, c, d, and e, respectively. The higher uncertainty on planet e reflects the lower precision in the radius determination (5 per cent uncertainty), which is based on the analysis of a single TESS transit, and highlights the importance of the high-precision CHEOPS photometry. In fact, with a single CHEOPS transit we managed to decrease the uncertainty on the radius of planet d from 5.1 per cent (L21, based on one TESS transit) to 2.5 per cent. Including also the improvement on the mass, this implied a decrease on the density uncertainty from 18.9 per cent to 10.2 per cent. We expect a similar improvement for planet e with future CHEOPS observations scheduled for 2022. The improvement in the radius of TOI-561 e is particularly important, since the planet is an interesting target for the study of the internal structure of cold sub-Neptunes. Its long period (|$P_{\rm d} = 77.03_{-0.24}^{+0.25}$| d) implies an insolation flux of Se = 4.96 ± 0.28 S⊕ and a relatively cool zero Bond albedo equilibrium temperature of Teq, e = 415 ± 6 K. As shown in Fig. 15, TOI-561 e is one of the few cool, long-period planets orbiting a star bright enough for precise RV characterization, and it is therefore an optimal test-case to refine tools and models that will be useful to characterize targets of future long-staring missions like PLATO.
V magnitude versus planetary periods for confirmed transiting exoplanets as reported in the Extrasolar Planets Encyclopaedia catalogue (http://exoplanet.eu/catalog/) in date 2021 October 18. The dashed vertical line marks V = 12 mag. TOI-561 e is one of the few long-period planets orbiting a star bright enough for precise RV characterization.
TOI-561 hosts one of the most intriguing USP planets discovered to date. As initially suggested by L21, our analysis confirms that TOI-561 b is the lowest density (ρb = 3.8 ± 0.5 g cm−3) USP super-Earth that we know of (see Fig. 12), and it paves the way for in-depth studies of interior composition, and formation and evolution processes of USP planets. Even though now the mass values are consistent within 1σ, contrary to what proposed by W21 (see Section 2.2) TOI-561 b is not consistent with a pure rocky composition, and to explain the planetary density our internal structure modelling (Section 6) predicts basically no H/He envelope, and a massive water layer. In this regard, an important point to consider is that, with an insolation flux of Sb ≃ 4745 S⊕, the planet receives more irradiation from the star than the theoretical runaway greenhouse limit (Kasting, Whitmire & Reynolds 1993; Goldblatt & Watson 2012; Kopparapu et al. 2013). In this case, a large water content would imply the presence of an extended steam atmosphere, which in turn would increase the measured radius with respect to a purely condensed water world, leading in our model to an overestimation of the bulk water content (Turbet et al. 2020). The presence of a water steam envelope could eventually be tested with the James Webb Space Telescope (JWST). In fact, with an Emission Spectroscopy Metric (ESM; Kempton et al. 2018) value of 8.2, TOI-561 b is a promising target for secondary eclipse and phase curve observations. More complex models, including a lighter core compositions (i.e. a Ca/Al enriched core), the modelling of water steam envelopes, or wet-melt solid interiors related to deep water reservoirs (Dorn & Lichtenberg 2021), could be an interesting step forward in the understanding of the planet structure and composition. The low density of TOI-561 b could also be related to the fact that the host star is a metal-poor, thick-disk star. Adibekyan et al. (2021a) showed that the composition of the rocky planets reflects the chemical abundances of the host star (even though not in a one-to-one relation), so implying a lighter composition for TOI-561 b with respect to other USP planets that orbit more metal-rich stars.13 According to Adibekyan et al. (2021a), the low density of TOI-561 b is consistent with the general ρ/ρEarth-like – |$f_{\rm iron}^{\rm star}$| trend and dispersion inferred from the sample of rocky planets analysed by the authors (see Figs. 2, 3 therein), where ρ/ρEarth-like is the planetary density normalised to that expected for an Earth-like composition, and |$f_{\rm iron}^{\rm star}$| is the iron-to-silicate mass fraction of the protoplanetary disk as inferred from the stellar properties. An additional interesting remark concerns the Galactic kinematics of the host star. According to our analysis, performed as described in Mustill, Lambrechts & Davies (2021), TOI-561 is located in a low-density region of the 6-dimensional Galactic phase space (see Winter et al. 2020, Mustill et al. 2021, and Kruijssen et al. 2021 for definition and discussion), which is not surprising given that TOI-561 is a thick disk star (Mustill et al. 2021). Kruijssen, Longmore & Chevance (2020) showed that stars in low-density regions seem to host no super-Earths, but only sub-Neptunes, i.e. planets having a significant H/He envelope and therefore located above the radius gap. In this context, TOI-561 b is an interesting object that runs counter to this finding. We point out that this result should be taken with some caution, since the Kruijssen et al. (2020) sample does not include planets with periods shorter than one day, and it excludes stars with ages >4.5 Gyr.14
All the four planets seem to host a large water layer (Section 6), although with high uncertainties, especially for planet c and d, due to the degeneracy related to the possible presence of a gas envelope. Also in this case, the presence of a considerable amount of water could be linked with the stellar properties. In fact, Santos et al. (2017) showed that metal-poor, thick disk stars are expected to form planetary building blocks with a higher water mass fraction (∼76 per cent) compared to metal-rich, thin disk stars (∼58 per cent). Therefore, we would expect these stars to produce water-rich planets, a result that is in agreement with our findings on the TOI-561 system.
Except for TOI-561 b, all the other planets are suggested to host a non-negligible H/He envelope. In particular, the gas content of planet c (∼1.3 wt per cent, the highest mass fraction among the four planets) implies a much lower density with respect to the density of planet d, even though the two planets have a similar size. This is reflected in the different positions of the planets in the mass-radius diagram (Fig. 11). The two planets show hints of a different evolution for what concerns their gas content. In fact, our atmospheric evolution model (Section 7) suggests that planet c underwent a strong envelope loss after the atmospheric accretion and the dispersal of the protoplanetary nebula, while planet d (as well as planet e) did not experience strong atmospheric escape, with a current gas content that is comparable to the original one. The surprising difference in gas mass fraction between planets c, d and e, not only at present time but also at the end of their formation phase, takes probably its origin in the conditions that prevailed during the protoplanetary disk phase. Planet c is indeed likely sub-critical because of its low mass, where sub-critical planets are those with masses below the critical value required to initiate runaway gas accretion (see Helled et al. 2014 for a recent review on the core accretion model), whereas planets d and e never accreted large amounts of gas as demonstrated in Section 7, and so they also remained always below the critical mass. The interpretation of the different gas mass fractions could therefore result from the structure of sub-critical planets. In this case, the gas mass fraction depends on the core mass, the thermodynamical properties in the disc, and more importantly the accretion rate of solids (lower accretion rate translating in larger gas mass fraction). Interpreting the internal structure of the four planets of the system in a global planetary system formation model could therefore constrain these parameters.
With its derived properties, TOI-561 c has a Transmission Spectroscopy Metric (TSM, Kempton et al. 2018) of 110.4, and is therefore a suitable target for atmospheric characterization with JWST.15 Instead, planets d and e have lower TSM values of 30.7 and 16.2, respectively. As the TSM is proportional to the equilibrium temperature, it is not surprising to obtain lower values for the two planets, given their longer periods.
In addition to the characterization of the four planets, we also identified a significant long-term signal (P ∼ 473 d) in the RVs. On the basis of our current data set, we are not able to distinguish between a stellar (magnetically-induced) or planetary origin. Long-term monitoring using both spectroscopic ground-based facilities and future long-staring missions like the PLATO spacecraft will allow us to shed light on the nature of this additional signal and to potentially find new outer companions. It is worth noting that, if the above-mentioned signal proves in future to be of planetary origin, there is a non-zero chance that, under the assumption of co-planarity, such a planet would transit. In fact, assuming the same inclination of planet e and using the semimajor axis |$a/{R_\star }= 279_{-10}^{+14}$| derived from our global fit, we infer an impact parameter of |$0.97_{-0.63}^{+0.49}$|. Moreover, the planet would orbit in TOI-561’s empirical habitable zone (175 ≲ P ≲ 652 d), as originally defined by Kasting et al. (1993) using a 1D climate model, and later updated in Kopparapu et al. (2013), Ramirez & Kaltenegger (2016) for main-sequence stars with 2600 < Teff |$\lt 10\, 000$| K.
This work bears witness to the fruitful results that can be obtained by the timely combination of data coming from different instruments. It adds to the works (Bonfanti et al. 2021b; Leleu et al. 2021; Delrez et al. 2021) that prove the potential of CHEOPS in precisely characterizing TESS-discovered exoplanets, as well as demonstrating the key role of high-precision spectrographs such as HARPS-N when working in synergy with space-based facilities.
SUPPORTING INFORMATION
Table 5. HARPS-N RV and activity indices measurements.
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.
ACKNOWLEDGEMENTS
We thank the referee for the useful comments that helped improving the quality of the manuscript. We gratefully acknowledge the MuSCAT2 team for the availability in collaborating with the CHEOPS Consortium on target monitoring, and the NGTS team for providing ground-based photometry that helped the scheduling of our observations. CHEOPS is an ESA mission in partnership with Switzerland with important contributions to the payload and the ground segment from Austria, Belgium, France, Germany, Hungary, Italy, Portugal, Spain, Sweden, and the United Kingdom. The CHEOPS Consortium gratefully acknowledge the support received by all the agencies, offices, universities, and industries involved. Their flexibility and willingness to explore new approaches were essential to the success of the mission. This work is based on observations made with the Italian Telescopio Nazionale Galileo (TNG) operated on the island of La Palma by the Fundación Galileo Galilei of the INAF at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofisica de Canarias (GTO program, and A40TAC_23 program from INAF-TAC). The HARPS-N project was funded by the Prodex Program of the Swiss Space Office (SSO), the Harvard University Origin of Life Initiative (HUOLI), the Scottish Universities Physics Alliance (SUPA), the University of Geneva, the Smithsonian Astrophysical Observatory (SAO), and the Italian National Astrophysical Institute (INAF), University of St. Andrews, Queen’s University Belfast and University of Edinburgh. This paper includes data collected by the TESS mission, which are publicly available from the Mikulski Archive for Space Telescopes (MAST). Funding for the TESS mission is provided by the NASA Explorer Program. Resources supporting this work were provided by the NASA High-End Computing (HEC) Program through the NASA Advanced Supercomputing (NAS) Division at Ames Research Center for the production of the SPOC data products. This research has made use of the NASA Exoplanet Archive, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program. This research has made use of data obtained from the portal http://www.exoplanet.eu/ of The Extrasolar Planets Encyclopaedia. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. GL acknowledges support by CARIPARO Foundation, according to the agreement CARIPARO-Università degli Studi di Padova (Pratica n. 2018/0098). TW and ACC acknowledge support from STFC consolidated grant numbers ST/R000824/1 and ST/V000861/1, and UKSA grant number ST/R003203/1. YA, MJH, B-OD, and ML acknowledge the support of the Swiss National Fundation under grant numbers 200020_172746, PP00P2-190080, and PCEFP2_194576. SH gratefully acknowledges CNES funding through the grant number 837319. GPi, VNa, GSs, IPa, LBo, and RRa acknowledge the funding support from Italian Space Agency (ASI) regulated by ‘Accordo ASI-INAF n. 2013-016-R.0 del 9 luglio 2013 e integrazione del 9 luglio 2015 CHEOPS Fasi A/B/C’. ADe acknowledges support from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (project Four Aces, grant agreement No. 724427), and from the National Centre for Competence in Research ‘PlanetS’ supported by the Swiss National Science Foundation (SNSF). KR is grateful for support from the UK STFC via grant number ST/V000594/1. This work has been supported by the National Aeronautics and Space Administration under grant number NNX17AB59G, issued through the Exoplanets Research Program. S.S. has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 833925, project STAREX). MG is an F.R.S.-FNRS Senior Research Associate. VVG is an F.R.S-FNRS Research Associate. LD is an F.R.S.-FNRS Postdoctoral Researcher. This work has been carried out within the framework of the NCCR PlanetS supported by the Swiss National Science Foundation. AMu and MF acknowledge support from the Swedish National Space Agency (career grant numbers 120/19C, DNR 65/19, 174/18). ABr was supported by the SNSA. We acknowledge support from the Spanish Ministry of Science and Innovation and the European Regional Development Fund through grant numbers ESP2016-80435-C2-1-R, ESP2016-80435-C2-2-R, PGC2018-098153-B-C33, PGC2018-098153-B-C31, ESP2017-87676-C5-1-R,MDM-2017-0737 Unidad de Excelencia Maria de Maeztu-Centro de Astrobiología (INTA-CSIC), as well as the support of the Generalitat de Catalunya/CERCA programme. The MOC activities have been supported by the ESA contract no. 4000124370. SGS, SCCB, and VA acknowledge support from FCT through FCT contract nr. CEECIND/00826/2018, POPH/FSE (EC), nr. IF/01312/2014/CP1215/CT0004, and IF/00650/2015/CP1273/CT0001, respectively. ODSD is supported in the form of work contract (DL 57/2016/CP1364/CT0004) funded by national funds through FCT. XB, SC, DG, MF, and JL acknowledge their role as ESA-appointed CHEOPS science team members. The Belgian participation to CHEOPS has been supported by the Belgian Federal Science Policy Office (BELSPO) in the framework of the PRODEX Program, and by the University of Liège through an ARC grant for Concerted Research Actions financed by the Wallonia-Brussels Federation. This work was supported by FCT – Fundação para a Ciência e a Tecnologia through national funds and by FEDER through COMPETE2020 – Programa Operacional Competitividade e Internacionalizacão by these grants UID/FIS/04434/2019, UIDB/04434/2020, UIDP/04434/2020, PTDC/FIS-AST/32113/2017 & POCI-01-0145-FEDER-032113,PTDC/FIS-AST/28953/2017 & POCI-01-0145-FEDER-028953,PTDC/FIS-AST/28987/2017 & POCI-01-0145-FEDER-028987. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (project Four Aces, grant agreement no. 724427). DG and LMS gratefully acknowledge financial support from the CRT foundation under grant number 2018.2323 ‘Gaseousor rocky? Unveiling the nature of small worlds’. KGI is the ESA CHEOPS Project Scientist and is responsible for the ESA CHEOPS Guest Observers Programme. She does not participate in, or contribute to, the definition of the Guaranteed Time Programme of the CHEOPS mission through which observations described in this paper have been taken, nor to any aspect of target selection for the programme. This work was granted access to the HPC resources of MesoPSL financed by the Region Ile de France and the project Equip@Meso (reference ANR-10-EQPX-29-01) of the programme Investissements d’Avenir supervised by the Agence Nationale pour la Recherche. PM acknowledges support from STFC research grant number ST/M001040/1. This work was also partially supported by a grant from the Simons Foundation (PI: Queloz, grant number 327127). GyMSz acknowledges the support of the Hungarian National Research, Development and Innovation Office (NKFIH) grant K-125015, a PRODEX Institute Agreement between the ELTE Eötvös Loránd University and the European Space Agency (ESA-D/SCI-LE-2021-0025), the Lendület LP2018-7/2021 grant of the Hungarian Academy of Science and the support of the city of Szombathely. This work is partly supported by JSPS KAKENHI grant number JP18H05439, JST CREST grant number JPMJCR1761, the Astrobiology Center of National Institutes of Natural Sciences (NINS) (grant number AB031010). EE-B acknowledges financial support from the European Union and the State Agency of Investigation of the Spanish Ministry of Science and Innovation (MICINN) under the grant number PRE2020-093107 of the Pre-Doc Program for the Training of Doctors (FPI-SO) through FSE funds.
DATA AVAILABILITY
HARPS-N observations and data products are available through the Data & Analysis Center for Exoplanets (DACE) at https://dace.unige.ch/. TESS data products can be accessed through the official NASA website https://heasarc.gsfc.nasa.gov/docs/tess/data-access.html. All underlying data are available either in the online supporting material or will be available via VizieR at CDS, where we will provide both the raw and detrended CHEOPS light curves.
Footnotes
From NASA Exoplanet Archive (Akeson et al. 2013), https://exoplanetarchive.ipac.caltech.edu/.
See TESS Data Release Notes: Sector 35, DR51 (https://archive.stsci.edu/tess/tess_drn.html).
We note that we obtained the same results when using uniform, uninformative priors, also for the five- and six-Keplerian fits.
According to Kass & Raftery (1995), a difference |$\Delta \ln \mathcal {Z} \gt 5$| sets a strong evidence against the null hypothesis, which in our case corresponds to the four-planet model.
All the USP planets shown in Fig. 11 have [Fe/H]>−0.14.
Kempton et al. (2018) suggest to select planets with TSM >92 for 1.5 R⊕< Rp <2.75 R⊕, and TSM >84 for 2.75 R⊕< Rp <4 R⊕.
REFERENCES
APPENDIX A: CHEOPS LIGHT CURVES AND TELEGRAPHIC PIXEL TREATMENT
As described in Section 3.2, the three CHEOPS visits of TOI-561 were reduced via the standard DRP processing. The light curves presented in this study, obtained using the RINF aperture size (RINF |$= 0.9 \, \times$| DEFAULT, where DEFAULT = 25 px; see also Section 3.2), are shown in Fig. A1. While for the two initial visits the automatic drp processes was performed, the appearance of some telegraphic pixels during the third visit required a more in-depth analysis.

CHEOPS RINF light curves of TOI-561 as extracted from the drp, with 4σ-clipping for outliers removal. Visits 1, 2, and 3 are shown from top to bottom.
In addition to the large number of known hot pixels present in the CHEOPS CCD (some of them visible in Fig. 2), some normal pixels can change their behaviour during the duration of a visit, for example becoming ‘hot’ after a SAA crossing. These pixels, called ‘telegraphic’ for their abnormal behaviour, can affect the photometry if located within the photometric aperture (see e.g. Leleu et al. 2021). During the third CHEOPS visit, we identified an unusual flux bump before the ingress of TOI-561 d transit, at BJD ∼2459318.75 (top panel, Fig. A2). After analysing the statistics of each pixel light curve within the photometric aperture, we detected a telegraphic pixel with a large flux variation (see second panel, Fig. A2) located within the CHEOPS PSF. The exact position of this pixel on the CHEOPS CCD is shown in Fig. 2. We masked the pixel flux and repeated the photometric extraction of the visit using the RINF aperture, so removing the flux jump in the light curve (bottom panel, Fig. A2). During this analysis, we detected two additional telegraphic pixels within the photometric aperture, inducing smaller, but still significant variations in the light curve flux (third panel, Fig. A2). We corrected for the effect of these pixels as described above.
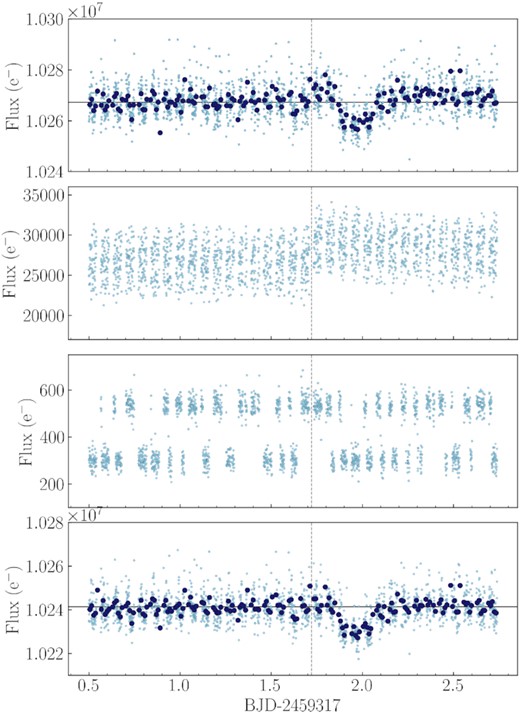
Top panel: TOI-561 RINF original light curve of the third visit (light blue dots) after the removal of 4σ outliers, with overplotted the 15-min binned light curve (dark blue dots). The start of the flux jump due to the telegraphic pixel is marked with the dashed vertical line. Second panel: Light curve of the telegraphic pixel located within the CHEOPS PSF. Third panel: Light curve of the two additional telegraphic pixels located within the RINF aperture. Bottom panel: Corrected light curve after masking the three telegraphic pixels.
While investigating the nature of the flux bump happening during the third visit, we also extracted the light curve using a PSF-photometry approach exploiting the pipe (PSF Imagette Photometric Extraction) software.16pipe is a photometric extraction package specifically developed to extract CHEOPS light curves by applying PSF photometry on the 60-pixel imagettes, complementing the official drp extraction. The use of PSF photometry makes usually easier to filter out the impact of hot pixels and cosmic rays, by either giving them a lower weight or masking them entirely in the fitting process. However, in this case the telegraphic pixel was located inside the CHEOPS PSF, requiring a careful manual masking. As for the drp light curve, the flux bump in the pipe photometry is reduced after masking the telegraphic pixel (bottom panel, Fig. A3). The pipe-extracted light curve resulted in a slightly lower mean absolute deviation (MAD) with respect to the drp photometry (top panel, Fig. A3), mainly due to the lower number of outliers present in the PSF photometry. For a more detailed comparison between pipe and drp photometries, see Morris et al. (2021b). We performed the same global analysis described in Section 5 using the pipe light curve instead of the drp one, obtaining consistent results and comparable uncertainties on the transit parameters of both planets b and d. We therefore decided to use the light curve obtained with the official drp extraction in our final analysis.
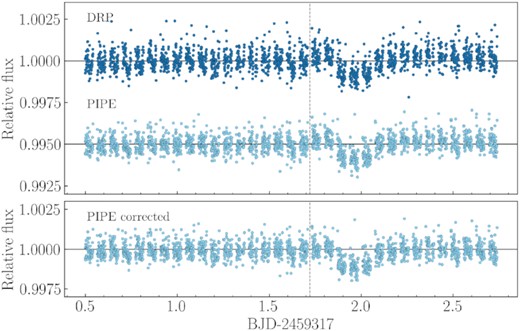
Top panel: Comparison between drp and pipe-extracted light curve of TOI-561 third visit, before the telegraphic pixel correction and with 4σ outliers removal. The DRP has an MAD of 371 ppm over the whole visit, while pipe of 325 ppm. Bottom panel: pipe light curve after the telegraphic pixel correction. The light curve gets slightly noisier (MAD = 331 ppm) because one less pixel is considered in the reduction, but more reliable thanks to the exclusion of the telegraphic pixel flux. In both panels, the beginning of the flux jump is highlighted with a vertical dashed line.
APPENDIX B: FLOATING CHUNK OFFSET METHOD ON TOI-561 B
In order to investigate the literature discrepancy on the mass of TOI-561 b (Section 2.2), we adopted a specific observing strategy with HARPS-N targeting the USP planet (Section 3.3), obtaining multiple observations during the same night for 22 nights. Multiple nightly observations can be used to precisely infer the mass of USP planets using the Floating Chunk Offset method (FCO; Hatzes 2014), which consists in applying a nightly offset to remove all the other signals present in the system, both of planetary and stellar origin (i.e. Howard et al. 2013; Pepe et al. 2013; Malavolta et al. 2018; Frustagli et al. 2020). The FCO method is only applicable when the separation between the USP period and the period of all the other signals is large enough, and the RV semi-amplitude has a similar or larger value with respect to the other signals. As demonstrated in L21, these conditions apply to TOI-561 b, for which the authors derived an FCO semi-amplitude of Kb, FCO = 1.80 ± 0.38 m s−1 (Mb, FCO = 1.83 ± 0.39 M⊕) exploiting multiple observations collected over ten nights.
Here, we applied the FCO method to TOI-561 b on a total of 22 HARPS-N nights, adding 12 novel nights to the 10 nights already presented in L21. Out of the total set, four nights have six multiple observations extending over more than 40 per cent of the orbital period of the planet, and span opposite orbital phases to provide an optimal phase coverage. We performed a pyde + emcee fit with pyorbit, assuming a fixed zero eccentricity and Gaussian priors on period and T0 coming from the global fit, and we added a jitter term to account for possible additional white noise. We derived a semi-amplitude of Kb = 1.81 ± 0.31 m s−1, corresponding to a mass of Mb = 1.86 ± 0.33 M⊕, with a jitter of |$0.96_{-0.23}^{+0.25}$| m s−1. Fig. B1 shows the resulting phase-folded RVs. The derived mass and semi-amplitude are nicely in agreement with the L21 values, and they support the values inferred from our joint photometric and RV modelling (Section 5), being consistent within 1σ. Given the higher number of RVs included in the joint fit, which led to smaller uncertainties on the derived parameters, we decided to adopt as final values for TOI-561 b the ones obtained from the global modelling, i.e. Kb = 1.93 ± 0.21 m s−1 and Mb = 1.99 ± 0.22 M⊕.
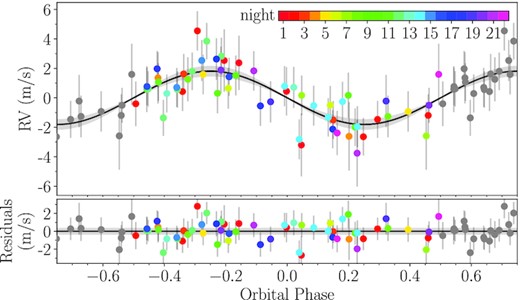
Phase-folded RVs of the 22 HARPS-N nights used to model TOI-561 b with the FCO method. The error bars include the jitter term added in quadrature.



