The spins of compact objects born from helium stars in binary systems

Fuller, Jim; Lu, Wenbin

doi:10.1093/mnras/stac317

ABSTRACT

The angular momentum (AM) content of massive stellar cores helps us to determine the natal spin rates of neutron stars and black holes. Asteroseismic measurements of low-mass stars have proven that stellar cores rotate slower than predicted by most prior work, so revised models are necessary. In this work, we apply an updated AM transport model based on the Tayler instability to massive helium stars in close binaries, in which tidal spin-up can greatly increase the star’s AM. Consistent with prior work, these stars can produce highly spinning black holes upon core-collapse if the orbital period is less than |$P_{\rm orb} \lesssim \! 1 \, {\rm d}$|⁠. For neutron stars, we predict a strong correlation between the pre-explosion mass and the neutron star rotation rate, with millisecond periods (⁠|$P_{\rm NS} \lesssim 5 \, {\rm ms}$|⁠) only achievable for massive (⁠|$M \gtrsim 10 \, M_\odot$|⁠) helium stars in tight (⁠|$P_{\rm orb} \lesssim 1 \, {\rm d}$|⁠) binaries. Finally, we discuss our models in relation to type Ib/c supernovae, superluminous supernove, gamma-ray bursts, and LIGO/Virgo measurements of black hole spins. Our models are roughly consistent with the rates and energetics of these phenomena, with the exception of broad-lined Ic supernovae, whose high rates and ejecta energies are difficult to explain.

stars: binaries: general, stars: black holes, stars: massive, stars: rotation, stars: supernovae: general, stars: Wolf-Rayet

1 INTRODUCTION

Rotation is a key player in the drama that unfolds upon the death of a massive star. The angular momentum (AM) contained in the iron core and overlying layers determines the rotation rate at core-collapse (CC), which could have a strong impact on the dynamics of CC and the subsequent supernova (SN) (see e.g. MacFadyen & Woosley 1999; Woosley, Heger & Weaver 2002; Yoon, Langer & Norman 2006). Rotation may help us determine the nature of the compact remnant, which could range from a slowly rotating neutron star (NS) to a millisecond magnetar or a rapidly spinning black hole (BH, see e.g. Heger, Langer & Woosley 2000; Heger, Woosley & Spruit 2005). The former could evolve into an ordinary pulsar, while the latter two outcomes offer exciting prospects for the engines that power long gamma-ray bursts (GRBs), broad-lined type Ic SNe (Ic-BL), and type Ic superluminous SNe (Woosley 1993; Maeda et al. 2007; Kasen & Bildsten 2010; Metzger et al. 2011).

In most cases, however, compact objects are probably born slowly rotating due to efficient AM transport within their progenitor stars. This is demonstrated by several lines of evidence. Asteroseismic measurements of core rotation rates of red giant stars (Beck et al. 2012; Mosser et al. 2012; Deheuvels et al. 2014, 2015; Triana et al. 2017; Gehan et al. 2018) indicate that they rotate much slower than predicted by most AM transport models (Cantiello et al. 2014; Fuller et al. 2014; Belkacem et al. 2015; Spada et al. 2016; Eggenberger et al. 2017; Ouazzani et al. 2019). White dwarfs typically rotate with periods of |$\sim 1 \, {\rm d}$| (Hermes et al. 2017), proving that the vast majority of their progenitors’ core AM is extracted by the time they form. Pulsar studies indicate that typical NSs are born with natal rotation periods of |$P_{\rm 0} \sim 50-100 \, {\rm ms}$| (Faucher-Giguère & Kaspi 2006; Popov et al. 2010; Popov & Turolla 2012; Gullón et al. 2014), again slower than predicted by many models (Heger et al. 2005). Finally, most BH spins measured by LIGO/Virgo are low (Zaldarriaga, Kushnir & Kollmeier 2018; The LIGO Scientific Collaboration 2019; Miller, Callister & Farr 2020; Roulet et al. 2021; Zevin et al. 2021), again indicating that strong AM transport within their progenitors extracts AM from the core and transports it to the envelope where it is lost by winds, binary interactions, or an SN explosion. This appears to conflict with the high BH spins measured for high-mass X-ray binaries (Miller & Miller 2015), an issue which is not yet understood (see Qin et al. 2019, Fishbach & Kalogera 2021, and Belczynski, Done & Lasota 2021 for recent discussion).

Fuller, Piro & Jermyn (2019) argued that magnetic fields generated by the Tayler instability create magnetic torques that can extract most of a stellar core’s AM and can approximately match asteroseismic observation rates (but see also Eggenberger et al. 2019). That model is a modified version of the Tayler–Spruit dynamo (Spruit 2002) used in many stellar models, in which weak magnetic fields are amplified by differential rotation. In the Fuller et al. (2019) version, the fields grow to larger strengths (creating more efficient AM transport) due to weaker non-linear dissipation via Alfvén waves in the saturated state. Ma & Fuller (2019) applied this model to massive single stars, predicting long NS rotation periods of tens to hundreds of milliseconds, while Fuller & Ma (2019) predicted low BH spins (a ∼ 10⁻²) for BHs born from single stars.

While compact object spins are slow in most cases, central engine models for energetic supernovae and GRBs suggest that rapid core rotation is possible in a small fraction of SN progenitors. A natural possibility to explore is stripped-envelope stars born in close binaries, where tidal spin-up replenishes the AM of the helium star, potentially spawning rapidly rotating compact objects (see e.g. Bogomazov & Popov 2009; Kushnir et al. 2017; Qin et al. 2018; Bavera et al. 2020; Belczynski et al. 2020; Olejak & Belczynski 2021). Here we investigate that possibility in detail by generating a suite of models in compact binary systems, including tidal torques and an updated AM transport prescription based on Fuller et al. (2019). We will find that rapid NS and BH spins are indeed possible, but that they are restricted to close binaries (orbital periods |$P_{\rm orb} \lesssim 1 \, {\rm d}$|⁠) and are most likely to originate from very massive helium stars (⁠|$M_{\rm He} \gtrsim 5-10 \, M_\odot$|⁠).

2 ANGULAR MOMENTUM TRANSPORT FOR LOW SHEAR

The Tayler–Spruit dynamo (Spruit 2002) produces magnetic torques by generating radial magnetic field from azimuthal fields via the Tayler instability. The azimuthal field B_ϕ is generated by winding up the radial field B_r via differential rotation. The azimuthal field grows until it becomes unstable to the Tayler instability (Spruit 1999), such that magnetic energy is then channeled into small-scale structures. The Tayler instability saturates when non-linear damping processes dissipate energy at the same rate that energy is added to the azimuthal field by winding. When the instability operates, it may also produce a magnetic dynamo that alters the mean radial magnetic field strength.

In prior descriptions of the Tayler instability (Spruit 2002; Fuller et al. 2019), it is not clear what happens when the shear q = |dln Ω/dln r| is below the minimum value q_min needed to sustain the saturated state, where r is radius and Ω is the local rotation rate of the star. According to the model of Spruit (2002), q_min = (N_eff/Ω)^7/4(η/r²Ω)^1/4, where N_eff is the effective buoyancy frequency and η is the magnetic diffusivity, while q_min ∼ (N_eff/Ω)^5/2(η/r²Ω)^3/4 in the model of Fuller et al. (2019), and both models assume that Ω ≪ N_eff. When q = q_min, the azimuthal magnetic field has an Alfvén frequency |$\omega _{\rm A} = B_\phi /\sqrt{4 \pi \rho r^2}$| that is equal to the minimum field strength needed for Tayler instability, ω_c ∼ Ω(N_eff/Ω)^1/2(η/r²Ω)^1/4.

When q < q_min, energy is added to the background field at a rate too slow to keep up with non-linear damping when the instability operates. The radial magnetic field B_r will still be wound up into a toroidal field B_ϕ by differential rotation, increasing the Alfvén frequency until it reaches ω_A ∼ ω_c. However, for q < q_min, the shear is not strong enough to maintain the saturated states found by Spruit (2002) or Fuller et al. (2019), so the instability likely occurs intermittently.

To estimate the torque provided by the intermittent action of the Tayler instability, we posit that the time-averaged torque is

$$\begin{eqnarray} T \sim \frac{q}{q_{\rm min}} B_r B_\phi \end{eqnarray}$$

(1)

when q < q_min and T ∼ B_rB_ϕ otherwise. This corresponds to a torque of the same magnitude as the saturated state, but acting on a duty cycle q/q_min. Assuming that B_r ∼ (ω_A/N)B_ϕ as used by both Fuller et al. (2019) and Spruit (2002), the time-averaged torque can be written

$$\begin{eqnarray} T \sim 4 \pi \rho r^2 \frac{q}{q_{\rm min}} \frac{\omega _{\rm A}^3}{N} \, . \end{eqnarray}$$

(2)

When the instability occurs intermittently, the time-averaged value of ω_A will be very close to the threshold ω_c, since field strengths above this will initiate the instability which will decrease B_ϕ faster than it can be generated due to winding. Using q_min ∼ α⁻³(N/Ω)^5/2(η/r²Ω)^3/4 from Fuller et al. (2019), where α is a constant of the order of unity, and the value of ω_c above, we find that the torque evaluates to

$$\begin{eqnarray} T \sim 4 \pi \alpha ^3 \rho r^2 q \Omega ^4/N^2 \, , \end{eqnarray}$$

(3)

i.e. the same value found when the instability operates continuously when q > q_min. Hence, the associated viscosity can always be written

$$\begin{eqnarray} \nu _{\rm AM} = \alpha ^3 r^2 \frac{\Omega ^3}{N^2} \, , \end{eqnarray}$$

(4)

the same as found by Fuller et al. (2019). The reason that the torque can reach the same value even when the instability operates intermittently is that the time-averaged value of B_ϕ is larger than it would be in the saturated state from Fuller et al. (2019). In other words, when q < q_min, ω_A ∼ ω_c > Ω(qΩ/N)^1/3, where the last value is the saturated value of ω_A from Fuller et al. (2019).

Although we recover the same viscosity law ν = α³r²Ω³/N², this now applies to the entire radiative region of the star where Ω < N, not just where q > q_min. Hence, the value of α needed to match asteroseismic observations will decrease. In prior models, Tayler torques would often enforce q ≃ q_min, but this is not the case in the updated prescription, so the rotation profiles are slightly different, but shear is still predicted to be largest where N is largest. Upon implementing this AM transport model into the same stellar models as Fuller et al. (2019), we find that a value of α ∼ 0.25 produces very similar core rotation rates as the prior prescription, which had α ∼ 1 but only operated when q > q_min. Since we expect α to be of the order of unity, a value of 0.25 is reasonable and suggests this model is viable. Hence we adopt α = 0.25 as an asteroseismically calibrated saturation coefficient for the models in this paper.

As discussed in Section 4 of Ma & Fuller (2019), the evolutionary time-scale of the star is always longer than the Tayler instability growth time such that we can assume the instability has reached the statistical equilibrium discussed above. In some cases, however, the AM transport time-scale can become longer than the stellar evolutionary time, such that Tayler torques become ineffective. In these cases, we expect AM to be nearly conserved in radiative regions, unless other processes such as wave-driven AM transport (e.g. Fuller et al. 2015) are important.

3 STELLAR EVOLUTION MODELS

Using the AM transport prescription described above, we run binary stellar evolution models using MESA (Paxton et al. 2011, 2013, 2015, 2018, 2019), version 10398. Our first step is to create a grid of helium star models to use in our binary evolution modelling. To do this, we begin with zero-age main sequence (ZAMS) stars of masses |$M_{\rm ZAMS} = \lbrace 14,16,18,20,25,30,40,50,60,70,80,90 \rbrace \, M_\odot$|⁠. All models are initialized with a rotation period of |$P_{\rm rot} = 2 \, {\rm d}$| (corresponding to rotational velocity |$v_{\rm rot} \sim 200 \, {\rm km\,s^{-1}}$|⁠) and have metallicity Z = 0.02, except the |$80 \, M_\odot$| and |$90 \, M_\odot$| models which have Z = 0.002. As discussed in Ma & Fuller (2019), the final core AM is not very sensitive to the initial rotational velocity, so we do not vary that parameter.

Throughout the evolution, wind mass-loss is included via MESA’s ‘Dutch’ wind prescription (de Jager, Nieuwenhuijzen & van der Hucht 1988; Nugis & Lamers 2000; Vink, de Koter & Lamers 2000; Vink, de Koter & Lamers 2001) with efficiency η = 0.5. Moderate exponential convective overshoot is included using overshoot_f=0.02. In convective zones, we adopt MESA’s default AM transport in which convection acts like an AM viscosity of ν ∼ Hv_con, where H and v_con are the scale height and convective velocity, such that rigid rotation is maintained. We also use MLT+ + (Paxton et al. 2013) and set the surface to an optical depth of 10³ in order to bypass structural issues related to super-Eddington luminosities in the near-surface layers. This decreases the radius of the star by a tiny amount and is unlikely to affect the core evolution or AM content. MESA inlists are provided at this Zenodo repository.¹

We then evolve these stars in a binary with initial orbital period of |$50 \, {\rm d}$| with a |$1.5 \, M_\odot$| point-mass companion. This choice allows the stars to effectively evolve as single stars until they overflow their Roche lobes when crossing the Hertzsprung gap, after they have exhausted hydrogen in their core but before helium burning has begun. Upon Roche lobe overflow, we simulate mass transfer by stripping off the hydrogen envelope using MESA’s relax_mass feature. This results in helium stars of masses |$M_{\rm He} = \lbrace 3.4,4.2,5.0,5.8,7.5,9.7,14,20,23,27.5,35,41 \rbrace \, M_\odot$|⁠, which are the template models we use for further calculations.

For each helium star model, we then relax its metallicity to either Z = 0.02 or Z = 0.002. While forming a Z = 0.002 model from a Z = 0.02 progenitor model (or vice versa) is not fully self-consistent, it allows us to explore a wider set of He star models. We shall see that the resulting spins depend primarily on final orbital period and final mass, with little memory of how the star got to that state (i.e. the initial mass, metallicity, companion mass, and orbital period). Next, we place the helium stars into an orbit with an equal-mass companion (treated as a point mass), with an orbital period of |$P_{\rm orb} = \lbrace 0.25, 0.5, 0.75, 1.0, 1.25, 1.5, 2.0, 99 \rbrace \, {\rm d}$|⁠. The period cannot be much smaller than |$0.25 \, {\rm d}$| without causing Roche lobe overflow during the He-burning stage, while periods longer than 2 d are uninteresting because tidal torques become negligible according to our tidal prescription. The 99-d models are effectively single helium stars.

For tidal torques, we use the same method as Qin et al. (2018) (see also Yoon, Woosley & Langer 2010; Kushnir et al. 2017) based on Zahn (1977). For a star of mass M and radius R, the tidal torque can be written

$$\begin{eqnarray} \dot{J}_{\rm tide} = 3 q^2 (\Omega _{\rm orb} - \Omega) M R^2 \left(\frac{R}{a}\right)^{\! 6} \frac{k}{T} \, , \end{eqnarray}$$

(5)

where Ω_orb is the angular orbital frequency, and q = M′/M is the mass ratio of the companion. Here, k/T describes how well the tidal forcing couples with internal gravity waves launched from the outer boundary of the convective core, which in Zahn’s notation is

$$\begin{eqnarray} \frac{k}{T} = \omega _{\rm d} (1 + q)^{5/6} \left(\frac{R}{a}\right)^{\! 5/2} E_2 \, , \end{eqnarray}$$

(6)

where |$\omega _{\rm d}= \sqrt{GM/R^3}$| is the star’s dynamical frequency, and E₂ scales strongly with the core radius. To evaluate this factor, we follow Kushnir et al. (2017) who show

$$\begin{eqnarray} \frac{k}{T} \simeq \frac{2}{3} \frac{\omega _{\rm d}^2}{\omega _{\rm c}} \left(\frac{r_{\rm c}}{R}\right)^{\! 5} \left(\frac{\omega _{\rm f}}{\omega _{\rm c}}\right)^{\! 5/3}\, \frac{\rho _{\rm c}}{\bar{\rho }_{\rm c}} \left(1 - \frac{\rho _{\rm c}}{\bar{\rho }_{\rm c}} \right)^2 \, , \end{eqnarray}$$

(7)

with |$\omega _{\rm c} = \sqrt{G m_{\rm c}/r_{\rm c}^3}$|⁠, ω_f = 2(Ω_orb − Ω), with m_c and r_c the convective core mass and radius, while ρ_c is the density at r_c and |$\bar{\rho }_{\rm c}$| is the average core density.

We use the same implementation as used in Qin et al. (2018), in which the torque is applied uniformly per unit mass to the radiative envelope, such that the rate of change of specific AM of each fluid element is

$$\begin{eqnarray} \dot{j} = \frac{2}{3 \kappa } \frac{r^2}{R^2} \frac{\dot{J}_{\rm tide}}{M} \, , \end{eqnarray}$$

(8)

and κ is the gyration radius κ = I/(MR²), with I the star’s moment of inertia. Technically, κ should be the gyration radius of the radiative envelope such that |$\int \mathrm{ d}m \dot{j} = \dot{J}_{\rm tide}$|⁠, but in our models this is nearly equal to κ so the distinction is unimportant. Another technical detail is that equation (8) is only appropriate if Ω is constant within the envelope. Since our AM transport prescription predicts nearly rigid rotation during core He burning when the tidal torque is important, this issue is not problematic. The tidal torque vanishes when the convective core disappears after core He burning and resumes when a convective C-burning core or He-burning shell appears, but this typically occurs in the final hundreds of years at which point tidal torques become negligible.

We then evolve these stars until the onset of CC. Some models halt due to numerical problems after oxygen burning, but we find that subsequent AM transport is negligible so the core AM content is very close to its value at CC. The |$3.4 \, M_\odot$| models lose a large fraction of their helium envelopes via case BB mass transfer, and they undergo off-centre neon burning, at which point their evolution is terminated. It is thus possible that their final core AM are slightly overestimated due to AM transport during Ne/O burning.

In subsequent sections, we will compute the time until merger due to gravitational wave emission after CC, in the absence of kicks. To compute the post-CC orbital semimajor axis, eccentricity, and orbital decay time, we follow the procedure described in Tauris et al. (2017) (see also Blaauw 1961). For BH formation, this entails no change in the eccentricity or semimajor axis because we assume the entire star collapses into the BH. For NS formation, we assume that all the progenitor mass, apart from |$1.6 \, M_\odot$|⁠, is instantaneously lost from the system.

3.1 Angular momentum extraction

The evolution of the star’s core AM provides useful insight into the AM transport processes affecting the rotation rate of the compact object born upon CC. Fig. 1 plots J_core (the AM contained within the inner |$1.6 \, M_\odot$|⁠) of several different helium star models, each initialized with Z = 0.002 at an orbital period of |$P_{\rm orb} = 0.5 \, {\rm d}$|⁠. The mass cut-off |$1.6 \, M_\odot$| is a reasonable estimate for the baryonic mass of an NS born in the case of a subsequent explosion. Assuming conservation of AM during CC and explosion, the corresponding NS rotation period is P_NS = 2πI_NS/J_core. We use an NS moment of inertia of |$I_{\rm NS} = 1.5 \times 10^{45} {\rm g} \, {\rm cm}^2$|⁠, reasonable for this mass (Worley, Krastev & Li 2008).

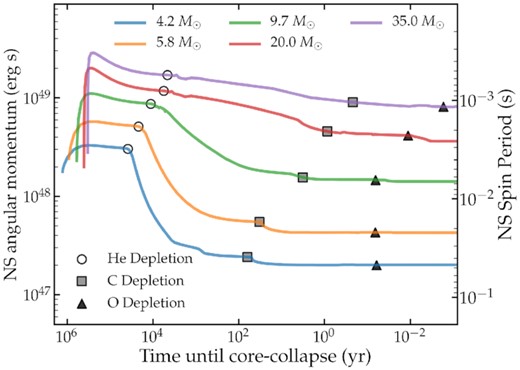
$The angular momentum (AM) content of the inner $1.6 \, M_\odot$ of helium stars of various masses, as a function of time. The right axis shows the corresponding NS rotation period. Each of these models is initialized with an orbital period of $P_{\rm orb} = 0.5 \, {\rm d}$. The core AM initially increases due to tidal spin-up, but it subsequently decreases as the core contracts and AM is transferred to the outer layers.$

Figure 1.

The angular momentum (AM) content of the inner |$1.6 \, M_\odot$| of helium stars of various masses, as a function of time. The right axis shows the corresponding NS rotation period. Each of these models is initialized with an orbital period of |$P_{\rm orb} = 0.5 \, {\rm d}$|⁠. The core AM initially increases due to tidal spin-up, but it subsequently decreases as the core contracts and AM is transferred to the outer layers.

Open in new tab Download slide

The helium star’s initial core AM is determined primarily by AM transport within the progenitor as it expands after the main sequence. As discussed in Ma & Fuller (2019), most of the core’s AM is lost during this phase, before the onset of envelope stripping. The core’s AM is nearly conserved during the stripping process, so our models self-consistently determine the initial spin rate of the helium star based on the progenitor’s evolution. In our models, the core’s AM is remarkably insensitive to the rotation rate of the progenitor because the internal torques are proportional to Ω⁴, so that the core’s spin reaches an ‘equilibrium’ spin rate at which spin-up via contraction is balanced by spin-down due to AM transport to the envelope.

At the short orbital period |$P_{\rm orb} = 0.5 \, {\rm d}$| in Fig. 1, tidal synchronization is fairly efficient and spins the stars up towards synchronous rotation, increasing J_core. The most massive models in Fig. 1 achieve nearly synchronous rotation due to their larger core radii (and hence stronger tidal torques), whereas the least massive models are only partially synchronized by the end of core He-burning. Each model remains rigidly rotating during core He-burning. Due to mass-loss via winds during this phase, the orbits widen slightly, decreasing the orbital/spin frequency. The core contracts slightly as He is depleted, reducing its moment of inertia and AM because it remains coupled with the radiative envelope. These effects combine to produce a slight reduction of J_core after tidal spin-up during core He-burning.

The largest extraction of core AM occurs between core He-depletion (denoted with open circles) and core C-depletion (denoted with grey circles). During this phase, the core contracts greatly but AM transport remains efficient, keeping the star nearly rigidly rotating until the beginning of C-burning. The large decrease in the core’s moment of inertia thus greatly decreases its AM content. During this phase, AM transport is efficient because the CO core has nearly uniform composition, hence there is not a strong composition gradient contributing to the compositional buoyancy frequency N_μ that restricts AM transport (see Fuller et al. 2019 for more detailed discussion).

During and after C-burning, large amounts of differential rotation begin to appear within the CO core, due to the large composition gradients that develop, and the shorter evolutionary times. However, the short remaining lifetime of the star means that only a small amount of AM can subsequently be extracted from the core before it collapses. Hence, J_core asymptotes to its final value soon after C-depletion, in spite of the fact that the rate at which the core loses AM generally continues to increase. We find that the AM extraction rates after He-depletion are similar between the low and high-mass models. However, the larger initial values of J_core and the much shorter evolution time-scales of the high-mass models means that much more core AM is retained at CC. Consequently, an NS produced from a |$4.2 \, M_\odot$| model is predicted to rotate with a period |$P_{\rm NS} \! \sim \! 50 \, {\rm ms}$|⁠, while an NS produced from a |$35 \, M_\odot$| model is predicted to rotate with a period |$P_{\rm NS} \! \sim \! 1 \, {\rm ms}$|⁠.

Fig. 2 shows the specific AM as a function of mass coordinate for a |$M_{\rm He} = 14 \, M_\odot$| model in a |$P_{\rm orb} = 0.5 \, {\rm d}$| binary, plotted at a few different evolutionary stages. This model has a |$\sim \! 3 \, M_\odot$| helium envelope and a radius of |$\sim \! 1.2 \, R_\odot$| at core-collapse. It would produce an NS with |$P_{\rm NS} \! \approx \! 4 \, {\rm ms}$| or a BH with a_BH ≈ 0.5 (see Section 4). The specific AM of the core decreases by a factor of a few between central helium depletion and central carbon burning, and decreases only slightly more before CC. Note that the specific AM of the outermost layers actually increases due to the AM transported outwards from inner layers. Only the outer |$\sim \! 1 \, M_\odot$| has enough AM (j > j_ISCO) to circularize outside of a BH formed from the interior layers (see Section 5.2 for calculation of j_ISCO).

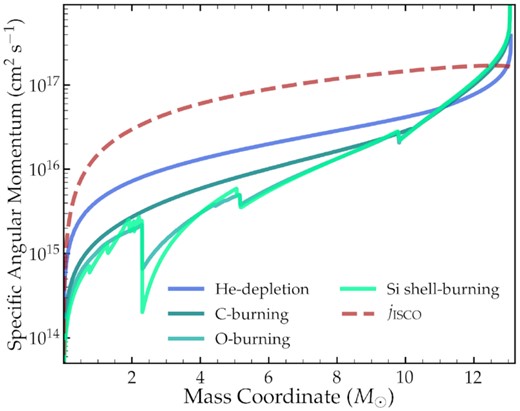
$Spherically averaged specific angular momentum as a function of mass coordinate within our $M_{\rm He} = 14 \, M_\odot$ ($M_{\rm ZAMS} = 40 \, M_\odot$), Z = 0.002 helium star with orbital period $P_{\rm orb} = 0.5 \, {\rm d}$. Lighter lines correspond to progressively later evolutionary stages, while the red dashed line corresponds to the specific angular momentum needed to circularize outside a black hole formed from the interior layers.$

Figure 2.

Spherically averaged specific angular momentum as a function of mass coordinate within our |$M_{\rm He} = 14 \, M_\odot$| (⁠|$M_{\rm ZAMS} = 40 \, M_\odot$|⁠), Z = 0.002 helium star with orbital period |$P_{\rm orb} = 0.5 \, {\rm d}$|⁠. Lighter lines correspond to progressively later evolutionary stages, while the red dashed line corresponds to the specific angular momentum needed to circularize outside a black hole formed from the interior layers.

Open in new tab Download slide

4 COMPACT OBJECT ROTATION RATES

4.1 Neutron star rotation rates

Fig. 3 shows our predictions for the natal NS rotation rates of each of our models, assuming (1) a successful explosion, (2) an NS of baryonic mass |$1.6 \, M_\odot$| and moment of inertia |$I_{\rm NS} = 1.5 \times 10^{45} {\rm g} \, {\rm cm}^2$|⁠, and (3) conservation of AM during CC and explosion. Our models predict a strong correlation between the pre-explosion mass and the NS rotation period, with higher mass stars producing NSs that rotate up to 50 times faster than low-mass stars, down to rotation periods of |$P_{\rm NS} \sim 1 \, {\rm ms}$| for the range of models considered here. While many of these stars likely produce BHs rather than NSs upon CC, those NSs that are born from massive stars in tight binaries are likely to be much more rapidly rotating than typical young NSs.

Figure 3.

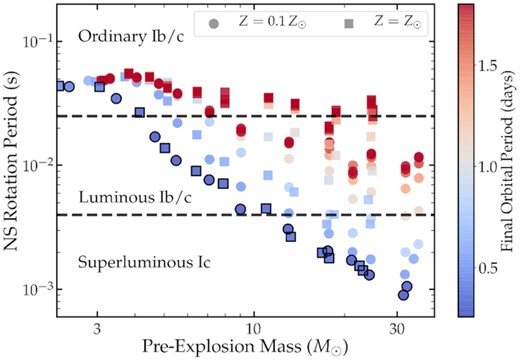
The natal neutron star rotation period for each of our models, calculated from the core angular momentum, as a function of the pre-explosion mass of its helium progenitor star. The colour of each symbol indicates the binary orbital period at core-collapse. The squares and circles denote solar metallicity and low-metallicity models, respectively. The black outlines denote models that would merge within a Hubble time. The dashed lines suggest the approximate boundaries between ordinary, luminous, and superluminous supernovae, given an appropriate magnetar field strength.

Open in new tab Download slide

There is also a strong correlation between pre-explosion orbital period and the NS rotation period, with rapidly rotating NSs arising from more compact binaries due to the more rapid rotation enforced by tidal synchronization during core He-burning. For stars in tight binaries, the progenitor metallicity only indirectly affects the NS rotation period, due to its affect on stellar winds which decrease M_exp and increase P_orb due to mass-loss during the He-burning phase. This makes rapid NS rotation more likely in low-metallicity environments, as also found for BH spin (e.g. Qin et al. 2018; Bavera et al. 2020). Because P_orb ≲ 1 d is required for millisecond NS periods in this scenario, many massive (⁠|$M \gtrsim 5 \, M_\odot$|⁠) main sequence companions are too large to fit within the orbit, and tidal spin-up is more likely to be achieved by a compact object or a low-mass companion star.

At orbital periods |$P_{\rm orb} \gtrsim 1 \, {\rm d}$|⁠, tidal synchronization does not occur and the NS rotation rate will depend on the progenitor rotation rate. We find relatively long NS rotation periods (⁠|$P_{\rm NS} \gtrsim 10 \, {\rm ms}$|⁠) for all the wide binary models considered here. Slower NS rotation may be possible for stars born less rapidly rotating or with higher mass loss rates due to higher metallicity. Faster NS rotation may be possible for stars born more rapidly rotating or with lower mass loss rates due to lower metallicity.

For NSs originating from low-mass progenitors with |$M_{\rm He} \lesssim 4 \, M_\odot$|⁠, the predicted NS rotation rate is |$P_{\rm NS} \sim 50 \, {\rm ms}$| with little dependence on mass and orbital period. This feature is similar to that found by Fuller et al. (2019) in which the predicted rotation rates of WDs are only weakly dependent on the progenitor’s rotation rate. The longer evolution time-scales in these stars allow the torques arising from Tayler instability to achieve ‘equilibrium’ in the sense that they reduce the core rotation rate until the AM transport time scale (which scales as Ω⁻³) becomes longer than the stellar evolution time-scale. Evidently this ‘equilibrium’ state is not reached in the advanced evolution of high-mass He stars because of their very short evolution time-scales, leading to a spread in NS rotation rates that depend on the progenitor rotation rate.

If NS baryonic masses from very massive stars are larger than |$1.6 \, M_\odot$|⁠, they will contain more AM and could spin faster than the models in Fig. 3. We find that using a baryonic mass of |$2.3 \, M_\odot$| and assuming I_NS ∝ M_NS results in spin periods that are smaller by a factor of ∼1.5. Smaller NS masses result in only slightly larger NS spin periods. Hence, the possible range of NS periods can only vary by a factor of ∼2 due to differences in the NS mass.

We note that the NS rotation periods of our single He stars models are a factor of ∼4 shorter than those born form H-rich stars in Ma & Fuller (2019), when comparing to the same ZAMS progenitor mass. There are two reasons. The first is that the helium core in H-rich stars is embedded in a H envelope that continues to extract AM from the He core, producing slightly slower core rotation rates. The second is that the updated AM transport prescription discussed in Section 2 leads to rotation rates faster by a factor of ∼2 compared to the prescription of Ma & Fuller (2019). As both of these prescriptions produce similar results for low-mass stars which approximately match asteroseismic data, this difference reflects the uncertainty of the models when extended to massive stars.

The NS rotation rates of our models can be reasonably approximated by a power-law relationship with the pre-explosion mass and orbital period, for pre-explosion masses |$M_{\rm exp} \gtrsim 5 \, M_\odot$| and |$P_{\rm orb} \lesssim 1 \, {\rm d}$|⁠. We find that

$$\begin{eqnarray} P_{\rm NS} = 1.4 {\rm ms} \left(\frac{M_{\rm exp}}{30 M_\odot } \right)^{\! -1.6} \left(\frac{P_{\rm orb}}{0.5 \, {\rm d}} \right)^{\! 1.0} \end{eqnarray}$$

(9)

provides a good fit to most of these models, with scatter at the level of |$\sim \! 50 {{\ \rm per\ cent}}$|⁠. Given that uncertainties in the physics of AM transport are larger than this scatter, this approximation is good enough to be used in binary population synthesis calculations. For low-mass progenitors with |$M_{\rm He} \lesssim 4 \, M_\odot$|⁠, a good approximation is simply |$P_{\rm NS} \approx 50 \, {\rm ms}$|⁠.

For He stars that are in binaries with |$P_{\rm orb} \gtrsim 1 \, {\rm d}$|⁠, we find that

$$\begin{eqnarray} P_{\rm NS} = 25 {\rm ms} \left(\frac{M_{\rm exp}}{30 M_\odot } \right)^{\! -0.25} \end{eqnarray}$$

(10)

provides a reasonable fit to our high-metallicity models, while

$$\begin{eqnarray} P_{\rm NS} = 10 {\rm ms} \left(\frac{M_{\rm exp}}{30 M_\odot } \right)^{\! -0.6} \end{eqnarray}$$

(11)

provides a reasonable fit to our low metallicity models. It is possible that the star’s initial rotation rate (which was not varied between our models) and mass-loss prescription could affect the NS rotation period in this case, especially for high-mass stars. The dependence on metallicity for single He stars reflects the difference in rotation rate due to AM loss via stellar winds: low metallicity stars lose less mass/AM via winds and remain more rapidly rotating, as discussed in many prior works (e.g. Georgy et al. 2013). However, the dependence on initial rotation rate and metallicity is weaker in our models due to the tendency for AM transport to push the core spin rate towards an equilibrium value as discussed in Sections 3.1 and 6.

4.2 Black hole spins

To estimate the spins of BHs formed from our models, we first compute the specific AM corresponding to the innermost stable circular orbit (ISCO)

$$\begin{eqnarray} j_{\rm ISCO} = \frac{2}{3^{3/2}} \left(1 + 2 \sqrt{3 r_{\rm ISCO}-2} \right) \frac{G m}{c} , \end{eqnarray}$$

(12)

where m is the interior mass and the ISCO radius r_ISCO is given by

$$\begin{eqnarray} r_{\rm ISCO} = 3 + z_2 - \sqrt{(3-z_1)(3 + z_1 + 2 z_2)} \, , \end{eqnarray}$$

(13)

with r_ISCO in units of Gm/c². Here

$$\begin{eqnarray} z_1 = 1 + (1-a^2)^{1/3}\left((1+a)^{1/3} + (1-a)^{1/3} \right) \, , \end{eqnarray}$$

(14)

|$z_2 = \sqrt{3 a^2 +z_1^2}$|⁠, and a = J_ac(m)c/(Gm²) is the spin of the BH with mass m and AM J_ac(m). For each infalling shell in the progenitor, we assume that all the underlying mass has fallen into the BH. However, for any mass with specific AM j > j_ISCO, we assume that the corresponding accreted specific AM is j_ISCO. Hence, the accreted AM is

$$\begin{eqnarray} J_{\rm ac}(m) = \int _0^m {\rm min} (j,j_{\rm ISCO}) \, \mathrm{ d}m \, . \end{eqnarray}$$

(15)

For j > j_ISCO, this crudely models accretion through a disc in which the accreted mass has the specific AM corresponding to the inner edge of the disc. The BH spin is then

$$\begin{eqnarray} a_{\rm BH} = \frac{J_{\rm ac}(M) c}{G M^2} \, , \end{eqnarray}$$

(16)

where M is the mass of the pre-collapse progenitor.

Only a small amount of mass is lost due to neutrino emission from He stars (Fernández et al. 2018), but there could be additional loss of BH AM due to material ejected during a failed explosion or via accretion feedback (Batta & Ramirez-Ruiz 2019). Conversely, the BH spin could be increased after accretion of fallback material that gains AM due to interaction with the companion (Batta, Ramirez-Ruiz & Fryer 2017; Schrøder, Batta & Ramirez-Ruiz 2018). In our simple accretion disc modelling of Section 5.2 (see Appendix A), most of the material that circularizes outside of ISCO is blown away by disc winds, slightly decreasing the BH mass and typically decreasing a_BH by ∼0.2 for high-spin models. Hence, our method above is likely to slightly overestimate BH spins.

Fig. 4 shows our predictions for BH spins as a function of progenitor mass and orbital period. We see that the predicted BH spin is nearly independent of progenitor mass or metallicity for |$M_{\rm exp} \gtrsim 5 \, M_\odot$| and |$P_{\rm orb} \lesssim 1 \, {\rm d}$| for which tidal synchronization occurs. In this regime, the spin is determined by the orbital period, with a_BH near unity for models with final orbital periods |$P_{\rm orb} \lesssim 0.5 \, {\rm d}$|⁠. This is because the progenitor’s spin frequency is approximately equal to the orbital frequency due to tidal synchronization at short orbital periods. An exception occurs for the lowest values of M_exp, which have much smaller values of a_BH. These stars have much smaller moments of inertia due to their more centrally concentrated structures, so that their AM content J is small even if they are tidally spun up. In most cases, however, we expect these stars to produce NSs rather than BHs.

Figure 4.

The same as Fig. 3, but showing the corresponding dimension-less black hole spin a_BH, computed via equation (16).

Open in new tab Download slide

While there is little explicit dependence of a_BH on metallicity when expressed in terms of the final orbital period, higher metallicity systems will lose more mass during core He-burning and hence evolve to longer orbital periods, as discussed above and in Qin et al. (2018) and Bavera et al. (2020). This can be seen in Fig. 4, as the low-metallicity models have systematically larger values of M_exp and a_BH even though they are initialized at the same helium star mass and with the same orbital periods. Hence, we expect higher spins in low-metallicity environments where there is less orbital widening.

Because of their large masses, most of the BH systems shown in Fig. 4 will merge within a Hubble time. Assuming equal mass BHs in a circular binary, the maximum orbital period for which a merger will occur within |$t_{\rm GW} = 13 \, {\rm Gyr}$| is

$$\begin{eqnarray} P_{\rm max} \simeq 2.3 \, {\rm d} \left(\frac{M_{\rm BH}}{10 M_\odot } \right)^{\!5/8} \, . \end{eqnarray}$$

(17)

Hence, all of the rapidly rotating BHs with |$P_{\rm orb} \lesssim 1 \, {\rm d}$| are expected to merge in much less than a Hubble time, while many slowly rotating BHs with |$P_{\rm orb} \gtrsim 1 \, {\rm d}$| are also expected to merge within a Hubble time. The observed spins of BHs are strongly dependent on the common envelope efficiency that sets their orbital period (or alternatively, the amount of orbital decay in the stable mass transfer scenario), with a more moderate dependence on progenitor metallicity.

Similar to the NS scenario discussed above, the short orbital periods required for high BH spins preclude many massive main sequence stars as the companion stars to tidally spun-up helium stars. Hence, the second BH can be more easily formed with high spin in this binary scenario, and we expect the first BH to have a low spin similar to the long-period systems in Fig. 4. Therefore, the expected χ_eff measured by LIGO/Virgo will likely be χ_eff ≲ 0.5 in most cases, assuming the second formed BH has lower mass than the first formed BH.

The values of a_BH of our models with |$P_{\rm orb} \lesssim 1 \, {\rm d}$| and |$M_{\rm exp} \gtrsim 5 \, M_\odot$| can be fairly well approximated by a simple power-law fit,

$$\begin{eqnarray} a_{\rm BH} = 1 \left(\frac{M_{\rm exp}}{30 M_\odot } \right)^{\! 0.5} \left(\frac{P_{\rm orb}}{0.43 \, {\rm d}} \right)^{\! -2.5} \, . \end{eqnarray}$$

(18)

Similar to our results for NSs, the scatter about these approximations is typically less than |$\sim 50{{\ \rm per\ cent}}$| such that they are good enough to be used in population synthesis calculations. See Bavera et al. (2021b) for a more complicated (but more accurate) fitting function.

For BHs born from He stars in single or wide binaries with |$P_{\rm orb} \gtrsim 1 \, {\rm d}$|⁠, we find fitting functions of

$$\begin{eqnarray} a_{\rm BH} = 0.013 \left(\frac{M_{\rm exp}}{30 M_\odot } \right)^{\! -0.6} \, \end{eqnarray}$$

(19)

for solar metallicity (Z = 0.02) and

$$\begin{eqnarray} a_{\rm BH} = 0.042 \left(\frac{M_{\rm exp}}{30 M_\odot }\right)^{\! -0.3} \, \end{eqnarray}$$

(20)

for low metallicity (Z = 0.002). As with NSs, the BH spin in this case depends on metallicity due to AM losses via winds during He-burning, as well as the initial rotation rate of the progenitor star. However, our results suggest that BHs born in wide binaries will generally be slowly rotating with a_BH ≲ 0.1. A possible exception is for BHs born via the chemically homogeneous evolution channel, which may be rapidly rotating at very low metallicity for single stars (e.g. Yoon et al. 2006) or stars in slightly wider binaries (de Mink & Mandel 2016; Mandel & de Mink 2016; Marchant et al. 2017).

The BH spins here are a few times faster than those of H-rich stars from Fuller & Ma (2019) because of the updated AM transport prescription and the continued loss of core AM to the envelope in H-rich stars. Our results for BH spin from He stars in tight binaries appear similar to those of Qin et al. (2018), Bavera et al. (2020, 2021a), when tidal spin-up occurs. We agree that a_BH can approach unity for stars with final orbital periods |$P_{\rm orb} \lesssim 0.4 \, {\rm d}$|⁠, and that a_BH ≲ 0.1 for final orbital periods |$P \gtrsim 1 \, {\rm d}$|⁠, with moderate spins at periods between these values. Like Bavera et al. (2021a), we find smaller spins for low-mass BHs due to the smaller progenitor moment of inertia during core He-burning, with a sharp falloff in spin for BH masses below |$\sim \! 5 \, M_\odot$|⁠. Similar to Bavera et al. (2021a), BHs born from our most massive models (⁠|$M_{\rm He} \gtrsim 35 \, M_\odot$|⁠) have smaller spin, because those stars typically lose so much mass that their orbital period widens and tidal spin-up becomes ineffective.

Overall, the differing AM transport prescription between our work and models employing the TS dynamo has little effect on BH spins from He stars in compact binaries, which are primarily determined by tidal spin-up. The difference may be larger for stars in wider binaries where the He star’s spin is primarily determined by AM transport within the hydrogen-rich progenitor, or when the He star is formed via chemically homogeneous evolution (see Section 6.2.2).

5 ENERGETIC SUPERNOVAE AND TRANSIENTS

Central engines are suspected to power energetic transients such as GRBs, type Ic-BL SNe, and superluminous type Ic SNe. Here, we examine the ability of our models to power these events through either accretion on to a BH after CC, or via the spin-down energy of a rapidly rotating magnetar. We also compare to observational inferences of magnetar rotation periods obtained by modelling type Ibc SNe.

5.1 Comparison with observed supernovae

Fig. 5 compares our predicted NS rotation periods (the same as shown in Fig. 3) to observationally inferred magnetar rotation periods, as a function of ejecta mass. Yu et al. (2017) and Blanchard et al. (2020) estimated ejecta masses, magnetar rotation periods, and magnetar field strengths by modelling SLSNe Ic light curves assuming they are powered by dipole spin-down of a rapidly rotating magnetar. Their inferred rotation periods and ejecta masses (teal/green stars in Fig. 5) show a similar trend to our predictions, with higher ejecta masses corresponding to more rapidly rotating magnetars. However, their inferred ejecta masses are several times lower than our predictions, for a given NS rotation period. Alternatively, their inferred spin periods are several times shorter than our predictions for a given ejecta mass, especially at low ejecta masses. One possibility for this discrepancy is that our model predicts too much AM extraction from massive stellar cores, and that NSs are born rotating several times faster than our predictions.

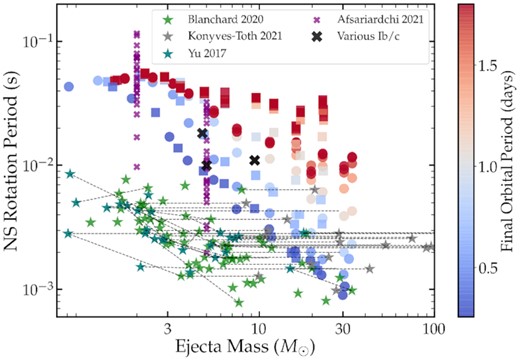
$The same as Fig. 3, but now in comparison with inferred magnetar rotation periods and ejecta masses for superluminous type Ic SNe taken from Yu et al. (2017) and Blanchard et al. (2020). When available, dashed lines connect different estimates for the same events, or with ejecta masses from Könyves-Tóth & Vinkó (2021). We also indicate possible magnetar spin periods from Afsariardchi et al. (2021), where the ejecta mass has been assumed to be $2 \, M_\odot$ or $5 \, M_\odot$. The black crosses correspond to a few individually modelled type Ib/c SNe discussed in the text.$

Figure 5.

The same as Fig. 3, but now in comparison with inferred magnetar rotation periods and ejecta masses for superluminous type Ic SNe taken from Yu et al. (2017) and Blanchard et al. (2020). When available, dashed lines connect different estimates for the same events, or with ejecta masses from Könyves-Tóth & Vinkó (2021). We also indicate possible magnetar spin periods from Afsariardchi et al. (2021), where the ejecta mass has been assumed to be |$2 \, M_\odot$| or |$5 \, M_\odot$|⁠. The black crosses correspond to a few individually modelled type Ib/c SNe discussed in the text.

Open in new tab Download slide

Another possibility is that the inferred ejecta masses of Yu et al. (2017) and Blanchard et al. (2020) are systematically too small. They used semi-analytic light-curve models with a constant opacity, assuming a magnetar central engine. Könyves-Tóth & Vinkó (2021) analysed many of the same events and estimated ejecta masses using Arnett’s rule (Arnett 1980, see also Khatami & Kasen 2019), remaining agnostic to the source of centralized heating. Their models also assumed a constant opacity and were coupled with spectroscopic ejecta velocity estimates. As shown in Fig. 5, their ejecta mass estimates are typically several times larger and are usually closer to the predictions of our models, though Könyves-Tóth & Vinkó (2021) did not estimate magnetar spin periods. In both cases, the use of a constant and grey opacity could lead to systematic errors when inferring the ejecta mass. Furthermore, the true ejecta masses could be larger than the measured ejecta masses in non-spherically symmetric SNe in which a massive but dim component of the ejecta is masked by a bright, low-mass, higher velocity component of the ejecta. It is safe to say that the ejecta masses are very uncertain, and we encourage more detailed photometric and spectroscopic modelling of these events to refine ejecta mass measurements.

Fig. 5 also shows a few magnetar rotation period estimates obtained by modelling ‘normal’ type Ib SNe, which likely arise from He stars formed in binaries (e.g. Zapartas et al. 2021). Afsariardchi et al. (2021) provided estimates for many events by assuming a typical ejecta mass of either |$2 \, M_\odot$| or |$5 \, M_\odot$|⁠. They found magnetar rotation periods very similar to those predicted by our models were consistent with helping to power the events they analysed. Ertl et al. (2020) came to a similar conclusion, showing that magnetars with periods of |$P_{\rm ns} \sim 20 \, {\rm ms}$| may help power the luminous end of type Ibc SNe. Hence, the faint end of the type Ibc distribution may arise from helium star progenitors in wide binaries that produce slower rotating NSs/magnetars, while the bright end could be powered by moderately rotating magnetars in tight binaries.

The inferred ejecta masses and magnetar rotation periods for a few detailed models of individual type Ib/c SNe are also shown in Fig. 5. Maeda et al. (2007) modelled the unusual type Ib SN 2005bf and concluded it could be powered by a magnetar with |$P_{\rm NS} \sim 10 \, {\rm ms}$| and came from a progenitor with |$M_{\rm ZAMS} \sim 20-25 \, M_\odot$|⁠, so we inferred an ejecta mass of |$M_{\rm ej} \sim 5 \, M_\odot$| based on our models for that mass range. Pandey et al. (2021) modelled the luminous type Ib SN 2012au and found that an ejecta mass of |$\approx \! 5 \, M_\odot$| and magnetar with |$P_{\rm NS} \approx 20 \, {\rm ms}$| could reproduce the data. Gutiérrez et al. (2021) modelled the double-peaked type Ic SN 2019cad and estimated a pre-explosion mass of |$11 \, M_\odot$| (⁠|$M_{\rm ej} \sim 9.4 \, M_\odot$|⁠) and a magnetar rotation period of |$P_{\rm NS} \sim 11 \, {\rm ms}$|⁠. Each of these events are consistent with our models for a final orbital period of |$P_{\rm orb} \sim 0.5-1 \, {\rm d}$|⁠.

5.2 Predictions for central engine models

5.2.1 Magnetar central engines

Our models also have implications for the progenitors of GRBs and type Ic-BL SNe. Many recent works (e.g. Metzger et al. 2011; Mazzali et al. 2014; Metzger et al. 2015; Beniamini, Giannios & Metzger 2017; Barnes et al. 2018; Margalit et al. 2018; Fryer et al. 2019; Aloy & Obergaulinger 2021; Shankar et al. 2021) have suggested rapidly rotating magnetars as the engines driving both of these events. To investigate this possibility, we compute the rotational energy E_rot = 0.5I_NS(2π/P_NS)² of a putative magnetar formed from the inner |$1.6 \, M_\odot$| of each of our models. We compare this to the typical energy |$E_{\rm Ic-BL} \approx 0.5 M_{\rm ej} v_{\rm ej}^2 \sim 10^{52} \, {\rm erg} \, (M_{\rm ej}/5 M_\odot) (v_{\rm ej}/1.5 \times 10^4 {\rm km\, s^{ -1}})^2$| associated with observed Ic-BL SNe. The bottom panel of Fig. 6 shows that the magnetar rotational energy of our models is less than 10⁵² erg for all but our most rapidly rotating models arising from the most massive progenitors. The discrepancy is even worse when one considers that the ejecta mass of our massive models would be far larger than |$5 \, M_\odot$|⁠, meaning that the ejecta velocity would be smaller than 15 000 km s⁻¹ and those SNe would not appear broad-lined. Another problem with this scenario is that such massive He stars may be less likely to form via a common envelope event (Klencki et al. 2020; Marchant et al. 2021; van Son et al. 2021), and less likely to explode (O’Connor & Ott 2011; Zapartas et al. 2021). This may disfavour magnetars as the power source of most Ic-BL SNe.

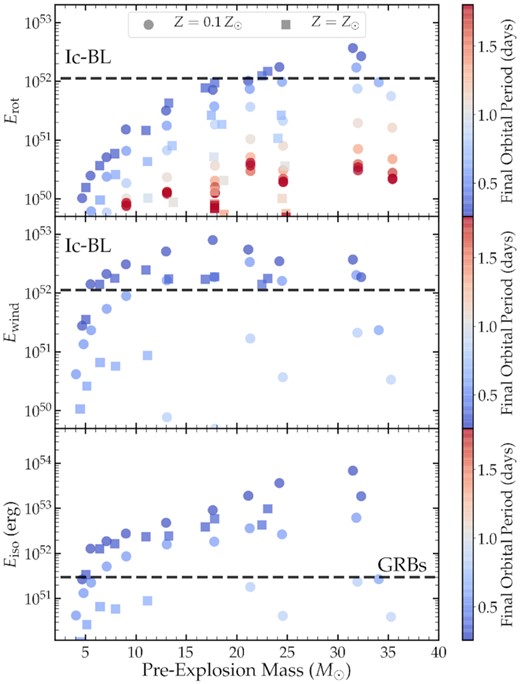
$Energetics of our models as a function of pre-explosion mass, with the same symbols as Fig. 3. Bottom: Isotropic GRB energy Eiso associated with accretion on to a newly formed BH for each of our models, as described in the text. Models with $E_{\rm iso} \gtrsim 3 \times 10^{51} \, {\rm erg}$ are good candidates to produce detectable GRBs. Middle: Energy released from an accretion disc wind in the case of BH formation. Top: Rotational energy Erot upon formation of a $1.6 \, M_\odot$ NS. Rotational or disc wind energies larger than the dashed line may be capable of powering a Ic-BL SN via magnetar spin-down or BH accretion, respectively. Our models struggle to power Ic-BL SNe via magnetar spin-down, unless there is significant magnetar spin-up due to fallback accretion (see the text).$

Figure 6.

Energetics of our models as a function of pre-explosion mass, with the same symbols as Fig. 3. Bottom: Isotropic GRB energy E_iso associated with accretion on to a newly formed BH for each of our models, as described in the text. Models with |$E_{\rm iso} \gtrsim 3 \times 10^{51} \, {\rm erg}$| are good candidates to produce detectable GRBs. Middle: Energy released from an accretion disc wind in the case of BH formation. Top: Rotational energy E_rot upon formation of a |$1.6 \, M_\odot$| NS. Rotational or disc wind energies larger than the dashed line may be capable of powering a Ic-BL SN via magnetar spin-down or BH accretion, respectively. Our models struggle to power Ic-BL SNe via magnetar spin-down, unless there is significant magnetar spin-up due to fallback accretion (see the text).

Open in new tab Download slide

There are two possibilities that may reconcile our models with the magnetar hypothesis. The first is that Ic-BL explosions are highly aspherical (e.g. bipolar jet-driven explosions, Maeda et al. 2002) such that a small fraction of mass absorbs most of the spin-down energy. This would drive larger ejecta velocities even for rotational energies less than |$\sim \! 10^{52} \, {\rm erg}$|⁠. The second possibility is that the magnetar is driven to large rotation rates by fallback accretion from outer layers of the star which lave larger specific AM. Piro & Ott (2011) (see also Metzger, Beniamini & Giannios 2018) showed that this can temporarily drive magnetars to |$\sim \! 1 \, {\rm ms}$| rotation periods (rotational energies |$E_{\rm rot} \gtrsim 10^{52} \, {\rm erg}$|⁠), even if the magnetar initially rotates much more slowly. After fallback accretion has slowed, the magnetar would subsequently spin-down via the propeller mechanism and/or dipole radiation, driving a type Ic-BL SN. In this scenario, Ic-BL can be produced by events with large magnetic fields of |$B \sim 10^{15} \, {\rm G}$| and short fallback times of |$t_{\rm fb} \sim 100 \, {\rm s}$|⁠, while SLSNe Ic can be produced by events with lower magnetic fields of |$B\sim 10^{14} \, {\rm G}$| and long fallback times of |$t_{\rm fb} \sim 10^4 \, {\rm s}$| (Lin et al. 2020, 2021).

Inspection of our models indicate that they do contain enough AM in their outer cores to spin-up a magnetar to |$P_{\rm NS} \sim \! 1 \, {\rm ms}$|⁠. For instance, this is easily achievable in many of our models if |$1 \, M_\odot$| of the inner |$\sim 5 \, M_\odot$| falls back on to an NS made from the iron core. Still, it is not clear how often that amount of fallback can occur, whether that mass can accrete on to the magnetar before being blown away by a disc wind, nor how often it can drive the magnetar to rapid rotation without making it collapse to a BH. Further investigation of this possibility for our models is deferred to future work.

5.2.2 Accreting black hole central engines

Perhaps a more appealing scenario for Ic-BL SNe is that they are powered by accretion on to a BH, i.e. the collapsar mechanism (MacFadyen & Woosley 1999; Kohri, Narayan & Piran 2005; Kumar, Narayan & Johnson 2008). In this model, the inner part of the star where the specific AM j < j_ISCO directly collapses to form a Kerr BH. Then, the outer layers with j > i_ISCO would circularize and form an accretion disc outside the ISCO. At high accretion rate, the disc may be sufficiently dense and hot to trigger URCA reactions and undergo neutrino cooling (Popham, Woosley & Fryer 1999; Narayan, Piran & Kumar 2001; Di Matteo, Perna & Narayan 2002; Kohri et al. 2005; Chen & Beloborodov 2007). In the case where the disc is strongly cooled due to neutrino emission, we expect that most of the mass will be viscously accreted to smaller radii (Shakura & Sunyaev 1973); whereas when the disc is not neutrino-cooled (in the advection-dominated accretion flow, or ADAF regime, Narayan & Yi 1994), then we expect most of the mass to be driven away from the system as disc wind (Blandford & Begelman 1999). The mechanical energy carried by the disc wind can drive a strong stellar explosion, and if this is the case, the supernova emission will be powered by the ⁵⁶Ni synthesized in the wind which mixes with the material in the outer envelope of the star during the explosion (MacFadyen & Woosley 1999).

To estimate the energy released through accretion on to the BH, E_ac, and the energy carried away by a disc wind, E_wind, we use a simple one-zone disc model as described in Appendix A. This model evolves the mass/AM of the disc by accounting for material accreting from the envelope of the stellar model, material lost through disc winds, and material falling through the ISCO on to the BH. The middle panel of Fig. 6 shows an estimate of the energy of the disc wind ejecta of our models. In slowly rotating (long orbital period) models, most of the stellar envelope plunges directly into the BH, so only a small amount of mass circularizes outside the ISCO, and the disc wind energy is small. However, many of our rapidly rotating models with short orbital periods |$P_{\rm orb} \lesssim 0.6 \, {\rm d}$| have energetic disc winds with energies exceeding |$10^{52} \, {\rm erg}$| and are capable of driving Ic-BL SNe. There is little progenitor mass dependence as long as the pre-explosion mass exceeds |$\sim \! 6 \, M_\odot$|⁠. The amount of mass that circularizes outside r_ISCO for models with energetic disc winds is typically |$M_{\rm ej} \sim 1-5 \, M_\odot$|⁠, most of which is ejected into the wind to form the SN ejecta rather than accreting on to the BH. This ejecta is hydrogen-free and helium-poor, as required to generate a Ic SN. Hence we consider our short-period models to be good candidates for the progenitors of Ic-BL SNe through the collapsar mechanism, but probably not through the millisecond magnetar mechanism.

Our models may also be good candidates to drive long GRBs via jets generated by the collapsar. To investigate this possibility, we compute the isotropic-equivalent GRB energy E_iso of material accreting on to the BH (e.g. Bavera et al. 2022)

$$\begin{eqnarray} E_{\rm iso} = \frac{\eta }{f_{\rm B}} E_{\rm ac} , \end{eqnarray}$$

(21)

where η is the fraction of accretion energy channeled into the jet and f_B is the beaming fraction. We take η = 0.01 and f_B = 0.01 such that η/f_B = 1, but we emphasize there is great uncertainty in these parameters. The top panel of Fig. 6 shows our calculations of E_iso for each of our models, along with an approximate detection threshold of |$E_{\rm iso} \sim 3 \times 10^{51} \, {\rm erg}$| that lies near the low end of detected GRBs (Perley et al. 2016). Our models with |$P_{\rm orb} \lesssim 0.75 \, {\rm d}$| and |$M_{\rm exp} \gtrsim 5 \, M_\odot$| (i.e. the same models that could generate Ic-BL SNe) are capable of driving long GRBs. More energetic GRBs are predicted to occur from more massive progenitors, with E_iso extending up to |$\sim \! 10^{54} \, {\rm erg}$| as observed. Since the progenitor models that can produce Ic-BL SNe are the same that produce long GRBs, our models naturally predict the association between long GRBs and Ic-BL SNe.

5.3 Rates

We have not performed binary population synthesis so detailed event rate estimates are beyond the scope of this work. Nevertheless, we can crudely extrapolate from observations and existing population synthesis calculations, if we assume that He stars in close binaries are the dominant channel for different types of events. Failure of our models to reach the observed rates may indicate that other channels (e.g. homogeneous evolution of stars spun up by accretion, Cantiello et al. 2007) are more important. The most recent BH merger rate from LIGO/Virgo is |$R_{\rm BBH} = 23.9^{+14.9}_{-8.6} \, {\rm Gpc}^{-3} \, {\rm yr}^{-1}$| and the NS merger rate is |$R_{\rm BNS} = 320^{+490}_{-240} \, {\rm Gpc}^{-3} \, {\rm yr}^{-1}$| (Abbott et al. 2021).

As can be seen from Fig. 3 and equation (17), the majority of merging NSs likely originate from binaries with pre-explosion orbital period |$P_{\rm orb} \lesssim 0.5 \, {\rm d}$| that are efficiently tidally spun-up. Hence, the NS merger rate provides a lower limit on the number of tidally spun-up He stars. Including NS-BH mergers will slightly increase this number. If we assume a Salpeter IMF, then helium stars with |$M_{\rm He} \! \gtrsim \! 10 \, M_\odot$| that originate from stars with |$M_{\rm ZAMS} \! \gtrsim \! 30 \, M_\odot$| are roughly |$30{{\ \rm per\ cent}}$| as common as helium stars with |$M_{\rm He} \! \gtrsim \! 4 \, M_\odot$| that originate from |$M_{\rm ZAMS} \! \gtrsim \! 12 \, M_\odot$|⁠. If these massive He stars (⁠|$M_{\rm He} \! \gtrsim \! 10 \, M_\odot$|⁠) all form highly magnetized NSs, the event rate of rotating magnetar-powered SNe would be |$\sim \! 100 \, {\rm Gpc}^{-3} \, {\rm yr}^{-1}$|⁠.

The estimate above can be compared with the observed rate of superluminous Ic SNe of |$R_{\rm SLSNe} = 35^{+25}_{-13} \, {\rm Gpc}^{-3} \, {\rm yr}^{-1}$| (Frohmaier et al. 2021) or |$R_{\rm SLSNe} \sim 40 \, {\rm Gpc}^{-3} \, {\rm yr}^{-1}$| (Zhao, Xue & Cao 2021). We thus conclude it is possible for our models to account for the rates of superluminous type Ic SNe. In reality, many of the massive He stars required for rapidly rotating magnetars likely collapse into BHs or produce NSs with too weak/strong fields and would therefore not generate a superluminous Ic SNe. Then again, the rate will be slightly increased by contributions from binaries with |$P_{\rm orb} \! \sim \! 0.75 \, {\rm d}$| that are tidally spun up but do not usually merge in a Hubble time. Future work will need to quantify these branching ratios in order to generate better rate estimates.

Our models struggle to match the observed rate of Ic-BL SNe if they are powered by magnetar rotation. While the volumetric rate is uncertain, Shivvers et al. (2017) (see also Modjaz et al. 2020) estimate that roughly |$4{{\ \rm per\ cent}}$| of stripped SNe are type Ic-BL. Given a stripped SNe rate of |$R_{\rm Ibc} = 2.4^{+0.8}_{-0.6} \times 10^{4} \, {\rm Gpc}^{-3} \, {\rm yr}^{-1}$| (Frohmaier et al. 2021), this entails |$R_{\rm Ic-BL} \! \sim \! 10^3 \, {\rm Gpc}^{-3} \, {\rm yr}^{-1}$|⁠, roughly 1 per cent of the total core-collapse SN rate. If only AM in the iron core contributes to the magnetar rotation period, then almost none of our models can reach the |$\sim \! 10^{52} \, {\rm erg}$| energy level inferred for type Ic-BL SNe, and we expect |$R_{\rm Ic-BL} \lt 10^2 \, {\rm Gpc}^{-3} \, {\rm yr}^{-1}$|⁠, far smaller than observationally inferred. One possibility to reconcile this difference is that fallback accretion very commonly spins up magnetars to millisecond periods, such that some of our less massive and longer orbital period models contribute to the Ic-BL SN population.

If Ic-BL SNe are instead powered by BH accretion via the collapsar mechanism, the same models in Fig. 6 that produce GRBs are those with |$E_{\rm ac} \gtrsim 10^{52} \, {\rm erg}$| that can produce Ic-BL SNe, and we might guess the rates of GRBs (after beaming corrections) and Ic-BL SNe to be similar. This is problematic because the uncorrected rate of long GRBs at low redshift is |$R_{\rm GRB} \sim 1 \, {\rm Gpc}^{-3} \, {\rm yr}^{-1}$| (Wanderman & Piran 2010), and using 1/f_B ∼ 100 implies a beaming-corrected volumetric rate of |$R_{\rm GRB} \sim \! 100 \, {\rm Gpc}^{-3} \, {\rm yr}^{-1}$|⁠. Hence, the observed GRB rate is a factor of ∼10 times smaller than that of Ic-BL SNe. It is possible that many GRB jets are choked or that the beaming fraction is smaller than f_B = 0.01, which could account for the lower observed rate of long GRBs compared to Ic-BL SNe. However, it is difficult for our models to simultaneously reproduce the long GRB rate and the much higher rate of Ic-BL SNe, as explained below.

Bavera et al. (2021a) performed population synthesis on their stellar models to predict BH merger rates in the range |$R_{\rm BBH} \sim \! 25-113 \, {\rm Gpc}^{-3} \, {\rm yr}^{-1}$|⁠, approximately consistent with the measured rate from LIGO/Virgo. Bavera et al. (2020) estimate that roughly |$20{{\ \rm per\ cent}}$|of these events will have moderate rotation with χ_eff > 0.1, which is also similar to the observed fraction of moderately spinning BH mergers (The LIGO Scientific Collaboration 2019). Since our models predict very similar BH spins as Bavera et al. (2020), we conclude that they can roughly account for the observed rate of of BH mergers, with both low and moderate χ_eff. The latter likely have one highly spinning BH like those in Fig. 6 capable of powering a GRB, corresponding to a crude local GRB rate estimate of |$R_{\rm GRB} \sim \! 10-40 \, {\rm Gpc}^{-3} \, {\rm yr}^{-1}$| if GRB jets are never choked. This is within a factor of a few of the observed GRB rate above, indicating that this binary channel may be able to account for most long GRBs, the same conclusion reached by Bavera et al. (2022).

However, this scenario cannot simultaneously explain the observed rate of Ic-BL SNe, given they are predicted to occur from the same models as those that generate long GRBs and moderate-χ_eff BH mergers. Scaling up the binary collapsar formation rate would help match the Ic-BL SN rate, but it would likely increase the BH merger rate above that observed. One possibility is that Ic-BL SNe are produced by collapsars formed through homogeneous evolution, which may not merge with a companion BH and could therefore increase the Ic-BL rate without increasing the BH merger rate. Another possibility is that most Ic-BL SNe (and perhaps most GRBs) are produced by the first-formed tidally spun-up He star in a short-period (⁠|$P \lesssim 1 \, {\rm d}$|⁠) binary with a main sequence secondary. The mass transfer at the end of the secondary’s life would likely be stable, widening the orbit so that the compact remnant (WD, NS, or BH) would not merge with the first-formed BH within a Hubble time, allowing these systems to enhance the rates of Ic-BL/GRBs without increasing the BH merger rate.

6 MODELLING UNCERTAINTIES

Several physical uncertainties affect our compact object spin predictions. Numerical convergence is only a minor source of uncertainty for these models, as shown in Section B.

One might expect that the predicted NS and BH spins are sensitive to the initial rotation rate of the progenitor star. However, that is not the case for these models. We ran a set of models in which the main sequence progenitor’s rotation rate was boosted to 80 per cent of its breakup rate at the end of the main sequence (e.g. to simulate accretion from a companion). We then constructed a He star model following the onset of Roche lobe overflow using the same technique described in Section 3. However, due to the very strong dependence of the AM viscosity with rotation rate (ν_AM ∝ Ω³), the core rotation rate reaches nearly the same value, regardless of the main sequence star’s total AM (see also Fuller et al. 2019; Ma & Fuller 2019). This evidently occurs even for massive stars which evolve very quickly across the HR gap, because we find the He star’s initial rotation rate (and subsequent NS and BH spin) is nearly the same, regardless of the spin rate of the main sequence progenitor.

Our models do not include rotational mixing via Eddington–Sweet circulation. To test its importance, we ran a set of models with a generous amount of rotational mixing (am_D_mix_factor = 1d-1 and D_ES_factor = 1) switched on for our helium star models. The resulting NS and BH spin rates are very similar, but slightly smaller for our highest mass models because of slightly increased wind mass-loss rates in these models.

A major assumption of our predictions for NS rotation rates is that of AM conservation during the core-collapse explosion. Multidimensional simulations (Müller et al. 2018; Chan, Müller & Heger 2020; Stockinger et al. 2020; Janka, Wongwathanarat & Kramer 2022) instead show that asymmetric explosions and fallback accretion can significantly alter the spin rate of the NS, spinning it up to spin periods as short as milliseconds. However, those simulations may also overestimate the spin-up via fallback because of numerical gridding effects or if fallback material is inefficiently accreted (Janka et al. 2022). Given the long NS spin periods predicted for our low-mass progenitor models, it is likely that the true spin periods for those NSs are set by fallback and are shorter than our predictions. However, given the rarity of engine-powered SNe, we are skeptical that a common process like asymmetric fallback accretion can explain the millisecond periods needed to power engine-driven transients, nor why those transients are associated with hydrogen-free progenitor stars.

6.1 AM transport uncertainties

Despite asteroseismically measured rotation rates of low-mass red giants, the physical mechanisms behind AM transport are not well understood, translating to substantial uncertainties for predictions of core rotation rates in high-mass stars. Our updated AM transport prescription based on the Tayler instability described in Section 2 yields similar predictions for low-mass red giants as the original prescription of Fuller et al. (2019), and it is therefore asteroseimically calibrated. However, this underpredicts the core rotation rates of low-mass sub-giant stars (Eggenberger et al. 2019), and it overpredicts the core rotation rates of secondary clump stars (Tayar et al. 2019). While our models match the data much better than models including the TS dynamo (Cantiello et al. 2014), they are clearly not perfect.

Moreover, the observed scatter (Gehan et al. 2018) in core rotation rates by a factor of ∼3 above and below the predictions of Fuller et al. (2019) for low-mass red giants likely entails diversity in the effective AM transport efficiency factor α. A similar scatter might be expected for high-mass stars. We find that the predicted NS rotation period scales roughly linearly with α for the models of this paper, with larger values of α creating more efficient AM transport and slower NS spin. Hence, real stars may exhibit a scatter in NS rotation periods by a factor of a few above or below our predictions. This may allow slightly lower mass stars to contribute substantially to rotation-powered energetic transients.

Our updated prescription predicts NS rotation periods roughly half that of Fuller et al. (2019) when applied to the H-poor stellar models of this paper. The difference is smaller for high-mass models but is slightly larger for our lowest mass models. For comparison, we ran several of our models with the original TS dynamo prescription of Spruit (2002). This predicts NS rotation rates ∼4 times faster than our low-mass models, with |$P_{\rm NS} \! \sim \! 10 \, {\rm ms}$| for |$M_{\rm exp} \lesssim 5 \, M_\odot$|⁠. Interestingly, however, both models predict similar NS rotation rates from high-mass stars. Hence, multiple proposed AM transport prescriptions coincidentally predict |$P_{\rm NS} \! \sim \! 1 \, {\rm ms}$| for short-period binaries with |$M_{\rm exp} \gtrsim 15 \, M_\odot$|⁠. For BH spin, both this work and models employing the TS dynamo now predict typical spins of a_BH ∼ 0.03 from BHs born from He stars in wide binaries (Qin et al. 2018; Bavera et al. 2020). This statement is dependent on the progenitor mass, rotation rate, metallicity, and mass-loss prescription, so it is largely coincidental.

In contrast to our models, Kissin & Thompson (2015) proposed that magnetic torques enforce nearly rigid rotation in radiative regions, while convective AM pumping causes differential rotation in thick convective layers (see also Takahashi & Langer 2021). Kissin & Thompson (2018) examined the core AM of massive stars in this scenario, predicting slowly rotating NSs in single stars, but finding that tidal spin-up of a red supergiant progenitor can lead to a rapidly rotating NS or BH. In their model, rapid rotation is possible for hydrogen-rich progenitors, in contrast to our models. They did not examine tidal spin-up of helium stars, nor did they investigate mass/metallicity dependence in detail. Future work should examine the convective AM pumping scenario to make distinguishing predictions from other models.

6.2 Helium stars from other evolutionary channels

6.2.1 Stable mass transfer

Several recent works (e.g. Pavlovskii et al. 2017; Klencki et al. 2020; Marchant et al. 2021; van Son et al. 2021) have argued that many merging BHs may form via orbital decay during stable mass transfer rather than common envelope evolution. Our models are agnostic to the progenitor channel as long as it produces a nearly hydrogen-free progenitor star in a short-period orbit, and as long as the envelope stripping occurs on a very short time-scale. The stable mass transfer scenario may leave a thicker hydrogen shell than used in our models, and it may proceed over a slightly longer (thermal) time-scale than the envelope stripping prescription that we use, so the resultant NS and BH spins may be somewhat different.

To explore the potential effect of a thin hydrogen envelope, we ran a few models identical to those above, but leaving a couple tenths of a solar mass of hydrogen after the stripping process. The results for high-mass stars (⁠|$M_{\rm ZAMS} \gtrsim 40 \, M_\odot$|⁠) are nearly unaffected because the residual hydrogen is quickly lost by winds. For lower mass stars, however, the hydrogen envelopes can be retained through helium core burning, causing the star to greatly inflate during helium shell burning (e.g. Laplace et al. 2020). The expanding hydrogen envelope extracts AM from the core, most of which is lost because this hydrogen envelope overflows the Roche lobe and is lost via case BB mass transfer (e.g. Tauris, Langer & Podsiadlowski 2015). In our models, this can cause the BH spin to be more than 50 per cent smaller, and in certain cases could also cause the NS spin period to be longer. Future work should investigate this scenario more thoroughly.

6.2.2 Helium stars from chemically homogeneous evolution

We have not examined massive helium stars formed through the homogeneous evolution channel (Maeder 1987; Woosley & Heger 2006; Yoon et al. 2006; Cantiello et al. 2007), in which there is no hydrogen envelope to absorb the core’s AM. Aguilera-Dena et al. (2018, 2020) examined the evolution of low-metallicity helium stars evolving through homogeneous evolution, adopting the TS dynamo (Spruit 2002) for AM transport. Those models also implemented rotational mixing enhanced by a factor of 10, such that they burned nearly all their helium and evolved into nearly homogeneous carbon–oxygen stars. Because those models did not include tidal spin-up, their total AM is determined by their initial spin rate and mass-loss history.

The AM of the iron core, however, is determined primarily by AM exchange with the overlying carbon–oxygen core and thus depends on the AM transport prescription. Our most massive tidally spun-up models (⁠|$M_{\rm exp} \! \sim \! 20 \, M_\odot$|⁠) have average core specific AM (within the inner |$1.6 \, M_\odot$|⁠) of |$j\approx 3 \times 10^{15} \, {\rm cm}^2 \, {\rm s}^{-1}$|⁠, similar to the models of Aguilera-Dena et al. (2020). However, our low-mass models (M_exp ≲ 5M_⊙) only have specific AM of |$j \! \sim \! 10^{14} \, {\rm cm}^2 \, {\rm s}^{-1}$|⁠, several times smaller than those of Aguilera-Dena et al. (2020). There are two reasons for this. First, the enhanced mixing of Aguilera-Dena et al. (2020) produces larger carbon–oxygen cores and more compact stars without extended helium envelopes, reducing the amount of AM transferred from the core to the helium envelope. Secondly, the less efficient AM transport from the TS dynamo extracts less AM from the core. We believe the core rotation rates of Aguilera-Dena et al. (2020) (especially for their low-mass models) could be overestimated because the TS dynamo underpredicts AM transport efficiency and overpredicts the core spin rates of low-mass red giants (Cantiello et al. 2014; Fuller et al. 2019). Additionally, the enhanced rotational mixing does not appear to be supported by measurements of nitrogen abundances of rotating stars (Brott et al. 2011).

7 CONCLUSION

We have generated a suite of detailed binary stellar evolution models, examining angular momentum (AM) transport and core rotation rates of massive helium stars in close binary systems. Such binaries could possibly be formed via common envelope evolution (e.g. Belczynski, Kalogera & Bulik 2002), or via stable mass transfer (e.g. Marchant et al. 2021), which may be more likely for massive helium stars (Klencki et al. 2020). Our models improve upon prior efforts by implementing an updated AM transport prescription based on magnetic torques associated with the Tayler instability (Fuller et al. 2019), which has been calibrated with asteroseismic core rotation rates of low-mass red giant stars. The models also include tidal torques from the companion star which greatly increase the AM content for binaries with orbital periods |$P_{\rm orb} \lesssim 1 \, {\rm d}$|⁠, allowing for rapid core rotation that could power various types of SNe and energetic transients. The efficient AM transport of our models allows most of the iron core’s AM to be extracted before core-collapse, predicting slower core rotation than most prior models.

Based on the core AM content just before core-collapse, we predict the rotation rates of neutron stars (NSs) born from binary helium stars (Fig. 3), assuming AM is conserved during collapse. We find that NSs born from low-mass progenitors (⁠|$M_{\rm exp} \lesssim 5 \, M_\odot$|⁠) and wide binaries |$(P_{\rm orb} \gtrsim 1 \, {\rm d}$|⁠) are generally slowly rotating, with initial rotation rates |$P_{\rm NS} \gtrsim 10 \, {\rm ms}$|⁠. The rotation periods of these NSs may instead be determined by asymmetric fallback accretion (e.g. Chan et al. 2020; Stockinger et al. 2020). NSs born from massive progenitors in close binaries can be rapidly rotating, with |$P_{\rm NS} \! \sim \! 1 \, {\rm ms}$| for the most massive progenitors in very tight binaries. Core contraction of very massive stars occurs so quickly that there is not enough time to remove the core AM before core-collapse, so our models predict a strong correlation between the NS rotation rate and progenitor/ejecta mass, with approximate scaling |$P_{\rm NS} \propto M_{\rm exp}^{-1.4} P_{\rm orb}^{0.8}$| for stars in tight binaries. A similar correlation has been observationally inferred from magnetar models for superluminous type Ic SNe (Blanchard et al. 2020), though our predicted ejecta masses are several times larger than many current estimates for observed events.

When a black hole (BH) is formed upon core-collapse, our models predict low spin (a ≲ 0.1) for BHs in wide binaries with |$P_{\rm orb} \gtrsim 1 \, {\rm d}$| (Fig. 4). However, tidal spin-up of the progenitor at shorter periods allows for rapid rotation, with a ∼ 1 possible at very short orbital periods, and an approximate scaling |$a \propto M_{\rm BH}^{0.5} P_{\rm orb}^{-2.5}$|⁠. Unlike NSs, the BH spin is nearly independent of AM transport and our models yield results similar to other recent work (e.g. Qin et al. 2018; Bavera et al. 2020). These models predict low values of χ_eff for most BH mergers observed by LIGO/Virgo, but with a significant fraction of moderate χ_eff events arising from BHs in close binaries. This appears consistent with the low/moderate measured values of χ_eff for most LIGO/Virgo events thus far.

Finally, we investigate the possibility of generating energetic transients (superluminous type Ic SNe, type Ic-BL SNe, and GRBs) via rotational or accretion power in our models. The AM content of the envelopes of our short-period binaries are likely sufficient to power GRBs via the collapsar model (Fig. 6). Using only the AM in the iron core, our massive models can create rapidly rotating magnetars capable of powering superluminous SNe, but only for very massive stars in very tight binaries with an appropriately tuned magnetar field strength, so it is unclear if they can account for the observed rates. This is more problematic for magnetar powering of Ic-BL SNe, which are more common and have larger explosion energies of |$\sim \! 10^{52} \, {\rm erg}$|⁠. These events require significant fallback accretion and spin-up of the magnetar to achieve the required rotational energy, or they must be powered by BH accretion rather than magnetar spin-down. While our models capable of powering GRBs are also predicted to power |$\sim \! 10^{52} \, {\rm erg}$| SNe Ic-BL via outflows from accretion disc winds, it is difficult to account for the much higher observed rate of SNe Ic-BL.

ACKNOWLEDGEMENTS

We thank the anonymous referee for a constructive review. JF is thankful for support through an Innovator Grant from The Rose Hills Foundation, and the Sloan Foundation through grant FG-2018-10515. WL is supported by the Lyman Spitzer, Jr. Fellowship at Princeton University.

DATA AVAILABILITY

MESA models and source code are available to download at https://zenodo.org/record/5778001#.YdSDDmjMLb1. Analysis scripts are available upon request to the authors.

Footnotes

1

https://zenodo.org/record/5778001#.YdSDDmjMLb1

2

Our code that models the BH accretion history can be downloaded from this URL: https://github.com/wenbinlu/collapsar.git

REFERENCES

Abbott

R.

et al. ,

2021

,

ApJ

,

913

,

L7

10.3847/2041-8213/abe949

Crossref

Search ADS

Afsariardchi

N.

,

Drout

M. R.

,

Khatami

D. K.

,

Matzner

C. D.

,

Moon

D.-S.

,

Ni

Y. Q.

,

2021

,

ApJ

,

918

,

89

10.3847/1538-4357/ac0aeb

Crossref

Search ADS

Aguilera-Dena

D. R.

,

Langer

N.

,

Moriya

T. J.

,

Schootemeijer

A.

,

2018

,

ApJ

,

858

,

115

10.3847/1538-4357/aabfc1

Crossref

Search ADS

Aguilera-Dena

D. R.

,

Langer

N.

,

Antoniadis

J.

,

Müller

B.

,

2020

,

ApJ

,

901

,

114

10.3847/1538-4357/abb138

Crossref

Search ADS

Aloy

M. Á.

,

Obergaulinger

M.

,

2021

,

MNRAS

,

500

,

4365

10.1093/mnras/staa3273

Crossref

Search ADS

Arnett

W. D.

,

1980

,

ApJ

,

237

,

541

10.1086/157898

Crossref

Search ADS

Barnes

J.

,

Duffell

P. C.

,

Liu

Y.

,

Modjaz

M.

,

Bianco

F. B.

,

Kasen

D.

,

MacFadyen

A. I.

,

2018

,

ApJ

,

860

,

38

10.3847/1538-4357/aabf84

Crossref

Search ADS

Batta

A.

,

Ramirez-Ruiz

E.

,

2019

,

preprint (arXiv:1904.04835)

Batta

A.

,

Ramirez-Ruiz

E.

,

Fryer

C.

,

2017

,

ApJ

,

846

,

L15

10.3847/2041-8213/aa8506

Crossref

Search ADS

Bavera

S. S.

et al. ,

2020

,

A&A

,

635

,

A97

10.1051/0004-6361/201936204

Crossref

Search ADS

Bavera

S. S.

et al. ,

2021a

,

A&A

,

647

,

A153

10.1051/0004-6361/202039804

Crossref

Search ADS

Bavera

S. S.

,

Zevin

M.

,

Fragos

T.

,

2021b

,

RNAAS

,

5

,

127

10.3847/2515-5172/ac053c

Crossref

Search ADS

Bavera

S. S.

et al. ,

2022

,

A&A

,

657

,

L8

10.1051/0004-6361/202141979

Crossref

Search ADS

Beck

P. G.

et al. ,

2012

,

Nature

,

481

,

55

10.1038/nature10612

Crossref

Search ADS

Belczynski

K.

,

Kalogera

V.

,

Bulik

T.

,

2002

,

ApJ

,

572

,

407

10.1086/340304

Crossref

Search ADS

Belczynski

K.

et al. ,

2020

,

A&A

,

636

,

A104

10.1051/0004-6361/201936528

Crossref

Search ADS

Belczynski

K.

,

Done

C.

,

Lasota

J. P.

,

2021

,

preprint (arXiv:2111.09401)

Belkacem

K.

et al. ,

2015

,

A&A

,

579

,

A31

10.1051/0004-6361/201526043

Crossref

Search ADS

Beniamini

P.

,

Giannios

D.

,

Metzger

B. D.

,

2017

,

MNRAS

,

472

,

3058

10.1093/mnras/stx2095

Crossref

Search ADS

Blaauw

A.

,

1961

,

Bull. Astron. Inst. Netherlands

,

15

,

265

Blanchard

P. K.

,

Berger

E.

,

Nicholl

M.

,

Villar

V. A.

,

2020

,

ApJ

,

897

,

114

10.3847/1538-4357/ab9638

Crossref

Search ADS

Blandford

R. D.

,

Begelman

M. C.

,

1999

,

MNRAS

,

303

,

L1

10.1046/j.1365-8711.1999.02358.x

Crossref

Search ADS

Bogomazov

A. I.

,

Popov

S. B.

,

2009

,

Astron. Rep.

,

53

,

325

10.1134/S1063772909040052

Crossref

Search ADS

Brott

I.

et al. ,

2011

,

A&A

,

530

,

A116

10.1051/0004-6361/201016114

Crossref

Search ADS

Cantiello

M.

,

Mankovich

C.

,

Bildsten

L.

,

Christensen-Dalsgaard

J.

,

Paxton

B.

,

2014

,

ApJ

,

788

,

93

10.1088/0004-637X/788/1/93

Crossref

Search ADS

Cantiello

M.

,

Yoon

S. C.

,

Langer

N.

,

Livio

M.

,

2007

,

A&A

,

465

,

L29

10.1051/0004-6361:20077115

Crossref

Search ADS

Chan

C.

,

Müller

B.

,

Heger

A.

,

2020

,

MNRAS

,

495

,

3751

10.1093/mnras/staa1431

Crossref

Search ADS

Chen

W.-X.

,

Beloborodov

A. M.

,

2007

,

ApJ

,

657

,

383

10.1086/508923

Crossref

Search ADS

de Jager

C.

,

Nieuwenhuijzen

H.

,

van der Hucht

K. A.

,

1988

,

A&AS

,

72

,

259

de Mink

S. E.

,

Mandel

I.

,

2016

,

MNRAS

,

460

,

3545

10.1093/mnras/stw1219

Crossref

Search ADS

Deheuvels

S.

et al. ,

2014

,

A&A

,

564

,

A27

10.1051/0004-6361/201322779

Crossref

Search ADS

Deheuvels

S.

,

Ballot

J.

,

Beck

P. G.

,

Mosser

B.

,

Østensen

R.

,

García

R. A.

,

Goupil

M. J.

,

2015

,

A&A

,

580

,

A96

10.1051/0004-6361/201526449

Crossref

Search ADS

Di Matteo

T.

,

Perna

R.

,

Narayan

R.

,

2002

,

ApJ

,

579

,

706

10.1086/342832

Crossref

Search ADS

Eggenberger

P.

et al. ,

2017

,

A&A

,

599

,

A18

10.1051/0004-6361/201629459

Crossref

Search ADS

Eggenberger

P.

,

den Hartogh

J. W.

,

Buldgen

G.

,

Meynet

G.

,

Salmon

S. J. A. J.

,

Deheuvels

S.

,

2019

,

A&A

,

631

,

L6

10.1051/0004-6361/201936348

Crossref

Search ADS

Ertl

T.

,

Woosley

S. E.

,

Sukhbold

T.

,

Janka

H. T.

,

2020

,

ApJ

,

890

,

51

10.3847/1538-4357/ab6458

Crossref

Search ADS

Faucher-Giguère

C.-A.

,

Kaspi

V. M.

,

2006

,

ApJ

,

643

,

332

10.1086/501516

Crossref

Search ADS

Fernández

R.

,

Quataert

E.

,

Kashiyama

K.

,

Coughlin

E. R.

,

2018

,

MNRAS

,

476

,

2366

10.1093/mnras/sty306

Crossref

Search ADS

Fishbach

M.

,

Kalogera

V.

,

2021

,

preprint (arXiv:2111.02935)

Frohmaier

C.

et al. ,

2021

,

MNRAS

,

500

,

5142

10.1093/mnras/staa3607

Crossref

Search ADS

Fryer

C. L.

,

Lloyd-Ronning

N.

,

Wollaeger

R.

,

Wiggins

B.

,

Miller

J.

,

Dolence

J.

,

Ryan

B.

,

Fields

C. E.

,

2019

,

Eur. Phys. J. A

,

55

,

132

10.1140/epja/i2019-12818-y

Crossref

Search ADS

Fuller

J.

,

Ma

L.

,

2019

,

ApJ

,

881

,

L1

10.3847/2041-8213/ab339b

Crossref

Search ADS

Fuller

J.

,

Lecoanet

D.

,

Cantiello

M.

,

Brown

B.

,

2014

,

ApJ

,

796

,

17

10.1088/0004-637X/796/1/17

Crossref

Search ADS

Fuller

J.

,

Cantiello

M.

,

Lecoanet

D.

,

Quataert

E.

,

2015

,

ApJ

,

810

,

101

10.1088/0004-637X/810/2/101

Crossref

Search ADS

Fuller

J.

,

Piro

A. L.

,

Jermyn

A. S.

,

2019

,

MNRAS

,

485

,

3661

10.1093/mnras/stz514

Crossref

Search ADS

Gehan

C.

,

Mosser

B.

,

Michel

E.

,

Samadi

R.

,

Kallinger

T.

,

2018

,

A&A

,

616

,

A24

10.1051/0004-6361/201832822

Crossref

Search ADS

Georgy

C.

,

Ekström

S.

,

Granada

A.

,

Meynet

G.

,

Mowlavi

N.

,

Eggenberger

P.

,

Maeder

A.

,

2013

,

A&A

,

553

,

A24

10.1051/0004-6361/201220558

Crossref

Search ADS

Gullón

M.

,

Miralles

J. A.

,

Viganò

D.

,

Pons

J. A.

,

2014

,

MNRAS

,

443

,

1891

10.1093/mnras/stu1253

Crossref

Search ADS

Gutiérrez

C. P.

et al. ,

2021

,

MNRAS

,

504

,

4907

10.1093/mnras/stab1009

Crossref

Search ADS

Heger

A.

,

Langer

N.

,

Woosley

S. E.

,

2000

,

ApJ

,

528

,

368

10.1086/308158

Crossref

Search ADS

Heger

A.

,

Woosley

S. E.

,

Spruit

H. C.

,

2005

,

ApJ

,

626

,

350

10.1086/429868

Crossref

Search ADS

Hermes

J. J.

et al. ,

2017

,

ApJS

,

232

,

23

10.3847/1538-4365/aa8bb5

Crossref

Search ADS

Janka

H. T.

,

Wongwathanarat

A.

,

Kramer

M.

,

2022

,

ApJ

,

926

,

9

10.3847/1538-4357/ac403c

Kasen

D.

,

Bildsten

L.

,

2010

,

ApJ

,

717

,

245

10.1088/0004-637X/717/1/245

Crossref

Search ADS

Khatami

D. K.

,

Kasen

D. N.

,

2019

,

ApJ

,

878

,

56

10.3847/1538-4357/ab1f09

Crossref

Search ADS

Kissin

Y.

,

Thompson

C.

,

2015

,

ApJ

,

808

,

35

10.1088/0004-637X/808/1/35

Crossref

Search ADS

Kissin

Y.

,

Thompson

C.

,

2018

,

ApJ

,

862

,

111

10.3847/1538-4357/aab1fb

Crossref

Search ADS

Klencki

J.

,

Nelemans

G.

,

Istrate

A. G.

,

Pols

O.

,

2020

,

A&A

,

638

,

A55

10.1051/0004-6361/202037694

Crossref

Search ADS

Kohri

K.

,

Narayan

R.

,

Piran

T.

,

2005

,

ApJ

,

629

,

341

10.1086/431354

Crossref

Search ADS

Könyves-Tóth

R.

,

Vinkó

J.

,

2021

,

ApJ

,

909

,

24

10.3847/1538-4357/abd6c8

Crossref

Search ADS

Kumar

P.

,

Narayan

R.

,

Johnson

J. L.

,

2008

,

MNRAS

,

388

,

1729

10.1111/j.1365-2966.2008.13493.x

Crossref

Search ADS

Kushnir

D.

,

Zaldarriaga

M.

,

Kollmeier

J. A.

,

Waldman

R.

,

2017

,

MNRAS

,

467

,

2146

10.1093/mnras/stx255

Crossref

Search ADS

Laplace

E.

,

Götberg

Y.

,

de Mink

S. E.

,

Justham

S.

,

Farmer

R.

,

2020

,

A&A

,

637

,

A6

10.1051/0004-6361/201937300

Crossref

Search ADS

Lin

W. L.

,

Wang

X. F.

,

Wang

L. J.

,

Dai

Z. G.

,

2020

,

ApJ

,

903

,

L24

10.3847/2041-8213/abc254

Crossref

Search ADS

Lin

W.

,

Wang

X.

,

Wang

L.

,

Dai

Z.

,

2021

,

ApJ

,

914

,

L2

10.3847/2041-8213/ac004a

Crossref

Search ADS

Ma

L.

,

Fuller

J.

,

2019

,

MNRAS

,

488

,

4338

10.1093/mnras/stz2009

Crossref

Search ADS

MacFadyen

A. I.

,

Woosley

S. E.

,

1999

,

ApJ

,

524

,

262

10.1086/307790

Crossref

Search ADS

Maeda

K.

,

Nakamura

T.

,

Nomoto

K.

,

Mazzali

P. A.

,

Patat

F.

,

Hachisu

I.

,

2002

,

ApJ

,

565

,

405

10.1086/324487

Crossref

Search ADS

Maeda

K.

et al. ,

2007

,

ApJ

,

666

,

1069

10.1086/520054

Crossref

Search ADS

Maeder

A.

,

1987

,

A&A

,

178

,

159

Mandel

I.

,

de Mink

S. E.

,

2016

,

MNRAS

,

458

,

2634

10.1093/mnras/stw379

Crossref

Search ADS

Marchant

P.

,

Langer

N.

,

Podsiadlowski

P.

,

Tauris

T. M.

,

de Mink

S.

,

Mandel

I.

,

Moriya

T. J.

,

2017

,

A&A

,

604

,

A55

10.1051/0004-6361/201630188

Crossref

Search ADS

Marchant

P.

,

Pappas

K. M. W.

,

Gallegos-Garcia

M.

,

Berry

C. P. L.

,

Taam

R. E.

,

Kalogera

V.

,

Podsiadlowski

P.

,

2021

,

A&A

,

650

,

A107

10.1051/0004-6361/202039992

Crossref

Search ADS

Margalit

B.

,

Metzger

B. D.

,

Thompson

T. A.

,

Nicholl

M.

,

Sukhbold

T.

,

2018

,

MNRAS

,

475

,

2659

10.1093/mnras/sty013

Crossref

Search ADS

Mazzali

P. A.

,

McFadyen

A. I.

,

Woosley

S. E.

,

Pian

E.

,

Tanaka

M.

,

2014

,

MNRAS

,

443

,

67

10.1093/mnras/stu1124

Crossref

Search ADS

Metzger

B. D.

,

Giannios

D.

,

Thompson

T. A.

,

Bucciantini

N.

,

Quataert

E.

,

2011

,

MNRAS

,

413

,

2031

10.1111/j.1365-2966.2011.18280.x

Crossref

Search ADS

Metzger

B. D.

,

Margalit

B.

,

Kasen

D.

,

Quataert

E.

,

2015

,

MNRAS

,

454

,

3311

10.1093/mnras/stv2224

Crossref

Search ADS

Metzger

B. D.

,

Beniamini

P.

,

Giannios

D.

,

2018

,

ApJ

,

857

,

95

10.3847/1538-4357/aab70c

Crossref

Search ADS

Miller

M. C.

,

Miller

J. M.

,

2015

,

Phys. Rep.

,

548

,

1

10.1016/j.physrep.2014.09.003

Crossref

Search ADS

Miller

S.

,

Callister

T. A.

,

Farr

W. M.

,

2020

,

ApJ

,

895

,

128

10.3847/1538-4357/ab80c0

Crossref

Search ADS

Modjaz

M.

et al. ,

2020

,

ApJ

,

892

,

153

10.3847/1538-4357/ab4185

Crossref

Search ADS

Mosser

B.

et al. ,

2012

,

A&A

,

548

,

A10

10.1051/0004-6361/201220106

Crossref

Search ADS

Müller

B.

et al. ,

2018

,

MNRAS

,

484

,

3307

10.1093/mnras/stz216

Crossref

Search ADS

Narayan

R.

,

Yi

I.

,

1994

,

ApJ

,

428

,

L13

10.1086/187381

Crossref

Search ADS

Narayan

R.

,

Piran

T.

,

Kumar

P.

,

2001

,

ApJ

,

557

,

949

10.1086/322267

Crossref

Search ADS

Nugis

T.

,

Lamers

H. J. G. L. M.

,

2000

,

A&A

,

360

,

227

O’Connor

E.

,

Ott

C. D.

,

2011

,

ApJ

,

730

,

70

10.1088/0004-637X/730/2/70

Crossref

Search ADS

Olejak

A.

,

Belczynski

K.

,

2021

,

ApJ

,

921

,

L2

10.3847/2041-8213/ac2f48

Ouazzani

R.-M.

,

Marques

J. P.

,

Goupil

M.

,

Christophe

S.

,

Antoci

V.

,

Salmon

S. J. A. J.

,

2019

,

A&A

,

626

,

A121

10.1051/0004-6361/201832607

Crossref

Search ADS

Pandey

S. B.

et al. ,

2021

,

MNRAS

,

507

,

1229

10.1093/mnras/stab1889

Pavlovskii

K.

,

Ivanova

N.

,

Belczynski

K.

,

Van

K. X.

,

2017

,

MNRAS

,

465

,

2092

10.1093/mnras/stw2786

Crossref

Search ADS

Paxton

B.

,

Bildsten

L.

,

Dotter

A.

,

Herwig

F.

,

Lesaffre

P.

,

Timmes

F.

,

2011

,

ApJS

,

192

,

3

10.1088/0067-0049/192/1/3

Crossref

Search ADS

Paxton

B.

et al. ,

2013

,

ApJS

,

208

,

4

10.1088/0067-0049/208/1/4

Crossref

Search ADS

Paxton

B.

et al. ,

2015

,

ApJS

,

220

,

15

10.1088/0067-0049/220/1/15

Crossref

Search ADS

Paxton

B.

et al. ,

2018

,

ApJS

,

234

,

34

10.3847/1538-4365/aaa5a8

Crossref

Search ADS

Paxton

B.

et al. ,

2019

,

ApJS

,

243

,

10

Perley

D. A.

et al. ,

2016

,

ApJ

,

817

,

8

10.3847/0004-637X/817/1/8

Crossref

Search ADS

Piro

A. L.

,

Ott

C. D.

,

2011

,

ApJ

,

736

,

108

10.1088/0004-637X/736/2/108

Crossref

Search ADS

Popham

R.

,

Woosley

S. E.

,

Fryer

C.

,

1999

,

ApJ

,

518

,

356

10.1086/307259

Crossref

Search ADS

Popov

S. B.

,

Turolla

R.

,

2012

,

Ap&SS

,

341

,

457

10.1007/s10509-012-1100-z

Crossref

Search ADS

Popov

S. B.

,

Pons

J. A.

,

Miralles

J. A.

,

Boldin

P. A.

,

Posselt

B.

,

2010

,

MNRAS

,

401

,

2675

10.1111/j.1365-2966.2009.15850.x

Crossref

Search ADS

Qin

Y.

,

Fragos

T.

,

Meynet

G.

,

Andrews

J.

,

Sørensen

M.

,

Song

H. F.

,

2018

,

A&A

,

616

,

A28

10.1051/0004-6361/201832839

Crossref

Search ADS

Qin

Y.

,

Marchant

P.

,

Fragos

T.

,

Meynet

G.

,

Kalogera

V.

,

2019

,

ApJ

,

870

,

L18

10.3847/2041-8213/aaf97b

Crossref

Search ADS

Roulet

J.

,

Chia

H. S.

,

Olsen

S.

,

Dai

L.

,

Venumadhav

T.

,

Zackay

B.

,

Zaldarriaga

M.

,

2021

,

Phys. Rev. D

,

104

,

83010

10.1103/PhysRevD.104.083010

Schrøder

S. L.

,

Batta

A.

,

Ramirez-Ruiz

E.

,

2018

,

ApJ

,

862

,

L3

10.3847/2041-8213/aacf8d

Crossref

Search ADS

Shakura

N. I.

,

Sunyaev

R. A.

,

1973

,

A&A

,

500

,

33

Shankar

S.

,

Mösta

P.

,

Barnes

J.

,

Duffell

P. C.

,

Kasen

D.

,

2021

,

MNRAS

,

508

,

5390

10.1093/mnras/stab2964

Shivvers

I.

et al. ,

2017

,

PASP

,

129

,

054201

10.1088/1538-3873/aa54a6

Crossref

Search ADS

Siegel

D. M.

,

Barnes

J.

,

Metzger

B. D.

,

2019

,

Nature

,

569

,

241

10.1038/s41586-019-1136-0

Crossref

Search ADS

PubMed

Spada

F.

,

Gellert

M.

,

Arlt

R.

,

Deheuvels

S.

,

2016

,

A&A

,

589

,

A23

10.1051/0004-6361/201527591

Crossref

Search ADS

Spruit

H. C.

,

1999

,

A&A

,

349

,

189

Spruit

H. C.

,

2002

,

A&A

,

381

,

923

10.1051/0004-6361:20011465

Crossref

Search ADS

Stockinger

G.

et al. ,

2020

,

MNRAS

,

496

,

2039

10.1093/mnras/staa1691

Crossref

Search ADS

Takahashi

K.

,

Langer

N.

,

2021

,

A&A

,

646

,

A19

10.1051/0004-6361/202039253

Crossref

Search ADS

Tauris

T. M.

,

Langer

N.

,

Podsiadlowski

P.

,

2015

,

MNRAS

,

451

,

2123

10.1093/mnras/stv990

Crossref

Search ADS

Tauris

T. M.

et al. ,

2017

,

ApJ

,

846

,

170

10.3847/1538-4357/aa7e89

Crossref

Search ADS

Tayar

J.

,

Beck

P. G.

,

Pinsonneault

M. H.

,

García

R. A.

,

Mathur

S.

,

2019

,

ApJ

,

887

,

203

10.3847/1538-4357/ab558a

The LIGO Scientific Collaboration

,

2019

,

ApJ

,

882

,

L24

10.3847/2041-8213/ab3800

Triana

S. A.

,

Corsaro

E.

,

De Ridder

J.

,

Bonanno

A.

,

Pérez Hernández

F.

,

García

R. A.

,

2017

,

A&A

,

602

,

A62

10.1051/0004-6361/201629186

Crossref

Search ADS

van Son

L. A. C.

et al. ,

2021

,

preprint (arXiv:2110.01634)

Vink

J. S.

,

de Koter

A.

,

Lamers

H. J. G. L. M.

,

2000

,

A&A

,

362

,

295

Vink

J. S.

,

de Koter

A.

,

Lamers

H. J. G. L. M.

,

2001

,

A&A

,

369

,

574

10.1051/0004-6361:20010127

Crossref

Search ADS

Wanderman

D.

,

Piran

T.

,

2010

,

MNRAS

,

406

,

1944

10.1111/j.1365-2966.2010.16787.x

Crossref

Search ADS

Woosley

S. E.

,

1993

,

ApJ

,

405

,

273

10.1086/172359

Crossref

Search ADS

Woosley

S. E.

,

Heger

A.

,

2006

,

ApJ

,

637

,

914

10.1086/498500

Crossref

Search ADS

Woosley

S. E.

,

Heger

A.

,

Weaver

T. A.

,

2002

,

Rev. Mod. Phys.

,

74

,

1015

10.1103/RevModPhys.74.1015

Crossref

Search ADS

Worley

A.

,

Krastev

P. G.

,

Li

B.-A.

,

2008

,

ApJ

,

685

,

390

10.1086/589823

Crossref

Search ADS

Yoon

S.-C.

,

Langer

N.

,

Norman

C.

,

2006

,

A&A

,

460

,

199

10.1051/0004-6361:20065912

Crossref

Search ADS

Yoon

S. C.

,

Woosley

S. E.

,

Langer

N.

,

2010

,

ApJ

,

725

,

940

10.1088/0004-637X/725/1/940

Crossref

Search ADS

Yu

Y.-W.

,

Zhu

J.-P.

,

Li

S.-Z.

,

Lü

H.-J.

,

Zou

Y.-C.

,

2017

,

ApJ

,

840

,

12

10.3847/1538-4357/aa6c27

Crossref

Search ADS

Yuan

F.

,

Narayan

R.

,

2014

,

ARA&A

,

52

,

529

10.1146/annurev-astro-082812-141003

Crossref

Search ADS

Zahn

J. P.

,

1977

,

A&A

,

500

,

121

Zaldarriaga

M.

,

Kushnir

D.

,

Kollmeier

J. A.

,

2018

,

MNRAS

,

473

,

4174

10.1093/mnras/stx2577

Crossref

Search ADS

Zapartas

E.

et al. ,

2021

,

A&A

,

656

,

L19

10.1051/0004-6361/202141506

Zevin

M.

et al. ,

2021

,

ApJ

,

910

,

152

10.3847/1538-4357/abe40e

Crossref

Search ADS

Zhao

W.-C.

,

Xue

X.-X.

,

Cao

X.-F.

,

2021

,

New Astron.

,

83

,

101506

10.1016/j.newast.2020.101506

Crossref

Search ADS

APPENDIX A: ACCRETION ENERGETICS

A crude one-zone model for the BH accretion disc and its time evolution is provided by Kumar et al. (2008), who included the combined actions of mass infall, viscous accretion, and disc wind. We adopt their model and briefly describe the procedure here.² At a given moment, the disc has mass M_d and AM J_d, so the characteristic radius is given by |$r_{\rm d}=J_{\rm d}^2/(GM_{\rm BH}M_{\rm d}^2)$| assuming Keplerian rotation. The time evolution of these two quantities are given by

$$\begin{eqnarray} \dot{M}_{\rm d} = \dot{M}_{\rm fb} - {M_{\rm d}\over t_{\rm vis}},\ \end{eqnarray}$$

(A1)

$$\begin{eqnarray} \dot{J}_{\rm d} = \dot{J}_{\rm fb} - \dot{M}_{\rm BH} j_{\rm ISCO} - f_{\rm AM} {J_{\rm d}\over t_{\rm vis}}, \end{eqnarray}$$

(A2)

where |$\dot{M}_{\rm fb}$| and |$\dot{J}_{\rm fb}$| are the mass and AM fallback rates of the envelope, |$t_{\rm vis}=\alpha _{\rm s}^{-1} \sqrt{r_{\rm d}^3/GM_{\rm BH}}$| is the viscous time-scale, α_s ∈ (0.01, 0.1) is the dimension-less viscous parameter (Shakura & Sunyaev 1973), and |$\dot{M}_{\rm BH}$| is the BH accretion rate at the inner edge of the disc. The parameter f_AM relates the specific AM of the mass lost through the disc wind to that of the disc, as described below.

To compute the mass/AM fallback rates from our progenitor model, we first calculate the free-fall time for each shell at radius r as |$t_{\rm ff}(r) = (\pi /2^{1/5}) \sqrt{r^3/GM(r)}$|⁠, where M(r) is the enclosed mass. Then, the mass fallback rate is given by

$$\begin{eqnarray} \dot{M}_{\rm fb} = \frac{\mathrm{ d}M}{\mathrm{ d}t_{\rm ff}} \, , \end{eqnarray}$$

(A3)

$$\begin{eqnarray} \dot{J}_{\rm fb} = \frac{2}{3} \Omega (r) r^2 \dot{M}_{\rm fb}. \end{eqnarray}$$

(A4)

These are the rates at which mass and AM are added to either the BH or the accretion disc at a given time t = t_ff(r). For the disc-forming radial shells with j > j_ISCO, we assume that only the regions >30° from the rotational axis manage to fallback to the disc whereas the regions with polar angles <30° is removed from the star by the mechanical feedback of the accretion disc wind/jet. This means that the mass and AM fallback rate are slightly reduced by a factor of cos 30° = 0.866 and (3/2)[cos 30° − (1/3)(cos 30°)³] = 0.974, respectively.

The key ingredient of the disc model is that at a given moment, the disc has a power-law radial mass accretion rate profile |$\dot{M}_{\rm acc}(r) = (M_{\rm d}/t_{\rm vis})(r/r_{\rm d})^s$| (Blandford & Begelman 1999), where s ∈ (0, 1) is a free parameter (likely between 0.3 and 0.8; Yuan & Narayan 2014). The power-law flattens below a transition radius r_t, where the disc starts to be neutrino-cooled, and there is no disc wind from radii r < r_t, i.e. |$\dot{M}_{\rm acc}(r\lt r_{\rm t})=\dot{M}_{\rm acc}(r_{\rm t})$|⁠. The transition radius is given by |$\dot{M}_{\rm acc}(r_{\rm t})=\dot{M}_{\rm ign} r_{\rm t}/r_{\rm s}$| (r_s = 2GM_BH/c² being the Schwarzschild radius), where |$\dot{M}_{\rm ign}$| is the critical accretion for URCA ignition that depends on the viscous parameter α_s, BH mass, and spin (see Chen & Beloborodov 2007; Siegel, Barnes & Metzger 2019). We adopt α_s = 0.03 and keep |$\dot{M}_{\rm ign}\simeq 10^{-2.5}\, M_\odot \rm \, yr^{-1}$| fixed in this paper. If r_t is in between r_ISCO and r_d, then the transition from ADAF to the neutrino-cooled regime indeed occurs, otherwise the radial profile of the accretion rate is either a single power law (if r_t < r_ISCO) or constant function (r_t > r_d). We further assume that the specific AM of the disc wind is equal to the local Keplerian value of |$\sqrt{GM_{\rm BH}r}$| at each radius r, which gives f_AM = (1 + 0.5/s)⁻¹[1 − (r_t/r_d)^{s + 0.5}]. Then, the mass and AM accretion rates of the BH are |$\dot{M}_{\rm BH}=\dot{M}_{\rm acc}(r_{\rm isco})$| and |$\dot{J}_{\rm BH}=j_{\rm ISCO}\dot{M}_{\rm BH}$|⁠. The total accretion luminosity of the disc is given by

$$\begin{eqnarray} L_{\rm ac}\simeq \eta _{\rm NT} \dot{M}_{\rm BH} c^2, \end{eqnarray}$$

(A5)

where the Novikov-Thorne efficiency |$\eta _{\rm NT}=1-\sqrt{1-r_{\rm s}/3r_{\rm isco}}$| is given by the energy difference between a particle at infinity and at the ISCO. Under the assumption that each wind fluid element lifted from radius r carries positive specific energy of GM_BH/2r, we estimate the total mechanical power of the disc wind to be

$$\begin{eqnarray} L_{\rm wind}\simeq {s\over 2(1-s)} {GM_{\rm BH}\over r_{\rm d}} {M_{\rm d}\over t_{\rm vis}}\left[(r_{\rm d}/r_{\rm t})^{1-s} - 1\right]. \end{eqnarray}$$

(A6)

Finally, we integrate over the entire evolution history and obtain the total energy generated by the accretion disc E_ac = ∫L_acdt as well as the mechanical energy carried by the disc wind E_wind = ∫L_winddt. Our nominal result in Fig. 6 uses s = 0.5, and for other choices of s ∈ (0.3, 0.8), E_wind differs by a factor of a few.

APPENDIX B: MODEL TESTING

B1 Resolution testing

It is important to check that our results are not spurious due to unstable or non-converged stellar models. To do this, we performed a few tests. First, we increased each model’s spatial resolution by a factor of ∼2 by decreasing mesh_delta_coeff and mesh_delta_coeff_for_highT. Fig. B1 shows that the predicted NS and BH rotation rates for all the models were very similar, within 10 per cent in most cases and never varying by more than 40 per cent. The differences appeared to be stochastic, with no systematic shift to higher or lower spins.

Figure B1.

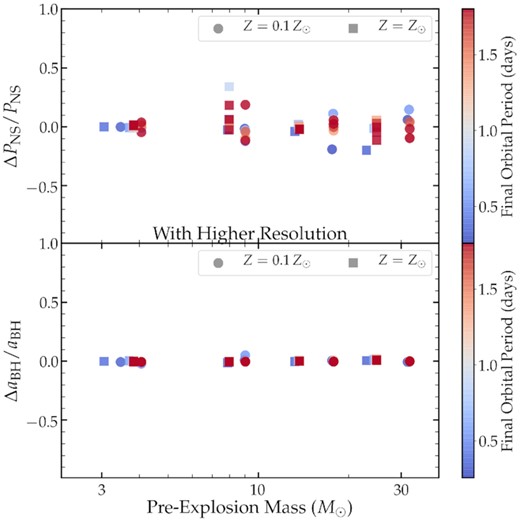
Fractional difference in the predicted NS rotation period (top) and BH spin (bottom) between models with our highest spatial resolution and slightly lower resolution.

Open in new tab Download slide

Secondly, we increased each model’s time resolution by requiring smaller changes in grid cell temperatures and chemical abundances by a factor of two. The corresponding differences in NS and BH spins are shown in Fig. B2. Again, no large or systematic changes were observed. Since the uncertainties in physical prescriptions (see below) are much larger than differences arising from numerical resolution, we consider the models to be sufficiently converged for our purposes.

Figure B2.

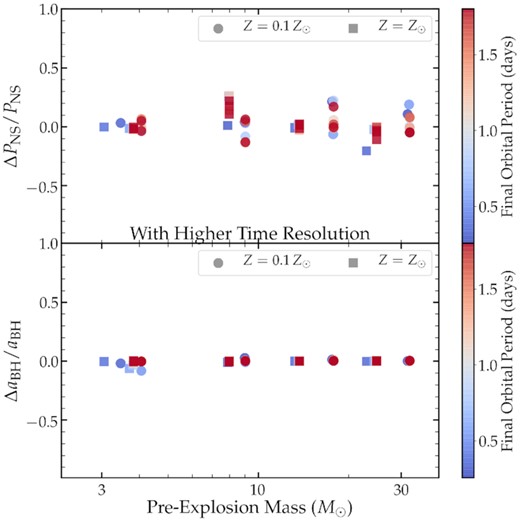
Same as Fig. B1 but for models with different time resolution.

Open in new tab Download slide

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Month:	Total Views:
February 2022	7
March 2022	42
April 2022	14
May 2022	20
June 2022	14
July 2022	17
August 2022	12
September 2022	8
October 2022	21
November 2022	7
December 2022	4
January 2023	16
February 2023	12
March 2023	10
April 2023	12
May 2023	1
June 2023	18
July 2023	4
August 2023	11
September 2023	4
October 2023	8
November 2023	9
December 2023	6
January 2024	13
February 2024	12
March 2024	17
April 2024	14
May 2024	29
June 2024	21
July 2024	23
August 2024	20
September 2024	32
October 2024	10
November 2024	14
December 2024	12
January 2025	14
February 2025	11
March 2025	23
April 2025	9
May 2025	18

Article Contents

The spins of compact objects born from helium stars in binary systems

ABSTRACT

1 INTRODUCTION

2 ANGULAR MOMENTUM TRANSPORT FOR LOW SHEAR

3 STELLAR EVOLUTION MODELS

3.1 Angular momentum extraction

4 COMPACT OBJECT ROTATION RATES

4.1 Neutron star rotation rates

4.2 Black hole spins

5 ENERGETIC SUPERNOVAE AND TRANSIENTS

5.1 Comparison with observed supernovae

5.2 Predictions for central engine models

5.2.1 Magnetar central engines

5.2.2 Accreting black hole central engines

5.3 Rates

6 MODELLING UNCERTAINTIES

6.1 AM transport uncertainties

6.2 Helium stars from other evolutionary channels

6.2.1 Stable mass transfer

6.2.2 Helium stars from chemically homogeneous evolution

7 CONCLUSION

ACKNOWLEDGEMENTS

DATA AVAILABILITY

Footnotes

REFERENCES

APPENDIX A: ACCRETION ENERGETICS

APPENDIX B: MODEL TESTING

B1 Resolution testing

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

The spins of compact objects born from helium stars in binary systems

ABSTRACT

1 INTRODUCTION

2 ANGULAR MOMENTUM TRANSPORT FOR LOW SHEAR

3 STELLAR EVOLUTION MODELS

3.1 Angular momentum extraction

4 COMPACT OBJECT ROTATION RATES

4.1 Neutron star rotation rates

4.2 Black hole spins

5 ENERGETIC SUPERNOVAE AND TRANSIENTS

5.1 Comparison with observed supernovae

5.2 Predictions for central engine models

5.2.1 Magnetar central engines

5.2.2 Accreting black hole central engines

5.3 Rates

6 MODELLING UNCERTAINTIES

6.1 AM transport uncertainties

6.2 Helium stars from other evolutionary channels

6.2.1 Stable mass transfer

6.2.2 Helium stars from chemically homogeneous evolution

7 CONCLUSION

ACKNOWLEDGEMENTS

DATA AVAILABILITY

Footnotes

REFERENCES

APPENDIX A: ACCRETION ENERGETICS

APPENDIX B: MODEL TESTING

B1 Resolution testing

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only