-
PDF
- Split View
-
Views
-
Cite
Cite
Ryan Endsley, Daniel P Stark, Stéphane Charlot, Jacopo Chevallard, Brant Robertson, Rychard J Bouwens, Mauro Stefanon, MMT spectroscopy of Lyman-alpha at z ≃ 7: evidence for accelerated reionization around massive galaxies, Monthly Notices of the Royal Astronomical Society, Volume 502, Issue 4, April 2021, Pages 6044–6063, https://doi.org/10.1093/mnras/stab432
Close - Share Icon Share
ABSTRACT
Reionization-era galaxies tend to exhibit weak Ly α emission, likely reflecting attenuation from an increasingly neutral IGM. Recent observations have begun to reveal exceptions to this picture, with strong Ly α emission now known in four of the most massive z = 7–9 galaxies in the CANDELS fields, all of which also exhibit intense [O iii]+H β emission (EW > 800 Å). To better understand why Ly α is anomalously strong in a subset of massive z ≃ 7–9 galaxies, we have initiated an MMT/Binospec survey targeting a larger sample (N = 22) of similarly luminous (≃1–6 L|$^{\ast }_{\mathrm{UV}}$|) z ≃ 7 galaxies selected over very wide-area fields (∼3 deg2). We confidently (>7σ) detect Ly α in 78 per cent (7/9) of galaxies with strong [O iii]+H β emission (EW > 800 Å) as opposed to only 8 per cent (1/12) of galaxies with more moderate (EW = 200–800 Å) [O iii]+H β. We argue that the higher Ly α EWs of the strong [O iii]+H β population likely reflect enhanced ionizing photon production efficiency owing to their large sSFRs (≳30 Gyr−1). We also find evidence that Ly α transmission from massive galaxies declines less rapidly over 6 < z < 7 than in low-mass lensed systems. In particular, our data suggest no strong evolution in Ly α transmission, consistent with a picture wherein massive z ≃ 7 galaxies often reside in large ionized regions. We detect three closely separated (R = 1.7 physical Mpc) z ≃ 7 Ly α emitters in our sample, conceivably tracing a large ionized structure that is consistent with this picture. We detect tentative evidence for an overdensity in this region, implying a large ionizing photon budget in the surrounding volume.
1 INTRODUCTION
Within the past decade, a number of concerted efforts have aimed at better understanding how and when the process of hydrogen reionization occurred. Such information provides insight into not only the growth of structure in the very early Universe, but also the nature of ionizing sources responsible for reionization (e.g. Loeb & Barkana 2001; Fan, Carilli & Keating 2006; Bouwens et al. 2015b; Robertson et al. 2015; Finkelstein 2016; Stark 2016; Dayal & Ferrara 2018; Naidu et al. 2020). Observationally, there has been great progress in identifying star-forming galaxies at z ∼ 6–10 (e.g. Ellis et al. 2013; McLure et al. 2013; Bowler et al. 2014, 2020; Atek et al. 2015; Bouwens et al. 2015a, 2019; Finkelstein et al. 2015; Livermore, Finkelstein & Lotz 2017; Oesch et al. 2018; Ono et al. 2018; Stefanon et al. 2017, 2019), revealing a population capable of generating copious amounts of ionizing photons in the early Universe.
The impact of these early ionizing agents on the IGM can be tracked independently using measurements of the timeline of the reionization process. Prominent detections of the Ly α and Ly β forests in quasar spectra at z ≲ 6 provide a model-independent constraint suggesting that reionization was largely complete by z = 5.9 (neutral fraction xH i ≲ 10 per cent; McGreer, Mesinger & D’Odorico 2015). However, the presence of a long neutral patch identified at z = 5.5 (Becker et al. 2015) suggests that reionization may have ended as late as z ≃ 5.2–5.3 (Kulkarni et al. 2019; Keating et al. 2020; Nasir & D’Aloisio 2020). At yet higher redshifts, strong damping wing signatures in the earliest known quasars (z ≃ 7.0–7.5) provide evidence for significant neutral hydrogen fractions (xH i ∼ 40–60 per cent; Greig et al. 2017; Bañados et al. 2018; Davies et al. 2018; Wang et al. 2020). Measurements of the Thomson scattering optical depth from the CMB are consistent with this reionization timeline, suggesting a reionization midpoint of z ∼ 7.7 (Planck Collaboration XLVII 2016; Planck Collaboration VI 2020).
High-redshift (z ≳ 6) galaxies have also long enabled complementary constraints on the timeline of reionization owing to the resonant nature of the Ly α emission line (e.g. Miralda-Escudé 1998; Malhotra & Rhoads 2004; Santos 2004; Mesinger & Furlanetto 2008; Dijkstra 2014). A number of studies have uncovered a marked decline in the fraction of star-forming galaxies showing strong Ly α (rest-frame equivalent width EW > 25 Å) at z > 6, consistent with expectations of an increasingly neutral IGM (e.g. Fontana et al. 2010; Stark et al. 2010; Vanzella et al. 2011; Ono et al. 2012; Treu et al. 2013; Caruana et al. 2014; Pentericci et al. 2014, 2018; Schenker et al. 2014; De Barros et al. 2017; Jung et al. 2017; Hoag et al. 2019; Mason et al. 2019). In a similar manner, the volume density of narrow-band selected Ly α emitters has been found to decrease rapidly from z ∼ 6 to z ∼ 7 (e.g. Malhotra & Rhoads 2004; Hu et al. 2010; Ouchi et al. 2010; Kashikawa et al. 2011; Konno et al. 2014; Ota et al. 2017; Zheng et al. 2017). Both these downturns suggest a highly neutral Universe (xH i > 0.4) at z ≃ 7 (e.g. Ota et al. 2017; Zheng et al. 2017; Mason et al. 2018a; Whitler et al. 2020), consistent with inferences from quasar spectra.
In the last 5 yr, attention has begun to focus on the Ly α properties of the most massive galaxies known in the reionization era. Recent spectroscopic observations have revealed a 100 per cent Ly α detection rate among four of the brightest1 (3–4 L|$_{\mathrm{UV}}^{\ast }$|) and most massive z = 7–9 galaxies selected over the CANDELS fields (Oesch et al. 2015; Zitrin et al. 2015; Roberts-Borsani et al. 2016, hereafter the RB16 sample; Stark et al. 2017), in marked contrast to the ≲10–20 per cent Ly α detection rate among typical (<L|$_{\mathrm{UV}}^{\ast }$|) galaxies at z ≳ 7 (e.g. Ono et al. 2012; Treu et al. 2013; Pentericci et al. 2014, 2018; Schenker et al. 2014). It is not yet clear why the Ly α photons emerging from the RB16 galaxies are so readily detectable given the highly neutral state of the IGM at z > 7. One likely possibility is that these massive galaxies trace strong overdensities (Zitrin et al. 2015) and are hence situated in large ionized regions in the IGM (e.g. Furlanetto, Zaldarriaga & Hernquist 2004; Wyithe & Loeb 2005; Lee et al. 2007; McQuinn et al. 2007; Weinberger et al. 2018). These bubbles enable Ly α photons to redshift further into the damping wing before encountering H i, boosting the transmission (e.g. Mesinger, Haiman & Cen 2004; Mason & Gronke 2020). On the other hand, the high-EW [O iii]+H β emission (>800 Å) of the RB16 sample may suggest that their Ly α detections were driven more by physics internal to each of the four galaxies (Stark et al. 2017). Strong [O iii]+H β typically signals a recent rapid upturn or burst in star formation activity, i.e. high specific star formation rate (sSFR; Tang et al. 2019; Endsley et al. 2021, hereafter E21), giving rise to very young stellar populations. The spectra of such galaxies are therefore dominated by extremely hot stars that produce ionizing photons very efficiently with respect to the far-UV continuum. Assuming these ionizing photons are reprocessed into recombination lines, this should also boost the production rate of Ly α relative to the rest-UV continuum.
To better understand the origin of strong Ly α from massive reionization-era galaxies, we have initiated an MMT/Binospec campaign targeting Ly α in a much larger sample of bright (1–6 L|$_{\mathrm{UV}}^{\ast }$|) z ≃ 7 systems. Here, we use the first results from our spectroscopic campaign to investigate to what extent strong [O iii]+H β (and hence large sSFRs) enhance Ly α detectability among bright reionization-era galaxies. Because our sources were selected over the very wide-area COSMOS and XMM3 fields (≈1.5 deg2 each), we are able to assemble a much larger sample of these rare systems relative to CANDELS (≈0.2 deg2 total; Grogin et al. 2011; Koekemoer et al. 2011).
We furthermore test whether our results are consistent with a picture wherein bright (and therefore likely massive; e.g. Barone-Nugent et al. 2014; Song et al. 2016a) z ≃ 7 galaxies often reside in large highly ionized bubbles, as would be expected if they preferentially trace overdensities. If this is the case, we would expect the transmission of Ly α photons from bright galaxies to show a substantially weaker decline at z ≳ 6 relative to much fainter sources. Recent observations suggest a sharp (factor of ∼10) decline in Ly α transmission for faint (∼0.1 L|$_{\mathrm{UV}}^{\ast }$|) lensed galaxies between z ≃ 6–7 (Hoag et al. 2019; Fuller et al. 2020). Our goal is to test whether our bright (1–6 L|$_{\mathrm{UV}}^{\ast }$|) z ≃ 7 galaxy sample exhibit a less rapid decline in Ly α transmission, building on earlier work targeting massive galaxies (e.g. Ono et al. 2012; Furusawa et al. 2016). For this investigation, we complement our z ≃ 7 targets with a collection of similarly bright z ≃ 6 sources that were observed simultaneously with the multiplex Binospec instrument.
This paper is organized as follows. In Section 2, we describe our observations including our sample selection, spectroscopic results, and the inferred [O iii]+H β EWs of each source. We present our analysis in Section 3, including an investigation of whether Ly α detectability is enhanced in bright z ≃ 7 systems with strong [O iii]+H β. We then discuss what our results imply for the presence of ionized regions around massive reionization-era galaxies in Section 4. Our main conclusions are summarized in Section 5.
All magnitudes are quoted in the AB system (Oke & Gunn 1983) and we adopt a flat ΛCDM cosmology with h = 0.7, ΩM = 0.3, and ΩΛ = 0.7, consistent with Planck results (Planck Collaboration VI 2020). All distances are quoted in physical units unless otherwise stated.
2 OBSERVATIONS
We have initiated a large spectroscopic Ly α survey of bright (≃1–6 L|$_{\mathrm{UV}}^{\ast }$|) galaxies at z ≃ 7 with MMT/Binospec. Our selection criteria are described in Section 2.1. We then detail our spectroscopic results and the photometric properties of galaxies in our spectroscopic sample in Section 2.2. Finally, we infer the physical properties (e.g. stellar mass and [O iii]+H β EW) of each spectroscopic target in Section 2.3.
2.1 Source selection and photometry
In this work, we aim to accomplish two goals focused on targeting Ly α in bright (≳L|$_{\mathrm{UV}}^{\ast }$|) galaxies at z ≃ 6–7. First, we seek to investigate whether strong [O iii]+H β (and hence large sSFRs) lead to enhanced Ly α emission among bright reionization-era galaxies. Secondly, we aim to quantify the evolution in the Ly α EW distribution of bright galaxies between z ≃ 6 and 7 to test whether our results are consistent with a picture wherein massive z ≃ 7 systems often reside in large ionized bubbles. Given the rarity of such luminous high-redshift galaxies, we select these sources over very wide-area fields, specifically the COSMOS and XMM3 fields that span 1.5 and 1.8 deg2, respectively. We describe our z ≃ 7 and z ≃ 6 source selection criteria in turn below.
2.1.1 Selection of z ≃ 7 sources
To ensure we can reliably identify z ≃ 7 galaxies and infer their [O iii]+H β EWs, we photometrically select our targets over wide-area (>1 deg2) fields with deep optical through mid-infrared imaging. Because of the exceptionally deep imaging over COSMOS, the majority of our sources are selected within this field. The Subaru/Hyper Surpime-Cam (HSC) Subaru Strategic Program (HSCSSP; Aihara et al. 2018, 2019) provides optical (0.4–1μm) imaging across COSMOS in the g, r, i, z, y broad-bands as well as the nb816 and nb921 narrow-bands. The near-infrared data come from the UltraVISTA survey (McCracken et al. 2012) that delivers imaging in VISTA/VIRCam Y, J, H, and Ks broad-bands. We use PDR2 and DR4 data from HSCSSP and UltraVISTA, respectively, both of which are already astrometrically calibrated to the Gaia frame that we adopt throughout this work.
Our z ≃ 7 source selection over COSMOS largely follows that described in E21 that utilizes, in part, the nb921 photometry to limit the selection to z ≳ 6.6 with high confidence. The specific adopted Lyman-break colour cuts are z−y > 1.5, z−Y > 1.5, nb921−Y > 1.0, and y−Y < 0.4 where we set fluxes in the z and nb921 dropout filters to their 1σ values in cases of non-detections, consistent with previous literature (e.g. Bouwens et al. 2015a; Stefanon et al. 2019). These z ≃ 7 selection criteria were designed by simulating the colours of z = 6–8 galaxies with flat rest-UV slopes (β = −2 where Fν ∝ λβ + 2) using the Inoue et al. (2014) IGM transmission function. As with any Lyman-break selection utilizing broad-band photometry, the exact redshift selection window depends slightly on the assumed Ly α EW. Galaxies with weak Ly α emission (≃0 Å EW) are only likely to satisfy the above criteria from z ≃ 6.6–6.9 because at higher redshifts the y−Y colour becomes too red. On the other hand, sources with strong Ly α satisfy our selection criteria to larger maximum redshifts – up to z ≃ 7.1 and z ≃ 7.2 for Ly α EW = 25 Å and 100 Å, respectively. This is because strong Ly α will boost the y-band flux resulting in bluer y−Y colours at a given redshift. We refer the interested reader to fig. 2 of E21 for a visualization of the impact of Ly α on our redshift selection window. Because only ∼10 per cent of bright z ≃ 7 galaxies show strong Ly α emission (EW > 25 Å; Ono et al. 2012; Schenker et al. 2014; Pentericci et al. 2018), the large majority of our sample will likely lie at z ≃ 6.6–6.9. None the less, we directly account for how our redshift selection window depends on Ly α strength when inferring the Ly α EW distribution as described in Section 2.2.4.
Along with the above colour cuts, we ensure that each z ≃ 7 source is real by requiring a > 3σ detection in y, Y, and J as well as a >5σ detection in at least one of those three bands. We also enforce non-detections (<2σ) in g and r since both these bands probe flux blueward of the Lyman-continuum limit at z ≥ 6.6. Finally, we clean our sample of T-type brown dwarfs (which can exhibit very strong z and nb921-drops) by preserving only those with Y−J < 0.45 or (J−H > 0 and J−Ks >0). These cuts are guided by brown dwarf spectra in the SPEX library (Burgasser 2014) that demonstrate that T-type brown drafts have red Y−J colours but blue J−H and J−Ks colours.
To build statistics on the brightest end, we also select galaxies over the XMM3 field. While the optical through mid-infrared coverage over XMM3 is significantly shallower relative to COSMOS, we are still able to identify the most luminous (J ≲ 24.5) z ≃ 7 galaxies within this field. Near-infrared imaging over XMM3 comes from DR3 of the VIDEO survey2 (Jarvis et al. 2013) that provides data from the Z, Y, J, H, and Ks VISTA/VIRCam broad-bands. For the optical imaging, we again use PDR2 of the HSCSSP that provides coverage in all the same bands as in COSMOS except for nb921. To compensate for the lack of nb921 imaging over XMM3, we enforce a much stronger dropout in the Z band, specifically requiring Z−y > 2.5 and Z−Y > 2.5 while maintaining the y−Y < 0.4 cut we applied in COSMOS. We found that such cuts select z ≃ 7 sources in a very similar redshift window as COSMOS after performing colour simulations of z = 6–8 galaxies similar to those described in E21. Here, we use VIRCam Z as the dropout band in XMM3 because the imaging in Z is often slightly deeper relative to z and both bands have very similar (normalized) transmission curves. All other selection criteria are equivalent to that over COSMOS.
To identify sources within each field, we run SExtractor (Bertin & Arnouts 1996) on a yYJHKs χ2 detection image (Szalay, Connolly & Szokoly 1999). We then calculate the optical and near-infrared photometry of each source in 1.2 arcsec diameter apertures which is ≈1.5 × the seeing in all bands. Aperture corrections are calculated from the median curve-of-growth of nearby isolated, unsaturated stars and photometric errors are determined using the standard deviation of flux within apertures randomly placed in nearby empty locations. As reported in E21, the typical 5σ depths in the COSMOS field are m = 27.7, 27.4, 27.3, 26.1, 26.9, 26.2, and 26.1 in g, r, i, nb816, z, nb921, and y, respectively. For the UltraVISTA data, the typical depths are m = 24.7, 24.5, 24.2, and 24.5 in Y, J, H, and Ks, respectively, for the deep stripes and m = 25.9, 25.8, 25.6, and 25.2, respectively, for the ultra-deep stripes. We are therefore able to identify z ≃ 7 galaxies as faint as J ∼ 26 in the ultra-deep stripes and J ∼ 25 in the deep stripes. In XMM3, the typical 5σ depths are m = 26.7, 26.3, 25.7, 25.3, 25.5, 24.3, 25.6, 25.0, 24.7, 24.3, and 23.9 in g, r, i, nb816, z, y, Z, Y, J, H, and Ks, respectively. We can therefore identify z ≃ 7 galaxies as faint as J ∼ 24.5 across XMM3.
2.1.2 Selection of z ≃ 6 sources
To quantify the evolution in the Ly α transmission for massive galaxies between z ≃ 6 and 7, we also observed bright z ≃ 6 sources that were photometrically selected as follows. Similar to our z ≃ 7 procedure, we design optimal z ≃ 6 selection criteria by simulating the HSC and VIRCam colours of z = 5–7 galaxies with rest-UV slope β = −2 and adopting the IGM transmission function from Inoue et al. (2014).
Our resulting z ≃ 6 selection criteria over COSMOS includes the following colour cuts:
nb816−z > 1.5
r− z > 1.5
z− y < 0.5
−0.5 <nb921−y < 0.5
Similar to our z ≃ 7 selection, fluxes in nb816 and r are set to their 1σ value in cases of non-detections. With these criteria, most selected bright z ≃ 6 sources (i.e. those with weak Ly α; Stark, Ellis & Ouchi 2011; De Barros et al. 2017) will lie at z ≃ 5.75–6.25 while strong Ly α emitters can be selected up to z ≃ 6.5. We have enforced the cut −0.5 <nb921−y < 0.5 to minimize the likelihood that strong z > 6.5 Ly α emitters are scattering into our z ≃ 6 selection. We additionally require a >5σ detection in z as well as a >3σ detection in nb921 and y to ensure each source is real. Finally, we enforce non-detections (<2σ) in g given that this band lies blueward of the Lyman-continuum break at z > 5.
In XMM3, our z ≃ 6 selection is largely similar. Specifically, we enforce nb816−Z > 1.5, r−Z > 1.5, and Z−Y < 0.5 (as detailed in Section 2.1.1, the Z and Y imaging are generally deeper than z and y, respectively, across XMM3). We also require a >5σ detection in Z as well as a >3σ detection in z and Y to ensure each source is real, in addition to non-detections (<2σ) in g. As in COSMOS, these cuts result in a redshift selection window of z ≃ 5.75–6.25 for sources with weak Ly α emission (EW ≃ 0 Å). Due to the lack of nb921 imaging across this field, sources with very strong Ly α emission (EW∼100 Å) can be selected up to z ≃ 6.6. However, our spectroscopic data confirm that all three of our z ≃ 6 XMM3 targets lie at z < 6.5 (Section 2.2) so this is not a concern for this work.
These z ≃ 6 sources are identified after running SExtractor on a znb921yYJHKs and zZyYJHK|$_s\, \chi ^2$| detection image over COSMOS and XMM3, respectively. Optical and near-infrared photometry are calculated in the same way as for the z ≃ 7 sources (1.2 arcsec diameter apertures). Given the depths in each field, we are able to identify z ≃ 6 sources down to y ∼ 26.5 in COSMOS3 and Y ∼ 25.5 in XMM3. Note that throughout this work, for the z ≃ 6 galaxies, we quote y-band magnitudes for those in COSMOS and Y-band magnitudes for those in XMM3 given the depth differences noted above.
2.1.3 IRAC photometry
To infer the [O iii]+H β EWs of our z ≃ 7 sample, we take advantage of the Spitzer/IRAC imaging over both COSMOS and XMM3. A full description of our procedure for generating IRAC mosaics in both the 3.6 μm and 4.5 μm filters is provided in E21. Briefly, we use the mopex software (Makovoz & Khan 2005) to coadd background-subtracted images (using SExtractor) and astrometrically match the output mosaics to the Gaia reference frame using the iraf package ccmap. In COSMOS, the IRAC data comes from a multitude of surveys: the Spitzer Extended Deep Survey (SEDS; Ashby et al. 2013), S-CANDELS (Ashby et al. 2015), Star Formation at 4<z<6 from the Spitzer Large Area Survey with Hyper Suprime-Cam (SPLASH; Steinhardt et al. 2014), Spitzer Matching survey of the UltraVISTA ultra-deep Stripes (SMUVS; Ashby et al. 2018), and Completing the Legacy of Spitzer/IRAC over COSMOS (P.I. I. Labbé). The IRAC data over XMM3 largely comes from the Spitzer Extragalactic Representative Volume Survey (SERVS; Mauduit et al. 2012) with deeper imaging on our z ≃ 7 targets from late-2019 observations led by P.I. M. Stefanon.
To compensate for the considerably broader IRAC PSF relative to the optical/near-infrared seeing, we measure IRAC photometry in 2.8 arcsec diameter apertures and utilize a deconfusion algorithm to remove contaminating flux from neighbouring sources. In XMM3, our deconfusion approach is equivalent to that detailed in E21. To summarize, we convolve the flux profile of every nearby source detected in the yYJHK|$_s\, \chi ^2$| image with a 2D Gaussian having full width at half-maximum (FWHM) equal to the quadrature difference of the IRAC FWHM and the median seeing from each band in our χ2 detection images. Flux profiles are calculated as the square root of the χ2 image using the SExtractor segmentation map to determine source footprints. The convolved flux profiles are fit to the IRAC image with total fluxes of each source as free parameters. Once this is done, the best-fitting flux profile of each neighbouring source is subtracted before measuring the IRAC photometry. We note that our XMM3 targets are not strongly confused and that residuals from the deconfusion algorithm are acceptably smooth. That is the S/N of the pixels inside the aperture do not appear to be systematically offset due to poor flux-profile fitting of the neighbouring sources upon visual inspection. We show the deconfused IRAC postage stamps of both sources in Fig. A1 (see Appendix) to illustrate this point.
In COSMOS, we take advantage of the very high-resolution HST F814W imaging across this field (Scoville et al. 2007) to calculate the flux profile of each neighbouring source. By convolving these flux profiles with IRAC PSFs calculated using unsaturated stars near each source (<3 arcmin separation), we are able to obtain much smoother residual images from the deconfusion algorithm for sources lying in crowded regions. For the purposes of this work, we remove sources from our sample that have poor IRAC residuals after employing our deconfusion algorithm, as is common in the literature (e.g. Labbé et al. 2013; Bouwens et al. 2015a; Smit et al. 2015; De Barros et al. 2019). One of our COSMOS targets (COS-862541) lies outside the F814W imaging and we therefore employ the same deconfusion approach as for XMM3, noting that this source is also not strongly confused. The deconfused IRAC postage stamp images of all our targets are shown in Fig. A1 (see Appendix).
2.2 MMT/Binospec spectroscopy
We have followed up a subset of our z ≃ 6 and z ≃ 7 galaxy samples described in Section 2.1 using the Binospec spectrograph (Fabricant et al. 2019) installed at the MMT. Binospec is a wide-field (240 arcmin2) and multi-object (up to ∼150 sources) spectrograph enabling wavelength coverage up to ≈1 μm with moderately high resolution (R ≈ 4400). As such, Binospec is an ideal instrument to target Ly α in large numbers of z ≃ 6–7 galaxies selected over wide-area fields. So far, we have observed seven masks with five in COSMOS and two in XMM3, totaling just over 31 h of integration time across all masks. In Table 1, we report the central coordinate, position angle, central wavelength, total exposure time, and average seeing for each mask. When choosing which sources would be assigned slits for each mask, we assigned higher priority to sources with brighter UV magnitudes to obtain a more homogeneous sample across luminosity. Because galaxy rest-UV slopes typically become bluer at higher redshifts (e.g. Bouwens et al. 2014), we also gave higher priority to z ≃ 6 sources with bluer rest-UV slopes to obtain z ≃ 6 and z ≃ 7 samples with more similar properties.
| Mask name . | RA . | Dec . | PA . | λcen . | Exposure time . | Average seeing . |
|---|---|---|---|---|---|---|
| . | . | . | (deg) . | (Å) . | (s) . | (arcsec) . |
| COSa | 10:02:29.53 | +02:17:24.58 | +45.0 | 8500 | 7200 | 1.0 |
| COSb | 10:00:28.37 | +01:53:50.84 | −98.5 | 8700 | 32 400 | 1.1 |
| COSc | 09:59:09.41 | +02:21:25.80 | −101.0 | 8700 | 7200 | 1.1 |
| COSd | 09:59:10.01 | +02:21:07.83 | −101.0 | 8700 | 18 900 | 1.0 |
| COSe | 10:00:39.92 | +02:35:16.12 | −20.0 | 8720 | 17 100 | 1.2 |
| XMM3a | 02:26:38.04 | −05:03:11.15 | −12.0 | 8700 | 10 200 | 0.9 |
| XMM3b | 02:27:22.70 | −04:19:35.44 | −116.2 | 8700 | 18 900 | 1.0 |
| Mask name . | RA . | Dec . | PA . | λcen . | Exposure time . | Average seeing . |
|---|---|---|---|---|---|---|
| . | . | . | (deg) . | (Å) . | (s) . | (arcsec) . |
| COSa | 10:02:29.53 | +02:17:24.58 | +45.0 | 8500 | 7200 | 1.0 |
| COSb | 10:00:28.37 | +01:53:50.84 | −98.5 | 8700 | 32 400 | 1.1 |
| COSc | 09:59:09.41 | +02:21:25.80 | −101.0 | 8700 | 7200 | 1.1 |
| COSd | 09:59:10.01 | +02:21:07.83 | −101.0 | 8700 | 18 900 | 1.0 |
| COSe | 10:00:39.92 | +02:35:16.12 | −20.0 | 8720 | 17 100 | 1.2 |
| XMM3a | 02:26:38.04 | −05:03:11.15 | −12.0 | 8700 | 10 200 | 0.9 |
| XMM3b | 02:27:22.70 | −04:19:35.44 | −116.2 | 8700 | 18 900 | 1.0 |
| Mask name . | RA . | Dec . | PA . | λcen . | Exposure time . | Average seeing . |
|---|---|---|---|---|---|---|
| . | . | . | (deg) . | (Å) . | (s) . | (arcsec) . |
| COSa | 10:02:29.53 | +02:17:24.58 | +45.0 | 8500 | 7200 | 1.0 |
| COSb | 10:00:28.37 | +01:53:50.84 | −98.5 | 8700 | 32 400 | 1.1 |
| COSc | 09:59:09.41 | +02:21:25.80 | −101.0 | 8700 | 7200 | 1.1 |
| COSd | 09:59:10.01 | +02:21:07.83 | −101.0 | 8700 | 18 900 | 1.0 |
| COSe | 10:00:39.92 | +02:35:16.12 | −20.0 | 8720 | 17 100 | 1.2 |
| XMM3a | 02:26:38.04 | −05:03:11.15 | −12.0 | 8700 | 10 200 | 0.9 |
| XMM3b | 02:27:22.70 | −04:19:35.44 | −116.2 | 8700 | 18 900 | 1.0 |
| Mask name . | RA . | Dec . | PA . | λcen . | Exposure time . | Average seeing . |
|---|---|---|---|---|---|---|
| . | . | . | (deg) . | (Å) . | (s) . | (arcsec) . |
| COSa | 10:02:29.53 | +02:17:24.58 | +45.0 | 8500 | 7200 | 1.0 |
| COSb | 10:00:28.37 | +01:53:50.84 | −98.5 | 8700 | 32 400 | 1.1 |
| COSc | 09:59:09.41 | +02:21:25.80 | −101.0 | 8700 | 7200 | 1.1 |
| COSd | 09:59:10.01 | +02:21:07.83 | −101.0 | 8700 | 18 900 | 1.0 |
| COSe | 10:00:39.92 | +02:35:16.12 | −20.0 | 8720 | 17 100 | 1.2 |
| XMM3a | 02:26:38.04 | −05:03:11.15 | −12.0 | 8700 | 10 200 | 0.9 |
| XMM3b | 02:27:22.70 | −04:19:35.44 | −116.2 | 8700 | 18 900 | 1.0 |
2.2.1 Sample description
Across these seven masks, we have targeted 22 z ≃ 7 sources satisfying the selection criteria described in Section 2.1. In Table 2, we report the coordinates, J-band magnitudes, 3.6 and 4.5 μm photometry, as well as the [3.6]−[4.5] colour for each targeted z ≃ 7 galaxy. We also note in Table 2 the mask containing each source, where four sources were placed on both the COSc and COSd masks for a total integration time of 26 100 s. The J-band magnitudes of our z ≃ 7 targets range from J = 24.3 to 26.3. The vast majority of these sources show blue [3.6]−[4.5] colours (<0), as expected given that z ≳ 7 galaxies typically possess strong [O iii]+H β emission (Labbé et al. 2013; Smit et al. 2014; De Barros et al. 2019; E21). Furthermore, 8 of our 22 z ≃ 7 targets have very blue [3.6]−[4.5] colours (|${\lt}-$|0.8) that translate to strong [O iii]+H β emission (EW ≳ 800 Å) assuming a flat rest-optical continuum slope and z = 6.75. This includes two sources (COS-221419 and COS-940214) that have 3.6 μm fluxes substantially above the 4.5 μm 2σ upper limit. Thus, even though these sources are not detected in 4.5 μm, the data still suggest that they likely possess strong [O iii]+H β emission.
z ≃ 7 galaxies targeted with MMT/Binospec across the ≈1.5 deg2 and 1.8 deg2 COSMOS and XMM3 fields, respectively. For sources with a non-detection (S/N<1) in one of the IRAC bands, we report the 2σ limiting magnitude and colour.
| Source ID . | RA . | Dec . | J . | 3.6 μm . | 4.5 μm . | [3.6]−[4.5] . | Masks . |
|---|---|---|---|---|---|---|---|
| COS-221419 | 10:00:26.28 | +01:46:03.22 | 26.07|$^{+0.29}_{-0.23}$| | 25.22|$^{+0.25}_{-0.21}$| | >26.30 | <−1.08 | COSb |
| COS-235129 | 10:00:39.21 | +01:46:43.68 | 25.75|$^{+0.26}_{-0.20}$| | 24.94|$^{+0.21}_{-0.18}$| | 25.03|$^{+0.16}_{-0.14}$| | −0.09|$^{+0.26}_{-0.24}$| | COSb |
| COS-237729 | 10:00:31.42 | +01:46:51.01 | 25.68|$^{+0.18}_{-0.15}$| | 24.84|$^{+0.20}_{-0.17}$| | 25.33|$^{+0.23}_{-0.19}$| | −0.49|$^{+0.28}_{-0.28}$| | COSb |
| COS-301652 | 10:00:54.82 | +01:50:05.18 | 25.65|$^{+0.22}_{-0.18}$| | 24.38|$^{+0.11}_{-0.10}$| | 24.67|$^{+0.13}_{-0.11}$| | −0.28|$^{+0.16}_{-0.16}$| | COSb |
| COS-469110 | 10:00:04.36 | +01:58:35.53 | 24.97|$^{+0.30}_{-0.23}$| | 24.28|$^{+0.10}_{-0.09}$| | 24.69|$^{+0.17}_{-0.14}$| | −0.40|$^{+0.18}_{-0.19}$| | COSb |
| COS-505871 | 10:00:21.35 | +02:00:30.93 | 25.51|$^{+0.16}_{-0.14}$| | 24.39|$^{+0.09}_{-0.09}$| | 24.54|$^{+0.13}_{-0.12}$| | −0.16|$^{+0.15}_{-0.16}$| | COSb |
| COS-534584 | 10:00:42.13 | +02:01:56.87 | 24.99|$^{+0.12}_{-0.11}$| | 24.02|$^{+0.10}_{-0.09}$| | 24.44|$^{+0.14}_{-0.13}$| | −0.42|$^{+0.16}_{-0.17}$| | COSb |
| COS-788571 | 09:59:21.68 | +02:14:53.02 | 25.27|$^{+0.11}_{-0.10}$| | 24.40|$^{+0.09}_{-0.08}$| | 25.32|$^{+0.23}_{-0.19}$| | −0.92|$^{+0.21}_{-0.24}$| | COSd |
| COS-851423 | 09:59:11.46 | +02:18:10.42 | 25.91|$^{+0.22}_{-0.19}$| | 24.82|$^{+0.15}_{-0.13}$| | 25.54|$^{+0.47}_{-0.32}$| | −0.72|$^{+0.36}_{-0.48}$| | COSc and COSd |
| COS-854905 | 09:59:09.13 | +02:18:22.38 | 25.75|$^{+0.28}_{-0.22}$| | 24.46|$^{+0.19}_{-0.16}$| | 24.90|$^{+0.32}_{-0.25}$| | −0.44|$^{+0.31}_{-0.35}$| | COSc and COSd |
| COS-856875 | 09:58:45.34 | +02:18:28.87 | 25.64|$^{+0.30}_{-0.24}$| | 25.09|$^{+0.25}_{-0.20}$| | 25.66|$^{+0.39}_{-0.28}$| | −0.57|$^{+0.38}_{-0.44}$| | COSc |
| COS-862541 | 10:03:05.25 | +02:18:42.75 | 24.49|$^{+0.26}_{-0.21}$| | 23.33|$^{+0.09}_{-0.08}$| | 24.65|$^{+0.30}_{-0.24}$| | −1.33|$^{+0.26}_{-0.32}$| | COSa |
| COS-940214 | 09:59:06.73 | +02:22:45.93 | 26.27|$^{+0.43}_{-0.31}$| | 25.06|$^{+0.29}_{-0.23}$| | >26.32 | <−1.26 | COSd |
| COS-955126 | 09:59:23.62 | +02:23:32.73 | 25.38|$^{+0.24}_{-0.20}$| | 24.20|$^{+0.14}_{-0.13}$| | 25.14|$^{+0.43}_{-0.30}$| | −0.94|$^{+0.33}_{-0.44}$| | COSd |
| COS-1009842 | 09:59:06.33 | +02:26:30.48 | 26.22|$^{+0.25}_{-0.20}$| | 25.16|$^{+0.24}_{-0.20}$| | 25.78|$^{+0.49}_{-0.34}$| | −0.61|$^{+0.42}_{-0.52}$| | COSc and COSd |
| COS-1048848 | 09:59:09.76 | +02:28:32.95 | 26.09|$^{+0.27}_{-0.22}$| | 26.11|$^{+0.65}_{-0.40}$| | >26.24 | <-0.13 | COSc and COSd |
| COS-1053257 | 09:58:46.20 | +02:28:45.76 | 24.79|$^{+0.08}_{-0.07}$| | 23.81|$^{+0.23}_{-0.19}$| | 24.13|$^{+0.30}_{-0.24}$| | −0.33|$^{+0.33}_{-0.36}$| | COSc and COSd |
| COS-1099982 | 10:00:23.37 | +02:31:14.80 | 25.45|$^{+0.14}_{-0.13}$| | 24.11|$^{+0.09}_{-0.09}$| | 25.43|$^{+0.26}_{-0.21}$| | −1.32|$^{+0.23}_{-0.28}$| | COSe |
| COS-1205190 | 10:00:45.44 | +02:36:48.81 | 25.82|$^{+0.20}_{-0.17}$| | 25.81|$^{+0.89}_{-0.48}$| | >25.82 | <−0.01 | COSe |
| COS-1235751 | 10:00:11.57 | +02:38:29.81 | 25.62|$^{+0.22}_{-0.18}$| | 24.27|$^{+0.14}_{-0.12}$| | 24.45|$^{+0.16}_{-0.14}$| | −0.18|$^{+0.19}_{-0.20}$| | COSe |
| XMM3-227436 | 02:26:46.19 | −04:59:53.57 | 24.67|$^{+0.21}_{-0.18}$| | 24.37|$^{+0.30}_{-0.23}$| | 23.78|$^{+0.18}_{-0.16}$| | 0.58|$^{+0.33}_{-0.30}$| | XMM3a |
| XMM3-504799 | 02:27:13.12 | −04:17:59.25 | 24.33|$^{+0.16}_{-0.14}$| | 23.37|$^{+0.11}_{-0.10}$| | 24.32|$^{+0.41}_{-0.30}$| | −0.95|$^{+0.32}_{-0.43}$| | XMM3b |
| Source ID . | RA . | Dec . | J . | 3.6 μm . | 4.5 μm . | [3.6]−[4.5] . | Masks . |
|---|---|---|---|---|---|---|---|
| COS-221419 | 10:00:26.28 | +01:46:03.22 | 26.07|$^{+0.29}_{-0.23}$| | 25.22|$^{+0.25}_{-0.21}$| | >26.30 | <−1.08 | COSb |
| COS-235129 | 10:00:39.21 | +01:46:43.68 | 25.75|$^{+0.26}_{-0.20}$| | 24.94|$^{+0.21}_{-0.18}$| | 25.03|$^{+0.16}_{-0.14}$| | −0.09|$^{+0.26}_{-0.24}$| | COSb |
| COS-237729 | 10:00:31.42 | +01:46:51.01 | 25.68|$^{+0.18}_{-0.15}$| | 24.84|$^{+0.20}_{-0.17}$| | 25.33|$^{+0.23}_{-0.19}$| | −0.49|$^{+0.28}_{-0.28}$| | COSb |
| COS-301652 | 10:00:54.82 | +01:50:05.18 | 25.65|$^{+0.22}_{-0.18}$| | 24.38|$^{+0.11}_{-0.10}$| | 24.67|$^{+0.13}_{-0.11}$| | −0.28|$^{+0.16}_{-0.16}$| | COSb |
| COS-469110 | 10:00:04.36 | +01:58:35.53 | 24.97|$^{+0.30}_{-0.23}$| | 24.28|$^{+0.10}_{-0.09}$| | 24.69|$^{+0.17}_{-0.14}$| | −0.40|$^{+0.18}_{-0.19}$| | COSb |
| COS-505871 | 10:00:21.35 | +02:00:30.93 | 25.51|$^{+0.16}_{-0.14}$| | 24.39|$^{+0.09}_{-0.09}$| | 24.54|$^{+0.13}_{-0.12}$| | −0.16|$^{+0.15}_{-0.16}$| | COSb |
| COS-534584 | 10:00:42.13 | +02:01:56.87 | 24.99|$^{+0.12}_{-0.11}$| | 24.02|$^{+0.10}_{-0.09}$| | 24.44|$^{+0.14}_{-0.13}$| | −0.42|$^{+0.16}_{-0.17}$| | COSb |
| COS-788571 | 09:59:21.68 | +02:14:53.02 | 25.27|$^{+0.11}_{-0.10}$| | 24.40|$^{+0.09}_{-0.08}$| | 25.32|$^{+0.23}_{-0.19}$| | −0.92|$^{+0.21}_{-0.24}$| | COSd |
| COS-851423 | 09:59:11.46 | +02:18:10.42 | 25.91|$^{+0.22}_{-0.19}$| | 24.82|$^{+0.15}_{-0.13}$| | 25.54|$^{+0.47}_{-0.32}$| | −0.72|$^{+0.36}_{-0.48}$| | COSc and COSd |
| COS-854905 | 09:59:09.13 | +02:18:22.38 | 25.75|$^{+0.28}_{-0.22}$| | 24.46|$^{+0.19}_{-0.16}$| | 24.90|$^{+0.32}_{-0.25}$| | −0.44|$^{+0.31}_{-0.35}$| | COSc and COSd |
| COS-856875 | 09:58:45.34 | +02:18:28.87 | 25.64|$^{+0.30}_{-0.24}$| | 25.09|$^{+0.25}_{-0.20}$| | 25.66|$^{+0.39}_{-0.28}$| | −0.57|$^{+0.38}_{-0.44}$| | COSc |
| COS-862541 | 10:03:05.25 | +02:18:42.75 | 24.49|$^{+0.26}_{-0.21}$| | 23.33|$^{+0.09}_{-0.08}$| | 24.65|$^{+0.30}_{-0.24}$| | −1.33|$^{+0.26}_{-0.32}$| | COSa |
| COS-940214 | 09:59:06.73 | +02:22:45.93 | 26.27|$^{+0.43}_{-0.31}$| | 25.06|$^{+0.29}_{-0.23}$| | >26.32 | <−1.26 | COSd |
| COS-955126 | 09:59:23.62 | +02:23:32.73 | 25.38|$^{+0.24}_{-0.20}$| | 24.20|$^{+0.14}_{-0.13}$| | 25.14|$^{+0.43}_{-0.30}$| | −0.94|$^{+0.33}_{-0.44}$| | COSd |
| COS-1009842 | 09:59:06.33 | +02:26:30.48 | 26.22|$^{+0.25}_{-0.20}$| | 25.16|$^{+0.24}_{-0.20}$| | 25.78|$^{+0.49}_{-0.34}$| | −0.61|$^{+0.42}_{-0.52}$| | COSc and COSd |
| COS-1048848 | 09:59:09.76 | +02:28:32.95 | 26.09|$^{+0.27}_{-0.22}$| | 26.11|$^{+0.65}_{-0.40}$| | >26.24 | <-0.13 | COSc and COSd |
| COS-1053257 | 09:58:46.20 | +02:28:45.76 | 24.79|$^{+0.08}_{-0.07}$| | 23.81|$^{+0.23}_{-0.19}$| | 24.13|$^{+0.30}_{-0.24}$| | −0.33|$^{+0.33}_{-0.36}$| | COSc and COSd |
| COS-1099982 | 10:00:23.37 | +02:31:14.80 | 25.45|$^{+0.14}_{-0.13}$| | 24.11|$^{+0.09}_{-0.09}$| | 25.43|$^{+0.26}_{-0.21}$| | −1.32|$^{+0.23}_{-0.28}$| | COSe |
| COS-1205190 | 10:00:45.44 | +02:36:48.81 | 25.82|$^{+0.20}_{-0.17}$| | 25.81|$^{+0.89}_{-0.48}$| | >25.82 | <−0.01 | COSe |
| COS-1235751 | 10:00:11.57 | +02:38:29.81 | 25.62|$^{+0.22}_{-0.18}$| | 24.27|$^{+0.14}_{-0.12}$| | 24.45|$^{+0.16}_{-0.14}$| | −0.18|$^{+0.19}_{-0.20}$| | COSe |
| XMM3-227436 | 02:26:46.19 | −04:59:53.57 | 24.67|$^{+0.21}_{-0.18}$| | 24.37|$^{+0.30}_{-0.23}$| | 23.78|$^{+0.18}_{-0.16}$| | 0.58|$^{+0.33}_{-0.30}$| | XMM3a |
| XMM3-504799 | 02:27:13.12 | −04:17:59.25 | 24.33|$^{+0.16}_{-0.14}$| | 23.37|$^{+0.11}_{-0.10}$| | 24.32|$^{+0.41}_{-0.30}$| | −0.95|$^{+0.32}_{-0.43}$| | XMM3b |
z ≃ 7 galaxies targeted with MMT/Binospec across the ≈1.5 deg2 and 1.8 deg2 COSMOS and XMM3 fields, respectively. For sources with a non-detection (S/N<1) in one of the IRAC bands, we report the 2σ limiting magnitude and colour.
| Source ID . | RA . | Dec . | J . | 3.6 μm . | 4.5 μm . | [3.6]−[4.5] . | Masks . |
|---|---|---|---|---|---|---|---|
| COS-221419 | 10:00:26.28 | +01:46:03.22 | 26.07|$^{+0.29}_{-0.23}$| | 25.22|$^{+0.25}_{-0.21}$| | >26.30 | <−1.08 | COSb |
| COS-235129 | 10:00:39.21 | +01:46:43.68 | 25.75|$^{+0.26}_{-0.20}$| | 24.94|$^{+0.21}_{-0.18}$| | 25.03|$^{+0.16}_{-0.14}$| | −0.09|$^{+0.26}_{-0.24}$| | COSb |
| COS-237729 | 10:00:31.42 | +01:46:51.01 | 25.68|$^{+0.18}_{-0.15}$| | 24.84|$^{+0.20}_{-0.17}$| | 25.33|$^{+0.23}_{-0.19}$| | −0.49|$^{+0.28}_{-0.28}$| | COSb |
| COS-301652 | 10:00:54.82 | +01:50:05.18 | 25.65|$^{+0.22}_{-0.18}$| | 24.38|$^{+0.11}_{-0.10}$| | 24.67|$^{+0.13}_{-0.11}$| | −0.28|$^{+0.16}_{-0.16}$| | COSb |
| COS-469110 | 10:00:04.36 | +01:58:35.53 | 24.97|$^{+0.30}_{-0.23}$| | 24.28|$^{+0.10}_{-0.09}$| | 24.69|$^{+0.17}_{-0.14}$| | −0.40|$^{+0.18}_{-0.19}$| | COSb |
| COS-505871 | 10:00:21.35 | +02:00:30.93 | 25.51|$^{+0.16}_{-0.14}$| | 24.39|$^{+0.09}_{-0.09}$| | 24.54|$^{+0.13}_{-0.12}$| | −0.16|$^{+0.15}_{-0.16}$| | COSb |
| COS-534584 | 10:00:42.13 | +02:01:56.87 | 24.99|$^{+0.12}_{-0.11}$| | 24.02|$^{+0.10}_{-0.09}$| | 24.44|$^{+0.14}_{-0.13}$| | −0.42|$^{+0.16}_{-0.17}$| | COSb |
| COS-788571 | 09:59:21.68 | +02:14:53.02 | 25.27|$^{+0.11}_{-0.10}$| | 24.40|$^{+0.09}_{-0.08}$| | 25.32|$^{+0.23}_{-0.19}$| | −0.92|$^{+0.21}_{-0.24}$| | COSd |
| COS-851423 | 09:59:11.46 | +02:18:10.42 | 25.91|$^{+0.22}_{-0.19}$| | 24.82|$^{+0.15}_{-0.13}$| | 25.54|$^{+0.47}_{-0.32}$| | −0.72|$^{+0.36}_{-0.48}$| | COSc and COSd |
| COS-854905 | 09:59:09.13 | +02:18:22.38 | 25.75|$^{+0.28}_{-0.22}$| | 24.46|$^{+0.19}_{-0.16}$| | 24.90|$^{+0.32}_{-0.25}$| | −0.44|$^{+0.31}_{-0.35}$| | COSc and COSd |
| COS-856875 | 09:58:45.34 | +02:18:28.87 | 25.64|$^{+0.30}_{-0.24}$| | 25.09|$^{+0.25}_{-0.20}$| | 25.66|$^{+0.39}_{-0.28}$| | −0.57|$^{+0.38}_{-0.44}$| | COSc |
| COS-862541 | 10:03:05.25 | +02:18:42.75 | 24.49|$^{+0.26}_{-0.21}$| | 23.33|$^{+0.09}_{-0.08}$| | 24.65|$^{+0.30}_{-0.24}$| | −1.33|$^{+0.26}_{-0.32}$| | COSa |
| COS-940214 | 09:59:06.73 | +02:22:45.93 | 26.27|$^{+0.43}_{-0.31}$| | 25.06|$^{+0.29}_{-0.23}$| | >26.32 | <−1.26 | COSd |
| COS-955126 | 09:59:23.62 | +02:23:32.73 | 25.38|$^{+0.24}_{-0.20}$| | 24.20|$^{+0.14}_{-0.13}$| | 25.14|$^{+0.43}_{-0.30}$| | −0.94|$^{+0.33}_{-0.44}$| | COSd |
| COS-1009842 | 09:59:06.33 | +02:26:30.48 | 26.22|$^{+0.25}_{-0.20}$| | 25.16|$^{+0.24}_{-0.20}$| | 25.78|$^{+0.49}_{-0.34}$| | −0.61|$^{+0.42}_{-0.52}$| | COSc and COSd |
| COS-1048848 | 09:59:09.76 | +02:28:32.95 | 26.09|$^{+0.27}_{-0.22}$| | 26.11|$^{+0.65}_{-0.40}$| | >26.24 | <-0.13 | COSc and COSd |
| COS-1053257 | 09:58:46.20 | +02:28:45.76 | 24.79|$^{+0.08}_{-0.07}$| | 23.81|$^{+0.23}_{-0.19}$| | 24.13|$^{+0.30}_{-0.24}$| | −0.33|$^{+0.33}_{-0.36}$| | COSc and COSd |
| COS-1099982 | 10:00:23.37 | +02:31:14.80 | 25.45|$^{+0.14}_{-0.13}$| | 24.11|$^{+0.09}_{-0.09}$| | 25.43|$^{+0.26}_{-0.21}$| | −1.32|$^{+0.23}_{-0.28}$| | COSe |
| COS-1205190 | 10:00:45.44 | +02:36:48.81 | 25.82|$^{+0.20}_{-0.17}$| | 25.81|$^{+0.89}_{-0.48}$| | >25.82 | <−0.01 | COSe |
| COS-1235751 | 10:00:11.57 | +02:38:29.81 | 25.62|$^{+0.22}_{-0.18}$| | 24.27|$^{+0.14}_{-0.12}$| | 24.45|$^{+0.16}_{-0.14}$| | −0.18|$^{+0.19}_{-0.20}$| | COSe |
| XMM3-227436 | 02:26:46.19 | −04:59:53.57 | 24.67|$^{+0.21}_{-0.18}$| | 24.37|$^{+0.30}_{-0.23}$| | 23.78|$^{+0.18}_{-0.16}$| | 0.58|$^{+0.33}_{-0.30}$| | XMM3a |
| XMM3-504799 | 02:27:13.12 | −04:17:59.25 | 24.33|$^{+0.16}_{-0.14}$| | 23.37|$^{+0.11}_{-0.10}$| | 24.32|$^{+0.41}_{-0.30}$| | −0.95|$^{+0.32}_{-0.43}$| | XMM3b |
| Source ID . | RA . | Dec . | J . | 3.6 μm . | 4.5 μm . | [3.6]−[4.5] . | Masks . |
|---|---|---|---|---|---|---|---|
| COS-221419 | 10:00:26.28 | +01:46:03.22 | 26.07|$^{+0.29}_{-0.23}$| | 25.22|$^{+0.25}_{-0.21}$| | >26.30 | <−1.08 | COSb |
| COS-235129 | 10:00:39.21 | +01:46:43.68 | 25.75|$^{+0.26}_{-0.20}$| | 24.94|$^{+0.21}_{-0.18}$| | 25.03|$^{+0.16}_{-0.14}$| | −0.09|$^{+0.26}_{-0.24}$| | COSb |
| COS-237729 | 10:00:31.42 | +01:46:51.01 | 25.68|$^{+0.18}_{-0.15}$| | 24.84|$^{+0.20}_{-0.17}$| | 25.33|$^{+0.23}_{-0.19}$| | −0.49|$^{+0.28}_{-0.28}$| | COSb |
| COS-301652 | 10:00:54.82 | +01:50:05.18 | 25.65|$^{+0.22}_{-0.18}$| | 24.38|$^{+0.11}_{-0.10}$| | 24.67|$^{+0.13}_{-0.11}$| | −0.28|$^{+0.16}_{-0.16}$| | COSb |
| COS-469110 | 10:00:04.36 | +01:58:35.53 | 24.97|$^{+0.30}_{-0.23}$| | 24.28|$^{+0.10}_{-0.09}$| | 24.69|$^{+0.17}_{-0.14}$| | −0.40|$^{+0.18}_{-0.19}$| | COSb |
| COS-505871 | 10:00:21.35 | +02:00:30.93 | 25.51|$^{+0.16}_{-0.14}$| | 24.39|$^{+0.09}_{-0.09}$| | 24.54|$^{+0.13}_{-0.12}$| | −0.16|$^{+0.15}_{-0.16}$| | COSb |
| COS-534584 | 10:00:42.13 | +02:01:56.87 | 24.99|$^{+0.12}_{-0.11}$| | 24.02|$^{+0.10}_{-0.09}$| | 24.44|$^{+0.14}_{-0.13}$| | −0.42|$^{+0.16}_{-0.17}$| | COSb |
| COS-788571 | 09:59:21.68 | +02:14:53.02 | 25.27|$^{+0.11}_{-0.10}$| | 24.40|$^{+0.09}_{-0.08}$| | 25.32|$^{+0.23}_{-0.19}$| | −0.92|$^{+0.21}_{-0.24}$| | COSd |
| COS-851423 | 09:59:11.46 | +02:18:10.42 | 25.91|$^{+0.22}_{-0.19}$| | 24.82|$^{+0.15}_{-0.13}$| | 25.54|$^{+0.47}_{-0.32}$| | −0.72|$^{+0.36}_{-0.48}$| | COSc and COSd |
| COS-854905 | 09:59:09.13 | +02:18:22.38 | 25.75|$^{+0.28}_{-0.22}$| | 24.46|$^{+0.19}_{-0.16}$| | 24.90|$^{+0.32}_{-0.25}$| | −0.44|$^{+0.31}_{-0.35}$| | COSc and COSd |
| COS-856875 | 09:58:45.34 | +02:18:28.87 | 25.64|$^{+0.30}_{-0.24}$| | 25.09|$^{+0.25}_{-0.20}$| | 25.66|$^{+0.39}_{-0.28}$| | −0.57|$^{+0.38}_{-0.44}$| | COSc |
| COS-862541 | 10:03:05.25 | +02:18:42.75 | 24.49|$^{+0.26}_{-0.21}$| | 23.33|$^{+0.09}_{-0.08}$| | 24.65|$^{+0.30}_{-0.24}$| | −1.33|$^{+0.26}_{-0.32}$| | COSa |
| COS-940214 | 09:59:06.73 | +02:22:45.93 | 26.27|$^{+0.43}_{-0.31}$| | 25.06|$^{+0.29}_{-0.23}$| | >26.32 | <−1.26 | COSd |
| COS-955126 | 09:59:23.62 | +02:23:32.73 | 25.38|$^{+0.24}_{-0.20}$| | 24.20|$^{+0.14}_{-0.13}$| | 25.14|$^{+0.43}_{-0.30}$| | −0.94|$^{+0.33}_{-0.44}$| | COSd |
| COS-1009842 | 09:59:06.33 | +02:26:30.48 | 26.22|$^{+0.25}_{-0.20}$| | 25.16|$^{+0.24}_{-0.20}$| | 25.78|$^{+0.49}_{-0.34}$| | −0.61|$^{+0.42}_{-0.52}$| | COSc and COSd |
| COS-1048848 | 09:59:09.76 | +02:28:32.95 | 26.09|$^{+0.27}_{-0.22}$| | 26.11|$^{+0.65}_{-0.40}$| | >26.24 | <-0.13 | COSc and COSd |
| COS-1053257 | 09:58:46.20 | +02:28:45.76 | 24.79|$^{+0.08}_{-0.07}$| | 23.81|$^{+0.23}_{-0.19}$| | 24.13|$^{+0.30}_{-0.24}$| | −0.33|$^{+0.33}_{-0.36}$| | COSc and COSd |
| COS-1099982 | 10:00:23.37 | +02:31:14.80 | 25.45|$^{+0.14}_{-0.13}$| | 24.11|$^{+0.09}_{-0.09}$| | 25.43|$^{+0.26}_{-0.21}$| | −1.32|$^{+0.23}_{-0.28}$| | COSe |
| COS-1205190 | 10:00:45.44 | +02:36:48.81 | 25.82|$^{+0.20}_{-0.17}$| | 25.81|$^{+0.89}_{-0.48}$| | >25.82 | <−0.01 | COSe |
| COS-1235751 | 10:00:11.57 | +02:38:29.81 | 25.62|$^{+0.22}_{-0.18}$| | 24.27|$^{+0.14}_{-0.12}$| | 24.45|$^{+0.16}_{-0.14}$| | −0.18|$^{+0.19}_{-0.20}$| | COSe |
| XMM3-227436 | 02:26:46.19 | −04:59:53.57 | 24.67|$^{+0.21}_{-0.18}$| | 24.37|$^{+0.30}_{-0.23}$| | 23.78|$^{+0.18}_{-0.16}$| | 0.58|$^{+0.33}_{-0.30}$| | XMM3a |
| XMM3-504799 | 02:27:13.12 | −04:17:59.25 | 24.33|$^{+0.16}_{-0.14}$| | 23.37|$^{+0.11}_{-0.10}$| | 24.32|$^{+0.41}_{-0.30}$| | −0.95|$^{+0.32}_{-0.43}$| | XMM3b |
Within these same seven masks, we have also targeted 30 z ≃ 6 galaxies satisfying the selection criteria from Section 2.1. The rest-UV apparent magnitudes4 of these z ≃ 6 targets range from |$m_{\mathrm{UV}}^{ }$| = 24.3–26.4, very similar to that of the z ≃ 7 targets (Fig. 1 top). The range of rest-UV slopes spanned by our z ≃ 6 spectroscopic targets (−1.2 ≤ β ≤ −3.5) is also very similar to that of the z ≃ 7 targets (−1.1 ≤ β ≤ −3.4). Furthermore, the typical rest-UV slopes of each sample are almost exactly equal – the median β of the z ≃ 7 sample is −2.07 and that of the z ≃ 6 sample is −2.09 (Fig. 1 bottom). For the z ≃ 7 sources, we calculate rest-UV slopes using YJHKs, while for the z ≃ 6 sources we use nb921yYJHKs and yYJHKs in COSMOS and XMM3, respectively.
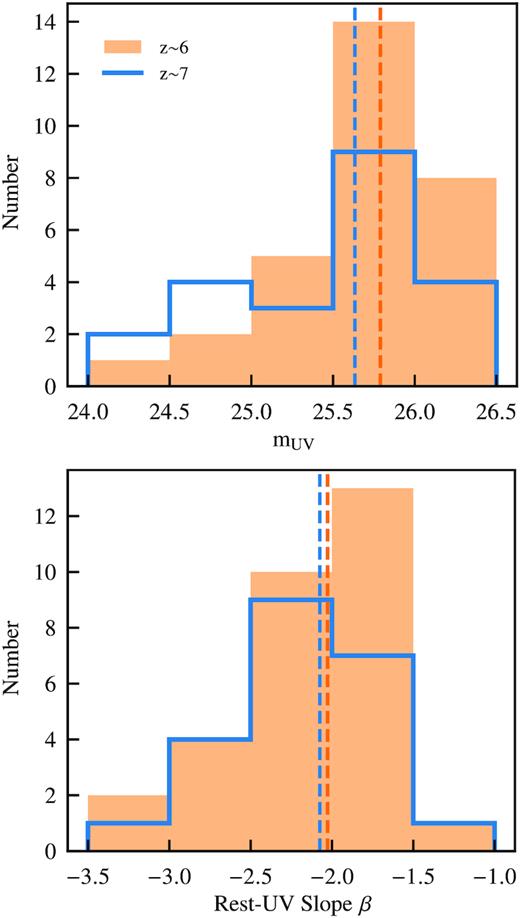
Figures comparing the distribution of apparent UV magnitudes (top) and rest-UV slopes (bottom) for our spectroscopic z ≃ 6 and z ≃ 7 samples. We show the z ≃ 6 distributions with a shaded orange histogram while the z ≃ 7 distributions are shown with a thick blue line. We show median values for each sample with vertical dashed lines. The range of UV magnitudes and rest-UV slopes, as well as their typical values, are very similar for these two spectroscopic samples.
2.2.2 Data reduction
To design our Binospec multi-object slit masks, we used the binomask software. We adopted a slit width of 1.0 arcsec and the 600 l/mm grating, yielding a resolving power of R ≈ 4360. Central wavelengths for each mask range from 8500 to 8720 Å (see Table 1) with the exact value chosen to optimize the red-end wavelength coverage of our z ≃ 7 targets. For all z ≃ 7 targets, the maximum wavelength coverage was ≥9635 Å meaning that our observations covered Ly α up to at least |${z}_{_{\mathrm{Ly\,\alpha }}}$| = 6.93. Furthermore, the typical wavelength coverage of our z ≃ 7 targets was 0.75–1.00 μm (|${z}_{_{\mathrm{Ly\,\alpha }}}$| = 5.17–7.23). For the z ≃ 6 targets, our observations covered at least 7890–9510 Å and therefore (assuming they all lie at z > 5) fully encompassed the Ly α redshift range |${z}_{_{\mathrm{Ly\,\alpha }}}$| ≃ 5.75–6.50 set by our selection criteria (Section 2.1.2).
We adopted a slit length of at least 20 arcsec (7 arcsec) for the z ≃ 7 (z ≃ 6) targets that we found leads to sufficient modelling of the sky background from ≈0.9–1 μm (≈0.8–0.9 μm). Each mask also included at least five stars off the primary field of views5 (FoVs) for guiding and monitoring seeing throughout the observations. In addition, we placed three stars within the primary FoVs to determine exposure weighting (see below) and absolute flux calibration.
Each individual exposure was reduced separately using the publicly available Binospec data reduction pipeline (Kansky et al. 2019). Exposures for each mask were then co-added using the weighting scheme from Kriek et al. (2015) that takes the height of the telluric-corrected 1D flux profile of bright stars on the mask as the relative weight. This accounts for both the average sky transmission and relative seeing in each exposure. The average seeing of each mask (calculated from the co-added spectra) is listed in Table 1 and ranges from 0.9 to 1.2 arcsec.
We extract 1D spectra using optimal extraction (Horne 1986) after fitting a Gaussian6 to the observed emission line profile along the spatial axis. As in E21, absolute flux calibration is determined by calculating the average scaling factor that matches the 1D spectra of the three stars placed on the mask to their mean PSF z-band magnitudes from the Pan-STARRS survey (Chambers et al. 2016). Given the relatively narrow wavelength range covered by these observations (≈0.75-1 μm), we assume that this factor does not evolve with wavelength.
To estimate slit loss factors, we adopt the size–luminosity relation of bright z = 6–7 galaxies found by Curtis-Lake et al. (2016) that assumes a Sérsic profile with n = 1.0 (consistent with the approach of Ono et al. 2013). The modelled Sérsic profile of each source is convolved with a 2D Gaussian with FWHM equal to the seeing of the respective mask, and the fraction of flux within the 1 arcsec Binospec slit is compared to that for a point source. The resulting relative slit loss correction factors range from 4 to 10 per cent for all z ≃ 6 and z ≃ 7 targets, with brighter sources having larger corrections due to their larger assumed half-light radius. We note that our results are not significantly altered if we instead calculate slit loss correction factors assuming the size–luminosity relation from Bowler et al. (2017) that mainly yields larger sizes (and hence larger correction factors) for the brightest (|$m_{\mathrm{UV}}^{ }$| < 25) sources.
We identify emission lines by first visually inspecting the 2D spectra of all sources. For emission features relatively clear of strong skylines, we calculate the flux in an aperture where the width along the wavelength axis is set by visual inspection of the 2D spectra with flux errors computed as described in E21. For these relatively clean emission features, we estimate that the fraction7 of flux potentially obscured by strong skylines is small (15–20 per cent) on average in both the z ≃ 6 and z ≃ 7 galaxies. We therefore conclude that our results on the evolution of the Ly α EW distribution between these two redshifts (Section 3.2) are not significantly impacted by this slight obscuration. Such small obscuration would furthermore only serve to slightly strengthen our conclusions8 on differences in the Ly α EW distribution for moderate versus strong [O iii]+H β emitters at z ≃ 7 (Section 3.1). Because the exact skyline obscuration fraction for a given source depends on the assumed line profile and accounting for it does not significantly alter our conclusions, we do not fold an obscuration correction for these relatively clean sources into our analysis.
For the few features that overlap more significantly with moderate-strength skylines, we adopt a slightly different approach to minimize the impact of skylines on the recovered flux (these sources are marked with asterisks in Tables 3 and 4). We fit the 1D spectra with a half-Gaussian (red-side only) convolved with the spectral resolution of our instrument (e.g. Hu et al. 2010) after masking portions of the spectrum contaminated by skylines. In this fitting procedure, we adopt a grid of three parameters describing the half-Gaussian (amplitude, standard deviation, and central wavelength) and compute the χ2 value for each point in the grid. The likelihood for a given set of parameters is then calculated as |$P(A,\sigma ,\lambda _0) \propto \mathrm{ e}^{-\chi ^2/2}$| which we convert to a probability distribution on the flux of the emission line. The flux and its uncertainty are then computed as the median value and standard deviation from this probability distribution. For all emission features, we subtract the continuum flux estimated from the photometry9 but compute the significance of the feature prior to this subtraction.
Information on confident (>7σ) Ly α detections in our z ≃ 7 sample. We quote the significance of each detection within parenthesis in the flux column where the fluxes have the continuum subtracted. Sources marked with asterisks are those with emission features close to moderate-strength skylines where we used a line-profile fitting technique to derive their total fluxes.
| Source ID . | |${z}_{_{\mathrm{Ly\,\alpha }}}$| . | Flux . | EW . |
|---|---|---|---|
| . | . | (10−18 erg s−1 cm−2) . | (Å) . |
| COS-469110 | 6.650 | 9.7 ± 1.3 (7.8σ) | 14.5 ± 5.0 |
| COS-940214* | 6.748 | 11.8 ± 1.8 (7.1σ) | 43.1 ± 14.7 |
| COS-1009842 | 6.761 | 12.3 ± 0.8 (15.4σ) | 41.6 ± 9.5 |
| COS-955126 | 6.813 | 8.2 ± 0.9 (10.4σ) | 12.3 ± 2.5 |
| COS-862541 | 6.850 | 15.3 ± 1.9 (9.0σ) | 11.8 ± 2.7 |
| XMM3-504799 | 6.883 | 5.1 ± 0.9 (7.1σ) | 3.7 ± 0.8 |
| COS-788571 | 6.884 | 16.3 ± 1.1 (15.9σ) | 30.6 ± 3.9 |
| COS-1205190 | 7.049 | 12.4 ± 1.6 (8.1σ) | 28.8 ± 6.0 |
| XMM3-227436 | 7.093 | 18.6 ± 2.3 (8.9σ) | 15.0 ± 3.2 |
| Source ID . | |${z}_{_{\mathrm{Ly\,\alpha }}}$| . | Flux . | EW . |
|---|---|---|---|
| . | . | (10−18 erg s−1 cm−2) . | (Å) . |
| COS-469110 | 6.650 | 9.7 ± 1.3 (7.8σ) | 14.5 ± 5.0 |
| COS-940214* | 6.748 | 11.8 ± 1.8 (7.1σ) | 43.1 ± 14.7 |
| COS-1009842 | 6.761 | 12.3 ± 0.8 (15.4σ) | 41.6 ± 9.5 |
| COS-955126 | 6.813 | 8.2 ± 0.9 (10.4σ) | 12.3 ± 2.5 |
| COS-862541 | 6.850 | 15.3 ± 1.9 (9.0σ) | 11.8 ± 2.7 |
| XMM3-504799 | 6.883 | 5.1 ± 0.9 (7.1σ) | 3.7 ± 0.8 |
| COS-788571 | 6.884 | 16.3 ± 1.1 (15.9σ) | 30.6 ± 3.9 |
| COS-1205190 | 7.049 | 12.4 ± 1.6 (8.1σ) | 28.8 ± 6.0 |
| XMM3-227436 | 7.093 | 18.6 ± 2.3 (8.9σ) | 15.0 ± 3.2 |
Information on confident (>7σ) Ly α detections in our z ≃ 7 sample. We quote the significance of each detection within parenthesis in the flux column where the fluxes have the continuum subtracted. Sources marked with asterisks are those with emission features close to moderate-strength skylines where we used a line-profile fitting technique to derive their total fluxes.
| Source ID . | |${z}_{_{\mathrm{Ly\,\alpha }}}$| . | Flux . | EW . |
|---|---|---|---|
| . | . | (10−18 erg s−1 cm−2) . | (Å) . |
| COS-469110 | 6.650 | 9.7 ± 1.3 (7.8σ) | 14.5 ± 5.0 |
| COS-940214* | 6.748 | 11.8 ± 1.8 (7.1σ) | 43.1 ± 14.7 |
| COS-1009842 | 6.761 | 12.3 ± 0.8 (15.4σ) | 41.6 ± 9.5 |
| COS-955126 | 6.813 | 8.2 ± 0.9 (10.4σ) | 12.3 ± 2.5 |
| COS-862541 | 6.850 | 15.3 ± 1.9 (9.0σ) | 11.8 ± 2.7 |
| XMM3-504799 | 6.883 | 5.1 ± 0.9 (7.1σ) | 3.7 ± 0.8 |
| COS-788571 | 6.884 | 16.3 ± 1.1 (15.9σ) | 30.6 ± 3.9 |
| COS-1205190 | 7.049 | 12.4 ± 1.6 (8.1σ) | 28.8 ± 6.0 |
| XMM3-227436 | 7.093 | 18.6 ± 2.3 (8.9σ) | 15.0 ± 3.2 |
| Source ID . | |${z}_{_{\mathrm{Ly\,\alpha }}}$| . | Flux . | EW . |
|---|---|---|---|
| . | . | (10−18 erg s−1 cm−2) . | (Å) . |
| COS-469110 | 6.650 | 9.7 ± 1.3 (7.8σ) | 14.5 ± 5.0 |
| COS-940214* | 6.748 | 11.8 ± 1.8 (7.1σ) | 43.1 ± 14.7 |
| COS-1009842 | 6.761 | 12.3 ± 0.8 (15.4σ) | 41.6 ± 9.5 |
| COS-955126 | 6.813 | 8.2 ± 0.9 (10.4σ) | 12.3 ± 2.5 |
| COS-862541 | 6.850 | 15.3 ± 1.9 (9.0σ) | 11.8 ± 2.7 |
| XMM3-504799 | 6.883 | 5.1 ± 0.9 (7.1σ) | 3.7 ± 0.8 |
| COS-788571 | 6.884 | 16.3 ± 1.1 (15.9σ) | 30.6 ± 3.9 |
| COS-1205190 | 7.049 | 12.4 ± 1.6 (8.1σ) | 28.8 ± 6.0 |
| XMM3-227436 | 7.093 | 18.6 ± 2.3 (8.9σ) | 15.0 ± 3.2 |
Information on confident (>7σ) Ly α detections in our z ≃ 6 sample. We report HSC y-band magnitudes for sources in COSMOS and VIRCam Y-band magnitudes in XMM3. Rest-UV slopes, β, are measured by fitting the nb921yYJHKs in COSMOS and yYJHKs in XMM3. We quote the significance of each detection within parenthesis in the flux column where the fluxes have the continuum subtracted. Sources marked with asterisks are those with emission features close to moderate-strength skylines where we used a line-profile fitting technique to derive their total fluxes.
| Source ID . | RA . | Dec . | y/Y . | β . | |${z}_{_{\mathrm{Ly\,\alpha }}}$| . | Flux . | EW . |
|---|---|---|---|---|---|---|---|
| . | . | . | . | . | . | (10−18 erg s−1 cm−2) . | (Å) . |
| XMM3-229059* | 02:26:22.67 | −05:05:31.13 | 24.31|$^{+0.13}_{-0.11}$| | −2.29 ± 0.19 | 5.824 | 27.6 ± 4.8 (7.6σ) | 13.6 ± 2.3 |
| COS-291078 | 10:00:41.08 | +01:47:18.54 | 25.73|$^{+0.23}_{-0.19}$| | −1.95 ± 0.39 | 5.863 | 10.9 ± 1.3 (8.5σ) | 16.0 ± 2.6 |
| COS-1131140 | 09:59:20.27 | +02:23:22.22 | 25.63|$^{+0.15}_{-0.13}$| | −1.66 ± 0.12 | 5.904 | 6.8 ± 0.7 (11.1σ) | 11.4 ± 1.8 |
| COS-1163498* | 09:59:18.45 | +02:24:53.93 | 26.21|$^{+0.27}_{-0.22}$| | −1.81 ± 0.30 | 5.909 | 10.2 ± 1.3 (8.9σ) | 29.2 ± 7.4 |
| COS-905289 | 09:59:44.62 | +02:13:29.21 | 25.79|$^{+0.20}_{-0.17}$| | −1.94 ± 0.80 | 5.915 | 6.9 ± 0.8 (9.0σ) | 13.4 ± 2.7 |
| COS-1181452 | 10:00:19.93 | +02:25:36.81 | 24.53|$^{+0.08}_{-0.08}$| | −1.91 ± 0.12 | 5.924 | 10.5 ± 1.4 (8.9σ) | 6.4 ± 0.9 |
| COS-881759 | 09:58:56.89 | +02:12:29.64 | 26.20|$^{+0.26}_{-0.20}$| | −2.03 ± 0.37 | 5.954 | 9.1 ± 0.8 (11.3σ) | 26.1 ± 6.0 |
| XMM3-569712* | 02:27:23.06 | −04:25:53.27 | 24.68|$^{+0.15}_{-0.13}$| | −2.06 ± 0.24 | 5.986 | 7.9 ± 2.0 (7.1σ) | 5.5 ± 1.0 |
| COS-282685 | 10:00:55.03 | +01:46:56.00 | 25.49|$^{+0.12}_{-0.11}$| | −1.89 ± 0.20 | 6.041 | 13.8 ± 1.5 (10.3σ) | 20.8 ± 3.0 |
| XMM3-198954 | 02:26:26.29 | −05:08:56.68 | 25.63|$^{+0.38}_{-0.28}$| | −3.40 ± 0.88 | 6.076 | 62.3 ± 2.7 (23.4σ) | 107 ± 32 |
| COS-1260899 | 09:58:54.84 | +02:29:12.33 | 25.66|$^{+0.16}_{-0.14}$| | −2.43 ± 0.29 | 6.143 | 22.8 ± 3.4 (7.0σ) | 40.7 ± 8.1 |
| COS-631233* | 10:00:07.02 | +02:01:48.85 | 26.42|$^{+0.34}_{-0.26}$| | −2.98 ± 0.73 | 6.212 | 31.7 ± 2.4 (13.2σ) | 113 ± 32 |
| COS-930465 | 09:58:48.31 | +02:14:33.66 | 25.68|$^{+0.15}_{-0.13}$| | −2.57 ± 0.52 | 6.303 | 9.9 ± 0.7 (14.1σ) | 18.4 ± 2.7 |
| Source ID . | RA . | Dec . | y/Y . | β . | |${z}_{_{\mathrm{Ly\,\alpha }}}$| . | Flux . | EW . |
|---|---|---|---|---|---|---|---|
| . | . | . | . | . | . | (10−18 erg s−1 cm−2) . | (Å) . |
| XMM3-229059* | 02:26:22.67 | −05:05:31.13 | 24.31|$^{+0.13}_{-0.11}$| | −2.29 ± 0.19 | 5.824 | 27.6 ± 4.8 (7.6σ) | 13.6 ± 2.3 |
| COS-291078 | 10:00:41.08 | +01:47:18.54 | 25.73|$^{+0.23}_{-0.19}$| | −1.95 ± 0.39 | 5.863 | 10.9 ± 1.3 (8.5σ) | 16.0 ± 2.6 |
| COS-1131140 | 09:59:20.27 | +02:23:22.22 | 25.63|$^{+0.15}_{-0.13}$| | −1.66 ± 0.12 | 5.904 | 6.8 ± 0.7 (11.1σ) | 11.4 ± 1.8 |
| COS-1163498* | 09:59:18.45 | +02:24:53.93 | 26.21|$^{+0.27}_{-0.22}$| | −1.81 ± 0.30 | 5.909 | 10.2 ± 1.3 (8.9σ) | 29.2 ± 7.4 |
| COS-905289 | 09:59:44.62 | +02:13:29.21 | 25.79|$^{+0.20}_{-0.17}$| | −1.94 ± 0.80 | 5.915 | 6.9 ± 0.8 (9.0σ) | 13.4 ± 2.7 |
| COS-1181452 | 10:00:19.93 | +02:25:36.81 | 24.53|$^{+0.08}_{-0.08}$| | −1.91 ± 0.12 | 5.924 | 10.5 ± 1.4 (8.9σ) | 6.4 ± 0.9 |
| COS-881759 | 09:58:56.89 | +02:12:29.64 | 26.20|$^{+0.26}_{-0.20}$| | −2.03 ± 0.37 | 5.954 | 9.1 ± 0.8 (11.3σ) | 26.1 ± 6.0 |
| XMM3-569712* | 02:27:23.06 | −04:25:53.27 | 24.68|$^{+0.15}_{-0.13}$| | −2.06 ± 0.24 | 5.986 | 7.9 ± 2.0 (7.1σ) | 5.5 ± 1.0 |
| COS-282685 | 10:00:55.03 | +01:46:56.00 | 25.49|$^{+0.12}_{-0.11}$| | −1.89 ± 0.20 | 6.041 | 13.8 ± 1.5 (10.3σ) | 20.8 ± 3.0 |
| XMM3-198954 | 02:26:26.29 | −05:08:56.68 | 25.63|$^{+0.38}_{-0.28}$| | −3.40 ± 0.88 | 6.076 | 62.3 ± 2.7 (23.4σ) | 107 ± 32 |
| COS-1260899 | 09:58:54.84 | +02:29:12.33 | 25.66|$^{+0.16}_{-0.14}$| | −2.43 ± 0.29 | 6.143 | 22.8 ± 3.4 (7.0σ) | 40.7 ± 8.1 |
| COS-631233* | 10:00:07.02 | +02:01:48.85 | 26.42|$^{+0.34}_{-0.26}$| | −2.98 ± 0.73 | 6.212 | 31.7 ± 2.4 (13.2σ) | 113 ± 32 |
| COS-930465 | 09:58:48.31 | +02:14:33.66 | 25.68|$^{+0.15}_{-0.13}$| | −2.57 ± 0.52 | 6.303 | 9.9 ± 0.7 (14.1σ) | 18.4 ± 2.7 |
Information on confident (>7σ) Ly α detections in our z ≃ 6 sample. We report HSC y-band magnitudes for sources in COSMOS and VIRCam Y-band magnitudes in XMM3. Rest-UV slopes, β, are measured by fitting the nb921yYJHKs in COSMOS and yYJHKs in XMM3. We quote the significance of each detection within parenthesis in the flux column where the fluxes have the continuum subtracted. Sources marked with asterisks are those with emission features close to moderate-strength skylines where we used a line-profile fitting technique to derive their total fluxes.
| Source ID . | RA . | Dec . | y/Y . | β . | |${z}_{_{\mathrm{Ly\,\alpha }}}$| . | Flux . | EW . |
|---|---|---|---|---|---|---|---|
| . | . | . | . | . | . | (10−18 erg s−1 cm−2) . | (Å) . |
| XMM3-229059* | 02:26:22.67 | −05:05:31.13 | 24.31|$^{+0.13}_{-0.11}$| | −2.29 ± 0.19 | 5.824 | 27.6 ± 4.8 (7.6σ) | 13.6 ± 2.3 |
| COS-291078 | 10:00:41.08 | +01:47:18.54 | 25.73|$^{+0.23}_{-0.19}$| | −1.95 ± 0.39 | 5.863 | 10.9 ± 1.3 (8.5σ) | 16.0 ± 2.6 |
| COS-1131140 | 09:59:20.27 | +02:23:22.22 | 25.63|$^{+0.15}_{-0.13}$| | −1.66 ± 0.12 | 5.904 | 6.8 ± 0.7 (11.1σ) | 11.4 ± 1.8 |
| COS-1163498* | 09:59:18.45 | +02:24:53.93 | 26.21|$^{+0.27}_{-0.22}$| | −1.81 ± 0.30 | 5.909 | 10.2 ± 1.3 (8.9σ) | 29.2 ± 7.4 |
| COS-905289 | 09:59:44.62 | +02:13:29.21 | 25.79|$^{+0.20}_{-0.17}$| | −1.94 ± 0.80 | 5.915 | 6.9 ± 0.8 (9.0σ) | 13.4 ± 2.7 |
| COS-1181452 | 10:00:19.93 | +02:25:36.81 | 24.53|$^{+0.08}_{-0.08}$| | −1.91 ± 0.12 | 5.924 | 10.5 ± 1.4 (8.9σ) | 6.4 ± 0.9 |
| COS-881759 | 09:58:56.89 | +02:12:29.64 | 26.20|$^{+0.26}_{-0.20}$| | −2.03 ± 0.37 | 5.954 | 9.1 ± 0.8 (11.3σ) | 26.1 ± 6.0 |
| XMM3-569712* | 02:27:23.06 | −04:25:53.27 | 24.68|$^{+0.15}_{-0.13}$| | −2.06 ± 0.24 | 5.986 | 7.9 ± 2.0 (7.1σ) | 5.5 ± 1.0 |
| COS-282685 | 10:00:55.03 | +01:46:56.00 | 25.49|$^{+0.12}_{-0.11}$| | −1.89 ± 0.20 | 6.041 | 13.8 ± 1.5 (10.3σ) | 20.8 ± 3.0 |
| XMM3-198954 | 02:26:26.29 | −05:08:56.68 | 25.63|$^{+0.38}_{-0.28}$| | −3.40 ± 0.88 | 6.076 | 62.3 ± 2.7 (23.4σ) | 107 ± 32 |
| COS-1260899 | 09:58:54.84 | +02:29:12.33 | 25.66|$^{+0.16}_{-0.14}$| | −2.43 ± 0.29 | 6.143 | 22.8 ± 3.4 (7.0σ) | 40.7 ± 8.1 |
| COS-631233* | 10:00:07.02 | +02:01:48.85 | 26.42|$^{+0.34}_{-0.26}$| | −2.98 ± 0.73 | 6.212 | 31.7 ± 2.4 (13.2σ) | 113 ± 32 |
| COS-930465 | 09:58:48.31 | +02:14:33.66 | 25.68|$^{+0.15}_{-0.13}$| | −2.57 ± 0.52 | 6.303 | 9.9 ± 0.7 (14.1σ) | 18.4 ± 2.7 |
| Source ID . | RA . | Dec . | y/Y . | β . | |${z}_{_{\mathrm{Ly\,\alpha }}}$| . | Flux . | EW . |
|---|---|---|---|---|---|---|---|
| . | . | . | . | . | . | (10−18 erg s−1 cm−2) . | (Å) . |
| XMM3-229059* | 02:26:22.67 | −05:05:31.13 | 24.31|$^{+0.13}_{-0.11}$| | −2.29 ± 0.19 | 5.824 | 27.6 ± 4.8 (7.6σ) | 13.6 ± 2.3 |
| COS-291078 | 10:00:41.08 | +01:47:18.54 | 25.73|$^{+0.23}_{-0.19}$| | −1.95 ± 0.39 | 5.863 | 10.9 ± 1.3 (8.5σ) | 16.0 ± 2.6 |
| COS-1131140 | 09:59:20.27 | +02:23:22.22 | 25.63|$^{+0.15}_{-0.13}$| | −1.66 ± 0.12 | 5.904 | 6.8 ± 0.7 (11.1σ) | 11.4 ± 1.8 |
| COS-1163498* | 09:59:18.45 | +02:24:53.93 | 26.21|$^{+0.27}_{-0.22}$| | −1.81 ± 0.30 | 5.909 | 10.2 ± 1.3 (8.9σ) | 29.2 ± 7.4 |
| COS-905289 | 09:59:44.62 | +02:13:29.21 | 25.79|$^{+0.20}_{-0.17}$| | −1.94 ± 0.80 | 5.915 | 6.9 ± 0.8 (9.0σ) | 13.4 ± 2.7 |
| COS-1181452 | 10:00:19.93 | +02:25:36.81 | 24.53|$^{+0.08}_{-0.08}$| | −1.91 ± 0.12 | 5.924 | 10.5 ± 1.4 (8.9σ) | 6.4 ± 0.9 |
| COS-881759 | 09:58:56.89 | +02:12:29.64 | 26.20|$^{+0.26}_{-0.20}$| | −2.03 ± 0.37 | 5.954 | 9.1 ± 0.8 (11.3σ) | 26.1 ± 6.0 |
| XMM3-569712* | 02:27:23.06 | −04:25:53.27 | 24.68|$^{+0.15}_{-0.13}$| | −2.06 ± 0.24 | 5.986 | 7.9 ± 2.0 (7.1σ) | 5.5 ± 1.0 |
| COS-282685 | 10:00:55.03 | +01:46:56.00 | 25.49|$^{+0.12}_{-0.11}$| | −1.89 ± 0.20 | 6.041 | 13.8 ± 1.5 (10.3σ) | 20.8 ± 3.0 |
| XMM3-198954 | 02:26:26.29 | −05:08:56.68 | 25.63|$^{+0.38}_{-0.28}$| | −3.40 ± 0.88 | 6.076 | 62.3 ± 2.7 (23.4σ) | 107 ± 32 |
| COS-1260899 | 09:58:54.84 | +02:29:12.33 | 25.66|$^{+0.16}_{-0.14}$| | −2.43 ± 0.29 | 6.143 | 22.8 ± 3.4 (7.0σ) | 40.7 ± 8.1 |
| COS-631233* | 10:00:07.02 | +02:01:48.85 | 26.42|$^{+0.34}_{-0.26}$| | −2.98 ± 0.73 | 6.212 | 31.7 ± 2.4 (13.2σ) | 113 ± 32 |
| COS-930465 | 09:58:48.31 | +02:14:33.66 | 25.68|$^{+0.15}_{-0.13}$| | −2.57 ± 0.52 | 6.303 | 9.9 ± 0.7 (14.1σ) | 18.4 ± 2.7 |
2.2.3 Detected emission lines
We detect confident (>7σ) emission features in 9 of the 22 z ≃ 7 galaxies in our sample (see Fig. 2). In all cases, we interpret these features as Ly α because all are fully consistent with such a solution given the expected redshift range of our sample and none are consistent with an [O ii]λ3727,3729 solution (two narrow peaks of roughly similar strength separated by ≈6.8 Å in the observed frame). We consider [O ii]λ3727,3729 as the primary alternative solution because it would be very difficult for anything but a Balmer break to mimic the strong nb921 and Z drops required by our selection criteria. We also find no other convincing features in the spectra of these sources (aside from the tentative features in COS-469110 consistent with NV emission; see below). The measured line fluxes and rest-frame EWs for sources with a Ly α detection are reported in Table 3. We also calculate the corresponding Ly α redshifts, |${z}_{_{\mathrm{Ly\,\alpha }}}$|, using the observed wavelength of peak flux in the 1D extraction and a rest-frame Ly α wavelength of 1215.67 Å. The detection for COS-862541 was previously reported in E21.
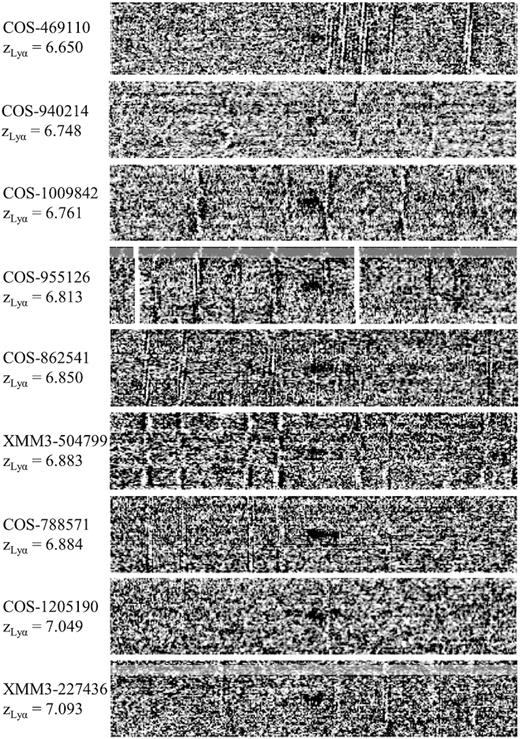
2D signal-to-noise ratio maps (black is positive) of our nine confident (>7σ) Ly α detections at z ≃ 7. These detections span a redshift range of |${z}_{_{\mathrm{Ly\,\alpha }}}$| = 6.650–7.093. Each sub-figure spans ±100 Å along the x-axis and ±7.3 arcsec along the y-axis. We mask the bright continuum from nearby sources in the spectra of COS-955126 and XMM3-227436 to improve clarity.
Our z ≃ 7 Ly α detections span redshifts of |${z}_{_{\mathrm{Ly\,\alpha }}}$| = 6.650–7.093. Measured fluxes and EWs range from (5.1–18.6) × 10−18 erg s−1 cm−2 and 3.7–43.1 Å, respectively. None of the detections lie at |${z}_{_{\mathrm{Ly\,\alpha }}}$| < 6.6, consistent with the strong nb921 and Z drops used in our selection. Furthermore, the large majority of detected targets lie at |${z}_{_{\mathrm{Ly\,\alpha }}}$| ≃ 6.6–6.9. While two of our sources (COS-1205190 and XMM3-227436) lie at z = 7.05–7.09, these redshifts are still consistent with our selection given the moderate-strength Ly α emission for these sources (EW = 15–29 Å; see Section 2.1.1).
We also detect confident (>7σ) emission features in 13 of our 30 z ≃ 6 targets. In Table 4, we report the coordinates, rest-UV slopes, Ly α redshifts, fluxes, EWs, and y/Y-band magnitudes of each detected z ≃ 6 source in COSMOS/XMM3. The 2D spectra of all z ≃ 6 detections are shown in Fig. 3 and span redshifts of |${z}_{_{\mathrm{Ly\,\alpha }}}$| = 5.824–6.303, consistent with expectations given their selection criteria (Section 2.1.2). We measure Ly α fluxes ranging from (6.8–62.3) × 10−18 erg s−1 cm−2 and EWs ranging from 5.5–113 Å.

2D signal-to-noise ratio maps of our 13 Ly α detections at z ≃ 6 where black is positive. These detections span a redshift range of |${z}_{_{\mathrm{Ly\,\alpha }}}$| = 5.824–6.303. Each sub-Fig. spans ±100 Å along the x-axis and ±2.5 arcsec along the y-axis.
Motivated by recent detections in similarly luminous z ≳ 7 galaxies (Tilvi et al. 2016; Laporte et al. 2017; Mainali et al. 2018; see also Hu et al. 2017), we search for NVλ1238.8,1242.8 emission in the spectra of our z ≃ 7 Ly α emitters. Given the very high ionization potential of this line (77 eV), any such detection would likely signal significant active galactic nucleus (AGN) activity. As shown in Fig. 4, we tentatively identify the NV doublet in COS-469110 (|$\mathrm{\mathit{ M}}_{\mathrm{UV}}^{ }$| = −21.7) where the emission is located at the exact expected spatial position of the source. We regard both these features as tentative because each is detected at <7σ significance, specifically 6.4σ and 5.2σ for the 1238.8 and 1242.8 Å components, respectively. However, we note that if we split our data into two distinct stacks,10 the NVλ1238.8 feature is significantly detected in each stack (5.2σ and 3.8σ), adding evidence that this feature is likely real.
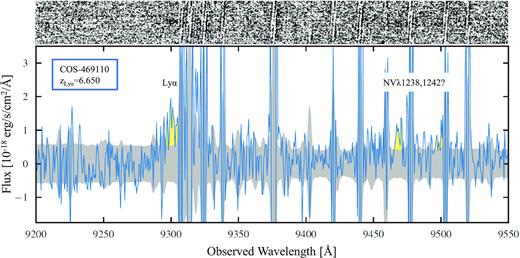
MMT/Binospec spectra of COS-469110 where we identify Ly α as well as tentative detections of the NVλ1238.8,1242.8 doublet, a signpost of significant AGN activity. The top and middle panels show the 2D and smoothed 2D signal-to-noise ratio maps, respectively, where black is positive. In the bottom panel, we show the 1D extraction centred on the expected spatial position of the source with the 1σ noise level in grey. The two NV doublet components are measured with a significance of 6.4σ and 5.2σ, respectively, and have peak wavelengths corresponding to the exact same redshift of z = 6.645. This translates to a Ly α velocity offset of ≈200 km s−1 that may help explain the exceptionally high NV to Ly α flux ratio of this source (see text).
The NVλ1238.8 component is clearly distinct from strong skylines and has a measured flux of (5.4 ± 1.0) × 10−18 erg s−1 cm−2 which, using the Y-band photometry for the continuum, corresponds to an EW of 8.4 ± 3.0 Å. The flux of the NVλ1242.8 component is measured to be (3.8 ± 0.8) × 10−18 erg s−1 cm−2 that corresponds to an EW of 5.9 ± 2.2 Å. While the 1242.8 Å component does rest up against a skyline, the peak wavelengths of both components correspond to the exact same redshift of z = 6.645 that is well consistent with the Ly α redshift of |${z}_{_{\mathrm{Ly\,\alpha }}}$| = 6.650 (we discuss the implied Ly α velocity offset below). Furthermore, the measured EWs of both components are consistent with that recently reported in three other similarly luminous z = 7–9 galaxies (Tilvi et al. 2016; Laporte et al. 2017; Mainali et al. 2018) as well as a 1:1 to 2:1 flux ratio for the doublet (Bickel 1969; Torres-Peimbert & Pena 1984). However, we do note that calculating this flux ratio is complicated by the partial skyline masking of the 1242.8 Å component.
While we do not detect any significant NV features in any of our other z ≃ 7 Ly α emitters, we are able to place 5σ NVλ1238.8 EW limits11 of ≤10 Å in six of our other 12 z ≃ 7 Ly α emitters, suggesting that the (tentative) NV emission from COS-469110 is likely exceptional among the bright z ≃ 7 population. This is perhaps further supported by the fact that the total NV flux we measure implies a line flux ratio of |$f_{_{\mathrm{NV}}}/f_{_{\mathrm{Ly}\,\alpha {}}}$| = 0.95 ± 0.19, much larger than typical upper limits recently placed on several other bright z > 6.5 Ly α emitters (|$f_{_{\mathrm{NV}}}/f_{_{\mathrm{Ly}\,\alpha {}}}\, \lesssim$| 0.2; Mainali et al. 2018; Shibuya et al. 2018). Because of the partial skyline obscuration of the 1242.8 Å component, this flux ratio for COS-469110 is likely a lower limit.
The Ly α velocity offset implied for COS-469110 is ≈200 km s−1, assuming that NV well traces the systemic redshift (Laporte et al. 2017). This velocity offset falls well within the range previously reported for similarly luminous (|$\mathrm{\mathit{ M}}_{\mathrm{UV}}^{ }$| |$\lt \, -$|21.5) galaxies at z > 6 (110–500 km s−1; Willott et al. 2015; Inoue et al. 2016; Pentericci et al. 2016; Laporte et al. 2017; Stark et al. 2017; Mainali et al. 2018; Matthee et al. 2020), though it does sit on the lower end of that range. This may help explain the exceptionally large NV to Ly α line flux ratio mentioned above as Ly α emission is more susceptible to strong scattering by the partially neutral IGM at lower velocity offsets (e.g. Miralda-Escudé 1998; Mason et al. 2018b).
2.2.4 Completeness simulations
When inferring the Ly α EW distribution in Section 3.2, we fold in constraints from non-detections. We do so by calculating the Ly α detection completeness of each non-detected source as a function of Ly α EW from EW = 0–100 Å in 1 Å steps. We insert 10 000 simulated 1D flux profiles for each value of EW into the fully reduced 1D spectrum of each source at its expected spatial position and determine what fraction of simulated features would be detected at >7σ. The observed wavelengths of these simulated features are randomly sampled using the redshift completeness distributions as a function of Ly α EW and rest-UV magnitude described in Section 2.1. In doing so, we account for the dependence of our redshift selection window on Ly α EW and for the impact of skyline obscuration. The profile of each simulated Ly α feature is a Gaussian with FWHM set to 220 km s−1, equal to the mean value measured from the two z ≃ 7 Ly α features detected with very high significance (>15σ) in our sample, namely COS-788571 (FWHM = 180 km s−1) and COS-1009842 (FWHM = 260 km s−1). This FWHM is also in excellent agreement with that found by Pentericci et al. (2018) using stacked spectra of fainter z ≃ 7 galaxies.
We plot the simulated spectroscopic completeness for a representative subset of the non-detected z ≃ 7 (z ≃ 6) galaxies in the top (bottom) panel of Fig. 5. The spectral constraints on most of these z ≃ 6–7 targets yield ≳50 per cent completeness at EW = 20 Å, increasing to ≳80 per cent at EW = 60 Å. For a small subset of the non-detected z ≃ 7 sources, the spectral completeness declines at high Ly α EW due to their lack of very red (≳9750 Å) spectral coverage that prohibits detecting Ly α at z ≳ 7.0. Such a high-redshift solution is only likely for strong Ly α emitters given our selection criteria (Section 2.1.1). All of this information is folded into our analysis when inferring the Ly α EW distributions (Section 3).
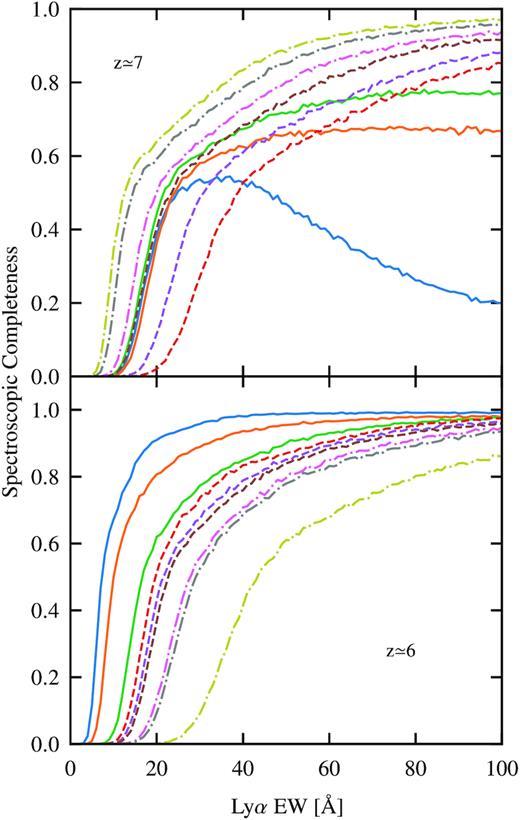
Figures showing our simulated spectroscopic completeness as a function of Ly α EW for non-detected sources at z ≃ 7 (top) and z ≃ 6 (bottom). To improve clarity, we only show the completeness curves for a representative subset of non-detected sources. For a small subset of the non-detected z ≃ 7 sources, the spectral completeness declines at high Ly α EW due to their lack of very red (≳9750 Å) spectral coverage that prohibits detecting Ly α at z ≳ 7.0 and such a high-redshift solution is only likely for strong Ly α emitters (Section 2.1.1). All of this information is folded into our analysis when inferring the Ly α EW distributions.
2.3 Photoionization modelling
We now infer the [O iii]+H β EWs of each of our z ≃ 7 targets to test whether we see a correlation with Ly α visibility. To infer the [O iii]+H β emission strength (as well as other physical properties such as stellar mass), we use the BayEsian Analysis of GaLaxy sEds (beagle; Chevallard & Charlot 2016) SED fitting code. beagle computes both the stellar and nebular emission of star-forming galaxies by adopting the photoionization models from Gutkin, Charlot & Bruzual (2016), which are derived by incorporating the latest version of Bruzual & Charlot (2003) stellar population synthesis models into cloudy (Ferland et al. 2013). Our SED fitting procedure with beagle matches that described in E21. Briefly, we assume a delayed star formation history (SFR ∝ t e−t/τ) with an allowed recent (<10 Myr) burst, a minimum age of 1 Myr, an sSFR ranging from 0.1 Gyr−1 to 1000 Gyr−1, and an SMC dust prescription.
We note that some of our spectroscopically confirmed sources lie at |${z}_{_{\mathrm{Ly\,\alpha }}}$| ≈ 6.85–6.9 (COS-788571, COS-862541, and XMM3-504799) where the transmission of [O iii]λ5007 through [3.6] (and hence the inferred [O iii]+H β EW) is very sensitive to the exact systemic redshift, zsys. At z ≳ 6, visible Ly α emission is often redshifted relative to systemic due to complex radiative transfer effects in the ISM, CGM, and IGM (see e.g. Dijkstra 2014 for a review). The current maximum observed velocity offset at z > 6 is 500 km s−1 (Willott et al. 2015) that translates to zsys = |${z}_{_{\mathrm{Ly\,\alpha }}}$|−0.013 at z = 6.6–7.1 where we have z ≃ 7 Ly α detections. Therefore, during the beagle fitting process, we allow zsys to range between |${z}_{_{\mathrm{Ly\,\alpha }}}$|−0.013 and |${z}_{_{\mathrm{Ly\,\alpha }}}$| for z ≃ 7 sources with a Ly α detection.
For sources with a Ly α detection, we furthermore exclude bands blueward of the Ly α break during the fitting process. We also do not fit to bands significantly impacted by Ly α emission for these sources as it is currently not possible to leave the effective Ly α transmission fraction through the IGM as a free parameter in beagle. This means we fit to all bands redder than and including Y for sources with |${z}_{_{\mathrm{Ly\,\alpha }}}$| < 6.9 and all bands redder than including J for sources with |${z}_{_{\mathrm{Ly\,\alpha }}}$| > 6.9. Sources without a Ly α detection are fit using all optical through mid-infrared photometry with a uniform redshift prior of z = 6–8 and we remove Ly α emission from the nebular templates given the low (∼10 per cent) fraction of strong Ly α emitters (EW > 25 Å) found among the bright z ≃ 7 population in previous works (e.g. Ono et al. 2012; Schenker et al. 2014; Pentericci et al. 2018). We report the inferred [O iii]+H β EWs of each z ≃ 7 source in Table 5, along with their inferred absolute UV magnitudes (at 1600 Å rest-frame), stellar masses, V-band optical depths, and sSFRs. In the final column, we report the inferred ionizing photon production efficiencies, |$\xi _{\mathrm{ion}}^{\ast }$|, computed using the intrinsic UV luminosity (at 1500 Å rest-frame) of the stellar population before processing through dust and gas (see Chevallard et al. 2018 for details). We also quote photometric redshifts for sources without a Ly α detection and |${z}_{_{\mathrm{Ly\,\alpha }}}$| for sources with a Ly α detection in Table 5.
Inferred properties of our z ≃ 7 sample targeted with MMT/Binospec. These properties were obtained by fitting photometry with a photoionization model using the beagle SED fitting code (Chevallard & Charlot 2016). The best-fitting values and errors are determined by calculating the median and inner 68 per cent confidence interval values marginalized over the posterior probability distribution function output by beagle. We report spectroscopic redshifts for sources with a confident (>7σ) Ly α detection and photometric redshifts otherwise.
| Source ID . | Redshift . | |$\mathrm{\mathit{ M}}_{\mathrm{UV}}^{ }$| . | log10 M* . | |$\tau _{_V}$| . | sSFR . | [O iii]+H β EW . | log10 |$\xi _{\mathrm{ion}}^{\ast }$| . |
|---|---|---|---|---|---|---|---|
| . | . | . | (M⊙) . | . | (Gyr−1) . | (Å) . | (erg−1 Hz) . |
| COS-221419 | 6.70|$^{+0.05}_{-0.04}$| | −21.0|$^{+0.1}_{-0.1}$| | 8.4|$^{+0.4}_{-0.4}$| | 0.01|$^{+0.02}_{-0.01}$| | 6.3|$^{+47.3}_{-5.8}$| | 690|$^{+760}_{-440}$| | 25.52|$^{+0.19}_{-0.25}$| |
| COS-235129 | 6.76|$^{+0.08}_{-0.07}$| | −21.4|$^{+0.1}_{-0.1}$| | 9.5|$^{+0.3}_{-1.0}$| | 0.03|$^{+0.08}_{-0.02}$| | 0.9|$^{+4.2}_{-0.7}$| | 200|$^{+230}_{-150}$| | 25.25|$^{+0.32}_{-0.39}$| |
| COS-237729 | 6.83|$^{+0.10}_{-0.09}$| | −21.1|$^{+0.1}_{-0.1}$| | 8.8|$^{+0.8}_{-0.7}$| | 0.05|$^{+0.09}_{-0.05}$| | 5.1|$^{+37.1}_{-4.5}$| | 650|$^{+530}_{-420}$| | 25.60|$^{+0.21}_{-0.29}$| |
| COS-301652 | 6.63|$^{+0.09}_{-0.03}$| | −21.2|$^{+0.1}_{-0.1}$| | 9.3|$^{+0.7}_{-1.1}$| | 0.08|$^{+0.10}_{-0.07}$| | 2.0|$^{+9.5}_{-1.5}$| | 520|$^{+330}_{-270}$| | 25.59|$^{+0.18}_{-0.25}$| |
| COS-469110 | 6.650 | −21.7|$^{+0.2}_{-0.1}$| | 8.8|$^{+0.8}_{-0.5}$| | 0.04|$^{+0.09}_{-0.04}$| | 5.3|$^{+32.4}_{-4.7}$| | 730|$^{+380}_{-320}$| | 25.58|$^{+0.22}_{-0.20}$| |
| COS-505871 | 6.67|$^{+0.12}_{-0.07}$| | −21.2|$^{+0.1}_{-0.1}$| | 10.0|$^{+0.2}_{-1.5}$| | 0.04|$^{+0.15}_{-0.03}$| | 1.2|$^{+3.4}_{-0.7}$| | 290|$^{+320}_{-190}$| | 25.50|$^{+0.24}_{-0.31}$| |
| COS-534584 | 6.60|$^{+0.01}_{-0.01}$| | −21.9|$^{+0.1}_{-0.1}$| | 9.2|$^{+0.5}_{-0.7}$| | 0.12|$^{+0.04}_{-0.06}$| | 5.7|$^{+26.2}_{-5.1}$| | 790|$^{+520}_{-390}$| | 25.50|$^{+0.20}_{-0.19}$| |
| COS-788571 | 6.884 | −21.5|$^{+0.1}_{-0.1}$| | 8.9|$^{+0.4}_{-0.3}$| | 0.02|$^{+0.06}_{-0.01}$| | 173.3|$^{+253.5}_{-124.7}$| | 3680|$^{+1940}_{-1660}$| | 25.91|$^{+0.06}_{-0.11}$| |
| COS-851423 | 6.65|$^{+0.05}_{-0.03}$| | −21.1|$^{+0.1}_{-0.1}$| | 8.3|$^{+0.7}_{-0.3}$| | 0.01|$^{+0.03}_{-0.01}$| | 9.5|$^{+55.8}_{-8.9}$| | 1030|$^{+730}_{-480}$| | 25.63|$^{+0.14}_{-0.19}$| |
| COS-854905 | 6.67|$^{+0.05}_{-0.03}$| | −21.4|$^{+0.1}_{-0.1}$| | 8.8|$^{+0.9}_{-0.6}$| | 0.02|$^{+0.05}_{-0.01}$| | 2.4|$^{+14.5}_{-2.0}$| | 560|$^{+490}_{-350}$| | 25.51|$^{+0.20}_{-0.28}$| |
| COS-856875 | 6.68|$^{+0.05}_{-0.03}$| | −21.2|$^{+0.1}_{-0.1}$| | 8.6|$^{+0.6}_{-0.5}$| | 0.01|$^{+0.03}_{-0.01}$| | 3.1|$^{+25.0}_{-2.7}$| | 540|$^{+430}_{-280}$| | 25.48|$^{+0.20}_{-0.22}$| |
| COS-862541 | 6.850 | −22.5|$^{+0.1}_{-0.1}$| | 9.1|$^{+0.4}_{-0.3}$| | 0.06|$^{+0.07}_{-0.05}$| | 155.6|$^{+193.2}_{-123.2}$| | 4160|$^{+1610}_{-1270}$| | 25.89|$^{+0.08}_{-0.08}$| |
| COS-940214 | 6.748 | −20.4|$^{+0.2}_{-0.2}$| | 8.0|$^{+0.4}_{-0.3}$| | 0.01|$^{+0.04}_{-0.01}$| | 134.1|$^{+238.5}_{-122.8}$| | 3210|$^{+1950}_{-1790}$| | 25.87|$^{+0.10}_{-0.16}$| |
| COS-955126 | 6.813 | −21.5|$^{+0.1}_{-0.1}$| | 8.5|$^{+0.6}_{-0.3}$| | 0.02|$^{+0.06}_{-0.02}$| | 29.2|$^{+97.5}_{-27.6}$| | 1620|$^{+980}_{-650}$| | 25.73|$^{+0.10}_{-0.11}$| |
| COS-1009842 | 6.761 | −20.6|$^{+0.2}_{-0.1}$| | 8.3|$^{+0.8}_{-0.4}$| | 0.03|$^{+0.07}_{-0.02}$| | 10.4|$^{+58.1}_{-9.3}$| | 910|$^{+720}_{-500}$| | 25.65|$^{+0.15}_{-0.22}$| |
| COS-1048848 | 6.69|$^{+0.11}_{-0.08}$| | −20.7|$^{+0.1}_{-0.1}$| | 8.4|$^{+0.3}_{-0.3}$| | 0.01|$^{+0.03}_{-0.01}$| | 2.1|$^{+15.8}_{-1.8}$| | 310|$^{+300}_{-180}$| | 25.35|$^{+0.24}_{-0.33}$| |
| COS-1053257 | 6.68|$^{+0.07}_{-0.05}$| | −22.0|$^{+0.1}_{-0.1}$| | 8.5|$^{+0.8}_{-0.2}$| | 0.04|$^{+0.06}_{-0.04}$| | 5.0|$^{+42.3}_{-4.6}$| | 630|$^{+530}_{-310}$| | 25.75|$^{+0.13}_{-0.23}$| |
| COS-1099982 | 6.68|$^{+0.03}_{-0.02}$| | −21.6|$^{+0.1}_{-0.1}$| | 8.6|$^{+0.5}_{-0.3}$| | 0.01|$^{+0.03}_{-0.01}$| | 72.7|$^{+112.0}_{-54.9}$| | 2470|$^{+1080}_{-690}$| | 25.76|$^{+0.09}_{-0.07}$| |
| COS-1205190 | 7.049 | −20.9|$^{+0.2}_{-0.2}$| | 8.6|$^{+0.4}_{-0.5}$| | 0.01|$^{+0.03}_{-0.01}$| | 2.8|$^{+25.4}_{-2.4}$| | 330|$^{+470}_{-220}$| | 25.42|$^{+0.27}_{-0.40}$| |
| COS-1235751 | 6.74|$^{+0.09}_{-0.07}$| | −21.3|$^{+0.1}_{-0.1}$| | 9.4|$^{+0.5}_{-0.6}$| | 0.32|$^{+0.06}_{-0.07}$| | 1.6|$^{+9.9}_{-1.3}$| | 300|$^{+240}_{-190}$| | 25.35|$^{+0.30}_{-0.34}$| |
| XMM3-227436 | 7.093 | −22.3|$^{+0.2}_{-0.1}$| | 9.0|$^{+0.7}_{-0.4}$| | 0.04|$^{+0.09}_{-0.03}$| | 6.6|$^{+56.5}_{-6.0}$| | 930|$^{+800}_{-510}$| | 25.84|$^{+0.28}_{-0.23}$| |
| XMM3-504799 | 6.883 | −22.5|$^{+0.1}_{-0.1}$| | 9.3|$^{+0.6}_{-0.4}$| | 0.05|$^{+0.10}_{-0.04}$| | 80.1|$^{+190.9}_{-71.3}$| | 2310|$^{+1830}_{-1150}$| | 26.22|$^{+0.25}_{-0.23}$| |
| Source ID . | Redshift . | |$\mathrm{\mathit{ M}}_{\mathrm{UV}}^{ }$| . | log10 M* . | |$\tau _{_V}$| . | sSFR . | [O iii]+H β EW . | log10 |$\xi _{\mathrm{ion}}^{\ast }$| . |
|---|---|---|---|---|---|---|---|
| . | . | . | (M⊙) . | . | (Gyr−1) . | (Å) . | (erg−1 Hz) . |
| COS-221419 | 6.70|$^{+0.05}_{-0.04}$| | −21.0|$^{+0.1}_{-0.1}$| | 8.4|$^{+0.4}_{-0.4}$| | 0.01|$^{+0.02}_{-0.01}$| | 6.3|$^{+47.3}_{-5.8}$| | 690|$^{+760}_{-440}$| | 25.52|$^{+0.19}_{-0.25}$| |
| COS-235129 | 6.76|$^{+0.08}_{-0.07}$| | −21.4|$^{+0.1}_{-0.1}$| | 9.5|$^{+0.3}_{-1.0}$| | 0.03|$^{+0.08}_{-0.02}$| | 0.9|$^{+4.2}_{-0.7}$| | 200|$^{+230}_{-150}$| | 25.25|$^{+0.32}_{-0.39}$| |
| COS-237729 | 6.83|$^{+0.10}_{-0.09}$| | −21.1|$^{+0.1}_{-0.1}$| | 8.8|$^{+0.8}_{-0.7}$| | 0.05|$^{+0.09}_{-0.05}$| | 5.1|$^{+37.1}_{-4.5}$| | 650|$^{+530}_{-420}$| | 25.60|$^{+0.21}_{-0.29}$| |
| COS-301652 | 6.63|$^{+0.09}_{-0.03}$| | −21.2|$^{+0.1}_{-0.1}$| | 9.3|$^{+0.7}_{-1.1}$| | 0.08|$^{+0.10}_{-0.07}$| | 2.0|$^{+9.5}_{-1.5}$| | 520|$^{+330}_{-270}$| | 25.59|$^{+0.18}_{-0.25}$| |
| COS-469110 | 6.650 | −21.7|$^{+0.2}_{-0.1}$| | 8.8|$^{+0.8}_{-0.5}$| | 0.04|$^{+0.09}_{-0.04}$| | 5.3|$^{+32.4}_{-4.7}$| | 730|$^{+380}_{-320}$| | 25.58|$^{+0.22}_{-0.20}$| |
| COS-505871 | 6.67|$^{+0.12}_{-0.07}$| | −21.2|$^{+0.1}_{-0.1}$| | 10.0|$^{+0.2}_{-1.5}$| | 0.04|$^{+0.15}_{-0.03}$| | 1.2|$^{+3.4}_{-0.7}$| | 290|$^{+320}_{-190}$| | 25.50|$^{+0.24}_{-0.31}$| |
| COS-534584 | 6.60|$^{+0.01}_{-0.01}$| | −21.9|$^{+0.1}_{-0.1}$| | 9.2|$^{+0.5}_{-0.7}$| | 0.12|$^{+0.04}_{-0.06}$| | 5.7|$^{+26.2}_{-5.1}$| | 790|$^{+520}_{-390}$| | 25.50|$^{+0.20}_{-0.19}$| |
| COS-788571 | 6.884 | −21.5|$^{+0.1}_{-0.1}$| | 8.9|$^{+0.4}_{-0.3}$| | 0.02|$^{+0.06}_{-0.01}$| | 173.3|$^{+253.5}_{-124.7}$| | 3680|$^{+1940}_{-1660}$| | 25.91|$^{+0.06}_{-0.11}$| |
| COS-851423 | 6.65|$^{+0.05}_{-0.03}$| | −21.1|$^{+0.1}_{-0.1}$| | 8.3|$^{+0.7}_{-0.3}$| | 0.01|$^{+0.03}_{-0.01}$| | 9.5|$^{+55.8}_{-8.9}$| | 1030|$^{+730}_{-480}$| | 25.63|$^{+0.14}_{-0.19}$| |
| COS-854905 | 6.67|$^{+0.05}_{-0.03}$| | −21.4|$^{+0.1}_{-0.1}$| | 8.8|$^{+0.9}_{-0.6}$| | 0.02|$^{+0.05}_{-0.01}$| | 2.4|$^{+14.5}_{-2.0}$| | 560|$^{+490}_{-350}$| | 25.51|$^{+0.20}_{-0.28}$| |
| COS-856875 | 6.68|$^{+0.05}_{-0.03}$| | −21.2|$^{+0.1}_{-0.1}$| | 8.6|$^{+0.6}_{-0.5}$| | 0.01|$^{+0.03}_{-0.01}$| | 3.1|$^{+25.0}_{-2.7}$| | 540|$^{+430}_{-280}$| | 25.48|$^{+0.20}_{-0.22}$| |
| COS-862541 | 6.850 | −22.5|$^{+0.1}_{-0.1}$| | 9.1|$^{+0.4}_{-0.3}$| | 0.06|$^{+0.07}_{-0.05}$| | 155.6|$^{+193.2}_{-123.2}$| | 4160|$^{+1610}_{-1270}$| | 25.89|$^{+0.08}_{-0.08}$| |
| COS-940214 | 6.748 | −20.4|$^{+0.2}_{-0.2}$| | 8.0|$^{+0.4}_{-0.3}$| | 0.01|$^{+0.04}_{-0.01}$| | 134.1|$^{+238.5}_{-122.8}$| | 3210|$^{+1950}_{-1790}$| | 25.87|$^{+0.10}_{-0.16}$| |
| COS-955126 | 6.813 | −21.5|$^{+0.1}_{-0.1}$| | 8.5|$^{+0.6}_{-0.3}$| | 0.02|$^{+0.06}_{-0.02}$| | 29.2|$^{+97.5}_{-27.6}$| | 1620|$^{+980}_{-650}$| | 25.73|$^{+0.10}_{-0.11}$| |
| COS-1009842 | 6.761 | −20.6|$^{+0.2}_{-0.1}$| | 8.3|$^{+0.8}_{-0.4}$| | 0.03|$^{+0.07}_{-0.02}$| | 10.4|$^{+58.1}_{-9.3}$| | 910|$^{+720}_{-500}$| | 25.65|$^{+0.15}_{-0.22}$| |
| COS-1048848 | 6.69|$^{+0.11}_{-0.08}$| | −20.7|$^{+0.1}_{-0.1}$| | 8.4|$^{+0.3}_{-0.3}$| | 0.01|$^{+0.03}_{-0.01}$| | 2.1|$^{+15.8}_{-1.8}$| | 310|$^{+300}_{-180}$| | 25.35|$^{+0.24}_{-0.33}$| |
| COS-1053257 | 6.68|$^{+0.07}_{-0.05}$| | −22.0|$^{+0.1}_{-0.1}$| | 8.5|$^{+0.8}_{-0.2}$| | 0.04|$^{+0.06}_{-0.04}$| | 5.0|$^{+42.3}_{-4.6}$| | 630|$^{+530}_{-310}$| | 25.75|$^{+0.13}_{-0.23}$| |
| COS-1099982 | 6.68|$^{+0.03}_{-0.02}$| | −21.6|$^{+0.1}_{-0.1}$| | 8.6|$^{+0.5}_{-0.3}$| | 0.01|$^{+0.03}_{-0.01}$| | 72.7|$^{+112.0}_{-54.9}$| | 2470|$^{+1080}_{-690}$| | 25.76|$^{+0.09}_{-0.07}$| |
| COS-1205190 | 7.049 | −20.9|$^{+0.2}_{-0.2}$| | 8.6|$^{+0.4}_{-0.5}$| | 0.01|$^{+0.03}_{-0.01}$| | 2.8|$^{+25.4}_{-2.4}$| | 330|$^{+470}_{-220}$| | 25.42|$^{+0.27}_{-0.40}$| |
| COS-1235751 | 6.74|$^{+0.09}_{-0.07}$| | −21.3|$^{+0.1}_{-0.1}$| | 9.4|$^{+0.5}_{-0.6}$| | 0.32|$^{+0.06}_{-0.07}$| | 1.6|$^{+9.9}_{-1.3}$| | 300|$^{+240}_{-190}$| | 25.35|$^{+0.30}_{-0.34}$| |
| XMM3-227436 | 7.093 | −22.3|$^{+0.2}_{-0.1}$| | 9.0|$^{+0.7}_{-0.4}$| | 0.04|$^{+0.09}_{-0.03}$| | 6.6|$^{+56.5}_{-6.0}$| | 930|$^{+800}_{-510}$| | 25.84|$^{+0.28}_{-0.23}$| |
| XMM3-504799 | 6.883 | −22.5|$^{+0.1}_{-0.1}$| | 9.3|$^{+0.6}_{-0.4}$| | 0.05|$^{+0.10}_{-0.04}$| | 80.1|$^{+190.9}_{-71.3}$| | 2310|$^{+1830}_{-1150}$| | 26.22|$^{+0.25}_{-0.23}$| |
Inferred properties of our z ≃ 7 sample targeted with MMT/Binospec. These properties were obtained by fitting photometry with a photoionization model using the beagle SED fitting code (Chevallard & Charlot 2016). The best-fitting values and errors are determined by calculating the median and inner 68 per cent confidence interval values marginalized over the posterior probability distribution function output by beagle. We report spectroscopic redshifts for sources with a confident (>7σ) Ly α detection and photometric redshifts otherwise.
| Source ID . | Redshift . | |$\mathrm{\mathit{ M}}_{\mathrm{UV}}^{ }$| . | log10 M* . | |$\tau _{_V}$| . | sSFR . | [O iii]+H β EW . | log10 |$\xi _{\mathrm{ion}}^{\ast }$| . |
|---|---|---|---|---|---|---|---|
| . | . | . | (M⊙) . | . | (Gyr−1) . | (Å) . | (erg−1 Hz) . |
| COS-221419 | 6.70|$^{+0.05}_{-0.04}$| | −21.0|$^{+0.1}_{-0.1}$| | 8.4|$^{+0.4}_{-0.4}$| | 0.01|$^{+0.02}_{-0.01}$| | 6.3|$^{+47.3}_{-5.8}$| | 690|$^{+760}_{-440}$| | 25.52|$^{+0.19}_{-0.25}$| |
| COS-235129 | 6.76|$^{+0.08}_{-0.07}$| | −21.4|$^{+0.1}_{-0.1}$| | 9.5|$^{+0.3}_{-1.0}$| | 0.03|$^{+0.08}_{-0.02}$| | 0.9|$^{+4.2}_{-0.7}$| | 200|$^{+230}_{-150}$| | 25.25|$^{+0.32}_{-0.39}$| |
| COS-237729 | 6.83|$^{+0.10}_{-0.09}$| | −21.1|$^{+0.1}_{-0.1}$| | 8.8|$^{+0.8}_{-0.7}$| | 0.05|$^{+0.09}_{-0.05}$| | 5.1|$^{+37.1}_{-4.5}$| | 650|$^{+530}_{-420}$| | 25.60|$^{+0.21}_{-0.29}$| |
| COS-301652 | 6.63|$^{+0.09}_{-0.03}$| | −21.2|$^{+0.1}_{-0.1}$| | 9.3|$^{+0.7}_{-1.1}$| | 0.08|$^{+0.10}_{-0.07}$| | 2.0|$^{+9.5}_{-1.5}$| | 520|$^{+330}_{-270}$| | 25.59|$^{+0.18}_{-0.25}$| |
| COS-469110 | 6.650 | −21.7|$^{+0.2}_{-0.1}$| | 8.8|$^{+0.8}_{-0.5}$| | 0.04|$^{+0.09}_{-0.04}$| | 5.3|$^{+32.4}_{-4.7}$| | 730|$^{+380}_{-320}$| | 25.58|$^{+0.22}_{-0.20}$| |
| COS-505871 | 6.67|$^{+0.12}_{-0.07}$| | −21.2|$^{+0.1}_{-0.1}$| | 10.0|$^{+0.2}_{-1.5}$| | 0.04|$^{+0.15}_{-0.03}$| | 1.2|$^{+3.4}_{-0.7}$| | 290|$^{+320}_{-190}$| | 25.50|$^{+0.24}_{-0.31}$| |
| COS-534584 | 6.60|$^{+0.01}_{-0.01}$| | −21.9|$^{+0.1}_{-0.1}$| | 9.2|$^{+0.5}_{-0.7}$| | 0.12|$^{+0.04}_{-0.06}$| | 5.7|$^{+26.2}_{-5.1}$| | 790|$^{+520}_{-390}$| | 25.50|$^{+0.20}_{-0.19}$| |
| COS-788571 | 6.884 | −21.5|$^{+0.1}_{-0.1}$| | 8.9|$^{+0.4}_{-0.3}$| | 0.02|$^{+0.06}_{-0.01}$| | 173.3|$^{+253.5}_{-124.7}$| | 3680|$^{+1940}_{-1660}$| | 25.91|$^{+0.06}_{-0.11}$| |
| COS-851423 | 6.65|$^{+0.05}_{-0.03}$| | −21.1|$^{+0.1}_{-0.1}$| | 8.3|$^{+0.7}_{-0.3}$| | 0.01|$^{+0.03}_{-0.01}$| | 9.5|$^{+55.8}_{-8.9}$| | 1030|$^{+730}_{-480}$| | 25.63|$^{+0.14}_{-0.19}$| |
| COS-854905 | 6.67|$^{+0.05}_{-0.03}$| | −21.4|$^{+0.1}_{-0.1}$| | 8.8|$^{+0.9}_{-0.6}$| | 0.02|$^{+0.05}_{-0.01}$| | 2.4|$^{+14.5}_{-2.0}$| | 560|$^{+490}_{-350}$| | 25.51|$^{+0.20}_{-0.28}$| |
| COS-856875 | 6.68|$^{+0.05}_{-0.03}$| | −21.2|$^{+0.1}_{-0.1}$| | 8.6|$^{+0.6}_{-0.5}$| | 0.01|$^{+0.03}_{-0.01}$| | 3.1|$^{+25.0}_{-2.7}$| | 540|$^{+430}_{-280}$| | 25.48|$^{+0.20}_{-0.22}$| |
| COS-862541 | 6.850 | −22.5|$^{+0.1}_{-0.1}$| | 9.1|$^{+0.4}_{-0.3}$| | 0.06|$^{+0.07}_{-0.05}$| | 155.6|$^{+193.2}_{-123.2}$| | 4160|$^{+1610}_{-1270}$| | 25.89|$^{+0.08}_{-0.08}$| |
| COS-940214 | 6.748 | −20.4|$^{+0.2}_{-0.2}$| | 8.0|$^{+0.4}_{-0.3}$| | 0.01|$^{+0.04}_{-0.01}$| | 134.1|$^{+238.5}_{-122.8}$| | 3210|$^{+1950}_{-1790}$| | 25.87|$^{+0.10}_{-0.16}$| |
| COS-955126 | 6.813 | −21.5|$^{+0.1}_{-0.1}$| | 8.5|$^{+0.6}_{-0.3}$| | 0.02|$^{+0.06}_{-0.02}$| | 29.2|$^{+97.5}_{-27.6}$| | 1620|$^{+980}_{-650}$| | 25.73|$^{+0.10}_{-0.11}$| |
| COS-1009842 | 6.761 | −20.6|$^{+0.2}_{-0.1}$| | 8.3|$^{+0.8}_{-0.4}$| | 0.03|$^{+0.07}_{-0.02}$| | 10.4|$^{+58.1}_{-9.3}$| | 910|$^{+720}_{-500}$| | 25.65|$^{+0.15}_{-0.22}$| |
| COS-1048848 | 6.69|$^{+0.11}_{-0.08}$| | −20.7|$^{+0.1}_{-0.1}$| | 8.4|$^{+0.3}_{-0.3}$| | 0.01|$^{+0.03}_{-0.01}$| | 2.1|$^{+15.8}_{-1.8}$| | 310|$^{+300}_{-180}$| | 25.35|$^{+0.24}_{-0.33}$| |
| COS-1053257 | 6.68|$^{+0.07}_{-0.05}$| | −22.0|$^{+0.1}_{-0.1}$| | 8.5|$^{+0.8}_{-0.2}$| | 0.04|$^{+0.06}_{-0.04}$| | 5.0|$^{+42.3}_{-4.6}$| | 630|$^{+530}_{-310}$| | 25.75|$^{+0.13}_{-0.23}$| |
| COS-1099982 | 6.68|$^{+0.03}_{-0.02}$| | −21.6|$^{+0.1}_{-0.1}$| | 8.6|$^{+0.5}_{-0.3}$| | 0.01|$^{+0.03}_{-0.01}$| | 72.7|$^{+112.0}_{-54.9}$| | 2470|$^{+1080}_{-690}$| | 25.76|$^{+0.09}_{-0.07}$| |
| COS-1205190 | 7.049 | −20.9|$^{+0.2}_{-0.2}$| | 8.6|$^{+0.4}_{-0.5}$| | 0.01|$^{+0.03}_{-0.01}$| | 2.8|$^{+25.4}_{-2.4}$| | 330|$^{+470}_{-220}$| | 25.42|$^{+0.27}_{-0.40}$| |
| COS-1235751 | 6.74|$^{+0.09}_{-0.07}$| | −21.3|$^{+0.1}_{-0.1}$| | 9.4|$^{+0.5}_{-0.6}$| | 0.32|$^{+0.06}_{-0.07}$| | 1.6|$^{+9.9}_{-1.3}$| | 300|$^{+240}_{-190}$| | 25.35|$^{+0.30}_{-0.34}$| |
| XMM3-227436 | 7.093 | −22.3|$^{+0.2}_{-0.1}$| | 9.0|$^{+0.7}_{-0.4}$| | 0.04|$^{+0.09}_{-0.03}$| | 6.6|$^{+56.5}_{-6.0}$| | 930|$^{+800}_{-510}$| | 25.84|$^{+0.28}_{-0.23}$| |
| XMM3-504799 | 6.883 | −22.5|$^{+0.1}_{-0.1}$| | 9.3|$^{+0.6}_{-0.4}$| | 0.05|$^{+0.10}_{-0.04}$| | 80.1|$^{+190.9}_{-71.3}$| | 2310|$^{+1830}_{-1150}$| | 26.22|$^{+0.25}_{-0.23}$| |
| Source ID . | Redshift . | |$\mathrm{\mathit{ M}}_{\mathrm{UV}}^{ }$| . | log10 M* . | |$\tau _{_V}$| . | sSFR . | [O iii]+H β EW . | log10 |$\xi _{\mathrm{ion}}^{\ast }$| . |
|---|---|---|---|---|---|---|---|
| . | . | . | (M⊙) . | . | (Gyr−1) . | (Å) . | (erg−1 Hz) . |
| COS-221419 | 6.70|$^{+0.05}_{-0.04}$| | −21.0|$^{+0.1}_{-0.1}$| | 8.4|$^{+0.4}_{-0.4}$| | 0.01|$^{+0.02}_{-0.01}$| | 6.3|$^{+47.3}_{-5.8}$| | 690|$^{+760}_{-440}$| | 25.52|$^{+0.19}_{-0.25}$| |
| COS-235129 | 6.76|$^{+0.08}_{-0.07}$| | −21.4|$^{+0.1}_{-0.1}$| | 9.5|$^{+0.3}_{-1.0}$| | 0.03|$^{+0.08}_{-0.02}$| | 0.9|$^{+4.2}_{-0.7}$| | 200|$^{+230}_{-150}$| | 25.25|$^{+0.32}_{-0.39}$| |
| COS-237729 | 6.83|$^{+0.10}_{-0.09}$| | −21.1|$^{+0.1}_{-0.1}$| | 8.8|$^{+0.8}_{-0.7}$| | 0.05|$^{+0.09}_{-0.05}$| | 5.1|$^{+37.1}_{-4.5}$| | 650|$^{+530}_{-420}$| | 25.60|$^{+0.21}_{-0.29}$| |
| COS-301652 | 6.63|$^{+0.09}_{-0.03}$| | −21.2|$^{+0.1}_{-0.1}$| | 9.3|$^{+0.7}_{-1.1}$| | 0.08|$^{+0.10}_{-0.07}$| | 2.0|$^{+9.5}_{-1.5}$| | 520|$^{+330}_{-270}$| | 25.59|$^{+0.18}_{-0.25}$| |
| COS-469110 | 6.650 | −21.7|$^{+0.2}_{-0.1}$| | 8.8|$^{+0.8}_{-0.5}$| | 0.04|$^{+0.09}_{-0.04}$| | 5.3|$^{+32.4}_{-4.7}$| | 730|$^{+380}_{-320}$| | 25.58|$^{+0.22}_{-0.20}$| |
| COS-505871 | 6.67|$^{+0.12}_{-0.07}$| | −21.2|$^{+0.1}_{-0.1}$| | 10.0|$^{+0.2}_{-1.5}$| | 0.04|$^{+0.15}_{-0.03}$| | 1.2|$^{+3.4}_{-0.7}$| | 290|$^{+320}_{-190}$| | 25.50|$^{+0.24}_{-0.31}$| |
| COS-534584 | 6.60|$^{+0.01}_{-0.01}$| | −21.9|$^{+0.1}_{-0.1}$| | 9.2|$^{+0.5}_{-0.7}$| | 0.12|$^{+0.04}_{-0.06}$| | 5.7|$^{+26.2}_{-5.1}$| | 790|$^{+520}_{-390}$| | 25.50|$^{+0.20}_{-0.19}$| |
| COS-788571 | 6.884 | −21.5|$^{+0.1}_{-0.1}$| | 8.9|$^{+0.4}_{-0.3}$| | 0.02|$^{+0.06}_{-0.01}$| | 173.3|$^{+253.5}_{-124.7}$| | 3680|$^{+1940}_{-1660}$| | 25.91|$^{+0.06}_{-0.11}$| |
| COS-851423 | 6.65|$^{+0.05}_{-0.03}$| | −21.1|$^{+0.1}_{-0.1}$| | 8.3|$^{+0.7}_{-0.3}$| | 0.01|$^{+0.03}_{-0.01}$| | 9.5|$^{+55.8}_{-8.9}$| | 1030|$^{+730}_{-480}$| | 25.63|$^{+0.14}_{-0.19}$| |
| COS-854905 | 6.67|$^{+0.05}_{-0.03}$| | −21.4|$^{+0.1}_{-0.1}$| | 8.8|$^{+0.9}_{-0.6}$| | 0.02|$^{+0.05}_{-0.01}$| | 2.4|$^{+14.5}_{-2.0}$| | 560|$^{+490}_{-350}$| | 25.51|$^{+0.20}_{-0.28}$| |
| COS-856875 | 6.68|$^{+0.05}_{-0.03}$| | −21.2|$^{+0.1}_{-0.1}$| | 8.6|$^{+0.6}_{-0.5}$| | 0.01|$^{+0.03}_{-0.01}$| | 3.1|$^{+25.0}_{-2.7}$| | 540|$^{+430}_{-280}$| | 25.48|$^{+0.20}_{-0.22}$| |
| COS-862541 | 6.850 | −22.5|$^{+0.1}_{-0.1}$| | 9.1|$^{+0.4}_{-0.3}$| | 0.06|$^{+0.07}_{-0.05}$| | 155.6|$^{+193.2}_{-123.2}$| | 4160|$^{+1610}_{-1270}$| | 25.89|$^{+0.08}_{-0.08}$| |
| COS-940214 | 6.748 | −20.4|$^{+0.2}_{-0.2}$| | 8.0|$^{+0.4}_{-0.3}$| | 0.01|$^{+0.04}_{-0.01}$| | 134.1|$^{+238.5}_{-122.8}$| | 3210|$^{+1950}_{-1790}$| | 25.87|$^{+0.10}_{-0.16}$| |
| COS-955126 | 6.813 | −21.5|$^{+0.1}_{-0.1}$| | 8.5|$^{+0.6}_{-0.3}$| | 0.02|$^{+0.06}_{-0.02}$| | 29.2|$^{+97.5}_{-27.6}$| | 1620|$^{+980}_{-650}$| | 25.73|$^{+0.10}_{-0.11}$| |
| COS-1009842 | 6.761 | −20.6|$^{+0.2}_{-0.1}$| | 8.3|$^{+0.8}_{-0.4}$| | 0.03|$^{+0.07}_{-0.02}$| | 10.4|$^{+58.1}_{-9.3}$| | 910|$^{+720}_{-500}$| | 25.65|$^{+0.15}_{-0.22}$| |
| COS-1048848 | 6.69|$^{+0.11}_{-0.08}$| | −20.7|$^{+0.1}_{-0.1}$| | 8.4|$^{+0.3}_{-0.3}$| | 0.01|$^{+0.03}_{-0.01}$| | 2.1|$^{+15.8}_{-1.8}$| | 310|$^{+300}_{-180}$| | 25.35|$^{+0.24}_{-0.33}$| |
| COS-1053257 | 6.68|$^{+0.07}_{-0.05}$| | −22.0|$^{+0.1}_{-0.1}$| | 8.5|$^{+0.8}_{-0.2}$| | 0.04|$^{+0.06}_{-0.04}$| | 5.0|$^{+42.3}_{-4.6}$| | 630|$^{+530}_{-310}$| | 25.75|$^{+0.13}_{-0.23}$| |
| COS-1099982 | 6.68|$^{+0.03}_{-0.02}$| | −21.6|$^{+0.1}_{-0.1}$| | 8.6|$^{+0.5}_{-0.3}$| | 0.01|$^{+0.03}_{-0.01}$| | 72.7|$^{+112.0}_{-54.9}$| | 2470|$^{+1080}_{-690}$| | 25.76|$^{+0.09}_{-0.07}$| |
| COS-1205190 | 7.049 | −20.9|$^{+0.2}_{-0.2}$| | 8.6|$^{+0.4}_{-0.5}$| | 0.01|$^{+0.03}_{-0.01}$| | 2.8|$^{+25.4}_{-2.4}$| | 330|$^{+470}_{-220}$| | 25.42|$^{+0.27}_{-0.40}$| |
| COS-1235751 | 6.74|$^{+0.09}_{-0.07}$| | −21.3|$^{+0.1}_{-0.1}$| | 9.4|$^{+0.5}_{-0.6}$| | 0.32|$^{+0.06}_{-0.07}$| | 1.6|$^{+9.9}_{-1.3}$| | 300|$^{+240}_{-190}$| | 25.35|$^{+0.30}_{-0.34}$| |
| XMM3-227436 | 7.093 | −22.3|$^{+0.2}_{-0.1}$| | 9.0|$^{+0.7}_{-0.4}$| | 0.04|$^{+0.09}_{-0.03}$| | 6.6|$^{+56.5}_{-6.0}$| | 930|$^{+800}_{-510}$| | 25.84|$^{+0.28}_{-0.23}$| |
| XMM3-504799 | 6.883 | −22.5|$^{+0.1}_{-0.1}$| | 9.3|$^{+0.6}_{-0.4}$| | 0.05|$^{+0.10}_{-0.04}$| | 80.1|$^{+190.9}_{-71.3}$| | 2310|$^{+1830}_{-1150}$| | 26.22|$^{+0.25}_{-0.23}$| |
Overall, we find a diverse range of galaxy properties within our sample as illustrated in Fig. 6. In particular, the inferred [O iii]+H β EWs range from 200 to 4000 Å and the sSFRs span ∼1–150 Gyr−1. Galaxies with inferred [O iii]+H β EW > 800 Å (and therefore similar to those in the RB16 sample) tend to possess very large sSFRs (≳30 Gyr−1), consistent with expectations of galaxies experiencing a recent strong upturn or burst in star formation activity (Atek et al. 2011; Amorín et al. 2015; Maseda et al. 2018; Tang et al. 2019; E21). As expected (Chevallard et al. 2018; Tang et al. 2019), we also find that |$\xi _{\mathrm{ion}}^{\ast }$| tends to increase with [O iii]+H β EW among our sample where sources with [O iii]+H β EW > 800 Å are inferred to produce ionizing photons 2.2× as efficiently as those with weaker [O iii]+H β. The median inferred [O iii]+H β EW of all sources is 710 Å, suggesting that our sample is reasonably well representative of the global z ≃ 7 galaxy population (typical EW = 692 Å; E21).
![Spectral energy distributions of a subset of z ≃ 7 sources in our spectroscopic sample. We select sources to display the variety of absolute UV magnitudes, $\mathrm{\mathit{ M}}_{\mathrm{UV}}^{ }$, and inferred [O iii]+H β EWs (generally increasing to the right) in this sample. In each panel, the median fit beagle SED model is overlaid in black with grey shading showing the inner 68 per cent confidence interval from the posterior output by beagle. Blue diamonds show the fitted photometry (with 2σ upper limits in cases of non-detections) while the red empty circles show the median model photometry from beagle with errors enclosing the 68 per cent confidence interval. We only show model photometry for bands used in the fitting process where we ignore bands impacted by Ly α emission or bluewards of the Ly α break for sources with a >7σ Ly α detection.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/502/4/10.1093_mnras_stab432/1/m_stab432fig6.jpeg?Expires=1749866341&Signature=Ze4exyBc3l4LADzHt5IFtkCAQJr1Y~c2CH5c~QXKP-1i~q8UaR4BvgjN0wCh9G2WK2bCOCGAE3sp2vJBMVd1n7YGnB9xNZJ3VpPEr5d1CwDnqhcO-q1YNMFIdUjFBcGg7zIkyJQihcvRyL2gzeQWYeHcaRbRmMQIdKuzdTFu9zOxUh5jG-f7Na~D3Yk1MZ1XFqenAJyR1CVwqyisUeZsSURFYJan4rRRduMy-uXTk7Ov17isoaTFTP38SlbaEfw7PP48UunG4DoPs828W-0I9fUf6rRBcRmyGghYjcfwi~HZrC118tF-pzP8Jh~x0Ze-IZ8qlfK6XGQS3q4Uc~8Ceg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Spectral energy distributions of a subset of z ≃ 7 sources in our spectroscopic sample. We select sources to display the variety of absolute UV magnitudes, |$\mathrm{\mathit{ M}}_{\mathrm{UV}}^{ }$|, and inferred [O iii]+H β EWs (generally increasing to the right) in this sample. In each panel, the median fit beagle SED model is overlaid in black with grey shading showing the inner 68 per cent confidence interval from the posterior output by beagle. Blue diamonds show the fitted photometry (with 2σ upper limits in cases of non-detections) while the red empty circles show the median model photometry from beagle with errors enclosing the 68 per cent confidence interval. We only show model photometry for bands used in the fitting process where we ignore bands impacted by Ly α emission or bluewards of the Ly α break for sources with a >7σ Ly α detection.
The absolute UV magnitudes of our z ≃ 7 targets also span −22.5 ≤ |$\mathrm{M}_{\mathrm{UV}}^{ }$| |$\le \, -$|20.4 that corresponds to a luminosity range of 0.8–5.8 L|$_{\mathrm{UV}}^{\ast }$| when adopting the z ≃ 7 |$\mathrm{M_{UV}^{\ast }}$| value12 of −20.6 from Bowler et al. (2017). Our survey is therefore capturing a subset of the most luminous reionization-era galaxies. Furthermore, over half the galaxies in our z ≃ 7 sample are >2 L|$_{\mathrm{UV}}^{\ast }$|, a population that has been largely missed by previous spectroscopy targeting this epoch. Considering the published literature of z ≃ 7 Ly α observations from Fontana et al. (2010), Pentericci et al. (2011, 2014), Vanzella et al. (2011), and Schenker et al. (2012, 2014), only 4 of 64 targeted galaxies were >2 L|$_{\mathrm{UV}}^{\ast }$|. The only previous spectroscopic z ≃ 7 studies with a comparable luminosity range to our sample are Ono et al. (2012) and Furusawa et al. (2016). Even so, our sample is at least twice as large as either of these previous studies.
The bright UV luminosities of our z ≃ 7 targets suggest that they are among the most massive galaxies present in the reionization era, given both clustering measurements (Barone-Nugent et al. 2014) as well as inferences of the |$\mathrm{\mathit{ M}}_{\mathrm{UV}}^{ }$|–M* relation (Song et al. 2016a). Stellar masses derived from our SED fitting procedure suggest a similar picture. Most of our z ≃ 7 galaxies are inferred to have log10(M*/M⊙) ∼ 9–10, which is significantly more massive than fainter z ≃ 7 galaxies identified over the GOODS fields (E21). Therefore, in what follows, we interchangeably use the terms ‘bright’ and ‘massive’ when describing our sample.
3 ANALYSIS
In this section, we first investigate how Ly α detectability correlates with [O iii]+H β emission (and hence sSFR) within our sample of 22 bright (L|$_{\mathrm{UV}}^{}\, \simeq$| 1–6 L|$_{\mathrm{UV}}^{\ast }$|) z ≃ 7 galaxies (Section 3.1). We then quantify evolution in the Ly α EW distribution of bright galaxies between z ≃ 6–7 to test whether our results are consistent with accelerated reionization around massive z ≃ 7 systems (Section 3.2). Finally, we investigate the spatial separations of our z ≃ 7 Ly α emitters to identify any potentially large ionized bubbles within our observed fields (Section 3.3).
3.1 The Connection between [O iii]+H β and Ly α at z ≃ 7
The number of Ly α detections among UV-continuum selected galaxies in the reionization era (z ≳ 7) has grown rapidly over the past decade (e.g. Vanzella et al. 2011; Ono et al. 2012; Schenker et al. 2012; Shibuya et al. 2012; Finkelstein et al. 2013; Pentericci et al. 2014, 2018; Song et al. 2016b; Jung et al. 2017, 2018; Castellano et al. 2018; Larson et al. 2018; Hoag et al. 2019; Fuller et al. 2020; Tilvi et al. 2020). One of the most surprising results from these campaigns was the 100 per cent Ly α detection rate among the four brightest (L|$_{\mathrm{UV}}^{}$| = 3–4 L|$_{\mathrm{UV}}^{\ast }$|) z > 7 galaxies selected over the CANDELS fields (i.e. the RB16 sample). While this led some to suggest that massive reionization-era systems may trace accelerated sites of reionization (Zitrin et al. 2015; Stark et al. 2017), this interpretation was complicated by the fact that the RB16 galaxies were selected to not only be very massive, but also to possess strong [O iii]+H β emission (EW > 800 Å). Such strong nebular emission signals the presence of intense radiation fields likely powered by a recent rapid upturn in star formation activity (i.e. high sSFR; Tang et al. 2019; E21). This therefore raises the possibility that the Ly α detections within the RB16 sample were not necessarily due to large ionized regions, but perhaps instead driven by physics internal to each of the four galaxies (Tang et al. 2019).
To better understand the origin of strong Ly α from the RB16 sample, we here analyse the Ly α constraints from our larger sample (N = 22) of similarly massive (L|$_{\mathrm{UV}}^{}\, \simeq$| 1–6 L|$_{\mathrm{UV}}^{\ast }$|) z ≃ 7 galaxies possessing a wide range of inferred [O iii]+H β EWs (200–4000 Å). This diversity of nebular emission strengths enables us to explore how the sSFRs of massive reionization-era galaxies impact their Ly α detectability. To this end, we divide our sample into galaxies with strong (EW > 800 Å) versus more moderate (EW = 200–800 Å) inferred [O iii]+H β emission. By this classification, galaxies in the strong [O iii]+H β emitter sub-sample will possess large sSFRs comparable to those in the RB16 sample while the moderate [O iii]+H β emitters are more representative of the typical massive z ≃ 7 population (E21). Here, we do not include COS-469110 in either sub-sample given its tentative NV detection (Fig. 4) that is a likely signpost of significant AGN activity. We do, however, discuss the potential implications of this unique source below.
An essential question for interpreting the RB16 result is whether our z ≃ 7 targets with strong [O iii]+H β emission show an increased Ly α detection rate. From our observations, we confidently (>7σ) detect Ly α in seven of nine (78 per cent) galaxies with strong [O iii]+H β emission, yet in only one of 12 (8 per cent) galaxies with more moderate [O iii]+H β (see Fig. 7). Our results therefore suggest that Ly α is indeed more easily detectable from massive z ≃ 7 galaxies possessing very large sSFRs (≳30 Gyr−1). We note that the two strong [O iii]+H β emitters in our sample that went undetected may exhibit prominent Ly α emission that is masked by skylines. This possibility is accounted for in our analysis below.
![Plot showing the inferred [O iii]+H β EWs and measured rest-UV slopes for each of our 22 massive (L$_{\mathrm{UV}}^{}\, \simeq$ 1–6 L$_{\mathrm{UV}}^{\ast }$) z ≃ 7 systems. We mark those with and without confident (>7σ) Ly α detections as shown in the legend. As indicated by the prominence of blue markers to the right of the plot, we confidently detect Ly α at a much higher rate from strong [O iii]+H β emitters (>800 Å EW; 78 per cent detection rate) than more moderate [O iii]+H β emitters (200–800 Å EW; 8 per cent detection rate). Our results therefore suggest that Ly α is more readily detectable from massive z ≃ 7 galaxies experiencing a rapid upturn in star formation activity (i.e. high sSFR). We also use a red star to show COS-469110 which likely harbors an AGN given its tentative NV detection (see Fig. 4).](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/502/4/10.1093_mnras_stab432/1/m_stab432fig7.jpeg?Expires=1749866341&Signature=Zdk8GHP5CXTdhBXuCYc8HLyqvZ~IN-sQ4j-P7hjO8whIZXSso14ogaa3gZM~i9weM47Fg2vid7HE7B5PVYQPGbjBTiJjB~kB7oAK6d4eV23MtnCAY-BipDDVbwNoXYv5yPFztU2SRqE7MJFztkRe9Mjx5sLmnufn7WbowuzwXzP3nBw~j47MdKKWJjuJnt6QshIafDkPHL0tlJcGjlC6YfljnHXgXU1E~3e99y1iwOxB8YBT~YrLYPgKXfRLzt~dPUusnGlIF3n~XZVuVmgRnJqeT8OoUaJ55mUwznJp2DQW1n5oYQ-3c0Xl2TyAZgL0ERS4mn9ziA7TwjQGr8b7XA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Plot showing the inferred [O iii]+H β EWs and measured rest-UV slopes for each of our 22 massive (L|$_{\mathrm{UV}}^{}\, \simeq$| 1–6 L|$_{\mathrm{UV}}^{\ast }$|) z ≃ 7 systems. We mark those with and without confident (>7σ) Ly α detections as shown in the legend. As indicated by the prominence of blue markers to the right of the plot, we confidently detect Ly α at a much higher rate from strong [O iii]+H β emitters (>800 Å EW; 78 per cent detection rate) than more moderate [O iii]+H β emitters (200–800 Å EW; 8 per cent detection rate). Our results therefore suggest that Ly α is more readily detectable from massive z ≃ 7 galaxies experiencing a rapid upturn in star formation activity (i.e. high sSFR). We also use a red star to show COS-469110 which likely harbors an AGN given its tentative NV detection (see Fig. 4).
We find that massive z ≃ 7 galaxies with strong [O iii]+H β emission typically exhibit much stronger Ly α (4.7× higher EW) relative to more moderate [O iii]+H β emitters when comparing the best-fitting μEW values for each sub-sample (see top panel of Fig. 8). Therefore, while uncertainties remain significant,15 our results suggest that galaxy sSFRs play a significant role in regulating Ly α emission from massive reionization-era galaxies. The recent results of Castellano et al. (2017) provide additional empirical support of this picture. In their study, they find that the stacked IRAC colours of z ≃ 6.8 Ly α emitters selected over the CANDELS fields indicate much stronger [O iii]+H β emission relative to galaxies that went undetected in Ly α. This is consistent with our results using [O iii]+H β EWs inferred for individual (and generally more massive) galaxies.
![Comparison of the inferred Ly α EW distributions for our z ≃ 7 sample as a function of physical properties. In the top panel, we compare the Ly α EW distributions for moderate (orange dashed curve) versus strong [O iii]+H β emitters (solid blue). In the bottom panel, we compare the inferred Ly α EW distributions for our z ≃ 7 galaxies with rest-UV slopes of β > −2.1 (dashed orange) versus the bluest sources with β < −2.1 (solid blue curve). These plots demonstrate that massive z ≃ 7 galaxies with strong [O iii]+H β emission and/or very blue rest-UV slopes show evidence for systematically higher EW Ly α emission.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/502/4/10.1093_mnras_stab432/1/m_stab432fig8.jpeg?Expires=1749866341&Signature=jswXgsRUIp~oScsgKX0EBDPgOXfLKh40L3boagXh6O7nPZiNi2yK9hZAVyWmowGyMkfvrgNvB5CmyhwPfQUlQGu6PbkUAs-G100w82UkPnKG6RsrvkicvCEqHNzH7tNMUvVIIhLAqK59G2cK6TFEOeQdZRxnHcX0q8Kuqu8NYINtPtx6aqaC3bTnb-epspeR2U9FS3vvXa2X6TC1wUu7EERcXs2d78KlARc318QTMfD1hXuVd363RFt1-ayUnMqt24dorUGJRmU3dj25q0A-rn5oxs-tJta6mTPnF0p1vgn8ueC1gSMhwZwlMOjzibjPlOmbdsIG8QAnN1Yg4UhkoA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Comparison of the inferred Ly α EW distributions for our z ≃ 7 sample as a function of physical properties. In the top panel, we compare the Ly α EW distributions for moderate (orange dashed curve) versus strong [O iii]+H β emitters (solid blue). In the bottom panel, we compare the inferred Ly α EW distributions for our z ≃ 7 galaxies with rest-UV slopes of β > −2.1 (dashed orange) versus the bluest sources with β < −2.1 (solid blue curve). These plots demonstrate that massive z ≃ 7 galaxies with strong [O iii]+H β emission and/or very blue rest-UV slopes show evidence for systematically higher EW Ly α emission.
Interestingly, two sources in our sample, COS-469100 and COS-1205190, both show fairly strong Ly α (EW = 15–29 Å), yet possess only moderate [O iii]+H β emission (EW = 200–800 Å). It is therefore of interest to explore whether there are other reasons to believe that these two sources may still possess unusually powerful radiation fields as expected in very large sSFR systems. Indeed, the tentative NV detection within COS-469110 (see Fig. 4) signals that this source likely harbors an AGN. We also find reason to believe that COS-1205190 may be powering an intense radiation field given its extremely blue rest-UV slope of β = −3.44 ± 1.03. Such a blue slope (the bluest in our sample; Table 6) is consistent with not only extremely low dust content, but also very low metallicity. This possible dearth of metals in COS-1205190 would naturally lead to relatively weak [O iii] emission16 even if it recently experienced a burst of star formation activity (sSFR ≳ 30 Gyr−1) as typically inferred for the strong [O iii]+H β emitters in our sample. If our above suspicions of COS-469100 and COS-1205190 are correct, all nine of our z ≃ 7 Ly α detections are from sources with intense radiation fields and we would infer that such systems typically exhibit substantially stronger (|$5.9_{-3.1}^{+4.3} \times $| higher EW) Ly α relative to the more typical massive z ≃ 7 population that has moderate [O iii]+H β (EW = 200–800 Å), moderately low metallicity (∼0.2 Z⊙; E21), and emission dominated by star formation.
Compiled information on our z ≃ 7 sample connecting their physical properties (i.e. [O iii]+H β EWs and rest-UV slopes) to their Ly α EWs. For sources without a Ly α detection, we quote the 7σ limiting EW in skyline-free regions.
| Source ID . | Ly α EW . | [O iii]+H β EW . | β . |
|---|---|---|---|
| . | (Å) . | (Å) . | . |
| COS-221419 | <11.8 | 690|$^{+760}_{-440}$| | −2.80 ± 0.62 |
| COS-235129 | <7.6 | 200|$^{+230}_{-150}$| | −2.09 ± 0.47 |
| COS-237729 | <12.9 | 650|$^{+530}_{-420}$| | −1.92 ± 0.34 |
| COS-301652 | <9.8 | 520|$^{+330}_{-270}$| | −2.08 ± 0.09 |
| COS-469110 | 12.5 ± 4.3 | 730|$^{+380}_{-320}$| | −1.69 ± 0.50 |
| COS-505871 | <11.5 | 290|$^{+320}_{-190}$| | −2.23 ± 0.62 |
| COS-534584 | <5.2 | 790|$^{+520}_{-390}$| | −1.76 ± 0.29 |
| COS-788571 | 30.6 ± 3.9 | 3680|$^{+1940}_{-1660}$| | −2.11 ± 0.53 |
| COS-851423 | <7.5 | 1030|$^{+730}_{-480}$| | −2.64 ± 0.38 |
| COS-854905 | <6.4 | 560|$^{+490}_{-350}$| | −1.95 ± 0.24 |
| COS-856875 | <20.0 | 540|$^{+430}_{-280}$| | −2.07 ± 0.37 |
| COS-862541 | 11.8 ± 2.7 | 4160|$^{+1610}_{-1270}$| | −1.90 ± 0.43 |
| COS-940214 | 43.1 ± 14.7 | 3210|$^{+1950}_{-1790}$| | −2.77 ± 0.54 |
| COS-955126 | 12.3 ± 2.5 | 1620|$^{+980}_{-650}$| | −2.44 ± 0.13 |
| COS-1009842 | 41.6 ± 9.5 | 910|$^{+720}_{-500}$| | −2.61 ± 0.44 |
| COS-1048848 | <11.2 | 310|$^{+300}_{-180}$| | −2.43 ± 0.35 |
| COS-1053257 | <3.2 | 630|$^{+530}_{-310}$| | −2.02 ± 0.20 |
| COS-1099982 | <12.5 | 2470|$^{+1080}_{-690}$| | −1.83 ± 0.08 |
| COS-1205190 | 28.8 ± 6.0 | 330|$^{+470}_{-220}$| | −3.44 ± 1.03 |
| COS-1235751 | <17.4 | 300|$^{+240}_{-190}$| | −1.10 ± 0.30 |
| XMM3-227436 | 15.0 ± 3.2 | 930|$^{+800}_{-510}$| | −1.85 ± 0.27 |
| XMM3-504799 | 3.7 ± 0.8 | 2310|$^{+1830}_{-1150}$| | −2.02 ± 0.42 |
| Source ID . | Ly α EW . | [O iii]+H β EW . | β . |
|---|---|---|---|
| . | (Å) . | (Å) . | . |
| COS-221419 | <11.8 | 690|$^{+760}_{-440}$| | −2.80 ± 0.62 |
| COS-235129 | <7.6 | 200|$^{+230}_{-150}$| | −2.09 ± 0.47 |
| COS-237729 | <12.9 | 650|$^{+530}_{-420}$| | −1.92 ± 0.34 |
| COS-301652 | <9.8 | 520|$^{+330}_{-270}$| | −2.08 ± 0.09 |
| COS-469110 | 12.5 ± 4.3 | 730|$^{+380}_{-320}$| | −1.69 ± 0.50 |
| COS-505871 | <11.5 | 290|$^{+320}_{-190}$| | −2.23 ± 0.62 |
| COS-534584 | <5.2 | 790|$^{+520}_{-390}$| | −1.76 ± 0.29 |
| COS-788571 | 30.6 ± 3.9 | 3680|$^{+1940}_{-1660}$| | −2.11 ± 0.53 |
| COS-851423 | <7.5 | 1030|$^{+730}_{-480}$| | −2.64 ± 0.38 |
| COS-854905 | <6.4 | 560|$^{+490}_{-350}$| | −1.95 ± 0.24 |
| COS-856875 | <20.0 | 540|$^{+430}_{-280}$| | −2.07 ± 0.37 |
| COS-862541 | 11.8 ± 2.7 | 4160|$^{+1610}_{-1270}$| | −1.90 ± 0.43 |
| COS-940214 | 43.1 ± 14.7 | 3210|$^{+1950}_{-1790}$| | −2.77 ± 0.54 |
| COS-955126 | 12.3 ± 2.5 | 1620|$^{+980}_{-650}$| | −2.44 ± 0.13 |
| COS-1009842 | 41.6 ± 9.5 | 910|$^{+720}_{-500}$| | −2.61 ± 0.44 |
| COS-1048848 | <11.2 | 310|$^{+300}_{-180}$| | −2.43 ± 0.35 |
| COS-1053257 | <3.2 | 630|$^{+530}_{-310}$| | −2.02 ± 0.20 |
| COS-1099982 | <12.5 | 2470|$^{+1080}_{-690}$| | −1.83 ± 0.08 |
| COS-1205190 | 28.8 ± 6.0 | 330|$^{+470}_{-220}$| | −3.44 ± 1.03 |
| COS-1235751 | <17.4 | 300|$^{+240}_{-190}$| | −1.10 ± 0.30 |
| XMM3-227436 | 15.0 ± 3.2 | 930|$^{+800}_{-510}$| | −1.85 ± 0.27 |
| XMM3-504799 | 3.7 ± 0.8 | 2310|$^{+1830}_{-1150}$| | −2.02 ± 0.42 |
Compiled information on our z ≃ 7 sample connecting their physical properties (i.e. [O iii]+H β EWs and rest-UV slopes) to their Ly α EWs. For sources without a Ly α detection, we quote the 7σ limiting EW in skyline-free regions.
| Source ID . | Ly α EW . | [O iii]+H β EW . | β . |
|---|---|---|---|
| . | (Å) . | (Å) . | . |
| COS-221419 | <11.8 | 690|$^{+760}_{-440}$| | −2.80 ± 0.62 |
| COS-235129 | <7.6 | 200|$^{+230}_{-150}$| | −2.09 ± 0.47 |
| COS-237729 | <12.9 | 650|$^{+530}_{-420}$| | −1.92 ± 0.34 |
| COS-301652 | <9.8 | 520|$^{+330}_{-270}$| | −2.08 ± 0.09 |
| COS-469110 | 12.5 ± 4.3 | 730|$^{+380}_{-320}$| | −1.69 ± 0.50 |
| COS-505871 | <11.5 | 290|$^{+320}_{-190}$| | −2.23 ± 0.62 |
| COS-534584 | <5.2 | 790|$^{+520}_{-390}$| | −1.76 ± 0.29 |
| COS-788571 | 30.6 ± 3.9 | 3680|$^{+1940}_{-1660}$| | −2.11 ± 0.53 |
| COS-851423 | <7.5 | 1030|$^{+730}_{-480}$| | −2.64 ± 0.38 |
| COS-854905 | <6.4 | 560|$^{+490}_{-350}$| | −1.95 ± 0.24 |
| COS-856875 | <20.0 | 540|$^{+430}_{-280}$| | −2.07 ± 0.37 |
| COS-862541 | 11.8 ± 2.7 | 4160|$^{+1610}_{-1270}$| | −1.90 ± 0.43 |
| COS-940214 | 43.1 ± 14.7 | 3210|$^{+1950}_{-1790}$| | −2.77 ± 0.54 |
| COS-955126 | 12.3 ± 2.5 | 1620|$^{+980}_{-650}$| | −2.44 ± 0.13 |
| COS-1009842 | 41.6 ± 9.5 | 910|$^{+720}_{-500}$| | −2.61 ± 0.44 |
| COS-1048848 | <11.2 | 310|$^{+300}_{-180}$| | −2.43 ± 0.35 |
| COS-1053257 | <3.2 | 630|$^{+530}_{-310}$| | −2.02 ± 0.20 |
| COS-1099982 | <12.5 | 2470|$^{+1080}_{-690}$| | −1.83 ± 0.08 |
| COS-1205190 | 28.8 ± 6.0 | 330|$^{+470}_{-220}$| | −3.44 ± 1.03 |
| COS-1235751 | <17.4 | 300|$^{+240}_{-190}$| | −1.10 ± 0.30 |
| XMM3-227436 | 15.0 ± 3.2 | 930|$^{+800}_{-510}$| | −1.85 ± 0.27 |
| XMM3-504799 | 3.7 ± 0.8 | 2310|$^{+1830}_{-1150}$| | −2.02 ± 0.42 |
| Source ID . | Ly α EW . | [O iii]+H β EW . | β . |
|---|---|---|---|
| . | (Å) . | (Å) . | . |
| COS-221419 | <11.8 | 690|$^{+760}_{-440}$| | −2.80 ± 0.62 |
| COS-235129 | <7.6 | 200|$^{+230}_{-150}$| | −2.09 ± 0.47 |
| COS-237729 | <12.9 | 650|$^{+530}_{-420}$| | −1.92 ± 0.34 |
| COS-301652 | <9.8 | 520|$^{+330}_{-270}$| | −2.08 ± 0.09 |
| COS-469110 | 12.5 ± 4.3 | 730|$^{+380}_{-320}$| | −1.69 ± 0.50 |
| COS-505871 | <11.5 | 290|$^{+320}_{-190}$| | −2.23 ± 0.62 |
| COS-534584 | <5.2 | 790|$^{+520}_{-390}$| | −1.76 ± 0.29 |
| COS-788571 | 30.6 ± 3.9 | 3680|$^{+1940}_{-1660}$| | −2.11 ± 0.53 |
| COS-851423 | <7.5 | 1030|$^{+730}_{-480}$| | −2.64 ± 0.38 |
| COS-854905 | <6.4 | 560|$^{+490}_{-350}$| | −1.95 ± 0.24 |
| COS-856875 | <20.0 | 540|$^{+430}_{-280}$| | −2.07 ± 0.37 |
| COS-862541 | 11.8 ± 2.7 | 4160|$^{+1610}_{-1270}$| | −1.90 ± 0.43 |
| COS-940214 | 43.1 ± 14.7 | 3210|$^{+1950}_{-1790}$| | −2.77 ± 0.54 |
| COS-955126 | 12.3 ± 2.5 | 1620|$^{+980}_{-650}$| | −2.44 ± 0.13 |
| COS-1009842 | 41.6 ± 9.5 | 910|$^{+720}_{-500}$| | −2.61 ± 0.44 |
| COS-1048848 | <11.2 | 310|$^{+300}_{-180}$| | −2.43 ± 0.35 |
| COS-1053257 | <3.2 | 630|$^{+530}_{-310}$| | −2.02 ± 0.20 |
| COS-1099982 | <12.5 | 2470|$^{+1080}_{-690}$| | −1.83 ± 0.08 |
| COS-1205190 | 28.8 ± 6.0 | 330|$^{+470}_{-220}$| | −3.44 ± 1.03 |
| COS-1235751 | <17.4 | 300|$^{+240}_{-190}$| | −1.10 ± 0.30 |
| XMM3-227436 | 15.0 ± 3.2 | 930|$^{+800}_{-510}$| | −1.85 ± 0.27 |
| XMM3-504799 | 3.7 ± 0.8 | 2310|$^{+1830}_{-1150}$| | −2.02 ± 0.42 |
The strong Ly α emission (EW = 29 Å) from our bluest source (COS-1205190) also motivates an investigation into how the observed Ly α EW is related to the rest-UV slope among massive z ≃ 7 galaxies. While it has been shown that Ly α becomes stronger in z ≃ 4 galaxies from β = −1.4 to β = −1.8 (Stark et al. 2010), it is not necessarily clear that such a prominent trend would continue to exist when the bulk of the galaxy population is very blue (β ≲ −2) as is the case at z ≃ 7 (Bouwens et al. 2014). To test for any such association, we split our sample (again ignoring COS-469110) into sources with β < −2.1 and β > −2.1, where we adopt a dividing point equal to the approximate median rest-UV slope of the entire sample (β = −2.07). Following the Bayesian approach used for the [O iii]+H β versus Ly α analysis above, we find that our bluest galaxies (−3.4 < β < −2.1) typically exhibit much stronger Ly α (|$4.0^{+4.1}_{-1.9} \times$| higher EW) relative to those more representative of the massive z ≃ 7 population (−1.1 < β < −2.1; E21) as illustrated in the bottom panel of Fig. 8. This trend likely reflects lower dust content (and therefore relatively little Ly α attenuation) within bluer sources as is the case at lower redshifts (e.g. Shapley et al. 2003; Pentericci et al. 2009; Kornei et al. 2010; Stark et al. 2010; Hathi et al. 2016; Trainor et al. 2016). Notably, our z ≃ 7 galaxies also follow a similar behaviour to the z ≃ 6 sources presented in De Barros et al. (2017) where our strongest Ly α emitters (EW > 25 Å) all possess very blue rest-UV slopes (β < −2.1; see Table 6) likely signaling particularly low dust content along the line of sight.
The overall picture emerging from these results is that the observed Ly α EW is substantially enhanced by a recent strong burst of star formation (or presence of an AGN) among massive reionization-era galaxies. Low dust content along the line of sight will further enhance visible Ly α similar to trends at lower redshifts. While we defer a more detailed physical interpretation until Section 4, we emphasize that our results demonstrate that Ly α can be detected with high success rate in massive z ≃ 7 galaxies possessing strong [O iii]+H β emission (>800 Å EW) and very blue rest-UV slopes (β < −2.1).
3.2 Evolution in the Ly α EW distribution of massive galaxies from z ≃ 6 to z ≃ 7
Over the past decade, a variety of observational campaigns have presented evidence that the IGM rapidly transitions from highly ionized at z ≃ 6 (xH i ∼ 10 per cent; e.g. McGreer et al. 2015) to substantially neutral at z ≃ 7 (xH i ∼ 50 per cent; e.g. Greig & Mesinger 2017; Zheng et al. 2017; Davies et al. 2018; Wang et al. 2020; Whitler et al. 2020). Such a rapid transition is naturally expected to reduce Ly α transmission between z ≃ 6–7 for the typical galaxy population. This is perhaps evidenced by the factor of ∼10 decline in the strong Ly α (EW > 25 Å) emitter fraction among the low-mass lensed population (∼0.1 L|$_{\mathrm{UV}}^{\ast }$|; Hoag et al. 2019; Fuller et al. 2020). One of the primary goals of our spectroscopic campaign is to build a sufficiently large sample of very bright z ≃ 6–7 galaxies to explicitly test whether Ly α transmission from massive systems is evolving at a slower pace, as would be expected if they commonly reside in large ionized bubbles (e.g. Wyithe & Loeb 2005; McQuinn et al. 2007; Weinberger et al. 2018). While this campaign is still ongoing, we here report our current constraints on the Ly α EW distribution evolution between z ≃ 6–7 using our sample of 30 and 22 massive (L|$_{\mathrm{UV}}^{}\, \simeq$| 1–6 L|$_{\mathrm{UV}}^{\ast }$|) galaxies at z ≃ 6 and z ≃ 7, respectively.
At each redshift, we infer the Ly α EW distribution following the Bayesian approach presented in Section 3.1 where we assume a lognormal function parametrized by a median EW, μEW, and standard deviation, σEW. Here, we also add a third parameter, A, quantifying the fraction of sources with Ly α EW > 0 Å because some galaxies may not show any Ly α in emission (e.g. Schenker et al. 2014; Mason et al. 2018a). Using the same grid for μEW and σEW as in Section 3.1 and allowing A to vary between 0 and 1 (with a spacing of 0.01), we calculate the probability for each set of parameters P(μEW, σEW, A) as in equation (1).
The Ly α EW distribution of our 22 massive z ≃ 7 galaxies is well characterized by a lognormal distribution with a median EW μEW = |$11.0^{+3.8}_{-3.2}$| Å and standard deviation σEW = |$0.37^{+0.15}_{-0.10}$| dex. The fraction of EW > 0 Å sources is found to be very high (A = |$0.88^{+0.09}_{-0.15}$|) with a best-fitting value of A = 1, suggesting that a large majority of massive z ≃ 7 galaxies show Ly α in emission. This EW distribution further implies that approximately 15 per cent of our z ≃ 7 galaxies exhibit strong (EW > 25 Å) Ly α, in agreement with previous studies quantifying this Ly α emitter fraction among the bright (|$\mathrm{\mathit{ M}}_{\mathrm{UV}}^{ }$| |$\lt \, -$|20.25) population (e.g. Ono et al. 2012; Schenker et al. 2014; Pentericci et al. 2018). Interestingly, the Ly α EW distribution inferred from our 30 massive z ≃ 6 galaxies is remarkably similar to that at z ≃ 7 with all three parameters agreeing well within 1σ uncertainties (see Table 7).
Parameters inferred describing the lognormal Ly α EW distribution of massive galaxies at z ≃ 7 and z ≃ 6. The three parameters μEW, σEW, and A are, respectively, the median EW, standard deviation, and fraction of sources with Ly α EW > 0 Å.
| . | μEW (Å) . | σEW (dex) . | A . |
|---|---|---|---|
| z ≃ 6 | |$12.0^{+2.8}_{-2.3}$| | |$0.31^{+0.11}_{-0.08}$| | |$0.89^{+0.08}_{-0.13}$| |
| z ≃ 7 | |$11.0^{+3.8}_{-3.2}$| | |$0.37^{+0.15}_{-0.10}$| | |$0.88^{+0.09}_{-0.15}$| |
| . | μEW (Å) . | σEW (dex) . | A . |
|---|---|---|---|
| z ≃ 6 | |$12.0^{+2.8}_{-2.3}$| | |$0.31^{+0.11}_{-0.08}$| | |$0.89^{+0.08}_{-0.13}$| |
| z ≃ 7 | |$11.0^{+3.8}_{-3.2}$| | |$0.37^{+0.15}_{-0.10}$| | |$0.88^{+0.09}_{-0.15}$| |
Parameters inferred describing the lognormal Ly α EW distribution of massive galaxies at z ≃ 7 and z ≃ 6. The three parameters μEW, σEW, and A are, respectively, the median EW, standard deviation, and fraction of sources with Ly α EW > 0 Å.
| . | μEW (Å) . | σEW (dex) . | A . |
|---|---|---|---|
| z ≃ 6 | |$12.0^{+2.8}_{-2.3}$| | |$0.31^{+0.11}_{-0.08}$| | |$0.89^{+0.08}_{-0.13}$| |
| z ≃ 7 | |$11.0^{+3.8}_{-3.2}$| | |$0.37^{+0.15}_{-0.10}$| | |$0.88^{+0.09}_{-0.15}$| |
| . | μEW (Å) . | σEW (dex) . | A . |
|---|---|---|---|
| z ≃ 6 | |$12.0^{+2.8}_{-2.3}$| | |$0.31^{+0.11}_{-0.08}$| | |$0.89^{+0.08}_{-0.13}$| |
| z ≃ 7 | |$11.0^{+3.8}_{-3.2}$| | |$0.37^{+0.15}_{-0.10}$| | |$0.88^{+0.09}_{-0.15}$| |

Plot showing the inferred Ly α EW distributions of our massive galaxy samples at z ≃ 7 (solid blue) and z ≃ 6 (dashed orange) using the Bayesian approach of equation (2). These two distributions are equivalent within uncertainties, suggesting that Ly α transmission is evolving less rapidly between z ≃ 6–7 for the massive population relative to low-mass lensed systems (Hoag et al. 2019; Fuller et al. 2020). This is consistent with a scenario wherein massive z ≃ 7 galaxies often reside in large highly ionized bubbles.
Our goal is to quantify evolution in the transmission of Ly α for massive galaxies between z ≃ 6–7. While the value of T inferred above does account for evolution in transmission, it also includes any evolution in the physical conditions that may be impacting Ly α production and escape within galaxies. Fortunately, we can take the first steps towards decoupling these internal factors using the insight gained from our analysis in Section 3.1. Therein, we found that the observed Ly α EW in massive z ≃ 7 galaxies correlates with rest-UV slope and [O iii]+H β EW. As detailed in Section 2.2, the typical rest-UV slopes of our z ≃ 6 (β = −2.09) and z ≃ 7 (β = −2.07) samples are essentially equal. Given this, we assume that the dust content of our two samples are similar enough to not cause a significant evolution in the Ly α EW distribution. As discussed further in Section 4, the trend between [O iii]+H β EW and Ly α EW seen in our sample is likely driven by the relationship between [O iii]+H β EW and the stellar ionizing photon production efficiency, |$\xi _{\mathrm{ion}}^{\ast }$| (Chevallard et al. 2018; Tang et al. 2019). Our SED fits with beagle suggests that the typical ionizing photon production efficiencies of our z ≃ 6 (|$\log _{10}[\xi _{\mathrm{ion}}^{\ast } / (\mathrm{erg}^{-1}\ \mathrm{Hz})]$| = 25.62) and z ≃ 7 (|$\log _{10}[\xi _{\mathrm{ion}}^{\ast } / (\mathrm{erg}^{-1}\ \mathrm{Hz})]$| = 25.59) samples are also similar enough to not significantly impact the evolution of the Ly α EW distribution. We therefore assume that our inferred value of T is dominated by the evolution in Ly α transmission.
Equipped with this knowledge, we find that our spectroscopic data rule out a strong decline in Ly α transmission (Tz ≃ 7 / Tz ≃ 6 < 0.5) with 98.5 per cent (≈2σ) confidence. This is in contrast to the ten-fold decrease in strong Ly α emitters among low-mass lensed galaxies over the same redshift interval (Hoag et al. 2019; Fuller et al. 2020). Therefore, while uncertainties are significant given our modest sample size, our results currently suggest that Ly α transmission is evolving less rapidly between z ≃ 6–7 for the massive population.
There are a number of possible explanations for this difference in Ly α transmission evolution as we enter the epoch of reionization. One is that massive z ≃ 7 galaxies may tend to possess larger Ly α velocity offsets, helping push the photons into the damping wing before escaping the host galaxy (Mason et al. 2018b). This may be expected given the positive correlation between Ly α velocity offset and rest-UV luminosity at z ∼ 2–3 (Erb et al. 2014), likely reflecting (in part) the ability of more massive galaxies to drive stronger outflows. Another explanation is that massive z ≃ 7 galaxies are more likely to reside in large ionized bubbles (Furlanetto et al. 2004; Wyithe & Loeb 2005; Lee et al. 2007; McQuinn et al. 2007; Weinberger et al. 2018) which enable Ly α photons to cosmologically redshift far into the damping wing and thus transmit more easily through a partially neutral IGM.
3.3 A possible large ionized region at z ≃ 7
As discussed in Section 3.2, our results are consistent with a scenario wherein massive z ≃ 7 systems often reside in large ionized regions. In this same picture, we might expect to find some of our z ≃ 7 Ly α emitters nearby one another if they reside in the same bubble. Interestingly, we do indeed find an instance where three of our massive z ≃ 7 Ly α emitters possess very similar redshifts (Δz ∼ 0.05) and are also closely separated in angular space (<5 arcmin).
Our spectroscopic results indicate that COS-940214 (|${z}_{_{\mathrm{Ly\alpha }}}$| = 6.748), COS-1009842 (|${z}_{_{\mathrm{Ly\alpha }}}$| = 6.761), and COS-995126 (|${z}_{_{\mathrm{Ly\,\alpha }}}$| = 6.813) all lie within a spherical volume with radius R = 1.7 physical Mpc (Fig. 10), consistent with the expected sizes of H ii regions at z = 7 (e.g. Furlanetto et al. 2004; Mesinger & Furlanetto 2007; Lin et al. 2016). These three sources have luminosities ranging from 0.8–2.3 L|$^{\ast }_{\mathrm{UV}}$| and therefore are likely among the most massive galaxies present at z ≃ 7. All three are also inferred to be actively forming stars with SFRs of 7–28 M⊙ yr−1 using the SED fitting procedure described in Section 2.3. Their very blue IRAC colours ([3.6]−[4.5] |$\lt \, -$|0.6) further suggest large sSFRs ranging from approximately 10–130 Gyr−1 (see Table 5). Because the typical sSFR at z ≃ 7 is 5 Gyr−1 (E21), these three galaxies are likely undergoing a burst of star formation.
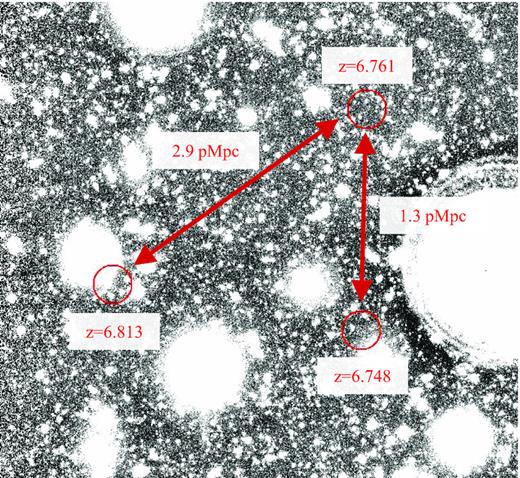
Illustration of three closely separated Ly α emitters in our z ≃ 7 sample. All three sources fall within a spherical region with radius R = 1.7 physical Mpc, consistent with the expected sizes of H ii regions at z ≃ 7 (e.g. Lin et al. 2016). The proximity of these Ly α emitters thus may plausibly reflect the presence of a large ionized bubble.
We estimate that the three aforementioned sources could individually power bubbles of sizes R = 0.29–0.41 physical Mpc, consistent with other estimates recently reported at z ≃ 7–8 (Castellano et al. 2018; Tilvi et al. 2020). The largest region (R = 0.41 Mpc) is estimated to come from COS-955126 given that it is inferred to produce more than twice as many ionizing photons as the other two sources, mainly due to its much higher luminosity. COS-940214 and COS-1009842 have very similar estimated bubble sizes (R = 0.30 and 0.29 Mpc, respectively) due to the similarity in their inferred |$\dot{N}_{\mathrm{ion}}$|. Notably, these estimated bubble sizes (|$R\, \sim$| 0.3 Mpc) are much smaller than the observed separation between the three galaxies (R = 1.7 Mpc).
One way in which a larger bubble may have grown around these sources is through the impact of a local overdensity (e.g. Furlanetto et al. 2004; Wyithe & Loeb 2005; Lee et al. 2007; McQuinn et al. 2007). Such a scenario may already be hinted at by the proximity of these ≳L|$^{\ast }_{\mathrm{UV}}$| galaxies. Using the z ≃ 7 luminosity function from Bowler et al. (2017), we would expect only N = 0.7 bright (≥0.8 L|$^{\ast }_{\mathrm{UV}}$|) galaxies on average within a 1.7 Mpc radius sphere. Because we know there are at least three such galaxies within this volume, our data suggest this region is likely a factor of ≳4 × overdense. Further evidence of an overdensity comes from investigating the surface density of photometrically selected z ≃ 7 galaxies over this region. In an ≈60 arcmin2 rectangular area encompassing the three Ly α emitters, we identify a total of nine galaxies satisfying our z ≃ 7 selection criteria (Section 2.1), a factor of 6× above that expected on average19 in the same area (N = 1.5). Future Ly α observations will enable us to better quantify the spectroscopic overdensity within this region.
4 DISCUSSION
Numerous observational studies over the past decade have demonstrated a low (≲10–20 per cent) Ly α detection rate among typical (<L|$^{\ast }_{\mathrm{UV}}$|) z ≳ 7 galaxies (e.g. Ono et al. 2012; Treu et al. 2013; Pentericci et al. 2014, 2018; Schenker et al. 2014; Tilvi et al. 2014). It was therefore a surprise when Ly α was detected in all four of the brightest (3–4 L|$^{\ast }_{\mathrm{UV}}$|) z > 7 galaxies selected over the CANDELS fields (i.e. the RB16 sample), particularly given that the IGM is thought to be highly neutral at these epochs (xH i > 40 per cent; e.g. Davies et al. 2018; Planck Collaboration VI 2020; Wang et al. 2020; Whitler et al. 2020). The unusual Ly α detectability of these sources hence suggested that their Ly α photons may be less sensitive to strong scattering by the IGM, as would be expected if these objects reside in large, highly ionized bubbles (e.g. Zitrin et al. 2015; Weinberger et al. 2018). However, it has been proposed that intense radiation fields may also be driving their enhanced Ly α detectability given that all four RB16 galaxies are inferred to possess strong [O iii]+H β emission (EW > 800 Å; Stark et al. 2017). In this section, we use our observations of a larger population (N = 22) of similarly bright (L|$^{}_{\mathrm{UV}}\, \simeq$| 1–6 L|$^{\ast }_{\mathrm{UV}}$|) z ≃ 7 galaxies with Spitzer/IRAC constraints on [O iii]+H β EWs to better understand the origin of strong Ly α within the RB16 sample.
We find that the detectability of Ly α depends strongly on the [O iii]+H β EW at z ≃ 7. We detect Ly α in 78 per cent (7/9) of bright z ≃ 7 galaxies possessing strong [O iii]+H β (EW > 800 Å) as opposed to only 8 per cent (1/12) of galaxies with more moderate [O iii]+H β (EW = 200–800 Å; Section 3.1). The much (4.7×) higher Ly α EWs of the strong [O iii]+H β population likely reflects, in part, a larger ionizing photon production efficiency associated with young stellar populations (Chevallard et al. 2018; Tang et al. 2019). The high sSFRs (≳30 Gyr−1) of these galaxies may also help drive low H i column density channels through the ISM/CGM (e.g. Clarke & Oey 2002; Ma et al. 2020) through which Ly α photons can efficiently escape (Jaskot et al. 2019; Gazagnes et al. 2020).
While we have shown that efficient ionizing photon production significantly boosted the Ly α detectability of the RB16 sample, our results also suggest that the IGM ionization may have played a significant role in enhancing their visibility as well. In particular, we find no evidence of strong evolution in the Ly α EW distribution of bright (L|$^{}_{\mathrm{UV}}\, \simeq$| 1–6 L|$^{\ast }_{\mathrm{UV}}$|) galaxies between z ≃ 6–7 (Section 3.2). This result stands in contrast to the rapid downturn in the fraction of strong Ly α emitters (>25 Å EW) among low-mass (∼0.1 L|$^{\ast }_{\mathrm{UV}}$|) lensed galaxies between z ≃ 6–7 (Hoag et al. 2019; Fuller et al. 2020), suggesting that Ly α in the bright population may evolve more slowly. Such findings are consistent with theoretical expectation that the brightest (and hence the most massive; e.g. Barone-Nugent et al. 2014) z ≃ 7 galaxies trace overdensities that are the first to create large, highly ionized bubbles (e.g. Furlanetto et al. 2004; Wyithe & Loeb 2005; Lee et al. 2007; McQuinn et al. 2007; Weinberger et al. 2018).
If massive z ≃ 7 galaxies do trace overdense regions, we may expect to find Ly α emitting galaxies in our sample nearby one another within the same ionized structure. Indeed, our results revealed three z ≃ 7 Ly α emitters separated by relatively small angular distances (<5 arcmin) and with similar redshifts (Section 3.3). The corresponding spatial separation of these Ly α emitters (R = 1.7 physical Mpc) is consistent with the expected sizes of H ii regions at z ≃ 7 (Furlanetto et al. 2004; Mesinger & Furlanetto 2007; Lin et al. 2016), suggesting that they may lie within the same large, highly ionized bubble. None the less, with our present data, it is not yet possible to characterize the extent of the ionized regions surrounding these z ≃ 7 Ly α emitters. There are two distinct possibilities consistent with our current data. On one hand, these massive z ≃ 7 galaxies may be tracing a large ionized region, with a size comparable to their spatial separation (R ≳ 2 Mpc). This would be expected if the galaxies trace a strongly overdense structure with larger-than-average ionizing photon output. In this case, we would expect to see enhanced Ly α from all systems within the ionized region. However, it is also possible that these systems are situated within distinct, moderate-sized (R ∼ 0.3 Mpc) bubbles in which they are the dominant contributors of ionizing photons. The smaller bubbles would lead to larger damping wing attenuation of Ly α from the IGM. But the corresponding reduction in the Ly α flux is countered by efficient production of nebular emission, as signaled by the large EW [O iii]+H β emission (and hence high sSFRs). The transmission could be further boosted if these massive systems have large velocity offsets (e.g. Erb et al. 2014; Stark et al. 2017; Mason et al. 2018b), redshifting the line further into the damping wing before it encounters hydrogen.
Which of these two pictures is true depends largely on whether the nearby Ly α emitting galaxies we have identified trace a strong overdensity in galaxies. In Section 3.3, we presented evidence that this may indeed be the case. The number density of spectroscopically confirmed >0.8 L|$^{\ast }_{\mathrm{UV}}$| systems in this region (N = 3) is ≈4 times the average (N = 0.7) expected from z ≃ 7 luminosity functions (e.g. Bowler et al. 2017). Furthermore, the surface density of photometrically selected z ≃ 7 galaxies surrounding the nearby Ly α emitters is 6× the average. This suggests that an overdense population of neighbouring galaxies may potentially help power a large ionized region.
These results add to two similar instances of grouped Ly α emitting galaxies that have been reported at z = 7.0–7.7 (Vanzella et al. 2011; Castellano et al. 2018; Tilvi et al. 2020). Both these previously identified regions contain at least one bright (>L|$^{\ast }_{\mathrm{UV}}$|) galaxy. Furthermore, one of these regions (the BDF) shows evidence of a host overdensity similar to that in our sample (Castellano et al. 2016). Interestingly, deep spectroscopic follow-up of relatively faint (<0.7 L|$^{\ast }_{\mathrm{UV}}$|) z ≃ 7 systems identified photometrically in the BDF revealed no Ly α detections (Castellano et al. 2018). As stated therein, this may suggest that many of the fainter systems reside outside the ionized region, though it is also possible that Ly α is preferentially seen in the brightest systems because of their larger velocity offsets. Ultimately, future Ly α spectroscopy of fainter sources (with known spatial positions via e.g. JWST rest-optical line detections) will be able to discern whether the Ly α EW distribution in the vicinity of these massive Ly α emitters is enhanced towards larger values as would be expected if they reside in large bubbles.
5 SUMMARY
We present the first results from a new spectroscopic MMT/Binospec program aimed at targeting Ly α in a large sample of bright (L|$^{}_{\mathrm{UV}}\, \simeq$| 1–6 L|$^{\ast }_{\mathrm{UV}}$|) z ≃ 7 galaxies selected over very wide-area fields (∼3 deg2 total). We use these results to investigate to what extent strong [O iii]+H β emission (and hence large sSFRs) boost Ly α detectability from bright reionization-era galaxies. We secondly test whether the decline in the visibility of Ly α emission is less rapid for massive galaxies, as might be expected if they trace strong overdensities that are situated in large ionized bubbles. Our conclusions are as follows:
From our 22 targeted bright z ≃ 7 galaxies, we confidently (>7σ) detect Ly α from nine sources. The redshifts of our z ≃ 7 Ly α emitters range from |${z}_{_{\mathrm{Ly\alpha }}}$| = 6.650–7.093, consistent with expectations given our photometric selection criteria. We measure Ly α fluxes ranging from (5.1–18.6)× 10−18 erg s−1 cm−2 and rest-frame EWs spanning 3.7–43.1 Å. For sources lacking a confident detection, the data typically place a (7σ) Ly α EW limit of ≲10 Å in skyline-free regions of the spectra.
We find that the detectability of Ly α depends strongly on [O iii]+H β EW among luminous z ≃ 7 galaxies. We confidently detect Ly α in 78 per cent (7/9) of sources with strong [O iii]+H β emission (EW > 800 Å) as opposed to only 8 per cent (1/12) of sources with more moderate [O iii]+H β (EW = 200–800 Å). The much (4.7×) higher Ly α EWs of the strong [O iii]+H β population likely reflect a larger ionizing photon production efficiency (and hence likely also a larger L|$_{\mathrm{Ly}\alpha}$|/L|$_{\text{UV}}$|) owing to extremely young, hot stars formed in a recent rapid upturn or burst in star formation activity (Chevallard et al. 2018; Tang et al. 2019). The high sSFRs (≳30 Gyr−1) of such galaxies may also help create low H i column density channels through the ISM/CGM (e.g. Clarke & Oey 2002; Ma et al. 2020) through which Ly α photons can efficiently escape (e.g. Jaskot et al. 2019; Gazagnes et al. 2020). Given the large variations in Ly α detectability within our data, it will be necessary to ensure that future samples be well matched in sSFR across cosmic time to well infer the evolution of the IGM neutral state.
We tentatively detect the nebular NVλ1238.8,1242.8 doublet, a signpost of significant AGN activity, in one of our z ≃ 7 Ly α emitters. This is the fifth tentative detection of NV so far reported in a z ≳ 7 Ly α emitter (Tilvi et al. 2016; Hu et al. 2017; Laporte et al. 2017; Mainali et al. 2018) suggesting that low-luminosity AGN are present in a subset of the most massive reionization-era galaxies. Further investigation of this population will ultimately help clarify the contribution of such AGN to cosmic reionization (Madau & Haardt 2015; Giallongo et al. 2019; Grazian et al. 2020).
We find no evidence for strong evolution in the transmission of Ly α emission for the massive (≃1–6 L|$^{\ast }_{\mathrm{UV}}$|) population between z ≃ 6–7 (Tz ≃ 7/Tz ≃ 6 = 1.04|$^{+0.39}_{-0.29}$|). This is in contrast to observations of low-mass (∼0.1 L|$^{\ast }_{\mathrm{UV}}$|) lensed galaxies which suggest a factor of ∼10 decline in transmission (Hoag et al. 2019; Fuller et al. 2020). With our current sample size, we can rule out a factor of ≥2 decline in Ly α transmission with 98.5 per cent (≈2σ) confidence among massive galaxies. We discuss a number of possible explanations for these findings, including the expectation that massive z ≃ 7 galaxies often reside within large, highly ionized bubbles (e.g. Furlanetto et al. 2004; McQuinn et al. 2007; Weinberger et al. 2018).
We find three Ly α emitters in our z ≃ 7 sample separated by relatively small angular distances (<5 arcmin) and with nearly identical redshifts (Δz ≈ 0.05). These small angular separations may be a signpost of an ionized bubble enhancing Ly α transmission. Indeed, the spatial separations of these Ly α emitters (R = 1.7 physical Mpc) are consistent with the expected sizes of H ii regions at z ≃ 7 (e.g. Furlanetto et al. 2004; Mesinger & Furlanetto 2007; Lin et al. 2016). With our present data, we cannot yet characterize the full extent of the ionized regions surrounding these closely separated Ly α emitters. However, we estimate that these Ly α emitters are individually capable of powering ionized bubbles with radii of R∼0.3 Mpc, consistent with other estimates recently reported at z ≃ 7–8 (Castellano et al. 2018; Tilvi et al. 2020). Future work targeting fainter galaxies in the region should be able to determine if the ionized region extends beyond these radii.
We find tentative evidence of an overdensity surrounding these closely separated Ly α emitters. The number density of spectroscopically confirmed >0.8 L|$^{\ast }_{\mathrm{UV}}$| systems in these regions (N = 3) is ≃4 times the average (N = 0.7) expected from z ≃ 7 luminosity functions. Furthermore, the surface density of photometrically selected z ≃ 7 galaxies surrounding the nearby Ly α emitters is 6× the average. Such an overdensity may help facilitate the growth of a large (R ≳ 2 physical Mpc) bubble around these sources.
As a next step towards understanding Ly α emission from massive reionziation-era galaxies, in future work we will combine this Binospec data set with recent results from a Cycle 7 ALMA Large Program, the Reionization Era Bright Emission Line Survey (REBELS; 2019.1.01634.L). REBELS has begun providing systemic redshifts via the [C ii]158 μm emission line as well as constraints on far-infrared dust continuum emission for a number of our z ≃ 7 targets. With this more complete rest-UV through far-infrared view, we will begin to better characterize the Ly α velocity offsets of massive z ≃ 7 galaxies as well as understand how their observed [C ii] and dust continuum emission relates to Ly α.
ACKNOWLEDGEMENTS
RE and DPS acknowledge funding from JWST/NIRCam contract to the University of Arizona, NAS5-02015. JC and SC acknowledge financial support from the European Research Council (ERC) via an Advanced Grant under grant agreement no. 321323 – NEOGAL. RJB and MS acknowledge support from the Nederlandse Organisatie voor Wetenschappelijk Onderzoek via TOP grant TOP1.16.057. BER was supported in part by NASA program HST-GO-14747, contract NNG16PJ25C, and grant 80NSSC18K0563, and NSF award 1828315. Observations reported here were obtained at the MMT Observatory, a joint facility of the University of Arizona and the Smithsonian Institution.
This research has benefited from the SpeX Prism Library (and/or SpeX Prism Library Analysis Toolkit), maintained by Adam Burgasser at http://www.browndwarfs.org/spexprism. This research also made use of astropy, a community-developed core python package for Astronomy (Astropy Collaboration 2013; Price-Whelan et al. 2018); matplotlib (Hunter 2007); numpy (Van Der Walt, Colbert & Varoquaux 2011); and scipy (Jones et al. 2001).
DATA AVAILABILITY
The optical through mid-infrared imaging data underlying this article are available through their respective data repositories. See https://hsc-release.mtk.nao.ac.jp/doc/ for HSC data, http://www.eso.org/rm/publicAccess#/dataReleases for UltraVISTA and VIDEO data, and https://sha.ipac.caltech.edu/applications/Spitzer/SHA/ for IRAC data. The MMT/Binospec data will be shared upon reasonable request to the corresponding author.
Footnotes
Throughout this work, we adopt M|$_{\mathrm{UV}}^{\ast }$| = −20.6 from the z ≃ 7 luminosity function results of Bowler et al. (2017).
We astrometrically correct the public VIDEO mosaics to the Gaia frame to bring into agreement with the optical HSC imaging.
Because our z ≃ 6 selection criteria in COSMOS does not utilize VIRCam photometry, the selection is equivalent for the deep and ultra-deep UltraVISTA stripes.
As discussed in Section 2.1.2, we use y and Y-band magnitudes to quote |$m_{\mathrm{UV}}^{ }$| for z ≃ 6 sources in COSMOS and XMM3, respectively.
Binospec’s FOV is composed of two separate 8 × 15 arcmin2 FoVs separated by a 3.2 arcmin gap.
The FWHM of this Gaussian is not allowed to be less than the seeing.
This fraction is calculated by assuming a fixed Ly α line profile shape equivalent to that used in our completeness simulations (Gaussian with FWHM = 220 km s−1; Section 2.2.4) and fitting this profile to the 1D spectra of each detected source.
This is because the Ly α EW for detected sources (which almost always lie in the strong [O iii]+H β emitter sub-sample; Section 3.1) would be pushed to higher values.
For z ≃ 7 sources with |${z}_{_{\mathrm{Ly\,\alpha }}}$|< 6.9, we use the Y-band photometry to estimate the continuum. For those with |${z}_{_{\mathrm{Ly\,\alpha }}}$| > 6.9, we use the J band because Y is partially contaminated by Ly α at these redshifts. For the z ≃ 6 sources, we adopt the y and Y-band photometry for the continuum in COSMOS and XMM3, respectively.
We divide our data such that the total weight of all exposures in each stack is roughly equal.
Here, we report the 5σ EW limit over the observed wavelength range corresponding to Ly α velocity offsets of 0–500 km s−1 similar to the approach of Mainali et al. (2018).
As appropriate for our work, we are using the (double-power law) luminosity function parameters obtained when treating ground-based as a single galaxy.
We adopt a lognormal EW distribution throughout our analysis because this function yields the best fit to our data when comparing to a Gaussian (e.g. Ouchi et al. 2008; Guaita et al. 2010) and exponentially declining (e.g. Jung et al. 2017; Mason et al. 2018a) function. None of our major conclusions are significantly altered if we adopt one of these other distributions instead.
The median and inner 68 per cent confidence interval of this ratio on median EWs from the marginalized P(μEW) of each sub-sample is 3.8|$^{+4.4}_{-2.4}$|. These uncertainties are largely due to our current sample size and non-detections in most moderate [O iii]+H β emitters.
While H β EW does increase with decreasing metallicity, it only reaches ∼300 Å at 0.01 Z⊙ even in extremely rapidly star-forming systems (sSFR ∼ 100 Gyr−1) according to the Gutkin et al. (2016) templates used in beagle.
This is assuming a clumping factor of C≈3 at z = 7 (e.g. Finlator et al. 2012; Shull et al. 2012; Pawlik, Schaye & Dalla Vecchia 2015). More recent, higher resolution simulations find that the clumping factor is temporarily increased to C ∼ 10–20 shortly (∼3–10 Myr) after a region becomes reionized (Park et al. 2016; D’Aloisio et al. 2020). Adopting such a higher value would yield smaller estimated bubble sizes, still insufficient to cover the observed separation between the three galaxies.
This ≈60 arcmin2 rectangular area is entirely contained within an UltraVISTA ultra-deep stripe. We identify 67 z ≃ 7 galaxies across all the ultra-deep stripes (0.73 deg2 total) translating to an average surface density of 0.0255 arcmin−2 (not corrected for completeness).
REFERENCES
APPENDIX A: IRAC IMAGING
We show the deconfused (Section 2.1.3) IRAC postage stamps of our z ≃ 7 targets in Fig. A1. The postage stamps for COS-862541 are shown in E21.
Deconfused IRAC 3.6 and 4.5 μm postage stamps of our z ≃ 7 targets. Each postage stamp is approximately 16.5 arcsec by 16.5 arcsec. The red circle indicates the 2.8 arcsec diameter aperture used to measure the photometry. The postage stamps for COS-862541 are shown in E21.



