-
PDF
- Split View
-
Views
-
Cite
Cite
H Abdalla, R Adam, F Aharonian, F Ait Benkhali, E O Angüner, M Arakawa, C Arcaro, C Armand, T Armstrong, H Ashkar, M Backes, V Baghmanyan, V Barbosa Martins, A Barnacka, M Barnard, Y Becherini, D Berge, K Bernlöhr, M Böttcher, C Boisson, J Bolmont, S Bonnefoy, J Bregeon, M Breuhaus, F Brun, P Brun, M Bryan, M Büchele, T Bulik, T Bylund, S Caroff, A Carosi, S Casanova, T Chand, S Chandra, A Chen, G Cotter, M Curyło, I D Davids, J Davies, C Deil, J Devin, P deWilt, L Dirson, A Djannati-Ataï, A Dmytriiev, A Donath, V Doroshenko, J Dyks, K Egberts, F Eichhorn, G Emery, J -P Ernenwein, K Feijen, S Fegan, A Fiasson, G Fontaine, S Funk, M Füßling, S Gabici, Y A Gallant, G Giavitto, L Giunti, D Glawion, J F Glicenstein, D Gottschall, M -H Grondin, J Hahn, M Haupt, G Hermann, J A Hinton, W Hofmann, C Hoischen, T L Holch, M Holler, M Hörbe, D Horns, D Huber, H Iwasaki, M Jamrozy, D Jankowsky, F Jankowsky, A Jardin-Blicq, V Joshi, I Jung-Richardt, M A Kastendieck, K Katarzyński, M Katsuragawa, U Katz, D Khangulyan, B Khélifi, S Klepser, W Kluźniak, Nu Komin, R Konno, K Kosack, D Kostunin, M Kreter, G Lamanna, A Lemière, M Lemoine-Goumard, J -P Lenain, E Leser, C Levy, T Lohse, I Lypova, J Mackey, J Majumdar, D Malyshev, D Malyshev, V Marandon, P Marchegiani, A Marcowith, A Mares, G Martí-Devesa, R Marx, G Maurin, P J Meintjes, R Moderski, M Mohamed, L Mohrmann, C Moore, P Morris, E Moulin, J Muller, T Murach, S Nakashima, K Nakashima, M de Naurois, H Ndiyavala, F Niederwanger, J Niemiec, L Oakes, P O’Brien, H Odaka, S Ohm, E de Oña Wilhelmi, M Ostrowski, M Panter, R D Parsons, B Peyaud, Q Piel, S Pita, V Poireau, A P Noel, D A Prokhorov, H Prokoph, G Pühlhofer, M Punch, A Quirrenbach, S Raab, R Rauth, A Reimer, O Reimer, Q Remy, M Renaud, F Rieger, L Rinchiuso, C Romoli, G Rowell, B Rudak, E Ruiz-Velasco, V Sahakian, S Sailer, S Saito, D A Sanchez, A Santangelo, M Sasaki, M Scalici, F Schüssler, H M Schutte, U Schwanke, S Schwemmer, M Seglar-Arroyo, M Senniappan, A S Seyffert, N Shafi, K Shiningayamwe, R Simoni, A Sinha, H Sol, A Specovius, S Spencer, M Spir-Jacob, Ł Stawarz, R Steenkamp, C Stegmann, C Steppa, T Takahashi, T Tavernier, A M Taylor, R Terrier, D Tiziani, M Tluczykont, L Tomankova, C Trichard, M Tsirou, N Tsuji, R Tuffs, Y Uchiyama, D J van der Walt, C van Eldik, C van Rensburg, B van Soelen, G Vasileiadis, J Veh, C Venter, P Vincent, J Vink, H J Völk, T Vuillaume, Z Wadiasingh, S J Wagner, J Watson, F Werner, R White, A Wierzcholska, R Yang, H Yoneda, M Zacharias, R Zanin, D Zargaryan, A A Zdziarski, A Zech, S J Zhu, J Zorn, N Żywucka, M Cerruti, (H.E.S.S. Collaboration), Very high energy γ-ray emission from two blazars of unknown redshift and upper limits on their distance, Monthly Notices of the Royal Astronomical Society, Volume 494, Issue 4, June 2020, Pages 5590–5602, https://doi.org/10.1093/mnras/staa999
Close - Share Icon Share
ABSTRACT
We report on the detection of very high energy (VHE; E > 100 GeV) γ-ray emission from the BL Lac objects KUV 00311−1938 and PKS 1440−389 with the High Energy Stereoscopic System (H.E.S.S.). H.E.S.S. observations were accompanied or preceded by multiwavelength observations with Fermi/LAT, XRT and UVOT onboard the Swift satellite, and ATOM. Based on an extrapolation of the Fermi/LAT spectrum towards the VHE γ-ray regime, we deduce a 95 per cent confidence level upper limit on the unknown redshift of KUV 00311−1938 of |$z$| < 0.98 and of PKS 1440−389 of |$z$| < 0.53. When combined with previous spectroscopy results, the redshift of KUV 00311−1938 is constrained to 0.51 ≤ |$z$| < 0.98 and of PKS 1440−389 to 0.14 ⪅ |$z$| < 0.53.
1 INTRODUCTION
The extragalactic γ-ray sky is strongly dominated by blazars, a class of radio-loud jet-dominated active galactic nuclei (AGNs) in which the relativistic jet is oriented at a small angle with respect to the line of sight. This alignment leads to strong Doppler enhancement of the observed flux across the entire electromagnetic spectrum as well as a shortening of the apparent variability, which has been observed to be as short as a few minutes (e.g. Gaidos et al. 1996; Aharonian et al. 2007; Albert et al. 2007; Arlen et al. 2013). The radio to γ-ray spectral energy distribution (SED) of blazars is dominated by two distinct, non-thermal radiation components, where the low-energy emission (from radio through UV or X-rays) is generally ascribed to synchrotron radiation from relativistic electrons/positrons in the jet. For the high-energy emission, both a Compton-scattering-based leptonic scenario and a hadronic scenario, where γ-ray emission results from proton synchrotron radiation and photo-pion-induced processes, are plausible (see, e.g. Böttcher et al. 2013, for a comparative study of both types of models).
The multiwavelength variability of blazars exhibits complex patterns on all time-scales, from years down to minutes, with variability at different frequencies sometimes being correlated, but sometimes also showing uncorrelated behaviour, such as “orphan” γ-ray flares without significant counterparts at lower frequencies (e.g. Krawczynski et al. 2004). The fast (intra-day) variability time-scales indicate that the broad-band emission, at least from optical to γ-ray frequencies, must originate in small, localised regions along the jet, with a radius no larger than |${c\, \tau \, \delta \, (1+z)^{-1} \simeq 1.8\times 10^{14}\, \tau _{\rm {10 min}}\, \delta _{10} (1+z)^{-1}}$| cm, where |$\tau _{\rm {10 min}} = \tau /\rm {10 \; min}$| is the observed variability time-scale, δ10 = δ/10 is the Doppler factor of the emitting region, and |$z$| is the redshift of the source. Measurements of blazar SEDs and their variability thus provide a unique laboratory for probing the microphysical processes of particle acceleration and radiative cooling in AGN jets.
Based on the location of the peak of the low-energy (synchrotron) spectral component, νsy, blazars are sub-divided into low-synchrotron-peaked (LSP, with νsy ≤ 1014 Hz), intermediate-synchrotron-peaked (ISP, with |$10^{14} \, {\rm Hz} \lt \nu _{\rm sy} \le 10^{15}$| Hz), and high-synchrotron-peaked (HSP) blazars (with νsy > 1015 Hz; Abdo et al. 2010). Blazars are also divided into BL Lacertae objects (BL Lacs) and Flat-Spectrum Radio-Quasars (FSRQs) on the basis of their optical/UV spectrum, which is almost featureless in BL Lacs, and shows broad emission lines in FSRQs. While FSRQs are all LSPs, BL Lacs are characterised by a variety of peak frequencies. The vast majority of blazars detected by ground-based Imaging Atmospheric Cherenkov telescope (IACT) facilities in very high energy (VHE; E ≥ 100 GeV) γ-rays are BL Lacs belonging to the HSP class.
As VHE γ-rays are subject to γγ absorption due to e+e− pair production on IR – optical photons, the extragalactic background light (EBL) limits the cosmic horizon out to which VHE γ-ray sources are detectable (e.g. Nikishov 1962; Gould & Schréder 1967; Stecker, de Jager & Salamon 1992; Aharonian et al. 2006a; Finke, Razzaque & Dermer 2010). In agreement with this expectation, no VHE γ-ray source has so far been detected at a redshift |$z$| > 1, the current record holder being the gravitationally lensed blazar S3 0218+35 at a redshift of |$z$| = 0.944 (Ahnen et al. 2016).
While the EBL absorption represents an intrinsic limit for VHE astrophysics, it is possible to probe the EBL itself through its absorption imprint on VHE spectra of blazars (e.g. H.E.S.S. Collaboration 2017; Fermi-LAT Collaboration 2018; Abeysekara et al. 2019; Acciari et al. 2019).
For such studies, as large a sample of VHE blazars as possible, over as large a redshift range as possible, is necessary in order to disentangle source-intrinsic high-energy cut-offs from the effect of absorption on the EBL, improve the statistical uncertainty on the measurement, and study the evolution of the EBL with the redshift. A high redshift by itself does not necessarily mean that a blazar is interesting for propagation studies, given that both the intrinsic brightness of the source and the hardness of its spectrum play a key role. This motivates continued programmes by all currently operating IACT arrays to detect new VHE blazars and characterise their spectral properties in the VHE band. The selection of targets for such searches is most commonly based on an extrapolation of the High Energy (HE; E > 100 MeV) γ-ray spectra as measured by the Fermi Large Area Telescope (LAT, Nolan et al. 2012; Acero et al. 2015), taking into account the expected attenuation due to EBL γγ absorption: bright and hard LAT sources are prime candidates for pointed observations with IACTs.
A major problem when studying blazars is that the measurement of a BL Lac’s redshift is not trivial, due to the weakness of the emission lines (if any) in the optical spectrum. It is possible to constrain the redshift via the identification of absorption lines from the host galaxy, or to provide a lower limit on it via the detection of absorption lines from intergalactic absorbers. If the redshift is unknown, it is possible to use the current knowledge of the EBL together with the information from Fermi/LAT to compute an upper limit on the redshift of the source.
In this paper we present the detection with H.E.S.S. in the VHE regime of two blazars, selected for their hard Fermi/LAT spectra and large upper limits on their redshift, KUV 00311−1938 and PKS 1440−389. We present new constraining upper limits on their distance using Fermi/LAT and H.E.S.S. spectral information. We describe the details of the H.E.S.S. observations and data analysis in Section 2, and results from multiwavelength observations in Section 3. Then in Section 4.1 we present the SEDs, and in Section 4.2 we discuss our redshift constraint. We conclude with a summary of our results in Section 5. Throughout this text, the results for KUV 00311−1938 and PKS 1440−389 are presented in separate subsections.
1.1 KUV 00311−1938
KUV 00311−1938 has been classified as a BL Lac firstly by a spectroscopic identification in the sample of bright, soft, high-Galactic-latitude X-ray sources from the ROSAT All-Sky Survey (Thomas et al. 1998; Voges et al. 1999). Later, Bauer et al. (2000) associated this bright (|$S_{\rm X} = 1.32^{-11} \, \rm ergs \; s^{-1} \; cm^{-2}$|) ROSAT source with a strong radio emitter (Condon et al. 1998, |$S_{1.4 \; \rm GHz} = \rm 18.8 \; mJy$|). Its extreme value of the X-ray to radio flux ratio and its high X-ray flux, led to its inclusion in the Sedentary Multi-Frequency Survey catalogue (Piranomonte et al. 2007), which primarily selected HSPs.
A first evaluation of the redshift of KUV 00311−1938 was performed by Piranomonte et al. (2007), where a value of 0.61 was quoted although flagged as ‘tentative’. Later, Pita et al. (2014) detected the MgII doubled with the X-Shooter spectrograph operating on the VLT to estimate a secure lower limit on the redshift of the source to 0.506, and used non-detection of the host galaxy to place an upper redshift limit of 1.54. Recently, Fernandez Alonso, Pichel & Rovero (2019) attempted to constrain the redshift of KUV 00311−1938, by estimating the range of EBL absorption allowed by the preliminary H.E.S.S. observations presented in Becherini et al. (2012) and matching this to existing EBL models. They conclude that a redshift around 0.5-0.6 is the most plausible.
KUV 00311−1938 has been imaged multiple times with VLBI by Piner & Edwards (2018), who observed superluminal apparent motions of a secondary jet component with βapp = 6 ± 2 relative to a fixed radio core at |$\rm \alpha _{\rm J2000} = 00^{h} 33 ^{m} 34.380^{s}$|, |$\rm \delta _{\rm J2000} = -19^{\circ } 21^{\prime } 33.131^{\prime \prime }$| (Piner & Edwards 2014). We take the position of the radio core as our nominal location for KUV 00311−1938.
The Fermi/LAT (Atwood et al. 2009) reported the detection of a very bright HE γ-ray source consistent with KUV 00311−1938 in all the catalogues, including the ones compiled with high energy events only (Acero et al. 2015; Ajello et al. 2017).
In the most-recent 4FGL (Fermi-LAT Collaboration 2020) catalogue this source has an integrated flux of 2.96 ± 0.11 × 10−9|$\rm ph\, cm^{-2}\, s^{-1}$| in the [1–100] GeV range and a photon power-law (PWL) spectrum with a hard (1.67 ± 0.02) spectral index. The spectrum is reported as curved, with both a log-parabola (LP, 4.68 σ) and a PWL with exponential cut-off (EC, 5.15 σ) being preferred over the simple PWL. The 4FGL reports modest fractional variance on both yearly (Fvar = 0.16 ± 0.06) and bi-monthly (Fvar = 0.33 ± 0.05) time-scales, with the larger variability seen on the shorter time-scale.
H.E.S.S. observations of this source started at the end of 2009 and were pursued until 2014, leading to the detection of VHE γ-ray emission from this distant BL Lac (see Section 2), reported here.
1.2 PKS 1440−389
PKS 1440−389 (|$\rm \alpha _{\rm J2000} = 14 ^{h} 43 ^{m} 57 ^{s}$| |$\rm \delta _{\rm J2000} = -39^{\circ } 08^{\prime } 39^{\prime \prime }$|; Jackson et al. 2002) was first detected as a bright radio source in the Parkes survey (Wright & Otrupcek 1990). The source has been observed repeatedly by the TANAMI (Tracking of AGN with Austral Milliarcsecond Interferometry, Ojha et al. 2010) project between 2010 and 2016. Krauß et al. (2016) present three quasi-simultaneous SEDs of PKS 1440−389, which indicate a synchrotron peak at 1015 Hz|$\, \lesssim \nu _{\rm sy} \lesssim 10^{16}$| Hz, consistent with an HSP classification.
In the first data release of the 6dF Galaxy Survey (Jones et al. 2004), the redshift of the source is listed as |$z$| = 0.065, but this redshift value is no longer included in the final version of the 6dF catalogue (Jones et al. 2009) due to the poor quality of the optical spectrum. Despite many follow-up observations in different wavelength regimes, the redshift of PKS 1440−389 remains uncertain due to its featureless continuum spectrum (e.g. Landoni et al. 2015).
The current constraint from optical spectroscopic observations is 0.14 < |$z$| < 2.2 (Shaw et al. 2013).
PKS 1440−389 stands out as a bright γ-ray HSP with a hard well-constrained Fermi/LAT spectrum, with the 4FGL reporting a PWL index of 1.82 ± 0.02 and an integrated flux (over [1–100] GeV) of 3.95 ± 0.13 × 10−9|$\rm ph\, cm^{-2}\, s^{-1}$|. Similar to KUV 00311−1938, here too the spectrum shows evidence of being curved, with both an LP (4.14 σ) and a PWL with EC (4.33 σ) being preferred over the simple PWL. The 4FGL also reports modest variability on both yearly (Fvar = 0.12 ± 0.05) and bi-monthly (Fvar = 0.16 ± 0.05) time-scales.
Assuming a redshift near the lower limit of the allowed range, the EBL-corrected extrapolation of the Fermi/LAT spectrum into the VHE regime appeared promising for detection, and H.E.S.S. observations in 2012 yielded the discovery of the source at VHE (Prokoph et al. 2015). Using that preliminary H.E.S.S. spectrum, Sahu et al. (2019) computed a model-dependent limit on the distance of PKS 1440−389, 0.14 |$ < z < $| 0.24, assuming a hadronic origin of the emission.
2 H.E.S.S. DATA ANALYSIS AND RESULTS
H.E.S.S. is an array of five IACTs located in the Khomas Highland in Namibia (S 23°16′18″, E 16°30′00″) at an altitude of about 1800 m above sea level. From January 2004 to October 2012, the array was a four-telescope instrument, with telescopes CT1-4. Each of the telescopes, located at the corners of a square with a side length of 120 m, has a mirror surface area of 107 m2 and a camera composed of 960 photomultipliers covering a large field of view (FoV) of 5° diameter. The stereoscopic system works in a coincidence mode, requiring at least two of the four telescopes to trigger the detection of an extended air shower. In its initial four-telescope configuration used here, H.E.S.S. is sensitive to γ-ray energies from 100 GeV to about 100 TeV (Aharonian et al. 2006b).
In October 2012, a fifth telescope (CT5), with a mirror surface area of 600 m2 and an improved camera (Bolmont et al. 2014), was installed at the centre of the original square.
All observations were done in wobble mode, where the source is observed with an offset of 0.5° with respect to the centre of the instrument’s FoV to allow for simultaneous background measurements (Fomin et al. 1994). The analysis of the γ-ray emission from the two sources was carried out with the analysis procedure described in Parsons & Hinton (2014), where an enhanced low-energy sensitivity with respect to standard analysis methods (Aharonian et al. 2006b) is achieved. Since these sources are potentially very distant and so likely have very soft spectra, a special analysis configuration with a charge value of |$\rm 40$| photo electrons is used as the minimal required total amplitude for the cleaned and reconstructed image in each telescope.
The statistical significance of the two detections was determined using the Reflected background modelling method (Aharonian et al. 2006b) and equation (17) of Li & Ma (1983). In the Reflected background method, α is the reciprocal of the number of OFF-source regions considered in a run. If the number of OFF regions vary from run to run, the average α for all the runs is used.
The time-averaged differential VHE γ-ray spectra of the sources were derived using the forward-folding technique described in Piron et al. (2001). The maximum energy for both fits was chosen to be 3 TeV, while the minimum energy was left free and therefore represents the threshold energy.
The systematic uncertainties have been estimated following the procedure described in Aharonian et al. (2006b), with the uncertainty from the selection cuts estimated using the difference between the lead and cross-check analysis. A fit of an LP did not significantly improve the fit.
2.1 KUV 00311−1938
H.E.S.S. started observing several high-redshift blazars in the last years of its 4-telescope configuration and continued after the addition of a fifth telescope. Among the blazars observed by H.E.S.S., KUV 00311−1938 had the largest lower limit on |$z$|, and preliminary results of the observations were published in Becherini et al. (2012).
Observations of KUV 00311−1938 were carried out with H.E.S.S. in a campaign between end of 2009 and end of 2014 (MJD 55145–56954), leading to 102.6 hours of good-quality data (after hardware and weather quality selection criteria were applied with a procedure similar to that described in Aharonian et al. 2006b). These observations were taken with an average zenith angle of 14°.
To keep consistency in the analysis of later data and the data taken mostly before the fifth telescope was added to the array, all data are analysed in the four telescope configuration, removing data from CT5.
The source is detected at a level of 5.2 standard deviations, with an excess of 340.8 counts from the ON region of 0.1° radius centred at the nominal position of the source. The total number of ON- and OFF-source events are |$\rm N_{ON} = 4273$| and |$\rm N_{OFF} = 53247$|, with a background normalization factor α = 0.073849. A fit to the uncorrelated excess map yields a position for the excess of |$\rm \alpha _{J2000} = 00^{h} 33 ^{m} 36^{s} \pm 06 ^{s}_{\rm stat}$| and |$\rm \delta _{J2000} = -19^{\circ } 21^{\prime } \pm 1^{\prime }_{\rm stat}$|, consistent with the position of the radio core seen by the VLA. The systematic uncertainty is estimated as |$\rm \alpha _{J2000} = \pm 1.3 ^{s}_{\rm sys}$| and |$\rm \delta _{J2000} = \pm 20^{\prime \prime }_{\rm sys}$|, smaller than the statistical one.
The light curve for KUV 00311−1938, assuming a fixed index and binned by observation period (between August and December), is shown in Fig. 1. A fit of a constant to these flux points finds no significant deviation from a steady flux (χ2/ndf = 4.2/5), nor is any variation found at daily time-scales.
![Light curves for KUV 00311−1938 (left) and PKS 1440−389 (right). Top panels:H.E.S.S. light curves showing the flux above $\rm 0.83 \, TeV$ per observing season (left) and above $\rm 0.147 \, TeV$ with daily binning (right). Only statistical errors are shown, and upper limits are calculated when the significance in a bin is below 1 σ. Middle panels: Light curve of Fermi/LAT observations in the energy range [100 MeV to 300 GeV] in 2-month binning (left). Fermi/LAT light curve in the energy range [300 MeV to 300 GeV] in monthly bins (right). The significance in each bin is at least 3 σ. Bottom panel: Light curve of atom observations with the R filter.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/494/4/10.1093_mnras_staa999/3/m_staa999fig1.jpeg?Expires=1749141784&Signature=et5UoyKcYw9ET8ACUx9HWtP42vDunPhUmf-2Vg0QRxxJKCTK-cvZynLLBUm-FxGOV02KgeM6-skuRahhGb8PGEYRKq9UIK4e9hd-5zHVUOUYiohS-o7JOa96y6GAOng7bMiq6wVHsKxUFh9Su6uYna09Yc9aok9i5vfTfeNZyhvaYwVQQoRn~Gyz6HnzkpNLgaYsArlWLgG~rLVaMq66BlNrlRROjAirNXaNVlBH-C4Eq6CzT246vbfkP6cKfinNzOGVF5xjiXPqkfZ6Gumt13zr2IyhxmHTzeuNOvwjL2NSBkzID0cjurbZ6vzxiAaprT34gaL5eNu58NtnCtVtSw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Light curves for KUV 00311−1938 (left) and PKS 1440−389 (right). Top panels:H.E.S.S. light curves showing the flux above |$\rm 0.83 \, TeV$| per observing season (left) and above |$\rm 0.147 \, TeV$| with daily binning (right). Only statistical errors are shown, and upper limits are calculated when the significance in a bin is below 1 σ. Middle panels: Light curve of Fermi/LAT observations in the energy range [100 MeV to 300 GeV] in 2-month binning (left). Fermi/LAT light curve in the energy range [300 MeV to 300 GeV] in monthly bins (right). The significance in each bin is at least 3 σ. Bottom panel: Light curve of atom observations with the R filter.
The KUV 00311−1938 time-averaged spectrum is presented in Fig. 2, and the fit results are presented in Table 1. The spectrum was fitted by a PWL function, see Table 2 for the full expression.
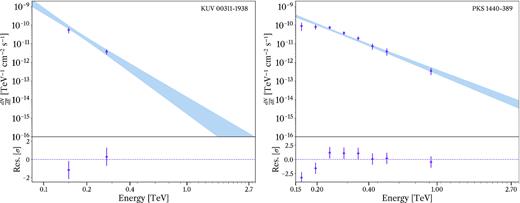
Left panel: Differential energy spectrum of the VHE γ-ray emission of KUV 00311−1938. right panel: Differential energy spectrum of the VHE γ-ray emission of PKS 1440−389. Upper plot: Time-averaged VHE spectrum measured from the two sources. Overlaid spectral points were rebinned, requiring a minimum point significance of 2 σ per bin. The butterfly represents the 1 σ confidence level error band of the fitted spectrum using a power-law hypothesis. Lower plot: Residuals of the reconstructed data points compared to the model.
Results of the spectral fitting of the H.E.S.S. data for the blazars KUV 00311−1938 and PKS 1440−389. The threshold energy, Eth, is defined as the energy at which the energy bias is less than 10 per cent. E0 is set to be the decorrelation energy of the fit. We give the integrated fluxes for both sources above the larger value of Eth.
| KUV 00311−1938 . | |
|---|---|
| Γ | 5.1 ± 0.6stat ± 0.3sys |
| N0 | |$(4.1 \pm 0.8_{\rm stat} \pm 1.7_{\rm sys}) \times 10^{-11}\rm TeV^{-1}cm^{-2}\, s^{-1}$| |
| E0 | 170 GeV |
| Eth | 83 GeV |
| |$F_{ (E \gt E_{\rm th}) }$| | (3 ± 1stat ± 1sys) × 10−11 cm−2 s−1 |
| F(E > 147 GeV) | |${\sim }0.9{{\,\rm per\, cent}}$| Crab flux >147 GeV |
| PKS 1440−389 | |
| Γ | 3.7 ± 0.2stat ± 0.3sys |
| N0 | |$(3.5 \pm 0.3_{\rm stat} \pm 1.2_{\rm sys}) \times 10^{-11} \rm TeV^{-1}cm^{-2}\, s^{-1}$| |
| E0 | 274 GeV |
| Eth | 147 GeV |
| |$F_{(E \gt E_{\rm th})}$| | (1.87 ± 0.21stat ± 0.8sys) × 10−11cm−2 s−1 |
| F(E > 147 GeV) | |${\sim }5.4{{\,\rm per\, cent}}$| Crab flux >147 GeV |
| KUV 00311−1938 . | |
|---|---|
| Γ | 5.1 ± 0.6stat ± 0.3sys |
| N0 | |$(4.1 \pm 0.8_{\rm stat} \pm 1.7_{\rm sys}) \times 10^{-11}\rm TeV^{-1}cm^{-2}\, s^{-1}$| |
| E0 | 170 GeV |
| Eth | 83 GeV |
| |$F_{ (E \gt E_{\rm th}) }$| | (3 ± 1stat ± 1sys) × 10−11 cm−2 s−1 |
| F(E > 147 GeV) | |${\sim }0.9{{\,\rm per\, cent}}$| Crab flux >147 GeV |
| PKS 1440−389 | |
| Γ | 3.7 ± 0.2stat ± 0.3sys |
| N0 | |$(3.5 \pm 0.3_{\rm stat} \pm 1.2_{\rm sys}) \times 10^{-11} \rm TeV^{-1}cm^{-2}\, s^{-1}$| |
| E0 | 274 GeV |
| Eth | 147 GeV |
| |$F_{(E \gt E_{\rm th})}$| | (1.87 ± 0.21stat ± 0.8sys) × 10−11cm−2 s−1 |
| F(E > 147 GeV) | |${\sim }5.4{{\,\rm per\, cent}}$| Crab flux >147 GeV |
Results of the spectral fitting of the H.E.S.S. data for the blazars KUV 00311−1938 and PKS 1440−389. The threshold energy, Eth, is defined as the energy at which the energy bias is less than 10 per cent. E0 is set to be the decorrelation energy of the fit. We give the integrated fluxes for both sources above the larger value of Eth.
| KUV 00311−1938 . | |
|---|---|
| Γ | 5.1 ± 0.6stat ± 0.3sys |
| N0 | |$(4.1 \pm 0.8_{\rm stat} \pm 1.7_{\rm sys}) \times 10^{-11}\rm TeV^{-1}cm^{-2}\, s^{-1}$| |
| E0 | 170 GeV |
| Eth | 83 GeV |
| |$F_{ (E \gt E_{\rm th}) }$| | (3 ± 1stat ± 1sys) × 10−11 cm−2 s−1 |
| F(E > 147 GeV) | |${\sim }0.9{{\,\rm per\, cent}}$| Crab flux >147 GeV |
| PKS 1440−389 | |
| Γ | 3.7 ± 0.2stat ± 0.3sys |
| N0 | |$(3.5 \pm 0.3_{\rm stat} \pm 1.2_{\rm sys}) \times 10^{-11} \rm TeV^{-1}cm^{-2}\, s^{-1}$| |
| E0 | 274 GeV |
| Eth | 147 GeV |
| |$F_{(E \gt E_{\rm th})}$| | (1.87 ± 0.21stat ± 0.8sys) × 10−11cm−2 s−1 |
| F(E > 147 GeV) | |${\sim }5.4{{\,\rm per\, cent}}$| Crab flux >147 GeV |
| KUV 00311−1938 . | |
|---|---|
| Γ | 5.1 ± 0.6stat ± 0.3sys |
| N0 | |$(4.1 \pm 0.8_{\rm stat} \pm 1.7_{\rm sys}) \times 10^{-11}\rm TeV^{-1}cm^{-2}\, s^{-1}$| |
| E0 | 170 GeV |
| Eth | 83 GeV |
| |$F_{ (E \gt E_{\rm th}) }$| | (3 ± 1stat ± 1sys) × 10−11 cm−2 s−1 |
| F(E > 147 GeV) | |${\sim }0.9{{\,\rm per\, cent}}$| Crab flux >147 GeV |
| PKS 1440−389 | |
| Γ | 3.7 ± 0.2stat ± 0.3sys |
| N0 | |$(3.5 \pm 0.3_{\rm stat} \pm 1.2_{\rm sys}) \times 10^{-11} \rm TeV^{-1}cm^{-2}\, s^{-1}$| |
| E0 | 274 GeV |
| Eth | 147 GeV |
| |$F_{(E \gt E_{\rm th})}$| | (1.87 ± 0.21stat ± 0.8sys) × 10−11cm−2 s−1 |
| F(E > 147 GeV) | |${\sim }5.4{{\,\rm per\, cent}}$| Crab flux >147 GeV |
All the results have been cross-checked and confirmed with the analysis method in De Naurois & Rolland (2009).
2.2 PKS 1440−389
H.E.S.S. observations of PKS 1440−389 were conducted during the 3-month period between February 28 and May 27, 2012 (MJD 55985−56074) at a mean zenith angle of 17°. After quality selection and dead time correction, the data sum up to a total observation time of 11.9 hours.
The source is detected at a level of 11.7 standard deviations, with an excess of 342 counts from the ON region of 0.1° radius centred at the nominal position of the source. The total number of ON- and OFF-source events being |$\rm N_{ON} = 999$| and |$\rm N_{OFF} = 6391$|, respectively, with a background normalization factor α = 0.102754.
A fit to the uncorrelated excess map yields a position for the excess of |$\rm \alpha _{\rm J2000} = 14 ^{h} 44 ^{m} 0.2 ^{s} \pm 2.6 ^{s}_{\rm stat} \pm 1.3 ^{s}_{\rm sys}$| and |$\rm \delta _{\rm J2000} = -39^{\circ } 08^{\prime } 21^{\prime \prime } \pm 31^{\prime \prime }_{\rm stat} \pm 20^{\prime \prime }_{\rm sys}$|, which is spatially consistent with the radio position of the BL Lac object PKS 1440−389 (Jackson et al. 2002).
A daily binned light curve was derived for energies above the energy threshold (147 GeV), assuming a fixed spectral index, and is shown in the top-right panel of Fig. 1. A fit with a constant to the flux points showed no significant deviation from a steady flux (χ2/ndf = 19.41/14), nor was any variation detected on monthly time-scales.
The photon spectrum in the energy range above 147 GeV (shown in Fig. 2), and the fit results are found in Table 1. The systematics were estimated in the same way as for the analysis of KUV 00311−1938.
All the results have been cross-checked and confirmed with the analysis method in Becherini et al. (2011).
3 DATA ANALYSIS AND RESULTS OF MULTIWAVELENGTH INSTRUMENTS
Complementary to the H.E.S.S. observations, multiwavelength data from observations with Fermi/LAT (20 MeV–300 GeV), Swift/XRT (0.2–10 keV), Swift/UVOT (170–650 nm) and atom (optical R filter) are presented in this section. Only for PKS 1440−389 are all data contemporaneous. Unfortunately, for KUV 00311−1938 no contemporaneous Swift observations are available.
3.1 Fermi/LAT
The Large Area Telescope (LAT) on board the Fermi satellite is a pair-conversion γ-ray detector, sensitive in the energy range from 20 MeV to above 300 GeV (Atwood et al. 2009).
Data contemporaneous to the H.E.S.S. observations were analysed with the LAT ScienceTools, version v11r5p3 for both sources. Source-class events in a circular region of interest of 10° radius centred at the positions of the sources are considered and the P8R2_SOURCE_V6 instrumental response functions were used. To remove γ-rays produced by cosmic-ray interactions in the Earth’s limb, events with zenith angles greater than 90° were rejected. The isotropic background, containing both the extragalactic diffuse γ-ray and residual instrumental background, is estimated through the iso_p8v2_SOURCE_V6_v06 model, while the Galactic diffuse emission is modelled with the spatial template gll_iem_v06. Spectral parameters were extracted by fitting a model containing the diffuse background and point sources from the 3FGL catalogue (Acero et al. 2015). The spectral parameters of sources within the inner 3° of the region of interest were left free during the fit, all others were fixed to their 3FGL values.
The spectral analysis was performed between different values of |$E_{\min}$| and |$E_{\max}$| assuming three different spectral models, a PWL, a PWL with EC, and an LP, see Table 2 for full expressions.
| Spectral shape . | Formula . | Parameter explanation . |
|---|---|---|
| Power-law (PWL) | |$\mathrm{ d}N/\mathrm{ d}E = {N_0 \cdot (E/E_0)^{-\Gamma }}$| | N0 = normalization at E = E0, Γ = photon index. N0 and Γ free in the minimization |
| Power-law with exponential cut-off (EC) | |$\mathrm{ d}N/\mathrm{ d}E = N_0 \cdot (E/E_0)^{-\Gamma }\cdot \exp{(-E/E_\mathrm{ c})}$| | Ec = cut-off energy, N0 and Γ as above. N0, Γ, Ec free in the minimization |
| Log-parabola (LP) | |$\mathrm{ d}N/\mathrm{ d}E = N_0 \cdot (E/E_b)^{-a-b\cdot \mathrm{log}(E/E_b)}$| | Eb = scale parameter, a = photon index at E = Eb, and b = curvature parameter. N0, a, and b free in the minimization |
| Spectral shape . | Formula . | Parameter explanation . |
|---|---|---|
| Power-law (PWL) | |$\mathrm{ d}N/\mathrm{ d}E = {N_0 \cdot (E/E_0)^{-\Gamma }}$| | N0 = normalization at E = E0, Γ = photon index. N0 and Γ free in the minimization |
| Power-law with exponential cut-off (EC) | |$\mathrm{ d}N/\mathrm{ d}E = N_0 \cdot (E/E_0)^{-\Gamma }\cdot \exp{(-E/E_\mathrm{ c})}$| | Ec = cut-off energy, N0 and Γ as above. N0, Γ, Ec free in the minimization |
| Log-parabola (LP) | |$\mathrm{ d}N/\mathrm{ d}E = N_0 \cdot (E/E_b)^{-a-b\cdot \mathrm{log}(E/E_b)}$| | Eb = scale parameter, a = photon index at E = Eb, and b = curvature parameter. N0, a, and b free in the minimization |
| Spectral shape . | Formula . | Parameter explanation . |
|---|---|---|
| Power-law (PWL) | |$\mathrm{ d}N/\mathrm{ d}E = {N_0 \cdot (E/E_0)^{-\Gamma }}$| | N0 = normalization at E = E0, Γ = photon index. N0 and Γ free in the minimization |
| Power-law with exponential cut-off (EC) | |$\mathrm{ d}N/\mathrm{ d}E = N_0 \cdot (E/E_0)^{-\Gamma }\cdot \exp{(-E/E_\mathrm{ c})}$| | Ec = cut-off energy, N0 and Γ as above. N0, Γ, Ec free in the minimization |
| Log-parabola (LP) | |$\mathrm{ d}N/\mathrm{ d}E = N_0 \cdot (E/E_b)^{-a-b\cdot \mathrm{log}(E/E_b)}$| | Eb = scale parameter, a = photon index at E = Eb, and b = curvature parameter. N0, a, and b free in the minimization |
| Spectral shape . | Formula . | Parameter explanation . |
|---|---|---|
| Power-law (PWL) | |$\mathrm{ d}N/\mathrm{ d}E = {N_0 \cdot (E/E_0)^{-\Gamma }}$| | N0 = normalization at E = E0, Γ = photon index. N0 and Γ free in the minimization |
| Power-law with exponential cut-off (EC) | |$\mathrm{ d}N/\mathrm{ d}E = N_0 \cdot (E/E_0)^{-\Gamma }\cdot \exp{(-E/E_\mathrm{ c})}$| | Ec = cut-off energy, N0 and Γ as above. N0, Γ, Ec free in the minimization |
| Log-parabola (LP) | |$\mathrm{ d}N/\mathrm{ d}E = N_0 \cdot (E/E_b)^{-a-b\cdot \mathrm{log}(E/E_b)}$| | Eb = scale parameter, a = photon index at E = Eb, and b = curvature parameter. N0, a, and b free in the minimization |
The three spectral models were used to assess the best spectral fit for a given analysis using the log likelihood ratio test. Results of the preferred spectral fits are summarized in Table 3. The event analysis presented here uses the binned likelihood method (Atwood et al. 2009) with Pass8 (version 2) data and the user contributed python tools Enrico (Sanchez & Deil 2015). The estimated systematic uncertainty on the flux in these analyses is 10 per cent at 0.1 GeV, 5 per cent at 0.5 GeV and 10 per cent at 10 GeV and above (Ackermann et al. 2011). The test positions of the sources were taken from the 3FGL and are consistent with the nominal positions given previously.
Results of the spectral fitting of the Fermi/LAT data for the blazars KUV 00311−1938 and PKS 1440−389. Only the most significant spectral shape of the various analyses presented, evaluated with the log-likelihood ratio test, is shown. We present the values of all the spectral parameters which were left free during the fit procedure. E0 is set to be the decorrelation energy of the fit.
| Source . | Model . | Energy range . | TS . | Spectral parameters . | Integrated flux . |
|---|---|---|---|---|---|
| . | . | (GeV) . | . | . | (|$\rm ph\, cm^{-2} s^{-1}$|) . |
| KUV 00311−1938 | EC | 0.1–300 | 2009 | Γ = 1.58 ± 0.05, | |$F_{(E \gt 100\, \mathrm{MeV})} = (1.15 \pm 0.1)\times 10^{-8}$| |
| |$N_{0} = (6.99 \pm 1.05)\times 10^{-11} \rm ph\, MeV^{-1}\, cm^{-2}\, s^{-1}$|, | |||||
| |$E_{\mathrm{ c}} = (54500 \pm 16200)\; \mathrm{ MeV}$| | |||||
| |$E_{0} = 100 ~\rm MeV$| | |||||
| KUV 00311−1938 | PWL | 0.1–10 | 1465 | Γ = 1.60 ± 0.05 | |$F_{(E \gt 100\, \mathrm{MeV})} = (1.1\pm 0.1)\times 10^{-8}$| |
| |$N_{0} = (4.46 \pm 0.23)\times 10^{-13} \, \rm ph\, MeV^{-1}\, cm^{-2}\, s^{-1}$|, | |||||
| |$E_{0} = 2398 ~\rm MeV$| | |||||
| PKS 1440−389 | PWL | 0.3–300 | 88.4 | Γ = 1.69 ± 0.15 | |$F_{(E \gt 300\, \mathrm{MeV})} = (6.5\pm 1.8)\times 10^{-9}$| |
| |$N_{0} = (3.57 \pm 0.79)\times 10^{-13} \, \rm ph\, MeV^{-1}\, cm^{-2}\, s^{-1}$|, | |||||
| |$E_{0} = 2753 ~\rm MeV$| | |||||
| PKS 1440−389 | PWL | 0.3–10 | 57.5 | Γ = 1.46 ± 0.30 | |$F_{(E \gt 300\, \mathrm{MeV})} = (5.4\pm 1.9)\times 10^{-9}$| |
| |$N_{0} = (4.04 \pm 0.98)\times 10^{-13} \, \rm ph\, MeV^{-1}\, cm^{-2}\, s^{-1}$|, | |||||
| |$E_{0} = 2753 ~\rm MeV$| |
| Source . | Model . | Energy range . | TS . | Spectral parameters . | Integrated flux . |
|---|---|---|---|---|---|
| . | . | (GeV) . | . | . | (|$\rm ph\, cm^{-2} s^{-1}$|) . |
| KUV 00311−1938 | EC | 0.1–300 | 2009 | Γ = 1.58 ± 0.05, | |$F_{(E \gt 100\, \mathrm{MeV})} = (1.15 \pm 0.1)\times 10^{-8}$| |
| |$N_{0} = (6.99 \pm 1.05)\times 10^{-11} \rm ph\, MeV^{-1}\, cm^{-2}\, s^{-1}$|, | |||||
| |$E_{\mathrm{ c}} = (54500 \pm 16200)\; \mathrm{ MeV}$| | |||||
| |$E_{0} = 100 ~\rm MeV$| | |||||
| KUV 00311−1938 | PWL | 0.1–10 | 1465 | Γ = 1.60 ± 0.05 | |$F_{(E \gt 100\, \mathrm{MeV})} = (1.1\pm 0.1)\times 10^{-8}$| |
| |$N_{0} = (4.46 \pm 0.23)\times 10^{-13} \, \rm ph\, MeV^{-1}\, cm^{-2}\, s^{-1}$|, | |||||
| |$E_{0} = 2398 ~\rm MeV$| | |||||
| PKS 1440−389 | PWL | 0.3–300 | 88.4 | Γ = 1.69 ± 0.15 | |$F_{(E \gt 300\, \mathrm{MeV})} = (6.5\pm 1.8)\times 10^{-9}$| |
| |$N_{0} = (3.57 \pm 0.79)\times 10^{-13} \, \rm ph\, MeV^{-1}\, cm^{-2}\, s^{-1}$|, | |||||
| |$E_{0} = 2753 ~\rm MeV$| | |||||
| PKS 1440−389 | PWL | 0.3–10 | 57.5 | Γ = 1.46 ± 0.30 | |$F_{(E \gt 300\, \mathrm{MeV})} = (5.4\pm 1.9)\times 10^{-9}$| |
| |$N_{0} = (4.04 \pm 0.98)\times 10^{-13} \, \rm ph\, MeV^{-1}\, cm^{-2}\, s^{-1}$|, | |||||
| |$E_{0} = 2753 ~\rm MeV$| |
Results of the spectral fitting of the Fermi/LAT data for the blazars KUV 00311−1938 and PKS 1440−389. Only the most significant spectral shape of the various analyses presented, evaluated with the log-likelihood ratio test, is shown. We present the values of all the spectral parameters which were left free during the fit procedure. E0 is set to be the decorrelation energy of the fit.
| Source . | Model . | Energy range . | TS . | Spectral parameters . | Integrated flux . |
|---|---|---|---|---|---|
| . | . | (GeV) . | . | . | (|$\rm ph\, cm^{-2} s^{-1}$|) . |
| KUV 00311−1938 | EC | 0.1–300 | 2009 | Γ = 1.58 ± 0.05, | |$F_{(E \gt 100\, \mathrm{MeV})} = (1.15 \pm 0.1)\times 10^{-8}$| |
| |$N_{0} = (6.99 \pm 1.05)\times 10^{-11} \rm ph\, MeV^{-1}\, cm^{-2}\, s^{-1}$|, | |||||
| |$E_{\mathrm{ c}} = (54500 \pm 16200)\; \mathrm{ MeV}$| | |||||
| |$E_{0} = 100 ~\rm MeV$| | |||||
| KUV 00311−1938 | PWL | 0.1–10 | 1465 | Γ = 1.60 ± 0.05 | |$F_{(E \gt 100\, \mathrm{MeV})} = (1.1\pm 0.1)\times 10^{-8}$| |
| |$N_{0} = (4.46 \pm 0.23)\times 10^{-13} \, \rm ph\, MeV^{-1}\, cm^{-2}\, s^{-1}$|, | |||||
| |$E_{0} = 2398 ~\rm MeV$| | |||||
| PKS 1440−389 | PWL | 0.3–300 | 88.4 | Γ = 1.69 ± 0.15 | |$F_{(E \gt 300\, \mathrm{MeV})} = (6.5\pm 1.8)\times 10^{-9}$| |
| |$N_{0} = (3.57 \pm 0.79)\times 10^{-13} \, \rm ph\, MeV^{-1}\, cm^{-2}\, s^{-1}$|, | |||||
| |$E_{0} = 2753 ~\rm MeV$| | |||||
| PKS 1440−389 | PWL | 0.3–10 | 57.5 | Γ = 1.46 ± 0.30 | |$F_{(E \gt 300\, \mathrm{MeV})} = (5.4\pm 1.9)\times 10^{-9}$| |
| |$N_{0} = (4.04 \pm 0.98)\times 10^{-13} \, \rm ph\, MeV^{-1}\, cm^{-2}\, s^{-1}$|, | |||||
| |$E_{0} = 2753 ~\rm MeV$| |
| Source . | Model . | Energy range . | TS . | Spectral parameters . | Integrated flux . |
|---|---|---|---|---|---|
| . | . | (GeV) . | . | . | (|$\rm ph\, cm^{-2} s^{-1}$|) . |
| KUV 00311−1938 | EC | 0.1–300 | 2009 | Γ = 1.58 ± 0.05, | |$F_{(E \gt 100\, \mathrm{MeV})} = (1.15 \pm 0.1)\times 10^{-8}$| |
| |$N_{0} = (6.99 \pm 1.05)\times 10^{-11} \rm ph\, MeV^{-1}\, cm^{-2}\, s^{-1}$|, | |||||
| |$E_{\mathrm{ c}} = (54500 \pm 16200)\; \mathrm{ MeV}$| | |||||
| |$E_{0} = 100 ~\rm MeV$| | |||||
| KUV 00311−1938 | PWL | 0.1–10 | 1465 | Γ = 1.60 ± 0.05 | |$F_{(E \gt 100\, \mathrm{MeV})} = (1.1\pm 0.1)\times 10^{-8}$| |
| |$N_{0} = (4.46 \pm 0.23)\times 10^{-13} \, \rm ph\, MeV^{-1}\, cm^{-2}\, s^{-1}$|, | |||||
| |$E_{0} = 2398 ~\rm MeV$| | |||||
| PKS 1440−389 | PWL | 0.3–300 | 88.4 | Γ = 1.69 ± 0.15 | |$F_{(E \gt 300\, \mathrm{MeV})} = (6.5\pm 1.8)\times 10^{-9}$| |
| |$N_{0} = (3.57 \pm 0.79)\times 10^{-13} \, \rm ph\, MeV^{-1}\, cm^{-2}\, s^{-1}$|, | |||||
| |$E_{0} = 2753 ~\rm MeV$| | |||||
| PKS 1440−389 | PWL | 0.3–10 | 57.5 | Γ = 1.46 ± 0.30 | |$F_{(E \gt 300\, \mathrm{MeV})} = (5.4\pm 1.9)\times 10^{-9}$| |
| |$N_{0} = (4.04 \pm 0.98)\times 10^{-13} \, \rm ph\, MeV^{-1}\, cm^{-2}\, s^{-1}$|, | |||||
| |$E_{0} = 2753 ~\rm MeV$| |
For each source, we present the analysis up to |$E_{\max}= 300 \; \mathrm{ GeV}$| and the analysis up to |$E_{\max}= 10 \; \mathrm{ GeV}$|. The former analysis is used to understand the agreement with the H.E.S.S. spectrum in the SED shown in Section 4.1. The latter is used to assess the shape of the spectrum up at the energies where EBL absorption effects are negligible, so that the upper limit on the redshift can be evaluated, see Section 4.2.
3.1.1 KUV 00311−1938
Fermi/LAT data contemporaneous to the H.E.S.S. observations, i.e. in the period from 2009-11-10 (MJD 55145) to 2014-08-25 (MJD 56894) were analysed in the [100 MeV–300 GeV] energy range and in the [100 MeV–10 GeV] energy range.
As the source has modest variability in the 4FGL catalogue (Section 1.1), a 2-month binning Fermi/LAT light curve was computed assuming a PWL shape, leaving the index free to vary (see Fig. 1).
[100 MeV–300 GeV]. No variability is detected during the H.E.S.S. observation period, as an excess variance calculation yields a value compatible with zero. The γ-ray emission from KUV 00311−1938 is therefore well described as constant in the Fermi/LAT energy range, implying that it is safe to combine the data from the full H.E.S.S. observation period into a single spectrum. All spectral models result in an excess with a significance of about ≈45 σ. A likelihood ratio test shows that the EC (Ec = 54.4 GeV) is preferred to the simple PWL shape at the 4.20 σ-level using five years of data, in line with the 5.15 σ for the whole 8-years Fermi/LAT 4FGL analysis. The reconstructed Fermi/LAT spectrum is shown alongside the H.E.S.S. spectrum in Fig. 3. The significance of the Fermi/LAT binned spectral points shown is at least 3 σ. If the significance of the bin is less than 3 σ, a 95 per cent upper limit on the flux in the bin is computed.
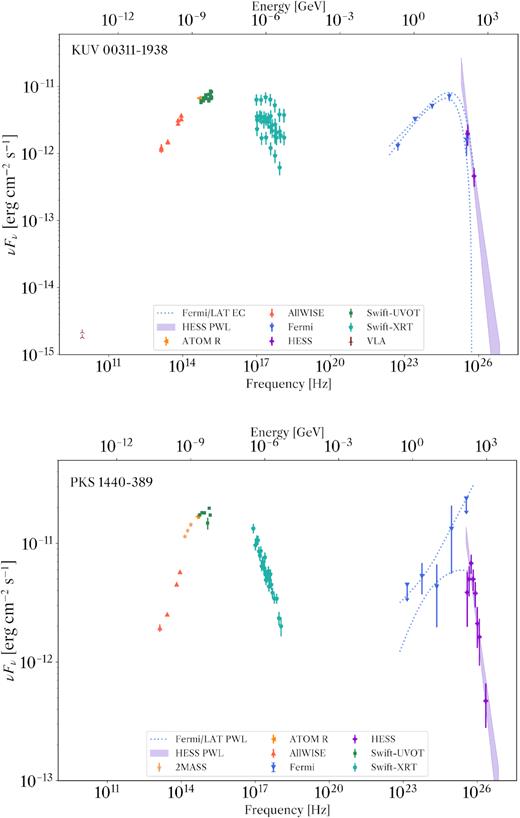
Top panel: Averaged multiwavelength spectral energy distribution of KUV 00311−1938. Bottom panel: Contemporaneous multiwavelength spectral energy distribution of PKS 1440−389. In both plots the H.E.S.S. spectrum is represented by the filled butterfly and purple points at the highest energies, indicating 1 σ statistical errors. The measured Fermi/LAT spectrum is represented by the blue dotted lines and points (see Section 3.1.1 for details). Upper limits are calculated if the significance of the energy bin is less than 3 σ. The Fermi/LAT butterflies include only statistical errors.
[100 MeV–10 GeV]. All spectral models result in an excess with a significance of about |${\approx }7.6\sigma$|. A likelihood ratio test shows that the PWL is the preferred shape in this energy range using the five years of data.
3.1.2 PKS 1440−389
Fermi/LAT data analysis has been performed for the 3-month data set contemporaneous with the H.E.S.S. observations (MJD 55985−56074) in the energy range [300 MeV–300 GeV] and [300 MeV–10 GeV]. The low-energy bound of 300 MeV was applied to avoid contamination from the bright, nearby quasar PKS B1424−418 due to the larger point spread function at low energies (Ackermann et al. 2013).
Since PKS 1440−389 has modest variability in the 4FGL catalogue (Section 1.2), a monthly binning Fermi/LAT light curve was computed assuming a PWL shape, leaving the index free to vary (see Fig. 1). The excess variance calculation over the Fermi/LAT light curve gives a value of 0.1 ± 0.3. Therefore data from the whole 3-month data set were combined into a single spectrum.
[300 MeV to 300 GeV]. All spectral models in this energy range result in an excess with a significance of about ≈9.4 σ and the favoured shape is the PWL. The reconstructed Fermi/LAT spectrum in this range is shown alongside the H.E.S.S. spectrum in Fig. 3.
[300 MeV to 10 GeV]. Spectral models in this energy range result in an excess with a significance of about |$7.6\sigma$| and the preferred spectral shape is the PWL.
3.2 Swift/XRT and UVOT
The X-ray telescope (XRT) onboard the Swift satellite is designed to measure X-rays in the 0.2–10 keV energy range (Burrows et al. 2005). Images in six filters (V and B in optical and U, UVW1, UVM2 and UVW2, in the ultraviolet, in order of increasing frequency) can be obtained simultaneously to XRT with the Swift/UVOT telescope (Roming et al. 2005).
Target of opportunity observations were obtained on 2012 April 29 (MJD 56046), following the H.E.S.S. detection of PKS 1440−389. Unfortunately that was not the case for KUV 00311−1938 and only a few observations exist, with none of these archival observations being within the time span of the overall H.E.S.S. observing campaign.
The X-ray observations were performed with the XRT detector in photon counting (PC) mode in the 0.3–10 keV energy range. The analysis was performed using the standard HEASoft (v6.16) and Xspec (v12.8.2) tools. Source counts were extracted using the xselect task from a circular region with a radius of 20 pixels (∼47 arcsec). Background counts were extracted from a 60-pixel circular region with no known X-ray sources. The data were grouped, requiring a minimum of 20 counts per bin and then fitted with a PWL model including photoelectric absorption with a fixed value for the Galactic column density
Sky-corrected images for all available Swift/UVOT filters were taken from the Swift archive, and aperture photometry was performed using the UVOT tasks included within the HEASoft package. Source counts were extracted using a 5″ radius for all single exposures and all filters, while the background was estimated from different positions more than 25″ away from the source. Count rates were then converted to fluxes using the standard photometric zero-points (Poole et al. 2008). The reported fluxes are de-reddened for Galactic extinction following the procedure in Roming et al. (2009), with E(B − V) estimate from the IRSA.1
3.2.1 KUV 00311−1938
We analysed all six Swift snapshot observations of KUV 00311−1938 that were unfortunately performed prior to the H.E.S.S. campaign, between 2008 November 9 and 2009 May 8, see Table 4.
The XRT spectra were fitted with a single PWL model with Galactic absorption NH fixed at 1.67 × 1020 cm−2 (Willingale et al. 2013). Results are given for each individual observation in Table 4, showing that the source is variable in the X-ray band.
Available Swift/XRT observations, IDs, corresponding dates, and exposure times for KUV 00311−1938 (rows 1–6) and PKS 1440−389 (the last row). Power-law parameters describing the differential photon flux obtained for the available XRT observations. |$N_{\rm H \rm }$| is fixed at the Galactic value, 1.67 × 1020 cm−2 for KUV 00311−1938 and 1.08 × 1021 cm−2 for PKS 1440−389.
| ID . | Start . | Exposure . | Γ . | Normalisation at 1 keV . | |$\chi ^2 /\rm d.o.f.$| . |
|---|---|---|---|---|---|
| . | . | (s) . | . | (10−3 cm−2 s−1 keV−1) . | . |
| 00037546001 | 2008-11-09 | 1655 | |$2.13^{+0.15}_{-0.15}$| | |$1.95^{+0.21}_{-0.18}$| | 8.6/10 |
| 00037546002 | 2008-11-11 | 2922 | |$2.29^{+0.11}_{-0.11}$| | |$1.76^{+0.12}_{-0.12}$| | 22.1/26 |
| 00037546003 | 2008-11-13 | 2790 | |$2.26^{+0.12}_{-0.12}$| | |$1.60^{+0.17}_{-0.18}$| | 23.4/23 |
| 00037546004 | 2008-11-15 | 3891 | |$2.37^{+0.10}_{-0.10}$| | |$1.61^{+0.15}_{-0.15}$| | 41.3/32 |
| 00038359001 | 2009-02-01 | 3349 | |$2.52^{+0.20}_{-0.21}$| | |$0.86^{+0.08}_{-0.08}$| | 16.2/15 |
| 00038359002 | 2009-05-08 | 4722 | |$2.23^{+0.07}_{-0.07}$| | |$3.54^{+0.19}_{-0.19}$| | 93.2/82 |
| 00041665002 | 2012-04-29 | 8551 | |$2.64^{+0.05}_{-0.05}$| | |$3.80^{+0.12}_{-0.12}$| | 124.4/108 |
| ID . | Start . | Exposure . | Γ . | Normalisation at 1 keV . | |$\chi ^2 /\rm d.o.f.$| . |
|---|---|---|---|---|---|
| . | . | (s) . | . | (10−3 cm−2 s−1 keV−1) . | . |
| 00037546001 | 2008-11-09 | 1655 | |$2.13^{+0.15}_{-0.15}$| | |$1.95^{+0.21}_{-0.18}$| | 8.6/10 |
| 00037546002 | 2008-11-11 | 2922 | |$2.29^{+0.11}_{-0.11}$| | |$1.76^{+0.12}_{-0.12}$| | 22.1/26 |
| 00037546003 | 2008-11-13 | 2790 | |$2.26^{+0.12}_{-0.12}$| | |$1.60^{+0.17}_{-0.18}$| | 23.4/23 |
| 00037546004 | 2008-11-15 | 3891 | |$2.37^{+0.10}_{-0.10}$| | |$1.61^{+0.15}_{-0.15}$| | 41.3/32 |
| 00038359001 | 2009-02-01 | 3349 | |$2.52^{+0.20}_{-0.21}$| | |$0.86^{+0.08}_{-0.08}$| | 16.2/15 |
| 00038359002 | 2009-05-08 | 4722 | |$2.23^{+0.07}_{-0.07}$| | |$3.54^{+0.19}_{-0.19}$| | 93.2/82 |
| 00041665002 | 2012-04-29 | 8551 | |$2.64^{+0.05}_{-0.05}$| | |$3.80^{+0.12}_{-0.12}$| | 124.4/108 |
Available Swift/XRT observations, IDs, corresponding dates, and exposure times for KUV 00311−1938 (rows 1–6) and PKS 1440−389 (the last row). Power-law parameters describing the differential photon flux obtained for the available XRT observations. |$N_{\rm H \rm }$| is fixed at the Galactic value, 1.67 × 1020 cm−2 for KUV 00311−1938 and 1.08 × 1021 cm−2 for PKS 1440−389.
| ID . | Start . | Exposure . | Γ . | Normalisation at 1 keV . | |$\chi ^2 /\rm d.o.f.$| . |
|---|---|---|---|---|---|
| . | . | (s) . | . | (10−3 cm−2 s−1 keV−1) . | . |
| 00037546001 | 2008-11-09 | 1655 | |$2.13^{+0.15}_{-0.15}$| | |$1.95^{+0.21}_{-0.18}$| | 8.6/10 |
| 00037546002 | 2008-11-11 | 2922 | |$2.29^{+0.11}_{-0.11}$| | |$1.76^{+0.12}_{-0.12}$| | 22.1/26 |
| 00037546003 | 2008-11-13 | 2790 | |$2.26^{+0.12}_{-0.12}$| | |$1.60^{+0.17}_{-0.18}$| | 23.4/23 |
| 00037546004 | 2008-11-15 | 3891 | |$2.37^{+0.10}_{-0.10}$| | |$1.61^{+0.15}_{-0.15}$| | 41.3/32 |
| 00038359001 | 2009-02-01 | 3349 | |$2.52^{+0.20}_{-0.21}$| | |$0.86^{+0.08}_{-0.08}$| | 16.2/15 |
| 00038359002 | 2009-05-08 | 4722 | |$2.23^{+0.07}_{-0.07}$| | |$3.54^{+0.19}_{-0.19}$| | 93.2/82 |
| 00041665002 | 2012-04-29 | 8551 | |$2.64^{+0.05}_{-0.05}$| | |$3.80^{+0.12}_{-0.12}$| | 124.4/108 |
| ID . | Start . | Exposure . | Γ . | Normalisation at 1 keV . | |$\chi ^2 /\rm d.o.f.$| . |
|---|---|---|---|---|---|
| . | . | (s) . | . | (10−3 cm−2 s−1 keV−1) . | . |
| 00037546001 | 2008-11-09 | 1655 | |$2.13^{+0.15}_{-0.15}$| | |$1.95^{+0.21}_{-0.18}$| | 8.6/10 |
| 00037546002 | 2008-11-11 | 2922 | |$2.29^{+0.11}_{-0.11}$| | |$1.76^{+0.12}_{-0.12}$| | 22.1/26 |
| 00037546003 | 2008-11-13 | 2790 | |$2.26^{+0.12}_{-0.12}$| | |$1.60^{+0.17}_{-0.18}$| | 23.4/23 |
| 00037546004 | 2008-11-15 | 3891 | |$2.37^{+0.10}_{-0.10}$| | |$1.61^{+0.15}_{-0.15}$| | 41.3/32 |
| 00038359001 | 2009-02-01 | 3349 | |$2.52^{+0.20}_{-0.21}$| | |$0.86^{+0.08}_{-0.08}$| | 16.2/15 |
| 00038359002 | 2009-05-08 | 4722 | |$2.23^{+0.07}_{-0.07}$| | |$3.54^{+0.19}_{-0.19}$| | 93.2/82 |
| 00041665002 | 2012-04-29 | 8551 | |$2.64^{+0.05}_{-0.05}$| | |$3.80^{+0.12}_{-0.12}$| | 124.4/108 |
During each XRT pointing, multiple exposures were taken with the Swift/UVOT instrument using all its filters. All available filters in each observation were searched for variability with the uvotmaghist tool. Since no variability was observed in any filter, the multiple images within each filter were stacked prior to performing aperture photometry. The reported fluxes in Table 5 are de-reddened for Galactic extinction with E(B − V) = 0.019 mag.
Swift/UVOT photometric fluxes in 10−12 erg cm−2 s−1. KUV 00311−1938, rows 1–6; PKS 1440−389, the last row.
| ID . | V . | B . | U . | UVM1 . | UVM2 . | UVW2 . |
|---|---|---|---|---|---|---|
| 00037546001 | 5.73 ± 0.25 | 6.62 ± 0.18 | 6.15 ± 0.18 | 6.07 ± 0.17 | 7.0 ± 0.19 | 6.76 ± 0.14 |
| 00037546002 | 5.96 ± 0.19 | 6.84 ± 0.14 | 6.35 ± 0.13 | 6.40 ± 0.13 | 7.03 ± 0.16 | 6.71 ± 0.03 |
| 00037546003 | 6.34 ± 0.20 | 6.68 ± 0.14 | 6.17 ± 0.14 | 6.12 ± 0.13 | 7.52 ± 0.17 | 6.70 ± 0.11 |
| 00037546004 | 5.82 ± 0.16 | 6.68 ± 0.10 | 6.22 ± 0.11 | 6.50 ± 0.10 | 6.81 ± 0.14 | 6.98 ± 0.80 |
| 00038359001 | 6.12 ± 0.13 | 6.57 ± 0.76 | 6.12 ± 0.84 | 6.22 ± 0.86 | – | 6.56 ± 0.75 |
| 00038359002 | 6.00 ± 0.15 | 7.52 ± 0.10 | 6.73 ± 0.10 | 7.60 ± 0.10 | 8.53 ± 0.13 | 8.32 ± 0.76 |
| 00041665002 | 17.34 ± 0.56 | 18.07 ± 0.42 | 18.11 ± 0.42 | 14.79 ± 0.17 | 19.77 ± 0.27 | 17.30 ± 0.36 |
| ID . | V . | B . | U . | UVM1 . | UVM2 . | UVW2 . |
|---|---|---|---|---|---|---|
| 00037546001 | 5.73 ± 0.25 | 6.62 ± 0.18 | 6.15 ± 0.18 | 6.07 ± 0.17 | 7.0 ± 0.19 | 6.76 ± 0.14 |
| 00037546002 | 5.96 ± 0.19 | 6.84 ± 0.14 | 6.35 ± 0.13 | 6.40 ± 0.13 | 7.03 ± 0.16 | 6.71 ± 0.03 |
| 00037546003 | 6.34 ± 0.20 | 6.68 ± 0.14 | 6.17 ± 0.14 | 6.12 ± 0.13 | 7.52 ± 0.17 | 6.70 ± 0.11 |
| 00037546004 | 5.82 ± 0.16 | 6.68 ± 0.10 | 6.22 ± 0.11 | 6.50 ± 0.10 | 6.81 ± 0.14 | 6.98 ± 0.80 |
| 00038359001 | 6.12 ± 0.13 | 6.57 ± 0.76 | 6.12 ± 0.84 | 6.22 ± 0.86 | – | 6.56 ± 0.75 |
| 00038359002 | 6.00 ± 0.15 | 7.52 ± 0.10 | 6.73 ± 0.10 | 7.60 ± 0.10 | 8.53 ± 0.13 | 8.32 ± 0.76 |
| 00041665002 | 17.34 ± 0.56 | 18.07 ± 0.42 | 18.11 ± 0.42 | 14.79 ± 0.17 | 19.77 ± 0.27 | 17.30 ± 0.36 |
Swift/UVOT photometric fluxes in 10−12 erg cm−2 s−1. KUV 00311−1938, rows 1–6; PKS 1440−389, the last row.
| ID . | V . | B . | U . | UVM1 . | UVM2 . | UVW2 . |
|---|---|---|---|---|---|---|
| 00037546001 | 5.73 ± 0.25 | 6.62 ± 0.18 | 6.15 ± 0.18 | 6.07 ± 0.17 | 7.0 ± 0.19 | 6.76 ± 0.14 |
| 00037546002 | 5.96 ± 0.19 | 6.84 ± 0.14 | 6.35 ± 0.13 | 6.40 ± 0.13 | 7.03 ± 0.16 | 6.71 ± 0.03 |
| 00037546003 | 6.34 ± 0.20 | 6.68 ± 0.14 | 6.17 ± 0.14 | 6.12 ± 0.13 | 7.52 ± 0.17 | 6.70 ± 0.11 |
| 00037546004 | 5.82 ± 0.16 | 6.68 ± 0.10 | 6.22 ± 0.11 | 6.50 ± 0.10 | 6.81 ± 0.14 | 6.98 ± 0.80 |
| 00038359001 | 6.12 ± 0.13 | 6.57 ± 0.76 | 6.12 ± 0.84 | 6.22 ± 0.86 | – | 6.56 ± 0.75 |
| 00038359002 | 6.00 ± 0.15 | 7.52 ± 0.10 | 6.73 ± 0.10 | 7.60 ± 0.10 | 8.53 ± 0.13 | 8.32 ± 0.76 |
| 00041665002 | 17.34 ± 0.56 | 18.07 ± 0.42 | 18.11 ± 0.42 | 14.79 ± 0.17 | 19.77 ± 0.27 | 17.30 ± 0.36 |
| ID . | V . | B . | U . | UVM1 . | UVM2 . | UVW2 . |
|---|---|---|---|---|---|---|
| 00037546001 | 5.73 ± 0.25 | 6.62 ± 0.18 | 6.15 ± 0.18 | 6.07 ± 0.17 | 7.0 ± 0.19 | 6.76 ± 0.14 |
| 00037546002 | 5.96 ± 0.19 | 6.84 ± 0.14 | 6.35 ± 0.13 | 6.40 ± 0.13 | 7.03 ± 0.16 | 6.71 ± 0.03 |
| 00037546003 | 6.34 ± 0.20 | 6.68 ± 0.14 | 6.17 ± 0.14 | 6.12 ± 0.13 | 7.52 ± 0.17 | 6.70 ± 0.11 |
| 00037546004 | 5.82 ± 0.16 | 6.68 ± 0.10 | 6.22 ± 0.11 | 6.50 ± 0.10 | 6.81 ± 0.14 | 6.98 ± 0.80 |
| 00038359001 | 6.12 ± 0.13 | 6.57 ± 0.76 | 6.12 ± 0.84 | 6.22 ± 0.86 | – | 6.56 ± 0.75 |
| 00038359002 | 6.00 ± 0.15 | 7.52 ± 0.10 | 6.73 ± 0.10 | 7.60 ± 0.10 | 8.53 ± 0.13 | 8.32 ± 0.76 |
| 00041665002 | 17.34 ± 0.56 | 18.07 ± 0.42 | 18.11 ± 0.42 | 14.79 ± 0.17 | 19.77 ± 0.27 | 17.30 ± 0.36 |
The source exhibits variability between different observations, reaching a maximum flux around 2009 May 8 in both X-rays and ultraviolet. The UVOT photometric points and XRT spectral points are shown in Fig. 3.
3.2.2 PKS 1440−389
The fit result of the XRT spectrum of the 8 ks exposure obtained on 2012 April 29 (MJD 56046) for a fixed Galactic column density of NH = 1.08 × 1021 cm−2 (Willingale et al. 2013), can be found in Table 4.
Results from the analysis of simultaneous Swift/UVOT observations in all six filters are given in Table 5. With UVW1 and UVM2 filter observations having four individual exposures, they were stacked prior to aperture photometry as the uvotmaghist task showed no variability between the individual exposures. The reported fluxes are de-reddened for Galactic absorption, E(B − V) = 0.103 mag.
3.3 ATOM
The Automatic Telescope for Optical Monitoring2 (ATOM) is a |$\rm 75\, cm$| optical support telescope for H.E.S.S., located at the H.E.S.S. site. Operating since 2005, it provides optical monitoring of γ-ray sources. KUV 00311−1938 was regularly monitored from April 2008 to December 2012 in the R band (|$\rm 640\, nm$|), while PKS 1440−389 was observed with high cadence during the whole 2012 H.E.S.S. campaign on the source.
The ATOM data were analysed using aperture photometry with custom calibrators in the FoV. We were able to use up to four calibrators in the case of KUV 00311−1938 and five for PKS 1440−389. The resulting magnitudes were de-reddened in the same manner as done for the UVOT data. The uncertainty on the absolute calibration is propagated into the evaluation of the flux errors.
The resulting R-band light curves, corrected for Galactic extinction, are presented in the bottom panel of Fig. 1 showing clear variability in the optical regime contemporaneous with the H.E.S.S. observations, for both KUV 00311−1938 and PKS 1440−389.
4 DISCUSSION
In this section, we present a brief discussion of the implications of our observational results. Specifically, considering the unknown redshift of the sources, we will derive an upper limit on the redshift based on the extrapolation of the Fermi/LAT spectrum into the VHE (H.E.S.S.) regime (Section 4.2).
4.1 Spectral energy distribution
Here we present the broad-band SED of the two sources, using both the observations presented above complemented by archival data at longer wavelengths and discuss them.
4.1.1 KUV 00311−1938
To find archival data to complement the observations mentioned in the previous section, the SSDC SEDBuilder tool3 was used to retrieve AllWISE (Wright et al. 2010) data from the time period from the start of the first Swift observations to the end of the H.E.S.S. observations, a time period spanning from November 2008 to November 2014. The optical light curve for KUV 00311−1938 is summarized as the average flux. In addition, radio fluxes of the central object as measured by the VLA (Piner & Edwards 2014) during the extended H.E.S.S. period are also included.
The resulting broad-band SED of KUV 00311−1938 is shown in Fig. 3, displaying the standard synchrotron and inverse Compton peaks of similar luminosity.
Grouping the Swift/XRT observation by date defines three flux states, and fitting the synchrotron peak at each of these three states with a third-order polynomial gives a peak frequency and a peak flux. The low-flux state results in a peak flux of ∼6.6 × 10−12 erg cm−2 s−1 at ∼2 × 1015 Hz, the intermediate-flux state results in ∼7 × 10−12 erg cm−2 s−1 at ∼3 × 1015 Hz and ∼9 × 10−12 erg cm−2 s−1 at ∼9 × 1015 Hz for the high-flux state.
Despite the variability in the X-rays, it is clear that the synchrotron peak is wider than the inverse Compton peak, a strong indication that the high energy bump has suffered some form of absorption at the higher energies. This is attributed to the effect of γ-γ pair-production on the EBL in the line of sight. This type of absorption becomes more important with increasing distance, and in the next section we use γ-ray observations and a model for the EBL to constrain the redshift range compatible with our observations. It is also possible to get a similar break in the inverse Compton part of the spectrum if Klein–Nishina effects are important (Kusunose & Takahara 2005).
4.1.2 PKS 1440−389
Using the multiwavelength data sets described in detail in the previous sections, a SED of PKS 1440−389 was constructed and is shown in Fig. 3. In addition to the data described in the previous sections, archival data from the 2MASS (Skrutskie et al. 2006; Mao 2011) and WISE catalogues (Wright et al. 2010) were used to complete the low-energy part of the SED, bearing in mind that those data are not contemporaneous with the rest of the SED.
Fitting the synchrotron peak with a third-order polynomial gives a peak frequency of 4 × 1015 Hz with a corresponding peak flux of 2 × 10−11 erg cm−2 s−1.
4.2 Redshift constraints
The combined Fermi/LAT and H.E.S.S. data set can be used to derive an upper limit on the redshift of the source, assuming that there is no upturn in the source-intrinsic γ-ray spectrum beyond the Fermi/LAT energy range. Under this assumption, the extrapolation of the HE γ-ray spectrum can be seen as an upper limit on the un-absorbed flux in the VHE regime. It therefore provides a conservative upper limit on the EBL absorption effect, which will be overestimated if there is any downward curvature in the intrinsic γ-ray spectrum.
To obtain the intrinsic source spectrum, the energy range for the Fermi/LAT analysis was restricted to energies for which EBL absorption is negligible and then extrapolated to VHEs. The ratio between this extrapolated flux, Fint(E), and the observed VHE flux, FVHE(E), then provides an upper limit on the optical depth τmax(E), as FVHE(E)/Fint(E) = exp (−τmax(E)).
Despite the small fraction of strictly overlapping HE and VHE observations, the Fermi/LAT spectra used for this calculation are a reasonable description of the intrinsic behaviour, because the light curves of both sources show only modest variability in the HESS observing periods, see Sections 3.1.1 and 3.1.2.
Once an upper limit on the optical depth is calculated, using either equation (1) or (2), the distance to a given blazar can be constrained by comparing it to the predictions of a specific EBL model. This is done by assuming a redshift, and then varying the assumed redshift until the difference between the predicted absorption and the observational upper limit is minimised. The EBL models considered in this study are: the model of Franceschini et al. (2008) and the model of Domínguez et al. (2011).
For the calculation of τmax below, we use equation (2). We then compare the obtained τmax with the predictions coming from the two models. We finally estimate a redshift by trying different source redshifts and then requiring that the EBL absorption by the models should be below the maximum permissible across the energy range.
4.2.1 KUV 00311−1938
A PWL fitted to the Fermi/LAT data below 10 GeV (see Table 3) and extrapolated to the 83 GeV to 3.0 TeV energy band was used as the intrinsic model, Fint. This was then compared to the H.E.S.S. observations via the measured FVHE and ΔFVHE.
We derive an upper limit of |$z$| < 0.93 using Domínguez et al. (2011). In comparison, using the Franceschini model we get a limit of |$z$| < 0.98.
The derived upper limit on the optical depth as a function of energy is shown on the left in Fig. 4, calculated with equation (2). The H.E.S.S. constraint together with the lower limit from optical spectroscopy, limits the redshift of KUV 00311−1938 to 0.51 ≤ |$z$| < 0.98 at the 95 per cent CL, improving on the previous upper limit of |$z$| < 1.54.
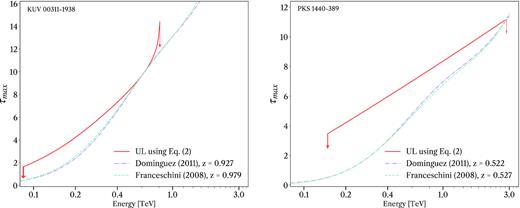
Left panel: Optical depth as a function of energy for KUV 00311−1938. The red line represents the upper limit at the 95 per cent CL as derived from the combined Fermi/LAT and H.E.S.S. data using equation (2) which includes the Fermi/LAT errors. Additionally shown by dashed and dot-dashed lines are the EBL model predictions from Domínguez et al. (2011) and Franceschini, Rodighiero & Vaccari (2008) that correspond to the upper limits on the redshift. Right panel: Optical depth as a function of energy for PKS 1440−389. The red line represents the upper limit at the 95 per cent CL as derived from the combined Fermi/LAT and H.E.S.S. data using equation (2). Additionally shown by dashed and dot-dashed lines are the EBL model predictions for the two upper limits on the redshift.
4.2.2 PKS 1440−389
To obtain the intrinsic source spectrum for PKS 1440−389, the energy range for the Fermi/LAT analysis was restricted to energies below 10 GeV. This was then extrapolated and used to estimate absorption in the energy range 147 GeV−3.0 TeV.
An upper limit of |$z$| < 0.53 can be put on the redshift at the 95 per cent CL when using the EBL model of Domínguez et al. (2011). Applying the Franceschini model yields a compatible redshift constraint. This result significantly reduces the redshift constraint of |$z$| < 2.2 obtained through optical spectroscopy by Shaw et al. (2013).
Combining our constraint with the lower limit from the non-detection of the host galaxy by Shaw et al. (2013), the redshift of PKS 1440−389 is found to be in the range of 0.14 ⪅|$z$| < 0.53 at the 95 per cent CL.
5 SUMMARY AND CONCLUSIONS
In this paper, we present the final H.E.S.S. results on the detection of the two blazars KUV 00311−1938 and PKS 1440−389 and their multiwavelength analysis. With the shape of the inverse Compton bump we also constrain the redshift of the sources.
The blazar KUV 00311−1938 has been observed by H.E.S.S. between 2009 and 2014, leading to the detection of its VHE emission with a significance of 5.2 standard deviations. The time-averaged VHE spectrum of this blazar is soft, with a photon index of Γ = 5.1 ± 0.6stat ± 0.3sys and a flux |${\sim }0.9{{\,\rm per\, cent}}$| of that of the Crab nebula above 147 GeV.
Observations at other wavelengths have been analysed in order to have a multiband view of the SED of this AGN detected in the VHE range. In particular, an analysis of the HE emission in Fermi/LAT data reveals a detection of this AGN at a significance level of about ≈45 σ standard deviations.
We reported also the detection of VHE γ-ray emission from the HSP PKS 1440−389 by H.E.S.S., accompanied by multiwavelength observations with Fermi/LAT, Swift/XRT and UVOT, and atom. The H.E.S.S. spectrum has a spectral index of 3.7 ± 0.2stat ± 0.3sys and a flux of |${\sim }5.4{{\ \rm per\, cent}}$| of that of the Crab nebula above 147 GeV. No evidence for short-term (day-scale or intra-day) variability has been found in the γ-ray regime (neither with Fermi/LAT nor with H.E.S.S.), but moderate variability on weekly time-scales is found in the optical light curve measured by atom.
By comparing the EBL absorption derived from models of intrinsic emission fitted to data, we constrain the redshift of KUV 00311−1938 to below |$z$| = 0.98, which combines with known spectroscopical constraints to give 0.51 ≤ |$z$| < 0.98. While VHE blazars have been detected up to |$z$| = 0.94, the most distant ones have been seen only during flaring states. The current most distant and, within the limited duty cycle of IACTs, that are monitoring the VHE sky at the current sensitivity level only for the last two decades, persistent (since observations began and within observational constraints), VHE blazar is PKS 1424+240 (Acciari et al. 2010) at |$z$| ≃ 0.6. KUV 00311−1938 can thus potentially be the most distant persistent emitter of VHE photons. The determination of its redshift via optical spectroscopy is thus of paramount importance for VHE astrophysics: once its distance is constrained, it will be one of the best sources to study the propagation of VHE photons in the Universe.
For the blazar PKS 1440−389 based on an extrapolation of the Fermi/LAT spectrum towards the measured H.E.S.S. VHE γ-ray spectrum, accounting for EBL absorption, we deduce an upper limit on the redshift of the source of |$z$| < 0.53. Combined with previous results, this constrains the redshift to the range 0.14 ⪅ |$z$| < 0.53. PKS 1440−389 is found to be a standard source within the VHE HSPs, fitting reasonably well into the current population.
ACKNOWLEDGEMENTS
The support of the Namibian authorities and of the University of Namibia in facilitating the construction and operation of H.E.S.S. is gratefully acknowledged, as is the support by the German Ministry for Education and Research (BMBF), the Max Planck Society, the German Research Foundation (DFG), the Helmholtz Association, the Alexander von Humboldt Foundation, the French Ministry of Higher Education, Research and Innovation, the Centre National de la Recherche Scientifique (CNRS/IN2P3 and CNRS/INSU), the Commissariat à l'Énergie Atomique et aux Énergies Alternatives (CEA), the U.K. Science and Technology Facilities Council (STFC), the Knut and Alice Wallenberg Foundation, the National Science Centre, Poland grant no. 2016/22/M/ST9/00382, the South African Department of Science and Technology and National Research Foundation, the University of Namibia, the National Commission on Research, Science and Technology of Namibia (NCRST), the Austrian Federal Ministry of Education, Science and Research and the Austrian Science Fund (FWF), the Australian Research Council (ARC), the Japan Society for the Promotion of Science, and the University of Amsterdam. We appreciate the excellent work of the technical support staff in Berlin, Zeuthen, Heidelberg, Palaiseau, Paris, Saclay, Tübingen, and in Namibia in the construction and operation of the equipment.
This work benefited from services provided by the H.E.S.S. Virtual Organisation, supported by the national resource providers of the EGI Federation.
The H.E.S.S. and Fermi/LAT analysis computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at Lunarc. Tomas Bylund and Yvonne Becherini wish to acknowledge the support of the Data Intensive Sciences and Applications (DISA) centre at Linnaeus University.
Matteo Cerruti has received financial support through the Postdoctoral Junior Leader Fellowship Programme from “la Caixa” Foundation (LCF/BQ/PI18/11630012).
This research made use of the NASA/IPAC Extragalactic Database (NED) and of the SIMBAD Astronomical Database, of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration.
We acknowledge the use of public data from the Swift data archive.
This research made use of Gammapy, a community- developed core Python package for gamma-ray astronomy (Deil et al. 2017).
This research has made use of data and software provided by the Fermi Science Support Center, managed by the HEASARC at the Goddard Space Flight Center.
Part of this work is based on archival data, software or online services provided by the Space Science Data Center - ASI.
This research has made use of the VizieR catalogue access tool, CDS, Strasbourg, France (doi:10.26093/cds/vizier). The original description of the VizieR service was published in A&AS143, 23.
This research has made use of the NASA/IPAC Infrared Science Archive, which is funded by the National Aeronautics and Space Administration and operated by the California Institute of Technology.
Footnotes
Available at https://tools.ssdc.asi.it/SED/



