The perturbed FLRW metric on all scales: Newtonian limit and top-hat collapse

Finke, Andreas

doi:10.1093/mnras/stz3145

ABSTRACT

The applicability of a linearized perturbed FLRW metric to the late, lumpy universe has been subject to debate. We consider in an elementary way the Newtonian limit of the Einstein equations with this ansatz for the case of structure formation in late-time cosmology, on small and large scales, and argue that linearizing the Einstein tensor produces only a small error down to arbitrarily small, decoupled scales (e.g. Solar system scales). On subhorizon patches, the metric scale factor becomes a coordinate choice equivalent to choosing the spatial curvature, and not a sign that the FLRW metric cannot perturbatively accommodate very different local physical expansion rates of matter; we distinguish these concepts, and show that they merge on large scales for the Newtonian limit to be globally valid. Furthermore, on subhorizon scales, a perturbed FLRW metric ansatz does not already imply assumptions on isotropy, and effects beyond an FLRW background, including those potentially caused by non-linearities of general relativity (GR), may be encoded into non-trivial boundary conditions. The corresponding cosmologies have already been developed in a Newtonian setting by Heckmann and Schücking and none of these boundary conditions can explain the accelerated expansion of the universe. Our analysis of the field equations is confirmed on the level of solutions by an example of pedagogical value, comparing a collapsing top-hat overdensity (embedded into a cosmological background) treated in such perturbative manner to the corresponding exact solution of GR, where we find good agreement even in the regimes of strong density contrast.

gravitation, large-scale structure of Universe, cosmology: theory

1 INTRODUCTION

The late universe, a slice of which is visible to galaxy surveys on our past light-cone, is very clumpy. This is in stark contrast to the earlier universe: the observed fluctuations in the cosmic microwave background (CMB) are small (Aghanim et al. 2018), allowing for a precise interpretation of their properties based on linearized, relativistic cosmological perturbation theory that is well established (Durrer 2008). However, gravitational collapse has transformed the smooth state into one that cannot be evolved anymore by effective fluid equations (Baumann et al. 2012) without removing short scales of comoving size of a couple of Mpc, and certainly not by linear equations.

The conceptually simple, but technically challenging, non-linear Newtonian Vlasov–Poisson system (Peebles 1980) describes the gravitational amplification of dark matter structures including smaller scales and large density contrasts. Newtonian N-body simulations have tackled the challenging prediction of the structures’ morphology, solving this system by sampling its characteristic curves. There is no doubt that Newtonian theory is capturing the gravitational physics of finite astrophysical systems such as galaxies or clusters of galaxies, where gravity is weak. We similarly expect Newtonian physics to approximate sufficiently localized cosmological patches when fields are weak and matter is moving slowly (Peebles 1980; Kaiser 2017), including the non-linear evolution of matter beyond linear cosmological perturbation theory. However, in cosmology, we are interested in global solutions, and the validity and generality of a Newtonian approximation is not immediately clear when going to large scales.

The Newtonian limit of general relativity (GR) may therefore be studied carefully in the context of large-scale structure in cosmology (Peebles 1980; Holz & Wald 1998; Green & Wald 2012). The limit involves linearizing the Einstein tensor for weak fields around a background. The choice of this global background solution is non-trivial. Instead, a local approach aims to avoid this step and it has been shown how gluing together patches close to the Minkowski space–time in a bottom-up construction yields cosmological solutions of GR (Sanghai & Clifton 2015), that is, the background emerges and can be compared to the predictions of Newtonian cosmology. Therefore, a local approach can help clarifying the generality of the Newtonian limit in cosmology, which is crucial when building simple models for reaching robust conclusions about our universe comparing to observations. For example, the report in Rácz et al. (2017) of large relativistic acceleration effects beyond Newtonian cosmology without the need for dark energy produced in simulations with a modified N-body code has recently received a critical reply Kaiser (2017) in which the backreaction proposal (see e.g. Buchert & Räsänen 2012) was discussed assuming a Newtonian setting. However, any significant differences of Newtonian and GR cosmological dynamics claimed to invalidate this reply (Buchert 2017) must be related to assumptions made when taking the Newtonian limit of GR, and the discussion can be supplemented by this step. Beyond foundational questions in GR, a Newtonian limit is still the foundation for obtaining the leading-order corrections to structure formation from covariantly formulated modified gravity theories, by using N-body simulations that have been modified accordingly. Furthermore, the Newtonian limit is the relevant approach for properly addressing cosmological effects on cosmologically very small systems, like the Solar system (or even an atom Bonnor 1999; Price & Romano 2012), both for GR (Dicke & Peebles 1964; Bonnor 1996; Cooperstock, Faraoni & Vollick 1998; Carrera & Giulini 2010; Nandra, Lasenby & Hobson 2012b) and modified gravity. Constraints on the time evolution of the Newton constant obtained in the Solar system (Pitjeva & Pitjev 2013; Hofmann & Müller 2018; Fienga et al. 2015) and therefore on modified gravity are already below one per cent of the Hubble rate, and are becoming stronger with observation time with dramatic implications for some models (Belgacem et al. 2019).

In this paper, we are concerned with a correct leading-order treatment of non-linear structures in late-time cosmology. This is complemented by recent works on more general expansions of GR for a highly accurate description of our universe (Adamek et al. 2013, 2016; Fidler et al. 2017; Milillo et al. 2015; Goldberg, Clifton & Malik 2017).

We base the discussion on a convenient standard tool, which is the FLRW metric with scalar and vector perturbations (Harrison 1967; Bertschinger 1995)

$$\begin{eqnarray*} \mathrm{ d}s^2 = -(1+2\Psi) \mathrm{d}t^2 + 2 \boldsymbol {B} \cdot \mathrm{d} \boldsymbol{x} \mathrm{d} t + a^2(t)(1-2\Phi)\mathrm{d}\boldsymbol{x}^2, \end{eqnarray*}$$

(1)

where Ψ, Φ, and |$\boldsymbol {B}$| are small in a way to be specified. The presence of the scale factor a(t) at an early stage of the theoretical description is intriguing. In contrast, in Newtonian cosmology, the starting point (before the continuum limit and without a cosmological constant) are simply the equations

$$\begin{eqnarray*} \ddot{\boldsymbol{r}}_\mathrm{ i} = \,\, G_\mathrm{ N} \, m\sum \frac{\boldsymbol{r}_\mathrm{ j}-\boldsymbol{r}_\mathrm{ i}}{|\boldsymbol{r}_\mathrm{ j}-\boldsymbol{r}_\mathrm{ i}|^3} \end{eqnarray*}$$

(2)

for particles of equal mass m. The scale factor can now appear in two familiar, but in principle different, ways. The first situation concerns the dynamics of a homogeneous ball of dust in the continuum limit, of finite or infinite size, for which the time dependence of the radial positions of the shells is a common factor. Here, the scale factor is related to the physical motion of matter, and it satisfies a Friedmann equation. The second situation is that of an inhomogeneous cosmos. Here, the scale factor is introduced into the Newtonian equations (2) by hand, adopting comoving spatial coordinates |$\boldsymbol{x}$| with

$$\begin{eqnarray*} \boldsymbol{r}=a(t)\boldsymbol{x}, \end{eqnarray*}$$

(3)

which is a coordinate gauge that has been discussed carefully in Kaiser (2017). As noted there, the most convenient, but by no means necessary, choice is to use the motion scale factor of the first situation that emerges when replacing the inhomogeneous cosmos by an averaged homogeneous ball.

On the other hand, it is usually stated that the metric scale factor in equation (1) should be the one of a best-fitting background universe. When perturbations in equation (1) are neglected ‘on average’, and if the background energy density is assumed to be the Newtonian spatial average of the physical density, the metric scale factor obeys the same Friedmann equation of the homogeneous ball of matter in Newtonian theory. Since the Einstein equations are non-linear, a background scale factor based on Newtonian averaging may seem as a shortcut lacking rigorous justification (Kolb, Marra & Matarrese 2010; Wiltshire 2011). Furthermore, if the ‘correct’ scale factor must be chosen in equation (1), corresponding to some average Hubble flow, the intuition may be that situations where matter locally moves with very different expansion rates (e.g. after turnaround) cannot be small perturbations as assumed in equation (1, Räsänen 2010). However, it has also been shown that Lemaître–Tolman–Bondi (LTB) solutions with locally different expansion rates of matter can be mapped to perturbed FLRW if the inhomogeneities are confined to subhorizon scale (Van Acoleyen 2008; Yamamoto et al. 2016). This supports the validity of the ansatz (1), but clearly questions the physical relevance of the scale factor in the metric on small scales, similarly to its introduction as a coordinate choice in Newtonian cosmology.

We therefore studied GR cosmology using a perturbed FLRW metric and guided by the observed properties of dark matter at low redshifts, emphasizing a local approach. To leading order, we recovered the validity of a linearization of the Einstein tensor and obtained a consistent Newtonian limit. These results can be illustrated by an explicit example: the simplest, most extreme (and therefore most interesting) space–time describing a collapsing object within the expanding universe is arguably that of a top-hat profile – a homogeneous core surrounded by an empty shell – embedded into a matter-dominated universe. We confirmed that the perturbed FLRW metric is able to describe this situation; it can thus simultaneously accommodate structures with very different expansion rates. As a key step in the argument, we derived explicit coordinate transformations that can change the scale factor non-perturbatively from being solution of one Friedmann equation to a solution of another Friedmann equation, while keeping the potentials perturbative. We also found that on subhorizon scales and allowing for Ψ ≠ Φ the scale factor in the metric (1) is arbitrary, whereas it emerges on large scales for a correct description of the geometry, where it eventually must correspond to the physical motion of matter. We checked this gauge freedom of a(t) by repeating the analysis of the top-hat example using the perturbed FLRW metric with another choice of scale factor.

Due to the local and constructive approach, the calculations are general enough to have implications for the backreaction proposal. On small scales, where the scale factor of the perturbed FLRW metric is arbitrary, the effect of GR solutions is constrained free of the assumption that the global background is an FLRW space–time. Since local cosmological tests take place in this regime, dark energy can be probed disentangled from potential relativistic effects on the dynamics.

The paper is structured as follows. Section 2 reviews the Newtonian limit for late-time cosmology and derives the starting point of Newtonian cosmology from GR in the general setting of arbitrary scale factor. Section 3 then introduces the top-hat space–time in detail in Section 3.1, tests the FLRW metric in the standard case in Section 3.2, and subsequently confirms the result of Section 2, for Ψ ≠ Φ with a non-standard choice of scale factor in Section 3.3. Before we conclude in Section 5 we discuss in Section 4 in some detail the large-scale limit (Section 4.1), the meaning of cosmic expansion for local systems (Section 4.2), the transition from covariance to inertial frames (Section 4.3), and the assumptions that have been made with the FLRW metric and the implications for the backreaction proposal (Section 4.4).

2 NEWTONIAN LIMIT

We start from GR with cosmological constant Λ and the metric (1)

$$\begin{eqnarray*} \mathrm{ d}s^2 = -(1+2\Psi) \mathrm{d}t^2 + 2 \boldsymbol {B} \cdot \mathrm{d} \boldsymbol{x} \mathrm{d} t + a^2(t)(1-2\Phi)\mathrm{d}\boldsymbol{x}^2 \end{eqnarray*}$$

(4)

without spherical symmetry, but neglecting tensor perturbations. One may think about this ansatz as being perturbative around a flat FLRW background, but this is an overly restrictive picture on small enough scales. We will shortly see that a ‘curvature’ term in the equation of motion for a(t) can be encoded into a quadratic difference of Ψ and Φ, corresponding to a Friedmann equation for universes with non-zero spatial curvature. This is a gauge freedom appearing when integrating the Einstein equations carefully. It implies that there must exist corresponding coordinate transformations that leave the form of the metric (1) invariant but that change the scale factor non-perturbatively by |$\mathcal {O}(1)$|⁠. These transformations preserve the right perturbative character of the potentials for late-time structure in cosmology. We derive them in for the top-hat example in Section 3 (equations 75, 76, 77, 78 and 89, 90, 91, 92). With a gauge change of a(t) for a fixed space–time the interpretation of the ‘comoving’ spatial coordinates |$\boldsymbol{x}$| changes as well. For this reason, these spatial coordinates are not necessarily aligned with the motion of matter. Locally, such a construction would indeed be ill defined in late-time cosmology because matter trajectories can cross; but even on average, some gauge freedom exists (see below around equation 14).

The source on the right-hand side of the Einstein equations,

$$\begin{eqnarray*} G_{\mu \nu } + \Lambda g_{\mu \nu } = 8 \pi G_\mathrm{ N} T_{\mu \nu }, \end{eqnarray*}$$

(5)

can conveniently be thought of as a collection of point masses that sample an initial phase-space sheet which is allowed to cross itself in real space. For simplicity, we neglect pressure. Then, matter motion is geodesic. We avoid both a fluid assumption and averaging. For completeness, in the continuum limit an explicit expression for the energy-momentum tensor is given by

$$\begin{eqnarray*} T^{\mu \nu }(x^\alpha) = \int \left[\mathrm{ d}p^1 \mathrm{ d}p^2 \mathrm{ d}p^3 \frac{\sqrt{-g}}{ p_0 } \right] f (x^\alpha , p^i) p^\mu p^\nu \end{eqnarray*}$$

(6)

where the integral is over the future-pointing part of the mass shell p^μp^νg_μν = −m² making p₀ and p⁰ functions of the integration variables pⁱ, the square brackets enclose an invariant measure on this space, and f is a scalar distribution function on one-particle phase space (the mass shell within the tangent bundle) which we do not need to specify further here (Ehlers & Sachs 1969).

2.1 Weak-field, slow-motion expansion scheme

We can develop an expansion scheme based on a non-relativistic velocity v ≪ 1 and anticipating that the potentials Ψ and Φ, in this section collectively denoted as ϕ, behave similarly to Newtonian potentials and obey a Poisson equation sourced dominantly by the matter density fluctuations corresponding to the observed morphology. For simplicity and because we are considering the late universe we shall set a ≈ 1 in the following explanation; comoving spatial coordinates x can be thought of as physical.

First, we make a weak-field assumption, neglecting neutron stars and black holes, and assume that the potentials are small of order v² ≪ 1. Here v plays the role of an escape velocity of a particle in the potential. It is numerically of order v ∼ 10⁻². In the following, we will drop relative corrections of order v² or higher, so e.g. |$\mathcal {O}(v^4)$| from the potentials. Second, spatial derivatives are large in the following sense. The linearity of the Poisson equation allows to decompose its solution into parts sourced by parts of the the hierarchy of structures of various sizes L_i and locations x_i. Picking a part ϕ_i of the solution that dominantly contributes at some point x, let us first assume |x − x_i| ∼ L_i (or closer). Since ϕ_i solves the Poisson equation, ϕ_i(x) = f_i((x − x₀)/L_i) where f_i is well approximated by a low-order Laurent polynomial in the modulus of its argument z ∼ 1 (or smaller) which ensures that |df_i(z)/dz| ∼ |f_i|/z ∼ |f_i| (or larger). Indeed, typical forms of f_i(z) are ∝ 1/z outside of an overdensity or ∝ z² in a region of homogeneous density (as below). By the chain rule, |∇ϕ_i| ∼ ϕ_i/L_i. For each relevant term, its size L_i naively is at most roughly the distance particles can have travelled in a Hubble time |$H_0^{-1}$|⁠. The largest voids will then have a size of roughly L_i ∼ v/H₀, but typical sizes of haloes, sheets and filaments (or even the Solar system) can be much smaller. This, a spatial derivative with respect to any component of x increases the value of ϕ by a factor of at least |$L_\mathrm{ i}^{-1}$| per term, so by at least H₀/v overall,

$$\begin{eqnarray*} \nabla \gtrsim H_0 v^{-1}. \end{eqnarray*}$$

(7)

Therefore, |$\nabla ^2 \phi \sim H_0^2$| or larger; indeed we were anticipating ∇²ϕ to be of order |$G_\mathrm{ N} \rho \gtrsim G_\mathrm{ N} \rho _b \sim H_0^2$| when saying the potentials are similar to the Newtonian one. If |x − x_i| ∼ L_i does not hold for some large perturbation, which may contribute significantly even at a greater distance, we again assume that the size of voids is bounded from above and, further, that the largest ones are abundant enough that at least one is in the vicinity of every point. Then, equation(7) still approximately holds. Third, compared to spatial derivatives, time derivatives are suppressed in all cases by a factor of v ≪ 1 if the potentials are changing due to the change of matter moving with such speed, leading to a quasi-static approximation. For simplicity we keep ‘cosmological’ terms like

$$\begin{eqnarray*} H_a^2 := (\dot{a} / a)^2 \end{eqnarray*}$$

(8)

in the equation on all scales, even though on small scales where |$\nabla ^2 \phi \gg H_0^2$| and thus |$\ddot{\phi } \gg H_0^2 v^2$|⁠, it is possible that |$\ddot{\phi }$| (which we drop in comparison to ∇²ϕ) is larger than |$H_a^2$| (which for the standard scale factor a is equal to |$H_0^2$| today). Proceeding in this way is still consistent, because in this case the cosmological terms similar to equation (8) are anyway strongly dominated by the second spatial derivatives ∇²ϕ by a factor of more than v⁻². These cosmological terms therefore and do not spoil the result, so removing them from the equations on very small scales is not necessary. A convenient consequence of this expansion scheme to leading order is that the equations become linear. A term quadratic in the potentials starts out at |$\mathcal {O}(v^4)$| and ends up at most at |$\mathcal {O}(v^2)$| after two spatial derivatives. Higher order derivatives do not appear in the Einstein equations.

We assume further that the vector perturbation |$\boldsymbol {B}$| is of order |$\mathcal {O}(v^3)$| and behaves similarly to the potentials under derivatives. For further discussion of the scheme and the literature, it is more practical to see the equations first.

2.2 Field equations

In the field equations in this section, we drop relative corrections of order |$\mathcal {O}(v^2)$|⁠. Given the expansion scheme, we obtain a Poisson equation

$$\begin{eqnarray*} 3 H_\mathrm{ a}^2 + 2 a^{-2} \nabla ^2 \Phi - \Lambda = 8 \pi G_\mathrm{ N} T_{00} \end{eqnarray*}$$

(9)

from the time–time component, validating the assumptions we have been making on Φ in the previous subsection for developing the expansion scheme.¹

Further we get

$$\begin{eqnarray*} (i\ne j): \partial _\mathrm{ i} \partial _\mathrm{ j} (\Psi -\Phi) = 0 \end{eqnarray*}$$

(10)

$$\begin{eqnarray*} (\partial _\mathrm{ i}^2 - \partial _\mathrm{ j}^2) (\Psi - \Phi) = 0, \end{eqnarray*}$$

(11)

$$\begin{eqnarray*} - 3 H_a^2 - 6 \frac{\ddot{a}}{a} + 3 \Lambda + 2a^{-2}\nabla ^2(\Psi - \Phi) &= 0 \end{eqnarray*}$$

(12)

with the first set of equations coming from the spatial off-diagonal Einstein equations and the rest from combining the spatial diagonal equations. The energy-momentum tensor can be neglected here if it is of order ρv² which would only give ∼v⁴ corrections for the potentials after integrating the Poisson equation.

This requires that either the coordinates are approximately adapted to the Hubble flow that emerged from the homogeneous history of the universe so that

$$\begin{eqnarray*} |\langle \boldsymbol{v} \rangle |^2 \ll 1 \end{eqnarray*}$$

(13)

where the components of |$\boldsymbol{v}$| are vⁱ = T⁰ⁱ/T⁰⁰ and where the average is over a statistical ensemble at any location, or we are in the subhorizon regime where any Hubble flow itself is small,

$$\begin{eqnarray*} |H_\mathrm{ a} \boldsymbol{x}|^2 \lesssim v^2 \ll 1, \nonumber \\ H_\mathrm{ a} \sim H_0. \end{eqnarray*}$$

(14)

Note that in the second case, |$\mathcal {O}(H_0)$| departures of H_a are allowed.

These equations determine the potentials. We check consistency with the space–time components below. The solution of equation (10) is

$$\begin{eqnarray*} \Psi = \Phi + f_1(x,t) + f_2(y,t) + f_3(z,t). \end{eqnarray*}$$

(15)

Most authors set the functions f_i = 0,² but staying general will allow us to understand the gauge freedom of the scale factor itself on small scales. Indeed, equations (11) only imply for the form of the functions f_i evaluated at a point (q, t)

$$\begin{eqnarray*} f_\mathrm{ i}(q, t) = \alpha (t) q^2/2 + \beta _\mathrm{ i}(t) q + \gamma _\mathrm{ i}(t), \end{eqnarray*}$$

(16)

and thus equation (12) becomes

$$\begin{eqnarray*} 2 \alpha (t) = a^2\left(H_\mathrm{ a}^2 + 2\frac{\ddot{a}}{a} - \Lambda \right) \equiv - k(t) \end{eqnarray*}$$

(17)

so that equation (15) is with equation (16)

$$\begin{eqnarray*} \Psi - \Phi = -k(t) \frac{x^2 + y^2 + z^2 }{4} + \gamma (t) , \end{eqnarray*}$$

(18)

where |$\gamma (t) = \sum _1^3 \gamma _\mathrm{ i}(t)$| and where we have dropped a linear part |$\boldsymbol {\beta }(t) \cdot \boldsymbol{x}$| as discussed in Section 4.3. We now also set γ(t) = 0. From comparison of equation (17) with the usual Friedmann equations derived on the homogeneous and isotropic background levels including spatial curvature explicitly, the term k(t) = −2α(t), which appears also in equation (18), admits an interpretation as time-dependent spatial curvature. Using equation (17), we can chose either a(t) and determine k(t) by differentiation or choose k(t) and determine a(t) by integration. This works as long as either

$$\begin{eqnarray*} |k(t)| \ll H_0^2, \end{eqnarray*}$$

(19)

or in the subhorizon regime (14), since then the difference (18) of the two potentials is much smaller than unity.

Reiterating on the comment around equation (8) above, on very small and fast scales, the result (18) should be thought of as Ψ − Φ ∼ 0 (to lowest order). The right-hand side is a cosmological term ∝ k(t)r² that automatically loses significance on small scales. In fact, near r = 0 the Laplacian of Ψ − Φ may actually be dominated by space-dependent post-Newtonian terms. These new terms arise from solving equations to next order containing now both terms like |$\ddot{\phi }$| in equation (12) as well as quadratic terms like ϕ∂²ϕ in (10) (which are of similar size). However, since ∂²ϕ still dominates ϕ∂²ϕ, the post-Newtonian terms are subleading and the statement Ψ = Φ (up to a constant) is now correct to leading order if the cosmological term ∝ k(t)r² is even smaller. This is for example true when restricting to Solar system scale, where we know how small the post-Newtonian corrections are. Therefore, while one could drop the cosmological term in e.g. equation (12) on such scales to emphasize it is not the largest subleading correction, it is not necessary when the goal is only a valid leading-order treatment. As written, the equation holds also on cosmological scales.

On the other hand, studying the full linearized Einstein equations including terms like |$\ddot{\phi }$| in equation (12) while setting Ψ = Φ, which removes spatial derivatives from equation (12, and which is obtained from excluding terms like ϕ∂²ϕ and gauging α(t) = 0) leads to unphysical results for large density contrasts (Räsänen 2010) and is incorrect given the physical setup because |$\ddot{\phi } \sim \phi \partial ^2 \phi$|⁠. Blind application of the standard cosmological perturbation theory treatment developed for small density contrasts, when a perturbative expansion in powers of the potential is well behaved, does break down for large-scale structure. This does not imply that proper leading-order physics cannot be obtained from a linearized treatment like ours. Instead of being forced to include quadratic terms or higher, the easier solution is to drop certain linear terms by changing to an expansion scheme that tracks powers of v.

The expansion scheme discussed here can also effectively be obtained in Fourier space of linear perturbation theory in a subhorizon limit, which we see a posteriori. By taking the leading terms when k → ∞ and before any manipulations that use δ ≪ 1 (and by selecting a Newtonian source) the expansion discussed here is recovered, but only for the special gauge of α(t) = 0. In the Fourier space approach polynomial growth in real space is easily missed. Typically, one introduces background equations to define sources of vanishing volume average to be able to divide by k².

2.3 Friedmann equations as a gauge choice

Comparing equations (18) and (17), it is immediate that the standard choice Ψ = Φ implies α(t) = 0 (and γ(t) = 0). On small scales, this is a gauge choice. Vanishing α(t) in equation (17) together with equation (9) means that a(t) satisfies both standard Friedmann equations for pressureless matter

$$\begin{eqnarray*} 3 H_\mathrm{ a}^2 = 8 \pi G_\mathrm{ N} \rho _\mathrm{b} + \Lambda \end{eqnarray*}$$

(20)

$$\begin{eqnarray*} 6 \frac{\ddot{a}}{a} = - 8\pi G_\mathrm{ N} \rho _\mathrm{ b} + 2 \Lambda \end{eqnarray*}$$

(21)

if Φ = 0 and T₀₀ = ρ_b is the background density, e.g. on average. However, α(t) = 0 in equation (17) alone already implies the sum of the two previous equations (20) and (21)

$$\begin{eqnarray*} H_\mathrm{ a}^2 + 2\frac{\ddot{a}}{a} = \Lambda \end{eqnarray*}$$

(22)

without invoking an averaging argument in the pressureless case considered here. The substitution a(t) = h^2/3(t) reduces this to an inverted harmonic oscillator equation for h. The solutions admitting a big bang (with a negative sign in front of the decaying exponential) are then

$$\begin{eqnarray*} a(t) = A \sinh \left(\frac{\sqrt{3 \Lambda }}{2} (t-t_0) + s \right)^{2/3}, \end{eqnarray*}$$

(23)

where the integration constants A, s can be fixed to have a(t₀) = 1 and H_a(t₀) = H₀ as

$$\begin{eqnarray*} A = (3 H_0^2 \Lambda ^{-1} - 1)^{1/3} \equiv (\Omega _\Lambda ^{-1} -1)^{1/3} \end{eqnarray*}$$

(24)

$$\begin{eqnarray*} s = \tanh ^{-1}\left(\sqrt{ \Lambda (3 H_0^2)^{-1}} \right)\equiv \tanh ^{-1}\left(\sqrt{ \Omega _\Lambda } \right), \end{eqnarray*}$$

(25)

which is already equivalent to the solution of the Friedmann equation (20) for pressureless matter ρ_b ∼ a⁻³. Note that for fixed Λ the normalization of the matter density enters indirectly into the integration constants via |$\Omega _\Lambda = \Lambda / 3 H_0^2 = (8\pi G_\mathrm{ N} \rho _{\mathrm{ b},0}/\Lambda + 1)^{-1}$|⁠, even if the differential equation did not contain a matter term. The a⁻³ scaling of ρ_b can be recovered from the solution (23) together with equation (20) [which was obtained from equation (9) on average].

From equation (18), any other gauge choice implies the set-in of a quadratic divergence for the difference of the two potentials, and therefore for at least one them in the metric. The Friedmann gauge choice is thus relevant when constructing a global perturbed FLRW solution, to be discussed below in Section 4.1.

If we are interested in a patch of the universe of size much smaller than the Hubble scale, a growth of the potentials |$\sim H_0^2 r^2$| is of no concern. In this case a(t) is allowed to depart from the Friedmann solution by |$\mathcal {O}(1)$|⁠. Instead of satisfying equation (22), a(t) may satisfy (17) for α(t) ≠ 0 chosen with |$\alpha (t) \sim H_0^2$|⁠. This preserves the condition for small peculiar velocities on subhorizon scales (14). The scale factor is therefore directly related to an arbitrary gauge freedom in the subhorizon limit.

As discussed above, Ψ − Φ also contains small non-linear terms and time derivatives of the potentials, which dominate the quadratic difference on sufficiently small scales, so Ψ ≃ Φ restricted to very small scales does not imply Friedmannian scale factor evolution. Instead, the scale factor remains unconstrained in its cosmological evolution. This is expected, because the choice of scale factor should become completely irrelevant on these local scales. In particular it may still be chosen to obey a gauge like equation (23) for a treatment unified with larger scales.

2.4 Motion of matter

We now show that we indeed obtain the proper Newtonian limit independent of the choice of scale factor.

First, the remaining time–space component of the field equations gives

$$\begin{eqnarray*} 2 H_\mathrm{ a} \nabla \Psi + 2 \partial _\mathrm{ t} \nabla \Phi +\frac{1}{2 a^2}\nabla \times (\nabla \times \boldsymbol {B}) = 8 \pi G_\mathrm{ N} T_{0\mathrm{ i}}. \end{eqnarray*}$$

(26)

Note that without a vector perturbation |$\boldsymbol {B}$| of the metric, the current T_0i would have to be longitudinal, which is not compatible with cosmological dynamics: neglecting the vorticity (small before stream crossing Jelic-Cizmek et al. 2018), |$\nabla \times (\rho \boldsymbol {v}) \approx (\nabla \rho) \times \boldsymbol {v}$| and there is no reason for density (not potential!) gradient and velocity to be aligned. We may choose the vector potential of the transverse part of 16πG_Na²T_0i at every instant to be transverse itself, and can set |$\boldsymbol {B}$| to be the vector potential of this quantity. Thus, |$\nabla \times (\nabla \times \boldsymbol {B})/2 a^2 = 8 \pi G_\mathrm{ N} T_{0\mathrm{ i}}^T$|⁠, and we have absorbed the transverse part of T_0i. |$\boldsymbol {B}$| may be chosen transverse as well (like in the Poisson gauge Bertschinger 1995). Then, the double-curl of |$\mathbf {B}$| equals the vector Laplacian of |$\boldsymbol {B}$|⁠.³ Since the Laplacian converts the other potentials from |$\mathcal {O}(v^2)$| to ∼ρ, when we assume the same type of spatial variation for |$\boldsymbol {B}$| it is indeed smaller of order |$\mathcal {O}(v^3)$| such that we have |$\nabla ^2 \boldsymbol {B} \sim T_{0\mathrm{ i}} \sim \rho v$|⁠. Subtracting the transverse part, we are left with

$$\begin{eqnarray*} 2 H_\mathrm{ a} \partial _\mathrm{ i} \Psi +2 \partial _\mathrm{ t} \partial _\mathrm{ i} \Phi = 8 \pi G_\mathrm{ N} T_{0\mathrm{ i}} \end{eqnarray*}$$

(27)

where the source can be assumed to be longitudinal. We therefore do not lose information when taking the divergence. We get with equation (18)

$$\begin{eqnarray*} (H_\mathrm{ a} +\partial _\mathrm{ t}) 2 \nabla ^2 \Phi + 3 a^2 H_\mathrm{ a} \left(H_\mathrm{ a}^2 + 2\frac{\ddot{a}}{a} - \Lambda \right)= 8 \pi G_\mathrm{ N}\partial _\mathrm{ i} T_{0\mathrm{ i}}. \end{eqnarray*}$$

(28)

Using the Poisson equation (9), we can replace |$2 \nabla ^2 \Phi = 8 \pi G_\mathrm{ N} a^2 T_{00} - 3 a^2 H_\mathrm{ a}^2 + a^2 \Lambda$|⁠, and it can be directly verified that many terms cancel to give the equation ∂_tT₀₀ + 3H_aT₀₀ = a⁻²∂_iT_0i, or, dropping terms of order |$\mathcal {O}(\partial _\mathrm{ t} T_{00} v^2)$| and |$\mathcal {O}(\partial _\mathrm{ i} T_{00} v^3)$| with respect to |$\mathcal {O}(\partial _\mathrm{ t} T_{00})$|⁠, that is, up to relative corrections of |$\mathcal {O}(v^2)$| which we must drop,

$$\begin{eqnarray*} \partial _\mathrm{ t} T^{00} + 3 H_\mathrm{ a} T^{00} = - \partial _\mathrm{ i} T^{0\mathrm{ i}} \end{eqnarray*}$$

(29)

where we have raised indices while the metric is still approximately diagonal. Going to physical (meaning not comoving) spatial coordinates with rⁱ = axⁱ and t unchanged does not change T⁰⁰, but T⁰ⁱ → −H_axⁱT⁰⁰ + T⁰ⁱ/a (using the same name for the tensor components in the new coordinates). Since ∂_i → a∂_i this gives simply the Newtonian continuity equation

$$\begin{eqnarray*} \partial _\mathrm{ t} T^{00} + \partial _\mathrm{ i} T^{0\mathrm{ i}} = 0. \end{eqnarray*}$$

(30)

To obtain a leading-order equation of motion for the matter it is easiest to expand the geodesic equation directly to required order. With the four-velocity u^μ = dx^μ/dτ, it can be written without Christoffel symbols as

$$\begin{eqnarray*} \frac{\mathrm{ d} u_\sigma }{\mathrm{ d} \tau } = \frac{1}{2} \partial _\sigma g_{\mu \nu } u^\mu u^\nu . \end{eqnarray*}$$

(31)

We are back in the comoving coordinates with scale factor a. With |$u^\mu = (-1, \partial _\mathrm{ t} x^i) + \mathcal {O}(v^2)$| we have |$u_\mathrm{ i} = a^2 \partial _\mathrm{ t} x^i + \mathcal {O}(v^3)$|⁠. The left-hand side of equation (31) with σ = i can be expressed with the physical coordinates |$\boldsymbol {r} = a \boldsymbol {x}$| as |$\partial _\mathrm{ t} (a^2 \partial _\mathrm{ t} \boldsymbol{x}) = a \partial _\mathrm{ t}^2 \boldsymbol{r} - \boldsymbol{r} \partial _\mathrm{ t}^2 a$|⁠. The right-hand side is |$(1+\mathcal {O}(v^2)) \nabla g_{00}/2 \approx - \nabla \Psi \rightarrow -a \nabla \Psi$| where the last gradient is with respect to |$\boldsymbol{r}$|⁠. This means that in physical coordinates

$$\begin{eqnarray*} \ddot{\boldsymbol{r}} = - \nabla \Psi + \frac{\ddot{a}}{a} \boldsymbol{r}. \end{eqnarray*}$$

(32)

We can compare this to the standard Newtonian case involving the gradient of a potential sourced by the total matter content as

$$\begin{eqnarray*} \nabla ^2 \phi _\mathrm{ N} = 4 \pi G_\mathrm{ N} T_{00}. \end{eqnarray*}$$

(33)

Comparison of the two Poisson equations (33) and (9) (absorbing the a² in the latter into the new Laplacian with respect to physical coordinates and assuming adapted boundary conditions) gives

$$\begin{eqnarray*} \Phi = \phi _\mathrm{ N} + (\Lambda - 3 H_\mathrm{ a}^2) \boldsymbol{r}^2/12 \end{eqnarray*}$$

(34)

$$\begin{eqnarray*} -\nabla \Phi = -\nabla \phi _\mathrm{ N} + (H_\mathrm{ a}^2 /2 - \Lambda /6) \boldsymbol {r}. \end{eqnarray*}$$

(35)

We can trade the Ψ potential in equation (32) for the Φ potential with equation (18) and finally for the Newton potential ϕ_N

$$\begin{eqnarray*} \ddot{\boldsymbol{r}} = - \nabla \Psi + \frac{\ddot{a}}{a} \boldsymbol{r} \end{eqnarray*}$$

(36)

$$\begin{eqnarray*} = - \nabla \Phi - \frac{1}{2} H_\mathrm{ a}^2 \boldsymbol{r} + \frac{1}{2} \Lambda \boldsymbol{r} \end{eqnarray*}$$

(37)

$$\begin{eqnarray*} = - \nabla \phi _\mathrm{ N} + \frac{1}{3} \Lambda \boldsymbol{r} . \end{eqnarray*}$$

(38)

We stress that the result is that for Λ = 0, there is no cosmic force on small scales at all, consistent with the starting point of Newtonian cosmology.

3 EMBEDDED TOP-HAT COLLAPSE

To test the gauge freedom of the scale factor and the applicability of the perturbed FLRW metric in situations of strong inhomogeneity, we consider a spherically symmetric example with Λ = 0 for simplicity. For radial motion, T_0i is irrotational and we can set |$\boldsymbol {B}=0$| in the following. In particular, we consider the collapse of a pressureless dust top-hat (core region), leaving behind a vacuum shell, embedded into the matter cosmos.

To understand our example, it is useful to be aware of the Einstein–Straus solution (Einstein & Straus 1945, 1946; Carrera & Giulini 2010). It serves as an even simpler toy model of a collapsed structure in the expanding universe and can be thought of as the end result of a spherical collapse in the following sense: it represents what is obtained from a matter-dominated universe by compressing the dust contained within a ball of arbitrary size into a black hole. The dust outside of the vacuum bubble created in this way continues its usual expansion not only in Newtonian gravity but also, exactly, in GR. The vacuum bubble is therefore bounded by a shell of fixed comoving radial coordinate and expanding in physical coordinates (for standard comoving coordinates adjusted to the initial Hubble flow). An observer entering the bubble from the outside trying to remain at fixed comoving or physical coordinates needs to compensate a gravitational pull towards the centre that is increasing with decreasing distance to the black hole (starting at zero for the comoving case) and ultimately diverging at the Schwarzschild horizon, but the crossover into the bubble is smooth. An explicit solution in a single coordinate system is rather unwieldy in terms of formulae (Schücking 1954; Laarakkers & Poisson 2001; Balbinot, Bergamini & Comastri 1988), considerably more so than the solution McVittie found by direct integration of the Einstein equations (McVittie 1933; Nandra, Lasenby & Hobson 2012a) with a similar goal of describing a point mass embedded in an expanding universe, but the physical picture is simpler for the Einstein–Straus solution.

Instead of imposing a central black hole, we will be concerned with the previous weak-field stage of the collapse, for which the black hole is smoothed to a collapsing top-hat core similar to the Oppenheimer–Snyder model (Oppenheimer & Snyder 1939). The Oppenheimer–Snyder model is in some sense the most extreme yet simple case of collapse. The exact solution of a top-hat undergoing turnaround and collapse is a portion of the closed FLRW space–time (Misner et al. 2017).⁴ The combined Einstein–Straus–Oppenheimer–Snyder collapse has been discussed by other authors within GR (Nottale 1982; Dai, Pajer & Schmidt 2015; Kim, Lasenby & Hobson 2018). The density profile and its evolution is schematically illustrated in Fig. 1.

Figure 1.

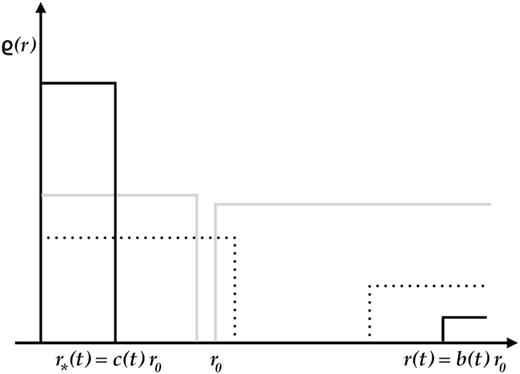
An example initial density profile is shown (grey) with a top-hat created by compressing the matter in a homogeneous universe within a spherical region. After some expansion (dotted), the top-hat turns around and collapses, whereas the outer universe continues to expand (black). The boundary of the top-hat is denoted as r_*(t) and the outer boundary of the vacuum region as r(t). Their time evolution is parametrized by two scale factors c(t) and b(t), respectively.

Open in new tab Download slide

We wish to model this space–time in the perturbed FLRW gauge, which will give a continuously differentiable but approximate solution in a single coordinate system by construction. Our strategy is to assess the quality of the approximation by comparing the result to the exact (closed FLRW, Schwarzschild, and flat FLRW) solutions separately for each of the three regions by finding appropriate coordinate transformations. This compliments the more complicated and less explicit result in Van Acoleyen (2008), which studies the validity of the perturbed FLRW solution by comparison to the exact LTB class of solutions, with the explicit top-hat collapse case that intuitively is the most challenging one for the perturbed FLRW metric.⁵

3.1 Newtonian top-hat collapse

We first use a physical radial coordinate r in which Newtonian theory holds in the usual way to describe some aspects of the collapse. Subsequently, we will work with two alternative choices of comoving coordinates.⁶ While it would be possible to stay entirely within the respective comoving coordinates for the calculations, this would double part of our work.

In physical coordinates, we can use Newtonian gravity according to Section (2.4). We let the initial radius of the ball be r₀, so the conserved mass in the top hat is

$$\begin{eqnarray*} M = \frac{4 \pi }{3} r^3_0 \rho _{\mathrm{ b},0} \end{eqnarray*}$$

(39)

where ρ_{b, 0} is the initial cosmic background density.⁷ The expansion of the boundary of the ball can be parametrized as r(t) = b(t)r₀ with b(t₀) = 1. Then, b(t) obeys

$$\begin{eqnarray*} H_\mathrm{ b}^2 = \frac{\dot{b}^2}{b^2} = \frac{2 G_\mathrm{ N} M}{r_0^3 b^3}, \end{eqnarray*}$$

(40)

which follows from setting the conserved total energy⁸ for the shell to zero so that |$\dot{r}^2(t) /2 = E_{\mathrm{ kin}} = - E_{\mathrm{ pot}} = G_\mathrm{ N}M/r(t)$|⁠, assuming shells do not cross so that |$M=M(r_0) \sim r_0^3$| is constant in time. No crossing is ensured if the shells further out at |$r_0^{\prime } \gt r_0$| expand with the same law |$r^{\prime }(t) = b(t) r_0^{\prime }$|⁠, or equivalently, if their total energy is also vanishing, which we assume as an initial condition.⁹

Equation (40) is equivalent to the Friedmann equation for the flat matter-dominated Einstein–de Sitter (EdS) universe with a Hubble parameter H₀ ≡ H_b(t₀) at the initial time¹⁰ obeying

$$\begin{eqnarray*} H_0^2 r_0^3 = 2 G_\mathrm{ N} M = \frac{8 \pi G_\mathrm{ N}}{3} r^3_0 \rho _{\mathrm{ b},0}, \end{eqnarray*}$$

(41)

so that

$$\begin{eqnarray*} H_\mathrm{ b}^2 = \frac{H_0^2}{b^3} = \frac{8 \pi G_\mathrm{ N}}{3} \rho _{b} \quad \text{where} \,\,\,\, \rho _\mathrm{ b} \equiv b^{-3} \rho _{\mathrm{ b},0} \end{eqnarray*}$$

(42)

that is, to equation (20) with vanishing cosmological constant, and therefore to equation (22), under the renaming b(t) → a(t). However, these equations a priori do not describe the same thing, since b(t) is related to the physical motion of matter shells in the outer region whereas a(t) is the particular metric scale factor choice for which the potentials do not diverge. However, if horizon scales are to be considered, we saw around equation (13) that the Hubble flow must be aligned to the coordinates to ensure small peculiar velocities, so the equations for a(t) and b(t) must approximately coincide. That is why we have chosen vanishing total shell energy at large distances here. Otherwise, there would be an additional term K/b² in equation (42), corresponding to a spatial curvature term in a Friedmann equation, which would only be consistent with a non-flat metric ansatz at large scales.

Locally, however, the Newtonian theory coming from the flat perturbed FLRW metric does allow for the set-up of the initial state corresponding to other value of the shell energies. In particular, we assume that the top hat is much smaller than the horizon size. The top-hat collapse evolution is independent of the dynamics outside and can be parametrized by another homogeneous scale factor c(t) with r_*(t) = c(t)r₀ where r_*(t) is the radial position of the outmost shell at time t. Choosing a negative total energy E for all top-hat shells, we easily find

$$\begin{eqnarray*} H_\mathrm{ c}^2 =\frac{\dot{c}^2}{c^2} = \frac{H_0^2}{c^3} + \frac{K}{c^2} \end{eqnarray*}$$

(43)

where |$K = 2 E / r_0^2 \lt 0$| by choice. Here the definition of H₀ is unchanged from before in terms of the mass M; H₀ is not necessarily to be understood as the value of H_c at t₀ (but still of H_b, as before). The actual value of H_c(t₀) depends on K and c(t₀). We could, for example, choose H_c(t₀) = H₀ by setting c(t₀) < 1 appropriately for a given K, corresponding to an initial state of a compressed top hat that velocity-wise is initially aligned with the previous Hubble flow. At later times, the motion of the matter described by c(t) does not correspond to the (parabolic) expansion law b(t) ∝ t^2/3 of the matter outside. Indeed, eventually c(t) will be a decreasing function with H_c < 0. We are not going to need the well-known exact (cycloidal) solutions to this Friedmann equation.

We now first explore the natural choice a(t) = b(t) and then the choice a(t) = c(t) for the metric scale factor. The latter choice can be valid if not only the top hat but the whole patch considered are small compared to the Hubble distance |$H_a^{-1}$| according to the discussion after equation (13).

3.2 Cosmological scale factor

First, we make the standard choice Ψ = Φ ≡ ϕ so that the metric scale factor is equation (23) in the Λ → 0 limit, which gives the EdS solution. That is, we chose a(t) = b(t). The metric (1) becomes

$$\begin{eqnarray*} \mathrm{ d}s^2 = -(1+2\phi) \mathrm{ d}t^2 + b^2(t) (1-2\phi) (\mathrm{ d}x^2 + x^2 \mathrm{ d}\Omega ^2) \end{eqnarray*}$$

(44)

where x = b⁻¹(t)r is the comoving radius,

$$\begin{eqnarray*} b(t) = (3 H_0 t / 2)^{2/3} \end{eqnarray*}$$

(45)

satisfies the Friedmann equation (42) and the Poisson equation (9) reads

$$\begin{eqnarray*} \nabla ^2 \phi = 4 \pi G_\mathrm{ N} b^2 (\rho - \rho _\mathrm{ b}). \end{eqnarray*}$$

(46)

We can solve this Poisson equation ensuring continuity of ϕ and ∂_xϕ at the two boundaries starting from the inside. To reduce clutter, in the following units are such that G_N = 1. We obtain

$$\begin{eqnarray*} \phi (x,t)&=&\left\lbrace \begin{array}{@{}l@{\quad }l@{}}\\ \\ \\ \\\end{array}\right.\nonumber\\ &&\quad\displaystyle\frac{1}{b(t)} \left(\frac{M}{2} \frac{ (x / x_*(t))^2 -3}{x_*(t)} -\frac{1}{4} H_0^2 \left(x^2 - 3 x_0^2\right) \right) \\ &&\quad\displaystyle -\frac{1}{b(t)} \left(M/x + \frac{1}{4} H_0^2 \left(x^2 - 3 x_0^2\right) \right) \\ &&\quad 0 \end{eqnarray*}$$

(47),(48),(49)

where the three formulae apply in the three regions x ≤ x_*(t), x_*(t) < x < x₀, and x ≥ x₀, respectively, and where x_*(t) = b(t)⁻¹r_*(t) is the comoving position of the boundary of the top hat and and x₀ = r₀ is the comoving position of the transition from vacuum to cosmological density. Here, ϕ has been shifted to zero outside. An exemplary ϕ is plotted in Fig. 2.

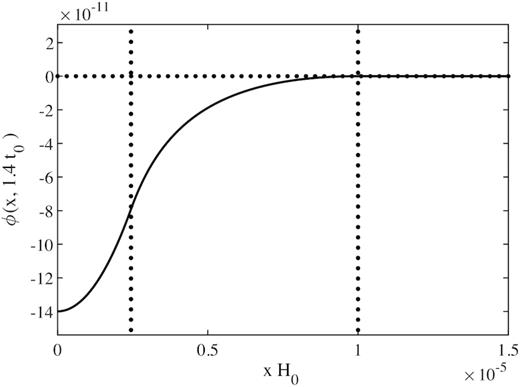
$This plot shows the three matched pieces of the solution for ϕ in equations (47)–(49) for an overdensity obtained from first compressing the dust in a ball of radius $r_0 = 10^{-5} H_0^{-1}$ to 0.4r0 (c(t0) = 0.4) and then letting it collapse until tf = 1.4t0. The vertical lines indicate the separation into core, vacuum, and outer cosmological region. The radial coordinate x is comoving with scale factor b(t). In the moment t = tf shown in the plot, b(tf) ≈ 1.66 (thus, if tf refers to today, t0 is at a redshift of 0.66). Initial velocities were aligned with the original Hubble flow; it follows that K = −2.34. The density contrast in the top-hat core, in the leftmost area of the plot, is δ = b3(tf)/c3(tf) − 1 ≈ 67, but the potential remains small everywhere.$

Figure 2.

This plot shows the three matched pieces of the solution for ϕ in equations (47)–(49) for an overdensity obtained from first compressing the dust in a ball of radius |$r_0 = 10^{-5} H_0^{-1}$| to 0.4r₀ (c(t₀) = 0.4) and then letting it collapse until t_f = 1.4t₀. The vertical lines indicate the separation into core, vacuum, and outer cosmological region. The radial coordinate x is comoving with scale factor b(t). In the moment t = t_f shown in the plot, b(t_f) ≈ 1.66 (thus, if t_f refers to today, t₀ is at a redshift of 0.66). Initial velocities were aligned with the original Hubble flow; it follows that K = −2.34. The density contrast in the top-hat core, in the leftmost area of the plot, is δ = b³(t_f)/c³(t_f) − 1 ≈ 67, but the potential remains small everywhere.

Open in new tab Download slide

3.2.1 External region x ≥ x₀

Since ϕ = 0, the metric (44) is the FLRW metric for the EdS cosmos.

3.2.2 Vacuum region x_*(t) < x < x₀

We first transform (44) to the areal radius r = (1 − ϕ)bx (to be distinguished from the function r(t) = b(t)r₀), which yields, to first order in ϕ,

$$\begin{eqnarray*} \mathrm{ d}s^2 &=&-(1+2\phi - (1-2\phi)A^2 B^{-2}) \mathrm{ d}t^2 \nonumber \\ &&-\, 2(1-2\phi)AB^{-2} \mathrm{ d}r \mathrm{ d}t \nonumber \\ &&+\, (1-2\phi)B^{-2} \mathrm{ d}r^2 + r^2 \mathrm{ d}\Omega ^2 \end{eqnarray*}$$

(50)

$$\begin{eqnarray*} A = H_\mathrm{ b} r - \phi _{,\mathrm{ t}} b x \end{eqnarray*}$$

(51)

$$\begin{eqnarray*} B = 1 - \phi - \phi _{,\mathrm{ x}} x \end{eqnarray*}$$

(52)

where the time derivative _{, t} in equation (51) is at constant x and where afterwards x should be eliminated in terms of r. This follows immediately from writing dr = Adt + bBdx⇔(bdx)² = B⁻²(dr − Adt)².

In the following, we keep |$H_\mathrm{ b}^2 r^2$| and M/r as the smallest terms. The first one is very small compared to one if the vacuum region is very small compared to the Hubble distance, |$r_0 \ll H_\mathrm{ b}^{-1}$|⁠, because x ≤ x₀ and |$b = \mathcal {O}(1)$|⁠; the second term is everywhere small under the weak-field assumption. We drop |$\sqrt{H_\mathrm{ b}^2 r^2} (M/r) = H_\mathrm{ b} M$| and smaller, and thus also H_brϕ ≪ v². In general, one cannot drop terms of order v³ (like |$\boldsymbol {B}$| itself) from the vector mode; however, only the transverse part of any vector mode enters in the continuity equation (26). We can therefore definitely ignore radial r − t off-diagonal terms of order v³ in the metric, corresponding to a longitudinal mode.

From the potential equations (47)–(49), A ≈ H_br. Also, |$B \approx 1 + 3 H_\mathrm{ b}^2 (r^2 - r^2(t))/4$|⁠. This leads to

$$\begin{eqnarray*} \mathrm{ d}s^2 &=& -\left(1-2M/r - \frac{3}{2} H_\mathrm{ b}^2 (r^2 - r^2(t))\right) \mathrm{ d}t^2 - 2H_\mathrm{ b}r \mathrm{ d}r \mathrm{ d}t \nonumber \\ &&+ \left(1+2M/r -H_\mathrm{ b}^2 r^2 \right) \mathrm{ d}r^2 + r^2 \mathrm{ d}\Omega ^2. \end{eqnarray*}$$

(53)

Our task is to remove the off-diagonal part by a transformation to a new time coordinate

$$\begin{eqnarray*} t^{\prime } = f(t,r), \end{eqnarray*}$$

(54)

since the radial coordinate is the areal radius already, just like in Schwarzschild coordinates. Let J denote the Jacobian of the new coordinates as a function of the old ones; the metric transforms as g → (J⁻¹)^tgJ⁻¹. Writing only the non-trivial (t, r) part, we have

$$\begin{eqnarray*} J = {\begin{pmatrix}f_{,\mathrm{ t}} & f_{,\mathrm{ r}} \\ 0 & 1 \end{pmatrix}} \quad \rightarrow \quad J^{-1} = \frac{1}{f_{,\mathrm{ t}} }{\begin{pmatrix}1 & -f_{,\mathrm{ r}} \\ 0 & f_{,\mathrm{ t}} \end{pmatrix}} \end{eqnarray*}$$

(55)

and find

$$\begin{eqnarray*} g \quad \rightarrow \quad \frac{1}{f_{,\mathrm{ t}}^2 }{\begin{pmatrix}g_{\mathrm{ tt}} & -f_{,\mathrm{ r}} g_{\mathrm{ tt}} + f_{,\mathrm{ t}} g_{\mathrm{ rt}} \\ -f_{,\mathrm{ r}} g_{\mathrm{ tt}} + f_{,\mathrm{ t}} g_{\mathrm{ rt}} & f_{,\mathrm{ r}}^2 g_{\mathrm{ tt}} - 2 f_{,\mathrm{ r}} f_{,\mathrm{ t}} g_{\mathrm{ rt}} + f_{,\mathrm{ t}}^2 g_{\mathrm{ rr}} \end{pmatrix}} \end{eqnarray*}$$

(56)

and can read off that for

$$\begin{eqnarray*} f_{,\mathrm{ r}} = \frac{g_{\mathrm{ rt}} }{g_{\mathrm{ tt}}} f_{,\mathrm{ t}} \end{eqnarray*}$$

(57)

the metric transforms as

$$\begin{eqnarray*} g \quad \rightarrow \quad {\begin{pmatrix}g_{\mathrm{ tt}} / f_{,\mathrm{ t}}^2& 0 \\ 0 & g_{\mathrm{ rr}} - g_{\mathrm{ rt}}^2/g_{\mathrm{ tt}} \end{pmatrix}} . \end{eqnarray*}$$

(58)

The condition (57) is a first-order linear PDE (that can be reduced to a non-linear ODE by the method of characteristics). It may be noted that evidently it is not necessary to solve the PDE to get the new g_rr, which does not depend on f in equation (58).

In the present case, any diagonalizing transformation adds |$-g_{\mathrm{ rt}}^2/ g_{\mathrm{ tt}} \approx g_{\mathrm{ rt}}^2 = H^2 r^2$| to g_rr which therefore becomes 1 + 2M/r. If the t′t′-element was −(1 − 2M/r), the metric would clearly be the weak-field limit of the Schwarzschild solution. All that is required for this is that

$$\begin{eqnarray*} f_{,\mathrm{ t}} = 1 - \frac{\delta g_{\mathrm{ tt}}}{2} \end{eqnarray*}$$

(59)

where δg_tt are the terms we want to remove, for then

$$\begin{eqnarray*} g_{\mathrm{ tt}} \quad &\rightarrow \qquad \quad g_{\mathrm{ tt}} \qquad \qquad f_{,\mathrm{ t}}^{-2} \nonumber \\ &\approx -\left(1-\frac{2M}{r} - \delta g_{\mathrm{ tt}} \right) (1+\delta g_{\mathrm{ tt}})\approx - \left(1-\frac{2M}{r}\right) , \end{eqnarray*}$$

(60)

so f_{, t} = 1 − 3H²(r² − r²(t))/4. On the other hand, the PDE is, to sufficient order and assuming f_{, t} = O(H²r²) (smallest possible transformation), simply f_{, r} ≈ g_rt/g_tt ≈ −g_rt = Hr so that f = Hr²/2 + h(t). Given that H = 2/(3t) and the form of b(t) we see that there indeed exists a solution f = t + Hr²/2 + 3(H₀x₀)²/(2Hb) with the required f_{, t}. In summary, the coordinate transformation

$$\begin{eqnarray*} x^{\prime } \equiv r = (1-\phi (x,t)) b(t) x \end{eqnarray*}$$

(61)

$$\begin{eqnarray*} t^{\prime } = t + \frac{1}{2} H_\mathrm{ b}(t) b^2(t) x^2 + \frac{3 H_0^2 x_0^2}{2 H_\mathrm{ b}(t) b(t)} \end{eqnarray*}$$

(62)

puts the perturbed FLRW metric (44) in the vacuum region (47)–(49) into the weak-field approximation of the Schwarzschild solution. Note in particular that the metric is now static.

3.2.3 Interior region x ≤ x_*(t)

We can play a similar game for the interior region. We first introduce a spatial coordinate

$$\begin{eqnarray*} x^{\prime } = (1-\phi - \epsilon)bx/c \approx (1-\phi)(1 - \epsilon) bx/c. \end{eqnarray*}$$

(63)

Here ϵ = ϵ(x, t) is assumed to be of the same order as ϕ. When ϵ vanishes, this is a straightforward coordinate change designed taking g_θθ from x²(1 − 2ϕ)b²(t) to x^′2c²(t). The role of ϵ is to compensate the effect of a given further time transformation to a new time t′, such that instead |$x^2 (1-2\phi) b^2(t) = x^{\prime 2} \tilde{c}^2(t^{\prime })$| for a given choice of the function |$\tilde{c}$|⁠. Thus,

$$\begin{eqnarray*} (1+2\epsilon) c^2(t) = \tilde{c}^2(t^{\prime }). \end{eqnarray*}$$

(64)

Again writing dx′ = Adt + bBdx, we have now that

$$\begin{eqnarray*} A &\approx &(H_\mathrm{ b} - H_\mathrm{ c}) x^{\prime } \nonumber \\ B &=& c^{-1}(1- (\phi + \epsilon) - (\phi +\epsilon)_{,\mathrm{ x}} x) \end{eqnarray*}$$

(65)

where we have anticipated that the rate of change |$\dot{\epsilon }/\epsilon = \mathcal {O}(H_0)$| to neglect terms.

Using the Friedmann equation for c, (43), the expression for ϕ in the interior region (47)–(49) can be written as

$$\begin{eqnarray*} \phi = \frac{1}{4} H_0^2 \left(b^2 x^2 (c^{-3} - b^{-3}) - 3 x_0^2 (c^{-1} - b^{-1})\right) \end{eqnarray*}$$

(66)

$$\begin{eqnarray*} = \frac{1}{4}\left[ (H_\mathrm{ c}^2 - H_\mathrm{ b}^2) c^2 x^{\prime 2} - K x^{\prime 2} + 3 H_0^2 x_0^2 (b^{-1} - c^{-1}) \right]. \end{eqnarray*}$$

(67)

With the definitions (65), the metric (44) becomes, under the transformation (63),

$$\begin{eqnarray*} g_{\mathrm{ tt}} &\approx & -(1+2 \phi - A^2 c^2) \nonumber \\ g_{\mathrm{ x}^{\prime } \mathrm{ t}} &\approx &- A c^2. \nonumber \\ g_{\mathrm{ x}^{\prime } \mathrm{ x}^{\prime }} &=& (1-2\phi) B^{-2} \end{eqnarray*}$$

(68)

Again, for integrating equation (57) (with x′ playing the role of r), the procedure reduces to integrating |$-g_{\mathrm{ x}^{\prime }\mathrm{ t} }$| in x′, to give

$$\begin{eqnarray*} t^{\prime } = f(x^{\prime }, t) = t + (H_\mathrm{ b} - H_\mathrm{ c}) c^2 x^{\prime 2} /2 + g(t). \end{eqnarray*}$$

(69)

For |$g_{\mathrm{ t}^{\prime }\mathrm{ t}^{\prime }} \approx -1$| we would like again that equation (59) is satisfied, with δg_tt now defined as all terms perturbing −1 in g_tt, which reads

$$\begin{eqnarray*} f_{,\mathrm{ t}} &=& 1 + \frac{c^2 (H_\mathrm{ c}^2 - H_\mathrm{ b}^2 - 2(H_\mathrm{ c}-H_\mathrm{ b})^2) - K}{4}x^{\prime 2} \nonumber \\ &&+ \,\frac{3 H_0^2 x_0^2 (b^{-1} - c^{-1})}{4}. \end{eqnarray*}$$

(70)

It can be shown, using the two Friedmann equations for b (42) and c (43) to eliminate time derivatives, that this is indeed consistent with equation (69) when we pick

$$\begin{eqnarray*} g(t) = (3/4) H_0^2 x_0^2 \int (b^{-1} - c^{-1}) \mathrm{ d}t . \end{eqnarray*}$$

(71)

The metric is now diagonal and g_tt = −1. We are ready to read off an ϵ after Taylor expanding the left-hand side of equation (64) around t′, defining δt = t′ − t,

$$\begin{eqnarray*} &&c^2(t) (1+2 \epsilon) \\ &\approx & \left([c^2]|_{t=t^{\prime }} - [c^2]_{,\mathrm{ t}} \delta t\right)(1+2\epsilon) \\ &\approx & c^2(t=t^{\prime }) + 2 c^2 \epsilon - c^4 x^{\prime 2} (H_\mathrm{ c} H_\mathrm{ b} - H_\mathrm{ c}^2) - 2 c^2 H_\mathrm{ c} g(t). \end{eqnarray*}$$

This means that

$$\begin{eqnarray*} \epsilon &=& H_\mathrm{ c} g(t) + c^2 x^{\prime 2} (H_\mathrm{ c} H_\mathrm{ b} - H_\mathrm{ c}^2)/2 \nonumber \\ &\approx & H_\mathrm{ c} g(t) + b^2 x^2 (H_\mathrm{ c} H_\mathrm{ b} - H_\mathrm{ c}^2)/2 \end{eqnarray*}$$

(72)

would imply that |$\tilde{c}(t^{\prime }) = c(t=t^{\prime })$| from equation (64). This is a convenient choice, for it means that |$\tilde{c}$| has been chosen to satisfy the same Friedmann equation (with the time derivative with respect to the new time variable t′!) for the closed universe, we have found earlier for c, because it is the same function of its argument as is c of its argument, so this is the natural choice we adopt.

Finally, we compute |$g_{\mathrm{ x}^{\prime }\mathrm{ x}^{\prime }}$|⁠, which picks up an additional |$+ g_{\mathrm{ x}^{\prime } \mathrm{ t}}^2$| compared to equation (68) under the diagonalizing time transformation. Thus,

$$\begin{eqnarray*} g_{\mathrm{ x}^{\prime } \mathrm{ x}^{\prime }} &=& (1-2\phi) B^{-2}+ g_{\mathrm{ x}^{\prime } \mathrm{ t}}^2 \nonumber \\ &\approx & c^2(t) (1+2(\phi + \epsilon)_{,\mathrm{ x}} x + 2 \epsilon) + g_{\mathrm{ x}^{\prime } \mathrm{ t}}^2 \nonumber \\ &\approx & \tilde{c}^2(t^{\prime }) (1+2(\phi + \epsilon)_{,\mathrm{ x}^{\prime }} x^{\prime }) + g_{\mathrm{ x}^{\prime } \mathrm{ t}}^2 \nonumber \\ &\approx & c^2(t^{\prime }) (1+2(\phi + \epsilon)_{,\mathrm{ x}^{\prime }} x^{\prime } + c^2 x^{\prime 2} (H_\mathrm{ c} - H_\mathrm{ b})^2). \end{eqnarray*}$$

(73)

This simplifies straightforwardly to |$g_{\mathrm{ x}^{\prime } \mathrm{ x}^{\prime }} = c^2(t^{\prime }) (1-K x^{\prime 2})$| for the choice of ϵ we have made. With the identification k = −K > 0, the metric is now

$$\begin{eqnarray*} \mathrm{ d}s^2 = - \mathrm{ d}t^{\prime 2} + c^2(t^{\prime })\left(\frac{\mathrm{ d}x^{\prime 2}}{1-kx^{\prime 2}} + x^{\prime 2} \mathrm{ d}\Omega ^2\right) \end{eqnarray*}$$

(74)

for 0 < kx^′2 ≪ 1, which was already assumed. This is the metric of the closed universe as well as the exact solution of the collapsing top hat.

In summary, the transformation

$$\begin{eqnarray*} x^{\prime } = x(1-\phi (x,t))\left(1 - H_\mathrm{ c}(t) \delta t(x,t)\right) \frac{b(t)}{c(t)} \end{eqnarray*}$$

(75)

$$\begin{eqnarray*} t^{\prime } = t + \delta t(x,t) \end{eqnarray*}$$

(76)

$$\begin{eqnarray*} \delta t(x,t) \equiv \frac{H_\mathrm{ b}(t) - H_\mathrm{ c}(t)}{2} b^2(t) x^2 + g(t) \end{eqnarray*}$$

(77)

$$\begin{eqnarray*} g(t) \equiv \frac{3}{4} H_0^2 x_0^2 \int (b^{-1} - c^{-1}) \mathrm{ d}t \end{eqnarray*}$$

(78)

puts the interior region of the perturbed FLRW metric above into the weak-field closed FLRW form (74) describing a collapsing top-hat dust profile.

3.3 Collapsing scale factor

We now choose a(t) = c(t) as the metric scale factor, that is, coordinates that are collapsing with the top hat. The metric ansatz equation (1) is then

$$\begin{eqnarray*} \mathrm{ d}s^2 = -(1+2\Psi) \mathrm{ d}t^2 + c^2(t) (1-2\Phi) (\mathrm{ d}x^2 + x^2 \mathrm{ d}\Omega ^2) \end{eqnarray*}$$

(79)

where x = c⁻¹(t)r is the comoving radius, c(t) satisfies the Friedmann equation (43) and the Poisson equation (9) reads

$$\begin{eqnarray*} \nabla ^2 \Phi = 4 \pi G_\mathrm{ N} c^2(t) \rho (x,t) - \frac{3}{2} c^2(t) H_\mathrm{ c}^2(t) . \end{eqnarray*}$$

(80)

We also need Ψ, which according to equation (18) is given by

$$\begin{eqnarray*} \Psi = \Phi + \frac{c^2}{2} \left(\frac{H_\mathrm{ c}^2}{2} + \frac{\ddot{c}}{c} \right) x^2 = \Phi + \frac{K}{4}x^2 \end{eqnarray*}$$

(81)

where the Friedmann equation for c was differentiated in time to obtain the result. The interpretation of the pre-factor of x²/4 in the difference Φ − Ψ as a spatial curvature term k(t) that was mentioned after equation (18) is of course recovered in this simple example, in which k = −K is time-independent.

The coordinate of the top-hat boundary x_* is no longer given by b⁻¹r_*(t) but by c⁻¹r_*(t) = r₀ and is time-independent. On the other hand, the boundary of the vacuum bubble is now time-dependent with

$$\begin{eqnarray*} x_0(t) = c^{-1} r(t) = c^{-1} b \,\,r_0 \ge r_0. \end{eqnarray*}$$

(82)

Then, the solutions for the potentials are,¹¹

$$\begin{eqnarray*} \Phi (x,t)&=&\left\lbrace \begin{array}{@{}l@{\quad }l@{}}\\ \\ \\\end{array}\right.\nonumber\\ &&\quad\displaystyle- \frac{K}{4}x^2 - \frac{3}{4} \frac{H_0^2 r_0^2}{c}\\ &&\quad\displaystyle-\frac{H_0^2 r_0^3}{2 c x} - \frac{c^2 H_\mathrm{ c}^2}{4}x^2\\ &&\quad\displaystyle \frac{c^2 H_0^2 }{4 b^3}x^2 - \frac{c^2 H_\mathrm{ c}^2}{4}x^2 - \frac{3H_0^2 r_0^2}{4b} \end{eqnarray*}$$

(83),(84),(85)

$$\begin{eqnarray*} \Psi (x,t)&=&\left\lbrace \begin{array}{@{}l@{\quad }l@{}}\\ \\ \\\end{array}\right. \nonumber\\ &&\quad\displaystyle- \frac{3}{4} \frac{H_0^2 r_0^2}{c}\\ &&\quad\displaystyle-\frac{H_0^2 r_0^3}{2c x} - \frac{H_0^2}{4 c}x^2\\ &&\quad\displaystyle\frac{H_0^2}{4} \left(\frac{c^2}{ b^3}x^2 - \frac{x^2}{c} - \frac{3 r_0^2}{b} \right) \end{eqnarray*}$$

(86),(87),(88)

where the formulae each again hold in the three regions now written as x ≤ r₀, r₀ < x < x₀(t), and x ≥ x₀(t), respectively. They are shown in Fig. 3. A comparison of the potentials Φ and ϕ from the previous section is shown in Fig. 4.

Figure 3.

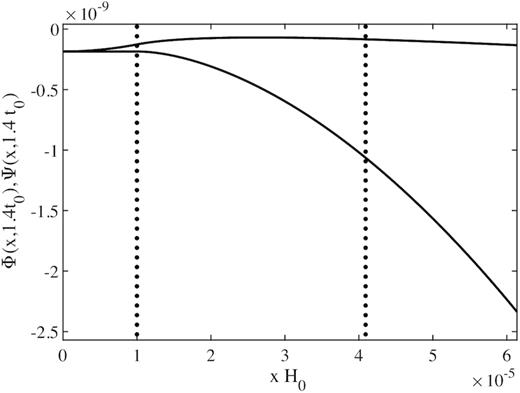
Shown are Φ (upper curve) and Ψ (lower curve) given by equations (83)–(86) for the same overdensity as in Fig. 2. Coordinates are now comoving with respect to scale factor c(t). Both potentials diverge quadratically on large scales since the scale factor does not correspond to the average motion there, but still remain small in a cosmological region of subhorizon size.

Open in new tab Download slide

Figure 4.

Comparison of ϕ from Fig. 2 (upper curve) and Φ from Fig. 3 (lower curve). To compare the values at the same physical points more easily, Φ has been re-expressed as a function of the comoving coordinates with respect to b(t).

Open in new tab Download slide

3.3.1 External region x ≥ x₀(t)

The discussion proceeds like in the previous case (Section 3.2.3) with b and c reversed in the formulae. First, the spatial coordinate is transformed analogously to equation (63). Next, of course, −δg_tt/2 = Ψ − A²b²/2 is a different expression, but one can again confirm that it is in fact equal to the time derivative of a δt chosen for diagonalization of the metric as given below, so it is again possible to simultaneously let |$g_{\mathrm{ tt}} \rightarrow g_{\mathrm{ t}^{\prime }\mathrm{ t}^{\prime }} = -1$| when diagonalizing the metric. The determination of ϵ for obtaining b²(t′) (instead of b²(t(t′)) [without ϵ] or |$b^2(t(t^{\prime })) (1+2\epsilon) \equiv \tilde{b}^2(t^{\prime })$| [for a generic ϵ]) in |$g_{\mathrm{ x}^{\prime }\mathrm{ x}^{\prime }}$| is analogous, and all terms perturbing b²(t′) cancel for this particular choice of ϵ in |$g_{\mathrm{ x}^{\prime } \mathrm{ x}^{\prime }}$| after the transformation to the new time coordinate. Therefore, the transformation

$$\begin{eqnarray*} x^{\prime } = x(1-\Phi (x,t))\left(1 - H_\mathrm{ b}(t) \delta t(x,t)\right) \frac{c(t)}{b(t)} \end{eqnarray*}$$

(89)

$$\begin{eqnarray*} t^{\prime } = t + \delta t(x,t) \end{eqnarray*}$$

(90)

$$\begin{eqnarray*} \delta t(x,t) \equiv \frac{H_\mathrm{ c}(t) - H_\mathrm{ b}(t)}{2} c^2(t) x^2 + g(t) \end{eqnarray*}$$

(91)

$$\begin{eqnarray*} g(t) \equiv -\frac{3}{4} H_0^2 r_0^2 \int b^{-1} \mathrm{ d}t \end{eqnarray*}$$

(92)

puts the exterior region of the perturbed FLRW metric equation (79) with collapsing scale factor into the EdS metric with its standard scale factor

$$\begin{eqnarray*} \mathrm{ d}s^2 = -\mathrm{ d}t^{\prime 2} + b^2(t^{\prime }) (\mathrm{ d}x^{\prime 2} + x^{\prime 2} \mathrm{ d}\Omega ^2). \end{eqnarray*}$$

(93)

It has to be noted that unlike before for the exterior region, this was shown only on subhorizon scales, because we have assumed smallness of the potentials which clearly both grow quadratically for this choice of scale factor. As discussed, on larger scales, the choice of a scale factor that leads to large peculiar velocities is not expected to be successful in the Newtonian limit.

3.3.2 Vacuum region r₀ ≤ x ≤ x₀(t)

The transformation to the Schwarzschild line element presents no difficulties following the previous discussion in Section 3.2.2. We find

$$\begin{eqnarray*} r = x (1-\Phi (x,t)) c(t) \end{eqnarray*}$$

(94)

$$\begin{eqnarray*} t^{\prime } = t + \frac{1}{2} H_\mathrm{ c}(t) c^2(t) x^2 \end{eqnarray*}$$

(95)

to put the perturbed FLRW metric equation (44) in the vacuum region into the weak-field approximation of the Schwarzschild solution.

3.3.3 Interior region x ≤ r₀

The transformation is a simple special case of the general transformation from the flat FLRW metric to the curved collapsing FLRW metric equations (75)–(78) for unchanging scale factor, so for b → c; non-negligible off-diagonal terms are not created and ϵ = H_cδt is not spatially dependent. We take

$$\begin{eqnarray*} x^{\prime } = (1-\Phi (x,t))(1- H_\mathrm{ c}(t) \delta t(t)) x \end{eqnarray*}$$

(96)

$$\begin{eqnarray*} t^{\prime } = t + \delta t(t) \end{eqnarray*}$$

(97)

$$\begin{eqnarray*} \delta t(t) = -\frac{3 H_0^2 r_0^2}{4} \int c^{-1} \mathrm{ d}t \end{eqnarray*}$$

(98)

and get

$$\begin{eqnarray*} g_{\mathrm{ rr}} &=& c^2(t^{\prime })(1 + 2 \Phi _{,\mathrm{ x}^{\prime }}x^{\prime }) \approx c^2(t^{\prime })(1+Kx^{\prime 2})^{-1} \nonumber \\ &=& c^2(t^{\prime })(1-k x^{\prime 2})^{-1}, \end{eqnarray*}$$

(99)

so that equation (74) is again recovered.

This case would have been even simpler, namely not requiring a time transformation δt = 0 = ϵ, had we shifted the potentials by a (time-dependent) constant setting Ψ = 0 in the inside. A similar trick was used zeroing ϕ in the expanding scale factor case a(t) = b(t), exploited in Section 3.2.1. Here, we have illustrated that a non-zero constant related to γ(t) in equation (18) can be removed.

4 DISCUSSION

The coordinate transformations derived in the previous section validate the perturbed FLRW description for the embedded top-hat example for different gauge choices of the scale factor for a specific example. Here, we address some subtle points of the general Newtonian limit: the validity on large scales in Section 4.1, the Newtonian picture of structure formation in Section 4.2 and the relation of the linear part of the gauge freedom Ψ − Φ in equation (16) to the Newtonian cosmology developed by Heckmann and Schücking (1955, 1956) as well as implications for backreaction in the remaining two sections.

4.1 Emergence of Friedmann scale factor

On scales comparable to or larger than the Hubble scale, we have seen that the Newtonian limit can work only under a list of assumptions.

First, we need Ψ ≃ Φ and α(t) ≃ 0, so we may demand simply α(t) = 0 with the corresponding Friedmann solution (23) for a(t). Otherwise, if H_a departs by |$\mathcal {O}(H_0)$| from the Friedmann evolution, the difference of the potentials, and therefore at least one of them, approaches |$\mathcal {O}(1)$| at the Hubble scale, contradicting the assumption of small potentials used to derive the Newtonian field equations in Section 2.

Second, in Section 2, we have also requested that the physical Hubble flow is described by a(t) on large scales so that peculiar velocities can remain small far away from the coordinate center.

These two conditions are compatible, because the Friedmann equation for a(t) from the Einstein equations for Ψ = Φ and the Friedmann equation for the matter background that can be derived from the geodesic equation (38, done in Section 3.1 for the special case of vanishing cosmological constant) are in fact equivalent.

Finally, another quadratic divergence that would spoil the Newtonian limit would arise when solving the Poisson equation (9) if the source (meaning all terms except the Laplacian) did not average to something small on large scales. This is a well-known issue with the solution of the Newtonian Poisson equation (33), for which

$$\begin{eqnarray*} \phi _\mathrm{ N} \sim 2 \pi G_\mathrm{ N}/3 \, \rho _\mathrm{ b} r^2 \end{eqnarray*}$$

(100)

reaches the non-perturbative |$\mathcal {O}(1)$| at the Hubble scale. The metric potential Φ differs from the Newtonian potential by a quadratic term (equation 34), and by an appropriate choice of scale factor this regularizes all or part of the divergence. This choice is fully compatible to the previous conditions. If we assume that at early times, when the universe was very homogeneous, the source does average to something small, it already follows from the previous assumptions that it is the case at all times: since matter moves on average with the Hubble flow described by a(t), the continuity equation for matter then implies that T₀₀ thins out as a⁻³, which is in fact proportional to the other source terms |$3H_\mathrm{ a}^2-\Lambda$| in equation (9). This can be checked explicitly from the solution (23) for a(t) obtained from Ψ = Φ.

The smallness of the average of the source of the Poisson equation at early times becomes a statement about the flatness of the universe on large scales. If the average is not small at an early time, a curvature term may be introduced to balance the resulting divergence. The argument of the time-preservation of the absence of the divergence can be generalized to this case.

One is of course free to introduce another scale factor and coordinate system when solving the Newtonian equations after they have been obtained as described, and discussed in Kaiser (2017). However, only the Friedmann scale factor a(t) will be valid in the expression for the metric to describe the geometry of the space−time. In this sense, the a(t) given by equation (23) is emerging on large scales as a quantity that is useful for the description of the geometry.

4.2 Cosmic expansion force acting on local systems?

Many workers have investigated the influence of the global cosmology on the local dynamics. The classic results of Einstein & Straus (1945, 1946) are in accordance with the more general result (38) reported here that there is no local effect in a matter-dominated universe that cannot be explained in a simple manner by Newtonian gravity. In particular, Newton’s laws do not have to be ‘corrected’ for the ‘expansion of space’.

The cosmological constant does have an effect, investigated for example in Nandra et al. (2012b). More generally, any modification of the background evolution, be it homogeneous dark energy or infrared-modified gravity, replaces the cosmological constant by a term that is time dependent in general. This term can simply be understood as the Newtonian ‘weight’ of the dark energy component seen as a perfect fluid, when taking as given that pressure gravitates as predicted by GR. Note that N-body simulations are sensitive to modification of the background evolution because of this mechanism.¹² All of this certainly has been known to some cosmologists for a long time (an early qualitative discussion is Dicke & Peebles 1964, see also Noerdlinger & Petrosian 1971), has been employed in studies of dynamics, e.g. in Lahav et al. (1991) and Falco et al. (2013), and forms the starting point of the success of Newtonian cosmology. An insightful discussion of the problem can be found in Dominguez & Gaite (2001), where the Newtonian shear effects are also investigated.

However, recent studies have sometimes come to more diffuse conclusions. These are often based on modelling the problem using exact solutions that contain a homogeneous component, like unperturbed FLRW for the the homogeneous universe (Cooperstock et al. 1998; Bonnor 1999; Price & Romano 2012), exact solutions describing a mass embedded into a universe with homogeneous density component like McVittie’s¹³ (Carrera & Giulini 2010; Nandra et al. 2012a), or others (Bonnor 1996), or they discuss several such models (Faraoni & Jacques 2007). On the other hand, the LTB solution does not contain a separate homogeneous component, and results directly agree with ours (Pavlidou, Tetradis & Tomaras 2014).

The homogeneous background components in the universe, more precisely a ball of cosmic fluids centred in the origin and extending up to a particle’s position, causes a force with magnitude proportional to |$\ddot{a} r / a$| according to Newton’s gravity, where a is the scale factor of the background cosmology obeying the Friedmann equations. (Indeed this is a valid way to derive the Friedmann equations, see Section 3.1 and Bertschinger 1995; Maggiore 2018.) The authors investigating local systems in cosmological backgrounds based on exact solutions often report such a force, but do not seem to appreciate that it can be understood in a simple Newtonian way. This is problematic when drawing conclusions about our realistic inhomogeneous universe. One must be aware of the local distribution of sources. For example, for vanishing cosmological constant, there is no cosmic force in the Solar system if and only if there is no dark matter in the Solar system, and conversely a force due to dark matter can be orders of magnitude larger than |$\ddot{a} r / a$| if the dark matter concentration is similarly higher. Regarding the cosmic effects on atoms, the importance of the nature of dark matter is then obvious.

In our view, it would be a particularly unnatural interpretation to attribute the effect instead to a long-range non-Newtonian force exerted from the ‘expansion of space’, which does not make sense in the Newtonian picture. Therefore, there is no need to argue against the validity of the physical picture given by the Einstein–Straus situation, even if it is not a realistic model neglecting the hierarchy of structures and demanding an exceedingly large vacuum bubble to compensate e.g. our sun (Carrera & Giulini 2010).

4.3 Newtonian inertial frames in cosmology

In an unperturbed Λ cold dark matter (ΛCDM) universe, the symmetry of homogeneity is incompatible with the Newtonian postulate of the existence of one particular class of inertial frames related by Galilean transformations. Two matter particles at two different locations feel a relative force and cannot both be at rest in, and define the origin of, an inertial frame of the same class. Clearly, there is no concept of a unique, global ‘absolute space’ for an infinite self-gravitating system. Even for a finite, expanding sphere there is no preferred inertial frame if observers at different locations are taken to be equivalently meaningful and ignorant of the boundary (McCrea 1955).

Newtonian cosmological theory can do without absolute space. Conceptually, one wants to adopt the local freely falling inertial frames familiar from GR. Mathematically, the breaking of the symmetry of homogeneity at the level of the specification of the theory can be avoided and postponed to the choice of integration constants at the level of solution. This has been achieved in Heckmann & Schücking (1956) by completing the Newtonian Poisson equation with the following boundary conditions at infinity

$$\begin{eqnarray*} \nabla ^2 \phi _N &=& 4 \pi G_\mathrm{ N} \rho (t)\nonumber \\ \left(\partial _\mathrm{ i} \partial _\mathrm{ j} - \frac{1}{3} \delta _{\mathrm{ ij}} \nabla ^2\right) \phi _\mathrm{ N} &=& A_{\mathrm{ ij}} (t), \end{eqnarray*}$$

(101)

where ρ(t) is the limit of the density at spatial infinity, assumed to exist, and A_ij(t) is a symmetric traceless matrix function that selects between various Newtonian cosmological models. The solution ϕ_N is then unique up to the addition of planes

$$\begin{eqnarray*} \phi _\mathrm{ N} \rightarrow \phi _\mathrm{ N} + \boldsymbol {\tilde{\beta }}(t) \cdot \boldsymbol{x}+ \gamma (t). \end{eqnarray*}$$

(102)

The linear term causes an additional time-dependent acceleration. This can be used to adapt the coordinates from one freely falling observer to another. More generally, any kind of global homogeneous acceleration can be achieved with the linear term. Unlike the effects of A_ij, however, the linear term is fundamentally unobservable in the present setting (Heckmann & Schücking 1955) because all of the material content of the universe including any lab equipment is affected by it in the same way. It amounts to describing the same physics from an accelerated frame.

In this paper, we are faced with the general-relativistic emergence of the situation captured by this modification of Newtonian theory. On the one hand, for the starting point of the (unperturbed) FLRW metric, the transformation from one free-fall observer to another is a trivial translation generated by the obvious spatial Killing vectors. All comoving observers are geodesic and therefore simultaneously unaccelerated from a GR point of view. On the other hand, the Newtonian limit involves the transition to expanding physical coordinates which necessarily singles out the coordinate origin, seemingly breaking the symmetry. But the theory of GR and the FLRW ansatz on small scales with free perturbations naturally do not ‘know’ that our goal is to find Newton’s familiar equations written out in any inertial frame at all and certainly do not choose the origin for us.

And indeed, GR manages to preserve the symmetry of homogeneity due to gauge freedom.¹⁴ The function |$\boldsymbol {\beta }(t)$| is a degree of freedom arising when integrating Einstein’s equations that adds a linear term |$\boldsymbol {\beta }(t) \cdot \boldsymbol {x}$| to Ψ (and |$- 2 \boldsymbol {\beta }(t) \cdot \boldsymbol {x}$| to g₀₀) according to equation (15). Again, in general, for |$\boldsymbol {\beta }(t)\ne 0$|⁠, the negative gradient generates a global acceleration |$-\boldsymbol {\beta }(t)$| on a particle, as can be easily seen from the geodesic equation in the form of equation (32). In this case, one may boost to that proper frame which, as seen from the original one, undergoes the same acceleration. In Minkowski space, so on sufficiently small scales, such a boost precisely removes the linear term from g₀₀ (Møller 1952), replacing it by the square |$(\boldsymbol {\beta }(t) \cdot \boldsymbol {x})^2$|⁠. The effect of this remaining term in the geodesic equation must be neglected at leading order if we assume the acceleration happens on cosmic time-scales |$|\boldsymbol {\beta }| \sim H_0 v$|⁠. While a detailed calculation of the boost for the perturbed FLRW metric on all scales goes beyond the scope of this discussion, we may conclude that the choice of |$\boldsymbol {\beta }(t)$| can be used on small scales and after taking the Newtonian limit to transform from one class of inertial frame to another, and in general, it allows for the description of the same physics from an accelerated frame. Therefore, setting |$\boldsymbol {\beta }(t) = 0$| (together with the assumptions in the next section) has the interpretation of selecting one of all the mutually accelerated classes of inertial frames compatible with homogeneity as our coordinate system.

It is worth pointing out a difference between the Newtonian and GR cosmology. Unlike in the Newtonian cosmology developed in Heckmann & Schücking (1956), the mathematically explicit homogeneity of the Newtonian cosmology obtained here from GR does not rely on the engineered boundary conditions (101), but emerges naturally from the field equations.

4.4 Boundary conditions and constraints on general-relativistic effects on the dynamics

In Section 2, we have argued that on the level of the field equations, which are local in real space, terms non-linear in the metric perturbations are subleading¹⁵ for late-time cosmology with relative corrections of only |$\mathcal {O}(v^2)$|⁠. We have shown that the remaining Newtonian limit is fully consistent and compatible with non-linear behaviour of matter, that is, density contrasts δ ≫ 1. That this picture carries over to the solutions received support from the explicit example considered in Section 3. In more general settings, in the solution, due to its integral nature, small non-linear terms in the differential equations may accumulate and grow to become large on very large scales, if they are coherent. However, due to the suppression of the non-linear source terms by v² with respect to the matter density, this growth is equally suppressed by a factor of v² compared to the growth of the unregularized Newtonian potential equation (100), and thus bounded by

$$\begin{eqnarray*} \phi _{\mathrm{ nl}} \lesssim v^2 G_\mathrm{ N} \rho _\mathrm{ b} r^2 \sim v^2 H_0^2 r^2. \end{eqnarray*}$$

(103)

On horizon scales, the scalar perturbations of the FLRW metric could thus be modified by a term of a size of up to v², comparable in magnitude to the regularized potentials. However, due to the large-scale growth, the implied force modification |$|\nabla \phi _{\mathrm{ nl}}|_{r=H_0^{-1}} \sim H_0 v^2$| is still suppressed by a factor of v with respect to local forces (|∇Φ| ∼ H₀v) and, more importantly, by a factor of v² with respect to the coherent Friedmann forces relating to the expansion [the first and the other terms in the geodesic equation (37), respectively]. Thus, even in this coherent case, this is not sufficient to explain the order-unity effect of the cosmological constant on the Friedmann dynamics at horizon scale. We conclude that the non-linear terms of the Einstein equations may really be dropped in a first-order analysis at least in a finite region of horizon size or smaller.

We can further develop the discussion of possible effects from GR on the dynamics, under the assumption that gravitational waves can be neglected. Restricted to small scales, we will see that the assumption of a perturbed FLRW metric is weak enough and that we can understand the effects of cosmological solutions beyond an FLRW background despite the formal use of this metric. Specifically, we ask the questions if, first, it is possible within the approach under consideration that ignorance of the ‘right’ global background solution could lead to an order-unity effect on the matter motion on scales large enough to have cosmological applications, and, secondly, if this effect could look like cosmic acceleration. We will find that the answers are yes and no, respectively.

It is important to be mathematically slightly more precise in the rest of this section. To obtain a well-posed Dirichlet problem from the Poisson equation (9) or its Newtonian analogue (33), we must prescribe boundary conditions. We can define a boundary of a finite-sized (but large) patch of the universe under consideration and prescribe the potential on it. At first, we may ignore the gravitational effects caused by matter outside a spherical patch and set the source to zero there; note first that in the homogeneous case the Newtonian forces from each outer spherical shell cancel exactly. In the inhomogeneous Newtonian setting, the shearing caused by structures beyond ∼1 Mpc, which affects only non-spherical objects, has been estimated in Dominguez & Gaite (2001) to be negligibly small.

Next, as an alternative to setting boundary conditions, we can specify a Green’s function that, convolved with the source, yields a unique solution for the potential, defining it also on the boundary. For Newtonian gravity, we would like this Green’s function to be

$$\begin{eqnarray*} G(\boldsymbol {x},\boldsymbol {x}^{\prime }) = - \frac{1}{4 \pi } \frac{1}{|\boldsymbol {x} - \boldsymbol {x^{\prime }} |}, \end{eqnarray*}$$

(104)

since taking the gradient of the convolution shows that this corresponds to applying Newton’s force law in the chosen patch.¹⁶

The effect of any different Green’s function (or boundary condition) is that of adding to the solution another homogeneous solution of the Poisson equation, i.e. a harmonic function. Among these are linear functions (planes). These have been fixed already in the previous section (e.g. to ensure that the centre of the spherical patch, where the potential gradient vanishes in the homogeneous setting, is the coordinate origin). The non-linear harmonic functions, on the other hand, have non-trivial gradients. For example, the small effect of the matter inhomogeneities outside the spherical patch could be reintroduced by a small deformation of the Green’s function. Furthermore, effects from the boundary at infinity¹⁷ in Newtonian cosmology or, as we will see below, from non-FLRW background solutions in GR are encoded in boundary conditions. Similarly, if the non-linear terms of GR were to conspire to give an effect at very large scales, this would have to appear as non-trivial boundary conditions of our patch.

In the complete theory of GR a choice of boundary conditions on a surface surrounding the region of interest is not required; providing initial data are enough.¹⁸ However, after taking the Newtonian limit, we have lost the information of the evolution of the boundaries. Thus, while the Green’s function is actually determined and cannot just be chosen to be equation (104), we are ignorant of it, also because we do not want to control the initial state in our approach on very large scales, preferring to restrict linearization to a subhorizon patch. Therefore, we simply consider the possibility of generic boundary conditions which can even be time-dependent. The only constraint we put on them is that they cause effects that are at most of order unity, that is, they cause additional forces comparable to the Newtonian forces, since even stronger effects are certainly not observed. Equivalently, we are allowed to add additional harmonic functions ϕ_h to the potential that have gradients comparable to those of the Newtonian potential obtained with equation (104).

It follows that these functions ϕ_h do not grow arbitrarily fast. Since we want |$| \nabla \phi _\mathrm{ h} | \lesssim H_0 v + H_0^2 r$| [again corresponding to the local forces and the Friedmann forces, respectively, equation (37)], they reach at most |$\mathcal {O}(1)$| at the horizon scale. Upon subtraction of an irrelevant constant, we therefore have ϕ_h ∼ v² on subhorizon scales ≲ v/H₀. This scale is already cosmological in the sense that the average matter density in a region of this size can be comparable to that of the cosmological constant, and the latter therefore effective in causing an accelerated Friedmann evolution of the patch. The approximations of Section 2 still hold. Furthermore, the choice of scale factor is irrelevant on this scale as discussed in Section 2.3 (cf. Section 4.1); in particular a = 1 is allowed, corresponding to an expansion around Minkowski space–time.¹⁹ It is clear that there is no additional input from the fact that the starting point was a perturbed FLRW metric. The situation is instead that locally a given metric, in fact general up to neglecting tensor modes and smallness of vector modes, satisfies Einstein’s equations for a given source to some required accuracy under the assumptions of Section 2, and uniqueness of the solution for given initial conditions implies that we are considering the right solution if the initial conditions are satisfied. Since we have encoded the non-trivial initial conditions in the scalar sector into the boundary conditions, which are still free, we are facing the general set of all relevant scalar sector solutions of GR for the local cosmological patch with a given dust source. In particular, as mentioned, there is no assumptions on isotropy at this point (within the limits of order-unity effects). As another example, locally, curvature of spatial slices can be realized perturbatively, as is clear from the example in Section 3, where the coordinate transformation between the curved FLRW metric for the collapsing core and the flat FLRW metric description was given. We conclude that on cosmological but subhorizon scales, the perturbed FLRW metric is a fully general ansatz for the relevant physics that does not imply a choice of background. On the other hand, we cannot trivially extend such a local treatment to horizon scales, because ϕ_h can become non-perturbative, just like Φ and Ψ − Φ for the wrong choice of metric scale factor. We have thus made the assumption of an FLRW background earlier when claiming that can Ψ and Φ remain small on large scales, making an implicit statement on their boundary conditions.

Despite the generality of the free boundary conditions, they cannot cause radial forces like the cosmic forces, including the accelerating one caused by a cosmological constant. To see this, note that the gradients of the harmonic functions ϕ_h are necessarily divergence-free. Therefore, by Gauss’ theorem, their flux through any closed surface must vanish, which is impossible for a radial force field. The gradients instead correspond to anisotropic (multipole) forces causing tidal shear. As mentioned above, the shear due to the inhomogeneity of the matter outside the patch is normally negligible in our universe (Dominguez & Gaite 2001). However, one can conceive cosmological models that are not based on an isotropic and homogeneous FLRW background. These effects can be modelled locally by non-linear harmonic functions ϕ_h since we have seen that this is the only remaining degree of freedom. It is interesting to note that these functions are in one-to-one correspondence with the different solutions of Heckmann–Schücking Newtonian cosmology selected by different boundary conditions (101) because those boundary conditions are precisely such that the solution to the Poisson equation is unique up to the addition of planes (Heckmann & Schücking 1956) and therefore they precisely fix the non-linear functions ϕ_h. Consequently, these general anisotropic Newtonian models, as well as their exact relativistic counterparts with non-trivial electric part of the Weyl tensor (Ellis 2009) in the Newtonian limit, admit a perturbed FLRW description by using some Green’s function different from equation (104) on subhorizon scales.

Conversely, if anisotropies are sufficiently constrained (which seems natural given the observed isotropy of the CMB), there cannot be large boundary conditions that break our perturbative treatment. The relevant solutions of GR are then restricted to be close to the FLRW type even on larger scales. We reserve a quantitative version of this argument for future work.

For a much more rigorous and more general discussion of backreaction, see Ishibashi & Wald (2005), and Green & Wald (2011, 2013, 2014).

5 SUMMARY AND CONCLUSION

We have justified and analysed the Newtonian limit of late-time GR cosmology with a perturbed FLRW ansatz including scalar and vector modes, following an approach in real space and implementing assumptions on the matter structures and motion based on observations. The vector mode of the metric can be used to absorb the transverse component of the time-space components of the energy-momentum tensor and does not enter elsewhere to leading order. The dynamics of CDM is Newtonian to leading order, which was discussed mostly assuming flatness and isotropy, although generalizations have been pointed out. The scale factor in the metric, or equivalently the spatial curvature at some instance, is a gauge choice on subhorizon scales and always drops out of the dynamical equations when they are formulated in a Newtonian frame. GR does not select the inertial frame; selecting it is another gauge choice. This can be understood as a consequence of the cosmological principle encoded in the FLRW geometry, and its implementation into Newtonian cosmology has previously been achieved in the Heckmann–Schücking formulation of the boundary conditions.

On large scales comparable or beyond the Hubble scale, given natural assumptions, the Newtonian limit works, but the scale factor appearing in the metric must be chosen to be close enough to the standard one compatible with the Friedmann equations with the right spatial curvature. In Fourier space, on horizon scales, one finds general-relativistic corrections which however correspond to Newtonian cosmology in changed variables (Green & Wald 2012). Since we work in real space to define accuracy, we are not concerned with these terms in this work.

Restricting to small vector perturbations and ignoring gravitational waves, GR does not allow for other dust cosmologies than those of Heckmann and Schücking (1956) on subhorizon scales. Therefore, comparing observations of structure on these scales to predictions derived with the perturbed FLRW metric are actually general if, in case it is of interest, anisotropic boundary conditions are allowed.

Consequently, measuring the cosmological dynamics on subhorizon scales can directly probe and disentangle the existence and nature of dark energy versus relativistic dynamical effects (encoded in boundary conditions). For example, one may study properties of galaxy clusters like the turnaround radius, see Hansen et al. (2019), and references therein. Less directly, one may restrict comparing clustering data to predictions based on the perturbed FLRW approach with various kinds of dark energy to subhorizon scales to restore model independence. On the other hand, supernova measurements of the expansion history have to extend to large distances of redshifts z ∼ 1 to make the effects of dark energy on the cosmological background dynamics visible, by going sufficiently far into the past on the light-cone instead of on particle trajectories, exceeding the subhorizon regime. On these larger scales, a more advanced treatment including GR cosmologies beyond FLRW backgrounds would be required to make the most of the data in particular if GR supports cosmologies that are both relevant for our universe and not simple large-scale extensions of the Heckmann–Schücking Newtonian cosmologies, such that new radial forces can emerge on large scales. However, this seems difficult to achieve without simultaneously violating observed isotropy already on smaller scales.

Furthermore, we fully agree with the Newtonian picture in Kaiser (2017) on the distinction of volume expansion and a scale factor that is a gauge freedom, and share the critique of the N-body simulation carried out in Rácz et al. (2017), where the two concepts were mixed, and the metric scale factor was locally adjusted to the expansion rate. We have shown that changing the metric scale factor in a patch must be accompanied by a change of metric curvature according to Einstein’s equations, and this in fact ensures that the Newtonian limit, which holds to leading order, is unchanged. Failing to do so simulates not relativistic physics beyond an FLRW background, but another theory than GR.

We conclude that the perturbed FLRW ansatz provides a consistent physical picture. It works as well as one could possibly hope for for the embedded top-hat model we have studied, for which the exact solution is known. From this analysis, there are no concerns for using the perturbed FLRW metric to simultaneously describe cosmology and much smaller scales like the Solar system.

The equations of motion for matter can be generalized e.g. to include frame dragging from the vector mode. In Castiblanco et al. (2019), the authors claim that the relativistic dynamical corrections beyond the Newtonian limit can have a very significant effect on the squeezed bispectrum due to the combination of different scales, at least when evaluated in perturbation theory. If confirmed by non-perturbative numerical studies, this would limit the success of Newtonian cosmology (amended with relativistic light propagation) in the perturbed FLRW metric (1) for late-time large scale structure.

ACKNOWLEDGEMENTS

I thank Michele Maggiore, Pierre Fleury, and Enis Belgacem for many crucial discussions and encouraging support and Pierre Fleury for a careful reading of the manuscript and insightful comments. Ruth Durrer, Steen Hansen, Nick Kaiser, David F. Mota, and Clément Stahl, as well as the anonymous referee, have also provided well-appreciated feedback on various aspects of this work. My work is supported by the Fonds National Suisse and the SwissMAP National Center of Competence in Research.

Footnotes

1

It should be noted at this point that seemingly circular reasoning like this is not problematic when solving differential equations as long as the final solution is self-consistent and satisfies all required boundary conditions under some assumptions ensuring uniqueness of the solution. (We also assume that an exact solution is obtainable continuously from minute deformations of the approximate result.) Instead of circular reasoning, this approach may be seen as an educated guess of a solution. There are however subtleties: besides not discussing tensor perturbations here, boundary conditions, required for uniqueness, will be addressed below. For now, we are still in the process of checking self-consistency.

2

It is also easy to miss these terms when working in Fourier space.

3

It appears that in this form the vector modes of FLRW were already discussed in Thomas, Bruni & Wands (2015).

4

The original interior Oppenheimer–Snyder solution (Oppenheimer & Snyder 1939) is actually equal to a patch of time-reversed flat EdS which does not allow for a turnaround.

5

A reader familiar with the LTB solutions may think that the embedded top-hat collapse should be a special case. Indeed, LTB solutions exactly describe more general inhomogeneous dust distributions with spherical symmetry. However, a single LTB metric is not able to cover the space–time considered with one set of coordinates. The gauge (g_tt = −1, diagonal) is too constraining for each region so that one inherits the discontinuities from the discontinuous source.

6

To be clear, again the word ‘comoving’ refers only to the use of FLRW coordinates with some scale factor of the metric (1) factored out from the physical spatial coordinates. Comoving coordinates in this sense do not guarantee vanishing or small peculiar velocities, because the scale factor may not be related to the physical motion of matter.

7

Conservation of mass is implied by the continuity equation (30). The flat-space expression for the volume of the ball follows only to leading order. Metric perturbations and perturbations of T₀₀ and of the time coordinate that would change the spatial slicing due to coordinate transformations relevant in the present work can be neglected at the required order, because the mass only enters into small terms that are themselves perturbative.

8

The energy conservation employed here is the first integral of the Newtonian form of the geodesics (38).

9

One may also check that the continuity equation preserves homogeneity of the density under the linear radial velocity profiles that the law r(t) = b(t)r₀ implies at an initial time, which in turn are preserved by the gravitational force of a homogeneous ball. Of course, this is unstable: gravitation amplifies small inhomogeneities. A real top-hat disintegrates into shocks; the present model is a smoothed idealization.

10

Note that t₀ may be chosen to be e.g. in the past and therefore H₀ may not mean the Hubble parameter today.

11

One can recycle the previous result for ϕ in equations (47)–(49). Compared to equation (46), at fixed time, the values of the source ρ = T₀₀ are the same in each region to leading order. One may rescale the terms quadratic in x by c²/b² and correct for the different Hubble rates by adding |$c^2(H_\mathrm{ b}^2- H_\mathrm{ c}^2) x^2/4$|⁠. For the matching, the latter difference can be ignored because it affects all regions in the same way. Then, at the two boundaries expressed in the new coordinates, the new potential evaluates to the same numerical value as before. The new homogeneous solutions required for matching properly at the (new) boundaries thus need to be numerically unchanged at the boundaries as well. Therefore the constants are unchanged (but we write x_*(t) → cr₀/b, its previous definition, to not confuse it with the new x_* = r₀), and the term ∝ 1/x in the middle region picks up a factor of b/c, since x at the boundary is rescaled by the same factor.

12

Of course in different coordinates like comoving space and supercomoving time, employed for numerical reasons, the physics may be less obvious.

13

Indeed, the energy-momentum tensor of McVittie’s solution shows that besides the central delta function there is a homogeneous cosmic fluid everywhere.

14

We do not specify any boundary conditions for Ψ. Here we assume Φ to be any fixed solution of equation (9), the boundary conditions of which we discuss below.

15

Of course, throughout, we assume that a perturbative treatment is valid, where the size of the non-linear terms is estimated using properties of the linear solution.

16

This Green’s function generates the isotropic Friedmann expansion in the homogeneous case. This is not happening for a non-spherical patch choice, but in this case we cannot expect the force from outside the patch to be negligible unless the total matter distribution is either finite and aspherical or the infinite limit of such a set-up, to be discussed below.

17

For example, one can consider the infinite limit of a aspherical, e.g. elliptical, matter distribution (Bertschinger 1995).

18

Beyond the Newtonian approximation, which is based on elliptic constraint equations, the boundary conditions are not a free choice but fixed by the initial state and the dynamics of GR. To illustrate causality, consider GR linearized around Minkowski spacetime (Maggiore 2008), g_μν = η_μν + h_μν with |$\bar{h}_{\mu \nu } = h_{\mu \nu } - \eta _{\mu \nu } h /2$| : in Lorenz gauge (which is exhibiting causality more explicitly) |$\partial _\mu \bar{h}_{\mu \nu } = 0$| one has |$\Box \bar{h}_{\mu \nu } = - 16 \pi G_\mathrm{ N} T_{\mu \nu }$| and therefore

$$\begin{eqnarray*} -\frac{1}{4} \bar{h}_{00} = -G_N \int d^3x^{\prime } \frac{T_{00}(t - |\boldsymbol{x} - \boldsymbol{x^{\prime }} |, \boldsymbol{x^{\prime }})}{|\boldsymbol{x} - \boldsymbol{x^{\prime }} |} \end{eqnarray*}$$

(105)

where the retarded Green’s function has been selected to causally propagate the initial state to the future. When the retardation and the other components of the source are neglected, equation (105) becomes the Newtonian potential obtained using the Green’s function (104)

$$\begin{eqnarray*} -\frac{1}{4} \bar{h}_{00} = -\frac{1}{2} h_{00} = -\frac{1}{2} h_{\mathrm{ i i}} = -G_\mathrm{ N} \int \mathrm{ d}^3x^{\prime } \frac{T_{00}(t, \boldsymbol{x^{\prime }})}{|\boldsymbol{x} - \boldsymbol{x^{\prime }} |} \end{eqnarray*}$$

(106)

$$\begin{eqnarray*} = 4 \pi G_\mathrm{ N} \int \mathrm{ d}^3x^{\prime } G(\boldsymbol {x}, \boldsymbol {x^{\prime }}) T_{00}(t, \boldsymbol {x^{\prime }}) \end{eqnarray*}$$

(107)

of the Laplacian, which fixes the value of the potential on any boundary. Similarly, in a standard global approach to cosmology, the boundary conditions in the Newtonian approximation are at least in principle fixed from GR assuming (almost) homogeneous FLRW at early times.

19

Note that for this case, and for Λ = 0, the usual Ψ = Φ follows from equation (18), with a = 1 corresponding to the solution of the second-order Friedmann equation (22) for H_a(t₀) = 0.

REFERENCES

Adamek

J.

,

Daverio

D.

,

Durrer

R.

,

Kunz

M.

,

2013

,

Phys. Rev. D

,

88

,

103527

10.1103/PhysRevD.88.103527

Crossref

Search ADS

Adamek

J.

,

Daverio

D.

,

Durrer

R.

,

Kunz

M.

,

2016

,

Nat. Phys.

,

12

,

346

10.1038/nphys3673

Crossref

Search ADS

Aghanim

N.

et al. .,

2018

,

preprint (arXiv:1807.06209)

Balbinot

R.

,

Bergamini

R.

,

Comastri

A.

,

1988

,

Phys. Rev. D

,

38

,

2415

10.1103/PhysRevD.38.2415

Crossref

Search ADS

Baumann

D.

,

Nicolis

A.

,

Senatore

L.

,

Zaldarriaga

M.

,

2012

,

J. Cosmol. Astropart. Phys.

,

2012

,

051

Crossref

Search ADS

Belgacem

E.

,

Finke

A.

,

Frassino

A.

,

Maggiore

M.

,

2019

,

J. Cosmol. Astropart. Phys.

,

2019

,

035

Crossref

Search ADS

Bertschinger

E.

,

1995

,

preprint (astro-ph/9503125)

Bonnor

W.

,

1996

,

MNRAS

,

282

,

1467

10.1093/mnras/282.4.1467

Crossref

Search ADS

Bonnor

W. B.

,

1999

,

Class. Quantum Gravity

,

16

,

1313

10.1088/0264-9381/16/4/020

Crossref

Search ADS

Buchert

T.

,

2017

,

MNRAS

,

473

,

L46

10.1093/mnrasl/slx160

Crossref

Search ADS

Buchert

T.

,

Räsänen

S.

,

2012

,

Annu. Rev. Nucl. Part. Sci.

,

62

,

57

10.1146/annurev.nucl.012809.104435

Crossref

Search ADS

Carrera

M.

,

Giulini

D.

,

2010

,

Rev. Mod. Phys.

,

82

,

169

10.1103/RevModPhys.82.169

Crossref

Search ADS

Castiblanco

L.

,

Gannouji

R.

,

Noreña

J.

,

Stahl

C.

,

2019

,

J. Cosmol. Astropart. Phys.

,

2019

,

030

Crossref

Search ADS

Cooperstock

F. I.

,

Faraoni

V.

,

Vollick

D. N.

,

1998

,

ApJ

,

503

,

61

10.1086/305956

Crossref

Search ADS

Dai

L.

,

Pajer

E.

,

Schmidt

F.

,

2015

,

J. Cosmol. Astropart. Phys.

,

2015

,

059

Crossref

Search ADS

Dicke

R. H.

,

Peebles

P. J. E.

,

1964

,

Phys. Rev. Lett.

,

12

,

435

10.1103/PhysRevLett.12.435

Crossref

Search ADS

Dominguez

A.

,

Gaite

J.

,

2001

,

EPL (Europhys. Lett.)

,

55

,

458

10.1209/epl/i2001-00437-y

Crossref

Search ADS

Durrer

R.

,

2008

,

The Cosmic Microwave Background, by Ruth Durrer. ISBN 978-0-521-84704-9 (HB)

.

Published by Cambridge University Press

,

Cambridge, UK

Ehlers

J.

,

Sachs

R.

,

1969

, in

Chretien

M.

,

Deser

S.

,

Goldstein

J.

, eds,

Brandeis University Summer Institute In Theoretical Physics 1968, Astrophysics and General Relativity, Vol. 2

.

Gordon and Breach Science Publishers

,

New York

, p.

331

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Einstein

A.

,

Straus

E.

,

1946

,

Rev. Mod. Phys.

,

18

,

148

10.1103/RevModPhys.18.148

Crossref

Search ADS

Einstein

A.

,

Straus

E. G.

,

1945

,

Rev. Mod. Phys.

,

17

,

120

10.1103/RevModPhys.17.120

Crossref

Search ADS

Ellis

G. F.

,

2009

,

Gen. Relativ. Gravit.

,

41

,

581

10.1007/s10714-009-0760-7

Crossref

Search ADS

Falco

M.

,

Mamon

G. A.

,

Wojtak

R.

,

Hansen

S. H.

,

Gottlöber

S.

,

2013

,

MNRAS

,

436

,

2639

10.1093/mnras/stt1768

Crossref

Search ADS

Faraoni

V.

,

Jacques

A.

,

2007

,

Phys. Rev. D

,

76

,

063510

10.1103/PhysRevD.76.063510

Crossref

Search ADS

Fidler

C.

,

Tram

T.

,

Rampf

C.

,

Crittenden

R.

,

Koyama

K.

,

Wands

D.

,

2017

,

J. Cosmol. Astropart. Phys.

,

2017

,

022

Crossref

Search ADS

Fienga

A.

,

Laskar

J.

,

Exertier

P.

,

Manche

H.

,

Gastineau

M.

,

2015

,

Celest. Mech. Dyn. Astron.

,

123

,

325

10.1007/s10569-015-9639-y

Crossref

Search ADS

Goldberg

S. R.

,

Clifton

T.

,

Malik

K. A.

,

2017

,

Phys. Rev. D

,

95

,

043503

10.1103/PhysRevD.95.043503

Crossref

Search ADS

Green

S. R.

,

Wald

R. M.

,

2011

,

Phys. Rev. D

,

83

,

084020

10.1103/PhysRevD.83.084020

Crossref

Search ADS

Green

S. R.

,

Wald

R. M.

,

2012

,

Phys. Rev. D

,

85

,

063512

10.1103/PhysRevD.85.063512

Crossref

Search ADS

Green

S. R.

,

Wald

R. M.

,

2013

,

Phys. Rev. D

,

87

,

124037

10.1103/PhysRevD.87.124037

Crossref

Search ADS

Green

S. R.

,

Wald

R. M.

,

2014

,

Class. Quantum Gravity

,

31

,

234003

10.1088/0264-9381/31/23/234003

Crossref

Search ADS

Hansen

S. H.

,

Hassani

F.

,

Lombriser

L.

,

Kunz

M.

,

2019

;

Harrison

E.

,

1967

,

Rev. Mod. Phys.

,

39

,

862

10.1103/RevModPhys.39.862

Crossref

Search ADS

Heckmann

O.

,

Schücking

E.

,

1955

,

Z. Astrophys.

,

38

,

95

Heckmann

O.

,

Schücking

E.

,

1956

,

Z. Astrophys.

,

40

,

81

Hofmann

F.

,

Müller

J.

,

2018

,

Class. Quantum Gravity

,

35

,

035015

10.1088/1361-6382/aa8f7a

Crossref

Search ADS

Holz

D. E.

,

Wald

R. M.

,

1998

,

Phys. Rev. D

,

58

,

063501

10.1103/PhysRevD.58.063501

Crossref

Search ADS

Ishibashi

A.

,

Wald

R. M.

,

2005

,

Class. Quantum Gravity

,

23

,

235

10.1088/0264-9381/23/1/012

Crossref

Search ADS

Jelic-Cizmek

G.

,

Lepori

F.

,

Adamek

J.

,

Durrer

R.

,

2018

,

J. Cosmol. Astropart. Phys.

,

2018

,

006

Crossref

Search ADS

Kaiser

N.

,

2017

,

MNRAS

,

469

,

744

10.1093/mnras/stx907

Crossref

Kim

D. Y.

,

Lasenby

A. N.

,

Hobson

M. P.

,

2018

,

Gen. Relativ. Gravit.

,

50

,

29

Crossref

Search ADS

Kolb

E. W.

,

Marra

V.

,

Matarrese

S.

,

2010

,

Gen. Relativ. Gravit.

,

42

,

1399

10.1007/s10714-009-0913-8

Crossref

Search ADS

Laarakkers

W. G.

,

Poisson

E.

,

2001

,

Phys. Rev. D

,

64

,

084008

10.1103/PhysRevD.64.084008

Crossref

Search ADS

Lahav

O.

,

Lilje

P. B.

,

Primack

J. R.

,

Rees

M. J.

,

1991

,

MNRAS

,

251

,

128

10.1093/mnras/251.1.128

Crossref

Search ADS

Maggiore

M.

,

2008

,

Gravitational Waves: Volume 1: Theory and Experiments

.

Oxford Univ. Press

,

Oxford

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Maggiore

M.

,

2018

,

Gravitational Waves: Volume 2: Astrophysics and Cosmology

,

Oxford Univ. Press

,

Oxford

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

McCrea

W.

,

1955

,

Math. Gaz.

,

39

,

287

Crossref

Search ADS

McVittie

G. C.

,

1933

,

MNRAS

,

93

,

325

10.1093/mnras/93.5.325

Crossref

Search ADS

Milillo

I.

,

Bertacca

D.

,

Bruni

M.

,

Maselli

A.

,

2015

,

Phys. Review D

,

92

,

023519

10.1103/PhysRevD.92.023519

Crossref

Search ADS

Misner

C. W.

,

Thorne

K. S.

,

Wheeler

J. A.

,

Kaiser

D. I.

,

2017

,

Gravitation

.

Princeton Univ. Press

,

Princeton, NJ

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Møller

C.

,

1952

,

The Theory of Relativity

.

Oxford Univ. Press

,

Oxford

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Nandra

R.

,

Lasenby

A. N.

,

Hobson

M. P.

,

2012a

,

MNRAS

,

422

,

2931

10.1111/j.1365-2966.2012.20618.x

Crossref

Search ADS

Nandra

R.

,

Lasenby

A. N.

,

Hobson

M. P.

,

2012b

,

MNRAS

,

422

,

2945

10.1111/j.1365-2966.2012.20617.x

Crossref

Search ADS

Noerdlinger

P. D.

,

Petrosian

V.

,

1971

,

ApJ

,

168

,

1

10.1086/151054

Crossref

Search ADS

Nottale

L.

,

1982

,

A&A

,

110

,

9

Oppenheimer

J. R.

,

Snyder

H.

,

1939

,

Phys. Rev.

,

56

,

455

10.1103/PhysRev.56.455

Crossref

Search ADS

Pavlidou

V.

,

Tetradis

N.

,

Tomaras

T.

,

2014

,

J. Cosmol. Astropart. Phys.

,

2014

,

017

Crossref

Search ADS

Peebles

P. J. E.

,

1980

,

The Large-Scale Structure of the Universe

.

Princeton Univ. Press

,

Princeton, NJ

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Pitjeva

E.

,

Pitjev

N.

,

2013

,

MNRAS

,

432

,

3431

10.1093/mnras/stt695

Crossref

Search ADS

Price

R. H.

,

Romano

J. D.

,

2012

,

Am. J. Phys.

,

80

,

376

10.1119/1.3699245

Crossref

Search ADS

Rácz

G.

,

Dobos

L.

,

Beck

R.

,

Szapudi

I.

,

Csabai

I.

,

2017

,

MNRAS

,

469

,

L1

10.1093/mnrasl/slx026

Crossref

Search ADS

Räsänen

S.

,

2010

,

Phys. Rev. D

,

81

,

103512

Crossref

Search ADS

Sanghai

V. A. A.

,

Clifton

T.

,

2015

,

Phys. Rev. D

,

91

,

103532

10.1103/PhysRevD.91.103532

Crossref

Search ADS

Schücking

E.

,

1954

,

Z. Phys.

,

137

,

595

Crossref

Search ADS

Thomas

D. B.

,

Bruni

M.

,

Wands

D.

,

2015

,

MNRAS

,

452

,

1727

10.1093/mnras/stv1390

Crossref

Search ADS

Van Acoleyen

K.

,

2008

,

J. Cosmol. Astropart. Phys.

,

2008

,

028

Crossref

Search ADS

Wiltshire

D. L.

,

2011

,

Class. Quantum Gravity

,

28

,

164006

10.1088/0264-9381/28/16/164006

Crossref

Search ADS

Yamamoto

K.

,

Marra

V.

,

Mukhanov

V.

,

Sasaki

M.

,

2016

,

J. Cosmol. Astropart. Phys.

,

2016

,

030

Crossref

Search ADS

APPENDIX A: NORMAL COORDINATES FOR EINSTEIN–DE SITTER SPACE–TIME

We can apply the methods developed above to the unperturbed FLRW metric. After going to r = a(t)x we have A = Hr, B = 1, and

$$\begin{eqnarray*} \mathrm{ d}s^2 = -(1-H^2 r^2) \mathrm{ d}t^2 - 2 H r \mathrm{ d}r \mathrm{ d}t + \mathrm{ d}r^2 + r^2 \mathrm{ d}\Omega ^2, \end{eqnarray*}$$

(A1)

which is exact. The most general exact diagonalizing transformation for the EDS case is now t′ = f(t, r) = F(9t^2/3/2 + r²t^−4/3); to get units of time we take F(x) = (2x/9)^3/2 such that t′ = t(1 + H²r²/2)^3/2. This of course again reduces to t′ = t + Hr²/2 in the subhorizon limit. In any case, g_rr → 1 + H²r²/(1 − H²r²) = 1/(1 − H²r²) . A short calculation gives g_tt → −((1 + H²r²/2)(1 − H²r²))⁻¹. Therefore

$$\begin{eqnarray*} \mathrm{ d}s^2 &=& -\displaystyle\frac{1}{(1+H^2r^2/2)(1-H^2 r^2)} \mathrm{ d}t^{\prime 2}\nonumber \\ && + \,\displaystyle\frac{1}{1-H^2 r^2} \mathrm{ d}r^2 \,\,+ r^2 \mathrm{ d}\Omega ^2. \end{eqnarray*}$$

(A2)

Note that the time t in H ∝ t⁻¹ has to be expressed via t′ and r from by solving the relation t′ = f(t, r) for t, and in terms of the new coordinates the metric appears very complicated. However, at the coordinate origin, the Christoffel symbols agree with those of flat space–time in spherical coordinates, since there are no linear corrections in r, and so the coordinates agree with Riemann normal coordinates for the central observer up to second order.

For a general FLRW metric (not necessarily matter-dominated) and this time approximating we still find f(r, t) = t + Hr²/2 + h(t), thus g_rr ≈ 1 + H²r². The time–time component becomes |$g_{\mathrm{ t}^{\prime }\mathrm{ t}^{\prime }} \approx -(1-H^2r^2)/(1+ \dot{H} r^2/2 + \dot{h})^2$|⁠. For h = 0, this is the weak-field de Sitter metric for |$\dot{H} = 0$|⁠; if on the other hand |$\dot{H} = -3 H^2 /2$| for EDS, g_tt ≈ (1 + H²r²/2) agrees with the weak-field limit of the previous exact result.

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Month:	Total Views:
November 2019	3
December 2019	18
January 2020	7
February 2020	9
March 2020	6
April 2020	5
May 2020	2
June 2020	3
August 2020	2
September 2020	1
November 2020	1
December 2020	1
January 2021	2
February 2021	3
March 2021	1
May 2021	2
June 2021	14
July 2021	1
September 2021	4
December 2021	3
February 2022	2
April 2022	3
July 2022	2
September 2022	2
November 2022	2
December 2022	2
January 2023	2
February 2023	7
March 2023	6
April 2023	6
May 2023	11
June 2023	11
July 2023	10
August 2023	7
September 2023	17
October 2023	5
November 2023	5
December 2023	12
January 2024	4
February 2024	1
March 2024	15
April 2024	10
May 2024	20
June 2024	18
July 2024	8
August 2024	17
September 2024	6
October 2024	18
November 2024	10
December 2024	9
January 2025	5
February 2025	11
March 2025	13
April 2025	11
May 2025	6

Article Contents

The perturbed FLRW metric on all scales: Newtonian limit and top-hat collapse

ABSTRACT

1 INTRODUCTION

2 NEWTONIAN LIMIT

2.1 Weak-field, slow-motion expansion scheme

2.2 Field equations

2.3 Friedmann equations as a gauge choice

2.4 Motion of matter

3 EMBEDDED TOP-HAT COLLAPSE

3.1 Newtonian top-hat collapse

3.2 Cosmological scale factor

3.2.1 External region x ≥ x₀

3.2.2 Vacuum region x_*(t) < x < x₀

3.2.3 Interior region x ≤ x_*(t)

3.3 Collapsing scale factor

3.3.1 External region x ≥ x₀(t)

3.3.2 Vacuum region r₀ ≤ x ≤ x₀(t)

3.3.3 Interior region x ≤ r₀

4 DISCUSSION

4.1 Emergence of Friedmann scale factor

4.2 Cosmic expansion force acting on local systems?

4.3 Newtonian inertial frames in cosmology

4.4 Boundary conditions and constraints on general-relativistic effects on the dynamics

5 SUMMARY AND CONCLUSION

ACKNOWLEDGEMENTS

Footnotes

REFERENCES

APPENDIX A: NORMAL COORDINATES FOR EINSTEIN–DE SITTER SPACE–TIME

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

The perturbed FLRW metric on all scales: Newtonian limit and top-hat collapse Free

ABSTRACT

1 INTRODUCTION

2 NEWTONIAN LIMIT

2.1 Weak-field, slow-motion expansion scheme

2.2 Field equations

2.3 Friedmann equations as a gauge choice

2.4 Motion of matter

3 EMBEDDED TOP-HAT COLLAPSE

3.1 Newtonian top-hat collapse

3.2 Cosmological scale factor

3.2.1 External region x ≥ x0

3.2.2 Vacuum region x*(t) < x < x0

3.2.3 Interior region x ≤ x*(t)

3.3 Collapsing scale factor

3.3.1 External region x ≥ x0(t)

3.3.2 Vacuum region r0 ≤ x ≤ x0(t)

3.3.3 Interior region x ≤ r0

4 DISCUSSION

4.1 Emergence of Friedmann scale factor

4.2 Cosmic expansion force acting on local systems?

4.3 Newtonian inertial frames in cosmology

4.4 Boundary conditions and constraints on general-relativistic effects on the dynamics

5 SUMMARY AND CONCLUSION

ACKNOWLEDGEMENTS

Footnotes

REFERENCES

APPENDIX A: NORMAL COORDINATES FOR EINSTEIN–DE SITTER SPACE–TIME

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

The perturbed FLRW metric on all scales: Newtonian limit and top-hat collapse

3.2.1 External region x ≥ x₀

3.2.2 Vacuum region x_*(t) < x < x₀

3.2.3 Interior region x ≤ x_*(t)

3.3.1 External region x ≥ x₀(t)

3.3.2 Vacuum region r₀ ≤ x ≤ x₀(t)

3.3.3 Interior region x ≤ r₀