-
PDF
- Split View
-
Views
-
Cite
Cite
I García-Bernete, C Ramos Almeida, A Alonso-Herrero, M J Ward, J A Acosta-Pulido, M Pereira-Santaella, A Hernán-Caballero, A Asensio Ramos, O González-Martín, N A Levenson, S Mateos, F J Carrera, C Ricci, P Roche, I Marquez, C Packham, J Masegosa, L Fuller, Torus model properties of an ultra-hard X-ray selected sample of Seyfert galaxies, Monthly Notices of the Royal Astronomical Society, Volume 486, Issue 4, July 2019, Pages 4917–4935, https://doi.org/10.1093/mnras/stz1003
Close - Share Icon Share
ABSTRACT
We characterize for the first time the torus properties of an ultra-hard X-ray (14–195 keV) volume-limited (DL < 40 Mpc) sample of 24 Seyfert (Sy) galaxies (BCS40 sample). The sample was selected from the Swift/BAT nine-month catalogue. We use high angular resolution nuclear infrared (IR) photometry and N-band spectroscopy, the CLUMPY torus models and a Bayesian tool to characterize the properties of the nuclear dust. In the case of the Sy1s, we estimate the accretion disc contribution to the subarcsecond resolution nuclear IR SEDs (∼0.4 arcsec) which is, on average, 46 ± 28, 23 ± 13, and 11 ± 5 per cent in the J, H, and K bands, respectively. This indicates that the accretion disc templates that assume a steep fall for longer wavelengths than 1 |$\mu$|m might underestimate its contribution to the near-IR emission. Using both optical (broad versus narrow lines) and X-ray (unabsorbed versus absorbed) classifications, we compare the global posterior distribution of the torus model parameters. We confirm that Sy2s have larger values of the torus covering factor (CT ∼ 0.95) than Sy1s (CT ∼ 0.65) in our volume-limited Seyfert sample. These findings are independent of whether we use an optical or X-ray classification. We find that the torus covering factor remains essentially constant within the errors in our luminosity range and there is no clear dependence with the Eddington ratio. Finally, we find tentative evidence that even an ultra-hard X-ray selection is missing a significant fraction of highly absorbed type 2 sources with very high covering factor tori.
1 INTRODUCTION
Active galactic nuclei (AGNs) are powered by accretion of material onto supermassive black holes (SMBHs), which release energy in the form of radiation and/or mechanical outflows to the host galaxy interstellar medium. Although they comprise just a small fraction of the galaxies in the local Universe (∼10 per cent), AGNs are now considered to be a short but recurrent phase in the overall lifetime of galaxies. Accordingly, galaxies are observed as AGN during an active phase when their SMBHs are accreting material at a relatively high rate (e.g. Bennert et al. 2011). Several studies found a correlation between the SMBH and host galaxy bulge mass (e.g. Kormendy & Ho 2013 and references therein) which is interpreted as a sign of coevolution of AGNs and their host galaxies. However, the study of the AGN–host galaxy connection is difficult due to the very different spatial and temporal scales involved. Therefore, it is of great importance to investigate the innermost regions of AGN to better understand this connection (see Ramos Almeida & Ricci 2017 and references therein).
The key piece of the AGN unified model (Antonucci 1993) is a dusty molecular torus that obscures the central engines of type 2, and allows a direct view in the case of type 1 sources. This dusty torus absorbs part of the AGN radiation and reprocesses it to emerge in the infrared (IR).
To correctly separate the nuclear emission from the foreground galaxy emission and be able to characterize the properties of the nuclear obscurer the highest possible spatial resolution is required. Since Seyfert (Sy) galaxies are intermediate-luminosity AGNs, and, in general, are relatively nearby, they are one of the best astrophysical laboratories to study the inner regions of active galaxies.
The torus radius has been constrained to be compact (∼0.1–10 pc) in the mid-IR (MIR; ∼5–30 |$\mu$|m). For example, using MIR direct imaging, Packham et al. (2005b) and Radomski et al. (2008) found for Circinus and Centaurus A that the MIR size of the torus is less than ∼4 pc (diameter). The modelling of MIR interferometric data shows a relatively compact torus of r < 10 pc (e.g. Jaffe et al. 2004; Tristram et al. 2007, 2009; Burtscher et al. 2009, 2013; Raban et al. 2009; López-Gonzaga et al. 2016). Atacama Large Millimeter/submillimeter Array (ALMA) observations of the archetypal Seyfert 2 galaxy NGC 1068 have spatially resolved for the first time the submillimetre (sub-mm) counterpart of the putative torus (Gallimore et al. 2016; García-Burillo et al. 2016; Imanishi et al. 2018). This is a disc of ∼7–10 pc diameter. More recently, Alonso-Herrero et al. (2018) and Combes et al. (2019) have found even larger nuclear molecular discs for other Seyfert galaxies and low-luminosity AGNs. Thus, as theoretically predicted (e.g. Schartmann et al. 2008; Stalevski et al. 2012), the radii measured in the sub-mm for the dusty and molecular torus are found to be larger than those inferred from IR observations. Therefore, to constrain the properties of the warm dust, we still need to compare torus models to the observed SEDs.
Torus models can be broadly grouped in two categories: physical (e.g. Wada & Norman 2002; Schartmann et al. 2008; Wada 2012) and geometrical (ad hoc; e.g. Pier & Krolik 1992; Efstathiou & Rowan-Robinson 1995; Nenkova et al. 2008a,b; Hönig et al. 2010; Stalevski et al. 2012; Siebenmorgen, Heymann & Efstathiou 2015; Hönig & Kishimoto 2017). Some of the geometrical models also include a polar component in the MIR range (e.g. Hönig & Kishimoto 2017). However, this polar emission has been detected so far in 6 Seyfert galaxies of the 23 observed using IR interferometry (López-Gonzaga et al. 2016; Leftley et al. 2018) and therefore more observations are needed in order to study whether this is a common feature in AGNs. The physical models are more realistic since they include important processes, such as supernovae and AGN feedback. However, they require large computational times and therefore it is more difficult to compare with observations. On the other hand, geometrical torus models are more degenerate, but they can be easily compared with the observations, assuming various geometries and compositions of the dust (see Ramos Almeida & Ricci 2017 for a review).
Recent studies reported good fits to the nuclear IR SED of nearby AGNs assuming a clumpy distribution of dust surrounding the central engine (e.g. Mason et al. 2006, 2009; Nikutta, Elitzur & Lacy 2009; Ramos Almeida et al. 2009; hereafter RA09; Ramos Almeida et al. 2011; hereafter RA11; Hönig et al. 2010; Alonso-Herrero et al. 2011; hereafter AH11; Sales et al. 2011; Lira et al. 2013; García-Bernete et al. 2015; Ichikawa et al. 2015; Siebenmorgen et al. 2015; Fuller et al. 2016; Audibert et al. 2017; García-González et al. 2017). Although the torus properties of nearby Seyfert galaxies have been extensively studied in the literature, to date there have been no studies based on an ultra-hard X-ray (14–195 keV) selected sample of these galaxies using high angular resolution IR data.
In this work, we use the Nenkova et al. (2008a,b) clumpy torus models, known as CLUMPY, and the Bayesian tool BayesClumpy (Asensio Ramos & Ramos Almeida 2009, 2013) to fit the nuclear IR emission of an ultra-hard X-ray selected sample of Seyfert galaxies. Our aim is to study the torus properties that are driving the Seyfert-type classification, the difference in the dusty torus of the various Seyfert types and how they vary with the central engine properties.
The paper is organized as follows. Sections 2 and 3 describe the sample selection, the observations and data compilation, respectively. The nuclear IR SED construction and modelling are presented in Section 4. In Section 5, we compare the torus properties for the different Seyfert subgroups. Finally, in Section 6 we summarize the main conclusions of this work. Throughout this paper, we assumed a cosmology with H0 = 73 km s−1 Mpc−1, Ωm = 0.27, and ΩΛ = 0.73, and a velocity-field corrected using the Mould et al. (2000) model, which includes the influence of the Virgo cluster, the Great Attractor, and the Shapley supercluster.
2 SAMPLE SELECTION
The sample studied here consists of 24 Seyfert galaxies previously presented in García-Bernete et al. (2016; hereafter GB16). It was drawn from the Swift/BAT nine-month catalogue (Tueller et al. 2008). The ultra-hard 14–195 keV band of the parent sample is far less sensitive to the effects of obscuration than optical or softer X-ray wavelengths, making this AGN selection one of the least biased for NH < 1024 cm−2 to date (see e.g. Winter et al. 2009, 2010; Weaver et al. 2010; Ichikawa et al. 2012; Ricci et al. 2015; Ueda et al. 2015).
We selected all the Seyfert galaxies in the nine-month catalogue with luminosity distances DL < 40 Mpc. We used this distance limit to ensure a resolution element of ≤50 pc in the MIR, considering the average angular resolution of 8–10 m-class ground-based telescopes (∼0.3 arcsec at 10 |$\mu$|m). This constraint provides us with a sample of 24 local Seyfert galaxies (hereafter BCS40 sample; GB16) containing 8 Sy1 (Sy1, Sy1.2 and Sy1.5), 6 Sy1.8/1.9, and 10 Sy2 galaxies. This sample covers an AGN luminosity range log(L|${_{\textrm{int}}^{2-10\, \textrm{keV}}})\,{\sim }$| 40.5–43.4 erg s−1. See GB16 for further details on the sample selection. The properties of the BCS40 sample are shown in Table 1.
BCS40 sample. Right ascension (RA), declination (Dec.), Seyfert type and galaxy inclination (b/a) were taken from the NASA/IPAC Extragalactic Database (NED). |$\mathit{ A}_{V}^{for}$| corresponds to the foreground extinction due to the host galaxy. References: (a) Veilleux, Goodrich & Hill (1997); (b) Reynolds et al. (1997); (c) Alloin et al. (1981); (d) Storchi-Bergmann et al. (1999); (e) Ward et al. (1987b); (f) Ward & Morris (1984); (g) Contini & Viegas (1999); (h) Rodríguez-Ardila et al. (2017); (i) Lira et al. (1999); (j) Packham et al. (1996); (k) Marconi et al. (2000); (l) Goodrich, Veilleux & Hill (1994); (m) Halpern & Filippenko (1984); (n) Winge et al. (2000).
| Name . | RA . | Dec. . | DL . | Spatial . | Seyfert . | b/a . | Foreground . |
|---|---|---|---|---|---|---|---|
| . | (J2000) . | (J2000) . | (Mpc) . | scale . | type . | . | extinction (A|$_{V}^{for}$|) . |
| . | . | . | . | (pc arcsec−1) . | . | . | (mag) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . |
| ESO 005-G004 | 06h05m41.6s | −86d37m55s | 24.1 | 116 | 2.0 | 0.21 | – |
| MCG-05-23-016 | 09h47m40.1s | −30h56m55s | 35.8 | 171 | 2.0 | 0.45 | >6 (a) |
| MCG-06-30-015 | 13h35m53.7s | −34d17m44s | 26.8 | 128 | 1.2 | 0.60 | ∼1.8–3.0 (b) |
| NGC 1365 | 03h33m36.4s | −36d08m25s | 21.5 | 103 | 1.8 | 0.55 | <5 (c) |
| NGC 2110 | 05h52m11.4s | −07d27m22s | 32.4 | 155 | 2.0 | 0.76 | 5.0 (d) |
| NGC 2992 | 09h45m42.0s | −14d19m35s | 34.4 | 164 | 1.9 | 0.31 | 3.8 (e) |
| NGC 3081 | 09h59m29.5s | −22d49m35s | 34.5 | 164 | 2.0 | 0.76 | – |
| NGC 3227 | 10h23m30.6s | + 19d51m54s | 20.4 | 98 | 1.5 | 0.67 | 2.3 (e) |
| NGC 3783 | 11h39m01.7s | −37d44m19s | 36.4 | 173 | 1.2 | 0.89 | 0.8 (f) |
| NGC 4051 | 12h03m09.6s | + 44d31m53s | 12.9 | 62 | 1.2 | 0.75 | 1.0 (g) |
| NGC 4138 | 12h09m29.8s | + 43d41m07s | 17.7 | 85 | 1.9 | 0.65 | – |
| NGC 4151 | 12h10m32.6s | + 39d24m21s | 20.0 | 96 | 1.5 | 0.71 | 1.0 (e) |
| NGC 4388a | 12h25m46.7s | + 12d39m44s | 17.0 | 82 | 2.0 | 0.19 | 5.9 (h) |
| NGC 4395 | 12h25m48.8s | + 33d32m49s | 3.84 | 19 | 1.8 | 0.83 | 0.4 (i) |
| NGC 4945 | 13h05m27.5s | −49d28m06s | 4.36 | 21 | 2.0 | 0.19 | – |
| NGC 5128 (CenA) | 13h25m27.6s | −43d01m09s | 4.28 | 21 | 2.0 | 0.78 | ∼7–8 (j, k) |
| NGC 5506 | 14h13m14.9s | −03d12m27s | 30.1 | 144 | 1.9 | 0.24 | ≥11 (l) |
| NGC 6300 | 17h16m59.5s | −62d49m14s | 14.0 | 68 | 2.0 | 0.67 | – |
| NGC 6814 | 19h42n40.6s | −10d19m25s | 25.8 | 123 | 1.5 | 0.93 | – |
| NGC 7172 | 22h02m01.9s | −31d52m11s | 37.9 | 180 | 2.0 | 0.56 | – |
| NGC 7213 | 22h09m16.3s | −47d10m00s | 25.1 | 120 | 1.5 | 0.90 | 0.6 (m) |
| NGC 7314 | 22h35m46.2s | −26d03m02s | 20.9 | 100 | 1.9 | 0.46 | – |
| NGC 7582 | 23h18m23.5s | −42d22m14s | 22.1 | 106 | 2.0 | 0.42 | ∼8–13 (n) |
| UGC 6728 | 11h45m16.0s | + 79d40m53s | 32.1 | 153 | 1.2 | 0.63 | – |
| Name . | RA . | Dec. . | DL . | Spatial . | Seyfert . | b/a . | Foreground . |
|---|---|---|---|---|---|---|---|
| . | (J2000) . | (J2000) . | (Mpc) . | scale . | type . | . | extinction (A|$_{V}^{for}$|) . |
| . | . | . | . | (pc arcsec−1) . | . | . | (mag) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . |
| ESO 005-G004 | 06h05m41.6s | −86d37m55s | 24.1 | 116 | 2.0 | 0.21 | – |
| MCG-05-23-016 | 09h47m40.1s | −30h56m55s | 35.8 | 171 | 2.0 | 0.45 | >6 (a) |
| MCG-06-30-015 | 13h35m53.7s | −34d17m44s | 26.8 | 128 | 1.2 | 0.60 | ∼1.8–3.0 (b) |
| NGC 1365 | 03h33m36.4s | −36d08m25s | 21.5 | 103 | 1.8 | 0.55 | <5 (c) |
| NGC 2110 | 05h52m11.4s | −07d27m22s | 32.4 | 155 | 2.0 | 0.76 | 5.0 (d) |
| NGC 2992 | 09h45m42.0s | −14d19m35s | 34.4 | 164 | 1.9 | 0.31 | 3.8 (e) |
| NGC 3081 | 09h59m29.5s | −22d49m35s | 34.5 | 164 | 2.0 | 0.76 | – |
| NGC 3227 | 10h23m30.6s | + 19d51m54s | 20.4 | 98 | 1.5 | 0.67 | 2.3 (e) |
| NGC 3783 | 11h39m01.7s | −37d44m19s | 36.4 | 173 | 1.2 | 0.89 | 0.8 (f) |
| NGC 4051 | 12h03m09.6s | + 44d31m53s | 12.9 | 62 | 1.2 | 0.75 | 1.0 (g) |
| NGC 4138 | 12h09m29.8s | + 43d41m07s | 17.7 | 85 | 1.9 | 0.65 | – |
| NGC 4151 | 12h10m32.6s | + 39d24m21s | 20.0 | 96 | 1.5 | 0.71 | 1.0 (e) |
| NGC 4388a | 12h25m46.7s | + 12d39m44s | 17.0 | 82 | 2.0 | 0.19 | 5.9 (h) |
| NGC 4395 | 12h25m48.8s | + 33d32m49s | 3.84 | 19 | 1.8 | 0.83 | 0.4 (i) |
| NGC 4945 | 13h05m27.5s | −49d28m06s | 4.36 | 21 | 2.0 | 0.19 | – |
| NGC 5128 (CenA) | 13h25m27.6s | −43d01m09s | 4.28 | 21 | 2.0 | 0.78 | ∼7–8 (j, k) |
| NGC 5506 | 14h13m14.9s | −03d12m27s | 30.1 | 144 | 1.9 | 0.24 | ≥11 (l) |
| NGC 6300 | 17h16m59.5s | −62d49m14s | 14.0 | 68 | 2.0 | 0.67 | – |
| NGC 6814 | 19h42n40.6s | −10d19m25s | 25.8 | 123 | 1.5 | 0.93 | – |
| NGC 7172 | 22h02m01.9s | −31d52m11s | 37.9 | 180 | 2.0 | 0.56 | – |
| NGC 7213 | 22h09m16.3s | −47d10m00s | 25.1 | 120 | 1.5 | 0.90 | 0.6 (m) |
| NGC 7314 | 22h35m46.2s | −26d03m02s | 20.9 | 100 | 1.9 | 0.46 | – |
| NGC 7582 | 23h18m23.5s | −42d22m14s | 22.1 | 106 | 2.0 | 0.42 | ∼8–13 (n) |
| UGC 6728 | 11h45m16.0s | + 79d40m53s | 32.1 | 153 | 1.2 | 0.63 | – |
aThis galaxy is part of the Virgo Cluster (Binggeli, Sandage & Tammann 1985).
BCS40 sample. Right ascension (RA), declination (Dec.), Seyfert type and galaxy inclination (b/a) were taken from the NASA/IPAC Extragalactic Database (NED). |$\mathit{ A}_{V}^{for}$| corresponds to the foreground extinction due to the host galaxy. References: (a) Veilleux, Goodrich & Hill (1997); (b) Reynolds et al. (1997); (c) Alloin et al. (1981); (d) Storchi-Bergmann et al. (1999); (e) Ward et al. (1987b); (f) Ward & Morris (1984); (g) Contini & Viegas (1999); (h) Rodríguez-Ardila et al. (2017); (i) Lira et al. (1999); (j) Packham et al. (1996); (k) Marconi et al. (2000); (l) Goodrich, Veilleux & Hill (1994); (m) Halpern & Filippenko (1984); (n) Winge et al. (2000).
| Name . | RA . | Dec. . | DL . | Spatial . | Seyfert . | b/a . | Foreground . |
|---|---|---|---|---|---|---|---|
| . | (J2000) . | (J2000) . | (Mpc) . | scale . | type . | . | extinction (A|$_{V}^{for}$|) . |
| . | . | . | . | (pc arcsec−1) . | . | . | (mag) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . |
| ESO 005-G004 | 06h05m41.6s | −86d37m55s | 24.1 | 116 | 2.0 | 0.21 | – |
| MCG-05-23-016 | 09h47m40.1s | −30h56m55s | 35.8 | 171 | 2.0 | 0.45 | >6 (a) |
| MCG-06-30-015 | 13h35m53.7s | −34d17m44s | 26.8 | 128 | 1.2 | 0.60 | ∼1.8–3.0 (b) |
| NGC 1365 | 03h33m36.4s | −36d08m25s | 21.5 | 103 | 1.8 | 0.55 | <5 (c) |
| NGC 2110 | 05h52m11.4s | −07d27m22s | 32.4 | 155 | 2.0 | 0.76 | 5.0 (d) |
| NGC 2992 | 09h45m42.0s | −14d19m35s | 34.4 | 164 | 1.9 | 0.31 | 3.8 (e) |
| NGC 3081 | 09h59m29.5s | −22d49m35s | 34.5 | 164 | 2.0 | 0.76 | – |
| NGC 3227 | 10h23m30.6s | + 19d51m54s | 20.4 | 98 | 1.5 | 0.67 | 2.3 (e) |
| NGC 3783 | 11h39m01.7s | −37d44m19s | 36.4 | 173 | 1.2 | 0.89 | 0.8 (f) |
| NGC 4051 | 12h03m09.6s | + 44d31m53s | 12.9 | 62 | 1.2 | 0.75 | 1.0 (g) |
| NGC 4138 | 12h09m29.8s | + 43d41m07s | 17.7 | 85 | 1.9 | 0.65 | – |
| NGC 4151 | 12h10m32.6s | + 39d24m21s | 20.0 | 96 | 1.5 | 0.71 | 1.0 (e) |
| NGC 4388a | 12h25m46.7s | + 12d39m44s | 17.0 | 82 | 2.0 | 0.19 | 5.9 (h) |
| NGC 4395 | 12h25m48.8s | + 33d32m49s | 3.84 | 19 | 1.8 | 0.83 | 0.4 (i) |
| NGC 4945 | 13h05m27.5s | −49d28m06s | 4.36 | 21 | 2.0 | 0.19 | – |
| NGC 5128 (CenA) | 13h25m27.6s | −43d01m09s | 4.28 | 21 | 2.0 | 0.78 | ∼7–8 (j, k) |
| NGC 5506 | 14h13m14.9s | −03d12m27s | 30.1 | 144 | 1.9 | 0.24 | ≥11 (l) |
| NGC 6300 | 17h16m59.5s | −62d49m14s | 14.0 | 68 | 2.0 | 0.67 | – |
| NGC 6814 | 19h42n40.6s | −10d19m25s | 25.8 | 123 | 1.5 | 0.93 | – |
| NGC 7172 | 22h02m01.9s | −31d52m11s | 37.9 | 180 | 2.0 | 0.56 | – |
| NGC 7213 | 22h09m16.3s | −47d10m00s | 25.1 | 120 | 1.5 | 0.90 | 0.6 (m) |
| NGC 7314 | 22h35m46.2s | −26d03m02s | 20.9 | 100 | 1.9 | 0.46 | – |
| NGC 7582 | 23h18m23.5s | −42d22m14s | 22.1 | 106 | 2.0 | 0.42 | ∼8–13 (n) |
| UGC 6728 | 11h45m16.0s | + 79d40m53s | 32.1 | 153 | 1.2 | 0.63 | – |
| Name . | RA . | Dec. . | DL . | Spatial . | Seyfert . | b/a . | Foreground . |
|---|---|---|---|---|---|---|---|
| . | (J2000) . | (J2000) . | (Mpc) . | scale . | type . | . | extinction (A|$_{V}^{for}$|) . |
| . | . | . | . | (pc arcsec−1) . | . | . | (mag) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . |
| ESO 005-G004 | 06h05m41.6s | −86d37m55s | 24.1 | 116 | 2.0 | 0.21 | – |
| MCG-05-23-016 | 09h47m40.1s | −30h56m55s | 35.8 | 171 | 2.0 | 0.45 | >6 (a) |
| MCG-06-30-015 | 13h35m53.7s | −34d17m44s | 26.8 | 128 | 1.2 | 0.60 | ∼1.8–3.0 (b) |
| NGC 1365 | 03h33m36.4s | −36d08m25s | 21.5 | 103 | 1.8 | 0.55 | <5 (c) |
| NGC 2110 | 05h52m11.4s | −07d27m22s | 32.4 | 155 | 2.0 | 0.76 | 5.0 (d) |
| NGC 2992 | 09h45m42.0s | −14d19m35s | 34.4 | 164 | 1.9 | 0.31 | 3.8 (e) |
| NGC 3081 | 09h59m29.5s | −22d49m35s | 34.5 | 164 | 2.0 | 0.76 | – |
| NGC 3227 | 10h23m30.6s | + 19d51m54s | 20.4 | 98 | 1.5 | 0.67 | 2.3 (e) |
| NGC 3783 | 11h39m01.7s | −37d44m19s | 36.4 | 173 | 1.2 | 0.89 | 0.8 (f) |
| NGC 4051 | 12h03m09.6s | + 44d31m53s | 12.9 | 62 | 1.2 | 0.75 | 1.0 (g) |
| NGC 4138 | 12h09m29.8s | + 43d41m07s | 17.7 | 85 | 1.9 | 0.65 | – |
| NGC 4151 | 12h10m32.6s | + 39d24m21s | 20.0 | 96 | 1.5 | 0.71 | 1.0 (e) |
| NGC 4388a | 12h25m46.7s | + 12d39m44s | 17.0 | 82 | 2.0 | 0.19 | 5.9 (h) |
| NGC 4395 | 12h25m48.8s | + 33d32m49s | 3.84 | 19 | 1.8 | 0.83 | 0.4 (i) |
| NGC 4945 | 13h05m27.5s | −49d28m06s | 4.36 | 21 | 2.0 | 0.19 | – |
| NGC 5128 (CenA) | 13h25m27.6s | −43d01m09s | 4.28 | 21 | 2.0 | 0.78 | ∼7–8 (j, k) |
| NGC 5506 | 14h13m14.9s | −03d12m27s | 30.1 | 144 | 1.9 | 0.24 | ≥11 (l) |
| NGC 6300 | 17h16m59.5s | −62d49m14s | 14.0 | 68 | 2.0 | 0.67 | – |
| NGC 6814 | 19h42n40.6s | −10d19m25s | 25.8 | 123 | 1.5 | 0.93 | – |
| NGC 7172 | 22h02m01.9s | −31d52m11s | 37.9 | 180 | 2.0 | 0.56 | – |
| NGC 7213 | 22h09m16.3s | −47d10m00s | 25.1 | 120 | 1.5 | 0.90 | 0.6 (m) |
| NGC 7314 | 22h35m46.2s | −26d03m02s | 20.9 | 100 | 1.9 | 0.46 | – |
| NGC 7582 | 23h18m23.5s | −42d22m14s | 22.1 | 106 | 2.0 | 0.42 | ∼8–13 (n) |
| UGC 6728 | 11h45m16.0s | + 79d40m53s | 32.1 | 153 | 1.2 | 0.63 | – |
aThis galaxy is part of the Virgo Cluster (Binggeli, Sandage & Tammann 1985).
3 OBSERVATIONS
Our aim is to construct high angular resolution IR SEDs for the whole sample. In the following, we describe the new and archival MIR and near-IR (NIR; ∼1–5 |$\mu$|m) observations used in this work.
3.1 New observations
3.1.1 Gran Telescopio CANARIAS/CanariCam
We obtained subarcsecond resolution N-band spectra (7.5–13 |$\mu$|m) of two Seyfert galaxies (NGC 4138 and UGC 6728) using the low spectral resolution (R ∼ 175) grating available in the instrument CanariCam (CC; Telesco et al. 2003; Packham et al. 2005a), on the 10.4-m Gran Telescopio CANARIAS (GTC). CC is an MIR (7.5–25 |$\mu$|m) imager with spectroscopic, coronagraphic and polarimetric capabilities. It uses an Si:As detector, which covers a field of view (FOV) of 26 × 19 arcsec2 on the sky and it has a pixel scale of 0.08 arcsec. NGC 4138 and UGC 6728 were observed in 2016 March and the slit, of width 0.52 arcsec, was oriented at PA = 145 and 150 deg, respectively. The total on-source integration times were 1061 and 1415 s, respectively. In both cases, the standard MIR chopping-nodding technique was used with chop and nod throws of 15 arcsec (see Table 2). The data were taken on 2016 March 14 and 15 as part of a Director’s Discretionary Time program (GTC04-15B DDT; PI: I. García-Bernete). Using the acquisition images of the standard stars used for NGC 4138 (HD 95121) and UGC 6728 (HD 105943), we measured for the standard stars full width at half-maximum (FWHM) values of 0.28 arcsec (at λ = 10.3 |$\mu$|m) and 0.34 arcsec (at λ = 8.7 |$\mu$|m), respectively.
Summary of the NIR fluxes and MIR spectroscopy employed in this work. Columns from 2 to 6 list the J-, H-, K-, L- and M-band fluxes available. Columns 7 and 8 correspond to their corresponding instruments/filters and references, respectively. Columns 9, 10, and 11 list the N-band spectroscopy slit widths, position angles (PA) and references. References: (a) Skrutskie et al. (2006); (b) Alonso-Herrero et al. (2001); (c) Kotilainen et al. (1992); (d) Carollo et al. (2002); (e) Sosa-Brito et al. (2001); (f) this work; (g) Alonso-Herrero et al. (1998); (h) Quillen et al. (2001); (i) Burtscher et al. (2015); (j) Kishimoto et al. (2007); (k) Alonso-Herrero et al. (2003); (l) Prieto et al. (2010); (m) Prieto, Reunanen & Kotilainen (2002); (n) Ward et al. (1987a); (o) Hönig et al. (2010); (p) González-Martín et al. (2013); (q) García-Bernete et al. (2015); (r) Alonso-Herrero et al. (2016); (s)Alonso-Herrero et al. (2011).
| Name . | NIR Flux Density (mJy) . | . | . | N-band Spectroscopy . | . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| . | J band . | H band . | Kband . | L band . | M band . | Filters . | Ref. . | Slit Width . | PA . | Ref. . |
| . | . | . | . | . | . | . | . | (arcsec) . | (deg) . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . |
| ESO 005-G004 | <14.3 | <28 | <39.6 | – | – | 2MASS/J, H, K | a | – | – | – |
| MCG-05-23-016 | 1.1 ± 0.2 | 3.7 ± 0.6 | 10.7 ± 1.6 | <79.5 | – | UKIRT/J, H, K, L | b | 0.75 | 50 | o |
| MCG-06-30-015 | 6.5 ± 1.0 | 11.8 ± 1.8 | 31.3 ± 4.7 | – | – | UKIRT/J, H, K | c | 0.75 | 80 | o |
| NGC 1365 | – | 8.3 ± 0.8 | <24.2 | – | – | HST/F160W, AAT/K | d, e | 0.35 | 15 | p |
| NGC 2110 | 6.6 ± 1.0 | 8.7 ± 1.3 | 12.2 ± 1.8 | <58.1 | – | CIRCE/J, H, K, UKIRT/L | f, g | 0.75 | 55 | o |
| NGC 2992 | 1.8 ± 0.3 | 2.3 ± 0.3 | 5.4 ± 0.8 | <22.7 | – | CIRCE/J, H, K, UKIRT/L | f, g | 0.52 | 30 | q, r |
| NGC 3081 | – | 0.22 ± 0.02 | <1.8 | <11.3 | – | HST/F160W, SINFONI/K, UKIRT/L | h, i, g | 0.65 | 0 | p |
| NGC 3227 | – | 7.8 ± 0.8 | 16.6 ± 1.7 | <46.7 | – | HST/F160W, F222M, NFSCam/L | j, k | 0.52 | 0 | r |
| NGC 3783 | 23 ± 3 | – | 73 ± 11 | <170 | – | NACO/J, K, L | l | 0.75 | 315 | o |
| NGC 4051 | – | 12.8 ± 1.9 | 15.1 ± 2.3 | <73.5 | – | WHT/H, SINFONI/K, NFSCam/L | e, i, k | 0.52 | 310 | r |
| NGC 4138 | – | – | 2.3 ± 0.4 | – | – | HST/F190N | f | 0.52 | 145 | f |
| NGC 4151 | 69 ± 7 | 103.6 ± 10.4 | 177.5 ± 17.8 | <325 | <449 | HST/F110W, F160W, F222M, KPNO/L, M | k, b | 0.36 | 60 | s |
| NGC 4388 | 0.06 ± 0.01 | 0.7 ± 0.1 | <7.5 | <40 | – | HST/F110W, F160W, SINFONI/K, UKIRT/L | k, i | 0.52 | 90 | r |
| NGC 4395 | – | 0.9 ± 0.1 | <1.1 | – | – | HST/F160W, NFSCam/K | k | – | – | – |
| NGC 4945 | – | <0.15 | <25.8 | – | – | HST/F160W, AAT/K | h, e | 0.65 | 45 | p |
| NGC 5128 | 1.3 ± 0.2 | 5.8 ± 0.6 | 30 ± 4 | 200 ± 30 | – | NACO/J, HST/F160W, NACO/K, L | l, h | 0.65 | 0 | p |
| NGC 5506 | 13 ± 2 | 53.1 ± 5.3 | 80 ± 12 | 290 ± 44 | <530 | NACO/J, HST/F160W, NACO/K, L, UKIRT/M | l, h, b | 0.35 | 60 | p |
| NGC 6300 | – | 2.0 ± 0.2 | <5.4 | – | – | HST/F160W, SINFONI/K | h, i | – | – | – |
| NGC 6814 | – | 6.2 ± 0.6 | 6.3 ± 1.0 | – | – | HST/F160W, SINFONI/K | h, i | – | – | – |
| NGC 7172 | 1.3 ± 0.2 | 8.8 ± 1.3 | 15 ± 2 | <30 | <61.4 | CIRCE/J, H, K, UKIRT/L, M | f, b | 0.35 | 60 | p |
| NGC 7213 | 1.8 ± 0.3 | 5.2 ± 0.8 | 14.7 ± 2.2 | – | – | SOFI/J, H, K | m | 0.75 | 300 | o |
| NGC 7314 | 1.9 ± 0.3 | 3.6 ± 0.5 | 7.1 ± 1.1 | <21.9 | – | CIRCE/J, H, K, UKIRT/L | f, n | – | – | – |
| NGC 7582 | – | <11 | <18 | – | – | HST/F160W, NACO/K | l | 0.70 | 0 | p |
| UGC 6728 | < 9.2 | <10.8 | <11.8 | – | – | 2MASS/J, H, K | a | 0.52 | 150 | f |
| Name . | NIR Flux Density (mJy) . | . | . | N-band Spectroscopy . | . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| . | J band . | H band . | Kband . | L band . | M band . | Filters . | Ref. . | Slit Width . | PA . | Ref. . |
| . | . | . | . | . | . | . | . | (arcsec) . | (deg) . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . |
| ESO 005-G004 | <14.3 | <28 | <39.6 | – | – | 2MASS/J, H, K | a | – | – | – |
| MCG-05-23-016 | 1.1 ± 0.2 | 3.7 ± 0.6 | 10.7 ± 1.6 | <79.5 | – | UKIRT/J, H, K, L | b | 0.75 | 50 | o |
| MCG-06-30-015 | 6.5 ± 1.0 | 11.8 ± 1.8 | 31.3 ± 4.7 | – | – | UKIRT/J, H, K | c | 0.75 | 80 | o |
| NGC 1365 | – | 8.3 ± 0.8 | <24.2 | – | – | HST/F160W, AAT/K | d, e | 0.35 | 15 | p |
| NGC 2110 | 6.6 ± 1.0 | 8.7 ± 1.3 | 12.2 ± 1.8 | <58.1 | – | CIRCE/J, H, K, UKIRT/L | f, g | 0.75 | 55 | o |
| NGC 2992 | 1.8 ± 0.3 | 2.3 ± 0.3 | 5.4 ± 0.8 | <22.7 | – | CIRCE/J, H, K, UKIRT/L | f, g | 0.52 | 30 | q, r |
| NGC 3081 | – | 0.22 ± 0.02 | <1.8 | <11.3 | – | HST/F160W, SINFONI/K, UKIRT/L | h, i, g | 0.65 | 0 | p |
| NGC 3227 | – | 7.8 ± 0.8 | 16.6 ± 1.7 | <46.7 | – | HST/F160W, F222M, NFSCam/L | j, k | 0.52 | 0 | r |
| NGC 3783 | 23 ± 3 | – | 73 ± 11 | <170 | – | NACO/J, K, L | l | 0.75 | 315 | o |
| NGC 4051 | – | 12.8 ± 1.9 | 15.1 ± 2.3 | <73.5 | – | WHT/H, SINFONI/K, NFSCam/L | e, i, k | 0.52 | 310 | r |
| NGC 4138 | – | – | 2.3 ± 0.4 | – | – | HST/F190N | f | 0.52 | 145 | f |
| NGC 4151 | 69 ± 7 | 103.6 ± 10.4 | 177.5 ± 17.8 | <325 | <449 | HST/F110W, F160W, F222M, KPNO/L, M | k, b | 0.36 | 60 | s |
| NGC 4388 | 0.06 ± 0.01 | 0.7 ± 0.1 | <7.5 | <40 | – | HST/F110W, F160W, SINFONI/K, UKIRT/L | k, i | 0.52 | 90 | r |
| NGC 4395 | – | 0.9 ± 0.1 | <1.1 | – | – | HST/F160W, NFSCam/K | k | – | – | – |
| NGC 4945 | – | <0.15 | <25.8 | – | – | HST/F160W, AAT/K | h, e | 0.65 | 45 | p |
| NGC 5128 | 1.3 ± 0.2 | 5.8 ± 0.6 | 30 ± 4 | 200 ± 30 | – | NACO/J, HST/F160W, NACO/K, L | l, h | 0.65 | 0 | p |
| NGC 5506 | 13 ± 2 | 53.1 ± 5.3 | 80 ± 12 | 290 ± 44 | <530 | NACO/J, HST/F160W, NACO/K, L, UKIRT/M | l, h, b | 0.35 | 60 | p |
| NGC 6300 | – | 2.0 ± 0.2 | <5.4 | – | – | HST/F160W, SINFONI/K | h, i | – | – | – |
| NGC 6814 | – | 6.2 ± 0.6 | 6.3 ± 1.0 | – | – | HST/F160W, SINFONI/K | h, i | – | – | – |
| NGC 7172 | 1.3 ± 0.2 | 8.8 ± 1.3 | 15 ± 2 | <30 | <61.4 | CIRCE/J, H, K, UKIRT/L, M | f, b | 0.35 | 60 | p |
| NGC 7213 | 1.8 ± 0.3 | 5.2 ± 0.8 | 14.7 ± 2.2 | – | – | SOFI/J, H, K | m | 0.75 | 300 | o |
| NGC 7314 | 1.9 ± 0.3 | 3.6 ± 0.5 | 7.1 ± 1.1 | <21.9 | – | CIRCE/J, H, K, UKIRT/L | f, n | – | – | – |
| NGC 7582 | – | <11 | <18 | – | – | HST/F160W, NACO/K | l | 0.70 | 0 | p |
| UGC 6728 | < 9.2 | <10.8 | <11.8 | – | – | 2MASS/J, H, K | a | 0.52 | 150 | f |
Summary of the NIR fluxes and MIR spectroscopy employed in this work. Columns from 2 to 6 list the J-, H-, K-, L- and M-band fluxes available. Columns 7 and 8 correspond to their corresponding instruments/filters and references, respectively. Columns 9, 10, and 11 list the N-band spectroscopy slit widths, position angles (PA) and references. References: (a) Skrutskie et al. (2006); (b) Alonso-Herrero et al. (2001); (c) Kotilainen et al. (1992); (d) Carollo et al. (2002); (e) Sosa-Brito et al. (2001); (f) this work; (g) Alonso-Herrero et al. (1998); (h) Quillen et al. (2001); (i) Burtscher et al. (2015); (j) Kishimoto et al. (2007); (k) Alonso-Herrero et al. (2003); (l) Prieto et al. (2010); (m) Prieto, Reunanen & Kotilainen (2002); (n) Ward et al. (1987a); (o) Hönig et al. (2010); (p) González-Martín et al. (2013); (q) García-Bernete et al. (2015); (r) Alonso-Herrero et al. (2016); (s)Alonso-Herrero et al. (2011).
| Name . | NIR Flux Density (mJy) . | . | . | N-band Spectroscopy . | . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| . | J band . | H band . | Kband . | L band . | M band . | Filters . | Ref. . | Slit Width . | PA . | Ref. . |
| . | . | . | . | . | . | . | . | (arcsec) . | (deg) . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . |
| ESO 005-G004 | <14.3 | <28 | <39.6 | – | – | 2MASS/J, H, K | a | – | – | – |
| MCG-05-23-016 | 1.1 ± 0.2 | 3.7 ± 0.6 | 10.7 ± 1.6 | <79.5 | – | UKIRT/J, H, K, L | b | 0.75 | 50 | o |
| MCG-06-30-015 | 6.5 ± 1.0 | 11.8 ± 1.8 | 31.3 ± 4.7 | – | – | UKIRT/J, H, K | c | 0.75 | 80 | o |
| NGC 1365 | – | 8.3 ± 0.8 | <24.2 | – | – | HST/F160W, AAT/K | d, e | 0.35 | 15 | p |
| NGC 2110 | 6.6 ± 1.0 | 8.7 ± 1.3 | 12.2 ± 1.8 | <58.1 | – | CIRCE/J, H, K, UKIRT/L | f, g | 0.75 | 55 | o |
| NGC 2992 | 1.8 ± 0.3 | 2.3 ± 0.3 | 5.4 ± 0.8 | <22.7 | – | CIRCE/J, H, K, UKIRT/L | f, g | 0.52 | 30 | q, r |
| NGC 3081 | – | 0.22 ± 0.02 | <1.8 | <11.3 | – | HST/F160W, SINFONI/K, UKIRT/L | h, i, g | 0.65 | 0 | p |
| NGC 3227 | – | 7.8 ± 0.8 | 16.6 ± 1.7 | <46.7 | – | HST/F160W, F222M, NFSCam/L | j, k | 0.52 | 0 | r |
| NGC 3783 | 23 ± 3 | – | 73 ± 11 | <170 | – | NACO/J, K, L | l | 0.75 | 315 | o |
| NGC 4051 | – | 12.8 ± 1.9 | 15.1 ± 2.3 | <73.5 | – | WHT/H, SINFONI/K, NFSCam/L | e, i, k | 0.52 | 310 | r |
| NGC 4138 | – | – | 2.3 ± 0.4 | – | – | HST/F190N | f | 0.52 | 145 | f |
| NGC 4151 | 69 ± 7 | 103.6 ± 10.4 | 177.5 ± 17.8 | <325 | <449 | HST/F110W, F160W, F222M, KPNO/L, M | k, b | 0.36 | 60 | s |
| NGC 4388 | 0.06 ± 0.01 | 0.7 ± 0.1 | <7.5 | <40 | – | HST/F110W, F160W, SINFONI/K, UKIRT/L | k, i | 0.52 | 90 | r |
| NGC 4395 | – | 0.9 ± 0.1 | <1.1 | – | – | HST/F160W, NFSCam/K | k | – | – | – |
| NGC 4945 | – | <0.15 | <25.8 | – | – | HST/F160W, AAT/K | h, e | 0.65 | 45 | p |
| NGC 5128 | 1.3 ± 0.2 | 5.8 ± 0.6 | 30 ± 4 | 200 ± 30 | – | NACO/J, HST/F160W, NACO/K, L | l, h | 0.65 | 0 | p |
| NGC 5506 | 13 ± 2 | 53.1 ± 5.3 | 80 ± 12 | 290 ± 44 | <530 | NACO/J, HST/F160W, NACO/K, L, UKIRT/M | l, h, b | 0.35 | 60 | p |
| NGC 6300 | – | 2.0 ± 0.2 | <5.4 | – | – | HST/F160W, SINFONI/K | h, i | – | – | – |
| NGC 6814 | – | 6.2 ± 0.6 | 6.3 ± 1.0 | – | – | HST/F160W, SINFONI/K | h, i | – | – | – |
| NGC 7172 | 1.3 ± 0.2 | 8.8 ± 1.3 | 15 ± 2 | <30 | <61.4 | CIRCE/J, H, K, UKIRT/L, M | f, b | 0.35 | 60 | p |
| NGC 7213 | 1.8 ± 0.3 | 5.2 ± 0.8 | 14.7 ± 2.2 | – | – | SOFI/J, H, K | m | 0.75 | 300 | o |
| NGC 7314 | 1.9 ± 0.3 | 3.6 ± 0.5 | 7.1 ± 1.1 | <21.9 | – | CIRCE/J, H, K, UKIRT/L | f, n | – | – | – |
| NGC 7582 | – | <11 | <18 | – | – | HST/F160W, NACO/K | l | 0.70 | 0 | p |
| UGC 6728 | < 9.2 | <10.8 | <11.8 | – | – | 2MASS/J, H, K | a | 0.52 | 150 | f |
| Name . | NIR Flux Density (mJy) . | . | . | N-band Spectroscopy . | . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| . | J band . | H band . | Kband . | L band . | M band . | Filters . | Ref. . | Slit Width . | PA . | Ref. . |
| . | . | . | . | . | . | . | . | (arcsec) . | (deg) . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . |
| ESO 005-G004 | <14.3 | <28 | <39.6 | – | – | 2MASS/J, H, K | a | – | – | – |
| MCG-05-23-016 | 1.1 ± 0.2 | 3.7 ± 0.6 | 10.7 ± 1.6 | <79.5 | – | UKIRT/J, H, K, L | b | 0.75 | 50 | o |
| MCG-06-30-015 | 6.5 ± 1.0 | 11.8 ± 1.8 | 31.3 ± 4.7 | – | – | UKIRT/J, H, K | c | 0.75 | 80 | o |
| NGC 1365 | – | 8.3 ± 0.8 | <24.2 | – | – | HST/F160W, AAT/K | d, e | 0.35 | 15 | p |
| NGC 2110 | 6.6 ± 1.0 | 8.7 ± 1.3 | 12.2 ± 1.8 | <58.1 | – | CIRCE/J, H, K, UKIRT/L | f, g | 0.75 | 55 | o |
| NGC 2992 | 1.8 ± 0.3 | 2.3 ± 0.3 | 5.4 ± 0.8 | <22.7 | – | CIRCE/J, H, K, UKIRT/L | f, g | 0.52 | 30 | q, r |
| NGC 3081 | – | 0.22 ± 0.02 | <1.8 | <11.3 | – | HST/F160W, SINFONI/K, UKIRT/L | h, i, g | 0.65 | 0 | p |
| NGC 3227 | – | 7.8 ± 0.8 | 16.6 ± 1.7 | <46.7 | – | HST/F160W, F222M, NFSCam/L | j, k | 0.52 | 0 | r |
| NGC 3783 | 23 ± 3 | – | 73 ± 11 | <170 | – | NACO/J, K, L | l | 0.75 | 315 | o |
| NGC 4051 | – | 12.8 ± 1.9 | 15.1 ± 2.3 | <73.5 | – | WHT/H, SINFONI/K, NFSCam/L | e, i, k | 0.52 | 310 | r |
| NGC 4138 | – | – | 2.3 ± 0.4 | – | – | HST/F190N | f | 0.52 | 145 | f |
| NGC 4151 | 69 ± 7 | 103.6 ± 10.4 | 177.5 ± 17.8 | <325 | <449 | HST/F110W, F160W, F222M, KPNO/L, M | k, b | 0.36 | 60 | s |
| NGC 4388 | 0.06 ± 0.01 | 0.7 ± 0.1 | <7.5 | <40 | – | HST/F110W, F160W, SINFONI/K, UKIRT/L | k, i | 0.52 | 90 | r |
| NGC 4395 | – | 0.9 ± 0.1 | <1.1 | – | – | HST/F160W, NFSCam/K | k | – | – | – |
| NGC 4945 | – | <0.15 | <25.8 | – | – | HST/F160W, AAT/K | h, e | 0.65 | 45 | p |
| NGC 5128 | 1.3 ± 0.2 | 5.8 ± 0.6 | 30 ± 4 | 200 ± 30 | – | NACO/J, HST/F160W, NACO/K, L | l, h | 0.65 | 0 | p |
| NGC 5506 | 13 ± 2 | 53.1 ± 5.3 | 80 ± 12 | 290 ± 44 | <530 | NACO/J, HST/F160W, NACO/K, L, UKIRT/M | l, h, b | 0.35 | 60 | p |
| NGC 6300 | – | 2.0 ± 0.2 | <5.4 | – | – | HST/F160W, SINFONI/K | h, i | – | – | – |
| NGC 6814 | – | 6.2 ± 0.6 | 6.3 ± 1.0 | – | – | HST/F160W, SINFONI/K | h, i | – | – | – |
| NGC 7172 | 1.3 ± 0.2 | 8.8 ± 1.3 | 15 ± 2 | <30 | <61.4 | CIRCE/J, H, K, UKIRT/L, M | f, b | 0.35 | 60 | p |
| NGC 7213 | 1.8 ± 0.3 | 5.2 ± 0.8 | 14.7 ± 2.2 | – | – | SOFI/J, H, K | m | 0.75 | 300 | o |
| NGC 7314 | 1.9 ± 0.3 | 3.6 ± 0.5 | 7.1 ± 1.1 | <21.9 | – | CIRCE/J, H, K, UKIRT/L | f, n | – | – | – |
| NGC 7582 | – | <11 | <18 | – | – | HST/F160W, NACO/K | l | 0.70 | 0 | p |
| UGC 6728 | < 9.2 | <10.8 | <11.8 | – | – | 2MASS/J, H, K | a | 0.52 | 150 | f |
The data reduction was carried out with the RedCan pipeline (González-Martín et al. 2013), which performs sky subtraction, stacking of individual observation, rejection of the bad frames (due to excess array of sky noise), wavelength and flux calibration, trace determination and spectral extraction. We extracted the nuclear spectra as a point source for both galaxies. Note that for point source extraction, RedCan uses an aperture that increases with wavelength to take into account the decreasing angular resolution, and it also performs a correction account for slit loses (see González-Martín et al. 2013 for further details on CC data reduction).
3.1.2 Gran Telescopio CANARIAS/CIRCE
We obtained NIR imaging data (J, H, and K bands) with the Canarias InfraRed Camera Experiment (CIRCE; Garner et al. 2014) on the 10.4-m GTC. The instrument was equipped with an engineering grade Hawaii2RG detector with a total FOV of 3.4 × 3.4 arcmin2 and a plate scale of 0.1 arcsec pixel−1. Note that all the observations were taken using a 5 dither pattern. See Table 3 for observation details.
| Name . | Filter . | Obs. . | Total . | PSF . | FWHM . |
|---|---|---|---|---|---|
| . | name . | Date . | on-source . | star . | PSF . |
| . | . | . | time (s) . | name . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . |
| NGC 2110 | J | 11/10/2016 | 75 | AS05 0 | 0.89 arcsec |
| H | 11/10/2016 | 75 | 0.75 arcsec | ||
| Ks | 11/10/2016 | 75 | 0.76 arcsec | ||
| NGC 2992 | J | 05/02/2017 | 125 | S708 D | 0.98 arcsec |
| H | 05/02/2017 | 125 | 0.78 arcsec | ||
| Ks | 05/02/2017 | 125 | 0.76 arcsec | ||
| NGC 7172 | J | 16/10/2016 | 125 | AS31 1 | 0.71 arcsec |
| H | 16/10/2016 | 125 | 0.70 arcsec | ||
| Ks | 16/10/2016 | 125 | 0.63 arcsec | ||
| NGC 7314 | J | 05/02/2017 | 150 | AS05 0 | 0.50 arcsec |
| H | 05/02/2017 | 150 | 0.54 arcsec | ||
| Ks | 05/02/2017 | 150 | 0.53 arcsec |
| Name . | Filter . | Obs. . | Total . | PSF . | FWHM . |
|---|---|---|---|---|---|
| . | name . | Date . | on-source . | star . | PSF . |
| . | . | . | time (s) . | name . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . |
| NGC 2110 | J | 11/10/2016 | 75 | AS05 0 | 0.89 arcsec |
| H | 11/10/2016 | 75 | 0.75 arcsec | ||
| Ks | 11/10/2016 | 75 | 0.76 arcsec | ||
| NGC 2992 | J | 05/02/2017 | 125 | S708 D | 0.98 arcsec |
| H | 05/02/2017 | 125 | 0.78 arcsec | ||
| Ks | 05/02/2017 | 125 | 0.76 arcsec | ||
| NGC 7172 | J | 16/10/2016 | 125 | AS31 1 | 0.71 arcsec |
| H | 16/10/2016 | 125 | 0.70 arcsec | ||
| Ks | 16/10/2016 | 125 | 0.63 arcsec | ||
| NGC 7314 | J | 05/02/2017 | 150 | AS05 0 | 0.50 arcsec |
| H | 05/02/2017 | 150 | 0.54 arcsec | ||
| Ks | 05/02/2017 | 150 | 0.53 arcsec |
| Name . | Filter . | Obs. . | Total . | PSF . | FWHM . |
|---|---|---|---|---|---|
| . | name . | Date . | on-source . | star . | PSF . |
| . | . | . | time (s) . | name . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . |
| NGC 2110 | J | 11/10/2016 | 75 | AS05 0 | 0.89 arcsec |
| H | 11/10/2016 | 75 | 0.75 arcsec | ||
| Ks | 11/10/2016 | 75 | 0.76 arcsec | ||
| NGC 2992 | J | 05/02/2017 | 125 | S708 D | 0.98 arcsec |
| H | 05/02/2017 | 125 | 0.78 arcsec | ||
| Ks | 05/02/2017 | 125 | 0.76 arcsec | ||
| NGC 7172 | J | 16/10/2016 | 125 | AS31 1 | 0.71 arcsec |
| H | 16/10/2016 | 125 | 0.70 arcsec | ||
| Ks | 16/10/2016 | 125 | 0.63 arcsec | ||
| NGC 7314 | J | 05/02/2017 | 150 | AS05 0 | 0.50 arcsec |
| H | 05/02/2017 | 150 | 0.54 arcsec | ||
| Ks | 05/02/2017 | 150 | 0.53 arcsec |
| Name . | Filter . | Obs. . | Total . | PSF . | FWHM . |
|---|---|---|---|---|---|
| . | name . | Date . | on-source . | star . | PSF . |
| . | . | . | time (s) . | name . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . |
| NGC 2110 | J | 11/10/2016 | 75 | AS05 0 | 0.89 arcsec |
| H | 11/10/2016 | 75 | 0.75 arcsec | ||
| Ks | 11/10/2016 | 75 | 0.76 arcsec | ||
| NGC 2992 | J | 05/02/2017 | 125 | S708 D | 0.98 arcsec |
| H | 05/02/2017 | 125 | 0.78 arcsec | ||
| Ks | 05/02/2017 | 125 | 0.76 arcsec | ||
| NGC 7172 | J | 16/10/2016 | 125 | AS31 1 | 0.71 arcsec |
| H | 16/10/2016 | 125 | 0.70 arcsec | ||
| Ks | 16/10/2016 | 125 | 0.63 arcsec | ||
| NGC 7314 | J | 05/02/2017 | 150 | AS05 0 | 0.50 arcsec |
| H | 05/02/2017 | 150 | 0.54 arcsec | ||
| Ks | 05/02/2017 | 150 | 0.53 arcsec |
We performed the data reduction by using the idl (Interactive Data Language) routines employed in D’Ammando et al. (2017). The first step in the data processing includes the subtraction of dark current frames. From twilight sky exposures, we obtained an illumination correction to compensate a decrease of about 40 per cent from the centre to the border of the FOV. At this point, we introduced a correction to remove a pattern of inclined stripes related to reading amplifiers. Once this pattern was removed, the images corresponding to each dither cycle were median combined to form a sky frame, which was subtracted for each frame of the cycle. We then combined all sky-subtracted images with the commonly used shift-and-add technique. During the combination of these frames, we applied a bad-pixel mask, which includes the two vertical bands corresponding to non-functional amplifiers. Finally, we obtained the photometric calibrations relative to photometric standard PSF stars using their Two-Micron All-Sky Survey (2MASS) photometry.
To estimate the NIR nuclear fluxes in the J, H, and K bands, we used the PSF subtraction method (see GB16 and references therein), which consists of subtracting the PSF star from the galaxy profiles. This method has been widely used in ground-based IR images (e.g. Soifer et al. 2000; Radomski et al. 2002, 2003; García-Bernete et al. 2015).
3.2 Archival data
We downloaded the fully reduced NIR imaging data of NGC 4138 (unpublished, to our knowledge) from the ESA Hubble Legacy Archive.1 This Seyfert 1.9 galaxy was observed in 2008 February with the Near Infrared Camera and Multi-Object Spectrometer (NICMOS) and the narrow F190N filter (λc = 1.9 |$\mu$|m). This observation was taken using the NIC3 camera, which has an FOV 51.2 × 51.2 arcsec2 on the sky and a pixel scale of 0.2 .arcsec This image was taken as part of the Hubble programs GO11080 (cycle:15, PI: D. Calzetti) and the exposure time was 13 474 s.
In order to accurately subtract the unresolved AGN component, first, we generated a theoretical Tiny Tim2 PSF (Krist 1995; Krist, Hook & Stoehr 2011) for the NIC3 camera F190N filter and, then, we used the PSF subtraction method.
3.3 Literature high angular resolution IR observations
We compiled the highest angular resolution IR (∼1–30 |$\mu$|m) nuclear fluxes available from the literature for our sample. The compiled nuclear NIR fluxes are from both ground- and space-based (i.e. Hubble Space Telescope; HST) data (see Table 2). In the case of the MIR nuclear fluxes, we used the measurements of the unresolved MIR emission (angular resolutions ranging from 0.2 to 0.6 arcsec) calculated in GB16, where we employed the PSF subtraction method on high angular resolution MIR images from 8–10 m-class ground-based telescopes (GTC/CanariCam, VLT/VISIR, Gemini/T-ReCS and MICHELLE; see table 2 of GB16).
We retrieved 31.5 |$\mu$|m high angular resolution (FWHM ∼ 3.1 arcsec) nuclear fluxes of six Seyfert galaxies (see Table 4), which were observed with the long-wavelength camera (LWC; λ > 25 |$\mu$|m) within the Faint Object Infrared Camera for the SOFIA Telescope (FORCAST; Herter et al. 2012) on the 2.5-m SOFIA telescope. These observations were obtained using the 31.5 |$\mu$|m filter (Δλ = 5.7 |$\mu$|m). See Fuller et al. (2016) for further details on the observations, data reduction, and obtention of unresolved nuclear fluxes.
Summary of the nuclear MIR emission derived from the AGN contribution based on spectral decomposition of Spitzer/IRS spectra and the SOFIA/FORCAST 31.5 |$\mu$|m fluxes. Column 1 corresponds to the galaxy name. Columns from 2 to 6 list the 4.5, 5.5, 18.0, 25.0, and 30.0 fluxes, respectively. The final column 7, corresponds to the SOFIA/FORCAST 31.5 |$\mu$|m fluxes, reported by Fuller et al. (2016).
| Name . | Flux density (mJy) . | |||||
|---|---|---|---|---|---|---|
| . | 4.5 |$\mu$|m . | 5.5 |$\mu$|m . | 18.0 |$\mu$|m . | 25.0 |$\mu$|m . | 30.0 |$\mu$|m . | 31.5 |$\mu$|m . |
| . | . | . | . | . | . | SOFIA/FORCAST . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| ESO 005-G004 | 2.9 ± 0.4 | 3.8 ± 0.6 | – | 141 ± 28 | 163 ± 33 | – |
| MCG-05-23-016 | – | 101.1 ± 15.2 | – | <1762.1 | <1898 | <1640 |
| MCG-06-30-015 | 57.3 ± 8.6 | 69.2 ± 10.4 | 308.5 ± 61.7 | 352.1 ± 70.4 | <519.8 | – |
| NGC 1365 | 39.3 ± 5.9 | 49.8 ± 7.5 | – | 514.5 ± 102.9 | 554.2 ± 110.8a | – |
| NGC 2110 | 112.8 ± 16.9 | 125.3 ± 18.8 | 508.9 ± 101.8 | 598.9 ± 119.8 | <858.1 | <860 |
| NGC 2992 | 16.1 ± 2.4 | 28.8 ± 4.3 | – | 773.2 ± 154.6 | 965 ± 193 | <810 |
| NGC 3081 | – | 18.8 ± 2.8 | – | 452.2 ± 90.4 | 520 ± 104 | <800 |
| NGC 3227 | – | 47 ± 7 | 839.7 ± 167.9 | 947 ± 189 | 1018.8 ± 203.8 | <1300 |
| NGC 3783 | – | 133.8 ± 20.1 | – | 1022.6 ± 204.5 | 1182.8 ± 236.6 | – |
| NGC 4051 | 76.5 ± 11.5 | 97 ± 15 | 661.3 ± 132.3 | 1001.1 ± 200.2 | <1354.7 | – |
| NGC 4138 | 5.8 ± 0.9 | 6.9 ± 1.0 | 30.9 ± 6.2 | 35.3 ± 7.1 | 37 ± 7a | – |
| NGC 4151 | – | 404 ± 61 | – | 3187.4 ± 637.5 | 2965.2 ± 593.0 | – |
| NGC 4388 | 23.5 ± 3.5 | 30.2 ± 4.5 | 788.6 ± 157.7 | 1127.1 ± 225.4 | 1305.7 ± 261.1 | <2040 |
| NGC 4395 | – | 1.4 ± 0.2 | 19.8 ± 4.0 | 25.6 ± 5.1 | 30.3 ± 6.1 | – |
| NGC 4945 | – | 4.9 ± 0.7 | – | 194.4 ± 38.9 | 252.5 ± 50.5 | – |
| NGC 5128 | – | 372.2 ± 55.8 | – | 3526.2 ± 705.2 | 4095.3 ± 819.1 | – |
| NGC 5506 | – | 490.6 ± 73.6 | – | <3273.3 | <3960.9 | <3660 |
| NGC 6300 | 11.4 ± 1.7 | 28.1 ± 4.2 | 614.3 ± 112.9 | 1831.1 ± 366.2 | <2694.1 | – |
| NGC 6814 | 12.2 ± 1.8 | 15.5 ± 2.3 | – | 160 ± 32 | <249.7 | – |
| NGC 7172 | – | 41.8 ± 6.3 | – | 146.6 ± 29.3 | 166.3 ± 33.3 | – |
| NGC 7213 | – | 19.2 ± 2.9 | – | <386.6 | <389.7 | – |
| NGC 7314 | – | <21.5 | – | 180.8 ± 36.2 | 203.8 ± 40.8 | – |
| NGC 7582 | – | 27.3 ± 4.1 | – | 649.7 ± 129.9 | 923.8 ± 184.8 | – |
| UGC 6728 | 12.1 ± 1.8 | 14.7 ± 2.2 | 57.2 ± 11.4 | 54.5 ± 10.9 | 51.7 ± 10.3 | – |
| Name . | Flux density (mJy) . | |||||
|---|---|---|---|---|---|---|
| . | 4.5 |$\mu$|m . | 5.5 |$\mu$|m . | 18.0 |$\mu$|m . | 25.0 |$\mu$|m . | 30.0 |$\mu$|m . | 31.5 |$\mu$|m . |
| . | . | . | . | . | . | SOFIA/FORCAST . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| ESO 005-G004 | 2.9 ± 0.4 | 3.8 ± 0.6 | – | 141 ± 28 | 163 ± 33 | – |
| MCG-05-23-016 | – | 101.1 ± 15.2 | – | <1762.1 | <1898 | <1640 |
| MCG-06-30-015 | 57.3 ± 8.6 | 69.2 ± 10.4 | 308.5 ± 61.7 | 352.1 ± 70.4 | <519.8 | – |
| NGC 1365 | 39.3 ± 5.9 | 49.8 ± 7.5 | – | 514.5 ± 102.9 | 554.2 ± 110.8a | – |
| NGC 2110 | 112.8 ± 16.9 | 125.3 ± 18.8 | 508.9 ± 101.8 | 598.9 ± 119.8 | <858.1 | <860 |
| NGC 2992 | 16.1 ± 2.4 | 28.8 ± 4.3 | – | 773.2 ± 154.6 | 965 ± 193 | <810 |
| NGC 3081 | – | 18.8 ± 2.8 | – | 452.2 ± 90.4 | 520 ± 104 | <800 |
| NGC 3227 | – | 47 ± 7 | 839.7 ± 167.9 | 947 ± 189 | 1018.8 ± 203.8 | <1300 |
| NGC 3783 | – | 133.8 ± 20.1 | – | 1022.6 ± 204.5 | 1182.8 ± 236.6 | – |
| NGC 4051 | 76.5 ± 11.5 | 97 ± 15 | 661.3 ± 132.3 | 1001.1 ± 200.2 | <1354.7 | – |
| NGC 4138 | 5.8 ± 0.9 | 6.9 ± 1.0 | 30.9 ± 6.2 | 35.3 ± 7.1 | 37 ± 7a | – |
| NGC 4151 | – | 404 ± 61 | – | 3187.4 ± 637.5 | 2965.2 ± 593.0 | – |
| NGC 4388 | 23.5 ± 3.5 | 30.2 ± 4.5 | 788.6 ± 157.7 | 1127.1 ± 225.4 | 1305.7 ± 261.1 | <2040 |
| NGC 4395 | – | 1.4 ± 0.2 | 19.8 ± 4.0 | 25.6 ± 5.1 | 30.3 ± 6.1 | – |
| NGC 4945 | – | 4.9 ± 0.7 | – | 194.4 ± 38.9 | 252.5 ± 50.5 | – |
| NGC 5128 | – | 372.2 ± 55.8 | – | 3526.2 ± 705.2 | 4095.3 ± 819.1 | – |
| NGC 5506 | – | 490.6 ± 73.6 | – | <3273.3 | <3960.9 | <3660 |
| NGC 6300 | 11.4 ± 1.7 | 28.1 ± 4.2 | 614.3 ± 112.9 | 1831.1 ± 366.2 | <2694.1 | – |
| NGC 6814 | 12.2 ± 1.8 | 15.5 ± 2.3 | – | 160 ± 32 | <249.7 | – |
| NGC 7172 | – | 41.8 ± 6.3 | – | 146.6 ± 29.3 | 166.3 ± 33.3 | – |
| NGC 7213 | – | 19.2 ± 2.9 | – | <386.6 | <389.7 | – |
| NGC 7314 | – | <21.5 | – | 180.8 ± 36.2 | 203.8 ± 40.8 | – |
| NGC 7582 | – | 27.3 ± 4.1 | – | 649.7 ± 129.9 | 923.8 ± 184.8 | – |
| UGC 6728 | 12.1 ± 1.8 | 14.7 ± 2.2 | 57.2 ± 11.4 | 54.5 ± 10.9 | 51.7 ± 10.3 | – |
aCorresponds to nuclear fluxes calculated at 28 |$\mu$|m instead of 30 |$\mu$|m. See Section 4.1 for further details.
Summary of the nuclear MIR emission derived from the AGN contribution based on spectral decomposition of Spitzer/IRS spectra and the SOFIA/FORCAST 31.5 |$\mu$|m fluxes. Column 1 corresponds to the galaxy name. Columns from 2 to 6 list the 4.5, 5.5, 18.0, 25.0, and 30.0 fluxes, respectively. The final column 7, corresponds to the SOFIA/FORCAST 31.5 |$\mu$|m fluxes, reported by Fuller et al. (2016).
| Name . | Flux density (mJy) . | |||||
|---|---|---|---|---|---|---|
| . | 4.5 |$\mu$|m . | 5.5 |$\mu$|m . | 18.0 |$\mu$|m . | 25.0 |$\mu$|m . | 30.0 |$\mu$|m . | 31.5 |$\mu$|m . |
| . | . | . | . | . | . | SOFIA/FORCAST . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| ESO 005-G004 | 2.9 ± 0.4 | 3.8 ± 0.6 | – | 141 ± 28 | 163 ± 33 | – |
| MCG-05-23-016 | – | 101.1 ± 15.2 | – | <1762.1 | <1898 | <1640 |
| MCG-06-30-015 | 57.3 ± 8.6 | 69.2 ± 10.4 | 308.5 ± 61.7 | 352.1 ± 70.4 | <519.8 | – |
| NGC 1365 | 39.3 ± 5.9 | 49.8 ± 7.5 | – | 514.5 ± 102.9 | 554.2 ± 110.8a | – |
| NGC 2110 | 112.8 ± 16.9 | 125.3 ± 18.8 | 508.9 ± 101.8 | 598.9 ± 119.8 | <858.1 | <860 |
| NGC 2992 | 16.1 ± 2.4 | 28.8 ± 4.3 | – | 773.2 ± 154.6 | 965 ± 193 | <810 |
| NGC 3081 | – | 18.8 ± 2.8 | – | 452.2 ± 90.4 | 520 ± 104 | <800 |
| NGC 3227 | – | 47 ± 7 | 839.7 ± 167.9 | 947 ± 189 | 1018.8 ± 203.8 | <1300 |
| NGC 3783 | – | 133.8 ± 20.1 | – | 1022.6 ± 204.5 | 1182.8 ± 236.6 | – |
| NGC 4051 | 76.5 ± 11.5 | 97 ± 15 | 661.3 ± 132.3 | 1001.1 ± 200.2 | <1354.7 | – |
| NGC 4138 | 5.8 ± 0.9 | 6.9 ± 1.0 | 30.9 ± 6.2 | 35.3 ± 7.1 | 37 ± 7a | – |
| NGC 4151 | – | 404 ± 61 | – | 3187.4 ± 637.5 | 2965.2 ± 593.0 | – |
| NGC 4388 | 23.5 ± 3.5 | 30.2 ± 4.5 | 788.6 ± 157.7 | 1127.1 ± 225.4 | 1305.7 ± 261.1 | <2040 |
| NGC 4395 | – | 1.4 ± 0.2 | 19.8 ± 4.0 | 25.6 ± 5.1 | 30.3 ± 6.1 | – |
| NGC 4945 | – | 4.9 ± 0.7 | – | 194.4 ± 38.9 | 252.5 ± 50.5 | – |
| NGC 5128 | – | 372.2 ± 55.8 | – | 3526.2 ± 705.2 | 4095.3 ± 819.1 | – |
| NGC 5506 | – | 490.6 ± 73.6 | – | <3273.3 | <3960.9 | <3660 |
| NGC 6300 | 11.4 ± 1.7 | 28.1 ± 4.2 | 614.3 ± 112.9 | 1831.1 ± 366.2 | <2694.1 | – |
| NGC 6814 | 12.2 ± 1.8 | 15.5 ± 2.3 | – | 160 ± 32 | <249.7 | – |
| NGC 7172 | – | 41.8 ± 6.3 | – | 146.6 ± 29.3 | 166.3 ± 33.3 | – |
| NGC 7213 | – | 19.2 ± 2.9 | – | <386.6 | <389.7 | – |
| NGC 7314 | – | <21.5 | – | 180.8 ± 36.2 | 203.8 ± 40.8 | – |
| NGC 7582 | – | 27.3 ± 4.1 | – | 649.7 ± 129.9 | 923.8 ± 184.8 | – |
| UGC 6728 | 12.1 ± 1.8 | 14.7 ± 2.2 | 57.2 ± 11.4 | 54.5 ± 10.9 | 51.7 ± 10.3 | – |
| Name . | Flux density (mJy) . | |||||
|---|---|---|---|---|---|---|
| . | 4.5 |$\mu$|m . | 5.5 |$\mu$|m . | 18.0 |$\mu$|m . | 25.0 |$\mu$|m . | 30.0 |$\mu$|m . | 31.5 |$\mu$|m . |
| . | . | . | . | . | . | SOFIA/FORCAST . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| ESO 005-G004 | 2.9 ± 0.4 | 3.8 ± 0.6 | – | 141 ± 28 | 163 ± 33 | – |
| MCG-05-23-016 | – | 101.1 ± 15.2 | – | <1762.1 | <1898 | <1640 |
| MCG-06-30-015 | 57.3 ± 8.6 | 69.2 ± 10.4 | 308.5 ± 61.7 | 352.1 ± 70.4 | <519.8 | – |
| NGC 1365 | 39.3 ± 5.9 | 49.8 ± 7.5 | – | 514.5 ± 102.9 | 554.2 ± 110.8a | – |
| NGC 2110 | 112.8 ± 16.9 | 125.3 ± 18.8 | 508.9 ± 101.8 | 598.9 ± 119.8 | <858.1 | <860 |
| NGC 2992 | 16.1 ± 2.4 | 28.8 ± 4.3 | – | 773.2 ± 154.6 | 965 ± 193 | <810 |
| NGC 3081 | – | 18.8 ± 2.8 | – | 452.2 ± 90.4 | 520 ± 104 | <800 |
| NGC 3227 | – | 47 ± 7 | 839.7 ± 167.9 | 947 ± 189 | 1018.8 ± 203.8 | <1300 |
| NGC 3783 | – | 133.8 ± 20.1 | – | 1022.6 ± 204.5 | 1182.8 ± 236.6 | – |
| NGC 4051 | 76.5 ± 11.5 | 97 ± 15 | 661.3 ± 132.3 | 1001.1 ± 200.2 | <1354.7 | – |
| NGC 4138 | 5.8 ± 0.9 | 6.9 ± 1.0 | 30.9 ± 6.2 | 35.3 ± 7.1 | 37 ± 7a | – |
| NGC 4151 | – | 404 ± 61 | – | 3187.4 ± 637.5 | 2965.2 ± 593.0 | – |
| NGC 4388 | 23.5 ± 3.5 | 30.2 ± 4.5 | 788.6 ± 157.7 | 1127.1 ± 225.4 | 1305.7 ± 261.1 | <2040 |
| NGC 4395 | – | 1.4 ± 0.2 | 19.8 ± 4.0 | 25.6 ± 5.1 | 30.3 ± 6.1 | – |
| NGC 4945 | – | 4.9 ± 0.7 | – | 194.4 ± 38.9 | 252.5 ± 50.5 | – |
| NGC 5128 | – | 372.2 ± 55.8 | – | 3526.2 ± 705.2 | 4095.3 ± 819.1 | – |
| NGC 5506 | – | 490.6 ± 73.6 | – | <3273.3 | <3960.9 | <3660 |
| NGC 6300 | 11.4 ± 1.7 | 28.1 ± 4.2 | 614.3 ± 112.9 | 1831.1 ± 366.2 | <2694.1 | – |
| NGC 6814 | 12.2 ± 1.8 | 15.5 ± 2.3 | – | 160 ± 32 | <249.7 | – |
| NGC 7172 | – | 41.8 ± 6.3 | – | 146.6 ± 29.3 | 166.3 ± 33.3 | – |
| NGC 7213 | – | 19.2 ± 2.9 | – | <386.6 | <389.7 | – |
| NGC 7314 | – | <21.5 | – | 180.8 ± 36.2 | 203.8 ± 40.8 | – |
| NGC 7582 | – | 27.3 ± 4.1 | – | 649.7 ± 129.9 | 923.8 ± 184.8 | – |
| UGC 6728 | 12.1 ± 1.8 | 14.7 ± 2.2 | 57.2 ± 11.4 | 54.5 ± 10.9 | 51.7 ± 10.3 | – |
aCorresponds to nuclear fluxes calculated at 28 |$\mu$|m instead of 30 |$\mu$|m. See Section 4.1 for further details.
Finally, we compiled N-band spectra (7.5–13 |$\mu$|m) for the majority of the sample (17/24 sources), which were obtained with different instruments (GTC/CC, VLT/VISIR, Gemini/T-ReCS, and MICHELLE). Details on these observations are given in Table 2, and we used the fully reduced and flux-calibrated spectra noted.
4 NUCLEAR IR SEDS
4.1 SED construction
To construct the entire nuclear IR SEDs sampling similar physical scales, we use NIR nuclear fluxes from our own GTC/CIRCE observations, HST archival data, or the highest angular resolution nuclear IR fluxes available in the literature. For those cases in which the angular resolution available is greater than 1 arcsec or there is evidence of a possible extra contribution from the host galaxy we used them as upper limits (see Table 2).
When available, we used the subarcsecond nuclear spectra extracted as a point source, resampling them to 50 points, following the same methodology as in previous works using N-band nuclear spectra and clumpy torus models (e.g. AH11; Ramos Almeida et al. 2014; García-Bernete et al. 2015). In general, there is a good agreement between the flux calibration of the nuclear spectra and the N-band nuclear fluxes. However, for consistency, we systematically scaled the spectra to the N-band nuclear fluxes, unless there is any evidence to discard them due to the possible contribution of either emission lines or PAH features in the specific spectral window of the filters (e.g. NGC 7582). We estimated a ∼15 per cent total uncertainty for the nuclear spectra by quadratically adding the errors in the flux calibration and point source extraction.
In addition, we estimated the AGN contribution at 5.5, 25, and 30 |$\mu$|m for all the galaxies based on spectral decomposition of Spitzer/IRS galaxies (see Table 4).3 To do so, we first scaled the AGN component to the N-band fluxes and then calculated homogeneous nuclear fluxes at 5.5, 25, and 30 |$\mu$|m using a 1 |$\mu$|m window in the scaled AGN component, using the same method as in GB16. We remark that when a specific rest-frame AGN template extends down to ∼4 |$\mu$|m, which occurs for roughly half of our sample (11/24 sources), we also derived the 4.5 |$\mu$|m nuclear fluxes (see Table 4). Finally, for those sources without Q-band (17–25 |$\mu$|m) photometry (e.g. NGC 4388), we calculated the 18 |$\mu$|m fluxes using the same methodology.
Five sources lack high angular resolution nuclear spectra (NGC 4395, NGC 6300, NGC 6814, NGC 7314, and ESO 005-G004). Nevertheless, we have high angular resolution photometry in the N and Q bands, and we then used the scaled AGN components derived from the IRS spectra to obtain N-band ‘pseudo-nuclear’ spectra (e.g. Hernán-Caballero et al. 2015). For consistency with the other 19 nuclear IR SEDs, we restricted the scaled AGN component to have the same wavelength range (7.5–13 |$\mu$|m) as the ground-based spectra and resampled to 50 points. Note that we also use the ‘pseudo-nuclear’ spectra for NGC 4138, NGC 4945, NGC 7172, and UGC 6728. In the case of NGC 4945 and NGC 7172, their nuclear spectra show a strong contribution from the host galaxy, while those of NGC 4138 and UGC 6728 are very noisy and practically identical in spectral shape to the AGN component.
4.2 SED observational properties
In Fig. 1, we present the nuclear IR SEDs (∼1–30 |$\mu$|m) of our sample of Seyfert galaxies. In these plots, we compare the spectral shapes and the average nuclear IR SEDs for the different Seyfert types considered in this study (Sy1, Sy1.8/1.9, and Sy2 galaxies). The average nuclear IR Sy1, Sy1.8/1.9, and Sy2 templates were constructed using the nuclear IR SEDs described in Section 4.1, but excluding the lowest angular resolution data (i.e. upper limits). For consistency, we used the same wavelength grid for all the photometry (1.6, 2.2, 5.5, 8.8, 18.0, 25.0, 30.0 |$\mu$|m). To do so, we performed a quadratic interpolation of nearby measurements for each galaxy. In this process, we avoid using L and M bands due to the large number of upper limits at these wavelengths. Note that we computed the interpolated fluxes for the sole purpose of deriving the average Seyfert templates. In addition, we used N-band spectra, either the subarcsecond angular resolution or the ‘pseudo-nuclear’ spectra (see Section 4.1).
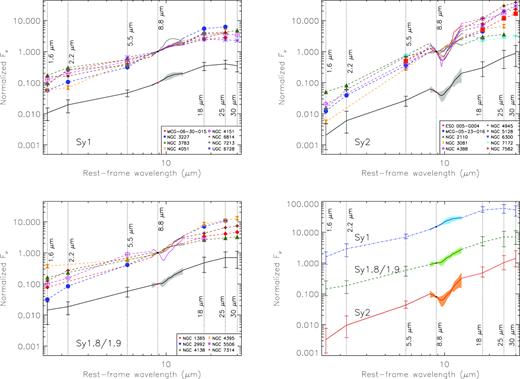
Observed nuclear IR SEDs for the Sy1, Sy1.8/1.9, and Sy2 galaxies in the BCS40 sample. Note that different colours and symbols correspond to the galaxies labelled in each panel. All SEDs have been normalized at 8.8 |$\mu$|m, and the average Sy1, Sy1.8/1.9, and Sy2 (black dashed line) have been shifted in the Y-axis for clarity. The error bars correspond to the standard deviation of each averaged point. Bottom-right panel: average Sy1, Sy1.8/1.9, and Sy2 nuclear IR SEDs. Blue dot–dashed, green dashed, and red solid lines correspond to the Sy1, Sy1.8/1.9, and Sy2 templates, respectively. The average SEDs have been shifted in the Y-axis.
We measured the NIR (1.6–8 |$\mu$|m), MIR (8–18 |$\mu$|m), and total IR (1.6–25 |$\mu$|m) spectral indices (fν α να), the H/N and N/Q flux ratios, and the strength of the silicate feature (9.7 |$\mu$|m) for each galaxy in the sample. We also repeated these measurements in the derived Sy1, Sy1.8/1.9, and Sy2 templates, which are representative of each group of SEDs (see Table 5). We find steeper IR slopes for Sy2 than for Sy1, and the Sy1.8/1.9 and Sy1 slopes are very similar. Steeper IR slopes for type 2 AGN have been previously reported in the literature for Seyfert galaxies (e.g. Alonso-Herrero et al. 2003, RA11 and references therein) and more luminous AGNs (e.g. Mateos et al. 2016). In addition, we measured practically the same MIR slopes for the three groups (αMIR ∼ −2) within the errors, in good agreement with the results reported by RA11. Following the same methodology as in RA09 and RA11, we also compare the spectral shapes of the different Seyfert types using the H/N and N/Q flux ratios. In agreement with the values reported by the latter authors, we found similar N/Q flux ratios (∼0.3–0.2). On the other hand, we found that Sy1 (0.11 ± 0.05) and Sy1.8/1.9 (0.15 ± 0.12) galaxies have slightly larger values of the H/N flux ratio than those of Sy2 (0.04 ± 0.05), but the values are consistent within the errors.
Spectral shape information of the nuclear IR SEDs. The strength of the 9.7 |$\mu$|m silicate feature is computed as SSil = ln (fcont/f9.7), where fcont and f9.7 are the flux densities of the continuum and the feature, which we measured at 9.7 |$\mu$|m.
| . | H/N . | N/Q . | αIR . | αNIR . | αMIR . | SSil . |
|---|---|---|---|---|---|---|
| . | 1.6/8.8 |$\mu$|m . | 8.8/18 |$\mu$|m . | 1.6–25 |$\mu$|m . | 1.6–8.0 |$\mu$|m . | 8–18 |$\mu$|m . | 9.7 |$\mu$|m . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| Average Sy1 | 0.11 ± 0.05 | 0.31 ± 0.08 | −1.4 ± 0.2 | −1.3 ± 0.3 | −1.7 ± 0.3 | 0.07 ± 0.14 |
| Average Sy1.8/1.9 | 0.15 ± 0.12 | 0.25 ± 0.11 | −1.5 ± 0.4 | −1.3 ± 0.5 | −1.9 ± 0.7 | −0.33 ± 0.45 |
| Average Sy2 | 0.04 ± 0.05 | 0.22 ± 0.13 | −2.0 ± 0.6 | −2.4 ± 0.6 | −1.8 ± 0.7 | −1.01 ± 0.65 |
| . | H/N . | N/Q . | αIR . | αNIR . | αMIR . | SSil . |
|---|---|---|---|---|---|---|
| . | 1.6/8.8 |$\mu$|m . | 8.8/18 |$\mu$|m . | 1.6–25 |$\mu$|m . | 1.6–8.0 |$\mu$|m . | 8–18 |$\mu$|m . | 9.7 |$\mu$|m . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| Average Sy1 | 0.11 ± 0.05 | 0.31 ± 0.08 | −1.4 ± 0.2 | −1.3 ± 0.3 | −1.7 ± 0.3 | 0.07 ± 0.14 |
| Average Sy1.8/1.9 | 0.15 ± 0.12 | 0.25 ± 0.11 | −1.5 ± 0.4 | −1.3 ± 0.5 | −1.9 ± 0.7 | −0.33 ± 0.45 |
| Average Sy2 | 0.04 ± 0.05 | 0.22 ± 0.13 | −2.0 ± 0.6 | −2.4 ± 0.6 | −1.8 ± 0.7 | −1.01 ± 0.65 |
Spectral shape information of the nuclear IR SEDs. The strength of the 9.7 |$\mu$|m silicate feature is computed as SSil = ln (fcont/f9.7), where fcont and f9.7 are the flux densities of the continuum and the feature, which we measured at 9.7 |$\mu$|m.
| . | H/N . | N/Q . | αIR . | αNIR . | αMIR . | SSil . |
|---|---|---|---|---|---|---|
| . | 1.6/8.8 |$\mu$|m . | 8.8/18 |$\mu$|m . | 1.6–25 |$\mu$|m . | 1.6–8.0 |$\mu$|m . | 8–18 |$\mu$|m . | 9.7 |$\mu$|m . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| Average Sy1 | 0.11 ± 0.05 | 0.31 ± 0.08 | −1.4 ± 0.2 | −1.3 ± 0.3 | −1.7 ± 0.3 | 0.07 ± 0.14 |
| Average Sy1.8/1.9 | 0.15 ± 0.12 | 0.25 ± 0.11 | −1.5 ± 0.4 | −1.3 ± 0.5 | −1.9 ± 0.7 | −0.33 ± 0.45 |
| Average Sy2 | 0.04 ± 0.05 | 0.22 ± 0.13 | −2.0 ± 0.6 | −2.4 ± 0.6 | −1.8 ± 0.7 | −1.01 ± 0.65 |
| . | H/N . | N/Q . | αIR . | αNIR . | αMIR . | SSil . |
|---|---|---|---|---|---|---|
| . | 1.6/8.8 |$\mu$|m . | 8.8/18 |$\mu$|m . | 1.6–25 |$\mu$|m . | 1.6–8.0 |$\mu$|m . | 8–18 |$\mu$|m . | 9.7 |$\mu$|m . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| Average Sy1 | 0.11 ± 0.05 | 0.31 ± 0.08 | −1.4 ± 0.2 | −1.3 ± 0.3 | −1.7 ± 0.3 | 0.07 ± 0.14 |
| Average Sy1.8/1.9 | 0.15 ± 0.12 | 0.25 ± 0.11 | −1.5 ± 0.4 | −1.3 ± 0.5 | −1.9 ± 0.7 | −0.33 ± 0.45 |
| Average Sy2 | 0.04 ± 0.05 | 0.22 ± 0.13 | −2.0 ± 0.6 | −2.4 ± 0.6 | −1.8 ± 0.7 | −1.01 ± 0.65 |
Taking advantage of the spectroscopy data, we compare the strength of the silicate feature (9.7 |$\mu$|m) for the different Seyfert types (see Table 5). The latter is computed as SSil = ln (fcont/f9.7), where fcont and f9.7 are the flux densities of the continuum and the feature, which we measured at 9.7 |$\mu$|m. As can be seen from the top-left panel of Fig. 1, the majority of the Sy1 galaxies show weak or moderate emission (SSil > 0; the only exception is NGC 3227, which has a value of −0.2 and it could be related to the emission of PAHs), whereas Sy1.8/1.9 and Sy2 galaxies have relatively deep silicate features (SSil = −0.3 and −1.0, respectively). This feature is normally observed in weak emission or absent in Sy1 and in shallow absorption in type 2 Seyfert galaxies when observed in subarcsecond resolution data (e.g. Alonso-Herrero et al. 2016, García-González et al. 2017 and references therein).
4.3 Accretion disc fitting
The NIR emission of AGN is mainly produced by the emission of very hot dust and the direct emission from the AGN (i.e. accretion disc) in the case of type 1s, although another important contribution can be stellar emission from the host galaxy. The contribution from the accretion disc declines with increasing wavelength. According to both theoretical models (e.g. Hubeny et al. 2001) and polarized light observations (e.g. Kishimoto et al. 2001) the NIR emission of the accretion disc can be explained by a power-law extension of the optical/UV spectrum to the NIR range. This power-law extrapolation is commonly used to fit the AGN direct emission in Seyfert 1 galaxies (e.g. Stalevski et al. 2012). However, the clumpy torus models of Nenkova et al. (2008a,b) assume a steep fall of the disc spectrum for wavelengths longer than 1 |$\mu$|m. We note that the CLUMPY models cannot reproduce the NIR bumps observed in the SEDs of some Sy1s (e.g. Mor, Netzer & Elitzur 2009; RA11; AH11). For example, Mateos et al. (2016) successfully reproduced the IR SEDs of a sample of X-ray selected quasars using a non-truncated disc component and the CLUMPY torus models.
In order to quantify the contribution from the accretion disc to the nuclear NIR emission, we follow the same procedure as described in Hernán-Caballero et al. (2016) using optical, NIR, and MIR photometry (see Tables 2, 4, and 6) to fit the accretion disc emission for all Sy1 galaxies4 in our sample. This method used a semi-empirical model consisting of a single template for the accretion disc and two blackbodies for the dust emission.
Accretion disc measurements derived from the fitting of Sy1s. Columns 2, 3, and 4 list the fractional contribution of the accretion disc component to the J-, H-, and K-band emission, respectively. References for the optical photometry: (a) Bentz et al. (2016a); (b) Muñoz Marín et al. (2007); (c) Ho & Peng (2001); (d) Prieto et al. (2010); (e) Bentz et al. (2013); (f) Lauer et al. (2005); (g) Bentz et al. (2016b). Note that for the average values we used only sources with subarcsecond resolution data.
| Name . | FJ . | FH . | FK . | Ref. . |
|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . |
| MCG-06-30-015 | 0.17 | 0.09 | 0.03 | a |
| NGC 3227 | 0.52 | 0.25 | 0.10 | b,c |
| NGC 3783 | 0.27 | 0.14 | 0.07 | d |
| NGC 4051 | 0.21 | 0.11 | 0.08 | c |
| NGC 4151 | 0.83 | 0.40 | 0.19 | c |
| NGC 6814 | 0.41 | 0.24 | 0.20 | e |
| NGC 7213 | 0.49 | 0.15 | 0.04 | f |
| UGC 6728 | 0.22a | 0.18a | 0.14a | h |
| Average Sy1 | 0.46 ± 0.28 | 0.23 ± 0.13 | 0.11 ± 0.05 | – |
| Name . | FJ . | FH . | FK . | Ref. . |
|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . |
| MCG-06-30-015 | 0.17 | 0.09 | 0.03 | a |
| NGC 3227 | 0.52 | 0.25 | 0.10 | b,c |
| NGC 3783 | 0.27 | 0.14 | 0.07 | d |
| NGC 4051 | 0.21 | 0.11 | 0.08 | c |
| NGC 4151 | 0.83 | 0.40 | 0.19 | c |
| NGC 6814 | 0.41 | 0.24 | 0.20 | e |
| NGC 7213 | 0.49 | 0.15 | 0.04 | f |
| UGC 6728 | 0.22a | 0.18a | 0.14a | h |
| Average Sy1 | 0.46 ± 0.28 | 0.23 ± 0.13 | 0.11 ± 0.05 | – |
aDerived from NIR upper limits.
Accretion disc measurements derived from the fitting of Sy1s. Columns 2, 3, and 4 list the fractional contribution of the accretion disc component to the J-, H-, and K-band emission, respectively. References for the optical photometry: (a) Bentz et al. (2016a); (b) Muñoz Marín et al. (2007); (c) Ho & Peng (2001); (d) Prieto et al. (2010); (e) Bentz et al. (2013); (f) Lauer et al. (2005); (g) Bentz et al. (2016b). Note that for the average values we used only sources with subarcsecond resolution data.
| Name . | FJ . | FH . | FK . | Ref. . |
|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . |
| MCG-06-30-015 | 0.17 | 0.09 | 0.03 | a |
| NGC 3227 | 0.52 | 0.25 | 0.10 | b,c |
| NGC 3783 | 0.27 | 0.14 | 0.07 | d |
| NGC 4051 | 0.21 | 0.11 | 0.08 | c |
| NGC 4151 | 0.83 | 0.40 | 0.19 | c |
| NGC 6814 | 0.41 | 0.24 | 0.20 | e |
| NGC 7213 | 0.49 | 0.15 | 0.04 | f |
| UGC 6728 | 0.22a | 0.18a | 0.14a | h |
| Average Sy1 | 0.46 ± 0.28 | 0.23 ± 0.13 | 0.11 ± 0.05 | – |
| Name . | FJ . | FH . | FK . | Ref. . |
|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . |
| MCG-06-30-015 | 0.17 | 0.09 | 0.03 | a |
| NGC 3227 | 0.52 | 0.25 | 0.10 | b,c |
| NGC 3783 | 0.27 | 0.14 | 0.07 | d |
| NGC 4051 | 0.21 | 0.11 | 0.08 | c |
| NGC 4151 | 0.83 | 0.40 | 0.19 | c |
| NGC 6814 | 0.41 | 0.24 | 0.20 | e |
| NGC 7213 | 0.49 | 0.15 | 0.04 | f |
| UGC 6728 | 0.22a | 0.18a | 0.14a | h |
| Average Sy1 | 0.46 ± 0.28 | 0.23 ± 0.13 | 0.11 ± 0.05 | – |
aDerived from NIR upper limits.
In Fig. 2, we present the fitting results and in Table 6 we list the fractional contribution of this component to the nuclear NIR emission. Using only the fits with subarcsecond resolution data, we find that the average contribution of the accretion disc to the J-, H-, and K-band emission are 46 ± 28, 23 ± 13, and 11 ± 5 per cent in ∼0.4 arcsec apertures, which are in good agreement with the values reported by Hernán-Caballero et al. (2016) for the rest-frame J, H, and Kband (48 ± 16, 27 ± 14, and 17 ± 1 per cent) using a sample of luminous quasars. We note that the largest contribution from the accretion disc to the NIR emission is found for NGC 4151. This is in agreement with previous works on this galaxy (e.g. Swain et al. 2003; Kishimoto et al. 2007; Riffel, Storchi-Bergmann & McGregor 2009).
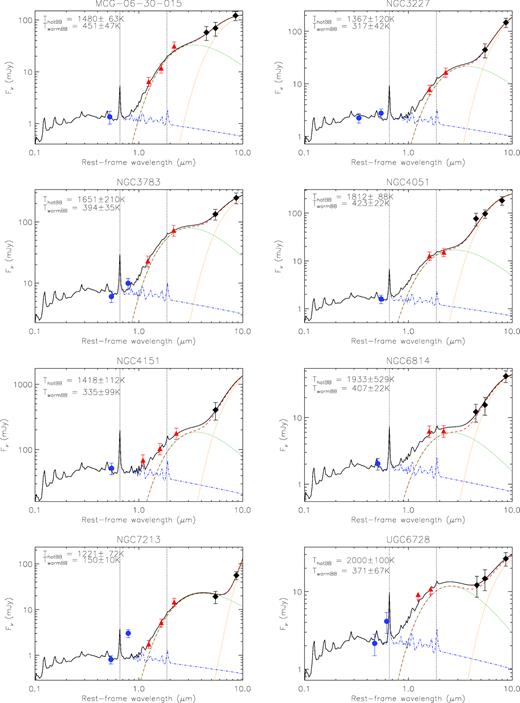
Accretion disc emission fits of Sy1s. Blue circles, red triangles, and black diamonds represent broadband photometry in the rest-frame optical, NIR, and MIR, respectively. We show the dust components (red dashed lines), accretion disc component (blue dot–dashed line) and best fits (black solid lines). Note that the dust component is modelled as a linear combination of two blackbodies at adjustable temperatures (green and orange dotted lines). The vertical dotted lines mark the rest-frame wavelength of Hα and Pa α.
Since we find a significant contribution of the accretion disc emission in the NIR range of Sy1, we subtracted this component in all Sy1 galaxies prior to fitting the nuclear IR SEDs with torus models.
4.4 SED modelling with the CLUMPY torus models
Using the CLUMPY models and BayesClumpy, we fit all the nuclear NIR-to-MIR SEDs in our sample (See Appendix A). A detailed description of the CLUMPY model parameters (see Table 8) can be found in Nenkova et al. (2008a,b). For approximately half of our sample (13/24 sources; see Table 7), we used Gaussian priors for σ (width of clouds angular distribution) based on the opening angle of the ionization cones from published [O III] and/or H α images or NLR kinematics modelling (see Table 7 for further details). In addition, we used the IR extinction curve of Chiar & Tielens (2006) of the local ISM to account for any possible foreground extinction from the host galaxy. This curve covers the range ∼1–35 |$\mu$|m and accounts for the two silicate features at 9.7 and 18 |$\mu$|m. We used different priors for the foreground extinction from the host galaxy (A|$_{V}^{for}$|) for the various Seyfert types, taking into account the values available in the literature (see Table 1). We used A|$_{V}^{for}$| = [0,2] mag for Sy1 and [0,8] mag for Sy1.8/1.9 and Sy2. Finally, we used uniform priors for the rest of the parameters. When the observed data introduce sufficient information into the fit, the resulting posteriors will clearly differ from the input uniform distributions, either showing trends or being centred at certain values within the considered intervals.
Constraints on the torus widths derived from ionization cone opening angles. References: (a) Mundell et al. (1995); (b) Fischer et al. (2013); (c) Müller-Sánchez et al. (2011); (d) Christopoulou et al. (1997); (e) Wilson & Tsvetanov (1994); (f) García-Lorenzo, Arribas & Mediavilla (2001); (g) Rosario et al. (2010); (h) Ferruit, Wilson & Mulchaey (2000); (i) Bryant & Hunstead (1999); (j) Wilson, Baldwin & Ulvestad (1985).
| Name . | σliterature . | Ref. . | Interval used . |
|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . |
| Sy1 galaxies | |||
| NGC 3227 | 55°–60° | a | [45°–65°] |
| NGC 3783 | 35°–56° | b, c | [35°–55°] |
| NGC 4051 | 67○a | d | [50°–70°] |
| NGC 4151 | 52°–62° | e | [45°–65°] |
| NGC 6814 | 43○a | c | [35°–55°] |
| Sy1.8/1.9 galaxies | |||
| NGC 1365 | 29°–49° | e | [30°–50°] |
| NGC 2992 | 25° | f | [15°–35°] |
| Sy2 galaxies | |||
| NGC 2110 | 45° | g | [35°–55°] |
| NGC 3081 | 75° | h | [50°–70°] |
| NGC 4388 | 65° | e | [50°–70°] |
| NGC 5128 | 55°–65○a | i | [50°–70°] |
| NGC 5506 | 45° | j | [35°–55°] |
| NGC 7582 | 42°–52° | e | [35°–55°] |
| Name . | σliterature . | Ref. . | Interval used . |
|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . |
| Sy1 galaxies | |||
| NGC 3227 | 55°–60° | a | [45°–65°] |
| NGC 3783 | 35°–56° | b, c | [35°–55°] |
| NGC 4051 | 67○a | d | [50°–70°] |
| NGC 4151 | 52°–62° | e | [45°–65°] |
| NGC 6814 | 43○a | c | [35°–55°] |
| Sy1.8/1.9 galaxies | |||
| NGC 1365 | 29°–49° | e | [30°–50°] |
| NGC 2992 | 25° | f | [15°–35°] |
| Sy2 galaxies | |||
| NGC 2110 | 45° | g | [35°–55°] |
| NGC 3081 | 75° | h | [50°–70°] |
| NGC 4388 | 65° | e | [50°–70°] |
| NGC 5128 | 55°–65○a | i | [50°–70°] |
| NGC 5506 | 45° | j | [35°–55°] |
| NGC 7582 | 42°–52° | e | [35°–55°] |
aDerived from NLR kinematics modelling.
Constraints on the torus widths derived from ionization cone opening angles. References: (a) Mundell et al. (1995); (b) Fischer et al. (2013); (c) Müller-Sánchez et al. (2011); (d) Christopoulou et al. (1997); (e) Wilson & Tsvetanov (1994); (f) García-Lorenzo, Arribas & Mediavilla (2001); (g) Rosario et al. (2010); (h) Ferruit, Wilson & Mulchaey (2000); (i) Bryant & Hunstead (1999); (j) Wilson, Baldwin & Ulvestad (1985).
| Name . | σliterature . | Ref. . | Interval used . |
|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . |
| Sy1 galaxies | |||
| NGC 3227 | 55°–60° | a | [45°–65°] |
| NGC 3783 | 35°–56° | b, c | [35°–55°] |
| NGC 4051 | 67○a | d | [50°–70°] |
| NGC 4151 | 52°–62° | e | [45°–65°] |
| NGC 6814 | 43○a | c | [35°–55°] |
| Sy1.8/1.9 galaxies | |||
| NGC 1365 | 29°–49° | e | [30°–50°] |
| NGC 2992 | 25° | f | [15°–35°] |
| Sy2 galaxies | |||
| NGC 2110 | 45° | g | [35°–55°] |
| NGC 3081 | 75° | h | [50°–70°] |
| NGC 4388 | 65° | e | [50°–70°] |
| NGC 5128 | 55°–65○a | i | [50°–70°] |
| NGC 5506 | 45° | j | [35°–55°] |
| NGC 7582 | 42°–52° | e | [35°–55°] |
| Name . | σliterature . | Ref. . | Interval used . |
|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . |
| Sy1 galaxies | |||
| NGC 3227 | 55°–60° | a | [45°–65°] |
| NGC 3783 | 35°–56° | b, c | [35°–55°] |
| NGC 4051 | 67○a | d | [50°–70°] |
| NGC 4151 | 52°–62° | e | [45°–65°] |
| NGC 6814 | 43○a | c | [35°–55°] |
| Sy1.8/1.9 galaxies | |||
| NGC 1365 | 29°–49° | e | [30°–50°] |
| NGC 2992 | 25° | f | [15°–35°] |
| Sy2 galaxies | |||
| NGC 2110 | 45° | g | [35°–55°] |
| NGC 3081 | 75° | h | [50°–70°] |
| NGC 4388 | 65° | e | [50°–70°] |
| NGC 5128 | 55°–65○a | i | [50°–70°] |
| NGC 5506 | 45° | j | [35°–55°] |
| NGC 7582 | 42°–52° | e | [35°–55°] |
aDerived from NLR kinematics modelling.
Clumpy torus model parameters. i = 0° is face-on and i = 90° is edge-on. We note that the foreground extinction is unrelated to the torus.
| Parameter . | Symbol . | Interval . |
|---|---|---|
| Radial extent of the torus | Y | [5, 100] |
| Width of clouds angular distribution | σ | [15°, 70°] |
| Number of clouds along an equatorial ray | N0 | [1, 15] |
| Index of the radial density profile | q | [0, 3] |
| Inclination angle of the torus | i | [0°, 90°] |
| Optical depth per single cloud | τV | [5, 150] |
| Foreground extinction | A|$_{V}^{for}$| | Sy1s: [0, 2] mag |
| Sy1.8/1.9/2s: [0, 8] mag | ||
| Parameter . | Symbol . | Interval . |
|---|---|---|
| Radial extent of the torus | Y | [5, 100] |
| Width of clouds angular distribution | σ | [15°, 70°] |
| Number of clouds along an equatorial ray | N0 | [1, 15] |
| Index of the radial density profile | q | [0, 3] |
| Inclination angle of the torus | i | [0°, 90°] |
| Optical depth per single cloud | τV | [5, 150] |
| Foreground extinction | A|$_{V}^{for}$| | Sy1s: [0, 2] mag |
| Sy1.8/1.9/2s: [0, 8] mag | ||
Clumpy torus model parameters. i = 0° is face-on and i = 90° is edge-on. We note that the foreground extinction is unrelated to the torus.
| Parameter . | Symbol . | Interval . |
|---|---|---|
| Radial extent of the torus | Y | [5, 100] |
| Width of clouds angular distribution | σ | [15°, 70°] |
| Number of clouds along an equatorial ray | N0 | [1, 15] |
| Index of the radial density profile | q | [0, 3] |
| Inclination angle of the torus | i | [0°, 90°] |
| Optical depth per single cloud | τV | [5, 150] |
| Foreground extinction | A|$_{V}^{for}$| | Sy1s: [0, 2] mag |
| Sy1.8/1.9/2s: [0, 8] mag | ||
| Parameter . | Symbol . | Interval . |
|---|---|---|
| Radial extent of the torus | Y | [5, 100] |
| Width of clouds angular distribution | σ | [15°, 70°] |
| Number of clouds along an equatorial ray | N0 | [1, 15] |
| Index of the radial density profile | q | [0, 3] |
| Inclination angle of the torus | i | [0°, 90°] |
| Optical depth per single cloud | τV | [5, 150] |
| Foreground extinction | A|$_{V}^{for}$| | Sy1s: [0, 2] mag |
| Sy1.8/1.9/2s: [0, 8] mag | ||
We note that for this study we used the updated version (2014 October) of the Nenkova et al. (2008a,b) clumpy torus models.5 Older versions of these models used the optical depth along the slab normal for the synthetic clouds. However, in a recent comparison with spherical clouds (3D radiative transfer), the calculations showed that the effective optical depth through a cloud was two times higher than in the former approach (Heymann, Nikutta, and Elitzur, in preparation). Although the absorption caused by clouds is not affected by this, the cloud emission does change since its source function is wavelength-dependent. As a consequence, a moderate change in the spectral shape has been reported on the CLUMPY webpage (less than 20 per cent at any given wavelength).
In Appendix A, we present the results of the nuclear IR SED fitting process with the CLUMPY models (see Section 4.4), which are the marginal posterior distributions of the six parameters that define these models plus the foreground extinction and vertical shift. This shift scales with the AGN bolometric luminosity. We can also translate the posterior distributions of the parameters into a best-fitting model described by the combination of parameters that maximizes the posterior (maximum-a-posteriori; MAP) and a median model, computed with the median value of each posterior (see Appendix A). We found different average models of each subgroup from the median fitted nuclear IR SEDs. The Sy1 average model including the accretion disc emission component (black dotted line of Fig. 3) shows a flat NIR slope and the shape for the Sy2 average model (red solid line of Fig. 3) is very steep. The Sy1.8/1.9 average model lies between those of the Sy1 and Sy2 models.
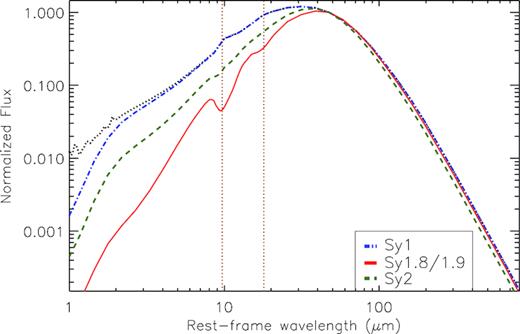
IR torus model emission as derived from the median-fitted nuclear IR SEDs. Blue dot–dashed, green dashed, and red solid lines represent the average of the median SEDs of Sy1, Sy1.8/1.9, and Sy2 galaxies, respectively. We plot the average median SEDs of Sy1 including the accretion disc emission, which corresponds as the black dotted line, for comparison. The SEDs are normalized at 50 |$\mu$|m. The brown vertical dotted lines correspond to silicate features.
In general, the CLUMPY models provide good fits (χ2/dof(degrees of freedom) < 2.0) to the majority (19/24) of the nuclear IR SEDs (see Appendix A). While the MIR emission is well fitted for practically all the SEDs, we found that 5/24 galaxies (i.e. NGC 3783, NGC 4395, NGC 5506, NGC 7172, and NGC 7314) show a clear excess of emission in the NIR. This likely indicates an extra hot dust component is needed to reproduce their IR SEDs (see also Mor et al. 2009). We note that the main goal of this work is to obtain a global statistical analysis of the clumpy torus model parameters of the various Seyfert galaxy types, rather than focusing on the individual fits (see Appendix A). As a sanity check, we repeated the analysis using only those galaxies with the best (χ2/dof < 1.0; ∼63 per cent of the sample) and good (χ2/dof < 2.0; ∼79 per cent of the sample) fits and we find the same results within 1σ.
5 COMPARISON OF THE TORUS PROPERTIES
In this section, we investigate the main differences between the clumpy torus model parameters for the BCS40 sample. Table 9 reports the main derived properties of the torus from the model parameters and the X-ray measurements for comparison.
AGN and torus model properties derived from the fits and X-ray properties. The torus model properties were derived from the median values of the marginal posterior distributions. Columns 2, 3, 4, 5, 6, and 7 list the AGN bolometric luminosity (L|$_{\mathrm{ bol}}^{\mathrm{ model}}$|), torus bolometric luminosity (L|$_{\mathrm{ bol}}^{\mathrm{ torus}}$|, obtained by integrating the corresponding model torus emission), torus gas mass (MTorus), torus outer radius (rTorus), escape probability (Pesc) and torus covering factor (CT) derived from the torus model. Note that median values are listed with their corresponding ±1σ values around the median. Columns 8, 9, and 10 correspond to the hydrogen column density, intrinsic 2–10 keV and absorption-corrected 14–195 keV X-ray luminosities taken from Ricci et al. (2017a). Columns 11 and 12 list the BH masses with their references and the derived Eddington Ratio following the same methodology as in Ricci et al. (2017b). References for MBH/M⊙: (a) this work; (b) Koss et al. (2017); (c) Vasudevan et al. (2010). See Appendix C for further information about the estimation of the BH masses.
| Name . | log(L|$_{\mathrm{ bol}}^{\mathrm{ model}}$|) . | log(L|$_{\mathrm{ bol}}^{\mathrm{ torus}}$|) . | MTorus . | rTorus . | Pesc . | CT . | log(N|$_{\textrm{H}}^{\mathrm{ X-rays}}$|) . | log(L|$_{\textrm{int}}^{2-10\, \textrm{keV}}$|) . | log(L|$_{\textrm{cor}}^{14-195\, \textrm{keV}}$|) . | log(MBH/M⊙) . | log(λEdd) . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (erg s−1) . | (erg s−1) . | (M⊙) . | (pc) . | (%) . | . | (cm−2) . | (erg s−1) . | (erg s−1) . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| Sy1 galaxies | |||||||||||
| MCG-06-30-015 | 43.33 | 43.02 | (0.2 ± 0.1) × 105 | 4.0|$\pm _{2.2}^{2.3}$| | 57|$\pm _{23}^{21}$| | 0.13|$\pm _{0.02}^{0.05}$| | 20.85 | 42.74 | 42.66 | 7.42 (a) | −1.52 |
| NGC 3227 | 42.91 | 43.08 | (1.1|$\pm _{0.3}^{0.6})\times 10^5$| | 1.2|$\pm _{0.2}^{0.3}$| | 24|$\pm _{6}^{12}$| | 0.86|$\pm _{0.07}^{0.04}$| | 20.95 | 42.10 | 42.58 | 6.62 (b) | −1.36 |
| NGC 3783 | 43.48 | 43.72 | (8.8|$\pm _{3.2}^{9.3})\times 10^5$| | 3.6|$\pm _{0.8}^{1.6}$| | 69|$\pm _{17}^{14}$| | 0.68|$\pm _{0.10}^{0.08}$| | 20.49 | 43.43 | 43.28 | 7.14 (a) | −0.55 |
| NGC 4051 | 42.59 | 42.72 | (0.3|$\pm _{0.1}^{0.9})\times 10^4$| | 0.3|$\pm _{0.1}^{0.5}$| | 31|$\pm _{13}^{17}$| | 0.80|$\pm _{0.06}^{0.05}$| | 20.00 | 41.33 | 41.47 | 5.60 (b) | −1.11 |
| NGC 4151 | 43.49 | 43.71 | (7.5|$\pm _{2.3}^{2.4})\times 10^5$| | 3.3|$\pm _{0.6}^{0.5}$| | 71|$\pm _{9}^{7}$| | 0.73|$\pm _{0.05}^{0.04}$| | 22.71 | 42.31 | 43.43 | 7.43 (a) | −1.96 |
| NGC 6814 | 42.40 | 42.56 | (1.9|$\pm _{1.2}^{7.0})\times 10^5$| | 2.1|$\pm _{0.8}^{2.6}$| | 80|$\pm _{22}^{12}$| | 0.51|$\pm _{0.12}^{0.10}$| | 20.97 | 42.31 | 42.80 | 6.46 (b) | −0.99 |
| NGC 7213 | 43.96 | 42.82 | (1.1|$\pm _{0.5}^{1.1})\times 10^5$| | 1.9|$\pm _{0.4}^{0.8}$| | 100 | 0.12|$\pm _{0.01}^{0.03}$| | 20.00 | 41.95 | 42.54 | 7.37 (c) | −2.26 |
| UGC 6728 | 42.40 | 43.39 | (0.4|$\pm _{0.3}^{0.5})\times 10^5$| | 2.8|$\pm _{1.5}^{1.7}$| | 24|$\pm _{20}^{49}$| | 0.58|$\pm _{0.27}^{0.19}$| | 20.00 | 41.80 | 42.44 | 5.32 (b) | −0.36 |
| Sy1.8/1.9 galaxies | |||||||||||
| NGC 1365 | 42.83 | 42.95 | (2.5|$\pm _{1.2}^{5.9})\times 10^5$| | 2.1|$\pm _{0.6}^{1.9}$| | 60|$\pm _{19}^{23}$| | 0.46|$\pm _{0.06}^{0.13}$| | 22.21 | 42.32 | 42.69 | 7.92 (a) | −2.44 |
| NGC 2992 | 43.57 | 43.32 | (1.2|$\pm _{0.5}^{1.4})\times 10^5$| | 1.9|$\pm _{0.5}^{1.1}$| | 0.7|$\pm _{0.5}^{0.8}$| | 0.46|$\pm _{0.07}^{0.05}$| | 21.72 | 42.00 | 42.53 | 5.42 (b) | −0.26 |
| NGC 4138 | 41.92 | 41.67 | (0.6|$\pm _{0.4}^{1.2})\times 10^4$| | 0.9|$\pm _{0.5}^{0.8}$| | 81|$\pm _{32}^{17}$| | 0.18|$\pm _{0.06}^{0.12}$| | 22.89 | 41.23 | 41.59 | 7.30 (b) | −2.91 |
| NGC 4395 | 39.98 | 39.97 | (0.2|$\pm _{0.1}^{0.3})\times 10^4$| | 0.2|$\pm _{0.1}^{0.2}$| | 0.4|$\pm _{0.3}^{0.4}$| | 0.74|$\pm _{0.22}^{0.16}$| | 21.04 | 40.50 | 40.63 | 4.88 (a) | −1.22 |
| NGC 5506 | 43.86 | 43.94 | (7.6|$\pm _{1.3}^{2.6})\times 10^5$| | 3.8|$\pm _{0.3}^{0.6}$| | 30|$\pm _{10}^{9}$| | 0.91|$\pm _{0.02}^{0.01}$| | 22.44 | 42.99 | 43.44 | 8.29 (a) | −2.14 |
| NGC 7314 | 42.26 | 42.40 | (1.4|$\pm _{0.5}^{2.4})\times 10^5$| | 1.3|$\pm _{0.3}^{0.9}$| | 33|$\pm _{13}^{16}$| | 0.84|$\pm _{0.31}^{0.05}$| | 21.60 | 42.33 | 42.44 | 7.24 (b) | −1.75 |
| Sy2 galaxies | |||||||||||
| ESO 005-G004 | 42.43 | 42.22 | (0.9|$\pm _{0.2}^{0.3})\times 10^5$| | 1.5|$\pm _{0.2}^{0.3}$| | 0.002|$\pm _{0.002}^{0.001}$| | 0.95|$\pm _{0.06}^{0.03}$| | 24.34 | 42.78 | 42.74 | 6.98 (c) | −1.04 |
| MCG-05-23-016 | 43.75 | 43.73 | (3.2|$\pm _{1.6}^{8.7})\times 10^5$| | 3.5|$\pm _{1.2}^{4.4}$| | 8|$\pm _{6}^{17}$| | 0.80|$\pm _{0.16}^{0.08}$| | 22.18 | 43.20 | 43.43 | 7.98 (a) | −1.62 |
| NGC 2110 | 43.28 | 43.37 | (3.9|$\pm _{2.3}^{11.3})\times 10^5$| | 4.5|$\pm _{1.9}^{5.7}$| | 54 ± 26 | 0.55|$\pm _{0.07}^{0.10}$| | 22.94 | 42.69 | 43.49 | 9.25 (b) | −3.40 |
| NGC 3081 | 43.15 | 43.10 | (6.6|$\pm _{2.7}^{2.4})\times 10^5$| | 13.5|$\pm _{5.6}^{5.2}$| | 0.4 ± 0.3 | 0.95|$\pm _{0.06}^{0.02}$| | 23.91 | 42.72 | 43.60 | 8.41 (b) | −2.53 |
| NGC 4388 | 43.04 | 42.97 | (1.6|$\pm _{0.2}^{0.3})\times 10^6$| | 4.8 ± 0.4 | 0.6|$\pm _{0.1}^{0.2}$| | 0.99|$\pm _{0.002}^{0.001}$| | 23.52 | 43.05 | 43.47 | 6.99 (b) | −0.78 |
| NGC 4945 | 41.05 | 40.86 | (1.3|$\pm _{0.4}^{1.4})\times 10^5$| | 2.2|$\pm _{0.4}^{1.0}$| | 0.001|$\pm _{0.001}^{0.007}$| | 0.97|$\pm _{0.03}^{0.02}$| | 24.80 | 42.69 | 42.53 | 7.78 (a) | −1.93 |
| NGC 5128 | 42.27 | 42.28 | (1.7|$\pm _{0.4}^{0.6})\times 10^5$| | 2.1 ± 0.3 | 10|$\pm _{3}^{6}$| | 0.94|$\pm _{0.02}^{0.01}$| | 23.02 | 42.39 | 43.09 | 7.94 (a) | −2.39 |
| NGC 6300 | 43.00 | 43.05 | (5.4|$\pm _{1.7}^{2.8})\times 10^5$| | 2.7|$\pm _{0.5}^{0.6}$| | 0.9|$\pm _{0.3}^{0.7}$| | 0.99|$\pm _{0.002}^{0.001}$| | 23.31 | 41.84 | 42.43 | 7.01 (a) | −2.01 |
| NGC 7172 | 42.91 | 42.91 | (1.0|$\pm _{0.3}^{0.7})\times 10^5$| | 2.1|$\pm _{0.4}^{0.6}$| | 5|$\pm _{5}^{10}$| | 0.98|$\pm _{0.03}^{0.02}$| | 22.91 | 42.76 | 43.36 | 8.45 (b) | −2.53 |
| NGC 7582 | 43.08 | 42.81 | (1.2|$\pm _{0.5}^{0.7})\times 10^6$| | 9.4|$\pm _{2.4}^{3.0}$| | 0.003|$\pm _{0.003}^{0.02}$| | 0.83|$\pm _{0.08}^{0.05}$| | 24.33 | 42.86 | 43.28 | 7.52 (a) | −1.50 |
| Name . | log(L|$_{\mathrm{ bol}}^{\mathrm{ model}}$|) . | log(L|$_{\mathrm{ bol}}^{\mathrm{ torus}}$|) . | MTorus . | rTorus . | Pesc . | CT . | log(N|$_{\textrm{H}}^{\mathrm{ X-rays}}$|) . | log(L|$_{\textrm{int}}^{2-10\, \textrm{keV}}$|) . | log(L|$_{\textrm{cor}}^{14-195\, \textrm{keV}}$|) . | log(MBH/M⊙) . | log(λEdd) . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (erg s−1) . | (erg s−1) . | (M⊙) . | (pc) . | (%) . | . | (cm−2) . | (erg s−1) . | (erg s−1) . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| Sy1 galaxies | |||||||||||
| MCG-06-30-015 | 43.33 | 43.02 | (0.2 ± 0.1) × 105 | 4.0|$\pm _{2.2}^{2.3}$| | 57|$\pm _{23}^{21}$| | 0.13|$\pm _{0.02}^{0.05}$| | 20.85 | 42.74 | 42.66 | 7.42 (a) | −1.52 |
| NGC 3227 | 42.91 | 43.08 | (1.1|$\pm _{0.3}^{0.6})\times 10^5$| | 1.2|$\pm _{0.2}^{0.3}$| | 24|$\pm _{6}^{12}$| | 0.86|$\pm _{0.07}^{0.04}$| | 20.95 | 42.10 | 42.58 | 6.62 (b) | −1.36 |
| NGC 3783 | 43.48 | 43.72 | (8.8|$\pm _{3.2}^{9.3})\times 10^5$| | 3.6|$\pm _{0.8}^{1.6}$| | 69|$\pm _{17}^{14}$| | 0.68|$\pm _{0.10}^{0.08}$| | 20.49 | 43.43 | 43.28 | 7.14 (a) | −0.55 |
| NGC 4051 | 42.59 | 42.72 | (0.3|$\pm _{0.1}^{0.9})\times 10^4$| | 0.3|$\pm _{0.1}^{0.5}$| | 31|$\pm _{13}^{17}$| | 0.80|$\pm _{0.06}^{0.05}$| | 20.00 | 41.33 | 41.47 | 5.60 (b) | −1.11 |
| NGC 4151 | 43.49 | 43.71 | (7.5|$\pm _{2.3}^{2.4})\times 10^5$| | 3.3|$\pm _{0.6}^{0.5}$| | 71|$\pm _{9}^{7}$| | 0.73|$\pm _{0.05}^{0.04}$| | 22.71 | 42.31 | 43.43 | 7.43 (a) | −1.96 |
| NGC 6814 | 42.40 | 42.56 | (1.9|$\pm _{1.2}^{7.0})\times 10^5$| | 2.1|$\pm _{0.8}^{2.6}$| | 80|$\pm _{22}^{12}$| | 0.51|$\pm _{0.12}^{0.10}$| | 20.97 | 42.31 | 42.80 | 6.46 (b) | −0.99 |
| NGC 7213 | 43.96 | 42.82 | (1.1|$\pm _{0.5}^{1.1})\times 10^5$| | 1.9|$\pm _{0.4}^{0.8}$| | 100 | 0.12|$\pm _{0.01}^{0.03}$| | 20.00 | 41.95 | 42.54 | 7.37 (c) | −2.26 |
| UGC 6728 | 42.40 | 43.39 | (0.4|$\pm _{0.3}^{0.5})\times 10^5$| | 2.8|$\pm _{1.5}^{1.7}$| | 24|$\pm _{20}^{49}$| | 0.58|$\pm _{0.27}^{0.19}$| | 20.00 | 41.80 | 42.44 | 5.32 (b) | −0.36 |
| Sy1.8/1.9 galaxies | |||||||||||
| NGC 1365 | 42.83 | 42.95 | (2.5|$\pm _{1.2}^{5.9})\times 10^5$| | 2.1|$\pm _{0.6}^{1.9}$| | 60|$\pm _{19}^{23}$| | 0.46|$\pm _{0.06}^{0.13}$| | 22.21 | 42.32 | 42.69 | 7.92 (a) | −2.44 |
| NGC 2992 | 43.57 | 43.32 | (1.2|$\pm _{0.5}^{1.4})\times 10^5$| | 1.9|$\pm _{0.5}^{1.1}$| | 0.7|$\pm _{0.5}^{0.8}$| | 0.46|$\pm _{0.07}^{0.05}$| | 21.72 | 42.00 | 42.53 | 5.42 (b) | −0.26 |
| NGC 4138 | 41.92 | 41.67 | (0.6|$\pm _{0.4}^{1.2})\times 10^4$| | 0.9|$\pm _{0.5}^{0.8}$| | 81|$\pm _{32}^{17}$| | 0.18|$\pm _{0.06}^{0.12}$| | 22.89 | 41.23 | 41.59 | 7.30 (b) | −2.91 |
| NGC 4395 | 39.98 | 39.97 | (0.2|$\pm _{0.1}^{0.3})\times 10^4$| | 0.2|$\pm _{0.1}^{0.2}$| | 0.4|$\pm _{0.3}^{0.4}$| | 0.74|$\pm _{0.22}^{0.16}$| | 21.04 | 40.50 | 40.63 | 4.88 (a) | −1.22 |
| NGC 5506 | 43.86 | 43.94 | (7.6|$\pm _{1.3}^{2.6})\times 10^5$| | 3.8|$\pm _{0.3}^{0.6}$| | 30|$\pm _{10}^{9}$| | 0.91|$\pm _{0.02}^{0.01}$| | 22.44 | 42.99 | 43.44 | 8.29 (a) | −2.14 |
| NGC 7314 | 42.26 | 42.40 | (1.4|$\pm _{0.5}^{2.4})\times 10^5$| | 1.3|$\pm _{0.3}^{0.9}$| | 33|$\pm _{13}^{16}$| | 0.84|$\pm _{0.31}^{0.05}$| | 21.60 | 42.33 | 42.44 | 7.24 (b) | −1.75 |
| Sy2 galaxies | |||||||||||
| ESO 005-G004 | 42.43 | 42.22 | (0.9|$\pm _{0.2}^{0.3})\times 10^5$| | 1.5|$\pm _{0.2}^{0.3}$| | 0.002|$\pm _{0.002}^{0.001}$| | 0.95|$\pm _{0.06}^{0.03}$| | 24.34 | 42.78 | 42.74 | 6.98 (c) | −1.04 |
| MCG-05-23-016 | 43.75 | 43.73 | (3.2|$\pm _{1.6}^{8.7})\times 10^5$| | 3.5|$\pm _{1.2}^{4.4}$| | 8|$\pm _{6}^{17}$| | 0.80|$\pm _{0.16}^{0.08}$| | 22.18 | 43.20 | 43.43 | 7.98 (a) | −1.62 |
| NGC 2110 | 43.28 | 43.37 | (3.9|$\pm _{2.3}^{11.3})\times 10^5$| | 4.5|$\pm _{1.9}^{5.7}$| | 54 ± 26 | 0.55|$\pm _{0.07}^{0.10}$| | 22.94 | 42.69 | 43.49 | 9.25 (b) | −3.40 |
| NGC 3081 | 43.15 | 43.10 | (6.6|$\pm _{2.7}^{2.4})\times 10^5$| | 13.5|$\pm _{5.6}^{5.2}$| | 0.4 ± 0.3 | 0.95|$\pm _{0.06}^{0.02}$| | 23.91 | 42.72 | 43.60 | 8.41 (b) | −2.53 |
| NGC 4388 | 43.04 | 42.97 | (1.6|$\pm _{0.2}^{0.3})\times 10^6$| | 4.8 ± 0.4 | 0.6|$\pm _{0.1}^{0.2}$| | 0.99|$\pm _{0.002}^{0.001}$| | 23.52 | 43.05 | 43.47 | 6.99 (b) | −0.78 |
| NGC 4945 | 41.05 | 40.86 | (1.3|$\pm _{0.4}^{1.4})\times 10^5$| | 2.2|$\pm _{0.4}^{1.0}$| | 0.001|$\pm _{0.001}^{0.007}$| | 0.97|$\pm _{0.03}^{0.02}$| | 24.80 | 42.69 | 42.53 | 7.78 (a) | −1.93 |
| NGC 5128 | 42.27 | 42.28 | (1.7|$\pm _{0.4}^{0.6})\times 10^5$| | 2.1 ± 0.3 | 10|$\pm _{3}^{6}$| | 0.94|$\pm _{0.02}^{0.01}$| | 23.02 | 42.39 | 43.09 | 7.94 (a) | −2.39 |
| NGC 6300 | 43.00 | 43.05 | (5.4|$\pm _{1.7}^{2.8})\times 10^5$| | 2.7|$\pm _{0.5}^{0.6}$| | 0.9|$\pm _{0.3}^{0.7}$| | 0.99|$\pm _{0.002}^{0.001}$| | 23.31 | 41.84 | 42.43 | 7.01 (a) | −2.01 |
| NGC 7172 | 42.91 | 42.91 | (1.0|$\pm _{0.3}^{0.7})\times 10^5$| | 2.1|$\pm _{0.4}^{0.6}$| | 5|$\pm _{5}^{10}$| | 0.98|$\pm _{0.03}^{0.02}$| | 22.91 | 42.76 | 43.36 | 8.45 (b) | −2.53 |
| NGC 7582 | 43.08 | 42.81 | (1.2|$\pm _{0.5}^{0.7})\times 10^6$| | 9.4|$\pm _{2.4}^{3.0}$| | 0.003|$\pm _{0.003}^{0.02}$| | 0.83|$\pm _{0.08}^{0.05}$| | 24.33 | 42.86 | 43.28 | 7.52 (a) | −1.50 |
AGN and torus model properties derived from the fits and X-ray properties. The torus model properties were derived from the median values of the marginal posterior distributions. Columns 2, 3, 4, 5, 6, and 7 list the AGN bolometric luminosity (L|$_{\mathrm{ bol}}^{\mathrm{ model}}$|), torus bolometric luminosity (L|$_{\mathrm{ bol}}^{\mathrm{ torus}}$|, obtained by integrating the corresponding model torus emission), torus gas mass (MTorus), torus outer radius (rTorus), escape probability (Pesc) and torus covering factor (CT) derived from the torus model. Note that median values are listed with their corresponding ±1σ values around the median. Columns 8, 9, and 10 correspond to the hydrogen column density, intrinsic 2–10 keV and absorption-corrected 14–195 keV X-ray luminosities taken from Ricci et al. (2017a). Columns 11 and 12 list the BH masses with their references and the derived Eddington Ratio following the same methodology as in Ricci et al. (2017b). References for MBH/M⊙: (a) this work; (b) Koss et al. (2017); (c) Vasudevan et al. (2010). See Appendix C for further information about the estimation of the BH masses.
| Name . | log(L|$_{\mathrm{ bol}}^{\mathrm{ model}}$|) . | log(L|$_{\mathrm{ bol}}^{\mathrm{ torus}}$|) . | MTorus . | rTorus . | Pesc . | CT . | log(N|$_{\textrm{H}}^{\mathrm{ X-rays}}$|) . | log(L|$_{\textrm{int}}^{2-10\, \textrm{keV}}$|) . | log(L|$_{\textrm{cor}}^{14-195\, \textrm{keV}}$|) . | log(MBH/M⊙) . | log(λEdd) . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (erg s−1) . | (erg s−1) . | (M⊙) . | (pc) . | (%) . | . | (cm−2) . | (erg s−1) . | (erg s−1) . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| Sy1 galaxies | |||||||||||
| MCG-06-30-015 | 43.33 | 43.02 | (0.2 ± 0.1) × 105 | 4.0|$\pm _{2.2}^{2.3}$| | 57|$\pm _{23}^{21}$| | 0.13|$\pm _{0.02}^{0.05}$| | 20.85 | 42.74 | 42.66 | 7.42 (a) | −1.52 |
| NGC 3227 | 42.91 | 43.08 | (1.1|$\pm _{0.3}^{0.6})\times 10^5$| | 1.2|$\pm _{0.2}^{0.3}$| | 24|$\pm _{6}^{12}$| | 0.86|$\pm _{0.07}^{0.04}$| | 20.95 | 42.10 | 42.58 | 6.62 (b) | −1.36 |
| NGC 3783 | 43.48 | 43.72 | (8.8|$\pm _{3.2}^{9.3})\times 10^5$| | 3.6|$\pm _{0.8}^{1.6}$| | 69|$\pm _{17}^{14}$| | 0.68|$\pm _{0.10}^{0.08}$| | 20.49 | 43.43 | 43.28 | 7.14 (a) | −0.55 |
| NGC 4051 | 42.59 | 42.72 | (0.3|$\pm _{0.1}^{0.9})\times 10^4$| | 0.3|$\pm _{0.1}^{0.5}$| | 31|$\pm _{13}^{17}$| | 0.80|$\pm _{0.06}^{0.05}$| | 20.00 | 41.33 | 41.47 | 5.60 (b) | −1.11 |
| NGC 4151 | 43.49 | 43.71 | (7.5|$\pm _{2.3}^{2.4})\times 10^5$| | 3.3|$\pm _{0.6}^{0.5}$| | 71|$\pm _{9}^{7}$| | 0.73|$\pm _{0.05}^{0.04}$| | 22.71 | 42.31 | 43.43 | 7.43 (a) | −1.96 |
| NGC 6814 | 42.40 | 42.56 | (1.9|$\pm _{1.2}^{7.0})\times 10^5$| | 2.1|$\pm _{0.8}^{2.6}$| | 80|$\pm _{22}^{12}$| | 0.51|$\pm _{0.12}^{0.10}$| | 20.97 | 42.31 | 42.80 | 6.46 (b) | −0.99 |
| NGC 7213 | 43.96 | 42.82 | (1.1|$\pm _{0.5}^{1.1})\times 10^5$| | 1.9|$\pm _{0.4}^{0.8}$| | 100 | 0.12|$\pm _{0.01}^{0.03}$| | 20.00 | 41.95 | 42.54 | 7.37 (c) | −2.26 |
| UGC 6728 | 42.40 | 43.39 | (0.4|$\pm _{0.3}^{0.5})\times 10^5$| | 2.8|$\pm _{1.5}^{1.7}$| | 24|$\pm _{20}^{49}$| | 0.58|$\pm _{0.27}^{0.19}$| | 20.00 | 41.80 | 42.44 | 5.32 (b) | −0.36 |
| Sy1.8/1.9 galaxies | |||||||||||
| NGC 1365 | 42.83 | 42.95 | (2.5|$\pm _{1.2}^{5.9})\times 10^5$| | 2.1|$\pm _{0.6}^{1.9}$| | 60|$\pm _{19}^{23}$| | 0.46|$\pm _{0.06}^{0.13}$| | 22.21 | 42.32 | 42.69 | 7.92 (a) | −2.44 |
| NGC 2992 | 43.57 | 43.32 | (1.2|$\pm _{0.5}^{1.4})\times 10^5$| | 1.9|$\pm _{0.5}^{1.1}$| | 0.7|$\pm _{0.5}^{0.8}$| | 0.46|$\pm _{0.07}^{0.05}$| | 21.72 | 42.00 | 42.53 | 5.42 (b) | −0.26 |
| NGC 4138 | 41.92 | 41.67 | (0.6|$\pm _{0.4}^{1.2})\times 10^4$| | 0.9|$\pm _{0.5}^{0.8}$| | 81|$\pm _{32}^{17}$| | 0.18|$\pm _{0.06}^{0.12}$| | 22.89 | 41.23 | 41.59 | 7.30 (b) | −2.91 |
| NGC 4395 | 39.98 | 39.97 | (0.2|$\pm _{0.1}^{0.3})\times 10^4$| | 0.2|$\pm _{0.1}^{0.2}$| | 0.4|$\pm _{0.3}^{0.4}$| | 0.74|$\pm _{0.22}^{0.16}$| | 21.04 | 40.50 | 40.63 | 4.88 (a) | −1.22 |
| NGC 5506 | 43.86 | 43.94 | (7.6|$\pm _{1.3}^{2.6})\times 10^5$| | 3.8|$\pm _{0.3}^{0.6}$| | 30|$\pm _{10}^{9}$| | 0.91|$\pm _{0.02}^{0.01}$| | 22.44 | 42.99 | 43.44 | 8.29 (a) | −2.14 |
| NGC 7314 | 42.26 | 42.40 | (1.4|$\pm _{0.5}^{2.4})\times 10^5$| | 1.3|$\pm _{0.3}^{0.9}$| | 33|$\pm _{13}^{16}$| | 0.84|$\pm _{0.31}^{0.05}$| | 21.60 | 42.33 | 42.44 | 7.24 (b) | −1.75 |
| Sy2 galaxies | |||||||||||
| ESO 005-G004 | 42.43 | 42.22 | (0.9|$\pm _{0.2}^{0.3})\times 10^5$| | 1.5|$\pm _{0.2}^{0.3}$| | 0.002|$\pm _{0.002}^{0.001}$| | 0.95|$\pm _{0.06}^{0.03}$| | 24.34 | 42.78 | 42.74 | 6.98 (c) | −1.04 |
| MCG-05-23-016 | 43.75 | 43.73 | (3.2|$\pm _{1.6}^{8.7})\times 10^5$| | 3.5|$\pm _{1.2}^{4.4}$| | 8|$\pm _{6}^{17}$| | 0.80|$\pm _{0.16}^{0.08}$| | 22.18 | 43.20 | 43.43 | 7.98 (a) | −1.62 |
| NGC 2110 | 43.28 | 43.37 | (3.9|$\pm _{2.3}^{11.3})\times 10^5$| | 4.5|$\pm _{1.9}^{5.7}$| | 54 ± 26 | 0.55|$\pm _{0.07}^{0.10}$| | 22.94 | 42.69 | 43.49 | 9.25 (b) | −3.40 |
| NGC 3081 | 43.15 | 43.10 | (6.6|$\pm _{2.7}^{2.4})\times 10^5$| | 13.5|$\pm _{5.6}^{5.2}$| | 0.4 ± 0.3 | 0.95|$\pm _{0.06}^{0.02}$| | 23.91 | 42.72 | 43.60 | 8.41 (b) | −2.53 |
| NGC 4388 | 43.04 | 42.97 | (1.6|$\pm _{0.2}^{0.3})\times 10^6$| | 4.8 ± 0.4 | 0.6|$\pm _{0.1}^{0.2}$| | 0.99|$\pm _{0.002}^{0.001}$| | 23.52 | 43.05 | 43.47 | 6.99 (b) | −0.78 |
| NGC 4945 | 41.05 | 40.86 | (1.3|$\pm _{0.4}^{1.4})\times 10^5$| | 2.2|$\pm _{0.4}^{1.0}$| | 0.001|$\pm _{0.001}^{0.007}$| | 0.97|$\pm _{0.03}^{0.02}$| | 24.80 | 42.69 | 42.53 | 7.78 (a) | −1.93 |
| NGC 5128 | 42.27 | 42.28 | (1.7|$\pm _{0.4}^{0.6})\times 10^5$| | 2.1 ± 0.3 | 10|$\pm _{3}^{6}$| | 0.94|$\pm _{0.02}^{0.01}$| | 23.02 | 42.39 | 43.09 | 7.94 (a) | −2.39 |
| NGC 6300 | 43.00 | 43.05 | (5.4|$\pm _{1.7}^{2.8})\times 10^5$| | 2.7|$\pm _{0.5}^{0.6}$| | 0.9|$\pm _{0.3}^{0.7}$| | 0.99|$\pm _{0.002}^{0.001}$| | 23.31 | 41.84 | 42.43 | 7.01 (a) | −2.01 |
| NGC 7172 | 42.91 | 42.91 | (1.0|$\pm _{0.3}^{0.7})\times 10^5$| | 2.1|$\pm _{0.4}^{0.6}$| | 5|$\pm _{5}^{10}$| | 0.98|$\pm _{0.03}^{0.02}$| | 22.91 | 42.76 | 43.36 | 8.45 (b) | −2.53 |
| NGC 7582 | 43.08 | 42.81 | (1.2|$\pm _{0.5}^{0.7})\times 10^6$| | 9.4|$\pm _{2.4}^{3.0}$| | 0.003|$\pm _{0.003}^{0.02}$| | 0.83|$\pm _{0.08}^{0.05}$| | 24.33 | 42.86 | 43.28 | 7.52 (a) | −1.50 |
| Name . | log(L|$_{\mathrm{ bol}}^{\mathrm{ model}}$|) . | log(L|$_{\mathrm{ bol}}^{\mathrm{ torus}}$|) . | MTorus . | rTorus . | Pesc . | CT . | log(N|$_{\textrm{H}}^{\mathrm{ X-rays}}$|) . | log(L|$_{\textrm{int}}^{2-10\, \textrm{keV}}$|) . | log(L|$_{\textrm{cor}}^{14-195\, \textrm{keV}}$|) . | log(MBH/M⊙) . | log(λEdd) . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (erg s−1) . | (erg s−1) . | (M⊙) . | (pc) . | (%) . | . | (cm−2) . | (erg s−1) . | (erg s−1) . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| Sy1 galaxies | |||||||||||
| MCG-06-30-015 | 43.33 | 43.02 | (0.2 ± 0.1) × 105 | 4.0|$\pm _{2.2}^{2.3}$| | 57|$\pm _{23}^{21}$| | 0.13|$\pm _{0.02}^{0.05}$| | 20.85 | 42.74 | 42.66 | 7.42 (a) | −1.52 |
| NGC 3227 | 42.91 | 43.08 | (1.1|$\pm _{0.3}^{0.6})\times 10^5$| | 1.2|$\pm _{0.2}^{0.3}$| | 24|$\pm _{6}^{12}$| | 0.86|$\pm _{0.07}^{0.04}$| | 20.95 | 42.10 | 42.58 | 6.62 (b) | −1.36 |
| NGC 3783 | 43.48 | 43.72 | (8.8|$\pm _{3.2}^{9.3})\times 10^5$| | 3.6|$\pm _{0.8}^{1.6}$| | 69|$\pm _{17}^{14}$| | 0.68|$\pm _{0.10}^{0.08}$| | 20.49 | 43.43 | 43.28 | 7.14 (a) | −0.55 |
| NGC 4051 | 42.59 | 42.72 | (0.3|$\pm _{0.1}^{0.9})\times 10^4$| | 0.3|$\pm _{0.1}^{0.5}$| | 31|$\pm _{13}^{17}$| | 0.80|$\pm _{0.06}^{0.05}$| | 20.00 | 41.33 | 41.47 | 5.60 (b) | −1.11 |
| NGC 4151 | 43.49 | 43.71 | (7.5|$\pm _{2.3}^{2.4})\times 10^5$| | 3.3|$\pm _{0.6}^{0.5}$| | 71|$\pm _{9}^{7}$| | 0.73|$\pm _{0.05}^{0.04}$| | 22.71 | 42.31 | 43.43 | 7.43 (a) | −1.96 |
| NGC 6814 | 42.40 | 42.56 | (1.9|$\pm _{1.2}^{7.0})\times 10^5$| | 2.1|$\pm _{0.8}^{2.6}$| | 80|$\pm _{22}^{12}$| | 0.51|$\pm _{0.12}^{0.10}$| | 20.97 | 42.31 | 42.80 | 6.46 (b) | −0.99 |
| NGC 7213 | 43.96 | 42.82 | (1.1|$\pm _{0.5}^{1.1})\times 10^5$| | 1.9|$\pm _{0.4}^{0.8}$| | 100 | 0.12|$\pm _{0.01}^{0.03}$| | 20.00 | 41.95 | 42.54 | 7.37 (c) | −2.26 |
| UGC 6728 | 42.40 | 43.39 | (0.4|$\pm _{0.3}^{0.5})\times 10^5$| | 2.8|$\pm _{1.5}^{1.7}$| | 24|$\pm _{20}^{49}$| | 0.58|$\pm _{0.27}^{0.19}$| | 20.00 | 41.80 | 42.44 | 5.32 (b) | −0.36 |
| Sy1.8/1.9 galaxies | |||||||||||
| NGC 1365 | 42.83 | 42.95 | (2.5|$\pm _{1.2}^{5.9})\times 10^5$| | 2.1|$\pm _{0.6}^{1.9}$| | 60|$\pm _{19}^{23}$| | 0.46|$\pm _{0.06}^{0.13}$| | 22.21 | 42.32 | 42.69 | 7.92 (a) | −2.44 |
| NGC 2992 | 43.57 | 43.32 | (1.2|$\pm _{0.5}^{1.4})\times 10^5$| | 1.9|$\pm _{0.5}^{1.1}$| | 0.7|$\pm _{0.5}^{0.8}$| | 0.46|$\pm _{0.07}^{0.05}$| | 21.72 | 42.00 | 42.53 | 5.42 (b) | −0.26 |
| NGC 4138 | 41.92 | 41.67 | (0.6|$\pm _{0.4}^{1.2})\times 10^4$| | 0.9|$\pm _{0.5}^{0.8}$| | 81|$\pm _{32}^{17}$| | 0.18|$\pm _{0.06}^{0.12}$| | 22.89 | 41.23 | 41.59 | 7.30 (b) | −2.91 |
| NGC 4395 | 39.98 | 39.97 | (0.2|$\pm _{0.1}^{0.3})\times 10^4$| | 0.2|$\pm _{0.1}^{0.2}$| | 0.4|$\pm _{0.3}^{0.4}$| | 0.74|$\pm _{0.22}^{0.16}$| | 21.04 | 40.50 | 40.63 | 4.88 (a) | −1.22 |
| NGC 5506 | 43.86 | 43.94 | (7.6|$\pm _{1.3}^{2.6})\times 10^5$| | 3.8|$\pm _{0.3}^{0.6}$| | 30|$\pm _{10}^{9}$| | 0.91|$\pm _{0.02}^{0.01}$| | 22.44 | 42.99 | 43.44 | 8.29 (a) | −2.14 |
| NGC 7314 | 42.26 | 42.40 | (1.4|$\pm _{0.5}^{2.4})\times 10^5$| | 1.3|$\pm _{0.3}^{0.9}$| | 33|$\pm _{13}^{16}$| | 0.84|$\pm _{0.31}^{0.05}$| | 21.60 | 42.33 | 42.44 | 7.24 (b) | −1.75 |
| Sy2 galaxies | |||||||||||
| ESO 005-G004 | 42.43 | 42.22 | (0.9|$\pm _{0.2}^{0.3})\times 10^5$| | 1.5|$\pm _{0.2}^{0.3}$| | 0.002|$\pm _{0.002}^{0.001}$| | 0.95|$\pm _{0.06}^{0.03}$| | 24.34 | 42.78 | 42.74 | 6.98 (c) | −1.04 |
| MCG-05-23-016 | 43.75 | 43.73 | (3.2|$\pm _{1.6}^{8.7})\times 10^5$| | 3.5|$\pm _{1.2}^{4.4}$| | 8|$\pm _{6}^{17}$| | 0.80|$\pm _{0.16}^{0.08}$| | 22.18 | 43.20 | 43.43 | 7.98 (a) | −1.62 |
| NGC 2110 | 43.28 | 43.37 | (3.9|$\pm _{2.3}^{11.3})\times 10^5$| | 4.5|$\pm _{1.9}^{5.7}$| | 54 ± 26 | 0.55|$\pm _{0.07}^{0.10}$| | 22.94 | 42.69 | 43.49 | 9.25 (b) | −3.40 |
| NGC 3081 | 43.15 | 43.10 | (6.6|$\pm _{2.7}^{2.4})\times 10^5$| | 13.5|$\pm _{5.6}^{5.2}$| | 0.4 ± 0.3 | 0.95|$\pm _{0.06}^{0.02}$| | 23.91 | 42.72 | 43.60 | 8.41 (b) | −2.53 |
| NGC 4388 | 43.04 | 42.97 | (1.6|$\pm _{0.2}^{0.3})\times 10^6$| | 4.8 ± 0.4 | 0.6|$\pm _{0.1}^{0.2}$| | 0.99|$\pm _{0.002}^{0.001}$| | 23.52 | 43.05 | 43.47 | 6.99 (b) | −0.78 |
| NGC 4945 | 41.05 | 40.86 | (1.3|$\pm _{0.4}^{1.4})\times 10^5$| | 2.2|$\pm _{0.4}^{1.0}$| | 0.001|$\pm _{0.001}^{0.007}$| | 0.97|$\pm _{0.03}^{0.02}$| | 24.80 | 42.69 | 42.53 | 7.78 (a) | −1.93 |
| NGC 5128 | 42.27 | 42.28 | (1.7|$\pm _{0.4}^{0.6})\times 10^5$| | 2.1 ± 0.3 | 10|$\pm _{3}^{6}$| | 0.94|$\pm _{0.02}^{0.01}$| | 23.02 | 42.39 | 43.09 | 7.94 (a) | −2.39 |
| NGC 6300 | 43.00 | 43.05 | (5.4|$\pm _{1.7}^{2.8})\times 10^5$| | 2.7|$\pm _{0.5}^{0.6}$| | 0.9|$\pm _{0.3}^{0.7}$| | 0.99|$\pm _{0.002}^{0.001}$| | 23.31 | 41.84 | 42.43 | 7.01 (a) | −2.01 |
| NGC 7172 | 42.91 | 42.91 | (1.0|$\pm _{0.3}^{0.7})\times 10^5$| | 2.1|$\pm _{0.4}^{0.6}$| | 5|$\pm _{5}^{10}$| | 0.98|$\pm _{0.03}^{0.02}$| | 22.91 | 42.76 | 43.36 | 8.45 (b) | −2.53 |
| NGC 7582 | 43.08 | 42.81 | (1.2|$\pm _{0.5}^{0.7})\times 10^6$| | 9.4|$\pm _{2.4}^{3.0}$| | 0.003|$\pm _{0.003}^{0.02}$| | 0.83|$\pm _{0.08}^{0.05}$| | 24.33 | 42.86 | 43.28 | 7.52 (a) | −1.50 |
5.1 Distributions of clumpy torus model parameters
5.1.1 Optical classification
In this section, we discuss the global posterior distributions and their mean values for Sy1, Sy1.8/1.9, and Sy2. To this end, we apply the hierarchical Bayesian approach also used in Ichikawa et al. (2015). To be more precise, we assume that the global properties of the objects are extracted from common prior distributions and we infer the hyperparameters of these priors. Because of its flexibility, we decided to use beta distributions as these prior distributions. To take advantage of the already computed sampling of the posterior for each individual object, we leverage the importance sampling trick developed by Brewer & Elliott (2014). Although one should ideally sample from the full hierarchical probabilistic model, we consider this approximate technique as sufficient for our purposes.
As can be seen from Fig. 4, the majority of the global distributions are clearly different. To quantify these differences, we use the Kullback–Leibler divergence (KLD; Kullback & Leibler 1951) as in RA11. This approach takes into account the overall shape of the posterior distribution and it always has a positive value. In the case of two identical distributions, it is equal to zero and the larger the values the more different the distributions. RA11 suggested that for values larger than 1 (bold face in Table 10), two posterior distributions may be considered to be significantly different. Following this, we find that the differences in σ, N0, and τV (see Fig. 4) between Sy1 and Sy2 are significant according to the KLD. The same applies to σ and τV between Sy1.8/1.9 and Sy2 galaxies. We note that RA11 found essentially the same differences between Sy1 and Sy2 galaxies. All these results are in good agreement with previous works (e.g. RA11, AH11, and Ichikawa et al. 2015). However, we find smaller values of the cloud optical depth for Sy2 (τV ∼ 56) than for Sy1 and Sy1.8/1.9 galaxies (τV ∼ 94–114) and smaller values of i for Sy1 (i=19 ± 16°).
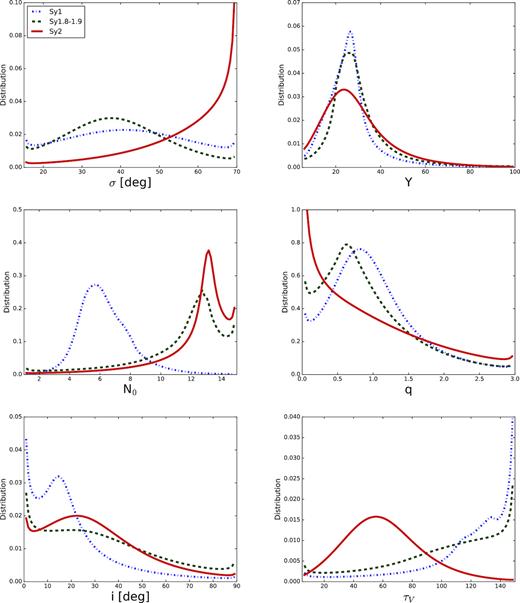
Comparison between the clumpy torus model parameter global posterior distributions for the optical classification. Blue dot–dashed, green dashed, and red solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, and Sy2 galaxies, respectively.
Kullback–Leibler divergence (KLD) results for comparison of the global posterior distribution of each parameter for the various subgroups. In bold we indicate the statistically significant differences.
| Subgroups . | σ . | Y . | N0 . | q . | τV . | i . | CT . |
|---|---|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . |
| Sy1s versus Sy2s | 1.16 | 0.19 | 5.07 | 0.27 | 5.56 | 0.47 | 5.11 |
| Sy1s versus Sy1.8/1.9 | 0.06 | 0.11 | 3.84 | 0.04 | 0.19 | 0.38 | 0.91 |
| Sy2s versus Sy1.8/1.9 | 1.73 | 0.10 | 0.17 | 0.13 | 3.63 | 0.13 | 3.21 |
| Absorbed versus unabsorbed | 0.86 | 0.42 | 1.74 | 0.95 | 2.11 | 0.10 | 1.88 |
| Subgroups . | σ . | Y . | N0 . | q . | τV . | i . | CT . |
|---|---|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . |
| Sy1s versus Sy2s | 1.16 | 0.19 | 5.07 | 0.27 | 5.56 | 0.47 | 5.11 |
| Sy1s versus Sy1.8/1.9 | 0.06 | 0.11 | 3.84 | 0.04 | 0.19 | 0.38 | 0.91 |
| Sy2s versus Sy1.8/1.9 | 1.73 | 0.10 | 0.17 | 0.13 | 3.63 | 0.13 | 3.21 |
| Absorbed versus unabsorbed | 0.86 | 0.42 | 1.74 | 0.95 | 2.11 | 0.10 | 1.88 |
Kullback–Leibler divergence (KLD) results for comparison of the global posterior distribution of each parameter for the various subgroups. In bold we indicate the statistically significant differences.
| Subgroups . | σ . | Y . | N0 . | q . | τV . | i . | CT . |
|---|---|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . |
| Sy1s versus Sy2s | 1.16 | 0.19 | 5.07 | 0.27 | 5.56 | 0.47 | 5.11 |
| Sy1s versus Sy1.8/1.9 | 0.06 | 0.11 | 3.84 | 0.04 | 0.19 | 0.38 | 0.91 |
| Sy2s versus Sy1.8/1.9 | 1.73 | 0.10 | 0.17 | 0.13 | 3.63 | 0.13 | 3.21 |
| Absorbed versus unabsorbed | 0.86 | 0.42 | 1.74 | 0.95 | 2.11 | 0.10 | 1.88 |
| Subgroups . | σ . | Y . | N0 . | q . | τV . | i . | CT . |
|---|---|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . |
| Sy1s versus Sy2s | 1.16 | 0.19 | 5.07 | 0.27 | 5.56 | 0.47 | 5.11 |
| Sy1s versus Sy1.8/1.9 | 0.06 | 0.11 | 3.84 | 0.04 | 0.19 | 0.38 | 0.91 |
| Sy2s versus Sy1.8/1.9 | 1.73 | 0.10 | 0.17 | 0.13 | 3.63 | 0.13 | 3.21 |
| Absorbed versus unabsorbed | 0.86 | 0.42 | 1.74 | 0.95 | 2.11 | 0.10 | 1.88 |
5.1.2 X-ray classification
So far, we have compared the torus properties for Seyfert galaxies with different optical classifications. In this section we obtained the global posterior distributions of the sample divided into unabsorbed (NH < 1022 cm−2) and absorbed (NH > 1022 cm−2) Seyfert galaxies in X-rays.
In Fig. 5, we show these distributions. We find essentially the same trends as when we divide the sample into Sy1 and Sy2 using an optical classification, but with less significance (see Table 10). This is due to the fact that the majority of optically classified Sy1 and Sy2 correspond to the unabsorbed and absorbed subgroups, respectively. Half of the Sy1.8/1.9 galaxies are classified as unabsorbed and the other half as absorbed, while only one Sy1 galaxy is absorbed (i.e. NGC 4151).
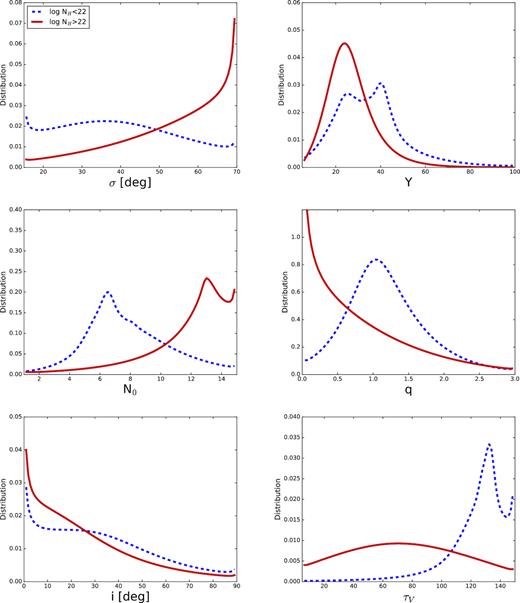
Comparison between the clumpy torus model parameter global posterior distributions for type 1 and type 2 Seyferts according to the X-ray classification. Blue dot–dashed and red solid lines represent the parameter distributions of unabsorbed and absorbed Seyfert galaxies, respectively.
5.2 Torus size, angular width, and mass
We find median values of 1.1 ± 3.5, 1.4 ± 2.8, and 3.9 ± 5.1 × 105 M⊙ for the torus gas masses of Sy1, Sy1.8/1.9, and Sy2 galaxies. Lira et al. (2013) found values of the torus masses ranging from 104 to 106 M⊙ using a sample of 48 Sy2 galaxies from the extended 12 |$\mu$|m Galaxy Sample (Rush, Malkan & Spinoglio 1993). For 5/8 Sy1 galaxies, we can compare the torus gas masses with measurements corresponding to the inner 30 pc (radius) reported by Hicks et al. (2009). They derived masses of M|$_{\mathrm{ gas}}^{\mathrm{ H}_2}$| = 3–20 × 106 M⊙ for NCG 3227, NCG 3783, NCG 4051, NCG 4151, and NCG 6814. These masses were obtained from the H2 1-0S(1) emission line at 2.12 |$\mu$|m. We do not have any Sy2 galaxy in common with Hicks et al. (2009), but we compare with the two Sy2 galaxies in their sample (Circinus and NGC 1068). For Circinus using a smaller radius of 9 pc, they found an M|$_{\mathrm{ gas}}^{\mathrm{ H}_2}$| = 1.9 × 106 M⊙. For NGC 1068, the latter authors reported a mass of M|$_{\mathrm{ gas}}^{\mathrm{ H}_2}$| = 2.3 × 107 M⊙ in the inner 30 pc. As expected, we found that the gas masses inferred from the fit of the nuclear IR SEDs in a smaller radius (∼0.5–15 pc) are smaller than those measured in the inner ∼30 pc. Using the CO(6-5) line observed with ALMA, García-Burillo et al. (2016) reported a smaller gas mass (1.2 × 105 M⊙) for the inner ∼7–10 pc of NGC 1068. Finally, using ALMA/CO(2-1) data, Alonso-Herrero et al. (2018) found that the nuclear disc of the Sy2 NGC 5643 is a factor of ∼10 more massive and larger (∼26 pc of diameter) than that of NGC 1068. Therefore, we obtain comparable values of the torus mass with those derived from the highest angular resolution data.
5.3 The covering factor
Clumpy torus models imply that the differences between type 1 and type 2 AGN depend of whether there is a direct view of the broad-line region (BLR; e.g. Nenkova et al. 2008a,b). Therefore, the observed classification is the result of the probability for an AGN-produced photon to escape through the torus along a viewing angle without being absorbed. As this probability is always non-zero, it is always possible to have a direct view of the BLR, regardless of the torus orientation. Therefore, the larger the covering factor (CT) the larger the probability of classifying an AGN as type 2. In fact, the geometrical covering factor gives the type 2/total fraction (e.g. Mateos et al. 2017).
In order to compare the covering factors for the three subgroups, we derived the combined probability distributions. To do so, we concatenated together the individual arrays of the CT values returned Bayesian modelling for all objects in subgroups and we computed the combined probability distributions since it is a non-linear function of the torus model parameters (σ and N0; see left-hand panel of Fig. 6). We note that we do not use the hierarchical Bayesian approach since if we use the generalized beta distribution as the prior we would introduce an extra prior in the CT derived quantities. Using our ultra-hard X-ray volume-limited sample of Seyfert galaxies, we confirm the results first reported by RA11 that the covering factors of Sy2 are larger than those of Sy1 galaxies. Indeed, using the optical classification, we find that Sy2 have larger median values of the covering factor combined probability distributions (C|$_T=0.95\pm _{0.18}^{0.04}$|) than Sy1 (C|$_T=0.66\pm _{0.52}^{0.16}$|) and Sy1.8/1.9 (C|$_T=0.53\pm _{0.37}^{0.21}$|) which is the same as for Sy1s, within the errors. These results are in good agreement with previous works (e.g. RA11; AH11; Ichikawa et al. 2015; Mateos et al. 2016). We also repeat the global posterior distribution for the covering factor using the X-ray classification (see Section 5.1.2) and we find the same trend (see right-hand panel of Fig. 6 and Table 10).
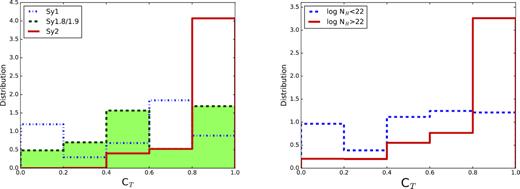
Left-hand panel: comparison between the torus covering factor (CT) combined probability distributions for the optical classification. Blue dot–dashed, green dashed, and red solid lines represent the parameter distributions of Sy1, Sy1.8/1.9, and Sy2, respectively. Right-hand panel: same as left-hand panel, but for the X-ray classification, unabsorbed (log NH < 22 cm−2) and absorbed Seyfert galaxies (log NH > 22 cm−2). Blue dot–dashed and red solid lines represent the parameter distributions of unabsorbed and absorbed Seyfert galaxies, respectively.
5.3.1 Dependence with AGN luminosity and Eddington ratio
To investigate the relation between the bolometric luminosity derived from the X-rays (2–10 and 14–195 keV; see Appendix B) and the covering factor (see top panels of Fig. 7), we divided our sample into several luminosity bins. In the first bin, we included the three sources with log(L|$_{bol}^{AGN})\lt $|43, while the rest of the sample was divided in two bins of equal logarithmic width (1 dex). We find that the σ parameter remains essentially constant within the errors, throughout our luminosity range [log(L|$_{bol}^{AGN})\,{\sim }$| 41–45 erg s−1; see top panels of Fig. 7]. The same applies for the covering factor (see top panels of Fig. 8). We find slightly larger values of CT (≳0.5) in the log(L|$_{bol}^{AGN})\,{\sim}$| 44–45 erg s−1 luminosity range because the majority of the sources in that bin are Sy2s. Thus, we do not find a statistically significant trend in the covering factor with AGN luminosity, which is in good agreement with recent studies (e.g. Mateos et al. 2016, 2017; Netzer et al. 2016; Stalevski et al. 2016; Lani, Netzer & Lutz 2017; Ichikawa et al. 2019).
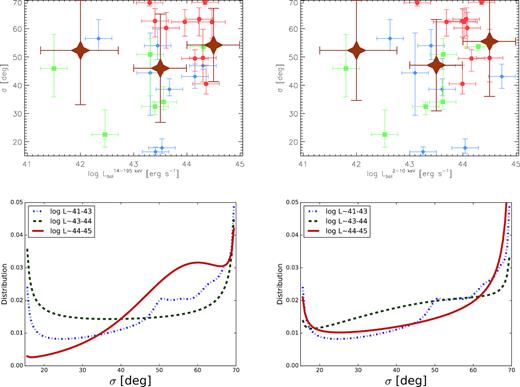
Top panels: luminosity dependence of the torus width for the BCS40 sample using the bolometric luminosities derived from the 14–195 keV and 2–10 keV bands. Blue diamonds, green squares, and red circles represent Sy1, Sy1.8/1.9, and Sy2, respectively. Brown stars correspond to values derived from the global posterior distribution of each bin subgroup. The error bars represent the ±1σ confidence interval for the individual and average measurements. Note that for the average values the error bars in the X-axis indicate the bin width. Bottom panels: comparison between the global posterior distributions of the torus width for three ranges of bolometric luminosities derived from the 14–195 keV and 2–10 keV bands.
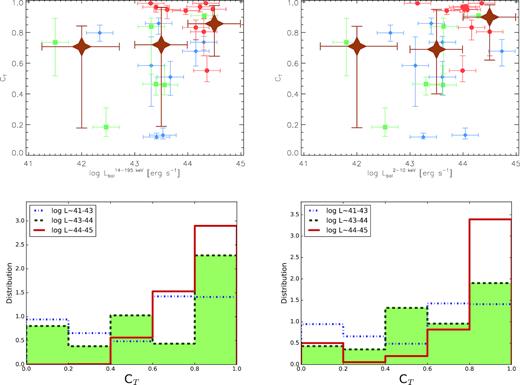
Same as Fig. 7 but for the covering factor (CT). Bottom panels: comparison between the covering factor combined probability distributions for three ranges of bolometric luminosities. The error bars represent the ±1σ confidence interval for the individual and median measurements. Note that for the median values the error bars in the X-axis indicate the bin width.
More recently it has been suggested that the Eddington ratio is the key parameter determining the covering factor, instead of the bolometric luminosity (e.g. Buchner & Bauer 2017; Ricci et al. 2017b). Ricci et al. (2017b) found that the covering factor rapidly decreases at higher Eddington ratios (see the orange solid line of Fig. 9). We derived Eddington ratios using the 2–10 keV bolometric X-ray luminosities and the black hole mass estimates from Ricci et al. (2017a) and Koss et al. (2017), respectively. For the remaining sources, we estimate the black hole masses (see Appendix C) as in Koss et al. (2017). The only exceptions are NGC 7213 and ESO 005-G004, for which we take their black hole masses from Vasudevan et al. (2010). The Eddington ratios of the sample are listed in Table 9.
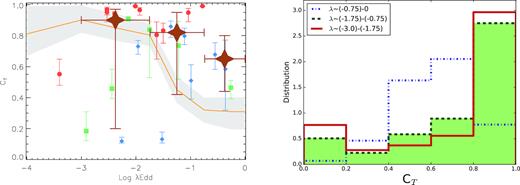
Left-hand panel: relation between the covering factor and the Eddington ratio for the BCS40 sample. The solid orange line is the relation derived by Ricci et al. (2017b) and the uncertainties are shown as grey shaded regions. Blue diamonds, green squares, and red circles represent Sy1, Sy1.8/1.9, and Sy2, respectively. Brown stars are the median values of the combined probability distribution of each Eddington ratio bin. The error bars represent the ±1σ confidence interval for the individual and median measurements. Note that for the median values the error bars in the X-axis indicate the bin width. Right-hand panel: comparison between the torus covering factor (CT) combined probability distributions of each bin.
Although we find higher values of the CT for lower Eddington ratios (see Fig. 9), we do not find a statistically significant dependence of the torus covering factor with the Eddington ratio. This result suggests, albeit for a small luminosity range and a limited number of galaxies, that the Eddington ratio would not be driving the geometrical covering factor.
5.3.2 Missing obscured Seyferts?
In Fig. 10, we show the Sy2 fraction in our sample as estimated by using two covering factor bins (0.5–0.8 and 0.8–1.0).6 To estimate the uncertainties, we used the bootstrap error estimation generating 106 mock samples of Sy1, Sy1.8/1.9, and Sy2s by randomly selecting sources using replacements, with their corresponding covering factor distributions from the original samples. Note that the number of Sy1, Sy1.8/1.9, and Sy2s in each mock sample keep constant the observed number of Seyferts (i.e. nSy1 + nSy1.8/1.9 + nSy2). Finally, for each source, we calculate the obscured fraction in each bin by integrating its probability distribution (see e.g. Mateos et al. 2017).
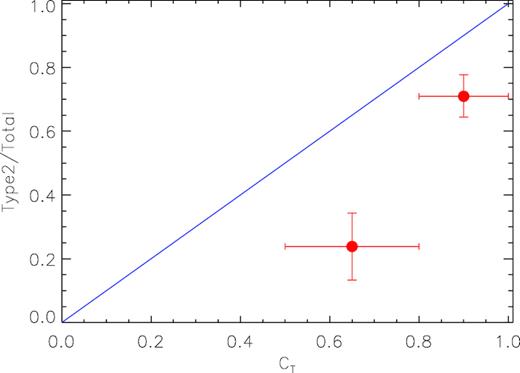
Sy2 fraction versus torus covering factor for the BCS40 sample grouped in two bins. The error bars in the X-axis indicate the bin width and in the Y-axis represent the ±1σ confidence interval.
Our data points should follow the 1:1 blue line shown in Fig. 10 if our sample did not miss any high covering factor source (covering factor values ∼1). However, the Sy2/total fraction is always below the 1:1 line. In general, we found that the most highly absorbed sources are the ones with higher torus covering factors (see also RA11, AH11 and Mateos et al. 2016). All this suggests that even an ultra-hard X-ray (14–195 keV) Swift/BAT selection is missing a significant fraction of highly absorbed type 2 sources with very high covering factor tori. This is expected since at column densities NH > 1023.5 cm−2, even high-energy photons (14–195 keV X-ray band) are absorbed. An example of these missing sources could be NGC 4418, which is a very highly obscured AGN at ∼30 Mpc. It has a compact IR bright core with the deepest known silicate absorption but it is not detected in the Swift/BAT hard X-ray band (e.g. Roche, Alonso-Herrero & Gonzalez-Martin 2015 and references therein). The result presented here agrees with those reported in Ricci et al. (2015) and Koss et al. (2016) at energies >10 keV and Mateos et al. (2017) at energies >4.5 keV. The latter authors inferred the existence of a population of X-ray undetected objects with high torus covering factor, especially at high bolometric luminosities (>1044 erg s−1).
6 CONCLUSIONS
We present for the first time a detailed modelling of the nuclear dust emission of an ultra-hard X-ray (14–195 keV) volume-limited (DL < 40 Mpc) sample of 24 Seyfert galaxies. We selected our targets from the Swift/BAT nine-month catalogue. Our sample covers an AGN luminosity range log(L|$_{\textrm{int}}^{2-10\, \textrm{keV}}){\sim }$| 40.5–43.4 erg s−1. We fitted the nuclear IR SEDs obtained with high angular resolution data (∼1–30 |$\mu$|m) with the CLUMPY models using a Bayesian approach. From these fits, we derived torus model parameters for the individual 24 galaxies. In the case of Seyfert 1s, we took special care to subtract the accretion disc contribution from the observed nuclear SEDs using the type 1 QSO accretion disc template from Hernán-Caballero et al. (2016). The main goal of this work was to obtain a global statistical analysis of the clumpy torus model parameters of type 1 and 2 Seyfert galaxies. We used both optical (broad versus narrow lines) and X-ray (unabsorbed versus absorbed) classifications for our analysis. Using these classifications, we compared the global posterior distribution of the torus model parameters, rather than focusing on the individual fits.
We verified our previous results that type 2 Seyferts have tori with larger widths and more clouds than type 1/1.8/1.9s. These findings are independent of whether we use an optical or X-ray classification. We found that the covering factor is likely the main parameter driving the classification of Seyfert galaxies. We derived compact torus sizes (radius <15 pc), and gas masses in the 104–106 M⊙ range for both types.
We derived geometrical covering factors for the individual galaxies and globally for Sy1s and Sy2s. In clumpy torus models, the geometrical covering factor is a function of the angular size and the number of clouds. Using these distributions, we confirmed that Seyfert 2 galaxies have larger values of the covering factor (C|$_T=0.95\pm _{0.18}^{0.04}$|) than type 1s (C|$_T=0.66\pm _{0.52}^{0.16}$|) using, for the first time, an ultra-hard X-ray selected sample of Seyferts. We found that the torus covering factor remains constant within the errors in our luminosity range and no clear dependence with the Eddington ratio. Finally, we compared the derived covering factor with the observed type 2 fraction for our sample. From this comparison, we found tentative evidence that even an ultra-hard X-ray selection is missing a significant fraction of highly absorbed type 2 sources with very high covering factor tori, as also concluded by Mateos et al. (2017) at lower X-ray energies using a more distant and luminous sample of AGN.
We note that detailed studies such as this, carried out not only using larger samples of galaxies but covering wider luminosity and redshift ranges are needed to improve the statistics of the results we report here. In the future, this methodology may be applied to AGN samples using high angular resolution and sensitive MIR data, observed with the combined spectral coverage of NIRSpec and MIRI aboard the James Webb Space Telescope (JWST).
SUPPORTING INFORMATION
online_appendices.pdf.
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.
ACKNOWLEDGEMENTS
IGB acknowledges financial support from the Instituto de Astrofísica de Canarias through Fundación La Caixa. IGB also acknowledges Oxford University and Durham University for their hospitality during his stays in 2017 August when this project was started and 2018 May, respectively. IGB also acknowledges Cardiff University for their hospitality from 2018 May to August. CRA and IGB acknowledge financial support from the Spanish Ministry of Science and Innovation (MICINN) through project AYA2016-76682-C3-2-P. IGB, AAH, and FJC also acknowledge financial support through grant PN AYA2015-64346-C2-1-P (MINECO/FEDER). Funded by the Agencia Estatal de Investigación, Unidad de Excelencia María de Maeztu. CRA also acknowledges the Ramón y Cajal Program of the Spanish Ministry of Economy and Competitiveness. MPS acknowledges support from STFC through grant ST/N000919/1. OGM thanks to the PAPIIT UNAM project IA103118. SM acknowledges financial support through grant AYA2016-76730-P (MINECO/FEDER). IM and JM acknowledge financial support from the research project AYA2016-76682-C3-1-P (AEI/FEDER, UE). LF and CP acknowledge support from the NSF- grant number 1616828.
Finally, we are extremely grateful to the GTC staff for their constant and enthusiastic support, and to the anonymous referee for useful comments.
Footnotes
Note that when the derived rest-frame AGN component does not extend as far as 30 |$\mu$|m, we calculated 28 |$\mu$|m fluxes (e.g. NGC 1365 and NGC 4138). If that is not possible, we used the Spitzer/IRS spectra to estimate the 30 |$\mu$|m fluxes and considered the IRS fluxes as upper limits, due to the low angular resolution of Spitzer. The latter also applies to the 25 |$\mu$|m fluxes. We note that the 25 and 30 |$\mu$|m fluxes could have some contribution from the host galaxy.
Note that we use CT values larger than 0.5 due to the lack of data in the lower CT range for Sy2 galaxies (see left-hand panel of Fig. 6).



