-
PDF
- Split View
-
Views
-
Cite
Cite
Holly P Preece, Christopher A Tout, C Simon Jeffery, Convection physics and tidal synchronization of the subdwarf binary NY Virginis, Monthly Notices of the Royal Astronomical Society, Volume 485, Issue 2, May 2019, Pages 2889–2894, https://doi.org/10.1093/mnras/stz547
Close - Share Icon Share
ABSTRACT
Asteroseismological analysis of NY Vir suggests that at least the outer 55 per cent of the star (in radius) rotates as a solid body and is tidally synchronized to the orbit. Detailed calculation of tidal dissipation rates in NY Vir fails to account for this synchronization. Recent observations of He core burning stars suggest that the extent of the convective core may be substantially larger than that predicted with theoretical models. We conduct a parametric investigation of sdB models generated with the Cambridge stars code to artificially extend the radial extent of the convective core. These models with extended cores still fail to account for the synchronization. Tidal synchronization may be achievable with a non-MLT treatment of convection.
1 INTRODUCTION
Hot subdwarf B (sdB) stars are core-helium burning stars which have had their hydrogen-rich envelopes stripped, most likely in a binary interaction. The stars are typically slow rotators. However, those in close binaries are somewhat spun up. The sdB stars in close binaries, with orbital periods less than |$10\, \rm {d}$|, have either low-mass main-sequence or white dwarf companions. The companions are unseen so it is not possible to measure the inclination of the observed systems unless they are eclipsing. If the system is tidally locked then the spin period and orbital period of the binaries should be the same and an observed rotation velocity would allow the inclination to be measured. Several observed sdB systems challenge this assumption (Pablo et al. 2012a; Pablo, Kawaler & Green 2012b; Schaffenroth et al. 2014). Theoretical calculations of tidal synchronization time-scales for sdB stars fail to account for synchronization via either the equilibrium or dynamical dissipation mechanisms (Preece, Tout & Jeffery 2018).
Of the observed pulsating sdB binaries, the eclipsing HW Vir type binary NY Vir (PG 1336−018) is the only object whose outer layers show evidence of synchronous rotation with the binary orbit (Charpinet et al. 2008). The star oscillates with p modes in its outer 55 per cent. Rotation in the deep interior is not constrained owing to the lack of sensitivity of p modes to these regions.
Charpinet et al. (2008) obtained a mass for the sdB component of |$0.459\pm 0.006\, \rm {M_\odot }$| from asteroseismology, while Van Grootel et al. (2013) measured an asteroseismic mass of |$0.471\, \pm \, 0.006\, \rm {M_\odot }$|. Vučković et al. (2007) obtained three equally probable solutions from photometry and radial velocities. These give sdB masses of 0.530, 0.466, or |$0.389\, \rm {M_\odot }$|. The companion mass M2 is either 0.11 or |$0.12\, \rm {M_\odot }$| and the orbital period of the binary |$P_{\rm {orb}} = 0.101016\, \rm {d}$|.
The tidal synchronization time-scale is inversely proportional to the ratio of the radius of the dissipative region to the binary separation to the sixth power (Darwin 1879; Eggleton 2006). Increasing the radius of the convective region reduces the tidal synchronization time. Observational asteroseismic data suggest the radial extent of the He burning core, as illustrated in Fig. 1, is substantially underestimated in stellar models (Van Grootel et al. 2010a,b; Charpinet et al. 2011; Giammichele et al. 2018). We investigate whether increasing the radius of the convective zone could reduce synchronization times sufficiently to account for the observed synchronization of NY Vir. We examine the effect that increasing the extent of the convective region has on all the quantities which go into the tidal synchronization calculations.
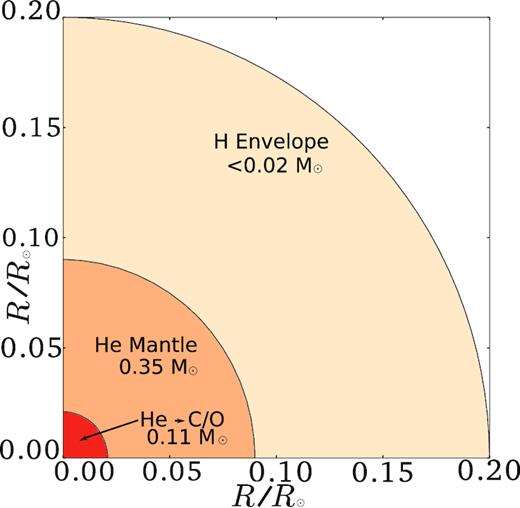
Scale diagram of a typical sdB star as predicted by stellar models. He → C/O (red) indicates the convective zone.
2 STELLAR MODELS
The evolutionary models used in this study were all constructed with the Cambridge STARS code as first described by Eggleton (1971) and subsequently updated by Pols et al. (1995) and Stancliffe & Eldridge (2009). Three classes of model were created, one with overshoot (labelled: δov = 0.12), one without overshoot (δov = 0), and one without overshooting but with a modified Schwarzschild criterion (Δ∇ + 0.15), where Δ∇ ≡ ∇r − ∇a, the difference between radiative and adiabatic thermodynamic gradients |$\rm {d}\, ln\, {\it T} / \rm {d}\, ln\, {\it P}$|. Under the standard Schwarzschild criterion, the convective region is defined as that where Δ∇ > 0 and hence includes the semiconvective region. The superadiabacity of the convective region that develops as the star evolves is very low and is in fact more likely a semiconvective region. For each of these classes, an early and a late model were compared. The early model was defined as the model obtained when the fractional core He abundance by mass drops to 0.9. The late model was defined to be the model where the convective core reached its maximal radial extent. The initial models were constructed without a modified Schwarzschild criterion by the same method used by Preece et al. (2018). We introduce several mechanisms for artificially increasing the convective region.
2.1 Modifying the Schwarzschild criterion
For the models labelled Δ∇ + 0.15, the extent of the convective region was artificially extended by modifying the Schwarzschild criterion for stability against convection from ∇r − ∇a > 0 to ∇r − ∇a + 0.15 > 0. This has the effect of forcing convection to occur in regions near to convective boundaries which would otherwise be radiative. The increment 0.15 was chosen because this was the largest which produced stable evolutionary models.
2.2 Semiconvection and overshooting
Eggleton (1972) implemented semiconvection in STARS as a diffusive process which follows Schwarzschild & Härm (1958)’s prescription. It assumes that the energy transport by convection in the semiconvective region is borderline negligible but that there is substantial chemical mixing which avoids any discontinuity in the chemical profile. Semiconvective regions then have ∇r ≈ ∇a.
For He-core burning models the inclusion of overshooting suppresses the growth of the semiconvective zone. This ultimately leads to the formation of a smaller combined convective and semiconvective region than if overshooting were not used. For the models with the modified Schwarzschild criterion, overshooting occurs where ∇r − ∇a + 0.15 > −δ
By contrast, the stellar evolution code mesa defines semiconvective regions as those which are unstable to convection according to the Schwarzschild criterion but stable according to the Ledoux criterion (Paxton et al. 2011, 2013). The mesa overshooting region is defined as lovHP where lov is user defined and HP is the pressure scale height. Because HP → ∞ as r → 0 the overshooting length can become very large for stars with small convective cores.
2.3 Mixing length theory
In the stars code mixing length theory as described by Böhm-Vitense (1958) is used. Near the core the pressure scale height HP → ∞. The mixing length l is defined to be αHP and sets the average distance travelled by convective elements. The mixing length parameter α is a user defined constant. Physically, convective elements cannot travel an infinite distance. As suggested by Eggleton (1972), the mixing length is modified such that it cannot exceed the distance to the edge of the convective zone. This also has a modest effect on the mixing velocity |$w$|.
3 CONVECTIVE TIDAL DISSIPATION
The most efficient mechanism for tidal dissipation in sdB stars in close binaries is convective dissipation. Convection implies the bulk movement of material over large distances within the star. Turbulent viscosity in the convective region causes the tidal bulge to move away from the line connecting the centres of mass of the two stars. Fig. 2 is a schematic diagram illustrating the dissipation.
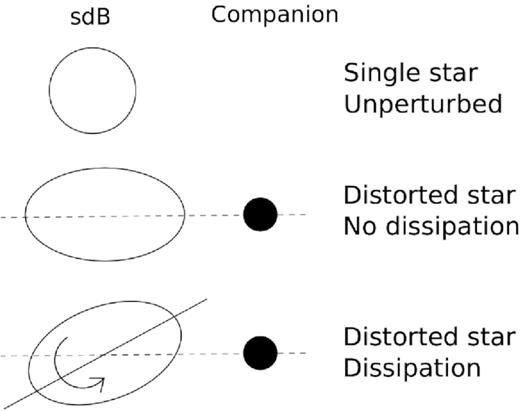
Schematic diagram of tidal interactions. The first panel shows a single, unperturbed star. The second panel shows a tidally distorted star which is either tidally synchronized or has no dissipation. The tidal bulge lies along the line connecting the centre of masses of the binary system. The final panel shows a non-synchronously rotating, tidally distorted star with a dissipation mechanism. The tidal bulge lags or leads the line connecting the centre of masses of the stars. This produces a torque which spins the star either up or down until it is rotating synchronously.
3.1 The tidal synchronization time-scale
As can be seen in Table 1, tidal synchronization time-scales for NY Vir predicted from standard models of sdB stars are close to or longer than the Hubble time. Tidal synchronization cannot occur before these models exhaust their core helium supplies, move off the EHB and on to a white dwarf cooling track. Because τsync is inversely proportional to the radius of the dissipative region to the sixth power, simple calculations suggest that increasing the convective radius rconv should substantially decrease the synchronization time. Somewhat surprisingly, increasing rconv by a factor of 2.5 by modifying the Schwarzschild criterion only reduces the synchronization time by about an order of magnitude. The changes in the structural properties of the star affect the quadrupole tensor and so too the tides. Increases in the viscous time and mass of the convective region and decreases in the quadrupole moment and moment of inertia term counteract the effect of increasing the fractional convective radius.
Convective mass, radius, dimensionless quadrupole moment, and synchronization time for the models considered.
| Model . | R1/R⊙ . | M1/M⊙ . | Q . | (1 − Q)2 . | |$\tau _{\rm {sync}}(\Psi _1)/\rm {Gyr}$| . | |$\tau _{\rm {sync}}(\Psi _2)/\rm {Gyr}$| . |
|---|---|---|---|---|---|---|
| |$\rm {Early} \, \delta _{\rm {ov}}=0$| | 0.021 | 0.113 | 0.013 85 | 0.972 50 | 36.47 | 588.63 |
| |$\rm {Late}\, \delta _{\rm {ov}}=0$| | 0.033 | 0.280 | 0.008 90 | 0.982 28 | 65.31 | 2448.11 |
| |$\rm {Early}\, \delta _{\rm {ov}}=0.12$| | 0.021 | 0.107 | 0.013 89 | 0.972 41 | 32.76 | 492.56 |
| |$\rm {Late}\, \delta _{\rm {ov}}=0.12$| | 0.024 | 0.151 | 0.008 02 | 0.984 02 | 62.78 | 1007.95 |
| |$\rm {Early} \, \Delta \nabla + 0.15$| | 0.042 | 0.317 | 0.010 78 | 0.978 56 | 74.02 | 4222.01 |
| Late Δ∇ + 0.15 | 0.053 | 0.441 | 0.008 67 | 0.982 74 | 12.52 | 60.24 |
| Model . | R1/R⊙ . | M1/M⊙ . | Q . | (1 − Q)2 . | |$\tau _{\rm {sync}}(\Psi _1)/\rm {Gyr}$| . | |$\tau _{\rm {sync}}(\Psi _2)/\rm {Gyr}$| . |
|---|---|---|---|---|---|---|
| |$\rm {Early} \, \delta _{\rm {ov}}=0$| | 0.021 | 0.113 | 0.013 85 | 0.972 50 | 36.47 | 588.63 |
| |$\rm {Late}\, \delta _{\rm {ov}}=0$| | 0.033 | 0.280 | 0.008 90 | 0.982 28 | 65.31 | 2448.11 |
| |$\rm {Early}\, \delta _{\rm {ov}}=0.12$| | 0.021 | 0.107 | 0.013 89 | 0.972 41 | 32.76 | 492.56 |
| |$\rm {Late}\, \delta _{\rm {ov}}=0.12$| | 0.024 | 0.151 | 0.008 02 | 0.984 02 | 62.78 | 1007.95 |
| |$\rm {Early} \, \Delta \nabla + 0.15$| | 0.042 | 0.317 | 0.010 78 | 0.978 56 | 74.02 | 4222.01 |
| Late Δ∇ + 0.15 | 0.053 | 0.441 | 0.008 67 | 0.982 74 | 12.52 | 60.24 |
Convective mass, radius, dimensionless quadrupole moment, and synchronization time for the models considered.
| Model . | R1/R⊙ . | M1/M⊙ . | Q . | (1 − Q)2 . | |$\tau _{\rm {sync}}(\Psi _1)/\rm {Gyr}$| . | |$\tau _{\rm {sync}}(\Psi _2)/\rm {Gyr}$| . |
|---|---|---|---|---|---|---|
| |$\rm {Early} \, \delta _{\rm {ov}}=0$| | 0.021 | 0.113 | 0.013 85 | 0.972 50 | 36.47 | 588.63 |
| |$\rm {Late}\, \delta _{\rm {ov}}=0$| | 0.033 | 0.280 | 0.008 90 | 0.982 28 | 65.31 | 2448.11 |
| |$\rm {Early}\, \delta _{\rm {ov}}=0.12$| | 0.021 | 0.107 | 0.013 89 | 0.972 41 | 32.76 | 492.56 |
| |$\rm {Late}\, \delta _{\rm {ov}}=0.12$| | 0.024 | 0.151 | 0.008 02 | 0.984 02 | 62.78 | 1007.95 |
| |$\rm {Early} \, \Delta \nabla + 0.15$| | 0.042 | 0.317 | 0.010 78 | 0.978 56 | 74.02 | 4222.01 |
| Late Δ∇ + 0.15 | 0.053 | 0.441 | 0.008 67 | 0.982 74 | 12.52 | 60.24 |
| Model . | R1/R⊙ . | M1/M⊙ . | Q . | (1 − Q)2 . | |$\tau _{\rm {sync}}(\Psi _1)/\rm {Gyr}$| . | |$\tau _{\rm {sync}}(\Psi _2)/\rm {Gyr}$| . |
|---|---|---|---|---|---|---|
| |$\rm {Early} \, \delta _{\rm {ov}}=0$| | 0.021 | 0.113 | 0.013 85 | 0.972 50 | 36.47 | 588.63 |
| |$\rm {Late}\, \delta _{\rm {ov}}=0$| | 0.033 | 0.280 | 0.008 90 | 0.982 28 | 65.31 | 2448.11 |
| |$\rm {Early}\, \delta _{\rm {ov}}=0.12$| | 0.021 | 0.107 | 0.013 89 | 0.972 41 | 32.76 | 492.56 |
| |$\rm {Late}\, \delta _{\rm {ov}}=0.12$| | 0.024 | 0.151 | 0.008 02 | 0.984 02 | 62.78 | 1007.95 |
| |$\rm {Early} \, \Delta \nabla + 0.15$| | 0.042 | 0.317 | 0.010 78 | 0.978 56 | 74.02 | 4222.01 |
| Late Δ∇ + 0.15 | 0.053 | 0.441 | 0.008 67 | 0.982 74 | 12.52 | 60.24 |
The equation for tidal synchronization has multiple terms, all of which have an allowed physically constrained ranges. The dependence of the radial extent of the convective zone on the individual terms and their allowed ranges is now examined.
3.2 The dimensionless quadrupole moment
The mass quadrupole tensor of an object describes the spatial distribution of the matter. If the object is a point source the quadrupole tensor vanishes. The dimensionless quadrupole moment Q is given in Table 1. Varying rconv/RsdB does not particularly change Q because the early and late models with convective overshooting have the same fractional convective radius. However, Q is sensitive to the total radius and density of the star and Q doesn’t particularly change for the evolving models with no overshooting and a modified Schwarzschild criterion (Δ∇ + 0.15). For the models tested (1 − Q)2 is between 0.97 and 0.99. Because (1 − Q)2 is close to unity in all cases considered it does not have a substantial influence on the tidal synchronization time-scale.
3.3 The mass and radius of the convective region
The sdB star He cores are small but dense. The H-rich envelope is radially extended but accounts for a small amount of the mass. The mass as a function of radius can be seen in Fig. 3. The outer regions of the star expand as the star evolves. In addition the high internal density means a small increase in the convective radius substantially increases the convective mass. When convective overshooting is used the radius of the convective region stays approximately the same but the mass increases by half. It is worth noting that whether a region is convective or radiative has little impact on the density profile. The models with the modified Schwarzschild criterion are denser than the standard models. Furthermore, the mass and radius term in equation (3) can be plotted as in Fig. 4. From this the mass and radius term can be constrained to be between 108 and |$7\times 10^9\, \rm {g^2\, cm^{-6}}$|.
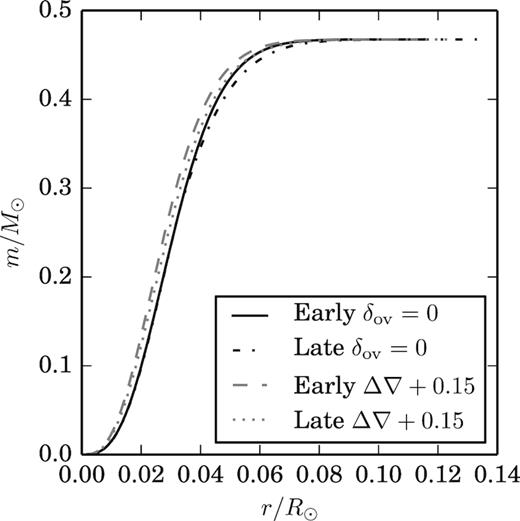
The mass m contained within a sphere of radius r. The models with semiconvection and no convective overshooting are plotted in black and labelled δov = 0. The models with no convective overshooting had the same profiles and thus are not plotted. The modified Schwarzschild criterion models, labelled Δ∇ + 0.15 and plotted in grey, are denser.
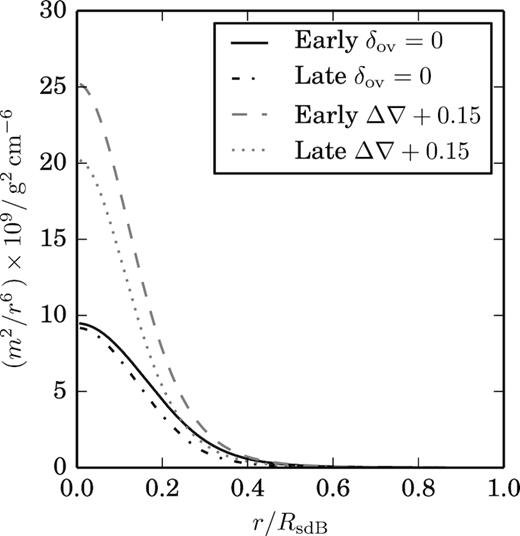
The mass to the second power over the radius to the sixth power as a function of fractional radius for the same models as in Fig. 3.
3.4 Moment of inertia term
For tidal calculations the ratio of the moment of inertia at the edge of the convective core to the moment of inertia if the mass were confided to a shell at the same radius is required. The overall dependence of the moment of inertia term on the fractional convective radius is displayed in Fig. 5. This term lies between 0.15 and 0.37.
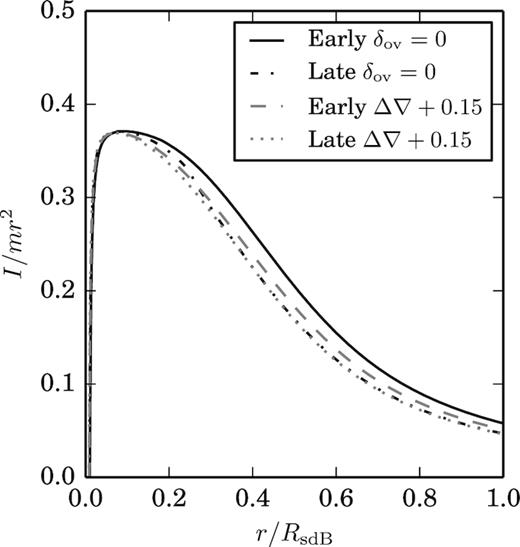
The ratio of the moment of inertia of the region enclosed to the moment of inertia if the matter were confined to a shell placed at the same radius as a function of fractional sdB radius.
3.5 The viscous time
Tidal interactions convert kinetic energy from tidal distortions into heat by dissipative processes whilst conserving angular momentum. This dissipation can be calculated from the square of the variation in the quadrupole tensor over time. As the companion moves around the sdB star the gravitational potential through the star changes cyclically. This changes the matter distribution and so affects the quadrupole tensor. If not synchronized, the tidal bulge moves around the star following the companion. This introduces a time-dependent velocity field in the dissipative regions. The dissipation has a time-scale of τvisc.
The viscous time as calculated by equation (4) with Ψ1 is shown in Fig. 6 for convective regions modified to extend throughout the star. The mixing length l used is the distance to the edge of the convective region such that at r = 0, l = R1, and at r = R1, l = 0. The time-scales at the models’ convective boundaries are also plotted. The δov = 0.12 models are again omitted because they are almost identical to the δov = 0 models. The mixing velocity |$w$| is not well defined for regions which would be radiative. If r < R1 we use |$w$| from the models. If r > R1, |$w$| was given the same distribution but over the extended region. The dip in the Late Δ∇ + 0.15 models is due to a large peak in γ(r) at the convective boundary. This is most likely an artefact of our modification to the Schwarzschild criterion. Without this peak the τvisc profile is almost identical to the Early Δ∇ + 0.15 profile. Overall, larger convective cores have longer viscous times.
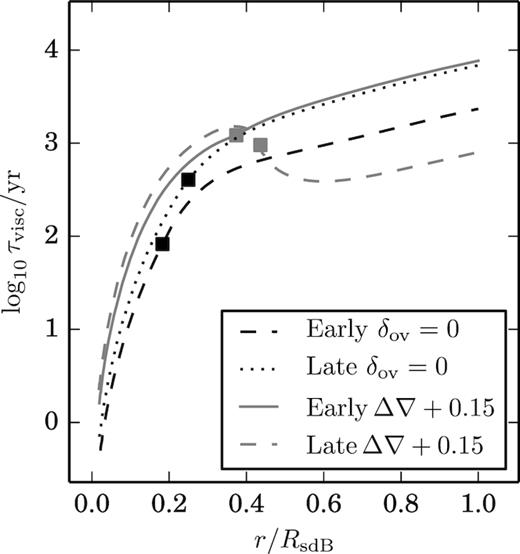
The viscous time-scale as a function of the convective radius as a fraction of the total radius. Each line represents a single evolutionary model. The points plotted are the viscous times predicted by the stellar models with each model’s convective core radius. Increasing the radius of the convective region increases the viscous time-scale. A damping factor of Ψ1 is used.
3.6 Critical viscous time
All terms on the right-hand side of equation (3) are known for any given mass and radius. The equation can be rearranged for the desired synchronization time. The maximum τvisc to synchronize the system in this time as a function of convective radius can be derived. The upper limit to the viscous time for synchronization within the EHB lifetime |$\tau _{\rm {EHB}}\, =\, 10^8\, \rm {yr}$| is plotted in Fig. 7. The viscous time as calculated with equation (4) for each of the evolutionary models in Table 1 is also plotted.
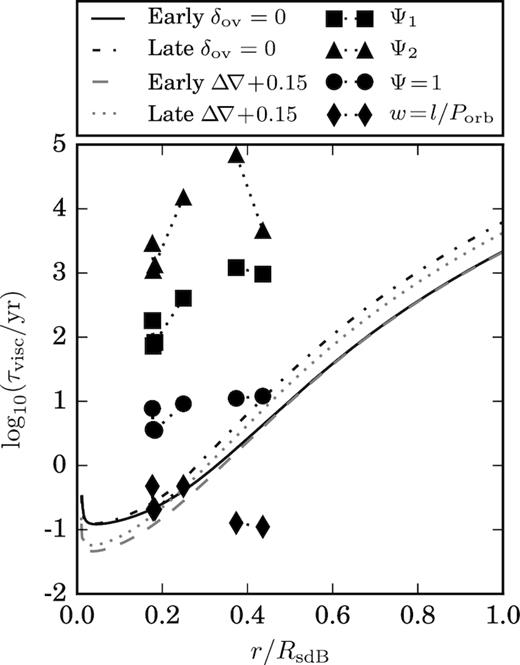
The viscous time-scale τvisc as a function of the fractional convective radius. The curves show the critical viscous time, for each convective radius, to achieve tidal synchronization during the EHB lifetime. Each line represents a single evolutionary model. The points plotted and connected with dotted lines are the viscous times predicted by the stellar models. The dotted lines connect the end points of evolutionary sequences with the same input physics (δov = 0, δov = 0.12, and Δ∇ + 0.15). For completeness the evolutionary models with convective overshoot are also plotted. The early models without a modified Schwarzschild criterion both start at almost identical places. The spread in the points is due to different damping factors. The squares use Ψ1, the triangles Ψ2, and the circles Ψ = 1. The diamonds have the convective velocity |$w$| = l/Porb, the minimum velocity required for the tides not to be considered fast. Increasing the fractional convective region increases the viscous time-scale.
The τvisc calculated for the models with equation (4) and the usual mixing theory estimates for the convective velocity are above the upper limits even when the damping factor is ignored. The τvisc increases as the convective core grows for all models with increasing radius owing to the high density of the material in the helium mantle. The damping factor is the most influential parameter. The choice of Ψ stratifies τvisc by orders of magnitude. When the damping factor is excluded τvisc does not vary much between the models and is about |$10\, \rm {yr}$|. Fig. 7 shows that doubling the radial extent of the convective region increases the viscous time-scale by approximately an order of magnitude. If the mixing velocity is increased such that |$w$| = l/Porb the tides are no longer considered fast and so are not damped. The convective velocity is driven by the heat flux. Increasing the velocity would cause a substantial increase in the heat flux which would then change the temperature gradient and hence the structure in other significant ways. If the convective cells turnover without releasing all of their energy to the surroundings higher velocities can be reached without changing the overall heat flux. Some 3D hydrodynamical simulations of convective regions in stars have typical velocities which are much larger than those predicted by mixing length theory (Arnett, Meakin & Young 2009; Gilkis & Soker 2016).
The derived upper limits are all within an order of magnitude of each other. If the radius of the dissipative region is small the viscous time must be less than a year for synchronization to be achieved. For convective regions which take up more than half of the sdB star by radius the critical viscous time is less than |$10\, \rm {yr}$|. This is more than the viscous time predicted when no damping is included.
4 DISCUSSION
J162256+473051 is another HW Vir type system with a lower mass companion in a shorter-period orbit than NY Vir. Observations show that this star is rotating sub-synchronously. Calculations of the tidal synchronization time indicate that this system should synchronize more rapidly than NY Vir owing to its substantially smaller orbital separation. If J162256+473051 is neither expected nor observed to be synchronized, why should NY Vir appear to be synchronized?
HW Vir type systems are most likely formed via a common-envelope interaction (Han et al. 2002). The spin of the outer regions of the sdB star that subsequently forms are affected during this process. NY Vir has p modes which propagate through the outer 55 per cent of the star. These p modes are consistent with synchronization. The presence of p modes means that the region must be radiative. However, synchronization could have been achieved during the common-envelope phase. NY Vir’s companion is more massive and more radially extended than that of J162256+473051 so its companion should have had more of an effect during this phase.
5 CONCLUSIONS
Asteroseismic evidence for rotational and orbital synchronization in the hot subdwarf binary NY Vir is at variance with our previous theoretical predictions of tidal synchronization in such stars. Because the tidal synchronization time-scale is inversely proportional to the radius of the convective region to the sixth power artificial extensions to the convection boundary have been examined to see whether a larger convective region could account for the observed synchronization. Increasing the radius of the convective region by a factor of 2.5 decreases tidal synchronization times by less than one order of magnitude, insufficient to bring NY Vir close to synchronization within its core-helium burning (or extended horizontal-branch) lifetime.
The individual terms of equation (3) were examined to test how much each contributes to the synchronization time and what constraints may be placed on the quantities contained in them. The boundary of the convective core was moved outwards to see if there was a radius at which tidal synchronization could occur without any modifications to the theory. It was found that even making the stars fully convective would not be sufficient because the orbital periods are shorter than the convective turnover time and consequently dissipation of the tides is damped. The damping factor and choice of mixing length theory are the areas of largest uncertainty. If the convective mixing velocity is increased such that |$w$| > l/Porb all the models predict tidal synchronization within the EHB lifetime. Some 3D hydrodynamical simulations of convective regions predict velocities substantially larger than those calculated with MLT. If these calculations prove correct, tidal synchronization might result from invocation of non-classical convection physics.
In seeking an alternative explanation for the synchronization of NY Vir, we note that the common-envelope phase is not well understood. If the tides do not synchronize on the EHB it is possible that at least the outer layers of the sdB star were synchronized during the common-envelope phase.
ACKNOWLEDGEMENTS
Research at the Armagh Observatory and Planetarium is supported by a grant-in-aid from the Northern Ireland Department for Communities. HPP acknowledges support from Nicky Saltiel, Churchill College and the UK Science and Technology Facilities Council (STFC) Grant No. ST/M502268/1. CSJ acknowledges support from STFC Grant No. ST/M000834/1. CAT thanks Churchill College for his fellowship.



