Search
Close
Search
Advanced Search
Search Menu
AI Discovery Assistant

ABSTRACT

The second law of thermodynamics is known to hold at small scales also when gravity plays a leading role, as in the case of black holes and self-gravitating radiation spheres. It has been suggested that it should as well at large scales. Here, by a purely kinematic analysis – based on the history of the Hubble factor and independent of any cosmological model – we explore if this law is fulfilled in the case of homogeneous and isotropic universes regardless of the sign of the spatial curvature.

gravitation, cosmology: theory

1 INTRODUCTION

At first sight, gravity and thermodynamics appear as practically disjoint, if not altogether unrelated, branches of Physics. However, as a closer look reveals, this is misleading. Recall, for instance, Tolman’s law of thermodynamic equilibrium in a stationary gravitational field (Tolman 1930, 1934), Unruh’s effect (Unruh 1976), the entropy associated to event (Hawking 1975, 1976; Gibbons & Hawking 1977; Wald 1994) and apparent horizons, (Bak & Rey 2000; Cai & Cao 2007), the generalized second law of thermodynamics for black holes (Bekenstein 1974, 1975), the equilibrium of self-gravitating radiation spheres (Sorkin, Wald & Jiu 1981; Pavón & Landsberg 1988), and, finally, the realization that the field equations of Einstein gravity can be understood as thermodynamic equations of state (Jacobson 1995; Padmanabhan 2005).

Therefore, the question arises: Is the Universe a thermodynamic system? To put it another way, Does it follow the laws of thermodynamics? In general relativity, and in most theories of gravity, the conservation of energy – i.e. the first law – emerges directly from the field equations of the theory in question, but to experimentally verify whether or not it is fulfilled at large scales appears far beyond present human capability. Here, we do not concern ourselves with this law; we simply assume its validity. As for the third law, we think it does not apply at large scales since the concept of ‘temperature of the Universe’ has no clear meaning. It is the second law that we are interested in.

At this point we feel expedient to recall it. As we witness on daily basis, macroscopic systems tend spontaneously to thermodynamic equilibrium. This is at the very basis of the second law. The latter encapsulates this by asserting that the entropy, |$\, S$|⁠, of isolated systems never decreases, S′ ≥ 0 and that, at least in the last stage of approaching equilibrium, it is concave, S″ < 0 (Callen 1960). The prime means derivative with respect to the relevant thermodynamic variable. In this paper, we shall tentatively apply this to cosmic expansion.

Before going any further, we wish to emphasize that sometimes the second law is found formulated by stating just the above condition on S′ but not on S″. While this mutilated version works well for many practical purposes, it is insufficient in general. Otherwise one would observe systems whose entropy increased without bound, which is at odds with daily experience. In this connection, it should be noted that this can arise in Newtonian gravity. A case in point is the gravothermal catastrophe: the entropy of a number of gravitating point masses confined to the interior of a rigid sphere, of perfectly reflecting walls, whose radius exceeds some critical value, diverges (Antonov 1962; Lynden-Bell, Wood & Royal 1968). This uncomfortable outcome hints that thermodynamics and Newtonian gravity are not fully consistent with each other. Nevertheless, it can be evaded by resorting to general relativity: The formation of a black hole at the centre of the sphere renders the entropy of the system to stay bounded.

Today, it is widely agreed that the entropy of the Universe (we mean that part of the Universe in causal contact with us) is overwhelmingly contributed by the entropy of the cosmic horizon (about 10122 times the Boltzmann constant). Supermassive black holes and the cosmic microwave radiation, alongside the cosmic sea of neutrinos, come behind by |$\, 18$| and 33 orders of magnitude, respectively. All the other sources of entropy contribute much less (Egan & Lineweaver 2010). Therefore, to ascertain whether the Universe fulfils the second law it suffices to see whether the entropy of the cosmic horizon, Sh, comply with |$S^{\prime }_{\rm h} \ge 0$| and |$S^{\prime \prime }_{\rm h} \le 0$|⁠. In homogeneous and isotropic universes one can define different causal horizons. We are interested in the apparent horizon (the boundary hypersurface of the space–time antitrapped region; Bak & Rey 2000), since it always exists in non-static universes, independently of whether it accelerates when t → ∞ or not. Neglecting possible (small) quantum corrections, the entropy of the horizon is found to be proportional to the area of the latter (Bak & Rey 2000; Cai & Cao 2007):
(1)
where |${\cal A} = 4 \pi \tilde{r}^{2}_{{\cal A}}$|⁠, |$\tilde{r}_{{\cal A}}= 1/\sqrt{H^{2} \, + \, k \, a^{-2}}\,$| the radius of the apparent horizon, k = +1, 0, −1 the normalized spatial curvature parameter, and ℓp the Planck length. Thereby, it follows that the Universe will comply with the second law provided that |$\, {\cal A}^{\prime } \ge 0$| and |$\, {\cal A}^{\prime \prime } \le 0$| (the prime means derivative with respect the scale factor of the Robertson–Walker metric).

The aim of this paper is to explore whether this is to be expected in view of the current data of the history of the Hubble factor. As it turns out, our study – which is purely kinematic – suggests that this may well be the case, i.e. that the Universe seems to tend to a state of maximum entropy in the long run. This outcome was suggested earlier (Ferreira & Pavón 2016). Here we strengthen this suggestion by employing an ampler data set and using a somewhat different analysis.

This result is also achievable from the ‘holographic equipartition principle’, i.e. the rate at which the three spatial volumes of the flat universe increase with expansion is proportional to the difference of the number of degrees of freedom between the horizon and the bulk (Krishna & Mathew 2017). However, our approach is more economical as we neither use temperatures at all nor assume equality beween them.

The paper is organized as follows. Next section presents the observational data and the best fit to them. Section 3 introduces three simple parametrizations of the Hubble function in terms of the scale factor. As we will see, the derivatives of the area of the apparent horizon associated to these parametrizations fulfil the inequalities expressed in the preceding paragraph. Section 4 studies, for the sake of comparison, the evolution of the apparent horizon for a handful of cosmological models that are known to fit reasonably well the data. Last section presents our conclusions and final comments.

2 H(z) DATA AND GAUSSIAN PROCESS

We shall use the set of 39 data of the Hubble factor, H(⁠|$z$|⁠), alongside their 1σ confidence interval, in terms of the redshift, compiled by Farooq et al. (2017) and Ryan, Doshi & Ratra (2018), listed in Table 1. These data come from different sources, also listed there, and were obtained using differential ages of red luminous galaxies, galaxy clustering, and baryon acoustic oscillation techniques – see references in the said table for details. Our study does not rely on any cosmological model at all. However, in Section 4, we compare the predictions of some successful models about the evolution of the area of the horizon with the outcome of our kinematic analysis.

Table 1.
Open in new tab

Hubble’s parameter versus redshift and scale factor.

|$z$|aH(⁠|$z$|⁠)  (km s−1 Mpc−1)Ref.
0.070.9369 ± 19.6Zhang et al. (2014)
0.090.9269 ± 12Simon, Verde & Jimenez (2005)
0.1000.9169 ± 12Simon et al. (2005)
0.1200.8968.6 ± 26.2Zhang et al. (2014)
0.1700.8583 ± 8Simon et al. (2005)
0.1790.8475 ± 4Moresco et al. (2012)
0.1990.8375 ± 5Moresco et al. (2012)
0.2000.8372.9 ± 29.6Zhang et al. (2014)
0.2700.7977 ± 14Simon et al. (2005)
0.2800.7888.8 ± 36.6Zhang et al. (2014)
0.3200.7579.2 ± 5.6Cuesta et al. (2016)
0.3520.7483 ± 14Moresco et al. (2012)
0.38020.7283 ± 13.5Moresco et al. (2012)
0.4000.7195 ± 17Simon et al. (2005)
0.40040.7177 ± 10.2Moresco et al. (2012)
0.42470.7087.1 ± 11.2Moresco et al. (2012)
0.4400.6982.6 ± 7.8Blake et al. (2012)
0.44970.6992.8 ± 12.9Moresco et al. (2012)
0.4700.6889 ± 50Ratsimbazafy et al. (2017)
0.47830.6880.9 ± 9Moresco et al. (2012)
0.4800.6897 ± 62Stern et al. (2010)
0.5700.64100.3 ± 3.7Cuesta et al. (2016)
0.5930.63104 ± 13Moresco et al. (2012)
0.6000.6387.9 ± 6.1Blake et al. (2012)
0.6800.6092 ± 8Moresco et al. (2012)
0.7300.5897.3 ± 7Blake et al. (2012)
0.7810.56105 ± 12Moresco et al. (2012)
0.8750.53125 ± 17Moresco et al. (2012)
0.8800.5390 ± 40Stern et al. (2010)
0.9000.52117 ± 23Simon et al. (2005)
1.0370.49154 ± 20Moresco et al. (2012)
1.3000.43168 ± 17Simon et al. (2005)
1.3630.42160 ± 33.6Moresco (2015)
1.4300.41177 ± 18Simon et al. (2005)
1.5300.40140 ± 14Simon et al. (2005)
1.7500.36202 ± 40Simon et al. (2005)
1.9650.34186.5 ± 50.4Moresco (2015)
2.3400.30222 ± 7Delubac et al. (2015)
2.3600.30226 ± 8Font-Ribera et al. (2014)
|$z$|aH(⁠|$z$|⁠)  (km s−1 Mpc−1)Ref.
0.070.9369 ± 19.6Zhang et al. (2014)
0.090.9269 ± 12Simon, Verde & Jimenez (2005)
0.1000.9169 ± 12Simon et al. (2005)
0.1200.8968.6 ± 26.2Zhang et al. (2014)
0.1700.8583 ± 8Simon et al. (2005)
0.1790.8475 ± 4Moresco et al. (2012)
0.1990.8375 ± 5Moresco et al. (2012)
0.2000.8372.9 ± 29.6Zhang et al. (2014)
0.2700.7977 ± 14Simon et al. (2005)
0.2800.7888.8 ± 36.6Zhang et al. (2014)
0.3200.7579.2 ± 5.6Cuesta et al. (2016)
0.3520.7483 ± 14Moresco et al. (2012)
0.38020.7283 ± 13.5Moresco et al. (2012)
0.4000.7195 ± 17Simon et al. (2005)
0.40040.7177 ± 10.2Moresco et al. (2012)
0.42470.7087.1 ± 11.2Moresco et al. (2012)
0.4400.6982.6 ± 7.8Blake et al. (2012)
0.44970.6992.8 ± 12.9Moresco et al. (2012)
0.4700.6889 ± 50Ratsimbazafy et al. (2017)
0.47830.6880.9 ± 9Moresco et al. (2012)
0.4800.6897 ± 62Stern et al. (2010)
0.5700.64100.3 ± 3.7Cuesta et al. (2016)
0.5930.63104 ± 13Moresco et al. (2012)
0.6000.6387.9 ± 6.1Blake et al. (2012)
0.6800.6092 ± 8Moresco et al. (2012)
0.7300.5897.3 ± 7Blake et al. (2012)
0.7810.56105 ± 12Moresco et al. (2012)
0.8750.53125 ± 17Moresco et al. (2012)
0.8800.5390 ± 40Stern et al. (2010)
0.9000.52117 ± 23Simon et al. (2005)
1.0370.49154 ± 20Moresco et al. (2012)
1.3000.43168 ± 17Simon et al. (2005)
1.3630.42160 ± 33.6Moresco (2015)
1.4300.41177 ± 18Simon et al. (2005)
1.5300.40140 ± 14Simon et al. (2005)
1.7500.36202 ± 40Simon et al. (2005)
1.9650.34186.5 ± 50.4Moresco (2015)
2.3400.30222 ± 7Delubac et al. (2015)
2.3600.30226 ± 8Font-Ribera et al. (2014)
Table 1.
Open in new tab

Hubble’s parameter versus redshift and scale factor.

|$z$|aH(⁠|$z$|⁠)  (km s−1 Mpc−1)Ref.
0.070.9369 ± 19.6Zhang et al. (2014)
0.090.9269 ± 12Simon, Verde & Jimenez (2005)
0.1000.9169 ± 12Simon et al. (2005)
0.1200.8968.6 ± 26.2Zhang et al. (2014)
0.1700.8583 ± 8Simon et al. (2005)
0.1790.8475 ± 4Moresco et al. (2012)
0.1990.8375 ± 5Moresco et al. (2012)
0.2000.8372.9 ± 29.6Zhang et al. (2014)
0.2700.7977 ± 14Simon et al. (2005)
0.2800.7888.8 ± 36.6Zhang et al. (2014)
0.3200.7579.2 ± 5.6Cuesta et al. (2016)
0.3520.7483 ± 14Moresco et al. (2012)
0.38020.7283 ± 13.5Moresco et al. (2012)
0.4000.7195 ± 17Simon et al. (2005)
0.40040.7177 ± 10.2Moresco et al. (2012)
0.42470.7087.1 ± 11.2Moresco et al. (2012)
0.4400.6982.6 ± 7.8Blake et al. (2012)
0.44970.6992.8 ± 12.9Moresco et al. (2012)
0.4700.6889 ± 50Ratsimbazafy et al. (2017)
0.47830.6880.9 ± 9Moresco et al. (2012)
0.4800.6897 ± 62Stern et al. (2010)
0.5700.64100.3 ± 3.7Cuesta et al. (2016)
0.5930.63104 ± 13Moresco et al. (2012)
0.6000.6387.9 ± 6.1Blake et al. (2012)
0.6800.6092 ± 8Moresco et al. (2012)
0.7300.5897.3 ± 7Blake et al. (2012)
0.7810.56105 ± 12Moresco et al. (2012)
0.8750.53125 ± 17Moresco et al. (2012)
0.8800.5390 ± 40Stern et al. (2010)
0.9000.52117 ± 23Simon et al. (2005)
1.0370.49154 ± 20Moresco et al. (2012)
1.3000.43168 ± 17Simon et al. (2005)
1.3630.42160 ± 33.6Moresco (2015)
1.4300.41177 ± 18Simon et al. (2005)
1.5300.40140 ± 14Simon et al. (2005)
1.7500.36202 ± 40Simon et al. (2005)
1.9650.34186.5 ± 50.4Moresco (2015)
2.3400.30222 ± 7Delubac et al. (2015)
2.3600.30226 ± 8Font-Ribera et al. (2014)
|$z$|aH(⁠|$z$|⁠)  (km s−1 Mpc−1)Ref.
0.070.9369 ± 19.6Zhang et al. (2014)
0.090.9269 ± 12Simon, Verde & Jimenez (2005)
0.1000.9169 ± 12Simon et al. (2005)
0.1200.8968.6 ± 26.2Zhang et al. (2014)
0.1700.8583 ± 8Simon et al. (2005)
0.1790.8475 ± 4Moresco et al. (2012)
0.1990.8375 ± 5Moresco et al. (2012)
0.2000.8372.9 ± 29.6Zhang et al. (2014)
0.2700.7977 ± 14Simon et al. (2005)
0.2800.7888.8 ± 36.6Zhang et al. (2014)
0.3200.7579.2 ± 5.6Cuesta et al. (2016)
0.3520.7483 ± 14Moresco et al. (2012)
0.38020.7283 ± 13.5Moresco et al. (2012)
0.4000.7195 ± 17Simon et al. (2005)
0.40040.7177 ± 10.2Moresco et al. (2012)
0.42470.7087.1 ± 11.2Moresco et al. (2012)
0.4400.6982.6 ± 7.8Blake et al. (2012)
0.44970.6992.8 ± 12.9Moresco et al. (2012)
0.4700.6889 ± 50Ratsimbazafy et al. (2017)
0.47830.6880.9 ± 9Moresco et al. (2012)
0.4800.6897 ± 62Stern et al. (2010)
0.5700.64100.3 ± 3.7Cuesta et al. (2016)
0.5930.63104 ± 13Moresco et al. (2012)
0.6000.6387.9 ± 6.1Blake et al. (2012)
0.6800.6092 ± 8Moresco et al. (2012)
0.7300.5897.3 ± 7Blake et al. (2012)
0.7810.56105 ± 12Moresco et al. (2012)
0.8750.53125 ± 17Moresco et al. (2012)
0.8800.5390 ± 40Stern et al. (2010)
0.9000.52117 ± 23Simon et al. (2005)
1.0370.49154 ± 20Moresco et al. (2012)
1.3000.43168 ± 17Simon et al. (2005)
1.3630.42160 ± 33.6Moresco (2015)
1.4300.41177 ± 18Simon et al. (2005)
1.5300.40140 ± 14Simon et al. (2005)
1.7500.36202 ± 40Simon et al. (2005)
1.9650.34186.5 ± 50.4Moresco (2015)
2.3400.30222 ± 7Delubac et al. (2015)
2.3600.30226 ± 8Font-Ribera et al. (2014)

Regrettably, a few of H(⁠|$z$|⁠) data are affected by uncomfortably big 1σ confidence intervals whereby some statistically based smoothing process must be applied to the whole data set if one wishes to draw sensible conclusions. We resort to the machine learning model Gaussian process, which infers a function from labelled training data (Rasmussen & Williams 2006). This process is capable of capturing a wide range of behaviours with only a set of parameters and admits a Bayesian interpretation (Zhao 2018). In this study, we are implementing the Gaussian process using the wolfram language(which includes a wide range machine learning capabilities), to be more specific we are using the predict function with the performance goal based on quality. All the numeric analysis is only based on the library given by the wolfram mathematica 10.4. See Seikel, Clarkson & Smith (2012) for a deep numerical analysis, with useful references, to this technique in a cosmological context.

Application of the Gaussian process to the data set results in the blue solid line – the ‘best fit’ – and its 1σ (grey shaded) confidence band, in terms of the scale factor, as shown in Fig. 1. Extrapolation to a = 1 gives H0 = 66.2 ± 16.6 km s−1 Mpc−1. This line suggests that |$\, H^{\prime}$| is negative in the whole interval |$\, 0.3 \le a \le 1.0\,$| and that |$\, H^{\prime \prime}$| is positive for |$\, a \ge 0.4$|⁠. Inspection of figs 1(c) and 3(a) of Carvalho & Alcaniz (2011) also supports this view. In principle there is no grounds to believe that this should be different for |$\, a \gt 1$|⁠.

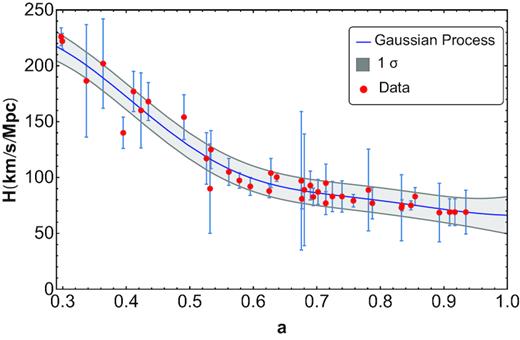
H(a) data (red points) and their 1σ confidence interval listed in Table 1. The blue solid line is the best fit to the data obtained by the Gaussian process. The grey shaded band corresponds to the 1σ confidence interval.
Figure 1.

H(a) data (red points) and their 1σ confidence interval listed in Table 1. The blue solid line is the best fit to the data obtained by the Gaussian process. The grey shaded band corresponds to the 1σ confidence interval.

Open in new tabDownload slide

Notice that H′ < 0 implies |${\cal A^{\prime }} > 0$| (at least, in spatially flat universes). Likewise, H″ > 0 leads to |${\cal A^{\prime \prime }} < 0$|⁠, which must be realized from some scale factor onwards if the entropy of the horizon is to approach a maximum in the long run (alongside |${\cal A^{\prime }} > 0$|⁠). As we will see below, in this regard, the impact of the spatial curvature will have little consequence (if at all) at late times.

3 PARAMETRIZING THE HUBBLE FUNCTION

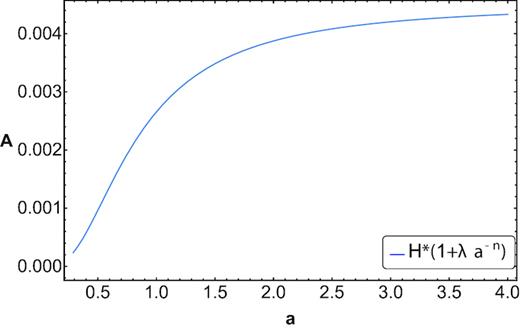
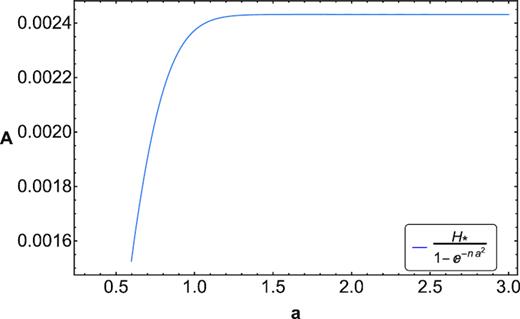
Here we essay three simple parametrizations of |$\, H(a)$| that comply with the conditions H′(a) < 0 and H″(a) > 0, mentioned above, in the interval covered by the H(⁠|$z$|⁠) data listed in Table 1, and that lead to |${\cal A}^{\prime } \gt 0$| and |${\cal A}^{\prime \prime } \le 0$| (the latter inequality is not necessarily valid when a < 0.5). We emphasize that these three Hubble functions are not meant to describe cosmic expansion for |$\, a \ll 1$|⁠, but we hope they will be qualitatively correct otherwise. We will contrast them with the best fit (blue solid line) shown in Fig. 1. We will take as the ‘goodness’ of a given parametrization the area enclosed by the said best-fitting line and the graph of the parametrization (the smaller the area, the better the parametrization).

3.1 Parametrization 1

Our first proposal is
(2)
By numerically fitting it to the best-fitting line with the 1σ confidence interval of Fig. 1, one obtains for the free parameters: H* = 41.15 ± 2.30 km s−1 Mpc−1 and λ = 0.51 ± 0.03. Then, H0 = 68.5 km s−1 Mpc−1, and the age of the universe, defined as |$t_{0} = \int _{0}^{1}{\mathrm{ d}a/(a\, H(a))}$|⁠, is 13 Gyr. On the other hand, the deceleration parameter, q = −1 − (aH′/H), evaluated at present gives q0 = −0.49 and the transition deceleration–acceleration occurs at atr = 0.51. The area between the graph of the parametrization and the blue solid line (best fit) obtained using the Gaussian process is 5.15.

Fig. 2 contrasts equation (2), black dashed line, with the best fit to the Hubble data. The dependence of the area of the apparent horizon on the scale factor for k = 0 is depicted in Fig. 3. The graphs for k = +1 and k = −1 show no significant difference with this one; all three are practically coincident (this is also true for parametrizations 2 and 3 considered below). From this graph we learn that |${\cal A}^{\prime } \ge 0$| in the range of scale factor considered and that |${\cal A}^{\prime \prime } \le 0$| from a ≃ 0.5 onward.

Same as Fig. 1 but including the curve (dashed line) corresponding to parametrization 1 (equation 2 with H* = 41.15 km s−1 Mpc−1 and λ = 0.51).
Figure 2.

Same as Fig. 1 but including the curve (dashed line) corresponding to parametrization 1 (equation 2 with H* = 41.15 km s−1 Mpc−1 and λ = 0.51).

Open in new tabDownload slide
Area of the apparent horizon of parametrization 1 assuming k = 0. The graphs for k = +1 and k = −1 are practically undistinguishable from this one and, therefore, not shown.
Figure 3.

Area of the apparent horizon of parametrization 1 assuming k = 0. The graphs for k = +1 and k = −1 are practically undistinguishable from this one and, therefore, not shown.

Open in new tabDownload slide

3.2 Parametrization 2

The second parametrization is
(3)
Proceeding as in the previous case, the best fits for the free parameters are found to be H* = 52.77 ± 3.18 km s−1 Mpc−1, λ = 0.30 ± 0.55, and n = 1.94 ± 0.09. Thus, t0 = 13.9 Gyr, H0 = 68.7 km s−1 Mpc−1, q0 = −0.54, and atr = 0.53. Fig. 4 compares this parametrization (black dashed line) with the best fit to the Hubble data. The area between the curves is 5.12. Fig. 5 shows the evolution of the area of the apparent horizon.
Same as Fig. 1 but including the curve (dashed line) of parametrization 2 (equation 3 with H* = 52.77 km s−1 Mpc−1, λ = 0.30, and $\, n=1.94$).
Figure 4.

Same as Fig. 1 but including the curve (dashed line) of parametrization 2 (equation 3 with H* = 52.77 km s−1 Mpc−1, λ = 0.30, and |$\, n=1.94$|⁠).

Open in new tabDownload slide
Area of the apparent horizon corresponding to parametrization 2.
Figure 5.

Area of the apparent horizon corresponding to parametrization 2.

Open in new tabDownload slide

3.3 Parametrization 3

As third parametrization, we propose
(4)
Proceeding as before yields H* = 67.81 ± 3.58 km s−1 Mpc−1 and n = 3.84 ± 0.32. Thus, t0 = 14 Gyr, H0 = 72.7 km s−1 Mpc−1, q0 = −0.89, and |$a_{\rm tr} = 0.54$|⁠. Fig. 6 contrasts the graph (black dashed line) corresponding to equation (4) with the best fit to the Hubble data. The area between the curves is 7.79. Fig. 7 shows the evolution of the area of the horizon.
Same as Fig. 1 but including the curve (dashed line) of parametrization 3 (equation 4 with H* = 67.81 km s−1 Mpc−1 and n = 3.84).
Figure 6.

Same as Fig. 1 but including the curve (dashed line) of parametrization 3 (equation 4 with H* = 67.81 km s−1 Mpc−1 and n = 3.84).

Open in new tabDownload slide
Area of the apparent horizon for parametrization 3.
Figure 7.

Area of the apparent horizon for parametrization 3.

Open in new tabDownload slide

The value for q0 derived from these three essay Hubble functions is quite consistent with the one measured by Daly et al. (2008) (q0 = −0.48 ± 0.11) by a model independent analysis. These authors based their study on the distances and redshifts to 192 supernovae, 30 radio galaxies, and 38 galaxy clusters. However, the quantity atr that follows from the said Hubble functions results slightly lower than the obtained by Daly et al., namely |$a_{\rm tr}= 0.56^{+0.10}_{-0.03}$|⁠.

All three parametrizations share the features that, regardless the sign of the curvature index k, the area, |${\cal A}$|⁠, of the apparent horizon never decreases and that |${\cal A}^{\prime \prime } \le 0$| from some value of the scale factor on. This hints that the universe described by each of them fulfils the second law of thermodynamics and tend asymptotically to state of maximum entropy of the order of |$H^{-2}_{*}$| in Planck units.

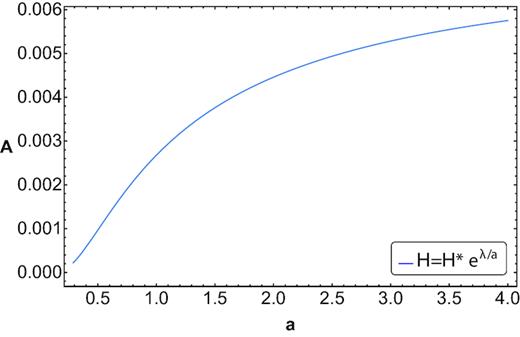
Nevertheless, Hubble functions that comply with H′ < 0 and H″ > 0 but fail to lead to |$\, {\cal A}^{\prime \prime } \le 0$|⁠, at late times (at least when k = 0) can be proposed. Consider for instance |$\, H = H_{*} \, [\exp (\lambda /a) \, - \, 1]$| and |$\, H = H_{*} \exp (-\lambda a)$|⁠, where λ is a positive definite constant. The entropy of spatially flat cosmological models whose expansion were governed by any of these two functions would increase unbounded to never reach a state of thermal equilibrium. However, as previously remarked (Pavón & Radicella 2013), both Hubble functions are at stark variance with observation. The first one corresponds to a universe that never accelerates. The second one to a universe that accelerates at early times (i.e. for a < λ−1) and decelerates forever afterward.

At this point one may wonder whether the evolution of the apparent horizon dictated by the three Hubble’s essay functions of above are qualitatively consistent with the corresponding evolution predicted by those cosmological models that fit reasonably well the observational data. This will be the subject of the next section. As it will turn out, the answer to this question is in the affirmative.

4 COSMOLOGICAL MODELS-DOMINATED PRESSURELESS MATTER AND DARK ENERGY

In this section, we briefly consider the evolution of the area of the apparent horizon in a homogeneous and isotropic universe governed by Einstein gravity and dominated by pressureless matter (baryonic plus dark) and dark energy. We also allow for the presence of a small spatial curvature. We first study the case in which dark energy is in the form of a positive cosmological constant, Λ, and then when it is given by a scalar field with constant equation of state parameter |$w_{\rm X} \ne -1$|⁠. In both cases we assume, in agreement with dynamical measurements (see e.g. Freedman 2001 for a short review and section V in Bartelmann 2010), that the matter component contributes to the total energy budget by about 30 per cent. The rest is in the form of dark energy (either a cosmological constant or a scalar field) plus spatial curvature. As stressed in Ryan et al. (2018), Ooba, Ratra & Sugiyama (2018), and Park & Ratra (2018a,b), the latter may well be non-negligible.

Nowadays there is a discrepancy between local and global measurements of the Hubble constant H0. The former yield 73.24 ± 1.74 km s−1 Mpc−1 (Riess et al. 2016), while the latter, based on the spatially flat Λ cold dark matter (ΛCDM) model, give |$\, 67.8 \pm 0.9$| km s−1 Mpc−1 (Ade 2016). Below, we will use in turn the result of Riess et al. and the prior 68 ± 2.8 km s−1 Mpc−1 employed by Ryan et al. (2018). As we will see, no major difference arises with regard to the overall evolution of the area of the horizon. At any rate, both values are somewhat above the best fit obtained by the Gaussian process (blue solid line in Fig. 1). As input data we will employ the cosmological parameter values obtained in Ryan et al. (2018) by constraining several simple cosmological models based in Einstein gravity (both with and without spatial curvature) using 31 |$\, H(z)$| data in the redshift range |$\, 0.07 \le z \le 1.965$| and 11 baryon acoustic oscillation distance measurements.

4.1 ΛCDM models

For this kind of models Friedamann’s equation reads
(5)
where Ωm0 and Ωk0 = 1 − Ωm0 − ΩΛ denote the present value of the density parameters of matter and spatial curvature, respectively, and ΩΛ the parameter density associated with the cosmological constant. From equation (5) it is seen that at large times the area of the apparent horizon is of the order of |$\, H^{-2}_{0} \Omega ^{-1}_{\Lambda}$|⁠.

We study two ΛCDM cases.

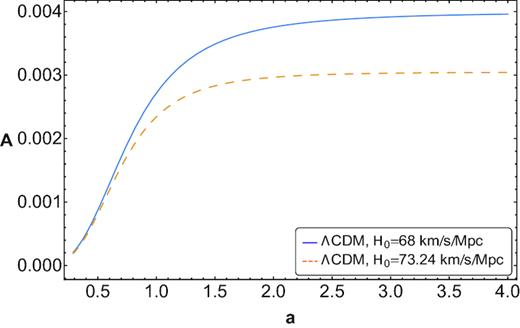
  • First case, H0 = 68 ± 2.8 km s−1 Mpc−1, Ωm0 = 0.29, and ΩΛ0 = 0.68 (see black dashed line in Fig. 8). Thus, t0 = 13.9 Gyr, q0 = −0.54, and atr = 0.60. The area between the curves is 3.25.

  • Second case, H0 = 73.24 ± 1.74 km s−1 Mpc−1, Ωm0 = 0.30, and Ωk0 = −0.07 (see orange dot–dashed line in Fig. 8). Thus, t0 = 13.2 Gyr, q0 = −0.62, and |$a_{\rm tr} = 0.58$|⁠. The area between the curves is 3.86.

The evolution of the area of the apparent horizon is shown, in each case, in Fig. 9.

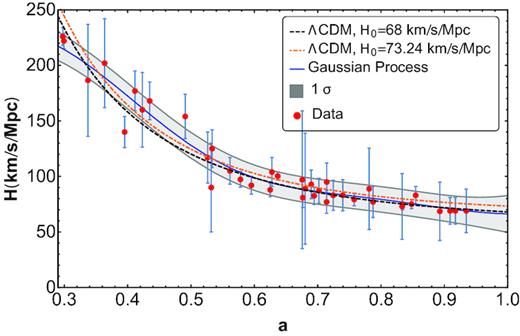
The Hubble factor for the two ΛCDM models contrasted with the best fit to the Hubble data in Table 1 using the Gaussian process.
Figure 8.

The Hubble factor for the two ΛCDM models contrasted with the best fit to the Hubble data in Table 1 using the Gaussian process.

Open in new tabDownload slide
Area of the apparent horizon in the ΛCDM models.
Figure 9.

Area of the apparent horizon in the ΛCDM models.

Open in new tabDownload slide

4.2 Flat XCDM models

We consider a generic dark energy model that, from the phenomenological viewpoint, essentially differs at first order from the ΛCDM in that the equation of state parameter, |$w$|X ≡ pX/ρX, is a constant different from −1. We study in turn two flat XCDM cases where
(6)

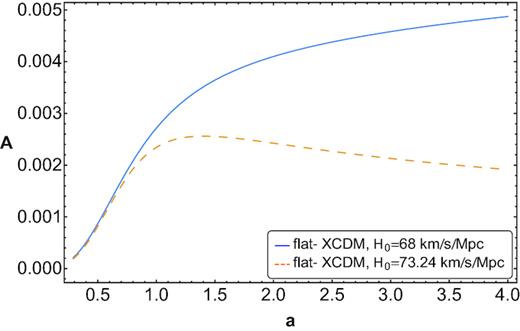
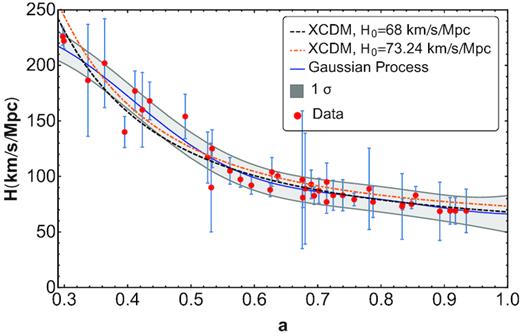
  • First case, H0 = 68 ± 2.8 ± 0.9 km s−1 Mpc−1, Ωm0 = 0.29, and |$w$|X = −0.94 (see black dashed line in Fig. 10). Thus, t0 = 13.9 Gyr, q0 = −0.50, and atr = 0.59. The area between the curves is 3.11.

  • Second case, H0 = 73.24 ± 1.74 km s−1 Mpc−1, Ωm0 = 0.29, and |$w$|X = −1.13 (see orange dot–dashed line in Fig. 10). Thus, t0 = 13.3 Gyr, q0 = −0.70, and |$a_{\rm tr} = 0.60$|⁠. The area between the curves is 3.57. Note – see Fig. 11 – that the area of the apparent horizon begins increasing but at some point (as soon as the dark energy takes over) it decreases. This violation of the second law (which occurs because, in this case, the dark energy is of ‘phantom’ type, |$w$|X < −1) goes hand in hand with the fact that phantom fields present classical (Dabrowski 2015) and quantum instabilities (Cline, Jeon & Moore 2004; Sbisà 2014) that render them implausible.

In both cases the evolution of the area of the horizon is shown Fig. 11.

Same as Fig. 8 but for the two flat XCDM models.
Figure 10.

Same as Fig. 8 but for the two flat XCDM models.

Open in new tabDownload slide
Area of the apparent horizon for the flat XCDM models.
Figure 11.

Area of the apparent horizon for the flat XCDM models.

Open in new tabDownload slide

4.3 Non-flat XCDM models

The Hubble factor of spatially curved XCDM models can be written as
(7)
\begin{eqnarray*} (\Omega _{\rm X0} = 1 - \Omega _{\rm m0} - \Omega _{\rm k0}). \end{eqnarray*}

  • First case, |$\, H_0= 68 \pm 2.8$| km s−1 Mpc−1, Ωm0 = 0.31, Ωk0 = −0.18, and |$w$|X = −0.76 (see black dashed line in Fig. 12). Thus, t0 = 13.8 Gyr, q0 = −0.40, and atr = 0.58. The area between the curves is 2.99.

  • Second case, H0 = 73.24 ± 1.74 km s−1 Mpc−1, Ωm0 = 0.32, Ωk0 = −0.21, and |$w$|X = −0.84 (see orange dot–dashed line in Fig. 12). Thus, t0 = 13 Gyr, q0 = −0.52, and |$a_{\rm tr} = 0.57$|⁠. The area between the curves is |$\, 4.29$|⁠.

Same as Fig. 8 but for the non-flat XCDM models.
Figure 12.

Same as Fig. 8 but for the non-flat XCDM models.

Open in new tabDownload slide

The evolution of the area of the apparent horizons is depicted in Fig. 13.

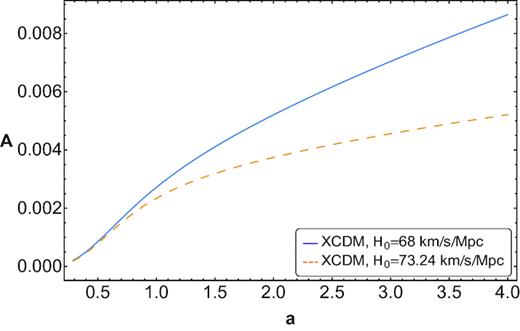
Evolution of the area of the horizon of the non-flat XCDM model.
Figure 13.

Evolution of the area of the horizon of the non-flat XCDM model.

Open in new tabDownload slide

Notice that the cosmological models considered in this section fit better (by about a factor of 2) the best fit (blue solid line) to the Hubble data set in Fig. 1 than any of the three parametrizations of Section 3 (i.e. the former have a lower value for the area between the curves than the latter) even though no fitting process to the said data has been applied to the cosmological models. This was to be expected with regard to the Hubble essay functions 1 and 3 because the models of this section have one or two more free parameters.

We have just considered a handful of simple cosmological models that fit observation reasonably well – see Ryan et al. (2018). More sophisticated models, as those beyond Einstein gravity, also deserve consideration. However, generally speaking, in that case the fit of the model parameters to the observational data is significantly affected by systematics.

We conclude this section by noting that the apparent horizon of homogeneous and isotropic cosmological models, regardless of their spatial curvature, that fit current observation and are classical and quantum-mechanically stable comply with the same conditions (⁠|${\cal A^{\prime }} \gt 0$| and |${\cal A^{\prime \prime }} \le 0$|⁠, the latter at least from some value of the scale factor onward) than the three essay Hubble functions (equations 2–4) of Section 3. These two conditions ensure that the corresponding cosmological model respects the second law. This suggests that from this preliminary H(⁠|$z$|⁠) data set, however scarce and of limited quality, one may glimpse that the universe fulfils the said law. Therefore, from this point of view, it appears to behave as a normal thermodynamic system. Recently, this conclusion was also attained by an altogether different route, namely by the analysis of the statistical fluctuations of the flux of energy on the apparent horizon (Mimoso & Pavón 2018). As it turns out, the strength of the fluctuations decreases with the area of the horizon and increases with the temperature of the latter. Just as in systems in which gravity is absent (Landau & Lifshitz 1971).

5 CONCLUDING REMARKS

The recent years have witnessed a reinforcement of the connection between gravity and thermodynamics. As two salient landmarks we mention the discovery that fully gravitationally collapsed objects possess a well-defined temperature and entropy (Hawking 1975, 1976), and the realization that the gravity field equations can be viewed as thermodynamic equations of state (Jacobson 1995; Padmanabhan 2005). In this context it is natural to ask whether the Universe behaves as a normal thermodynamic system; that is to say, whether it satisfies the laws of thermodynamics; most importantly the second law. Actually, this amount to consider whether the aforesaid law also holds at cosmic scales.

To answer this question we assumed the Universe is homogeneous and isotropic at sufficiently large scales and, based on the history of the Hubble function as specified in Table 1, made a kinematic analysis independent of any cosmological model. In Section 2, by applying the Gaussian process we obtained a best fit to the data (blue solid line in Fig. 1). The latter suggests that H′(a) < 0 and H″(a) > 0. Then, in Section 3 we essayed three simple Hubble functions (equations 2–4) that comply with these two inequalities, and are consistent with the second law as applied to the area of the apparent horizon (i.e. |${\cal A^{\prime }} \gt 0 \,$| and |$\, {\cal A^{\prime \prime }} \lt 0$|⁠), and reproduce reasonably well (especially for a ≥ 0.55) the best fit to the Hubble data – Figs 2, 4, and 6. As illustrated by two examples, Hubble functions that imply |$\, {\cal A^{\prime \prime }} \gt 0$| in the long run strongly disagree with observation at the background level. In Section 4, we contrasted the evolution of the Hubble function predicted by some simple, flat, and non-flat cosmological models that fit observation reasonably well (Ryan et al. 2018) with the best fit to the Hubble data set (Figs 8, 10, and 12). These fits are only somewhat better than those of the three parametrizations proposed in Section 3. Except for the second flat XCDM model, which is of ‘phantom’ type and presents instabilities at the classical and quantum level, the area of the apparent horizon is always increasing and with second derivative negative in the long run. In this regard, it mimics the evolution of the area of the apparent horizon associated to the three essay Hubble functions of Section 3.

Our overall conclusion is that the second law of thermodynamics seems to be obeyed by the Universe we observe today and, therefore, that this law also holds at cosmic scales. However, this conclusion, extracted from a scarce number of Hubble data of not great quality, cannot be but preliminary. Nevertheless, we hope that in the not distant future a much more ample set of data of better quality will be available whence we will make able to reach a firmer conclusion. This improvement in the quality and number of data may arise not only from a refinement of the current techniques but also from measuring the drift of the redshift of distant sources (Sandage 1962; Loeb 1998). This seems feasible thanks to the future European Extreme Large Telescope alongside advanced spectrographs like CODEX (2018).

Finally, as is apparent, our approach is purely classical in nature. Nevertheless, it is worthy to emphasize that it is also robust against quantum fluctuations since, as demonstrated by Oshita (2018), these do not invalidate the generalized second law because cosmological decoherence prevents it in the case of de Sitter expansion.

ACKNOWLEDGEMENTS

MG-E acknowledges support from a PUCV doctoral scholarship and DI-VRIEA-PUCV for financial support.

REFERENCES

Ade
P.
,
2016
,
A&A
,
594
,
A13

Crossref
Search ADS
 

Antonov
V.
,
1962
,
Vest. Leningrad Gos. Univ.
,
7
,
135

 

Bak
D.
,
Rey
S.-J.
,
2000
,
Classical Quantum Gravity
,
17
,
L83
10.1088/0264-9381/17/15/101

Crossref
Search ADS
 

Bartelmann
M.
,
2010
,
Rev. Modern Phys.
,
82
,
331
10.1103/RevModPhys.82.331

Crossref
Search ADS
 

Bekenstein
J. D.
,
1974
,
Phys. Rev. D
,
9
,
3292
10.1103/PhysRevD.9.3292

Crossref
Search ADS
 

Bekenstein
J. D.
,
1975
,
Phys. Rev. D
,
12
,
3077
10.1103/PhysRevD.12.3077

Crossref
Search ADS
 

Blake
C.
et al. ,
2012
,
MNRAS
,
425
,
405

Crossref
Search ADS
 

Cai
R.
,
Cao
L.
,
2007
,
Phys. Rev. D
,
75
,
064008
10.1103/PhysRevD.75.064008

Crossref
Search ADS
 

Callen
H.
,
1960
,
Thermodynamics and an Introduction to Thermostatistics
, 2nd edn.
Wiley
,
New York

Google Scholar

OpenURL Placeholder Text

 

Carvalho
J. C.
,
Alcaniz
J. S.
,
2011
,
MNRAS
,
418
,
1873

Crossref
Search ADS
 

Cline
J. M.
,
Jeon
S.
,
Moore
G. D.
,
2004
,
Phys. Rev. D
,
70
,
043543
10.1103/PhysRevD.70.043543

Crossref
Search ADS
 

CODEX
,
2018
,
An Ultra-Stable, High-Resolution Optical Spectrograph for the E-ELT
. (www.iac.es/proyecto/codex)

 

Cuesta
A. J.
et al. ,
2016
,
MNRAS
,
457
,
1770

Crossref
Search ADS
 

Dabrowski
M. P.
,
2015
,
European J. Phys.
,
36
,
065017
10.1088/0143-0807/36/6/065017

Crossref
Search ADS
 

Daly
R. A.
,
Djorgovski
S.
,
Freeman
K. A.
,
Mory
M. P.
,
O dea
C.
,
Kharb
P.
,
Baum
S.
,
2008
,
ApJ
,
677
,
1
10.1086/528837

Crossref
Search ADS
 

Delubac
T.
et al. ,
2015
,
A&A
,
574
,
A59

Crossref
Search ADS
 

Egan
C. A.
,
Lineweaver
C. H.
,
2010
,
ApJ
,
710
,
1825
10.1088/0004-637X/710/2/1825

Crossref
Search ADS
 

Farooq
O.
,
Madiyar
F. R.
,
Crandall
S.
,
Ratra
B.
,
2017
,
ApJ
,
835
,
26
10.3847/1538-4357/835/1/26

Crossref
Search ADS
 

Ferreira
P. C.
,
Pavón
D.
,
2016
,
Universe
,
2
,
27
10.3390/universe2040027

Crossref
Search ADS
 

Font-Ribera
A.
et al. ,
2014
,
J. Cosmol. Astropart. Phys.
,
05
,
027
10.1088/1475-7516/2014/05/027

Crossref
Search ADS
 

Freedman
W. L.
,
2001
, in
Bergström
L.
,
Fransson
C.
,
Carlson
P.
, eds,
Particle Physics and the Universe
.
World Scientific Press
,
Singapore
, p.
37

Google Scholar

OpenURL Placeholder Text

 

Gibbons
G. W.
,
Hawking
S. W.
,
1977
,
Phys. Rev. D
,
15
,
2752
10.1103/PhysRevD.15.2752

Crossref
Search ADS
 

Hawking
S.
,
1975
,
Commun. Math. Phys.
,
43
,
199
10.1007/BF02345020

Crossref
Search ADS
 

Hawking
S.
,
1976
,
Phys. Rev. D
,
13
,
191
10.1103/PhysRevD.13.191

Crossref
Search ADS
 

Jacobson
T.
,
1995
,
Phys. Rev. Lett.
,
75
,
1260
10.1103/PhysRevLett.75.1260

Crossref
Search ADS
PubMed
 

Krishna
P.
,
Mathew
T. K.
,
2017
,
Phys. Rev. D
,
96
,
063513
10.1103/PhysRevD.96.063513

Crossref
Search ADS
 

Landau
L.
,
Lifshitz
E.
,
1971
,
Mécanique des Fluides
.
MIR
,
Moscow

 

Loeb
A.
,
1998
,
ApJ
,
499
,
L111
10.1086/311375

Crossref
Search ADS
 

Lynden-Bell
D.
,
Wood
R.
,
Royal
A.
,
1968
,
MNRAS
,
138
,
495

Crossref
Search ADS
 

Mimoso
J. P.
,
Pavón
D.
,
2018
,
Phys. Rev. D
,
97
,
103537
10.1103/PhysRevD.97.103537

Crossref
Search ADS
 

Moresco
M.
,
2015
,
MNRAS
,
450
,
L16

Crossref
Search ADS
 

Moresco
M.
et al. ,
2012
,
J. Cosmol. Astropart. Phys.
,
08
,
006
10.1088/1475-7516/2012/08/006

Crossref
Search ADS
 

Ooba
J.
,
Ratra
B.
,
Sugiyama
N.
,
2018
,
ApJ
,
864
,
80

Crossref
Search ADS
 

Oshita
N.
,
2018
,
Phys. Rev. D
,
97
,
023510
10.1103/PhysRevD.97.023510

Crossref
Search ADS
 

Padmanabhan
T.
,
2005
,
Phys. Rep.
,
406
,
49
10.1016/j.physrep.2004.10.003

Crossref
Search ADS
 

Park
C.-G.
,
Ratra
B.
,
2018a
,
preprint(arXiv:1803.05522)

Park
C.-G.
,
Ratra
B.
,
2018b
,
preprint(arXiv:1809.03598)

Pavón
D.
,
Landsberg
P. T.
,
1988
,
Gen. Relativ. Gravitation
,
20
,
457
10.1007/BF00758121

Crossref
Search ADS
 

Pavón
D.
,
Radicella
N.
,
2013
,
Gen. Relativ. Gravitation
,
45
,
63
10.1007/s10714-012-1457-x

Crossref
Search ADS
 

Rasmussen
C. E.
,
Williams
C. K.
,
2006
,
Gaussian Process for Machine Learning
.
The MIT Press
,
Cambridge, MA

Google Scholar

OpenURL Placeholder Text

 

Ratsimbazafy
A.
,
Loubser
S.
,
Crawford
S.
,
Cress
C.
,
Bassett
B.
,
Nichol
R.
,
Väisänen
P.
,
2017
,
MNRAS
,
467
,
3239

Crossref
Search ADS
 

Riess
A. G.
et al. ,
2016
,
ApJ
,
826
,
56
10.3847/0004-637X/826/1/56

Crossref
Search ADS
 

Ryan
J.
,
Doshi
S.
,
Ratra
B.
,
2018
,
MNRAS
,
480
,
759

Crossref
Search ADS
 

Sandage
L.
,
1962
,
ApJ
,
136
,
319
10.1086/147385

Crossref
Search ADS
 

Sbisà
F.
,
2014
,
European J. Phys.
,
36
,
015009
10.1088/0143-0807/36/1/015009

Crossref
Search ADS
 

Seikel
M.
,
Clarkson
C.
,
Smith
M.
,
2012
,
J. Cosmol. Astropart. Phys.
,
06
,
036
10.1088/1475-7516/2012/06/036

Crossref
Search ADS
 

Simon
J.
,
Verde
L.
,
Jimenez
R.
,
2005
,
Phys. Rev. D
,
71
,
123001
10.1103/PhysRevD.71.123001

Crossref
Search ADS
 

Sorkin
R. D.
,
Wald
R. M.
,
Jiu
Z. Z.
,
1981
,
Gen. Relativ. Gravitation
,
13
,
1127
10.1007/BF00759862

Crossref
Search ADS
 

Stern
D.
,
Jimenez
R.
,
Verde
L.
,
Kamionkowski
M.
,
Stanford
S. A.
,
2010
,
J. Cosmol. Astropart. Phys.
,
02
,
008
10.1088/1475-7516/2010/02/008

Crossref
Search ADS
 

Tolman
R. C.
,
1930
,
Phys. Rev.
,
35
,
904
10.1103/PhysRev.35.904

Crossref
Search ADS
 

Tolman
R. C.
,
1934
,
Relativity, Thermodynamics, and Cosmology
.
Clarendon Press
,
Oxford

 

Unruh
W. G.
,
1976
,
Phys. Rev. D
,
14
,
870
10.1103/PhysRevD.14.870

Crossref
Search ADS
 

Wald
R. M.
,
1994
,
Quantum Field Theory in Curved Spacetime and Black Hole Thermodynamics
.
Univ. Chicago Press
,
Chicago, IL

Google Scholar

OpenURL Placeholder Text

 

Zhang
C.
,
Zhang
H.
,
Yuan
S.
,
Liu
S.
,
Zhang
T.-J.
,
Sun
Y.-C.
,
2014
,
Res. Astron. Astrophys.
,
14
,
1221
10.1088/1674-4527/14/10/002

Crossref
Search ADS
 

Zhao
Z.
,
2018
,
preprint(arXiv:1812.04877)

© 2019 The Author(s) Published by Oxford University Press on behalf of the Royal Astronomical Society
This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)
Issue Section:
Article
Download all slides