-
PDF
- Split View
-
Views
-
Cite
Cite
Maryam Samadi, Shahram Abbassi, Wei-Min Gu, Accretion flows with comparable radiation and gas pressures, Monthly Notices of the Royal Astronomical Society, Volume 484, Issue 3, April 2019, Pages 2915–2923, https://doi.org/10.1093/mnras/stz141
Close - Share Icon Share
Abstract
By taking into account photon absorption, we investigate the vertical structure of accretion flows with comparable radiation and gas pressures. We consider two separate energy equations for matter and radiation in the diffusion limit. In order to solve the set of radiation hydrodynamic equations in steady state and axisymmetric configuration, we employ self-similar technique in the radial direction. We need the reflection symmetry about the mid-plane to find gas density at the equator. For a typical solution, we assume that the gas pressure has 10–50 per cent portion of the total pressure. In this paper, since the radiation energy is involved directly, we are able to estimate how much energy of viscous heating is transported in the radial direction and advected towards the central object. Our results show that although the mass accretion rate does not approach the Eddington limit, the energy advection is rather high. Moreover, in a disc with greater accretion rate and less portion of gas pressure at the total pressure, more energy is advected to its centre. In addition, as we expect the accretion flow becomes thicker with greater values of gas pressure. Based on Solberg–Høiland conditions, we notice that the flow is convectively stable in all parts of such a disc.
1 INTRODUCTION
In active galactic nuclei, the major part of energy originates from the vicinity of the central black hole that is occupied by an optically thick accretion flow. Any realistic accretion flow has sufficient angular momentum to form a rotationally supported disc. Due to the liberation of gravitational energy and the existence of turbulent viscosity, the disc can become visible for us. Modelling of such a disc that surrounds a black hole started by pioneers such as Zeldovich (1964), Salpeter (1964), and Zeldovich & Novikov (1967). Lynden-Bell (1969) explained that the energy source of quasars is a viscous accretion disc. The standard accretion disc model proposed by Shakura & Sunyaev (1973) became very successful to describe optically thick and geometrically thin accretion discs observed in X-ray binaries. However, this model turned out to be unable to clarify some observational features arising from very hot plasma around black holes. After that popular model, slim disc model was introduced by Abramowicz et al. (1988), who presented the properties of those optically thick discs with high-mass accretion rates close to its critical values. A few years before it, another popular model had been gradually forming (Ichimaru 1977, Rees et al. 1982), and finally became comprehensive and identified as radiatively inefficient accretion flows (RIAFs) (Narayan & Yi 1994, 1995; Abramowicz et al. 1995; Chen et al. 1997). This model was applied to explain very hard radiation, such as hard X-rays and gamma-rays (up to 100keVwhich were not perceptible by the standard disc model. In the slim discs and RIAFs, the heat energy released by viscous dissipation is stored in the gas and it is advected onto the disc's center. Therefore, they both belong to advection-dominated accretion flows and can be appropriately described by the self-similar solutions in the radial direction (Narayan & Yi 1994). On the other hand, the presence of radiation can influence significantly the dynamics of the accretion system. Moreover, we expect the radiation pressure exceeds the gas pressure in the central regions, since the accretion rate is greater than about 1% of the Eddington value (Turner 2004, Shakura & Sunyaev 1973; Pringle 1981). It seems that without including radiation pressure in the definition of α- prescription, we can not explain observed X-ray luminosities of some compact objects. Near Eddington limit, photons carry a significant fraction of the total momentum, hence radiation also associates with matter for transportation of the angular momentum out of the disc (Jiang et al. 2013). So far, some simulations have been done by several athours (e.g. Eggum et al. 1987, 1988; Okuda, Fujita & Sakashita 1997; Fujita & Okuda 1998; Kley & Lin 1999; Takeuchi, Mineshige & Ohsuga 2009; Sadowski et al. 2014) to study slim discs, especially in supercritical accretion regime. Fujita & Okuda (1998) performed 2D calculations to examine subcritical accretion discs with a luminosity comparable with Eddington one. Okuda (2002) noticed that it is possible for a flow that has supercritical accretion rate in the outer boundary layers to become subcritical near the black hole. An analytical investigation for a time-independent case has been done by Gu (2012; Gu12) that had drawn attention towards the vertical structure of such a flow with dominant radiation pressure. In the pioneer theoretical works of Shakura–Sunyaev and slim discs, it is common to consider asymptotic states of the accreting systems, which one of the two pressures of gas or radiation is dominant, and also they assume just electron scattering has the main role in the opacity of disc. In the standard model, in the region close to the central mass, the radiation pressure reaches its ultimate limit, and the high amount of luminosity comes out from this part of disc. Further that luminous part, the main assumption changes to the other ultimate limit of pressure where the gas pressure becomes more significant than the radiation one. Therefore, we do not expect these ultimate limits to occur between two completely discrete neighbourhood regions; it does not sound unreasonable to have an expectation to find a transition area between these two territories with both considerable pressures of photons and real particles. On the other hand, we think of another probable situation that is related to being an independent area extended from r = 10rg to several tens of Schwarzschild radius with pr ≈ pg. Another point related to luminosity of the mentioned region might come to our mind: whether the high luminosity can also be produced by a part of the flow where both gas and radiation have comparable portions and a non-negligible number of photons are trapped, and therefore this might affect the flow’s dynamics. Moreover, one of the basic assumptions of the standard disc is the local energy balance between viscous heating and cooling via radiation but a bit deviation from it leads to extra energy for advection. If we consider conservation energy of matter and radiation separately, we will be able to investigate the variation of energy advection at the intermediate area with mass accretion rate.
In this paper, we follow the similar procedure of Gu12 and employ self-similar solutions to remove r-dependence of the system quantities, but we aim to study the mentioned different situation where both radiation and gas have comparable portions to form the total pressure of system. The accretion disc’s thickness has been examined by Gu et al. (2009) with assumption of semipolytropic relationship, p(θ) = Kρ(θ)γ, where p, ρ, and γ are gas pressure, density, and the ratio of specific heats. The important result of that work was to show that the accretion flows in advection-dominated regime tend to be quite thick. In our earlier studies (Samadi, Abbassi & Khajavi 2014; Samadi & Abbassi 2017), we focused on the effect of magnetic field with toroidal and poloidal configurations, separately. For both cases, the magnetic force acted in the opposite direction of the gas pressure force and made the disc thinner. In this work, we might expect the radiation pressure behaves like gas pressure and decreases towards the polar axis. The main purpose of this paper is to revisit vertical structure of optically thick accretion flows with rather high accretion rates (saying, several tens of percent of Eddington mass accretion rate) by taking into account photon absorption. The outline of this paper is as follows. In Section 2, we present the basic radiation hydrodynamics equations, which include the two separate equations for energies of gas and radiation. Self-similar equations are employed for a typical radius of r = 30rg in Section 3. Section 4 is devoted to boundary conditions and the permissible values of density at the equatorial plane regarding the gas temperature. The results of the numerical solution and a derivation of the disc thickness are presented in Section 5 and, finally, discussions and conclusions are given in Section 6.
2 EQUATIONS AND ASSUMPTIONS
We study an accreting flow around a black hole with mass M, in a steady-state regime that is assumed to be axisymmetric and non-relativistic. We define the system in spherical coordinates (r, θ, ϕ), and we use Newtonian potential, that is, Ψ = GM/r. The basic equations to describe such a system consist of
- continuity equationwhere ρ is the density and v is the time-averaged flow velocity;(1)\begin{eqnarray*} \frac{\partial \rho }{\partial t}+\nabla \cdot (\rho {\boldsymbol v})=0, \end{eqnarray*}
- the momentum conservationwhere D/Dt = ∂/∂t + v.∇, pg is the gas pressure, Tν is the stress tensor, c is the light speed, F0 is the radiation flux. The total opacity χ has two parts including Thomson scattering and absorption:(2)\begin{eqnarray*} \rho \frac{D{\boldsymbol v}}{Dt}=-\nabla p_\mathrm{ g}-\rho \nabla \Psi -\nabla \cdot {\boldsymbol T}^\nu +\frac{\chi }{c}{\boldsymbol F}_0 , \end{eqnarray*}where |$\sigma _T=6.652\times 10^{-25}cm^2$| is the Thomson cross-section, mp is the proton mass, and κ is the absorption opacity. In this problem, we consider two kinds of absorption, free–free and bound–free, as(3)\begin{eqnarray*} \chi =\frac{\sigma _T}{m_\mathrm{ p}}\rho +\kappa, \end{eqnarray*}\begin{equation*} \kappa _{\mathrm{ ff}}=1.7\times 10^{-25} T^{-7/2}(\frac{\rho }{m_\mathrm{ p}})^2\mathrm{ cm}^{-1}, \end{equation*}So, we can find the total absorption opacity as κ = κff + κbf;\begin{equation*} \kappa _{\mathrm{ bf}}=4.8\times 10^{-24} T^{-7/2}\frac{Z}{Z_\odot }(\frac{\rho }{m_\mathrm{ p}})^2\mathrm{ cm}^{-1}. \end{equation*}
- the energy equation of gaswhere e is the internal energy density, Φvis is the viscous dissipative function, B is the blackbody intensity, and E0 is the radiation energy density. (4) and finally based on conservation of radiation energy density (Mihalas & Mihalas 1984), we have(4)\begin{eqnarray*} \frac{\partial e}{\partial t}+\nabla \cdot (e{\boldsymbol v})=-p_\mathrm{ g}\nabla \cdot {\boldsymbol v}+\Phi _{\mathrm{ vis}}-4\pi \kappa B+c\kappa E_0, \end{eqnarray*}where P0 is the radiation pressure tensor. It might be helpful to point out the physical interpretation of new terms that has appeared in equation (5) due to considering radiation and also the interaction between photons and gas particles. For instance, ∇v|$\colon$|P0 shows the rate at which radiation pressure is doing work, ∇ · F0 specifies the rate of transport of radiation energy, 4πκB is the rate at which energy of matter is being added to the radiation field (the same term in equation 4 appears with negative sign which means decreasing energy of matter due to its radiation), and finally −cκE0 denotes the amount of radiation energy that is removed from the total radiation energy and transported to the energy of matter in the unit of time (all terms are per unit volume). In the spherical coordinates, the velocity field has these three components, (|$v$|r, |$v$|θ, |$v$|ϕ), but we follow Narayan & Yi (1995), and assume |$v$|θ = 0.1 With steady-state, axisymmetric flow, and neglecting |$v$|θ, equation (1) yields(5)\begin{eqnarray*} \frac{\partial E_0}{\partial t}+\nabla \cdot (E_0{\boldsymbol v})=-\nabla {\boldsymbol v:}{\bf P}_0-\nabla \cdot {\boldsymbol F}_0+4\pi \kappa B-c\kappa E_0, \end{eqnarray*}(6)\begin{eqnarray*} \frac{1}{r^2}\frac{\partial }{\partial r}(r^2\rho v_\mathrm{ r})=0. \end{eqnarray*}
3 SELF-SIMILAR SOLUTIONS
4 SOLUTIONS AT THE EQUATOR
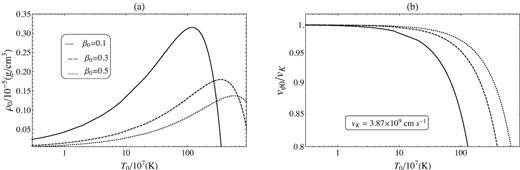
Solutions at the equatorial plane corresponding to |$M=10\, \mathrm{M}_\odot , \alpha =0.3, \gamma =1.5$|, and several values of β0. The radius of these solutions is r = 30rg, where rg = 2GM/c2 is the Schwarzschild radius. Here, |$v$|K is Keplerian velocity and equals to 3.87 × 109cm s−1.
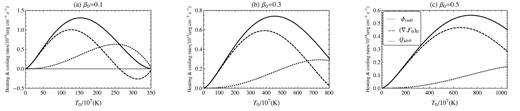
The heating (Φvis0) and cooling (Qadv0, (∇ · F0)0) rates at the equatorial plane corresponding to r = 30rg, |$M=10\, \mathrm{M}_\odot , \alpha =0.3, \gamma =1.5$|, and several values of β0.
5 VERTICAL STRUCTURE
Fig. 3 shows the angular variation of dimensionless density, radial, and azimuthal components of the flow’s velocity and also the two pressures of gas and radiation. All quantities in this figure have been scaled by their boundary values at the equatorial plane, which are listed in Table 1. According to Fig. 3(a), the density of gas starts from a maximum value at the mid-plane and tends to its minimum at the surface angle. Comparing the minimum value of our density here with most of those in ADAFs we have faced with in our previous works, we notice this minimum cannot reach zero and just becomes about 20 per cent of its equatorial value. However, this result is not strange for theoretical solutions since similar little ascending trend can be seen in fig. 3 of Jiao & Wu (2011; the minimum value of ρ is about 0.4ρ0 and also in fig. 1 of Narayan & Yi 1995), ρ varies by only 10 per cent from the polar axis to the mid-plane with ε′ = 0.1 and for ε′ = 1 we see ρ(θ = 90°) ∼ 2ρ(θ = 0). In profile (b), it can be seen that the rotational velocity is decreasing outwards, whereas the accretion velocity is minimum at the mid-plane and ends up maximum at the surface. The gas temperature, T (equivalently the sound speed squared |$c_\mathrm{ s}^2=k_\mathrm{ B} T/\mu m_\mathrm{ p}$|) peaks at θ = 90°, which is the same as ADAF’s solutions in other works (such as figs 1 and 4 of Samadi et al. 2014; fig. 1 of Gu et al. 2009). The two pressures appear somehow different, pr does not show noticeable change inside the disc especially for lower value of β0, i.e. 0.1. As we expect for gas pressure, it faces a rather sharp decrease towards the surface of disc.
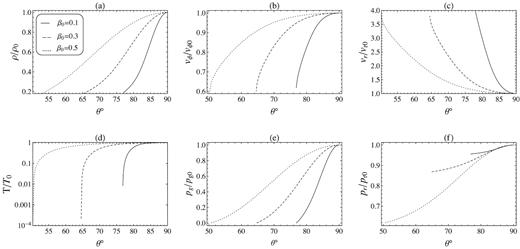
Angular profile of the physical variables at r = 30rg corresponding to |$\alpha =0.3, \gamma =1.5, M=10\, \mathrm{M}_\odot$|, and several values of β0.
| β0 . | 0.1 . | 0.3 . | 0.5 . |
|---|---|---|---|
| T0/109 (K) | 0.5 | 2 | 5 |
| ρ0/10−6 (g cm−3) | 2.64 | 1.65 | 1.37 |
| |$v$|ϕ0/|$v$|K | 0.93 | 0.90 | 0.85 |
| −|$v$|r0/|$v$|K | 0.02 | 0.03 | 0.05 |
| pg0/1011 (dyn cm−2) | 2.18 | 5.46 | 11.29 |
| pr0/1012 (dyn cm−2) | 1.96 | 1.27 | 1.13 |
| β0 . | 0.1 . | 0.3 . | 0.5 . |
|---|---|---|---|
| T0/109 (K) | 0.5 | 2 | 5 |
| ρ0/10−6 (g cm−3) | 2.64 | 1.65 | 1.37 |
| |$v$|ϕ0/|$v$|K | 0.93 | 0.90 | 0.85 |
| −|$v$|r0/|$v$|K | 0.02 | 0.03 | 0.05 |
| pg0/1011 (dyn cm−2) | 2.18 | 5.46 | 11.29 |
| pr0/1012 (dyn cm−2) | 1.96 | 1.27 | 1.13 |
| β0 . | 0.1 . | 0.3 . | 0.5 . |
|---|---|---|---|
| T0/109 (K) | 0.5 | 2 | 5 |
| ρ0/10−6 (g cm−3) | 2.64 | 1.65 | 1.37 |
| |$v$|ϕ0/|$v$|K | 0.93 | 0.90 | 0.85 |
| −|$v$|r0/|$v$|K | 0.02 | 0.03 | 0.05 |
| pg0/1011 (dyn cm−2) | 2.18 | 5.46 | 11.29 |
| pr0/1012 (dyn cm−2) | 1.96 | 1.27 | 1.13 |
| β0 . | 0.1 . | 0.3 . | 0.5 . |
|---|---|---|---|
| T0/109 (K) | 0.5 | 2 | 5 |
| ρ0/10−6 (g cm−3) | 2.64 | 1.65 | 1.37 |
| |$v$|ϕ0/|$v$|K | 0.93 | 0.90 | 0.85 |
| −|$v$|r0/|$v$|K | 0.02 | 0.03 | 0.05 |
| pg0/1011 (dyn cm−2) | 2.18 | 5.46 | 11.29 |
| pr0/1012 (dyn cm−2) | 1.96 | 1.27 | 1.13 |
which is approximately equal to 0.15. In Fig. 7, we have plotted (a) the half-thickness of disc, (b) the total mass accretion rate, and (c) the advection parameter versus radius for three values of β0. As seen in panels of this figure, all these quantities increase at larger radii. Furthermore, in the last figure of this section, Fig. 8, we see a direct effect from mass accretion rate on the advection factor. The similar result has been presented by Gu (2012) in fig. 4 of his paper.
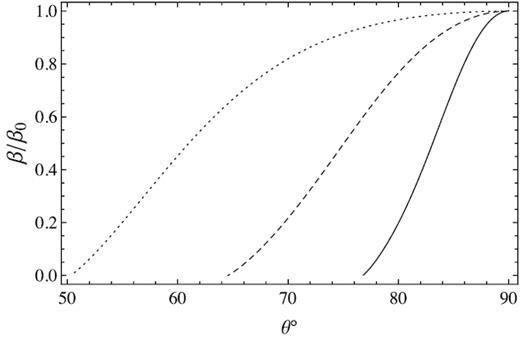
The angular variation of β’s at r = 30rg, which shows how much the ratio of gas pressure to the total pressure of disc reduces towards the surface and tends to even zero at the outer layers. The solid, dashed, and dotted lines refer to β0 = 0.1, 0.3, and 0.5, respectively.
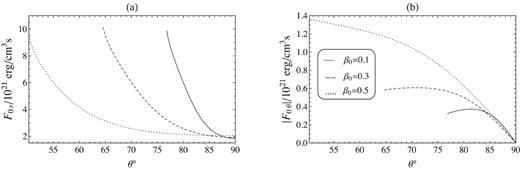
Angular profile of radiation flux’s components for a typical solution at r = 30rg with |$\alpha =0.3, \gamma =1.5, M=10\, \mathrm{M}_\odot$|, and three different values of β0.
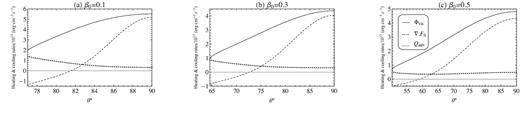
The angular variation of heating (Φvis) and cooling (Qadv, ∇ · F0) rates at r = 30rg with α = 0.3, γ = 1.5, and |$M=10\, \mathrm{M}_\odot$| with different β0’s.
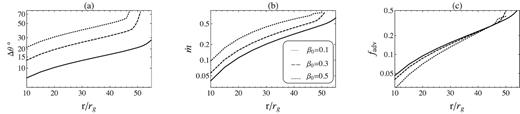
Variation of (a) the disc’s half-thickness, (b) mass accretion rate, and (c) advection parameter with respect to radius. The equatorial value of gas temperature and density are different for each β0.
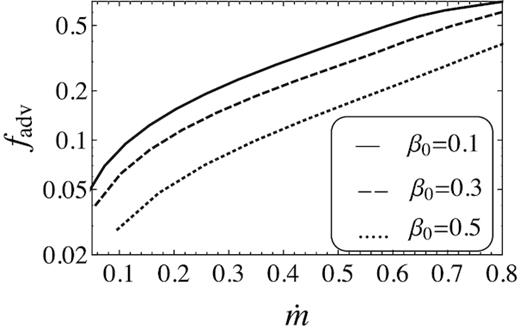
Variation of the advection parameter, fadv with respect to the mass accretion rate, |$\dot{m}$|.
| β0 . | 0.1 . | 0.3 . | 0.5 . |
|---|---|---|---|
| |$\dot{m}$| | 0.20 | 0.28 | 0.44 |
| Δθ° | 13.17 | 25.46 | 39.72 |
| H/r | 0.23 | 0.43 | 0.64 |
| fadv | 0.15 | 0.14 | 0.13 |
| Qvis/1021 (erg cm−3 s−1) | 0.86 | 1.17 | 1.80 |
| |$Q_{\mathrm{ adv}}/10^{20}\, \rm (erg\ cm^{-3}\, s^{-1})$| | 1.33 | 1.72 | 2.37 |
| |$Q_c/10^{20}\ \rm (erg\ cm^{-3}\ s^{-1})$| | 3.14 | 5.25 | 10.5 |
| β0 . | 0.1 . | 0.3 . | 0.5 . |
|---|---|---|---|
| |$\dot{m}$| | 0.20 | 0.28 | 0.44 |
| Δθ° | 13.17 | 25.46 | 39.72 |
| H/r | 0.23 | 0.43 | 0.64 |
| fadv | 0.15 | 0.14 | 0.13 |
| Qvis/1021 (erg cm−3 s−1) | 0.86 | 1.17 | 1.80 |
| |$Q_{\mathrm{ adv}}/10^{20}\, \rm (erg\ cm^{-3}\, s^{-1})$| | 1.33 | 1.72 | 2.37 |
| |$Q_c/10^{20}\ \rm (erg\ cm^{-3}\ s^{-1})$| | 3.14 | 5.25 | 10.5 |
| β0 . | 0.1 . | 0.3 . | 0.5 . |
|---|---|---|---|
| |$\dot{m}$| | 0.20 | 0.28 | 0.44 |
| Δθ° | 13.17 | 25.46 | 39.72 |
| H/r | 0.23 | 0.43 | 0.64 |
| fadv | 0.15 | 0.14 | 0.13 |
| Qvis/1021 (erg cm−3 s−1) | 0.86 | 1.17 | 1.80 |
| |$Q_{\mathrm{ adv}}/10^{20}\, \rm (erg\ cm^{-3}\, s^{-1})$| | 1.33 | 1.72 | 2.37 |
| |$Q_c/10^{20}\ \rm (erg\ cm^{-3}\ s^{-1})$| | 3.14 | 5.25 | 10.5 |
| β0 . | 0.1 . | 0.3 . | 0.5 . |
|---|---|---|---|
| |$\dot{m}$| | 0.20 | 0.28 | 0.44 |
| Δθ° | 13.17 | 25.46 | 39.72 |
| H/r | 0.23 | 0.43 | 0.64 |
| fadv | 0.15 | 0.14 | 0.13 |
| Qvis/1021 (erg cm−3 s−1) | 0.86 | 1.17 | 1.80 |
| |$Q_{\mathrm{ adv}}/10^{20}\, \rm (erg\ cm^{-3}\, s^{-1})$| | 1.33 | 1.72 | 2.37 |
| |$Q_c/10^{20}\ \rm (erg\ cm^{-3}\ s^{-1})$| | 3.14 | 5.25 | 10.5 |
5.1 Convective stability
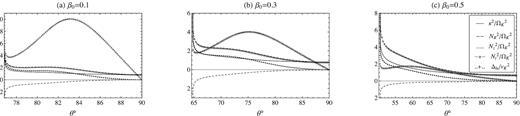
The angular variation of κ2 (thick solid line), |$N_\mathrm{ R}^2$| (dashed line), |$N_Z^2$| (dotted line), |$N_t^2$| (dashed line with asterix), and Δls (dotted line with plus sign) at r = 30rg with |$M=10\, \mathrm{M}_\odot , \alpha =0.3, \gamma =1.5$|, and for three values of β0.
6 SUMMARY AND CONCLUSIONS
We studied the vertical structure of optically thick accretion flows in the presence of both radiation and gas pressures. We did not employ radiative transfer, instead of that we adopted the separated energy equation similar to the internal energy of gas based on diffusion approximation in radiation field. The self-similar solutions in the radial direction helped us to convert the partial differential equations into a set of algebraic equations and ODE’s. Solving equations on the equator and considering some basic assumptions such as high optical depth, we could obtain proper values of density and gas temperature. At the typical radius of r = 30rg, we assumed the gas pressure had 10–50 per cent portion of the total pressure and calculated the θ -dependence of physical quantities. With a permissible gas temperature at mid-plane (T0/109K = 0.5, 2, 5), we calculated corresponding gas pressure that yields β0 = 0.1, 0.3, 0.5. The velocity’s components at the equatorial plane were found from two algebraic equations. With these known quantities, we could start integrating the differential equations and then stopped calculation because of gas pressure that tended to negative values. In fact, the gas pressure showed a descending behaviour, and it became gradually zero at a certain angle (0 < θ0 < 90°) before approaching the vertical axis, whereas the radiation pressure faced a little change at this angular distance. Therefore, we expect to find accretion discs with two vertical parts, one is located inside from the mid-plane to θ0, and affected by both pg and pr, and the other one as a surrounding layer of the equatorial part whose radiation pressure is dominant and hence it has different features. Although the temperature of gas at the inside region was rather high at the equator, it became negligible at the surface of the disc, meanwhile the temperature at the outer layer is determined based on radiation and it must be very high. Furthermore, we found out with greater accretion rate and less portion of gas pressure in the total pressure, more energy was advected to the central object. In our solutions, we realized that despite the outward direction of radiation flux, it is possible that divergence of the radiation flux becomes negative. However, our results for other input parameters are not practical at outer regions (especially for hotter discs) because we neglected the meridional component of the velocity, and it is just ignorable near the mid-plane but |$v$|θ is very effective to make |$v$|r positive and change significantly the angular profile of energy transportation outside the flow. Moreover, the typical accretion flows presented here with temperatues of 0.5 - 5 × 109 K were found out to be convectively stable. Our results here are useful to apply for intermediate cases between slim and thin discs that include two parts, one part near the mid-plane that has non-ignorable gas pressure and the other part with dominant radiation pressure and negligible gas pressure (about three order of magnitude smaller). The vertical structure of inner part can be found by the presented method, but it is incomplete. The outer part can be described by omitting the gas pressure and use one energy equation for the total energy of the flow like that has been done by Gu12. We can use the surface value of quantities as boundary conditions for solving differential equations in the outer part.
ACKNOWLEDGEMENTS
We are grateful to the anonymous referee for his/her thoughtful and constructive comments, which helped us to improve the first version of this paper. Maryam Samadi also wishes to thank Faride Danesh-Manesh for her kind help in some parts of this project. This work has been supported financially by Research Institute for Astronomy and Astrophysics of Maragha (RIAAM) under research project No. 1/6025-21.
Footnotes
This assumption is often used for all kinds of accretion discs.



