Dependence of Hall coefficient on grain size and cosmic ray rate and implication for circumstellar disc formation

Dust grain model parameters.

Model	a_min (⁠\|$\rm {\mu m}$\|⁠)	a_single (⁠\|$\rm {\mu m}$\|⁠)	a_max (⁠\|$\rm {\mu m}$\|⁠)	s_max	f_dg	σ_tot/n_H (⁠\|$\rm {cm^5}$\|⁠)
s1a	0.005		0.25	10	0.01	2.830 52 × 10⁻²¹
s1b	0.005		0.25	10	0.005	1.415 26 × 10⁻²¹
s1c	0.005		0.25	10	0.02	5.661 05 × 10⁻²¹
s2	0.0181		0.9049	10	0.0341	2.666 49 × 10⁻²¹
s3		0.3		1	0.01	5.835 31 × 10⁻²²
s4		0.1		1	0.01	1.744 86 × 10⁻²¹
s5		0.075		1	0.01	2.336 44 × 10⁻²¹
s6		0.05		1	0.01	3.5035 × 10⁻²¹
s7		0.025		1	0.01	7.000 06 × 10⁻²¹
s8		0.01		1	0.01	1.744 86 × 10⁻²⁰

Model	a_min (⁠\|$\rm {\mu m}$\|⁠)	a_single (⁠\|$\rm {\mu m}$\|⁠)	a_max (⁠\|$\rm {\mu m}$\|⁠)	s_max	f_dg	σ_tot/n_H (⁠\|$\rm {cm^5}$\|⁠)
s1a	0.005		0.25	10	0.01	2.830 52 × 10⁻²¹
s1b	0.005		0.25	10	0.005	1.415 26 × 10⁻²¹
s1c	0.005		0.25	10	0.02	5.661 05 × 10⁻²¹
s2	0.0181		0.9049	10	0.0341	2.666 49 × 10⁻²¹
s3		0.3		1	0.01	5.835 31 × 10⁻²²
s4		0.1		1	0.01	1.744 86 × 10⁻²¹
s5		0.075		1	0.01	2.336 44 × 10⁻²¹
s6		0.05		1	0.01	3.5035 × 10⁻²¹
s7		0.025		1	0.01	7.000 06 × 10⁻²¹
s8		0.01		1	0.01	1.744 86 × 10⁻²⁰

Table 1.

Dust grain model parameters.

Model	a_min (⁠\|$\rm {\mu m}$\|⁠)	a_single (⁠\|$\rm {\mu m}$\|⁠)	a_max (⁠\|$\rm {\mu m}$\|⁠)	s_max	f_dg	σ_tot/n_H (⁠\|$\rm {cm^5}$\|⁠)
s1a	0.005		0.25	10	0.01	2.830 52 × 10⁻²¹
s1b	0.005		0.25	10	0.005	1.415 26 × 10⁻²¹
s1c	0.005		0.25	10	0.02	5.661 05 × 10⁻²¹
s2	0.0181		0.9049	10	0.0341	2.666 49 × 10⁻²¹
s3		0.3		1	0.01	5.835 31 × 10⁻²²
s4		0.1		1	0.01	1.744 86 × 10⁻²¹
s5		0.075		1	0.01	2.336 44 × 10⁻²¹
s6		0.05		1	0.01	3.5035 × 10⁻²¹
s7		0.025		1	0.01	7.000 06 × 10⁻²¹
s8		0.01		1	0.01	1.744 86 × 10⁻²⁰

Model	a_min (⁠\|$\rm {\mu m}$\|⁠)	a_single (⁠\|$\rm {\mu m}$\|⁠)	a_max (⁠\|$\rm {\mu m}$\|⁠)	s_max	f_dg	σ_tot/n_H (⁠\|$\rm {cm^5}$\|⁠)
s1a	0.005		0.25	10	0.01	2.830 52 × 10⁻²¹
s1b	0.005		0.25	10	0.005	1.415 26 × 10⁻²¹
s1c	0.005		0.25	10	0.02	5.661 05 × 10⁻²¹
s2	0.0181		0.9049	10	0.0341	2.666 49 × 10⁻²¹
s3		0.3		1	0.01	5.835 31 × 10⁻²²
s4		0.1		1	0.01	1.744 86 × 10⁻²¹
s5		0.075		1	0.01	2.336 44 × 10⁻²¹
s6		0.05		1	0.01	3.5035 × 10⁻²¹
s7		0.025		1	0.01	7.000 06 × 10⁻²¹
s8		0.01		1	0.01	1.744 86 × 10⁻²⁰

2.4 Chemical reactions and networks

Calculation of the Hall coefficient also required determination of the fractional abundance of each charged species, x_ν (see equations 10 and 11). In this subsection, we describe the method by which the chemical abundance of each charged particle was determined, based on a series of papers by Umebayashi & Nakano (1990). In these calculations, the relative abundance of each neutral species (H₂, He, CO, O₂, O, and Mg) relative to the number of hydrogen atoms was fixed as shown in Table 2.

Table 2.

Abundance of each neutral species relative to the number of hydrogen atoms (Sano et al. 2000). δ indicates the fraction of each element remaining in the gas phase. The fractional abundances of molecules, δm, and of metal ions, δM, in the interstellar gas phase are δm = 0.2 and δM = 0.02, respectively, while the abundance of oxygen molecules in the gas phase is δO₂ = 0.7 (Morton 1974).

Chemical species	Relative abundances
\|$\rm {H_2}$\|	x\|$\rm {H_2} = 0.5$\|
He	xHe = 9.75 × 10⁻²
CO	xCO = 3.62 × 10⁻⁴ δm
\|$\rm {O_2}$\|	x\|$\rm {O_2}$\| = 0.5 δO₂ (8.53 − 3.62) × 10⁻⁴δm
O	\|$\rm {xO} = (1-\delta {\rm O}_2) (8.53-3.62) \times 10^{-4} \delta {\rm m}$\|
Mg	xMg = 7.97 × 10⁻⁵δM

Chemical species	Relative abundances
\|$\rm {H_2}$\|	x\|$\rm {H_2} = 0.5$\|
He	xHe = 9.75 × 10⁻²
CO	xCO = 3.62 × 10⁻⁴ δm
\|$\rm {O_2}$\|	x\|$\rm {O_2}$\| = 0.5 δO₂ (8.53 − 3.62) × 10⁻⁴δm
O	\|$\rm {xO} = (1-\delta {\rm O}_2) (8.53-3.62) \times 10^{-4} \delta {\rm m}$\|
Mg	xMg = 7.97 × 10⁻⁵δM

Table 2.

Abundance of each neutral species relative to the number of hydrogen atoms (Sano et al. 2000). δ indicates the fraction of each element remaining in the gas phase. The fractional abundances of molecules, δm, and of metal ions, δM, in the interstellar gas phase are δm = 0.2 and δM = 0.02, respectively, while the abundance of oxygen molecules in the gas phase is δO₂ = 0.7 (Morton 1974).

Chemical species	Relative abundances
\|$\rm {H_2}$\|	x\|$\rm {H_2} = 0.5$\|
He	xHe = 9.75 × 10⁻²
CO	xCO = 3.62 × 10⁻⁴ δm
\|$\rm {O_2}$\|	x\|$\rm {O_2}$\| = 0.5 δO₂ (8.53 − 3.62) × 10⁻⁴δm
O	\|$\rm {xO} = (1-\delta {\rm O}_2) (8.53-3.62) \times 10^{-4} \delta {\rm m}$\|
Mg	xMg = 7.97 × 10⁻⁵δM

Chemical species	Relative abundances
\|$\rm {H_2}$\|	x\|$\rm {H_2} = 0.5$\|
He	xHe = 9.75 × 10⁻²
CO	xCO = 3.62 × 10⁻⁴ δm
\|$\rm {O_2}$\|	x\|$\rm {O_2}$\| = 0.5 δO₂ (8.53 − 3.62) × 10⁻⁴δm
O	\|$\rm {xO} = (1-\delta {\rm O}_2) (8.53-3.62) \times 10^{-4} \delta {\rm m}$\|
Mg	xMg = 7.97 × 10⁻⁵δM

As described in Section 2.2, |$\rm {{H_3}^+,m^+,Mg^+,He^+,C^+, and \ H^+}$| were considered as the charged species in addition to the charged dust grains (see below), where m⁺ represents molecular ions other than |${\rm H_3^+}$|⁠. Because the most abundant charged molecular ion species is HCO⁺, we identified m⁺ with HCO⁺ (Marchand et al. 2016). A total of 25 chemical reactions was considered.

The four types of charged particle reactions incorporated in the calculations were

|$\rm {j \rightarrow i+e^{-}}$| (ionization of neutral particles),
|$\rm {i + e^{-} \rightarrow j}$| (recombination of positive ions and electrons),
|$\rm {i + k \rightarrow j+ \ast}$| (recombination of charged ions), and
|$\rm {G({\it q})+ i/e^- \ ({\rm ion \ or \ electron}) \rightarrow G({\it q} \pm 1)}$| (absorption of charged particles on to dust grains following collisions).

Here, i indicates a charged species, j and k represent different neutral species, * is the product of a charged species, and G(q) is dust having charge q. In the following discussions, for convenience, we assign a number to each charged particle (ion or electron), as shown in Table 3.

Table 3.

Chemical species considered in this study and assigned numbers.

Species	Assigned number i
e⁻	0
H\|$_3^+$\|	1
m⁺	2
Mg⁺	3
He⁺	4
C⁺	5
H⁺	6

Table 3.

Chemical species considered in this study and assigned numbers.

Species	Assigned number i
e⁻	0
H\|$_3^+$\|	1
m⁺	2
Mg⁺	3
He⁺	4
C⁺	5
H⁺	6

In the case of reaction (1), cosmic rays represent the ionization source. Here, the parameter ζ is applied, equal to the total ionization rate of a hydrogen molecule, and we set the reaction rate of |$\rm {H_2}$| and He as shown in table 2 in Umebayashi & Nakano (1990). The cosmic ray rates employed in this study are provided in Table 4, with ζ = 10⁻¹⁷ s⁻¹ as the fiducial value.

Table 4.

Cosmic ray rates employed in this study.

		ζ ( s⁻¹ )
10⁻¹⁸	10^−17.5	10⁻¹⁷	10^−16.5	10⁻¹⁶

Table 4.

Cosmic ray rates employed in this study.

		ζ ( s⁻¹ )
10⁻¹⁸	10^−17.5	10⁻¹⁷	10^−16.5	10⁻¹⁶

The chemical reactions and the associated reaction rates in points (2) and (3), above, are taken from the UMIST database (McElroy et al. 2013) and are summarized in Table A1 in Appendix A.

Since dust grains absorb charged particles, they play a significant role in determining the fractional abundances of such particles. In addition, because the dust grains themselves are charged, they also contribute to the Hall coefficient. In Appendix B, we discuss reaction (4), which is based on collisions between dust grains and charged particles with subsequent absorption of the charged particles on the grain surfaces.

At this point, we explain the calculations used to derive the abundances of charged particles and dust grains. For the sake of convenience, these calculations are based on the abundance of charged particles and dust grains relative to the number of hydrogen atoms, and so the abundances of each charged species and dust grain is described as x_i = n_i/n_H and x_d = n_d/n_H. In this process, the maximum and minimum charges of the dust grains at each gas density are determined (for details, see Okuzumi 2009), and the time-derivative equation for each species is provided in Appendix C. The fractional abundance of each charged particle and dust grain as a function of the gas density was calculated according to the following procedure:

beginning from the initial chemical abundance values in Table 2, the equations given in Appendix C were implicitly solved for a fixed gas density and gas temperature (see Section 2.5) until an equilibrium state was realized, and the initial dust grains abundance values were pre-calculated for each dust distribution model (using equation 22 for MRN models and equation 24 for single-sized models), following which
the gas density was increased by 0.1 dex and step (a) was repeated.

Using this procedure, the fractional abundance of each species was derived over the range of |$10^4\, {\rm cm}^{-3} \lt n_{\rm H} \lt 10^{14}\, {\rm cm}^{-3}$|⁠. It should be noted that we confirmed that the elapsed time required to obtain an equilibrium state was much shorter than the freefall time-scale t_ff (= |$(3\pi /(32\, G\, \rho))^{1/2}$|⁠) in the density range considered in this study. We compare the elapsed time-scale and freefall time-scale and show that equilibrium time is much shorter than freefall time in Appendix D. Finally, using the abundance of each species and the equations described in Section 2.2, we derived the Hall coefficient, η_H, for each gas density. Employing 10 different dust grain models (Table 1) and five different cosmic ray rates (Table 4), we calculated the chemical abundance values and the Hall coefficients for 50 models in total.

2.5 Gas temperature and magnetic field strength

When solving the chemical network for a given gas density, it is necessary to assume the gas temperature. According to Larson (1969), Masunaga & Inutsuka (2000), and Tomida et al. (2013), the gas temperature can be obtained using the barotropic equation of state

\begin{eqnarray*} T = 10 \left[1+\gamma \left(\dfrac{n_{\rm H}}{10^{11}\, {\rm cm}^{-3} }\right)^{\gamma -1} \right] \rm K, \end{eqnarray*}

(26)

where n_H and γ (= 5/3) are the number density and specific heat ratio of hydrogen. Because the Hall coefficient depends on the magnetic field strength, B, as discussed in Section 2, we also need to assume the magnetic field strength. In this work, the plasma beta, β, was employed as an index of the magnetic field, defined as

\begin{eqnarray*} \beta \equiv \frac{P_{\rm th}}{P_{\rm mag}}, \end{eqnarray*}

(27)

where the thermal P_th and magnetic P_mag pressures are, respectively, written as

\begin{eqnarray*} P_{\rm th} = \frac{\rho _{\rm g} \, k_B T}{\mu m_{\rm H}} \end{eqnarray*}

(28)

and

\begin{eqnarray*} P_{\rm mag} = {\frac{B^2}{8 \pi }}. \end{eqnarray*}

(29)

Here, ρ_g, k_B, μ, and m_H are the fluid density, Boltzmann constant, mean molecular weight, and proton mass, respectively. In this study, a constant mean molecular weight of μ = 2.4 was adopted because the work focused solely on the low-temperature region of the collapsing cloud (see Section 4.1). Based on equations (28) and (29), the magnetic field strength can be written as

\begin{eqnarray*} B = \sqrt{\dfrac{8\pi \rho _{\rm g} k_{\rm B} T }{\mu m_{\rm H} \beta } }. \end{eqnarray*}

(30)

The gas density is related to the number density according to the relationship ρ_g = 1.4n_Hm_H. Thus, the gas temperature is a function of the (number) density (equation 26) and the magnetic field strength is a function of both the number density, n_H, and the plasma beta, β. Because the plasma beta is not uniquely determined, we referred to recent publications regarding non-ideal MHD simulations (e.g. Wurster et al. 2018b), and on this basis adopted β = 100 as the fiducial value. Note that the effect of varying β on the Hall coefficient is discussed in Section 5.3.

Fig. 1 plots the gas temperatures (left) derived from equation (26) and the magnetic field strengths (right) derived from equation (30) with β = 100 against the number density. These plots are in good agreement with recently published one-dimensional and multidimensional simulations (Tomida et al. 2015 ;Tsukamoto et al. 2015a).

Figure 1.

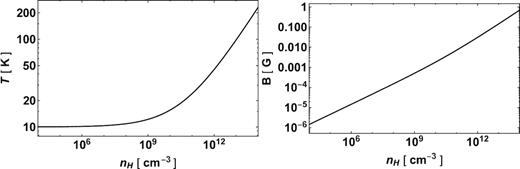
Gas temperature (left) and magnetic field strength (right) as functions of number density.

3 RESULTS OF CHEMICAL REACTION CALCULATIONS

Chemical reactions were calculated according to the method outlined in Section 2. To begin with, we present the chemical abundance results obtained using different dust models in conjunction with ζ = 10⁻¹⁸ (Fig. 2), 10⁻¹⁷ (Fig. 3), and 10⁻¹⁶ s⁻¹ (Fig. 4). These data indicate that the chemical abundances are significantly affected by both the dust distribution and cosmic ray rate. As the grain size becomes smaller, the adsorption of charge on to the grains becomes more effective, such that the number of ions and electrons decreases, as shown in Fig. 3. In addition, we checked the relation between the number of grains and f_dg comparing models s1a, s1b, and s1c, and confirmed that the fractional abundances of grains increase as f_dg decreases. Figs 2–4 also show that the fractional abundances of dust grains in single-sized models s3–s8 are roughly proportional to a⁻³ because the total mass of grains is fixed. Models s1a and s7 in Fig. 3 give similar results because the average size in MRN model s1a is 0.035|$\,\rm {\mu m}$| (as calculated using equation 20), which is close to the grain size assumed in model s7 (0.025 μm). In contrast, models s3 (a_single = 0.3 μm) and s8 (a_single = 0.01 μm) provide noticeably different results, with the abundances of Mg⁺ and e⁻ at |$n_{\rm H}=10^8\, {\rm cm}^{-3}$| from model s3 being two and four orders of magnitudes higher, respectively, than those from model s8. These large differences in the fractional abundances of charged species greatly affects the Hall coefficient. In addition, a comparison of Figs 2, 3, and 4 shows that the cosmic ray ionization rate significantly affects the fractional abundances of charged particles. To a first approximation, the fractional abundances of charged particles scale linearly with the ionization rate.

Figure 2.

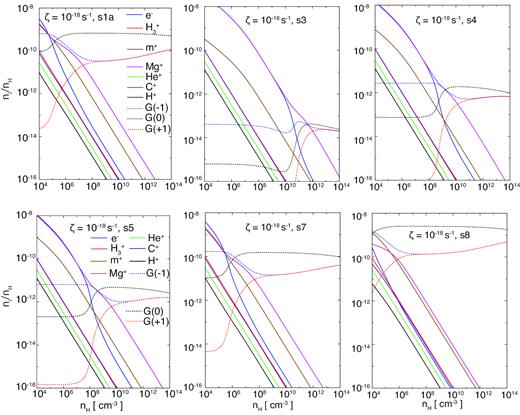
Chemical abundances of charged species, neutral species, and charged dust grains (Z = ±1) for different dust models (s1a, s3, s4, s5, s7, and s8), obtained using a constant ionization rate of ζ = 10⁻¹⁸ s⁻¹, as functions of the number density.

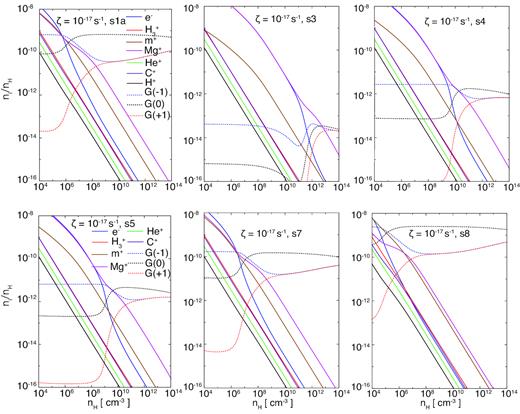
$The same data as in Fig. 2 but for $\zeta =10^{-17} \rm {s^{-1}}$ using models (s1a, s3, s4, s5, s7, and s8).$

Figure 3.

The same data as in Fig. 2 but for |$\zeta =10^{-17} \rm {s^{-1}}$| using models (s1a, s3, s4, s5, s7, and s8).

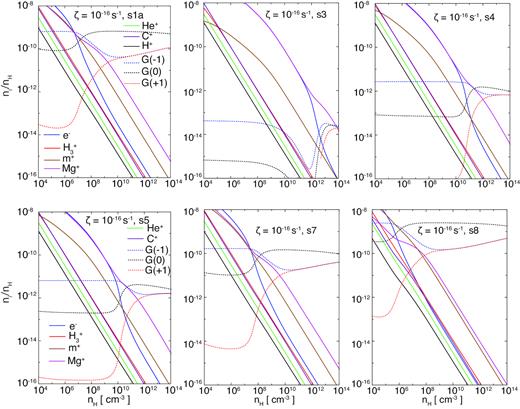
$The same data as in Fig. 2 but for $\zeta =10^{-16}\, \rm {s^{-1}}$ using models (s1a, s3, s4, s5, s7, and s8).$

Figure 4.

The same data as in Fig. 2 but for |$\zeta =10^{-16}\, \rm {s^{-1}}$| using models (s1a, s3, s4, s5, s7, and s8).

Figs 5 and 6 show the Hall coefficients calculated for the different dust models using equations (5)–(16). These plots indicate that the absolute value of the Hall coefficient is modified by both the grain size and grain size distribution, as well as by the cosmic ray strength. Furthermore, as seen in Figs 5 and 6, the sign of the Hall coefficient can change depending on the grain size or grain size distribution. As an example, in the centre panel of Fig. 5 (ζ = 10⁻¹⁷ s⁻¹), the Hall coefficient is positive over the entire range of |$10^4\, {\rm cm}^{-3} \lesssim n_{\rm H} \lesssim 10^{14}\, {\rm cm}^{-3}$| for model s3, while it is positive only in the range of |$n_{\rm H} \gt 10^{13}\, {\rm cm}^{-3}$| for model s5. Thus, even a change in the grain size by a factor of 4 can cause a flip in the sign of the Hall coefficient at |$n_{\rm H} \sim 10^{13}\, {\rm cm}^{-3}$|⁠. Zhao, Caselli & Li (2018) also showed that large-sized grains (or removal of small-sized grains; |${\lesssim } 0.1\, \rm {\mu m}$|⁠) noticeably decrease the Hall coefficient, which agrees well with our results (see the centre panel of Fig. 5).

Hall coefficients for single-sized dust models at ζ = 10−18 (left), 10−17 (centre), and 10−16 s−1 (right). The results from models s3, s4, s5, s6, s7, and s8 are plotted in blue, red, green, yellow, orange, and purple. For each line, the positive and negative values of ηH are indicated by broken and solid lines, respectively.

Figure 5.

Hall coefficients for single-sized dust models at ζ = 10⁻¹⁸ (left), 10⁻¹⁷ (centre), and 10⁻¹⁶ s⁻¹ (right). The results from models s3, s4, s5, s6, s7, and s8 are plotted in blue, red, green, yellow, orange, and purple. For each line, the positive and negative values of η_H are indicated by broken and solid lines, respectively.

Figure 6.

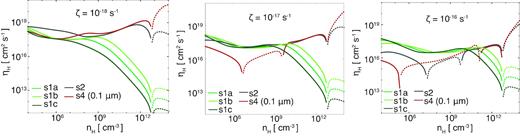
Hall coefficients for various MRN dust distributions. Models s1a, s1b, s1c, s2, and s4 are plotted in green, light green, dark green, grey, and red, respectively. For each line, positive and negative values of η_H are indicated by solid and broken lines, respectively.

4 APPLICATION: DISC SIZE INDUCED BY THE HALL EFFECT

As described in Section 1, the purpose of this study was to estimate the disc size considering solely the Hall effect. To correctly determine the disc size, non-ideal MHD simulations were required (e.g. Tsukamoto et al. 2015b). However, during the star formation process, a small disc formed around a protostar gradually evolves. Thus, at minimum, the spatial scale of the protostar should be resolved (Vaytet et al. 2018) when examining the formation and evolution of the circumstellar disc. Despite this, the time-scale becomes extremely short when resolving the protostar, and so it is impossible to simulate disc evolution and determine the disc size with adequate spatial resolution. As an example, a very recent simulation managed to calculate the disc evolution over a time span of several months following protostar formation (e.g. Tomida et al. 2015; Masson et al. 2016; Tsukamoto et al. 2017). In contrast, observations have indicated that the main accretion phase, during which the disc evolves via mass accretion, lasts for ∼10⁵ yr (Andre & Montmerle 1994; Enoch et al. 2008). In addition, the Hall coefficient, which is related to the angular momentum associated with transport in the infalling gas and disc evolution, is greatly affected by specific dust properties and the environmental effects of the ionization source (or the cosmic ray strength). Thus, to determine the disc size, it is necessary to calculate the disc evolution over a span of at least ∼10⁵ yr, while resolving the protostar using the grain size and cosmic ray strength as parameters. Since such calculations are difficult to execute even using the fastest supercomputers presently available, we analytically estimated the disc size by referring to the simulation results.

Because the Hall coefficient is determined by the abundance of charged particles, the charged particle properties and chemical networks were discussed in the previous sections. Below, in order to simplify our assumptions, we estimate and discuss the influence of the Hall effect on the evolution and formation of the circumstellar disc. This discussion begins with an explanation of the process used to estimate the disc size induced by the Hall effect.

The (specific) angular momentum of the infalling gas resulting from the Hall effect must first be evaluated, as this determines the disc size. Note that the angular momentum is redistributed in the disc and a part of the angular momentum is also ejected by protostellar outflow, meaning that the estimates provided herein actually refer to the upper limit of the disc size. Even so, it is useful to assess the effects of both the dust properties and cosmic ray strength on the Hall coefficient and resultant disc size. Our approach to estimating the disc size is illustrated schematically in Fig. 7. To begin, we assume a non-rotating prestellar cloud. Although this assumption is not actually correct, it is a useful approach to estimating the angular momentum resulting solely from the Hall effect. Next, we calculate the chemical networks and derive the Hall coefficient as a function of cloud density, which can be converted to a length-scale (or Jeans length). Subsequently, the angular momentum of the infalling gas is derived by defining r_Hall and assuming that the infalling gas instantaneously acquires the angular momentum at r_Hall. In this study, we use the term r_Hall for the Hall radius or Hall point and employ a value of r_Hall = 300 au, which is similar to the pseudo-disc size (Tsukamoto et al. 2017). A Jeans length of r_Hall = 300 au corresponds to a number density of n_Hall = 10⁸ cm⁻³.

Figure 7.

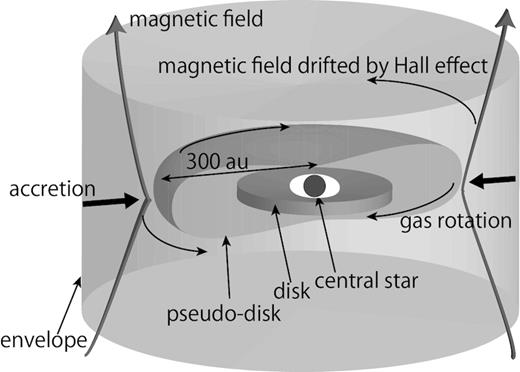
Schematic of the envelope, pseudo-disc, and disc.

Even without rotation, the magnetic field is twisted by the Hall effect such that a toroidal component is produced. Subsequently, after coupling between the neutral gas and magnetic field (or charged particles) is recovered, the magnetic tension force caused by the toroidal component of the magnetic field imparts a rotational motion. This is the reason why the non-rotating gas acquires an angular momentum as a result of the Hall effect.

4.1 Hall velocity

We assume that the gas velocity passing through the Hall radius (r = r_Hall) converges to the Hall drift velocity. Thus, the azimuthal component of the gas velocity can be written as

\begin{eqnarray*} v_\phi &\sim & -\boldsymbol {v}_{\rm Hall,\phi }, \nonumber \\ &=& \eta _H \frac{(\nabla \times \boldsymbol {B})_\phi }{|B_z|}. \end{eqnarray*}

(31)

The same definition of the Hall drift velocity is also used in Tsukamoto (2016). The convergence of the gas rotation velocity is explained in Section 2.1, and the validity of the gas velocity assumption is demonstrated in fig. 3 of Krasnopolsky et al. (2011), which confirms that the azimuthal gas velocity converges to the Hall drift velocity. The time-scale of the |$\boldsymbol {v}_\phi$| change is discussed in Section 5.2.1.

Using a cylindrical coordinate system, the Hall-induced rotational velocity can be written as

\begin{eqnarray*} v_{\phi } = \frac{\eta _H}{B_z} \left(\frac{\partial B_{r,s}}{\partial z}-\frac{\partial B_z}{\partial r} \right), \end{eqnarray*}

(32)

where B_{r, s} is the magnetic field strength in the radial direction at the surface of the pseudo-disc. These calculations allow the approximation |∂B_{r, s}/∂|$z$|| ∼ B_{r, s}/H_env, where H_env is the scaleheight of the infalling envelope. In addition, the radial derivative term is assumed to be zero (i.e. |$\frac{\partial B_{r,s}}{\partial z} \gg \frac{\partial B_z}{\partial r}$|⁠; Lubow, Papaloizou & Pringle 1994). Thus, equation (32) can in turn be approximated by

\begin{eqnarray*} v_{\phi } = \frac{\eta _H}{|B_z|} \frac{B_{r,s}}{H_{\rm env}}. \end{eqnarray*}

(33)

In these calculations, B_{r, s} is rewritten in terms of the mass-to-flux ratio. The magnetic flux threading the core is given by

\begin{eqnarray*} \Phi _{\rm tot} =2 \pi r^2 B_{r,s}, \end{eqnarray*}

(34)

based on the monopole approximation employed in Contopoulos, Ciolek & Königl (1998) and Braiding & Wardle (2012).

We also define the mass-to-flux ratio normalized by the critical value as

\begin{eqnarray*} \mu _{\rm tot} \equiv \left(\frac{M_{\rm tot}}{\Phi _{\rm tot}} \right) / \left(\frac{M}{\Phi } \right)_{\rm crit}, \end{eqnarray*}

(35)

where (M/Φ)_crit = (0.53/3π)(5/G)^1/2 is the critical mass-to-flux ratio (Mouschovias & Spitzer 1976; Mac Low & Klessen 2004) and M_tot is the total core mass, as discussed below (see equation 42). Using these equations, equation (33) can be rewritten as

\begin{eqnarray*} v_{\phi } &=& \frac{\eta _{\rm H}}{|B_z|} \frac{B_{r,s}}{H_{\rm env}} \frac{(M/\Phi)_{\rm tot}}{\mu _{\rm tot} (M/\Phi)_{\rm crit}} \nonumber \\ &=& \frac{\eta _{\rm H}}{|B_z|} \frac{1}{\mu _{\rm tot} (M/\Phi)_{\rm crit}} \frac{M_{\rm tot}}{2 \pi r^2 H_{\rm env}}. \end{eqnarray*}

(36)

Here, μ_tot = 1 is adopted based on the simulation results of Machida & Matsumoto (2011). The vertical direction of the magnetic field is given by equation (30), using B = B_|$z$|.

According to Saigo & Hanawa (1998), the scaleheight of the envelope can be approximated by

\begin{eqnarray*} H_{\rm env}=\frac{\sqrt{2} c_s}{\sqrt{\pi G \rho _{\rm env}}} \sim \frac{c_s}{\sqrt{G \rho _{\rm env}}}, \end{eqnarray*}

(37)

where ρ_env = 3.8 × 10⁻¹⁶ g|$\, {\rm cm}^{-3}$| (⁠|$n_{\rm env}=10^8\, {\rm cm}^{-3}$|⁠) is adopted on the basis of Tsukamoto et al. (2017). The speed of sound is determined employing equation (26). Using this approach, the scaleheight of the envelope is estimated to be H_env = 360 au, in good agreement with recently reported simulation results (e.g. Tsukamoto et al. 2017).

4.2 Disc model and angular momentum estimated using the Hall effect

Recent simulations of disc formation have indicated that the circumstellar disc in the early star formation phase is massive (Inutsuka, Machida & Matsumoto 2010; Tomida et al. 2015; Tsukamoto et al. 2015a; Vaytet et al. 2018). Thus, Toomre’s Q-parameter, which is given by Q = c_sΩ_kep/(πGΣ_disc), is expected to be small. Using the Q-parameter, we can represent the disc surface density as

\begin{eqnarray*} \Sigma _{\rm disc}=\frac{c_s \Omega _K}{\pi G Q}, \end{eqnarray*}

(38)

where the value of Q is assumed to be constant over the entire disc. According to Kusaka, Nakano & Hayashi (1970) and Chiang & Goldreich (1997), the disc temperature can be determined using the equation

\begin{eqnarray*} T_{\rm disc} = 150 \left(\frac{r}{1\, \rm {au}} \right)^{- {3}/{7}} \ \ \ {\rm K}. \end{eqnarray*}

(39)

Substituting the temperature, T_disc, and Keplerian angular velocity, Ω_k, the dimensional surface density of the disc can be described as

\begin{eqnarray*} \Sigma _{\rm disc}= c_{\rm sd} \Sigma _0 \left(\frac{Q}{1} \right)^{-1} \left(\frac{M_{\rm star}}{0.1 \mathrm{ M}_\odot } \right)^{{1}/{2}} \left(\frac{r}{100\, \rm {au}} \right)^{-{12}/{7}} \rm {g}\, {\rm cm}^{-2}, \end{eqnarray*}

(40)

where M_star is the protostellar mass, Σ₀ is a constant estimated to have a value of Σ₀ = 8.2 g cm⁻² based on the above equations, and c_sd is a control parameter used to adjust the disc surface density. Using equation (40), the disc mass is estimated as

\begin{eqnarray*} M_{\rm disc}=\int _0^r \Sigma _{\rm disc}\, 2 \pi r \mathrm{ d}r. \end{eqnarray*}

(41)

In addition, we define the total mass (which includes the disc and protostellar masses) as

\begin{eqnarray*} M_{\rm tot}=M_{\rm star}+M_{\rm disc}. \end{eqnarray*}

(42)

The total mass, M_tot, should equal the overall mass of the infalling gas passing through the Hall radius. Note that we ignore mass ejection via protostellar outflow in this study. The infalling gas passing through the Hall radius, r_Hall, is assumed to acquire an angular momentum via the Hall effect, and this momentum can be estimated as

\begin{eqnarray*} J_{\rm Hall} &\sim & M_{\rm tot} j_{\rm Hall} \nonumber \\ &=& M_{\rm tot} r_{\rm Hall} v_{\phi }, \end{eqnarray*}

(43)

where r = r_Hall and equation (36) are employed to obtain |$v$|_ϕ. Thus, the Hall angular momentum, J_Hall, can be written as |$J_{\rm Hall} \sim M_{\rm tot}\, r_{\rm Hall}\, v_{\rm Hall,\phi}$|⁠.

To determine the size of the circumstellar disc, the angular momentum induced by the Hall effect is assumed to produce a Keplerian disc around the protostar. Consequently, the infalling mass is distributed into the protostar and Keplerian disc, although only the Keplerian disc is assumed to have angular momentum. This angular momentum is given by

\begin{eqnarray*} \begin{split} J_{\rm Kepler}&=\int _0^r \Sigma _{\rm disc}(r) 2 \pi r j_{\rm Kepler}\, \mathrm{ d}r \\ &=\int _0^r \Sigma _{\rm disc}(r) 2 \pi r^2 v_{\rm Kepler} \, \mathrm{ d}r \\ &=\int _0^r \Sigma _{\rm disc}(r) 2 \pi r^2 \sqrt{\frac{G M_{\rm star}}{r}} \mathrm{ d}r. \end{split} \end{eqnarray*}

(44)

Therefore, using solely the total and protostellar masses, we can determine the size of the disc outer edge at which the Keplerian angular momentum corresponds to the angular momentum of the total gas that has already undergone infall. Hereafter, we define the size of disc’s outer edge as r_disc.

As described above, the disc surface density is determined based on the Q-parameter. However, since disc fragmentation may occur when Q ≲ 1, it is difficult to retain a simple disc. Thus, we consider that c_sd = 1 (i.e. Q = 1) gives the maximum surface density. In reality, because the disc surface density is expected to be less than c_sd = 1, c_sd is parametrized and the value adopted in this study is provided in Table 5. The protostellar mass, which is also employed as a parameter to determine the disc radius, is included in the same table.

Table 5.

Parameters determining the disc surface density and protostellar mass.

c_sd	1, 0.1, 0.01
M_star (M_⊙)	0.03, 0.05, 0.07, 0.1, 0.3, 0.5, 0.7

Table 5.

Parameters determining the disc surface density and protostellar mass.

c_sd	1, 0.1, 0.01
M_star (M_⊙)	0.03, 0.05, 0.07, 0.1, 0.3, 0.5, 0.7

4.3 Keplerian disc induced by the Hall effect

The disc size induced by the Hall effect was determined according to the procedure:

the protostellar mass, M_star, was assumed to determine the total mass, M_tot (equation 42),
the specific angular momentum, |$j_{\rm Hall}= r_{\rm Hall}\, v_{\rm Hall, \phi}$|⁠, was estimated using equation (36),
the total angular momentum of the accreted material was calculated as |$J_{\rm Hall}=M_{\rm tot}\, j_{\rm Hall}$|⁠,
the total angular momentum of the Keplerian disc was estimated based on equation (44), assuming that the disc extends to a very large radius, and
the disc size, r_disc, at which the angular momentum of the Keplerian disc equals that of the accreted material [the rotation of which is determined by the Hall effect as in steps (i)–(ii)] was determined.

After varying the protostellar mass, steps (i)–(v) were repeated using the different models listed in Tables 1 and 4, to determine r_disc for each model. The resulting values are presented in Fig. 8 as filled magenta circles. As an example of the estimation of the disc induced by the Hall effect, Fig. 8 plots the angular momentum values for Keplerian and Hall discs (hereafter, we refer to discs formed by the Hall effect as Hall discs). These values were obtained using c_sd = 1 and ζ = 10⁻¹⁷ s⁻¹ for different grain size models and assuming a protostellar mass of |$M_{\rm star}=0.1\, \mathrm{ M}_\odot$|⁠. Additionally, the specific angular momentum induced by the Hall effect, j_Hall, was calculated for each model (see Section 4.2). For each line (that is, each grain size model) in this figure, the angular momentum of the Hall disc is less than that of the Keplerian disc outside the point denoted by the purple circle, meaning that a rotationally supported disc will not form in such regions. Conversely, in the region (or at the radius) inside the purple circle, the angular momentum of the Hall disc is greater than that of the Keplerian disc and so a rotationally supported disc (i.e. a Keplerian disc) can form. Because angular momentum can be transferred inside the disc, it is difficult to precisely determine the disc radius values in this study. Even so, a comparison of the angular momenta of the Hall disc and the Keplerian disc allows a rough estimation of the disc size for a given grain size and protostellar mass. The data in this figure indicate that the disc size is r_disc = 2.13 au in the case of model s4 (⁠|$a_{\rm single}=0.1\, {\rm \mu m}$|⁠) and 5.01 au in the case of model s8 (⁠|$a_{\rm single}=0.01\, {\rm \mu m}$|⁠).

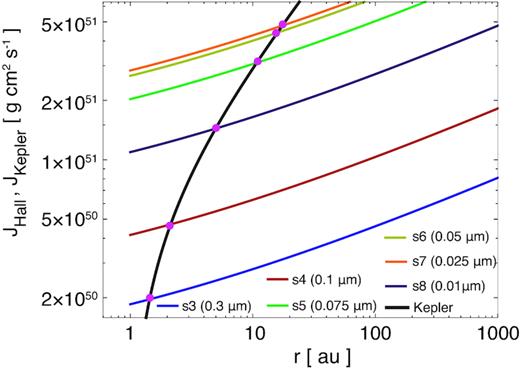
$The angular momentum values of the Hall discs for different grain size models versus the radius, as obtained using csd = 1 and ζ = 10−17 s−1, with a protostellar mass of $M_{\rm star}=0.1\, \mathrm{ M}_\odot$. The thick black solid line corresponds to the angular momentum of the Keplerian disc. The filled magenta circles indicate the intersections of the angular momenta of Hall and Keplerian discs, and correspond to the radii of the Hall discs.$

Figure 8.

The angular momentum values of the Hall discs for different grain size models versus the radius, as obtained using c_sd = 1 and ζ = 10⁻¹⁷ s⁻¹, with a protostellar mass of |$M_{\rm star}=0.1\, \mathrm{ M}_\odot$|⁠. The thick black solid line corresponds to the angular momentum of the Keplerian disc. The filled magenta circles indicate the intersections of the angular momenta of Hall and Keplerian discs, and correspond to the radii of the Hall discs.

While varying the protostellar mass, M_star, we derived the corresponding disc sizes according to the procedure described above. Fig. 9 plots the disc sizes obtained using the single-sized (left) and MRN (right) dust grain size distribution models as functions of the protostellar mass, based on using c_sd = 1 and ζ = 10⁻¹⁷ s⁻¹. These plots demonstrate that the size of the Keplerian disc varies considerably depending on the grain size (distribution), even if the protostellar mass is kept constant. As an example, at |$M_{\rm ps}=0.7\, \mathrm{ M}_\odot$|⁠, the disc size for a_single = 0.025 μm (model s7) is r_disc = 80 au, while the size for 0.3 μm (model s3) is r_disc = 3 au (left-hand panel of Fig. 9), corresponding to a variation in the disc size by a factor of 27. This result indicates that both the Hall effect and dust properties can affect the formation and evolution of the circumstellar disc.

Figure 9.

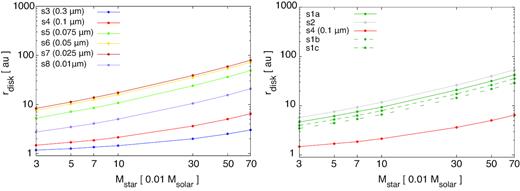
Disc sizes obtained using single-sized (left) and MRN (right) grain distributions as functions of the protostellar mass, as calculated with c_sd = 1 and ζ = 10⁻¹⁷ s⁻¹.

4.4 Parameter effects

The effects of the various parameters on the size of the Keplerian disc induced by the Hall effect were examined by constructing a fiducial model with the surface density parameter c_sd = 1, protostellar mass M_star = 0.1 M_⊙ and a cosmic ray ionization rate of ζ = |$10^{-17} \rm {s^{-1}}$|⁠. In this subsection, we discuss the results.

Fig. 10 plots the disc sizes as functions of c_sd for each dust model listed in Tables 1 and 5, obtained using a protostellar mass of |$M_{\rm star}=0.1\, \mathrm{ M}_\odot$| and an ionization rate of ζ = |$10^{-17} \rm {s^{-1}}$|⁠. As described in Section 4.2, we constructed the disc model on the basis of Q = 1, which corresponds to a marginally gravitationally unstable disc. Subsequently, we calculated the disc sizes, while adjusting the disc surface density using the parameter c_sd. As can be seen from these data, the disc size increases as the disc surface density decreases. This occurs because a less massive disc requires a large radius to have the same angular momentum as a more massive disc. However, the disc size is not strongly correlated with the surface density or with c_sd. As demonstrated by Fig. 10, the disc radius increases by approximately one order of magnitude when the disc surface density is reduced by about two orders of magnitude (c_sd = 0.01).

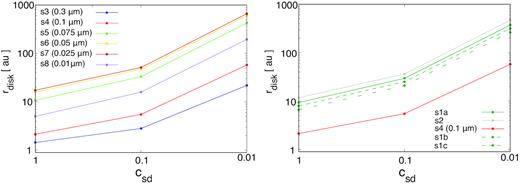
$Disc sizes obtained from the single-sized (left) and MRN (right) dust grain distributions versus the disc surface density control parameter csd, obtained using a prestellar mass of $M_{\rm star}=0.1\, \mathrm{ M}_\odot$ and a cosmic ray ionization rate of ζ = 10−17 s−1.$

Figure 10.

Disc sizes obtained from the single-sized (left) and MRN (right) dust grain distributions versus the disc surface density control parameter c_sd, obtained using a prestellar mass of |$M_{\rm star}=0.1\, \mathrm{ M}_\odot$| and a cosmic ray ionization rate of ζ = 10⁻¹⁷ s⁻¹.

Fig. 11 summarizes the effect of the cosmic ray ionization rate ζ on the disc size for different grain size models. Basically, the disc size decreases as ζ increases, because the non-ideal effect (or the Hall effect) becomes ineffective in an environment in which the ionization intensity is strong. However, an exception is also evident such that, in the case of the small dust grain models (models s1a, s1c and s8), a disc radius peak is seen in the vicinity of ζ ∼ 10^−17.5–10^−16.5 s⁻¹. These three models have greater proportions of small dust particles than the other seven models (as seen in Table 1) along with a smaller proportion of electrons, and the peak is attributed to these differences. The calculations required to obtain the Hall coefficient are highly complex and so at present we cannot conclusively identify the cause of the peak. However, this phenomenon will be addressed in a forthcoming paper.

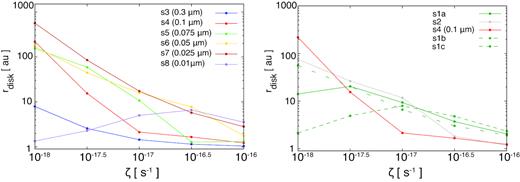
$Disc sizes for the single-sized (left) and MRN (right) dust grain distributions as functions of the cosmic ray ionization rate, ζ, obtained using csd = 1 and $M_{\rm star}=0.1\, \mathrm{ M}_\odot$.$

Figure 11.

Disc sizes for the single-sized (left) and MRN (right) dust grain distributions as functions of the cosmic ray ionization rate, ζ, obtained using c_sd = 1 and |$M_{\rm star}=0.1\, \mathrm{ M}_\odot$|⁠.

5 CAVEATS

As reported in Section 2, previous simulation studies have identified the possible importance of the Hall effect during the star formation process. However, long-term simulations (up to the formation of a mature circumstellar disc) cannot be performed because the whistler waves propagating to the star-forming cloud must be resolved using a very short time-steps to properly estimate the Hall effect during simulations (e.g. Sano & Stone 2002). Thus, in this study, we analytically estimated the impact of the Hall effect on disc evolution in star-forming clouds, and found that this effect significantly influences the star and disc formation processes depending on the dust properties and the strength of ionization sources. However, there are some caveats associated with this investigation of the circumstellar disc induced by the Hall effect. In this section, we discuss the validity of the assumptions used in this study.

5.1 Other non-ideal MHD effects

In this study, we ignored ambipolar diffusion and Ohmic dissipation in the induction equation. Only considering the ambipolar diffusion, Hennebelle et al. (2016) also analytically estimated the disc radius as

\begin{eqnarray*} r \sim 18 \ \rm {au} \left(\frac{\eta _{\rm AD}}{0.1 \rm {s}} \right)^{{2}/{9}} \left(\frac{B_{\rm z}}{0.1 \rm {G}} \right)^{-{4}/{9}} \left(\frac{M}{0.1 M_\odot } \right)^{{1}/{3}}, \end{eqnarray*}

(45)

where M is the total mass of disc and protostar and η_AD¹ is the ambipolar diffusion coefficient. When the protostellar mass is M_star = 0.1M_solar, the disc radius derived from Hennebelle et al. (2016) is comparable to that derived from this study (see Fig. 9), which implies that we cannot ignore both ambipolar diffusion and the Hall effect when considering the disc formation.

In addition to the Hall effect and ambipolar diffusion, Ohmic dissipation also affects the disc formation (e.g. Machida, Inutsuka & Matsumoto 2011). Moreover, in analytical works, we ignored some mechanisms of angular momentum transfer such as protostellar outflow that significantly reduces the angular momentum of the disc. Thus, in order to fully investigate the disc evolution, we need to execute non-ideal MHD simulations including all the non-ideal MHD terms in future.

5.2 Assumptions and limitations of the disc model

In this subsection, we discuss the assumptions and limitations used in this study. Especially, we focus on the time-scale for convergence of the Hall velocity, the initial rotation, and the size growth of grains.

5.2.1 Convergence time-scale of the Hall velocity

In Section 4.1, we assumed that gas particles instantaneously receive the angular momentum (or the Hall velocity) at the moment at which they pass through the Hall radius (see Section 4.2). In the collapsing cloud, the Hall velocity results from the Lorenz force of the toroidal field component induced by the Hall effect. We assumed the toroidal field produced by the Hall effect at a specific, constant value. However, it is necessary to estimate the saturation time-scale in order to confirm that the gas particles indeed obtain the Hall velocity estimated in Section 4.1.

The specific angular momentum of the gas fluid induced by the Hall effect is estimated from the magnetic torque exerted by the magnetic tension and is described as

\begin{eqnarray*} \begin{split} j(t_{\rm Hall}) &= \left[\boldsymbol {r} \times \left(\frac{(\nabla \times \boldsymbol {B}) \times \boldsymbol {B}}{4 \pi \rho } \right) \right]_z t_{\rm Hall}, \\ &\sim \frac{r}{4 \pi \rho } \frac{B_{r,s} B_z}{H} t_{\rm Hall}, \end{split} \end{eqnarray*}

(46)

where t_Hall is the time-scale until a constant (or time-independent) toroidal field is induced by the magnetic tension force or Hall effect. We use the same approximation as used in the derivation of the Hall velocity (see equations 32 and 33). In these calculations, a Hall radius of |$r_{\rm Hall}=300\, \rm {au}$| and a density of |$\rho =10^{-15}\rm {g \ cm^{-3}}$| are employed (as per Section 4.1). Using B_|$z$| (equation 30), H (equation 37), and B_{r, s} (equation 34) and their fiducial values, equation (46) can be written as

\begin{eqnarray*} j(t_{\rm Hall}) \sim 4.0 \times 10^{11}\, \left(\frac{t_{\rm Hall}}{1\, \rm s}\right) \ \rm {cm^2 \ s^{-1}}. \end{eqnarray*}

(47)

In addition, using the saturated Hall velocity (equation 36), we can write the specific angular momentum at r_Hall = 300 au as

\begin{eqnarray*} j(t_{\rm sat}) = r v_\phi \sim 2.1 \times 10^{18} \ \rm {cm^2 \ s^{-1}}. \end{eqnarray*}

(48)

When the steady state (or saturation) is reached, j(t_Hall) = j(t_sat) is established. Thus, the saturation timescale is estimated as

\begin{eqnarray*} t_{\rm Hall} \sim 5.1 \times 10^6 \ \rm {s}. \end{eqnarray*}

(49)

The dynamic time-scale of the collapsing cloud roughly corresponds to the freefall time-scale, t_ff. The t_ff at |$n_{\rm {Hall}} = 10^8\, \rm {cm^{-3}}$| is given by

\begin{eqnarray*} t_{\rm ff} = \sqrt{\frac{3 \pi }{32 G \rho }} = 1.4 \times 10^{11} \ \rm {s}. \end{eqnarray*}

(50)

Thus, the saturation time-scale is much shorter than the freefall time-scale t_Hall ≪ t_ff, suggesting that the (saturated) toroidal field is instantaneously generated under a given set of cloud parameters, and supplies the Hall velocity estimated in this study to the infalling gas particles.

5.2.2 Initial rotation

In this study, we ignored the rotation of prestellar clouds for simplicity. Observations show that molecular cloud cores have non-negligible rotations or angular momenta (e.g. Goodman et al. 1993; Caselli et al. 2002). Thus, our assumption of non-rotating cores is not very correct. However, we could estimate the angular momentum purely induced by the Hall effect, and found that the Hall effect significantly influences the disc formation. This indicates that the Hall effect cannot be ignored to investigate the disc formation, independent of the initial cloud rotation.

5.2.3 Grain growth during star formation process

We do not include the time-dependent grain growth. However, in reality, grains would grow by collisions between grains or sticking molecules on to grains. In addition, collisional destruction should be occurred in the star-forming cloud.

Chiaki et al. (2014) executed the simulations to estimate the dust growth under very low metallicity environments. They showed that the grain growth can change the star formation process under such environments. Our results showed that the grain sizes strongly affect the Hall effect and resulting disc size. Thus, we require simulations including the time-dependent change of grain sizes (or grain growth) in a future study.

5.3 The effect of magnetic field strength

A value of β = 100 was used to estimate the magnetic field strength in conjunction with equation (30), which is consistent with recent numerical simulations (e.g. Wurster et al. 2018b). However, since only the very early phase of disc formation has been investigated by simulations, the magnetic field strength and plasma beta of the disc would be expected to vary over time.

In this subsection, we assess the effect of the magnetic field strength (or plasma beta) on the disc size. Based on Section 4.2, we again calculated the disc size, employing β values over the range of 1 ≤ β ≤ 500. Fig. 12 plots the disc size values against the plasma beta, as determined using the fiducial parameters a_single = 0.1 μ m and |$\zeta = 10^{-17}\, \rm {s^{-1}}$|⁠. This figure confirms that the disc size decreases as β increases over the range of 1 ≲ β ≲ 50, but increases in the case of β values in the range of β ≳ 50. At |$n_{\rm {Hall}} = 10^8\, \rm {cm^{-3}}$|⁠, the Hall coefficient, η_H, becomes large as the magnetic field is strengthened (see fig. 6 in Marchand et al. 2016). In the present analysis, when 1 ≲ β ≲ 50, variations in η_H are primarily responsible for changes in β . In contrast, when 50 ≲ β ≲ 500, the decrease in the vertical component of the magnetic field, B_|$z$|, determines the disc size (see equation 36). However, the dependence of the magnetic field on η_H is not straightforward (see equations 6–9), and thus we cannot provide a simple explanation of the trend seen in Fig. 12. During the star formation process, although the fluctuations in the magnetic field strength are complex, our results suggest that it is important to consider the magnetic field strength when assessing the Hall effect.

Figure 12.

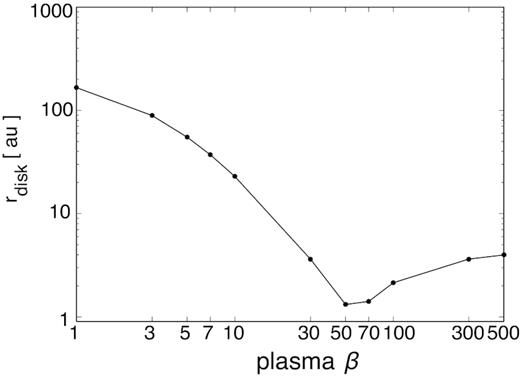
Calculated disc size as function of plasma β.

It is evident that the disc size varies with the magnetic field strength, and that the magnetic field is accumulated and amplified in the disc because it is coupled with the infalling matter. In contrast, the magnetic field is dissipated by Ohmic dissipation and ambipolar diffusion in the disc, and the magneto-rotational instability plays a role in determining the magnetic field strength in the disc. These effects are beyond the scope of this study, and the determination of magnetic field strength in the disc would not be possible even using state-of-art simulations. The results of this work imply that the magnetic field strength is important for investigating the angular momentum induced by the Hall effect. Thus, both the magnetic field strength and Hall effect would influence the formation and evolution of circumstellar discs.

6 SUMMARY

In this study, we analytically estimated the influence of the Hall effect on the formation and evolution of circumstellar discs. The chemical reactions in the collapsing cloud were initially determined to derive the Hall coefficient based on prior publications, but using a variety of dust grain models and ionization intensities. The results show that the Hall coefficient strongly depends both on the assumed dust model and the ionization intensity.

Subsequently, a simple disc model was employed to evaluate the size of the circumstellar disc solely on the basis of the Hall effect. Depending on the grain size and ionization intensity values selected, disc sizes of ∼3–100 au (∼2–20 au) were obtained for a protostar mass of |$0.5\, \mathrm{ M}_\odot$| (⁠|$0.1\, \mathrm{ M}_\odot$|⁠). It was expected that at n_Hall = 10⁸ cm⁻³, which number density is used in the disc model, smaller dust grains tend to form a larger disc in the grain size range of |$0.025\,\rm {\mu }m \lesssim a_{\rm {single}} \lesssim 0.3\,\rm {\mu }m$|⁠, because small grains significantly reduce the fraction of charged particles and amplify the non-ideal MHD effects. Conversely, in the range of |$0.01\,\rm {\mu }m \lesssim a_{\rm {single}} \lesssim 0.025\,\rm {\mu }m$|⁠, the disc size decreases as the grain size becomes smaller, because charged dust grains are much more abundant than charged particles. As such, a peak in the disc size change data appears at |$a_{\rm {single}}=0.025\,\rm {\mu }m$| in the case of |$\zeta =10^{-17} \rm {s^{-1}}$|⁠. In addition, large discs tend to be associated with weak ionization intensities, as a result of coupling between charged species and neutral gas.

The Keplerian discs observed around Class 0 objects have a size of ∼10–100 au, which is comparable to the disc size induced by the Hall effect. Thus, the Hall effect evidently contributes to the disc evolution, depending on the star-forming environment. It is important to note that the simple disc model in the work reported herein was not comprehensive. In particular, the time required for the growth of dust grains was neglected. Nevertheless, this work demonstrates that the Hall coefficient is significantly dependent on the average grain size, and so investigations of disc evolution must take into account the growth of dust particles.

ACKNOWLEDGEMENTS

We thank the referee for his/her useful comments. The authors gratefully acknowledge helpful discussions with K. Tomida. This work was supported by JSPS KAKENHI grants (numbers 17H02869, JP17K05387, JP17H06360, and 17KK0096). This research used computational resources within the high-performance computing infrastructure (HPCI) system provided by the Cyberscience Center, Tohoku University, the Cybermedia Center, Osaka University, and the Earth Simulator, JAMSTEC via the HPCI System Research Project (project numbers hp170047 and hp180001). Simulations were also performed by 2017 and 2018 Koubo Kadai on the Earth Simulator (NEC SX-ACE) at JAMSTEC.

Footnotes

1

The unit of η_AD in equation (45) differs from the unit used in this study (⁠|$\rm cm^2 s^{-1}$|⁠). The difference in resistivities between them is c²/4π (for detailed definition, see Marchand et al. 2016).

REFERENCES

Andre

P.

,

Montmerle

T.

,

1994

,

ApJ

,

420

,

837

10.1086/173608

10.3847/1538-4357/836/1/46

Bai

X.-N.

,

Stone

J. M.

,

2017

,

ApJ

,

836

,

46

Bate

M. R.

,

1998

,

ApJ

,

508

,

L95

10.1086/311719

10.1111/j.1365-2966.2012.20601.x

Braiding

C. R.

,

Wardle

M.

,

2012

,

MNRAS

,

422

,

261

Caselli

P.

,

Benson

P. J.

,

Myers

P. C.

,

Tafalla

M.

,

2002

,

ApJ

,

572

,

238

10.1086/340195

Chiaki

G.

,

Schneider

R.

,

Nozawa

T.

,

Omukai

K.

,

Limongi

M.

,

Yoshida

N.

,

Chieffi

A.

,

2014

,

MNRAS

,

439

,

3121

10.1093/mnras/stu178

Chiang

E. I.

,

Goldreich

P.

,

1997

,

ApJ

,

490

,

368

10.1086/304869

Contopoulos

I.

,

Ciolek

G. E.

,

Königl

A.

,

1998

,

ApJ

,

504

,

247

10.1086/306075

10.1088/0004-637X/725/1/466

Crutcher

R. M.

,

Wandelt

B.

,

Heiles

C.

,

Falgarone

E.

,

Troland

T. H.

,

2010

,

ApJ

,

725

,

466

Draine

B. T.

,

Sutin

B.

,

1987

,

ApJ

,

320

,

803

10.1086/165596

Draine

B. T.

,

Roberge

W. G.

,

Dalgarno

A.

,

1983

,

ApJ

,

264

,

485

10.1086/160617

10.1088/0004-637X/706/1/L46

Duffin

D. F.

,

Pudritz

R. E.

,

2009

,

ApJ

,

706

,

L46

Enoch

M. L.

,

Evans

N. J.

II,

Sargent

A. I.

,

Glenn

J.

,

Rosolowsky

E.

,

Myers

P.

,

2008

,

ApJ

,

684

,

1240

10.1086/589963

Farquhar

P. R. A.

,

Millar

T. J.

,

Herbst

E.

,

1994

,

MNRAS

,

269

,

641

10.1093/mnras/269.3.641

Goodman

A. A.

,

Benson

P. J.

,

Fuller

G. A.

,

Myers

P. C.

,

1993

,

ApJ

,

406

,

528

10.1086/172465

10.3847/2041-8205/830/1/L8

Hennebelle

P.

,

Commerçon

B.

,

Chabrier

G.

,

Marchand

P.

,

2016

,

ApJ

,

830

,

L8

10.1088/2041-8205/718/2/L58

Hirashita

H.

,

Lin

C.-Y.

,

2018

,

preprint(arXiv:1804.00848)

Inutsuka

S.-i.

,

Machida

M. N.

,

Matsumoto

T.

,

2010

,

ApJ

,

718

,

L58

10.1088/0004-637X/733/1/54

Krasnopolsky

R.

,

Li

Z.-Y.

,

Shang

H.

,

2011

,

ApJ

,

733

,

54

Kusaka

T.

,

Nakano

T.

,

Hayashi

C.

,

1970

,

Prog. Theor. Phys.

,

44

,

1580

10.1143/PTP.44.1580

Larson

R. B.

,

1969

,

MNRAS

,

145

,

271

10.1093/mnras/145.3.271

Lubow

S. H.

,

Papaloizou

J. C. B.

,

Pringle

J. E.

,

1994

,

MNRAS

,

267

,

235

10.1093/mnras/267.2.235

10.1051/0004-6361/201220465

McElroy

D.

,

Walsh

C.

,

Markwick

A. J.

,

Cordiner

M. A.

,

Smith

K.

,

Millar

T. J.

,

2013

,

A&A

,

550

,

A36

10.1103/RevModPhys.76.125

Mac Low

M.-M.

,

Klessen

R. S.

,

2004

,

Rev. Mod. Phys.

,

76

,

125

10.1111/j.1365-2966.2011.18349.x

Machida

M. N.

,

Matsumoto

T.

,

2011

,

MNRAS

,

413

,

2767

Machida

M. N.

,

Inutsuka

S.-i.

,

Matsumoto

T.

,

2006

,

ApJ

,

647

,

L151

10.1086/507179

Machida

M. N.

,

Inutsuka

S.-i.

,

Matsumoto

T.

,

2007

,

ApJ

,

670

,

1198

10.1086/521779

10.1088/0004-637X/724/2/1006

Machida

M. N.

,

Inutsuka

S.-i.

,

Matsumoto

T.

,

2010

,

ApJ

,

724

,

1006

Machida

M. N.

,

Inutsuka

S.-I.

,

Matsumoto

T.

,

2011

,

PASJ

,

63

,

555

10.1093/pasj/63.3.555

Machida

M. N.

,

Inutsuka

S.-i.

,

Matsumoto

T.

,

2014

,

MNRAS

,

438

,

2278

10.1093/mnras/stt2343

10.1051/0004-6361/201526780

Marchand

P.

,

Masson

J.

,

Chabrier

G.

,

Hennebelle

P.

,

Commerçon

B.

,

Vaytet

N.

,

2016

,

A&A

,

592

,

A18

Marchand

P.

,

Commerçon

B.

,

Chabrier

G.

,

2018

,

A&A

,

619

,

A37

10.1051/0004-6361/201526371

Masson

J.

,

Chabrier

G.

,

Hennebelle

P.

,

Vaytet

N.

,

Commerçon

B.

,

2016

,

A&A

,

587

,

A32

Masunaga

H.

,

Inutsuka

S.-i.

,

2000

,

ApJ

,

531

,

350

10.1086/308439

Mathis

J. S.

,

Rumpl

W.

,

Nordsieck

K. H.

,

1977

,

ApJ

,

217

,

425

10.1086/155591

Mellon

R. R.

,

Li

Z.-Y.

,

2008

,

ApJ

,

681

,

1356

10.1086/587542

Morton

D. C.

,

1974

,

ApJ

,

193

,

L35

10.1086/181625

Mouschovias

T. C.

,

Spitzer

L.

, Jr,

1976

,

ApJ

,

210

,

326

10.1086/154835

Nakano

T.

,

1984

,

Fundam. Cosm. Phys.

,

9

,

139

Nakano

T.

,

Nishi

R.

,

Umebayashi

T.

,

2002

,

ApJ

,

573

,

199

10.1086/340587

10.1088/0004-637X/698/2/1122

Okuzumi

S.

,

2009

,

ApJ

,

698

,

1122

10.1051/0004-6361/200911794

Padovani

M.

,

Galli

D.

,

Glassgold

A. E.

,

2009

,

A&A

,

501

,

619

Saigo

K.

,

Hanawa

T.

,

1998

,

ApJ

,

493

,

342

10.1086/305093

Sano

T.

,

Stone

J. M.

,

2002

,

ApJ

,

570

,

314

10.1086/339504

Sano

T.

,

Miyama

S. M.

,

Umebayashi

T.

,

Nakano

T.

,

2000

,

ApJ

,

543

,

486

10.1086/317075

10.1088/0004-637X/763/1/6

Tomida

K.

,

Tomisaka

K.

,

Matsumoto

T.

,

Hori

Y.

,

Okuzumi

S.

,

Machida

M. N.

,

Saigo

K.

,

2013

,

ApJ

,

763

,

6

10.1088/0004-637X/801/2/117

Tomida

K.

,

Okuzumi

S.

,

Machida

M. N.

,

2015

,

ApJ

,

801

,

117

Tomisaka

K.

,

1998

,

ApJ

,

502

,

L163

10.1086/311504

Tomisaka

K.

,

2000

,

ApJ

,

528

,

L41

10.1086/312417

Tomisaka

K.

,

2002

,

ApJ

,

575

,

306

10.1086/341133

Tsukamoto

Y.

,

2016

,

PASA

,

33

,

e010

10.1017/pasa.2016.6

Tsukamoto

Y.

,

Iwasaki

K.

,

Okuzumi

S.

,

Machida

M. N.

,

Inutsuka

S.

,

2015a

,

MNRAS

,

452

,

278

10.1093/mnras/stv1290

10.1088/2041-8205/810/2/L26

Tsukamoto

Y.

,

Iwasaki

K.

,

Okuzumi

S.

,

Machida

M. N.

,

Inutsuka

S.

,

2015b

,

ApJ

,

810

,

L26

Tsukamoto

Y.

,

Okuzumi

S.

,

Iwasaki

K.

,

Machida

M. N.

,

Inutsuka

S.-i.

,

2017

,

PASJ

,

69

,

95

10.1093/pasj/psx113

Tsukamoto

Y.

,

Okuzumi

S.

,

Iwasaki

K.

,

Machida

M. N.

,

Inutsuka

S.

,

2018

,

ApJ

,

868

,

22

10.3847/1538-4357/aae4dc

Umebayashi

T.

,

Nakano

T.

,

1980

,

PASJ

,

32

,

405

Umebayashi

T.

,

Nakano

T.

,

1990

,

MNRAS

,

243

,

103

10.1093/mnras/243.1.103

Vaytet

N.

,

Commerçon

B.

,

Masson

J.

,

González

M.

,

Chabrier

G.

,

2018

,

A&A

,

615

,

A5

10.1046/j.1365-8711.1999.02211.x

Wardle

M.

,

Ng

C.

,

1999

,

MNRAS

,

303

,

239

Wurster

J.

,

Price

D. J.

,

Bate

M. R.

,

2016

,

MNRAS

,

457

,

1037

10.1093/mnras/stw013

Wurster

J.

,

Bate

M. R.

,

Price

D. J.

,

2018a

,

MNRAS

,

475

,

1859

10.1093/mnras/stx3339

Wurster

J.

,

Bate

M. R.

,

Price

D. J.

,

2018b

,

MNRAS

,

476

,

2063

10.1093/mnras/sty392

Zhao

B.

,

Caselli

P.

,

Li

Z.-Y.

,

2018

,

MNRAS

,

478

,

2723

10.1093/mnras/sty1165

APPENDIX A: REACTION RATES

All the reactions used in this study, along with the associated reaction rates, are summarized in Table A1. The reaction between a charged particle i (that is, an ion) and an electron, e⁻, is written as k_i, while k_ij represents the reaction rate between charged species i and neutral species j, as in Table 3. Note that the HCO⁺ reaction rate was used as the m⁺ reaction rate, because HCO⁺ is the most abundant molecular ion after H|$_3^+$|⁠. In the case that a single charged species could undergo multiple reactions, these were distinguished using the symbols a − e. As an example, H|$_3^+$| can participate in five different reactions, with reaction rates k_12a, k_12b, k_12c, k_12d, and k_12e. As described in Section 2.4, these reaction rates were acquired from the UMIST database (McElroy et al. 2013).

Table A1.

Reactions and reaction rates used in this study.

Reaction	Rate (⁠\|$\rm {cm^3\, s^{-1}}$\|⁠)
\|$\rm {H_3^+ + e^- \rightarrow H_2 + H}$\|	\|$k_{1a}=2.34 \times 10^{-8} (\frac{T}{300})^{-0.5}$\|
\|$\rm {H_3^+ + e^- \rightarrow H+H+H}$\|	\|$k_{1b}=4.36 \times 10^{-8} (\frac{T}{300})^{-0.5}$\|
\|$\rm {HCO^+ + e^- \rightarrow CO + H}$\|	\|$k_2=2.4 \times 10^{-7} (\frac{T}{300})^{-0.7}$\|
\|$\rm {Mg^+ + e^- \rightarrow Mg}$\| + hν	\|$k_3=2.78 \times 10^{-12} (\frac{T}{300})^{-0.7}$\|
\|$\rm {He^+ + e^- \rightarrow He}$\| + hν	\|$k_4=5.36 \times 10^{-12} (\frac{T}{300})^{-0.5}$\|
\|$\rm {C^+ + e^- \rightarrow C}$\| + hν	\|$k_5=2.36 \times 10^{-12} (\frac{T}{300})^{-0.3} \rm {exp}(\frac{-17.6}{T})$\|
\|$\rm {H^+ + e^- \rightarrow H}$\| + hν	\|$k_6=3.50 \times 10^{-12} (\frac{T}{300})^{-0.8}$\|
\|$\rm {H_3^+ + O \rightarrow H_2O^+ + H}$\|	\|$k_{12a}=3.42 \times 10^{-10} (\frac{T}{300})^{-0.2} \rm {xO}$\|
\|$\rm {H_3^+ + O \rightarrow OH^+ + H_2}$\|	\|$k_{12b}=7.98 \times 10^{-10} (\frac{T}{300})^{-0.2} \rm {xO}$\|
\|$\rm {H_3^+ + CO \rightarrow HCO^+ + H_2}$\|	\|$k_{12c}=1.36 \times 10^{-9} (\frac{T}{300})^{-0.1} \rm {exp}(\frac{3.40}{T}) \rm {xCO}$\|
\|$\rm {H_3^+ + CO \rightarrow HOC^+ + H_2}$\|	\|$k_{12d}=8.49 \times 10^{-10} (\frac{T}{300})^{0.1} \rm {exp}(\frac{-5.20}{T}) \rm {xCO}$\|
\|$\rm {H_3^+ + O_2 \rightarrow O_2H^+ + H_2}$\|	\|$k_{12e}=9.30 \times 10^{-10} \rm {exp}(\frac{-100.00}{T}) \rm {xO_2}$\|
\|$\rm {H_3^+ + Mg \rightarrow Mg^+ + H + H_2}$\|	\|$k_{13}=1.0 \times 10^{-9} \rm {xM}$\|
\|$\rm {HCO^+ + Mg \rightarrow Mg^+ + HCO}$\|	\|$k_{23}=2.9 \times 10^{-9} \rm {xM}$\|
\|$\rm {He^+ + O_2 \rightarrow O^+ + O + He}$\|	\|$k_{42}=1.1 \times 10^{-9} \rm {xO_2}$\|
\|$\rm {He^+ + CO \rightarrow C^+ + O + He}$\|	\|$k_{45}=1.6 \times 10^{-9} \rm {xCO}$\|
\|$\rm {He^+ + H_2 \rightarrow H^+ + H + He}$\|	\|$k_{46}=3.7 \times 10^{-14} \rm {exp}(\frac{-35.0}{T}) \rm {xH_2}$\|
\|$\rm {C^+ + H_2 \rightarrow CH_2^+}$\| + hν	\|$k_{52a}=4.0 \times 10^{-16} \left(\frac{T}{300} \right)^{-0.2} \rm {xH_2}$\|
\|$\rm {C^+ + O_2 \rightarrow CO^+ + O}$\|	\|$k_{52b}=3.42 \times 10^{-10} \rm {xO_2}$\|
\|$\rm {C^+ + O_2 \rightarrow CO + O^+}$\|	\|$k_{52c}=4.54 \times 10^{-10} \rm {xO_2}$\|
\|$\rm {C^+ + Mg \rightarrow Mg^+ + C}$\|	\|$k_{53}=1.1 \times 10^{-9} \rm {xM}$\|
\|$\rm {H^+ + O \rightarrow O^+ + H}$\|	\|$k_{62a}=6.86 \times 10^{-10} (\frac{T}{300})^{0.3} \rm {exp} (\frac{-224.30}{T}) \rm {xO}$\|
\|$\rm {H^+ + O_2 \rightarrow O_2^+ + H}$\|	\|$k_{62b}=2.00 \times 10^{-9} \rm {xO_2}$\|
\|$\rm {H^+ + Mg \rightarrow Mg^+ + H}$\|	\|$k_{63}=1.1 \times 10^{-9} \rm {xM}$\|
\|$\rm {He^+ + H_2 \rightarrow H_2^+ + He}$\|	\|$k_{41}=7.2 \times 10^{-15} \rm {xH_2}$\|

Reaction	Rate (⁠\|$\rm {cm^3\, s^{-1}}$\|⁠)
\|$\rm {H_3^+ + e^- \rightarrow H_2 + H}$\|	\|$k_{1a}=2.34 \times 10^{-8} (\frac{T}{300})^{-0.5}$\|
\|$\rm {H_3^+ + e^- \rightarrow H+H+H}$\|	\|$k_{1b}=4.36 \times 10^{-8} (\frac{T}{300})^{-0.5}$\|
\|$\rm {HCO^+ + e^- \rightarrow CO + H}$\|	\|$k_2=2.4 \times 10^{-7} (\frac{T}{300})^{-0.7}$\|
\|$\rm {Mg^+ + e^- \rightarrow Mg}$\| + hν	\|$k_3=2.78 \times 10^{-12} (\frac{T}{300})^{-0.7}$\|
\|$\rm {He^+ + e^- \rightarrow He}$\| + hν	\|$k_4=5.36 \times 10^{-12} (\frac{T}{300})^{-0.5}$\|
\|$\rm {C^+ + e^- \rightarrow C}$\| + hν	\|$k_5=2.36 \times 10^{-12} (\frac{T}{300})^{-0.3} \rm {exp}(\frac{-17.6}{T})$\|
\|$\rm {H^+ + e^- \rightarrow H}$\| + hν	\|$k_6=3.50 \times 10^{-12} (\frac{T}{300})^{-0.8}$\|
\|$\rm {H_3^+ + O \rightarrow H_2O^+ + H}$\|	\|$k_{12a}=3.42 \times 10^{-10} (\frac{T}{300})^{-0.2} \rm {xO}$\|
\|$\rm {H_3^+ + O \rightarrow OH^+ + H_2}$\|	\|$k_{12b}=7.98 \times 10^{-10} (\frac{T}{300})^{-0.2} \rm {xO}$\|
\|$\rm {H_3^+ + CO \rightarrow HCO^+ + H_2}$\|	\|$k_{12c}=1.36 \times 10^{-9} (\frac{T}{300})^{-0.1} \rm {exp}(\frac{3.40}{T}) \rm {xCO}$\|
\|$\rm {H_3^+ + CO \rightarrow HOC^+ + H_2}$\|	\|$k_{12d}=8.49 \times 10^{-10} (\frac{T}{300})^{0.1} \rm {exp}(\frac{-5.20}{T}) \rm {xCO}$\|
\|$\rm {H_3^+ + O_2 \rightarrow O_2H^+ + H_2}$\|	\|$k_{12e}=9.30 \times 10^{-10} \rm {exp}(\frac{-100.00}{T}) \rm {xO_2}$\|
\|$\rm {H_3^+ + Mg \rightarrow Mg^+ + H + H_2}$\|	\|$k_{13}=1.0 \times 10^{-9} \rm {xM}$\|
\|$\rm {HCO^+ + Mg \rightarrow Mg^+ + HCO}$\|	\|$k_{23}=2.9 \times 10^{-9} \rm {xM}$\|
\|$\rm {He^+ + O_2 \rightarrow O^+ + O + He}$\|	\|$k_{42}=1.1 \times 10^{-9} \rm {xO_2}$\|
\|$\rm {He^+ + CO \rightarrow C^+ + O + He}$\|	\|$k_{45}=1.6 \times 10^{-9} \rm {xCO}$\|
\|$\rm {He^+ + H_2 \rightarrow H^+ + H + He}$\|	\|$k_{46}=3.7 \times 10^{-14} \rm {exp}(\frac{-35.0}{T}) \rm {xH_2}$\|
\|$\rm {C^+ + H_2 \rightarrow CH_2^+}$\| + hν	\|$k_{52a}=4.0 \times 10^{-16} \left(\frac{T}{300} \right)^{-0.2} \rm {xH_2}$\|
\|$\rm {C^+ + O_2 \rightarrow CO^+ + O}$\|	\|$k_{52b}=3.42 \times 10^{-10} \rm {xO_2}$\|
\|$\rm {C^+ + O_2 \rightarrow CO + O^+}$\|	\|$k_{52c}=4.54 \times 10^{-10} \rm {xO_2}$\|
\|$\rm {C^+ + Mg \rightarrow Mg^+ + C}$\|	\|$k_{53}=1.1 \times 10^{-9} \rm {xM}$\|
\|$\rm {H^+ + O \rightarrow O^+ + H}$\|	\|$k_{62a}=6.86 \times 10^{-10} (\frac{T}{300})^{0.3} \rm {exp} (\frac{-224.30}{T}) \rm {xO}$\|
\|$\rm {H^+ + O_2 \rightarrow O_2^+ + H}$\|	\|$k_{62b}=2.00 \times 10^{-9} \rm {xO_2}$\|
\|$\rm {H^+ + Mg \rightarrow Mg^+ + H}$\|	\|$k_{63}=1.1 \times 10^{-9} \rm {xM}$\|
\|$\rm {He^+ + H_2 \rightarrow H_2^+ + He}$\|	\|$k_{41}=7.2 \times 10^{-15} \rm {xH_2}$\|

Table A1.

Reactions and reaction rates used in this study.

Reaction	Rate (⁠\|$\rm {cm^3\, s^{-1}}$\|⁠)
\|$\rm {H_3^+ + e^- \rightarrow H_2 + H}$\|	\|$k_{1a}=2.34 \times 10^{-8} (\frac{T}{300})^{-0.5}$\|
\|$\rm {H_3^+ + e^- \rightarrow H+H+H}$\|	\|$k_{1b}=4.36 \times 10^{-8} (\frac{T}{300})^{-0.5}$\|
\|$\rm {HCO^+ + e^- \rightarrow CO + H}$\|	\|$k_2=2.4 \times 10^{-7} (\frac{T}{300})^{-0.7}$\|
\|$\rm {Mg^+ + e^- \rightarrow Mg}$\| + hν	\|$k_3=2.78 \times 10^{-12} (\frac{T}{300})^{-0.7}$\|
\|$\rm {He^+ + e^- \rightarrow He}$\| + hν	\|$k_4=5.36 \times 10^{-12} (\frac{T}{300})^{-0.5}$\|
\|$\rm {C^+ + e^- \rightarrow C}$\| + hν	\|$k_5=2.36 \times 10^{-12} (\frac{T}{300})^{-0.3} \rm {exp}(\frac{-17.6}{T})$\|
\|$\rm {H^+ + e^- \rightarrow H}$\| + hν	\|$k_6=3.50 \times 10^{-12} (\frac{T}{300})^{-0.8}$\|
\|$\rm {H_3^+ + O \rightarrow H_2O^+ + H}$\|	\|$k_{12a}=3.42 \times 10^{-10} (\frac{T}{300})^{-0.2} \rm {xO}$\|
\|$\rm {H_3^+ + O \rightarrow OH^+ + H_2}$\|	\|$k_{12b}=7.98 \times 10^{-10} (\frac{T}{300})^{-0.2} \rm {xO}$\|
\|$\rm {H_3^+ + CO \rightarrow HCO^+ + H_2}$\|	\|$k_{12c}=1.36 \times 10^{-9} (\frac{T}{300})^{-0.1} \rm {exp}(\frac{3.40}{T}) \rm {xCO}$\|
\|$\rm {H_3^+ + CO \rightarrow HOC^+ + H_2}$\|	\|$k_{12d}=8.49 \times 10^{-10} (\frac{T}{300})^{0.1} \rm {exp}(\frac{-5.20}{T}) \rm {xCO}$\|
\|$\rm {H_3^+ + O_2 \rightarrow O_2H^+ + H_2}$\|	\|$k_{12e}=9.30 \times 10^{-10} \rm {exp}(\frac{-100.00}{T}) \rm {xO_2}$\|
\|$\rm {H_3^+ + Mg \rightarrow Mg^+ + H + H_2}$\|	\|$k_{13}=1.0 \times 10^{-9} \rm {xM}$\|
\|$\rm {HCO^+ + Mg \rightarrow Mg^+ + HCO}$\|	\|$k_{23}=2.9 \times 10^{-9} \rm {xM}$\|
\|$\rm {He^+ + O_2 \rightarrow O^+ + O + He}$\|	\|$k_{42}=1.1 \times 10^{-9} \rm {xO_2}$\|
\|$\rm {He^+ + CO \rightarrow C^+ + O + He}$\|	\|$k_{45}=1.6 \times 10^{-9} \rm {xCO}$\|
\|$\rm {He^+ + H_2 \rightarrow H^+ + H + He}$\|	\|$k_{46}=3.7 \times 10^{-14} \rm {exp}(\frac{-35.0}{T}) \rm {xH_2}$\|
\|$\rm {C^+ + H_2 \rightarrow CH_2^+}$\| + hν	\|$k_{52a}=4.0 \times 10^{-16} \left(\frac{T}{300} \right)^{-0.2} \rm {xH_2}$\|
\|$\rm {C^+ + O_2 \rightarrow CO^+ + O}$\|	\|$k_{52b}=3.42 \times 10^{-10} \rm {xO_2}$\|
\|$\rm {C^+ + O_2 \rightarrow CO + O^+}$\|	\|$k_{52c}=4.54 \times 10^{-10} \rm {xO_2}$\|
\|$\rm {C^+ + Mg \rightarrow Mg^+ + C}$\|	\|$k_{53}=1.1 \times 10^{-9} \rm {xM}$\|
\|$\rm {H^+ + O \rightarrow O^+ + H}$\|	\|$k_{62a}=6.86 \times 10^{-10} (\frac{T}{300})^{0.3} \rm {exp} (\frac{-224.30}{T}) \rm {xO}$\|
\|$\rm {H^+ + O_2 \rightarrow O_2^+ + H}$\|	\|$k_{62b}=2.00 \times 10^{-9} \rm {xO_2}$\|
\|$\rm {H^+ + Mg \rightarrow Mg^+ + H}$\|	\|$k_{63}=1.1 \times 10^{-9} \rm {xM}$\|
\|$\rm {He^+ + H_2 \rightarrow H_2^+ + He}$\|	\|$k_{41}=7.2 \times 10^{-15} \rm {xH_2}$\|

Reaction	Rate (⁠\|$\rm {cm^3\, s^{-1}}$\|⁠)
\|$\rm {H_3^+ + e^- \rightarrow H_2 + H}$\|	\|$k_{1a}=2.34 \times 10^{-8} (\frac{T}{300})^{-0.5}$\|
\|$\rm {H_3^+ + e^- \rightarrow H+H+H}$\|	\|$k_{1b}=4.36 \times 10^{-8} (\frac{T}{300})^{-0.5}$\|
\|$\rm {HCO^+ + e^- \rightarrow CO + H}$\|	\|$k_2=2.4 \times 10^{-7} (\frac{T}{300})^{-0.7}$\|
\|$\rm {Mg^+ + e^- \rightarrow Mg}$\| + hν	\|$k_3=2.78 \times 10^{-12} (\frac{T}{300})^{-0.7}$\|
\|$\rm {He^+ + e^- \rightarrow He}$\| + hν	\|$k_4=5.36 \times 10^{-12} (\frac{T}{300})^{-0.5}$\|
\|$\rm {C^+ + e^- \rightarrow C}$\| + hν	\|$k_5=2.36 \times 10^{-12} (\frac{T}{300})^{-0.3} \rm {exp}(\frac{-17.6}{T})$\|
\|$\rm {H^+ + e^- \rightarrow H}$\| + hν	\|$k_6=3.50 \times 10^{-12} (\frac{T}{300})^{-0.8}$\|
\|$\rm {H_3^+ + O \rightarrow H_2O^+ + H}$\|	\|$k_{12a}=3.42 \times 10^{-10} (\frac{T}{300})^{-0.2} \rm {xO}$\|
\|$\rm {H_3^+ + O \rightarrow OH^+ + H_2}$\|	\|$k_{12b}=7.98 \times 10^{-10} (\frac{T}{300})^{-0.2} \rm {xO}$\|
\|$\rm {H_3^+ + CO \rightarrow HCO^+ + H_2}$\|	\|$k_{12c}=1.36 \times 10^{-9} (\frac{T}{300})^{-0.1} \rm {exp}(\frac{3.40}{T}) \rm {xCO}$\|
\|$\rm {H_3^+ + CO \rightarrow HOC^+ + H_2}$\|	\|$k_{12d}=8.49 \times 10^{-10} (\frac{T}{300})^{0.1} \rm {exp}(\frac{-5.20}{T}) \rm {xCO}$\|
\|$\rm {H_3^+ + O_2 \rightarrow O_2H^+ + H_2}$\|	\|$k_{12e}=9.30 \times 10^{-10} \rm {exp}(\frac{-100.00}{T}) \rm {xO_2}$\|
\|$\rm {H_3^+ + Mg \rightarrow Mg^+ + H + H_2}$\|	\|$k_{13}=1.0 \times 10^{-9} \rm {xM}$\|
\|$\rm {HCO^+ + Mg \rightarrow Mg^+ + HCO}$\|	\|$k_{23}=2.9 \times 10^{-9} \rm {xM}$\|
\|$\rm {He^+ + O_2 \rightarrow O^+ + O + He}$\|	\|$k_{42}=1.1 \times 10^{-9} \rm {xO_2}$\|
\|$\rm {He^+ + CO \rightarrow C^+ + O + He}$\|	\|$k_{45}=1.6 \times 10^{-9} \rm {xCO}$\|
\|$\rm {He^+ + H_2 \rightarrow H^+ + H + He}$\|	\|$k_{46}=3.7 \times 10^{-14} \rm {exp}(\frac{-35.0}{T}) \rm {xH_2}$\|
\|$\rm {C^+ + H_2 \rightarrow CH_2^+}$\| + hν	\|$k_{52a}=4.0 \times 10^{-16} \left(\frac{T}{300} \right)^{-0.2} \rm {xH_2}$\|
\|$\rm {C^+ + O_2 \rightarrow CO^+ + O}$\|	\|$k_{52b}=3.42 \times 10^{-10} \rm {xO_2}$\|
\|$\rm {C^+ + O_2 \rightarrow CO + O^+}$\|	\|$k_{52c}=4.54 \times 10^{-10} \rm {xO_2}$\|
\|$\rm {C^+ + Mg \rightarrow Mg^+ + C}$\|	\|$k_{53}=1.1 \times 10^{-9} \rm {xM}$\|
\|$\rm {H^+ + O \rightarrow O^+ + H}$\|	\|$k_{62a}=6.86 \times 10^{-10} (\frac{T}{300})^{0.3} \rm {exp} (\frac{-224.30}{T}) \rm {xO}$\|
\|$\rm {H^+ + O_2 \rightarrow O_2^+ + H}$\|	\|$k_{62b}=2.00 \times 10^{-9} \rm {xO_2}$\|
\|$\rm {H^+ + Mg \rightarrow Mg^+ + H}$\|	\|$k_{63}=1.1 \times 10^{-9} \rm {xM}$\|
\|$\rm {He^+ + H_2 \rightarrow H_2^+ + He}$\|	\|$k_{41}=7.2 \times 10^{-15} \rm {xH_2}$\|

APPENDIX B: DUST REACTIONS

In this appendix, we address collisions between dust grains and charged particles and the absorption of charged particles on to the surfaces of dust grains. Three types of dust grains are considered: positively charged, negatively charged, and neutral. The reactions of these grains with ions and electrons are also considered, such that six reactions are required, as described below. According to Draine & Sutin (1987), the reaction rates can be summarized as itemized below.

The collisional rate between charged grains and ions (i = 1–6), written as
\begin{eqnarray*} k_{id} (s,z)= \left\lbrace \begin{array}{l}\sqrt{\frac{8 k_B T}{\pi m_i}} \sigma _s \ \rm {exp} \left(-\frac{{\it z}}{(1+|{\it z}|^{-1/2})\tau _s} \right) \ \left\lbrace 1+ \left(\frac{1}{4\tau _s+3{\it z}} \right)^{1/2} \right\rbrace ^2 \qquad ({\it z} \ \rm {\gt 0}) \\ \sqrt{\frac{8 k_B T}{\pi m_i}} \sigma _s \ \left(1-\frac{z}{\tau _s} \right) \ \left\lbrace 1+ \left(\frac{2}{\tau _s-2z} \right)^{1/2} \right\rbrace \qquad (z\lt 0). \end{array} \right. \end{eqnarray*}
(B1)
The collisional rate between charged grains and electrons (i = 0), written as
\begin{eqnarray*} k_{id} (s,z)= \left\lbrace \begin{array}{l}\sqrt{\frac{8 k_B T}{\pi m_e}} \sigma _s \ \left(1+\frac{z}{\tau _s} \right) \left\lbrace 1+\left(\frac{2}{\tau _s+2z} \right)^{1/2} \right\rbrace \qquad (z\gt 0) \\ \sqrt{\frac{8 k_B T}{\pi m_e}} \sigma _s \ \rm {exp} \left(\frac{{\it z}}{(1+|{\it z}|^{-1/2})\tau _s} \right) \ \left\lbrace 1+ \left(\frac{1}{4\tau _s-3{\it z}} \right)^{1/2} \right\rbrace ^2 \qquad ({\it z} \ \rm {\lt 0}). \end{array} \right. \end{eqnarray*}
(B2)
The collisional rate between neutral grains, electrons, and ions (i = 0–6), written as
\begin{eqnarray*} k_{nd} (s,0) =\sqrt{\frac{8 k_B T}{\pi m_e}} \sigma _s \left\lbrace 1+ \left(\frac{\pi }{2 \tau _s} \right)^{1/2} \right\rbrace . \end{eqnarray*}
(B3)

Here, |$z$|⁠, m_e, σ_s, and τ_s indicate the charge on the dust particles, the electron mass, the collision cross-section and the reduced temperature, respectively. The reduced temperature, τ_s, is described as

\begin{eqnarray*} \tau _{s}=\frac{a_s k_B T}{e^2}, \end{eqnarray*}

(B4)

and the collision cross-section, σ_s, is

\begin{eqnarray*} \sigma _s=\pi {a_{s}}^2, \end{eqnarray*}

(B5)

where the suffix s indicates the dust grains in the s-th bin (see Section 2.3).

APPENDIX C: REACTION EQUATIONS

The reaction equations used in this study were as follows. The term x_i (i = 0–6) refers to the fractional abundance of each charged species (for each index, see Table 3) and x_d(s, |$z$|⁠) refers to the fractional abundance of dust grains, where s is the bin number and |$z$| is the charge of dust grains. The reaction rates are summarized in Appendix A and the cosmic ray rates, ζ, can be found in Section 2.4.

\begin{eqnarray*} \begin{aligned} \frac{\mathrm{ d}x_0}{\mathrm{ d}t} =&\, \, (0.97+0.84+0.03) \zeta - n_{\rm H} (k_1 x_1 +k_2 x_2 +k_3 x_3 +k_4 x_4 + k_5 x_5 +k_6 x_6) x_0 \\ & - n_{\rm H} \biggl (\displaystyle \sum _{s=1}^{s_{\rm max}} \Bigl (\displaystyle \sum _{z=z_{\rm min}}^{-1} k_{ed}(s,z) x_{\rm d}(s,z) + k_{nd}(s)x_{\rm d}(s,0) +\displaystyle \sum _{z=1}^{z_{\rm max}} k_{ed}(s,z)x_{\rm d}(s,z) \Bigr) \biggr) x_0. \end{aligned} \end{eqnarray*}

(C1)

\begin{eqnarray*} \begin{aligned} \frac{\mathrm{ d}x_1}{\mathrm{ d}t} &= 0.97\zeta - n_{\rm H} \bigl ((k_{1a}+k_{1b}) x_0 + (k_{12a}+k_{12b}+k_{12c}+k_{12d}+k_{12e}) x_2 - k_{41} x_4 \bigr) x_1 - \delta _{1,\rm {d}}. \end{aligned} \end{eqnarray*}

(C2)

\begin{eqnarray*} \begin{aligned} \frac{\mathrm{ d}x_2}{\mathrm{ d}t} =& -\, n_{\rm H} \Bigl (k_2 x_0 - (k_{12a}+k_{12b}+k_{12c}+k_{12d}+k_{12e}) x_1 + k_{23} x_3 - k_{42} x_4 \\ & - (k_{52a}+k_{52b}+k_{52c}) x_5 - (k_{62a}+k_{62b}) x_6 \Bigr) x_2 - \delta _{2,\rm {d}}. \end{aligned} \end{eqnarray*}

(C3)

\begin{eqnarray*} \begin{aligned} \frac{\mathrm{ d}x_3}{\mathrm{ d}t} = - n_{\rm H} \left(k_3 x_0 - k_{13} x_1 - k_{23} x_2 - k_{53} x_5 - k_{63} x_6 \right) x_3 - \delta _{3,\rm {d}}. \end{aligned} \end{eqnarray*}

(C4)

\begin{eqnarray*} \begin{aligned} \frac{\mathrm{ d}x_4}{\mathrm{ d}t} = 0.84 \zeta - n_{\rm H} \left(k_4 x_0 + k_{42} x_2 + k_{45} x_5 + k_{46} x_6 + k_{41} x_1 \right) x_4 - \delta _{4,\rm {d}}. \end{aligned} \end{eqnarray*}

(C5)

\begin{eqnarray*} \begin{aligned} \frac{\mathrm{ d}x_5}{\mathrm{ d}t} = - n_{\rm H} \left(k_5 x_0 - k_{45} x_4 + (k_{52a}+k_{52b}+k_{52c}) x_2 + k_{53} x_3 \right) x_5 - \delta _{5,\rm {d}}. \end{aligned} \end{eqnarray*}

(C6)

\begin{eqnarray*} \begin{aligned} \frac{\mathrm{ d}x_6}{\mathrm{ d}t} =0.03 \zeta - n_{\rm H} \left(k_6 x_0 - k_{46} x_4 + (k_{62a}+k_{62b}) x_2 + k_{63} x_3 \right) x_6 - \delta _{6,\rm {d}}. \end{aligned} \end{eqnarray*}

(C7)

\begin{eqnarray*} \begin{aligned} \frac{\mathrm{ d}x_{\rm d}(z)}{\mathrm{ d}t} =& \,\, n_{\rm H} \displaystyle \sum _{s=1}^{s_{\rm {max}}} \Bigl (-k_{ed} (s,z) x_{\rm d}(s,z) x_0 - \displaystyle \sum _{i=1}^6 k_{id} (s,z) x_{\rm d}(s,z) x_i \\ &+ k_{ed}(s,z+1) x_{\rm d}(s,z+1) x_0 + k_{id}(s,z-1) x_{\rm d}(s,z-1) x_i \Bigr), \end{aligned} \end{eqnarray*}

(C8)

In the above, δ_{i, d} indicates the reaction following a collision between a charged particle i and a dust grain, and is given by

\begin{eqnarray*} \begin{aligned} \delta _{i,{\rm d}} &= n_{\rm H} \left\lbrace \displaystyle \sum _{s=1}^{s_{\rm {max}}} \left(\displaystyle \sum _{z=z_{min}}^{-1} k_{i-d}(s,z) x_{\rm d}(s,z) +k_{nd}(s)x_d(s,0) +\displaystyle \sum _{z=1}^{z_{max}} x_{i+d}(s,z)x_{\rm d}(s,z) \right) \right\rbrace x_i. \end{aligned} \end{eqnarray*}

(C9)

APPENDIX D: EQUILIBRIUM TIME-SCALE VERSUS FREEFALL TIME-SCALE

In this appendix, we compare the elapsed time required to obtain an equilibrium state with the freefall time-scale at a given density. Fig. D1 shows that chemical abundances of charged species considered in this study reach an equilibrium state within the freefall time-scale.

$Chemical abundances of charged species for different gas number density $10^4, 10^8, 10^{11}, 10^{14}\, \rm {cm^{-3}}$ as a function of ζt ($\zeta = 10^{-17} \rm {s^{-1}}$). The freefall time-scale is given by $t_{\rm ff} = \sqrt{\frac{3 \pi }{32 G \rho }}$.$

Figure D1.

Chemical abundances of charged species for different gas number density |$10^4, 10^8, 10^{11}, 10^{14}\, \rm {cm^{-3}}$| as a function of ζt (⁠|$\zeta = 10^{-17} \rm {s^{-1}}$|⁠). The freefall time-scale is given by |$t_{\rm ff} = \sqrt{\frac{3 \pi }{32 G \rho }}$|⁠.