Interplay between physics and geometry in Balmer filaments: the case of SN 1006 Free

Best-fitting parameters to our kinetic models [columns (4)–(10)]; derived integrated I_b/I_n ratio (11); same ratio, from more realistic simulated observations as in Morlino et al. (2012) (12); correction factor, as from equation (37) (13). Symbols are defined in the text, and the compression factor r is taken to be equal to 4.

V_sh	T_e/T_p	f_n,u	f_n,0	f_b,0	h_Rn₀	g_i,n	g_i,b/g_i,n	ε_n	ε_b	I_b/I_n	I_b/I_n	α
(⁠\|${\rm km\, s^{-1}}$\|⁠)					(⁠\|$\times 10^{14}\, {\rm cm^{-2}}$\|⁠)					present	M + 12
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)
2500	0.01	0.10	0.102	0.020	5.184	0.057	0.157	0.088	0.027	0.52	0.72	0.087
2500	0.10	0.10	0.102	0.021	5.504	0.044	0.097	0.079	0.026	0.68	1.24	0.216
3000	0.01	0.10	0.101	0.012	6.837	0.017	0.065	0.106	0.037	0.42	0.52	0.061
3000	0.10	0.10	0.101	0.012	7.452	0.010	0.028	0.097	0.040	0.63	0.69	0.012
3500	0.01	0.10	0.100	0.009	8.838	0.007	0.041	0.121	0.044	0.29	0.31	0.021
3500	0.10	0.10	0.100	0.006	9.708	0.018	0.069	0.113	0.047	0.47	0.47	0.000

V_sh	T_e/T_p	f_n,u	f_n,0	f_b,0	h_Rn₀	g_i,n	g_i,b/g_i,n	ε_n	ε_b	I_b/I_n	I_b/I_n	α
(⁠\|${\rm km\, s^{-1}}$\|⁠)					(⁠\|$\times 10^{14}\, {\rm cm^{-2}}$\|⁠)					present	M + 12
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)
2500	0.01	0.10	0.102	0.020	5.184	0.057	0.157	0.088	0.027	0.52	0.72	0.087
2500	0.10	0.10	0.102	0.021	5.504	0.044	0.097	0.079	0.026	0.68	1.24	0.216
3000	0.01	0.10	0.101	0.012	6.837	0.017	0.065	0.106	0.037	0.42	0.52	0.061
3000	0.10	0.10	0.101	0.012	7.452	0.010	0.028	0.097	0.040	0.63	0.69	0.012
3500	0.01	0.10	0.100	0.009	8.838	0.007	0.041	0.121	0.044	0.29	0.31	0.021
3500	0.10	0.10	0.100	0.006	9.708	0.018	0.069	0.113	0.047	0.47	0.47	0.000

Table 1.

Best-fitting parameters to our kinetic models [columns (4)–(10)]; derived integrated I_b/I_n ratio (11); same ratio, from more realistic simulated observations as in Morlino et al. (2012) (12); correction factor, as from equation (37) (13). Symbols are defined in the text, and the compression factor r is taken to be equal to 4.

V_sh	T_e/T_p	f_n,u	f_n,0	f_b,0	h_Rn₀	g_i,n	g_i,b/g_i,n	ε_n	ε_b	I_b/I_n	I_b/I_n	α
(⁠\|${\rm km\, s^{-1}}$\|⁠)					(⁠\|$\times 10^{14}\, {\rm cm^{-2}}$\|⁠)					present	M + 12
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)
2500	0.01	0.10	0.102	0.020	5.184	0.057	0.157	0.088	0.027	0.52	0.72	0.087
2500	0.10	0.10	0.102	0.021	5.504	0.044	0.097	0.079	0.026	0.68	1.24	0.216
3000	0.01	0.10	0.101	0.012	6.837	0.017	0.065	0.106	0.037	0.42	0.52	0.061
3000	0.10	0.10	0.101	0.012	7.452	0.010	0.028	0.097	0.040	0.63	0.69	0.012
3500	0.01	0.10	0.100	0.009	8.838	0.007	0.041	0.121	0.044	0.29	0.31	0.021
3500	0.10	0.10	0.100	0.006	9.708	0.018	0.069	0.113	0.047	0.47	0.47	0.000

V_sh	T_e/T_p	f_n,u	f_n,0	f_b,0	h_Rn₀	g_i,n	g_i,b/g_i,n	ε_n	ε_b	I_b/I_n	I_b/I_n	α
(⁠\|${\rm km\, s^{-1}}$\|⁠)					(⁠\|$\times 10^{14}\, {\rm cm^{-2}}$\|⁠)					present	M + 12
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)
2500	0.01	0.10	0.102	0.020	5.184	0.057	0.157	0.088	0.027	0.52	0.72	0.087
2500	0.10	0.10	0.102	0.021	5.504	0.044	0.097	0.079	0.026	0.68	1.24	0.216
3000	0.01	0.10	0.101	0.012	6.837	0.017	0.065	0.106	0.037	0.42	0.52	0.061
3000	0.10	0.10	0.101	0.012	7.452	0.010	0.028	0.097	0.040	0.63	0.69	0.012
3500	0.01	0.10	0.100	0.009	8.838	0.007	0.041	0.121	0.044	0.29	0.31	0.021
3500	0.10	0.10	0.100	0.006	9.708	0.018	0.069	0.113	0.047	0.47	0.47	0.000

A direct consequence of the above equations is the conservation of the total particle flux:

\begin{eqnarray*} f_\mathrm{ n}(z) + \left[ f_\mathrm{ b}(z) + f_{\mathrm{ p}}(z) \right]/r=1. \end{eqnarray*}

(16)

In general, κ_ce, κ_{i, n}, κ_{i, b}, and r should change with space, but from here on we will assume all these quantities to be spatially constant. Let us introduce κ_R = κ_ce + κ_{i, n} as a reference reaction rate, and scale all reaction rates with it:

\begin{eqnarray*} \kappa _{\mathrm{ ce}} = g_{\mathrm{ i,n}} \kappa _\mathrm{ R}; \end{eqnarray*}

(17)

\begin{eqnarray*} \kappa _{\mathrm{ i,n}} = (1-g_{\mathrm{ i,n}})\kappa _\mathrm{ R}; \end{eqnarray*}

(18)

\begin{eqnarray*} \kappa _{\mathrm{ i,b}} = (1-g_{\mathrm{ i,b}})\kappa _\mathrm{ R}/r. \end{eqnarray*}

(19)

The newly defined quantities g_{i, n} and g_{i, b} are dimensionless constants, suitably chosen to simplify the following expressions.

Equations (13)–(15) do not generally allow an analytic solution with respect to the variable |$z$|⁠, but they do with respect to f_n, taken as the independent variable (⁠|$z$| then disappears, since it is not explicitly present in the equations). The general solution is:

\begin{eqnarray*} \frac{f_\mathrm{ b}(f_\mathrm{ n})}{f_\mathrm{ n}}=\left(\frac{f_{\mathrm{ b},0}}{f_{\mathrm{ n},0}}+\frac{r\, g_{\mathrm{ i,n}}}{g_{\mathrm{ i,b}}}\right)\left(\frac{f_\mathrm{ n}}{f_{\mathrm{ n},0}}\right)^{-g_{\mathrm{ i,n}}} -\frac{r\, g_{\mathrm{ i,n}}}{g_{\mathrm{ i,b}}}. \end{eqnarray*}

(20)

In the special case of a low neutral fraction, we can assume f_p to be constant (and equal to r); in which case equation (13) can be easily solved giving:

\begin{eqnarray*} f_\mathrm{ n}(z)=f_{\mathrm{ n},0}\exp \left(-\frac{z}{h_\mathrm{ R}}\right), \end{eqnarray*}

(21)

with h_R = V_sh/(rκ_Rn₀) being the reference scale length; and therefore:

\begin{eqnarray*} \frac{f_\mathrm{ b}(z)}{f_\mathrm{ n}(z)}=\left(\frac{f_{\mathrm{ b},0}}{f_{\mathrm{ n},0}}+\frac{r\, g_{\mathrm{ i,n}}}{g_{\mathrm{ i,b}}}\right)\exp \left(\frac{g_{\mathrm{ i,n}}z}{h_\mathrm{ R}}\right) -\frac{r\, g_{\mathrm{ i,n}}}{g_{\mathrm{ i,b}}}. \end{eqnarray*}

(22)

Once all density profiles have been derived, the emissivities in the narrow- and broad-line components can be approximated as:

\begin{eqnarray*} j_\mathrm{ n}(z) = \epsilon _{\mathrm{ n}}f_\mathrm{ n}(z)f_{\mathrm{ p}}(z)\, \kappa _\mathrm{ R}\, n_0^2; \end{eqnarray*}

(23)

\begin{eqnarray*} j_\mathrm{ b}(z) = \epsilon _{\mathrm{ b}}f_\mathrm{ b}(z)f_{\mathrm{ p}}(z)\, \kappa _\mathrm{ R}\, n_0^2, \end{eqnarray*}

(24)

where we have parametrized the physics of the emission with the parameters ε_n and ε_b, which are dimensionless (since the emissivities are in |${\, \rm photons\, cm^{-3}s^{-1}}$|⁠), and that for simplicity, we also assume to be constant. The ratio of the line components is then:

\begin{eqnarray*} \frac{I_\mathrm{ b}(z)}{I_\mathrm{ n}(z)} &=& \frac{\epsilon _{\mathrm{ b}}}{\epsilon _{\mathrm{ n}}}\frac{f_\mathrm{ b}(z)}{f_\mathrm{ n}(z)} \\ &=& \frac{\epsilon _{\mathrm{ b}}}{\epsilon _{\mathrm{ n}}}\left[\left(\frac{f_{\mathrm{ b},0}}{f_{\mathrm{ n},0}}+\frac{r\, g_{\mathrm{ i,n}}}{g_{\mathrm{ i,b}}}\right)\exp \left(\frac{g_{\mathrm{ i,n}}z}{h_\mathrm{ R}}\right)-\frac{r\, g_{\mathrm{ i,n}}}{g_{\mathrm{ i,b}}}\right] \end{eqnarray*}

(25),(26)

(hereafter we will use the symbols j_{n, b} only for the emissivities, while I_{n, b} represents the volume-integrated emission).

The spatially integrated emissions, scaled with their dimensional part, are then:

\begin{eqnarray*} \frac{I_\mathrm{ n}}{n_0f_{\mathrm{ n,u}}V_\mathrm{sh}} = \epsilon _{\mathrm{ n}}\frac{f_{\mathrm{ n},0}}{f_{\mathrm{ n,u}}}; \end{eqnarray*}

(27)

\begin{eqnarray*} \frac{I_\mathrm{ b}}{n_0f_{\mathrm{ n,u}}V_\mathrm{sh}} = \frac{\epsilon _{\mathrm{ b}} }{(1-g_{\mathrm{ i,n}})}\left(\frac{r\, g_{\mathrm{ i,n}}^2}{g_{\mathrm{ i,b}}}\frac{f_{\mathrm{ n},0}}{f_{\mathrm{ n,u}}}+\frac{f_{\mathrm{ b},0}}{f_{\mathrm{ n,u}}}\right), \end{eqnarray*}

(28)

where f_{n, u} the upstream neutral fraction (which, in the presence of a precursor, may be slightly different from f_{n, 0}, the value right at shock front). From the above equations, one can derive the line ratio I_b/I_n. When the shock structure is not resolved, these two quantities are the only ones that can be measured.

We want to stress that the above approximated model will only be used to fit profiles calculated with our numerical simulations. Therefore, the assumptions behind it, like the constancy of several parameters and first of all the fluid-like treatment, are simply justified by how effectively it fits, with a limited number of ‘physical-like’ parameters, the results of our kinetic models (as in Section 2). For instance, the non-Gaussianity of the velocity distribution of neutrals leads to some spatial changes for r different from what we have assumed. In addition, the use of equation (24) for modelling the emissivity in the broad component is in general not justified, because also CE reactions with slow and fast neutral lead to fast neutrals in excited states, and could be acceptable only in the limit of low neutral fractions. We have found anyway reasonable fits for both the particle distributions and the emission in the two line components. Table 1 gives, in columns (4)–(10), the best-fitting parameters to some kinetic models. Figs 1 and 2 also show the quality of the fit for one of the models.

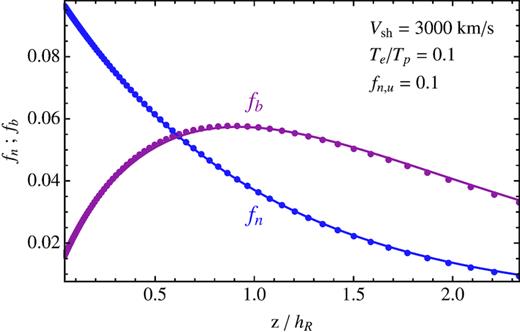
$Comparison between numerical profiles (dots) of fn (blue) and fb (red) (computed using the model presented in Blasi et al. 2012, and following papers), together with fits (solid lines) obtained using our approximate model. These profiles are for $V_\mathrm{sh}=3000{\, \rm km\, s^{-1}}$, unit total density and $10{{\ \rm per\ cent}}$ neutral fraction upstream, and Te/Tp = 0.1.$

Figure 1.

Comparison between numerical profiles (dots) of f_n (blue) and f_b (red) (computed using the model presented in Blasi et al. 2012, and following papers), together with fits (solid lines) obtained using our approximate model. These profiles are for |$V_\mathrm{sh}=3000{\, \rm km\, s^{-1}}$|⁠, unit total density and |$10{{\ \rm per\ cent}}$| neutral fraction upstream, and T_e/T_p = 0.1.

Figure 2.

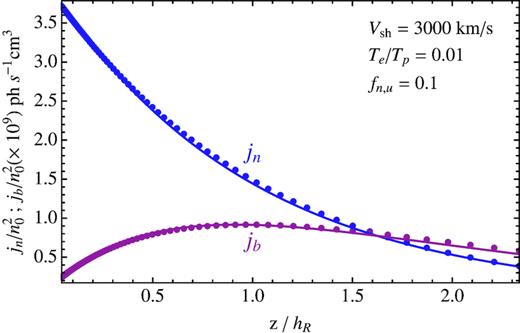
Same as Fig. 1, but for the emissivity in the two line components.

3.2 A parametric model

Even the above simplified model may be too involved for a direct comparison with the data, due to possible degeneracies among some physical parameters. We then prefer to use a parametrization closer to what is actually observed, in terms of polynomials of |$z$| times an exponential function.

Here, we discuss a very simple but non-trivial case, which already contains a number of features present in real cases. Let us assume that the downstream profile of the emissivity in the narrow- and broad-line components are respectively described by:

\begin{eqnarray*} j_\mathrm{ n}(z) = n_0f_{\mathrm{ n,u}}V_\mathrm{sh}\frac{A_\mathrm{ n}}{h_\mathrm{ R}}\exp \left(-\frac{z}{h_\mathrm{ R}}\right); \end{eqnarray*}

(29)

\begin{eqnarray*} j_\mathrm{ b}(z) = n_0f_{\mathrm{ n,u}}V_\mathrm{sh}\left(\frac{A_\mathrm{ b}}{h_\mathrm{ R}}+\frac{B_\mathrm{ b}z}{h_\mathrm{ R}^2}\right)\exp \left(-\frac{z}{h_\mathrm{ R}}\right); \end{eqnarray*}

(30)

the former formula is equivalent to that of our three-fluid model (equation 23), in the limit of small neutral fractions; while the latter one, much simpler than that (equation 24) in the previous section, is anyway a good approximation. In particular, the assumption of the same exponential length-scale h_R for both emissivities is justified by the fact that, in equation (22), the parameter g_{i, n} is always very small, so that a linear expansion of the exponential factor is accurate till large |$z$|/h_R values; but as shown below the most direct justification comes the fact that fits to the kinetic models are very good.

It is possible to relate the quantities A_n, A_b, and B_b to the parameters used in the three-fluid model described above. From a comparison with a power expansion in |$z$| of equations (23) and (24), from our models one derives:

\begin{eqnarray*} A_{\mathrm{ n}} = \epsilon _{\mathrm{ n}}f_{\mathrm{ n},0}/f_{\mathrm{ n,u}}; \end{eqnarray*}

(31)

\begin{eqnarray*} A_{\mathrm{ b}} = \epsilon _{\mathrm{ b}}f_{\mathrm{ b},0}/f_{\mathrm{ n,u}}; \end{eqnarray*}

(32)

\begin{eqnarray*} B_{\mathrm{ b}} = g_{\mathrm{ i,n}}\left(\frac{f_{\mathrm{ b},0}}{f_{\mathrm{ n,u}}}+\frac{r\, g_{\mathrm{ i,n}}}{g_{\mathrm{ i,b}}}\frac{f_{\mathrm{ n},0}}{f_{\mathrm{ n,u}}}\right)\epsilon _{\mathrm{ b}}. \end{eqnarray*}

(33)

These three quantities are listed for all the models presented in Table 2, at columns from (4) to (6).

Table 2.

Derived parameters for the parametric model [columns (4)–(6)]; same parameters, corrected with using equations (38)–(40) [columns (7)–(9)].

V_sh	T_e/T_p	f_n,u	A_n	A_b/A_n	B_b/A_n	A_n	A_b/A_n	B_b/A_n
(⁠\|${\rm km\, s^{-1}}$\|⁠)						(obs)	(obs)	(obs)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
2500	0.01	0.10	0.089	0.061	0.46	0.081	0.162	0.50
2500	0.10	0.10	0.080	0.068	0.61	0.063	0.362	0.78
3000	0.01	0.10	0.107	0.042	0.38	0.100	0.110	0.40
3000	0.10	0.10	0.097	0.050	0.58	0.096	0.063	0.59
3500	0.01	0.10	0.122	0.031	0.26	0.119	0.053	0.26
3500	0.10	0.10	0.113	0.027	0.44	0.113	0.027	0.44

V_sh	T_e/T_p	f_n,u	A_n	A_b/A_n	B_b/A_n	A_n	A_b/A_n	B_b/A_n
(⁠\|${\rm km\, s^{-1}}$\|⁠)						(obs)	(obs)	(obs)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
2500	0.01	0.10	0.089	0.061	0.46	0.081	0.162	0.50
2500	0.10	0.10	0.080	0.068	0.61	0.063	0.362	0.78
3000	0.01	0.10	0.107	0.042	0.38	0.100	0.110	0.40
3000	0.10	0.10	0.097	0.050	0.58	0.096	0.063	0.59
3500	0.01	0.10	0.122	0.031	0.26	0.119	0.053	0.26
3500	0.10	0.10	0.113	0.027	0.44	0.113	0.027	0.44

Table 2.

Derived parameters for the parametric model [columns (4)–(6)]; same parameters, corrected with using equations (38)–(40) [columns (7)–(9)].

V_sh	T_e/T_p	f_n,u	A_n	A_b/A_n	B_b/A_n	A_n	A_b/A_n	B_b/A_n
(⁠\|${\rm km\, s^{-1}}$\|⁠)						(obs)	(obs)	(obs)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
2500	0.01	0.10	0.089	0.061	0.46	0.081	0.162	0.50
2500	0.10	0.10	0.080	0.068	0.61	0.063	0.362	0.78
3000	0.01	0.10	0.107	0.042	0.38	0.100	0.110	0.40
3000	0.10	0.10	0.097	0.050	0.58	0.096	0.063	0.59
3500	0.01	0.10	0.122	0.031	0.26	0.119	0.053	0.26
3500	0.10	0.10	0.113	0.027	0.44	0.113	0.027	0.44

V_sh	T_e/T_p	f_n,u	A_n	A_b/A_n	B_b/A_n	A_n	A_b/A_n	B_b/A_n
(⁠\|${\rm km\, s^{-1}}$\|⁠)						(obs)	(obs)	(obs)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
2500	0.01	0.10	0.089	0.061	0.46	0.081	0.162	0.50
2500	0.10	0.10	0.080	0.068	0.61	0.063	0.362	0.78
3000	0.01	0.10	0.107	0.042	0.38	0.100	0.110	0.40
3000	0.10	0.10	0.097	0.050	0.58	0.096	0.063	0.59
3500	0.01	0.10	0.122	0.031	0.26	0.119	0.053	0.26
3500	0.10	0.10	0.113	0.027	0.44	0.113	0.027	0.44

It can be seen that, within this approximation, the spatially integrated emissions divided by (n₀f_{n, u}V_sh) are A_n and A_b + B_b for the narrow and the broad component, respectively (see for comparison equations 27 and 28). So, their ratio is I_b/I_n = (A_b + B_b)/A_n. Another consequence of this formulation is that the line components ratio along |$z$| must follow a linear trend, namely:

\begin{eqnarray*} \frac{j_\mathrm{ b}}{j_\mathrm{ n}} = \frac{A_\mathrm{ b}}{A_\mathrm{ n}}+\frac{B_\mathrm{ b}}{A_\mathrm{ n}}z. \end{eqnarray*}

(34)

This is valid only as a first approximation (see equation 26 for a more accurate one), but it can be verified that, for the |$z$| values of interest, it is a reasonably good approximation (see Fig. 3).

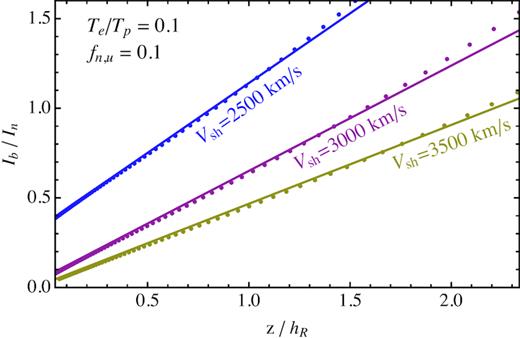
$Profiles of Ib/In for three models, respectively with Vsh = 2500, 3000, and $3500{\, \rm km\, s^{-1}}$ (and fn, u = 0.1, Te/Tp = 0.1), all corrected using equation (37). The dots are from the kinetic models (whose locations are very well reproduced by our three-fluid model), while the lines show their linear approximations, provided by equation (34).$

Figure 3.

Profiles of I_b/I_n for three models, respectively with V_sh = 2500, 3000, and |$3500{\, \rm km\, s^{-1}}$| (and f_{n, u} = 0.1, T_e/T_p = 0.1), all corrected using equation (37). The dots are from the kinetic models (whose locations are very well reproduced by our three-fluid model), while the lines show their linear approximations, provided by equation (34).

It is worthwhile to stress that when information on narrow- and broad-line components is not available separately, the quantities A_b/A_n and B_b/A_n cannot be inferred observationally. One can proceed fitting the total line flux, in which case the simplest (and, as we shall see below, sufficiently accurate) fit is that using a pure exponential law, namely:

\begin{eqnarray*} j_\mathrm{ n}+j_\mathrm{ b} = C\exp \left(-\frac{z}{h_\mathrm{exp}}\right). \end{eqnarray*}

(35)

In this case, one then needs to relate the exponential length-scale (h_exp) to the previously defined h_R. Since the exact functional dependencies using h_R and h_exp are different, the best-fitting relation would depend on the interval of |$z$| used for the fit. Anyway, we have found that a simple and rather accurate relation is:

\begin{eqnarray*} \frac{h_\mathrm{exp}}{h_\mathrm{ R}} = 1+\frac{B_\mathrm{ b}}{A_\mathrm{ n}+A_\mathrm{ b}}. \end{eqnarray*}

(36)

Fig. 4 compares the results obtained with this formula and those of exponential fits to our parametric model.

Figure 4.

Contour plot giving the value of the ratio h_exp/h_R as a function of A_b/A_n and B_b/A_n. The black solid lines trace the results of exponential best fits to the profiles (down to 5 per cent of their peak values). The red dashed lines trace instead the approximated values, obtained using equation (36).

3.3 Matching the observed I_b/I_n ratio

The values of the integrated I_b/I_n ratios, as derived from our models and listed in column (11) of Table 1, are always lower than those we had computed in Morlino et al. (2012), shown in fig. 16 therein, and listed in column (12) of Table 1. The reason of this discrepancy is that in Morlino et al. (2012), the synthesized line profiles have been fitted with a two-component model in a very similar way to what is usually done in the analysis of actual observations (with a simulated instrumental spectral resolution |${\sim }150{\, \rm km\, s^{-1}}$|⁠): this approach is feasible on spatially integrated models, but rather cumbersome and less reliable if one wants to apply it to each spatial step of our model.

Instead, what we dub here as ‘narrow’ component is the composition of two different kinds of populations: the truly ‘cold’ neutrals, namely those directly coming from the upstream and with thermal velocities |${\sim }10{\, \rm km\, s^{-1}}$|⁠, and those originated instead from a charge exchange with a warm proton in the neutral precursor, having thermal velocities typically in the 100–300|${\, \rm km\, s^{-1}}$| range; this latter population is the one emitting the ‘intermediate component’, as described in our past papers, and clearly detected in N103B by Ghavamian et al. (2017) and in Tycho’s SNR by Knežević et al. (2017).

However, in all cases in which the quality of the observation is not good enough to detect the intermediate component, we expect that, after the line profile fit, a fraction of the flux of the intermediate component is partly ascribed to the narrow component, and partly to the broad component.

Since in the downstream the spatial behaviours of cold and intermediate neutrals are very similar, we assume that a spatially constant fraction α of the I_n, as calculated by the model, is contributing to the observed broad component, so that the observed I_b/I_n ratio, in terms of the model fluxes, reads:

\begin{eqnarray*} \left.\frac{I_\mathrm{ b}}{I_\mathrm{ n}}\right|_\mathrm{obs}=\frac{I_\mathrm{ b}/I_\mathrm{ n}+\alpha }{(1-\alpha)}. \end{eqnarray*}

(37)

The last two columns of Table 1 show the ratio between the integrated broad and narrow components, respectively, as it would be observed (see fig. 16 in Morlino et al. 2012), and the value of α required for the correction. The fact that the values of α decrease for increasing shock velocity is easily explained by a decrease, with increasing V_sh, of the relative effectiveness of CE processes, so that less warm neutrals may cross back the shock, therefore forming a less prominent neutral precursor, and consequently, a weaker intermediate component.

As for our parametric model, using equation (37), the expected values for the observed quantities, as functions of the model ones, are:

\begin{eqnarray*} A_{\mathrm{ n},\mathrm{obs}} = (1-\alpha)A_{\mathrm{ n}}; \end{eqnarray*}

(38)

\begin{eqnarray*} A_{\mathrm{ b},\mathrm{obs}} = A_{\mathrm{ b}}+\alpha A_{\mathrm{ n}}; \end{eqnarray*}

(39)

\begin{eqnarray*} B_{\mathrm{ b},\mathrm{obs}} = B_{\mathrm{ b}}. \end{eqnarray*}

(40)

These quantities are listed in Table 2, at columns from (7) to (9). From here on, when referring to the quantities A_{n, obs}, A_{b, obs}, and B_{b, obs}, for simplicity we will omit the suffix ‘obs’.

4 ANALYTIC PROJECTED PROFILES

In equations (29) and (30), we have introduced the simplest non trivial way to model parametrically the emissivity profiles in the two line components. On the other hand, virtually any profile could be approximated with arbitrary accuracy, by increasing the order of the polynomials (now respectively 0 and 1) in those formulae. In this section, we set the mathematical basis to model, for any intrinsic downstream profile, the actual observed profiles by taking into account projection effects.

4.1 The limit of large curvature radii

The general problem of connecting the downstream emissivity profiles to their transformation into observed surface brightness profiles, for a generically curved shock surface, is numerically complex and heavy. Therefore, performing a best-fitting analysis on data profiles may become a difficult task.

We present here an analytic treatment that can be used to considerably simplify this problem. To do so, we assume that the curvature radii of the shock surface are always much larger than the projected shock distance (δ|$z$|⁠; again oriented to the downstream) that we are considering: this allows us to neglect its component along the LOS (δy) when computing the distance of a point from the shock surface, which is equivalent to limiting to the first order all expansions in |$z$|_r/R_curv, where |$z$|_r is the actual distance of the point from shock (positive downstream) and R_curv is the local radius of curvature (positive for a convex curvature), namely:

\begin{eqnarray*} z_\mathrm{ r}\simeq \delta z = z-Z_\mathrm{sh}(y), \end{eqnarray*}

(41)

where Z_sh(y) describes the shock surface, with y being the LOS coordinate.

The surface brightnesses of the narrow and broad components, I_n(⁠|$z$|⁠) and I_b(⁠|$z$|⁠) respectively, can be computed by integrating along the LOS the downstream emissivities j_n(⁠|$z$|⁠) and j_b(⁠|$z$|⁠):

\begin{eqnarray*} I_{\mathrm{ n,b}}(z)=\int {j_{\mathrm{ n,b}}(z-Z_\mathrm{sh}(y))\, \mathrm{ d}y}, \end{eqnarray*}

(42)

where the integration limits are derived by solving in y the equation |$z$| = Z_sh(y), and retaining only the downstream segment(s) along the LOS.

4.2 Analysis of the constant-curvature case

For a constant curvature, in the limit of large R_curv, one gets:

\begin{eqnarray*} Z_\mathrm{sh}(y) = R_\mathrm{curv}\left(1-\sqrt{1-\frac{y^2}{R_\mathrm{curv}^2}}\right)\simeq \frac{y^2}{2R_\mathrm{curv}} \end{eqnarray*}

(43)

where, for simplicity, we have chosen y = 0 as the reference point along the LOS, and Z_sh(0) = 0. Note that R_curv must be taken with its sign, and therefore Z_sh ≥ 0 in the convex case, while ≤0 in the concave one.

The intersections with the shock surface are respectively |$y_{1,2}=\pm \sqrt{2zR_\mathrm{curv}}$|⁠. This means that, in the convex case, the surface brightness is positive only for |$z$| > 0, and the integration must be performed along the path between these intersections. In the concave case, instead, for |$z$| < 0, the integration must be performed in the two outer paths, while for |$z$| > 0, the integration must be performed over all y values.

Let us now assume that the emissivity profiles j_{n, b}(⁠|$z$|⁠) can be reasonably well approximated as a linear combination of (a sufficiently small number of) terms;

\begin{eqnarray*} \chi _\mathrm{ m}(z, h)=(z/h)^m\exp (-z/h). \end{eqnarray*}

(44)

Here below we shall show that, in the case of a constant curvature, either positive or negative, each one of these terms allows an analytic solution; and, therefore, an analytic solution is also possible for any linear combination of them.

Let us first consider the case of a positive curvature (convex case). In general, it holds:

\begin{eqnarray*} \Sigma _\mathrm{ m}^{+,d}(z) &=& \int _{y_1}^{y_2}{\!\!\!\!\chi _\mathrm{ m}\left(z-\frac{y^2}{2R_\mathrm{curv}},h\right)\, \mathrm{ d}y}\nonumber \\ &=& \Sigma _\mathrm{D}\left[P_\mathrm{ m}(z/h)\, 2F_\mathrm{D}\left(\!\sqrt{z/h}\, \right)-Q_\mathrm{ m}(z/h)\sqrt{z/h}\right], \end{eqnarray*}

(45)

where |$\Sigma _\mathrm{D}=\sqrt{2hR_\mathrm{curv}}$| is the dimensional scaling, namely an ‘equivalent path length’, and F_D(⁠|$z$|⁠) is the Dawson’s integral, defined as:

\begin{eqnarray*} F_\mathrm{D}(z)=\exp (-z^2)\int _0^z{\exp (y^2)\, \mathrm{ d}y}=\frac{\sqrt{\pi }}{2}\exp (-z^2)\operatorname{erfi}(z), \end{eqnarray*}

(46)

while the polynomials P_m(⁠|$z$|⁠) and Q_m(⁠|$z$|⁠) are given in Table 3 for some values of m. In this case the surface brightness from the projected upstream region vanishes; while the profiles in the projected downstream are shown in Fig. 5.

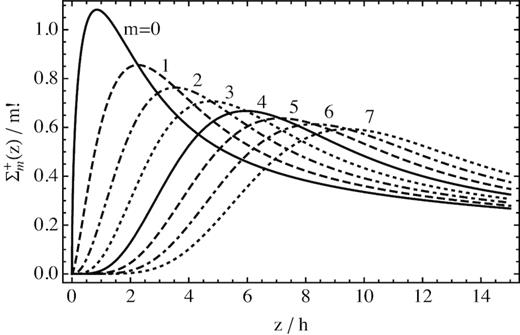
$Profiles of $\Sigma _\mathrm{ m}^{+,d}(x)$ (only projected downstream), scaled with m! to give the same asymptotic solution at all values of m.$

Figure 5.

Profiles of |$\Sigma _\mathrm{ m}^{+,d}(x)$| (only projected downstream), scaled with m! to give the same asymptotic solution at all values of m.

Table 3.

Explicit forms of the first P_m(⁠|$z$|⁠) and Q_m(⁠|$z$|⁠) polynomials, which have been introduced in equations from (45) to (49).

m	P_m(⁠\|$z$\|⁠)	Q_m(⁠\|$z$\|⁠)
0	1	0
1	\|$z+\frac{1}{2}$\|	1
2	\|$z^2+z+\frac{3}{4}$\|	\|$z+\frac{3}{2}$\|
3	\|$z^3+\frac{3}{2}z^2+\frac{9}{4}z+\frac{15}{8}$\|	\|$z^2+2z+\frac{15}{4}$\|
4	\|$z^4+2z^3+\frac{9}{2}z^2+\frac{15}{2}z+\frac{105}{16}$\|	\|$z^3+\frac{5}{2}z^2+\frac{25}{4}z+\frac{105}{8}$\|

m	P_m(⁠\|$z$\|⁠)	Q_m(⁠\|$z$\|⁠)
0	1	0
1	\|$z+\frac{1}{2}$\|	1
2	\|$z^2+z+\frac{3}{4}$\|	\|$z+\frac{3}{2}$\|
3	\|$z^3+\frac{3}{2}z^2+\frac{9}{4}z+\frac{15}{8}$\|	\|$z^2+2z+\frac{15}{4}$\|
4	\|$z^4+2z^3+\frac{9}{2}z^2+\frac{15}{2}z+\frac{105}{16}$\|	\|$z^3+\frac{5}{2}z^2+\frac{25}{4}z+\frac{105}{8}$\|

Table 3.

Explicit forms of the first P_m(⁠|$z$|⁠) and Q_m(⁠|$z$|⁠) polynomials, which have been introduced in equations from (45) to (49).

m	P_m(⁠\|$z$\|⁠)	Q_m(⁠\|$z$\|⁠)
0	1	0
1	\|$z+\frac{1}{2}$\|	1
2	\|$z^2+z+\frac{3}{4}$\|	\|$z+\frac{3}{2}$\|
3	\|$z^3+\frac{3}{2}z^2+\frac{9}{4}z+\frac{15}{8}$\|	\|$z^2+2z+\frac{15}{4}$\|
4	\|$z^4+2z^3+\frac{9}{2}z^2+\frac{15}{2}z+\frac{105}{16}$\|	\|$z^3+\frac{5}{2}z^2+\frac{25}{4}z+\frac{105}{8}$\|

m	P_m(⁠\|$z$\|⁠)	Q_m(⁠\|$z$\|⁠)
0	1	0
1	\|$z+\frac{1}{2}$\|	1
2	\|$z^2+z+\frac{3}{4}$\|	\|$z+\frac{3}{2}$\|
3	\|$z^3+\frac{3}{2}z^2+\frac{9}{4}z+\frac{15}{8}$\|	\|$z^2+2z+\frac{15}{4}$\|
4	\|$z^4+2z^3+\frac{9}{2}z^2+\frac{15}{2}z+\frac{105}{16}$\|	\|$z^3+\frac{5}{2}z^2+\frac{25}{4}z+\frac{105}{8}$\|

In an analogous way, one can compute the case of a negative curvature (concave case). Now the emission comes both from the projected upstream (⁠|$z$| < 0) and the projected downstream (⁠|$z$| > 0).

For |$z$| < 0, we have:

\begin{eqnarray*} \Sigma _\mathrm{ m}^{-,u}(z) &=& \int _{-\infty }^{y_1}{\chi _\mathrm{ m}\left(z+\frac{y^2}{2R_\mathrm{curv}},h\right)\, \mathrm{ d}y}\nonumber \\ &&+ \, \int _{y_2}^{\infty }{\chi _\mathrm{ m}\left(z+\frac{y^2}{2R_\mathrm{curv}},h\right)\, \mathrm{ d}y}\nonumber \\ &=& \Sigma _\mathrm{D}\left[P_\mathrm{ m}(z/h)\, 2F_\mathrm{X}\left(\sqrt{-z/h}\right)+Q_\mathrm{ m}(z/h)\sqrt{-z/h}\right], \nonumber \\ \end{eqnarray*}

(47)

where:

\begin{eqnarray*} F_\mathrm{X}(z)=\exp (z^2)\int _z^\infty {\exp (-y^2)\, \mathrm{ d}y}=\frac{\sqrt{\pi }}{2}\exp (z^2)\operatorname{erfc}(z), \end{eqnarray*}

(48)

while the polynomials P_m(⁠|$z$|⁠) and Q_m(⁠|$z$|⁠) are the same as in the previous case. Instead, for |$z$| > 0, we simply have:

\begin{eqnarray*} \Sigma _\mathrm{ m}^{-,d}(z) = \int _{-\infty }^{\infty }\!{\chi _\mathrm{ m}\!\left(\!z+\frac{y^2}{2R_\mathrm{curv}},h\!\right) \!\mathrm{ d}y}=\Sigma _\mathrm{D}P_\mathrm{ m}(z/h)\sqrt{\pi }\,{\mathrm e}^{-z/h}\!. \end{eqnarray*}

(49)

The global projected profiles are then obtained by combining |$\Sigma _\mathrm{ m}^{-,u}(z)$| for negative |$z$| values and |$\Sigma _\mathrm{ m}^{-,d}(z)$| for positive |$z$| values: the results are shown in Fig. 6.

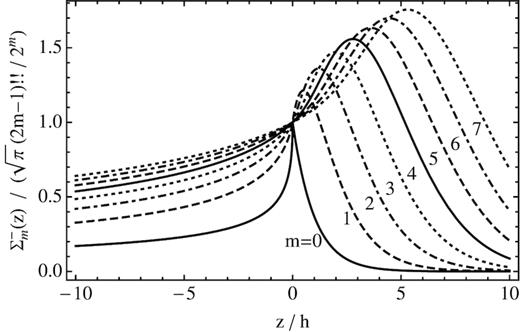
$Profiles of $\Sigma _\mathrm{ m}^{-}(z)$ (both projected upstream and downstream), scaled with $\sqrt{\pi }(2m-1)!!/2^m$ to normalize their value at $z$ = 0.$

Figure 6.

Profiles of |$\Sigma _\mathrm{ m}^{-}(z)$| (both projected upstream and downstream), scaled with |$\sqrt{\pi }(2m-1)!!/2^m$| to normalize their value at |$z$| = 0.

The linear combination of the projected profiles, obtained in this way for this basis of functions, will allow us to treat in a rather simple way a wide range of cases.

5 SPATIALLY RESOLVED PROFILES

The solutions derived in the previous section are adequate to treat generally complex profiles in the shock transition zone. However, with the limited quality of the observations available so far one could hardly go beyond the simplest non-trivial level, which we have labelled as parametric model, and described by equations (29) and (30), so that

\begin{eqnarray*} \frac{j_\mathrm{ n}}{n_0f_{\mathrm{ n,u}}V_\mathrm{sh}} = \frac{2A_\mathrm{ n}}{h_\mathrm{ R}}\chi _0(z,h_\mathrm{ R}); \end{eqnarray*}

(50)

\begin{eqnarray*} \frac{j_\mathrm{ b}}{n_0f_{\mathrm{ n,u}}V_\mathrm{sh}} = \frac{2A_\mathrm{ b}}{h_\mathrm{ R}}\chi _0(z,h_\mathrm{ R})+\frac{B_\mathrm{ b}}{h_\mathrm{ R}}\chi _1(z,h_\mathrm{ R}). \end{eqnarray*}

(51)

Within this framework, we will discuss here some simple configurations. At this stage, we do not aim at a quantitative match of existing cases, but rather at outlining their qualitative behaviour. However, we will use the case A_b/A_n = 0.063 and B_b/A_n = 0.59, for consistency with Section 7.1, where we will analyse a specific Balmer filament of SN 1006.

5.1 The case of a constant convex curvature

In the convex case, one can use equation (45) to derive:

\begin{eqnarray*} \frac{I_\mathrm{ n}}{n_0f_{\mathrm{ n,u}}V_\mathrm{sh}\Sigma _\mathrm{D}} = \frac{2A_\mathrm{ n}}{h_\mathrm{ R}}F_\mathrm{D}\left(\sqrt{\frac{z}{h_\mathrm{ R}}}\right); \end{eqnarray*}

(52)

\begin{eqnarray*} \frac{I_\mathrm{ b}}{n_0f_{\mathrm{ n,u}}V_\mathrm{sh}\Sigma _\mathrm{D}} &=& \frac{2A_\mathrm{ b}}{h_\mathrm{ R}}F_\mathrm{D}\left(\sqrt{\frac{z}{h_\mathrm{ R}}}\right) \nonumber \\ &&+\, \frac{B_\mathrm{ b}}{h_\mathrm{ R}}\left[\left(\frac{2z}{h_\mathrm{ R}}+1\right)F_\mathrm{D}\left(\sqrt{\frac{z}{h_\mathrm{ R}}}\right)+\sqrt{\frac{z}{h_\mathrm{ R}}}\,\right] \end{eqnarray*}

(53)

in the projected downstream. These curves are shown in Fig. 7, together with I_b/I_n.

Figure 7.

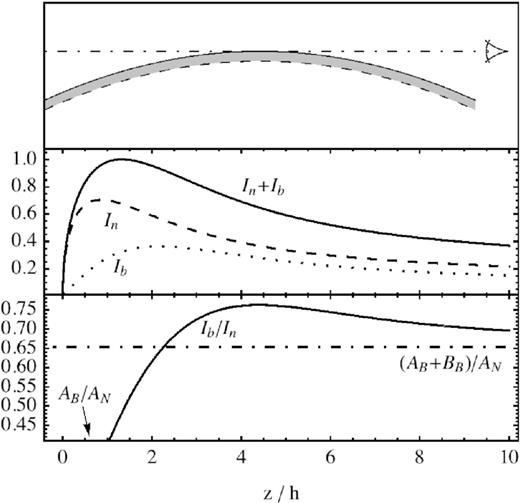
Upper panel: sketch of the geometry for a convex case with constant curvature, where the solid line represents the shock surface, the dashed line qualitatively represents the end of the transition zone, and the dotted–dashed line represents the LOS corresponding to the projected limb (⁠|$z$| = 0). Mid panel: model intensity profiles, normalized to the maximum value of the total intensity. Lower panel: associated I_b/I_n ratio; note the early increase, and the asymptotic convergence to the integrated ratio.

In the case of a constant curvature, the ratio between the surface brightness in the broad and narrow components (I_b/I_n) near the apex (0 < |$z$| ≪ h_R) increases as:

\begin{eqnarray*} \frac{I_\mathrm{ b}}{I_\mathrm{ n}}\simeq \frac{A_\mathrm{ b}}{A_\mathrm{ n}}+\frac{2}{3}\frac{B_\mathrm{ b}}{A_\mathrm{ n}}\frac{z}{h_\mathrm{ R}}; \end{eqnarray*}

(54)

while, for large values of |$z$|⁠, it reaches the asymptotic value (A_b + B_b)/A_n.

Therefore, already from a fit to the total emission, one could verify the presence of such a geometry, estimating the scale length h_exp, and then h_R. Observations of the line profile, with adequate angular resolution, allow one to trace the gradual increase of I_b/I_n, and to constrain separately A_b/A_n and B_b/A_n.

5.2 The case of a constant concave curvature

For the concave case, we have:

\begin{eqnarray*} \frac{I_\mathrm{ n}}{n_0f_{\mathrm{ n,u}}V_\mathrm{sh}\Sigma _\mathrm{D}} = \frac{2A_\mathrm{ n}}{h_\mathrm{ R}}F_\mathrm{X}\left(\sqrt{-\frac{z}{h_\mathrm{ R}}}\right); \end{eqnarray*}

(55)

\begin{eqnarray*} \frac{I_\mathrm{ b}}{n_0f_{\mathrm{ n,u}}V_\mathrm{sh}\Sigma _\mathrm{D}} &=& \frac{2A_\mathrm{ b}}{h_\mathrm{ R}}F_\mathrm{X}\left(\sqrt{-\frac{z}{h_\mathrm{ R}}}\right)\nonumber \\ &&+\, \frac{B_\mathrm{ b}}{h_\mathrm{ R}}\left(\left(-\frac{2z}{h_\mathrm{ R}}+1\right)F_\mathrm{X}\left(\sqrt{-\frac{z}{h_\mathrm{ R}}}\right)+\sqrt{-\frac{z}{h_\mathrm{ R}}}\right) \nonumber \\ \end{eqnarray*}

(56)

in the projected upstream, while:

\begin{eqnarray*} \frac{I_\mathrm{ n}}{n_0f_{\mathrm{ n,u}}V_\mathrm{sh}\Sigma _\mathrm{D}} = \frac{A_\mathrm{ n}}{h_\mathrm{ R}}\sqrt{\pi }\,\mathrm{ e}^{-z/h_R}; \end{eqnarray*}

(57)

\begin{eqnarray*} \frac{I_\mathrm{ b}}{n_0f_{\mathrm{ n,u}}V_\mathrm{sh}\Sigma _\mathrm{D}} = \left(\frac{A_\mathrm{ b}}{h_\mathrm{ R}}+\frac{B_\mathrm{ b}}{h_\mathrm{ R}}\left(\frac{z}{h_\mathrm{ R}}+\frac{1}{2}\right)\right)\sqrt{\pi }\,\mathrm{ e}^{-z/h_R} \end{eqnarray*}

(58)

in the projected downstream (as shown in Fig. 8).

Figure 8.

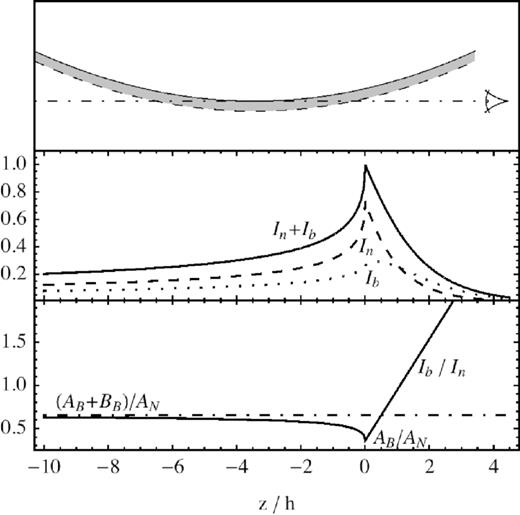
Same as Fig. 7, for a concave case with constant curvature; note the upstream asymptotic value, the early decrease near the interface between projected upstream and downstream, and finally the linear divergence in the projected downstream.

In the case of a constant curvature, (A_b + B_b)/A_n is the I_b/I_n asymptotic value at large negative values of |$z$|⁠, while for |$z$| approaching zero it decreases to A_b/A_n. Finally, for the projected downstream regions, this simple model implies the following linear trend:

\begin{eqnarray*} \frac{I_\mathrm{ b}}{I_\mathrm{ n}}=\frac{A_\mathrm{ b}}{A_\mathrm{ n}}+\frac{B_\mathrm{ b}}{A_\mathrm{ n}}\left(\frac{1}{2}+\frac{z}{h_\mathrm{ R}}\right). \end{eqnarray*}

(59)

Then also in this case, with adequate spatial and spectral resolutions, A_b/A_n, B_b/A_n and h_R could be extracted from the observations.

5.3 A non-constant concave curvature

However, how we shall see below, rather often a concave model with constant curvature does not match the data well, so that a more sophisticated model is required. Here, we present a mild generalization of the constant curvature case, achieved by combining it with a 1D model seen edge-on: this is similar to a sheet that does not follow a purely cylindrical geometry, but exhibits a tangent point to the LOS extending a significant distance along the LOS (Fig. 9). The results for this case are shown in Fig. 10, for different values of the C parameter: C is a dimensionless parameter, which gives the length of the straight section in units of Σ_D. This still simple model does not match the data well, but shows some important facts: first, an extra edge-on layer, or more generally some deviations from a pure constant curvature which produce some wiggling near the tangent point, would enhance the magnitude of the peak compared to the surface brightness in the projected upstream; on the other hand, the profile of I_b/I_n would undergo only minor changes.

Figure 9.

Same as Figs 7 and 8, for a concave case with non-constant curvature, sketched by adding a straight line to the previous case. Here, the I_n + I_b profile is sensibly sharper, while the I_b/I_n presents only minor changes.

Figure 10.

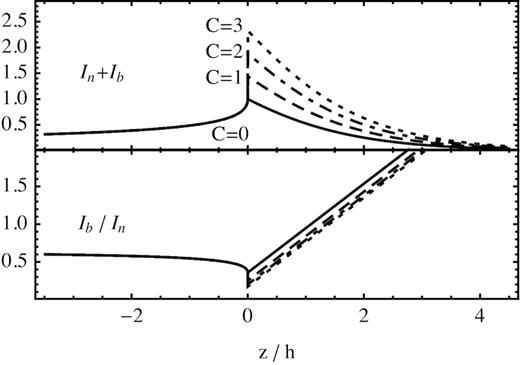
Upper panel: model total intensity profile in the constant curvature, concave case plus and edge-on straight component, for various values of C (C = 0 gives the same case as in Fig. 8). Changing the value of C, the intensity profiles can change considerably. On the other hand (lower panel), the I_b/I_n ratio is only slightly dependent on C.

6 APPLICATION TO A REAL CASE: SN 1006

6.1 Why SN 1006

In the following, we shall apply the methods derived so far to a real case, refining them whenever required. The Balmer emission along the northwestern limb of SN 1006 represents for this an almost perfect case: observations with high spatial and/or spectral resolution, on which to test and use our models, are available; a shock velocity (⁠|${\simeq } 3000{\, \rm km\, s^{-1}}$|⁠) high enough to limit the role of CE processes (this simplifies the models and makes them more reliable); structures near the limb that appear rather well ordered; no evidence of efficient CR acceleration, which justifies neglecting the effect of CRs in the analysis.

With reference to the shock speed, Ghavamian et al. (2001) measured a spectral width of |$2290\pm 80{\, \rm km\, s^{-1}}$|⁠, from which for a low T_e/T_p ratio they derived a shock speed of |$2890\pm 100{\, \rm km\, s^{-1}}$|⁠. A lower shock velocity, |${\sim }2500{\, \rm km\, s^{-1}}$|⁠, follows instead from the model of Morlino et al. (2013b): for a more detailed and updated discussion, see Raymond et al. (2017). In the following analysis, we shall fix V_sh to |$3000{\, \rm km\, s^{-1}}$|⁠.

With reference to CR acceleration, a low efficiency in the northwestern limb can be deduced from several results of observations: (1) the absence of non-thermal X-ray emission (Bamba et al. 2003; Winkler et al. 2014); (2) a non-detection of TeV (Acero et al. 2010) and GeV gamma-rays (Xing et al. 2016); moreover, from the analysis of Balmer emission, two additional pieces of information point towards a low CR acceleration efficiency: (3) the FWHM (full width at half-maximum) of the narrow line is |${\sim } 21 {\, \rm km\, s^{-1}}$| (Sollerman et al. 2003), compatible with being produced by unperturbed ISM with T = 10⁴ K, pointing toward the absence of a CR precursor able to heat the upstream plasma; and (4) an absence of evidence of any Hα precursor in front of the shock (R + 07).

6.2 Some recent high-quality observations

In this section we summarize some results of two relevant papers, Raymond et al. (2007, hereafter R + 07) and Nikolić et al. (2013, hereafter N + 13), in which Balmer emission from some areas along the northwestern limb of SN 1006 has been observed in great detail, and that contain a wealth of information, which will be used in the present work. The former paper is based on a very deep HST/ACS image covering most of the Hα emission from that limb, and the superb spatial resolution of that image (an FWHM of about 0.13 arcsec, corresponding to about |$4\times 10^{15}d_2{\, \rm cm}$|⁠, where d₂ is the distance of SN 1006 in units of |$2{\, \rm kpc}$|⁠) allows one to probe scales shorter than the collisional mean-free paths, and therefore to resolve the physical structure of the filaments.

The latter paper, instead, presents a map of a selected portion of the northwestern Hα limb of SN1006, roughly corresponding to ‘Regions 26–29’ (as dubbed by R + 07). The instrument used, VIMOS in the IFU mode on the Very Large Telescope (VLT), allows both good spatial resolution (with a pixel size 0.67 arcsec, corresponding to about |$2.0\times 10^{16}d_2{\, \rm cm}$|⁠; and a typical seeing ≃ 1 arcsec, namely |${\simeq }3\times 10^{16}d_2{\, \rm cm}$|⁠), and a spectral resolution R ≃ 2650 (equivalent to about |$110{\, \rm km\, s^{-1}}$|⁠).

These newer data are complementary to those shown by R + 07: now the spatial resolution is not as good as that of the HST; but the HST does not contain any information on the Hα line shape, while in VIMOS/VLT, the spectral resolution is more than sufficient to measure the width of the broad-line component (W), the intensity ratio between broad and narrow components (I_b/I_n), as well as the velocity shift of the centroid of the broad Hα component with respect to the narrow one (ΔV).

Let us first briefly report and discuss some conclusions in R + 07, one of the main goals of which was to estimate the upstream medium density. With the aim of analysing the spatial structure of the H α emission in the vicinity of the shock front, R + 07 for the first time also discussed how the geometrical structure of the emitting region may affect the observations. The approach of R + 07 was to approximate a ripple in the shock surface as a concave portion of a cylindrical surface, and to try in this way a fit to the projected profile of a filament. Within this framework, and with the help of a model for the physics in the downstream of the shock, the length-scale of the inner part of the profile has been used to infer the total gas density; while the scale length of the outer part of the filament’s profile, being mostly related to the curvature radius of the cylinder. In turn, since the curvature radius is related to the effective emission length along the LOS, combining this information with a photometric measurement of the surface brightness R + 07 also infer the gas neutral density (with the obvious constraint that it cannot be larger than the total density). Therefore, from a combined fit to filament brightness and spatial profile, one could aim at estimating independently curvature radius, total density, and neutral fraction.

While this method is very powerful, the results presented in that paper were not definitive, in the sense that no combination of parameters was found, allowing for an exact match of the shape of the radial profiles (respectively ‘Position 10’ and ‘Position 28’, in that paper). In addition, in both cases better fits have been obtained only with very small values for the curvature radius: about |$10^{17}{\, \rm cm}$|⁠, namely 100 times smaller than the observed length of the filament itself. In order to justify this large discrepancy between the two scale lengths, the authors suggested the presence of a magnetic field oriented near the plane of the sky, as the reason for a strongly anisotropic pattern for the ripples.

In addition to all this, R + 07 for the first time mentioned two effects, which in the following we will find to be very important: (i) the possibility of more than one tangency point along the LOS, to explain the profile without requiring a too small curvature radius; and (ii) the possibility of bulk velocity contributions to the measured broad-line width, if more than one layer intercepts the LOS.

The second paper, namely N + 13, presented a number of observed effects, unexpected before then, that surely deserve an explanation. First of all, it showed clear evidence of significant spatial variations in W (of order 10–20 per cent across the limb) and I_b/I_n (ranging from ∼0.4 to ∼1.6), over just a few arcseconds on the plane of the sky. In particular, both spatial variations of W and I_b/I_n have rather distinctive behaviours across the rim: W reaches larger values outwards of the bright filament, while I_b/I_n stays rather constant (with typical values of 0.7–0.8) outwards of that filament, but then shows strong variations right across the filament, reaching there both its lowest and its highest values within the field (see Fig. 19 for an overall view of all these trends).

The authors concluded that for the observed spatial variations one cannot simply invoke density variations, because variations up to 40 per cent would be required on small length-scales (only tens of atomic mean-free paths), and this would not be compatible with the smoothness of the shock observed even on much larger scales; instead, they proposed that these variations arise from the microphysics and that, in particular, the presence in some locations of very low values of the intensity ratio could motivate the need to include in the models suprathermal particles and CRs.

Another clearly observed effect is the velocity shifts between broad and narrow components, with values ranging from about |$-300$| to |$+300{\, \rm km\, s^{-1}}$|⁠: these shifts have been interpreted in terms of slightly different orientations of the local shock front, deviating in half of the cases by less than ∼2 deg from the pure edge-on orientation (see their table S1). These estimates were based on the assumption of a single emitting layer along the LOS; while as we shall see below a different interpretation may be more plausible.

In the following, we shall adapt and generalize some of the concepts introduced by R + 07, and we will show how effectively one can naturally explain, just in terms of geometrical effects, most of the phenomena mentioned above.

7 RE-ANALYSIS OF RAYMOND ET AL. DATA

In order to study in detail the filament’s profile, and to extract further information from it, a higher spatial resolution is required, which in this case is provided by the HST. The field considered here contains the area labelled as ‘Regions 26–29’ in R + 07 (see Fig. 11). In this zone, the Balmer emission shows the following spatial structure: a stripe of about 10 arcsec width and, on its inner side, a much brighter and well-defined filament, with a width of ∼1 arcsec. Since in the following, we analyse independently the two sectors, we use two different techniques for the data handling.

Figure 11.

Locations of the two HST fields used for the analysis of the outer limb (green, solid line rectangle), and the inner filament (yellow, dashed line rectangle). A broader area has been chosen for the outer limb, in order to increase the signal-to-noise ratio, while the analysed portion of the inner filament is smaller and limited to the region where the filament is sharper.

For the outer boundary, we aim at reaching very low surface brightnesses. For this reason, we have chosen a wider area (shown in the figure by a green, solid line rectangle), and we have removed the regions containing stars. As for the inner filament, instead, we have chosen a narrower area (outlined in the figure by a yellow, dashed line rectangle, and rather close to Position 28, in R + 07) to minimize blurring effects on the filament profile.

In all the fits shown below we will assume A_b/A_n = 0.063 and B_b/A_n = 0.59, as in Table 2, corresponding to |$V_\mathrm{sh}=3000{\, \rm km\, s^{-1}}$|⁠, T_e/T_p = 0.1, and f_{n, u} = 0.1. We will check the consistency of the data with this assumption a posteriori.

7.1 Fitting the outer projected boundary

Fig. 12 shows the intensity profile of the outer edge together with the fit results. One may notice that the profile shows some limb brightening, which can be nicely fitted by a model with positive curvature. We interpret residual oscillations in the observed profile as the effect of secondary, low-amplitude ripples.

Figure 12.

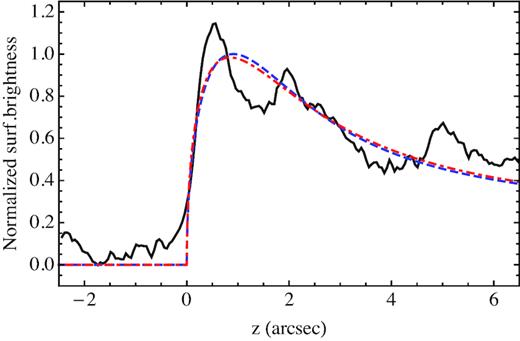
Comparison of the total intensity profile of the outer edge of the emission region, together with a fit obtained by using our parametric model (blue, dashed line) and with a fit using a simple exponential profile (red, dotted–dashed line): note that the exponential fit gives already a reasonably good profile.

For one of the fits (blue dashed line), we have used our parametric model (sum of the equations 52 and 53), obtaining a length-scale h_R = 0.69 arcsec, which corresponds to an ambient density |$n_0=0.033\, d_2^{-1}{\, \rm cm^{-3}}$|⁠.

Also the result of a pure exponential profile (equation 35) is shown (red dotted–dashed line), for which we have derived a best-fitting value h_exp = 0.99 arcsec that, using equation (36), translates into h_R = 0.64 arcsec: this, together with the almost coincidence of the two fitting curves, shows that a fit with an exponential profile is accurate enough. Please notice that our fits also include secondary parameters such as the background level, the intensity scale, and the offset position of the limb.

Differently from the approach by R + 07, here we cannot use the photometry to estimate the ambient density, because we do not have any way to estimate independently the path length along the LOS. Instead, by taking our previously estimated values for n₀ and h_R and using equations (52) and (53), we can infer the ambient neutral fraction f_{n, u}, as a function of the local R_curv along the LOS. The normalized surface brightness profile shown in Fig. 12 can be converted into |${\, \rm photons\, cm^{-2}\,s^{-1}\,arcsec^{-2}}$| multiplying it by a factor 2.69 × 10⁻⁵. In this way, we derive:

\begin{eqnarray*} f_{\mathrm{ n,u}}=0.23\, (R_\mathrm{curv}/1{\, \rm arcsec})^{-1/2}. \end{eqnarray*}

(60)

If along the LOS, the curvature is similar to those seen on the plane of the sky, of order 50–500 arcsec, a neutral fraction of order 0.01–0.03 would be inferred, namely smaller than typically assumed.

7.2 The effect of ripples on the shock surface

The fit in Fig. 12 actually shows a series of oscillations that are not reproduced by the smoother fit. Therefore, one may wonder whether, rather than the best-fitting scale length h_R (or alternatively h_exp for an exponential fit), one sees instead the composition of structures with much smaller scale lengths (and therefore associated to much higher ambient densities). In principle, one may find an infinite number of mathematically valid solutions, which involve small-scale changes of the shock surface profile, and/or the ambient medium density, and/or the upstream neutral fraction. The problem is how to match the observed radial profile with spatial distributions that are not clearly ‘ad hoc’, and that are described by a rather small number of free parameters. In this section, we will focus on the possibility that what is observed can be simply explained as a geometrical effect, due to the presence of small amplitude ripples.

For this, let us generalize equation (43) with the addition of a sinusoidal modulation:

\begin{eqnarray*} Z_\mathrm{sh}(y)=\frac{y^2}{2R_\mathrm{curv}}+H\cos (k y+\phi)+Z_\mathrm{offs} \end{eqnarray*}

(61)

(a small Z_offs may be required for optimize the alignment to the data). Note that also here we use the limit of large R_curv values, in which case we cannot extract from the data information on y, k, and R_curv separately, but only on |$\tilde{y}=y\sqrt{2R_\mathrm{curv}}$| and |$\tilde{k}=k/\sqrt{2R_\mathrm{curv}}$|⁠.

We have then computed a least-squares fitting to the observed profile of the outer limb, using the formula above for the profile of the shock surface, plus an exponential trend for the downstream emissivity profile. The best-fitting parameters are:

\begin{eqnarray*} h_\mathrm{exp}&=&1.09{\, \rm arcsec}; \quad \, \, \,\, H=0.24{\, \rm arcsec}; \nonumber \\ \tilde{k}&=&8.0{\, \rm arcsec^{1/2}}; \quad \,\, \phi =201{\, \rm deg}, Z_\mathrm{offs}=-0.1{\, \rm arcsec}, \end{eqnarray*}

(62)

and the resulting fit is shown in Fig. 13. The quality of the fit is in a sense surprising, because in the reality, one would not expect a pure sinusoidal behaviour, but rather random oscillations with some power spectrum. The information that one could infer from the best-fitting parameters is the following: the value of h_exp is consistent within 10 per cent with that derived in the previous section,without including oscillations, and therefore it must be taken as a rather robust result; the required amplitude of the oscillations (H) is very small; the wavelength of the oscillations λ = 2π/k is unknown, but can be rather long and scales as |$R_\mathrm{curv}^{1/2}$|⁠.

Figure 13.

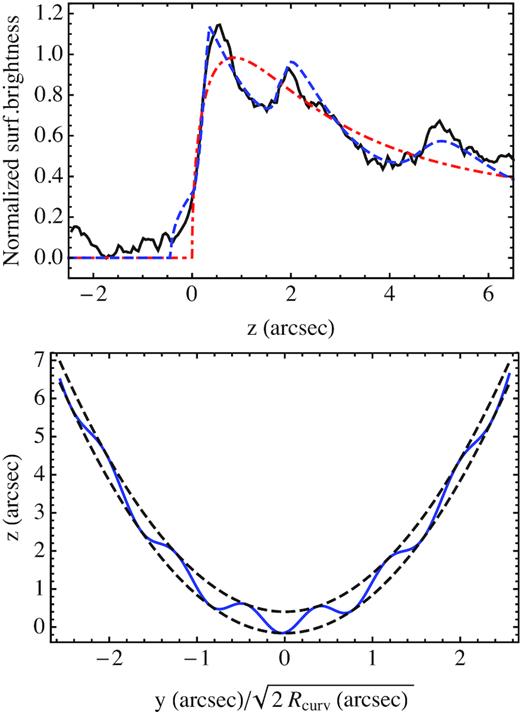
Results of the best fit for a shock surface with sinusoidal ripples. The upper panel shows the new fit (blue dashed line), compared to the data (black solid line) and the exponential fit (red dotted line), as already shown in Fig. 12. The lower panel shows instead the shape of the shock surface (blue solid line), together with its upper and lower boundaries (black dashed line) to make the oscillation more visible. Note that the horizontal and vertical scales are not the same: for the real shape, the horizontal scale must be considerably stretched.

A further clue in favour of a purely geometrical effect can be derived from an inspection of the map in Fig. 11. One may recognize the main peaks in the profile as stripes in the map, oriented ‘almost’ parallel to the outer boundary. Incidentally, the fact that these features look almost parallel to the limb does not necessarily imply that the oscillations have a preferential orientation with respect to us, but simply that the value of R_curv is large (say, of order |$10^3{\, \rm arcsec}$|⁠).

We have also attempted analogous best fits, by first assuming a sinusoidal oscillation (of about |$\pm 60{{\ \rm per\ cent}}$|⁠) of only the ambient density, and then only of the neutral fraction (by an amount of |$\pm 80{{\ \rm per\ cent}}$|⁠). The results are shown in Fig. 14: in either case, the secondary peaks look smoother that those obtained by perturbing the shock surface. In fact, the data show some peaks, like for instance that one at |$z\simeq 2{\, \rm arcsec}$|⁠, which are even sharper than the fit in Fig. 13. Of course, a better fit could be obtained by allowing a more complex power spectrum than a simply monochromatic one, but this would require further free parameters and is beyond the scope of the present analysis.

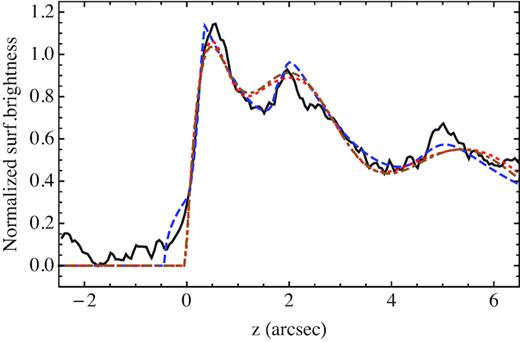
$Comparison of best fits to the radial profile, by using respectively: (a) oscillations in shape from the constant-curvature case (blue dashed curve); (b) oscillations in density (red dotted colour); and (c) oscillations in neutral fraction (brown dotted–dashed curve). It is apparent that the first fit is slightly more accurate, and in particular that it is more effective in producing sharper secondary peaks.$

Figure 14.

Comparison of best fits to the radial profile, by using respectively: (a) oscillations in shape from the constant-curvature case (blue dashed curve); (b) oscillations in density (red dotted colour); and (c) oscillations in neutral fraction (brown dotted–dashed curve). It is apparent that the first fit is slightly more accurate, and in particular that it is more effective in producing sharper secondary peaks.

7.3 On the validity of the derived length-scale

Since the density estimate that we have obtained is significantly smaller than most of the previous estimated in the literature, it is worth discussing under which conditions our approach may overestimate the length-scale h, therefore underestimating n₀.

To this purpose let us consider a limit case, in which a layer with vanishing h mimics the case of an infinite h. This may occur, for instance, if the layer has exactly a triangular shape, with its vertex at the projected position of the outer edge: in this case, we would see a sharp edge with a constant surface brightness inside. However, it would be sufficient to have a slightly roundish vertex to get a very sharp peak of surface brightness near the projected limb, which then flattens to a low surface brightness value when the two flat shoulders are reached.

Since it is very unlikely (although possible) having such a sharp vertex, in the presence of a small value of h, one should likely see a very sharp peak followed by a stripe with a surface brightnesses much lower than those predicted by the constant curvature model (as from Fig. 7). Anyway, by a suitable combination of many such components with different offsets, one could manage to reproduce also the general profile as shown in Fig. 12. But, in our opinion, it is not justified to assume such a fine-tuned model to reproduce a general trend that is instead naturally reproduced by a constant curvature model.

To conclude, even if our estimated value |$h_\mathrm{ R}=0.64{\, \rm arcsec}$| is formally just an upper limit, we believe that it is a rather reliable estimate.

7.4 Fitting the inner bright filament

The total intensity profile of the inner filament is shown in Fig. 15: as we have mentioned before, a constant concave curvature does not allow one to adequately describe its structure. Here, we present a method to fit its structure in detail, and to extract another independent estimate of the ambient density.

Figure 15.

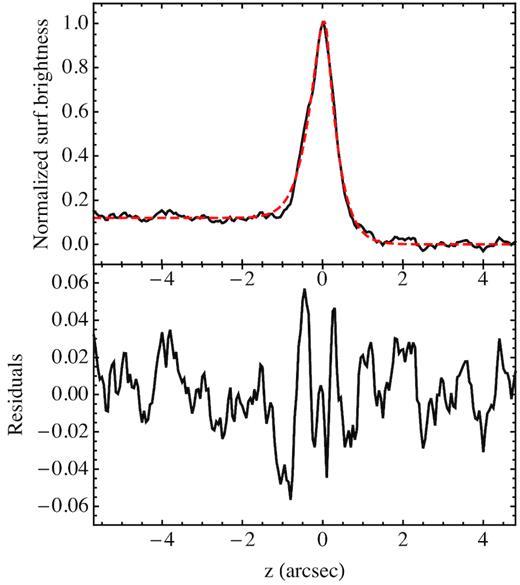
The upper panel shows the total line intensity profile of the inner filament, normalized to its maximum value (black line – the origin of the coordinate is set at the peak position), together with our best-fitting profile (red dashed line). The lower panel shows instead the fit residuals.

In order to perform this task, let us release our former assumptions about the shape of the shock front, and focus only on the distribution on the sky of the shock front positions, |${\cal P}(z)$|⁠. Assuming that the emission profile across the transition zone (j_t(⁠|$z$|⁠) = j_n(⁠|$z$|⁠) + j_b(⁠|$z$|⁠)) is the same for all positions along the shock, the observed profile can be written as the convolution |${\cal P}(z)\ast j_\mathrm{ t}(z)$|⁠. The inverse problem seems in principle unsolvable, because from one function (the observed profile), we aim at extracting two.

To allow a treatment of this problem, we then proceed with two further assumptions. First, that j_t(⁠|$z$|⁠) follows our parametric model:

\begin{eqnarray*} j_\mathrm{ t}(z)=\frac{1+(A_\mathrm{ b}/A_\mathrm{ n})+(B_\mathrm{ b}/A_\mathrm{ n})(z/h_\mathrm{ R})}{1+(A_\mathrm{ b}/A_\mathrm{ n})+(B_\mathrm{ b}/A_\mathrm{ n})}\frac{\exp (-z/h_\mathrm{ R})}{h_\mathrm{ R}}, \end{eqnarray*}

(63)

(scaled such that |$\int _0^\infty j_\mathrm{ t}(z)\, \mathrm{ d}z=1$|⁠), where we assume A_b/A_n and B_b/A_n to be known, while leaving only h_R as a free parameter. The other assumption is that the |${\cal P}(z)$| distribution vanishes at all |$z$| > |$z$|_max: this constraint retains the idea that the overall shape of the shock surface is concave there, and we shall see how adding this assumption a solution may be obtained. One may find in fact that the profile in the projected downstream depends on |${\cal P}(z)$| through the following expression:

\begin{eqnarray*} I_{\mathrm{ t,D}}(z)=\left(C_{0,\mathrm{ D}}+C_{1,\mathrm{ D}}\frac{z-z_\mathrm{max}}{h_\mathrm{ R}}\right)\exp \left(-\frac{z-z_\mathrm{max}}{h_\mathrm{ R}}\right), \end{eqnarray*}

(64)

where:

\begin{eqnarray*} C_{0,\mathrm{ D}}=\frac{(1+A_\mathrm{ b}/A_\mathrm{ n}){\cal I}_{(0)}-(B_\mathrm{ b}/A_\mathrm{ n}){\cal I}_{(1)}}{1+(A_\mathrm{ b}/A_\mathrm{ n})+(B_\mathrm{ b}/A_\mathrm{ n})}; \end{eqnarray*}

(65)

\begin{eqnarray*} C_{1,\mathrm{ D}}=\frac{(B_\mathrm{ b} /A_\mathrm{ n}){\cal I}_{(0)}}{1+(A_\mathrm{ b}/A_\mathrm{ n})+(B_\mathrm{ b}/A_\mathrm{ n})}, \end{eqnarray*}

(66)

with:

\begin{eqnarray*} {\cal I}_{(n)}=\int _{-\infty }^{z_\mathrm{max}}{\left(\frac{z^{\prime }}{h_\mathrm{ R}}\right)^n\exp \left(\frac{z^{\prime }}{h_\mathrm{ R}}\right){\cal P}(z^{\prime })\, \mathrm{ d}z^{\prime }}; \end{eqnarray*}

(67)

unfortunately, |${\cal I}_{(0)}$| and |${\cal I}_{(1)}$| can be evaluated only if the profile of |${\cal P}(z)$| is known. In the projected upstream, the evaluation is similar but more complex, since the upper limit of the integrals is now |$z$|⁠, therefore changing with position.

The problem can be further simplified making a guess for the function |${\cal P}(z)$|⁠. We have tried the following form:

\begin{eqnarray*} {\cal P}(z)=\left(a+b(z-z_\mathrm{max})\right)\exp \left(\frac{z-z_\mathrm{max}}{h}\right)+c,\quad \hbox{for}\,\,z\lt z_\mathrm{max}\nonumber \\ \end{eqnarray*}

(68)

(which will be justified a posteriori), where the best values for a, b, c, and h have to be evaluated. The choice of this profile is purely phenomenological, and has been inspired by the data shape. It can be shown that in the projected upstream:

\begin{eqnarray*} I_{\mathrm{ t,U}}(z)=\left(C_{0,\mathrm{ U}}+C_{1,\mathrm{ U}}\frac{z-z_\mathrm{max}}{h_\mathrm{ R}}\right)\exp \left(\frac{z-z_\mathrm{max}}{h}\right)+c. \end{eqnarray*}

(69)

The quantities C_{0, U}, C_{1, U}, C_{0, D}, and C_{1, D} can be written as functions of a, b, c, h, and h_R (plus of course of A_b/A_n and A_b/A_n, which here have been given a priori). By least-squares fitting at the same time to the upstream and downstream data, and leaving also free the quantity |$z$|_max, we finally obtain:

\begin{eqnarray*} z_\mathrm{max} &=& 0.14{\, \rm arcsec};\,\,h_\mathrm{ R}=0.24{\, \rm arcsec}\nonumber \\ a &=& -0.18;\,\,b=-14.43;\,\,c=0.12;\,\,h=0.24{\, \rm arcsec}, \end{eqnarray*}

(70)

implying an ambient density |$n_0=0.095\, d_2{\, \rm cm^{-3}}$|⁠. As shown by Fig. 15, the fit to the filament’s profile is quite good: this already can be taken as a proof of the validity of the shape introduced with equation (68).

An independent test of the goodness of the function |${\cal P}(z)$| can be performed comparing the fitted expression with a ‘brute-force’ deconvolution, obtained using a number of parameters equal to the number of data points (therefore without any treatment of the errors): these are shown in Fig. 16, and apart from the scatter the profiles look virtually identical.

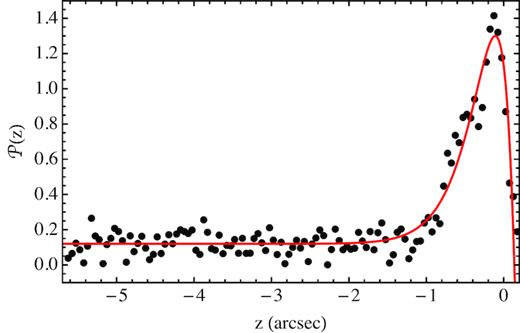
$Comparison of our model ${\cal P}(z)$, as from equation (68) (red line), and the distribution computed to match exactly the data (black dots).$

Figure 16.

Comparison of our model |${\cal P}(z)$|⁠, as from equation (68) (red line), and the distribution computed to match exactly the data (black dots).

The most relevant result concerns the value of h_R, which is almost 3 times smaller than previously derived from the outer part of the external filament: this implies that at the location of the brightest filament the shock is really moving through a medium that is ∼3 times denser than in the outer edge, provided that the other physical parameters do not change significantly. This is a first evidence of density changes, even if such density changes alone cannot be responsible for the huge variations observed in surface brightness.

Our assumption of the existence of a given |$z$|_max is formally incorrect, in the sense that shock is a closed surface, so that sooner or later its projection should turn towards the centre of the SNR. Our assumption therefore is equivalent to assume that, before this happens, the face-on surface brightness must almost vanish. The fact that, as it will be shown below, the observed profile of I_b/I_n in the projected downstream presents a steady increase of the I_b/I_n ratio as long as some emission is detected, namely a behaviour similar to that in Fig. 8, seems to justify the correctness of our assumption.

Now, the normalized surface brightness profile shown in Fig. 15 can be converted into |${\, \rm photons\, cm^{-2}\,s^{-1}\,arcsec^{-2}}$| multiplying it by a factor 1.17 × 10⁻⁴. In this way, we derive:

\begin{eqnarray*} f_{\mathrm{ n,u}}=1.7 \, (\lambda _\mathrm{LOS}/1{\, \rm arcsec})^{-1}, \end{eqnarray*}

(71)

where λ_LOS is the effective length of the emission region along the LOS (again expressed in arcseconds, to allow a direct comparison with the size of the structures seen on the map). For instance, an upstream neutral fraction 0.01–0.03 would imply λ_LOS to be in the range 60–170 arcsec corresponding to about 0.6–1.7 pc.

7.5 Multiplicity of the brightest filaments

In the previous section, we have shown that the assumption of a rippled surface, rather than one with a constant curvature, can successfully reproduce the available data without assuming local curvatures along the LOS much smaller than those measurable on the plane of the sky, as done by R + 07.

The only remaining issue is if the assumption of ripples, i.e. of multiple shock intersections along the LOS, should be considered or not as a ‘fine-tuning’. The purpose of this section is to justify the idea that multiple intersections occur quite naturally, once one has selected from the whole field of view only those locations with the brightest (projected) filaments.

To this purpose, let us present here some results of a simulation of the projection effect a rippled surface. The spirit of these numerical simulations is, in a sense, like that of the model of distorted sheet presented by Hester (1987), in order to justify the observed structures present in middle-aged SNRs, and in particular in the Cygnus Loop.

While a forthcoming paper will be devoted to a more detailed statistical analysis, let us present here, for the sake of illustration, just the results of a single realization of small radial fluctuations of an otherwise spherical surface (representing the blast wave). The radial fluctuations have been simulated with an isotropic Kolmogorov spectrum (δr(k) ∝ k^−5/3); a separation of one decade between the lowest and the highest wavelength has been chosen to give a better by-eye match to real cases. These radial fluctuations have been then mapped onto a portion of a sphere, and observed edge-on: the resulting projected image shows the presence of several filaments, of all intensities (see Fig. 17). Here, the local surface brightnesses are simply proportional to the total length of the layers crossing a given ray path: this is equivalent to the assumption of a constant face-on surface on this emitting sheet.

Figure 17.

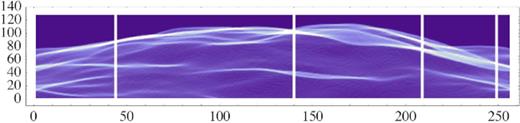
Simulated map, obtained by a single realization of a spherical sheet with random radial fluctuations (see the text for details) and shown in projection. The four vertical stripes have been chosen among those containing the brightest portions of filaments, and the profiles for them are displayed in Fig. 18. The coordinate units, being arbitrary, are expressed here just in pixels.

Then we have examined separately all the columns in the map (256, in the case shown), and ranked all these slices according to the highest brightness measurable in each of them. This process has been conducted automatically, to avoid subjective choices; only at a later stage, since the brightest slices have shown the tendency to cluster spatially, we have manually selected just one slice as representative for each cluster. The selected slices are marked by vertical segments in Fig. 17, while the various panels in Fig. 18 show the shapes of the corrugated limb in each slice: from them, it is apparent that the multiple intersections, in correspondence of the brightest projected filaments, are not the exception but rather the rule.

Figure 18.

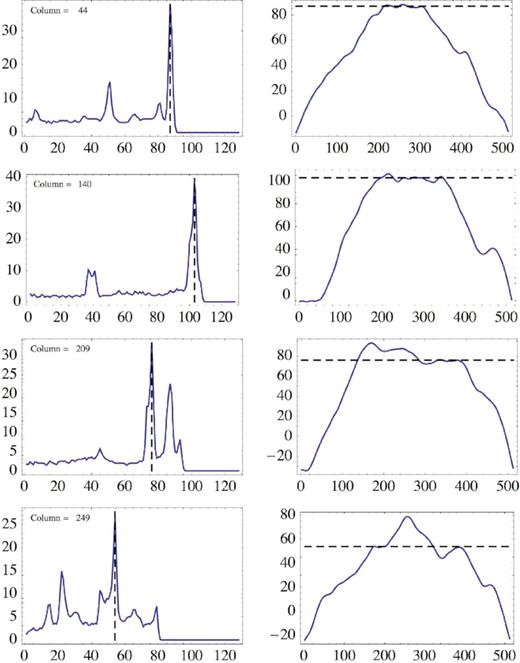
Profiles corresponding to the four vertical stripes shown in Fig. 17, each of them labelled by the corresponding column in the map. The left-side column shows the intensity profiles, under the assumption of a constant face-on surface brightness on the emitting sheet (the upwards direction in the map is now rightwards). The right-side column shows, instead, the profiles of the distorted limb, sectioned at the respective columns (the scales of the x and y coordinates are different, in order to enhance the effects of the ripples). The dashed lines refer to the position of the brightest peak in each cut.

As a final comment, it is worth noticing that when the shock is not spatially resolved no bias is introduced in the estimation of the upstream neutral density. This is due to the fact that in the case of a corrugated shock the map shows both brighter regions and regions of depleted emission. Hence, when the shock is not resolved, the total luminosity remains the same with respect to a non-corrugated shock.

8 RE-ANALYSIS OF NIKOLIC ET AL. DATA

The model parameters derived from the analysis of the HST image, performed in the previous section, should be tested on the data from N + 13 (their table S1) that, in spite of having a lower resolution, allow one to follow the I_b/I_n spatial changes across the shock. While the data in table S1 are reported to be correct, the authors acknowledged in the arXiv version of the paper (arXiv:1302.4328v2) that the reference direction of the inner shock rim in fig. 3 in N + 13 was chosen incorrectly which mostly affected the I_b/I_n ratio trend, as plotted in that figure. For this reason, our present analysis directly refers to their table. In addition, the authors provided us with the measured intensities of the narrow (I_n) and broad (I_b) components separately, together with the broad-line centroid offset with respect to the narrow-line centroid. In order to derive suitable I_b + I_n and I_b/I_n profiles we have proceeded as follows: first, the coordinates of the bin centroids have been rotated (by 38 deg, anticlockwise), in order to orientate the axes respectively parallel to the filament and orthogonal to it.

Since we have noticed some trend in the brightness along the filament, in order to get a neater radial profile we have first corrected for a smooth trend along the filament, by fitting it with a (third-degree) polynomial: this correction has been then applied just to improve the average profile for the total line intensity across the filament; while obviously the intensity ratio I_b/I_n is not affected.

Finally, in order to provide a higher homogeneity between the points used to draw the profiles, we have selected the central 15 arcsec along the filament (89 selected positions, out of the original 133). The final results of this procedure are shown in Fig. 19 for W_obs, I_n + I_b, and I_b/I_n.

Figure 19.

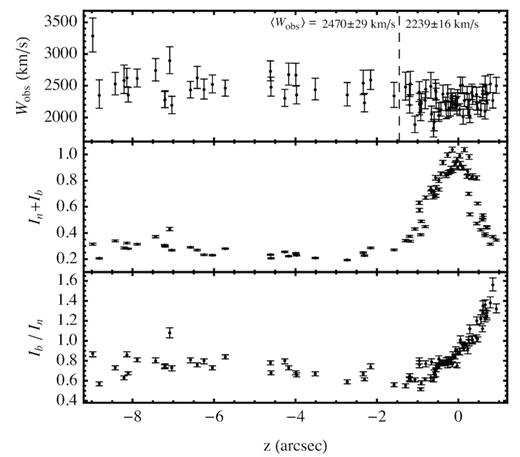
Profiles of the total intensity (upper panel) and of I_b/I_n (lower panel), as derived from the data of N + 13 (see the text). The intensity profile is normalized to its peak, while the origin of the coordinate corresponds to the intensity peak.

8.1 Matching the observed I_b/I_n ratio

Let us now take the model of spatial profile of the total emission, as derived in the previous section, and downgrade it to fit the same profile, at the lower resolution as in N + 13. The best match is reached after convolving the original profile with a Gaussian function with an FWHM of 0.95 arcsec, compatible with the average spatial resolution of the N + 13 data (see the upper panel of Fig. 20; we had also to optimize spatial offset, flux scale, and background level).

Figure 20.

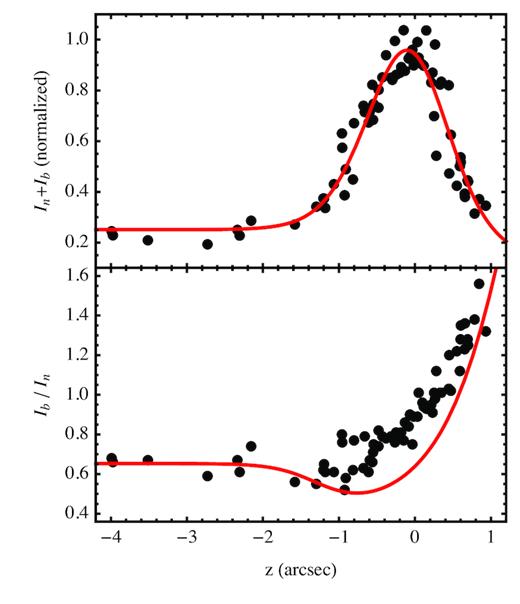
Simulated I_n + I_b and I_b/I_n profiles for the spatial resolution of N + 13 (solid red lines), compared with actual observations in that work (black dots). The upper panel shows the result of the fit to the total line flux, needed to set the spatial resolution. The lower panel compares instead the prediction for the I_b/I_n profile, compared with the data.

Then we have calculated the expected profile of I_b/I_n, shown in Fig. 20. The main spectroscopic trend, namely the increase of I_b/I_n in the projected downstream, is rather well reproduced: the asymptotic increase is well matched, and also the small dip of I_b/I_n with respect to the upstream limit is marginally detected; moreover, the bending in the downstream trend as well as the start of an increase of I_b/I_n before the peak in I_b + I_n are clearly effects resulting from the limited spatial resolution.

The only observational effect that is not correctly reproduced by our model is the prompt increase of I_b/I_n right after its minimum (at |$z$| ≃ 1 arcsec, in the figure). This effect is probably the result of the superposition of layers with different densities, and therefore different h_R values, while for the denser layer, I_n goes down promptly in the downstream, I_b survives a bit longer, with the effect of slightly increasing the line components ratio, in the intermediate region. Unfortunately, this kind of modelling is not quantitatively viable, due to the limitations of the presently available data.

8.2 Width of the broad-line component

Another important diagnostic tool is the width of the broad-line component, which is directly linked to the shock velocity, even though with some dependence on the thermal equilibration level (see e.g. fig. 10 in Morlino et al. 2012). However, N + 13 showed that there is a variation of the broad-line FWHM along the Balmer filament that increases from |$W_\mathrm{ b} = 2357.7{\, \rm km\, s^{-1}}$| in the inner part, up to |$W_\mathrm{ b} =2555.4{\, \rm km\, s^{-1}}$| in the outer one (see fig. 1 in that paper). The average line widths given in the upper panel of Fig. 19, 2239 ± 16 and |$2470\pm 29{\, \rm km\, s^{-1}}$| respectively, are slightly different only because we used a different selection. If such a variation were simply due to a different shock velocity in different parts of the shock, the required velocity difference should be |$\Delta V_\mathrm{sh}\simeq 500{\, \rm km\, s^{-1}}$|⁠. But, as also noticed by N + 13, this would be incompatible with the almost unchanged profile of the shock over two decades of observations.

In order to put an upper limit on ΔV_sh, we reused the data in Winkler, Gupta & Long (2003), taken from the sector F of their fig. 2, which almost completely overlaps with the portion of filament analysed by N + 13. For this sector, Winkler et al. (2003) estimated a mean proper motion of |$283.2\pm 1.0{\, \rm mas\, yr^{-1}}$|⁠, which is equivalent to a shock velocity |$2685\pm 9\, d_2{\, \rm km\, s^{-1}}$|⁠. We have compared the filament profiles at years 1987.32 and 1998.48, as shown in their fig. 3, after shifting the 1998 profile backwards by 3.16 arcsec in order to match the inner peak of the 1987 profile. As shown in Fig. 21, the whole profile between the two epochs is almost unchanged. A small displacement of ∼0.1 arcsec between the outer edges of the two profiles is visible which is, however, smaller than the image resolution and compatible with the pixel size of 0.1 arcsec. As a consequence, the upper limit on the differential proper motion in the plane of the sky between the inner and the outer edges, taking into account also the measurement uncertainties, is ∼16 mas yr⁻¹, which corresponds to |$\Delta V_{\rm sh,\perp }\lesssim 150\, d_2{\, \rm km\, s^{-1}}$|⁠. Such a low value cannot account by itself for the observed difference in W_b. In fact, even a difference of |$150{\, \rm km\, s^{-1}}$| would imply a difference in W_b ≃ 70–|$80{\, \rm km\, s^{-1}}$|⁠, much less than the |${\simeq }230{\, \rm km\, s^{-1}}$| difference, measured between the bright filament and the outer region (see Fig. 19), then strengthening the idea that a contribution of bulk velocities to the line widths at the outer edge may be substantial.

Figure 21.

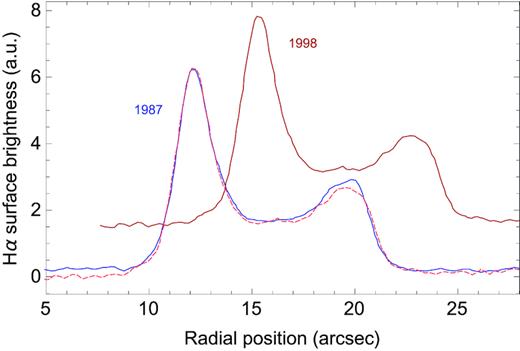
Radial profile of the total Hα emission of a portion of northwestern filament of SN 1006 at epochs 1987.32 and 1998.48 from Winkler et al. (2003). The dashed line corresponds to the 1998 profile shifted backwards by 3.16 arcsec. The shapes of the two profiles are virtually identical with the exception of a small displacement of the outer edge in the 1998 profile of ∼0.1 arcsec which is, however, compatible with the spatial resolution.

On the other hand, as we will show in Section 8.3, the larger FWHM in the outer edge can be well explained by projection effects, while the FWHM of the inner edge is the observable to be compared with the one calculated by 1D models. At this point, we can proceed to an estimate of SN1006 shock speed using the model in Section 2. Assuming the lowest possible value of T_e/T_p = m_e/m_p, we can infer the lowest value for the shock speed given by equation (10) in Morlino et al. (2013b), which corresponds to 2599|${\, \rm km\, s^{-1}}$|⁠. This translates into a lowest boundary for the distance d ≳ 1.9 kpc.

As for an upper bound to V_sh, and therefore to the distance, one should first set an upper limit to other sinks of energy (like, for instance, an efficient CR production), and then explore what range of values for T_e/T_i is consistent with the relative behaviour of broad- and narrow-line components. We have found before that the observed I_b/I_n ratio is consistent with |${\sim }10{{\ \rm per\ cent}}$| of the proton energy to be shared with electrons, then increasing the estimate of the shock speed, and therefore of the distance, by about 5 per cent. Due to all this, the shock speed that that we have assumed throughout this paper, namely |$3000{\, \rm km\, s^{-1}}$|⁠, is probably too large, by about 10 per cent. But, in consideration of the uncertainties involved and on the negligible effects on our main conclusions, in this work we have preferred to keep this reference value for that speed, rather than attempting a combined optimization that involves also V_sh.

8.3 Modelling broad-line widths and shifts

In this section, we propose a rather natural explanation for the origin of the variations in space of the width of the broad-line component (W), as well as for the observed shifts of the broad-line barycentre with respect to that of the narrow one (ΔV), both effects measured by N + 13. We show that they do not necessarily follow from changes in the physical conditions, but are more likely consequence of the geometrical structure of the shock surface. We follow and extend a concept introduced by R + 07, namely that the measured spectral width of the broad-line component is the combined effect of thermal spreads and bulk motions.

Let us investigate the case in which two layers (labelled as ‘a’ and ‘b’) intercept the LOS. We indicate with A_a and A_b their respective face-on surface brightnesses of the broad-line component, while θ_a and θ_b are their inclination angles with respect to the observer (where θ = 0 means a layer seen edge on). In addition, we assume the individual layers to be thin enough to neglect their internal structure. Finally, we assume that the velocity distribution of the hot emitting neutrals is a Gaussian with an isotropic thermal dispersion σ₀ and an average bulk velocity V₂, constant in value and always orthogonal to the shock surface. By integrating over the radial velocity, one gets:

\begin{eqnarray*} A_\mathrm{obs} = A_\mathrm{ a}/|\sin (\theta _\mathrm{ a})|+A_\mathrm{ b}/|\sin (\theta _\mathrm{ b})|; \end{eqnarray*}

(72)

\begin{eqnarray*} \Delta V_\mathrm{obs} = \frac{A_\mathrm{ a}-A_\mathrm{ b}}{A_\mathrm{obs}}V_2; \end{eqnarray*}

(73)

\begin{eqnarray*} \sigma _\mathrm{obs}^2 = \sigma _0^2+V_2^2\frac{A_\mathrm{ a}A_\mathrm{ b}\left(|\sin (\theta _\mathrm{ a})|+|\sin (\theta _\mathrm{ b})|\right)^2}{A_\mathrm{obs}^2|\sin (\theta _\mathrm{ a})\sin (\theta _\mathrm{ b})|}, \end{eqnarray*}

(74)

where A_obs is the observed surface brightness, ΔV_obs the observed velocity shift (with respect to the position of the narrow component), and σ_obs the observed Gaussian dispersion (with the FWHM being |$W\simeq 2.35\, \sigma$|⁠). We also take sin (θ_a) to be positive and sin (θ_b) to be negative; namely one layer moving towards the observer and the other moving away.

It should be noticed from equation (73) that, if A_a = A_b, necessarily the broad-to-narrow component velocity shift must be zero: therefore, the measurement by N + 13 of both positive and negative shifts requires some spatial variability in the face-on surface brightness.

If θ_a and θ_b are close to each other, in absolute value (let us use the symbol θ for both), then we have:

\begin{eqnarray*} \Delta V_\mathrm{obs} = S_\mathrm{ A}|\sin (\theta)|V_2; \end{eqnarray*}

(75)

\begin{eqnarray*} \sigma _\mathrm{obs}^2 = \sigma _0^2+(1-S_\mathrm{ A}^2)\sin (\theta)^2V_2^2, \end{eqnarray*}

(76)

where S_A = (A_a − A_b)/(A_a + A_b). Note that the lack of a clear correlation between W and ΔV suggests that |sin (θ)| and S_A are statistically independent quantities.

For the following analysis, we use a large number of Monte Carlo simulations, in which we assume a Gaussian distribution with zero mean for ln (A_a/A_b), and an independent Gaussian distribution with zero mean for sin (θ)V₂. Every time we use equations (75) and (76) to derive |$\Delta V_\mathrm{obs}^2$| and |$\sigma _\mathrm{obs}^2-\sigma _0^2$|⁠, respectively. Although the distribution of points in the |$\left\lbrace \Delta V_\mathrm{obs}^2,\sigma _\mathrm{obs}^2-\sigma _0^2\right\rbrace$| parameter plane does not shown any evident correlation, one may try derive a best-fitting relation |$\sigma _\mathrm{obs}^2-\sigma _0^2=K_0^2+K_1\Delta V_\mathrm{obs}^2$|⁠.

From simulations, one may find that K₀ is linearly proportional to the assumed standard deviation for the stochastic variable sin (θ)V₂, while K₁ is independent from it, depending only on the spread of the A_a/A_b distribution. We also find that the best-fitting K₁ has typically a positive sign, and that its uncertainty could be made very small by increasing considerably the number of points.

Unfortunately, the data on which to test this trend are rather limited in number: the number of points to the left of the dashed line in Fig. 19 (namely excluding the bright inner filament, where the layers on the LOS are likely more than two) is only 29. With these data, one finds |$\sigma _\mathrm{obs}^2=(1062.)^2+0.795(\Delta V_\mathrm{obs})^2$|⁠, where both σ_obs and ΔV_obs are expressed in |${\, \rm km\, s^{-1}}$|⁠.

By performing a large number of Monte Carlo simulations, with the same number of points, we have produced Fig. 22: it shows the dependence of the best-fitting value of K₁ on the spread of the A_a/A_b distribution (expressed in terms of the median value of A_a/A_b, with A_a taken conventionally to be the layer with the higher face-on surface brightness). In this figure, the 1σ and 2σ ranges compatible with the 29-point case are also displayed. Within 1σ, the observed value K₁ = 0.795 is compatible with the median of A_a/A_b being in the range [1.84,3.53]; within 2σ the median is anyway larger than 1.53 (which means that in half of the cases the layer a has a face-on surface brightness at least 53 per cent brighter than the layer b). This is a further evidence of the presence of consistent surface density fluctuations along the shock surface.

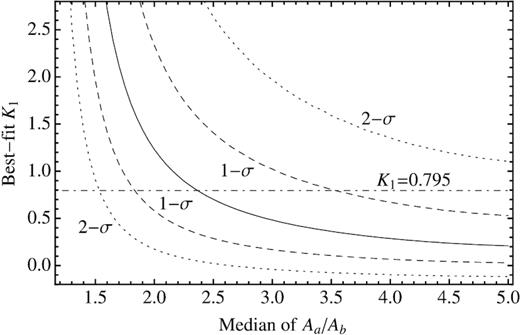
Dependence of the best-fitting value of K1 on the spread of the Aa/Ab distribution (expressed in terms of the median value of Aa/Ab, with Aa > Ab).

Figure 22.

Dependence of the best-fitting value of K₁ on the spread of the A_a/A_b distribution (expressed in terms of the median value of A_a/A_b, with A_a > A_b).

Instead, for the value of K₀, our simulations (see Fig. 23) show that it has a 1σ range of about 0.3–0.8 times the standard deviation of |$\sin (\theta)\, V_2$|⁠, and is nearly independent of the typical value of the A_a/A_b ratio. If we assume that the broad-line width in the region of the bright limb is not appreciably affected by bulk motion effects, we can infer σ₀ from it, and therefore estimate an average value for |sin (θ)|, which would give a 1σ range for θ of about 10–30 deg. These values are about one order of magnitude larger than the inclination angles from the pure edge-on case, as from table S1 in N + 13, simply because they refer to different scenarios (two layers with unbalanced face-on surface brightnesses, versus a single layer).

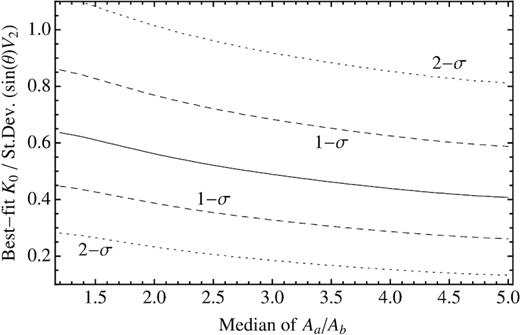
$Dependence of the best-fitting value of K0, scaled with the standard deviation of $\sin (\theta)\, V_2$, on the spread of the Aa/Ab distribution.$

Figure 23.

Dependence of the best-fitting value of K₀, scaled with the standard deviation of |$\sin (\theta)\, V_2$|⁠, on the spread of the A_a/A_b distribution.

For this range of values, a further estimate of f_{n, u} can be obtained with a photometric approach: a typical surface brightness in the region between the outer limb and the bright filament is about |$1.6\times 10^{-5}{\, \rm photons\, cm^{-2}\,s^{-1}\,arcsec^{-2}}$|⁠, so that by assuming a density of |$0.033{\, \rm cm^{-3}}$| like in the outer limb, it comes out |$f_{\mathrm{ n,u}}=0.216\, |\sin (\theta)|$|⁠, which implies typical values of 0.03–0.1 for f_{n, u}. All these estimates are uncertain, none the less they show a consistency of the present scenario.

Such face-on surface brightness variations should take place on rather large density scales, of at least ∼10″, namely ⪞ |$0.1{\, \rm pc}$|⁠. A feel of this can be obtained also by looking at Fig. 24, where the centres of the bins in which N + 13 have measured ΔV are displayed with three different symbols and colours. Variations in the face-on surface brightness do not necessarily imply ambient density variations (and especially of the same level), but just variations in the density of the upstream neutral component (n₀f_{n, u}).

Figure 24.

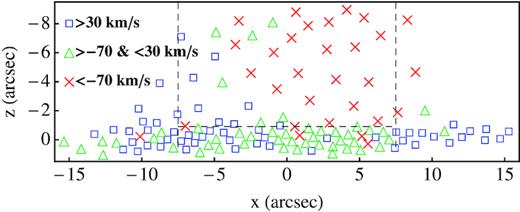
Map of the positions of the N + 13 data points, labelled with three different symbols, depending on the measured value of the broad-line velocity offset. The figure shows some spatial coherence of the offset, with a length-scale ∼10 arcsec. The vertical dashed lines enclose the area that we have selected for our general analysis; while the points used to investigate the relation between broad-line widths and shifts are only those above the horizontal line.

10.1051/0004-6361:20077742

One plausible guess would be that f_{n, u} is proportional to n₀ if the ambient gas is photoionized by the Galactic radiation field, so that the n₀ fluctuations would be |${\sim }20{{\ \rm per\ cent}}$|⁠. However, the variations could be entirely due to n₀, or entirely due to f_{n, u}. In fact, if n₀ and f_{n, u} are anticorrelated due to photoionization from the local shock itself, the density fluctuations could be larger.

The scenario presented in this section is in a sense similar to that discussed by Shimoda et al. (2015), but with opposite results. Namely we find that, in the case of two (or more) oblique layers along the LOS, the effective width of the broad component is increasing because of the composition of the thermal width with the bulk velocities of the two components; in doing this, we have assumed that the shock velocity is always aligned with the shock normal (even though this condition does not seem to be strictly required). Instead, in Shimoda et al. (2015), the dominant effect is the decrease of the effective shock velocity, with respect to that estimated from astrometric measurements, because in the presence of ripples, the shock is oblique almost everywhere. A close comparison of these two results is difficult, because the conclusion of Shimoda et al. (2015) is based on the output of a numerical simulation. However, we believe that our approach is better justified here, because the ripples are at a rather low level (as derived from our model, as well as from a direct inspection of the edge shape). And, in fact, the increased width outside the bright filament is more naturally explained in our scenario. We do not exclude that, in cases in which turbulence is more important, the scheme proposed by Shimoda et al. (2015) could be more appropriate.

9 COMPARING DENSITY ESTIMATES

In this section, we will focus on one of the main outcomes of this work, namely the estimates of the ambient density in the northwestern limb. In the above sections, we have derived ambient densities ranging from an average value of |$0.03{\, \rm cm^{-3}}$| in the outer edge to about |$0.10{\, \rm cm^{-3}}$| in the bright filament. These values are a factor 3–10 lower than previous estimates that can be found in literature, hence it is worth discussing possible reasons for such a discrepancy. A commonly accepted scenario is that SN 1006 expands in a tenuous ambient medium, with a density gradient directed towards the northwestern side, and/or with a denser cloud located near the northwestern limb. Nevertheless, there is not a general agreement on the absolute value of the density.

Analyses of the X-ray thermal emission on the southeastern side lead to very low ambient densities, such as Winkler et al. (2014) who measured |$n_0=0.045_{-0.020}^{+0.049}{\, \rm cm^{-3}}$|⁠; similar or even lower densities are found by Miceli et al. (2012). With such low ambient densities, it is not at all a surprise that SN 1006 is still in the ejecta-dominated (ED) regime in that region. This means that in spite of the large SNR size, the total mass of the swept up material is still moderate. Using a model from Chevalier (1982), in which the ejecta density distribution has a flat inner core and a power-law outer profile proportional to r⁻ⁿ with an index n = 7, and assuming that the SNR is near the end of its ED phase, one can set the following upper limit for the ambient density:

\begin{eqnarray*} n_0\le 0.035\, d_2^{-3}\Big (M_\mathrm{ej}/1.4 {\rm M}_\odot \Big){\, \rm cm^{-3}}. \end{eqnarray*}

(77)

The Balmer filament in the southeast region is very well approximated by a circle. With respect to this circle, the northwest filament has a radial distances smaller by about 8 per cent. One could naturally explain such a distortion level by assuming that the ambient density is higher on the northwestern side, and possibly also that the shock on that side is entering the Sedov–Taylor phase. Indeed, the lower expansion velocity on that side would be consistent with a later phase (see e.g. Winkler et al. 2014). Since at a given time during the ED phase, the SNR radius is proportional to |$n_0^{1/n}$|⁠, for n = 7, a density factor ≃ 2 would be sufficient to account for the small distortion on the northwestern side. The required density difference would be even smaller if the remnant were in a later evolutionary phase.

In the case of an isolated higher density cloud, the limb distortion does not allow any stringent limit, but the shock velocity does. Let us use the simple argument that the ram pressure in the shock downstream is everywhere a constant fraction of that upstream, so that the V_sh ∝ n^−1/2 scaling can be applied. In this case, a lower expansion velocity by |${\simeq }40{{\ \rm per\ cent}}$| on the northwestern side would allow an overdensity no higher than a factor ∼3. Since both the indentation and the lower velocity must be fitted simultaneously, a likely possibility is that both effects occur at the same time. Alternatively, a cloud with 3 times higher density would naturally account for both the indentation and the lower proper motion, provided that the blast wave reached it when the SNR was about |$20{{\ \rm per\ cent}}$| smaller than its present size. Therefore, from these kinds of arguments, one should be surprised to measure ambient densities larger than |${\simeq }0.1{\, \rm cm^{-3}}$| on the northwestern side.

Let us now come to direct measurements, and begin with Balmer observations: R + 07, on the basis of the modelling that we have mentioned in Section 6.2, have derived |$0.25{\, \rm cm^{-3}}\le n_0\le 0.4{\, \rm cm^{-3}}$|⁠; while Heng et al. (2007), re-analysing the same HST image, corrected the R + 07 density estimate to the range 0.15–|$0.3{\, \rm cm^{-3}}$|⁠. However, we have already discussed above the reasons why this kind of analysis can be misleading.

Let us consider the results of some X-ray analyses. Winkler & Long (1997) derived a pre-shock density |${\sim }1.0{\, \rm cm^{-3}}$| based on the comparison of the relative position between optical and ROSAT X-ray emission. Analysing Chandra data, Long et al. (2003) derived an ionization time scale of |$220{\, \rm cm^{-3}\, yr}$| for the northwestern limb; measuring a thickness of |$17{\, \rm arcsec}$| for the X-ray emitting layer and assuming |$(1/4)\times 3000{\, \rm km\, s^{-1}}$| for the post-shock flow velocity, they estimated a characteristic time of |$240{\, \rm yr}$|⁠, and therefore an ambient density of |${\sim }0.25{\, \rm cm^{-3}}$|⁠. One should notice though that, if the contact discontinuity is not too far from the forward shock the downstream velocity decreases in the downstream, so that the characteristic time must be longer and therefore the ambient density should be lower.

A similar analysis has been performed by Acero, Ballet & Decourchelle (2007), on the basis of XMM–Newton data. An interesting aspect of that work is that it measured not only a region of the bright limb (labelled as NW-1), but also an area of faint emission in front of the bright filament (labelled as NWf). While for the bright filament an ambient density of about |$0.15{\, \rm cm^{-3}}$| was derived, the ambient density for the outer faint region was estimated to about |$0.05{\, \rm cm^{-3}}$|⁠. The authors suggested that a density of |$0.05{\, \rm cm^{-3}}$| is representative of the ambient medium around SN 1006, except for the bright northwestern filament. Our proposed scenario of a shock moving through a patchy ambient medium would be consistent with these observations.¹

Using Spitzer-IR data, together with a model for the destruction of grains in the post-shock gas, Winkler et al. (2013) derived a plasma density of about |$1.0{\, \rm cm^{-3}}$|⁠, and therefore an ambient density |${\sim }0.25{\, \rm cm^{-3}}$|⁠. However, the observed IR radial profiles cannot be adequately reproduced by their model: this has been interpreted as a sign that the ambient density is not uniform. But in this case, it becomes unclear how reliable the density estimate itself could be.

Rather extreme estimates are made by Dubner et al. (2002) of nearly |$0.3{\, \rm cm^{-3}}$| for the neutral component based only on H I radio emission (this estimate refers to the average density of the cloud that the northwestern shock has just started to interact with and not necessarily to the density of the presently shocked medium), and by Laming et al. (1996), |${\sim }0.04{\, \rm cm^{-3}}$|⁠, based on the relative intensity of ultraviolet (UV) lines. The latter low estimate is consistent with a more recent one by Raymond et al. (2017), for a nearby bow-shock-like structure, grounded on the measured flux in the |$\mathrm{He\, II}\, \lambda 1640$| line. One should notice however that the last two results may be affected by the fact that in both UV observations the instrument aperture intercepts only part of the emission.

To conclude, the density estimates present in the literature give a rather wide range of values and, sometimes, the assumptions to derive them are not fully justified. On the other hand our density estimates, roughly in the range 0.03–|$0.1{\, \rm cm^{-3}}$|⁠, are based on fits of the Hα radial profiles from which a reliable physical length is deduced. Such a method is quite model insensitive; our result is only mildly dependent on model parameters as shown in Table 1. In addition, our estimates would lead to an evolutionary scenario that is in reasonable agreement with the expectations. Finally, we note that the total density that we have derived is consistent with estimates from global models of the Galactic gas distribution (see e.g. Ferrière 2001, for a review): at a distance of about |$500{\, \rm pc}$| from the Galactic plane (which corresponds to the location of SN 1006 for a 2 kpc distance) the mean density is about |$10^{-2}{\, \rm cm^{-3}}$| (of course with an expected wide spread on local values).

10 DISCUSSION AND CONCLUSIONS

The main goal of this work is to show the importance to disentangle geometrical effects from the shock dynamics, in order to extract reasonable values for the physical parameters. With this in mind, the results of the present work are twofold.

On one side, we have introduced a number of techniques that are particularly effective to analyse observations of Balmer filaments when the spatial resolution is good enough to resolve the physical structure of the shock transition zone. Such techniques are especially useful if the information on the total line emission is complemented with further information on the line profile. To this respect, we have first approached the problem in a rather general way while, in the second part of the work, we showed how to further refine these techniques applying them to actual data from a portion of the northwestern filament of SN 1006. In this analysis, a crucial aspect is a proper treatment of the geometry of the emitting region. The type of bending of the shock surface may affect the observed spatial profile of the total emission, the profile of the I_b/I_n ratio, and even the observed width of the broad-line component; and in some cases, the structure of bending can be too complex to be modelled by a constant curvature profile. For such complications, photometry cannot be used as the primary method to estimate densities, because of the uncertainties on the path length of the emitting region along the LOS. In addition, spectral offsets of the barycentre of the broad-line component, once combined with other information, can be used to estimate the level of density inhomogeneities, and their spatial scales, in the ambient medium reached by the shock.

On the other side, we have obtained estimates of some physical parameters for the analysed region of the limb of SN 1006, which are not at all trivial, and that in some cases are considerably different from what has been estimated or assumed in previous works.

In the previous section, we have already discussed the matter of the ambient density. Another important parameter is the upstream neutral fraction. Our results are consistent with low upstream neutral fractions, more likely in the range 0.01–0.1. This range could be compared with an outcome of Ghavamian et al. (2002), which analysed a very deep optical spectrum of a nearby portion of the northwestern rim of SN 1006. That observation allowed those authors to detect not only the Hα line, but also the Hβ and Hγ lines, and for the first time the |$\mathrm{He\, I}\, \lambda 6678$| and (marginally) the |$\mathrm{He\, II}\, \lambda 4686$| lines. Among others, they have presented a diagnostic diagram that links the |$\mathrm{He\, I}/{\mathrm{H}}\alpha$| ratio, the equilibration fraction, and the neutral fraction (see their fig. 7). On the basis of that diagram, Ghavamian et al. (2002) estimate into 10 per cent the upstream neutral fraction for hydrogen, even though a neutral fraction as low as 3 per cent would still be compatible with the data, and then with our results. Moreover, we notice that a low neutral fraction is indeed expected when the total density is low because, while the radiative ionization time is independent of density, the recombination time-scales like the inverse of the density. In principle one could estimate the actual neutral density knowing the local radiation field, which goes, however, beyond the scope of the present work.

Finally, we have shown several pieces of evidence of the presence of consistent ambient density variations over length scales of some tenths of a pc: this follows for instance from the density estimates different by a factor ∼3 between the outer limb and the bright inner filament; from the measurements of offsets of the broad-line barycentre that lead to variations larger than 50 per cent; from the rather smooth spatial dependence of these offsets, over scales of about 0.1–0.2 pc, as well as from an observed I_b/I_n spatial profile that is not well fitted by a single-density model.

If one uses the approximate proportionality |$V_\mathrm{sh}\propto n_0^{-1/2}$| (see above), this result may seems in conflict with the stringent upper limit measured for the difference between the shock velocity in the outer limb and that in the bright filament. But this is not straightforward: being the thickness of the layer smaller than the typical length-scales of the observed perturbations of the shock surface (as from the Hα image), the sound crossing time may be too long to ensure an effective pressure balance. In addition, if ambient density fluctuations (or other causes) trigger small stable oscillations about a steady state, it is consequent that the instantaneous velocity differences with respect to the steady-state solution vanish when the elongation is maximum. Only a more detailed analysis, which is beyond the scopes of this work, could aim at clarifying this sort of issues.

In the present work, we kept fixed the assumed shock velocity (V_sh), and the level of temperature equilibration between electrons and protons (T_e/T_p), in order to calculate the numerical model that we have then used in our fits to the data. We have then found a rather good match to the data so that the most likely values for V_sh and T_e/T_p should not be very different from those we have used here. A further more accurate analysis would be advisable; an analysis based on a much finer grid of numerical models, able to refine at the same time also the two quantities above. However, in order to improve sufficiently the models one should take also into account the effect of Lyβ scattering on the spatial profile of the emission of the Hα narrow-line component: a full treatment of it will be presented in a forthcoming paper. This effect, and all its consequences on spatially resolved emission models, will be the subject of a forthcoming paper.

To conclude, the physical and geometrical models discussed in this paper are important for estimating the degree of ambiguity in the physical interpretation of existing data; but the kind of analysis presented here can develop its maximal diagnostic potential only in the presence of data with at the same time a very high spatial resolution and a sufficient spectral resolution to clearly resolve the line profile in each point. Such data quality level will be hopefully reached in a near future using, for instance, a combination of adaptive optics and integral field spectrometry. Another requirement for the shock transition zone to be resolved is that the SNR under investigation is a very close one and/or expands in a low-density medium: the best such sources are SN 1006 and the Cygnus Loop, plus possibly a few other nearby Galactic SNRs. In addition, previous works have also shown the huge diagnostic potential of combined analyses of H and He optical lines (e.g. Ghavamian et al. 2002), as well as of UV lines (e.g. Laming et al. 1996; Raymond et al. 2017): an optimal diagnostic analysis should then be able to effectively combine all these different pieces of information.

ACKNOWLEDGEMENTS

We are grateful to an anonymous referee for a careful reading of the paper and for all the suggestions that allowed us to improve the quality of the paper. GM and RB acknowledge the financial support from the ASI-INAF agreement no. 2017-14-H.0 ‘Attività di Studio per la comunità scientifica di Astrofisica delle Alte Energie e Fisica Astroparticellare – Analisi dati, Teoria e Simulazioni’. SK was supported by the Ministry of Education, Science and Technological Development of the Republic of Serbia through project no. 176021, ‘Visible and Invisible Matter in Nearby Galaxies: Theory and Observations’. JCR was supported by Guest Investigator grant HST-GO-13435.001 from the Space Telescope Science Institute.

Finally, we thank Anita Morlino for not being born too soon, giving us enough time to finish this work.

Footnotes

1

Notice that, if the ram-pressure scaling law is applied to the NW filament, the upper limit on the proper motion difference between the front and back edges shown in Fig. 21 seems in contradiction with the measured density contrast. Nevertheless, such a scaling law cannot be used straightforwardly in the case of a curved shock front: indeed, convex or concave curvatures give rise to divergent or convergent flows immediately downstream, a fact that can produce turbulence, affecting the velocity and pressure patterns. Hence, a more detailed model is required before drawing firm conclusions.

REFERENCES

Acero

F.

,

Ballet

J.

,

Decourchelle

A.

,

2007

,

A&A

,

475

,

883

10.1051/0004-6361/200913916

Acero

F.

, et al. ,

2010

,

A&A

,

516

,

A62

Bamba

A.

,

Yamazaki

R.

,

Ueno

M.

,

Koyama

K.

,

2003

,

ApJ

,

589

,

827

10.1086/374687

10.1088/0004-637X/755/2/121

Blasi

P.

,

Morlino

G.

,

Bandiera

R.

,

Amato

E.

,

Caprioli

D.

,

2012

,

ApJ

,

755

,

121

Chevalier

R. A.

,

1982

,

ApJ

,

258

,

790

10.1086/160126

Chevalier

R. A.

,

Raymond

J. C.

,

1978

,

ApJ

,

225

,

27L

10.1086/182785

Chevalier

R. A.

,

Kirshner

R. P.

,

Raymond

J. C.

,

1980

,

ApJ

,

235

,

186

10.1086/157623

10.1088/0034-4885/46/8/002

Drury

L’O. C.

,

1983

,

Rep. Prog. Phys.

,

49

,

973

10.1051/0004-6361:20020365

Dubner

G. M.

,

Giacani

E. B.

,

Goss

W. M.

,

Green

A. J.

,

Nyman

L.

,

2002

,

A&A

,

387

,

1047

10.1103/RevModPhys.73.1031

Ferrière

K. M.

,

2001

,

Rev. Mod. Phys.

,

73

,

1031

Ghavamian

P.

,

Raymond

J.

,

Smith

R. C.

,

Hartigan

P.

,

2001

,

ApJ

,

47

,

995

10.1086/318408

Ghavamian

P.

,

Winkler

P. F.

,

Raymond

J. C.

,

Long

K. S.

,

2002

,

ApJ

,

572

,

888

10.1086/340437

Ghavamian

P.

,

Laming

J. M.

,

Rakowski

C. E.

,

2007

,

ApJ

,

654

,

L69

10.1086/510740

10.1007/s11214-013-9999-0

Ghavamian

P.

,

Schwartz

S. J.

,

Mitchell

J.

,

Masters

A.

,

Laming

J. M.

,

2013

,

Space Sci. Rev.

,

178

,

633

Ghavamian

P.

,

Seitenzahl

I. R.

,

Vogt

F. P. A.

,

Dopita

M. A.

,

Terry

J. P.

,

Williams

B. J.

,

Winkler

P. F.

,

Laming

J. M.

,

2017

,

ApJ

,

847

,

122

10.3847/1538-4357/aa83b8

10.1088/2041-8205/719/2/L140

Helder

E. A.

,

Kosenko

D.

,

Vink

J.

,

2010

,

ApJ

,

719

,

L140

Helder

E. A.

,

Vink

J.

,

Bamba

A.

,

Bleeker

J. A. M.

,

Burrows

D. N.

,

Ghavamian

P.

,

Yamazaki

R.

,

2013

,

MNRAS

,

435

,

910

10.1093/mnras/stt993

Heng

K.

,

McCray

R.

,

2007

,

ApJ

,

654

,

923

10.1086/509601

Heng

K.

,

van Adelsberg

M.

,

McCray

R.

,

Raymond

J. C.

,

2007

,

ApJ

,

668

,

27

10.1086/521298

Hester

J. J.

,

1987

,

ApJ

,

314

,

187

10.1086/165049

Hester

J. J.

,

Raymond

J. C.

,

Blair

W. P.

,

1994

,

ApJ

,

420

,

721

10.1086/173598

10.3847/2041-8205/819/2/L32

Katsuda

S.

et al. ,

2016

,

ApJ

,

819

,

L32

Knežević

S.

et al. ,

2017

,

ApJ

,

846

,

167

10.3847/1538-4357/aa8323

Korreck

K. E.

,

Raymond

J. C.

,

Zurbuchen

T. H.

,

Ghavamian

P.

,

2004

,

ApJ

,

615

,

280

10.1086/424481

Laming

J. M.

,

Raymond

J. C.

,

McLaughlin

B. M.

,

Blair

W. P.

,

1996

,

ApJ

,

472

,

267

10.1086/178061

Lee

J.-J.

et al. ,

2007

,

ApJ

,

659

,

L133

10.1086/517520

10.1088/2041-8205/715/2/L146

Lee

J.-J.

et al. ,

2010

,

ApJ

,

715

,

L146

Lim

A. J.

,

Raga

A. C.

,

1996

,

MNRAS

,

280

,

103

10.1093/mnras/280.1.103

Long

K. S.

,

Reynolds

S. P.

,

Raymond

J. C.

,

Winkler

P. F.

,

Dyer

K. K.

,

Petre

R.

,

2003

,

ApJ

,

586

,

1162

10.1086/367832

10.1051/0004-6361/201219766

Miceli

M.

,

Bocchino

F.

,

Decourchelle

A.

,

Maurin

G.

,

Vink

J.

,

Orlando

S.

,

Reale

F.

,

Broersen

S.

,

2012

,

A&A

,

546

,

A66

10.1088/0004-637X/760/2/137

Morlino

G.

,

Bandiera

R.

,

Blasi

P.

,

Amato

E.

,

2012

,

ApJ

,

760

,

137

10.1088/0004-637X/768/2/148

Morlino

G.

,

Blasi

P.

,

Bandiera

R.

,

Amato

E.

,

Caprioli

D.

,

2013a

,

ApJ

,

768

,

148

10.1051/0004-6361/201322006

Morlino

G.

,

Blasi

P.

,

Bandiera

R.

,

Amato

E.

,

2013b

,

A&A

,

558

,

A25

10.1051/0004-6361/201322986

Morlino

G.

,

Blasi

P.

,

Bandiera

R.

,

Amato

E.

,

2014

,

A&A

,

562

,

A141

Nikolić

S.

,

van de Ven

G

,

Heng

K.

,

Kupko

D.

,

Husemann

B.

,

Raymond

J. C.

,

Hughes

J. P.

,

Falcón-Barroso

J.

,

2013

,

Science

,

340

,

45

10.1126/science.1228297

PubMed

Rakowski

C. E.

,

Ghavamian

P.

,

Hughes

J. P.

,

2003

,

ApJ

,

590

,

846

10.1086/375162

Raymond

J. C.

,

Korreck

K. E.

,

Sedlacek

Q. C.

,

Blair

W. P.

,

Ghavamian

P.

,

Sankrit

R.

,

2007

,

ApJ

,

659

,

1257

10.1086/512483

Raymond

J. C.

,

Winkler

P. F.

,

Blair

W. P.

,

Laming

J. M.R.

,

2017

,

ApJ

,

851

,

12

10.3847/1538-4357/aa998f

10.1088/0004-637X/803/2/98

Shimoda

J.

,

Inoue

T.

,

Ohira

Y.

,

Yamazaki

R.

,

Bamba

A.

,

Vink

J.

,

2015

,

ApJ

,

803

,

98

Skilling

J.

,

1971

,

ApJ

,

170

,

265

10.1086/151210

Smith

R. C.

,

Kirshner

R. P.

,

Blair

W. P.

,

Winkler

P. F.

,

1991

,

ApJ

,

375

,

652

10.1086/170228

Smith

R. C.

,

Raymond

J. C.

,

Laming

J. M.

,

1994

,

ApJ

,

420

,

286

10.1086/173558

Sollerman

J.

,

Ghavamian

P.

,

Lundqvist

P.

,

Smith

R. C.

,

2003

,

A&A

,

407

,

249

van Adelsberg

M.

,

Heng

K.

,

McCray

R.

,

Raymond

J. C.

,

2008

,

ApJ

,

689

,

1089

10.1086/592680

Winkler

P. F.

,

Long

K. S.

,

1997

,

ApJ

,

491

,

829

10.1086/304969

Winkler

P. F.

,

Gupta

G.

,

Long

K. S.

,

2003

,

ApJ

,

585

,

324

10.1086/345985

10.1088/0004-637X/764/2/156

Winkler

P. F.

,

Williams

B. J.

,

Blair

W. P.

,

Borkowski

K. J.

,

Ghavamian

P.

,

Long

K. S.

,

Raymond

J. C.

,

Reynolds

S. P.

,

2013

,

ApJ

,

764

,

156

10.1088/0004-637X/781/2/65

Winkler

P. F.

,

Williams

B. J.

,

Reynolds

S. P.

,

Petre

R.

,

Long

K. S.

,

Katsuda

S.

,

Hwang

U.

,

2014

,

ApJ

,

781

,

65

10.3847/0004-637X/823/1/44

Xing

Y.

,

Wang

Z.

,

Zhang

X.

,

Chen

Y.

,

2016

,

ApJ

,

823

,

44