-
PDF
- Split View
-
Views
-
Cite
Cite
Masaaki Otsuka, Physical properties of the fullerene C60-containing planetary nebula SaSt2-3, Monthly Notices of the Royal Astronomical Society, Volume 482, Issue 2, January 2019, Pages 2354–2373, https://doi.org/10.1093/mnras/sty2733
Close - Share Icon Share
ABSTRACT
We perform a detailed analysis of the fullerene C60-containing planetary nebula (PN) SaSt2-3 to investigate the physical properties of the central star (B0-1II) and nebula based on our own Subaru/HDS spectra and multiwavelength archival data. By assessing the stellar absorption, we derive the effective temperature, surface gravity, and photospheric abundances. For the first time, we report time variability of the central star’s radial velocity, strongly indicating a binary central star. Comparison between the derived elemental abundances and those predicted values by asymptotic giant branch (AGB) star nucleosynthesis models indicates that the progenitor is a star with initial mass of ∼1.25 M|$\odot$| and metallicity Z = 0.001/α-element/Cl-rich ([α,Cl/Fe] ∼ +0.3–0.4). We determine the distance (11.33 kpc) to be consistent with the post-AGB evolution of 1.25 M|$\odot$| initial mass stars with Z = 0.001. Using the photoionization model, we fully reproduce the derived quantities by adopting a cylindrically shaped nebula. We derive the mass fraction of the C-atoms present in atomic gas, graphite grain, and C60. The highest mass fraction of C60 (∼0.19 per cent) indicates that SaSt2-3 is the C60-richest PN amongst Galactic PNe. From comparison of stellar/nebular properties with other C60 PNe, we conclude that the C60 formation depends on the central star’s properties and its surrounding environment (e.g. binary disc), rather than the amount of C-atoms produced during the AGB phase.
1 INTRODUCTION
Mid-infrared (mid-IR) spectroscopic observations made by the Spitzer/Infrared Spectrograph (IRS, Houck et al. 2004) have recently detected fullerene C60 and C70 in a variety of space environments such as R Coronae Borealis stars (García-Hernández, Kameswara Rao & Lambert 2011a), reflection nebulae (Sellgren et al. 2010), young stellar objects (Roberts, Smith & Sarre 2012), post-asymptotic giant branch (AGB) stars (Gielen et al. 2011a,b), proto-planetary nebula (PNe; Zhang & Kwok 2011), and PN (Cami et al. 2010; García-Hernández et al. 2010, 2011b, 2012; Otsuka et al. 2013, 2014, 2016). At the moment, PNe represent the largest fraction of fullerene detection; since the first detection of the mid-IR C60 and C70 bands in the C-rich PN Tc1 by Cami et al. (2010), 24 fullerene-containing PNe have been identified in the Milky Way and the Large and Small Magellanic Clouds (LMC and SMC, respectively).
In general, C60 PNe show very similar IR dust features and stellar/nebular properties; their mid-IR spectra display broad 6−9, 11, and 30 |$\mu$|m features in addition to C60 bands at 7.0, 8.5, 17.4, and 18.9 |$\mu$|m, and they have cool central stars and low-excitation nebulae, indicating that their age after the AGB phase is very young (e.g. Otsuka et al. 2014). The excitation mechanisms (e.g. Bernard-Salas et al. 2012) and the formation paths (e.g. Duley & Hu 2012; Berné, Montillaud & Joblin 2015) are not well understood and are still a subject of debate. However, it remains unclear why these objects exhibit the C60 features – is the span of time during which spectral features of C60 are present a short-lived phase that all C-rich PNe go through, or are C60 PNe distinct objects in terms of their stellar/nebular properties and/or evolution? This is directly linked to the question of how C60 forms in evolved star environments. We would like to answer this fundamental question by investigating the physical properties of C60 PNe and comparing them with non-C60 PNe.
Amongst C60 PNe, SaSt2-3 (PN G232.0+05.7, Acker et al. 1992) first identified by Sanduleak & Stephenson (1972) is a particularly interesting object to that we should pay more attention. Otsuka et al. (2014) discovered C60 bands in this PN for the first time. Surprisingly, the mid-IR C60 band strengths in SaSt2-3 and Tc1 are the strongest amongst all the fullerene-containing objects. This strongly indicates that the fullerene formation in these two PNe is particularly efficient. Tc1 has been extensively studied since the discovery of C60. However, SaSt2-3 is not entirely understood due to the lack of available data for the central star and nebula and its uncertain distance (D). The uncertain D towards SaSt2-3 has led to different estimates of the central star luminosity (L*) and effective temperature (Teff); accordingly, this has led to inconsistencies in understanding the evolutionary status of this PN (Gesicki & Zijlstra 2007; Otsuka et al. 2014). What we know from the prior studies is that this object has low-metallicity (ε(S) = 5.48,1 Pereira & Miranda 2007) and is (possibly) a Type IV PN (i.e., halo population, Pereira & Miranda 2007).
If we obtain the UV to optical wavelength spectra of the central star as well as the nebula, we can resolve issues raised and verify conclusions from previous studies of SaSt2-3; by so doing, we can hope to gain insights into the C60 formation. Fortunately, the UV-optical photometry data from the AAVSO Photometric All Sky Survey (APASS, Henden et al. 2016) can rigorously constrain L*, and Frew, Parker & Bojičić (2016) improved its distance estimate (D = 14.86 ± 4.26 kpc). Therefore, we perform a comprehensive analysis on our own high-dispersion spectra of SaSt2-3 taken using the 8.2 m Subaru telescope/high-dispersion spectrograph (HDS, Noguchi et al. 2002) and archived multiwavelength data.
We organize the next sections as follows. In Section 2, we describe our HDS spectroscopy and near-IR imaging using the NOAO WIYN 3.5 m/WIYN High-Resolution Infrared Camera (WHIRC, Meixner et al. 2010) and the reduction of this data. The Spitzer/IRS observation and its data reduction are described in Otsuka et al. (2014). In Fig. 1, we plot all the data used in the present work. In Section 3, we perform plasma diagnostics and derive ionic/elemental abundances. In Section 4, we derive photospheric elemental abundances, Teff, and surface gravity |$\log \, g$| by fitting the stellar absorption using the theoretical stellar atmosphere code tlusty (Hubeny 1988). In Section 5, we compare the derived nebular and stellar elemental abundances with those values predicted by AGB nucleosynthesis models in order to infer the initial mass of the progenitor star. In Section 6, we build the spectral energy distribution (SED) model using the photoionization code Cloudy (v.13.05, Ferland et al. 2013) to be consistent with all the derived quantities based on our determined D. In Section 7, we discuss the origin and evolution of SaSt2-3 and the C60 formation in PNe by comparison of the derived nebular/stellar properties with other non-C60 and C60-containing PNe. Finally, we summarize the present work.
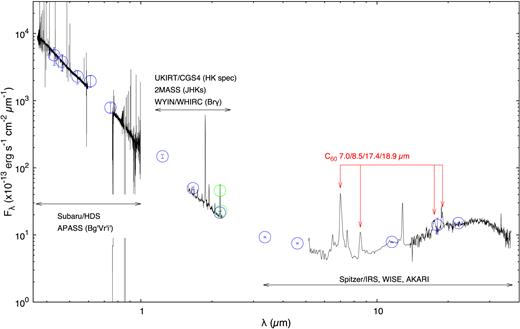
Panchromatic data of SaSt2-3 used in the present work. The green (WHIRC Brγ-on/off bands) and blue circles (the other bands) are the photometry data and the black lines are the spectra, respectively. The flux density of the Subaru/HDS spectrum is scaled to match the APASS Bg′Vr′i′-bands. The UKIRT 3.8 m/Cooled Grating Spectrometer 4 (CGS4) HK-band spectrum (we downloaded the raw data of the spectrum presented in Lumsden, Puxley & Hoare (2001) from the UKIRT archive data website and reduced them using iraf) is scaled to match the 2MASS Ks-band. The Spitzer/IRS spectrum is scaled to match the WISE/W3 and W4 and AKARI L18W bands.
2 DATA SET AND REDUCTION
2.1 Subaru/HDS observation
We secured high-dispersion Echelle spectra using the HDS located at one of the Nasmyth loci of the 8.2 m Subaru Telescope at the top of Mauna Kea in Hawai’i. We summarize our observations in Table 1. We selected the 2 × 2 on-chip binning pattern. We set the slit-width to be 1.2″. We used the blue cross disperser for the 3640−5390 Å observation and the red one for the 4740−7490 Å and 7190−9960 Å observations, respectively. We utilized the atmospheric dispersion corrector (ADC) during the observations. In all the observations, we observed the standard star Hiltner 600 for correcting Echelle blaze functions and flux density simultaneously. In the 7190−9960 Å observation, we observed the telluric standard stars HD 61017 (B9III, mV = 6.68) and HD 62217 (B9V, mV = 8.26) at similar airmass.
| Date . | λ (Å) . | |$\lambda /\delta \, \lambda$| (ave.) . | Exp. time . | Condition/Seeing . |
|---|---|---|---|---|
| 2013/10/06 | 3640−5390 | 33 500 | 2 × 200 s, 2600 s | Thin cloud, ∼0.7″ |
| 2013/12/10 | 4740−7490 | 33 300 | 100, 500, 900 s | Clear, ∼0.7″ |
| 2016/02/01 | 7190−9960 | 32 300 | 180 s, 4 × 1600 s | Clear, ∼0.7−1.0″ |
| Date | Band | Pixel scale | Exp. time | Condition/Seeing |
| 2013/04/24 | Brγ, Brγ45 | 0.1″ × 0.1″ | 5 pts × 120 s | Clear, ∼0.6−0.7″ |
| Date . | λ (Å) . | |$\lambda /\delta \, \lambda$| (ave.) . | Exp. time . | Condition/Seeing . |
|---|---|---|---|---|
| 2013/10/06 | 3640−5390 | 33 500 | 2 × 200 s, 2600 s | Thin cloud, ∼0.7″ |
| 2013/12/10 | 4740−7490 | 33 300 | 100, 500, 900 s | Clear, ∼0.7″ |
| 2016/02/01 | 7190−9960 | 32 300 | 180 s, 4 × 1600 s | Clear, ∼0.7−1.0″ |
| Date | Band | Pixel scale | Exp. time | Condition/Seeing |
| 2013/04/24 | Brγ, Brγ45 | 0.1″ × 0.1″ | 5 pts × 120 s | Clear, ∼0.6−0.7″ |
| Date . | λ (Å) . | |$\lambda /\delta \, \lambda$| (ave.) . | Exp. time . | Condition/Seeing . |
|---|---|---|---|---|
| 2013/10/06 | 3640−5390 | 33 500 | 2 × 200 s, 2600 s | Thin cloud, ∼0.7″ |
| 2013/12/10 | 4740−7490 | 33 300 | 100, 500, 900 s | Clear, ∼0.7″ |
| 2016/02/01 | 7190−9960 | 32 300 | 180 s, 4 × 1600 s | Clear, ∼0.7−1.0″ |
| Date | Band | Pixel scale | Exp. time | Condition/Seeing |
| 2013/04/24 | Brγ, Brγ45 | 0.1″ × 0.1″ | 5 pts × 120 s | Clear, ∼0.6−0.7″ |
| Date . | λ (Å) . | |$\lambda /\delta \, \lambda$| (ave.) . | Exp. time . | Condition/Seeing . |
|---|---|---|---|---|
| 2013/10/06 | 3640−5390 | 33 500 | 2 × 200 s, 2600 s | Thin cloud, ∼0.7″ |
| 2013/12/10 | 4740−7490 | 33 300 | 100, 500, 900 s | Clear, ∼0.7″ |
| 2016/02/01 | 7190−9960 | 32 300 | 180 s, 4 × 1600 s | Clear, ∼0.7−1.0″ |
| Date | Band | Pixel scale | Exp. time | Condition/Seeing |
| 2013/04/24 | Brγ, Brγ45 | 0.1″ × 0.1″ | 5 pts × 120 s | Clear, ∼0.6−0.7″ |
We reduced the data using iraf2 in a standard manner, including over-scan subtraction, scattered light subtraction between Echelle orders, and telluric absorption removal. We adopted the atmospheric extinction correction function measured by Buton et al. (2013) at Mauna Kea. We measured the actual spectral resolution (|$R = \lambda /\delta {\lambda } =$| 32 300−33 500, see Table 1) using >300 Th–Ar comparison lines. The signal-to-noise ratio (S/N) for continuum reaches ∼40 at ∼3640 Å and ∼11 at ∼9950 Å. In ∼3700−4800 Å (this range is important in stellar absorption fittings), S/N is >70. We scaled both spectra to the average flux density in the overlapping regions (4740−5390 Å and 7190−7490 Å), and we connected these scaled spectra into a single 3640−9960 Å spectrum. The resultant spectrum is presented in Fig. 1.
2.2 Flux measurements and interstellar extinction correction
We determine c(Hβ) values by comparing the observed Balmer and Paschen line ratios to Hβ with the theoretical ratios of Storey & Hummer (1995) for the case with an electron temperature Te = 104 K and an electron density ne = 2000 cm−3 under the Case B assumption. We calculate this ne using the [O ii] F(3726 Å)/F(3729 Å) and the [Cl iii] F(5517 Å)/F(5537 Å) ratios. For the 3640−5390 Å spectrum, we obtain c(Hβ) = 0.20 ± 0.01, which is the intensity-weight average amongst the Hγ, Hδ, Hε, and Hη to the Hβ ratios. For the 4740−7490 Å spectrum, we obtain c(Hβ) = 0.40 ± 0.01 from the Hα/Hβ ratio. For the 7190−9960 Å spectrum, we determine c(Hβ) = 0.24 ± 0.03 from the Paschen H i 9014 Å (P10) to the Hβ ratio. For all HDS spectra, we adopt the average c(Hβ) = 0.28 ± 0.11 amongst three HDS observations.
Tylenda et al. (1992) reported c(Hβ) = 1.11 (observation date is unknown). We derive the average c(Hβ) = 1.11 ± 0.26 using the ratio of F(Hα), F(Hγ), and F(Hδ) to F(Hβ) measured from their spectra.3 Based on the F(Hα) and F(Hβ) reported by Dopita & Hua (1997), we obtain c(Hβ) = 0.43 ± 0.04 (obs date: 1997 March). Pereira & Miranda (2007) reported E(B − V) = 0.11 ± 0.02, which corresponds to c(Hβ) = 0.13−0.19 (obs date: 2005 Feb.). Using the line flux table of Pereira & Miranda (2007), we obtain the average c(Hβ) = 0.41 ± 0.23 calculated from F(Hα), F(Hγ), and F(P10) to F(Hβ). Using the archived ESO Faint Object Spectrograph and Camera (EFOSC) spectrum taken on 2000 April,4 we obtain a c(Hβ) = 0.68 ± 0.11 measured from the F(Hα)/F(Hβ) ratio. A time variation of c(Hβ) seen between 1992 and 2016 might be due to the effect of stellar H i absorption to corresponding nebular H i and also orbital motion of the binary central star (Section 4.2).
We scale the Spitzer/IRS spectrum to match the Wide-field Infrared Survey Explorer (WISE) W3/W4 band flux densities of Cutri (2013) and the L18W AKARI/IRC mid-infrared all-sky survey of Ishihara et al. (2010) (see Section 2.4). For this scaled Spitzer/IRS spectrum, we do not correct interstellar extinction because the interstellar extinction is negligibly small in the mid-IR wavelength. It is common practice in nebular analyses to scale all line intensities in such a way that Hβ has a line flux of 100. To achieve this, we first normalize the line fluxes with respect to the complex of the H i 7.46 |$\mu$|m (n = 5−6, n is the quantum number) and 7.50 |$\mu$|m (n = 6−8) lines. F(7.48/7.50 |$\mu$|m) is (4.87 ± 0.30) × 10−15 erg s−1 cm−2 (A(−B) means A × 10−B hereafter). According to Storey & Hummer (1995) for the Case B assumption with Te = 104 K and ne = 2000 cm−3, the ratio of H iI(7.48/7.50 |$\mu$|m)/I(Hβ) = 3.102/100. Finally, we multiply all the normalized line fluxes by 3.102 to express them relative to Hβ with I(Hβ) = 100.
In Appendix Table A1, we list the identified emission lines in the Subaru/HDS and Spitzer/IRS spectra. The first column is the laboratory wavelength in air. Here, I(Hβ) is 100. The last column δ I(λ) corresponds to 1-σ.
2.3 NOAO/WHIRC near-IR imaging observation
We took the high-resolution images using NOAO WIYN 3.5 m/WHIRC. We summarize the observation log in Table 1. We took the two narrowband images using the Brγ (λc = 2.162 |$\mu$|m, effective bandwidth (Weff) = 0.210 |$\mu$|m), and Brγ45 (λc = 2.188 |$\mu$|m, Weff = 0.245 |$\mu$|m) filters.5 We selected a 5 pts dithering pattern. We followed a standard manner for near-IR imaging data reductions using iraf, including background sky and dark current subtraction, bad pixel masking, flat-fielding, and distortion correction. Finally, we obtained a single averaged image for each band.
For the flux calibration, we utilized the SED of the standard star 2MASS07480394−1407155 based on its photometry between the 2 micron all sky survey (2MASS, Cutri et al. 2003) JHKs and WISE bands W1/W2. The SED of this star can be well fitted with a single blackbody temperature of 3510 K. Then, we derived the flux density in each band by taking each filter transmission curve into account. Next, we measured the respective count of the standard star in the Brγ and Brγ45 images. Thus, we obtained the conversion factor from the counts in ADU to flux density in erg s−1 cm−2 |$\mu$|m−1. The measured flux density in each band is listed in Appendix Table A2 and plotted in Fig. 1 (green circles).
2.4 Photometry data
To support the present work, we collected the data taken from APASS, 2MASS, WISE, and AKARI/Infrared Camera (IRC). In Table A2, we list the observed and reddening corrected flux densities Fλ and Iλ, respectively. We obtain Iλ using equation (1) and the average c(Hβ) = 0.28 ± 0.11 amongst three HDS observations (Section 2.2). Due to negligibly small reddening effect, we do not correct Fλ in the longer wavelength than WISE W1 band (3.35 |$\mu$|m).
3 NEBULAR LINE ANALYSIS
3.1 Systemic nebular radial velocity
We obtain the average heliocentric radial velocity of +166.6 km s−1 measured from the identified 128 nebular lines in the HDS spectrum (the standard deviation is 3.2 km s−1 amongst all these lines and that of each radial velocity is 0.52 km s−1 in the average). The LSR radial velocity vr(LSR) of +149.1 km s−1 is much faster than vr(LSR) in other Galactic PNe towards l ∼220−240° and b ≲ ±10° (≲ +80 km s−1; Quireza, Rocha-Pinto & Maciel 2007). vr(LSR) of +105 km s−1 in the C60 PN M1-9 (PN G214.0+04.3, Otsuka et al. 2014) is the closest to SaSt2-3’s vr(LSR) (Quireza et al. 2007). Peculiar velocity relative to Galactic rotation is calculated using vr(LSR) and D in order to classify PNe into Type I-IV (i.e. thin/thick disc and halo; see e.g. Peimbert 1978). We discuss classification of SaSt2-3 in Section 7.1. We do not find a time-variation of the radial velocity measured by the nebular lines. We report the radial velocity measurements from the stellar absorption in Section 4.2.
3.2 H β flux of the entire nebula
From the measured F(H i 7.48/7.50 |$\mu$|m) and the theoretical I(H i 7.48/7.50 |$\mu$|m)/I(Hβ) ratio = 3.102/100 (see Section 2.2), we obtain I(Hβ) of the entire nebula to be (1.57 ± 0.28)(−12) erg s−1 cm−2. F(Hα) and F(H β) using the 5″ wide slit observation by Dopita & Hua (1997) and c(Hβ) = 0.43 ± 0.04 (Section 2.2) yields I(Hβ) = (1.97 ± 0.20)(−12) erg s−1 cm−2, which is consistent with ours. In the present work, we adopt our own calculated I(Hβ) for the entire nebula because our I(Hβ) is based on interstellar extinction-free and stellar H i absorption effect less mid-IR H i 7.48/7.50 |$\mu$|m.
3.3 Plasma diagnostics
We determine ne and Te using diagnostic line ratios listed in Table 2, with the resulting ne – Te diagnostic curves for the collisionally excited lines (CELs) shown in Fig. 2. The roughly vertical (blue) lines can be used to determine ne; more horizontal (grey) lines Te. Although the other diagnostic curves (red) yield both ne and Te, we use them as Te indicators here. Since the emission of each ion originates from regions of different Te and ne, we need to determine both parameters for each ion independently so that we can determine accurate ionic abundances later on. This involves several steps. First, we note that Te ∼9000 K from Te([Ar iii]), Te([S iii])opt, and Te([N ii]) curves. Next, we adopt Te = 9000 K to solve each equation of population at ≥ 5 multiple energy levels for each ne sensitive ions; from this, we then calculate ne from the corresponding diagnostic line ratios for [N i], [S ii], [O ii], [Cl iii], and [S iii] (see Table 2). Note that the precise Te we assume here does not matter much, since these ne diagnostic line ratios are fairly insensitive to Te. With the ne values established, we then determine Te by adopting the derived ne values corresponding to each ion. We adopt ne([O ii]) for Te([N ii]) derivation. Our derived values are in agreement with those by Pereira & Miranda (2007) who found ne([S ii]) = 2100 ± 600 cm−3 and Te([N ii]) = 9600 ± 930 K.
![ne – Te diagram of SaSt2-3. ne, Te, and both ne and Te diagnostic curves are indicated by the blue, grey, and red lines, respectively. Te([S iii])opt and Te([S iii])opt/ir curves are the result of the [S iii] I(9069 Å)/I(6313 Å) and [S iii] I(9069 Å)/I(18.71/33.47 $\mu$m) ratios, respectively. See also Table 2.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/482/2/10.1093_mnras_sty2733/2/m_sty2733fig2.jpeg?Expires=1749907934&Signature=EwilIAoWqNHXlLa11s576GBTrIaoD75Ea09ZbLA~qBV8faHNkUWfVLIvY0aPc8gCBDizxjsKCJdvMzW9~9DeUMIgZBD6wxnbnrnnKa4wl76nlwYiM2XDdPHEDdQgF0XTHNADNRhh5Depay3YSHK9LnfPPI~J3xiifG2mKl0vY1QX3DjbgXEXuIlKC1IPNJNuTf4hDhWk-MdD9f7mtPMxRMtn-LetjVur6gJqbCfkHbt-foJ4cT6tNq~MaKlWWrhTyO7NYdHD5Mpc4bdhir-kdr08EOEhRwxEoIcnwXcgSdasvBON7Y7kEY0aiFwC-cU0O~fCkdBCyKkhPgwehAyZQQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
ne – Te diagram of SaSt2-3. ne, Te, and both ne and Te diagnostic curves are indicated by the blue, grey, and red lines, respectively. Te([S iii])opt and Te([S iii])opt/ir curves are the result of the [S iii] I(9069 Å)/I(6313 Å) and [S iii] I(9069 Å)/I(18.71/33.47 |$\mu$|m) ratios, respectively. See also Table 2.
Summary of plasma diagnostics. Since the lower limit [N i] I(5198 Å)/I(5200 Å) ratio is out of the range of the ne([N i]) derivation, we give the upper limit ne([N i]) = 1460 cm−3.
| CEL ne-diagnostic line ratio . | Ratio . | Result (cm−3) . |
|---|---|---|
| N i I(5198 Å)/I(5200 Å) | 1.088 ± 0.498 | 460 |
| [S ii] I(6717 Å)/I(6731 Å) | 0.663 ± 0.074 | 2680 ± 1070 |
| [O ii] I(3726 Å)/I(3729 Å) | 1.440 ± 0.163 | 1560 ± 490 |
| [Cl iii] I(5517 Å)/I(5537 Å) | 1.048 ± 0.130 | 2180 ± 1070 |
| [S iii] I(18.71 |$\mu$|m)/I(33.47 |$\mu$|m) | 1.314 ± 0.334 | 1190 ± 570 |
| CEL Te-diagnostic line ratio | Ratio | Result (K) |
| [N ii] I(6548/83 Å)/I(5755 Å) | 114.881 ± 8.621 | 9200 ± 260 |
| [S iii] I(9069 Å)/I(6313 Å) | 14.443 ± 2.558 | 8530 ± 570 |
| [Ar iii] I(7135/7751 Å)/I(8.99 |$\mu$|m) | 0.952 ± 0.197 | 8250 ± 790 |
| CEL ne & Te-diagnostic line ratio | Ratio | Result (K) |
| [S ii] I(6717/31 Å)/I(4069 Å) | 10.322 ± 0.958 | 7220 ± 430 |
| [O ii] I(3726/3729 Å)/I(7320/30 Å) | 26.725 ± 2.103 | 9670 ± 430 |
| [S iii] I(9069 Å)/I(18.71/33.47 |$\mu$|m) | 0.278 ± 0.054 | 11 040 ± 1860 |
| RL Te-diagnostic line ratio | Ratio | Result (K) |
| |$[I_{\lambda }(8194\, {\mathring{\rm A} }) - I_{\lambda }(8169\, {\mathring{\rm A} })]/I$|(P11) | 0.022 ± 0.004 | 7340 ± 2610 |
| He i I(7281 Å)/I(6678 Å) | 0.256 ± 0.036 | 11 830 ± 1790 |
| CEL ne-diagnostic line ratio . | Ratio . | Result (cm−3) . |
|---|---|---|
| N i I(5198 Å)/I(5200 Å) | 1.088 ± 0.498 | 460 |
| [S ii] I(6717 Å)/I(6731 Å) | 0.663 ± 0.074 | 2680 ± 1070 |
| [O ii] I(3726 Å)/I(3729 Å) | 1.440 ± 0.163 | 1560 ± 490 |
| [Cl iii] I(5517 Å)/I(5537 Å) | 1.048 ± 0.130 | 2180 ± 1070 |
| [S iii] I(18.71 |$\mu$|m)/I(33.47 |$\mu$|m) | 1.314 ± 0.334 | 1190 ± 570 |
| CEL Te-diagnostic line ratio | Ratio | Result (K) |
| [N ii] I(6548/83 Å)/I(5755 Å) | 114.881 ± 8.621 | 9200 ± 260 |
| [S iii] I(9069 Å)/I(6313 Å) | 14.443 ± 2.558 | 8530 ± 570 |
| [Ar iii] I(7135/7751 Å)/I(8.99 |$\mu$|m) | 0.952 ± 0.197 | 8250 ± 790 |
| CEL ne & Te-diagnostic line ratio | Ratio | Result (K) |
| [S ii] I(6717/31 Å)/I(4069 Å) | 10.322 ± 0.958 | 7220 ± 430 |
| [O ii] I(3726/3729 Å)/I(7320/30 Å) | 26.725 ± 2.103 | 9670 ± 430 |
| [S iii] I(9069 Å)/I(18.71/33.47 |$\mu$|m) | 0.278 ± 0.054 | 11 040 ± 1860 |
| RL Te-diagnostic line ratio | Ratio | Result (K) |
| |$[I_{\lambda }(8194\, {\mathring{\rm A} }) - I_{\lambda }(8169\, {\mathring{\rm A} })]/I$|(P11) | 0.022 ± 0.004 | 7340 ± 2610 |
| He i I(7281 Å)/I(6678 Å) | 0.256 ± 0.036 | 11 830 ± 1790 |
Summary of plasma diagnostics. Since the lower limit [N i] I(5198 Å)/I(5200 Å) ratio is out of the range of the ne([N i]) derivation, we give the upper limit ne([N i]) = 1460 cm−3.
| CEL ne-diagnostic line ratio . | Ratio . | Result (cm−3) . |
|---|---|---|
| N i I(5198 Å)/I(5200 Å) | 1.088 ± 0.498 | 460 |
| [S ii] I(6717 Å)/I(6731 Å) | 0.663 ± 0.074 | 2680 ± 1070 |
| [O ii] I(3726 Å)/I(3729 Å) | 1.440 ± 0.163 | 1560 ± 490 |
| [Cl iii] I(5517 Å)/I(5537 Å) | 1.048 ± 0.130 | 2180 ± 1070 |
| [S iii] I(18.71 |$\mu$|m)/I(33.47 |$\mu$|m) | 1.314 ± 0.334 | 1190 ± 570 |
| CEL Te-diagnostic line ratio | Ratio | Result (K) |
| [N ii] I(6548/83 Å)/I(5755 Å) | 114.881 ± 8.621 | 9200 ± 260 |
| [S iii] I(9069 Å)/I(6313 Å) | 14.443 ± 2.558 | 8530 ± 570 |
| [Ar iii] I(7135/7751 Å)/I(8.99 |$\mu$|m) | 0.952 ± 0.197 | 8250 ± 790 |
| CEL ne & Te-diagnostic line ratio | Ratio | Result (K) |
| [S ii] I(6717/31 Å)/I(4069 Å) | 10.322 ± 0.958 | 7220 ± 430 |
| [O ii] I(3726/3729 Å)/I(7320/30 Å) | 26.725 ± 2.103 | 9670 ± 430 |
| [S iii] I(9069 Å)/I(18.71/33.47 |$\mu$|m) | 0.278 ± 0.054 | 11 040 ± 1860 |
| RL Te-diagnostic line ratio | Ratio | Result (K) |
| |$[I_{\lambda }(8194\, {\mathring{\rm A} }) - I_{\lambda }(8169\, {\mathring{\rm A} })]/I$|(P11) | 0.022 ± 0.004 | 7340 ± 2610 |
| He i I(7281 Å)/I(6678 Å) | 0.256 ± 0.036 | 11 830 ± 1790 |
| CEL ne-diagnostic line ratio . | Ratio . | Result (cm−3) . |
|---|---|---|
| N i I(5198 Å)/I(5200 Å) | 1.088 ± 0.498 | 460 |
| [S ii] I(6717 Å)/I(6731 Å) | 0.663 ± 0.074 | 2680 ± 1070 |
| [O ii] I(3726 Å)/I(3729 Å) | 1.440 ± 0.163 | 1560 ± 490 |
| [Cl iii] I(5517 Å)/I(5537 Å) | 1.048 ± 0.130 | 2180 ± 1070 |
| [S iii] I(18.71 |$\mu$|m)/I(33.47 |$\mu$|m) | 1.314 ± 0.334 | 1190 ± 570 |
| CEL Te-diagnostic line ratio | Ratio | Result (K) |
| [N ii] I(6548/83 Å)/I(5755 Å) | 114.881 ± 8.621 | 9200 ± 260 |
| [S iii] I(9069 Å)/I(6313 Å) | 14.443 ± 2.558 | 8530 ± 570 |
| [Ar iii] I(7135/7751 Å)/I(8.99 |$\mu$|m) | 0.952 ± 0.197 | 8250 ± 790 |
| CEL ne & Te-diagnostic line ratio | Ratio | Result (K) |
| [S ii] I(6717/31 Å)/I(4069 Å) | 10.322 ± 0.958 | 7220 ± 430 |
| [O ii] I(3726/3729 Å)/I(7320/30 Å) | 26.725 ± 2.103 | 9670 ± 430 |
| [S iii] I(9069 Å)/I(18.71/33.47 |$\mu$|m) | 0.278 ± 0.054 | 11 040 ± 1860 |
| RL Te-diagnostic line ratio | Ratio | Result (K) |
| |$[I_{\lambda }(8194\, {\mathring{\rm A} }) - I_{\lambda }(8169\, {\mathring{\rm A} })]/I$|(P11) | 0.022 ± 0.004 | 7340 ± 2610 |
| He i I(7281 Å)/I(6678 Å) | 0.256 ± 0.036 | 11 830 ± 1790 |
We compute Te(He i) using singlet He i lines. To calculate Te(PJ) from the Paschen continuum discontinuity by utilizing the equation (7) of Fang & Liu (2011), first we determine the He+ abundance of 1.09(−2) ± 2.28(−4) under the obtained Te(He i). Eventually, we utilize Te(He i) for both He+ and C2+ abundance calculations due to higher Te(PJ) uncertainty.
3.4 Ionic abundance derivations
We calculate the CEL ionic abundances by solving an equation of population at multiple energy levels under the adopted Te and ne as listed in Table 3; Te = 9270 K is the average value amongst two Te([S iii]) and Te([Ar iii]), Te = 9790 K is the average value amongst two Te([S iii]), Te = 9440 K is the average between Te([N ii]) and Te([O ii]), and ne = 1690 cm−3 is the average between ne([Cl iii]) and ne([S iii]). For the recombination line (RL) He+ and C2+, we adopt Te(He i) and ne = 104 cm−3. Our choice of the Te–ne pair of each ion depends on the potential (IP) of the targeting ion. Except for the CEL N+, O+, 2+, and S+ which Pereira & Miranda (2007) already measured, the first measurements of all the ionic abundances are done by us. We summarize the resultant CEL and RL ionic abundances in Appendix Table A3. We calculate each ionic abundance using each line intensity. Then, we adopt the weight-average value as the representative ionic abundance as listed in the last line of each ion. We give 1-σ uncertainty of each ionic abundance, which accounts for the uncertainties of line fluxes (including c(Hβ) uncertainty), Te, and ne.
| Ion . | Te (K) . | ne (cm−3) . |
|---|---|---|
| N0, O0, S+ | Te([S ii]) | ne([S ii]) |
| N+ | Te([N ii]) | ne([O ii]) |
| O+ | Te([O ii]) | ne([O ii]) |
| O2+, Ne+ | 9270 ± 1070 | 1690 ± 820 |
| S2+ | 9790 ± 1220 | ne([S iii]) |
| Ar2+ | Te([Ar iii]) | 1690 ± 820 |
| Cl+, Fe2+ | 9440 ± 350 | ne([O ii]) |
| Cl2+ | 9270 ± 1070 | ne([Cl iii]) |
| Ion . | Te (K) . | ne (cm−3) . |
|---|---|---|
| N0, O0, S+ | Te([S ii]) | ne([S ii]) |
| N+ | Te([N ii]) | ne([O ii]) |
| O+ | Te([O ii]) | ne([O ii]) |
| O2+, Ne+ | 9270 ± 1070 | 1690 ± 820 |
| S2+ | 9790 ± 1220 | ne([S iii]) |
| Ar2+ | Te([Ar iii]) | 1690 ± 820 |
| Cl+, Fe2+ | 9440 ± 350 | ne([O ii]) |
| Cl2+ | 9270 ± 1070 | ne([Cl iii]) |
| Ion . | Te (K) . | ne (cm−3) . |
|---|---|---|
| N0, O0, S+ | Te([S ii]) | ne([S ii]) |
| N+ | Te([N ii]) | ne([O ii]) |
| O+ | Te([O ii]) | ne([O ii]) |
| O2+, Ne+ | 9270 ± 1070 | 1690 ± 820 |
| S2+ | 9790 ± 1220 | ne([S iii]) |
| Ar2+ | Te([Ar iii]) | 1690 ± 820 |
| Cl+, Fe2+ | 9440 ± 350 | ne([O ii]) |
| Cl2+ | 9270 ± 1070 | ne([Cl iii]) |
| Ion . | Te (K) . | ne (cm−3) . |
|---|---|---|
| N0, O0, S+ | Te([S ii]) | ne([S ii]) |
| N+ | Te([N ii]) | ne([O ii]) |
| O+ | Te([O ii]) | ne([O ii]) |
| O2+, Ne+ | 9270 ± 1070 | 1690 ± 820 |
| S2+ | 9790 ± 1220 | ne([S iii]) |
| Ar2+ | Te([Ar iii]) | 1690 ± 820 |
| Cl+, Fe2+ | 9440 ± 350 | ne([O ii]) |
| Cl2+ | 9270 ± 1070 | ne([Cl iii]) |
The He+ abundance of 9.72(−3) in SaSt2-3 is 10 times smaller than in evolved PNe (e.g. |$T_{\rm eff} \gtrsim 50\, 000$| K). For instance, in the C60 PN M1-20 (|$T_{\rm eff} = 45\, 880$| K, Otsuka et al. 2014), Wang & Liu (2007) find He+ abundance of 9.50(−2). Moreover, the He+ abundance is also significantly lower than in other Galactic C60 PNe with |$T_{\rm eff} \lesssim 40\, 000$| K where He+ abundances have been determined: 6.99(−2) in IC418 (Hyung, Aller & Feibelman 1994), 6.57(−2) in M1-6 (Otsuka in prep), 3.93(−2) in M1-11 (Otsuka et al. 2013), 3.5(−2) in M1-12 (Henry et al. 2010), and 6.0(−2) in Tc1 (Pottasch, Surendiranath & Bernard-Salas 2011). Similar to the C60 PN Lin49 in the SMC (Otsuka et al. 2016), the low He+ abundance is due to the smaller number of ionizing photons for He+ ( ≥ 21 eV): using the spectra synthesized by tlusty (with L* = 7000 L|$\odot$|, |$\log \, g$| = 3.11 cm s−2, metallicity Z = 1/10 Z|$\odot$|, see below), we estimate the number of photons with energy ≥ 21 eV to be 8.3(+45) s−1 in a |$T_{\rm eff} = 28\, 100$|K star-like SaSt2-3 (see Section 4) and 4.8(+46) s−1 in |$T_{\rm eff} = 32\, 000$|K stars like M1-11 and M1-12. Thus, the majority of the He atoms in SaSt2-3 are in the neutral state.
The higher multiplet C ii lines are generally reliable because these lines are less affected by resonance fluorescence. However, the higher C2+ abundances from the C ii 3918.98/20.69 Å (4s2S − 3p2P) and 7231.32/36.42 Å (3d2D − 3p2P) are likely due to the enhancement by resonance from the 635.25/636.99 Å (4s2S − 2p2P) and the 687 Å (3d2D − 2p2P), respectively. Thus, we exclude the C2 + abundances from these C ii lines and C ii 6451.95 Å6 in the representative RL C2+ determination.
Our N+ and O+, 2+ are comparable with Pereira & Miranda (2007), who calculated N+ = 2.42(−5), O+ = 1.87(−4), O2+ = 1.22(−6), and S+ = 3.0(−7) (they note that their derived ionic abundances has ±30|${{\ \rm per\ cent}}$| uncertainty) under Te([N ii]) = 9600 K and ne([S ii]) = 2100 cm−3. The discrepancy between their and our S+ (5.89(−7)) is caused by Te selection; if we adopt Te = 9600 K and ne = 2100 cm−3, we obtain S+ = 3.48(−7).
3.5 Elemental abundance derivations using the ICFs
To obtain the elemental abundances using the derived ionic abundances, we introduce the ionization correction factors (ICFs, see e.g. Delgado-Inglada, Morisset & Stasińska 2014, for details). Here, the number density ratio of the element X with respect to the hydrogen, n(X)/n(H) is equal to ICF(X) · ∑m = 1 n(Xm+)/n(H+). The ICFs have been empirically determined based on the fraction of observed ion number densities with similar ionization potentials to the target element, and have also been determined based on the fractions of the ions calculated by photoionization models. Since SaSt2-3 is very low-excitation PN, the ICFs (He in particular) adopted for more highly excited PNe do not work well. Therefore, we need a special treatment for SaSt2-3. Thus, in addition to the ICFs established by photoionization grid models of Delgado-Inglada et al. (2014), we refer to ICFs used in Lin49 by Otsuka et al. (2016).
In Lin49, the C2+/C ratio is similar to the Ar2+/Ar ratio. For SaSt2-3, we adopt equation (A6) of Otsuka et al. (2016) for C and Ar. Both ICF(C) and ICF(Ar) are 2.7 · (Cl/Cl2+) = 5.12 ± 1.41. For He derivation, we adopt two ICF(He) calculated using the equation (42) of Peimbert & Costero (1969, 11.57) and from the ratio of Ar/Ar2 + (5.12). ICF(N) = 1.04 ± 0.13 is from Delgado-Inglada et al. (2014). ICF(Fe) = 1.31 ± 0.16 is from Delgado-Inglada & Rodríguez (2014) based on the observation results. ICF of the other elements is unity. We verify whether the adopted ICFs here are proper by comparing with Cloudy photoionization model (Section 6).
In the second and third columns of Table 4, we present the resultant elemental abundances with 1-σ uncertainty, except for ε(He), where we adopt its range. The two columns are the relative abundance to the solar value by Lodders (2010) and the ε(X) by Pereira & Miranda (2007). Our ε(N) and ε(O) are consistent with Pereira & Miranda (2007). As explained in Section 3.4, ε(S) discrepancy between theirs and ours is attributed to the S+ abundance. By the Cloudy model under D = 6 kpc, Otsuka et al. (2014) derived ε(N/O/Ne/S/Ar) = 7.49, 8.23, 7.68, 6.17, and 5.93 based on the optical spectrum of Pereira & Miranda (2007) and the Spitzer/IRS spectrum. Otsuka et al. (2014) estimated an expected CEL ε(C) = 8.72 using a [C/H]−[C/Ar] relation established amongst 115 Galactic PNe. Delgado-Inglada & Rodríguez (2014) reported that the RL C2+ to the CEL C2+ ratio in IC418 is 2.4. Applying this value to SaSt2-3, we obtain an expected CEL ε(C) = 8.83 ± 0.12, which is consistent with Otsuka et al. (2014). We attempt to obtain more plausible expected CEL ε(C) using the stellar ε(C) and ε(O) in Section 4.1. The [Ne/H] is comparable with the [O/H] because Ne together with O had been synthesized in the He-rich intershell during the AGB phase. The Ne enhancement would be due to the increase of 22Ne.
Nebular elemental abundances using the ICFs. The last column (PM07) is the ε(X) value derived by Pereira & Miranda (2007).
| X . | n(X)/n(H) . | ε(X) . | ε(X) − ε(X|$\odot$|) . | ε(X) . |
|---|---|---|---|---|
| . | (Ours) . | (Ours) . | (Ours) . | (PM07) . |
| He | 5.58(−2) – 1.26(−1) | 10.75 – 11.10 | −0.15 – +0.20 | ··· |
| C | 1.61(−3) ± 4.61(−4) | 9.21 ± 0.12 | +0.82 ± 0.13 | ··· |
| N | 2.95(−5) ± 4.09(−6) | 7.47 ± 0.06 | −0.36 ± 0.13 | 7.38 ± 0.14 |
| O | 1.30(−4) ± 1.10(−5) | 8.11 ± 0.04 | −0.58 ± 0.06 | 8.27 ± 0.14 |
| Ne | 2.91(−5) ± 2.85(−6) | 7.46 ± 0.04 | −0.41 ± 0.11 | ··· |
| S | 1.26(−6) ± 8.80(−8) | 6.10 ± 0.03 | −1.09 ± 0.05 | 5.48 ± 0.14 |
| Cl | 3.68(−8) ± 5.51(−9) | 4.57 ± 0.07 | −0.69 ± 0.09 | ··· |
| Ar | 4.62(−7) ± 1.43(−7) | 5.66 ± 0.13 | −0.89 ± 0.16 | ··· |
| Fe | 1.94(−7) ± 2.74(−8) | 5.29 ± 0.06 | −2.18 ± 0.07 | ··· |
| X . | n(X)/n(H) . | ε(X) . | ε(X) − ε(X|$\odot$|) . | ε(X) . |
|---|---|---|---|---|
| . | (Ours) . | (Ours) . | (Ours) . | (PM07) . |
| He | 5.58(−2) – 1.26(−1) | 10.75 – 11.10 | −0.15 – +0.20 | ··· |
| C | 1.61(−3) ± 4.61(−4) | 9.21 ± 0.12 | +0.82 ± 0.13 | ··· |
| N | 2.95(−5) ± 4.09(−6) | 7.47 ± 0.06 | −0.36 ± 0.13 | 7.38 ± 0.14 |
| O | 1.30(−4) ± 1.10(−5) | 8.11 ± 0.04 | −0.58 ± 0.06 | 8.27 ± 0.14 |
| Ne | 2.91(−5) ± 2.85(−6) | 7.46 ± 0.04 | −0.41 ± 0.11 | ··· |
| S | 1.26(−6) ± 8.80(−8) | 6.10 ± 0.03 | −1.09 ± 0.05 | 5.48 ± 0.14 |
| Cl | 3.68(−8) ± 5.51(−9) | 4.57 ± 0.07 | −0.69 ± 0.09 | ··· |
| Ar | 4.62(−7) ± 1.43(−7) | 5.66 ± 0.13 | −0.89 ± 0.16 | ··· |
| Fe | 1.94(−7) ± 2.74(−8) | 5.29 ± 0.06 | −2.18 ± 0.07 | ··· |
Nebular elemental abundances using the ICFs. The last column (PM07) is the ε(X) value derived by Pereira & Miranda (2007).
| X . | n(X)/n(H) . | ε(X) . | ε(X) − ε(X|$\odot$|) . | ε(X) . |
|---|---|---|---|---|
| . | (Ours) . | (Ours) . | (Ours) . | (PM07) . |
| He | 5.58(−2) – 1.26(−1) | 10.75 – 11.10 | −0.15 – +0.20 | ··· |
| C | 1.61(−3) ± 4.61(−4) | 9.21 ± 0.12 | +0.82 ± 0.13 | ··· |
| N | 2.95(−5) ± 4.09(−6) | 7.47 ± 0.06 | −0.36 ± 0.13 | 7.38 ± 0.14 |
| O | 1.30(−4) ± 1.10(−5) | 8.11 ± 0.04 | −0.58 ± 0.06 | 8.27 ± 0.14 |
| Ne | 2.91(−5) ± 2.85(−6) | 7.46 ± 0.04 | −0.41 ± 0.11 | ··· |
| S | 1.26(−6) ± 8.80(−8) | 6.10 ± 0.03 | −1.09 ± 0.05 | 5.48 ± 0.14 |
| Cl | 3.68(−8) ± 5.51(−9) | 4.57 ± 0.07 | −0.69 ± 0.09 | ··· |
| Ar | 4.62(−7) ± 1.43(−7) | 5.66 ± 0.13 | −0.89 ± 0.16 | ··· |
| Fe | 1.94(−7) ± 2.74(−8) | 5.29 ± 0.06 | −2.18 ± 0.07 | ··· |
| X . | n(X)/n(H) . | ε(X) . | ε(X) − ε(X|$\odot$|) . | ε(X) . |
|---|---|---|---|---|
| . | (Ours) . | (Ours) . | (Ours) . | (PM07) . |
| He | 5.58(−2) – 1.26(−1) | 10.75 – 11.10 | −0.15 – +0.20 | ··· |
| C | 1.61(−3) ± 4.61(−4) | 9.21 ± 0.12 | +0.82 ± 0.13 | ··· |
| N | 2.95(−5) ± 4.09(−6) | 7.47 ± 0.06 | −0.36 ± 0.13 | 7.38 ± 0.14 |
| O | 1.30(−4) ± 1.10(−5) | 8.11 ± 0.04 | −0.58 ± 0.06 | 8.27 ± 0.14 |
| Ne | 2.91(−5) ± 2.85(−6) | 7.46 ± 0.04 | −0.41 ± 0.11 | ··· |
| S | 1.26(−6) ± 8.80(−8) | 6.10 ± 0.03 | −1.09 ± 0.05 | 5.48 ± 0.14 |
| Cl | 3.68(−8) ± 5.51(−9) | 4.57 ± 0.07 | −0.69 ± 0.09 | ··· |
| Ar | 4.62(−7) ± 1.43(−7) | 5.66 ± 0.13 | −0.89 ± 0.16 | ··· |
| Fe | 1.94(−7) ± 2.74(−8) | 5.29 ± 0.06 | −2.18 ± 0.07 | ··· |
The [S,Cl,Ar/H] abundances are low, and if these represent the stellar abundances, then SaSt2-3 is the lowest metallicity object amongst the Galactic C60 PNe, and we infer Z ∼0.1 Z|$\odot$| from the average [S,Cl,Ar/H]. While most Ar is probably in the gas phase in this object, S could be incorporated into dust grains (e.g. MgS, suggested to be a candidate for the carrier of the broad 30 |$\mu$|m feature that is observed in the C60 PNe). Fe is even more depleted, but it is unlikely that this represents the initial abundance given the other elemental abundances. Rather, a fraction of the Fe will be incorporated into dust grains. We discuss further the elemental abundances in Section 5.
4 STELLAR ABSORPTION ANALYSIS
4.1 Stellar parameter derivations
We perform stellar absorption analysis of the HDS spectra taken on 2013 Oct 6 and Dec 10 using the non-local thermodynamic equilibrium (non-LTE) stellar atmosphere modelling code tlusty. We detect strong Si iii,iv and He ii absorption lines. From our tlusty modelling, Teff of the central star is 28 100 K (Table 5), which is cooler than |$T_{\rm eff} \ge 30\, 000$|K in the O-type stars. Thus, we classify the stellar spectrum of SaSt2-3 into early B-type giant B0-1II rather than O-type. Thus, we use comprehensive grid of 1540 metal line-blanketed, non-LTE, plane-parallel, hydrostatic model atmospheres of B-type stars BSTAR20067 by Lanz & Hubeny (2007).
| Parameter . | Value . | Parameter . | Value . |
|---|---|---|---|
| Teff (K) | 28 100 ± 300 | ε(He) | 10.99 ± 0.09 |
| |$\log \, g$| (cm s−2) | 3.11 ± 0.05 | ε(C) | 8.56 ± 0.10 |
| vt (km s−1) | 10 ± 2 | ε(N) | 7.26 ± 0.16 |
| |$v\, \sin (i)$| (km s−1) | 56 ± 4 | ε(O) | 8.10 ± 0.17 |
| ε(Si) | 6.81 ± 0.10 |
| Parameter . | Value . | Parameter . | Value . |
|---|---|---|---|
| Teff (K) | 28 100 ± 300 | ε(He) | 10.99 ± 0.09 |
| |$\log \, g$| (cm s−2) | 3.11 ± 0.05 | ε(C) | 8.56 ± 0.10 |
| vt (km s−1) | 10 ± 2 | ε(N) | 7.26 ± 0.16 |
| |$v\, \sin (i)$| (km s−1) | 56 ± 4 | ε(O) | 8.10 ± 0.17 |
| ε(Si) | 6.81 ± 0.10 |
| Parameter . | Value . | Parameter . | Value . |
|---|---|---|---|
| Teff (K) | 28 100 ± 300 | ε(He) | 10.99 ± 0.09 |
| |$\log \, g$| (cm s−2) | 3.11 ± 0.05 | ε(C) | 8.56 ± 0.10 |
| vt (km s−1) | 10 ± 2 | ε(N) | 7.26 ± 0.16 |
| |$v\, \sin (i)$| (km s−1) | 56 ± 4 | ε(O) | 8.10 ± 0.17 |
| ε(Si) | 6.81 ± 0.10 |
| Parameter . | Value . | Parameter . | Value . |
|---|---|---|---|
| Teff (K) | 28 100 ± 300 | ε(He) | 10.99 ± 0.09 |
| |$\log \, g$| (cm s−2) | 3.11 ± 0.05 | ε(C) | 8.56 ± 0.10 |
| vt (km s−1) | 10 ± 2 | ε(N) | 7.26 ± 0.16 |
| |$v\, \sin (i)$| (km s−1) | 56 ± 4 | ε(O) | 8.10 ± 0.17 |
| ε(Si) | 6.81 ± 0.10 |
We find the average nebular [Cl,S,Ar/H] of −0.89 ± 0.12 (Section 3.5). Assuming that the metallicity Z of the central star and the nebula is roughly the same as seen in the case of IC 418 by Morisset & Georgiev (2009), we adopt the Z = 0.1 Z|$\odot$| model grid from BSTAR2006. All of the initial abundances in this model grid are set to ε(He) = 11.00 and [X/H] = −1 except for He. Based on the Z = 0.1 Z|$\odot$| model grid, we vary ε(X) to yield each equivalent width (EW) of element X to compare with each EW(X) measured from the observed HDS spectra. Throughout our tlusty synthesis analysis, we do not set [He,C,N,O,Si/H] = −1 and we do not adopt the derived nebular He,C,N,O/H] as the stellar photospheric ones. Based on the measured EW of the identified 9 He i,ii, 4 C iii,iv, 2 N ii,iii, 13 O ii, and 5 Si iii,iv absorption, we derive the photospheric He/C/N/O/Si abundances, microturbulent velocity (vt), rotational velocity (|$v\, \sin (i)$|; i is the angle between the rotation axis and the line of sight), Teff, and |$\log\, g$| of the central star. These absorption lines are lesser affected by the nearby nebular lines and absorption lines of the other elements. As we report later, the central wavelength of the stellar absorption lines changes between observing dates whereas those of the nebular lines remain constant. Before analysis, we convert heliocentric wavelength frame of the HDS spectrum into rest frame using the radial velocity determined by the He ii4686 Å for the 2013 Oct 6 data (+154.8 ± 2.3 km s−1) and the He ii5411 Å for the 2013 Dec 10 data (+182.3 ± 4.0 km s−1).
First, we set the basic parameters characterizing the stellar atmosphere, i.e. Z, vt, Teff, and |$\log\, g$|. By setting |$T_{\rm eff} = 28\, 000$| K and |$\log \, g = 3.10$| cm s−2, we investigate ε(O) versus selected 8 O ii lines’ EW to determine vt using synfit. For each absorption, we set instrumental line broadening determined by measuring Th-Ar line widths. Since vt ≥ 10 km s−1 gives minimization of the scatter in ε(O) versus EW, we adopt vt = 10 km s−1. As a reference, Morisset & Georgiev (2009) adopted vt = 10 km s−1 for IC418.
We determine Teff and |$\log\, g$| using the |$T_{ \mathrm{ eff}} - \log\, g$| curves generated by the model atmosphere with vt = 10 km s−1, Z = 0.1 Z|$\odot$|, and ε(He) = 10.90. The |$T_{ \mathrm{ eff}} - \log\, g$| curves are generated by the following process; for a fixed Teff, we vary |$\log \, g$| from 2.90 − 3.30 cm s−2 in a constant 0.01 cm s−2 step to find the best fit value for each observed He i,ii’s EW. We test the range of Teff from 27 500 − 28 500 K (200 K step).
Based on the determined vt, Teff, and |$\log\, g$|, we further constrain ε(He) and calculate ε(C/N/O/Si) abundances by comparing the observed and model predicted EWs of each line by synabund.8 We summarise the result in Table 5. In Appendix Table A4, we list the elemental abundances using each line. We adopt the average value as the representative abundance as listed in the last line of each element. The uncertainty of elemental abundances includes errors from the measured EWs, Teff, |$\log\, g$|, and the uncertainty when we adopt the model atmosphere with the [Z/H] = −0.90 or −1.10 and when we assume the uncertainty of vt of 2 km s−1. We determine |$v\, \sin (i)$| by line-profile fittings of the selected He i,ii and H i in 4000−4700 Å using synfit9
In Fig. 3, we show the synthetic stellar spectrum generated using synspec.10 We identify the absorption lines (except for H i) with the model predicted EW ≥ 10 mÅ by the blue lines. The synthetic spectrum in 3700−4750 Å is presented in Appendix Fig. A1. Stellar Ne, S, Ar, Mg, Ca, and Ti (α-elements) and Ni, Fe, and Zn are not derived in optical HDS spectra of SaSt2-3. These abundances are not small and also they are very important in characterizing the spectrum of the central star and its radiation hardness (in particular, X-ray to UV wavelength). We know that the central star radiation is suppressed by the metal line-blanket effect and also it is very important in subsequent Cloudy modelling. Thus, it is worth simulating these elements, too. We adopt the nebular Ne, S, Cl, and Ar abundances due to no detection of stellar absorption of these elements. We adopt ε(Fe) = 6.38 ([Fe/H] = −1.1, see Section 3.5). Based on the discussion in Section 5, for the other elements up to Fe except for α-elements Mg, Ca, and Ti, we adopt the predicted values by the AGB nucleosynthesis model of initially 1.25 M|$\odot$| and Z = 0.001 stars by Fishlock et al. (2014). For Mg, Ca, and Ti, we adopt ε(Mg) = 6.80, ε(Ca) = 5.43, and ε(Ti) = 4.05, respectively (i.e. [Mg,Ca,Ti/H] = −0.7).
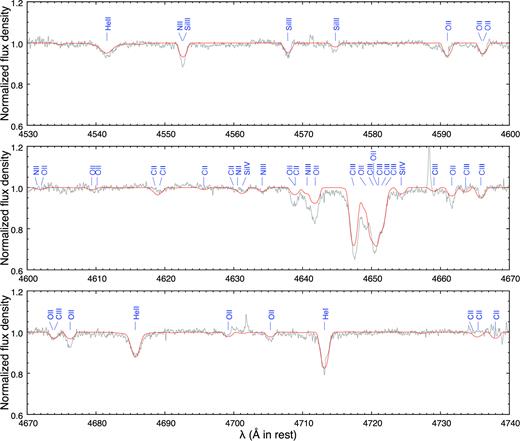
Comparison between the observed HDS (grey line) and the tlusty synthetic spectrum (red line) in the range between 4530 and 4740 Å. The absorption lines (except for H i) with the model predicted EW ≥ 10 mÅ are indicated by the blue lines. The input parameters are listed in Table 5.
The stellar ε(He/N/O) is in agreement with the nebular ε(He/N/O) within their uncertainties. The stellar C/O ratio (2.93 ± 1.33) indicates that SaSt2-3 is definitely a C-rich PN. Based on the consistency between the stellar and the nebular elemental abundances, we obtain an expected CEL ε(C) = 8.58 ± 0.20 using the CEL ε(O) and the stellar C/O ratio.
4.2 Time variation of line profile and radial velocity; Evidence of a binary central star
Our important discovery is that the central wavelength of the stellar absorption lines varies from date to date whereas there is no wavelength shift of the nebular emission lines.
We compute the heliocentric radial velocities vr of the central star via Fourier cross-correlation between the observed spectra and the synthetic tlusty spectrum using fxcor in iraf. FXCOR calculates the velocity shift between two different spectra in the selected wavelength regions.11 Here, we select good S/N regions. In Table 6, we list vr and vr − vsys, where vsys is the systemic radial velocity measured from the 128 nebular emission lines ( +166.6 km s−1, see Section 3.1). In Fig. 4, we show the singlet He i 5015/7281 Å absorption and the tlusty synthetic spectrum as the guide.
Heliocentric radial velocity vr of the central star. The systemic radial velocity vsys is +166.6 km s−1 (Section 3.1).
| Obs Date . | JD (– 2456000.0) . | vr (km s−1) . | vr − vsys (km s−1) . |
|---|---|---|---|
| 2013/10/06 | 573.096 | +152.8 ± 0.6 | −13.76 |
| 2013/12/10 | 637.917 | +183.6 ± 0.4 | +16.95 |
| 2016/02/01 | 1420.831 | +156.2 ± 0.6 | −10.39 |
| Obs Date . | JD (– 2456000.0) . | vr (km s−1) . | vr − vsys (km s−1) . |
|---|---|---|---|
| 2013/10/06 | 573.096 | +152.8 ± 0.6 | −13.76 |
| 2013/12/10 | 637.917 | +183.6 ± 0.4 | +16.95 |
| 2016/02/01 | 1420.831 | +156.2 ± 0.6 | −10.39 |
Heliocentric radial velocity vr of the central star. The systemic radial velocity vsys is +166.6 km s−1 (Section 3.1).
| Obs Date . | JD (– 2456000.0) . | vr (km s−1) . | vr − vsys (km s−1) . |
|---|---|---|---|
| 2013/10/06 | 573.096 | +152.8 ± 0.6 | −13.76 |
| 2013/12/10 | 637.917 | +183.6 ± 0.4 | +16.95 |
| 2016/02/01 | 1420.831 | +156.2 ± 0.6 | −10.39 |
| Obs Date . | JD (– 2456000.0) . | vr (km s−1) . | vr − vsys (km s−1) . |
|---|---|---|---|
| 2013/10/06 | 573.096 | +152.8 ± 0.6 | −13.76 |
| 2013/12/10 | 637.917 | +183.6 ± 0.4 | +16.95 |
| 2016/02/01 | 1420.831 | +156.2 ± 0.6 | −10.39 |
We interpret that the radial velocity time-variation is caused by orbital motion in a binary system. Méndez, Forte & López (1986) reported the photometric and radial velocity variations of the CSPN of C60 PN IC418. They measured the radial velocities using the stellar C iii 5695 Å and C iv 5801/11 Å. The systemic radial velocity was derived using the nebular [N ii] 5755 Å line. Later, Méndez (1989) concluded that the central star is not likely to be a binary because the orbital motion alone (if present) would not be enough to explain the observed variations. We note that the C iii 5695 Å and C iv 5801/11 Å lines are good indicators of the stellar activity (e.g. wind velocity) and these lines would be unlikely to give more accurate radial velocity of the central star. Thus, as far as we know, this would be the firm detection case of the binary central stars amongst all the C60 PNe. Since we have only three periods of the binary motion, we do not determine any parameters of the binary central star yet.
We expected near-IR excess from the binary circumstellar disc from Otsuka et al. (2016) who detected near-IR excess in most of the SMC C60 PNe and discussed possible links between near-IR excess, disc, and fullerene formation; since the ejected material from the central star can be stably harboured for a long time, even smaller molecules could aggregate into much larger molecules. However, in SaSt2-3, we do not find near-IR excess in the observed SED (Fig. 1). No near-IR excess might mean a possibility of a nearly edge-on disc rather an inclined disc.
5 COMPARISON WITH AGB MODEL PREDICTIONS
In Table 7, we compile the derived abundances. The nebular CEL ε(C) is an expected value by our analysis (Section 4.1). As the comparisons, we list the AGB nucleosynthesis model predictions by Fishlock et al. (2014) for initially 1.25 M|$\odot$| stars with Z = 0.001 and Karakas (2010) for initially 1.50 M|$\odot$| stars with Z = 0.004. Note that Fishlock et al. (2014) and Karakas (2010) set the initial [X/H] to be −1.1 and −0.7, respectively. We calculate reduced chi-squared values (|$\chi _{\nu }^{2}$|, ν is degree of freedom) between the nebular ε(X) and the AGB model predicted values for each of 1.00 − 3.25 M|$\odot$| star with Z = 0.001 (nine models in total). We use |$\chi _{\nu }^{2}$| as the guide to find out which AGB model’s predicted abundances is the closest to the derived abundances. The aim of this analysis is to infer the initial mass of the progenitor. We should note that these AGB grid models do not aim to explain the observed elemental abundances of SaSt2-3. We exclude Fe in |$\chi _{\nu }^{2}$| evaluation. We adopt the nebular ε(X) values. For ε(He) and ε(C), we adopt 10.96 ± 0.17 (intermediate value, 9.10(−2) ± 3.52(−3)) and 8.58 ± 0.20 (an expected nebular CEL C value, 3.80(−4) ± 1.76(−4)), respectively.
| X . | Nebular . | Stellar . | 1.25 M|$\odot$| . | 1.50 M|$\odot$| . |
|---|---|---|---|---|
| . | . | . | Z = 0.001 . | Z = 0.004 . |
| He | 10.75 – 11.10 | 10.99 ± 0.09 | 11.01 | 10.97 |
| C(RL) | 9.21 ± 0.12 | 8.55 ± 0.10 | 8.56 | 8.46 |
| C(CEL) | 8.58 ± 0.20 | ··· | ||
| N | 7.47 ± 0.06 | 7.25 ± 0.16 | 7.26 | 7.65 |
| O | 8.11 ± 0.04 | 8.10 ± 0.17 | 7.68 | 8.23 |
| Ne | 7.46 ± 0.04 | ··· | 7.37 | 7.42 |
| Si | ··· | 6.81 ± 0.10 | 6.39 | 6.85 |
| S | 6.10 ± 0.03 | ··· | 6.00 | 6.70 |
| Cl | 4.57 ± 0.07 | ··· | 4.08 | ··· |
| Ar | 5.66 ± 0.13 | ··· | 5.28 | ··· |
| Fe | 5.29 ± 0.06 | ··· | 6.38 | 6.80 |
| X . | Nebular . | Stellar . | 1.25 M|$\odot$| . | 1.50 M|$\odot$| . |
|---|---|---|---|---|
| . | . | . | Z = 0.001 . | Z = 0.004 . |
| He | 10.75 – 11.10 | 10.99 ± 0.09 | 11.01 | 10.97 |
| C(RL) | 9.21 ± 0.12 | 8.55 ± 0.10 | 8.56 | 8.46 |
| C(CEL) | 8.58 ± 0.20 | ··· | ||
| N | 7.47 ± 0.06 | 7.25 ± 0.16 | 7.26 | 7.65 |
| O | 8.11 ± 0.04 | 8.10 ± 0.17 | 7.68 | 8.23 |
| Ne | 7.46 ± 0.04 | ··· | 7.37 | 7.42 |
| Si | ··· | 6.81 ± 0.10 | 6.39 | 6.85 |
| S | 6.10 ± 0.03 | ··· | 6.00 | 6.70 |
| Cl | 4.57 ± 0.07 | ··· | 4.08 | ··· |
| Ar | 5.66 ± 0.13 | ··· | 5.28 | ··· |
| Fe | 5.29 ± 0.06 | ··· | 6.38 | 6.80 |
| X . | Nebular . | Stellar . | 1.25 M|$\odot$| . | 1.50 M|$\odot$| . |
|---|---|---|---|---|
| . | . | . | Z = 0.001 . | Z = 0.004 . |
| He | 10.75 – 11.10 | 10.99 ± 0.09 | 11.01 | 10.97 |
| C(RL) | 9.21 ± 0.12 | 8.55 ± 0.10 | 8.56 | 8.46 |
| C(CEL) | 8.58 ± 0.20 | ··· | ||
| N | 7.47 ± 0.06 | 7.25 ± 0.16 | 7.26 | 7.65 |
| O | 8.11 ± 0.04 | 8.10 ± 0.17 | 7.68 | 8.23 |
| Ne | 7.46 ± 0.04 | ··· | 7.37 | 7.42 |
| Si | ··· | 6.81 ± 0.10 | 6.39 | 6.85 |
| S | 6.10 ± 0.03 | ··· | 6.00 | 6.70 |
| Cl | 4.57 ± 0.07 | ··· | 4.08 | ··· |
| Ar | 5.66 ± 0.13 | ··· | 5.28 | ··· |
| Fe | 5.29 ± 0.06 | ··· | 6.38 | 6.80 |
| X . | Nebular . | Stellar . | 1.25 M|$\odot$| . | 1.50 M|$\odot$| . |
|---|---|---|---|---|
| . | . | . | Z = 0.001 . | Z = 0.004 . |
| He | 10.75 – 11.10 | 10.99 ± 0.09 | 11.01 | 10.97 |
| C(RL) | 9.21 ± 0.12 | 8.55 ± 0.10 | 8.56 | 8.46 |
| C(CEL) | 8.58 ± 0.20 | ··· | ||
| N | 7.47 ± 0.06 | 7.25 ± 0.16 | 7.26 | 7.65 |
| O | 8.11 ± 0.04 | 8.10 ± 0.17 | 7.68 | 8.23 |
| Ne | 7.46 ± 0.04 | ··· | 7.37 | 7.42 |
| Si | ··· | 6.81 ± 0.10 | 6.39 | 6.85 |
| S | 6.10 ± 0.03 | ··· | 6.00 | 6.70 |
| Cl | 4.57 ± 0.07 | ··· | 4.08 | ··· |
| Ar | 5.66 ± 0.13 | ··· | 5.28 | ··· |
| Fe | 5.29 ± 0.06 | ··· | 6.38 | 6.80 |
Since the reduced-χ2 for the 1.25 M|$\odot$| model marks the minimum (|$\chi _{7}^{2}$| = 14 (= 99/(8 – 1)) in 8 elements), this model is the closet to the derived ε(X). |$\chi _{4}^{2}$| is 17 (= 66/(5 – 1)) limited to ε(He/C/N/O/Ne). Next, we compare the AGB models for the same mass stars with Z = 0.004 because these models could account for the derived abundances except for S (no predictions for Cl and Ar, however). The model for 1.5 M|$\odot$| initial mass stars with Z = 0.004 gives the closest fit to the observation (|$\chi _{5}^{2}$| = 360 (=1800/(6 – 1))in 6 elements). Limited to ε(He/C/N/O/Ne), |$\chi _{4}^{2}$| is 7 (=28/(5 – 1)).
The B-type central star indicates that SaSt2-3 is an extremely young PN and just finished the AGB phase. The presence of H absorption lines (Fig. 3) indicates that SaSt2-3 did not experience very late thermal pulse evolution, so this PN is probably in the course of H-burning post-AGB evolution. According to the H-burning post-AGB evolution model of Vassiliadis & Wood (1994), stars with initially 1.5 M|$\odot$| and Z = 0.004 would evolve into hot stars with the core mass (M*) of 0.64 M|$\odot$|. L* of such stars is ∼7380 L|$\odot$| when Teff is ∼28 100 K in ∼1050 years after the AGB phase. Whereas, we infer that 1.25 M|$\odot$| stars with Z = 0.001 would evolve into stars with M* of 0.649 M|$\odot$|; their L* and Teff is ∼7765 L|$\odot$| and ∼28 100 K, respectively in ∼1770 yr after the AGB-phase based on the models of Fishlock et al. (2014) and Vassiliadis & Wood (1994). The main difference in the post-AGB evolution of 1.50 M|$\odot$|/Z = 0.004 stars and 1.25 M|$\odot$|/Z = 0.001 stars is evolutionary time-scale.
Through these discussions, we summarise as follows. The Z = 0.001 model gives the closest values to the derived elemental abundances, although there is systematically ∼0.3–0.4 dex discrepancy of ε(O,Cl,Ar). The Z = 0.004 model shows excellent fit to the derived nebular and stellar ε(He/C/N/O/Si). Considering initial settings of [X/H] in the models, we conclude that the progenitor of SaSt2-3 would be a ∼1.25 M|$\odot$| star with initially Z∼0.001 ([Fe/H] ∼ −1.1) and [α,Cl/Fe] ∼ +0.3–0.4. This is consistent or comparable with the Galaxy chemical evolution model of Kobayashi, Karakas & Umeda (2011); in the Galactic thick disc, the predicted [Si/Fe], [S/Fe], [Cl/Fe], and [Ar/Fe] are ∼+0.6, ∼+0.4, ∼−0.3, and ∼ +0.3 in [Fe/H] < −1, respectively.
6 PHOTOIONIZATION MODEL
In the previous sections, we characterized the central star and dusty nebula. In this section, we build the photoionization model using Cloudy and tlusty to be consistent with all the derived quantities, AGB nucleosynthesis model, and post-AGB evolution model. Below, we explain how to set each parameter in the model, and then we show the result.
6.1 Modelling approach
6.1.1 Distance
Since the distance D is an important parameter, we estimate it by our own method as explained below. We first extract the stellar spectrum from the observed HDS spectrum because the observed spectrum is the sum of the nebular emission lines and continuum and the central star’s continuum. For this purpose, we scale the HDS spectrum flux density to match the APASS Bg′Vr′i′ bands. Then, we subtract the theoretically calculated nebular continuum from the scaled HDS spectrum. We utilize the nebcont code in the Dispo package of starlink v.2015A12 to generate the nebular continuum under adopting I(Hβ) = 1.57(−12) erg s−1 cm−2 (Section 3.2), Te = 104 K, ne = 2000 cm−3 (Table 2), and n(He+)/n(H+) = 1.09(−2) (Table A3). In Fig. 5(a), we show the scaled HDS spectrum and the synthetic nebular continuum. Fig. 5(b) displays the tlusty synthetic spectrum of the central star (in the case of |$T_{\rm eff} = 28\, 100$| K) scaled to match the residual spectrum generated by subtracting the nebular continuum from the HDS spectrum.
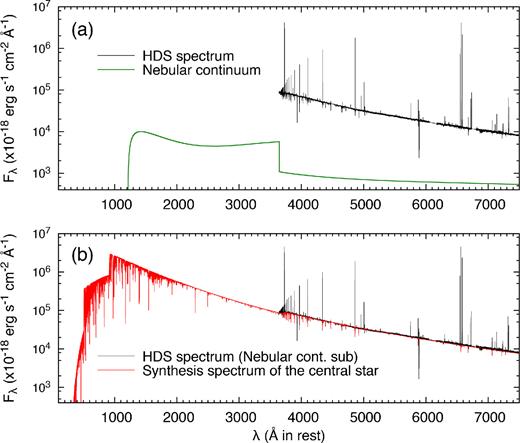
(Upper panel) The de-reddened HDS spectrum scaled up to the flux density at the APASS Bg′Vr′i′ bands and the calculated nebular continuum by nebcont. (Lower panel) The synthetic spectrum of the central star by tlusty (Section 4.1) scaled to match the residual spectrum produced by subtracting the nebular continuum from the HDS spectrum.
Assuming that the progenitor is an initially 1.25 M|$\odot$|/Z = 0.001 star and its luminosity is currently 7765 L|$\odot$| (Section 5), we obtain D = 9.90 − 12.76 kpc. If we assume an initially 1.5 M|$\odot$| progenitor star with Z = 0.004, D is 9.66 − 12.44 kpc.
In our Cloudy model, we adopt D = 11.33 kpc, which is the intermediate value of D when we assume that the central star evolved from a star with initially 1.25 M|$\odot$| and Z = 0.001. Adopting our measured Galactocentric distance of 17.35 kpc, the predicted ε(O/Ne/Cl/S/Ar) from the Galaxy ε(O/Ne/Cl/S/Ar) gradient established amongst Galactic PN nebular abundances by Henry, Kwitter & Balick (2004) are 8.33 ± 0.21, 7.61 ± 0.35, 6.22 ± 0.25, 4.67 ± 0.34, and 6.06 ± 0.25, respectively. These values are in line with the derived nebular abundances (Table 7). Our adopted D = 11.33 kpc is in agreement with Frew et al. (2016), who reported 14.86 ± 4.26 kpc. Our derived D is also comparable with the value (14.31 ± 8.54 kpc) determined from the parallax measured using Gaia DR2 (σπ = 0.0699 ± 0.0417 mas; Gaia Collaboration et al. 2018). Thus, we simultaneously justify our estimated D and nebular ε(O/Ne/Cl/S/Ar).
6.1.2 Central star
As input to Cloudy, we use the tlusty synthetic spectrum of the central star, adopting the parameters from Table 5. In our iterations here, we only vary Teff in the range of |$27\, 800-28\, 500$| K and L* in the range of 7300 − 8300 L|$\odot$|.
6.1.3 Nebula geometry and boundary condition
We plot the observed data and its interpolated curve in Fig. 6. The continuum spectrum in the wavelength ≲ 0.36 |$\mu$|m corresponds to the sum of (1) the nebular continuum (green line in Fig. 5(a)) and (2) the synthetic spectrum of the central star (red line in Fig. 5(b)). The far-IR flux density at 65, 90, 100, 120, and 140 |$\mu$|m is an expected value obtained by fitting for the 15−40 |$\mu$|m Spitzer/IRS spectrum.
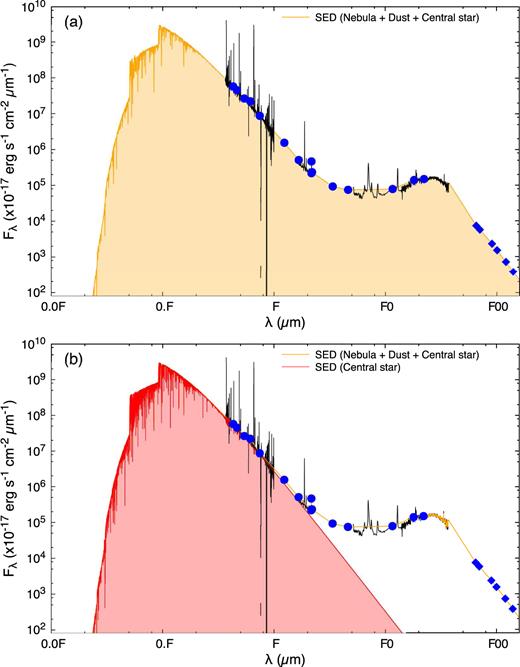
(Upper panel) SED based on the observed data (black lines and blue filled circles) and its interpolated curve (orange line). The far-IR flux density at 65, 90, 100, 120, and 140 |$\mu$|m (the blue diamonds) is an expected value. The integrated flux density between ∼5(−3) to 140|$\mu$|m (indicated by the orange region) is ∼8215 L|$\odot$| in D = 11.33 kpc. (Lower panel) SED based on the observed data and its interpolated curve, and the synthetic spectrum of the central star. The integrated flux density of the central star within the same wavelength range (indicated by the red region) is ∼7765 L|$\odot$| in D = 11.33 kpc. See text in details.
We use equations (2) and (3) by Otsuka et al. (2014), who fitted the Spitzer/IRS spectra of Galactic C60 PNe in 15−40|$\mu$|m with the synthetic absorption coefficient Qλ value. For SaSt2-3, we set the minimum dust temperature = 20 K and adopt p = q = 2 and α = 0 which are the same values used in Otsuka et al. (2014). From the fitting, we derive the maximum dust temperature of 136.2 ± 0.4 K, the expected Fν at 65, 90, 100, 120, and 140 |$\mu$|m are 105.3, 63.5, 51.6, 35.0, and 24.6 mJy, respectively.
From integrating this SED (i.e., the orange region in Fig. 6(a)), we find a total luminosity of ∼8215 L|$\odot$|. The luminosity of each component is
Central star: ∼7765 L|$\odot$|,
Nebular continuum + dust continuum: ∼392 L|$\odot$|,
Nebular emission line: ∼58 L|$\odot$|.
Here, the luminosity of nebular emission line is the sum of all the detected emission lines in the HDS and Spitzer spectra. We obtain L* of ∼7765 L|$\odot$| by integrating flux density of the central star’s SED within the same wavelength range, indicated by the red region in Fig. 6(b). Thus, we find that only ∼6 per cent of the central star’s radiation (= (392 + 58)/7765) seems to be absorbed by the nebula.
To check whether nebula boundary is determined by the power of the stellar radiation (i.e. ionization bound) or material distribution (i.e. material bound), we tested both the ionization boundary model and the material boundary model. The WHIRC Brγ and Brγ45 images in Fig. 7 display the central bright region and the compact nebula. From the Brγ – Brγ45 image (Fig. 7(c)), we measure the radius of the ionized nebula extended up to be 1.2″.
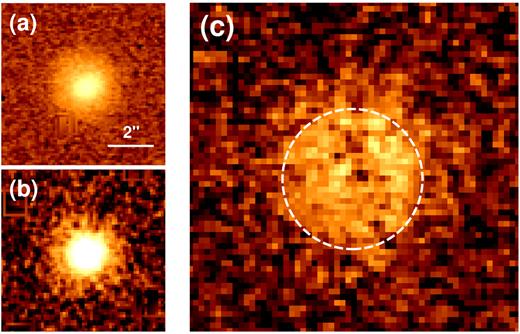
(LEFT two panels) The Br γ and Br γ45 images of SaSt2-3. (RIGHT panel) The Br γ minus Br γ45 image. The radius of the dashed circle is 1.2″. North is up and east is left in these images.
The material boundary model (the model calculation is stopped at the outer radius of 1.2″) gives a good fit except for underestimates of the [O i] and [N i] line fluxes. However, when we adopt an open geometry such as a cylinder in the ionization boundary model (the model calculation is stopped when Te is dropped down to ∼4000 K where most of the ionized species are not emitted), we explained well the balance between the input energy from the central star and the output energy from the nebula plus dust (i.e. L* ≫ Lneb + dust) and the observed [O i] and [N i] line fluxes. Although the WHIRC images do not clearly show a cylinder or bipolar nebula, it is plausible judging from the [O i] 6300 Å line-profile. Fig. 8 shows the [O i] 6300 Å line-profile fitting by two Gaussian components with vr = +154.6 and +170.6 km s−1 at the peak intensity of each component. The [O i] lines emitted from the most outer part of the nebula show blue-shifted asymmetry. Such asymmetric profiles are seen in e.g. PN Wray 16-423 (Otsuka 2015); Wray16-423 has a bright cylindrical structure surrounded by an elliptically extended nebula shell.
![Fitting for the [O i] 6300 Å line. This line can be fitted with two Gaussian components (dashed lines). The red line is the sum of these components.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/482/2/10.1093_mnras_sty2733/2/m_sty2733fig8.jpeg?Expires=1749907934&Signature=3V0ronhjiE8cqOYNiWVyW8R6Yd9OEVir1igAwfJGQ7rt41iaTNwdreVxr6OIac3acoj5GPEyT98a8reZi-CsUUlL7T0X~bf8XS4p-ch2zoTDxUkVr046ZLIZb56-tPNBhp-3IPuFsOxzd8IcYs73TaWydVgNOtSQGiPRaHA7KkwLq3cEQYIzL5fQ56kH-QWwdo8RGt6q4Mrxll99VpTWEaIry4tBpgLOMx5ETBUjKsce0P-4aqhnzxGkVuCnuFlIpzx5xjgKgvbF-EHKBDTrNLVTDs9gI1l-s~AnroGufGwctWwyH3I-bdf55T3AHgQJcL2fT9zJCqUrW-NG5eavKQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Fitting for the [O i] 6300 Å line. This line can be fitted with two Gaussian components (dashed lines). The red line is the sum of these components.
From these discussions, we adopt the cylinder geometry with the height = 0.8″. We determined this scale height through a small grid model, and we found that the cylinder height ≥ 0.8″ is necessary. We adopt ionization bounded condition, assuming the ionization front radius of 1.2″.
6.1.4 Elemental abundances and hydrogen density
We adopt the nebular value of ε(N/O/Ne/S/Cl/Ar/Fe) (Table 7) as the initial value and then refine via model iterations within 0.2 dex of the input values so that the best-fit abundances would reproduce the observed emission line intensities. We adopt the nebular ε(He) = 10.96 as the first guess, and vary it in range from 10.75 to 11.10. We keep an expected CEL ε(C) = 8.58 (c.f. stellar ε(C) = 8.55) and stellar ε(Si) = 6.81 through the model iterations. For α-elements Mg, Ca, and Ti (not derived, though), we fix the [Mg,Ca,Ti/Fe] = +0.3, where [Fe/H] is −1.1 (Section 5). We adopt a constant hydrogen number density (nH) radial profile. We first guess that nH is equal to ne; we adopt the average ne amongst the measured ne except for ne([N i]) (Table 2), then we vary nH to get the best fit.
6.1.5 Dust grains
We assume that the underlying continuum is due to graphite grains based on the fact that SaSt2-3 shows the spectral signature of carbon-rich species.
We use the optical data of Martin & Rouleau (1991) for randomly oriented graphite spheres, and we assume the ‘1/3 − 2/3’ approximation (Draine & Malhotra 1993). We adopt the grain radius a = 0.05 − 0.25 |$\mu$|m and a−3.5 size distribution. If we set the smallest a = 0.005 |$\mu$|m, the maximum grain temperature is over the sublimation temperature of 1750 K. Thus, we set the smallest a = 0.05 |$\mu$|m. We resolve the size distribution into 20 bins (the smallest is 0.05 − 0.054 |$\mu$|m and the largest is ∼0.23 − 0.25 |$\mu$|m). We do not attempt to fit the broad 6−9|$\mu$|m and 11 |$\mu$|m features because the carriers of these features are not determined yet and also these profiles are different from typical band profile of the polycyclic aromatic hydrocarbons (PAHs) in the same wavelengths.
6.2 Modelling results
The input parameters of the best fitting result and the derived quantities are summarized in Table 8. In total, we varied 12 parameters within a given range; L*, ε(He/N/O/Ne/S/Cl/Ar/Fe), inner radius (rin), nH, and grain abundance until |$\chi _{\nu }^{2}$| calculated from I(Hβ), 76 emission line fluxes, 25 broadband fluxes, 4 mid-IR flux densities, and ionization-bound radius (i.e. outer radius rout). Since there is no observed far-IR data, we stop the model calculation at the ionization front, where Te is dropped down to ∼4000 K. To evaluate the goodness of the model fitting, we refer to |$\chi _{\nu }^{2}$|. For the [O i] and [N i] lines, we adopt 30 per cent relative uncertainty because these lines are mostly from the PDRs. For the higher order Balmer lines H i (B24 - B14), we set 10 per cent relative uncertainty by considering into account the uncertainty of these lines largely affected by the stellar absorption. The reduced-χ2 value in the best model is 12. The relatively large reduced-χ2 value even in the best fitting would be due to the uncertainty of the atomic data which we cannot control. Therefore, we conclude that our best fitting result reproduces observations very well. The predicted line fluxes, broadband fluxes, and flux densities are compiled in Appendix Table A5. For references, we list expected Fν at 65, 90, 100, 120, and 140 μm obtained by fitting for the 15−40|$\mu$|m Spitzer/IRS spectrum (Section 6.1.3). In Figs. 9 and 10, we compare the model SED with the observed one.
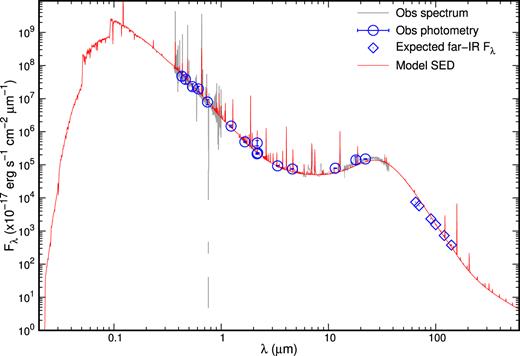
Comparison between the observed SED (blue circles and grey lines) and the SED predicted by the best-fit model (red line). The spectral resolution (R) of the model SED is a constant 1000.
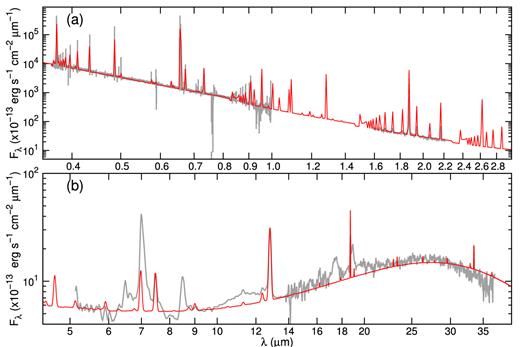
Comparison between the observed SED and the SED predicted by the best fit model in 0.35−3.0|$\mu$|m (upper panel) and in 4.4−40|$\mu$|m (lower panel). The legends in both panels are the same used in Fig. 9. R of the model SED in 0.35−3.0|$\mu$|m is a constant 1000. R is a constant 90 in 4.4−14|$\mu$|m (low-resolution module) and 570 in 14−40|$\mu$|m (high-resolution one), which correspond to the Spitzer/IRS resolution.
| Central star . | Value . |
|---|---|
| L* / Teff / |$\log \, g$| / D | 7400 L|$\odot$| / 28 170 K / 3.11 cm s−2 / 11.33 kpc |
| MV / R* /m* | −2.10 / 3.606 R|$\odot$| / 0.611 M|$\odot$| |
| Nebula | Value |
| Geometry | Cylinder with height = 0.8″ (8600 AU) |
| Radius | rin:0.006″ (63 AU), rout:1.25″ (14 162 AU) |
| ε(X) | He:10.83, C:8.58, N:7.46, O:8.27, Ne:7.46, |
| Mg:6.80, Si:6.84, S:6.10, Cl:4.51, Ar:5.65, | |
| Ca:5.43, Ti:4.05, Fe:5.41, | |
| Others: Fishlock et al. (2014) | |
| nH | 3098 cm−3 |
| log I(H β) | −11.804 erg s−1 cm−2 |
| mg | 6.13(−2) M|$\odot$| |
| Dust | Value |
| Grain size | 0.05 − 0.25 |$\mu$|m |
| Td / md / DGR (md/mg) | 66 − 909 K / 2.08(−5) M|$\odot$| / 3.39(−4) |
| Central star . | Value . |
|---|---|
| L* / Teff / |$\log \, g$| / D | 7400 L|$\odot$| / 28 170 K / 3.11 cm s−2 / 11.33 kpc |
| MV / R* /m* | −2.10 / 3.606 R|$\odot$| / 0.611 M|$\odot$| |
| Nebula | Value |
| Geometry | Cylinder with height = 0.8″ (8600 AU) |
| Radius | rin:0.006″ (63 AU), rout:1.25″ (14 162 AU) |
| ε(X) | He:10.83, C:8.58, N:7.46, O:8.27, Ne:7.46, |
| Mg:6.80, Si:6.84, S:6.10, Cl:4.51, Ar:5.65, | |
| Ca:5.43, Ti:4.05, Fe:5.41, | |
| Others: Fishlock et al. (2014) | |
| nH | 3098 cm−3 |
| log I(H β) | −11.804 erg s−1 cm−2 |
| mg | 6.13(−2) M|$\odot$| |
| Dust | Value |
| Grain size | 0.05 − 0.25 |$\mu$|m |
| Td / md / DGR (md/mg) | 66 − 909 K / 2.08(−5) M|$\odot$| / 3.39(−4) |
Note. – Nebular ε(He/N/O/Ne/S/Cl/Ar/Fe) abundances derived by empirical method (Section 3.5) are 10.75 − 11.10/7.47/8.11/7.46/6.10/4.57/5.66/5.29, respectively.
| Central star . | Value . |
|---|---|
| L* / Teff / |$\log \, g$| / D | 7400 L|$\odot$| / 28 170 K / 3.11 cm s−2 / 11.33 kpc |
| MV / R* /m* | −2.10 / 3.606 R|$\odot$| / 0.611 M|$\odot$| |
| Nebula | Value |
| Geometry | Cylinder with height = 0.8″ (8600 AU) |
| Radius | rin:0.006″ (63 AU), rout:1.25″ (14 162 AU) |
| ε(X) | He:10.83, C:8.58, N:7.46, O:8.27, Ne:7.46, |
| Mg:6.80, Si:6.84, S:6.10, Cl:4.51, Ar:5.65, | |
| Ca:5.43, Ti:4.05, Fe:5.41, | |
| Others: Fishlock et al. (2014) | |
| nH | 3098 cm−3 |
| log I(H β) | −11.804 erg s−1 cm−2 |
| mg | 6.13(−2) M|$\odot$| |
| Dust | Value |
| Grain size | 0.05 − 0.25 |$\mu$|m |
| Td / md / DGR (md/mg) | 66 − 909 K / 2.08(−5) M|$\odot$| / 3.39(−4) |
| Central star . | Value . |
|---|---|
| L* / Teff / |$\log \, g$| / D | 7400 L|$\odot$| / 28 170 K / 3.11 cm s−2 / 11.33 kpc |
| MV / R* /m* | −2.10 / 3.606 R|$\odot$| / 0.611 M|$\odot$| |
| Nebula | Value |
| Geometry | Cylinder with height = 0.8″ (8600 AU) |
| Radius | rin:0.006″ (63 AU), rout:1.25″ (14 162 AU) |
| ε(X) | He:10.83, C:8.58, N:7.46, O:8.27, Ne:7.46, |
| Mg:6.80, Si:6.84, S:6.10, Cl:4.51, Ar:5.65, | |
| Ca:5.43, Ti:4.05, Fe:5.41, | |
| Others: Fishlock et al. (2014) | |
| nH | 3098 cm−3 |
| log I(H β) | −11.804 erg s−1 cm−2 |
| mg | 6.13(−2) M|$\odot$| |
| Dust | Value |
| Grain size | 0.05 − 0.25 |$\mu$|m |
| Td / md / DGR (md/mg) | 66 − 909 K / 2.08(−5) M|$\odot$| / 3.39(−4) |
Note. – Nebular ε(He/N/O/Ne/S/Cl/Ar/Fe) abundances derived by empirical method (Section 3.5) are 10.75 − 11.10/7.47/8.11/7.46/6.10/4.57/5.66/5.29, respectively.
In Fig. 11, we show the location of the CSPN predicted by our Cloudy model on the post-AGB evolutionary tracks for initially Z = 0.001 and 1.0, 1.25, and 1.50 M|$\odot$| (Vassiliadis & Wood 1994). We generate this 1.25 M|$\odot$| track by linear interpolation between the 1.00 and 1.50 M|$\odot$| tracks of (Vassiliadis & Wood 1994). Our Cloudy model predicts L* = 7400 L|$\odot$|, |$T_{\rm eff} = 28\, 170$| K, and m* = 0.611 M|$\odot$|. L* and m* are justly close to predicted values (∼7765 L|$\odot$| and 0.649 M|$\odot$|) based on the models of initially 1.25 M|$\odot$| stars with Z = 0.001 (Vassiliadis & Wood 1994; Fishlock et al. 2014). In Fig. 11, we plot the model results of Gesicki & Zijlstra (2007) and Otsuka et al. (2014) as well. These two models show a large discrepancy from the predicted post-AGB evolution track, but our model completely improves this.
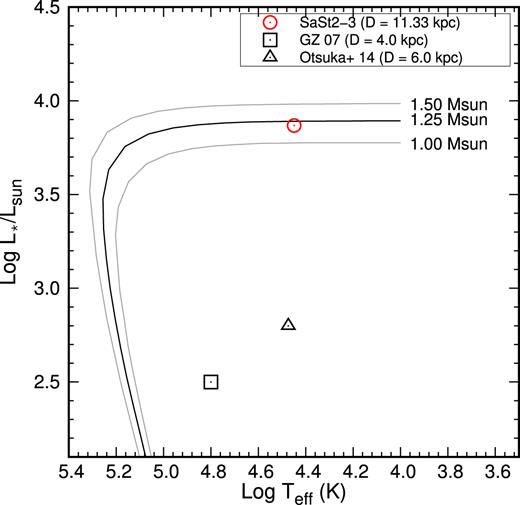
The location of the central star on the post-AGB evolutionary tracks for initially Z = 0.001 and 1.0, 1.25, and 1.50 M|$\odot$| (Vassiliadis & Wood 1994). We generate this 1.25 M|$\odot$| track by linear interpolation between the 1.00 and 1.50 M|$\odot$| tracks of Vassiliadis & Wood (1994). For comparisons, we plot Teff and L* of the central star derived by Gesicki & Zijlstra (2007) (GZ07, square; |$T_{\rm eff} = 63\, 095$| K and L* = 316 L|$\odot$| under D = 4 kpc) and Otsuka et al. (2014) (Otsuka + 14, triangle; |$T_{\rm eff} = 29\, 750$| K and L* = 630 L|$\odot$| under D = 6 kpc).
Our model succeeds in reproducing the derived ε(X), the volume average Te (9150 K, while 8930 K in the observation), and I(Hβ). In Table 9, we present the fraction of each ion in each element. Except for C and Ar, the model predicted ICF is well consistent with the empirically determined ICF.
Ionic abundance fraction predicted by our model and comparison between the predicted ICFs (ICFmodel) and the empirically determined ICFs (ICFemp).
| X . | X0 . | X+ . | X2+ . | X3+ . | ICFmodel . | ICFemp . |
|---|---|---|---|---|---|---|
| He | 0.845 | 0.155 | <0.001 | 6.70 | 5.12 − 11.57 | |
| C | <0.001 | 0.883 | 0.116 | <0.001 | 8.61 | 5.12 ± 1.41 |
| N | 0.002 | 0.948 | 0.050 | <0.001 | 1.05 | 1.04 ± 0.13 |
| O | 0.010 | 0.982 | 0.008 | <0.001 | 1.01 | 1.00 |
| Ne | 0.012 | 0.988 | <0.001 | <0.001 | 1.01 | 1.00 |
| S | <0.001 | 0.244 | 0.756 | <0.001 | 1.00 | 1.00 |
| Cl | <0.001 | 0.383 | 0.617 | <0.001 | 1.00 | 1.00 |
| Ar | 0.003 | 0.867 | 0.131 | <0.001 | 7.66 | 5.12 ± 1.41 |
| Fe | <0.001 | 0.062 | 0.923 | 0.015 | 1.08 | 1.31 ± 0.16 |
| X . | X0 . | X+ . | X2+ . | X3+ . | ICFmodel . | ICFemp . |
|---|---|---|---|---|---|---|
| He | 0.845 | 0.155 | <0.001 | 6.70 | 5.12 − 11.57 | |
| C | <0.001 | 0.883 | 0.116 | <0.001 | 8.61 | 5.12 ± 1.41 |
| N | 0.002 | 0.948 | 0.050 | <0.001 | 1.05 | 1.04 ± 0.13 |
| O | 0.010 | 0.982 | 0.008 | <0.001 | 1.01 | 1.00 |
| Ne | 0.012 | 0.988 | <0.001 | <0.001 | 1.01 | 1.00 |
| S | <0.001 | 0.244 | 0.756 | <0.001 | 1.00 | 1.00 |
| Cl | <0.001 | 0.383 | 0.617 | <0.001 | 1.00 | 1.00 |
| Ar | 0.003 | 0.867 | 0.131 | <0.001 | 7.66 | 5.12 ± 1.41 |
| Fe | <0.001 | 0.062 | 0.923 | 0.015 | 1.08 | 1.31 ± 0.16 |
Ionic abundance fraction predicted by our model and comparison between the predicted ICFs (ICFmodel) and the empirically determined ICFs (ICFemp).
| X . | X0 . | X+ . | X2+ . | X3+ . | ICFmodel . | ICFemp . |
|---|---|---|---|---|---|---|
| He | 0.845 | 0.155 | <0.001 | 6.70 | 5.12 − 11.57 | |
| C | <0.001 | 0.883 | 0.116 | <0.001 | 8.61 | 5.12 ± 1.41 |
| N | 0.002 | 0.948 | 0.050 | <0.001 | 1.05 | 1.04 ± 0.13 |
| O | 0.010 | 0.982 | 0.008 | <0.001 | 1.01 | 1.00 |
| Ne | 0.012 | 0.988 | <0.001 | <0.001 | 1.01 | 1.00 |
| S | <0.001 | 0.244 | 0.756 | <0.001 | 1.00 | 1.00 |
| Cl | <0.001 | 0.383 | 0.617 | <0.001 | 1.00 | 1.00 |
| Ar | 0.003 | 0.867 | 0.131 | <0.001 | 7.66 | 5.12 ± 1.41 |
| Fe | <0.001 | 0.062 | 0.923 | 0.015 | 1.08 | 1.31 ± 0.16 |
| X . | X0 . | X+ . | X2+ . | X3+ . | ICFmodel . | ICFemp . |
|---|---|---|---|---|---|---|
| He | 0.845 | 0.155 | <0.001 | 6.70 | 5.12 − 11.57 | |
| C | <0.001 | 0.883 | 0.116 | <0.001 | 8.61 | 5.12 ± 1.41 |
| N | 0.002 | 0.948 | 0.050 | <0.001 | 1.05 | 1.04 ± 0.13 |
| O | 0.010 | 0.982 | 0.008 | <0.001 | 1.01 | 1.00 |
| Ne | 0.012 | 0.988 | <0.001 | <0.001 | 1.01 | 1.00 |
| S | <0.001 | 0.244 | 0.756 | <0.001 | 1.00 | 1.00 |
| Cl | <0.001 | 0.383 | 0.617 | <0.001 | 1.00 | 1.00 |
| Ar | 0.003 | 0.867 | 0.131 | <0.001 | 7.66 | 5.12 ± 1.41 |
| Fe | <0.001 | 0.062 | 0.923 | 0.015 | 1.08 | 1.31 ± 0.16 |
The gas mass mg is the sum of the ionized and neutral atomic/molecular gas species. Note that we stopped the model calculation at the ionization front. Our mg is ∼18 per cent of the ejected mass at the last thermal pulse (TP) of 1.25 M|$\odot$| initial mass stars with Z = 0.001 (0.334 M|$\odot$|, Fishlock et al. 2014). If we increase the emitting volume by adopting a closed-geometry such as a spherical nebula, the situation is slightly improved (we trace ∼35 per cent of the ejected mass) but the fitting model becomes worse as we explained. According to Fishlock et al. (2014), such stars experienced the superwind phase in the final few TPs during which the mass-loss rate reaches a plateau of ∼10−5 M|$\odot$| yr−1. One might think that our underestimated mg might be caused by excluding the neutral gas and molecular gas regions. However, it is unlikely that SaSt2-3 has the molecular gas rich envelope because the molecular hydrogen H2 lines in K-band are not detected (Lumsden et al. 2001). Indeed, we confirm this fact by analysis of the UKIRT CGS4 HK-band spectrum of SaSt2-3 (Fig. 1). Since our mg is greater than the ejected mass 2.7(–3) M|$\odot$| at the last TP of initially 1.00 M|$\odot$| stars with Z = 0.001, we can conclude that the progenitor should be a >1.00 M|$\odot$| initial mass star. Fishlock et al. (2014) predicts that 1.00 M|$\odot$| stars lost the majority of its stellar envelope before it reaches the superwind phase. The 1.25 M|$\odot$| progenitor that we infer might have experienced such mass loss. If this is true, non-detection of the H2 lines might be because thin circumstellar envelope does not shield UV radiation from the CSPN and H2 is dissociated. As an other explanation for the estimated small mg, the ejected mass during the AGB phase might be efficiently transported to the stellar surface of a companion star. Our small mg would be largely improved by taking cold gas/dust components that can be traced by far-IR observation.
As presented in Fig. 10(b), our Cloudy model predicts an emission line around 7 |$\mu$|m. This line is the complex of the [Ar ii] 6.99 |$\mu$|m and H i 6.95/7.09 |$\mu$|m lines. In the Spitzer/IRS spectrum, we measure the total line-flux of the [Ar ii] 6.99 |$\mu$|m, H i 6.95/7.09 |$\mu$|m, and C60 7.0 |$\mu$|m to be 28.67 ± 3.23, where I(Hβ) = 100. The model predicts I([Ar ii] 6.99 |$\mu$|m + H i 6.95/7.09 |$\mu$|m)/I(Hβ) = 4.173 (I(Hβ) = 100). The contribution of the atomic line complex to the C60 7.0 |$\mu$|m band (14.6 |${{\ \rm per\ cent}}$|) is not as significant as Otsuka et al. (2014) expected (30.3 |${{\ \rm per\ cent}}$|). We estimate I(C60 7.0 |$\mu$|m)/I(Hβ) to be 24.5 ± 2.8.
7 DISCUSSIONS
7.1 Evolution of SaSt2-3
Using the Galactic rotation velocity based on the distance scale of Cahn, Kaler & Stanghellini (1992), van de Steene & Zijlstra (1995), and Zhang (1995), vr(LSR) = +149.1 km s−1, and D = 11.33 kpc, we obtain ΔV = 68.2 − 77.9 km s−1. The height above the Galactic plane |z| is 1.13 kpc. These results are in agreement with the Type III PN classification of Quireza et al. (2007). ΔV and |z| do not exceed 120 km s−1 and 1.99 kpc for the Type IV PN classification of Quireza et al. (2007), respectively. The metallicity of SaSt2-3 is much richer than typical halo PNe such as K648, BoBn1, and H4-1 showing [Ar/H] ≲ –2 (Otsuka et al. 2010; Otsuka, Hyung & Tajitsu 2015; Otsuka & Tajitsu 2013). Thus, we conclude that SaSt2-3 belongs to the thick disc younger population and a Type III PN rather than a Type IV PN (Pereira & Miranda 2007). Note that classification of PN type does not matter whether the central star is binary or not.
SaSt2-3 would have evolved from a binary composed of a ∼1.25 M|$\odot$| initial mass star and an companion star. However, any parameters on binary motion are unknown yet. According to the simulation using the binary_c 13 code by Izzard et al. (2004), an initially 1.25 M|$\odot$| single star with Z = 0.001 will enter the PN phase within 3.5 Gyr after the progenitor was in the main-sequence. Perhaps, evolutionary time required to reach the AGB phase would be shortened by binary interaction (i.e. < 3.47 Gyr).
SaSt2-3 composes of a ∼0.61 M|$\odot$| B-type cool central star with |$T_{\rm eff} = 28\, 100$| K and a companion star. We find the Ca I absorption centred at 6616.62 Å and 6689.28 Å in heliocentric wavelength (6613.13 and 6685.6 Å in rest wavelength, respectively). vr using these two absorption lines is +165.5 km s−1 and +152.1 km s−1, respectively. These vr is close to vr of the central star (+183.6 km s−1, Table 6). Thus, we assume that these lines could be originated from the envelope in the companion star. However, since there is only one spectrum covering 6600 − 6690 Å we have (Table 1), we do not yet find radial velocity variations of this absorption. We suppose that the companion star might be a F-K spectral type star in the main-sequence in terms of the initial mass by referring to De Marco et al. (2013).
7.2 Comparisons with non-C60 and C60-containing PNe
Our study can fully characterize the physical properties of SaSt2-3. Thus, we are able to compare nebular elemental abundances and central star properties with those of other C60 PNe, and we attempt to gain insights into the C60 formation in PNe. For this purpose, we select C60 PNe Tc1 and IC418 because they were previously modelled using Cloudy, and they have been extensively studied. In Table 10, we compile their properties. Due to the lack of existing UV spectra, the CEL ε(C) in SaSt2-3 is not determined yet. However, since we adopt an expected CEL ε(C) (= (C/O)* × OCEL) from the stellar C/O ratio, the reliability of the discussion here is not compromised. We adopt the results of Tc1 and IC418 by Pottasch et al. (2011) and Morisset & Georgiev (2009), respectively. For Tc1, since Pottasch et al. (2011) calculated ε(Ar) by the sum of the Ar+ and Ar2+ abundances without subtracting C60 7.0 |$\mu$|m and H i lines from the complex line at 7 |$\mu$|m, their calculated ε(Ar) is certainly overestimated. Therefore, we compute ε(Ar) from Ar2+ (7.0(–7)) and ICF(Ar) = S/S2+ (1.71). ε(He) in Tc1 is predicted by their Cloudy model.
Nebular and central star’s properties of C60-containing PNe IC418, Tc1 and SaSt2-3 and non C60-containing C-rich PNe, IC2165 and Me2-1. ε(He) in SaSt2-3 listed in this table is the intermediate value of ε(He) derived by empirical method. Mini. is the initial mass of the progenitor inferred from the plot of L* and Teff on the post-AGB evolutionary tracks (Fig. 12) based on Vassiliadis & Wood (1994).
| Nebula . | ε(He) . | ε(C) . | ε(N) . | ε(O) . | ε(Ne) . | ε(S) . | ε(Cl) . | ε(Ar) . | ε(Fe) . | Z . | |$\log \, L_{\ast }/L_{\odot}$| . | Teff (K) . | |$\log \, g$| (cm s−2) . | Mini. (M|$\odot$|) . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IC418 | 11.08 | 8.90 | 8.00 | 8.60 | 8.00 | 6.65 | 5.00 | 6.20 | 4.60 | 0.008 | 3.88 | 36 700 | 3.55 | ∼1.8 |
| Tc1 | 10.92 | 8.56 | 7.56 | 8.41 | 7.80 | 6.45 | 4.97 | 6.08 | 5.19 | 0.004 | 3.85 | 32 000 | 3.30 | ∼1.5 |
| SaSt2-3 | 10.96 | 8.58 | 7.47 | 8.11 | 7.46 | 6.10 | 4.57 | 5.66 | 5.29 | 0.001 | 3.87 | 28 170 | 3.11 | ∼1.3 |
| IC2165 | 11.05 | 8.62 | 8.07 | 8.53 | 7.73 | 6.26 | ··· | 6.00 | ··· | 0.004 | 3.73 | 181 000 | 7.0 | ∼2.1 |
| Me2-1 | 11.00 | 8.85 | 7.71 | 8.72 | 7.97 | 6.96 | ··· | 6.20 | ··· | 0.008 | 3.56 | 170 000 | 7.0 | ∼1.8 |
| Nebula . | ε(He) . | ε(C) . | ε(N) . | ε(O) . | ε(Ne) . | ε(S) . | ε(Cl) . | ε(Ar) . | ε(Fe) . | Z . | |$\log \, L_{\ast }/L_{\odot}$| . | Teff (K) . | |$\log \, g$| (cm s−2) . | Mini. (M|$\odot$|) . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IC418 | 11.08 | 8.90 | 8.00 | 8.60 | 8.00 | 6.65 | 5.00 | 6.20 | 4.60 | 0.008 | 3.88 | 36 700 | 3.55 | ∼1.8 |
| Tc1 | 10.92 | 8.56 | 7.56 | 8.41 | 7.80 | 6.45 | 4.97 | 6.08 | 5.19 | 0.004 | 3.85 | 32 000 | 3.30 | ∼1.5 |
| SaSt2-3 | 10.96 | 8.58 | 7.47 | 8.11 | 7.46 | 6.10 | 4.57 | 5.66 | 5.29 | 0.001 | 3.87 | 28 170 | 3.11 | ∼1.3 |
| IC2165 | 11.05 | 8.62 | 8.07 | 8.53 | 7.73 | 6.26 | ··· | 6.00 | ··· | 0.004 | 3.73 | 181 000 | 7.0 | ∼2.1 |
| Me2-1 | 11.00 | 8.85 | 7.71 | 8.72 | 7.97 | 6.96 | ··· | 6.20 | ··· | 0.008 | 3.56 | 170 000 | 7.0 | ∼1.8 |
Note. – We estimated L|$\odot$| of Tc1 using D = 3.0 kpc (cf. 2.67 kpc, Frew, Bojičić & Parker 2013), a theoretical model spectrum of Lanz & Hubeny (2007) for O-type stars with |$T_{\rm eff} = 32\, 000$| K, |$\log \, g = 3.3$| cm s−2 (Mendez, Kudritzki & Herrero 1992), and Z = 0.008 to match with the interstellar extinction corrected HST/STIS spectrum of the central star (Khan & Worthey 2018). We estimated Teff of IC2165 and Me2-1 based the energy balance method of Dopita & Meatheringham (1991). L* is estimated using theoretical model spectra of Rauch (2003) with the derived Teff and assumed |$\log \, g = 7.0$| cm s−2 to match with the dereddened HST/WFPC2 F547M/F555W (V-band) magnitude of the central stars measured by Wolff, Code & Groth (2000), and D of Frew et al. (2013).
Nebular and central star’s properties of C60-containing PNe IC418, Tc1 and SaSt2-3 and non C60-containing C-rich PNe, IC2165 and Me2-1. ε(He) in SaSt2-3 listed in this table is the intermediate value of ε(He) derived by empirical method. Mini. is the initial mass of the progenitor inferred from the plot of L* and Teff on the post-AGB evolutionary tracks (Fig. 12) based on Vassiliadis & Wood (1994).
| Nebula . | ε(He) . | ε(C) . | ε(N) . | ε(O) . | ε(Ne) . | ε(S) . | ε(Cl) . | ε(Ar) . | ε(Fe) . | Z . | |$\log \, L_{\ast }/L_{\odot}$| . | Teff (K) . | |$\log \, g$| (cm s−2) . | Mini. (M|$\odot$|) . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IC418 | 11.08 | 8.90 | 8.00 | 8.60 | 8.00 | 6.65 | 5.00 | 6.20 | 4.60 | 0.008 | 3.88 | 36 700 | 3.55 | ∼1.8 |
| Tc1 | 10.92 | 8.56 | 7.56 | 8.41 | 7.80 | 6.45 | 4.97 | 6.08 | 5.19 | 0.004 | 3.85 | 32 000 | 3.30 | ∼1.5 |
| SaSt2-3 | 10.96 | 8.58 | 7.47 | 8.11 | 7.46 | 6.10 | 4.57 | 5.66 | 5.29 | 0.001 | 3.87 | 28 170 | 3.11 | ∼1.3 |
| IC2165 | 11.05 | 8.62 | 8.07 | 8.53 | 7.73 | 6.26 | ··· | 6.00 | ··· | 0.004 | 3.73 | 181 000 | 7.0 | ∼2.1 |
| Me2-1 | 11.00 | 8.85 | 7.71 | 8.72 | 7.97 | 6.96 | ··· | 6.20 | ··· | 0.008 | 3.56 | 170 000 | 7.0 | ∼1.8 |
| Nebula . | ε(He) . | ε(C) . | ε(N) . | ε(O) . | ε(Ne) . | ε(S) . | ε(Cl) . | ε(Ar) . | ε(Fe) . | Z . | |$\log \, L_{\ast }/L_{\odot}$| . | Teff (K) . | |$\log \, g$| (cm s−2) . | Mini. (M|$\odot$|) . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IC418 | 11.08 | 8.90 | 8.00 | 8.60 | 8.00 | 6.65 | 5.00 | 6.20 | 4.60 | 0.008 | 3.88 | 36 700 | 3.55 | ∼1.8 |
| Tc1 | 10.92 | 8.56 | 7.56 | 8.41 | 7.80 | 6.45 | 4.97 | 6.08 | 5.19 | 0.004 | 3.85 | 32 000 | 3.30 | ∼1.5 |
| SaSt2-3 | 10.96 | 8.58 | 7.47 | 8.11 | 7.46 | 6.10 | 4.57 | 5.66 | 5.29 | 0.001 | 3.87 | 28 170 | 3.11 | ∼1.3 |
| IC2165 | 11.05 | 8.62 | 8.07 | 8.53 | 7.73 | 6.26 | ··· | 6.00 | ··· | 0.004 | 3.73 | 181 000 | 7.0 | ∼2.1 |
| Me2-1 | 11.00 | 8.85 | 7.71 | 8.72 | 7.97 | 6.96 | ··· | 6.20 | ··· | 0.008 | 3.56 | 170 000 | 7.0 | ∼1.8 |
Note. – We estimated L|$\odot$| of Tc1 using D = 3.0 kpc (cf. 2.67 kpc, Frew, Bojičić & Parker 2013), a theoretical model spectrum of Lanz & Hubeny (2007) for O-type stars with |$T_{\rm eff} = 32\, 000$| K, |$\log \, g = 3.3$| cm s−2 (Mendez, Kudritzki & Herrero 1992), and Z = 0.008 to match with the interstellar extinction corrected HST/STIS spectrum of the central star (Khan & Worthey 2018). We estimated Teff of IC2165 and Me2-1 based the energy balance method of Dopita & Meatheringham (1991). L* is estimated using theoretical model spectra of Rauch (2003) with the derived Teff and assumed |$\log \, g = 7.0$| cm s−2 to match with the dereddened HST/WFPC2 F547M/F555W (V-band) magnitude of the central stars measured by Wolff, Code & Groth (2000), and D of Frew et al. (2013).
Comparisons with theoretical AGB nucleosynthesis models of Karakas (2010) indicate that the initial mass (Mini.) is ∼1.90 − 2.10 M|$\odot$| for IC418 and ∼1.50 − 1.90 M|$\odot$| for Tc1, respectively. From plots of L* and Teff on the post-AGB evolutionary tracks based on Vassiliadis & Wood (1994) (Fig. 12), we have the same estimate for IC418 (∼1.8 M|$\odot$|) and Tc1 (∼1.5 M|$\odot$|). Based on our estimates for the initial mass and metallicity, the age of IC418 and Tc1 after the main sequence is ∼2 − 3 Gyr. Thus, we attest that SaSt2-3 is the most metal-deficient and oldest Galactic C60 PN.
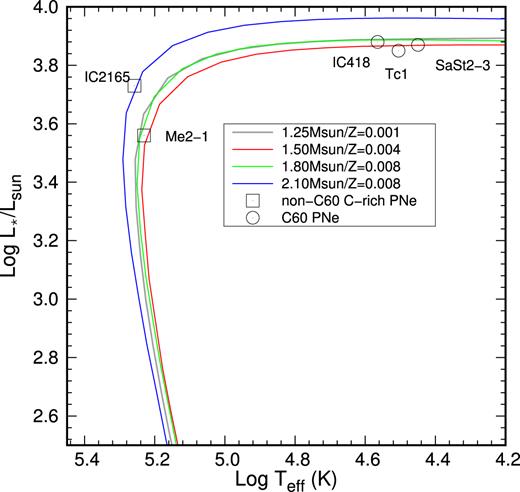
The location of C60-containing PNe IC418, Tc1, and SaSt2-3 and non-C60 C-rich PNe IC2165 and Me2-1 on the post-AGB evolutionary tracks based on Vassiliadis & Wood (1994).
Our findings in elemental abundances are as follows; (i) the values of ε(C) in these C60 PNe are not peculiar values that can be explained by the AGB nucleosynthesis models, (ii) despite that the C60 band strength in SaSt2-3 and Tc1 is much stronger than that in IC418 (see Table 10 of Otsuka et al. 2014), and ε(C) in Tc1 and SaSt2-3 is smaller than that in IC418, and (iii) the C/O ratio (an indicator of the amount of the C-atoms unlocked in dust and molecules) in Tc1 is smaller than that in IC418. Supporting (i), non C60-containing C-rich PNe IC2165 (Miller et al. 2019) and Me2-1 (Pottasch & Bernard-Salas 2010) (they are selected based on metallicity and initial mass) show similar abundances (including ε(C)) to C60 PNe. The difference between non-C60 and C60 PNe is Teff only, supporting that the weak radiation field from the central star is in favour of the C60 formation. The time during which C60 is present might be a short-lived phase that C-rich PNe go through, but we do not yet have firm observational evidence of this. These findings would result in our conclusion that the C60 formation does not largely depend on the amount of the C-atoms produced during the AGB phase, and Tc1 and SaSt2-3 efficiently produced the C60 molecule by some mechanisms not present in IC418.
It is noticeable that Fe abundance is highly depleted in all C60 PNe. The highly deficient Fe is possibly due to selective depletion in a binary disc (e.g. Otsuka et al. 2016, reference therein). If C60 PNe have a disc around the central star, they can harbour mass-loss including AGB products for a long time and shield C60 molecules from the intense central star’s UV radiation. Then, most of the Fe-atoms might be tied up in dust grains (e.g. FeO) within a disc. Accordingly, an environment suitable for large carbon molecule formation might be created. This would be in the case of SaSt2-3. The central star of IC418 would be not a binary (e.g. Méndez 1989). There are no reports on the binary central star of Tc1 so far.
If it is the case, is C60 formation dependent on the central star’s properties and its surrounding environment, such as a binary disc? To answer this question, we need to calculate the mass of the C-atoms present in atomic gas, dust and C60 by a fair means. From a more global perspective, the fraction of the C-atoms would be a critically important parameter to understand how much mass carbon PN progenitors had returned to their host galaxies. However, we find that the excitation diagram based on the observed C60 8.5/17.4/18.9 |$\mu$|m fluxes and the expected C60 7.0 |$\mu$|m flux (I(C60 7.0 |$\mu$|m)/I(Hβ) = 24.5 ± 2.8, see Section 6.2) in SaSt2-3 indicates non-LTE conditions. The same situation exists in other C60 PNe including Tc1 (Cami et al. 2010) and IC418 (Otsuka et al. 2014). Therefore, we sought other ways not involving the excitation diagrams. Of these, the method proposed by Berné & Tielens (2012) is seemingly suitable to our aim; this method requires the observed/modelled IR SED, all four mid-IR C60 band fluxes, and dust mass. These three parameters are already determined in SaSt2-3 and IC418.
In Table 11, we summarize the mass of the C-atoms present in atomic gas, dust, and C60 in SaSt2-3, IC418, and Lin49 in the SMC (as a comparison of the possible binary C60 PN). For SaSt2-3 and Lin49, we obtain I(IR) by integrating the atomic gas emission free SED (generated by the Cloudy best model) in the range from 4 to 200 |$\mu$|m. Then, we calculate the total C60 flux I(C60) (Table A1). Finally, assuming that the dust and C60 are emitted in the same regions, we estimate the C60 mass (=md × I(C60)/I(IR)). The column density and total number of C60 in SaSt2-3 are 8.57(+12) cm−2 and 7.53(+47), respectively. By applying the method to IC418 (but using the combined Infrared Space Observatory (ISO)/Short Wavelength Spectrometer (SWS)/Long-Wave Spectrometer (LWS) and Spitzer combined spectrum), we obtain their C60 mass.
| Nebula . | atomic C . | graphite grains . | C60 . | Mass frac. . |
|---|---|---|---|---|
| . | (×10−4 M|$\odot$|) . | (× 10−5 M|$\odot$|) . | (×10−7 M|$\odot$|) . | of C60 (%) . |
| IC418 | 3.99 | 1.70 | 2.26 | 0.05 |
| Lin49 | 3.00 | 4.15 − 4.29 | 3.05 − 4.64 | 0.09 − 0.14 |
| SaSt2-3 | 2.17 | 2.08 | 4.53 | 0.19 |
| Nebula . | atomic C . | graphite grains . | C60 . | Mass frac. . |
|---|---|---|---|---|
| . | (×10−4 M|$\odot$|) . | (× 10−5 M|$\odot$|) . | (×10−7 M|$\odot$|) . | of C60 (%) . |
| IC418 | 3.99 | 1.70 | 2.26 | 0.05 |
| Lin49 | 3.00 | 4.15 − 4.29 | 3.05 − 4.64 | 0.09 − 0.14 |
| SaSt2-3 | 2.17 | 2.08 | 4.53 | 0.19 |
Note. – Mass of C60 is determined by (graphite grain mass for Lin49 and SaSt2-3) or (the total dust mass 7.76(−5) M|$\odot$| including graphite grain for IC418; Gómez-Llanos et al. 2018) × I(C60)/I(IR). I(C60) is the total flux of the mid-IR C60 bands measured by Otsuka et al. (2014, 1.03(−10) erg s−1 cm−2 for IC 418 using the ISO/SWS/LWS and Spitzer combined spectrum), Otsuka et al. (2016, 9.26(−14) erg s−1 cm−2 for Lin 49), and the present work for SaSt2-3 ( 9.43(−13) erg s−1 cm−2). I(IR) in IC418, Lin49, and SaSt2-3 is 3.53(−8), 1.26(−11) (two-shell model)/8.56(−12) (single shell model), and 4.33(−11) in erg s−1 cm−2, respectively.
| Nebula . | atomic C . | graphite grains . | C60 . | Mass frac. . |
|---|---|---|---|---|
| . | (×10−4 M|$\odot$|) . | (× 10−5 M|$\odot$|) . | (×10−7 M|$\odot$|) . | of C60 (%) . |
| IC418 | 3.99 | 1.70 | 2.26 | 0.05 |
| Lin49 | 3.00 | 4.15 − 4.29 | 3.05 − 4.64 | 0.09 − 0.14 |
| SaSt2-3 | 2.17 | 2.08 | 4.53 | 0.19 |
| Nebula . | atomic C . | graphite grains . | C60 . | Mass frac. . |
|---|---|---|---|---|
| . | (×10−4 M|$\odot$|) . | (× 10−5 M|$\odot$|) . | (×10−7 M|$\odot$|) . | of C60 (%) . |
| IC418 | 3.99 | 1.70 | 2.26 | 0.05 |
| Lin49 | 3.00 | 4.15 − 4.29 | 3.05 − 4.64 | 0.09 − 0.14 |
| SaSt2-3 | 2.17 | 2.08 | 4.53 | 0.19 |
Note. – Mass of C60 is determined by (graphite grain mass for Lin49 and SaSt2-3) or (the total dust mass 7.76(−5) M|$\odot$| including graphite grain for IC418; Gómez-Llanos et al. 2018) × I(C60)/I(IR). I(C60) is the total flux of the mid-IR C60 bands measured by Otsuka et al. (2014, 1.03(−10) erg s−1 cm−2 for IC 418 using the ISO/SWS/LWS and Spitzer combined spectrum), Otsuka et al. (2016, 9.26(−14) erg s−1 cm−2 for Lin 49), and the present work for SaSt2-3 ( 9.43(−13) erg s−1 cm−2). I(IR) in IC418, Lin49, and SaSt2-3 is 3.53(−8), 1.26(−11) (two-shell model)/8.56(−12) (single shell model), and 4.33(−11) in erg s−1 cm−2, respectively.
From this analysis, we quantitatively demonstrate that SaSt2-3 and Lin49 produced C60 more efficiently than IC418. Thus, we conclude that the C60 formation depends upon the central star’s properties and its surrounding environment (e.g. a binary disc), rather than the amount of C-atoms.
8 SUMMARY
We have studied the fullerene-containing PN SaSt2-3 in order to investigate its physical properties and gain insights into the C60 formation in PN progenitors. We derived the nine and four elemental abundances from nebular line and stellar absorption analysis, respectively. The derived elemental abundances indicate that the progenitor is an initially ∼1.25 M|$\odot$| star with Z = 0.001 and α-element and Cl enhanced ([α,Cl/Fe] ∼ +0.3–0.4). The distance D of 11.33 kpc is determined by comparing the derived luminosity as a function of D and Teff with the predicted luminosity by the post-AGB evolution model for the 1.25 M|$\odot$| stars with Z = 0.001. SaSt2-3 is classified as part of the thick disc population with an early B-type central star with |$T_{\rm eff} = 28\, 100$| K, |$\log \, {g} = 3.11$| cm s−2, and the core-mass of ∼0.61 M|$\odot$|. We discovered the binary central star of SaSt2-3 from time-variation of the stellar radial velocity. Further observations are necessary to understand the binary system. We built the comprehensive photoionization model. The calculated gas mass is much smaller than the AGB model prediction for the single 1.25 M|$\odot$| stars with Z = 0.001. The lower gas mass could be due to the short duration time of the superwind phase or efficient mass-transfer into the stellar surface of the companion star during the AGB phase. From the simple analysis, we quantitatively demonstrate that SaSt2-3 produced C60 more efficiently than other C60 PNe. The C60 formation would depend on the central star’s properties and its surrounding environment. There might be a link between the C60 formation efficiency and the binary central star. Spatially resolved spectral maps of the atomic carbon, carbon dust, and C60 are necessary to identify the locations of C60 and investigate the abundance distribution of these species within dusty nebula. We succeed to demonstrate what type of and how much mass of stars can produce how much C60 molecules. We will further investigate stellar/nebular properties and C60 in order to find what parameters are of critical importance in the C60 formation.
ACKNOWLEDGEMENTS
I am grateful to the anonymous referee for carefully reading and the useful suggestions which greatly improved this article. I learned a lot of things from his/her comments. I was supported by the research fund 104-2811-M-001-138 and 104-2112-M-001-041-MY3 from the Ministry of Science and Technology (MOST), R.O.C. I thank Dr. Akito Tajitsu for supporting my Subaru HDS observations. I sincerely thank Drs. Benjamin Sargent, Peter Scicluna, and Toshiya Ueta for critically reading the paper and giving suggestions. This work was partly based on archival data obtained with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. This research is in part based on observations with AKARI, a JAXA project with the participation of ESA. A portion of this work was based on the use of the ASIAA clustering computing system.
Footnotes
Based on observations made with NAOJ Subaru Telescope under the programme IDs: S13B-188S and S16A-227S (PI of both programme is M. Otsuka) and made with NOAO/WIYN telescope (programme ID: 2013A-0429, PI: M. Meixner)
ε(X) equals to 12 + log10 n(X)/n(H), where X is the target element and n(X)/n(H) is the number density ratio relative to hydrogen.
iraf is distributed by the National Optical Astronomy Observatories, operated by the Association of Universities for Research in Astronomy (AURA), Inc., under a cooperative agreement with the National Science Foundation.
We downloaded this spectrum from HASH PN database. http://202.189.117.101:8999/gpne/index.php.
The spectrum was taken by Acker et al (Programme ID: 64.H-0279(A)).
Because the C2 + abundance from this line is about three time larger than that from the C ii 4267 Å. The C ii 4267 Å is the most reliable RL C2 + indicator.
synabund is a code developed by Prof. I. Hubeny in order to calculate EWs under tlusty stellar model atmosphere.
synfit is a code developed by Prof. I. Hubeny in order to synthesise line-profiles under tlusty stellar model atmosphere.
The wavelength ranges we set are as follows; for the 2013 Oct 6 spectrum, 3911−3932, 4002−4036, 4082−4096, 4112−4182, 4302−4330, 4357−4442, and 4533−4730 Å. For the 2013 Dec 10, 5014−5023, 4920−4934, 5043−5056, 5403−5420, and 5589−5599 Å. For the 2016 Feb 1, 7280−7293 Å.
This code can simulate single star evolution by adopting a large binary separation and a small companion star. Here, we adopted an initial binary separation of 1(+6) R|$\odot$| and the initial companion star mass of 0.1 M|$\odot$|.
REFERENCES
APPENDIX A: SUPPORTING RESULTS
The following tables and figure support our works.
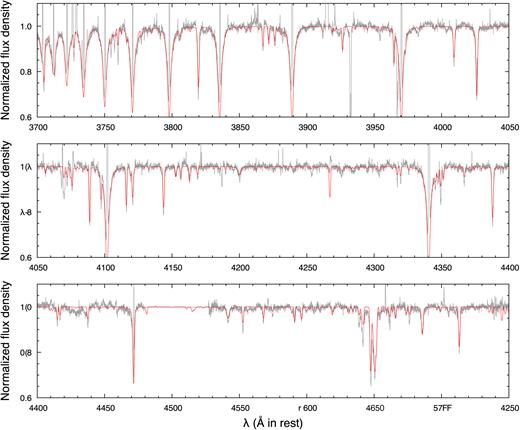
Comparison between the observed HDS (grey line) and the tlusty synthetic spectrum (red line) of SaSt2-3. The input parameters are listed in Table 5.
Identified emission lines in the HDS and IRS spectra. f(λ) is reddening law of Cardelli et al. (1989), F(λ) and I(λ) are observed and interstellar extinction corrected line fluxes normalized to F(Hβ) and I(Hβ), respectively.
| λlab. (Å) . | Line . | f(λ) . | F(λ) . | δ F(λ) . | I(λ) . | δ I(λ) . |
|---|---|---|---|---|---|---|
| 3656.66 | B37 | 0.336 | 0.015 | 0.010 | 0.019 | 0.013 |
| 3657.27 | B36 | 0.336 | 0.062 | 0.019 | 0.077 | 0.024 |
| 3657.92 | B35 | 0.336 | 0.048 | 0.013 | 0.060 | 0.017 |
| 3658.64 | B34 | 0.336 | 0.076 | 0.012 | 0.094 | 0.017 |
| 3659.42 | B32 | 0.336 | 0.131 | 0.015 | 0.162 | 0.023 |
| 3660.28 | B33 | 0.335 | 0.162 | 0.014 | 0.201 | 0.024 |
| 3661.22 | B31 | 0.335 | 0.265 | 0.021 | 0.330 | 0.038 |
| 3662.26 | B30 | 0.335 | 0.324 | 0.028 | 0.402 | 0.048 |
| 3663.40 | B29 | 0.335 | 0.377 | 0.032 | 0.469 | 0.055 |
| 3664.68 | B28 | 0.334 | 0.762 | 0.052 | 0.945 | 0.101 |
| 3666.09 | B27 | 0.334 | 0.676 | 0.049 | 0.839 | 0.092 |
| 3667.68 | B26 | 0.334 | 0.623 | 0.039 | 0.773 | 0.080 |
| 3669.46 | B25 | 0.334 | 0.581 | 0.032 | 0.721 | 0.071 |
| 3671.48 | B24 | 0.333 | 0.593 | 0.029 | 0.735 | 0.070 |
| 3673.76 | B23 | 0.333 | 0.733 | 0.030 | 0.909 | 0.083 |
| 3676.36 | B22 | 0.332 | 0.739 | 0.033 | 0.916 | 0.085 |
| 3679.35 | B21 | 0.332 | 0.844 | 0.031 | 1.046 | 0.094 |
| 3682.81 | B20 | 0.331 | 0.897 | 0.034 | 1.111 | 0.100 |
| 3686.83 | B19 | 0.330 | 1.121 | 0.031 | 1.388 | 0.119 |
| 3691.55 | B18 | 0.329 | 1.184 | 0.023 | 1.465 | 0.122 |
| 3697.15 | B17 | 0.328 | 1.298 | 0.027 | 1.605 | 0.134 |
| 3703.85 | B16 | 0.327 | 1.778 | 0.031 | 2.196 | 0.181 |
| 3709.65 | He i | 0.326 | 0.039 | 0.013 | 0.049 | 0.016 |
| 3711.97 | B15 | 0.325 | 1.665 | 0.032 | 2.054 | 0.169 |
| 3721.94 | B14 | 0.323 | 2.167 | 0.040 | 2.671 | 0.218 |
| 3726.03 | [O ii] | 0.322 | 107.494 | 1.338 | 132.411 | 10.617 |
| 3728.81 | [O ii] | 0.322 | 74.678 | 0.644 | 91.955 | 7.314 |
| 3733.01 | He i | 0.321 | 0.071 | 0.010 | 0.088 | 0.014 |
| 3734.37 | B13 | 0.321 | 2.375 | 0.036 | 2.922 | 0.235 |
| 3750.15 | B12 | 0.317 | 3.125 | 0.027 | 3.836 | 0.301 |
| 3770.63 | B11 | 0.313 | 4.076 | 0.033 | 4.991 | 0.386 |
| 3797.90 | B10 | 0.307 | 5.102 | 0.035 | 6.224 | 0.472 |
| 3819.60 | He i | 0.302 | 0.089 | 0.011 | 0.108 | 0.015 |
| 3835.38 | B9 (Hη) | 0.299 | 6.491 | 0.037 | 7.876 | 0.580 |
| 3889.05 | B8 | 0.286 | 9.595 | 0.191 | 11.547 | 0.844 |
| 3918.97 | C ii | 0.279 | 0.065 | 0.011 | 0.078 | 0.014 |
| 3920.68 | C ii | 0.279 | 0.142 | 0.011 | 0.170 | 0.018 |
| 3970.07 | B7 (Hε) | 0.266 | 14.294 | 0.071 | 16.977 | 1.113 |
| 4068.60 | [S ii] | 0.239 | 0.808 | 0.035 | 0.944 | 0.069 |
| 4101.73 | B6 (Hδ) | 0.230 | 23.318 | 0.106 | 27.051 | 1.531 |
| 4267.00 | C ii | 0.180 | 0.210 | 0.030 | 0.236 | 0.035 |
| 4340.46 | B5 (Hγ) | 0.157 | 42.854 | 0.195 | 47.420 | 1.837 |
| 4471.47 | He i | 0.115 | 0.569 | 0.013 | 0.613 | 0.022 |
| 4571.10 | Mg i] | 0.084 | 0.106 | 0.019 | 0.112 | 0.020 |
| 4658.05 | [Fe iii] | 0.058 | 0.391 | 0.015 | 0.406 | 0.017 |
| 4701.53 | [Fe iii] | 0.045 | 0.093 | 0.008 | 0.096 | 0.009 |
| 4754.69 | [Fe iii] | 0.030 | 0.077 | 0.013 | 0.079 | 0.014 |
| 4769.43 | [Fe iii] | 0.025 | 0.025 | 0.008 | 0.025 | 0.008 |
| 4861.33 | B4 (Hβ) | 0.000 | 100.000 | 0.251 | 100.000 | 0.251 |
| 4881.00 | [Fe iii] | −0.005 | 0.131 | 0.009 | 0.130 | 0.009 |
| 4888.87 | [Fe iii] | −0.007 | 0.021 | 0.007 | 0.021 | 0.007 |
| 4921.93 | He i | −0.016 | 0.130 | 0.008 | 0.129 | 0.008 |
| 4958.91 | [O iii] | −0.026 | 1.127 | 0.008 | 1.109 | 0.011 |
| 5006.84 | [O iii] | −0.038 | 3.408 | 0.015 | 3.326 | 0.034 |
| 5015.68 | He i | −0.040 | 0.385 | 0.010 | 0.375 | 0.011 |
| 5055.98 | Si ii | −0.050 | 0.097 | 0.031 | 0.094 | 0.030 |
| 5067.52 | Ni iii | −0.052 | 0.065 | 0.010 | 0.062 | 0.009 |
| 5197.90 | [N i] | −0.082 | 0.059 | 0.022 | 0.056 | 0.021 |
| 5200.26 | [N i] | −0.083 | 0.055 | 0.015 | 0.052 | 0.014 |
| 5270.40 | [Fe iii] | −0.098 | 0.183 | 0.011 | 0.172 | 0.011 |
| 5273.24 | Ne ii | −0.098 | 0.031 | 0.012 | 0.029 | 0.011 |
| 5517.72 | [Cl iii] | −0.145 | 0.128 | 0.013 | 0.116 | 0.012 |
| 5537.89 | [Cl iii] | −0.149 | 0.122 | 0.006 | 0.111 | 0.007 |
| 5754.64 | [N ii] | −0.185 | 1.489 | 0.017 | 1.322 | 0.062 |
| 5875.60 | He i | −0.203 | 1.786 | 0.029 | 1.566 | 0.082 |
| 5886.05 | C ii | −0.205 | 0.061 | 0.010 | 0.054 | 0.009 |
| 5891.60 | C ii | −0.205 | 0.056 | 0.008 | 0.049 | 0.007 |
| 5912.58 | C i | −0.208 | 0.058 | 0.005 | 0.051 | 0.005 |
| 5931.78 | N ii | −0.211 | 0.068 | 0.008 | 0.059 | 0.007 |
| 5950.71 | Fe iii | −0.214 | 0.040 | 0.009 | 0.035 | 0.008 |
| 6300.30 | [O i] | −0.263 | 0.638 | 0.018 | 0.538 | 0.038 |
| 6312.10 | [S iii] | −0.264 | 0.212 | 0.013 | 0.179 | 0.016 |
| 6347.03 | Ni ii | −0.269 | 0.070 | 0.010 | 0.059 | 0.009 |
| 6363.78 | [O i] | −0.271 | 0.195 | 0.014 | 0.164 | 0.016 |
| 6379.58 | O ii | −0.273 | 0.098 | 0.023 | 0.082 | 0.020 |
| 6461.95 | C ii | −0.284 | 0.074 | 0.009 | 0.061 | 0.008 |
| 6548.04 | [N ii] | −0.296 | 45.988 | 0.395 | 37.985 | 2.778 |
| 6562.80 | B3 (Hα) | −0.298 | 375.888 | 1.958 | 310.085 | 22.731 |
| 6578.05 | C ii | −0.300 | 0.317 | 0.008 | 0.261 | 0.020 |
| 6583.46 | [N ii] | −0.300 | 138.238 | 1.323 | 113.836 | 8.471 |
| 6678.15 | He i | −0.313 | 0.588 | 0.012 | 0.480 | 0.038 |
| 6716.44 | [S ii] | −0.318 | 4.770 | 0.047 | 3.884 | 0.306 |
| 6730.81 | [S ii] | −0.320 | 7.203 | 0.078 | 5.857 | 0.465 |
| 7065.18 | He i | −0.364 | 0.494 | 0.011 | 0.391 | 0.036 |
| 7135.80 | [Ar iii] | −0.374 | 0.740 | 0.009 | 0.581 | 0.054 |
| 7231.32 | C ii | −0.387 | 0.352 | 0.018 | 0.274 | 0.024 |
| 7236.42 | C ii | −0.387 | 0.741 | 0.034 | 0.576 | 0.042 |
| 7281.35 | He i | −0.393 | 0.159 | 0.010 | 0.123 | 0.014 |
| 7318.92 | [O ii] | −0.398 | 1.465 | 0.061 | 1.132 | 0.120 |
| 7319.99 | [O ii] | −0.398 | 4.560 | 0.057 | 3.524 | 0.348 |
| 7329.66 | [O ii] | −0.400 | 2.382 | 0.026 | 1.839 | 0.182 |
| 7330.73 | [O ii] | −0.400 | 2.460 | 0.029 | 1.899 | 0.188 |
| 7751.10 | [Ar iii] | −0.455 | 0.187 | 0.009 | 0.139 | 0.017 |
| 7769.23 | Ca i | −0.458 | 0.122 | 0.007 | 0.091 | 0.012 |
| 7771.94 | O i | −0.458 | 0.084 | 0.006 | 0.063 | 0.008 |
| 7874.65 | [Fe ii] | −0.471 | 0.032 | 0.004 | 0.023 | 0.004 |
| 8240.19 | P45 | −0.515 | 0.067 | 0.008 | 0.048 | 0.008 |
| 8241.88 | P44 | −0.516 | 0.090 | 0.008 | 0.064 | 0.010 |
| 8243.69 | P43 | −0.516 | 0.055 | 0.006 | 0.039 | 0.007 |
| 8245.64 | P42 | −0.516 | 0.023 | 0.005 | 0.016 | 0.004 |
| 8247.73 | P41 | −0.516 | 0.071 | 0.006 | 0.051 | 0.008 |
| 8249.97 | P40 | −0.517 | 0.037 | 0.003 | 0.027 | 0.004 |
| 8252.40 | P39 | −0.517 | 0.077 | 0.008 | 0.055 | 0.009 |
| 8255.02 | P38 | −0.517 | 0.093 | 0.008 | 0.066 | 0.010 |
| 8257.85 | P37 | −0.517 | 0.093 | 0.007 | 0.066 | 0.010 |
| 8260.93 | P36 | −0.518 | 0.103 | 0.010 | 0.074 | 0.012 |
| 8264.28 | P35 | −0.518 | 0.107 | 0.009 | 0.076 | 0.012 |
| 8267.94 | P34 | −0.519 | 0.114 | 0.008 | 0.082 | 0.012 |
| 8271.93 | P33 | −0.519 | 0.118 | 0.012 | 0.084 | 0.014 |
| 8276.31 | P32 | −0.520 | 0.120 | 0.011 | 0.086 | 0.014 |
| 8281.12 | P31 | −0.520 | 0.114 | 0.010 | 0.081 | 0.013 |
| 8286.43 | P30 | −0.521 | 0.135 | 0.011 | 0.096 | 0.015 |
| 8292.31 | P29 | −0.521 | 0.190 | 0.012 | 0.135 | 0.019 |
| 8298.83 | P28 | −0.522 | 0.164 | 0.010 | 0.117 | 0.017 |
| 8306.11 | P27 | −0.523 | 0.207 | 0.012 | 0.148 | 0.021 |
| 8333.78 | P24 | −0.526 | 0.307 | 0.017 | 0.218 | 0.031 |
| 8340.80 | C ii | −0.527 | 0.018 | 0.005 | 0.013 | 0.004 |
| 8345.47 | P23 | −0.527 | 0.296 | 0.017 | 0.211 | 0.030 |
| 8359.00 | P22 | −0.529 | 0.385 | 0.021 | 0.274 | 0.038 |
| 8374.48 | P21 | −0.531 | 0.366 | 0.020 | 0.260 | 0.037 |
| 8392.40 | P20 | −0.533 | 0.382 | 0.020 | 0.271 | 0.038 |
| 8413.32 | P19 | −0.535 | 0.449 | 0.021 | 0.318 | 0.044 |
| 8502.48 | P16 | −0.544 | 0.668 | 0.031 | 0.470 | 0.067 |
| 8665.02 | P13 | −0.560 | 1.274 | 0.057 | 0.887 | 0.128 |
| 8750.47 | P12 | −0.568 | 1.558 | 0.069 | 1.079 | 0.158 |
| 8776.83 | He i | −0.571 | 0.046 | 0.005 | 0.032 | 0.006 |
| 8862.78 | P11 | −0.578 | 1.903 | 0.085 | 1.309 | 0.195 |
| 9014.91 | P10 | −0.590 | 2.554 | 0.113 | 1.744 | 0.264 |
| 9068.60 | [S iii] | −0.594 | 3.789 | 0.170 | 2.581 | 0.394 |
| 9123.60 | [Cl ii] | −0.598 | 0.128 | 0.010 | 0.087 | 0.014 |
| 9545.97 | P8 | −0.626 | 4.546 | 0.202 | 3.033 | 0.486 |
| 70000.0 | C60/[Ar ii]/H i | 28.665 | 3.226 | |||
| 74578.2 | H i | 3.102 | 0.226 | |||
| 85000.0 | C60 | 7.003 | 0.545 | |||
| 89889.3 | [Ar iii] | 0.757 | 0.145 | |||
| 123800.0 | H i | 1.029 | 0.271 | |||
| 128100.6 | [Ne ii] | 20.607 | 1.555 | |||
| 174000.0 | C60/C70 | 12.131 | 1.654 | |||
| C60 | 9.399 | 1.282 | ||||
| 187079.3 | [S iii] | 5.263 | 0.724 | |||
| 189000.0 | C60/C70 | <21.253 | ||||
| C60 | <19.188 | |||||
| 334719.0 | [S iii] | 4.004 | 0.857 |
| λlab. (Å) . | Line . | f(λ) . | F(λ) . | δ F(λ) . | I(λ) . | δ I(λ) . |
|---|---|---|---|---|---|---|
| 3656.66 | B37 | 0.336 | 0.015 | 0.010 | 0.019 | 0.013 |
| 3657.27 | B36 | 0.336 | 0.062 | 0.019 | 0.077 | 0.024 |
| 3657.92 | B35 | 0.336 | 0.048 | 0.013 | 0.060 | 0.017 |
| 3658.64 | B34 | 0.336 | 0.076 | 0.012 | 0.094 | 0.017 |
| 3659.42 | B32 | 0.336 | 0.131 | 0.015 | 0.162 | 0.023 |
| 3660.28 | B33 | 0.335 | 0.162 | 0.014 | 0.201 | 0.024 |
| 3661.22 | B31 | 0.335 | 0.265 | 0.021 | 0.330 | 0.038 |
| 3662.26 | B30 | 0.335 | 0.324 | 0.028 | 0.402 | 0.048 |
| 3663.40 | B29 | 0.335 | 0.377 | 0.032 | 0.469 | 0.055 |
| 3664.68 | B28 | 0.334 | 0.762 | 0.052 | 0.945 | 0.101 |
| 3666.09 | B27 | 0.334 | 0.676 | 0.049 | 0.839 | 0.092 |
| 3667.68 | B26 | 0.334 | 0.623 | 0.039 | 0.773 | 0.080 |
| 3669.46 | B25 | 0.334 | 0.581 | 0.032 | 0.721 | 0.071 |
| 3671.48 | B24 | 0.333 | 0.593 | 0.029 | 0.735 | 0.070 |
| 3673.76 | B23 | 0.333 | 0.733 | 0.030 | 0.909 | 0.083 |
| 3676.36 | B22 | 0.332 | 0.739 | 0.033 | 0.916 | 0.085 |
| 3679.35 | B21 | 0.332 | 0.844 | 0.031 | 1.046 | 0.094 |
| 3682.81 | B20 | 0.331 | 0.897 | 0.034 | 1.111 | 0.100 |
| 3686.83 | B19 | 0.330 | 1.121 | 0.031 | 1.388 | 0.119 |
| 3691.55 | B18 | 0.329 | 1.184 | 0.023 | 1.465 | 0.122 |
| 3697.15 | B17 | 0.328 | 1.298 | 0.027 | 1.605 | 0.134 |
| 3703.85 | B16 | 0.327 | 1.778 | 0.031 | 2.196 | 0.181 |
| 3709.65 | He i | 0.326 | 0.039 | 0.013 | 0.049 | 0.016 |
| 3711.97 | B15 | 0.325 | 1.665 | 0.032 | 2.054 | 0.169 |
| 3721.94 | B14 | 0.323 | 2.167 | 0.040 | 2.671 | 0.218 |
| 3726.03 | [O ii] | 0.322 | 107.494 | 1.338 | 132.411 | 10.617 |
| 3728.81 | [O ii] | 0.322 | 74.678 | 0.644 | 91.955 | 7.314 |
| 3733.01 | He i | 0.321 | 0.071 | 0.010 | 0.088 | 0.014 |
| 3734.37 | B13 | 0.321 | 2.375 | 0.036 | 2.922 | 0.235 |
| 3750.15 | B12 | 0.317 | 3.125 | 0.027 | 3.836 | 0.301 |
| 3770.63 | B11 | 0.313 | 4.076 | 0.033 | 4.991 | 0.386 |
| 3797.90 | B10 | 0.307 | 5.102 | 0.035 | 6.224 | 0.472 |
| 3819.60 | He i | 0.302 | 0.089 | 0.011 | 0.108 | 0.015 |
| 3835.38 | B9 (Hη) | 0.299 | 6.491 | 0.037 | 7.876 | 0.580 |
| 3889.05 | B8 | 0.286 | 9.595 | 0.191 | 11.547 | 0.844 |
| 3918.97 | C ii | 0.279 | 0.065 | 0.011 | 0.078 | 0.014 |
| 3920.68 | C ii | 0.279 | 0.142 | 0.011 | 0.170 | 0.018 |
| 3970.07 | B7 (Hε) | 0.266 | 14.294 | 0.071 | 16.977 | 1.113 |
| 4068.60 | [S ii] | 0.239 | 0.808 | 0.035 | 0.944 | 0.069 |
| 4101.73 | B6 (Hδ) | 0.230 | 23.318 | 0.106 | 27.051 | 1.531 |
| 4267.00 | C ii | 0.180 | 0.210 | 0.030 | 0.236 | 0.035 |
| 4340.46 | B5 (Hγ) | 0.157 | 42.854 | 0.195 | 47.420 | 1.837 |
| 4471.47 | He i | 0.115 | 0.569 | 0.013 | 0.613 | 0.022 |
| 4571.10 | Mg i] | 0.084 | 0.106 | 0.019 | 0.112 | 0.020 |
| 4658.05 | [Fe iii] | 0.058 | 0.391 | 0.015 | 0.406 | 0.017 |
| 4701.53 | [Fe iii] | 0.045 | 0.093 | 0.008 | 0.096 | 0.009 |
| 4754.69 | [Fe iii] | 0.030 | 0.077 | 0.013 | 0.079 | 0.014 |
| 4769.43 | [Fe iii] | 0.025 | 0.025 | 0.008 | 0.025 | 0.008 |
| 4861.33 | B4 (Hβ) | 0.000 | 100.000 | 0.251 | 100.000 | 0.251 |
| 4881.00 | [Fe iii] | −0.005 | 0.131 | 0.009 | 0.130 | 0.009 |
| 4888.87 | [Fe iii] | −0.007 | 0.021 | 0.007 | 0.021 | 0.007 |
| 4921.93 | He i | −0.016 | 0.130 | 0.008 | 0.129 | 0.008 |
| 4958.91 | [O iii] | −0.026 | 1.127 | 0.008 | 1.109 | 0.011 |
| 5006.84 | [O iii] | −0.038 | 3.408 | 0.015 | 3.326 | 0.034 |
| 5015.68 | He i | −0.040 | 0.385 | 0.010 | 0.375 | 0.011 |
| 5055.98 | Si ii | −0.050 | 0.097 | 0.031 | 0.094 | 0.030 |
| 5067.52 | Ni iii | −0.052 | 0.065 | 0.010 | 0.062 | 0.009 |
| 5197.90 | [N i] | −0.082 | 0.059 | 0.022 | 0.056 | 0.021 |
| 5200.26 | [N i] | −0.083 | 0.055 | 0.015 | 0.052 | 0.014 |
| 5270.40 | [Fe iii] | −0.098 | 0.183 | 0.011 | 0.172 | 0.011 |
| 5273.24 | Ne ii | −0.098 | 0.031 | 0.012 | 0.029 | 0.011 |
| 5517.72 | [Cl iii] | −0.145 | 0.128 | 0.013 | 0.116 | 0.012 |
| 5537.89 | [Cl iii] | −0.149 | 0.122 | 0.006 | 0.111 | 0.007 |
| 5754.64 | [N ii] | −0.185 | 1.489 | 0.017 | 1.322 | 0.062 |
| 5875.60 | He i | −0.203 | 1.786 | 0.029 | 1.566 | 0.082 |
| 5886.05 | C ii | −0.205 | 0.061 | 0.010 | 0.054 | 0.009 |
| 5891.60 | C ii | −0.205 | 0.056 | 0.008 | 0.049 | 0.007 |
| 5912.58 | C i | −0.208 | 0.058 | 0.005 | 0.051 | 0.005 |
| 5931.78 | N ii | −0.211 | 0.068 | 0.008 | 0.059 | 0.007 |
| 5950.71 | Fe iii | −0.214 | 0.040 | 0.009 | 0.035 | 0.008 |
| 6300.30 | [O i] | −0.263 | 0.638 | 0.018 | 0.538 | 0.038 |
| 6312.10 | [S iii] | −0.264 | 0.212 | 0.013 | 0.179 | 0.016 |
| 6347.03 | Ni ii | −0.269 | 0.070 | 0.010 | 0.059 | 0.009 |
| 6363.78 | [O i] | −0.271 | 0.195 | 0.014 | 0.164 | 0.016 |
| 6379.58 | O ii | −0.273 | 0.098 | 0.023 | 0.082 | 0.020 |
| 6461.95 | C ii | −0.284 | 0.074 | 0.009 | 0.061 | 0.008 |
| 6548.04 | [N ii] | −0.296 | 45.988 | 0.395 | 37.985 | 2.778 |
| 6562.80 | B3 (Hα) | −0.298 | 375.888 | 1.958 | 310.085 | 22.731 |
| 6578.05 | C ii | −0.300 | 0.317 | 0.008 | 0.261 | 0.020 |
| 6583.46 | [N ii] | −0.300 | 138.238 | 1.323 | 113.836 | 8.471 |
| 6678.15 | He i | −0.313 | 0.588 | 0.012 | 0.480 | 0.038 |
| 6716.44 | [S ii] | −0.318 | 4.770 | 0.047 | 3.884 | 0.306 |
| 6730.81 | [S ii] | −0.320 | 7.203 | 0.078 | 5.857 | 0.465 |
| 7065.18 | He i | −0.364 | 0.494 | 0.011 | 0.391 | 0.036 |
| 7135.80 | [Ar iii] | −0.374 | 0.740 | 0.009 | 0.581 | 0.054 |
| 7231.32 | C ii | −0.387 | 0.352 | 0.018 | 0.274 | 0.024 |
| 7236.42 | C ii | −0.387 | 0.741 | 0.034 | 0.576 | 0.042 |
| 7281.35 | He i | −0.393 | 0.159 | 0.010 | 0.123 | 0.014 |
| 7318.92 | [O ii] | −0.398 | 1.465 | 0.061 | 1.132 | 0.120 |
| 7319.99 | [O ii] | −0.398 | 4.560 | 0.057 | 3.524 | 0.348 |
| 7329.66 | [O ii] | −0.400 | 2.382 | 0.026 | 1.839 | 0.182 |
| 7330.73 | [O ii] | −0.400 | 2.460 | 0.029 | 1.899 | 0.188 |
| 7751.10 | [Ar iii] | −0.455 | 0.187 | 0.009 | 0.139 | 0.017 |
| 7769.23 | Ca i | −0.458 | 0.122 | 0.007 | 0.091 | 0.012 |
| 7771.94 | O i | −0.458 | 0.084 | 0.006 | 0.063 | 0.008 |
| 7874.65 | [Fe ii] | −0.471 | 0.032 | 0.004 | 0.023 | 0.004 |
| 8240.19 | P45 | −0.515 | 0.067 | 0.008 | 0.048 | 0.008 |
| 8241.88 | P44 | −0.516 | 0.090 | 0.008 | 0.064 | 0.010 |
| 8243.69 | P43 | −0.516 | 0.055 | 0.006 | 0.039 | 0.007 |
| 8245.64 | P42 | −0.516 | 0.023 | 0.005 | 0.016 | 0.004 |
| 8247.73 | P41 | −0.516 | 0.071 | 0.006 | 0.051 | 0.008 |
| 8249.97 | P40 | −0.517 | 0.037 | 0.003 | 0.027 | 0.004 |
| 8252.40 | P39 | −0.517 | 0.077 | 0.008 | 0.055 | 0.009 |
| 8255.02 | P38 | −0.517 | 0.093 | 0.008 | 0.066 | 0.010 |
| 8257.85 | P37 | −0.517 | 0.093 | 0.007 | 0.066 | 0.010 |
| 8260.93 | P36 | −0.518 | 0.103 | 0.010 | 0.074 | 0.012 |
| 8264.28 | P35 | −0.518 | 0.107 | 0.009 | 0.076 | 0.012 |
| 8267.94 | P34 | −0.519 | 0.114 | 0.008 | 0.082 | 0.012 |
| 8271.93 | P33 | −0.519 | 0.118 | 0.012 | 0.084 | 0.014 |
| 8276.31 | P32 | −0.520 | 0.120 | 0.011 | 0.086 | 0.014 |
| 8281.12 | P31 | −0.520 | 0.114 | 0.010 | 0.081 | 0.013 |
| 8286.43 | P30 | −0.521 | 0.135 | 0.011 | 0.096 | 0.015 |
| 8292.31 | P29 | −0.521 | 0.190 | 0.012 | 0.135 | 0.019 |
| 8298.83 | P28 | −0.522 | 0.164 | 0.010 | 0.117 | 0.017 |
| 8306.11 | P27 | −0.523 | 0.207 | 0.012 | 0.148 | 0.021 |
| 8333.78 | P24 | −0.526 | 0.307 | 0.017 | 0.218 | 0.031 |
| 8340.80 | C ii | −0.527 | 0.018 | 0.005 | 0.013 | 0.004 |
| 8345.47 | P23 | −0.527 | 0.296 | 0.017 | 0.211 | 0.030 |
| 8359.00 | P22 | −0.529 | 0.385 | 0.021 | 0.274 | 0.038 |
| 8374.48 | P21 | −0.531 | 0.366 | 0.020 | 0.260 | 0.037 |
| 8392.40 | P20 | −0.533 | 0.382 | 0.020 | 0.271 | 0.038 |
| 8413.32 | P19 | −0.535 | 0.449 | 0.021 | 0.318 | 0.044 |
| 8502.48 | P16 | −0.544 | 0.668 | 0.031 | 0.470 | 0.067 |
| 8665.02 | P13 | −0.560 | 1.274 | 0.057 | 0.887 | 0.128 |
| 8750.47 | P12 | −0.568 | 1.558 | 0.069 | 1.079 | 0.158 |
| 8776.83 | He i | −0.571 | 0.046 | 0.005 | 0.032 | 0.006 |
| 8862.78 | P11 | −0.578 | 1.903 | 0.085 | 1.309 | 0.195 |
| 9014.91 | P10 | −0.590 | 2.554 | 0.113 | 1.744 | 0.264 |
| 9068.60 | [S iii] | −0.594 | 3.789 | 0.170 | 2.581 | 0.394 |
| 9123.60 | [Cl ii] | −0.598 | 0.128 | 0.010 | 0.087 | 0.014 |
| 9545.97 | P8 | −0.626 | 4.546 | 0.202 | 3.033 | 0.486 |
| 70000.0 | C60/[Ar ii]/H i | 28.665 | 3.226 | |||
| 74578.2 | H i | 3.102 | 0.226 | |||
| 85000.0 | C60 | 7.003 | 0.545 | |||
| 89889.3 | [Ar iii] | 0.757 | 0.145 | |||
| 123800.0 | H i | 1.029 | 0.271 | |||
| 128100.6 | [Ne ii] | 20.607 | 1.555 | |||
| 174000.0 | C60/C70 | 12.131 | 1.654 | |||
| C60 | 9.399 | 1.282 | ||||
| 187079.3 | [S iii] | 5.263 | 0.724 | |||
| 189000.0 | C60/C70 | <21.253 | ||||
| C60 | <19.188 | |||||
| 334719.0 | [S iii] | 4.004 | 0.857 |
Note. We measured the flux of the C60, 70 18.9 |$\mu$|m by adopting FWHM of 0.347 |$\mu$|m measured in Tc1 (Otsuka et al. 2014) because this line seems to be partially lacked due to spike noise. We estimated the expected solo intensity of the C60 17.4/18.9 |$\mu$|m using the C60/C70 ratio at 17.4 |$\mu$|m = 3.44 and the C60/C70 ratio at 18.9 |$\mu$|m = 9.29 measured in Tc1 (Cami et al. 2010).
Identified emission lines in the HDS and IRS spectra. f(λ) is reddening law of Cardelli et al. (1989), F(λ) and I(λ) are observed and interstellar extinction corrected line fluxes normalized to F(Hβ) and I(Hβ), respectively.
| λlab. (Å) . | Line . | f(λ) . | F(λ) . | δ F(λ) . | I(λ) . | δ I(λ) . |
|---|---|---|---|---|---|---|
| 3656.66 | B37 | 0.336 | 0.015 | 0.010 | 0.019 | 0.013 |
| 3657.27 | B36 | 0.336 | 0.062 | 0.019 | 0.077 | 0.024 |
| 3657.92 | B35 | 0.336 | 0.048 | 0.013 | 0.060 | 0.017 |
| 3658.64 | B34 | 0.336 | 0.076 | 0.012 | 0.094 | 0.017 |
| 3659.42 | B32 | 0.336 | 0.131 | 0.015 | 0.162 | 0.023 |
| 3660.28 | B33 | 0.335 | 0.162 | 0.014 | 0.201 | 0.024 |
| 3661.22 | B31 | 0.335 | 0.265 | 0.021 | 0.330 | 0.038 |
| 3662.26 | B30 | 0.335 | 0.324 | 0.028 | 0.402 | 0.048 |
| 3663.40 | B29 | 0.335 | 0.377 | 0.032 | 0.469 | 0.055 |
| 3664.68 | B28 | 0.334 | 0.762 | 0.052 | 0.945 | 0.101 |
| 3666.09 | B27 | 0.334 | 0.676 | 0.049 | 0.839 | 0.092 |
| 3667.68 | B26 | 0.334 | 0.623 | 0.039 | 0.773 | 0.080 |
| 3669.46 | B25 | 0.334 | 0.581 | 0.032 | 0.721 | 0.071 |
| 3671.48 | B24 | 0.333 | 0.593 | 0.029 | 0.735 | 0.070 |
| 3673.76 | B23 | 0.333 | 0.733 | 0.030 | 0.909 | 0.083 |
| 3676.36 | B22 | 0.332 | 0.739 | 0.033 | 0.916 | 0.085 |
| 3679.35 | B21 | 0.332 | 0.844 | 0.031 | 1.046 | 0.094 |
| 3682.81 | B20 | 0.331 | 0.897 | 0.034 | 1.111 | 0.100 |
| 3686.83 | B19 | 0.330 | 1.121 | 0.031 | 1.388 | 0.119 |
| 3691.55 | B18 | 0.329 | 1.184 | 0.023 | 1.465 | 0.122 |
| 3697.15 | B17 | 0.328 | 1.298 | 0.027 | 1.605 | 0.134 |
| 3703.85 | B16 | 0.327 | 1.778 | 0.031 | 2.196 | 0.181 |
| 3709.65 | He i | 0.326 | 0.039 | 0.013 | 0.049 | 0.016 |
| 3711.97 | B15 | 0.325 | 1.665 | 0.032 | 2.054 | 0.169 |
| 3721.94 | B14 | 0.323 | 2.167 | 0.040 | 2.671 | 0.218 |
| 3726.03 | [O ii] | 0.322 | 107.494 | 1.338 | 132.411 | 10.617 |
| 3728.81 | [O ii] | 0.322 | 74.678 | 0.644 | 91.955 | 7.314 |
| 3733.01 | He i | 0.321 | 0.071 | 0.010 | 0.088 | 0.014 |
| 3734.37 | B13 | 0.321 | 2.375 | 0.036 | 2.922 | 0.235 |
| 3750.15 | B12 | 0.317 | 3.125 | 0.027 | 3.836 | 0.301 |
| 3770.63 | B11 | 0.313 | 4.076 | 0.033 | 4.991 | 0.386 |
| 3797.90 | B10 | 0.307 | 5.102 | 0.035 | 6.224 | 0.472 |
| 3819.60 | He i | 0.302 | 0.089 | 0.011 | 0.108 | 0.015 |
| 3835.38 | B9 (Hη) | 0.299 | 6.491 | 0.037 | 7.876 | 0.580 |
| 3889.05 | B8 | 0.286 | 9.595 | 0.191 | 11.547 | 0.844 |
| 3918.97 | C ii | 0.279 | 0.065 | 0.011 | 0.078 | 0.014 |
| 3920.68 | C ii | 0.279 | 0.142 | 0.011 | 0.170 | 0.018 |
| 3970.07 | B7 (Hε) | 0.266 | 14.294 | 0.071 | 16.977 | 1.113 |
| 4068.60 | [S ii] | 0.239 | 0.808 | 0.035 | 0.944 | 0.069 |
| 4101.73 | B6 (Hδ) | 0.230 | 23.318 | 0.106 | 27.051 | 1.531 |
| 4267.00 | C ii | 0.180 | 0.210 | 0.030 | 0.236 | 0.035 |
| 4340.46 | B5 (Hγ) | 0.157 | 42.854 | 0.195 | 47.420 | 1.837 |
| 4471.47 | He i | 0.115 | 0.569 | 0.013 | 0.613 | 0.022 |
| 4571.10 | Mg i] | 0.084 | 0.106 | 0.019 | 0.112 | 0.020 |
| 4658.05 | [Fe iii] | 0.058 | 0.391 | 0.015 | 0.406 | 0.017 |
| 4701.53 | [Fe iii] | 0.045 | 0.093 | 0.008 | 0.096 | 0.009 |
| 4754.69 | [Fe iii] | 0.030 | 0.077 | 0.013 | 0.079 | 0.014 |
| 4769.43 | [Fe iii] | 0.025 | 0.025 | 0.008 | 0.025 | 0.008 |
| 4861.33 | B4 (Hβ) | 0.000 | 100.000 | 0.251 | 100.000 | 0.251 |
| 4881.00 | [Fe iii] | −0.005 | 0.131 | 0.009 | 0.130 | 0.009 |
| 4888.87 | [Fe iii] | −0.007 | 0.021 | 0.007 | 0.021 | 0.007 |
| 4921.93 | He i | −0.016 | 0.130 | 0.008 | 0.129 | 0.008 |
| 4958.91 | [O iii] | −0.026 | 1.127 | 0.008 | 1.109 | 0.011 |
| 5006.84 | [O iii] | −0.038 | 3.408 | 0.015 | 3.326 | 0.034 |
| 5015.68 | He i | −0.040 | 0.385 | 0.010 | 0.375 | 0.011 |
| 5055.98 | Si ii | −0.050 | 0.097 | 0.031 | 0.094 | 0.030 |
| 5067.52 | Ni iii | −0.052 | 0.065 | 0.010 | 0.062 | 0.009 |
| 5197.90 | [N i] | −0.082 | 0.059 | 0.022 | 0.056 | 0.021 |
| 5200.26 | [N i] | −0.083 | 0.055 | 0.015 | 0.052 | 0.014 |
| 5270.40 | [Fe iii] | −0.098 | 0.183 | 0.011 | 0.172 | 0.011 |
| 5273.24 | Ne ii | −0.098 | 0.031 | 0.012 | 0.029 | 0.011 |
| 5517.72 | [Cl iii] | −0.145 | 0.128 | 0.013 | 0.116 | 0.012 |
| 5537.89 | [Cl iii] | −0.149 | 0.122 | 0.006 | 0.111 | 0.007 |
| 5754.64 | [N ii] | −0.185 | 1.489 | 0.017 | 1.322 | 0.062 |
| 5875.60 | He i | −0.203 | 1.786 | 0.029 | 1.566 | 0.082 |
| 5886.05 | C ii | −0.205 | 0.061 | 0.010 | 0.054 | 0.009 |
| 5891.60 | C ii | −0.205 | 0.056 | 0.008 | 0.049 | 0.007 |
| 5912.58 | C i | −0.208 | 0.058 | 0.005 | 0.051 | 0.005 |
| 5931.78 | N ii | −0.211 | 0.068 | 0.008 | 0.059 | 0.007 |
| 5950.71 | Fe iii | −0.214 | 0.040 | 0.009 | 0.035 | 0.008 |
| 6300.30 | [O i] | −0.263 | 0.638 | 0.018 | 0.538 | 0.038 |
| 6312.10 | [S iii] | −0.264 | 0.212 | 0.013 | 0.179 | 0.016 |
| 6347.03 | Ni ii | −0.269 | 0.070 | 0.010 | 0.059 | 0.009 |
| 6363.78 | [O i] | −0.271 | 0.195 | 0.014 | 0.164 | 0.016 |
| 6379.58 | O ii | −0.273 | 0.098 | 0.023 | 0.082 | 0.020 |
| 6461.95 | C ii | −0.284 | 0.074 | 0.009 | 0.061 | 0.008 |
| 6548.04 | [N ii] | −0.296 | 45.988 | 0.395 | 37.985 | 2.778 |
| 6562.80 | B3 (Hα) | −0.298 | 375.888 | 1.958 | 310.085 | 22.731 |
| 6578.05 | C ii | −0.300 | 0.317 | 0.008 | 0.261 | 0.020 |
| 6583.46 | [N ii] | −0.300 | 138.238 | 1.323 | 113.836 | 8.471 |
| 6678.15 | He i | −0.313 | 0.588 | 0.012 | 0.480 | 0.038 |
| 6716.44 | [S ii] | −0.318 | 4.770 | 0.047 | 3.884 | 0.306 |
| 6730.81 | [S ii] | −0.320 | 7.203 | 0.078 | 5.857 | 0.465 |
| 7065.18 | He i | −0.364 | 0.494 | 0.011 | 0.391 | 0.036 |
| 7135.80 | [Ar iii] | −0.374 | 0.740 | 0.009 | 0.581 | 0.054 |
| 7231.32 | C ii | −0.387 | 0.352 | 0.018 | 0.274 | 0.024 |
| 7236.42 | C ii | −0.387 | 0.741 | 0.034 | 0.576 | 0.042 |
| 7281.35 | He i | −0.393 | 0.159 | 0.010 | 0.123 | 0.014 |
| 7318.92 | [O ii] | −0.398 | 1.465 | 0.061 | 1.132 | 0.120 |
| 7319.99 | [O ii] | −0.398 | 4.560 | 0.057 | 3.524 | 0.348 |
| 7329.66 | [O ii] | −0.400 | 2.382 | 0.026 | 1.839 | 0.182 |
| 7330.73 | [O ii] | −0.400 | 2.460 | 0.029 | 1.899 | 0.188 |
| 7751.10 | [Ar iii] | −0.455 | 0.187 | 0.009 | 0.139 | 0.017 |
| 7769.23 | Ca i | −0.458 | 0.122 | 0.007 | 0.091 | 0.012 |
| 7771.94 | O i | −0.458 | 0.084 | 0.006 | 0.063 | 0.008 |
| 7874.65 | [Fe ii] | −0.471 | 0.032 | 0.004 | 0.023 | 0.004 |
| 8240.19 | P45 | −0.515 | 0.067 | 0.008 | 0.048 | 0.008 |
| 8241.88 | P44 | −0.516 | 0.090 | 0.008 | 0.064 | 0.010 |
| 8243.69 | P43 | −0.516 | 0.055 | 0.006 | 0.039 | 0.007 |
| 8245.64 | P42 | −0.516 | 0.023 | 0.005 | 0.016 | 0.004 |
| 8247.73 | P41 | −0.516 | 0.071 | 0.006 | 0.051 | 0.008 |
| 8249.97 | P40 | −0.517 | 0.037 | 0.003 | 0.027 | 0.004 |
| 8252.40 | P39 | −0.517 | 0.077 | 0.008 | 0.055 | 0.009 |
| 8255.02 | P38 | −0.517 | 0.093 | 0.008 | 0.066 | 0.010 |
| 8257.85 | P37 | −0.517 | 0.093 | 0.007 | 0.066 | 0.010 |
| 8260.93 | P36 | −0.518 | 0.103 | 0.010 | 0.074 | 0.012 |
| 8264.28 | P35 | −0.518 | 0.107 | 0.009 | 0.076 | 0.012 |
| 8267.94 | P34 | −0.519 | 0.114 | 0.008 | 0.082 | 0.012 |
| 8271.93 | P33 | −0.519 | 0.118 | 0.012 | 0.084 | 0.014 |
| 8276.31 | P32 | −0.520 | 0.120 | 0.011 | 0.086 | 0.014 |
| 8281.12 | P31 | −0.520 | 0.114 | 0.010 | 0.081 | 0.013 |
| 8286.43 | P30 | −0.521 | 0.135 | 0.011 | 0.096 | 0.015 |
| 8292.31 | P29 | −0.521 | 0.190 | 0.012 | 0.135 | 0.019 |
| 8298.83 | P28 | −0.522 | 0.164 | 0.010 | 0.117 | 0.017 |
| 8306.11 | P27 | −0.523 | 0.207 | 0.012 | 0.148 | 0.021 |
| 8333.78 | P24 | −0.526 | 0.307 | 0.017 | 0.218 | 0.031 |
| 8340.80 | C ii | −0.527 | 0.018 | 0.005 | 0.013 | 0.004 |
| 8345.47 | P23 | −0.527 | 0.296 | 0.017 | 0.211 | 0.030 |
| 8359.00 | P22 | −0.529 | 0.385 | 0.021 | 0.274 | 0.038 |
| 8374.48 | P21 | −0.531 | 0.366 | 0.020 | 0.260 | 0.037 |
| 8392.40 | P20 | −0.533 | 0.382 | 0.020 | 0.271 | 0.038 |
| 8413.32 | P19 | −0.535 | 0.449 | 0.021 | 0.318 | 0.044 |
| 8502.48 | P16 | −0.544 | 0.668 | 0.031 | 0.470 | 0.067 |
| 8665.02 | P13 | −0.560 | 1.274 | 0.057 | 0.887 | 0.128 |
| 8750.47 | P12 | −0.568 | 1.558 | 0.069 | 1.079 | 0.158 |
| 8776.83 | He i | −0.571 | 0.046 | 0.005 | 0.032 | 0.006 |
| 8862.78 | P11 | −0.578 | 1.903 | 0.085 | 1.309 | 0.195 |
| 9014.91 | P10 | −0.590 | 2.554 | 0.113 | 1.744 | 0.264 |
| 9068.60 | [S iii] | −0.594 | 3.789 | 0.170 | 2.581 | 0.394 |
| 9123.60 | [Cl ii] | −0.598 | 0.128 | 0.010 | 0.087 | 0.014 |
| 9545.97 | P8 | −0.626 | 4.546 | 0.202 | 3.033 | 0.486 |
| 70000.0 | C60/[Ar ii]/H i | 28.665 | 3.226 | |||
| 74578.2 | H i | 3.102 | 0.226 | |||
| 85000.0 | C60 | 7.003 | 0.545 | |||
| 89889.3 | [Ar iii] | 0.757 | 0.145 | |||
| 123800.0 | H i | 1.029 | 0.271 | |||
| 128100.6 | [Ne ii] | 20.607 | 1.555 | |||
| 174000.0 | C60/C70 | 12.131 | 1.654 | |||
| C60 | 9.399 | 1.282 | ||||
| 187079.3 | [S iii] | 5.263 | 0.724 | |||
| 189000.0 | C60/C70 | <21.253 | ||||
| C60 | <19.188 | |||||
| 334719.0 | [S iii] | 4.004 | 0.857 |
| λlab. (Å) . | Line . | f(λ) . | F(λ) . | δ F(λ) . | I(λ) . | δ I(λ) . |
|---|---|---|---|---|---|---|
| 3656.66 | B37 | 0.336 | 0.015 | 0.010 | 0.019 | 0.013 |
| 3657.27 | B36 | 0.336 | 0.062 | 0.019 | 0.077 | 0.024 |
| 3657.92 | B35 | 0.336 | 0.048 | 0.013 | 0.060 | 0.017 |
| 3658.64 | B34 | 0.336 | 0.076 | 0.012 | 0.094 | 0.017 |
| 3659.42 | B32 | 0.336 | 0.131 | 0.015 | 0.162 | 0.023 |
| 3660.28 | B33 | 0.335 | 0.162 | 0.014 | 0.201 | 0.024 |
| 3661.22 | B31 | 0.335 | 0.265 | 0.021 | 0.330 | 0.038 |
| 3662.26 | B30 | 0.335 | 0.324 | 0.028 | 0.402 | 0.048 |
| 3663.40 | B29 | 0.335 | 0.377 | 0.032 | 0.469 | 0.055 |
| 3664.68 | B28 | 0.334 | 0.762 | 0.052 | 0.945 | 0.101 |
| 3666.09 | B27 | 0.334 | 0.676 | 0.049 | 0.839 | 0.092 |
| 3667.68 | B26 | 0.334 | 0.623 | 0.039 | 0.773 | 0.080 |
| 3669.46 | B25 | 0.334 | 0.581 | 0.032 | 0.721 | 0.071 |
| 3671.48 | B24 | 0.333 | 0.593 | 0.029 | 0.735 | 0.070 |
| 3673.76 | B23 | 0.333 | 0.733 | 0.030 | 0.909 | 0.083 |
| 3676.36 | B22 | 0.332 | 0.739 | 0.033 | 0.916 | 0.085 |
| 3679.35 | B21 | 0.332 | 0.844 | 0.031 | 1.046 | 0.094 |
| 3682.81 | B20 | 0.331 | 0.897 | 0.034 | 1.111 | 0.100 |
| 3686.83 | B19 | 0.330 | 1.121 | 0.031 | 1.388 | 0.119 |
| 3691.55 | B18 | 0.329 | 1.184 | 0.023 | 1.465 | 0.122 |
| 3697.15 | B17 | 0.328 | 1.298 | 0.027 | 1.605 | 0.134 |
| 3703.85 | B16 | 0.327 | 1.778 | 0.031 | 2.196 | 0.181 |
| 3709.65 | He i | 0.326 | 0.039 | 0.013 | 0.049 | 0.016 |
| 3711.97 | B15 | 0.325 | 1.665 | 0.032 | 2.054 | 0.169 |
| 3721.94 | B14 | 0.323 | 2.167 | 0.040 | 2.671 | 0.218 |
| 3726.03 | [O ii] | 0.322 | 107.494 | 1.338 | 132.411 | 10.617 |
| 3728.81 | [O ii] | 0.322 | 74.678 | 0.644 | 91.955 | 7.314 |
| 3733.01 | He i | 0.321 | 0.071 | 0.010 | 0.088 | 0.014 |
| 3734.37 | B13 | 0.321 | 2.375 | 0.036 | 2.922 | 0.235 |
| 3750.15 | B12 | 0.317 | 3.125 | 0.027 | 3.836 | 0.301 |
| 3770.63 | B11 | 0.313 | 4.076 | 0.033 | 4.991 | 0.386 |
| 3797.90 | B10 | 0.307 | 5.102 | 0.035 | 6.224 | 0.472 |
| 3819.60 | He i | 0.302 | 0.089 | 0.011 | 0.108 | 0.015 |
| 3835.38 | B9 (Hη) | 0.299 | 6.491 | 0.037 | 7.876 | 0.580 |
| 3889.05 | B8 | 0.286 | 9.595 | 0.191 | 11.547 | 0.844 |
| 3918.97 | C ii | 0.279 | 0.065 | 0.011 | 0.078 | 0.014 |
| 3920.68 | C ii | 0.279 | 0.142 | 0.011 | 0.170 | 0.018 |
| 3970.07 | B7 (Hε) | 0.266 | 14.294 | 0.071 | 16.977 | 1.113 |
| 4068.60 | [S ii] | 0.239 | 0.808 | 0.035 | 0.944 | 0.069 |
| 4101.73 | B6 (Hδ) | 0.230 | 23.318 | 0.106 | 27.051 | 1.531 |
| 4267.00 | C ii | 0.180 | 0.210 | 0.030 | 0.236 | 0.035 |
| 4340.46 | B5 (Hγ) | 0.157 | 42.854 | 0.195 | 47.420 | 1.837 |
| 4471.47 | He i | 0.115 | 0.569 | 0.013 | 0.613 | 0.022 |
| 4571.10 | Mg i] | 0.084 | 0.106 | 0.019 | 0.112 | 0.020 |
| 4658.05 | [Fe iii] | 0.058 | 0.391 | 0.015 | 0.406 | 0.017 |
| 4701.53 | [Fe iii] | 0.045 | 0.093 | 0.008 | 0.096 | 0.009 |
| 4754.69 | [Fe iii] | 0.030 | 0.077 | 0.013 | 0.079 | 0.014 |
| 4769.43 | [Fe iii] | 0.025 | 0.025 | 0.008 | 0.025 | 0.008 |
| 4861.33 | B4 (Hβ) | 0.000 | 100.000 | 0.251 | 100.000 | 0.251 |
| 4881.00 | [Fe iii] | −0.005 | 0.131 | 0.009 | 0.130 | 0.009 |
| 4888.87 | [Fe iii] | −0.007 | 0.021 | 0.007 | 0.021 | 0.007 |
| 4921.93 | He i | −0.016 | 0.130 | 0.008 | 0.129 | 0.008 |
| 4958.91 | [O iii] | −0.026 | 1.127 | 0.008 | 1.109 | 0.011 |
| 5006.84 | [O iii] | −0.038 | 3.408 | 0.015 | 3.326 | 0.034 |
| 5015.68 | He i | −0.040 | 0.385 | 0.010 | 0.375 | 0.011 |
| 5055.98 | Si ii | −0.050 | 0.097 | 0.031 | 0.094 | 0.030 |
| 5067.52 | Ni iii | −0.052 | 0.065 | 0.010 | 0.062 | 0.009 |
| 5197.90 | [N i] | −0.082 | 0.059 | 0.022 | 0.056 | 0.021 |
| 5200.26 | [N i] | −0.083 | 0.055 | 0.015 | 0.052 | 0.014 |
| 5270.40 | [Fe iii] | −0.098 | 0.183 | 0.011 | 0.172 | 0.011 |
| 5273.24 | Ne ii | −0.098 | 0.031 | 0.012 | 0.029 | 0.011 |
| 5517.72 | [Cl iii] | −0.145 | 0.128 | 0.013 | 0.116 | 0.012 |
| 5537.89 | [Cl iii] | −0.149 | 0.122 | 0.006 | 0.111 | 0.007 |
| 5754.64 | [N ii] | −0.185 | 1.489 | 0.017 | 1.322 | 0.062 |
| 5875.60 | He i | −0.203 | 1.786 | 0.029 | 1.566 | 0.082 |
| 5886.05 | C ii | −0.205 | 0.061 | 0.010 | 0.054 | 0.009 |
| 5891.60 | C ii | −0.205 | 0.056 | 0.008 | 0.049 | 0.007 |
| 5912.58 | C i | −0.208 | 0.058 | 0.005 | 0.051 | 0.005 |
| 5931.78 | N ii | −0.211 | 0.068 | 0.008 | 0.059 | 0.007 |
| 5950.71 | Fe iii | −0.214 | 0.040 | 0.009 | 0.035 | 0.008 |
| 6300.30 | [O i] | −0.263 | 0.638 | 0.018 | 0.538 | 0.038 |
| 6312.10 | [S iii] | −0.264 | 0.212 | 0.013 | 0.179 | 0.016 |
| 6347.03 | Ni ii | −0.269 | 0.070 | 0.010 | 0.059 | 0.009 |
| 6363.78 | [O i] | −0.271 | 0.195 | 0.014 | 0.164 | 0.016 |
| 6379.58 | O ii | −0.273 | 0.098 | 0.023 | 0.082 | 0.020 |
| 6461.95 | C ii | −0.284 | 0.074 | 0.009 | 0.061 | 0.008 |
| 6548.04 | [N ii] | −0.296 | 45.988 | 0.395 | 37.985 | 2.778 |
| 6562.80 | B3 (Hα) | −0.298 | 375.888 | 1.958 | 310.085 | 22.731 |
| 6578.05 | C ii | −0.300 | 0.317 | 0.008 | 0.261 | 0.020 |
| 6583.46 | [N ii] | −0.300 | 138.238 | 1.323 | 113.836 | 8.471 |
| 6678.15 | He i | −0.313 | 0.588 | 0.012 | 0.480 | 0.038 |
| 6716.44 | [S ii] | −0.318 | 4.770 | 0.047 | 3.884 | 0.306 |
| 6730.81 | [S ii] | −0.320 | 7.203 | 0.078 | 5.857 | 0.465 |
| 7065.18 | He i | −0.364 | 0.494 | 0.011 | 0.391 | 0.036 |
| 7135.80 | [Ar iii] | −0.374 | 0.740 | 0.009 | 0.581 | 0.054 |
| 7231.32 | C ii | −0.387 | 0.352 | 0.018 | 0.274 | 0.024 |
| 7236.42 | C ii | −0.387 | 0.741 | 0.034 | 0.576 | 0.042 |
| 7281.35 | He i | −0.393 | 0.159 | 0.010 | 0.123 | 0.014 |
| 7318.92 | [O ii] | −0.398 | 1.465 | 0.061 | 1.132 | 0.120 |
| 7319.99 | [O ii] | −0.398 | 4.560 | 0.057 | 3.524 | 0.348 |
| 7329.66 | [O ii] | −0.400 | 2.382 | 0.026 | 1.839 | 0.182 |
| 7330.73 | [O ii] | −0.400 | 2.460 | 0.029 | 1.899 | 0.188 |
| 7751.10 | [Ar iii] | −0.455 | 0.187 | 0.009 | 0.139 | 0.017 |
| 7769.23 | Ca i | −0.458 | 0.122 | 0.007 | 0.091 | 0.012 |
| 7771.94 | O i | −0.458 | 0.084 | 0.006 | 0.063 | 0.008 |
| 7874.65 | [Fe ii] | −0.471 | 0.032 | 0.004 | 0.023 | 0.004 |
| 8240.19 | P45 | −0.515 | 0.067 | 0.008 | 0.048 | 0.008 |
| 8241.88 | P44 | −0.516 | 0.090 | 0.008 | 0.064 | 0.010 |
| 8243.69 | P43 | −0.516 | 0.055 | 0.006 | 0.039 | 0.007 |
| 8245.64 | P42 | −0.516 | 0.023 | 0.005 | 0.016 | 0.004 |
| 8247.73 | P41 | −0.516 | 0.071 | 0.006 | 0.051 | 0.008 |
| 8249.97 | P40 | −0.517 | 0.037 | 0.003 | 0.027 | 0.004 |
| 8252.40 | P39 | −0.517 | 0.077 | 0.008 | 0.055 | 0.009 |
| 8255.02 | P38 | −0.517 | 0.093 | 0.008 | 0.066 | 0.010 |
| 8257.85 | P37 | −0.517 | 0.093 | 0.007 | 0.066 | 0.010 |
| 8260.93 | P36 | −0.518 | 0.103 | 0.010 | 0.074 | 0.012 |
| 8264.28 | P35 | −0.518 | 0.107 | 0.009 | 0.076 | 0.012 |
| 8267.94 | P34 | −0.519 | 0.114 | 0.008 | 0.082 | 0.012 |
| 8271.93 | P33 | −0.519 | 0.118 | 0.012 | 0.084 | 0.014 |
| 8276.31 | P32 | −0.520 | 0.120 | 0.011 | 0.086 | 0.014 |
| 8281.12 | P31 | −0.520 | 0.114 | 0.010 | 0.081 | 0.013 |
| 8286.43 | P30 | −0.521 | 0.135 | 0.011 | 0.096 | 0.015 |
| 8292.31 | P29 | −0.521 | 0.190 | 0.012 | 0.135 | 0.019 |
| 8298.83 | P28 | −0.522 | 0.164 | 0.010 | 0.117 | 0.017 |
| 8306.11 | P27 | −0.523 | 0.207 | 0.012 | 0.148 | 0.021 |
| 8333.78 | P24 | −0.526 | 0.307 | 0.017 | 0.218 | 0.031 |
| 8340.80 | C ii | −0.527 | 0.018 | 0.005 | 0.013 | 0.004 |
| 8345.47 | P23 | −0.527 | 0.296 | 0.017 | 0.211 | 0.030 |
| 8359.00 | P22 | −0.529 | 0.385 | 0.021 | 0.274 | 0.038 |
| 8374.48 | P21 | −0.531 | 0.366 | 0.020 | 0.260 | 0.037 |
| 8392.40 | P20 | −0.533 | 0.382 | 0.020 | 0.271 | 0.038 |
| 8413.32 | P19 | −0.535 | 0.449 | 0.021 | 0.318 | 0.044 |
| 8502.48 | P16 | −0.544 | 0.668 | 0.031 | 0.470 | 0.067 |
| 8665.02 | P13 | −0.560 | 1.274 | 0.057 | 0.887 | 0.128 |
| 8750.47 | P12 | −0.568 | 1.558 | 0.069 | 1.079 | 0.158 |
| 8776.83 | He i | −0.571 | 0.046 | 0.005 | 0.032 | 0.006 |
| 8862.78 | P11 | −0.578 | 1.903 | 0.085 | 1.309 | 0.195 |
| 9014.91 | P10 | −0.590 | 2.554 | 0.113 | 1.744 | 0.264 |
| 9068.60 | [S iii] | −0.594 | 3.789 | 0.170 | 2.581 | 0.394 |
| 9123.60 | [Cl ii] | −0.598 | 0.128 | 0.010 | 0.087 | 0.014 |
| 9545.97 | P8 | −0.626 | 4.546 | 0.202 | 3.033 | 0.486 |
| 70000.0 | C60/[Ar ii]/H i | 28.665 | 3.226 | |||
| 74578.2 | H i | 3.102 | 0.226 | |||
| 85000.0 | C60 | 7.003 | 0.545 | |||
| 89889.3 | [Ar iii] | 0.757 | 0.145 | |||
| 123800.0 | H i | 1.029 | 0.271 | |||
| 128100.6 | [Ne ii] | 20.607 | 1.555 | |||
| 174000.0 | C60/C70 | 12.131 | 1.654 | |||
| C60 | 9.399 | 1.282 | ||||
| 187079.3 | [S iii] | 5.263 | 0.724 | |||
| 189000.0 | C60/C70 | <21.253 | ||||
| C60 | <19.188 | |||||
| 334719.0 | [S iii] | 4.004 | 0.857 |
Note. We measured the flux of the C60, 70 18.9 |$\mu$|m by adopting FWHM of 0.347 |$\mu$|m measured in Tc1 (Otsuka et al. 2014) because this line seems to be partially lacked due to spike noise. We estimated the expected solo intensity of the C60 17.4/18.9 |$\mu$|m using the C60/C70 ratio at 17.4 |$\mu$|m = 3.44 and the C60/C70 ratio at 18.9 |$\mu$|m = 9.29 measured in Tc1 (Cami et al. 2010).
| Band . | λc . | Fλ (reddened) . | Iλ (de-reddened) . |
|---|---|---|---|
| . | . | (erg s−1 cm−2|$\mu$|m−1) . | (erg s−1 cm−2|$\mu$|m−1) . |
| B | 0.4297 |$\mu$|m | 2.24(−10) ± 5.99(−12) | 4.75(−10) ± 1.41(−10) |
| g′ | 0.4640 |$\mu$|m | 1.93(−10) ± 1.42(−12) | 3.81(−10) ± 1.03(−10) |
| V | 0.5394 |$\mu$|m | 1.31(−10) ± 3.25(−12) | 2.29(−10) ± 5.14(−11) |
| r′ | 0.6122 |$\mu$|m | 1.05(−10) ± 2.61(−12) | 1.96(−10) ± 3.82(−11) |
| i′ | 0.7440 |$\mu$|m | 3.89(−11) ± 3.29(−12) | 7.89(−11) ± 1.35(−11) |
| J | 1.235 |$\mu$|m | 1.27(−11) ± 3.03(−13) | 1.48(−11) ± 9.94(−13) |
| H | 1.662 |$\mu$|m | 4.49(−12) ± 1.24(−13) | 4.95(−12) ± 2.36(−13) |
| Ks | 2.159 |$\mu$|m | 2.01(−12) ± 6.86(−14) | 2.15(−12) ± 9.13(−14) |
| Brγ | 2.162 |$\mu$|m | 4.29(−12) ± 7.66(−13) | 4.57(−12) ± 8.25(−13) |
| Brγ45 | 2.188 |$\mu$|m | 2.15(−12) ± 4.14(−14) | 2.28(−12) ± 7.21(−14) |
| W1 | 3.353 |$\mu$|m | 9.28(−13) ± 1.97(−14) | |
| W2 | 4.602 |$\mu$|m | 7.49(−13) ± 1.45(−14) | |
| W3 | 11.56 |$\mu$|m | 7.87(−13) ± 1.09(−14) | |
| L18W | 18.00 |$\mu$|m | 1.40(−12) ± 3.71(−13) | |
| W4 | 22.09 |$\mu$|m | 1.50(−12) ± 3.04(−14) |
| Band . | λc . | Fλ (reddened) . | Iλ (de-reddened) . |
|---|---|---|---|
| . | . | (erg s−1 cm−2|$\mu$|m−1) . | (erg s−1 cm−2|$\mu$|m−1) . |
| B | 0.4297 |$\mu$|m | 2.24(−10) ± 5.99(−12) | 4.75(−10) ± 1.41(−10) |
| g′ | 0.4640 |$\mu$|m | 1.93(−10) ± 1.42(−12) | 3.81(−10) ± 1.03(−10) |
| V | 0.5394 |$\mu$|m | 1.31(−10) ± 3.25(−12) | 2.29(−10) ± 5.14(−11) |
| r′ | 0.6122 |$\mu$|m | 1.05(−10) ± 2.61(−12) | 1.96(−10) ± 3.82(−11) |
| i′ | 0.7440 |$\mu$|m | 3.89(−11) ± 3.29(−12) | 7.89(−11) ± 1.35(−11) |
| J | 1.235 |$\mu$|m | 1.27(−11) ± 3.03(−13) | 1.48(−11) ± 9.94(−13) |
| H | 1.662 |$\mu$|m | 4.49(−12) ± 1.24(−13) | 4.95(−12) ± 2.36(−13) |
| Ks | 2.159 |$\mu$|m | 2.01(−12) ± 6.86(−14) | 2.15(−12) ± 9.13(−14) |
| Brγ | 2.162 |$\mu$|m | 4.29(−12) ± 7.66(−13) | 4.57(−12) ± 8.25(−13) |
| Brγ45 | 2.188 |$\mu$|m | 2.15(−12) ± 4.14(−14) | 2.28(−12) ± 7.21(−14) |
| W1 | 3.353 |$\mu$|m | 9.28(−13) ± 1.97(−14) | |
| W2 | 4.602 |$\mu$|m | 7.49(−13) ± 1.45(−14) | |
| W3 | 11.56 |$\mu$|m | 7.87(−13) ± 1.09(−14) | |
| L18W | 18.00 |$\mu$|m | 1.40(−12) ± 3.71(−13) | |
| W4 | 22.09 |$\mu$|m | 1.50(−12) ± 3.04(−14) |
| Band . | λc . | Fλ (reddened) . | Iλ (de-reddened) . |
|---|---|---|---|
| . | . | (erg s−1 cm−2|$\mu$|m−1) . | (erg s−1 cm−2|$\mu$|m−1) . |
| B | 0.4297 |$\mu$|m | 2.24(−10) ± 5.99(−12) | 4.75(−10) ± 1.41(−10) |
| g′ | 0.4640 |$\mu$|m | 1.93(−10) ± 1.42(−12) | 3.81(−10) ± 1.03(−10) |
| V | 0.5394 |$\mu$|m | 1.31(−10) ± 3.25(−12) | 2.29(−10) ± 5.14(−11) |
| r′ | 0.6122 |$\mu$|m | 1.05(−10) ± 2.61(−12) | 1.96(−10) ± 3.82(−11) |
| i′ | 0.7440 |$\mu$|m | 3.89(−11) ± 3.29(−12) | 7.89(−11) ± 1.35(−11) |
| J | 1.235 |$\mu$|m | 1.27(−11) ± 3.03(−13) | 1.48(−11) ± 9.94(−13) |
| H | 1.662 |$\mu$|m | 4.49(−12) ± 1.24(−13) | 4.95(−12) ± 2.36(−13) |
| Ks | 2.159 |$\mu$|m | 2.01(−12) ± 6.86(−14) | 2.15(−12) ± 9.13(−14) |
| Brγ | 2.162 |$\mu$|m | 4.29(−12) ± 7.66(−13) | 4.57(−12) ± 8.25(−13) |
| Brγ45 | 2.188 |$\mu$|m | 2.15(−12) ± 4.14(−14) | 2.28(−12) ± 7.21(−14) |
| W1 | 3.353 |$\mu$|m | 9.28(−13) ± 1.97(−14) | |
| W2 | 4.602 |$\mu$|m | 7.49(−13) ± 1.45(−14) | |
| W3 | 11.56 |$\mu$|m | 7.87(−13) ± 1.09(−14) | |
| L18W | 18.00 |$\mu$|m | 1.40(−12) ± 3.71(−13) | |
| W4 | 22.09 |$\mu$|m | 1.50(−12) ± 3.04(−14) |
| Band . | λc . | Fλ (reddened) . | Iλ (de-reddened) . |
|---|---|---|---|
| . | . | (erg s−1 cm−2|$\mu$|m−1) . | (erg s−1 cm−2|$\mu$|m−1) . |
| B | 0.4297 |$\mu$|m | 2.24(−10) ± 5.99(−12) | 4.75(−10) ± 1.41(−10) |
| g′ | 0.4640 |$\mu$|m | 1.93(−10) ± 1.42(−12) | 3.81(−10) ± 1.03(−10) |
| V | 0.5394 |$\mu$|m | 1.31(−10) ± 3.25(−12) | 2.29(−10) ± 5.14(−11) |
| r′ | 0.6122 |$\mu$|m | 1.05(−10) ± 2.61(−12) | 1.96(−10) ± 3.82(−11) |
| i′ | 0.7440 |$\mu$|m | 3.89(−11) ± 3.29(−12) | 7.89(−11) ± 1.35(−11) |
| J | 1.235 |$\mu$|m | 1.27(−11) ± 3.03(−13) | 1.48(−11) ± 9.94(−13) |
| H | 1.662 |$\mu$|m | 4.49(−12) ± 1.24(−13) | 4.95(−12) ± 2.36(−13) |
| Ks | 2.159 |$\mu$|m | 2.01(−12) ± 6.86(−14) | 2.15(−12) ± 9.13(−14) |
| Brγ | 2.162 |$\mu$|m | 4.29(−12) ± 7.66(−13) | 4.57(−12) ± 8.25(−13) |
| Brγ45 | 2.188 |$\mu$|m | 2.15(−12) ± 4.14(−14) | 2.28(−12) ± 7.21(−14) |
| W1 | 3.353 |$\mu$|m | 9.28(−13) ± 1.97(−14) | |
| W2 | 4.602 |$\mu$|m | 7.49(−13) ± 1.45(−14) | |
| W3 | 11.56 |$\mu$|m | 7.87(−13) ± 1.09(−14) | |
| L18W | 18.00 |$\mu$|m | 1.40(−12) ± 3.71(−13) | |
| W4 | 22.09 |$\mu$|m | 1.50(−12) ± 3.04(−14) |
| Ion(Xm+) . | λlab. . | I(λ) (I(Hβ) = 100) . | n(Xm+)/n(H+) . |
|---|---|---|---|
| He+ | 4471.47 Å | 0.613 ± 0.022 | 1.11(−2) ± 4.43(−4) |
| 4921.93 Å | 0.129 ± 0.008 | 9.44(−3) ± 6.10(−4) | |
| 5015.68 Å | 0.375 ± 0.011 | 1.20(−2) ± 4.04(−4) | |
| 5875.60 Å | 1.566 ± 0.082 | 9.58(−3) ± 5.33(−4) | |
| 6678.15 Å | 0.480 ± 0.038 | 1.19(−2) ± 9.72(−4) | |
| 7065.18 Å | 0.391 ± 0.036 | 6.49(−3) ± 6.06(−4) | |
| 7281.35 Å | 0.123 ± 0.014 | 1.06(−2) ± 1.21(−3) | |
| 1.09(−2) ± 2.28(−4) | |||
| C2+ | 4267.00 Å | 0.236 ± 0.035 | 2.39(−4) ± 3.58(−5) |
| 5891.60 Å | 0.049 ± 0.007 | 3.35(−4) ± 4.56(−5) | |
| 6461.95 Å | 0.061 ± 0.008 | 6.03(−4) ± 8.07(−5) | |
| 6578.05 Å | 0.261 ± 0.020 | 3.16(−4) ± 2.60(−5) | |
| 7231.34 Å | 0.274 ± 0.024 | 6.11(−4) ± 8.85(−5) | |
| 7236.42 Å | 0.576 ± 0.042 | 6.68(−4) ± 6.13(−5) | |
| 3.14(−4) ± 2.49(−5) | |||
| N0 | 5197.90 Å | 0.056 ± 0.021 | 7.60(−7) ± 2.85(−7) |
| 5200.26 Å | 0.052 ± 0.014 | 4.04(−7) ± 1.35(−7) | |
| 5.82(−7) ± 2.51(−7) | |||
| N+ | 5754.64 Å | 1.322 ± 0.062 | 2.88(−5) ± 5.08(−6) |
| 6548.04 Å | 37.985 ± 2.778 | 2.83(−5) ± 2.93(−6) | |
| 6583.46 Å | 113.836 ± 8.471 | 2.86(−5) ± 3.00(−6) | |
| 2.85(−5) ± 1.94(−6) | |||
| O0 | 6300.30 Å | 0.538 ± 0.038 | 4.37(−6) ± 1.25(−6) |
| 6363.78 Å | 0.164 ± 0.016 | 4.16(−6) ± 1.22(−6) | |
| 4.26(−6) ± 8.72(−7) | |||
| O+ | 3726.03 Å | 132.411 ± 10.617 | 1.29(−4) ± 2.56(−5) |
| 3728.81 Å | 91.955 ± 7.314 | 1.25(−4) ± 1.38(−5) | |
| 7318.92 Å | 1.132 ± 0.120 | 1.38(−4) ± 5.23(−5) | |
| 7319.99 Å | 3.524 ± 0.348 | 1.37(−4) ± 5.16(−5) | |
| 7329.66 Å | 1.839 ± 0.182 | 1.35(−4) ± 5.11(−5) | |
| 7330.73 Å | 1.899 ± 0.188 | 1.41(−4) ± 5.31(−5) | |
| 1.28(−4) ± 1.10(−5) | |||
| O2+ | 4958.91 Å | 1.109 ± 0.011 | 1.68(−6) ± 6.82(−7) |
| 5006.84 Å | 3.326 ± 0.034 | 1.75(−6) ± 7.08(−7) | |
| 1.72(−6) ± 4.91(−7) | |||
| Ne+ | 12.81 |$\mu$|m | 20.607 ± 1.555 | 2.91(−5) ± 2.85(−6) |
| S+ | 4068.60 Å | 0.944 ± 0.069 | 6.22(−7) ± 1.08(−7) |
| 6716.44 Å | 3.884 ± 0.306 | 6.47(−7) ± 6.72(−8) | |
| 6730.81 Å | 5.857 ± 0.465 | 6.38(−7) ± 7.27(−8) | |
| 6.39(−7) ± 4.49(−8) | |||
| S2+ | 18.71 |$\mu$|m | 5.263 ± 0.724 | 6.08(−7) ± 9.80(−8) |
| 33.47 |$\mu$|m | 4.004 ± 0.857 | 5.93(−7) ± 1.63(−7) | |
| 6312.10 Å | 0.179 ± 0.016 | 5.84(−7) ± 3.00(−7) | |
| 9068.60 Å | 2.581 ± 0.394 | 7.28(−7) ± 2.17(−7) | |
| 6.18(−7) ± 7.57(−8) | |||
| Cl+ | 9123.60 Å | 0.087 ± 0.014 | 1.74(−8) ± 3.20(−9) |
| Cl2+ | 5517.72 Å | 0.116 ± 0.012 | 2.12(−8) ± 8.45(−9) |
| 5537.89 Å | 0.111 ± 0.007 | 1.87(−8) ± 5.29(−9) | |
| 1.94(−8) ± 4.48(−9) | |||
| Ar2+ | 8.99 |$\mu$|m | 0.757 ± 0.145 | 8.79(−8) ± 1.74(−8) |
| 7135.80 Å | 0.581 ± 0.054 | 9.30(−8) ± 2.58(−8) | |
| 7751.10 Å | 0.139 ± 0.017 | 9.29(−8) ± 2.68(−8) | |
| 9.02(−8) ± 1.27(−8) | |||
| Fe2+ | 4658.05 Å | 0.406 ± 0.017 | 1.93(−7) ± 2.49(−8) |
| 4701.53 Å | 0.096 ± 0.009 | 1.45(−7) ± 2.40(−8) | |
| 4754.69 Å | 0.079 ± 0.014 | 2.00(−7) ± 4.24(−8) | |
| 4769.43 Å | 0.025 ± 0.008 | 1.10(−7) ± 3.71(−8) | |
| 4881.00 Å | 0.130 ± 0.009 | 1.09(−7) ± 1.99(−8) | |
| 5270.40 Å | 0.172 ± 0.011 | 1.61(−7) ± 2.06(−8) | |
| 1.48(−7) ± 1.03(−8) |
| Ion(Xm+) . | λlab. . | I(λ) (I(Hβ) = 100) . | n(Xm+)/n(H+) . |
|---|---|---|---|
| He+ | 4471.47 Å | 0.613 ± 0.022 | 1.11(−2) ± 4.43(−4) |
| 4921.93 Å | 0.129 ± 0.008 | 9.44(−3) ± 6.10(−4) | |
| 5015.68 Å | 0.375 ± 0.011 | 1.20(−2) ± 4.04(−4) | |
| 5875.60 Å | 1.566 ± 0.082 | 9.58(−3) ± 5.33(−4) | |
| 6678.15 Å | 0.480 ± 0.038 | 1.19(−2) ± 9.72(−4) | |
| 7065.18 Å | 0.391 ± 0.036 | 6.49(−3) ± 6.06(−4) | |
| 7281.35 Å | 0.123 ± 0.014 | 1.06(−2) ± 1.21(−3) | |
| 1.09(−2) ± 2.28(−4) | |||
| C2+ | 4267.00 Å | 0.236 ± 0.035 | 2.39(−4) ± 3.58(−5) |
| 5891.60 Å | 0.049 ± 0.007 | 3.35(−4) ± 4.56(−5) | |
| 6461.95 Å | 0.061 ± 0.008 | 6.03(−4) ± 8.07(−5) | |
| 6578.05 Å | 0.261 ± 0.020 | 3.16(−4) ± 2.60(−5) | |
| 7231.34 Å | 0.274 ± 0.024 | 6.11(−4) ± 8.85(−5) | |
| 7236.42 Å | 0.576 ± 0.042 | 6.68(−4) ± 6.13(−5) | |
| 3.14(−4) ± 2.49(−5) | |||
| N0 | 5197.90 Å | 0.056 ± 0.021 | 7.60(−7) ± 2.85(−7) |
| 5200.26 Å | 0.052 ± 0.014 | 4.04(−7) ± 1.35(−7) | |
| 5.82(−7) ± 2.51(−7) | |||
| N+ | 5754.64 Å | 1.322 ± 0.062 | 2.88(−5) ± 5.08(−6) |
| 6548.04 Å | 37.985 ± 2.778 | 2.83(−5) ± 2.93(−6) | |
| 6583.46 Å | 113.836 ± 8.471 | 2.86(−5) ± 3.00(−6) | |
| 2.85(−5) ± 1.94(−6) | |||
| O0 | 6300.30 Å | 0.538 ± 0.038 | 4.37(−6) ± 1.25(−6) |
| 6363.78 Å | 0.164 ± 0.016 | 4.16(−6) ± 1.22(−6) | |
| 4.26(−6) ± 8.72(−7) | |||
| O+ | 3726.03 Å | 132.411 ± 10.617 | 1.29(−4) ± 2.56(−5) |
| 3728.81 Å | 91.955 ± 7.314 | 1.25(−4) ± 1.38(−5) | |
| 7318.92 Å | 1.132 ± 0.120 | 1.38(−4) ± 5.23(−5) | |
| 7319.99 Å | 3.524 ± 0.348 | 1.37(−4) ± 5.16(−5) | |
| 7329.66 Å | 1.839 ± 0.182 | 1.35(−4) ± 5.11(−5) | |
| 7330.73 Å | 1.899 ± 0.188 | 1.41(−4) ± 5.31(−5) | |
| 1.28(−4) ± 1.10(−5) | |||
| O2+ | 4958.91 Å | 1.109 ± 0.011 | 1.68(−6) ± 6.82(−7) |
| 5006.84 Å | 3.326 ± 0.034 | 1.75(−6) ± 7.08(−7) | |
| 1.72(−6) ± 4.91(−7) | |||
| Ne+ | 12.81 |$\mu$|m | 20.607 ± 1.555 | 2.91(−5) ± 2.85(−6) |
| S+ | 4068.60 Å | 0.944 ± 0.069 | 6.22(−7) ± 1.08(−7) |
| 6716.44 Å | 3.884 ± 0.306 | 6.47(−7) ± 6.72(−8) | |
| 6730.81 Å | 5.857 ± 0.465 | 6.38(−7) ± 7.27(−8) | |
| 6.39(−7) ± 4.49(−8) | |||
| S2+ | 18.71 |$\mu$|m | 5.263 ± 0.724 | 6.08(−7) ± 9.80(−8) |
| 33.47 |$\mu$|m | 4.004 ± 0.857 | 5.93(−7) ± 1.63(−7) | |
| 6312.10 Å | 0.179 ± 0.016 | 5.84(−7) ± 3.00(−7) | |
| 9068.60 Å | 2.581 ± 0.394 | 7.28(−7) ± 2.17(−7) | |
| 6.18(−7) ± 7.57(−8) | |||
| Cl+ | 9123.60 Å | 0.087 ± 0.014 | 1.74(−8) ± 3.20(−9) |
| Cl2+ | 5517.72 Å | 0.116 ± 0.012 | 2.12(−8) ± 8.45(−9) |
| 5537.89 Å | 0.111 ± 0.007 | 1.87(−8) ± 5.29(−9) | |
| 1.94(−8) ± 4.48(−9) | |||
| Ar2+ | 8.99 |$\mu$|m | 0.757 ± 0.145 | 8.79(−8) ± 1.74(−8) |
| 7135.80 Å | 0.581 ± 0.054 | 9.30(−8) ± 2.58(−8) | |
| 7751.10 Å | 0.139 ± 0.017 | 9.29(−8) ± 2.68(−8) | |
| 9.02(−8) ± 1.27(−8) | |||
| Fe2+ | 4658.05 Å | 0.406 ± 0.017 | 1.93(−7) ± 2.49(−8) |
| 4701.53 Å | 0.096 ± 0.009 | 1.45(−7) ± 2.40(−8) | |
| 4754.69 Å | 0.079 ± 0.014 | 2.00(−7) ± 4.24(−8) | |
| 4769.43 Å | 0.025 ± 0.008 | 1.10(−7) ± 3.71(−8) | |
| 4881.00 Å | 0.130 ± 0.009 | 1.09(−7) ± 1.99(−8) | |
| 5270.40 Å | 0.172 ± 0.011 | 1.61(−7) ± 2.06(−8) | |
| 1.48(−7) ± 1.03(−8) |
| Ion(Xm+) . | λlab. . | I(λ) (I(Hβ) = 100) . | n(Xm+)/n(H+) . |
|---|---|---|---|
| He+ | 4471.47 Å | 0.613 ± 0.022 | 1.11(−2) ± 4.43(−4) |
| 4921.93 Å | 0.129 ± 0.008 | 9.44(−3) ± 6.10(−4) | |
| 5015.68 Å | 0.375 ± 0.011 | 1.20(−2) ± 4.04(−4) | |
| 5875.60 Å | 1.566 ± 0.082 | 9.58(−3) ± 5.33(−4) | |
| 6678.15 Å | 0.480 ± 0.038 | 1.19(−2) ± 9.72(−4) | |
| 7065.18 Å | 0.391 ± 0.036 | 6.49(−3) ± 6.06(−4) | |
| 7281.35 Å | 0.123 ± 0.014 | 1.06(−2) ± 1.21(−3) | |
| 1.09(−2) ± 2.28(−4) | |||
| C2+ | 4267.00 Å | 0.236 ± 0.035 | 2.39(−4) ± 3.58(−5) |
| 5891.60 Å | 0.049 ± 0.007 | 3.35(−4) ± 4.56(−5) | |
| 6461.95 Å | 0.061 ± 0.008 | 6.03(−4) ± 8.07(−5) | |
| 6578.05 Å | 0.261 ± 0.020 | 3.16(−4) ± 2.60(−5) | |
| 7231.34 Å | 0.274 ± 0.024 | 6.11(−4) ± 8.85(−5) | |
| 7236.42 Å | 0.576 ± 0.042 | 6.68(−4) ± 6.13(−5) | |
| 3.14(−4) ± 2.49(−5) | |||
| N0 | 5197.90 Å | 0.056 ± 0.021 | 7.60(−7) ± 2.85(−7) |
| 5200.26 Å | 0.052 ± 0.014 | 4.04(−7) ± 1.35(−7) | |
| 5.82(−7) ± 2.51(−7) | |||
| N+ | 5754.64 Å | 1.322 ± 0.062 | 2.88(−5) ± 5.08(−6) |
| 6548.04 Å | 37.985 ± 2.778 | 2.83(−5) ± 2.93(−6) | |
| 6583.46 Å | 113.836 ± 8.471 | 2.86(−5) ± 3.00(−6) | |
| 2.85(−5) ± 1.94(−6) | |||
| O0 | 6300.30 Å | 0.538 ± 0.038 | 4.37(−6) ± 1.25(−6) |
| 6363.78 Å | 0.164 ± 0.016 | 4.16(−6) ± 1.22(−6) | |
| 4.26(−6) ± 8.72(−7) | |||
| O+ | 3726.03 Å | 132.411 ± 10.617 | 1.29(−4) ± 2.56(−5) |
| 3728.81 Å | 91.955 ± 7.314 | 1.25(−4) ± 1.38(−5) | |
| 7318.92 Å | 1.132 ± 0.120 | 1.38(−4) ± 5.23(−5) | |
| 7319.99 Å | 3.524 ± 0.348 | 1.37(−4) ± 5.16(−5) | |
| 7329.66 Å | 1.839 ± 0.182 | 1.35(−4) ± 5.11(−5) | |
| 7330.73 Å | 1.899 ± 0.188 | 1.41(−4) ± 5.31(−5) | |
| 1.28(−4) ± 1.10(−5) | |||
| O2+ | 4958.91 Å | 1.109 ± 0.011 | 1.68(−6) ± 6.82(−7) |
| 5006.84 Å | 3.326 ± 0.034 | 1.75(−6) ± 7.08(−7) | |
| 1.72(−6) ± 4.91(−7) | |||
| Ne+ | 12.81 |$\mu$|m | 20.607 ± 1.555 | 2.91(−5) ± 2.85(−6) |
| S+ | 4068.60 Å | 0.944 ± 0.069 | 6.22(−7) ± 1.08(−7) |
| 6716.44 Å | 3.884 ± 0.306 | 6.47(−7) ± 6.72(−8) | |
| 6730.81 Å | 5.857 ± 0.465 | 6.38(−7) ± 7.27(−8) | |
| 6.39(−7) ± 4.49(−8) | |||
| S2+ | 18.71 |$\mu$|m | 5.263 ± 0.724 | 6.08(−7) ± 9.80(−8) |
| 33.47 |$\mu$|m | 4.004 ± 0.857 | 5.93(−7) ± 1.63(−7) | |
| 6312.10 Å | 0.179 ± 0.016 | 5.84(−7) ± 3.00(−7) | |
| 9068.60 Å | 2.581 ± 0.394 | 7.28(−7) ± 2.17(−7) | |
| 6.18(−7) ± 7.57(−8) | |||
| Cl+ | 9123.60 Å | 0.087 ± 0.014 | 1.74(−8) ± 3.20(−9) |
| Cl2+ | 5517.72 Å | 0.116 ± 0.012 | 2.12(−8) ± 8.45(−9) |
| 5537.89 Å | 0.111 ± 0.007 | 1.87(−8) ± 5.29(−9) | |
| 1.94(−8) ± 4.48(−9) | |||
| Ar2+ | 8.99 |$\mu$|m | 0.757 ± 0.145 | 8.79(−8) ± 1.74(−8) |
| 7135.80 Å | 0.581 ± 0.054 | 9.30(−8) ± 2.58(−8) | |
| 7751.10 Å | 0.139 ± 0.017 | 9.29(−8) ± 2.68(−8) | |
| 9.02(−8) ± 1.27(−8) | |||
| Fe2+ | 4658.05 Å | 0.406 ± 0.017 | 1.93(−7) ± 2.49(−8) |
| 4701.53 Å | 0.096 ± 0.009 | 1.45(−7) ± 2.40(−8) | |
| 4754.69 Å | 0.079 ± 0.014 | 2.00(−7) ± 4.24(−8) | |
| 4769.43 Å | 0.025 ± 0.008 | 1.10(−7) ± 3.71(−8) | |
| 4881.00 Å | 0.130 ± 0.009 | 1.09(−7) ± 1.99(−8) | |
| 5270.40 Å | 0.172 ± 0.011 | 1.61(−7) ± 2.06(−8) | |
| 1.48(−7) ± 1.03(−8) |
| Ion(Xm+) . | λlab. . | I(λ) (I(Hβ) = 100) . | n(Xm+)/n(H+) . |
|---|---|---|---|
| He+ | 4471.47 Å | 0.613 ± 0.022 | 1.11(−2) ± 4.43(−4) |
| 4921.93 Å | 0.129 ± 0.008 | 9.44(−3) ± 6.10(−4) | |
| 5015.68 Å | 0.375 ± 0.011 | 1.20(−2) ± 4.04(−4) | |
| 5875.60 Å | 1.566 ± 0.082 | 9.58(−3) ± 5.33(−4) | |
| 6678.15 Å | 0.480 ± 0.038 | 1.19(−2) ± 9.72(−4) | |
| 7065.18 Å | 0.391 ± 0.036 | 6.49(−3) ± 6.06(−4) | |
| 7281.35 Å | 0.123 ± 0.014 | 1.06(−2) ± 1.21(−3) | |
| 1.09(−2) ± 2.28(−4) | |||
| C2+ | 4267.00 Å | 0.236 ± 0.035 | 2.39(−4) ± 3.58(−5) |
| 5891.60 Å | 0.049 ± 0.007 | 3.35(−4) ± 4.56(−5) | |
| 6461.95 Å | 0.061 ± 0.008 | 6.03(−4) ± 8.07(−5) | |
| 6578.05 Å | 0.261 ± 0.020 | 3.16(−4) ± 2.60(−5) | |
| 7231.34 Å | 0.274 ± 0.024 | 6.11(−4) ± 8.85(−5) | |
| 7236.42 Å | 0.576 ± 0.042 | 6.68(−4) ± 6.13(−5) | |
| 3.14(−4) ± 2.49(−5) | |||
| N0 | 5197.90 Å | 0.056 ± 0.021 | 7.60(−7) ± 2.85(−7) |
| 5200.26 Å | 0.052 ± 0.014 | 4.04(−7) ± 1.35(−7) | |
| 5.82(−7) ± 2.51(−7) | |||
| N+ | 5754.64 Å | 1.322 ± 0.062 | 2.88(−5) ± 5.08(−6) |
| 6548.04 Å | 37.985 ± 2.778 | 2.83(−5) ± 2.93(−6) | |
| 6583.46 Å | 113.836 ± 8.471 | 2.86(−5) ± 3.00(−6) | |
| 2.85(−5) ± 1.94(−6) | |||
| O0 | 6300.30 Å | 0.538 ± 0.038 | 4.37(−6) ± 1.25(−6) |
| 6363.78 Å | 0.164 ± 0.016 | 4.16(−6) ± 1.22(−6) | |
| 4.26(−6) ± 8.72(−7) | |||
| O+ | 3726.03 Å | 132.411 ± 10.617 | 1.29(−4) ± 2.56(−5) |
| 3728.81 Å | 91.955 ± 7.314 | 1.25(−4) ± 1.38(−5) | |
| 7318.92 Å | 1.132 ± 0.120 | 1.38(−4) ± 5.23(−5) | |
| 7319.99 Å | 3.524 ± 0.348 | 1.37(−4) ± 5.16(−5) | |
| 7329.66 Å | 1.839 ± 0.182 | 1.35(−4) ± 5.11(−5) | |
| 7330.73 Å | 1.899 ± 0.188 | 1.41(−4) ± 5.31(−5) | |
| 1.28(−4) ± 1.10(−5) | |||
| O2+ | 4958.91 Å | 1.109 ± 0.011 | 1.68(−6) ± 6.82(−7) |
| 5006.84 Å | 3.326 ± 0.034 | 1.75(−6) ± 7.08(−7) | |
| 1.72(−6) ± 4.91(−7) | |||
| Ne+ | 12.81 |$\mu$|m | 20.607 ± 1.555 | 2.91(−5) ± 2.85(−6) |
| S+ | 4068.60 Å | 0.944 ± 0.069 | 6.22(−7) ± 1.08(−7) |
| 6716.44 Å | 3.884 ± 0.306 | 6.47(−7) ± 6.72(−8) | |
| 6730.81 Å | 5.857 ± 0.465 | 6.38(−7) ± 7.27(−8) | |
| 6.39(−7) ± 4.49(−8) | |||
| S2+ | 18.71 |$\mu$|m | 5.263 ± 0.724 | 6.08(−7) ± 9.80(−8) |
| 33.47 |$\mu$|m | 4.004 ± 0.857 | 5.93(−7) ± 1.63(−7) | |
| 6312.10 Å | 0.179 ± 0.016 | 5.84(−7) ± 3.00(−7) | |
| 9068.60 Å | 2.581 ± 0.394 | 7.28(−7) ± 2.17(−7) | |
| 6.18(−7) ± 7.57(−8) | |||
| Cl+ | 9123.60 Å | 0.087 ± 0.014 | 1.74(−8) ± 3.20(−9) |
| Cl2+ | 5517.72 Å | 0.116 ± 0.012 | 2.12(−8) ± 8.45(−9) |
| 5537.89 Å | 0.111 ± 0.007 | 1.87(−8) ± 5.29(−9) | |
| 1.94(−8) ± 4.48(−9) | |||
| Ar2+ | 8.99 |$\mu$|m | 0.757 ± 0.145 | 8.79(−8) ± 1.74(−8) |
| 7135.80 Å | 0.581 ± 0.054 | 9.30(−8) ± 2.58(−8) | |
| 7751.10 Å | 0.139 ± 0.017 | 9.29(−8) ± 2.68(−8) | |
| 9.02(−8) ± 1.27(−8) | |||
| Fe2+ | 4658.05 Å | 0.406 ± 0.017 | 1.93(−7) ± 2.49(−8) |
| 4701.53 Å | 0.096 ± 0.009 | 1.45(−7) ± 2.40(−8) | |
| 4754.69 Å | 0.079 ± 0.014 | 2.00(−7) ± 4.24(−8) | |
| 4769.43 Å | 0.025 ± 0.008 | 1.10(−7) ± 3.71(−8) | |
| 4881.00 Å | 0.130 ± 0.009 | 1.09(−7) ± 1.99(−8) | |
| 5270.40 Å | 0.172 ± 0.011 | 1.61(−7) ± 2.06(−8) | |
| 1.48(−7) ± 1.03(−8) |
The measurements of the equivalent width (EW) of the stellar absorption and the derived elemental abundances.
| Line . | λlab. (Å) . | EW (mÅ) . | n(X)/n(H) . | ε(X) . |
|---|---|---|---|---|
| He i | 3652.90 | 29.24 ± 1.87 | 8.92(−2) ± 2.77(−2) | 10.95 ± 0.14 |
| 3867.45 | 104.20 ± 1.30 | 9.30(−2) ± 1.41(−2) | 10.97 ± 0.07 | |
| 4009.24 | 188.70 ± 1.56 | 7.85(−2) ± 9.76(−3) | 10.89 ± 0.05 | |
| 4120.78 | 184.40 ± 2.10 | 1.20(−1) ± 2.12(−2) | 11.08 ± 0.08 | |
| 4143.68 | 266.70 ± 1.65 | 1.13(−1) ± 1.47(−2) | 11.05 ± 0.06 | |
| 4168.99 | 39.69 ± 1.48 | 8.60(−2) ± 1.96(−2) | 10.93 ± 0.10 | |
| He ii | 4541.62 | 129.90 ± 2.34 | 1.01(−1) ± 2.23(−2) | 11.01 ± 0.10 |
| 4685.71 | 210.00 ± 1.96 | 9.85(−2) ± 2.12(−2) | 10.99 ± 0.09 | |
| 5411.52 | 136.90 ± 2.21 | 9.85(−2) ± 2.27(−2) | 10.99 ± 0.10 | |
| 9.76(−2) ± 1.93(−3) | 10.99 ± 0.09 | |||
| C iii | 4156.56 | 65.84 ± 1.68 | 3.83(−4) ± 8.75(−5) | 8.58 ± 0.10 |
| 4162.96 | 75.54 ± 1.79 | 3.39(−4) ± 7.42(−5) | 8.53 ± 0.10 | |
| 4665.92 | 67.63 ± 1.49 | 3.47(−4) ± 7.07(−5) | 8.54 ± 0.09 | |
| C iv | 5801.31 | 44.60 ± 1.60 | 3.96(−4) ± 1.12(−4) | 8.60 ± 0.12 |
| 3.66(−4) ± 8.60(−5) | 8.56 ± 0.10 | |||
| N ii | 3995.00 | 15.58 ± 1.45 | 1.68(−5) ± 7.90(−6) | 7.23 ± 0.20 |
| N iii | 4634.12 | 26.21 ± 1.47 | 1.91(−5) ± 5.61(−6) | 7.28 ± 0.13 |
| 1.85(−5) ± 6.76(−6) | 7.25 ± 0.16 | |||
| O ii | 3882.17 | 38.17 ± 1.34 | 8.77(−5) ± 3.08(−5) | 7.94 ± 0.15 |
| 3954.21 | 37.06 ± 0.93 | 1.66(−4) ± 3.19(−5) | 8.22 ± 0.08 | |
| 3982.72 | 26.86 ± 1.89 | 8.70(−5) ± 5.19(−5) | 7.94 ± 0.26 | |
| 4092.89 | 22.34 ± 1.23 | 6.36(−5) ± 4.62(−5) | 7.80 ± 0.32 | |
| 4119.22 | 54.49 ± 1.67 | 1.38(−4) ± 2.93(−5) | 8.14 ± 0.09 | |
| 4132.79 | 24.40 ± 1.15 | 1.99(−4) ± 4.91(−5) | 8.30 ± 0.11 | |
| 4189.75 | 30.55 ± 1.22 | 2.24(−4) ± 4.86(−5) | 8.35 ± 0.09 | |
| 4366.77 | 53.74 ± 1.13 | 1.17(−4) ± 1.92(−5) | 8.07 ± 0.08 | |
| 4590.83 | 63.35 ± 2.44 | 8.57(−5) ± 2.01(−5) | 7.93 ± 0.10 | |
| 4596.07 | 62.17 ± 1.51 | 1.07(−4) ± 1.92(−5) | 8.03 ± 0.08 | |
| 4661.53 | 61.34 ± 1.25 | 1.43(−4) ± 2.35(−5) | 8.16 ± 0.06 | |
| 4673.84 | 10.44 ± 1.19 | 7.75(−5) ± 5.31(−5) | 7.89 ± 0.30 | |
| 4676.14 | 45.04 ± 1.22 | 1.27(−4) ± 2.30(−5) | 8.10 ± 0.08 | |
| 1.25(−4) ± 4.86(−5) | 8.10 ± 0.17 | |||
| Si iii | 4552.57 | 83.11 ± 1.22 | 6.61(−6) ± 9.81(−7) | 6.82 ± 0.06 |
| 4567.77 | 62.27 ± 1.10 | 7.33(−6) ± 1.14(−6) | 6.87 ± 0.07 | |
| 4574.57 | 21.00 ± 1.31 | 5.90(−6) ± 1.65(−6) | 6.77 ± 0.12 | |
| Si iv | 4116.11 | 162.50 ± 1.29 | 4.33(−6) ± 6.08(−7) | 6.64 ± 0.06 |
| 4631.08 | 42.81 ± 2.00 | 8.41(−6) ± 2.47(−6) | 6.93 ± 0.13 | |
| 6.52(−6) ± 1.54(−6) | 6.81 ± 0.10 |
| Line . | λlab. (Å) . | EW (mÅ) . | n(X)/n(H) . | ε(X) . |
|---|---|---|---|---|
| He i | 3652.90 | 29.24 ± 1.87 | 8.92(−2) ± 2.77(−2) | 10.95 ± 0.14 |
| 3867.45 | 104.20 ± 1.30 | 9.30(−2) ± 1.41(−2) | 10.97 ± 0.07 | |
| 4009.24 | 188.70 ± 1.56 | 7.85(−2) ± 9.76(−3) | 10.89 ± 0.05 | |
| 4120.78 | 184.40 ± 2.10 | 1.20(−1) ± 2.12(−2) | 11.08 ± 0.08 | |
| 4143.68 | 266.70 ± 1.65 | 1.13(−1) ± 1.47(−2) | 11.05 ± 0.06 | |
| 4168.99 | 39.69 ± 1.48 | 8.60(−2) ± 1.96(−2) | 10.93 ± 0.10 | |
| He ii | 4541.62 | 129.90 ± 2.34 | 1.01(−1) ± 2.23(−2) | 11.01 ± 0.10 |
| 4685.71 | 210.00 ± 1.96 | 9.85(−2) ± 2.12(−2) | 10.99 ± 0.09 | |
| 5411.52 | 136.90 ± 2.21 | 9.85(−2) ± 2.27(−2) | 10.99 ± 0.10 | |
| 9.76(−2) ± 1.93(−3) | 10.99 ± 0.09 | |||
| C iii | 4156.56 | 65.84 ± 1.68 | 3.83(−4) ± 8.75(−5) | 8.58 ± 0.10 |
| 4162.96 | 75.54 ± 1.79 | 3.39(−4) ± 7.42(−5) | 8.53 ± 0.10 | |
| 4665.92 | 67.63 ± 1.49 | 3.47(−4) ± 7.07(−5) | 8.54 ± 0.09 | |
| C iv | 5801.31 | 44.60 ± 1.60 | 3.96(−4) ± 1.12(−4) | 8.60 ± 0.12 |
| 3.66(−4) ± 8.60(−5) | 8.56 ± 0.10 | |||
| N ii | 3995.00 | 15.58 ± 1.45 | 1.68(−5) ± 7.90(−6) | 7.23 ± 0.20 |
| N iii | 4634.12 | 26.21 ± 1.47 | 1.91(−5) ± 5.61(−6) | 7.28 ± 0.13 |
| 1.85(−5) ± 6.76(−6) | 7.25 ± 0.16 | |||
| O ii | 3882.17 | 38.17 ± 1.34 | 8.77(−5) ± 3.08(−5) | 7.94 ± 0.15 |
| 3954.21 | 37.06 ± 0.93 | 1.66(−4) ± 3.19(−5) | 8.22 ± 0.08 | |
| 3982.72 | 26.86 ± 1.89 | 8.70(−5) ± 5.19(−5) | 7.94 ± 0.26 | |
| 4092.89 | 22.34 ± 1.23 | 6.36(−5) ± 4.62(−5) | 7.80 ± 0.32 | |
| 4119.22 | 54.49 ± 1.67 | 1.38(−4) ± 2.93(−5) | 8.14 ± 0.09 | |
| 4132.79 | 24.40 ± 1.15 | 1.99(−4) ± 4.91(−5) | 8.30 ± 0.11 | |
| 4189.75 | 30.55 ± 1.22 | 2.24(−4) ± 4.86(−5) | 8.35 ± 0.09 | |
| 4366.77 | 53.74 ± 1.13 | 1.17(−4) ± 1.92(−5) | 8.07 ± 0.08 | |
| 4590.83 | 63.35 ± 2.44 | 8.57(−5) ± 2.01(−5) | 7.93 ± 0.10 | |
| 4596.07 | 62.17 ± 1.51 | 1.07(−4) ± 1.92(−5) | 8.03 ± 0.08 | |
| 4661.53 | 61.34 ± 1.25 | 1.43(−4) ± 2.35(−5) | 8.16 ± 0.06 | |
| 4673.84 | 10.44 ± 1.19 | 7.75(−5) ± 5.31(−5) | 7.89 ± 0.30 | |
| 4676.14 | 45.04 ± 1.22 | 1.27(−4) ± 2.30(−5) | 8.10 ± 0.08 | |
| 1.25(−4) ± 4.86(−5) | 8.10 ± 0.17 | |||
| Si iii | 4552.57 | 83.11 ± 1.22 | 6.61(−6) ± 9.81(−7) | 6.82 ± 0.06 |
| 4567.77 | 62.27 ± 1.10 | 7.33(−6) ± 1.14(−6) | 6.87 ± 0.07 | |
| 4574.57 | 21.00 ± 1.31 | 5.90(−6) ± 1.65(−6) | 6.77 ± 0.12 | |
| Si iv | 4116.11 | 162.50 ± 1.29 | 4.33(−6) ± 6.08(−7) | 6.64 ± 0.06 |
| 4631.08 | 42.81 ± 2.00 | 8.41(−6) ± 2.47(−6) | 6.93 ± 0.13 | |
| 6.52(−6) ± 1.54(−6) | 6.81 ± 0.10 |
The measurements of the equivalent width (EW) of the stellar absorption and the derived elemental abundances.
| Line . | λlab. (Å) . | EW (mÅ) . | n(X)/n(H) . | ε(X) . |
|---|---|---|---|---|
| He i | 3652.90 | 29.24 ± 1.87 | 8.92(−2) ± 2.77(−2) | 10.95 ± 0.14 |
| 3867.45 | 104.20 ± 1.30 | 9.30(−2) ± 1.41(−2) | 10.97 ± 0.07 | |
| 4009.24 | 188.70 ± 1.56 | 7.85(−2) ± 9.76(−3) | 10.89 ± 0.05 | |
| 4120.78 | 184.40 ± 2.10 | 1.20(−1) ± 2.12(−2) | 11.08 ± 0.08 | |
| 4143.68 | 266.70 ± 1.65 | 1.13(−1) ± 1.47(−2) | 11.05 ± 0.06 | |
| 4168.99 | 39.69 ± 1.48 | 8.60(−2) ± 1.96(−2) | 10.93 ± 0.10 | |
| He ii | 4541.62 | 129.90 ± 2.34 | 1.01(−1) ± 2.23(−2) | 11.01 ± 0.10 |
| 4685.71 | 210.00 ± 1.96 | 9.85(−2) ± 2.12(−2) | 10.99 ± 0.09 | |
| 5411.52 | 136.90 ± 2.21 | 9.85(−2) ± 2.27(−2) | 10.99 ± 0.10 | |
| 9.76(−2) ± 1.93(−3) | 10.99 ± 0.09 | |||
| C iii | 4156.56 | 65.84 ± 1.68 | 3.83(−4) ± 8.75(−5) | 8.58 ± 0.10 |
| 4162.96 | 75.54 ± 1.79 | 3.39(−4) ± 7.42(−5) | 8.53 ± 0.10 | |
| 4665.92 | 67.63 ± 1.49 | 3.47(−4) ± 7.07(−5) | 8.54 ± 0.09 | |
| C iv | 5801.31 | 44.60 ± 1.60 | 3.96(−4) ± 1.12(−4) | 8.60 ± 0.12 |
| 3.66(−4) ± 8.60(−5) | 8.56 ± 0.10 | |||
| N ii | 3995.00 | 15.58 ± 1.45 | 1.68(−5) ± 7.90(−6) | 7.23 ± 0.20 |
| N iii | 4634.12 | 26.21 ± 1.47 | 1.91(−5) ± 5.61(−6) | 7.28 ± 0.13 |
| 1.85(−5) ± 6.76(−6) | 7.25 ± 0.16 | |||
| O ii | 3882.17 | 38.17 ± 1.34 | 8.77(−5) ± 3.08(−5) | 7.94 ± 0.15 |
| 3954.21 | 37.06 ± 0.93 | 1.66(−4) ± 3.19(−5) | 8.22 ± 0.08 | |
| 3982.72 | 26.86 ± 1.89 | 8.70(−5) ± 5.19(−5) | 7.94 ± 0.26 | |
| 4092.89 | 22.34 ± 1.23 | 6.36(−5) ± 4.62(−5) | 7.80 ± 0.32 | |
| 4119.22 | 54.49 ± 1.67 | 1.38(−4) ± 2.93(−5) | 8.14 ± 0.09 | |
| 4132.79 | 24.40 ± 1.15 | 1.99(−4) ± 4.91(−5) | 8.30 ± 0.11 | |
| 4189.75 | 30.55 ± 1.22 | 2.24(−4) ± 4.86(−5) | 8.35 ± 0.09 | |
| 4366.77 | 53.74 ± 1.13 | 1.17(−4) ± 1.92(−5) | 8.07 ± 0.08 | |
| 4590.83 | 63.35 ± 2.44 | 8.57(−5) ± 2.01(−5) | 7.93 ± 0.10 | |
| 4596.07 | 62.17 ± 1.51 | 1.07(−4) ± 1.92(−5) | 8.03 ± 0.08 | |
| 4661.53 | 61.34 ± 1.25 | 1.43(−4) ± 2.35(−5) | 8.16 ± 0.06 | |
| 4673.84 | 10.44 ± 1.19 | 7.75(−5) ± 5.31(−5) | 7.89 ± 0.30 | |
| 4676.14 | 45.04 ± 1.22 | 1.27(−4) ± 2.30(−5) | 8.10 ± 0.08 | |
| 1.25(−4) ± 4.86(−5) | 8.10 ± 0.17 | |||
| Si iii | 4552.57 | 83.11 ± 1.22 | 6.61(−6) ± 9.81(−7) | 6.82 ± 0.06 |
| 4567.77 | 62.27 ± 1.10 | 7.33(−6) ± 1.14(−6) | 6.87 ± 0.07 | |
| 4574.57 | 21.00 ± 1.31 | 5.90(−6) ± 1.65(−6) | 6.77 ± 0.12 | |
| Si iv | 4116.11 | 162.50 ± 1.29 | 4.33(−6) ± 6.08(−7) | 6.64 ± 0.06 |
| 4631.08 | 42.81 ± 2.00 | 8.41(−6) ± 2.47(−6) | 6.93 ± 0.13 | |
| 6.52(−6) ± 1.54(−6) | 6.81 ± 0.10 |
| Line . | λlab. (Å) . | EW (mÅ) . | n(X)/n(H) . | ε(X) . |
|---|---|---|---|---|
| He i | 3652.90 | 29.24 ± 1.87 | 8.92(−2) ± 2.77(−2) | 10.95 ± 0.14 |
| 3867.45 | 104.20 ± 1.30 | 9.30(−2) ± 1.41(−2) | 10.97 ± 0.07 | |
| 4009.24 | 188.70 ± 1.56 | 7.85(−2) ± 9.76(−3) | 10.89 ± 0.05 | |
| 4120.78 | 184.40 ± 2.10 | 1.20(−1) ± 2.12(−2) | 11.08 ± 0.08 | |
| 4143.68 | 266.70 ± 1.65 | 1.13(−1) ± 1.47(−2) | 11.05 ± 0.06 | |
| 4168.99 | 39.69 ± 1.48 | 8.60(−2) ± 1.96(−2) | 10.93 ± 0.10 | |
| He ii | 4541.62 | 129.90 ± 2.34 | 1.01(−1) ± 2.23(−2) | 11.01 ± 0.10 |
| 4685.71 | 210.00 ± 1.96 | 9.85(−2) ± 2.12(−2) | 10.99 ± 0.09 | |
| 5411.52 | 136.90 ± 2.21 | 9.85(−2) ± 2.27(−2) | 10.99 ± 0.10 | |
| 9.76(−2) ± 1.93(−3) | 10.99 ± 0.09 | |||
| C iii | 4156.56 | 65.84 ± 1.68 | 3.83(−4) ± 8.75(−5) | 8.58 ± 0.10 |
| 4162.96 | 75.54 ± 1.79 | 3.39(−4) ± 7.42(−5) | 8.53 ± 0.10 | |
| 4665.92 | 67.63 ± 1.49 | 3.47(−4) ± 7.07(−5) | 8.54 ± 0.09 | |
| C iv | 5801.31 | 44.60 ± 1.60 | 3.96(−4) ± 1.12(−4) | 8.60 ± 0.12 |
| 3.66(−4) ± 8.60(−5) | 8.56 ± 0.10 | |||
| N ii | 3995.00 | 15.58 ± 1.45 | 1.68(−5) ± 7.90(−6) | 7.23 ± 0.20 |
| N iii | 4634.12 | 26.21 ± 1.47 | 1.91(−5) ± 5.61(−6) | 7.28 ± 0.13 |
| 1.85(−5) ± 6.76(−6) | 7.25 ± 0.16 | |||
| O ii | 3882.17 | 38.17 ± 1.34 | 8.77(−5) ± 3.08(−5) | 7.94 ± 0.15 |
| 3954.21 | 37.06 ± 0.93 | 1.66(−4) ± 3.19(−5) | 8.22 ± 0.08 | |
| 3982.72 | 26.86 ± 1.89 | 8.70(−5) ± 5.19(−5) | 7.94 ± 0.26 | |
| 4092.89 | 22.34 ± 1.23 | 6.36(−5) ± 4.62(−5) | 7.80 ± 0.32 | |
| 4119.22 | 54.49 ± 1.67 | 1.38(−4) ± 2.93(−5) | 8.14 ± 0.09 | |
| 4132.79 | 24.40 ± 1.15 | 1.99(−4) ± 4.91(−5) | 8.30 ± 0.11 | |
| 4189.75 | 30.55 ± 1.22 | 2.24(−4) ± 4.86(−5) | 8.35 ± 0.09 | |
| 4366.77 | 53.74 ± 1.13 | 1.17(−4) ± 1.92(−5) | 8.07 ± 0.08 | |
| 4590.83 | 63.35 ± 2.44 | 8.57(−5) ± 2.01(−5) | 7.93 ± 0.10 | |
| 4596.07 | 62.17 ± 1.51 | 1.07(−4) ± 1.92(−5) | 8.03 ± 0.08 | |
| 4661.53 | 61.34 ± 1.25 | 1.43(−4) ± 2.35(−5) | 8.16 ± 0.06 | |
| 4673.84 | 10.44 ± 1.19 | 7.75(−5) ± 5.31(−5) | 7.89 ± 0.30 | |
| 4676.14 | 45.04 ± 1.22 | 1.27(−4) ± 2.30(−5) | 8.10 ± 0.08 | |
| 1.25(−4) ± 4.86(−5) | 8.10 ± 0.17 | |||
| Si iii | 4552.57 | 83.11 ± 1.22 | 6.61(−6) ± 9.81(−7) | 6.82 ± 0.06 |
| 4567.77 | 62.27 ± 1.10 | 7.33(−6) ± 1.14(−6) | 6.87 ± 0.07 | |
| 4574.57 | 21.00 ± 1.31 | 5.90(−6) ± 1.65(−6) | 6.77 ± 0.12 | |
| Si iv | 4116.11 | 162.50 ± 1.29 | 4.33(−6) ± 6.08(−7) | 6.64 ± 0.06 |
| 4631.08 | 42.81 ± 2.00 | 8.41(−6) ± 2.47(−6) | 6.93 ± 0.13 | |
| 6.52(−6) ± 1.54(−6) | 6.81 ± 0.10 |
Comparison of the observed line intensities, band fluxes, and flux densities between the cloudy model and the observation. The band width for the integrated band flux is as follows; 0.084, 0.116, 0.087, 0.111, 0.104 |$\mu$|m in B, |$g^{^{\prime }}$|, V, |$r^{^{\prime }}$|, and |$i^{^{\prime }}$|, respectively. 0.162, 0.251, 0.260, 0.626, 1.042 |$\mu$|m in J, H, Ks, W1, and W2, respectively. 0.36, 0.40, 0.60, 1.00, 0.25, 1.00, 2.00, 0.70, 0.40, 0.50, 0.50, 0.50, 0.50, 0.50, and 1.00 |$\mu$|m in IRS-1 to -15, respectively.
| Line . | λlab. . | I(Cloudy) . | I(Obs) . | Line . | λlab. . | I(Cloudy) . | I(Obs) . |
|---|---|---|---|---|---|---|---|
| . | . | I(Hβ) = 100 . | I(Hβ) = 100 . | . | . | I(Hβ) = 100 . | I(Hβ) = 100 . |
| B24 | 3671 Å | 0.439 | 0.735 | [Cl iii] | 5538 Å | 0.122 | 0.111 |
| B23 | 3674 Å | 0.487 | 0.909 | [N ii] | 5755 Å | 1.293 | 1.322 |
| B22 | 3676 Å | 0.545 | 0.916 | He i | 5876 Å | 1.673 | 1.566 |
| B21 | 3679 Å | 0.613 | 1.046 | [O i] | 6300 Å | 0.951 | 0.538 |
| B20 | 3683 Å | 0.696 | 1.111 | [S iii] | 6312 Å | 0.392 | 0.179 |
| B19 | 3687 Å | 0.798 | 1.388 | [O i] | 6363 Å | 0.303 | 0.164 |
| B18 | 3692 Å | 0.924 | 1.465 | [N ii] | 6548 Å | 35.039 | 37.985 |
| B17 | 3697 Å | 1.081 | 1.605 | B3 | 6563 Å | 289.424 | 310.085 |
| B16 | 3704 Å | 1.282 | 2.196 | [N ii] | 6584 Å | 103.400 | 113.836 |
| B15 | 3712 Å | 1.541 | 2.054 | He i | 6678 Å | 0.467 | 0.480 |
| B14 | 3722 Å | 1.882 | 2.671 | [S ii] | 6716 Å | 2.688 | 3.884 |
| [O ii] | 3726 Å | 139.511 | 132.411 | [S ii] | 6731 Å | 4.311 | 5.857 |
| [O ii] | 3729 Å | 76.585 | 91.955 | He i | 7065 Å | 0.541 | 0.391 |
| B13 | 3734 Å | 2.340 | 2.922 | [Ar iii] | 7135 Å | 0.592 | 0.581 |
| B12 | 3750 Å | 2.966 | 3.836 | He i | 7281 Å | 0.110 | 0.123 |
| B11 | 3771 Å | 3.849 | 4.991 | [O ii] | 7323 Å | 6.193 | 4.657 |
| B10 | 3798 Å | 5.130 | 6.224 | [O ii] | 7332 Å | 4.939 | 3.739 |
| He i | 3820 Å | 0.138 | 0.108 | [Ar iii] | 7751 Å | 0.143 | 0.139 |
| B9 | 3835 Å | 7.068 | 7.876 | P24 | 8334 Å | 0.145 | 0.218 |
| B8 | 3889 Å | 10.143 | 11.547 | P23 | 8346 Å | 0.162 | 0.211 |
| B7 | 3970 Å | 15.359 | 16.977 | P22 | 8359 Å | 0.182 | 0.274 |
| [S ii] | 4070 Å | 1.019 | 0.944 | P21 | 8374 Å | 0.206 | 0.260 |
| B6 | 4102 Å | 25.012 | 27.051 | P20 | 8392 Å | 0.235 | 0.271 |
| B5 | 4340 Å | 45.252 | 47.420 | P19 | 8413 Å | 0.271 | 0.318 |
| He i | 4471 Å | 0.556 | 0.613 | P16 | 8502 Å | 0.441 | 0.470 |
| [Fe iii] | 4659 Å | 0.323 | 0.401 | P13 | 8665 Å | 0.815 | 0.887 |
| [Fe iii] | 4702 Å | 0.108 | 0.112 | P12 | 8750 Å | 1.036 | 1.079 |
| [Fe iii] | 4755 Å | 0.059 | 0.079 | P11 | 8863 Å | 1.347 | 1.309 |
| [Fe iii] | 4770 Å | 0.036 | 0.025 | P10 | 9015 Å | 1.798 | 1.744 |
| [Fe iii] | 4881 Å | 0.106 | 0.130 | [S iii] | 9069 Å | 4.858 | 2.581 |
| He i | 4922 Å | 0.155 | 0.129 | [Cl ii] | 9124 Å | 0.058 | 0.087 |
| [O iii] | 4959 Å | 1.095 | 1.109 | P8 | 9546 Å | 3.568 | 3.033 |
| [O iii] | 5007 Å | 3.296 | 3.326 | H i | 7.48/50 |$\mu$|m | 3.153 | 3.102 |
| He i | 5016 Å | 0.427 | 0.375 | [Ar iii] | 8.99 |$\mu$|m | 0.618 | 0.757 |
| [N i] | 5198 Å | 0.036 | 0.056 | H i | 12.38 |$\mu$|m | 1.067 | 1.029 |
| [N i] | 5200 Å | 0.022 | 0.052 | [Ne ii] | 12.81 |$\mu$|m | 20.002 | 20.607 |
| [Fe iii] | 5271 Å | 0.187 | 0.172 | [S iii] | 18.71 |$\mu$|m | 6.684 | 5.263 |
| [Cl iii] | 5518 Å | 0.113 | 0.116 | [S iii] | 33.47 |$\mu$|m | 2.941 | 4.004 |
| Band | λc | I(Cloudy) | I(Obs) | Band | λc | I(Cloudy) | I(Obs) |
| I(Hβ) = 100 | I(Hβ) = 100 | I(Hβ) = 100 | I(Hβ) = 100 | ||||
| B | 0.4297 |$\mu$|m | 3112.550 | 2569.843 | IRS-04 | 14.50 |$\mu$|m | 42.844 | 53.079 |
| |$g^{^{\prime }}$| | 0.4640 |$\mu$|m | 3502.697 | 2831.786 | IRS-05 | 15.00 |$\mu$|m | 11.085 | 13.975 |
| V | 0.5394 |$\mu$|m | 1401.690 | 1280.855 | IRS-06 | 16.50 |$\mu$|m | 50.613 | 64.398 |
| |$r^{^{\prime }}$| | 0.6122 |$\mu$|m | 2097.757 | 1395.011 | IRS-07 | 22.00 |$\mu$|m | 145.937 | 177.499 |
| |$i^{^{\prime }}$| | 0.7440 |$\mu$|m | 603.378 | 527.513 | IRS-08 | 23.35 |$\mu$|m | 53.640 | 64.324 |
| J | 1.235 |$\mu$|m | 168.908 | 153.285 | IRS-09 | 27.00 |$\mu$|m | 32.776 | 37.026 |
| H | 1.662 |$\mu$|m | 82.062 | 79.281 | IRS-10 | 28.00 |$\mu$|m | 41.138 | 45.412 |
| Ks | 2.159 |$\mu$|m | 45.506 | 35.859 | IRS-11 | 29.00 |$\mu$|m | 40.587 | 44.158 |
| W1 | 3.353 |$\mu$|m | 38.985 | 36.990 | IRS-12 | 30.00 |$\mu$|m | 39.898 | 42.550 |
| W2 | 4.603 |$\mu$|m | 43.688 | 49.748 | IRS-13 | 31.00 |$\mu$|m | 38.834 | 40.629 |
| IRS-01 | 8.100 |$\mu$|m | 10.832 | 10.822 | IRS-14 | 32.00 |$\mu$|m | 37.647 | 38.441 |
| IRS-02 | 10.00 |$\mu$|m | 12.494 | 13.062 | IRS-15 | 34.50 |$\mu$|m | 73.392 | 64.405 |
| IRS-03 | 13.50 |$\mu$|m | 23.575 | 28.543 | ||||
| ID | λc | Fν(Cloudy) | Fν(Model) | ID | λc | Fν(Cloudy) | Fν(Model) |
| (Jy) | (Jy) | (Jy) | (Jy) | ||||
| MIR-01 | 15.00 |$\mu$|m | 0.052 | 0.066 | FIR-02 | 90.00 |$\mu$|m | 0.081 | 0.063 |
| MIR-02 | 20.00 |$\mu$|m | 0.135 | 0.172 | FIR-03 | 100.0 |$\mu$|m | 0.060 | 0.052 |
| MIR-03 | 25.00 |$\mu$|m | 0.262 | 0.306 | FIR-04 | 120.0 |$\mu$|m | 0.035 | 0.035 |
| MIR-04 | 30.00 |$\mu$|m | 0.375 | 0.401 | FIR-05 | 140.0 |$\mu$|m | 0.023 | 0.025 |
| FIR-01 | 65.00 |$\mu$|m | 0.201 | 0.105 |
| Line . | λlab. . | I(Cloudy) . | I(Obs) . | Line . | λlab. . | I(Cloudy) . | I(Obs) . |
|---|---|---|---|---|---|---|---|
| . | . | I(Hβ) = 100 . | I(Hβ) = 100 . | . | . | I(Hβ) = 100 . | I(Hβ) = 100 . |
| B24 | 3671 Å | 0.439 | 0.735 | [Cl iii] | 5538 Å | 0.122 | 0.111 |
| B23 | 3674 Å | 0.487 | 0.909 | [N ii] | 5755 Å | 1.293 | 1.322 |
| B22 | 3676 Å | 0.545 | 0.916 | He i | 5876 Å | 1.673 | 1.566 |
| B21 | 3679 Å | 0.613 | 1.046 | [O i] | 6300 Å | 0.951 | 0.538 |
| B20 | 3683 Å | 0.696 | 1.111 | [S iii] | 6312 Å | 0.392 | 0.179 |
| B19 | 3687 Å | 0.798 | 1.388 | [O i] | 6363 Å | 0.303 | 0.164 |
| B18 | 3692 Å | 0.924 | 1.465 | [N ii] | 6548 Å | 35.039 | 37.985 |
| B17 | 3697 Å | 1.081 | 1.605 | B3 | 6563 Å | 289.424 | 310.085 |
| B16 | 3704 Å | 1.282 | 2.196 | [N ii] | 6584 Å | 103.400 | 113.836 |
| B15 | 3712 Å | 1.541 | 2.054 | He i | 6678 Å | 0.467 | 0.480 |
| B14 | 3722 Å | 1.882 | 2.671 | [S ii] | 6716 Å | 2.688 | 3.884 |
| [O ii] | 3726 Å | 139.511 | 132.411 | [S ii] | 6731 Å | 4.311 | 5.857 |
| [O ii] | 3729 Å | 76.585 | 91.955 | He i | 7065 Å | 0.541 | 0.391 |
| B13 | 3734 Å | 2.340 | 2.922 | [Ar iii] | 7135 Å | 0.592 | 0.581 |
| B12 | 3750 Å | 2.966 | 3.836 | He i | 7281 Å | 0.110 | 0.123 |
| B11 | 3771 Å | 3.849 | 4.991 | [O ii] | 7323 Å | 6.193 | 4.657 |
| B10 | 3798 Å | 5.130 | 6.224 | [O ii] | 7332 Å | 4.939 | 3.739 |
| He i | 3820 Å | 0.138 | 0.108 | [Ar iii] | 7751 Å | 0.143 | 0.139 |
| B9 | 3835 Å | 7.068 | 7.876 | P24 | 8334 Å | 0.145 | 0.218 |
| B8 | 3889 Å | 10.143 | 11.547 | P23 | 8346 Å | 0.162 | 0.211 |
| B7 | 3970 Å | 15.359 | 16.977 | P22 | 8359 Å | 0.182 | 0.274 |
| [S ii] | 4070 Å | 1.019 | 0.944 | P21 | 8374 Å | 0.206 | 0.260 |
| B6 | 4102 Å | 25.012 | 27.051 | P20 | 8392 Å | 0.235 | 0.271 |
| B5 | 4340 Å | 45.252 | 47.420 | P19 | 8413 Å | 0.271 | 0.318 |
| He i | 4471 Å | 0.556 | 0.613 | P16 | 8502 Å | 0.441 | 0.470 |
| [Fe iii] | 4659 Å | 0.323 | 0.401 | P13 | 8665 Å | 0.815 | 0.887 |
| [Fe iii] | 4702 Å | 0.108 | 0.112 | P12 | 8750 Å | 1.036 | 1.079 |
| [Fe iii] | 4755 Å | 0.059 | 0.079 | P11 | 8863 Å | 1.347 | 1.309 |
| [Fe iii] | 4770 Å | 0.036 | 0.025 | P10 | 9015 Å | 1.798 | 1.744 |
| [Fe iii] | 4881 Å | 0.106 | 0.130 | [S iii] | 9069 Å | 4.858 | 2.581 |
| He i | 4922 Å | 0.155 | 0.129 | [Cl ii] | 9124 Å | 0.058 | 0.087 |
| [O iii] | 4959 Å | 1.095 | 1.109 | P8 | 9546 Å | 3.568 | 3.033 |
| [O iii] | 5007 Å | 3.296 | 3.326 | H i | 7.48/50 |$\mu$|m | 3.153 | 3.102 |
| He i | 5016 Å | 0.427 | 0.375 | [Ar iii] | 8.99 |$\mu$|m | 0.618 | 0.757 |
| [N i] | 5198 Å | 0.036 | 0.056 | H i | 12.38 |$\mu$|m | 1.067 | 1.029 |
| [N i] | 5200 Å | 0.022 | 0.052 | [Ne ii] | 12.81 |$\mu$|m | 20.002 | 20.607 |
| [Fe iii] | 5271 Å | 0.187 | 0.172 | [S iii] | 18.71 |$\mu$|m | 6.684 | 5.263 |
| [Cl iii] | 5518 Å | 0.113 | 0.116 | [S iii] | 33.47 |$\mu$|m | 2.941 | 4.004 |
| Band | λc | I(Cloudy) | I(Obs) | Band | λc | I(Cloudy) | I(Obs) |
| I(Hβ) = 100 | I(Hβ) = 100 | I(Hβ) = 100 | I(Hβ) = 100 | ||||
| B | 0.4297 |$\mu$|m | 3112.550 | 2569.843 | IRS-04 | 14.50 |$\mu$|m | 42.844 | 53.079 |
| |$g^{^{\prime }}$| | 0.4640 |$\mu$|m | 3502.697 | 2831.786 | IRS-05 | 15.00 |$\mu$|m | 11.085 | 13.975 |
| V | 0.5394 |$\mu$|m | 1401.690 | 1280.855 | IRS-06 | 16.50 |$\mu$|m | 50.613 | 64.398 |
| |$r^{^{\prime }}$| | 0.6122 |$\mu$|m | 2097.757 | 1395.011 | IRS-07 | 22.00 |$\mu$|m | 145.937 | 177.499 |
| |$i^{^{\prime }}$| | 0.7440 |$\mu$|m | 603.378 | 527.513 | IRS-08 | 23.35 |$\mu$|m | 53.640 | 64.324 |
| J | 1.235 |$\mu$|m | 168.908 | 153.285 | IRS-09 | 27.00 |$\mu$|m | 32.776 | 37.026 |
| H | 1.662 |$\mu$|m | 82.062 | 79.281 | IRS-10 | 28.00 |$\mu$|m | 41.138 | 45.412 |
| Ks | 2.159 |$\mu$|m | 45.506 | 35.859 | IRS-11 | 29.00 |$\mu$|m | 40.587 | 44.158 |
| W1 | 3.353 |$\mu$|m | 38.985 | 36.990 | IRS-12 | 30.00 |$\mu$|m | 39.898 | 42.550 |
| W2 | 4.603 |$\mu$|m | 43.688 | 49.748 | IRS-13 | 31.00 |$\mu$|m | 38.834 | 40.629 |
| IRS-01 | 8.100 |$\mu$|m | 10.832 | 10.822 | IRS-14 | 32.00 |$\mu$|m | 37.647 | 38.441 |
| IRS-02 | 10.00 |$\mu$|m | 12.494 | 13.062 | IRS-15 | 34.50 |$\mu$|m | 73.392 | 64.405 |
| IRS-03 | 13.50 |$\mu$|m | 23.575 | 28.543 | ||||
| ID | λc | Fν(Cloudy) | Fν(Model) | ID | λc | Fν(Cloudy) | Fν(Model) |
| (Jy) | (Jy) | (Jy) | (Jy) | ||||
| MIR-01 | 15.00 |$\mu$|m | 0.052 | 0.066 | FIR-02 | 90.00 |$\mu$|m | 0.081 | 0.063 |
| MIR-02 | 20.00 |$\mu$|m | 0.135 | 0.172 | FIR-03 | 100.0 |$\mu$|m | 0.060 | 0.052 |
| MIR-03 | 25.00 |$\mu$|m | 0.262 | 0.306 | FIR-04 | 120.0 |$\mu$|m | 0.035 | 0.035 |
| MIR-04 | 30.00 |$\mu$|m | 0.375 | 0.401 | FIR-05 | 140.0 |$\mu$|m | 0.023 | 0.025 |
| FIR-01 | 65.00 |$\mu$|m | 0.201 | 0.105 |
Comparison of the observed line intensities, band fluxes, and flux densities between the cloudy model and the observation. The band width for the integrated band flux is as follows; 0.084, 0.116, 0.087, 0.111, 0.104 |$\mu$|m in B, |$g^{^{\prime }}$|, V, |$r^{^{\prime }}$|, and |$i^{^{\prime }}$|, respectively. 0.162, 0.251, 0.260, 0.626, 1.042 |$\mu$|m in J, H, Ks, W1, and W2, respectively. 0.36, 0.40, 0.60, 1.00, 0.25, 1.00, 2.00, 0.70, 0.40, 0.50, 0.50, 0.50, 0.50, 0.50, and 1.00 |$\mu$|m in IRS-1 to -15, respectively.
| Line . | λlab. . | I(Cloudy) . | I(Obs) . | Line . | λlab. . | I(Cloudy) . | I(Obs) . |
|---|---|---|---|---|---|---|---|
| . | . | I(Hβ) = 100 . | I(Hβ) = 100 . | . | . | I(Hβ) = 100 . | I(Hβ) = 100 . |
| B24 | 3671 Å | 0.439 | 0.735 | [Cl iii] | 5538 Å | 0.122 | 0.111 |
| B23 | 3674 Å | 0.487 | 0.909 | [N ii] | 5755 Å | 1.293 | 1.322 |
| B22 | 3676 Å | 0.545 | 0.916 | He i | 5876 Å | 1.673 | 1.566 |
| B21 | 3679 Å | 0.613 | 1.046 | [O i] | 6300 Å | 0.951 | 0.538 |
| B20 | 3683 Å | 0.696 | 1.111 | [S iii] | 6312 Å | 0.392 | 0.179 |
| B19 | 3687 Å | 0.798 | 1.388 | [O i] | 6363 Å | 0.303 | 0.164 |
| B18 | 3692 Å | 0.924 | 1.465 | [N ii] | 6548 Å | 35.039 | 37.985 |
| B17 | 3697 Å | 1.081 | 1.605 | B3 | 6563 Å | 289.424 | 310.085 |
| B16 | 3704 Å | 1.282 | 2.196 | [N ii] | 6584 Å | 103.400 | 113.836 |
| B15 | 3712 Å | 1.541 | 2.054 | He i | 6678 Å | 0.467 | 0.480 |
| B14 | 3722 Å | 1.882 | 2.671 | [S ii] | 6716 Å | 2.688 | 3.884 |
| [O ii] | 3726 Å | 139.511 | 132.411 | [S ii] | 6731 Å | 4.311 | 5.857 |
| [O ii] | 3729 Å | 76.585 | 91.955 | He i | 7065 Å | 0.541 | 0.391 |
| B13 | 3734 Å | 2.340 | 2.922 | [Ar iii] | 7135 Å | 0.592 | 0.581 |
| B12 | 3750 Å | 2.966 | 3.836 | He i | 7281 Å | 0.110 | 0.123 |
| B11 | 3771 Å | 3.849 | 4.991 | [O ii] | 7323 Å | 6.193 | 4.657 |
| B10 | 3798 Å | 5.130 | 6.224 | [O ii] | 7332 Å | 4.939 | 3.739 |
| He i | 3820 Å | 0.138 | 0.108 | [Ar iii] | 7751 Å | 0.143 | 0.139 |
| B9 | 3835 Å | 7.068 | 7.876 | P24 | 8334 Å | 0.145 | 0.218 |
| B8 | 3889 Å | 10.143 | 11.547 | P23 | 8346 Å | 0.162 | 0.211 |
| B7 | 3970 Å | 15.359 | 16.977 | P22 | 8359 Å | 0.182 | 0.274 |
| [S ii] | 4070 Å | 1.019 | 0.944 | P21 | 8374 Å | 0.206 | 0.260 |
| B6 | 4102 Å | 25.012 | 27.051 | P20 | 8392 Å | 0.235 | 0.271 |
| B5 | 4340 Å | 45.252 | 47.420 | P19 | 8413 Å | 0.271 | 0.318 |
| He i | 4471 Å | 0.556 | 0.613 | P16 | 8502 Å | 0.441 | 0.470 |
| [Fe iii] | 4659 Å | 0.323 | 0.401 | P13 | 8665 Å | 0.815 | 0.887 |
| [Fe iii] | 4702 Å | 0.108 | 0.112 | P12 | 8750 Å | 1.036 | 1.079 |
| [Fe iii] | 4755 Å | 0.059 | 0.079 | P11 | 8863 Å | 1.347 | 1.309 |
| [Fe iii] | 4770 Å | 0.036 | 0.025 | P10 | 9015 Å | 1.798 | 1.744 |
| [Fe iii] | 4881 Å | 0.106 | 0.130 | [S iii] | 9069 Å | 4.858 | 2.581 |
| He i | 4922 Å | 0.155 | 0.129 | [Cl ii] | 9124 Å | 0.058 | 0.087 |
| [O iii] | 4959 Å | 1.095 | 1.109 | P8 | 9546 Å | 3.568 | 3.033 |
| [O iii] | 5007 Å | 3.296 | 3.326 | H i | 7.48/50 |$\mu$|m | 3.153 | 3.102 |
| He i | 5016 Å | 0.427 | 0.375 | [Ar iii] | 8.99 |$\mu$|m | 0.618 | 0.757 |
| [N i] | 5198 Å | 0.036 | 0.056 | H i | 12.38 |$\mu$|m | 1.067 | 1.029 |
| [N i] | 5200 Å | 0.022 | 0.052 | [Ne ii] | 12.81 |$\mu$|m | 20.002 | 20.607 |
| [Fe iii] | 5271 Å | 0.187 | 0.172 | [S iii] | 18.71 |$\mu$|m | 6.684 | 5.263 |
| [Cl iii] | 5518 Å | 0.113 | 0.116 | [S iii] | 33.47 |$\mu$|m | 2.941 | 4.004 |
| Band | λc | I(Cloudy) | I(Obs) | Band | λc | I(Cloudy) | I(Obs) |
| I(Hβ) = 100 | I(Hβ) = 100 | I(Hβ) = 100 | I(Hβ) = 100 | ||||
| B | 0.4297 |$\mu$|m | 3112.550 | 2569.843 | IRS-04 | 14.50 |$\mu$|m | 42.844 | 53.079 |
| |$g^{^{\prime }}$| | 0.4640 |$\mu$|m | 3502.697 | 2831.786 | IRS-05 | 15.00 |$\mu$|m | 11.085 | 13.975 |
| V | 0.5394 |$\mu$|m | 1401.690 | 1280.855 | IRS-06 | 16.50 |$\mu$|m | 50.613 | 64.398 |
| |$r^{^{\prime }}$| | 0.6122 |$\mu$|m | 2097.757 | 1395.011 | IRS-07 | 22.00 |$\mu$|m | 145.937 | 177.499 |
| |$i^{^{\prime }}$| | 0.7440 |$\mu$|m | 603.378 | 527.513 | IRS-08 | 23.35 |$\mu$|m | 53.640 | 64.324 |
| J | 1.235 |$\mu$|m | 168.908 | 153.285 | IRS-09 | 27.00 |$\mu$|m | 32.776 | 37.026 |
| H | 1.662 |$\mu$|m | 82.062 | 79.281 | IRS-10 | 28.00 |$\mu$|m | 41.138 | 45.412 |
| Ks | 2.159 |$\mu$|m | 45.506 | 35.859 | IRS-11 | 29.00 |$\mu$|m | 40.587 | 44.158 |
| W1 | 3.353 |$\mu$|m | 38.985 | 36.990 | IRS-12 | 30.00 |$\mu$|m | 39.898 | 42.550 |
| W2 | 4.603 |$\mu$|m | 43.688 | 49.748 | IRS-13 | 31.00 |$\mu$|m | 38.834 | 40.629 |
| IRS-01 | 8.100 |$\mu$|m | 10.832 | 10.822 | IRS-14 | 32.00 |$\mu$|m | 37.647 | 38.441 |
| IRS-02 | 10.00 |$\mu$|m | 12.494 | 13.062 | IRS-15 | 34.50 |$\mu$|m | 73.392 | 64.405 |
| IRS-03 | 13.50 |$\mu$|m | 23.575 | 28.543 | ||||
| ID | λc | Fν(Cloudy) | Fν(Model) | ID | λc | Fν(Cloudy) | Fν(Model) |
| (Jy) | (Jy) | (Jy) | (Jy) | ||||
| MIR-01 | 15.00 |$\mu$|m | 0.052 | 0.066 | FIR-02 | 90.00 |$\mu$|m | 0.081 | 0.063 |
| MIR-02 | 20.00 |$\mu$|m | 0.135 | 0.172 | FIR-03 | 100.0 |$\mu$|m | 0.060 | 0.052 |
| MIR-03 | 25.00 |$\mu$|m | 0.262 | 0.306 | FIR-04 | 120.0 |$\mu$|m | 0.035 | 0.035 |
| MIR-04 | 30.00 |$\mu$|m | 0.375 | 0.401 | FIR-05 | 140.0 |$\mu$|m | 0.023 | 0.025 |
| FIR-01 | 65.00 |$\mu$|m | 0.201 | 0.105 |
| Line . | λlab. . | I(Cloudy) . | I(Obs) . | Line . | λlab. . | I(Cloudy) . | I(Obs) . |
|---|---|---|---|---|---|---|---|
| . | . | I(Hβ) = 100 . | I(Hβ) = 100 . | . | . | I(Hβ) = 100 . | I(Hβ) = 100 . |
| B24 | 3671 Å | 0.439 | 0.735 | [Cl iii] | 5538 Å | 0.122 | 0.111 |
| B23 | 3674 Å | 0.487 | 0.909 | [N ii] | 5755 Å | 1.293 | 1.322 |
| B22 | 3676 Å | 0.545 | 0.916 | He i | 5876 Å | 1.673 | 1.566 |
| B21 | 3679 Å | 0.613 | 1.046 | [O i] | 6300 Å | 0.951 | 0.538 |
| B20 | 3683 Å | 0.696 | 1.111 | [S iii] | 6312 Å | 0.392 | 0.179 |
| B19 | 3687 Å | 0.798 | 1.388 | [O i] | 6363 Å | 0.303 | 0.164 |
| B18 | 3692 Å | 0.924 | 1.465 | [N ii] | 6548 Å | 35.039 | 37.985 |
| B17 | 3697 Å | 1.081 | 1.605 | B3 | 6563 Å | 289.424 | 310.085 |
| B16 | 3704 Å | 1.282 | 2.196 | [N ii] | 6584 Å | 103.400 | 113.836 |
| B15 | 3712 Å | 1.541 | 2.054 | He i | 6678 Å | 0.467 | 0.480 |
| B14 | 3722 Å | 1.882 | 2.671 | [S ii] | 6716 Å | 2.688 | 3.884 |
| [O ii] | 3726 Å | 139.511 | 132.411 | [S ii] | 6731 Å | 4.311 | 5.857 |
| [O ii] | 3729 Å | 76.585 | 91.955 | He i | 7065 Å | 0.541 | 0.391 |
| B13 | 3734 Å | 2.340 | 2.922 | [Ar iii] | 7135 Å | 0.592 | 0.581 |
| B12 | 3750 Å | 2.966 | 3.836 | He i | 7281 Å | 0.110 | 0.123 |
| B11 | 3771 Å | 3.849 | 4.991 | [O ii] | 7323 Å | 6.193 | 4.657 |
| B10 | 3798 Å | 5.130 | 6.224 | [O ii] | 7332 Å | 4.939 | 3.739 |
| He i | 3820 Å | 0.138 | 0.108 | [Ar iii] | 7751 Å | 0.143 | 0.139 |
| B9 | 3835 Å | 7.068 | 7.876 | P24 | 8334 Å | 0.145 | 0.218 |
| B8 | 3889 Å | 10.143 | 11.547 | P23 | 8346 Å | 0.162 | 0.211 |
| B7 | 3970 Å | 15.359 | 16.977 | P22 | 8359 Å | 0.182 | 0.274 |
| [S ii] | 4070 Å | 1.019 | 0.944 | P21 | 8374 Å | 0.206 | 0.260 |
| B6 | 4102 Å | 25.012 | 27.051 | P20 | 8392 Å | 0.235 | 0.271 |
| B5 | 4340 Å | 45.252 | 47.420 | P19 | 8413 Å | 0.271 | 0.318 |
| He i | 4471 Å | 0.556 | 0.613 | P16 | 8502 Å | 0.441 | 0.470 |
| [Fe iii] | 4659 Å | 0.323 | 0.401 | P13 | 8665 Å | 0.815 | 0.887 |
| [Fe iii] | 4702 Å | 0.108 | 0.112 | P12 | 8750 Å | 1.036 | 1.079 |
| [Fe iii] | 4755 Å | 0.059 | 0.079 | P11 | 8863 Å | 1.347 | 1.309 |
| [Fe iii] | 4770 Å | 0.036 | 0.025 | P10 | 9015 Å | 1.798 | 1.744 |
| [Fe iii] | 4881 Å | 0.106 | 0.130 | [S iii] | 9069 Å | 4.858 | 2.581 |
| He i | 4922 Å | 0.155 | 0.129 | [Cl ii] | 9124 Å | 0.058 | 0.087 |
| [O iii] | 4959 Å | 1.095 | 1.109 | P8 | 9546 Å | 3.568 | 3.033 |
| [O iii] | 5007 Å | 3.296 | 3.326 | H i | 7.48/50 |$\mu$|m | 3.153 | 3.102 |
| He i | 5016 Å | 0.427 | 0.375 | [Ar iii] | 8.99 |$\mu$|m | 0.618 | 0.757 |
| [N i] | 5198 Å | 0.036 | 0.056 | H i | 12.38 |$\mu$|m | 1.067 | 1.029 |
| [N i] | 5200 Å | 0.022 | 0.052 | [Ne ii] | 12.81 |$\mu$|m | 20.002 | 20.607 |
| [Fe iii] | 5271 Å | 0.187 | 0.172 | [S iii] | 18.71 |$\mu$|m | 6.684 | 5.263 |
| [Cl iii] | 5518 Å | 0.113 | 0.116 | [S iii] | 33.47 |$\mu$|m | 2.941 | 4.004 |
| Band | λc | I(Cloudy) | I(Obs) | Band | λc | I(Cloudy) | I(Obs) |
| I(Hβ) = 100 | I(Hβ) = 100 | I(Hβ) = 100 | I(Hβ) = 100 | ||||
| B | 0.4297 |$\mu$|m | 3112.550 | 2569.843 | IRS-04 | 14.50 |$\mu$|m | 42.844 | 53.079 |
| |$g^{^{\prime }}$| | 0.4640 |$\mu$|m | 3502.697 | 2831.786 | IRS-05 | 15.00 |$\mu$|m | 11.085 | 13.975 |
| V | 0.5394 |$\mu$|m | 1401.690 | 1280.855 | IRS-06 | 16.50 |$\mu$|m | 50.613 | 64.398 |
| |$r^{^{\prime }}$| | 0.6122 |$\mu$|m | 2097.757 | 1395.011 | IRS-07 | 22.00 |$\mu$|m | 145.937 | 177.499 |
| |$i^{^{\prime }}$| | 0.7440 |$\mu$|m | 603.378 | 527.513 | IRS-08 | 23.35 |$\mu$|m | 53.640 | 64.324 |
| J | 1.235 |$\mu$|m | 168.908 | 153.285 | IRS-09 | 27.00 |$\mu$|m | 32.776 | 37.026 |
| H | 1.662 |$\mu$|m | 82.062 | 79.281 | IRS-10 | 28.00 |$\mu$|m | 41.138 | 45.412 |
| Ks | 2.159 |$\mu$|m | 45.506 | 35.859 | IRS-11 | 29.00 |$\mu$|m | 40.587 | 44.158 |
| W1 | 3.353 |$\mu$|m | 38.985 | 36.990 | IRS-12 | 30.00 |$\mu$|m | 39.898 | 42.550 |
| W2 | 4.603 |$\mu$|m | 43.688 | 49.748 | IRS-13 | 31.00 |$\mu$|m | 38.834 | 40.629 |
| IRS-01 | 8.100 |$\mu$|m | 10.832 | 10.822 | IRS-14 | 32.00 |$\mu$|m | 37.647 | 38.441 |
| IRS-02 | 10.00 |$\mu$|m | 12.494 | 13.062 | IRS-15 | 34.50 |$\mu$|m | 73.392 | 64.405 |
| IRS-03 | 13.50 |$\mu$|m | 23.575 | 28.543 | ||||
| ID | λc | Fν(Cloudy) | Fν(Model) | ID | λc | Fν(Cloudy) | Fν(Model) |
| (Jy) | (Jy) | (Jy) | (Jy) | ||||
| MIR-01 | 15.00 |$\mu$|m | 0.052 | 0.066 | FIR-02 | 90.00 |$\mu$|m | 0.081 | 0.063 |
| MIR-02 | 20.00 |$\mu$|m | 0.135 | 0.172 | FIR-03 | 100.0 |$\mu$|m | 0.060 | 0.052 |
| MIR-03 | 25.00 |$\mu$|m | 0.262 | 0.306 | FIR-04 | 120.0 |$\mu$|m | 0.035 | 0.035 |
| MIR-04 | 30.00 |$\mu$|m | 0.375 | 0.401 | FIR-05 | 140.0 |$\mu$|m | 0.023 | 0.025 |
| FIR-01 | 65.00 |$\mu$|m | 0.201 | 0.105 |




