Search
Close
Search
Advanced Search
Search Menu
AI Discovery Assistant

Abstract

The low-order kinematic moments of galaxies, namely bulk flow and shear, enables us to test whether theoretical models can accurately describe the evolution of the mass density field in the nearby Universe. We use the so-called ηMLE maximum likelihood estimator in log-distance space to measure these moments from a combined sample of the 2MASS Tully–Fisher (2MTF) survey and the cosmicflows-3 (CF3) compilation. Galaxies common between 2MTF and CF3 demonstrate a small zero-point difference of −0.016 ± 0.002 dex. We test the ηMLE on 16 mock 2MTF survey catalogues in order to explore how well the ηMLE recovers the true moments, and the effect of sample anisotropy. On the scale size of 37 h−1 Mpc, we find that the bulk flow of the local Universe is 259 ± 15 km s−1 in the direction is (l, b) = (300 ± 4°, 23 ± 3°) (Galactic coordinates). The average shear amplitude is 1.7 ± 0.4 h km s−1 Mpc−1. We use a variable window function to explore the bulk and shear moments as a function of depth. In all cases, the measurements are consistent with the predictions of the Λ cold dark matter (ΛCDM) model.

surveys, galaxies: statistics, large-scale structure of Universe, cosmology: observations

1 INTRODUCTION

In the local Universe, the gravitational effects of mass density fluctuations exert perturbations on galaxies’ redshifts on top of Hubble’s Law, called ‘peculiar velocities’. The dipole and the quadruple of the peculiar velocity field, namely ‘bulk flow’ and ‘shear’, respectively, enable us to trace the matter density fluctuations and test whether the cosmological model accurately describes the motion of galaxies in the nearby Universe.

In previous work related to the measurement of the bulk and shear moments (Staveley-Smith & Davies 1989; Jaffe & Kaiser 1995; Willick & Strauss 1998; Parnovsky et al. 2001; Feldman, Watkins & Hudson 2010; Hong et al. 2014; Scrimgeour et al. 2016; Qin et al. 2018), the results largely agree with the ΛCDM prediction. However, some studies have measured large values for the bulk flow, in apparent disagreement with the ΛCDM prediction. For example, Watkins, Feldman & Hudson (2009) measure 407 ± 81 km s−1 on the scale size of 50 h−1 Mpc.

The bulk and shear moments are usually measured in velocity space (⁠|$v$|-space) or log-distance space (η-space). In |$v$|-space, the main measurement techniques are (Kaiser 1988; Sarkar, Feldman & Watkins 2007; Watkins et al. 2009; Feldman et al. 2010; Hong et al. 2014): log-linear χ2 minimization, minimum variance (MV) estimation and maximum likelihood estimation (MLE). Some of these |$v$|-space estimation techniques assume that the measured peculiar velocities have Gaussian errors, which is not the case for the usual estimator of peculiar velocity. Watkins & Feldman (2015) therefore introduced a peculiar velocity estimator which has Gaussian errors and, under some circumstances is unbiased. Alternatively, as shown by previous authors including Nusser & Davis (1995, 2011) and Qin et al. (2018), the bulk and shear moments in the local Universe can be measured in η-space using the ‘ηMLE’ technique. Nusser & Davis (2011) convert the model bulk flow into magnitudes analytically, using linear approximations, then convert to log-distance ratio and compare to the measurements, while Qin et al. (2018), convert the model bulk flow into log-distance ratio numerically without any approximations, then compare to the measurements.

In this work, we extend the ηMLE in Qin et al. (2018) to quadrupole (shear) measurements and, through weighting functions, compare the measured shear moments with ΛCDM prediction at different depths. We measure the bulk and shear moments from the combined dataset of cosmicflows-3 (CF3; Tully, Courtois & Sorce 2016) and 2MASS Tully–Fisher (2MTF; Hong et al. 2014).

The paper is structured as follows: in Section 2, we introduce the data: 2MTF, CF3, and their combination. The theory associated with the low-order moments (bulk and shear) is introduced in Section 3. In Section 4, we summarize how these are estimated from the data. In Section 5, we discuss the bulk and shear moments obtained from the 2MTF mocks. The final results are presented in Section 6. We provide a conclusion in Section 7.

This paper assumes spatially flat cosmology with parameters from the Planck Collaboration XVI (2014): Ωm = 0.3175, σ8 = 0.8344, ΩΛ = 0.6825, and H0 = 100 h km s−1 Mpc−1. We use these parameters to calculate the expected ΛCDM bulk flow and shear as well as the comoving distances.

2 DATA

2.1 CF3 and 2MTF

cosmicflows-3 (CF3) is a full-sky compilation of distances and velocities (Tully et al. 2016), containing 17  669 galaxies reach |$cz = 34\, 755$| km s−1. The data sources are heterogeneous, and include distances obtained from the luminosity-linewidth (Tully–Fisher) relation, the Fundamental Plane (FP), surface-brightness fluctuations, from Type Ia supernova (SNIa) observations, the tip of the Red Giant Branch (TRGB), with the largest recent increment being the FP sample of the Six-degree-Field Galaxy Survey (6dFGS) of Springob et al. (2014). We removed those galaxies with CMB frame redshift lower than 600 km s−1, leaving 17  407.

2MTF is a Tully–Fisher sample derived from the Two Micron All-Sky Survey (2MASS). The Tully–Fisher relation is measured using H i rotation widths (Springob et al. 2005; Haynes et al. 2011; Hong et al. 2013; Masters et al. 2014) for galaxies at redshifts measured in the 2MASS Redshift Survey (Huchra et al. 2012). The final 2MTF catalogue contains 2 062 galaxies with a redshift cut 600 km s−1 < cz < 1.2 × 104 km s−1. The 2MTF K-band magnitude limit is 11.25 mag.

2.2 The combination of CF3 and 2MTF

The combination of CF3 and 2MTF data offers the following advantages. First, the combined data set is much deeper than 2MTF alone (CF3 extends out to three times the redshift of 2MTF). Secondly, the combined data set is more isotropic than CF3 alone (the projected sky density of CF3 is greater in the southern sky by a factor of 2.4, and the projected density of 2MTF is greater in the northern sky by 1.6).

In order to find the common galaxies in the two catalogue and calibrate out any zero-points, we need to cross-compare the estimated distances in the 2MTF and the CF3 data. The ‘logarithmic distance ratio’ for a galaxy, η is defined as
(1)
where d|$z$| is the apparent distance of a galaxy and is inferred from the observed redshift of the galaxy. The true comoving distance, dh is calculated from a redshift-independent measurement of the galaxy (Strauss & Willick 1995). 2MTF uses the Tully–Fisher distance estimator, while CF3 uses a compilation of Fundamental Plane, Tully–Fisher and Type Ia supernovae. The CF3 catalogue does not have log-distance ratio data, but it lists distance modulus μ, corresponding to h = 0.75. We convert μ to η, assuming h = 0.75, and assign an error for η corresponding to 1/5 of the error for μ.
There are 1117 common galaxies in the 2MTF and the CF3. These galaxies are identified as having CF3 and 2MTF heliocentric velocity differences |Δ|$v$|hel| < 150 km s−1. The CF3 distance estimator for these galaxies is mostly Tully–Fisher. For each galaxy, we calculate log10dh(2MTF) and log10dh(CF3) then apply a linear fit with a 3σ clip. This removes 21 galaxies, leaving 1 096 (we used the hyperfit package; Robotham & Obreschkow 2015). In Fig. 1, we plot log10dh(2MTF) against log10dh(CF3) for these galaxies. The average difference is
(2)
representing a 4 per cent difference in distance.
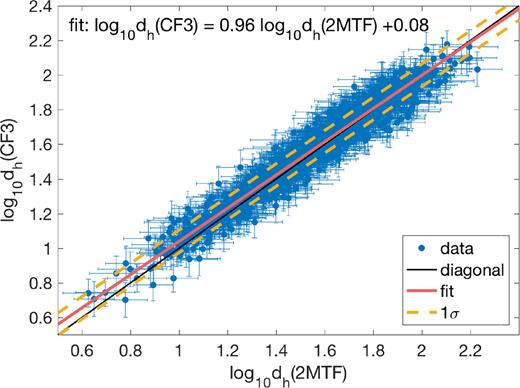
Comparing the CF3 distances to the 2MTF distances for 1 096 common galaxies. The expected 1:1 relation for perfect agreement is shown in the solid black line. The hyperfit line is shown in the solid red line. The ±1σ is indicated by the yellow dashed lines, and σ = 0.07.
Figure 1.

Comparing the CF3 distances to the 2MTF distances for 1 096 common galaxies. The expected 1:1 relation for perfect agreement is shown in the solid black line. The hyperfit line is shown in the solid red line. The ±1σ is indicated by the yellow dashed lines, and σ = 0.07.

Open in new tabDownload slide

Removing the 1 117 common galaxies from CF3, and adding a zero-point correction of −0.016 to the log-distance ratio data in CF3, we obtain a combined data set, which has 18 352 galaxies. The sky coverage and the redshift distribution of the combined CF3 and 2MTF is shown in Figs 2 and 3, respectively.

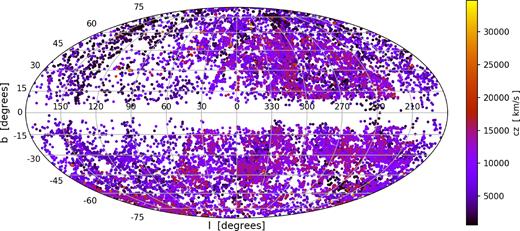
Distribution of 18 352 galaxies in the combined 2MTF and CF3 data set in Galactic coordinates. The galaxy redshift is indicated by the colour of the points, based on the right-hand colour bar. The majority of galaxies lie at recession velocities cz < 16 000 km s−1.
Figure 2.

Distribution of 18 352 galaxies in the combined 2MTF and CF3 data set in Galactic coordinates. The galaxy redshift is indicated by the colour of the points, based on the right-hand colour bar. The majority of galaxies lie at recession velocities cz < 16 000 km s−1.

Open in new tabDownload slide
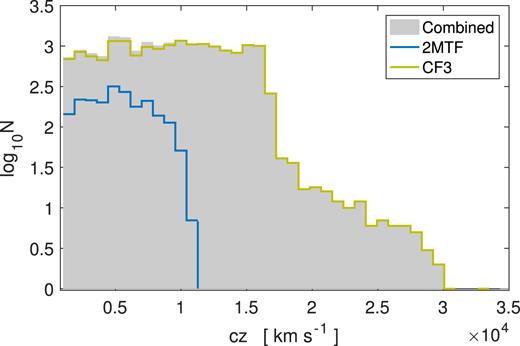
The redshift (in CMB frame) distribution of the datasets. The light-green/yellow and the blue line are for the CF3 and 2MTF data, respectively. The Combined dataset is represented by the grey bars.
Figure 3.

The redshift (in CMB frame) distribution of the datasets. The light-green/yellow and the blue line are for the CF3 and 2MTF data, respectively. The Combined dataset is represented by the grey bars.

Open in new tabDownload slide

3 BULK FLOW AND SHEAR MOMENTS

Following the argument in Kaiser (1988) and Jaffe & Kaiser (1995), using the Taylor series expansion, we expand the line-of-sight total velocity field, V(dh) to first order:
(3)
(hereafter, repeated indices represent summation), where dh is the comoving distance, and |$\lbrace {\bf \hat{r}}_x,{\bf \hat{r}}_y,{\bf \hat{r}}_z\rbrace$| represents the projections for the unit vector of dh in the three Cartesian directions. Then, following Staveley–Smith & Davies (1989) and Parnovsky et al. (2001), we can decompose the tensor, Aij into a summation of trace part Hδij and traceless part Qij:
(4)
We then can write equation (3) as
(5)
where Hdh corresponds to the Hubble law with the Hubble constant H (Parnovsky et al. 2001).
The left-hand side of equation (5), which is the difference between the total velocity field, V(dh) and the Hubble recession velocity Hdh, describes the line-of-sight peculiar motion of the galaxies. Denoting this by |$v$|(dh) gives:
(6)
The three zeroth-order components, Bi are known as ‘bulk flow’. The first-order tensor, Qij describes the ‘shear’ moments and is traceless, i.e.
(7)
The line-of-sight peculiar velocity (PV) field only has radial components, i.e. it is curl-free. Therefore, Qij is a symmetric tensor (Feldman et al. 2010), Qij = Qji, so that there are 5 independent shear components, giving eight independent moment components for the first-order expansion in equation (6).
To simplify equation (6), we follow Jaffe & Kaiser (1995) and Feldman et al. (2010) and rewrite as follows:
(8)
where Up are the nine moment components given by
(9)
and the mode functions are given by
(10)
In this paper, we use the measured log-distance ratio η from the individual and combined CF3 and 2MTF samples to estimate the nine moments Up.

4 MAXIMUM LIKELIHOOD ESTIMATION

To preserve the Gaussian nature of the measurement errors, there are two methods that can be applied to obtain maximum likelihood estimates of the bulk flow velocity and shear moments.

The first (ηMLE) calculates the model log-distance ratio from the model Up and compares to the measured value (Nusser & Davis 1995, 2011; Qin et al. 2018).

The second method (⁠|$w$|MLE) converts the measured η into |$v$|-space to obtain the peculiar velocities, |$v$| using the PV estimator of Watkins & Feldman (2015), then compares to the model Up under the assumption that the measured |$v$| has Gaussian error (Kaiser 1988).

One caveat is that the PV estimator in Watkins & Feldman (2015) only strictly estimates an unbiased peculiar velocity under the assumption that the cz of the galaxy is much greater than the true peculiar velocity (not the measured peculiar velocity) for that galaxy (Watkins & Feldman 2015). By contrast, the ηMLE can avoid assumptions about the galaxy’s unknown true PV compared to its redshift.

4.1 ηMLE

A galaxy’s line-of-sight peculiar velocity can be related to its observed redshift |$z$| through (Colless et al. 2001; Hui & Greene 2006; Davis & Scrimgeour 2014)
(11)
where redshift |$z$|h corresponds to the true comoving distance, dh of the galaxy, and c is the speed of light. The above equation neglects the effects of gravitational lensing and relativistic motions (Davis & Scrimgeour 2014). In the spatially flat ΛCDM model, the comoving distance is given by
(12)
where
(13)
and H0, Ωm, and ΩΛ are the present epoch Hubble constant, matter and dark energy densities, respectively. The apparent comoving distance d|$z$| can be related to the observed redshift |$z$| through a similar expression.
Substituting equation (6) into equation (11) to replace |$v$|⁠, then using the low-redshift approximation |$z$|h ≈ H0dh(⁠|$z$|h)/c to replace |$z$|h, we can obtain the relationship between dh and {Bi, Qij}:
(14)
This equation is used to calculate the model-predicted dh for the ηMLE and the |$w$|MLE. The model dh is then combined with d|$z$| to compute a model log-distance ratio. One caveat is that, since Qij in equation (14) is traceless, the element Qzz is computed from Qxx and Qyy using equation (7), rather than setting Qzz as an independent shear component. A Taylor expansion of dh in equation (14) around the position of |$(B_i=0, \, Q_{ij} {\bf \hat{r}}_i {\bf \hat{r}}_j=0)$| confirms that dh = d|$z$|, as would be expected in the absence of any peculiar velocity.
Finally, assuming that for a given set of galaxies, the measured log-distance ratios are independent and Gaussian, for a set of n log-distance ratios, the likelihood can be written (Qin et al. 2018):
(15)
where |$\tilde{\eta }_n(U_p)$| is the model log-distance ratio for each galaxy, ηn is the measured log-distance ratio with error of εn, and ε⋆, n is given by (Hui & Greene 2006; Johnson et al. 2014):
(16)
where σ⋆ is the 1D velocity dispersion (Scrimgeour et al. 2016). Similar to the PV estimator in Watkins & Feldman (2015) (or our equation 21), equation (16) also uses the approximation that the cz of the galaxy is much greater than the true peculiar velocity for that galaxy. However, in ηMLE, this approximation is less important since σ⋆ is set to be a free parameter.

The maximum likelihood Up cannot be obtained analytically due to the non-linear relationship between the model Up and the model predicted log-distance ratio. Instead, we follow the method of Qin et al. (2018), combining flat priors on the σ⋆ and Up (excluding Qzz) with the likelihood in equation (15), enabling us to write the posterior probability of these nine independent parameters given the cosmological model and the data. Here, we use the Metropolis–Hastings Markov chain Monte Carlo (MCMC) algorithm with flat priors in the interval Bi ∈ [−1200, +1200] km s−1 and Qij ∈ [−100, +100] h km s−1 Mpc −1 to explore the posterior.

Feldman et al. (2010) use the MV method to estimate Up. In their estimator, they set Qzz as an independent component rather than using equation (7) to compute Qzz from Qxx and Qyy. In our paper, we also tested the ηMLE on mocks by setting Qzz as an independent component (see Appendix  A), but found this led to larger reduced χ2.

The measurement error of the bulk flow amplitude, eB can be calculated use the Jacobian, J and the covariance matrix of the bulk flow velocity, |$R^{\epsilon }_{ij}$| through
(17)
where |$J=\partial B/\partial B_i$| and |$R^{\epsilon }_{ij}$| is calculated using the MCMC chains. For comparison to theory, the ‘MLE depth’, which is the characteristic scale of cosmic flow measurement, is defined as (Scrimgeour et al. 2016)
(18)
where the weight factors |$W_n=1/(\sigma _n^2+\sigma ^2_{\star })$|⁠. For the purpose of this comparison, the measurement errors of peculiar velocities, σn are given by (Hui & Greene 2006; Johnson et al. 2014; Howlett et al. 2017):
(19)
which is similar to equation (16). The theoretical expected bulk flow is compared to the measured value at the scale of dMLE.

4.2 wMLE: estimation in v-space

Assuming peculiar velocities have Gaussian errors, the likelihood of n peculiar velocities |$v$|n given Up is (Kaiser 1988):
(20)
where |$\tilde{v}_n(U_p)$| is the model PV for each observed galaxy .
To preserve the above Gaussian assumption, Watkins & Feldman (2015) developed the following estimator to calculate peculiar velocities as the input to the above likelihood function,
(21)
where dl is the luminosity distance, and |$z$|mod is given by
(22)
The acceleration parameter is q0 = 0.5(Ωm − 2ΩΛ). The |$w$|MLE method refers to the combination of PV estimator in equation (21) and the likelihood in equation (20). However, equation (21) only estimates an unbiased PV under the assumption that the galaxy’s cz is much larger than its true peculiar velocity, |$v$|t(Watkins & Feldman 2015).
To compute the peculiar velocity, we can first calculate the true comoving distance, dh from the measured η and the inferred comoving distance, d|$z$| using
(23)
then converting to luminosity distance using dl = (1 + |$z$|⁠)dh, calculating |$z$|mod from the observed redshift |$z$| using equation (22). Equation (21) can then be solved to obtain |$v$|⁠. The |$\tilde{v}_n(U_p)$| in equation (20) can be computed by first calculating the model-predicted dh from equation (14), then solving equation (6) to obtain |$\tilde{v}_n(U_p)$|⁠. Similar to the ηMLE method, we use MCMC with uniform priors in the interval Bi ∈ [−1200, +1200] km s−1 and Qij ∈ [−100, +100] h km s−1 Mpc −1. Qzz is also computed from Qxx and Qyy using equation (7), rather than setting it as an independent component.

5 BULK AND SHEAR MOMENTS IN THE 2MTF MOCKS

In order to test how well the ηMLE and the |$w$|MLE are expected to recover the true moments from the observational data, we applied the two estimators to 16 mock 2MTF catalogues (Howlett et al. 2017). We use the SURFS simulations (Elahi et al. 2018) and the GiggleZ (Poole et al. 2015) to generate these mocks. The SURFS simulation uses cosmological parameters of Ωm = 0.3121, Ωb = 0.0488, and h = 0.6751. while the GiggleZ simulation uses cosmological parameters of Ωm = 0.273, Ωb = 0.0456, and h = 0.705. This also allows us to explore whether the two estimators give consistent answers under different cosmologies. Each mock catalogue contains |$\sim 2\, 000$| galaxies, and matches the survey geometry (i.e. sky coverage and the distance distribution) and the selection function of the 2MTF survey (Qin et al. 2018).

The true velocity, vt of each galaxy are known from the simulation. Within each mock, the ‘true’ bulk flow velocity, Bt is defined as the average of the true galaxy velocities along orthogonal axes
(24)
The ‘true’ shear moments within each mock are defined as the traceless part of
(25)
The true comoving distance of each galaxy, dh, n is known from the simulations, and |${\bf \hat{r}}_{j,n}$| is the projection, in the j-direction, of the corresponding unit vector.
As shown in Fig. 4, in Cartesian equatorial coordinates, we compare the measured bulk flow of the 16 2MTF mocks to their true bulk flow. To compare the ηMLE to |$w$|MLE, we calculate the reduced χ2 between true bulk flow, Bt and the measured bulk flow, Bm using
(26)
where the vector Bm and Bt contain 48 elements, including 3 directions × 16 mocks. The covariance matrix |$\boldsymbol{\mathsf {C}}$| contains 48 × 48 elements (16 3 × 3 diagonal blocks, and zero elsewhere). The 16 3 × 3 diagonal blocks of |$\boldsymbol{\mathsf {C}}$| are computed from the 16 MCMC samples for both |$w$|MLE and ηMLE. For ηMLE we find |$\chi ^2_{\mathrm{ red}}({\bf B}) = 3.70$|⁠, which is slightly lower than for |$w$|MLE (where |$\chi ^2_{\mathrm{ red}}({\bf B}) = 4.04$|⁠). These |$\chi ^2_{\mathrm{ red}}({\bf B})$| are smaller compared to the results in Qin et al. (2018) (where |$\chi ^2_{\mathrm{ red}}({\bf B})=4.02$| for ηMLE and 4.23 for |$w$|MLE). This is because, in this work, both the ηMLE estimator and the |$w$|MLE estimator have more parameters (due to the shear moments) which will reduce the scatter in |$\boldsymbol{B}_m$| about |$\boldsymbol{B}_{t}$| and increase the length of the error bars.
The measured bulk flow for the 16 2MTF mocks in equatorial coordinates. The upper and bottom panels are for the $w$MLE estimator and the ηMLE estimator, respectively.
Figure 4.

The measured bulk flow for the 16 2MTF mocks in equatorial coordinates. The upper and bottom panels are for the |$w$|MLE estimator and the ηMLE estimator, respectively.

Open in new tabDownload slide
The estimated shear moments from the mocks are compared to the true shear moments in Fig. 5. Similarly, the reduced χ2 between the measured shear moments, Qm and true shear moments, Qt is given by
(27)
where the Qm and Qt contain 80 elements (16 mocks and 5 independent elements without Qzz). The covariance matrix |$\boldsymbol{\mathsf {C}}$| is an 80 × 80 matrix with 16 5 × 5 diagonal blocks and zero elsewhere. Also, we use the 16 MCMC samples to calculate the diagonal blocks. For ηMLE we find |$\chi _{\mathrm{ red}}^2({\bf Q}) =3.10$|⁠, which is almost the same as the |$w$|MLE methods (where |$\chi _{\mathrm{ red}}^2({\bf Q}) = 3.14$|⁠).
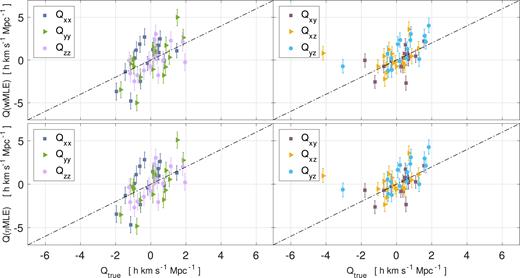
The measured shear moments for the 16 2MTF mocks. The (x, y, $z$) measurements are in equatorial coordinates. The upper and lower panels are for the $w$MLE estimator and the ηMLE estimator, respectively.
Figure 5.

The measured shear moments for the 16 2MTF mocks. The (x, y, |$z$|⁠) measurements are in equatorial coordinates. The upper and lower panels are for the |$w$|MLE estimator and the ηMLE estimator, respectively.

Open in new tabDownload slide
The reduced χ2 for all the eight moments (excluding Qzz) is given by
(28)
where the measured moments, Um and the true moments, Ut contain 128 elements (8 independent elements and 16 mocks). The covariance matrix |$\boldsymbol{\mathsf {C}}$| is an 128 × 128 matrix with 16 8 × 8 diagonal blocks and zero elsewhere. The 16 MCMC samples are used to calculate the 16 8 × 8 diagonal blocks. For ηMLE we find |$\chi _{\mathrm{ red}}^2({\bf U}) =3.49$|⁠, for |$w$|MLE, we find |$\chi _{\mathrm{ red}}^2({\bf U}) = 3.58$|⁠.

Generally, for both the bulk flow measurements and the shear measurements, the |$w$|MLE and ηMLE perform similarly and return unbiased measurements of bulk flow and shear moments. However, due to the Watkins & Feldman (2015) estimator having a necessary assumption of |$v$|true ≪ cz, some systematic errors are introduced for the closest galaxies in the mocks. As a result, the |$\chi ^2_{\mathrm{ red}}({\bf B})$| of |$w$|MLE is slightly higher compared to the ηMLE. Overall, we find ηMLE performs better than |$w$|MLE for the 2MTF mocks, and for the subsequent parts of this paper, ηMLE is the one we shall adopt to measure the bulk flow and shear moments from the data sets.

The reasons for the reduced chi-squared values far from 1 are most likely due to: (i) the assumption that the standard deviation of true velocities in the mocks is σ⋆ (or ε⋆, n in the ηMLE method); (ii) the fitted values of bulk and shear flow are weighted in a different manner to the ‘true’ values, leading to different effective depths; and (iii) the moment model is only a low-order approximation of a more complex velocity field.

6 RESULTS AND DISCUSSION

6.1 Results and comparison with ΛCDM theory

The resultant bulk and shear moments measurements (in Galactic coordinates) for 2MTF, CF3, and the combined data are presented in Table 1. The measurement errors of the bulk flow velocity and shear moments for the combined data set (and CF3) are much smaller compared to 2MTF. This is mainly due to the combined data set covering a much larger cosmological volume. CF3 also combines distances using the weighted average of multiple measurements, if available.

Table 1.
Open in new tab

Bulk flow and shear moments measurements for 2MTF, CF3, and the combined data set in Galactic coordinates. The CRMS column gives expected cosmic variance due to ΛCDM. The last row lists the depth of the measurement.

2MTFCF3Combined
ηMLECRMSηMLECRMSηMLECRMS
Bx (km s−1)130.6 ± 39.5±164.8134.5 ± 17.4±160.4120.6 ± 17.7±155.6
By (km s−1)−340.3 ± 37.0±172.1−282.7 ± 15.7±169.4−206.5 ± 16.1±164.2
B|$z$| (km s−1)85.4 ± 30.5±185.676.6 ± 11.9±178.399.5 ± 12.1±173.4
Qxx (h km s−1 Mpc−1)3.69 ± 1.35±2.530.73 ± 0.43±1.782.12 ± 0.44±1.68
Qxy (h km s−1 Mpc−1)−4.16 ± 1.16±1.45−1.41 ± 0.36±0.95−1.16 ± 0.36±0.89
Qxz (h km s−1 Mpc−1)−0.96 ± 0.97±1.321.13 ± 0.28±0.860.17 ± 0.27±0.80
Qyy (h km s−1 Mpc−1)0.36 ± 1.30±3.200.83 ± 0.41±1.841.94 ± 0.41±1.74
Qyz (h km s−1 Mpc−1)−1.47 ± 1.01±1.54−0.14 ± 0.29±0.890.47 ± 0.29±0.83
Qzz (h km s−1 Mpc−1)−4.05 ± 1.18±2.68−1.56 ± 0.36±2.02−4.06 ± 0.36±1.85
dMLE (h−1 Mpc)323537
2MTFCF3Combined
ηMLECRMSηMLECRMSηMLECRMS
Bx (km s−1)130.6 ± 39.5±164.8134.5 ± 17.4±160.4120.6 ± 17.7±155.6
By (km s−1)−340.3 ± 37.0±172.1−282.7 ± 15.7±169.4−206.5 ± 16.1±164.2
B|$z$| (km s−1)85.4 ± 30.5±185.676.6 ± 11.9±178.399.5 ± 12.1±173.4
Qxx (h km s−1 Mpc−1)3.69 ± 1.35±2.530.73 ± 0.43±1.782.12 ± 0.44±1.68
Qxy (h km s−1 Mpc−1)−4.16 ± 1.16±1.45−1.41 ± 0.36±0.95−1.16 ± 0.36±0.89
Qxz (h km s−1 Mpc−1)−0.96 ± 0.97±1.321.13 ± 0.28±0.860.17 ± 0.27±0.80
Qyy (h km s−1 Mpc−1)0.36 ± 1.30±3.200.83 ± 0.41±1.841.94 ± 0.41±1.74
Qyz (h km s−1 Mpc−1)−1.47 ± 1.01±1.54−0.14 ± 0.29±0.890.47 ± 0.29±0.83
Qzz (h km s−1 Mpc−1)−4.05 ± 1.18±2.68−1.56 ± 0.36±2.02−4.06 ± 0.36±1.85
dMLE (h−1 Mpc)323537
Table 1.
Open in new tab

Bulk flow and shear moments measurements for 2MTF, CF3, and the combined data set in Galactic coordinates. The CRMS column gives expected cosmic variance due to ΛCDM. The last row lists the depth of the measurement.

2MTFCF3Combined
ηMLECRMSηMLECRMSηMLECRMS
Bx (km s−1)130.6 ± 39.5±164.8134.5 ± 17.4±160.4120.6 ± 17.7±155.6
By (km s−1)−340.3 ± 37.0±172.1−282.7 ± 15.7±169.4−206.5 ± 16.1±164.2
B|$z$| (km s−1)85.4 ± 30.5±185.676.6 ± 11.9±178.399.5 ± 12.1±173.4
Qxx (h km s−1 Mpc−1)3.69 ± 1.35±2.530.73 ± 0.43±1.782.12 ± 0.44±1.68
Qxy (h km s−1 Mpc−1)−4.16 ± 1.16±1.45−1.41 ± 0.36±0.95−1.16 ± 0.36±0.89
Qxz (h km s−1 Mpc−1)−0.96 ± 0.97±1.321.13 ± 0.28±0.860.17 ± 0.27±0.80
Qyy (h km s−1 Mpc−1)0.36 ± 1.30±3.200.83 ± 0.41±1.841.94 ± 0.41±1.74
Qyz (h km s−1 Mpc−1)−1.47 ± 1.01±1.54−0.14 ± 0.29±0.890.47 ± 0.29±0.83
Qzz (h km s−1 Mpc−1)−4.05 ± 1.18±2.68−1.56 ± 0.36±2.02−4.06 ± 0.36±1.85
dMLE (h−1 Mpc)323537
2MTFCF3Combined
ηMLECRMSηMLECRMSηMLECRMS
Bx (km s−1)130.6 ± 39.5±164.8134.5 ± 17.4±160.4120.6 ± 17.7±155.6
By (km s−1)−340.3 ± 37.0±172.1−282.7 ± 15.7±169.4−206.5 ± 16.1±164.2
B|$z$| (km s−1)85.4 ± 30.5±185.676.6 ± 11.9±178.399.5 ± 12.1±173.4
Qxx (h km s−1 Mpc−1)3.69 ± 1.35±2.530.73 ± 0.43±1.782.12 ± 0.44±1.68
Qxy (h km s−1 Mpc−1)−4.16 ± 1.16±1.45−1.41 ± 0.36±0.95−1.16 ± 0.36±0.89
Qxz (h km s−1 Mpc−1)−0.96 ± 0.97±1.321.13 ± 0.28±0.860.17 ± 0.27±0.80
Qyy (h km s−1 Mpc−1)0.36 ± 1.30±3.200.83 ± 0.41±1.841.94 ± 0.41±1.74
Qyz (h km s−1 Mpc−1)−1.47 ± 1.01±1.54−0.14 ± 0.29±0.890.47 ± 0.29±0.83
Qzz (h km s−1 Mpc−1)−4.05 ± 1.18±2.68−1.56 ± 0.36±2.02−4.06 ± 0.36±1.85
dMLE (h−1 Mpc)323537
In Table 1, we also list the ΛCDM prediction, which has zero mean and ‘cosmic root mean square’ (CRMS) variation (Feldman et al. 2010), for each data set. Assuming ΛCDM, the CRMS is given by the diagonal elements of the following covariance matrix (Feldman et al. 2010; Ma, Gordon & Feldman 2011; Johnson et al. 2014):
(29)
The indices p and q range from 1 to 9, corresponding to the nine moment modes in equation (10). The linear density power spectrum |$\mathcal {P}(k)$| is generated using the camb package (Lewis, Challinor & Lasenby 2000). The window function, |$\mathcal {W}_{pq}(k)$| for the individual moments Up is given by (Feldman et al. 2010; Ma et al. 2011; Johnson et al. 2014)
(30)
The analytic expression of the angle-averaged window function, fmn(k) is given by Ma et al. (2011) (also, see equation 5 in Johnson et al. 2014). Assuming PVs have a Gaussian distribution (see equation 20), the weight factors, |$w$|p, n in equation (30) are given by (Kaiser 1988; Jaffe & Kaiser 1995; Feldman & Watkins 2008):
(31)
The above Gaussian assumption is true for the |$w$|MLE. Since the |$w$|MLE and the ηMLE give almost the same Up measurements (or almost the same |$\chi ^2_{red}$|⁠, see Fig. 4), it is rational to compare the ‘CRMS’, inferred from equation (31), to the ηMLE measurements in Table 1, even though the weight factors correspond to velocities rather than log-distance ratios. In Galactic coordinates, the |$\mathcal {W}_{pq}^2(k)$| of equation (30) for 2MTF, CF3, and the combined data sets is shown in Fig. 6.
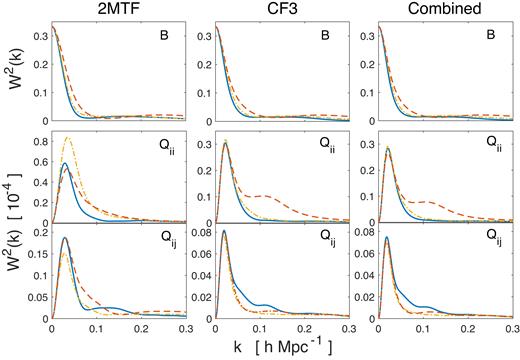
The window functions for 2MTF, CF3, and the combined data set, all in Galactic coordinates. In the top panels are the bulk flow x (blue solid curve), y (yellow dot-dashed curve), and $z$ (red dashed curve) components. In the middle panels are the Qxx (blue solid curve), Qyy (yellow dot-dashed curve), Qzz (red dashed curve) components. In the bottom panels are the Qxy (blue solid curve), Qxz (yellow dot-dashed curve), Qyz (red dashed curve) components. The left-hand side panels are for 2MTF, the middle panels are for CF3, the right-hand side panels are for the combined data set.
Figure 6.

The window functions for 2MTF, CF3, and the combined data set, all in Galactic coordinates. In the top panels are the bulk flow x (blue solid curve), y (yellow dot-dashed curve), and |$z$| (red dashed curve) components. In the middle panels are the Qxx (blue solid curve), Qyy (yellow dot-dashed curve), Qzz (red dashed curve) components. In the bottom panels are the Qxy (blue solid curve), Qxz (yellow dot-dashed curve), Qyz (red dashed curve) components. The left-hand side panels are for 2MTF, the middle panels are for CF3, the right-hand side panels are for the combined data set.

Open in new tabDownload slide

The estimation procedure of CMRS follows the arguments in Feldman et al. (2010) (see also Watkins et al. 2009; Scrimgeour et al. 2016). To reiterate, to obtain the estimates of the CMRS expected within our survey under the ΛCDM cosmological model, we perform the following steps:

  • Use the positions and errors of galaxies within the 2MTF (CF3) survey to calculate the weight factors in equation (31).

  • Combine these with the fmn term in equation (30) (which also only depends on the 2MTF (CF3) galaxy positions) to calculate the window function of the data.

  • Integrate this window function along with the ΛCDM power spectrum to calculate the matrix Rpq in equation (29).

  • The CMRS values are then given by the diagonal elements of Rpq.

As the above procedure depends only on the positions and errors of the galaxies within 2MTF (CF3) data and the ΛCDM cosmological model, we are testing the agreement between our data and the cosmological model without the need for any simulations.

From Table 1, for the CF3, 2MTF and the combined sample, we find that the majority of our Qij measurements are consistent with the CRMS calculated from ΛCDM theory. After combining the CRMS predictions with measurement errors, the largest deviations are the Qxy component in 2MTF at 2.2σ and the Qzz component in the combined data set at 2.2σ too.

We also need to compare the measured bulk flow amplitude to the ΛCDM prediction. Unlike the individual components of the bulk flow and shear, the bulk flow amplitude is non-Gaussian, following instead a Maxwell–Boltzmann distribution. The rms of the bulk flow amplitude, σB can be calculated from |$R_{ij}^{v}$| of equation (29) using the Jacobian. The probability distribution of the bulk flow amplitude B is given by (Li et al. 2012; Hong et al. 2014; Scrimgeour et al. 2016)
(32)
where the most likely B is expressed as |$B_p=\sqrt{2/3}\sigma _B$|⁠, and the cosmic variance of B is given by |${B_p}^{+0.419\sigma _B}_{-0.356\sigma _B}$| (68 per cent confidence level) and |${B_p}^{+0.891\sigma _B}_{-0.619\sigma _B}$| (95 per cent confidence level)1 (Scrimgeour et al. 2016). The theoretical bulk flow amplitude prediction for the 2MTF, CF3, and combined data set is given in Table 2. All bulk flows are consistent with ΛCDM predictions.
Table 2.
Open in new tab

The ηMLE measured bulk flows are compared to the prediction of ΛCDM and its cosmic variance.

ΛCDM |B| (km s−1)ηMLE |B| (km s−1)
CF3238|$^{+122}_{-104}$|322 ± 15
2MTF243|$^{+125}_{-106}$|374 ± 36
Combined231|$^{+118}_{-101}$|259 ± 15
ΛCDM |B| (km s−1)ηMLE |B| (km s−1)
CF3238|$^{+122}_{-104}$|322 ± 15
2MTF243|$^{+125}_{-106}$|374 ± 36
Combined231|$^{+118}_{-101}$|259 ± 15
Table 2.
Open in new tab

The ηMLE measured bulk flows are compared to the prediction of ΛCDM and its cosmic variance.

ΛCDM |B| (km s−1)ηMLE |B| (km s−1)
CF3238|$^{+122}_{-104}$|322 ± 15
2MTF243|$^{+125}_{-106}$|374 ± 36
Combined231|$^{+118}_{-101}$|259 ± 15
ΛCDM |B| (km s−1)ηMLE |B| (km s−1)
CF3238|$^{+122}_{-104}$|322 ± 15
2MTF243|$^{+125}_{-106}$|374 ± 36
Combined231|$^{+118}_{-101}$|259 ± 15

6.2 Cosmic flow as a function of depth

The bulk flow amplitudes, measured from 2MTF and the CF3 individually and combined, are plotted against the survey depth in Fig. 7. Usually, comparing bulk flow measurements between different surveys on a single figure is difficult, since those surveys have differing survey geometries and depths. Therefore, it is necessary to standardize the window function, and in this paper, we used the spherical top-hat window function: |$\mathcal {W}(k)=3(\sin kR-kR\cos kR)/(kR)^3$|⁠. In Fig. 7, we also compare our bulk flow measurements with the measurements of others (Watkins et al. 2009; Colin et al. 2011; Dai, Kinney & Stojkovic 2011; Nusser & Davis 2011; Turnbull et al. 2012; Ma & Scott 2013; Hong et al. 2014; Scrimgeour et al. 2016; Qin et al. 2018). The black solid curve represents the most likely bulk flow predicted by the ΛCDM using the spherical top-hat window function. From Fig. 7, we find most of the measured bulk flows are consistent with the ΛCDM prediction at the 68 per cent confidence level.

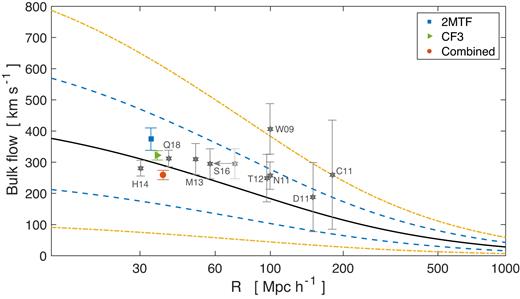
The ηMLE measured bulk flow amplitudes (filled circles •) for 2MTF, CF3, and the combined data set are compared to values from other authors. The most probable bulk flow from the ΛCDM prediction is shown as the solid line. The yellow and blue dashed lines indicate 95 per cent and 68 per cent confidence levels, respectively. Other measurements are indicated by the grey stars (⋆) (Q18: Qin et al. 2018; H14: Hong et al. 2014; T12: Turnbull et al. 2012; W09: Watkins et al. 2009; N11: Nusser & Davis 2011; M13: Ma & Scott 2013; D11: Dai et al. 2011; C11: Colin et al. 2011; S16: Scrimgeour et al. 2016). Following Scrimgeour et al. (2016), W09 and T12 are plotted at twice their quoted radius since they use Gaussian windows. To account for the half-sky coverage of 6dFGSv, the S16 (Scrimgeour et al. 2016) measurement is shifted as shown by the grey arrow.
Figure 7.

The ηMLE measured bulk flow amplitudes (filled circles •) for 2MTF, CF3, and the combined data set are compared to values from other authors. The most probable bulk flow from the ΛCDM prediction is shown as the solid line. The yellow and blue dashed lines indicate 95 per cent and 68 per cent confidence levels, respectively. Other measurements are indicated by the grey stars (⋆) (Q18: Qin et al. 2018; H14: Hong et al. 2014; T12: Turnbull et al. 2012; W09: Watkins et al. 2009; N11: Nusser & Davis 2011; M13: Ma & Scott 2013; D11: Dai et al. 2011; C11: Colin et al. 2011; S16: Scrimgeour et al. 2016). Following Scrimgeour et al. (2016), W09 and T12 are plotted at twice their quoted radius since they use Gaussian windows. To account for the half-sky coverage of 6dFGSv, the S16 (Scrimgeour et al. 2016) measurement is shifted as shown by the grey arrow.

Open in new tabDownload slide

In Fig. 8, the bulk flow directions are compared in Galactic coordinates. The bulk flow directions from different surveys are mainly in agreement except S16 (Scrimgeour et al. 2016). This discrepancy appears to come from their imperfect Malmquist bias correction to the 6dFGSv data, based on the assumption that peculiar velocities, estimated from equation (11), have Gaussian errors (see Qin et al. 2018). The bulk flow direction converges towards the CMB dipole, and appears to be due to local effects combined with more distant gravitational perturbations, including the Shapley supercluster.

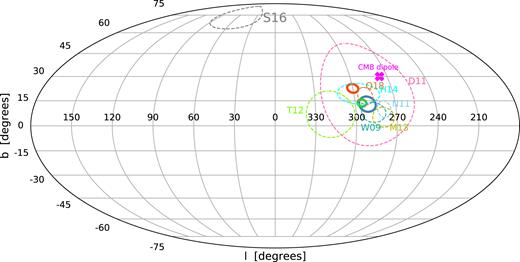
The direction of bulk flow from different measurements are compared in Galactic coordinates. The ηMLE results for 2MTF, CF3, and the combined data set are shown in the blue, green, and the red solid circles, respectively. The coloured dashed circles indicate other recent measurements (Q18: Qin et al. 2018; H14: Hong et al. 2014; T12: Turnbull et al. 2012; W09: Watkins et al. 2009; N11: Nusser & Davis 2011; M13: Ma & Scott 2013; D11: Dai et al. 2011; S16: Scrimgeour et al. 2016). The 1σ error is indicated by the radius of the circles. The CMB dipole direction is shown as the pink cross.
Figure 8.

The direction of bulk flow from different measurements are compared in Galactic coordinates. The ηMLE results for 2MTF, CF3, and the combined data set are shown in the blue, green, and the red solid circles, respectively. The coloured dashed circles indicate other recent measurements (Q18: Qin et al. 2018; H14: Hong et al. 2014; T12: Turnbull et al. 2012; W09: Watkins et al. 2009; N11: Nusser & Davis 2011; M13: Ma & Scott 2013; D11: Dai et al. 2011; S16: Scrimgeour et al. 2016). The 1σ error is indicated by the radius of the circles. The CMB dipole direction is shown as the pink cross.

Open in new tabDownload slide
We can also use the data to explore how the measured and theoretical moments compare at different depths. By changing galaxy’s contribution to the likelihood of equation (15), the measured bulk and shear moments will change along with the survey depth. Using the combined data set, in order to adjust each galaxy’s contribution to equation (15), we multiply the logarithmic likelihood of the n-th galaxy by the following weight factors
(33)
By changing the value of KR, we can change the distribution of d|$z$|, as shown in Fig. 9. Given KR, the survey depth is calculated from a modified version of equation (18):
(34)
In Fig. 10, we plot the measured absolute amplitudes of the moments against R. The black solid curves are the CRMS for each of the moments generated using the combined data set by multiplying equation (31) by the weight factors, αn:
(35)
then repeating the steps given in Section 6.1. As shown in Table 3, corresponding to Fig. 10, we list the χ2 difference between the measured and the theoretical moments, and the probability of obtaining a larger χ2, P(> χ2) at different depths. In all cases we do not find sufficient evidence to reject ΛCDM with average level of 40 per cent.
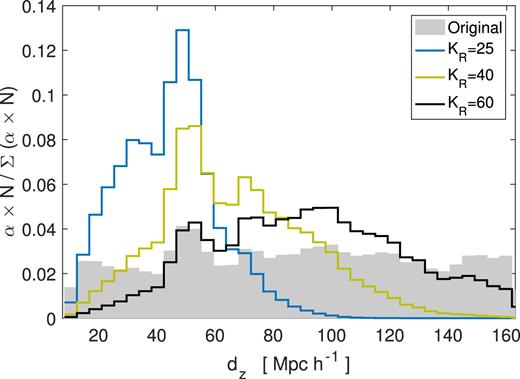
The distribution of d$z$ setting KR = 25, 40, and 60, respectively. The grey bars are the original distribution of d$z$ without any weighting.
Figure 9.

The distribution of d|$z$| setting KR = 25, 40, and 60, respectively. The grey bars are the original distribution of d|$z$| without any weighting.

Open in new tabDownload slide
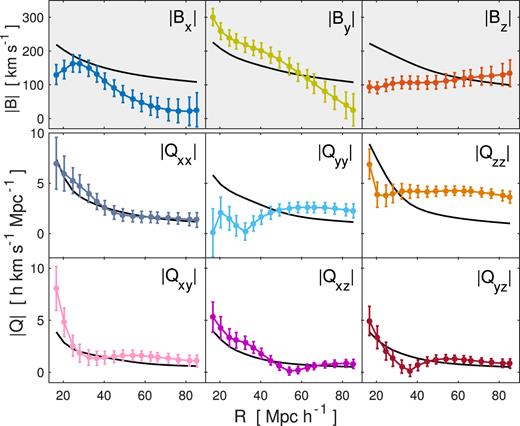
The absolute amplitude of the moments as a function of survey depth. The upper panels are for the bulk flow, the middle panels are for the diagonal elements of the shear tensor, and the bottom panels are for the non-diagonal elements of the shear tensor. The black solid curves are the ΛCDM CRMS predictions for each moment. The measurement points for the components are highly correlated, so their covariance must be taken into account when comparing to the black curves.
Figure 10.

The absolute amplitude of the moments as a function of survey depth. The upper panels are for the bulk flow, the middle panels are for the diagonal elements of the shear tensor, and the bottom panels are for the non-diagonal elements of the shear tensor. The black solid curves are the ΛCDM CRMS predictions for each moment. The measurement points for the components are highly correlated, so their covariance must be taken into account when comparing to the black curves.

Open in new tabDownload slide
Table 3.
Open in new tab

The χ2 and probability P(> χ2) of the measured moments at different depths. The degrees of freedom for B, Q and U are 3, 5, and 8, respectively.

RBQU
h−1 Mpcχ2Pχ2Pχ2P
202.2840.527.0510.229.01600.34
282.7930.424.7740.446.71610.57
362.7610.433.9890.556.27780.62
452.4540.483.7780.586.29260.61
542.1230.555.2040.398.15390.42
581.9790.586.0830.309.32310.32
631.8820.606.8690.2310.37670.24
661.8030.617.3270.2010.93420.21
711.7260.637.7800.1711.43800.18
761.6710.647.8040.1711.19890.19
811.6750.647.6850.1710.70170.22
851.7390.637.0290.229.77840.28
RBQU
h−1 Mpcχ2Pχ2Pχ2P
202.2840.527.0510.229.01600.34
282.7930.424.7740.446.71610.57
362.7610.433.9890.556.27780.62
452.4540.483.7780.586.29260.61
542.1230.555.2040.398.15390.42
581.9790.586.0830.309.32310.32
631.8820.606.8690.2310.37670.24
661.8030.617.3270.2010.93420.21
711.7260.637.7800.1711.43800.18
761.6710.647.8040.1711.19890.19
811.6750.647.6850.1710.70170.22
851.7390.637.0290.229.77840.28
Table 3.
Open in new tab

The χ2 and probability P(> χ2) of the measured moments at different depths. The degrees of freedom for B, Q and U are 3, 5, and 8, respectively.

RBQU
h−1 Mpcχ2Pχ2Pχ2P
202.2840.527.0510.229.01600.34
282.7930.424.7740.446.71610.57
362.7610.433.9890.556.27780.62
452.4540.483.7780.586.29260.61
542.1230.555.2040.398.15390.42
581.9790.586.0830.309.32310.32
631.8820.606.8690.2310.37670.24
661.8030.617.3270.2010.93420.21
711.7260.637.7800.1711.43800.18
761.6710.647.8040.1711.19890.19
811.6750.647.6850.1710.70170.22
851.7390.637.0290.229.77840.28
RBQU
h−1 Mpcχ2Pχ2Pχ2P
202.2840.527.0510.229.01600.34
282.7930.424.7740.446.71610.57
362.7610.433.9890.556.27780.62
452.4540.483.7780.586.29260.61
542.1230.555.2040.398.15390.42
581.9790.586.0830.309.32310.32
631.8820.606.8690.2310.37670.24
661.8030.617.3270.2010.93420.21
711.7260.637.7800.1711.43800.18
761.6710.647.8040.1711.19890.19
811.6750.647.6850.1710.70170.22
851.7390.637.0290.229.77840.28

7 CONCLUSIONS

We have measured the bulk and shear moments in the individual and combined 2MTF and CF3 surveys. We applied the ηMLE to the catalogues in order to preserve the Gaussian nature of the measurement errors of the peculiar velocities. Using the galaxies common between 2MTF and CF3, we demonstrate a small zero-point difference of −0.016 ± 0.002 dex.

We have tested the ηMLE on 2MTF mocks and compare to the |$w$|MLE results. We find ηMLE performs better than |$w$|MLE in both the bulk and shear moment estimation. In addition, by performing tests on anisotropic mocks, we found that leaving Qzz (or the trace of shear tensor) as a free parameter in the MCMC routine of ηMLE is not desirable, and increases the measurement error of Qzz significantly.

We compare the measured bulk and shear components to the predictions from ΛCDM model and the measurements to be consistent with the ΛCDM prediction, with no substantial deviation from the cosmic RMS values predicted by ΛCDM. Using the combined data set, we have also explored the change of bulk and shear moments with survey depth and again find consistency with ΛCDM at all depths between 20 and 85 Mpc h−1. Using the combined sample, we measured the amplitude (depth) of the bulk flow to be 259 ± 15 km s−1 (37h−1 Mpc), the result again being consistent with the ΛCDM prediction at the 68 per cent confidence level.

ACKNOWLEDGEMENTS

FQ has received financial support from China Scholarship Council (CSC). TH is supported by the Open Project Program of the Key Laboratory of FAST, NAOC, Chinese Academy of Sciences. Parts of this research were conducted by the Australian Research Council Centre of Excellence for All-sky Astrophysics (CAASTRO), through project number CE110001020 and the Australian Research Council Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), through project number CE170100013.

Footnotes

1

The upper and lower limits mean that the integral of equation (32) in the interval [Bp − 0.356σB, Bp + 0.419σB] is 0.68. The integral in the interval [Bp − 0.619σB, Bp + 0.891σB] is 0.95. The interesting question is if we were to calculate the bulk flow around N random ΛCDM observers, what would be the expected value of the bulk flow (the answer is Bp) and where would 68 per cent (95 per cent) of the measurements lie about this point. Then comparing this statistic to our measured local bulk flow as a test of whether or not our measurement would be expected within a ΛCDM universe.

REFERENCES

Colin
J.
,
Mohayaee
R.
,
Sarkar
S.
,
Shafieloo
A.
,
2011
,
MNRAS
,
414
,
264
10.1111/j.1365-2966.2011.18402.x

Crossref
Search ADS
 

Colless
M.
,
Saglia
R. P.
,
Burstein
D.
,
Davies
R. L.
,
McMahan
R. K.
,
Wegner
G.
,
2001
,
MNRAS
,
321
,
277
10.1046/j.1365-8711.2001.04044.x

Crossref
Search ADS
 

Dai
D.-C.
,
Kinney
W. H.
,
Stojkovic
D.
,
2011
,
J. Cosmol. Astropart. Phys.
,
4
,
015
10.1088/1475-7516/2011/04/015

Crossref
Search ADS
 

Davis
T. M.
,
Scrimgeour
M. I.
,
2014
,
MNRAS
,
442
,
1117
10.1093/mnras/stu920

Crossref
Search ADS
 

Elahi
P. J.
,
Welker
C.
,
Power
C.
,
Lagos
C. d. P.
,
Robotham
A. S. G.
,
Cañas
R.
,
Poulton
R.
,
2018
,
MNRAS
,
475
,
5338
10.1093/mnras/sty061

Crossref
Search ADS
 

Feldman
H. A.
,
Watkins
R.
,
2008
,
MNRAS
,
387
,
825
10.1111/j.1365-2966.2008.13288.x

Crossref
Search ADS
 

Feldman
H. A.
,
Watkins
R.
,
Hudson
M. J.
,
2010
,
MNRAS
,
407
,
2328
10.1111/j.1365-2966.2010.17052.x

Crossref
Search ADS
 

Haynes
M. P.
et al. ,
2011
,
AJ
,
142
,
170
10.1088/0004-6256/142/5/170

Crossref
Search ADS
 

Hong
T.
et al. ,
2013
,
MNRAS
,
432
,
1178
10.1093/mnras/stt555

Crossref
Search ADS
 

Hong
T.
et al. ,
2014
,
MNRAS
,
445
,
402
10.1093/mnras/stu1774

Crossref
Search ADS
 

Howlett
C.
et al. ,
2017
,
MNRAS
,
471
,
3135
10.1093/mnras/stx1521

Crossref
Search ADS
 

Huchra
J. P.
et al. ,
2012
,
ApJS
,
199
,
26
10.1088/0067-0049/199/2/26

Crossref
Search ADS
 

Hui
L.
,
Greene
P. B.
,
2006
,
Phys. Rev. D
,
73
,
123526
10.1103/PhysRevD.73.123526

Crossref
Search ADS
 

Jaffe
A. H.
,
Kaiser
N.
,
1995
,
ApJ
,
455
,
26
10.1086/176551

Crossref
Search ADS
 

Johnson
A.
et al. ,
2014
,
MNRAS
,
444
,
3926
10.1093/mnras/stu1615

Crossref
Search ADS
 

Kaiser
N.
,
1988
,
MNRAS
,
231
,
149
10.1093/mnras/231.2.149

Crossref
Search ADS
 

Lewis
A.
,
Challinor
A.
,
Lasenby
A.
,
2000
,
ApJ
,
538
,
473
10.1086/309179

Crossref
Search ADS
 

Li
M.
et al. ,
2012
,
ApJ
,
761
,
151
10.1088/0004-637X/761/2/151

Crossref
Search ADS
 

Ma
Y.-Z.
,
Scott
D.
,
2013
,
MNRAS
,
428
,
2017
10.1093/mnras/sts178

Crossref
Search ADS
 

Ma
Y.-Z.
,
Gordon
C.
,
Feldman
H. A.
,
2011
,
Phys. Rev. D
,
83
,
103002
10.1103/PhysRevD.83.103002

Crossref
Search ADS
 

Masters
K. L.
,
Crook
A.
,
Hong
T.
,
Jarrett
T. H.
,
Koribalski
B. S.
,
Macri
L.
,
Springob
C. M.
,
Staveley-Smith
L.
,
2014
,
MNRAS
,
443
,
1044
10.1093/mnras/stu1225

Crossref
Search ADS
 

Nusser
A.
,
Davis
M.
,
1995
,
MNRAS
,
276
,
1391
10.1093/mnras/276.4.1391

Crossref
Search ADS
 

Nusser
A.
,
Davis
M.
,
2011
,
ApJ
,
736
,
93
10.1088/0004-637X/736/2/93

Crossref
Search ADS
 

Parnovsky
S. L.
,
Kudrya
Y. N.
,
Karachentseva
V. E.
,
Karachentsev
I. D.
,
2001
,
Astron. Lett.
,
27
,
765
10.1134/1.1424358

Crossref
Search ADS
 

Planck Collaboration XVI
,
2014
,
A&A
,
571
,
A16
10.1051/0004-6361/201321591

Crossref
Search ADS
 

Poole
G. B.
et al. ,
2015
,
MNRAS
,
449
,
1454
10.1093/mnras/stv314

Crossref
Search ADS
 

Qin
F.
,
Howlett
C.
,
Staveley-Smith
L.
,
Hong
T.
,
2018
,
MNRAS
,
477
,
5150
10.1093/mnras/sty928

Crossref
Search ADS
 

Robotham
A. S. G.
,
Obreschkow
D.
,
2015
,
PASA
,
32
,
e033
10.1017/pasa.2015.33

Crossref
Search ADS
 

Sarkar
D.
,
Feldman
H. A.
,
Watkins
R.
,
2007
,
MNRAS
,
375
,
691
10.1111/j.1365-2966.2006.11334.x

Crossref
Search ADS
 

Scrimgeour
M. I.
et al. ,
2016
,
MNRAS
,
455
,
386
10.1093/mnras/stv2146

Crossref
Search ADS
 

Springob
C. M.
,
Haynes
M. P.
,
Giovanelli
R.
,
Kent
B. R.
,
2005
,
ApJS
,
160
,
149
10.1086/431550

Crossref
Search ADS
 

Springob
C. M.
et al. ,
2014
,
MNRAS
,
445
,
2677
10.1093/mnras/stu1743

Crossref
Search ADS
 

Staveley-Smith
L.
,
Davies
R. D.
,
1989
,
MNRAS
,
241
,
787
10.1093/mnras/241.4.787

Crossref
Search ADS
 

Strauss
M. A.
,
Willick
J. A.
,
1995
,
Phys. Rep.
,
261
,
271
10.1016/0370-1573(95)00013-7

Crossref
Search ADS
 

Tully
R. B.
,
Courtois
H. M.
,
Sorce
J. G.
,
2016
,
AJ
,
152
,
50
10.3847/0004-6256/152/2/50

Crossref
Search ADS
 

Turnbull
S. J.
,
Hudson
M. J.
,
Feldman
H. A.
,
Hicken
M.
,
Kirshner
R. P.
,
Watkins
R.
,
2012
,
MNRAS
,
420
,
447
10.1111/j.1365-2966.2011.20050.x

Crossref
Search ADS
 

Watkins
R.
,
Feldman
H. A.
,
2015
,
MNRAS
,
450
,
1868
10.1093/mnras/stv651

Crossref
Search ADS
 

Watkins
R.
,
Feldman
H. A.
,
Hudson
M. J.
,
2009
,
MNRAS
,
392
,
743
10.1111/j.1365-2966.2008.14089.x

Crossref
Search ADS
 

Willick
J. A.
,
Strauss
M. A.
,
1998
,
ApJ
,
507
,
64
10.1086/306314

Crossref
Search ADS
 

APPENDIX A: SETTING Qzz AS AN INDEPENDENT PARAMETER IN ηMLE

In the MCMC routine of ηMLE, by setting Qzz as an independent shear component, we measured the bulk flow for the 16 2MTF mocks in equatorial coordinates, and compare to the true bulk flow in the top panel of Fig. A1. We find |$\chi ^2_{\mathrm{ red}}({\bf B}) = 3.73$|⁠. The measured shear moments from the mocks are shown in middle and bottom panels of Fig. A1. Correspondingly, the true shear moments is calculated directly from equation (25) without removing the trace. The |$\chi ^2_{\mathrm{ red}}({\bf Q})$| is 3.63. For all the eight moments, we find |$\chi ^2_{\mathrm{ red}}({\bf U})$| is 3.80. Compared with the |$\chi ^2_{\mathrm{ red}}$| values from ηMLE in Section 5, we find that setting Qzz as an independent component in the MCMC routine, results in larger |$\chi ^2_{\mathrm{ red}}$| values. There therefore appears to be no gain in setting Qzz as an independent component.

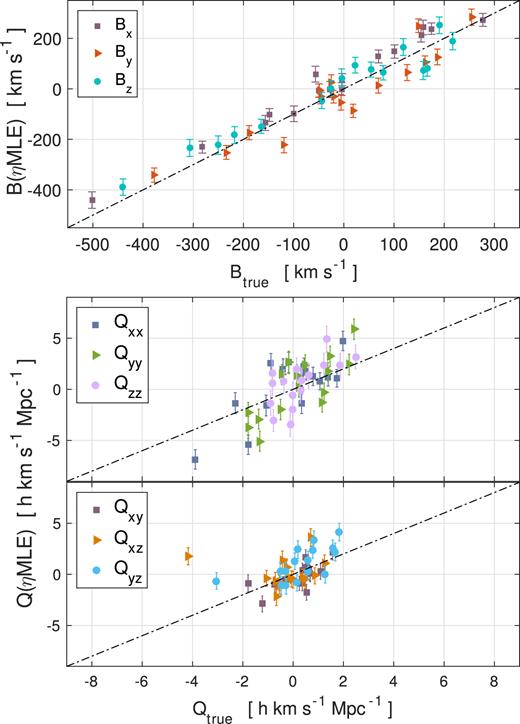
The measured bulk flow and shear for 16 2MTF mocks in equatorial coordinates. Qzz is set to be an independent component in the MCMC routine of the estimators. The top panel is for the bulk flow measurements; the middle and bottom panels are for the shear measurements.
Figure A1.

The measured bulk flow and shear for 16 2MTF mocks in equatorial coordinates. Qzz is set to be an independent component in the MCMC routine of the estimators. The top panel is for the bulk flow measurements; the middle and bottom panels are for the shear measurements.

Open in new tabDownload slide

For anisotropic sky coverage, setting Qzz as an independent component in the MCMC routine of ηMLE results in worse biases from the true values. As an example, we removed mock galaxies in the northern sky (Dec > 0°) to obtain a half-sky 2MTF mocks. Then we used the true log-distance ratio, ηt to measure the diagonal elements of the shear tensor Q. In each mock, ηt is known from the simulations and is not affected by any selection effects or measurement errors. As shown in the top panel of Fig. A2, the resultant Qzz has very large scatter about the true Qzz, and the error bars are very large. By contrast, as show in the bottom panel of Fig. A2, where Qzz is not an independent component (and calculated instead from Qxx and Qyy as in equation 7), the measured Qzz is consistent with the true values.

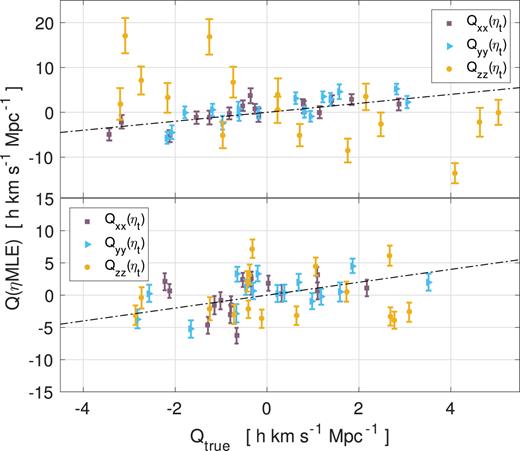
The measurements of the diagonal elements of Q for the half-sky 2MTF mocks using ηMLE. In the upper panel, we set Qzz as an independent component in the MCMC routine. In the bottom panel, Qzz is not independent in the MCMC routine.
Figure A2.

The measurements of the diagonal elements of Q for the half-sky 2MTF mocks using ηMLE. In the upper panel, we set Qzz as an independent component in the MCMC routine. In the bottom panel, Qzz is not independent in the MCMC routine.

Open in new tabDownload slide
© 2018 The Author(s) Published by Oxford University Press on behalf of the Royal Astronomical Society
This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)
Issue Section:
Article
Download all slides