Spatially dependent modelling of pulsar wind nebula G0.9+0.1

van Rensburg, C; Krüger, P P; Venter, C

doi:10.1093/mnras/sty826

Abstract

We present results from a leptonic emission code that models the spectral energy distribution of a pulsar wind nebula by solving a Fokker–Planck-type transport equation and calculating inverse Compton and synchrotron emissivities. We have created this time-dependent, multizone model to investigate changes in the particle spectrum as they traverse the pulsar wind nebula, by considering a time and spatially dependent B-field, spatially dependent bulk particle speed implying convection and adiabatic losses, diffusion, as well as radiative losses. Our code predicts the radiation spectrum at different positions in the nebula, yielding the surface brightness versus radius and the nebular size as function of energy. We compare our new model against more basic models using the observed spectrum of pulsar wind nebula G0.9+0.1, incorporating data from H.E.S.S. as well as radio and X-ray experiments. We show that simultaneously fitting the spectral energy distribution and the energy-dependent source size leads to more stringent constraints on several model parameters.

radiation mechanisms: non-thermal, pulsars: individual (PSR J1747-2809), gamma-rays: general

1 INTRODUCTION

Pulsar wind nebulae (PWNe) are true multiwavelength objects, observable from the highest γ-ray energies down to the radio waveband, sometimes exhibiting complex morphologies in the different energy domains. Discoveries during the last decade by ground-based Imaging Atmospheric Cherenkov Telescopes (IACTs) have increased the number of known very high energy (VHE; E > 100 GeV) γ-ray sources to nearly 200.¹ Hewitt & Lemoine-Goumard (2015) note that nearly 40 of these are confirmed PWNe. Following the 9 yr H.E.S.S. Galactic Plane Survey (HGPS; Carrigan et al. 2013), H.E.S.S. published a paper describing the properties of 19 PWNe and 10 strong PWN candidates, as well as empirical trends between several PWN/pulsar parameters (Abdalla et al. 2018). It is expected that the future Cherenkov Telescope Array (CTA), with its order-of-magnitude increase in sensitivity and improvement in angular resolution, will discover several more (older and fainter) PWNe and reveal many more morphological details. A systematic search with the Fermi Large Area Telescope (LAT) for GeV emission in the vicinity of TeV-detected sources yielded 5 high-energy γ-ray PWNe and 11 PWN candidates (Ferrara et al. 2015). In the X-ray to VHE γ-ray energy range, there are 85 PWNe or PWN candidates with 71 of them having associated pulsars (Kargaltsev, Pavlov & Durant 2012).

For slower moving pulsars, one might observe a composite supernova remnant (SNR), with nebular and shell emission visible in both radio and X-ray bands. Such young systems (having ages of a few thousand years) exhibit a high degree of spherical symmetry and it is possible that the SNR reverse shock has not yet interacted with the PWN (e.g. SNR G11.2−0.3 and G21.5−0.9). The PWN around PSR B1509−58 provides a counter example, exhibiting a strong anticorrelation between the radio and X-ray emission morphology. This system is reminiscent of older PWNe associated with fast-moving pulsars and γ-ray sources that exhibit complex morphologies (e.g. the Rabbit Nebula and G327.1−1.1; Roberts et al. 2005; Slane 2017). In even older PWNe (with ages of tens of thousands of years), a rapidly decreasing B-field may lead to γ-ray emission dominating the observed radio and X-ray emission (e.g. HESS J1825−137; Slane 2017).

High-resolution observations by Chandra X-ray Observatory have furthermore revealed complex substructures such as toroidal structures, bipolar jets, and filaments (Helfand, Gotthelf & Halpern 2001; Roberts et al. 2003). Similarly, high-resolution radio images sometimes reveal complex PWN morphology including filaments, knots, and holes (Dubner, Giacani & Decourchelle 2008). Complementary optical and infrared observations may uncover spectral features in the particle spectrum, information about the shocked supernova ejecta, and newly formed dust (Temim & Slane 2017).

PWNe (plerions) have historically been identified based on their observational properties, i.e. having a filled-centre emission morphology, a flat spectrum at radio wavelengths, and a very broad spectrum of non-thermal emission ranging from the radio band to high-energy γ-rays (e.g. Weiler & Panagia 1978; de Jager & Djannati-Ataï 2009; Amato 2014). Apart from the Galactic population of PWNe, H.E.S.S. has detected a powerful extragalactic PWN in the Large Magellanic Cloud lying at a distance of ∼50 kpc (Abramowski et al. 2012). Galactic PWNe are interesting laboratories due to the fact that they are nearby sources that are well resolved, especially in the X-ray band. The knowledge that we gain from studying them also has a strong impact in many other fields, ranging from γ-ray bursts (GRBs) to active galactic nuclei.

Current spectral models (mostly leptonic) attempt to reproduce the observed spectral energy distributions (SEDs) of PWNe. These models, however, differ slightly from one another. Most of them model the structure of the PWN as a single sphere (i.e. one-zone models) by assuming spherical symmetry (see e.g. Venter & de Jager 2007; Zhang, Chen & Fang 2008; Tanaka & Takahara 2011; Martín, Torres & Rea 2012; Torres et al. 2014), although time dependence is an important feature of these models. The majority of models assume that the injection spectrum of particles is in the form of a broken power law. Using a particle-in-cell code, Sironi & Spitkovsky (2011) found that the particle injection spectrum may be a modified Maxwellian with a power-law tail with index ∼1.5. This is the result of magnetic reconnection at the termination shock due to the striped wind of the PWN. Vorster et al. (2013), on the other hand, model the injection of particles as a type of broken power law, with the exception that the flux at the break energy may vary discontinuously (i.e. assuming a multicomponent injection spectrum). Some authors model the injection of particles including acceleration due to the SNR shock and their subsequent emission. This is also known as thermal leakage, see Fang & Zhang (2010).

The particle transport is also handled differently. Some works calculate the particle population solving a differential equation involving diffusion, convection, and adiabatic and radiation losses (e.g. Tanaka & Takahara 2011; Torres et al. 2014), while other models only consider particle escape (e.g. Zhang, Chen & Fang 2008; Qiao, Zhang & Fang 2009). Some models omit adiabatic losses (e.g. Venter & de Jager 2007), and there are different specifications for the time-dependent PWN B-field. Different models also consider different types of emission; for example, Tanaka & Takahara (2011) take synchrotron-self-Compton (SSC) emission into account and others consider bremsstrahlung (e.g. Martín et al. 2012) in addition to inverse Compton (IC) scattering and synchrotron radiation (SR). While these models have been reasonably successful at reproducing observed SEDs, these one-zone spectral models cannot reproduce any of the observed morphological properties of PWNe.

Conversely, magnetohydrodynamic (MHD) models are also being developed that can model the morphology of PWNe in great detail (e.g. Bucciantini 2014), but they in turn cannot predict the SED from the PWNe. These models describe the geometry and environment of the PWN and not the high-energy particle spectrum and therefore the information about the radiation spectrum is lost. There are, however, models that follow a hybrid approach (e.g. Porth et al. 2016): they model the morphology of the PWN in great detail using an MHD code, and then use a steady-state spectral model to produce the SED of the PWN.

In light of the above, there is a void in the current modelling landscape for a spatiotemporal and energy-dependent PWN model that models both morphology and the SED of a PWN. By adding a spatial dimension to an emission code, one is able to constrain the model more significantly using available data such as surface brightness profiles, spectral index versus radius, and energy-dependent source size, and thus probe the PWN physics more deeply. For example, current spectral models have degenerate best-fitting parameters. Since they are not spatially dependent, they cannot constrain functional dependences such as B-field and diffusion coefficient profiles. Our newly developed time-dependent, multizone model aids in breaking some degeneracies by first constraining the profiles of, e.g. the PWN B-field and then fitting the observed SED in a more constrained parameter space, thus making use of both spectral and spatial data. Further motivation to develop this type of model comes from observations of a PWN population. Kargaltsev et al. (2015) found that the measured γ-ray luminosity (1–10 TeV) of PWNe does not correlate with the spin-down luminosity of their embedded pulsars. Alternatively, they found that the X-ray luminosity (0.5–8 keV) is correlated with the pulsar spin-down luminosity. Furthermore, there are indications that a strong correlation exists between the TeV surface brightness of the PWNe and the spin-down luminosity of their embedded pulsars (Abdalla et al. 2018). A spatially dependent spectral model will yield the flux as a function of radius, allowing one to model the surface brightness and thus probe this and other relationships. Furthermore, one would be in a position to interpret the anticipated morphological details that will be measured by future experiments. In light of the above, we implemented such a model (Van Rensburg, Kruger & Venter 2014; Van Rensburg 2015) and discuss its behaviour in this paper.²

In this paper, we describe the development of our PWN model. In Section 2, we describe some technical details and assumptions of our model. Section 3 details the calibration of our code against independent models, while we perform a parameter study in Section 4. We discuss spatially dependent results in Section 5, and our conclusions follow in Section 6.

2 THE MODEL

In this section, the development and implementation of the multizone, time-dependent code, which models the transport of particles through a PWN, is described. We make the simplifying assumption that the geometrical structure of the PWN may be modelled as a sphere into which particles are injected and allowed to diffuse and undergo energy losses. Another assumption is that particle transport is spherically symmetric and thus the only changes in the particle spectrum will be in the radial direction (apart from changes in the particle energy). The model therefore consists of three dimensions in which the transport equation is solved: the spatial or radial dimension, the lepton energy dimension, and the time dimension.

2.1 The transport equation

We solve a Fokker–Planck-type equation that includes diffusion, convection, energy losses (radiative and adiabatic), as well as a particle source term. We start from the following form of the transport equation (Moraal 2013)

\begin{eqnarray} \frac{{\partial} f}{{\partial} t} = -\nabla \cdot \boldsymbol {S} + \frac{1}{p^2}\frac{{\partial} }{{\partial} p}\left(p^2\left\langle \dot{p}\right\rangle _{\rm {tot}} f\right) + Q(\boldsymbol {r}, \boldsymbol {p},t), \end{eqnarray}

(1)

with f the distribution function (number of particles per six-dimensional unit phase-space volume, spanning three spatial and three momentum directions), |$Q(\boldsymbol {r}, \boldsymbol {p},t)$| the particle injection spectrum, r the radial dimension, p the particle momentum, and |$\langle \dot{p}\rangle _{\rm {tot}}$| the total rate of change of p. The term |$\nabla \cdot \boldsymbol {S} = \nabla \cdot \left(\boldsymbol {V}f - \boldsymbol {\underline{K}} \nabla f\right)$| describes the general movement of particles in the PWN, with |$\boldsymbol {V}$| the bulk motion of particles, |$\boldsymbol {\underline{K}}$| the diffusion tensor, and |$\boldsymbol {S}$| the streaming density. However, we rewrite equation (1) in terms of energy and also transform the distribution function to a particle spectrum per unit volume U_p as is more customary. Following Moraal (2013), we use the relation |$U_{\rm {p}}(\boldsymbol {r},p,t) = 4 {\pi} p^2 f(\boldsymbol {r}, \boldsymbol {p},t)$| (with the units of U_p being number of particles per three-dimensional volume per momentum interval) to convert f to a particle spectrum, and |$E^2 = p^2c^2 + E_0^2$| to convert equation (1) from momentum to energy space, with E₀ = m_ec², m_e the electron mass, and c the speed of light in vacuum. We also assume that the diffusion is only energy dependent, |$\boldsymbol {\underline{K}} = \kappa (E_{\rm {e}})$|⁠, with E_e the lepton energy. Thus, equation (1) becomes

\begin{eqnarray} \frac{{\partial} N_{\rm {e}}}{{\partial} t} &=& -\boldsymbol {V} \cdot (\nabla N_{\rm {e}}) + \kappa \nabla ^2 N_{\rm {e}} \nonumber\\ &&+ \frac{1}{3}(\nabla \cdot \boldsymbol {V})\left( \left[\frac{{\partial} N_{\rm {e}}}{{\partial} \ln E_{\rm {e}}} \right] - 2N_{\rm {e}} \right) \nonumber\\ &&+ \frac{{\partial} }{{\partial} E}(\dot{E}_{\rm {e,tot}}N_{\rm {e}}) + Q(\boldsymbol {r},E_{\rm {e}},t), \end{eqnarray}

(2)

with |$\dot{E}_{\rm {e,tot}}$| total energy loss rate, including radiation and adiabatic energy losses. The units of |$N_{\rm {e}} \equiv U_{\rm {E}}(\boldsymbol {r},E_{\rm {e}},t)$| are the number of particles per unit energy and volume. See Van Rensburg (2015) for more details.

2.2 The particle injection spectrum

Following Venter & de Jager (2007), we use a broken power law for the particle injection spectrum

\begin{eqnarray} Q(E_{\rm {e}},t) = \left\lbrace {\begin{array}{c@{\quad}c}Q_0(t)\left(\frac{E_{\rm {e}}}{E_{\rm {b}}}\right)^{\alpha _1} \qquad E_{\rm {e,min}} \le E_{\rm {e}}<E_{\rm {b}}\\ Q_0(t)\left(\frac{E_{\rm {e}}}{E_{\rm {b}}}\right)^{\alpha _2} \qquad E_{\rm {b}} < E_{\rm {e}} \le E_{\rm {e,max}}. \end{array}}\right. \end{eqnarray}

(3)

Here, Q₀(t) is the time-dependent normalization constant, E_b is the break energy, α₁ and α₂ are the spectral indices. To obtain Q₀ we use the following form for the spin-down luminosity of the pulsar: L(t) = L₀/(1 + t/τ₀)² assuming a braking index of n = 3 (e.g. Reynolds & Chevalier 1984). The birth characteristic age is |$\tau _{0} = P_0/(n-1)\dot{P}_0$|⁠, t is the time, L₀ is the initial spin-down luminosity, and P₀ and |$\dot{P_0}$| are the pulsar’s initial period and time derivative of the period. From the current value of P and |$\dot{P}$|⁠, we first calculate |$\tau _{\rm {c}} = P/(n-1)\dot{P}$|⁠, which is the characteristic age of the pulsar (Gaensler & Slane 2006). Next, we use τ₀ = τ_c − t_age, with t_age the age of the PWN. From this follows L(t) for constant n, with t_age the only free parameter (see the Appendix). To solve for Q₀, we set

\begin{eqnarray} \epsilon L(t) = \int _{E_{\rm {min}}}^{E_{\rm {b}}}QE_{\rm {e}}{\rm d}E_{\rm {e}} + \int _{E_{\rm {b}}}^{E_{\rm {max}}}QE_{\rm {e}}{\rm d}E_{\rm {e}}, \end{eqnarray}

(4)

with ε = 1/(1 + σ) the constant conversion efficiency of the spin-down luminosity to particle power, and σ the ratio of electromagnetic to particle energy density.

2.3 Energy losses

Energy losses in our model are due to two main processes: radiative and adiabatic energy losses. For radiative energy losses, we incorporated SR and IC scattering,³ similar to calculations done by Kopp et al. (2013) in their globular cluster model. The SR losses are given by Blumenthal & Gould (1970)

\begin{eqnarray} \left(\frac{{\rm d}E_{\rm {e}}}{{\rm d}t}\right)_{\rm {SR}} = -\frac{\sigma _T c}{6 {\pi} E_0^2} E_{\rm {e}}^2B_{\bot }^2, \end{eqnarray}

(5)

with |$\sigma _T = (8 {\pi} /3)r_{\rm {e}}^2 = 6.65 \times 10^{-25}\, \rm {cm}^2$| the Thomson cross-section, B_⊥ the average perpendicular PWN B-field at a certain time and radius, and r_e = e²/m_ec² the classical electron radius. The IC scattering energy loss rate of leptons scattering blackbody (BB) photons is given by

\begin{eqnarray} && \left(\frac{{\rm d}E_{\rm {e}}}{{\rm d}t}\right)_{\rm {IC}} &=& \, \,\frac{g_{\rm {IC}}}{E_{\rm {e}}^2} \sum _{l=1}^{3} \int\!\!\!\int n_{\varepsilon ,l}(r, \varepsilon ,T_l)\, \nonumber \\ &&\times\,\frac{E_\gamma }{\varepsilon } \zeta (E_{\rm {e}},E_{\gamma }, \varepsilon ) {\rm d} \varepsilon {\rm d}E_\gamma , \end{eqnarray}

(6)

with n_{ε, l}(r, ε, T_l) the BB photon number density of the lth BB component, |$g_{\rm {IC}} = 2 {\pi} {\rm e}^4c$|⁠, ε the soft-photon energy, T_l the BB temperature, E_γ the TeV upscattered photon energy, and ζ the collision rate

\begin{eqnarray} \zeta (E_{\rm {e}},E_{\gamma }, \varepsilon ) = \zeta _0 \hat{\zeta }(E_{\rm {e}},E_{\gamma }, \varepsilon ), \end{eqnarray}

(7)

with |$\zeta _0 = 2 {\pi} e^4E_0c/\varepsilon E_{\rm {e}}^2$|⁠, and |$\hat{\zeta }$| given by Jones (1968)

\begin{eqnarray} \hat{\zeta }(E_{\rm {e}},E_{\gamma }, \varepsilon ) =\left\lbrace {\begin{array}{ccc}0 &\rm {if} &E_{\gamma } \le \frac{\varepsilon E_0^2}{4 E_{\rm {e}}^2}, \\ \frac{E_{\gamma }}{\varepsilon }-\frac{E_0^2}{4 E_{\rm {e}}^2} &\rm {if} &\frac{\varepsilon E_0^2}{4 E_{\rm {e}}^2} \le E_{\gamma } \le \varepsilon , \\ f(q,g_0) &\rm {if} &\varepsilon \le E_{\gamma } \le \frac{4\varepsilon E_{\rm {e}}^2}{E_0^2 + 4\varepsilon E_{\rm {e}}}, \\ 0 &\rm {if} &E_{\gamma } \ge \frac{4\varepsilon E_{\rm {e}}^2}{E_0^2 + 4\varepsilon E_{\rm {e}}}. \end{array}}\right. \end{eqnarray}

(8)

Here, f(q, g₀) = 2qlnq + (1 − q)(1 + (2 + g₀)q), |$q=E_0^2E_{\gamma }/(4\varepsilon E_{\rm {e}}(E_{\rm {e}}-E_{\gamma }))$|⁠, and |$g_0(\varepsilon ,E_{\gamma }) = 2\varepsilon E_{\gamma }/E_0^2$|⁠.

The particles in the PWN also lose energy due to adiabatic processes caused by the bulk motion of the particles in the PWN as energy is expended to expand the PWN. The adiabatic energy losses are given by |$\dot{E}_{\rm {e,ad}} = \frac{1}{3}(\nabla \cdot \boldsymbol {V})E_{\rm {e}}$| (e.g. Zhang et al. 2008). The two radiation loss rates and the adiabatic energy loss rate can be added to find the total loss rate |$\dot{E}_{\rm {e,tot}}$| used in equation (2).

2.4 Diffusion

The particle diffusion is assumed to be Bohm-type diffusion, with the scalar diffusion coefficient κ given by

\begin{eqnarray} \kappa (E_{\rm {e}}) = \kappa _B\frac{E_{\rm {e}}}{B}, \end{eqnarray}

(9)

with κ_B = c/3e, e denotes the elementary charge. We are currently unaware how turbulent the B-field is inside the PWN, although we have some constraints from the polarized radio spectrum. Due to this uncertainty, we are not sure what form of diffusion coefficient to use and therefore we choose Bohm diffusion as a first approximation when fitting spectral and spatial data. This is a fairly common practice as it describes slow diffusion that is perpendicular to the local B-field.⁴

In the parameter study, we perform in Section 4; however, we parametrize the diffusion coefficient as

\begin{eqnarray} \kappa (E_{\rm {e}}) = \kappa _0 \left( \frac{E_{\rm {e}}}{E^{\prime }_0} \right)^q, \end{eqnarray}

(10)

with |$E^{\prime }_0 = 1$| TeV (with Bohm diffusion being a special case of this general parametric form). This allowed us to change the normalization of the diffusion coefficient using κ₀, and also the energy dependence using q, to evaluate the effects that these changes have on both the particle and emission spectra and the size of the PWN.

2.5 Bulk particle motion and magnetic field

The bulk particle speed inside the PWN is parametrized by

\begin{eqnarray} V(r) = V_0\left(\frac{r}{r_0}\right)^{\alpha _{{V}}}, \end{eqnarray}

(11)

with α_V the velocity profile parameter. Here, V₀ is the speed at r₀. In modelling the bulk particle motion, the adiabatic energy loss time-scale was set constant as done by Torres et al. (2014) as we used their results to calibrate our model. This was done by fixing

\begin{eqnarray} \tau _{\rm {ad}} \equiv \frac{E_{\rm {e}}}{\dot{E}_{\rm {ad}}}, \end{eqnarray}

(12)

where |$\dot{E}_{\rm {ad}} = (\nabla \cdot \boldsymbol {V})E_{\rm {e}}/3$| and using the analytical form of the term |$(\nabla \cdot \boldsymbol {V})$| that follows from equation (11):

\begin{eqnarray} (\nabla \cdot \boldsymbol {V}) = \left( \alpha _{{V}} + 2 \right) \left( \frac{V}{r} \right). \end{eqnarray}

(13)

Thus, we find V₀ = r₀/τ_ad and α_V = 1 in this case.

We also use a parametrized form of the B-field given by

\begin{eqnarray} B(r,t) = B_{\rm {age}}\left(\frac{r}{r_0}\right)^{\alpha _{{B}}}\left(\frac{t}{t_{\rm {age}}}\right)^{\beta _{{B}}}, \end{eqnarray}

(14)

with B_age the present-day B-field at r = r₀ and t = t_age, t the time since the PWN’s birth, t_age is the PWN age, and α_B and β_B the B-field parameters. This parametrized⁵ form of the B-field goes to infinity if t = 0 and therefore we limit the B-field to B_max = 10B_age. Although this is an arbitrary assumption, we found that limiting the B-field to larger values (B_max = 100B_age and B_max = 1000B_age) has a negligible effect on the predicted SED, but significantly increases the computation time. This parametrized form of the B-field is mainly used to see what effect changes in the B-field will have on the SED and the size of the PWN. The B-field and bulk motion are linked by Faraday’s law of induction (e.g. Ferreira & de Jager 2008)

\begin{eqnarray} \frac{{\partial} \boldsymbol {B}}{{\partial} t} = \nabla \times \left(\boldsymbol {V} \times \boldsymbol {B} \right). \end{eqnarray}

(15)

The Lorentz force |$\boldsymbol {F} = q(\boldsymbol {E} + \boldsymbol {V} \times \boldsymbol {B})$| is set to zero, assuming that the plasma is a good conductor and thus provides a force-free environment for the leptons. This assumption together with the Maxwell equation

\begin{eqnarray} \frac{{\partial} \boldsymbol {B}}{{\partial} t} = -\nabla \times \boldsymbol {E} \end{eqnarray}

(16)

yields equation (15). Assuming that the temporal change of the B-field is slow, we set (Kennel & Coroniti 1984; Sefako & de Jager 2003; Schöck et al. 2010)

\begin{eqnarray} \frac{{\partial} \boldsymbol {B}}{{\partial} t} \simeq 0 \end{eqnarray}

(17)

so that

\begin{eqnarray} \nabla \times \left(\boldsymbol {V} \times \boldsymbol {B} \right) \simeq 0. \end{eqnarray}

(18)

From this, and assuming spherical symmetry, equation (15) reduces to (e.g. Kennel & Coroniti 1984; Schöck et al. 2010)

\begin{eqnarray} VBr={\rm {constant}}=V_0B_0r_0. \end{eqnarray}

(19)

It can now be shown that by inserting equations (11) and (14) into equation (19), the following relation holds

\begin{eqnarray} \alpha _{{V}}+\alpha _{{B}}=-1. \end{eqnarray}

(20)

We added the spatial dimension and in this adding two new parameters, α_B and α_V. We use the relationship in equation (20) to reduce these two free parameters in our model to one.

2.6 Numerical solution to the transport equation

To calculate the numerical solution to the transport equation given in equation (2), we have to discretize this equation. We assume spherical symmetry, thus |${\partial} /{\partial} \theta = 0$| and |${\partial} /{\partial} \phi = 0$|⁠, so that |$\nabla ^2 N_{\rm {e}} = 1/r^2\left({\partial} /{\partial} r\left[r^2{\partial} N_{\rm {e}}/{\partial} r\right]\right)$|⁠. We first approached the discretization process by using a simple Euler method. It soon became clear that this method was numerically unstable. We then decided to use a DuFort–Frankel scheme to discretize equation (2) giving

\begin{eqnarray} &&{(1-z+\beta )(N_{\rm {e}})_{i,j+1,k} }\nonumber\\ \quad &=& 2Q_{i,j,1} \triangle t + (1+z-\beta )(N_{\rm {e}})_{i,j-1,k} + (\beta +\gamma -\eta )(N_{\rm {e}})_{i,j,k+1} \nonumber\\ && +\, (\beta -\gamma +\eta )(N_{\rm {e}})_{i,j,k-1} -2(\nabla \cdot \boldsymbol {V})_{i,j,k}\triangle t (N_{\rm {e}})_{i,j,k}\nonumber\\ && + \frac{2}{\left\lbrace ({\rm d}E_{\rm {e}})_{i+1,j,k}+({\rm d}E_{\rm {e}})_{i,j,k})\right\rbrace } \nonumber\\ &&\times\,\left\lbrace r_{\rm {a}} \left({\rm d}E_{\rm {e,loss}}\right)_{i+1,j,k}(N_{\rm {e}})_{i+1,j,k} \right. \nonumber\\ && - \left. \frac{1}{r_{\rm {a}}}\left({\rm d}E_{\rm {e,loss}}\right)_{i-1,j,k}(N_{\rm {e}})_{i-1,j,k}\right\rbrace , \end{eqnarray}

(21)

with β = 2κΔt/(Δr)², γ = 2κΔt/(rΔr), η = V_kΔt/Δr, Δr the bin size of the spatial dimension, Δt the bin size of the time dimension, |${\rm d}E_{\rm {e,loss}}=\dot{E}_{\rm {e,tot}}\Delta t$|⁠, and V_k the bulk particle motion in the current radial bin. Also, r_a = (ΔE_e)_{i + 1, j, k}/(ΔE_e)_{i, j, k} with

\begin{eqnarray} z = \left(\frac{1}{(\Delta E_{\rm {e}})_{{i+1,j,k}}-(\Delta E_{\rm {e}})_{{i,j,k}}}\right)\left(\frac{1}{r_{\rm {a}}}-r_{\rm {a}}\right)(\dot{E_{\rm {e}}})_{{i,j,k}}. \end{eqnarray}

(22)

Here, i, j, k are the indices for energy, time, and space, respectively, with the energy being logarithmically binned, the spatial dimension linearly binned, and the time dimension dynamically binned to optimize the runtime of the code. See Van Rensburg (2015) for more details.

We limit the particle energy following Venter & de Jager (2007),

\begin{eqnarray} E_{\rm {max}} = \frac{e}{2}\sqrt{\frac{L(t)\sigma }{c(1+\sigma )}}. \end{eqnarray}

(23)

This is a containment argument, limiting the Larmor radius r_L ≲ 0.5r_s with r_s the shock radius. Particles with E_e > E_max are assumed to have escaped from the PWN.

2.7 Boundary conditions

The boundary conditions of our model are handled as follows. The multizone model divides the PWN into spherical shells to solve equation (21) numerically. The particles are injected into the innermost zone/annulus (r_min) and allowed to propagate through the different zones, with the spectral evolution being governed by equation (21). As the initial condition, all zones are assumed to be devoid of any particles, i.e. N_e = 0 at t = 0, and a set of ‘ghost points’ that are also devoid of particles are defined outside the boundaries in time, as the DuFort–Frankel scheme requires two previous time steps. For the spatial dimension, the boundary conditions are reflective at the inner boundary to avoid losing particles towards the pulsar past the termination shock and at the outer boundary r_max the particles are allowed to escape. To model the escape of particles at the outer boundary, the particle spectrum is set to zero there, while for the reflective inner boundary we need zero flux through the innermost radial shell. Therefore, we set

\begin{eqnarray} S &=& -\kappa \left(\frac{(N_{\rm {e}})_{i,j,1} - (N_{\rm {e}})_{i,j,0}}{\Delta r}\right) + V_{i,j,1}\nonumber\\ &&\times\, \left(\frac{(N_{\rm {e}})_{i,j,1} + (N_{\rm {e}})_{i,j,0}}{2} \right) = 0, \end{eqnarray}

(24)

leading to

\begin{eqnarray} (N_{\rm {e}})_{i,j,0} = (N_{\rm {e}})_{i,j,1} \times \frac{\kappa /\Delta r-V_{i,j,1}/2}{\kappa /\Delta r+V_{i,j,1}/2}. \end{eqnarray}

(25)

We solve N_e for a minimum particle energy of E_min = 1 × 10⁻⁷ erg by allowing particles with smaller energies to escape. The maximum particles energy is limited by equation (23). The injection of particles into the PWN can also be seen as a boundary condition. We inject the particles at a certain rate and assume that the particle injection spectrum Q″ is uniformly distributed in the first zone. Thus,

\begin{eqnarray} \frac{Q^{\prime \prime }}{V^1_{\rm {shell}}} = Q, \end{eqnarray}

(26)

where |$V^1_{\rm {shell}}$| is the volume of the first zone and Q the injection spectrum per unit energy, time, and volume as used in equation (21).

2.8 Radiation spectrum

A time-dependent photon spectrum of each zone can now be calculated, using the electron spectrum N_e(r, E_e) solved for each zone. For IC, we have (Kopp et al. 2013)

\begin{eqnarray} && \left(\frac{{\rm d}N_\gamma }{{\rm d}E_\gamma }\right)_{IC} &=& \, \, \frac{g_{{\rm IC}}}{A} \sum _{l=1}^{3} \int \!\!\!\! \int n_{\varepsilon ,l}(r, \varepsilon ,T_l) \nonumber\\ &&\times \frac{\mathcal {N}_{\rm {e}}}{\varepsilon E_{\rm {e}}^2}\zeta (E_{\rm {e}},E_\gamma , \varepsilon ) {\rm d}\varepsilon {\rm d}E_{\rm {e}}, \end{eqnarray}

(27)

where |$A=4 {\pi} d^2$| (d the distance to the source) and |$\mathcal {N}_{\rm {e}} = N_{\rm {e}}V_{\rm {shell}}$| is the number of electrons per energy in a spherical shell at radius r. We consider l = 3 BB components of target photons, i.e. the cosmic background radiation (CMB), Galactic background infrared (IR) photons, and starlight.

For SR, we have

\begin{eqnarray} && \left(\frac{{\rm d}N_\gamma }{{\rm d}E_\gamma }\right)_{\rm {SR}} &=&\, \, \frac{1}{A}\frac{1}{hE_\gamma }\frac{\sqrt{3}e^3B(r,t)}{E_0} \int \!\!\!\! \int _0^{ {\pi} /2} \mathcal {N}_{\rm {e}}(E_{\rm {e}},r)\nonumber\\ &&\times F \left(\frac{\nu }{\nu _{\rm {cr}}(E_{\rm {e}}, \alpha ,r)}\right)\sin ^2 \alpha {\rm d}\alpha {\rm d}E_{\rm {e}}, \end{eqnarray}

(28)

with ν_cr the critical frequency (with pitch angle α, which we assume to be |$ {\pi} /2$| so that sin ²α = 1) given by

\begin{eqnarray} \nu _{\rm {cr}}(E_{\rm {e}},r) = \frac{3ec}{4 {\pi} E_0^3}E_{\rm {e}}^2 B_{\perp }(r,t), \end{eqnarray}

(29)

and

\begin{eqnarray} F(x) = x\int _x^\infty K_{5/3}(y){\rm d}y, \end{eqnarray}

(30)

where K_5/3 is the modified Bessel function of order 5/3. The total radiation spectrum at Earth is found by calculating equations (27) and (28) for each zone in the model and adding them.

2.9 Line-of-sight calculation

Next, the radiation per unit volume can be calculated by dividing the radiation spectrum by the volume of the zone where the radiation originated. This is used to perform the line-of-sight (LOS) calculation to project the radiation on to the plane of the sky in order to find the surface brightness and flux as a function of 2D projected radius. This allows us to estimate the size of the PWN and also study this size as a function of energy.

We multiply the radiation per unit volume by the volume in a particular LOS (V_LOS) as viewed from Earth (Fig. 1).

Figure 1.

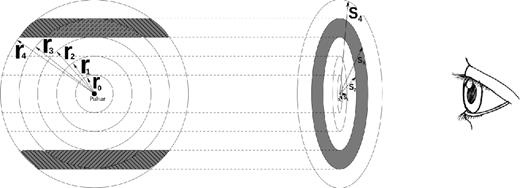
Schematic for the geometry of the LOS calculation.

Open in new tab Download slide

The pulsar plus the multizone model of the surrounding PWN are on the left-hand side of Fig. 1 and the right-hand side shows how ‘LOS cylinders’ are chosen through the PWN, with the observer looking on from the right. The source is very far from Earth and cylinders instead of cones are chosen as a good first approximation. Cylinders, with radii s, intersecting the spherical zones and the spherical shells, with radii r, are assumed to have the same bin sizes. This results in the observer viewing the projected PWN as several 2D ‘annuli’, for example the shaded region in Fig. 1, all with different radii. The radiation in a certain annulus can thus be calculated if the volume of the intersection (V_LOS) between a particular hollow cylinder and the spheres is known. Setting |$a \equiv \sqrt{r^2-s^2}$|⁠, we find that the volume of intersection between a cylinder and sphere V(s) is

\begin{eqnarray} V(s) = \frac{4 {\pi} }{3}\left[-\left(r^2-s^2\right)^{\frac{3}{2}} + r^3\right]. \end{eqnarray}

(31)

The LOS volume (V_LOS) can now be calculated by subtracting the correct volumes from one another. For example, the intersection volume of an annulus with radius s_k and sphere with r_i is

\begin{eqnarray} V_{\rm {LOS}} = \left(V_{i,k} - V_{i,k-1}\right) - \left(V_{i-1,k} - V_{i-1,k-1}\right). \end{eqnarray}

(32)

This expression, however, holds only when s < r. If s is larger or equal to r, then the intersection volume will simply be the volume of the sphere of radius r. The total radiation for the specific LOS, or annulus, can be calculated by adding the radiation for all the segments (Fig. 1). To find the total radiation at Earth from the PWN, the radiation from all the different LOSs (annuli) may be added.

As a test of this LOS calculation, we summed the total flux from all the spheres to find the total flux from the PWN and then also added the flux from all the cylinders after the LOS calculation. Both these calculations yielded the same flux. We can now use this projected flux to calculate the surface brightness profile and thus calculate the size of the PWN (Section 5).

3 CODE CALIBRATION VIA SED FITS

PWN G0.9+0.1 will be used as a case study to calibrate our newly developed code and here we briefly summarize some of its observational properties. Becker & Helfand (1987) observed G0.9+0.1 for 45-min integrations at 20 and 6 cm, which led to the discovery of the composite nature of this bright, extended source near the Galactic Centre (GC) in the radio band. SNR G0.9+0.1 has since become a well-known SNR, with an estimated age of a few thousand years. This source exhibits a flat-spectrum radio core (∼2 arcmin across) corresponding to the PWN, and also clearly shows steeper shell components (⁠|$\sim\!\! {} 8{\rm \,arcmin}$| diameter shell). While performing a survey on the GC, Sidoli et al. (2004) serendipitously observed SNR G0.9+0.1 using the XMM–Newton telescope. Their observations provided the first evidence of X-ray emission from PWN G0.9+0.1. Sidoli et al. (2004) fit an absorbed power-law spectrum that yielded a photon index of Γ ∼ 1.9 and an energy flux of F = 4.8 × 10⁻¹² erg cm⁻² s⁻¹ in the 2–10 keV energy band. This translates to a luminosity of L_X ∼ 5 × 10³⁴ erg s⁻¹ for a distance of 10 kpc. Aharonian et al. (2005) studied VHE γ rays from the GC with the H.E.S.S. telescope. During the observation of Sgr A*, two sources of VHE gamma rays were clearly visible, with SNR G0.9+0.1 being one of these sources. They performed a power-law fit to the observed spectrum and found a photon index of 2.29 ± 0.14_stat with a photon flux of (5.5 ± 0.8_stat) × 10⁻¹² cm⁻² s⁻¹ for energies above 200 GeV. This flux is only |$\sim\! {} 2 \,{per\,cent}$| of the flux from the Crab nebula, making PWN G0.9+0.1 one of the weakest sources detected at TeV energies to date. Some years later, the radio pulsar PSR J1747−2809 was discovered in PWN G0.9+0.1 with period⁶P = 52 ms and |$\dot{P} = 1.85\times 10^{-13}$| (Camilo et al. 2009).

In the next section, we calibrate our new model against a previous more basic model (Venter & de Jager 2007). This model only assumed a parametric form for the B-field, and did not take into account work done by the B-field and the effect thereof on its time dependence. The calibration with this older model is a first point of reference and is also done for historical reasons, since our new model incorporates many of the basic elements of the Venter & de Jager (2007) model. We also calibrated our new model against a more modern model (Torres et al. 2014). Both of these earlier works assumed one-zone models (no spatial dependence). We decided to add another calibration using the model of Lu et al. (2017, results not shown since we focused on PWN G0.9+0.1). The fact that the respective predicted spectra are in reasonable agreement increases our confidence in the accuracy of our model.

3.1 Calibration against the model of Venter & de Jager (2007)

The assumed model parameters used to calibrate our model against that of Venter & de Jager (2007) are listed in Table 1. In Table 1, n is the braking index given by |$n = \Omega \ddot{\Omega }/\dot{\Omega }^2$|⁠, with |$\Omega = 2 {\pi} /P$| the angular speed and P the period of rotation of the pulsar; β_VdJ is the B-field parameter as in equation (33); and B(t_age) is the present-day B-field. In this first calibration with Venter & de Jager (2007), we use |$B(t_{\rm {age}})=40.0\, {\mu}$|G, noting that their model was developed before the discovery of PSR J1747−2809 associated with PWN G0.9+0.1. The more reasonable value for the present-day B-field, 14.0 |${\mu}$|G, is used in the calibration against the model of Torres et al. (2014) in the next section as we now know P and |$\dot{P}$| for the embedded pulsar, as mentioned above. Also, ε is the conversion efficiency as mentioned in equation (4), t_age is the age of the PWN, τ₀ is the characteristic spin-down time-scale of the pulsar, d is the distance to the PWN, α₁ and α₂ are the spectral indices, and L₀ is the birth spin-down luminosity. The sigma parameter (σ) is the ratio of the electromagnetic to particle energy density and is used to calculate the maximum particle energy. We chose three soft-photon components: the CMB with a temperature of T₁ = 2.76 K and an average energy density of u₁ = 0.23 eV cm⁻³, Galactic background infrared photons as component 2, and optical starlight as component 3 (with T_i and u_i as given in Table 1). For these assumed model parameters, we find the SED as shown in Fig. 2. The radio data are from Becker & Helfand (1987), the X-ray data from Porquet, Decourchelle & Warwick (2003) and Sidoli et al. (2004), and the gamma-ray data from Aharonian et al. (2005). The solid line represents our predicted SED, while the dashed line shows the output from the model of Venter & de Jager (2007).

Figure 2.

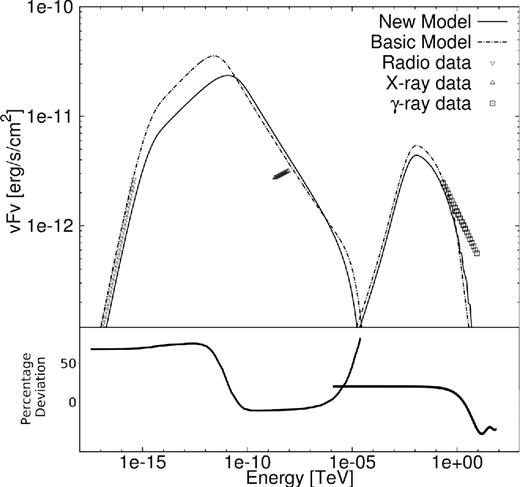
Calibration against the model of Venter & de Jager (2007) for PWN G0.9+0.1. Bottom panel indicates the percentage deviation between the two SEDs.

Open in new tab Download slide

Table 1.

Open in new tab

Values of model parameters as used in the calibration against the model of Venter & de Jager (2007) for PWN G0.9+0.1.

Model parameter	Symbol	Value
Braking index	n	3
B-field parameter	β_VdJ	0.5
Present-day B-field	B(t_age)	40.0 \|${\mu} \rm {G}$\|
Conversion efficiency	ε	0.6
Age	t_age	1 900 yr
Characteristic time-scale	τ₀	3 681 yr
Distance	d	8.5 kpc
Q index 1	α₁	−1.0
Q index 2	α₂	−2.6
Initial spin-down power (⁠\|$10^{38}\,\rm {erg}$\|\|$\rm {s^{-1}}$\|⁠)	L₀	0.99
Sigma parameter	σ	0.2
Soft-photon component 1	T₁ and u₁	2.76 K, \|$0.23\, \rm {eV\,cm^{-3}}$\|
Soft-photon component 2	T₂ and u₂	35 K, \|$0.5\, \rm {eV\,cm^{-3}}$\|
Soft-photon component 3	T₃ and u₃	4500 K, \|$50\, \rm {eV\,cm^{-3}}$\|

Model parameter	Symbol	Value
Braking index	n	3
B-field parameter	β_VdJ	0.5
Present-day B-field	B(t_age)	40.0 \|${\mu} \rm {G}$\|
Conversion efficiency	ε	0.6
Age	t_age	1 900 yr
Characteristic time-scale	τ₀	3 681 yr
Distance	d	8.5 kpc
Q index 1	α₁	−1.0
Q index 2	α₂	−2.6
Initial spin-down power (⁠\|$10^{38}\,\rm {erg}$\|\|$\rm {s^{-1}}$\|⁠)	L₀	0.99
Sigma parameter	σ	0.2
Soft-photon component 1	T₁ and u₁	2.76 K, \|$0.23\, \rm {eV\,cm^{-3}}$\|
Soft-photon component 2	T₂ and u₂	35 K, \|$0.5\, \rm {eV\,cm^{-3}}$\|
Soft-photon component 3	T₃ and u₃	4500 K, \|$50\, \rm {eV\,cm^{-3}}$\|

Table 1.

Open in new tab

Values of model parameters as used in the calibration against the model of Venter & de Jager (2007) for PWN G0.9+0.1.

Model parameter	Symbol	Value
Braking index	n	3
B-field parameter	β_VdJ	0.5
Present-day B-field	B(t_age)	40.0 \|${\mu} \rm {G}$\|
Conversion efficiency	ε	0.6
Age	t_age	1 900 yr
Characteristic time-scale	τ₀	3 681 yr
Distance	d	8.5 kpc
Q index 1	α₁	−1.0
Q index 2	α₂	−2.6
Initial spin-down power (⁠\|$10^{38}\,\rm {erg}$\|\|$\rm {s^{-1}}$\|⁠)	L₀	0.99
Sigma parameter	σ	0.2
Soft-photon component 1	T₁ and u₁	2.76 K, \|$0.23\, \rm {eV\,cm^{-3}}$\|
Soft-photon component 2	T₂ and u₂	35 K, \|$0.5\, \rm {eV\,cm^{-3}}$\|
Soft-photon component 3	T₃ and u₃	4500 K, \|$50\, \rm {eV\,cm^{-3}}$\|

Model parameter	Symbol	Value
Braking index	n	3
B-field parameter	β_VdJ	0.5
Present-day B-field	B(t_age)	40.0 \|${\mu} \rm {G}$\|
Conversion efficiency	ε	0.6
Age	t_age	1 900 yr
Characteristic time-scale	τ₀	3 681 yr
Distance	d	8.5 kpc
Q index 1	α₁	−1.0
Q index 2	α₂	−2.6
Initial spin-down power (⁠\|$10^{38}\,\rm {erg}$\|\|$\rm {s^{-1}}$\|⁠)	L₀	0.99
Sigma parameter	σ	0.2
Soft-photon component 1	T₁ and u₁	2.76 K, \|$0.23\, \rm {eV\,cm^{-3}}$\|
Soft-photon component 2	T₂ and u₂	35 K, \|$0.5\, \rm {eV\,cm^{-3}}$\|
Soft-photon component 3	T₃ and u₃	4500 K, \|$50\, \rm {eV\,cm^{-3}}$\|

To compare our new model to the model of Venter & de Jager (2007), we had to remove the effects of the bulk particle motion, as their model did not incorporate such motion and only considered diffusion, SR losses, and particle escape. Thus, their model did not include adiabatic losses nor convection (see below). The way the effects of these processes are removed from the new model is by simply setting the bulk speed inside the PWN to zero. Venter & de Jager (2007) also modelled the B-field by parametrizing it as

\begin{eqnarray} B(t) = \frac{B_0}{1+\left( t / \tau _0 \right)^{\beta _{{VdJ}}}}. \end{eqnarray}

(33)

Our model was adapted to also parametrize the B-field using this same time-dependent form. These two simple changes to our model allowed us to calibrate our model against theirs as seen in Fig. 2. In Table 1, the present-day B-field B_age.

Our time-dependent, multizone PWN model does not reproduce the results of Venter & de Jager (2007) exactly, but the SEDs are quite close. The reason for this is the fact that the older model did not take into account IC losses in the particle transport, since it assumed SR losses to dominate. This led to particle energy losses being underestimated, leaving an excess of high-energy particles. Their IC radiation is therefore slightly higher than our new model prediction. Other differences may result from our very different treatment of the particle transport as we solved a full transport equation and Venter & de Jager (2007) solved a linearized transport equation using energy losses, diffusion and effective time-scales.

One thing to note here is that in Table 1, the two variables ε and σ are independent. They are, however, in reality related by ε = 1/(1 + σ). This inconsistency is only present in the calibration with Venter & de Jager (2007) and is correctly implemented in the rest of the paper.

Our model fits the data quite well, but still has trouble in fitting the slope of the X-ray spectrum. Vorster et al. (2013) modelled PWN G21.5−0.9 where they also encountered this problem when using a broken-power-law injection spectrum that connects smoothly at some break energy. They therefore used a two-component particle injection spectrum that does not transition smoothly (instead the low-energy component cuts off steeply in order to connect to the lower-flux, high-energy component), allowing them to fit both the radio and X-ray spectral slopes. This is something worth noting for future development of our code.

3.2 Calibration against the model of Torres et al. (2014)

As a second calibration, we used results from a more recent study by Torres et al. (2014), who created a time-dependent model of young PWNe by modelling them as a single sphere. We again use PWN G0.9+0.1 as the calibration source. The assumed model parameters for this second calibration are given in Table 2. The B-field is now modelled according to equation (14), hence the values of α_B and β_B in Table 2. Some of the parameters are different from those used during the calibration with the model of Venter & de Jager (2007). One of these changes is the present-day B-field that is now set to |$14 \,{\mu} {\rm G}$|⁠, versus the previous value of |$40\,{\mu} {\rm G}$|⁠. Furthermore, the discovery of pulsar PSR J1747−2809 in the PWN G0.9+0.1 yielded P and |$\dot{P}$| which pin down the value of L(t_age) (see the Appendix). The B-field is parametrized using α_B = 0 and β_B = −1.3, which, from equation (14), indicates that the B-field is constant in the spatial dimension. Torres et al. (2014) model the time dependence of the B-field using

\begin{eqnarray} \int _0^t (1-\epsilon ) L(t^{\prime })R_{\rm {PWN}}(t^{\prime }){\rm d}t^{\prime } = W_{B}R_{\rm {PWN}}, \end{eqnarray}

(34)

where

\begin{eqnarray} W_{B}=\frac{4 {\pi} }{3}R^3_{\rm {PWN}}(t)\frac{B^2(t)}{8 {\pi} }, \end{eqnarray}

(35)

and mention that if the age of the PWN is less than the characteristic age (t_age < τ₀), then B(t) ∝ t^−1.3. Therefore, we set the value of β_B = −1.3. While Torres et al. (2014) solved B(t) numerically, we can approximate the early-age limit of B(t) using such a power law. One thing to note here is the usage of R_PWN. Torres et al. (2014) explicitly use a time-dependent PWN radius for G0.9+0.1, setting R_PWN(t_age) = 2.5 pc. However, we do not. Instead we choose⁷ an escape boundary r_max ≫ R_PWN, and then later calculate the observable size of the PWN by noting where the surface brightness has decreased by two thirds from the value at r_min (from an observer’s point of view; this is possible since we have information about the morphology of the PWN). Our approach is admittedly different from the standard one, but with a very particular motivation. If we assume a standard expression for R_PWN(t) and if the age of the PWN is much smaller than the radiation loss time-scale, one would expect no evolution of PWN size with energy, contrary to what is observed in some PWNe.⁸ Conversely, we calculate the energy-dependent PWN size using the predicted surface brightness profile. However, this approach does not ignore the dynamical evolution of the PWN. While we determine R_PWN(t) from the emission properties, we do take into account the effect of evolution on the B-field profile by choosing β_B = −1.3. Our parametric approach captures the essence of the evolution (e.g. as assumed by Torres et al. 2014) in a simplified way, but allows us the freedom to infer this profile, should the data require a somewhat different behaviour for the decline of the B-field with radius. As a test we performed alternative runs of our code, in which we included the formalism of Torres et al. (2014) to calculate the B-field. We found no significant difference in the predicted SED when using these two different approaches (Fig. 3), justifying our usage of the parametric approach when modelling young PWNe.

Figure 3.

Comparison of the predicted SED for the parametric versus analytical treatment of the temporal evolution of the B-field.

Open in new tab Download slide

Table 2.

Open in new tab

Values of model parameters as used in the calibration against the model of Torres et al. (2014) for PWN G0.9+0.1.

Model parameter	Symbol	Value
Braking index	n	3
B-field parameter	α_B	0.0
B-field parameter	β_B	−1.3
V parameter	α_V	1.0
Present-day B-field	B(t_age)	14.0 \|${\mu} \rm {G}$\|
Conversion efficiency	ε	0.99
Age	t_age	2 000 yr
Characteristic time-scale	τ₀	3 305 yr
Distance	d	8.5 kpc
Q index 1	α₁	−1.4
Q index 2	α₂	−2.7
Initial spin-down power (⁠\|$10^{38}\,\rm {erg}$\|\|$\rm {s^{-1}}$\|⁠)	L₀	1.1
Sigma parameter	σ	0.01
Soft-photon component 1	T₁ and u₁	2.76 K, \|$0.23\, \rm {eV\,cm^{-3}}$\|
Soft-photon component 2	T₂ and u₂	30 K, \|$2.5\, \rm {eV\,cm^{-3}}$\|
Soft-photon component 3	T₃ and u₃	3000 K, \|$25\, \rm {eV\,cm^{-3}}$\|

Model parameter	Symbol	Value
Braking index	n	3
B-field parameter	α_B	0.0
B-field parameter	β_B	−1.3
V parameter	α_V	1.0
Present-day B-field	B(t_age)	14.0 \|${\mu} \rm {G}$\|
Conversion efficiency	ε	0.99
Age	t_age	2 000 yr
Characteristic time-scale	τ₀	3 305 yr
Distance	d	8.5 kpc
Q index 1	α₁	−1.4
Q index 2	α₂	−2.7
Initial spin-down power (⁠\|$10^{38}\,\rm {erg}$\|\|$\rm {s^{-1}}$\|⁠)	L₀	1.1
Sigma parameter	σ	0.01
Soft-photon component 1	T₁ and u₁	2.76 K, \|$0.23\, \rm {eV\,cm^{-3}}$\|
Soft-photon component 2	T₂ and u₂	30 K, \|$2.5\, \rm {eV\,cm^{-3}}$\|
Soft-photon component 3	T₃ and u₃	3000 K, \|$25\, \rm {eV\,cm^{-3}}$\|

Table 2.

Open in new tab

Values of model parameters as used in the calibration against the model of Torres et al. (2014) for PWN G0.9+0.1.

Model parameter	Symbol	Value
Braking index	n	3
B-field parameter	α_B	0.0
B-field parameter	β_B	−1.3
V parameter	α_V	1.0
Present-day B-field	B(t_age)	14.0 \|${\mu} \rm {G}$\|
Conversion efficiency	ε	0.99
Age	t_age	2 000 yr
Characteristic time-scale	τ₀	3 305 yr
Distance	d	8.5 kpc
Q index 1	α₁	−1.4
Q index 2	α₂	−2.7
Initial spin-down power (⁠\|$10^{38}\,\rm {erg}$\|\|$\rm {s^{-1}}$\|⁠)	L₀	1.1
Sigma parameter	σ	0.01
Soft-photon component 1	T₁ and u₁	2.76 K, \|$0.23\, \rm {eV\,cm^{-3}}$\|
Soft-photon component 2	T₂ and u₂	30 K, \|$2.5\, \rm {eV\,cm^{-3}}$\|
Soft-photon component 3	T₃ and u₃	3000 K, \|$25\, \rm {eV\,cm^{-3}}$\|

Model parameter	Symbol	Value
Braking index	n	3
B-field parameter	α_B	0.0
B-field parameter	β_B	−1.3
V parameter	α_V	1.0
Present-day B-field	B(t_age)	14.0 \|${\mu} \rm {G}$\|
Conversion efficiency	ε	0.99
Age	t_age	2 000 yr
Characteristic time-scale	τ₀	3 305 yr
Distance	d	8.5 kpc
Q index 1	α₁	−1.4
Q index 2	α₂	−2.7
Initial spin-down power (⁠\|$10^{38}\,\rm {erg}$\|\|$\rm {s^{-1}}$\|⁠)	L₀	1.1
Sigma parameter	σ	0.01
Soft-photon component 1	T₁ and u₁	2.76 K, \|$0.23\, \rm {eV\,cm^{-3}}$\|
Soft-photon component 2	T₂ and u₂	30 K, \|$2.5\, \rm {eV\,cm^{-3}}$\|
Soft-photon component 3	T₃ and u₃	3000 K, \|$25\, \rm {eV\,cm^{-3}}$\|

The bulk motion of the particles is parametrized by equation (11) using model parameters α_V, V₀, and r₀ = r_min and the velocity is parametrized by setting α_V = 1.0, with V₀ = r₀/t_age. This is done so that our model can have the same adiabatic energy loss rate assumed by Torres et al. (2014). They have a constant adiabatic energy loss time-scale and to reproduce this in our model, we have to set α_V = 1 (see equation 13). This leads to a value for V₀ from the adiabatic time-scale:

\begin{eqnarray} \tau _{\rm {ad}} = \frac{E}{\dot{E}_{\rm {ad}}}, \end{eqnarray}

(36)

where |$\dot{E}_{\rm {ad}} = (\nabla \cdot \boldsymbol {V})E_{\rm {e}}/3$|⁠. By using the analytical form of |$(\nabla \cdot \boldsymbol {V})$| in equation (13), we find that V₀ = r₀/τ_ad. This is, however, not physical, if the relationship between V(r) and B(r, t) in equation (20) holds. From these equations, it is clear that α_V = −1 when α_B = 0. The conversion efficiency (ε) is very large, but there exists a degeneracy between ε and L₀ and therefore this is still a preliminary value. The changes in B(r, t) and V(r) are the only substantial differences between the model of Torres et al. (2014) and our model. The rest of the parameters are very similar to the previous case, e.g. the indices of the injection spectrum and the soft-photon components used in the calculation of the IC spectrum.

Fig. 4 compares our predicted SED with the model prediction of Torres et al. (2014), with their results shown by the dashed–dotted line and our model SED shown as the solid line. The differences between the two models stem from the different ways in which the transport of particles is handled. In our code we incorporated a Fokker–Planck-type transport equation, and Torres et al. (2014) modelled the transport by using average time-scales.

Figure 4.

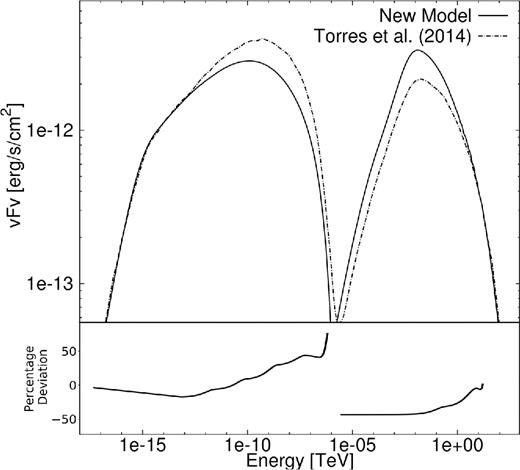
Calibration against the model of Torres et al. (2014) for PWN G0.9+0.1. Bottom panel indicates the percentage deviation between the two SEDs.

Open in new tab Download slide

During the calibration of the code, other sources were also modelled (e.g. G21.5-0.9, G54.1+0.3, and HESS J1356-645). We found that the model yields reasonable fits for most of the chosen sources as long as they are young PWNe. These results will be shown in a subsequent paper where we will perform a more detailed PWN population study.

4 PARAMETER STUDY

We can now investigate the effects of several of the free model parameters on the predicted particle spectrum and SED. As a reference model for this section, we use the same parameters that were used in the calibration against Torres et al. (2014) for G0.9+0.1, as in Fig. 4. The SED of the PWN is calculated at Earth for each spherical zone and then these are added to find the total flux from the PWN.

4.1 Time evolution (age)

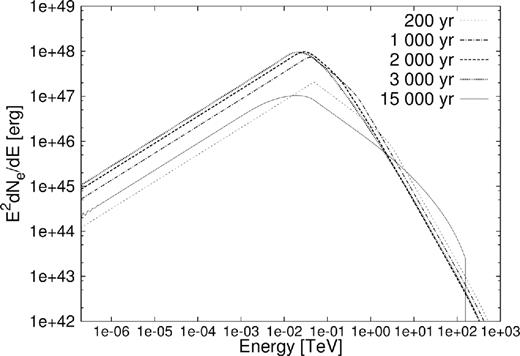
In Fig. 5, the time evolution of the lepton spectrum is shown. From this figure, it can be seen that when the PWN is still very young (t_age ∼ 200 yr) the particle spectrum closely resembles the shape of the injection spectrum apart from the spectral break at a few TeV that develops due to radiation losses. As the PWN ages, however, it starts to fill up with particles (giving an increased |$E^2_{\rm {e}}{\rm d}N_{\rm {e}}/{\rm d}E_{\rm {e}}$|⁠) and at some stage the PWN is totally filled, at an age in the order of a few thousand years. After this the level of the particle spectrum decreases. This is due to the particles losing energy over time due to SR, IC, adiabatic energy losses, and escape, and also due to the fact that the embedded pulsar is spinning down, resulting in fewer particles being injected into the PWN. The effect of the spun-down pulsar can be clearly seen in Fig. 5 by observing the spectrum at 15 000 yr. By this time, the embedded pulsar has significantly spun down so that the total particle spectrum is lower than it was at ≈200 yr due to the fact that now more particles are escaping from the modelled region at r_max than are being injected by the pulsar. Also, note the leftward shift of E_b due to radiative losses. The bump at high energies for 15 000 yr is due to a pile-up of particles. This occurs due to the decreased B-field B(t), resulting in an increased diffusion coefficient and also decreased SR energy losses. These losses are energy dependent and therefore the high-energy particles will be most affected. The increased diffusion will cause the particles to resemble the injection spectrum more and more due to suppressed SR losses.

Figure 5.

Time evolution of the lepton spectrum.

Open in new tab Download slide

The particle spectrum in Fig. 5 not only goes up and down as the PWN ages, but the whole spectrum shifts to lower energies. This can be seen by looking at where the spectrum peaks and also at the tails at high and low energies. This is due to the fact that the particles lose energy through previously mentioned mechanisms. Due to the SR energy losses, the particle spectrum will develop a high energy break at some break energy. By using |$\dot{E}_{\rm {SR}}$| as in equation (5), we can calculate the time-scale for synchrotron losses (τ_SR) and by setting it equal to the age of the PWN (t_age), one may estimate where this second break is expected in the spectrum:

\begin{eqnarray} \tau _{\rm {SR}} = \frac{E_{\rm {e}}}{\dot{E}_{\rm {SR}}} = t_{\rm {age}} \Rightarrow E_{\rm {e}} \propto \frac{1}{t_{\rm {age}} \langle B \rangle ^2}. \end{eqnarray}

(37)

Thus, from equation (37), we can see that the break should move to lower energies as the PWN ages. In equation (37), we have to use the average B-field 〈B〉 over the lifetime of the PWN as the present-day B-field is too small. This is visible in Fig. 5 where the break for 200 yr is at ≈ 2 TeV, for 1000 yr at ≈ 0.6 TeV, for 2000 yr at ≈ 0.2 TeV, and for 5000 yr at ≈ 0.15 TeV. By inserting these values into equation (37), we find a reasonable value of |$\langle B \rangle \sim 150\,{\mu}$|G. These results are similar to those found by Torres et al. (2014).

4.2 Magnetic field

The B-field B(r, t) inside the PWN (which determines the diffusion) plays a large role in determining the shape of the SED (level and break energy of SR and IC component), and is characterized by the free parameters B_age, α_B, and β_B (Table 2). As a default, the present-day B-field is set to |$14 \,{\mu} {\rm G}$| and is then changed to 10, to 20, and to |$40\,{\mu} {\rm G}$| to see what effect this will have. Here, we fix the values for α_B and β_B to 0.0 and −1.3, respectively, as mentioned earlier, so only the value of B_age was changed (see Section 5.2 for a discussion on the changes in α_V and α_B). As the B-field increases from 10 to 40 |${\mu} {\rm G}$|⁠, the particle spectrum becomes softer at high energies, since |$\dot{E}_{\rm {SR}} \propto E_{\rm {e}}^2B^2$|⁠. Thus, higher energy particles lose more energy so that there are fewer particles at high energies left to radiate. The high-energy tail of the IC spectrum in Fig. 6 is therefore lower for a larger B-field. The SR power is directly proportional to the B-field strength squared and thus as the B-field increases, so does the SR.

Figure 6.

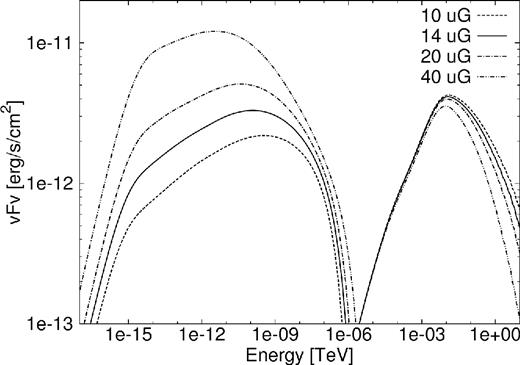
SED for PWN G0.9+0.1 with a change in the present-day B-field.

Open in new tab Download slide

4.3 Bulk particle motion

The bulk particle motion (particle speed) in the PWN is modelled by equation (11) and the value for α_V = 1 is kept constant here, although the value of V₀ is changed to V₀ = 0, 2V₀, and V₀/2 as can be seen in Figs 7 and 8. To compare our results with those of Torres et al. (2014), we need the same form for the bulk particle motion (see equation 36). The adiabatic time-scale that Torres et al. (2014) used for G0.9+0.1 was ∼2000 yr, giving V₀ = 5 × 10⁻⁵ pc yr⁻¹ for r₀ = 0.1 pc and τ_ad = 2000 yr.

Figure 7.

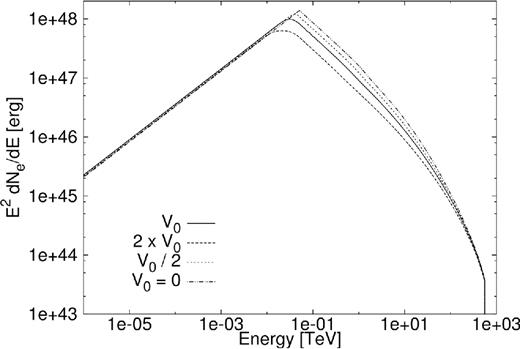
Particle spectrum for PWN G0.9+0.1 for a change in the bulk speed of the particles.

Open in new tab Download slide

Figure 8.

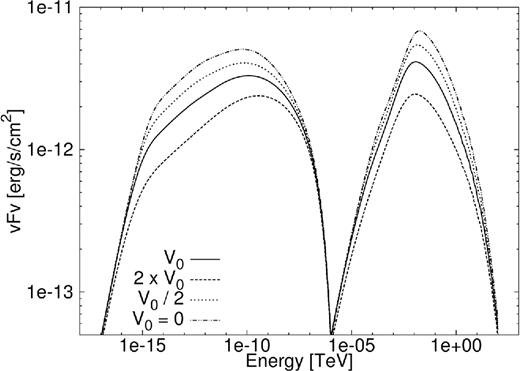
SED for PWN G0.9+0.1 for a change in the bulk speed of the particles.

Open in new tab Download slide

In Fig. 7, the particle spectrum increases as V₀ is lowered. This is due to the fact that for a lower speed, the particles lose less energy due to adiabatic losses. The adiabatic energy losses also account for the leftward shift of the peak in the particle spectrum. The radiation spectrum is linked to the particle spectrum and therefore a lower particle spectrum results in a lower radiation spectrum. This effect can be seen in Fig. 8 where the radiation decreases with an increase in the bulk speed of the particles. For high energies, SR energy losses dominate over adiabatic losses and therefore the high-energy tail of the radiation spectrum is independent of changes in V₀ and the tails converge.

4.4 Injection rate/initial spin-down rate

The particles in the PWN are injected from the embedded pulsar and the injected spectrum is normalized using the time-dependent spin-down power of the pulsar, which is given by (see the Appendix)

\begin{eqnarray} L(t) = L_0 \left(1+\frac{t}{\tau _0}\right)^{-(n+1)/(n-1)}. \end{eqnarray}

(38)

The number of injected particles is assumed to be directly proportional to this spin-down power. We can thus change L₀ to inject more or fewer particles into the PWN. If more particles are injected into the PWN, the whole particle spectrum of the PWN will increase and thus also the radiation spectrum and vice versa (not shown). This change does not influence the shape of either the particle or the radiation spectrum. The same effect is seen when the value of the conversion efficiency (ε) is changed (see equation 4). Another parameter is the characteristic spin-down time-scale at birth (τ₀) given in equation (38) that characterizes how fast the pulsar spins down. When this characteristic time is shorter, the pulsar spins down faster, resulting in fewer particles being injected into the PWN and thus both the particle and radiation spectrum are lower. The opposite happens when τ₀ is longer. Furthermore, the braking index n in equation (38) is usually set to 3 for rotating dipoles. If the braking index is decreased, the number of particles injected into the PWN increases due to the reduced spin-down of the pulsar (since both the index (n + 1)/(n − 1) as well as τ₀ change). Therefore, more particles are injected for longer periods into the PWN. Due to this, the particle and radiation spectrum will increase with a decreased n. These effects are similar to changing the normalization of the injection spectrum.

4.5 Soft-photon fields

Table 2 shows the three different soft-photon components used to model the IC scattering in the PWN. These components can be turned on and off at will, and Fig. 9 shows the contribution of each of these components. The CMB target field produces a flat spectrum that causes the first small bump on the left-hand side of the total IC flux component. The starlight at 3000 K, with an energy density of 25 eV cm⁻³, produces the highest peak and plays the largest role in the overall IC flux.

Figure 9.

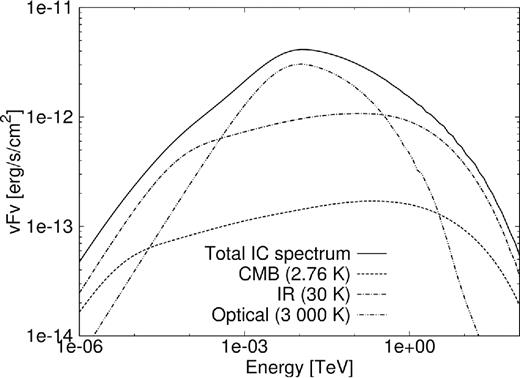
IC spectrum for PWN G0.9+0.1 showing the contribution of different soft-photon components in Table 2. The solid line is the total radiation, dashed line is the 2.76K CMB component, dashed–dotted line is the 30 K component, and the dashed-dot–dotted line shows the 3000 K component.

Open in new tab Download slide

The effect of changes in the energy densities u_l and the temperatures T_l (l = 1, 2, 3) of the soft-photon components can be understood as follows. For a single blackbody (BB), we have a spectral photon number density

\begin{eqnarray} n_{\nu } = \frac{8 {\pi} \nu ^2}{c^3}\frac{1}{e^{h\nu /kT_l}-1}. \end{eqnarray}

(39)

For a given total photon energy density u_l at a particular position in the PWN, we need a number N_BB of individual black bodies at a temperature T_l to reach u_l, i.e.

\begin{eqnarray} N_{\rm {BB}} = \frac{u_l}{u_{\rm {BB}}(T_l)}, \end{eqnarray}

(40)

with the energy density of a single BB

\begin{eqnarray} u_{\rm {BB}}(T_l) = \int u_{\nu }{\rm d}{\nu } = \int h \nu n_{\nu } {\rm d} \nu \propto T_l^4 \end{eqnarray}

(41)

the frequency-integrated energy density of a single BB and

\begin{eqnarray} \int n_{\nu } {\rm d} \nu \propto T_l^3. \end{eqnarray}

(42)

Thus, the IC flux from the PWN scales as (see also equation 27, using n_ν instead of n_ε)

\begin{eqnarray} && \left( {\frac{{\rm d}N}{{\rm d}E}}\right)_{\rm {IC}} \propto N_{\rm {BB}} \int n_{\nu } {\rm d}\nu \propto \frac{u_l}{T_l}. \end{eqnarray}

(43)

Thus, if the total energy density u_l is increased or decreased, the IC radiation will also increase or decrease linearly. However, when the temperature is increased or decreased for a constant u_l, the IC flux scales in the opposite direction. This is due to the fact that when the temperature is increased, fewer photons are needed to reach the same energy density u_l (since the average photon energy is now larger), leading to a lower normalization for the cumulative BB spectrum.

4.6 The effect of changing other parameters

The effects of changing most of the major parameters have been described, but the following are also free parameters worth noting. The free parameters α₁ and α₂ will influence the slopes and the normalization of the particle and radiation spectrum. Lastly, the flux from the PWN at Earth scales as 1/d² and the sizes of the spatial bins are also linearly dependent on d (influencing the diffusion and convection time-scales for each zone), but the latter is a small effect on the emitted SED.

5 SPATIALLY DEPENDENT RESULTS FROM OUR PWN MODEL

In the previous sections, we showed the total particle spectrum and SED predicted by the code for different parameter choices. These calculations, however, were not the main aim of the code that we have developed, as we are especially interested in the spatial dependence of the radiation from the PWN. In this section, we will study the effects that changing some of the parameters have on the energy-dependent size of the PWN.

5.1 Effects of changes in the diffusion coefficient and bulk particle motion on the PWN’s morphology

The diffusion coefficient contains two free parameters, which can be seen in equation (10). Here, we consider the effects of changing the parameters κ₀ and q (for Bohm diffusion, q = 1), with |$E^{\prime }_0$| set to 1 TeV (changing |$E^{\prime }_0$| is similar to changing κ₀). We can now increase or decrease the value of κ₀ (assuming it is not linked with the magnitude of the B-field) and thus change the normalization of the diffusion coefficient. We can also change q that has an influence on the energy dependence of the diffusion coefficient:

Fig. 10 shows how the size of the PWN changes with energy for three different scenarios. The thin solid lines indicate 5κ₀, the thick solid lines indicate κ₀, and the dashed lines indicate κ₀/5. The left graphs show SR and the right graphs IC emission. For this set of scenarios, the size of the PWN increases with increased energy. In the first two scenarios, diffusion dominates the particle transport and causes the high-energy particles to diffuse outward faster than low-energy particles, filling up the outer zones and resulting in a larger size for the PWN at high energies. This effect is larger for high-energy particles due to the energy dependence of the diffusion coefficient (q > 0). For κ₀/5, we see that the effect is not as pronounced. Here, the diffusion coefficient is so small that the SR energy loss rate starts to dominate diffusion. The particles therefore ‘burn off’ or expend their energy before they can reach the outer zones (cooling therefore dominates). Changes to q have similar effects on the SED than changes to κ₀ but are more pronounced at higher energies.

Figure 10.

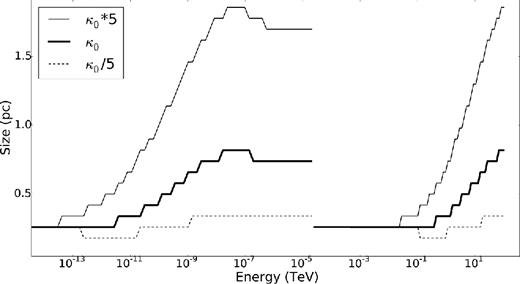
Size of the PWN as a function of energy when the normalization constant of the diffusion coefficient is changed.

Open in new tab Download slide

Next, we studied the effect of varying the bulk motion on the energy-dependent size of the PWN by varying V₀ for two different cases: the first as seen in Fig. 11 is for the model parameters given in Table 2, while the second as seen in Fig. 12 is for the parameters given in Table 3. If we consider V₀ = 0 (Fig. 11), indicated by the dashed line, we find that the size of the PWN is determined by the energy-dependent diffusion and therefore the size increases with increasing energy. Adding a bulk flow to the code (e.g. non-zero V₀ and thick solid line) increases the size of the PWN irrespective of the energy of the particles. However, for a very large bulk flow speed (e.g. 10V₀ and thin solid line), the radio size is significantly larger than the X-ray size. This is due to the energy dependence of the SR energy losses that dominate at higher energies, thereby reducing the lifetime of these X-ray-emitting particles and resulting in a smaller source compared to the radio. In this first case, α_V = 1, which is non-physical as mentioned in the discussion following equation (36). The bulk flow speed becomes so large in the outer zones that particle escape becomes significant. Therefore, if the normalization is increased beyond 10V₀, the radio source size in fact starts to decrease. Next, we do a similar study by using the more physical set of parameters given in Table 3, where α_V = −1. Fig. 12 shows the effect of changes to the normalization of the bulk motion of particles.

Figure 11.

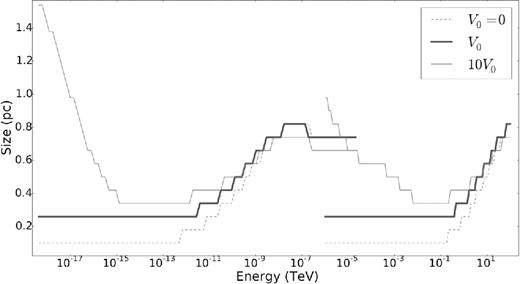
Size of the PWN as a function of energy for different normalizations of the bulk particle speed for the model parameters given in Table 2.

Open in new tab Download slide

Figure 12.

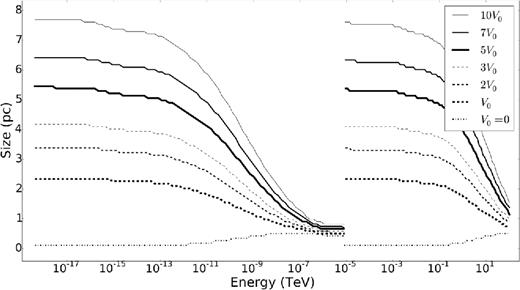
Size of the PWN as a function of energy for different normalisations of the bulk particle speed for the model parameters given in Table 3.

Open in new tab Download slide

Table 3.

Open in new tab

Modified parameters for PWN G0.9+0.1 for fitting the SED as well as the energy-dependent size of the PWN.

Model parameter	Symbol	Value	Torres et al. (2014)
Present-day B-field	B(t_age)	15.98.0 \|${\mu} \rm {G}$\|	14.0 \|${\mu} \rm {G}$\|
Age of the PWN	t_age	\|$3 227\, \rm {yr}$\|	\|$2 000 \rm {\,yr}$\|
Initial spin-down power (⁠\|$10^{38}\,\rm {erg}$\|\|$\rm {s^{-1}}$\|⁠)	L₀	1.44	1.0
B-field parameter	α_B	0.0	0
B-field parameter	β_B	−1.0	−1.3
V parameter	α_V	−1.0	1.0
Particle bulk motion	V₀	0.0615c	1.63 × 10⁻⁴c
Diffusion	κ₀	3.356	1.0

Model parameter	Symbol	Value	Torres et al. (2014)
Present-day B-field	B(t_age)	15.98.0 \|${\mu} \rm {G}$\|	14.0 \|${\mu} \rm {G}$\|
Age of the PWN	t_age	\|$3 227\, \rm {yr}$\|	\|$2 000 \rm {\,yr}$\|
Initial spin-down power (⁠\|$10^{38}\,\rm {erg}$\|\|$\rm {s^{-1}}$\|⁠)	L₀	1.44	1.0
B-field parameter	α_B	0.0	0
B-field parameter	β_B	−1.0	−1.3
V parameter	α_V	−1.0	1.0
Particle bulk motion	V₀	0.0615c	1.63 × 10⁻⁴c
Diffusion	κ₀	3.356	1.0

Table 3.

Open in new tab

Modified parameters for PWN G0.9+0.1 for fitting the SED as well as the energy-dependent size of the PWN.

Model parameter	Symbol	Value	Torres et al. (2014)
Present-day B-field	B(t_age)	15.98.0 \|${\mu} \rm {G}$\|	14.0 \|${\mu} \rm {G}$\|
Age of the PWN	t_age	\|$3 227\, \rm {yr}$\|	\|$2 000 \rm {\,yr}$\|
Initial spin-down power (⁠\|$10^{38}\,\rm {erg}$\|\|$\rm {s^{-1}}$\|⁠)	L₀	1.44	1.0
B-field parameter	α_B	0.0	0
B-field parameter	β_B	−1.0	−1.3
V parameter	α_V	−1.0	1.0
Particle bulk motion	V₀	0.0615c	1.63 × 10⁻⁴c
Diffusion	κ₀	3.356	1.0

Model parameter	Symbol	Value	Torres et al. (2014)
Present-day B-field	B(t_age)	15.98.0 \|${\mu} \rm {G}$\|	14.0 \|${\mu} \rm {G}$\|
Age of the PWN	t_age	\|$3 227\, \rm {yr}$\|	\|$2 000 \rm {\,yr}$\|
Initial spin-down power (⁠\|$10^{38}\,\rm {erg}$\|\|$\rm {s^{-1}}$\|⁠)	L₀	1.44	1.0
B-field parameter	α_B	0.0	0
B-field parameter	β_B	−1.0	−1.3
V parameter	α_V	−1.0	1.0
Particle bulk motion	V₀	0.0615c	1.63 × 10⁻⁴c
Diffusion	κ₀	3.356	1.0

Again, if V₀ = 0 (dashed–dotted line, the same line as in Fig. 11), the PWN has a smaller size at lower energies than at higher energies. The size increases monotonically with V₀. At the lower energies convection dominates the radiative energy losses and therefore the particles have a very long lifetime, allowing them to diffuse to the outer zones and still be able to radiate, resulting in a large source size. In contrast to this, at high energies, the SR losses dominate the convection, resulting in a very short lifetime for the high-energy particles; therefore, these particles radiate all their energy before they have time to convect to the outer zones. This leads to a relatively smaller X-ray source size.

5.2 Different cases of α_V and α_B

In equations (11) and (14), we assumed that the B-field may have a spatial and time dependences and that the bulk motion only has a spatial dependence. In this section, the effects of different spatial dependences for B(r, t) and V(r) are studied. Note that we have assumed the diffusion coefficient to be spatially independent throughout this work. However, since we are now considering the spatial dependence of the B-field in this paragraph, and κ ∝ 1/B(r, t), this assumption is technically violated here. The effect is small when the divergence of |$\vec{\kappa }$| is small, which we will assume to be the case in this section. This spatial dependence of the diffusion coefficient can be implemented in future by adding another convective term to the transport equation.

From equation (20), the following relationship is assumed to hold: α_V + α_B = −1. For this section, the time dependence of the B-field is kept unchanged, with β_B = −1.3, and four different scenarios for α_B and α_V are shown. Here, the first situation is the same as Torres et al. (2014), with α_B = 0 and α_V = 1. We also considered the following three situations: α_B = 0 and α_V = −1, α_B = −0.5 and α_V = −0.5, and α_B = −1 and α_V = 0. These three situations all comply with equation (20), with the B-field kept constant in the first spatial zone. The B-field was limited to a maximum value, as the parametrization resulted in the B-field growing infinitely large during the early epochs of the PWN’s lifespan.

In Fig. 13, the particle spectrum is shown for the four different scenarios, with the solid line showing the result for α_B = 0 and α_V = 1 as is effectively assumed by Torres et al. (2014). In this case, the B-field is spatially constant over the entire PWN, but the bulk speed increases linearly with r. The particles move extremely fast, as they propagate farther from the centre of the PWN. They therefore lose more energy due to adiabatic energy losses relative to the other cases. Thus, the solid line is lower than the other situations and the peak of the spectrum is also shifted to the left.

Figure 13.

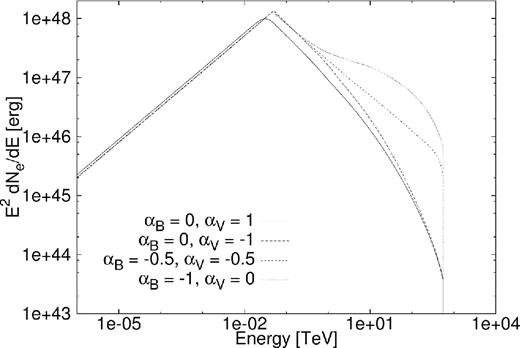
Particle spectrum for PWN G0.9+0.1 with a change in the parametrized B-field and bulk particle motion.

Open in new tab Download slide

We can see from both Figs 13 and 14 that changes to the B-field have a more profound impact on the particle spectrum and SED than changes to the radially dependent speed. If the spatial dependence of the B-field changes from α_B = 0 to α_B = −0.5 and α_B = −1, the B-field is first constant over all space and then decreases as r^−0.5 and finally it reduces rapidly as r⁻¹. The effect of this can be seen in the particle spectrum, as the number of high-energy particles increases for a decreased B-field and hence a lower SR loss rate. This effect is emphasized in the situation where α_B = −1, resulting in a very small B-field at the outer edges of the PWN. This can also be seen in the radiation spectrum in Fig. 14 where a decreased B-field results in reduced radiation in the SR band (since |$\dot{E}_{\rm {SR}} \propto B^2$|⁠), and the increased radiation in the IC band is due to more particles being present at those energies. This increase in the high-energy particles is quite large for α_B = −1, though (possibly indicating a violation of our assumption that the divergence of |$\vec{\kappa }$| is small in this case). We note that our model currently does not take into account the fact that the cut-off energy due to particle escape (E_max) should also be a function of the B-field. This is because in reality σ ∝ B² (we have assumed σ to be constant), and therefore |$E_{\rm {max}} \sim \sqrt{B^2/(1+B^2)}$|⁠, which will have the effect that if the B-field is reduced, σ and therefore E_max will decrease. This may cause the high-energy particles to be cut-off at lower energies as the B-field decreases due to more efficient particle escape, and therefore the build-up of high-energy particles may be partially removed (we say ‘partially’ since the Larmor radius of the most energetic particles in the outer zones is still smaller than the PWN size by a factor of a few, inhibiting efficient escape of particles from the PWN). The question of particle escape may also be addressed by refining our outer boundary condition in future.

Figure 14.

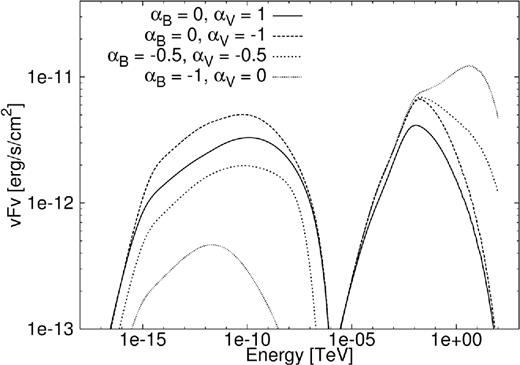
SED for PWN G0.9+0.1 with a change in the parametrized B-field and bulk particle motion.

Open in new tab Download slide

From Fig. 15, we can see that in scenario one (dashed line, α_B = 0 and α_V = 1) the PWN size for low energies is always larger than for all the other scenarios. This is due to the bulk speed being directly proportional to r in this case, resulting in the particles moving faster as they move farther out from the centre of the PWN. This will result in the outer zones filling up with particles, while not escaping. This may point to our outer boundary that was chosen to be much larger than the radius of the PWN (r_max ≫ R_PWN). For scenario two (thick solid line, α_B = 0 and α_V = −1), the size of the PWN at low energies follows the same pattern as for both low-energy and high-energy photons, since the energy-dependent diffusion now dominates convection. At lower energies, we see that PWN is smaller than in scenario one, as the speed is now proportional to r⁻¹, which results in a slower bulk motion and thus fewer low-energy particles moving to the outer zones. In scenario three (thin solid line, α_B = −0.5 and α_V = −0.5) and four (dotted line, α_B = −1 and α_V = 0), the B-field has a spatial dependence, reducing as one moves farther away from the centre of the PWN. This reduced B-field will lead to increased diffusion and decreased SR losses as mentioned in the first part of this section. For these two scenarios, the dependence of the bulk motion on radius is weaker and therefore diffusion dominates the particle transport. Once again we can see the energy dependence of the diffusion, since the PWN is initially smaller and then increases for higher energies. At very high energies, the PWN size becomes very large, which is not the case for the SR component. The first is due to the pile up of high-energy particles (leading to substantially increased IC emission, Fig. 14), while the second is due to the fact that SR is severely inhibited for the very low B-field.

Figure 15.

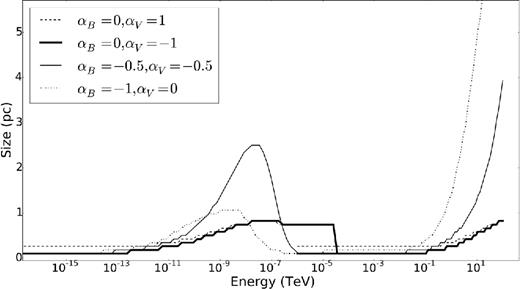
Size of PWN G0.9+0.1 as a function of energy for changes in α_B and α_V.

Open in new tab Download slide

5.3 Size versus energy fits

Figs 16 and 17 show the radiation spectrum and the size versus energy graphs for PWN G0.9+0.1 for the calibration parameters (black lines) as in Table 2 modelled by Torres et al. (2014), with the dots indicating the estimated radio and the square the estimated X-ray size.⁹ The upper limit on the predicted TeV size is 10.4 pc, i.e. we use the point spread function of the H.E.S.S. telescope (not shown). The radio data are from Becker & Helfand (1987) and Dubner et al. (2008), the X-ray data are from Porquet et al. (2003) and the TeV data from Aharonian et al. (2005). The model provides reasonable fits to the spectral radio, X-ray, and TeV data; however, it is clear that the predicted size of the PWN does not fit the data at all. After adjusting some parameters, we found a better fit and this can also be seen in Figs 16 and 17 (grey lines). Table 3 shows the new parameters used for this fit.

Figure 16.

SED for PWN G0.9+0.1 for the parameters used by Torres et al. (2014) (Table 2) and the fitted parameters as in Table 3. The radio (Becker & Helfand 1987), X-ray (Porquet et al. 2003), and γ-ray data (Aharonian et al. 2005) are also shown.

Open in new tab Download slide

Figure 17.

Size of the PWN as a function of energy for the calibration parameters in Table 2 and the fitted parameters in Table 3. The observed radio (Dubner et al. 2008) and X-ray sizes (Porquet et al. 2003) are also indicated.

Open in new tab Download slide

The process of finding a better fit to the both the SED of the PWN and the energy-dependent size was facilitated by our prior parameter study. The only way in which we could increase the size of the PWN at lower energies was to increase the bulk speed of the particles. This, however, increased the adiabatic energy losses, and resulted in a lower radiation spectrum. This was then countered by increasing the age of the PWN (which effectively leads to an increase in L₀). The bulk speed of the particles had to be increased substantially to fit the data, but given the large errors on the size of the PWN in the radio band, we could still fit the data with a bulk speed as small as 0.073c. The profile trends for the B-field as well as the bulk speed of the particles were also changed. To increase the size of the PWN further we also increased the normalization of the diffusion coefficient of the particles. This is not a bad assumption as the diffusion was originally modelled to be Bohm-type diffusion, which is a very slow perpendicular diffusion with respect to the B-field. All these changes produced the grey lines in Figs 16 and 17. Here, we see that we have a good fit for the radio size, which according to data, does not change with energy and the model reproduces this trend as well as the trend where the size of the PWN decreases with increasing energy. This is a common feature of PWNe.

In a future paper, a more robust statistical method may be used to find the best fit to this source’s SED and energy-dependent size and to also investigate the parameter degeneracy.

6 CONCLUSIONS

This study focused on modelling the evolution of PWNe, with the main aim being to create a spatially dependent temporal code to model the radiation morphology of PWNe. We solved a Fokker–Planck-type transport equation to model the particle evolution inside a PWN, injecting a broken power-law particle spectrum and allowing this spectrum to evolve over time taking into account energy losses due to SR, IC scattering, and adiabatic cooling of the PWN due to expansion. We also took into account particle diffusion and convection in the form of a bulk particle motion.

We calibrated the code by comparing it to results by two independent codes (Venter & de Jager 2007; Torres et al. 2014), using PWN G0.9+0.1 as calibration source. We found that our model was well calibrated. Our model is now able to not only fit the observed radiation spectra from the PWN but also yields results concerning the morphology of the PWN (i.e. it is able to reproduce the size of the PWN as a function of energy). Thus, we can potentially derive stronger constraints on key quantities characterizing the PWN.

The spatiotemporal-energetic model we presented is a first approach to modelling PWNe for multiple spatial bins, thus there are a number of improvements that can be made. For example, the code currently has a problem with a build-up of particles at high energies when the B-field decreases rapidly with radius. This is partially due to the fact that we chose a fixed r_max ≫ R_PWN. We will revise this boundary condition in future. One way in which this could be refined is by using an MHD code to model the morphology of the PWN in more detail and to find a more realistic time-dependent radius of the PWN. This will allow us to use this radius as the outer boundary that will enable the particles to escape more efficiently from the PWN. One can also obtain more realistic spatial and time dependences for the B-field and bulk flow speeds using an MHD code. This will yield refined SR and adiabatic losses and convection. Furthermore, treating σ as being dependent on the B-field will aid by lowering the maximum energy of particles that are contained within the PWN. The code should also be generalized in future to handle a spatially dependent diffusion coefficient by adding another convective term to the transport equation.

In future, we will perform a population study to investigate currently known trends, e.g. the X-ray luminosity that correlates with the pulsar spin-down luminosity and its anticorrelation with the characteristic age of the pulsar. We could also probe other trends, e.g. investigate whether there is a correlation between the TeV surface brightness of the PWN and the spin-down luminosity of the pulsar (Abdalla et al. 2018), as well as the surface brightness versus age. Some follow-up projects or refinements to the model are as follows. The code currently assumes spherical symmetry. This can be revised by expanding the model to two or three spatial dimensions. One could also add anisotropic effects such as considering distinct equatorial and polar outflows (injection) of particles. Some older PWNe are offset from the pulsar, revealing a bullet shape. This is either due to an inhomogeneity in the interstellar medium (ISM) in which the PWN expands causing an asymmetric reverse shock and thus an offset PWN, or to the pulsar receiving some kick velocity at birth, thus moving away from the PWN centre. The radiation peaks at the pulsar position, thus also causing the bullet shape. These effects could be added to the model to simulate a more realistic situation. The code is currently only applicable to young PWNe. This should be addressed so that all ages of PWNe can be modelled, e.g., by including a more complex parametrization of the B-field and adding the effect of an asymmetric reverse shock to the code.

The CTA will reveal more sources and more information regarding the morphology of PWNe due to its improved sensitivity and angular resolution. This will necessitate the continued development, application, and refinement of spatially dependent PWN codes such as the one discussed here.

Acknowledgements

We gratefully acknowledge fruitful discussions with Andreas Kopp, Harm Moraal, and Stefan Ferreira. This work is based on the research supported wholly/in part by the National Research Foundation (NRF) of South Africa (grant numbers 87613, 90822, 92860, 93278, and 99072). The grantholder acknowledges that opinions, findings, and conclusions or recommendations expressed in any publication generated by the NRF supported research is that of the author(s), and that the NRF accepts no liability whatsoever in this regard.

Footnotes

1

http://tevcat2.uchicago.edu/

2

It has come to our attention during the final stages of our code development that an independent study has recently been published by Lu, Gao & Zhang (2017) describing a spatially dependent PWN model. Their code models the electron spectrum using a Fokker–Planck equation, similar to our code, and then predicts the SED from the PWN. They also assume spherical symmetry and take into account SR, IC, and adiabatic energy losses. They use free expansion to determine the radius of the PWN, while we in contrast use the surface brightness of the PWN to predict its size. Although they calculate the surface brightness, they only predict this for the X-ray band. We model the surface brightness for the entire electromagnetic spectrum and thus we predict the size of the PWN as a function of energy. We also perform a thorough parameter study to show the effects of all the model parameters. Lastly, they applied their model to MSH 15-52, while we studied G0.9+0.1. We therefore believe that our results are complementary to their work. Indeed, their work provides another independent calibration of our model, and we find very similar spectra for the same input parameters for MSH 15-52. See Section 3 for other calibrations of our code.

3

We neglect SSC and Bremsstrahlung as the energy losses due to these two effects are orders of magnitude smaller than SR and IC scattering for PWN G0.9+0.1.

4

We treat the B-field as predominantly azimuthal as is standard practice (e.g. Schöck et al. 2010; Vorster & Moraal 2014). This assumption is based on several arguments: in this case |$\nabla \cdot \boldsymbol {B} = 0$|⁠, at typical PWN scales any dipolar field components have all but died out compared to the toroidal components (given their respective 1/r³ versus 1/r decay), and X-ray observations show ubiquitous polar and equatorial outflows supporting an azimuthal structure winding around the pulsar in the equatorial plane. Lastly, radio polarization measurements indicate that the magnetic field must be very ordered.

5

We assumed the parametric form for the B-field for mathematical expedience assuming the PWN is young. In fact, it is explicitly stated in the Torres et al. (2014) that at earlier times the B-field may be approximated using a power law in time [B ∼ t^−1.3; see also Vorster et al. (2013) and references therein]. One could use the numerical solution as done by Torres et al. (2014), but the question then is what the effect of uncertainty on R_PWN(t) will be on the eventual B(t); i.e. this approach is also not without some assumptions. Our simple approach of using a parametrized B-field is meant to be an approximation to the output of a complex MHD code. The solution to such a code is beyond the scope of the current paper and is avoided for the reason that we are focusing on emission physics. In future, one may consider the combination of emission and MHD codes to obtain even more realistic results. To test the effect of parametrizing the B-field versus calculating it numerically, we implemented the latter approach and found that respective results are very close (see Section 3.2). For older PWNe, a numeric approach will be better and the effect of the reverse shock will also have to be taken into account.

6

Below we discuss calibration of our model against that of Venter & de Jager (2007). To closer align with their procedure, for the sake of calibration, we fixed the value of L₀ and birth period P₀ = 43 ms van der Swaluw & Wu 2001, assuming no decay of the pulsar B-field, i.e. |$P_0 \dot{P}_0=PP_0$|⁠. In the rest of the paper, however, we calculate τ_c using P and |$\dot{P}$|⁠, we assume t_age, and from this follows τ₀ and L₀ (without the need to calculate P₀ and |$\dot{P}_0$| explicitly).

7

For simplicity, we assume this distant boundary for the PWN where particles escape. We restrict ourselves to modelling young PWN where free expansion of the wind should be justified. Later evolutionary phases may be characterized by a reverse shock, or reverberation phase where interaction with the ambient medium is much more important. If we would enforce particle escape at a moving boundary R_PWN rather than following our approach of escape at a distant boundary, the particle density may be somewhat lower, leading to slightly lower fluxes than predicted by our model.

8

Whether a PWN’s morphology is energy-dependent seems to be closely linked with the evolutionary stage of the PWN and to whether particles efficiently escape from the system beyond R_PWN(t). As mentioned in the Introduction section, young systems with slow moving embedded pulsars may manifest as composite SNRs with a high degree of spherical symmetry, prior to the interaction with the SNR reverse shock. In such systems, particles may not have had time to cool significantly due to radiation losses, leading to a morphology that seems to be largely energy independent. Middle-aged PWNe may exhibit complex morphologies (e.g. collimated X-ray emission versus more diffuse ambient radio emission), while in older PWNe, the γ-ray emission may dominate the radio and X-ray emission. This is probably due to the fact that high-energy particles are the ones that preferentially cool and escape from the PWN. Hinton et al. (2011) argue that while confinement of particles in PWNe may be effective during the early stages of evolution, the interaction with the SNR reverse shock may disrupt the PWN via, e.g. the growth of Rayleigh–Taylor instabilities, and diffusion of particles out of the PWN becomes possible. In the case of PWN G0.9+0.1, we may be witnessing an intermediate case. While this PWN is quite young and the radio and X-ray sizes are very similar, the X-ray morphology seems to be slightly smaller than the radio (Dubner et al. 2008). This hint of morphological evolution (Fig. 17) is consistent with the observed softening of the X-ray spectrum as one moves from the inner to outer regions of the PWN, indicating the effect of SR losses in this system (Porquet et al. 2003).

9

We directly infer the source sizes for the radio and X-rays bands from the respective images in the original papers. This procedure may be somewhat arbitrary and prone to error, and also dependent on the presentational choices or assumptions made in the original papers. The best way to determine these sizes would be to redo the data analysis and infer them in a systematic way. However, this is beyond the scope of the current modelling paper. Furthermore, we note that our model is spherically symmetric, while the data indicate that the source is not. To account for these uncertainties (i.e. source asymmetry and actual energy-dependent source size), we specified a sizable error on our estimated values.

REFERENCES

Abdalla

H.

et al. ,

2018

,

A&AS

,

612

,

A2

Abramowski

A.

et al. ,

2012

,

A&A

,

545

,

L2

Crossref

Search ADS

Aharonian

F.

et al. ,

2005

,

A&AS

,

432

,

L25

Crossref

Search ADS

Amato

E.

,

2014

,

Int. J. Mod. Phys. Conf. Ser.

,

28

,

60160

10.1142/S2010194514601604

Crossref

Search ADS

Becker

R. H.

,

Helfand

D. J.

,

1987

,

ApJ

,

316

,

660

10.1086/165231

Crossref

Search ADS

Blumenthal

G. R.

,

Gould

R. J.

,

1970

,

Rev. Mod. Phys.

,

42

,

237

10.1103/RevModPhys.42.237

Crossref

Search ADS

Bucciantini

N.

,

2014

,

Int. J. Mod. Phys. Conf. Ser.

,

28

,

60162

10.1142/S2010194514601628

Crossref

Search ADS

Camilo

F.

,

Ransom

S. M.

,

Gaensler

B. M.

,

Lorimer

D. R.

,

2009

,

ApJ

,

700

,

L34

10.1088/0004-637X/700/1/L34

Crossref

Search ADS

Carrigan

S.

et al. ,

2013

, in

Saa

A.

,

ed., Proceedings of the 33rd International Cosmic Ray Conference

.

Rio de Janeiro

(arXiv:1307.4690)

de Jager

O. C.

,

Djannati-Ataï

A.

,

2009

, in

Becker

W.

, ed.,

Neutron Stars and Pulsars, Astrophysics and Space Science Library, Vol. 357

.

Springer

,

Berlin

, p.

451

doi:10.1007/978-3-540-76965-1_17

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Dubner

G.

,

Giacani

E.

,

Decourchelle

A.

,

2008

,

A&A

,

487

,

1033

Crossref

Search ADS

Fang

J.

,

Zhang

L.

,

2010

,

ApJ

,

718

,

467

10.1088/0004-637X/718/1/467

Crossref

Search ADS

Ferrara

E. C.

,

Ballet

J.

,

Cavazzuti

E.

,

Digel

S.

,

2015

,

IAU General Assembly

,

22

,

2255765

Ferreira

S. E. S.

,

de Jager

O. C.

,

2008

,

A&A

,

478

,

17

Crossref

Search ADS

Gaensler

B. M.

,

Slane

P. O.

,

2006

,

ARA&A

,

44

,

17

Crossref

Search ADS

Helfand

D. J.

,

Gotthelf

E. V.

,

Halpern

J. P.

,

2001

,

ApJ

,

556

,

380

10.1086/321533

Crossref

Search ADS

Hewitt

J. W.

,

Lemoine-Goumard

M.

,

2015

,

C. R. Phys.

,

16

,

674

10.1016/j.crhy.2015.08.015

Crossref

Search ADS

Hinton

J. A.

,

Funk

S.

,

Parsons

R. D.

,

Ohm

S.

,

2011

,

ApJ

,

743

,

L7

10.1088/2041-8205/743/1/L7

Crossref

Search ADS

Jones

F. C.

,

1968

,

Phys. Rev.

,

167

,

1159

10.1103/PhysRev.167.1159

Crossref

Search ADS

Kargaltsev

O.

,

Pavlov

G. G.

,

Durant

M.

,

2012

, in

Lewandowski

W.

,

Maron

O.

,

Kijak

J.

, eds,

ASP Conf. Ser. Vol. 466, Electromagnetic Radiation from Pulsars and Magnetars

.

Astron. Soc. Pac.

,

San Francisco

, p.

167

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Kargaltsev

O.

,

Cerutti

B.

,

Lyubarsky

Y.

,

Striani

E.

,

2015

,

Space Sci. Rev.

,

191

,

391

10.1007/s11214-015-0171-x

Crossref

Search ADS

Kennel

C. F.

,

Coroniti

F. V.

,

1984

,

ApJ

,

283

,

710

10.1086/162357

Crossref

Search ADS

Kopp

A.

,

Venter

C.

,

Büsching

I.

,

de Jager

O. C.

,

2013

,

ApJ

,

779

,

126

10.1088/0004-637X/779/2/126

Crossref

Search ADS

Lu

F.-W.

,

Gao

Q.-G.

,

Zhang

L.

,

2017

,

ApJ

,

834

,

43

10.3847/1538-4357/834/1/43

Crossref

Search ADS

Martín

J.

,

Torres

D. F.

,

Rea

N.

,

2012

,

MNRAS

,

427

,

415

10.1111/j.1365-2966.2012.22014.x

Crossref

Search ADS

Moraal

H.

,

2013

,

Space Sci. Rev.

,

176

,

299

10.1007/s11214-011-9819-3

Crossref

Search ADS

Pacini

F.

,

Salvati

M.

,

1973

,

ApJ

,

186

,

249

10.1086/152495

Crossref

Search ADS

Porquet

D.

,

Decourchelle

A.

,

Warwick

R. S.

,

2003

,

A&AS

,

401

,

197

Crossref

Search ADS

Porth

O.

,

Vorster

M. J.

,

Lyutikov

M.

,

Engelbrecht

N. E.

,

2016

,

MNRAS

,

460

,

4135

10.1093/mnras/stw1152

Crossref

Search ADS

Qiao

W.-F.

,

Zhang

L.

,

Fang

J.

,

2009

,

Res. Astron. Astrophys.

,

9

,

449

10.1088/1674-4527/9/4/007

Crossref

Search ADS

Rees

M. J.

,

Gunn

J. E.

,

1974

,

MNRAS

,

167

,

1

10.1093/mnras/167.1.1

Crossref

Search ADS

Reynolds

S. P.

,

Chevalier

R. A.

,

1984

,

ApJ

,

278

,

630

10.1086/161831

Crossref

Search ADS

Roberts

M. S. E.

,

Tam

C. R.

,

Kaspi

V. M.

,

Lyutikov

M.

,

Vasisht

G.

,

Pivovaroff

M.

,

Gotthelf

E. V.

,

Kawai

N.

,

2003

,

ApJ

,

588

,

992

10.1086/374266

Crossref

Search ADS

Roberts

M. S. E.

,

Lyutikov

M.

,

Gaensler

B. M.

,

Brogan

C. L.

,

Tam

C. R.

,

Romani

R. W.

,

2005

, in

Sjouwerman

L. O.

,

Dyer

K. K.

, eds,

X-Ray and Radio Connections

. id.

#5.06

.

Available at: http://www.aoc.nrao.edu/events/xraydio

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Schöck

F. M.

,

Büsching

I.

,

de Jager

O. C.

,

Eger

P.

,

Vorster

M. J.

,

2010

,

A&A

,

515

,

A109

Crossref

Search ADS

Sefako

R. R.

,

de Jager

O. C.

,

2003

,

ApJ

,

593

,

1013

10.1086/376567

Crossref

Search ADS

Sidoli

L.

,

Bocchino

F.

,

Mereghetti

S.

,

Bandiera

R.

,

2004

,

MmSAI

,

75

,

507

Sironi

L.

,

Spitkovsky

A.

,

2011

,

ApJ

,

741

,

39

10.1088/0004-637X/741/1/39

Crossref

Search ADS

Slane

P.

,

2017

, in

Alsabti

A. W.

,

Murdin

P.

, eds,

Handbook of Supernovae

.

Springer International Publishing AG

, p.

2159

Tanaka

S. J.

,

Takahara

F.

,

2011

,

ApJ

,

741

,

40

10.1088/0004-637X/741/1/40

Crossref

Search ADS

Temim

T.

,

Slane

P.

,

2017

, in

Torres

D. F.

, ed.,

Astrophysics and Space Science Library, Vol. 446

,

Modelling Pulsar Wind Nebulae

.

Springer

,

Switzerland

, p.

29

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Torres

D. F.

,

Cillis

A.

,

Martín

J.

,

de Oña Wilhelmi

E.

,

2014

,

High Energy Phys. Nucl. Phys.

,

1

,

31

van der Swaluw

E.

,

Wu

Y.

,

2001

,

ApJ

,

555

,

L49

10.1086/321733

Crossref

Search ADS

Van Rensburg

C.

,

2015

,

MSc thesis

,

North-West Univ.

(Unpublished

)

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Van Rensburg

C.

,

Kruger

P. P.

,

Venter

C.

,

2014

, in

Engelbrecht

C.

,

Karataglidis

S.

, eds,

Proceedings of SAIP2014, the 59th Annual Conference of the South African Institute of Physics

(arXiv:1504.05043

). p.

377

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Venter

C.

,

de Jager

O. C.

,

2007

, in

Becker

W.

,

Huang

H. H.

, eds,

WE-Heraeus Seminar on Neutron Stars and Pulsars 40 years after the Discovery

.

801

,

MPE Report 291

, p.

40

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Vorster

M. J.

,

Moraal

H.

,

2014

,

ApJ

,

788

,

132

10.1088/0004-637X/788/2/132

Crossref

Search ADS

Vorster

M. J.

,

Tibolla

O.

,

Ferreira

S. E. S.

,

Kaufmann

S.

,

2013

, in

Saa

A.

,

ed., Proceedings of the 33rd International Cosmic Ray Conference. (arXiv:1308.1626)

Weiler

K. W.

,

Panagia

N.

,

1978

,

A&AS

,

70

,

419

Zhang

L.

,

Chen

S. B.

,

Fang

J.

,

2008

,

ApJ

,

676

,

1210

10.1086/527466

Crossref

Search ADS

APPENDIX

We derive expressions for L(t) and L₀(τ₀) to show that τ₀ = τ_c − t_age. We make two assumptions: the first is that the B-field of the pulsar does not decay over short time-scales, i.e. |$\dot{P}P^{n-2} = \dot{P}_0P_0^{n-2}$| (e.g. Venter & de Jager 2007) and the second is a braking law of the form |$\dot{\Omega } = k \Omega ^n$| (e.g. Pacini & Salvati 1973; Rees & Gunn 1974; Gaensler & Slane 2006).

The spin-down luminosity L(t) of the pulsar can be constructed by using the second assumption and the following definition |$L(t) = I \Omega \dot{\Omega }$|⁠, thus L(t) = kIΩ^n + 1. We can integrate |$\dot{\Omega }$| to find

\begin{eqnarray} \int _{\Omega _0}^{\Omega } \Omega ^{-n}{\rm d}\Omega =\int _0^t{\rm d}t, \end{eqnarray}

(A1)

thus

\begin{eqnarray} \frac{1}{1-n}\left(\Omega ^{1-n}-\Omega _0^{1-n}\right) = kt \end{eqnarray}

(A2)

leaving us with

\begin{eqnarray} \Omega = \left(\frac{1}{(1-n)kt+\Omega _0^{1-n}}\right)^{\frac{1}{n-1}}. \end{eqnarray}

(A3)

Now we can obtain L(t) by replacing the Ω with equation (A3). Thus,

\begin{eqnarray} L(t) = kI\left(\frac{1}{(1-n)kt+\Omega _0^{1-n}} \right)^{\frac{n+1}{n-1}}. \end{eqnarray}

(A4)

We set β = (n + 1)/(n − 1) and do some manipulation to find

\begin{eqnarray} L(t) = kI\Omega _0^{n+1}\left( 1+\frac{(1-n)kt}{\Omega _0^{1-n}} \right)^{-\beta }. \end{eqnarray}

(A5)

We know from the definition of L(t) that |$L_0(t) = kI\Omega _0^{n+1}$| (assuming a constant value for I and k) and also that |$(1-n)k/\Omega _0^{1-n} = (1-n)\dot{\Omega }_0/\Omega _0 = 1/\tau _0$| and thus

\begin{eqnarray} L(t) = \frac{L_0}{\left( 1+\frac{t}{\tau _0} \right)^{\beta }}. \end{eqnarray}

(A6)

In this first part, we have shown how the spin-down luminosity is derived from the second assumption. When substituting t = t_age and |$L_{\rm {age}} = L(t_{\rm {age}}) = 4 {\pi} ^2I\dot{P}/P^3$|⁠, we find a first expression for L₀:

\begin{eqnarray} L_0 = L_{\rm {age}}\left( 1+\frac{t_{\rm {age}}}{\tau _0} \right)^{\beta }. \end{eqnarray}

(A7)

We will now obtain another expression for L₀(τ₀) using the first assumption |$\dot{P}P^{n-2} = \dot{P}_0P_0^{n-2} = K$|⁠, with K a constant. We rewrite this assumption as

\begin{eqnarray} P_0 = \left(\frac{K}{\dot{P}_0}\right)^{\frac{1}{n-2}}. \end{eqnarray}

(A8)

Since |$L_0 = 4 {\pi} ^2I\dot{P}_0/P_0^3$|

\begin{eqnarray} L_0=\frac{4 {\pi} ^2I\dot{P}_0}{\left(\frac{K}{\dot{P}_0} \right)^{3/(n-2)}}. \end{eqnarray}

(A9)

Following some manipulations, we find

\begin{eqnarray} L_0 = \frac{4 {\pi} ^2I}{K^{3/(n-2)}} \cdot \dot{P}_0^{\frac{n+1}{n-2}}. \end{eqnarray}

(A10)

We can also find |$\dot{P}_0$| as a function of τ₀ by using the definition for the birth characteristic age of the pulsar given by |$\tau _0 = P_0/(n-1)\dot{P}_0$|⁠. Thus, we have

\begin{eqnarray} \tau _0 = \frac{(K/\dot{P}_0)^{1/(n-2)}}{(n-1)\dot{P}_0}, \end{eqnarray}

(A11)

and once again we solve for |$\dot{P}_0$|⁠, leaving us with

\begin{eqnarray} \dot{P}_0 = \left( \frac{K^{1/(n-2)}}{(n-1)\tau _0} \right)^{\frac{n-2}{n-1}}. \end{eqnarray}

(A12)

We can now substitute equation (A12) into equation (A10) to find L₀ as a function of τ₀. We are thus left with

\begin{eqnarray} L_0 = \left( \frac{4 {\pi} ^2I}{K^{3/(n-2)}} \right)\left( \left[ \frac{K^{1/(n-2)}}{(n-1)\tau _0} \right]^{\frac{n-2}{n-1}} \right)^{\frac{n+1}{n-2}}, \end{eqnarray}

(A13)

resulting in

\begin{eqnarray} L_0 = 4 {\pi} ^2I K^{-2/(n-1)}\left( \frac{1}{(n-1)\tau _0} \right)^{\frac{n+1}{n-1}}. \end{eqnarray}

(A14)

By substituting the constant |$K=\dot{P}P^{n-2}$| back, we find

\begin{eqnarray} L_0 = 4 {\pi} ^2I \dot{P}^{\frac{-2}{(n-1)}} P^{\frac{-2(n-2)}{(n-1)}} \left( \frac{1}{(n-1)\tau _0} \right)^{\frac{n+1}{n-1}}, \end{eqnarray}

(A15)

and by using the definition for the current spin-down luminosity |$L_{\rm {age}}=4 {\pi} ^2I\dot{P}/P^3$|⁠, we find

\begin{eqnarray} L_0 = L_{\rm {age}} \frac{P^3}{\dot{P}} \dot{P}^{\frac{-2}{(n-1)}} P^{\frac{-2(n-2)}{(n-1)}} \left( \frac{1}{(n-1)\tau _0} \right)^{\frac{n+1}{n-1}}. \end{eqnarray}

(A16)

Upon simplification, we find

\begin{eqnarray} L_0 = L_{\rm {age}}\left( \frac{P}{\dot{P}(n-1)\tau _0} \right)^{\frac{n+1}{n-1}}. \end{eqnarray}

(A17)

We can simplify this further by using the definition for the characteristic age of the pulsar; thus,

\begin{eqnarray} L_0 = L_{\rm {age}}\left( \frac{\tau _c}{\tau _0} \right)^{\beta }. \end{eqnarray}

(A18)

We now have two forms for the birth spin-down luminosity of the pulsar in equations (A7) and (A18) and by setting them equal

\begin{eqnarray} \left(\frac{\tau _c}{\tau _0} \right)^{\beta } = \left( 1+\frac{t_{\rm {age}}}{\tau _0} \right)^{\beta } \end{eqnarray}

(A19)

we find

\begin{eqnarray} \tau _0 = \tau _{\rm {c}} - t_{\rm {age}}. \end{eqnarray}

(A20)

This equation is used in Section 2.2. Therefore, we choose t_age and n, calculate τ_c and L_age using the measured value of P and |$\dot{P}$|⁠, calculate τ₀ from equation (A20) and lastly L₀ from equation (A18). All parameters are now known and we can obtain L(t) from equation (A6).

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/about_us/legal/notices)

Download all slides

Month:	Total Views:
April 2018	8
May 2018	17
June 2018	14
July 2018	8
August 2018	9
September 2018	5
October 2018	6
November 2018	3
December 2018	13
March 2019	2
April 2019	3
May 2019	12
June 2019	5
July 2019	4
August 2019	2
September 2019	1
October 2019	7
November 2019	9
December 2019	3
January 2020	12
March 2020	2
April 2020	2
June 2020	7
July 2020	11
October 2020	3
December 2020	2
March 2021	1
May 2021	1
June 2021	2
July 2021	4
August 2021	1
September 2021	3
October 2021	6
November 2021	3
December 2021	6
January 2022	11
February 2022	11
March 2022	7
April 2022	17
May 2022	6
June 2022	14
July 2022	25
August 2022	24
September 2022	19
October 2022	5
November 2022	14
December 2022	3
January 2023	9
February 2023	6
March 2023	14
April 2023	5
May 2023	5
June 2023	3
July 2023	5
August 2023	14
September 2023	1
October 2023	13
November 2023	10
December 2023	10
January 2024	9
February 2024	6
March 2024	17
April 2024	5
May 2024	9
June 2024	5
July 2024	10
August 2024	11
September 2024	8
October 2024	26
November 2024	8
December 2024	3
January 2025	13
February 2025	2
March 2025	15
April 2025	5
May 2025	2

Article Contents

Spatially dependent modelling of pulsar wind nebula G0.9+0.1

Abstract

1 INTRODUCTION

2 THE MODEL

2.1 The transport equation

2.2 The particle injection spectrum

2.3 Energy losses

2.4 Diffusion

2.5 Bulk particle motion and magnetic field

2.6 Numerical solution to the transport equation

2.7 Boundary conditions

2.8 Radiation spectrum

2.9 Line-of-sight calculation

3 CODE CALIBRATION VIA SED FITS

3.1 Calibration against the model of Venter & de Jager (2007)

3.2 Calibration against the model of Torres et al. (2014)

4 PARAMETER STUDY

4.1 Time evolution (age)

4.2 Magnetic field

4.3 Bulk particle motion

4.4 Injection rate/initial spin-down rate

4.5 Soft-photon fields

4.6 The effect of changing other parameters

5 SPATIALLY DEPENDENT RESULTS FROM OUR PWN MODEL

5.1 Effects of changes in the diffusion coefficient and bulk particle motion on the PWN’s morphology

5.2 Different cases of αV and αB

5.3 Size versus energy fits

6 CONCLUSIONS

Acknowledgements

Footnotes

REFERENCES

APPENDIX

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

5.2 Different cases of α_V and α_B