-
PDF
- Split View
-
Views
-
Cite
Cite
Hiroki Yoneda, Chris Done, Frits Paerels, Tadayuki Takahashi, Shin Watanabe, Search for gravitational redshifted absorption lines in LMXB Serpens X-1, Monthly Notices of the Royal Astronomical Society, Volume 475, Issue 2, April 2018, Pages 2194–2203, https://doi.org/10.1093/mnras/stx3328
Close - Share Icon Share
Abstract
The equation of state for ultradense matter can be tested from observations of the ratio of mass to radius of neutron stars. This could be measured precisely from the redshift of a narrow line produced on the surface. X-rays bursts have been intensively searched for such features, but so far without detection. Here instead we search for redshifted lines in the persistent emission, where the accretion flow dominates over the surface emission. We discuss the requirements for narrow lines to be produced, and show that narrow absorption lines from highly ionized iron can potentially be observable in accreting low-mass X-ray binaries (LMXBs; low B field) that have either low spin or low inclination so that Doppler broadening is small. This selects Serpens X-1 as the only potential candidate persistent LMXB due to its low inclination. Including surface models in the broad-band accretion flow model predicts that the absorption line from He-like iron at 6.7 keV should be redshifted to ∼5.1–5.7 keV (10–15 km for 1.4 M⊙) and have an equivalent width of 0.8–8 eV for surface temperatures of 7–10 × 106 K. We use the high-resolution Chandra grating data to give a firm upper limit of 2–3 eV for an absorption line at ∼5 keV. We discuss possible reasons for this lack of detection (the surface temperature and the geometry of the boundary layer etc.). Future instruments with better sensitivity are required in order to explore the existence of such features.
1 INTRODUCTION
Neutron star (NS) masses and radii are determined by the equation of state (EoS) of dense matter, described by quantum chromodynamics (QCD) at the quark–gluon interaction level. However, this is not a theory that is well understood. Only small portions of the two-dimensional phase space (temperature and chemical potential or equivalently pressure) are satisfactorily described by theory and accessible to experiment. NS cores have mean densities that are much higher than can be produced in current laboratory conditions, 2–8 times larger than the nuclear saturation density. They are also relatively cool and in equilibrium with both strong and weak force (unlike heavy ion collider experiments) and are neutron rich (unlike normal nuclei that are approximately symmetric in neutrons and protons). Thus measuring the macroscopic properties of NSs gives insight into the fundamental QCD interactions in a new regime (e.g. Lattimer 2012).
The most stringent constraints so far come from the firm detection of NSs with masses of ∼2 M⊙ (Demorest et al. 2010; Antoniadis et al. 2013), directly ruling out any EoS that has a maximum mass below this value. This was first thought to exclude a significant contribution of hyperons (Demorest et al. 2010), which is puzzling as they are energetically favourable at high densities. However, more recent calculations of the effect of hyperons show that these were not necessarily inconsistent with the data (e.g. Whittenbury et al. 2014).
Ideally, the full EoS can be traced out from measuring both mass and radius for a sample of NSs of different masses. Some of the best current constraints for this come from thermal emission from the surface of quiescent low-mass X-ray binaries (LMXBs), the cooling tails of thermonuclear bursts, and pulse profile modelling of accreting millisecond pulsars (e.g. the review by Özel & Freire 2016). However, there are multiple caveats for each technique (see e.g. Miller & Lamb 2016), and even the best determinations have uncertainties of the order of 10–20 per cent.
We review the requirements for such absorption line features to be produced, and show that the only feasible persistent source where these might be detected is the LMXB Serpens X-1 (Section 2). We describe the expected features from models of the surface (Section 3), and use these models combined with the Suzaku broad-band data to predict the equivalent width (EW) of the most prominent absorption line, Fe xxv (Section 4). Section 5 shows that these predictions are already challenged by upper limits on this feature from Chandra grating data for a high-temperature surface. We discuss physical implications of our results on the thermal conductivity of NSs and other physical parameters, and conclude by summarizing our results.
2 REQUIREMENTS FOR OBSERVABLE NARROW ABSORPTION LINES FROM THE NEUTRON STAR SURFACE
We follow the discussion in the Astro-H White Paper on Low-mass X-ray Binaries (Done et al. 2014). To see narrow absorption lines from the NS surface require that there are heavy elements in the photosphere, that these are not completely ionized, that the photosphere is not buried beneath an optically thick accretion flow, and that the resulting atomic features are not substantially broadened.
Heavy elements are deposited on to the NS surface by the accretion flow. They are stopped by collisional processes, which are more efficient for higher mass/charge ions. Hence iron and other heavy elements are halted higher up in the photosphere than lower atomic number elements. They can then be destroyed by spallation bombardment (by the still energetic helium and hydrogen ions, transforming the iron nuclei to lower Z elements) or sink under gravity. The deposition and destruction rate both depend linearly on |$\dot{M}$| so the steady state Fe column is around the solar abundance, independent of |$\dot{M}$| for Lx > 6 × 1032 erg s−1 (Bildsten, Chang & Paerels 2003; Chang, Bildsten & Wasserman 2005). Thus there can be iron and other heavy elements in the photosphere of an accreting NS, but not in an isolated or very quiescent NS.
Accreting NSs can have either low- or high-mass companion stars. The NSs in high-mass X-ray binaries are young, and the NSs typically have very high magnetic fields. These broaden any potential atomic features via Zeeman splitting, with ΔE ∼ 12B/(109 G) eV (Loeb 2003). By contrast, the LMXBs typically have low fields with B ≤ 109 G, so narrow atomic features can possibly form in these systems.
The surface of a NS in an LMXB can only be seen if it is not hidden beneath the accretion flow. This depends on the geometry of the accreting material and its optical depth. In the truncated disc/hot accretion flow models, the accretion geometry changes dramatically at the spectral transition between the island and banana branches (see e.g. Done, Gierliński & Kubota 2007; Kajava et al. 2014). At low accretion rates, the accretion flow is hot and quasi-spherical interior to some truncation radius at which the thin disc evaporates (island state). There is additional luminosity from the boundary layer where the flow settles on to the surface, but the flow and boundary layer merge together, forming a single hot (∼30–50 keV), optically thin(ish) (τ ∼ 1.5–2) structure (Medvedev & Narayan 2001). A fraction e−τ of the surface emission should escape without scattering, so ∼10–20 per cent of the intrinsic NS photosphere should be seen directly (see Figs 1a and 1b). The temperature of this surface emission can also be seen imprinted on to the low energy rollover of the Compton spectrum and is only ∼0.5–0.6 keV (e.g. Sakurai et al. 2014). Fig. 2 shows the ion fraction of Fe in the NS atmosphere assuming local thermodynamic equilibrium. At 0.5–0.6 keV, there should be a considerable fraction of iron that is not completely ionized, so atomic features could be seen (Rauch, Suleimanov & Werner 2008) though X-ray irradiation from the optically thin boundary layer could give a more complex photosphere temperature structure.

The geometry of the accretion flow on to the NS surface depending on the accretion rate. L/LEdd is ∼10−4 (a), ∼10−2 (b), ∼0.1 (c), and ∼1 (d) from left to right (Done et al. 2014).
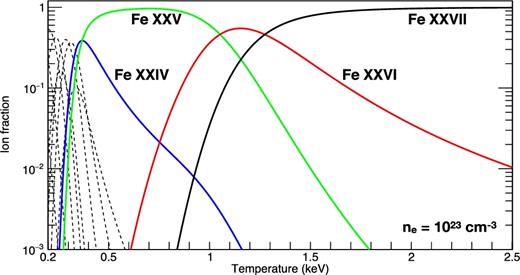
Ion fraction of Fe in the neutron star (NS) atmosphere. The electron density is fixed to 1023 cm−3 that is the typical value in the NS atmosphere (Özel 2013). It is calculated using the Saha equation. We include the effect of pressure ionization by lowering the ionization potential due to Debye shielding.
At higher mass accretion rates (L ≥ 0.1–0.5LEdd), the thin disc extends down to the NS surface, forming a boundary layer where it impacts around the NS equator. The boundary layer is now optically thick (τ ∼ 5–10) so hides the surface beneath it. The boundary layer itself is at the local Eddington temperature of ∼2.5 keV (Revnivtsev, Suleimanov & Poutanen 2013). This is high enough that iron should be almost completely ionized (Fig. 2; Rauch et al. 2008), so no atomic features are expected from the luminous accretion flow. However, the vertical extent of the boundary layer depends on the accretion rate, and it only forms an equatorial belt for L ≲ 0.3LEdd (Suleimanov & Poutanen 2006, Fig. 1c). The pole is uncovered, so this part of the NS surface can be seen directly. It is heated mainly by thermal conduction from the equatorial accretion belt, so its temperature is probably cool enough for H- and He-like iron to exist.
At still higher mass accretion rates, the spreading layer extends up to the pole and the surface is completely covered by the optically thick, completely ionized accretion flow (upper banana branch and Z sources: Fig. 1d). Hence the largest fraction of surface emission should be seen from a pole-on view of a lower banana branch source, where the optically thick accretion flow is confined to an equatorial belt, or in an island state, where the accretion flow covers most of the surface but is optically thin (e.g. Sakurai et al. 2014).
The final requirement is that the atomic features are not broadened by rotation, where ΔE ∼ 1600νspin/(600 Hz)sin i eV (Özel 2013). This is a stringent constraint as typical LMXBs have νspin = 185–650 Hz (Altamirano et al. 2012; Patruno & Watts 2012).
There is one system, Serpens X-1, where optical spectroscopy of the 2 h binary orbit indicates a low inclination, i ≤ 10° (Cornelisse et al. 2013). A low inclination is also consistent with the non-detection of dips in the X-ray light curves, and the lack of any burst oscillations in the X-ray burst light curves (Galloway et al. 2008). This persistent system is always in the soft state (mid banana branch, L/LEdd ∼ 0.5; Chiang et al. 2016a), so the boundary layer should not extend over the pole. Additionally, this is a very bright source ∼300 mCrab. Thus Serpens X-1 is the only currently known persistent source where it may be possible to detect gravitationally redshifted lines from the surface during normal (non-burst) accretion.
3 NEUTRON STAR SURFACE BLACKBODY MODEL
The emission from the hot NS surface should contain atomic features, which depend on the temperature, gravity, and chemical composition of the photosphere. Rauch et al. (2008) show calculations for a NS of a mass of 1.4 M⊙ and a radius of 10 km (i.e. log g = 14.39, redshift parameter z = 0.306) and the solar abundance over the temperature range 1–20 × 106 K (∼0.1–2 keV). The focus of their work was on the claimed detection of iron n = 3–2 absorption lines in EXO 0748−676 (Cottam et al. 2002), but they also show the Fe n = 2–1 absorption lines that are in a simpler part of the spectrum where there is less ambiguity in interpretation. These show that these H- and He-like K shell absorption lines are strongest around surface temperatures of 1 keV as iron is mostly ionized for temperatures above 2 keV (Fig. 2). When the temperature is below 0.3 keV, the luminosity of the surface blackbody is (0.3/1)4, i.e. 100 times weaker so that it is difficult to observe the lines.
The NS surface temperature can be seen in NSs at low mass accretion rates (island state) as it is imprinted on the Comptonized boundary layer emission as the seed photon temperature, and distinctly hotter than the disc photons. Sakurai et al. (2014) show that this is ∼0.5 keV for Aql X-1 in the brighter island states, and similar seed photon temperatures (0.5–0.7 keV) are seen in other NSs in similar states (Gierliński & Done 2002; Di Salvo et al. 2015). Higher temperatures of 1–1.6 keV are seen (again from seed photons) in the higher mass accretion rate (banana branch) states (Oosterbroek et al. 2001; Gierliński & Done 2002; Sakurai et al. 2014; Di Salvo et al. 2015), though these are for the heated surface underneath the boundary layer rather than measuring the temperature at the uncovered pole where the temperature should be somewhat lower. Hence we use two models for the NS with effective temperatures of 7 × 106 and 10 × 106 K (Fig. 3) to explore their predictions for the visibility of the iron absorption line from the surface. These are calculated as in Rauch et al. (2008); Suleimanov, private communication. The spectra are given as intrinsic (unredshifted) surface Eddington flux H(E) = F(E)/4π so we convert these to surface luminosity L(E) = (4πR)2H(E).
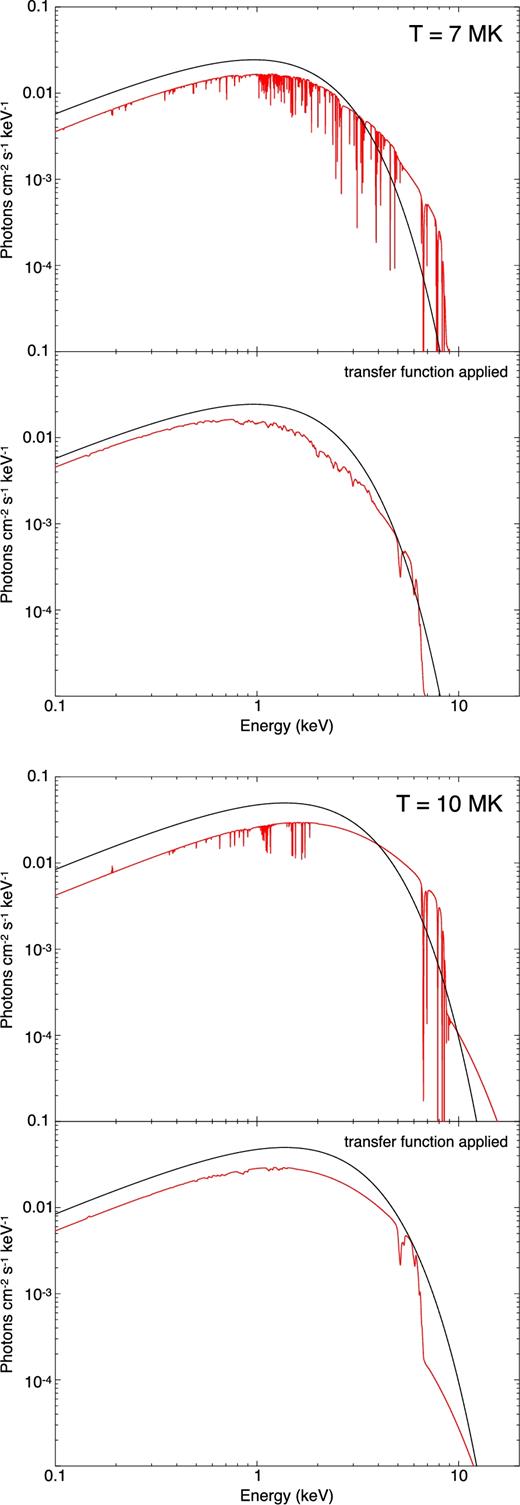
Neutron star atmosphere models with T = 7 × 106 and 10 × 106 K. The red curve in the top is the spectrum without the redshift and the broadening effect. The bottom is the spectrum after the transfer function is applied. The black curves are the blackbody spectra with T = 7 × 106 and 10 × 106 K.
We predict their spectra at infinity using the calculated relativistic transfer functions of Bauböck, Psaltis & Özel (2013). These include the Doppler effects from spin and gravity, so they depend on inclination and spin frequency and surface gravity. We assume the system inclination of 10° together with a typical NS spin frequency of 400 Hz for the same log g as above, so z = 0.307, and convolve the NS spectra with this transfer function (Bauböck, private communication).
4 ESTIMATION OF THE ABSORPTION LINE INTENSITY WITH SUZAKU
4.1 Observations and data reduction
Suzaku observed Serpens X-1 for ∼30 ks on 2006 October 24 (Obs ID: 401048010). The observation of X-ray Imaging Spectrometer (XIS)/Suzaku was taken in 1/4 window with 1 s burst clock mode at the XIS nominal pointing position. We correct the images by using aeattcor2 in the HEAsoft package. The CCD data are still affected by pile-up (Yamada et al. 2012), so we remove the data from a circle of radius 60 pixels centred on the brightest pixel, corresponding to a 3 per cent pile-up fraction. We sum XIS0, XIS2, and XIS3 using addascaspec in the HEAsoft package and reprocessed HXD PIN data following the standard analysis procedure and adopted ae_hxd_pinxinome3_20080129.rsp as the response file. The non-X-ray background is estimated following the standard analysis thread described in The Suzaku Data Reduction Guide and the cosmic X-ray background is ignored because the source is very bright. The spectra were rebinned so that each bin contains more than 20 counts.
We used xspec version 12.9.0 to fit the spectra. The fitting was performed from 1.0 to 9.0 keV in the XIS and from 15.0 to 20.0 keV in the HXD PIN. The region from 1.5 to 2.5 keV was ignored due to the large calibration uncertainties coming from the instrumental edges. We set the normalization of PIN data relative to XIS data as a free parameter. The best-fitting values of it are consistent with the value (1.16) in The Suzaku Data Reduction Guide in the ∼1σ confidence level (Tables 1 and 2).
Best-fitting parameters for kerrbb+nthcomp without the surface blackbody models using Suzaku spectrum.
| Component . | Parameter . | . |
|---|---|---|
| tbnew_gas | NH (1022 cm−2) | (0.44) |
| kerrbb | η | (0.0) |
| a | (0.2) | |
| i (° ) | (10.0) | |
| Mbh (M⊙) | (1.4) | |
| Mdd (1018 g/s) | |$0.637_{-0.009}^{+0.010}$| | |
| Dbh (kpc) | (10.0) | |
| hd | |$1.653_{-0.019}^{+0.019}$| | |
| rflag | (1.0) | |
| lflag | (0.0) | |
| norm | (1.0) | |
| nthcomp | Gamma | |$6.3_{-3.3}^{+0.3}$| |
| kTe (keV) | >3.1 | |
| kTbb (keV) | |$1.76_{-0.14}^{+0.03}$| | |
| Ldisc/LBL | |$0.943_{-0.029}^{+0.022}$| | |
| Gaussian | Line E (keV) | |$6.656_{-0.031}^{+0.031}$| |
| σ (keV) | |$0.233_{-0.036}^{+0.040}$| | |
| norm (10−3) | |$2.58_{-0.33}^{+0.36}$| | |
| constant (HXD PIN) | |$1.205_{-0.044}^{+0.045}$| | |
| χ2/dof | 2097.5/1918 |
| Component . | Parameter . | . |
|---|---|---|
| tbnew_gas | NH (1022 cm−2) | (0.44) |
| kerrbb | η | (0.0) |
| a | (0.2) | |
| i (° ) | (10.0) | |
| Mbh (M⊙) | (1.4) | |
| Mdd (1018 g/s) | |$0.637_{-0.009}^{+0.010}$| | |
| Dbh (kpc) | (10.0) | |
| hd | |$1.653_{-0.019}^{+0.019}$| | |
| rflag | (1.0) | |
| lflag | (0.0) | |
| norm | (1.0) | |
| nthcomp | Gamma | |$6.3_{-3.3}^{+0.3}$| |
| kTe (keV) | >3.1 | |
| kTbb (keV) | |$1.76_{-0.14}^{+0.03}$| | |
| Ldisc/LBL | |$0.943_{-0.029}^{+0.022}$| | |
| Gaussian | Line E (keV) | |$6.656_{-0.031}^{+0.031}$| |
| σ (keV) | |$0.233_{-0.036}^{+0.040}$| | |
| norm (10−3) | |$2.58_{-0.33}^{+0.36}$| | |
| constant (HXD PIN) | |$1.205_{-0.044}^{+0.045}$| | |
| χ2/dof | 2097.5/1918 |
Best-fitting parameters for kerrbb+nthcomp without the surface blackbody models using Suzaku spectrum.
| Component . | Parameter . | . |
|---|---|---|
| tbnew_gas | NH (1022 cm−2) | (0.44) |
| kerrbb | η | (0.0) |
| a | (0.2) | |
| i (° ) | (10.0) | |
| Mbh (M⊙) | (1.4) | |
| Mdd (1018 g/s) | |$0.637_{-0.009}^{+0.010}$| | |
| Dbh (kpc) | (10.0) | |
| hd | |$1.653_{-0.019}^{+0.019}$| | |
| rflag | (1.0) | |
| lflag | (0.0) | |
| norm | (1.0) | |
| nthcomp | Gamma | |$6.3_{-3.3}^{+0.3}$| |
| kTe (keV) | >3.1 | |
| kTbb (keV) | |$1.76_{-0.14}^{+0.03}$| | |
| Ldisc/LBL | |$0.943_{-0.029}^{+0.022}$| | |
| Gaussian | Line E (keV) | |$6.656_{-0.031}^{+0.031}$| |
| σ (keV) | |$0.233_{-0.036}^{+0.040}$| | |
| norm (10−3) | |$2.58_{-0.33}^{+0.36}$| | |
| constant (HXD PIN) | |$1.205_{-0.044}^{+0.045}$| | |
| χ2/dof | 2097.5/1918 |
| Component . | Parameter . | . |
|---|---|---|
| tbnew_gas | NH (1022 cm−2) | (0.44) |
| kerrbb | η | (0.0) |
| a | (0.2) | |
| i (° ) | (10.0) | |
| Mbh (M⊙) | (1.4) | |
| Mdd (1018 g/s) | |$0.637_{-0.009}^{+0.010}$| | |
| Dbh (kpc) | (10.0) | |
| hd | |$1.653_{-0.019}^{+0.019}$| | |
| rflag | (1.0) | |
| lflag | (0.0) | |
| norm | (1.0) | |
| nthcomp | Gamma | |$6.3_{-3.3}^{+0.3}$| |
| kTe (keV) | >3.1 | |
| kTbb (keV) | |$1.76_{-0.14}^{+0.03}$| | |
| Ldisc/LBL | |$0.943_{-0.029}^{+0.022}$| | |
| Gaussian | Line E (keV) | |$6.656_{-0.031}^{+0.031}$| |
| σ (keV) | |$0.233_{-0.036}^{+0.040}$| | |
| norm (10−3) | |$2.58_{-0.33}^{+0.36}$| | |
| constant (HXD PIN) | |$1.205_{-0.044}^{+0.045}$| | |
| χ2/dof | 2097.5/1918 |
Best-fitting parameters for kerrbb+nthcomp with the surface blackbody models using Suzaku spectrum. NH is 4.4 × 1021 cm−2 (fixed).
| . | . | Surface temperature . | |
|---|---|---|---|
| Component . | Parameter . | 7 × 106 K . | 10 × 106 K . |
| kerrbb | Mdd (1018 g s−1) | |$0.620_{-0.010}^{+0.010}$| | |$0.592_{-0.007}^{+0.008}$| |
| hd | |$1.651_{-0.020}^{+0.020}$| | |$1.601_{-0.015}^{+0.017}$| | |
| nthcomp | Gamma | |$6.2_{-3.3}^{+0.3}$| | |$6.4_{-3.3}^{+0.4}$| |
| kTe (keV) | >3.0 | >3.2 | |
| kTbb (keV) | |$1.75_{-0.15}^{+0.03}$| | |$1.79_{-0.11}^{+0.03}$| | |
| Ldisc/LBL | |$0.913_{-0.028}^{+0.029}$| | |$0.870_{-0.020}^{+0.023}$| | |
| Gaussian | Line E (keV) | |$6.657_{-0.032}^{+0.030}$| | |$6.675_{-0.023}^{+0.023}$| |
| σ (keV) | |$0.233_{-0.036}^{+0.039}$| | |$0.244_{-0.027}^{+0.029}$| | |
| norm (10−3) | |$2.62_{-0.33}^{+0.35}$| | |$3.43_{-0.33}^{+0.35}$| | |
| constant (HXD PIN) | |$1.208_{-0.044}^{+0.045}$| | |$1.16_{-0.041}^{+0.043}$| | |
| χ2/dof | 2080.5/1918 | 2131.4/1918 | |
| . | . | Surface temperature . | |
|---|---|---|---|
| Component . | Parameter . | 7 × 106 K . | 10 × 106 K . |
| kerrbb | Mdd (1018 g s−1) | |$0.620_{-0.010}^{+0.010}$| | |$0.592_{-0.007}^{+0.008}$| |
| hd | |$1.651_{-0.020}^{+0.020}$| | |$1.601_{-0.015}^{+0.017}$| | |
| nthcomp | Gamma | |$6.2_{-3.3}^{+0.3}$| | |$6.4_{-3.3}^{+0.4}$| |
| kTe (keV) | >3.0 | >3.2 | |
| kTbb (keV) | |$1.75_{-0.15}^{+0.03}$| | |$1.79_{-0.11}^{+0.03}$| | |
| Ldisc/LBL | |$0.913_{-0.028}^{+0.029}$| | |$0.870_{-0.020}^{+0.023}$| | |
| Gaussian | Line E (keV) | |$6.657_{-0.032}^{+0.030}$| | |$6.675_{-0.023}^{+0.023}$| |
| σ (keV) | |$0.233_{-0.036}^{+0.039}$| | |$0.244_{-0.027}^{+0.029}$| | |
| norm (10−3) | |$2.62_{-0.33}^{+0.35}$| | |$3.43_{-0.33}^{+0.35}$| | |
| constant (HXD PIN) | |$1.208_{-0.044}^{+0.045}$| | |$1.16_{-0.041}^{+0.043}$| | |
| χ2/dof | 2080.5/1918 | 2131.4/1918 | |
Best-fitting parameters for kerrbb+nthcomp with the surface blackbody models using Suzaku spectrum. NH is 4.4 × 1021 cm−2 (fixed).
| . | . | Surface temperature . | |
|---|---|---|---|
| Component . | Parameter . | 7 × 106 K . | 10 × 106 K . |
| kerrbb | Mdd (1018 g s−1) | |$0.620_{-0.010}^{+0.010}$| | |$0.592_{-0.007}^{+0.008}$| |
| hd | |$1.651_{-0.020}^{+0.020}$| | |$1.601_{-0.015}^{+0.017}$| | |
| nthcomp | Gamma | |$6.2_{-3.3}^{+0.3}$| | |$6.4_{-3.3}^{+0.4}$| |
| kTe (keV) | >3.0 | >3.2 | |
| kTbb (keV) | |$1.75_{-0.15}^{+0.03}$| | |$1.79_{-0.11}^{+0.03}$| | |
| Ldisc/LBL | |$0.913_{-0.028}^{+0.029}$| | |$0.870_{-0.020}^{+0.023}$| | |
| Gaussian | Line E (keV) | |$6.657_{-0.032}^{+0.030}$| | |$6.675_{-0.023}^{+0.023}$| |
| σ (keV) | |$0.233_{-0.036}^{+0.039}$| | |$0.244_{-0.027}^{+0.029}$| | |
| norm (10−3) | |$2.62_{-0.33}^{+0.35}$| | |$3.43_{-0.33}^{+0.35}$| | |
| constant (HXD PIN) | |$1.208_{-0.044}^{+0.045}$| | |$1.16_{-0.041}^{+0.043}$| | |
| χ2/dof | 2080.5/1918 | 2131.4/1918 | |
| . | . | Surface temperature . | |
|---|---|---|---|
| Component . | Parameter . | 7 × 106 K . | 10 × 106 K . |
| kerrbb | Mdd (1018 g s−1) | |$0.620_{-0.010}^{+0.010}$| | |$0.592_{-0.007}^{+0.008}$| |
| hd | |$1.651_{-0.020}^{+0.020}$| | |$1.601_{-0.015}^{+0.017}$| | |
| nthcomp | Gamma | |$6.2_{-3.3}^{+0.3}$| | |$6.4_{-3.3}^{+0.4}$| |
| kTe (keV) | >3.0 | >3.2 | |
| kTbb (keV) | |$1.75_{-0.15}^{+0.03}$| | |$1.79_{-0.11}^{+0.03}$| | |
| Ldisc/LBL | |$0.913_{-0.028}^{+0.029}$| | |$0.870_{-0.020}^{+0.023}$| | |
| Gaussian | Line E (keV) | |$6.657_{-0.032}^{+0.030}$| | |$6.675_{-0.023}^{+0.023}$| |
| σ (keV) | |$0.233_{-0.036}^{+0.039}$| | |$0.244_{-0.027}^{+0.029}$| | |
| norm (10−3) | |$2.62_{-0.33}^{+0.35}$| | |$3.43_{-0.33}^{+0.35}$| | |
| constant (HXD PIN) | |$1.208_{-0.044}^{+0.045}$| | |$1.16_{-0.041}^{+0.043}$| | |
| χ2/dof | 2080.5/1918 | 2131.4/1918 | |
We assumed a neutral hydrogen column density as 4.4 × 1021 cm−2 (Dickey & Lockman 1990) via the tbnew_gas model that is a new and improved version of the X-ray absorption model tbabs (Wilms, Allen & McCray 2000) and set the photoelectric absorption cross-sections as ‘vern’ and the metal abundances as ‘wilm’. Errors in this paper are given at 90 per cent confidence level unless otherwise stated.
4.2 Identification of the spectral components
We fit the spectrum with a continuum model consisting of a disc and Comptonized boundary layer (Fig. 4). There is considerable spectral degeneracy in decomposing a broadly curving continuum into two smoothly curving components (e.g. Done, Życki & Smith 2002; Revnivtsev & Gilfanov 2006), so we use the best physical models for the emission. We describe the disc by the kerrbb model (Li et al. 2005) that includes relativistic smearing of the sum of colour temperature corrected blackbody components with luminosity given by the fully relativistic emissivity. We fix the inclination angle of 10° (Cornelisse et al. 2013) and the mass of 1.4 M⊙ and assume a distance of 10 kpc (the X = 0 limit from type 1 X-ray burst observations; Galloway et al. 2008). We describe the Comptonization using the nthcomp model (Zdziarski, Johnson & Magdziarz 1996). This should produce a reflection component from illumination of the disc, but this can be complex (Bhattacharyya & Strohmayer 2007; Cackett et al. 2008; Miller et al. 2013; Chiang et al. 2016a,b; Matranga et al. 2017). Here our focus is to describe the continuum shape for a simulation of the narrow redshifted absorption lines, so we simply use a Gaussian emission line to fit the data. The resulting parameters are shown in Table 1.
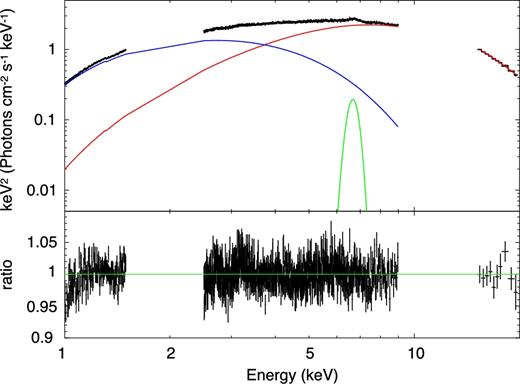
Unfolded Suzaku spectrum with kerrbb+nthcomp without the surface blackbody models. The blue curve is kerrbb, the red one is nthcomp, and the green one is Gaussian for the iron line.
While the temperature of electrons in the boundary layer, Te(>3.1 keV) is poorly constrained due to the lack of data in high-energy band, the temperature of the surface beneath it, |$T_{\mathrm{BL}} (=1.76_{-0.14}^{+0.03}\,\mathrm{keV})$|, is close to those derived for the boundary layer in similarly bright LMXBs spectra by Revnivtsev & Gilfanov (2006), where they break the spectral degeneracies by Fourier resolved spectroscopy. Thus our spectral decomposition appears reasonable.
The luminosity ratio of the disc emission to the boundary layer emission is |$0.943_{-0.029}^{+0.022}$|. This potentially already provides some constraints on the EoS modulo NS spin (Sibgatullin & Sunyaev 2000). The boundary layer dissipates the remaining kinetic power of the accretion flow, which will depend on the difference in spin frequency between the disc inner edge and the surface. However, it also depends on the EoS, especially where the NS is smaller than the radius of the last stable circular orbit as the boundary layer luminosity is enhanced by the additional kinetic energy of the radially plunging material. The calculations of Sibgatullin & Sunyaev (2000, their fig. 1) give a spin of 540 Hz for a luminosity ratio of 0.943 with their assumed EoS (R = 11.3 km for a 1.4 M⊙ NS). This is a reasonable spin frequency, but it is probably overestimated as our models for the boundary layer luminosity neglected the reflection continuum.
The expected efficiency of accretion is ∼0.14 (fig. 1 of Sibgatullin & Sunyaev 2000). Combining this with the mass accretion rate through the disc of 0.64 × 1018 g s−1 (Table 1) gives a total luminosity that is ∼ 45 per cent of the Eddington mass accretion rate for a 1.4 M⊙ NS. The total absorption-corrected bolometric flux from the data is instead 1.0 × 10−8 erg cm−2 s−1, giving a luminosity of 1.2 × 1038 erg s−1 for the assumed distance of 10 kpc, which is ∼ 70 per cent of the Eddington luminosity. This discrepancy is less than a factor of 2, but could indicate either that the distance is 7.7 kpc, as derived from assuming the solar abundance for the X-ray bursts (Galloway et al. 2008), or that the EoS is different to that assumed in Sibgatullin & Sunyaev (2000).
4.3 Estimation of the equivalent width of the iron absorption line
We add each of the two different temperature surface spectra described in Section 3 to the emission model derived above. This is the maximum possible contribution from the surface, as it assumes that the entire star is directly visible rather than being partly covered by the boundary layer and partly obscured by the disc. However, these effects are minimized for a pole on view so this represents a reasonable contribution of the surface emission for Serpens X-1. The results are shown in Table 2 and Fig. 5. The luminosity of the surface blackbody for the 7 × 106 and 10 × 106 K models is 0.8 and 3.3 per cent of the total luminosity, respectively, so its inclusion makes a difference in the best-fitting continuum parameters. This is most marked for the disc, as the shape of the surface emission overlaps most with this component, so its inclusion reduces the mass accretion rate and Ldisc/LBL.
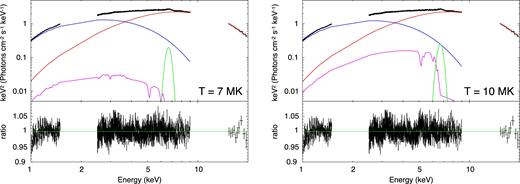
Unfolded Suzaku spectrum with kerrbb+nthcomp with the surface blackbody models. The magenta is the surface model and the blue curve is kerrbb, the red one is nthcomp, and the green one is Gaussian for the iron line. The effective temperature of the surface is 7 × 106 K in the left-hand figure and 10 × 106 K in the right-hand figure.
We use these models to determine the EW of the iron absorption lines from the surface against the brighter continuum emission from the accretion flow. We used fakeit command in xspec without errors to produce a model spectrum on a dummy (diagonal) response matrix from 1 to 15 keV with energy resolution of 1 eV. We then fit this over the very restricted energy range of 4.7–5.7 keV with a powerlaw+Gaussian+Gaussian model. A single Gaussian is a good representation of the multiple n = 2–1 transitions in each ion state as the substructure is blended due to the Doppler shifts (see Section 3). Table 3 shows the resulting equivalent and intrinsic widths. The intrinsic width is higher for the Fe xxv as there is a larger energy range between the multiple transitions (forbidden, intercombination, and resonance) than for Fe xxvi (just spin–orbit splitting). Both lines increase in EW for higher temperature, as the contribution of the surface emission increases, but Fe xxv always has higher EW than Fe xxvi, from 0.8 to 7.7 eV as the temperature increases from 7 × 106 to 10 × 106 K. In the next section, we search the higher resolution Chandra transmission grating data for the absorption lines, and compare the result with these model predictions.
Estimation of the equivalent width of the iron absorption line with different surface temperatures.
| . | Effective temperature . | EW (eV) . | Energy (keV) . | σ (eV) . |
|---|---|---|---|---|
| Fe xxvx + y, w, z | 7 × 106 K | 0.76 | 5.11 | 83 |
| Fe xxvi Lyα | 0.05 | 5.35 | 39 | |
| Fe xxvx + y, w, z | 10 × 106 K | 7.7 | 5.12 | 86 |
| Fe xxvi Lyα | 2.0 | 5.35 | 53 |
| . | Effective temperature . | EW (eV) . | Energy (keV) . | σ (eV) . |
|---|---|---|---|---|
| Fe xxvx + y, w, z | 7 × 106 K | 0.76 | 5.11 | 83 |
| Fe xxvi Lyα | 0.05 | 5.35 | 39 | |
| Fe xxvx + y, w, z | 10 × 106 K | 7.7 | 5.12 | 86 |
| Fe xxvi Lyα | 2.0 | 5.35 | 53 |
Estimation of the equivalent width of the iron absorption line with different surface temperatures.
| . | Effective temperature . | EW (eV) . | Energy (keV) . | σ (eV) . |
|---|---|---|---|---|
| Fe xxvx + y, w, z | 7 × 106 K | 0.76 | 5.11 | 83 |
| Fe xxvi Lyα | 0.05 | 5.35 | 39 | |
| Fe xxvx + y, w, z | 10 × 106 K | 7.7 | 5.12 | 86 |
| Fe xxvi Lyα | 2.0 | 5.35 | 53 |
| . | Effective temperature . | EW (eV) . | Energy (keV) . | σ (eV) . |
|---|---|---|---|---|
| Fe xxvx + y, w, z | 7 × 106 K | 0.76 | 5.11 | 83 |
| Fe xxvi Lyα | 0.05 | 5.35 | 39 | |
| Fe xxvx + y, w, z | 10 × 106 K | 7.7 | 5.12 | 86 |
| Fe xxvi Lyα | 2.0 | 5.35 | 53 |
5 LINE SEARCH WITH CHANDRA
5.1 Observations and data reduction
Chandra observed Serpens X-1 with the High Energy Transmission Grating Spectrometer (HETGS) twice on 2014 June 27–29 and August 25–26 (Obs ID: 16208, 16209) each with ∼150 ks exposure. These data were taken in continuous clocking (CC) mode in which the data are transferred every 2.85 ms in order to avoid pile-up. The HETG consists of two sets of gratings, the Medium Energy Grating (MEG) and the High Energy Gratings (HEG; Canizares et al. 2005). The two gratings have different grating periods, 4001.41 Å in MEG and 2000.81 Å in HEG. Since the MEG's grating period is almost exactly twice as long as the HEG's, the scattering angle for the Nth order HEG is very close to that of 2Nth order MEG. The alignment angles for MEG and HEG are very similar (−5|$_{.}^{\circ}$|19 in HEG and 4|$_{.}^{\circ}$|74 in MEG), so the position along the X-axis of the Nth order HEG and 2Nth order MEG is almost the same as each other.
In the standard [timed exposure (TE)] mode, the full imaging is retained, and the MEG and HEG grating orders are separated in Y- and X-axis values and so do not overlap. However, in CC mode, the information about the position in the columns (CHIPY) is lost because events are read out continuously and the frame image is collapsed into one row. Thus the Nth order HEG and 2Nth order MEG overlap. Normally, in order to avoid this, the source point is placed with a Y-axis offset from the centre of the chip so that the MEG positive order and HEG negative order (or MEG negative order and HEG positive order) are excluded from the chips. However, in our data set, the source point is set at the centre of the Y-axis, so MEG±2 are intermixed with HEG±1 and the response files (which assume HEG and MEG are separated) are not appropriate. Hence we use only MEG±1 in our analysis. The MEG effective area is comparable to that of the HEG at 5 keV, so this is not a big loss of signal (see Fig. 6).
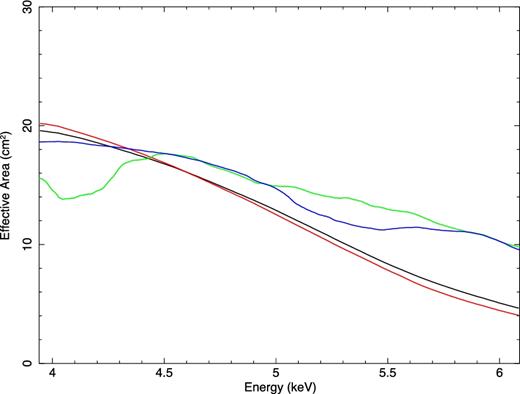
Chandra HETG effective areas. The black curve is MEG−1, the red one is MEG+1, the green one is HEG−1, and the blue one is HEG+1.
We processed the data using chandra_repro command in ciao v4.8 software package and combined data from both observations to produce spectra for MEG+1 and MEG−1 (there are no MEG±2 data from this tool due to the overlap with HEG±1 discussed above). There is one weak type I burst during the observations, but we did not exclude it because it contributes only ∼0.5 per cent of the total counts (Chiang et al. 2016a). We fixed the hydrogen column density, photoelectric absorption cross-sections, and the metal abundances, as for the Suzaku analysis.
5.2 Method of absorption line search
We do a blind search on the Chandra MEG±1 data. The target of the search is the combination of Fe xxvx + y, w, z (6.7 keV) since it is the strongest absorption feature in the NS atmosphere model over the expected temperature range. We set the range of search redshift as z = 0.1–0.7, corresponding to an energy for Fe xxv of 6.09–3.94 keV (though the most likely range of NS radii is 10–15 km, i.e. z = 0.31–0.17). No discrete structures are seen in the MEG±1 effective areas in this range (Fig. 6).
We fit the MEG±1 spectra separately with separate powerlaw models from 3.90 to 6.13 keV (i.e. extended by 0.04 keV from the central energy range so that the line would be fully resolved by the data even at the edge of the redshift range). This adequately describes the continuum over this narrow energy range (see Fig. 7). We save the parameters of the best-fitting model and the chi-squared values (|$\chi ^2_0$|). The parameters are not tied between the two spectra as there are differences of a few per cent in the flux. This is considered to be due to the scattering halo effect or clocking background that is associated with CC-mode (Schulz 2014). They do not affect the structure of the absorption line because they make the continuous background. Thus they are of no significance in this analysis.
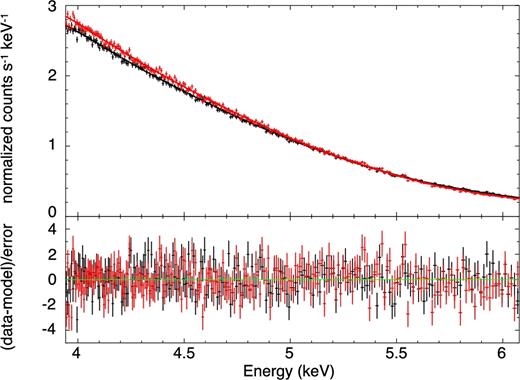
Chandra MEG±1 count rate spectrum and the best-fitting continuum model. The black curve is MEG−1 and the red one is MEG+1.
We fix the power-law continuum and add in a Gaussian line, parametrized by the centre energy (E), standard deviation (σ), and equivalent width (EW). We fix σ at 80 eV (see Table 3) and vary E from 3.94 to 6.09 keV in steps of 0.01 keV (much smaller than the expected intrinsic width of the line of 0.08 keV). Thus the only free parameter in the fitting is the EW, which can be either negative or positive, corresponding to absorption and emission lines, respectively. We calculate the difference of the chi-squared values from |$\chi ^2_0$| and save it (Δχ2(E)) together with the EW of the best-fitting model (EW(E)).
We determine the 3σ confidence limit on the detection of a line, i.e. find the Δχ2 that corresponds to a probability of 0.0027 of getting a false positive. This is not straightforward due to the multiple energies searched. We approach this in two different ways. First, we simulate MEG±1 spectra from a simple powerlaw continuum. We fit these with powerlaw+Gaussian stepping the centre energy of the Gaussian over the same energy range as for the real data. We repeat this 10 000 times and rank the resulting Δχ2(E), picking the 27th highest (as 10 000 × 0.0027 is 27). This gives |$\Delta \chi ^2_{3\sigma } = 15.12$|.
We use the same simulations as before and find 〈N(c0)〉 = 4.42. This implies |$\Delta \chi ^2_{3\sigma }=15.37$|, very similar to the standard simulation result. Hereafter this value is used for the blind search because the first result has a relatively large Poisson error ∼0.3.
5.3 Results of absorption line search
The maximum observed value of Δχ2(E) is 5.41 (upper panel in Fig. 8). This is substantially smaller than the value of 15.37 derived above for a 3σ detection. Therefore we did not find any absorption lines at the 3σ confidence level. The 3σ upper limit of the EW was found at each energy by increasing the intensity until Δχ2(E) = 15.37 was reached. These are plotted in the lower panel of Fig. 8. The decrease in effective area at higher energies means that this upper limit on any absorption line goes from −8 eV for z = 0.1 to ∼−2 eV for z ≥ 0.3. However, there are broad features present that probably indicate residual continuum curvature that is not well modelled by the assumed power law. A more accurate measure of the upper limit of the line with respect to a more complex continuum is half the difference between the upper and lower limit to EW. This gives ∼−6, −4, −3, −1.5 eV at z = 0.1, 0.2, 0.3, 0.7.
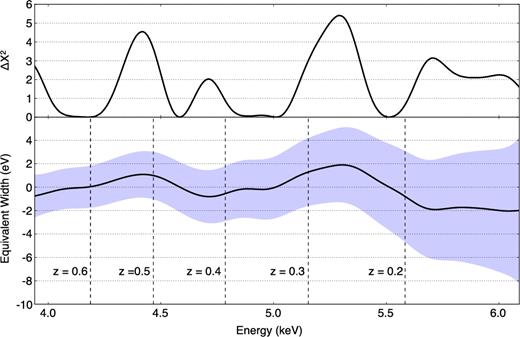
Top: Δχ2 at different line energy in the search range. Bottom: best-fitting value of the equivalent width (the black solid line) and 3σ upper limit of it.
The upper limit from the Chandra data is −3 eV at ∼5.1 keV. This rules out an absorption line at ∼5.1 keV with an EW as large as 7.7 eV as predicted by the 10 × 106 K surface model. It is instead consistent with the predicted absorption line EW of 0.8 eV for the lower surface temperature of 7 × 106 K. We simulated this photosphere model through the Chandra response using the fakeit command, and estimate that such a line could be detected at the 3σ confidence level with a 3–4 Ms exposure.
6 DISCUSSION
The Chandra data clearly show that either the NS surface temperature is lower than 10 × 106 K or some other mechanism suppresses the absorption line. We first assess the expected surface temperature, and then examine the other assumptions that determine the absorption line strength.
6.1 Surface temperature
We measured the surface temperature beneath the boundary layer as ∼1.7 keV from the seed photon energy of the Comptonization component in the broad-band Suzaku data (Table 1). However the temperature at the pole is not necessarily the same. The equator is illuminated by the boundary layer and subject to ram pressure heating, whereas the pole is largely unaffected by these. Instead, the pole is heated by thermal conduction from the equator and from the interior of the star (though this is probably negligible in comparison).
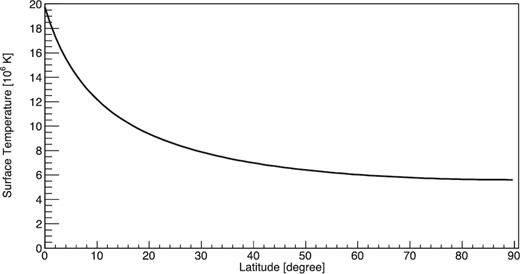
Thermal distribution along the latitude. We set T0 as 1.7 keV and κ as 1023 erg cm−1 K−1 s−1.
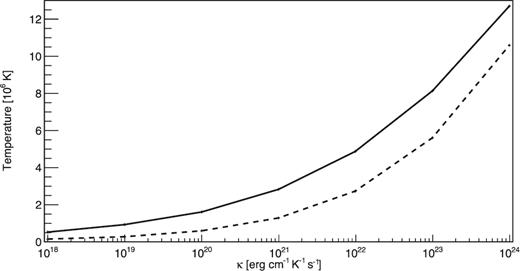
Dependence of the surface temperature on κ: the solid line is the temperature averaged over the surface, Tave. The dashed line is the temperature at the pole, Tθ = 0. The range of κ is derived from Geppert et al. (2004).
These low temperatures are very close to the temperatures observed for the NS surface cooling after a transient accretion episode (Heinke 2013; Degenaar et al. 2015). This emission is powered by deep crustal heating by pycnonuclear reactions during accretion, and sets a lower limit to the temperature of the pole even when thermal conductivity is low. This points to the need for more sophisticated calculations that include the energy exchanged with the inner part of the star. Nonetheless, it appears feasible that the surface temperature of the NS surface near the pole is less than 7 × 106 K and so produces an Fe xxv absorption line EW that is less than 1 eV, undetectable with current data. However, there are other possible issues that could suppress the line EW. We explore them below.
6.2 Uncovered surface area and metallicity
The disc accretion on to the NS surface terminates in a boundary layer, where the deceleration takes place in an equatorial belt with meridional extent set by the mass accretion rate (Inogamov & Sunyaev 1999). The boundary layer is optically thick, so shields the surface from view, and is hot enough that iron should be completely ionized so it produces no atomic features. The extent of the boundary layer depends on mass accretion rate, and for the 0.3–0.6LEdd (distance of 7.7–10 kpc) derived for Serpens X-1 in Section 4, the accretion belt will cover around half of the visible NS surface. This will halve the predicted line EW for a given temperature, but a surface as hot as 107 K would still be marginally inconsistent with the Chandra upper limits for a 10–13 km NS. However, the geometry of the boundary layer also depends on other physical parameters. For example, in the case that the disc thickness on the NS surface is relatively thick, the boundary layer can reach the pole if LBL > 0.25–0.4LEdd (Suleimanov & Poutanen 2006). Thus we cannot rule out the possibility that the NS surface is totally covered by the optically thick corona.
The extent of the boundary layer also determines the metallicity of the photosphere at the pole. Heavy metals sink on a time-scale of ∼10 s due to the strong gravity of the NS (Bildsten et al. 2003), but even low levels of accretion are sufficient to replenish iron in the photosphere (Özel 2013). The meridional structure of the boundary layer means that the deposition of fresh material takes place in the equatorial belt rather than at the pole. Hence it is possible that there is an abundance gradient with polar angle, with the pole being mostly hydrogen while the metals are confined to the hot boundary layer. This anticorrelation of metallicity with ‘bare’ (uncovered by the boundary layer) NS surface would mean that no iron absorption lines could be seen whatever the polar temperature. However, the amount of accretion required to replenish the photosphere is very small, and the maximum polar angle extent of the boundary layer is not sharp. There is a ‘dark layer’ of material beyond the bright boundary layer that extends closer towards the poles, especially for the fairly high accretion rates considered here (Inogamov & Sunyaev 1999), so it seems unlikely that metals are absent from the surface.
6.3 Boundary layer illumination of atmosphere
The model atmosphere calculations in Section 3 assume that there is no additional heating from illumination. Plainly the boundary layer will illuminate the surface at the pole to some extent, though the equatorial belt geometry means that only a small fraction of the boundary layer flux will be intercepted by the polar regions. While this could contribute to heating the surface, increasing the expected absorption line depth, irradiation can produce a temperature inversion that switches the line into emission. There are no current calculations of this effect, but we note that our Chandra upper limits are equally stringent for emission as for absorption.
6.4 Inclination offset and spin frequency
The binary inclination is small, ∼10° (Cornelisse et al. 2013), but the NS spin axis could be misaligned from the binary orbit due to the supernovae kick at its formation (Brandt & Podsiadlowski 1995). This leads to both misalignment of the spin and orbit, and high orbital eccentricity but both of these are removed by tidal forces, often before the companion fills its Roche lobe and the system becomes an LMXB (Hut 1981). Thus the NS spin in Serpens X-1 should be aligned with the binary orbit, and the binary orbit inclination is low (Cornelisse et al. 2013). However, measurements of the inclination from sophisticated fitting of the reflected signature from the boundary layer illumination of the accretion disc give a significantly larger value, i ∼ 27° (Matranga et al. 2017), which would be sufficient to broaden the line beyond detectability as a narrow feature. Inclination is difficult to measure precisely by reflection, as it depends on the spectral modelling (compare to Miller et al. 2013 who used less physical models but derived i ∼ 9° from the same data). We conclude that the inclination angle to the NS spin axis is most likely low, so this is not the origin of the loss of narrow line.
The spin frequency of Serpens X-1 has not been detected. In our model prediction, we assume that it is 400 Hz. This is a typical value in observed LMXBs (Altamirano et al. 2012; Patruno & Watts 2012). In the spectral analysis in Section 4.2, the spin frequency is estimated as ∼500 Hz using the luminosity ratio of the disc emission to the boundary layer emission, and it is consistent with that of LMXBs. However if this object is a peculiar source and the spin frequency is over than ∼1 kHz, the absorption lines would be totally broadened.
7 CONCLUSIONS
We show that atomic features from highly ionized iron are potentially observable in the persistent (non-burst) emission of accreting LMXB for low-inclination or low-spin NSs. Serpens X-1 is the only known non-transient system that fulfils these constraints, having low orbital inclination. This is on the middle banana branch, so the accretion flow geometry is probably an accretion disc that forms a boundary layer around the NS equator, leaving the polar surface directly visible. We use the Suzaku broad-band data to model the continuum emission, and then use this as a baseline to add in the predicted surface emission. We model this for two temperatures that span a reasonable range for the polar surface of 7–10 × 106 K. These predict an absorption line from Fe xxv Kα with EW of 0.8–8 eV for a completely equatorial boundary layer, or 0.4–4 eV if the boundary layer covers half of the NS surface. We search for this line in existing Chandra grating data, and find an upper limit of 2–3 eV. We discuss potential reasons for this non-detection (the surface temperature, the geometry of the boundary layer, the metallicity in the atmosphere, the inclination angle, and the spin frequency of the star). Our conclusion is that the line is likely there at the level of 1 eV, a combination of the boundary layer obscuring half of the surface, and the polar temperature being lower than 10 × 106 K. However, to detect such a line at 3σ confidence would require 3–4 Ms exposure time with the Chandra gratings. Thus it is unlikely that current instrumentation can obtain substantially better constraints. The effective area of X-ray Astronomy Recovery Mission (XARM; the Hitomi recovery mission) is ∼10 times as large as that of Chandra around 5 keV, so the line could be detected at 3σ confidence in ∼300 ks. The future X-ray mission Athena has a much larger effective area (fig. 4 in Barret et al. 2013), so should be able to constrain such a small EW with an observation of around 2 × 104 s. The potential of such future observations motivates more theoretical work on the NS surface emission (including a two-dimensional analysis of the temperature, abundances, and effect of illumination) in order to obtain a better understanding of the expected features.
Acknowledgements
The authors would like to express their thanks to V. Suleimanov and M. Bauböck for making their available to us, and K. Ishibashi for advice on Chandra data analysis. HY acknowledges the support of the Advanced Leading Graduate Course for Photon Science (ALPS). CD acknowledges the support from STFC under grant ST/L00075X/1 and a JSPS long-term fellowship. This work was supported by the Grant-in-Aid for Scientific Research on Innovative Areas ‘Nuclear Matter in Neutron Stars Investigated by Experiments and Astronomical Observations’ (KAKENHI 24105007).
REFERENCES
APPENDIX: MEG±1 AND HEG±1
Just for reference, we show the result in Figs A1 and A2 when HEG±1 data are included to the analysis. We obtained 〈N(0.5)〉 = 4.20 and |${\Delta \chi ^2_\mathrm{3\sigma }} = 15.27$|. (The number of trials of the simulation of MEG±1 spectra in Section 5.2 is 1000.) As shown in Fig. A1, the HEG+1 spectrum is rolling and the powerlaw model does not fit it well. Because of this, a large Δχ2 is seen in Fig. A2 around 4.7 keV where the residuals is significant in HEG+1. Therefore the Δχ2 around 4.7 keV is larger than |$\Delta \chi ^2_\mathrm{3\sigma }$| but this does not mean that we have detected the absorption line. Considering that the other spectra are fitted well simply with the powerlaw model, it is natural that the spectrum data or the response files are not correct due to the mixing. If we use the response file that considers that the HEG+1 spectrum is intermixed with the MEG+2, the matters might be improved.
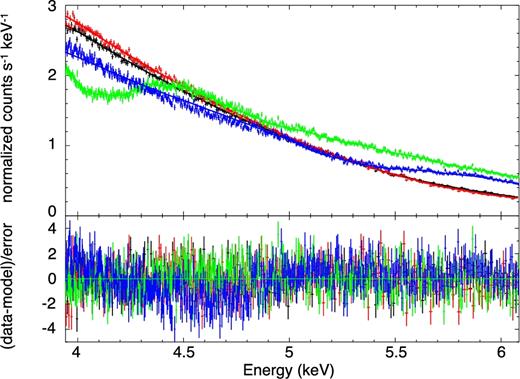
Chandra MEG±1 and HEG±1 count rate spectrum and the best-fitting continuum model. The black curve is MEG−1, the red one is MEG+1, the green one is HEG−1, and the blue one is HEG+1.
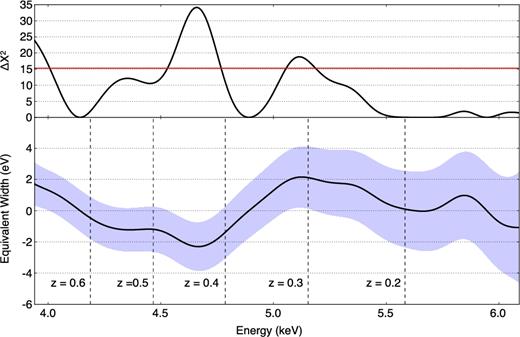
Top: Δχ2 at different line energy in the search range. Bottom: best-fitting value of the equivalent width (the black solid line) and 3σ upper limit of it. The red line represents for 3σ detection level (|${\Delta \chi ^2_\mathrm{3\sigma }} = 15.27$|).



