Search
Close
Search
Advanced Search
Search Menu
AI Discovery Assistant

Abstract

The observed motion of stars close to galaxy nuclei shows that the resulting velocities are small of the order of a few hundred of km s−1. In these regions of strong gravity, the Newtonian gravitational field or even a post-Newtonian approximation may not be adequate to describe the motion of stars. In this paper, we study the possibility that the rotation curves problem may be explained mostly in the realm of Einstein's general relativity in a nearly weak field regime. By using the geodesic equations to obtain a gravitational potential generated from a point-like source, we end up in the concept of a nearly Newtonian gravity, and we show that its resulting potential responds to the dark halo mostly attributed to dark matter. We show that it comes essentially from the propagation of the non-linear effects of the obtained effective velocity field. As a test, we study a sample of 27 low surface brightness galaxies (LSBGs) and nine dwarf galaxies obtaining rotation curve shapes in nearly agreement with observations.

gravitation, galaxies: general

1 INTRODUCTION

The recent analysis of observations in astrophysics and cosmology indicates the existence of constraints on the nature of the gravitational field produced by dark matter: first, the third peak in the power spectrum of the cosmic microwave background (CMB) radiation in the Planck mission (Planck Collaboration XVI 2014) reveals that such gravitational field cannot be generated by any theory of baryons only. Secondly, optical, X-ray and gravitational lensing observations of the bullet cluster (Dietrich et al. 2012) indicate that the centre of mass of the cluster components cannot be explained by simulations of some alternative theories without dark matter. Thirdly, the observations of galactic cores indicate the gravitational field in these regions is strong not unlike that of the ones produced by a supermassive black holes at their centres. Since any form of dark matter interacts with ordinary matter by its own gravitational field, the nature of dark matter depends on a previously defined gravitational field compatible with the above-mentioned observations. Because of this difficulty, the existence of dark matter turned to be one of the challenging problems of contemporary cosmology, astrophysics and particle physics. Similar effects on gravitational perturbations are also verified at scales of galaxies, the so-called rotation curve problem (Rubin & Kent Ford 1970), where the observed velocities in the faint outskirts of galaxies differ from those ones expected from Newtonian predictions of having at least the same magnitude of the top speed observed in their bright starlight cores. This was corroborated with the observations of lines of 21-cm neutron hydrogen synthesis that extents farther than the limit of the luminous baryonic galactic disc that confirms the mass versus velocity discrepancy in these regions. Accordingly, an additional non-baryonic huge amount of dark matter mass should be included to justify the observed pattern (Bosma 1981a,b; de Blok 2010; Arun, Gudennavar & Sivaram 2017).

One successful theoretical scheme for explanation of this effect resides in the cosmological constant (Λ) cold dark matter (CDM) parametrization (Padmanabhan 2003; Peebles & Ratra 2003), for short ΛCDM. It tries to explain both formation and growth of large structures in Universe as well the accelerated expansion problem (for review, see Spergel 2015; Arun et al. 2017). One fundamental point that favours the ΛCDM model concerns its applications to cosmological scale and provides a simulation of the growth of the larger structures of the universe consistent with the observations on large-scale structure (LSS) surveys (Springel 2005).

On the other hand, the situation is problematic at galaxy scale. For instance, the CDM simulations predict the existence of a dark matter halo core larger than the scale length of the galactic disc due to subgalactic central cusp structures (Navarro, Frenk & White 1997), which conflicts the observations. This is commonly known as the cusp and core problem (Salucci 2001; Spekkens, Giovanelli & Haynes 2005; de Blok 2010; Ogiya & Mori 2014). Another situation occurs at Local Group where observations of dwarf neighbouring galaxies exhibit a flattened core density profile but simulations regarding the ΛCDM model provide orders of magnitude larger than observed for dwarf populations, as known as the missing satellite problem (Klypin et al. 1999; Moore et al. 1999). These facts also motivated a variety of alternative explanations to the dark matter issue, e.g. modifications of standard Newton's gravity (Milgrom 1983; Bekenstein & Milgrom 1984; Brownstein & Moffat 2006) and Einstein's gravity (Katsuragawa & Matsuzaki 2007; Mannheim & O'Brien 2012; Capozziello, Cardone & Troisi 2016), including the possible existence of new essences and of specific scalar fields (Briscece 2011; Harko 2011; Martinez-Medina & Matos 2014), or the higher dimensional space–times (Capozziello et al. 2009; Gergerly et al. 2011; Capistrano & Cabral 2014).

In this paper, we focus on the observed gravitational effect as verified in rotation curves of galaxies without going into debate whether dark matter does exist or not. On the contrary, we look for discussing that the relativistic effects may respond to a larger part of the observed effect on the rotation curve shapes. To our proposes, we start simple without assuming a dark matter mass for the present study and analyse how the model responds to this constraint. Differently from the models in recent literature, we propose a simple theoretical mechanism essentially in the realm of general relativity (GR). In Section 2, we argue that we can obtain useful information from the gravitational field produced from the Einstein gravity. In doing so, we study the relativistic slow motion in the sense that we use only the geodesic equations alone, leaving the deviation equation intact (Infeld & Plebanski 1960; Capistrano, Roque & Valada 2014; Capistrano, Penagos & Alárcon 2016). With those features, the resulting potential strength lies somewhere between GR and Newtonian gravity. Hence, we use the nearly Newtonian approximation (Misner, Thorne & Wheeler 1973) to investigate gravitational phenomena in astrophysical scale (Capistrano et al. 2014, 2016) being the rotation curves problem a fundamental test for the model.

To this aim, we focus our investigation on a selected sample of 25 low surface brightness galaxies (LSBGs) based on high resolution of smooth hybrid alpha–H i rotation curves (de Blok et al. 2001) in Section 3, and two more giant LSBGs from Lelli, Fratenelli & Sancisi (2010). Particularly, LSBGs exhibit rotation curves in which the mass–velocity discrepancy is more evident and the corresponding curves are steeper. Chiefly, they constitute an important constraint on theoretical models of galaxy formation and evolution. As a complementary test, we investigate how the model also responds to a set of nine dwarf galaxies (Karukes & Salucci 2017), which dynamics has been increasingly gotten attention as an important constraint to deal with the dark matter problem (Oman 2015). In the present model, we neglect inclination and projection effects. In conclusion section, we present the final remarks.

2 THE NEARLY NEWTONIAN GRAVITY

To introduce the methodology, in this paper we concentrate our attention on LSBGs and dwarf galaxies (to be discussed in Section 3) that are better suited for later comparisons. The LSBGs and dwarf galaxies are very interesting for a first study using this approach since they share some common attributes. They are regarded a dark-matter-dominated systems. For LSBGs, even in small scale lengths are considered (Swaters, Madore & Trewhella 2000; de Blok, Mcgaugh & Rubin 2001; Salucci, Walter & Borriello 2003; Swaters et al. 2003a; Swaters 2003b), since most of their contents are made of neutron hydrogen and relic stars, and 95 per cent of its content is commonly attributed to non-baryonic CDM and they have a central bulge with a surface brightness fainter than μ0, B ∼ 23 mag arsec−2B-band, which is in general slightly higher than dwarf galaxies (Vorobyov et al. 2009; de Blok 2010). The dwarf galaxies have been caught attention due to a possible breakdown of ΛCDM at Milk Way Local Group scale that does not provide a fair population of these systems exceeding at least as much as 10 times larger than observed. This is known as the missing satellite problem (Klypin et al. 1999; Moore et al. 1999). Likewise, LSBGs are regarded as a dark-dominated faintness system with relic stars. Chiefly, the necessity to study such systems is to understand star formation in low-mass haloes (Karachentsev, Makarov & Kaisina 2013; Nierenberg et al. 2016; Stierwalt et al. 2017).

These general characteristics make LSBGs and dwarf galaxies entirely compatible to the assumption of a disc condition with a vanishing source. We assume that a test particle is embedded in a pressureless galactic fluid with low density that interacts only through its gravitational field. Hence, due to the LSBGs and dwarf galaxies relic stars, a test particle does not evince any interaction with near particles (stars) and the bulge looks like a point-like source. Thus, let us consider the bulge of a galaxy in the centre of the circular basis of a cylinder and a test particle with a unitary mass orbiting by its edge. In order to describe an axially symmetric motion of a test particle we use Weyl's line element (Weyl 1917):
(1)
where λ = λ(r, z) and σ = σ(r, z). The exterior gravitational field in the cylinder outskirts is given by Einstein's vacuum equations:
(2)
(3)
(4)
where the terms (, r), (, z) and (, rr), (, zz) denote, respectively, the first and the second derivatives with respect to the variables r and z. It is worth noting that Weyl's metric has a particular interest for astrophysical applications since the metric does not lose its asymptotes when reduced to Schwarzschild symmetry (Weyl 1917; Rosen 1949; Zipoy 1966) and is also asymptotically flat metric (Weyl 1917; Rosen 1949; Zipoy 1966; Gautreau, Hoffman & Armenti 1972; Stephani et al. 2003). Hence, the resulting gravitational field produces will be different from the Schwarzschild one under specific conditions according to Cartan's equivalence problem1 (Cartan 1927; Stephani et al. 2003; MacCallum 2006).
It is interesting to note that regardless of velocity arguments, the diffeomorphism invariance of GR is also broken down by the condition that the cylinder thickness h0 is smaller than its radius R0, i.e. h0 ≪ R0 being reduced to its circular basis that can be smoothly perturbed by the expansion of the metric parameters. In order to analyse effects of the lack of the diffeomorphism invariance, we start with solving the non-linear system given by equations (2)–(4). Differently as proposed in Ujevic & Letelier (2004, 2007); González, Gutiérrez-Piñeres & Ospina (2008); Vogt & Letelier (2008) and Gutiérrez-Piñeres, González & Quevedo (2013) for a mass distribution with Weyl's exact solutions of Einstein equations, we study approximate solutions of this metric by expanding its coefficient functions (or potentials) that essentially refers to the particle's orbit and not to the distribution of matter in galaxy. To this end, we expand the coefficients λ(r, z) and σ(r, z) into a Taylor's series in such a way
(5)
(6)
and considering the approximation up to the second order (to keep aspects of the non-linearity of the system), we define
(7)
where we denote A(r) = σ(r, 0), |$a(r)= {\left. {{{\mathrm{\partial} \sigma (r,z)} \over {\mathrm{\partial} z}}} \right|_{z = 0}}$| and |$c(r)=\left.{{{{\mathrm{\partial} ^2}\sigma (r,z)} \over {\mathrm{\partial} {z^2}}}} \right|_{z = 0}$|⁠.
In addition, we use the same procedure as in equation (7) to the coefficient λ(r, z) and define
(8)
where we denote B(r) = λ(r, 0), |$b(r)= {\left. {{{\mathrm{\partial} \lambda (r,z)} \over {\mathrm{\partial} z}}} \right|_{z = 0}}$| and |${\rm d}(r)=\left.{{{{\mathrm{\partial} ^2}\lambda (r,z)} \over {\mathrm{\partial} {z^2}}}} \right|_{z = 0}$|⁠.
Substituting the coefficients given by equations (7) and (8) in the system given by equations (2)–(4) one obtains the final form of the coefficient σ(r, z):
(9)
and also a closed form for the coefficient λ(r, z) given by
(10)
where c1 and d1 are true integration constants. It is worth nothing that for superior orders, the terms in the coefficients σ(r, z) and λ(r, z) turn to be redundant (Capistrano et al. 2014) due to the reduction of the cylinder geometry to a circular basis. Moreover, it was found that the initial functions a(r) and c(r) can be reduced to constants a0 and c0, respectively, and k0 also is a constant factor. The functions b(r) and d(r) are given by
(11)
(12)

2.1 The effective velocity field

The small deviation from Minkowski's metric does not depend on the velocity of the particle. Since v ≪ c, we can use Newtonian coordinates (with x4 = t, t being the Newtonian time), so that the spatial components of the geodesic equation become
(13)
where the Latin indices run from 1 to 3. A gravitational scalar field Φ is defined by the relation
(14)
and comparing equations (13) and (14) we obtain an equation to determine the field Φ:
(15)
where δij is the Kronecker delta. Notice that the potential Φ is defined by this equation so far but it is not necessarily the Newtonian gravitational field because the gravitational field was not assumed to be weak. On the other hand, if one looks at the gravitational field itself as the particle continues its fall, the gravitational pull continuously builds up by small increments of the metric as
\begin{equation*} g_{\mu \nu } \approx \eta _{\mu \nu } +\delta h_{\mu \nu }+ (\delta h_{\mu \nu })^2 +\cdots . \end{equation*}
Naturally, there is no way to stop this process without applying an external force. Thus, equation (15) can be integrated along the geodesic, where the set of increments δhμν continuously increases up to a finite value hμν, leading to a scalar gravitational potential (named the nearly Newtonian potential by Misner et al. 1973):
(16)
Notice that the weak Newtonian gravitational field was not an imposed condition, except at the beginning of the free fall. The component g44 of the metric is obtained from an exact solution of Einstein's equations whose solutions count with the contribution of all metric components (and not just g44). Since the potential depends only on the determination of the coefficient σ(r, z) and the coefficient λ(z, r) is a null quantity.

The symmetry group of equation (15) is similar to the generalized Galilean group, where the Newtonian potential is replaced by equation (16). Since the system is no longer diffeomorphic invariant, so that the metric should be written in coordinates that are consistent with the metric symmetry of the local gravitational field.

It is worth noting that the component g44 is an exact and non-approximated solution due to integration of the original gravitational field. This gravitational field is a strong one in a sense we have one full component of the Einstein's gravitational field. This qualitative interpretation may shed light mainly on studies of astrophysical purposes where the level of the strength of the gravitational field plays an important role. In this paper, we are not proposing a modification of Einstein's theory, but only reviewing the slow motion problem starting from the whole GR not under the a priori assumption of a weak gravitational field. Rather than semantics, the term ‘nearly Newtonian’ denotes an intermediate gravitational field regime to differ from the standard parametrized post-Newtonian (PPN) approximation. It is important to point out that the usual PPN expansion is not uniformly valid for large distances (Burke 1969) and limitations for the study of the dynamics of pulsars with complex gravitational regimes (e.g. so-called quasi-stationary weak-field, strong-field, the highly dynamical strong-field regime – particularly, it is the case of black holes and neutron stars – and also the radiation regime) represent a serious constraints on the PPN approximation (Wex 2015).

Chiefly, under imposed conditions, this recovers all results learned from traditional GR textbooks. For instance, if we assume the slow motion condition v ≪ c plus equation (16), under a symmetric spherical metric with g44 = −(1 − 2M/r), it invariably will lead us to its linear Newtonian limit once the Gauss equation is restored (Infeld & Plebanski 1960). Moreover, the observed correlation between the highest energy cosmic rays sources and active galactic nuclei (The Pierre Auger Collaboration 2007) appears to suggest that there are strong gravitational fields in those nuclei, not unlike that of a supermassive black hole (Richstone et al 1949; Ferrarese & Merrit 2002; Ferrarese & Ford 2005). Nonetheless, on what concerns the motion itself, the observed motion of stars close to those nuclei shows that the resulting velocities are small of the order of a few hundreds of km s−1. Hence, in these regions of strong gravity the Newtonian gravitational field or even a post-Newtonian approximation may not be adequate to describe the motion of stars. In reality, the motion of stars in spiral galaxies tells that we need a gravitational model capable of describing a slow motion also valid for gravitational fields of any strength. In order to test this nearly Newtonian limit, using equations (9) and (16), one can calculate in the galactic plane the related gravitational potential generated by a point-like mass at a distance r given by
(17)
On the other hand, in a previous publication (Capistrano et al. 2014), it was argued that at Solar system scale the constant c0 ≪ 1 given by |$c_0 = \pm \frac{1}{4\pi }\nu$|⁠, where ν is the Keplerian mean motion given by |$\nu =\sqrt{\frac{GM}{\gamma ^3}}$| being γ the semimajor axis. Since the constant c0 has such a small value, in a larger scale, e.g. galactic scale, the exponential term approaches to unity that makes dominant the monomial k0th power term in equation (17) and we can obtain a simpler expression:
(18)
The corresponding potential is felt by the test particle with a mass m that revolves in a circular orbit the bulge treated as a point mass source with mass M. Interestingly, the form of the potential in equation (18) might resemble the Yukawa potential (Quandt & Schmidt 1991) in the context of the conformal gravity unless a radial decaying in the exponential term should given, but actually the exponential term in this formula is just an integration constant and the resulting potential is a polynomial function of k0th order.
Thus, using the Newtonian velocity formula for an orbiting particle |$v(r) = \sqrt{r \frac{\mathrm{\partial} \Phi }{\mathrm{\partial} r}}$| one can obtain the related nearly Newtonian velocity:
(19)
where R0 is the optical disc scale length and all the constants were aggregated in the factor β0. Since the gravitational potential in equation (18) has a relativistic origin and may respond to the dark non-baryonic sector, hence it must dominate over the Newtonian term at the largest radial distances that are currently of relevance to the studies of galactic rotation curves.
Interestingly, note that for the value k0 = −1 and β0 = 1 we obtain the standard Newtonian velocity formula |$v=\sqrt{\frac{GM}{r}}$|⁠. Because of the fact that equation (19) has its origin from a cylindrical symmetry, it cannot reproduce the Newtonian term unless we set strictly the values of the parameter k0. In fact, this is a relic from the non-linear subtleties of the original GR gravitational field that affects over the system that does not allow to make a linear superposition rule with a summation over the values of k0. Accordingly, equation (19) responds only to the non-Newtonian part for values of k0 ≠ −1. Moreover, it is well known that any fit to a galactic rotation curves has to include both terms for asymptotically large enough radial distances where the Newtonian term would be negligible. In doing so, we propose the total effective velocity given by
(20)
which the terms vN and vnN are the Newtonian velocity and the nearly Newtonian velocities, respectively. To connect these regions, we resort to a Blumenthal's exponential mass thin disc model (Blumenthal et al. 1986), where the optical radial distribution is extended in the galactic plane decaying into an exponential profile from the galactic centre of the orbit (de Blok 2010). The passage from the point-like source to extended one is correct in a linearized framework with a Newtonian mass M(r). Hence, we have the corresponding relation of our test particle to total net luminous mass given by m → M(r). The total mass M(r) represents the visible mass profile that decays exponentially within a distance r from the centre. Accordingly,
(21)
where rc is the galaxy scale length parameter and M⋆ = Mgas + Mdisc. Again, even if the form of equation (21) may resemble an Yukawa-like potential, Blumenthal's mass model keeps no relation with Yukawa potential itself. This model was heuristically destined to a specific end concerning to tackle the problem of the infall of the baryonic distribution in a disc galaxy. The parameter rc also refers to a particular characteristic of a galaxy and this does not emerge as a fundamental scale length, since one can use different configurations of mass models to galaxy parameters. As we will see in conjunction with the parameters β0 and k0, the parameter rc will play an important role in the stabilization of the curve shapes in the outskirts regions of the galaxies.
It is worth noting that the dark baryon mass is neglected. We consider here only the mass of gas and the mass of the galactic disc. The mass scale for the primordial He is given by |$M_{{\rm gas}} = 1.4 M_{\rm H\, \small {I}}$|⁠, where |$M_{\rm H\, \small {I}}$| is the mass of the hydrogenous 21-cm lines that go through the galactic disc up to outer disc. Thus, we rewrite the effective velocity as
(22)
Accordingly, equation (22) evinces some important requirement of the effective velocity vanishes asymptotically. From the theoretical point of view, the effective velocity vanishes in an infinite radius for an asymptotically flat rotation curve but, in practice, this is interpreted as a maximum finite radius according to observations as the influence of a gravitational area of the galaxy itself ceases to be. It is important to point out that we have obtained a model with only three parameters (considering the additional parameter from the related mass model) to be fixed in a case-by-case basis, due to the particularities of each galaxy.

3 RESULTS AND DISCUSSION

3.1 LSBGs sample

The main criterion used to choose an appropriated sample was to study galaxies with low brightness profile to test the present methodology what concerns the dark sector away from the outer luminous optical disc. To this end, we have chosen a sample of 25 LSBGs varying their maximum radial distance from 1.7 up to 62.7 kpc. As well known, the LSBGs are regarded as dark-dominated system and they provide a good test for a gravitational theory (de Blok et al. 2001; Mannheim & O'Brien 2012). The present sample was extracted from de Blok et al. (2001). The authors in de Blok et al. (2001) investigated a large sample of 30 galaxies based on the analysis of high resolution of smooth hybrid alpha–H i rotation curves. The measurements were obtained from a long-slit major axis spectra at Las Campanas Observatory. The adopted distances were computed assuming a Hubble flow with H0 = 75 km s−1 Mpc−1. The results are presented in the shapes shown in Figs 1, 2 and 3.

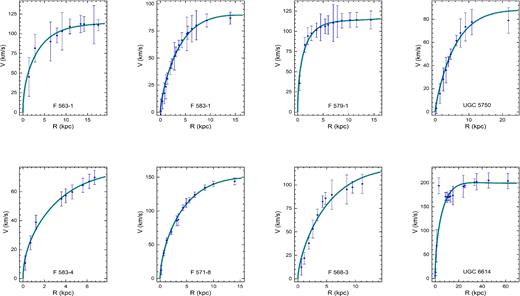
Rotation curves of a sample of eight LSBGs galaxies with photometry.
Figure 1.

Rotation curves of a sample of eight LSBGs galaxies with photometry.

Open in new tabDownload slide
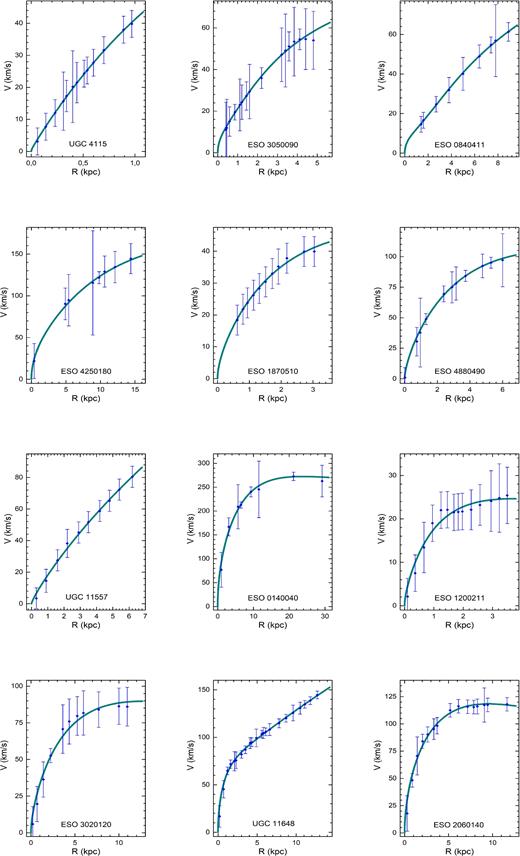
Second sample of LSBGs galaxies without photometry.
Figure 2.

Second sample of LSBGs galaxies without photometry.

Open in new tabDownload slide
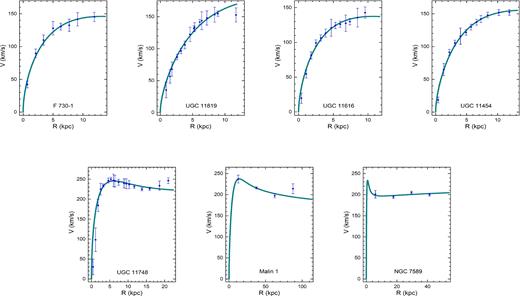
Third sample of LSBGs galaxies without photometry.
Figure 3.

Third sample of LSBGs galaxies without photometry.

Open in new tabDownload slide

Table 1 shows the main values considered to fit rotation curves. The data of disc scale length R0, the H i gas mass |$M_{\rm H\, \small {I}}$| (that extends beyond optical disc) and the stellar disc mass Mdisc were extracted from Mannheim & O'Brien (2012). In addition, the adopted distances D measured in units of Mpc, the maximum radius Rmax in kpc units for adopted distance and the observed smoothed velocities V were obtained from de Blok et al. (2001) and divided in small groups of photometric and non-photometric galaxies as shown in Figs 1, 2 and 3, respectively.

Table 1.
Open in new tab

Relevant galaxy properties of a set of 25 objects extracted from de Blok et al. (2001) and Mannheim & O'Brien (2012). The adopted distance D is measured in units of Mpc, the galaxy core distance R0 and the maximum distance Rmax are in units of kpc. Moreover, the H i mass |$M_{\rm H\, \small {I}}$| and visible disc mass Mdisc are in units of mass (1010 M⊙), where M⊙ is the Sun mass. The average top velocity V is in units of km s−1. The data of the giant LSBGs NGC  7589 and Malin 1 were extracted from Lelli et al. (2010).

GalaxiesDR0Rmax|$M_{\rm H\, \small {I}}$|MdiscV
UGC  41155.50.31.7–0.0139.8
ESO  305009013.21.35.6–0.0654.6
ESO  084041182.43.59.1–0.0661.3
ESO  425018088.37.314.6–4.79144.5
ESO  187051016.82.12.8–0.0939.9
ESO  488049028.71.67.8–0.4397.1
UGC  1155723.73.06.70.250.3780.4
ESO  01400040217.810.130.0–20.7272.7
F563-146.82.914.10.291.35112.4
ESO  120021115.22.03.5–0.0125.4
ESO  302012070.93.411.2–0.7786.3
UGC  1164849.04.013.0–2.57144.6
F583-132.41.614.10.180.1586.9
ESO  206014059.65.111.6–3.51118.0
F579-186.95.214.70.213.33114.4
UGC  575056.13.38.60.10.178.9
F583-450.82.87.00.060.3169.9
F571-850.35.414.60.164.48143.9
F730-1148.35.812.2–5.95145.3
UGC  1181961.54.711.9–4.83154.7
UGC  1161674.93.19.8–2.43142.8
UGC  1145493.93.412.3–3.15152.2
F568-380.04.211.60.31.2101.1
UGC  1174849.02.613–9.67250.0
UGC  661486.28.262.72.079.7205.2
NGC  758913020.741.3–1.5200.1
Malin 13772.987.5–6.7214.1
GalaxiesDR0Rmax|$M_{\rm H\, \small {I}}$|MdiscV
UGC  41155.50.31.7–0.0139.8
ESO  305009013.21.35.6–0.0654.6
ESO  084041182.43.59.1–0.0661.3
ESO  425018088.37.314.6–4.79144.5
ESO  187051016.82.12.8–0.0939.9
ESO  488049028.71.67.8–0.4397.1
UGC  1155723.73.06.70.250.3780.4
ESO  01400040217.810.130.0–20.7272.7
F563-146.82.914.10.291.35112.4
ESO  120021115.22.03.5–0.0125.4
ESO  302012070.93.411.2–0.7786.3
UGC  1164849.04.013.0–2.57144.6
F583-132.41.614.10.180.1586.9
ESO  206014059.65.111.6–3.51118.0
F579-186.95.214.70.213.33114.4
UGC  575056.13.38.60.10.178.9
F583-450.82.87.00.060.3169.9
F571-850.35.414.60.164.48143.9
F730-1148.35.812.2–5.95145.3
UGC  1181961.54.711.9–4.83154.7
UGC  1161674.93.19.8–2.43142.8
UGC  1145493.93.412.3–3.15152.2
F568-380.04.211.60.31.2101.1
UGC  1174849.02.613–9.67250.0
UGC  661486.28.262.72.079.7205.2
NGC  758913020.741.3–1.5200.1
Malin 13772.987.5–6.7214.1
Table 1.
Open in new tab

Relevant galaxy properties of a set of 25 objects extracted from de Blok et al. (2001) and Mannheim & O'Brien (2012). The adopted distance D is measured in units of Mpc, the galaxy core distance R0 and the maximum distance Rmax are in units of kpc. Moreover, the H i mass |$M_{\rm H\, \small {I}}$| and visible disc mass Mdisc are in units of mass (1010 M⊙), where M⊙ is the Sun mass. The average top velocity V is in units of km s−1. The data of the giant LSBGs NGC  7589 and Malin 1 were extracted from Lelli et al. (2010).

GalaxiesDR0Rmax|$M_{\rm H\, \small {I}}$|MdiscV
UGC  41155.50.31.7–0.0139.8
ESO  305009013.21.35.6–0.0654.6
ESO  084041182.43.59.1–0.0661.3
ESO  425018088.37.314.6–4.79144.5
ESO  187051016.82.12.8–0.0939.9
ESO  488049028.71.67.8–0.4397.1
UGC  1155723.73.06.70.250.3780.4
ESO  01400040217.810.130.0–20.7272.7
F563-146.82.914.10.291.35112.4
ESO  120021115.22.03.5–0.0125.4
ESO  302012070.93.411.2–0.7786.3
UGC  1164849.04.013.0–2.57144.6
F583-132.41.614.10.180.1586.9
ESO  206014059.65.111.6–3.51118.0
F579-186.95.214.70.213.33114.4
UGC  575056.13.38.60.10.178.9
F583-450.82.87.00.060.3169.9
F571-850.35.414.60.164.48143.9
F730-1148.35.812.2–5.95145.3
UGC  1181961.54.711.9–4.83154.7
UGC  1161674.93.19.8–2.43142.8
UGC  1145493.93.412.3–3.15152.2
F568-380.04.211.60.31.2101.1
UGC  1174849.02.613–9.67250.0
UGC  661486.28.262.72.079.7205.2
NGC  758913020.741.3–1.5200.1
Malin 13772.987.5–6.7214.1
GalaxiesDR0Rmax|$M_{\rm H\, \small {I}}$|MdiscV
UGC  41155.50.31.7–0.0139.8
ESO  305009013.21.35.6–0.0654.6
ESO  084041182.43.59.1–0.0661.3
ESO  425018088.37.314.6–4.79144.5
ESO  187051016.82.12.8–0.0939.9
ESO  488049028.71.67.8–0.4397.1
UGC  1155723.73.06.70.250.3780.4
ESO  01400040217.810.130.0–20.7272.7
F563-146.82.914.10.291.35112.4
ESO  120021115.22.03.5–0.0125.4
ESO  302012070.93.411.2–0.7786.3
UGC  1164849.04.013.0–2.57144.6
F583-132.41.614.10.180.1586.9
ESO  206014059.65.111.6–3.51118.0
F579-186.95.214.70.213.33114.4
UGC  575056.13.38.60.10.178.9
F583-450.82.87.00.060.3169.9
F571-850.35.414.60.164.48143.9
F730-1148.35.812.2–5.95145.3
UGC  1181961.54.711.9–4.83154.7
UGC  1161674.93.19.8–2.43142.8
UGC  1145493.93.412.3–3.15152.2
F568-380.04.211.60.31.2101.1
UGC  1174849.02.613–9.67250.0
UGC  661486.28.262.72.079.7205.2
NGC  758913020.741.3–1.5200.1
Malin 13772.987.5–6.7214.1

To control the systematics, we use GnuPlot 5.0 software to compute non-linear least-squares fitting applying the Levenberg–Marquardt algorithm that is a simpler and good reference to analysis on the goodness-of-fit to data. Table 2 presents the obtained values for the parameters and the related reduced chi-squared (⁠|$\chi ^2_{{\rm red}}$|⁠) and the probability p. The sequence of galaxies as shown in Table 2 is according to their increasing chi-squared values. Interestingly, the overall values indicate small values of the reduced chi-squared.

Table 2.
Open in new tab

The obtained fitting values for the parameters (β0, rc, k0) and reduced |$\chi ^2_{{\rm red}}$| and the probability p.

Galaxiesβ0rck0|$\chi ^2_{{\rm red}}$|p
UGC  411511.105 ± 13.8101.186 ± 0.7280.002 ± 0.2520.0051
ESO  30500901.585 ± 0.3681.343 ± 0.1280.638 ± 0.1580.0151
ESO  08404113.825 ± 0.3092.019 ± 0.1061.090 ± 0.07820.0070.999
ESO  42501801.302 ± 0.3615.873 ± 0.7170.259 ± 0.2630.0180.999
ESO  18705103.196 ± 11.4801.769 ± 3.749−0.269 ± 2.3930.0250.999
ESO  48804904.311 ± 3.9433.050 ± 1.351−0.381 ± 0.3360.0350.999
UGC  1155727.786 ± 183.10017.056 ± 57.73−0.221 ± 0.6520.0730.999
ESO  014000401.324 ± 0.2725.117 ± 0.5680.025 ± 0.2180.1070.991
F563-10.510 ± 0.2142.844 ± 0.4720.263 ± 0.2380.1120.998
ESO  12002116.695 ± 18.6300.938 ± 2.652−0.262 ± 2.9100.1420.999
ESO  30201202.871 ± 9.5213.894 ± 6.616−0.395 ± 1.7600.1430.998
UGC  116480.288 ± 0.02282.504 ± 0.04471.266 ± 0.0760.1580.999
F583-12.486 ± 5.7563.687 ± 3.460−0.220 ± 0.8950.1600.999
ESO  20601401.199 ± 5.6663.959 ± 8.298−0.590 ± 3.3710.2000.998
F579-v10.279 ± 0.07712.522 ± 0.1170.645 ± 0.3360.2120.997
UGC  57505.836 ± 14.7704.872 ± 6.525−0.082 ± 1.1520.3110.962
F583-41.076 ± 0.4132.021 ± 0.2820.306 ± 0.3950.3200.927
F571-82.105 ± 3.8106.048 ± 5.132−0.472 ± 0.9790.4180.939
F730-V11.477 ± 7.2915.280 ± 11.740−0.582 ± 3.0170.5680.725
UGC  118192.417 ± 13.3605.802 ± 15.140−0.347 ± 2.8460.7180.735
UGC  116162.101 ± 8.7973.726 ± 7.152−0.491 ± 2.1510.9000.532
UGC  114542.601 ± 6.5604.820 ± 5.623−0.4923 ± 1.1641.4340.167
F568-33.0517 ± 34.2006.037 ± 32.64−0.354 ± 5.0591.4700.162
UGC  117480.423 ± 0.1171.771 ± 0.1870.082 ± 0.1622.6180.000
NGC  758924.307 ± 1.2790.269 ± 0.0000.088 ± 0.1103.3110.069
UGC  66140.850 ± 0.5205.906 ± 1.5970.114 ± 0.3933.9150.000
Malin 11.409 ± 0.7243.479 ± 2.173−0.193 ± 0.1903.9940.046
Galaxiesβ0rck0|$\chi ^2_{{\rm red}}$|p
UGC  411511.105 ± 13.8101.186 ± 0.7280.002 ± 0.2520.0051
ESO  30500901.585 ± 0.3681.343 ± 0.1280.638 ± 0.1580.0151
ESO  08404113.825 ± 0.3092.019 ± 0.1061.090 ± 0.07820.0070.999
ESO  42501801.302 ± 0.3615.873 ± 0.7170.259 ± 0.2630.0180.999
ESO  18705103.196 ± 11.4801.769 ± 3.749−0.269 ± 2.3930.0250.999
ESO  48804904.311 ± 3.9433.050 ± 1.351−0.381 ± 0.3360.0350.999
UGC  1155727.786 ± 183.10017.056 ± 57.73−0.221 ± 0.6520.0730.999
ESO  014000401.324 ± 0.2725.117 ± 0.5680.025 ± 0.2180.1070.991
F563-10.510 ± 0.2142.844 ± 0.4720.263 ± 0.2380.1120.998
ESO  12002116.695 ± 18.6300.938 ± 2.652−0.262 ± 2.9100.1420.999
ESO  30201202.871 ± 9.5213.894 ± 6.616−0.395 ± 1.7600.1430.998
UGC  116480.288 ± 0.02282.504 ± 0.04471.266 ± 0.0760.1580.999
F583-12.486 ± 5.7563.687 ± 3.460−0.220 ± 0.8950.1600.999
ESO  20601401.199 ± 5.6663.959 ± 8.298−0.590 ± 3.3710.2000.998
F579-v10.279 ± 0.07712.522 ± 0.1170.645 ± 0.3360.2120.997
UGC  57505.836 ± 14.7704.872 ± 6.525−0.082 ± 1.1520.3110.962
F583-41.076 ± 0.4132.021 ± 0.2820.306 ± 0.3950.3200.927
F571-82.105 ± 3.8106.048 ± 5.132−0.472 ± 0.9790.4180.939
F730-V11.477 ± 7.2915.280 ± 11.740−0.582 ± 3.0170.5680.725
UGC  118192.417 ± 13.3605.802 ± 15.140−0.347 ± 2.8460.7180.735
UGC  116162.101 ± 8.7973.726 ± 7.152−0.491 ± 2.1510.9000.532
UGC  114542.601 ± 6.5604.820 ± 5.623−0.4923 ± 1.1641.4340.167
F568-33.0517 ± 34.2006.037 ± 32.64−0.354 ± 5.0591.4700.162
UGC  117480.423 ± 0.1171.771 ± 0.1870.082 ± 0.1622.6180.000
NGC  758924.307 ± 1.2790.269 ± 0.0000.088 ± 0.1103.3110.069
UGC  66140.850 ± 0.5205.906 ± 1.5970.114 ± 0.3933.9150.000
Malin 11.409 ± 0.7243.479 ± 2.173−0.193 ± 0.1903.9940.046
Table 2.
Open in new tab

The obtained fitting values for the parameters (β0, rc, k0) and reduced |$\chi ^2_{{\rm red}}$| and the probability p.

Galaxiesβ0rck0|$\chi ^2_{{\rm red}}$|p
UGC  411511.105 ± 13.8101.186 ± 0.7280.002 ± 0.2520.0051
ESO  30500901.585 ± 0.3681.343 ± 0.1280.638 ± 0.1580.0151
ESO  08404113.825 ± 0.3092.019 ± 0.1061.090 ± 0.07820.0070.999
ESO  42501801.302 ± 0.3615.873 ± 0.7170.259 ± 0.2630.0180.999
ESO  18705103.196 ± 11.4801.769 ± 3.749−0.269 ± 2.3930.0250.999
ESO  48804904.311 ± 3.9433.050 ± 1.351−0.381 ± 0.3360.0350.999
UGC  1155727.786 ± 183.10017.056 ± 57.73−0.221 ± 0.6520.0730.999
ESO  014000401.324 ± 0.2725.117 ± 0.5680.025 ± 0.2180.1070.991
F563-10.510 ± 0.2142.844 ± 0.4720.263 ± 0.2380.1120.998
ESO  12002116.695 ± 18.6300.938 ± 2.652−0.262 ± 2.9100.1420.999
ESO  30201202.871 ± 9.5213.894 ± 6.616−0.395 ± 1.7600.1430.998
UGC  116480.288 ± 0.02282.504 ± 0.04471.266 ± 0.0760.1580.999
F583-12.486 ± 5.7563.687 ± 3.460−0.220 ± 0.8950.1600.999
ESO  20601401.199 ± 5.6663.959 ± 8.298−0.590 ± 3.3710.2000.998
F579-v10.279 ± 0.07712.522 ± 0.1170.645 ± 0.3360.2120.997
UGC  57505.836 ± 14.7704.872 ± 6.525−0.082 ± 1.1520.3110.962
F583-41.076 ± 0.4132.021 ± 0.2820.306 ± 0.3950.3200.927
F571-82.105 ± 3.8106.048 ± 5.132−0.472 ± 0.9790.4180.939
F730-V11.477 ± 7.2915.280 ± 11.740−0.582 ± 3.0170.5680.725
UGC  118192.417 ± 13.3605.802 ± 15.140−0.347 ± 2.8460.7180.735
UGC  116162.101 ± 8.7973.726 ± 7.152−0.491 ± 2.1510.9000.532
UGC  114542.601 ± 6.5604.820 ± 5.623−0.4923 ± 1.1641.4340.167
F568-33.0517 ± 34.2006.037 ± 32.64−0.354 ± 5.0591.4700.162
UGC  117480.423 ± 0.1171.771 ± 0.1870.082 ± 0.1622.6180.000
NGC  758924.307 ± 1.2790.269 ± 0.0000.088 ± 0.1103.3110.069
UGC  66140.850 ± 0.5205.906 ± 1.5970.114 ± 0.3933.9150.000
Malin 11.409 ± 0.7243.479 ± 2.173−0.193 ± 0.1903.9940.046
Galaxiesβ0rck0|$\chi ^2_{{\rm red}}$|p
UGC  411511.105 ± 13.8101.186 ± 0.7280.002 ± 0.2520.0051
ESO  30500901.585 ± 0.3681.343 ± 0.1280.638 ± 0.1580.0151
ESO  08404113.825 ± 0.3092.019 ± 0.1061.090 ± 0.07820.0070.999
ESO  42501801.302 ± 0.3615.873 ± 0.7170.259 ± 0.2630.0180.999
ESO  18705103.196 ± 11.4801.769 ± 3.749−0.269 ± 2.3930.0250.999
ESO  48804904.311 ± 3.9433.050 ± 1.351−0.381 ± 0.3360.0350.999
UGC  1155727.786 ± 183.10017.056 ± 57.73−0.221 ± 0.6520.0730.999
ESO  014000401.324 ± 0.2725.117 ± 0.5680.025 ± 0.2180.1070.991
F563-10.510 ± 0.2142.844 ± 0.4720.263 ± 0.2380.1120.998
ESO  12002116.695 ± 18.6300.938 ± 2.652−0.262 ± 2.9100.1420.999
ESO  30201202.871 ± 9.5213.894 ± 6.616−0.395 ± 1.7600.1430.998
UGC  116480.288 ± 0.02282.504 ± 0.04471.266 ± 0.0760.1580.999
F583-12.486 ± 5.7563.687 ± 3.460−0.220 ± 0.8950.1600.999
ESO  20601401.199 ± 5.6663.959 ± 8.298−0.590 ± 3.3710.2000.998
F579-v10.279 ± 0.07712.522 ± 0.1170.645 ± 0.3360.2120.997
UGC  57505.836 ± 14.7704.872 ± 6.525−0.082 ± 1.1520.3110.962
F583-41.076 ± 0.4132.021 ± 0.2820.306 ± 0.3950.3200.927
F571-82.105 ± 3.8106.048 ± 5.132−0.472 ± 0.9790.4180.939
F730-V11.477 ± 7.2915.280 ± 11.740−0.582 ± 3.0170.5680.725
UGC  118192.417 ± 13.3605.802 ± 15.140−0.347 ± 2.8460.7180.735
UGC  116162.101 ± 8.7973.726 ± 7.152−0.491 ± 2.1510.9000.532
UGC  114542.601 ± 6.5604.820 ± 5.623−0.4923 ± 1.1641.4340.167
F568-33.0517 ± 34.2006.037 ± 32.64−0.354 ± 5.0591.4700.162
UGC  117480.423 ± 0.1171.771 ± 0.1870.082 ± 0.1622.6180.000
NGC  758924.307 ± 1.2790.269 ± 0.0000.088 ± 0.1103.3110.069
UGC  66140.850 ± 0.5205.906 ± 1.5970.114 ± 0.3933.9150.000
Malin 11.409 ± 0.7243.479 ± 2.173−0.193 ± 0.1903.9940.046

The most galaxies present a good fitting (p > 0.95) from UGC  4115 to UGC  5750. Average fits (0.95 > p > 0.05) were obtaining from the galaxies F583-4 to F568-3, including NGC  7589. Even so, in their cases the rotation curves did not worsen, which is the case of UGC  11819 that did not cover the last error bar providing a slight higher value for the final velocity data point as shown in Fig. 3. On another extreme, we have the results for the UGC  11748 and UGC  6614. These galaxies present a probability value lower than 0.05 indicating a bad fitting (p < 0.05) with large value of the reduced chi-squared, which means that the systematics possibly may affected the model (the errors had been overestimated) or an amount of dark matter may be necessary to consider and the analysis is fairly inconclusive. On the other hand, the shape of their curves was not badly affected as depicted in Figs 1 and 2.

For UGC  11748 mimics the case of UGC  11819 in Fig 3 that did not cover the last error bar but differently from UGC  11819, we have obtained a slight lower value for the final velocity data point. For the giant LSBG UGC  6614, its bulge amounts for most of the observed inner part velocity with a large velocity peak, which the only one non-covered error bar value may happen due to the adopted model of a mass profile. It is noteworthy to point out that for these galaxies, we have obtained similar results as those obtained in de Blok et al. (2001). Using a pseudo-isotherm and a Navarro–Frenk–White (NFW) halo profiles it was also reported in de Blok et al. (2001) a similar pattern as we have shown with χ2 value larger than 1 and vanishing chance p in all models (minimum disc, minimum disc+gas and maximum disc) checked by the authors in de Blok et al. (2001). In the case of UGC  11819 the ‘best-fitting’ occurred for the pseudo-isotherm profile with chi-squared lower than 1.

Another two giant LSBGs studied were Malin 1 and NGC 7589. These galaxies are two examples that exceed a typical length scale for a LSBGs type of the order of 50  kpc. Lelli et al. (2010) assumed H0 = 70 km s−1 Mpc−1 for the obtained H i velocity fields. An important fact relies on that Lelli et al. (2010) ascertained a variation in velocity due to inclination (about 3o) of 14 and 5 km s−1 for Malin 1 and NGC  7589, respectively.

In addition, we have adopt the calculated mass model as shown in Lelli et al. (2010) with the lowest χ2 value as a reference to obtain the related mass and radial distances of these galaxies as the values shown in Table 1. Whereas we have obtained reasonable results for NGC  7589 with a satisfactory rotation curve shape, Malin 1 is a challenge for this model with the highest χ2 value around 3.99 that might represent a limiting case for this model, but the shape of its rotation curve was not heavily affected as one can see in Fig. 3. Likewise in aforementioned cases for UGC  11819 and UGC  11748, the Malin 1 rotation curve did not cover the last error bar and we have obtained a slight lower value for the final velocity data point. Possibly, the inclination and the so-called luminous blob in Malin 1 may also have affected our fitting and up to now a smooth shape of the rotation curve was not warranted to correct the last data point. Actually, as reported in Lelli et al. (2010), the giant LSBGs appear to be closer to high surface brightness galaxies (HSBGs) with respect to their physical properties and steeply rising curves that may be a relevant case to take into account.

3.2 Analysis on dwarf galaxies sample

For the dwarf galaxies, we used a sample of eight galaxies from Karukes & Salucci (2017) with average optical disc velocity about 61 km s−1 and low-mass bulgeless systems (they have just a simple stellar disc) as shown in Table 3. We also test the model regarding the dwarf galaxy NGC  1560, which is considered a dark-dominated system based on Hα and H i analysis. The data were extracted from Broeils (1992) for a Hubble flow H0 = 75 km s−1 Mpc−1 in Westerbork Synthesis Radio Telescope using optical surface photometry and observations on 21-cm neutral hydrogen lines for H0 = 75 km s−1 Mpc−1.

Table 3.
Open in new tab

Relevant galaxy properties of a set of eight objects extracted from Karukes & Salucci (2017). The adopted distance D is measured in units of Mpc, the galaxy core distance R0. Moreover, the H i mass |$M_{\rm H\, \small {I}}$| and visible disc mass Mdisc are in units of mass (1010 M⊙), where  M⊙ is the Sun mass. The average top (optical) velocity V is in units of km s−1. The data of NGC 1560 were extracted from Broeils (1992). In this case, the top speed was assumed to be as the value of the correct velocity for asymmetric drift.

GalaxiesDR0|$M_{\rm H\, \small {I}}$|MdiscV
DDO 52 (UGC 4426)10.284.240.06430.019860.0
DDO 101 (UGC 6900)16.12.710.04470.013858.8
UGC 75594.882.460.01680.005237.4
WLM0.971.290.008230.0017933.0
UGC 88377.215.40.04820.014947.6
DDO 43 (UGC 3860)5.731.350.009720.00335.3
IC 1613 (UGC 668)0.731.460.0030.0009219.0
UGC 12814.942.930.03950.012253.8
NGC 15603.01.60.120.1778.7
GalaxiesDR0|$M_{\rm H\, \small {I}}$|MdiscV
DDO 52 (UGC 4426)10.284.240.06430.019860.0
DDO 101 (UGC 6900)16.12.710.04470.013858.8
UGC 75594.882.460.01680.005237.4
WLM0.971.290.008230.0017933.0
UGC 88377.215.40.04820.014947.6
DDO 43 (UGC 3860)5.731.350.009720.00335.3
IC 1613 (UGC 668)0.731.460.0030.0009219.0
UGC 12814.942.930.03950.012253.8
NGC 15603.01.60.120.1778.7
Table 3.
Open in new tab

Relevant galaxy properties of a set of eight objects extracted from Karukes & Salucci (2017). The adopted distance D is measured in units of Mpc, the galaxy core distance R0. Moreover, the H i mass |$M_{\rm H\, \small {I}}$| and visible disc mass Mdisc are in units of mass (1010 M⊙), where  M⊙ is the Sun mass. The average top (optical) velocity V is in units of km s−1. The data of NGC 1560 were extracted from Broeils (1992). In this case, the top speed was assumed to be as the value of the correct velocity for asymmetric drift.

GalaxiesDR0|$M_{\rm H\, \small {I}}$|MdiscV
DDO 52 (UGC 4426)10.284.240.06430.019860.0
DDO 101 (UGC 6900)16.12.710.04470.013858.8
UGC 75594.882.460.01680.005237.4
WLM0.971.290.008230.0017933.0
UGC 88377.215.40.04820.014947.6
DDO 43 (UGC 3860)5.731.350.009720.00335.3
IC 1613 (UGC 668)0.731.460.0030.0009219.0
UGC 12814.942.930.03950.012253.8
NGC 15603.01.60.120.1778.7
GalaxiesDR0|$M_{\rm H\, \small {I}}$|MdiscV
DDO 52 (UGC 4426)10.284.240.06430.019860.0
DDO 101 (UGC 6900)16.12.710.04470.013858.8
UGC 75594.882.460.01680.005237.4
WLM0.971.290.008230.0017933.0
UGC 88377.215.40.04820.014947.6
DDO 43 (UGC 3860)5.731.350.009720.00335.3
IC 1613 (UGC 668)0.731.460.0030.0009219.0
UGC 12814.942.930.03950.012253.8
NGC 15603.01.60.120.1778.7

As shown in Table 4, it was found an interesting compatibility with the results presented in Karukes & Salucci (2017) with small values of the reduced chi-squared smaller than 1. Only two cases (UGC  8837 and UGC  3860) present probability around ∼0.8 indicating a reasonable fitting but the shapes show a good pattern and they are not worsen as compared to the expected shapes so is the same case for UGC  1281.

Table 4.
Open in new tab

The obtained fitting values for the parameters (β0, rc, k0) and reduced |$\chi ^2_{{\rm red}}$| and the probability p for the related dwarf galaxies.

Galaxiesβ0rck0|$\chi ^2_{{\rm red}}$|p
DDO 52 (UGC 4426)8.534 ± 9.6171.919 ± 2.34−0.094 ± 1.2440.0860.999
DDO 101 (UGC 6900)5.182 ± 0.2690.819 ± 0.0600.297 ± 0.07800.1040.996
UGC 75597.989 ± 14.041.538 ± 2.228−0.116 ± 1.3950.3050.985
WLM9.050 ± 12.421.027 ± 1.044−0.186 ± 0.8190.3730.989
UGC 883735.645 ± 107.44.569 ± 10.120.180 ± 1.170.4110.847
DDO 43 (UGC 3860)7.344 ± 48.590.996 ± 4.829−0.0007 ± 4.6560.4380.822
IC 1613 (UGC 668)5.493 ± 5.5791.114 ± 0.7420.539 ± 0.8470.5000.926
UGC 12818.759 ± 27.731.737 ± 4.73−0.0326 ± 2.6651.5360.129
NGC 15600.526 ± 0.2260.519 ± 0.2271.685 ± 0.2463.7180.000
Galaxiesβ0rck0|$\chi ^2_{{\rm red}}$|p
DDO 52 (UGC 4426)8.534 ± 9.6171.919 ± 2.34−0.094 ± 1.2440.0860.999
DDO 101 (UGC 6900)5.182 ± 0.2690.819 ± 0.0600.297 ± 0.07800.1040.996
UGC 75597.989 ± 14.041.538 ± 2.228−0.116 ± 1.3950.3050.985
WLM9.050 ± 12.421.027 ± 1.044−0.186 ± 0.8190.3730.989
UGC 883735.645 ± 107.44.569 ± 10.120.180 ± 1.170.4110.847
DDO 43 (UGC 3860)7.344 ± 48.590.996 ± 4.829−0.0007 ± 4.6560.4380.822
IC 1613 (UGC 668)5.493 ± 5.5791.114 ± 0.7420.539 ± 0.8470.5000.926
UGC 12818.759 ± 27.731.737 ± 4.73−0.0326 ± 2.6651.5360.129
NGC 15600.526 ± 0.2260.519 ± 0.2271.685 ± 0.2463.7180.000
Table 4.
Open in new tab

The obtained fitting values for the parameters (β0, rc, k0) and reduced |$\chi ^2_{{\rm red}}$| and the probability p for the related dwarf galaxies.

Galaxiesβ0rck0|$\chi ^2_{{\rm red}}$|p
DDO 52 (UGC 4426)8.534 ± 9.6171.919 ± 2.34−0.094 ± 1.2440.0860.999
DDO 101 (UGC 6900)5.182 ± 0.2690.819 ± 0.0600.297 ± 0.07800.1040.996
UGC 75597.989 ± 14.041.538 ± 2.228−0.116 ± 1.3950.3050.985
WLM9.050 ± 12.421.027 ± 1.044−0.186 ± 0.8190.3730.989
UGC 883735.645 ± 107.44.569 ± 10.120.180 ± 1.170.4110.847
DDO 43 (UGC 3860)7.344 ± 48.590.996 ± 4.829−0.0007 ± 4.6560.4380.822
IC 1613 (UGC 668)5.493 ± 5.5791.114 ± 0.7420.539 ± 0.8470.5000.926
UGC 12818.759 ± 27.731.737 ± 4.73−0.0326 ± 2.6651.5360.129
NGC 15600.526 ± 0.2260.519 ± 0.2271.685 ± 0.2463.7180.000
Galaxiesβ0rck0|$\chi ^2_{{\rm red}}$|p
DDO 52 (UGC 4426)8.534 ± 9.6171.919 ± 2.34−0.094 ± 1.2440.0860.999
DDO 101 (UGC 6900)5.182 ± 0.2690.819 ± 0.0600.297 ± 0.07800.1040.996
UGC 75597.989 ± 14.041.538 ± 2.228−0.116 ± 1.3950.3050.985
WLM9.050 ± 12.421.027 ± 1.044−0.186 ± 0.8190.3730.989
UGC 883735.645 ± 107.44.569 ± 10.120.180 ± 1.170.4110.847
DDO 43 (UGC 3860)7.344 ± 48.590.996 ± 4.829−0.0007 ± 4.6560.4380.822
IC 1613 (UGC 668)5.493 ± 5.5791.114 ± 0.7420.539 ± 0.8470.5000.926
UGC 12818.759 ± 27.731.737 ± 4.73−0.0326 ± 2.6651.5360.129
NGC 15600.526 ± 0.2260.519 ± 0.2271.685 ± 0.2463.7180.000

The overall pattern shows an outer steep rise in the shapes as shown in Fig. 4. For the galaxies UGC  3680 and IC  1613 are on currently discussion about their dark matter content (Oman et al. 2016) but in both cases we have found reasonable rotation curves. For the IC  1613 galaxy, the resulting rotation curve presents a reasonable adjustment with probability p = 0.926 and as the same case of UGC  11819, UGC  11748, Malin 1 and WLM, the adjustment did not cover the last error bar. Accordingly, the case for NGC  1560 has been revealed to be a defiant example for the model due to its characteristics with a rapid rise (until 4  kpc) and a later dip (around 5  kpc) in its observed rotation curve. Even so, our model shows compatibility with dark halo models as compared to the best fit by Broeils (1992).

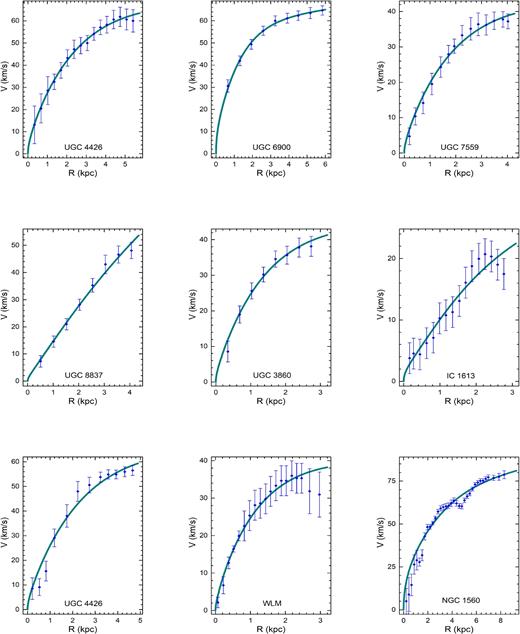
Sample of nine dwarf galaxies.
Figure 4.

Sample of nine dwarf galaxies.

Open in new tabDownload slide

4 FINAL REMARKS

Traditionally, GR has been excluded as the appropriate gravitational theory for the local dark matter gravitational field because it has been assumed that only its Newtonian limit would be effective near galaxies and clusters. In this paper, we have tried to recover the idea that the dark matter problem at least what concerns the local galactic scale may have a huge relativistic component as our results suggest in the observed rotation curve shapes leaving the dark matter component, whatever it is, a small amount to play. We have argued that the observational evidence of strong gravitational fields near the core of galaxies is inconsistent with the Newtonian limit argument. The obvious thing to do is to examine (again) the equations of slow motion in GR. We have reviewed this subject showing that the metric component g44 dominates the gravitational force, leading to the nearly Newtonian potential as shown in equation (16). It was shown that when considering the slow motion of stars near galaxies, including near the core, the slow motion breaks the general covariance of GR but not Einstein's equations.

Since dark matter gravity dominates over baryons gravity, it follows that the gravitational field of dark matter haloes surrounding large structures inherits the same symmetry evidenced by the visible shape of that object, so that spiral galaxies would not be spherically symmetric. It reinforces the cornerstone idea of this method that we need a gravitational model capable of describing a slow motion being valid for gravitational fields of any strength. The necessity of this aspect of gravity is reinforced by the observable effects of local dark matter gravity are the gravitational microlensing effect and the motion of stars and plasma in the vicinity of large structures such as galaxies and clusters. It is natural to suppose that the gravitational field produced by dark matter applies to both cosmological and local situations. Indeed, the dark matter gravitational field is supposed to be of the same nature and described by the same fundamental law, regardless if it is local or cosmological.

It is noteworthy two preliminary considerations both based on the observational facts. First, dark matter gravity predominant over the baryons gravity. This implies that the visible disc shape of a spiral galaxy is an indication that the dark matter gravitational field must be approximately a disc-symmetric field. Indeed, it would be difficult to conciliate a spherically symmetric predominant dark matter gravitational field not influencing the shape of a visible disc galaxy. Secondly, in cosmology the only effective effect of dark matter was the perturbation that its gravitational field produced on the geometry and hence on the visible matter density. Therefore, admitting that the nature of the dark matter gravitational field is the same, and that it is predominant over baryons, we are led to consider only the vacuum gravitational field, again as a first approximation. The resulting vnN maintains the asymptotically profile for a rotation curve when extended to infinity with a flat or nearly flat curve for a maximum radius.

In the course of this study, we realized that it was possible to construct a model with only one parameter (without considering the mass model) generated by setting the integration constant c1 = 0 in equation (9) but this was revealed to be a very constrained assumption. For the case of Malin 1, its related rotation curve was compromised but a better shape was obtained for the two-parameters case with c1 ≠ 0 plus the additional parameter from the adopted mass model. For these cases the present model revealed to be sensitive to the adopted mass profile. Accordingly, the exponential disc modelled by Blumenthal's profile revealed to be a tolerable approximation. Whereas the k0 parameter fluctuates in real number range, β0 is a strictly positive parameter.

The model represents an initially idealized approach to the actual detailed complex galactic dynamics that prevails but it allows a solution in the context of GR. Differently from the PPN approximation, we have presented an effective model with only three parameters constrained case-by-case with observations with promising results. Specifically for the cases of UGC  11819, UGC  11748, Malin 1, WLM IC  1613 galaxies, the resulting rotation curve presents a reasonable shapes but they presented the last error bar uncovered, which may be due to the choice of the mass model or possibly due to systematics, and should be investigated further. The good fits presented fortify our confidence to improve and expand this methodology to a more realistic approach on this problem with the study of HSBGs and comparisons of density profiles. A further development must take into account a detailed mechanism on galaxy formation to be confronted to ΛCDM model, which is a fundamental issue to investigate in order to understand a bottom-up scenario according to observations (Gao et al. 2005; Springel et al. 2005).

Acknowledgements

We thank Ekaterina Karukes and Paolo Salucci for gently providing their data base on dwarf galaxies.

Footnotes

1

The Riemann tensors and their covariant derivatives up to the seventh order must be equal.

REFERENCES

Arun
K.
,
Gudennavar
S. B.
,
Sivaram
C.
,
2007
,
Adv. Space Res.
,
60
,
166

Crossref
Search ADS
 

Bekenstein
J.
,
Milgrom
M.
,
1984
,
ApJ
,
286
,
7

Crossref
Search ADS
 

Blumenthal
G. R.
,
Faber
S. M.
,
Flores
R.
,
Primack
J. R.
,
1986
,
ApJ
,
301
,
27

Crossref
Search ADS
 

Bosma
A.
,
1981a
,
AJ
,
86
,
1791

Crossref
Search ADS
 

Bosma
A.
,
1981b
,
AJ
,
86
,
1825

Crossref
Search ADS
 

Briscece
F.
,
2011
,
Phys. Lett. B
,
696
,
315

Crossref
Search ADS
 

Broeils
A. H.
,
1992
,
A&A
,
256
,
19

 

Brownstein
J. R.
,
Moffat
J. W.
,
2006
,
ApJ
,
636
,
721

Crossref
Search ADS
 

Burke
W. L.
,
1969
,
PhD thesis
,
California Institute of Technology

Google Scholar

OpenURL Placeholder Text

 

Capistrano
A. J. S.
,
Cabral
L. A.
,
2014
,
Ann. Phys.
,
384
,
64

Crossref
Search ADS
 

Capistrano
A. J. S.
,
Roque
W. L.
,
Valada
R. S.
,
2014
,
MNRAS
,
444
,
1639

Crossref
Search ADS
 

Capistrano
A. J. S.
,
Penagos
J. A. M.
,
Alárcon
M. S.
,
2016
,
MNRAS
,
463
,
1587

Crossref
Search ADS
 

Capozziello
S.
,
Cardone
V. F.
,
Troisi
A.
,
2007
,
MNRAS
,
375
,
1423

Crossref
Search ADS
 

Capozziello
S.
,
Piedipalumbo
E.
,
Rubano
C.
,
Scudellaro
P.
,
2009
,
A&A
,
505
,
21

Crossref
Search ADS
 

Cartan
E.
,
1927
,
Ann. Soc. Polonaise Math.
,
6
,
1

 

de Blok
W. J. G.
,
2010
,
Adv. Astron.
,
2010
,
789293

Crossref
Search ADS
 

de Blok
W. J. G.
,
McGaugh
S. S.
,
Rubin
V. C.
,
2001
,
AJ
,
122
,
2396

Crossref
Search ADS
 

Dietrich
J. P.
,
Werner
N.
,
Clowe
D.
,
Finoguenov
A.
,
Kitching
T.
,
Miller
L.
,
Simionescu
A.
,
2012
,
Nature
,
487
,
202

Crossref
Search ADS
PubMed
 

Ferrarese
L.
,
Ford
H.
,
2005
,
Space Sci. Rev.
,
116
,
523

Crossref
Search ADS
 

Ferrarese
L.
Merrit
D.
,
2002
,
preprint (arXiv:astro-ph/0206222)

Gao
L.
White
S. D. M.
Jenkins
A.
Frenk
C. S.
Springel
V.
,
2005
,
MNRAS
,
363
,
379

Crossref
Search ADS
 

Gautreau
R.
,
Hoffman
R. B.
,
Armenti
A.
,
1972
,
Il Nuovo Cimento B
,
7
,
71

Crossref
Search ADS
 

Gergerly
L. Á.
,
Harko
T.
,
Dwornik
M.
,
Kupi
G.
,
Keresztes
Z.
,
2011
,
MNRAS
,
415
,
3275

Crossref
Search ADS
 

González
G. A.
,
Gutiérrez-Piñeres
A. C.
,
Ospina
P. A.
,
2008
,
Phys. Rev. D
,
78
,
064058

Crossref
Search ADS
 

Gutiérrez-Piñeres
A. C.
González
G. A.
Quevedo
H.
,
2013
,
Phys. Rev. D
,
87
,
044010

Crossref
Search ADS
 

Harko
T.
,
2011
,
MNRAS
,
413
,
3095

Crossref
Search ADS
 

Infeld
L.
Plebanski
J.
,
1960
,
Motion and Relativity
.
Pergamon Press
,
New York

Google Scholar

OpenURL Placeholder Text

 

Karachentsev
I. D.
Makarov
D. I.
Kaisina
E. I.
,
2013
,
AJ
,
145
,
101

Crossref
Search ADS
 

Karukes
E. V.
,
Salucci
P.
,
2017
,
MNRAS
,
465
,
4703

Crossref
Search ADS
 

Katsuragawa
T.
,
Matsuzaki
S.
,
2017
,
Phys. Rev. D
,
95
,
044040

Crossref
Search ADS
 

Klypin
A.
,
Kravtsov
A.
,
Valenzuela
O.
,
Prada
F.
,
1999
,
ApJ
,
522
,
89

Crossref
Search ADS
 

Lelli
F.
,
Fratenelli
F.
,
Sancisi
R.
,
2010
,
A&A
,
516
,
A11

Crossref
Search ADS
 

MacCallum
M. A. H.
,
2006
, in
Mornas
L.
Alonso
J. D.
, eds,
AIP Conf. Proc. Vol. 841, A Century of Relativity Physics: ERE 2005; XXVIII Spanish Relativity Meeting
.
Am. Inst. Phys.
,
New York
, p.
129

Google Scholar

OpenURL Placeholder Text

 

Mannheim
P. D.
,
O'Brien
J. G.
,
2012
,
Phys. Rev. D
,
85
,
124020

Crossref
Search ADS
 

Martinez-Medina
L. A.
,
Matos
T.
,
2014
,
MNRAS
,
444
,
185

Crossref
Search ADS
 

Milgrom
M.
,
1983
,
ApJ
,
270
,
365

Crossref
Search ADS
 

Misner
C.
Thorne
K. S.
Wheeler
J. A.
,
1973
,
Gravitation
.
Freeeman & Co.
,
San Francisco

Google Scholar

OpenURL Placeholder Text

 

Moore
B.
,
Ghigna
S.
,
Governato
F.
,
Lake
G.
,
Quinn
T.
,
Stadel
J.
,
Tozzi
P.
,
1999
,
ApJ
,
524
,
L19

Crossref
Search ADS
 

Navarro
J. F.
,
Frenk
C. S.
,
White
S. D. M.
,
1997
,
ApJ
,
490
,
493

Crossref
Search ADS
 

Nierenberg
A. M.
,
Treu
T.
,
Menci
N.
,
Lu
Y.
,
Torrey
P.
,
Vogelsberger
M.
,
2016
,
MNRAS
,
462
,
4473

Crossref
Search ADS
 

Ogiya
G.
Mori
M.
,
2014
,
ApJ
,
793
,
46

Crossref
Search ADS
 

Oman
K. A.
,
2015
,
MNRAS
,
452
,
3650

Crossref
Search ADS
 

Oman
K. A.
,
Navarro
J. F.
,
Sales
L. V.
,
Fattahi
A.
,
Frenk
C. S.
,
Sawala
T.
,
Schaller
M.
,
White
S. D. M.
,
2016
,
MNRAS
,
460
,
3610

Crossref
Search ADS
 

Padmanabhan
T.
,
2003
,
Phys. Rep.
,
380
,
235

Crossref
Search ADS
 

Peebles
P. J. E.
,
Ratra
B.
,
2003
,
Rev. Modern Phys.
,
75
,
559

Crossref
Search ADS
 

Planck Collaboration XVI
,
2014
,
A&A
,
571
,
A16

Crossref
Search ADS
 

Quandt
I.
,
Schmidt
H.-J.
,
1991
,
Astron. Nachr.
,
312
,
97

Crossref
Search ADS
 

Richstone
D.
et al. ,
1998
,
Nature
,
395
,
A14

 

Rosen
N.
,
1949
,
Rev. Modern Phys.
,
21
,
503

Crossref
Search ADS
 

Rubin
V. C.
,
Kent Ford
W.
,
Jr
,
1970
,
ApJ
,
159
,
379

Crossref
Search ADS
 

Salucci
P.
,
2001
,
MNRAS
,
344
,
L1

Crossref
Search ADS
 

Salucci
P.
,
Walter
F.
,
Borriello
A.
,
2003
,
A&A
,
409
,
53

Crossref
Search ADS
 

Spekkens
K.
,
Giovanelli
R.
,
Haynes
M. P.
,
2005
,
AJ
,
129
,
2119

Crossref
Search ADS
 

Spergel
D. N.
,
2015
,
Science
,
347
,
1100

Crossref
Search ADS
PubMed
 

Springel
V.
,
2005
,
MNRAS
,
364
,
1105

Crossref
Search ADS
 

Springel
V.
et al. ,
2005
,
Nature
,
435
,
629

Crossref
Search ADS
PubMed
 

Stephani
H.
Kramer
D.
MacCallum
M.
Hoenselaers
C.
Herlt
E.
,
2003
,
Exact Solutions of Einstein's Field Equations, 2nd edn
.
Cambridge Univ. Press
,
Cambridge

Google Scholar

Crossref
Search ADS

 

Stierwalt
S.
,
Liss
S. E.
,
Johnson
K. E.
,
Patton
D. R.
,
Privon
G. C.
,
Besla
G.
,
Kallivayalil
N.
,
Putman
M.
,
2017
,
Nat. Astron
,
1
,
0025

Crossref
Search ADS
 

Swaters
R. A.
,
Madore
B. F.
,
Trewhella
M.
,
2000
,
ApJ
,
531
,
L107

Crossref
Search ADS
 

Swaters
R. A.
,
Madore
B. F.
,
Van den Bosch
F. C.
,
Balcells
M.
,
2003a
,
ApJ
,
583
,
732

Crossref
Search ADS
 

Swaters
R. A.
,
Verheijen
M. A. W.
,
Bershady
M. A.
,
Andersen
D. R.
,
2003b
,
ApJ
,
587
,
L19

Crossref
Search ADS
 

The Pierre Auger Collaboration
,
2007
,
Science
,
318
,
938

Crossref
Search ADS
PubMed
 

Ujevic
M.
Letelier
P. S.
,
2004
,
Phys. Rev. D
,
70
,
084015

Crossref
Search ADS
 

Ujevic
M.
Letelier
P. S.
,
2007
,
Gen. Relativ. Gravitation
,
39
,
1345

Crossref
Search ADS
 

Vogt
D.
,
Letelier
P. S.
,
2008
,
MNRAS
,
384
,
834

Crossref
Search ADS
 

Vorobyov
E. I.
Shchekinov
Yu.
Bizyaev
D.
Bomans
D.
Dettmar
R.-J.
,
2009
,
A&A
,
505
,
483

Crossref
Search ADS
 

Wex
N.
,
2015
, in
Puetzfeld
D.
Lämmerzahl
C.
Schutz
B.
, eds,
Equations of Motion in Relativistic Gravity
.
Springer-Verlag
,
Berlin
, p.
651

Google Scholar

Crossref
Search ADS

 

Weyl
H.
,
1917
,
Ann. Phys.
,
54
,
117

Crossref
Search ADS
 

Zipoy
M. D.
,
1966
,
J. Math. Phys.
,
7
,
1137

Crossref
Search ADS
 
© 2017 The Authors Published by Oxford University Press on behalf of the Royal Astronomical Society
Issue Section:
Article
Download all slides