Tidal disruption by extreme mass ratio binaries and application to ASASSN-15lh

Abstract

1 INTRODUCTION

Galaxy mergers lead to the formation of supermassive black hole (SMBH) binaries, which coalesce due to stellar scattering, interactions with nuclear gas, and gravitational wave losses (e.g. Begelman, Blandford & Rees 1980; Kelley, Blecha & Hernquist 2017). Although this scenario is theoretically compelling, observational tests have been frustrated by the difficulty of identifying galaxies with multiple SMBHs. Imaging and spectroscopic surveys provide powerful tools for identifying samples of relatively wide separation dual active galactic nuclei (AGNs; Komossa et al. 2003; Comerford et al. 2009), but the number of confirmed binaries at pc-scale separation is much smaller (Rodriguez et al. 2006). At even smaller separations, surveys of AGN variability have the potential to discover binaries approaching or entering the gravitational wave dominated phase of inspiral (Hayasaki, Mineshige & Sudou 2007; MacFadyen & Milosavljević 2008; Cuadra et al. 2009; D’Orazio & Haiman 2017), with recent surveys identifying a number of candidates (Charisi et al. 2016; Liu et al. 2016).

Tidal disruption events (TDEs; Lacy, Townes & Hollenbach 1982; Rees 1988) – when a star is destroyed by the tidal field of a SMBH – offer a complementary route to SMBH binary discovery. While the number of observed TDEs is presently of the order of dozens (Komossa 2015), current surveys such as the Panoramic Survey Telescope and Rapid Response System (Kaiser et al. 2010; Gezari et al. 2012; Chambers et al. 2016), the All-Sky Automated Survey for SuperNovae (Holoien et al. 2014; Shappee et al. 2014), and the Palomar Transient Factory (Law et al. 2009; Arcavi et al. 2014; Blagorodnova et al. 2017) are discovering events at an increasing rate. Future surveys such as the Zwicky Transient Facility (Bellm 2014) and the Large Synoptic Survey Telescope (Ivezic et al. 2008) are predicted to yield hundreds of new candidates. Some fraction of these TDEs will occur in galaxies containing binaries, which may affect the light curve in distinct and predictable ways.

The detectability of SMBH binaries from TDE surveys is a strong function of the binary mass and separation. A binary modifies the fallback rate from the standard result for a single black hole, |$\dot{M}_{\rm fb} \propto t^{-5/3}$| (Phinney 1989), if the bound debris has an orbit that is large enough to experience a significant perturbation from the binary. For moderate mass ratio binaries with q = M₂/M₁ ∼ 0.2, M₂ ≤ M₁ being the masses of the SMBHs, this requirement favours systems with relatively low-mass SMBHs (M_h ≲ 10⁶ M_⊙) (Coughlin et al. 2017). More massive SMBH binary systems would still perturb the fallback rate, but only for separations where the gravitational wave inspiral time is short and the probability of a coincident TDE small.

Coughlin et al. (2017) used a combination of three-body integrations and hydrodynamic simulations to identify the observable characteristics of TDEs in moderate mass ratio binary systems. Their results suggested that a binary of the appropriate separation can introduce a variety of strong perturbations to the light curve, including ‘dips’ when fallback on to the disrupting hole is interrupted (Liu, Li & Chen 2009; Ricarte et al. 2016), bursts of accretion, and quasi-periodic variability. In this paper, we extend our prior study to the case of extreme mass ratio SMBH binaries. Our motivations are two-fold. From a theoretical perspective, disruptions by the secondary represent the only channel for TDEs in large galaxies where the primary has a mass M₁ ≳ 10⁸ M_⊙ that is too large to tidally disrupt Solar-type (and smaller) stars. Minor mergers could result in a significant population of extreme mass ratio binaries in such galaxies, and because the gravitational wave inspiral time increases for a fixed primary mass approximately as τ_GW ∝ 1/q (Peters & Mathews 1963), TDEs by the secondary could be perturbed by the presence of a primary on observable time-scales. Observationally, we investigate whether a TDE by the secondary in an extreme mass ratio system provides a possible interpretation for the light curve of the event ASASSN-15lh. Initially classified as an extremely luminous supernova (Dong et al. 2016), the physical nature of ASASSN-15lh remains unclear, with different lines of evidence supporting either a supernova (Godoy-Rivera et al. 2017) or TDE (Margutti et al. 2017) interpretation. If ASASSN-15lh was a TDE, the likely mass of the primary SMBH in the observed galaxy is close to the maximum allowable value, leading to suggestions that the black hole is most likely rotating rapidly (Leloudas et al. 2016). Here we study whether the characteristics of the event – including its perplexing rebrightening at ∼100  d after detection – could instead be consistent with the tidal disruption of a star by a binary companion with much lower mass.

The layout of the paper is as follows. In Section 2 we provide the basic time-scales over which we expect variability to occur in TDEs resulting from extreme-q SMBH binaries. We use our arguments to constrain the properties of the putative binary system that could explain ASASSN-15lh. To substantiate these general arguments, in Section 3 we describe the results of a number of hydrodynamic simulations of the disruption of a star by an SMBH binary, with binary properties appropriate to those anticipated for ASASSN-15lh. In Section 4 we discuss the implications of our findings, and we summarize and conclude in Section 5.

2 GENERAL TIME-SCALES

For an isolated SMBH, the accretion rate eventually transitions to a power law that is well-matched by the analytically predicted, t^−5/3 scaling (Phinney 1989).¹ Matters can be considerably more complicated when the disrupting black hole is part of a binary system (Coughlin et al. 2017); the accretion rate on to one or both SMBHs can often increase or decrease by orders of magnitude after the start of the decline. These changes to the accretion rate can also be quite erratic, and occur on time-scales that are much shorter than the orbital period of the binary (though long-term accretion curves generally exhibit peaks in their power spectra at frequencies comparable to the orbital period). Moreover, in some extreme cases the accretion rate never follows the t^−5/3 fallback rate – even after a large number of T_ret.

3 HYDRODYNAMIC SIMULATIONS

To test the reasoning outlined in the previous section, we simulate, using the smoothed-particle hydrodynamics (SPH) code phantom (Price et al. 2017), the tidal disruption of a star by an SMBH binary.

3.1 Setup

The star is approximated as a γ = 5/3 polytrope with a Solar mass and radius by first placing ∼5 × 10⁵ particles on a close-packed sphere. The sphere is then stretched to achieve a nearly polytropic density distribution, and it is thereafter dynamically relaxed for 10 sound crossing times to smooth out any numerical perturbations. The relaxed polytrope is subsequently placed on an orbit that will take it within the tidal radius of a 5 × 10⁵ M_⊙ SMBH, which is the secondary SMBH in a circular binary with a primary of mass M₁ = 10⁸ M_⊙. We consider cases where the semimajor axis of the binary orbit is a = 500 GM₁/c² ≃ 2.5 mpc (30 simulations), and a = 5 mpc (20 simulations).

To further establish the orbit of the to-be-disrupted star we use the same procedure outlined in Coughlin et al. (2017): we assume that the star originally comes from near or beyond the sphere of influence of the binary on a parabolic orbit about the binary centre of mass, its initial position randomly distributed over a sphere of radius 50a and its pericentre uniformly distributed between 0 and 2a. We integrate the orbit of the star, assumed to be a point mass, about the binary until it is either ejected (recedes to beyond 100 times the separation of the binary) or passes through the tidal radius of either SMBH. If a star is disrupted by the secondary, we trace its orbit back to the point where it was five times the tidal radius away from the hole – just prior to disruption – and use its location and velocity at that time to initialize the SPH simulation.

By following this route we avoid simulating the hydrodynamics of the entire encounter of the star with the binary, which would be prohibitively expensive and would not yield much new information about the evolution of the star prior to disruption. As pointed out by Coughlin et al. (2017), this method also highlights the fact that the orbital energy and angular momentum of the star can change as it orbits the binary. These changes can then impact the evolution of the TDE, and can introduce some intrinsic scatter to, e.g. the time to peak. As was also done in Coughlin et al. (2017), we do not simulate any encounters that have β = r_t/r_p ≥ 5, where r_p is the pericentre distance of the star and r_t is the tidal radius, as these encounters are difficult to resolve and can introduce numerical artefacts that affect the energy distribution of the debris.

The evolution of the tidally disrupted debris is followed for roughly an orbital period of the binary, which is of the order of a year, and self-gravity is included at all stages using a k–D tree (Gafton & Rosswog 2011); the gas maintains a polytropic equation of state, and so cooling and heating through shocks are ignored. Particles that enter within 0.5r_t of either black hole, with r_t appropriately scaled to the size of the hole, are ‘accreted’, and contribute to the accretion rate of the black hole. We assessed the sensitivity of our accretion rates to this choice of accretion radius by decreasing it by a factor of two, and this resulted in only small differences (see Fig. 3).

3.2 Results

Of the 30 disruptions with a = 2.5 mpc and q = 0.005, 23 generated a completely unbound stream, thereby resulting in no accretion, or a stream on a wide orbit about the binary that, in some instances, encircled the system in a circumbinary ring of gas that eventually spread into a disc (Coughlin & Armitage 2017). These 23 cases had little to no accretion at all times, bearing little resemblance to a ‘normal’ TDE.

As pointed out in Coughlin et al. (2017), the reason for these ejections and atypical stream distributions is that the specific energy of the centre of mass of the star is modified by the motion of the secondary. In particular, in the rest frame of the secondary, the star has an approximate energy of |$\epsilon \simeq \boldsymbol {v}_{{\rm app}}^2/2-GM/r$|⁠, where |$\boldsymbol {v}_{{\rm app}}^2$| is the square of the vector difference between the velocity of the star and the velocity of the secondary. In general, |$\boldsymbol {v}_{{\rm app}}^2$| contains cross terms that depend on the relative orientation of the star and the secondary at the time of disruption, and will be smaller (larger) if the star and the secondary are moving parallel (antiparallel) to one another when the star enters within the tidal radius. However, these cross terms sum to approximately zero when averaged over the ensemble of disruptions, and the net contribution to the average energy of the star is given by the kinetic energy of the secondary. In the small-q limit, ε = GM_p/(2a), M_p being the mass of the primary, and the ratio of this energy to the tidal energy spread Δε is ε/Δε ≃ q^−1/3(M_p/M_*)^1/3/(2k), where k is the ratio of the binary separation to the tidal radius of the primary (see also equation 8 of Coughlin et al. 2017). For the present setup, this ratio is ε/Δε ≃ 6 when a = 2.5 mpc (≃ 3 when a = 5 mpc), meaning that the orientation of the disrupted star must be favourable in order to cancel the relatively large contribution to the energy that results from the motion of the secondary. Instances in which the alignment is not favourable result in a completely unbound stream, and it is therefore not surprising that the majority of the simulated disruptions generate little to no accretion.

The other seven yielded accretion at early times, with some likelihood of appearing like a TDE from an isolated SMBH, and the top-left, top-right, and middle-left panels of Fig. 1 illustrate the accretion rate on to the secondary SMBH that results from these disruptions. Each curve represents a different simulation, except for the dashed curve in the top-left hand panel, which shows the solution that follows from the impulse approximation for comparison, and the horizontal, dot–dashed line in the same panel, which gives the Eddington limit of the hole assuming |$L = 0.1\dot{M}c^2$|⁠. The accretion curves were broken up into separate panels for clarity.

Figure 1.

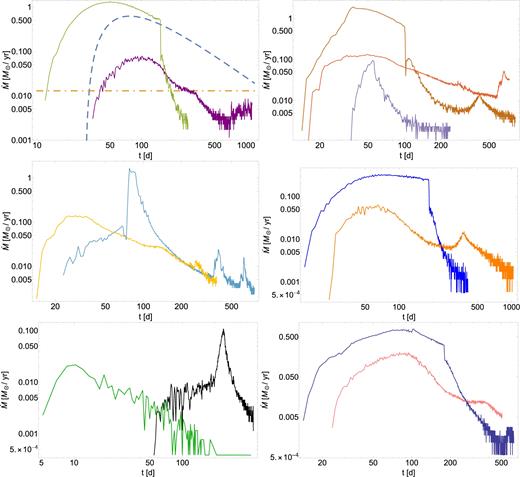
The top-left, top-right, and middle-left plots show the accretion rate in Solar masses per year as a function of time in days for q = 0.005 and a = 2.5 mpc, which is the setup most favoured by the scaling arguments for the event ASASSN-15lh. The dashed curve in the top-left panel shows the analytic prediction that follows from the impulse approximation, and the horizontal, dot–dashed line shows the Eddington limit assuming |$L = 0.1\dot{M}c^2$|⁠. The different curves in each panel – aside from the analytic solution – are from different simulations, and are only plotted separately for the sake of clarity. The middle-right, bottom-left, and bottom-right panels illustrate the accretion rate in Solar masses per year as a function of time in days for q = 0.005 and a = 5 mpc.

Open in new tabDownload slide

It is obvious that the accretion curves do not match the impulse approximation exactly, and there are a number of reasons for this discrepancy; for one, the impulse approximation measures the ‘fallback rate’, being the rate at which material returns to pericentre. On the other hand, material that accretes on to the black hole in the simulation must first transfer its angular momentum outwards and dissipate its kinetic energy. It is also apparent that the return time of the most bound debris is either earlier or later than that predicted analytically, and this results not only from the fact that the star is already tidally distorted at the time it passes through the tidal radius (Coughlin & Nixon 2015), but also because the binding energy of the centre of mass is not exactly equal to zero. In particular, the three-body interactions change the specific energy of the star from its original, parabolic value, meaning that the most bound debris has an energy that deviates from the value imposed by the tidal force and thus returns at an earlier or later time.

For the same reason, the peak accretion rate can differ from the analytically predicted one by over an order of magnitude, and the total mass accreted can exceed or fall below the expected value of ≃  M_⊙/2. Nevertheless, the time to peak measured from the start of accretion is typically around the same value, and corresponds to roughly the value that results from the impulse approximation (∼30–40 d). Consistent with this observation, one can show, by extending the analysis in Lodato et al. (2009) and Coughlin & Begelman (2014) to include a non-zero centre of mass energy ε_c, that the time to rise is generally insensitive to ε_c as long as ε_c ≲ Δε, where |$\Delta \epsilon = GM_{\rm h}R_*/r_{\rm t}^2$|⁠.

The presence of the binary companion also generates a number of perturbations on the accretion rate, including, as was noted in Coughlin et al. (2017), sudden and drastic increases and decreases in its magnitude. We also see from each of the three panels that there is a time at which the accretion rate first exhibits a large change, and this corresponds roughly to a time of 100–150 d following the disruption of the star. We will return to a more in depth discussion of this point and its implications for ASASSN-15lh in Sections 4.1 and 4.2.

The middle-right, bottom-left, and bottom-right panels of Fig. 1 show the accretion rates from disruptions by a binary with q = 0.005 and a = 5 mpc; as was true for those with q = 0.005 and a = 2.5 mpc, the six shown in this figure looked like standard disruptions and had prompt accretion, while the other 14 resulted in completely ejected streams or low-amplitude, variable, and late-time accretion. The main features of these plots are similar to those with a = 5 mpc, but we note that the time at which the accretion rate starts to show significant variability is typically closer to 200 d.

The morphology of the accretion flows that result from these simulations are similar in appearance to those in Coughlin et al. (2017), with a small-scale accretion disc around the secondary (disrupting) SMBH and a larger-scale, extended cloud of debris that surrounds the binary; see Fig. 2. However, while accretion on to both black holes occurred most of the time for the moderate-q binaries considered in Coughlin et al. (2017) (see their fig. 12 and the online, supplementary material), the simulations here generally did not result in accretion on to the primary (or, if it did, it was at late times and was very low). This could be due either to the difference in mass ratio or to the wider separations considered here – Coughlin et al. (2017) let a = 100 r_{t, 1}, while here a = 500–1000 r_{t, 1}.

Figure 2.

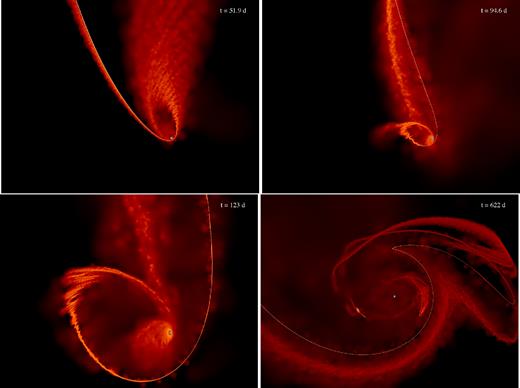
The top-left, top-right, and bottom-left show an example of the accretion disc that forms around the secondary SMBH from a TDE. This simulation corresponds to the accretion rate shown by the blue curve in the middle-left panel of Fig. 1, and the time since disruption is shown in the top-right corner of each panel. Colour scales with density, and brighter (darker) colours indicate denser (less dense) regions. The bottom-right panel of this figure shows the same simulation at a later time, and expanded in scale to demonstrate that, in addition to maintaining a small-scale accretion disc around the secondary, some debris expands to large radii and surrounds the binary. The blue points show the positions of the SMBHs.

Open in new tabDownload slide

4 DISCUSSION

4.1 Accretion rates and morphology

It is apparent from Fig. 1 that, for the simulations that result in prompt accretion on to the secondary black hole, there is an initial rise, peak, and decay in the accretion rate that resembles the isolated-SMBH, canonical-TDE picture. After a finite amount of time, however, the accretion rate changes drastically, and can decrease (e.g. the green curve in the top-left panel of Fig. 1) or increase (e.g. the blue curve in the middle-left panel of Fig. 1) by an order of magnitude and do so rather abruptly.

We argued in Section 2 that, when a TDE occurs by the secondary SMBH, such deviations are expected to occur in systems with small q, the reason being that the accreting debris recedes outside the Hill sphere of the secondary and affects the accretion rate on a time-scale given by equation (3). Using a = 2.5 mpc and M₁ = 10⁸ M_⊙ in this expression gives T_σ ≃ 90  d, which is in rough agreement with Fig. 1. We also find T_σ ≃ 250  d for a = 5 mpc and M₁ = 10⁸ M_⊙, which is approximately the time-scale at which changes start to occur in the accretion curves shown in the middle-right, bottom-left, and bottom-right panels of Fig. 1.

The relative orientation of the returning debris stream, the secondary black hole, and the centre of mass of the binary – approximately at the location of the primary – determine the magnitude of the change in the accretion rate. Furthermore, if this interpretation is correct, the orientation and physical extent of the accretion disc around the secondary should reflect these changes, as the angular momentum profile of the incoming debris, relative to the secondary, starts to differ from the material initially comprising the disc.

In support of this notion, the top-left, top-right, and bottom-left panels of Fig. 2 show the accretion disc around the secondary SMBH at three different times, those times given in the top-right corner of each panel; in this figure, colours scale with the density, with brighter (darker) colours representing denser (more rarefied) material. This simulation corresponds to the accretion rate shown by the blue curve in the middle-left panel of Fig. 1. We see that initially a large-scale, elliptical disc forms around the SMBH, and the accretion rate starts to rise and resemble the situation from an isolated TDE. However, after ∼90  d, the orientation of the debris stream starts to change, and material is funnelled into a much closer region around the black hole. After this time, a new, much more compact disc forms around the SMBH, and its rotation profile is retrograde with respect to the accretion disc that originally formed. In this case, the debris stream, the secondary, and the centre of mass are nearly aligned, and this alignment results in a decrease in the angular momentum of the incoming material and a corresponding increase in the accretion rate by over an order of magnitude. The bottom-right panel shows a zoomed-out version of the same simulation at a later time, demonstrating that some debris is flung to larger distance and generates a cloud of debris that encompasses the binary.

In addition to an initial, major increase or decrease in the accretion rate, many of the simulations exhibit variability at later times. This behaviour was also seen in the simulations run by Coughlin et al. (2017), and these additional variations could occur when the secondary SMBH comes close to the debris stream; while Liu et al. (2009) and Ricarte et al. (2016) argued that these instances should cause dips in the accretion rate of the primary, here we see – not surprisingly – that they can also result in an increase in the accretion rate of the secondary.

Some of the changes in the accretion rates in Fig. 1 are likely due to the specific choice of accretion radius; for example, the near-vertical spikes occur when the stream passes into or out of the accretion radius of the hole. However, these changes are ultimately caused by the change in the orientation of the stream, as evidenced by Fig. 2, and choosing a smaller accretion radius would likely serve to reflect the same features but smoothed out temporally. Additionally, we speculate that the more gradual changes in the accretion curves are less sensitive to the accretion radius, and Fig. 3 confirms this notion: the red curve shows the accretion rate when the accretion radius is set to r_t/2 (and is identical to the yellow curve shown in the middle-left panel of Fig. 1), and the black curve illustrates the accretion rate when the accretion radius is set to half that value. It is apparent that, for this TDE, only small changes in the accretion rate are induced by adopting a smaller accretion radius.

Figure 3.

The accretion rate on to the SMBH for two values of the accretion radius, as shown in the legend. The red curve in this figure is the same as the yellow curve in the middle-left panel of Fig. 1.

Open in new tabDownload slide

Before moving on, we note that the relatively modest particle number (5 × 10⁵ particles – chosen because higher resolution would be substantially more expensive) results in numerical dissipation in the immediate vicinity of the accreting SMBH. This likely leads to faster stream circularization and disc formation than would be the case if there were only physical sources of dissipation. In the physical situation, apsidal precession due to general relativity is responsible for stream self-intersection and circularization, and without this effect there would be a significant delay in the onset of accretion (Shiokawa et al. 2015; Bonnerot et al. 2016; Hayasaki, Stone & Loeb 2016). In the case of close binaries, the binary potential will cause additional precession that increases with distance from the disrupting black hole. Circularization will therefore occur on a time-scale that is no longer (and possibly shorter) than for the case of an isolated black hole. Thus, while disc formation may be artificially enhanced by numerical effects in our models, there are physical sources of precession that correspondingly generate physical dissipation on time-scales comparable to the fallback time.

4.2 Application to ASASSN-15lh

ASASSN-15lh was among the brightest supernovae ever detected, with an estimated peak bolometric luminosity of L ≃ 10⁴⁵ erg s⁻¹ and a total radiated energy in excess of 10⁵² erg (Dong et al. 2016; Godoy-Rivera et al. 2017). In addition, the event rebrightened – only in the UV bands – around day ∼120 after first detection, reached a second peak around day ∼200, and then continued to decline (Brown et al. 2016; Godoy-Rivera et al. 2017). As noted by Margutti et al. (2017), who found that the source was emitting in the soft X-ray in addition to the optical and UV, ASASSN-15lh also exhibited a significant degree of variability in the UV bands during the rebrightening phase; there may have also been a second rebrightening, only in the shortest wavelengths, around 260 d post-detection (Brown et al. 2016).

Dong et al. (2016) pointed out that the lack of any hydrogen emission lines means that the rebrightening is likely unassociated with the interaction between the ejecta from a supernova and circumstellar material (but see Chatzopoulos et al. 2016); time-scale arguments also suggest that this association is unlikely (Margutti et al. 2017). Likewise, the peak luminosity of ASASSN-15lh would require a very large amount (≳ 30 M_⊙) of ⁵⁶Ni, and the decline in luminosity is inconsistent with the radioactive decay time-scale (Quimby et al. 2011; Dong et al. 2016). While a magnetar-powered explosion is still possible, there is only a narrow range of permissible properties of the neutron star if one is to accommodate all aspects of the observations (Chatzopoulos et al. 2016). Finally, the properties of the host galaxy, being very massive with little star formation, are inconsistent with those of other, superluminous supernovae (Neill et al. 2011).

While the proximity of the event with the nucleus of the host galaxy (Brown et al. 2016) favours the tidal disruption scenario for the origin of ASASSN-15lh (the lack of hydrogen emission lines is also consistent, depending on the orientation of the disrupted debris; Guillochon, Manukian & Ramirez-Ruiz 2014; Roth et al. 2016), arguably the biggest criticism of this model is that the mass–luminosity relation implies an SMBH mass of ∼10⁸ M_⊙ (McConnell & Ma 2013). A straightforward calculation shows that SMBHs of such mass (and larger) consume-Solar type stars (and smaller) whole. Nevertheless, the tidal radius can be pushed slightly outside the event horizon if the hole is rapidly rotating in a prograde sense with respect to the angular momentum vector of the stellar orbit (Kesden 2012), and such a scenario was invoked by Leloudas et al. (2016) to explain ASASSN-15lh.

On the other hand, if one posits that a lower mass, companion SMBH was the disrupting hole, then such a black hole can have a mass well below the maximum-allowable mass for disruption. As we showed above, one can use the rise time, which was successfully inferred for this event, to constrain the mass of the secondary to M_h ≃ 5 × 10⁵ M_⊙, and the time at which rebrightening occurs gives a ≃ 3.6 mpc.

Our hydrodynamic simulations with a = 2.5 mpc, q = 0.005, and M₁ = 10⁸ M_⊙ generated a number of interesting fallback signatures, and many of them do not look like ASASSN-15lh. A few, however, do bear a very similar resemblance to the event. For example, the yellow accretion curve middle-left panel of Fig. 1 (see also Fig. 3) has a rise time of the order of ∼30  d, a power-law decay following the initial peak, and a second rebrightening that starts around ∼100  d. This rebrightening event lasts for roughly 60 d, after which the accretion rate resumes its power-law decline until much later times. The purple curve in the top-left panel of Fig. 1 also has many of the same features, with an initial peak after ∼60  d, a second brightening starting at ∼150  d that lasts ∼100  d, and otherwise an approximate power-law decline (again, until much later times).

As can be seen from Fig. 2, the increase in the accretion rate corresponds to a substantial restructuring of the accretion disc around the hole, with more material being funnelled to small radii. If the disc remains thin, then a natural consequence of such a small-scale accretion disc would not only be an increase in the accretion rate, but also an increase in the effective temperature (Shakura & Sunyaev 1973). Therefore, this model immediately incorporates the larger UV flux seen from ASASSN-15lh.

The peak luminosity of the event reached L ≃ 10⁴⁵ erg s⁻¹, which, for an SMBH mass of 5 × 10⁵ M_⊙ and a radiative efficiency of 0.1, corresponds to a few times the Eddington limit of the hole. Accretion rates of this magnitude are achieved by our simulations, and the fact that the luminosity is only mildly supercritical is consistent with the lack of hard X-ray emission that would be expected from highly super-Eddington TDEs (such as, for example, Swift J1644+57; e.g. Bloom et al. 2011; Burrows et al. 2011; Cannizzo, Troja & Lodato 2011; Levan et al. 2011; Zauderer et al. 2011). Furthermore, the total radiated energy, E ≃ few × 10⁵² erg, is manifestly obtained if the disrupted star is Solar-like and half of the star is accreted (again, with a radiative efficiency of 0.1). While the shift in centre of mass energy means that some of our simulations accrete more or less of half of a Solar mass, the scale of the total radiated energy is always of the order few × 10⁵² erg.

Finally, many of the curves in Fig. 1 show some degree of variability in the accretion rate near the time at which the rebrightening occurs. While the magnitude of the variations are certainly somewhat dependent on the size of the accretion radius and the resolution of the simulation, since the change in accretion morphology during the rebrightening is rather drastic, we expect some intrinsic, physical variability around this time, which is consistent with that seen in ASASSN-15lh (Margutti et al. 2017). Additionally, most of the accretion rates show some other resurgence over the roughly power-law decline at even later times (i.e. after the rebrightening that we expect to occur on the time-scale given by equation 3). As noted by Brown et al. (2016), there is some evidence that ASASSN-15lh underwent a second rebrightening around day ∼260, but only in the highest-energy bands. Not only are such additional variations in line with the binary SMBH interpretation, we might also expect – if the binary SMBH interpretation is correct – the event to exhibit some fluctuations in its light curve at later times still.

4.3 Rate of TDEs

In our model, the star is tidally disrupted by the secondary, which has a mass M₂ = 0.005M₁. As shown by Coughlin et al. (2017), who performed a more systematic study of the effects of q on the properties of TDEs by SMBHs in binaries, the relative probability of disruption by the secondary SMBH is approximately λ₂ ≃ q/2. Thus, the vast majority of stars in systems with q = 0.005 should be disrupted by the primary.

In the setup considered here, where the primary mass is 10⁸ M_⊙, all of the stars that are ‘disrupted’ by the primary are actually swallowed whole, as r_{g, 1} = GM₁/c² ≃ r_{t, 1}. Thus, while it would seem unlikely that any observed TDE in such a small-q system should be committed by the secondary, we circumvent this issue – stars are much more likely to enter within the tidal radius of the primary, but the act of doing so generates no observable emission.

Nevertheless, the total rate of tidal disruption for the systems considered here is rather low: of a total of 6 × 10⁶ encounters with a = 2.5 mpc, the restricted three-body integrations resulted in only 44 disruptions by the secondary (and we simulated the hydrodynamic evolution for 30 of those). Using the fact that the separation of the binary is 500r_{t, 1}, the rate of disruption by the binary is λ_{TDE, binary} ≃ 44 × 500/(6 × 10⁶)λ_TDE ≃ 0.004λ_TDE, where λ_TDE is the rate of disruption by an isolated SMBH. Moreover, if we only consider the seven disruptions that generated prompt accretion, then the observable rate of disruption falls by an additional factor of ∼ 7. If λ_TDE = 10⁻⁴ gal⁻¹ yr⁻¹ (Frank & Rees 1976; Stone & Metzger 2016), then we expect roughly 0.2 TDEs over the lifetime of the binary, and even fewer that result in observable accretion. When a = 5 mpc, the total number of expected TDEs increases to ∼3 before the binary inspirals due to gravitational wave losses. Thus, the likelihood of tidally disrupting a Solar-like star is somewhat low over the lifetime of the binary.

On the one hand, superluminous supernovae are quite rare, and ASASSN-15lh is among the most extraordinary within that class. It would therefore not be overly surprising if the event itself also required a set of extraordinary conditions. Given the large number of relatively low-mass satellite galaxies, it also seems plausible that there may exist a significant population of low-mass black holes spiraling into the centres of larger galaxies.

Another possibility is that our initial conditions for the three-body encounters – a star approaching the binary centre of mass on a parabolic trajectory – were too restrictive. As shown by Chen et al. (2009), if there is a significant population of bound stars to the primary, this can boost the TDE rate by a factor of ∼10⁴. Stars bound to the secondary could also undergo Kozai oscillations, and those with large orbital inclinations could be driven to such high eccentricities (the eccentric Kozai mechanism) that they plunge within the tidal radius of the secondary (Ivanov, Polnarev & Saha 2005; Li et al. 2015); this could also significantly augment the TDE rate. Finally, as shown by Madigan et al. (2017), an eccentric disc of stars maintains its stability by pushing some stellar orbits to high eccentricities, which – if such a population of stars is present, and some studies suggest they may be somewhat common (Lauer et al. 2005) – further increases the TDE rate.

4.4 Other sources of emission: winds and accretion on to the primary

From Fig. 1, we see that accretion on to the secondary often proceeds at a super-Eddington rate. While most of the time the rate is only mildly super-Eddington, satisfying |$\dot{M} = N\times \dot{M}_{{\rm Edd}}$| with N ≃ few, in some cases, and particularly towards the peak in the accretion rate, N can approach and even exceed 100. While these hyper-Eddington periods are predicted analytically (Rees 1988; Evans & Kochanek 1989), the peak accretion rates in Fig. 1 can actually exceed the analytical one (shown by the dashed curve in the top-left panel in this figure), which is a consequence of self-gravity (Coughlin & Nixon 2015) and the non-zero energy of the stellar centre of mass.

In these highly supercritical regimes, one might expect winds (Strubbe & Quataert 2009; Metzger & Stone 2016) or, in the more extreme cases, jets (Giannios & Metzger 2011; Coughlin & Begelman 2014; Tchekhovskoy et al. 2014; Coughlin & Begelman 2015) to be launched from the vicinity of the accreting SMBH. From these outflows one would expect an additional source of radiation, with properties distinct from the disc. While it is unlikely that this scenario explains the rebrightening seen in ASASSN-15lh – the accretion rate would have been super-Eddington prior to the increase, and the constancy of the X-ray emission (Margutti et al. 2017) suggests that there was no change in the source of harder photons – changes in the luminosity induced by a sudden super-Eddington surge of accretion would be possible in other systems.

5 SUMMARY AND CONCLUSIONS

In this paper we analysed the tidal disruption of Solar-like stars by the secondary black hole in binary systems with high mass primaries and extreme mass ratios (q = M₂/M₁ = 0.005). These systems are interesting because (1) for sufficiently high primary masses no TDEs from the primary are expected, and (2) for extreme mass ratios the binary can be tight enough to perturb a secondary TDE while the gravitational wave inspiral time is still moderately long (1–10 Myr for our specific parameters). We argued heuristically that these events should display light curves that initially rise, peak, and decay in a manner similar to those of TDEs by isolated SMBHs. However, after a time |$T_{\sigma } \propto {a^{3/2}}/\sqrt{GM_1}$|⁠, where a is the separation of the binary and M₁ is the mass of the primary, the accretion on to the secondary should exhibit some deviation from the canonical-TDE scenario, resulting in a variation in the light curve.

Using a combination of three-body integrations and hydrodynamic simulations, we studied the properties of the fallback from TDEs by the secondary in systems with black hole masses of 10⁸ and 5 × 10⁵ M_⊙, and a = 2.5 or 5 mpc. The most common outcome – occurring in about 2/3 to 3/4 of realizations – was the formation of an unbound debris stream that would not result in any accretion (though it may mimic a supernova as it slams into the circumnuclear environment; Guillochon et al. 2016), or a very weakly bound stream with accretion at late times that would not yield a recognizable TDE signal. The subset of bound debris events, however, produced simulated accretion curves that displayed structure on approximately the analytically predicted time-scales. As in the case of more nearly equal mass binaries, studied by Coughlin et al. (2017), a variety of morphologies were produced, including cases where the accretion rate showed sudden declines or excesses at late times. We associate these features with binary-induced changes in the specific angular momentum of the fallback material.

Based on our results, we suggest that two classes of SMBH binaries are potentially detectable from their effect on TDE light curves. The first is systems with low mass primaries (M₁ ∼ 10⁶ M_⊙) and moderate q, characteristic of sub-Milky Way mass galaxies. Disruptions by either the primary or the secondary might occur in these systems, though the rate of primary disruptions dominates. The second is systems with primary masses above the mass where Solar-type stars are swallowed whole (about 10⁸ M_⊙, though with some dependence on the spin). There could be a significant population of extreme mass ratio secondaries in such systems, and these secondaries could generate TDEs with distinctive ‘binary’ light curves at separations of the order of 1–10 mpc. The rate is uncertain, though probably low, but such events might be identifiable given a large enough sample of massive host galaxies where primary TDEs are not possible.

Finally we applied our results to the puzzling transient ASASSN-15lh, which has variously been identified as an exceptionally luminous SN or as a TDE. If it is a TDE, the host galaxy properties imply a primary mass that is close to or above the critical value of 10⁸ M_⊙, making the alternate hypothesis of a secondary disruption conceivable. We make no strong claims, but note that some of the features of the ASASSN-15lh event – most particularly its rebrightening about 100 d after detection – are reasonably common outcomes of our simulations. ASASSN-15lh could be an example of a TDE by a low-mass secondary in a tight binary with a massive primary.

Acknowledgements

Support for this work was provided by NASA through the Einstein Fellowship Program, grant PF6-170150. PJA acknowledges support from NASA through grant NNX16AI40G. We thank the referee for useful comments and suggestions. We used splash (Price 2007) for the visualization. This research used the Savio computational cluster resource provided by the Berkeley Research Computing program at the University of California, Berkeley (supported by the UC Berkeley Chancellor, Vice Chancellor for Research, and Chief Information Officer).

Footenotes

REFERENCES