-
PDF
- Split View
-
Views
-
Cite
Cite
Kevin D Wilk, D John Hillier, Luc Dessart, Ejecta mass diagnostics of Type Ia supernovae, Monthly Notices of the Royal Astronomical Society, Volume 474, Issue 3, March 2018, Pages 3187–3211, https://doi.org/10.1093/mnras/stx2816
Close - Share Icon Share
Abstract
We present one-dimensional non-local thermodynamic equilibrium time-dependent radiative transfer simulations (using cmfgen) of two sub-Chandrasekhar (sub-MCh), one MCh and one super-MCh Type Ia SN ejecta models. Three originate from MCh delayed detonation models, and the fourth is a sub-MCh detonation model. Ejecta masses are 1.02, 1.04, 1.40 and 1.70 M⊙, and all models have 0.62 M⊙ of 56Ni. Sub-MCh model light curves evolve faster, reaching bolometric maximum 2–3 d earlier and having 3–4 d shorter bolometric half-light widths. The models vary by ∼12 per cent at maximum bolometric luminosity and by 0.17 mag in Bmax. While ΔM15(B) increases with ejecta mass, it only varies by ∼5 per cent around 1 mag. Sub-MCh models are 0.25 mag bluer in B − R at Bmax. Optical spectra share many similarities, but lower mass models exhibit less UV line blanketing during the photospheric phase. At nebular times, significant near-infrared (NIR) spectroscopic differences are seen. In particular, emission lines of the Ca ii NIR triplet; [S iii] λλ9068,9530; [Ca ii] λλ7291,7324; [Ar iii] λλ7135,7751 and [Ni ii] 1.939 μm are stronger in higher mass models. The [Ni ii] 1.939 μm line is absent in the sub-MCh detonation model, and provides a valuable potential tool to distinguish sub-MCh explosions from MCh explosions. In general, the nebular phase models are too highly ionized. We attribute this to the neglect of clumping and/or the distribution of intermediate mass and iron group elements. The two sub-MCh models, while exploded by different mechanisms, can be distinguished in the J and H bands at late times (e.g. +200 d).
1 INTRODUCTION
Type Ia supernovae (SNe Ia) are thought to be thermonuclear runaway explosions of carbon-oxygen (C/O) white dwarfs (WDs; Hoyle & Fowler 1960), but the formation channel of the progenitor remains uncertain. Determining the progenitor channel(s) of SNe Ia, and their diversity, is of crucial importance since it will improve their use as probes of cosmological parameters (Riess et al. 1998; Perlmutter et al. 1999). Further, understanding the progenitor channel allows us to probe stellar evolution of binary systems prior to the SN occurring, and hence place constraints on both binary synthesis models and binary evolution.
There are two main progenitor channels invoked to explain the origin of SNe Ia – the single degenerate (SD) channel and double degenerate channel. In the ‘classic SD channel, the WD accretes matter (usually hydrogen and/or helium) from a non-degenerate star due to binary interaction via Roche lobe overflow. However, mass transfer in the SD channel is not limited to Roche lobe overflow – it can also be mediated by wind mass-loss as, for example, in symbiotic systems (see Maoz, Mannucci & Nelemans 2014, for a review). In the SD channel matter accumulates on the WD, where stable burning can occur, until the star approaches the Chandrasekhar mass (MCh≈1.4 M⊙) and explodes leading to an SN Ia (Whelan & Iben 1973; Nomoto 1982).
How the WD explodes has long been a matter of study within the astrophysics community. The different explosion mechanisms include pure detonation (Arnett 1969; Sim et al. 2010), pure deflagration (Nomoto, Sugimoto & Neo 1976), delayed detonation and pulsating delayed detonation (Khokhlov 1991a,b; Gamezo, Khokhlov & Oran 2005; Livne, Asida & Höflich 2005; Röpke & Niemeyer 2007; Jackson et al. 2010; Seitenzahl et al. 2013) and gravitationally confined detonation (GCD; Plewa, Calder & Lamb 2004). More recent research on the GCD, including three-dimensional (3D) full star simulations, was presented by Seitenzahl et al. (2016). For sub-MCh WD masses, a double detonation scenario has been explored (Woosley & Weaver 1994; Livne & Arnett 1995; Fink, Hillebrandt & Röpke 2007; Fink et al. 2010).
One of the most successful theories at reproducing the properties of standard SNe Ia is the delayed-detonation transition (DDT) model, where the WD first undergoes a subsonic deflagration phase. The resulting expansion of the WD creates lower density fuel, which is necessary for the production of intermediate mass elements (IMEs). At a particular density, the burning switches from subsonic to supersonic (Khokhlov 1991a,b). This scenario is required to recreate the observed chemical stratification. Pure detonation models produce too many iron group elements (IGEs) such as iron and nickel but not enough IMEs at high velocities to reproduce SN Ia spectra. On the other hand, deflagration models produce abundant amounts of IMEs but not enough 56Ni to power the SN luminosity. This mechanism is a possible channel for underluminous SNe Ia (Travaglio et al. 2004; Phillips et al. 2007; Jordan et al. 2012; Kromer et al. 2013). One-dimensional (1D) DDT models have been very successful in reproducing the observed properties of SNe Ia. However, these models describe the turbulent flame propagation only in a parametrized way. Three-dimensional models better capture the fluid instabilities and mixing. This lead to different ejecta structures that do not reproduce observables as well as 1D models (see e.g. Seitenzahl et al. 2013; Sim et al. 2013).
The double degenerate scenario corresponds to the merger of two WDs through loss of angular momentum by gravitational wave emission. It is not understood how the merger triggers the explosion, although it is thought that during the merger the smaller mass WD donates matter to the more massive WD. Recently, modelling by Sato et al. (2015) has shown that, depending on the masses of the two WDs, explosions can occur either during the merger phase, provided both WDs are within a mass range between 0.9 and 1.1 M⊙, or within the merger remnant phase when the more massive object reaches MCh. From their models, the authors estimate that 9 per cent of galactic SNe Ia can be attributed to mergers. One problem in this scenario is that rapid mass accretion of carbon and oxygen leads to an off-centre carbon ignition and subsequently an O/Ne/Mg WD (Saio & Nomoto 1985). Accretion-induced collapse creates additional problems for high accretion rates, leading to the formation of a neutron star instead of an SN Ia. For an extensive review about progenitors of SNe Ia, see Maoz et al. (2014).
When almost the entire C/O WD has burnt, releasing ∼1051 erg (more energy than the gravitational binding energy of a MCh WD), the energy liberated unbinds the WD, producing an ejecta with no remnant. Ejecta velocities of the order of ∼10 000 km s−1 are produced, and within minutes, the ejecta reaches a homologous coasting phase (radiation pressure from 56Ni decay produces second-order effects). At early times, the ejecta is radiation dominated and heated by the decay of 56Ni (56Co for post-maximum evolution). It is because of this, main decay chain of 56Ni→56Co→56Fe, with roughly 1.7 MeV of energy release per decay for 56Ni and 3.7 MeV per decay for 56Co, that these objects are so luminous. However, Dessart et al. (2014a) show the importance of heating the outer (≥20 000 km s−1) ejecta from other decay channels.
Early work by Stritzinger et al. (2006) suggested sub-MCh WDs as progenitors for some SNe Ia based on comparisons of UVOIR light curves (LCs) of 16 SNe with analytical models of nuclear decay luminosities and energy deposition. Scalzo et al. (2014a), Scalzo, Ruiter & Sim (2014b), Sim et al. (2010, 2011) and Blondin et al. (2017) have shown that there is both observational and theoretical evidence for sub-MCh explosions. From photometric model fitting, Scalzo et al. (2014a,b) shows that the mass distribution for SNe Ia includes both sub-MCh and super-MCh events. Scalzo et al. (2014b) argue that 25–50 per cent of SN Ia events deviate from MCh events, with most of these occurring as sub-MCh explosions. Therefore, for given measured 56Ni masses, one can compare SNe Ia to better understand how ejecta mass affects LCs and spectral evolution.
Sim et al. (2010, 2011) found good agreement with photometric observations at maximum and reproduced IME features in synthetic spectra at maximum with 1D pure detonations of sub-MCh explosions. However, these models decline too rapidly post-maximum. This idealized approach ignores the influence of any accreted helium layer. Previous works (Woosley & Weaver 1994; Livne & Arnett 1995; Hoeflich & Khokhlov 1996; Hoeflich et al. 1996; Nugent et al. 1997; Kromer et al. 2010) found difficulties reproducing the observed LCs, colours and spectral evolution after treating the burnt helium layer, which synthesizes a significant amount of 56Ni.
Woosley et al. (2007) explored a grid of SN Ia models coming from 1.38 M⊙ WDs with varying amounts of mixing and 56Ni, finding models of similar 56Ni to have large variations of decline rates [ΔM15(B) – which is the change in B-band magnitude 15 d after B-band maximum (Phillips 1993)] and antiwidth–luminosity relationships. Woosley & Kasen (2011) computed hydrodynamic and radiative transfer simulations of sub-MCh mass models for helium-accreting WDs, but the authors only found reasonable agreement with spectra and LCs of common SNe Ia for the most massive WDs with the smallest helium layers they considered. Blondin et al. (2017) looks at broadening our understanding of the width–luminosity relation (WLR) using pure detonations of sub-MCh WDs. Their work shows promising agreement with observations of faint SNe Ia, confirming the need for two WD populations to explain the full behaviour of the WLR seen at high- and low-SN Ia brightness.
Observations have shown high-velocity features (HVFs) in early-time spectra of SNe Ia. These features have been used to constrain the explosion scenario (Mazzali et al. 2005a,b; Tanaka et al. 2006; Blondin et al. 2013; Childress et al. 2013, 2014; Pan et al. 2015; Silverman et al. 2015; Zhao et al. 2015). Studying the formation of these features as well as their correlation with galaxy environment can improve our understanding of Type Ia progenitors. We can gain insights, for example, into the density and temperature structure of the outer layers. The latter will reveal itself through changes in ionization and hence the strength of spectral features.
In this paper, we study two sub-MCh models (∼1 M⊙), a MCh model (∼1.4 M⊙), and a super-MCh model (∼1.7 M⊙), all with the same 56Ni mass by design, to determine the effects of ejecta mass. One model is a standard DDT model, two models are standard DDT models whose density have been scaled to give the desired ejecta mass, while the final model arises from a pure detonation in a sub-MCh model. The original DDT models are also somewhat artificial. For example, the onset of detonation in a DDT model is a free parameter. Further, it is impossible in current models to resolve and adequately model the thermonuclear flame [see Ciaraldi-Schoolmann, Seitenzahl & Röpke (2013) and references therein]. We consider evolution over more than 200 d in time – from ∼1 d after the explosion until approximately 220 d after the explosion, and look for diagnostics of ejecta mass (Mej) for our 56Ni mass that can be used to distinguish between the different models. Since the precise explosion mechanism is uncertain, the two sub-MCh models were exploded using different assumptions. Spectra and LCs were computed using non-LTE and time-dependent radiative transfer. Looking for SN Ia diagnostics, we wanted to remove sensitivity of 56Ni while focusing on ejecta mass to uncover insights in SN Ia evolution, both spectroscopically and photometrically.
The paper is organized as follows. In Section 2, we discuss the techniques used and initial ejecta properties. We compare the bolometric LCs as well as synthetic photometric LCs in Section 3. We discuss the spectral evolution, highlighting the strong spectral differences, in Section 4. In Section 5, we further highlight the distinctions between our two sub-MCh models. In Section 6.1, we comment on the lack of HVFs. Section 6.2 shows spectral comparison to a few SNe Ia that are close in measured Mej and 56Ni mass. In Section 6.3, we discuss shortcomings of our models in reproducing spectral characteristics of SNe Ia beyond 20 d post-maximum. Section 7 summarizes our results and conclusions.
2 TECHNIQUE
To determine spectral and LC diagnostics, we utilize hydrodynamical models that have been evolved from explosion until 0.75 d. Homologous expansion of the ejecta is well established at 100 s, and it is assumed to strictly hold at all times thereafter. We allow for non-local thermodynamic equilibrium (non-LTE) and solve the spherically symmetric, time-dependent, relativistic radiative transfer equation in order to produce emergent synthetic spectra from which synthetic LCs can be produced.
2.1 Ejecta and radiative transfer modelling
Our models correspond to scaled ejecta of model DDC0 (density scaled by 0.73, model SUB2) and DDC15 (density scaled by 1.22, model SUP), complemented with models DDC10 (no scaling applied, model CHAN; see Blondin et al. 2013) and SCH5p5 (density scaled by 0.98, model SUB1; see Blondin et al. 2017). This density scaling is applied to produce ejecta with the same 56Ni mass initially (0.62 M⊙), but differing in ejecta mass so that they lie below, at and above the MCh. This scaling, applied exclusively to the density at 10 s after explosion, is obviously artificial. An advantage of this scaling method is that, while the mass varies, the chemical stratification does not. This ensures the models retain their fundamental characteristic of all SN Ia ejecta. We do not compute the combustion nor make any claim that a flame would behave in the way adopted for the corresponding WD mass (i.e. deflagration followed by detonation in the DDC models; pure detonation in the SCH model). Even in the original (unscaled) model, the treatment of combustion is largely imposed rather than computed from first principles. The purpose of the study is to investigate the signatures sensitive to variations in ejecta mass, keeping the 56Ni mass the same between all models in order to retain only one variable quantity. Model masses, kinetic energies and important species masses are summarized in Table 1.
Model summary. Listed are the masses in M⊙, ejecta kinetic energies in 1051 ergs, and the root mean square of the velocity in km s−1. Also listed is model mass information in M⊙ at 0.75 d post-explosion. The parentheses (#) correspond to |$\times 10^{\#}$|
| Model . | Mass . | EKin . | υrms . | C . | O . | Na . | Mg . | Si . | S . | Ar . |
|---|---|---|---|---|---|---|---|---|---|---|
| . | (M⊙) . | (1051 ergs) . | (km s−1) . | (M⊙) . | (M⊙) . | (M⊙) . | (M⊙) . | (M⊙) . | (M⊙) . | (M⊙) . |
| SUB1 | 1.04 | 1.22 | 10821 | 3.295(−3) | 5.196(−2) | 1.306(−5) | 2.441(−3) | 1.553(−1) | 1.022(−1) | 2.248(−2) |
| SUB2 | 1.02 | 1.17 | 10695 | 8.803(−4) | 3.906(−2) | 4.466(-6) | 2.615(−3) | 1.185(−1) | 7.488(−2) | 1.654(−2) |
| CHAN | 1.40 | 1.51 | 10415 | 2.419(−3) | 9.595(−2) | 1.244(−5) | 9.557(−3) | 2.551(−1) | 1.661(−1) | 3.693(−2) |
| SUP | 1.70 | 1.81 | 10351 | 3.333(−3) | 1.293(−1) | 2.044(−5) | 1.387(−2) | 3.805(−1) | 2.443(−1) | 5.223(−2) |
| Model | Ca | Ti | Cr | Fe | Co | 58Ni + 60Ni | 56Ni | |||
| (M⊙) | (M⊙) | (M⊙) | (M⊙) | (M⊙) | (M⊙) | (M⊙) | ||||
| SUB1 | 2.361(−2) | 2.665(−5) | 1.030(−2) | 2.226(−2) | 5.526(−2) | 1.1(−2) | 5.684(−1) | |||
| SUB2 | 1.822(−2) | 1.083(−4) | 1.516(−2) | 6.654(−2) | 5.680(−2) | 2.6(−2) | 5.710(−1) | |||
| CHAN | 4.120(−2) | 1.486(−4) | 2.689(−2) | 1.020(−1) | 5.713(−2) | 2.5(−2) | 5.708(−1) | |||
| SUP | 5.562(−2) | 1.828(−4) | 2.977(−2) | 1.224(−1) | 5.777(−2) | 3.0(−2) | 5.707(−1) |
| Model . | Mass . | EKin . | υrms . | C . | O . | Na . | Mg . | Si . | S . | Ar . |
|---|---|---|---|---|---|---|---|---|---|---|
| . | (M⊙) . | (1051 ergs) . | (km s−1) . | (M⊙) . | (M⊙) . | (M⊙) . | (M⊙) . | (M⊙) . | (M⊙) . | (M⊙) . |
| SUB1 | 1.04 | 1.22 | 10821 | 3.295(−3) | 5.196(−2) | 1.306(−5) | 2.441(−3) | 1.553(−1) | 1.022(−1) | 2.248(−2) |
| SUB2 | 1.02 | 1.17 | 10695 | 8.803(−4) | 3.906(−2) | 4.466(-6) | 2.615(−3) | 1.185(−1) | 7.488(−2) | 1.654(−2) |
| CHAN | 1.40 | 1.51 | 10415 | 2.419(−3) | 9.595(−2) | 1.244(−5) | 9.557(−3) | 2.551(−1) | 1.661(−1) | 3.693(−2) |
| SUP | 1.70 | 1.81 | 10351 | 3.333(−3) | 1.293(−1) | 2.044(−5) | 1.387(−2) | 3.805(−1) | 2.443(−1) | 5.223(−2) |
| Model | Ca | Ti | Cr | Fe | Co | 58Ni + 60Ni | 56Ni | |||
| (M⊙) | (M⊙) | (M⊙) | (M⊙) | (M⊙) | (M⊙) | (M⊙) | ||||
| SUB1 | 2.361(−2) | 2.665(−5) | 1.030(−2) | 2.226(−2) | 5.526(−2) | 1.1(−2) | 5.684(−1) | |||
| SUB2 | 1.822(−2) | 1.083(−4) | 1.516(−2) | 6.654(−2) | 5.680(−2) | 2.6(−2) | 5.710(−1) | |||
| CHAN | 4.120(−2) | 1.486(−4) | 2.689(−2) | 1.020(−1) | 5.713(−2) | 2.5(−2) | 5.708(−1) | |||
| SUP | 5.562(−2) | 1.828(−4) | 2.977(−2) | 1.224(−1) | 5.777(−2) | 3.0(−2) | 5.707(−1) |
Model summary. Listed are the masses in M⊙, ejecta kinetic energies in 1051 ergs, and the root mean square of the velocity in km s−1. Also listed is model mass information in M⊙ at 0.75 d post-explosion. The parentheses (#) correspond to |$\times 10^{\#}$|
| Model . | Mass . | EKin . | υrms . | C . | O . | Na . | Mg . | Si . | S . | Ar . |
|---|---|---|---|---|---|---|---|---|---|---|
| . | (M⊙) . | (1051 ergs) . | (km s−1) . | (M⊙) . | (M⊙) . | (M⊙) . | (M⊙) . | (M⊙) . | (M⊙) . | (M⊙) . |
| SUB1 | 1.04 | 1.22 | 10821 | 3.295(−3) | 5.196(−2) | 1.306(−5) | 2.441(−3) | 1.553(−1) | 1.022(−1) | 2.248(−2) |
| SUB2 | 1.02 | 1.17 | 10695 | 8.803(−4) | 3.906(−2) | 4.466(-6) | 2.615(−3) | 1.185(−1) | 7.488(−2) | 1.654(−2) |
| CHAN | 1.40 | 1.51 | 10415 | 2.419(−3) | 9.595(−2) | 1.244(−5) | 9.557(−3) | 2.551(−1) | 1.661(−1) | 3.693(−2) |
| SUP | 1.70 | 1.81 | 10351 | 3.333(−3) | 1.293(−1) | 2.044(−5) | 1.387(−2) | 3.805(−1) | 2.443(−1) | 5.223(−2) |
| Model | Ca | Ti | Cr | Fe | Co | 58Ni + 60Ni | 56Ni | |||
| (M⊙) | (M⊙) | (M⊙) | (M⊙) | (M⊙) | (M⊙) | (M⊙) | ||||
| SUB1 | 2.361(−2) | 2.665(−5) | 1.030(−2) | 2.226(−2) | 5.526(−2) | 1.1(−2) | 5.684(−1) | |||
| SUB2 | 1.822(−2) | 1.083(−4) | 1.516(−2) | 6.654(−2) | 5.680(−2) | 2.6(−2) | 5.710(−1) | |||
| CHAN | 4.120(−2) | 1.486(−4) | 2.689(−2) | 1.020(−1) | 5.713(−2) | 2.5(−2) | 5.708(−1) | |||
| SUP | 5.562(−2) | 1.828(−4) | 2.977(−2) | 1.224(−1) | 5.777(−2) | 3.0(−2) | 5.707(−1) |
| Model . | Mass . | EKin . | υrms . | C . | O . | Na . | Mg . | Si . | S . | Ar . |
|---|---|---|---|---|---|---|---|---|---|---|
| . | (M⊙) . | (1051 ergs) . | (km s−1) . | (M⊙) . | (M⊙) . | (M⊙) . | (M⊙) . | (M⊙) . | (M⊙) . | (M⊙) . |
| SUB1 | 1.04 | 1.22 | 10821 | 3.295(−3) | 5.196(−2) | 1.306(−5) | 2.441(−3) | 1.553(−1) | 1.022(−1) | 2.248(−2) |
| SUB2 | 1.02 | 1.17 | 10695 | 8.803(−4) | 3.906(−2) | 4.466(-6) | 2.615(−3) | 1.185(−1) | 7.488(−2) | 1.654(−2) |
| CHAN | 1.40 | 1.51 | 10415 | 2.419(−3) | 9.595(−2) | 1.244(−5) | 9.557(−3) | 2.551(−1) | 1.661(−1) | 3.693(−2) |
| SUP | 1.70 | 1.81 | 10351 | 3.333(−3) | 1.293(−1) | 2.044(−5) | 1.387(−2) | 3.805(−1) | 2.443(−1) | 5.223(−2) |
| Model | Ca | Ti | Cr | Fe | Co | 58Ni + 60Ni | 56Ni | |||
| (M⊙) | (M⊙) | (M⊙) | (M⊙) | (M⊙) | (M⊙) | (M⊙) | ||||
| SUB1 | 2.361(−2) | 2.665(−5) | 1.030(−2) | 2.226(−2) | 5.526(−2) | 1.1(−2) | 5.684(−1) | |||
| SUB2 | 1.822(−2) | 1.083(−4) | 1.516(−2) | 6.654(−2) | 5.680(−2) | 2.6(−2) | 5.710(−1) | |||
| CHAN | 4.120(−2) | 1.486(−4) | 2.689(−2) | 1.020(−1) | 5.713(−2) | 2.5(−2) | 5.708(−1) | |||
| SUP | 5.562(−2) | 1.828(−4) | 2.977(−2) | 1.224(−1) | 5.777(−2) | 3.0(−2) | 5.707(−1) |
The use of scaled DDT models for SUB2 and SUP is problematical since the explosion properties will depend on the mass of the WD. For example, differences in the initial central densities before the explosion will likely lead to different abundance profiles within the ejecta. In particular, sub-MCh WDs, unlike their MCh counterpart with stable IGEs in their inner ejecta, do not exhibit a ‘56Ni hole’ which is a low 56Ni abundance inside an expansion velocity of 2500 km s−1. However, a comparison of SUB2 with SUB1 will allow us to test the sensitivity of the results to the adopted explosion model. The explosion mechanism for ejecta with super-Chandrasekhar masses is extremely uncertain, and any adopted model will have limitations.
The radiative transfer models have been computed using cmfgen (Hillier & Miller 1998; Hillier & Dessart 2012; Dessart et al. 2014a,b), which solves the spherically symmetric, non-local thermodynamic equilibrium (non-LTE), time-dependent, relativistic radiative transfer equation in the comoving frame. To advance in time, we used a 10 per cent time step for each model starting from 0.75 d until ∼100 d, after which we used a time step of 10 d. At early times (≲7 d) during the time sequence, we assumed that γ-ray photons created from radioactive decays are locally deposited. Otherwise, we approximate the γ-ray deposition as grey, adopting the procedure from Swartz, Sutherland & Harkness (1995) and a κγ = 0.06Ye cm2 g−1. The kinetic energy of decay positrons is locally deposited at all epochs. cmfgen currently treats both one- and two-step decay chains for calculating non-thermal heating.
2.2 Ejecta conditions for radiative transfer
Table 1 shows the yields for the most abundant species in our ejecta models at 0.75 d. Since the 56Ni mass is fixed, there are substantial variations in the mass of the IMEs. In particular, the mass of individual IMEs in model SUP is a factor of 3–5 larger than in model SUB2; model SUB1 has ∼1.3–1.4 times the mass of IMEs and ∼1/3 times the iron mass of SUB2. The initial iron abundance in SUB1 is almost a factor of 6 lower than in SUP. The mass of stable nickel (58Ni and 60Ni) is 0.011, 0.026, 0.025 and 0.030 M⊙ for SUB1, SUB2, CHAN and SUP. The presence of stable nickel features in nebular spectra, and the ability to measure the nickel abundance, is discussed in Sections 4 and 6.3.
In Fig. 1, we show the outward cumulative mass as a function of velocity. Less than 1 per cent of the mass lies beyond 25 000 km s−1 for all models, and hence we restrict future model ejecta comparisons to velocities less than 30 000 km s−1. Higher velocity material makes very minor contributions to synthetic spectra.
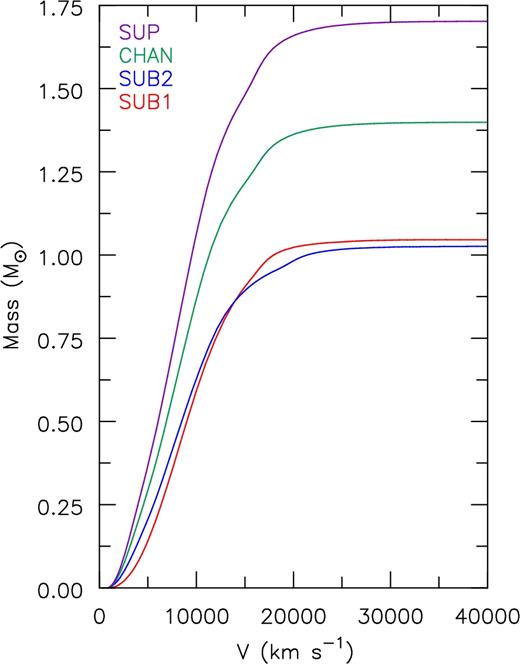
Illustration of the outward cumulative mass as a function of velocity. The cumulative mass begins to flatten off around 25 000 km s−1 for all models, the velocity at which the density begins to decrease rapidly. Less than 1 per cent of the total mass is exterior to this velocity.
Fig. 2 compares the initial mass fraction at 0.75 d for all models. All but model SUB1 exhibit an ‘56Ni hole’ at velocities less than ∼2500 km s−1. As noted earlier, the hole in SUB2 is artificial, and arises since the model was scaled from a model based on the explosion of a MCh WD that has a higher central density.

The initial abundance as a function of velocity for carbon, oxygen, silicon, iron, cobalt and nickel for model SUB1 (top left), SUB2 (top right), CHAN (bottom left) and SUP (bottom right). Notice the absence of the ‘56Ni hole’ in model SUB1 (i.e. presence of 56Ni), a result of having lower densities during the initial explosion. Also apparent is the overlap of the nickel distribution with IMEs around 8000–12 000 km s−1 in all models.
3 LIGHT CURVES
The LCs and colour evolution of Type Ia models depend on the progenitor system and potentially offer a means to distinguish between progenitor systems. Due to differences in ejecta mass, the diffusion time varies between models, giving rise to morphological separations in both the width of each bolometric LC and the peak luminosity. However, from work by Pinto & Eastman (2000a,b), we expect this effect to be small.
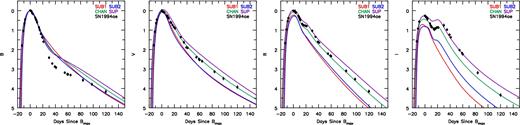
Fig. 3shows the bolometric LCs of all models relative to the time of explosion. Decreasing ejecta mass (shorter diffusion time) corresponds to a faster evolving SN. In days since explosion, the bolometric luminosity maximum occurs at 14.4 (3.80× 109 L⊙), 14.4 (3.96× 109 L⊙), 15.84 (3.63× 109 L⊙) and 17.42 (3.47× 109 L⊙) for models SUB1, SUB2, CHAN and SUP, respectively. To characterize the bolometric LCs, we list tmax (time of bolometric maximum), t−1/2 and t+1/2 [the times to rise from half bolometric maximum luminosity to maximum and to decline from bolometric maximum back to half of maximum – see Contardo, Leibundgut & Vacca (2000)] in Table 2. Between ∼1 and 1.7 M⊙, we have roughly a 1 d difference in half-light rise times (t−1/2), with SUB ejecta models rising faster. After bolometric maximum, the SUP ejecta model takes roughly ∼3.5 d longer than the SUB ejecta models to decline to half light (t+1/2). With precise measurement determinations of the rise time in Lbol, we can put stronger constraints on the ejecta mass for a given 56Ni mass.
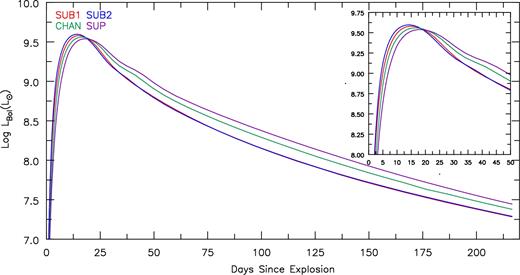
The bolometric luminosities for all models as a function of age since explosion. Lower mass models evolve faster in their bolometric LCs compared with higher mass models – the lower the ejecta mass, the earlier the time of bolometric maximum (Table 2).
LC parameters such as absolute magnitude maximum (MX), time of maximum (t(Xmax)) and decline parameter (ΔM15(X)) for band X. Also included are half-light rise and decline times for Lbol (t−1/2 and t+1/2), time of bolometric maximum (tmax), and maximum bolometric light (Lbol).
| Model . | MU . | t(Umax) . | ΔM15(U) . | MB . | t(Bmax) . | ΔM15(B) . | MV . | t(Vmax) . | ΔM15(V) . | MR . | t(Rmax) . | ΔM15(R) . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (mag) . | (d) . | (mag) . | (mag) . | (d) . | (mag) . | (mag) . | (d) . | (mag) . | (mag) . | (d) . | (mag) . |
| SUB1 | −19.89 | 14.13 | 1.07 | −19.39 | 16.97 | 0.95 | −19.36 | 17.99 | 0.88 | −19.17 | 17.40 | 0.89 |
| SUB2 | −19.96 | 13.35 | 1.08 | −19.41 | 15.64 | 0.94 | −19.36 | 16.48 | 0.96 | −19.14 | 17.01 | 0.91 |
| CHAN | −19.78 | 14.90 | 1.06 | −19.31 | 18.54 | 0.94 | −19.31 | 19.91 | 0.68 | −19.24 | 18.92 | 0.76 |
| SUP | −19.67 | 15.92 | 1.03 | −19.25 | 19.86 | 0.99 | −19.31 | 21.89 | 0.60 | −19.29 | 20.48 | 0.59 |
| MI | t(Imax) | ΔM15(I) | MJ | t(Jmax) | ΔM15(J) | MH | t(Hmax) | ΔM15(H) | MK | t(Kmax) | ΔM15(K) | |
| (mag) | (d) | (mag) | (mag) | (d) | (mag) | (mag) | (d) | (mag) | (mag) | (d) | (mag) | |
| SUB1 | −18.68 | 12.86 | 0.70 | −18.24 | 9.60 | 1.54 | −17.87 | 8.76 | 0.29 | −17.90 | 9.62 | 0.08 |
| SUB2 | −18.60 | 13.76 | 0.64 | −18.06 | 8.39 | 1.03 | −17.70 | 7.81 | 0.09 | −17.77 | 9.27 | −0.08 |
| CHAN | −18.87 | 16.41 | 0.44 | −18.48 | 12.73 | 1.26 | −18.08 | 10.73 | 0.10 | −18.10 | 12.40 | −0.02 |
| SUP | −18.99 | 19.01 | 0.27 | −18.67 | 15.29 | 1.17 | −18.30 | 12.91 | 0.02 | −18.28 | 15.25 | −0.07 |
| t−1/2 | t+1/2 | tmax | Lbol | |||||||||
| (mag) | (d) | (d) | (109L⊙) | |||||||||
| SUB1 | 8.18 | 13.0 | 14.4 | 3.80 | ||||||||
| SUB2 | 8.02 | 12.44 | 14.4 | 3.96 | ||||||||
| CHAN | 8.83 | 14.75 | 15.84 | 3.63 | ||||||||
| SUP | 9.27 | 16.57 | 17.42 | 3.47 |
| Model . | MU . | t(Umax) . | ΔM15(U) . | MB . | t(Bmax) . | ΔM15(B) . | MV . | t(Vmax) . | ΔM15(V) . | MR . | t(Rmax) . | ΔM15(R) . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (mag) . | (d) . | (mag) . | (mag) . | (d) . | (mag) . | (mag) . | (d) . | (mag) . | (mag) . | (d) . | (mag) . |
| SUB1 | −19.89 | 14.13 | 1.07 | −19.39 | 16.97 | 0.95 | −19.36 | 17.99 | 0.88 | −19.17 | 17.40 | 0.89 |
| SUB2 | −19.96 | 13.35 | 1.08 | −19.41 | 15.64 | 0.94 | −19.36 | 16.48 | 0.96 | −19.14 | 17.01 | 0.91 |
| CHAN | −19.78 | 14.90 | 1.06 | −19.31 | 18.54 | 0.94 | −19.31 | 19.91 | 0.68 | −19.24 | 18.92 | 0.76 |
| SUP | −19.67 | 15.92 | 1.03 | −19.25 | 19.86 | 0.99 | −19.31 | 21.89 | 0.60 | −19.29 | 20.48 | 0.59 |
| MI | t(Imax) | ΔM15(I) | MJ | t(Jmax) | ΔM15(J) | MH | t(Hmax) | ΔM15(H) | MK | t(Kmax) | ΔM15(K) | |
| (mag) | (d) | (mag) | (mag) | (d) | (mag) | (mag) | (d) | (mag) | (mag) | (d) | (mag) | |
| SUB1 | −18.68 | 12.86 | 0.70 | −18.24 | 9.60 | 1.54 | −17.87 | 8.76 | 0.29 | −17.90 | 9.62 | 0.08 |
| SUB2 | −18.60 | 13.76 | 0.64 | −18.06 | 8.39 | 1.03 | −17.70 | 7.81 | 0.09 | −17.77 | 9.27 | −0.08 |
| CHAN | −18.87 | 16.41 | 0.44 | −18.48 | 12.73 | 1.26 | −18.08 | 10.73 | 0.10 | −18.10 | 12.40 | −0.02 |
| SUP | −18.99 | 19.01 | 0.27 | −18.67 | 15.29 | 1.17 | −18.30 | 12.91 | 0.02 | −18.28 | 15.25 | −0.07 |
| t−1/2 | t+1/2 | tmax | Lbol | |||||||||
| (mag) | (d) | (d) | (109L⊙) | |||||||||
| SUB1 | 8.18 | 13.0 | 14.4 | 3.80 | ||||||||
| SUB2 | 8.02 | 12.44 | 14.4 | 3.96 | ||||||||
| CHAN | 8.83 | 14.75 | 15.84 | 3.63 | ||||||||
| SUP | 9.27 | 16.57 | 17.42 | 3.47 |
LC parameters such as absolute magnitude maximum (MX), time of maximum (t(Xmax)) and decline parameter (ΔM15(X)) for band X. Also included are half-light rise and decline times for Lbol (t−1/2 and t+1/2), time of bolometric maximum (tmax), and maximum bolometric light (Lbol).
| Model . | MU . | t(Umax) . | ΔM15(U) . | MB . | t(Bmax) . | ΔM15(B) . | MV . | t(Vmax) . | ΔM15(V) . | MR . | t(Rmax) . | ΔM15(R) . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (mag) . | (d) . | (mag) . | (mag) . | (d) . | (mag) . | (mag) . | (d) . | (mag) . | (mag) . | (d) . | (mag) . |
| SUB1 | −19.89 | 14.13 | 1.07 | −19.39 | 16.97 | 0.95 | −19.36 | 17.99 | 0.88 | −19.17 | 17.40 | 0.89 |
| SUB2 | −19.96 | 13.35 | 1.08 | −19.41 | 15.64 | 0.94 | −19.36 | 16.48 | 0.96 | −19.14 | 17.01 | 0.91 |
| CHAN | −19.78 | 14.90 | 1.06 | −19.31 | 18.54 | 0.94 | −19.31 | 19.91 | 0.68 | −19.24 | 18.92 | 0.76 |
| SUP | −19.67 | 15.92 | 1.03 | −19.25 | 19.86 | 0.99 | −19.31 | 21.89 | 0.60 | −19.29 | 20.48 | 0.59 |
| MI | t(Imax) | ΔM15(I) | MJ | t(Jmax) | ΔM15(J) | MH | t(Hmax) | ΔM15(H) | MK | t(Kmax) | ΔM15(K) | |
| (mag) | (d) | (mag) | (mag) | (d) | (mag) | (mag) | (d) | (mag) | (mag) | (d) | (mag) | |
| SUB1 | −18.68 | 12.86 | 0.70 | −18.24 | 9.60 | 1.54 | −17.87 | 8.76 | 0.29 | −17.90 | 9.62 | 0.08 |
| SUB2 | −18.60 | 13.76 | 0.64 | −18.06 | 8.39 | 1.03 | −17.70 | 7.81 | 0.09 | −17.77 | 9.27 | −0.08 |
| CHAN | −18.87 | 16.41 | 0.44 | −18.48 | 12.73 | 1.26 | −18.08 | 10.73 | 0.10 | −18.10 | 12.40 | −0.02 |
| SUP | −18.99 | 19.01 | 0.27 | −18.67 | 15.29 | 1.17 | −18.30 | 12.91 | 0.02 | −18.28 | 15.25 | −0.07 |
| t−1/2 | t+1/2 | tmax | Lbol | |||||||||
| (mag) | (d) | (d) | (109L⊙) | |||||||||
| SUB1 | 8.18 | 13.0 | 14.4 | 3.80 | ||||||||
| SUB2 | 8.02 | 12.44 | 14.4 | 3.96 | ||||||||
| CHAN | 8.83 | 14.75 | 15.84 | 3.63 | ||||||||
| SUP | 9.27 | 16.57 | 17.42 | 3.47 |
| Model . | MU . | t(Umax) . | ΔM15(U) . | MB . | t(Bmax) . | ΔM15(B) . | MV . | t(Vmax) . | ΔM15(V) . | MR . | t(Rmax) . | ΔM15(R) . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (mag) . | (d) . | (mag) . | (mag) . | (d) . | (mag) . | (mag) . | (d) . | (mag) . | (mag) . | (d) . | (mag) . |
| SUB1 | −19.89 | 14.13 | 1.07 | −19.39 | 16.97 | 0.95 | −19.36 | 17.99 | 0.88 | −19.17 | 17.40 | 0.89 |
| SUB2 | −19.96 | 13.35 | 1.08 | −19.41 | 15.64 | 0.94 | −19.36 | 16.48 | 0.96 | −19.14 | 17.01 | 0.91 |
| CHAN | −19.78 | 14.90 | 1.06 | −19.31 | 18.54 | 0.94 | −19.31 | 19.91 | 0.68 | −19.24 | 18.92 | 0.76 |
| SUP | −19.67 | 15.92 | 1.03 | −19.25 | 19.86 | 0.99 | −19.31 | 21.89 | 0.60 | −19.29 | 20.48 | 0.59 |
| MI | t(Imax) | ΔM15(I) | MJ | t(Jmax) | ΔM15(J) | MH | t(Hmax) | ΔM15(H) | MK | t(Kmax) | ΔM15(K) | |
| (mag) | (d) | (mag) | (mag) | (d) | (mag) | (mag) | (d) | (mag) | (mag) | (d) | (mag) | |
| SUB1 | −18.68 | 12.86 | 0.70 | −18.24 | 9.60 | 1.54 | −17.87 | 8.76 | 0.29 | −17.90 | 9.62 | 0.08 |
| SUB2 | −18.60 | 13.76 | 0.64 | −18.06 | 8.39 | 1.03 | −17.70 | 7.81 | 0.09 | −17.77 | 9.27 | −0.08 |
| CHAN | −18.87 | 16.41 | 0.44 | −18.48 | 12.73 | 1.26 | −18.08 | 10.73 | 0.10 | −18.10 | 12.40 | −0.02 |
| SUP | −18.99 | 19.01 | 0.27 | −18.67 | 15.29 | 1.17 | −18.30 | 12.91 | 0.02 | −18.28 | 15.25 | −0.07 |
| t−1/2 | t+1/2 | tmax | Lbol | |||||||||
| (mag) | (d) | (d) | (109L⊙) | |||||||||
| SUB1 | 8.18 | 13.0 | 14.4 | 3.80 | ||||||||
| SUB2 | 8.02 | 12.44 | 14.4 | 3.96 | ||||||||
| CHAN | 8.83 | 14.75 | 15.84 | 3.63 | ||||||||
| SUP | 9.27 | 16.57 | 17.42 | 3.47 |
As the 56Ni mass is the same for all models, differences in the bolometric LC evolution are primarily due to ejecta mass. However, despite differences in ejecta mass of ∼70 per cent, the differences are relatively small, though measurable. This effect of ejecta mass should be clearly visible from a statistical sample of deep high cadence observations of SNe Ia.
Fig. 4 shows synthetic LCs plotted in days since B-band maximum. The LCs for the two sub-MCh ejecta models tend to be more luminous at maximum [with the exception of the near-infrared (NIR) bands] but have fainter nebular luminosities. The former arises because at bolometric maximum Lbol ≈ Ldecay and since the peak is earlier, the decay rate is greater. The latter arises because of the less efficient trapping of γ-rays. Table 2 also lists the peak LC absolute magnitudes for different Johnson bands (MU → MK), rise times (in days since explosion), and decline parameter ΔM15(X) for a given band X. All bands show a faster rise time for lower-mass ejecta models, just as they do for Lbol.

The plots show all LCs as a function of age since B-band maximum. Unlike the bolometric luminosity (Fig. 3), the B-band LCs for SUB1 and SUB2 are different – SUB1 is roughly 0.2 mag brighter than SUB2 between ∼25 and 60 d post-B-band maximum. This difference in evolution arises because SUB1 lacks the ‘56Ni hole’ (Fig. 2), and hence is hotter, and has higher ionization, at lower velocities than SUB2. The H-band shows a triple peak for model SUB2 as the ionization shifts downwards, enhancing charge 2+ and then 1+ ion abundances of IGEs like cobalt and iron.
Observational evidence suggests that H-band photometry for SNe Ia can provide higher accuracy than the B-band calibration galactic distances (Krisciunas et al. 2004, 2007; Wood-Vasey et al. 2008). However, our models have a spread of almost one magnitude in the H-band at the time of B-band maximum light. Following the temperature separation between models (higher mass → cooler ejecta), the higher mass ejecta also show larger flux in the H-band at all epochs. Our LCs still show two peaks in the H-band as normal SNe Ia do, a consequence of the ionization shift in iron (and other IGEs) going from ionization states 2+ → 1+ (Kasen 2006). The second peak is of the same brightness for our SUB models compared to higher ejecta mass models. Past the second H-band peak, we see roughly a constant decline in all models until close to 150 d past maximum light.
Fig. 5 shows the U − B, B − V and B − R colour evolution relative to B-band maximum. It shows that the lower mass models are bluer at most epochs. There is over a magnitude difference in B − R from sub-MCh to super-MCh around 25 d after Bmax. SUB models are bluest in colour post-B-band maximum compared to higher mass models. Post-maximum, model SUP remains the most red of all the models, while SUB1 remains bluer than other models after +40 d, a result of higher temperatures and ionization due to larger M(56Ni)/Mej. This is explored in Figs 6 and 7 and then in Section 4 where we discuss the spectral evolution.
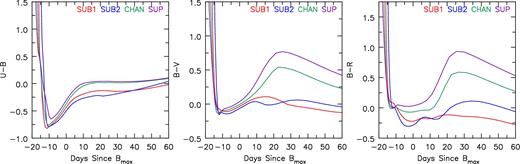
The U − B, B − V and B − R colours relative to B-band maximum. Models SUB1 and SUB2 show bluer colours for all epochs. Ten days before B-band maximum all models have similar colours. As the ejecta ages, differences in the B − R colour become much larger – at B-band maximum, the B − R colour differs by ∼0.3 mag between SUB2 and SUP, while at later epochs the colour difference between SUB1 and SUP can be in excess of 1 mag.
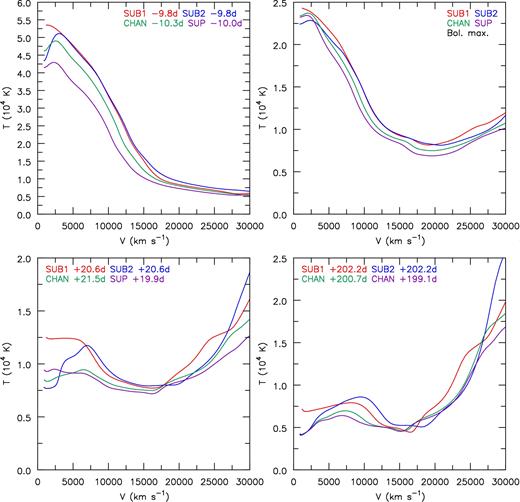
Temperature evolution as a function of velocity for models SUB1, SUB2, CHAN and SUP at epochs −10, +0, +20 and +200 d relative to bolometric maximum. SUB1 exhibits higher temperatures at low velocities compared to SUB2, CHAN and SUP – the higher temperature arises because of the much higher 56Ni abundance in the innermost ejecta of SUB1 (Fig. 2).

Average ionization state for bolometric maximum (left) and 216 d post-explosion (right) for IGEs. The average ionization is defined as the total number of free electrons from each species divided by the total species population. At bolometric maximum, the average ionization rises beyond 20 000 km s−1 due to the low densities inhibiting recombination. The average ionization state is higher for sub-MCh models, a result of more heating per unit mass. At nebular times, SUB1 remains at a higher average ionization in the inner region due to a larger deposition of energy by positrons arising from the higher 56Co mass fraction in the inner region (see Fig. 8).
Fig. 6 shows the temperature evolution of our models, with SUB1 and SUB2 maintaining higher temperatures at all epochs. Fig. 7 shows the average ionization for a few IGEs such as iron, cobalt and nickel. SUB models show a higher ionization compared to higher mass models, producing ejecta with bluer colours. The monotonic temperature distribution of SUB1 below 5000 km s−1 is due to the lack of a ‘56Ni hole’. Fig. 8 shows the fraction of the energy deposition from positrons to the total energy deposition at about 216 d post-explosion. At late times, SUB1 maintains a higher ionization in the innermost ejecta due to more assumed local positron energy deposition. Generally speaking, SUB1 and SUB2 have higher temperatures at comparable epochs than those of CHAN and SUP. We further discuss the implications of higher temperatures in Section 4.
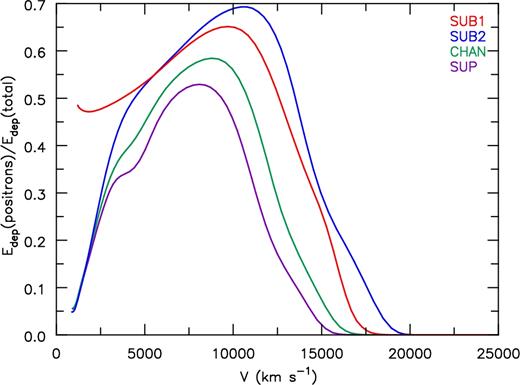
Ratio of the locally deposited energy from positrons (mainly from 56Co) to the energy deposited by nuclear decays in the ejecta at about 216 d post-explosion. SUB1 shows a much higher ratio shortward of 5000 km s−1 due to the lack of a ‘56Ni hole’ and higher 56Ni production in the core. This leads to higher ionization and a higher temperature in the inner region (in combination with lower densities) compared to other models.
4 SPECTRAL DIAGNOSTICS
Spectra provide important constraints for distinguishing progenitor and explosion models. However, despite a 70 per cent difference in mass, model optical spectra (Figs 9–13) at most phases are similar, consistent with work by Blondin et al. (2013) who concluded that SNe Ia are mainly distinguished by their 56Ni mass. This similarity is observed for classical SNe Ia where differences in optical spectra are generally rather subtle (Filippenko 1997), which presumably occurs because of similarities in composition. Interestingly, optical spectra of models SUB1 and SUB2 are remarkably similar for most phases of evolution, despite the different methods to produce these ejecta models. However, there are differences between models, particularly in the infrared, and these do give rise to useful diagnostics. We investigate these diagnostics by comparing model spectra at time steps of approximately −10, −5, 0, +5, +10, +20, +50, +100 and +200 d from bolometric maximum (Figs 9–13). Thus, when comparing observational spectra of SNe Ia from comparable 56Ni mass, these diagnostics will separate events by ejecta mass. Note that model spectra are plotted for vacuum wavelengths; however, wavelengths ≥2000 Å listed are quoted in air.
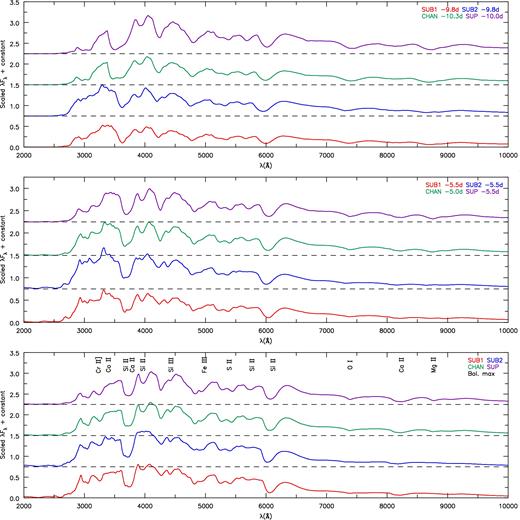
Spectral comparisons between models in the pre-maximum (−10 and −5 d relative to bolometric maximum) and bolometric maximum plotted in λFλ versus λ in order to contrast the NIR tail of the spectrum. All models have been scaled by the same factor, and we have added an offset to allow spectra to be more easily distinguished. During these phases, the optical spectra (3500 to 7000 Å) are very similar. However, there are differences in the amount of UV blanketing occurring shortward of 3500 Å, and in the strength of O i and the Ca ii NIR triplet. We also see that the strength of the O i feature decreases with age while the Ca ii NIR triplet increases in strength.
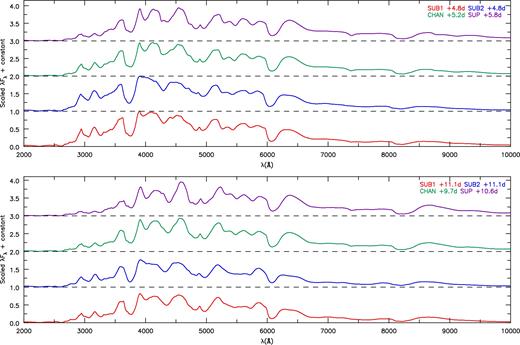
Spectral comparisons between models in the post-maximum phases (+5 and +10 d) relative to bolometric maximum plotted in λFλ versus λ space in order to contrast the NIR tail of the spectrum. In each plot, all models have been scaled by the same value, and we have added a multiple of the offset to more easily distinguish the models. The optical spectra is again similar showing still the strong Si ii doublet at ∼6100 Å. The UV spectrum shows stronger blanketing in higher mass models. The strength of the Ca ii NIR triplet deviates between the models, showing stronger absorption/emission in the cooler (higher mass) models.
Spectral comparisons between models in the post-maximum phases at roughly +20 and +50 d relative to bolometric maximum. Each separate plot shows spectra scaled by the same value. At around +20 d, we continue to see a relatively homogeneous class of objects in the optical but stronger differences emerge in the NIR, such as the strength of the Ca ii NIR triplet and the growth of Fe ii and Co ii lines – see Section 4.2.2. Despite the lack of Fe ii and Co ii features in SUB1 (a consequence of having lower densities and higher temperatures/ionization in the inner ejecta), spectra of SUB1 and SUB2 are still fairly similar.
![Spectral comparison between models in the nebular phase at roughly +100 d after bolometric maximum. We have scaled all models by the same value, and plot Fλ versus λ. All models exhibit roughly the same amount of emission in the [Fe iii] λ4658 line, but show substantial flux differences in the NIR. Unlike the other models, SUB1 lacks NIR Fe ii and Co ii features. Emission lines of [S iii] λλ9068, 9530, and [Ar iii] λλ7135, 7751 are present, and increase in strength relative to [Fe iii] λ4658 as the ejecta mass, and equivalently, as the mass of IMEs, increases.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/474/3/10.1093_mnras_stx2816/1/m_stx2816fig12.jpeg?Expires=1749346109&Signature=rzdY6awaHHPIxToEr~lL-OeRBOq0T0ddmRMW1FYAYdFPsZqXW6juc2GABDm~QvBDW-gSYlp4yriZfJjRfiAUKF~QR4q345ixns2OzM-i-vdRytxKOt97pwN8BQrPfoS3cHFw3PLuslY4KQ9SDyCyk6n15Dc-DqcSmNBILVd9h2we-08ppDrrdZ4r87cQu5PrzKod7gQJMBo5IYtze0lXNS0wSkY7Xr4J1lFhF-MCEz-pj8xM5yd5ZW5kJq2HSySfqMQZik8QEYUu05gY6DHKcYkW~eY-g8uux0Nibl~OE9hMwYjPtI79Ft8n9O8I2gUHlJ6q6dN1Aal1FovtdQb2Ow__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Spectral comparison between models in the nebular phase at roughly +100 d after bolometric maximum. We have scaled all models by the same value, and plot Fλ versus λ. All models exhibit roughly the same amount of emission in the [Fe iii] λ4658 line, but show substantial flux differences in the NIR. Unlike the other models, SUB1 lacks NIR Fe ii and Co ii features. Emission lines of [S iii] λλ9068, 9530, and [Ar iii] λλ7135, 7751 are present, and increase in strength relative to [Fe iii] λ4658 as the ejecta mass, and equivalently, as the mass of IMEs, increases.
![Spectral comparison between models in the nebular phase at roughly +200 d after bolometric maximum. We have scaled all models by the same value, and plot Fλ versus λ. As at 100 d, SUB1 shows no prominent [Fe ii] or [Co ii] lines. Further, spectra of SUB1 in the J and H bands are now substantially different from those of SUB2. The [S iii] λλ9068, 9530 and the [Ar iii] λλ7135, 7751 features have increased in strength relative to [Fe iii] λ4658. The broad emission feature covering 7000 through 7500 Å is a blend of [Ar iii] λ7135, [Ni ii] λ7378 and [Ca ii] λλ7291, 7324.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/474/3/10.1093_mnras_stx2816/1/m_stx2816fig13.jpeg?Expires=1749346109&Signature=SD1uECBOnBW3pfWio9TjUlrEVa2QXirDlAYnQzQM3rM0TwrbMd0RoG9F~DpbrA-DehAco-FD0dUKKOL-mL2KuEHkczKga1CPeWNID~ogzilFlogBoJvwGAmsiPv-58wwL2oArujhjzWb3b8vcm3SIwcRsKwzcznAtu9NouIcBPJp7oqNugQlvSbdnsQCIYUnfD1LspYJIutNwYbKBMo~yz-vdJlhWkqbrSx-qorfLPxLN1v2xIXAaF1EcnGhrU5tO-DdVdD2-VJ2XpO-ohF6GGSFHmPCCradxDuAxzFDuUfQaT6SAiT68pR~b4OQrNg1rNjQIGK-4koCVU6cXN8hhg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Spectral comparison between models in the nebular phase at roughly +200 d after bolometric maximum. We have scaled all models by the same value, and plot Fλ versus λ. As at 100 d, SUB1 shows no prominent [Fe ii] or [Co ii] lines. Further, spectra of SUB1 in the J and H bands are now substantially different from those of SUB2. The [S iii] λλ9068, 9530 and the [Ar iii] λλ7135, 7751 features have increased in strength relative to [Fe iii] λ4658. The broad emission feature covering 7000 through 7500 Å is a blend of [Ar iii] λ7135, [Ni ii] λ7378 and [Ca ii] λλ7291, 7324.
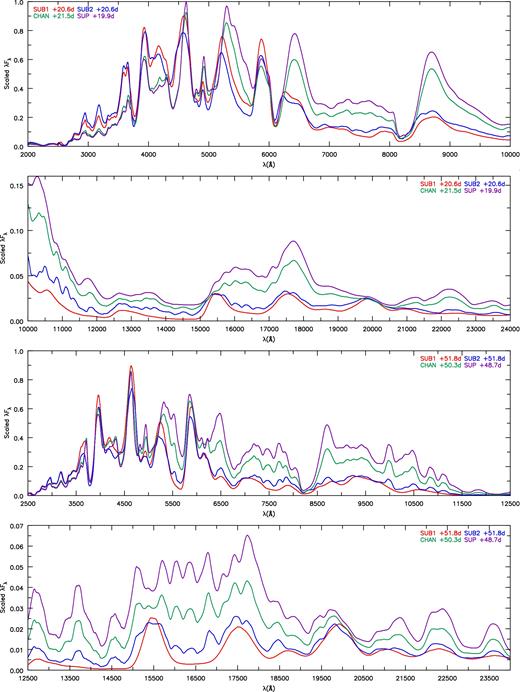
Fig. 9 shows the early spectral evolution (−10, −5 and 0 d relative to bolometric maximum) plotted in λFλ (arbitrary units). We label the contributions of important species at bolometric maximum. Figs 10 and 11 show the post-maximum photospheric phase (+5, +10, +20, +50) plotted in λFλ (arbitrary units). Figs 12 and 13 show nebular spectra at +100 and +200 d post-bolometric maximum plotted in Fλ (arbitrary units). Contributions from important species are labelled. Notice the transition towards predominantly forbidden lines in nebular spectra. These figures are used to highlight important diagnostics.
4.1 [Ni ii] 1.939 μm
In SNe Ia, the nickel abundance is sensitive to the progenitor mass and/or explosion scenario. In 1D explosion modelling, higher central densities have higher neutronization that leads to more stable 58Ni being produced during nuclear burning (Nomoto 1984; Khokhlov 1991a,b). This 1D modelling implies that sub-MCh SNe Ia will show a lower abundance of 58Ni compared to MCh SNe Ia (for the same 56Ni mass). However, 3D DDT modelling suggests that the 56Ni hole predicted in 1D MCh WD DDT models may be absent, and both 56Ni and 58Ni extend from the lowest velocities to about 10 000 km s−1(Kasen, Röpke & Woosley 2009; Seitenzahl et al. 2013). 22Ne settling in sub-MCh has also been proposed as a way to enhance the neutronization; however, the time-scale for gravitational settling can be ∼109–1010 yr (Bildsten & Hall 2001). Therefore, nickel diagnostics, particularly at nebular times, may constrain the progenitor scenario, nucleosynthesis, and explosion mechanism (Woosley 1997; Iwamoto et al. 1999; Stehle et al. 2005; Mazzali & Podsiadlowski 2006; Gerardy et al. 2007; Maeda et al. 2010; Mazzali et al. 2011; Mazzali & Hachinger 2012; Mazzali et al. 2015). At nebular times, most of the 56Ni will have decayed, and any nickel emission features are due to stable nickel, and in particular 58Ni and 60Ni, which are expected to be underabundant in (1D) sub-MCh DDT models compared with MCh models. The width of any observed nebular nickel feature will constrain the hydrodynamic width of the emitting region, thus testing model predictions about the presence of a 56Ni hole. Therefore, nickel features may offer the best diagnostic for ejecta masses below MCh if ejecta do or do not have 56Ni holes as predicted by 1D modelling.
In the optical nebular spectra at +100 and +200 d (Figs 12 and 13), the [Ni ii] λλ7378,7412 lines are blended, and hence not very useful for abundance determinations. However, in the NIR there is a forbidden [Ni ii] transition (3d8(3F)4s2 F7/2 − 3d8(3F)4s4 F9/2) at 1.939 μm which in our synthetic spectra is relatively blend free. It overlaps with telluric lines in low-redshift SNe, but higher redshift (z > 0.08) SNe avoid telluric absorption. While observations of this line appear to be rare, Friesen et al. (2014) find evidence for this line in spectra of SN2011fe, SN2014J and SN2003du.
In our models, SUB1 shows no evidence of [Ni ii] 1.939 μm. On the other hand, SUB2, CHAN and SUP show the line, with a strength that correlates with ejecta mass. The absence of [Ni ii] 1.939 μm in SUB1 arises from two effects — SUB1 has a smaller amount of stable nickel (see Table 1) and a higher ionization than the other models. The presence of 56Co under ∼3000 km s−1 in SUB1 means that there is a great amount of heating from positrons, which deposit their energy locally (Fig. 8). This, combined with the lower densities, leads to both a higher temperature, and a higher ionization (Figs 6 and 7). Surprisingly, and despite their similar ionization potentials, Fe ii cannot be used as an ionization tracer for Ni ii. In SUB1 Ni iii/Ni ii is significantly larger than Fe iii/Fe ii. This arises because the photoionization of Ni ii is dominated by large resonances in its photoionization cross-section. Therefore, the absence of [Ni ii] 1.939 μm in SN Ia spectra at 100–200 d indicates that the mass of the progenitor is below MCh. However, we re-emphasize that SUB2 is a scaled MCh model, so it is not a true sub-MCh model. SUB2 has a stable nickel core and shows [Ni ii] 1.939 μm.
4.2 Ionization
Once the 56Ni mass is determined via ‘Arnett's rule, which states that the luminosity at bolometric maximum is equal to the 56Ni decay chain luminosity, or using LC fitting like that of Scalzo et al. (2014a,b), one can separate different SNe Ia based on ejecta mass using differences in ionization/temperature (see Fig. 6). This result follows from the heating per gram available to the gas. The greater the ejecta mass is, the lower the heating rate per gram is. Consequently, ejecta with a larger M(56Ni)/Mej are hotter (see Blondin et al. 2017) for |$\dot{e}_{\rm decay}\equiv L_{\rm decay}/M_{\rm tot}$|. Indeed, our models indicate that low-mass WD models, for a given 56Ni mass, maintain higher ionizations throughout their spectral evolution.
4.2.1 UV blanketing
Previous studies focused on the UV variability and used the UV spectral region for understanding SNe Ia. These studies looked at the role of metallicity on UV blanketing (Lentz et al. 2000; Walker et al. 2012; Wang et al. 2012; Foley & Kirshner 2013), finding that lower metallicities shift the blanketing blueward. Foley et al. (2016) looked at a sample of SNe Ia and found the UV diversity linearly correlates with the optical LC shape. In particular, the strength of UV line flux measurements (∼2030 and 2535 Å) increases with increasing Δm15(B). Other studies of UV variation hope to use it as a cosmological utility (Ellis et al. 2008; Sullivan et al. 2009) to improve standardizability. Therefore, understanding how Mej for a given 56Ni mass influences the UV spectrum is important to the astronomical community.
Until the ejecta begins entering its nebular phase (∼100 d), we see larger UV blanketing shortward of 4000 Å for larger mass ejecta. This effect is attributed to a temperature difference between models. We see in Figs 6 and 7 that below 25 000 km s−1models with higher temperatures have higher ionizations, seen as a shift in the line blanketing to higher frequencies. Pre-maximum spectra show the Ca ii feature (H & K lines near λ3500) is affected by UV blanketing, making it difficult to distinguish in SUP and CHAN (Fig. 9). Ti ii contributes to much of the blanketing more than 5 d before maximum, while Ti ii, Fe ii and Fe iii shape the UV spectra just prior to maximum. Around maximum, Co ii contributes much of the UV blanketing (below 3500 Å) with the strongest blanketing occurring in model SUP. Looking inwards of 25 000 km s−1, SUB1 and SUB2 show a higher ionization of cobalt than that of models SUP and CHAN. For Co ii there is about a half dex difference in ionization between SUB1 and SUP. These Co ii differences show up as absorption affecting the slope of the feature at ∼3500 Å. Post-maximum (Figs 10 and 11), there is less variation in UV blanketing between the models.
If we compare the peak fluxes at bolometric maximum (Fig. 9) of three UV features (namely the features near ∼2850, ∼3150 and ∼3550 Å), we can characterize the level of blanketing by comparing the flux at peak in each feature. For all ejecta models, the flux ratio F(3150)/F(2850) is close to unity (0.93, 1.07, 1.03 and 1.11 for SUB1, SUB2, CHAN and SUP). However, comparing these lines to the feature just short of the Ca ii H&K and Si ii ∼λ3660 Å absorption profile, we see that the flux ratio F(3550)/F(2850) is strongly dependent on ejecta mass. This flux ratio F(3550)/F(2850) is 0.99, 1.01, 1.20 and 1.75 for SUB1, SUB2, CHAN and SUP. These UV features reflect the temperature and ionization of the ejecta and offer a diagnostic of ejecta mass for a given 56Ni mass.
4.2.2 Optical and IR
Besides variations in UV blanketing, other ionization diagnostics are seen in optical and infrared spectra. For instance, leading up to maximum (Fig. 9), each model shows a different strength of the Si iii triplet (λλ4553, 4568, 4575) absorption, which is the strongest in models SUB1 and SUB2. SNe Ia typically classified as normal, such as SN2011fe, show the Si iii feature around 4400 Å (Pereira et al. 2013) as our model CHAN does. SNe Ia such as SN2003hv, thought to be a sub-MCh event (Mazzali et al. 2011), show this absorption feature much more strongly (Leloudas et al. 2009), as in our SUB models.
Post-maximum (Fig. 11), the NIR part of the spectrum begins to show prominent permitted [Fe ii] (9997.58, 10501.50, 10862.64, 16787.18 and 16873.20 Å) and Co ii features (11829.72, 15758.43, 16064.48, 16360.46, 16687.30, 21344.70, 21503.28, 22202.92, 22475.63 and 23612.53 Å), as well as forbidden [Fe iii] (22178.21, 22420.43 and 23478.80 Å) and [Co iii] (12724.19, 15483.56, 17408.66, 19575.24, 20022.57 and 20973.15 Å) lines. Many of the Co ii and Fe ii features are absent in SUB1, a result of the higher ionization.
Optical nebular spectra typically exhibit emission lines of Fe iii and Co iii (Figs 12 and 13). In the NIR S2 + and Ar2 + show up in our model spectra as [S iii] λλ9068, 9530 and [Ar iii] λλ7135, 7751, with the strength of these features relative to [Fe iii] λ4658 correlating with higher ejecta mass. As will be discussed in Section 6.3, our model spectra tend to exhibit too high an ionization, especially after 40 d. In particular, they lack strong [Fe ii] (e.g. [Fe ii] ∼4350 Å). However, [Fe ii] and [Co ii] features are readily identified in the IR, except for model SUB1. Since SUB1 comes from the explosion of a sub-MCh WD, its inner density is lower throughout its evolution compared to SUB2, and this hinders recombination. Further, SUB1 lacks the ‘56Ni hole’ seen in the later models, and hence the temperature in the inner region is higher than in the other models (see Figs 6–8).
4.3 C/O and IMEs
As the mass of C/O and IMEs is strongly correlated (by design from the density scalings) with the ejecta mass for a given 56Ni mass (see Table 1), one should expect that lines from C/O and IMEs will provide a useful diagnostic tool for ejecta mass. As to be expected, our models show stronger absorption features for oxygen and IMEs for increasing ejecta mass. For example, the strength of absorption due to the O i λλ7772, 7774, 7775 triplet absorption correlates with ejecta mass in pre-maximum spectrum (Fig. 9). The feature fades by a few weeks post-bolometric maximum. Mg ii λλ9218, 9244 is another feature whose strength correlates with high ejecta mass – see Table 3 that lists the pseudo-equivalent widths (pEWs) measured by a straight line across the maxima of the absorption profile; it also fades within a few weeks post-bolometric maximum.
Si iiλλ5958, 5979, observed roughly around ∼λ5750, is a spectroscopic classification diagnostic for SNe Ia (|$\mathcal {R}$|(Si) ≡ pEW(Si ii λ5750)/pEW(Si ii λ6100)) and, like other IME features, its strength correlates with ejecta mass. Table 3 highlights the correlation of pEWs of various features with ejecta mass of our models. Post-maximum (Figs 10 and 11), we see the strength of the emission increase, giving a large morphological separation between models. Calcium (as Ca ii) also shows the same behaviour as Si ii. The absorption and emission strength of the Ca ii NIR triplet distinguishes models throughout the spectral evolution. We find that the strength of this feature correlates with ejecta mass. We further discuss the Ca ii NIR triplet and the Si ii λλ6347, 6371 doublet in Section 6.1.
Approximate pEW (Å) based on a straight line across the profile of the absorption feature.
| Model . | Si ii λ5750 . | Si ii λ6100 . | O i λ7400 . | Mg ii λ8700 . |
|---|---|---|---|---|
| SUB1 | 10 | 139 | 17 | ≲1 |
| SUB2 | 8 | 160 | 9 | ∼1 |
| CHAN | 20 | 156 | 32 | 32 |
| SUP | 30 | 158 | 50 | 53 |
| Model . | Si ii λ5750 . | Si ii λ6100 . | O i λ7400 . | Mg ii λ8700 . |
|---|---|---|---|---|
| SUB1 | 10 | 139 | 17 | ≲1 |
| SUB2 | 8 | 160 | 9 | ∼1 |
| CHAN | 20 | 156 | 32 | 32 |
| SUP | 30 | 158 | 50 | 53 |
Approximate pEW (Å) based on a straight line across the profile of the absorption feature.
| Model . | Si ii λ5750 . | Si ii λ6100 . | O i λ7400 . | Mg ii λ8700 . |
|---|---|---|---|---|
| SUB1 | 10 | 139 | 17 | ≲1 |
| SUB2 | 8 | 160 | 9 | ∼1 |
| CHAN | 20 | 156 | 32 | 32 |
| SUP | 30 | 158 | 50 | 53 |
| Model . | Si ii λ5750 . | Si ii λ6100 . | O i λ7400 . | Mg ii λ8700 . |
|---|---|---|---|---|
| SUB1 | 10 | 139 | 17 | ≲1 |
| SUB2 | 8 | 160 | 9 | ∼1 |
| CHAN | 20 | 156 | 32 | 32 |
| SUP | 30 | 158 | 50 | 53 |
5 EXPLOSION SCENARIO: SUB1 VERSUS SUB2
Since the explosion process and progenitor system are unknown, we highlight and summarize useful diagnostics for distinguishing our models of the same Mej. As mentioned earlier, SUB1 comes from a detonation model of a sub-MCh WD, while SUB2 comes from the DDT of a MCh WD, which was scaled in density to have the same mass as SUB1 and the same 56Ni mass. Since SUB1 was detonated as a sub-MCh WD, it had lower densities when exploded compared to SUB2 and lacks the ‘56Ni hole’. Without the ‘56Ni hole’, SUB1 has a larger (assumed) local deposition fraction from decay positrons compared to the total decay energy deposition (Fig. 8) for velocities less than 5000 km s−1. This keeps the inner region of SUB1 hotter than SUB2, which shows stronger features of higher ionization states of IGEs as the ejecta evolves past the photospheric phase and exposes the inner iron-rich material. At nebular times, the strength of [Ni ii] 1.939 μm gives a clear distinction between SUB1 and SUB2, as lower density ejecta model SUB1 does not show this feature.
Up to maximum light, SUB1 and SUB2 possess very similar spectra (Fig. 9), especially in the optical. However, as the photosphere begins to recede inwards, differences are seen in the NIR – Fe ii and Co ii features are absent in SUB1 but present in SUB2 (Figs 10 and 11). Below 5000 km s−1, the densities in SUB1 are roughly a factor of 3 lower than in SUB2. Further, SUB1 has a larger fraction of local radioactive heating from positrons. These factors inhibit recombination and a higher ionization persists in SUB1 compared to SUB2. The NIR region is potentially the best diagnostic for the ionization state of the ejecta in SNe Ia (shown in Figs 12 and 13).
This higher ionization, seen in post-maximum spectra (Figs 10 and 11), yields lower fluxes in the NIR. We see roughly half a magnitude difference in the post-maximum I, J and H bands. However, the magnitude difference between J and H grows to ∼2 mag difference by 200 d post-maximum.
6 ADDITIONAL INVESTIGATIONS
In this section, we present additional investigations of our ejecta models focusing on HVFs and comparisons to observational data. We also explore shortcomings with our ejecta models.
6.1 High velocity features – Si ii and Ca ii
HVFs are absorption features, seen in the strongest lines, that show a distinct difference in velocity (often early and prior to maximum), by more than a few thousand km s−1 from the lower velocity, photospheric component (Gerardy et al. 2004; Mazzali et al. 2005a,b). Note the two strongest components of the Ca ii NIR triplet (λ8542 & λ8662) are separated by ∼4000 km s−1. Thus, any single Ca ii NIR profile may show an absorption feature with two components separated by a few thousand km s−1 that is different from an HVF. In many SNe Ia, HVFs have even been observed at maximum for the Ca ii NIR triplet but not for Si ii λλ6347, 6371 (Childress et al. 2014). There is no clear indication when HVFs start to disappear in all observed cases. Silverman et al. (2015) state that the HVF Ca ii triplet begins to disappear around −1 d prior to maximum for ΔM15(B) = 1.4–1.6 mag; however, discoveries of HVFs are potentially biased towards those that persist closer to maximum light.
Shown in Figs 14 and 15 is the evolution of the Si ii doublet and the Ca ii NIR triplet, with a vertical line at −15 000 km s−1 as a reference. In all models, Ca ii HVFs are seen before bolometric maximum (≲ − 11 d). However, no HVF for Si ii λλ6347, 6371 is seen. Notice the striking difference in the pre-maximum Ca ii triplet profile (≲ − 11 d) and the profile at later dates. The lack of a Si ii doublet HVF could just be a by-product of atomic physics. Although both the Ca ii NIR triplet and the Si ii doublet are not resonance transitions, the lower level of the Ca ii triplet is metastable. The lower level of the Si ii λ6355 doublet is the 4s state that is coupled to the ground state by a permitted transition. Therefore, when compared to the Si ii λ6355 doublet, the Ca ii NIR triplet persists longer because the metastable lower level population persists longer.
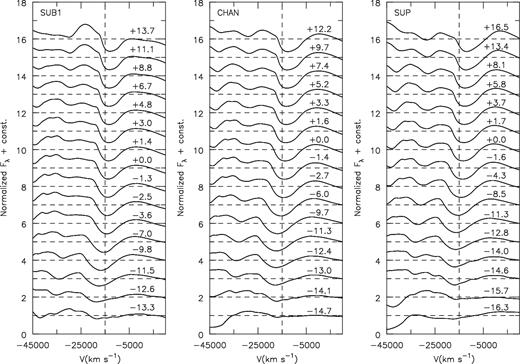
Normalized flux (according to equation 1 between 5800 and 6500 Å) of the Si ii λλ6347, 6371 doublet relative to bolometric maximum plotted in velocity space shifted relative to λ6355. Note the lack of Si ii HVFs. A vertical line at −15 000 km s−1 is included as a reference.
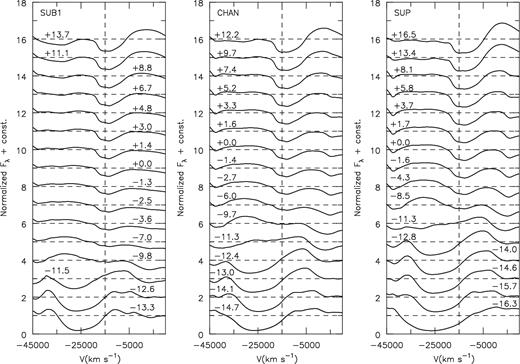
Normalized flux (according to equation 1 between 7000 and 9000 Å) of the Ca ii triplet relative to bolometric maximum plotted in velocity space shifted relative to λ8662. Note prior to ≲−11 d, HVFs are present without a photospheric component. After the HVF disappears, the photospheric component becomes visible. A vertical line at −15 000 km s−1 is included as a reference.
By defining a straight line between the maxima on either side of the absorption profiles of these Si ii features, we are able to compute our models’ pEWs (listed in Table 3). Comparing our work to fig. 8 of Blondin et al. (2012), we find our spectra are clustered around those labelled broad-lined Ia as seen in Fig. 16. Branch et al. (2006) looked at the pEWs of Si ii features near λ6100 and λ5750 in these spectra at maximum in order to group these spectra in different classifications: ‘core-normal, ‘broad-line’, ‘shallow-silicon’ and ‘cool’. For the most massive model (SUP), it might fall under the ‘cool’ classification from Branch et al. (2006), but it lacks the strong Ti ii absorption.

6.2 Comparison to data
6.2.1 SN1994ae
SN1994ae exploded in NGC 3370 (z = 0.0043 – Riess et al. 1999; Jha, Riess & Kirshner 2007) and was first discovered on 1994 November 14 by van Dyk et al. (1994). It reached B-band maximum (mB = 13.21 mag) on MJD 49685.5 with Δm15(B) = 0.96 mag (Riess et al. 1999; Jha et al. 2007). For comparison, we reddened our models using E(B − V) = 0.0226 mag and RV = 3.1 (Jha et al. 2007). Fig. 17 shows the spectral comparison of SN1994ae at +0.0, +10.0 and +152.7 d after B-band maximum and normalized LCs relative to band maximum are shown in Fig. 18.
![SN1994ae compared to our models at epochs +0.0, +10.0, and +152.7 d relative to B-band maximum, which occurred on MJD 49685.5. For comparison, we reddened our models using E(B − V) = 0.0226 mag and RV = 3.1 (Jha et al. 2007). All fluxes have been normalized between 4000 and 7000 Å according to equation (1). The observational data were taken from public CfA data (https://www.cfa.harvard.edu/supernova/SNarchive.html). At +0 d, we see that our model spectra do not reproduce the velocity of the Si ii λ6347, 6371 doublet and the UV Si ii triplet. The spectra show evidence of the Si iii triplet (λλ4553, 4568, 4575) absorption as do our SUB models (an indication of high ionization). Spectra at later epochs indicate cooler ejecta and model SUP is closest to reproducing the features. However, at nebular times (+152.7 d), our model optical Fe iii lines appear too strong and the [S iii] λλ9068, 9530 lines appear to be absent in observed spectra.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/474/3/10.1093_mnras_stx2816/1/m_stx2816fig17.jpeg?Expires=1749346110&Signature=lgjRtdKmD0f1hN-zbkgk2Woo-gnmEXc-CFie88NDplMPVZtKd6OsD7-pExHc-VZR-7MYp12ZdBvlS8kgakphY3BzhF-XxPxJr0685hW6Nrn26mroxamISe8S7lOpRo5V6f92DDCvU8iQQH8ei9Sd3~l6k39kY~0mom0oe24GWgXsAXMNRvoW9XmoHnzzUGmGbkotxXefQEHke66CQoojyI2DdEemRXCb2z0f6fkTEisivrjGhA3y6doRobvsMi38UXpznVqQP52oEwfPm9PgzV5ILPdvJ~V34xhsw6nM499lDuNS3sqAUgyAcuXLtMHdxYlXMPooxMvI3lZLcpT0Tw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
SN1994ae compared to our models at epochs +0.0, +10.0, and +152.7 d relative to B-band maximum, which occurred on MJD 49685.5. For comparison, we reddened our models using E(B − V) = 0.0226 mag and RV = 3.1 (Jha et al. 2007). All fluxes have been normalized between 4000 and 7000 Å according to equation (1). The observational data were taken from public CfA data (https://www.cfa.harvard.edu/supernova/SNarchive.html). At +0 d, we see that our model spectra do not reproduce the velocity of the Si ii λ6347, 6371 doublet and the UV Si ii triplet. The spectra show evidence of the Si iii triplet (λλ4553, 4568, 4575) absorption as do our SUB models (an indication of high ionization). Spectra at later epochs indicate cooler ejecta and model SUP is closest to reproducing the features. However, at nebular times (+152.7 d), our model optical Fe iii lines appear too strong and the [S iii] λλ9068, 9530 lines appear to be absent in observed spectra.
SN1994ae multiband LCs normalized to Bmax and corrected for reddening (see Section 6.2.1). Our B-band LC agrees until 20 d post-maximum. Afterwards, our LCs show roughly half a magnitude more flux. The V/R-band LC agrees with our model CHAN. Our models disagree with observations in the location of the I-band's second peak and more so for models with lower ejecta mass. Archived LC photometry is taken from Open Supernova Catalog (Guillochon et al. 2017), with references from the CfA Supernova Archive (https://www.cfa.harvard.edu/supernova/SNarchive.html) and (Riess et al. 2005).
At +0 d, our model spectra do not reproduce the velocity of the Si ii λ6355 doublet and UV Si ii triplet. Results by Dessart et al. (2014a) suggest SNe Ia resulting from pulsational-delayed detonations (PDD) retain more unburnt carbon and have little mass at high velocity (≳15 000 km s−1) due to pulsations. Therefore, spectral features of SN1994ae might be best explained by PDD modelling, and would resemble similar radiative properties of DDT models. The spectra also show evidence of the Si iii triplet (λλ4553, 4568, 4575) absorption as in our SUB models (an indication of high ionization). Later spectra show cooler ejecta and model SUP is closest to reproducing the features. However, at nebular times (+152.7 d) our model optical [Fe iii] lines appear too strong and [S iii] λλ9068, 9530 are absent in the observational data.
For the LC comparison, we shifted the LCs to give the same time of Bmax and reddened the models with AB = 0.091, AV = 0.070, AR = 0.057 and AI = 0.041 mag, obtained using E(B − V) = 0.0226 mag and RV = 3.1 from Jha et al. (2007). We normalized the LCs to 0 mag at Bmax and shifted the observational data by 12.98 mag. We see in Fig. 18 that our B-band LC is consistent until 20 d post-maximum, where our LCs begin showing roughly half a magnitude more flux. Model CHAN matches well the V/R-band observations. However, our models fail to reproduce the second peak in the I-band, and the disagreement is greater in lower mass models.
6.2.2 SN1995D
SN1995D exploded in NGC 2962 and was discovered on 1995 February 10 (Nakano, Kushida & Kushida 1995). Its redshift is z = 0.0067, and it reached B-band maximum (mB = 13.44 mag) on MJD 49768.7 (Riess et al. 1999; Jha et al. 2007). SN1995D has been argued as having a 56Ni mass of about 0.58 M⊙ and an ejecta mass around 1.45 M⊙ (Childress et al. 2015). For comparison, we reddened our models using E(B − V) = 0.026 mag and RV = 3.1 (Jha et al. 2007).
Fig. 19shows the spectral comparison of SN1995D at +3.6, +42.5 and +93.5 d after B-band maximum. The early epochs (+3.6 d) show good qualitative agreement with SUB1 except our model shows a larger blueshifted Si ii doublet. This may be best explained by a PDD model (Dessart et al. 2014a). SUB1 also matches the UV spectrum shortward of 4000 Å. At later epochs like +42.5 and +93.5 d, we see a better agreement to model SUP and to CHAN, due to lower temperatures and ionization. Roughly all features at +93.5 d are matched by SUP. Despite the calculated 56Ni and ejecta mass being closest to CHAN, SN1995D shows only moderate qualitative agreement at later epochs. SN1995D transitions from looking like our SUB1 into that of SUP from early to late epochs.
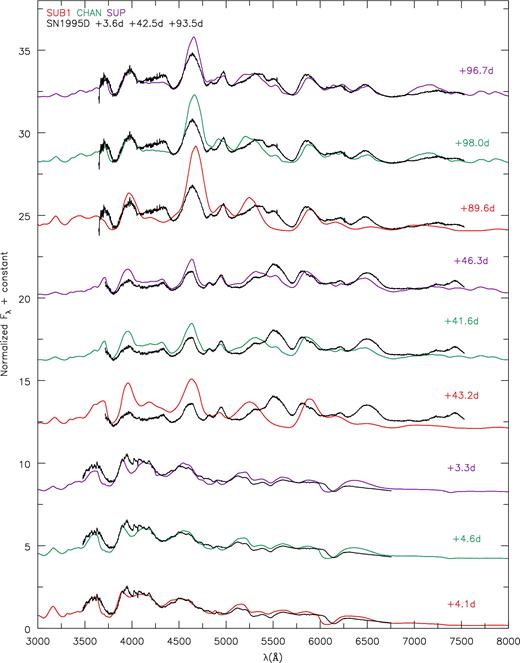
SN1995D compared to models at times +3.6, +42.5 and +93.5 d relative to B-band maximum that occurred on MJD 49768.7. We have corrected for redshift with a value of 0.0067. We reddened the models with E(B − V) = 0.026 mag and RV = 3.1. All fluxes have been normalized between 4000 and 7000 Å according to equation (1). The observational data were taken from public CfA data (https://www.cfa.harvard.edu/supernova/SNarchive.html). +3.6 d shows good qualitative agreement with SUB1, except our models have the Si ii λ6355 doublet formed at a higher velocity. SUB1 also matches the UV spectrum shortward of 4000 Å. Later epochs (+42.5 and +93.5 d) show a better agreement to model SUP and to CHAN, due to lower temperatures and ionization. Roughly all features at +93.5 d are matched by SUP.
To compare LCs, we shifted the LCs to give the same time of Bmax and reddened the models with AB = 0.106, AV = 0.081, AR = 0.066 and AI = 0.048 mag, obtained using E(B − V) = 0.026 mag and RV = 3.1 (Jha et al. 2007). We normalized the LCs to 0 mag at Bmax and shift the observational data by 13.35 mag.
In Fig. 20, we see that our B-band LC is consistent with all models until ∼12 d post-maximum, where our LCs then begin showing roughly half a magnitude more flux. Model CHAN matches well the V/R-band observations. Our models fail to reproduce the second peak in the I band (it occurs 10–20 d too early), although the SUP model matches the data at late times. Model SUP also seems consistent with the peak flux ratios in SN1995D.
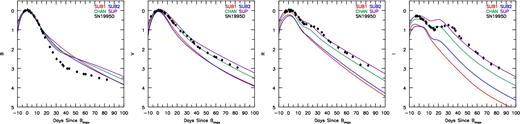
SN1995D multiband LCs normalized to Bmax and corrected for reddening (see Section 6.2.2). B-band LC agrees until ∼12 d post-maximum. Afterwards, our LCs show roughly half a magnitude more flux. The V/R-band LCs qualitatively agree with our CHAN model, although our models fail to reproduce the second peak in the I band. However, model SUP agrees with the observational data at late times. Archived LC photometry is taken from Open Supernova Catalog (Guillochon et al. 2017), with references from CfA Supernova Archive (https://www.cfa.harvard.edu/supernova/SNarchive.html) and (Riess et al. 1999).
6.2.3 SN2001ay
SN2001ay exploded outside IC 4423 and was discovered on 2001 April 18 by Swift, Li & Schwartz (2001). Krisciunas et al. (2011) and references therein cite its redshift as z = 0.0302 and indicate that it reached B-band maximum (MB = −19.19 mag) on 23 April 2001. For spectral comparison, we reddened our model spectra using E(B − V)MW = 0.026 mag, E(B − V)host = 0.072 mag, and RV = 3.1 (Krisciunas et al. 2011). Krisciunas et al. (2011) states a M(56Ni) of (0.58 ± 0.15)/α M⊙, for an α = Lmax/ENi, typically between 1 and 1.2. Given the close proximity between the estimated 56Ni mass for SN2001ay and that of our model set, we explore the spectral similarities.
Fig. 21shows the spectral comparison for epochs −1.5, +9.3 and +56.3 d relative to B-band maximum. All models provide a good qualitative fit to the optical spectrum at −1.5 d, with SUP exhibiting the worst fit. While all models fit the Si ii λλ6347, 6371 doublet in absorption strength and velocity, our models show stronger absorption in the Si ii λλ5041, 5056, 5056.3 triplet around 4800 Å. Blended with this feature is absorption arising from Fe ii λ5018, and this is also somewhat too strong in the models. The biggest discrepancy between model and observation for the blend occurs for model SUP. SUB1 lacks absorption at ∼4000 Å, which is clearly present in the observations, and all of the other models. No model reproduces the shape of the UV absorption near 3700 Å, which could be due to a discrepancy with the Ca ii H&K lines.
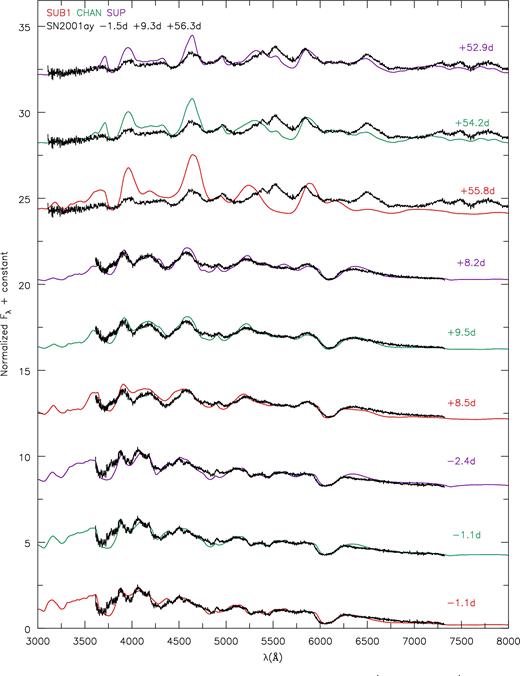
SN2001ay compared to models at epochs −1.5, +9.3 and +56.3 d relative to B-band maximum. Observed spectra have been corrected for a redshift of z = 0.0302. Models are reddened using E(B − V)MW = 0.026 mag, E(B − V)host = 0.072 mag and RV = 3.1. All fluxes are normalized in the range of 4000–7000 Å according to equation (1). Observational data were taken from public CfA data (https://www.cfa.harvard.edu/supernova/SNarchive.html). Early on, models reproduce velocity of the Si ii λλ6347, 6371 doublet. Models show stronger Si ii λλ5041, 5056, 5056.3 triplet absorption seen around 4800 Å, and also show discrepancies in Fe ii λ5018, seen around 4900 Å. SN2001ay shows similar Si iii λλ4553, 4568, 4575 triplet absorption as CHAN. No model reproduces the shape of the UV feature, most likely a discrepancy of formation velocity for the Ca ii H&K lines. Later spectral phases (+9.3 and +56 d) are best reproduced by SUP, indicating much lower temperature towards the innermost ejecta. SUP, however, shows a stronger absorption feature of the Ca ii NIR triplet. Given the discrepancies, we see at −1.5 d with the Ca ii H&K lines, SN2001ay shows a lack of strong Ca ii features.
Later, model SUP qualitatively agrees the SN2001ay spectra at +9.3 and +56.3 d best. At +9.3 d, SUP shows agreement despite its stronger Fe ii absorption lines around 4800 Å. At +56.3 d, the spectra is dominated by Fe ii features, which SUP matches well, given its cooler temperatures and lower ionization. Models SUB1, SUB2 and CHAN are too highly ionized and exhibit too much emission from higher ionization states such as Fe iii. Despite matching much of the optical spectrum, SUP does not match well the absorption features associated with the Ca ii NIR triplet and the Ca ii H&K lines. Given the discrepancy with calcium at −1.5 d, this may indicate that the calcium abundance is too high or that the distribution in velocity space is incorrect.
For the LC comparison, we reddened the models with AB = 0.397, AV = 0.307, AR = 0.148 and AI = 0.178 mag, by combining host and MW values as E(B − V) = 0.098 mag and RV = 3.1 (Krisciunas et al. 2011). We normalize the LCs to 0 mag at Bmax and shift the observed data by 16.35 mag. Fig. 22 shows our models fail to reproduce the post-maximum decline except for U/B bands. Our models show too little V/R/I flux in the decline post-maximum, but SUP agrees in peak flux ratios between bands with SN2001ay.
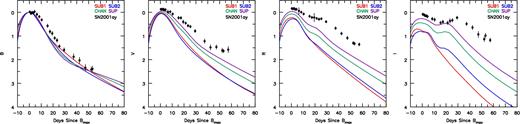
Multiband LCs for SN2001ay normalized to Bmax and corrected for reddening (see Section 6.2.3). Our models fail to reproduce the post-maximum decline except for U/B bands. Models show too little V/R/I flux in the decline post-maximum. However, the peak flux ratio between bands matches to model SUP. A larger reddening and an adjustment of the time of B-band maximum would improve the comparison. Archived LC photometry is taken from Open Supernova Catalog (Guillochon et al. 2017), with references from Ganeshalingam et al. (2010) and Silverman et al. (2012).
6.2.4 SN2005el
SN2005el exploded in NGC 1819 and was discovered on 2005 September 19 (Madison, Baek & Li 2005) at a redshift of z = 0.0148 (Hicken et al. 2009). It reached B-band maximum (mB = 14.84 mag) on MJD 53646.4 (Hicken et al. 2009). Scalzo et al. (2014a) classified SN2005el as having 0.9 M⊙ of ejecta as well as 0.54 M⊙ of 56Ni, which, considering the errors in the determinations, are close to our models SUB1 and SUB2. For comparison, we applied reddening to our models using E(B − V) = 0.136 mag and RV = 3.1 [an E(B − V) value that is higher than that stated in Scalzo et al. (2014a)].
Fig. 23shows our spectral comparison to SN2005el. The early epochs of −5.9 and +2.1 d show some qualitative agreement, mostly with SUB1 and SUB2. At this epoch, our models do not reproduce the Si ii λλ6347, 6371 doublet. Our models indicate a Si ii λλ6347, 6371 doublet formed at higher velocities. Therefore, spectral features of SN2005el may be best explained by a PDD model. Unlike the Si ii doublet, models CHAN and SUP do reproduce the S ii ‘w’ feature. Since our models show a higher blue-shifted Si ii doublet, it is not surprising that our UV does not match, given other Si ii and Ca ii H&K features in this region. If the Ca ii H&K lines and Si ii λλ3854, 3856, 3862 triplet are separated by thousands of km s−1, then it is likely to result in the spike seen at the bottom of the 3700 Å absorption feature, whereas our models show one broad absorption feature around 3700 Å (seen in SN2008ec, for example). Given the strong absorption profile around 4400 Å, we suggest this is the Si iii λλ4553, 4568, 4575 triplet, indicating a high ionization at this epoch.
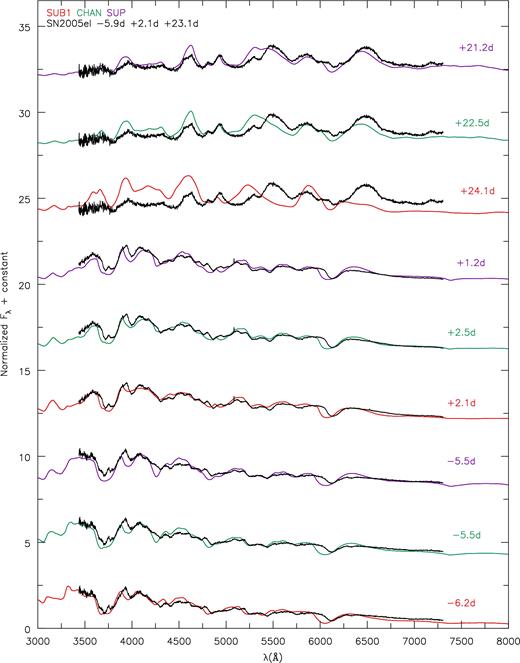
SN2005el compared to models at times −5.9, −4.9 and +23.1 d relative to B-band maximum. Observed spectrum is corrected for a redshift of 0.0148. Models are reddened with E(B − V) = 0.136 mag and RV = 3.1. All fluxes are normalized between 4000 and 7000 Å according to equation (1). This observational data were taken from public CFA data (https://www.cfa.harvard.edu/supernova/SNarchive.html). Around −5 d, our models do not reproduce the Si ii λλ6347, 6371 doublet. Models show line formation at higher velocities. Unlike the Si ii doublet, CHAN and SUP do reproduce the S ii ‘w’ feature. UV spectra is poorly reproduced due to formation velocities of Si ii and Ca ii H&K features in this region. If the Ca ii H&K lines are formed a few thousand km s−1 away from the Si ii λλ3854, 3856, 3862 triplet (which our models show both sum to the broad absorption feature around 3700 Å), it is likely to result in the spike seen at the bottom of the 3700 Å absorption feature. SN2005el also shows a strong absorption profile around 4400 Å, which we suggest to be the Si iii λλ4553, 4568, 4575 triplet, indicating a high ionization. At +24.9 d, model SUP agrees qualitatively in almost all spectral features. At this epoch, SUP has the coolest inner ejecta. This agreement is surprising, given the 70 per cent difference in claimed ejecta mass. The discrepancy around 5300 Å could be the result of differences in the Fe ii or Cr ii absorption.
At +24.9 d, we see that model SUP agrees qualitatively in almost all features. Other models are too blue compared to the cooler SUP model. This is surprising given the claim that SN2005el is a sub-MCh SN with an ejecta mass of only 0.9 M⊙. The discrepancy around 5300 Å could be the result of differences in the Fe ii or Cr ii absorption.
One should expect SUB1 or SUB2 to resemble the spectral evolution of SN2005el; however, we only see that SUB1 matches prior to maximum and does not match SN2005el at late epochs, where SUP shows best agreement. There are several possible explanations for the inconsistencies. First, the 56Ni mass may be lower than 0.54 M⊙. Secondly, the poor agreement in the extent of the Si ii λλ6347, 6371 doublet could indicate a different explosion scenario (such as PDD mentioned earlier – little mass at high velocity).
To compare LCs, we shifted the LCs relative to the time of Bmax and reddened the models with AB = 0.543, AV = 0.414, AR = 0.339, AI = 0.245, AJ = 0.122 and AH = 0.077 mag, obtained using E(B − V) = 0.136 mag and RV = 3.1 slightly higher than Scalzo et al. (2014a). The LCs were normalized to 0 mag at Bmax and we adjust the observational data by 14.76 mag. In Fig. 24, we see the optical bands are reproduced well with our SUB models (except B beyond 20 d). Although the late time behaviour in the H-band is reproduced, the NIR LCs do not generally agree with the SUB models. The double peak structure in the J-band observations is well produced by the models, although in the H-band it less evident.
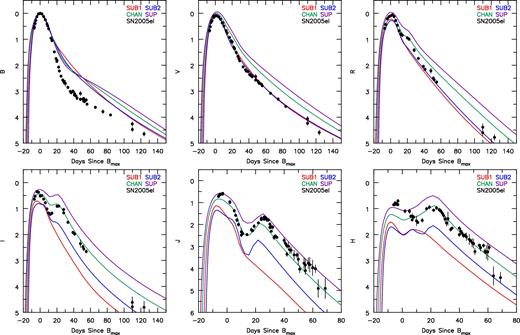
Multiband LCs corrected for reddening and normalized to Bmax (see Section 6.2.4). Optical band normalized LCs of SN2005el agree in morphology with our SUB models. The NIR LCs do not agree with SUB models. Instead, the NIR LCs show better agreement with CHAN and SUP. Archived LC photometry is taken from Open Supernova Catalog (Guillochon et al. 2017), with references from (Contreras et al. 2010; Ganeshalingam et al. 2010; Silverman et al. 2012; Friedman et al. 2015).
6.3 Model setbacks and theoretical problems
When compared to observation data, our models do show a higher ionization, especially in the nebular phase. The strength of the [Fe iii] λ4658 feature is too strong compared to other optical/NIR features. Further, optical spectra lack emission such as [Fe ii] ∼λ4350 emission, seen in nebular spectra of SNe Ia of Taubenberger et al. (2013) and Black, Fesen & Parrent (2016), for example. Other researchers have also had difficulty modelling the Fe ii feature near 4350 Å (Spyromillo 2016, private communication; Sim 2016, private communication; Mazzali et al. 2015; Friesen et al. 2017). It is not surprising that these models struggle to get the ionization correct – there are no free parameters and the density structure and element distribution is set by the adopted initial model.
At late times, the super-MCh model was generally in better agreement with observation – a result of the model being cooler with lower ionization. Since we know that most of the observed SNe we discussed are not super-MCh, there is a fundamental problem with the models. This problem might arise from the adopted explosion models, be related to assumptions about mixing and clumping, and/or be a problem in the ionization calculations. Since nebular spectra show strong [Fe ii] and [Fe iii], the Fe+/Fe2 + ratio must be of order unity, and consequently, it is sensitive to the Fe atomic models (and the density structure).
The disconnection between early and late time modelling is not unexpected. Early time spectra are dependent on the outer ejecta whereas late time spectra are primarily dependent on the inner ejecta. Further, the processes determining the observed spectra in the photospheric and nebular phases are distinct, and subject to different uncertainties in the atomic data.
Another problem is the strong nebular [S iii] λλ9068, 9530 and [Ar iii] λλ7135, 7751 lines. The [S iii] λλ9068, 9530 does not seem to appear in nebular spectra. However, it is not clear if [Ar iii] λ7135 is present. There are three additional transitions contributing to that overall feature between 7000 and 7500 Å. There are two [Fe ii] λλ7155, 7172 lines that overlap [Ar iii] λ7135, and depending on the ionization structure of the ejecta, it becomes difficult to determine the source of the feature in observations. However, atomic physics of the [Ar iii] λλ7135, 7751 lines requires that the line ratio, I(7135)/I(7751), should be a factor of 4.2, so if spectral detections of [Ar iii] λ7751 are possible, then one can determine the strength of the blended [Ar iii] λ7135 line. However, observed SN Ia nebular spectra appear absent of IME lines. This could be due to an absence of 56Ni in the IME zone. In our models, the presence of some 56Ni in the IME zone means that positrons are available as a heating source after the ejecta has become optically thin to grey photons. One would expect some level of mixing to occur through Rayleigh–Taylor instabilities between these layers – see Hicks (2015) and references therein. To address the problem of too high an ionization, clumping, arising from radiation hydrodynamic instabilities, should be considered in future studies. Our preliminary work shows that, as expected, clumping lowers the ionization, and we will address this issue in a future paper.
Another possible explanation concerns the validity of the explosion models. We have considered only four models, and only two of the explosion models were obtained from ‘first principles’, and even these were derived from 1D explosions. Alternative explosion mechanisms might give rise to different density and abundance profiles, and in particular, the spatial distribution of 56Ni. The later will influence the amount of UV line blanketing, potentially introducing degeneracies with the ejecta mass. However, other diagnostics (e.g. the NIR nickel line) provide additional information, and can break the degeneracies. Further, despite the deficiencies, the models have highlighted important diagnostics and questions that can help facilitate future progress towards understanding Type Ia SNe.
7 CONCLUSION
We have presented four 1D SN Ia models – three delayed detonation models with masses of 1.02, 1.40 and 1.70 M⊙ and one detonation sub-MCh model with a mass of 1.04 M⊙. By design, the models have the same 56Ni mass of ∼0.62 M⊙ that allows us to investigate the dependence of LCs and spectra on ejecta mass. Despite the smallness of the model grid they serve to highlight important diagnostics that can help facilitate future progress towards understanding Type Ia SNe.
Our results show that despite large differences in ejecta mass, the optical flux throughout the photospheric phase shows less than 0.3 mag difference in peak brightness in the LCs, as well as nearly identical spectral features. We have seen that the peak bolometric luminosity of each model is similar to within about 15 per cent, and the difference in rise time is less than ∼20 per cent. Due to differences in diffusion time, however, the two sub-MCh mass models do evolve faster (pre-maximum) by a day as seen from the bolometric luminosity and synthetic B-band LCs. There is only a slight difference (∼5 per cent) in the decline parameter, ΔM15(B), between sub-MCh and super-MCh models. Our sub-MCh models have much bluer colours at all epochs compared with SUP (B − R difference of ≈0.3 mag at maximum and a difference in B − R ≳1 mag roughly 20 d post-maximum). Our models show larger differences in NIR LCs, particularly with the H-band's ∼1 mag difference at maximum light between sub-MCh and super-MCh.
Spectroscopically, at most photospheric phases, the optical spectra show the same gross features. However, the strength of UV blanketing between 2000 and 4000 Å is found to correlate with ejecta mass. Lower mass models have higher temperature and ionization (as more heating per gram), and hence lower UV blanketing between 2000 and 4000 Å. M(56Ni)/Mej is the leading parameter controlling this study. Higher mass models produce stronger IME features, such as the Ca ii NIR triplet and the Si ii λ6347, 6371 doublet prior to the nebular phase, and stronger [S ii] λλ9530, 9068, [Ca ii] λλ7291, 7324, and [Ar iii] λ7135 in the nebular phase. Lower mass models have higher ionization, as indicated by the presence of the Si iii λλ4553, 4568, 4575 triplet near maximum and the lack of strong Fe ii and Co ii lines in the optical post-photospheric/nebular phase. Model SUB1, unlike SUB2, is dominated by strong [Fe iii] and [Co iii] lines, such as [Fe iii] λ4658, [Fe iii] λ5270, [Co iii] λ5888 and [Co iii] 1.5484 μm.
In the nebular phase, the [Ni ii] 1.939 μm line is absent in our sub-MCh detonation model, but readily visible in the three other models. Potentially, the [Ni ii] 1.939 μm line provides us with a diagnostic of the amount of stable nickel (58Ni & 60Ni), unlike the blended optical [Ni ii] λλ7378, 7412 lines. Its absence in NIR spectra would provide strong evidence for a lack of a ‘56Ni hole’ and potentially sub-Chandrasekhar mass ejecta (given 1D modelling). However, complex ionization issues can influence the strength of all [Ni ii] lines, making absolute determinations of the abundance model dependent. Overall the NIR provides the best diagnostics for distinguishing between our different SN Ia progenitor models.
In comparing our spectra to observation at times greater than 20 d post-maximum, we consistently find better qualitative fits with our cooler, high-mass super-MCh model. Given that there is a ∼20–70 per cent difference in claimed ejecta mass between our compared observational objects and our super-MCh model, we suggest clumping as a way to lower the high ionization and high temperatures observed in our models. While it is difficult to reproduce all observational features due to the diversity of SNe Ia, we are able to match some features shown in our comparison to observations. Prior to maximum, the best choice of model varies. Agreement depends on the velocity structure of the ejecta. For instance, the photospheric features Si ii λλ6347, 6371 and the Ca ii NIR triplet expose the difficulty of reproducing the velocity structure of SN Ia (Figs 21 and 23, for example). Future efforts to reproduce the diversity of these features requires a better understanding of the outer ejecta and explosion mechanism.
Parallel work has been undertaken by Blondin et al. (submitted to MNRAS) who studied SN 1999by using a low-mass model (0.9 M⊙) and a model with a Chandrasekhar mass (both with 0.12 M⊙of 56Ni). They find that the lower mass model provides a better match to the LC and exhibits a faster rise and a brighter maximum. As in our study, the lower mass model does not show the [Ni ii] 1.939 μm line, which is seen in their Chandrasekhar model
To determine more accurate diagnostic signatures of SN Ia progenitors, we need to understand clumping and inhomogeneities in Ia ejecta. Some insights can be obtained from multidimensional explosion modelling, while additional insight might be obtained from studies of young SN remnants that are not interacting with the surrounding ISM. During the photospheric phase, more UV spectral data will help to constrain the ionization and temperature of the gas. More NIR spectral data will help to test our diagnostics, such as the NIR Ca ii triplet (or nebular [Ca ii] λλ7291, 7324), the nebular features between 9000 Åand 1 μm (such as [S iii] λλ9068, 9530) and the [Ni ii] 1.939 μm line (requiring SNe Ia at a high enough redshift to avoid the telluric absorption). These nebular features can provide leverage on the progenitor channel by constraining initial densities ([Ni ii]), the overlap between IMEs and IGEs ([Ca ii]), and the ionization structure.
As many more SN spectra become available it will be possible to do systematic statistical comparisons between SNe that have a similar initial 56Ni mass. As discussed above, our studies show that Type Ia SN will exhibit systematic differences in spectra and multiband LCs as a function of ejecta mass, thus providing fundamental constraints on the nature of the progenitors.
Acknowledgements
We thank Stéphane Blondin for providing feedback for this work as well as everyone at the ‘Supernovae Through the Ages: Understanding the Past to Prepare for the Future’ conference who presented work and talked with us about our research. We also thank the referee for providing very detailed and useful comments and questions. This research has made use of the CfA Supernova Archive, which is funded in part by the National Science Foundation through grant AST 0907903. DJH acknowledges partial support from STScI theory grant HST-AR-12640.001-A, and DJH and KDW thank NASA for partial support through theory grant NNX14AB41G.
REFERENCES



