-
PDF
- Split View
-
Views
-
Cite
Cite
Daisuke Taniguchi, Noriyuki Matsunaga, Naoto Kobayashi, Kei Fukue, Satoshi Hamano, Yuji Ikeda, Hideyo Kawakita, Sohei Kondo, Hiroaki Sameshima, Chikako Yasui, Method to estimate the effective temperatures of late-type giants using line-depth ratios in the wavelength range 0.97–1.32 μm, Monthly Notices of the Royal Astronomical Society, Volume 473, Issue 4, February 2018, Pages 4993–5001, https://doi.org/10.1093/mnras/stx2691
Close - Share Icon Share
Abstract
The effective temperature, one of the most fundamental atmospheric parameters of a star, can be estimated using various methods; here, we focus on a method using line-depth ratios (LDRs). This method combines low- and high-excitation lines and makes use of relations between LDRs of these line pairs and the effective temperature. It has an advantage, for example, of being minimally affected by interstellar reddening, which changes stellar colours. We report 81 relations between LDRs and effective temperature established with high-resolution, λ/Δλ ∼ 28 000, spectra of nine G- to M-type giants in the Y and J bands. Our analysis gives the first comprehensive set of LDR relations for this wavelength range. The combination of all these relations can be used to determine the effective temperatures of stars that have 3700 < Teff < 5400 K and −0.5 < [Fe/H] < +0.3 dex, to a precision of ±10 K in the best cases.
1 INTRODUCTION
Stellar atmospheres are characterized mainly by effective temperature (Teff), surface gravity (log g) and metallicity ([Fe/H]), of which Teff has a particularly strong impact on spectra and is often the first parameter to be estimated during spectral analysis. Among many methods of measuring Teff, we focus on the line-depth ratio (LDR) method in this article. In cool stars (around solar temperature and below), the depths of low-excitation lines of neutral atoms are sensitive to Teff, while those of high-excitation lines are relatively insensitive (Gray 2008) and hence their ratios are good temperature indicators (Gray & Johanson 1991; Fukue et al. 2015 and references therein). This method has a few advantages: LDRs are not affected by interstellar reddening, and atmospheric parameters other than Teff are expected to have no, or at least relatively weak, effects on LDRs.
Sasselov & Lester (1990) used LDRs between C i and Si i lines around 1.1 μm to measure the temperatures and reddenings of Cepheids in a relative way. This pioneering work, however, had a limited impact on later applications, due to the small number of standard stars and line pairs. In contrast, previous works on the LDR method mostly used visible spectral ranges (e.g. Kovtyukh et al. 2003, 2006; Kovtyukh 2007). With the development of infrared facilities in recent years, it has become possible to make more comprehensive studies using high-resolution infrared spectra. Recently, Fukue et al. (2015) established the LDR method for H-band spectra, 1.50–1.65 μm. In this wavelength range, however, the small number of low-excitation lines and severe blending between molecular and metal lines make it difficult to find a large number of useful LDR pairs. As a result, the precision of Teff after taking an average of the values from available pairs is only ∼50 K for each star in the best case, while the LDR method in the visible range can achieve a precision of ∼5 K (Kovtyukh et al. 2006). Here, we investigate Y- and J-band spectra to find the LDR–Teff relations for the first time. This wavelength range has a number of both low- and high-excitation lines (e.g. Meléndez & Barbuy 1999) and thus one can expect many useful LDR pairs that will enable us to achieve high precision.
2 OBSERVATION
The ten targets listed in Table 1 were selected mainly from Gaia FGK benchmark stars (Blanco-Cuaresma et al. 2014; Jofré et al. 2014; Heiter et al. 2015), in addition to a few prototypes of red giants such as Arcturus. All of our targets are giants with luminosity class III or II and have spectral types between early G and early M (3700 K < Teff < 5400 K). Their metallicities are between −0.45 and +0.25 dex in [Fe/H] except for Arcturus, −0.52 dex.
The target stars and their atmospheric parameters. Spectral types are from SIMBAD (Wenger et al. 2000). The temperatures of μ Leo and Aldebaran were estimated in both references (1) and (2) and we use the weighted means. The last column gives the dates of our WINERED observations.
| Object . | HD . | Sp. Type . | Teff [K] . | [Fe/H] [dex] . | log g [dex] . | Obs. Date . |
|---|---|---|---|---|---|---|
| ε Leo | 84441 | G1II | 5398 ± 31[2] | −0.06 ± 0.04[2] | 2.02 ± 0.08[2] | 2014 Jan 23 |
| κ Gem | 62345 | G8IIIa | 5029 ± 47[2] | −0.01 ± 0.05[2] | 2.61 ± 0.12[2] | 2013 Dec 8 |
| ε Vir | 113226 | G8III | 4983 ± 61[1] | |$+0.15\pm 0.16_{}^{\text{[1]}}$| | 2.77 ± 0.02[1] | 2014 Jan 23 |
| Pollux | 62509 | K0III | 4858 ± 60[1] | +0.13 ± 0.16[1] | 2.90 ± 0.08[1] | 2013 Feb 28 |
| μ Leo | 85503 | K2IIIb | 4470 ± 40[1,2] | +0.25 ± 0.15[1] | 2.51 ± 0.11[1] | 2013 Feb 23 |
| Alphard | 81797 | K3II-III | 4171 ± 52[2] | +0.08 ± 0.07[2] | 1.56 ± 0.20[2] | 2013 Nov 30 |
| Aldebaran | 29139 | K5III | 3882 ± 19[1,2] | −0.37 ± 0.17[1] | 1.11 ± 0.19[1] | 2013 Feb 24 |
| α Cet | 18884 | M1.5IIIa | 3796 ± 65[1] | −0.45 ± 0.47[1] | 0.68 ± 0.23[1] | 2013 Nov 30 |
| δ Oph | 146051 | M0.5III | 3783 ± 20[2] | −0.03 ± 0.06[2] | 1.45 ± 0.19[2] | 2014 Jan 23 |
| Arcturus | 124897 | K0III | 4286 ± 35[1] | −0.52 ± 0.08[1] | 1.64 ± 0.09[1] | 2013 Feb 23 |
| Object . | HD . | Sp. Type . | Teff [K] . | [Fe/H] [dex] . | log g [dex] . | Obs. Date . |
|---|---|---|---|---|---|---|
| ε Leo | 84441 | G1II | 5398 ± 31[2] | −0.06 ± 0.04[2] | 2.02 ± 0.08[2] | 2014 Jan 23 |
| κ Gem | 62345 | G8IIIa | 5029 ± 47[2] | −0.01 ± 0.05[2] | 2.61 ± 0.12[2] | 2013 Dec 8 |
| ε Vir | 113226 | G8III | 4983 ± 61[1] | |$+0.15\pm 0.16_{}^{\text{[1]}}$| | 2.77 ± 0.02[1] | 2014 Jan 23 |
| Pollux | 62509 | K0III | 4858 ± 60[1] | +0.13 ± 0.16[1] | 2.90 ± 0.08[1] | 2013 Feb 28 |
| μ Leo | 85503 | K2IIIb | 4470 ± 40[1,2] | +0.25 ± 0.15[1] | 2.51 ± 0.11[1] | 2013 Feb 23 |
| Alphard | 81797 | K3II-III | 4171 ± 52[2] | +0.08 ± 0.07[2] | 1.56 ± 0.20[2] | 2013 Nov 30 |
| Aldebaran | 29139 | K5III | 3882 ± 19[1,2] | −0.37 ± 0.17[1] | 1.11 ± 0.19[1] | 2013 Feb 24 |
| α Cet | 18884 | M1.5IIIa | 3796 ± 65[1] | −0.45 ± 0.47[1] | 0.68 ± 0.23[1] | 2013 Nov 30 |
| δ Oph | 146051 | M0.5III | 3783 ± 20[2] | −0.03 ± 0.06[2] | 1.45 ± 0.19[2] | 2014 Jan 23 |
| Arcturus | 124897 | K0III | 4286 ± 35[1] | −0.52 ± 0.08[1] | 1.64 ± 0.09[1] | 2013 Feb 23 |
The target stars and their atmospheric parameters. Spectral types are from SIMBAD (Wenger et al. 2000). The temperatures of μ Leo and Aldebaran were estimated in both references (1) and (2) and we use the weighted means. The last column gives the dates of our WINERED observations.
| Object . | HD . | Sp. Type . | Teff [K] . | [Fe/H] [dex] . | log g [dex] . | Obs. Date . |
|---|---|---|---|---|---|---|
| ε Leo | 84441 | G1II | 5398 ± 31[2] | −0.06 ± 0.04[2] | 2.02 ± 0.08[2] | 2014 Jan 23 |
| κ Gem | 62345 | G8IIIa | 5029 ± 47[2] | −0.01 ± 0.05[2] | 2.61 ± 0.12[2] | 2013 Dec 8 |
| ε Vir | 113226 | G8III | 4983 ± 61[1] | |$+0.15\pm 0.16_{}^{\text{[1]}}$| | 2.77 ± 0.02[1] | 2014 Jan 23 |
| Pollux | 62509 | K0III | 4858 ± 60[1] | +0.13 ± 0.16[1] | 2.90 ± 0.08[1] | 2013 Feb 28 |
| μ Leo | 85503 | K2IIIb | 4470 ± 40[1,2] | +0.25 ± 0.15[1] | 2.51 ± 0.11[1] | 2013 Feb 23 |
| Alphard | 81797 | K3II-III | 4171 ± 52[2] | +0.08 ± 0.07[2] | 1.56 ± 0.20[2] | 2013 Nov 30 |
| Aldebaran | 29139 | K5III | 3882 ± 19[1,2] | −0.37 ± 0.17[1] | 1.11 ± 0.19[1] | 2013 Feb 24 |
| α Cet | 18884 | M1.5IIIa | 3796 ± 65[1] | −0.45 ± 0.47[1] | 0.68 ± 0.23[1] | 2013 Nov 30 |
| δ Oph | 146051 | M0.5III | 3783 ± 20[2] | −0.03 ± 0.06[2] | 1.45 ± 0.19[2] | 2014 Jan 23 |
| Arcturus | 124897 | K0III | 4286 ± 35[1] | −0.52 ± 0.08[1] | 1.64 ± 0.09[1] | 2013 Feb 23 |
| Object . | HD . | Sp. Type . | Teff [K] . | [Fe/H] [dex] . | log g [dex] . | Obs. Date . |
|---|---|---|---|---|---|---|
| ε Leo | 84441 | G1II | 5398 ± 31[2] | −0.06 ± 0.04[2] | 2.02 ± 0.08[2] | 2014 Jan 23 |
| κ Gem | 62345 | G8IIIa | 5029 ± 47[2] | −0.01 ± 0.05[2] | 2.61 ± 0.12[2] | 2013 Dec 8 |
| ε Vir | 113226 | G8III | 4983 ± 61[1] | |$+0.15\pm 0.16_{}^{\text{[1]}}$| | 2.77 ± 0.02[1] | 2014 Jan 23 |
| Pollux | 62509 | K0III | 4858 ± 60[1] | +0.13 ± 0.16[1] | 2.90 ± 0.08[1] | 2013 Feb 28 |
| μ Leo | 85503 | K2IIIb | 4470 ± 40[1,2] | +0.25 ± 0.15[1] | 2.51 ± 0.11[1] | 2013 Feb 23 |
| Alphard | 81797 | K3II-III | 4171 ± 52[2] | +0.08 ± 0.07[2] | 1.56 ± 0.20[2] | 2013 Nov 30 |
| Aldebaran | 29139 | K5III | 3882 ± 19[1,2] | −0.37 ± 0.17[1] | 1.11 ± 0.19[1] | 2013 Feb 24 |
| α Cet | 18884 | M1.5IIIa | 3796 ± 65[1] | −0.45 ± 0.47[1] | 0.68 ± 0.23[1] | 2013 Nov 30 |
| δ Oph | 146051 | M0.5III | 3783 ± 20[2] | −0.03 ± 0.06[2] | 1.45 ± 0.19[2] | 2014 Jan 23 |
| Arcturus | 124897 | K0III | 4286 ± 35[1] | −0.52 ± 0.08[1] | 1.64 ± 0.09[1] | 2013 Feb 23 |
We observed these ten stars between 2013 February 23 and 2014 January 23 using near-infrared high-resolution spectrograph WINERED attached to the Nasmyth platform of the 1.3-m Araki Telescope at Koyama Astronomical Observatory of Kyoto Sangyo University in Japan (Ikeda et al. 2016). WINERED can collect spectra covering the wavelength range from 0.90–1.35 μm (z΄, Y and J bands) with a spectral resolution of R ∼ 28 000 with one integration. All of our targets are bright, −2.3 < J < 2.0 mag, and the total integration time with each target within the slit was between 12 and 240 s to achieve a signal-to-noise ratio (S/N) of 100 or higher. We describe the resultant S/N in Section 3.1. For every target star, we also observed a telluric standard star (an A0V star in most cases) for subtracting telluric absorption.
3 DATA ANALYSIS
3.1 Spectra reduction
Basic data reduction was performed automatically using the pipeline software prepared by the WINERED team based on pyraf.1 The pipeline process includes the standard analysis steps for echelle spectra: bad pixel masking, sky subtraction, flat-fielding, scattered light subtraction, transformation of each two-dimensional echelle image into images with the space and wavelength axes orthogonal to each other for individual orders, spectrum extraction, wavelength calibration and continuum normalization. In addition, it was necessary to correct for time-dependent wavelength shifts as follows. We used ThAr lamp data as the initial wavelength calibration in the pipeline software, but we found that some spectra had wavelength offsets, probably caused by varying ambient temperature.2 In this work, such offsets are not critical, because we are not interested in radial velocities, but the adjustment of the wavelength scale of individual frames was necessary to avoid the artificial broadening of the line spread function in a combined spectrum of each target. The relative offsets between individual spectra were measured using almost isolated telluric absorption lines and were removed before combining the spectra. Then, telluric absorption lines in the combined spectrum of each target were removed using the spectrum of a telluric-standard star, except for the 53rd–55th orders, 1.01–1.07 μm, in which almost no significant telluric lines are present. The wavelength scale of each telluric-corrected spectrum was converted to the rest frame of each star using its intrinsic absorption lines. Our wavelengths are in the standard air scale. Finally, we renormalize the spectra using pyraf to adjust the continuum level to unity. In the following discussions, we consider 12 orders listed in Table 2. We ignore other orders (42nd, 49th–51st and 58th–61st), which are around gaps between atmospheric windows. In the analysis to find and calibrate the LDR–Teff relations, we ignore Arcturus because, according to Fukue et al. (2015), its low metallicity causes offsets from the trends between LDR and effective temperature. Table 2 shows the S/N of each order of each star calculated from the variance of the normalized counts in continuum regions, as an indicator of spectral quality. The spectral resolution was stable and quite constant for all of our spectra. The full width at half-maximum (FWHM) values measured with most stellar lines correspond to λ/Δλ between 26 000 and 30 000. Fig. 1 shows a small range of the spectra obtained. This range has a line pair that shows a clear temperature dependence, as we discuss below.

Part of the spectra for the 55th order, drawn in order of decreasing effective temperature (from top), except for Arcturus at the bottom, which was not included in establishing the LDR–Teff relations. The two lines in the graph show a clear dependence on temperature (the high-excitation line on the left and the low-excitation line on the right).
S/N of the reduced spectra in each echelle order (52–57th in the Y band and 43–48th in the J band).
| Object . | 57 . | 56 . | 55 . | 54 . | 53 . | 52 . | 48 . | 47 . | 46 . | 45 . | 44 . | 43 . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ε Leo | 321 | 293 | 581 | 266 | 332 | 207 | 173 | 178 | 194 | 224 | 198 | 178 |
| κ Gem | 102 | 154 | 385 | 406 | 248 | 192 | 141 | 269 | 170 | 359 | 245 | 233 |
| ε Vir | 99 | 86 | 289 | 532 | 290 | 172 | 111 | 200 | 204 | 329 | 220 | 225 |
| Pollux | 134 | 117 | 150 | 160 | 287 | 126 | 121 | 120 | 143 | 261 | 152 | 187 |
| μ Leo | 87 | 82 | 175 | 353 | 226 | 126 | 102 | 118 | 99 | 166 | 119 | 144 |
| Alphard | 128 | 119 | 263 | 254 | 291 | 155 | 103 | 89 | 124 | 223 | 97 | 146 |
| Aldebaran | 49 | 153 | 173 | 176 | 141 | 192 | 185 | 137 | 174 | 312 | 166 | 181 |
| α Cet | 125 | 134 | 143 | 226 | 290 | 229 | 166 | 165 | 151 | 342 | 241 | 171 |
| δ Oph | 195 | 140 | 142 | 301 | 368 | 186 | 103 | 177 | 165 | 405 | 186 | 293 |
| Arcturus | 118 | 192 | 246 | 248 | 264 | 191 | 128 | 99 | 188 | 193 | 158 | 278 |
| Object . | 57 . | 56 . | 55 . | 54 . | 53 . | 52 . | 48 . | 47 . | 46 . | 45 . | 44 . | 43 . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ε Leo | 321 | 293 | 581 | 266 | 332 | 207 | 173 | 178 | 194 | 224 | 198 | 178 |
| κ Gem | 102 | 154 | 385 | 406 | 248 | 192 | 141 | 269 | 170 | 359 | 245 | 233 |
| ε Vir | 99 | 86 | 289 | 532 | 290 | 172 | 111 | 200 | 204 | 329 | 220 | 225 |
| Pollux | 134 | 117 | 150 | 160 | 287 | 126 | 121 | 120 | 143 | 261 | 152 | 187 |
| μ Leo | 87 | 82 | 175 | 353 | 226 | 126 | 102 | 118 | 99 | 166 | 119 | 144 |
| Alphard | 128 | 119 | 263 | 254 | 291 | 155 | 103 | 89 | 124 | 223 | 97 | 146 |
| Aldebaran | 49 | 153 | 173 | 176 | 141 | 192 | 185 | 137 | 174 | 312 | 166 | 181 |
| α Cet | 125 | 134 | 143 | 226 | 290 | 229 | 166 | 165 | 151 | 342 | 241 | 171 |
| δ Oph | 195 | 140 | 142 | 301 | 368 | 186 | 103 | 177 | 165 | 405 | 186 | 293 |
| Arcturus | 118 | 192 | 246 | 248 | 264 | 191 | 128 | 99 | 188 | 193 | 158 | 278 |
S/N of the reduced spectra in each echelle order (52–57th in the Y band and 43–48th in the J band).
| Object . | 57 . | 56 . | 55 . | 54 . | 53 . | 52 . | 48 . | 47 . | 46 . | 45 . | 44 . | 43 . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ε Leo | 321 | 293 | 581 | 266 | 332 | 207 | 173 | 178 | 194 | 224 | 198 | 178 |
| κ Gem | 102 | 154 | 385 | 406 | 248 | 192 | 141 | 269 | 170 | 359 | 245 | 233 |
| ε Vir | 99 | 86 | 289 | 532 | 290 | 172 | 111 | 200 | 204 | 329 | 220 | 225 |
| Pollux | 134 | 117 | 150 | 160 | 287 | 126 | 121 | 120 | 143 | 261 | 152 | 187 |
| μ Leo | 87 | 82 | 175 | 353 | 226 | 126 | 102 | 118 | 99 | 166 | 119 | 144 |
| Alphard | 128 | 119 | 263 | 254 | 291 | 155 | 103 | 89 | 124 | 223 | 97 | 146 |
| Aldebaran | 49 | 153 | 173 | 176 | 141 | 192 | 185 | 137 | 174 | 312 | 166 | 181 |
| α Cet | 125 | 134 | 143 | 226 | 290 | 229 | 166 | 165 | 151 | 342 | 241 | 171 |
| δ Oph | 195 | 140 | 142 | 301 | 368 | 186 | 103 | 177 | 165 | 405 | 186 | 293 |
| Arcturus | 118 | 192 | 246 | 248 | 264 | 191 | 128 | 99 | 188 | 193 | 158 | 278 |
| Object . | 57 . | 56 . | 55 . | 54 . | 53 . | 52 . | 48 . | 47 . | 46 . | 45 . | 44 . | 43 . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ε Leo | 321 | 293 | 581 | 266 | 332 | 207 | 173 | 178 | 194 | 224 | 198 | 178 |
| κ Gem | 102 | 154 | 385 | 406 | 248 | 192 | 141 | 269 | 170 | 359 | 245 | 233 |
| ε Vir | 99 | 86 | 289 | 532 | 290 | 172 | 111 | 200 | 204 | 329 | 220 | 225 |
| Pollux | 134 | 117 | 150 | 160 | 287 | 126 | 121 | 120 | 143 | 261 | 152 | 187 |
| μ Leo | 87 | 82 | 175 | 353 | 226 | 126 | 102 | 118 | 99 | 166 | 119 | 144 |
| Alphard | 128 | 119 | 263 | 254 | 291 | 155 | 103 | 89 | 124 | 223 | 97 | 146 |
| Aldebaran | 49 | 153 | 173 | 176 | 141 | 192 | 185 | 137 | 174 | 312 | 166 | 181 |
| α Cet | 125 | 134 | 143 | 226 | 290 | 229 | 166 | 165 | 151 | 342 | 241 | 171 |
| δ Oph | 195 | 140 | 142 | 301 | 368 | 186 | 103 | 177 | 165 | 405 | 186 | 293 |
| Arcturus | 118 | 192 | 246 | 248 | 264 | 191 | 128 | 99 | 188 | 193 | 158 | 278 |
3.2 Line selection and measurement of line depth
As the candidates of atomic lines to be used for LDRs, we consider the lines identified in our Arcturus spectrum. Here we outline its line identification, but details of the analysis and the entire line list will be published in a forthcoming article (Ikeda et al., in preparation). First, we produced a synthesized spectrum of Arcturus, the parameters of which are assumed to be Teff = 4275 K, log g = 1.7 and [Fe/H] = −0.4 dex (Smith et al. 2013), using the ATLAS9 atmospheric models and codes given by Kurucz (1993). As the input list of atomic lines for the synthetic spectrum, the Vienna Atomic Line Database (VALD3; Ryabchikova et al. 2015) was used. Secondly, the observed and synthetic spectra were compared closely with each other in order to identify lines with depth larger than ∼1 per cent. Although the S/N of the Arcturus spectrum is higher than 200 at all wavelengths, CN molecular lines often make the identification of shallow lines less certain. In such cases, to confirm the contribution of weak atomic lines around molecular lines, we further compared the observed spectrum with a synthetic spectrum, but with only CN lines included. Thus we obtained approximately 800 atomic lines.
Among the lines identified in Arcturus, here we include relatively isolated neutral lines of Fe, Ti, Si, Cr, Ca, Ni, Mg, Na, Co, Al, Mn and K in our analysis for LDRs. Ion lines and lines of C, N and O were not included (Kovtyukh et al. 2006). Moreover, we excluded lines based on the following criteria: deep lines that appear deeper than ∼0.5 in Arcturus and lines blended with molecular CN lines or other atomic lines, which have different elements and/or excitation potentials. These criteria left 125 and 99 lines in the Y and J bands, respectively. We refer to VALD3 for line parameters such as excitation potential and oscillator strength.
For the 125 and 99 lines we selected, we used a quadratic function to fit three (or four) pixels near the bottom of each line, rather than fitting the entire line profile, e.g. by the Gaussian or the Voigt function (Strassmeier & Schordan 2000). We define |$d_{i}^{(n)}$| as a line depth from the continuum level to the bottom of the fitted function, where i indicates the ID number of the line and (n) indicates the ID number of the star. Weak lines with |$d_{i}^{(n)}<0.02$| are ignored in the following analysis.
3.3 Line pair selection
We calculated the LDR, |$r_{j}^{(n)}=d_{i}^{(n)}/d_{i^{\prime }}^{(n)}$|, for any line pair, j, of approximately 1500 pairs for which the both lines were detected in more than four stars and have excitation potentials separated by more than 1 eV. We treated each order independently, i.e. we did not combine lines in different orders, and divided the depth of the low-excitation line, di, by that of the high-excitation line, |$d_{i^{\prime }}$|. For each line pair, j, we plotted the effective temperatures Teff against the common logarithms of the LDRs, log rj, and determined the regression line, Teff = ajlog rj + bj, using the weighted total least-squares method (see Markovsky & Van Huffel 2007 for a review). The weight of a line pair, j, of star (n) was calculated by |$w_{j}^{(n)}=[(\sigma _{y}^{(n)})^{2}+{a_{j}}^{2}(\sigma _{x,j}^{(n)})^{2}]^{-1}$|, where |$\sigma _{x,j}^{(n)}$| and |$\sigma _{y}^{(n)}$| indicate the standard error of |$\log r_{j}^{(n)}$| calculated using the S/N and that of the literature Teff(n) for each star, respectively. The dispersion around each regression line is defined as σj2. The effective temperature and its error for each star based on each relation are given as |$T_{j}^{(n)}\pm \Delta T_{j}^{(n)}$|, for which the error was determined using the variance–covariance matrix of coefficients (aj, bj) of the regression line and the error of |$\log r_{j}^{(n)}$|. In the subsequent analysis, about 900 line pairs that have σj > 150 K were not included. Moreover, 21 line pairs that have aj > 0 were excluded. A large fraction of the rejected pairs include a weak iron line at 10350.77 Å (6.145 eV) in the Y band. This line may be blended by other line(s), which causes the unexpected dependence of the LDR on effective temperature, though the presence of such blended lines is not clear in the available line lists. The rest of the line pairs with aj > 0 have Ti i lines for both low- and high-excitation potentials.3 LDR–Teff relations for the majority of Ti i–Ti i pairs are not tight enough to be selected and their slopes can be negative, positive or not well determined. The reason for the opposite slopes for a small number of Ti i–Ti i pairs is unclear.
There is a large number of possible combinations of line pairs and we selected a set of pairs as follows. One condition is that each line is used only once, i.e. it is not included in more than one line pair. This ensures that statistical errors in |$r_{j}^{(n)}$| values in different LDR–Teff relations are independent of each other and makes it easy to calculate the statistical errors of combined effective temperatures (TLDR in Section 4). In fact, the final set of relations we discuss in Section 4 makes use of 162 lines, which is about 70 per cent of the selected lines. This condition for the line-pair selection has no large impact on the statistical error, which would be better only by ∼15 per cent even if we used all the pre-selected pairs.
The basic idea of the process is to select line pairs that meet the following conditions as much as possible: (i) high precision in reproducing the effective temperatures of our sample stars and (ii) small difference in wavelength between the two lines of each line pair. With the latter condition fulfilled, the possibility of other instruments detecting both lines of a line pair in the same echelle order becomes high and the error in the LDR introduced in the continuum normalization is expected to be smaller.
4 RESULTS
We applied the procedure described above to our 224 nodes (i.e. lines) and 603 edges (i.e. line pairs). By changing the coefficient e from 0 to 2 K Å− 1, we searched for the optimized matching, Mk(e), that gives the smallest E at each e value and observed how e affects the solutions. Fig. 2 plots the values of ET and Eλ for Mk(e) with varying e. By increasing e, the weight of Eλ increases relative to ET in the evaluation function and then the optimal matching and the values of ET and Eλ change. At around e = 0.5 K Å− 1, ET is only slightly larger compared with the case with e = 0 K Å− 1 for most orders (the exception being the order 48), which optimizes the precision in the redetemined temperature by ignoring the difference in wavelength, while Eλ improves to some extent by changing e from 0 to 0.5 K Å− 1. The number of line pairs in the 48th order is only four and, with e = 0.5 K Å− 1, the wavelength separations of the individual pairs become significantly small, with only a small increase in ET. We selected e = 0.5 K Å− 1 and Table 3 lists the resultant values of the evaluation functions and other parameters in our analysis.
![The dependence of ET(Mk(e)) and Eλ(Mk(e)) on the parameter e in equation (1). The evaluation functions are defined in the text. Variations of ET(Mk(e)) (top row) and Eλ(Mk(e)) (bottom row) are presented for a group of echelle orders in each band (52nd–57th in the Y band on the left and 43rd–48th in the J band on the right). Each solid line represents the evaluation function and the vertical dashed line represents the value e = 0.5 K Å− 1 that we used for the final solutions. Legends show which colour corresponds to which echelle order. [The colour version of this figure is available in the online journal.]](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/473/4/10.1093_mnras_stx2691/1/m_stx2691fig2.jpeg?Expires=1749909460&Signature=qdq2ZJLrvwImVOT~96Qil3RpAWSd28pLbJGb6rURPkxL9RpU2PJnsvbG~jCdJiEpJBCYeKnIUQHA60oqDOZY5myIPm17ilt845wgz5NZ5bMMIjmvj-IRgsMkRXh4DqrSlR2YXpDrkMtHGKfKS~xY4icYhqU0sG573Yh2BPXC~mwtugbAOOAZdmxYYeMveWYHHnrwxJ2e5FhIN4oN6YIxZLFKdWBu~mUMXJ4oA~gQY6y81kyPY4sru8deteh7FObCLgJnc4O8fFmpK6LkvpW~rNqn31oaGJY~mwHGrkoHP3oTT90olB~2q8SP8QKUE78OrnsgGuq0R~HTKHPR4XD0ag__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The dependence of ET(Mk(e)) and Eλ(Mk(e)) on the parameter e in equation (1). The evaluation functions are defined in the text. Variations of ET(Mk(e)) (top row) and Eλ(Mk(e)) (bottom row) are presented for a group of echelle orders in each band (52nd–57th in the Y band on the left and 43rd–48th in the J band on the right). Each solid line represents the evaluation function and the vertical dashed line represents the value e = 0.5 K Å− 1 that we used for the final solutions. Legends show which colour corresponds to which echelle order. [The colour version of this figure is available in the online journal.]
Parameters of the selected line pairs in individual orders (52–57th in Y and 43–48th in J): wavelength range λmin < λ < λmax from the WINERED website (http://merlot.kyoto-su.ac.jp/LIH/WINERED/), the number of lines Nline considered to make pairs, the number of line pairs Npair included in the final solutions and values of the evaluation functions. In addition, the last column gives the same parameters, but for all the orders combined.
| Order . | 57 . | 56 . | 55 . | 54 . | 53 . | 52 . | 48 . | 47 . | 46 . | 45 . | 44 . | 43 . | Combined . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| λmin [μm] | 0.976 | 0.992 | 1.010 | 1.028 | 1.048 | 1.068 | 1.156 | 1.180 | 1.205 | 1.232 | 1.260 | 1.290 | 0.976 |
| λmax [μm] | 0.992 | 1.010 | 1.028 | 1.048 | 1.068 | 1.089 | 1.180 | 1.205 | 1.232 | 1.260 | 1.290 | 1.319 | 1.319 |
| Nline | 4 | 23 | 19 | 30 | 17 | 32 | 13 | 11 | 19 | 14 | 16 | 26 | 224 |
| Npair | 1 | 10 | 4 | 10 | 8 | 14 | 3 | 3 | 4 | 5 | 7 | 12 | 81 |
| ET(e = 0.5) [K] | 47 | 24 | 106 | 30 | 29 | 61 | 60 | 80 | 76 | 77 | 28 | 46 | 28.6 |
| Eλ(e = 0.5) [Å] | 9 | 47 | 40 | 66 | 39 | 53 | 9 | 68 | 72 | 79 | 73 | 111 | 68.0 |
| E(e = 0.5) [K] | 51 | 48 | 126 | 63 | 49 | 87 | 64 | 114 | 112 | 117 | 64 | 101 | 62.6 |
| Order . | 57 . | 56 . | 55 . | 54 . | 53 . | 52 . | 48 . | 47 . | 46 . | 45 . | 44 . | 43 . | Combined . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| λmin [μm] | 0.976 | 0.992 | 1.010 | 1.028 | 1.048 | 1.068 | 1.156 | 1.180 | 1.205 | 1.232 | 1.260 | 1.290 | 0.976 |
| λmax [μm] | 0.992 | 1.010 | 1.028 | 1.048 | 1.068 | 1.089 | 1.180 | 1.205 | 1.232 | 1.260 | 1.290 | 1.319 | 1.319 |
| Nline | 4 | 23 | 19 | 30 | 17 | 32 | 13 | 11 | 19 | 14 | 16 | 26 | 224 |
| Npair | 1 | 10 | 4 | 10 | 8 | 14 | 3 | 3 | 4 | 5 | 7 | 12 | 81 |
| ET(e = 0.5) [K] | 47 | 24 | 106 | 30 | 29 | 61 | 60 | 80 | 76 | 77 | 28 | 46 | 28.6 |
| Eλ(e = 0.5) [Å] | 9 | 47 | 40 | 66 | 39 | 53 | 9 | 68 | 72 | 79 | 73 | 111 | 68.0 |
| E(e = 0.5) [K] | 51 | 48 | 126 | 63 | 49 | 87 | 64 | 114 | 112 | 117 | 64 | 101 | 62.6 |
Parameters of the selected line pairs in individual orders (52–57th in Y and 43–48th in J): wavelength range λmin < λ < λmax from the WINERED website (http://merlot.kyoto-su.ac.jp/LIH/WINERED/), the number of lines Nline considered to make pairs, the number of line pairs Npair included in the final solutions and values of the evaluation functions. In addition, the last column gives the same parameters, but for all the orders combined.
| Order . | 57 . | 56 . | 55 . | 54 . | 53 . | 52 . | 48 . | 47 . | 46 . | 45 . | 44 . | 43 . | Combined . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| λmin [μm] | 0.976 | 0.992 | 1.010 | 1.028 | 1.048 | 1.068 | 1.156 | 1.180 | 1.205 | 1.232 | 1.260 | 1.290 | 0.976 |
| λmax [μm] | 0.992 | 1.010 | 1.028 | 1.048 | 1.068 | 1.089 | 1.180 | 1.205 | 1.232 | 1.260 | 1.290 | 1.319 | 1.319 |
| Nline | 4 | 23 | 19 | 30 | 17 | 32 | 13 | 11 | 19 | 14 | 16 | 26 | 224 |
| Npair | 1 | 10 | 4 | 10 | 8 | 14 | 3 | 3 | 4 | 5 | 7 | 12 | 81 |
| ET(e = 0.5) [K] | 47 | 24 | 106 | 30 | 29 | 61 | 60 | 80 | 76 | 77 | 28 | 46 | 28.6 |
| Eλ(e = 0.5) [Å] | 9 | 47 | 40 | 66 | 39 | 53 | 9 | 68 | 72 | 79 | 73 | 111 | 68.0 |
| E(e = 0.5) [K] | 51 | 48 | 126 | 63 | 49 | 87 | 64 | 114 | 112 | 117 | 64 | 101 | 62.6 |
| Order . | 57 . | 56 . | 55 . | 54 . | 53 . | 52 . | 48 . | 47 . | 46 . | 45 . | 44 . | 43 . | Combined . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| λmin [μm] | 0.976 | 0.992 | 1.010 | 1.028 | 1.048 | 1.068 | 1.156 | 1.180 | 1.205 | 1.232 | 1.260 | 1.290 | 0.976 |
| λmax [μm] | 0.992 | 1.010 | 1.028 | 1.048 | 1.068 | 1.089 | 1.180 | 1.205 | 1.232 | 1.260 | 1.290 | 1.319 | 1.319 |
| Nline | 4 | 23 | 19 | 30 | 17 | 32 | 13 | 11 | 19 | 14 | 16 | 26 | 224 |
| Npair | 1 | 10 | 4 | 10 | 8 | 14 | 3 | 3 | 4 | 5 | 7 | 12 | 81 |
| ET(e = 0.5) [K] | 47 | 24 | 106 | 30 | 29 | 61 | 60 | 80 | 76 | 77 | 28 | 46 | 28.6 |
| Eλ(e = 0.5) [Å] | 9 | 47 | 40 | 66 | 39 | 53 | 9 | 68 | 72 | 79 | 73 | 111 | 68.0 |
| E(e = 0.5) [K] | 51 | 48 | 126 | 63 | 49 | 87 | 64 | 114 | 112 | 117 | 64 | 101 | 62.6 |
We obtained 47 LDR–Teff relations in the Y band and 34 in the J band, with e = 0.5 K Å− 1. Tables 4 and 5 list the line pairs and relations and Fig. 3 shows some examples of these relations. We redetermined the effective temperatures using our final relations (TLDR in Table 6) and compared them with Teff in the literature in Fig. 4. The difference, TLDR − Teff, has no clear dependence on Teff or [Fe/H], suggesting that this LDR method is effective across the parameter range covered by the nine calibrating stars, i.e. 3700 < Teff < 5400 K and −0.5 < [Fe/H] < +0.3 dex. In order to evaluate the power of the LDR method, considering all orders available, we consider the evaluation function of equation (1) but including all orders and line pairs, i.e. we use TLDR(n) instead of the temperatures for an individual order, |$T_{M_{k(e)}}^{(n)}$|, and consider the wavelength differences of all line pairs. Thus the calculated evaluation functions are |$E_{T}^{\mathrm{all}}=28.6\, \mathrm{K}$| and |$E_{\lambda }^{\mathrm{all}}=68.0\, \mathrm{{\rm \mathring{\rm A} }}$|. These values are, for example, smaller than those4 for the result by Fukue et al. (2015), who used nine line pairs in the H band and obtained |$E_{T}^{\mathrm{IRCS}}=85.5\, \mathrm{K}$| and |$E_{\lambda }^{\mathrm{IRCS}}=295.6\, \mathrm{{\rm \mathring{\rm A} }}$|.
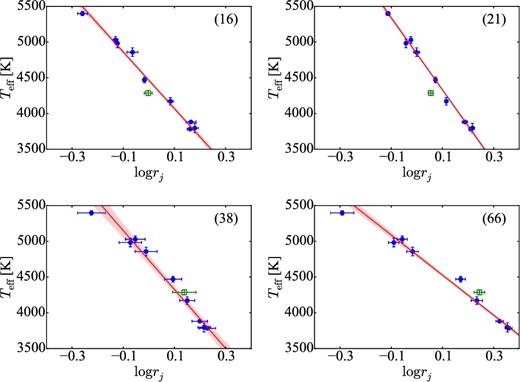
Examples of LDR–Teff relations. The ID of the line pair is given in each panel. Arcturus, indicated by a green open square in each panel, was not used for the relation that was obtained; other objects are indicated by blue filled circles. Plots for all 81 relations are available as online material – see the Supporting Information.
![Differences between the redetermined effective temperatures TLDR from our LDR method and the literature temperatures Teff plotted against Teff (left panel) and [Fe/H] (right panel). Symbols are the same as in Fig. 3. The size of the vertical error bars is dominated by the error in the literature temperature, except for high-temperature stars (ε Leo and κ Gem) and Arcturus.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/473/4/10.1093_mnras_stx2691/1/m_stx2691fig4.jpeg?Expires=1749909460&Signature=qHhxSYCKopu2rzVSb2WlXpU0O3ooeEVW-q5Ns8rZR6yjhuh58f4tE8A7gsUbC4r9htNeBMPEQsi9lWJi3RyM20VQB5Kfthgbhs~05v8F~dZusf4wyMQzFItokVEmYS32cTig7HYNFs4RuGIWpwgBfswbZwoH3IXhMrby9vM7iw38OzDnORdGQe7R944ONbCxADclO4RfS1xijhGOlj6C2Iersw7j7MQVQfk3Wl5TpS8Uz9GhSrDV1Z~pUtfGIpyjTGQeQvUMjUlJfFomblDunvOwdgx3J2wtQAkNELNj-16UBreeLgcP7cz20cjLjz3akPvi5Gvcc2~x9U5OSHMZqQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Differences between the redetermined effective temperatures TLDR from our LDR method and the literature temperatures Teff plotted against Teff (left panel) and [Fe/H] (right panel). Symbols are the same as in Fig. 3. The size of the vertical error bars is dominated by the error in the literature temperature, except for high-temperature stars (ε Leo and κ Gem) and Arcturus.
List of low- and high-excitation lines and LDR–Teff relations in the Y band. a and b represent the coefficients of Teff = a log r + b, N represents the number of stars used in fitting and σ represents the dispersion of the relation. If more than one line is listed at the same wavelength in the original line catalogue, information for the line with the largest log gf value is adopted here. The flag in the last column indicates the line pairs that are used in the analysis without the telluric correction in Section 5.
| . | . | Low-excitation line . | High-excitation line . | LDR–Teff relation . | . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID . | Order . | λ [Å] . | El. . | E.P. [eV] . | λ [Å] . | El. . | E.P. [eV] . | a [K] . | b [K] . | N . | σ [K] . | flag . |
| (1) | 57 | 9879.583 | Ti i | 1.873 | 9889.035 | Fe i | 5.033 | − 1462 | 3543 | 5 | 43 | |
| (2) | 56 | 9927.351 | Ti i | 1.879 | 9944.207 | Fe i | 5.012 | − 2390 | 4837 | 8 | 112 | |
| (3) | 56 | 9946.320 | Cr i | 3.556 | 9953.471 | Fe i | 5.446 | − 2635 | 4223 | 6 | 125 | 1 |
| (4) | 56 | 10003.09 | Ti i | 2.160 | 9961.256 | Na i | 3.617 | − 2645 | 4339 | 6 | 86 | 1 |
| (5) | 56 | 10081.39 | Fe i | 2.424 | 9980.463 | Fe i | 5.033 | − 2687 | 4586 | 9 | 74 | |
| (6) | 56 | 10005.66 | Ti i | 1.067 | 9987.869 | Fe i | 2.176 | − 961 | 3955 | 5 | 27 | |
| (7) | 56 | 9997.959 | Ti i | 1.873 | 10077.17 | Fe i | 2.990 | − 2297 | 4848 | 8 | 121 | |
| (8) | 56 | 10011.74 | Ti i | 2.154 | 10041.47 | Fe i | 5.012 | − 2477 | 5189 | 9 | 87 | |
| (9) | 56 | 10034.49 | Ti i | 1.460 | 10086.24 | Fe i | 2.949 | − 2433 | 4953 | 8 | 42 | |
| (10) | 56 | 10059.90 | Ti i | 1.430 | 10068.33 | Si i | 6.099 | − 1088 | 4837 | 6 | 99 | |
| (11) | 56 | 10066.51 | Ti i | 2.160 | 10065.05 | Fe i | 4.835 | − 1801 | 3631 | 9 | 79 | 1 |
| (12) | 55 | 10155.16 | Fe i | 2.176 | 10216.31 | Fe i | 4.733 | − 3116 | 3758 | 9 | 148 | |
| (13) | 55 | 10167.47 | Fe i | 2.198 | 10193.22 | Ni i | 4.089 | − 4235 | 4587 | 9 | 143 | |
| (14) | 55 | 10189.15 | Ti i | 1.460 | 10195.11 | Fe i | 2.728 | − 1654 | 3522 | 6 | 78 | |
| (15) | 55 | 10273.68 | Ca i | 4.535 | 10230.80 | Fe i | 6.119 | − 2179 | 4584 | 9 | 102 | |
| (16) | 54 | 10423.74 | Fe i | 3.071 | 10288.94 | Si i | 4.920 | − 3964 | 4465 | 9 | 69 | 1 |
| (17) | 54 | 10333.18 | Fe i | 4.593 | 10313.20 | Si i | 6.399 | − 2830 | 5109 | 5 | 68 | 1 |
| (18) | 54 | 10321.06 | Ni i | 5.525 | 10414.91 | Si i | 6.619 | − 3392 | 4482 | 5 | 132 | 1 |
| (19) | 54 | 10332.33 | Fe i | 3.635 | 10353.81 | Fe i | 5.393 | − 4499 | 4779 | 9 | 96 | 1 |
| (20) | 54 | 10396.80 | Ti i | 0.848 | 10340.89 | Fe i | 2.198 | − 4433 | 5016 | 9 | 110 | 1 |
| (21) | 54 | 10343.82 | Ca i | 2.933 | 10371.26 | Si i | 4.930 | − 5040 | 4836 | 9 | 49 | 1 |
| (22) | 54 | 10423.03 | Fe i | 2.692 | 10347.97 | Fe i | 5.393 | − 3912 | 5346 | 9 | 127 | 1 |
| (23) | 54 | 10382.31 | Co i | 2.871 | 10388.75 | Fe i | 5.446 | − 2256 | 4454 | 7 | 97 | 1 |
| (24) | 54 | 10395.80 | Fe i | 2.176 | 10469.65 | Fe i | 3.884 | − 8570 | 4524 | 9 | 146 | 1 |
| (25) | 54 | 10460.05 | Ti i | 2.256 | 10435.35 | Fe i | 4.733 | − 2058 | 4693 | 8 | 117 | 1 |
| (26) | 53 | 10486.25 | Cr i | 3.011 | 10530.51 | Ni i | 4.105 | − 3839 | 5192 | 9 | 70 | 1 |
| (27) | 53 | 10496.11 | Ti i | 0.836 | 10535.71 | Fe i | 6.206 | − 1832 | 5620 | 9 | 107 | 1 |
| (28) | 53 | 10510.01 | Cr i | 3.013 | 10555.65 | Fe i | 5.446 | − 2015 | 5081 | 9 | 92 | 1 |
| (29) | 53 | 10551.76 | Ti i | 1.887 | 10532.24 | Fe i | 3.929 | − 1475 | 3325 | 5 | 39 | 1 |
| (30) | 53 | 10552.97 | Ti i | 2.249 | 10582.16 | Si i | 6.223 | − 936 | 4393 | 7 | 44 | 1 |
| (31) | 53 | 10577.14 | Fe i | 3.301 | 10611.69 | Fe i | 6.169 | − 4007 | 4805 | 9 | 106 | 1 |
| (32) | 53 | 10607.72 | Ti i | 0.848 | 10672.14 | Cr i | 3.013 | − 2069 | 4236 | 8 | 91 | 1 |
| (33) | 53 | 10616.72 | Fe i | 3.267 | 10627.65 | Si i | 5.863 | − 2750 | 3799 | 9 | 106 | 1 |
| (34) | 52 | 10677.05 | Ti i | 0.836 | 10721.66 | Fe i | 5.507 | − 1297 | 5420 | 7 | 117 | |
| (35) | 52 | 10692.73 | Fe i | 3.071 | 10689.72 | Si i | 5.954 | − 2088 | 2691 | 6 | 113 | |
| (36) | 52 | 10753.00 | Fe i | 3.960 | 10694.25 | Si i | 5.964 | − 3586 | 3739 | 9 | 103 | |
| (37) | 52 | 10746.45 | Na i | 3.191 | 10717.81 | Fe i | 5.539 | − 4899 | 6654 | 7 | 133 | |
| (38) | 52 | 10725.19 | Fe i | 3.640 | 10849.47 | Fe i | 5.539 | − 4120 | 4739 | 9 | 97 | |
| (39) | 52 | 10726.39 | Ti i | 0.813 | 10785.39 | Fe i | 5.621 | − 1685 | 5490 | 8 | 144 | |
| (40) | 52 | 10783.05 | Fe i | 3.111 | 10727.41 | Si i | 5.984 | − 3629 | 3936 | 9 | 69 | |
| (41) | 52 | 10732.86 | Ti i | 0.826 | 10762.26 | Ni i | 4.154 | − 1681 | 5364 | 8 | 70 | |
| (42) | 52 | 10742.55 | Fe i | 3.642 | 10749.38 | Si i | 4.930 | − 4284 | − 120 | 5 | 145 | |
| (43) | 52 | 10774.87 | Ti i | 0.818 | 10838.97 | Ca i | 4.878 | − 1628 | 4756 | 8 | 74 | |
| (44) | 52 | 10780.69 | Fe i | 3.237 | 10843.86 | Si i | 5.863 | − 2479 | 3308 | 9 | 146 | |
| (45) | 52 | 10834.85 | Na i | 3.617 | 10784.56 | Si i | 5.964 | − 3081 | 4923 | 9 | 123 | |
| (46) | 52 | 10801.36 | Cr i | 3.011 | 10811.12 | Mg i | 5.946 | − 2476 | 2985 | 9 | 136 | |
| (47) | 52 | 10816.91 | Cr i | 3.013 | 10827.09 | Si i | 4.954 | − 2020 | 3002 | 8 | 131 | |
| . | . | Low-excitation line . | High-excitation line . | LDR–Teff relation . | . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID . | Order . | λ [Å] . | El. . | E.P. [eV] . | λ [Å] . | El. . | E.P. [eV] . | a [K] . | b [K] . | N . | σ [K] . | flag . |
| (1) | 57 | 9879.583 | Ti i | 1.873 | 9889.035 | Fe i | 5.033 | − 1462 | 3543 | 5 | 43 | |
| (2) | 56 | 9927.351 | Ti i | 1.879 | 9944.207 | Fe i | 5.012 | − 2390 | 4837 | 8 | 112 | |
| (3) | 56 | 9946.320 | Cr i | 3.556 | 9953.471 | Fe i | 5.446 | − 2635 | 4223 | 6 | 125 | 1 |
| (4) | 56 | 10003.09 | Ti i | 2.160 | 9961.256 | Na i | 3.617 | − 2645 | 4339 | 6 | 86 | 1 |
| (5) | 56 | 10081.39 | Fe i | 2.424 | 9980.463 | Fe i | 5.033 | − 2687 | 4586 | 9 | 74 | |
| (6) | 56 | 10005.66 | Ti i | 1.067 | 9987.869 | Fe i | 2.176 | − 961 | 3955 | 5 | 27 | |
| (7) | 56 | 9997.959 | Ti i | 1.873 | 10077.17 | Fe i | 2.990 | − 2297 | 4848 | 8 | 121 | |
| (8) | 56 | 10011.74 | Ti i | 2.154 | 10041.47 | Fe i | 5.012 | − 2477 | 5189 | 9 | 87 | |
| (9) | 56 | 10034.49 | Ti i | 1.460 | 10086.24 | Fe i | 2.949 | − 2433 | 4953 | 8 | 42 | |
| (10) | 56 | 10059.90 | Ti i | 1.430 | 10068.33 | Si i | 6.099 | − 1088 | 4837 | 6 | 99 | |
| (11) | 56 | 10066.51 | Ti i | 2.160 | 10065.05 | Fe i | 4.835 | − 1801 | 3631 | 9 | 79 | 1 |
| (12) | 55 | 10155.16 | Fe i | 2.176 | 10216.31 | Fe i | 4.733 | − 3116 | 3758 | 9 | 148 | |
| (13) | 55 | 10167.47 | Fe i | 2.198 | 10193.22 | Ni i | 4.089 | − 4235 | 4587 | 9 | 143 | |
| (14) | 55 | 10189.15 | Ti i | 1.460 | 10195.11 | Fe i | 2.728 | − 1654 | 3522 | 6 | 78 | |
| (15) | 55 | 10273.68 | Ca i | 4.535 | 10230.80 | Fe i | 6.119 | − 2179 | 4584 | 9 | 102 | |
| (16) | 54 | 10423.74 | Fe i | 3.071 | 10288.94 | Si i | 4.920 | − 3964 | 4465 | 9 | 69 | 1 |
| (17) | 54 | 10333.18 | Fe i | 4.593 | 10313.20 | Si i | 6.399 | − 2830 | 5109 | 5 | 68 | 1 |
| (18) | 54 | 10321.06 | Ni i | 5.525 | 10414.91 | Si i | 6.619 | − 3392 | 4482 | 5 | 132 | 1 |
| (19) | 54 | 10332.33 | Fe i | 3.635 | 10353.81 | Fe i | 5.393 | − 4499 | 4779 | 9 | 96 | 1 |
| (20) | 54 | 10396.80 | Ti i | 0.848 | 10340.89 | Fe i | 2.198 | − 4433 | 5016 | 9 | 110 | 1 |
| (21) | 54 | 10343.82 | Ca i | 2.933 | 10371.26 | Si i | 4.930 | − 5040 | 4836 | 9 | 49 | 1 |
| (22) | 54 | 10423.03 | Fe i | 2.692 | 10347.97 | Fe i | 5.393 | − 3912 | 5346 | 9 | 127 | 1 |
| (23) | 54 | 10382.31 | Co i | 2.871 | 10388.75 | Fe i | 5.446 | − 2256 | 4454 | 7 | 97 | 1 |
| (24) | 54 | 10395.80 | Fe i | 2.176 | 10469.65 | Fe i | 3.884 | − 8570 | 4524 | 9 | 146 | 1 |
| (25) | 54 | 10460.05 | Ti i | 2.256 | 10435.35 | Fe i | 4.733 | − 2058 | 4693 | 8 | 117 | 1 |
| (26) | 53 | 10486.25 | Cr i | 3.011 | 10530.51 | Ni i | 4.105 | − 3839 | 5192 | 9 | 70 | 1 |
| (27) | 53 | 10496.11 | Ti i | 0.836 | 10535.71 | Fe i | 6.206 | − 1832 | 5620 | 9 | 107 | 1 |
| (28) | 53 | 10510.01 | Cr i | 3.013 | 10555.65 | Fe i | 5.446 | − 2015 | 5081 | 9 | 92 | 1 |
| (29) | 53 | 10551.76 | Ti i | 1.887 | 10532.24 | Fe i | 3.929 | − 1475 | 3325 | 5 | 39 | 1 |
| (30) | 53 | 10552.97 | Ti i | 2.249 | 10582.16 | Si i | 6.223 | − 936 | 4393 | 7 | 44 | 1 |
| (31) | 53 | 10577.14 | Fe i | 3.301 | 10611.69 | Fe i | 6.169 | − 4007 | 4805 | 9 | 106 | 1 |
| (32) | 53 | 10607.72 | Ti i | 0.848 | 10672.14 | Cr i | 3.013 | − 2069 | 4236 | 8 | 91 | 1 |
| (33) | 53 | 10616.72 | Fe i | 3.267 | 10627.65 | Si i | 5.863 | − 2750 | 3799 | 9 | 106 | 1 |
| (34) | 52 | 10677.05 | Ti i | 0.836 | 10721.66 | Fe i | 5.507 | − 1297 | 5420 | 7 | 117 | |
| (35) | 52 | 10692.73 | Fe i | 3.071 | 10689.72 | Si i | 5.954 | − 2088 | 2691 | 6 | 113 | |
| (36) | 52 | 10753.00 | Fe i | 3.960 | 10694.25 | Si i | 5.964 | − 3586 | 3739 | 9 | 103 | |
| (37) | 52 | 10746.45 | Na i | 3.191 | 10717.81 | Fe i | 5.539 | − 4899 | 6654 | 7 | 133 | |
| (38) | 52 | 10725.19 | Fe i | 3.640 | 10849.47 | Fe i | 5.539 | − 4120 | 4739 | 9 | 97 | |
| (39) | 52 | 10726.39 | Ti i | 0.813 | 10785.39 | Fe i | 5.621 | − 1685 | 5490 | 8 | 144 | |
| (40) | 52 | 10783.05 | Fe i | 3.111 | 10727.41 | Si i | 5.984 | − 3629 | 3936 | 9 | 69 | |
| (41) | 52 | 10732.86 | Ti i | 0.826 | 10762.26 | Ni i | 4.154 | − 1681 | 5364 | 8 | 70 | |
| (42) | 52 | 10742.55 | Fe i | 3.642 | 10749.38 | Si i | 4.930 | − 4284 | − 120 | 5 | 145 | |
| (43) | 52 | 10774.87 | Ti i | 0.818 | 10838.97 | Ca i | 4.878 | − 1628 | 4756 | 8 | 74 | |
| (44) | 52 | 10780.69 | Fe i | 3.237 | 10843.86 | Si i | 5.863 | − 2479 | 3308 | 9 | 146 | |
| (45) | 52 | 10834.85 | Na i | 3.617 | 10784.56 | Si i | 5.964 | − 3081 | 4923 | 9 | 123 | |
| (46) | 52 | 10801.36 | Cr i | 3.011 | 10811.12 | Mg i | 5.946 | − 2476 | 2985 | 9 | 136 | |
| (47) | 52 | 10816.91 | Cr i | 3.013 | 10827.09 | Si i | 4.954 | − 2020 | 3002 | 8 | 131 | |
List of low- and high-excitation lines and LDR–Teff relations in the Y band. a and b represent the coefficients of Teff = a log r + b, N represents the number of stars used in fitting and σ represents the dispersion of the relation. If more than one line is listed at the same wavelength in the original line catalogue, information for the line with the largest log gf value is adopted here. The flag in the last column indicates the line pairs that are used in the analysis without the telluric correction in Section 5.
| . | . | Low-excitation line . | High-excitation line . | LDR–Teff relation . | . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID . | Order . | λ [Å] . | El. . | E.P. [eV] . | λ [Å] . | El. . | E.P. [eV] . | a [K] . | b [K] . | N . | σ [K] . | flag . |
| (1) | 57 | 9879.583 | Ti i | 1.873 | 9889.035 | Fe i | 5.033 | − 1462 | 3543 | 5 | 43 | |
| (2) | 56 | 9927.351 | Ti i | 1.879 | 9944.207 | Fe i | 5.012 | − 2390 | 4837 | 8 | 112 | |
| (3) | 56 | 9946.320 | Cr i | 3.556 | 9953.471 | Fe i | 5.446 | − 2635 | 4223 | 6 | 125 | 1 |
| (4) | 56 | 10003.09 | Ti i | 2.160 | 9961.256 | Na i | 3.617 | − 2645 | 4339 | 6 | 86 | 1 |
| (5) | 56 | 10081.39 | Fe i | 2.424 | 9980.463 | Fe i | 5.033 | − 2687 | 4586 | 9 | 74 | |
| (6) | 56 | 10005.66 | Ti i | 1.067 | 9987.869 | Fe i | 2.176 | − 961 | 3955 | 5 | 27 | |
| (7) | 56 | 9997.959 | Ti i | 1.873 | 10077.17 | Fe i | 2.990 | − 2297 | 4848 | 8 | 121 | |
| (8) | 56 | 10011.74 | Ti i | 2.154 | 10041.47 | Fe i | 5.012 | − 2477 | 5189 | 9 | 87 | |
| (9) | 56 | 10034.49 | Ti i | 1.460 | 10086.24 | Fe i | 2.949 | − 2433 | 4953 | 8 | 42 | |
| (10) | 56 | 10059.90 | Ti i | 1.430 | 10068.33 | Si i | 6.099 | − 1088 | 4837 | 6 | 99 | |
| (11) | 56 | 10066.51 | Ti i | 2.160 | 10065.05 | Fe i | 4.835 | − 1801 | 3631 | 9 | 79 | 1 |
| (12) | 55 | 10155.16 | Fe i | 2.176 | 10216.31 | Fe i | 4.733 | − 3116 | 3758 | 9 | 148 | |
| (13) | 55 | 10167.47 | Fe i | 2.198 | 10193.22 | Ni i | 4.089 | − 4235 | 4587 | 9 | 143 | |
| (14) | 55 | 10189.15 | Ti i | 1.460 | 10195.11 | Fe i | 2.728 | − 1654 | 3522 | 6 | 78 | |
| (15) | 55 | 10273.68 | Ca i | 4.535 | 10230.80 | Fe i | 6.119 | − 2179 | 4584 | 9 | 102 | |
| (16) | 54 | 10423.74 | Fe i | 3.071 | 10288.94 | Si i | 4.920 | − 3964 | 4465 | 9 | 69 | 1 |
| (17) | 54 | 10333.18 | Fe i | 4.593 | 10313.20 | Si i | 6.399 | − 2830 | 5109 | 5 | 68 | 1 |
| (18) | 54 | 10321.06 | Ni i | 5.525 | 10414.91 | Si i | 6.619 | − 3392 | 4482 | 5 | 132 | 1 |
| (19) | 54 | 10332.33 | Fe i | 3.635 | 10353.81 | Fe i | 5.393 | − 4499 | 4779 | 9 | 96 | 1 |
| (20) | 54 | 10396.80 | Ti i | 0.848 | 10340.89 | Fe i | 2.198 | − 4433 | 5016 | 9 | 110 | 1 |
| (21) | 54 | 10343.82 | Ca i | 2.933 | 10371.26 | Si i | 4.930 | − 5040 | 4836 | 9 | 49 | 1 |
| (22) | 54 | 10423.03 | Fe i | 2.692 | 10347.97 | Fe i | 5.393 | − 3912 | 5346 | 9 | 127 | 1 |
| (23) | 54 | 10382.31 | Co i | 2.871 | 10388.75 | Fe i | 5.446 | − 2256 | 4454 | 7 | 97 | 1 |
| (24) | 54 | 10395.80 | Fe i | 2.176 | 10469.65 | Fe i | 3.884 | − 8570 | 4524 | 9 | 146 | 1 |
| (25) | 54 | 10460.05 | Ti i | 2.256 | 10435.35 | Fe i | 4.733 | − 2058 | 4693 | 8 | 117 | 1 |
| (26) | 53 | 10486.25 | Cr i | 3.011 | 10530.51 | Ni i | 4.105 | − 3839 | 5192 | 9 | 70 | 1 |
| (27) | 53 | 10496.11 | Ti i | 0.836 | 10535.71 | Fe i | 6.206 | − 1832 | 5620 | 9 | 107 | 1 |
| (28) | 53 | 10510.01 | Cr i | 3.013 | 10555.65 | Fe i | 5.446 | − 2015 | 5081 | 9 | 92 | 1 |
| (29) | 53 | 10551.76 | Ti i | 1.887 | 10532.24 | Fe i | 3.929 | − 1475 | 3325 | 5 | 39 | 1 |
| (30) | 53 | 10552.97 | Ti i | 2.249 | 10582.16 | Si i | 6.223 | − 936 | 4393 | 7 | 44 | 1 |
| (31) | 53 | 10577.14 | Fe i | 3.301 | 10611.69 | Fe i | 6.169 | − 4007 | 4805 | 9 | 106 | 1 |
| (32) | 53 | 10607.72 | Ti i | 0.848 | 10672.14 | Cr i | 3.013 | − 2069 | 4236 | 8 | 91 | 1 |
| (33) | 53 | 10616.72 | Fe i | 3.267 | 10627.65 | Si i | 5.863 | − 2750 | 3799 | 9 | 106 | 1 |
| (34) | 52 | 10677.05 | Ti i | 0.836 | 10721.66 | Fe i | 5.507 | − 1297 | 5420 | 7 | 117 | |
| (35) | 52 | 10692.73 | Fe i | 3.071 | 10689.72 | Si i | 5.954 | − 2088 | 2691 | 6 | 113 | |
| (36) | 52 | 10753.00 | Fe i | 3.960 | 10694.25 | Si i | 5.964 | − 3586 | 3739 | 9 | 103 | |
| (37) | 52 | 10746.45 | Na i | 3.191 | 10717.81 | Fe i | 5.539 | − 4899 | 6654 | 7 | 133 | |
| (38) | 52 | 10725.19 | Fe i | 3.640 | 10849.47 | Fe i | 5.539 | − 4120 | 4739 | 9 | 97 | |
| (39) | 52 | 10726.39 | Ti i | 0.813 | 10785.39 | Fe i | 5.621 | − 1685 | 5490 | 8 | 144 | |
| (40) | 52 | 10783.05 | Fe i | 3.111 | 10727.41 | Si i | 5.984 | − 3629 | 3936 | 9 | 69 | |
| (41) | 52 | 10732.86 | Ti i | 0.826 | 10762.26 | Ni i | 4.154 | − 1681 | 5364 | 8 | 70 | |
| (42) | 52 | 10742.55 | Fe i | 3.642 | 10749.38 | Si i | 4.930 | − 4284 | − 120 | 5 | 145 | |
| (43) | 52 | 10774.87 | Ti i | 0.818 | 10838.97 | Ca i | 4.878 | − 1628 | 4756 | 8 | 74 | |
| (44) | 52 | 10780.69 | Fe i | 3.237 | 10843.86 | Si i | 5.863 | − 2479 | 3308 | 9 | 146 | |
| (45) | 52 | 10834.85 | Na i | 3.617 | 10784.56 | Si i | 5.964 | − 3081 | 4923 | 9 | 123 | |
| (46) | 52 | 10801.36 | Cr i | 3.011 | 10811.12 | Mg i | 5.946 | − 2476 | 2985 | 9 | 136 | |
| (47) | 52 | 10816.91 | Cr i | 3.013 | 10827.09 | Si i | 4.954 | − 2020 | 3002 | 8 | 131 | |
| . | . | Low-excitation line . | High-excitation line . | LDR–Teff relation . | . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID . | Order . | λ [Å] . | El. . | E.P. [eV] . | λ [Å] . | El. . | E.P. [eV] . | a [K] . | b [K] . | N . | σ [K] . | flag . |
| (1) | 57 | 9879.583 | Ti i | 1.873 | 9889.035 | Fe i | 5.033 | − 1462 | 3543 | 5 | 43 | |
| (2) | 56 | 9927.351 | Ti i | 1.879 | 9944.207 | Fe i | 5.012 | − 2390 | 4837 | 8 | 112 | |
| (3) | 56 | 9946.320 | Cr i | 3.556 | 9953.471 | Fe i | 5.446 | − 2635 | 4223 | 6 | 125 | 1 |
| (4) | 56 | 10003.09 | Ti i | 2.160 | 9961.256 | Na i | 3.617 | − 2645 | 4339 | 6 | 86 | 1 |
| (5) | 56 | 10081.39 | Fe i | 2.424 | 9980.463 | Fe i | 5.033 | − 2687 | 4586 | 9 | 74 | |
| (6) | 56 | 10005.66 | Ti i | 1.067 | 9987.869 | Fe i | 2.176 | − 961 | 3955 | 5 | 27 | |
| (7) | 56 | 9997.959 | Ti i | 1.873 | 10077.17 | Fe i | 2.990 | − 2297 | 4848 | 8 | 121 | |
| (8) | 56 | 10011.74 | Ti i | 2.154 | 10041.47 | Fe i | 5.012 | − 2477 | 5189 | 9 | 87 | |
| (9) | 56 | 10034.49 | Ti i | 1.460 | 10086.24 | Fe i | 2.949 | − 2433 | 4953 | 8 | 42 | |
| (10) | 56 | 10059.90 | Ti i | 1.430 | 10068.33 | Si i | 6.099 | − 1088 | 4837 | 6 | 99 | |
| (11) | 56 | 10066.51 | Ti i | 2.160 | 10065.05 | Fe i | 4.835 | − 1801 | 3631 | 9 | 79 | 1 |
| (12) | 55 | 10155.16 | Fe i | 2.176 | 10216.31 | Fe i | 4.733 | − 3116 | 3758 | 9 | 148 | |
| (13) | 55 | 10167.47 | Fe i | 2.198 | 10193.22 | Ni i | 4.089 | − 4235 | 4587 | 9 | 143 | |
| (14) | 55 | 10189.15 | Ti i | 1.460 | 10195.11 | Fe i | 2.728 | − 1654 | 3522 | 6 | 78 | |
| (15) | 55 | 10273.68 | Ca i | 4.535 | 10230.80 | Fe i | 6.119 | − 2179 | 4584 | 9 | 102 | |
| (16) | 54 | 10423.74 | Fe i | 3.071 | 10288.94 | Si i | 4.920 | − 3964 | 4465 | 9 | 69 | 1 |
| (17) | 54 | 10333.18 | Fe i | 4.593 | 10313.20 | Si i | 6.399 | − 2830 | 5109 | 5 | 68 | 1 |
| (18) | 54 | 10321.06 | Ni i | 5.525 | 10414.91 | Si i | 6.619 | − 3392 | 4482 | 5 | 132 | 1 |
| (19) | 54 | 10332.33 | Fe i | 3.635 | 10353.81 | Fe i | 5.393 | − 4499 | 4779 | 9 | 96 | 1 |
| (20) | 54 | 10396.80 | Ti i | 0.848 | 10340.89 | Fe i | 2.198 | − 4433 | 5016 | 9 | 110 | 1 |
| (21) | 54 | 10343.82 | Ca i | 2.933 | 10371.26 | Si i | 4.930 | − 5040 | 4836 | 9 | 49 | 1 |
| (22) | 54 | 10423.03 | Fe i | 2.692 | 10347.97 | Fe i | 5.393 | − 3912 | 5346 | 9 | 127 | 1 |
| (23) | 54 | 10382.31 | Co i | 2.871 | 10388.75 | Fe i | 5.446 | − 2256 | 4454 | 7 | 97 | 1 |
| (24) | 54 | 10395.80 | Fe i | 2.176 | 10469.65 | Fe i | 3.884 | − 8570 | 4524 | 9 | 146 | 1 |
| (25) | 54 | 10460.05 | Ti i | 2.256 | 10435.35 | Fe i | 4.733 | − 2058 | 4693 | 8 | 117 | 1 |
| (26) | 53 | 10486.25 | Cr i | 3.011 | 10530.51 | Ni i | 4.105 | − 3839 | 5192 | 9 | 70 | 1 |
| (27) | 53 | 10496.11 | Ti i | 0.836 | 10535.71 | Fe i | 6.206 | − 1832 | 5620 | 9 | 107 | 1 |
| (28) | 53 | 10510.01 | Cr i | 3.013 | 10555.65 | Fe i | 5.446 | − 2015 | 5081 | 9 | 92 | 1 |
| (29) | 53 | 10551.76 | Ti i | 1.887 | 10532.24 | Fe i | 3.929 | − 1475 | 3325 | 5 | 39 | 1 |
| (30) | 53 | 10552.97 | Ti i | 2.249 | 10582.16 | Si i | 6.223 | − 936 | 4393 | 7 | 44 | 1 |
| (31) | 53 | 10577.14 | Fe i | 3.301 | 10611.69 | Fe i | 6.169 | − 4007 | 4805 | 9 | 106 | 1 |
| (32) | 53 | 10607.72 | Ti i | 0.848 | 10672.14 | Cr i | 3.013 | − 2069 | 4236 | 8 | 91 | 1 |
| (33) | 53 | 10616.72 | Fe i | 3.267 | 10627.65 | Si i | 5.863 | − 2750 | 3799 | 9 | 106 | 1 |
| (34) | 52 | 10677.05 | Ti i | 0.836 | 10721.66 | Fe i | 5.507 | − 1297 | 5420 | 7 | 117 | |
| (35) | 52 | 10692.73 | Fe i | 3.071 | 10689.72 | Si i | 5.954 | − 2088 | 2691 | 6 | 113 | |
| (36) | 52 | 10753.00 | Fe i | 3.960 | 10694.25 | Si i | 5.964 | − 3586 | 3739 | 9 | 103 | |
| (37) | 52 | 10746.45 | Na i | 3.191 | 10717.81 | Fe i | 5.539 | − 4899 | 6654 | 7 | 133 | |
| (38) | 52 | 10725.19 | Fe i | 3.640 | 10849.47 | Fe i | 5.539 | − 4120 | 4739 | 9 | 97 | |
| (39) | 52 | 10726.39 | Ti i | 0.813 | 10785.39 | Fe i | 5.621 | − 1685 | 5490 | 8 | 144 | |
| (40) | 52 | 10783.05 | Fe i | 3.111 | 10727.41 | Si i | 5.984 | − 3629 | 3936 | 9 | 69 | |
| (41) | 52 | 10732.86 | Ti i | 0.826 | 10762.26 | Ni i | 4.154 | − 1681 | 5364 | 8 | 70 | |
| (42) | 52 | 10742.55 | Fe i | 3.642 | 10749.38 | Si i | 4.930 | − 4284 | − 120 | 5 | 145 | |
| (43) | 52 | 10774.87 | Ti i | 0.818 | 10838.97 | Ca i | 4.878 | − 1628 | 4756 | 8 | 74 | |
| (44) | 52 | 10780.69 | Fe i | 3.237 | 10843.86 | Si i | 5.863 | − 2479 | 3308 | 9 | 146 | |
| (45) | 52 | 10834.85 | Na i | 3.617 | 10784.56 | Si i | 5.964 | − 3081 | 4923 | 9 | 123 | |
| (46) | 52 | 10801.36 | Cr i | 3.011 | 10811.12 | Mg i | 5.946 | − 2476 | 2985 | 9 | 136 | |
| (47) | 52 | 10816.91 | Cr i | 3.013 | 10827.09 | Si i | 4.954 | − 2020 | 3002 | 8 | 131 | |
| . | . | Low-excitation line . | High-excitation line . | LDR–Teff relation . | . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID . | Order . | λ [Å] . | El. . | E.P. [eV] . | λ [Å] . | El. . | E.P. [eV] . | a [K] . | b [K] . | N . | σ [K] . | flag . |
| (48) | 48 | 11638.26 | Fe i | 2.176 | 11640.94 | Si i | 6.274 | − 2932 | 6052 | 9 | 129 | |
| (49) | 48 | 11667.23 | Ti i | 2.345 | 11681.59 | Fe i | 3.547 | − 983 | 3668 | 5 | 49 | |
| (50) | 48 | 11797.19 | Ti i | 1.430 | 11793.04 | Ca i | 4.535 | − 1792 | 4315 | 8 | 94 | |
| (51) | 47 | 11884.08 | Fe i | 2.223 | 11984.20 | Si i | 4.930 | − 4890 | 4172 | 9 | 103 | |
| (52) | 47 | 11955.95 | Ca i | 4.131 | 12005.40 | Fe i | 5.587 | − 3333 | 3862 | 9 | 142 | |
| (53) | 47 | 12000.97 | Cr i | 3.435 | 12039.82 | Mg i | 5.753 | − 1954 | 3329 | 6 | 39 | |
| (54) | 46 | 12105.84 | Ca i | 4.554 | 12178.34 | Si i | 6.269 | − 2366 | 4660 | 9 | 116 | |
| (55) | 46 | 12255.70 | Ti i | 3.921 | 12133.99 | Si i | 5.984 | − 1971 | 4202 | 5 | 90 | |
| (56) | 46 | 12190.10 | Fe i | 3.635 | 12175.73 | Si i | 6.619 | − 3204 | 5735 | 9 | 144 | |
| (57) | 46 | 12267.89 | Fe i | 3.274 | 12283.30 | Fe i | 6.169 | − 1948 | 4368 | 6 | 140 | |
| (58) | 45 | 12340.48 | Fe i | 2.279 | 12390.15 | Si i | 5.082 | − 2374 | 4091 | 9 | 69 | 1 |
| (59) | 45 | 12388.37 | Ti i | 2.160 | 12393.07 | Fe i | 4.956 | − 2413 | 4345 | 8 | 114 | 1 |
| (60) | 45 | 12557.00 | Fe i | 2.279 | 12423.03 | Mg i | 5.932 | − 4690 | 4993 | 9 | 144 | |
| (61) | 45 | 12532.84 | Cr i | 2.709 | 12457.13 | Mg i | 6.431 | − 1892 | 5119 | 9 | 84 | |
| (62) | 45 | 12510.52 | Fe i | 4.956 | 12583.92 | Si i | 6.616 | − 1965 | 4468 | 9 | 129 | |
| (63) | 44 | 12600.28 | Ti i | 1.443 | 12720.15 | Co i | 3.530 | − 1302 | 4869 | 8 | 76 | |
| (64) | 44 | 12671.10 | Ti i | 1.430 | 12789.45 | Fe i | 5.010 | − 1637 | 4885 | 8 | 68 | |
| (65) | 44 | 12744.91 | Ti i | 2.488 | 12679.17 | Na i | 3.617 | − 2061 | 3314 | 5 | 145 | |
| (66) | 44 | 12831.44 | Ti i | 1.430 | 12807.15 | Fe i | 3.640 | − 2806 | 4808 | 9 | 76 | |
| (67) | 44 | 12821.67 | Ti i | 1.460 | 12808.24 | Fe i | 4.988 | − 3021 | 5954 | 8 | 93 | |
| (68) | 44 | 12811.48 | Ti i | 2.160 | 12870.04 | Mg i | 6.588 | − 1913 | 5418 | 8 | 121 | |
| (69) | 44 | 12847.03 | Ti i | 1.443 | 12840.57 | Fe i | 4.956 | − 4468 | 5627 | 9 | 65 | |
| (70) | 43 | 12910.09 | Cr i | 2.708 | 12896.12 | Fe i | 4.913 | − 3182 | 5019 | 9 | 88 | |
| (71) | 43 | 12921.81 | Cr i | 2.709 | 12909.07 | Ca i | 4.430 | − 3019 | 3422 | 8 | 61 | |
| (72) | 43 | 12919.90 | Ti i | 2.154 | 13014.84 | Fe i | 5.446 | − 1428 | 4822 | 8 | 48 | |
| (73) | 43 | 12927.48 | Ti i | 2.154 | 13134.94 | Ca i | 4.451 | − 1181 | 3268 | 5 | 134 | |
| (74) | 43 | 12932.31 | Ni i | 2.740 | 12934.67 | Fe i | 5.393 | − 5366 | 5703 | 9 | 122 | |
| (75) | 43 | 12937.02 | Cr i | 2.710 | 13098.88 | Fe i | 5.010 | − 2800 | 4811 | 9 | 140 | |
| (76) | 43 | 12975.91 | Mn i | 2.888 | 13029.52 | Si i | 6.083 | − 2655 | 6276 | 9 | 111 | |
| (77) | 43 | 12987.57 | Ti i | 2.506 | 13147.92 | Fe i | 5.393 | − 1723 | 3694 | 6 | 101 | |
| (78) | 43 | 13005.36 | Ti i | 2.175 | 13152.74 | Si i | 4.920 | − 1807 | 3864 | 6 | 84 | |
| (79) | 43 | 13006.68 | Fe i | 2.990 | 13030.92 | Si i | 6.079 | − 2665 | 4735 | 9 | 75 | |
| (80) | 43 | 13011.90 | Ti i | 1.443 | 13123.41 | Al i | 3.143 | − 1819 | 3313 | 8 | 126 | |
| (81) | 43 | 13033.55 | Ca i | 4.441 | 13102.06 | Si i | 6.083 | − 3156 | 4148 | 8 | 149 | |
| . | . | Low-excitation line . | High-excitation line . | LDR–Teff relation . | . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID . | Order . | λ [Å] . | El. . | E.P. [eV] . | λ [Å] . | El. . | E.P. [eV] . | a [K] . | b [K] . | N . | σ [K] . | flag . |
| (48) | 48 | 11638.26 | Fe i | 2.176 | 11640.94 | Si i | 6.274 | − 2932 | 6052 | 9 | 129 | |
| (49) | 48 | 11667.23 | Ti i | 2.345 | 11681.59 | Fe i | 3.547 | − 983 | 3668 | 5 | 49 | |
| (50) | 48 | 11797.19 | Ti i | 1.430 | 11793.04 | Ca i | 4.535 | − 1792 | 4315 | 8 | 94 | |
| (51) | 47 | 11884.08 | Fe i | 2.223 | 11984.20 | Si i | 4.930 | − 4890 | 4172 | 9 | 103 | |
| (52) | 47 | 11955.95 | Ca i | 4.131 | 12005.40 | Fe i | 5.587 | − 3333 | 3862 | 9 | 142 | |
| (53) | 47 | 12000.97 | Cr i | 3.435 | 12039.82 | Mg i | 5.753 | − 1954 | 3329 | 6 | 39 | |
| (54) | 46 | 12105.84 | Ca i | 4.554 | 12178.34 | Si i | 6.269 | − 2366 | 4660 | 9 | 116 | |
| (55) | 46 | 12255.70 | Ti i | 3.921 | 12133.99 | Si i | 5.984 | − 1971 | 4202 | 5 | 90 | |
| (56) | 46 | 12190.10 | Fe i | 3.635 | 12175.73 | Si i | 6.619 | − 3204 | 5735 | 9 | 144 | |
| (57) | 46 | 12267.89 | Fe i | 3.274 | 12283.30 | Fe i | 6.169 | − 1948 | 4368 | 6 | 140 | |
| (58) | 45 | 12340.48 | Fe i | 2.279 | 12390.15 | Si i | 5.082 | − 2374 | 4091 | 9 | 69 | 1 |
| (59) | 45 | 12388.37 | Ti i | 2.160 | 12393.07 | Fe i | 4.956 | − 2413 | 4345 | 8 | 114 | 1 |
| (60) | 45 | 12557.00 | Fe i | 2.279 | 12423.03 | Mg i | 5.932 | − 4690 | 4993 | 9 | 144 | |
| (61) | 45 | 12532.84 | Cr i | 2.709 | 12457.13 | Mg i | 6.431 | − 1892 | 5119 | 9 | 84 | |
| (62) | 45 | 12510.52 | Fe i | 4.956 | 12583.92 | Si i | 6.616 | − 1965 | 4468 | 9 | 129 | |
| (63) | 44 | 12600.28 | Ti i | 1.443 | 12720.15 | Co i | 3.530 | − 1302 | 4869 | 8 | 76 | |
| (64) | 44 | 12671.10 | Ti i | 1.430 | 12789.45 | Fe i | 5.010 | − 1637 | 4885 | 8 | 68 | |
| (65) | 44 | 12744.91 | Ti i | 2.488 | 12679.17 | Na i | 3.617 | − 2061 | 3314 | 5 | 145 | |
| (66) | 44 | 12831.44 | Ti i | 1.430 | 12807.15 | Fe i | 3.640 | − 2806 | 4808 | 9 | 76 | |
| (67) | 44 | 12821.67 | Ti i | 1.460 | 12808.24 | Fe i | 4.988 | − 3021 | 5954 | 8 | 93 | |
| (68) | 44 | 12811.48 | Ti i | 2.160 | 12870.04 | Mg i | 6.588 | − 1913 | 5418 | 8 | 121 | |
| (69) | 44 | 12847.03 | Ti i | 1.443 | 12840.57 | Fe i | 4.956 | − 4468 | 5627 | 9 | 65 | |
| (70) | 43 | 12910.09 | Cr i | 2.708 | 12896.12 | Fe i | 4.913 | − 3182 | 5019 | 9 | 88 | |
| (71) | 43 | 12921.81 | Cr i | 2.709 | 12909.07 | Ca i | 4.430 | − 3019 | 3422 | 8 | 61 | |
| (72) | 43 | 12919.90 | Ti i | 2.154 | 13014.84 | Fe i | 5.446 | − 1428 | 4822 | 8 | 48 | |
| (73) | 43 | 12927.48 | Ti i | 2.154 | 13134.94 | Ca i | 4.451 | − 1181 | 3268 | 5 | 134 | |
| (74) | 43 | 12932.31 | Ni i | 2.740 | 12934.67 | Fe i | 5.393 | − 5366 | 5703 | 9 | 122 | |
| (75) | 43 | 12937.02 | Cr i | 2.710 | 13098.88 | Fe i | 5.010 | − 2800 | 4811 | 9 | 140 | |
| (76) | 43 | 12975.91 | Mn i | 2.888 | 13029.52 | Si i | 6.083 | − 2655 | 6276 | 9 | 111 | |
| (77) | 43 | 12987.57 | Ti i | 2.506 | 13147.92 | Fe i | 5.393 | − 1723 | 3694 | 6 | 101 | |
| (78) | 43 | 13005.36 | Ti i | 2.175 | 13152.74 | Si i | 4.920 | − 1807 | 3864 | 6 | 84 | |
| (79) | 43 | 13006.68 | Fe i | 2.990 | 13030.92 | Si i | 6.079 | − 2665 | 4735 | 9 | 75 | |
| (80) | 43 | 13011.90 | Ti i | 1.443 | 13123.41 | Al i | 3.143 | − 1819 | 3313 | 8 | 126 | |
| (81) | 43 | 13033.55 | Ca i | 4.441 | 13102.06 | Si i | 6.083 | − 3156 | 4148 | 8 | 149 | |
| . | . | Low-excitation line . | High-excitation line . | LDR–Teff relation . | . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID . | Order . | λ [Å] . | El. . | E.P. [eV] . | λ [Å] . | El. . | E.P. [eV] . | a [K] . | b [K] . | N . | σ [K] . | flag . |
| (48) | 48 | 11638.26 | Fe i | 2.176 | 11640.94 | Si i | 6.274 | − 2932 | 6052 | 9 | 129 | |
| (49) | 48 | 11667.23 | Ti i | 2.345 | 11681.59 | Fe i | 3.547 | − 983 | 3668 | 5 | 49 | |
| (50) | 48 | 11797.19 | Ti i | 1.430 | 11793.04 | Ca i | 4.535 | − 1792 | 4315 | 8 | 94 | |
| (51) | 47 | 11884.08 | Fe i | 2.223 | 11984.20 | Si i | 4.930 | − 4890 | 4172 | 9 | 103 | |
| (52) | 47 | 11955.95 | Ca i | 4.131 | 12005.40 | Fe i | 5.587 | − 3333 | 3862 | 9 | 142 | |
| (53) | 47 | 12000.97 | Cr i | 3.435 | 12039.82 | Mg i | 5.753 | − 1954 | 3329 | 6 | 39 | |
| (54) | 46 | 12105.84 | Ca i | 4.554 | 12178.34 | Si i | 6.269 | − 2366 | 4660 | 9 | 116 | |
| (55) | 46 | 12255.70 | Ti i | 3.921 | 12133.99 | Si i | 5.984 | − 1971 | 4202 | 5 | 90 | |
| (56) | 46 | 12190.10 | Fe i | 3.635 | 12175.73 | Si i | 6.619 | − 3204 | 5735 | 9 | 144 | |
| (57) | 46 | 12267.89 | Fe i | 3.274 | 12283.30 | Fe i | 6.169 | − 1948 | 4368 | 6 | 140 | |
| (58) | 45 | 12340.48 | Fe i | 2.279 | 12390.15 | Si i | 5.082 | − 2374 | 4091 | 9 | 69 | 1 |
| (59) | 45 | 12388.37 | Ti i | 2.160 | 12393.07 | Fe i | 4.956 | − 2413 | 4345 | 8 | 114 | 1 |
| (60) | 45 | 12557.00 | Fe i | 2.279 | 12423.03 | Mg i | 5.932 | − 4690 | 4993 | 9 | 144 | |
| (61) | 45 | 12532.84 | Cr i | 2.709 | 12457.13 | Mg i | 6.431 | − 1892 | 5119 | 9 | 84 | |
| (62) | 45 | 12510.52 | Fe i | 4.956 | 12583.92 | Si i | 6.616 | − 1965 | 4468 | 9 | 129 | |
| (63) | 44 | 12600.28 | Ti i | 1.443 | 12720.15 | Co i | 3.530 | − 1302 | 4869 | 8 | 76 | |
| (64) | 44 | 12671.10 | Ti i | 1.430 | 12789.45 | Fe i | 5.010 | − 1637 | 4885 | 8 | 68 | |
| (65) | 44 | 12744.91 | Ti i | 2.488 | 12679.17 | Na i | 3.617 | − 2061 | 3314 | 5 | 145 | |
| (66) | 44 | 12831.44 | Ti i | 1.430 | 12807.15 | Fe i | 3.640 | − 2806 | 4808 | 9 | 76 | |
| (67) | 44 | 12821.67 | Ti i | 1.460 | 12808.24 | Fe i | 4.988 | − 3021 | 5954 | 8 | 93 | |
| (68) | 44 | 12811.48 | Ti i | 2.160 | 12870.04 | Mg i | 6.588 | − 1913 | 5418 | 8 | 121 | |
| (69) | 44 | 12847.03 | Ti i | 1.443 | 12840.57 | Fe i | 4.956 | − 4468 | 5627 | 9 | 65 | |
| (70) | 43 | 12910.09 | Cr i | 2.708 | 12896.12 | Fe i | 4.913 | − 3182 | 5019 | 9 | 88 | |
| (71) | 43 | 12921.81 | Cr i | 2.709 | 12909.07 | Ca i | 4.430 | − 3019 | 3422 | 8 | 61 | |
| (72) | 43 | 12919.90 | Ti i | 2.154 | 13014.84 | Fe i | 5.446 | − 1428 | 4822 | 8 | 48 | |
| (73) | 43 | 12927.48 | Ti i | 2.154 | 13134.94 | Ca i | 4.451 | − 1181 | 3268 | 5 | 134 | |
| (74) | 43 | 12932.31 | Ni i | 2.740 | 12934.67 | Fe i | 5.393 | − 5366 | 5703 | 9 | 122 | |
| (75) | 43 | 12937.02 | Cr i | 2.710 | 13098.88 | Fe i | 5.010 | − 2800 | 4811 | 9 | 140 | |
| (76) | 43 | 12975.91 | Mn i | 2.888 | 13029.52 | Si i | 6.083 | − 2655 | 6276 | 9 | 111 | |
| (77) | 43 | 12987.57 | Ti i | 2.506 | 13147.92 | Fe i | 5.393 | − 1723 | 3694 | 6 | 101 | |
| (78) | 43 | 13005.36 | Ti i | 2.175 | 13152.74 | Si i | 4.920 | − 1807 | 3864 | 6 | 84 | |
| (79) | 43 | 13006.68 | Fe i | 2.990 | 13030.92 | Si i | 6.079 | − 2665 | 4735 | 9 | 75 | |
| (80) | 43 | 13011.90 | Ti i | 1.443 | 13123.41 | Al i | 3.143 | − 1819 | 3313 | 8 | 126 | |
| (81) | 43 | 13033.55 | Ca i | 4.441 | 13102.06 | Si i | 6.083 | − 3156 | 4148 | 8 | 149 | |
| . | . | Low-excitation line . | High-excitation line . | LDR–Teff relation . | . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID . | Order . | λ [Å] . | El. . | E.P. [eV] . | λ [Å] . | El. . | E.P. [eV] . | a [K] . | b [K] . | N . | σ [K] . | flag . |
| (48) | 48 | 11638.26 | Fe i | 2.176 | 11640.94 | Si i | 6.274 | − 2932 | 6052 | 9 | 129 | |
| (49) | 48 | 11667.23 | Ti i | 2.345 | 11681.59 | Fe i | 3.547 | − 983 | 3668 | 5 | 49 | |
| (50) | 48 | 11797.19 | Ti i | 1.430 | 11793.04 | Ca i | 4.535 | − 1792 | 4315 | 8 | 94 | |
| (51) | 47 | 11884.08 | Fe i | 2.223 | 11984.20 | Si i | 4.930 | − 4890 | 4172 | 9 | 103 | |
| (52) | 47 | 11955.95 | Ca i | 4.131 | 12005.40 | Fe i | 5.587 | − 3333 | 3862 | 9 | 142 | |
| (53) | 47 | 12000.97 | Cr i | 3.435 | 12039.82 | Mg i | 5.753 | − 1954 | 3329 | 6 | 39 | |
| (54) | 46 | 12105.84 | Ca i | 4.554 | 12178.34 | Si i | 6.269 | − 2366 | 4660 | 9 | 116 | |
| (55) | 46 | 12255.70 | Ti i | 3.921 | 12133.99 | Si i | 5.984 | − 1971 | 4202 | 5 | 90 | |
| (56) | 46 | 12190.10 | Fe i | 3.635 | 12175.73 | Si i | 6.619 | − 3204 | 5735 | 9 | 144 | |
| (57) | 46 | 12267.89 | Fe i | 3.274 | 12283.30 | Fe i | 6.169 | − 1948 | 4368 | 6 | 140 | |
| (58) | 45 | 12340.48 | Fe i | 2.279 | 12390.15 | Si i | 5.082 | − 2374 | 4091 | 9 | 69 | 1 |
| (59) | 45 | 12388.37 | Ti i | 2.160 | 12393.07 | Fe i | 4.956 | − 2413 | 4345 | 8 | 114 | 1 |
| (60) | 45 | 12557.00 | Fe i | 2.279 | 12423.03 | Mg i | 5.932 | − 4690 | 4993 | 9 | 144 | |
| (61) | 45 | 12532.84 | Cr i | 2.709 | 12457.13 | Mg i | 6.431 | − 1892 | 5119 | 9 | 84 | |
| (62) | 45 | 12510.52 | Fe i | 4.956 | 12583.92 | Si i | 6.616 | − 1965 | 4468 | 9 | 129 | |
| (63) | 44 | 12600.28 | Ti i | 1.443 | 12720.15 | Co i | 3.530 | − 1302 | 4869 | 8 | 76 | |
| (64) | 44 | 12671.10 | Ti i | 1.430 | 12789.45 | Fe i | 5.010 | − 1637 | 4885 | 8 | 68 | |
| (65) | 44 | 12744.91 | Ti i | 2.488 | 12679.17 | Na i | 3.617 | − 2061 | 3314 | 5 | 145 | |
| (66) | 44 | 12831.44 | Ti i | 1.430 | 12807.15 | Fe i | 3.640 | − 2806 | 4808 | 9 | 76 | |
| (67) | 44 | 12821.67 | Ti i | 1.460 | 12808.24 | Fe i | 4.988 | − 3021 | 5954 | 8 | 93 | |
| (68) | 44 | 12811.48 | Ti i | 2.160 | 12870.04 | Mg i | 6.588 | − 1913 | 5418 | 8 | 121 | |
| (69) | 44 | 12847.03 | Ti i | 1.443 | 12840.57 | Fe i | 4.956 | − 4468 | 5627 | 9 | 65 | |
| (70) | 43 | 12910.09 | Cr i | 2.708 | 12896.12 | Fe i | 4.913 | − 3182 | 5019 | 9 | 88 | |
| (71) | 43 | 12921.81 | Cr i | 2.709 | 12909.07 | Ca i | 4.430 | − 3019 | 3422 | 8 | 61 | |
| (72) | 43 | 12919.90 | Ti i | 2.154 | 13014.84 | Fe i | 5.446 | − 1428 | 4822 | 8 | 48 | |
| (73) | 43 | 12927.48 | Ti i | 2.154 | 13134.94 | Ca i | 4.451 | − 1181 | 3268 | 5 | 134 | |
| (74) | 43 | 12932.31 | Ni i | 2.740 | 12934.67 | Fe i | 5.393 | − 5366 | 5703 | 9 | 122 | |
| (75) | 43 | 12937.02 | Cr i | 2.710 | 13098.88 | Fe i | 5.010 | − 2800 | 4811 | 9 | 140 | |
| (76) | 43 | 12975.91 | Mn i | 2.888 | 13029.52 | Si i | 6.083 | − 2655 | 6276 | 9 | 111 | |
| (77) | 43 | 12987.57 | Ti i | 2.506 | 13147.92 | Fe i | 5.393 | − 1723 | 3694 | 6 | 101 | |
| (78) | 43 | 13005.36 | Ti i | 2.175 | 13152.74 | Si i | 4.920 | − 1807 | 3864 | 6 | 84 | |
| (79) | 43 | 13006.68 | Fe i | 2.990 | 13030.92 | Si i | 6.079 | − 2665 | 4735 | 9 | 75 | |
| (80) | 43 | 13011.90 | Ti i | 1.443 | 13123.41 | Al i | 3.143 | − 1819 | 3313 | 8 | 126 | |
| (81) | 43 | 13033.55 | Ca i | 4.441 | 13102.06 | Si i | 6.083 | − 3156 | 4148 | 8 | 149 | |
The literature values of effective temperatures, redetermined effective temperatures using all available line pairs (TLDR) and those based on uncorrected spectra (TLDRnott). The numbers in round brackets indicate the numbers of line pairs used for the LDR temperatures. The literature Teff is same as in Table 1.
| Object . | Teff [K] . | TLDR [K] . | TLDRnott [K] . |
|---|---|---|---|
| ε Leo | 5398 ± 31 | 5429 ± 24 (42) | 5395 ± 46 (14) |
| κ Gem | 5029 ± 47 | 4982 ± 13 (60) | 4971 ± 15 (19) |
| ε Vir | 4983 ± 61 | 4996 ± 11 (65) | 5024 ± 19 (20) |
| Pollux | 4858 ± 60 | 4829 ± 12 (73) | 4836 ± 23 (22) |
| µ Leo | 4470 ± 40 | 4434 ± 15 (80) | 4454 ± 27 (23) |
| Alphard | 4171 ± 52 | 4143 ± 9 (79) | 4169 ± 13 (23) |
| Aldebaran | 3882 ± 19 | 3887 ± 6 (78) | 3860 ± 13 (21) |
| α Cet | 3796 ± 65 | 3780 ± 9 (79) | 3780 ± 14 (21) |
| δ Oph | 3783 ± 20 | 3812 ± 4 (79) | 3806 ± 7 (21) |
| Arcturus | 4286 ± 35 | 4312 ± 36 (71) | 4261 ± 72 (18) |
| Object . | Teff [K] . | TLDR [K] . | TLDRnott [K] . |
|---|---|---|---|
| ε Leo | 5398 ± 31 | 5429 ± 24 (42) | 5395 ± 46 (14) |
| κ Gem | 5029 ± 47 | 4982 ± 13 (60) | 4971 ± 15 (19) |
| ε Vir | 4983 ± 61 | 4996 ± 11 (65) | 5024 ± 19 (20) |
| Pollux | 4858 ± 60 | 4829 ± 12 (73) | 4836 ± 23 (22) |
| µ Leo | 4470 ± 40 | 4434 ± 15 (80) | 4454 ± 27 (23) |
| Alphard | 4171 ± 52 | 4143 ± 9 (79) | 4169 ± 13 (23) |
| Aldebaran | 3882 ± 19 | 3887 ± 6 (78) | 3860 ± 13 (21) |
| α Cet | 3796 ± 65 | 3780 ± 9 (79) | 3780 ± 14 (21) |
| δ Oph | 3783 ± 20 | 3812 ± 4 (79) | 3806 ± 7 (21) |
| Arcturus | 4286 ± 35 | 4312 ± 36 (71) | 4261 ± 72 (18) |
The literature values of effective temperatures, redetermined effective temperatures using all available line pairs (TLDR) and those based on uncorrected spectra (TLDRnott). The numbers in round brackets indicate the numbers of line pairs used for the LDR temperatures. The literature Teff is same as in Table 1.
| Object . | Teff [K] . | TLDR [K] . | TLDRnott [K] . |
|---|---|---|---|
| ε Leo | 5398 ± 31 | 5429 ± 24 (42) | 5395 ± 46 (14) |
| κ Gem | 5029 ± 47 | 4982 ± 13 (60) | 4971 ± 15 (19) |
| ε Vir | 4983 ± 61 | 4996 ± 11 (65) | 5024 ± 19 (20) |
| Pollux | 4858 ± 60 | 4829 ± 12 (73) | 4836 ± 23 (22) |
| µ Leo | 4470 ± 40 | 4434 ± 15 (80) | 4454 ± 27 (23) |
| Alphard | 4171 ± 52 | 4143 ± 9 (79) | 4169 ± 13 (23) |
| Aldebaran | 3882 ± 19 | 3887 ± 6 (78) | 3860 ± 13 (21) |
| α Cet | 3796 ± 65 | 3780 ± 9 (79) | 3780 ± 14 (21) |
| δ Oph | 3783 ± 20 | 3812 ± 4 (79) | 3806 ± 7 (21) |
| Arcturus | 4286 ± 35 | 4312 ± 36 (71) | 4261 ± 72 (18) |
| Object . | Teff [K] . | TLDR [K] . | TLDRnott [K] . |
|---|---|---|---|
| ε Leo | 5398 ± 31 | 5429 ± 24 (42) | 5395 ± 46 (14) |
| κ Gem | 5029 ± 47 | 4982 ± 13 (60) | 4971 ± 15 (19) |
| ε Vir | 4983 ± 61 | 4996 ± 11 (65) | 5024 ± 19 (20) |
| Pollux | 4858 ± 60 | 4829 ± 12 (73) | 4836 ± 23 (22) |
| µ Leo | 4470 ± 40 | 4434 ± 15 (80) | 4454 ± 27 (23) |
| Alphard | 4171 ± 52 | 4143 ± 9 (79) | 4169 ± 13 (23) |
| Aldebaran | 3882 ± 19 | 3887 ± 6 (78) | 3860 ± 13 (21) |
| α Cet | 3796 ± 65 | 3780 ± 9 (79) | 3780 ± 14 (21) |
| δ Oph | 3783 ± 20 | 3812 ± 4 (79) | 3806 ± 7 (21) |
| Arcturus | 4286 ± 35 | 4312 ± 36 (71) | 4261 ± 72 (18) |
It is worthwhile discussing TLDR for Arcturus, which was not included in the calibration. Fukue et al. (2015) found that Arcturus tends to show offsets from LDR–Teff relations of other stars. They suggested that this is owing to the low metallicity and/or non-solar abundance ratios of Arcturus, [Fe/H] = −0.52, [Ti/H] = −0.313, [Si/H] = −0.252 by Jofré et al. (2015). The results in Table 6 appear to show that the temperature from our method (TLDR = 4312 ± 36 K) is consistent with the literature Teff, but a closer look reveals the peculiarity of Arcturus's TLDR. If we use only 22 line pairs composed of Ti i (low excitation) and Fe i (high excitation), we obtain a temperature of 4120 ± 60 K. If we use only 14 line pairs of Si i (high excitation) and Fe i (low excitation), in contrast, the temperature is estimated at 4485 ± 35 K. These deviations can be understood as the effect of non-solar [Ti/Fe] and [Si/Fe] values. These offsets of the two major groups of line pairs cancelled each other out and the average TLDR became close to the literature temperature, but giving a relatively large error in the case of Arcturus. Such deviations are not observed in other objects in this study. Follow-up spectroscopic data for a larger sample of stars with known temperatures and abundances would be useful to discuss the abundance dependences of the LDR–Teff relations further.
5 DISCUSSION
It is useful to know what spectral quality is needed to measure the effective temperature based on our LDR method for planning future observations. Here, we discuss how the precision of TLDR depends on the S/N of a spectrum and on whether or not we can make the telluric correction.
First, considering a common S/N fixed for all orders, we calculate a feasible precision using |$\Delta {T^{\prime }_{\mathrm{LDR}}}^{(n)}=\sqrt{1/\sum _{j}(1/\Delta T_{j}^{(n)})^{2}}$|, where |$\Delta T_{j}^{(n)}$| is the temperature error for each star obtained in the same way described in Section 3, except that the given S/N is used instead of the S/N obtained from our observed spectrum. It is straightforward to calculate |$\Delta T^{\prime }_{\mathrm{LDR}}$| as a function of S/N and we can estimate the S/N for which the precision reaches two target values, 10 and 20 K. As illustrated in Fig. 5, in order to estimate the effective temperature of 4000 K within a precision of 10 K, for example, one needs to obtain spectra with S/N higher than 100. Although the required S/N values also depend on the metallicity and the resolution, which change the line depths, Fig. 5 can be used as a guideline for estimating the necessary observational times for solar-metal stars approximately, using an instrument with resolution ∼28 000. The statistical error will become larger if limited wavelength coverage allows one to use a smaller number of lines.
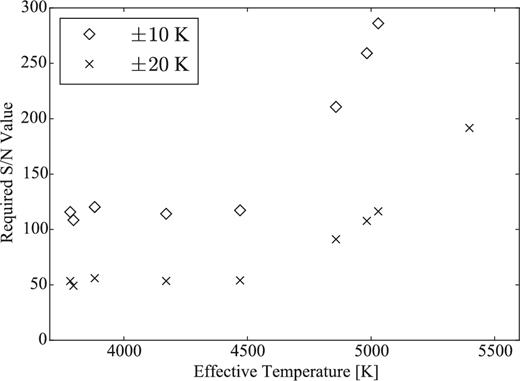
The value of S/N required for estimating TLDR with specific precision: 10 K (open diamond) and 20 K (cross). See more details in the text.
Next, we compare the precision that can be achieved with telluric-corrected or uncorrected spectra. We found that all the metal lines used in this work in the 53–55th orders and also a significant number of lines in other orders are free from blending with telluric lines for our objects. When the LDR method is applied to other stars, however, one needs to take radial velocities into account when considering the blending. For example, some of the lines in the 53rd–55th orders could have been blended with telluric lines if our targets were offset by a particular redshift. For 23 line pairs marked in Tables 4 and 5 (21 in the Y band and two in the J band), both lines of each pair have no telluric absorption line deeper than 3 per cent, with the spectral range corresponding to the redshift within 200 km s−1. We considered the absorption depths of a telluric standard spectrum of ó Aur taken on 2013 November 30. Table 6 compares the redetermined effective temperatures obtained with all line pairs in telluric-corrected spectra (TLDR) and the values obtained with the above 23 line pairs in telluric-uncorrected spectra (TLDRnott). The error propagation was calculated in the same way as for TLDR, as mentioned above, and S/N values in Table 2 were also used for telluric-uncorrected spectra. We found that TLDRnott values are consistent with TLDR. Even with significantly fewer line pairs, the precision of TLDRnott is still moderately high. Our LDR method can be used even without the telluric correction, with slightly lower precision, which may give efficient access to stellar temperatures with shorter observational times and analytical works.
The accuracy of the continuum normalization is another important factor that may affect the accuracy of the LDR measurements. For example, Jofré et al. (2017) found that offsets between re-normalized continuum levels obtained with different methods are as large as 0.05 in the worst case for optical lines of Arcturus (see their fig. 4). If we add (or subtract) such a large offset to the depth of each line, the LDR temperatures could change by 100–200 K. However, the effect of normalization is expected to be smaller in the LDR method, because the lines selected in this work tend to be in relatively uncrowded spectral parts for which the continuum is easily traced. In addition, the LDR–Teff relations are based on the empirical calibration and the line depths are not compared with a theoretical prediction in which the continuum is perfectly defined. Even if there were some offsets between the true and apparent continuum levels, the LDR values for stars with similar temperatures should be similar. In fact, the statistics of the LDR–Teff relations we obtained indicate that the continuum normalization has little impact on the precision of our LDRs. The scatters around individual LDR–Teff relations are 10–150 K and can be explained by statistical errors relating to the spectral quality, S/N, and precision of the reference temperatures. Nonetheless, when LDRs are measured in spectra with a significantly different resolution, the continuum normalization may cause systematic temperature offsets of the order of 100–200 K in the worst cases and re-calibration with a homogeneous data set is recommended.
6 SUMMARY AND CONCLUSION
We developed a method to estimate the effective temperature using the LDR in the Y and J bands. This method enables us to estimate the effective temperatures of G, K and M giants with a precision of ±10 K in the best cases, using 81 line pairs. Roughly speaking, a S/N of 100 is needed to estimate the effective temperature to a precision of ±10 K for a solar-metal star with Teff = 4000 K, while without the telluric correction the error would get twice as large. Although our set of line pairs is optimized for use with WINERED in terms of resolution and wavelength range of the individual orders, this set should also be useful for other instruments. Recalibration of the LDR–Teff relations would be useful for other instruments, although LDRs are expected to be insensitive to the spectral resolution under no blending effects of neighbouring lines.
Acknowledgements
We acknowledge the useful comments from the referee, Ulrike Heiter. We are grateful to Masaomi Kinoshita, Kenshi Nakanishi, Tetsuya Nakaoka and Yoshiharu Shinnaka for observing some of our targets. We also thank the staff of Koyama Astronomical Observatory for their support during our observations. This work has been supported by Grants-in-Aid, KAKENHI, from Japan Society for the Promotion of Science (JSPS; Nos. 16684001, 20340042, 21840052 and 26287028) and MEXT Supported Programs for the Strategic Research Foundation at Private Universities (Nos. S0801061 and S1411028). NK also acknowledges support through the Japan–India Science Cooperative Program between 2013 and 2018 under an agreement between the JSPS and the Department of Science and Technology (DST) in India. KF is grateful to KAKENHI (16H07323) Grant-in-Aid for Research Activity Start-up.
pyraf is a prodict of the Space Telescope Science Institute, which is operated by AURA for NASA.
In late 2016, we made an instrumental upgrade to minimize such offsets.
We found relatively tight LDR–Teff relations, with unexpected slopes for six pairs of Ti i lines (for each pair, the first is the low-excitation line): 10496.11–10551.76 Å, 10607.72–10551.76 Å, 12671.10–12744.91 Å, 12821.67–12744.91 Å, 12831.44–12744.91 Å and 12847.03–12744.91 Å.
REFERENCES
SUPPORTING INFORMATION
Supplementary data are available at MNRAS online.
Figure 3. LDR–Teff plots for all 81 relations.
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.



