-
PDF
- Split View
-
Views
-
Cite
Cite
A. Owens, S. N. Yurchenko, V. Špirko, Anomalous phosphine sensitivity coefficients as probes for a possible variation of the proton-to-electron mass ratio, Monthly Notices of the Royal Astronomical Society, Volume 473, Issue 4, February 2018, Pages 4986–4992, https://doi.org/10.1093/mnras/stx2696
Close - Share Icon Share
Abstract
A robust variational approach is used to investigate the sensitivity of the rotation–vibration spectrum of phosphine (PH3) to a possible cosmological variation of the proton-to-electron mass ratio, μ. Whilst the majority of computed sensitivity coefficients, T, involving the low-lying vibrational states acquire the expected values of T ≈ −1 and T ≈ −1/2 for rotational and ro-vibrational transitions, respectively, anomalous sensitivities are uncovered for the A1 − A2 splittings in the ν2/ν4, ν1/ν3 and |$2\nu _4^{\ell =0}/2\nu _4^{\ell =2}$| manifolds of PH3. A pronounced Coriolis interaction between these states in conjunction with accidentally degenerate A1 and A2 energy levels produces a series of enhanced sensitivity coefficients. Phosphine is expected to occur in a number of different astrophysical environments and has potential for investigating a drifting constant. Furthermore, the displayed behaviour hints at a wider trend in molecules of |$\boldsymbol {C}_{3\mathrm{v}}\mathrm{(M)}$| symmetry, thus demonstrating that the splittings induced by higher-order ro-vibrational interactions are well suited for probing μ in other symmetric top molecules in space, since these low-frequency transitions can be straightforwardly detected by radio telescopes.
1 INTRODUCTION
Recently, the J = 2 − 1 rotational transition of phosphine (PH3) was detected in the carbon star envelope IRC +10216 (Agúndez et al. 2014), thus confirming the presence of PH3 in the outflows of evolved stars but more significantly outside of the Solar system. The appearance of PH3 has been predicted in numerous other astrophysical environments (see the discussion by Sousa-Silva et al. 2015 and references therein), and because of prominent ‘irregularities’ displayed by its rotation–vibration spectrum, it is a promising system for investigating the cosmological variability of the proton-to-electron mass ratio, μ = mp/me. Observing PH3 outside of our Galaxy is no easy feat; however, nearby Galactic molecular clouds offer a means to constrain μ through the so-called chameleon scenario (Brax et al. 2004; Khoury & Weltman 2004) as evidenced by studies of ammonia (Levshakov et al. 2010b,a) and methanol (Daprà et al. 2017).
At present, the most robust constraint on a temporal variation of μ was determined from methanol absorption spectra observed in the lensing galaxy PKS1830−211 (Kanekar et al. 2015). The three measured transitions possessed sensitivity coefficients, T, ranging from −7.4 to −1.0 and resulted in a constraint of |$\dot{\mu }/\mu < 2\times 10^{-17}\,$|yr−1 assuming a linear rate of change. This translates to no change in μ over the past ≈7.5 billion years and is in agreement with the best laboratory constraint to date, which measured optical transitions in 171Yb+ ions to derive |$\dot{\mu }/\mu = (0.2\pm 1.1)\times 10^{-16}\,$|yr−1 (Godun et al. 2014) again assuming a linear rate of change. Whilst the use of methanol has led to several astronomical constraints (Jansen et al. 2011; Levshakov, Kozlov & Reimers 2011; Bagdonaite et al. 2013a,b; Thompson 2013; Kanekar et al. 2015), it is worthwhile identifying other molecular absorbers with notable sensitivities to expand the search for a drifting μ.
Due to the small difference between its rotational constants B and C, and also because of the strong x − y Coriolis interaction between the coinciding ν2/ν4, ν1/ν3 and |$2\nu _4^{\ell =0}/2\nu _4^{\ell =2}$| states (see Fig. 1), phosphine is a potential candidate system for probing μ. Notably, the spectrum of PH3, and presumably other molecules of |$\boldsymbol {C}_{3\mathrm{v}}\mathrm{(M)}$| symmetry, is special due to the anomalous behaviour of the A1 − A2 splittings (Ulenikov et al. 2002). A large number of spectroscopic studies of PH3 have been reported in the literature (see Müller 2013 and references therein) and highly accurate data is available for the majority of its states. Furthermore, a robust theoretical description of this molecule, which we utilize for this work, has been developed over the years (Yurchenko et al. 2003, 2005, 2006; Ovsyannikov et al. 2008a,b; Sousa-Silva, Yurchenko & Tennyson 2013; Sousa-Silva et al. 2014, 2015; Sousa-Silva, Tennyson & Yurchenko 2016), culminating in the construction of a comprehensive rotation–vibration line list applicable for elevated temperatures (Sousa-Silva et al. 2015).
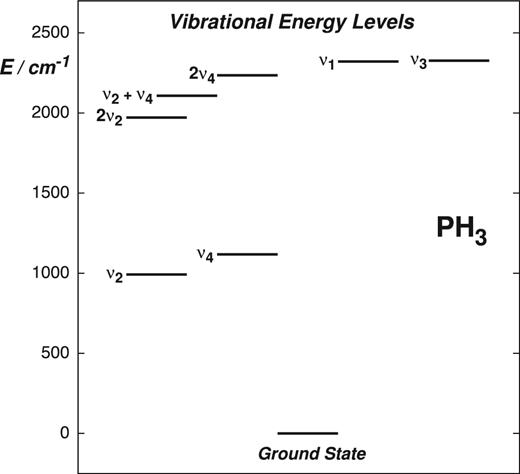
Model radiative transfer calculations of phosphine excitation in the envelope of IRC +10216 (Cernicharo et al. 1999; Agúndez et al. 2014) highlighted the importance of infrared pumping from the ground to the first excited vibrational states, helping explain the presence of strong emission bands in the observed spectra. We therefore find it useful to investigate the sensitivity of the ground, fundamental and low-lying combination and overtone vibrational states of PH3 (see Fig. 1) to a possible space–time variation of μ using a robust variational approach. The paper is structured as follows: in Section 2, we describe the variational approach used to compute sensitivity coefficients. The results for the phosphine molecule are presented and discussed in Section 3. Concluding remarks are given in Section 4.
2 VARIATIONAL APPROACH
Sensitivity coefficients for PH3 have been computed with the same variational approach as was previously employed for ammonia (Owens et al. 2015a, 2016) and the hydronium cation (Owens et al. 2015b). Calculations were carried out with the nuclear motion program trove (Yurchenko, Thiel & Jensen 2007; Yachmenev & Yurchenko 2015; Yurchenko, Yachmenev & Ovsyannikov 2017) and utilized the potential energy surface (PES), dipole moment surface (DMS) and computational set-up of Sousa-Silva et al. (2015), which have all undergone rigorous testing and are known to be reliable. We refer the reader to Sousa-Silva et al. (2015) for further details of the nuclear motion computations. All sensitivity coefficients, equation (1), have been determined with calculated frequencies, Eu − El, as oppose to experimental values when available. This was done for consistency and to verify the trend in sensitivities displayed by PH3, which we will discuss further in Section 3.
3 RESULTS AND DISCUSSION
In general, as shown in Table 1, Figs 2 and 3, the majority of the calculated sensitivity coefficients for the low-lying vibrational states acquire the expected values of T ≈ −1 and T ≈ −1/2 for rotational and ro-vibrational transitions, respectively. Notably, this is the case for the J = 2 − 1 and J = 1 − 0 rotational transitions observed in the carbon star envelope IRC +10216 (Agúndez et al. 2008, 2014). For a small fraction of the probed transitions, the sensitivities deviate from the usual values. Accidental coincidences between ro-vibrational states can cause the magnitude of these ‘irregularities’ to strongly increase with vibrational excitation, as illustrated in Fig. 4.
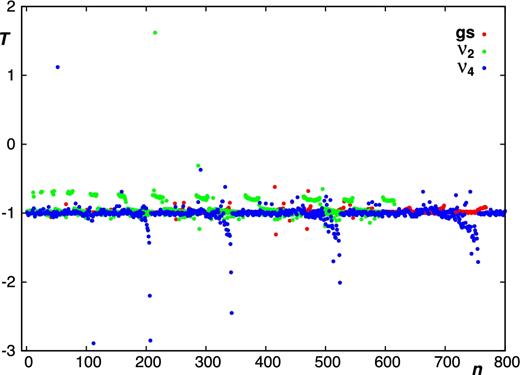
Sensitivity coefficients T for pure rotational transitions in the ground, ν2, and ν4 vibrational states of PH3. Here, n is a running number which counts the number of transitions.
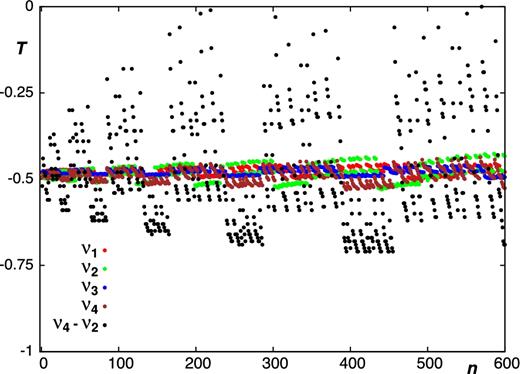
Sensitivity coefficients T for ro-vibrational transitions from the ground to the lowest vibrational states of PH3. Here, n is a running number which counts the number of transitions.
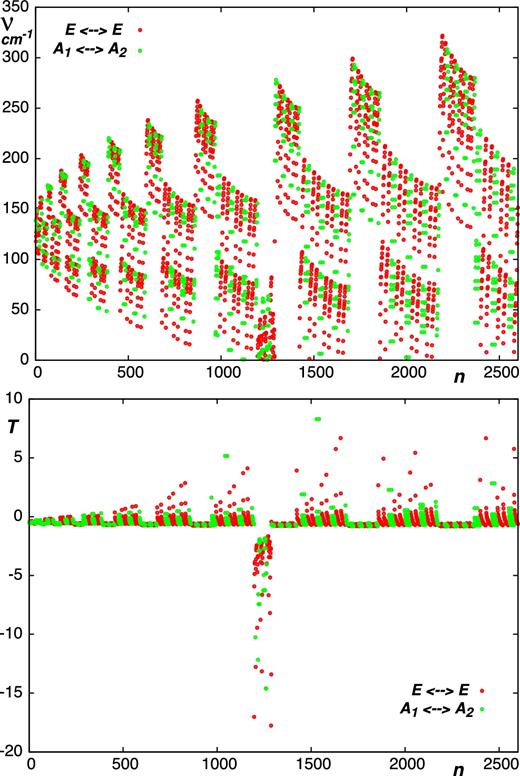
The wavenumbers ν (in cm−1) and sensitivity coefficients T of the ν4 ← ν2 ro-vibrational transitions of PH3. Here, n is a running number which counts the number of transitions.
Calculated frequency νcalc (in MHz), frequency difference Δc − e (in MHz) compared to experimental value from Belov et al. (1981), Einstein A coefficient (in s−1) and sensitivity coefficient T for vibrational ground-state transitions of PH3.
| Γ΄ . | J΄ . | K΄ . | Γ″ . | J″ . | K″ . | νcalc . | Δc − e . | A . | T . |
|---|---|---|---|---|---|---|---|---|---|
| Allowed | |||||||||
| A2 | 1 | 0 | A1 | 0 | 0 | 266 947.2 | 2.7 | 0.253E-04 | −0.99 |
| E | 2 | 1 | E | 1 | 1 | 533 819.4 | 4.2 | 0.182E-03 | −0.99 |
| A1 | 2 | 0 | A2 | 1 | 0 | 533 795.5 | 0.9 | 0.242E-03 | −1.00 |
| E | 3 | 2 | E | 2 | 2 | 800 586.8 | 6.9 | 0.486E-03 | −1.00 |
| E | 3 | 1 | E | 2 | 1 | 800 490.8 | 3.7 | 0.778E-03 | −0.99 |
| A2 | 3 | 0 | A1 | 2 | 0 | 800 463.8 | 7.7 | 0.875E-03 | −0.99 |
| A1 | 4 | 3 | A2 | 3 | 3 | 1067 210.2 | 3.9 | 0.940E-03 | −0.99 |
| A2 | 4 | 3 | A1 | 3 | 3 | 1067 210.2 | 3.9 | 0.940E-03 | −0.99 |
| E | 4 | 2 | E | 3 | 2 | 1067 006.3 | 6.0 | 0.161E-02 | −0.99 |
| E | 4 | 1 | E | 3 | 1 | 1066 886.4 | 9.5 | 0.201E-02 | −1.00 |
| A1 | 4 | 0 | A2 | 3 | 0 | 1066 844.4 | 8.5 | 0.215E-02 | −1.00 |
| Forbidden | |||||||||
| E | 6 | 1 | E | 6 | 2 | 47 409.2 | 18.0 | 0.780E-12 | −0.87 |
| E | 7 | 1 | E | 7 | 2 | 47 199.3 | 20.7 | 0.140E-11 | −0.95 |
| E | 8 | 1 | E | 8 | 2 | 46 962.5 | 23.4 | 0.232E-11 | −0.96 |
| E | 9 | 1 | E | 9 | 2 | 46 695.7 | 24.2 | 0.362E-11 | −1.08 |
| E | 10 | 1 | E | 10 | 2 | 46 404.9 | 27.1 | 0.540E-11 | −0.85 |
| E | 11 | 1 | E | 11 | 2 | 46 090.1 | 31.6 | 0.775E-11 | −0.85 |
| E | 12 | 1 | E | 12 | 2 | 45 748.3 | 33.5 | 0.108E-10 | −0.86 |
| E | 13 | 1 | E | 13 | 2 | 45 382.6 | 34.7 | 0.146E-10 | −0.83 |
| E | 14 | 1 | E | 14 | 2 | 44 995.8 | 37.2 | 0.193E-10 | −0.96 |
| E | 15 | 1 | E | 15 | 2 | 44 591.1 | 42.2 | 0.251E-10 | −0.92 |
| A2 | 3 | 0 | A1 | 3 | 3 | 143 750.5 | 48.9 | 0.152E-11 | −0.98 |
| A1 | 4 | 0 | A2 | 4 | 3 | 143 384.7 | 53.7 | 0.636E-11 | −1.01 |
| A2 | 5 | 0 | A1 | 5 | 3 | 142 923.1 | 53.1 | 0.169E-10 | −1.01 |
| A1 | 6 | 0 | A2 | 6 | 3 | 142 377.4 | 58.4 | 0.361E-10 | −0.96 |
| A2 | 7 | 0 | A1 | 7 | 3 | 141 744.9 | 65.8 | 0.674E-10 | −0.96 |
| A1 | 8 | 0 | A2 | 8 | 3 | 141 022.4 | 71.9 | 0.115E-09 | −0.96 |
| A2 | 9 | 0 | A1 | 9 | 3 | 140 209.9 | 76.8 | 0.182E-09 | −0.96 |
| A1 | 10 | 0 | A2 | 10 | 3 | 139 307.6 | 81.0 | 0.275E-09 | −0.97 |
| A2 | 11 | 0 | A1 | 11 | 3 | 138 318.2 | 90.2 | 0.398E-09 | −0.95 |
| A1 | 12 | 0 | A2 | 12 | 3 | 137 230.0 | 95.3 | 0.557E-09 | −0.93 |
| A2 | 13 | 0 | A1 | 13 | 3 | 136 045.8 | 104.4 | 0.756E-09 | −0.90 |
| A1 | 14 | 0 | A2 | 14 | 3 | 134 750.7 | 109.3 | 0.100E-08 | −0.93 |
| E | 6 | 2 | E | 6 | 5 | 333 977.8 | 137.8 | 0.903E-10 | −0.99 |
| E | 7 | 2 | E | 7 | 5 | 332 493.8 | 148.9 | 0.225E-09 | −0.97 |
| E | 8 | 2 | E | 8 | 5 | 330 815.0 | 163.3 | 0.452E-09 | −0.97 |
| E | 9 | 2 | E | 9 | 5 | 328 941.3 | 176.9 | 0.801E-09 | −0.96 |
| E | 10 | 2 | E | 10 | 5 | 326 884.7 | 194.4 | 0.130E-08 | −0.98 |
| E | 11 | 2 | E | 11 | 5 | 324 645.2 | 209.3 | 0.199E-08 | −0.95 |
| E | 12 | 2 | E | 12 | 5 | 322 237.9 | 228.9 | 0.290E-08 | −0.95 |
| E | 13 | 2 | E | 13 | 5 | 319 665.7 | 247.9 | 0.406E-08 | −0.96 |
| E | 14 | 2 | E | 14 | 5 | 316 940.6 | 268.7 | 0.552E-08 | −0.93 |
| E | 15 | 2 | E | 15 | 5 | 314 068.6 | 288.1 | 0.731E-08 | −0.92 |
| A1 | 7 | 3 | A2 | 7 | 6 | 429 296.8 | 188.4 | 0.249E-09 | −0.99 |
| A2 | 7 | 3 | A1 | 7 | 6 | 429 284.8 | 189.2 | 0.249E-09 | −1.00 |
| A1 | 8 | 3 | A2 | 8 | 6 | 427 132.3 | 205.7 | 0.613E-09 | −0.98 |
| A2 | 8 | 3 | A1 | 8 | 6 | 427 105.3 | 207.2 | 0.613E-09 | −0.98 |
| A1 | 9 | 3 | A2 | 9 | 6 | 424 728.0 | 227.1 | 0.122E-08 | −0.98 |
| A2 | 9 | 3 | A1 | 9 | 6 | 424 671.0 | 227.0 | 0.122E-08 | −0.98 |
| A1 | 10 | 3 | A2 | 10 | 6 | 422 092.8 | 249.8 | 0.213E-08 | −0.96 |
| A2 | 10 | 3 | A1 | 10 | 6 | 421 984.9 | 247.2 | 0.213E-08 | −0.96 |
| A1 | 11 | 3 | A2 | 11 | 6 | 419 238.8 | 271.7 | 0.343E-08 | −0.96 |
| A2 | 11 | 3 | A1 | 11 | 6 | 419 052.9 | 269.8 | 0.343E-08 | −0.96 |
| A1 | 12 | 3 | A2 | 12 | 6 | 416 186.9 | 297.6 | 0.519E-08 | −0.95 |
| A2 | 12 | 3 | A1 | 12 | 6 | 415 878.1 | 294.8 | 0.518E-08 | −0.94 |
| A1 | 13 | 3 | A2 | 13 | 6 | 412 949.1 | 320.2 | 0.748E-08 | −0.94 |
| A2 | 13 | 3 | A1 | 13 | 6 | 412 457.5 | 316.6 | 0.747E-08 | −0.95 |
| A1 | 14 | 3 | A2 | 14 | 6 | 409 558.5 | 350.2 | 0.104E-07 | −0.94 |
| A2 | 14 | 3 | A1 | 14 | 6 | 408 797.0 | 341.3 | 0.104E-07 | −0.94 |
| A1 | 15 | 3 | A2 | 15 | 6 | 406 029.9 | 377.3 | 0.140E-07 | −0.93 |
| A2 | 15 | 3 | A1 | 15 | 6 | 404 893.7 | 366.7 | 0.139E-07 | −0.92 |
| Γ΄ . | J΄ . | K΄ . | Γ″ . | J″ . | K″ . | νcalc . | Δc − e . | A . | T . |
|---|---|---|---|---|---|---|---|---|---|
| Allowed | |||||||||
| A2 | 1 | 0 | A1 | 0 | 0 | 266 947.2 | 2.7 | 0.253E-04 | −0.99 |
| E | 2 | 1 | E | 1 | 1 | 533 819.4 | 4.2 | 0.182E-03 | −0.99 |
| A1 | 2 | 0 | A2 | 1 | 0 | 533 795.5 | 0.9 | 0.242E-03 | −1.00 |
| E | 3 | 2 | E | 2 | 2 | 800 586.8 | 6.9 | 0.486E-03 | −1.00 |
| E | 3 | 1 | E | 2 | 1 | 800 490.8 | 3.7 | 0.778E-03 | −0.99 |
| A2 | 3 | 0 | A1 | 2 | 0 | 800 463.8 | 7.7 | 0.875E-03 | −0.99 |
| A1 | 4 | 3 | A2 | 3 | 3 | 1067 210.2 | 3.9 | 0.940E-03 | −0.99 |
| A2 | 4 | 3 | A1 | 3 | 3 | 1067 210.2 | 3.9 | 0.940E-03 | −0.99 |
| E | 4 | 2 | E | 3 | 2 | 1067 006.3 | 6.0 | 0.161E-02 | −0.99 |
| E | 4 | 1 | E | 3 | 1 | 1066 886.4 | 9.5 | 0.201E-02 | −1.00 |
| A1 | 4 | 0 | A2 | 3 | 0 | 1066 844.4 | 8.5 | 0.215E-02 | −1.00 |
| Forbidden | |||||||||
| E | 6 | 1 | E | 6 | 2 | 47 409.2 | 18.0 | 0.780E-12 | −0.87 |
| E | 7 | 1 | E | 7 | 2 | 47 199.3 | 20.7 | 0.140E-11 | −0.95 |
| E | 8 | 1 | E | 8 | 2 | 46 962.5 | 23.4 | 0.232E-11 | −0.96 |
| E | 9 | 1 | E | 9 | 2 | 46 695.7 | 24.2 | 0.362E-11 | −1.08 |
| E | 10 | 1 | E | 10 | 2 | 46 404.9 | 27.1 | 0.540E-11 | −0.85 |
| E | 11 | 1 | E | 11 | 2 | 46 090.1 | 31.6 | 0.775E-11 | −0.85 |
| E | 12 | 1 | E | 12 | 2 | 45 748.3 | 33.5 | 0.108E-10 | −0.86 |
| E | 13 | 1 | E | 13 | 2 | 45 382.6 | 34.7 | 0.146E-10 | −0.83 |
| E | 14 | 1 | E | 14 | 2 | 44 995.8 | 37.2 | 0.193E-10 | −0.96 |
| E | 15 | 1 | E | 15 | 2 | 44 591.1 | 42.2 | 0.251E-10 | −0.92 |
| A2 | 3 | 0 | A1 | 3 | 3 | 143 750.5 | 48.9 | 0.152E-11 | −0.98 |
| A1 | 4 | 0 | A2 | 4 | 3 | 143 384.7 | 53.7 | 0.636E-11 | −1.01 |
| A2 | 5 | 0 | A1 | 5 | 3 | 142 923.1 | 53.1 | 0.169E-10 | −1.01 |
| A1 | 6 | 0 | A2 | 6 | 3 | 142 377.4 | 58.4 | 0.361E-10 | −0.96 |
| A2 | 7 | 0 | A1 | 7 | 3 | 141 744.9 | 65.8 | 0.674E-10 | −0.96 |
| A1 | 8 | 0 | A2 | 8 | 3 | 141 022.4 | 71.9 | 0.115E-09 | −0.96 |
| A2 | 9 | 0 | A1 | 9 | 3 | 140 209.9 | 76.8 | 0.182E-09 | −0.96 |
| A1 | 10 | 0 | A2 | 10 | 3 | 139 307.6 | 81.0 | 0.275E-09 | −0.97 |
| A2 | 11 | 0 | A1 | 11 | 3 | 138 318.2 | 90.2 | 0.398E-09 | −0.95 |
| A1 | 12 | 0 | A2 | 12 | 3 | 137 230.0 | 95.3 | 0.557E-09 | −0.93 |
| A2 | 13 | 0 | A1 | 13 | 3 | 136 045.8 | 104.4 | 0.756E-09 | −0.90 |
| A1 | 14 | 0 | A2 | 14 | 3 | 134 750.7 | 109.3 | 0.100E-08 | −0.93 |
| E | 6 | 2 | E | 6 | 5 | 333 977.8 | 137.8 | 0.903E-10 | −0.99 |
| E | 7 | 2 | E | 7 | 5 | 332 493.8 | 148.9 | 0.225E-09 | −0.97 |
| E | 8 | 2 | E | 8 | 5 | 330 815.0 | 163.3 | 0.452E-09 | −0.97 |
| E | 9 | 2 | E | 9 | 5 | 328 941.3 | 176.9 | 0.801E-09 | −0.96 |
| E | 10 | 2 | E | 10 | 5 | 326 884.7 | 194.4 | 0.130E-08 | −0.98 |
| E | 11 | 2 | E | 11 | 5 | 324 645.2 | 209.3 | 0.199E-08 | −0.95 |
| E | 12 | 2 | E | 12 | 5 | 322 237.9 | 228.9 | 0.290E-08 | −0.95 |
| E | 13 | 2 | E | 13 | 5 | 319 665.7 | 247.9 | 0.406E-08 | −0.96 |
| E | 14 | 2 | E | 14 | 5 | 316 940.6 | 268.7 | 0.552E-08 | −0.93 |
| E | 15 | 2 | E | 15 | 5 | 314 068.6 | 288.1 | 0.731E-08 | −0.92 |
| A1 | 7 | 3 | A2 | 7 | 6 | 429 296.8 | 188.4 | 0.249E-09 | −0.99 |
| A2 | 7 | 3 | A1 | 7 | 6 | 429 284.8 | 189.2 | 0.249E-09 | −1.00 |
| A1 | 8 | 3 | A2 | 8 | 6 | 427 132.3 | 205.7 | 0.613E-09 | −0.98 |
| A2 | 8 | 3 | A1 | 8 | 6 | 427 105.3 | 207.2 | 0.613E-09 | −0.98 |
| A1 | 9 | 3 | A2 | 9 | 6 | 424 728.0 | 227.1 | 0.122E-08 | −0.98 |
| A2 | 9 | 3 | A1 | 9 | 6 | 424 671.0 | 227.0 | 0.122E-08 | −0.98 |
| A1 | 10 | 3 | A2 | 10 | 6 | 422 092.8 | 249.8 | 0.213E-08 | −0.96 |
| A2 | 10 | 3 | A1 | 10 | 6 | 421 984.9 | 247.2 | 0.213E-08 | −0.96 |
| A1 | 11 | 3 | A2 | 11 | 6 | 419 238.8 | 271.7 | 0.343E-08 | −0.96 |
| A2 | 11 | 3 | A1 | 11 | 6 | 419 052.9 | 269.8 | 0.343E-08 | −0.96 |
| A1 | 12 | 3 | A2 | 12 | 6 | 416 186.9 | 297.6 | 0.519E-08 | −0.95 |
| A2 | 12 | 3 | A1 | 12 | 6 | 415 878.1 | 294.8 | 0.518E-08 | −0.94 |
| A1 | 13 | 3 | A2 | 13 | 6 | 412 949.1 | 320.2 | 0.748E-08 | −0.94 |
| A2 | 13 | 3 | A1 | 13 | 6 | 412 457.5 | 316.6 | 0.747E-08 | −0.95 |
| A1 | 14 | 3 | A2 | 14 | 6 | 409 558.5 | 350.2 | 0.104E-07 | −0.94 |
| A2 | 14 | 3 | A1 | 14 | 6 | 408 797.0 | 341.3 | 0.104E-07 | −0.94 |
| A1 | 15 | 3 | A2 | 15 | 6 | 406 029.9 | 377.3 | 0.140E-07 | −0.93 |
| A2 | 15 | 3 | A1 | 15 | 6 | 404 893.7 | 366.7 | 0.139E-07 | −0.92 |
Calculated frequency νcalc (in MHz), frequency difference Δc − e (in MHz) compared to experimental value from Belov et al. (1981), Einstein A coefficient (in s−1) and sensitivity coefficient T for vibrational ground-state transitions of PH3.
| Γ΄ . | J΄ . | K΄ . | Γ″ . | J″ . | K″ . | νcalc . | Δc − e . | A . | T . |
|---|---|---|---|---|---|---|---|---|---|
| Allowed | |||||||||
| A2 | 1 | 0 | A1 | 0 | 0 | 266 947.2 | 2.7 | 0.253E-04 | −0.99 |
| E | 2 | 1 | E | 1 | 1 | 533 819.4 | 4.2 | 0.182E-03 | −0.99 |
| A1 | 2 | 0 | A2 | 1 | 0 | 533 795.5 | 0.9 | 0.242E-03 | −1.00 |
| E | 3 | 2 | E | 2 | 2 | 800 586.8 | 6.9 | 0.486E-03 | −1.00 |
| E | 3 | 1 | E | 2 | 1 | 800 490.8 | 3.7 | 0.778E-03 | −0.99 |
| A2 | 3 | 0 | A1 | 2 | 0 | 800 463.8 | 7.7 | 0.875E-03 | −0.99 |
| A1 | 4 | 3 | A2 | 3 | 3 | 1067 210.2 | 3.9 | 0.940E-03 | −0.99 |
| A2 | 4 | 3 | A1 | 3 | 3 | 1067 210.2 | 3.9 | 0.940E-03 | −0.99 |
| E | 4 | 2 | E | 3 | 2 | 1067 006.3 | 6.0 | 0.161E-02 | −0.99 |
| E | 4 | 1 | E | 3 | 1 | 1066 886.4 | 9.5 | 0.201E-02 | −1.00 |
| A1 | 4 | 0 | A2 | 3 | 0 | 1066 844.4 | 8.5 | 0.215E-02 | −1.00 |
| Forbidden | |||||||||
| E | 6 | 1 | E | 6 | 2 | 47 409.2 | 18.0 | 0.780E-12 | −0.87 |
| E | 7 | 1 | E | 7 | 2 | 47 199.3 | 20.7 | 0.140E-11 | −0.95 |
| E | 8 | 1 | E | 8 | 2 | 46 962.5 | 23.4 | 0.232E-11 | −0.96 |
| E | 9 | 1 | E | 9 | 2 | 46 695.7 | 24.2 | 0.362E-11 | −1.08 |
| E | 10 | 1 | E | 10 | 2 | 46 404.9 | 27.1 | 0.540E-11 | −0.85 |
| E | 11 | 1 | E | 11 | 2 | 46 090.1 | 31.6 | 0.775E-11 | −0.85 |
| E | 12 | 1 | E | 12 | 2 | 45 748.3 | 33.5 | 0.108E-10 | −0.86 |
| E | 13 | 1 | E | 13 | 2 | 45 382.6 | 34.7 | 0.146E-10 | −0.83 |
| E | 14 | 1 | E | 14 | 2 | 44 995.8 | 37.2 | 0.193E-10 | −0.96 |
| E | 15 | 1 | E | 15 | 2 | 44 591.1 | 42.2 | 0.251E-10 | −0.92 |
| A2 | 3 | 0 | A1 | 3 | 3 | 143 750.5 | 48.9 | 0.152E-11 | −0.98 |
| A1 | 4 | 0 | A2 | 4 | 3 | 143 384.7 | 53.7 | 0.636E-11 | −1.01 |
| A2 | 5 | 0 | A1 | 5 | 3 | 142 923.1 | 53.1 | 0.169E-10 | −1.01 |
| A1 | 6 | 0 | A2 | 6 | 3 | 142 377.4 | 58.4 | 0.361E-10 | −0.96 |
| A2 | 7 | 0 | A1 | 7 | 3 | 141 744.9 | 65.8 | 0.674E-10 | −0.96 |
| A1 | 8 | 0 | A2 | 8 | 3 | 141 022.4 | 71.9 | 0.115E-09 | −0.96 |
| A2 | 9 | 0 | A1 | 9 | 3 | 140 209.9 | 76.8 | 0.182E-09 | −0.96 |
| A1 | 10 | 0 | A2 | 10 | 3 | 139 307.6 | 81.0 | 0.275E-09 | −0.97 |
| A2 | 11 | 0 | A1 | 11 | 3 | 138 318.2 | 90.2 | 0.398E-09 | −0.95 |
| A1 | 12 | 0 | A2 | 12 | 3 | 137 230.0 | 95.3 | 0.557E-09 | −0.93 |
| A2 | 13 | 0 | A1 | 13 | 3 | 136 045.8 | 104.4 | 0.756E-09 | −0.90 |
| A1 | 14 | 0 | A2 | 14 | 3 | 134 750.7 | 109.3 | 0.100E-08 | −0.93 |
| E | 6 | 2 | E | 6 | 5 | 333 977.8 | 137.8 | 0.903E-10 | −0.99 |
| E | 7 | 2 | E | 7 | 5 | 332 493.8 | 148.9 | 0.225E-09 | −0.97 |
| E | 8 | 2 | E | 8 | 5 | 330 815.0 | 163.3 | 0.452E-09 | −0.97 |
| E | 9 | 2 | E | 9 | 5 | 328 941.3 | 176.9 | 0.801E-09 | −0.96 |
| E | 10 | 2 | E | 10 | 5 | 326 884.7 | 194.4 | 0.130E-08 | −0.98 |
| E | 11 | 2 | E | 11 | 5 | 324 645.2 | 209.3 | 0.199E-08 | −0.95 |
| E | 12 | 2 | E | 12 | 5 | 322 237.9 | 228.9 | 0.290E-08 | −0.95 |
| E | 13 | 2 | E | 13 | 5 | 319 665.7 | 247.9 | 0.406E-08 | −0.96 |
| E | 14 | 2 | E | 14 | 5 | 316 940.6 | 268.7 | 0.552E-08 | −0.93 |
| E | 15 | 2 | E | 15 | 5 | 314 068.6 | 288.1 | 0.731E-08 | −0.92 |
| A1 | 7 | 3 | A2 | 7 | 6 | 429 296.8 | 188.4 | 0.249E-09 | −0.99 |
| A2 | 7 | 3 | A1 | 7 | 6 | 429 284.8 | 189.2 | 0.249E-09 | −1.00 |
| A1 | 8 | 3 | A2 | 8 | 6 | 427 132.3 | 205.7 | 0.613E-09 | −0.98 |
| A2 | 8 | 3 | A1 | 8 | 6 | 427 105.3 | 207.2 | 0.613E-09 | −0.98 |
| A1 | 9 | 3 | A2 | 9 | 6 | 424 728.0 | 227.1 | 0.122E-08 | −0.98 |
| A2 | 9 | 3 | A1 | 9 | 6 | 424 671.0 | 227.0 | 0.122E-08 | −0.98 |
| A1 | 10 | 3 | A2 | 10 | 6 | 422 092.8 | 249.8 | 0.213E-08 | −0.96 |
| A2 | 10 | 3 | A1 | 10 | 6 | 421 984.9 | 247.2 | 0.213E-08 | −0.96 |
| A1 | 11 | 3 | A2 | 11 | 6 | 419 238.8 | 271.7 | 0.343E-08 | −0.96 |
| A2 | 11 | 3 | A1 | 11 | 6 | 419 052.9 | 269.8 | 0.343E-08 | −0.96 |
| A1 | 12 | 3 | A2 | 12 | 6 | 416 186.9 | 297.6 | 0.519E-08 | −0.95 |
| A2 | 12 | 3 | A1 | 12 | 6 | 415 878.1 | 294.8 | 0.518E-08 | −0.94 |
| A1 | 13 | 3 | A2 | 13 | 6 | 412 949.1 | 320.2 | 0.748E-08 | −0.94 |
| A2 | 13 | 3 | A1 | 13 | 6 | 412 457.5 | 316.6 | 0.747E-08 | −0.95 |
| A1 | 14 | 3 | A2 | 14 | 6 | 409 558.5 | 350.2 | 0.104E-07 | −0.94 |
| A2 | 14 | 3 | A1 | 14 | 6 | 408 797.0 | 341.3 | 0.104E-07 | −0.94 |
| A1 | 15 | 3 | A2 | 15 | 6 | 406 029.9 | 377.3 | 0.140E-07 | −0.93 |
| A2 | 15 | 3 | A1 | 15 | 6 | 404 893.7 | 366.7 | 0.139E-07 | −0.92 |
| Γ΄ . | J΄ . | K΄ . | Γ″ . | J″ . | K″ . | νcalc . | Δc − e . | A . | T . |
|---|---|---|---|---|---|---|---|---|---|
| Allowed | |||||||||
| A2 | 1 | 0 | A1 | 0 | 0 | 266 947.2 | 2.7 | 0.253E-04 | −0.99 |
| E | 2 | 1 | E | 1 | 1 | 533 819.4 | 4.2 | 0.182E-03 | −0.99 |
| A1 | 2 | 0 | A2 | 1 | 0 | 533 795.5 | 0.9 | 0.242E-03 | −1.00 |
| E | 3 | 2 | E | 2 | 2 | 800 586.8 | 6.9 | 0.486E-03 | −1.00 |
| E | 3 | 1 | E | 2 | 1 | 800 490.8 | 3.7 | 0.778E-03 | −0.99 |
| A2 | 3 | 0 | A1 | 2 | 0 | 800 463.8 | 7.7 | 0.875E-03 | −0.99 |
| A1 | 4 | 3 | A2 | 3 | 3 | 1067 210.2 | 3.9 | 0.940E-03 | −0.99 |
| A2 | 4 | 3 | A1 | 3 | 3 | 1067 210.2 | 3.9 | 0.940E-03 | −0.99 |
| E | 4 | 2 | E | 3 | 2 | 1067 006.3 | 6.0 | 0.161E-02 | −0.99 |
| E | 4 | 1 | E | 3 | 1 | 1066 886.4 | 9.5 | 0.201E-02 | −1.00 |
| A1 | 4 | 0 | A2 | 3 | 0 | 1066 844.4 | 8.5 | 0.215E-02 | −1.00 |
| Forbidden | |||||||||
| E | 6 | 1 | E | 6 | 2 | 47 409.2 | 18.0 | 0.780E-12 | −0.87 |
| E | 7 | 1 | E | 7 | 2 | 47 199.3 | 20.7 | 0.140E-11 | −0.95 |
| E | 8 | 1 | E | 8 | 2 | 46 962.5 | 23.4 | 0.232E-11 | −0.96 |
| E | 9 | 1 | E | 9 | 2 | 46 695.7 | 24.2 | 0.362E-11 | −1.08 |
| E | 10 | 1 | E | 10 | 2 | 46 404.9 | 27.1 | 0.540E-11 | −0.85 |
| E | 11 | 1 | E | 11 | 2 | 46 090.1 | 31.6 | 0.775E-11 | −0.85 |
| E | 12 | 1 | E | 12 | 2 | 45 748.3 | 33.5 | 0.108E-10 | −0.86 |
| E | 13 | 1 | E | 13 | 2 | 45 382.6 | 34.7 | 0.146E-10 | −0.83 |
| E | 14 | 1 | E | 14 | 2 | 44 995.8 | 37.2 | 0.193E-10 | −0.96 |
| E | 15 | 1 | E | 15 | 2 | 44 591.1 | 42.2 | 0.251E-10 | −0.92 |
| A2 | 3 | 0 | A1 | 3 | 3 | 143 750.5 | 48.9 | 0.152E-11 | −0.98 |
| A1 | 4 | 0 | A2 | 4 | 3 | 143 384.7 | 53.7 | 0.636E-11 | −1.01 |
| A2 | 5 | 0 | A1 | 5 | 3 | 142 923.1 | 53.1 | 0.169E-10 | −1.01 |
| A1 | 6 | 0 | A2 | 6 | 3 | 142 377.4 | 58.4 | 0.361E-10 | −0.96 |
| A2 | 7 | 0 | A1 | 7 | 3 | 141 744.9 | 65.8 | 0.674E-10 | −0.96 |
| A1 | 8 | 0 | A2 | 8 | 3 | 141 022.4 | 71.9 | 0.115E-09 | −0.96 |
| A2 | 9 | 0 | A1 | 9 | 3 | 140 209.9 | 76.8 | 0.182E-09 | −0.96 |
| A1 | 10 | 0 | A2 | 10 | 3 | 139 307.6 | 81.0 | 0.275E-09 | −0.97 |
| A2 | 11 | 0 | A1 | 11 | 3 | 138 318.2 | 90.2 | 0.398E-09 | −0.95 |
| A1 | 12 | 0 | A2 | 12 | 3 | 137 230.0 | 95.3 | 0.557E-09 | −0.93 |
| A2 | 13 | 0 | A1 | 13 | 3 | 136 045.8 | 104.4 | 0.756E-09 | −0.90 |
| A1 | 14 | 0 | A2 | 14 | 3 | 134 750.7 | 109.3 | 0.100E-08 | −0.93 |
| E | 6 | 2 | E | 6 | 5 | 333 977.8 | 137.8 | 0.903E-10 | −0.99 |
| E | 7 | 2 | E | 7 | 5 | 332 493.8 | 148.9 | 0.225E-09 | −0.97 |
| E | 8 | 2 | E | 8 | 5 | 330 815.0 | 163.3 | 0.452E-09 | −0.97 |
| E | 9 | 2 | E | 9 | 5 | 328 941.3 | 176.9 | 0.801E-09 | −0.96 |
| E | 10 | 2 | E | 10 | 5 | 326 884.7 | 194.4 | 0.130E-08 | −0.98 |
| E | 11 | 2 | E | 11 | 5 | 324 645.2 | 209.3 | 0.199E-08 | −0.95 |
| E | 12 | 2 | E | 12 | 5 | 322 237.9 | 228.9 | 0.290E-08 | −0.95 |
| E | 13 | 2 | E | 13 | 5 | 319 665.7 | 247.9 | 0.406E-08 | −0.96 |
| E | 14 | 2 | E | 14 | 5 | 316 940.6 | 268.7 | 0.552E-08 | −0.93 |
| E | 15 | 2 | E | 15 | 5 | 314 068.6 | 288.1 | 0.731E-08 | −0.92 |
| A1 | 7 | 3 | A2 | 7 | 6 | 429 296.8 | 188.4 | 0.249E-09 | −0.99 |
| A2 | 7 | 3 | A1 | 7 | 6 | 429 284.8 | 189.2 | 0.249E-09 | −1.00 |
| A1 | 8 | 3 | A2 | 8 | 6 | 427 132.3 | 205.7 | 0.613E-09 | −0.98 |
| A2 | 8 | 3 | A1 | 8 | 6 | 427 105.3 | 207.2 | 0.613E-09 | −0.98 |
| A1 | 9 | 3 | A2 | 9 | 6 | 424 728.0 | 227.1 | 0.122E-08 | −0.98 |
| A2 | 9 | 3 | A1 | 9 | 6 | 424 671.0 | 227.0 | 0.122E-08 | −0.98 |
| A1 | 10 | 3 | A2 | 10 | 6 | 422 092.8 | 249.8 | 0.213E-08 | −0.96 |
| A2 | 10 | 3 | A1 | 10 | 6 | 421 984.9 | 247.2 | 0.213E-08 | −0.96 |
| A1 | 11 | 3 | A2 | 11 | 6 | 419 238.8 | 271.7 | 0.343E-08 | −0.96 |
| A2 | 11 | 3 | A1 | 11 | 6 | 419 052.9 | 269.8 | 0.343E-08 | −0.96 |
| A1 | 12 | 3 | A2 | 12 | 6 | 416 186.9 | 297.6 | 0.519E-08 | −0.95 |
| A2 | 12 | 3 | A1 | 12 | 6 | 415 878.1 | 294.8 | 0.518E-08 | −0.94 |
| A1 | 13 | 3 | A2 | 13 | 6 | 412 949.1 | 320.2 | 0.748E-08 | −0.94 |
| A2 | 13 | 3 | A1 | 13 | 6 | 412 457.5 | 316.6 | 0.747E-08 | −0.95 |
| A1 | 14 | 3 | A2 | 14 | 6 | 409 558.5 | 350.2 | 0.104E-07 | −0.94 |
| A2 | 14 | 3 | A1 | 14 | 6 | 408 797.0 | 341.3 | 0.104E-07 | −0.94 |
| A1 | 15 | 3 | A2 | 15 | 6 | 406 029.9 | 377.3 | 0.140E-07 | −0.93 |
| A2 | 15 | 3 | A1 | 15 | 6 | 404 893.7 | 366.7 | 0.139E-07 | −0.92 |
The most striking sensitivities are displayed by the A1 − A2 doublets of PH3. As is well known for a molecule with |$\boldsymbol {C}_{3\mathrm{v}}\mathrm{(M)}$| symmetry, all rotation–vibration energy levels corresponding to the same K ≡ |k| ≠ 0 rotational quantum number and having overall A1, A2 symmetry are split into doublets due to different ro-vibrational interactions (see, for example, Chen & Oka 1989). For the non-degenerate vibrational states, the A1 − A2 splittings occur for rotational levels with K = 3n (n = 1, 2, …). For the doubly degenerate fundamental vibrational states characterized by the vibrational angular momentum quantum number ℓ ≠ 0, the splittings occur for the K = 1, 2, 4, 5, 7, 8… levels.
In Tables 2–9, we have computed sensitivity coefficients for a large number of the A1 − A2 doublets for low-lying vibrational states. The results suggest that sensitivities of the A1 − A2 splittings for non-coinciding ro-vibrational states possess values dependent on the rotational quantum number J. For example, T ≈ −1.5, −2, −3 for k = 1, 2, 3, respectively (see Tables 2–5). It would be interesting to see if this trend is present in other molecules of |$\boldsymbol {C}_{3\mathrm{v}}\mathrm{(M)}$| symmetry. For the sensitivities corresponding to coinciding states, there is a strong and irregular dependence on the x − y Coriolis interaction that can produce values at least one order of magnitude larger than the respective Coriolis-free predictions. This behaviour is similar to that of NH3 (Špirko 2014; Owens et al. 2015a, 2016) and H3O+ (Owens et al. 2015b) .
Calculated and experimental k = 3, A1 − A2 splittings (in MHz) and their sensitivities in the ground (gs) and ν2 vibrational states of PH3.
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| gs | |${\boldsymbol{\nu _2}}$| | |||||
| 4 | 0.43409a | 0.450 | 3.60b | 3.568 | ||
| 5 | 1.73413a | 1.769 | 13.096b | 13.371 | ||
| 6 | 5.19570a | 5.246 | 36.627b | 37.384 | ||
| 7 | 12.9690a | 13.101 | 78c | 86.640 | −3.6 | |
| 8 | 28.4825a | 28.780 | −2.9 | 174c | 176.19 | −3.6 |
| 9 | 56.8550a | 57.440 | −2.7 | 318c | 325.12 | −3.5 |
| 10 | 106.46 | −2.90 | 531c | 557.13 | −3.4 | |
| 11 | 185.90 | −3.00 | 872c | 900.40 | −3.3 | |
| 12 | 309.03 | −3.02 | 1412c | 1388.2 | −3.3 | |
| 13 | 493.04 | −3.04 | 2009c | 2059.6 | −3.3 | |
| 14 | 759.76 | −3.03 | 2896c | 2959.6 | −3.17 | |
| 15 | 1136.1 | −3.02 | 4686c | 4139.8 | −3.13 | |
| 16 | 1654.8 | −3.03 | 5660.3 | −3.10 | ||
| 17 | 2355.8 | −3.03 | 7588.6 | −3.07 | ||
| 18 | 3285.9 | −3.03 | 10002 | −3.06 |
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| gs | |${\boldsymbol{\nu _2}}$| | |||||
| 4 | 0.43409a | 0.450 | 3.60b | 3.568 | ||
| 5 | 1.73413a | 1.769 | 13.096b | 13.371 | ||
| 6 | 5.19570a | 5.246 | 36.627b | 37.384 | ||
| 7 | 12.9690a | 13.101 | 78c | 86.640 | −3.6 | |
| 8 | 28.4825a | 28.780 | −2.9 | 174c | 176.19 | −3.6 |
| 9 | 56.8550a | 57.440 | −2.7 | 318c | 325.12 | −3.5 |
| 10 | 106.46 | −2.90 | 531c | 557.13 | −3.4 | |
| 11 | 185.90 | −3.00 | 872c | 900.40 | −3.3 | |
| 12 | 309.03 | −3.02 | 1412c | 1388.2 | −3.3 | |
| 13 | 493.04 | −3.04 | 2009c | 2059.6 | −3.3 | |
| 14 | 759.76 | −3.03 | 2896c | 2959.6 | −3.17 | |
| 15 | 1136.1 | −3.02 | 4686c | 4139.8 | −3.13 | |
| 16 | 1654.8 | −3.03 | 5660.3 | −3.10 | ||
| 17 | 2355.8 | −3.03 | 7588.6 | −3.07 | ||
| 18 | 3285.9 | −3.03 | 10002 | −3.06 |
Calculated and experimental k = 3, A1 − A2 splittings (in MHz) and their sensitivities in the ground (gs) and ν2 vibrational states of PH3.
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| gs | |${\boldsymbol{\nu _2}}$| | |||||
| 4 | 0.43409a | 0.450 | 3.60b | 3.568 | ||
| 5 | 1.73413a | 1.769 | 13.096b | 13.371 | ||
| 6 | 5.19570a | 5.246 | 36.627b | 37.384 | ||
| 7 | 12.9690a | 13.101 | 78c | 86.640 | −3.6 | |
| 8 | 28.4825a | 28.780 | −2.9 | 174c | 176.19 | −3.6 |
| 9 | 56.8550a | 57.440 | −2.7 | 318c | 325.12 | −3.5 |
| 10 | 106.46 | −2.90 | 531c | 557.13 | −3.4 | |
| 11 | 185.90 | −3.00 | 872c | 900.40 | −3.3 | |
| 12 | 309.03 | −3.02 | 1412c | 1388.2 | −3.3 | |
| 13 | 493.04 | −3.04 | 2009c | 2059.6 | −3.3 | |
| 14 | 759.76 | −3.03 | 2896c | 2959.6 | −3.17 | |
| 15 | 1136.1 | −3.02 | 4686c | 4139.8 | −3.13 | |
| 16 | 1654.8 | −3.03 | 5660.3 | −3.10 | ||
| 17 | 2355.8 | −3.03 | 7588.6 | −3.07 | ||
| 18 | 3285.9 | −3.03 | 10002 | −3.06 |
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| gs | |${\boldsymbol{\nu _2}}$| | |||||
| 4 | 0.43409a | 0.450 | 3.60b | 3.568 | ||
| 5 | 1.73413a | 1.769 | 13.096b | 13.371 | ||
| 6 | 5.19570a | 5.246 | 36.627b | 37.384 | ||
| 7 | 12.9690a | 13.101 | 78c | 86.640 | −3.6 | |
| 8 | 28.4825a | 28.780 | −2.9 | 174c | 176.19 | −3.6 |
| 9 | 56.8550a | 57.440 | −2.7 | 318c | 325.12 | −3.5 |
| 10 | 106.46 | −2.90 | 531c | 557.13 | −3.4 | |
| 11 | 185.90 | −3.00 | 872c | 900.40 | −3.3 | |
| 12 | 309.03 | −3.02 | 1412c | 1388.2 | −3.3 | |
| 13 | 493.04 | −3.04 | 2009c | 2059.6 | −3.3 | |
| 14 | 759.76 | −3.03 | 2896c | 2959.6 | −3.17 | |
| 15 | 1136.1 | −3.02 | 4686c | 4139.8 | −3.13 | |
| 16 | 1654.8 | −3.03 | 5660.3 | −3.10 | ||
| 17 | 2355.8 | −3.03 | 7588.6 | −3.07 | ||
| 18 | 3285.9 | −3.03 | 10002 | −3.06 |
Calculated and experimental (Ulenikov et al. 2002) k = 3, A1 − A2 splittings (in MHz) and their sensitivities in the ν1 and |$2\nu _4^{\ell =2}$| vibrational states of PH3.
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| |${\boldsymbol{\nu _1}}$| | |${\boldsymbol{2\nu _{4}^{\ell =2}}}$| | |||||
| 4 | 2.10 | 573 | 503.6 | −2.6 | ||
| 5 | 7.88 | 1811 | 1561 | −2.6 | ||
| 6 | 21.62 | 3906 | 3337 | −2.5 | ||
| 7 | 47.37 | −5 | 6763 | 5792 | −2.33 | |
| 8 | 45 | 87.18 | −3.8 | 9719 | 8885 | −2.25 |
| 9 | 114 | 140.0 | −3.84 | 14 429 | 12 504 | −2.15 |
| 10 | 201.9 | −2.97 | 17 649 | 15 241 | −1.54 | |
| 11 | 195 | 261.9 | −2.05 | 19 460 | 17 519 | −3.17 |
| 12 | 342 | 480.0 | −3.38 | 29 539 | 26 118 | −2.15 |
| 13 | 255 | 810.2 | −3.65 | 32 465 | −2.03 | |
| 14 | 6706 | 959.2 | 21.3 | 38 781 | −1.98 | |
| 15 | 6665 | 3.83 | 45 247 | −1.89 | ||
| 16 | 1756 | −14.17 | 51 606 | −1.86 | ||
| 17 | 3405 | −5.39 | 57 544 | −1.76 | ||
| 18 | 5880 | −10.61 | 52 187 | 0.15 |
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| |${\boldsymbol{\nu _1}}$| | |${\boldsymbol{2\nu _{4}^{\ell =2}}}$| | |||||
| 4 | 2.10 | 573 | 503.6 | −2.6 | ||
| 5 | 7.88 | 1811 | 1561 | −2.6 | ||
| 6 | 21.62 | 3906 | 3337 | −2.5 | ||
| 7 | 47.37 | −5 | 6763 | 5792 | −2.33 | |
| 8 | 45 | 87.18 | −3.8 | 9719 | 8885 | −2.25 |
| 9 | 114 | 140.0 | −3.84 | 14 429 | 12 504 | −2.15 |
| 10 | 201.9 | −2.97 | 17 649 | 15 241 | −1.54 | |
| 11 | 195 | 261.9 | −2.05 | 19 460 | 17 519 | −3.17 |
| 12 | 342 | 480.0 | −3.38 | 29 539 | 26 118 | −2.15 |
| 13 | 255 | 810.2 | −3.65 | 32 465 | −2.03 | |
| 14 | 6706 | 959.2 | 21.3 | 38 781 | −1.98 | |
| 15 | 6665 | 3.83 | 45 247 | −1.89 | ||
| 16 | 1756 | −14.17 | 51 606 | −1.86 | ||
| 17 | 3405 | −5.39 | 57 544 | −1.76 | ||
| 18 | 5880 | −10.61 | 52 187 | 0.15 |
Calculated and experimental (Ulenikov et al. 2002) k = 3, A1 − A2 splittings (in MHz) and their sensitivities in the ν1 and |$2\nu _4^{\ell =2}$| vibrational states of PH3.
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| |${\boldsymbol{\nu _1}}$| | |${\boldsymbol{2\nu _{4}^{\ell =2}}}$| | |||||
| 4 | 2.10 | 573 | 503.6 | −2.6 | ||
| 5 | 7.88 | 1811 | 1561 | −2.6 | ||
| 6 | 21.62 | 3906 | 3337 | −2.5 | ||
| 7 | 47.37 | −5 | 6763 | 5792 | −2.33 | |
| 8 | 45 | 87.18 | −3.8 | 9719 | 8885 | −2.25 |
| 9 | 114 | 140.0 | −3.84 | 14 429 | 12 504 | −2.15 |
| 10 | 201.9 | −2.97 | 17 649 | 15 241 | −1.54 | |
| 11 | 195 | 261.9 | −2.05 | 19 460 | 17 519 | −3.17 |
| 12 | 342 | 480.0 | −3.38 | 29 539 | 26 118 | −2.15 |
| 13 | 255 | 810.2 | −3.65 | 32 465 | −2.03 | |
| 14 | 6706 | 959.2 | 21.3 | 38 781 | −1.98 | |
| 15 | 6665 | 3.83 | 45 247 | −1.89 | ||
| 16 | 1756 | −14.17 | 51 606 | −1.86 | ||
| 17 | 3405 | −5.39 | 57 544 | −1.76 | ||
| 18 | 5880 | −10.61 | 52 187 | 0.15 |
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| |${\boldsymbol{\nu _1}}$| | |${\boldsymbol{2\nu _{4}^{\ell =2}}}$| | |||||
| 4 | 2.10 | 573 | 503.6 | −2.6 | ||
| 5 | 7.88 | 1811 | 1561 | −2.6 | ||
| 6 | 21.62 | 3906 | 3337 | −2.5 | ||
| 7 | 47.37 | −5 | 6763 | 5792 | −2.33 | |
| 8 | 45 | 87.18 | −3.8 | 9719 | 8885 | −2.25 |
| 9 | 114 | 140.0 | −3.84 | 14 429 | 12 504 | −2.15 |
| 10 | 201.9 | −2.97 | 17 649 | 15 241 | −1.54 | |
| 11 | 195 | 261.9 | −2.05 | 19 460 | 17 519 | −3.17 |
| 12 | 342 | 480.0 | −3.38 | 29 539 | 26 118 | −2.15 |
| 13 | 255 | 810.2 | −3.65 | 32 465 | −2.03 | |
| 14 | 6706 | 959.2 | 21.3 | 38 781 | −1.98 | |
| 15 | 6665 | 3.83 | 45 247 | −1.89 | ||
| 16 | 1756 | −14.17 | 51 606 | −1.86 | ||
| 17 | 3405 | −5.39 | 57 544 | −1.76 | ||
| 18 | 5880 | −10.61 | 52 187 | 0.15 |
Calculated and experimental k = 1 and k = 2, A1 − A2 splittings (in MHz) and their sensitivities in the ν4 vibrational state of PH3.
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| k = 1 | k = 2 | |||||
| 1 | 10 498.9a | 10 429.5 | −1.51 | |||
| 2 | 31 269.7a | 31 058.4 | −1.50 | 30b | 30.16 | |
| 3 | 61 876.0c | 61 444.7 | −1.49 | 150b | 149.12 | −2.51 |
| 4 | 101 889.7d | 101 152 | −1.48 | 438b | 436.62 | −2.37 |
| 5 | 150 200e | 149 480 | −1.47 | 986b | 975.97 | −2.35 |
| 6 | 207 700e | 205 747 | −1.45 | 1850b | 1827.4 | −2.37 |
| 7 | 271 300e | 269 219 | −1.44 | 3034b | 3004.9 | −2.32 |
| 8 | 342 600e | 339 148 | −1.43 | 4521b | 4471.7 | −2.22 |
| 9 | 419 000e | 414 689 | −1.40 | 6175b | 6156.9 | −2.17 |
| 10 | 502 300e | 497 112 | −1.38 | 7989b | 7980.1 | −2.11 |
| 11 | 588 700e | 581 763 | −1.37 | 9875b | 9868.3 | −2.03 |
| 12 | 679 300e | 671 136 | −1.35 | 11 700e | 11 762 | −1.97 |
| 13 | 772 300e | 764 108 | −1.34 | 12 600e | 13 613 | −1.93 |
| 14 | 869 600e | 860 215 | −1.32 | 17 900e | 15 378 | −1.88 |
| 15 | 967 700e | 959 068 | −1.31 | 19 600e | 16 754 | −1.68 |
| 16 | 1060 200 | −1.30 | 12 454 | −4.48 | ||
| 17 | 1162 100 | −1.27 | 18 172 | −1.81 | ||
| 18 | 1273 400 | −1.27 | 19 568 | −1.67 |
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| k = 1 | k = 2 | |||||
| 1 | 10 498.9a | 10 429.5 | −1.51 | |||
| 2 | 31 269.7a | 31 058.4 | −1.50 | 30b | 30.16 | |
| 3 | 61 876.0c | 61 444.7 | −1.49 | 150b | 149.12 | −2.51 |
| 4 | 101 889.7d | 101 152 | −1.48 | 438b | 436.62 | −2.37 |
| 5 | 150 200e | 149 480 | −1.47 | 986b | 975.97 | −2.35 |
| 6 | 207 700e | 205 747 | −1.45 | 1850b | 1827.4 | −2.37 |
| 7 | 271 300e | 269 219 | −1.44 | 3034b | 3004.9 | −2.32 |
| 8 | 342 600e | 339 148 | −1.43 | 4521b | 4471.7 | −2.22 |
| 9 | 419 000e | 414 689 | −1.40 | 6175b | 6156.9 | −2.17 |
| 10 | 502 300e | 497 112 | −1.38 | 7989b | 7980.1 | −2.11 |
| 11 | 588 700e | 581 763 | −1.37 | 9875b | 9868.3 | −2.03 |
| 12 | 679 300e | 671 136 | −1.35 | 11 700e | 11 762 | −1.97 |
| 13 | 772 300e | 764 108 | −1.34 | 12 600e | 13 613 | −1.93 |
| 14 | 869 600e | 860 215 | −1.32 | 17 900e | 15 378 | −1.88 |
| 15 | 967 700e | 959 068 | −1.31 | 19 600e | 16 754 | −1.68 |
| 16 | 1060 200 | −1.30 | 12 454 | −4.48 | ||
| 17 | 1162 100 | −1.27 | 18 172 | −1.81 | ||
| 18 | 1273 400 | −1.27 | 19 568 | −1.67 |
Calculated and experimental k = 1 and k = 2, A1 − A2 splittings (in MHz) and their sensitivities in the ν4 vibrational state of PH3.
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| k = 1 | k = 2 | |||||
| 1 | 10 498.9a | 10 429.5 | −1.51 | |||
| 2 | 31 269.7a | 31 058.4 | −1.50 | 30b | 30.16 | |
| 3 | 61 876.0c | 61 444.7 | −1.49 | 150b | 149.12 | −2.51 |
| 4 | 101 889.7d | 101 152 | −1.48 | 438b | 436.62 | −2.37 |
| 5 | 150 200e | 149 480 | −1.47 | 986b | 975.97 | −2.35 |
| 6 | 207 700e | 205 747 | −1.45 | 1850b | 1827.4 | −2.37 |
| 7 | 271 300e | 269 219 | −1.44 | 3034b | 3004.9 | −2.32 |
| 8 | 342 600e | 339 148 | −1.43 | 4521b | 4471.7 | −2.22 |
| 9 | 419 000e | 414 689 | −1.40 | 6175b | 6156.9 | −2.17 |
| 10 | 502 300e | 497 112 | −1.38 | 7989b | 7980.1 | −2.11 |
| 11 | 588 700e | 581 763 | −1.37 | 9875b | 9868.3 | −2.03 |
| 12 | 679 300e | 671 136 | −1.35 | 11 700e | 11 762 | −1.97 |
| 13 | 772 300e | 764 108 | −1.34 | 12 600e | 13 613 | −1.93 |
| 14 | 869 600e | 860 215 | −1.32 | 17 900e | 15 378 | −1.88 |
| 15 | 967 700e | 959 068 | −1.31 | 19 600e | 16 754 | −1.68 |
| 16 | 1060 200 | −1.30 | 12 454 | −4.48 | ||
| 17 | 1162 100 | −1.27 | 18 172 | −1.81 | ||
| 18 | 1273 400 | −1.27 | 19 568 | −1.67 |
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| k = 1 | k = 2 | |||||
| 1 | 10 498.9a | 10 429.5 | −1.51 | |||
| 2 | 31 269.7a | 31 058.4 | −1.50 | 30b | 30.16 | |
| 3 | 61 876.0c | 61 444.7 | −1.49 | 150b | 149.12 | −2.51 |
| 4 | 101 889.7d | 101 152 | −1.48 | 438b | 436.62 | −2.37 |
| 5 | 150 200e | 149 480 | −1.47 | 986b | 975.97 | −2.35 |
| 6 | 207 700e | 205 747 | −1.45 | 1850b | 1827.4 | −2.37 |
| 7 | 271 300e | 269 219 | −1.44 | 3034b | 3004.9 | −2.32 |
| 8 | 342 600e | 339 148 | −1.43 | 4521b | 4471.7 | −2.22 |
| 9 | 419 000e | 414 689 | −1.40 | 6175b | 6156.9 | −2.17 |
| 10 | 502 300e | 497 112 | −1.38 | 7989b | 7980.1 | −2.11 |
| 11 | 588 700e | 581 763 | −1.37 | 9875b | 9868.3 | −2.03 |
| 12 | 679 300e | 671 136 | −1.35 | 11 700e | 11 762 | −1.97 |
| 13 | 772 300e | 764 108 | −1.34 | 12 600e | 13 613 | −1.93 |
| 14 | 869 600e | 860 215 | −1.32 | 17 900e | 15 378 | −1.88 |
| 15 | 967 700e | 959 068 | −1.31 | 19 600e | 16 754 | −1.68 |
| 16 | 1060 200 | −1.30 | 12 454 | −4.48 | ||
| 17 | 1162 100 | −1.27 | 18 172 | −1.81 | ||
| 18 | 1273 400 | −1.27 | 19 568 | −1.67 |
Calculated and experimental (Ulenikov et al. 2002) k = 1 and k = 2, A1 − A2 splittings (in MHz) and their sensitivities in the ν3 vibrational state of PH3.
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| k = 1 | k = 2 | |||||
| 1 | 333 | 533 | −1.57 | |||
| 2 | 1004 | 1596 | −1.45 | 54 | 59.48 | −3.7 |
| 3 | 2015 | 3177 | −1.46 | 288 | 293.89 | −3.4 |
| 4 | 3385 | 5256 | −1.45 | 914 | 864.93 | −3.22 |
| 5 | 5081 | 7788 | −1.46 | 2078 | 1959.3 | −3.13 |
| 6 | 7069 | 10 686 | −1.44 | 3990 | 3747.7 | −3.08 |
| 7 | 9156 | 13 763 | −1.38 | 6799 | 6301.6 | −2.96 |
| 8 | 11 368 | 16 604 | −1.20 | 10 460 | 9453.3 | −2.75 |
| 9 | 12 825 | 18 371 | −0.79 | 14 558 | 12 583 | −2.36 |
| 10 | 12 894 | 37 630 | −0.72 | 18 386 | 34 468 | −1.61 |
| 11 | 10 736 | 41 212 | −0.86 | 21 441 | 42 221 | −1.95 |
| 12 | 39 033 | 45 466 | −0.84 | 56 796 | 52 692 | −2.17 |
| 13 | 44 078 | 49 330 | −0.61 | 71 518 | 66 005 | −2.41 |
| 14 | 49 924 | 51 045 | 0.08 | 83 884 | −2.99 | |
| 15 | 51 214 | 48 059 | 0.58 | 224 180 | 1.45 | |
| 16 | 34 359 | −32.8 | 73 345 | −7.15 | ||
| 17 | 128 720 | 3.81 | 86 681 | 5.34 | ||
| 18 | 128 190 | −1.23 | 110 930 | −3.44 |
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| k = 1 | k = 2 | |||||
| 1 | 333 | 533 | −1.57 | |||
| 2 | 1004 | 1596 | −1.45 | 54 | 59.48 | −3.7 |
| 3 | 2015 | 3177 | −1.46 | 288 | 293.89 | −3.4 |
| 4 | 3385 | 5256 | −1.45 | 914 | 864.93 | −3.22 |
| 5 | 5081 | 7788 | −1.46 | 2078 | 1959.3 | −3.13 |
| 6 | 7069 | 10 686 | −1.44 | 3990 | 3747.7 | −3.08 |
| 7 | 9156 | 13 763 | −1.38 | 6799 | 6301.6 | −2.96 |
| 8 | 11 368 | 16 604 | −1.20 | 10 460 | 9453.3 | −2.75 |
| 9 | 12 825 | 18 371 | −0.79 | 14 558 | 12 583 | −2.36 |
| 10 | 12 894 | 37 630 | −0.72 | 18 386 | 34 468 | −1.61 |
| 11 | 10 736 | 41 212 | −0.86 | 21 441 | 42 221 | −1.95 |
| 12 | 39 033 | 45 466 | −0.84 | 56 796 | 52 692 | −2.17 |
| 13 | 44 078 | 49 330 | −0.61 | 71 518 | 66 005 | −2.41 |
| 14 | 49 924 | 51 045 | 0.08 | 83 884 | −2.99 | |
| 15 | 51 214 | 48 059 | 0.58 | 224 180 | 1.45 | |
| 16 | 34 359 | −32.8 | 73 345 | −7.15 | ||
| 17 | 128 720 | 3.81 | 86 681 | 5.34 | ||
| 18 | 128 190 | −1.23 | 110 930 | −3.44 |
Calculated and experimental (Ulenikov et al. 2002) k = 1 and k = 2, A1 − A2 splittings (in MHz) and their sensitivities in the ν3 vibrational state of PH3.
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| k = 1 | k = 2 | |||||
| 1 | 333 | 533 | −1.57 | |||
| 2 | 1004 | 1596 | −1.45 | 54 | 59.48 | −3.7 |
| 3 | 2015 | 3177 | −1.46 | 288 | 293.89 | −3.4 |
| 4 | 3385 | 5256 | −1.45 | 914 | 864.93 | −3.22 |
| 5 | 5081 | 7788 | −1.46 | 2078 | 1959.3 | −3.13 |
| 6 | 7069 | 10 686 | −1.44 | 3990 | 3747.7 | −3.08 |
| 7 | 9156 | 13 763 | −1.38 | 6799 | 6301.6 | −2.96 |
| 8 | 11 368 | 16 604 | −1.20 | 10 460 | 9453.3 | −2.75 |
| 9 | 12 825 | 18 371 | −0.79 | 14 558 | 12 583 | −2.36 |
| 10 | 12 894 | 37 630 | −0.72 | 18 386 | 34 468 | −1.61 |
| 11 | 10 736 | 41 212 | −0.86 | 21 441 | 42 221 | −1.95 |
| 12 | 39 033 | 45 466 | −0.84 | 56 796 | 52 692 | −2.17 |
| 13 | 44 078 | 49 330 | −0.61 | 71 518 | 66 005 | −2.41 |
| 14 | 49 924 | 51 045 | 0.08 | 83 884 | −2.99 | |
| 15 | 51 214 | 48 059 | 0.58 | 224 180 | 1.45 | |
| 16 | 34 359 | −32.8 | 73 345 | −7.15 | ||
| 17 | 128 720 | 3.81 | 86 681 | 5.34 | ||
| 18 | 128 190 | −1.23 | 110 930 | −3.44 |
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| k = 1 | k = 2 | |||||
| 1 | 333 | 533 | −1.57 | |||
| 2 | 1004 | 1596 | −1.45 | 54 | 59.48 | −3.7 |
| 3 | 2015 | 3177 | −1.46 | 288 | 293.89 | −3.4 |
| 4 | 3385 | 5256 | −1.45 | 914 | 864.93 | −3.22 |
| 5 | 5081 | 7788 | −1.46 | 2078 | 1959.3 | −3.13 |
| 6 | 7069 | 10 686 | −1.44 | 3990 | 3747.7 | −3.08 |
| 7 | 9156 | 13 763 | −1.38 | 6799 | 6301.6 | −2.96 |
| 8 | 11 368 | 16 604 | −1.20 | 10 460 | 9453.3 | −2.75 |
| 9 | 12 825 | 18 371 | −0.79 | 14 558 | 12 583 | −2.36 |
| 10 | 12 894 | 37 630 | −0.72 | 18 386 | 34 468 | −1.61 |
| 11 | 10 736 | 41 212 | −0.86 | 21 441 | 42 221 | −1.95 |
| 12 | 39 033 | 45 466 | −0.84 | 56 796 | 52 692 | −2.17 |
| 13 | 44 078 | 49 330 | −0.61 | 71 518 | 66 005 | −2.41 |
| 14 | 49 924 | 51 045 | 0.08 | 83 884 | −2.99 | |
| 15 | 51 214 | 48 059 | 0.58 | 224 180 | 1.45 | |
| 16 | 34 359 | −32.8 | 73 345 | −7.15 | ||
| 17 | 128 720 | 3.81 | 86 681 | 5.34 | ||
| 18 | 128 190 | −1.23 | 110 930 | −3.44 |
Calculated and experimental (Ulenikov et al. 2002) k = 4 and k = 5, A1 − A2 splittings (in MHz) and their sensitivities in the ν3 vibrational state of PH3.
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| k = 4 | k = 5 | |||||
| 8 | 97.79 | −2.94 | ||||
| 9 | 295.8 | −2.70 | ||||
| 10 | 563 | 889.3 | −2.81 | 135.1 | −2.87 | |
| 11 | 2215 | 2988 | −2.36 | 186 | 267.1 | −2.81 |
| 12 | 5546 | 35905 | −2.45 | 216 | 278.9 | 2.02 |
| 13 | 3439 | 6242 | −2.91 | 306 | 16.1 | 461 |
| 14 | 3663 | 6172 | −5.8 | 6171 | −25.50 | |
| 15 | 6098 | −5.4 | 15175 | 18.1 |
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| k = 4 | k = 5 | |||||
| 8 | 97.79 | −2.94 | ||||
| 9 | 295.8 | −2.70 | ||||
| 10 | 563 | 889.3 | −2.81 | 135.1 | −2.87 | |
| 11 | 2215 | 2988 | −2.36 | 186 | 267.1 | −2.81 |
| 12 | 5546 | 35905 | −2.45 | 216 | 278.9 | 2.02 |
| 13 | 3439 | 6242 | −2.91 | 306 | 16.1 | 461 |
| 14 | 3663 | 6172 | −5.8 | 6171 | −25.50 | |
| 15 | 6098 | −5.4 | 15175 | 18.1 |
Calculated and experimental (Ulenikov et al. 2002) k = 4 and k = 5, A1 − A2 splittings (in MHz) and their sensitivities in the ν3 vibrational state of PH3.
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| k = 4 | k = 5 | |||||
| 8 | 97.79 | −2.94 | ||||
| 9 | 295.8 | −2.70 | ||||
| 10 | 563 | 889.3 | −2.81 | 135.1 | −2.87 | |
| 11 | 2215 | 2988 | −2.36 | 186 | 267.1 | −2.81 |
| 12 | 5546 | 35905 | −2.45 | 216 | 278.9 | 2.02 |
| 13 | 3439 | 6242 | −2.91 | 306 | 16.1 | 461 |
| 14 | 3663 | 6172 | −5.8 | 6171 | −25.50 | |
| 15 | 6098 | −5.4 | 15175 | 18.1 |
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| k = 4 | k = 5 | |||||
| 8 | 97.79 | −2.94 | ||||
| 9 | 295.8 | −2.70 | ||||
| 10 | 563 | 889.3 | −2.81 | 135.1 | −2.87 | |
| 11 | 2215 | 2988 | −2.36 | 186 | 267.1 | −2.81 |
| 12 | 5546 | 35905 | −2.45 | 216 | 278.9 | 2.02 |
| 13 | 3439 | 6242 | −2.91 | 306 | 16.1 | 461 |
| 14 | 3663 | 6172 | −5.8 | 6171 | −25.50 | |
| 15 | 6098 | −5.4 | 15175 | 18.1 |
Calculated and experimental k = 4 and k = 7, A1 − A2 splittings (in MHz) and their sensitivities in the ν4 vibrational state of PH3.
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| k = 4 | k = 7 | |||||
| 5 | 582a | 582.08 | −2.08 | |||
| 6 | 1292a | 1310.2 | −2.18 | |||
| 7 | 2278a | 2418.6 | −2.13 | |||
| 8 | 3897a | 3916.4 | −2.15 | |||
| 9 | 5762a | 5788.4 | −2.11 | 210b | 211.7 | −5.25 |
| 10 | 7971a | 8019.5 | −2.08 | 1190b | 1363.3 | 1.04 |
| 11 | 10 530a | 10 610 | −2.07 | 618b | 646.3 | −2.09 |
| 12 | 13 730a | 13 580 | −2.06 | 651b | 671.4 | −2.33 |
| 13 | 16 793a | 16 966 | −2.06 | 767b | 796.7 | −2.54 |
| 14 | 20 686a | 20 821 | −2.08 | 959b | 987.3 | −2.67 |
| 15 | 23 800c | 25 211 | −2.09 | 1157b | 1246.5 | −2.71 |
| 16 | 30 209 | −2.10 | 1589.1 | −2.84 | ||
| 17 | 35 900 | −2.12 | 2038.3 | −2.87 | ||
| 18 | 42 378 | −2.15 | 2625.3 | −2.94 |
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| k = 4 | k = 7 | |||||
| 5 | 582a | 582.08 | −2.08 | |||
| 6 | 1292a | 1310.2 | −2.18 | |||
| 7 | 2278a | 2418.6 | −2.13 | |||
| 8 | 3897a | 3916.4 | −2.15 | |||
| 9 | 5762a | 5788.4 | −2.11 | 210b | 211.7 | −5.25 |
| 10 | 7971a | 8019.5 | −2.08 | 1190b | 1363.3 | 1.04 |
| 11 | 10 530a | 10 610 | −2.07 | 618b | 646.3 | −2.09 |
| 12 | 13 730a | 13 580 | −2.06 | 651b | 671.4 | −2.33 |
| 13 | 16 793a | 16 966 | −2.06 | 767b | 796.7 | −2.54 |
| 14 | 20 686a | 20 821 | −2.08 | 959b | 987.3 | −2.67 |
| 15 | 23 800c | 25 211 | −2.09 | 1157b | 1246.5 | −2.71 |
| 16 | 30 209 | −2.10 | 1589.1 | −2.84 | ||
| 17 | 35 900 | −2.12 | 2038.3 | −2.87 | ||
| 18 | 42 378 | −2.15 | 2625.3 | −2.94 |
Calculated and experimental k = 4 and k = 7, A1 − A2 splittings (in MHz) and their sensitivities in the ν4 vibrational state of PH3.
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| k = 4 | k = 7 | |||||
| 5 | 582a | 582.08 | −2.08 | |||
| 6 | 1292a | 1310.2 | −2.18 | |||
| 7 | 2278a | 2418.6 | −2.13 | |||
| 8 | 3897a | 3916.4 | −2.15 | |||
| 9 | 5762a | 5788.4 | −2.11 | 210b | 211.7 | −5.25 |
| 10 | 7971a | 8019.5 | −2.08 | 1190b | 1363.3 | 1.04 |
| 11 | 10 530a | 10 610 | −2.07 | 618b | 646.3 | −2.09 |
| 12 | 13 730a | 13 580 | −2.06 | 651b | 671.4 | −2.33 |
| 13 | 16 793a | 16 966 | −2.06 | 767b | 796.7 | −2.54 |
| 14 | 20 686a | 20 821 | −2.08 | 959b | 987.3 | −2.67 |
| 15 | 23 800c | 25 211 | −2.09 | 1157b | 1246.5 | −2.71 |
| 16 | 30 209 | −2.10 | 1589.1 | −2.84 | ||
| 17 | 35 900 | −2.12 | 2038.3 | −2.87 | ||
| 18 | 42 378 | −2.15 | 2625.3 | −2.94 |
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| k = 4 | k = 7 | |||||
| 5 | 582a | 582.08 | −2.08 | |||
| 6 | 1292a | 1310.2 | −2.18 | |||
| 7 | 2278a | 2418.6 | −2.13 | |||
| 8 | 3897a | 3916.4 | −2.15 | |||
| 9 | 5762a | 5788.4 | −2.11 | 210b | 211.7 | −5.25 |
| 10 | 7971a | 8019.5 | −2.08 | 1190b | 1363.3 | 1.04 |
| 11 | 10 530a | 10 610 | −2.07 | 618b | 646.3 | −2.09 |
| 12 | 13 730a | 13 580 | −2.06 | 651b | 671.4 | −2.33 |
| 13 | 16 793a | 16 966 | −2.06 | 767b | 796.7 | −2.54 |
| 14 | 20 686a | 20 821 | −2.08 | 959b | 987.3 | −2.67 |
| 15 | 23 800c | 25 211 | −2.09 | 1157b | 1246.5 | −2.71 |
| 16 | 30 209 | −2.10 | 1589.1 | −2.84 | ||
| 17 | 35 900 | −2.12 | 2038.3 | −2.87 | ||
| 18 | 42 378 | −2.15 | 2625.3 | −2.94 |
Calculated and experimental (Ulenikov et al. 2002) k = 7 and k = 8, A1 − A2 splittings (in MHz) and their sensitivities in the ν3 vibrational state of PH3.
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| k = 7 | k = 8 | |||||
| 12 | 30.55 | −64 | 1340 | 743.7 | −91 | |
| 13 | 1260170 | 1.44 | 18210 | 34 | ||
| 14 | 1817 | 8766 | 0.21 | 3136 | 10565 | −4.91 |
| 15 | 2585.5 | 27.6 | 1344.4 | −22.3 | ||
| 16 | 807.4 | −1.11 | 1370.2 | 11.7 | ||
| 17 | 1485.1 | −22.9 | 5056.4 | −16.8 | ||
| 18 | 1315.0 | −417 | 73.0 | −3.1 |
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| k = 7 | k = 8 | |||||
| 12 | 30.55 | −64 | 1340 | 743.7 | −91 | |
| 13 | 1260170 | 1.44 | 18210 | 34 | ||
| 14 | 1817 | 8766 | 0.21 | 3136 | 10565 | −4.91 |
| 15 | 2585.5 | 27.6 | 1344.4 | −22.3 | ||
| 16 | 807.4 | −1.11 | 1370.2 | 11.7 | ||
| 17 | 1485.1 | −22.9 | 5056.4 | −16.8 | ||
| 18 | 1315.0 | −417 | 73.0 | −3.1 |
Calculated and experimental (Ulenikov et al. 2002) k = 7 and k = 8, A1 − A2 splittings (in MHz) and their sensitivities in the ν3 vibrational state of PH3.
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| k = 7 | k = 8 | |||||
| 12 | 30.55 | −64 | 1340 | 743.7 | −91 | |
| 13 | 1260170 | 1.44 | 18210 | 34 | ||
| 14 | 1817 | 8766 | 0.21 | 3136 | 10565 | −4.91 |
| 15 | 2585.5 | 27.6 | 1344.4 | −22.3 | ||
| 16 | 807.4 | −1.11 | 1370.2 | 11.7 | ||
| 17 | 1485.1 | −22.9 | 5056.4 | −16.8 | ||
| 18 | 1315.0 | −417 | 73.0 | −3.1 |
| J . | νexp . | νcalc . | T . | νexp . | νcalc . | T . |
|---|---|---|---|---|---|---|
| k = 7 | k = 8 | |||||
| 12 | 30.55 | −64 | 1340 | 743.7 | −91 | |
| 13 | 1260170 | 1.44 | 18210 | 34 | ||
| 14 | 1817 | 8766 | 0.21 | 3136 | 10565 | −4.91 |
| 15 | 2585.5 | 27.6 | 1344.4 | −22.3 | ||
| 16 | 807.4 | −1.11 | 1370.2 | 11.7 | ||
| 17 | 1485.1 | −22.9 | 5056.4 | −16.8 | ||
| 18 | 1315.0 | −417 | 73.0 | −3.1 |
Calculated and experimental (Ulenikov et al. 2002) k = 1, A1 − A2 splittings (in MHz) and their sensitivities in the |$2\nu _4^{\ell =2}$| vibrational state of PH3. The splitting |$\nu =\Delta E_{A_1/A_2}=(E_{A_2}-E_{A_1}\cdot (-1)^J)$|. The sensitivity Texp is obtained using the frequencies from Ulenikov et al. (2002) instead of the computed values.
| J . | νcalc . | Tcalc . | νexp . | Texp . |
|---|---|---|---|---|
| 1 | 221.7055 | −2.5 | 216.7499 | −2.6 |
| 2 | 592.9445 | −2.3 | 573.2032 | −2.4 |
| 3 | 653.0709 | −1.8 | 604.0818 | −1.9 |
| 4 | 286.2628 | −0.6 | 220.3475 | −0.7 |
| 5 | 48.8692 | 1.7 | −62.0570 | 1.4 |
| 6 | 31.0615 | −4.3 | −115.4201 | −1.2 |
| 7 | 150.8825 | −3.8 | −23.3838 | −24.4 |
| 8 | 370.1448 | −3.1 | 160.3890 | −7.2 |
| 9 | 656.5515 | −2.7 | 413.1140 | −4.2 |
| 10 | 964.8880 | −2.3 | 757.2757 | −3.0 |
| 11 | 1240.5502 | −2.0 | 1072.9572 | −2.3 |
| 12 | 1432.5733 | −1.5 | 1087.6470 | −1.9 |
| 13 | 1495.6166 | −3.1 | 1141.3099 | −4.1 |
| J . | νcalc . | Tcalc . | νexp . | Texp . |
|---|---|---|---|---|
| 1 | 221.7055 | −2.5 | 216.7499 | −2.6 |
| 2 | 592.9445 | −2.3 | 573.2032 | −2.4 |
| 3 | 653.0709 | −1.8 | 604.0818 | −1.9 |
| 4 | 286.2628 | −0.6 | 220.3475 | −0.7 |
| 5 | 48.8692 | 1.7 | −62.0570 | 1.4 |
| 6 | 31.0615 | −4.3 | −115.4201 | −1.2 |
| 7 | 150.8825 | −3.8 | −23.3838 | −24.4 |
| 8 | 370.1448 | −3.1 | 160.3890 | −7.2 |
| 9 | 656.5515 | −2.7 | 413.1140 | −4.2 |
| 10 | 964.8880 | −2.3 | 757.2757 | −3.0 |
| 11 | 1240.5502 | −2.0 | 1072.9572 | −2.3 |
| 12 | 1432.5733 | −1.5 | 1087.6470 | −1.9 |
| 13 | 1495.6166 | −3.1 | 1141.3099 | −4.1 |
Calculated and experimental (Ulenikov et al. 2002) k = 1, A1 − A2 splittings (in MHz) and their sensitivities in the |$2\nu _4^{\ell =2}$| vibrational state of PH3. The splitting |$\nu =\Delta E_{A_1/A_2}=(E_{A_2}-E_{A_1}\cdot (-1)^J)$|. The sensitivity Texp is obtained using the frequencies from Ulenikov et al. (2002) instead of the computed values.
| J . | νcalc . | Tcalc . | νexp . | Texp . |
|---|---|---|---|---|
| 1 | 221.7055 | −2.5 | 216.7499 | −2.6 |
| 2 | 592.9445 | −2.3 | 573.2032 | −2.4 |
| 3 | 653.0709 | −1.8 | 604.0818 | −1.9 |
| 4 | 286.2628 | −0.6 | 220.3475 | −0.7 |
| 5 | 48.8692 | 1.7 | −62.0570 | 1.4 |
| 6 | 31.0615 | −4.3 | −115.4201 | −1.2 |
| 7 | 150.8825 | −3.8 | −23.3838 | −24.4 |
| 8 | 370.1448 | −3.1 | 160.3890 | −7.2 |
| 9 | 656.5515 | −2.7 | 413.1140 | −4.2 |
| 10 | 964.8880 | −2.3 | 757.2757 | −3.0 |
| 11 | 1240.5502 | −2.0 | 1072.9572 | −2.3 |
| 12 | 1432.5733 | −1.5 | 1087.6470 | −1.9 |
| 13 | 1495.6166 | −3.1 | 1141.3099 | −4.1 |
| J . | νcalc . | Tcalc . | νexp . | Texp . |
|---|---|---|---|---|
| 1 | 221.7055 | −2.5 | 216.7499 | −2.6 |
| 2 | 592.9445 | −2.3 | 573.2032 | −2.4 |
| 3 | 653.0709 | −1.8 | 604.0818 | −1.9 |
| 4 | 286.2628 | −0.6 | 220.3475 | −0.7 |
| 5 | 48.8692 | 1.7 | −62.0570 | 1.4 |
| 6 | 31.0615 | −4.3 | −115.4201 | −1.2 |
| 7 | 150.8825 | −3.8 | −23.3838 | −24.4 |
| 8 | 370.1448 | −3.1 | 160.3890 | −7.2 |
| 9 | 656.5515 | −2.7 | 413.1140 | −4.2 |
| 10 | 964.8880 | −2.3 | 757.2757 | −3.0 |
| 11 | 1240.5502 | −2.0 | 1072.9572 | −2.3 |
| 12 | 1432.5733 | −1.5 | 1087.6470 | −1.9 |
| 13 | 1495.6166 | −3.1 | 1141.3099 | −4.1 |
A detailed study of the A1 − A2 splittings in the |$2\nu _4^{\ell =2}$| state was presented by Ulenikov et al. (2002) where it was shown that the dependence of the splitting on J in the K = 1 rotational sub-levels was anomalous between J = 3–8. This anomaly is caused by an interaction with the closely lying |$2\nu _4^{\ell =0}$| state (K = 0). In Fig. 5 and Table 9, we show the A1 − A2 splittings in the |$2\nu _4^{\ell =2}$| state and corresponding sensitivity coefficients with respect to J. Aside from the J = 7 sensitivity coefficient, which greatly increases when using the experimental frequency value, there is good agreement with the work of Ulenikov et al. (2002) and the sensitivities are highly anomalous.
It should be stated that for very energetically close coinciding states, our variational approach may not be capable of a truly quantitative description. This is the reason why sensitivities have not been computed for certain extremely small A1 − A2 splittings. Also, where computed frequencies noticeably differ from the experimental values the resultant sensitivities should only be regarded as illustrative, for example, in Table 8. We have encountered this problem before (Owens et al. 2016) and whilst the underlying numerical derivatives are relatively stable, it is safer to regard the predicted sensitivity coefficients with caution. Despite this, a large number of the computed A1 − A2 splittings are in good agreement with experiment and, more importantly, reside in the radio frequency region.
4 CONCLUSION
The sensitivity of the rotation–vibration spectrum of PH3 to a possible variation of μ has been probed using an accurate variational approach. Calculations utilized the nuclear motion program trove in conjunction with an established empirically refined PES and ab initio DMS. The low-lying vibrational states were studied as they play an important role in phosphine excitation in the carbon star envelope IRC +10216. Whilst the majority of computed sensitivity coefficients assumed their expected values, anomalous sensitivities were displayed by the A1 − A2 splittings in the ν2/ν4, ν1/ν3 and |$2\nu _4^{\ell =0}/2\nu _4^{\ell =2}$| manifolds. This behaviour arises due to strong Coriolis interactions between states and may be present in other molecules with |$\boldsymbol {C}_{3\mathrm{v}}\mathrm{(M)}$| symmetry. The fact that molecules with highly sensitive transitions such as ammonia are already being used in advanced terrestrial experiments (Cheng et al. 2016) suggests that PH3 may not be a primary candidate for constraining μ in laboratory studies. Its merit as a probe for a drifting constant is more likely to be in cosmological settings as it is a relevant astrophysical molecule with a well-documented spectrum and a negligible hyperfine splitting (Müller 2013). However, it is hard to comment on the necessary conditions for its detection since its presence and formation are not well understood (see the discussion by Sousa-Silva et al. 2015 and references therein). Despite this, PH3 as a model system shows that the splittings caused by higher-order rotation–vibration interactions, which are essentially low-frequency transitions that can be measured using radio telescopes, have real potential for investigating a possible variation of μ.
ACKNOWLEDGEMENTS
AO acknowledges support from the Deutsche Forschungsgemeinschaft (DFG) through the excellence cluster ‘The Hamburg Center for Ultrafast Imaging - Structure, Dynamics and Control of Matter at the Atomic Scale’ (CUI, EXC1074). SY acknowledges support from the COST action MOLIM No. CM1405. VS acknowledges the research project RVO:61388963 (IOCB) and support from the Czech Science Foundation (grant P209/15-10267S).
REFERENCES




