-
PDF
- Split View
-
Views
-
Cite
Cite
De-Hua Wang, Cheng-Min Zhang, Jin-Lu Qu, Yi-Yan Yang, Correlations between the frequencies of twin kHz QPOs and spins of neutron stars in LMXBs, Monthly Notices of the Royal Astronomical Society, Volume 473, Issue 4, February 2018, Pages 4862–4867, https://doi.org/10.1093/mnras/stx2578
Close - Share Icon Share
Abstract
We investigate the correlation between the frequencies of twin kilohertz quasi-periodic oscillations (kHz QPOs) and neutron star (NS) spins in low-mass X-ray binaries (LMXBs), based on the data sets of 12 sources with simultaneously detected twin kHz QPOs and NS spins, and find that the histogram of the ratio between the frequency difference of twin kHz QPOs (Δν ≡ ν2 − ν1) and NS spin νs shows a non-uniform distribution with a gap at Δν/νs ∼ 0.65. We try to classify the 12 sources into two categories according to this gap: (I) slow rotators with 〈νs〉 ∼ 311 Hz, XTE J1807.4−294, 4U 1915−05, IGR J17191−2821, 4U 1702−43, 4U 1728−34 and 4U 0614+09 follow a relation Δν/νs > 0.65; (II) fast rotators with 〈νs〉 ∼ 546 Hz, SAX J1808.4−3658, KS 1731−260, Aql X−1, 4U 1636−53, SAX J1750.8−2900 and 4U 1608−52 satisfy the relation Δν/νs < 0.65. However, the linear fittings of Δν versus νs relations of groups (I) and (II) are unsatisfactory to ensure any certain correlations. We suggest that this phenomenon may arise from the fact that most measured kHz QPOs and spins satisfy the conditions of 1.1 νs ≤ ν2 < 1300 Hz and Δν decreasing with ν2. Apparently, the diversified distribution of Δν/νs refutes the simple beat-frequency model, and the statistical correlations between the twin kHz QPOs and NS spins may arise from the magnetosphere–disc boundary environments, e.g. co-rotation radius and NS radius, that modulate the occurrences of X-ray signals. Furthermore, we also find a distribution of the ratio of ν2 to ν1 clusters around the value of 〈ν2/ν1〉 ∼ 3: 2, which shows no obvious correlation with NS spins.
1 INTRODUCTION
The launch of the Rossi X-ray Timing Explorer (RXTE) has led to the discovery of kilohertz quasi-periodic oscillations (kHz QPOs) in neutron star low-mass X-ray binaries (NS-LMXBs) (Strohmayer et al. 1996; van der Klis et al. 1996). The frequencies of these QPOs cover a range from ∼100 Hz to ∼1300 Hz (van der Klis 2000, 2006) and correlate with other timing and spectral features (Wijnands et al. 1997a,b; Homan et al. 2002; Ford & van der Klis 1998; Kaaret et al. 1998; Méndez et al. 1999; Ford et al. 2000; Psaltis, Belloni & van der Klis 1999; Belloni, Psaltis & van der Klis 2002). These high-frequency QPOs usually appear in pairs (upper ν2 and lower ν1), with the frequencies showing a nonlinear relation (Belloni, Méndez & Homan 2005; Zhang et al. 2006a; Belloni, Méndez & Homan 2007); so far over 20 LMXBs have shown twin kHz QPOs in accreting millisecond X-ray pulsars (AMXP), atoll and Z sources (Hasinger & van der Klis 1989; van der Klis 2000, 2006; Wang et al. 2014).
It is believed that twin kHz QPOs may reflect the matter motion around the inner accretion disc dozens of kilometres away from the neutron star (Kluźniak, Michelson & Wagoner 1990; van der Klis 2000 and references therein; Zhang & Wang 2013; Wang et al. 2015, 2017), which can be used to probe the strong gravitational field and the strong magnetic field around the neutron star, and to constrain the NS mass–radius relation (Kluźniak et al. 1990; van der Klis 2006; Wang et al. 2013; Miller & Miller 2015). Although several theoretical interpretations have been proposed, such as relativistic precession (Stella & Vietri 1999; Stella, Vietri & Morsink 1999; Török et al. 2016), a magnetohydrodynamic wave (Zhang 2004) or nonlinear resonance (Kluźniak & Abramowicz 2001; Abramowicz et al. 2003a,b) within an accretion disc and sonic-point beat frequency (SPBF) (Miller, Lamb & Psaltis 1998; Lamb & Miller 2001), there is currently no consensus as to the origin of kHz QPOs.
The sonic-point beat-frequency model interprets the frequency separation of twin kHz QPOs as being close to the NS spin (Miller et al. 1998; Lamb & Miller 2001). However, the following observations show that the averaged peak separations are found to be either close to the spin frequency or to its half (Lamb & Miller 2001; Wijnands et al. 2003; van der Klis 2006). In addition, the resonance model also suggests the frequency of kHz QPOs to be related to the NS spin (Lee, Abramowicz & Kluźniak 2004). Thanks to the high timing revolution of RXTE, there are ∼30 NS-LMXBs with observed NS spin signals (Burderi & Di Salvo 2013; van der Klis 2016), in which some sources have even been observed as NS-spin derivative (e.g. Burderi et al. 2006); 12 sources have also been detected for twin kHz QPOs, making it possible to further analyse the correlation between the frequencies of twin kHz QPOs and NS spins.
The goal of this paper is to analyse the frequency correlation between the twin kHz QPOs and NS spins; its structure is organized as follows. In Section 2, we introduce the data on simultaneously detected twin kHz QPOs and NS spins of the 12 sources used in the analysis, and their correlations are studied and investigated in Section 3. Finally, we present the discussion and conclusions in Section 4.
2 THE PUBLISHED SAMPLES OF THE SIMULTANEOUSLY DETECTED TWIN KHZ QPO AND NS SPIN FREQUENCIES
We focus on the 12 NS-LMXBs for which twin kHz QPOs and NS spins have been simultaneously detected, and collect the data for these QPO and spin frequencies from the published literature. The samples contain 26 pairs of twin kHz QPOs from two accreting millisecond X-ray pulsars (XTE J1807.4−294 and SAX J1808.4−3658), and 177 ones from 10 atoll sources. The NS spin frequencies of the 12 sources are inferred from either the periodic or nearly periodic X-ray burst oscillations (van der Klis 2006; Boutloukos & Lamb 2008).
The frequency ranges of the twin kHz QPOs from the 12 NS-LMXBs are reported in Table 1, from which it can be seen that the lower kHz QPOs show a frequency range of ν1 ∼ 106–979 Hz, while the upper kHz QPOs show a frequency range of ν2 ∼ 337–1253 Hz. Table 1 also shows the NS spin frequencies of the 12 sources, with a range of νs ∼ 191–619 Hz and an average value of ∼428 Hz. It is also noticed from Table 1 that XTE J1807.4−294 shows relatively lower frequencies for the twin kHz QPOs and NS spin than other sources, i.e. ν1 ∼ 106–370 Hz, ν2 ∼ 337–587 Hz and νs ∼ 191 Hz, respectively.
| Source (12)a . | ν1b . | ν2c . | νsd . | Δνe . | 〈Δν〉f . | Δν/νs . | ν2/ν1 . | Referencesg . |
|---|---|---|---|---|---|---|---|---|
| . | (Hz) . | (Hz) . | (Hz) . | (Hz) . | (Hz) . | . | . | . |
| XTE J1807.4−294 | 106–370 | 337–587 | 191 (A) | 179–247 | 197 | 0.94–1.29 | 1.51–3.18 | [1, 13] |
| 4U 1915−05 | 224–707 | 514–1055 | 270 (N) | 290–353 | 299 | 1.07–1.31 | 1.49–2.30 | [2, 13] |
| IGR J17191−2821 | 681–870 | 1037–1185 | 294 (N) | 315–362 | 349 | 1.07–1.23 | 1.36–1.53 | [3, 13] |
| 4U 1702−43 | 722 | 1055 | 330 (N) | 333 | 333 | 1.00 | 1.46 | [4, 13] |
| 4U 1728−34 | 308–894 | 582–1183 | 363 (N) | 231–363 | 341 | 0.64–1.00 | 1.31–1.89 | [5, 13] |
| SAX J1808.4−3658 | 435–567 | 599–737 | 401 (AN) | 164–195 | 185 | 0.41–0.49 | 1.30–1.39 | [6, 13] |
| 4U 0614+09 | 153–843 | 449–1162 | 415 (N) | 238–382 | 317 | 0.57–0.92 | 1.36–2.93 | [7, 14] |
| KS 1731−260 | 898–903 | 1159–1183 | 524 (N) | 260–283 | 272 | 0.50–0.54 | 1.29–1.31 | [8, 13] |
| Aql X−1 | 795–803 | 1074–1083 | 550 (AN) | 278–280 | 279 | ∼0.51 | ∼1.35 | [9, 13] |
| 4U 1636−53 | 529–979 | 823–1228 | 581 (N) | 230–341 | 277 | 0.40–0.59 | 1.23–1.56 | [10, 13] |
| SAX J1750.8−2900 | 936 | 1253 | 601 (N) | 317 | 317 | 0.53 | 1.34 | [11, 13] |
| 4U 1608−52 | 473–867 | 799–1104 | 619 (N) | 225–326 | 304 | 0.36–0.53 | 1.26–1.69 | [12, 13] |
| Source (12)a . | ν1b . | ν2c . | νsd . | Δνe . | 〈Δν〉f . | Δν/νs . | ν2/ν1 . | Referencesg . |
|---|---|---|---|---|---|---|---|---|
| . | (Hz) . | (Hz) . | (Hz) . | (Hz) . | (Hz) . | . | . | . |
| XTE J1807.4−294 | 106–370 | 337–587 | 191 (A) | 179–247 | 197 | 0.94–1.29 | 1.51–3.18 | [1, 13] |
| 4U 1915−05 | 224–707 | 514–1055 | 270 (N) | 290–353 | 299 | 1.07–1.31 | 1.49–2.30 | [2, 13] |
| IGR J17191−2821 | 681–870 | 1037–1185 | 294 (N) | 315–362 | 349 | 1.07–1.23 | 1.36–1.53 | [3, 13] |
| 4U 1702−43 | 722 | 1055 | 330 (N) | 333 | 333 | 1.00 | 1.46 | [4, 13] |
| 4U 1728−34 | 308–894 | 582–1183 | 363 (N) | 231–363 | 341 | 0.64–1.00 | 1.31–1.89 | [5, 13] |
| SAX J1808.4−3658 | 435–567 | 599–737 | 401 (AN) | 164–195 | 185 | 0.41–0.49 | 1.30–1.39 | [6, 13] |
| 4U 0614+09 | 153–843 | 449–1162 | 415 (N) | 238–382 | 317 | 0.57–0.92 | 1.36–2.93 | [7, 14] |
| KS 1731−260 | 898–903 | 1159–1183 | 524 (N) | 260–283 | 272 | 0.50–0.54 | 1.29–1.31 | [8, 13] |
| Aql X−1 | 795–803 | 1074–1083 | 550 (AN) | 278–280 | 279 | ∼0.51 | ∼1.35 | [9, 13] |
| 4U 1636−53 | 529–979 | 823–1228 | 581 (N) | 230–341 | 277 | 0.40–0.59 | 1.23–1.56 | [10, 13] |
| SAX J1750.8−2900 | 936 | 1253 | 601 (N) | 317 | 317 | 0.53 | 1.34 | [11, 13] |
| 4U 1608−52 | 473–867 | 799–1104 | 619 (N) | 225–326 | 304 | 0.36–0.53 | 1.26–1.69 | [12, 13] |
Notes. a: The sources are listed in the order of NS spin frequency.
b: ν1: frequency of the lower kHz QPO.
c: ν2: frequency of the upper kHz QPO.
d: νs: NS spin frequency inferred from periodic or nearly periodic X-ray oscillations. A: accretion-powered millisecond pulsar. N: nuclear-powered millisecond pulsar.
e: Δν: Δν ≡ ν2 − ν1.
f: 〈Δν〉: weighted mean value of Δν calculated by equation (1).
g: [1] Linares et al. (2005), Zhang et al. (2006b); [2] Boirin et al. (2000); [3] Altamirano et al. (2010); [4] Markwardt, Strohmayer & Swank (1999); [5] Di Salvo et al. (2001), van Straaten et al. (2002), Strohmayer et al. (1996), Migliari, van der Klis & Fender (2003), Jonker, Méndez & van der Klis (2000), Méndez & van der Klis (1999); [6] van Straaten, van der Klis & Wijnands (2005), Wijnands et al. (2003), Bult & van der Klis (2015); [7] van Straaten et al. (2000), van Straaten et al. (2002), Boutelier, Barret & Miller (2009); [8] Wijnands & van der Klis (1997); [9] Barret, Boutelier & Miller (2008); [10] Altamirano et al. (2008), Wijnands et al. (1997a), Bhattacharyya (2010), Di Salvo et al. (2003), Jonker et al. (2000), Jonker, Méndez & van der Klis (2002), Lin et al. (2011), Sanna et al. (2014); [11] Kaaret et al. (2002); [12] van Straaten, van der Klis & Méndez (2003), Barret et al. (2005), Jonker et al. (2000), Méndez et al. (1998); [13] Reference in Boutloukos & Lamb (2008); [14] Strohmayer, Markwardt & Kuulkers (2008).
| Source (12)a . | ν1b . | ν2c . | νsd . | Δνe . | 〈Δν〉f . | Δν/νs . | ν2/ν1 . | Referencesg . |
|---|---|---|---|---|---|---|---|---|
| . | (Hz) . | (Hz) . | (Hz) . | (Hz) . | (Hz) . | . | . | . |
| XTE J1807.4−294 | 106–370 | 337–587 | 191 (A) | 179–247 | 197 | 0.94–1.29 | 1.51–3.18 | [1, 13] |
| 4U 1915−05 | 224–707 | 514–1055 | 270 (N) | 290–353 | 299 | 1.07–1.31 | 1.49–2.30 | [2, 13] |
| IGR J17191−2821 | 681–870 | 1037–1185 | 294 (N) | 315–362 | 349 | 1.07–1.23 | 1.36–1.53 | [3, 13] |
| 4U 1702−43 | 722 | 1055 | 330 (N) | 333 | 333 | 1.00 | 1.46 | [4, 13] |
| 4U 1728−34 | 308–894 | 582–1183 | 363 (N) | 231–363 | 341 | 0.64–1.00 | 1.31–1.89 | [5, 13] |
| SAX J1808.4−3658 | 435–567 | 599–737 | 401 (AN) | 164–195 | 185 | 0.41–0.49 | 1.30–1.39 | [6, 13] |
| 4U 0614+09 | 153–843 | 449–1162 | 415 (N) | 238–382 | 317 | 0.57–0.92 | 1.36–2.93 | [7, 14] |
| KS 1731−260 | 898–903 | 1159–1183 | 524 (N) | 260–283 | 272 | 0.50–0.54 | 1.29–1.31 | [8, 13] |
| Aql X−1 | 795–803 | 1074–1083 | 550 (AN) | 278–280 | 279 | ∼0.51 | ∼1.35 | [9, 13] |
| 4U 1636−53 | 529–979 | 823–1228 | 581 (N) | 230–341 | 277 | 0.40–0.59 | 1.23–1.56 | [10, 13] |
| SAX J1750.8−2900 | 936 | 1253 | 601 (N) | 317 | 317 | 0.53 | 1.34 | [11, 13] |
| 4U 1608−52 | 473–867 | 799–1104 | 619 (N) | 225–326 | 304 | 0.36–0.53 | 1.26–1.69 | [12, 13] |
| Source (12)a . | ν1b . | ν2c . | νsd . | Δνe . | 〈Δν〉f . | Δν/νs . | ν2/ν1 . | Referencesg . |
|---|---|---|---|---|---|---|---|---|
| . | (Hz) . | (Hz) . | (Hz) . | (Hz) . | (Hz) . | . | . | . |
| XTE J1807.4−294 | 106–370 | 337–587 | 191 (A) | 179–247 | 197 | 0.94–1.29 | 1.51–3.18 | [1, 13] |
| 4U 1915−05 | 224–707 | 514–1055 | 270 (N) | 290–353 | 299 | 1.07–1.31 | 1.49–2.30 | [2, 13] |
| IGR J17191−2821 | 681–870 | 1037–1185 | 294 (N) | 315–362 | 349 | 1.07–1.23 | 1.36–1.53 | [3, 13] |
| 4U 1702−43 | 722 | 1055 | 330 (N) | 333 | 333 | 1.00 | 1.46 | [4, 13] |
| 4U 1728−34 | 308–894 | 582–1183 | 363 (N) | 231–363 | 341 | 0.64–1.00 | 1.31–1.89 | [5, 13] |
| SAX J1808.4−3658 | 435–567 | 599–737 | 401 (AN) | 164–195 | 185 | 0.41–0.49 | 1.30–1.39 | [6, 13] |
| 4U 0614+09 | 153–843 | 449–1162 | 415 (N) | 238–382 | 317 | 0.57–0.92 | 1.36–2.93 | [7, 14] |
| KS 1731−260 | 898–903 | 1159–1183 | 524 (N) | 260–283 | 272 | 0.50–0.54 | 1.29–1.31 | [8, 13] |
| Aql X−1 | 795–803 | 1074–1083 | 550 (AN) | 278–280 | 279 | ∼0.51 | ∼1.35 | [9, 13] |
| 4U 1636−53 | 529–979 | 823–1228 | 581 (N) | 230–341 | 277 | 0.40–0.59 | 1.23–1.56 | [10, 13] |
| SAX J1750.8−2900 | 936 | 1253 | 601 (N) | 317 | 317 | 0.53 | 1.34 | [11, 13] |
| 4U 1608−52 | 473–867 | 799–1104 | 619 (N) | 225–326 | 304 | 0.36–0.53 | 1.26–1.69 | [12, 13] |
Notes. a: The sources are listed in the order of NS spin frequency.
b: ν1: frequency of the lower kHz QPO.
c: ν2: frequency of the upper kHz QPO.
d: νs: NS spin frequency inferred from periodic or nearly periodic X-ray oscillations. A: accretion-powered millisecond pulsar. N: nuclear-powered millisecond pulsar.
e: Δν: Δν ≡ ν2 − ν1.
f: 〈Δν〉: weighted mean value of Δν calculated by equation (1).
g: [1] Linares et al. (2005), Zhang et al. (2006b); [2] Boirin et al. (2000); [3] Altamirano et al. (2010); [4] Markwardt, Strohmayer & Swank (1999); [5] Di Salvo et al. (2001), van Straaten et al. (2002), Strohmayer et al. (1996), Migliari, van der Klis & Fender (2003), Jonker, Méndez & van der Klis (2000), Méndez & van der Klis (1999); [6] van Straaten, van der Klis & Wijnands (2005), Wijnands et al. (2003), Bult & van der Klis (2015); [7] van Straaten et al. (2000), van Straaten et al. (2002), Boutelier, Barret & Miller (2009); [8] Wijnands & van der Klis (1997); [9] Barret, Boutelier & Miller (2008); [10] Altamirano et al. (2008), Wijnands et al. (1997a), Bhattacharyya (2010), Di Salvo et al. (2003), Jonker et al. (2000), Jonker, Méndez & van der Klis (2002), Lin et al. (2011), Sanna et al. (2014); [11] Kaaret et al. (2002); [12] van Straaten, van der Klis & Méndez (2003), Barret et al. (2005), Jonker et al. (2000), Méndez et al. (1998); [13] Reference in Boutloukos & Lamb (2008); [14] Strohmayer, Markwardt & Kuulkers (2008).
3 FREQUENCY CORRELATION BETWEEN THE TWIN KHZ QPOS AND NS SPINS
3.1 The correlation between ν2 and νs
First, we try to probe the correlation between ν2 and νs with the collected data of kHz QPOs and NS spins for the 12 NS-LMXBs; these data are shown in Fig. 1, where we notice that the upper limit of ν2 is around ν2 < 1300 Hz. It is also noticed from Table 1 and Fig. 1 that the NS spin frequency of each source is smaller than its upper kHz QPO frequencies, and the kHz QPO data are constrained in the region of ν2 ≥ 1.1 νs. The distribution of the ν2 versus νs relation is quite dispersive and there is no obvious concentrated phenomenon.
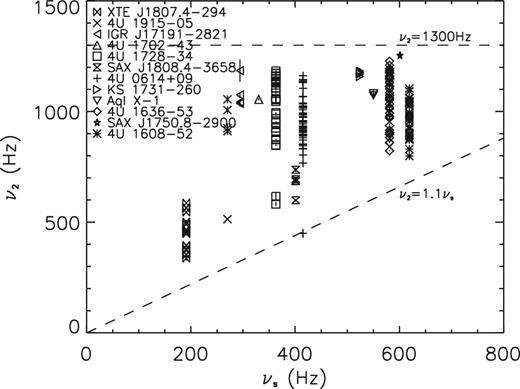
Plot of the upper kHz QPO (ν2) versus NS spin (νs). The upper frequency ν2 of the 12 sources have a range of ∼337–1253 Hz; this is constrained in the region of νs ≤ ν2 < 1300 Hz by the dashed straight lines.
3.2 The correlation between Δν and νs
The sonic-point beat-frequency model suggests that the frequency difference between the upper and lower kHz QPOs (Δν ≡ ν2 − ν1) may be related to the NS spin frequency νs (Miller et al. 1998; Lamb & Miller 2001; Lamb 2003). The resonance model predicts that the ratio between Δν and νs (Δν/νs) is approximately equal to small integers, e.g. Δν/νs ∼ 0.5, ∼2/3 or ∼1, etc. (Lee et al. 2004). However, there is currently no consensus as to these correlations. Here we calculate the values of Δν for all the twin kHz QPOs and show the results in Table 1. The range of Δν is ∼164–382 Hz, where SAX J1808.4−3658 and XTE J1807.4−294 show the lower Δν values of ∼164–195 Hz and ∼179–247 Hz, respectively. We probe the correlation between Δν and νs from the following aspects.
We calculate the ratio between Δν and νs and show the results in Table 1, where the range of Δν/νs spans a lot of values from 0.36 to 1.31. Fig. 2(a) shows the histogram of Δν/νs, where the bump distribution is noticed. The Kolmogorov–Smirnov (K–S) test suggests that the Δν/νs distribution is not uniform at the 95 per cent confidence level, implying that there may exist a possible dependence of Δν on νs. It can be seen from Fig. 2(a) that there exists a distribution gap at Δν/νs ∼ 0.65; we suspect that the 12 sources can be classified into two categories by this gap, and we also make a test of the double-Gaussian function fitting that presents the central values of the two peaks at ∼0.5 and ∼0.8, respectively, as shown in Table 2. Furthermore, we find that the Δν/νs distribution from 0.7 to 1.3 is quite dispersive, which is not sufficiently obvious to classify them as a group. Moreover, we also notice that the Δν/νs distribution shown in Fig. 2(a) is partly similar to the expectation of the resonance model (see fig. 4 of Lee et al. 2004), which predicts a peak at Δν/νs ∼ 0.5 and other values; however, its predicted peak Δν/νs ∼ 2/3 is not found in Fig. 2(a).
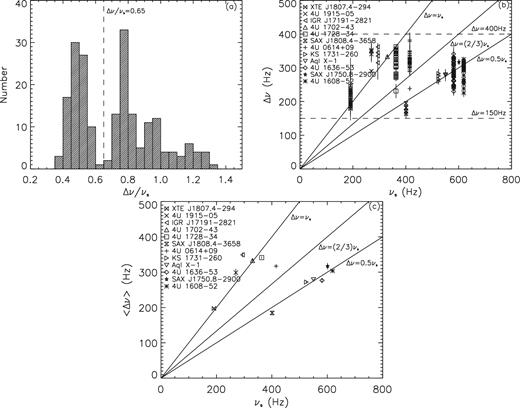
(a) A histogram of Δν/νs, where Δν is the frequency difference between the upper and lower kHz QPOs (Δν = ν2 − ν1) and νs is the NS spin. (b) Plot of Δν versus νs, where the lines of Δν = 0.5 νs, Δν = (2/3) νs and Δν = νs predicted by the resonance model (Lee et al. 2004) are also plotted. (c) Plot of the weighted mean values of Δν (〈Δν〉) versus νs.
| Relation . | Function . | Parameter . | χ2/d.o.f. . |
|---|---|---|---|
| Δν/νs | f (x) = | a1 = 32 ± 11 | 1.5 |
| b1 = 0.78 ± 0.02 | |||
| |$a_1*{\rm e}^{-((x-b_1)/c_1)^2}+$| | c1 = 0.05 ± 0.02 | ||
| a2 = 32 ± 10 | |||
| |$a_2*{\rm e}^{-((x-b_2)/c_2)^2}$| | b2 = 0.49 ± 0.02 | ||
| c2 = 0.08 ± 0.03 | |||
| Δν ∼ νs | (I) Δν = a1 νs + b1 | a1 = 0.3 ± 0.1 | 5.3 |
| b1 = 200 ± 45 | |||
| (II) Δν = a2 νs + b2 | a2 = 0.5 ± 0.1 | 3.0 | |
| b2 = −22 ± 65 | |||
| ν2/ν1 ∼ νs | |$\nu _2/\nu _1=a\nu _{\rm s}^b$| | a = 2.4 ± 0.6 | 0.04 |
| b = −0.08 ± 0.04 |
| Relation . | Function . | Parameter . | χ2/d.o.f. . |
|---|---|---|---|
| Δν/νs | f (x) = | a1 = 32 ± 11 | 1.5 |
| b1 = 0.78 ± 0.02 | |||
| |$a_1*{\rm e}^{-((x-b_1)/c_1)^2}+$| | c1 = 0.05 ± 0.02 | ||
| a2 = 32 ± 10 | |||
| |$a_2*{\rm e}^{-((x-b_2)/c_2)^2}$| | b2 = 0.49 ± 0.02 | ||
| c2 = 0.08 ± 0.03 | |||
| Δν ∼ νs | (I) Δν = a1 νs + b1 | a1 = 0.3 ± 0.1 | 5.3 |
| b1 = 200 ± 45 | |||
| (II) Δν = a2 νs + b2 | a2 = 0.5 ± 0.1 | 3.0 | |
| b2 = −22 ± 65 | |||
| ν2/ν1 ∼ νs | |$\nu _2/\nu _1=a\nu _{\rm s}^b$| | a = 2.4 ± 0.6 | 0.04 |
| b = −0.08 ± 0.04 |
| Relation . | Function . | Parameter . | χ2/d.o.f. . |
|---|---|---|---|
| Δν/νs | f (x) = | a1 = 32 ± 11 | 1.5 |
| b1 = 0.78 ± 0.02 | |||
| |$a_1*{\rm e}^{-((x-b_1)/c_1)^2}+$| | c1 = 0.05 ± 0.02 | ||
| a2 = 32 ± 10 | |||
| |$a_2*{\rm e}^{-((x-b_2)/c_2)^2}$| | b2 = 0.49 ± 0.02 | ||
| c2 = 0.08 ± 0.03 | |||
| Δν ∼ νs | (I) Δν = a1 νs + b1 | a1 = 0.3 ± 0.1 | 5.3 |
| b1 = 200 ± 45 | |||
| (II) Δν = a2 νs + b2 | a2 = 0.5 ± 0.1 | 3.0 | |
| b2 = −22 ± 65 | |||
| ν2/ν1 ∼ νs | |$\nu _2/\nu _1=a\nu _{\rm s}^b$| | a = 2.4 ± 0.6 | 0.04 |
| b = −0.08 ± 0.04 |
| Relation . | Function . | Parameter . | χ2/d.o.f. . |
|---|---|---|---|
| Δν/νs | f (x) = | a1 = 32 ± 11 | 1.5 |
| b1 = 0.78 ± 0.02 | |||
| |$a_1*{\rm e}^{-((x-b_1)/c_1)^2}+$| | c1 = 0.05 ± 0.02 | ||
| a2 = 32 ± 10 | |||
| |$a_2*{\rm e}^{-((x-b_2)/c_2)^2}$| | b2 = 0.49 ± 0.02 | ||
| c2 = 0.08 ± 0.03 | |||
| Δν ∼ νs | (I) Δν = a1 νs + b1 | a1 = 0.3 ± 0.1 | 5.3 |
| b1 = 200 ± 45 | |||
| (II) Δν = a2 νs + b2 | a2 = 0.5 ± 0.1 | 3.0 | |
| b2 = −22 ± 65 | |||
| ν2/ν1 ∼ νs | |$\nu _2/\nu _1=a\nu _{\rm s}^b$| | a = 2.4 ± 0.6 | 0.04 |
| b = −0.08 ± 0.04 |
Fig. 2(b) shows a plot of Δν versus νs, and a big range of Δν is found: ∼150–400 Hz. So, the distribution of Δν versus νs is quite dispersive; however, clustering phenomena separated by Δν/νs ∼ 0.65 can be seen, i.e. group (I) with Δν/νs > 0.65: XTE J1807.4−294, 4U 1915−05, IGR J17191−2821, 4U 1702−43, 4U 1728−34 and 4U 0614+09; and group (II) with Δν/νs < 0.65: SAX J1808.4−3658, KS 1731−260, Aql X−1, 4U 1636−53, SAX J1750.8−2900 and 4U 1608−52. Furthermore, we try to find non-biased linear correlations between Δν and νs of groups (I) and (II), respectively, by fitting them with linear functions. The fitting results are shown in Table 2, where the reduced χ2 values of fitting on the two groups are χ2/d.o.f. ∼ 5.3 and χ2/d.o.f. ∼ 3.0, respectively, implying the unsatisfactory fittings to show any certain correlations. In addition, Fig. 2(b) also shows the predicted relations of Δν = 0.5 νs, Δν = (2/3)νs and Δν = νs by the resonance model (Lee et al. 2004); however, it can be seen that the predicted correlations seem to be partly consistent with the data, except for the lack of data around the line Δν = (2/3) νs.
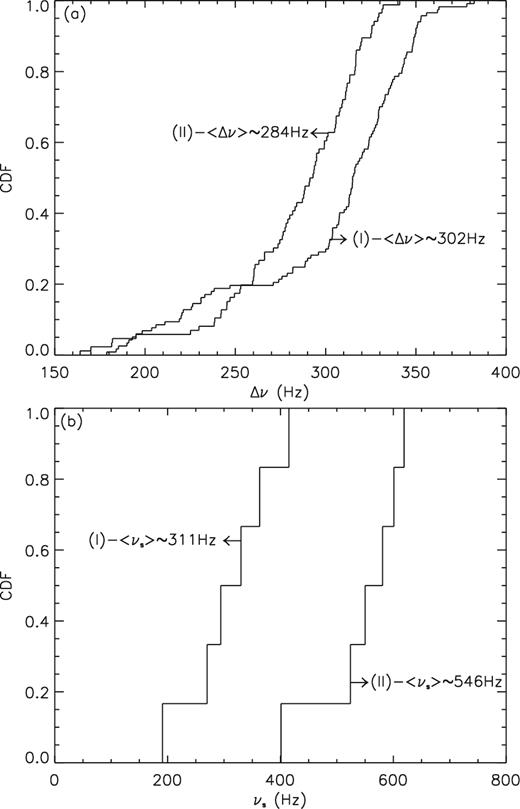
(a) The CDF curves of Δν for group (I) and group (II) (see Section 3.2). (b) Similar to (a), but for the NS spins (νs).
3.3 The correlation between ν2/ν1 and νs
The nonlinear resonance model by Abramowicz et al. (2003a,b, 2005) claimed that the ratio relation between the frequencies of pairs of high-frequency QPOs in compact X-ray binaries approximately peaks about 3:2, which has been observed in both stellar and intermediate black hole (BH) binaries (Pasham, Strohmayer & Mushotzky 2014); however, this 3:2 phenomenon is not so sharp in the twin kHz QPOs of NS-LMXBs (Belloni et al. 2005, 2007).
Here, we calculate the values of ν2/ν1 and show the results in Table 1; we find that the range of ν2/ν1 is ∼1.23–3.18 with a mean value of 〈ν2/ν1〉 ∼ 3: 2. XTE J1807.4−294 shows relatively larger values of ν2/ν1 (∼1.51–3.18) than other sources. Fig. 4(a) shows the histogram of ν2/ν1, from which a ratio-clustering phenomenon around 3:2 is noticed, as noted by the nonlinear resonance model (see fig. 4 of Abramowicz et al. 2003a). Fig. 4(b) shows a diagram of ν2/ν1 versus νs, where the distribution is quite dispersive. We fit the relation with a power-law function |$\nu _2/\nu _1=a\nu _{\rm s}^b$| and show the results in Table 2. However, the reduced χ2 value of the fitting is quite poor (χ2/d.o.f. ∼ 0.04), which means that there is no obvious correlation between ν2/ν1 and νs.
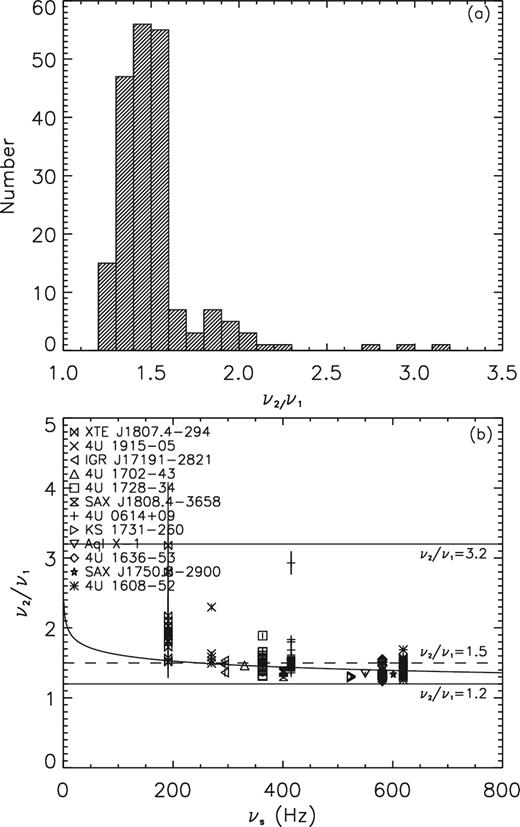
(a) A histogram of the frequency ratio of twin kHz QPOs (ν2/ν1). (b) Plot of ν2/ν1 versus NS spin frequency (νs), where the power-law curve fitting results are shown in Table 2.
4 DISCUSSION AND CONCLUSIONS
Based on the data sets of 12 sources with simultaneously detected twin kHz QPOs and NS spins, we investigate the correlation between the twin kHz QPOs and the NS spins, and find that there exists a gap at Δν/νs ∼ 0.65 in the Δν/νs distribution. The distribution of the ratio of ν2 to ν1 clusters around the mean value of 〈ν2/ν1〉 ∼ 3: 2, which shows no obvious correlation with NS spins. The details of the conclusions are discussed and summarized as follows:
The upper frequencies of twin kHz QPOs satisfy the conditions of 1.1 νs ≤ ν2 < 1300 Hz (see Table 1 and Fig. 1), where the maximum value of 1300 Hz may arise from the constraint by the NS stellar surface (van der Klis 2006) and the relation ν2 ≥ 1.1 νs may arise from the fact that the appearance of the twin kHz QPOs needs a critical orbital Keplerian velocity of the accretion matter at the NS co-rotational radius (Wang et al. 2017). It should also be noticed that the lower kHz QPO frequencies ν1 are larger or smaller than the NS spin frequency νs (see Table 1 and Wang et al. 2014). As the NS cannot rotate faster than the Keplerian frequency at the equator, the relation of ν2 > νs and ν1 > or < νs is compatible with the fact that the upper kHz QPO should be intimately involved in the Keplerian orbital frequency; thus, the lower kHz QPO might not be directly given by the orbital frequency.
We focus on statistical tests about how the relations proposed by various kHz QPO models compile with the detected data. First, the relativistic precession model predicts no correlation of the twin kHz QPO frequency difference with NS spin (Stella & Vietri 1999; Stella et al. 1999; Török et al. 2016). The histogram of Δν/νs shows the bump phenomenon (see Fig. 2(a)), which is not compatible with a uniform distribution by the K–S test. So, we suspect that the frequencies of twin kHz QPOs and NS spins may obey an indirect relation, which may arise from the magnetosphere–disc boundary environments, e.g. co-rotation radius and NS radius. Secondly, the sonic-point beat-frequency model interprets the frequency difference of twin kHz QPOs as being close to the NS spin frequency (Miller et al. 1998; Lamb & Miller 2001). However, the Δν/νs histogram in Fig. 2(a) shows a diversified distribution, which obviously rejects the idea of claiming Δν/νs ∼ 1; therefore a simple beat-frequency model should be refused. Thirdly, the forced resonance model by Lee et al. (2004) predicts peaks at Δν/νs ∼ 0.5, ∼2/3 and ∼1, etc. It is noticed that the Δν/νs distributions of the detected data at 0.5 and 1 seem to be consistent with the expectations of the model; however, the values around 2/3 are short of the detected samples.
We try to classify the 12 sources into two categories based on the gap value at Δν/νs = 0.65. (I) As slow rotators with 〈νs〉 ∼ 311 Hz, XTE J1807.4−294, 4U 1915−05, IGR J17191−2821, 4U 1702−43, 4U 1728−34 and 4U 0614+09 follow a relation Δν/νs > 0.65. (II) As fast rotators with 〈νs〉 ∼ 546 Hz, SAX J1808.4−3658, KS 1731−260, Aql X−1, 4U 1636−53, SAX J1750.8−2900 and 4U 1608−52 satisfy the relation Δν/νs < 0.65 (see Figs 2(b) and 2(c)). Because of the condition ν2 ≥ 1.1 νs (Wang et al. 2017) and with Δν decreasing with ν2 (van der Klis 2006; Zhang et al. 2006a), the slow rotators (Lamb & Boutloukos 2008) with smaller νs show big Δν, which causes the big Δν/νs value of >0.65. In contrast, the fast rotators with big spin frequencies νs correspond to small Δν, which causes the smaller Δν/νs value of <0.65. However, it is not clear if a bimodal distribution of Δν/νs is possible, nor what physical process can explain the gap around Δν/νs ∼ 0.65. If the correlation of Δν versus νs can be confirmed, it may be applied to estimate the NS spin frequencies in LMXBs.
As known, various bands of QPO frequencies in BH-LMXBs and NS-LMXBs follow tight relations (Belloni et al. 2005, 2007), and a pair of high-frequency QPOs in stellar and intermediate black hole binaries follows, approximately, a 3:2 ratio relation, which may be a particular phenomenon from the innermost stable circular orbit (Abramowicz et al. 2003a,b; Pasham et al. 2014). In fact, there has been a suggestion in the literature for the 3:2 ratio as a parametric resonance between two particular modes of torus oscillations (Bursa et al. 2004; Kluźniak 2005; Kluźniak et al. 2007). However, we find that the distribution of the ratio of ν2 to ν1 of the 12 NS-LMXBs sources clusters around a value of ∼3:2 (see Fig. 4(a)), which shows no obvious correlation with NS spin. The statistical result of the ∼3:2 QPO ratio relation shares a similar conclusion from the nonlinear resonance model (see fig. 4 of Abramowicz et al. 2003a), implying that the ∼3:2 relation may be a common property of compact X-ray binaries around some particular radius. Why the ratios of the pair QPOs of NS-LMXBs and BH-LMXBs show ∼3:2 correlations is still unclear, and more effort is needed to uncover this secret by analysing more QPO data in future detections.
ACKNOWLEDGEMENTS
This work is supported by the National Program on Key Research and Development Project (Grant No. 2016YFA0400803), the National Natural Science Foundation of China (Grant No. 11173034, No. 11673023 and No. 11703003), the Science and Technology Foundation of Guizhou Province (Grant No. J[2015]2113 and No. LH[2016]7226) and the Doctoral Starting up Foundation of Guizhou Normal University 2014. We are grateful for the critical comments and suggestions by the anonymous referee, which have significantly improved the quality of the paper.
REFERENCES



