-
PDF
- Split View
-
Views
-
Cite
Cite
Bo Zhao, Paola Caselli, Zhi-Yun Li, Ruben Krasnopolsky, Decoupling of magnetic fields in collapsing protostellar envelopes and disc formation and fragmentation, Monthly Notices of the Royal Astronomical Society, Volume 473, Issue 4, February 2018, Pages 4868–4889, https://doi.org/10.1093/mnras/stx2617
Close - Share Icon Share
Abstract
Efficient magnetic braking is a formidable obstacle to the formation of rotationally supported discs (RSDs) around protostars in magnetized dense cores. We have previously shown, through 2D (axisymmetric) non-ideal magnetohydrodynamic simulations, that removing very small grains (VSGs: ∼10 Å to few 100 Å) can greatly enhance ambipolar diffusion and enable the formation of RSDs. Here, we extend the simulations of disc formation enabled by VSG removal to 3D. We find that the key to this scenario of disc formation is that the drift velocity of the magnetic field almost cancels out the infall velocity of the neutrals in the 102–103 au scale ‘pseudo-disc’ where the field lines are most severely pinched and most of protostellar envelope mass infall occurs. As a result, the bulk neutral envelope matter can collapse without dragging much magnetic flux into the disc-forming region, which lowers the magnetic braking efficiency. We find that the initial discs enabled by VSG removal tend to be Toomre-unstable, which leads to the formation of prominent spiral structures that function as centrifugal barriers. The piling-up of infall material near the centrifugal barrier often produces dense fragments of tens of Jupiter masses, especially in cores that are not too strongly magnetized. Some fragments accrete on to the central stellar object, producing bursts in mass accretion rate. Others are longer lived, although whether they can survive for a long term to produce multiple systems remains to be ascertained. Our results highlight the importance of dust grain evolution in determining the formation and properties of protostellar discs and potentially multiple systems.
1 INTRODUCTION
Angular momentum lies in the heart of the formation of rotationally supported discs (RSDs), which is strongly affected by the magnetic flux harboured in the central disc-forming region. The winding of pinched magnetic field lines by gas rotation can cause large magnetic torques that transport angular momentum away from the equatorial region (Mestel & Spitzer 1956; Mouschovias 1977; Mouschovias & Paleologou 1980; Basu & Mouschovias 1994), preventing the formation of RSDs. This is the so-called magnetic braking problem (Allen, Li & Shu 2003; Mellon & Li 2008; Li, Krasnopolsky & Shang 2011), which is in tension with recent high-resolution observations of ∼100 au discs and spirals around young protostellar objects (Tobin et al. 2012, 2013; Tokuda et al. 2014; Pérez et al. 2016; Tobin et al. 2016).
Recent theoretical studies on disc formation often resort to non-ideal magnetohydrodynamic (MHD) effects to avert the magnetic braking ‘catastrophe’ (Mouschovias & Paleologou 1986; Königl 1987; Mellon & Li 2009; Dapp & Basu 2010; Krasnopolsky, Li & Shang 2011; Li, Krasnopolsky & Shang 2011; Dapp, Basu & Kunz 2012; Tomida et al. 2013; Masson et al. 2015; Tomida, Okuzumi & Machida 2015; Tsukamoto et al. 2015a,b; Wurst, Price & Bate 2016), based on the principle that magnetic fields are partially decoupled from neutral matter in weakly ionized dense cores (Bergin & Tafalla 2007). However, most studies focus on the decoupling of the magnetic field at very high densities within a few to tens of au scale around the central star. The RSDs formed in this fashion, if any, are of limited size (at most ∼30 au in radius) and have no clear sign of growth to the ∼50–100 au Keplerian discs observed around Class 0 protostars (Murillo et al. 2013; Codella et al. 2014; Tobin et al. 2016; Lee et al. 2017).
In our previous two-dimensional (2D) study, Zhao et al. (2016, Zhao+16 hereafter), we have shown that large (axisymmetric) RSDs and self-gravitating rings are able to form in the absence of very small grains (VSGs) of ∼10 Å to few 100 Å. In fact, it is the large population of VSGs in the MRN size distribution that dominates the coupling of the bulk neutral matter to the magnetic field at densities below 1010 cm−3. The removal of VSGs can enhance the ambipolar diffusion of magnetic field in the envelope by ∼1–2 orders of magnitude, so that the amount of magnetic flux dragged by the collapse into the central disc-forming region is reduced. Because the decoupling of magnetic fields occurs much earlier, magnetic braking operating in the central equatorial region becomes inefficient in transporting away angular momentum. Therefore, the high specific angular momentum in the infalling gas eventually leads to the formation and growth of early RSDs.
According to Zhao+16, the key requirement for magnetized disc formation is the lack of VSGs in dense cores, which has been confirmed by recent CARMA centimetre survey searching for emission of spinning dust grains (Tibbs et al. 2016). They show a depletion of nanometre grains (≲100 Å) in all dense molecular cores in their survey. The depletion of VSGs can occur either in the pre-stellar or protostellar phase, through both accretion of VSGs on to dust grain mantles (process analogous to molecular freeze-out, e.g. Tielens & Hagen 1982; Hasegawa, Herbst & Leung 1992) and grain coagulation (e.g. Chokshi, Tielens & Hollenbach 1993; Dominik & Tielens 1997). Grain coagulation has been shown to be rather efficient in removing small grains (<0.1 μm) within a few 106 yr (Ossenkopf 1993; Hirashita 2012). Furthermore, the time-scale for coagulation of VSGs on to big grains has shown to be the shortest (∼1.6 × 103 yr; Köhler et al. 2012). Hence, prior to the birth of the protostellar disc, the collapsing envelope is likely to have a greatly reduced abundance of VSGs, which enhances ambipolar diffusion.
In this study, we extend our previous study of AD-induced disc formation to three-dimension (3D) and provide conditions for the formation of RSDs and multiple systems. We confirm the crucial role of removing VSGs in the formation of RSDs, as found in Zhao+16. Particularly, we find that the infall velocity of the magnetic field decreases to nearly zero over a wide equatorial region in the envelope, where magnetic field lines are strongly pinched by the collapsing flow. Unlike Hennebelle et al. (2016), the self-regulation of magnetic fields by AD actually occurs on much larger scales, and is due to the vertical gradient of the radial magnetic field (field pinching and the associated magnetic tension force) instead of the radial gradient of poloidal fields (and the associated magnetic pressure gradient). Efficient decoupling of magnetic fields in the envelope leads to sufficient angular momentum influx into the disc-forming region, triggering the formation of an early RSD or ring (∼10–40 au) which evolves into a small circumstellar disc(∼20 au) surrounded by large spiral structures (a few 100 au). We also confirm that both rotation speed and magnetic field strength of the initial core can affect the morphology and size of the disc. For cores with lower magnetization, multiple companion objects can form from spiral or ring structures via material piling up near the centrifugal barrier, which belongs to the type of fragmentation driven by rapid accretion (Kratter et al. 2010; Kratter & Lodato 2016). The models that produce large spirals and multiple systems in 3D correspond to the models with ring structures found in the 2D axisymmetric calculations of Zhao+16.
The rest of the paper is organized as follows. Section 2 describes the initial conditions of the simulation set, together with an overview of the results. In Section 3, we present and analyse the simulation results. The comparison with existing theories of disc formation and a case study of B335 are given in Section 4. Finally, we summarize the results in Section 5.
2 INITIAL CONDITION
We carry out 3D numerical simulations1 using zeustw code (Krasnopolsky, Li & Shang 2010), focusing on the ambipolar diffusion for the diffusion of magnetic field in collapsing cloud cores. We adopt the same chemical network as in Zhao+16, which computes the magnetic diffusivities2 at every hydrodynamic time-step and at each spatial point.
The initial conditions are similar to Zhao+16, except for a more accurate equation of state (EOS) that is described in Appendix A. We initialize a uniform, isolated spherical core with total mass Mc = 1.0 M⊙, and radius Rc = 1017 cm ≈6684 au. This corresponds to an initial mass density ρ0 = 4.77 × 10−19 g cm−3 and a number density for molecular hydrogen n(H2) = 1.2 × 105 cm−3 (assuming mean molecular weight μ = 2.36). The free-fall time of the core is thus tff = 3 × 1012 s ≈ 9.6 × 104 yr. The initial core is rotating as a solid body with angular speed ω0 = 1 × 10−13 s−1 for slow rotating case, and 2 × 10−13 s−1 for fast rotating case, corresponding to a ratio of rotational to gravitational energy βrot ≈ 0.025 and 0.1 (Goodman et al. 1993), respectively. The initial core is threaded by a uniform magnetic field along the rotation axis with a constant strength B0 of 4.25 × 10−5 G for strong field case and 2.13 × 10−5 G for weak field case, which gives a dimensionless mass-to-flux ratio λ (|${\equiv} {M_{\rm c} \over \pi R_{\rm c}^2 B_0}2\pi \sqrt{G}$|) of 2.4 and 4.8, respectively. It is consistent with the mean value of λ inferred from the OH Zeeman observations by Troland & Crutcher (2008).
We adopt the spherical coordinate system (r, θ, ϕ) and non-uniform grid to provide high resolution towards the innermost region of simulation domain. The inner boundary has a radius rin = 3 × 1013 cm = 2 au and the outer has rout = 1017 cm. At both boundaries, we impose standard outflow boundary conditions to allow matter to leave the computational domain. The mass accreted across the inner boundary is collected at the centre as the stellar object. We use a total of 120 × 96 × 96 grid points. The grid is uniform in the ϕ direction, non-uniform in the θ direction with δθ = 0|$_{.}^{\circ}$|6713 near the equator, and non-uniform in the r direction with a spacing δr = 0.1 au next to the inner boundary. The r-direction spacing increases geometrically outward by a constant factor of ∼1.0733, and the θ-direction spacing increases geometrically from the equator to either pole by a constant factor of ∼1.0387.
In most models of this study, we fix the cosmic ray ionization rate at the cloud edge to be |$\zeta _0^{\rm H_2}=1.0\times 10^{-17}$| s−1, with a characteristic attenuation length of 96 g cm−2. We do not consider the high cosmic ray ionization case of |$\zeta _0^{\rm H_2}=5.0\times 10^{-17}$| s−1 of Zhao+16, where disc formation is strongly suppressed unless both βrot and λ are high. We choose two grain size distributions, MRN and tr-MRN for the computation of non-ideal MHD diffusivities. Both size distributions have the same power-law index −3.5 and maximum grain size amax = 0.25 μm, but different minimum grain sizes amin = 0.005 μm (MRN) and 0.1 μm (tr-MRN). As compared to Zhao+16, we dropped the large grain case, as we find its effect on disc formation is in between the MRN and tr-MRN cases. The simulation models are summarized in Table 1.
| Model . | Grain size . | λ . | βrot . | Morphology . | Initial disc/ring . | Spiral structure . | Circumstellar disc . |
|---|---|---|---|---|---|---|---|
| . | . | . | . | . | Radius (au) . | Radius (au) . | Average radius (au) . |
| 2.4Slw-MRN | MRN | 2.4 | 0.025 | DEMS | – | – | – |
| 2.4Slw-trMRN | tr-MRN | 2.4 | 0.025 | Disc+Spiral | ∼15 | ∼40 | ∼20 |
| 2.4Fst-MRN | MRN | 2.4 | 0.1 | DEMS | – | – | – |
| 2.4Fst-trMRN | tr-MRN | 2.4 | 0.1 | Ring→Disc+Spiral | ∼30 | ∼100↑ | ∼15 |
| 4.8Slw-MRN | MRN | 4.8 | 0.025 | DEMS+DiscTrans | ∼15 | – | – |
| 4.8Slw-trMRN | tr-MRN | 4.8 | 0.025 | Ring→Disc+SpiralFrag | ∼25 | ∼150↑ | ∼20 |
| 4.8Fst-MRN | MRN | 4.8 | 0.1 | DiscShrink→DEMS | ∼20 | – | ∼10→0 |
| 4.8Fst-trMRN | tr-MRN | 4.8 | 0.1 | RingFrag | ∼40 | ∼200↑ | ∼10 |
| HydroSlw | – | ∞ | 0.025 | RingFrag→Multiples | ∼50–100 | ∼500↑ | ∼20 |
| HydroFst | – | ∞ | 0.1 | RingFrag→Multiples | ∼70–150 | ∼1000↑ | ∼20 |
| Model . | Grain size . | λ . | βrot . | Morphology . | Initial disc/ring . | Spiral structure . | Circumstellar disc . |
|---|---|---|---|---|---|---|---|
| . | . | . | . | . | Radius (au) . | Radius (au) . | Average radius (au) . |
| 2.4Slw-MRN | MRN | 2.4 | 0.025 | DEMS | – | – | – |
| 2.4Slw-trMRN | tr-MRN | 2.4 | 0.025 | Disc+Spiral | ∼15 | ∼40 | ∼20 |
| 2.4Fst-MRN | MRN | 2.4 | 0.1 | DEMS | – | – | – |
| 2.4Fst-trMRN | tr-MRN | 2.4 | 0.1 | Ring→Disc+Spiral | ∼30 | ∼100↑ | ∼15 |
| 4.8Slw-MRN | MRN | 4.8 | 0.025 | DEMS+DiscTrans | ∼15 | – | – |
| 4.8Slw-trMRN | tr-MRN | 4.8 | 0.025 | Ring→Disc+SpiralFrag | ∼25 | ∼150↑ | ∼20 |
| 4.8Fst-MRN | MRN | 4.8 | 0.1 | DiscShrink→DEMS | ∼20 | – | ∼10→0 |
| 4.8Fst-trMRN | tr-MRN | 4.8 | 0.1 | RingFrag | ∼40 | ∼200↑ | ∼10 |
| HydroSlw | – | ∞ | 0.025 | RingFrag→Multiples | ∼50–100 | ∼500↑ | ∼20 |
| HydroFst | – | ∞ | 0.1 | RingFrag→Multiples | ∼70–150 | ∼1000↑ | ∼20 |
Notes. (a) MRN: full MRN distribution with amin = 0.005 μm and amax = 0.25 μm.
(b) tr-MRN: truncated MRN with amin = 0.1 μm and amax = 0.25 μm.
(c) DEMS: Decoupling-Enabled Magnetic Structures (Zhao et al. 2011).
(d) RSDTrans: a transient RSD appears early on due to the high angular momentum initially, but disappears within 103 yr.
(e) RSDShrink: initially forms a RSD but shrinks in size over time (∼103 yr).
(f) SpiralFrag or RingFrag: fragmentation occurs in spirals or rings, leading to the formation of binary and multiple systems.
(g) The symbol (↑) denotes that the radius of the spiral structure (or centrifugal radius) continues to increase over time.
| Model . | Grain size . | λ . | βrot . | Morphology . | Initial disc/ring . | Spiral structure . | Circumstellar disc . |
|---|---|---|---|---|---|---|---|
| . | . | . | . | . | Radius (au) . | Radius (au) . | Average radius (au) . |
| 2.4Slw-MRN | MRN | 2.4 | 0.025 | DEMS | – | – | – |
| 2.4Slw-trMRN | tr-MRN | 2.4 | 0.025 | Disc+Spiral | ∼15 | ∼40 | ∼20 |
| 2.4Fst-MRN | MRN | 2.4 | 0.1 | DEMS | – | – | – |
| 2.4Fst-trMRN | tr-MRN | 2.4 | 0.1 | Ring→Disc+Spiral | ∼30 | ∼100↑ | ∼15 |
| 4.8Slw-MRN | MRN | 4.8 | 0.025 | DEMS+DiscTrans | ∼15 | – | – |
| 4.8Slw-trMRN | tr-MRN | 4.8 | 0.025 | Ring→Disc+SpiralFrag | ∼25 | ∼150↑ | ∼20 |
| 4.8Fst-MRN | MRN | 4.8 | 0.1 | DiscShrink→DEMS | ∼20 | – | ∼10→0 |
| 4.8Fst-trMRN | tr-MRN | 4.8 | 0.1 | RingFrag | ∼40 | ∼200↑ | ∼10 |
| HydroSlw | – | ∞ | 0.025 | RingFrag→Multiples | ∼50–100 | ∼500↑ | ∼20 |
| HydroFst | – | ∞ | 0.1 | RingFrag→Multiples | ∼70–150 | ∼1000↑ | ∼20 |
| Model . | Grain size . | λ . | βrot . | Morphology . | Initial disc/ring . | Spiral structure . | Circumstellar disc . |
|---|---|---|---|---|---|---|---|
| . | . | . | . | . | Radius (au) . | Radius (au) . | Average radius (au) . |
| 2.4Slw-MRN | MRN | 2.4 | 0.025 | DEMS | – | – | – |
| 2.4Slw-trMRN | tr-MRN | 2.4 | 0.025 | Disc+Spiral | ∼15 | ∼40 | ∼20 |
| 2.4Fst-MRN | MRN | 2.4 | 0.1 | DEMS | – | – | – |
| 2.4Fst-trMRN | tr-MRN | 2.4 | 0.1 | Ring→Disc+Spiral | ∼30 | ∼100↑ | ∼15 |
| 4.8Slw-MRN | MRN | 4.8 | 0.025 | DEMS+DiscTrans | ∼15 | – | – |
| 4.8Slw-trMRN | tr-MRN | 4.8 | 0.025 | Ring→Disc+SpiralFrag | ∼25 | ∼150↑ | ∼20 |
| 4.8Fst-MRN | MRN | 4.8 | 0.1 | DiscShrink→DEMS | ∼20 | – | ∼10→0 |
| 4.8Fst-trMRN | tr-MRN | 4.8 | 0.1 | RingFrag | ∼40 | ∼200↑ | ∼10 |
| HydroSlw | – | ∞ | 0.025 | RingFrag→Multiples | ∼50–100 | ∼500↑ | ∼20 |
| HydroFst | – | ∞ | 0.1 | RingFrag→Multiples | ∼70–150 | ∼1000↑ | ∼20 |
Notes. (a) MRN: full MRN distribution with amin = 0.005 μm and amax = 0.25 μm.
(b) tr-MRN: truncated MRN with amin = 0.1 μm and amax = 0.25 μm.
(c) DEMS: Decoupling-Enabled Magnetic Structures (Zhao et al. 2011).
(d) RSDTrans: a transient RSD appears early on due to the high angular momentum initially, but disappears within 103 yr.
(e) RSDShrink: initially forms a RSD but shrinks in size over time (∼103 yr).
(f) SpiralFrag or RingFrag: fragmentation occurs in spirals or rings, leading to the formation of binary and multiple systems.
(g) The symbol (↑) denotes that the radius of the spiral structure (or centrifugal radius) continues to increase over time.
3 SIMULATION RESULTS
As shown in Table 1, the conditions for disc formation are largely similar to Zhao+16, with formation of rotational supported structures occurring in all tr-MRN cases, compared to no disc, transient disc or shrinking disc in the MRN cases. The main difference from Zhao+16 is the variety of disc morphologies shown in 3D, ranging from DEMS (Decoupling-Enabled Magnetic Structures; Zhao et al. 2011) to RSDs, and from spiral to ring structures. In cases with lower magnetization (λ = 4.8), fragmentation often occurs within spirals and rings that leads to the initial formation of binary and multiple systems.
3.1 AD-enabled disc formation: field decoupling in the envelope
Despite existing literature on field decoupling in the high-density disc itself, we find the key for disc formation lies in the field decoupling in the protostellar envelope. Particularly, an enhanced AD in the absence of VSGs (Zhao+16) ensures sufficient magnetic flux to be decoupled in the low-density envelope before reaching the inner tens-of-au stellar vicinity, thus preventing the ‘catastrophic’ magnetic braking and preserving sufficient angular momentum for disc assembly.
3.1.a Truncated tr-MRN model: 2.4Slw-trMRN
Fig. 1 shows the face-on view of the equatorial disc-spiral structure in the 2.4Slw-trMRN model at 131.096 kyr, about 4.56 kyr after the formation of first core. The velocity profile clearly shows that the inner ∼20 au disc is rotating with Keplerian speed. The spiral structure is likely infall streams on to the Keplerian disc. The effective centrifugal pressure |$P_{\rm cent}={1 \over 2} \rho {\rm v}_\phi ^2$| in the disc is ∼10 times higher than the thermal pressure, indicating that the disc is primarily rotationally supported (see Fig. 2). The plasma-β (|${\equiv} {P_{\rm th} \over P_{\rm B}}$|, where Pth is the thermal pressure and PB the magnetic pressure) in the disc is of the order of ∼102. The disc rotation also wraps up magnetic field lines over time, producing the well-developed toroidal magnetic field components shown in the top-right panel of Fig. 1.
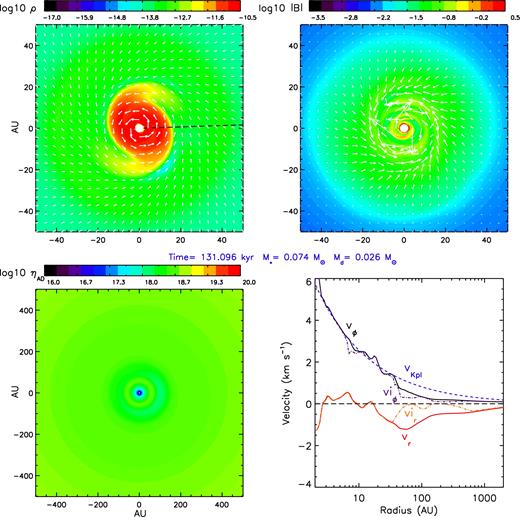
Distributions of logarithmic mass density ρ (g cm−3), magnetic field strength |B| (G), and ambipolar diffusivity ηAD (cm2 s−1) within 0|$_{.}^{\circ}$|336 of the equator, and velocity profile along the ϕ = 1|$_{.}^{\circ}$|9 line cut (black dashed line in the top-left panel) for the 2.4Slw-trMRN model at time t ≈ 131.1 kyr = 1.36tff. The projected velocity field (top left) and magnetic field (top right) are shown as white arrows. Length unit of the axes is in au. The typical temperature in the disc is around 100 K.

Profile of thermal Pth, magnetic PB, ram Pram and effective centrifugal Pcent pressures within 0|$_{.}^{\circ}$|336 of the equator, along the same line cut as the velocity profile in Fig. 1.
The direct evidence of magnetic decoupling in the envelope is the significant separation between the infall velocity of neutral gas vr and that of the ions vir (bottom-right panel of Fig. 1). The ion velocity is in fact an ‘effective ion velocity’ defined as |$\boldsymbol {vi} \equiv \boldsymbol {v}+\boldsymbol {v}_{\rm d}$|, where |$\boldsymbol {v}_{\rm d}$| is the drift velocity of the magnetic field given in equa-tion (1). Because AD in zeustw is treated using an explicit method (Mac Low et al. 1995; Li et al. 2011) and |$\boldsymbol {vi}$| is directly used to evolve the magnetic field, hence |$\boldsymbol {vi}$| actually denotes the velocity of the magnetic field.3 The nearly zero effective ion velocity4vir at ∼50–300 au implies that magnetic fields have almost decoupled from the bulk infall motion of neutral gas and are left behind in the envelope. Such an efficient decoupling is a result of the enhanced AD at low-density regimes (≲1010 cm−2) in the absence of VSGs (Zhao+16; see their section 4 and fig. 2). It is clearly manifested in the bottom-left panel of Fig. 1 that the AD diffusivity on the ∼500 au scale is already well above 1018 cm2 s−1, which is at least one order of magnitude higher than the infalling region in the 2.4Slw-MRN model (shown in the next section).
3.1.b MRN grain model: 2.4Slw-MRN
In the 2.4Slw-MRN model, the physical structure of the central region is drastically different. No obvious RSD forms at all (Fig. 3); instead, large torus-shaped DEMS occupy the inner ∼150 au, which consist essentially of the decoupled flux from the accreted matter (Zhao et al. 2011; Krasnopolsky et al. 2012). Accordingly, the magnetic field strength is also higher in the low-density DEMS. Such a structure expands over time from a few au to a few 100 au, which blocks infall and obstructs rotation over a large region on the equator. Gas finds other paths to reach the centre, however, dragging in most magnetic field lines as well (bottom-right panel of Fig. 3, plotted along a line cut in the positive x direction). Unlike the 2.4Slw-trMRN model, the effective ion velocity is almost indistinguishable from the bulk neutral velocity beyond 70 au; There is only a partial separation between vir and vr in the inner ∼20–70 au; yet the separation is not as large as in the 2.4Slw-trMRN model. As most of the magnetic field is dragged all the way to the centre and eventually decouples at the inner boundary (∼2 au) from the accreted matter that enters the sink hole5 it joins the existing DEMS or creates new DEMS in directions of least resistance.
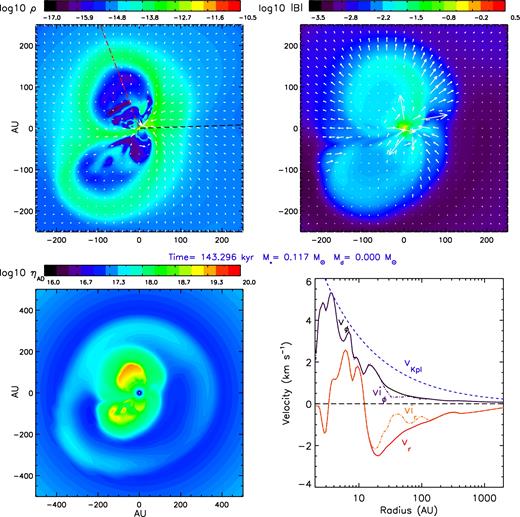
Distributions of logarithmic mass density ρ (g cm−3), magnetic field strength |B| (G) and ambipolar diffusivity ηAD (cm2 s−1) within 0|$_{.}^{\circ}$|336 of the equator, and velocity profile along the ϕ = 1|$_{.}^{\circ}$|9 line cut (black dashed line in the top-left panel) for the 2.4Slw-MRN model at time t ≈ 143.3 kyr = 1.49tff. The projected velocity field (top left) and magnetic field (top right) are shown as white arrows. Length unit of the axes is in au. The red dashed line in the top-left panel is the line cut used in Fig. 4.
As shown in Fig. 4, the infall velocity for the northern DEMS component shows clear expansion with vr and vir being positive between ∼50 and 200 au. Very little rotation is present across the DEMS. The equatorial region within ∼30–200 au is dominated by magnetic pressure PB; and the innermost ∼30 au is dominated by both magnetic and ram pressures, which implies magnetic instability of the interchange type (rising of more strongly magnetized material against less strongly magnetized collapsing flow, e.g. Parker 1979).
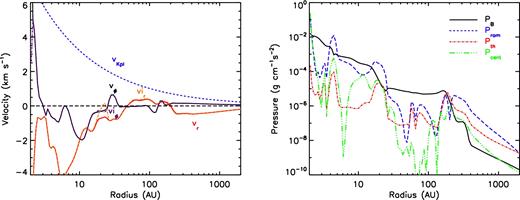
Left-hand panel: profile of equatorial infall and rotation speed in the 2.4Slw-MRN model at t ≈ 143.3 kyr (same time as in Fig. 3). The Keplerian speed is plotted based on the central mass. Right-hand panel: profile of equatorial thermal Pth, magnetic PB, ram Pram and effective centrifugal Pcent pressures. Both panels are plotted along a line cut through the DEMS with ϕ = 111° (red dashed line in the top-left panel of Fig. 3).
In comparison to the 2.4Slw-trMRN model above, the primary reason for the failure of disc formation and the presence of DEMS is that too much magnetic flux has been brought to the centre. It is a direct consequence of the low ambipolar diffusivity in the infalling envelope beyond ∼102 au (number density ∼107–1010 g cm−3). Apart from the expanding DEMS, the ηAD is mostly around 1017 cm2 s−1 within the 500 au region (bottom-left panel of Fig. 3) – at least one order of magnitude lower than the values in the 2.4Slw-trMRN model. This leads to very little decoupling of magnetic field from the infall flow, and hence an excessive amount of magnetic flux reaching the centre. Although a certain degree of field decoupling indeed occurs in the inner few tens of au, it does not prevent enough magnetic flux from accumulating in the central region and hence is unable to save the disc. The drastic difference between the two models is simply caused by changing a single parameter – the grain size distribution.
3.1.c Collapse-induced pinching of B-fields and B-field decoupling in the envelope
In the tr-MRN cases where VSGs are absent, the regions of field decoupling expand over time from a few tens of au to a few 103 au into the envelope. As shown in Fig. 5, the effective infall velocity of ions vir is close to 0 between 30 and 80 au at an early time t ≈ 127.4 kyr (∼850 yr after the formation of the first core), along with a well-decoupled zone between 20 and 100 au. At t ≈ 132.1 kyr, regions of zero vir are located between 40 and 400 au, and the decoupling region extends further to 20–600 au. At the later time t ≈ 146.0 kyr, vir has reached 0 in a wide equatorial region between 70 and 2000 au, and is mostly separated from the neutral infall velocity vr between 20 and 2000 au. Note that the effective rotational velocity of ions viϕ is mostly identical to the neutral vϕ, with a moderate separation in the inner ∼100 au, where poloidal magnetic fields start to wind up to generate the toroidal field components and a corresponding radial currents across the ‘pseudo-disc’ (Galli & Shu 1993).
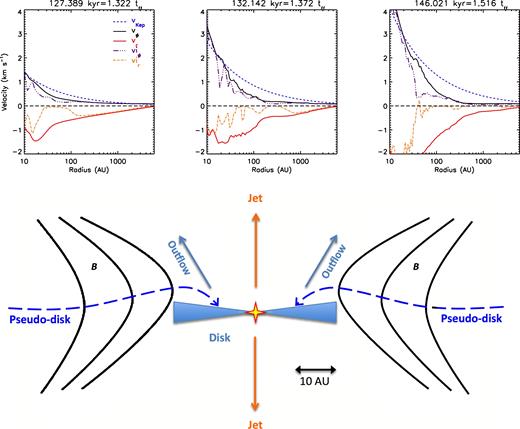
Top row: velocity profiles for the 2.4Slw-trMRN model at time t = 1.322 tff, 1.372 tff and 1.516 tff, along the curved infall stream or the pseudo-disc where field pinching are the strongest. Bottom row: illustration of the equatorial RSD and the curved pseudo-disc for the 2.4Slw-trMRN model (see also Fig. 19). Such a configuration is persistent rather than transient.
The large separation between vir and vr in the tr-MRN case indicates a notable radial drift of magnetic field relative to the neutrals, i.e. field decoupling from the collapsing flow. We show below that the location of the decoupling region is tied closely to the regions with strong pinching of magnetic field by the collapsing flow. Therefore, the expansion of the decoupling region is a natural consequence of the inside-out collapse that gradually induces the field pinching at larger and larger radii along the equator.
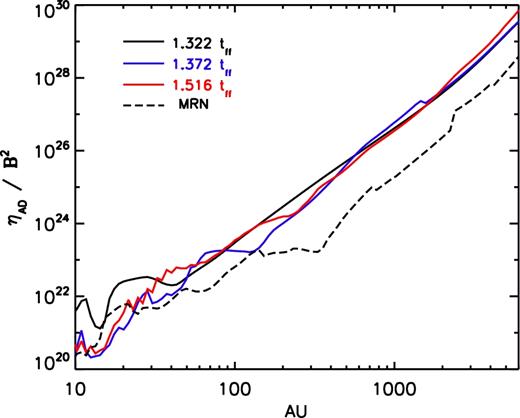
|$\eta _{\rm AD}/\boldsymbol {B}^2$| for three different times of the 2.4Slw-trMRN model, along with the 2.4Slw-MRN model at 1.487tff. The values are plotted along the curved infall stream or the pseudo-disc.
After eliminating the role of |$\eta _{\rm AD}/\boldsymbol {B}^2$|, we are left with only one possibility to account for the expansion of the decoupling region – the tension force (Bθ/r)(∂Br/∂θ). In Fig. 7, we plot the different terms of the Lorenz force based on equations (2) and (3), along a line through the curved infall stream (or pseudo-disc, see sketch in the bottom panel of Fig. 5) that properly captures the positions with the most severe pinching of magnetic field lines. When comparing curves of different times, the tension term (Bθ/r)(∂Br/∂θ) clearly shows larger values in the corresponding decoupling regions. For instance, at t ≈ 1.372tff, the tension term between 100 and 600 au is about 10 times higher than that at an early time t ≈ 1.322tff that has a decoupling region between 20 and 100 au. Hence, the total decoupling zone at t ≈ 1.372tff is combined into 20–600 au, which matches the velocity separation in Fig. 5. A similar reasoning applies to t ≈ 1.516tff that yields an even wider decoupling zone between 20 and 2000 au; this again matches the above-mentioned velocity separation.
![Lorenz force terms (Bθ/r)(∂Br/∂θ), ($-\nabla \times \boldsymbol {B}$)ϕBθ, [($\nabla \times \boldsymbol {B}$)$\times \boldsymbol {B}$]r, (Bθ/r)(∂rBθ/∂r) and ($\nabla \times \boldsymbol {B}$)θBϕ for the three different times of the 2.4Slw-trMRN model, along with the 2.4Slw-MRN model at 1.487tff. Solid lines represent positive values and dot–dashed ones represent negative values. The values are plotted along the curved infall stream or the pseudo-disc.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/473/4/10.1093_mnras_stx2617/2/m_stx2617fig7.jpeg?Expires=1750565664&Signature=NFdqTdbQP~QKJtnEEE~SPQiEpgs4aCQnNwOwbEz3FcDSLLyfn5QbViu0JyYYEGO7RF800N-MjnnAxQmCfM4-DNr91ATlaPdRdjUAwQOSNLUizq8PfjTantM2oxYghLOMoMxNIFvhL5AJ5cOcZiy6hMiZPDS58WmDNU0Zv46Q3Kr0MkMps-OJcFVxepRedoBNBQl~mE75OSTo~-vInKeFXTLqj8R01GIG~7atdM6NI6cmRco5yy~sA-ywmak9nPFjZgM-M8L2qRYsQQkxj2GtBbRD9eNMOK5lEKP~kGjJZnxJPxufvZmQbPJTKb-i7axoQy2jolaP4dTgEzIl9J~fVQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Lorenz force terms (Bθ/r)(∂Br/∂θ), (|$-\nabla \times \boldsymbol {B}$|)ϕBθ, [(|$\nabla \times \boldsymbol {B}$|)|$\times \boldsymbol {B}$|]r, (Bθ/r)(∂rBθ/∂r) and (|$\nabla \times \boldsymbol {B}$|)θBϕ for the three different times of the 2.4Slw-trMRN model, along with the 2.4Slw-MRN model at 1.487tff. Solid lines represent positive values and dot–dashed ones represent negative values. The values are plotted along the curved infall stream or the pseudo-disc.
Note that the three terms (Bθ/r)(∂Br/∂θ), (|$-\nabla \times \boldsymbol {B}$|)ϕBθ and [(|$\nabla \times \boldsymbol {B}$|)|$\times \boldsymbol {B}$|]r are almost identical to each other, with only very small discrepancies in the inner 20 au. This validates the approximations we made in equations (2) and (3). Indeed, the gradient of Bθ and the whole term (|$\nabla \times \boldsymbol {B}_\theta$|)Bϕ are more chaotic and orders of magnitude smaller than their respective counterparts. The dominance of tension force among the Lorenz force terms and its expansion in radius over time therefore proves the collapse triggered field pinching to be the main reason for the large expanding decoupling region in the envelope. The mechanism of this type of field decoupling is summarized in Fig. 8.
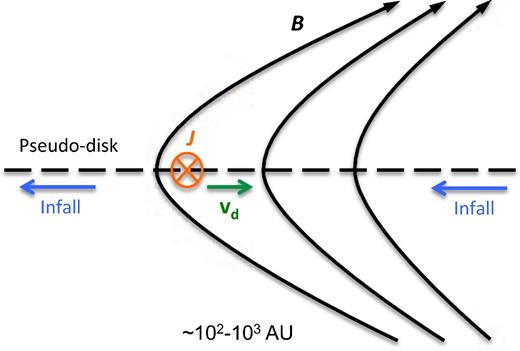
Illustration of AD drift in the collapsing envelope, in which |$\boldsymbol {J}={c \over 4\pi } \nabla \times \boldsymbol {B}$| is the current induced by the field pinching across the pseudo-disc, and |${\boldsymbol v}_{\rm d}$| is the ambipolar drift velocity.
As collapse proceeds, the efficient field decoupling prevents a large fraction of the magnetic flux from moving inward with the collapsing neutral flow. We thus expect the mass-to-flux ratio λ to increase over time, which is exactly the case in Fig. 9. λ increases from 2–3 at the cloud edge to ∼10, ∼100 and ∼200 near the centre at time 1.322tff, 1.372tff and 1.516tff, respectively. In comparison, λ in the MRN model at time 1.487tff kyr is a few times lower than that of the tr-MRN cases outside ∼100 au. For regions inside ∼100 au, we compare the MRN case with the tr-MRN case at time 1.372tff, in that they are similar in terms of total star plus disc mass.
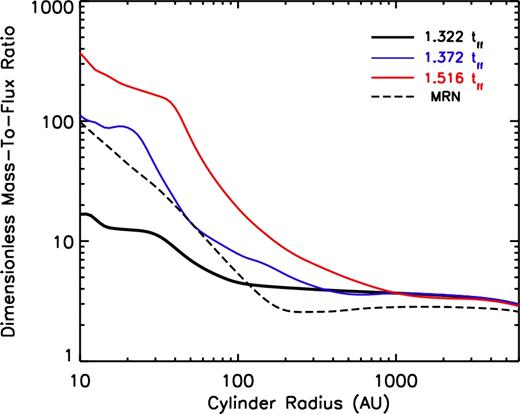
Dimensionless mass-to-flux ratio λ, for three different times of the 2.4Slw-trMRN model, along with the 2.4Slw-MRN model at 1.487tff.
The mass-to-flux ratio λ in the tr-MRN model at 1.372tff is no less than the MRN model at 1.487tff. It is indeed caused by a difference in magnetic flux (inside a given cylinder) shown in Fig. 10, since the two cases are comparable in mass evolution. Inside ∼2000 au, the specific angular momentum is already a factor of a few higher in the tr-MRN case than in the MRN case, which is consistent with the result in Zhao+16. Such a difference is even larger in the inner ∼200 au where DEMS reside. Note that the infalling gas piles up at ∼200–300 au outside the DEMS in the MRN case, and hence resulting in a small plateau in the specific angular momentum outside the DEMS. Therefore, the excessive magnetic flux in the MRN model both lowers the specific angular momentum of the infalling gas in a wide region, and results in the magnetically dominated DEMS that obstruct the rotation in the innermost disc-forming region.
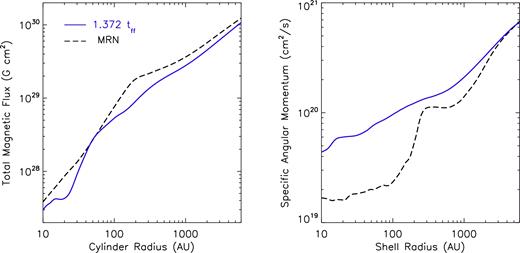
Total magnetic flux inside cylinders of different radii (left), and specific angular momentum inside shells at different radii (right), for the 2.4Slw-trMRN model at 1.372tff and the 2.4Slw-MRN model at 1.487tff. The two chosen frames have a similar total mass of star plus disc.
To conclude, it is worth noting that the decoupling region occurs preferentially in the vicinity of the infall channel where field pinching is the strongest (similar to Krasnopolsky & Königl 2002). In an axisymmetric collapse, such a channel is along the equator. Larger than ∼3° (with respect to the origin) above or below the equator, the separation of infall velocity between the magnetic field and the neutrals nearly disappears in either the MRN or tr-MRN models. Besides, the AD decoupling of magnetic fields triggered by collapse requires a lack of VSGs before the onset of discs, in order to provide enough ambipolar diffusivity in the envelope. Therefore, the process of removing VSGs must have already taken place in the 103 au scale envelope or even in the pre-stellar phase.
3.2 Trapping and escaping of early DEMS in discs
As shown in Zhao et al. (2011) and Krasnopolsky et al. (2012) for both the ideal MHD limit and non-ideal MHD cases, DEMS are inevitable structures once magnetic flux is by any means decoupled from the accreted matter (on to the star). In Section 3.1.b, we have demonstrated the catastrophic role of DEMS in suppressing disc formation and obstructing disc rotation in the MRN cases. However, in the tr-MRN models, the DEMS are still present, but are less destructive and play a less important role.
In the tr-MRN models, the DEMS are most prominent in early phases shortly after the first core formation, as gas in the cloud centre that has the lowest specific angular momentum is quickly accreted by the star. As shown in Fig. 11, the corresponding decoupled magnetic flux remains in the stellar vicinity, and is surrounded by the early RSD formed from the infalling gas with higher specific angular momentum (second to fifth panels from the left).
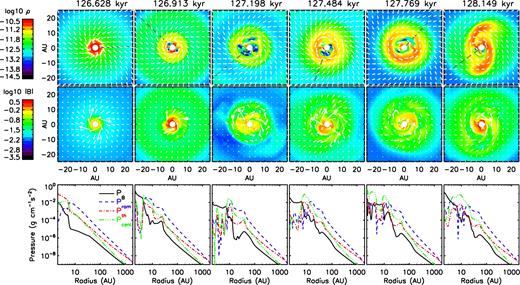
Early evolution of disc and DEMS for 2.4Slw-trMRN model. Top row: distribution of mass density ρ (g cm−3) and velocity field vectors within 0|$_{.}^{\circ}$|336 of the equator. Middle row: distribution of magnetic field strength |B| and magnetic field vectors on the same surface. Bottom row: thermal Pth, magnetic PB, ram Pram and effective centrifugal Pcent pressures along the same surface; the line cuts are drawn from the origin and pass through the low-density DEMS, with azimuthal angle ϕ = 1|$_{.}^{\circ}$|9, 137°, 219°, 249°, 47° and 216°, respectively (black dashed lines in the top row).
At the beginning, the axisymmetric first core (first panel from the left) breaks into filamentary accretion flows (second panel from the left) in between DEMS under the so-called magnetic interchange instability (Parker 1979; Kaisig, Tajima & Lovelace 1992; Stehle & Spruit 2001; Krasnopolsky et al. 2012). The DEMS (high magnetic field strength and low-density regions dominated by PB) tend to expand as the central star grows in mass and more magnetic flux is decoupled (third panel from the left); however, the structures are quickly contained and squeezed by the ∼10 au initial ring-shaped RSD (fourth panel from the left). The RSD (high-density disc regions dominated by Pcent), which is unrelated to the already disrupted first core, is formed by assembling infalling gas with large enough centrifugal radius, thanks to the efficient decoupling of magnetic flux at larger radii that allows gas to retain enough angular momentum along their way to the centre (as discussed above in Section 3.1.c). Within a few 100 yr, the RSD quickly grows and becomes massive enough (≳50 per cent of stellar mass) to be self-gravitating (Toomre Q parameter ∼0.2, see Fig. 12) and develops spiral structures that open up escape channels for DEMS (sixth panel from the left).
At later times, the DEMS are less obvious and become even less disruptive to disc evolution, as most magnetic flux is excluded from the thermally and rotationally dominated disc.6 In other words, a sizeable RSD (≳10 au) further prevents magnetic flux from reaching the very centre and minimizes the development of DEMS around the star. Recall that to form and retain such an RSD requires enough angular momentum in the infalling gas, which is achieved in the tr-MRN models. We will show a shrinking disc example in the MRN model in Section 3.4 where the initial RSD can quickly shrink into the central sink hole by accreting gas with low specific angular momentum; in such a case, large DEMS re-appear at later times.
It is worth clarifying that the development of DEMS is a natural result of magnetic flux conservation and does not depend on the detailed decoupling mechanisms (Ohmic, AD or Hall; see Krasnopolsky et al. 2012). The results in this section also imply that
the first hydrostatic core (Larson 1969) is prone to disruption by magnetic instabilities and is unlikely the origin of the RSD formed later, in contrast to the claims by previous studies (Bate 1998, 2010, 2011; Machida & Matsumoto 2011);
the onset of RSD takes place outside the DEMS region, which is enabled by the sufficient angular momentum in the infalling gas;
after a sizeable RSD (≳10–15 au) is in place, most magnetic flux can be further kept outside the disc, or the centrifugal radius of the infalling gas (definition given in equation 6) if it is smaller than the disc radius.
3.3 Disc fragmentation and formation of multiple systems
Until recently, disc fragmentation has shown to be difficult if the initial core is moderately or strongly magnetized (λ ≲ 10) (e.g. Lewis & Bate 2017). In contrast, we find that fragmentation can indeed occur on spirals or rings in the tr-MRN models (Table 1) with a relatively strong initial magnetic field (λ = 4.8). Note that the spiral or ring structures themselves are clear signs of high specific angular momentum entering the inner disc-forming region.
density is above certain critical value ρcr, i.e. ρ > ρcr = 10−13 g cm−3;
azimuthal velocity dominates over radial velocity, i.e. vϕ > fthresvr;
rotational support dominates over both thermal and magnetic support, i.e. |$\rho {v}_\phi ^2/2$| > fthresPth, and |$\rho {v}_\phi ^2/2$| > fthresPmag.
We choose fthres = 2 in our analysis. Note that the criterion of low magnetic support is generally not important, because the high-density regions satisfying criterion (i) generally have plasma-β of the order of ∼101–104 (e.g. Fig. 2).7 For the same reason, the magnetic Toomre parameter (Kim & Ostriker 2001; Seifried et al. 2013) is almost identical to the standard Toomre Q parameter under the above criteria.
We apply these analyses to both the non-fragmenting (2.4Fst-trMRN) and fragmenting (4.8Slw-trMRN and 4.8Fst-trMRN) models. We confirm that the criterion Q ≲ 1 alone is insufficient for the occurrence of fragmentation; the instability induced spiral structures also have to accrete materials from the envelope more rapidly than it could transport them inward (Kratter et al. 2010). In our simulation, we observe that the fragments usually form at the local centrifugal barrier (sections of the spiral or ring structures, shown below) where the infall material piles up.
3.3.a Spiral structures and centrifugal barrier: model 2.4Fst-trMRN
In the 2.4Fst-trMRN model (higher magnetization), no obvious fragmentation takes place throughout the simulation even though Toomre Q < 1 (see detailed discussion in Section 3.3.d); instead, a grand spiral structure steadily develops in the central 100 au region. As shown in Fig. 13, the early evolution is very similar to the 2.4Slw-trMRN model (slower rotation) above. The ∼5 au first core (first panel from the left) is quickly disrupted within ∼600 yr and the inner ∼10 au region is occupied by the DEMS. Surrounding the DEMS, an RSD is assembled and gradually grows as gas with high specific angular momentum falls in (second panel from the left). This stage lasts about ∼1.2 kyr until the RSD grows more massive than the central star and becomes gravitationally unstable. As shown in Fig. 12, the disc mass catches up and overtakes the stellar mass around t ∼ 160 kyr, and the Q parameter decreases rapidly from ∼1.0 to ∼0.2. In the third panel from the left, the RSD is compressed by the infall into a ring shape and starts to wobble. The northern and southern sections of the ring accumulates materials faster than other ring sections, which rapidly breaks the ring symmetry. Within 1/4 orbit, the two mass-gaining regions are turned into two spirals while the other ring sections fall to the centre. During the process, the DEMS find open channels to escape from the inner region, similar to the 2.4Slw-MRN case. Thereafter, accretion streams are able to wrap around the central star to form a well-defined disc. In another ∼1000 yr, the whole disc-spiral structure extends to ∼100 au.
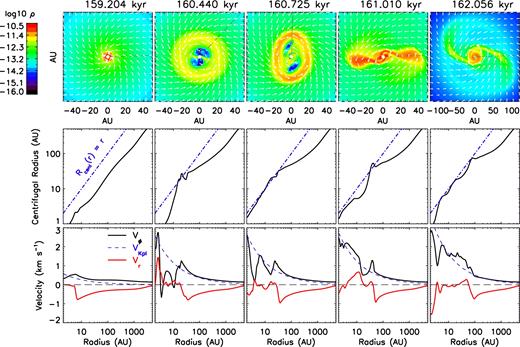
Early evolution of spiral structures for 2.4Fst-trMRN model. Top row: distribution of mass density ρ (g cm−3) and velocity field vectors within 0|$_{.}^{\circ}$|336 of the equator. Middle row: estimated centrifugal radius. Bottom row: velocity profile along the same surface; the line cuts are drawn from the origin with azimuthal angle ϕ = 1|$_{.}^{\circ}$|9, 47°, 88°, 1|$_{.}^{\circ}$|9 and 1|$_{.}^{\circ}$|9, respectively (black dashed lines in the top row).
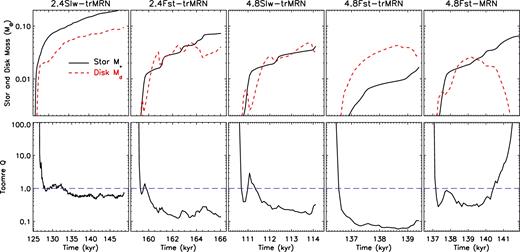
Evolution of mass of star and disc (top row), and Toomre Q (bottom row) for models with prominent discs. Dashed blue lines represent Q = 1. For models with formation of companion objects, 4.8Slw-trMRN and 4.8Fst-trMRN, we only show the quantities before the formation of companions.
The distribution of Rcent(r) is plotted in the second row of Fig. 13 for the corresponding snapshots in the top row. Except for the first core phase (M* ≲ 10−3 M⊙), the rest has a common ‘plateau’ feature in the Rcent curve. It is a typical signature of the ‘so-called’ centrifugal barrier (Zhao+16) because the infalling gas at different radii along the ‘plateau’ tends to arrive at the same radius Rcent. Such centrifugal radii are around 20–30 au (second panel from the left), 30–40 au (third panel from the left), 40–50 au (fourth panel from the left) and 70–80 au (fifth panel from the left) for the respective snapshots. As collapse continues to bring the envelope gas with higher angular momentum (initial solid-body rotation), the location of the centrifugal barrier moves outward.
The centrifugal barrier can also be identified from the kinematic profiles. As the envelope gas falls towards the central region, its rotation speed vϕ suddenly rises and infall speed vr almost vanishes across the centrifugal barrier. Interior to the centrifugal barrier (post shock), vϕ tends to decrease to the local Keplerian speed, unless the inner regions are dominated by the DEMS. It is worth pointing out that the centrifugal barrier at later times (fourth and fifth panels from the left) coincides with the outer arm of the spiral structures, as compared to the rigid rings formed by piling up infall material shown in Zhao+16 (2D). In this sense, the centrifugal barrier in 3D is much less stiff or obstructive to the infall flows than in 2D.
3.3.b Fragmentation of spirals and accretion bursts: model 4.8Slw-trMRN
In the 4.8Slw-trMRN model with a low magnetization and slow rotation, fragmentation frequently occurs on the outer arm of the spiral structures, producing transient companion clumps with tens of Jupiter mass. In most cases, the companion clumps spiral inward and tidally interact with the circumstellar disc, leading to episodic accretion events (Fig. 14; see also Vorobyov & Basu 2006, 2015). However, the orbital evolution of companion objects is not well followed in this study due to a lack of sink particle treatment (except for the stationary sink hole in the centre, which can violate the linear momentum conservation).
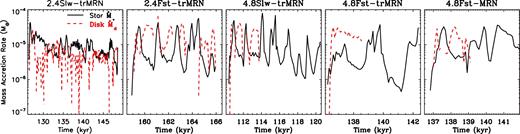
Evolution of mass accretion rate of the star and disc for models with prominent discs. In comparison to Fig. 12, we also show |$\dot{M}_*$| at later times for model 4.8Slw-trMRN and 4.8Fst-trMRN after the formation of companion objects.
The early evolution of 4.8Slw-trMRN model is similar to that of the 2.4Slw-trMRN and 2.4Fst-trMRN models, in which the first core is disrupted by DEMS and an unstable RSD (Q ∼ 0.3 at 111.7–120.1 kyr; see Fig. 12) forms outside the DEMS from the infalling rotating materials. In Fig. 15, we present the phase when the spiral structure is already developed from the wobbling massive RSD (first panel from the left, ∼2.8 kyr after the formation of the first core). A slight asymmetry causes the northern spiral arm to accumulate materials faster than the southern arm. Such a perturbation runs away rapidly within half orbital time, causing the northern arm to grow into a massive clump as it rotates to the southern position (second panel from the left). The massive clump, about 60 per cent of the stellar mass of 0.042 M⊙, tidally disrupts the circumstellar disc. It is then followed by an accretion burst (|$\dot{M}_* \approx$| 6–7 × 10−5 M⊙ yr−1) when materials flow along the stream from the clump on to the central star. Part of the clump wraps around the star to form a new circumstellar disc, and the rest continues to rotate and stretch into an arc shape. After another half orbit (third panel from the left), infalling materials pile up at the stretched northern arc at r ∼ 70–80 au, i.e. the centrifugal barrier, where two companion objects form with a total mass of ∼0.017 M⊙ (∼30 per cent of the stellar mass). The two companion clumps quickly merge into one clump with a mass of ∼0.022 M⊙, which spirals inward towards the star. After another 1/4 orbit (fourth panel from the left), the circumstellar disc is disrupted again. The 0.028 M⊙ clump near the 0.068 M⊙ star causes another episode of accretion burst (|$\dot{M}_* \approx$| 6–7 × 10−5 M⊙ yr−1). The situation afterwards is very similar to that of the first burst, where part of the clump wraps into a new circumstellar disc and the rest stretches out into long arc-shaped streams. Another 3/4 orbit later, a new clump of ∼0.011 M⊙ (∼15 per cent of the stellar mass) forms near the ∼100 au centrifugal barrier.
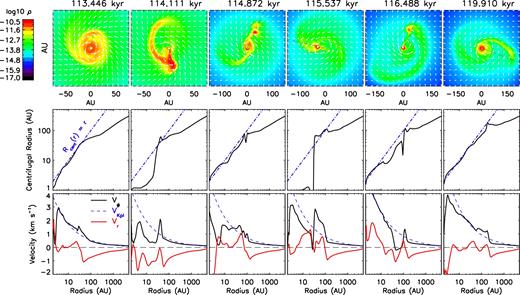
Evolution of spiral structures for 4.8Slw-trMRN model. Top row: distribution of mass density ρ (g cm−3) and velocity field vectors within 0|$_{.}^{\circ}$|336 of the equator. Middle row: estimated centrifugal radius. Bottom row: velocity profile along the same surface; the line cuts are drawn from the origin with azimuthal angle ϕ = 81°, 279°, 66°, 167°, 66° and 339°, respectively (black dashed lines in the top row).
The subsequent evolution repeats the previous episodes in a similar fashion; and after two more accretion burst episodes, the system evolves into a more standard disc plus spiral configuration which extends to ∼150 au. However, the outer spiral arm located near the centrifugal barrier is still susceptible to the formation of 10−2 M⊙ companion clumps.
It is worth verifying the location of the centrifugal barrier from both the centrifugal radius and the velocity profile (plotted along a line passing through the clumps). Basically the locations of the ‘plateau’ on the Rcent curve and the sharp change in vϕ and vr coincide well with each other; and the location of such a centrifugal barrier also coincides with that of the companion clumps in the top panels. This indicates that the companion clumps are indeed formed from piling up infall material at the centrifugal barrier. Note that the curves of centrifugal radius inner to the centrifugal barrier are heavily affected by the companion objects at later times.
3.3.c Fragmentation of rings and multiple systems: model 4.8Fst-trMRN
In the faster rotating model 4.8Fst-trMRN, fragmentation of rings (formed due to high angular momentum influx) frequently produces multiple companion clumps. The early evolution of model 4.8Fst-trMRN, however, has much smaller DEMS than the other cases, due to a lack of accretion on to the central star. Until t = 138.828 kyr (second panel from the left of Fig. 16, ∼2.2 kyr after the formation of the first core), the stellar accretion rate is only around 4 × 10−7 M⊙ yr−1. It is caused by the large angular momentum in the innermost ∼5 au that prevents the gas from falling further below their large centrifugal orbits. Nevertheless, small DEMS can still develop in the inner 5 au (first panel from the left), which have disrupted the first core (similar to Section 3.2). Surrounding the DEMS is a ∼10–15 au RSD with ∼0.006 M⊙ formed from the gas with high specific angular momentum; Further out between 25 and 35 au, a massive ring (0.024 M⊙) is growing outside the RSD by assembling gas from larger radii with even higher specific angular momentum. The ring has four times the mass of the inner RSD and three times the mass of the star, thus creating a gap between 15 and 25 au by gradually attracting materials in the gap on to it (first panel from the left). The massive ring quickly becomes gravitationally unstable, and wobbles and deforms within a few hundred years (about one orbital time). Tidal streams then develop, which connect the ring to the inner RSD (second panel from the left).
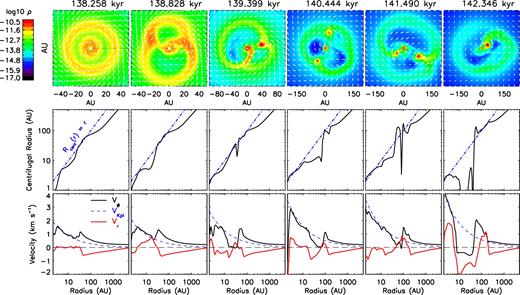
Evolution of spiral and ring structures for model 4.8Fst-trMRN. Top row: distribution of mass density ρ (g cm−3) and velocity field vectors within 0|$_{.}^{\circ}$|336 of the equator. Middle row: estimated centrifugal radius. Bottom row: velocity profile along the same surface; the line cuts are drawn from the origin with azimuthal angle ϕ = 1|$_{.}^{\circ}$|9, 1|$_{.}^{\circ}$|9, 13°, 73°, 328° and 36°, respectively (black dashed lines in the top row).
The eastern and western sections of the ring preferentially accrete the infall matter. After another 1/2 orbit, the original western ring section stretches into an arm around the inner disc, while the original eastern section forms a 0.016 M⊙ companion clump that equals the stellar mass (third panel from the left). Gas near the clump also tends to orbit around it. However, the companion clump fails to survive the close approach 1/2 orbit later; it is tidally disrupted by the central star and produces an accretion burst with |$\dot{M}_*\sim 3\times 10^{-5}$| M⊙ yr−1. Note that the original 40 au ring structure keeps expanding to 100 and 200 au scales concurrently. About 500 yr after the accretion burst (fourth panel from the left), two well-separated companion clumps develop within the ring structure, with mass ∼0.008 (northern) and 0.010 M⊙ (southern), respectively. They sum up to 2/3 of the stellar mass. Subsequently, the triple system undergoes dynamic interactions, with the northern lighter companion spiralling inward and the southern companion growing more massive. In 1/4 orbit (fifth panel from the left), the masses of the triple system are 0.009 (eastern), 0.022 (western) and 0.029 M⊙ (primary). The western massive companion continues to accrete and becomes equal mass with the central primary (0.030 M⊙). The lighter companion is tidally stretched when it rotates in between the two massive objects; it is eventually merged on to the western companion to form a 0.036 M⊙ secondary, the same mass as the primary star (sixth panel from the left). The secondary later merges with the primary and leads to another accretion burst; however, since we do not have full sink particle treatment (except for the stationary sink hole in the centre), the result could otherwise be a tight binary system with mass ratio ∼1 or a hierarchical triple system (Reipurth et al. 2014).
Throughout the evolution, the location of centrifugal barrier moves outward with time (middle row of Fig. 16), which matches with the radius of the large ring structure well. A second ‘plateau’ also appears at 10 au scale, corresponding to the centrifugally supported inner disc around the primary. Similar to the 4.8Slw-trMRN model above, the curves of centrifugal radius interior to the barrier are affected by the companion objects. The velocity profiles are plotted along lines passing through the companion objects, which show the usual ‘bump’ feature in vϕ and sudden decrease in vr for a typical centrifugal barrier. Again, it confirms that the most probable sites for the formation of companion objects are the centrifugal barriers where the infall material piles up.
3.3.d Disc stability analysis
We conclude the section with a general analysis of disc stability. Recall that the criterion Q < 1 only implies the growth of spiral waves in the disc. Indeed in Fig. 12, all four tr-MRN models satisfy the Q < 1 criterion, yet only the two models with lower magnetization (λ = 4.8) show prominent fragmentation because the disc (or ring) is more massive and hence more unstable gravitationally. In these two models, new fragments often appear in the outer part of the spiral or ring structures, where infall material from the envelope piles up. In this sense, these piling-up spots are indeed the centrifugal barriers.
Interestingly, models 2.4Fst-trMRN and 4.8Slw-trMRN have very similar Toomre Q values at the early times, yet only the latter shows fragmentation. This is in fact consistent with the principles derived in Kratter et al. (2010, see their equations 1 and 2 and fig. 2). We compare the model 2.4Fst-trMRN at t = 162.1 kyr (Fig. 13) and model 4.8Slw-trMRN at t = 113.4 kyr (Fig. 15), both having a stellar mass of ∼0.03 M⊙. While both discs have similar accretion rate (∼10−5 M⊙ yr−1) and hence similar thermal parameter ζ,8 the rotation speed of the spiral structure (not the envelope) in the 4.8Slw-trMRN model (tighter spiral) is twice faster than in the 2.4Fst-trMRN model (grand spiral). Accordingly, the 4.8Slw-trMRN model has a smaller rotational parameter Γ,8 which makes fragmentation easier according to fig. 2 of Kratter et al. (2010). In other words, faster rotation (of the disc-spiral structure) promotes fragmentation.
3.4 Failed disc: shrinking disc
In Table 1, the 4.8Fst-MRN model is of particular interest, in which a 10–20 au RSD forms initially but shrinks over time and disappears within ∼3.7 kyr. The same case has been discussed in our 2D study Zhao+16 (see their section 5.4). Despite the advantage of weaker magnetization and faster rotation, the AD in the envelope is much less efficient than the tr-MRN models. As a result, an increasing amount of magnetic flux is being dragged into the inner disc-forming region as collapse continues. The magnetic braking in this case still operates efficiently to torque down the gas rotation, leading to an insufficient supply of specific angular momentum to maintain the current disc size. Therefore, the RSD shrinks in size and the disc material gradually falls into the central star due to a lack of rotational support.
As shown in Fig. 17, the early evolution of the 4.8Fst-MRN model is similar to the tr-MRN models: DEMS ‘hatches’ in the inner ∼10 au after disrupting the first core; and an RSD assembles between 10 and 20 au (second panel from the left). The unstable ring-shaped RSD then deforms and wraps around the star to form the usual disc-spiral configuration. However, in contrast to the large spirals in the tr-MRN models, the spiral structure in this case quickly disappears within ∼600 yr, leaving only a compact disc of 10–15 au radius (fourth panel from the left). The suppression of spiral structures is a sign of reduced angular momentum influx. Notably, in the next ∼500 yr, the infall flow gradually moves away from the equatorial plane, making the pseudo-disc to curve towards the upper hemisphere (recall that a similar phenomenon appears in the 2.4Slw-trMRN model as well). It is a natural outcome of the low angular momentum in the infalling gas; the gas flow finds alternative channels to reach their centrifugal radius that is much smaller than the disc radius. In this fashion, the disc accretes mass but little angular momentum, which causes the disc to shrink in size over time.

Evolution of the shrinking disc for model 4.8Fst-MRN. Top row: distribution of mass density ρ (g cm−3) and velocity field vectors within 0|$_{.}^{\circ}$|336 of the equator. Middle row: distribution of mass density ρ (g cm−3) and velocity field vectors on the meridian plane with azimuthal angle ϕ = 1|$_{.}^{\circ}$|9. Bottom row: estimated centrifugal radius.
The change of disc radius can also be identified from the evolution of centrifugal radius, particularly the secondary ‘plateau’ for the inner tens of au radius. Across different times, the value of Rcent indicated by the secondary ‘plateau’ well follows the disc radius. It first increases from ∼5 to ∼20 au at early times (first to third panels from the left), but later decreases from ∼10 au (fourth panel from the left) to ∼3 au (fifth panel from the left) and quickly vanishes in another 200 yr (sixth panel from the left). The lack of the inner ‘plateau’ denotes the absence of RSD, which is exactly the case in the top row. At this time, the central region is instead occupied by the familiar DEMS.
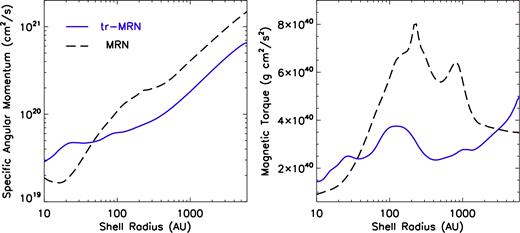
Comparison of specific angular momentum and magnetic torque for 4.8Fst-MRN and 2.4Slw-trMRN models at a similar evolutionary epoch 141.3 kyr and 128.5 kyr, respectively. The two chosen frames have similar total mass of star plus disc (∼0.06 M⊙).
The magnetic torque in the 4.8Fst-MRN case peaks between 200 and 300 au, near which the specific angular momentum curve flattens (conservation of angular momentum; Goodman et al. 1993; Belloche 2013). It implies that the magnetic torque is enhanced by the increasing rotational motion there. The magnitude of magnetic torque in the 4.8Fst-MRN case is also a few times higher than the 2.4Slw-trMRN case, indicating a stronger magnetic braking in the former. Consequently, the specific angular momentum inside ∼200 au decreases more rapidly in the MRN model. Such a quick slowing down in gas rotation in turn weakens the magnetic braking. In contrast, the strength of magnetic braking keeps at a relatively low level throughout the core. As a result, the decrease in specific angular momentum is more gradual. Even in the inner tens of au, there is still an adequate amount of angular momentum to maintain the RSD. Therefore, the effect of removing VSGs is more significant on maintaining a long-lived RSD than that of increasing the initial core rotation or mass-to-flux ratio (for λ of a few).
3.5 Outflow
The formation and evolution of RSDs are naturally accompanied by magnetically driven outflows. However, most outflows in our 3D models have multiple components, some of which can be asymmetric. Thus, different launching mechanisms may be in play for different outflow components. Note that we use an Alfvén dt floor9 to avoid extremely small time-steps, which may artificially add tiny mass to the outflow regions and can alter the momentum of the outflow. Therefore, the discussion in this section is more qualitative than quantitative.
As shown in Fig. 19, the outflow in the 2.4Slw-trMRN model has two components: one is centrally collimated and the other fanning out sideways. The former bipolar component may correspond to the jet or ‘X-wind’ type (Shu et al. 2000); yet simulations with much higher resolution are required to understand its nature, which is beyond the scope of this study. The latter fan-like component, however, only appears in the upper hemisphere (similar to the 4.8Fst-MRN model). The origin of this outflow component is likely to be the magneto-centrifugal (slingshot) mechanism (Blandford & Payne 1982), in that its launching point coincides with the landing site of the ‘curved’ infall stream, where magnetic field lines are strongly pinched. The bottom row of the first panel from the left clearly shows that the pinching locations of magnetic field lines are shifted towards the upper hemisphere, following the curved infall stream. Therefore, the pseudo-disc is also curved instead of a plane along the equator. Note that the edge-on picture is very similar to the shrinking disc model (4.8Fst-MRN) discussed above, except that the landing site of the infall stream is at ∼10 au compared with ≲3 au in the shrinking disc model, thanks to the high angular momentum influx in the absence of VSGs.
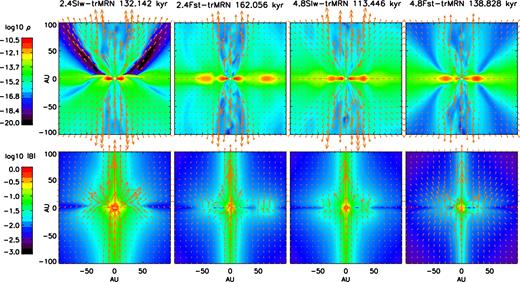
Comparison of outflow structures in the bipolar region (top row) and magnetic field configurations (bottom row) among the disc-forming models. The colour contours are logarithmic mass density ρ (g cm−3) and magnetic field strength |B| (G) for top and bottom rows, respectively. The red arrows are velocity field and magnetic field vectors on the meridian plane for the top and bottom rows, respectively.
In the other three tr-MRN models, the outer fan-like component of the outflow is not as prominent as the 2.4Slw-trMRN model; while the inner collimated component is clearly visible. The reason can be numerical (Alfvén dt floor) as well as physical. As shown in the bottom rows of second to fourth panels from the left, magnetic field lines indeed pile up at the centrifugal barrier, which is in the form of spiral (second to third panels from the left) or ring (fourth panel from the left) structures (see corresponding frames in Figs 12–14). However, the ‘ring-type’ centrifugal barrier shows more obvious fan-like outflow cavities than the ‘spiral-type’ centrifugal barrier; this is because the former barrier is more efficient in blocking infall and piling up field lines, while the spiral structure still allow materials and field lines to further fall and spiral along it. Nevertheless, the fan-like outflow should be visible if the accretion flow from the envelope lands on a narrow region of the disc or ring, which can be an explanation to the outflow offset recently observed by Bjerkeli et al. (2016) and Alves et al. (2017). In this paradigm, asymmetric (one-sided) outflows can be more common than symmetric ones.
4 DISCUSSION
4.1 DEMS and AD shock
The main difference of our work with previous studies is the relatively efficient decoupling of magnetic field in the collapsing envelope. It not only promotes the formation of RSDs, but also avoids the abrupt decoupling of the large amount of magnetic flux dragged into the stellar vicinity. Otherwise, as we have demonstrated in models with MRN grains, sooner or later, DEMS will dominate the inner tens to hundreds of au regions, obstructing the gas rotation further. Similarly, if efficient AD only occurs in the inner tens of AU, the ‘so-called’ AD shock (Li & McKee 1996) is also inevitable. Therefore, the magnetic flux problem and magnetic braking catastrophe in star formation are closely related. Averting the former will simultaneously alleviate the latter, which can be achieved by the removal of VSGs in the collapsing protostellar envelope or even earlier, during the pre-stellar core.
4.2 Disc size
Among the tr-MRN models, the inner RSDs (or circumstellar discs) at later times are of ∼20 au in radius and are surrounded by the extended spiral structures. This picture seemingly matches the self-regulated disc formation model by Hennebelle et al. (2016). However, even the non-magnetic models (Table 1) produce small circumstellar discs with ∼20 au radius; yet their rotation-dominated spiral structures are much larger. Hence, the small disc radius is unlikely to result from magnetic effects. In fact, the size of the circumstellar disc is mainly determined by the thermal support (Fig. 20) and is sensitive to the adiabatic index (see Appendix A). In comparison, the extended spiral structures are as thick as 100–150 au in the vertical direction and are not in hydrostatic equilibrium at large-scale heights; the outer layers are largely infalling towards the mid-plane. Therefore, the extended spiral structure may not be strictly defined as part of the disc, but a transition zone between the envelope and the circumstellar disc, where infalling gas starts to spiral inward. Furthermore, when considering the magnetic flux distribution during the collapse, the dominant term should be |${\mathrm{\partial} B_r \over \mathrm{\partial} z}$|, i.e. field pinching along the infall plane as we have shown in Section 3.1.c, instead of |$\mathrm{\partial} B_z \over \mathrm{\partial} r$| considered in Hennebelle et al. (2016).
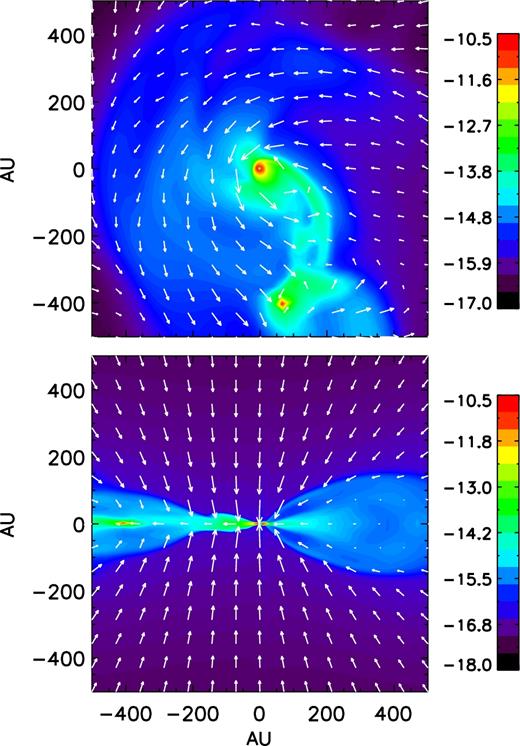
Binary system formed in the HydroSlw model at t ≈ 119.5 kyr, with the central object of 0.087 M⊙. Both circumstellar discs are ∼10–20 au in radius. The bulk part of the circumstellar disc has a temperature of 50–100 K. The distribution of logarithmic mass density and vectors of velocity fields are plotted within 0|$_{.}^{\circ}$|336 of the equator (top) and on the meridian plane (bottom).
The main difference between the non-magnetic and magnetic models is the size of the spiral structure, which is much larger in the non-magnetic models (Table 1). The spiral structure marks the regions where rotation starts to dominate over infall (hints of large spiral structures in recent observations: Tokuda et al. 2014, Pérez et al. 2016 and Yen et al. 2017). Thus, the outer edge of the spiral structure is generally the location where the specific angular momentum curve starts to flatten (e.g. Goodman et al. 1993; Belloche 2013), or the plateau of the centrifugal radius curve. Because of the quickening of rotational motion, the magnetic braking is also the strongest inside the spiral regions (e.g. Fig. 18), which makes the spiral structure smaller over time in models with stronger magnetic field.
4.3 Lower limit for βrot and the case of B335
As we have shown that both initial rotation and magnetization can affect the formation of RSDs, we thus explore the lower limit of initial rotation speed below which an RSD is hard to form. From the test simulations we carried out for tr-MRN grains,10 we find that, in order for discs to form, the ratio of rotational to gravitational energy βrot should be higher than ∼1.5–1.6 per cent for initial magnetization of λ = 2.4 and ∼0.5–0.6 per cent for magnetization of λ = 4.8, which corresponds to a lower limit of angular speed ω0 = 8 × 10−14 and 5 × 10−14 s−1, respectively. Note that these values only apply to dense cores with initial solid-body rotation profile.11
When the initial rotation is slower than the lower limit, the infalling gas will reach a centrifugal radius of <10 au, dragging a large amount of magnetic flux to the stellar vicinity (even under the enhanced AD due to removal of VSGs). Therefore, the central ∼10 au region is inevitably dominated by DEMS, which constantly disrupt the disc structure and suppress the formation of a well-defined RSD. As shown in Fig. 21, the central object is surrounded by filamentary accretion streams rather than a disc (face-on view). In the edge-on view, the infall stream curves towards the upper hemisphere and lands on to the disc from above, which results in an one-sided outflow (similar to the 2.4Slw-trMRN and 4.8Fst-MRN models above12). The curve of centrifugal radius decreases nearly monotonically towards the inner 10 au, only showing a small plateau at ∼5 au. It is consistent with the landing radius of the infall stream.
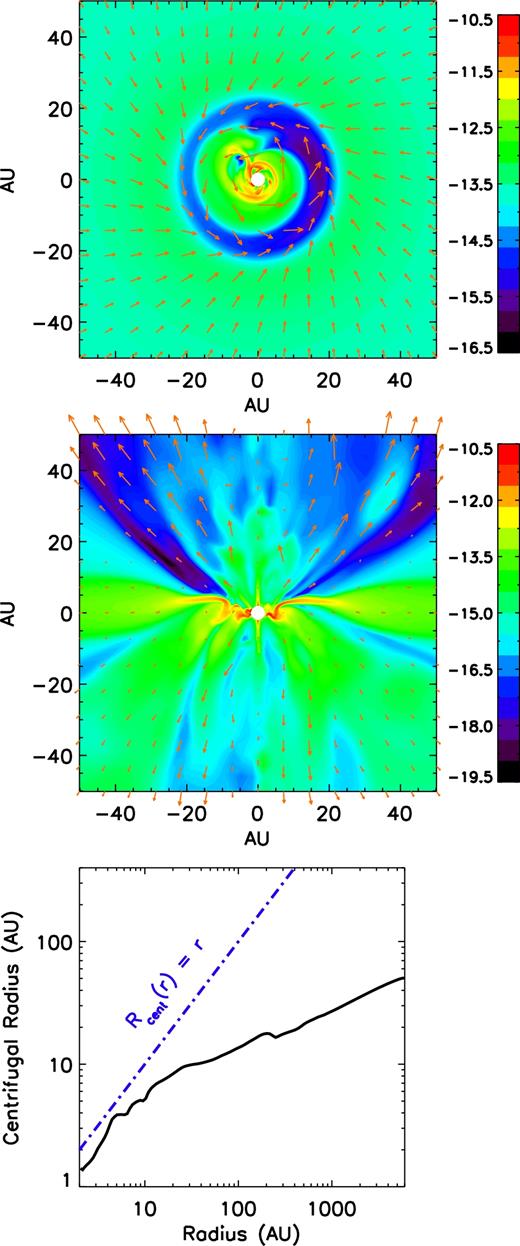
Distribution of logarithmic mass density ρ (g cm−3) within 0|$_{.}^{\circ}$|336 of the equator (top) and on the meridian plane (middle) for a slow rotating core (ω0 = 4 × 10−14 s−1) with λ = 4.8 at t ≈ 107.9 kyr. The mass of the central object is ∼0.06 M⊙. Orange vectors are velocity fields. The DEMS are constantly disrupting the disc structure (<10 au) in the centre. Outflows are yet prominent. Bottom: estimated centrifugal radius.
This particular model matches to some extent the observation of B335, where no Keplerian disc >10 au is found around the protostar (Evans et al. 2015; Yen et al. 2015b) yet CO outflows are clearly visible (Yen, Shigehisa & Nagayoshi 2010). The estimated angular speed of the host core is about 2.6 × 10−14 s−1, which is a few times lower than other protostellar sources with disc detection (Yen et al. 2015a). This value is close to the lower limit of angular speed we find for λ = 4.8 cores. It is likely that B335 is already in lack of VSGs during the collapse process; otherwise, a much larger angular speed (>10−13 s−1) or mass-to-flux ratio (>10) of the host core is required with the full MRN distribution to form even a small, short-lived (or shrinking) disc (Section 3.4). Nevertheless, a disc, even a small one, is necessary to power the ordered, wide-angle outflows observed in B335; a fully magnetically dominated inner region with no disc at all generally produces chaotic morphologies in the bipolar region, which is unlikely the case for B335.
4.4 VSGs in dense cores
The lack of VSGs in dense cores (Tibbs et al. 2016) can be caused by either (1) grain evolution or (2) magnetic selection effect. The former includes accretion of VSGs on to grain mantles (process analogous to molecular freeze-out, e.g. Tielens & Hagen 1982; Hasegawa et al. 1992) and grain coagulation (Chokshi et al. 1993; Dominik & Tielens 1997); and the latter refers to the differential coupling of grains to the magnetic field based on their size (Ciolek & Mouschovias 1996). While grain evolution can start from the quiescent pre-stellar phase, magnetic selection normally occurs during the collapse phase. We will leave the more complete chemistry model including grain evolution and multifluid non-ideal MHD to future studies.
4.5 Numerical limitations
Finally, we raise cautions for the potential limitations of our numerical treatment.
First, we use Alfvén dt floor to limit the velocity of MHD waves, which will add tiny mass to certain grid cells with low density but strong magnetic field (the total added mass for the entire computational domain is of the order of ∼10−3–10−2 of the central point mass). The floor is most likely to trigger in the bipolar regions, which can affect the outflow dynamics and more specifically, slowing down the outflow.
Secondly, we set an AD dt floor (dtfloor, AD) to avoid intolerably small AD time-steps. The result is that the AD diffusivity ηAD is capped13 in the outflow region and bulk part of the disc (if any), which causes the matter there to be better coupled to the magnetic fields than it should be. This cap on ηAD should not affect our main result that disc formation is enabled by ambipolar diffusion in the infalling envelope. We have explored smaller values of dtfloor, AD (=1 × 106 and 3 × 105) using a lower resolution in r direction (δr = 0.33 au), and find that large DEMS still dominate the central regions around the star and disc formation is strongly suppressed as in Section 3.1.b. Therefore, in terms of forming RSDs, the specific angular momentum of the infalling gas being accreted by the disc plays a dominant role over the decoupling process in the disc itself.
Thirdly, the code has no sink particle treatment (except for the stationary sink hole in the centre), and hence is not ideal for following orbital evolution of binary and multiple systems. We only confirm the onset of fragmentation and the formation of companion stellar masses.
Fourthly, we have not included Ohmic and Hall effect in this study, but their corresponding diffusivities are computed regardlessly. We found in the tr-MRN models the Ohmic diffusivity is about ∼10 times smaller than the ambipolar diffusivity inside the circumstellar discs. As we have shown in Zhao+16, Ohmic dissipation has negligible effect on disc formation because (1) with the full MRN distribution, the lack of dense long-lived disc in the first place makes it difficult for Ohmic dissipation to dominate; while (2) in the absence of VSGs, ambipolar diffusivity always dominates over Ohmic diffusivity at densities below 1014–1015 cm−3. Once we further decrease the radius of the inner boundary (e.g. below 1 au), the inclusion of Ohmic dissipation will become crucial. Besides, Hall effect is very sensitive to the polarity of magnetic field (Krasnopolsky et al. 2011; Braiding & Wardle 2012; Tsukamoto et al. 2015b; Wurster et al. 2016), which adds another twist to the formation of protostellar discs. We will investigate the interplay between the three non-ideal MHD effects in future studies.
5 SUMMARY
We have extended our 2D study of protostellar disc formation (Zhao+16) to 3D, using the same equilibrium chemical network. We have verified the main result found in Zhao+16 that the removal of VSGs enables the formation of RSDs of tens of au through the enhanced ambipolar diffusion of magnetic fields in the collapsing envelope. Because of the reduction of magnetic flux dragged into the central disc-forming region, magnetic braking becomes less efficient and the key ingredient for disc formation – angular momentum – is sufficiently retained. Further conclusions are listed below.
(1) Collapse pinches magnetic field lines along the infall plane (pseudo-disc plane) where ambipolar drift is the strongest (|${\propto}{\mathrm{\partial} B_r \over \mathrm{\partial} \theta }$|). With the enhanced ηAD (VSGs absent), the ‘effective’ ion velocity (or the magnetic field velocity) nearly vanishes along the infall plane even at 102–103 au scales. This indicates that magnetic fields are gradually left behind in the envelope by the collapsing neutral matter.
(2) The so-called DEMS (formed by the decoupled magnetic flux from the accreted matter) can still suppress disc formation and obstruct disc rotation if the full MRN distribution is used. Even in the absence of VSGs, DEMS are still present at early times. They play the role of disrupting the first core, preventing it from directly evolving into a circumstellar disc. Disc formation in such cases relies on the supply of high angular momentum material from the infalling envelope.
(3) High specific angular momentum entering the inner region enables both the formation of RSDs and the development of spiral (or ring) structures. The size of spirals (or rings) matches the centrifugal radius of the infalling gas. The outer edge of the spirals (or rings) is also the location where the specific angular momentum curve starts to flatten.
(4) When the initial core is relatively weakly magnetized (with a dimensionless mass-to-flux ratio of 4.8 rather than 2.4), fragmentation frequently occurs on the outer spiral arms (or on the rings), where infall material from the envelope piles up. Such fragments of tens of Jupiter mass could mark the early onset of multiple systems. Some of the fragments, particularly when the core rotation is relatively slow, merge quickly with the central stellar object, producing bursts of mass accretion. Others are longer lived, and can potentially survive as multiple stellar systems, although sink particles are needed to better follow their long-term evolution.
(5) Magnetically driven outflows have multiple components. The central bipolar component is more symmetric and collimated, which may correspond to jet or ‘X-wind’. The outer fan-like component can be more asymmetric (one-sided). Its launching location coincides with the landing site of the infalling gas on the disc or ring.
ACKNOWLEDGEMENTS
We thank Kengo Tomida for providing the data of evolutionary track. BZ and PC acknowledge support from the European Research Council (ERC; project PALs 320620). Z-Y L is supported in part by National Aeronautics and Space Administration (NASA) NNX14AB38G, National Science Foundation (NSF) AST-1313083 and NSF AST-1716259. Numerical simulations are carried out on the Center for Astrochemical Studies (CAS) group cluster at Max-Planck-Institute for Extraterrestrial Physics (MPE).
Merely for convenience, we follow the axisymmetric pre-stellar collapse in 2D until well before the formation of a first hydrostatic core (Larson 1969), and restart the simulation in full 3D thereafter.
The momentum transfer rate coefficients are parametrized as a function of temperature according to table 1 of Pinto & Galli (2008).
The velocity profile is plotted along a line cut within 0|$_{.}^{\circ}$|336 of the equator; however, the infall stream in this model does not lie on the equator and lands upon the disc from the upper hemisphere (see Section 3.1.c and Fig. 5) Therefore, the actual decoupling region along the infall stream should be slightly bigger and a moderate decoupling indeed occurs near 20 au as well.
When magnetic field lines are dragged to the inner boundary, they are free to move around after detaching from the accreted matter. Therefore, the total magnetic flux is conserved (unlike Wurst, Price & Bate 2017).
Note that the RSD and the pseudo-disc in the 2.4Slw-trMRN model are non-coplanar (Fig. 5, see also Li et al. 2014). Despite the unusual geometry, the infall stream along the pseudo-disc still lands relatively far from the central star, with a radial distance between 10 and 15 au (centrifugal radius, see also Section 3.4 for detailed discussions).
The high-density part of the spiral structures generally have plasma-β of the order of ∼101, while the plasma-β in the disc is at least a few 102.
ζ and Γ are dimensionless parameters used in Kratter et al. (2010).
The minimum density allowed for any given cell is set to |${|\boldsymbol {B}|^2 \over 4\pi (|\Delta x|_{\rm min}/{\rm d}t_{\rm floor,\, {Alfv{\acute{e}}n}})^2}$|, where |Δx|min is the smallest of the cell's sizes along r, θ and ϕ directions, and d|$t_{\rm floor,\, {Alfv{\acute{e}}n}}$| is set to 3 × 105 s. As a result, artificial mass is added to cells with densities below the minimum density. Such a floor usually triggers in the bipolar regions with very large Alfvén speeds and often very tiny |Δx|ϕ.
The initial angular speed ω0 tested includes 8 × 10−14 and 7.2 × 10−14 s−1 for initial magnetization of λ = 2.4, and 6.4 × 10−14, 5 × 10−14 and 4 × 10−14 s−1 for initial magnetization of λ = 4.8.
The lower limit of βrot found here is likely to be the key for the small discs (≲10 au) formed in Dapp et al. (2012). In fig. 2 of Dapp et al. (2012), they showed very similar trend of enhanced AD in the absence of VSGs as we presented in Zhao+16; however, they did not elaborate on its effect on disc formation. The initial rotation speed used in Dapp et al. (2012) as well as in Dapp & Basu (2010, 1 km s−1 pc−1 ≈ 3.2 × 10−14 s−1) seems to be too slow to produce discs larger than 10 au. It corresponds to βrot ∼0.6 per cent for their λ = 2 core, which is well below the lower limit we found for the λ = 2.4 case.
In some test simulations, the infall stream can also curve towards the lower hemisphere and land on to the disc from below.
The cap of ηAD is computed for each cell as |${\rm CFL_{AD}} {|\Delta x|_{\rm min}^2 \over 4 {\rm d}t_{\rm floor,AD}}$|, where CFLAD = 0.4 is the Courant–Friedrichs–Lewy number for AD, |Δx|min is the smallest of the cell's sizes along r, θ and ϕ directions, and dtfloor, AD is set to 3 × 106 s. Such an ηAD cap based on dtfloor, AD behaves approximately as a constant ηAD cap of ∼1019 cm2 s−1 in the bulk part of the circumstellar disc.
We find that stiffening the EOS at 3 × 10−13 g cm−3 offers a more realistic thermal pressure than at 1 × 10−13 g cm−3 for the single 5/3 power law.
REFERENCES
APPENDIX A: EQUATION OF STATE
Function fitting (red solid curve) for the evolutionary track from Tomida et al. (2013, black solid curve). The barotropic EOS with adiabatic indices of 5/3 and 7/5 is shown in blue dashed and purple dashed lines.



