The most massive galaxies in clusters are already fully grown at z ∼ 0.5

Oldham, L. J.; Houghton, R. C. W.; Davies, Roger L.

doi:10.1093/mnras/stw2791

Abstract

By constructing scaling relations for galaxies in the massive cluster MACSJ0717.5 at z = 0.545 and comparing with those of Coma, we model the luminosity evolution of the stellar populations and the structural evolution of the galaxies. We calculate magnitudes, surface brightnesses and effective radii using Hubble Space Telescope (HST)/ACS images and velocity dispersions using Gemini/GMOS spectra, and present a catalogue of our measurements for 17 galaxies. We also generate photometric catalogues for ∼3000 galaxies from the HST imaging. With these, we construct the colour–magnitude relation, the Fundamental Plane, the mass-to-light versus mass relation, the mass–size relation and the mass–velocity dispersion relation for both clusters. We present a new, coherent way of modelling these scaling relations simultaneously using a simple physical model in order to infer the evolution in luminosity, size and velocity dispersion as a function of redshift, and show that the data can be fully accounted for with this model. We find that (a) the evolution in size and velocity dispersion undergone by these galaxies between z ∼ 0.5 and z ∼ 0 is mild, with R_e(z) ∼ (1 + z)^{−0.40 ± 0.32} and σ(z) ∼ (1 + z)^{0.09 ± 0.27}, and (b) the stellar populations are old, ∼10 Gyr, with a ∼3 Gyr dispersion in age, and are consistent with evolving purely passively since z ∼ 0.5 with |$\Delta \log M/L_{\rm B} = -0.55_{-0.07}^{+0.15} z$|⁠. The implication is that these galaxies formed their stars early and subsequently grew dissipationlessly so as to have their mass already in place by z ∼ 0.5, and suggests a dominant role for dry mergers, which may have accelerated the growth in these high-density cluster environments.

galaxies: clusters: individual: MACSJ0717.5, galaxies: elliptical and lenticular, cD, galaxies: evolution, galaxies: kinematics and dynamics

1 INTRODUCTION

Observations of early-type galaxies (ETGs) at high redshifts indicate that they are massive, bright and compact (e.g. van Dokkum et al. 2008), and must therefore evolve through a series of minor mergers and accretion events into the large, passive systems that we see today. However, they also obey tight scaling relations, such as the Fundamental Plane (FP), out to redshifts z ∼ 1 (e.g. Holden et al. 2010), with a small scatter that is much more in keeping with stellar populations that formed early, then faded passively. As such, there remain a number of unanswered questions about how these systems have evolved: for instance, when did they undergo most of their evolution? Do all ETGs experience significant size growth? Luckily, ETGs retain observable imprints of their past which help us to answer these questions.

The FP (Djorgovski & Davis 1987; Dressler et al. 1987) is one such tool. The virial theorem predicts the existence of a plane of the form

\begin{equation} \log R_{\rm e} = \alpha \log \sigma + \beta \langle \mu _{\rm e}\rangle + \gamma , \end{equation}

(1)

where R_e, σ and 〈μ_e〉 are the half-light radius, velocity dispersion and effective surface brightness (the mean surface brightness within R_e), respectively, with α = 2 and β = 1, which should be tightly obeyed by all galaxies. The fact that ETGs fall on such a plane implies a high degree of uniformity in how these systems have evolved, but the tilt of the FP relative to the virial prediction – with α = 1.24 and β = 0.33 in the local Universe (Jørgensen, Franx & Kjaergaard 1995) – also indicates some systematic variations across the plane, which may be either structural – with, for instance, some mass dependence in the luminous-to-dark matter ratio or the mass profile shape – or related to the stellar populations, with more massive galaxies having more bottom-heavy initial mass functions (IMFs). The evolution of the FP therefore holds a great deal of information about the evolution of the structure and stellar populations of ETGs themselves.

In the past, the evolution of the zero-point of the FP has been taken as evidence for the passive fading of the stellar populations and used to measure stellar age (e.g. Bender, Ziegler & Bruzual 1996; van Dokkum & Franx 1996; van Dokkum & Ellis 2003; Jørgensen et al. 2006), generally implying a mean star formation redshift z_f > 2. However, the FP is also sensitive to evolution in velocity dispersion and size, and while more recent studies have attempted to account for this, no consensus has yet been reached on the strength of this evolution. For instance, Saglia et al. (2010) measured the structural evolution of a sample of field galaxies out to z ∼ 0.9 and found it to be significant, with its inclusion in the zero-point analysis increasing the stellar age by 1–4 Gyr (depending on morphology and redshift). On the other hand, Jørgensen & Chiboucas (2013) and Jørgensen et al. (2014) found only very small differences in size and velocity dispersion for cluster galaxies across similar redshifts – roughly one-third that of Saglia et al. (2010) – and made the suggestion that structural evolution may depend on environment, with accelerated growth in dense clusters. However, Newman et al. (2014) found no evidence for size differences between field and cluster galaxies at z = 1.8 – indicating that any changes must imprint themselves in a narrow redshift window – while Valentinuzzi et al. (2010) identified large numbers of compact galaxies in clusters at 0 < z < 1, which suggests the evolutionary scheme of ETGs in clusters is diverse. The question of how and when any growth occurs, then, and how it relates to the stellar populations, remains open, and it is important to try to answer this further using independent samples and methods.

Another extremely simple but useful scaling relation that can be used to give a measure of the ETG formation epoch is the colour–magnitude relation (CMR; Baum 1959; Sandage 1972; Visvanathan & Sandage 1977), in which the ETGs fall along a tight red sequence, whose intrinsic scatter is mainly determined by the distribution of stellar age. In contrast to the FP, which contains information on dark matter content and galaxy structure, the CMR depends almost wholly on the properties of the stellar populations. Several studies out to redshifts z ∼ 1.3 have shown the intrinsic scatter about the CMR to be consistently small (generally <0.1 mag: see Stanford, Eisenhardt & Dickinson 1995; Ellis et al. 1997; Bower, Kodama & Terlevich 1998; Stanford, Eisenhardt & Dickinson 1998; Mei et al. 2009), suggestive of generally old stellar populations, with a redshift of formation z_f > 2 and a small spread in age. However, it is hard to disentangle these two degenerate factors, given that the scatter decreases with both increasing age – as stars become asymptotically redder – and increasing synchronicity – as stars with similar ages have similar colours. It is therefore possible for a stellar population with recent, synchronized star formation to have the same small scatter as one in which the star formation happened longer ago but was dispersed. Clearly, if this degeneracy can be broken, it can provide informative complementary constraints on the FP.

The aim of this work is to construct these scaling relations for the cluster MACSJ0717.5+3745 (hereafter MACSJ0717) at z = 0.545, and to compare with those of the Coma galaxies to investigate their evolution in terms of galaxy structure and stellar populations. The paper is organized as follows: in Section 2, we introduce the data and explain our reduction methods; in Section 3, we construct the scaling relations and in Section 4, we interpret these in terms of stellar population models. Sections 5 and 6 then give a discussion and summary. We assume Ω_m = 0.3, Ω_Λ = 0.7 and H₀ = 71 kms⁻¹ Mpc⁻¹ throughout, and calculate magnitudes in the AB system.

2 DATA SOURCES AND REDUCTION

2.1 Sources

For both MACSJ0717 and Coma, we construct the CMR, the FP and mass-to-light versus mass (MLM) relation and the mass–size and mass–velocity dispersion relations. We therefore require colours, surface photometry and kinematics in each case.

For MACSJ0717, we measure photometry using archival Hubble Space Telescope (HST)/ACS images that were observed as part of the Cluster Lensing And Supernova survey with Hubble (CLASH; Postman et al. 2012). For size and surface brightness measurements, we use the F475W (exposure time: 4064 s) and F625W bands (exposure time: 4128 s) in order to bracket the Balmer break in the rest frame. For catalogue generation using SExtractor (Bertin 1996), we additionally use the multiband image (summing all 16 CLASH filters) as the reference image for object detection (as explained in more detail in Section 2.2). These data are available from the CLASH archive, and have been previously corrected for galactic extinction and redrizzled to a pixel scale of 0.065 arcsec pixel⁻¹. We measure velocity dispersions using Gemini/GMOS spectra, available in the Gemini archive for a subsample of 31 galaxies. These spectra, along with associated flat and bias frames, were taken over four dates between 2003 February 4 and 2003 March 2, using GMOS in multi-object mode with the B600_G5303 grating (which has a resolution R = 1688 for a 0.5 arcsec slit width at 461 nm), as part of the science program GN-2002B-Q-44.

For Coma, we use the kinematic data from Jørgensen et al. (1999); integrated photometry, observed in the Johnson U and V bands, from Terlevich, Caldwell & Bower (2001); and the surface photometry in the Gunn r΄ band from Jørgensen et al. (1995). We refer the reader to these papers for further information, though we note that the photometry has been previously corrected for galactic extinction, and that we convert the Gunn r΄ photometry to AB magnitudes using the corrections listed in Frei & Gunn (1994).

2.2 Photometry

The CLASH data base (Postman et al. 2012) provides a SExtractor-generated catalogue of isophotal magnitudes for ∼8000 objects detected in the HST images; however, in order to calculate colours precisely for the CMR and avoid underestimating the flux of the largest low-surface-brightness galaxies, we use SExtractor to generate a catalogue of integrated aperture magnitudes, taking advantage of SExtractor's dual-image mode to use the multiband image for source detection and the single-band images for measurement. We use an aperture radius of 1.3 arcsec in both wavebands, and select objects according to the following criteria:

stellarity < 0.95 and full width at half-maximum > 0.2 arcsec, to avoid contamination from stars;
magnitude uncertainty < 0.2 mag and flag > 4, to avoid objects that may not have been properly deblended or do not have reliable photometry;
F625W magnitude < 25 mag, as a luminosity cut-off.

We cross-correlate our SExtractor catalogue with the existing CLASH catalogue, which provides photometric redshifts based on the full set of 16 ACS/HST filters, and further rejects all objects whose redshift range does not satisfy z_min < 0.545 < z_max for the 95 per cent confidence intervals z_min and z_max.

We model the surface brightnesses of the galaxies in the F625W image using single-component Sérsic profiles, with

\begin{equation} I(R) = I_{\rm e} \exp {{\Bigg [-k_n\Big (\frac{R}{R_{\rm e}}\Big )^{{1}/{n}}- 1\Bigg ]}} \end{equation}

(2)

for Sérsic index n, effective radius R_e, k_n = 2n − 0.324 and radius R² = q²(x − x₀)² + (y − y₀)²/q² for axis ratio q and galaxy centroid (x₀, y₀) (with both R_e and R being circularized, projected quantities). To test for and eliminate systematics in our size measurements, we proceed via two different methods. First, we use the curve-of-growth fitting (COG) code presented in Houghton et al. (2012), which has been rigorously tested and shown to reproduce simulated images to high accuracy (see the appendix of that paper). This masks bright regions close to the galaxy to create a ‘clean’ cutout, whose circularized integrated light profile is then fitted using a chi-squared minimization. Secondly, we use a surface-fitting code based on that developed for Oldham et al. (2016), which explores the six-dimensional parameter space represented by (x₀, y₀, R_e, n, q, θ) – where (x₀, y₀) is the centroid of the Sérsic profile, θ is the position angle and q is the ellipticity – using the Markov Chain Monte Carlo (MCMC) sampler emcee (Foreman-Mackey et al. 2013). In this case, for objects with crowded fields, we model all bright objects simultaneously. For both the COG and the surface-fitting routines, we convolve the model with the radial profile of an unsaturated star in the image to account for the point-spread function, and we find very good agreement between the two sets of results. For Coma, we use the sizes and surface brightnesses presented in Jørgensen et al. (1995), which were measured using de Vaucouleurs COGs.

Of the 31 MACSJ0717 objects in the spectroscopic sample, only 19 of these overlap with the CLASH field; of these, a further two are in fact stars (as can be clearly seen in both the imaging and the spectra), and so are excluded from the analysis. We therefore end up with a final sample of 17 galaxies. The completeness of the spectroscopic sample relative to the galaxy population is illustrated in Fig. 2. Three of the systems in the final sample (object IDs 11, 13 and 22) have clear extended stellar haloes or bulge+disc morphologies which mean that we are unable to construct satisfactory models using a single Sérsic component; for these, we add a second component and find that this enables us to model their light profiles down to the noise. It is important to do this sparingly in order that all our measured sizes are directly comparable.

The galaxy cutouts and model residuals are presented in Fig. A1 in Appendix A, and the effective radii and surface brightnesses are included in Table 1, with the latter corrected for cosmological dimming as 10 log (1 + z) and extinction. Fig. 1 shows the CLASH footprint, with our final galaxy sample marked. We also calculate synthetic rest-frame absolute magnitudes in the Johnson U and B bands, using the stellar population models of Bruzual & Charlot (2003) (under the same assumptions as those stated in Section 4); these are included in Table A1.

HST/ACS F625W image of MACSJ0717, with a pixel scale of 0.065 arcsec pixel−1 and dimensions 325 arcsec × 325 arcsec; black circles show the final sample of 17 galaxies.

Figure 1.

HST/ACS F625W image of MACSJ0717, with a pixel scale of 0.065 arcsec pixel⁻¹ and dimensions 325 arcsec × 325 arcsec; black circles show the final sample of 17 galaxies.

Open in new tab Download slide

Table 1.

Open in new tab

Photometry, kinematics and stellar and dynamical masses for the galaxies in the final MACSJ0717 sample. The photometry has been corrected for extinction and effective surface brightnesses 〈μ_e〉 are corrected for cosmological dimming as 10 log (1 + z); F625W magnitudes are calculated from surface fitting the HST/ACS image as described in Section 2.1, while F475W–F625W colours are calculated from the SExtractor catalogues, also described in Section 2.1. Dynamical and stellar masses M_dyn and M_⋆ are calculated as described in Sections 3.3 and 3.4. We note that a number of objects have M_⋆ > M_dyn, which may be a result of the assumptions made to measure stellar masses, or the fact that M_dyn is not the total dynamical mass but the mass measured in some ill-defined aperture. It also reflects the findings of a number of other studies of non-local ETGs (e.g. Stockton et al. 2014). We discuss this further in Section 5.3. We also compute synthetic rest-frame absolute magnitudes in the Johnson U and B bands; these are included in Table A1.

ID	RA (deg)	Dec. (deg)	R_e (kpc)	σ (km s⁻¹)	〈μ_e〉 (mag)	F625W (mag)	F475W–F625W (mag)	log (M_⋆/M_⊙)	log (M_dyn/M_⊙)
2	109.4079	37.7363	3.04 ± 0.18	220.9 ± 4.0	19.92 ± 0.11	21.46 ± 0.03	1.88 ± 0.03	11.40 ± 0.06	11.24 ± 0.03
4	109.3952	37.7316	3.42 ± 0.20	198.8 ± 5.4	19.93 ± 0.10	21.24 ± 0.04	1.86 ± 0.03	11.42 ± 0.09	11.20 ± 0.03
5	109.3943	37.7358	1.69 ± 0.06	220.2 ± 4.8	18.44 ± 0.05	21.27 ± 0.01	1.80 ± 0.02	11.28 ± 0.09	10.98 ± 0.01
7	109.3981	37.7515	4.06 ± 0.12	298.7 ± 3.0	19.57 ± 0.05	20.49 ± 0.05	1.89 ± 0.02	11.73 ± 0.11	11.63 ± 0.02
8	109.3986	37.7548	9.51 ± 0.30	157.8 ± 2.4	20.68 ± 0.54	18.48 ± 0.01	1.90 ± 0.01	12.51 ± 0.11	11.44 ± 0.02
9	109.3857	37.7454	14.55 ± 0.33	274.7 ± 4.7	21.37 ± 0.02	19.54 ± 0.01	1.70 ± 0.01	11.61 ± 0.15	12.11 ± 0.01
10	109.3892	37.7514	2.68 ± 0.11	159.1 ± 3.6	19.25 ± 0.07	21.07 ± 0.02	1.75 ± 0.03	11.22 ± 0.10	10.90 ± 0.02
11	109.3831	37.7535	2.52 ± 0.97	184.8 ± 3.9	20.51 ± 0.09	20.59 ± 0.03	1.77 ± 0.02	11.42 ± 0.10	11.00 ± 0.03
12	109.3707	37.7523	5.07 ± 0.24	216.5 ± 4.1	20.44 ± 0.08	20.88 ± 0.02	1.79 ± 0.02	11.39 ± 0.09	11.44 ± 0.02
13	109.3690	37.7577	2.41 ± 0.88	109.4 ± 3.1	20.66 ± 0.08	20.84 ± 0.05	1.69 ± 0.03	11.08 ± 0.15	10.52 ± 0.03
14	109.3601	37.7584	10.26 ± 0.94	223.2 ± 4.1	21.28 ± 0.16	20.20 ± 0.05	1.85 ± 0.02	11.80 ± 0.11	11.77 ± 0.04
16	109.3529	37.7672	11.31 ± 0.42	302.8 ± 3.8	20.82 ± 0.05	19.52 ± 0.04	1.89 ± 0.02	11.99 ± 0.12	12.08 ± 0.02
22	109.4019	37.7341	3.40 ± 0.38	205.1 ± 5.9	20.79 ± 0.02	20.22 ± 0.01	1.97 ± 0.02	12.01 ± 0.08	11.22 ± 0.02
23	109.3754	37.7511	3.33 ± 0.13	227.1 ± 6.7	19.88 ± 0.05	21.25 ± 0.02	1.92 ± 0.03	11.57 ± 0.07	11.30 ± 0.01
24	109.3629	37.7653	3.79 ± 0.17	187.6 ± 4.7	20.14 ± 0.08	21.21 ± 0.02	1.80 ± 0.03	11.31 ± 0.10	11.19 ± 0.02
28	109.4188	37.7439	0.21 ± 0.00	166.1 ± 5.2	17.52 ± 0.18	24.77 ± 0.14	1.34 ± 0.03	8.51 ± 0.06	9.84 ± 0.01

ID	RA (deg)	Dec. (deg)	R_e (kpc)	σ (km s⁻¹)	〈μ_e〉 (mag)	F625W (mag)	F475W–F625W (mag)	log (M_⋆/M_⊙)	log (M_dyn/M_⊙)
2	109.4079	37.7363	3.04 ± 0.18	220.9 ± 4.0	19.92 ± 0.11	21.46 ± 0.03	1.88 ± 0.03	11.40 ± 0.06	11.24 ± 0.03
4	109.3952	37.7316	3.42 ± 0.20	198.8 ± 5.4	19.93 ± 0.10	21.24 ± 0.04	1.86 ± 0.03	11.42 ± 0.09	11.20 ± 0.03
5	109.3943	37.7358	1.69 ± 0.06	220.2 ± 4.8	18.44 ± 0.05	21.27 ± 0.01	1.80 ± 0.02	11.28 ± 0.09	10.98 ± 0.01
7	109.3981	37.7515	4.06 ± 0.12	298.7 ± 3.0	19.57 ± 0.05	20.49 ± 0.05	1.89 ± 0.02	11.73 ± 0.11	11.63 ± 0.02
8	109.3986	37.7548	9.51 ± 0.30	157.8 ± 2.4	20.68 ± 0.54	18.48 ± 0.01	1.90 ± 0.01	12.51 ± 0.11	11.44 ± 0.02
9	109.3857	37.7454	14.55 ± 0.33	274.7 ± 4.7	21.37 ± 0.02	19.54 ± 0.01	1.70 ± 0.01	11.61 ± 0.15	12.11 ± 0.01
10	109.3892	37.7514	2.68 ± 0.11	159.1 ± 3.6	19.25 ± 0.07	21.07 ± 0.02	1.75 ± 0.03	11.22 ± 0.10	10.90 ± 0.02
11	109.3831	37.7535	2.52 ± 0.97	184.8 ± 3.9	20.51 ± 0.09	20.59 ± 0.03	1.77 ± 0.02	11.42 ± 0.10	11.00 ± 0.03
12	109.3707	37.7523	5.07 ± 0.24	216.5 ± 4.1	20.44 ± 0.08	20.88 ± 0.02	1.79 ± 0.02	11.39 ± 0.09	11.44 ± 0.02
13	109.3690	37.7577	2.41 ± 0.88	109.4 ± 3.1	20.66 ± 0.08	20.84 ± 0.05	1.69 ± 0.03	11.08 ± 0.15	10.52 ± 0.03
14	109.3601	37.7584	10.26 ± 0.94	223.2 ± 4.1	21.28 ± 0.16	20.20 ± 0.05	1.85 ± 0.02	11.80 ± 0.11	11.77 ± 0.04
16	109.3529	37.7672	11.31 ± 0.42	302.8 ± 3.8	20.82 ± 0.05	19.52 ± 0.04	1.89 ± 0.02	11.99 ± 0.12	12.08 ± 0.02
22	109.4019	37.7341	3.40 ± 0.38	205.1 ± 5.9	20.79 ± 0.02	20.22 ± 0.01	1.97 ± 0.02	12.01 ± 0.08	11.22 ± 0.02
23	109.3754	37.7511	3.33 ± 0.13	227.1 ± 6.7	19.88 ± 0.05	21.25 ± 0.02	1.92 ± 0.03	11.57 ± 0.07	11.30 ± 0.01
24	109.3629	37.7653	3.79 ± 0.17	187.6 ± 4.7	20.14 ± 0.08	21.21 ± 0.02	1.80 ± 0.03	11.31 ± 0.10	11.19 ± 0.02
28	109.4188	37.7439	0.21 ± 0.00	166.1 ± 5.2	17.52 ± 0.18	24.77 ± 0.14	1.34 ± 0.03	8.51 ± 0.06	9.84 ± 0.01

Table 1.

Open in new tab

Photometry, kinematics and stellar and dynamical masses for the galaxies in the final MACSJ0717 sample. The photometry has been corrected for extinction and effective surface brightnesses 〈μ_e〉 are corrected for cosmological dimming as 10 log (1 + z); F625W magnitudes are calculated from surface fitting the HST/ACS image as described in Section 2.1, while F475W–F625W colours are calculated from the SExtractor catalogues, also described in Section 2.1. Dynamical and stellar masses M_dyn and M_⋆ are calculated as described in Sections 3.3 and 3.4. We note that a number of objects have M_⋆ > M_dyn, which may be a result of the assumptions made to measure stellar masses, or the fact that M_dyn is not the total dynamical mass but the mass measured in some ill-defined aperture. It also reflects the findings of a number of other studies of non-local ETGs (e.g. Stockton et al. 2014). We discuss this further in Section 5.3. We also compute synthetic rest-frame absolute magnitudes in the Johnson U and B bands; these are included in Table A1.

ID	RA (deg)	Dec. (deg)	R_e (kpc)	σ (km s⁻¹)	〈μ_e〉 (mag)	F625W (mag)	F475W–F625W (mag)	log (M_⋆/M_⊙)	log (M_dyn/M_⊙)
2	109.4079	37.7363	3.04 ± 0.18	220.9 ± 4.0	19.92 ± 0.11	21.46 ± 0.03	1.88 ± 0.03	11.40 ± 0.06	11.24 ± 0.03
4	109.3952	37.7316	3.42 ± 0.20	198.8 ± 5.4	19.93 ± 0.10	21.24 ± 0.04	1.86 ± 0.03	11.42 ± 0.09	11.20 ± 0.03
5	109.3943	37.7358	1.69 ± 0.06	220.2 ± 4.8	18.44 ± 0.05	21.27 ± 0.01	1.80 ± 0.02	11.28 ± 0.09	10.98 ± 0.01
7	109.3981	37.7515	4.06 ± 0.12	298.7 ± 3.0	19.57 ± 0.05	20.49 ± 0.05	1.89 ± 0.02	11.73 ± 0.11	11.63 ± 0.02
8	109.3986	37.7548	9.51 ± 0.30	157.8 ± 2.4	20.68 ± 0.54	18.48 ± 0.01	1.90 ± 0.01	12.51 ± 0.11	11.44 ± 0.02
9	109.3857	37.7454	14.55 ± 0.33	274.7 ± 4.7	21.37 ± 0.02	19.54 ± 0.01	1.70 ± 0.01	11.61 ± 0.15	12.11 ± 0.01
10	109.3892	37.7514	2.68 ± 0.11	159.1 ± 3.6	19.25 ± 0.07	21.07 ± 0.02	1.75 ± 0.03	11.22 ± 0.10	10.90 ± 0.02
11	109.3831	37.7535	2.52 ± 0.97	184.8 ± 3.9	20.51 ± 0.09	20.59 ± 0.03	1.77 ± 0.02	11.42 ± 0.10	11.00 ± 0.03
12	109.3707	37.7523	5.07 ± 0.24	216.5 ± 4.1	20.44 ± 0.08	20.88 ± 0.02	1.79 ± 0.02	11.39 ± 0.09	11.44 ± 0.02
13	109.3690	37.7577	2.41 ± 0.88	109.4 ± 3.1	20.66 ± 0.08	20.84 ± 0.05	1.69 ± 0.03	11.08 ± 0.15	10.52 ± 0.03
14	109.3601	37.7584	10.26 ± 0.94	223.2 ± 4.1	21.28 ± 0.16	20.20 ± 0.05	1.85 ± 0.02	11.80 ± 0.11	11.77 ± 0.04
16	109.3529	37.7672	11.31 ± 0.42	302.8 ± 3.8	20.82 ± 0.05	19.52 ± 0.04	1.89 ± 0.02	11.99 ± 0.12	12.08 ± 0.02
22	109.4019	37.7341	3.40 ± 0.38	205.1 ± 5.9	20.79 ± 0.02	20.22 ± 0.01	1.97 ± 0.02	12.01 ± 0.08	11.22 ± 0.02
23	109.3754	37.7511	3.33 ± 0.13	227.1 ± 6.7	19.88 ± 0.05	21.25 ± 0.02	1.92 ± 0.03	11.57 ± 0.07	11.30 ± 0.01
24	109.3629	37.7653	3.79 ± 0.17	187.6 ± 4.7	20.14 ± 0.08	21.21 ± 0.02	1.80 ± 0.03	11.31 ± 0.10	11.19 ± 0.02
28	109.4188	37.7439	0.21 ± 0.00	166.1 ± 5.2	17.52 ± 0.18	24.77 ± 0.14	1.34 ± 0.03	8.51 ± 0.06	9.84 ± 0.01

ID	RA (deg)	Dec. (deg)	R_e (kpc)	σ (km s⁻¹)	〈μ_e〉 (mag)	F625W (mag)	F475W–F625W (mag)	log (M_⋆/M_⊙)	log (M_dyn/M_⊙)
2	109.4079	37.7363	3.04 ± 0.18	220.9 ± 4.0	19.92 ± 0.11	21.46 ± 0.03	1.88 ± 0.03	11.40 ± 0.06	11.24 ± 0.03
4	109.3952	37.7316	3.42 ± 0.20	198.8 ± 5.4	19.93 ± 0.10	21.24 ± 0.04	1.86 ± 0.03	11.42 ± 0.09	11.20 ± 0.03
5	109.3943	37.7358	1.69 ± 0.06	220.2 ± 4.8	18.44 ± 0.05	21.27 ± 0.01	1.80 ± 0.02	11.28 ± 0.09	10.98 ± 0.01
7	109.3981	37.7515	4.06 ± 0.12	298.7 ± 3.0	19.57 ± 0.05	20.49 ± 0.05	1.89 ± 0.02	11.73 ± 0.11	11.63 ± 0.02
8	109.3986	37.7548	9.51 ± 0.30	157.8 ± 2.4	20.68 ± 0.54	18.48 ± 0.01	1.90 ± 0.01	12.51 ± 0.11	11.44 ± 0.02
9	109.3857	37.7454	14.55 ± 0.33	274.7 ± 4.7	21.37 ± 0.02	19.54 ± 0.01	1.70 ± 0.01	11.61 ± 0.15	12.11 ± 0.01
10	109.3892	37.7514	2.68 ± 0.11	159.1 ± 3.6	19.25 ± 0.07	21.07 ± 0.02	1.75 ± 0.03	11.22 ± 0.10	10.90 ± 0.02
11	109.3831	37.7535	2.52 ± 0.97	184.8 ± 3.9	20.51 ± 0.09	20.59 ± 0.03	1.77 ± 0.02	11.42 ± 0.10	11.00 ± 0.03
12	109.3707	37.7523	5.07 ± 0.24	216.5 ± 4.1	20.44 ± 0.08	20.88 ± 0.02	1.79 ± 0.02	11.39 ± 0.09	11.44 ± 0.02
13	109.3690	37.7577	2.41 ± 0.88	109.4 ± 3.1	20.66 ± 0.08	20.84 ± 0.05	1.69 ± 0.03	11.08 ± 0.15	10.52 ± 0.03
14	109.3601	37.7584	10.26 ± 0.94	223.2 ± 4.1	21.28 ± 0.16	20.20 ± 0.05	1.85 ± 0.02	11.80 ± 0.11	11.77 ± 0.04
16	109.3529	37.7672	11.31 ± 0.42	302.8 ± 3.8	20.82 ± 0.05	19.52 ± 0.04	1.89 ± 0.02	11.99 ± 0.12	12.08 ± 0.02
22	109.4019	37.7341	3.40 ± 0.38	205.1 ± 5.9	20.79 ± 0.02	20.22 ± 0.01	1.97 ± 0.02	12.01 ± 0.08	11.22 ± 0.02
23	109.3754	37.7511	3.33 ± 0.13	227.1 ± 6.7	19.88 ± 0.05	21.25 ± 0.02	1.92 ± 0.03	11.57 ± 0.07	11.30 ± 0.01
24	109.3629	37.7653	3.79 ± 0.17	187.6 ± 4.7	20.14 ± 0.08	21.21 ± 0.02	1.80 ± 0.03	11.31 ± 0.10	11.19 ± 0.02
28	109.4188	37.7439	0.21 ± 0.00	166.1 ± 5.2	17.52 ± 0.18	24.77 ± 0.14	1.34 ± 0.03	8.51 ± 0.06	9.84 ± 0.01

2.3 Spectroscopy

We reduce the spectra of all 31 galaxies using the GMOS package in iraf (Tody 1993), calibrating the wavelength using the skylines in the exposures, according to the UVES sky emission atlas (Hanuschik 2003). To attain a higher signal-to-noise ratio, we stack the 12 exposures slitlet by slitlet.

We model each spectrum as the sum of a galaxy and a continuum component. For the former, we use stellar templates for G, K, A and F stars from the Indo-US Stellar Library of Coudé Feed Stellar Spectra (Valdes et al. 2004), which we redshift and convolve with a dispersion |$\sigma _{{\rm model}}^2 = \sigma _{{\rm true}}^2 + \sigma _{{\rm inst}}^2 - \sigma _{{\rm tmp}}^2$|⁠, where σ_true is the physical velocity dispersion of the system, σ_inst is the instrument resolution and σ_tmp is the intrinsic resolution of the templates (which is 1.2 Å for the Indo-US templates). We measure the resolution in each spectrum by fitting Gaussians to the skylines, and find this to be constant across the slitlets, with λ/dλ = 3030. The continuum is an order-6 polynomial which accounts for the difference in shape between the templates and the true spectrum, and regions where atmospheric absorption dominates the spectrum are masked. We therefore have two free non-linear parameters – the redshift and velocity dispersion for the galaxy – and 15 linear parameters – the weights of each of the nine stellar templates, and the coefficients of the order-6 polynomial. We construct a likelihood of the data given the model

\begin{equation} \ln L = -\frac{1}{2}\sum _k \Big (\frac{F_{k,{\rm obs}} - F_{k,{\rm mod}}}{\delta F_k}\Big )^2, \end{equation}

(3)

where the sum is over k pixels along the wavelength axis, and F_mod, F_obs and δF are the model flux, observed flux and observed variance, respectively. We then explore the posterior probability distribution of the model given the data using the MCMC package emcee (Foreman-Mackey et al. 2013).

Our kinematic models are shown in the far-right panels of Fig. A1, and the resulting velocity dispersions are included in Table 1. We test the robustness of our kinematic inference by repeating the exercise using the lower resolution galaxy templates of Bruzual & Charlot (2003) and find that the typical uncertainty in the velocity dispersion is of order 5 per cent; as this is significantly larger than our statistical uncertainties, we impose this as the uncertainty on all our velocity dispersion measurements (though we note that the statistical uncertainties are given in Table 1). We also check the robustness of our method by modelling the spectra independently using the penalized pixel fitting (ppxf) software of Cappellari & Emsellem (2004) (v4.15, also using the INDO-US library), and find the uncertainty to be less than 5 per cent. To our inferred velocity dispersions, we apply aperture corrections following the prescription in Jørgensen et al. (1995), correcting the dispersions from the 1 arcsec apertures over which we extracted the spectra to a standard aperture size of 3.4 arcsec at the distance of Coma.

3 SCALING RELATIONS

3.1 The colour–magnitude relation

We use a mixture model (Hogg, Bovy & Lang 2010) to fit for the slope α_CMD, intercept β_CMD and intrinsic scatter σ_CMR of the red sequence according to the equation

\begin{equation} M_1 - M_2 = \alpha _{{\rm CMD}} M_2 + \beta _{{\rm CMD}}, \end{equation}

(4)

where M₁ and M₂ represent the ‘blue’ and ‘red’ magnitudes, respectively, with M₁, M₂ = U, V for Coma and M₁, M₂ = F475W, F625W for MACSJ0717. Our model assigns every point a probability of belonging to either the linear distribution of the red sequence or a distribution of outliers that is Gaussian in colour, and seeks the best fit via an MCMC exploration.

We test this routine by applying it to the data for Coma, and obtain a value for the scatter σ = 0.065 ± 0.009, which agrees with the value σ = 0.069 ± 0.01 quoted in Terlevich et al. (2001). We note that, in that study, different morphological groupings of galaxies have their scatters measured separately and give significantly different results; however, in our sample we do not make any cuts based on morphology. Also, we find that our model is very sensitive to the choice of upper magnitude limit, with stricter magnitude limits leading to smaller inferred scatters. This may be a sign of the inadequacy of a single Gaussian for describing the outlier distribution. To compare the scatter of the two clusters, then, it is important to cut both samples at the same physical magnitude, and it is the smaller sample of higher redshift galaxies, with generally fewer galaxies at the faint end, that dictates where this should be. This sets an apparent magnitude cut-off for the higher redshift cluster of F625W = 24 mag, which we convert to an r-band cut-off for the Coma galaxies using the stellar population models of Section 4.

We find the red sequence of MACSJ0717 to have a shallower slope than Coma, consistent with the fact that Coma is being observed in bluer filters. The scatter is consistent with that of Coma, though slightly smaller, indicating that the stellar populations are already old and red in the MACSJ0717 galaxies, as explored in Section 4.1 and discussed in Section 5.1. This may also be affected by the smaller interval sampled by the U and V filters in Coma's rest frame than by the MACSJ0717 filters. We also note that the MACSJ0717 galaxies appear to extend to brighter magnitudes than the Coma sample (the brightest Coma galaxy has an absolute magnitude M_U = −20.2, whereas the MACSJ0717 galaxies extend to M_U = −19.42 ± 0.18, as shown in Table A1); though this is partly an effect of the different filters with which each cluster has been observed, the filters and redshifts are such that this would in fact be amplified by a filter correction. This is a point that we return to in the analysis of other scaling relations in Section 3.3. The fitted red sequence of MACSJ0717 is shown in Fig. 2 and a summary of the results is given in Table 2.

Figure 2.

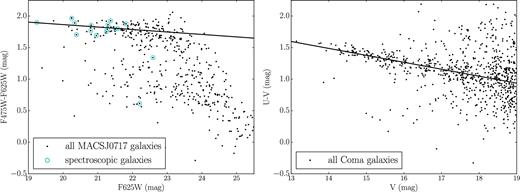
The CMRs for MACSJ0717 (left) and Coma (right), with all apparent magnitudes measured in the observed frame. The 17 galaxies included in the MACSJ0717 spectroscopic sample are circled in turquoise, and indicate that our spectroscopic subsample is 50 per cent complete down to an absolute magnitude of −21.5 mag in the F625W band. The fits to the red sequences are also plotted.

Open in new tab Download slide

Table 2.

Open in new tab

The inferred parameters for the CMR, FP, MLM, MR and MS relations of MACSJ0717, modelled as described in Section 3.

Parameter	CMR	FP	FP	MLM	MLM	M_⋆–σ	M_⋆–R_e	ALL
			(parallel)		(parallel)	(parallel)	(parallel)
α_CMR	−0.03 ± 0.01	–	–	–	–	–	–	–
β_CMR	1.17 ± 0.01	–	–	–	–	–	–	–
σ_CMR	0.055 ± 0.009	–	–	–	–	–	–	–
α_FP	–	1.15 ± 0.43	1.08 ± 0.07	–	–	–	–	1.10 ± 0.18
β_FP	–	0.34 ± 0.05	0.32 ± 0.01	–	–	–	–	0.34 ± 0.03
γ_FP	–	0.18 ± 0.15	0.20 ± 0.05	–	–	–	–	–
ν_{FP, log σ}	–	0.31 ± 0.03	0.31 ± 0.03	–	–	–	–	0.31 ± 0.03
\|$\nu _{{\rm FP},\mu _{\rm e}}$\|	–	0.10 ± 0.28	0.08 ± 0.30	–	–	—	–	0.10 ± 0.29
τ_{FP, log σ}	–	0.12 ± 0.03	0.12 ± 0.03	–	–	–	–	0.12 ± 0.03
\|$\tau _{{\rm FP},\mu _{\rm e}}$\|	–	1.13 ± 0.25	1.15 ± 0.25	–	–	–	–	1.15 ± 0.26
ρ	–	0.11 ± 0.25	0.12 ± 0.27	–	–	–	—	0.12 ± 0.26
σ_FP	–	0.17 ± 0.05	0.16 ± 0.04	–	—	–	–	0.12 ± 0.06
α_ML	–	–	–	0.12 ± 0.11	0.25 ± 0.02	—	–	0.25 ± 0.04
β_ML	–	–	–	0.52 ± 0.15	0.36 ± 0.06	–	–	–
ν_ML	–	–	–	1.24 ± 0.15	1.24 ± 0.15	—	–	1.25 ± 0.16
τ_ML	–	–	–	0.60 ± 0.14	0.59 ± 0.14	—	–	0.60 ± 0.14
σ_ML	–	–	–	0.22 ± 0.05	0.22 ± 0.05	–	–	0.22 ± 0.05
β_MR	–	–	–	–	–	–	−0.21 ± 0.07	–
ν_MR	–	–	–	–	–	–	1.39 ± 0.22	1.39 ± 0.15
τ_MR	–	–	–	–	–	–	0.90 ± 0.20	0.86 ± 0.13
σ_MR	–	–	–	–	–	–	0.24 ± 0.06	0.24 ± 0.06
β_MS	–	–	–	–	–	−0.01 ± 0.05	–	–
ν_MS	–	–	–	–	–	1.39 ± 0.23	–	1.39 ± 0.15
τ_MS	–	–	–	–	–	0.92 ± 0.20	–	0.86 ± 0.13
σ_MS	–	–	–	–	–	0.20 ± 0.05	–	0.20 ± 0.04
ξ	–	–	–	–	–	–	−0.37 ± 0.39	−0.40 ± 0.32
η	–	–	–	–	–	0.06 ± 0.28	–	0.09 ± 0.27
Δm	–	–	–	–	–	–	–	0.59 ± 0.26

Parameter	CMR	FP	FP	MLM	MLM	M_⋆–σ	M_⋆–R_e	ALL
			(parallel)		(parallel)	(parallel)	(parallel)
α_CMR	−0.03 ± 0.01	–	–	–	–	–	–	–
β_CMR	1.17 ± 0.01	–	–	–	–	–	–	–
σ_CMR	0.055 ± 0.009	–	–	–	–	–	–	–
α_FP	–	1.15 ± 0.43	1.08 ± 0.07	–	–	–	–	1.10 ± 0.18
β_FP	–	0.34 ± 0.05	0.32 ± 0.01	–	–	–	–	0.34 ± 0.03
γ_FP	–	0.18 ± 0.15	0.20 ± 0.05	–	–	–	–	–
ν_{FP, log σ}	–	0.31 ± 0.03	0.31 ± 0.03	–	–	–	–	0.31 ± 0.03
\|$\nu _{{\rm FP},\mu _{\rm e}}$\|	–	0.10 ± 0.28	0.08 ± 0.30	–	–	—	–	0.10 ± 0.29
τ_{FP, log σ}	–	0.12 ± 0.03	0.12 ± 0.03	–	–	–	–	0.12 ± 0.03
\|$\tau _{{\rm FP},\mu _{\rm e}}$\|	–	1.13 ± 0.25	1.15 ± 0.25	–	–	–	–	1.15 ± 0.26
ρ	–	0.11 ± 0.25	0.12 ± 0.27	–	–	–	—	0.12 ± 0.26
σ_FP	–	0.17 ± 0.05	0.16 ± 0.04	–	—	–	–	0.12 ± 0.06
α_ML	–	–	–	0.12 ± 0.11	0.25 ± 0.02	—	–	0.25 ± 0.04
β_ML	–	–	–	0.52 ± 0.15	0.36 ± 0.06	–	–	–
ν_ML	–	–	–	1.24 ± 0.15	1.24 ± 0.15	—	–	1.25 ± 0.16
τ_ML	–	–	–	0.60 ± 0.14	0.59 ± 0.14	—	–	0.60 ± 0.14
σ_ML	–	–	–	0.22 ± 0.05	0.22 ± 0.05	–	–	0.22 ± 0.05
β_MR	–	–	–	–	–	–	−0.21 ± 0.07	–
ν_MR	–	–	–	–	–	–	1.39 ± 0.22	1.39 ± 0.15
τ_MR	–	–	–	–	–	–	0.90 ± 0.20	0.86 ± 0.13
σ_MR	–	–	–	–	–	–	0.24 ± 0.06	0.24 ± 0.06
β_MS	–	–	–	–	–	−0.01 ± 0.05	–	–
ν_MS	–	–	–	–	–	1.39 ± 0.23	–	1.39 ± 0.15
τ_MS	–	–	–	–	–	0.92 ± 0.20	–	0.86 ± 0.13
σ_MS	–	–	–	–	–	0.20 ± 0.05	–	0.20 ± 0.04
ξ	–	–	–	–	–	–	−0.37 ± 0.39	−0.40 ± 0.32
η	–	–	–	–	–	0.06 ± 0.28	–	0.09 ± 0.27
Δm	–	–	–	–	–	–	–	0.59 ± 0.26

Table 2.

Open in new tab

The inferred parameters for the CMR, FP, MLM, MR and MS relations of MACSJ0717, modelled as described in Section 3.

Parameter	CMR	FP	FP	MLM	MLM	M_⋆–σ	M_⋆–R_e	ALL
			(parallel)		(parallel)	(parallel)	(parallel)
α_CMR	−0.03 ± 0.01	–	–	–	–	–	–	–
β_CMR	1.17 ± 0.01	–	–	–	–	–	–	–
σ_CMR	0.055 ± 0.009	–	–	–	–	–	–	–
α_FP	–	1.15 ± 0.43	1.08 ± 0.07	–	–	–	–	1.10 ± 0.18
β_FP	–	0.34 ± 0.05	0.32 ± 0.01	–	–	–	–	0.34 ± 0.03
γ_FP	–	0.18 ± 0.15	0.20 ± 0.05	–	–	–	–	–
ν_{FP, log σ}	–	0.31 ± 0.03	0.31 ± 0.03	–	–	–	–	0.31 ± 0.03
\|$\nu _{{\rm FP},\mu _{\rm e}}$\|	–	0.10 ± 0.28	0.08 ± 0.30	–	–	—	–	0.10 ± 0.29
τ_{FP, log σ}	–	0.12 ± 0.03	0.12 ± 0.03	–	–	–	–	0.12 ± 0.03
\|$\tau _{{\rm FP},\mu _{\rm e}}$\|	–	1.13 ± 0.25	1.15 ± 0.25	–	–	–	–	1.15 ± 0.26
ρ	–	0.11 ± 0.25	0.12 ± 0.27	–	–	–	—	0.12 ± 0.26
σ_FP	–	0.17 ± 0.05	0.16 ± 0.04	–	—	–	–	0.12 ± 0.06
α_ML	–	–	–	0.12 ± 0.11	0.25 ± 0.02	—	–	0.25 ± 0.04
β_ML	–	–	–	0.52 ± 0.15	0.36 ± 0.06	–	–	–
ν_ML	–	–	–	1.24 ± 0.15	1.24 ± 0.15	—	–	1.25 ± 0.16
τ_ML	–	–	–	0.60 ± 0.14	0.59 ± 0.14	—	–	0.60 ± 0.14
σ_ML	–	–	–	0.22 ± 0.05	0.22 ± 0.05	–	–	0.22 ± 0.05
β_MR	–	–	–	–	–	–	−0.21 ± 0.07	–
ν_MR	–	–	–	–	–	–	1.39 ± 0.22	1.39 ± 0.15
τ_MR	–	–	–	–	–	–	0.90 ± 0.20	0.86 ± 0.13
σ_MR	–	–	–	–	–	–	0.24 ± 0.06	0.24 ± 0.06
β_MS	–	–	–	–	–	−0.01 ± 0.05	–	–
ν_MS	–	–	–	–	–	1.39 ± 0.23	–	1.39 ± 0.15
τ_MS	–	–	–	–	–	0.92 ± 0.20	–	0.86 ± 0.13
σ_MS	–	–	–	–	–	0.20 ± 0.05	–	0.20 ± 0.04
ξ	–	–	–	–	–	–	−0.37 ± 0.39	−0.40 ± 0.32
η	–	–	–	–	–	0.06 ± 0.28	–	0.09 ± 0.27
Δm	–	–	–	–	–	–	–	0.59 ± 0.26

Parameter	CMR	FP	FP	MLM	MLM	M_⋆–σ	M_⋆–R_e	ALL
			(parallel)		(parallel)	(parallel)	(parallel)
α_CMR	−0.03 ± 0.01	–	–	–	–	–	–	–
β_CMR	1.17 ± 0.01	–	–	–	–	–	–	–
σ_CMR	0.055 ± 0.009	–	–	–	–	–	–	–
α_FP	–	1.15 ± 0.43	1.08 ± 0.07	–	–	–	–	1.10 ± 0.18
β_FP	–	0.34 ± 0.05	0.32 ± 0.01	–	–	–	–	0.34 ± 0.03
γ_FP	–	0.18 ± 0.15	0.20 ± 0.05	–	–	–	–	–
ν_{FP, log σ}	–	0.31 ± 0.03	0.31 ± 0.03	–	–	–	–	0.31 ± 0.03
\|$\nu _{{\rm FP},\mu _{\rm e}}$\|	–	0.10 ± 0.28	0.08 ± 0.30	–	–	—	–	0.10 ± 0.29
τ_{FP, log σ}	–	0.12 ± 0.03	0.12 ± 0.03	–	–	–	–	0.12 ± 0.03
\|$\tau _{{\rm FP},\mu _{\rm e}}$\|	–	1.13 ± 0.25	1.15 ± 0.25	–	–	–	–	1.15 ± 0.26
ρ	–	0.11 ± 0.25	0.12 ± 0.27	–	–	–	—	0.12 ± 0.26
σ_FP	–	0.17 ± 0.05	0.16 ± 0.04	–	—	–	–	0.12 ± 0.06
α_ML	–	–	–	0.12 ± 0.11	0.25 ± 0.02	—	–	0.25 ± 0.04
β_ML	–	–	–	0.52 ± 0.15	0.36 ± 0.06	–	–	–
ν_ML	–	–	–	1.24 ± 0.15	1.24 ± 0.15	—	–	1.25 ± 0.16
τ_ML	–	–	–	0.60 ± 0.14	0.59 ± 0.14	—	–	0.60 ± 0.14
σ_ML	–	–	–	0.22 ± 0.05	0.22 ± 0.05	–	–	0.22 ± 0.05
β_MR	–	–	–	–	–	–	−0.21 ± 0.07	–
ν_MR	–	–	–	–	–	–	1.39 ± 0.22	1.39 ± 0.15
τ_MR	–	–	–	–	–	–	0.90 ± 0.20	0.86 ± 0.13
σ_MR	–	–	–	–	–	–	0.24 ± 0.06	0.24 ± 0.06
β_MS	–	–	–	–	–	−0.01 ± 0.05	–	–
ν_MS	–	–	–	–	–	1.39 ± 0.23	–	1.39 ± 0.15
τ_MS	–	–	–	–	–	0.92 ± 0.20	–	0.86 ± 0.13
σ_MS	–	–	–	–	–	0.20 ± 0.05	–	0.20 ± 0.04
ξ	–	–	–	–	–	–	−0.37 ± 0.39	−0.40 ± 0.32
η	–	–	–	–	–	0.06 ± 0.28	–	0.09 ± 0.27
Δm	–	–	–	–	–	–	–	0.59 ± 0.26

3.2 The Fundamental Plane

Initially, we fit the FPs for the two clusters independently; as we find their slopes to be consistent with no evolution, we then model them simultaneously, requiring both to be parallel, in order to infer the offset between the two. We assume each data set to lie on a plane

\begin{eqnarray} &&{\log R_{{\rm e},z} = \alpha _{{\rm FP},z} \log \sigma _z + \beta _{{\rm FP},z} \langle \mu _{{\rm e},z} \rangle + \gamma _{{\rm FP},z}} \nonumber\\ &&{\quad\log R_{{\rm e},0} = \alpha _{{\rm FP},0} \log \sigma _0 + \beta _{{\rm FP},0} \langle \mu _{{\rm e},0} \rangle + \gamma _{{\rm FP},0} } \end{eqnarray}

(5)

where the subscript x₀ refers to quantities relating to the low-redshift cluster (Coma), and the subscript x_z corresponds to the high-redshift cluster. To reduce the scale of the degeneracy between the plane parameters, we redefine σ_FP = σ/100 km s⁻¹ and 〈μ_{e, FP}〉 = 〈μ_e〉 − 20. We further assume the independent variables to be drawn from a multivariate Gaussian distribution with mean |$\vec{\nu }_{{\rm FP}} = (\nu _{\log \sigma }, \nu _{{\rm FP},\mu _{\rm e}})$| and variance

\begin{equation} \vec{\tau }_{{\rm FP}}^2 = \left(\begin{array}{cc}\tau _{\log \sigma }^2 & \rho \tau _{\log \sigma }\tau _{\mu _{\rm e}} \\ \rho \tau _{\log \sigma }\tau _{\mu _{\rm e}} & \tau _{\mu _{\rm e}}^2 \end{array} \right)\!. \end{equation}

(6)

This is appropriate as it deals with the fact that the galaxies in each sample are almost certainly drawn from different intrinsic distributions, with the higher redshift MACSJ0717 galaxies likely to be drawn from the most massive and luminous end of their population. More details on the model are provided in Kelly (2007), which presents the formalism, but essentially, we construct the likelihood for the data given a particular set of plane and Gaussian parameters, and obtain the posterior distribution using an MCMC exploration of the parameter space. The median values of the marginalized distributions are presented in Table 3, together with 16th and 84th percentile uncertainties, and the fitted FP is shown in both edge-on and face-on projections in Fig. 3. We demonstrate that the MACSJ0717 galaxies are indeed drawn from a distribution with a higher mean velocity dispersion, with ν_log σ = 0.31 ± 0.03 for MACSJ0717 and ν_log σ = 0.21 ± 0.02 for Coma – consistent with the idea that the former extend to brighter magnitudes and higher masses. When we model the two planes simultaneously, we find the clusters to be offset, with γ_z − γ₀ = −0.14 ± 0.06.

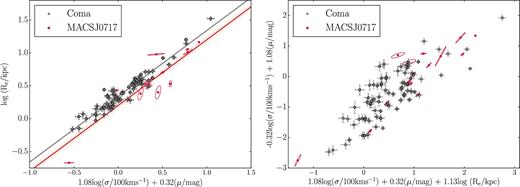
The FPs of the Coma and MACSJ0717 galaxies, with σ in units of 100 km s−1, 〈μe〉 in magnitudes and Re in kpc. The FP of MACSJ0717 is slightly offset from that of Coma, which we show to be the result of two effects: the evolution of the stellar populations and the evolution of the structure of the galaxies. Note that the surface brightnesses here are measured in the observed-frame F625W and r΄ filters for MACSJ0717 and Coma, respectively, and have been corrected for cosmological dimming as 10 log (1 + z). Two complementary projections are shown in order to highlight the different regions occupied by the two galaxy populations. Left: an edge-on projection. Right: a face-on projection.

Figure 3.

The FPs of the Coma and MACSJ0717 galaxies, with σ in units of 100 km s⁻¹, 〈μ_e〉 in magnitudes and R_e in kpc. The FP of MACSJ0717 is slightly offset from that of Coma, which we show to be the result of two effects: the evolution of the stellar populations and the evolution of the structure of the galaxies. Note that the surface brightnesses here are measured in the observed-frame F625W and r΄ filters for MACSJ0717 and Coma, respectively, and have been corrected for cosmological dimming as 10 log (1 + z). Two complementary projections are shown in order to highlight the different regions occupied by the two galaxy populations. Left: an edge-on projection. Right: a face-on projection.

Open in new tab Download slide

Table 3.

Open in new tab

The inferred parameters for the CMR, FP, MLM, MR and MS relations of Coma, modelled as described in Section 3.

Parameter	CMR	FP	FP	MLM	MLM	M_⋆–σ	M_⋆–R_e	ALL
			(parallel)		(parallel)	(parallel)	(parallel)
α_CMR	−0.11 ± 0.01	–	–	–	–	–
β_CMR	−0.82 ± 0.01	–	–	–	–	–	–
σ_CMR	0.065 ± 0.005	–	–	–	–	–	–
α_FP	–	1.09 ± 0.07	1.08 ± 0.07	–	–	–	–	1.10 ± 0.18
β_FP	–	0.32 ± 0.01	0.32 ± 0.01	–	–	–	–	0.34 ± 0.03
γ_FP	–	0.34 ± 0.02	0.34 ± 0.02	–	–	–	–	0.35 ± 0.04
ν_{FP, log σ}	–	0.21 ± 0.02	0.21 ± 0.02	–	–	–	–	0.19 ± 0.02
\|$\nu _{{\rm FP},\mu _e}$\|	–	−0.48 ± 0.09	−0.48 ± 0.09	–	–	–	–	−0.53 ± 0.10
τ_{FP, log σ}	–	0.14 ± 0.01	0.14 ± 0.01	–	–	–	–	0.12 ± 0.01
\|$\tau _{{\rm FP},\mu _e}$\|	–	0.78 ± 0.07	0.78 ± 0.06	–	–	–	–	0.82 ± 0.08
ρ	–	−0.09 ± 0.11	−0.09 ± 0.11	–	–	–	–	−0.24 ± 0.13
σ_FP	–	0.07 ± 0.01	0.08 ± 0.01	–	–	–	–	0.05 ± 0.03
α_ML	–	–	–	0.25 ± 0.04	0.25 ± 0.02	–	–	0.25 ± 0.04
β_ML	–	–	–	0.36 ± 0.04	0.37 ± 0.02	–	–	0.37 ± 0.03
ν_ML	–	–	–	0.88 ± 0.05	0.88 ± 0.06	–	–	0.82 ± 0.05
τ_ML	–	–	–	0.49 ± 0.04	0.48 ± 0.04	–	–	0.39 ± 0.04
σ_ML	–	–	–	0.07 ± 0.01	0.10 ± 0.01	–	–	0.10 ± 0.01
α_MR	–	–	–	–	–	–	–	–
β_MR	–	–	–	–	–	–	−0.14 ± 0.03	−0.14 ± 0.02
ν_MR	–	–	–	–	–	–	0.93 ± 0.05	0.93 ± 0.04
τ_MR	–	–	–	–	–	–	0.38 ± 0.04	0.38 ± 0.03
σ_MR	–	–	–	–	–	–	0.19 ± 0.02	0.19 ± 0.02
α_MS	–	–	–	–	–	–	–	–
β_MS	–	–	–	–	–	−0.02 ± 0.01	–	−0.02 ± 0.01
ν_MS	–	–	–	–	–	0.93 ± 0.05	–	0.93 ± 0.04
τ_MS	–	–	–	–	–	0.38 ± 0.04	–	0.38 ± 0.03
σ_MS	–	–	–	–	–	0.08 ± 0.01	–	0.08 ± 0.01
ξ	–	–	–	–	–	–	−0.37 ± 0.39	−0.40 ± 0.32
η	–	–	–	–	–	0.06 ± 0.28	–	0.09 ± 0.27
Δm	–	–	–	–	–	–	–	0.59 ± 0.26

Parameter	CMR	FP	FP	MLM	MLM	M_⋆–σ	M_⋆–R_e	ALL
			(parallel)		(parallel)	(parallel)	(parallel)
α_CMR	−0.11 ± 0.01	–	–	–	–	–
β_CMR	−0.82 ± 0.01	–	–	–	–	–	–
σ_CMR	0.065 ± 0.005	–	–	–	–	–	–
α_FP	–	1.09 ± 0.07	1.08 ± 0.07	–	–	–	–	1.10 ± 0.18
β_FP	–	0.32 ± 0.01	0.32 ± 0.01	–	–	–	–	0.34 ± 0.03
γ_FP	–	0.34 ± 0.02	0.34 ± 0.02	–	–	–	–	0.35 ± 0.04
ν_{FP, log σ}	–	0.21 ± 0.02	0.21 ± 0.02	–	–	–	–	0.19 ± 0.02
\|$\nu _{{\rm FP},\mu _e}$\|	–	−0.48 ± 0.09	−0.48 ± 0.09	–	–	–	–	−0.53 ± 0.10
τ_{FP, log σ}	–	0.14 ± 0.01	0.14 ± 0.01	–	–	–	–	0.12 ± 0.01
\|$\tau _{{\rm FP},\mu _e}$\|	–	0.78 ± 0.07	0.78 ± 0.06	–	–	–	–	0.82 ± 0.08
ρ	–	−0.09 ± 0.11	−0.09 ± 0.11	–	–	–	–	−0.24 ± 0.13
σ_FP	–	0.07 ± 0.01	0.08 ± 0.01	–	–	–	–	0.05 ± 0.03
α_ML	–	–	–	0.25 ± 0.04	0.25 ± 0.02	–	–	0.25 ± 0.04
β_ML	–	–	–	0.36 ± 0.04	0.37 ± 0.02	–	–	0.37 ± 0.03
ν_ML	–	–	–	0.88 ± 0.05	0.88 ± 0.06	–	–	0.82 ± 0.05
τ_ML	–	–	–	0.49 ± 0.04	0.48 ± 0.04	–	–	0.39 ± 0.04
σ_ML	–	–	–	0.07 ± 0.01	0.10 ± 0.01	–	–	0.10 ± 0.01
α_MR	–	–	–	–	–	–	–	–
β_MR	–	–	–	–	–	–	−0.14 ± 0.03	−0.14 ± 0.02
ν_MR	–	–	–	–	–	–	0.93 ± 0.05	0.93 ± 0.04
τ_MR	–	–	–	–	–	–	0.38 ± 0.04	0.38 ± 0.03
σ_MR	–	–	–	–	–	–	0.19 ± 0.02	0.19 ± 0.02
α_MS	–	–	–	–	–	–	–	–
β_MS	–	–	–	–	–	−0.02 ± 0.01	–	−0.02 ± 0.01
ν_MS	–	–	–	–	–	0.93 ± 0.05	–	0.93 ± 0.04
τ_MS	–	–	–	–	–	0.38 ± 0.04	–	0.38 ± 0.03
σ_MS	–	–	–	–	–	0.08 ± 0.01	–	0.08 ± 0.01
ξ	–	–	–	–	–	–	−0.37 ± 0.39	−0.40 ± 0.32
η	–	–	–	–	–	0.06 ± 0.28	–	0.09 ± 0.27
Δm	–	–	–	–	–	–	–	0.59 ± 0.26

Table 3.

Open in new tab

The inferred parameters for the CMR, FP, MLM, MR and MS relations of Coma, modelled as described in Section 3.

Parameter	CMR	FP	FP	MLM	MLM	M_⋆–σ	M_⋆–R_e	ALL
			(parallel)		(parallel)	(parallel)	(parallel)
α_CMR	−0.11 ± 0.01	–	–	–	–	–
β_CMR	−0.82 ± 0.01	–	–	–	–	–	–
σ_CMR	0.065 ± 0.005	–	–	–	–	–	–
α_FP	–	1.09 ± 0.07	1.08 ± 0.07	–	–	–	–	1.10 ± 0.18
β_FP	–	0.32 ± 0.01	0.32 ± 0.01	–	–	–	–	0.34 ± 0.03
γ_FP	–	0.34 ± 0.02	0.34 ± 0.02	–	–	–	–	0.35 ± 0.04
ν_{FP, log σ}	–	0.21 ± 0.02	0.21 ± 0.02	–	–	–	–	0.19 ± 0.02
\|$\nu _{{\rm FP},\mu _e}$\|	–	−0.48 ± 0.09	−0.48 ± 0.09	–	–	–	–	−0.53 ± 0.10
τ_{FP, log σ}	–	0.14 ± 0.01	0.14 ± 0.01	–	–	–	–	0.12 ± 0.01
\|$\tau _{{\rm FP},\mu _e}$\|	–	0.78 ± 0.07	0.78 ± 0.06	–	–	–	–	0.82 ± 0.08
ρ	–	−0.09 ± 0.11	−0.09 ± 0.11	–	–	–	–	−0.24 ± 0.13
σ_FP	–	0.07 ± 0.01	0.08 ± 0.01	–	–	–	–	0.05 ± 0.03
α_ML	–	–	–	0.25 ± 0.04	0.25 ± 0.02	–	–	0.25 ± 0.04
β_ML	–	–	–	0.36 ± 0.04	0.37 ± 0.02	–	–	0.37 ± 0.03
ν_ML	–	–	–	0.88 ± 0.05	0.88 ± 0.06	–	–	0.82 ± 0.05
τ_ML	–	–	–	0.49 ± 0.04	0.48 ± 0.04	–	–	0.39 ± 0.04
σ_ML	–	–	–	0.07 ± 0.01	0.10 ± 0.01	–	–	0.10 ± 0.01
α_MR	–	–	–	–	–	–	–	–
β_MR	–	–	–	–	–	–	−0.14 ± 0.03	−0.14 ± 0.02
ν_MR	–	–	–	–	–	–	0.93 ± 0.05	0.93 ± 0.04
τ_MR	–	–	–	–	–	–	0.38 ± 0.04	0.38 ± 0.03
σ_MR	–	–	–	–	–	–	0.19 ± 0.02	0.19 ± 0.02
α_MS	–	–	–	–	–	–	–	–
β_MS	–	–	–	–	–	−0.02 ± 0.01	–	−0.02 ± 0.01
ν_MS	–	–	–	–	–	0.93 ± 0.05	–	0.93 ± 0.04
τ_MS	–	–	–	–	–	0.38 ± 0.04	–	0.38 ± 0.03
σ_MS	–	–	–	–	–	0.08 ± 0.01	–	0.08 ± 0.01
ξ	–	–	–	–	–	–	−0.37 ± 0.39	−0.40 ± 0.32
η	–	–	–	–	–	0.06 ± 0.28	–	0.09 ± 0.27
Δm	–	–	–	–	–	–	–	0.59 ± 0.26

Parameter	CMR	FP	FP	MLM	MLM	M_⋆–σ	M_⋆–R_e	ALL
			(parallel)		(parallel)	(parallel)	(parallel)
α_CMR	−0.11 ± 0.01	–	–	–	–	–
β_CMR	−0.82 ± 0.01	–	–	–	–	–	–
σ_CMR	0.065 ± 0.005	–	–	–	–	–	–
α_FP	–	1.09 ± 0.07	1.08 ± 0.07	–	–	–	–	1.10 ± 0.18
β_FP	–	0.32 ± 0.01	0.32 ± 0.01	–	–	–	–	0.34 ± 0.03
γ_FP	–	0.34 ± 0.02	0.34 ± 0.02	–	–	–	–	0.35 ± 0.04
ν_{FP, log σ}	–	0.21 ± 0.02	0.21 ± 0.02	–	–	–	–	0.19 ± 0.02
\|$\nu _{{\rm FP},\mu _e}$\|	–	−0.48 ± 0.09	−0.48 ± 0.09	–	–	–	–	−0.53 ± 0.10
τ_{FP, log σ}	–	0.14 ± 0.01	0.14 ± 0.01	–	–	–	–	0.12 ± 0.01
\|$\tau _{{\rm FP},\mu _e}$\|	–	0.78 ± 0.07	0.78 ± 0.06	–	–	–	–	0.82 ± 0.08
ρ	–	−0.09 ± 0.11	−0.09 ± 0.11	–	–	–	–	−0.24 ± 0.13
σ_FP	–	0.07 ± 0.01	0.08 ± 0.01	–	–	–	–	0.05 ± 0.03
α_ML	–	–	–	0.25 ± 0.04	0.25 ± 0.02	–	–	0.25 ± 0.04
β_ML	–	–	–	0.36 ± 0.04	0.37 ± 0.02	–	–	0.37 ± 0.03
ν_ML	–	–	–	0.88 ± 0.05	0.88 ± 0.06	–	–	0.82 ± 0.05
τ_ML	–	–	–	0.49 ± 0.04	0.48 ± 0.04	–	–	0.39 ± 0.04
σ_ML	–	–	–	0.07 ± 0.01	0.10 ± 0.01	–	–	0.10 ± 0.01
α_MR	–	–	–	–	–	–	–	–
β_MR	–	–	–	–	–	–	−0.14 ± 0.03	−0.14 ± 0.02
ν_MR	–	–	–	–	–	–	0.93 ± 0.05	0.93 ± 0.04
τ_MR	–	–	–	–	–	–	0.38 ± 0.04	0.38 ± 0.03
σ_MR	–	–	–	–	–	–	0.19 ± 0.02	0.19 ± 0.02
α_MS	–	–	–	–	–	–	–	–
β_MS	–	–	–	–	–	−0.02 ± 0.01	–	−0.02 ± 0.01
ν_MS	–	–	–	–	–	0.93 ± 0.05	–	0.93 ± 0.04
τ_MS	–	–	–	–	–	0.38 ± 0.04	–	0.38 ± 0.03
σ_MS	–	–	–	–	–	0.08 ± 0.01	–	0.08 ± 0.01
ξ	–	–	–	–	–	–	−0.37 ± 0.39	−0.40 ± 0.32
η	–	–	–	–	–	0.06 ± 0.28	–	0.09 ± 0.27
Δm	–	–	–	–	–	–	–	0.59 ± 0.26

3.3 The M_dyn/L–M_dyn relation

To construct the MLM relation, we calculate the dynamical mass-to-light ratio within R_e, M_dyn/L, in the F625W band (MACSJ0717) and r band (Coma) using the virial estimator

\begin{equation} \frac{M_{{\rm dyn}}}{L}(<\!R_{\rm e}) = \frac{\beta \sigma ^2R_{\rm e}}{G L} \end{equation}

(7)

(e.g. Cappellari et al. 2006). This assumes virial equilibrium, consistent with the assumptions of the FP. The value of the coefficient β depends on the mass distribution of the galaxy, and can be either calculated from theoretical models (in which case it is dependent on the Sérsic index n) or calibrated from galaxy samples for which multiple M_dyn/L estimates are available. As our size measurements for the Coma galaxies come from de Vaucouleurs models, we do not have Sérsic indices from which to calculate β(n) (though we do for the MACSJ0717 galaxies); we therefore adopt the best-fitting value of β = 5 presented in Cappellari et al. (2006), which was calibrated by comparing virial and Schwarzschild M_dyn/L estimates for a sample of 25 E and S0 galaxies. We then construct a ‘dynamical’ mass

\begin{equation} M_{{\rm dyn}} = \frac{\beta \sigma ^2R_{\rm e}}{G} \end{equation}

(8)

though we note that this is not intended to represent the total dynamical mass within any physically meaningful aperture. For instance, according to equation (6), the half-light dynamical mass should use β = 2.5, whereas Wolf et al. (2010) suggests that β = 4 is more appropriate. Clearly, there remains uncertainty here, and we therefore continue to use β = 5 in order to facilitate comparisons with other studies. Given that we are interested in the offset between the two galaxy samples rather than the absolute relations, the choice of any constant β does not affect our conclusions (though this is not true if β varies across the plane).

We calculate the bandpass luminosities relative to that of the Sun (based on a redshifted CALSPEC solar spectrum) from the surface brightnesses using the equation

\begin{equation} \mathcal {M}_{{\rm gal}} - \mathcal {M}_{{\odot }} = -2.5\log \Big (\frac{L_{{\rm gal}}}{L_{{\odot }}}\Big ), \end{equation}

(9)

where |$\mathcal {M}$| represents an absolute magnitude and |$\mathcal {M}_{{\odot }} (z=0,r) = 4.58$| and |$\mathcal {M}_{{\odot }} (z=0.545,F625W) = 5.17$|⁠, and construct the MLM relations for the Coma and MACSJ0717 galaxies, as can be seen in Fig. 4. Again modelling the masses and mass-to-light ratios as being drawn from a multivariate Gaussian distribution, we infer both these underlying distributions and the slope, intercept and scatter of the linear relation

\begin{equation} \log \frac{M_{{\rm dyn}}}{L} = \alpha _{{\rm ML}} \log M_{{\rm dyn}} + \beta _{{\rm ML}}, \end{equation}

(10)

where mass M_dyn and luminosity L are measured in units of 10¹⁰ M_⊙ and L_⊙; our inference is presented in Table 2. This time, modelling the clusters independently leads us to find marginally different slopes (in addition to an offset), with β_ML = 0.25 ± 0.02 for Coma and β_ML = 0.12 ± 0.11 for MACSJ0717, though the uncertainties of the MACSJ0717 relation are large, making them consistent at the 1σ level. The point here is that our high-redshift sample lacks the dynamic range that would be needed to robustly infer both the slope and intercept of the MLM relation; these two parameters suffer degeneracies, making them hard to constrain. When we model the two populations together, we find that the Coma data dominate the fit to the slope – which is not surprising, given that we have ∼6 times more galaxies in the latter – such that β_ML = 0.25 ± 0.02; the MLM relation for MACSJ0717 then lies virtually on top of that of Coma, with β_z − β₀ = −0.01 ± 0.06. We also confirm that the MACSJ0717 galaxies are drawn from a more massive distribution, with ν_ML = 1.24 ± 0.15 compared to ν_ML = 0.88 ± 0.05 for Coma. This is a selection effect that we would expect, given that the former is at a higher redshift and that magnitude limits mean that we are only able to observe the most massive end of the mass distribution. Nevertheless, Fig. 5 suggests there are genuinely more high-mass galaxies in MACSJ0717 than in Coma – this is an interesting result that may be connected with the higher cluster mass of MACSJ0717 (see Section 5.4). Fig. 4 also shows more generally that the two populations have similar trends between their dynamical masses and mass-to-light ratios, with the main difference being that the MACSJ0717 galaxies have higher masses. The results of this modelling are summarized in Table 2.

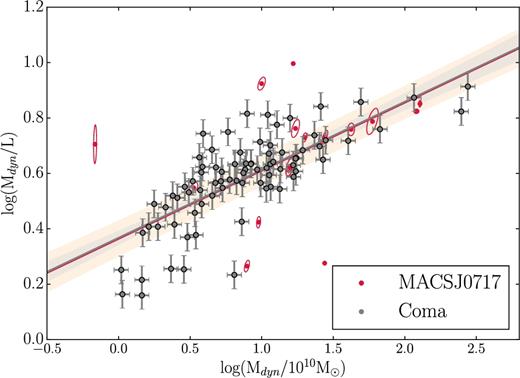
The MLM relation for the galaxies in Coma and MACSJ0717, with Mdyn in units of 1010 M⊙ and Mdyn/L in units of M⊙/L⊙. When the MACSJ0717 galaxies are constrained to be parallel to those of Coma, the relations lie virtually on top of each other (though note that the luminosity is measured in a different filter and at a different redshift for each cluster).

Figure 4.

The MLM relation for the galaxies in Coma and MACSJ0717, with M_dyn in units of 10¹⁰ M_⊙ and M_dyn/L in units of M_⊙/L_⊙. When the MACSJ0717 galaxies are constrained to be parallel to those of Coma, the relations lie virtually on top of each other (though note that the luminosity is measured in a different filter and at a different redshift for each cluster).

Open in new tab Download slide

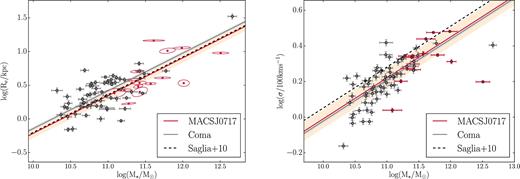
Mass–size and mass–velocity dispersion relations for the two clusters, with stellar masses in units 1010 M⊙, sizes in kpc and velocity dispersions in units of 100 km s−1. In both cases, the scaling relations of the two clusters are consistent with being parallel but offset, with the high-redshift galaxies being both marginally smaller and having marginally higher velocity dispersions. The dashed lines show the relations given in Saglia et al. (2010), evaluated at z = 0.545. Both are consistent with our MACSJ0717 sample within 2σ (though we do not show the uncertainties on the Saglia et al. 2010 relations here).

Figure 5.

Mass–size and mass–velocity dispersion relations for the two clusters, with stellar masses in units 10¹⁰ M_⊙, sizes in kpc and velocity dispersions in units of 100 km s⁻¹. In both cases, the scaling relations of the two clusters are consistent with being parallel but offset, with the high-redshift galaxies being both marginally smaller and having marginally higher velocity dispersions. The dashed lines show the relations given in Saglia et al. (2010), evaluated at z = 0.545. Both are consistent with our MACSJ0717 sample within 2σ (though we do not show the uncertainties on the Saglia et al. 2010 relations here).

Open in new tab Download slide

3.4 The M_⋆–σ and M_⋆–R_e relations

As discussed in Section 1, any structural evolution of the galaxy population with redshift would also have an impact on the offset of the FP. We therefore attempt to measure the evolution in size and velocity dispersion between the two ETG samples using two independent methods. First, we fit the M_⋆–R_e and M_⋆–σ relations to infer the difference in size and velocity dispersion of galaxies of any given mass, that is the subject of this section. Later, we model the FP and MLM, M_⋆–R_e and M_⋆–σ relations simultaneously in order to infer the evolution in size, velocity dispersion and luminosity all at once. That is the topic of Section 4.5.

We use stellar masses here as opposed to the dynamical masses calculated in the previous section to avoid the obvious degeneracies between M_dyn, σ and R_e. We calculate stellar masses for Coma cluster and MACS0717 galaxies by comparing the u–g and F475W–F625W colours, respectively, to the same colours calculated from the simple stellar population (SSP) models of Bruzual & Charlot (2003, BC03). In order to break the degeneracy between age and metallicity, we make the assumption that galaxies on the red sequence are coeval to first order and that the slope of the red sequence is driven by a systematic change in metallicity with luminosity (as found by Kodama & Arimoto 1997). By assuming an average age of the red sequence, we interpolate between SSP models of fixed age and varying metallicity to convert the CMR of the red sequence into a metallicity–luminosity relation; this provides a metallicity for each galaxy, based on its luminosity and not its colour. With this metallicity, we use the observed colour to infer the age and stellar mass-to-light ratio M_⋆/L of each galaxy. In practice, for each galaxy, we interpolate between the two SSPs that bracket the metallicity derived from the CMR to calculate the age and M_⋆/L. We do not apply any luminosity weighting corrections as these are deemed second order. Nor do we limit the derived ages to be younger than the age of the Universe (although this is not a significant issue).

For young star-forming galaxies, M_⋆/L is far smaller, and the luminosity far greater, than that of an old passive galaxy of the same mass, leading us to dramatically overestimate of the metallicity from the luminosity–metallicity relation we derived above for red sequence galaxies. However, at young ages (<1 Gyr), colour is primarily determined by age, not metallicity. Thus, curves of colour versus M_⋆/L for different metallicities only diverge at old ages; at younger ages, the curves converge and the dominant factor in determining M_⋆/L is age; metallicity has virtually no effect. Thus, for luminous blue star-forming galaxies, although our luminosity–metallicity relation overestimates the metallicity, the M_⋆/L and stellar masses remain accurate. Hence, we find no need to iterate the estimation of the metallicity once the age and M_⋆/L (the real parameters of interest) have been calculated.

Adopting this method, we calculate the M_⋆/L for the Coma galaxies assuming red sequence ages of 8, 10 and 12 Gyr. We then adopt the average of the M_⋆/L values and use the scatter from the variation of input age as the formal error on the M_⋆/L values. We find Coma cluster galaxies to be around solar metallicity and (by construction) around 10 Gyr old. When calculating the M_⋆/L of the galaxies in MACS0717, we adopt red sequence ages of (8, 10, 12) – 5.3 Gyr. We find that the MACSJ0717 galaxies are slightly higher metallicity (around 1.5 × solar) than Coma galaxies (around solar). Note that although the derived stellar masses depend slightly on the initial age assumed for Coma (and for MACS0717, forced to be 5.3 Gyr younger), the relative ratio between the Coma and MACS0717 masses is almost constant, if we assume an age >8 Gyr for Coma. For ages below 8 Gyr, the stellar masses for MACSJ0717 galaxies drop rapidly compared to the stellar masses for Coma galaxies (to the extent that if we assume an age of 6 Gyr for Coma, the average stellar masses in both clusters become the same). But such young ages (implying ages of <1 Gyr for the MACSJ0717 stellar populations) are unrealistic and ruled out by both the CMR and FP or MLM results.

The stellar masses are included in Table 2; we note that the stellar masses reveal the general mass differences of the two samples even more clearly than the dynamical masses of the previous section, with almost all the high-z galaxies containing more stellar mass than nearly all the low-z galaxies. As discussed previously, this indicates a genuine excess of high-mass galaxies in MACSJ0717 relative to Coma.

We assume the size and velocity dispersion to follow power laws in the total mass and fit

\begin{equation} \log R_{\rm e} = \alpha _{{\rm MR}} \log M_{\star } + \beta _{{\rm MR}} \end{equation}

(11)

and

\begin{equation} \log \sigma = \alpha _{{\rm MS}} \log M_{\star } + \beta _{{\rm MS}} \end{equation}

(12)

using the same formalism as in earlier sections in which the slope, intercept and intrinsic scatter are inferred together with the properties of the underlying Gaussian distribution of log M_⋆. The limited dynamic range in mass of each population makes it difficult to make meaningful inference on both the slope and intercept of these relations (especially for the size–mass relation) and break the strong degeneracy that exists between them; we therefore fix the slope of the size–mass relation to α_MR = 0.56, as found in Shen et al. (2003), and that of the sigma–mass relation to α_MS = 0.23 as in Saglia et al. (2010), both of which were measured using significantly bigger galaxy samples. Our inference is shown in Fig. 5 and demonstrates that the two populations look extremely similar in both respects. This implies that a very small amount of evolution has taken place between the z ∼ 0.5 and z ∼ 0 galaxies.

We also compare our M_⋆–R_e and M_⋆–σ relations with those of Saglia et al. (2010) – in which these relations were constructed for galaxies from 26 clusters out to redshifts z ∼ 0.9 – and find that we are consistent with both at the 2σ level. With regard to the slightly poorer agreement between the M_⋆–σ relations relative to the M_⋆–R_e relations, we note that MACSJ0717 has a high velocity dispersion |$\sigma _{{\rm cluster}} = 1660_{-130}^{+120}$| km s⁻¹ (Ebeling et al. 2007) relative to the mean velocity dispersion |$\bar{\sigma }_{{\rm cluster}} = 525 \pm 210$| km s⁻¹ of the EDisCS clusters used in that study. This may be evidence for the more rapid evolution of galaxies in denser environments, such that the galaxy velocity dispersions in higher mass clusters at z = 0.5 more closely resemble those of z = 0 galaxies than do those in lower mass clusters at z = 0.5. We discuss this further in Section 5.2, though we cannot make any strong claims on the basis of the data used in this paper.

Following van der Wel et al. (2008) and Saglia et al. (2010), we relate the offsets between the clusters to measure the evolution as a function of redshift:

\begin{equation} \beta _{{\rm MR},z} - \beta _{{\rm MR},0} = \xi \log (1+z) \end{equation}

(13)

and

\begin{equation} \beta _{{\rm MS},z} - \beta _{{\rm MS},0} = \eta \log (1+z) \end{equation}

(14)

and therefore find ξ = −0.37 ± 0.39, η = 0.06 ± 0.28 as summarized in Table 2. We note that the evolution we find here is weaker than the ξ = −0.98 ± 0.11 found by van der Wel et al. (2008) for field ellipticals, but consistent with the ξ = −0.53 ± 0.04 inferred by Delaye et al. (2014) for cluster ellipticals, and moreover that the evolution in both size and velocity dispersion is consistent with zero (see also Saglia et al. 2010; Jørgensen et al. 2014; Saracco et al. 2014, for indications of mild structural evolution of cluster ETGs). The implication is that only a small amount of evolution has taken place in these galaxies between z = 0.545 and the present day. We use these in Section 4.4 to account for the effects of size evolution in the FP and MLM relations.

4 STELLAR POPULATION MODELS

The key idea of using the changes in our scaling relations to understand the underlying stellar populations is that the scaling relations themselves are simply a convenient way of characterizing the observable properties of galaxies – in our case, this means luminosities, colours, sizes, velocity dispersions – and that these properties are governed in turn by the stars they contain. We can then use stellar population synthesis (SPS) models, under particular, astrophysically motivated assumptions regarding the age, metallicity, IMF and star formation history (SFH) of the population, to connect the changes we observe to the evolution of the stellar populations. The assumptions we make as to the SFHs in the CMR, and the FP and M_dyn/L analyses are different and are simplifications of the real, much more complex and extended processes that we know ETGs are subject to; however, both are motivated by the data, and can be interpreted together to provide a fuller picture of these galaxies’ evolution. The other main assumption we make here is that the ETGs in MACSJ0717 are directly comparable to those in Coma, such that the former represent the Coma population at an earlier stage in their evolution.

Historically, the differences due to the redshifts of the two galaxy populations and the filters in which they have been observed have been accounted for by correcting the data; specifically, by applying K-corrections to the data and then comparing the FP zero-points as if both galaxy populations had been observed at the same redshift and with the same filter. However, this requires some galaxy ‘template’ to be chosen and assumptions to be made regarding the spectral energy distribution (SED) and age of the galaxies, and therefore introduces significant uncertainty and possible bias. We therefore refrain from doing this, and, rather than correcting the data, we entirely forward-model the observations. In a development of the methods introduced in Houghton et al. (2012), we use the BC03 SPS models, assuming a Salpeter IMF (based on evidence that massive ETGs may have IMFs that are more heavier than the Milky Way like Chabrier IMF, e.g. Auger et al. 2010) and solar metallicity, and entirely forward-model the data by evaluating the SPS models in the same redshifted filters as those with which the latter were observed (though we do subtract the cosmological dimming term 10 log (1 + z) from the surface brightnesses, as stated in Section 2.2). This removes the need to apply any ad hoc colour or bandpass ‘corrections’ to the data (see e.g. Hogg et al. 2002) based on assumptions about the SED. Any further assumptions that we make regarding the stellar populations in the case of specific scaling relations are explained in the relevant section.

4.1 Luminosity evolution from the CMR

To constrain the stellar ages from the evolution in the CMR scatter, we assume an SFH in which each galaxy comprises an SSP, but allow for a spread in SSP ages between galaxies. This allows us to write the colour scatter as a Taylor expansion

\begin{equation} \frac{\mathrm{d}\textrm {col}}{\mathrm{d}t} \approx \frac{\sigma _{{\rm CMR}}}{\sigma _{{\rm age}}} \approx \frac{3.5 \sigma _{{\rm CMR}}}{\Delta t}, \end{equation}

(15)

where dcol/dt is the rate of change of colour at the mean stellar age of the galaxies, σ_CMR is the intrinsic colour scatter measured from the CMR, σ_age is the intrinsic scatter in stellar age between galaxies (assuming a Gaussian distribution) which translates to the equivalent width of Δt ≈ 3.5σ_age of a population of galaxies that form their SSPs uniformly between t_start and t_stop. Relating t_start and t_stop by the ratio b of the SSP formation period to the total time available,

\begin{equation} \Delta t = t_{{\rm stop}} - t_{{\rm start}} = b t_{{\rm stop}}, \end{equation}

(16)

we can rewrite the mean formation time t_f = (1/2)(t_start + t_stop) in terms of Δt and so derive an equation for the evolution in colour of a galaxy's stars:

\begin{equation} \frac{\mathrm{d}\textrm {col}}{\mathrm{d}t} = 3.5\sigma _{{\rm CMR}} \frac{b ^{-1} - \frac{1}{2}}{t_{\rm f}} \end{equation}

(17)

(see also Bower, Lucey & Ellis 1992; Bower, Kodama & Terlevich 1998; Houghton et al. 2012). Note that this model has all the stars in a single galaxy forming simultaneously, but distributes the formation times for different galaxies uniformly with a dispersion b and mean age t_f. Thus b = 0 corresponds to a cluster whose galaxies all formed at once, whereas b = 1 allows the cluster galaxies to have formed their stars from the beginning of the Universe until t_stop.

Given that we have inferred the intrinsic scatter σ_CMR for the CMRs of the two clusters, and that we can use SPS models to calculate the rate of change of colour as a function of stellar age, we can thus infer the stellar age dispersion b and mean stellar age 13.6 − t_f Gyr of the cluster galaxies. We do this by constructing a chi-squared likelihood from equation (16), accounting for the uncertainties in σ_CMR that are given in Table 2. As shown in Fig. 6, we find a mean age |$9.44_{-0.57}^{+0.46}$| Gyr and dispersion |$b = 0.83_{-0.12}^{+0.11}$|⁠, indicating that the stellar populations are fairly old but formed with a significant dispersion ∼3 Gyr. Note that this is a strong constraint compared to the lower limits that have been previously obtained from the CMR (Bower et al. 1992, 1998; Houghton et al. 2012); this is mainly due to the fact that we have measured the intrinsic scatter for two clusters rather than one, and can therefore break the degeneracy between b and t_f, which would otherwise be unconstrained. The strength of our constraint relative to Houghton et al. (2012), who did use two clusters, comes from the wider redshift separation of our clusters. The constraint obtained here could therefore be further improved by the addition of higher redshift clusters to this analysis.

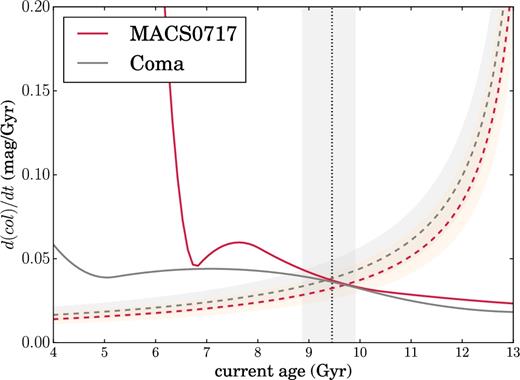
$Inferring the mean stellar age and age dispersion of the cluster galaxies from the evolution of the CMR's intrinsic scatter. Assuming each galaxy to consist of an SSP, with a spread formation times between galaxies, we compare the implied rate of change of colour with that predicted by SSP models. The solid curves show the rate of change of colour that for a solar metallicity SSP with a Salpeter IMF in the BC03 models as a function of the current age of the stars; the dashed curves show the right-hand side of equation (16) for the value $b = 0.83_{-0.12}^{+0.11}$ that we infer, and the vertical black line shows the inferred mean age $9.44_{-0.57}^{+0.46}$ Gyr.$

Figure 6.

Inferring the mean stellar age and age dispersion of the cluster galaxies from the evolution of the CMR's intrinsic scatter. Assuming each galaxy to consist of an SSP, with a spread formation times between galaxies, we compare the implied rate of change of colour with that predicted by SSP models. The solid curves show the rate of change of colour that for a solar metallicity SSP with a Salpeter IMF in the BC03 models as a function of the current age of the stars; the dashed curves show the right-hand side of equation (16) for the value |$b = 0.83_{-0.12}^{+0.11}$| that we infer, and the vertical black line shows the inferred mean age |$9.44_{-0.57}^{+0.46}$| Gyr.

Open in new tab Download slide

4.2 Luminosity evolution from the Fundamental Plane

We have observed that there is a change in the zero-point of the FP with time. This could be due to an evolution in any or all of the plane variables – indeed, at fixed mass, all are understood to change with redshift, though the evolution in R_e and σ, as discussed in Section 1, is understood to be a small effect. Similarly to Saglia et al. (2010) and van der Wel et al. (2008), we derive a general expression relating the FP offset to the evolution of the FP variables, and apply this, first under the assumption of no size evolution, and then using a parametrization for size evolution which we constrain directly from our data. In contrast to the CMR analysis, we now assume that all the stars in all the galaxies formed in a single event, with one SSP characterizing the whole cluster. We can then compare the luminosity evolution we observe with the predictions of SPS models to obtain a further estimate of the stellar age.

By requiring that the FP of MACSJ0717 be parallel to that of Coma, we have been able to measure its displacement, Δγ_FP = γ_{FP, z} − γ_{FP, 0} = −0.14 ± 0.06, in the direction of log R_e, where subscripts x₀ and x_z denote quantities measured with respect to the low- and high-redshift clusters, respectively, as before. Given the FP equation and the construction of the surface brightness as |$\langle \mu _{\rm e}\rangle = -2.5\log (\frac{L}{2\pi R_{\rm e}^2})$|⁠, we have

\begin{equation} \gamma _z - \gamma _0 = \Delta \log R_{\rm e} - \alpha \Delta \log \sigma - \beta \Delta \langle \mu _{\rm e}\rangle , \end{equation}

(18)

where we have dropped the subscript x_FP for clarity, and ΔX = X_z − X₀, i.e. ΔX > 0 means that X has decreased between redshift z and today. This translates into a magnitude evolution Δm

\begin{equation} \Delta m = \frac{(1-5\beta )\Delta \log R_{\rm e} - \alpha \Delta \log \sigma - \Delta \gamma }{\beta }. \end{equation}

(19)

In Section 4.5, we use the full machinery of equation (19) to both investigate and treat the effects of size evolution. Here, though, we proceed under the first approximation that R_e and σ are constant with redshift, in which case equation (19) simplifies dramatically.

The measured change between γ_z and γ₀ translates to an evolution in magnitude of Δm = 0.44 ± 0.10 mag (in the different filters), which we include in Table 4. This implies that, for a particular position on the FP, the stars in a MACSJ0717 galaxy are actually dimmer than those in Coma. While, at first glance, this appears contrary to our expectation of ageing stellar populations, we emphasize that the high- and low-redshift filters are not matched, meaning that each is being sampled in a different region of the spectrum. The purpose of our SPS model comparison is to account for these filter effects in addition to the effects of the intrinsic luminosity evolution of the population.

Table 4.

Open in new tab

Inferences on the size, magnitude and velocity dispersion evolution from the FP, MLM and M–R_e and M–σ relations and the CMR, and the implied formation times of the stellar populations. All models recover a stellar age ∼10 Gyr, though the MLM relation implies slightly larger ages than the FP and the joint analysis. The final two columns provide the implied magnitude evolution in the rest-frame Johnson B and V bands, according to the ages given in the sixth column.

Scaling	Size evolution	ξ	η	Observed-frame magnitude	Age	Rest-frame B-band	Rest-frame V-band
relation	corrected?			evolution (mag)	(Gyr)	magnitude evolution (mag)	magnitude evolution (mag)
CMR	–	–	–	–	\|$9.44_{-0.57}^{+0.46}$\|	–	–
FP	N	–	–	0.44 ± 0.19	\|$9.12_{-0.80}^{+1.22}$\|	\|$-0.86_{-0.16}^{+0.15}$\|	\|$-0.78_{-0.16}^{+0.14}$\|
FP	Y	−0.37 ± 0.39	0.06 ± 0.28	0.54 ± 0.29	\|$9.72_{-1.40}^{+3.17}$\|	\|$-0.78_{-0.24}^{+0.21}$\|	\|$-0.69_{-0.23}^{+0.18}$\|
MLM	N	–	–	0.57 ± 0.18	\|$9.89_{-0.98}^{+1.73}$\|	\|$-0.75_{-0.15}^{+0.14}$\|	\|$-0.67_{-0.15}^{+0.12}$\|
MLM	Y	−0.37 ± 0.39	0.06 ± 0.28	0.66 ± 0.19	\|$10.64_{-1.34}^{+2.50}$\|	\|$-0.69_{-0.15}^{+0.13}$\|	\|$-0.61_{-0.14}^{+0.11}$\|
MLM and FP	Y	−0.40 ± 0.32	0.09 ± 0.27	0.59 ± 0.26	\|$10.00_{-1.32}^{+3.14}$\|	\|$-0.74_{-0.09}^{+0.19}$\|	\|$-0.65_{-0.08}^{+0.15}$\|

Scaling	Size evolution	ξ	η	Observed-frame magnitude	Age	Rest-frame B-band	Rest-frame V-band
relation	corrected?			evolution (mag)	(Gyr)	magnitude evolution (mag)	magnitude evolution (mag)
CMR	–	–	–	–	\|$9.44_{-0.57}^{+0.46}$\|	–	–
FP	N	–	–	0.44 ± 0.19	\|$9.12_{-0.80}^{+1.22}$\|	\|$-0.86_{-0.16}^{+0.15}$\|	\|$-0.78_{-0.16}^{+0.14}$\|
FP	Y	−0.37 ± 0.39	0.06 ± 0.28	0.54 ± 0.29	\|$9.72_{-1.40}^{+3.17}$\|	\|$-0.78_{-0.24}^{+0.21}$\|	\|$-0.69_{-0.23}^{+0.18}$\|
MLM	N	–	–	0.57 ± 0.18	\|$9.89_{-0.98}^{+1.73}$\|	\|$-0.75_{-0.15}^{+0.14}$\|	\|$-0.67_{-0.15}^{+0.12}$\|
MLM	Y	−0.37 ± 0.39	0.06 ± 0.28	0.66 ± 0.19	\|$10.64_{-1.34}^{+2.50}$\|	\|$-0.69_{-0.15}^{+0.13}$\|	\|$-0.61_{-0.14}^{+0.11}$\|
MLM and FP	Y	−0.40 ± 0.32	0.09 ± 0.27	0.59 ± 0.26	\|$10.00_{-1.32}^{+3.14}$\|	\|$-0.74_{-0.09}^{+0.19}$\|	\|$-0.65_{-0.08}^{+0.15}$\|

Table 4.

Open in new tab

Inferences on the size, magnitude and velocity dispersion evolution from the FP, MLM and M–R_e and M–σ relations and the CMR, and the implied formation times of the stellar populations. All models recover a stellar age ∼10 Gyr, though the MLM relation implies slightly larger ages than the FP and the joint analysis. The final two columns provide the implied magnitude evolution in the rest-frame Johnson B and V bands, according to the ages given in the sixth column.

Scaling	Size evolution	ξ	η	Observed-frame magnitude	Age	Rest-frame B-band	Rest-frame V-band
relation	corrected?			evolution (mag)	(Gyr)	magnitude evolution (mag)	magnitude evolution (mag)
CMR	–	–	–	–	\|$9.44_{-0.57}^{+0.46}$\|	–	–
FP	N	–	–	0.44 ± 0.19	\|$9.12_{-0.80}^{+1.22}$\|	\|$-0.86_{-0.16}^{+0.15}$\|	\|$-0.78_{-0.16}^{+0.14}$\|
FP	Y	−0.37 ± 0.39	0.06 ± 0.28	0.54 ± 0.29	\|$9.72_{-1.40}^{+3.17}$\|	\|$-0.78_{-0.24}^{+0.21}$\|	\|$-0.69_{-0.23}^{+0.18}$\|
MLM	N	–	–	0.57 ± 0.18	\|$9.89_{-0.98}^{+1.73}$\|	\|$-0.75_{-0.15}^{+0.14}$\|	\|$-0.67_{-0.15}^{+0.12}$\|
MLM	Y	−0.37 ± 0.39	0.06 ± 0.28	0.66 ± 0.19	\|$10.64_{-1.34}^{+2.50}$\|	\|$-0.69_{-0.15}^{+0.13}$\|	\|$-0.61_{-0.14}^{+0.11}$\|
MLM and FP	Y	−0.40 ± 0.32	0.09 ± 0.27	0.59 ± 0.26	\|$10.00_{-1.32}^{+3.14}$\|	\|$-0.74_{-0.09}^{+0.19}$\|	\|$-0.65_{-0.08}^{+0.15}$\|

Scaling	Size evolution	ξ	η	Observed-frame magnitude	Age	Rest-frame B-band	Rest-frame V-band
relation	corrected?			evolution (mag)	(Gyr)	magnitude evolution (mag)	magnitude evolution (mag)
CMR	–	–	–	–	\|$9.44_{-0.57}^{+0.46}$\|	–	–
FP	N	–	–	0.44 ± 0.19	\|$9.12_{-0.80}^{+1.22}$\|	\|$-0.86_{-0.16}^{+0.15}$\|	\|$-0.78_{-0.16}^{+0.14}$\|
FP	Y	−0.37 ± 0.39	0.06 ± 0.28	0.54 ± 0.29	\|$9.72_{-1.40}^{+3.17}$\|	\|$-0.78_{-0.24}^{+0.21}$\|	\|$-0.69_{-0.23}^{+0.18}$\|
MLM	N	–	–	0.57 ± 0.18	\|$9.89_{-0.98}^{+1.73}$\|	\|$-0.75_{-0.15}^{+0.14}$\|	\|$-0.67_{-0.15}^{+0.12}$\|
MLM	Y	−0.37 ± 0.39	0.06 ± 0.28	0.66 ± 0.19	\|$10.64_{-1.34}^{+2.50}$\|	\|$-0.69_{-0.15}^{+0.13}$\|	\|$-0.61_{-0.14}^{+0.11}$\|
MLM and FP	Y	−0.40 ± 0.32	0.09 ± 0.27	0.59 ± 0.26	\|$10.00_{-1.32}^{+3.14}$\|	\|$-0.74_{-0.09}^{+0.19}$\|	\|$-0.65_{-0.08}^{+0.15}$\|

We use the BC03 stellar population models to interpret this, again assuming an SSP with solar metallicity and a Salpeter IMF. As explained at the beginning of Section 4, we take account of both the different filters used and the age difference by modelling the colour Δm = F625W(z = 0.545, T − 5.33) − r(z = 0, T), where z is the redshift and T is the age of the Universe in Gyr. The evolution of Δm in this setup is shown in Fig. 7, with the magnitude offset Δm = 0.44 ± 0.19 determined from the FP overplotted in red, along with its 1σ upper and lower bounds. The intersection of this measured offset with the model lines gives an estimate for the age as |$9.12_{-0.80}^{+1.22}$| Gyr, and is in good agreement with the constraints from the CMR that were obtained in the previous section, plotted in grey in the figure. This is old, and implies that the stellar populations are already highly evolved by the time we observed them in MACSJ0717.

Figure 7.

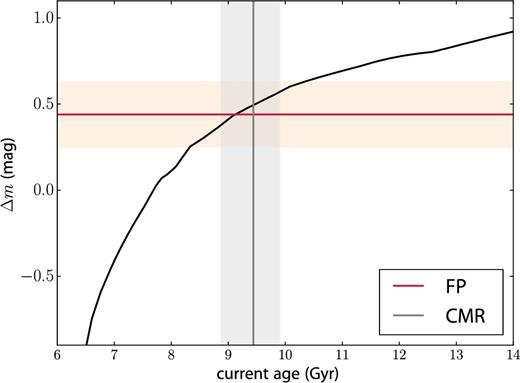
SSP prediction for the evolution of the observed magnitude difference between the Coma and MACSJ0717 galaxies as a function of cluster age. Overplotted in red is the offset inferred from the evolution of the FP, as described in Section 4.2; the grey vertical line shows the inference on age from the CMR, which agrees remarkably well. In both cases, the shaded regions show the 1σ uncertainties.

Open in new tab Download slide

4.3 Luminosity evolution from the M_dyn/L–M_dyn relation

As for the FP, we assume that both populations can be described by the same power-law index (the individual cluster slopes are consistent at the 1σ level) and, under the same assumption of one universal SSP, we use our simultaneous fit to the two clusters and compare the offset between them with that predicted by SSP models in order to make another estimate of the stellar age. Here, given that the mass scales as M ∼ σ²R_e, we have

\begin{equation} \Delta \log (M/L) = 2 \Delta \log \sigma + \Delta \log R_{\rm e} - \Delta \log L, \end{equation}

(20)

which can be related to the offset using equation (9) to give

\begin{eqnarray} \Delta m = \Delta \mathcal {M_{{\odot }}} + 2.5\big [ \Delta \beta _{{\rm ML}} + (\alpha _{{\rm ML}} - 1)(2 \Delta \log \sigma + \Delta \log R_{\rm e})\big ]\!, \nonumber\\ \end{eqnarray}

(21)

where |$\Delta \mathcal {M_{{\odot }}}$| is the difference in absolute solar magnitude in the (blueshifted) filters.

As with the FP, we initially assume zero structural evolution, and calculate the magnitude offset and corresponding stellar age. From our best fit to the two cluster populations, we then find Δm = 0.57 ± 0.18, consistent with our earlier FP result and included in Table 4. This implies a stellar age of |$9.89_{-0.98}^{+1.73}$| Gyr.

4.4 Combining size and luminosity evolution

To apply our inference on size evolution from the mass–size and mass–velocity dispersion relations of Section 3.4 to our scaling relations using equations (16) and (18), we define

\begin{equation} \Delta \log R_{\rm e} = \xi \log (1+z) \end{equation}

(22)

and

\begin{equation} \Delta \log \sigma = \eta \log (1+z), \end{equation}

(23)

using the values of ξ and η as defined in equations (11) and (12) and tabulated in Tables 2 and 3.

Using our calculated values for ξ and η alongside equations (16) and (18), we can now calculate the magnitude evolution Δm that must have taken place between the two clusters according to the FP and the MLM relation. We can write the magnitude offset as

\begin{equation} \Delta m = \frac{\log (1+z) [(1-5\beta )\xi - \alpha \eta ] - \Delta \gamma }{\beta } \end{equation}

(24)

for the FP, and

\begin{equation} \Delta m = \Delta \mathcal {M_{{\odot }}} + 2.5 [ \Delta \beta + (\alpha -1)(2\eta +\xi )\log (1+z)] \end{equation}

(25)

for the MLM relation.

In Table 4, we summarize η, ξ, Δm and the corresponding stellar age, according to our stellar population models, both with and without allowing for structural evolution. The final two columns of that table give the implied magnitude evolution in the rest-frame Johnson B and V bands, assuming the stellar age that has been inferred in each case. We note that we do not attempt to account for progenitor bias that may arise from the fact that relatively young galaxies included in the local sample would be missing at higher redshifts, where they would not yet appear passive; we do not have the data to constrain it here. However, Valentinuzzi et al. (2010) and Saglia et al. (2010) investigated this for their larger samples of field galaxies at comparable redshifts, and found the effect to be small. We therefore assume the same to be true for our cluster galaxy samples. The MLM relation generally implies ages that are between 0.5 and 1 Gyr older than the FP, though the results are formally consistent and imply a stellar age of ∼10 Gyr.

4.5 Combining scaling relations: inferring size and luminosity evolution

In the previous sections, we analysed each scaling relation separately, using assumptions the size evolution measured from the M_⋆–R_e (MR) and M_⋆–σ (MS) relations to infer the evolution in luminosity and so the stellar age. Here, we model the FP and the MLM, MR and MS relations simultaneously, using both clusters so as to infer not only the scaling relation parameters and the underlying (Gaussian) distributions as before, but also the magnitude, size and dynamical evolution between z = 0.545 and the present day. This has a number of significant advantages, including that (a) it ensures that the inferred scaling relations are all consistent, (b) it allows us to infer the physical parameters ξ, η and Δm (which were previously calculated after the modelling) in addition to those describing the scaling relations themselves and (c) it fully explores degeneracies between the physical parameters, as is not possible to do when they are calculated postmodelling.

To do this, we use the same formalism as before. We assume the MLM relations for the two clusters can be described according to the following equations:

\begin{equation} \log \frac{M_{{\rm dyn}}}{L} = \alpha _{{\rm ML}} \log M_{{\rm dyn}} + \beta _{{\rm ML}} (z), \end{equation}

(26)

where the intercept for the low-redshift cluster is

\begin{equation} \beta _{{\rm ML}} (0) = \beta _{{\rm ML}} \end{equation}

(27)

and for MACSJ0717, we now explicitly account for size, magnitude and velocity dispersion evolution with

\begin{eqnarray} \beta _{{\rm ML}} (z) &=& \beta _{{\rm ML}} + 0.4(\Delta m - \Delta \mathcal {M_{{\odot }}}) \nonumber\\ && +\, (1-\alpha _{{\rm ML}})(2\eta + \xi )\log (1+z). \end{eqnarray}

(28)

As before, we take the slope α_ML to be the same for both clusters. Also as before, each cluster has a distribution in log M_dyn given by a normal distribution with mean ν_ML and variance |$\tau _{ML}^2$|⁠.

We also assume the FPs for the two clusters can be described according to

\begin{equation} \log R_{\rm e} = \alpha _{{\rm FP}} \log \sigma + \beta _{{\rm FP}} \langle \mu _{\rm e}\rangle + \gamma _{{\rm FP}} (z), \end{equation}

(29)

where the intercept of the low-redshift cluster is

\begin{equation} \gamma _{{\rm FP}} (0) = \gamma _{{\rm FP}} \end{equation}

(30)

and for MACSJ0717

\begin{equation} \gamma _{{\rm FP}} (z) = \gamma _{{\rm FP}} + [ \xi (1 - 5\beta _{{\rm FP}}) - \alpha \eta]\log (1+z) - \beta _{{\rm FP}} \Delta m. \end{equation}

(31)

Again, the slopes α_FP and β_FP are the same for both clusters, and the independent variables log σ and 〈μ_e〉 are drawn from multivariate normal distributions as described in Section 3.2.

Finally, we include the MR and MS relations, retaining our definition of η and ξ as being measured at constant stellar mass, to give

\begin{equation} \beta _{{\rm MR}}(z) = \beta _{{\rm MR},0} + \xi \log (1+z) \end{equation}

(32)

and

\begin{equation} \beta _{{\rm MS}}(z) = \beta _{{\rm MS},0} + \eta \log (1+z) \end{equation}

(33)

for the MR and MS relations, respectively, with log M_⋆ being drawn from a normal distribution with mean |$\nu _{M_{\star }}$| and variance |$\tau _{M_{\star }}^2$|⁠. This model now has the advantage of allowing us to infer the amount of size evolution and magnitude evolution that best describe our whole data set, and guarantees that all four scaling relations are treated in a consistent way. It also sidesteps some of the potential dangers of our earlier method for constraining the structural evolution, as it does not assume that the stellar mass remains constant with redshift.

Our results are summarized in Table 2; encouragingly, the parameters of the FP and MLM relations are consistent with those inferred in our previous, simpler models. However, we now have additional constraints on the evolution of R_e, σ and the luminosity. Although ξ, η and Δm have degeneracies within each relation, the modelling of all four relations at once breaks this degeneracy and we are able to infer Δm = 0.59 ± 0.26, ξ = −0.40 ± 0.32 and η = 0.09 ± 0.27. The fact that the uncertainties on these parameters are comparable to – and, in a number of cases, smaller than – the uncertainties on the same parameters when each scaling relation is modelled separately, indicates that the degeneracies are not significant, and that the scheme we have set up is indeed internally consistent. These results correspond to a stellar age |$10.00_{-1.32}^{+3.14}$| Gyr.

5 DISCUSSION

5.1 Old, passively evolving stellar populations

The FP and its evolution with redshift contain a wealth of information about ETG formation and evolution; however, in order to extract this information meaningfully, it is important to understand the contributions due to different processes – that is, the luminosity evolution of the stellar populations and the structural evolution of the galaxies themselves – and to find a way to disentangle them. In this work, we have combined the FP with a number of other scaling relations in order to break these degeneracies and make inference on both the luminous and structural evolution. We are now in a position to tie together what we have found.

Initially, we used the evolution of the intrinsic scatter of the CMR to infer the mean stellar age, allowing for some dispersion. There, we assumed an SFH in which each galaxy is composed of an SSP with some dispersion in age across the galaxy population, and used the small evolution in the intrinsic scatter to infer a mean age |$9.44_{-0.57}^{+0.46}$| Gyr and a dispersion of ∼3 Gyr. This dispersion is significant but still implies some coordination in the star formation times of the different galaxies; together with the small intrinsic scatter of the FP and the MLM relation, this justified our treatment of the latter assuming that all the galaxies’ stars formed in a single burst. We then modelled the FP, MLM, MS and MR relations in two ways: first, treating each separately, constraining the slopes to be parallel for the two clusters and using the offsets between them to measure the evolution in size, velocity dispersion and luminosity and hence the stellar age; secondly, by requiring all four relations to have evolved in a consistent way with regard to the structures and luminosities of the galaxies. In both cases, we find very clearly that only a small amount of evolution has taken place, with the high-redshift galaxies only marginally smaller and with marginally higher velocity dispersions than the Coma galaxies, and the luminosity evolution consistent with the passive fading of old populations.

In Table 4, we present the magnitude evolution that was inferred in each case, both in the observed-frame r΄ (Coma) and F625W (MACSJ0717) filters and the rest-frame U- and V-band filters (though we note that the latter are more uncertain due to assumptions made in calculating K-corrections). In the joint analysis, we find |$\Delta m_{{\rm B}} = -0.74_{-0.09}^{+0.19}$| mag, or equivalently, |$\Delta \log M/L_{{\rm B}} = -0.30_{-0.04}^{+0.08} = -0.55_{-0.07}^{+0.15} z = -1.59_{-0.21}^{+0.42} \log (1+z)$|⁠. This is consistent with the findings of Saglia et al. (2010) and Holden et al. (2010), indicating that the stellar populations in these ETGs have been evolving passively. Our inferred mean age of |$10.00_{-1.32}^{+3.14}$| Gyr, corresponding to a formation redshift |$z_{{\rm form}} = 1.87_{-0.58}^{+>10}$|⁠, is also in agreement with the measurements of Jørgensen et al. (2014), which examined the FP of a z = 1.27 cluster, and implies that these galaxies are dominated by old stars which formed ∼10 Gyr ago with some dispersion. Thus, we are seeing galaxies which are already significantly evolved when we look at MACSJ0717, consistent with a picture in which massive ETGs form their stars early and then grow passively and dissipationlessly, e.g. by minor mergers and accretion.

5.2 Accelerated growth?

The extremely small amount of structural evolution that we find to have taken place indicates that the galaxies in MACSJ0717 must have undergone the majority of their structural changes at earlier times. This may be a result of the very dense environment in which they are residing: indeed, other studies of galaxies in rich clusters out to z ∼ 1 have also found no evidence for significant size or velocity dispersion evolution (Stott et al. 2011; Jørgensen & Chiboucas 2013; Jørgensen et al. 2014; Saracco et al. 2014). Moreover, when we compare these results with those from similar studies focusing on galaxies in lower density clusters, in which stronger structural evolution is found (e.g. Saglia et al. 2010) – and further, with those from studies of field ellipticals, which show evidence for yet stronger evolutionary trends (e.g. van der Wel et al. 2008, 2014) – a tentative picture emerges of an environment-dependent growth time-scale, with galaxies in denser environments reaching their present-day sizes at earlier epochs than those in lower density environments. While we cannot comment quantitatively on this hypothesis based on the data in this paper, we note that this would also be in line with the majority of studies that have directly compared the sizes of passive galaxies in high- and low-density environments (e.g. Lani et al. 2013; Delaye et al. 2014) and found the galaxies in higher density environments to be up to 50 per cent bigger (though see also Newman et al. 2014).

If it is indeed the case that the growth of these galaxies has been accelerated by the dense cluster environment, this would also be strong evidence in favour of merger-driven growth – which is likely to be enhanced in clusters – as opposed to growth by internal processes such as adiabatic expansion due to quasar outflows (e.g. Fan et al. 2010). It would therefore be interesting to take a deeper census of the MACSJ0717 cluster in order to establish whether the implied rate of mergers and accretion is consistent with the rate of evolution that we have observed. Of course, it is possible that our spectroscopic galaxy sample in MACSJ0717 is biased towards the largest radius systems, in which case the cluster may also host a number of other massive but smaller galaxies which are still undergoing some structural evolution. While a deeper census would again be necessary before this could be ruled out, it is nevertheless clear that a significant population of large, massive, apparently fully evolved galaxies are already in place by z ∼ 0.5. We also note that MACSJ0717 is an extremely massive cluster – indeed, the CLASH survey exclusively targeted strong lensing clusters – and that it may therefore be an extreme example of accelerated growth.

5.3 Can we trust the stellar and dynamical masses?

The stellar masses derived in Section 3.4 are on average higher than the dynamical masses, for the galaxies in both clusters (see Table 1) – implying that all the mass in these systems should be luminous. For Coma, the median ratio of stellar to dynamical mass is 1.39, while for MACSJ0717 the median ratio is 1.48. At face value, this is unphysical. However, recall that the dynamical mass given by equation (7) is not the total dynamical mass, but is really twice the dynamical mass within one effective radius. Furthermore, with β = 5, it calculates the dynamical mass for a specific mass profile. In fact, variations in β may be as large as a factor of two for typical mass profiles of ETGs. Furthermore, when calculating the mass-to-light ratios from the BC03 stellar populations, we adopted a Salpeter IMF. Mass-to-light ratios in the r band for old, solar metallicity SSPs are typically in the ratio 2:3 for Chabrier : Salpeter IMFs. Thus had we adopted a Chabrier (2003) or Kroupa (2001) IMF, the stellar masses would be roughly equal to the dynamical masses. We further note that we are not the first to identify stellar masses larger than dynamical masses; Peralta de Arriba et al. (2014) attribute an evolution in the stellar-to-dynamical mass being due to an evolving non-homology due to size evolution.

One caveat with our analysis is that we have attributed all the evolution to an evolution of the luminous matter as opposed to the dark matter, and the discrepancies between M_dyn and M_⋆ mean that we are unable to estimate the dark matter fractions in these galaxies and so obtain a measure of how important this assumption might be. However, more detailed studies of individual galaxies have shown that the dark matter content of ETGs only dominates at large projected radii R > R_e (e.g. Oldham & Auger 2016), and so should not significantly affect stellar velocity dispersions that are measured in the central regions. It is therefore unlikely to be a significant problem in this study.

5.4 Can we compare MACSJ0717 with Coma?

The assumption at the foundation of this work is that the galaxies in MACSJ0717 represent an earlier evolutionary stage of the Coma galaxies: this allows us to compare their stellar populations and so make statements about the ages of their stars and the time-scales of their formation. If this assumption is not valid, it could lead to systematic errors in our age calculations, so it is important to examine it closely.

One possible problem could be the differing masses of the two clusters, with the X-ray luminosity of MACSJ0717 being more than three times greater than that of Coma – compare L_MACS = 24.6 × 10⁴⁴ erg s⁻¹ (Ebeling et al. 2007) with L_Coma = 7.21 × 10⁴⁴ erg s⁻¹ (Ebeling et al. 1996). In the hierarchical paradigm, more massive dark matter haloes like that of MACSJ0717 are expected to collapse earlier and so have older stars. Further, if growth is accelerated in higher mass, higher density systems as we have suggested, this could also lead to inconsistencies in our framework. However, the evolution that we infer is sufficiently small that even an underlying age difference of ∼1 Gyr would not make it significant. It is therefore extremely unlikely that either of these effects would bias our inference on scales larger than our uncertainties. We also note that the good agreement between our different age measurements suggests that the framework we have set up is consistent.

6 CONCLUSIONS

We have constructed the CMR, the FP and the M_dyn/L–M_dyn, M_⋆–σ and M_⋆–R_e relations for galaxies in the cluster MACSJ0717, at z ∼ 0.5, using archived data from the CLASH and Gemini data bases, and for Coma using existing data sets. By analysing these evolution between these relations, we have reached the following conclusions.

The galaxies fall on an FP and an M_dyn/L–M_dyn relation which are offset relative to those of Coma. The luminosity evolution implied by these offsets is Δm ∼ 0.6 mag, corresponding to a star formation epoch of ∼10 Gyr followed by passive fading.
The galaxies fall on M_⋆–σ and M_⋆–R_e relations which are only marginally offset from those of Coma. The structural evolution implied by this is minimal, with R_e(z) ∼ (1 + z)^{−0.40 ± 0.32} and σ(z) ∼ (1 + z)^{0.09 ± 0.27}, corresponding to galaxies which have undergone the majority of their evolution at earlier times.
The FP and M_dyn/L–M_dyn, M_⋆–σ and M_⋆–R_e relations, modelled together, confirm these results. Importantly, the fact that all four relations can be modelled simultaneously and consistently imply that degeneracies between the physical parameters are not significant and that the physical scenario we have established, with evolution in luminosity, size and velocity dispersion, is consistent with and can fully account for the data. The fact that the inference from the independent CMR – which is also based on different assumptions about the star formation histories of the galaxies – is also consistent with these results further underlines this conclusion.
The small amount of structural evolution that we find in these galaxies is consistent with other studies of size evolution in cluster galaxies, but seems to be in tension with that found in studies of field ellipticals. This suggests that growth may be accelerated in high-density environments, where the rate of merging may be increased. If so, this is strong evidence that dry merging is a dominant channel of growth in these systems.
Taken together, these results lead to a very clear picture in which these z ∼ 0.5 galaxies have already experienced most of their star formation and structural evolution at earlier stages in their lives.

Acknowledgments

We thank the referee for their helpful comments. LJO thanks the Science and Technology Facilities Council (STFC) for the award of a studentship; RCWH was also supported by STFC [STFC grant numbers ST/H002456/1, ST/K00106X/1 and ST/J002216/1]. RLD acknowledges travel and computer grants from Christ Church, Oxford and support from the Oxford Centre for Astrophysical Surveys which is funded by the Hintze Family Charitable Foundation.

This work was based on observations obtained at the Gemini Observatory (Program ID GN-2002B-Q-44; acquired through the Gemini Science Archive and processed using the Gemini iraf package), which is operated by the Association of Universities for Research in Astronomy, Inc., under a cooperative agreement with the NSF on behalf of the Gemini partnership: the National Science Foundation (United States), the National Research Council (Canada), CONICYT (Chile), Ministerio de Ciencia, Tecnologa e Innovacin Productiva (Argentina) and Ministrio da Cincia, Tecnologia e Inovao (Brazil).

This work was also based on observations made with the NASA/ESA Hubble Space Telescope, obtained from the Data Archive at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-26555. These observations are associated with the CLASH Multi-Cycle Treasury Program (GO-12065).

REFERENCES

Auger

M. W.

,

Treu

T.

,

Gavazzi

R.

,

Bolton

A. S.

,

Koopmans

L. V. E.

,

Marshall, P. J.

,

2010

,

ApJ

,

721

,

L163

Crossref

Search ADS

Baum

W. A.

,

1959

,

PASP

,

71

,

106

Crossref

Search ADS

Bender

R.

,

Ziegler

B.

,

Bruzual

G.

,

1996

,

ApJ

,

463

Bertin

E.

,

Arnouts

S.

,

1996

,

A&AS

,

117

,

393

Crossref

Search ADS

Bower

R. G.

,

Lucey

J. R.

,

Ellis

R. S.

,

1992

,

MNRAS

,

254

,

601

Crossref

Search ADS

Bower

R. G.

,

Kodama

T.

,

Terlevich

A.

,

1998

,

MNRAS

,

299

,

1193

Crossref

Search ADS

Bruzual

G.

,

Charlot

S.

,

2003

,

MNRAS

,

344

,

1000

(BC03)

Crossref

Search ADS

Cappellari

M.

,

Emsellem

E.

,

2004

,

PASP

,

116

,

138

Crossref

Search ADS

Cappellari

M.

et al. ,

2006

,

MNRAS

,

366

,

1126

Crossref

Search ADS

Chabrier

G.

,

2003

,

PASP

,

115

,

763

Crossref

Search ADS

Delaye

L.

et al. ,

2014

,

MNRAS

,

441

,

203

Crossref

Search ADS

Djorgovski

S.

,

Davis

M.

,

1987

,

ApJ

,

313

,

59

Crossref

Search ADS

Dressler

A.

,

Lynden-Bell

D.

,

Burstein

D.

,

Davies

R. L.

,

Faber

S. M.

,

Terlevich

R.

,

Wegner

G.

,

1987

,

ApJ

,

313

,

42

Crossref

Search ADS

Ebeling

H.

,

Voges

W.

,

Bohringer

H.

,

Edge

A. C.

,

Huchra

J. P.

,

Briel

U. G.

,

1996

,

MNRAS

,

281

,

799

Crossref

Search ADS

Ebeling

H.

,

Barrett

E.

,

Donovan

D.

,

Ma

C.-J.

,

Edge

A. C.

,

van Speybroeck

L.

,

2007

,

ApJ

,

661

Ellis

R. S.

,

Smail

I.

,

Dressler

A.

,

Couch

W. J.

,

Oemler

A.

,

Jr

,

Butcher

H.

,

Sharples

R. M.

,

1997

,

ApJ

,

483

,

582

Crossref

Search ADS

Fan

L.

,

Lapi

A.

,

Bressan

A.

,

Bernardi

M.

,

De Zotti

G.

,

Danese

L.

,

2010

,

ApJ

,

718

,

1460

Crossref

Search ADS

Foreman-Mackey

D.

,

Hogg

D. W.

,

Lang

D.

,

Goodman

J.

,

2013

,

Publ. Astron. Soc. Pacific

,

125

,

306

Crossref

Search ADS

Frei

Z.

,

Gunn

J. E.

,

1994

,

AJ

,

108

,

1476

Crossref

Search ADS

Hanuschik

R. W.

,

2003

,

A&A

,

407

,

1157

Crossref

Search ADS

Hogg

D. W.

,

Baldry

I. K.

,

Blanton

M. R.

,

Eisenstein

D. J.

,

2002

,

preprint (arXiv:astro-ph/0210394)

Hogg

D. W.

,

Bovy

J.

,

Lang

D.

,

2010

,

preprint (arXiv:e-prints)

Holden

B. P.

,

van der Wel

A.

,

Kelson

D. D.

,

Franx

M.

,

Illingworth

G. D.

,

2010

,

ApJ

,

724

,

714

Crossref

Search ADS

Houghton

R. C. W.

,

Davies

R. L.

,

Dalla Bont

E.

,

Masters

R.

,

2012

,

MNRAS

,

423

,

256

Crossref

Search ADS

Jørgensen

I.

,

Chiboucas

K.

,

2013

,

AJ

,

145

,

77

Crossref

Search ADS

Jørgensen

I.

,

Franx

M.

,

Kjaergaard

P.

,

1995

,

MNRAS

,

273

,

1097

Crossref

Search ADS

Jørgensen

I.

,

Franx

M.

,

Hjorth

J.

,

van Dokkum

P. G.

,

1999

,

MNRAS

,

308

,

833

Crossref

Search ADS

Jørgensen

I.

,

Chiboucas

K.

,

Flint

K.

,

Bergmann

M.

,

Barr

J.

,

Davies

R.

,

2006

,

ApJ

,

639

Jørgensen

I.

,

Chiboucas

K.

,

Toft

S.

,

Bergmann

M.

,

Zirm

A.

,

Schiavon

R. P.

,

Grützbauch

R.

,

2014

,

AJ

,

148

,

117

Crossref

Search ADS

Kelly

B. C.

,

2007

,

ApJ

,

665

,

1489

Crossref

Search ADS

Kodama

T.

,

Arimoto

N.

,

1997

,

A&A

,

320

,

41

Kroupa

P.

,

2001

,

MNRAS

,

322

,

231

Crossref

Search ADS

Lani

C.

et al. ,

2013

,

MNRAS

,

435

,

207

Crossref

Search ADS

Mei

S.

et al. ,

2009

,

ApJ

,

690

,

42

Crossref

Search ADS

Newman

A. B.

,

Ellis

R. S.

,

Andreon

S.

,

Treu

T.

,

Raichoor

A.

,

Trinchieri

G.

,

2014

,

ApJ

,

788

,

51

Crossref

Search ADS

Oldham

L. J.

,

Auger

M. W.

,

2016

,

MNRAS

,

457

,

421

Crossref

Search ADS

Oldham

L. J.

et al. ,

2016

,

MNRAS

,

in press

Peralta

de Arriba L.

,

Balcells

M.

,

Falcón-Barroso

J.

,

Trujillo

I.

,

2014

,

MNRAS

,

440

,

1634

Crossref

Search ADS

Postman

M.

et al. ,

2012

,

ApJS

,

199

,

25

Crossref

Search ADS

Saglia

R. P.

et al. ,

2010

,

A&A

,

524

,

A6

Crossref

Search ADS

Sandage

A.

,

1972

,

ApJ

,

176

,

21

Crossref

Search ADS

Saracco

P.

et al. ,

2014

,

A&A

,

567

,

A94

Crossref

Search ADS

Shen

S.

,

Mo

H. J.

,

White

S. D. M.

,

Blanton

M. R.

,

Kauffmann

G.

,

Voges

W.

,

Brinkmann

J.

,

Csabai

I.

,

2003

,

MNRAS

,

343

,

978

Crossref

Search ADS

Stanford

S. A.

,

Eisenhardt

P. R.

,

Dickinson

M.

,

1995

,

ApJ

,

450

,

512

Crossref

Search ADS

Stanford

S. A.

,

Eisenhardt

P. R.

,

Dickinson

M.

,

1998

,

ApJ

,

492

,

461

Crossref

Search ADS

Stockton

A.

,

Shih

H.-Y.

,

Larson

K.

,

Mann

A. W.

,

2014

,

ApJ

,

780

,

134

Crossref

Search ADS

Stott

J. P.

,

Collins

C. A.

,

Burke

C.

,

Hamilton-Morris

V.

,

Smith

G. P.

,

2011

,

MNRAS

,

414

,

445

Crossref

Search ADS

Terlevich

A. I.

,

Caldwell

N.

,

Bower

R. G.

,

2001

,

MNRAS

,

326

,

1547

Crossref

Search ADS

Tody

D.

,

1993

, in

Hanisch

R. J.

,

Brissenden

R. J. V.

,

Barnes

J.

, eds,

ASP Conf. Ser. Vol. 52

,

Astronomical Data Analysis Software and Systems II

.

Astron. Soc. Pac.

,

San Francisco

, p.

173

van der Wel

A.

,

Holden

B. P.

,

Zirm

A. W.

,

Franx

M.

,

Rettura

A.

,

Illingworth

G. D.

,

Ford

H. C.

,

2008

,

ApJ

,

688

,

48

Crossref

Search ADS

van der Wel

A.

et al. ,

2014

,

ApJ

,

788

,

28

Crossref

Search ADS

van Dokkum

P. G.

,

Ellis

R. S.

,

2003

,

ApJ

,

592

van Dokkum

P. G.

,

Franx

M.

,

1996

,

MNRAS

,

281

,

985

Crossref

Search ADS

van Dokkum

P. G.

et al. ,

2008

,

ApJ

,

677

,

L5

Crossref

Search ADS

Valdes

F.

,

Gupta

R.

,

Rose

J. A.

,

Singh

H. P.

,

Bell

D. J.

,

2004

,

ApJS

,

152

,

251

Crossref

Search ADS

Valentinuzzi

T.

et al. ,

2010

,

ApJ

,

721

,

L19

Crossref

Search ADS

Visvanathan

N.

,

Sandage

A.

,

1977

,

ApJ

,

216

,

214

Crossref

Search ADS

Wolf

J.

,

Martinez

G. D.

,

Bullock

J. S.

,

Kaplinghat

M.

,

Geha

M.

,

Muñoz

R. R.

,

Simon

J. D.

,

Avedo

F. F.

,

2010

,

MNRAS

,

406

,

1220

APPENDIX A

Figure A1.

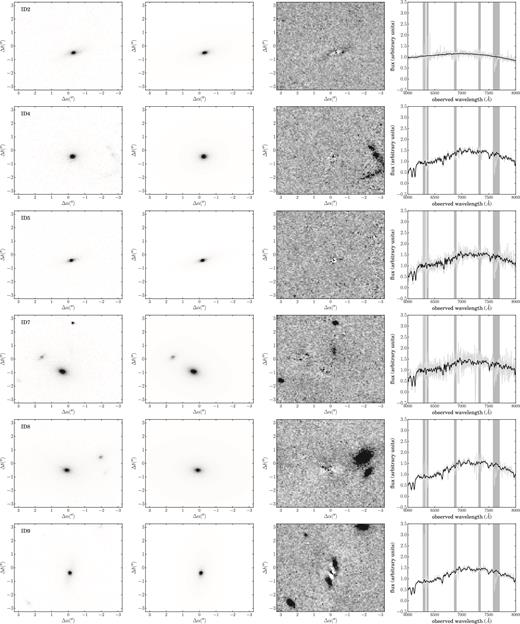
For each object in our final MACSJ0717 sample, from left to right: HST/ACS F625W data; model; signal-to-noise residuals; fitted spectrum. Image cutouts are 6.5 arcsec on a side; spectra show the extracted spectrum in grey and the model in black, with masked regions in dark grey.

Open in new tab Download slide

Figure A1

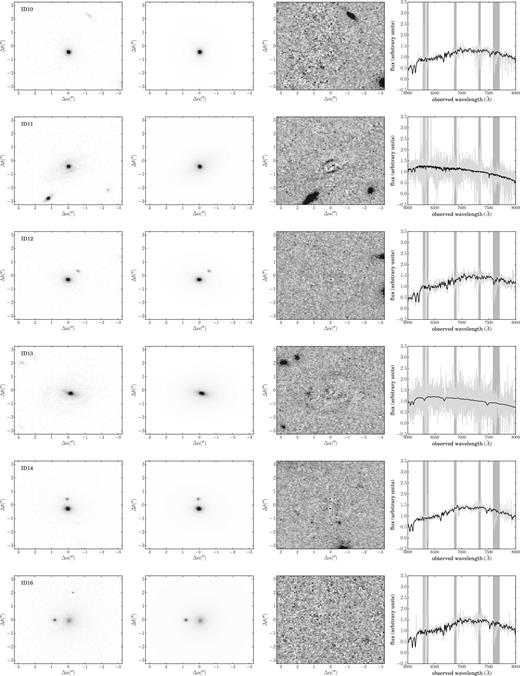
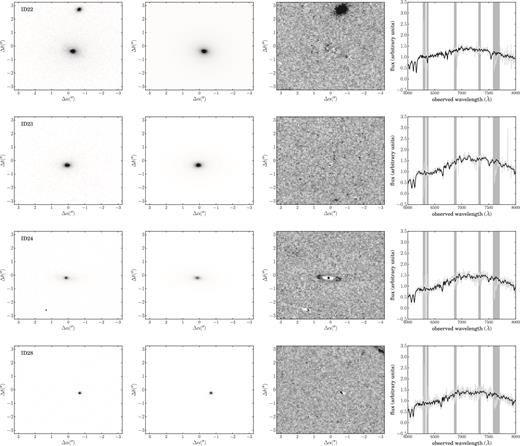
– continued

Open in new tab Download slide

Figure A1

– continued

Open in new tab Download slide

Table A1.

Open in new tab

Rest-frame absolute magnitudes for the MACSJ0717 galaxies in the Johnson U and B bands. We calculate these by fitting Bruzual & Charlot (2003) SPS models to the F625W and F475W magnitudes and colours, assuming a Salpeter IMF and solar metallicity as in Section 4; this allows us to infer a stellar mass and age. We then evaluate these models in the rest-frame U and V filters.

ID	U (mag)	B (mag)
2	−19.65 ± 0.08	−21.09 ± 0.08
4	−19.88 ± 0.09	−21.32 ± 0.09
5	−19.89 ± 0.05	−21.25 ± 0.05
7	−20.61 ± 0.06	−22.07 ± 0.06
8	−22.62 ± 0.08	−24.08 ± 0.08
9	−21.68 ± 0.09	−22.94 ± 0.09
10	−20.20 ± 0.06	−21.30 ± 0.06
11	−20.59 ± 0.06	−21.92 ± 0.06
12	−20.39 ± 0.08	−21.49 ± 0.08
13	−20.39 ± 0.08	−21.64 ± 0.08
14	−21.06 ± 0.10	−22.17 ± 0.10
16	−21.59 ± 0.06	−23.05 ± 0.06
22	−21.04 ± 0.09	−22.15 ± 0.09
23	−20.01 ± 0.06	−21.12 ± 0.06
24	−19.96 ± 0.09	−21.32 ± 0.09
28	−19.42 ± 0.18	−19.94 ± 0.18

ID	U (mag)	B (mag)
2	−19.65 ± 0.08	−21.09 ± 0.08
4	−19.88 ± 0.09	−21.32 ± 0.09
5	−19.89 ± 0.05	−21.25 ± 0.05
7	−20.61 ± 0.06	−22.07 ± 0.06
8	−22.62 ± 0.08	−24.08 ± 0.08
9	−21.68 ± 0.09	−22.94 ± 0.09
10	−20.20 ± 0.06	−21.30 ± 0.06
11	−20.59 ± 0.06	−21.92 ± 0.06
12	−20.39 ± 0.08	−21.49 ± 0.08
13	−20.39 ± 0.08	−21.64 ± 0.08
14	−21.06 ± 0.10	−22.17 ± 0.10
16	−21.59 ± 0.06	−23.05 ± 0.06
22	−21.04 ± 0.09	−22.15 ± 0.09
23	−20.01 ± 0.06	−21.12 ± 0.06
24	−19.96 ± 0.09	−21.32 ± 0.09
28	−19.42 ± 0.18	−19.94 ± 0.18

Table A1.

Open in new tab

Rest-frame absolute magnitudes for the MACSJ0717 galaxies in the Johnson U and B bands. We calculate these by fitting Bruzual & Charlot (2003) SPS models to the F625W and F475W magnitudes and colours, assuming a Salpeter IMF and solar metallicity as in Section 4; this allows us to infer a stellar mass and age. We then evaluate these models in the rest-frame U and V filters.

ID	U (mag)	B (mag)
2	−19.65 ± 0.08	−21.09 ± 0.08
4	−19.88 ± 0.09	−21.32 ± 0.09
5	−19.89 ± 0.05	−21.25 ± 0.05
7	−20.61 ± 0.06	−22.07 ± 0.06
8	−22.62 ± 0.08	−24.08 ± 0.08
9	−21.68 ± 0.09	−22.94 ± 0.09
10	−20.20 ± 0.06	−21.30 ± 0.06
11	−20.59 ± 0.06	−21.92 ± 0.06
12	−20.39 ± 0.08	−21.49 ± 0.08
13	−20.39 ± 0.08	−21.64 ± 0.08
14	−21.06 ± 0.10	−22.17 ± 0.10
16	−21.59 ± 0.06	−23.05 ± 0.06
22	−21.04 ± 0.09	−22.15 ± 0.09
23	−20.01 ± 0.06	−21.12 ± 0.06
24	−19.96 ± 0.09	−21.32 ± 0.09
28	−19.42 ± 0.18	−19.94 ± 0.18

ID	U (mag)	B (mag)
2	−19.65 ± 0.08	−21.09 ± 0.08
4	−19.88 ± 0.09	−21.32 ± 0.09
5	−19.89 ± 0.05	−21.25 ± 0.05
7	−20.61 ± 0.06	−22.07 ± 0.06
8	−22.62 ± 0.08	−24.08 ± 0.08
9	−21.68 ± 0.09	−22.94 ± 0.09
10	−20.20 ± 0.06	−21.30 ± 0.06
11	−20.59 ± 0.06	−21.92 ± 0.06
12	−20.39 ± 0.08	−21.49 ± 0.08
13	−20.39 ± 0.08	−21.64 ± 0.08
14	−21.06 ± 0.10	−22.17 ± 0.10
16	−21.59 ± 0.06	−23.05 ± 0.06
22	−21.04 ± 0.09	−22.15 ± 0.09
23	−20.01 ± 0.06	−21.12 ± 0.06
24	−19.96 ± 0.09	−21.32 ± 0.09
28	−19.42 ± 0.18	−19.94 ± 0.18

Download all slides

Month:	Total Views:
January 2017	6
February 2017	7
March 2017	18
April 2017	5
May 2017	7
June 2017	6
July 2017	8
August 2017	7
September 2017	3
October 2017	5
November 2017	1
December 2017	2
January 2018	5
February 2018	4
March 2018	4
May 2018	6
June 2018	3
July 2018	2
August 2018	4
October 2018	1
December 2018	2
January 2019	1
February 2019	2
March 2019	7
July 2019	1
September 2019	1
October 2019	5
December 2019	2
January 2020	3
March 2020	2
April 2020	3
May 2020	3
June 2020	5
July 2020	11
August 2020	2
September 2020	1
October 2020	2
December 2020	1
February 2021	3
March 2021	8
April 2021	2
June 2021	5
July 2021	2
September 2021	3
October 2021	3
November 2021	1
December 2021	1
January 2022	3
February 2022	1
March 2022	2
April 2022	34
May 2022	1
June 2022	2
July 2022	6
August 2022	12
September 2022	7
October 2022	1
November 2022	5
December 2022	2
January 2023	2
February 2023	2
March 2023	3
April 2023	2
May 2023	4
June 2023	3
July 2023	2
August 2023	4
September 2023	5
October 2023	4
November 2023	2
December 2023	12
January 2024	5
February 2024	18
March 2024	3
April 2024	6
May 2024	3
June 2024	14
July 2024	13
August 2024	8
September 2024	10
October 2024	10
November 2024	11
December 2024	3
January 2025	7
February 2025	10
March 2025	16
May 2025	2

Article Contents

The most massive galaxies in clusters are already fully grown at z ∼ 0.5

Abstract

1 INTRODUCTION

2 DATA SOURCES AND REDUCTION

2.1 Sources

2.2 Photometry

2.3 Spectroscopy

3 SCALING RELATIONS

3.1 The colour–magnitude relation

3.2 The Fundamental Plane

3.3 The M_dyn/L–M_dyn relation

3.4 The M_⋆–σ and M_⋆–R_e relations

4 STELLAR POPULATION MODELS

4.1 Luminosity evolution from the CMR

4.2 Luminosity evolution from the Fundamental Plane

4.3 Luminosity evolution from the M_dyn/L–M_dyn relation

4.4 Combining size and luminosity evolution

4.5 Combining scaling relations: inferring size and luminosity evolution

5 DISCUSSION

5.1 Old, passively evolving stellar populations

5.2 Accelerated growth?

5.3 Can we trust the stellar and dynamical masses?

5.4 Can we compare MACSJ0717 with Coma?

6 CONCLUSIONS

Acknowledgments

REFERENCES

APPENDIX A

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

The most massive galaxies in clusters are already fully grown at z ∼ 0.5 Free

Abstract

1 INTRODUCTION

2 DATA SOURCES AND REDUCTION

2.1 Sources

2.2 Photometry

2.3 Spectroscopy

3 SCALING RELATIONS

3.1 The colour–magnitude relation

3.2 The Fundamental Plane

3.3 The Mdyn/L–Mdyn relation

3.4 The M⋆–σ and M⋆–Re relations

4 STELLAR POPULATION MODELS

4.1 Luminosity evolution from the CMR

4.2 Luminosity evolution from the Fundamental Plane

4.3 Luminosity evolution from the Mdyn/L–Mdyn relation

4.4 Combining size and luminosity evolution

4.5 Combining scaling relations: inferring size and luminosity evolution

5 DISCUSSION

5.1 Old, passively evolving stellar populations

5.2 Accelerated growth?

5.3 Can we trust the stellar and dynamical masses?

5.4 Can we compare MACSJ0717 with Coma?

6 CONCLUSIONS

Acknowledgments

REFERENCES

APPENDIX A

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

The most massive galaxies in clusters are already fully grown at z ∼ 0.5

3.3 The M_dyn/L–M_dyn relation

3.4 The M_⋆–σ and M_⋆–R_e relations

4.3 Luminosity evolution from the M_dyn/L–M_dyn relation