-
PDF
- Split View
-
Views
-
Cite
Cite
K. Pavlovskii, N. Ivanova, K. Belczynski, K. X. Van, Stability of mass transfer from massive giants: double black hole binary formation and ultraluminous X-ray sources, Monthly Notices of the Royal Astronomical Society, Volume 465, Issue 2, February 2017, Pages 2092–2100, https://doi.org/10.1093/mnras/stw2786
Close - Share Icon Share
Abstract
Mass transfer in binaries with massive donors and compact companions, when the donors rapidly evolve after their main sequence, determines the formation rates of merging double stellar-mass black hole (BH) binaries formed outside clusters. This mass transfer was previously postulated to be unstable and was expected to lead to a common envelope event. The common envelope event then ends with either the merger of the two stars or formation of a binary that eventually may become a merging double BH. We revisit the stability of this mass transfer and find an unanticipated third outcome: for a large range of binary orbital separations, this mass transfer is stable. This newly found stability allows us to reconcile the empirical rate obtained by LIGO, 9-240 Gpc−3 yr−1, with the theoretical rate for double BH binary mergers predicted by population synthesis studies by excluding a channel that predicts a merger rate above 1000 Gpc−3 yr−1. Furthermore, the stability of the mass transfer leads to the formation of ultraluminous X-ray sources. The theoretically predicted formation rates of bright ultraluminous X-ray sources powered by a stellar-mass BH are high enough to explain the number of observed bright ultraluminous X-ray sources.
1 INTRODUCTION
Understanding the formation channels of close black hole–black hole (BH–BH) binaries is important, on one hand, for understanding the nature of the gravitational wave signals, and, inversely, for constraining binary evolution theory from the observed rate and flavour of double compact object mergers (Abbott et al. 2016). There are two theoretically dominant formation channels that can form a close double BH binary that can merge within a Hubble time in isolation, in addition to scenarios in which a close double BH binary can be formed via dynamical interactions in dense stellar systems (e.g. Rodriguez, Chatterjee & Rasio 2016). In the first isolated scenario, the formation depends crucially on the development of at least one common envelope phase during the evolution of a double BH progenitor binary (Belczynski et al. 2010). The stability of mass transfer (MT) from massive giants may alter the fate of a binary, and in particular it may prohibit double BH formation. In the second isolated formation scenario, a double BH can be formed from an initially tight massive binary with fast rotating stars. If both stars in that binary remain fully mixed, neither star will ever become a giant. The chemically homogeneous evolution of rapidly rotating stars was studied in de Mink et al. (2009), and this formation scenario was proposed in Mandel & de Mink (2016) and Marchant et al. (2016). In this work, we will reevaluate the plausibility of the first isolated formation channel.
In this scenario, the episode of the MT that most affects BH–BH formation rates takes place when the initially more massive companion has already become a compact object. The second companion, now more massive, starts to evolve from its main sequence, and overfills its Roche lobe. At the moment the MT starts, the mass ratio (of donor star to compact object) in this system with one compact object is large. By the conventional MT stability criterion for either convective or radiative donors, the MT is deemed to be dynamically unstable and must result in a common envelope event. Depending on the energy balance, the outcome of the common envelope event is either the merger of the two components or the ejection of the common envelope. In the latter case, the close binary thus produced may evolve into a double BH and merge within a Hubble time, thus becoming a source of detectable gravitational waves.
For BH–BH progenitor binaries, the decisive episode of MT that initiates a common envelope phase was found to predominantly take place when the massive donor is at its Hertzsprung gap (HG), which is before the star is deemed to appear as a well-developed convective giant (Belczynski et al. 2007, 2010). In this paper, we will refer to stars being on the HG in the same manner as Hurley, Pols & Tout (2000) and Dominik et al. (2012), even if those stars may already have the next stages of core and/or shell burning. A donor in this case does not necessarily have a well-developed density contrast between the core and the envelope. While the outcome of a common envelope event in the case of a well-developed giant donor is not yet well understood and is commonly parametrized with the energy budget formalism (for a review, see Ivanova et al. 2013), the applicability of the energy formalism for a donor with a poorly developed density contrast is even less justified. The uncertainty over whether this unstable MT results in a merger or creates a close binary was most recently investigated with the startrack population synthesis code (Dominik et al. 2012, 2013, 2015; Belczynski et al. 2016b). It was found that the merger rate for double BHs changes by more than an order of magnitude depending on whether, assuming that the energy formalism can be applied, a binary survives common envelope or if a merger takes place.
In this paper, we propose a third outcome: we find that the MT is stable for a large range of donor radii and mass ratios. We discuss here why the MT is stable and present the detailed MT calculations covering a limited parameter space. This allows us to derive the parametrized criterion for stability, suitable for the future studies using population synthesis codes. We show that this newly identified MT stability between a massive donor during HG or early core helium burning and a BH: (i) does not lead to the formation of close BH–BH binaries, but (ii) does lead to the appearance of the binary systems as ultraluminous X-ray sources (ULXs).
2 UNDERSTANDING THE STABILITY OF THE MT FROM HG DONORS
To treat the MT, a population synthesis approach needs parametrized stability thresholds. These thresholds can be based on whether the donor is convective or radiative, the mass ratio of the binary companions at the onset of the Roche lobe overflow (RLOF), the mode of MT (which is the assumption on how conservative the MT is) and sometimes on additional features of the donor and/or of the accretor.
It was suggested in past that the donor's response ζdon is low if not negative for stars with convective envelopes – indeed, the simplified polytropic stars were found to expand upon mass-loss (Hjellming & Webbink 1987). That led to a classical understanding that if the donor has a convective envelope at the moment of RLOF, the mass ratio is above the critical value, ∼0.78 and the MT is fully conservative, then the ensuing MT will be dynamically unstable (Hjellming & Webbink 1987; Soberman, Phinney & van den Heuvel 1997). Later, when the reaction of realistic stellar models was studied, it was shown that the convective envelopes do not necessarily expand upon the mass-loss, and the critical mass ratio for stable MT can even be larger than 1 (Woods & Ivanova 2011). Note that the mass ratio as is usually defined in MT stability studies – donor mass to accretor mass – differs from that adopted in some population synthesis studies or from the definition used by LIGO (the ratio of the more massive star's mass to that of the less massive star; thus the mass ratio is always ≥1). In radiative donors, ζdon is positive, and MT in systems with as large a mass ratio as 3.5 is known to be initially dynamically stable (Ivanova & Taam 2004; Ge et al. 2010). We clarify that the startrack population synthesis code uses mass–radius exponents to determine the stability of the MT (Belczynski et al. 2008).
The difference in the response between radiative and convective donors is bound to their entropy profiles. The flat entropy profile of the convective donors leads to insignificant shrinkage or expansion, while the increase with mass of the entropy profile of radiative donors provides the shrinkage as a result of mass removal. One of the plausible consequences is a delayed dynamical instability (see e.g. Ivanova & Taam 2004; Ge et al. 2010). A delayed dynamical instability may take place in systems with a radiative donor, in the cases when the MT is determined initially as stable. As the MT strips off the donor's mass, it may expose the mass layer that had a flat entropy profile before the start of MT. Then the donor response suddenly changes, leading to dynamically unstable MT.
Recently, a new MT framework was developed (Pavlovskii & Ivanova 2015). This approach adopts that the stellar material, which currently has expanded outside the Roche lobe of its donor, cannot be immediately relocated into the accretor's Roche lobe, as the MT rate via the L1 neighbourhood is finite. The framework can follow the MT beyond the L1 overflow by calculating the current RLOF MT rate until L2/L3 overflow occurs, if the latter does happen. A model that has overfilled its outer Lagrangian point can still be simulated, but the MT through this point is not taken into account. Usually by the time this happens, the MT itself is already dynamically unstable and the Euler term is comparable to the centrifugal term, i.e. the Roche lobe approximation itself breaks down. As an immediate application, it was found that for donors with deep convective envelopes, the critical mass ratio is about twice what was previously thought, i.e. above 1.6. This allows for more massive donors to have MT without initiating a common envelope event. If a giant donor has a shallow (in mass) convective envelope, it may respond almost like a radiative donor, i.e. the MT could be stable for mass ratios up to 3.5 (Pavlovskii & Ivanova 2015). It follows that treating arbitrary, including very large, L1 overflow in a self-consistent way, provides an overall increase of stability of the MT for convective donors. It can be expected that allowing for L1 overflow for radiative donors can provide the same effect on the stability of the MT, although no specific study for radiative donors has been made before this paper.
This drastic change of the critical mass ratio that separates stable and unstable binary systems is especially important for the HG donors that play a role in BH–BH binary formation. We note however that a massive donor's structure can be in general quite complex and include both formally radiative layers with only slightly increasing specific entropy in mass, and formally convective layers in which the entropy decreases quite fast. The response of the donor is not solely defined by whether a convective or radiative layer is being removed during MT, but is a complex function of the donor's structure as a whole, which can be only determined with detailed simulations. A donor with a shallow or absent convective envelope, may still contain a shell with a relatively flat entropy profile. When, during the MT, the donor's outer layers are steadily eaten to expose the shell with a sufficiently flat entropy profile, ζdon decreases dramatically, which might lead in some cases to the delayed dynamical instability, if the mass ratio at this time has not been decreased enough.
Therefore, the simplified prescription that was supplied in Pavlovskii & Ivanova (2015) for convective donors less massive than 30 M⊙ is not useful for the case of very massive donors at their HG. In this paper, we will perform detailed simulations for such massive donors using the MT framework from Pavlovskii & Ivanova (2015). The aim is to find the range of donor radii at the moment of RLOF, such that the MT, for a given mass ratio, will not be affected by either of the following instabilities.
Expansion instability appears in donors which at the moment of RLOF are experiencing a period of fast thermal-time-scale expansion. In some donors, this almost immediately (within a few thousand years) leads to extremely fast MT and dynamical instability. We define the radius that a donor should reach before RLOF to avoid this instability as RS: donors which are larger than RS at the start of the MT, will experience stable MT.
Convection instability appears in donors with a sufficiently developed convective envelope. We define the minimum critical radius, which a donor should reach before RLOF to experience this instability, as RU: donors which are larger than RU at the start of the MT, will experience unstable MT.
3 DETAILED MT SIMULATIONS
To calculate the detailed evolution of the giants and their behaviour during the RLOF, we use the MT framework described in Pavlovskii & Ivanova (2015). This MT code is a custom extension to the MESA/binary module that uses the MESA/star stellar code for the evolution of single stars (Paxton et al. 2011, 2013, 2015). Specifically, we use MESA SDK revision 245, and our changes were implemented for MESA version 7736.1
For donors, we consider stars of several initial masses – 20, 30, 40, 60 and 80 M⊙ – with solar metallicity taken as Z = 0.02 and with the metallicity 0.1 Z⊙. The stars are evolved employing the Vink wind prescription (Vink, de Koter & Lamers 2001). Luminous blue variable winds and eruptions are not taken into account. It is known that high-mass stars are very sensitive to input parameters. The evolutionary tracks produced by MESA can differ vastly from other stellar codes unless fine-tuned for their input parameters, especially overshooting and wind loss (Choi et al. 2016). For our stability criteria, it is the state of the donor at the start of the MT that is important, not the adopted prescription of the overshooting or wind loss (donors of different masses can reach that point depending on the adopted prescriptions). Therefore, rather than simply providing the donor's and BH masses and the orbital period at the start of the MT, we provide detailed descriptions of the donor stars’ states (see Table 1).
We place each star in a binary containing a BH, varying the BH mass from 7 M⊙ to 14 M⊙. We considered the range of the initial binary separation at the start of MT from a few tenths of R⊙ (this corresponds to the RLOF right after the end of the donor's main sequence) to a few thousands of R⊙ (when the donor starts to develop a deep convective envelope). We clarify that for this exercise, the orbital separation is a secondary variable, and we search for the outcomes in the parameter space of the donor's radius at the start of the MT. The initial scan is done with a dozen choices of initial radii within the range described above. Then, the radii at which the MT can become unstable are clarified by running a more refined mesh between the points where the stability/instability border was found initially. In most of the cases, the final values were fine-tuned using models where the donor's radius differed by only 1 per cent of the donor's radius.
After the start of the MT, and during the continuing MT, we examine whether or not the MT is dynamically unstable. For this, we employ the modified criterion outlined in Pavlovskii & Ivanova (2015), namely, |${\dot{M}}P/M > 2{\rm per cent}$|, where P is the orbital period and M is the donor's mass. This way, we can detect either immediate or delayed dynamical instability, whichever takes place in a given system. As the initial MT rate in the systems which are close to the stability/instability region is expected to be very high, we test the stability border in the non-conservative (above the Eddington accretion limit) MT regime with isotropic re-emission for angular momentum loss, where the lost material carries away the specific angular momentum of the accretor.
The third type of instability – delayed dynamical instability – might take place in some donors that overfill their Roche lobe when their radius is inside the stability region – between RS and RU. The method we use detects whether the MT becomes unstable, and, if it is, we check whether the reason could be related to delayed dynamical instability. In all simulations that were done for this study, the delayed dynamical instability was not detected.
The radii that border the stability region, RS and RU, are thus subject to the same uncertainty as the evolution of high-mass stars in general. The plausible reasons include, but are not limited to, the adopted prescription for mixing; the inapplicability of the (simplified) chosen atmospheric conditions; winds, instabilities and eruptions; treatment of convection in the outer layers of massive stars; rotation of the envelope; core overshooting and more (see discussion of uncertainties and how they can affect population studies in section 2 of Belczynski et al. 2014, and some details on how MESA outcomes in particular can vary depending on the input can be found in Choi et al. 2016).
The complete results for solar and sub-solar metallicities are presented in Table 1. The values for the stability borders are provided as two evolutionary points, where one point is for a model that is certainly stable, and another point for the model that is certainly unstable. The actual stability border should be located between these two points. Frequently, the behaviour between the two points cannot be classified in terms of certain stability or instability. The mapping provided in Table 1 between the donor's radius, the mass at the moment of RLOF and the stability of the ensuing MT may be directly used by the population synthesis codes. Below we provide analyses of the results.
| Md, zams . | MBH . | RS . | Md, S . | MHe, S . | |${\rm H_{\rm sh,S}}$| . | |${\rm He_{\rm c,S}}$| . | RU . | Md, U . | MHe, U . | Mconv . | Teff, U . | Hsh, U . | Heco, U . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Z = 0.1 Z⊙ | |||||||||||||
| 20 | 7 | stable | 686–721 | 19.6 | 7.0 | 1.8-3.8 | 4369–4251 | ✓ | ✓ | ||||
| 30 | 7 | 44–51 | 29.4 | 7.7–7.6 | ✓ | – | 1004–1111 | 29.1–29.2 | 8.1–8.2 | 1.6*–3.9 | 4483–4268 | ✓ | ✓ |
| 40 | 7 | 309–354 | 38.6 | 11.5 | ✓ | ✓ | 1260–1327 | 38.6–38.7 | 11.4 | 1.7*–2.7 | 5244–5709 | ✓ | ✓ |
| 60 | 7 | unstable | |||||||||||
| 60 | 10 | 346–364 | 56.8 | 20.4–20.5 | ✓ | – | 1705–1790 | 56.8 | 19.8 | 6.0*–6.9* | 4473–4387 | ✓ | ✓ |
| 60 | 12 | 140–156 | 56.8 | 21.1–20.9 | ✓ | – | 1768–1879 | 56.8 | 19.8–19.7 | 6.8*–8.2* | 4409–4323 | ✓ | ✓ |
| 80 | 7 | unstable | |||||||||||
| 80 | 10 | stable | 2217–2241 | 74.5 | 32.6 | 18.2*–18.2* | 4285–4276 | ✓ | ✓ | ||||
| 80 | 14 | 134–155 | 74.6 | 34.6–34.3 | ✓ | – | 2122–2179 | 74.5 | 32.7–32.6 | 18.2*–18.2* | 4345–4304 | ✓ | ✓ |
| Z = Z⊙ | |||||||||||||
| 20 | 7 | stable | 729–743 | 19.6 | 5.7 | 2.3-2.7 | 3936–3886 | ✓ | ✓ | ||||
| 30 | 7 | stable | 1144–1174 | 26.6 | 9.8 | 5.0*–5.5* | 3835–3789 | ✓ | – | ||||
| 40 | 7 | stable | 1381–1434 | 32.5 | 14.7 | 4.4*–5.2* | 3872–3804 | ✓ | – | ||||
| 60 | 10 | stable | 2035–2172 | 41.0 | 23.8 | 3.7*–5.0* | 3868–3776 | ✓ | – | ||||
| 60 | 12 | stable | 2009–2057 | 41.0 | 23.8 | 3.5*–3.9* | 3886–3851 | ✓ | – | ||||
| 80 | 10 | stable | stable | ||||||||||
| 80 | 14 | stable | stable |
| Md, zams . | MBH . | RS . | Md, S . | MHe, S . | |${\rm H_{\rm sh,S}}$| . | |${\rm He_{\rm c,S}}$| . | RU . | Md, U . | MHe, U . | Mconv . | Teff, U . | Hsh, U . | Heco, U . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Z = 0.1 Z⊙ | |||||||||||||
| 20 | 7 | stable | 686–721 | 19.6 | 7.0 | 1.8-3.8 | 4369–4251 | ✓ | ✓ | ||||
| 30 | 7 | 44–51 | 29.4 | 7.7–7.6 | ✓ | – | 1004–1111 | 29.1–29.2 | 8.1–8.2 | 1.6*–3.9 | 4483–4268 | ✓ | ✓ |
| 40 | 7 | 309–354 | 38.6 | 11.5 | ✓ | ✓ | 1260–1327 | 38.6–38.7 | 11.4 | 1.7*–2.7 | 5244–5709 | ✓ | ✓ |
| 60 | 7 | unstable | |||||||||||
| 60 | 10 | 346–364 | 56.8 | 20.4–20.5 | ✓ | – | 1705–1790 | 56.8 | 19.8 | 6.0*–6.9* | 4473–4387 | ✓ | ✓ |
| 60 | 12 | 140–156 | 56.8 | 21.1–20.9 | ✓ | – | 1768–1879 | 56.8 | 19.8–19.7 | 6.8*–8.2* | 4409–4323 | ✓ | ✓ |
| 80 | 7 | unstable | |||||||||||
| 80 | 10 | stable | 2217–2241 | 74.5 | 32.6 | 18.2*–18.2* | 4285–4276 | ✓ | ✓ | ||||
| 80 | 14 | 134–155 | 74.6 | 34.6–34.3 | ✓ | – | 2122–2179 | 74.5 | 32.7–32.6 | 18.2*–18.2* | 4345–4304 | ✓ | ✓ |
| Z = Z⊙ | |||||||||||||
| 20 | 7 | stable | 729–743 | 19.6 | 5.7 | 2.3-2.7 | 3936–3886 | ✓ | ✓ | ||||
| 30 | 7 | stable | 1144–1174 | 26.6 | 9.8 | 5.0*–5.5* | 3835–3789 | ✓ | – | ||||
| 40 | 7 | stable | 1381–1434 | 32.5 | 14.7 | 4.4*–5.2* | 3872–3804 | ✓ | – | ||||
| 60 | 10 | stable | 2035–2172 | 41.0 | 23.8 | 3.7*–5.0* | 3868–3776 | ✓ | – | ||||
| 60 | 12 | stable | 2009–2057 | 41.0 | 23.8 | 3.5*–3.9* | 3886–3851 | ✓ | – | ||||
| 80 | 10 | stable | stable | ||||||||||
| 80 | 14 | stable | stable |
Notes.RS is the stability border during the post-main-sequence expansion. The lower provided values indicate the models with the largest radius which have unstable MT, and the upper provided values indicated the models with the smallest radius which have stable MT. RU is the upper stability border during the outer convective envelope development. The lower provided values indicated the models with the largest radius which have stable MT, and the upper value indicated the model with the smallest radius which has unstable MT. Md, S, Md, U are the donor masses at the moment they reached the corresponding stability border. MHe, S and MHe, U are the He core masses at the same moments, defined as the mass coordinate of the donor where hydrogen is below 0.01 × (1 − Z). Currently present nuclear burning is indicated with check-marks for Hydrogen shell burning (|$\rm H_{sh,S},\rm H_{sh,U}$|), He core burning (|$\rm He_{co,S},\rm He_{co,U}$|), at RS or RU correspondingly. ‘Unstable’ means that the binary is always unstable. ‘Stable’ in the column for RS means that a binary will be always stable with respect to the MT after the donor left its main sequence and before it develops convective envelope. If ‘stable’ is also indicated in the column for RU, the MT is always stable. Mconv is the mass of the outer convective layer. Masses of convective envelopes with asterisks refer to those convective envelopes which have radiative layers within them. All masses are in M⊙ and radii are in R⊙. Teff, U is the effective temperature at the lower and upper values of RU, in K.
| Md, zams . | MBH . | RS . | Md, S . | MHe, S . | |${\rm H_{\rm sh,S}}$| . | |${\rm He_{\rm c,S}}$| . | RU . | Md, U . | MHe, U . | Mconv . | Teff, U . | Hsh, U . | Heco, U . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Z = 0.1 Z⊙ | |||||||||||||
| 20 | 7 | stable | 686–721 | 19.6 | 7.0 | 1.8-3.8 | 4369–4251 | ✓ | ✓ | ||||
| 30 | 7 | 44–51 | 29.4 | 7.7–7.6 | ✓ | – | 1004–1111 | 29.1–29.2 | 8.1–8.2 | 1.6*–3.9 | 4483–4268 | ✓ | ✓ |
| 40 | 7 | 309–354 | 38.6 | 11.5 | ✓ | ✓ | 1260–1327 | 38.6–38.7 | 11.4 | 1.7*–2.7 | 5244–5709 | ✓ | ✓ |
| 60 | 7 | unstable | |||||||||||
| 60 | 10 | 346–364 | 56.8 | 20.4–20.5 | ✓ | – | 1705–1790 | 56.8 | 19.8 | 6.0*–6.9* | 4473–4387 | ✓ | ✓ |
| 60 | 12 | 140–156 | 56.8 | 21.1–20.9 | ✓ | – | 1768–1879 | 56.8 | 19.8–19.7 | 6.8*–8.2* | 4409–4323 | ✓ | ✓ |
| 80 | 7 | unstable | |||||||||||
| 80 | 10 | stable | 2217–2241 | 74.5 | 32.6 | 18.2*–18.2* | 4285–4276 | ✓ | ✓ | ||||
| 80 | 14 | 134–155 | 74.6 | 34.6–34.3 | ✓ | – | 2122–2179 | 74.5 | 32.7–32.6 | 18.2*–18.2* | 4345–4304 | ✓ | ✓ |
| Z = Z⊙ | |||||||||||||
| 20 | 7 | stable | 729–743 | 19.6 | 5.7 | 2.3-2.7 | 3936–3886 | ✓ | ✓ | ||||
| 30 | 7 | stable | 1144–1174 | 26.6 | 9.8 | 5.0*–5.5* | 3835–3789 | ✓ | – | ||||
| 40 | 7 | stable | 1381–1434 | 32.5 | 14.7 | 4.4*–5.2* | 3872–3804 | ✓ | – | ||||
| 60 | 10 | stable | 2035–2172 | 41.0 | 23.8 | 3.7*–5.0* | 3868–3776 | ✓ | – | ||||
| 60 | 12 | stable | 2009–2057 | 41.0 | 23.8 | 3.5*–3.9* | 3886–3851 | ✓ | – | ||||
| 80 | 10 | stable | stable | ||||||||||
| 80 | 14 | stable | stable |
| Md, zams . | MBH . | RS . | Md, S . | MHe, S . | |${\rm H_{\rm sh,S}}$| . | |${\rm He_{\rm c,S}}$| . | RU . | Md, U . | MHe, U . | Mconv . | Teff, U . | Hsh, U . | Heco, U . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Z = 0.1 Z⊙ | |||||||||||||
| 20 | 7 | stable | 686–721 | 19.6 | 7.0 | 1.8-3.8 | 4369–4251 | ✓ | ✓ | ||||
| 30 | 7 | 44–51 | 29.4 | 7.7–7.6 | ✓ | – | 1004–1111 | 29.1–29.2 | 8.1–8.2 | 1.6*–3.9 | 4483–4268 | ✓ | ✓ |
| 40 | 7 | 309–354 | 38.6 | 11.5 | ✓ | ✓ | 1260–1327 | 38.6–38.7 | 11.4 | 1.7*–2.7 | 5244–5709 | ✓ | ✓ |
| 60 | 7 | unstable | |||||||||||
| 60 | 10 | 346–364 | 56.8 | 20.4–20.5 | ✓ | – | 1705–1790 | 56.8 | 19.8 | 6.0*–6.9* | 4473–4387 | ✓ | ✓ |
| 60 | 12 | 140–156 | 56.8 | 21.1–20.9 | ✓ | – | 1768–1879 | 56.8 | 19.8–19.7 | 6.8*–8.2* | 4409–4323 | ✓ | ✓ |
| 80 | 7 | unstable | |||||||||||
| 80 | 10 | stable | 2217–2241 | 74.5 | 32.6 | 18.2*–18.2* | 4285–4276 | ✓ | ✓ | ||||
| 80 | 14 | 134–155 | 74.6 | 34.6–34.3 | ✓ | – | 2122–2179 | 74.5 | 32.7–32.6 | 18.2*–18.2* | 4345–4304 | ✓ | ✓ |
| Z = Z⊙ | |||||||||||||
| 20 | 7 | stable | 729–743 | 19.6 | 5.7 | 2.3-2.7 | 3936–3886 | ✓ | ✓ | ||||
| 30 | 7 | stable | 1144–1174 | 26.6 | 9.8 | 5.0*–5.5* | 3835–3789 | ✓ | – | ||||
| 40 | 7 | stable | 1381–1434 | 32.5 | 14.7 | 4.4*–5.2* | 3872–3804 | ✓ | – | ||||
| 60 | 10 | stable | 2035–2172 | 41.0 | 23.8 | 3.7*–5.0* | 3868–3776 | ✓ | – | ||||
| 60 | 12 | stable | 2009–2057 | 41.0 | 23.8 | 3.5*–3.9* | 3886–3851 | ✓ | – | ||||
| 80 | 10 | stable | stable | ||||||||||
| 80 | 14 | stable | stable |
Notes.RS is the stability border during the post-main-sequence expansion. The lower provided values indicate the models with the largest radius which have unstable MT, and the upper provided values indicated the models with the smallest radius which have stable MT. RU is the upper stability border during the outer convective envelope development. The lower provided values indicated the models with the largest radius which have stable MT, and the upper value indicated the model with the smallest radius which has unstable MT. Md, S, Md, U are the donor masses at the moment they reached the corresponding stability border. MHe, S and MHe, U are the He core masses at the same moments, defined as the mass coordinate of the donor where hydrogen is below 0.01 × (1 − Z). Currently present nuclear burning is indicated with check-marks for Hydrogen shell burning (|$\rm H_{sh,S},\rm H_{sh,U}$|), He core burning (|$\rm He_{co,S},\rm He_{co,U}$|), at RS or RU correspondingly. ‘Unstable’ means that the binary is always unstable. ‘Stable’ in the column for RS means that a binary will be always stable with respect to the MT after the donor left its main sequence and before it develops convective envelope. If ‘stable’ is also indicated in the column for RU, the MT is always stable. Mconv is the mass of the outer convective layer. Masses of convective envelopes with asterisks refer to those convective envelopes which have radiative layers within them. All masses are in M⊙ and radii are in R⊙. Teff, U is the effective temperature at the lower and upper values of RU, in K.
3.1 Expansion instability
The first critical point, RS, happens during the fast thermal-time-scale expansion of the star during the HG. Most stars that reach RLOF between the end of the main sequence and this critical point experience unstable MT almost immediately, in a few thousand years after the start of the RLOF. However, MT in some binaries is always stable after the end of the donor's main sequence.
For example, for a binary with a BH of 7 M⊙ and a donor with an initial mass 30 M⊙ and Z = 0.1 Z⊙, RS is located between the radii of 44 and 51 R⊙ at the moment of RLOF. 44 R⊙ corresponds to immediately unstable MT, and 51 R⊙ to stable MT (see Table 1). At the same time, a binary with a donor with the initial mass of 20 M⊙ of any metallicity always shows stable MT after the end of the donor's main sequence. Also, all solar metallicity donors produce stable MT if they reach RLOF after the end of the donor's main sequence.
The stability increases as the initial mass ratio decreases. This is a very well-known effect (see e.g. Soberman et al. 1997), which is caused by the increase of ζRL. We have analysed whether the rate of radial expansion after the main sequence can in a direct and simple way explain the instability. However, we found that the higher rate of expansion is not always associated with this type of instability, and it is likely a hidden function of the envelope density and entropy gradient at the start of the MT.
3.2 Convective instability
The second critical point, RU, corresponds to the moment when the donor expands large enough on the giant branch to develop a deep outer convective envelope. The emergence of an initial convective layer in the donor's outer layers does not initiate the convective instability.
For example, in a binary with a 7 MBH and a 30 M⊙ red giant of Z = 0.1 Z⊙, RU is located between 1004 R⊙ and 1112 R⊙ at RLOF (see Table 1). If the radius of the donor at the start of the MT is less than 1004 R⊙, the MT is stable even though the donor's outer convective zone is already 1.6 M⊙ in mass. If the 30 M⊙ donor's radius is ≥ RU = 1112 R⊙ at RLOF, the MT is unstable. The L1 MT rate reaches about 0.27 M⊙ yr−1; at this fast MT the condition |${\dot{M}}P/M < 2{\rm per cent}$| is not satisfied anymore, and we flag it as dynamical-time-scale MT. The mass of the donor at this moment is reduced to 26.4 M⊙. The dynamical MT in this case leads to a common envelope which will start with a less-massive envelope, and with different initial orbital parameters at the MT onset, than if the whole envelope were present.
We observe that this type of instability requires a sufficiently developed convective envelope to be present in the donor. For example, the binary with a 10 MBH and a 80 M⊙ red giant of Z = 0.1 Z⊙ is stable until the convective envelope has increased to 18.2 M⊙ despite having a mass ratio of 7.5 (see Table 1). One can notice from the data in Table 1 that the boundary of this type of instability quite often, albeit not always, is located when the convective envelope is still formed of convective layers which did not yet merge (see Fig. 1 for a visual depiction, and Table 1 where the models with a layered convective envelope are indicated with asterisks).
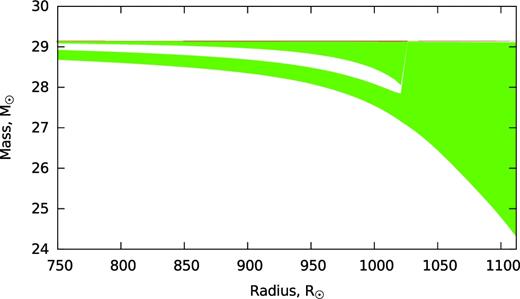
Development of the convective envelope (shaded area), which leads to the convection instability at RU in a 30 M⊙ giant, Z = 0.1 Z⊙. This star will have stable MT with a 7 M⊙ BH companion if it is smaller than 1004 R⊙ at the moment of RLOF. The MT with a 7 M⊙ BH companion is immediately unstable if the donor is larger than 1111 R⊙ at the moment RLOF.
Solar-metallicity donors have stronger winds than donors with Z = 0.1 Z⊙. These strong winds further increase the stability of the MT for the 80 M⊙ donors: solar metallicity 80 M⊙ donors never reach radii higher than 100 R⊙ (or 300 R⊙ if their models are calculated with MLT++, as described in Paxton et al. 2013) and never develop a convective envelope. For that reason, the second type of instability is not applicable to them, and binaries with 80 M⊙ donors will have stable MT even with a 10 M⊙ BH.
3.3 Behaviour in the stability region
Stars that experience RLOF between the first and the second critical point proceed with dynamically stable MT. We note that the donors between two critical points can experience L2/L3 overflow, which can be detected by our framework, but is not treated (we do not calculate the mass-loss through the L2/L3 nozzle). This overflow is not likely to lead to dynamically unstable MT because the outer layers of these stars are quite rarefied and the corresponding mass-loss rates are too low to cause any dynamical instability. To warrant that the systems are stable, we test binaries applying fully conservative MT evolution – in real binaries, the fraction of the transferred material that is accreted can be anywhere between 0 and 1, but if the MT is stable in the fully conservative case, it will be also be stable in the non-conservative case, assuming isotropic re-emission for angular momentum loss. We also consider the case of non-conservative MT.
We checked the stability of the MT by considering donors with five initial masses of 20, 30, 40, 60 and 80 M⊙, and metallicity 0.1 Z⊙. For each mass, the donors were taken to be distributed uniformly in the logarithm of radius at RLOF between RS (if applicable, otherwise, the radius at the end of the main sequence) and RU. We use 10 M⊙ BHs as accretors for the 60 and 80 M⊙ donors, and 7 M⊙ BHs for the 20 and 30 M⊙ donors. All sequences were found to be stable. We did not notice a significant difference between the conservative and non-conservative MT sequences in terms of the MT duration or the MT rate, while the final orbital separations in the case of the non-conservative MT are smaller than in the conservative case.
For example, let us consider a binary with a 7 MBH and a 30 M⊙ donor of Z = 0.1 Z⊙, with a radius of 750 R⊙ at the moment of RLOF. At the start of RLOF, the outer envelope of the star is radiative, and the star has a convective core with a mass ≈ 5 M⊙ and an inner convective layer stretching in mass coordinate from ≈8 to 14 M⊙. The rest of the star is radiative. A dynamical time-scale MT in this donor can be estimated as 1 M⊙ yr−1, while the maximum attained MT rate does not exceed even 1 per cent of that. The relative RLOF (by what fraction the donor exceeds its Roche lobe radius, in units of the Roche lobe radius) reaches 37 per cent, but the mass of the star outside of the Roche lobe is less than 0.5 per cent of the donor mass. The binary experiences a brief period of L2/L3 overflow during which the MT rate reaches 0.005 M⊙ yr−1. In total, 4.1 M⊙ was transferred via the L1 point during the L2/L3 overflow that lasted ∼1000 yr. Note, that the stream of matter via the L2/L3 nozzles (lost from the system) is negligible in mass when compared to the stream flowing via L1. Similar equatorial outflows have been observed in SS 433, an X-ray binary that has a very high MT rate (Blundell et al. 2001).
After the giant's ζdon becomes larger than ζRL, and the degree of the donor's RLOF becomes small, the MT rate falls to ≈10−5 M⊙ yr−1. In this state, the system remains for about 2 × 105 yr. By the time the donor detaches, ≈11.6 M⊙ has been removed, leaving a core of ∼10 M⊙ and an envelope of 7.5 M⊙. The envelope is predominantly radiative with a convective layer located between 10.5 M⊙ to 12.3 M⊙. The mass ratio of the donor to the BH, by the time the MT stops, is ∼2.5. The binary has shrunk, and the donor radius at the end is only about 107 compared to 750 R⊙ at the moment of RLOF. We note that a strong shrinkage is a common property for the binaries we consider. However, for most systems, their final separation does not enable future formation of a double BH that can merge within a Hubble time.
For most cases, the L2/L3 overflow is very short (significantly less than a thousand years) and its duration grows as the system approaches RU. We clarify here that under L2/L3 outflow we only consider the mass-loss from the donor, not the mass-loss from the disc around the accretor. L2/L3 overflow is only detected in our models when the donor is more massive than the accretor, and hence for clarity we will refer to it as L3 overflow.
We find that the most massive donors, 60 M⊙ and 80 M⊙, either do not develop L3 overflow at all, or we find that L3 overflow never occurs for more than a few tens of years, even for very wide systems. Presumably, more massive systems are removed from this regime, as they start dynamically unstable MT rather than suffer prolonged L3 overflow, and are not identified as stable systems.
For example, let us consider a system with an initial donor of 40 M⊙ with a BH accretor of 7 M⊙. We take the system where the donor radius was 1106 R⊙ at the first RLOF, hence close to RU. This system had one of the longest durations of L3 overflow among the studied systems, 1550 yr in total. L3 overflow started when the radius of the donor decreased to 580 R⊙. When the donor expands to reach the L3 point, the deviation of the Roche potential at its surface from the spherically symmetric potential (as in the evolutionary code) reaches about 25 per cent. Here, the potential with which a 1D star is evolved in |$\tt MESA$| is less negative. Therefore, the 1D approach allows a star to expand more than the same star could expand when placed in a binary potential. We therefore cannot be sure that this donor indeed reaches the L3 point at the time when our code detects this.
Let us estimate the mass-loss via L3 assuming that the donor has expanded to and beyond L3. A simplification we make is that the cross-section of the nozzle in the L3 neighbourhood is not larger than the cross-section of the nozzle in the L1 neighbourhood. Adopting the same approach as for obtaining the L1 MT rate, the mass-loss rate via L3 should depend on the cross-section through which the matter flows, the sonic velocity at this cross-section and the density of the material at this cross-section. We find that if the L1 and L3 cross-sections have the same area, then the L1 MT rate exceeds the L3 mass-loss rate by at least a factor of 30 during the L3 overflow episode.
For the particular binary system described above, if L3 outflow creates a circumbinary disc, the binary will shrink a few percent faster. This small factor does not provide a compelling argument that the system will not survive L3 overflow.
We conclude that if the binary systems start the MT when their donor's radii are between RS and RU, they do not experience unstable MT. It means that they are unlikely to experience the common envelope phase, unless the donor reattaches again to the Roche lobe in the future and loses enough mass to reach the delayed dynamical instability (a theoretical possibility that we did not encounter in our models, but cannot exclude completely). This rules out the possibility that such binaries can produce double BH mergers. The range of the radii, and therefore of the initial orbital periods at which that MT can be initiated, covers almost the entire parameter space between the end of the main sequence and a ‘convective’ giant stage.
4 ULX SOURCES
There are two dominant ways to explain ULXs. One is to assume that the accretor is an intermediate mass BH (100 M⊙ or more) that accretes at (or below) its Eddington limit (Colbert & Mushotzky 1999). Alternatively, it can be a binary with an neutron star or a stellar mass BH where the MT rate exceeds the Eddington limit by a factor of up to a few dozens, and the radiation is beamed (Rappaport, Podsiadlowski & Pfahl 2005; King 2009). If the MT rate is very high, such as produced by thermal-time-scale MT, then relativistic beaming is not required to explain the observed ULX luminosities. Strong relativistic beaming is also not expected for BH accretors when the MT rates exceed strongly their Eddington limit, unlike the case with neutron stars accretors (King 2008; King & Lasota 2016). The binary systems considered in this paper can produce the last mentioned type of ULXs, with a stellar mass BH accretor and very high MT rates, where the novelty is that the mass ratio is very large.
There are at least two important observational examples of a ULX with an accretor having a mass of only a few solar masses, where the observed luminosity exceeds the accretor's Eddington limit, and where the mass ratio between the donor and the accretor is large (note that our study should not be used to explain all ULXs observed to date). The first example is SS 433, which is a well-known X-ray binary in the Milky Way. SS 433 most likely has a stellar mass BH accretor (Fabrika 2004; Cherepashchuk et al. 2013). This system contains a massive donor of 12.3 ± 3.3 M⊙ and a BH of 4.3 ± 0.8 M⊙ (Hillwig & Gies 2008). SS 433 is a non-conservative system, and the rate of mass outflow exceeds the Eddington accretion limit by a factor of several hundred to a few thousands (e.g. King, Taam & Begelman 2000; Okuda, Lipunova & Molteni 2009). This system is our local ‘misaligned’ ULX, and the beamed emission is coming out of a cone with a half opening angle of about 20° (Begelman, King & Pringle 2006; Khabibullin & Sazonov 2016).
The second example is ULX M82 X-2, discovered by Ptak & Griffiths (1999) in the nearby galaxy M82. The observed luminosity of ULX M82 X-2 is 1.8 × 1040 erg s−1. It has been shown recently, via the discovery of X-ray pulsations, that the accretor in M82 X-2 is a neutron star (Bachetti et al. 2014); thus, the luminosity in this system exceeds the Eddington limit for a 1.4 M⊙ neutron star by a factor of 100.
Interestingly, the population studies of ULXs, until recently, mostly involved the consideration of an intermediate-mass BH with a stellar mass donor (e.g. Hopman, Portegies Zwart & Alexander 2004; Kalogera et al. 2004; Portegies Zwart, Dewi & Maccarone 2004; Madhusudhan et al. 2006, 2008), as the MT in systems with very massive donors and stellar mass BH accretors was thought to be dynamically unstable. However, observations showed that ULX M82 X-2 consists of a massive giant donor and a neutron star accretor orbiting each other with a period of 2.5 d and a minimum companion mass of 5.2 M⊙, with the mass ratio exceeding 3.7 (Bachetti et al. 2014).
Fragos et al. (2015) have shown that it is possible to obtain such systems assuming non-conservative MT from a hydrogen-rich giant donor that fills its Roche lobe to a neutron star accretor. They used an implicit MT scheme that is built such that the donor is always kept within its Roche lobe. Our study is somewhat similar albeit we have less technical constraints on which MT systems can be modelled through the MT.
Our MT framework can handle MT rates which are up to a few per cent of the dynamical time-scale MT rate – up to a dozen of M⊙ yr−1, while Fragos et al. (2015) had to assume that any system where the MT rate exceeded |$10^{-2}\rm\, {M_{{\odot }}}\,yr^{-1}$| is bound to start a common envelope.
Our MT framework allows for high degrees of RLOF, all the way to L2/L3 (outer Lagrangian point of the donor) overflow.
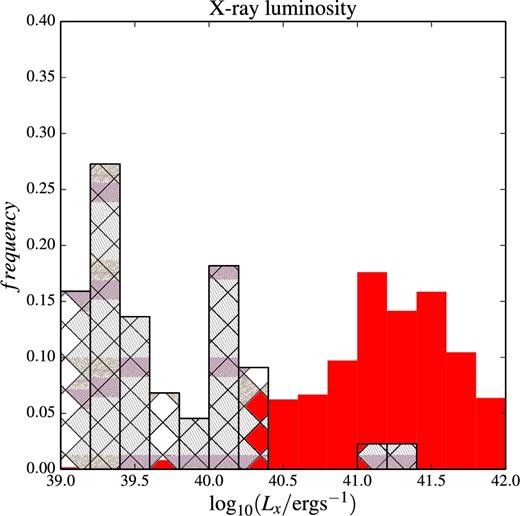
The time-averaged distribution of ULXs formed in our simulations (through conservative MT) is shown with the red histogram. The distribution of X-ray luminosities of 33 ULXs in nearby ( ≲ 5 Mpc) galaxies, as taken from Gladstone et al. (2013), is shown with the hatched area. LX is X-ray luminosity. For modelled ULXs, LX is calculated using MT rate via L1, |$\dot{M}_{L1}$| and equation (7) with f = 1. It indicates therefore the upper range of possible LX.
We find that the average time our models spend in the ULX state is ∼105 yr. We regularly obtain MT rates which exceed the Eddington luminosity by a factor of ∼ 1000 (see e.g. the history of MT shown in Fig. 3 ). The time-averaged distribution of X-ray luminosities obtained from the simulations can explain the luminosities of the observed ULXs even if the accreting BHs are non-rotating. The donors which are initially more massive than 30 M⊙ dominate above Lx ≥ 1041 ergs s−1 (this value is smaller by a factor of 6 if the BH accretors are non-rotating).
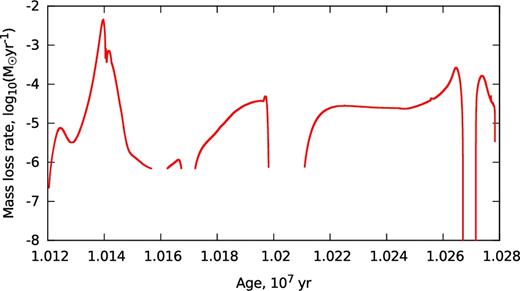
History of the MT in a binary system with a 20 M⊙ giant and a 7 M⊙ BH. At the RLOF the donor has a radius of 144 R⊙, and has Z = 0.1 Z⊙. Interruptions of the line indicate that the donor's radius is smaller than the Roche lobe volume radius (e.g. the donor detaches). It does not mean that the mass-loss rate is zero, because the donor produces a stellar wind.
These systems with massive donors can nicely explain, for instance, ULX1 located in NGC 5643. That ULX has a luminosity of 4 × 1040 erg s−1 and was argued to have a BH accretor (Pintore et al. 2016). We note, though, that our study shows that the accretor does not require a BH as massive as 30 M⊙ emitting at 10 times the Eddington limit, but this system may only have a 10 M⊙ BH, while having a much higher MT rate.
Let us estimate the rates at which we can produce detectable ULXs via our channel. Our ULXs are produced in place of the common envelope events during an HG leading to merging BH–BH, and therefore we will be using those rates for our estimate. Dominik et al. (2012) have provided a suite of 16 population synthesis models that are also available online at syntheticuniverse.org. For each model, two submodels were presented. In one subset, it was assumed that common envelope initiated by an HG donor is allowed, and energy balance was applied to check if a given system has survived or merged (submodels A). In the other subset, it was assumed that each common envelope initiated by an HG donor leads to a merger of two stars, aborting binary evolution (submodels B). Not every RLOF with an HG donor in the Dominik et al. (2012) simulations leads to a common envelope: some MTs with the HG donors are stable events in both submodels.
For submodels A, Dominik et al. (2012) found that the formation rate of BH–BH mergers can be up to 26 Myr−1 per star formation unit of 1 M⊙ yr−1 for metallicity Z = 0.002, and up to 8.5 Myr−1 per star formation unit of 1 M⊙ yr−1 for solar-type metallicity of Z = 0.02. These rates assume that if the MT starts when a massive donor crosses the HG, a common envelope event can take place, and that it may potentially result in the formation of a double BH. In models where this formation channel is inhibited (submodels B), the resulting merger rate drops dramatically, indicating that the BH–BH merger rates are dominated by common envelopes with the HG donors. For example, the BH–BH merger rates for submodels B are up to 8.2 Myr−1 per star formation unit of 1 M⊙ yr−1 for metallicity Z = 0.002, and up to 1.2 Myr−1 per star formation unit of 1 M⊙ yr−1 for metallicity Z = 0.02 (Dominik et al. 2012). Not all MTs that are initiated during the HG and result in a common envelope event lead to BH–BH formation, but the difference in merger rates between submodels A and B (quoted above) gives an approximate estimate for the number of MT events that took place, and therefore provides the lower limit on the theoretically expected rate of MTs during the HG. On the other hand, we have used the upper limits on BH–BH merger rates from Dominik et al. (2012) to limit how large the rates inferred using submodels A may reach.
Our ULXs are therefore formed at the rate 18 Myr−1 per unit of star formation for sub-solar metallicity Z = 0.002, while the rate drops down to 7.3 Myr−1 per unit of star formation for solar-like metallicity Z = 0.02. With the average lifetime of ∼105 yr, and assuming, as in Dominik et al. (2012), that the star formation rate in the Milky Way is 3.5 M⊙ yr−1, the theoretical rates above result in ∼2.6 ULX systems can be present in a galaxy similar to the Milky Way at a solar metallicity. Note that in Milky Way two ULX systems were tentatively identified (SS 433 and GRS 1915+105), where one observed system, SS 433, resembles our model of a massive donor and a substantially less massive BH. A synthetic galaxy similar to the Milky Way with the same star formation rate, but with sub-solar metallicity of Z = 0.002 would contain ∼6.3 ULX systems. Summing up, the theoretically expected numbers of ULXs per star formation unit of 1 M⊙ yr−1, are ∼1.8 ULXs for Z = 0.002 and ∼0.7 for Z = 0.02. A more accurate estimate can be made only with a future full-scale population synthesis study.
Observationally, ULXs are detected at numbers in range 0.2–2 per star formation rate of 1 M⊙ yr−1 (Swartz et al. 2011; Luangtip et al. 2015), where the larger value is determined from the sample of all galaxies within 14.5 Mpc, and the smaller value is determined from the sample of 17 luminous infrared galaxies within 60 Mpc (these galaxies presumably have a higher metallicity). A part of the observed ULXs can potentially be interpreted as systems with intermediate-mass BHs, especially for nearby galaxies where more constraints on the spectrum of ULXs were obtained (Gladstone et al. 2013). More importantly, a fraction of ULXs can be powered by accreting neutron stars, such as ULX M82 X-2. Adopting that half of the observed ULXs have a stellar mass BH accretor, observationally, ULXs are detected at about 1 per star formation rate of 1 M⊙ yr−1, similar to our theoretically predicted rates.
We mainly produce ULXs at the higher end of the ULX luminosity function (LX ≳ 1041 erg s−1). Even after taking into account the inefficiency f, or considering that some matter can outflow from the system, as observed in SS 433, and thus cannot be converted into radiation, our systems likely will produce predominantly LX ≳ 1040 erg s−1. The considered formation channel can produce such bright ULXs with reasonable values of inefficiency f, 5–10. We note that this channel cannot explain the majority of the observed ULXs – those having LX ≈ 2–3 × 1039 erg s−1 – unless the inefficiency is extremely large, f ≳ 100. We therefore only apply our channel to explain the formation of bright ULXs. The observed formation rate of similarly bright ULXs is about five times less than the overall ULX formation rate, or 0.4 per star formation rate of 1 M⊙ yr−1, or even less, if the observed sample contains also ULXs powered by intermediate mass BHs or NSs.
It is important that some geometrical collimation of the emission cone, for BHs that accrete at rates exceeding vastly their Eddington limits, is expected. The fraction of the sky covered by the beamed radiation can be as low as 0.1 (King 2009). Therefore, it is possible that observationally, only 10 per cent of the existing bright ULXs are detected. Then the intrinsic formation rate of bright ULXs can be as high as four ULXs per star formation rate of 1 M⊙ yr−1.
We conclude that our theoretical formation rate of bright stellar-mass BH ULXs is similar to the observed one. The theoretical rate might even be increased if all MT events that take place during the HG are taken into account, not just those that were assumed to result in the formation of BH–BH mergers from the HG common envelope channel. Additionally, it is also very likely that other channels (not involving HG donors) may produce high-luminosity ULXs (Wiktorowicz et al. 2015). We find that as metallicity increases, the number of produced ULXs drops, which may explain the deficit of ULXs per star formation unit in luminous infrared galaxies found in Luangtip et al. (2015).
5 CONCLUSIONS
We analysed the MT in binary systems with massive donors (20–80 M⊙) and stellar-mass BHs (7–14 M⊙) for two metallicities: solar (Z⊙ = 0.02) and sub-solar (0.1 Z⊙). The considered binary systems have high mass ratios, and the MT in these systems was previously considered to be unstable. We found the regions where the MT is stable, including systems with an initial (onset of MT) mass ratio as high as 7.5. The stability regions are bordered by two key instabilities. First is the instability that develops during fast post-main-sequence expansion; this instability is avoided in a number of donors, especially by those of solar metallicity. Second is the instability that takes place when a sufficiently deep outer convective zone is developed; this instability starts well after the initial development of the outer convective envelope. However, in most of the parameter space where donor stars are on the HG (as adopted for this study, this includes early core helium burning stars), the binaries are found to evolve through fast but stable MT.
Unstable MT takes place only in very expanded giants with well-developed envelopes. In those cases, by the onset of the common envelope, a substantial part of the envelope had been transferred via the initial stage of the MT. The effect of the donor's envelope ‘reduction’ on the common envelope outcomes, in principle, can be tested in population synthesis with common envelope energy prescription parameters, as it might be important. A typical case that leads to the formation of a BH–BH merger resembling GW150914 in an isolated binary, without the requirement of homogeneous evolution, involves a core helium-burning giant with a mass of 82.2 M⊙ which enters CE phase at a radius of 1665 R⊙ (see fig. 1 of Belczynski et al. 2016a). This typical binary simulated with the population synthesis code startrack is outside the range of parameters tested in our study; it originates at a very low metallicity Z = 0.0006, and at the onset of CE the BH mass is 35.1 M⊙. The CE leads to significant orbital decay (the orbital separation decreases from a = 3780 R⊙ to a = 43.8 R⊙) as the large envelope (mass of 45.4 M⊙) is ejected [with the adopted α = 1.0 and the estimated λ = 0.15 from Xu & Li (2010)]. This binary survives and forms a massive BH–BH merger (two BHs with mass ∼30 M⊙) at the end of its evolution.
In the past, and in the majority of the present studies, it is assumed that post-main-sequence stars (including HG stars) may evolve through, and survive, a common envelope (Tutukov & Yungelson 1993; Lipunov, Postnov & Prokhorov 1997; Nelemans, Yungelson & Portegies Zwart 2001; Voss & Tauris 2003; Mennekens & Vanbeveren 2014; Eldridge & Stanway 2016). Since a significant fraction of stellar expansion is encountered during the HG, the most likely formation scenarios of BH–BH mergers in population synthesis studies involve HG donors in the common envelope phase. With our findings, the BH–BH merger rates obtained in simulations that allow for common envelopes with HG donors are subject to drastic reduction. This effect was approximately quantified with the use of the startrack population synthesis code. For solar-like metallicity, the effect is overwhelming, producing a factor of 750 decrease in the predicted BH–BH merger rates. For sub-solar metallicity, this produces however only a factor of 14 decrease (see table 1 of Belczynski et al. 2010).
Most BH–BH mergers are estimated to originate from low-metallicity environments, and a population synthesis calculation that takes into account the forbidden common envelope development predicts a merger rate of 220 Gpc−3 yr−1, and the most likely detection of BH–BH mergers with a total mass of 20–80 M⊙ (Belczynski et al. 2016a). In the same study, the model in which common envelope is allowed for HG donors generates BH–BH merger rates of ≳ 1000 Gpc−3 yr−1. The LIGO empirical estimate of the local Universe BH–BH merger rate is in the range 9–240 Gpc−3 yr−1, and the three BH–BH mergers are found with total (the sum of the two merging BH masses) masses in the range 22–65 M⊙(The LIGO Scientific Collaboration et al. 2016). The LIGO results indicate therefore that a population synthesis approach in which HG donors will initiate a common envelope is not valid. Here, we provide a previously missing theoretical foundation that allows us to reconcile the theory and observations.
We also demonstrate that the MT binaries with HG donors that avoid the common envelope event will become ULXs. High thermal time-scale MT rates lead to very high X-ray luminosities, which may even exceed 1042 erg s−1 (see also Wiktorowicz et al. 2015). The theoretically expected formation rate of ULXs that are powered by accretion on to a stellar-mass BH is found to be 0.7–1.8 per star formation unit of 1 M⊙ yr−1, for the metallicity range Z = 0.02–0.002. The binaries that produce bright ULXs consist of donors that are initially 20–80 M⊙, and significantly less massive BHs. This rate may explain the observed formation rate of bright ULXs, which is 0.4–4 per star formation unit of 1 M⊙ yr−1.
Acknowledgments
NI thanks NSERC Discovery and Canada Research Chairs Program. KB acknowledges support from the Polish NCN grants: Sonata Bis 2 (DEC-2012/07/E/ST9/01360), OPUS (2015/19/B/ST9/01099) and OPUS (2015/19/B/ST9/03188). The authors thank C. Heinke for checking the English in the manuscript. This research has been enabled by the use of computing resources provided by WestGrid and Compute/Calcul Canada. A part of this work was performed at the Aspen Center for Physics, which is supported by National Science Foundation grant PHY-1066293.
The modifed version of MESA, including the Roche lobe tables and examples of inlists, are available at www.ualberta.ca/∼ivanova1/mesa_l1_mt/



