-
PDF
- Split View
-
Views
-
Cite
Cite
Sergiy Silich, Guillermo Tenorio-Tagle, Gas expulsion versus gas retention: what process dominates in young massive clusters?, Monthly Notices of the Royal Astronomical Society, Volume 465, Issue 2, February 2017, Pages 1375–1383, https://doi.org/10.1093/mnras/stw2879
Close - Share Icon Share
Abstract
The ability of young stellar clusters to expel or retain the gas left over after a first episode of star formation is a central issue in all models aiming to explain multiple stellar populations and the peculiar light element abundance patterns in globular clusters. Recent attempts to detect the gas left over from star formation in present-day clusters with masses similar to those of globular clusters did not reveal a significant amount of gas in the majority of them, which strongly restricts the scenarios of multiple stellar population formation. Here the conditions required to retain the gas left over from star formation within the natal star-forming cloud are revised. It is shown that the usually accepted concept regarding the thermalization of the star cluster kinetic energy due to nearby stellar winds and supernova ejecta collisions must be taken with care in the case of very compact and dense star-forming clouds where three star formation regimes are possible if one considers different star formation efficiencies and mass concentrations. The three possible regimes are well separated in the half-mass radius and in the natal gas central density versus pre-stellar cloud mass parameter space. The two gas-free clusters in the Antennae galaxies and the gas-rich cluster with a similar mass and age in the galaxy NGC 5253 appear in different zones in these diagrams. The critical lines obtained for clusters with a solar and a primordial gas metallicity are compared.
1 INTRODUCTION
Globular clusters (GCs), considered for a long time to be chemically homogeneous stellar systems, formed instantaneously in young assembling galaxies, are now confirmed to have a much more complex structure. Deep photometric observations and detailed spectroscopy with Hubble Space Telescope have revealed that all of them have distinct main-sequence subpopulations and large star-to-star abundance variations in light elements with well-documented anti-correlations between O and Na, Mg and Al (see Bedin et al. 2004; Marino et al. 2008; Carretta et al. 2009; Piotto et al. 2012; Renzini et al. 2015, and references therein). At the same time, the majority of GCs remain mono-metallic regarding the iron group elements. Only the most massive ones (e.g. ω Cen, M22, Terzan 5) exhibit multiple [Fe/H] populations which strongly restricts the ability of young proto-GCs to retain the iron-enriched supernova (SN) ejecta (see Renzini 2013, and references therein). Despite many efforts to solve this problem, the discovery of multiple stellar populations in GCs remains one of the most challenging results of the last decade in the context of the origin and evolution of stellar populations in galaxies.
There are three main candidates which potentially reach the right hydrogen burning conditions to explain the abundance anomalies in GCs. These are (a) asymptotic giant branch (AGB) stars (D'Antona & Caloi 2004; D'Ercole et al. 2008); (b) fast rotating massive stars (FRMS; Prantzos & Charbonnel 2006; Decressin et al. 2007; Bastian et al. 2013) and interacting massive binaries (IMB; de Mink et al. 2009; Tenorio-Tagle et al. 2016).
The applicability of the FRMS and IMB scenarios requires that young proto-GCs retain some of the pristine gas left over from the formation of a first stellar population for some time (20–40 Myr) whereas in the AGB scenario this gas is removed by stellar winds and SN explosions. The second stellar population in this latter case is formed after the end of SN explosions from the slow AGB winds retained in the potential well of the cluster mixed with some matter accreted late in the evolution of the cluster.
Recently, Bastian et al. (2013) and Bastian, Hollyhead & Cabrera-Ziri (2014) attempted to find the matter left over from star formation in nearby young massive clusters, but did not detect any significant amount of gas (down to 1–2 per cent limits of the star cluster mass) in their target clusters. This led them to claim that even high-mass clusters with masses 106 M⊙ or more expel their natal gas within a few Myr after their formation, which strongly restricts scenarios for multiple stellar population formation. However, observations of nearby galaxies provided in infrared, millimetre and radio wavelengths revealed several very luminous and compact regions which are believed to be young stellar clusters still embedded into their natal gaseous clouds (Turner, Beck & Ho 2000; Turner et al. 2003; Beck 2015).
1D and 3D numerical simulations provided by D'Ercole et al. (2008) and Calura et al. (2015) show that stellar winds effectively remove gas from star-forming regions and completely clean them up of the pristine matter no later than 15 Myr after their formation. However, calculations provided by Krause et al. (2012, 2016) with a 1D thin layer approximation led to the conclusion that in most cases the expanding star cluster wind-blown shells are destroyed via Rayleigh–Taylor (RT) instabilities before reaching the escape velocity which prevents gas expulsion from the star-forming region.
Another approach has been recently discussed by Tenorio-Tagle et al. (2015, 2016) who considered a model in which the negative feedback provided by stellar winds is suppressed because all massive stars compose close binary systems. The major implications of this are that the large collection of IMB are likely to hold the remaining cloud against gravitational collapse while contaminating the gas left over from star formation. This would happen without disrupting the centrally concentrated density distribution even during the early evolution of GCs. Under such conditions, blast waves from sequential SN explosions are likely to undergo blowout expelling the SN products into the ambient interstellar medium (ISM) keeping most clusters mono-metallic regarding the iron group elements.
Here we show that bubbles formed by stellar winds and single SN explosions in the central zones of compact and massive young stellar clusters may stall before merging with their neighbours. This naturally allows for the retention and enrichment of the gas left over from the formation of a 1G and likely would lead to the formation of a second generation of stars with a peculiar abundance pattern. The fate of the gas left over from star formation depends then not only on the proto-stellar cloud mass and the star formation efficiency (SFE), but also on the gas concentration (or the central gas density) in the proto-stellar cloud. The major output from our study is critical lines which separate the gas expulsion and the gas retention regimes in the star-forming cloud size and in the central gas density versus the star-forming cloud mass parameter space and the dependence of these critical lines on the SFE.
Radiative pressure effects are presumably small in the dynamics of bubbles formed around single OB stars (Krumholz & Matzner 2009). They may be significant only for a short while in the dynamics of shells formed around star clusters (e.g. Silich & Tenorio-Tagle 2013; Martínez-González, Silich & Tenorio-Tagle 2014; Gupta et al. 2016). Such shells are driven by a high thermal pressure, which is boosted when individual stellar winds begin to collide and convert their kinetic energy into thermal energy of the injected matter. We leave the detailed analysis of radiation pressure effects on our model to a forthcoming communication.
The paper is organized as follows. In Section 2, we introduce the models adopted for the initial gas and stellar density distributions in the star-forming cloud and determine the rate of mechanical energy injected by massive stars into the intracluster medium. In this section, we also discuss the dynamics of bubbles driven by individual stellar winds and individual SN explosions and derive the conditions for them to stall before merging with their neighbours. In Section 3, we split the half-mass radius versus star-forming cloud mass and the central gas density versus star-forming cloud mass parameter space on to three regions. In the first case, neighbouring wind-driven bubbles merge and upon the collisions their shells fragment leaving the swept-up matter as a collection of dense clumps. Neighbouring stellar winds begin then to interact directly causing the large overpressure which evolves into a cluster wind. The fragmented original gas will then be mass-loaded by the cluster wind and finally expelled out of the star-forming volume. In the second case, the wind-driven bubbles are unable to merge and are thus not able to cause the conditions for the generation of a cluster wind and the removal of the leftover gas. In this regime, individual SNe may engulf neighbouring wind sources. The energy input rate to the supernova remnant (SNR) then grows with time causing a continuous acceleration and eventually the SNR destruction. This immediately leads to the expelling of SN products out of the cluster. In the third region, SNRs stall before merging with nearby wind-driven bubbles. The natal gas is then contaminated with the iron group elements and retained in the central zones of the star-forming cloud. Here we also discuss how the SFE and the stellar metallicity affect the critical lines which separate clusters evolving in different regimes. We also show that three clusters with similar masses and ages, two gas-less clusters in the Antennae galaxies and the gas-rich cluster in the dwarf galaxy NGC 5253, are located in different regions of our half-mass radius versus star-forming cloud mass diagram. Finally, in Section 4 we summarize our major results and conclusions.
2 MODEL SETUP
2.1 Stellar and gas density distributions
2.2 Input energy
Note that the number of massive stars N decreases after the onset of SN explosions (it is assumed that the rate of SN explosions follows the starburst99 model predictions). The mean separation between nearby massive stars Δ then increases with time. Clusters which were not able to form a wind and expel the leftover gas after the first SN explosion should retain it when the separation between nearby energy sources becomes larger. Therefore, hereafter we do not consider the star cluster mechanical luminosity time evolution.
The results obtained below should not be restricted to the Plummer model. For example, in the case of mass segregation (e.g. Dib et al. 2008), the assumption that the gas and massive stars are equally distributed does not hold. The mean separation between massive stars in the central zones of the cluster then would be smaller than that predicted by equation (4). This will reduce the critical radii obtained in the next sections and enhance the gas critical densities, but does not change our major conclusions.
2.3 Wind-driven bubbles
Inside the central zone with radius r < R2G, the 1G stars contaminate the pristine gas left over after their formation with different H-burning products providing the conditions to form a polluted 2G. Note that wind-driven bubbles do not stall in the outskirts of the cloud where they instead accelerate into a sharp density gradient and then blow out into the surrounding ISM. This restricts the size of the polluted zone and results in a centrally concentrated second subpopulation.
2.4 SN-driven bubbles
In young stellar clusters with a normal IMF, stellar winds represent a dominant negative feedback mechanism only for a short while, unless the most massive stars do not explode as SNe, but directly form black holes (see Decressin et al. 2010; Krause et al. 2012, and references therein). It is usually assumed that in massive star clusters the first SN explodes at an age of about 3.5 Myr and since then SN explosions become the most energetic negative feedback events responsible for the gas expulsion from the recently formed clusters. In this section, we discuss the impact which SNe provide on the gas which a cluster wind did not expel from the star-forming region and the conditions required to form a second subpopulation enriched with the iron group elements.
As the SN expands into the rarefied gas left by a previous stellar wind, the initial radius R0 could be approximated by the radius of the stalling wind-driven bubble: R0 ≈ Rstall,w (Wheeler et al. 1980).
SN-driven bubbles sweep up the gas left over from star formation and if they stall at the distance larger than the mean separation between nearby massive stars, the stellar winds formerly separated by the dense matter left over from star formation merge and add their energy to the thermal energy of the hot bubble formed after an SN explosion. A coherent shell which sweeps up the gas left over from star formation is then formed inside the cluster. The energy input rate in such a bubble grows rapidly as it overtakes neighbouring wind sources. One can show (see Appendix A) that in this case the expanding shell accelerates even if it moves into a constant density ambient medium. Such an accelerating shell becomes destroyed via RT instabilities. The hot gas then finally escapes from the cloud carrying away all SN products whereas fragments from the broken shell are likely to remain bound within a gravitational well of the cluster (Krause et al. 2012). Massive stars not affected by the SN blast wave then continue to contaminate the collection of RT clumps formed after blowout of previous SNRs as well as the rest of the gas left over after the formation of a first stellar generation.
In the central zones of even more compact and dense star-forming clouds, SNRs stall before merging with nearby wind-driven bubbles. Only in this case and with the help of the global turbulent pressure, SNe are able to eventually enrich the pristine gas left over from the 1G formation with iron group elements. The radius of this zone, Renrich, is determined by the critical half-mass radius RhmSN,crit and the actual half-mass radius of the proto-stellar cloud.
3 GAS EXPULSION VERSUS GAS RETENTION IN YOUNG STELLAR CLUSTERS
As mentioned above, some models of multiple populations in GCs require the star cluster volume to be cleaned up whereas other require the primordial gas to be retained. In this section, the critical lines which allow one to distinguish between clusters which expel or retain the gas left over from star formation are presented. Also, how these critical lines are affected by the proto-stellar gas metallicity and by the SFE are here discussed.
3.1 Young clusters in present-day galaxies
Fig. 1 presents the critical radii, Rhmw,crit and RhmSN,crit (upper panels), and the critical gas central densities (lower panels) as a function of the star-forming cloud mass, all assuming a solar gas metallicity. The left-hand and right-hand panels in Fig. 1 correspond to different SFE: ε = 0.3 and 0.7, respectively. The critical radii and critical gas central densities for the wind-dominated and SN-dominated regimes are displayed by solid and dashed lines, respectively.
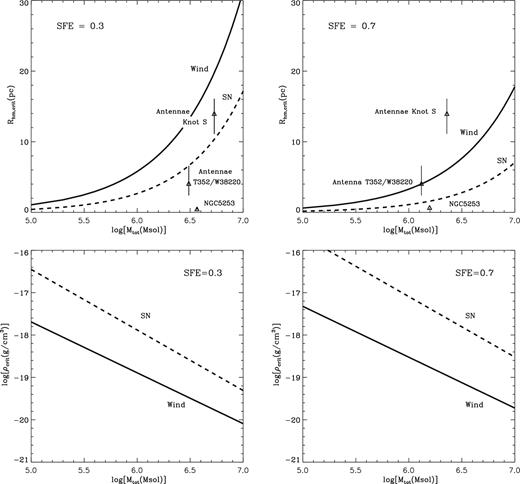
Critical radii and gas central densities for proto-stellar clouds with solar gas metallicity. The left-hand panels show how the critical half-mass radius and the central gas density change with the total mass of the proto-stellar cloud if the SFE ε = 0.3. The right-hand column shows the same in the case of the larger SFE ε = 0.7. In all panels, solid and dashed lines display the critical cloud parameters derived for a stellar wind-dominated regime and after the onset of the SN explosions, respectively. Labelled symbols in the upper panels give the location of three selected clusters (see Table 1) with their corresponding error bars.
There are three zones in these diagrams. In clusters located above the solid line in the top panels and below the solid lines in the bottom panels, individual wind-driven bubbles merge with neighbouring sources and form a collection of dense clumps in the whole star-forming volume. Nearby stellar winds then begin to collide heating up the injected matter and forming a mass-loaded star cluster wind which eventually cleans up the star-forming cloud. Stellar winds are not able to merge in more compact and denser star-forming clouds located in between the solid and dashed lines in these diagrams. However, SNRs formed in such clusters engulf neighbouring wind sources. They gain then more energy which results in their acceleration and eventually leads to the development of RT instabilities and the SN shell destruction. It is likely that RT clumps left over from the disrupted shells remain bound to the cluster (Krause et al. 2012) while the iron-enriched gas escapes into the ambient ISM through the broken shells and does not pollute the gas available for a 2G. The fundamental difference between these two regimes is that individual SN explosions are not synchronized in time and space. They do not act coherently and have little effect on the leftover gas distribution (Tenorio-Tagle et al. 2015). On the other hand, if wind-driven bubbles merge, they do merge simultaneously in the whole star-forming volume and eventually form a powerful, mass-loaded star cluster wind. The coherence of energy sources is a fundamental ingredient as was already stressed by Calura et al. (2015) and Sharma et al. (2014).
The most massive and compact star clusters located below the dashed lines in the top panels and above the dashed lines in the bottom panels retain the pristine gas and some SN products. In this case, the 2G should present an enhanced iron abundance.
The comparison of the left-hand and right-hand panels in Fig. 1 shows that the regime of star formation strongly depends on the SFE of the 1G. The critical lines go down in the top panels and up in the bottom panels as the considered SFE for the 1G becomes larger. This implies that natal clouds with a large SFE must be more compact and denser compared to their counterparts with a low SFE in order to form the 2G subpopulation. Note also that the critical lines mark clouds which retain primordial gas only in a small central zone. However, the size of this zone and the amount of the retained gas available for the 2G formation grow rapidly in more compact clusters with an Rhm < Rhm,crit.
The critical gas central densities are presented in the bottom panels. At first glance, they look too large if one takes as a reference value the interstellar gas density in the Milky Way or another nearby galaxy. However, the stellar mass density in GCs with multiple stellar populations reaches 105 M⊙ pc−3 which corresponds to a number density of atoms about n ≈ 107 cm−3 (Renzini 2013). This value is comparable and in many cases even larger than the critical densities shown in Fig. 1. Thus, it is likely that many young, massive and compact clusters may retain the gas left over from star formation in their central zones. This seems to be in conflict with the recent results by Bastian et al. (2013, 2014) who did not detect a significant amount of gas in many young (ages less than 20 Myr) massive (masses about 106 M⊙ or more) clusters located in different nearby galaxies and claimed that even high-mass clusters expel their natal gas within a few Myr after formation. Note, however, that not all nearby young massive clusters are free of gas. Probably the best example of an equally young and massive star cluster which still remains embedded within its natal cloud is a ∼106 M⊙, ∼4 Myr old cluster, in the dwarf galaxy NGC 5253 (see Turner et al. 2000, 2003, 2015; Beck 2015). In order to understand what determines such a profound difference between this cluster and those studied by Bastian and collaborators, we selected from the list of Bastian et al. (2014) two clusters whose ages and masses are similar to the massive cluster in NGC 5253. Following Krause et al. (2016), we transformed the half-light radii of the selected clusters into half-mass radii (see Table 1). Note that the half-mass radii may be even larger if one accounts for a possible mass segregation in the observed clusters. As the cluster in NGC 5253 is still embedded into a dense molecular cloud and is not visible at optical or UV wavelengths, we adopted the size of the radio supernebula detected around the cluster (see Turner et al. 2000; Beck 2015) as the maximum value for the star cluster half-mass radius and then accommodated all clusters in our diagram.
| Galaxy . | Cluster . | Age . | Mass . | Half-mass radius . |
|---|---|---|---|---|
| . | . | (Myr) . | (106 M⊙) . | (pc) . |
| The Antennae | ||||
| T352/W38220 | 4 | 0.92 | |$4.1^{+2.5}_{-1.7}$| | |
| Knot S | 5 | 1.6 | |$13.6^{+2.5}_{-2.5}$| | |
| NGC 5253 | Super star cluster | |||
| in cloud D | 4.4 | 1.1 | |$0.5^{+0.15}_{-0.15}$| |
| Galaxy . | Cluster . | Age . | Mass . | Half-mass radius . |
|---|---|---|---|---|
| . | . | (Myr) . | (106 M⊙) . | (pc) . |
| The Antennae | ||||
| T352/W38220 | 4 | 0.92 | |$4.1^{+2.5}_{-1.7}$| | |
| Knot S | 5 | 1.6 | |$13.6^{+2.5}_{-2.5}$| | |
| NGC 5253 | Super star cluster | |||
| in cloud D | 4.4 | 1.1 | |$0.5^{+0.15}_{-0.15}$| |
| Galaxy . | Cluster . | Age . | Mass . | Half-mass radius . |
|---|---|---|---|---|
| . | . | (Myr) . | (106 M⊙) . | (pc) . |
| The Antennae | ||||
| T352/W38220 | 4 | 0.92 | |$4.1^{+2.5}_{-1.7}$| | |
| Knot S | 5 | 1.6 | |$13.6^{+2.5}_{-2.5}$| | |
| NGC 5253 | Super star cluster | |||
| in cloud D | 4.4 | 1.1 | |$0.5^{+0.15}_{-0.15}$| |
| Galaxy . | Cluster . | Age . | Mass . | Half-mass radius . |
|---|---|---|---|---|
| . | . | (Myr) . | (106 M⊙) . | (pc) . |
| The Antennae | ||||
| T352/W38220 | 4 | 0.92 | |$4.1^{+2.5}_{-1.7}$| | |
| Knot S | 5 | 1.6 | |$13.6^{+2.5}_{-2.5}$| | |
| NGC 5253 | Super star cluster | |||
| in cloud D | 4.4 | 1.1 | |$0.5^{+0.15}_{-0.15}$| |
In the case of a low SFE (see the upper-left panel in Fig. 1), T353/W38220 and NGC 5253 clusters are located in the parameter space where clusters should retain gas left over from star formation even in the SN-dominated regime. Even the older and less concentrated cluster Knot S is located in between the wind and the SN critical lines and thus should expel SN products, but retain the primordial gas and the dense RT clumps caused by blowout events. However, in the case of a larger SFE (the upper-right panel in Fig. 1), only NGC 5253 cluster remains in the total gas retention parameter space, while the Antennae clusters are to disperse their primordial gas during the wind-dominated stage. Therefore, we suggest that the SFE in the Antennae clusters must have been large. The major difference between these three clusters, very similar in their mass and age, is then their compactness: the most compact cluster in the NGC 5253 galaxy remains embedded into its natal cloud whereas the less compact clusters in the Antennae are not. The stalling bubble model may also explain the lack of non-thermal radio emission from the NGC 5253 cluster (Beck et al. 1996; Martín-Hernández, Schaerer & Sauvage 2005) because in this case shock waves vanish rapidly, the Fermi acceleration mechanism does not work and therefore high-energy particles cannot survive for a long time after SN explosions.
3.2 Young clusters in ancient low-metallicity galaxies
There is a common belief that stellar winds driven by stars with low metal abundances are less energetic than those driven by their metal-rich counterparts. Taking into account this difference, one can calculate the critical half-mass radii and the critical central densities for young proto-stellar clouds with a low gas metallicity as was done in the previous section for present-day young massive clusters. Critical lines calculated with stellar wind mechanical luminosities as derived by D'Ercole et al. (2008) for stars with extremely low metal abundances, L⋆ = 3 × 1039(M⋆/106 M⊙) erg s−1, are shown in Fig. 2.
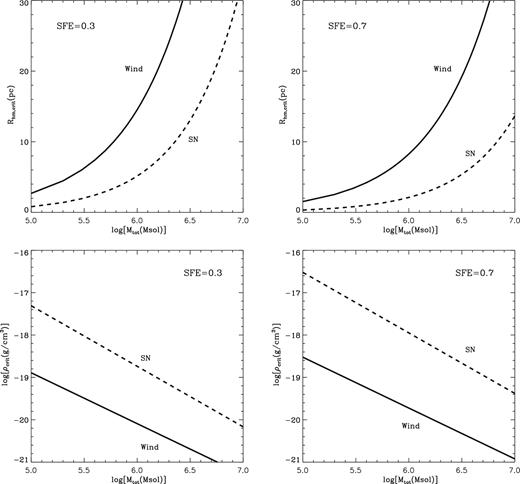
The same as in Fig. 1, but calculated for proto-stellar clouds with a primordial gas metallicity Z = 0.001 Z⊙.
An inspection of Fig. 2 and its comparison with Fig. 1 lead one to conclude that the requirements for proto-GCs to retain pristine gas left over from star formation are less stringent than those derived for present-day massive clusters. Much less dense (about an order of magnitude) and less compact proto-GCs may retain gas left over after the 1G stars have formed. This is because stars with low metal abundances have less energetic winds and their wind-driven bubbles stall without merging with their neighbours in lower density star-forming clouds (compare the bottom panels in Figs 1 and 2). In this case, SNRs also stall before merging with nearby stellar winds in less dense star-forming clouds as they explode inside wind-driven bubbles with a smaller size. This significantly extends the window of opportunity to form a second stellar population in low-metallicity clouds.
Clouds located below the solid lines in the top panels and above the solid lines in the bottom panels in Figs 1 and 2 are able to form multiple stellar populations. The mass ratio M1G/M2G depends on the SFE (see Tenorio-Tagle et al. 2016) and on the cluster compactness. Proto-globular clouds form more massive 2G population when located further away from the wind-driven bubble critical line in the gas retention parameter space. However, only very massive and compact clusters located below the dashed lines in the top panels and above the dashed lines in the bottom panels in Figs 1 and 2 are able to retain SN products and form stellar populations with different metallicities regarding the iron group elements.
4 CONCLUDING REMARKS
The common belief that stellar winds and SNRs in compact, young stellar clusters rapidly merge due to a small separation between nearby massive stars and expel the gas left over from star formation into the ambient ISM should be taken with care. Four major parameters (total mass, size, SFE and the natal gas metallicity) determine which one of the two processes – gas expulsion or gas retention – dominates in each star-forming cloud and select one of the three possible star formation regimes.
If the central gas density in the star-forming cloud is small (ρg < ρw,crit), the collection of individual wind-driven bubbles merge and fragment. Neighbouring stellar winds then collide, heat up the injected matter and form a powerful mass-loaded star cluster wind which eventually cleans out the cluster. In this case, 2G stars are not formed unless the cluster accretes a sufficient amount of gas during the late stages of its evolution, as suggested in the AGB scenario (D'Ercole et al. 2008, 2010) for GC formation.
If the central gas density falls into the range ρw,crit < ρg < ρSN,crit, stellar winds do not merge. However, shells formed after individual SN explosions engulf neighbouring massive stars, gain their stellar wind energy, accelerate and eventually are disrupted via RT instabilities. As individual SN explosions are not synchronized in time and space, they have little effect on the gas distribution in the rest of the star-forming cloud. RT clumps are likely to remain bound within the gravitational well of the cluster. This collection of clumps and the gas unused for the 1G formation are continuously contaminated by the 1G stars and likely form finally a second subpopulation. The hot, iron-enriched gas however escapes from the cluster into the ambient ISM through the broken shells and does not pollute the 2G with products of SN explosions. All stellar subpopulations in such clusters should present the same iron group metallicity.
If the central gas density in the proto-stellar cloud is large enough, ρg > ρSN,crit, SNRs in the central zones of the star-forming cloud stall before merging with nearby stellar winds. Such clusters retain metals injected into the intracluster medium by SNe. Only in this case, clusters with an [Fe/H] spread could be formed.
Clusters with the same mass, SFE and the natal gas metallicity but different mass concentrations evolve in different hydrodynamic regimes. More compact clusters retain the natal gas left over from the 1G formation whereas less compact ones expel it into the ambient ISM. This justifies the presence of natal gas in the most compact super star cluster in NGC 5253 and the non-detection of gas left over from star formation in the less compact clusters T352/W38220 and Knot S, in the Antennae galaxies.
Acknowledgments
We thank J. Turner for her detailed comments regarding the size of the NGC 5253 super star cluster and the surrounding molecular cloud properties. SS thanks E. Ramirez-Ruiz and colleagues from the Astronomy and Astrophysics Department for discussions, support and hospitality during his stay at UC Santa Cruz. We also thank our anonymous referee for a detailed report full of valuable comments which helped to clarify our model and improve the paper significantly. This study has been supported by CONACYT – México, research grant 167169.



