The Milky Way's rotation curve out to 100 kpc and its constraint on the Galactic mass distribution

Huang, Y.; Liu, X.-W.; Yuan, H.-B.; Xiang, M.-S.; Zhang, H.-W.; Chen, B.-Q.; Ren, J.-J.; Wang, C.; Zhang, Y.; Hou, Y.-H.; Wang, Y.-F.; Cao, Z.-H.

doi:10.1093/mnras/stw2096

Abstract

The rotation curve (RC) of the Milky Way out to ∼100 kpc has been constructed using ∼16 000 primary red clump giants (PRCGs) in the outer disc selected from the LAMOST Spectroscopic Survey of the Galactic Anti-centre (LSS-GAC) and the Sloan Digital Sky Survey (SDSS)-III/APOGEE survey, combined with ∼5700 halo K giants (HKGs) selected from the SDSS/SEGUE survey. To derive the RC, the PRCG sample of the warm disc population and the HKG sample of halo stellar population are, respectively, analysed using a kinematical model allowing for the asymmetric drift corrections and re-analysed using the spherical Jeans equation along with measurements of the anisotropic parameter β currently available. The typical uncertainties of RC derived from the PRCG and HKG samples are, respectively, 5–7 km s⁻¹ and several tens km s⁻¹. We determine a circular velocity at the solar position, V_c(R₀) = 240 ± 6 km s⁻¹ and an azimuthal peculiar speed of the Sun, V_⊙ = 12.1 ± 7.6 km s⁻¹, both in good agreement with the previous determinations. The newly constructed RC has a generally flat value of 240 km s⁻¹ within a Galactocentric distance r of 25 kpc and then decreases steadily to 150 km s⁻¹ at r ∼ 100 kpc. On top of this overall trend, the RC exhibits two prominent localized dips, one at r ∼ 11 kpc and another at r ∼ 19 kpc. From the newly constructed RC, combined with other constraints, we have built a parametrized mass model for the Galaxy, yielding a virial mass of the Milky Way's dark matter halo of |$0.90^{+0.07}_{-0.08} \times 10^{12}$| M_⊙ and a local dark matter density, |$\rho _{\rm {\odot }, dm} = 0.32^{+0.02}_{-0.02}$| GeV cm⁻³.

Galaxy: disc, Galaxy: fundamental parameters, Galaxy: halo, Galaxy: kinematics and dynamics, Galaxy: structure

1 INTRODUCTION

The rotation curve (hereafter RC) of the Milky Way gives the measured circular velocity V_c as a function of the Galactocentric distance r. The RC provides important constraints on the mass distribution of our Galaxy, including its dark matter (DM) content, as well as the local DM density (e.g. Salucci et al. 2010; Weber & de Boer 2010). The latter is crucial for the interpretation of any signals that DM search experiments, direct or indirect, are expected to detect. The RC can also be used to construct realistic Galactic mass model by fitting the RC with a parametrized multicomponent Milky Way, consisting of, for instance, a bulge, a disc and a DM halo (e.g. Sofue, Honma & Omodaka 2009; Xin & Zheng 2013).

Generally speaking, for the inner region (i.e. inside the solar circle) of the Galactic disc, the RC can be accurately measured simply using the so-called tangent-point (TP) method with the H i 21 cm or the CO 2.6 mm gas emissions in the Galactic plane as tracer (Burton & Gordon 1978; Gunn, Knapp & Tremaine 1979; Clemens 1985; Fich, Blitz & Stark 1989; Levine, Heiles & Blitz. 2008; Sofue et al. 2009). In principle, a well-defined RC could be established by this method for the entire Galactic inner region if one assumes that the gas moves in perfect circular orbits around the Galactic Centre (GC). However, the distribution and kinematics of gas can be easily perturbed by non-axisymmetric structures, in particular by the bar near the centre. Given the presence of those perturbations, the TP method only works well in deriving the RC for the projected Galactocentric distance R from ∼4.5 kpc to R₀ (Galactocentric distance of the Sun; Chemin, Renaud & Soubiran 2015). For the outer disc beyond the solar circle, the TP method cannot be used to derive the RC. Instead, the RC is derived using a variety of tracers belonging to the cold disc populations from the measured line-of-sight velocities (V_los) and estimated distances, such as the thickness of H i gas (Merrifield 1992; Honma & Sofue 1997), H ii regions (Fich et al. 1989; Brand & Blitz 1993; Turbide & Moffat 1993), OB stars (Frink et al. 1996; Uemura et al. 2000; Bobylev & Bajkova 2015), carbon stars (Demers & Battinelli 2007; Battinelli et al. 2013) and classical cepheids (Pont et al. 1997). However, two important issues limit the accuracy of RC derived from those disc tracers. First, it is difficult to determine the distances of those disc tracers and the poorly determined distances could lead large uncertainties (generally of the order of tens km s⁻¹, see, e.g. the fig. 1 of Sofue et al. 2009) in the derived circular velocity V_c. Another issue is that, similar to the TP method, the underlying assumption that the disc tracers used move in purely circular orbits can be easily broken. Disc tracers belonging to the cold populations, especially those young objects, are generally associated with the spiral arms and thus their kinematics are often perturbed by the arms. At present, it is difficult to correct for the effects of those perturbations given the properties including dynamics of arms are still poorly understood. Recently, accurate distances and values of V_los have been measured for a number of masers¹ by the Bar and Spiral Structure Legacy (BeSSeL) survey (Brunthaler et al. 2011), allowing, in principle, the determination of RC to a very high precision, say better than few km s⁻¹ (e.g. Xin & Zheng 2013; Reid et al. 2014). However, in deriving the RC from those measurements, possible perturbations to the measured velocities caused by the spiral arms remain to be properly accounted for.

Figure 1.

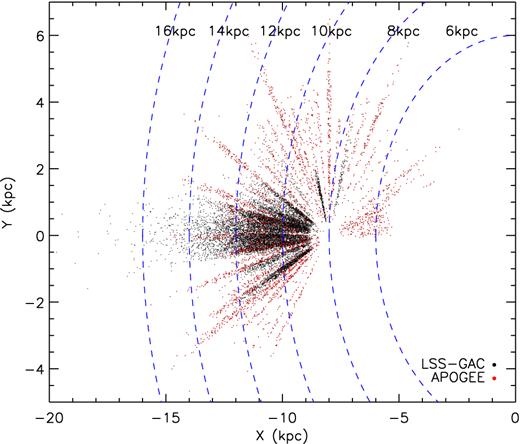
Spatial distribution of PRCG sample stars in the X–Y plane. Black and red dots represent stars selected from LSS-GAC and APOGEE, respectively. Blue dash lines denote different Galactocentric radii.

Open in new tab Download slide

For regions beyond the Galactic disc, the RC needs to be measured using halo stars, such as the blue horizontal branch (BHB) stars (Xue et al. 2008; Deason, Belokurov & Evans 2012; Kafle et al. 2012; Williams & Evans 2015) and the K giants (Bhattacharjee, Chaudhury & Kundu 2014, hereafter BCK14), globular clusters or dwarf galaxies. For those tracers of halo populations (assuming isotropically distributed), the radial velocity dispersion σ_r, number density ν and velocity anisotropy parameter |$\beta \equiv 1 - \sigma ^2_t/\sigma ^2_r$|⁠, are linked to the circular velocity V_c through the Jeans equation (see, e.g. Binney & Tremaine 2008, p. 349) for spherical systems. For halo tracers, profile of the radial velocity dispersion σ_r can be easily estimated from the line-of-sight velocity dispersion σ_los (Battaglia et al. 2005; Dehnen, McLaughlin & Sachania 2006), while their number density is found to follow a double power law with a break radius r_b around 20 kpc (Bell et al. 2008; Watkins et al. 2009; Deason, Belokurov & Evans 2011; Sesar, Jurić & Ivezić 2011). However, the anisotropy parameter β has only been accurately measured in the solar neighbourhood, with a radially biased value between 0.5 and 0.7 (Kepley et al. 2007; Smith et al. 2009; Bond et al. 2010; Brown et al. 2010). Due to the lack of accurate proper motion measurements of distant halo tracers, the anisotropy parameter β is still poorly constrained beyond the solar neighbourhood, particularly for the outer halo (>25 kpc). Hence, the existing determinations of RC suffer from the so-called RC/mass–anisotropy degeneracy. To solve this problem, various values of the anisotropy parameter, either of arbitrary nature (e.g. BCK14) or predicted by numerical simulations (e.g. Xue et al. 2008; BCK14) have been adopted in the spherical Jeans equation to derive the RC. Only more recently, some constraints on the anisotropy parameter, mainly for the inner halo (≤25 kpc), have become available, based on some direct/indirect measurements (e.g. Deason et al. 2012, 2013; Kafle et al. 2012).

In this paper, we report a newly constructed RC of our Galaxy, the Milky Way, extending out to 100 kpc, derived from ∼16 000 primary red clump giants (PRCGs) selected from the LAMOST Spectroscopic Survey of the Galactic Anti-centre (LSS-GAC; Liu et al. 2014; Yuan et al. 2015) and the Sloan Digital Sky Survey (SDSS)-III/APOGEE survey (Eisenstein et al. 2011; Majewski et al. 2015) in the (outer) disc, as well as from ∼5700 halo K giants (HKGs) selected from the SDSS/SEGUE survey (Yanny et al. 2009) for the halo region. The usage of PRCGs in deriving the RC in the outer disc region help solve the above described two issues neatly. First, PRCGs are considered as excellent standard candles given that their intrinsic luminosities are insensitive to the stellar populations (i.e. metallicity and age; e.g. Cannon 1970; Paczyński & Stanek 1998). Thus their distances can be determined to a much higher precision (typically 5–10 percent) than for most other tracers belonging to cold disc population. Secondly, PRCGs are of intermediate- to old-age stellar populations. Thus they have enough time to dynamically mix in the disc and are therefore less affected by non-axisymmetric structures than those cold gaseous or young stellar tracers. On the other hand, given that our PRCG sample stars are of relative old-age (i.e. warm), they need to be corrected the so-called asymmetric drifts (the offsets between the circular velocity and the mean rotational speed of the population concerned), which can be calculated from the velocity dispersions of our sample stars. The large number of PRCGs employed in the current study dramatically reduces the random errors of the newly derived RC. To derive the RC for the halo region, we have chosen SEGUE HKGs as tracers considering that, (1) they are intrinsically bright and also span about 4 mag in r-band absolute magnitude (M_r ∼ −1 to 3 mag), allowing one to determine the RC out to a distance as far as 100 kpc; (2) they are abundantly observed in the SDSS/SEGUE survey. We note that BCK14 have analysed the same SEGUE HKG sample (and other two halo tracer samples) using the spherical Jeans equation and derived the RC in the halo region. However, the analysis either assumes a constant anisotropy parameter β or takes its value from numerical simulations, and thus could be liable to potential systematic uncertainties. To break the RC/mass–anisotropy degeneracy, we have re-analysed the SEGUE HKG sample to derive the RC in the halo region using measurements of β now available in the literature (see Section 4.1). Finally, we have constructed a new parametrized mass model for the Milky Way by combining constraints provided by the current, newly constructed RC and other available data.

The paper is organized as follows. In Section 2, we describe the LSS-GAC and SDSS data sets. We derive the RC by modelling the PRCG and HKG samples in Sections 3 and 4, respectively. The combined, final RC out to 100 kpc is presented in Section 5. A Galactic mass model derived by fitting the newly constructed RC is presented in Section 6. Finally, we summarize in Section 7.

2 DATA

2.1 Coordinate systems

In this study, we use three sets of coordinate systems: (1) a right-handed Cartesian system (X, Y, Z) positioned at the GC with X pointing in the direction opposite to the Sun, Y in the direction of Galactic rotation and Z towards the North Galactic Pole; (2) a Galactocentric cylindrical system (R, ϕ, Z) with R, the projected Galactocentric distance, increasing radially outwards, ϕ in the direction of Galactic rotation and Z the same as that in the Cartesian system; (3) a Galactocentric spherical coordinate system (r, θ, ϕ) with r, the Galactocentric distance, increasing radially outwards, θ towards the South Galactic Pole and ϕ in the direction of Galactic counter-rotation. The Sun is assumed to be at the Galactic mid-plane (i.e. Z = 0 pc) and has a value of R₀ of 8.34 kpc (Reid et al. 2014). The former two coordinate systems are mainly used for disc stars and the spherical coordinate system is used for halo stars. The three velocity components are represented by (U, V, W) in the Cartesian system centred on the Sun, (V_R, V_ϕ, V_Z) in the Galactocentric cylindrical system and (V_r, V_θ, V_ϕ) in the Galactocentric spherical system.

2.2 LSS-GAC, SDSS/SEGUE and SDSS-III/APOGEE data

In this work, we use the second release of value-added catalogues of LSS-GAC (LSS-GAC DR2; Xiang et al. 2016), the ninth SDSS/SEGUE public data release (SDSS/SEGUE DR9; Ahn et al. 2012) and the twelfth SDSS-III/APOGEE public data release (SDSS-III/APOGEE DR12; Alam et al. 2015).

LSS-GAC is a major component of the on-going LAMOST Experiment for Galactic Understanding and Exploration (LEGUE; Deng et al. 2012). LSS-GAC aims to collect optical (λλ 3800–9000), low-resolution (R ∼ 1800) spectra under dark and grey lunar conditions for a statistically complete sample of over three million stars of all colours and of magnitudes 14.0 ≤ r < 17.8 mag (18.5 mag for limited fields), in a continuous sky area of ∼3400 square degrees, centred on the GAC, covering Galactic longitudes 150 < l < 210° and latitudes |b| < 30°. Over 2.5 million spectra of very bright stars (9 < r < 14.0 mag) in the equatorial Declination range −10 < δ < 60° will also be obtained under bright lunar conditions. The survey, initiated in the fall of 2012, is expected to last for 5 yr. Details about the survey, including the scientific motivations, target selections and data reduction, can be found in Liu et al. (2014) and Yuan et al. (2015). The stellar atmospheric parameters and line-of-sight velocity V_los of LSS-GAC targets are derived with the LAMOST Stellar Parameter Pipeline at Peking University (LSP3; Xiang et al. 2015) using template matching with empirical spectral libraries. LSP3 achieves an accuracy of 5.0 km s⁻¹, 150 K, 0.25 dex, 0.15 dex for V_los, effective temperature, surface gravity and metallicity [Fe/H], respectively, for spectra of FGK stars of signal-to-noise ratios (SNRs) per pixel at 4650 Å higher than 10.

SDSS/SEGUE survey, a Galactic extension of the SDSS-II/III surveys, has obtained a total of about 360 000 optical (λλ3820–9100), low-resolution (R ∼ 2000) spectra of Galactic stars at different distances, from 0.5 to 100 kpc (Yanny et al. 2009). The spectra are processed with SEGUE Stellar Parameter Pipeline (SSPP; Allende Prieto et al. 2008; Lee et al. 2008a,b; Smolinski et al. 2011), providing estimates of stellar parameters and V_los. The typical external errors of the stellar atmospheric parameters yielded by SSPP are ∼5 km s⁻¹ in V_los, 180 K in T_eff, 0.24 dex in log g and 0.23 dex in [Fe/H] (Smolinski et al. 2011).

The SDSS-III/APOGEE survey collects high-resolution (R ∼ 22 500) and high SNRs (∼100 per pixel) spectra in the near-infrared (H band; 1.51–1.70 μm) for over one hundred thousand stars (mainly the red giant stars) in the Milky Way. The scientific motivations and target selections are described in Majewski et al. (2015) and Zasowski et al. (2013), respectively. The data reduction and stellar parameter determinations are introduced by Nidever et al. (2015) and García Pérez et al. (2016), respectively. Calibrated with open clusters, the accuracy of APOGEE stellar parameters are better than 150 K in T_eff, 0.2 dex in log g and 0.1 dex in [Fe/H] (Mészáros et al. 2013). Benefited from the high resolution and high SNRs of APOGEE spectra, the random errors of V_los delivered for APOGEE stars are at the level of ∼0.1 km s⁻¹ with a zero-point uncertainty at the level of ∼0.5 km s⁻¹ (Nidever et al. 2015).

2.3 PRCG and HKG samples

Specifically, as mentioned earlier, we use PRCGs selected from LSS-GAC and SDSS-III/APOGEE to derive the RC in the (outer) disc and HKGs selected from SDSS/SEGUE to derive that in the halo. The PRCG stars are selected based on their positions in the metallicity dependent effective temperature-surface gravity and colour–metallicity stellar parameters spaces, as developed by Bovy et al. (2014) and applied to the APOGEE data. From SDSS DR12, a total of 19 937 PRCGs are identified. Huang et al. (2015a) apply the same method to the LSS-GAC DR2 and identify over 0.11 million PRCGs. The almost constant absolutes magnitude of PRCGs allow us to assign distances to the individual PRCGs with an accuracy of 5–10 per cent. For consistency of analysis, we have applied a zero-point correction to V_los values of LSS-GAC PRCG sample stars by adding a constant 2.7 km s⁻¹ to those values. This zero-point offset between LSS-GAC and APOGEE V_los values is derived from a comparison of the two sets of measurements for 1500 common PRCG sample stars. The correction is consistent with the finding of Xiang et al. (2015) who compare the values of V_los for the LSS-GAC DR1 and APOGEE full samples that have about 3800 common sources. To ignore the vertical motions in the following kinematic analysis and to minimize the contamination of halo stars, we have restricted the PRCG sample to stars of |b| ≤ 3° and [Fe/H] ≥−1.0. Finally, a total of 15 634 PRCGs are selected, with 11 572 stars from LSS-GAC and 3792 stars from APOGEE. As Fig. 1 shows, our PRCG sample spans from R = 6 to 16 kpc in the Galactic plane.

The HKGs used here are taken from the SEGUE K giant catalogue compiled by Xue et al. (2014). The catalogue provides unbiased distance estimates with a typical precision of 16 per cent, as well as values of V_los and metallicities for a total of 6036 K giant stars. To exclude possible contamination from the disc population, we have selected only those HKGs of |Z| ≥ 4 kpc from the catalogue. In addition, we cull of r ≤ 8.0 kpc considering that only a few stars are found inside that radius. Finally, a total of 5733 HKGs are selected. As Fig. 2 shows, the sample HKGs span a large range in Galactocentric radius r, from 8 to about 100 kpc.

Figure 2.

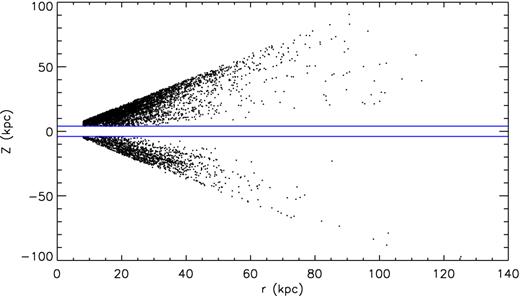
Spatial distribution of the SEGUE HKG sample stars in the r–Z plane. The two blue lines represent |Z| = 4 kpc.

Open in new tab Download slide

3 RC FROM PRCGs

3.1 Kinematical model

For the PRCGs, our approach to determine the RC is relied on the imprint that the Galactic rotation leaves in the observed heliocentric line-of-sight velocity |$V_{\rm los}^{\rm helio}$|⁠, as illustrated in Fig. 3. Specifically, the Galactic rotation yields a significant sinusoidal dependence on the Galactic longitude l of the observed |$V_{\rm los}^{\rm helio}$| at a certain value of R. Accordingly, one can derive the RC by fitting the observed |$V_{\rm los}^{\rm helio}$| as a function of l of the PRCG sample stars at different Galactocentric radii using a kinematical, axisymmetric model constructed as follows. Note that throughout the paper, the vertical motions are ignored and only those in the Galactic plane are considered since the sample includes only PRCGs of |b| ≤ 3° (see Section 2.3). As a result of the Galactic rotation, the average heliocentric line-of-sight velocities |$\overline{V}_{\rm los}^{\rm helio}$| of stars at a given position (R, l) in the Galactic plane in the Galactocentric cylindrical frame is given by

\begin{eqnarray} \overline{{V}}_{\rm los}^{\rm helio} &=& \overline{{V}}_{\phi } {(R)}\sin \beta - V_{\phi ,{\odot }}\sin l\nonumber\\ && +\, \overline{{V}}_{R} {(R)}\cos \beta + {V}_{R,{\odot }} \cos l, \end{eqnarray}

(1)

where |$\overline{{V}}_{\phi } {(R)}= V_{\rm c} {(R)}- V_{\rm a} {(R)}$|⁠. V_ϕ,⊙ and V_R,⊙ are the Sun's azimuthal velocity and the radial component of its peculiar velocity, respectively. |$\overline{V}_{{R}}$| is the mean radial motion. β is the angle between the Sun and the GC with respect to the given position and the value of this angle is given by (see Fig. 3),

\begin{equation} \beta = \sin ^{-1} \left(\frac{R_{0}}{R}\sin l\right). \end{equation}

(2)

V_a(R) is the so-called asymmetric drift and is given by (e.g. Binney & Tremaine 2008)

\begin{eqnarray} V_{\rm a} {(R)}&=& \frac{\sigma _{R}^{2} {(R)}}{2V_{\rm c} {(R)}} \Big[\frac{\sigma _{\phi }^{2} {(R)}}{\sigma _{R}^{2} {(R)}} - 1 + R \left(\frac{1}{R_{\rm d}} + \frac{2}{R_{\sigma }}\right) \nonumber\\ && - \frac{R}{\sigma _{R}^{2} {(R)}} \frac{\mathrm{\partial} \overline{V_{R}V_{Z}}}{\mathrm{\partial} Z}\Big], \end{eqnarray}

(3)

assuming that both the number density ν of tracers and their (projected) radial velocity dispersion σ_R are exponentially declining as a function of R with scalelengths of R_d and R_σ, respectively. The covariance |$\overline{V_{R}V_{Z}}$| does not show obvious variations with Z since our data are very close to the Galactic plane (Büdenbender, van de Ven & Watkins 2015). Therefore, we can ignore the last term in the above equation in the following analysis.

Figure 3.

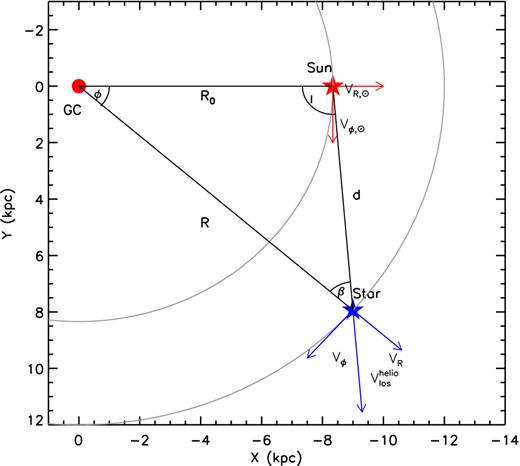
Schematic diagram showing the observed heliocentric line-of-sight velocity of a star in the Galactic plane at position (R, l), where R is the Galactocentric radius and l the Galactic longitude. The velocities are defined in cylindrical coordinates centred on the GC.

Open in new tab Download slide

From equation (1), |$\overline{V}_{\rm los}^{\rm helio}$| of stars at a certain R are essentially described by two trends of variations: (1) a sinusoidal dependence on the Galactic longitude governed by the mean Galactic rotation |$\overline{V}_{\phi }$| of the (warm) stellar populations at the given R and the azimuthal velocity of the Sun V_ϕ,⊙; (2) a cosinusoidal dependence on the Galactic longitude governed by the mean radial motion²|$\overline{V}_{{R}}$| of the (warm) stellar populations at the given R and the Sun's peculiar velocity in the radial direction V_R,⊙. For the first trend of variations, the mean Galactic rotation is a combination of the circular velocity (that we want to determine) and the asymmetric drift (that we need to correct for). With R_d, |$\sigma _{\phi }^{2} {(R)}$|/|$\sigma _{{R}}^{2} {(R)}$| and σ_R(R) known, the asymmetric drift V_a(R) becomes dependent on V_c only (see equation 3). The scalelength of the exponential disc, R_d, has been studied extensively and is generally known as about 2.5 kpc (e.g. Benjamin et al. 2005; Jurić et al. 2008). For |$\sigma _{\phi }^{2} {(R)}$|/|$\sigma _{{R}}^{2} {(R)}$|⁠, we assume it is independent of R and has a fixed value of 0.5, approximately the mean value of existing measurements in the solar neighbourhood (e.g. Dehnen & Binney 1998b; Bovy et al. 2012). The main unknown of equation (3) is σ_R(R), i.e. the value of the exponentially declining radial velocity dispersion as a function of R. Fortunately, from the existing data of APOGEE in the GC area (i.e. l ∼ 0°) and those from LSS-GAC in the GAC area (i.e. l ∼ 180°), we can measure the profile of σ_R directly from the line-of-sight velocity dispersion σ_los, since for those two areas, σ_R is essentially identical to σ_los. For this purpose, a total of ∼4900 PRCG disc stars of [Fe/H] ≥ −1.0 are selected from LSS-GAC and APOGEE with |l − 180| ≤ 3|$_{.}^{\circ}$|5 for the area towards the GAC and with |l| ≤ 3|$_{.}^{\circ}$|5 for that towards the GC. In doing so, we have also widened the cut on Galactic latitude by slightly, to |b| ≤ 5° in order to include more stars. Then we divide those stars into different bins in the radial direction and derive the line-of-sight velocity dispersion σ_los for each bin. The binsize in the radial direction is allowed to vary to contain a sufficient number of stars in each bin. We require that the binsizes are no smaller than 0.3 kpc and each bin contains at least 80 stars. As the blue dots in Fig. 4 show, σ_los shows a clear trend of declining with R. The profile is not well constrained, given the limited range of R covered, 10 ≤ R ≤ 14 kpc (no data points available from APOGEE). To better constrain the profile, we have replaced the requirement |b| ≤ 5° with |Z| ≤ 0.5 kpc in selecting the stars. For distant stars, the effect of the new requirement is similar to the original one, but it allows us to include more nearby stars of relative high Galactic latitudes that are still close enough to the Galactic plane such that their vertical motions can be ignored. Again, we derive σ_los by binning the stars in the radial direction and the results are overplotted in Fig. 4 by red dots. As expected, the new profile is similar to the original one for R ≥ 10 kpc, except that now it has data points in the inner disc (R ∼ 7–10 kpc). To quantitively describe the profile of σ_R, we fit the measured data points of σ_los obtained with the requirement of |Z| ≤ 0.5 kpc with an exponential function,

\begin{equation} \sigma _{{R}} {(R)}= \sigma _{{R}_{0}}exp \left(-\frac{R-R_{0}}{R_{\sigma }}\right), \end{equation}

(4)

where |$\sigma _{{R}_{0}}$| is the radial velocity dispersion at the solar position and R_σ the scalelength. As shown by the red line in Fig. 4, the best fit yields |$\sigma _{{R}_{0}} = 35.32 \pm 0.52$| km s⁻¹ and R_σ = 16.40 ± 1.25 kpc. The value of |$\sigma _{{R}_{0}}$| found here is consistent with the previous measurements for stars in the solar neighbourhood (e.g. Dehnen & Binney 1998b; Bensby, Feltzing & Lundström 2003; Soubiran, Bienaymé & Siebert 2003). The value of R_σ agrees well with the recent determination of Sharma et al. (2014), who report R_σ ∼ 14 kpc based on the RAVE (Steinmetz et al. 2006) data.

Figure 4.

Profile of line-of-sight velocity dispersion given by PRCG disc stars of [Fe/H] ≥ −1.0 in the direction of GC (l ∼ 0°) selected from APOGEE and in the direction of GAC (l ∼ 180°) selected from LSS-GAC with the requirement of |b| ≤ 5° (blue dots) or |Z| ≤ 0.5 kpc (red dots). The red line represents an exponential best fit to the data points of requirement |Z| ≤ 0.5 kpc as described by equation (4).

Open in new tab Download slide

In principle, the mean radial motion |$\overline{V}_{{R}}$| involved in the second trend of variations should be zero under our axisymmetric assumption. However, based on the RAVE data, Siebert et al. (2011) and Williams et al. (2013) recently show that the mean radial motion |$\overline{V}_{{R}}$| in the solar neighbourhood is not zero and has a gradient in the radial direction. To accomodate the possibility of a non-zero mean radial motion, we have left |$\overline{V}_{{R}}$| as a free parameter in our kinematical modelling. We note that the effect of mean radial motion on |$\overline{V}_{\rm los}^{\rm helio}$| can be easily disentangled from that of mean Galactic rotation considering that they have an opposite dependence on the Galactic longitude. Finally, we fix the values of the azimuthal velocity of the Sun V_ϕ,⊙ (involved in the first trend of variations), as well as the radial peculiar velocity, V_R,⊙ (involved in the second trend of variations), using the measurements in the literature. For V_ϕ,⊙, it is identical to Ω_⊙R₀. As mentioned earlier, R₀ has been set to 8.34 kpc (Reid et al. 2014). The value of Ω_⊙ is well constrained by the proper motions of Sgr A* measured by Reid & Brunthaler (2004). For V_R,⊙, we take the value of −7.01 km s⁻¹ determined by Huang et al. (2015b). Table 1 summaries all the fixed parameters employed in our kinematical model.

Table 1.

Open in new tab

Parameters of the kinematical model employed.

Parameter	Adopted value
R_d (kpc)	2.5 ± 0.5
\|$\sigma _{\phi }^{2}$\|/\|$\sigma _{R}^{2}$\|	0.5 ± 0.3
R_σ (kpc)	16.40 ± 1.25
\|$\sigma _{R_{0}}$\| (km s⁻¹)	35.32 ± 0.52
R₀ (kpc)	8.34 ± 0.16
Ω_⊙ (km s⁻¹ kpc⁻¹)	30.24 ± 0.11
V_R,⊙ (km s⁻¹)	−7.01 ± 0.20

Parameter	Adopted value
R_d (kpc)	2.5 ± 0.5
\|$\sigma _{\phi }^{2}$\|/\|$\sigma _{R}^{2}$\|	0.5 ± 0.3
R_σ (kpc)	16.40 ± 1.25
\|$\sigma _{R_{0}}$\| (km s⁻¹)	35.32 ± 0.52
R₀ (kpc)	8.34 ± 0.16
Ω_⊙ (km s⁻¹ kpc⁻¹)	30.24 ± 0.11
V_R,⊙ (km s⁻¹)	−7.01 ± 0.20

Table 1.

Open in new tab

Parameters of the kinematical model employed.

Parameter	Adopted value
R_d (kpc)	2.5 ± 0.5
\|$\sigma _{\phi }^{2}$\|/\|$\sigma _{R}^{2}$\|	0.5 ± 0.3
R_σ (kpc)	16.40 ± 1.25
\|$\sigma _{R_{0}}$\| (km s⁻¹)	35.32 ± 0.52
R₀ (kpc)	8.34 ± 0.16
Ω_⊙ (km s⁻¹ kpc⁻¹)	30.24 ± 0.11
V_R,⊙ (km s⁻¹)	−7.01 ± 0.20

Parameter	Adopted value
R_d (kpc)	2.5 ± 0.5
\|$\sigma _{\phi }^{2}$\|/\|$\sigma _{R}^{2}$\|	0.5 ± 0.3
R_σ (kpc)	16.40 ± 1.25
\|$\sigma _{R_{0}}$\| (km s⁻¹)	35.32 ± 0.52
R₀ (kpc)	8.34 ± 0.16
Ω_⊙ (km s⁻¹ kpc⁻¹)	30.24 ± 0.11
V_R,⊙ (km s⁻¹)	−7.01 ± 0.20

3.2 Fitting and results

With the asymmetric drift properly modelled and a series of parameters fixed as described above, we are now left with two free parameters, i.e. the circular velocity V_c(R) and the mean radial motion |$\overline{V}_{{R}} {(R)}$|⁠, to be determined by fitting |$V_{\rm los}^{\rm helio}$|(l) measurements of our PRCG sample. To do so, we divide the stars into annuli in the radial direction with width 0.5 kpc from R₀ to 12.34 kpc, with width 1 kpc from 12.34 to 14.34 kpc and with width 2 kpc for the last annulus, i.e. 14.34 < R < 16.34 kpc. The choice of the width are consistent with the typical distance uncertainties of our PRCG sample (i.e. 5 per cent). For most annuli, the stars span from ∼100° to 210° in Galactic longitude, wide enough to simultaneously obtain robust estimates of V_c(R) and |$\overline{V}_{{R}} {(R)}$|⁠. Stars of R ≤ R₀ in our sample are excluded given their narrow range of distribution in Galactic longitude. For each annulus, with the kinematical model described above, we fit the |$\overline{V}_{\rm los}^{\rm helio}$| as a function of Galactic longitude. To calculate the average heliocentric line-of-sight velocities at different Galactic longitudes, |$\overline{V}_{\rm los}^{\rm helio}$| (l) measurements, we divide the stars of each annulus into bins of Galactic longitude. The binsize is allowed to vary but set to be no less than 2|$_{.}^{\circ}$|5 and each bin contains no less than 20 stars. Finally, the best-fitting values of V_c(R) and |$\overline{V}_{{R}} {(R)}$| of each annulus are found by non-linear fitting that minimizes χ² defined as

\begin{equation} \chi ^{2} = \sum _{i=1}^{N} \frac{\left[\overline{V}_{\rm los, obs}^{\rm helio} (l_{i}, R) - \overline{V}_{\rm los, model}^{\rm helio} (l_{i}, R |\,{\boldsymbol {p}})\right]^{2}}{ \sigma _{\overline{V}_{\rm los, obs}^{\rm helio} (l_{i})}^{2}}, \end{equation}

(5)

where N is the total number of data points to be fitted, |$\sigma _{\overline{V}_{\rm los, obs}^{\rm helio} (l_{i})}$| is the uncertainty of |$\overline{V}_{\rm los}^{\rm helio}$| (l_i), l_i the mean longitude of the ith Galactic longitude bin, and |${\boldsymbol p}$| represents the parameters in the kinematical model (see equation 1), including those of fixed values as listed in Table 1 and, the circular velocity and mean radial motion to be derived from the fitting.

The fits are presented in Fig. 5. The derived RC, i.e. circular velocity V_c as a function of R, is presented in Fig. 6. To properly evaluate the errors of the derived V_c, we consider not only the fitting error |$\sigma _{V_{\rm c}}^{\rm fit}$| but also the error |$\sigma _{V_{\rm c}}^{\rm para}$| that propagates from the uncertainties of parameters fixed in the kinematical model (see Table 1) as measured by previous or current work. Values of the latter are calculated using Monte Carlo simulations. In practice, we obtain a distribution of the derived values of V_c by repeating the fitting 5000 times, and infer the error |$\sigma _{V_{\rm c}}^{\rm para}$| from the distribution. For each fit, values of those fixed parameters are randomly sampled assuming Gaussian distributions of values with uncertainties as listed in Table 1. The final error of the derived V_c is then given by |$\sqrt{(\sigma _{V_{\rm c}}^{\rm fit})^{2} + (\sigma _{V_{\rm c}}^{\rm para})^{2}}$|⁠. The typical error of RC thus derived is only 5–7 km s⁻¹. The relatively large errors (few tens km s⁻¹) in the few annuli of large R are due to the relatively poor sampling in Galactic longitude for those annuli. The newly derived RC shows a smooth trend of variations with R, except for a clear dip at R around 11 kpc. To infer the circular velocity at the solar position, V_c(R₀), we apply a linear fit to the data point inside the dip, i.e. R ≤ 11 kpc (Fig. 6). The fit yields V_c(R₀) = 239.89 ± 5.92 km s⁻¹, along with a local estimate of the slope of RC, i.e. ∂V_c/∂R, of −6.85 ± 3.90 km s⁻¹ kpc⁻¹. Combining this estimate of V_c(R₀) and the known V_{ϕ, ⊙}, we find an azimuthal peculiar velocity of the Sun, V_⊙, of 12.09 ± 7.61 km s⁻¹. As defined in Section 2.1, the current analysis assumes R₀ = 8.34 kpc as determined by Reid et al. (2014). Actually, as evident from equation (1), the current data set also provide some constraints on R₀ and therefore can be used to check whether they are consistent with the adopted value of R₀. For this purpose, we have calculated |$\chi ^{2}_{\rm tot}$|⁠, the sum of the reduced χ² values of the fit for the 11 annuli defined in Fig. 5, for various assumed values of R₀ ranging from 7.2 to 10.0 kpc with a constant step 0.1 kpc. The results, plotted in Fig. 7, show a clear minimum around 8.3 kpc, identical to the value assumed above. Finally, we present the mean radial motions |$\overline{V}_{{R}} {(R)}$| deduced from the fitting in Fig. 8. The mean radial motion increases from ∼1 km s⁻¹ at R = 8.5 kpc to ∼9 km s⁻¹ at R = 12.5 kpc, and then decrease to ∼4 km s⁻¹ at R = 15 kpc. This trend of variations of |$\overline{V}_{R}$| found here, together with a negative gradient of the radial motion found previously from the RAVE data for 7 ≲ R ≲ 8.5 kpc (Siebert et al. 2011; Williams et al. 2013), suggest that the value of mean radial motion oscillates with R. This interesting result is worth of further investigations but is out of the scope of the current study.

$Distributions of the heliocentric line-of-sight velocities ($V_{\rm los}^{\rm helio}$) as a function of the Galactic longitude in the individual annuli of R for the PRCG sample. Back and red dots represent LSS-GAC and APOGEE PRCGs, respectively. Blue dots in each annulus represent the mean heliocentric line-of-sight velocities of the individual Galactic longitude bins. Red lines show the best fits to the data of the kinematical model described in the text.$

Figure 5.

Distributions of the heliocentric line-of-sight velocities (⁠|$V_{\rm los}^{\rm helio}$|⁠) as a function of the Galactic longitude in the individual annuli of R for the PRCG sample. Back and red dots represent LSS-GAC and APOGEE PRCGs, respectively. Blue dots in each annulus represent the mean heliocentric line-of-sight velocities of the individual Galactic longitude bins. Red lines show the best fits to the data of the kinematical model described in the text.

Open in new tab Download slide

Figure 6.

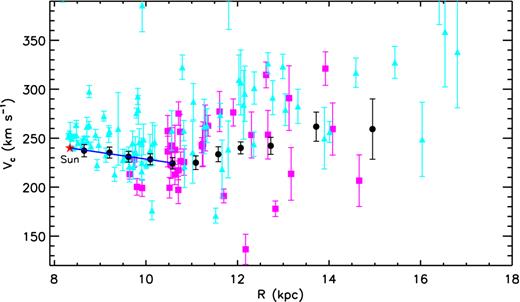
Circular velocities of the Milky Way derived from our PRCG sample for the Galactocentric radius range 8 ≤ R ≤ 16 kpc (black dots). Blue line is a linear fit to the RC for R ≤ 11 kpc. The red star denotes the circular velocity at the solar position as predicted by the linear fit. Also overplotted cyan triangles and magenta boxes represent, respectively, measurements based H ii regions (Fich et al. 1989) and carbon stars of 60 ≤ l ≤ 150° (Demers & Battinelli 2007).

Open in new tab Download slide

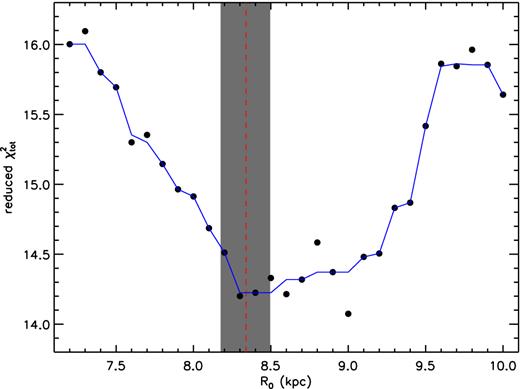
$$\chi ^{2}_{\rm tot}$, sum of the reduced χ2 values of fit for the 11 annuli defined in Fig. 5, as a function of the assumed value of R0. The blue line connecting the dots has been smoothed over three adjacent points. Red dashed line represents the adopted value 8.34 kpc of R0 and the 1σ error of the adopted value of R0 as estimated by Reid et al. (2014) is shown in grey shade.$

Figure 7.

|$\chi ^{2}_{\rm tot}$|⁠, sum of the reduced χ² values of fit for the 11 annuli defined in Fig. 5, as a function of the assumed value of R₀. The blue line connecting the dots has been smoothed over three adjacent points. Red dashed line represents the adopted value 8.34 kpc of R₀ and the 1σ error of the adopted value of R₀ as estimated by Reid et al. (2014) is shown in grey shade.

Open in new tab Download slide

Figure 8.

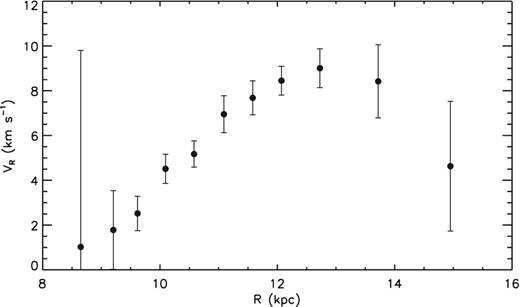
Mean radial motion as a function of R deduced from the PRCG sample.

Open in new tab Download slide

3.3 Discussion

3.3.1 Systematics

To assess the systematic uncertainties of the newly derived RC, we first examine whether our choices of values of those fixed parameters in the kinematical model affect the results significantly. To check the possible effects of |$\sigma _{\phi }^{2}$|/|$\sigma _{R}^{2}$| on the derived RC, we have tried two values, i.e. a lowest value 0.35 and a highest value 0.70 reported in the literature, and redo the fitting. The relative differences between the original RC, i.e. V_c, that derived assuming the canonical values of those parameters, and those derived after changing the canonical value of |$\sigma _{\phi }^{2}$|/|$\sigma _{{R}}^{2}$| to the two extreme values above, denoted by |$V^\ast _{\rm c}$|⁠, are presented in Fig. 9. The differences are all smaller than 0.5 per cent (∼1.25 km s⁻¹). Similarly, by choosing a large-scale length R_d = 3.7 kpc from Chang, Ko & Peng (2011) and an almost flat radial velocity dispersion profile (⁠|$\sigma _{R_{0}} = 31.4$| km s⁻¹ and R_σ = 270 kpc) from Bovy et al. (2012), we find that the resultant changes in our results (cf. Fig. 9) are again very small, less than 2 per cent (∼5 km s⁻¹). As discussed in the above section, our adopted value of R₀ is self-consistent with the current data set, suggesting our derived RC should suffer from negligible systematics, if any, as a result of our chosen value of R₀. Finally, at present, the best constraint on the V_ϕ,⊙ comes from the proper motion measurements of Sgr A*, yielding a value that is also in accordance with other most recent independent determinations (e.g. Bovy et al. 2012; Reid et al. 2014; Sharma et al. 2014). Therefore, we have assumed that there are no systematic errors arising from our adopted value of V_ϕ,⊙ in deriving the RC. To conclude, the systematic errors of RC resultant as a consequence of our adopted canonical values of parameters are likely to be smaller than 2 per cent (∼5 km s⁻¹).

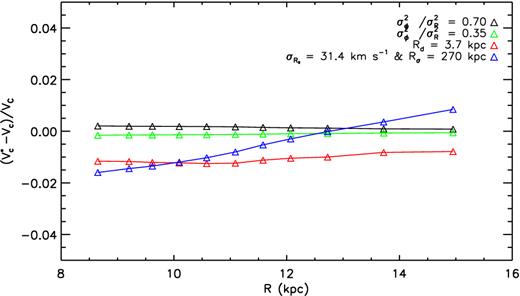
$Relative difference, $(V^{{\ast }}_{{\rm c}} - V_{\rm c})/V_{\rm c}$, between the value of RC deduced by varying the assumed value of parameters fixed in the kinematical model, i.e. $V^\ast _{\rm c}$, and that derived assuming the canonical values of those parameters, i.e. Vc. Different colours of triangles represent the results for different sets of parameters as labelled in the top-right corner of the diagram. Lines of different colours are used to connect triangles of the same colour to guide the eye.$

Figure 9.

Relative difference, |$(V^{{\ast }}_{{\rm c}} - V_{\rm c})/V_{\rm c}$|⁠, between the value of RC deduced by varying the assumed value of parameters fixed in the kinematical model, i.e. |$V^\ast _{\rm c}$|⁠, and that derived assuming the canonical values of those parameters, i.e. V_c. Different colours of triangles represent the results for different sets of parameters as labelled in the top-right corner of the diagram. Lines of different colours are used to connect triangles of the same colour to guide the eye.

Open in new tab Download slide

The kinematical model described above assumes a simplified Gaussian distribution of azimuthal velocity V_ϕ. In reality, for stars of warm population (such as those of our PRCG sample), the distribution of V_ϕ is significantly skewed (e.g. Schönrich & Binney 2012, hereafter SB12). However, the simplification is expected to have only minor effects on our derived RC. As pointed out by Bovy et al. (2012), only at the TP the non-Gaussianity of V_ϕ distribution is fully visible as at those points the line-of-sight velocity is identical to V_ϕ. The PRCG sample employed in the current study are mostly spread over the Galactic longitudes between 90° and 240°. There is no TP in within this Galactic longitude range, hence the skewness of V_ϕ distribution is much less significant for our sample. To check the validity of the above simplification, we have further performed tests using mock-data, as presented in Appendix. When generating the mock-data sets, the line-of-sight velocities are no longer sampled assuming a Gaussian distribution of V_ϕ but using a distribution calculated from the analytic formula given by SB12 (that well describes the skewness of V_ϕ distribution). A detailed description of the mock-data sets and the tests can be found in Appendix. We fit the mock-data sets using the above kinematical model (assuming a simplified Gaussian distribution of V_ϕ). The results show that the simplification does not introduce any significant bias in the derived RC.

In constructing the kinematical model, we have assumed an axisymmetric Galactic disc. In reality, there are prominent non-axisymmetric structures in the Milky Way, such as the central bar and spiral arms, that may bias the derived RC. In principle, as discussed earlier, the PRCGs belong to relatively old and warm populations, and consequently should be relatively insensitive to perturbations by non-axisymmetric structures. It is thus notable that, for the current PRCG sample, we have detected a non-zero mean radial motions, increasing from ∼1 km s⁻¹ at R = 8.5 kpc to ∼9 km s⁻¹ at R = 12.5 kpc, and then decreasing to ∼4 km s⁻¹ at R = 15 kpc (see Fig. 8). Generally, non-axisymmetric structures could induce such streaming motions, both in the radial and azimuthal directions. Therefore, the possibility that the derived RC is affected by the non-axisymmetric structures cannot be ruled out, considering that the trend seen in |$\overline{V}_{R}$| may be caused by such perturbations. By numerical simulations, one can quantitatively examine the effects of non-axisymmetric perturbations on warm populations, such as the PRCGs analysed here, and figure out how large are the effects on the derived RC. However, we leave this to future work.

Finally, we note that the systematics caused by uncertainties in our determinations of distance and V_los of our PRCG sample stars are likely to be negligible, given the high accuracies of the current distance and V_los estimates.

3.3.2 Comparisons with other work

As introduced, there have already many determinations of the RC in the disc based on data of various disc tracers of cold populations. To compare those earlier results with ours, we have used the data (i.e. distances, radial velocities and errors) of H ii regions published by Fich et al. (1989) and those of carbon stars of 60 ≤ l ≤ 150° published by Demers & Battinelli (2007), and recalculate the circular velocities, adopting the same value of R₀ assumed in the current study, the value of V_c(R₀) deduced from the current study, as well as the solar peculiar velocities in the radial and vertical directions (U_⊙, W_⊙) from Huang et al. (2015b) for consistency reason. The results are presented in Fig. 6. In generally, they show a trend of variations similar to our new measurements but with much large scatters. The large scatters are possibly due to the large distance errors in those data, or the perturbations of the non-axisymmetric structures, or both of them. More recently, Bovy et al. (2012) derive the RC for R from 4 to 14 kpc with a kinematical model³ quite similar to ours, using data of 3365 stars of warm populations selected from APOGEE. In their analysis, they have assumed a flat and a power-law form of the RC when fitting the data. Both approaches yield similar results and give V_c(R₀) = 218 ± 6 km s⁻¹. This estimate of circular velocity at the solar position is substantially smaller than our value of V_c(R₀) = 239.89 ± 5.92 km s⁻¹, which is in excellent agreement with most of the recent independent determinations (e.g. McMillan 2011; Schönrich 2012; Reid et al. 2014; Sharma et al. 2014). Their analysis also yields an estimate of V_⊙ of 26 ± 3 km s⁻¹. A very similar value, about 24 km s⁻¹, is obtained by Bovy et al. (2015), using a sample of 8155 PRCG stars within 250 pc from the Galactic mid-plane selected from the APOGEE, quite similar to the sample employed in the current analysis. Both estimates are more than 10 km s⁻¹ higher than the values estimated from stars in the solar neighbourhood (e.g. Schönrich, Binney & Dehnen 2010; Huang et al. 2015b) as well as the value deduced in the current study. We note however, the analyses of both Bovy et al. (2012, 2015) assume a certain shape of the RC – a flat RC in fact. The analyses also adopt a flat radial velocity dispersion profile. Both assumptions have a major impact on the estimated value of V_⊙ yet are not supported by the current data.

3.3.3 The dip at R ∼ 11 kpc

Our newly derived RC shows a prominent dip at R ∼ 11 kpc. Such a similar feature (dip at R ∼ 11 kpc) of RC has also been noted and studied by many previous studies (e.g. Sikivie 2003; Duffy & Sikivie 2008; Sofue et al. 2009; de Boer & Weber 2011). Sikivie (2003) and Duffy & Sikivie (2008) interpret the dip by the existence of hypothetical caustic rings of DM in the Galactic plane, with ring radii predicted at |$a_{n} \simeq \frac{40\,{\rm kpc}}{n}$| (n = 1, 2, 3, 4, …) for the Milky Way. In this model, the n = 3 hypothetical caustic ring is located at a₃ ≃ 13 kpc, and is interpreted to be responsible for the dip of RC at R ∼ 11 kpc. Alternatively, de Boer & Weber (2011) fit the dip with a donut-like ring of DM in the Galactic plane and conclude that the ring is actually at R ∼ 12.4 kpc with a total mass of ∼10¹⁰M_⊙. We will address this feature as revealed by our more accurate RC in a quantitatively way in Section 6. Finally, we note that the possibility that some unknown perturbations, such as those induced by non-axisymmetric structures discussed above, are actually responsible for this localized dip at 11 kpc, cannot be ruled out, considering that the derived RC is based on survey data that encompass only limited volumes of the whole Galaxy.

4 RC FROM HKGS

4.1 Spherical jeans model and results

To derive the RC in the halo region, the spherical Jeans equation is applied to the HKG stars to estimate the circular velocity V_c(R) in equilibrium through the relation,

\begin{equation} V_{\rm c}^{2} {(R)}= - \sigma _{r}^{2} \left(\frac{{\rm d}\,{\rm ln}\nu }{{\rm d}\,{\rm ln}r} + \frac{{\rm d}\,{\rm ln}\sigma _{r}^{2}}{{\rm d}\,{\rm ln}r} + 2\beta \right), \end{equation}

(6)

where σ_r is the radial velocity dispersion of the HKGs and ν the number density of HKGs. The velocity anisotropy parameter β is defined as

\begin{equation} \beta = 1 - \frac{\sigma _{\theta }^{2} + \sigma _{\phi }^{2}}{2\sigma _{r}^{2}}, \end{equation}

(7)

where σ_θ and σ_ϕ are the polar and azimuthal velocity dispersions in the spherical coordinate system defined in Section 2.1.

Recent extensive studies show that the number density of halo stellar population follows a broken power-law (ν ∝ r^−α) distribution with a minor- to major-axis ratio q = 0.5–1, and a shallow slope of α ∼ 2–3 out to a break radius r_b ∼ 16–27 kpc followed by a steeper slope of α ∼ 3.8–5 beyond r_b (e.g. Bell et al. 2008; Watkins et al. 2009; Deason 2011; Sesar et al. 2011, 2013; Faccioli et al. 2014; Xue et al. 2015). Similar to Kafle et al. (2014), here we adopt a spherical (i.e. q = 1), broken power-law distribution for the stellar halo, assuming α = 2.4 for the inner halo (r ≤ r_b) and α = 4.5 for the outer halo (r > r_b) from Watkins et al. (2009). In agreement with the recent measurements (e.g. Bell et al. 2008; Sesar et al. 2013; Kafle et al. 2014; Xue et al. 2015), we set the broken radius r_b to 20 kpc.

As mentioned earlier, determinations of the RC for the halo region suffer from the so-called RC–anisotropy degeneracy because of the poorly constrained velocity anisotropy parameter β, especially for the outer halo. There are however some recent progress in the measurements of β to large distances, using direct or indirect methods that help break the degeneracy. For the inner halo (r ≤ 12 kpc), β is well, both directly and indirectly, measured and is found to have a radial biased value around 0.5 (e.g. Smith et al. 2009; Brown et al. 2010; Kalfe et al. 2012). For the region 12 < r ≤ 18 kpc, based on a sample of ∼4600 BHB stars, Kafle et al. (2012) find that β declines steadily, reaching a tangential value of ∼− 1.1 at ∼17 kpc. From the proper motions of main-sequence stars measured by HST, Deason et al. (2013) find the halo is isotropic (⁠|$\beta = 0.0^{+0.2}_{-0.4}$|⁠) at r = 24 ± 6 kpc. The halo beyond 50 kpc is again found to be radially biased with β = 0.4 ± 0.2, based on the most recent study of Kafle et al. (2014). Table 2 summarizes these latest measurements of β. The table is used to infer β at any given r by interpolation in our following analysis.

Table 2.

Open in new tab

The velocity anisotropy parameter β at different radii.

r	β
(kpc)
[8.0, 12.0]	\|$+0.50^{+0.10}_{-0.10}$\|
13.2	\|$+0.47^{+0.23}_{-0.29}$\|
14.0	\|$+0.21^{+0.32}_{-0.23}$\|
15.1	\|$-0.23^{+0.51}_{-0.60}$\|
16.1	\|$-0.64^{+0.68}_{-0.87}$\|
16.9	\|$-1.08^{+0.78}_{-1.01}$\|
17.9	\|$-0.62^{+0.74}_{-0.98}$\|
[18.0, 30.0]	\|$+0.00^{+0.20}_{-0.40}$\|
>50	\|$+0.40^{+0.20}_{-0.20}$\|

r	β
(kpc)
[8.0, 12.0]	\|$+0.50^{+0.10}_{-0.10}$\|
13.2	\|$+0.47^{+0.23}_{-0.29}$\|
14.0	\|$+0.21^{+0.32}_{-0.23}$\|
15.1	\|$-0.23^{+0.51}_{-0.60}$\|
16.1	\|$-0.64^{+0.68}_{-0.87}$\|
16.9	\|$-1.08^{+0.78}_{-1.01}$\|
17.9	\|$-0.62^{+0.74}_{-0.98}$\|
[18.0, 30.0]	\|$+0.00^{+0.20}_{-0.40}$\|
>50	\|$+0.40^{+0.20}_{-0.20}$\|

Table 2.

Open in new tab

The velocity anisotropy parameter β at different radii.

r	β
(kpc)
[8.0, 12.0]	\|$+0.50^{+0.10}_{-0.10}$\|
13.2	\|$+0.47^{+0.23}_{-0.29}$\|
14.0	\|$+0.21^{+0.32}_{-0.23}$\|
15.1	\|$-0.23^{+0.51}_{-0.60}$\|
16.1	\|$-0.64^{+0.68}_{-0.87}$\|
16.9	\|$-1.08^{+0.78}_{-1.01}$\|
17.9	\|$-0.62^{+0.74}_{-0.98}$\|
[18.0, 30.0]	\|$+0.00^{+0.20}_{-0.40}$\|
>50	\|$+0.40^{+0.20}_{-0.20}$\|

r	β
(kpc)
[8.0, 12.0]	\|$+0.50^{+0.10}_{-0.10}$\|
13.2	\|$+0.47^{+0.23}_{-0.29}$\|
14.0	\|$+0.21^{+0.32}_{-0.23}$\|
15.1	\|$-0.23^{+0.51}_{-0.60}$\|
16.1	\|$-0.64^{+0.68}_{-0.87}$\|
16.9	\|$-1.08^{+0.78}_{-1.01}$\|
17.9	\|$-0.62^{+0.74}_{-0.98}$\|
[18.0, 30.0]	\|$+0.00^{+0.20}_{-0.40}$\|
>50	\|$+0.40^{+0.20}_{-0.20}$\|

Finally, we determine the last unknown term in the Jeans equation – the profile of radial velocity dispersion. To do so, we first convert the observed |$V_{\rm los}^{\rm helio}$| to the Galactic standard of rest (GSR) frame by

\begin{eqnarray} V_{\rm GSR} = V_{\rm los}^{\rm helio} + {\rm U}_{{\odot }}\cos b \cos l + V_{\phi , {\odot }}\cos b \sin l + {\rm W}_{{\odot }}\sin b, \nonumber\\ \end{eqnarray}

(8)

where U_⊙ and W_⊙ are taken from Huang et al. (2015b), and V_ϕ,⊙ is again set to the value as adopted in Section 3.1. Next, we calculate the GSR line-of-sight velocity dispersion, σ_GSR, by dividing HKGs into different radial bins. The binsize in radial direction is allowed to vary such that each bin contains at least 40 stars. We require that the radial binsizes are no smaller than 1.0 kpc for r ≤ 20 kpc, 2.5 kpc for 20 < r ≤ 50 kpc and 5.0 kpc for r > 50 kpc, respectively, to match with the typical distance uncertainties of our HKG sample stars (i.e. 16 per cent). The results are presented in Fig. 10. Then values of the radial velocity dispersion σ_r can be obtained by applying a correction factor (Dehnen et al. 2006) to σ_GSR,

\begin{equation} \sigma _{{r}} = \frac{\sigma _{\rm GSR}}{\sqrt{1 - \beta A(r)}}, \end{equation}

(9)

where

\begin{equation} A(r) = \frac{r^{2} + R_{0}^{2}}{4r^{2}} - \frac{(r^{2} - R_{0}^{2})^{2}}{8r^{3}R_{0}}{\rm ln}\left|\frac{r+R_{0}}{r-R_{0}}\right|. \end{equation}

(10)

The profile of σ_r, estimated from the above equations, is also presented in Fig. 10. The uncertainty of σ_GSR for each bin is estimated by the classical method, |$\Delta \sigma _{\rm GSR} = \sqrt{1/[2(N-1)]}\sigma _{\rm GSR}$|⁠, where N is the total number of stars in the bin. Then the uncertainty of σ_r for each bin is propagated from that of σ_GSR using equation (9). To account for possible uncertainties induced by the correction factor for σ_r, we run Monte Carlo simulations. This is realized using the uncertainties of the input quantities (β, r and σ_GSR) in equation (9) for a given bin and randomly sampling those quantities assuming Gaussian error distributions. For each bin, we obtain a distribution of σ_r by repeating the sampling 1000 times, and infer the error of σ_r for that bin from the distribution. Similar to the density profile, the profile of σ_r also shows a broken radius around 20 kpc, with a steeper slope inside the broken radius than beyond. To better describe the profile, we apply a double power-law fit (σ_r ∝ r^−γ) to the profile with a broken radius of 20 kpc. The fit yields an inner slope of γ = 0.43 and an outer slope of γ = 0.24.

Figure 10.

Velocity dispersions derived from the HKG sample. Green triangles and black circles represent the values of line-of-sight velocity dispersion in the GSR frame σ_GSR, and those of radial velocity dispersions σ_r, respectively. The dotted line indicates the broken radius (r = 20 kpc) of the σ_r profile. Red and blue lines show the best power-laws fits to the profile within and beyond the broken radius, respectively.

Open in new tab Download slide

We now can obtain the RC by solving the spherical Jeans equation (6) with values of ν, β and σ_r for the HKG sample properly specified above. The derived RC is presented in Fig. 11. The uncertainty of circular velocity V_c in each bin is again calculated using a Monte Carlo approach similar to that described above. The typical errors of the RC are several tens km s⁻¹. The largest errors found at radii around 20 kpc are due to the poorly constrained velocity anisotropy parameter β around that region. In the region 8 ≤ r ≤ 25 kpc, the RC shows two localized dips at radii ∼11 and ∼19 kpc, respectively. The inner one is exactly that already found above from the PRCG sample.

Figure 11.

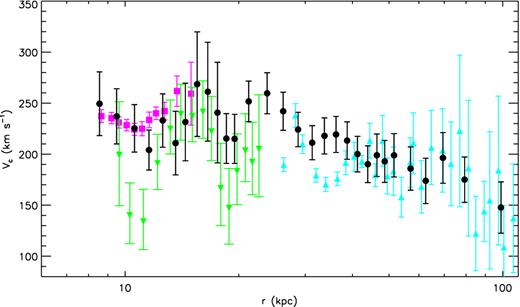
Circular velocities of the Milky Way derived from the HKG sample for the range 8 ≤ r ≤ 100 kpc (black circles). Magenta boxes are values derived from the PRCG sample. Also overplotted as green downward triangles and cyan triangles are, respectively, determinations taken from Kafle et al. (2012) and BCK14.

Open in new tab Download slide

4.2 Discussion

4.2.1 Systematics

As evident from equation (6), varying the power-law indexes of stellar density of the inner and/or the outer halo change the circular velocities derived systematically. To explore the sensitivity of the newly derived RC to the density profile adopted, we have repeated the analysis using another two sets of indexes, corresponding, respectively, the lower and upper limits allowed by the current available measurements. For the lower limit, we use a power-law index of 2.0 and 3.8 for the inner and outer halo, respectively. We find that the circular velocities thus derived are on average 8 per cent smaller than the original values in both the inner and outer halo regions. For the upper limit, we adopt a power-law index of 3.0 and 5.0 for the inner and outer halo, respectively, and find that the circular velocities deduced in the inner and outer halo regions are, respectively, 9 and 6 per cent larger than the original ones on average. Thus, the errors of the newly derived RC resultant from the possible uncertainties in density profile are probably less than 10 per cent as a whole (i.e. ∼20 km s⁻¹), which are comparable to the random errors of the newly derived RC.

In the current study, we assume that all the HKGs in our sample are of a single halo population in the Jeans equation. Recently, some studies (Hattori et al. 2013; Kafle et al. 2013) claim that there is a correlation between the metallicity and kinematics of halo stars such that metal-rich ([Fe/H] > −2) and metal-poor ([Fe/H] < −2) halo stars may actually belong to different populations. The correlation, if exists, may potentially affect our analysis. On the other hand, a revisit of the problem by Fermani & Schörich (2013) find no correlation at all. In the future, with even larger halo samples than the current available, it is possible to examine this effect quantitatively by modelling metal-rich and metal-poor populations separately using the Jeans equation.

Finally, we note that the current analysis assumes a spherical stellar halo. It may well be that the stellar halo is not spherical. We will however leave the determination of the RC in a non-spherical halo to future studies.

4.2.2 Comparisons with other work

We first compare the circular velocities derived from the HKG sample to those from the PRCG sample in the overlap region 8 ≤ r ≤ 15 kpc. As Fig. 11 shows, they are in good agreement within the errors and the dip at r ∼ 11 kpc discussed above is again revealed by data from the HKG sample. The close agreement between the two sets of independent determinations suggests the robustness of our analysis based on two types of tracer of different populations. Recently, Kafle et al. (2012) estimate the RC in the region 8 ≤ r ≤ 25 kpc with the spherical Jeans equation using 4664 BHB stars. Their results are overplotted in Fig. 11. Again, as Fig. 11 shows, the measurements also show two prominent dips at r ∼ 11 and ∼19 kpc, consistent with our result. We notice that the two dips revealed by their data are much deeper than ours, especially for the first dip. The discrepancies are largely caused by the differences in the radial velocity profiles between their BHB and our HKG samples. As mentioned earlier, BCK14 have recently derived the RC in the outer halo of 25 ≤ r ≤ 200 kpc, also with the spherical Jeans equation, using three halo tracer samples, including the HKG sample used in the current work. We overplot in Fig. 11 their values that are the combined results from the three halo tracer samples deduced by setting R₀ = 8.3 kpc, V_c(R₀) = 244 km s⁻¹, and assuming a β profile taken from the numerical simulation of Rashkov et al. (2013). As one can see in Fig. 11, their circular velocities are somewhat smaller than ours for r ≤ 30 kpc. Beyond this, they are in good agreement. The discrepancies inside 30 kpc are largely due to the differences of β adopted – they use β ∼ 0.6 as given by the simulation while we set it to 0.0 based on the direct measurement of Deason et al. (2013). For r ≥ 30 kpc, the values of β given by the simulation, between 0.50 and 0.75, are close to the value of 0.4 adopted by us. Thus, it is not surprising that the sets of two RC agree in general within the errors.

4.2.3 The dip at r ∼ 19 kpc

In addition to the significant, localized dip at r ∼ 11 kpc discussed in Section 3.3.3, another prominent dip at r ∼ 19 kpc is revealed in the RC derived by the current HKG sample. As mentioned above, the latter is also seen in the RC derived by Kafle et al. (2012) using over 4000 BHB stars. Recall that the profiles of stellar number density, velocity anisotropy and radial velocity dispersion, described in Section 4.1, all have a break around 20 kpc. Thus, it is tempting to conjecture that the dip seen in RC at r ∼ 19 kpc is a direct consequence of the breaks in those profiles that may all have a common cause. On the other hand, the possibility that the dip is artificial cannot be completely ruled out, given the current measurement uncertainties of the break radii as well as the slopes of those profiles. Finally, note that the position of the dip at r ∼ 19 kpc coincides roughly with an n = 2 ring radius, a₂ ≃ 20 kpc, of a hypothetical caustic ring of DM in the Galactic plane proposed by Sikivie (2003) and Duffy & Sikivie (2008). In Section 6, we will present further quantitive analysis of this dip.

5 FINAL COMBINED RC

In this section, we combine the two segments of RC derived above from, respectively, a sample of PRCGs selected from LSS-GAC and APOGEE (Fig. 6) and from a sample of HKGs selected from SEGUE (Fig. 11). For the overlap region (i.e. 8 ≤ r ≤ 15 kpc) of the two segments, the circular velocities derived from the PRCGs are adopted as the final values given their high accuracy almost an order of magnitude higher than those derived from the HKGs. In addition, to provide circular velocities for the inner disc region (inside the solar circle), we take the H i measurements of Fich et al. (1989) based on the TP method described above. We only provide H i data for the region between ∼4.5 kpc and R₀, believed to be less affected by the non-axisymmetric structures (e.g. the central bar; Chemin et al. 2015). For consistency, we have recalculated the circular velocities from those H i data adopting R₀ = 8.34 kpc and V_c(R₀) = 239.89 km s⁻¹ described above. The circular velocities for the inner disc region are provided by taking the mean of circular velocities derived from the H i data in every 0.5 kpc radial bin. The uncertainties of the mean circular velocities are assumed to be 7.0 km s⁻¹. The final combined values of circular velocity at different radius r, their associated 1σ errors (⁠|$\sigma _{V_{\rm c}}$|⁠) and the tracer used, are presented in Table 3. This final combined RC is plotted in Fig. 12. Generally, the combined RC has a flat value 240 km s⁻¹ within r ∼ 25 kpc. Beyond this, it starts to decline steadily, reaching 150 km s⁻¹ at r ∼ 100 kpc. In addition to the overall trend, two prominent localized dips, as described earlier, are clearly seen in the RC, with one at r ∼ 11 kpc and another at r ∼ 19 kpc.

Figure 12.

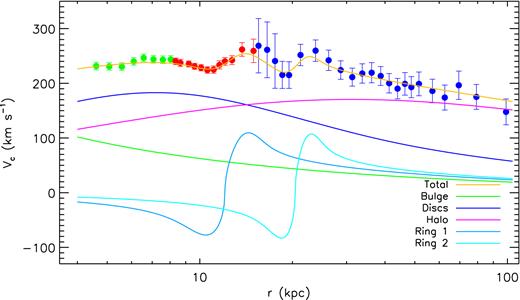
Final combined RC of the Milky Way to ∼100 kpc derived from H i data (green dots), PRCGs (red dots) and HKGs (blue dots). Lines of different colours as labelled in the bottom-right corner of the diagram represent the best-fitting RCs contributions to the components of the Milky Way, with the line in gold representing the sum of contributions from all the mass components (see Section 6.1 for details).

Open in new tab Download slide

Table 3.

Open in new tab

Final combined RC of the Milky Way.

r	V_c	\|$\sigma _{V_{\rm c}}$\|	Tracer	r	V_c	\|$\sigma _{V_{\rm c}}$\|	Tracer
(kpc)	(km s⁻¹)	(km s⁻¹)		(kpc)	(km s⁻¹)	(km s⁻¹)
4.60	231.24	7.00	H i	17.56	240.66	49.91	HKG
5.08	230.46	7.00	H i	18.54	215.31	24.80	HKG
5.58	230.01	7.00	H i	19.50	214.99	24.42	HKG
6.10	239.61	7.00	H i	21.25	251.68	19.50	HKG
6.57	246.27	7.00	H i	23.78	259.65	19.62	HKG
7.07	243.49	7.00	H i	26.22	242.02	18.66	HKG
7.58	242.71	7.00	H i	28.71	224.11	16.97	HKG
8.04	243.23	7.00	H i	31.29	211.20	16.43	HKG
8.34	239.89	5.92	PRCG	33.73	217.93	17.66	HKG
8.65	237.26	6.29	PRCG	36.19	219.33	18.44	HKG
9.20	235.30	5.60	PRCG	38.73	213.31	17.29	HKG
9.62	230.99	5.49	PRCG	41.25	200.05	17.72	HKG
10.09	228.41	5.62	PRCG	43.93	190.15	18.65	HKG
10.58	224.26	5.87	PRCG	46.43	198.95	20.70	HKG
11.09	224.94	7.02	PRCG	48.71	192.91	19.24	HKG
11.58	233.57	7.65	PRCG	51.56	198.90	21.74	HKG
12.07	240.02	6.17	PRCG	57.03	185.88	21.56	HKG
12.73	242.21	8.64	PRCG	62.55	173.89	22.87	HKG
13.72	261.78	14.89	PRCG	69.47	196.36	25.89	HKG
14.95	259.26	30.84	PRCG	79.27	175.05	22.71	HKG
15.52	268.57	49.67	HKG	98.97	147.72	23.55	HKG
16.55	261.17	50.91	HKG	–	–	–	–

r	V_c	\|$\sigma _{V_{\rm c}}$\|	Tracer	r	V_c	\|$\sigma _{V_{\rm c}}$\|	Tracer
(kpc)	(km s⁻¹)	(km s⁻¹)		(kpc)	(km s⁻¹)	(km s⁻¹)
4.60	231.24	7.00	H i	17.56	240.66	49.91	HKG
5.08	230.46	7.00	H i	18.54	215.31	24.80	HKG
5.58	230.01	7.00	H i	19.50	214.99	24.42	HKG
6.10	239.61	7.00	H i	21.25	251.68	19.50	HKG
6.57	246.27	7.00	H i	23.78	259.65	19.62	HKG
7.07	243.49	7.00	H i	26.22	242.02	18.66	HKG
7.58	242.71	7.00	H i	28.71	224.11	16.97	HKG
8.04	243.23	7.00	H i	31.29	211.20	16.43	HKG
8.34	239.89	5.92	PRCG	33.73	217.93	17.66	HKG
8.65	237.26	6.29	PRCG	36.19	219.33	18.44	HKG
9.20	235.30	5.60	PRCG	38.73	213.31	17.29	HKG
9.62	230.99	5.49	PRCG	41.25	200.05	17.72	HKG
10.09	228.41	5.62	PRCG	43.93	190.15	18.65	HKG
10.58	224.26	5.87	PRCG	46.43	198.95	20.70	HKG
11.09	224.94	7.02	PRCG	48.71	192.91	19.24	HKG
11.58	233.57	7.65	PRCG	51.56	198.90	21.74	HKG
12.07	240.02	6.17	PRCG	57.03	185.88	21.56	HKG
12.73	242.21	8.64	PRCG	62.55	173.89	22.87	HKG
13.72	261.78	14.89	PRCG	69.47	196.36	25.89	HKG
14.95	259.26	30.84	PRCG	79.27	175.05	22.71	HKG
15.52	268.57	49.67	HKG	98.97	147.72	23.55	HKG
16.55	261.17	50.91	HKG	–	–	–	–

Table 3.

Open in new tab

Final combined RC of the Milky Way.

r	V_c	\|$\sigma _{V_{\rm c}}$\|	Tracer	r	V_c	\|$\sigma _{V_{\rm c}}$\|	Tracer
(kpc)	(km s⁻¹)	(km s⁻¹)		(kpc)	(km s⁻¹)	(km s⁻¹)
4.60	231.24	7.00	H i	17.56	240.66	49.91	HKG
5.08	230.46	7.00	H i	18.54	215.31	24.80	HKG
5.58	230.01	7.00	H i	19.50	214.99	24.42	HKG
6.10	239.61	7.00	H i	21.25	251.68	19.50	HKG
6.57	246.27	7.00	H i	23.78	259.65	19.62	HKG
7.07	243.49	7.00	H i	26.22	242.02	18.66	HKG
7.58	242.71	7.00	H i	28.71	224.11	16.97	HKG
8.04	243.23	7.00	H i	31.29	211.20	16.43	HKG
8.34	239.89	5.92	PRCG	33.73	217.93	17.66	HKG
8.65	237.26	6.29	PRCG	36.19	219.33	18.44	HKG
9.20	235.30	5.60	PRCG	38.73	213.31	17.29	HKG
9.62	230.99	5.49	PRCG	41.25	200.05	17.72	HKG
10.09	228.41	5.62	PRCG	43.93	190.15	18.65	HKG
10.58	224.26	5.87	PRCG	46.43	198.95	20.70	HKG
11.09	224.94	7.02	PRCG	48.71	192.91	19.24	HKG
11.58	233.57	7.65	PRCG	51.56	198.90	21.74	HKG
12.07	240.02	6.17	PRCG	57.03	185.88	21.56	HKG
12.73	242.21	8.64	PRCG	62.55	173.89	22.87	HKG
13.72	261.78	14.89	PRCG	69.47	196.36	25.89	HKG
14.95	259.26	30.84	PRCG	79.27	175.05	22.71	HKG
15.52	268.57	49.67	HKG	98.97	147.72	23.55	HKG
16.55	261.17	50.91	HKG	–	–	–	–

r	V_c	\|$\sigma _{V_{\rm c}}$\|	Tracer	r	V_c	\|$\sigma _{V_{\rm c}}$\|	Tracer
(kpc)	(km s⁻¹)	(km s⁻¹)		(kpc)	(km s⁻¹)	(km s⁻¹)
4.60	231.24	7.00	H i	17.56	240.66	49.91	HKG
5.08	230.46	7.00	H i	18.54	215.31	24.80	HKG
5.58	230.01	7.00	H i	19.50	214.99	24.42	HKG
6.10	239.61	7.00	H i	21.25	251.68	19.50	HKG
6.57	246.27	7.00	H i	23.78	259.65	19.62	HKG
7.07	243.49	7.00	H i	26.22	242.02	18.66	HKG
7.58	242.71	7.00	H i	28.71	224.11	16.97	HKG
8.04	243.23	7.00	H i	31.29	211.20	16.43	HKG
8.34	239.89	5.92	PRCG	33.73	217.93	17.66	HKG
8.65	237.26	6.29	PRCG	36.19	219.33	18.44	HKG
9.20	235.30	5.60	PRCG	38.73	213.31	17.29	HKG
9.62	230.99	5.49	PRCG	41.25	200.05	17.72	HKG
10.09	228.41	5.62	PRCG	43.93	190.15	18.65	HKG
10.58	224.26	5.87	PRCG	46.43	198.95	20.70	HKG
11.09	224.94	7.02	PRCG	48.71	192.91	19.24	HKG
11.58	233.57	7.65	PRCG	51.56	198.90	21.74	HKG
12.07	240.02	6.17	PRCG	57.03	185.88	21.56	HKG
12.73	242.21	8.64	PRCG	62.55	173.89	22.87	HKG
13.72	261.78	14.89	PRCG	69.47	196.36	25.89	HKG
14.95	259.26	30.84	PRCG	79.27	175.05	22.71	HKG
15.52	268.57	49.67	HKG	98.97	147.72	23.55	HKG
16.55	261.17	50.91	HKG	–	–	–	–

6 GALACTIC MASS MODELS BASED ON THE COMBINED RC

6.1 Galactic mass models and the fit results

Modelling the mass distribution of the Milky Way is a fundamental task of Galactic astronomy (e.g. Dehnen & Binney 1998a, hereafter DB98a; Klypin, Zhao & Somerville 2002). It is also of vital importance for understanding the Galaxy formation and evolution, bearing fundamental questions such as whether the Galactic disc is maximal (e.g. Sackett 1997), whether there is a ‘missing baryon problem’ in our Galaxy (e.g. Klypin et al. 1999) and whether our Galaxy is an archetypical spiral galaxy comparing to other local spiral galaxies (e.g. Hammer et al. 2007). As introduced in Section 1, the RC provides the most fundamental, direct probe of the mass distribution of the Milky Way. In doing this, we have constructed a parametrized Galactic mass model by fitting the model predicted RC to our newly derived combined one presented above. This parametrized Galactic mass model consists of four major components, i.e. three discs, a bulge, a DM halo and two rings. The model predicted circular velocities as a function of Galactic radius are contributed by the four components as given by

\begin{equation} V_{\rm c}^{2} = {V_{{\rm c}, \rm disc}^{2} + V_{{\rm c}, \rm bulge}^{2} + V_{{\rm c}, \rm halo}^{2} + V_{{\rm c}, \rm ring}^{2}}. \end{equation}

(11)

Except for the rings, we adopt density profiles of the other three major components similar to those employed by DB98a and McMillan (2011). They are briefly described below.

(1) The discs. Three subcomponents are included in the disc component, i.e. a gas, a thin and a thick stellar disc. Their surface densities are all described by

\begin{equation} \Sigma (R) = \Sigma _{\rm d, 0}\exp \left(-\frac{R}{R_{\rm d}} - \frac{R_{\rm hole}}{R}\right), \end{equation}

(12)

with a central surface density Σ_d,0 and a scalelength R_d. The parameter R_hole is used specially for the gas disc to create a central cavity in the surface density that match with the observations (e.g. Dame et al. 1987). As in DB98a, we adopt R_hole = 4 kpc for the gas disc and R_hole = 0 for the stellar discs. We further fix the surface density for the individual subdiscs to the local measurements, denoted by |$\Sigma _{{R}_{0}}$|⁠. We adopt |$\Sigma _{{R}_{0}, {\rm gas}} = 17.0\,{\rm M}_{{\odot }}$| pc⁻² from Read (2014) and |$\Sigma _{{R}_{0}, {\rm thick}} = 7.0\,{\rm M}_{{\odot }}$| pc⁻² from Flynn et al. (2006). The local surface density of the thin disc can be derived from the total local stellar surface density |$\Sigma _{{R}_{0}, {\rm stellar}} = 38.0\,{\rm M}_{{\odot }}$| pc⁻² estimated by Bovy et al. (2013) by subtracting contributions from the thick disc and the stellar halo (⁠|$\Sigma _{{R}_{0}, {\rm halo}} = 0.6\,{\rm M}_{{\odot }}$| pc⁻²; Flynn et al. 2006). Then, for each subdiscs, the central surface density can be calculated from |$\Sigma _{\rm d, 0} = \Sigma _{R_{0}}\exp (R_{0}/R_{\rm d} + R_{\rm hole}/R_{0})$|⁠. Moreover, we fix the ratio of gas disc scalelength to the thin disc scalelength to 2. For any axisymmetric component with surface density |$\Sigma (R^{^{\prime }})$|⁠, the circular velocity is given by (Binney & Tremaine 2008; Xin & Zheng 2013),

\begin{equation} V_{\rm c}^{2} (R) = -4G \int _{0}^{R} \frac{a^{2}{\rm d}a}{\sqrt{R^{2} - a^{2}}} \int _{a}^{\infty } \frac{{\rm d}\Sigma (R^{^{\prime }})}{\sqrt{{R^{^{\prime }2}}-a^{2}}}. \end{equation}

(13)

Specifically, for the exponential razor-thin stellar discs, equation (13) has analytic solution given by

\begin{equation} V_{\rm c}^{2} (R) = 4\pi G\Sigma _{\rm d, 0}R_{\rm d}y^{2}[I_{0}(y)K_{0}(y) - I_{1}(y)K_{1}(y)], \end{equation}

(14)

where y = R/(2R_d). I_n and K_n (n = 0, 1) are the first and second kind modified Bessel functions, respectively. Finally, the circular velocity of main disc component is given by quadratic sum of contributions from the three subdiscs, |$V_{{\rm c},\,{\rm disc}}^{2} = V_{{\rm c},\,{\rm thin}}^{2} + V_{{\rm c},\,{\rm thick}}^{2} + V_{{\rm c},\,{\rm gas}}^{2}$|⁠.

(2) The bulge and DM halo. The density distributions of the bulge and the DM halo are each described by

\begin{equation} \rho (R, Z) = \frac{\rho _{0}}{m^{\gamma }(1+m)^{\beta - \gamma }} \exp [-(mr_{0}/r_{\rm t})^{2}], \end{equation}

(15)

where,

\begin{equation} m (R, Z) = \sqrt{(R/r_{0})^{2} + (Z/qr_{0})^{2}}, \end{equation}

(16)

with scale radius r₀, scale density ρ₀, axis ratio q and truncated radius r_t. The indexes γ and β describe, respectively, the inner (r ≪ r₀) and outer (r₀ ≪ r ≪ r_t) slopes of the radial density profile.

Following McMillan (2011), we set our bulge mass model similar to that constructed by Bissantz & Gerhard (2002) given that we have no data to constrain the bulge mass distribution. The model has parameters γ_b = 0, β_b = 1.8, r_b,0 = 0.075 kpc, r_b,t = 2.1 kpc, an axis ratio q = 0.5 and a scale density ρ_b,0 = 9.93 × 10¹⁰M_⊙ kpc⁻³. The total bulge mass corresponding to these parameters is 8.9 × 10⁹M_⊙. The contribution to circular velocity of this bulge component can be calculated numerically (Binney & Tremaine 2008, p. 92).

For the DM halo, a spherical NFW density profile is adopted with q_h = 1, γ_h = 1, β_h = 3 and r_t ≃ ∞. The free parameter ρ_h,0, also denoted as ρ_s, is given by

\begin{equation} \rho _{{\rm s}} = \frac{\rho _{\rm cr}\Omega _{\rm m}\delta _{\rm th}}{3}\frac{c^{3}}{{\rm ln}(1 + c) - c/(1 + c)}, \end{equation}

(17)

where ρ_cr = 3H²/8πG is the critical density of the Universe, Ω_m the contribution of (dark and baryonic) matter to the critical density, δ_th the critical overdensity at virialization and c the concentration parameter (the ratio of the virial radius r_vir to the scale radius r_h,0, also denoted as r_s). In the following analysis, we adopt Ω_m = 0.28 and H₀ = 69.7 km s⁻¹ Mpc⁻¹ from Hinshaw et al. (2013), and set δ_th = 340 (Bryan & Norman 1998). The enclosed virial mass within the virial radius of the NFW DM halo is given by

\begin{equation} M_{\rm vir} = \frac{4\pi }{3}\rho _{\rm cr}\Omega _{\rm m}\delta _{\rm th}r_{\rm vir}^{3}. \end{equation}

(18)

The contribution to circular velocity of the NFW DM halo can be calculated as

\begin{equation} V_{\rm c}^{2} (r) = 4\pi G\rho _{{\rm s}}r_{{\rm s}}^{3}\frac{\ln (1 + x) - x/(1 + x)}{r}, \end{equation}

(19)

where x = r/r_s.

(3) The mass rings. As discussed earlier, there are two prominent localized dips in the RC, one at r ∼ 11 kpc and another at r ∼ 19 kpc. By chance or not, the two dips are almost at the exact positions of the n = 3 and 2 hypothetical caustic rings of DM, at a₃ ≃ 13 kpc and a₂ ≃ 20 kpc, respectively, as proposed by Sikivie (2003) and Duffy & Sikivie (2008). To quantify the mass distributions that may be associated with the two dips, we consider two ring-like structures in the Galactic plane in our mass models. Following de Boer & Weber (2011), the surface density profiles of the two rings are each described by

\begin{equation} \Sigma (R) = \Sigma _{\rm 0, ring}\exp \left[-\frac{(R - R_{\rm ring})^{2}}{2\sigma ^{2}_{\rm ring}}\right]. \end{equation}

(20)

This Gaussian-like ring has a central surface density Σ_0,ring, a ring radius R_ring and a Gaussian width σ_ring. The contribution to circular velocity of the ring component is given by the quadratic sum of contributions of the two rings, |$V_{{\rm c}, {\rm ring}}^{2} = V_{{\rm c}, {\rm ring1}}^{2} + V_{{\rm c}, {\rm ring2}}^{2}$| and can be calculated numerically with equation (13).

In total, there are 10 free parameters in our Galactic mass model: two for the discs (R_d,thin and R_d,thick), two for the DM halo (r_s and ρ_s), and six for the rings (Σ_0,ring1,2, R_ring1,2 and σ_ring1,2). To derive the 10 free parameters, we fit the model circular velocities given by equation (11), to match our newly derived values (see Table 3 & Fig. 12). We note that the latter six parameters are only sensitive to the two localized features (i.e. the dips) in the RC and thus do not affect the overall fit controlled by the former four parameters. To efficiently explore the parameter space in searching for the best mass model, we use a Markov Chain Monte Carlo (MCMC) technique to sample the likelihood of the data, which is defined as

\begin{equation} \mathcal {L} = \prod _{i=1}^{N}\frac{1} {\sqrt{2\pi }\sigma _{V_{{\rm c}, {R}_{i}}^{\rm obs} }}\exp {\frac{-[V_{{\rm c}, {R}_{i}}^{\rm obs} - V_{{{\rm c}, R}_{i}}^{\rm model} ({\boldsymbol p})]^{2}}{2\sigma _{V_{{{\rm c}, R}_{i}}^{\rm obs}}^{2}}}, \end{equation}

(21)

where N is the total data points, |$\sigma _{V_{{{\rm c}, R}_{i}}^{\rm obs}}$| is the uncertainty of the observed circular velocity and p represents the 10 free parameters of the above Galactic mass model that we want to determine. The parameters after post-burn period in the MCMC chain give the probability distribution functions (PDFs) of the 10 free parameters. We present the marginalized one- and two-dimensional PDFs of the model parameters in Fig. 13. The joint PDFs clearly show some correlations amongst the parameters. For example, R_ring1 is strongly correlated with σ_ring1. In addition, anticorrelations are found between R_{d, thin} and R_d,thick, and between ρ_s and r_s. Other pairwise parameters are generally independent of each other. Finally, the best-fitting values of model parameters are estimated by the median values of their marginalized PDFs. The uncertainties are computed from the 68 per cent probability intervals of the marginalized PDF of each parameter. The final best-fitting values of parameters of our mass models and other derived quantities (e.g. mass of each component), together with their corresponding uncertainties, are presented in Table 4. As Fig. 12 shows, the best-fitting RC is in excellent agreement with the observed one. The contributions to RC from each of the components corresponding to the best-fitting parameters are also overplotted in Fig. 12.

Figure 13.

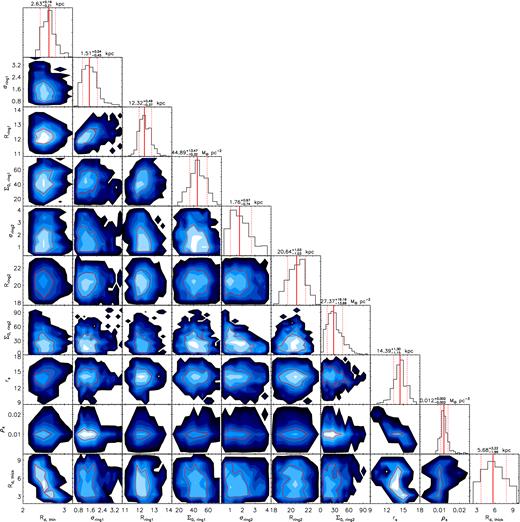
Two-dimensional marginalized PDFs for the 10 model parameters (described in detail in Section 6.1) obtained from the MCMC. Histograms on top of each column show the one-dimensional marginalized PDFs of each parameter labelled at the bottom of the column. The red contour in each panel delineates the 1σ confidence level. The red solid and dotted lines in each histogram represent, respectively, the best-fitting value and the 68 per cent probability intervals of the parameter concerned. The best-fitting values and uncertainties of the model parameters are also labelled near the top of the individual columns.

Open in new tab Download slide

Table 4.

Open in new tab

Best-fitting mass model parameters and derived quantities.

Galactic component	Parameter	Value	Unit	Note^a
Bulge	M_b	8.9	10⁹M_⊙	Fixed
discs	Σ_d,0,thin	\|$726.9_{-123.6}^{+203.5}$\|	M_⊙ pc⁻²	Fixed
	R_d,thin	\|$2.63^{+0.16}_{-0.21}$\|	kpc	Fitted
	M_d,thin	\|$3.15_{-0.19}^{+0.35}$\|	10¹⁰M_⊙	Derived
	Σ_d,0,thick	\|$30.4_{-10.3}^{+36.2}$\|	M_⊙ pc⁻²	Fixed
	R_d,thick	\|$5.68^{+2.22}_{-1.99}$\|	kpc	Fitted
	M_d,thick	\|$0.62_{-0.06}^{+0.16}$\|	10¹⁰ M_⊙	Derived
	Σ_d,0,gas	\|$134.3_{-12.1}^{+18.8}$\|	M_⊙ pc⁻²	Fixed
	R_d,gas	\|$5.26^{+0.32}_{-0.42}$\|	kpc	Fixed
	M_d,gas	\|$0.55_{-0.02}^{+0.02}$\|	10¹⁰ M_⊙	Derived
	M_d,total	\|$4.32^{+0.39}_{-0.20}$\|	10¹⁰ M_⊙	Derived
DM halo	r_s	\|$14.39^{+1.30}_{-1.15}$\|	kpc	Fitted
	ρ_s	\|$0.0121_{-0.0016}^{+0.0021}$\|	M_⊙ pc⁻³	Fitted
	ρ_⊙	\|$0.0083^{+0.0005}_{-0.0005}$\|	M_⊙ pc⁻³	Derived
	c	\|$18.06_{-0.90}^{+1.26}$\|	–	Derived
	r_vir	\|$255.69_{-7.67}^{+7.67}$\|	kpc	Derived
	M_vir	\|$0.90_{-0.08}^{+0.07}$\|	10¹² M_⊙	Derived
Rings	Σ_{0, ring1}	\|$44.89^{+13.47}_{-10.32}$\|	M_⊙ pc⁻²	Fitted
	R_ring1	\|$12.32^{+0.49}_{-0.37}$\|	kpc	Fitted
	σ_ring1	\|$1.51^{+0.54}_{-0.45}$\|	kpc	Fitted
	M_ring1	\|$1.32^{+0.71}_{-0.50}$\|	10¹⁰ M_⊙	Derived
	Σ_{0, ring2}	\|$27.37^{+19.16}_{-13.69}$\|	M_⊙ pc⁻²	Fitted
	R_ring2	\|$20.64^{+1.03}_{-1.03}$\|	kpc	Fitted
	σ_ring2	\|$1.76^{+0.97}_{-0.74}$\|	kpc	Fitted
	M_ring2	\|$1.57^{+0.83}_{-0.75}$\|	10¹⁰ M_⊙	Derived
All	M_total	\|$0.97^{+0.07}_{-0.08}$\|	10¹² M_⊙	Derived

Galactic component	Parameter	Value	Unit	Note^a
Bulge	M_b	8.9	10⁹M_⊙	Fixed
discs	Σ_d,0,thin	\|$726.9_{-123.6}^{+203.5}$\|	M_⊙ pc⁻²	Fixed
	R_d,thin	\|$2.63^{+0.16}_{-0.21}$\|	kpc	Fitted
	M_d,thin	\|$3.15_{-0.19}^{+0.35}$\|	10¹⁰M_⊙	Derived
	Σ_d,0,thick	\|$30.4_{-10.3}^{+36.2}$\|	M_⊙ pc⁻²	Fixed
	R_d,thick	\|$5.68^{+2.22}_{-1.99}$\|	kpc	Fitted
	M_d,thick	\|$0.62_{-0.06}^{+0.16}$\|	10¹⁰ M_⊙	Derived
	Σ_d,0,gas	\|$134.3_{-12.1}^{+18.8}$\|	M_⊙ pc⁻²	Fixed
	R_d,gas	\|$5.26^{+0.32}_{-0.42}$\|	kpc	Fixed
	M_d,gas	\|$0.55_{-0.02}^{+0.02}$\|	10¹⁰ M_⊙	Derived
	M_d,total	\|$4.32^{+0.39}_{-0.20}$\|	10¹⁰ M_⊙	Derived
DM halo	r_s	\|$14.39^{+1.30}_{-1.15}$\|	kpc	Fitted
	ρ_s	\|$0.0121_{-0.0016}^{+0.0021}$\|	M_⊙ pc⁻³	Fitted
	ρ_⊙	\|$0.0083^{+0.0005}_{-0.0005}$\|	M_⊙ pc⁻³	Derived
	c	\|$18.06_{-0.90}^{+1.26}$\|	–	Derived
	r_vir	\|$255.69_{-7.67}^{+7.67}$\|	kpc	Derived
	M_vir	\|$0.90_{-0.08}^{+0.07}$\|	10¹² M_⊙	Derived
Rings	Σ_{0, ring1}	\|$44.89^{+13.47}_{-10.32}$\|	M_⊙ pc⁻²	Fitted
	R_ring1	\|$12.32^{+0.49}_{-0.37}$\|	kpc	Fitted
	σ_ring1	\|$1.51^{+0.54}_{-0.45}$\|	kpc	Fitted
	M_ring1	\|$1.32^{+0.71}_{-0.50}$\|	10¹⁰ M_⊙	Derived
	Σ_{0, ring2}	\|$27.37^{+19.16}_{-13.69}$\|	M_⊙ pc⁻²	Fitted
	R_ring2	\|$20.64^{+1.03}_{-1.03}$\|	kpc	Fitted
	σ_ring2	\|$1.76^{+0.97}_{-0.74}$\|	kpc	Fitted
	M_ring2	\|$1.57^{+0.83}_{-0.75}$\|	10¹⁰ M_⊙	Derived
All	M_total	\|$0.97^{+0.07}_{-0.08}$\|	10¹² M_⊙	Derived

^aHere, ‘fixed’, ‘fitted’ and ‘derived’ denote the parameter/quantity of concern is either fixed or fitted in our mass model, or derived from the resultant model.

Table 4.

Open in new tab

Best-fitting mass model parameters and derived quantities.

Galactic component	Parameter	Value	Unit	Note^a
Bulge	M_b	8.9	10⁹M_⊙	Fixed
discs	Σ_d,0,thin	\|$726.9_{-123.6}^{+203.5}$\|	M_⊙ pc⁻²	Fixed
	R_d,thin	\|$2.63^{+0.16}_{-0.21}$\|	kpc	Fitted
	M_d,thin	\|$3.15_{-0.19}^{+0.35}$\|	10¹⁰M_⊙	Derived
	Σ_d,0,thick	\|$30.4_{-10.3}^{+36.2}$\|	M_⊙ pc⁻²	Fixed
	R_d,thick	\|$5.68^{+2.22}_{-1.99}$\|	kpc	Fitted
	M_d,thick	\|$0.62_{-0.06}^{+0.16}$\|	10¹⁰ M_⊙	Derived
	Σ_d,0,gas	\|$134.3_{-12.1}^{+18.8}$\|	M_⊙ pc⁻²	Fixed
	R_d,gas	\|$5.26^{+0.32}_{-0.42}$\|	kpc	Fixed
	M_d,gas	\|$0.55_{-0.02}^{+0.02}$\|	10¹⁰ M_⊙	Derived
	M_d,total	\|$4.32^{+0.39}_{-0.20}$\|	10¹⁰ M_⊙	Derived
DM halo	r_s	\|$14.39^{+1.30}_{-1.15}$\|	kpc	Fitted
	ρ_s	\|$0.0121_{-0.0016}^{+0.0021}$\|	M_⊙ pc⁻³	Fitted
	ρ_⊙	\|$0.0083^{+0.0005}_{-0.0005}$\|	M_⊙ pc⁻³	Derived
	c	\|$18.06_{-0.90}^{+1.26}$\|	–	Derived
	r_vir	\|$255.69_{-7.67}^{+7.67}$\|	kpc	Derived
	M_vir	\|$0.90_{-0.08}^{+0.07}$\|	10¹² M_⊙	Derived
Rings	Σ_{0, ring1}	\|$44.89^{+13.47}_{-10.32}$\|	M_⊙ pc⁻²	Fitted
	R_ring1	\|$12.32^{+0.49}_{-0.37}$\|	kpc	Fitted
	σ_ring1	\|$1.51^{+0.54}_{-0.45}$\|	kpc	Fitted
	M_ring1	\|$1.32^{+0.71}_{-0.50}$\|	10¹⁰ M_⊙	Derived
	Σ_{0, ring2}	\|$27.37^{+19.16}_{-13.69}$\|	M_⊙ pc⁻²	Fitted
	R_ring2	\|$20.64^{+1.03}_{-1.03}$\|	kpc	Fitted
	σ_ring2	\|$1.76^{+0.97}_{-0.74}$\|	kpc	Fitted
	M_ring2	\|$1.57^{+0.83}_{-0.75}$\|	10¹⁰ M_⊙	Derived
All	M_total	\|$0.97^{+0.07}_{-0.08}$\|	10¹² M_⊙	Derived

Galactic component	Parameter	Value	Unit	Note^a
Bulge	M_b	8.9	10⁹M_⊙	Fixed
discs	Σ_d,0,thin	\|$726.9_{-123.6}^{+203.5}$\|	M_⊙ pc⁻²	Fixed
	R_d,thin	\|$2.63^{+0.16}_{-0.21}$\|	kpc	Fitted
	M_d,thin	\|$3.15_{-0.19}^{+0.35}$\|	10¹⁰M_⊙	Derived
	Σ_d,0,thick	\|$30.4_{-10.3}^{+36.2}$\|	M_⊙ pc⁻²	Fixed
	R_d,thick	\|$5.68^{+2.22}_{-1.99}$\|	kpc	Fitted
	M_d,thick	\|$0.62_{-0.06}^{+0.16}$\|	10¹⁰ M_⊙	Derived
	Σ_d,0,gas	\|$134.3_{-12.1}^{+18.8}$\|	M_⊙ pc⁻²	Fixed
	R_d,gas	\|$5.26^{+0.32}_{-0.42}$\|	kpc	Fixed
	M_d,gas	\|$0.55_{-0.02}^{+0.02}$\|	10¹⁰ M_⊙	Derived
	M_d,total	\|$4.32^{+0.39}_{-0.20}$\|	10¹⁰ M_⊙	Derived
DM halo	r_s	\|$14.39^{+1.30}_{-1.15}$\|	kpc	Fitted
	ρ_s	\|$0.0121_{-0.0016}^{+0.0021}$\|	M_⊙ pc⁻³	Fitted
	ρ_⊙	\|$0.0083^{+0.0005}_{-0.0005}$\|	M_⊙ pc⁻³	Derived
	c	\|$18.06_{-0.90}^{+1.26}$\|	–	Derived
	r_vir	\|$255.69_{-7.67}^{+7.67}$\|	kpc	Derived
	M_vir	\|$0.90_{-0.08}^{+0.07}$\|	10¹² M_⊙	Derived
Rings	Σ_{0, ring1}	\|$44.89^{+13.47}_{-10.32}$\|	M_⊙ pc⁻²	Fitted
	R_ring1	\|$12.32^{+0.49}_{-0.37}$\|	kpc	Fitted
	σ_ring1	\|$1.51^{+0.54}_{-0.45}$\|	kpc	Fitted
	M_ring1	\|$1.32^{+0.71}_{-0.50}$\|	10¹⁰ M_⊙	Derived
	Σ_{0, ring2}	\|$27.37^{+19.16}_{-13.69}$\|	M_⊙ pc⁻²	Fitted
	R_ring2	\|$20.64^{+1.03}_{-1.03}$\|	kpc	Fitted
	σ_ring2	\|$1.76^{+0.97}_{-0.74}$\|	kpc	Fitted
	M_ring2	\|$1.57^{+0.83}_{-0.75}$\|	10¹⁰ M_⊙	Derived
All	M_total	\|$0.97^{+0.07}_{-0.08}$\|	10¹² M_⊙	Derived

^aHere, ‘fixed’, ‘fitted’ and ‘derived’ denote the parameter/quantity of concern is either fixed or fitted in our mass model, or derived from the resultant model.

6.2 Discussion

6.2.1 DM halo

From the best-fitting values of ρ_s and r_s, we estimate a virial mass of the DM halo, |$M_{\rm vir} = 0.90^{+0.07}_{-0.08} \times 10^{12} {\rm M}_{{\odot }}$| within the virial radius |$r_{\rm vir} = 255.69^{+7.67}_{-7.67}$| kpc. The results are in excellent agreement with the recent measurements of Kafle et al. (2014). The concentration parameter c is |$18.06^{+1.26}_{-0.90}$|⁠, which also agrees well with the recent determinations of Kafle et al. (2014) and Piffl et al. (2014). As expected from equation (18), there is a strong anticorrelation between c and M_vir as shown in Fig. 14. The M_vir–c joint PDF is presented in Fig. 14. Also overplotted in the figure is the relation predicted by Λ cold dark matter (ΛCDM) simulations taken from Bullock et al. (2001). The values of c predicted by the simulations are systematically smaller than that yielded by our newly derived RC. However, as argued by Kafle et al. (2014) and Piffl et al. (2014), the theoretical relation is constructed from simulations with DM only. The presence of baryons, not considered in the simulations, is expected to increase the concentration. Finally, we note that the slightly lighter DM halo estimated here could lessen tension in hierarchical structure formation in the ΛCDM cosmological paradigm imposed by the so-called missing satellite and too big to fail problems (e.g. Springel et al. 2008; Vera-Ciro et al. 2013).

Figure 14.

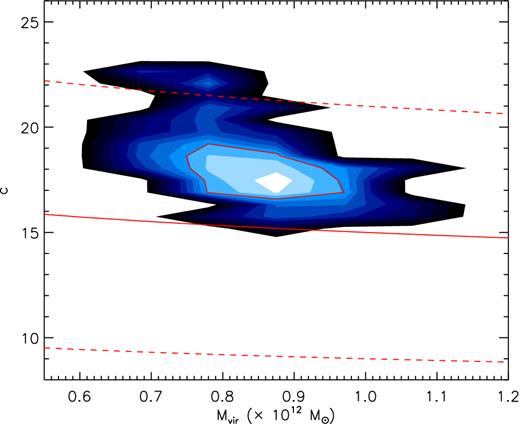
Two-dimensional PDF of virial mass M_vir and concentration parameter c. The red solid line delineates the M_vir–c relation predicted by the ΛCDM simulations of Bullock et al. (2001). The dashed red lines border the scatters of the relation. The red contour represents the 1σ confidence level.

Open in new tab Download slide

From ρ_s and r_s, we also find a local DM density, |$\rho _{\rm {\odot }, dm} = 0.0083^{+0.0005}_{-0.0005}$| M_⊙ pc⁻³ (⁠|$0.32^{+0.02}_{-0.02}$| Ge V cm⁻³). The very small uncertainty (only 5 per cent) is due to the strong anticorrelation between ρ_s and r_s. Our estimate of ρ_⊙,dm is in good agreement with the previous global (e.g. Catena & Ullio 2010; Salucci et al. 2010; McMillan 2011) as well as local determinations (e.g. Bovy & Tremaine 2012 Bovy & Rix 2013; Zhang et al. 2013), pointing to a nearly spherical local Milky Way DM halo (Read 2014).

6.2.2 The rings

As Fig. 12 shows, the two localized dips in our RC are fitted quite well by two Gaussian-like ring structures in the Galactic plane. The best-fitting values of the radii of the two rings are, respectively, |$12.32^{+0.49}_{-0.37}$| and |$20.64^{+1.03}_{-1.03}$| kpc, in good agreement with the radii of the n = 3 and 2 hypothetical caustic rings of DM, at a₃ ≃ 13 kpc and a₂ ≃ 20 kpc, respectively, as proposed by Sikivie (2003) and Duffy & Sikivie (2008). The radius of the inner ring is also in excellent agreement with the value of 12.4 kpc estimated by de Boer & Weber (2011). The rings are quite massive, of the order of 10¹⁰ M_⊙, again matching well with estimate of de Boer & Weber (2011). At present, observational evidence linking the dips seen in the RC to hypothetical caustic rings of DM is still marginal. To better understand the origin of the rings (or the dips in the RC), further observations and simulations are needed.

7 SUMMARY

Based on 16 000 PRCGs selected from LSS-GAC and SDSS-III/APOGEE, and 5700 HKGs selected from SDSS/SEGUE, we have derived the RC of the Milky Way out to ∼100 kpc. For the warm disc tracers PRCGs, a kinematic model with asymmetric drift correction is used to drive the RC. Benefited from the high accuracy of distances and line-of-sight velocities of the PRCG sample, the typical uncertainties of the newly derived circular velocities are only 5–7 km s⁻¹. From the new accurate RC yielded by the PRCG sample, we have also obtained an estimate of the circular velocity of 240 ± 6 km s⁻¹ at the solar position, of the solar peculiar velocity in the rotation direction of 12.1 ± 7.6 km s⁻¹. For the HGK halo tracers, we derive the RC by spherical Jeans equation. We use the current available measurements of the velocity anisotropy parameter β to break the so-called RC/mass-anisotropy degeneracy. The typical uncertainties of the derived circular velocities are several tens km s⁻¹.

By combining circular velocities from H i measurements for the inner disc inside the solar circle, we present a combined RC for Galactocentric distance r ranging from ∼4 to ∼100 kpc. The combined RC show an overall flat value of ∼240 km s⁻¹ within r ∼ 25 kpc, beyond which it declines steadily to 150 km s⁻¹ at r ∼ 100 kpc. The newly derived RC also established the existence of significant localized dips at r ∼ 11 and ∼19 kpc, respectively. The dips are possibly related to the n = 3 and 2 hypothetical caustic rings of DM with ring radii at a₂ ≃ 20 kpc and a₃ ≃ 13 kpc, respectively, as proposed by Sikivie (2003) and Duffy & Sikivie (2008).

Finally, we construct a parametrized Galactic mass model constrained by the newly derived RC and other available constraints. The best-fitting yields a virial mass of the DM halo |$M_{\rm vir} = 0.90^{+0.07}_{-0.08} \times 10^{12}$| M_⊙, a concentration parameter |$c = 18.06^{+1.26}_{-0.90}$| and a local DM density |$\rho _{\rm {\odot }, dm} = 0.32^{+0.02}_{-0.02}$| GeV cm⁻³. We also find the two RC dips can be well described by two Gaussian-like ring structures with the ring radii almost identical to the ones predicted by the hypothetical n = 2 and 3 caustic rings of DM. The two rings have a mass of the order of 10¹⁰M_⊙.

Acknowledgments

This work is supported by the National Key Basic Research Program of China 2014CB845700 and the National Natural Science Foundation of China 11473001 and 11233004. We thank Zuhui Fan and Xiangkun Liu for valuable discussions. We also thank Prajwal Raj Kafle for kindly providing his circular velocity measurements. The LAMOST FELLOWSHIP is supported by Special Funding for Advanced Users, budgeted and administrated by Center for Astronomical Mega-Science, Chinese Academy of Sciences (CAMS).

The Guoshoujing Telescope (the Large Sky Area Multi-Object Fibre Spectroscopic Telescope, LAMOST) is a National Major Scientific Project built by the Chinese Academy of Sciences. Funding for the project has been provided by the National Development and Reform Commission. LAMOST is operated and managed by the National Astronomical Observatories, Chinese Academy of Sciences.

This work has made use of data products from the SDSS.

1

The masers are generally associated with young massive stars and compact H ii regions in the spiral arms.

2

Actually, |$\overline{V}_{\rm los}^{\rm helio}$| also varies with angle β in a cosinusoidal form, as a result of the mean radial motion. Given that cos β = −cos (ϕ + l) ∝ − cos l, there is also an approximately cosinusoidal dependence of |$\overline{V}_{\rm los}^{\rm helio}$|on the Galactic longitude l governed by the mean radial motion.

3

We note that there is actually some differences between the kinematical analyses of Bovy et al. (2012) and ours that their analysis has to assume a certain shape of RC (either flat or power law) while ours does not.

REFERENCES

Ahn

C. P.

et al. .

2012

.

ApJS

,

203

,

21

Crossref

Search ADS

Alam

S.

et al. .

2015

.

ApJS

,

219

,

12

Crossref

Search ADS

Allende Prieto

C.

et al. .

2008

.

AJ

,

136

,

2070

Crossref

Search ADS

Battaglia

G.

et al. .

2005

.

MNRAS

,

364

,

433

Crossref

Search ADS

Battinelli

P.

,

Demers

S.

,

Rossi

C.

,

Gigoyan

K. S.

.

2013

.

Astrophysics

,

56

,

68

Crossref

Search ADS

Bell

E. F.

et al. .

2008

.

ApJ

,

680

,

295

Crossref

Search ADS

Benjamin

R. A.

et al. .

2005

.

ApJ

,

630

,

L149

Crossref

Search ADS

Bensby

T.

,

Feltzing

S.

,

Lundström

I.

.

2003

.

A&A

,

410

,

527

Crossref

Search ADS

Bhattacharjee

P.

,

Chaudhury

S.

,

Kundu

S.

.

2014

.

ApJ

,

785

,

63

Crossref

Search ADS

Binney

J.

,

Tremaine

S.

.

2008

.

Galactic Dynamics

. 2nd edn,

Princeton Univ. Press

,

Princeton, NJ

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Bissantz

N.

,

Gerhard

O.

.

2002

.

MNRAS

,

330

,

591

Crossref

Search ADS

Bobylev

V. V.

,

Bajkova

A. T.

.

2015

.

Astron. Lett.

,

41

,

473

Crossref

Search ADS

Bond

N. A.

et al. .

2010

.

ApJ

,

716

,

1

Crossref

Search ADS

Bovy

J.

,

Rix

H.-W.

.

2013

.

ApJ

,

779

,

115

Crossref

Search ADS

Bovy

J.

,

Tremaine

S.

.

2012

.

ApJ

,

756

,

89

Crossref

Search ADS

Bovy

J.

et al. .

2012

.

ApJ

,

759

,

131

Crossref

Search ADS

Bovy

J.

et al. .

2014

.

ApJ

,

790

,

127

Crossref

Search ADS

Bovy

J.

,

Bird

J. C.

,

García Pérez

A. E.

,

Majewski

S. R.

,

Nidever

D. L.

,

Zasowski

G.

.

2015

.

ApJ

,

800

,

83

Crossref

Search ADS

Brand

J.

,

Blitz

L.

.

1993

.

A&A

,

275

,

67

Brown

W. R.

,

Geller

M. J.

,

Kenyon

S. J.

,

Diaferio

A.

.

2010

.

AJ

,

139

,

59

Crossref

Search ADS

Brunthaler

A. M.

et al. .

2011

.

Astron. Nachr.

,

332

,

461

Crossref

Search ADS

Bryan

G. L.

,

Norman

M. L.

.

1998

.

ApJ

,

495

,

80

Crossref

Search ADS

Büdenbender

A.

,

van de Ven

G.

,

Watkins

L. L.

.

2015

.

MNRAS

,

452

,

956

Crossref

Search ADS

Bullock

J. S.

,

Kolatt

T. S.

,

Sigad

Y.

,

Somerville

R. S.

,

Kravstsov

A. V.

,

Klypin

A. A.

,

Primack

J. R.

,

Dekel

A.

.

2001

.

MNRAS

,

321

,

559

Crossref

Search ADS

Burton

W. B.

,

Gordon

M. A.

.

1978

.

A&A

,

63

,

7

Cannon

R. D.

.

1970

.

MNRAS

,

150

,

111

Crossref

Search ADS

Catena

R.

,

Ullio

P.

.

2010

.

J. Cosmol. Astropart. Phys.

,

8

,

004

Crossref

Search ADS

Chang

C.-K.

,

Ko

C.-M.

,

Peng

T.-H.

.

2011

.

ApJ

,

740

,

34

Crossref

Search ADS

Chemin

L.

,

Renaud

F.

,

Soubiran

C.

.

2015

.

A&A

,

578

,

A14

Crossref

Search ADS

Clemens

D. P.

.

1985

.

ApJ

,

295

,

422

Crossref

Search ADS

Dame

T. M.

et al. .

1987

.

ApJ

,

322

,

706

Crossref

Search ADS

de Boer

W.

,

Weber

M.

.

2011

.

J. Cosmol. Astropart. Phys.

,

4

,

002

Crossref

Search ADS

Deason

A. J.

,

Belokurov

V.

,

Evans

N. W.

.

2011

.

MNRAS

,

416

,

2903

Crossref

Search ADS

Deason

A. J.

,

Belokurov

V.

,

Evans

N. W.

,

An

J.

.

2012

.

MNRAS

,

424

,

L44

Crossref

Search ADS

Deason

A. J.

,

Van der Marel

R. P.

,

Guhathakurta

P.

,

Sohn

S. T.

,

Brown

T. M.

.

2013

.

ApJ

,

766

,

24

Crossref

Search ADS

Dehnen

W.

,

Binney

J. J.

.

1998a

.

MNRAS

,

294

,

429

Crossref

Search ADS

Dehnen

W.

,

Binney

J. J.

.

1998b

.

MNRAS

,

298

,

387

Crossref

Search ADS

Dehnen

W.

,

McLaughlin

D. E.

,

Sachania

J.

.

2006

.

MNRAS

,

369

,

1688

Crossref

Search ADS

Demers

S.

,

Battinelli

P.

.

2007

.

A&A

,

473

,

143

Crossref

Search ADS

Deng

L.-C.

et al. .

2012

.

Res. Astron. Astrophys.

,

12

,

735

Crossref

Search ADS

Duffy

L. D.

,

Sikivie

P.

.

2008

.

Phys. Rev. D

,

78

,

063508

Crossref

Search ADS

Eisenstein

D. J.

et al. .

2011

.

AJ

,

142

,

72

Crossref

Search ADS

Faccioli

L.

,

Smith

M. C.

,

Yuan

H.-B.

,

Zhang

H.-H.

,

Liu

X.-W.

,

Zhao

H.-B.

,

Yao

J.-S.

.

2014

.

ApJ

,

788

,

105

Crossref

Search ADS

Fermani

F.

,

Schönrich

R.

.

2013

.

MNRAS

,

432

,

2402

Crossref

Search ADS

Fich

M.

,

Blitz

L.

,

Stark

A. A.

.

1989

.

ApJ

,

342

,

272

Crossref

Search ADS

Flynn

C.

,

Holmberg

J.

,

Portinari

L.

,

Fuchs

B.

,

Jahreiß

H.

.

2006

.

MNRAS

,

372

,

1149

Crossref

Search ADS

Frink

S.

,

Fuchs

B.

,

Röser

S.

,

Wielen

R.

.

1996

.

A&A

,

314

,

430

García Pérez

A. E.

et al. .

2016

.

AJ

,

151

,

144

Crossref

Search ADS

Gunn

J. E.

,

Knapp

G. R.

,

Tremaine

S. D.

.

1979

.

AJ

,

84

,

1181

Crossref

Search ADS

Hammer

F.

,

Puech

M.

,

Chemin

L.

,

Flores

H.

,

Lehnert

M. D.

.

2007

.

ApJ

,

662

,

322

Crossref

Search ADS

Hattori

K.

,

Yoshii

Y.

,

Beers

T. C.

,

Carollo

D.

,

Lee

Y. S.

.

2013

.

ApJ

,

763

,

L17

Crossref

Search ADS

Hinshaw

G.

et al. .

2013

.

ApJS

,

208

,

19

Crossref

Search ADS

Honma

M.

,

Sofue

Y.

.

1997

.

PASJ

,

49

,

453

Huang

Y.

et al. .

2015a

.

Res. Astron. Astrophys.

,

15

,

1240

Crossref

Search ADS

Huang

Y.

,

Liu

X.-W.

,

Yuan

H.-B.

,

Xiang

M.-S.

,

Huo

Z.-Y.

,

Chen

B.-Q.

,

Zhang

Y.

,

Hou

Y.-Y.

.

2015b

.

MNRAS

,

449

,

162

Crossref

Search ADS

Jurić

M.

et al. .

2008

.

ApJ

,

673

,

864

Crossref

Search ADS

Kafle

P. R.

,

Sharma

S.

,

Lewis

G. F.

,

Bland-Hawthorn

J.

.

2012

.

ApJ

,

761

,

98

Crossref

Search ADS

Kafle

P. R.

,

Sharma

S.

,

Lewis

G. F.

,

Bland-Hawthorn

J.

.

2013

.

MNRAS

,

430

,

2973

Crossref

Search ADS

Kafle

P. R.

,

Sharma

S.

,

Lewis

G. F.

,

Bland-Hawthorn

J.

.

2014

.

ApJ

,

794

,

59

Crossref

Search ADS

Kepley

A. A.

et al. .

2007

.

AJ

,

134

,

1579

Crossref

Search ADS

Klypin

A.

,

Kravtsov

A. V.

,

Valenzuela

O.

,

Prada

F.

.

1999

.

ApJ

,

522

,

82

Crossref

Search ADS

Klypin

A.

,

Zhao

H.

,

Somerville

R. S.

.

2002

.

ApJ

,

573

,

597

Crossref

Search ADS

Lee

Y. S.

et al. .

2008a

.

AJ

,

136

,

2022

Crossref

Search ADS

Lee

Y. S.

et al. .

2008b

.

AJ

,

136

,

2050

Crossref

Search ADS

Levine

E. S.

,

Heiles

C.

,

Blitz

L.

.

2008

.

ApJ

,

679

,

1288

Crossref

Search ADS

Liu

X.-W.

et al. .

2014

, in

Feltzing

S.

,

Zhao

G.

,

Walton

N.

,

Whitelock

P.

.

Proc. IAU Symp. 298, Setting the Scene for Gaia and LAMOST

Cambridge Univ. Press

,

Cambridge

,

310

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

McMillan

P. J.

.

2011

.

MNRAS

,

414

,

2446

Crossref

Search ADS

Majewski

S. R.

et al. .

2015

.

preprint (arXiv:1509.05420)

Markwardt

C. B.

.

2009

, in

Bohlender

D. A.

,

Durand

D.

,

Dowler

P.

.

ASP Conf. Ser. Vol. 411, Astronomical Data Analysis Software and Systems XVIII

Astron. Soc. Pac.

,

San Francisco

,

251

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Merrifield

M. R.

.

1992

.

AJ

,

103

,

1552

Crossref

Search ADS

Mészáros

S.

et al. .

2013

.

AJ

,

146

,

133

Crossref

Search ADS

Nidever

D. L.

et al. .

2015

.

AJ

,

150

,

173

Crossref

Search ADS

Paczyński

B.

,

Stanek

K. Z.

.

1998

.

ApJ

,

494

,

L219

Crossref

Search ADS

Piffl

T.

et al. .

2014

.

MNRAS

,

445

,

3133

Crossref

Search ADS

Pont

F.

,

Queloz

D.

,

Bratschi

P.

,

Mayor

M.

.

1997

.

A&A

,

318

,

41

Rashkov

V.

,

Pillepich

A.

,

Deason

A. J.

,

Madau

P.

,

Rockosi

C. M.

,

Guedes

J.

,

Mayer

L.

.

2013

.

ApJ

,

773

,

L32

Crossref

Search ADS

Read

J. I.

.

2014

.

J. Phys. G: Nucl. Part. Phys.

,

41

,

063101

Crossref

Search ADS

Reid

M. J.

,

Brunthaler

A.

.

2004

.

ApJ

,

616

,

872

Crossref

Search ADS

Reid

M. J.

et al. .

2014

.

ApJ

,

783

,

130

Crossref

Search ADS

Sackett

P. D.

.

1997

.

ApJ

,

483

,

103

Crossref

Search ADS

Salucci

P.

,

Nesti

F.

,

Gentile

G.

,

Frigerio Martins

C.

.

2010

.

A&A

,

523

,

A83

Crossref

Search ADS

Schönrich

R.

.

2012

.

MNRAS

,

427

,

274

Crossref

Search ADS

Schönrich

R.

,

Binney

J.

,

Dehnen

W.

.

2010

.

MNRAS

,

403

,

1829

Crossref

Search ADS

Sesar

B.

,

Jurić

M.

,

Ivezić

Ž.

.

2011

.

ApJ

,

731

,

4

Crossref

Search ADS

Sesar

B.

et al. .

2013

.

AJ

,

146

,

21

Crossref

Search ADS

Sharma

S.

et al. .

2014

.

ApJ

,

793

,

51

Crossref

Search ADS

Siebert

A.

et al. .

2011

.

MNRAS

,

412

,

2026

Crossref

Search ADS

Sikivie

P.

.

2003

.

Phys. Lett. B

,

567

,

1

Crossref

Search ADS

Smith

M. C.

et al. .

2009

.

MNRAS

,

399

,

1223

Crossref

Search ADS

Smolinski

J. P.

et al. .

2011

.

AJ

,

141

,

89

Crossref

Search ADS

Sofue

Y.

,

Honma

M.

,

Omodaka

T.

.

2009

.

PASJ

,

61

,

227

Soubiran

C.

,

Bienaymé

O.

,

Siebert

A.

.

2003

.

A&A

,

398

,

141

Crossref

Search ADS

Springel

V.

et al. .

2008

.

MNRAS

,

391

,

1685

Crossref

Search ADS

Steinmetz

M.

et al. .

2006

.

AJ

,

132

,

1645

Crossref

Search ADS

Turbide

L.

,

Moffat

A. F. J.

.

1993

.

AJ

,

105

,

1831

Crossref

Search ADS

Uemura

M.

,

Ohashi

H.

,

Hayakawa

T.

,

Ishida

E.

,

Kato

T.

,

Hirata

R.

.

2000

.

PASJ

,

52

,

143

Vera-Ciro

C. A.

,

Helmi

A.

,

Starkenburg

E.

,

Breddels

M. A.

.

2013

.

MNRAS

,

428

,

169

Crossref

Search ADS

Watkins

L. L.

et al. .

2009

.

MNRAS

,

398

,

1757

Crossref

Search ADS

Weber

M.

,

de Boer

W.

.

2010

.

A&A

,

509

,

A25

Crossref

Search ADS

Williams

A. A.

,

Evans

N. W.

.

2015

.

MNRAS

,

454

,

698

Crossref

Search ADS

Williams

M. E. K.

et al. .

2013

.

MNRAS

,

436

,

101

Crossref

Search ADS

Xiang

M.-S.

et al. .

2015

.

MNRAS

,

448

,

822

Crossref

Search ADS

Xiang

M.-S.

et al. .

2016

.

MNRAS

,

in press

Xin

X.-S.

,

Zheng

X.-W.

.

2013

.

Res. Astron. Astrophys.

,

13

,

849

Crossref

Search ADS

Xue

X. X.

et al. .

2008

.

ApJ

,

684

,

1143

Crossref

Search ADS

Xue

X.-X.

et al. .

2014

.

ApJ

,

784

,

170

Crossref

Search ADS

Xue

X.-X.

,

Rix

H.-W.

,

Ma

Z.

,

Morrison

H.

,

Bovy

J.

,

Sesar

B.

,

Janesh

W.

.

2015

.

ApJ

,

809

,

144

Crossref

Search ADS

Yanny

B.

et al. .

2009

.

AJ

,

137

,

4377

Crossref

Search ADS

Yuan

H.-B.

et al. .

2015

.

MNRAS

,

448

,

855

Crossref

Search ADS

Zasowski

G.

et al. .

2013

.

AJ

,

146

,

81

Crossref

Search ADS

Zhang

L.

,

Rix

H.-W.

,

van de Ven

G.

,

Bovy

J.

,

Liu

C.

,

Zhang

G.

.

2013

.

ApJ

,

772

,

108

Crossref

Search ADS

APPENDIX: MOCK-DATA TESTS

Here, we use mock-data to test the effects of the approximations used in our kinematical model and the performance of the whole methodology described in Section 3 on deriving V_c(R) and |$\overline{V}_{{R}} (R)$|⁠. The mock-data sets are created by re-sampling the heliocentric line-of-sight velocity, |$V^{\rm helio}_{\rm los}$|⁠, for each data point from the PDF p(V_los|l, b, d, R₀, V_R,⊙, V_ϕ,⊙, V_ϕ(R), V_R(R), σ_R(R)). The positions (l, b, d) of the stars in the PDF are taken as exactly as those of the real data, i.e. 15 634 PRCGs. The values of Galactic constants (R₀, V_{ϕ, ⊙}, V_R,⊙) are the same as those fixed in Table 1 and the radial velocity dispersion profile, σ_R(R), is taken from the one derived in Section 3.1 by ourselves. At each R, a Gaussian distribution is used for V_R with a velocity dispersion, σ_R(R), as just mentioned. The centre of the Gaussian distribution, i.e. the mean radial velocity |$\overline{V}_{{R}}$|⁠, is a function of R given by

\begin{equation} \overline{V}_{{R}} = -10 \times \cos (2\pi R / 10 + 2). \end{equation}

(A1)

Rather than using a simplified Gaussian distribution of azimuthal-velocities assumed in our kinematical modelling described in Section 3.1, here, we use an azimuthal-velocity distribution generated from an analytic formula given by SB12. As argued by SB12, the analytic formula can nicely and naturally reproduce the non-Gaussianity of the observed azimuthal velocity distribution of the Geneva–Copenhagen Survey (GCS) local sample of stars with accurate space velocities. In addition, the distribution of V_ϕ given by this analytic formula also yields excellent fit to the distribution of V_ϕ produced by rigorous torus-based dynamics modelling (Binney & McMillan 2011). The distribution of V_ϕ generated from this formula is given by

\begin{eqnarray} n (V_{\phi } | R, z) &=& \mathcal {N} \exp {\left(-\frac{R_{\rm g} - R_{0}}{R_{\rm d}}\right)}\frac{2\pi R_{\rm g}K}{\sigma _{{R}} (R_{\rm g})}\nonumber\\ &&\times \,\exp {\left[-\frac{\Delta \Phi _{\rm ad}}{\sigma _{{R}}^{2} (R_{\rm g})}\right]}f(z, R_{\rm g} - R), \end{eqnarray}

(A2)

where |$\mathcal {N}$| is a normalization factor. R_g is the guiding-centre radius given by R_g = RV_ϕ/V_c. K is a factor that can be numerically calculated (cf. equation 12 of SB12). ΔΦ_ad and f(z, R_g − R) are the so-called adiabatic potential and z factor, respectively (cf. section 3 of SB12 for detailed descriptions of the two terms). The values of R_d and R₀ are adopted from Table 1. The profile of radial velocity dispersion, σ_R(R_g), is again the same as the one derived in Section 3.1 by ourselves. For the RC, V_c(R), two types of shape are assumed and tested: (1) a flat one,

\begin{equation} V_{\rm c} = 220; \end{equation}

(A3)

and (2) a parabolic curve,

\begin{equation} V_{\rm c} = 3 \times (R -12)^2 + 220. \end{equation}

(A4)

Using the PDF of |$V_{\rm los}^{\rm helio}$| described above, we create five mock-data sets, two with the flat and three with the parabolic RC. Then the same fitting technique used for the real data as described in Section 3.2 is applied to the mock-data sets. The RCs derived from the five mock-data sets are plotted in the left-hand panel of Fig. A1. The mean radial motions as a function of R derived from the mock-data sets are also shown in the right-hand panel of Fig. A1. For both assumed shapes of RC, the true values of circular velocity are all excellently recovered by our methodology described in Section 3. In addition, as we expect, the true values of the mean radial motions as a function of R are also recovered quite well.

Figure A1.

The left- and right-hand panels show the RCs and mean radial motions, respectively, recovered from the five mock-data sets using the exactly the same fitting method as applied to the real data. Red lines in the left and right panels plot the true RCs and mean radial motions as a function of R, respectively, that are assumed in generating the mock-data sets. The top two rows show the case of mock-data sets assuming a flat RC of value of 220 km s⁻¹ [see equation (A3)], while the bottom rows are parabolic RC described by equation (A4). The true mean radial motions as a function of R are described by equation (A1).

Open in new tab Download slide

Download all slides

Month:	Total Views:
December 2016	2
January 2017	12
February 2017	32
March 2017	21
April 2017	14
May 2017	27
June 2017	47
July 2017	34
August 2017	13
September 2017	18
October 2017	18
November 2017	21
December 2017	19
January 2018	11
February 2018	13
March 2018	30
April 2018	21
May 2018	18
June 2018	9
July 2018	15
August 2018	10
September 2018	13
October 2018	28
November 2018	15
December 2018	14
January 2019	3
February 2019	17
March 2019	22
April 2019	32
May 2019	13
June 2019	12
July 2019	5
August 2019	7
September 2019	10
October 2019	8
November 2019	20
December 2019	18
January 2020	14
February 2020	25
March 2020	15
April 2020	24
May 2020	4
June 2020	18
July 2020	12
August 2020	12
September 2020	25
October 2020	23
November 2020	31
December 2020	22
January 2021	38
February 2021	23
March 2021	48
April 2021	36
May 2021	22
June 2021	19
July 2021	32
August 2021	36
September 2021	24
October 2021	24
November 2021	44
December 2021	17
January 2022	32
February 2022	23
March 2022	55
April 2022	44
May 2022	46
June 2022	30
July 2022	33
August 2022	37
September 2022	45
October 2022	60
November 2022	59
December 2022	42
January 2023	31
February 2023	43
March 2023	56
April 2023	76
May 2023	43
June 2023	37
July 2023	25
August 2023	47
September 2023	40
October 2023	44
November 2023	35
December 2023	51
January 2024	94
February 2024	57
March 2024	74
April 2024	106
May 2024	62
June 2024	41
July 2024	54
August 2024	44
September 2024	77
October 2024	91
November 2024	104
December 2024	112
January 2025	94
February 2025	91
March 2025	121
April 2025	87
May 2025	58

Article Contents

The Milky Way's rotation curve out to 100 kpc and its constraint on the Galactic mass distribution

Abstract

1 INTRODUCTION

2 DATA

2.1 Coordinate systems

2.2 LSS-GAC, SDSS/SEGUE and SDSS-III/APOGEE data

2.3 PRCG and HKG samples

3 RC FROM PRCGs

3.1 Kinematical model

3.2 Fitting and results

3.3 Discussion

3.3.1 Systematics

3.3.2 Comparisons with other work

3.3.3 The dip at R ∼ 11 kpc

4 RC FROM HKGS

4.1 Spherical jeans model and results

4.2 Discussion

4.2.1 Systematics

4.2.2 Comparisons with other work

4.2.3 The dip at r ∼ 19 kpc

5 FINAL COMBINED RC

6 GALACTIC MASS MODELS BASED ON THE COMBINED RC

6.1 Galactic mass models and the fit results

6.2 Discussion

6.2.1 DM halo

6.2.2 The rings

7 SUMMARY

Acknowledgments

REFERENCES

APPENDIX: MOCK-DATA TESTS

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

The Milky Way's rotation curve out to 100 kpc and its constraint on the Galactic mass distribution Free

Abstract

1 INTRODUCTION

2 DATA

2.1 Coordinate systems

2.2 LSS-GAC, SDSS/SEGUE and SDSS-III/APOGEE data

2.3 PRCG and HKG samples

3 RC FROM PRCGs

3.1 Kinematical model

3.2 Fitting and results

3.3 Discussion

3.3.1 Systematics

3.3.2 Comparisons with other work

3.3.3 The dip at R ∼ 11 kpc

4 RC FROM HKGS

4.1 Spherical jeans model and results

4.2 Discussion

4.2.1 Systematics

4.2.2 Comparisons with other work

4.2.3 The dip at r ∼ 19 kpc

5 FINAL COMBINED RC

6 GALACTIC MASS MODELS BASED ON THE COMBINED RC

6.1 Galactic mass models and the fit results

6.2 Discussion

6.2.1 DM halo

6.2.2 The rings

7 SUMMARY

Acknowledgments

REFERENCES

APPENDIX: MOCK-DATA TESTS

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

The Milky Way's rotation curve out to 100 kpc and its constraint on the Galactic mass distribution