Large covariance matrices: smooth models from the two-point correlation function

O'Connell, Ross; Eisenstein, Daniel; Vargas, Mariana; Ho, Shirley; Padmanabhan, Nikhil

doi:10.1093/mnras/stw1821

Abstract

We introduce a new method for estimating the covariance matrix for the galaxy correlation function in surveys of large-scale structure. Our method combines simple theoretical results with a realistic characterization of the survey to dramatically reduce noise in the covariance matrix. For example, with an investment of only ≈1000 CPU hours we can produce a model covariance matrix with noise levels that would otherwise require ∼35 000 mocks. Non-Gaussian contributions to the model are calibrated against mock catalogues, after which the model covariance is found to be in impressive agreement with the mock covariance matrix. Since calibration of this method requires fewer mocks than brute force approaches, we believe that it could dramatically reduce the number of mocks required to analyse future surveys.

large-scale structure of Universe

1 INTRODUCTION

Covariance matrix estimation is a fundamental challenge in precision cosmology. In the standard approach many artificial or ‘mock’ catalogues are created that mimic the properties of the cosmological data set, the analysis is performed on each mock catalogue, and a sample covariance computed using those results. From a certain point of view this approach is very simple, since the mock catalogues are statistically independent of one another. The potential stumbling block is that the sample covariance provides a noisy estimate of the true covariance, and covariance matrix noise can degrade the final measurement. Reducing noise in the covariance matrix to acceptable levels generally requires a large number of mock catalogues, and covariance matrix estimation can consume the majority of computational resources for current analyses. Moreover, there is a clear trade-off between the number of mock catalogues required and the accuracy of any individual mock. We aim to improve this situation with a new method for covariance matrix estimation that combines simple theoretical results with a realistic characterization of the survey, and that can be calibrated against a relatively small number of mocks. We will demonstrate that this approach produces a covariance matrix suitable for analysis of baryon acoustic oscillations (BAO) in modern surveys.

The consequences of covariance matrix noise have been a subject of recent interest (Dodelson & Schneider 2013; Taylor, Joachimi & Kitching 2013; Percival et al. 2014). It is generally true that when cosmological parameters are determined from an observable estimated in N_bins (for example a correlation function or power spectrum), and the corresponding covariance matrix is estimated using N_mocks mock catalogues, then there is a fractional increase in the uncertainty in the cosmological parameters, relative to an ideal measurement, of |$\mathcal {O}\left(1/\left(N_{\mathrm{mocks}}-N_{\mathrm{bins}}\right)\right)$|⁠. In other words, having N_mocks ∼ 10 × N_bins (rather than much larger) has an impact on the final parameter estimates comparable to reducing the volume of a survey by ∼10 per cent. When the covariance matrix is estimated using a sample covariance of mock catalogues, there is thus an incentive to make N_mocks − N_bins as large as possible.

While some current surveys have achieved N_mocks ∼ 100 × N_bins, we are concerned that this may not be achievable in future surveys. First, we expect that many future analyses will attempt to utilize more accurate mocks, for example incorporating realistic light cones, and that this will raise the computational cost of a single mock. In addition, many future surveys [e.g. Euclid (Laureijs et al. 2011), DESI (Levi et al. 2013), WFIRST-AFTA (Spergel et al. 2015)] have proposed to perform tomographic analyses, rather than analysing a single redshift range; where current analyses might estimate the correlation function using 40 bins, a tomographic analysis using 10 redshift slices will necessarily use 400 bins.

A number of approaches have been developed to mitigate this problem. Many authors have focused on decreasing the computational time required to generate a mock, thus enabling a larger number of mocks. For a discussion of this line of research, and a comparison of different methods, we refer the reader to Chuang et al. (2015). We emphasize that while available computing resources may increase at a pace that accommodates increasing mock requirements, there will always be an opportunity cost to producing large numbers of mocks – given fixed computing resources, reducing the number of mocks required by a factor of 100 means that the amount of computing time that can be spent on each mock increases by a factor of 100.

It is also possible to address the problem by reducing N_bins, rather than increasing N_mocks. For example, current BAO analyses typically compress the angular dependence of the correlation function into two multipole moments or a small number of angular wedges, rather than retaining the full angular dependence of the correlation function. Proposals have also been made for an analogous compression of redshift-dependence for tomographic analyses (Zhu, Padmanabhan & White 2015). While these approaches provide an intriguing complement to the method we will describe, we point out that there may be tension between the optimal modes for compressing the signal, and the characteristic modes associated with systematic effects. For example, reducing the angular dependence of the redshift space galaxy correlation function to monopole and quadrupole modes provides highly efficient compression of the underlying correlation function, but systematic effects tend to depend on line-of-sight or transverse separations between points and thus compress poorly into the monopole and quadrupole modes.

Rather than directly change N_mocks or N_bins, one can move beyond a simple sample covariance matrix. For recent efforts to develop phenomenological models of the power spectrum covariance matrix, see Pearson & Samushia (2016). Methods that take advantage of the sparsity of the precision matrix also present a promising avenue (Padmanabhan et al. 2016), as they provide low noise estimates of the covariance from a small number of mocks. For both of these approaches (and in the approach developed in this paper), it is important to understand if discrepancies between the approximated covariance matrix and the true covariance matrix will have an impact on the estimation of cosmological parameters.

The approach we will develop in this paper builds on a simple observation: that the covariance of a two-point function is an appropriately integrated four-point function. The foundational work on this approach is provided by Bernstein (1994), who provided explicit formulas for the covariance of the two-point correlation function of a non-Gaussian field observed in a finite volume with uniform number density. These integrals were recast in terms of the power spectrum by Cohn (2006), and Smith et al. and Sanchez et al. used these results to produce covariance matrices for a Gaussian field Poisson sampled in real space with uniform number density (Sanchez, Baugh & Angulo 2008; Smith, Scoccimarro & Sheth 2008). These efforts were primarily focused on producing covariance matrices suitable for use in forecasts, rather than analyses of existing data. They were later extended by Grieb et al. (2016) to redshift space, and to accommodate higher multipoles. Xu et al. (2012, 2013) used a similar model covariance matrix to analyse the clustering of luminous red galaxies in SDSS DR7. In order to bring the model into better agreement with mock catalogues, Xu et al. more carefully modelled the redshift space power spectrum and introduced modifications to the shot noise term, eventually fitting a four-parameter model to 160 mock catalogues. The resulting model covariance was found to be in good agreement with the mock covariance.

The approach we take in this paper is to work entirely in position space, using the correlation function instead of the power spectrum. We extend the results of Bernstein to accommodate a non-uniform number density and accompanying non-uniform weights, so that our model accurately reflects the geometry of a modern survey. We find that the necessary integrals can be performed with a relatively small investment of computational time – for the specific example considered in this paper, a noise level that otherwise would have required ∼35 000 mocks was achieved using only 1000 CPU hours. Rather than directly model the connected three- and four-point correlation functions, we find that their effects can be modelled by adjusting the level of shot noise in the model covariance matrix. We fit this single parameter using 1000 QPM mocks, although we find that a much smaller number of mocks would suffice to constrain the parameter. Extensive comparisons between our model covariance and the QPM mock covariance indicate that the model is suitable for use in cosmological analysis.

This paper is organized as follows. In Section 2 we provide a simple analytic expression for the covariance matrix of a galaxy correlation function. This extends the results of Bernstein (1994) to incorporate position-dependent number densities and weights. In Section 3 we numerically integrate this expression over a realistic survey geometry, assuming that the underlying galaxy field is Gaussian. We find reasonable agreement between our results and a sample covariance computed from 1000 quick particle mesh (QPM; White, Tinker & McBride 2014) mocks produced using the same survey geometry. In Section 4 we show that increasing the level of shot noise in the Gaussian model covariance matrix brings it closer to the full, non-Gaussian covariance matrix. After fitting the shot noise increase using the QPM mocks, we find exceptional agreement between our method and the QPM sample covariance. The methods developed here for comparing covariance matrices may be of interest to other researchers working on the covariance matrix problem.

2 N-Point Functions and the Covariance Matrix

The basic observation that motivates this work is that the covariance matrix of an n-point function can be written as a combination of 2n − and lower-point functions. As a simple example, consider the correlation function ξ_ij of a density field δ_i:

\begin{equation} \xi _{ij}=\delta _{i}\delta _{j}\,. \end{equation}

(1)

The covariance between two observations of the correlation function is simply

\begin{eqnarray} \mathrm{cov}\left(\xi _{ij},\xi _{k\ell }\right) & = & \left\langle \xi _{ij}\xi _{kl}\right\rangle -\left\langle \xi _{ij}\right\rangle \left\langle \xi _{k\ell }\right\rangle \end{eqnarray}

(2)

\begin{eqnarray} & = & \left\langle \delta _{i}\delta _{j}\delta _{k}\delta _{\ell }\right\rangle -\left\langle \delta _{i}\delta _{j}\right\rangle \left\langle \delta _{k}\delta _{\ell }\right\rangle \end{eqnarray}

(3)

\begin{eqnarray} & = & \left\langle \xi _{ijk\ell }\right\rangle +\left\langle \xi _{ik}\right\rangle \left\langle \xi _{j\ell }\right\rangle +\left\langle \xi _{i\ell }\right\rangle \left\langle \xi _{jk}\right\rangle , \end{eqnarray}

(4)

where we have used ξ_ijkℓ to denote the connected four-point function. For fields that are Gaussian or nearly Gaussian, the value of expressions like (4) should be clear: they allow us to convert an estimate of the two-point correlation function into an estimate of that correlation function's covariance matrix.

In the following, we will demonstrate how to extend this simple result to correlation functions estimated in bins |$\Theta _{ij}^{a}$|⁠; how to modify it for a Poisson-sampled density field, and how to incorporate the inhomogeneous number density and non-uniform weighting that occur in realistic surveys. We build on the foundational work of Bernstein (1994), who derived an integral expression for the covariance matrix of the correlation function of a non-Gaussian field estimated from a survey with finite volume and finite, uniform number density. Our introduction of inhomogeneous number density and non-uniform weighting are novel extensions of that work.

2.1 Poisson sampling

Suppose that we have divided the volume of a galaxy survey into many cells, each small enough that it contains at most one galaxy. The overdensity in cell i is then

\begin{equation} \delta _{i}=\frac{b_{i}}{n_{i}}-1\,, \end{equation}

(5)

where b_i = 1 if the cell contains a galaxy and b_i = 0 otherwise, and n_i is the expected number of galaxies in the cell (note that this may vary from cell to cell). Since the choice of cell size is arbitrary we can choose n_i ≪ 1, and in this limit the overdensity satisfies a useful identity:

\begin{equation} \delta _{i}^{2}\approx \frac{1}{n_{i}}\left(1+\delta _{i}\right). \end{equation}

(6)

This identity encodes our intuitive understanding of Poisson sampling, which is that at sufficiently short separations |$\left(\delta _{i}\delta _{j}\rightarrow \ \delta _{i}^{2}\right)$| the correlation function is replaced by shot noise (∼1/n_i).

We estimate the correlation function as

\begin{eqnarray} \hat{\xi }^{a} & = & \left(RR^{a}\right)^{-1}\sum _{i\ne j}\Theta _{ij}^{a}n_{i}n_{j}\delta _{i}\delta _{j}\,, \end{eqnarray}

(7)

\begin{eqnarray} RR^{a} & \equiv & \sum _{i\ne j}\Theta _{ij}^{a}n_{i}n_{j}\,. \end{eqnarray}

(8)

The binning matrices |$\Theta _{ij}^{a}$| are one for pairs of points i, j that fall in bin a, and zero otherwise. We assume that the bins require finite separation, so that both sums run over distinct points i, j. Note that RR^a coincides with the usual notion of RR pair counts. The covariance of |$\hat{\xi }^{a}$| is then

\begin{equation} \left\langle \hat{\xi }^{a}\hat{\xi }^{b}\right\rangle -\left\langle \hat{\xi }^{a}\right\rangle \left\langle \hat{\xi }^{b}\right\rangle =\left(RR^{a}RR^{b}\right)^{-1}\sum _{i\ne j,k\ne \ell }\Theta _{ij}^{a}\Theta _{k\ell }^{b}n_{i}n_{j}n_{k}n_{\ell }\left[\left\langle \delta _{i}\delta _{j}\delta _{k}\delta _{\ell }\right\rangle -\left\langle \delta _{i}\delta _{j}\right\rangle \left\langle \delta _{k}\delta _{\ell }\right\rangle \right]. \end{equation}

(9)

To relate these quantities to the usual n-point functions, we must rewrite the sum in terms of non-coincident points,

\begin{equation} \sum _{i\ne j,k\ne \ell }\Theta _{ij}^{a}\Theta _{k\ell }^{b}n_{i}n_{j}n_{k}n_{\ell }\left\langle \delta _{i}\delta _{j}\delta _{k}\delta _{\ell }\right\rangle =\sum _{i\ne j\ne k\ne \ell }\Theta _{ij}^{a}\Theta _{k\ell }^{b}n_{i}n_{j}n_{k}n_{\ell }\left\langle \delta _{i}\delta _{j}\delta _{k}\delta _{\ell }\right\rangle +S_{\mathrm{single}}+S_{\mathrm{double}}, \end{equation}

(10)

with S_single containing single contractions,

\begin{eqnarray} S_{\mathrm{single}} & = & \sum _{i\ne j\ne k}\Theta _{ij}^{a}\Theta _{ki}^{b}n_{i}^{2}n_{j}n_{k}\left\langle \delta _{i}^{2}\delta _{j}\delta _{k}\right\rangle \end{eqnarray}

(11)

\begin{eqnarray} & = & \sum _{i\ne j\ne k}\Theta _{ij}^{a}\Theta _{ki}^{b}n_{i}n_{j}n_{k}\left[\left\langle \delta _{j}\delta _{k}\right\rangle +\left\langle \delta _{i}\delta _{j}\delta _{k}\right\rangle \right], \end{eqnarray}

(12)

and S_double containing double contractions,

\begin{eqnarray} S_{\mathrm{double}} & = & \delta ^{ab}\sum _{i\ne j}\Theta _{ij}^{a}n_{i}^{2}n_{j}^{2}\left\langle \delta _{i}^{2}\delta _{j}^{2}\right\rangle \end{eqnarray}

(13)

\begin{eqnarray} & = & \delta ^{ab}\sum _{i\ne j}\Theta _{ij}^{a}n_{i}n_{j}\left[1+\left\langle \delta _{i}\delta _{j}\right\rangle \right]. \end{eqnarray}

(14)

We have used (6) to simplify these expressions, and δ^ab are Kronecker deltas. These contractions can be visualized with the diagrams in Fig. 1.

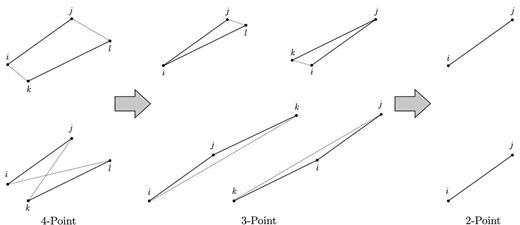
$Configurations of points that contribute to the covariance matrix integrals. Starting from the two four-point configurations that contribute to C4, single contractions generate the four possible three-point configurations of C3, and double contractions generate the two-point configuration of C2. Solid lines indicate pairs of points that are governed by a binning function, $\Theta ^{a}\left({\boldsymbol r}_{i}-{\boldsymbol r}_{j}\right)$, while dotted lines indicate pairs of points that are governed by a factor of the correlation function, $\xi \left({\boldsymbol r}_{i}-{\boldsymbol r}_{k}\right)$.$

Figure 1.

Configurations of points that contribute to the covariance matrix integrals. Starting from the two four-point configurations that contribute to C₄, single contractions generate the four possible three-point configurations of C₃, and double contractions generate the two-point configuration of C₂. Solid lines indicate pairs of points that are governed by a binning function, |$\Theta ^{a}\left({\boldsymbol r}_{i}-{\boldsymbol r}_{j}\right)$|⁠, while dotted lines indicate pairs of points that are governed by a factor of the correlation function, |$\xi \left({\boldsymbol r}_{i}-{\boldsymbol r}_{k}\right)$|⁠.

Open in new tab Download slide

After considering the possible contractions, we arrive at the following expression for C^ab, the model covariance matrix:

\begin{eqnarray} C^{ab} & = & C_{4}^{ab}+C_{3}^{ab}+C_{2}^{ab}\,, \end{eqnarray}

(15)

\begin{eqnarray} C_{4}^{ab} & \equiv & \left(RR^{a}RR^{b}\right)^{-1}\sum _{i\ne j\ne k\ne \ell }\Theta _{ij}^{a}\Theta _{k\ell }^{b}n_{i}n_{j}n_{k}n_{\ell }\left[\xi _{ijk\ell }+\xi _{ik}\xi _{j\ell }+\xi _{i\ell }\xi _{jk}\right], \end{eqnarray}

(16)

\begin{eqnarray} C_{3}^{ab} & \equiv & 4\times \left(RR^{a}RR^{b}\right)^{-1}\sum _{i\ne j\ne k}\Theta _{ij}^{a}\Theta _{ki}^{b}n_{i}n_{j}n_{k}\left[\xi _{ijk}+\xi _{jk}\right], \end{eqnarray}

(17)

\begin{eqnarray} C_{2}^{ab} & \equiv & 2\times \delta _{ab}\left(RR^{a}RR^{b}\right)^{-1}\sum _{i\ne j}\Theta _{ij}^{a}n_{i}n_{j}\left[\xi _{jk}+1\right], \end{eqnarray}

(18)

where ξ_ijk and ξ_ijkℓ denote the connected three- and four-point functions, respectively. A continuum limit yields

\begin{eqnarray} C_{4}^{ab} & = & (RR^{a}RR^{b})^{-1}\int d^{3}{\boldsymbol r}_{i}d^{3}{\boldsymbol r}_{j}d^{3}{\boldsymbol r}_{k}d^{3}{\boldsymbol r}_{\ell }\Theta ^{a}({\boldsymbol r}_{i}-{\boldsymbol r}_{j})\Theta ^{b}({\boldsymbol r}_{k}-{\boldsymbol r}_{\ell })n({\boldsymbol r}_{i})n({\boldsymbol r}_{j})n({\boldsymbol r}_{k})n({\boldsymbol r}_{\ell })\nonumber \\ & & \times \left[\xi _{4}({\boldsymbol r}_{i},{\boldsymbol r}_{j},{\boldsymbol r}_{k},{\boldsymbol r}_{\ell })+\xi ({\boldsymbol r}_{i}-{\boldsymbol r}_{k})\xi ({\boldsymbol r}_{j}-{\boldsymbol r}_{\ell })+\xi ({\boldsymbol r}_{i}-{\boldsymbol r}_{k})\xi ({\boldsymbol r}_{j}-{\boldsymbol r}_{\ell })\right], \end{eqnarray}

(19)

\begin{eqnarray} C_{3}^{ab} & = & 4\times (RR^{a}RR^{b})^{-1}\int d^{3}{\boldsymbol r}_{i}d^{3}{\boldsymbol r}_{j}d^{3}{\boldsymbol r}_{k}\Theta ^{a}({\boldsymbol r}_{i}-{\boldsymbol r}_{j})\Theta ^{b}({\boldsymbol r}_{k}-{\boldsymbol r}_{i})n({\boldsymbol r}_{i})n({\boldsymbol r}_{j})n({\boldsymbol r}_{k})\nonumber \\ & & \times \left[\xi _{3}({\boldsymbol r}_{i},{\boldsymbol r}_{j},{\boldsymbol r}_{k})+\xi ({\boldsymbol r}_{i}-{\boldsymbol r}_{k})\right], \end{eqnarray}

(20)

\begin{eqnarray} C_{2}^{ab} & = & 2\delta _{ab}\times (RR^{a}RR^{b})^{-1}\int d^{3}{\boldsymbol r}_{i}d^{3}{\boldsymbol r}_{j}\Theta ^{a}({\boldsymbol r}_{i}-{\boldsymbol r}_{j})n({\boldsymbol r}_{i})n({\boldsymbol r}_{j})\nonumber \\ & & \times \left[\xi ({\boldsymbol r}_{i}-{\boldsymbol r}_{j})+1\right], \end{eqnarray}

(21)

\begin{eqnarray} RR^{a} & = & \int d^{3}{\boldsymbol r}_{i}d^{3}{\boldsymbol r}_{j}\Theta ^{a}({\boldsymbol r}_{i}-{\boldsymbol r}_{j})n({\boldsymbol r}_{i})n({\boldsymbol r}_{j}), \end{eqnarray}

(22)

with ξ₃ and ξ₄ now denoting the connected three- and four-point functions and |$n\left({\boldsymbol r}\right)$| the expected number density at |${\boldsymbol r}$|⁠.

We can introduce a final complication, which is a non-uniform weighting scheme [e.g. FKP weights (Feldman, Kaiser & Peacock 1994)]. The basic observation is that a factor of w_iw_j is added to (7) and (8), leading to an additional factor of w_iw_jw_kw_ℓ in (9), but that (6) is unmodified. We therefore find

\begin{eqnarray} C_{4}^{ab} & = & (RR^{a}RR^{b})^{-1}\int d^{3}{\boldsymbol r}_{i}d^{3}{\boldsymbol r}_{j}d^{3}{\boldsymbol r}_{k}d^{3}{\boldsymbol r}_{\ell }\Theta ^{a}({\boldsymbol r}_{i}-{\boldsymbol r}_{j})\Theta ^{b}({\boldsymbol r}_{k}-{\boldsymbol r}_{\ell })\nonumber \\ & & \times\, n({\boldsymbol r}_{i})n({\boldsymbol r}_{j})n({\boldsymbol r}_{k})n({\boldsymbol r}_{\ell })w({\boldsymbol r}_{i})w({\boldsymbol r}_{j})w({\boldsymbol r}_{k})w({\boldsymbol r}_{\ell }) \nonumber \\ & & \times \left[\xi _{4}({\boldsymbol r}_{i},{\boldsymbol r}_{j},{\boldsymbol r}_{k},{\boldsymbol r}_{\ell })+\xi ({\boldsymbol r}_{i}-{\boldsymbol r}_{k})\xi ({\boldsymbol r}_{j}-{\boldsymbol r}_{\ell })+\xi ({\boldsymbol r}_{i}-{\boldsymbol r}_{\ell })\xi ({\boldsymbol r}_{j}-{\boldsymbol r}_{k})\right], \end{eqnarray}

(23)

\begin{eqnarray} C_{3}^{ab} & = & 4\times (RR^{a}RR^{b})^{-1}\int d^{3}{\boldsymbol r}_{i}d^{3}{\boldsymbol r}_{j}d^{3}{\boldsymbol r}_{k}\Theta ^{a}({\boldsymbol r}_{i}-{\boldsymbol r}_{j})\Theta ^{b}({\boldsymbol r}_{k}-{\boldsymbol r}_{i})n({\boldsymbol r}_{i})n({\boldsymbol r}_{j})n({\boldsymbol r}_{k})\nonumber \\ & & \times\, w^{2}({\boldsymbol r}_{i})w({\boldsymbol r}_{j})w({\boldsymbol r}_{k})\left[\xi _{3}({\boldsymbol r}_{i},{\boldsymbol r}_{j},{\boldsymbol r}_{k})+\xi ({\boldsymbol r}_{i}-{\boldsymbol r}_{k})\right], \end{eqnarray}

(24)

\begin{eqnarray} C_{2}^{ab} & = & 2\delta _{ab}\times (RR^{a}RR^{b})^{-1}\int d^{3}{\boldsymbol r}_{i}d^{3}{\boldsymbol r}_{j}\Theta ^{a}({\boldsymbol r}_{i}-{\boldsymbol r}_{j})n({\boldsymbol r}_{i})n({\boldsymbol r}_{j})\nonumber \\ & & \times\, w^{2}({{\boldsymbol r}_{i}})w^{2}({{\boldsymbol r}_{j}})\left[\xi ({\boldsymbol r}_{i}-{\boldsymbol r}_{j})+1\right], \end{eqnarray}

(25)

\begin{eqnarray} RR^{a} & = & \int d^{3}{\boldsymbol r}_{i}d^{3}{\boldsymbol r}_{j}\Theta ^{a}({\boldsymbol r}_{i}-{\boldsymbol r}_{j})n({\boldsymbol r}_{i})n({\boldsymbol r}_{j})w({{\boldsymbol r}_{i}})w({{\boldsymbol r}_{j}}). \end{eqnarray}

(26)

C₂, C₃, and C₄ all scale as 1/Vol, and are independent of overall rescalings of the weights. They also exhibit a simple scaling with the number density

\begin{equation} C_{m}^{ab}\propto n^{m-4}\,. \end{equation}

(27)

In Section 3 we will numerically integrate the Gaussian terms in (23)–(25). Rather than attempt to integrate the non-Gaussian terms involving ξ₃ and ξ₄, in Section 4 we will develop a simple method that uses increased shot noise to approximate the effects of non-Gaussianity.

3 INTEGRATING THE GAUSSIAN MODEL

In order to test the value of equations (23)–(26) for generating covariance matrices, we will attempt to reproduce the covariance matrix of a set of mock catalogues. Specifically, we will use 1000 QPM mocks (White et al. 2014) that mimic the CMASS sample of the Baryon Oscillation Spectroscopic Survey (BOSS). Redshift space distortions (RSD) are included, but no reconstruction algorithms have been applied to these mocks.

We use a correlation function estimated in 35 radial bins of width δr = 4 h⁻¹ Mpc, covering r = 40–180 h⁻¹ Mpc, and 10 angular bins of width δμ = 0.1, covering μ = 0–1. This is more bins, by at least a factor of 5, than would be used in a typical multipole analysis of BAO in the galaxy correlation function. A more aggressive binning was chosen in part because it makes the covariance matrix problem more challenging and makes the noise in the sample covariance matrix more readily apparent.

The numerical integration is performed with a new software package,¹ ‘rascal: A Rapid Sampler for Large Covariance Matrices’. It allows flexible specification of the cosmology, redshift distribution, and model correlation function, and can accept angular completeness masks in the mangle format (Swanson et al. 2008). The sampling algorithm is described in Section 3.3.

3.1 Survey geometry

The QPM mocks have a flat ΛCDM cosmology with Ω_m = 0.29. The geometry of the mock catalogues can be decomposed into radial and angular components. In the radial direction, the redshift-dependent number density |$\overline{n}\left(z\right)$| and weights w(z) are calibrated to the QPM mocks. We set |$\overline{n}\left(z\right)=0$| outside of the redshift bounds of the CMASS sample, i.e. for z < 0.43 and z > 0.7. In the angular directions, the survey mask specifies the completeness of the survey, c(Ω). The number density at a point in the survey is thus given by

\begin{equation} n\left(z,\Omega \right)=\overline{n}\left(z\right)c\left(\Omega \right). \end{equation}

(28)

In order to compare our implementation of the survey geometry with that of the mock catalogues, we compare the values of RR^a that we compute with the values taken from the mock random catalogues. The results are shown in Fig. 2. We find a small offset between our integration and the mocks which varies as a function of r_⊥. This arises because the mocks are generated using a ‘veto mask’ which replicates holes in the survey smaller than the telescope field-of-view (e.g. areas obscured by bright stars). Querying this mask is quite time-consuming, and we have not used it when generating the samples in this paper.

Figure 2.

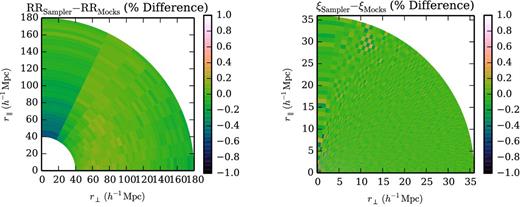
Using RR pair counts as a test of the survey geometry, we see that the representation of the survey in our sampler is in good agreement with the survey geometry in the mocks. We test the correlation function in our sampler by integrating it over the same bins used in the mocks, and find the two to be in excellent agreement.

Open in new tab Download slide

3.2 Correlation function

In order to integrate equations (23)–(25) we must specify a model correlation function (not to be confused with the estimated correlation function, whose covariance matrix we are computing). Rather than use the linear theory correlation function, or one derived from perturbation theory, we use the non-linear correlation function estimated from the 1000 QPM mocks. This ensures that the correlation function we use for integration agrees at relatively short scales (r ≳ 1 h⁻¹ Mpc) with the mocks, faithfully reproducing non-linear features such as the ‘finger-of-God’.

In the mocks, the correlation function is evaluated with radial bins that are 1 h⁻¹ Mpc wide and 120 angular bins covering μ = 0–1. A potential problem is that we then have estimates of the correlation function averaged over a bin, while the interpolation scheme used in our code assumes that the correlation function is specified at the centre of the bin. In order to address this we adopted an iterative scheme. We first treated the bin-averaged values ξ_mock^m from the mocks as bin-centre values, then performed the analogous bin-averaged integrals using our code,

\begin{equation} \xi _{\mathrm{out}}^{m}=(RR^{a})^{-1}\int d{\boldsymbol r}_{i}d{\boldsymbol r}_{j}\Theta ^{m}({\boldsymbol r}_{i}-{\boldsymbol r}_{j})n({\boldsymbol r}_{i})w({\boldsymbol r}_{i})n({\boldsymbol r}_{j})w({\boldsymbol r}_{j})\xi _{in}({\boldsymbol r}_{i}-{\boldsymbol r}_{j}). \end{equation}

(29)

We then rescaled the bin-centred input values of ξ according to ξ_out^m/ξ_mock^m and repeated the procedure. After three iterations, we arrived at sub-per-cent agreement between our implementation of the correlation function, as measured by its bin-averages, and the correlation function in the mocks. This is demonstrated in Fig. 2.

3.3 Importance Sampling

The integral (23) is 12-dimensional. It also has relatively limited support, so that the simplest Monte Carlo approaches converge quite slowly. We achieve acceptable convergence rates by using importance sampling. We begin by choosing a bin |$\Theta ^{a}\left({\boldsymbol r}_{i}-{\boldsymbol r}_{j}\right)$|⁠, then generate uniform draws of the separation |${\boldsymbol r}_{i}-{\boldsymbol r}_{j}$| within that bin. We then draw |$\left|{\boldsymbol r}_{j}-{\boldsymbol r}_{k}\right|$| and |$\left|{\boldsymbol r}_{i}-{\boldsymbol r}_{\ell }\right|$| from a pdf proportional to r²|ξ₀(r)|, where ξ₀(r) is the spherically averaged correlation function. The angular components of |${\boldsymbol r}_{j}-{\boldsymbol r}_{k}$| and |${\boldsymbol r}_{i}-{\boldsymbol r}_{\ell }$| are again determined by uniform draws. Finally, we sort the sets of four points according to which bin |$\Theta ^{b}\left({\boldsymbol r}_{k}-{\boldsymbol r}_{\ell }\right)$| they fall in. We therefore are able to estimate one column of |$C_{4}^{ab}$| from a set of draws. Since the integration proceeds column-by-column, this approach is trivially parallelizable. Moreover, the same draws can be used to determine |$C_{3}^{ab}$| and |$C_{2}^{aa}$|⁠.

In Fig. 3 we show portions of the C₄, C₃, and C₂ that we computed using this method and the inputs described above. These runs were completed on a desktop computer, requiring ≈1000 CPU hours to complete. Although the noise in our samples is not Wishart distributed, we can characterize our results in terms of an effective number of mocks by choosing a range of bins where the precision matrix should be very close to zero, then measuring the noise in those bins. Inverse Wishart statistics would imply

\begin{equation} \mathrm{var}(\Psi ^{ab})\approx \frac{\Psi ^{aa}\Psi ^{bb}}{N_{\mathrm{mocks}}-N_{\mathrm{bins}}} \end{equation}

(30)

for bins where Ψ^ab ≈ 0. We therefore define the effective number of mocks as

\begin{equation} N_{\mathrm{eff}}\equiv N_{\mathrm{bins}}+\left[\mathrm{var}\left(\frac{\Psi ^{ab}}{\sqrt{\Psi ^{aa}\Psi ^{bb}}}\right)\right]^{-1}, \end{equation}

(31)

with the variance taken across bins with Ψ^ab ≈ 0 from a single realization. Using bins with r^a ≥ 142 h⁻¹ Mpc and r^b ≤ 82 h⁻¹ Mpc, we find N_eff ∼ 35 000 for the C₄, C₃, and C₂ generated for this paper. The convergence of the sampler is easily characterized in terms of N_eff, with a roughly linear relationship between CPU time used running the sampler and N_eff.

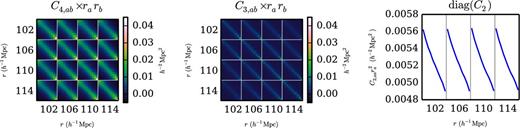
The three covariance matrix templates defined in (23)–(25), as evaluated using our sampler. The Gaussian covariance matrix is the sum of C4, C3, and the diagonal matrix C2. The correlation function is evaluated in bins with δr = 4 h−1 Mpc and δμ = 0.1. In these plots bins are ordered first in r (covering r = 102 h−1 Mpc to r = 114 h−1 Mpc), then in μ (μ = 0 to μ = 1). We show only a small portion of the covariance matrix, but this is sufficient to illustrate the high degree of convergence achieved in ∼1000 CPU hours with our sampler.

Figure 3.

The three covariance matrix templates defined in (23)–(25), as evaluated using our sampler. The Gaussian covariance matrix is the sum of C₄, C₃, and the diagonal matrix C₂. The correlation function is evaluated in bins with δr = 4 h⁻¹ Mpc and δμ = 0.1. In these plots bins are ordered first in r (covering r = 102 h⁻¹ Mpc to r = 114 h⁻¹ Mpc), then in μ (μ = 0 to μ = 1). We show only a small portion of the covariance matrix, but this is sufficient to illustrate the high degree of convergence achieved in ∼1000 CPU hours with our sampler.

Open in new tab Download slide

3.4 Comparison with mocks

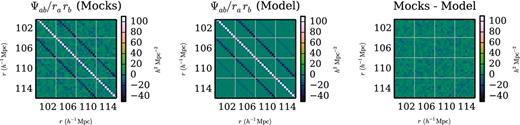
We have constructed a simple Gaussian model for the covariance matrix, taking as inputs the survey geometry and non-linear correlation function. Given the modesty of these inputs and the simplicity of the Gaussian model, the close agreement between our model covariance matrix and the covariance matrix determined using 1000 QPM mock catalogues with the same geometry and correlation function is remarkable. In Fig. 4 we plot a portion of the precision matrix as determined from the mocks, as computed in the Gaussian model, and the difference between the two. We observe discrepancies between the two at the ∼10 per cent level, most noticeable for diagonal entries in the precision matrix and in entries for bins with the same μ that are adjacent in r, and we now investigate the consequences of these discrepancies.

Figure 4.

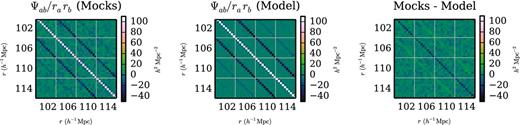
A small portion of the precision (inverse covariance) matrix, as determined from mock catalogues and from our Gaussian model (without fitting). The correlation function is evaluated in bins with δr = 4 h⁻¹ Mpc and δμ = 0.1. In these plots bins are ordered first in r (covering r = 102 h⁻¹ Mpc to r = 114 h⁻¹ Mpc), then in μ (μ = 0 to μ = 1). The reduction in noise in the model precision matrix, relative to the mock precision matrix, is readily apparent. The residuals in the rightmost plot are surprisingly small, given that we are using the purely Gaussian model, but also indicate the need for non-Gaussian corrections to the model (see Fig. 6).

Open in new tab Download slide

There are two reasons for using the precision matrix rather than the covariance matrix in this comparison. First, the structure of the precision matrix is considerably simpler than the structure of the covariance matrix, as can be seen by comparing Figs 3 and 4. Secondly, the precision matrix, rather than the covariance matrix, is what is used to compute χ² statistics, and thus is the quantity that is most relevant in analysis. Finally, we point out that large eigenvalues of the precision matrix correspond to small eigenvalues of the covariance matrix, and vice versa, so agreement between precision matrices cannot easily be established by comparing the corresponding covariance matrices directly.

We have chosen two approaches to a more detailed comparison of the precision matrices. In the first approach we begin by computing weighted residuals between the two precision matrices,

\begin{equation} \mathrm{resid}^{ab}=\frac{\Psi _{\mathrm{model}}^{ab}-\Psi _{\mathrm{mock}}^{ab}}{r_{a}r_{b}}\,, \end{equation}

(32)

with the r-weighting chosen to remove the naive r-dependence of the precision matrix. We then compute for each bin

\begin{eqnarray} \Delta r^{ab} & = & r^{a}-r^{b}\,, \end{eqnarray}

(33)

\begin{eqnarray} \Delta \mu ^{ab} & = & \mu ^{a}-\mu ^{b}, \end{eqnarray}

(34)

and average together the residuals for all bins with the same values of Δr and Δμ. The result is shown in Fig. 5 , where it is clear that we observe significant discrepancies when Δr = Δμ = 0 and when Δr = 4 h⁻¹ Mpc, Δμ = 0. We also observe small residuals for bins with Δr = 0 h⁻¹ Mpc, Δμ = 0.1, which were not readily apparent in Fig. 4.

Figure 5.

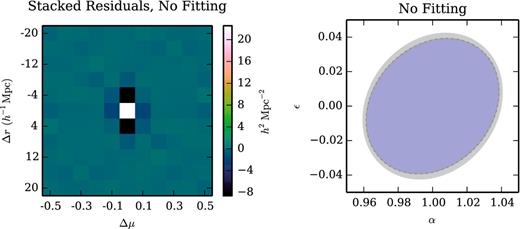
Comparison between the mock precision matrix and our (unfit) Gaussian model precision. Stacking the residuals reveals discrepancies on the diagonal of the precision matrix, and also for bins that share a μ range and are adjacent in r. Error ellipses for the BAO parameters α and ϵ show small discrepancies between the mocks (grey), model (blue), and noisy realizations of the model (dashed). The purely Gaussian model performs surprisingly well for BAO error estimation, but the discrepancies can be reduced with a non-Gaussian extension of the model (see Fig. 9).

Open in new tab Download slide

While the first method of comparison provides a direct check on the precision matrix, at least for modest Δr and Δμ, the second method uses a Fisher matrix to focus on modes of interest in BAO analyses. We assume a simple model for the correlation function,

\begin{equation} \xi _{\mathrm{Fisher}}\left(r,\mu \right)=\xi _{0}\left(b,\beta ,\alpha ,\epsilon ;r\right)P_{0}\left(\mu \right)+\xi _{2}\left(b,\beta ,\alpha ,\epsilon ;r\right)P_{2}\left(\mu \right)+\sum _{i=0}^{2}\left(a_{0,i}r^{i-2}P_{0}\left(\mu \right)+a_{2,i}r^{i-2}P_{2}\left(\mu \right)\right). \end{equation}

(35)

This correlation function depends on 10 parameters: the correlation function bias b, RSD parameter β, isotropic BAO rescaling factor α, anisotropic BAO rescaling factor ϵ, and the six systematic parameters a_{0, i}, a_{2, i}. P₀ and P₂ are Legendre polynomials. For further details on this model correlation function, see Xu et al. (2013). We then use the usual Fisher matrix formula to relate the precision matrix for these parameters to the precision matrix for the correlation function:

\begin{equation} \Psi _{\mathrm{Parameters}}^{ij}=\frac{\mathrm{\partial} \xi _{\mathrm{Fisher}}^{T}}{\mathrm{\partial} p_{i}}\Psi _{\mathrm{\xi }}\frac{\mathrm{\partial} \xi _{\mathrm{Fisher}}}{\mathrm{\partial} p_{j}}\,, \end{equation}

(36)

with p_i running over the 10 parameters. We invert Ψ_Parameters to find C_Parameters, then marginalize over b, β, and the systematic parameters to find a covariance matrix for isotropic and anisotropic BAO rescalings α and ϵ alone. The resulting error ellipses are shown in Fig. 5, and the parameters that define those ellipses are shown in Table 2. Again, discrepancies are readily apparent, though we defer a quantitative discussion of those discrepancies to Section 4.3.

It is telling that the discrepancies we observe between the mock and model precision matrices appear primarily on the diagonal of the precision matrix, and for bins that are adjacent to one another. Referring back to the integral in (23), we see that e.g. |$\left|{\boldsymbol r}_{i}-{\boldsymbol r}_{k}\right|$| and |$\left|{\boldsymbol r}_{j}-{\boldsymbol r}_{\ell }\right|$| can only reach very small values for overlapping or adjacent bins. We therefore interpret these discrepancies as a sign that our model is missing a contribution at short scales; since we know the two-point correlation function at short scales very well, it seems most likely that the observed discrepancies are a consequence of dropping the non-Gaussian terms involving ξ₃ and ξ₄. In the following we will attempt to model the non-Gaussian contributions without building explicit models for ξ₃ and ξ₄.

4 A SIMPLE MODEL FOR NON-GAUSSIANITY

We now attempt to improve the results of the previous section by introducing a one-parameter model to accommodate the effects of non-Gaussianity. Roughly speaking, we expect the connected three- and four-point functions to be large at small separations, then fall off rapidly at larger separations. A simple way of making the galaxy field ‘more correlated’ at short scales is to increase the amount of shot noise. Recall from (27) that C_m ∝ n^m−4, so that we can implement this rescaling using the integrals performed in the previous section:

\begin{equation} C_{\mathrm{NG}}\left(a\right)=C_{4}+aC_{3}+a^{2}C_{2}\,. \end{equation}

(37)

As illustrated in Figs 6 and 7, this simple rescaling yields a precision matrix that is in excellent agreement with the mock precision matrix. For applications of a similar model to the covariance of the power spectrum, see Carron, Wolk & Szapudi (2015).

$A small portion of the precision matrix, as determined from mock catalogues and from our non-Gaussian model (fit using the $\mathcal {L}_{2}$ likelihood). The correlation function is evaluated in bins with δr = 4 h−1 Mpc and δμ = 0.1. In these plots bins are ordered first in r (covering r = 102 h−1 Mpc to r = 114 h−1 Mpc), then in μ (μ = 0 to μ = 1). The difference in the final plot shows that fitting has removed the residuals found in Fig. 4, so that the non-Gaussian model precision matrix is now in excellent agreement with the mock precision matrix.$

Figure 6.

A small portion of the precision matrix, as determined from mock catalogues and from our non-Gaussian model (fit using the |$\mathcal {L}_{2}$| likelihood). The correlation function is evaluated in bins with δr = 4 h⁻¹ Mpc and δμ = 0.1. In these plots bins are ordered first in r (covering r = 102 h⁻¹ Mpc to r = 114 h⁻¹ Mpc), then in μ (μ = 0 to μ = 1). The difference in the final plot shows that fitting has removed the residuals found in Fig. 4, so that the non-Gaussian model precision matrix is now in excellent agreement with the mock precision matrix.

Open in new tab Download slide

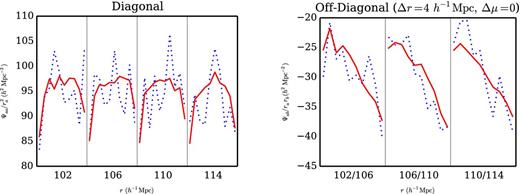
$We plot here the most prominent parts of the precision matrices in Fig. 6, both from the mocks (blue, dotted) and from our non-Gaussian model (red, fit using the $\mathcal {L}_{2}$ likelihood). The correlation function is evaluated in bins with δr = 4 h−1 Mpc and δμ = 0.1. In these plots bins are ordered first in r (covering r = 102 h−1 Mpc to r = 114 h−1 Mpc on), then in μ (μ = 0 to μ = 1).$

Figure 7.

We plot here the most prominent parts of the precision matrices in Fig. 6, both from the mocks (blue, dotted) and from our non-Gaussian model (red, fit using the |$\mathcal {L}_{2}$| likelihood). The correlation function is evaluated in bins with δr = 4 h⁻¹ Mpc and δμ = 0.1. In these plots bins are ordered first in r (covering r = 102 h⁻¹ Mpc to r = 114 h⁻¹ Mpc on), then in μ (μ = 0 to μ = 1).

Open in new tab Download slide

In the following, we will develop two approaches for fitting C_NG to the mocks. While the two approaches have distinct advantages and disadvantages, they will lead to substantially similar error ellipses for the BAO parameters α and ϵ.

4.1 |$\mathcal {L}_{1}$| likelihood

If we consider the mock correlation functions as noisy draws from a distribution described by Ψ_NG(a) = C_NG^{− 1}(a), the likelihood for a is

\begin{eqnarray} \mathcal {L}_{1}\left(a\right) & = & \prod _{\mathrm{\alpha \in mocks}}\sqrt{\frac{\det \Psi _{\mathrm{NG}}\left(a\right)}{\left(2\pi \right)^{N_{\mathrm{bins}}}}}\exp \left[-\frac{1}{2}\xi _{\alpha }^{T}\Psi _{\mathrm{NG}}\left(a\right)\xi _{\alpha }\right]. \end{eqnarray}

(38)

With a bit of rearranging, this becomes

\begin{equation} -\log \mathcal {L}_{1}\left(a\right)=\frac{N_{\mathrm{mocks}}}{2}\left[\mathrm{tr}\left(\Psi _{\mathrm{NG}}\left(a\right)C_{\mathrm{mocks}}\right)-\log \det \Psi _{\mathrm{NG}}\left(a\right)\right]+\cdots \,, \end{equation}

(39)

where the omitted terms are independent of a. Given our expression (37) for the model covariance matrix and the mock covariance matrix, it is straightforward to find the maximum likelihood value for a. This fitting dramatically reduces the residuals between the model and mock precision matrices, as shown in Fig. 8, and brings the mock and model α − ϵ error ellipses into better agreement, as show in Fig. 9.

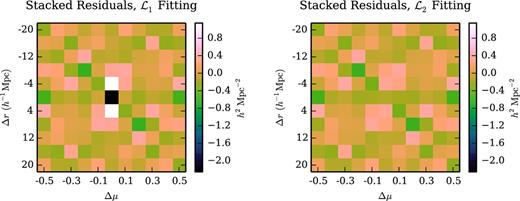
$Stacked residuals between our non-Gaussian (fit) models and the mocks. Fitting the non-Gaussian model using the $\mathcal {L}_{1}$ likelihood significantly reduces the stacked residuals relative to the (unfit) Gaussian model (see Fig. 5), while fitting with the $\mathcal {L}_{2}$ likelihood effectively eliminates the residuals. The absence of residuals indicates that the model precision matrix could replace the mock precision matrix in a variety of applications.$

Figure 8.

Stacked residuals between our non-Gaussian (fit) models and the mocks. Fitting the non-Gaussian model using the |$\mathcal {L}_{1}$| likelihood significantly reduces the stacked residuals relative to the (unfit) Gaussian model (see Fig. 5), while fitting with the |$\mathcal {L}_{2}$| likelihood effectively eliminates the residuals. The absence of residuals indicates that the model precision matrix could replace the mock precision matrix in a variety of applications.

Open in new tab Download slide

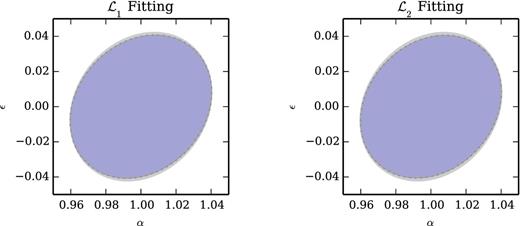
$Error ellipses for the BAO parameters α and ϵ from the mocks (grey), the non-Gaussian (fit) models (blue), and noisy realizations of those models (dashed). The discrepancies between the mocks and the Gaussian (fit) model are reduced, though a 3 per cent discrepancy persists in σϵ. The similarity between the two error ellipses indicates that choice of likelihood ($\mathcal {L}_{1}$ or $\mathcal {L}_{2}$) for fitting the non-Gaussian model has very little impact on BAO error estimation.$

Figure 9.

Error ellipses for the BAO parameters α and ϵ from the mocks (grey), the non-Gaussian (fit) models (blue), and noisy realizations of those models (dashed). The discrepancies between the mocks and the Gaussian (fit) model are reduced, though a 3 per cent discrepancy persists in σ_ϵ. The similarity between the two error ellipses indicates that choice of likelihood (⁠|$\mathcal {L}_{1}$| or |$\mathcal {L}_{2}$|⁠) for fitting the non-Gaussian model has very little impact on BAO error estimation.

Open in new tab Download slide

In order to better understand how this fitting works, we expand around a solution Ψ_NG → Ψ_NG + δΨ_NG, finding

\begin{eqnarray} \delta \left[-\log \mathcal {L}_{1}\right] & = & \frac{N_{\mathrm{mocks}}}{2}\left[\mathrm{tr}\left(\delta \Psi _{\mathrm{NG}}C_{\mathrm{mocks}}\right)-\log \det \left(1+C_{\mathrm{NG}}\delta \Psi _{\mathrm{NG}}\right)\right] \end{eqnarray}

(40)

\begin{eqnarray} \approx \frac{N_{\mathrm{mocks}}}{2}\,\mathrm{tr}\left[\delta \Psi _{\mathrm{NG}}\left(C_{\mathrm{mocks}}-C_{\mathrm{NG}}\right)\right], \end{eqnarray}

(41)

so that the likelihood |$\mathcal {L}_{1}$| is maximized when C_mocks = C_NG.

The principal benefit of the likelihood |$\mathcal {L}_{1}$| is that it does not require that we invert C_mocks. Indeed, this likelihood provides effective constraints on a (or other parameters, should we choose to fit a more elaborate model) even when C_mocks is degenerate, i.e. when N_mocks < N_bins. Although we will continue to use the full 1000 QPM mocks in our analysis, a much smaller number would have led to a very similar Ψ_NG. We anticipate that because this approach alleviates the need to have very large numbers of mock catalogues, it could be useful in a wide variety of cosmological analyses.

4.2 |$\mathcal {L}_{2}$| likelihood

The |$\mathcal {L}_{1}$| is not the only possible way to fit one covariance matrix to another. If we consider the goal to be comparison of two matrices, a plethora of methods are available. Noting that our goal is not to compare to arbitrary matrices, but instead to compare the two distributions described by those matrices, significantly narrows the field. One prominent candidate is the Kullback–Leibler (KL) divergence (Kullback 1951), which for two multivariate normal distributions (with the same means) specified by Ψ_a and C_b simplifies to

\begin{equation} KL\left(\Psi _{a},C_{b}\right)=\mathrm{tr}\left(\Psi _{a}C_{b}\right)-\log \det \Psi _{a}-\log \det C_{b}-N_{\mathrm{bins}}\,. \end{equation}

(42)

Note that if we take Ψ_a = Ψ_NG(a) and C_b = C_mocks, the result is proportional to (39), so that we have arrived back at the |$\mathcal {L}_{1}$| likelihood.

The KL divergence is notoriously non-symmetric, so that KL(Ψ_a, C_b) ≠ KL(Ψ_b, C_a). We can therefore formulate a second likelihood,

\begin{equation} -\log \mathcal {L}_{2}\left(a\right)= KL\left(\Psi _{\mathrm{mocks}},C_{\mathrm{NG}}\left(a\right)\right), \end{equation}

(43)

which will lead to a slightly different maximum likelihood value for a. Varying this likelihood as above, we find

\begin{equation} \delta \left[-\log \mathcal {L}_{2}\right]=\mathrm{tr}\left[\delta C_{\mathrm{NG}}\left(\Psi _{\mathrm{mocks}}-\Psi _{\mathrm{NG}}\right)\right], \end{equation}

(44)

so that where |$\mathcal {L}_{1}$| required agreement between C_mocks and C_NG, |$\mathcal {L}_{2}$| requires agreement between Ψ_mocks and Ψ_NG. While this should not be an issue when the space of distributions spanned by C_NG(a) includes the distribution that gives rise to C_mocks, when this is not the case we cannot expect |$\mathcal {L}_{1}$| and |$\mathcal {L}_{2}$| to yield the same maximum likelihood values. Indeed, by examining Fig. 8, which shows the residuals between the mocks and the model precision matrixes, we can see that the |$\mathcal {L}_{1}$| leaves significant residuals while |$\mathcal {L}_{2}$| does not.

The principal benefit of the |$\mathcal {L}_{2}$| likelihood is that it produces better agreement between the mock and model precision matrices than the |$\mathcal {L}_{1}$| likelihood, as shown in Fig. 8. Note that most (but not all) applications will require the precision matrix, rather than the covariance matrix. The principal drawback is that it requires that we invert C_mocks, and so requires that N_mocks > N_bins. In our case this requirement is satisfied, and so we prefer the |$\mathcal {L}_{2}$| likelihood. This preference is however slight, as the resulting α − ϵ error ellipses, shown in Fig. 9, are quite similar.

4.3 Results

After using both likelihoods to fit our model to the mock catalogues, we find

\begin{eqnarray} a_{1} & = & 1.145\pm 0.002\,, \end{eqnarray}

(45)

\begin{eqnarray} a_{2} & = & 1.131\pm 0.005, \end{eqnarray}

(46)

where a₁ is the shot noise rescaling determined using |$\mathcal {L}_{1}$| and a₂ is determined using |$\mathcal {L}_{2}$|⁠. We emphasize that this rescaling should not be interpreted as a mismatch between the number density in our code and the actual number density in the mocks, but rather as the additional shot noise required to mimic the effects of short-scale non-Gaussianity for the covariance matrix. The error bars for a₁ and a₂ are determined by jackknife resampling on the mocks, and establish that given 1000 mocks, the |$\mathcal {L}_{1}$| and |$\mathcal {L}_{2}$| likelihoods do lead to different rescalings of the shot noise.

One way to test the goodness-of-fit of our models is to determine what distribution of the KL divergence would result from noisy realizations of our best-fitting models. In order to ensure that the distributions we generate are comparable to the mocks, we do the following.

Draw 1000 correlation functions that follow our best-fitting covariance matrix.
Compute the sample covariance, C_noisy, and corresponding precision matrix for those draws.
Fit C_noisy or Ψ_noisy as appropriate, to generate C_refit and Ψ_refit.
Compute the KL divergence between the C_noisy/Ψ_noisy and Ψ_refit/C_refit.

The results of these tests are collected in Table 1. We see that fitting with either likelihood provides a significant improvement over the purely Gaussian model. As anticipated, we find that fitting with the two likelihoods leads to small discrepancies in the resulting KL divergences. We also find that after fitting, the differences between the mock and model covariance matrices are too large to be consistent with noise, indicating that there is room for further improvement in our models.

Table 1.

Open in new tab

KL divergences between our models (Gaussian, and Non-Gaussian fit using |$\mathcal {L}_{1}$| and |$\mathcal {L}_{2}$|⁠) and the mock catalogues. In order to calibrate, we have also computed KL divergences between each model and fits to noisy realizations of that model. With 1000 mocks it is clear that the mock covariance matrix is not consistent with noisy realizations of our models.

	C_test = C_mock	C_test = C_noisy
KL(Ψ_G, C_test)	42.14	35.13 ± 0.17
KL(Ψ_NG(a₁), C_test)	37.66	35.13 ± 0.17
KL(Ψ_NG(a₂), C_test)	37.69	35.13 ± 0.17
KL(Ψ_test, C_G)	45.76	40.59 ± 0.27
KL(Ψ_test, C_NG(a₁))	42.70	40.59 ± 0.27
KL(Ψ_test, C_NG(a₂))	42.66	40.59 ± 0.27

	C_test = C_mock	C_test = C_noisy
KL(Ψ_G, C_test)	42.14	35.13 ± 0.17
KL(Ψ_NG(a₁), C_test)	37.66	35.13 ± 0.17
KL(Ψ_NG(a₂), C_test)	37.69	35.13 ± 0.17
KL(Ψ_test, C_G)	45.76	40.59 ± 0.27
KL(Ψ_test, C_NG(a₁))	42.70	40.59 ± 0.27
KL(Ψ_test, C_NG(a₂))	42.66	40.59 ± 0.27

Table 1.

Open in new tab

KL divergences between our models (Gaussian, and Non-Gaussian fit using |$\mathcal {L}_{1}$| and |$\mathcal {L}_{2}$|⁠) and the mock catalogues. In order to calibrate, we have also computed KL divergences between each model and fits to noisy realizations of that model. With 1000 mocks it is clear that the mock covariance matrix is not consistent with noisy realizations of our models.

	C_test = C_mock	C_test = C_noisy
KL(Ψ_G, C_test)	42.14	35.13 ± 0.17
KL(Ψ_NG(a₁), C_test)	37.66	35.13 ± 0.17
KL(Ψ_NG(a₂), C_test)	37.69	35.13 ± 0.17
KL(Ψ_test, C_G)	45.76	40.59 ± 0.27
KL(Ψ_test, C_NG(a₁))	42.70	40.59 ± 0.27
KL(Ψ_test, C_NG(a₂))	42.66	40.59 ± 0.27

	C_test = C_mock	C_test = C_noisy
KL(Ψ_G, C_test)	42.14	35.13 ± 0.17
KL(Ψ_NG(a₁), C_test)	37.66	35.13 ± 0.17
KL(Ψ_NG(a₂), C_test)	37.69	35.13 ± 0.17
KL(Ψ_test, C_G)	45.76	40.59 ± 0.27
KL(Ψ_test, C_NG(a₁))	42.70	40.59 ± 0.27
KL(Ψ_test, C_NG(a₂))	42.66	40.59 ± 0.27

In order to determine whether our model is sufficient to be used in studies of BAO, we return to the Fisher matrix approach introduced in Section 3.4. After computing the error ellipses, we would like to know whether the error ellipse from the mocks is consistent with a noisy draw from the model covariance matrix. To determine this we follow a procedure similar to the one described above: we generate sets of 1000 mock correlation functions drawn following the model covariance matrix, compute the sample covariance for those noisy draws, and then compute the error ellipse from that sample covariance. By repeating this procedure, we can arrive at uncertainties in the uncertainties in α and ϵ, σ_α and σ_ϵ, as well as the uncertainty in their correlation coefficient, r_αϵ. These results are tabulated in Table 2. We find that when focusing only on the α − ϵ error ellipses, and with only 1000 mocks, the models fit using |$\mathcal {L}_{1}$| and |$\mathcal {L}_{2}$| are indistinguishable, and are consistent at the 1σ level with the QPM mocks. This constitutes an improvement over the unfit Gaussian model, which is >2σ discrepant from the QPM mocks. Thus, while we would be reluctant to use the Gaussian model in some applications, the simple non-Gaussian model introduced here is suitable for use in contemporary BAO studies.

Table 2.

Open in new tab

Fisher matrix results for the uncertainties σ_α and σ_ϵ, as well as the correlation coefficient r_αϵ. Even the Gaussian (unfit) model produces reasonable agreement in these parameters, and the level of agreement improves for the non-Gaussian (fit) models. When we restrict our attention to the BAO parameters, we find that the mock precision matrix is consistent with a noisy realization of our fit models, at least when we are limited to 1000 mocks.

	σ_α	σ_ϵ	r_αϵ	σ_α (noisy)	σ_ϵ (noisy)	r_αϵ (noisy)
C_mock	–	–	–	0.0403	0.0422	0.189
C_G	0.0384	0.0391	0.216	0.0387 ± 0.0011	0.0394 ± 0.0011	0.217 ± 0.038
C_NG(a₁)	0.0400	0.0405	0.203	0.0403 ± 0.0011	0.0409 ± 0.0012	0.204 ± 0.038
C_NG(a₂)	0.0399	0.0404	0.204	0.0401 ± 0.0011	0.0407 ± 0.0011	0.205 ± 0.038

	σ_α	σ_ϵ	r_αϵ	σ_α (noisy)	σ_ϵ (noisy)	r_αϵ (noisy)
C_mock	–	–	–	0.0403	0.0422	0.189
C_G	0.0384	0.0391	0.216	0.0387 ± 0.0011	0.0394 ± 0.0011	0.217 ± 0.038
C_NG(a₁)	0.0400	0.0405	0.203	0.0403 ± 0.0011	0.0409 ± 0.0012	0.204 ± 0.038
C_NG(a₂)	0.0399	0.0404	0.204	0.0401 ± 0.0011	0.0407 ± 0.0011	0.205 ± 0.038

Table 2.

Open in new tab

Fisher matrix results for the uncertainties σ_α and σ_ϵ, as well as the correlation coefficient r_αϵ. Even the Gaussian (unfit) model produces reasonable agreement in these parameters, and the level of agreement improves for the non-Gaussian (fit) models. When we restrict our attention to the BAO parameters, we find that the mock precision matrix is consistent with a noisy realization of our fit models, at least when we are limited to 1000 mocks.

	σ_α	σ_ϵ	r_αϵ	σ_α (noisy)	σ_ϵ (noisy)	r_αϵ (noisy)
C_mock	–	–	–	0.0403	0.0422	0.189
C_G	0.0384	0.0391	0.216	0.0387 ± 0.0011	0.0394 ± 0.0011	0.217 ± 0.038
C_NG(a₁)	0.0400	0.0405	0.203	0.0403 ± 0.0011	0.0409 ± 0.0012	0.204 ± 0.038
C_NG(a₂)	0.0399	0.0404	0.204	0.0401 ± 0.0011	0.0407 ± 0.0011	0.205 ± 0.038

	σ_α	σ_ϵ	r_αϵ	σ_α (noisy)	σ_ϵ (noisy)	r_αϵ (noisy)
C_mock	–	–	–	0.0403	0.0422	0.189
C_G	0.0384	0.0391	0.216	0.0387 ± 0.0011	0.0394 ± 0.0011	0.217 ± 0.038
C_NG(a₁)	0.0400	0.0405	0.203	0.0403 ± 0.0011	0.0409 ± 0.0012	0.204 ± 0.038
C_NG(a₂)	0.0399	0.0404	0.204	0.0401 ± 0.0011	0.0407 ± 0.0011	0.205 ± 0.038

We have not addressed the question of precisely when this model can be used. It is possible that as the number density of a survey increases the actual structure of the three- and four-point functions will be detectable in the covariance matrix. This is an intriguing question, and one we anticipate addressing in future work. We emphasize that numerically evaluating the integrals 23 and 24 with the full 3- and 4-point functions would not require substantially more computational time, so that the general approach described in this paper would still be effective in a very dense surveys, even if the model described in this section were to break down. We also emphasize that in the QPM mocks²nP_BAO ∼ 1, i.e. these mocks are not dominated by shot-noise. That our model is effective in this regime is very encouraging.

In the above we have used all 1000 QPM mocks to test our model precision matrix, since these are the most stringent tests we can perform with the mocks we have in hand. We can also imagine a scenario where we are interested in determining how many mock catalogues are required to appropriately calibrate our model precision matrix. A full treatment of this question requires that we specify accuracy goals for the precision matrix, and also raises the possibility that our model is better calibrated against something besides full-survey mocks (e.g. simulations of smaller sub-volumes of the survey, or against the survey data itself). We defer such a treatment for future work, focusing for now on the question of how the uncertainty in a depends on the number of mock catalogues used.

In Fig. 10 we show jackknife error bars for a computed using subsets of the full set of QPM mocks of size N_mocks. Because the fitting with the |$\mathcal {L}_1$| likelihood does not require that we invert the mock covariance matrix, we find the uncertainty in a is only weakly dependent on N_mocks. Indeed, we can achieve <1 per cent uncertainty in a with only 100 mocks, in spite of the fact that our covariance matrix has 350 bins. Fitting with the |$\mathcal {L}_2$| likelihood does require that we invert the mock precision matrix, and so we do require that N_mocks > 350, although we again achieve <1 per cent precision on a with only 600 mocks. As discussed above, fitting with the |$\mathcal {L}_2$| likelihood does provide a more accurate model precision matrix (Fig. 8), though this level of accuracy is not ultimately necessary for applications to BAO measurements (Table 2).

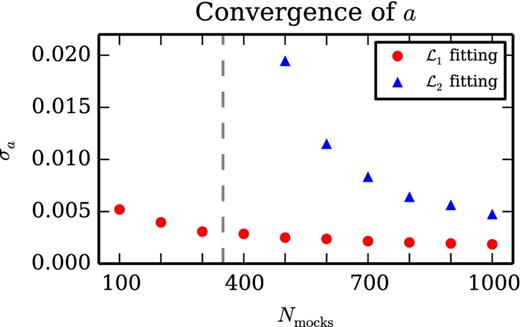
$The uncertainty in the shot noise rescaling parameter a versus the number of mocks used to calibrate it. Our covariance matrix has 350 bins, and so we indicate with a vertical dashed line Nmocks = 350. As the $\mathcal {L}_1$ likelihood (see equation 39) does not require that we invert the mock covariance matrix, it yields a precise estimate of a even with $\mathcal {O}(100)$ mocks. The $\mathcal {L}_2$ likelihood (see equation 43) does require that we invert the mock covariance matrix, and so only yields a precise estimate of a for Nmocks well above 350. Typical values for a in our model, calibrated against the QPM mocks, were 1.14, so 1 per cent precision on a can be achieved with a small number of mocks.$

Figure 10.

The uncertainty in the shot noise rescaling parameter a versus the number of mocks used to calibrate it. Our covariance matrix has 350 bins, and so we indicate with a vertical dashed line N_mocks = 350. As the |$\mathcal {L}_1$| likelihood (see equation 39) does not require that we invert the mock covariance matrix, it yields a precise estimate of a even with |$\mathcal {O}(100)$| mocks. The |$\mathcal {L}_2$| likelihood (see equation 43) does require that we invert the mock covariance matrix, and so only yields a precise estimate of a for N_mocks well above 350. Typical values for a in our model, calibrated against the QPM mocks, were 1.14, so 1 per cent precision on a can be achieved with a small number of mocks.

Open in new tab Download slide

5 OUTLOOK

We have demonstrated that integrating a simple Gaussian model for the covariance matrix of the galaxy correlation function yields a result that is in surprising agreement with that obtained from sample statistics applied to mock catalogues. A simple extension of that model, wherein the shot noise is allowed to vary and calibrated against mock catalogues, further improves that agreement, so that for the purposes of BAO measurements the mock and model covariance matrices are statistically consistent with each other. This was accomplished with an effective number of mocks N_eff ∼ 35 000 using just ≈1000 CPU hours, rather than the hundreds of thousands of CPU hours required to generate and analyse 1000 QPM mocks. Based on these results, we consider this method of covariance matrix estimation to be a strong alternative to producing very large numbers of mock catalogues. While |$\mathcal {O}\left(100\right)$| mocks will continue to be necessary for estimating systematic errors, we believe those |$\mathcal {O}\left(100\right)$| mocks will be sufficient to calibrate our model, or successors to it. With a reduction in the number of mocks required, we anticipate greater effort (both human and computational) can be devoted to improving the accuracy of the mocks, ultimately improving the reliability of error estimates from future analyses.

For the sake of simplicity we have focused on reproducing the mock covariance matrix. This is a somewhat artificial goal, since the mock catalogues are themselves imperfect representations of an actual survey. Turning our attention to the survey covariance matrix, we find an opportunity and a challenge. In our method, the mocks are only used to calibrate non-Gaussian corrections, in the form of increased shot noise, to the covariance matrix. Since we expect the effects of non-Gaussianity to be confined to relatively short scales, we can imagine performing this calibration step against simulations with a smaller volume and higher resolution, compared to the mocks. At the same time, we face the challenging question of how to bound possible discrepancies between our model covariance matrix and the true survey covariance matrix. While the accuracy requirements for a covariance matrix (whether derived from mocks or from a model) are ultimately determined by the science goals of a survey, the question of how to determine those requirements and assess whether they have been reached seems largely open.

A clear benefit of mock catalogues is that the same set of mocks can be used for measurement using a variety of observables (e.g. the power spectrum) and cosmological parameters (e.g. fσ₈, often measured using RSDs). While we have constructed a model covariance matrix suitable for analysis of the galaxy correlation function at BAO scales, our goal of reducing the number of mocks required for future surveys cannot be realized until analogous methods are developed for the other analyses typical of modern surveys. The covariance matrix of the power spectrum has received theoretical attention from many authors (Takahashi et al. 2009, 2011; de Putter et al. 2012; Mohammed & Seljak 2014). Recent efforts (Carron et al. 2015; Grieb et al. 2016) have come close to presenting a usable model for the covariance matrix of the power spectrum, though the effects of a non-uniform window function have not yet been incorporated. We are optimistic that the necessary extensions of those models can be performed, reducing the required number of mocks for power spectrum analyses to be in line with the |$\mathcal {O}\left(100\right)$| necessary for correlation function analyses.

RCO is supported by a grant from the Templeton Foundation. DJE is supported by grant DE-SC0013718 from the U.S. Department of Energy. SH is supported by NASA NNH12ZDA001N- EUCLID and NSF AST1412966. NP is supported in part by DOE DE-SC0008080.

Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the U.S. Department of Energy Office of Science. The SDSS-III web site is http://www.sdss3.org/. SDSS-III is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS-III Collaboration including the University of Arizona, the Brazilian Participation Group, Brookhaven National Laboratory, Carnegie Mellon University, University of Florida, the French Participation Group, the German Participation Group, Harvard University, the Instituto de Astrofisica de Canarias, the Michigan State/Notre Dame/JINA Participation Group, Johns Hopkins University, Lawrence Berkeley National Laboratory, Max Planck Institute for Astrophysics, Max Planck Institute for Extraterrestrial Physics, New Mexico State University, New York University, Ohio State University, Pennsylvania State University, University of Portsmouth, Princeton University, the Spanish Participation Group, University of Tokyo, University of Utah, Vanderbilt University, University of Virginia, University of Washington, and Yale University.

This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231.

1

An introduction to the package, as well as the python code, is available at: https://github.com/rcoconnell/Rascal.

2

We have not performed a careful study of the PATCHY mocks, which cover the same survey volume as the QPM mocks and were also created for the analysis of the BOSS survey. They differ in some quantitative aspects from the QPM mocks, and in particular more accurately reflect the bispectrum of the CMASS sample from BOSS (Kitaura et al. 2016). While it would be interesting to assess the impact of these quantitative discrepancies, in the absence of qualitative differences between the two sets of mocks we do not anticipate a qualitative difference in the performance of this model.

REFERENCES

Bernstein

G. M.

1994

ApJ

424

569

Month:	Total Views:
November 2016	1
January 2017	2
February 2017	7
March 2017	1
April 2017	1
May 2017	1
June 2017	6
July 2017	1
August 2017	3
September 2017	8
January 2018	1
February 2018	4
March 2018	2
April 2018	3
May 2018	3
July 2018	2
August 2018	7
September 2018	8
October 2018	5
November 2018	4
December 2018	1
February 2019	1
April 2019	2
May 2019	7
June 2019	4
July 2019	2
August 2019	2
September 2019	2
October 2019	3
November 2019	14
December 2019	9
January 2020	7
February 2020	7
March 2020	5
April 2020	11
May 2020	1
June 2020	4
July 2020	6
August 2020	8
September 2020	5

Article Contents

Large covariance matrices: smooth models from the two-point correlation function Free

Abstract

1 INTRODUCTION

2 N-Point Functions and the Covariance Matrix

2.1 Poisson sampling

3 INTEGRATING THE GAUSSIAN MODEL

3.1 Survey geometry

3.2 Correlation function

3.3 Importance Sampling

3.4 Comparison with mocks

4 A SIMPLE MODEL FOR NON-GAUSSIANITY

4.1 |$\mathcal {L}_{1}$| likelihood

4.2 |$\mathcal {L}_{2}$| likelihood

4.3 Results

5 OUTLOOK

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Large covariance matrices: smooth models from the two-point correlation function