-
PDF
- Split View
-
Views
-
Cite
Cite
Shotaro Yamasaki, Tomonori Totani, Norita Kawanaka, A blind search for prompt gamma-ray counterparts of fast radio bursts with Fermi-LAT data, Monthly Notices of the Royal Astronomical Society, Volume 460, Issue 3, 11 August 2016, Pages 2875–2880, https://doi.org/10.1093/mnras/stw1206
Close - Share Icon Share
Abstract
Fast radio bursts (FRBs) are a mysterious flash phenomenon detected in radio wavelengths with a duration of only a few milliseconds, and they may also have prompted gamma-ray flashes. Here, we carry out a blind search for ms-duration gamma-ray flashes using the 7-yr Fermi Large Area Telescope all-sky gamma-ray data. About 100 flash candidates are detected, but after removing those associated with bright steady point sources, we find no flash events at high Galactic latitude region (|b| > 20°). Events at lower latitude regions are consistent with statistical flukes originating from the diffuse gamma-ray background. From these results, we place an upper limit on the GeV gamma-ray to radio flux ratio of FRBs as ξ ≡ (νLν)γ/(νLν)radio ≲ (4.2–12) × 107, depending on the assumed FRB rate evolution index β = 0–4 [cosmic FRB rate ΦFRB ∝ (1 + z)β]. This limit is comparable with the largest value found for pulsars, though ξ of pulsars is distributed in a wide range. We also compare this limit with the spectral energy distribution of the 2004 giant flare of the magnetar SGR 1806−20.
1 INTRODUCTION
Fast radio bursts (FRBs) are a population of radio transients with durations of only about 1 ms. Since the discovery of the so-called Lorimer Burst (Lorimer et al. 2007), 17 FRBs have been reported by radio transient surveys to date (15 by Parkes radio telescope, Lorimer et al. 2007; Keane et al. 2012; Thornton et al. 2013; Burke-Spolaor & Bannister 2014; Champion et al. 2016; Petroff et al. 2015; Ravi, Shannon & Jameson 2015; Keane et al. 2016; 1 by Arecibo, Spitler et al. 2014, 2016; Scholz et al. 2016; and 1 by Green Bank Telescope, Masui et al. 2015). Their dispersion measures (DMs) are much larger than those expected for objects in our Galaxy, and a cosmological distance scale of z ∼ 0.5–1 is inferred if the dominant contribution to DMs is from electrons in intergalactic medium. A recent study of FRB150418 has identified its radio afterglow associated with an elliptical galaxy, whose redshift (z = 0.492) is consistent with that expected by its DM (Keane et al. 2016). However, no counterparts in other wavelengths have been detected. There are various progenitor models proposed for FRBs; some of them are related to young stellar populations, while others to old. The former includes giant flares from soft gamma-ray repeaters (SGRs; Popov & Postnov 2010; Thornton et al. 2013; Kulkarni et al. 2014; Lyubarsky 2014), collapsing supermassive neutron stars (‘blitzar’ model; Falcke & Rezzolla 2014), and giant radio pulses from pulsars (Connor, Sievers & Pen 2016; Cordes & Wasserman 2016). The latter includes binary neutron star (or black hole) mergers (Totani 2013; Mingarelli, Levin & Lazio 2015), and binary white dwarf mergers (Kashiyama, Ioka & Mészáros 2013).
Whatever the progenitor is, it is reasonable to expect corresponding ms-duration radiations of FRBs in other wavelengths. Here, we search for gamma-ray counterparts of FRBs using the 7-yr Fermi Large Area Telescope (Fermi-LAT) data. Radio telescopes finding FRBs at cosmological distances have narrower field of views (FoVs) [∼15 arcmin beam size for Parkes] than Fermi-LAT, and hence we expect that Fermi-LAT detects FRBs at smaller distances than those found in radio bands. Therefore, rather than examining the Fermi-LAT data at known FRB locations, we perform a blind search of ms-duration gamma-ray flashes (MGFs), without prior information about FRBs in radio bands. Then, we can derive more stringent constraints on the GeV gamma-ray to radio flux ratio of FRBs, than that from upper limits on gamma-ray flux set by Fermi-LAT for individual radio-detected FRBs.
The outline of this paper is as follows. In Section 2, we describe the details of the gamma-ray data set and our search method. We then present the results of the MGF search in Section 3. Constraints on the gamma-ray to radio flux ratio of FRBs will be derived in Section 4, followed by discussion for implications. Throughout this paper, we assume a flat-universe Λcold dark matter model with H0 = 67.8 km s− 1 Mpc− 1, ΩM = 0.308, ΩΛ = 0.692 (Planck Collaboration XIII 2015).
2 DATA AND SEARCH METHOD
The Fermi-LAT is a pair-conversion gamma-ray telescope designed to cover the energy band from 20 MeV to greater than 300 GeV. In this work, we use the Pass 7 Reprocessed weekly data publicly available at the Fermi mission website.1 The analysis spans the time period of 6.8 yr from 2008 July 31 (UTC) to 2015 June 18 (UTC), corresponding to the mission elapsed time (MET) from 239 557 417 to 455 059 763 s and the Fermi mission week from 1 to 368. We use P7SOURCE class photons with reconstructed energies from 1 to 100 GeV. We used the Fermi science tools version v9r32p5 package2 and the P7REP instrument response functions in our analysis. In accordance with the data analysis procedure outlined in Fermi mission website, we first selected 1 GeV< E < 100 GeV photons of ‘P7SOURCE’ class. There is another ‘Transient class’, which is for gamma-ray events with looser cuts than P7SOURCE and hence includes more background particle contamination. Though this class is useful for bright transients during which background contamination is negligible, we use P7SOURCE because we will search faint (i.e. small number statistics) transient events, to which background contamination is crucial. We also set the Earth relative zenith angle cut of 100° to reduce the bright earth-limb gamma-rays. Finally, we select gamma-rays only in the good time intervals (GTIs) when the data quality is good, by excluding the bad time intervals due to the spacecraft events. The total amount of GTIs is 79 per cent of the MET.
In order to search for MGF candidates, we apply a search algorithm as follows. First, we define the search time window Δt, and four values of Δt = 1, 2, 5, and 10 ms are tried here. We consider a reference gamma-ray event, and other gamma-ray events are searched within 2° radius from the reference in the time interval of Δt starting from the reference event. The radius is determined considering the per-photon angular resolution, ∼0| $_{.}^{\circ}$|8 [68 per cent containment of the point spread function (PSF)] at 1 GeV (Atwood et al. 2009; Acero et al. 2015). The number of gamma-rays in this time window and the circle, including the first reference photon itself, is denoted as Nph. Then, we repeat this procedure for all the gamma-ray events of the Fermi data set that we use. It is possible that a gamma-ray event is included in different MGFs as defined above, but we present all MGF candidates as different events in the following if they are different as a combination of photons. The detector deadtime per event of Fermi-LAT is < 100 μs, and it is negligible in our analysis.
3 RESULT
3.1 MGFs associated with known gamma-ray sources
The result of our blind search for MGFs is shown in Table 1 (see columns of ‘No cut’). For Nph = 2, there are 17, 33, 68, and 133 MGF candidates for Δt = 1, 2, 5, and 10 ms, respectively, as shown in the Table. Only one MGF event was found for Nph = 3 and Δt = 5 or 10 ms, and there were no events of Nph ≥ 4 for any value of Δt. We examined the Nph = 3 event, and found that it is associated with GRB 090510 (Ackermann et al. 2010), which shows photon clusterings within a time-scale of <10 ms. The total duration of detected LAT gamma-rays for GRB 090510 is 0.1 s, which is much longer than FRBs. Therefore, we remove this event from our sample in the following, and the results after this ‘1st cut’ are shown in Table 1. Only Nph = 2 events remain.
The number of detected MGF candidates (|$N_{\rm {obs}}^{\rm {2ph}}$| and |$N_{\rm {obs}}^{\rm {3ph}}$| for Nph = 2 and 3, respectively). ‘No cut’ is the result of our blind search for MGFs without any event cut. The ‘1st cut’ is to remove MGF candidates associated with GRB 090519. The ‘2nd cut’ is the result after removing MGF events that are caused by nearby bright sources [brighter than a photon flux of 4 × 10− 9 photons cm− 2 s− 1 (1 GeV < E < 100 GeV) with angular separation less than 2| $_{.}^{\circ}$|0]. The ‘3rd cut’ is removing regions close to the Galactic disc (|b| < 20°). The expected numbers of false events caused by the Poisson statistics of the diffuse gamma-ray background flux are shown as |$N_{\rm pred}^{\rm 2ph}$| in the 2nd and 3rd cut results.
| Cuts . | . | No cut . | . | 1st cut . | . | 2nd cut . | . | 3rd cut . | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| fskya . | . | 1.0 . | . | 1.0 . | . | 0.96 . | . | 0.68 . | ||||
| . | . | |$N_{\rm {obs}}^{\rm {2ph}}$| . | |$N_{\rm {obs}}^{\rm {3ph}}$| . | . | |$N_{\rm {obs}}^{\rm {2ph}}$| . | |$N_{\rm {obs}}^{\rm {3ph}}$| . | . | |$N_{\rm {obs}}^{\rm {2ph}}\;(N_{\rm {pred}}^{\rm {2ph}})$| . | |$N_{\rm {obs}}^{\rm {3ph}}$| . | . | |$N_{\rm {obs}}^{\rm {2ph}}\;(N_{\rm {pred}}^{\rm {2ph}})$| . | |$N_{\rm {obs}}^{\rm {3ph}}$| . |
| Δt = 1 ms | 17 | 0 | 14 | 0 | 1 (2.7) | 0 | 0 (1.2 × 10−1) | 0 | ||||
| Δt = 2 ms | 33 | 0 | 29 | 0 | 4 (5.3) | 0 | 0 (2.3 × 10−1) | 0 | ||||
| Δt = 5 ms | 68 | 1 | 62 | 0 | 17 (13) | 0 | 0 (5.8 × 10−1) | 0 | ||||
| Δt = 10 ms | 133 | 1 | 127 | 0 | 38 (27) | 0 | 0 (1.0) | 0 | ||||
| Cuts . | . | No cut . | . | 1st cut . | . | 2nd cut . | . | 3rd cut . | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| fskya . | . | 1.0 . | . | 1.0 . | . | 0.96 . | . | 0.68 . | ||||
| . | . | |$N_{\rm {obs}}^{\rm {2ph}}$| . | |$N_{\rm {obs}}^{\rm {3ph}}$| . | . | |$N_{\rm {obs}}^{\rm {2ph}}$| . | |$N_{\rm {obs}}^{\rm {3ph}}$| . | . | |$N_{\rm {obs}}^{\rm {2ph}}\;(N_{\rm {pred}}^{\rm {2ph}})$| . | |$N_{\rm {obs}}^{\rm {3ph}}$| . | . | |$N_{\rm {obs}}^{\rm {2ph}}\;(N_{\rm {pred}}^{\rm {2ph}})$| . | |$N_{\rm {obs}}^{\rm {3ph}}$| . |
| Δt = 1 ms | 17 | 0 | 14 | 0 | 1 (2.7) | 0 | 0 (1.2 × 10−1) | 0 | ||||
| Δt = 2 ms | 33 | 0 | 29 | 0 | 4 (5.3) | 0 | 0 (2.3 × 10−1) | 0 | ||||
| Δt = 5 ms | 68 | 1 | 62 | 0 | 17 (13) | 0 | 0 (5.8 × 10−1) | 0 | ||||
| Δt = 10 ms | 133 | 1 | 127 | 0 | 38 (27) | 0 | 0 (1.0) | 0 | ||||
Note. aThe remaining sky fraction after each event cut.
The number of detected MGF candidates (|$N_{\rm {obs}}^{\rm {2ph}}$| and |$N_{\rm {obs}}^{\rm {3ph}}$| for Nph = 2 and 3, respectively). ‘No cut’ is the result of our blind search for MGFs without any event cut. The ‘1st cut’ is to remove MGF candidates associated with GRB 090519. The ‘2nd cut’ is the result after removing MGF events that are caused by nearby bright sources [brighter than a photon flux of 4 × 10− 9 photons cm− 2 s− 1 (1 GeV < E < 100 GeV) with angular separation less than 2| $_{.}^{\circ}$|0]. The ‘3rd cut’ is removing regions close to the Galactic disc (|b| < 20°). The expected numbers of false events caused by the Poisson statistics of the diffuse gamma-ray background flux are shown as |$N_{\rm pred}^{\rm 2ph}$| in the 2nd and 3rd cut results.
| Cuts . | . | No cut . | . | 1st cut . | . | 2nd cut . | . | 3rd cut . | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| fskya . | . | 1.0 . | . | 1.0 . | . | 0.96 . | . | 0.68 . | ||||
| . | . | |$N_{\rm {obs}}^{\rm {2ph}}$| . | |$N_{\rm {obs}}^{\rm {3ph}}$| . | . | |$N_{\rm {obs}}^{\rm {2ph}}$| . | |$N_{\rm {obs}}^{\rm {3ph}}$| . | . | |$N_{\rm {obs}}^{\rm {2ph}}\;(N_{\rm {pred}}^{\rm {2ph}})$| . | |$N_{\rm {obs}}^{\rm {3ph}}$| . | . | |$N_{\rm {obs}}^{\rm {2ph}}\;(N_{\rm {pred}}^{\rm {2ph}})$| . | |$N_{\rm {obs}}^{\rm {3ph}}$| . |
| Δt = 1 ms | 17 | 0 | 14 | 0 | 1 (2.7) | 0 | 0 (1.2 × 10−1) | 0 | ||||
| Δt = 2 ms | 33 | 0 | 29 | 0 | 4 (5.3) | 0 | 0 (2.3 × 10−1) | 0 | ||||
| Δt = 5 ms | 68 | 1 | 62 | 0 | 17 (13) | 0 | 0 (5.8 × 10−1) | 0 | ||||
| Δt = 10 ms | 133 | 1 | 127 | 0 | 38 (27) | 0 | 0 (1.0) | 0 | ||||
| Cuts . | . | No cut . | . | 1st cut . | . | 2nd cut . | . | 3rd cut . | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| fskya . | . | 1.0 . | . | 1.0 . | . | 0.96 . | . | 0.68 . | ||||
| . | . | |$N_{\rm {obs}}^{\rm {2ph}}$| . | |$N_{\rm {obs}}^{\rm {3ph}}$| . | . | |$N_{\rm {obs}}^{\rm {2ph}}$| . | |$N_{\rm {obs}}^{\rm {3ph}}$| . | . | |$N_{\rm {obs}}^{\rm {2ph}}\;(N_{\rm {pred}}^{\rm {2ph}})$| . | |$N_{\rm {obs}}^{\rm {3ph}}$| . | . | |$N_{\rm {obs}}^{\rm {2ph}}\;(N_{\rm {pred}}^{\rm {2ph}})$| . | |$N_{\rm {obs}}^{\rm {3ph}}$| . |
| Δt = 1 ms | 17 | 0 | 14 | 0 | 1 (2.7) | 0 | 0 (1.2 × 10−1) | 0 | ||||
| Δt = 2 ms | 33 | 0 | 29 | 0 | 4 (5.3) | 0 | 0 (2.3 × 10−1) | 0 | ||||
| Δt = 5 ms | 68 | 1 | 62 | 0 | 17 (13) | 0 | 0 (5.8 × 10−1) | 0 | ||||
| Δt = 10 ms | 133 | 1 | 127 | 0 | 38 (27) | 0 | 0 (1.0) | 0 | ||||
Note. aThe remaining sky fraction after each event cut.
In order to examine the possibility that the detected Nph = 2 events are caused by bright point sources, we examined the nearest point source from each MGF event. We use the Fermi Large Area Telescope Third Source Catalog (3FGL; Acero et al. 2015) which consists of ∼3000 gamma-ray sources. Fig. 1 presents the photon flux distribution of the nearest point sources, in comparison with that of all the 3FGL catalogue point sources. The 3FGL sources nearest to the MGF candidates have obviously much brighter fluxes compared with the general 3FGL sources, indicating that most MGF candidates are caused by bright point sources. Fig. 2 is the histogram of angular distance from the MGF candidates to the nearest 3FGL sources. The angular distribution is similar to the Fermi-LAT PSFs (Atwood et al. 2009; Acero et al. 2015), and much smaller than the distribution expected for the case that the MGF candidates are randomly distributed in the sky, again indicating that these are caused by bright point sources. The classes of the nearest sources include a variety of populations for which ms scale variability is physically unlikely (e.g. blazars), and the most likely origin of the MGF candidates is simply statistical flukes induced by the Poisson statistics of a steady gamma-ray flux. Indeed, we confirmed that the number expected by Poisson statistics and point source fluxes is in rough agreement with that of the detected MGF candidates.
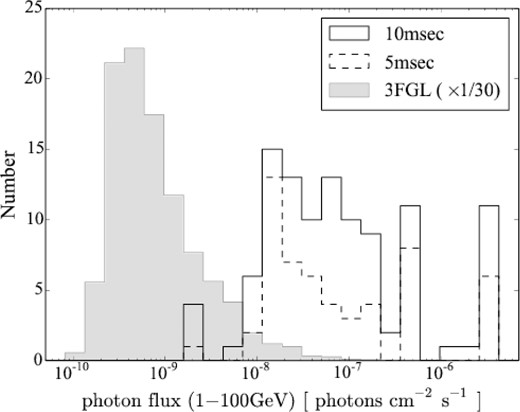
The photon flux (1 GeV < E < 100 GeV) distribution of the nearest point source to each MGF candidate with Nph = 2 and Δt = 5 or 10 ms, in comparison with that of all sources in the 3FGL catalogue. The histogram for the 3FGL sources is multiplied by a factor of 1/30 for the presentation purpose.

Angular separation distribution from each MGF candidate (Nph = 2) to the nearest 3FGL catalogue source, for Δt = 5 and 10 ms. The Fermi-LAT point spread function profile (at 1 GeV, 68 per cent containment) is also shown by the dashed curves (two same profiles scaled to the histograms of two Δt values). For comparison, the expected distribution when MGFs are randomly distributed on the sky is also shown.
There is an excess of the MGF distribution in Fig. 2 at θ ≳ 2| $_{.}^{\circ}$|0 compared with PSF, which implies a contribution of MGFs that are not caused by point sources. We will see that these are likely caused by the diffuse gamma-ray background (see below). To remove MGF candidates related to bright point sources, MGF candidates are excluded from the final sample if their nearest 3FGL source flux is larger than 4 × 10− 9 photons cm− 2 s− 1 and angular separation is smaller than 2| $_{.}^{\circ}$|0. The number of 3FGL sources exceeding this flux threshold is 293. The result of this cut is shown in Table 1 as ‘2nd cut’.
3.2 False MGFs by the diffuse background
Even after removing the regions affected by bright point sources, MGF candidates remain. These may be statistical flukes caused by Poisson statistics of constant gamma-ray flux of the diffuse gamma-ray background. Here, we estimate the number of MGF candidates expected by this. For this purpose, we first divide all sky into 72 × 36 regular square pixels in x- and y-axis directions on the Aitoff projection (i.e. a pixel scale of ∼5°), and the spatial direction and surface area of the j-th pixel are denoted by solid angle Ωj and ΔΩj. We then create a count map and an exposure map of gamma-rays selected by the criteria described in Section 2 using the Fermi analysis tool of GTLTCUBE and GTEXPCUBE. By dividing the count map (in photons) by the exposure map (in |$\rm {cm}^{2}\:\rm {s}$|) and the surface area ΔΩj, we get an intensity map (in photons |$\rm {cm}^{-2}\:\rm {s}^{-1} \ \rm {sr}^{-1}$|) of the diffuse gamma-ray background, J(Ωj).
The expected event numbers of false MGFs calculated in this way are compared with the observed numbers after the 2nd cut in Table 1, and also in Fig. 3 as a histogram along the Galactic latitude. The agreement between the expected and observed numbers is good, and hence most of the observed Nph = 2 events after the 2nd cut are considered to be produced by Poisson statistics of the diffuse background. It should be noted that all these events are found at low latitude regions of |b| < 20°. Therefore, we make the final 3rd cut to remove events of |b| < 20°. Then, the final result is that we found no MGF candidates after the three event cuts, and this will be used to set a limit on the gamma-ray/radio flux ratio of FRBs in Section 4.
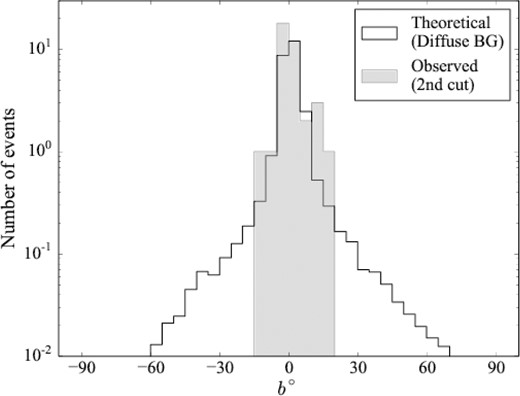
The Galactic latitude distribution of the MGF candidates with Nph = 2 and Δt = 10 ms after the 2nd cut (grey histogram). The expected distribution from the Poisson statistics of the diffuse gamma-ray background is shown as solid histogram.
4 IMPLICATIONS FOR FRBs
4.1 Modelling the population of FRBs
To set limits on physical quantities of FRBs by the no detection of MGFs, we first model the luminosity and rate evolution of FRBs. The luminosity function of FRBs is totally unknown, and here we simply use the standard candle approximation. Based on the typical peak flux Fν = 0.5 Jy of FRBs at observing frequency of ν = 1.4 GHz, and taking z ∼ 0.5 as FRB redshifts (Keane & Petroff 2015), we set the radio luminosity of FRBs to be (νLν)r = 1.1 × 1043 erg s− 1 at the rest-frame reference frequency νr = 2.1 GHz.
4.2 Upper-limit on gamma-ray/radio luminosity ratio
The expected number |$N_{\rm MGF}^{\rm tot}$| increases with increasing ξ because FRBs can be detected to larger distances. Then, no MGF detection after the 3rd event cut sets an upper limit on ξ, which is estimated by equating |$N_{\rm MGF}^{\rm tot}(\xi ) = 3.09$|, corresponding to 95 per cent upper limit on the expected value of the Poisson statistics. The results are summarized in Table 2, and the upper limits are found to be ξ = (4.2–12) × 107 for 0 ≤ β ≤ 4. The maximum redshift zmax depends on the direction to an FRB with respect to the Fermi-LAT FoV centre, and it is 0.02 for ξ ∼ 108 when an FRB is located at the FoV centre. This is much smaller than that of FRBs detected in radio bands (z ≳ 0.5), confirming that Fermi-LAT is sensitive to FRBs at smaller distances than those detected in radio bands. Correspondingly, our limit on ξ is stronger than that obtained from non-detection of radio-detected FRBs by Fermi-LAT (typically ξ ≲ 4 × 1010). For comparison, Tendulkar, Kaspi & Patel (2016) investigated Fermi-Gamma-ray Burst Monitor, Swift-Burst Alert Telescope, and Konus-Wind data at detected 16 FRB fields, setting an upper limit on soft gamma-ray to radio flux ratio of ξsoftγ ≲ 108–1010.
The 2σ upper limits on gamma-ray to radio flux ratio (ξ) for β = 0–4. The normalization of the volumetric FRB rate at z = 0 (Φ0) is also shown. FRB duration is assumed to be Δt = 3 ms.
| β . | . | Φ0 . | ξ . |
|---|---|---|---|
| . | . | (Gpc− 3 yr− 1) . | ( ≡ (νLν)γ/(νLν)r) . |
| 0 | |$1.2_{-0.8}^{+1.5}\times 10^4$| | |$<\!\!4.2_{-1.7}^{+2.4} \times 10^7$| | |
| 1 | |$7.4_{-4.7}^{+9.4}\times 10^3$| | |$<\!\!5.2_{-2.0}^{+4.3} \times 10^7$| | |
| 2 | |$4.5_{-2.9}^{+5.7}\times 10^3$| | |$<\!\!7.0_{-2.8}^{+5.0} \times 10^7$| | |
| 3 | |$2.7_{-1.7}^{+3.5}\times 10^3$| | |$<\!\!9.2_{-3.8}^{+7.8} \times 10^7$| | |
| 4 | |$1.6_{-1.0}^{+2.1}\times 10^3$| | |$<\!\!1.2_{-0.4}^{+1.2} \times 10^8$| |
| β . | . | Φ0 . | ξ . |
|---|---|---|---|
| . | . | (Gpc− 3 yr− 1) . | ( ≡ (νLν)γ/(νLν)r) . |
| 0 | |$1.2_{-0.8}^{+1.5}\times 10^4$| | |$<\!\!4.2_{-1.7}^{+2.4} \times 10^7$| | |
| 1 | |$7.4_{-4.7}^{+9.4}\times 10^3$| | |$<\!\!5.2_{-2.0}^{+4.3} \times 10^7$| | |
| 2 | |$4.5_{-2.9}^{+5.7}\times 10^3$| | |$<\!\!7.0_{-2.8}^{+5.0} \times 10^7$| | |
| 3 | |$2.7_{-1.7}^{+3.5}\times 10^3$| | |$<\!\!9.2_{-3.8}^{+7.8} \times 10^7$| | |
| 4 | |$1.6_{-1.0}^{+2.1}\times 10^3$| | |$<\!\!1.2_{-0.4}^{+1.2} \times 10^8$| |
The 2σ upper limits on gamma-ray to radio flux ratio (ξ) for β = 0–4. The normalization of the volumetric FRB rate at z = 0 (Φ0) is also shown. FRB duration is assumed to be Δt = 3 ms.
| β . | . | Φ0 . | ξ . |
|---|---|---|---|
| . | . | (Gpc− 3 yr− 1) . | ( ≡ (νLν)γ/(νLν)r) . |
| 0 | |$1.2_{-0.8}^{+1.5}\times 10^4$| | |$<\!\!4.2_{-1.7}^{+2.4} \times 10^7$| | |
| 1 | |$7.4_{-4.7}^{+9.4}\times 10^3$| | |$<\!\!5.2_{-2.0}^{+4.3} \times 10^7$| | |
| 2 | |$4.5_{-2.9}^{+5.7}\times 10^3$| | |$<\!\!7.0_{-2.8}^{+5.0} \times 10^7$| | |
| 3 | |$2.7_{-1.7}^{+3.5}\times 10^3$| | |$<\!\!9.2_{-3.8}^{+7.8} \times 10^7$| | |
| 4 | |$1.6_{-1.0}^{+2.1}\times 10^3$| | |$<\!\!1.2_{-0.4}^{+1.2} \times 10^8$| |
| β . | . | Φ0 . | ξ . |
|---|---|---|---|
| . | . | (Gpc− 3 yr− 1) . | ( ≡ (νLν)γ/(νLν)r) . |
| 0 | |$1.2_{-0.8}^{+1.5}\times 10^4$| | |$<\!\!4.2_{-1.7}^{+2.4} \times 10^7$| | |
| 1 | |$7.4_{-4.7}^{+9.4}\times 10^3$| | |$<\!\!5.2_{-2.0}^{+4.3} \times 10^7$| | |
| 2 | |$4.5_{-2.9}^{+5.7}\times 10^3$| | |$<\!\!7.0_{-2.8}^{+5.0} \times 10^7$| | |
| 3 | |$2.7_{-1.7}^{+3.5}\times 10^3$| | |$<\!\!9.2_{-3.8}^{+7.8} \times 10^7$| | |
| 4 | |$1.6_{-1.0}^{+2.1}\times 10^3$| | |$<\!\!1.2_{-0.4}^{+1.2} \times 10^8$| |
4.3 Discussion
The extremely high brightness temperature of FRBs implies that their radio emission is likely coherent radiation, and it is reasonable to expect that it is similar to that of radio pulsars. The gamma-ray to radio ratio is ξ = 104–108 for gamma-ray pulsars in the Second Fermi Large Area Telescope Catalog of Gamma-Ray Pulsars (2PC; Abdo et al. 2013). Some radio pulsars exhibit radio efficiencies of ∼10−2–10−4 with respect to spin-down luminosity (Szary et al. 2014), indicating that ξ should be smaller than 104 assuming that gamma-ray luminosity cannot exceed the spin-down luminosity. Therefore, ξ of pulsars are distributed in a wide range, and our upper limit of ξ ≲ 108 does not exclude a possibility that FRBs have a similar GeV gamma-ray to radio flux ratio to pulsars. Recently, repeating bursts were discovered from FRB 121102 (Spitler et al. 2014, 2016; Scholz et al. 2016), and the top candidate progenitor model would be supergiant pulses from pulsars. This is also consistent with our results if the gamma-ray to radio flux ratio of giant pulses is similar to that of normal pulsar emission.
Giant flares from SGRs (magnetars) are also discussed as a popular hypothesis for the FRB origin (Popov & Postnov 2010; Thornton et al. 2013; Kulkarni et al. 2014; Lyubarsky 2014). Tendulkar et al. (2016) placed an upper limit of <1.1 MJy on the radio flux by the non-detection of a radio single pulse event from the giant flare event of SGR 1806−20 on 2004 December 27, and it is interesting to compare our limit to that of this giant magnetar flare. Unfortunately, there is no direct GeV observation of the SGR 1806−20 giant flare in 2004, but we can estimate a reasonable flux level as follows. Frederiks et al. 2007 reported 20 keV–10 MeV spectrum of the giant flare using the Compton reflection from the Moon. Though non-thermal emission was not detected for the initial flare, a power-law component extending to 10 MeV with a photon index Γ = 1.7 was detected in the pulsating tail phase. The energy flux of the non-thermal component in 1–10 MeV is 1.9 per cent of the thermal component in 20–300 keV. If we assume the same percentage for the initial flare, the non-thermal flux of the initial flare is estimated to be 0.21 erg cm− 2 s− 1, which is much lower than the thermal flux at <MeV and hence consistent with no detection. Assuming that the power-law spectrum is extending to GeV with the same photon index, we estimate νFν flux at 1 GeV to be 0.51 erg cm− 2 s− 1, and combined with the radio upper limit, we obtain a lower limit to the GeV to radio flux ratio as ξ ≳ 107.5. This is marginally consistent with the upper limit on ξ derived by our work, and hence our result does not exclude a possibility that FRBs have a similar GeV to radio flux ratio to magnetar giant flares.
Binary neutron star mergers are also proposed as a possible candidate for catastrophic FRB events, and in this case we may expect associations between FRBs and short gamma-ray bursts (sGRBs; Totani 2013; Zhang 2014). Only one short GRB 090510 was detected in our MGF search in GeV, and note that sGRBs are efficiently detected in soft gamma-rays with a trigger time-scale much longer than the search made here. This means that our search is not optimized to constraining sGRBs. Furthermore, the upper limits on ξ derived in this work are valid only for sources whose event rate is similar to that of FRBs, but it is known that the event rate of sGRBs ( ∼ 10 yr− 1 Gpc− 3; Coward et al. 2012) is much smaller than that of FRBs ( ∼ 104 yr− 1 Gpc− 3). Therefore, our results do not strongly constrain the possible sGRB–FRB connection, and it is possible that a small fraction of FRBs are observed as sGRBs.
5 CONCLUSION
In this paper, we searched MGFs in the 7-yr Fermi-LAT data, motivated by the possible gamma-ray counterpart to FRBs. Since Fermi-LAT is observing wider FoV compared with radio telescopes finding FRBs, FRBs at shorter distances are expected to be detected in the Fermi-LAT, which are out of search fields of view of radio telescopes. Therefore, we performed a blind search of multiple gamma-ray events within a circle of point spread function and a time interval Δt = 1–10 ms, and found about 100 MGF candidates. There is only one event detected with three photons or more, and it is related to a bright short-duration gamma-ray burst GRB 090519. Examination of other events indicates that all of them can be explained by the Poisson statistics of steady gamma-ray flux from bright point sources or diffuse gamma-ray background. After removing regions of bright point sources, there is no MGF event in high Galactic latitude regions of |b| > 20°.
We then used this result to place an upper limit on the gamma-ray to radio flux ratio of FRBs, ξ( ≡ (νLν)γ/(νLν)r). In the calculation, we need to assume the comoving rate density and its evolution of FRBs, and assuming a power-law type evolution, ΦFRB = Φ0(1 + z)β, we derived ξ < (4.2–12) × 107 for β = 1–4. This limit is stronger than those obtained by no gamma-ray detection of known FRBs by about three orders of magnitude. The limit is comparable with the largest values found for pulsars. However, ξ of pulsars is distributed widely in many orders of magnitudes, and we cannot exclude that FRBs have similar values of ξ to pulsars in general. We also compared our limit with the spectral energy distribution of the 2004 giant flare of SGR 1806−20. The upper bound on the radio flux for this flare is marginally consistent with our limit of ξ, if a non-thermal power-law component up to GeV exists in the initial flare phase and its energy fraction with respect to the thermal emission is similar to that of pulsating tail phase emission.
We thank the anonymous Referee for the helpful remarks and suggestions. This work was supported by JSPS KAKENHI Grant Numbers 15K05018 and 40197778.
REFERENCES



