The paper ‘A semi-analytic dynamical friction model that reproduces core-stalling’ was published in MNRAS, 454, 3778 (2015). In Section 6.1, we presented a calculation of the inspiral of a satellite in a sharply truncated constant density core. We have discovered an error in the normalization of the background density for this model. This caused the central density to be underestimated by a factor of 10 and caused the satellite to stall artificially far out. The corrected calculation is shown in Fig. 1, as well as the erroneous calculation from Petts, Gualandris & Read (2015, hereafter P15). In the corrected model, the satellite stalls when it encloses its own mass, contrary to what is found in Read et al. (2006).
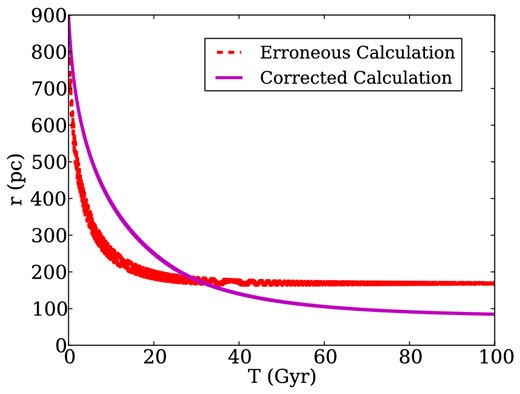
Inspiral of a satellite on an initially circular orbit in a cored galaxy modelled as in Section 6.1 of P15. The erroneous calculation (dotted red line) is shown as well as the corrected calculation using the correct background density (magenta line).
The Hénon model was composed of 224 equal mass particles. The units were G = Mg = RV = 1, where G is the gravitational constant and RV is the virial radius of the galaxy, defined as RV = −GMg2/2U, where U is the total potential energy of the system. The satellite had a mass of 1.6 × 10−4 and is initially placed on a circular orbit at the scale radius of the galaxy (∼0.237RV). Fig. 2 shows the results of the N-body simulation and the semi-analytic model from P15.
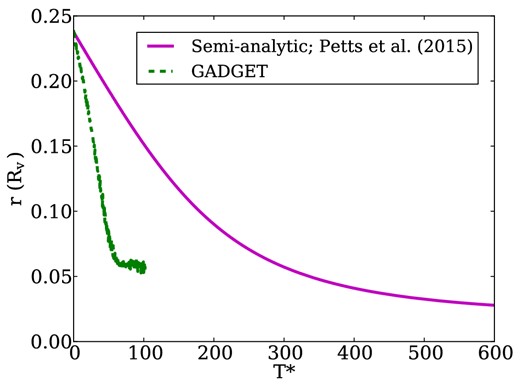
Inspiral of a satellite on an initially circular orbit in a cored galaxy modelled by Hénon's Isochrone model. The dashed green line is the result from the N-body model, and the magenta line is computed using the semi-analytic model from P15.
In P15, we did not claim to accurately match the inspiral (see figs 14 and 20 in P15 and relevant discussions), as it was evident from previous work that in cored galaxies, the standard Chandrasekhar formula underpredicts the frictional force (Read et al. 2006). However, we did claim that the stalling was captured by our model. Fig. 2 shows that our semi-analytic model does predict stalling, but at a smaller radius than the N-body model shows.
The model presented in P15 gives an excellent fit to the stalling radius in a Dehnen distribution of background stars, even for the case γ = 0 (Dehnen 1993). However, it is clear that it performs less well for large and particularly flat density cores such as in the Hénon model. We will present an improved dynamical friction model that gives better performance for both the inspiral and stalling for cored models in a forthcoming paper (Petts, Read & Gualandris 2016).
REFERENCES
