-
PDF
- Split View
-
Views
-
Cite
Cite
R. Raddi, S. Catalán, B. T. Gänsicke, J. J. Hermes, R. Napiwotzki, D. Koester, P.-E. Tremblay, G. Barentsen, H. J. Farnhill, M. Mohr-Smith, J. E. Drew, P. J. Groot, L. Guzman-Ramirez, Q. A. Parker, D. Steeghs, A. Zijlstra, A search for white dwarfs in the Galactic plane: the field and the open cluster population, Monthly Notices of the Royal Astronomical Society, Volume 457, Issue 2, 01 April 2016, Pages 1988–2004, https://doi.org/10.1093/mnras/stw042
Close - Share Icon Share
Abstract
We investigated the prospects for systematic searches of white dwarfs at low Galactic latitudes, using the VLT Survey Telescope H α Photometric Survey of the Galactic plane and Bulge (VPHAS+). We targeted 17 white dwarf candidates along sightlines of known open clusters, aiming to identify potential cluster members. We confirmed all the 17 white dwarf candidates from blue/optical spectroscopy, and we suggest five of them to be likely cluster members. We estimated progenitor ages and masses for the candidate cluster members, and compare our findings to those for other cluster white dwarfs. A white dwarf in NGC 3532 is the most massive known cluster member (1.13 M⊙), likely with an oxygen–neon core, for which we estimate an |$8.8_{-4.3}^{+1.2}$| M⊙ progenitor, close to the mass-divide between white dwarf and neutron star progenitors. A cluster member in Ruprecht 131 is a magnetic white dwarf, whose progenitor mass exceeded 2–3 M⊙. We stress that wider searches, and improved cluster distances and ages derived from data of the ESA Gaia mission, will advance the understanding of the mass-loss processes for low- to intermediate-mass stars.
1 INTRODUCTION
Main-sequence stars of masses below ≈8–10 M⊙ end their lives as white dwarfs (Herwig 2005; Smartt 2009), producing the most common stellar remnants. Up to 90 per cent of the mass of white dwarf progenitors is lost on the asymptotic giant branch (AGB), and then dispersed in to the interstellar medium (Iben & Renzini 1983), enriched with the yields of the nucleosynthesis s-processes (Busso, Gallino & Wasserburg 1999; Nomoto, Kobayashi & Tominaga 2013, and references therein).
Quantifying the mass-loss is crucial for a number of reasons. It allows us to: (i) estimate the amount of stellar yields (e.g. Marigo 2001; Karakas 2010; Siess 2010), and the dust output on the red giant branch and AGB (e.g. Matsuura et al. 2009; McDonald et al. 2011); (ii) infer the mass-to-light ratio of galaxies (e.g. Maraston 1998; Kotulla et al. 2009); (iii) date old stellar populations in open (García-Berro et al. 2010) and globular clusters (Richer et al. 1997; Hansen et al. 2004), or in the different constituents of the Milky Way, i.e. the disc (Winget et al. 1987; Oswalt et al. 1996), the bulge (Calamida et al. 2014; Gesicki et al. 2014), and the halo (Kalirai 2012). Modelling the final stages of evolution for white dwarf progenitors is complex, especially in the super-AGB regime – that is when 8–10 M⊙ stars could burn carbon under conditions of partial electron degeneracy, leading either to the formation of stable oxygen– neon core white dwarfs or neutron stars via electron-capture supernovae (e.g. Nomoto 1984; García-Berro, Ritossa & Iben 1997; Ritossa, García-Berro & Iben 1999; Farmer, Fields & Timmes 2015). In this range of masses, the separation between white dwarf and neutron star progenitors is expected to depend on stellar properties (metallicity above all; Eldridge & Tout 2004) that influence the mass growth of the core, as well as the mass-loss during the thermally pulsing AGB (TP-AGB) phase (e.g. Siess 2007, 2010; Doherty et al. 2015).
Cluster white dwarfs can help to study the correlation between their masses and those of the progenitors, known as the initial-to-final mass relation (Weidemann 1977; Koester & Weidemann 1980). The initial-to-final mass relation can also be studied using white dwarfs in wide binaries (i.e. main-sequence star plus white dwarf; Catalán et al. 2008a; or two white dwarfs; Girven et al. 2010; Andrews et al. 2015), but star clusters are the most favourable test benches as they can contain samples of white dwarfs, which formed from a coeval population of stars (Portegies Zwart et al. 2001). Ground-based follow-up spectroscopy is achievable for numerous cluster white dwarfs, enabling to assess a wide range of white dwarf progenitor masses, from 1.5–2 M⊙ (e.g. Kalirai et al. 2008) to ≳7 M⊙, which are useful to constrain the demarcation between white dwarf and neutron star progenitors (Williams, Bolte & Koester 2009). Although the white dwarf mass distribution is quite well constrained (Tremblay et al. 2013, and references therein), the general trend of the empirical initial-to-final mass relation remains approximate (Weidemann 2000), especially for low- and high-mass progenitors. Stellar parameters (e.g. metallicity, convection, rotation, magnetic fields) and environmental effects (e.g. binarity and intracluster dynamical interactions) are suggested to add intrinsic scatter to the shape of the initial-to-final mass relation (e.g. Ferrario et al. 2005; Catalán et al. 2008b; Romero, Campos & Kepler 2015).
At present, the study of the cluster initial-to-final mass relation is limited to about 10 clusters, with ≈50 spectroscopically confirmed white dwarf members (Salaris et al. 2009). There are presumably only three open clusters approaching a fully retrieved white dwarf cooling sequence: the Pleiades (Wegner, Reid & McMahan 1991; Dobbie et al. 2006), the Hyades (Schilbach & Röser 2012) and Praesepe (Casewell et al. 2009), which are all three nearby (d < 200 pc) and above the densest regions of the Galactic plane (|b| > 10 deg). While some new cluster members were discovered recently (Dobbie et al. 2012; Cummings et al. 2015, in NGC 3532 and M 37, respectively), several observational factors have worked against the identification of complete white dwarf populations. First, most clusters are in crowded, reddened areas of the Galactic plane. Secondly, the early dispersal of clusters causes the number of old clusters to be relatively small (Goodwin & Bastian 2006). Thirdly, no blue photometric survey, with sufficient magnitude depth (≲10 mag fainter than the cluster turn-off) and angular resolution, covered the Galactic plane until recently.
Here, we test the efficiency of the new VLT Survey Telescope (VST) H α Photometric Survey of the Southern Galactic Plane and Bulge (VPHAS+; Drew et al. 2014) at identifying white dwarfs. We selected white dwarf candidates in the direction of 11 relatively old open clusters, aiming to confirm new cluster members. We describe the selection method and observations in Section 2. The spectral analysis is presented in Section 3, while the estimates of white dwarf parameters and the confirmation of cluster membership are discussed in Section 4. Finally, in Section 5, we derive the progenitor masses for the suggested cluster members, and compare the new data with initial-to-final mass relations from previous studies. In the concluding remarks, we discuss the future perspectives for white dwarf searches in the Galactic plane.
2 THE DATA
2.1 VPHAS+ photometry
VPHAS+ started operations in 2011 December 28 and, once completed, will cover the southern Galactic plane between +210° ≲ ℓ ≲ +40° and −5° < b < 5°, and the Galactic bulge between |ℓ|, |b| < 10°. It combines ugri broad-band filters and a narrow-band H α filter, reaching down to 20 mag (at 10σ limit). The observing strategy of VPHAS+ separately groups (blue) ugr and (red) rH αi frames covering the same field, due to different requirements of lunar phase. Therefore, blue and red filters might be observed at different epochs. To cover the gaps between CCDs and the cross-shaped shadow cast by the segmented H α filter, every uri field is observed at two offset pointings, separated by −588 arcsec and +660 arcsec in the RA and declination directions, respectively, while every gH α field is observed at three offset pointings, including an intermediate position.
Here, we use the primary detections of the VPHAS+ data release 2 (DR2), accessible through the ESO Science Archive. It delivers PSF magnitudes, expressed in the Vega system, for 24 per cent of the survey area. Details on the source detection, photometry, and field merging are given in the data release document.1 The VPHAS+ DR2 photometry is delivered with a provisional uniform calibration, computed relative to the AAVSO Photometric All-Sky Survey Data Release 8 (APASS; Henden et al. 2012), following the prescriptions given in section 6 of Drew et al. (2014). The u band is calibrated separately as explained in section 6 and fig. 20 of Drew et al. (2014). The zero-points for the H α magnitudes are offset with respect to the r-band zero-points, based on the (r − H α) colours of main-sequence stars. While VPHAS+ DR2 photometry is currently suggested to be consistent with that of the Sloan Digital Sky Survey (SDSS; Abazajian et al. 2009) within 0.05 mag, there are known systematic errors ≥0.1 mag in isolated regions of the sky, probably inherited from APASS or due to patchy cloud coverage.
2.2 Clusters
The open clusters were drawn from the Dias et al. (2002) catalogue, setting the following criteria:
Cluster age ≥100 Myr, corresponding to the lifetime of a 5 M⊙ white dwarf progenitor.
Distance modulus ≤9.5 mag, to have a significant fraction of the white dwarf cooling sequence within the magnitude limits of VPHAS+.
VPHAS+ ugr photometry covering at least part of the cluster.
Of the 45 clusters, cluster remnants, and stellar associations, which fulfil the first two constraints, only 11 currently have VPHAS+ DR2 ugr photometry. We list in Table 1 their relevant properties, and the bibliographic references. Distances, reddenings, ages, and metallicities are from Dias et al. (2002) and Kharchenko et al. (2013). The data from Dias et al. (2002) are compiled from a number of sources, while Kharchenko et al. (2013) estimated cluster parameters and cluster membership using PPMXL (Roeser, Demleitner & Schilbach 2010) and the Two Micron All Sky Survey (2MASS; Skrutskie et al. 2006). Kharchenko et al. (2013) estimated typical errors of 11, 7, and 39 per cent for their measures of distances, reddenings, and ages, respectively, via comparison of the cluster parameters with data published in the literature. In Table 1, we list r1 and r2, which are the angular radius of the central part and the total radius of the clusters, respectively (r1 is defined as the angular separation from the cluster centre where the stellar surface density declines abruptly, while r2 is the angular separation where the cluster stellar density merges with that of the field; Kharchenko et al. 2005). We note here that Platais 9 and 10, which have r1 and r2 in the range of 1 deg, are presumably stellar associations rather than open clusters, as suggested by Dias et al. (2002) and Kharchenko et al. (2013). The total masses of the clusters, Moc, were determined by Piskunov et al. (2008) from the inferred tidal radii of the clusters.
Parameters of the 11 open clusters proposed to host the white dwarf candidates. We add a tickmark to the last column if at least one new cluster member is identified (Section 4).
| Name . | RA . | Dec . | ℓ . | b . | r1, r2 . | Da, b . | E(B − V)a, b . | |$t_{\rm {oc}}^{a,b}$| . | [Fe/H] . | |$M_{\rm {oc}}^{c}$| . | New . | . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (h:m:s) . | (°:′:″) . | (deg) . | (deg) . | (arcmin) . | (pc) . | (mag) . | (Myr) . | . | log (M⊙) . | . | . |
| NGC 2527 | 08:04:58 | −28:08:48 | 246.09 | 1.85 | 9, 20 | 601, 642 | 0.04 | 445, 800 | −0.10, 0.20 | 2.5 | |$\checkmark$| | |
| BH 23 | 08:14:24 | −36:23:00 | 254.08 | −0.96 | 9, 20 | 414, 480 | 0.06 | 250 | 1.7 | |||
| Platais 9 | 09:13:47 | −43:44:24 | 266.87 | 3.38 | 60, 126 | 174, 200 | 0.00 | 100 | ||||
| ASCC 59 | 10:20:13 | −57:39:00 | 283.78 | −0.51 | 12, 20 | 509, 550 | 0.05 | 290, 400 | ||||
| Loden 143 | 10:28:54 | −58:47:00 | 285.35 | −0.86 | 10, 18 | 600, 616 | 0.10, 0.12 | 281, 288 | |$\checkmark$| | |||
| NGC 3532 | 11:05:39 | −58:45:12 | 289.57 | 1.35 | 12, 25 | 492d | 0.03, 0.04 | 300d | 0.02 | 2.6 | |$\checkmark$| | |
| Platais 10 | 13:43:28 | −59:07:18 | 309.57 | 3.08 | 31, 60 | 246 | 0.00 | 100, 210 | ||||
| Johansson 1 | 15:46:20 | −52:22:54 | 327.90 | 1.80 | 11, 18 | 570, 869 | 0.17 | 200, 500 | |$\checkmark$| | |||
| ASCC 83 | 15:50:13 | −52:48:00 | 328.10 | 1.11 | 12, 20 | 600, 619 | 0.12, 0.15 | 125, 250 | ||||
| Ruprecht 131 | 17:49:15 | −29:15:00 | 0.14 | −0.84 | 5, 10 | 600, 614 | 0.10 | 1480 | 1.1 | |$\checkmark$| | ||
| Ruprecht 139 | 18:01:03 | −23:32:00 | 6.41 | −0.24 | 5, 10 | 550, 593 | 0.10, 0.15 | 1120 | ||||
| Name . | RA . | Dec . | ℓ . | b . | r1, r2 . | Da, b . | E(B − V)a, b . | |$t_{\rm {oc}}^{a,b}$| . | [Fe/H] . | |$M_{\rm {oc}}^{c}$| . | New . | . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (h:m:s) . | (°:′:″) . | (deg) . | (deg) . | (arcmin) . | (pc) . | (mag) . | (Myr) . | . | log (M⊙) . | . | . |
| NGC 2527 | 08:04:58 | −28:08:48 | 246.09 | 1.85 | 9, 20 | 601, 642 | 0.04 | 445, 800 | −0.10, 0.20 | 2.5 | |$\checkmark$| | |
| BH 23 | 08:14:24 | −36:23:00 | 254.08 | −0.96 | 9, 20 | 414, 480 | 0.06 | 250 | 1.7 | |||
| Platais 9 | 09:13:47 | −43:44:24 | 266.87 | 3.38 | 60, 126 | 174, 200 | 0.00 | 100 | ||||
| ASCC 59 | 10:20:13 | −57:39:00 | 283.78 | −0.51 | 12, 20 | 509, 550 | 0.05 | 290, 400 | ||||
| Loden 143 | 10:28:54 | −58:47:00 | 285.35 | −0.86 | 10, 18 | 600, 616 | 0.10, 0.12 | 281, 288 | |$\checkmark$| | |||
| NGC 3532 | 11:05:39 | −58:45:12 | 289.57 | 1.35 | 12, 25 | 492d | 0.03, 0.04 | 300d | 0.02 | 2.6 | |$\checkmark$| | |
| Platais 10 | 13:43:28 | −59:07:18 | 309.57 | 3.08 | 31, 60 | 246 | 0.00 | 100, 210 | ||||
| Johansson 1 | 15:46:20 | −52:22:54 | 327.90 | 1.80 | 11, 18 | 570, 869 | 0.17 | 200, 500 | |$\checkmark$| | |||
| ASCC 83 | 15:50:13 | −52:48:00 | 328.10 | 1.11 | 12, 20 | 600, 619 | 0.12, 0.15 | 125, 250 | ||||
| Ruprecht 131 | 17:49:15 | −29:15:00 | 0.14 | −0.84 | 5, 10 | 600, 614 | 0.10 | 1480 | 1.1 | |$\checkmark$| | ||
| Ruprecht 139 | 18:01:03 | −23:32:00 | 6.41 | −0.24 | 5, 10 | 550, 593 | 0.10, 0.15 | 1120 | ||||
Parameters of the 11 open clusters proposed to host the white dwarf candidates. We add a tickmark to the last column if at least one new cluster member is identified (Section 4).
| Name . | RA . | Dec . | ℓ . | b . | r1, r2 . | Da, b . | E(B − V)a, b . | |$t_{\rm {oc}}^{a,b}$| . | [Fe/H] . | |$M_{\rm {oc}}^{c}$| . | New . | . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (h:m:s) . | (°:′:″) . | (deg) . | (deg) . | (arcmin) . | (pc) . | (mag) . | (Myr) . | . | log (M⊙) . | . | . |
| NGC 2527 | 08:04:58 | −28:08:48 | 246.09 | 1.85 | 9, 20 | 601, 642 | 0.04 | 445, 800 | −0.10, 0.20 | 2.5 | |$\checkmark$| | |
| BH 23 | 08:14:24 | −36:23:00 | 254.08 | −0.96 | 9, 20 | 414, 480 | 0.06 | 250 | 1.7 | |||
| Platais 9 | 09:13:47 | −43:44:24 | 266.87 | 3.38 | 60, 126 | 174, 200 | 0.00 | 100 | ||||
| ASCC 59 | 10:20:13 | −57:39:00 | 283.78 | −0.51 | 12, 20 | 509, 550 | 0.05 | 290, 400 | ||||
| Loden 143 | 10:28:54 | −58:47:00 | 285.35 | −0.86 | 10, 18 | 600, 616 | 0.10, 0.12 | 281, 288 | |$\checkmark$| | |||
| NGC 3532 | 11:05:39 | −58:45:12 | 289.57 | 1.35 | 12, 25 | 492d | 0.03, 0.04 | 300d | 0.02 | 2.6 | |$\checkmark$| | |
| Platais 10 | 13:43:28 | −59:07:18 | 309.57 | 3.08 | 31, 60 | 246 | 0.00 | 100, 210 | ||||
| Johansson 1 | 15:46:20 | −52:22:54 | 327.90 | 1.80 | 11, 18 | 570, 869 | 0.17 | 200, 500 | |$\checkmark$| | |||
| ASCC 83 | 15:50:13 | −52:48:00 | 328.10 | 1.11 | 12, 20 | 600, 619 | 0.12, 0.15 | 125, 250 | ||||
| Ruprecht 131 | 17:49:15 | −29:15:00 | 0.14 | −0.84 | 5, 10 | 600, 614 | 0.10 | 1480 | 1.1 | |$\checkmark$| | ||
| Ruprecht 139 | 18:01:03 | −23:32:00 | 6.41 | −0.24 | 5, 10 | 550, 593 | 0.10, 0.15 | 1120 | ||||
| Name . | RA . | Dec . | ℓ . | b . | r1, r2 . | Da, b . | E(B − V)a, b . | |$t_{\rm {oc}}^{a,b}$| . | [Fe/H] . | |$M_{\rm {oc}}^{c}$| . | New . | . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (h:m:s) . | (°:′:″) . | (deg) . | (deg) . | (arcmin) . | (pc) . | (mag) . | (Myr) . | . | log (M⊙) . | . | . |
| NGC 2527 | 08:04:58 | −28:08:48 | 246.09 | 1.85 | 9, 20 | 601, 642 | 0.04 | 445, 800 | −0.10, 0.20 | 2.5 | |$\checkmark$| | |
| BH 23 | 08:14:24 | −36:23:00 | 254.08 | −0.96 | 9, 20 | 414, 480 | 0.06 | 250 | 1.7 | |||
| Platais 9 | 09:13:47 | −43:44:24 | 266.87 | 3.38 | 60, 126 | 174, 200 | 0.00 | 100 | ||||
| ASCC 59 | 10:20:13 | −57:39:00 | 283.78 | −0.51 | 12, 20 | 509, 550 | 0.05 | 290, 400 | ||||
| Loden 143 | 10:28:54 | −58:47:00 | 285.35 | −0.86 | 10, 18 | 600, 616 | 0.10, 0.12 | 281, 288 | |$\checkmark$| | |||
| NGC 3532 | 11:05:39 | −58:45:12 | 289.57 | 1.35 | 12, 25 | 492d | 0.03, 0.04 | 300d | 0.02 | 2.6 | |$\checkmark$| | |
| Platais 10 | 13:43:28 | −59:07:18 | 309.57 | 3.08 | 31, 60 | 246 | 0.00 | 100, 210 | ||||
| Johansson 1 | 15:46:20 | −52:22:54 | 327.90 | 1.80 | 11, 18 | 570, 869 | 0.17 | 200, 500 | |$\checkmark$| | |||
| ASCC 83 | 15:50:13 | −52:48:00 | 328.10 | 1.11 | 12, 20 | 600, 619 | 0.12, 0.15 | 125, 250 | ||||
| Ruprecht 131 | 17:49:15 | −29:15:00 | 0.14 | −0.84 | 5, 10 | 600, 614 | 0.10 | 1480 | 1.1 | |$\checkmark$| | ||
| Ruprecht 139 | 18:01:03 | −23:32:00 | 6.41 | −0.24 | 5, 10 | 550, 593 | 0.10, 0.15 | 1120 | ||||
The distances of the 11 clusters, given in Dias et al. (2002) and Kharchenko et al. (2013) mostly differ by less than 10 per cent, with the exception of Johansson 1 (570 pc; Dias et al. 2002, and 890 pc; Kharchenko et al. 2013), probably due to the difficulty of determining cluster membership. The cluster ages agree all within ≈40 per cent.
In the following paragraphs, we briefly review the available information for five of the 11 open clusters, in which we confirm new white dwarf members (Section 4). In Fig. 1, we show the mosaics of VPHAS+ g-band frames, covering the central parts of the five clusters, and we mark the positions of the new white dwarfs we identify as well as those of known white dwarfs.
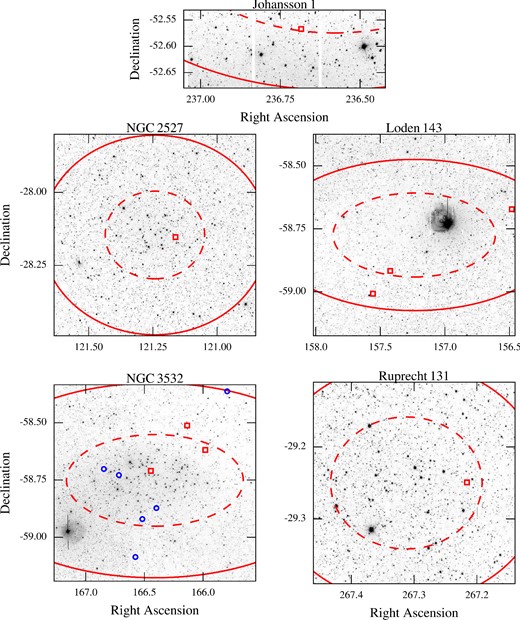
VPHAS+ g-band mosaics of five open clusters in our sample, for which we identify likely white dwarf members. Just a small part of Johanson 1 is covered by VPHAS+ imaging. The dashed curves represent the central part of the cluster, r1, while the solid curves trace the total cluster area, r2 (these radii are from Kharchenko et al. 2013, see Table 1). Red squares mark the positions of the white dwarf candidates, blue circles show the confirmed white dwarfs in NGC 3532 (Dobbie et al. 2012).
2.2.1 NGC 2527
The cluster is well populated with early A-type stars (Lindoff 1973; Houk & Cowley 1975), which are the brightest stars in Fig. 1. The range of ages for this cluster (Table 1) corresponds to turn-off mass of ≈2.2–3.5 M⊙, i.e. approximately to spectral types A3–B9. With a total stellar mass of ≈500 M⊙, we estimated from the Scalo (1986) initial mass function that NGC 2527 could host 13 ± 6 white dwarfs. From the VPHAS+ DR2 photometry, we selected for follow-up one white dwarf candidate towards the cluster centre.
2.2.2 Loden 143
Like other groups of stars described by Loden (1979), the presence of an open cluster appears in question. The VPHAS+ frames (Fig. 1) do not show a clearly visible clustering of bright stars. The very bright, saturated star, which creates an extended reflection in the mosaic of frames, defines the putative giant branch of the cluster in the colour–magnitude diagrams by Kharchenko et al. (2013). The authors comment on the sparse appearance of the cluster and suggest its parameters to be poorly constrained. We observed three white dwarf candidates in the cluster area.
2.2.3 NGC 3532
This is the only cluster in our list with known white dwarf members (seven; Reimers & Koester 1989; Koester & Reimers 1993; Dobbie et al. 2009, 2012). In the most recent photometric study of the cluster, Clem et al. (2011) confirmed a distance of 492 ± 12 pc and an age of 300 ± 100 Myr. Using the cluster age, the total mass of the cluster (Piskunov et al. 2008), and the initial mass function by Scalo (1986), we expect ≈7 ± 4 white dwarf members. Given the margin for a few more white dwarfs to be found in this cluster, we followed up three candidates. Six of the known white dwarfs are shown in Fig. 1 (the seventh is outside the figure) along with the three white dwarf candidates we have observed.
2.2.4 Johansson 1
The spread in distances and ages reported by Dias et al. (2002) and Kharchenko et al. (2013) is large, and it is probably due to sparse appearance of the cluster that can be also noticed in images from 2MASS and the VISTA Variables in the Via Lactea (VVV) survey (Saito et al. 2012). Several bright stars in the cluster area guided the cluster identification by Kharchenko et al. (2013), but the cluster main sequence was identified mistakenly by Johansson (1981) from the study of a few stars in the area of another cluster, Loden 2326. Unfortunately, VPHAS+ observations do not cover the whole cluster area yet. The white dwarf candidates we identified are within the suggested central part of the cluster.
2.2.5 Ruprecht 131
This cluster is the oldest in our sample and it is found in the Bulge section of the VPHAS+ footprint, not far from the crowded, young star-forming region of the Lagoon nebula. Dias et al. (2002) suggested the identification of Ruprecht 131 as being dubious. Kharchenko et al. (2013) determined its parameters using the bright stars that are visible in 2MASS images, and also recognizable in the VPHAS+ mosaic of the cluster area. This cluster is suggested to be old enough for stars down to ≈2 M⊙ to have become white dwarfs (total age < 1.5 Gyr). Considering the total stellar mass to be less than a hundred solar masses (Piskunov et al. 2008), it is likely that this cluster has few white dwarfs. We followed up one white dwarf candidate.
2.3 Photometric selection
White dwarfs occupy a limited part of the (u − g, g − r) colour plane that is also populated by hot subdwarfs, O- and B-type stars, and quasars (e.g. Girven et al. 2011; Greiss et al. 2012; Verbeek et al. 2012), whose contamination can be efficiently suppressed by applying reduced proper-motion selection criteria (Gentile Fusillo, Gänsicke & Greiss 2015). Furthermore, in the Galactic plane, the contamination by quasars is expected to be insignificant, due to the blocking effect of the interstellar reddening. Hot subdwarfs and high-mass main-sequence stars have redder colours than white dwarfs, because they are more distant (e.g. Mohr-Smith et al. 2015).
We identified about 70 white dwarf candidates, towards the 11 selected clusters, via cuts in the (u − g, g − r) colour–colour diagram, based on the synthetic colours of hydrogen- (DA) and helium-dominated (DB) white dwarfs (see example in Fig. 2). To guide our selection, we corrected the white dwarf tracks according to the interstellar reddening of the open clusters (Table 1). The absolute magnitudes of white dwarfs were computed in the VPHAS+ Vega system, convolving the transmission curves of the filters with a grid of Koester (2010) synthetic spectra. The fluxes of model spectra were calibrated to an absolute scale following Holberg & Bergeron (2006), and using the mass–radius relation adopted by the Montreal group.2 The absolute g-band magnitudes and intrinsic colours in the VPHAS+ Vega system are given in Appendix A, for a range of atmospheric temperatures (Teff = 6000–100 000 K) and surface gravities (log g = 7–9 dex).
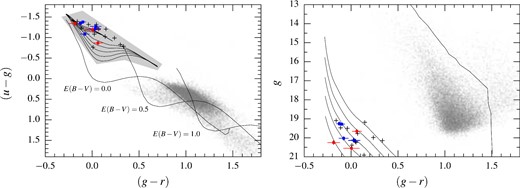
Colour–colour (left) and colour–magnitude (right) diagrams displaying the point sources identified in the VPHAS+ field 1739, within one cluster radius (18 arcmin) from the centre of NGC 3532. On the left, we represent the colour cuts we applied to select white dwarf candidates (black crosses) as a grey shaded area. The stars we followed up are overplotted as red squares with error bars, and the known cluster white dwarfs (Dobbie et al. 2012) with VPHAS+ DR2 photometry are represented by blue squares with error bars. The main sequence (Drew et al. 2014) is shown as a black curve, which is displaced by three different magnitudes of interstellar reddening, i.e. E(B − V) = 0.0, 0.5, 1.0. The white dwarf tracks for DA and DB white dwarfs (Appendix A) are plotted as black curves, with E(B − V) = 0.03. On the right, in the colour–magnitude diagram, the main sequence and the DA white dwarf cooling sequence for an assumed cluster distance of 492 pc, and E(B − V) = 0.03 (Table 1).
To maximize the chance of identifying cluster members and to prioritize the targets for the spectroscopic follow-up, we estimated photometric distances and cooling ages of the white dwarf candidates. Using DA models at fixed log g = 8, we estimated the Teff by fitting the VPHAS+ ugr photometry. Next, we inferred the absolute magnitudes of the white dwarf candidates interpolating the tables in Appendix A, and we estimated their cooling ages from the cooling models of the Montreal group (Fontaine, Brassard & Bergeron 2001). Finally, we estimated their photometric parallaxes. We chose to follow up 17 targets (see next section), having photometric distances and cooling ages broadly consistent with those of the selected open clusters. We summarize the relevant VPHAS+ data for the 17 spectroscopic targets in Table 2.
Details for the 17 white dwarf candidates confirmed by this study, including their photometry with 1σ errors, VPHAS+ field ID numbers, and observing dates for the red and blue frames. The naming convention for VPHAS+ sources is VPHAS Jhhmmss.ss+ddmmss.s, which includes the Epoch 2000 coordinates in sexagesimal format. In the text, we use an abbreviated version, VPHAS Jhhmm+ddmm.
| Name . | u . | g . | rblue . | rred . | H α . | i . | field . | date-obs . | |
|---|---|---|---|---|---|---|---|---|---|
| . | (mag) . | (mag) . | (mag) . | (mag) . | (mag) . | (mag) . | . | (blue) . | (red) . |
| VPHAS J080438.8−280914.0 | 19.56 ± 0.05 | 20.45 ± 0.04 | 20.47 ± 0.08 | 20.45 ± 0.07 | 20.47 ± 0.20 | 20.61 ± 0.15 | 0764 | 2013-04-13 | 2012-11-13 |
| VPHAS J081528.4−362535.9 | 18.13 ± 0.02 | 19.56 ± 0.02 | 19.66 ± 0.04 | 19.73 ± 0.05 | 19.71 ± 0.08 | 19.70 ± 0.06 | 0992 | 2013-05-13 | 2012-03-31 |
| VPHAS J090004.7−455613.4 | 18.53 ± 0.03 | 19.92 ± 0.02 | 20.01 ± 0.05 | 20.13 ± 0.08 | 20.03 ± 0.13 | 1266 | 2013-05-02 | 2012-04-30 | |
| VPHAS J101831.3−575211.0 | 19.92 ± 0.06 | 20.80 ± 0.04 | 20.96 ± 0.11 | 21.07 ± 0.13 | 20.64 ± 0.15 | 1678 | 2012-01-22 | 2012-04-29 | |
| VPHAS J102139.0−572939.8 | 18.83 ± 0.03 | 19.73 ± 0.02 | 19.63 ± 0.04 | 19.61 ± 0.05 | 19.74 ± 0.09 | 19.58 ± 0.06 | 1679 | 2012-01-22 | 2012-04-29 |
| VPHAS J102554.7−584106.0 | 18.94 ± 0.04 | 19.77 ± 0.03 | 19.59 ± 0.03 | 19.66 ± 0.04 | 19.77 ± 0.10 | 19.54 ± 0.06 | 1734 | 2012-02-14 | 2012-04-29 |
| VPHAS J102939.4−585527.4 | 18.62 ± 0.02 | 20.13 ± 0.04 | 20.25 ± 0.06 | 20.33 ± 0.08 | 20.30 ± 0.15 | 20.29 ± 0.12 | 1735 | 2012-02-14 | 2012-04-29 |
| VPHAS J103012.0−590048.6 | 18.70 ± 0.03 | 19.82 ± 0.03 | 19.86 ± 0.03 | 19.78 ± 0.05 | 19.88 ± 0.10 | 19.92 ± 0.06 | 1735 | 2012-02-14 | 2012-04-29 |
| VPHAS J110358.0−583709.2 | 19.36 ± 0.05 | 20.55 ± 0.05 | 20.54 ± 0.07 | 20.66 ± 0.12 | 20.58 ± 0.14 | 1739 | 2012-02-14 | 2012-05-30 | |
| VPHAS J110434.5−583047.4 | 18.91 ± 0.04 | 20.25 ± 0.03 | 20.43 ± 0.06 | 20.56 ± 0.10 | 20.17 ± 0.13 | 20.38 ± 0.11 | 1739 | 2012-02-14 | 2012-05-30 |
| VPHAS J110547.2−584241.8 | 18.79 ± 0.04 | 19.66 ± 0.03 | 19.60 ± 0.04 | 19.56 ± 0.05 | 19.93 ± 0.12 | 19.44 ± 0.06 | 1739 | 2012-02-14 | 2012-05-30 |
| VPHAS J133741.0−612110.2 | 19.16 ± 0.04 | 20.36 ± 0.04 | 20.30 ± 0.04 | 20.27 ± 0.05 | 20.30 ± 0.15 | 20.21 ± 0.10 | 1900 | 2012-02-26 | 2012-03-24 |
| VPHAS J134436.3−613419.2 | 19.37 ± 0.04 | 20.71 ± 0.04 | 20.53 ± 0.06 | 20.51 ± 0.06 | 20.78 ± 0.19 | 20.50 ± 0.13 | 1900 | 2012-02-26 | 2012-03-24 |
| VPHAS J154644.6−523359.0 | 20.18 ± 0.06 | 21.20 ± 0.06 | 21.19 ± 0.11 | 21.04 ± 0.10 | 20.84 ± 0.18 | 1501 | 2012-08-14 | 2012-07-13 | |
| VPHAS J154922.9−525158.3 | 19.88 ± 0.06 | 20.92 ± 0.05 | 20.96 ± 0.11 | 20.94 ± 0.08 | 20.86 ± 0.16 | 20.77 ± 0.13 | 1501 | 2012-08-14 | 2012-07-13 |
| VPHAS J174851.9−291456.8 | 20.32 ± 0.09 | 21.21 ± 0.06 | 20.86 ± 0.08 | 20.84 ± 0.09 | 20.58 ± 0.16 | 20.60 ± 0.18 | 0800 | 2012-08-10 | 2012-06-25 |
| VPHAS J180042.0−233238.5 | 17.16 ± 0.01 | 18.32 ± 0.01 | 18.20 ± 0.02 | 18.30 ± 0.02 | 18.28 ± 0.03 | 18.11 ± 0.03 | 0676 | 2012-08-14 | 2012-06-10 |
| Name . | u . | g . | rblue . | rred . | H α . | i . | field . | date-obs . | |
|---|---|---|---|---|---|---|---|---|---|
| . | (mag) . | (mag) . | (mag) . | (mag) . | (mag) . | (mag) . | . | (blue) . | (red) . |
| VPHAS J080438.8−280914.0 | 19.56 ± 0.05 | 20.45 ± 0.04 | 20.47 ± 0.08 | 20.45 ± 0.07 | 20.47 ± 0.20 | 20.61 ± 0.15 | 0764 | 2013-04-13 | 2012-11-13 |
| VPHAS J081528.4−362535.9 | 18.13 ± 0.02 | 19.56 ± 0.02 | 19.66 ± 0.04 | 19.73 ± 0.05 | 19.71 ± 0.08 | 19.70 ± 0.06 | 0992 | 2013-05-13 | 2012-03-31 |
| VPHAS J090004.7−455613.4 | 18.53 ± 0.03 | 19.92 ± 0.02 | 20.01 ± 0.05 | 20.13 ± 0.08 | 20.03 ± 0.13 | 1266 | 2013-05-02 | 2012-04-30 | |
| VPHAS J101831.3−575211.0 | 19.92 ± 0.06 | 20.80 ± 0.04 | 20.96 ± 0.11 | 21.07 ± 0.13 | 20.64 ± 0.15 | 1678 | 2012-01-22 | 2012-04-29 | |
| VPHAS J102139.0−572939.8 | 18.83 ± 0.03 | 19.73 ± 0.02 | 19.63 ± 0.04 | 19.61 ± 0.05 | 19.74 ± 0.09 | 19.58 ± 0.06 | 1679 | 2012-01-22 | 2012-04-29 |
| VPHAS J102554.7−584106.0 | 18.94 ± 0.04 | 19.77 ± 0.03 | 19.59 ± 0.03 | 19.66 ± 0.04 | 19.77 ± 0.10 | 19.54 ± 0.06 | 1734 | 2012-02-14 | 2012-04-29 |
| VPHAS J102939.4−585527.4 | 18.62 ± 0.02 | 20.13 ± 0.04 | 20.25 ± 0.06 | 20.33 ± 0.08 | 20.30 ± 0.15 | 20.29 ± 0.12 | 1735 | 2012-02-14 | 2012-04-29 |
| VPHAS J103012.0−590048.6 | 18.70 ± 0.03 | 19.82 ± 0.03 | 19.86 ± 0.03 | 19.78 ± 0.05 | 19.88 ± 0.10 | 19.92 ± 0.06 | 1735 | 2012-02-14 | 2012-04-29 |
| VPHAS J110358.0−583709.2 | 19.36 ± 0.05 | 20.55 ± 0.05 | 20.54 ± 0.07 | 20.66 ± 0.12 | 20.58 ± 0.14 | 1739 | 2012-02-14 | 2012-05-30 | |
| VPHAS J110434.5−583047.4 | 18.91 ± 0.04 | 20.25 ± 0.03 | 20.43 ± 0.06 | 20.56 ± 0.10 | 20.17 ± 0.13 | 20.38 ± 0.11 | 1739 | 2012-02-14 | 2012-05-30 |
| VPHAS J110547.2−584241.8 | 18.79 ± 0.04 | 19.66 ± 0.03 | 19.60 ± 0.04 | 19.56 ± 0.05 | 19.93 ± 0.12 | 19.44 ± 0.06 | 1739 | 2012-02-14 | 2012-05-30 |
| VPHAS J133741.0−612110.2 | 19.16 ± 0.04 | 20.36 ± 0.04 | 20.30 ± 0.04 | 20.27 ± 0.05 | 20.30 ± 0.15 | 20.21 ± 0.10 | 1900 | 2012-02-26 | 2012-03-24 |
| VPHAS J134436.3−613419.2 | 19.37 ± 0.04 | 20.71 ± 0.04 | 20.53 ± 0.06 | 20.51 ± 0.06 | 20.78 ± 0.19 | 20.50 ± 0.13 | 1900 | 2012-02-26 | 2012-03-24 |
| VPHAS J154644.6−523359.0 | 20.18 ± 0.06 | 21.20 ± 0.06 | 21.19 ± 0.11 | 21.04 ± 0.10 | 20.84 ± 0.18 | 1501 | 2012-08-14 | 2012-07-13 | |
| VPHAS J154922.9−525158.3 | 19.88 ± 0.06 | 20.92 ± 0.05 | 20.96 ± 0.11 | 20.94 ± 0.08 | 20.86 ± 0.16 | 20.77 ± 0.13 | 1501 | 2012-08-14 | 2012-07-13 |
| VPHAS J174851.9−291456.8 | 20.32 ± 0.09 | 21.21 ± 0.06 | 20.86 ± 0.08 | 20.84 ± 0.09 | 20.58 ± 0.16 | 20.60 ± 0.18 | 0800 | 2012-08-10 | 2012-06-25 |
| VPHAS J180042.0−233238.5 | 17.16 ± 0.01 | 18.32 ± 0.01 | 18.20 ± 0.02 | 18.30 ± 0.02 | 18.28 ± 0.03 | 18.11 ± 0.03 | 0676 | 2012-08-14 | 2012-06-10 |
Details for the 17 white dwarf candidates confirmed by this study, including their photometry with 1σ errors, VPHAS+ field ID numbers, and observing dates for the red and blue frames. The naming convention for VPHAS+ sources is VPHAS Jhhmmss.ss+ddmmss.s, which includes the Epoch 2000 coordinates in sexagesimal format. In the text, we use an abbreviated version, VPHAS Jhhmm+ddmm.
| Name . | u . | g . | rblue . | rred . | H α . | i . | field . | date-obs . | |
|---|---|---|---|---|---|---|---|---|---|
| . | (mag) . | (mag) . | (mag) . | (mag) . | (mag) . | (mag) . | . | (blue) . | (red) . |
| VPHAS J080438.8−280914.0 | 19.56 ± 0.05 | 20.45 ± 0.04 | 20.47 ± 0.08 | 20.45 ± 0.07 | 20.47 ± 0.20 | 20.61 ± 0.15 | 0764 | 2013-04-13 | 2012-11-13 |
| VPHAS J081528.4−362535.9 | 18.13 ± 0.02 | 19.56 ± 0.02 | 19.66 ± 0.04 | 19.73 ± 0.05 | 19.71 ± 0.08 | 19.70 ± 0.06 | 0992 | 2013-05-13 | 2012-03-31 |
| VPHAS J090004.7−455613.4 | 18.53 ± 0.03 | 19.92 ± 0.02 | 20.01 ± 0.05 | 20.13 ± 0.08 | 20.03 ± 0.13 | 1266 | 2013-05-02 | 2012-04-30 | |
| VPHAS J101831.3−575211.0 | 19.92 ± 0.06 | 20.80 ± 0.04 | 20.96 ± 0.11 | 21.07 ± 0.13 | 20.64 ± 0.15 | 1678 | 2012-01-22 | 2012-04-29 | |
| VPHAS J102139.0−572939.8 | 18.83 ± 0.03 | 19.73 ± 0.02 | 19.63 ± 0.04 | 19.61 ± 0.05 | 19.74 ± 0.09 | 19.58 ± 0.06 | 1679 | 2012-01-22 | 2012-04-29 |
| VPHAS J102554.7−584106.0 | 18.94 ± 0.04 | 19.77 ± 0.03 | 19.59 ± 0.03 | 19.66 ± 0.04 | 19.77 ± 0.10 | 19.54 ± 0.06 | 1734 | 2012-02-14 | 2012-04-29 |
| VPHAS J102939.4−585527.4 | 18.62 ± 0.02 | 20.13 ± 0.04 | 20.25 ± 0.06 | 20.33 ± 0.08 | 20.30 ± 0.15 | 20.29 ± 0.12 | 1735 | 2012-02-14 | 2012-04-29 |
| VPHAS J103012.0−590048.6 | 18.70 ± 0.03 | 19.82 ± 0.03 | 19.86 ± 0.03 | 19.78 ± 0.05 | 19.88 ± 0.10 | 19.92 ± 0.06 | 1735 | 2012-02-14 | 2012-04-29 |
| VPHAS J110358.0−583709.2 | 19.36 ± 0.05 | 20.55 ± 0.05 | 20.54 ± 0.07 | 20.66 ± 0.12 | 20.58 ± 0.14 | 1739 | 2012-02-14 | 2012-05-30 | |
| VPHAS J110434.5−583047.4 | 18.91 ± 0.04 | 20.25 ± 0.03 | 20.43 ± 0.06 | 20.56 ± 0.10 | 20.17 ± 0.13 | 20.38 ± 0.11 | 1739 | 2012-02-14 | 2012-05-30 |
| VPHAS J110547.2−584241.8 | 18.79 ± 0.04 | 19.66 ± 0.03 | 19.60 ± 0.04 | 19.56 ± 0.05 | 19.93 ± 0.12 | 19.44 ± 0.06 | 1739 | 2012-02-14 | 2012-05-30 |
| VPHAS J133741.0−612110.2 | 19.16 ± 0.04 | 20.36 ± 0.04 | 20.30 ± 0.04 | 20.27 ± 0.05 | 20.30 ± 0.15 | 20.21 ± 0.10 | 1900 | 2012-02-26 | 2012-03-24 |
| VPHAS J134436.3−613419.2 | 19.37 ± 0.04 | 20.71 ± 0.04 | 20.53 ± 0.06 | 20.51 ± 0.06 | 20.78 ± 0.19 | 20.50 ± 0.13 | 1900 | 2012-02-26 | 2012-03-24 |
| VPHAS J154644.6−523359.0 | 20.18 ± 0.06 | 21.20 ± 0.06 | 21.19 ± 0.11 | 21.04 ± 0.10 | 20.84 ± 0.18 | 1501 | 2012-08-14 | 2012-07-13 | |
| VPHAS J154922.9−525158.3 | 19.88 ± 0.06 | 20.92 ± 0.05 | 20.96 ± 0.11 | 20.94 ± 0.08 | 20.86 ± 0.16 | 20.77 ± 0.13 | 1501 | 2012-08-14 | 2012-07-13 |
| VPHAS J174851.9−291456.8 | 20.32 ± 0.09 | 21.21 ± 0.06 | 20.86 ± 0.08 | 20.84 ± 0.09 | 20.58 ± 0.16 | 20.60 ± 0.18 | 0800 | 2012-08-10 | 2012-06-25 |
| VPHAS J180042.0−233238.5 | 17.16 ± 0.01 | 18.32 ± 0.01 | 18.20 ± 0.02 | 18.30 ± 0.02 | 18.28 ± 0.03 | 18.11 ± 0.03 | 0676 | 2012-08-14 | 2012-06-10 |
| Name . | u . | g . | rblue . | rred . | H α . | i . | field . | date-obs . | |
|---|---|---|---|---|---|---|---|---|---|
| . | (mag) . | (mag) . | (mag) . | (mag) . | (mag) . | (mag) . | . | (blue) . | (red) . |
| VPHAS J080438.8−280914.0 | 19.56 ± 0.05 | 20.45 ± 0.04 | 20.47 ± 0.08 | 20.45 ± 0.07 | 20.47 ± 0.20 | 20.61 ± 0.15 | 0764 | 2013-04-13 | 2012-11-13 |
| VPHAS J081528.4−362535.9 | 18.13 ± 0.02 | 19.56 ± 0.02 | 19.66 ± 0.04 | 19.73 ± 0.05 | 19.71 ± 0.08 | 19.70 ± 0.06 | 0992 | 2013-05-13 | 2012-03-31 |
| VPHAS J090004.7−455613.4 | 18.53 ± 0.03 | 19.92 ± 0.02 | 20.01 ± 0.05 | 20.13 ± 0.08 | 20.03 ± 0.13 | 1266 | 2013-05-02 | 2012-04-30 | |
| VPHAS J101831.3−575211.0 | 19.92 ± 0.06 | 20.80 ± 0.04 | 20.96 ± 0.11 | 21.07 ± 0.13 | 20.64 ± 0.15 | 1678 | 2012-01-22 | 2012-04-29 | |
| VPHAS J102139.0−572939.8 | 18.83 ± 0.03 | 19.73 ± 0.02 | 19.63 ± 0.04 | 19.61 ± 0.05 | 19.74 ± 0.09 | 19.58 ± 0.06 | 1679 | 2012-01-22 | 2012-04-29 |
| VPHAS J102554.7−584106.0 | 18.94 ± 0.04 | 19.77 ± 0.03 | 19.59 ± 0.03 | 19.66 ± 0.04 | 19.77 ± 0.10 | 19.54 ± 0.06 | 1734 | 2012-02-14 | 2012-04-29 |
| VPHAS J102939.4−585527.4 | 18.62 ± 0.02 | 20.13 ± 0.04 | 20.25 ± 0.06 | 20.33 ± 0.08 | 20.30 ± 0.15 | 20.29 ± 0.12 | 1735 | 2012-02-14 | 2012-04-29 |
| VPHAS J103012.0−590048.6 | 18.70 ± 0.03 | 19.82 ± 0.03 | 19.86 ± 0.03 | 19.78 ± 0.05 | 19.88 ± 0.10 | 19.92 ± 0.06 | 1735 | 2012-02-14 | 2012-04-29 |
| VPHAS J110358.0−583709.2 | 19.36 ± 0.05 | 20.55 ± 0.05 | 20.54 ± 0.07 | 20.66 ± 0.12 | 20.58 ± 0.14 | 1739 | 2012-02-14 | 2012-05-30 | |
| VPHAS J110434.5−583047.4 | 18.91 ± 0.04 | 20.25 ± 0.03 | 20.43 ± 0.06 | 20.56 ± 0.10 | 20.17 ± 0.13 | 20.38 ± 0.11 | 1739 | 2012-02-14 | 2012-05-30 |
| VPHAS J110547.2−584241.8 | 18.79 ± 0.04 | 19.66 ± 0.03 | 19.60 ± 0.04 | 19.56 ± 0.05 | 19.93 ± 0.12 | 19.44 ± 0.06 | 1739 | 2012-02-14 | 2012-05-30 |
| VPHAS J133741.0−612110.2 | 19.16 ± 0.04 | 20.36 ± 0.04 | 20.30 ± 0.04 | 20.27 ± 0.05 | 20.30 ± 0.15 | 20.21 ± 0.10 | 1900 | 2012-02-26 | 2012-03-24 |
| VPHAS J134436.3−613419.2 | 19.37 ± 0.04 | 20.71 ± 0.04 | 20.53 ± 0.06 | 20.51 ± 0.06 | 20.78 ± 0.19 | 20.50 ± 0.13 | 1900 | 2012-02-26 | 2012-03-24 |
| VPHAS J154644.6−523359.0 | 20.18 ± 0.06 | 21.20 ± 0.06 | 21.19 ± 0.11 | 21.04 ± 0.10 | 20.84 ± 0.18 | 1501 | 2012-08-14 | 2012-07-13 | |
| VPHAS J154922.9−525158.3 | 19.88 ± 0.06 | 20.92 ± 0.05 | 20.96 ± 0.11 | 20.94 ± 0.08 | 20.86 ± 0.16 | 20.77 ± 0.13 | 1501 | 2012-08-14 | 2012-07-13 |
| VPHAS J174851.9−291456.8 | 20.32 ± 0.09 | 21.21 ± 0.06 | 20.86 ± 0.08 | 20.84 ± 0.09 | 20.58 ± 0.16 | 20.60 ± 0.18 | 0800 | 2012-08-10 | 2012-06-25 |
| VPHAS J180042.0−233238.5 | 17.16 ± 0.01 | 18.32 ± 0.01 | 18.20 ± 0.02 | 18.30 ± 0.02 | 18.28 ± 0.03 | 18.11 ± 0.03 | 0676 | 2012-08-14 | 2012-06-10 |
Three white dwarf candidates in the area of NGC 3532 also have Johnson–Kron–Cousins BVRcIc photometry (Clem et al. 2011), listed in Table 3. The B and V magnitudes are in good agreement with VPHAS+ DR2 photometry. The Rc and Ic magnitudes carry larger errors, but they appear to hint at small systematic differences with VPHAS+ DR2 at the faintest magnitudes.
Johnson–Kron–Cousins for the three white dwarfs in NGC 3532 (Clem et al. 2011).
| Name . | B . | V . | Rc . | Ic . |
|---|---|---|---|---|
| . | (mag) . | (mag) . | (mag) . | (mag) . |
| VPHAS J1103−5837 | 20.435 ± 0.024 | 20.560 ± 0.027 | 20.776 ± 0.081 | 20.756 ± 0.660 |
| VPHAS J1104−5830 | 20.141 ± 0.032 | 20.321 ± 0.021 | 20.512 ± 0.036 | 20.561 ± 0.178 |
| VPHAS J1105−5842 | 19.713 ± 0.019 | 19.581 ± 0.011 | 19.639 ± 0.018 | 19.615 ± 0.053 |
| Name . | B . | V . | Rc . | Ic . |
|---|---|---|---|---|
| . | (mag) . | (mag) . | (mag) . | (mag) . |
| VPHAS J1103−5837 | 20.435 ± 0.024 | 20.560 ± 0.027 | 20.776 ± 0.081 | 20.756 ± 0.660 |
| VPHAS J1104−5830 | 20.141 ± 0.032 | 20.321 ± 0.021 | 20.512 ± 0.036 | 20.561 ± 0.178 |
| VPHAS J1105−5842 | 19.713 ± 0.019 | 19.581 ± 0.011 | 19.639 ± 0.018 | 19.615 ± 0.053 |
Johnson–Kron–Cousins for the three white dwarfs in NGC 3532 (Clem et al. 2011).
| Name . | B . | V . | Rc . | Ic . |
|---|---|---|---|---|
| . | (mag) . | (mag) . | (mag) . | (mag) . |
| VPHAS J1103−5837 | 20.435 ± 0.024 | 20.560 ± 0.027 | 20.776 ± 0.081 | 20.756 ± 0.660 |
| VPHAS J1104−5830 | 20.141 ± 0.032 | 20.321 ± 0.021 | 20.512 ± 0.036 | 20.561 ± 0.178 |
| VPHAS J1105−5842 | 19.713 ± 0.019 | 19.581 ± 0.011 | 19.639 ± 0.018 | 19.615 ± 0.053 |
| Name . | B . | V . | Rc . | Ic . |
|---|---|---|---|---|
| . | (mag) . | (mag) . | (mag) . | (mag) . |
| VPHAS J1103−5837 | 20.435 ± 0.024 | 20.560 ± 0.027 | 20.776 ± 0.081 | 20.756 ± 0.660 |
| VPHAS J1104−5830 | 20.141 ± 0.032 | 20.321 ± 0.021 | 20.512 ± 0.036 | 20.561 ± 0.178 |
| VPHAS J1105−5842 | 19.713 ± 0.019 | 19.581 ± 0.011 | 19.639 ± 0.018 | 19.615 ± 0.053 |
2.4 Optical spectra
We acquired optical spectroscopy for 17 white dwarf candidates on 2014 April 28–30 with the visual and near-UV FOcal Reducer and low dispersion Spectrograph (FORS2; Appenzeller et al. 1998), mounted on the Very Large Telescope (VLT) UT1 (Antu). We used the blue sensitive E2V CCDs, with a pixel size of 15 μm, and the Grism 600B+22, which give a dispersion of 50 Å mm−1. The SR collimator (f1233 mm) was used with the standard 2 × 2 binned readout mode, giving a plate scale of 0.25 arcsec. With a 0.7 arcsec wide slit, we obtained a resolving power of R ≈ 1000 at H β. The relevant spectral coverage is 3500–6100 Å, allowing us to cover all the Balmer series from H β to the Balmer jump.
Weather conditions were overall good, but not photometric, with seeing varying between 0.5–1.6 arcsec. The exposure times ranged over 300–1200 s, and we achieved a signal-to-noise ratio (S/N) of ≥10 at H β for most stars (see Table 4). One spectrophotometric standard was observed each night, to allow for relative flux calibration. Standard calibrations were taken at the end of the night (bias, flat-fields, HeAr arc lamps).
The 2D images were reduced in a standard fashion to remove the bias, to apply flat-field correction and wavelength calibration, to extract the 1D spectrum, and to apply the flux calibration. The reduction steps were undertaken with the software developed by T. R. Marsh, pamela (Marsh 1989) and molly.3 The extracted spectra are shown in Fig. 3. Due to the relatively large sky background and faint magnitudes of the targets, some of the extracted spectra show residual sky-lines at 5577 Å.
The flux calibrated spectra follow relatively well the slope of the VPHAS+ DR2 ugr photometry, although some slight differences are apparent in the u band. Since our observations do not extend below 3500 Å, we cannot fully determine the flux contribution to the u band from the observed spectra. For one object, VPHAS J1021−5732, the slope inferred from the photometry appears to be ≈0.15 mag redder than that of the VLT/FORS2 spectrum. As it remains unclear whether it is a problem in the flux calibration of the spectrum or it is related to the DR2 photometry, the distance determined in Section 4 could be affected.
3 SPECTRAL ANALYSIS
We confirmed all 17 targets to be white dwarfs. Inspection of the spectra (Fig. 4) reveals 13 hydrogen-line (DA) white
dwarfs, one helium-line (DB) white dwarf (VPHAS J0900−4556), two likely magnetic (DAH) white dwarfs (VPHAS J1029−5855, VPHAS J1748−2914) with visible Zeeman splitting of the hydrogen lines, and a continuum (DC) white dwarf (VPHAS J1104−5830).
The atmospheric parameters (Teff, log g) of the DA white dwarfs were determined via comparison with two sets of model spectra. First, we used the fitsb2 program (Napiwotzki et al. 2004) with Koester (2010) model spectra. fitsb2 performs a fit to the spectral lines, minimizing the χ2 with a downhill simplex algorithm (derived from the AMOEBA routine; Press et al. 1992). The adopted grid of synthetic spectra spans Teff = 6000–100 000 K and log g = 5–9. The errors were assessed via a bootstrap method. Secondly, we used the set of model spectra by Tremblay, Bergeron & Gianninas (2011) and followed the fitting procedure detailed for DA white dwarfs in Bergeron, Saffer & Liebert (1992). Both the Koester (2010) and Tremblay et al. (2011) model spectra implement improved Stark broadening profiles of the hydrogen lines computed by Tremblay & Bergeron (2009). The Tremblay et al. (2011) models also account for NLTE effects, more appropriate for the study of hot white dwarfs like VPHAS J1344−6134. Here, we adopted for both sets of model atmospheres the mixing-length prescription ML2/α = 0.8. Due to the inaccurate treatment of convection, parametrized by the mixing-length theory in 1D model atmospheres, the log g measured from line-profile fits tends to be overestimated. Therefore, following Tremblay et al. (2013), we corrected the measured Teff and log g of DA white dwarfs with Teff < 15 000 K.
We measured the atmospheric parameters, using the following five transitions: H β, 4861.3 Å; H δ, 4340.5 Å; H γ, 4101.7 Å; H ϵ, 3970.4 Å; H8, 3889.05 Å. We achieved an accuracy of 200–850 K and 0.06–0.13, for the estimates of Teff and log g, with reduced χ2 of the order of unity. Given that the atmospheric parameters we measured using the two grids of models agreed to better than 2σ in all cases, we adopted the average values. To illustrate the quality of the data, we display the normalized Balmer lines of two observed spectra, VPHAS J0804−2809 and VPHAS J1546−5233, and the corresponding best-fitting model spectra, in Fig. 4. In some cases, the fitting procedure led to two possible solutions due to a degeneracy between Teff and log g, namely the hot and cool solutions. We compared the results with the observed photometry in order to choose the most likely correct solution.
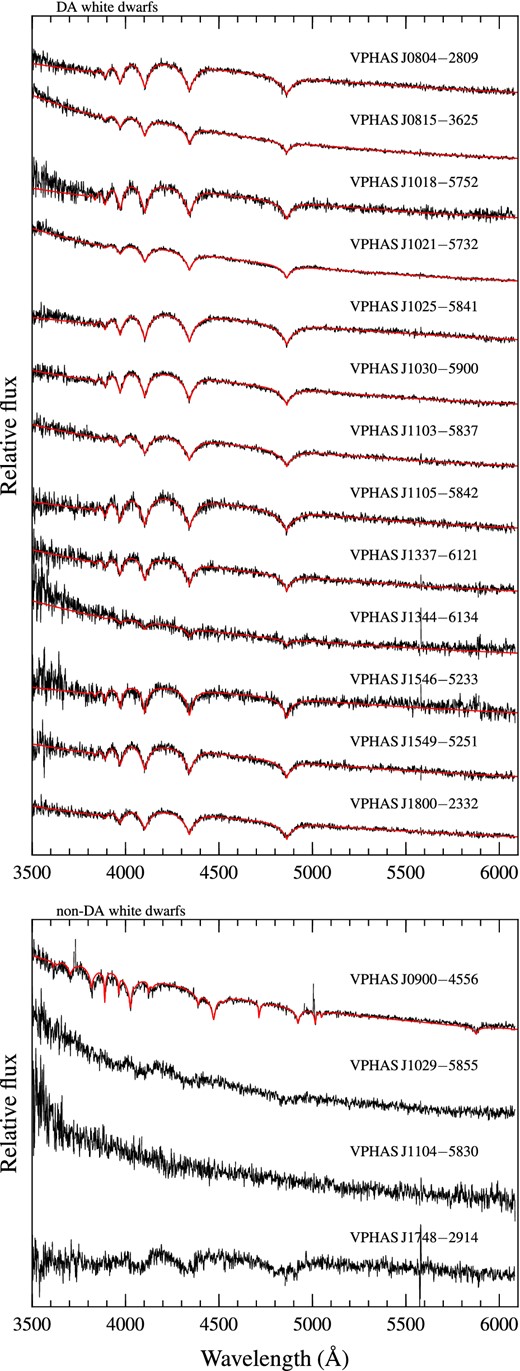
Top panel: in black, the observed spectra of DA white dwarfs (top panel) and, in red, the best-fitting models, normalized to the observed spectra. Bottom panel: as before, from top to bottom, the DB, DAH, DC, and DAH white dwarfs. The mismatch between some observed and model spectra at ≈3600 Å is likely due to calibration issues.
For some of the noisiest spectra, with S/N ≤ 20, the line profiles appear distorted and could arise from the superposition of two DA white dwarfs. Due to the quality of the data and the wavelength coverage of our spectra, we cannot rule out the presence of unseen, close white dwarf companions, suggested to be ≈25 per cent of the field population (Nelemans et al. 2001), or more in old open clusters (Portegies Zwart et al. 2001). Existing near-infrared data seem to exclude the presence of low-mass late-type companions (see next section for further discussion).
To determine the atmospheric parameters of VPHAS J0900−4556, we used fitsb2 with Koester (2010) DB model spectra, fitting the following He i lines: 4921.9, 4713.1, 4471.5, 4026.2, and 3888.7 Å. The DB grid of spectra spans Teff = 10 000–40 000 K and log g = 7–9. For the two DAH and the DC white dwarfs, we estimated photometric Teff from the available VPHAS+ DR2 magnitudes, with DA and DB model spectra, respectively. This precluded a determination of log g and interstellar reddening. To assess the Teff uncertainty, we considered log g = 8.00 ± 0.25 dex, corresponding to a white dwarf mass of 0.60 ± 0.15 M⊙. Given the high Teff we estimated for VPHAS J1104−5830, which is anomalous for typical DC white dwarfs, we suspect this star to be also magnetic. In presence of strong magnetic fields, the energy levels of the dominant atmospheric elements are characterized by large shifts, which would make the low S/N spectrum of VPHAS J1546−5233 look featureless.
We list the atmospheric parameters of all the observed white dwarfs in Table 4 and we overplot the corresponding model spectra on the VLT data in Fig. 3.
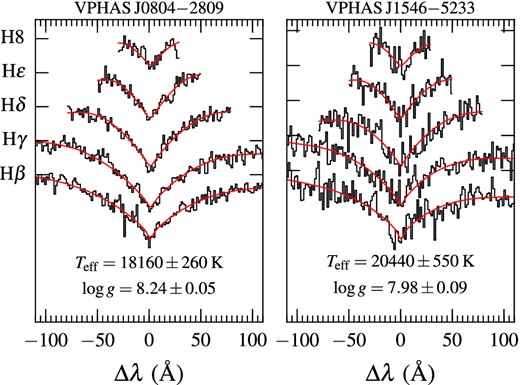
Normalized Balmer-line profiles for two spectra in our sample (black), and best-fitting model spectra (red).
Physical parameters of the 17 white dwarfs confirmed via spectroscopic follow-up. The S/N is measured at H β. δτWD is the fractional difference in cooling ages, between Montreal and BaSTI models (see Section 4.1 for details).
| Name . | Cluster . | S/N . | Type . | Teff . | log g . | Mg . | E(B − V) . | d . | MWD . | τWD . | δτWD . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | . | (K) . | (cgs) . | (mag) . | (mag) . | (pc) . | (M⊙) . | (Gyr) . | . |
| VPHAS J0804−2809 | NGC 2527 | 20 | DA | 18 160 ± 260 | 8.24 ± 0.05 | |$11.27_{-0.07}^{+0.09}$| | 0.05 ± 0.07 | 630 ± 77 | |$0.77_{-0.03}^{+0.03}$| | |$0.185_{-0.016}^{+0.016}$| | 0.12 |
| VPHAS J0815−3625 | BH 23 | 28 | DA | 31 870 ± 210 | 8.04 ± 0.04 | |$9.79_{-0.06}^{+0.06}$| | 0.12 ± 0.03 | 734 ± 40 | |$0.68_{-0.02}^{+0.02}$| | |$0.011_{-0.002}^{+0.002}$| | 0.10 |
| VPHAS J0900−4556 | Platais 9 | 23 | DB | 19 040 ± 450 | 8.13 ± 0.10 | |$10.94_{-0.14}^{+0.14}$| | 0.01 ± 0.05 | 615 ± 59 | |$0.70_{-0.06}^{+0.06}$| | |$0.130_{-0.029}^{+0.029}$| | 0.11 |
| VPHAS J1018−5752 | ASCC 59 | 10 | DA | 17 430 ± 390 | 7.79 ± 0.08 | |$10.66_{-0.12}^{+0.13}$| | 0.00 ± 0.04 | 1066 ± 86 | |$0.52_{-0.04}^{+0.04}$| | |$0.095_{-0.010}^{+0.010}$| | 0.00 |
| VPHAS J1021−5732 | ASCC 59 | 27 | DA | 30 110 ± 160 | 8.56 ± 0.03 | |$10.79_{-0.05}^{+0.05}$| | 0.28 ± 0.04 | 382 ± 27 | |$0.98_{-0.02}^{+0.02}$| | |$0.059_{-0.006}^{+0.006}$| | 0.10 |
| VPHAS J1025−5841 | Loden 143 | 21 | DA | 13 280 ± 240 | 8.44 ± 0.04 | |$12.23_{-0.07}^{+0.07}$| | 0.12 ± 0.04 | 263 ± 19 | |$0.89_{-0.03}^{+0.03}$| | |$0.580_{-0.028}^{+0.028}$| | 0.04 |
| VPHAS J1029−5855 | Loden 143 | 14 | DAH | a35 000 ± 5000 | 8.00 ± 0.25 | |$9.52_{-0.46}^{+0.46}$| | 1326 ± 214 | |$0.66_{-0.11}^{+0.15}$| | |$0.006_{-0.002}^{+0.009}$| | −0.12 | |
| VPHAS J1030−5900 | Loden 143 | 22 | DA | 19 780 ± 250 | 8.04 ± 0.04 | |$10.81_{-0.06}^{+0.06}$| | 0.07 ± 0.04 | 565 ± 41 | |$0.65_{-0.02}^{+0.02}$| | |$0.084_{-0.011}^{+0.011}$| | 0.00 |
| VPHAS J1103−5837 | NGC 3532 | 19 | DA | 23 910 ± 360 | 8.87 ± 0.05 | |$11.89_{-0.11}^{+0.11}$| | 0.13 ± 0.07 | 433 ± 54 | |$1.13_{-0.03}^{+0.03}$| | |$^{b}0.270_{-0.025}^{+0.034}$| | |
| VPHAS J1104−5830 | NGC 3532 | 8 | DC | a29 500 ± 300 | 8.00 ± 0.25 | |$9.90_{-0.44}^{+0.44}$| | 1174 ± 174 | |$0.64_{-0.11}^{+0.15}$| | |$0.011_{-0.003}^{+0.021}$| | −0.19 | |
| VPHAS J1105−5842 | NGC 3532 | 15 | DA | 14 230 ± 1160 | 8.16 ± 0.10 | |$11.64_{-0.16}^{+0.17}$| | 0.06 ± 0.04 | 363 ± 36 | |$0.71_{-0.06}^{+0.06}$| | |$0.323_{-0.066}^{+0.086}$| | 0.11 |
| VPHAS J1337−6121 | Platais 10 | 14 | DA | 24 100 ± 530 | 8.01 ± 0.08 | |$10.37_{-0.13}^{+0.13}$| | 0.20 ± 0.05 | 709 ± 67 | |$0.64_{-0.04}^{+0.05}$| | |$0.032_{-0.005}^{+0.013}$| | 0.00 |
| VPHAS J1344−6134 | Platais 10 | 10 | DA | 49 670 ± 2520 | 7.92 ± 0.19 | |$8.87_{-0.37}^{+0.37}$| | 0.39 ± 0.06 | 1202 ± 169 | |$0.66_{-0.08}^{+0.09}$| | 0.002 | −0.81 |
| VPHAS J1546−5233 | Johansson 1 | 12 | DA | 20 440 ± 550 | 7.98 ± 0.09 | |$10.65_{-0.15}^{+0.15}$| | 0.12 ± 0.11 | 1052 ± 204 | |$0.62_{-0.04}^{+0.05}$| | |$0.063_{-0.006}^{+0.019}$| | −0.01 |
| VPHAS J1549−5251 | ASCC 83 | 14 | DA | 20 320 ± 390 | 8.05 ± 0.07 | |$10.77_{-0.11}^{+0.11}$| | 0.07 ± 0.10 | 951 ± 165 | |$0.66_{-0.04}^{+0.04}$| | |$0.078_{-0.014}^{+0.017}$| | 0.01 |
| VPHAS J1748−2914 | Ruprecht 131 | 12 | DAH | a8750 ± 1200 | 8.00 ± 0.25 | |$12.84_{-0.52}^{+0.61}$| | 471 ± 102 | |$0.60_{-0.12}^{+0.16}$| | |$0.854_{-0.243}^{+0.672}$| | 0.05 | |
| VPHAS J1800−2332 | Ruprecht 139 | 21 | DA | 24 030 ± 360 | 8.60 ± 0.05 | |$11.36_{-0.09}^{+0.09}$| | 0.24 ± 0.02 | 165 ± 7 | |$0.99_{-0.03}^{+0.03}$| | |$0.153_{-0.019}^{+0.019}$| | 0.21 |
| Name . | Cluster . | S/N . | Type . | Teff . | log g . | Mg . | E(B − V) . | d . | MWD . | τWD . | δτWD . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | . | (K) . | (cgs) . | (mag) . | (mag) . | (pc) . | (M⊙) . | (Gyr) . | . |
| VPHAS J0804−2809 | NGC 2527 | 20 | DA | 18 160 ± 260 | 8.24 ± 0.05 | |$11.27_{-0.07}^{+0.09}$| | 0.05 ± 0.07 | 630 ± 77 | |$0.77_{-0.03}^{+0.03}$| | |$0.185_{-0.016}^{+0.016}$| | 0.12 |
| VPHAS J0815−3625 | BH 23 | 28 | DA | 31 870 ± 210 | 8.04 ± 0.04 | |$9.79_{-0.06}^{+0.06}$| | 0.12 ± 0.03 | 734 ± 40 | |$0.68_{-0.02}^{+0.02}$| | |$0.011_{-0.002}^{+0.002}$| | 0.10 |
| VPHAS J0900−4556 | Platais 9 | 23 | DB | 19 040 ± 450 | 8.13 ± 0.10 | |$10.94_{-0.14}^{+0.14}$| | 0.01 ± 0.05 | 615 ± 59 | |$0.70_{-0.06}^{+0.06}$| | |$0.130_{-0.029}^{+0.029}$| | 0.11 |
| VPHAS J1018−5752 | ASCC 59 | 10 | DA | 17 430 ± 390 | 7.79 ± 0.08 | |$10.66_{-0.12}^{+0.13}$| | 0.00 ± 0.04 | 1066 ± 86 | |$0.52_{-0.04}^{+0.04}$| | |$0.095_{-0.010}^{+0.010}$| | 0.00 |
| VPHAS J1021−5732 | ASCC 59 | 27 | DA | 30 110 ± 160 | 8.56 ± 0.03 | |$10.79_{-0.05}^{+0.05}$| | 0.28 ± 0.04 | 382 ± 27 | |$0.98_{-0.02}^{+0.02}$| | |$0.059_{-0.006}^{+0.006}$| | 0.10 |
| VPHAS J1025−5841 | Loden 143 | 21 | DA | 13 280 ± 240 | 8.44 ± 0.04 | |$12.23_{-0.07}^{+0.07}$| | 0.12 ± 0.04 | 263 ± 19 | |$0.89_{-0.03}^{+0.03}$| | |$0.580_{-0.028}^{+0.028}$| | 0.04 |
| VPHAS J1029−5855 | Loden 143 | 14 | DAH | a35 000 ± 5000 | 8.00 ± 0.25 | |$9.52_{-0.46}^{+0.46}$| | 1326 ± 214 | |$0.66_{-0.11}^{+0.15}$| | |$0.006_{-0.002}^{+0.009}$| | −0.12 | |
| VPHAS J1030−5900 | Loden 143 | 22 | DA | 19 780 ± 250 | 8.04 ± 0.04 | |$10.81_{-0.06}^{+0.06}$| | 0.07 ± 0.04 | 565 ± 41 | |$0.65_{-0.02}^{+0.02}$| | |$0.084_{-0.011}^{+0.011}$| | 0.00 |
| VPHAS J1103−5837 | NGC 3532 | 19 | DA | 23 910 ± 360 | 8.87 ± 0.05 | |$11.89_{-0.11}^{+0.11}$| | 0.13 ± 0.07 | 433 ± 54 | |$1.13_{-0.03}^{+0.03}$| | |$^{b}0.270_{-0.025}^{+0.034}$| | |
| VPHAS J1104−5830 | NGC 3532 | 8 | DC | a29 500 ± 300 | 8.00 ± 0.25 | |$9.90_{-0.44}^{+0.44}$| | 1174 ± 174 | |$0.64_{-0.11}^{+0.15}$| | |$0.011_{-0.003}^{+0.021}$| | −0.19 | |
| VPHAS J1105−5842 | NGC 3532 | 15 | DA | 14 230 ± 1160 | 8.16 ± 0.10 | |$11.64_{-0.16}^{+0.17}$| | 0.06 ± 0.04 | 363 ± 36 | |$0.71_{-0.06}^{+0.06}$| | |$0.323_{-0.066}^{+0.086}$| | 0.11 |
| VPHAS J1337−6121 | Platais 10 | 14 | DA | 24 100 ± 530 | 8.01 ± 0.08 | |$10.37_{-0.13}^{+0.13}$| | 0.20 ± 0.05 | 709 ± 67 | |$0.64_{-0.04}^{+0.05}$| | |$0.032_{-0.005}^{+0.013}$| | 0.00 |
| VPHAS J1344−6134 | Platais 10 | 10 | DA | 49 670 ± 2520 | 7.92 ± 0.19 | |$8.87_{-0.37}^{+0.37}$| | 0.39 ± 0.06 | 1202 ± 169 | |$0.66_{-0.08}^{+0.09}$| | 0.002 | −0.81 |
| VPHAS J1546−5233 | Johansson 1 | 12 | DA | 20 440 ± 550 | 7.98 ± 0.09 | |$10.65_{-0.15}^{+0.15}$| | 0.12 ± 0.11 | 1052 ± 204 | |$0.62_{-0.04}^{+0.05}$| | |$0.063_{-0.006}^{+0.019}$| | −0.01 |
| VPHAS J1549−5251 | ASCC 83 | 14 | DA | 20 320 ± 390 | 8.05 ± 0.07 | |$10.77_{-0.11}^{+0.11}$| | 0.07 ± 0.10 | 951 ± 165 | |$0.66_{-0.04}^{+0.04}$| | |$0.078_{-0.014}^{+0.017}$| | 0.01 |
| VPHAS J1748−2914 | Ruprecht 131 | 12 | DAH | a8750 ± 1200 | 8.00 ± 0.25 | |$12.84_{-0.52}^{+0.61}$| | 471 ± 102 | |$0.60_{-0.12}^{+0.16}$| | |$0.854_{-0.243}^{+0.672}$| | 0.05 | |
| VPHAS J1800−2332 | Ruprecht 139 | 21 | DA | 24 030 ± 360 | 8.60 ± 0.05 | |$11.36_{-0.09}^{+0.09}$| | 0.24 ± 0.02 | 165 ± 7 | |$0.99_{-0.03}^{+0.03}$| | |$0.153_{-0.019}^{+0.019}$| | 0.21 |
Notes. aEffective temperatures of DAH and DC white dwarfs are estimated from photometric fitting; no E(B−V) estimates.
bCooling age determined from Althaus et al. (2007) oxygen–neon core models.
Physical parameters of the 17 white dwarfs confirmed via spectroscopic follow-up. The S/N is measured at H β. δτWD is the fractional difference in cooling ages, between Montreal and BaSTI models (see Section 4.1 for details).
| Name . | Cluster . | S/N . | Type . | Teff . | log g . | Mg . | E(B − V) . | d . | MWD . | τWD . | δτWD . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | . | (K) . | (cgs) . | (mag) . | (mag) . | (pc) . | (M⊙) . | (Gyr) . | . |
| VPHAS J0804−2809 | NGC 2527 | 20 | DA | 18 160 ± 260 | 8.24 ± 0.05 | |$11.27_{-0.07}^{+0.09}$| | 0.05 ± 0.07 | 630 ± 77 | |$0.77_{-0.03}^{+0.03}$| | |$0.185_{-0.016}^{+0.016}$| | 0.12 |
| VPHAS J0815−3625 | BH 23 | 28 | DA | 31 870 ± 210 | 8.04 ± 0.04 | |$9.79_{-0.06}^{+0.06}$| | 0.12 ± 0.03 | 734 ± 40 | |$0.68_{-0.02}^{+0.02}$| | |$0.011_{-0.002}^{+0.002}$| | 0.10 |
| VPHAS J0900−4556 | Platais 9 | 23 | DB | 19 040 ± 450 | 8.13 ± 0.10 | |$10.94_{-0.14}^{+0.14}$| | 0.01 ± 0.05 | 615 ± 59 | |$0.70_{-0.06}^{+0.06}$| | |$0.130_{-0.029}^{+0.029}$| | 0.11 |
| VPHAS J1018−5752 | ASCC 59 | 10 | DA | 17 430 ± 390 | 7.79 ± 0.08 | |$10.66_{-0.12}^{+0.13}$| | 0.00 ± 0.04 | 1066 ± 86 | |$0.52_{-0.04}^{+0.04}$| | |$0.095_{-0.010}^{+0.010}$| | 0.00 |
| VPHAS J1021−5732 | ASCC 59 | 27 | DA | 30 110 ± 160 | 8.56 ± 0.03 | |$10.79_{-0.05}^{+0.05}$| | 0.28 ± 0.04 | 382 ± 27 | |$0.98_{-0.02}^{+0.02}$| | |$0.059_{-0.006}^{+0.006}$| | 0.10 |
| VPHAS J1025−5841 | Loden 143 | 21 | DA | 13 280 ± 240 | 8.44 ± 0.04 | |$12.23_{-0.07}^{+0.07}$| | 0.12 ± 0.04 | 263 ± 19 | |$0.89_{-0.03}^{+0.03}$| | |$0.580_{-0.028}^{+0.028}$| | 0.04 |
| VPHAS J1029−5855 | Loden 143 | 14 | DAH | a35 000 ± 5000 | 8.00 ± 0.25 | |$9.52_{-0.46}^{+0.46}$| | 1326 ± 214 | |$0.66_{-0.11}^{+0.15}$| | |$0.006_{-0.002}^{+0.009}$| | −0.12 | |
| VPHAS J1030−5900 | Loden 143 | 22 | DA | 19 780 ± 250 | 8.04 ± 0.04 | |$10.81_{-0.06}^{+0.06}$| | 0.07 ± 0.04 | 565 ± 41 | |$0.65_{-0.02}^{+0.02}$| | |$0.084_{-0.011}^{+0.011}$| | 0.00 |
| VPHAS J1103−5837 | NGC 3532 | 19 | DA | 23 910 ± 360 | 8.87 ± 0.05 | |$11.89_{-0.11}^{+0.11}$| | 0.13 ± 0.07 | 433 ± 54 | |$1.13_{-0.03}^{+0.03}$| | |$^{b}0.270_{-0.025}^{+0.034}$| | |
| VPHAS J1104−5830 | NGC 3532 | 8 | DC | a29 500 ± 300 | 8.00 ± 0.25 | |$9.90_{-0.44}^{+0.44}$| | 1174 ± 174 | |$0.64_{-0.11}^{+0.15}$| | |$0.011_{-0.003}^{+0.021}$| | −0.19 | |
| VPHAS J1105−5842 | NGC 3532 | 15 | DA | 14 230 ± 1160 | 8.16 ± 0.10 | |$11.64_{-0.16}^{+0.17}$| | 0.06 ± 0.04 | 363 ± 36 | |$0.71_{-0.06}^{+0.06}$| | |$0.323_{-0.066}^{+0.086}$| | 0.11 |
| VPHAS J1337−6121 | Platais 10 | 14 | DA | 24 100 ± 530 | 8.01 ± 0.08 | |$10.37_{-0.13}^{+0.13}$| | 0.20 ± 0.05 | 709 ± 67 | |$0.64_{-0.04}^{+0.05}$| | |$0.032_{-0.005}^{+0.013}$| | 0.00 |
| VPHAS J1344−6134 | Platais 10 | 10 | DA | 49 670 ± 2520 | 7.92 ± 0.19 | |$8.87_{-0.37}^{+0.37}$| | 0.39 ± 0.06 | 1202 ± 169 | |$0.66_{-0.08}^{+0.09}$| | 0.002 | −0.81 |
| VPHAS J1546−5233 | Johansson 1 | 12 | DA | 20 440 ± 550 | 7.98 ± 0.09 | |$10.65_{-0.15}^{+0.15}$| | 0.12 ± 0.11 | 1052 ± 204 | |$0.62_{-0.04}^{+0.05}$| | |$0.063_{-0.006}^{+0.019}$| | −0.01 |
| VPHAS J1549−5251 | ASCC 83 | 14 | DA | 20 320 ± 390 | 8.05 ± 0.07 | |$10.77_{-0.11}^{+0.11}$| | 0.07 ± 0.10 | 951 ± 165 | |$0.66_{-0.04}^{+0.04}$| | |$0.078_{-0.014}^{+0.017}$| | 0.01 |
| VPHAS J1748−2914 | Ruprecht 131 | 12 | DAH | a8750 ± 1200 | 8.00 ± 0.25 | |$12.84_{-0.52}^{+0.61}$| | 471 ± 102 | |$0.60_{-0.12}^{+0.16}$| | |$0.854_{-0.243}^{+0.672}$| | 0.05 | |
| VPHAS J1800−2332 | Ruprecht 139 | 21 | DA | 24 030 ± 360 | 8.60 ± 0.05 | |$11.36_{-0.09}^{+0.09}$| | 0.24 ± 0.02 | 165 ± 7 | |$0.99_{-0.03}^{+0.03}$| | |$0.153_{-0.019}^{+0.019}$| | 0.21 |
| Name . | Cluster . | S/N . | Type . | Teff . | log g . | Mg . | E(B − V) . | d . | MWD . | τWD . | δτWD . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | . | (K) . | (cgs) . | (mag) . | (mag) . | (pc) . | (M⊙) . | (Gyr) . | . |
| VPHAS J0804−2809 | NGC 2527 | 20 | DA | 18 160 ± 260 | 8.24 ± 0.05 | |$11.27_{-0.07}^{+0.09}$| | 0.05 ± 0.07 | 630 ± 77 | |$0.77_{-0.03}^{+0.03}$| | |$0.185_{-0.016}^{+0.016}$| | 0.12 |
| VPHAS J0815−3625 | BH 23 | 28 | DA | 31 870 ± 210 | 8.04 ± 0.04 | |$9.79_{-0.06}^{+0.06}$| | 0.12 ± 0.03 | 734 ± 40 | |$0.68_{-0.02}^{+0.02}$| | |$0.011_{-0.002}^{+0.002}$| | 0.10 |
| VPHAS J0900−4556 | Platais 9 | 23 | DB | 19 040 ± 450 | 8.13 ± 0.10 | |$10.94_{-0.14}^{+0.14}$| | 0.01 ± 0.05 | 615 ± 59 | |$0.70_{-0.06}^{+0.06}$| | |$0.130_{-0.029}^{+0.029}$| | 0.11 |
| VPHAS J1018−5752 | ASCC 59 | 10 | DA | 17 430 ± 390 | 7.79 ± 0.08 | |$10.66_{-0.12}^{+0.13}$| | 0.00 ± 0.04 | 1066 ± 86 | |$0.52_{-0.04}^{+0.04}$| | |$0.095_{-0.010}^{+0.010}$| | 0.00 |
| VPHAS J1021−5732 | ASCC 59 | 27 | DA | 30 110 ± 160 | 8.56 ± 0.03 | |$10.79_{-0.05}^{+0.05}$| | 0.28 ± 0.04 | 382 ± 27 | |$0.98_{-0.02}^{+0.02}$| | |$0.059_{-0.006}^{+0.006}$| | 0.10 |
| VPHAS J1025−5841 | Loden 143 | 21 | DA | 13 280 ± 240 | 8.44 ± 0.04 | |$12.23_{-0.07}^{+0.07}$| | 0.12 ± 0.04 | 263 ± 19 | |$0.89_{-0.03}^{+0.03}$| | |$0.580_{-0.028}^{+0.028}$| | 0.04 |
| VPHAS J1029−5855 | Loden 143 | 14 | DAH | a35 000 ± 5000 | 8.00 ± 0.25 | |$9.52_{-0.46}^{+0.46}$| | 1326 ± 214 | |$0.66_{-0.11}^{+0.15}$| | |$0.006_{-0.002}^{+0.009}$| | −0.12 | |
| VPHAS J1030−5900 | Loden 143 | 22 | DA | 19 780 ± 250 | 8.04 ± 0.04 | |$10.81_{-0.06}^{+0.06}$| | 0.07 ± 0.04 | 565 ± 41 | |$0.65_{-0.02}^{+0.02}$| | |$0.084_{-0.011}^{+0.011}$| | 0.00 |
| VPHAS J1103−5837 | NGC 3532 | 19 | DA | 23 910 ± 360 | 8.87 ± 0.05 | |$11.89_{-0.11}^{+0.11}$| | 0.13 ± 0.07 | 433 ± 54 | |$1.13_{-0.03}^{+0.03}$| | |$^{b}0.270_{-0.025}^{+0.034}$| | |
| VPHAS J1104−5830 | NGC 3532 | 8 | DC | a29 500 ± 300 | 8.00 ± 0.25 | |$9.90_{-0.44}^{+0.44}$| | 1174 ± 174 | |$0.64_{-0.11}^{+0.15}$| | |$0.011_{-0.003}^{+0.021}$| | −0.19 | |
| VPHAS J1105−5842 | NGC 3532 | 15 | DA | 14 230 ± 1160 | 8.16 ± 0.10 | |$11.64_{-0.16}^{+0.17}$| | 0.06 ± 0.04 | 363 ± 36 | |$0.71_{-0.06}^{+0.06}$| | |$0.323_{-0.066}^{+0.086}$| | 0.11 |
| VPHAS J1337−6121 | Platais 10 | 14 | DA | 24 100 ± 530 | 8.01 ± 0.08 | |$10.37_{-0.13}^{+0.13}$| | 0.20 ± 0.05 | 709 ± 67 | |$0.64_{-0.04}^{+0.05}$| | |$0.032_{-0.005}^{+0.013}$| | 0.00 |
| VPHAS J1344−6134 | Platais 10 | 10 | DA | 49 670 ± 2520 | 7.92 ± 0.19 | |$8.87_{-0.37}^{+0.37}$| | 0.39 ± 0.06 | 1202 ± 169 | |$0.66_{-0.08}^{+0.09}$| | 0.002 | −0.81 |
| VPHAS J1546−5233 | Johansson 1 | 12 | DA | 20 440 ± 550 | 7.98 ± 0.09 | |$10.65_{-0.15}^{+0.15}$| | 0.12 ± 0.11 | 1052 ± 204 | |$0.62_{-0.04}^{+0.05}$| | |$0.063_{-0.006}^{+0.019}$| | −0.01 |
| VPHAS J1549−5251 | ASCC 83 | 14 | DA | 20 320 ± 390 | 8.05 ± 0.07 | |$10.77_{-0.11}^{+0.11}$| | 0.07 ± 0.10 | 951 ± 165 | |$0.66_{-0.04}^{+0.04}$| | |$0.078_{-0.014}^{+0.017}$| | 0.01 |
| VPHAS J1748−2914 | Ruprecht 131 | 12 | DAH | a8750 ± 1200 | 8.00 ± 0.25 | |$12.84_{-0.52}^{+0.61}$| | 471 ± 102 | |$0.60_{-0.12}^{+0.16}$| | |$0.854_{-0.243}^{+0.672}$| | 0.05 | |
| VPHAS J1800−2332 | Ruprecht 139 | 21 | DA | 24 030 ± 360 | 8.60 ± 0.05 | |$11.36_{-0.09}^{+0.09}$| | 0.24 ± 0.02 | 165 ± 7 | |$0.99_{-0.03}^{+0.03}$| | |$0.153_{-0.019}^{+0.019}$| | 0.21 |
Notes. aEffective temperatures of DAH and DC white dwarfs are estimated from photometric fitting; no E(B−V) estimates.
bCooling age determined from Althaus et al. (2007) oxygen–neon core models.
3.1 Interstellar reddening
In Fig. 5 , we display the model spectra (derived either from spectroscopic or photometric fit) of the 17 white dwarfs along with the observed photometry, while the measured reddenings are given in Table 4. The agreement between photometry and model atmospheres is overall good, although some disagreement is seen in the u band, which is calibrated following the prescriptions given by Drew et al. (2014). The calibration may be problematic in some reddened field, due to the sparse appearance of the colour–colour diagram. Thus, the u magnitudes carry larger systematic uncertainties, because their calibration depends on that of g and r magnitudes, and it is also more subject to variations of atmospheric transparency.
The i-band fluxes of a few objects appear to be slightly above the predictions given by the model atmospheres. Thus, we checked if the observed white dwarfs display excess in the near-infrared, i.e. 2MASS, WISE (Wright et al. 2010), and VVV, signalling the presence of low-mass late-type companions. We note a bright infrared source at 1.25 arcsec from VPHAS J1800−2332 (Fig. 6). The flux from this object is not likely to affect the i magnitudes of the white dwarf, therefore we suspect that in this and other cases the calibration might suffer with systematically larger offsets, arising from the APASS-based calibration.
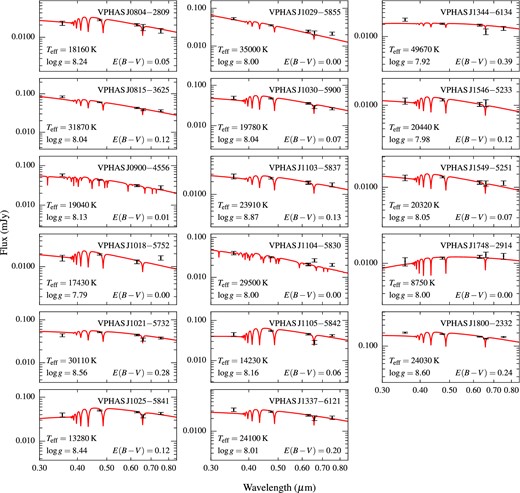
Observed fluxes (black error bars) and best-fitting models to the spectral lines (red). Model parameters and interstellar reddening are indicated in each panel. The model spectra of DA white dwarfs are reddened to match the (g − r) colour. DB models are plotted for VPHAS J0900−4556, and the DC white dwarf, VPHAS J1104−5830, whose low S/N spectrum does not reveal any noticeable spectral line. DA models are also plotted for the two DAH white dwarfs, VPHAS J1029−5855 and VPHAS J1748−2914, whose Teff are estimated from photometric fit, keeping log g = 8 and E(B − V) = 0.

Image cut-outs of VPHAS J1800−2332. The infrared flux in the J band is likely associated with another star at 1.25 arcsec from VPHAS J1800−2332, which is just visible in i-band frame, but it is already bright in the z band.
For VPHAS J1103−5837 and VPHAS J1105−5842, in NGC 3532, we also estimated the interstellar reddening from their (B − V) colours (Clem et al. 2011, Table 3), obtaining 0.07 ± 0.04 and 0.08 ± 0.02 mag, respectively, compatible with those we measure from VPHAS+ data.
4 MASSES, COOLING AGES, AND DISTANCES
To establish the cluster membership of white dwarfs, we need to estimate their distances and verify that the cooling ages are compatible with the cluster ages.
We determined the white dwarf spectroscopic parallaxes, using the appropriate intrinsic magnitudes from Appendix A, the observed magnitudes, and the interstellar extinction as Ag = 3.68 × E(B − V). The absolute magnitudes and distances are given in Table 4. Then, we estimated white dwarf masses and cooling ages from the cooling tracks of the Montreal group (Fontaine et al. 2001, see Fig. 7 and Table 4). For DA white dwarfs, we used the cooling models with thick hydrogen atmospheres (10−4 M⊙) and carbon–oxygen cores (Bergeron, Leggett & Ruiz 2001). Above 30 000 K, the carbon-core cooling models by Wood (1995) were used instead. For DB white dwarfs, we used the cooling models with a thinner hydrogen layer of 10−10 M⊙.
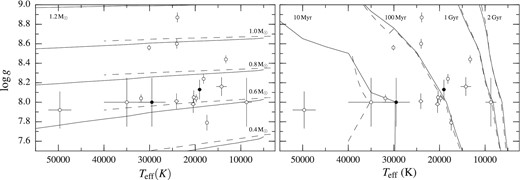
Mass (left-hand panel) and ages (right-hand panel) are estimated via interpolation of Teff and log g on to the white dwarf cooling tracks of Fontaine et al. (2001). DA tracks are plotted as solid lines, while dashed curves represent DB tracks. The filled dots are the DB and DC white dwarfs, i.e. VPHAS J0900−4556 and VPHAS J1104−5830.
Salaris et al. (2009) assessed the effect of systematic differences introduced by different treatments of neutrino cooling, core composition, and envelope thickness, for their cooling models. Referring to their table 4, we found that an increased neutrino cooling rate would produce a difference of 7–34 per cent in the white dwarf cooling ages of our sample, depending on Teff and log g. Smaller uncertainties are derived for different conductive opacities, core composition, and hydrogen-layer thickness, of the order of 2–6 per cent. We took these uncertainties into account when determining the progenitor lifetimes and masses, in the following section. In order to assess the effect of different cooling tracks on the age estimates, we also computed white dwarf cooling ages using the BaSTI models (Salaris et al. 2010), which use different formulations with respect to those of Fontaine et al. (2001) for the equation of state and opacities. In Table 4, we list the fractional difference in cooling ages, expressed as δτWD = [τWD(Montreal) − τWD(BaSTI)]/τWD(Montreal). The effect is comparable to the other uncertainties, and it is mostly in the range of 0.10 dex.
One white dwarf, VPHAS J1103−5837, could have an oxygen–neon core (M > 1.06 M⊙; García-Berro et al. 1997). Thus, we used the Althaus et al. (2007) cooling models for oxygen–neon cores, which suggest a cooling age ≈10 per cent shorter than that of a carbon–oxygen core white dwarf with the same mass.
4.1 Cluster membership
Comparing the white dwarf distances (Table 4) with the cluster distances (Table 1) in Fig. 8, we find that five of the 17 white dwarfs overlap within 1σ with the putative clusters (Table 5). The five white dwarfs have cooling ages younger than the cluster ages, which is also a necessary requirement for cluster membership.
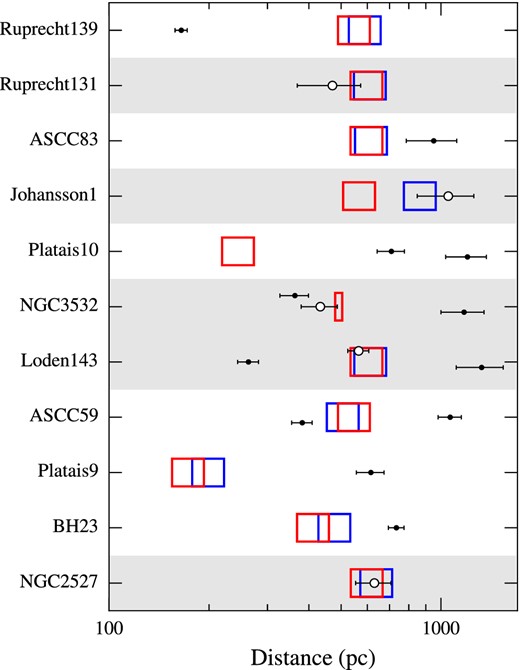
Assessment of cluster membership for the 17 white dwarfs. Red boxes indicate cluster distances of Dias et al. (2002), blue boxes those of Kharchenko et al. (2013), and points with error bars the white dwarf distances. The box sizes correspond to an uncertainty of 11 per cent of the cluster distance (Kharchenko et al. 2013). The candidate cluster members are represented by white circles with error bars, and the corresponding rows are highlighted by a grey shaded area.
Physical parameters of the white dwarf progenitors for the five likely cluster members, determined via interpolation of the progenitor ages with the BaSTI and Ekström et al. (2012) isochrones for rotating stars. The lower limits on progenitor ages and the upper limits on progenitor masses are represented by −− and ++ symbols, respectively.
| WD . | Cluster . | WWD . | tprog . | Mprog (BaSTI) . | Mprog (rot.) . |
|---|---|---|---|---|---|
| . | . | (M⊙) . | (Gyr) . | (M⊙) . | (M⊙) . |
| VPHAS J0804−2809 | NGC 2527 | |$0.77_{-0.03}^{+0.03}$| | |$0.441_{+0.188}^{+0.188}$| | |$3.06_{-0.35}^{+0.72}$| | |$3.13_{-0.30}^{+0.70}$| |
| VPHAS J1030−5900 | Loden 143 | |$0.65_{-0.02}^{+0.02}$| | |$0.200_{+0.023}^{+0.023}$| | |$4.02_{-0.12}^{+0.21}$| | |$4.22_{-0.18}^{+0.21}$| |
| VPHAS J1103−5837 | NGC 3532 | |$1.13_{-0.03}^{+0.03}$| | |$0.030_{\text{-}}^{+0.123}$| | |$8.80_{-4.31}^{++}$| | |$9.78_{-5.08}^{++}$| |
| VPHAS J1546−5233 | Johansson 1 | |$0.62_{-0.05}^{+0.05}$| | |$0.437_{+0.196}^{+0.195}$| | |$3.07_{-0.36}^{+0.75}$| | |$3.14_{-0.31}^{+0.78}$| |
| VPHAS J1748−2914 | Ruprecht 131 | |$0.60_{-0.12}^{+0.16}$| | |$0.626_{\text{-}}^{+0.660}$| | |$2.72_{-0.64}^{++}$| | |$2.84_{-0.79}^{++}$| |
| WD . | Cluster . | WWD . | tprog . | Mprog (BaSTI) . | Mprog (rot.) . |
|---|---|---|---|---|---|
| . | . | (M⊙) . | (Gyr) . | (M⊙) . | (M⊙) . |
| VPHAS J0804−2809 | NGC 2527 | |$0.77_{-0.03}^{+0.03}$| | |$0.441_{+0.188}^{+0.188}$| | |$3.06_{-0.35}^{+0.72}$| | |$3.13_{-0.30}^{+0.70}$| |
| VPHAS J1030−5900 | Loden 143 | |$0.65_{-0.02}^{+0.02}$| | |$0.200_{+0.023}^{+0.023}$| | |$4.02_{-0.12}^{+0.21}$| | |$4.22_{-0.18}^{+0.21}$| |
| VPHAS J1103−5837 | NGC 3532 | |$1.13_{-0.03}^{+0.03}$| | |$0.030_{\text{-}}^{+0.123}$| | |$8.80_{-4.31}^{++}$| | |$9.78_{-5.08}^{++}$| |
| VPHAS J1546−5233 | Johansson 1 | |$0.62_{-0.05}^{+0.05}$| | |$0.437_{+0.196}^{+0.195}$| | |$3.07_{-0.36}^{+0.75}$| | |$3.14_{-0.31}^{+0.78}$| |
| VPHAS J1748−2914 | Ruprecht 131 | |$0.60_{-0.12}^{+0.16}$| | |$0.626_{\text{-}}^{+0.660}$| | |$2.72_{-0.64}^{++}$| | |$2.84_{-0.79}^{++}$| |
Physical parameters of the white dwarf progenitors for the five likely cluster members, determined via interpolation of the progenitor ages with the BaSTI and Ekström et al. (2012) isochrones for rotating stars. The lower limits on progenitor ages and the upper limits on progenitor masses are represented by −− and ++ symbols, respectively.
| WD . | Cluster . | WWD . | tprog . | Mprog (BaSTI) . | Mprog (rot.) . |
|---|---|---|---|---|---|
| . | . | (M⊙) . | (Gyr) . | (M⊙) . | (M⊙) . |
| VPHAS J0804−2809 | NGC 2527 | |$0.77_{-0.03}^{+0.03}$| | |$0.441_{+0.188}^{+0.188}$| | |$3.06_{-0.35}^{+0.72}$| | |$3.13_{-0.30}^{+0.70}$| |
| VPHAS J1030−5900 | Loden 143 | |$0.65_{-0.02}^{+0.02}$| | |$0.200_{+0.023}^{+0.023}$| | |$4.02_{-0.12}^{+0.21}$| | |$4.22_{-0.18}^{+0.21}$| |
| VPHAS J1103−5837 | NGC 3532 | |$1.13_{-0.03}^{+0.03}$| | |$0.030_{\text{-}}^{+0.123}$| | |$8.80_{-4.31}^{++}$| | |$9.78_{-5.08}^{++}$| |
| VPHAS J1546−5233 | Johansson 1 | |$0.62_{-0.05}^{+0.05}$| | |$0.437_{+0.196}^{+0.195}$| | |$3.07_{-0.36}^{+0.75}$| | |$3.14_{-0.31}^{+0.78}$| |
| VPHAS J1748−2914 | Ruprecht 131 | |$0.60_{-0.12}^{+0.16}$| | |$0.626_{\text{-}}^{+0.660}$| | |$2.72_{-0.64}^{++}$| | |$2.84_{-0.79}^{++}$| |
| WD . | Cluster . | WWD . | tprog . | Mprog (BaSTI) . | Mprog (rot.) . |
|---|---|---|---|---|---|
| . | . | (M⊙) . | (Gyr) . | (M⊙) . | (M⊙) . |
| VPHAS J0804−2809 | NGC 2527 | |$0.77_{-0.03}^{+0.03}$| | |$0.441_{+0.188}^{+0.188}$| | |$3.06_{-0.35}^{+0.72}$| | |$3.13_{-0.30}^{+0.70}$| |
| VPHAS J1030−5900 | Loden 143 | |$0.65_{-0.02}^{+0.02}$| | |$0.200_{+0.023}^{+0.023}$| | |$4.02_{-0.12}^{+0.21}$| | |$4.22_{-0.18}^{+0.21}$| |
| VPHAS J1103−5837 | NGC 3532 | |$1.13_{-0.03}^{+0.03}$| | |$0.030_{\text{-}}^{+0.123}$| | |$8.80_{-4.31}^{++}$| | |$9.78_{-5.08}^{++}$| |
| VPHAS J1546−5233 | Johansson 1 | |$0.62_{-0.05}^{+0.05}$| | |$0.437_{+0.196}^{+0.195}$| | |$3.07_{-0.36}^{+0.75}$| | |$3.14_{-0.31}^{+0.78}$| |
| VPHAS J1748−2914 | Ruprecht 131 | |$0.60_{-0.12}^{+0.16}$| | |$0.626_{\text{-}}^{+0.660}$| | |$2.72_{-0.64}^{++}$| | |$2.84_{-0.79}^{++}$| |
Our sample of photometrically selected white dwarfs is dominated by the field population, given that the preliminary identification (Section 2.3) does not allow us to estimate accurate parallaxes. The inclusion of proper motions is a valuable tool, which can be considered in future for discriminating with higher accuracy between field and cluster members, although there may not be available data for the faint white dwarf studied here.
In order to estimate the contamination of field white dwarfs at the distance of each cluster, we used the white dwarf luminosity function derived from SDSS (see fig. 4 in Harris et al. 2006), which gives a space density of 0.0046 white dwarfs per pc−3. Since the luminosity function expresses the space density of white dwarfs in function of their bolometric magnitudes, we converted it to an apparent magnitude scale using the distances and the reddenings of the five open clusters, for which we identify white dwarf member candidates. Then, we integrated the luminosity functions between the range of apparent magnitudes for white dwarfs with cooling ages compatible to those of the clusters, providing they are within the VPHAS+ magnitude limits (13 ≤ g ≤ 22). Given the extension of the five open clusters (≈0.125 deg2), we expect ≤1–2 field white dwarfs within the angular radius r2 of each cluster (Fig. 1). We note that this number is small with respect to the number of expected white dwarfs in old clusters of 500–1000 M⊙, therefore we consider the contamination by field white dwarfs to be negligible.
Four stars, including three cluster members, deserve further mention. The first is VPHAS J1103−5837, in NGC 3532. The interstellar reddening we measure for this white dwarf from VPHAS+ DR2 colours, E(B − V) = 0.13 ± 0.07, is slightly larger (2σ) than that of the cluster (Table 1). Using the Clem et al. (2011) photometry in Table 3, we measure E(B − V) = 0.07 ± 0.04, enabling a better comparison with the cluster reddening. These small differences in interstellar reddening do not modify much the white dwarf distance, and its location within the central part of the cluster (dashed curve in Fig. 1) adds further evidence that this massive white dwarf may belong to NGC 3532. Secondly, for VPHAS J1546−5233 in Johansson 1, we measured distance and reddening that are compatible with those measured by Kharchenko et al. (2013), therefore we used their cluster age to infer the progenitor parameters for this white dwarf in the following section. Thirdly, for VPHAS J1748−2914, which is a magnetic white dwarf in Ruprecht 131, we estimated the Teff via a photometric fit, assuming a value of log g = 8.00 ± 0.25 based on the typical mass distribution of field white dwarfs (Tremblay et al. 2013). Since magnetic white dwarfs are often suggested to be slightly more massive than non-magnetic white dwarfs (Ferrario, de Martino & Gänsicke 2015, and references therein), they are more compact and less luminous at a given Teff. This implies that VPHAS J1748−2914 could be at a shorter distance, which may not be compatible with the cluster distance. Thus, the association of this white dwarf to Ruprecht 131 needs a stronger confirmation, via higher quality spectroscopy allowing more precise typing. Finally, VPHAS J1104−5830 that we also speculated to be a magnetic white dwarf in Section 3, could be closer than 1174 pc. However, it is worth noting that, even for log g = 8.5, corresponding to M ≈ 0.94 M⊙, its distance would be ≈800 pc, which is still further away than NGC 3532.
5 DISCUSSION
5.1 Progenitor ages and masses
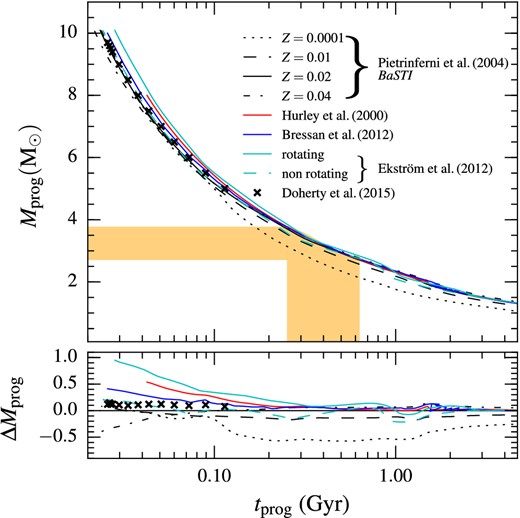
It is possible to estimate the initial mass of the white dwarf progenitor, Mi, comparing tprog with evolutionary models for single stars. For this purpose, we adopted cluster parameters from the available literature (Table 1) and the BaSTI isochrones (Pietrinferni et al. 2004). The error budget for the progenitor masses takes into account the uncertainties described in Section 4 and the cluster age uncertainties. It is important to note that, at least for progenitor masses below 4 M⊙, and down to 2 M⊙, different sets of isochrones give similar results. To substantiate this, we give a visual representation of the progenitor lifetimes for stars of ≤10 M⊙ in Fig. 9, where we also represent the difference in Mi obtain using different sets of isochrones. To show how the masses are inferred from the models, we display graphically the determination of Mi for one of the cluster members (VPHAS J0804−2809). The BaSTI isochrones take into account a standard Reimers (1975) parametrization of mass-loss, with η = 0.4, and core convective overshooting during the main sequence, but they do not include other effects like gravitational settling, radiative acceleration, and rotational mixing. The effect of metallicity is relatively subtle, but it becomes evident for very metal-poor models (Z = 0.0001), for which stars less massive than 5 M⊙ evolve much faster. Although not all the studied clusters have accurate measures of metallicity (Table 1), the progenitor age uncertainties are too large to enable a sensible distinction between progenitor lifetimes for different metallicities. Thus, we have added a further term in the error budget, which includes the differences in progenitor lifetimes due to a choice of isochrones with Z = 0.01, 0.02, 0.04, corresponding to the range of [Fe/H] for <4 Gyr old clusters in the Solar neighbourhood (see e.g. Region II of table 2 in Magrini et al. 2009). In Table 5, we list the progenitor masses of the five cluster members.
Top panel: comparison between different isochrones for stars with M ≤ 10 M⊙, showing the progenitor mass as a function of the progenitor lifetime, from the main sequence to the tip of the thermally pulsing AGB. The little bump near 2–2.5 M⊙ corresponds to the different evolutionary rate of stars experiencing the core helium-flash in degenerate (low-mass range) or non-degenerate conditions (high-mass range). To illustrate with an example the determination of the progenitor mass, we show the procedure for VPHAS J0804−2809 with the light-colour shaded area. Bottom panel: difference between progenitor masses inferred from different isochrones with respect to the BaSTI Z = 0.02 model, in function of the progenitor lifetime.
A comparison with the analytical formulation by Hurley, Pols & Tout (2000), and the PARSEC isochrones (Bressan et al. 2012), shows them to favour a slightly slower evolution for stars of ≥4 M⊙. These two models use different efficiencies for the mass-loss (η = 0.5, 0.2, respectively), and the PARSEC models include a somewhat more up-to-date physics with a different solar model, which determines their Z⊙ and mixing-length (see Bressan et al. 2012, for a discussion). For comparison in Fig. 9, we also plot the lifetimes for the Doherty et al. (2015) super-AGB stars and the Ekström et al. (2012) non-rotating models, which all fall in between the Hurley et al. (2000) and BaSTI curves. A more extreme case, however, is represented by the Ekström et al. (2012) rotating models, which consider an initial rotation rate on the zero-age main sequence of 0.4 times the critical escape velocity. Progenitors of our white dwarfs could have been stars with main-sequence masses of ≥2 M⊙, i.e. B- or A-type stars. These are typically fast rotators, whose main-sequence lifetime is prolonged in the Ekström et al. (2012) formulation due to radial mixing of stellar material, bringing unprocessed hydrogen in to the core. Therefore, for a given mass, a rotating model has a longer lasting main sequence than a non-rotating one. The effect of rotation becomes evident for stars with masses larger than 2 M⊙, and introduces a difference of up to 1 M⊙ when the progenitor mass is estimated at a given progenitor age (Fig 9, bottom panel). From the point of view of white dwarf structure, stellar rotation is suggested to be important as it could cause a lifting effect that keeps the core temperature of AGB stars below the critical ignition of carbon off-centre, allowing stable, massive carbon–oxygen white dwarf to exist (Dominguez et al. 1996). Since rotation would influence the core mass, and thus the white dwarf structure, we also list the progenitor masses interpolated from the Ekström et al. (2012) rotating models in Table 5.
5.2 Initial-to-final mass relation
The initial-to-final mass relation determined from Galactic open clusters suffers from relatively large scatter, mostly arising from the mutual interplay of intrinsic stellar properties. Binary evolution and interactions with other cluster members can also influence stellar evolution, adding a further source of uncertainty. All this can be worsened by model-dependent systematics, affecting the determination of cluster parameters and stellar evolution. In Fig. 10, we compare the initial and final masses of the five new cluster members to the 50 well-established cluster white dwarfs discussed by Salaris et al. (2009, and references therein). The authors used BaSTI evolutionary models to determine the cluster distances and ages, via interpolation with main-sequence isochrones, and white dwarf cooling ages via Salaris et al. (2010, and references therein) cooling models. Their approach insured that the progenitor ages and masses are estimated from a well-defined set of initial and final conditions. In the left-hand panel, we plot the initial masses interpolated from BaSTI isochrones. We note satisfying agreement for VPHAS J0804−2809, VPHAS J1103−5837, VPHAS J1546−5233, with the empirical relations by other authors.
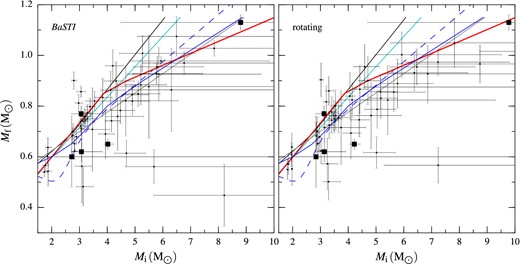
Left: initial-to-final mass relation using the data from Salaris et al. (2009), small dots, and the five new white dwarfs studied here, large squares. Right: initial-to-final mass relation with progenitor masses computed from the Ekström et al. (2012) rotating models. Error bars extending beyond 10 M⊙ indicate upper limits. Initial-to-final mass relations from the literature are: black, Catalán et al. (2008a); cyan Casewell et al. (2009); red, Salaris et al. (2009); grey, Gesicki et al. (2014); solid blue, Weidemann (2000). The dashed-blue curve is the core mass at the first thermal pulse (PARSEC isochrones), using the Marigo et al. (2013) parametrization.
The DAH white dwarf, VPHAS J1748−2914, overlaps the theoretical curve representing the core mass at the first thermal pulse (Marigo et al. 2013), which is the dominant factor in determining the white dwarf mass (Weidemann 2000). However, for this white dwarf the errors on the progenitor age are too large to derive a meaningful mass and we only give a lower limit. It is very important to find magnetic white dwarfs in open clusters, as they can be used to constrain the mass of their progenitors, yet unknown (Külebi et al. 2013), helping to understand the debated origin of magnetic fields in white dwarfs (Ferrario et al. 2015).
The progenitor mass of the remaining cluster white dwarf, VPHAS J1030−5900, falls below most of the other white dwarfs and the various initial-to-final mass relation curves. In the past, a few interpretations have been given to explain such outliers, including differential mass-loss on the giant branches due to metallicity, and binary interactions (Weidemann 2000). We note that at least two of the white dwarfs considered in Salaris et al. (2009) also have large progenitor masses, but final masses below 0.6 M⊙. As we suggested in Section 2, the physical parameters of Loden 143 might be rather uncertain, due to the ambiguous nature of the cluster, and the initial mass we derive for VPHAS J1030−5900 may not be correct. Nevertheless, we would like to stress that binarity may have a relevant effect on the scatter seen in the initial-to-final mass relation, especially at the large progenitor-mass end. In fact, white dwarf progenitors of Mi ≥ 2 M⊙ are characterized by a relatively high binary fraction in their pre-main sequence (e.g. ≈68–73 per cent; Baines et al. 2006) and later evolutionary stages (25–50 per cent; see e.g. Abt & Levy 1978; Oudmaijer & Parr 2010). Although we suggested the five new cluster white dwarfs not to have late-type, low-mass companions, some other white dwarfs displayed in Fig. 10 might be or may have been in binary systems.
In the right-hand panel of Fig. 10, for illustrative purposes we show again the 50 cluster white dwarfs studied in Salaris et al. (2009) and the five cluster white dwarf from this study, but we determine the progenitor masses of both samples from the Ekström et al. (2012) isochrones. As we noted in the previous section, there is a shift towards larger initial masses (up to 1 M⊙) for stars with Mi ≥ 2 M⊙, due to the prolonged lifetime as effect of rotational mixing. The two panels of Fig. 10 may not be directly comparable, as the cluster ages that we used are typically determined from evolutionary models that do not include stellar rotation. Given the importance that rotation has for the evolution of the most massive white dwarf progenitors, it should not be neglected when studying the evolution of stellar populations, and it would be worth to assess in future work its impact on the determination on cluster ages.
5.2.1 Upper mass limit of white dwarf progenitors
For the most massive cluster white dwarf in our study, VPHAS J1103−5837, we derived an |$8.8_{-4.3}^{+1.2}$| M⊙ progenitor, near the mass-boundary between white dwarf and neutron star progenitors (Smartt 2009). To place VPHAS J1103−5837 in context with the other white dwarfs of NGC 3532, we display in Fig. 11 their most up-to-date census by Dobbie et al. (2009, 2012). The new white dwarf seems to be genuinely the cluster member with the most massive progenitor. Since the cluster age uncertainty (±100 Myr; Clem et al. 2011) dominates the error propagation, we cannot derive a more accurate measure of the progenitor mass, due to the steep rise of the curves in Fig. 9. However, since massive white dwarfs could also be produced via binary interaction (Dominguez, Tornambe & Isern 1993) and we do not have information on the past history of VPHAS J1103−5837, we cannot discard that this white dwarf was produced through binary evolution (merger).
Considering the single star evolution channel, this result is very interesting, since it adds further empirical evidence to previous theoretical and observational works, suggesting the dividing mass to be Mi ≳ 7 M⊙ (e.g. García-Berro et al. 1997; Williams et al. 2009). The key ingredients influencing the final mass of white dwarfs are sensitive to stellar parameters like metallicity, and need to be tested on observed data. In the high-mass range, theoretical results show that high dredge-up efficiency couple to a moderate mass-loss (≈10−7 M⊙ yr−1), during the AGB phase, and appear to dominate the evolution of white dwarf progenitors (e.g. Siess 2007, 2010; Doherty et al. 2015). Observations suggest that the most intense core-mass growth occurs between Mi = 1.6 and 3.4 M⊙ (30 per cent), while it is appears to be smaller (≈10 per cent) for stars of Mi ≈ 4 M⊙ (Kalirai, Marigo & Tremblay 2014). However, the core-mass growth of massive white dwarf progenitors still needs to be confirmed. Thus, the search of other massive cluster white dwarfs should be prioritized, in order to better constrain the high-mass end of the initial-to-final mass relation. The evolutionary models for super-AGB stars (Mi ≥ 5 M⊙) become very resource consuming, due to extensive time- and spatial-resolution requirements for modelling the TP-AGB phase, and some approximations are taken in to account. Stars like VPHAS J1103−5837 could help to constrain the main uncertainties in the models, due to the treatment of convection, mass-loss, and third dredge-up efficiency (Doherty et al. 2015, and references therein).
6 SUMMARY AND CONCLUSIONS
We proved the efficient selection of white dwarfs from VPHAS+ DR2 ugr photometry, enabling the study of faint stellar remnants in the most crowded regions of the Galactic plane. We confirmed 17 white dwarf candidates with VLT/FORS2 spectroscopy. We identified 13 DA, one DB, two DAH, and one DC white dwarfs. Their atmospheric parameters, masses, ages, and distances, derived from model atmosphere analysis, suggest that five of them are likely members of open clusters.
The progenitor masses for the five new cluster members are broadly consistent with the known trend of the initial-to-final mass relation. VPHAS J1103−5837, in NGC 3532, is possibly the most massive white dwarf known in an open cluster (1.13 ± 0.03 M⊙), likely with an oxygen–neon core. Its progenitor mass, |$8.8_{-4.3}^{+1.2}$| M⊙, is close to the mass-divide with core-collapse supernovae. Finding more massive cluster white dwarfs, like VPHAS J1103−5837, is important to derive firmer constraints at the high progenitor-mass end of the initial-to-final mass relation. The DAH white dwarf, VPHAS J1748−2914, is suggested to belong to Ruprecht 131. Future observations of this star, with higher S/N, will be needed to confirm its cluster membership and to measure its progenitor mass, now only defined as a lower limit of 2–3 M⊙.
VPHAS+ and its twin surveys in the Northern hemisphere (IPHAS, and UVEX; Drew et al. 2005; Groot et al. 2009) are ideal tools for the successful identification of the missing population of faint stellar remnants of low- to intermediate-mass stars in the Galactic plane. Optical follow-up spectroscopy, with moderate resolution and S/N >20, is sufficient to confirm the white dwarfs and to measure their atmospheric parameters, but higher quality data are necessary if more accurate spectroscopic parallaxes are to be sought. The upcoming multi-object spectrographs, WEAVE on WHT (Dalton et al. 2012) and 4MOST on VISTA (de Jong et al. 2012), will play an important role in confirming more cluster white dwarfs and measuring accurate physical parameters. The ESA Gaia mission will deliver parallaxes for several hundred thousand white dwarfs down to 18–20 mag (Jordan 2007; Carrasco et al. 2014; Gaensicke et al. 2015), with an accuracy of ≈30 per cent (de Bruijne, Rygl & Antoja 2015). ESA Gaia will supply a crucial improvement to open clusters science, as it will determine stellar membership via the measure of parallaxes and proper motions, allowing the accurate determination of cluster distances and ages, and thus significantly improving the study of the initial-to-final mass relation
Based on data products from observations made with ESO telescopes at the La Silla Paranal Observatory under programme ID 177.D-3023, as part of the VST Photometric H α Survey of the Southern Galactic plane and Bulge (http://www.vphas.eu), and programme ID 093.D-0838.
We would like to thank Jorick Vink and Dimitri Veras for useful discussion, and Nick Wright for helpful advice on the use of Montage. We would like to thank Israel Blanchard, Dimitri Gadotti, Patricia Guajardo, and Roger Wesson for their support at Paranal. We would also like to thank the referee, Pierre Bergeron, for his useful comments.
The research leading to these results has received funding from the European Research Council under the European Union's Seventh Framework Programme (FP/2007-2013) / ERC Grant Agreement No. 320964 (WDTracer).
This research was made possible through the use of the AAVSO Photometric All-Sky Survey (APASS), funded by the Robert Martin Ayers Sciences Fund. The VPHAS+ mosaics were produced with Montage. It is funded by the National Science Foundation under Grant Number ACI-1440620, and was previously funded by the National Aeronautics and Space Administration's Earth Science Technology Office, Computation Technologies Project, under Cooperative Agreement Number NCC5-626 between NASA and the California Institute of Technology.
Available at: http://www.astro.umontreal.ca/∼bergeron/CoolingModels.
pamela is part of the starlink distribution at http://starlink.eao.hawaii.edu/starlink. molly is available at http://www.warwick.ac.uk/go/trmarsh/software/.
REFERENCES
APPENDIX: WHITE DWARF COOLING TRACKS
g-band absolute magnitudes and colours of DA white dwarfs in the VPHAS+ Vega system.
| . | log g = 7.00 . | log g = 7.50 . | log g = 8.00 . | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Teff . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . |
| 100 000 | 6.114 | −1.603 | −0.317 | −0.173 | 0.045 | 7.209 | −1.603 | −0.315 | −0.172 | 0.040 | 8.255 | −1.604 | −0.313 | −0.172 | 0.035 |
| 90 000 | 6.289 | −1.595 | −0.313 | −0.171 | 0.044 | 7.349 | −1.595 | −0.311 | −0.171 | 0.039 | 9.338 | −1.599 | −0.307 | −0.169 | 0.026 |
| 80 000 | 6.473 | −1.585 | −0.308 | −0.169 | 0.042 | 7.511 | −1.586 | −0.306 | −0.169 | 0.036 | 9.450 | −1.590 | −0.302 | −0.167 | 0.022 |
| 75 000 | 6.580 | −1.579 | −0.306 | −0.168 | 0.041 | 7.597 | −1.580 | −0.304 | −0.167 | 0.034 | 9.511 | −1.585 | −0.299 | −0.166 | 0.019 |
| 70 000 | 6.698 | −1.572 | −0.303 | −0.167 | 0.039 | 7.686 | −1.574 | −0.301 | −0.166 | 0.032 | 9.578 | −1.579 | −0.295 | −0.165 | 0.016 |
| 65 000 | 6.818 | −1.564 | −0.300 | −0.165 | 0.037 | 7.781 | −1.566 | −0.297 | −0.165 | 0.030 | 9.649 | −1.573 | −0.292 | −0.163 | 0.013 |
| 60 000 | 6.939 | −1.555 | −0.296 | −0.164 | 0.035 | 7.884 | −1.557 | −0.294 | −0.164 | 0.027 | 9.726 | −1.565 | −0.288 | −0.162 | 0.009 |
| 55 000 | 7.063 | −1.544 | −0.292 | −0.163 | 0.032 | 7.997 | −1.547 | −0.289 | −0.162 | 0.023 | 9.813 | −1.555 | −0.283 | −0.160 | 0.003 |
| 50 000 | 7.197 | −1.530 | −0.287 | −0.161 | 0.028 | 8.127 | −1.533 | −0.284 | −0.160 | 0.018 | 9.911 | −1.543 | −0.277 | −0.158 | −0.003 |
| 45 000 | 7.352 | −1.512 | −0.281 | −0.158 | 0.022 | 8.274 | −1.516 | −0.278 | −0.158 | 0.012 | 10.027 | −1.528 | −0.269 | −0.155 | −0.013 |
| 40 000 | 7.540 | −1.485 | −0.273 | −0.155 | 0.014 | 8.451 | −1.490 | −0.269 | −0.154 | 0.002 | 10.172 | −1.505 | −0.259 | −0.151 | −0.026 |
| 35 000 | 7.803 | −1.441 | −0.261 | −0.150 | 0.001 | 8.685 | −1.448 | −0.256 | −0.149 | −0.014 | 10.372 | −1.469 | −0.244 | −0.146 | −0.047 |
| 30 000 | 8.182 | −1.347 | −0.240 | −0.141 | −0.024 | 9.058 | −1.360 | −0.233 | −0.140 | −0.043 | 10.695 | −1.393 | −0.216 | −0.135 | −0.087 |
| 28 000 | 8.365 | −1.293 | −0.227 | −0.134 | −0.033 | 9.235 | −1.307 | −0.219 | −0.133 | −0.054 | 10.858 | −1.346 | −0.200 | −0.128 | −0.104 |
| 26 000 | 8.549 | −1.236 | −0.210 | −0.126 | −0.038 | 9.413 | −1.251 | −0.202 | −0.125 | −0.062 | 11.025 | −1.294 | −0.180 | −0.120 | −0.115 |
| 24 000 | 8.734 | −1.174 | −0.192 | −0.117 | −0.043 | 9.591 | −1.192 | −0.183 | −0.116 | −0.068 | 11.186 | −1.238 | −0.159 | −0.111 | −0.123 |
| 22 000 | 8.928 | −1.105 | −0.172 | −0.108 | −0.049 | 9.776 | −1.124 | −0.162 | −0.106 | −0.075 | 11.358 | −1.176 | −0.135 | −0.101 | −0.133 |
| 20 000 | 9.134 | −1.023 | −0.150 | −0.098 | −0.058 | 9.973 | −1.045 | −0.139 | −0.096 | −0.085 | 11.542 | −1.103 | −0.108 | −0.090 | −0.145 |
| 19 000 | 9.246 | −0.977 | −0.138 | −0.092 | −0.063 | 10.078 | −0.999 | −0.126 | −0.090 | −0.091 | 11.640 | −1.062 | −0.093 | −0.083 | −0.153 |
| 18 000 | 9.364 | −0.925 | −0.125 | −0.086 | −0.069 | 10.189 | −0.949 | −0.112 | −0.084 | −0.099 | 11.744 | −1.017 | −0.077 | −0.076 | −0.163 |
| 17 000 | 9.487 | −0.867 | −0.111 | −0.079 | −0.077 | 10.306 | −0.894 | −0.096 | −0.077 | −0.108 | 11.856 | −0.969 | −0.058 | −0.068 | −0.174 |
| 16 000 | 9.621 | −0.803 | −0.095 | −0.072 | −0.086 | 10.432 | −0.833 | −0.079 | −0.069 | −0.119 | 11.975 | −0.922 | −0.035 | −0.059 | −0.183 |
| 15 000 | 9.766 | −0.732 | −0.077 | −0.063 | −0.097 | 10.567 | −0.767 | −0.058 | −0.060 | −0.132 | 12.105 | −0.883 | −0.008 | −0.046 | −0.187 |
| 14 000 | 9.924 | −0.654 | −0.055 | −0.053 | −0.111 | 10.716 | −0.698 | −0.033 | −0.049 | −0.146 | 12.239 | −0.857 | 0.023 | −0.029 | −0.188 |
| 13 000 | 10.101 | −0.573 | −0.027 | −0.041 | −0.126 | 10.884 | −0.634 | −0.001 | −0.034 | −0.156 | 12.367 | −0.837 | 0.053 | −0.012 | −0.188 |
| 12 000 | 10.303 | −0.500 | 0.011 | −0.024 | −0.137 | 11.065 | −0.602 | 0.044 | −0.013 | −0.158 | 12.547 | −0.810 | 0.093 | 0.010 | −0.180 |
| 11 000 | 10.524 | −0.481 | 0.068 | 0.003 | −0.134 | 11.273 | −0.595 | 0.096 | 0.015 | −0.146 | 12.793 | −0.780 | 0.138 | 0.039 | −0.157 |
| 10 000 | 10.839 | −0.495 | 0.141 | 0.043 | −0.101 | 11.596 | −0.602 | 0.163 | 0.057 | −0.102 | 13.123 | −0.774 | 0.194 | 0.077 | −0.108 |
| 9500 | 11.053 | −0.518 | 0.183 | 0.070 | −0.070 | 11.802 | −0.620 | 0.203 | 0.082 | −0.069 | 13.320 | −0.774 | 0.226 | 0.100 | −0.075 |
| 9000 | 11.297 | −0.552 | 0.230 | 0.099 | −0.031 | 12.031 | −0.641 | 0.246 | 0.108 | −0.031 | 13.530 | −0.770 | 0.262 | 0.122 | −0.042 |
| 8500 | 11.565 | −0.583 | 0.279 | 0.129 | 0.009 | 12.277 | −0.654 | 0.291 | 0.135 | 0.007 | 13.756 | −0.756 | 0.301 | 0.145 | −0.012 |
| 8000 | 11.852 | −0.600 | 0.333 | 0.159 | 0.048 | 12.541 | −0.652 | 0.341 | 0.163 | 0.041 | 13.996 | −0.727 | 0.346 | 0.169 | 0.017 |
| 7500 | 12.159 | −0.594 | 0.392 | 0.191 | 0.081 | 12.824 | −0.629 | 0.397 | 0.193 | 0.069 | 14.257 | −0.678 | 0.399 | 0.198 | 0.043 |
| 7000 | 12.492 | −0.559 | 0.460 | 0.225 | 0.105 | 13.135 | −0.580 | 0.462 | 0.227 | 0.096 | 14.544 | −0.595 | 0.463 | 0.229 | 0.074 |
| 6500 | 12.861 | −0.485 | 0.537 | 0.264 | 0.134 | 13.482 | −0.489 | 0.541 | 0.265 | 0.126 | 14.877 | −0.453 | 0.547 | 0.266 | 0.113 |
| 6000 | 13.286 | −0.352 | 0.637 | 0.310 | 0.166 | 13.888 | −0.325 | 0.644 | 0.311 | 0.162 | 15.274 | −0.187 | 0.654 | 0.310 | 0.156 |
| log g = 8.50 | log g = 9.00 | ||||||||||||||
| Teff | g | (u − g) | (g − r) | (r − i) | (r − H α) | g | (u − g) | (g − r) | (r − i) | (r − H α) | |||||
| 100 000 | 9.238 | −1.606 | −0.311 | −0.171 | 0.029 | 10.299 | −1.608 | −0.309 | −0.170 | 0.022 | |||||
| 90 000 | 9.338 | −1.599 | −0.307 | −0.169 | 0.026 | 10.388 | −1.601 | −0.305 | −0.168 | 0.018 | |||||
| 80 000 | 9.450 | −1.590 | −0.302 | −0.167 | 0.022 | 10.492 | −1.593 | −0.299 | −0.166 | 0.014 | |||||
| 75 000 | 9.511 | −1.585 | −0.299 | −0.166 | 0.019 | 10.549 | −1.589 | −0.296 | −0.165 | 0.011 | |||||
| 70 000 | 9.578 | −1.579 | −0.295 | −0.165 | 0.016 | 10.610 | −1.583 | −0.293 | −0.163 | 0.008 | |||||
| 65 000 | 9.649 | −1.573 | −0.292 | −0.163 | 0.013 | 10.677 | −1.577 | −0.289 | −0.162 | 0.004 | |||||
| 60 000 | 9.726 | −1.565 | −0.288 | −0.162 | 0.009 | 10.752 | −1.570 | −0.284 | −0.160 | −0.001 | |||||
| 55 000 | 9.813 | −1.555 | −0.283 | −0.160 | 0.003 | 10.834 | −1.561 | −0.279 | −0.158 | −0.007 | |||||
| 50 000 | 9.911 | −1.543 | −0.277 | −0.158 | −0.003 | 10.928 | −1.550 | −0.273 | −0.156 | −0.015 | |||||
| 45 000 | 10.027 | −1.528 | −0.269 | −0.155 | −0.013 | 11.039 | −1.535 | −0.265 | −0.153 | −0.026 | |||||
| 40 000 | 10.172 | −1.505 | −0.259 | −0.151 | −0.026 | 11.178 | −1.515 | −0.254 | −0.149 | −0.041 | |||||
| 35 000 | 10.372 | −1.469 | −0.244 | −0.146 | −0.047 | 11.372 | −1.481 | −0.237 | −0.143 | −0.065 | |||||
| 30 000 | 10.695 | −1.393 | −0.216 | −0.135 | −0.087 | 11.677 | −1.413 | −0.207 | −0.132 | −0.110 | |||||
| 28 000 | 10.858 | −1.346 | −0.200 | −0.128 | −0.104 | 11.838 | −1.370 | −0.189 | −0.125 | −0.130 | |||||
| 26 000 | 11.025 | −1.294 | −0.180 | −0.120 | −0.115 | 12.005 | −1.320 | −0.167 | −0.116 | −0.143 | |||||
| 24 000 | 11.186 | −1.238 | −0.159 | −0.111 | −0.123 | 12.163 | −1.267 | −0.145 | −0.108 | −0.153 | |||||
| 22 000 | 11.358 | −1.176 | −0.135 | −0.101 | −0.133 | 12.335 | −1.208 | −0.119 | −0.097 | −0.163 | |||||
| 20 000 | 11.542 | −1.103 | −0.108 | −0.090 | −0.145 | 12.519 | −1.139 | −0.091 | −0.085 | −0.176 | |||||
| 19 000 | 11.640 | −1.062 | −0.093 | −0.083 | −0.153 | 12.618 | −1.101 | −0.074 | −0.078 | −0.185 | |||||
| 18 000 | 11.744 | −1.017 | −0.077 | −0.076 | −0.163 | 12.723 | −1.061 | −0.056 | −0.071 | −0.194 | |||||
| 17 000 | 11.856 | −0.969 | −0.058 | −0.068 | −0.174 | 12.835 | −1.023 | −0.034 | −0.061 | −0.201 | |||||
| 16 000 | 11.975 | −0.922 | −0.035 | −0.059 | −0.183 | 12.950 | −0.993 | −0.010 | −0.048 | −0.203 | |||||
| 15 000 | 12.105 | −0.883 | −0.008 | −0.046 | −0.187 | 13.065 | −0.971 | 0.016 | −0.034 | −0.203 | |||||
| 14 000 | 12.239 | −0.857 | 0.023 | −0.029 | −0.188 | 13.175 | −0.950 | 0.040 | −0.021 | −0.203 | |||||
| 13 000 | 12.367 | −0.837 | 0.053 | −0.012 | −0.188 | 13.323 | −0.922 | 0.070 | −0.002 | −0.199 | |||||
| 12 000 | 12.547 | −0.810 | 0.093 | 0.010 | −0.180 | 13.524 | −0.885 | 0.109 | 0.021 | −0.190 | |||||
| 11 000 | 12.793 | −0.780 | 0.138 | 0.039 | −0.157 | 13.780 | −0.853 | 0.150 | 0.050 | −0.165 | |||||
| 10 000 | 13.123 | −0.774 | 0.194 | 0.077 | −0.108 | 14.112 | −0.841 | 0.201 | 0.086 | −0.115 | |||||
| 9500 | 13.320 | −0.774 | 0.226 | 0.100 | −0.075 | 14.303 | −0.833 | 0.231 | 0.106 | −0.085 | |||||
| 9000 | 13.530 | −0.770 | 0.262 | 0.122 | −0.042 | 14.505 | −0.818 | 0.264 | 0.126 | −0.056 | |||||
| 8500 | 13.756 | −0.756 | 0.301 | 0.145 | −0.012 | 14.719 | −0.793 | 0.301 | 0.148 | −0.027 | |||||
| 8000 | 13.996 | −0.727 | 0.346 | 0.169 | 0.017 | 14.950 | −0.752 | 0.345 | 0.172 | −0.002 | |||||
| 7500 | 14.257 | −0.678 | 0.399 | 0.198 | 0.043 | 15.199 | −0.687 | 0.396 | 0.199 | 0.028 | |||||
| 7000 | 14.544 | −0.595 | 0.463 | 0.229 | 0.074 | 15.481 | −0.582 | 0.463 | 0.229 | 0.064 | |||||
| 6500 | 14.877 | −0.453 | 0.547 | 0.266 | 0.113 | 15.814 | −0.404 | 0.550 | 0.266 | 0.109 | |||||
| 6000 | 15.274 | −0.187 | 0.654 | 0.310 | 0.156 | 16.211 | −0.043 | 0.665 | 0.308 | 0.156 | |||||
| . | log g = 7.00 . | log g = 7.50 . | log g = 8.00 . | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Teff . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . |
| 100 000 | 6.114 | −1.603 | −0.317 | −0.173 | 0.045 | 7.209 | −1.603 | −0.315 | −0.172 | 0.040 | 8.255 | −1.604 | −0.313 | −0.172 | 0.035 |
| 90 000 | 6.289 | −1.595 | −0.313 | −0.171 | 0.044 | 7.349 | −1.595 | −0.311 | −0.171 | 0.039 | 9.338 | −1.599 | −0.307 | −0.169 | 0.026 |
| 80 000 | 6.473 | −1.585 | −0.308 | −0.169 | 0.042 | 7.511 | −1.586 | −0.306 | −0.169 | 0.036 | 9.450 | −1.590 | −0.302 | −0.167 | 0.022 |
| 75 000 | 6.580 | −1.579 | −0.306 | −0.168 | 0.041 | 7.597 | −1.580 | −0.304 | −0.167 | 0.034 | 9.511 | −1.585 | −0.299 | −0.166 | 0.019 |
| 70 000 | 6.698 | −1.572 | −0.303 | −0.167 | 0.039 | 7.686 | −1.574 | −0.301 | −0.166 | 0.032 | 9.578 | −1.579 | −0.295 | −0.165 | 0.016 |
| 65 000 | 6.818 | −1.564 | −0.300 | −0.165 | 0.037 | 7.781 | −1.566 | −0.297 | −0.165 | 0.030 | 9.649 | −1.573 | −0.292 | −0.163 | 0.013 |
| 60 000 | 6.939 | −1.555 | −0.296 | −0.164 | 0.035 | 7.884 | −1.557 | −0.294 | −0.164 | 0.027 | 9.726 | −1.565 | −0.288 | −0.162 | 0.009 |
| 55 000 | 7.063 | −1.544 | −0.292 | −0.163 | 0.032 | 7.997 | −1.547 | −0.289 | −0.162 | 0.023 | 9.813 | −1.555 | −0.283 | −0.160 | 0.003 |
| 50 000 | 7.197 | −1.530 | −0.287 | −0.161 | 0.028 | 8.127 | −1.533 | −0.284 | −0.160 | 0.018 | 9.911 | −1.543 | −0.277 | −0.158 | −0.003 |
| 45 000 | 7.352 | −1.512 | −0.281 | −0.158 | 0.022 | 8.274 | −1.516 | −0.278 | −0.158 | 0.012 | 10.027 | −1.528 | −0.269 | −0.155 | −0.013 |
| 40 000 | 7.540 | −1.485 | −0.273 | −0.155 | 0.014 | 8.451 | −1.490 | −0.269 | −0.154 | 0.002 | 10.172 | −1.505 | −0.259 | −0.151 | −0.026 |
| 35 000 | 7.803 | −1.441 | −0.261 | −0.150 | 0.001 | 8.685 | −1.448 | −0.256 | −0.149 | −0.014 | 10.372 | −1.469 | −0.244 | −0.146 | −0.047 |
| 30 000 | 8.182 | −1.347 | −0.240 | −0.141 | −0.024 | 9.058 | −1.360 | −0.233 | −0.140 | −0.043 | 10.695 | −1.393 | −0.216 | −0.135 | −0.087 |
| 28 000 | 8.365 | −1.293 | −0.227 | −0.134 | −0.033 | 9.235 | −1.307 | −0.219 | −0.133 | −0.054 | 10.858 | −1.346 | −0.200 | −0.128 | −0.104 |
| 26 000 | 8.549 | −1.236 | −0.210 | −0.126 | −0.038 | 9.413 | −1.251 | −0.202 | −0.125 | −0.062 | 11.025 | −1.294 | −0.180 | −0.120 | −0.115 |
| 24 000 | 8.734 | −1.174 | −0.192 | −0.117 | −0.043 | 9.591 | −1.192 | −0.183 | −0.116 | −0.068 | 11.186 | −1.238 | −0.159 | −0.111 | −0.123 |
| 22 000 | 8.928 | −1.105 | −0.172 | −0.108 | −0.049 | 9.776 | −1.124 | −0.162 | −0.106 | −0.075 | 11.358 | −1.176 | −0.135 | −0.101 | −0.133 |
| 20 000 | 9.134 | −1.023 | −0.150 | −0.098 | −0.058 | 9.973 | −1.045 | −0.139 | −0.096 | −0.085 | 11.542 | −1.103 | −0.108 | −0.090 | −0.145 |
| 19 000 | 9.246 | −0.977 | −0.138 | −0.092 | −0.063 | 10.078 | −0.999 | −0.126 | −0.090 | −0.091 | 11.640 | −1.062 | −0.093 | −0.083 | −0.153 |
| 18 000 | 9.364 | −0.925 | −0.125 | −0.086 | −0.069 | 10.189 | −0.949 | −0.112 | −0.084 | −0.099 | 11.744 | −1.017 | −0.077 | −0.076 | −0.163 |
| 17 000 | 9.487 | −0.867 | −0.111 | −0.079 | −0.077 | 10.306 | −0.894 | −0.096 | −0.077 | −0.108 | 11.856 | −0.969 | −0.058 | −0.068 | −0.174 |
| 16 000 | 9.621 | −0.803 | −0.095 | −0.072 | −0.086 | 10.432 | −0.833 | −0.079 | −0.069 | −0.119 | 11.975 | −0.922 | −0.035 | −0.059 | −0.183 |
| 15 000 | 9.766 | −0.732 | −0.077 | −0.063 | −0.097 | 10.567 | −0.767 | −0.058 | −0.060 | −0.132 | 12.105 | −0.883 | −0.008 | −0.046 | −0.187 |
| 14 000 | 9.924 | −0.654 | −0.055 | −0.053 | −0.111 | 10.716 | −0.698 | −0.033 | −0.049 | −0.146 | 12.239 | −0.857 | 0.023 | −0.029 | −0.188 |
| 13 000 | 10.101 | −0.573 | −0.027 | −0.041 | −0.126 | 10.884 | −0.634 | −0.001 | −0.034 | −0.156 | 12.367 | −0.837 | 0.053 | −0.012 | −0.188 |
| 12 000 | 10.303 | −0.500 | 0.011 | −0.024 | −0.137 | 11.065 | −0.602 | 0.044 | −0.013 | −0.158 | 12.547 | −0.810 | 0.093 | 0.010 | −0.180 |
| 11 000 | 10.524 | −0.481 | 0.068 | 0.003 | −0.134 | 11.273 | −0.595 | 0.096 | 0.015 | −0.146 | 12.793 | −0.780 | 0.138 | 0.039 | −0.157 |
| 10 000 | 10.839 | −0.495 | 0.141 | 0.043 | −0.101 | 11.596 | −0.602 | 0.163 | 0.057 | −0.102 | 13.123 | −0.774 | 0.194 | 0.077 | −0.108 |
| 9500 | 11.053 | −0.518 | 0.183 | 0.070 | −0.070 | 11.802 | −0.620 | 0.203 | 0.082 | −0.069 | 13.320 | −0.774 | 0.226 | 0.100 | −0.075 |
| 9000 | 11.297 | −0.552 | 0.230 | 0.099 | −0.031 | 12.031 | −0.641 | 0.246 | 0.108 | −0.031 | 13.530 | −0.770 | 0.262 | 0.122 | −0.042 |
| 8500 | 11.565 | −0.583 | 0.279 | 0.129 | 0.009 | 12.277 | −0.654 | 0.291 | 0.135 | 0.007 | 13.756 | −0.756 | 0.301 | 0.145 | −0.012 |
| 8000 | 11.852 | −0.600 | 0.333 | 0.159 | 0.048 | 12.541 | −0.652 | 0.341 | 0.163 | 0.041 | 13.996 | −0.727 | 0.346 | 0.169 | 0.017 |
| 7500 | 12.159 | −0.594 | 0.392 | 0.191 | 0.081 | 12.824 | −0.629 | 0.397 | 0.193 | 0.069 | 14.257 | −0.678 | 0.399 | 0.198 | 0.043 |
| 7000 | 12.492 | −0.559 | 0.460 | 0.225 | 0.105 | 13.135 | −0.580 | 0.462 | 0.227 | 0.096 | 14.544 | −0.595 | 0.463 | 0.229 | 0.074 |
| 6500 | 12.861 | −0.485 | 0.537 | 0.264 | 0.134 | 13.482 | −0.489 | 0.541 | 0.265 | 0.126 | 14.877 | −0.453 | 0.547 | 0.266 | 0.113 |
| 6000 | 13.286 | −0.352 | 0.637 | 0.310 | 0.166 | 13.888 | −0.325 | 0.644 | 0.311 | 0.162 | 15.274 | −0.187 | 0.654 | 0.310 | 0.156 |
| log g = 8.50 | log g = 9.00 | ||||||||||||||
| Teff | g | (u − g) | (g − r) | (r − i) | (r − H α) | g | (u − g) | (g − r) | (r − i) | (r − H α) | |||||
| 100 000 | 9.238 | −1.606 | −0.311 | −0.171 | 0.029 | 10.299 | −1.608 | −0.309 | −0.170 | 0.022 | |||||
| 90 000 | 9.338 | −1.599 | −0.307 | −0.169 | 0.026 | 10.388 | −1.601 | −0.305 | −0.168 | 0.018 | |||||
| 80 000 | 9.450 | −1.590 | −0.302 | −0.167 | 0.022 | 10.492 | −1.593 | −0.299 | −0.166 | 0.014 | |||||
| 75 000 | 9.511 | −1.585 | −0.299 | −0.166 | 0.019 | 10.549 | −1.589 | −0.296 | −0.165 | 0.011 | |||||
| 70 000 | 9.578 | −1.579 | −0.295 | −0.165 | 0.016 | 10.610 | −1.583 | −0.293 | −0.163 | 0.008 | |||||
| 65 000 | 9.649 | −1.573 | −0.292 | −0.163 | 0.013 | 10.677 | −1.577 | −0.289 | −0.162 | 0.004 | |||||
| 60 000 | 9.726 | −1.565 | −0.288 | −0.162 | 0.009 | 10.752 | −1.570 | −0.284 | −0.160 | −0.001 | |||||
| 55 000 | 9.813 | −1.555 | −0.283 | −0.160 | 0.003 | 10.834 | −1.561 | −0.279 | −0.158 | −0.007 | |||||
| 50 000 | 9.911 | −1.543 | −0.277 | −0.158 | −0.003 | 10.928 | −1.550 | −0.273 | −0.156 | −0.015 | |||||
| 45 000 | 10.027 | −1.528 | −0.269 | −0.155 | −0.013 | 11.039 | −1.535 | −0.265 | −0.153 | −0.026 | |||||
| 40 000 | 10.172 | −1.505 | −0.259 | −0.151 | −0.026 | 11.178 | −1.515 | −0.254 | −0.149 | −0.041 | |||||
| 35 000 | 10.372 | −1.469 | −0.244 | −0.146 | −0.047 | 11.372 | −1.481 | −0.237 | −0.143 | −0.065 | |||||
| 30 000 | 10.695 | −1.393 | −0.216 | −0.135 | −0.087 | 11.677 | −1.413 | −0.207 | −0.132 | −0.110 | |||||
| 28 000 | 10.858 | −1.346 | −0.200 | −0.128 | −0.104 | 11.838 | −1.370 | −0.189 | −0.125 | −0.130 | |||||
| 26 000 | 11.025 | −1.294 | −0.180 | −0.120 | −0.115 | 12.005 | −1.320 | −0.167 | −0.116 | −0.143 | |||||
| 24 000 | 11.186 | −1.238 | −0.159 | −0.111 | −0.123 | 12.163 | −1.267 | −0.145 | −0.108 | −0.153 | |||||
| 22 000 | 11.358 | −1.176 | −0.135 | −0.101 | −0.133 | 12.335 | −1.208 | −0.119 | −0.097 | −0.163 | |||||
| 20 000 | 11.542 | −1.103 | −0.108 | −0.090 | −0.145 | 12.519 | −1.139 | −0.091 | −0.085 | −0.176 | |||||
| 19 000 | 11.640 | −1.062 | −0.093 | −0.083 | −0.153 | 12.618 | −1.101 | −0.074 | −0.078 | −0.185 | |||||
| 18 000 | 11.744 | −1.017 | −0.077 | −0.076 | −0.163 | 12.723 | −1.061 | −0.056 | −0.071 | −0.194 | |||||
| 17 000 | 11.856 | −0.969 | −0.058 | −0.068 | −0.174 | 12.835 | −1.023 | −0.034 | −0.061 | −0.201 | |||||
| 16 000 | 11.975 | −0.922 | −0.035 | −0.059 | −0.183 | 12.950 | −0.993 | −0.010 | −0.048 | −0.203 | |||||
| 15 000 | 12.105 | −0.883 | −0.008 | −0.046 | −0.187 | 13.065 | −0.971 | 0.016 | −0.034 | −0.203 | |||||
| 14 000 | 12.239 | −0.857 | 0.023 | −0.029 | −0.188 | 13.175 | −0.950 | 0.040 | −0.021 | −0.203 | |||||
| 13 000 | 12.367 | −0.837 | 0.053 | −0.012 | −0.188 | 13.323 | −0.922 | 0.070 | −0.002 | −0.199 | |||||
| 12 000 | 12.547 | −0.810 | 0.093 | 0.010 | −0.180 | 13.524 | −0.885 | 0.109 | 0.021 | −0.190 | |||||
| 11 000 | 12.793 | −0.780 | 0.138 | 0.039 | −0.157 | 13.780 | −0.853 | 0.150 | 0.050 | −0.165 | |||||
| 10 000 | 13.123 | −0.774 | 0.194 | 0.077 | −0.108 | 14.112 | −0.841 | 0.201 | 0.086 | −0.115 | |||||
| 9500 | 13.320 | −0.774 | 0.226 | 0.100 | −0.075 | 14.303 | −0.833 | 0.231 | 0.106 | −0.085 | |||||
| 9000 | 13.530 | −0.770 | 0.262 | 0.122 | −0.042 | 14.505 | −0.818 | 0.264 | 0.126 | −0.056 | |||||
| 8500 | 13.756 | −0.756 | 0.301 | 0.145 | −0.012 | 14.719 | −0.793 | 0.301 | 0.148 | −0.027 | |||||
| 8000 | 13.996 | −0.727 | 0.346 | 0.169 | 0.017 | 14.950 | −0.752 | 0.345 | 0.172 | −0.002 | |||||
| 7500 | 14.257 | −0.678 | 0.399 | 0.198 | 0.043 | 15.199 | −0.687 | 0.396 | 0.199 | 0.028 | |||||
| 7000 | 14.544 | −0.595 | 0.463 | 0.229 | 0.074 | 15.481 | −0.582 | 0.463 | 0.229 | 0.064 | |||||
| 6500 | 14.877 | −0.453 | 0.547 | 0.266 | 0.113 | 15.814 | −0.404 | 0.550 | 0.266 | 0.109 | |||||
| 6000 | 15.274 | −0.187 | 0.654 | 0.310 | 0.156 | 16.211 | −0.043 | 0.665 | 0.308 | 0.156 | |||||
g-band absolute magnitudes and colours of DA white dwarfs in the VPHAS+ Vega system.
| . | log g = 7.00 . | log g = 7.50 . | log g = 8.00 . | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Teff . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . |
| 100 000 | 6.114 | −1.603 | −0.317 | −0.173 | 0.045 | 7.209 | −1.603 | −0.315 | −0.172 | 0.040 | 8.255 | −1.604 | −0.313 | −0.172 | 0.035 |
| 90 000 | 6.289 | −1.595 | −0.313 | −0.171 | 0.044 | 7.349 | −1.595 | −0.311 | −0.171 | 0.039 | 9.338 | −1.599 | −0.307 | −0.169 | 0.026 |
| 80 000 | 6.473 | −1.585 | −0.308 | −0.169 | 0.042 | 7.511 | −1.586 | −0.306 | −0.169 | 0.036 | 9.450 | −1.590 | −0.302 | −0.167 | 0.022 |
| 75 000 | 6.580 | −1.579 | −0.306 | −0.168 | 0.041 | 7.597 | −1.580 | −0.304 | −0.167 | 0.034 | 9.511 | −1.585 | −0.299 | −0.166 | 0.019 |
| 70 000 | 6.698 | −1.572 | −0.303 | −0.167 | 0.039 | 7.686 | −1.574 | −0.301 | −0.166 | 0.032 | 9.578 | −1.579 | −0.295 | −0.165 | 0.016 |
| 65 000 | 6.818 | −1.564 | −0.300 | −0.165 | 0.037 | 7.781 | −1.566 | −0.297 | −0.165 | 0.030 | 9.649 | −1.573 | −0.292 | −0.163 | 0.013 |
| 60 000 | 6.939 | −1.555 | −0.296 | −0.164 | 0.035 | 7.884 | −1.557 | −0.294 | −0.164 | 0.027 | 9.726 | −1.565 | −0.288 | −0.162 | 0.009 |
| 55 000 | 7.063 | −1.544 | −0.292 | −0.163 | 0.032 | 7.997 | −1.547 | −0.289 | −0.162 | 0.023 | 9.813 | −1.555 | −0.283 | −0.160 | 0.003 |
| 50 000 | 7.197 | −1.530 | −0.287 | −0.161 | 0.028 | 8.127 | −1.533 | −0.284 | −0.160 | 0.018 | 9.911 | −1.543 | −0.277 | −0.158 | −0.003 |
| 45 000 | 7.352 | −1.512 | −0.281 | −0.158 | 0.022 | 8.274 | −1.516 | −0.278 | −0.158 | 0.012 | 10.027 | −1.528 | −0.269 | −0.155 | −0.013 |
| 40 000 | 7.540 | −1.485 | −0.273 | −0.155 | 0.014 | 8.451 | −1.490 | −0.269 | −0.154 | 0.002 | 10.172 | −1.505 | −0.259 | −0.151 | −0.026 |
| 35 000 | 7.803 | −1.441 | −0.261 | −0.150 | 0.001 | 8.685 | −1.448 | −0.256 | −0.149 | −0.014 | 10.372 | −1.469 | −0.244 | −0.146 | −0.047 |
| 30 000 | 8.182 | −1.347 | −0.240 | −0.141 | −0.024 | 9.058 | −1.360 | −0.233 | −0.140 | −0.043 | 10.695 | −1.393 | −0.216 | −0.135 | −0.087 |
| 28 000 | 8.365 | −1.293 | −0.227 | −0.134 | −0.033 | 9.235 | −1.307 | −0.219 | −0.133 | −0.054 | 10.858 | −1.346 | −0.200 | −0.128 | −0.104 |
| 26 000 | 8.549 | −1.236 | −0.210 | −0.126 | −0.038 | 9.413 | −1.251 | −0.202 | −0.125 | −0.062 | 11.025 | −1.294 | −0.180 | −0.120 | −0.115 |
| 24 000 | 8.734 | −1.174 | −0.192 | −0.117 | −0.043 | 9.591 | −1.192 | −0.183 | −0.116 | −0.068 | 11.186 | −1.238 | −0.159 | −0.111 | −0.123 |
| 22 000 | 8.928 | −1.105 | −0.172 | −0.108 | −0.049 | 9.776 | −1.124 | −0.162 | −0.106 | −0.075 | 11.358 | −1.176 | −0.135 | −0.101 | −0.133 |
| 20 000 | 9.134 | −1.023 | −0.150 | −0.098 | −0.058 | 9.973 | −1.045 | −0.139 | −0.096 | −0.085 | 11.542 | −1.103 | −0.108 | −0.090 | −0.145 |
| 19 000 | 9.246 | −0.977 | −0.138 | −0.092 | −0.063 | 10.078 | −0.999 | −0.126 | −0.090 | −0.091 | 11.640 | −1.062 | −0.093 | −0.083 | −0.153 |
| 18 000 | 9.364 | −0.925 | −0.125 | −0.086 | −0.069 | 10.189 | −0.949 | −0.112 | −0.084 | −0.099 | 11.744 | −1.017 | −0.077 | −0.076 | −0.163 |
| 17 000 | 9.487 | −0.867 | −0.111 | −0.079 | −0.077 | 10.306 | −0.894 | −0.096 | −0.077 | −0.108 | 11.856 | −0.969 | −0.058 | −0.068 | −0.174 |
| 16 000 | 9.621 | −0.803 | −0.095 | −0.072 | −0.086 | 10.432 | −0.833 | −0.079 | −0.069 | −0.119 | 11.975 | −0.922 | −0.035 | −0.059 | −0.183 |
| 15 000 | 9.766 | −0.732 | −0.077 | −0.063 | −0.097 | 10.567 | −0.767 | −0.058 | −0.060 | −0.132 | 12.105 | −0.883 | −0.008 | −0.046 | −0.187 |
| 14 000 | 9.924 | −0.654 | −0.055 | −0.053 | −0.111 | 10.716 | −0.698 | −0.033 | −0.049 | −0.146 | 12.239 | −0.857 | 0.023 | −0.029 | −0.188 |
| 13 000 | 10.101 | −0.573 | −0.027 | −0.041 | −0.126 | 10.884 | −0.634 | −0.001 | −0.034 | −0.156 | 12.367 | −0.837 | 0.053 | −0.012 | −0.188 |
| 12 000 | 10.303 | −0.500 | 0.011 | −0.024 | −0.137 | 11.065 | −0.602 | 0.044 | −0.013 | −0.158 | 12.547 | −0.810 | 0.093 | 0.010 | −0.180 |
| 11 000 | 10.524 | −0.481 | 0.068 | 0.003 | −0.134 | 11.273 | −0.595 | 0.096 | 0.015 | −0.146 | 12.793 | −0.780 | 0.138 | 0.039 | −0.157 |
| 10 000 | 10.839 | −0.495 | 0.141 | 0.043 | −0.101 | 11.596 | −0.602 | 0.163 | 0.057 | −0.102 | 13.123 | −0.774 | 0.194 | 0.077 | −0.108 |
| 9500 | 11.053 | −0.518 | 0.183 | 0.070 | −0.070 | 11.802 | −0.620 | 0.203 | 0.082 | −0.069 | 13.320 | −0.774 | 0.226 | 0.100 | −0.075 |
| 9000 | 11.297 | −0.552 | 0.230 | 0.099 | −0.031 | 12.031 | −0.641 | 0.246 | 0.108 | −0.031 | 13.530 | −0.770 | 0.262 | 0.122 | −0.042 |
| 8500 | 11.565 | −0.583 | 0.279 | 0.129 | 0.009 | 12.277 | −0.654 | 0.291 | 0.135 | 0.007 | 13.756 | −0.756 | 0.301 | 0.145 | −0.012 |
| 8000 | 11.852 | −0.600 | 0.333 | 0.159 | 0.048 | 12.541 | −0.652 | 0.341 | 0.163 | 0.041 | 13.996 | −0.727 | 0.346 | 0.169 | 0.017 |
| 7500 | 12.159 | −0.594 | 0.392 | 0.191 | 0.081 | 12.824 | −0.629 | 0.397 | 0.193 | 0.069 | 14.257 | −0.678 | 0.399 | 0.198 | 0.043 |
| 7000 | 12.492 | −0.559 | 0.460 | 0.225 | 0.105 | 13.135 | −0.580 | 0.462 | 0.227 | 0.096 | 14.544 | −0.595 | 0.463 | 0.229 | 0.074 |
| 6500 | 12.861 | −0.485 | 0.537 | 0.264 | 0.134 | 13.482 | −0.489 | 0.541 | 0.265 | 0.126 | 14.877 | −0.453 | 0.547 | 0.266 | 0.113 |
| 6000 | 13.286 | −0.352 | 0.637 | 0.310 | 0.166 | 13.888 | −0.325 | 0.644 | 0.311 | 0.162 | 15.274 | −0.187 | 0.654 | 0.310 | 0.156 |
| log g = 8.50 | log g = 9.00 | ||||||||||||||
| Teff | g | (u − g) | (g − r) | (r − i) | (r − H α) | g | (u − g) | (g − r) | (r − i) | (r − H α) | |||||
| 100 000 | 9.238 | −1.606 | −0.311 | −0.171 | 0.029 | 10.299 | −1.608 | −0.309 | −0.170 | 0.022 | |||||
| 90 000 | 9.338 | −1.599 | −0.307 | −0.169 | 0.026 | 10.388 | −1.601 | −0.305 | −0.168 | 0.018 | |||||
| 80 000 | 9.450 | −1.590 | −0.302 | −0.167 | 0.022 | 10.492 | −1.593 | −0.299 | −0.166 | 0.014 | |||||
| 75 000 | 9.511 | −1.585 | −0.299 | −0.166 | 0.019 | 10.549 | −1.589 | −0.296 | −0.165 | 0.011 | |||||
| 70 000 | 9.578 | −1.579 | −0.295 | −0.165 | 0.016 | 10.610 | −1.583 | −0.293 | −0.163 | 0.008 | |||||
| 65 000 | 9.649 | −1.573 | −0.292 | −0.163 | 0.013 | 10.677 | −1.577 | −0.289 | −0.162 | 0.004 | |||||
| 60 000 | 9.726 | −1.565 | −0.288 | −0.162 | 0.009 | 10.752 | −1.570 | −0.284 | −0.160 | −0.001 | |||||
| 55 000 | 9.813 | −1.555 | −0.283 | −0.160 | 0.003 | 10.834 | −1.561 | −0.279 | −0.158 | −0.007 | |||||
| 50 000 | 9.911 | −1.543 | −0.277 | −0.158 | −0.003 | 10.928 | −1.550 | −0.273 | −0.156 | −0.015 | |||||
| 45 000 | 10.027 | −1.528 | −0.269 | −0.155 | −0.013 | 11.039 | −1.535 | −0.265 | −0.153 | −0.026 | |||||
| 40 000 | 10.172 | −1.505 | −0.259 | −0.151 | −0.026 | 11.178 | −1.515 | −0.254 | −0.149 | −0.041 | |||||
| 35 000 | 10.372 | −1.469 | −0.244 | −0.146 | −0.047 | 11.372 | −1.481 | −0.237 | −0.143 | −0.065 | |||||
| 30 000 | 10.695 | −1.393 | −0.216 | −0.135 | −0.087 | 11.677 | −1.413 | −0.207 | −0.132 | −0.110 | |||||
| 28 000 | 10.858 | −1.346 | −0.200 | −0.128 | −0.104 | 11.838 | −1.370 | −0.189 | −0.125 | −0.130 | |||||
| 26 000 | 11.025 | −1.294 | −0.180 | −0.120 | −0.115 | 12.005 | −1.320 | −0.167 | −0.116 | −0.143 | |||||
| 24 000 | 11.186 | −1.238 | −0.159 | −0.111 | −0.123 | 12.163 | −1.267 | −0.145 | −0.108 | −0.153 | |||||
| 22 000 | 11.358 | −1.176 | −0.135 | −0.101 | −0.133 | 12.335 | −1.208 | −0.119 | −0.097 | −0.163 | |||||
| 20 000 | 11.542 | −1.103 | −0.108 | −0.090 | −0.145 | 12.519 | −1.139 | −0.091 | −0.085 | −0.176 | |||||
| 19 000 | 11.640 | −1.062 | −0.093 | −0.083 | −0.153 | 12.618 | −1.101 | −0.074 | −0.078 | −0.185 | |||||
| 18 000 | 11.744 | −1.017 | −0.077 | −0.076 | −0.163 | 12.723 | −1.061 | −0.056 | −0.071 | −0.194 | |||||
| 17 000 | 11.856 | −0.969 | −0.058 | −0.068 | −0.174 | 12.835 | −1.023 | −0.034 | −0.061 | −0.201 | |||||
| 16 000 | 11.975 | −0.922 | −0.035 | −0.059 | −0.183 | 12.950 | −0.993 | −0.010 | −0.048 | −0.203 | |||||
| 15 000 | 12.105 | −0.883 | −0.008 | −0.046 | −0.187 | 13.065 | −0.971 | 0.016 | −0.034 | −0.203 | |||||
| 14 000 | 12.239 | −0.857 | 0.023 | −0.029 | −0.188 | 13.175 | −0.950 | 0.040 | −0.021 | −0.203 | |||||
| 13 000 | 12.367 | −0.837 | 0.053 | −0.012 | −0.188 | 13.323 | −0.922 | 0.070 | −0.002 | −0.199 | |||||
| 12 000 | 12.547 | −0.810 | 0.093 | 0.010 | −0.180 | 13.524 | −0.885 | 0.109 | 0.021 | −0.190 | |||||
| 11 000 | 12.793 | −0.780 | 0.138 | 0.039 | −0.157 | 13.780 | −0.853 | 0.150 | 0.050 | −0.165 | |||||
| 10 000 | 13.123 | −0.774 | 0.194 | 0.077 | −0.108 | 14.112 | −0.841 | 0.201 | 0.086 | −0.115 | |||||
| 9500 | 13.320 | −0.774 | 0.226 | 0.100 | −0.075 | 14.303 | −0.833 | 0.231 | 0.106 | −0.085 | |||||
| 9000 | 13.530 | −0.770 | 0.262 | 0.122 | −0.042 | 14.505 | −0.818 | 0.264 | 0.126 | −0.056 | |||||
| 8500 | 13.756 | −0.756 | 0.301 | 0.145 | −0.012 | 14.719 | −0.793 | 0.301 | 0.148 | −0.027 | |||||
| 8000 | 13.996 | −0.727 | 0.346 | 0.169 | 0.017 | 14.950 | −0.752 | 0.345 | 0.172 | −0.002 | |||||
| 7500 | 14.257 | −0.678 | 0.399 | 0.198 | 0.043 | 15.199 | −0.687 | 0.396 | 0.199 | 0.028 | |||||
| 7000 | 14.544 | −0.595 | 0.463 | 0.229 | 0.074 | 15.481 | −0.582 | 0.463 | 0.229 | 0.064 | |||||
| 6500 | 14.877 | −0.453 | 0.547 | 0.266 | 0.113 | 15.814 | −0.404 | 0.550 | 0.266 | 0.109 | |||||
| 6000 | 15.274 | −0.187 | 0.654 | 0.310 | 0.156 | 16.211 | −0.043 | 0.665 | 0.308 | 0.156 | |||||
| . | log g = 7.00 . | log g = 7.50 . | log g = 8.00 . | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Teff . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . |
| 100 000 | 6.114 | −1.603 | −0.317 | −0.173 | 0.045 | 7.209 | −1.603 | −0.315 | −0.172 | 0.040 | 8.255 | −1.604 | −0.313 | −0.172 | 0.035 |
| 90 000 | 6.289 | −1.595 | −0.313 | −0.171 | 0.044 | 7.349 | −1.595 | −0.311 | −0.171 | 0.039 | 9.338 | −1.599 | −0.307 | −0.169 | 0.026 |
| 80 000 | 6.473 | −1.585 | −0.308 | −0.169 | 0.042 | 7.511 | −1.586 | −0.306 | −0.169 | 0.036 | 9.450 | −1.590 | −0.302 | −0.167 | 0.022 |
| 75 000 | 6.580 | −1.579 | −0.306 | −0.168 | 0.041 | 7.597 | −1.580 | −0.304 | −0.167 | 0.034 | 9.511 | −1.585 | −0.299 | −0.166 | 0.019 |
| 70 000 | 6.698 | −1.572 | −0.303 | −0.167 | 0.039 | 7.686 | −1.574 | −0.301 | −0.166 | 0.032 | 9.578 | −1.579 | −0.295 | −0.165 | 0.016 |
| 65 000 | 6.818 | −1.564 | −0.300 | −0.165 | 0.037 | 7.781 | −1.566 | −0.297 | −0.165 | 0.030 | 9.649 | −1.573 | −0.292 | −0.163 | 0.013 |
| 60 000 | 6.939 | −1.555 | −0.296 | −0.164 | 0.035 | 7.884 | −1.557 | −0.294 | −0.164 | 0.027 | 9.726 | −1.565 | −0.288 | −0.162 | 0.009 |
| 55 000 | 7.063 | −1.544 | −0.292 | −0.163 | 0.032 | 7.997 | −1.547 | −0.289 | −0.162 | 0.023 | 9.813 | −1.555 | −0.283 | −0.160 | 0.003 |
| 50 000 | 7.197 | −1.530 | −0.287 | −0.161 | 0.028 | 8.127 | −1.533 | −0.284 | −0.160 | 0.018 | 9.911 | −1.543 | −0.277 | −0.158 | −0.003 |
| 45 000 | 7.352 | −1.512 | −0.281 | −0.158 | 0.022 | 8.274 | −1.516 | −0.278 | −0.158 | 0.012 | 10.027 | −1.528 | −0.269 | −0.155 | −0.013 |
| 40 000 | 7.540 | −1.485 | −0.273 | −0.155 | 0.014 | 8.451 | −1.490 | −0.269 | −0.154 | 0.002 | 10.172 | −1.505 | −0.259 | −0.151 | −0.026 |
| 35 000 | 7.803 | −1.441 | −0.261 | −0.150 | 0.001 | 8.685 | −1.448 | −0.256 | −0.149 | −0.014 | 10.372 | −1.469 | −0.244 | −0.146 | −0.047 |
| 30 000 | 8.182 | −1.347 | −0.240 | −0.141 | −0.024 | 9.058 | −1.360 | −0.233 | −0.140 | −0.043 | 10.695 | −1.393 | −0.216 | −0.135 | −0.087 |
| 28 000 | 8.365 | −1.293 | −0.227 | −0.134 | −0.033 | 9.235 | −1.307 | −0.219 | −0.133 | −0.054 | 10.858 | −1.346 | −0.200 | −0.128 | −0.104 |
| 26 000 | 8.549 | −1.236 | −0.210 | −0.126 | −0.038 | 9.413 | −1.251 | −0.202 | −0.125 | −0.062 | 11.025 | −1.294 | −0.180 | −0.120 | −0.115 |
| 24 000 | 8.734 | −1.174 | −0.192 | −0.117 | −0.043 | 9.591 | −1.192 | −0.183 | −0.116 | −0.068 | 11.186 | −1.238 | −0.159 | −0.111 | −0.123 |
| 22 000 | 8.928 | −1.105 | −0.172 | −0.108 | −0.049 | 9.776 | −1.124 | −0.162 | −0.106 | −0.075 | 11.358 | −1.176 | −0.135 | −0.101 | −0.133 |
| 20 000 | 9.134 | −1.023 | −0.150 | −0.098 | −0.058 | 9.973 | −1.045 | −0.139 | −0.096 | −0.085 | 11.542 | −1.103 | −0.108 | −0.090 | −0.145 |
| 19 000 | 9.246 | −0.977 | −0.138 | −0.092 | −0.063 | 10.078 | −0.999 | −0.126 | −0.090 | −0.091 | 11.640 | −1.062 | −0.093 | −0.083 | −0.153 |
| 18 000 | 9.364 | −0.925 | −0.125 | −0.086 | −0.069 | 10.189 | −0.949 | −0.112 | −0.084 | −0.099 | 11.744 | −1.017 | −0.077 | −0.076 | −0.163 |
| 17 000 | 9.487 | −0.867 | −0.111 | −0.079 | −0.077 | 10.306 | −0.894 | −0.096 | −0.077 | −0.108 | 11.856 | −0.969 | −0.058 | −0.068 | −0.174 |
| 16 000 | 9.621 | −0.803 | −0.095 | −0.072 | −0.086 | 10.432 | −0.833 | −0.079 | −0.069 | −0.119 | 11.975 | −0.922 | −0.035 | −0.059 | −0.183 |
| 15 000 | 9.766 | −0.732 | −0.077 | −0.063 | −0.097 | 10.567 | −0.767 | −0.058 | −0.060 | −0.132 | 12.105 | −0.883 | −0.008 | −0.046 | −0.187 |
| 14 000 | 9.924 | −0.654 | −0.055 | −0.053 | −0.111 | 10.716 | −0.698 | −0.033 | −0.049 | −0.146 | 12.239 | −0.857 | 0.023 | −0.029 | −0.188 |
| 13 000 | 10.101 | −0.573 | −0.027 | −0.041 | −0.126 | 10.884 | −0.634 | −0.001 | −0.034 | −0.156 | 12.367 | −0.837 | 0.053 | −0.012 | −0.188 |
| 12 000 | 10.303 | −0.500 | 0.011 | −0.024 | −0.137 | 11.065 | −0.602 | 0.044 | −0.013 | −0.158 | 12.547 | −0.810 | 0.093 | 0.010 | −0.180 |
| 11 000 | 10.524 | −0.481 | 0.068 | 0.003 | −0.134 | 11.273 | −0.595 | 0.096 | 0.015 | −0.146 | 12.793 | −0.780 | 0.138 | 0.039 | −0.157 |
| 10 000 | 10.839 | −0.495 | 0.141 | 0.043 | −0.101 | 11.596 | −0.602 | 0.163 | 0.057 | −0.102 | 13.123 | −0.774 | 0.194 | 0.077 | −0.108 |
| 9500 | 11.053 | −0.518 | 0.183 | 0.070 | −0.070 | 11.802 | −0.620 | 0.203 | 0.082 | −0.069 | 13.320 | −0.774 | 0.226 | 0.100 | −0.075 |
| 9000 | 11.297 | −0.552 | 0.230 | 0.099 | −0.031 | 12.031 | −0.641 | 0.246 | 0.108 | −0.031 | 13.530 | −0.770 | 0.262 | 0.122 | −0.042 |
| 8500 | 11.565 | −0.583 | 0.279 | 0.129 | 0.009 | 12.277 | −0.654 | 0.291 | 0.135 | 0.007 | 13.756 | −0.756 | 0.301 | 0.145 | −0.012 |
| 8000 | 11.852 | −0.600 | 0.333 | 0.159 | 0.048 | 12.541 | −0.652 | 0.341 | 0.163 | 0.041 | 13.996 | −0.727 | 0.346 | 0.169 | 0.017 |
| 7500 | 12.159 | −0.594 | 0.392 | 0.191 | 0.081 | 12.824 | −0.629 | 0.397 | 0.193 | 0.069 | 14.257 | −0.678 | 0.399 | 0.198 | 0.043 |
| 7000 | 12.492 | −0.559 | 0.460 | 0.225 | 0.105 | 13.135 | −0.580 | 0.462 | 0.227 | 0.096 | 14.544 | −0.595 | 0.463 | 0.229 | 0.074 |
| 6500 | 12.861 | −0.485 | 0.537 | 0.264 | 0.134 | 13.482 | −0.489 | 0.541 | 0.265 | 0.126 | 14.877 | −0.453 | 0.547 | 0.266 | 0.113 |
| 6000 | 13.286 | −0.352 | 0.637 | 0.310 | 0.166 | 13.888 | −0.325 | 0.644 | 0.311 | 0.162 | 15.274 | −0.187 | 0.654 | 0.310 | 0.156 |
| log g = 8.50 | log g = 9.00 | ||||||||||||||
| Teff | g | (u − g) | (g − r) | (r − i) | (r − H α) | g | (u − g) | (g − r) | (r − i) | (r − H α) | |||||
| 100 000 | 9.238 | −1.606 | −0.311 | −0.171 | 0.029 | 10.299 | −1.608 | −0.309 | −0.170 | 0.022 | |||||
| 90 000 | 9.338 | −1.599 | −0.307 | −0.169 | 0.026 | 10.388 | −1.601 | −0.305 | −0.168 | 0.018 | |||||
| 80 000 | 9.450 | −1.590 | −0.302 | −0.167 | 0.022 | 10.492 | −1.593 | −0.299 | −0.166 | 0.014 | |||||
| 75 000 | 9.511 | −1.585 | −0.299 | −0.166 | 0.019 | 10.549 | −1.589 | −0.296 | −0.165 | 0.011 | |||||
| 70 000 | 9.578 | −1.579 | −0.295 | −0.165 | 0.016 | 10.610 | −1.583 | −0.293 | −0.163 | 0.008 | |||||
| 65 000 | 9.649 | −1.573 | −0.292 | −0.163 | 0.013 | 10.677 | −1.577 | −0.289 | −0.162 | 0.004 | |||||
| 60 000 | 9.726 | −1.565 | −0.288 | −0.162 | 0.009 | 10.752 | −1.570 | −0.284 | −0.160 | −0.001 | |||||
| 55 000 | 9.813 | −1.555 | −0.283 | −0.160 | 0.003 | 10.834 | −1.561 | −0.279 | −0.158 | −0.007 | |||||
| 50 000 | 9.911 | −1.543 | −0.277 | −0.158 | −0.003 | 10.928 | −1.550 | −0.273 | −0.156 | −0.015 | |||||
| 45 000 | 10.027 | −1.528 | −0.269 | −0.155 | −0.013 | 11.039 | −1.535 | −0.265 | −0.153 | −0.026 | |||||
| 40 000 | 10.172 | −1.505 | −0.259 | −0.151 | −0.026 | 11.178 | −1.515 | −0.254 | −0.149 | −0.041 | |||||
| 35 000 | 10.372 | −1.469 | −0.244 | −0.146 | −0.047 | 11.372 | −1.481 | −0.237 | −0.143 | −0.065 | |||||
| 30 000 | 10.695 | −1.393 | −0.216 | −0.135 | −0.087 | 11.677 | −1.413 | −0.207 | −0.132 | −0.110 | |||||
| 28 000 | 10.858 | −1.346 | −0.200 | −0.128 | −0.104 | 11.838 | −1.370 | −0.189 | −0.125 | −0.130 | |||||
| 26 000 | 11.025 | −1.294 | −0.180 | −0.120 | −0.115 | 12.005 | −1.320 | −0.167 | −0.116 | −0.143 | |||||
| 24 000 | 11.186 | −1.238 | −0.159 | −0.111 | −0.123 | 12.163 | −1.267 | −0.145 | −0.108 | −0.153 | |||||
| 22 000 | 11.358 | −1.176 | −0.135 | −0.101 | −0.133 | 12.335 | −1.208 | −0.119 | −0.097 | −0.163 | |||||
| 20 000 | 11.542 | −1.103 | −0.108 | −0.090 | −0.145 | 12.519 | −1.139 | −0.091 | −0.085 | −0.176 | |||||
| 19 000 | 11.640 | −1.062 | −0.093 | −0.083 | −0.153 | 12.618 | −1.101 | −0.074 | −0.078 | −0.185 | |||||
| 18 000 | 11.744 | −1.017 | −0.077 | −0.076 | −0.163 | 12.723 | −1.061 | −0.056 | −0.071 | −0.194 | |||||
| 17 000 | 11.856 | −0.969 | −0.058 | −0.068 | −0.174 | 12.835 | −1.023 | −0.034 | −0.061 | −0.201 | |||||
| 16 000 | 11.975 | −0.922 | −0.035 | −0.059 | −0.183 | 12.950 | −0.993 | −0.010 | −0.048 | −0.203 | |||||
| 15 000 | 12.105 | −0.883 | −0.008 | −0.046 | −0.187 | 13.065 | −0.971 | 0.016 | −0.034 | −0.203 | |||||
| 14 000 | 12.239 | −0.857 | 0.023 | −0.029 | −0.188 | 13.175 | −0.950 | 0.040 | −0.021 | −0.203 | |||||
| 13 000 | 12.367 | −0.837 | 0.053 | −0.012 | −0.188 | 13.323 | −0.922 | 0.070 | −0.002 | −0.199 | |||||
| 12 000 | 12.547 | −0.810 | 0.093 | 0.010 | −0.180 | 13.524 | −0.885 | 0.109 | 0.021 | −0.190 | |||||
| 11 000 | 12.793 | −0.780 | 0.138 | 0.039 | −0.157 | 13.780 | −0.853 | 0.150 | 0.050 | −0.165 | |||||
| 10 000 | 13.123 | −0.774 | 0.194 | 0.077 | −0.108 | 14.112 | −0.841 | 0.201 | 0.086 | −0.115 | |||||
| 9500 | 13.320 | −0.774 | 0.226 | 0.100 | −0.075 | 14.303 | −0.833 | 0.231 | 0.106 | −0.085 | |||||
| 9000 | 13.530 | −0.770 | 0.262 | 0.122 | −0.042 | 14.505 | −0.818 | 0.264 | 0.126 | −0.056 | |||||
| 8500 | 13.756 | −0.756 | 0.301 | 0.145 | −0.012 | 14.719 | −0.793 | 0.301 | 0.148 | −0.027 | |||||
| 8000 | 13.996 | −0.727 | 0.346 | 0.169 | 0.017 | 14.950 | −0.752 | 0.345 | 0.172 | −0.002 | |||||
| 7500 | 14.257 | −0.678 | 0.399 | 0.198 | 0.043 | 15.199 | −0.687 | 0.396 | 0.199 | 0.028 | |||||
| 7000 | 14.544 | −0.595 | 0.463 | 0.229 | 0.074 | 15.481 | −0.582 | 0.463 | 0.229 | 0.064 | |||||
| 6500 | 14.877 | −0.453 | 0.547 | 0.266 | 0.113 | 15.814 | −0.404 | 0.550 | 0.266 | 0.109 | |||||
| 6000 | 15.274 | −0.187 | 0.654 | 0.310 | 0.156 | 16.211 | −0.043 | 0.665 | 0.308 | 0.156 | |||||
g-band absolute magnitudes and colours of DB white dwarfs in the VPHAS+ Vega system.
| . | log g = 7.00 . | log g = 7.50 . | log g = 8.00 . | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Teff . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . |
| 40 000 | 7.672 | −1.467 | −0.260 | −0.148 | 0.073 | 8.710 | −1.466 | −0.254 | −0.144 | 0.071 | 9.557 | −1.469 | −0.250 | −0.141 | 0.069 |
| 35 000 | 8.016 | −1.407 | −0.234 | −0.135 | 0.076 | 9.008 | −1.409 | −0.228 | −0.132 | 0.074 | 9.824 | −1.413 | −0.223 | −0.128 | 0.070 |
| 30 000 | 8.375 | −1.334 | −0.205 | −0.122 | 0.078 | 9.317 | −1.337 | −0.198 | −0.118 | 0.075 | 10.105 | −1.345 | −0.192 | −0.112 | 0.070 |
| 28 000 | 8.530 | −1.299 | −0.191 | −0.115 | 0.079 | 9.447 | −1.304 | −0.183 | −0.111 | 0.075 | 10.225 | −1.317 | −0.177 | −0.105 | 0.070 |
| 26 000 | 8.691 | −1.263 | −0.175 | −0.108 | 0.079 | 9.585 | −1.273 | −0.168 | −0.103 | 0.075 | 10.349 | −1.291 | −0.161 | −0.096 | 0.071 |
| 24 000 | 8.861 | −1.227 | −0.158 | −0.099 | 0.080 | 9.730 | −1.242 | −0.150 | −0.094 | 0.076 | 10.467 | −1.269 | −0.145 | −0.088 | 0.073 |
| 22 000 | 9.043 | −1.191 | −0.139 | −0.090 | 0.082 | 9.863 | −1.218 | −0.134 | −0.087 | 0.078 | 10.553 | −1.257 | −0.133 | −0.083 | 0.075 |
| 20 000 | 9.179 | −1.174 | −0.127 | −0.087 | 0.082 | 9.957 | −1.212 | −0.123 | −0.083 | 0.080 | 10.662 | −1.248 | −0.117 | −0.077 | 0.080 |
| 19 000 | 9.245 | −1.174 | −0.119 | −0.085 | 0.084 | 10.039 | −1.209 | −0.112 | −0.078 | 0.085 | 10.753 | −1.242 | −0.105 | −0.072 | 0.085 |
| 18 000 | 9.351 | −1.174 | −0.106 | −0.079 | 0.090 | 10.149 | −1.207 | −0.097 | −0.072 | 0.091 | 10.862 | −1.236 | −0.090 | −0.067 | 0.092 |
| 17 000 | 9.466 | −1.177 | −0.088 | −0.070 | 0.096 | 10.279 | −1.205 | −0.080 | −0.064 | 0.098 | 10.989 | −1.230 | −0.073 | −0.060 | 0.100 |
| 16 000 | 9.626 | −1.178 | −0.067 | −0.060 | 0.104 | 10.427 | −1.201 | −0.059 | −0.055 | 0.106 | 11.133 | −1.221 | −0.054 | −0.052 | 0.108 |
| 15 000 | 9.805 | −1.173 | −0.040 | −0.048 | 0.111 | 10.595 | −1.191 | −0.034 | −0.044 | 0.113 | 11.295 | −1.207 | −0.031 | −0.041 | 0.114 |
| 14 000 | 10.006 | −1.159 | −0.009 | −0.032 | 0.118 | 10.779 | −1.172 | −0.004 | −0.028 | 0.119 | 11.471 | −1.184 | −0.003 | −0.027 | 0.120 |
| 13 000 | 10.225 | −1.134 | 0.029 | −0.013 | 0.125 | 10.982 | −1.142 | 0.031 | −0.011 | 0.125 | 11.665 | −1.149 | 0.032 | −0.010 | 0.126 |
| 12 000 | 10.466 | −1.095 | 0.071 | 0.009 | 0.132 | 11.203 | −1.099 | 0.072 | 0.010 | 0.132 | 11.877 | −1.102 | 0.072 | 0.011 | 0.132 |
| 11 000 | 10.732 | −1.033 | 0.118 | 0.032 | 0.139 | 11.449 | −1.034 | 0.119 | 0.032 | 0.138 | 12.115 | −1.035 | 0.119 | 0.032 | 0.138 |
| 10 000 | 11.048 | −0.950 | 0.180 | 0.061 | 0.148 | 11.745 | −0.950 | 0.180 | 0.061 | 0.147 | 12.403 | −0.950 | 0.180 | 0.060 | 0.148 |
| log g = 8.50 | log g = 9.00 | ||||||||||||||
| Teff | g | (u − g) | (g − r) | (r − i) | (r − H α) | g | (u − g) | (g − r) | (r − i) | (r − H α) | |||||
| 40 000 | 10.403 | −1.474 | −0.246 | −0.136 | 0.066 | 11.396 | −1.479 | −0.245 | −0.130 | 0.062 | |||||
| 35 000 | 10.661 | −1.420 | −0.219 | −0.122 | 0.066 | 11.644 | −1.429 | −0.218 | −0.115 | 0.061 | |||||
| 30 000 | 10.933 | −1.359 | −0.188 | −0.105 | 0.065 | 11.898 | −1.378 | −0.187 | −0.097 | 0.062 | |||||
| 28 000 | 11.042 | −1.336 | −0.173 | −0.097 | 0.066 | 11.989 | −1.362 | −0.173 | −0.090 | 0.065 | |||||
| 26 000 | 11.145 | −1.317 | −0.157 | −0.089 | 0.069 | 12.067 | −1.348 | −0.161 | −0.083 | 0.068 | |||||
| 24 000 | 11.232 | −1.303 | −0.144 | −0.083 | 0.071 | 12.135 | −1.336 | −0.152 | −0.078 | 0.070 | |||||
| 22 000 | 11.306 | −1.294 | −0.134 | −0.078 | 0.074 | 12.240 | −1.320 | −0.137 | −0.071 | 0.075 | |||||
| 20 000 | 11.448 | −1.275 | −0.114 | −0.071 | 0.081 | 12.407 | −1.301 | −0.115 | −0.065 | 0.084 | |||||
| 19 000 | 11.545 | −1.266 | −0.103 | −0.067 | 0.086 | 12.511 | −1.291 | −0.102 | −0.063 | 0.090 | |||||
| 18 000 | 11.657 | −1.257 | −0.090 | −0.063 | 0.094 | 12.629 | −1.281 | −0.089 | −0.060 | 0.097 | |||||
| 17 000 | 11.784 | −1.250 | −0.075 | −0.058 | 0.101 | 12.760 | −1.269 | −0.074 | −0.056 | 0.104 | |||||
| 16 000 | 11.927 | −1.241 | −0.058 | −0.051 | 0.108 | 12.903 | −1.252 | −0.055 | −0.049 | 0.110 | |||||
| 15 000 | 12.084 | −1.222 | −0.035 | −0.041 | 0.114 | 13.058 | −1.229 | −0.032 | −0.039 | 0.116 | |||||
| 14 000 | 12.259 | −1.195 | −0.005 | −0.027 | 0.120 | 13.226 | −1.197 | −0.003 | −0.025 | 0.121 | |||||
| 13 000 | 12.445 | −1.159 | 0.024 | −0.012 | 0.125 | 13.409 | −1.156 | 0.032 | −0.008 | 0.126 | |||||
| 12 000 | 12.662 | −1.111 | 0.063 | 0.003 | 0.130 | 13.614 | −1.104 | 0.072 | 0.011 | 0.132 | |||||
| 11 000 | 12.892 | −1.035 | 0.119 | 0.032 | 0.139 | 13.848 | −1.035 | 0.120 | 0.032 | 0.139 | |||||
| 10 000 | 13.176 | −0.950 | 0.181 | 0.059 | 0.148 | 14.130 | −0.950 | 0.181 | 0.059 | 0.148 | |||||
| . | log g = 7.00 . | log g = 7.50 . | log g = 8.00 . | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Teff . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . |
| 40 000 | 7.672 | −1.467 | −0.260 | −0.148 | 0.073 | 8.710 | −1.466 | −0.254 | −0.144 | 0.071 | 9.557 | −1.469 | −0.250 | −0.141 | 0.069 |
| 35 000 | 8.016 | −1.407 | −0.234 | −0.135 | 0.076 | 9.008 | −1.409 | −0.228 | −0.132 | 0.074 | 9.824 | −1.413 | −0.223 | −0.128 | 0.070 |
| 30 000 | 8.375 | −1.334 | −0.205 | −0.122 | 0.078 | 9.317 | −1.337 | −0.198 | −0.118 | 0.075 | 10.105 | −1.345 | −0.192 | −0.112 | 0.070 |
| 28 000 | 8.530 | −1.299 | −0.191 | −0.115 | 0.079 | 9.447 | −1.304 | −0.183 | −0.111 | 0.075 | 10.225 | −1.317 | −0.177 | −0.105 | 0.070 |
| 26 000 | 8.691 | −1.263 | −0.175 | −0.108 | 0.079 | 9.585 | −1.273 | −0.168 | −0.103 | 0.075 | 10.349 | −1.291 | −0.161 | −0.096 | 0.071 |
| 24 000 | 8.861 | −1.227 | −0.158 | −0.099 | 0.080 | 9.730 | −1.242 | −0.150 | −0.094 | 0.076 | 10.467 | −1.269 | −0.145 | −0.088 | 0.073 |
| 22 000 | 9.043 | −1.191 | −0.139 | −0.090 | 0.082 | 9.863 | −1.218 | −0.134 | −0.087 | 0.078 | 10.553 | −1.257 | −0.133 | −0.083 | 0.075 |
| 20 000 | 9.179 | −1.174 | −0.127 | −0.087 | 0.082 | 9.957 | −1.212 | −0.123 | −0.083 | 0.080 | 10.662 | −1.248 | −0.117 | −0.077 | 0.080 |
| 19 000 | 9.245 | −1.174 | −0.119 | −0.085 | 0.084 | 10.039 | −1.209 | −0.112 | −0.078 | 0.085 | 10.753 | −1.242 | −0.105 | −0.072 | 0.085 |
| 18 000 | 9.351 | −1.174 | −0.106 | −0.079 | 0.090 | 10.149 | −1.207 | −0.097 | −0.072 | 0.091 | 10.862 | −1.236 | −0.090 | −0.067 | 0.092 |
| 17 000 | 9.466 | −1.177 | −0.088 | −0.070 | 0.096 | 10.279 | −1.205 | −0.080 | −0.064 | 0.098 | 10.989 | −1.230 | −0.073 | −0.060 | 0.100 |
| 16 000 | 9.626 | −1.178 | −0.067 | −0.060 | 0.104 | 10.427 | −1.201 | −0.059 | −0.055 | 0.106 | 11.133 | −1.221 | −0.054 | −0.052 | 0.108 |
| 15 000 | 9.805 | −1.173 | −0.040 | −0.048 | 0.111 | 10.595 | −1.191 | −0.034 | −0.044 | 0.113 | 11.295 | −1.207 | −0.031 | −0.041 | 0.114 |
| 14 000 | 10.006 | −1.159 | −0.009 | −0.032 | 0.118 | 10.779 | −1.172 | −0.004 | −0.028 | 0.119 | 11.471 | −1.184 | −0.003 | −0.027 | 0.120 |
| 13 000 | 10.225 | −1.134 | 0.029 | −0.013 | 0.125 | 10.982 | −1.142 | 0.031 | −0.011 | 0.125 | 11.665 | −1.149 | 0.032 | −0.010 | 0.126 |
| 12 000 | 10.466 | −1.095 | 0.071 | 0.009 | 0.132 | 11.203 | −1.099 | 0.072 | 0.010 | 0.132 | 11.877 | −1.102 | 0.072 | 0.011 | 0.132 |
| 11 000 | 10.732 | −1.033 | 0.118 | 0.032 | 0.139 | 11.449 | −1.034 | 0.119 | 0.032 | 0.138 | 12.115 | −1.035 | 0.119 | 0.032 | 0.138 |
| 10 000 | 11.048 | −0.950 | 0.180 | 0.061 | 0.148 | 11.745 | −0.950 | 0.180 | 0.061 | 0.147 | 12.403 | −0.950 | 0.180 | 0.060 | 0.148 |
| log g = 8.50 | log g = 9.00 | ||||||||||||||
| Teff | g | (u − g) | (g − r) | (r − i) | (r − H α) | g | (u − g) | (g − r) | (r − i) | (r − H α) | |||||
| 40 000 | 10.403 | −1.474 | −0.246 | −0.136 | 0.066 | 11.396 | −1.479 | −0.245 | −0.130 | 0.062 | |||||
| 35 000 | 10.661 | −1.420 | −0.219 | −0.122 | 0.066 | 11.644 | −1.429 | −0.218 | −0.115 | 0.061 | |||||
| 30 000 | 10.933 | −1.359 | −0.188 | −0.105 | 0.065 | 11.898 | −1.378 | −0.187 | −0.097 | 0.062 | |||||
| 28 000 | 11.042 | −1.336 | −0.173 | −0.097 | 0.066 | 11.989 | −1.362 | −0.173 | −0.090 | 0.065 | |||||
| 26 000 | 11.145 | −1.317 | −0.157 | −0.089 | 0.069 | 12.067 | −1.348 | −0.161 | −0.083 | 0.068 | |||||
| 24 000 | 11.232 | −1.303 | −0.144 | −0.083 | 0.071 | 12.135 | −1.336 | −0.152 | −0.078 | 0.070 | |||||
| 22 000 | 11.306 | −1.294 | −0.134 | −0.078 | 0.074 | 12.240 | −1.320 | −0.137 | −0.071 | 0.075 | |||||
| 20 000 | 11.448 | −1.275 | −0.114 | −0.071 | 0.081 | 12.407 | −1.301 | −0.115 | −0.065 | 0.084 | |||||
| 19 000 | 11.545 | −1.266 | −0.103 | −0.067 | 0.086 | 12.511 | −1.291 | −0.102 | −0.063 | 0.090 | |||||
| 18 000 | 11.657 | −1.257 | −0.090 | −0.063 | 0.094 | 12.629 | −1.281 | −0.089 | −0.060 | 0.097 | |||||
| 17 000 | 11.784 | −1.250 | −0.075 | −0.058 | 0.101 | 12.760 | −1.269 | −0.074 | −0.056 | 0.104 | |||||
| 16 000 | 11.927 | −1.241 | −0.058 | −0.051 | 0.108 | 12.903 | −1.252 | −0.055 | −0.049 | 0.110 | |||||
| 15 000 | 12.084 | −1.222 | −0.035 | −0.041 | 0.114 | 13.058 | −1.229 | −0.032 | −0.039 | 0.116 | |||||
| 14 000 | 12.259 | −1.195 | −0.005 | −0.027 | 0.120 | 13.226 | −1.197 | −0.003 | −0.025 | 0.121 | |||||
| 13 000 | 12.445 | −1.159 | 0.024 | −0.012 | 0.125 | 13.409 | −1.156 | 0.032 | −0.008 | 0.126 | |||||
| 12 000 | 12.662 | −1.111 | 0.063 | 0.003 | 0.130 | 13.614 | −1.104 | 0.072 | 0.011 | 0.132 | |||||
| 11 000 | 12.892 | −1.035 | 0.119 | 0.032 | 0.139 | 13.848 | −1.035 | 0.120 | 0.032 | 0.139 | |||||
| 10 000 | 13.176 | −0.950 | 0.181 | 0.059 | 0.148 | 14.130 | −0.950 | 0.181 | 0.059 | 0.148 | |||||
g-band absolute magnitudes and colours of DB white dwarfs in the VPHAS+ Vega system.
| . | log g = 7.00 . | log g = 7.50 . | log g = 8.00 . | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Teff . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . |
| 40 000 | 7.672 | −1.467 | −0.260 | −0.148 | 0.073 | 8.710 | −1.466 | −0.254 | −0.144 | 0.071 | 9.557 | −1.469 | −0.250 | −0.141 | 0.069 |
| 35 000 | 8.016 | −1.407 | −0.234 | −0.135 | 0.076 | 9.008 | −1.409 | −0.228 | −0.132 | 0.074 | 9.824 | −1.413 | −0.223 | −0.128 | 0.070 |
| 30 000 | 8.375 | −1.334 | −0.205 | −0.122 | 0.078 | 9.317 | −1.337 | −0.198 | −0.118 | 0.075 | 10.105 | −1.345 | −0.192 | −0.112 | 0.070 |
| 28 000 | 8.530 | −1.299 | −0.191 | −0.115 | 0.079 | 9.447 | −1.304 | −0.183 | −0.111 | 0.075 | 10.225 | −1.317 | −0.177 | −0.105 | 0.070 |
| 26 000 | 8.691 | −1.263 | −0.175 | −0.108 | 0.079 | 9.585 | −1.273 | −0.168 | −0.103 | 0.075 | 10.349 | −1.291 | −0.161 | −0.096 | 0.071 |
| 24 000 | 8.861 | −1.227 | −0.158 | −0.099 | 0.080 | 9.730 | −1.242 | −0.150 | −0.094 | 0.076 | 10.467 | −1.269 | −0.145 | −0.088 | 0.073 |
| 22 000 | 9.043 | −1.191 | −0.139 | −0.090 | 0.082 | 9.863 | −1.218 | −0.134 | −0.087 | 0.078 | 10.553 | −1.257 | −0.133 | −0.083 | 0.075 |
| 20 000 | 9.179 | −1.174 | −0.127 | −0.087 | 0.082 | 9.957 | −1.212 | −0.123 | −0.083 | 0.080 | 10.662 | −1.248 | −0.117 | −0.077 | 0.080 |
| 19 000 | 9.245 | −1.174 | −0.119 | −0.085 | 0.084 | 10.039 | −1.209 | −0.112 | −0.078 | 0.085 | 10.753 | −1.242 | −0.105 | −0.072 | 0.085 |
| 18 000 | 9.351 | −1.174 | −0.106 | −0.079 | 0.090 | 10.149 | −1.207 | −0.097 | −0.072 | 0.091 | 10.862 | −1.236 | −0.090 | −0.067 | 0.092 |
| 17 000 | 9.466 | −1.177 | −0.088 | −0.070 | 0.096 | 10.279 | −1.205 | −0.080 | −0.064 | 0.098 | 10.989 | −1.230 | −0.073 | −0.060 | 0.100 |
| 16 000 | 9.626 | −1.178 | −0.067 | −0.060 | 0.104 | 10.427 | −1.201 | −0.059 | −0.055 | 0.106 | 11.133 | −1.221 | −0.054 | −0.052 | 0.108 |
| 15 000 | 9.805 | −1.173 | −0.040 | −0.048 | 0.111 | 10.595 | −1.191 | −0.034 | −0.044 | 0.113 | 11.295 | −1.207 | −0.031 | −0.041 | 0.114 |
| 14 000 | 10.006 | −1.159 | −0.009 | −0.032 | 0.118 | 10.779 | −1.172 | −0.004 | −0.028 | 0.119 | 11.471 | −1.184 | −0.003 | −0.027 | 0.120 |
| 13 000 | 10.225 | −1.134 | 0.029 | −0.013 | 0.125 | 10.982 | −1.142 | 0.031 | −0.011 | 0.125 | 11.665 | −1.149 | 0.032 | −0.010 | 0.126 |
| 12 000 | 10.466 | −1.095 | 0.071 | 0.009 | 0.132 | 11.203 | −1.099 | 0.072 | 0.010 | 0.132 | 11.877 | −1.102 | 0.072 | 0.011 | 0.132 |
| 11 000 | 10.732 | −1.033 | 0.118 | 0.032 | 0.139 | 11.449 | −1.034 | 0.119 | 0.032 | 0.138 | 12.115 | −1.035 | 0.119 | 0.032 | 0.138 |
| 10 000 | 11.048 | −0.950 | 0.180 | 0.061 | 0.148 | 11.745 | −0.950 | 0.180 | 0.061 | 0.147 | 12.403 | −0.950 | 0.180 | 0.060 | 0.148 |
| log g = 8.50 | log g = 9.00 | ||||||||||||||
| Teff | g | (u − g) | (g − r) | (r − i) | (r − H α) | g | (u − g) | (g − r) | (r − i) | (r − H α) | |||||
| 40 000 | 10.403 | −1.474 | −0.246 | −0.136 | 0.066 | 11.396 | −1.479 | −0.245 | −0.130 | 0.062 | |||||
| 35 000 | 10.661 | −1.420 | −0.219 | −0.122 | 0.066 | 11.644 | −1.429 | −0.218 | −0.115 | 0.061 | |||||
| 30 000 | 10.933 | −1.359 | −0.188 | −0.105 | 0.065 | 11.898 | −1.378 | −0.187 | −0.097 | 0.062 | |||||
| 28 000 | 11.042 | −1.336 | −0.173 | −0.097 | 0.066 | 11.989 | −1.362 | −0.173 | −0.090 | 0.065 | |||||
| 26 000 | 11.145 | −1.317 | −0.157 | −0.089 | 0.069 | 12.067 | −1.348 | −0.161 | −0.083 | 0.068 | |||||
| 24 000 | 11.232 | −1.303 | −0.144 | −0.083 | 0.071 | 12.135 | −1.336 | −0.152 | −0.078 | 0.070 | |||||
| 22 000 | 11.306 | −1.294 | −0.134 | −0.078 | 0.074 | 12.240 | −1.320 | −0.137 | −0.071 | 0.075 | |||||
| 20 000 | 11.448 | −1.275 | −0.114 | −0.071 | 0.081 | 12.407 | −1.301 | −0.115 | −0.065 | 0.084 | |||||
| 19 000 | 11.545 | −1.266 | −0.103 | −0.067 | 0.086 | 12.511 | −1.291 | −0.102 | −0.063 | 0.090 | |||||
| 18 000 | 11.657 | −1.257 | −0.090 | −0.063 | 0.094 | 12.629 | −1.281 | −0.089 | −0.060 | 0.097 | |||||
| 17 000 | 11.784 | −1.250 | −0.075 | −0.058 | 0.101 | 12.760 | −1.269 | −0.074 | −0.056 | 0.104 | |||||
| 16 000 | 11.927 | −1.241 | −0.058 | −0.051 | 0.108 | 12.903 | −1.252 | −0.055 | −0.049 | 0.110 | |||||
| 15 000 | 12.084 | −1.222 | −0.035 | −0.041 | 0.114 | 13.058 | −1.229 | −0.032 | −0.039 | 0.116 | |||||
| 14 000 | 12.259 | −1.195 | −0.005 | −0.027 | 0.120 | 13.226 | −1.197 | −0.003 | −0.025 | 0.121 | |||||
| 13 000 | 12.445 | −1.159 | 0.024 | −0.012 | 0.125 | 13.409 | −1.156 | 0.032 | −0.008 | 0.126 | |||||
| 12 000 | 12.662 | −1.111 | 0.063 | 0.003 | 0.130 | 13.614 | −1.104 | 0.072 | 0.011 | 0.132 | |||||
| 11 000 | 12.892 | −1.035 | 0.119 | 0.032 | 0.139 | 13.848 | −1.035 | 0.120 | 0.032 | 0.139 | |||||
| 10 000 | 13.176 | −0.950 | 0.181 | 0.059 | 0.148 | 14.130 | −0.950 | 0.181 | 0.059 | 0.148 | |||||
| . | log g = 7.00 . | log g = 7.50 . | log g = 8.00 . | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Teff . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . | g . | (u − g) . | (g − r) . | (r − i) . | (r − H α) . |
| 40 000 | 7.672 | −1.467 | −0.260 | −0.148 | 0.073 | 8.710 | −1.466 | −0.254 | −0.144 | 0.071 | 9.557 | −1.469 | −0.250 | −0.141 | 0.069 |
| 35 000 | 8.016 | −1.407 | −0.234 | −0.135 | 0.076 | 9.008 | −1.409 | −0.228 | −0.132 | 0.074 | 9.824 | −1.413 | −0.223 | −0.128 | 0.070 |
| 30 000 | 8.375 | −1.334 | −0.205 | −0.122 | 0.078 | 9.317 | −1.337 | −0.198 | −0.118 | 0.075 | 10.105 | −1.345 | −0.192 | −0.112 | 0.070 |
| 28 000 | 8.530 | −1.299 | −0.191 | −0.115 | 0.079 | 9.447 | −1.304 | −0.183 | −0.111 | 0.075 | 10.225 | −1.317 | −0.177 | −0.105 | 0.070 |
| 26 000 | 8.691 | −1.263 | −0.175 | −0.108 | 0.079 | 9.585 | −1.273 | −0.168 | −0.103 | 0.075 | 10.349 | −1.291 | −0.161 | −0.096 | 0.071 |
| 24 000 | 8.861 | −1.227 | −0.158 | −0.099 | 0.080 | 9.730 | −1.242 | −0.150 | −0.094 | 0.076 | 10.467 | −1.269 | −0.145 | −0.088 | 0.073 |
| 22 000 | 9.043 | −1.191 | −0.139 | −0.090 | 0.082 | 9.863 | −1.218 | −0.134 | −0.087 | 0.078 | 10.553 | −1.257 | −0.133 | −0.083 | 0.075 |
| 20 000 | 9.179 | −1.174 | −0.127 | −0.087 | 0.082 | 9.957 | −1.212 | −0.123 | −0.083 | 0.080 | 10.662 | −1.248 | −0.117 | −0.077 | 0.080 |
| 19 000 | 9.245 | −1.174 | −0.119 | −0.085 | 0.084 | 10.039 | −1.209 | −0.112 | −0.078 | 0.085 | 10.753 | −1.242 | −0.105 | −0.072 | 0.085 |
| 18 000 | 9.351 | −1.174 | −0.106 | −0.079 | 0.090 | 10.149 | −1.207 | −0.097 | −0.072 | 0.091 | 10.862 | −1.236 | −0.090 | −0.067 | 0.092 |
| 17 000 | 9.466 | −1.177 | −0.088 | −0.070 | 0.096 | 10.279 | −1.205 | −0.080 | −0.064 | 0.098 | 10.989 | −1.230 | −0.073 | −0.060 | 0.100 |
| 16 000 | 9.626 | −1.178 | −0.067 | −0.060 | 0.104 | 10.427 | −1.201 | −0.059 | −0.055 | 0.106 | 11.133 | −1.221 | −0.054 | −0.052 | 0.108 |
| 15 000 | 9.805 | −1.173 | −0.040 | −0.048 | 0.111 | 10.595 | −1.191 | −0.034 | −0.044 | 0.113 | 11.295 | −1.207 | −0.031 | −0.041 | 0.114 |
| 14 000 | 10.006 | −1.159 | −0.009 | −0.032 | 0.118 | 10.779 | −1.172 | −0.004 | −0.028 | 0.119 | 11.471 | −1.184 | −0.003 | −0.027 | 0.120 |
| 13 000 | 10.225 | −1.134 | 0.029 | −0.013 | 0.125 | 10.982 | −1.142 | 0.031 | −0.011 | 0.125 | 11.665 | −1.149 | 0.032 | −0.010 | 0.126 |
| 12 000 | 10.466 | −1.095 | 0.071 | 0.009 | 0.132 | 11.203 | −1.099 | 0.072 | 0.010 | 0.132 | 11.877 | −1.102 | 0.072 | 0.011 | 0.132 |
| 11 000 | 10.732 | −1.033 | 0.118 | 0.032 | 0.139 | 11.449 | −1.034 | 0.119 | 0.032 | 0.138 | 12.115 | −1.035 | 0.119 | 0.032 | 0.138 |
| 10 000 | 11.048 | −0.950 | 0.180 | 0.061 | 0.148 | 11.745 | −0.950 | 0.180 | 0.061 | 0.147 | 12.403 | −0.950 | 0.180 | 0.060 | 0.148 |
| log g = 8.50 | log g = 9.00 | ||||||||||||||
| Teff | g | (u − g) | (g − r) | (r − i) | (r − H α) | g | (u − g) | (g − r) | (r − i) | (r − H α) | |||||
| 40 000 | 10.403 | −1.474 | −0.246 | −0.136 | 0.066 | 11.396 | −1.479 | −0.245 | −0.130 | 0.062 | |||||
| 35 000 | 10.661 | −1.420 | −0.219 | −0.122 | 0.066 | 11.644 | −1.429 | −0.218 | −0.115 | 0.061 | |||||
| 30 000 | 10.933 | −1.359 | −0.188 | −0.105 | 0.065 | 11.898 | −1.378 | −0.187 | −0.097 | 0.062 | |||||
| 28 000 | 11.042 | −1.336 | −0.173 | −0.097 | 0.066 | 11.989 | −1.362 | −0.173 | −0.090 | 0.065 | |||||
| 26 000 | 11.145 | −1.317 | −0.157 | −0.089 | 0.069 | 12.067 | −1.348 | −0.161 | −0.083 | 0.068 | |||||
| 24 000 | 11.232 | −1.303 | −0.144 | −0.083 | 0.071 | 12.135 | −1.336 | −0.152 | −0.078 | 0.070 | |||||
| 22 000 | 11.306 | −1.294 | −0.134 | −0.078 | 0.074 | 12.240 | −1.320 | −0.137 | −0.071 | 0.075 | |||||
| 20 000 | 11.448 | −1.275 | −0.114 | −0.071 | 0.081 | 12.407 | −1.301 | −0.115 | −0.065 | 0.084 | |||||
| 19 000 | 11.545 | −1.266 | −0.103 | −0.067 | 0.086 | 12.511 | −1.291 | −0.102 | −0.063 | 0.090 | |||||
| 18 000 | 11.657 | −1.257 | −0.090 | −0.063 | 0.094 | 12.629 | −1.281 | −0.089 | −0.060 | 0.097 | |||||
| 17 000 | 11.784 | −1.250 | −0.075 | −0.058 | 0.101 | 12.760 | −1.269 | −0.074 | −0.056 | 0.104 | |||||
| 16 000 | 11.927 | −1.241 | −0.058 | −0.051 | 0.108 | 12.903 | −1.252 | −0.055 | −0.049 | 0.110 | |||||
| 15 000 | 12.084 | −1.222 | −0.035 | −0.041 | 0.114 | 13.058 | −1.229 | −0.032 | −0.039 | 0.116 | |||||
| 14 000 | 12.259 | −1.195 | −0.005 | −0.027 | 0.120 | 13.226 | −1.197 | −0.003 | −0.025 | 0.121 | |||||
| 13 000 | 12.445 | −1.159 | 0.024 | −0.012 | 0.125 | 13.409 | −1.156 | 0.032 | −0.008 | 0.126 | |||||
| 12 000 | 12.662 | −1.111 | 0.063 | 0.003 | 0.130 | 13.614 | −1.104 | 0.072 | 0.011 | 0.132 | |||||
| 11 000 | 12.892 | −1.035 | 0.119 | 0.032 | 0.139 | 13.848 | −1.035 | 0.120 | 0.032 | 0.139 | |||||
| 10 000 | 13.176 | −0.950 | 0.181 | 0.059 | 0.148 | 14.130 | −0.950 | 0.181 | 0.059 | 0.148 | |||||




