Alignment of interstellar grains by mechanical torques: suprathermally rotating Gaussian random spheres

Das, Indrajit; Weingartner, Joseph C.

doi:10.1093/mnras/stw146

Abstract

Collisions of gas particles with a drifting grain give rise to a mechanical torque on the grain. Recent work by Lazarian & Hoang showed that mechanical torques might play a significant role in aligning helical grains along the interstellar magnetic field direction, even in the case of subsonic drift. We compute the mechanical torques on 13 different irregular grains and examine their resulting rotational dynamics, assuming steady rotation about the principal axis of greatest moment of inertia. We find that the alignment efficiency in the subsonic drift regime depends sensitively on the grain shape, with more efficient alignment for shapes with a substantial mechanical torque even in the case of no drift. The alignment is typically more efficient for supersonic drift. A more rigorous analysis of the dynamics is required to definitively appraise the role of mechanical torques in grain alignment.

dust, extinction, ISM: magnetic fields

1 INTRODUCTION

Observations of starlight polarization and polarized thermal emission from dust indicate that interstellar grains are non-spherical and aligned. Despite over 60 years of effort, the theory of grain alignment is not yet complete; see Lazarian (2007) and Andersson (2015) for reviews.

Among the early proposals for alignment mechanisms, Gold (1952a,b) considered ‘mechanical torques’ arising from collisions of gas particles with an elongated grain moving through the gas supersonically. Numerous authors have further elaborated and extended this model; see references in Lazarian & Hoang (2007b). While the alignment described by Gold is a stochastic process, Lazarian (2007) and Lazarian & Hoang (2007a) noted that irregularly shaped grains could experience systematic mechanical torques associated with their helicity. Lazarian & Hoang (2007b) examined the torque on a highly idealized helical grain. They concluded that the resulting alignment can be efficient even for grains moving subsonically, likely dominates over Gold-type alignment, and aligns grains with their long axes perpendicular to the magnetic field.

Lazarian & Hoang (2007b) noted that detailed studies of the mechanical torques on irregular grains are needed to clarify the efficiency of helicity-related mechanical torques, since the helicities of realistic grain shapes are unknown. That is our aim in this work. We examine the mechanical torques, for a variety of gas-grain drift speeds, on 13 irregular grains, whose shapes are described in Section 2. We describe the theoretical and computational aspects of the torque calculations in Sections 3 and 4, respectively. The results of these calculations are presented in Section 5. In Section 6, we examine the grain rotational dynamics under the influence of the mechanical, drag, and magnetic torques, assuming that the grain rotates about its principal axis of greatest moment of inertia, |${\hat{\boldsymbol a}}_1$|⁠. We discuss the implications for the efficiency of grain alignment by helicity-induced mechanical torques, but defer a detailed examination to an upcoming study, where the assumption of rotation about |${\hat{\boldsymbol a}}_1$| will be relaxed. Conclusions and future work are summarized in Section 7.

2 GRAIN SHAPES

We examine Gaussian random spheres (GRSs) using a slightly modified version of the prescription of Muinonen et al. (1996). Consider a coordinate system (x, y, z) fixed with respect to the grain with the origin located inside the grain. In spherical coordinates, the distance from the origin to the surface of the GRS, as a function of the polar angle θ (with |${\hat{\boldsymbol z}}$| as the reference axis) and azimuthal angle ϕ (with |${\hat{\boldsymbol x}}$| as the reference axis), is

\begin{equation} r_{\mathrm{surf}}(\theta , \phi ) = a (1 + \sigma ^2)^{-1/2} \exp [w_1(\theta , \phi )], \end{equation}

(1)

where

\begin{equation} w_1(\theta , \phi ) = \sum _{l=1}^{l_{\mathrm{max}}} \sum _{m=0}^l P_l^m(\cos \theta ) \, (a_{lm} \cos m \phi + b_{lm} \sin m \phi ) \end{equation}

(2)

and |$P_l^m(u)$| denotes the associated Legendre functions. The expansion coefficients a_lm and b_lm are taken as independent Gaussian random variables with zero means and equal variances |$\beta _{lm}^2$| given by

\begin{equation} \beta _{lm}^2 = (2 - \delta _{m0}) \frac{(l-m)!}{(l+m)!} c_l \ln (1 + \sigma ^2) \end{equation}

(3)

with

\begin{equation} c_l = l^{- \alpha } \ \left( \sum _{l=1}^{l_{\mathrm{max}}} l^{- \alpha } \right)^{ -1}. \end{equation}

(4)

For a given direction (θ, ϕ), the mean and variance of the distance r to the surface, over an ensemble of realizations of the grain geometry, are given by a and a²σ², respectively (in the limit l_max → ∞). Thus, the parameter σ controls the amplitude of deviations from sphericity, while α controls the angular scale of the deviations.

We generated 20 different grains, each with σ = 0.5 and half with α = 2 and the other half with α = 3. In each case, we took l_max = 8 and used a slightly modified version of the Gaussian deviate routine gasdev from Press et al. (1992) to select values for the coefficients a_lm and b_lm. If the ratio of the maximum to minimum principal moments of inertia of the resulting grain was less than 1.5 or greater than 3, then the shape was discarded as too symmetric or too extreme. (Preliminary scattering calculations indicate that these grains can produce polarization consistent with that observed in the ISM. This will be examined in detail in a study of radiative torques on these grains.) Also, we required that the centre of mass lies within the grain. Of the 13 grains that satisfied these criteria, grains 1–7 have α = 2 and grains 8–13 have α = 3. The values of a_lm and b_lm for these grains are given in Table 1. The resulting shape for grain 1 is displayed in Fig. 1.

Figure 1.

Views of grain 1 from two opposite directions.

Open in new tab Download slide

Table 1.

Open in new tab

GRS expansion coefficients. The full table is available online.

Grain	l	m	a_lm	b_lm
1	1	0	0.566 669 585	−0.085 194 1355
1	1	1	−0.367 041 01	0.213 834 444
1	2	0	−0.053 580 3218	−0.089 512 2548
1	2	1	−0.005 563 869 57	−0.008 703 381 94
1	2	2	−0.066 820 0056	0.088 286 5188

Grain	l	m	a_lm	b_lm
1	1	0	0.566 669 585	−0.085 194 1355
1	1	1	−0.367 041 01	0.213 834 444
1	2	0	−0.053 580 3218	−0.089 512 2548
1	2	1	−0.005 563 869 57	−0.008 703 381 94
1	2	2	−0.066 820 0056	0.088 286 5188

Table 1.

Open in new tab

GRS expansion coefficients. The full table is available online.

Grain	l	m	a_lm	b_lm
1	1	0	0.566 669 585	−0.085 194 1355
1	1	1	−0.367 041 01	0.213 834 444
1	2	0	−0.053 580 3218	−0.089 512 2548
1	2	1	−0.005 563 869 57	−0.008 703 381 94
1	2	2	−0.066 820 0056	0.088 286 5188

Grain	l	m	a_lm	b_lm
1	1	0	0.566 669 585	−0.085 194 1355
1	1	1	−0.367 041 01	0.213 834 444
1	2	0	−0.053 580 3218	−0.089 512 2548
1	2	1	−0.005 563 869 57	−0.008 703 381 94
1	2	2	−0.066 820 0056	0.088 286 5188

The volume V, coordinates of the centre of mass x_{i, cm}, and components of the inertia tensor |${\boldsymbol I}_{ij}$| are given by

\begin{equation} V = \frac{1}{3} \int _0^{2 \pi } \mathrm{d}\phi \int _{-1}^1 \mathrm{d}(\cos \theta ) \left[r_{\mathrm{surf}}(\theta , \phi )\right]^3, \end{equation}

(5)

\begin{equation} x_{i, \mathrm{cm}} = \frac{1}{4V} \int _0^{2\pi } \mathrm{d}\phi \int _{-1}^1 \mathrm{d}(\cos \theta ) [r_{\mathrm{surf}}(\theta , \phi )]^3 x_{i, \mathrm{surf}}(\theta , \phi ), \end{equation}

(6)

\begin{equation} I_{ii} = \int _0^{2\pi } \mathrm{d}\phi \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{r_{\mathrm{surf}}(\theta , \phi )} r^2 \mathrm{d}r [(x_j - x_{j, \mathrm{cm}})^2 + (x_k - x_{k, \mathrm{cm}})^2], \end{equation}

(7)

and

\begin{equation} {\boldsymbol I}_{ij} = - \int _0^{2\pi } \mathrm{d}\phi \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{r_{\mathrm{surf}}(\theta , \phi )} r^2 \mathrm{d}r \, x_i x_j, \end{equation}

(8)

where x₁ = x, x₂ = y, and x₃ = z. In equation (7), j and k stand for the two index values that are not equal to the value of index i.

For a given (θ, ϕ), the direction normal to the grain surface is found by taking the cross-product of the tangent vectors |${\boldsymbol T}_{\theta }$| and |${\boldsymbol T}_{\phi }$| along |${\hat{\boldsymbol \theta }}$| and |${\hat{\boldsymbol \phi }}$|⁠, respectively. For a GRS,

\begin{eqnarray} {\boldsymbol T}_{\theta } \times {\boldsymbol T}_{\phi } &=& [r_{\mathrm{surf}}(\theta , \phi )]^2 \sin \theta \biggl \lbrace \left[ \sin \theta \cos \phi + w_2(\theta , \phi ) \sin \theta \cos \theta \cos \phi + w_3 (\theta , \phi ) \csc \theta \sin \phi \right]{\hat{\boldsymbol x}} \nonumber\\ &&+ \left[ \sin \theta \sin \phi + w_2(\theta , \phi ) \sin \theta \cos \theta \sin \phi - w_3(\theta , \phi ) \csc \theta \cos \phi \right]{\hat{\boldsymbol y}} + \left[ \cos \theta - w_2(\theta , \phi ) \sin ^2 \theta \right]{\hat{\boldsymbol z}} \biggr \rbrace , \end{eqnarray}

(9)

where

\begin{equation} w_2(\theta , \phi ) = \sum _{l=1}^{l_{\mathrm{max}}} \sum _{m=0}^l \frac{ \mathrm{d}P_l^m(\cos \theta )}{\mathrm{d}(\cos \theta )} \, (a_{lm} \cos m \phi + b_{lm} \sin m \phi ) \end{equation}

(10)

and

\begin{equation} w_3(\theta , \phi ) = \sum _{l=1}^{l_{\mathrm{max}}} \sum _{m=0}^l m P_l^m(\cos \theta ) \, (- a_{lm} \sin m \phi + b_{lm} \cos m \phi ). \end{equation}

(11)

The surface area of the grain is given by

\begin{equation} S = \int _0^{\pi } \mathrm{d}\theta \int _0^{2\pi } \mathrm{d}\phi \, |{\boldsymbol T}_{\theta } \times {\boldsymbol T}_{\phi }| = \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2 \pi } \mathrm{d}\phi \, \eta _S(\theta , \phi ), \end{equation}

(12)

where

\begin{equation} \eta _S(\theta , \phi ) = [r_{\mathrm{surf}}(\theta , \phi )]^2 \left\lbrace 1 + [w_2(\theta , \phi ) \sin \theta ]^2 + [w_3(\theta , \phi ) \csc \theta ]^2 \right\rbrace ^{1/2}. \end{equation}

(13)

The outward pointing unit normal to the grain surface is given by

\begin{equation} {\hat{\boldsymbol N}} = \frac{({\boldsymbol T}_{\theta } \times {\boldsymbol T}_{\phi }) \, \nu _N}{\sin \theta \, \eta _S}, \end{equation}

(14)

where ν_N = 1 if |${\hat{\boldsymbol r}} {\cdot } ({\boldsymbol T}_{\theta } \times {\boldsymbol T}_{\phi }) > 0$| and ν_N = −1 if |${\hat{\boldsymbol r}} {\cdot } ({\boldsymbol T}_{\theta } \times {\boldsymbol T}_{\phi }) < 0$|⁠.

The effective radius a_eff is defined as the radius of a sphere with volume equal to that of the grain:

\begin{equation} a_{\mathrm{eff}} = \left( \frac{3V}{4 \pi } \right)^{1/3}. \end{equation}

(15)

The grain principal axes are denoted |${\hat{\boldsymbol a}}_i$| such that the associated moments of inertia satisfy I₁ ≥ I₂ ≥ I₃. We define shape parameters α_i by

\begin{equation} I_i = \frac{2}{5} \alpha _i \rho V a_{\mathrm{eff}}^2, \end{equation}

(16)

where ρ is the density of the grain material, assumed to be constant throughout the grain volume.

We take 8000 values (each) of cos θ and ϕ in performing the integrals for V, S, and x_{i, cm} and 4000 values (each) of cos θ, ϕ, and r in performing the integrals for the inertia tensor. We use the recurrence relation

\begin{equation} (l-m) P_l^m(x) = (2l-1) x P_{l-1}^m(x) - (l+m-1) P_{l-2}^m(x) \end{equation}

(17)

and the expressions

\begin{equation} P_m^m(x) = (-1)^m (2m-1)!! (1-x^2)^{m/2} \end{equation}

(18)

and

\begin{equation} P_{m+1}^m(x) = (2m+1) x P_m^m(x) \end{equation}

(19)

to efficiently compute |$P_l^m(\cos \theta )$| and |$\mathrm{d}P_l^m(\cos \theta )/\mathrm{d}(\cos \theta )$| for the 44 combinations (l, m) with l = 1 through l = 8. During the volume integration, we keep track of the largest value of r_surf(θ, ϕ), which we denote r_max.

The derived quantities that characterize the 13 grains examined in this study are given in Tables 2 and 3.

Table 2.

Open in new tab

GRS derived quantities.

Grain	Va⁻³(1 + σ²)^3/2	r_max/a_eff	\|$S/(4 \pi a^2_{\mathrm{eff}})$\|	\|$\boldsymbol {r}_{\mathrm{cm}}/a_{\mathrm{eff}}$\|	α₁	α₂	α₃
1	10.568	2.2349	1.3430	(0.289 92, −0.195 59, 0.504 64)	1.7130	1.2900	1.0919
2	7.3329	2.4285	1.4011	(0.024 61, 0.193 39, −0.449 91)	2.1253	1.9392	0.811 56
3	8.7756	1.9046	1.2935	(0.125 17, −0.313 83, 0.201 20)	1.8185	1.5170	0.822 55
4	16.336	1.9635	1.2528	(−0.595 78, −0.050 17, 0.198 73)	1.9565	1.9084	0.690 20
5	6.8640	1.9173	1.2684	(0.212 08, −0.325 22, −0.308 08)	1.4298	1.3524	0.819 91
6	6.6200	2.1619	1.2632	(−0.127 06, 0.463 37, 0.186 07)	1.4923	1.3382	0.882 05
7	7.4806	2.2211	1.3596	(0.082 03, −0.440 95, −0.126 76)	1.8843	1.4960	0.897 30
8	7.4378	1.6693	1.1266	(0.333 62, 0.184 62, −0.285 30)	1.5227	1.1675	0.854 52
9	10.468	2.1160	1.1180	(0.456 35, 0.097 77, −0.476 34)	1.4005	1.2106	0.870 44
10	7.0687	1.8321	1.0893	(−0.267 18, 0.170 87, 0.362 27)	1.3109	1.1339	0.862 01
11	8.6542	1.9723	1.1240	(0.139 15, 0.281 40, 0.487 41)	1.4962	1.1479	0.878 68
12	12.710	2.1524	1.0968	(−0.740 42, 0.259 73, 0.179 26)	1.4447	1.3281	0.737 23
13	5.6324	1.5987	1.1207	(0.026 09, −0.196 23, 0.086 27)	1.5328	1.4072	0.722 68

Grain	Va⁻³(1 + σ²)^3/2	r_max/a_eff	\|$S/(4 \pi a^2_{\mathrm{eff}})$\|	\|$\boldsymbol {r}_{\mathrm{cm}}/a_{\mathrm{eff}}$\|	α₁	α₂	α₃
1	10.568	2.2349	1.3430	(0.289 92, −0.195 59, 0.504 64)	1.7130	1.2900	1.0919
2	7.3329	2.4285	1.4011	(0.024 61, 0.193 39, −0.449 91)	2.1253	1.9392	0.811 56
3	8.7756	1.9046	1.2935	(0.125 17, −0.313 83, 0.201 20)	1.8185	1.5170	0.822 55
4	16.336	1.9635	1.2528	(−0.595 78, −0.050 17, 0.198 73)	1.9565	1.9084	0.690 20
5	6.8640	1.9173	1.2684	(0.212 08, −0.325 22, −0.308 08)	1.4298	1.3524	0.819 91
6	6.6200	2.1619	1.2632	(−0.127 06, 0.463 37, 0.186 07)	1.4923	1.3382	0.882 05
7	7.4806	2.2211	1.3596	(0.082 03, −0.440 95, −0.126 76)	1.8843	1.4960	0.897 30
8	7.4378	1.6693	1.1266	(0.333 62, 0.184 62, −0.285 30)	1.5227	1.1675	0.854 52
9	10.468	2.1160	1.1180	(0.456 35, 0.097 77, −0.476 34)	1.4005	1.2106	0.870 44
10	7.0687	1.8321	1.0893	(−0.267 18, 0.170 87, 0.362 27)	1.3109	1.1339	0.862 01
11	8.6542	1.9723	1.1240	(0.139 15, 0.281 40, 0.487 41)	1.4962	1.1479	0.878 68
12	12.710	2.1524	1.0968	(−0.740 42, 0.259 73, 0.179 26)	1.4447	1.3281	0.737 23
13	5.6324	1.5987	1.1207	(0.026 09, −0.196 23, 0.086 27)	1.5328	1.4072	0.722 68

Table 2.

Open in new tab

GRS derived quantities.

Grain	Va⁻³(1 + σ²)^3/2	r_max/a_eff	\|$S/(4 \pi a^2_{\mathrm{eff}})$\|	\|$\boldsymbol {r}_{\mathrm{cm}}/a_{\mathrm{eff}}$\|	α₁	α₂	α₃
1	10.568	2.2349	1.3430	(0.289 92, −0.195 59, 0.504 64)	1.7130	1.2900	1.0919
2	7.3329	2.4285	1.4011	(0.024 61, 0.193 39, −0.449 91)	2.1253	1.9392	0.811 56
3	8.7756	1.9046	1.2935	(0.125 17, −0.313 83, 0.201 20)	1.8185	1.5170	0.822 55
4	16.336	1.9635	1.2528	(−0.595 78, −0.050 17, 0.198 73)	1.9565	1.9084	0.690 20
5	6.8640	1.9173	1.2684	(0.212 08, −0.325 22, −0.308 08)	1.4298	1.3524	0.819 91
6	6.6200	2.1619	1.2632	(−0.127 06, 0.463 37, 0.186 07)	1.4923	1.3382	0.882 05
7	7.4806	2.2211	1.3596	(0.082 03, −0.440 95, −0.126 76)	1.8843	1.4960	0.897 30
8	7.4378	1.6693	1.1266	(0.333 62, 0.184 62, −0.285 30)	1.5227	1.1675	0.854 52
9	10.468	2.1160	1.1180	(0.456 35, 0.097 77, −0.476 34)	1.4005	1.2106	0.870 44
10	7.0687	1.8321	1.0893	(−0.267 18, 0.170 87, 0.362 27)	1.3109	1.1339	0.862 01
11	8.6542	1.9723	1.1240	(0.139 15, 0.281 40, 0.487 41)	1.4962	1.1479	0.878 68
12	12.710	2.1524	1.0968	(−0.740 42, 0.259 73, 0.179 26)	1.4447	1.3281	0.737 23
13	5.6324	1.5987	1.1207	(0.026 09, −0.196 23, 0.086 27)	1.5328	1.4072	0.722 68

Grain	Va⁻³(1 + σ²)^3/2	r_max/a_eff	\|$S/(4 \pi a^2_{\mathrm{eff}})$\|	\|$\boldsymbol {r}_{\mathrm{cm}}/a_{\mathrm{eff}}$\|	α₁	α₂	α₃
1	10.568	2.2349	1.3430	(0.289 92, −0.195 59, 0.504 64)	1.7130	1.2900	1.0919
2	7.3329	2.4285	1.4011	(0.024 61, 0.193 39, −0.449 91)	2.1253	1.9392	0.811 56
3	8.7756	1.9046	1.2935	(0.125 17, −0.313 83, 0.201 20)	1.8185	1.5170	0.822 55
4	16.336	1.9635	1.2528	(−0.595 78, −0.050 17, 0.198 73)	1.9565	1.9084	0.690 20
5	6.8640	1.9173	1.2684	(0.212 08, −0.325 22, −0.308 08)	1.4298	1.3524	0.819 91
6	6.6200	2.1619	1.2632	(−0.127 06, 0.463 37, 0.186 07)	1.4923	1.3382	0.882 05
7	7.4806	2.2211	1.3596	(0.082 03, −0.440 95, −0.126 76)	1.8843	1.4960	0.897 30
8	7.4378	1.6693	1.1266	(0.333 62, 0.184 62, −0.285 30)	1.5227	1.1675	0.854 52
9	10.468	2.1160	1.1180	(0.456 35, 0.097 77, −0.476 34)	1.4005	1.2106	0.870 44
10	7.0687	1.8321	1.0893	(−0.267 18, 0.170 87, 0.362 27)	1.3109	1.1339	0.862 01
11	8.6542	1.9723	1.1240	(0.139 15, 0.281 40, 0.487 41)	1.4962	1.1479	0.878 68
12	12.710	2.1524	1.0968	(−0.740 42, 0.259 73, 0.179 26)	1.4447	1.3281	0.737 23
13	5.6324	1.5987	1.1207	(0.026 09, −0.196 23, 0.086 27)	1.5328	1.4072	0.722 68

Table 3.

Open in new tab

GRS principal axes.

Grain	\|${\hat{\boldsymbol a}}_1$\|	\|${\hat{\boldsymbol a}}_2$\|	\|${\hat{\boldsymbol a}}_3$\|
1	(0.865 99, −0.102 72, −0.489 39)	(0.498 15, 0.262 64, 0.826 36)	(0.043 66, −0.959 41, 0.278 61)
2	(0.473 29, 0.818 76, 0.325 01)	(0.831 96, −0.536 73, 0.140 58)	(0.289 54, 0.203 86, −0.935 20)
3	(0.663 04, −0.085 54, 0.743 68)	(0.745 08, 0.171 39, −0.644 57)	(−0.072 32, 0.981 48, 0.177 37)
4	(0.224 58, −0.271 27, −0.935 93)	(0.763 16, 0.646 20, −0.004 17)	(0.605 93, −0.713 33, 0.352 15)
5	(0.164 10, 0.698 32, −0.696 73)	(0.668 26, 0.440 84, 0.599 24)	(0.725 61, −0.563 93, −0.394 31)
6	(0.663 50, −0.353 68, 0.659 30)	(0.745 49, 0.237 98, −0.622 58)	(0.063 30, 0.904 58, 0.421 57)
7	(0.411 90, 0.056 21, −0.909 49)	(0.852 98, −0.374 91, 0.363 14)	(−0.320 56, −0.925 36, −0.202 37)
8	(0.297 77, 0.864 30, 0.405 35)	(0.475 72, 0.233 79, −0.847 96)	(−0.827 66, 0.445 33, −0.341 55)
9	(0.545 70, 0.832 19, −0.098 33)	(0.714 75, −0.400 99, 0.573 01)	(0.437 42, −0.382 97, −0.813 63)
10	(0.693 00, −0.720 83, 0.011 97)	(0.619 14, 0.603 58, 0.502 35)	(−0.369 33, −0.340 72, 0.864 58)
11	(0.947 10, 0.317 92, 0.043 84)	(0.018 55, −0.190 59, 0.981 49)	(0.320 39, −0.928 76, −0.186 41)
12	(0.497 03, −0.305 07, 0.812 34)	(0.600 56, 0.796 66, −0.068 27)	(−0.626 33, 0.521 79, 0.579 18)
13	(0.478 66, −0.353 95, −0.803 49)	(0.332 35, 0.920 09, −0.207 33)	(0.812 67, −0.167 80, 0.558 04)

Grain	\|${\hat{\boldsymbol a}}_1$\|	\|${\hat{\boldsymbol a}}_2$\|	\|${\hat{\boldsymbol a}}_3$\|
1	(0.865 99, −0.102 72, −0.489 39)	(0.498 15, 0.262 64, 0.826 36)	(0.043 66, −0.959 41, 0.278 61)
2	(0.473 29, 0.818 76, 0.325 01)	(0.831 96, −0.536 73, 0.140 58)	(0.289 54, 0.203 86, −0.935 20)
3	(0.663 04, −0.085 54, 0.743 68)	(0.745 08, 0.171 39, −0.644 57)	(−0.072 32, 0.981 48, 0.177 37)
4	(0.224 58, −0.271 27, −0.935 93)	(0.763 16, 0.646 20, −0.004 17)	(0.605 93, −0.713 33, 0.352 15)
5	(0.164 10, 0.698 32, −0.696 73)	(0.668 26, 0.440 84, 0.599 24)	(0.725 61, −0.563 93, −0.394 31)
6	(0.663 50, −0.353 68, 0.659 30)	(0.745 49, 0.237 98, −0.622 58)	(0.063 30, 0.904 58, 0.421 57)
7	(0.411 90, 0.056 21, −0.909 49)	(0.852 98, −0.374 91, 0.363 14)	(−0.320 56, −0.925 36, −0.202 37)
8	(0.297 77, 0.864 30, 0.405 35)	(0.475 72, 0.233 79, −0.847 96)	(−0.827 66, 0.445 33, −0.341 55)
9	(0.545 70, 0.832 19, −0.098 33)	(0.714 75, −0.400 99, 0.573 01)	(0.437 42, −0.382 97, −0.813 63)
10	(0.693 00, −0.720 83, 0.011 97)	(0.619 14, 0.603 58, 0.502 35)	(−0.369 33, −0.340 72, 0.864 58)
11	(0.947 10, 0.317 92, 0.043 84)	(0.018 55, −0.190 59, 0.981 49)	(0.320 39, −0.928 76, −0.186 41)
12	(0.497 03, −0.305 07, 0.812 34)	(0.600 56, 0.796 66, −0.068 27)	(−0.626 33, 0.521 79, 0.579 18)
13	(0.478 66, −0.353 95, −0.803 49)	(0.332 35, 0.920 09, −0.207 33)	(0.812 67, −0.167 80, 0.558 04)

Table 3.

Open in new tab

GRS principal axes.

Grain	\|${\hat{\boldsymbol a}}_1$\|	\|${\hat{\boldsymbol a}}_2$\|	\|${\hat{\boldsymbol a}}_3$\|
1	(0.865 99, −0.102 72, −0.489 39)	(0.498 15, 0.262 64, 0.826 36)	(0.043 66, −0.959 41, 0.278 61)
2	(0.473 29, 0.818 76, 0.325 01)	(0.831 96, −0.536 73, 0.140 58)	(0.289 54, 0.203 86, −0.935 20)
3	(0.663 04, −0.085 54, 0.743 68)	(0.745 08, 0.171 39, −0.644 57)	(−0.072 32, 0.981 48, 0.177 37)
4	(0.224 58, −0.271 27, −0.935 93)	(0.763 16, 0.646 20, −0.004 17)	(0.605 93, −0.713 33, 0.352 15)
5	(0.164 10, 0.698 32, −0.696 73)	(0.668 26, 0.440 84, 0.599 24)	(0.725 61, −0.563 93, −0.394 31)
6	(0.663 50, −0.353 68, 0.659 30)	(0.745 49, 0.237 98, −0.622 58)	(0.063 30, 0.904 58, 0.421 57)
7	(0.411 90, 0.056 21, −0.909 49)	(0.852 98, −0.374 91, 0.363 14)	(−0.320 56, −0.925 36, −0.202 37)
8	(0.297 77, 0.864 30, 0.405 35)	(0.475 72, 0.233 79, −0.847 96)	(−0.827 66, 0.445 33, −0.341 55)
9	(0.545 70, 0.832 19, −0.098 33)	(0.714 75, −0.400 99, 0.573 01)	(0.437 42, −0.382 97, −0.813 63)
10	(0.693 00, −0.720 83, 0.011 97)	(0.619 14, 0.603 58, 0.502 35)	(−0.369 33, −0.340 72, 0.864 58)
11	(0.947 10, 0.317 92, 0.043 84)	(0.018 55, −0.190 59, 0.981 49)	(0.320 39, −0.928 76, −0.186 41)
12	(0.497 03, −0.305 07, 0.812 34)	(0.600 56, 0.796 66, −0.068 27)	(−0.626 33, 0.521 79, 0.579 18)
13	(0.478 66, −0.353 95, −0.803 49)	(0.332 35, 0.920 09, −0.207 33)	(0.812 67, −0.167 80, 0.558 04)

Grain	\|${\hat{\boldsymbol a}}_1$\|	\|${\hat{\boldsymbol a}}_2$\|	\|${\hat{\boldsymbol a}}_3$\|
1	(0.865 99, −0.102 72, −0.489 39)	(0.498 15, 0.262 64, 0.826 36)	(0.043 66, −0.959 41, 0.278 61)
2	(0.473 29, 0.818 76, 0.325 01)	(0.831 96, −0.536 73, 0.140 58)	(0.289 54, 0.203 86, −0.935 20)
3	(0.663 04, −0.085 54, 0.743 68)	(0.745 08, 0.171 39, −0.644 57)	(−0.072 32, 0.981 48, 0.177 37)
4	(0.224 58, −0.271 27, −0.935 93)	(0.763 16, 0.646 20, −0.004 17)	(0.605 93, −0.713 33, 0.352 15)
5	(0.164 10, 0.698 32, −0.696 73)	(0.668 26, 0.440 84, 0.599 24)	(0.725 61, −0.563 93, −0.394 31)
6	(0.663 50, −0.353 68, 0.659 30)	(0.745 49, 0.237 98, −0.622 58)	(0.063 30, 0.904 58, 0.421 57)
7	(0.411 90, 0.056 21, −0.909 49)	(0.852 98, −0.374 91, 0.363 14)	(−0.320 56, −0.925 36, −0.202 37)
8	(0.297 77, 0.864 30, 0.405 35)	(0.475 72, 0.233 79, −0.847 96)	(−0.827 66, 0.445 33, −0.341 55)
9	(0.545 70, 0.832 19, −0.098 33)	(0.714 75, −0.400 99, 0.573 01)	(0.437 42, −0.382 97, −0.813 63)
10	(0.693 00, −0.720 83, 0.011 97)	(0.619 14, 0.603 58, 0.502 35)	(−0.369 33, −0.340 72, 0.864 58)
11	(0.947 10, 0.317 92, 0.043 84)	(0.018 55, −0.190 59, 0.981 49)	(0.320 39, −0.928 76, −0.186 41)
12	(0.497 03, −0.305 07, 0.812 34)	(0.600 56, 0.796 66, −0.068 27)	(−0.626 33, 0.521 79, 0.579 18)
13	(0.478 66, −0.353 95, −0.803 49)	(0.332 35, 0.920 09, −0.207 33)	(0.812 67, −0.167 80, 0.558 04)

3 TORQUE CALCULATIONS: THEORY

3.1 Collisions of gas particles with the grain

The first step in evaluating the effects of gas-particle collisions with a grain is to determine which gas-particle trajectories, as observed in the rest frame of the grain, hit the grain. To this end, consider an enclosing sphere that is at rest relative to the GRS, is centred on the origin used in constructing the GRS, and has a radius r_sph that exceeds the maximum value of r_surf(θ, ϕ). When a gas particle strikes the enclosing sphere, its position |$\boldsymbol {r}_0 = r_{\mathrm{sph}} {\hat{\boldsymbol r}}$| is represented by spherical coordinates (r_sph, θ_sph, ϕ_sph) and its velocity |${\boldsymbol v} = v_{\mathrm{th}} s \, {\hat{\boldsymbol s}}$| is represented by spherical coordinates (v_ths, θ_in, ϕ_in), where the radial vector |${\hat{\boldsymbol r}}$| is the reference axis for the polar angle θ_in, the vector |${\hat{\boldsymbol \theta }}$| is the reference axis for the azimuthal angle ϕ_in, and the ‘reduced speed’ s is the particle's speed divided by the gas thermal speed,

\begin{equation} v_{\mathrm{th}} = \left( \frac{2 k T_{\mathrm{gas}}}{m} \right)^{1/2}; \end{equation}

(20)

k is Boltzmann's constant, T_gas is the gas temperature, and m is the mass of the gas particle. Explicitly,

\begin{equation} {\hat{\boldsymbol r}} = \sin \theta _{\mathrm{sph}} \cos \phi _{\mathrm{sph}} \, {\hat{\boldsymbol x}} + \sin \theta _{\mathrm{sph}} \sin \phi _{\mathrm{sph}} \, {\hat{\boldsymbol y}} + \cos \theta _{\mathrm{sph}} \, {\hat{\boldsymbol z}}, \end{equation}

(21)

\begin{equation} {\hat{\boldsymbol s}} = - (\sin \theta _{\mathrm{in}} \cos \phi _{\mathrm{in}} \, {\hat{\boldsymbol \theta }} + \sin \theta _{\mathrm{in}} \sin \phi _{\mathrm{in}} \, {\hat{\boldsymbol \phi }} + \cos \theta _{\mathrm{in}} \, {\hat{\boldsymbol r}}). \end{equation}

(22)

Assuming T_gas ≳ 20 K, |$v_{\mathrm{th}} \gtrsim 6 \times 10^4 \, \mathrm{cm} \, \mathrm{s}^{-1}$| for incoming H atoms. Even for highly suprathermal rotation, we expect grain angular rotational speeds |$\omega \lesssim 10^7 \, \mathrm{rad} \, \mathrm{s}^{-1}$| (Draine & Weingartner 1997), corresponding to linear speeds of the grain surface |$v_{\mathrm{surf}} \sim \omega a_{\mathrm{eff}} \lesssim 2 \times 10^2 \, \mathrm{cm} \, \mathrm{s}^{-1}$| for a_eff ≈ 0.2 μm. Since v_surf ≪ v_th, the grain rotation can be neglected during the time that the gas particle traverses the enclosing sphere. In other words, we neglect the curvature of the gas-particle trajectories as observed in the rest frame of the grain.

A gas particle that approaches the grain and enclosing sphere along a radial path has θ_in = 0 and will hit the grain. A gas particle that approaches with θ_in = π/2 will not hit the grain. By construction, there is a unique distance from the origin to the grain surface for each direction (θ, ϕ). Thus, for each set of angles (θ_sph, ϕ_sph, ϕ_in), there is a critical value u_c of cos θ_in such that a gas particle hits the grain when cos θ_in ≥ u_c and does not hit when cos θ_in < u_c. Our computational approach for determining u_c as a function of (θ_sph, ϕ_sph, ϕ_in) is described in Section 4.1.

3.2 Torque due to incoming and reflected atoms

In this section, we calculate the torque due to gas particles (hereafter referred to as ‘atoms’, though the analysis is equally valid for molecules) that strike the grain, assuming that they stick to the grain or reflect specularly. In the next section, we will examine the torque associated with atoms or molecules that depart the grain after sticking to the surface.

Consider atoms with mass m and number density n in a gas with temperature T_gas. An atom's velocity in the rest frame of the gas is |${\boldsymbol v}_{\rm g} = v_{\mathrm{th}} \, {\boldsymbol s}_{\rm g}$|⁠; the thermal speed v_th was defined in equation (20). The Maxwell velocity distribution is

\begin{equation} P_{\rm g}({\boldsymbol s}_{\rm g}) s_{\rm g}^2 \, \mathrm{d}s_{\rm g} \, \mathrm{d}\Omega _{\rm g} = \pi ^{-3/2} \exp (-s_{\rm g}^2) s_{\rm g}^2 \, \mathrm{d}s_{\rm g} \, \mathrm{d}\Omega _{\rm g}, \end{equation}

(23)

where dΩ_g is the solid angle element. The subscript ‘g’ indicates that the quantities are evaluated in the rest frame of the gas.

Now suppose the grain moves through the gas with velocity |$v_{\mathrm{th}} {\boldsymbol s}_{\rm d}$| where

\begin{equation} {\boldsymbol s}_{\rm d} = s_{\rm d} (\sin \theta _{\mathrm{gr}} \cos \phi _{\mathrm{gr}} \, {\hat{\boldsymbol x}} + \sin \theta _{\mathrm{gr}} \sin \phi _{\mathrm{gr}} \, {\hat{\boldsymbol y}} + \cos \theta _{\mathrm{gr}} \, {\hat{\boldsymbol z}}). \end{equation}

(24)

The reduced velocity of the gas atom as observed in the rest frame of the grain is |${\boldsymbol s} = {\boldsymbol s}_{\rm g} - {\boldsymbol s}_{\rm d}$|⁠. Since |${\boldsymbol s}_{\rm d}$| is constant,

\begin{equation} s^2 \mathrm{d}s \, \mathrm{d}\Omega = s_{\rm g}^2 \mathrm{d}s_{\rm g} \, \mathrm{d}\Omega _{\rm g} \end{equation}

(25)

and the distribution of atom velocities as observed in the rest frame of the grain is

\begin{equation} P({\boldsymbol s}) s^2 \mathrm{d}s \, \mathrm{d}\Omega = \pi ^{-3/2} \exp (- |{\boldsymbol s} + {\boldsymbol s}_{\rm d}|^2) s^2 \mathrm{d}s \, \mathrm{d}\Omega \end{equation}

(26)

with

\begin{equation} |{\boldsymbol s} + {\boldsymbol s}_{\rm d}|^2 = s^2 + s_{\rm d}^2 - 2 \beta s s_{\rm d} \end{equation}

(27)

and

\begin{equation} \beta = \beta _1 \cos \theta _{\mathrm{in}} + \beta _2 \sin \theta _{\mathrm{in}} \end{equation}

(28)

with

\begin{equation} \beta _1 = \sin \theta _{\mathrm{sph}} \sin \theta _{\mathrm{gr}} \cos (\phi _{\mathrm{sph}} - \phi _{\mathrm{gr}}) + \cos \theta _{\mathrm{sph}} \cos \theta _{\mathrm{gr}} \end{equation}

(29)

and

\begin{equation} \beta _2 = [\cos \theta _{\mathrm{sph}} \sin \theta _{\mathrm{gr}} \cos (\phi _{\mathrm{sph}} - \phi _{\mathrm{gr}}) - \sin \theta _{\mathrm{sph}} \cos \theta _{\mathrm{gr}}] \cos \phi _{\mathrm{in}} - \sin \theta _{\mathrm{gr}} \sin (\phi _{\mathrm{sph}} - \phi _{\mathrm{gr}}) \sin \phi _{\mathrm{in}}. \end{equation}

(30)

Note that −1 ≤ β ≤ 1. It is convenient to define the functions

\begin{equation} I_s(p, s_{\rm d}, \beta ) = \int _0^{\infty } \mathrm{d}s \, s^p \exp [-(s^2 + s_{\rm d}^2 - 2 \beta s s_{\rm d})]. \end{equation}

(31)

The rate at which gas atoms arrive at a surface element on the enclosing sphere with area |$r_{\mathrm{sph}}^2 \mathrm{d}(\cos \theta _{\mathrm{sph}}) \, \mathrm{d} \phi _{\mathrm{sph}}$|⁠, with reduced speeds between s and s + ds and from within a solid angle element d(cos θ_in) dϕ_in around direction (θ_in, ϕ_in), is

\begin{equation} \mathrm{d}R_{\mathrm{arr}} = n v_{\mathrm{th}} [\boldsymbol {s} {\cdot } (-{\hat{\boldsymbol r}})] \pi ^{-3/2} s^2 \exp [-(s^2 + s_{\rm d}^2 - 2 \beta s s_{\rm d})] \, \mathrm{d}s \, \mathrm{d}(\cos \theta _{\mathrm{in}}) \, \mathrm{d}\phi _{\mathrm{in}} \, r_{\mathrm{sph}}^2 \, \mathrm{d}(\cos \theta _{\mathrm{sph}}) \, \mathrm{d}\phi _{\mathrm{sph}}; \end{equation}

(32)

\begin{equation} {\boldsymbol s} {\cdot } (- {\hat{\boldsymbol r}}) = s \cos \theta _{\mathrm{in}}. \end{equation}

(33)

The total rate at which gas atoms strike the grain (to be used in Section 3.3) is thus

\begin{equation} R_{\mathrm{arr}} = n v_{\mathrm{th}} a_{\mathrm{eff}}^2 Q_{\mathrm{arr}} \end{equation}

(34)

with

\begin{equation} Q_{\mathrm{arr}} = \pi ^{-3/2} \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^2 \int _{-1}^1 \mathrm{d}(\cos \theta _{\mathrm{sph}}) \int _0^{2\pi } \mathrm{d} \phi _{\mathrm{sph}} \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \int _{u_{\rm c}}^1 \mathrm{d} (\cos \theta _{\mathrm{in}}) \cos \theta _{\mathrm{in}} I_s(3, s_{\rm d}, \beta ). \end{equation}

(35)

Each atom that strikes and sticks to the grain transfers angular momentum (relative to the grain's centre of mass) |$\Delta \boldsymbol {J}_{\mathrm{arr}} = m (\boldsymbol {r}_0 - \boldsymbol {r}_{\mathrm{cm}}) \times v_{\mathrm{th}} {\boldsymbol s}$|⁠. The mean torque due to arriving atoms is |$\boldsymbol {\Gamma }_{\mathrm{arr}} = \int \mathrm{d}R_{\mathrm{arr}} \, \Delta \boldsymbol {J}_{\mathrm{arr}}$|⁠. Thus,

\begin{equation} \boldsymbol {\Gamma }_{\mathrm{arr}} = \pi ^{-3/2} m n v_{\mathrm{th}}^2 r_{\mathrm{sph}}^3 \int _{-1}^1 \mathrm{d}(\cos \theta _{\mathrm{sph}}) \int _0^{2\pi } \mathrm{d} \phi _{\mathrm{sph}} \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \int _{u_{\rm c}}^1 \mathrm{d} (\cos \theta _{\mathrm{in}}) \int _0^{\infty } \mathrm{d}s \, s^2 \exp [-(s^2 + s_{\rm d}^2 - 2 \beta s s_{\rm d})] \, s \cos \theta _{\mathrm{in}} \left( {\hat{\boldsymbol r}} - \frac{\boldsymbol {r}_{\mathrm{cm}}}{r_{\mathrm{sph}}} \right) \times {\boldsymbol s}. \end{equation}

(36)

Expressing the mean torque in terms of an efficiency factor |$\boldsymbol {Q}_{\Gamma , \mathrm{arr}}$|⁠,

\begin{equation} \boldsymbol {\Gamma }_{\mathrm{arr}} = m n v_{\mathrm{th}}^2 a_{\mathrm{eff}}^3 \boldsymbol {Q}_{\Gamma , \mathrm{arr}} \end{equation}

(37)

with

\begin{equation} \boldsymbol {Q}_{\Gamma , \mathrm{arr}} = \pi ^{-3/2} \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^3 \int _{-1}^1 \mathrm{d}(\cos \theta _{\mathrm{sph}}) \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{sph}} \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \int _{u_{\rm c}}^1 \mathrm{d}(\cos \theta _{\mathrm{in}}) \cos \theta _{\mathrm{in}} \left( {\hat{\boldsymbol r}} - \frac{\boldsymbol {r}_{\mathrm{cm}}}{r_{\mathrm{sph}}} \right) \times {\hat{\boldsymbol s}} \, I_s(4, s_{\rm d}, \beta ). \end{equation}

(38)

See Appendix A1 for explicit expressions for |$[({\hat{\boldsymbol r}} - \boldsymbol {r}_{\mathrm{cm}}/r_{\mathrm{sph}}) \times {\hat{\boldsymbol s}}]_i$|⁠.

We calculate the components of the mean torque along the |${\hat{\boldsymbol x}}$|⁠, |${\hat{\boldsymbol y}}$|⁠, and |${\hat{\boldsymbol z}}$| directions that are fixed relative to the grain body. Of course, these are identical to the components in an inertial frame with basis vectors that are instantaneously aligned with those of the grain frame. When these quantities are used to examine the grain rotational dynamics, they will be transformed to a single inertial frame and averaged over the grain rotation.

Now consider the case that atoms reflect specularly from the grain surface. Following a reflection, the atom may escape the grain or strike the grain surface at another location. In the latter case, the atom undergoes another specular reflection; this continues until the atom ultimately escapes the grain.

Since the speed of the atom does not change upon reflection, the recoil angular momentum delivered to the grain is

\begin{equation} \Delta \boldsymbol {J}_{\mathrm{spec}} = - m v_{\mathrm{th}} s r_{\mathrm{sph}} \left( {\hat{\boldsymbol r}}_{\rm f} - \frac{\boldsymbol {r}_{\mathrm{cm}}}{r_{\mathrm{sph}}} \right) \times {\hat{\boldsymbol s}}_{\rm f}, \end{equation}

(39)

where |$r_{\mathrm{sph}} \, {\hat{\boldsymbol r}}_{\rm f}$| and |$s {\hat{\boldsymbol s}}_{\rm f}$| are the final position and reduced velocity of the reflected atom as it leaves the enclosing sphere. Thus, the mean recoil torque associated with specular reflection is

\begin{equation} \boldsymbol {\Gamma }_{\mathrm{spec}} = m n v_{\mathrm{th}}^2 a_{\mathrm{eff}}^3 \boldsymbol {Q}_{\Gamma , \mathrm{spec}} \end{equation}

(40)

with

\begin{equation} \boldsymbol {Q}_{\Gamma , \mathrm{spec}} = - \pi ^{-3/2} \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^3 \int _{-1}^1 \mathrm{d}(\cos \theta _{\mathrm{sph}}) \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{sph}} \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \int _{u_{\rm c}}^1 \mathrm{d}(\cos \theta _{\mathrm{in}}) \cos \theta _{\mathrm{in}} \left( {\hat{\boldsymbol r}}_{\rm f} - \frac{\boldsymbol {r}_{\mathrm{cm}}}{r_{\mathrm{sph}}} \right) \times {\hat{\boldsymbol s}}_{\rm f} \, I_s(4, s_{\rm d}, \beta ). \end{equation}

(41)

3.3 Mechanical torque due to outgoing atoms or molecules

We assume that the rate at which H atoms depart the grain (either in atomic form or as part of an H₂ molecule) equals the rate at which they arrive at the grain. In this section, we consider only particles that stick to the grain surface upon arrival (as opposed to those that reflect specularly). We further assume that these outgoing particles depart along the direction |${\hat{\boldsymbol N}}(\theta , \phi )$| normal to the grain surface (see equation 14). In order to keep the computational time manageable, we do not consider a distribution of outgoing directions for atoms/molecules that have been accommodated on the grain surface. We consider the following scenarios for the departing particles.

(1) Atoms or molecules depart from an arbitrary location on the grain surface. The rate of departure from a surface element is proportional to its area.

(2) Atoms or molecules depart from approximately the same location where they arrived on the grain surface.

In future work we will also examine the case that molecules depart from a set of special sites of molecule formation on the grain surface.

The angular momentum imparted to the grain when an atom or molecule departs is

\begin{equation} \Delta \boldsymbol {J}_{\mathrm{out}} = - m_{\mathrm{out}} v_{\mathrm{out}} a_{\mathrm{eff}} \left( \frac{\boldsymbol {r}_{\mathrm{surf}} - \boldsymbol {r}_{\mathrm{cm}}}{a_{\mathrm{eff}}} \right) \times {\hat{\boldsymbol N}}, \end{equation}

(42)

where m_out and v_out are the mass and speed of the outgoing particle, respectively. Next, we introduce a function κ_esc(θ, ϕ) such that κ_esc = 1 if an atom or molecule that departs the surface along |${\hat{\boldsymbol N}}$| at (θ, ϕ) escapes to infinity and κ_esc = 0 if the departing particle instead strikes the grain at another location on the surface.

For scenario (1), the rate at which particles depart a surface element is

\begin{equation} \mathrm{d}R_{\mathrm{out}, (1)} = g R_{\mathrm{arr}} S_{\mathrm{esc}}^{-1} \kappa _{\mathrm{esc}}(\theta , \phi ) \mathrm{d}(\cos \theta ) \mathrm{d}\phi \, \eta _S(\theta , \phi ), \end{equation}

(43)

where g = 1 if the departing species is an H atom and g = 1/2 if it is an H₂ molecule;

\begin{equation} S_{\mathrm{esc}} = \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2\pi } \mathrm{d}\phi \, \eta _S(\theta , \phi ) \kappa _{\mathrm{esc}}(\theta , \phi ). \end{equation}

(44)

Thus, the mean torque is

\begin{equation} \boldsymbol {\Gamma }_{\mathrm{out}, (1)} = g m_{\mathrm{out}} n v_{\mathrm{th}} v_{\mathrm{out}} a_{\mathrm{eff}}^3 \boldsymbol {Q}_{\Gamma , \mathrm{out}, (1)} = m n v_{\mathrm{th}} v_{\mathrm{out}} a_{\mathrm{eff}}^3 \boldsymbol {Q}_{\Gamma , \mathrm{out}, (1)} \end{equation}

(45)

with

\begin{equation} \boldsymbol {Q}_{\Gamma , \mathrm{out}, (1)} = - Q_{\mathrm{arr}} S_{\mathrm{esc}}^{-1} \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2\pi } \mathrm{d}\phi \, \eta _S(\theta , \phi ) \kappa _{\mathrm{esc}}(\theta , \phi ) \left( \frac{\boldsymbol {r}_{\mathrm{surf}} - \boldsymbol {r}_{\mathrm{cm}}}{a_{\mathrm{eff}}} \right) \times {\hat{\boldsymbol N}}. \end{equation}

(46)

The relation gm_out = m follows from the assumption that H atoms depart the grain at the same rate at which they arrive.

For scenario (2), consider a gas-phase atom arriving at the enclosing sphere at (θ_sph, ϕ_sph, ϕ_in, θ_in). After arriving at the grain surface, it departs along the surface normal. Its path either takes it away from the grain (beyond r_sph) or intersects the grain at another surface location, from which it then departs along the local normal. After some number of surface intersections, the departing particle hits the surface at a location (θ′, ϕ′) such that its path along |${\hat{\boldsymbol N}}(\theta ^{\prime }, \phi ^{\prime })$| takes it away from the grain. Thus, the mean torque due to outgoing atoms or molecules in scenario (2) is

\begin{equation} \boldsymbol {\Gamma }_{\mathrm{out}, (2)} = g \int \mathrm{d}R_{\mathrm{arr}} (\theta _{\mathrm{sph}}, \phi _{\mathrm{sph}}, \phi _{\mathrm{in}}, \theta _{\mathrm{in}}) \Delta \boldsymbol {J}_{\mathrm{out}}( \theta ^{\prime }, \phi ^{\prime }) = m n v_{\mathrm{th}} v_{\mathrm{out}} a_{\mathrm{eff}}^3 \boldsymbol {Q}_{\Gamma , \mathrm{out}, (2)} \end{equation}

(47)

with

\begin{equation} \boldsymbol {Q}_{\Gamma , \mathrm{out}, (2)} = - \pi ^{-3/2} \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^2 \int _{-1}^1 \mathrm{d}(\cos \theta _{\mathrm{sph}}) \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{sph}} \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \int _{u_{\rm c}}^1 \mathrm{d}(\cos \theta _{\mathrm{in}}) \cos \theta _{\mathrm{in}} \left[ \frac{\boldsymbol {r}_{\mathrm{surf}}(\theta ^{\prime }, \phi ^{\prime }) - \boldsymbol {r}_{\mathrm{cm}}}{a_{\mathrm{eff}}} \right] \times {\hat{\boldsymbol N}}(\theta ^{\prime }, \phi ^{\prime }) \, I_s(3, s_{\rm d}, \beta ). \end{equation}

(48)

3.4 Total mechanical torque

If a fraction f_spec of the gas-phase atoms that strike the grain surface reflect specularly, then the total mechanical torque is

\begin{equation} \boldsymbol {\Gamma }_{\mathrm{mech}} = m n v^2_{\mathrm{th}} a_{\mathrm{eff}}^3 \boldsymbol {Q}_{\Gamma , \mathrm{mech}} \end{equation}

(49)

with

\begin{equation} \boldsymbol {Q}_{\Gamma , \mathrm{mech}} = \boldsymbol {Q}_{\Gamma , \mathrm{arr}} + f_{\mathrm{spec}} \boldsymbol {Q}_{\Gamma , \mathrm{spec}} + (1 - f_{\mathrm{spec}}) \frac{v_{\mathrm{out}}}{v_{\mathrm{th}}} \, \boldsymbol {Q}_{\Gamma , \mathrm{out}}, \end{equation}

(50)

where |$\boldsymbol {Q}_{\Gamma , \mathrm{out}}$| is the efficiency factor for one of the scenarios (1 or 2) for outgoing particles.

3.5 Rotational averaging

We assume that the grain rotates steadily about |${\hat{\boldsymbol a}}_1$|⁠, as is appropriate for suprathermal rotation, and average the torque efficiency factors over this rotation.

Consider a coordinate system (x_v, y_v, z_v) fixed in space with |${\hat{\boldsymbol z}}_v$| along the direction of the grain's velocity and with |${\hat{\boldsymbol a}}_1$| lying in the x_v–z_v plane. From equation (24),

\begin{equation} \sin \theta _{\mathrm{gr}} \cos \phi _{\mathrm{gr}} = {\hat{\boldsymbol z}}_v {\cdot } {\hat{\boldsymbol x}}, \end{equation}

(51)

\begin{equation} \sin \theta _{\mathrm{gr}} \sin \phi _{\mathrm{gr}} = {\hat{\boldsymbol z}}_v {\cdot } {\hat{\boldsymbol y}}, \end{equation}

(52)

\begin{equation} \cos \theta _{\mathrm{gr}} = {\hat{\boldsymbol z}}_v {\cdot } {\hat{\boldsymbol z}}. \end{equation}

(53)

Take the angle between |${\hat{\boldsymbol v}}_{\mathrm{gr}}$| and |${\hat{\boldsymbol a}}_1$| to be θ_va. Since |${\hat{\boldsymbol a}}_1$| lies in the x_v–z_v plane,

\begin{equation} {\hat{\boldsymbol a}}_1 = \sin \theta _{va} \, {\hat{\boldsymbol x}}_v + \cos \theta _{va} \, {\hat{\boldsymbol z}}_v. \end{equation}

(54)

Next introduce angle Φ₂ to describe the rotation of |${\hat{\boldsymbol a}}_2$| about |${\hat{\boldsymbol a}}_1$|⁠. Define it such that |${\hat{\boldsymbol a}}_2$| lies along the y_v-axis when Φ₂ = 0 and in the x_v–z_v plane when Φ₂ = π/2. Specifically, |${\hat{\boldsymbol a}}_2 = {\hat{\boldsymbol y}}_v$| when Φ₂ = 0 and |${\hat{\boldsymbol a}}_2 = - \cos \theta _{va} \, {\hat{\boldsymbol x}}_v + \sin \theta _{va} \, {\hat{\boldsymbol z}}_v$| when Φ₂ = π/2. Thus,

\begin{equation} {\hat{\boldsymbol a}}_2 = \cos \Phi _2 \, {\hat{\boldsymbol y}}_v + \sin \Phi _2 (- \cos \theta _{va} \, {\hat{\boldsymbol x}}_v + \sin \theta _{va} \, {\hat{\boldsymbol z}}_v) \end{equation}

(55)

and

\begin{equation} {\hat{\boldsymbol a}}_3 = {\hat{\boldsymbol a}}_1 \times {\hat{\boldsymbol a}}_2 = \cos \Phi _2 (- \cos \theta _{va} \, {\hat{\boldsymbol x}}_v + \sin \theta _{va} \, {\hat{\boldsymbol z}}_v) - \sin \Phi _2 \, {\hat{\boldsymbol y}}_v. \end{equation}

(56)

Expressing the principal axes in equations (54)–(56) in terms of their components in the (x, y, z) system,

\begin{equation} a_{1x} \, {\hat{\boldsymbol x}} + a_{1y} \, {\hat{\boldsymbol y}} + a_{1z} \, {\hat{\boldsymbol z}} = \sin \theta _{va} \, {\hat{\boldsymbol x}}_v + \cos \theta _{va} \, {\hat{\boldsymbol z}}_v, \end{equation}

(57)

\begin{equation} a_{2x} \, {\hat{\boldsymbol x}} + a_{2y} \, {\hat{\boldsymbol y}} + a_{2z} \, {\hat{\boldsymbol z}} = \cos \Phi _2 \, {\hat{\boldsymbol y}}_v + \sin \Phi _2 (- \cos \theta _{va} \, {\hat{\boldsymbol x}}_v + \sin \theta _{va} \, {\hat{\boldsymbol z}}_v), \end{equation}

(58)

\begin{equation} a_{3x} \, {\hat{\boldsymbol x}} + a_{3y} \, {\hat{\boldsymbol y}} + a_{3z} \, {\hat{\boldsymbol z}} = \cos \Phi _2 (- \cos \theta _{va} \, {\hat{\boldsymbol x}}_v + \sin \theta _{va} \, {\hat{\boldsymbol z}}_v) - \sin \Phi _2 \, {\hat{\boldsymbol y}}_v. \end{equation}

(59)

Taking the dot product of equations (57)–(59) with |${\hat{\boldsymbol x}}$| yields

\begin{equation} a_{1x} = \sin \theta _{va} ({\hat{\boldsymbol x}}_v {\cdot } {\hat{\boldsymbol x}}) + \cos \theta _{va} ({\hat{\boldsymbol z}}_v {\cdot } {\hat{\boldsymbol x}}), \end{equation}

(60)

\begin{equation} a_{2x} = - \sin \Phi _2 \cos \theta _{va} ({\hat{\boldsymbol x}}_v {\cdot } {\hat{\boldsymbol x}}) + \cos \Phi _2 ({\hat{\boldsymbol y}}_v {\cdot } {\hat{\boldsymbol x}}) + \sin \Phi _2 \sin \theta _{va} ({\hat{\boldsymbol z}}_v {\cdot } {\hat{\boldsymbol x}}), \end{equation}

(61)

\begin{equation} a_{3x} = - \cos \Phi _2 \cos \theta _{va} ({\hat{\boldsymbol x}}_v {\cdot } {\hat{\boldsymbol x}}) - \sin \Phi _2 ({\hat{\boldsymbol y}}_v {\cdot } {\hat{\boldsymbol x}}) + \cos \Phi _2 \sin \theta _{va} ({\hat{\boldsymbol z}}_v {\cdot } {\hat{\boldsymbol x}}). \end{equation}

(62)

Equations of identical structure result when taking the dot product with |${\hat{\boldsymbol y}}$| or |${\hat{\boldsymbol z}}$|⁠. Solving for the dot products,

\begin{equation} {\hat{\boldsymbol x}}_v {\cdot } {\hat{\boldsymbol x}}_i = a_{1i} \sin \theta _{va} - (a_{2i} \sin \Phi _2 + a_{3i} \cos \Phi _2) \cos \theta _{va}, \end{equation}

(63)

\begin{equation} {\hat{\boldsymbol y}}_v {\cdot } {\hat{\boldsymbol x}}_i = a_{2i} \cos \Phi _2 - a_{3i} \sin \Phi _2, \end{equation}

(64)

\begin{equation} {\hat{\boldsymbol z}}_v {\cdot } {\hat{\boldsymbol x}}_i = a_{1i} \cos \theta _{va} + (a_{2i} \sin \Phi _2 + a_{3i} \cos \Phi _2) \sin \theta _{va}. \end{equation}

(65)

In equations (63)–(65), the subscript i = 1–3 denotes coordinates x, y, z in the original coordinate system used to define the GRS.

Substituting the expressions in equation (65) into equations (51)–(53) yields (θ_gr, ϕ_gr) as functions of (θ_va, Φ₂):

\begin{equation} \sin \theta _{\mathrm{gr}} \cos \phi _{\mathrm{gr}} = a_{1x} \cos \theta _{va} + (a_{2x} \sin \Phi _2 + a_{3x} \cos \Phi _2) \sin \theta _{va}, \end{equation}

(66)

\begin{equation} \sin \theta _{\mathrm{gr}} \sin \phi _{\mathrm{gr}} = a_{1y} \cos \theta _{va} + (a_{2y} \sin \Phi _2 + a_{3y} \cos \Phi _2) \sin \theta _{va}, \end{equation}

(67)

\begin{equation} \cos \theta _{\mathrm{gr}} = a_{1z} \cos \theta _{va} + (a_{2z} \sin \Phi _2 + a_{3z} \cos \Phi _2) \sin \theta _{va}. \end{equation}

(68)

The rotationally averaged value of the scalar efficiency factor Q_arr is

\begin{equation} \overline{Q}_{\mathrm{arr}}(\theta _{va}) = \frac{1}{2 \pi } \int _0^{2\pi } \mathrm{d} \Phi _2 \, Q_{\mathrm{arr}}(\theta _{va}, \Phi _2). \end{equation}

(69)

The rotationally averaged value of the x_v-component of a vector efficiency factor |$\boldsymbol {Q}_i$| (i equals, e.g. ‘Γ, arr’) is

\begin{equation} \overline{Q}_{i, x_v}(\theta _{va}) = \frac{1}{2 \pi } \int _0^{2\pi } \mathrm{d}\Phi _2 \, Q_{i, x_v}(\theta _{va}, \Phi _2), \end{equation}

(70)

\begin{equation} Q_{i, x_v}(\theta _{va}, \Phi _2) = \sum _{j=1}^3 Q_{i, j}(\theta _{\mathrm{gr}}, \phi _{\mathrm{gr}}) \, ({\hat{\boldsymbol x}}_v {\cdot } {\hat{\boldsymbol x}}_j). \end{equation}

(71)

Similarly for the y_v- and z_v-components.

It is convenient to express the averaged torque components in terms of spherical unit vectors |${\hat{\boldsymbol a}}_1$|⁠, |${\hat{\boldsymbol \theta }}_v = {\hat{\boldsymbol x}}_v \cos \theta _{va} - {\hat{\boldsymbol z}}_v \sin \theta _{va}$|⁠, and |${\hat{\boldsymbol \phi }}_v = {\hat{\boldsymbol y}}_v$|⁠.

3.6 Drag torque

A rotating grain experiences a drag torque. Only the outgoing particles (reflected or otherwise) contribute since the angular momenta of the incoming atoms (as observed in an inertial frame) are not affected by the grain rotation. In scenarios (1) and (2), the outgoing particle departs along the local surface normal |${\hat{\boldsymbol N}}$|⁠. After some number of times intersecting the grain surface (possibly zero), the particle's path along the local |${\hat{\boldsymbol N}}$| leads it to escape the grain. The outgoing particle's velocity in the torque expressions is |$v_{\mathrm{out}} {\hat{\boldsymbol N}}$|⁠. For a rotating grain, this velocity is replaced with |$v_{\mathrm{out}} {\hat{\boldsymbol N}} + {\boldsymbol v}_{\mathrm{surf}}$|⁠, where |${\boldsymbol v}_{\mathrm{surf}} = \omega \times (\boldsymbol {r}_{\mathrm{surf}} - \boldsymbol {r}_{\mathrm{cm}})$| is the velocity of the surface element due to the grain rotation. Thus, the expressions for the drag torque efficiency factors are identical to those for the mechanical torque except that |$v_{\mathrm{out}} {\hat{\boldsymbol N}}$| is replaced with |${\boldsymbol v}_{\mathrm{surf}}$|⁠.

Since the orientation (θ_gr, ϕ_gr) of a rotating grain relative to the direction of the drift velocity is not constant, the drag torque efficiency factors must be averaged over the rotation. For steady rotation about |${\hat{\boldsymbol a}}_1$|⁠, this is done as described in Section 3.5.

Since the motion of the grain can be neglected during the time interval that an outgoing particle is in the grain vicinity and the outgoing particle is always assumed to travel along |${\hat{\boldsymbol N}}$| in scenarios (1) and (2), the details of whether and where an outgoing particle strikes the grain surface are unaffected by the grain rotation. However, the velocity vector of the reflected particle does depend on rotation in the case of specular reflection, since the law of reflection applies in the rest frame of the surface element. This would introduce a major computational burden, since the particle paths would have to be traced anew for each value of the angular velocity. Thus, we do not compute the drag torque for the case of specular reflection.

For steady rotation about |${\hat{\boldsymbol a}}_1$|⁠,

\begin{equation} \boldsymbol {\Gamma }_{\mathrm{drag, \, out}, (i)} = m n v_{\mathrm{th}} a_{\mathrm{eff}}^4 \omega \boldsymbol {Q}_{\Gamma , \mathrm{drag, \, out}, (i)} \end{equation}

(72)

with

\begin{equation} \boldsymbol {Q}_{\Gamma , \mathrm{drag, \, out}, (1)} = - Q_{\mathrm{arr}} S_{\mathrm{esc}}^{-1} \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2\pi } \mathrm{d}\phi \, \eta _S(\theta , \phi ) \kappa _{\mathrm{esc}}(\theta , \phi ) \left[ \frac{r^2_{\mathrm{surf}} + r^2_{\mathrm{cm}} - 2 \boldsymbol {r}_{\mathrm{cm}} {\cdot } \boldsymbol {r}_{\mathrm{surf}}}{a_{\mathrm{eff}}^2} \ {\hat{\boldsymbol a}}_1 - {\hat{\boldsymbol a}}_1 {\cdot } \left( \frac{\boldsymbol {r}_{\mathrm{surf}} - \boldsymbol {r}_{\mathrm{cm}}}{a_{\mathrm{eff}}} \right) \frac{(\boldsymbol {r}_{\mathrm{surf}} - \boldsymbol {r}_{\mathrm{cm}})}{a_{\mathrm{eff}}} \right] \end{equation}

(73)

and

\begin{eqnarray} \boldsymbol {Q}_{\Gamma , \mathrm{drag, \, out}, (2)} &=& - \pi ^{-3/2} \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^2 \int _{-1}^1 \mathrm{d} (\cos \theta _{\mathrm{sph}}) \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{sph}} \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \int _{u_{\rm c}}^1 \mathrm{d}(\cos \theta _{\mathrm{in}}) \cos \theta _{\mathrm{in}} \, I_s(3, s_{\rm d}, \beta ) \nonumber\\ &&\times\left\lbrace \frac{r^2_{\mathrm{surf}}(\theta ^{\prime }, \phi ^{\prime }) + r^2_{\mathrm{cm}} - 2 \boldsymbol {r}_{\mathrm{cm}} {\cdot } \boldsymbol {r}_{\mathrm{surf}}(\theta ^{\prime }, \phi ^{\prime })}{a^2_{\mathrm{eff}}} \ {\hat{\boldsymbol a}}_1 - {\hat{\boldsymbol a}}_1 {\cdot } \left[ \frac{ \boldsymbol {r}_{\mathrm{surf}}(\theta ^{\prime }, \phi ^{\prime }) - \boldsymbol {r}_{\mathrm{cm}}}{a_{\mathrm{eff}}} \right] \frac{[\boldsymbol {r}_{\mathrm{surf}}(\theta ^{\prime }, \phi ^{\prime }) - \boldsymbol {r}_{\mathrm{cm}}]}{a_{\mathrm{eff}}} \right\rbrace . \end{eqnarray}

(74)

The above expressions must be averaged over the rotation about |${\hat{\boldsymbol a}}_1$| as described in Section 3.5.

In the case of a spherical grain at rest relative to the gas, u_c = 0, r_sph = a_eff, |$\boldsymbol {r}_{\mathrm{cm}} = 0$|⁠, s_d = 0, and equation (74) simply evaluates to |$\boldsymbol {Q}_{\Gamma , \mathrm{drag, \, out}, (2)} = - 4 \pi ^{1/2} {\hat{\boldsymbol a}}_1 /3$|⁠, which is a well-known result (see e.g. Draine & Weingartner 1996).

3.7 Extreme subsonic limit

When the grain's motion through the gas is highly subsonic (s_d ≪ 1), simple approximations for the integrals over s are available:

\begin{equation} I_s(3, s_{\rm d}, \beta ) \approx \frac{1}{2} + \frac{3 \sqrt{\pi }}{4} \, \beta s_{\rm d}, \end{equation}

(75)

\begin{equation} I_s(4, s_{\rm d}, \beta ) \approx \frac{3 \sqrt{\pi }}{8} + 2 \beta s_{\rm d}. \end{equation}

(76)

The efficiency factors associated with arriving atoms simplify to

\begin{equation} Q_{\mathrm{arr}} \approx Q_{\mathrm{arr}}(s_{\rm d} = 0) + Q^{\prime }_{\mathrm{arr}} \ s_{\rm d}, \end{equation}

(77)

\begin{equation} Q_{\mathrm{arr}}(s_{\rm d} = 0) = \frac{\pi ^{-3/2}}{4} \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^2 \int _{-1}^1 \mathrm{d}(\cos \theta _{\mathrm{sph}}) \int _0^{2 \pi } \mathrm{d}\phi _{\mathrm{sph}} \int _0^{2 \pi } \mathrm{d}\phi _{\mathrm{in}} \left(1-u_{\rm c}^2\right), \end{equation}

(78)

\begin{equation} Q^{\prime }_{\mathrm{arr}} = \frac{1}{4 \pi } \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^2 \int _{-1}^1 \mathrm{d}(\cos \theta _{\mathrm{sph}}) \int _0^{2 \pi } \mathrm{d}\phi _{\mathrm{sph}} \int _0^{2 \pi } \mathrm{d}\phi _{\mathrm{in}} \left[ \beta _1 \left(1 - u_{\rm c}^3\right) + \beta _2 \left(1-u_{\rm c}^2\right)^{3/2} \right], \end{equation}

(79)

\begin{equation} \boldsymbol {Q}_{\Gamma , \mathrm{arr}} \approx \boldsymbol {Q}_{\Gamma , \mathrm{arr}}(s_{\rm d} = 0) + \boldsymbol {Q}^{\prime }_{\Gamma , \mathrm{arr}} \ s_{\rm d}, \end{equation}

(80)

\begin{equation} \boldsymbol {Q}_{\Gamma , \mathrm{arr}}(s_{\rm d} = 0) = \frac{3}{8 \pi } \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^3 \int _{-1}^1 \mathrm{d}(\cos \theta _{\mathrm{sph}}) \int _0^{2\pi } \mathrm{d} \phi _{\mathrm{sph}} \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \int _{u_{\rm c}}^1 \mathrm{d} (\cos \theta _{\mathrm{in}}) \cos \theta _{\mathrm{in}} \left( {\hat{\boldsymbol r}} - \frac{\boldsymbol {r}_{\mathrm{cm}}}{r_{\mathrm{sph}}} \right) \times {\hat{\boldsymbol s}}, \end{equation}

(81)

\begin{equation} \boldsymbol {Q}^{\prime }_{\Gamma , \mathrm{arr}} = 2 \pi ^{-3/2} \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^3 \int _{-1}^1 \mathrm{d}(\cos \theta _{\mathrm{sph}}) \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{sph}} \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \int _{u_{\rm c}}^1 \mathrm{d}(\cos \theta _{\mathrm{in}}) \cos \theta _{\mathrm{in}} \left( {\hat{\boldsymbol r}} - \frac{\boldsymbol {r}_{\mathrm{cm}}}{r_{\mathrm{sph}}} \right) \times {\hat{\boldsymbol s}} \, \beta . \end{equation}

(82)

See Appendix A3 for explicit expressions that simplify the calculation of |$\boldsymbol {Q}_{\Gamma , \mathrm{arr}}(s_{\rm d} = 0)$| and |$\boldsymbol {Q}^{\prime }_{\Gamma , \mathrm{arr}}$|⁠. Although it is not evident from equations (79) and (81) or (A11), both |$Q^{\prime }_{\mathrm{arr}}$| and |$\boldsymbol {Q}_{\Gamma , \mathrm{arr}}(s_{\rm d} = 0)$| vanish, as shown in Appendix B.

For specular reflection,

\begin{equation} \boldsymbol {Q}_{\Gamma , \mathrm{spec}} \approx \boldsymbol {Q}_{\Gamma , \mathrm{spec}} (s_{\rm d} = 0) + \boldsymbol {Q}^{\prime }_{\Gamma , \mathrm{spec}} \ s_{\rm d} \end{equation}

(83)

with

\begin{equation} \boldsymbol {Q}_{\Gamma , \mathrm{spec}}(s_{\rm d} = 0) = - \frac{3}{8 \pi } \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^3 \int _{-1}^1 \mathrm{d}(\cos \theta _{\mathrm{sph}}) \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{sph}} \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \int _{u_{\rm c}}^1 \mathrm{d}(\cos \theta _{\mathrm{in}}) \cos \theta _{\mathrm{in}} \left( {\hat{\boldsymbol r}}_f - \frac{\boldsymbol {r}_{\mathrm{cm}}}{r_{\mathrm{sph}}} \right) \times {\hat{\boldsymbol s}}_{\rm f}, \end{equation}

(84)

\begin{equation} \boldsymbol {Q}^{\prime }_{\Gamma , \mathrm{spec}} = - 2 \pi ^{-3/2} \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^3 \int _{-1}^1 \mathrm{d}(\cos \theta _{\mathrm{sph}}) \int _0^{2\pi } d\phi _{\mathrm{sph}} \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \int _{u_{\rm c}}^1 \mathrm{d}(\cos \theta _{\mathrm{in}}) \cos \theta _{\mathrm{in}} \left( {\hat{\boldsymbol r}}_f - \frac{\boldsymbol {r}_{\mathrm{cm}}}{r_{\mathrm{sph}}} \right) \times {\hat{\boldsymbol s}}_{\rm f} \, \beta . \end{equation}

(85)

When s_d = 0, and in the limit that the grain rotation can be neglected during the collision, for every specularly reflected atom, there is an arriving atom whose velocity has the same magnitude but opposite sign. Thus, |$\boldsymbol {Q}_{\Gamma , \mathrm{spec}}(s_{\rm d} = 0) = \boldsymbol {Q}_{\Gamma , \mathrm{arr}} (s_{\rm d} = 0) = 0$|⁠.

As a check of our computer codes, we implement equations (79), (A11), and (84) to compute |$Q^{\prime }_{\mathrm{arr}}$|⁠, |$\boldsymbol {Q}_{\Gamma , \mathrm{arr}}(s_{\rm d} = 0)$|⁠, and |$\boldsymbol {Q}_{\Gamma , \mathrm{spec}}(s_{\rm d} = 0)$| and verify that they tend to zero as the numerical resolution improves.

The efficiency factors for outgoing scenario (1) depend on s_d only through Q_arr. For scenario (2),

\begin{equation} \boldsymbol {Q}_{\Gamma , \mathrm{out}, (2)} \approx \boldsymbol {Q}_{\Gamma , \mathrm{out}, (2)}(s_{\rm d} = 0) + \boldsymbol {Q}^{\prime }_{\Gamma , \mathrm{out}, (2)} \ s_{\rm d} \end{equation}

(86)

with

\begin{equation} \boldsymbol {Q}_{\Gamma , \mathrm{out}, (2)}(s_{\rm d} = 0) = - \frac{\pi ^{-3/2}}{2} \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^2 \int _{-1}^1 \mathrm{d}(\cos \theta _{\mathrm{sph}}) \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{sph}} \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \int _{u_{\rm c}}^1 \mathrm{d}(\cos \theta _{\mathrm{in}}) \cos \theta _{\mathrm{in}} \left[ \frac{\boldsymbol {r}_{\mathrm{surf}}(\theta ^{\prime }, \phi ^{\prime }) - \boldsymbol {r}_{\mathrm{cm}}}{a_{\mathrm{eff}}} \right] \times {\hat{\boldsymbol N}}(\theta ^{\prime }, \phi ^{\prime }), \end{equation}

(87)

\begin{equation} \boldsymbol {Q}^{\prime }_{\Gamma , \mathrm{out}, (2)} = - \frac{3}{4 \pi } \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^2 \int _{-1}^1 \mathrm{d}(\cos \theta _{\mathrm{sph}}) \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{sph}} \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \int _{u_{\rm c}}^1 \mathrm{d}(\cos \theta _{\mathrm{in}}) \cos \theta _{\mathrm{in}} \left[ \frac{\boldsymbol {r}_{\mathrm{surf}}(\theta ^{\prime }, \phi ^{\prime }) - \boldsymbol {r}_{\mathrm{cm}}}{a_{\mathrm{eff}}} \right] \times {\hat{\boldsymbol N}}(\theta ^{\prime }, \phi ^{\prime }) \, \beta , \end{equation}

(88)

and

\begin{equation} \boldsymbol {Q}_{\Gamma , \mathrm{drag, \, out}, (2)} \approx \boldsymbol {Q}_{\Gamma , \mathrm{drag, \, out}, (2)}(s_{\rm d} = 0) + \boldsymbol {Q}^{\prime }_{\Gamma , \mathrm{out}, (2)} \ s_{\rm d} \end{equation}

(89)

with

\begin{eqnarray} \boldsymbol {Q}_{\Gamma , \mathrm{drag, \, out}, (2)}(s_{\rm d} = 0) &=& - \frac{\pi ^{-3/2}}{2} \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^2 \int _{-1}^1 \mathrm{d} (\cos \theta _{\mathrm{sph}}) \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{sph}} \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \int _{u_{\rm c}}^1 \mathrm{d}(\cos \theta _{\mathrm{in}}) \cos \theta _{\mathrm{in}} \nonumber\\ &&\times \left\lbrace \frac{r^2_{\mathrm{surf}}(\theta ^{\prime }, \phi ^{\prime }) + r^2_{\mathrm{cm}} - 2 \boldsymbol {r}_{\mathrm{cm}} {\cdot } \boldsymbol {r}_{\mathrm{surf}}(\theta ^{\prime }, \phi ^{\prime })}{a^2_{\mathrm{eff}}} \ {\hat{\boldsymbol a}}_1 - {\hat{\boldsymbol a}}_1 {\cdot } \left[ \frac{ \boldsymbol {r}_{\mathrm{surf}}(\theta ^{\prime }, \phi ^{\prime }) - \boldsymbol {r}_{\mathrm{cm}}}{a_{\mathrm{eff}}} \right] \frac{[\boldsymbol {r}_{\mathrm{surf}}(\theta ^{\prime }, \phi ^{\prime }) - \boldsymbol {r}_{\mathrm{cm}}]}{a_{\mathrm{eff}}} \right\rbrace , \end{eqnarray}

(90)

\begin{eqnarray} \boldsymbol {Q}^{\prime }_{\Gamma , \mathrm{drag, \, out}, (2)} &=& - \frac{3}{4 \pi } \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^2 \int _{-1}^1 \mathrm{d} (\cos \theta _{\mathrm{sph}}) \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{sph}} \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \int _{u_{\rm c}}^1 \mathrm{d}(\cos \theta _{\mathrm{in}}) \cos \theta _{\mathrm{in}} \nonumber\\ &&\times \left\lbrace \frac{r^2_{\mathrm{surf}}(\theta ^{\prime }, \phi ^{\prime }) + r^2_{\mathrm{cm}} - 2 \boldsymbol {r}_{\mathrm{cm}} {\cdot } \boldsymbol {r}_{\mathrm{surf}}(\theta ^{\prime }, \phi ^{\prime })}{a^2_{\mathrm{eff}}} \ {\hat{\boldsymbol a}}_1 - {\hat{\boldsymbol a}}_1 {\cdot } \left[ \frac{ \boldsymbol {r}_{\mathrm{surf}}(\theta ^{\prime }, \phi ^{\prime }) - \boldsymbol {r}_{\mathrm{cm}}}{a_{\mathrm{eff}}} \right] \frac{[\boldsymbol {r}_{\mathrm{surf}}(\theta ^{\prime }, \phi ^{\prime }) - \boldsymbol {r}_{\mathrm{cm}}]}{a_{\mathrm{eff}}} \right\rbrace \beta . \end{eqnarray}

(91)

3.8 Extreme supersonic limit

If the grain motion is highly supersonic (s_d ≫ 1), then we can neglect the thermal motion of the gas atoms. In this case, all of the atoms move along |$- {\hat{\boldsymbol s}}_{\rm d}$|⁠. The simplest and most efficient computational approach dispenses with the enclosing sphere. The rate at which gas-phase particles arrive at a patch on the grain surface is

\begin{equation} \mathrm{d}R_{\mathrm{arr}} \approx n v_{\mathrm{th}} s_{\rm d} \, \mathrm{d}(\cos \theta ) \, \mathrm{d}\phi \, \eta _S(\theta , \phi ) [{\hat{\boldsymbol s}}_{\rm d} {\cdot } {\hat{\boldsymbol N}}(\theta , \phi )] \mu _{\mathrm{hit}}, \end{equation}

(92)

where μ_hit = 1 (0) if gas atoms do (do not) strike the patch. Gas atoms do not strike the patch if they are moving in the wrong direction (⁠|${\hat{\boldsymbol s}}_{\rm d} {\cdot } {\hat{\boldsymbol N}} < 0$|⁠) or if the patch is obstructed by another portion of the grain. Thus,

\begin{equation} Q_{\mathrm{arr}} \approx s_{\rm d} \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2 \pi } \mathrm{d}\phi \, \frac{\eta _S(\theta , \phi )}{a_{\mathrm{eff}}^2} [{\hat{\boldsymbol s}}_{\rm d} {\cdot } {\hat{\boldsymbol N}}(\theta , \phi )] \mu _{\mathrm{hit}}. \end{equation}

(93)

The angular momentum of the arriving particle is

\begin{equation} \Delta \boldsymbol {J}_{\mathrm{arr}} = m v_{\mathrm{th}} s_{\rm d}(\boldsymbol {r}_{\mathrm{surf}} - \boldsymbol {r}_{\mathrm{cm}}) \times (- {\hat{\boldsymbol s}}_{\rm d}). \end{equation}

(94)

Thus,

\begin{equation} \boldsymbol {Q}_{\Gamma , \mathrm{arr}} \approx s_{\rm d}^2 \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2 \pi } \mathrm{d}\phi \, \frac{\eta _S(\theta , \phi )}{a_{\mathrm{eff}}^2} [{\hat{\boldsymbol s}}_{\rm d} {\cdot } {\hat{\boldsymbol N}}(\theta , \phi )] \mu _{\mathrm{hit}} \frac{(\boldsymbol {r}_{\mathrm{surf}} - \boldsymbol {r}_{\mathrm{cm}})}{a_{\mathrm{eff}}} \times (- {\hat{\boldsymbol s}}_{\rm d}). \end{equation}

(95)

Similarly, for specular reflection,

\begin{equation} \boldsymbol {Q}_{\Gamma , \mathrm{spec}} \approx - s_{\rm d}^2 \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2 \pi } \mathrm{d}\phi \, \frac{\eta _S(\theta , \phi )}{a_{\mathrm{eff}}^2} [{\hat{\boldsymbol s}}_{\rm d} {\cdot } {\hat{\boldsymbol N}}(\theta , \phi )] \mu _{\mathrm{hit}} \frac{(\boldsymbol {r}_{\mathrm{surf, \, f}} - \boldsymbol {r}_{\mathrm{cm}})}{a_{\mathrm{eff}}} \times {\hat{\boldsymbol s}}_{\rm f}, \end{equation}

(96)

where |$\boldsymbol {r}_{\mathrm{surf, \, f}}$| is the position on the surface from which the departing particle escapes to infinity.

As noted in Section 3.7, the efficiency factors for outgoing scenario (1) depend on s_d only through Q_arr. For scenario (2),

\begin{equation} \boldsymbol {Q}_{\Gamma , \mathrm{out}, (2)} \approx - s_{\rm d} \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2 \pi } \mathrm{d}\phi \frac{\eta _S(\theta , \phi )}{a_{\mathrm{eff}}^2} [{\hat{\boldsymbol s}}_{\rm d} {\cdot } {\hat{\boldsymbol N}}(\theta , \phi )] \mu _{\mathrm{hit}} \left[ \frac{\boldsymbol {r}_{\mathrm{surf}}(\theta ^{\prime }, \phi ^{\prime }) - \boldsymbol {r}_{\mathrm{cm}}}{a_{\mathrm{eff}}} \right] \times {\hat{\boldsymbol N}} (\theta ^{\prime }, \phi ^{\prime }) \end{equation}

(97)

and

\begin{eqnarray} \boldsymbol {Q}_{\Gamma , \mathrm{drag, \, out}, (2)} &\approx& - s_{\rm d} \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2 \pi } \mathrm{d}\phi \frac{\eta _S(\theta , \phi )}{a_{\mathrm{eff}}^2} [{\hat{\boldsymbol s}}_{\rm d} {\cdot } {\hat{\boldsymbol N}}(\theta , \phi )] \mu _{\mathrm{hit}} \nonumber\\ &&\times \left\lbrace \frac{r^2_{\mathrm{surf}}(\theta ^{\prime }, \phi ^{\prime }) + r^2_{\mathrm{cm}} - 2 \boldsymbol {r}_{\mathrm{cm}} {\cdot } \boldsymbol {r}_{\mathrm{surf}} (\theta ^{\prime }, \phi ^{\prime })}{a_{\mathrm{eff}}^2} \ {\hat{\boldsymbol a}}_1 - {\hat{\boldsymbol a}}_1 {\cdot } \left[ \frac{\boldsymbol {r}_{\mathrm{surf}}(\theta ^{\prime }, \phi ^{\prime }) - \boldsymbol {r}_{\mathrm{cm}}}{a_{\mathrm{eff}}} \right] \frac{[\boldsymbol {r}_{\mathrm{surf}} (\theta ^{\prime }, \phi ^{\prime }) - \boldsymbol {r}_{\mathrm{cm}}]}{a_{\mathrm{eff}}} \right\rbrace . \end{eqnarray}

(98)

3.9 Mechanical/drag force

Of course, collisions with gas atoms give rise to a force as well as a torque on a grain. Although the grain rotational dynamics is our primary concern, for completeness and code verification purposes we provide expressions for the force in this section.

An arriving gas particle deposits momentum |$\Delta {\boldsymbol p} = m v_{\mathrm{th}} s \, {\hat{\boldsymbol s}}$| on the grain. The force due to arriving atoms is

\begin{equation} \boldsymbol {F}_{\mathrm{arr}} = \int \mathrm{d}R_{\mathrm{arr}} \, \Delta {\boldsymbol p} = m n v_{\mathrm{th}}^2 a_{\mathrm{eff}}^2 \boldsymbol {Q}_{F, \mathrm{arr}} \end{equation}

(99)

with

\begin{equation} \boldsymbol {Q}_{F, \mathrm{arr}} = - \pi ^{-3/2} \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^2 \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2\pi } \mathrm{d}\phi \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \int _{u_{\rm c}}^1 \mathrm{d} (\cos \theta _{\mathrm{in}}) \cos \theta _{\mathrm{in}} (- {\hat{\boldsymbol s}}) I_s(4, s_{\rm d}, \beta ). \end{equation}

(100)

See Section 4.1 for an explicit expression for |$- {\hat{\boldsymbol s}}$|⁠.

For specular reflection, there is an additional term

\begin{equation} \boldsymbol {Q}_{F, \mathrm{spec}} = - \pi ^{-3/2} \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^2 \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2\pi } \mathrm{d}\phi \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \int _{u_{\rm c}}^1 \mathrm{d} (\cos \theta _{\mathrm{in}}) \cos \theta _{\mathrm{in}} \, {\hat{\boldsymbol s}}_f I_s(4, s_{\rm d}, \beta ). \end{equation}

(101)

For scenarios (1) and (2) for the outgoing particles, the force is given by

\begin{equation} \boldsymbol {F}_{\mathrm{out}, (i)} = m n v_{\mathrm{th}} v_{\mathrm{out}} a_{\mathrm{eff}}^2 \boldsymbol {Q}_{F, \mathrm{out}, (i)} \end{equation}

(102)

with

\begin{equation} \boldsymbol {Q}_{F, \mathrm{out}, (1)} = - Q_{\mathrm{arr}} S_{\mathrm{esc}}^{-1} \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2\pi } \mathrm{d}\phi \, \eta _S(\theta , \phi ) \kappa _{\mathrm{esc}}(\theta , \phi ) {\hat{\boldsymbol N}}(\theta , \phi ), \end{equation}

(103)

\begin{equation} \boldsymbol {Q}_{F, \mathrm{out}, (2)} = - \pi ^{-3/2} \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^2 \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2\pi } \mathrm{d}\phi \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \int _{u_{\rm c}}^1 \mathrm{d} (\cos \theta _{\mathrm{in}}) \cos \theta _{\mathrm{in}} {\hat{\boldsymbol N}}(\theta ^{\prime }, \phi ^{\prime }) \, I_s(3, s_{\rm d}, \beta ). \end{equation}

(104)

Refer to Section 3.3 for the meaning of (θ′, ϕ′) for scenario (2).

The total force is

\begin{equation} \boldsymbol {F} = m n v^2_{\mathrm{th}} a_{\mathrm{eff}}^2 \left[ \boldsymbol {Q}_{F, \mathrm{arr}} + f_{\mathrm{spec}} \boldsymbol {Q}_{F, \mathrm{spec}} + (1 - f_{\mathrm{spec}}) \frac{v_{\mathrm{out}}}{v_{\mathrm{th}}} \, \boldsymbol {Q}_{F, \mathrm{out}} \right], \end{equation}

(105)

where |$\boldsymbol {Q}_{F, \mathrm{out}}$| is the efficiency factor for one of the scenarios (1 or 2) for outgoing particles.

In the extreme subsonic limit,

\begin{equation} \boldsymbol {Q}_{F, \mathrm{arr}} \approx \boldsymbol {Q}_{F, \mathrm{arr}}(s_{\rm d} = 0) + \boldsymbol {Q}^{\prime }_{F, \mathrm{arr}} \, s_{\rm d} \end{equation}

(106)

with

\begin{equation} \boldsymbol {Q}_{F, \mathrm{arr}}(s_{\rm d} = 0) = - \frac{3}{8 \pi } \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^2 \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2\pi } \mathrm{d}\phi \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \int _{u_{\rm c}}^1 \mathrm{d}(\cos \theta _{\mathrm{in}}) \cos \theta _{\mathrm{in}} (- {\hat{\boldsymbol s}}), \end{equation}

(107)

\begin{equation} \boldsymbol {Q}^{\prime }_{F, \mathrm{arr}} = - 2 \pi ^{-3/2} \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^2 \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2\pi } \mathrm{d}\phi \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \int _{u_{\rm c}}^1 \mathrm{d} (\cos \theta _{\mathrm{in}}) \cos \theta _{\mathrm{in}} (- {\hat{\boldsymbol s}}) \, \beta . \end{equation}

(108)

See Appendix A4 for explicit integration over cos θ_in. The expressions for |$\boldsymbol {Q}_{F, \mathrm{spec}}$| are identical except that |$(- {\hat{\boldsymbol s}}_{\rm d})$| is replaced with |${\hat{\boldsymbol s}}_{\rm f}$|⁠. From the arguments given in Section 3.7 (but with momentum in place of angular momentum), the force associated with arriving and specularly reflected atoms vanishes when s_d = 0. In other words, these processes result exclusively in a drag force. As with the torques, we implement the formulas above in our computer code and check that |$\boldsymbol {Q}_{F, \mathrm{arr}}(s_{\rm d} = 0)$| and |$\boldsymbol {Q}_{F, \mathrm{spec}}(s_{\rm d} = 0)$| are consistent with zero.

The efficiency factors for outgoing scenario (1) depend on s_d only through Q_arr. For scenario (2),

\begin{equation} \boldsymbol {Q}_{F, \mathrm{out}, (2)} \approx \boldsymbol {Q}_{F, \mathrm{out}, (2)}(s_{\rm d} = 0) + \boldsymbol {Q}^{\prime }_{F, \mathrm{out}, (2)} \ s_{\rm d} \end{equation}

(109)

with

\begin{equation} \boldsymbol {Q}_{F, \mathrm{out}, (2)}(s_{\rm d} = 0) = - \frac{\pi ^{-3/2}}{2} \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^2 \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2\pi } \mathrm{d}\phi \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \int _{u_{\rm c}}^1 \mathrm{d}(\cos \theta _{\mathrm{in}}) \cos \theta _{\mathrm{in}} {\hat{\boldsymbol N}}(\theta ^{\prime }, \phi ^{\prime }), \end{equation}

(110)

\begin{equation} \boldsymbol {Q}^{\prime }_{F, \mathrm{out}, (2)} = - \frac{3}{4\pi } \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^2 \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2\pi } \mathrm{d}\phi \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \int _{u_{\rm c}}^1 \mathrm{d}(\cos \theta _{\mathrm{in}}) \cos \theta _{\mathrm{in}} {\hat{\boldsymbol N}}(\theta ^{\prime }, \phi ^{\prime }) \, \beta . \end{equation}

(111)

In the extreme supersonic limit,

\begin{equation} \boldsymbol {Q}_{F, \mathrm{arr}} \approx - s_{\rm d} Q_{\mathrm{arr}} \, {\hat{\boldsymbol s}}_{\rm d}, \end{equation}

(112)

\begin{equation} \boldsymbol {Q}_{F, \mathrm{spec}} \approx - s_{\rm d}^2 \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2 \pi } \mathrm{d}\phi \, \frac{\eta _S(\theta , \phi )}{a_{\mathrm{eff}}^2} [{\hat{\boldsymbol s}}_{\rm d} {\cdot } {\hat{\boldsymbol N}}(\theta , \phi )] \mu _{\mathrm{hit}} \, {\hat{\boldsymbol s}}_{\rm f}, \end{equation}

(113)

and

\begin{equation} \boldsymbol {Q}_{F, \mathrm{out}, (2)} \approx - s_{\rm d} \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2 \pi } \mathrm{d}\phi \, \frac{\eta _S(\theta , \phi )}{a_{\mathrm{eff}}^2} [{\hat{\boldsymbol s}}_{\rm d} {\cdot } {\hat{\boldsymbol N}}(\theta , \phi )] \mu _{\mathrm{hit}} \, {\hat{\boldsymbol N}}(\theta ^{\prime }, \phi ^{\prime }). \end{equation}

(114)

4 TORQUE CALCULATIONS: COMPUTATIONAL APPROACH

4.1 Incoming trajectories

We take the radius r_sph of the enclosing sphere to be 1.01 r_max. (See the text following equation 19 for the definition of r_max.)

A gas atom incident on the enclosing sphere has initial position |$\boldsymbol {r}_0 = r_{\mathrm{sph}} {\hat{\boldsymbol r}}$| (see equation 21) and velocity |${\boldsymbol v} = v_{\mathrm{th}} s \, {\hat{\boldsymbol s}}$|⁠. From equation (22),

\begin{eqnarray} &&{{\boldsymbol v} = -v_{\mathrm{th}} s \left[ (\sin \theta _{\mathrm{in}} \cos \phi _{\mathrm{in}} \cos \theta _{\mathrm{sph}} \cos \phi _{\mathrm{sph}} - \sin \theta _{\mathrm{in}} \sin \phi _{\mathrm{in}} \sin \phi _{\mathrm{sph}} + \cos \theta _{\mathrm{in}} \sin \theta _{\mathrm{sph}} \cos \phi _{\mathrm{sph}}) {\hat{\boldsymbol x}} \right. +} \nonumber\\ &&{ \qquad\left. (\sin \theta _{\mathrm{in}} \cos \phi _{\mathrm{in}} \cos \theta _{\mathrm{sph}} \sin \phi _{\mathrm{sph}} + \sin \theta _{\mathrm{in}} \sin \phi _{\mathrm{in}} \cos \phi _{\mathrm{sph}} + \cos \theta _{\mathrm{in}} \sin \theta _{\mathrm{sph}} \sin \phi _{\mathrm{sph}}) {\hat{\boldsymbol y}} + (- \sin \theta _{\mathrm{in}} \cos \phi _{\mathrm{in}} \sin \theta _{\mathrm{sph}} + \cos \theta _{\mathrm{in}} \cos \theta _{\mathrm{sph}}) {\hat{\boldsymbol z}} \right].} \end{eqnarray}

(115)

Given (θ_sph, ϕ_sph, ϕ_in), the plane containing atom trajectories for arbitrary θ_in is spanned by the vectors |${\hat{\boldsymbol r}}$| and |${\hat{\boldsymbol s}}(\theta _{\mathrm{in}} = \pi /2)$|⁠. Now consider plane polar coordinates in this plane with μ the polar angle; μ = 0 along |${\hat{\boldsymbol r}}$| and μ = π/2 along |${\hat{\boldsymbol s}}(\theta _{\mathrm{in}} = \pi /2)$|⁠. The origin remains at the position within the grain originally adopted in defining the GRS. Positions along an atom trajectory have 0 ≤ μ ≤ π. The unit vector |${\hat{\boldsymbol V}}$| characterized by angle μ is

\begin{equation} {\hat{\boldsymbol V}} = {\hat{\boldsymbol r}} \cos \mu + {\hat{\boldsymbol s}} (\theta _{\mathrm{in}} = \pi /2) \sin \mu . \end{equation}

(116)

The spherical coordinates (θ, ϕ) of |${\hat{\boldsymbol V}}$| are found by equating expressions for the x-, y-, and z-components in both systems:

\begin{equation} \sin \theta \cos \phi = \sin \theta _{\mathrm{sph}} \cos \phi _{\mathrm{sph}} \cos \mu + (\sin \phi _{\mathrm{in}} \sin \phi _{\mathrm{sph}} - \cos \phi _{\mathrm{in}} \cos \theta _{\mathrm{sph}} \cos \phi _{\mathrm{sph}}) \sin \mu , \end{equation}

(117)

\begin{equation} \sin \theta \sin \phi = \sin \theta _{\mathrm{sph}} \sin \phi _{\mathrm{sph}} \cos \mu - (\sin \phi _{\mathrm{in}} \cos \phi _{\mathrm{sph}} + \cos \phi _{\mathrm{in}} \cos \theta _{\mathrm{sph}} \sin \phi _{\mathrm{sph}}) \sin \mu , \end{equation}

(118)

\begin{equation} \cos \theta = \cos \theta _{\mathrm{sph}} \cos \mu + \cos \phi _{\mathrm{in}} \sin \theta _{\mathrm{sph}} \sin \mu . \end{equation}

(119)

For each μ, there is a unique distance r_surf(μ) from the origin to the grain surface. A straight line that passes through |$\boldsymbol {r}_0$| and the point on the grain surface characterized by μ has

\begin{equation} \cos \theta _{\mathrm{in}}(\mu ) = \left\lbrace 1 + \sin ^2 \mu \left[ r_{\mathrm{sph}}/r_{\mathrm{surf}}(\mu ) - \cos \mu \right]^{-2} \right\rbrace ^{-1/2}. \end{equation}

(120)

Wherever cos θ_in(μ) has a local minimum, the line is tangent to the grain surface. The critical value u_c of cos θ_in is, of course, the global minimum. To find it, we first isolate the local minima by calculating cos θ_in(μ) for 1000 values of μ (evenly spaced between 0 and π). Then, we apply the routine brent from Press et al. (1992) to the lowest local minimum to find u_c. We tabulate u_c and the position where the corresponding trajectory strikes the grain surface as a function of (θ_sph, ϕ_sph, ϕ_in) for N₁ + 1 values of θ_sph (spaced evenly in cos θ_sph) and N₁ values of ϕ_sph and ϕ_in (spaced evenly between 0 and 2π, but excluding 2π). We discuss the adopted value of N₁, as well as the values of other parameters affecting the convergence of the results, in Section 5.1.

4.2 Arrival at the grain surface and reflection

Given u_c as a function of (θ_sph, ϕ_sph, ϕ_in), we next examine trajectories for (θ_sph, ϕ_sph, ϕ_in, θ_in), with N₁ + 1 values of θ_in spaced evenly in cos θ_in ∈ [u_c, 1]. For each incoming trajectory, we tabulate the values of |$- {\hat{\boldsymbol s}}$| and |$({\hat{\boldsymbol r}} - \boldsymbol {r}_{\mathrm{cm}}/r_{\mathrm{sph}}) \times {\hat{\boldsymbol s}}$| for use in evaluating |$\boldsymbol {Q}_{F, \mathrm{arr}}$| and |$\boldsymbol {Q}_{\Gamma , \mathrm{arr}}$| (equations 100 and 38).

Next, we determine where the trajectory strikes the grain surface. Starting with the incoming particle's position and velocity on the enclosing sphere (as described in Section 4.1), we advance the particle along its trajectory, in steps of length 10⁻³r_sph, until the particle reaches the grain interior. The final and penultimate steps bracket the intersection of the trajectory with the grain surface. The intersection point is then accurately found by 10 repeated bisections of this bracketing interval. This trajectory-tracing algorithm is not employed for the cases where cos θ_in = u_c (since the arrival location on the grain surface was obtained when u_c was determined) and cos θ_in = 1 [since the trajectory is radial in this case, it reaches the surface at (θ, ϕ) = (θ_sph, ϕ_sph)].

Finally, we determine the values of |$- {\hat{\boldsymbol s}}_{\rm f}$| and |$({\hat{\boldsymbol r}}_{\rm f} - \boldsymbol {r}_{\mathrm{cm}}/r_{\mathrm{sph}}) \times {\hat{\boldsymbol s}}_{\rm f}$| for use in evaluating |$\boldsymbol {Q}_{F, \mathrm{spec}}$| and |$\boldsymbol {Q}_{\Gamma , \mathrm{spec}}$| (equations 101 and 41). The surface normal vector |${\hat{\boldsymbol N}}$| at the point where the particle arrives at the grain is calculated using equation (14). Since |$|{\boldsymbol T}_{\theta } \times {\boldsymbol T}_{\phi }| = 0$| when sin θ = 0, this case must be treated differently. Instead, we evaluate |${\hat{\boldsymbol N}}$| for a small value of sin θ and several evenly spaced values of ϕ and take the average of these for |${\hat{\boldsymbol N}}$| when sin θ = 0. The velocity |${\boldsymbol v}_{\rm r}$| of the reflected particle is related to the velocity |${\boldsymbol v}_{\rm i}$| of the incoming particle by the law of reflection:

\begin{equation} {\boldsymbol v}_{\rm r} = {\boldsymbol v}_{\rm i} - 2 ({\boldsymbol v}_{\rm i} {\cdot } {\hat{\boldsymbol N}}) {\hat{\boldsymbol N}}. \end{equation}

(121)

We employ the same procedure as described in the previous paragraph to follow the trajectory of the reflected particle until it ultimately reaches the enclosing sphere (perhaps after multiple reflections on the grain surface).

4.3 Integrals over the reduced speed

Prior to computing torques, we generate, using mathematica, interpolation tables for the function I_s(p, s_d, β) defined in equation (31) with 20 001 values of β for the value of s_d under consideration and p = 3 and 4.

4.4 Characterization of the grain surface

We divide the grain surface into N₂ × N₂ patches, evenly spaced in cos θ and ϕ. Using the approach described in Section 4.2, we follow the trajectory of a particle departing the surface along the normal vector at the centre of each patch. We record whether or not the departing particle escapes to infinity or strikes the grain elsewhere (κ_esc = 1 or 0). If it escapes, then we record the vectors |${\hat{\boldsymbol N}}$|⁠, |$\boldsymbol {r}_{\mathrm{surf}}$|⁠, and |$(\boldsymbol {r}_{\mathrm{surf}} - \boldsymbol {r}_{\mathrm{cm}})/a_{\mathrm{eff}}$| for use in evaluating the force and torque associated with outgoing particles. If the departing particle strikes the grain elsewhere, then we record the index values of the patch that it strikes.

4.5 Torque evaluations

With the computational results from the preceding sections in hand, it is now straightforward to evaluate all of the efficiency factors. For outgoing scenario (2), we take the departure point for the outgoing particle to be the centre of the surface patch in which the incoming particle arrived. Similarly, when an outgoing particle strikes the grain surface elsewhere, we assume that the particle immediately departs along the surface normal in the centre of the patch that was struck.

We compute torques for (N₃ + 1, N₃) values of (θ_gr, ϕ_gr) and average over N₃ values of Φ₂ (when averaging over rotation about |${\hat{\boldsymbol a}}_1$|⁠). For Q_arr, |$\boldsymbol {Q}_{\Gamma , \mathrm{arr}}$|⁠, |$\boldsymbol {Q}_{\Gamma , \mathrm{spec}}$|⁠, |$\boldsymbol {Q}_{F, \mathrm{arr}}$|⁠, |$\boldsymbol {Q}_{F, \mathrm{spec}}$|⁠, |$\boldsymbol {Q}_{\Gamma , \mathrm{spec}}(s_{\rm d}=0)$|⁠, |$\boldsymbol {Q}^{\prime }_{\Gamma , \mathrm{spec}}$|⁠, |$\boldsymbol {Q}_{F, \mathrm{spec}}(s_{\rm d}=0)$|⁠, |$\boldsymbol {Q}^{\prime }_{F, \mathrm{spec}}$|⁠, |$\boldsymbol {Q}_{\Gamma , \mathrm{out}, (2)}$|⁠, |$\boldsymbol {Q}_{F, \mathrm{out}, (2)}$|⁠, |$\boldsymbol {Q}_{\Gamma , \mathrm{out}, (2)}(s_{\rm d} = 0)$|⁠, |$\boldsymbol {Q}^{\prime }_{\Gamma , \mathrm{out}, (2)}$|⁠, |$\boldsymbol {Q}_{\Gamma , \mathrm{drag, \, out}, (2)}(s_{\rm d} = 0)$|⁠, and |$\boldsymbol {Q}^{\prime }_{\Gamma , \mathrm{drag, \, out}, (2)}$|⁠, integrals are evaluated with (N₁ + 1, N₁, N₁, N₁ + 1) values of (θ_sph, ϕ_sph, ϕ_in, θ_in). For Q_arr(s_d = 0), |$Q^{\prime }_{\mathrm{arr}}$|⁠, |$\boldsymbol {Q}_{\Gamma , \mathrm{arr}}(s_{\rm d}=0)$|⁠, |$\boldsymbol {Q}^{\prime }_{\Gamma , \mathrm{arr}}$|⁠, |$\boldsymbol {Q}_{F, \mathrm{arr}}(s_{\rm d}=0)$|⁠, and |$\boldsymbol {Q}^{\prime }_{F, \mathrm{arr}}$|⁠, integrals are evaluated with (N₁ + 1, N₁, N₁) values of (θ_sph, ϕ_sph, ϕ_in). Integrals for |$\boldsymbol {Q}_{\Gamma , \mathrm{out}, (1)}/Q_{\mathrm{arr}}$|⁠, |$\boldsymbol {Q}_{\Gamma , \mathrm{drag, \, out}, (1)}/Q_{\mathrm{arr}}$|⁠, and |$\boldsymbol {Q}_{F, \mathrm{out}, (1)}/Q_{\mathrm{arr}}$| are evaluated with (4096, 4096) values of (θ_surf, ϕ_surf).

For the efficiency factors in the extreme supersonic limit, we first evaluate μ_hit for (N₁ + 1, N₁, N₃ + 1, N₃) values of (θ, ϕ, θ_gr, ϕ_gr). We employ the trajectory-tracing algorithm described in Section 4.2, except that we start at location (θ, ϕ) on the surface and move outwards along |${\hat{\boldsymbol N}}(\theta , \phi )$| to determine whether or not (θ, ϕ) is shadowed by another part of the grain. The integrals in equations (93) and (95–98) are then easily evaluated.

4.6 Code verification: spherical grains

Consider a uniform, spherical grain that drifts through the gas but does not spin. All of the contributions to the torque vanish and analytical results for the arrival rate and force are available as functions of s_d. From Baines & Williams (1965),

\begin{equation} Q_{\mathrm{arr}} = \pi ^{1/2} \exp (-s_{\rm d}^2) + \pi \left( s_{\rm d} + \frac{1}{2 s_{\rm d}} \right) \mathrm{erf}(s_{\rm d}) \end{equation}

(122)

where ‘erf’ denotes the error function. Taking asymptotic limits,

\begin{equation} Q_{\mathrm{arr}}(s_{\rm d} = 0) = 2 \pi ^{1/2}, \end{equation}

(123)

\begin{equation} Q^{\prime }_{\mathrm{arr}} = 0, \end{equation}

(124)

and

\begin{equation} Q_{\mathrm{arr}}(\mathrm{supersonic}) = \pi s_{\rm d}. \end{equation}

(125)

Baines, Williams & Asebiomo (1965) found that |$\boldsymbol {Q}_{F, \mathrm{spec}} = 0$| and

\begin{equation} \boldsymbol {Q}_{F, \mathrm{arr}} = - \pi ^{1/2} \left[ \left( s_{\rm d} + \frac{1}{2 s_{\rm d}} \right) \exp \left(- s_{\rm d}^2\right) + \left( 1 + s_{\rm d}^2 - \frac{1}{4 s_{\rm d}^2} \right) \pi ^{1/2} \mathrm{erf}(s_{\rm d}) \right]{\hat{\boldsymbol s}}_{\rm d}. \end{equation}

(126)

This reduces to the classic Epstein drag formula in the extreme subsonic limit, with |$\boldsymbol {Q}_{F, \mathrm{arr}}(s_{\rm d} = 0) = 0$| and

\begin{equation} \boldsymbol {Q}^{\prime }_{F, \mathrm{arr}} = - \frac{8}{3} \pi ^{1/2} \, {\hat{\boldsymbol s}}_{\rm d}. \end{equation}

(127)

In the extreme supersonic limit, |$\boldsymbol {Q}_{F, \mathrm{arr}} = - \pi s_{\rm d}^2 \, {\hat{\boldsymbol s}}_{\rm d}$|⁠.

Our codes reproduce all of these results for a spherical grain, for which all of the GRS expansion coefficients a_lm and b_lm vanish. We tested for numerous combinations of (θ_gr, ϕ_gr), in the extreme subsonic and supersonic limits and with s_d = 1.

5 TORQUE CALCULATIONS: COMPUTATIONAL RESULTS

5.1 Arrival rate and torques

In this section, we present computational results for grain 1.

In order to check for convergence of the numerical integrals that appear in the expressions for the efficiency factors, we first construct a table of data used in computing the integrands with N₁ = 2⁷ = 128. Recall that there are N₁ values of ϕ_sph and ϕ_in and N₁ + 1 values of cos θ_sph and cos θ_in. Since N₁ is a power of 2, the tabulated data can be used to evaluate the integrals with N₁ = 16, 32, 64, and 128. We find that 64 is often sufficient, though 128 is sometimes required. For s_d = 10, even N₁ = 128 is not sufficient for full convergence. For efficiency factors associated with outgoing particles, we typically adopt N₂ = 256 (recall that we divide the surface into |$N_2^2$| patches when examining the trajectories of outgoing particles). We also ran some computations with N₂ = 128 and 512 to check for convergence in this parameter. The number of orientations (θ_gr, ϕ_gr) (of the grain body relative to the drift velocity) for which quantities are computed affects the convergence of the rotationally averaged values. We have tried N₃ = 32, 64, and 128 (as well as 256 in the case of the supersonic limit).

Fig. 2 shows |$\overline{Q}_{\mathrm{arr}}$| for various values of s_d; from equation (78), Q_arr(s_d = 0) = 4.57. The dashed curves in Fig. 2 are for the extreme supersonic limit, scaled to s_d = 3 and 10. Recall that, for the subsonic limit, the first-order dependence on s_d (⁠|$Q^{\prime }_{\mathrm{arr}}$|⁠) vanishes. Since |${\hat{\boldsymbol a}}_1$| is the principal axis of greatest moment of inertia, the grain presents its largest cross-sectional area to the flowing gas when |${\hat{\boldsymbol a}}_1$| lies along the velocity vector. This explains the dependence of |$\overline{Q}_{\mathrm{arr}}$| on cos θ_va, which is most pronounced in the supersonic limit.

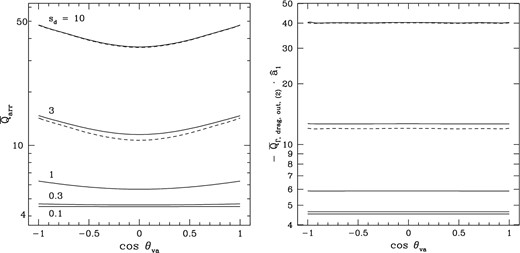
$Left: the grain 1 efficiency factor $\overline{Q}_{\mathrm{arr}}$ for the rate at which gas atoms arrive at the grain surface, averaged over rotation about ${\hat{\boldsymbol a}}_1$, as a function of the angle θva between ${\hat{\boldsymbol a}}_1$ and the grain velocity for various values of the reduced grain drift speed sd. Right: the drag torque efficiency factor $\boldsymbol {Q}_{\Gamma , \mathrm{drag, \, out}, (2)}$ (component along ${\hat{\boldsymbol a}}_1$) for the same values of sd (higher curves are for higher sd). In both cases, dashed curves are the result for the extreme supersonic limit, scaled to sd = 3 and 10.$

Figure 2.

Left: the grain 1 efficiency factor |$\overline{Q}_{\mathrm{arr}}$| for the rate at which gas atoms arrive at the grain surface, averaged over rotation about |${\hat{\boldsymbol a}}_1$|⁠, as a function of the angle θ_va between |${\hat{\boldsymbol a}}_1$| and the grain velocity for various values of the reduced grain drift speed s_d. Right: the drag torque efficiency factor |$\boldsymbol {Q}_{\Gamma , \mathrm{drag, \, out}, (2)}$| (component along |${\hat{\boldsymbol a}}_1$|⁠) for the same values of s_d (higher curves are for higher s_d). In both cases, dashed curves are the result for the extreme supersonic limit, scaled to s_d = 3 and 10.

Open in new tab Download slide

Figs 3 –5 show the components of the rotationally averaged efficiency factor for the torque due to arriving atoms (⁠|$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}}$|⁠), specular reflection (⁠|$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{spec}}$|⁠), and outgoing scenario 2 (⁠|$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{out, (2)}}$|⁠), along |${\hat{\boldsymbol a}}_1$|⁠, |${\hat{\boldsymbol \theta }}_v$|⁠, and |${\hat{\boldsymbol \phi }}_v$| (defined in the last sentence in Section 3.5). In the absence of an interstellar magnetic field, these components drive rotation about |${\hat{\boldsymbol a}}_1$|⁠, alignment of |${\hat{\boldsymbol a}}_1$| with respect to the direction |${\hat{\boldsymbol s}}_{\rm d}$| of the grain drift, and precession of |${\hat{\boldsymbol a}}_1$| about |${\hat{\boldsymbol s}}_{\rm d}$|⁠. The solid curves are results for s_d = 0.1, 0.3, 1.0, 3.0, and 10.0. Results computed in the extreme subsonic limit and scaled to s_d = 0.1, 0.3, and 1.0 are displayed as long-dashed curves. Similarly, results computed in the extreme supersonic limit and scaled to s_d = 1.0, 3.0, and 10.0 are displayed as short-dashed curves.

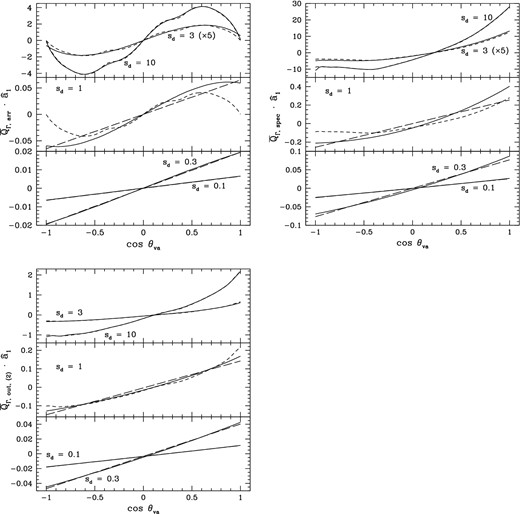
$Rotationally averaged grain 1 efficiency factor for the torque component along ${\hat{\boldsymbol a}}_1$ due to the arrival of gas atoms ($\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}}$), specular reflection ($\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{spec}}$), and outgoing scenario 2 ($\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{out, (2)}}$). The lower, middle, and upper subpanels are for sd = (0.1, 0.3), 1.0, and (3.0, 10.0), respectively. Long-dashed (short-dashed) curves are results for the extreme supersonic (subsonic) limits, scaled to the corresponding value of sd.$

Figure 3.

Rotationally averaged grain 1 efficiency factor for the torque component along |${\hat{\boldsymbol a}}_1$| due to the arrival of gas atoms (⁠|$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}}$|⁠), specular reflection (⁠|$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{spec}}$|⁠), and outgoing scenario 2 (⁠|$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{out, (2)}}$|⁠). The lower, middle, and upper subpanels are for s_d = (0.1, 0.3), 1.0, and (3.0, 10.0), respectively. Long-dashed (short-dashed) curves are results for the extreme supersonic (subsonic) limits, scaled to the corresponding value of s_d.

Open in new tab Download slide

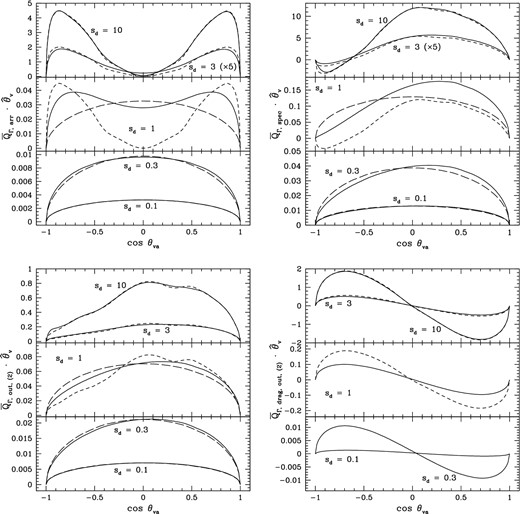
$Same as Fig. 3, except for the component along ${\hat{\boldsymbol \theta }}_v$ and including the drag torque efficiency $\boldsymbol {Q}_{\Gamma , \mathrm{drag, \, out}, (2)}$.$

Figure 4.

Same as Fig. 3, except for the component along |${\hat{\boldsymbol \theta }}_v$| and including the drag torque efficiency |$\boldsymbol {Q}_{\Gamma , \mathrm{drag, \, out}, (2)}$|⁠.

Open in new tab Download slide

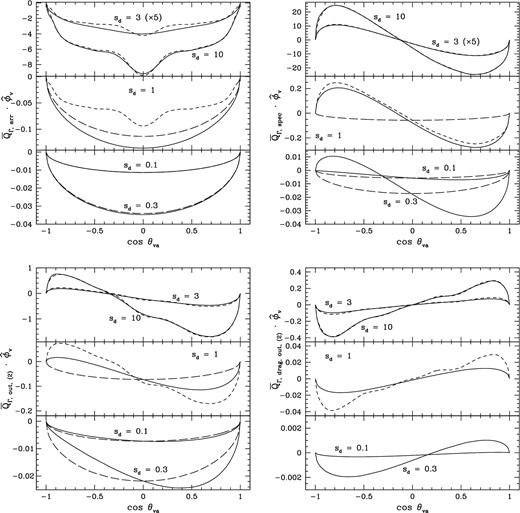
$Same as Fig. 4, except for the component along ${\hat{\boldsymbol \phi }}_v$.$

Figure 5.

Same as Fig. 4, except for the component along |${\hat{\boldsymbol \phi }}_v$|⁠.

Open in new tab Download slide

As seen in Figs 2–5, results associated with arriving atoms for s_d = 0.1 and 0.3 agree very well with those for the subsonic limit and results for s_d = 3 and 10 agree very well with those for the supersonic limit. Different computer codes are used for computing results in the cases of a specified value of s_d, the extreme subsonic limit, and the extreme supersonic limit. As described in the previous sections, the algorithm for the subsonic (supersonic) limit is somewhat (very) different from that for a specified s_d. Thus, the agreement of the results is confirmation of the validity of the codes.

The following features of |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}}$| exhibited in Figs 3 and 4 are worth noting: 1. |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}} {\cdot } {\hat{\boldsymbol a}}_1$| is an odd function of cos θ_va and is proportional to cos θ_va for subsonic drift, 2. |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}} {\cdot } {\hat{\boldsymbol \theta }}_v$| is an even function of cos θ_va and is proportional to sin θ_va for subsonic drift, 3. |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}} {\cdot } {\hat{\boldsymbol a}}_1$| and |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}} {\cdot } {\hat{\boldsymbol \theta }}_v$| have the same sign when cos θ_va > 0, 4. |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}} {\cdot } {\hat{\boldsymbol \theta }}_v (\cos \theta _{va} = 0) \rightarrow 0$| as s_d → ∞, 5. |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}} {\cdot } {\hat{\boldsymbol a}}_1 (\cos \theta _{va} = \pm 1) \rightarrow 0$| as s_d → ∞, 6. |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}} {\cdot } {\hat{\boldsymbol \theta }}_v (\cos \theta _{va} = \pm 1) = 0$|⁠. As shown in Appendix B, these properties are satisfied for all grain shapes. Our computational results exhibit most of these features for all 13 grains, providing further evidence that the code is robust. There are slight deviations from the expected form for |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}} {\cdot } {\hat{\boldsymbol \theta }}_v$| in the subsonic regime for grains 3, 10, and 11, and somewhat larger deviations for grains 5 and 9, suggesting that the computations are not fully converged in these cases. In addition, the computational result for |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}} {\cdot } {\hat{\boldsymbol a}}_1$| is always slightly offset in cos θ_va; i.e. it passes through zero at a value of cos θ_va slightly different from zero.

In producing the curves in Figs 2–5, we adopted N₁ = 128 for s_d = 0.1–3.0 and N₁ = 256 for s_d = 10. Given the close agreement between the results for s_d = 10 with the supersonic results scaled to s_d = 10, we will simply adopt the latter for grains 2–13. This greatly reduces the computational time.

Appendix C notes some features that characterize all of the rotationally averaged torque efficiencies in the extreme subsonic limit. We have verified that our results display these features for all 13 grain shapes.

Fig. 2 also displays the |${\hat{\boldsymbol a}}_1$|-component of the rotationally averaged drag torque efficiency factor |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{drag, \, out}, (2)}$| computed for outgoing scenario (2). These results agree well with those computed in the extreme supersonic limit and scaled to s_d = 3 and 10. In the limit of low s_d, the results tend towards that found for s_d = 0: |$\boldsymbol {Q}_{\Gamma , \mathrm{drag, \, out}, (2)} {\cdot } {\hat{\boldsymbol a}}_1 = -4.51$|⁠. We found an extremely weak first-order dependence of |$\boldsymbol {Q}_{\Gamma , \mathrm{drag, \, out}, (2)}$| on s_d; i.e. |$\boldsymbol {Q}^{\prime }_{\Gamma , \mathrm{drag, \, out}, (2)} {\cdot } {\hat{\boldsymbol a}}_1 \ll 1$| (and likewise for the other components). We computed the second-order term and found that its inclusion substantially overestimates Q_{Γ, drag, out, (2)} for small s_d. Evidently a power-series expansion converges slowly in the low-s_d limit. Figs 4 and 5 display |${\hat{\boldsymbol \theta }}_v$|- and |${\hat{\boldsymbol \phi }}_v$|-components of |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{drag, \, out}, (2)}$|⁠. Curves for the subsonic limit are not displayed because of the poor convergence behaviour.

For grains 2–13, plots of the rotationally averaged arrival efficiency |$\overline{Q}_{\mathrm{arr}}$| versus cos θ_va look very similar to that for grain 1, but with somewhat smaller magnitudes when α = 3 than when α = 2. Plots of the various torque efficiencies versus cos θ_va generally show a wide diversity of shapes, again with the magnitudes often smaller when α = 3 than when α = 2. The components of the drag torque efficiency along |${\hat{\boldsymbol a}}_1$| and |${\hat{\boldsymbol \theta }}_v$| are broadly similar, but the component along |${\hat{\boldsymbol \phi }}_v$| varies considerably among the grain shapes.

In outgoing scenario (1), the torque and drag efficiencies are both proportional to the arrival efficiency Q_arr. Since the angle θ_va does not change when the grain rotates around |${\hat{\boldsymbol a}}_1$|⁠, |$\overline{Q}_{\mathrm{arr}}$| remains constant for this motion. Thus, the components of |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{out}, (1)}$| and |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{drag, out}, (1)}$| along |${\hat{\boldsymbol \theta }}_v$| and |${\hat{\boldsymbol \phi }}_v$| vanish. (We assume that the time when an atom or molecule departs the grain surface is uncorrelated with the arrival time of the atom.) The components of the drag efficiency along |${\hat{\boldsymbol a}}_1$| are given in Table 4. For most of the grain shapes, |$\boldsymbol {Q}_{\Gamma , \mathrm{out}, (1)} {\cdot } {\hat{\boldsymbol a}}_1 / Q_{\mathrm{arr}}$| is consistent with zero, having not converged when evaluated using (4096)² patches on the surface. The exceptions are grain 4, for which |$\boldsymbol {Q}_{\Gamma , \mathrm{out}, (1)} {\cdot } {\hat{\boldsymbol a}}_1 / Q_{\mathrm{arr}} = 0.001\,22$|⁠, and grains 2 and 3, for which |$\boldsymbol {Q}_{\Gamma , \mathrm{out}, (1)} {\cdot } {\hat{\boldsymbol a}}_1 / Q_{\mathrm{arr}}$| appears to converge to ∼ −3 × 10⁻⁵ and ∼6 × 10⁻⁶, respectively.

Table 4.

Open in new tab

Drag efficiency factors in outgoing scenario (1).

Grain index	\|$\boldsymbol {Q}_{\Gamma , \mathrm{drag, out}, (1)} {\cdot } {\hat{\boldsymbol a}}_1 / Q_{\mathrm{arr}}$\|
1	−0.979
2	−1.091
3	−1.004
4	−1.052
5	−0.821
6	−0.888
7	−1.054
8	−0.904
9	−0.864
10	−0.819
11	−0.911
12	−0.873
13	−0.907

Grain index	\|$\boldsymbol {Q}_{\Gamma , \mathrm{drag, out}, (1)} {\cdot } {\hat{\boldsymbol a}}_1 / Q_{\mathrm{arr}}$\|
1	−0.979
2	−1.091
3	−1.004
4	−1.052
5	−0.821
6	−0.888
7	−1.054
8	−0.904
9	−0.864
10	−0.819
11	−0.911
12	−0.873
13	−0.907

Table 4.

Open in new tab

Drag efficiency factors in outgoing scenario (1).

Grain index	\|$\boldsymbol {Q}_{\Gamma , \mathrm{drag, out}, (1)} {\cdot } {\hat{\boldsymbol a}}_1 / Q_{\mathrm{arr}}$\|
1	−0.979
2	−1.091
3	−1.004
4	−1.052
5	−0.821
6	−0.888
7	−1.054
8	−0.904
9	−0.864
10	−0.819
11	−0.911
12	−0.873
13	−0.907

Grain index	\|$\boldsymbol {Q}_{\Gamma , \mathrm{drag, out}, (1)} {\cdot } {\hat{\boldsymbol a}}_1 / Q_{\mathrm{arr}}$\|
1	−0.979
2	−1.091
3	−1.004
4	−1.052
5	−0.821
6	−0.888
7	−1.054
8	−0.904
9	−0.864
10	−0.819
11	−0.911
12	−0.873
13	−0.907

5.2 Forces

As noted in Section 3.9, |$\boldsymbol {Q}_{F, \mathrm{arr}}$| and |$\boldsymbol {Q}_{F, \mathrm{spec}}$| both vanish when s_d = 0. Thus, the force is entirely drag when f_spec = 1. The component of the rotationally averaged drag force antiparallel to the grain's velocity is comparable in magnitude to that on a sphere (ranging between about 75 and 230 per cent of that for a sphere in all cases) but varies with θ_va, with its maximum value when cos θ_va = ±1 and minimum near cos θ_va = 0. There is also a component perpendicular to the grain's velocity which vanishes at cos θ_va = ±1 and near cos θ_va = 0 and can reach values as high as about 30 per cent of the drag force on a spherical grain.

For outgoing scenario (2), the force can be non-zero when s_d = 0. However, we have found that this term does not contribute substantially even when s_d = 0.1. The drag force in this case is qualitatively and quantitatively similar to that in the case of specular reflection.

For outgoing scenario (1), |$\boldsymbol {Q}_{F, \mathrm{out}, (1)}$| is proportional to Q_arr and its direction is fixed in grain-body coordinates; only the component along |${\hat{\boldsymbol a}}_1$| is non-zero when averaged over the grain rotation. For most shapes, |$\boldsymbol {Q}_{F, \mathrm{out}, (1)} {\cdot } {\hat{\boldsymbol a}}_1 / Q_{\mathrm{arr}}$| is consistent with zero, having not converged when evaluated using (4096)² patches on the surface. The exceptions are grains 3 and 4, for which |$\boldsymbol {Q}_{F, \mathrm{out}, (1)} {\cdot } {\hat{\boldsymbol a}}_1 / Q_{\mathrm{arr}} = 0.001\,28$| and −0.003 44, respectively, and grain 2, for which |$\boldsymbol {Q}_{F, \mathrm{out}, (1)} {\cdot } {\hat{\boldsymbol a}}_1 / Q_{\mathrm{arr}}$| appears to converge to ∼2 × 10⁻⁵. The drag force associated with the arriving atoms only is similar to that for the above cases, with a somewhat smaller range of magnitudes.

6 DYNAMICS

6.1 Equations of motion

Consider a coordinate system (x_B, y_B, z_B) with the interstellar magnetic field aligned along |${\hat{\boldsymbol z}}_B$|⁠. Take the velocity |${\boldsymbol s}_{\rm d}$| of the grain relative to the gas to lie in the x_B–z_B plane, at angle ψ_v to |${\hat{\boldsymbol z}}_B$|⁠. Assume that the grain rotates steadily about |${\hat{\boldsymbol a}}_1$|⁠, whose orientation is described by spherical coordinates (ξ, ϕ_B):

\begin{equation} {\hat{\boldsymbol a}}_1 = \sin \xi \cos \phi _B \, {\hat{\boldsymbol x}}_B + \sin \xi \sin \phi _B \, {\hat{\boldsymbol y}}_B + \cos \xi \, {\hat{\boldsymbol z}}_B. \end{equation}

(128)

With these definitions, the angle between the grain velocity and |${\hat{\boldsymbol a}}_1$| is given by

\begin{equation} \cos \theta _{va} = \sin \psi _v \sin \xi \cos \phi _B + \cos \psi _v \cos \xi . \end{equation}

(129)

The transformation between the coordinates (θ_v, ϕ_v) introduced at the end of Section 3.5 and (ξ, ϕ_B) is given by

\begin{equation} {\hat{\boldsymbol \xi }} {\cdot } {\hat{\boldsymbol \theta }}_v = {\hat{\boldsymbol \phi }}_B {\cdot } {\hat{\boldsymbol \phi }}_v = b_1 \equiv \frac{\cos \psi _v \sin \xi - \sin \psi _v \cos \xi \cos \phi _B}{\sin \theta _{va}}, \end{equation}

(130)

\begin{equation} - {\hat{\boldsymbol \xi }} {\cdot } {\hat{\boldsymbol \phi }}_v = {\hat{\boldsymbol \phi }}_B {\cdot } {\hat{\boldsymbol \theta }}_v = b_2 \equiv \frac{\sin \psi _v \sin \phi _B}{\sin \theta _{va}}. \end{equation}

(131)

When sin θ_va = 0, |${\hat{\boldsymbol \theta }}_v = {\hat{\boldsymbol \xi }}$| and |${\hat{\boldsymbol \phi }}_v = {\hat{\boldsymbol \phi }}_B$| (i.e. b₁ = 1 and b₂ = 0).

In spherical coordinates, the rotationally averaged mechanical torque is given by

\begin{equation} \overline{\boldsymbol {\Gamma }}_{\mathrm{mech}} = m n v^2_{\mathrm{th}} a_{\mathrm{eff}}^3 \left[ J^0_v(\xi , \phi _B) \, {\hat{\boldsymbol \xi }} + G^0_v(\xi , \phi _B) \, {\hat{\boldsymbol \phi }}_B + H^0_v(\xi , \phi _B) \, {\hat{\boldsymbol a}}_1 \right]; \end{equation}

(132)

from equations (49) and (50),

\begin{equation} J^0_v(\xi , \phi _B) = b_1 \overline{\boldsymbol {Q}}_{\Gamma , \mathrm{mech}} {\cdot } {\hat{\boldsymbol \theta }}_v - b_2 \overline{\boldsymbol {Q}}_{\Gamma , \mathrm{mech}} {\cdot } {\hat{\boldsymbol \phi }}_v, \end{equation}

(133)

\begin{equation} G^0_v(\xi , \phi _B) = b_2 \overline{\boldsymbol {Q}}_{\Gamma , \mathrm{mech}} {\cdot } {\hat{\boldsymbol \theta }}_v + b_1 \overline{\boldsymbol {Q}}_{\Gamma , \mathrm{mech}} {\cdot } {\hat{\boldsymbol \phi }}_v, \end{equation}

(134)

\begin{equation} H^0_v(\xi , \phi _B) = \overline{\boldsymbol {Q}}_{\Gamma , \mathrm{mech}} {\cdot } {\hat{\boldsymbol a}}_1. \end{equation}

(135)

Like the mechanical torque, the drag torque can vary as a function of θ_va and may have components along |${\hat{\boldsymbol \xi }}$| and |${\hat{\boldsymbol \phi }}_B$| as well as along |${\hat{\boldsymbol a}}_1$|⁠. Defining

\begin{equation} Q_{\Gamma , \mathrm{drag}, 0} = - \overline{\boldsymbol {Q}}_{\Gamma , \mathrm{drag}}(\cos \theta _{va} = 0) {\cdot } {\hat{\boldsymbol a}}_1 \end{equation}

(136)

and the drag time-scale as

\begin{equation} \tau _{\mathrm{drag}} = \frac{I_1}{m n v_{\mathrm{th}} a_{\mathrm{eff}}^4 Q_{\Gamma , \mathrm{drag}, 0}} = 2.47 \times 10^5 \, \mathrm{yr} \left( \frac{\rho }{3 \, \mathrm{g} \, \mathrm{cm}^{-3}} \right) \left( \frac{a_{\mathrm{eff}}}{0.2 \, \mu \mathrm{m}} \right) \left( \frac{T_{\mathrm{gas}}}{100 \, \mathrm{K}} \right)^{-1/2} \left( \frac{m}{m_p} \right)^{-1/2} \left( \frac{n}{30 \, \mathrm{cm}^{-3}} \right)^{-1} \frac{\alpha _1}{Q_{\Gamma , \mathrm{drag}, 0}}, \end{equation}

(137)

the rotationally averaged drag torque can be expressed as

\begin{equation} \overline{\boldsymbol {\Gamma }}_{\mathrm{drag}} = \frac{I_1 \omega }{\tau _{\mathrm{drag}}} \ \frac{\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{drag}}}{Q_{\Gamma , \mathrm{drag}, 0}}. \end{equation}

(138)

In analogy with the mechanical torque,

\begin{equation} \overline{\boldsymbol {\Gamma }}_{\mathrm{drag}} = \frac{I_1 \omega }{\tau _{\mathrm{drag}}} \left[ - H^0_{\mathrm{drag}}(\xi , \phi _B) \, {\hat{\boldsymbol a}}_1 + J^0_{\mathrm{drag}} (\xi , \phi _B) \, {\hat{\boldsymbol \xi }} + G^0_{\mathrm{drag}}(\xi , \phi _B) \, {\hat{\boldsymbol \phi }}_B \right] \end{equation}

(139)

with

\begin{equation} H^0_{\mathrm{drag}}(\xi , \phi _B) = - \frac{\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{drag}} {\cdot } {\hat{\boldsymbol a}}_1}{Q_{\Gamma , \mathrm{drag}, 0}}, \end{equation}

(140)

\begin{equation} J^0_{\mathrm{drag}}(\xi , \phi _B) = \frac{b_1 (\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{drag}} {\cdot } {\hat{\boldsymbol \theta }}_v) - b_2 (\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{drag}} {\cdot } {\hat{\boldsymbol \phi }}_v)}{Q_{\Gamma , \mathrm{drag}, 0}}, \end{equation}

(141)

\begin{equation} G^0_{\mathrm{drag}}(\xi , \phi _B) = \frac{b_2 (\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{drag}} {\cdot } {\hat{\boldsymbol \theta }}_v) + b_1 (\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{drag}} {\cdot } {\hat{\boldsymbol \phi }}_v)}{Q_{\Gamma , \mathrm{drag}, 0}}. \end{equation}

(142)

We will consider five separate cases for the mechanical torque. In the first, f_spec = 1, i.e. all of the arriving atoms reflect specularly. In the other cases, f_spec = 0; we consider both outgoing scenarios (1) and (2) with the outgoing particles either H atoms or H₂ molecules. Since we have not evaluated the drag torque for specular reflection, we will simply adopt the drag efficiency for outgoing atoms under scenario (2) in this case.

In order to ascertain the potential of the mechanical torque in aligning grains, we will examine the rotational dynamics under the action of only the mechanical, drag, and magnetic torques. This final torque, due to the interaction of the grain's Barnett magnetic moment with the interstellar magnetic field, is given by

\begin{equation} \boldsymbol {\Gamma }_B = {\hat{\boldsymbol \phi }}_B I_1 \Omega _B \omega \sin \xi , \end{equation}

(143)

where the precession frequency is (see e.g. Weingartner & Draine 2003)

\begin{equation} \Omega _B \approx 25 \, \mathrm{yr}^{-1} \left( \frac{a}{0.1 \, \mu \mathrm{m}} \right)^{-2} \left( \frac{\alpha _1 \rho }{3 \, \mathrm{g} \, \mathrm{cm}^{-3}} \right)^{-1} \left( \frac{\chi _0}{3.3 \times 10^{-4}} \right) \left( \frac{B}{5\, \mu \mathrm{G}} \right); \end{equation}

(144)

χ₀ is the static magnetic susceptibility of the grain material. The following analysis closely follows that in Draine & Weingartner (1997) with mechanical torques taking the place of radiative torques. The equation of motion,

\begin{equation} \frac{\mathrm{d}\boldsymbol {J}}{\mathrm{d}t} = I_1 \frac{\mathrm{d}}{\mathrm{d}t}\left(\omega {\hat{\boldsymbol a}}_1 \right) = \overline{\boldsymbol {\Gamma }}_{\mathrm{mech}} + \overline{\boldsymbol {\Gamma }}_{\mathrm{drag}} + \boldsymbol {\Gamma }_B \end{equation}

(145)

yields three component equations:

\begin{equation} \frac{\mathrm{d}\omega ^{\prime }}{\mathrm{d}t^{\prime }} = M_v H^0_v(\xi , \phi _B) - H^0_{\mathrm{drag}}(\xi , \phi _B) \, \omega ^{\prime }, \end{equation}

(146)

\begin{equation} \frac{\mathrm{d}\xi }{\mathrm{d}t^{\prime }} = M_v \ \frac{J^0_v(\xi , \phi _B)}{\omega ^{\prime }} + J^0_{\mathrm{drag}}(\xi , \phi _B), \end{equation}

(147)

\begin{equation} \frac{\mathrm{d}\phi _B}{\mathrm{d}t^{\prime }} = \Omega _B \tau _{\mathrm{drag}} + M_v \ \frac{G^0_v(\xi , \phi _B)}{\omega ^{\prime } \sin \xi } + \frac{G^0_{\mathrm{drag}} (\xi , \phi _B)}{\sin \xi }, \end{equation}

(148)

where

\begin{equation} t^{\prime } = \frac{t}{\tau _{\mathrm{drag}}}, \end{equation}

(149)

\begin{equation} \omega ^{\prime } = \frac{\omega }{\omega _T}, \end{equation}

(150)

the thermal rotation rate is given by (see e.g. Draine & Weingartner 1997)

\begin{equation} \omega _T = \left( \frac{15 kT_{\mathrm{gas}}}{8 \pi \alpha _1 \rho a_{\mathrm{eff}}^5} \right)^{1/2} = 1.66 \times 10^5 \, \mathrm{s}^{-1} \, \alpha _1^{-1/2} \left( \frac{T_{\mathrm{gas}}}{100 \, \mathrm{K}} \right)^{1/2} \left( \frac{\rho }{3 \, \mathrm{g} \, \mathrm{cm}^{-3}} \right)^{-1/2} \left( \frac{a_{\mathrm{eff}}}{0.1 \, \mu \mathrm{m}} \right)^{-2.5}, \end{equation}

(151)

and

\begin{equation} M_v = \frac{4}{Q_{\Gamma , \mathrm{drag}, 0}} \left( \frac{\pi \alpha _1 \rho a_{\mathrm{eff}}^3}{15 m} \right)^{1/2} = 7.75 \times 10^4 \left( \frac{a_{\mathrm{eff}}}{0.1 \, \mu \mathrm{m}} \right)^{3/2} \left( \frac{\rho }{3 \, \mathrm{g} \, \mathrm{cm}^{-3}} \right)^{1/2} \left( \frac{m}{m_p} \right)^{-1/2} \frac{\alpha _1^{1/2}}{Q_{\Gamma , \mathrm{drag}, 0}}. \end{equation}

(152)

Typically, Ω_Bτ_drag greatly exceeds all of the other terms on the right-hand sides in equations (146)–(148). Thus, we will approximate the motion in ϕ_B as uniform precession and average over this motion in equations (146) and (147):

\begin{equation} \frac{\mathrm{d}\omega ^{\prime }}{\mathrm{d}t^{\prime }} = M_v H_v(\xi ) - H_{\mathrm{drag}}(\xi ) \, \omega ^{\prime }, \end{equation}

(153)

\begin{equation} \frac{\mathrm{d}\xi }{\mathrm{d}t^{\prime }} = M_v \ \frac{J_v(\xi )}{\omega ^{\prime }} + J_{\mathrm{drag}}(\xi ) \end{equation}

(154)

with

\begin{equation} H_v(\xi ) = \frac{1}{2 \pi } \int _0^{2\pi } \mathrm{d}\phi _B \, H^0_v(\xi , \phi _B) \end{equation}

(155)

and likewise for J(ξ), H_drag(ξ), and J_drag(ξ). Of course, when ξ ≪ 1, the terms in equation (148) with sin ξ in the denominator cannot be neglected compared with Ω_Bτ_drag. However, in this case the orientation of the grain in space hardly depends on ϕ_B, so the assumption of a uniform distribution in ϕ_B does not introduce significant error. The terms in equations (147) and (148) with ω′ in the denominator can be comparable to Ω_Bτ_drag for sufficiently small ω′. However, the analysis already fails for such small ω′ since the assumption of steady rotation about |${\hat{\boldsymbol a}}_1$| is only justified in the limit of suprathermal rotation.

6.2 Stationary points

Setting dξ/dt′ = 0 and dω′/dt′ = 0 in equations (153) and (154), we find that stationary points |$(\xi _s, \omega ^{\prime }_s)$| occur where ξ_s is a zero of the function

\begin{equation} Z_v(\xi ) = J_v(\xi ) H_{\mathrm{drag}}(\xi ) + J_{\mathrm{drag}}(\xi ) H_v(\xi ). \end{equation}

(156)

Since J_v and J_drag both vanish at ξ = 0 and π, there are always stationary points at these ξ. For a given ξ_s,

\begin{equation} \omega ^{\prime }_s = \frac{M_v H_v(\xi _s)}{H_{\mathrm{drag}}(\xi _s)}. \end{equation}

(157)

A stationary point is characterized by linearizing equations (153) and (154) about |$(\xi _s, \omega ^{\prime }_s)$|⁠:

\begin{equation} \frac{\mathrm{d}\xi }{\mathrm{d}t^{\prime }} \approx A_l (\xi - \xi _s) + B_l (\omega ^{\prime } - \omega ^{\prime }_s), \end{equation}

(158)

\begin{equation} \frac{\mathrm{d}\omega ^{\prime }}{\mathrm{d}t^{\prime }} \approx C_l (\xi - \xi _s) + D_l (\omega ^{\prime } - \omega ^{\prime }_s) \end{equation}

(159)

with

\begin{equation} A_l = \frac{M_v}{\omega ^{\prime }_s} \left. \frac{\mathrm{d}J_v}{\mathrm{d}\xi } \right|_{\xi = \xi _s} + \left. \frac{\mathrm{d} J_{\mathrm{drag}}}{\mathrm{d}\xi } \right|_{\xi = \xi _s}, \end{equation}

(160)

\begin{equation} B_l = - \frac{M_v J_v(\xi _s)}{(\omega ^{\prime }_s)^2}, \end{equation}

(161)

\begin{equation} C_l = M_v \left. \frac{\mathrm{d}H_v}{\mathrm{d}\xi } \right|_{\xi = \xi _s} - \omega ^{\prime }_s \left. \frac{\mathrm{d}H_{\mathrm{drag}}}{\mathrm{d}\xi } \right|_{\xi = \xi _s}, \end{equation}

(162)

\begin{equation} D_l = - H_{\mathrm{drag}}(\xi _s). \end{equation}

(163)

The displacement from the stationary point is proportional to exp (λ_lt′) where

\begin{equation} \lambda _l = \frac{A_l + D_l \pm [ (A_l + D_l)^2 - 4 (A_l D_l - B_l C_l)]^{1/2}}{2}. \end{equation}

(164)

Thus, the stationary point is stable (an ‘attractor’) if

\begin{equation} A_l + D_l < 0 \ \ \ \mathrm{and} \ \ \ B_l C_l - A_l D_l < 0 ; \end{equation}

(165)

otherwise it is unstable (a ‘repeller’). The time-scale for approach to the stationary point is −[Re(λ_l)]⁻¹. We expect the alignment to be characterized by the longer relaxation time and have verified this by numerically integrating equations (153) and (154) for various values of s_d and ψ_v. Thus, the alignment time is

\begin{equation} \tau _{\mathrm{align}} = - \frac{2 \tau _{\mathrm{drag}}}{A_l + D_l + [(A_l - D_l)^2 + 4 B_l C_l]^{1/2}}. \end{equation}

(166)

6.3 Crossover points

Crossover points, where ω′ crosses zero, can only occur at angles ξ_c where J_v(ξ_c) = 0; otherwise there is a singularity in equation (154). Since J_v(ξ) vanishes at ξ = 0 and π, crossovers are always found at these angles. The polarity of a crossover is the sign of dω′/dt′; from equation (153),

\begin{equation} \mathrm{polarity} \ = \ \mathrm{sign}[H_v(\xi _c)]. \end{equation}

(167)

A crossover attractor is a crossover for which trajectories with ξ near ξ_c converge to the crossover, whereas the trajectories diverge from ξ_c for a crossover repeller. At a crossover repeller, only the single trajectory with ξ = ξ_c passes through the crossover. Since this occurs with infinitesimal probability, physical crossovers only occur at crossover attractors. For (ξ, ω′) near a crossover (ξ_c, 0),

\begin{equation} \frac{\mathrm{d}\xi }{\mathrm{d}t^{\prime }} \approx J_{\mathrm{drag}}(\xi _c) + \left[ \frac{M_v}{\omega ^{\prime }} \left. \frac{\mathrm{d}J_v}{\mathrm{d} \xi } \right|_{\xi = \xi _c} + \left. \frac{\mathrm{d}J_{\mathrm{drag}}}{\mathrm{d}\xi } \right|_{\xi = \xi _c} \right] (\xi - \xi _c). \end{equation}

(168)

As a trajectory with ξ near ξ_c approaches ω′ = 0, the first term in brackets dominates. For a crossover with positive polarity, trajectories converge on the crossover if d²ξ/d(t′)² < 0 when ω′ < 0 and d²ξ/d(t′)² > 0 when ω′ > 0. The opposite conditions apply for a crossover of negative polarity. Thus, a crossover is a crossover attractor if

\begin{equation} \frac{1}{H_v(\xi _c)} \left. \frac{\mathrm{d}J_v}{\mathrm{d}\xi } \right|_{\xi = \xi _c} > 0. \end{equation}

(169)

6.4 Results

We have examined the grain rotational dynamics for s_d = 0.1, 0.3, 1.0, 3.0, and 10.0. Table 5 gives the adopted values of the relevant parameters. The speed of the outgoing particle is v_out = (2kT_dust/m_p)^1/2 for H atoms (with T_dust the temperature of the grain) and v_out = (E_H2/m_p)^1/2 for H₂ molecules.

Table 5.

Open in new tab

Adopted parameter values for grain rotational dynamics.

a_eff

0.2 μm

ρ

3.0 g cm⁻³

χ₀

3.3 × 10⁻⁴

B

5.0 μG

T_dust

15 K

T_gas

100 K

E_H2

0.2 eV

n_H

30 cm⁻¹

Fig. 6 is a ‘trajectory map’, which shows how (cos ξ, ω′) evolves for grain 1 with s_d = 0.1 when the outgoing particles are H atoms in scenario (2) and ψ_v = 89°. This map features an attractor at (cos ξ, ω′) = (1, −31.7), a repellor at (−1, −58.4), a crossover attractor at cos ξ = −1 and a crossover repellor at cos ξ = 1. Draine & Weingartner (1997) classified trajectory maps in three categories. This is an example of a non-cyclic map, in which all of the trajectories land on the attractor, and it exhibits perfect alignment with the magnetic field, since ξ = 0 for the attractor. The other categories are cyclic maps, which exhibit no attractors, so that the grain state must cycle between crossovers indefinitely, and semicyclic maps, for which the grain state may either land on an attractor or cycle between crossovers. Since our analysis assumes that the grain angular momentum always lies along |${\hat{\boldsymbol a}}_1$|⁠, we cannot follow the dynamics through the crossovers and determine which of these possibilities actually occurs for semicyclic maps.

Figure 6.

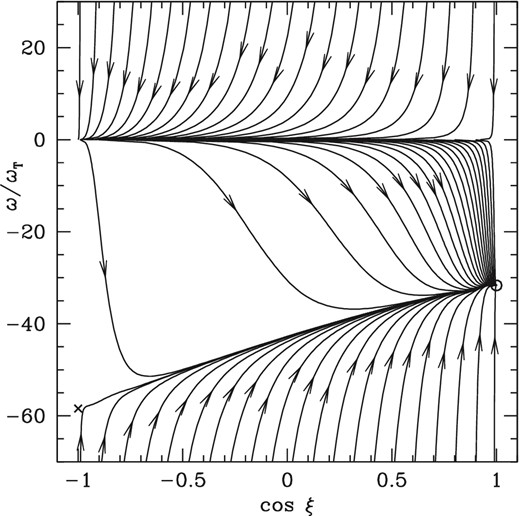
Trajectory map for grain 1, s_d = 0.1, ψ_v = 89°, and atoms as the outgoing particles in scenario (2). The rotational speed ω is normalized to the thermal value ω_T (equation 151); ξ is the alignment angle. The attractor (repeller) is indicated by the open circle (cross).

Open in new tab Download slide

In future work, we will relax the assumption that the angular momentum always lies along |${\hat{\boldsymbol a}}_1$|⁠, enabling a firm conclusion regarding the effectiveness of mechanical torques in aligning grains. Here we attempt to gain some insight by examining the incidence of attractors satisfying the following three conditions that are conducive to alignment: (1) |cos ξ| ≥ 1/3, ensuring that the ‘Rayleigh reduction factor’ characterizing the alignment effectiveness is positive (Lee & Draine 1985); (2) τ_align ≤ 10⁶ yr, in order to be competitive with radiative torques (Draine & Weingartner 1997); (3) ω/ω_T ≥ 3, so as to avoid disalignment due to collisions with gas particles (Lazarian & Hoang 2007b; Hoang & Lazarian 2008). For each of the 13 grain shapes, five assumptions regarding the outgoing particles, and five values of s_d, we consider 100 values of ψ_v between 0 and π/2, uniformly spaced in cos ψ_v. Fig. 7 shows f_attract, the fraction of values of ψ_v for which the trajectory map contains one or more attractors (making it non-cyclic or semicyclic) satisfying the above three conditions.

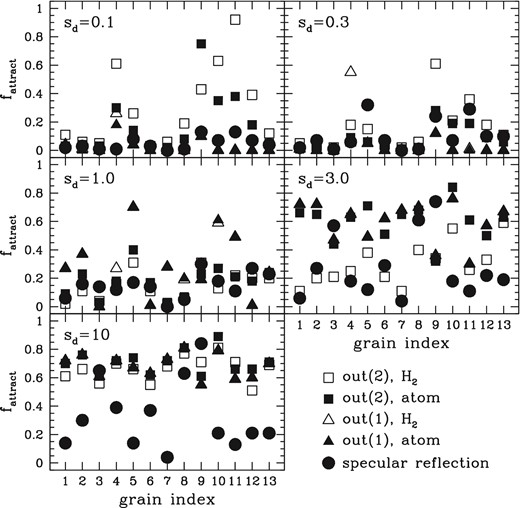
$For each of 65 cases (13 grain shapes and five assumptions regarding outgoing particles) and with five values of sd as indicated in each panel, the fraction fattract of values of ψv (uniformly distributed in cos ψv) for which the trajectory map contains one or more attractors satisfying the alignment-conducive conditions described in the text.$

Figure 7.

For each of 65 cases (13 grain shapes and five assumptions regarding outgoing particles) and with five values of s_d as indicated in each panel, the fraction f_attract of values of ψ_v (uniformly distributed in cos ψ_v) for which the trajectory map contains one or more attractors satisfying the alignment-conducive conditions described in the text.

Open in new tab Download slide

With the exception of grain 4, we include only the torque associated with the arriving atoms in the case of outgoing scenario (1), since |$\boldsymbol {Q}_{\Gamma , \mathrm{out}, (1)} {\cdot } {\hat{\boldsymbol a}}_1 / Q_{\mathrm{arr}}$| is consistent with zero for most of the shapes. Thus, except for grain 4, the open and filled triangles are coincident in Fig. 7. As noted in Section 5.1, |$\boldsymbol {Q}_{\Gamma , \mathrm{out}, (1)} {\cdot } {\hat{\boldsymbol a}}_1 / Q_{\mathrm{arr}}$| appears to converge to a small but non-zero value for grains 2 and 3. Including the associated torque does not alter the value of f_attract in any case for grain 3, but does alter its value for grain 2 by ±0.01 in some cases.

The fraction f_attract varies considerably depending on grain shape, outgoing particle characteristics, and s_d. On the whole, f_attract is larger for supersonic drift than for subsonic drift, suggesting more effective alignment in the former case. This may be partially offset by the result that maps with attractors tend to be non-cyclic in cases of subsonic drift and semicyclic in cases of supersonic drift (except that semicyclic character always dominates in the case of specular reflection). Even for subsonic drift, f_attract can approach unity for some grain shapes and outgoing scenarios. Thus, the simple analysis assuming that |$\boldsymbol {J} \parallel {\hat{\boldsymbol a}}_1$| indicates that alignment via mechanical torques may be viable for both subsonic and supersonic drift; a more detailed study that relaxes this assumption is needed.

6.5 Analysis

We have found that the increase in f_attract with s_d is commonly due to an increase in the number of attractors as s_d increases rather than an increase in the fraction of attractors that satisfy the three imposed conditions. To gain some insight into this observation, consider how the overall magnitudes and the shapes of the torques (i.e. plots of the rotationally averaged efficiency factor components as functions of cos θ_va) vary with s_d and how these affect the incidence of attractors and the associated values of ω/ω_T and τ_align.

Denote the overall magnitudes of the mechanical and drag torque efficiencies by |$\tilde{Q}_{\Gamma , \mathrm{mech}}$| and |$\tilde{Q}_{\Gamma , \mathrm{drag}}$|⁠, respectively. Both of these tend to increase with s_d. As noted in Section 3.8, in the extreme supersonic limit, the torques associated with arriving atoms and specular reflection increase in proportion to |$s_{\rm d}^2$| and the outgoing-particle and drag torques increase in proportion to s_d. In the subsonic limit (Section 3.7), |$\boldsymbol {Q}_{\Gamma , \mathrm{arr}} \propto s_{\rm d}$|⁠. The other mechanical torques can be non-vanishing when s_d = 0; thus, their overall magnitude does not necessarily increase monotonically with s_d in the subsonic limit (though this happens to be the case for grain 1). As seen in Fig. 2 (recall that |$\boldsymbol {Q}_{\Gamma , \mathrm{drag, out, (1)}} \propto Q_{\mathrm{arr}}$|⁠), |$\tilde{Q}_{\Gamma , \mathrm{drag}}$| increases very slowly with s_d in the subsonic limit and |$\tilde{Q}_{\Gamma , \mathrm{drag}} \propto s_{\rm d}$| in the supersonic limit.

If only the arriving atoms contributed to the mechanical torque, then its shape would not depend on s_d in either the extreme subsonic or supersonic limits, though it would depend on s_d for intermediate values of s_d. The shape of the total mechanical torque can vary in all of the regimes that we examine since it is the sum of two terms (arrival plus specular reflection or outgoing scenario 1 or 2) that vary with s_d in different ways. (Of course, for sufficiently large s_d, the shape does not depend on s_d, but at s_d = 10 the magnitude of |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}}$| does not yet overwhelm that of |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{out}}$|⁠. Also, the shapes of |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{spec}}$| and |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{out}}$| individually can vary with s_d at low s_d since they do not necessarily vanish when s_d = 0.) The shape of the drag torque also varies with s_d, but we have found that the dynamics is not greatly modified if the drag components perpendicular to |${\hat{\boldsymbol a}}_1$| are ignored. Furthermore, the variation of |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{drag, out}, (2)} \cdot {\hat{\boldsymbol a}}_1$| with θ_va is mild.

Now consider how the various quantities that affect the dynamics depend on |$\tilde{Q}_{\Gamma , \mathrm{mech}}$| and |$\tilde{Q}_{\Gamma , \mathrm{drag}}$|⁠: J_v and H_v are both proportional to |$\tilde{Q}_{\Gamma , \mathrm{mech}}$|⁠, τ_drag and M_v are both proportional to |$\tilde{Q}^{-1}_{\Gamma , \mathrm{drag}}$|⁠, and J_drag and H_drag are both independent of the overall torque magnitudes.

Thus, the function Z_v(ξ) (equation 156) is proportional to |$\tilde{Q}_{\Gamma , \mathrm{mech}}$|⁠. Since stationary points are located at ξ for which Z_v(ξ) = 0, the incidence of stationary points depends only on the shapes of the torques, not on their overall magnitudes. We have found that the great majority of the attractors lie at ξ = 0 or π, where stationary points are always located. Since the suprathermality |$\omega ^{\prime }_s \propto \tilde{Q}_{\Gamma , \mathrm{mech}} / \tilde{Q}_{\Gamma , \mathrm{drag}}$|⁠, it tends to increase with s_d and approaches values as large as 10⁵ in some cases when s_d = 10.

The terms A_l and D_l that appear in the linearized dynamical equations (equations 158–163) are independent of the overall torque magnitudes while |$B_l \propto \tilde{Q}_{\Gamma , \mathrm{drag}} \tilde{Q}^{-1}_{\Gamma , \mathrm{mech}}$| and |$C_l \propto \tilde{Q}_{\Gamma , \mathrm{mech}} \tilde{Q}^{-1}_{\Gamma , \mathrm{drag}}$|⁠. Thus, the conditions for a stationary point to be an attractor (equation 165) are independent of the overall torque magnitude. The increase in the number of attractors with s_d must result from the change in the shape of the mechanical torque as s_d increases.

Recall that |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{drag}}$| can usually be approximated as constant and antiparallel to |${\hat{\boldsymbol a}}_1$| without dramatically altering the dynamics. With this assumption, B_l = 0 and D_l = −1. Thus, the condition for a stationary point to be an attractor (equation 165) is A_l < 0. For a given value of ψ_v (except sin ψ_v = 0) and the stationary point at ξ = 0, C_l = 0 and

\begin{equation} A_l = \frac{Q_{\theta }(\cos \psi _v) \cot \psi _v - Q^{\prime }_{\theta }(\cos \psi _v) \sin \psi _v}{2 Q_{a1}(\cos \psi _v)}, \end{equation}

(170)

where |$Q_{\theta }(\cos \theta _{va}) = \overline{\boldsymbol {Q}}_{\Gamma , \mathrm{mech}} (\cos \theta _{va}) {\cdot } {\hat{\boldsymbol \theta }}_v$|⁠, |$Q^{\prime }_{\theta }(\cos \theta _{va}) = \mathrm{d}Q_{\theta }(\cos \theta _{va}) /\mathrm{d}(\cos \theta _{va})$|⁠, and |$Q_{a1}(\cos \theta _{va}) = \overline{\boldsymbol {Q}}_{\Gamma , \mathrm{mech}}(\cos \theta _{va}) {\cdot } {\hat{\boldsymbol a}}_1$|⁠. Note that we take cos θ_va as the argument of the rotationally averaged efficiency factors here. If sin ψ_v = 0, then

\begin{equation} A_l = {-} \sin \psi _v \, \frac{Q^{\prime }_{\theta }(\cos \psi _v)}{Q_{a1}(\cos \psi _v)} = \frac{1}{Q_{a1}(\cos \psi _v)} \left. \frac{\mathrm{d} Q_{\theta }(\cos \theta _{va})}{\mathrm{d} \theta _{va}} \right|_{\theta _{va} = \psi _v}. \end{equation}

(171)

Thus, if sin ψ_v ≠ 0 and Q_a1(cos ψ_v) ≠ 0, then, for a given ψ_v, the condition to have an attractor at ξ = 0 (A_l < 0) can be expressed in terms of the shape of the a₁- and θ_v-components of the rotationally averaged mechanical torque efficiency factor as

\begin{equation} Q_{a1}(\cos \psi _v) \left[ Q^{\prime }_{\theta }(\cos \psi _v) \sin ^2 \psi _v - Q_{\theta }(\cos \psi _v) \cos \psi _v \right] > 0 \end{equation}

(172)

(cf. section 6.3.2 of Lazarian & Hoang 2007a). The condition for the stationary point at ξ = π to be an attractor is identical except that cos ψ_v is replaced with −cos ψ_v. Of course, an attractor at ξ = 0 or π characterized by suprathermal rotation will not arise when Q_a1(cos ψ_v) = 0. Evidently the range of values of cos θ_va for which inequality (172) is satisfied varies considerably among GRS shapes for a given value of s_d and tends to increase with s_d for a given grain shape.

Since the denominator in the expression for τ_align in equation (166) does not depend on the overall torque magnitudes, the alignment time varies with s_d in exactly the same way as the drag time, namely in proportion to |$\tilde{Q}^{-1}_{\Gamma , \mathrm{drag}}$|⁠. Thus, the distribution of alignment times does not vary substantially as s_d increases through the subsonic regime but does decrease with s_d in the supersonic regime.

Now we will apply the above observations to the dynamics in the case of outgoing scenario (1). Except for grain 4, the torque associated with the outgoing atoms/molecules is negligible compared with the torque associated with the incoming atoms in this scenario. Thus, |$Q_{a1}(\cos \theta _{va}) = \overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}}(\cos \theta _{va}) {\cdot } {\hat{\boldsymbol a}}_1$| and |$Q_{\theta }(\cos \theta _{va}) = \overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}}(\cos \theta _{va}) {\cdot } {\hat{\boldsymbol \theta }}_v$|⁠. The incidence of attractors at ξ = 0 or π as a function of s_d can be explained from the grain-shape-independent properties of Q_a1 and Q_θ derived in Appendix B. (For the remainder of this discussion, it will be implicit that the attractors under discussion lie at ξ = 0 or π.)

First, since Q_a1(0) = 0, no attractors with suprathermal rotation are expected for cos ψ_v = 0. Secondly, when cos ψ_v = ±1, the condition for an attractor is that A_l given by equation (171) must be less than zero. Since Q_a1 and Q_θ have the same sign when cos θ_va > 0 and Q_θ(cos θ_va = ±1) = 0, dQ_θ/dθ_va has the same sign as Q_a1 for the stationary point at ξ = 0. Thus, A_l > 0 and this point is not an attractor. A similar analysis shows that the stationary point at ξ = π is also not an attractor.

Aside from the above special cases, the condition for an attractor is inequality (172). Suppose Q_a1(cos θ_va) > 0 when X₁ < cos θ_va < X₂. In this case, inequality (172) is equivalent to

\begin{equation} Q_{\theta }(\cos \psi _v) < \csc \psi _v \, Q_{\theta }(X_0) , \ \ X_1 < \cos \psi _v < X_0 , \end{equation}

(173)

\begin{equation} Q_{\theta }(\cos \psi _v) > \csc \psi _v \, Q_{\theta }(X_0), \ \ X_0 < \cos \psi _v < X_2 \end{equation}

(174)

for some X₀ such that X₁ < X₀ < X₂. If Q_a1(cos θ_va) < 0, then the inequality signs relating Q_θ(cos ψ_v) and |$\csc \psi _v \, Q_{\theta }(X_0)$| are reversed in the above condition.

For 9 of the 13 grain shapes, including grain 1, Q_θ(cos θ_va) has the same sign for the entire range of cos θ_va (−1 to 1). Thus, if Q_a1(cos θ_va) > 0 when cos θ_va > 0, then Q_θ(cos θ_va) > 0 when cos θ_va > 0 and, for a given ψ_v, the condition for an attractor at ξ = 0 is

\begin{equation} Q_{\theta }(\cos \psi _v) > \csc \psi _v \, Q_{\theta }(\cos \theta _{va} = 0). \end{equation}

(175)

If Q_a1(cos θ_va > 0) < 0, then Q_θ(cos θ_va > 0) < 0 and the condition for an attractor at ξ = 0 is

\begin{equation} Q_{\theta }(\cos \psi _v) < \csc \psi _v \, Q_{\theta }(\cos \theta _{va} = 0). \end{equation}

(176)

Thus, the condition for an attractor at ξ = 0 (assuming Q_θ has the same sign for the entire range of cos θ_va) is

\begin{equation} |Q_{\theta }(\cos \psi _v)| > \csc \psi _v \, |Q_{\theta }(\cos \theta _{va} = 0)|. \end{equation}

(177)

The condition for an attractor at ξ = π is identical. In the extreme subsonic regime, |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}} {\cdot } {\hat{\boldsymbol \theta }_v} (\cos \theta _{va}) \propto \sin \theta _{va}$|⁠, so the condition for an attractor is sin ψ_v > 1. Thus, for the idealized conditions considered here for outgoing scenario (1), i.e. only the torque associated with the arriving atoms is significant and only attractors at ξ = 0 and π are considered, we expect f_attract = 0 in the subsonic regime. In the extreme supersonic limit, |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}} {\cdot } {\hat{\boldsymbol \theta }_v} (\cos \theta _{va} = 0) \rightarrow 0$| and condition (177) is satisfied for an expanding range of values of ψ_v. As a result, f_attract increases dramatically as s_d increases.

As seen in Fig. 7, our computed f_attract for outgoing scenario (1) does not equal zero in the subsonic regime for grains 2, 5, and 9. For grain 2, this occurs because the computational result for Q_a1(cos θ_va) crosses zero at cos θ_va ≈ −0.018 rather than at zero. As a result, Q_a1 has the wrong sign for a small range of cos θ_va, yielding spurious attractors at ξ = π for ψ_v very close to 90°. Although this slight offset in Q_a1(cos θ_va) afflicts the computational results for all grains, it is only large enough to affect f_attract for grain 2. For grains 5 and 9, deviations of the shape of the computed Q_θ(cos θ_va) from sin θ_va are responsible for the spurious attractors. We have generated a version of Fig. 7 for the subsonic regime using torques computed with N₁ = 64 rather than 128. (Recall that there are N₁ values of ϕ_sph and ϕ_in and N₁ + 1 values of cos θ_sph and cos θ_in.) With N₁ = 64, f_attract for outgoing scenario (1) is somewhat higher for grains 2, 5, and 9 and also non-zero for grains 3, 6, 10, and 11. Thus, f_attract approaches zero as the numerical resolution increases, in agreement with our idealized model.

In the case of grain 4, |$\boldsymbol {Q}_{\Gamma , \mathrm{out}, (1)} {\cdot } {\hat{\boldsymbol a}}_1$| is not negligible. For s_d = 0.1, |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}} {\cdot } {\hat{\boldsymbol a}_1} \approx -7 \times 10^{-3} \cos \theta _{va}$|⁠, |$\boldsymbol {Q}_{\Gamma , \mathrm{out}, (1)} {\cdot } {\hat{\boldsymbol a}}_1 / Q_{\mathrm{arr}} = 0.001\,22$|⁠, and Q_arr ≈ 4.3. Evaluating v_out/v_th for the cases of atomic and molecular outgoing particles using the parameter values in Table 5, we find that Q_a1 ≈ Q₀ − 7 × 10⁻³cos θ_va with Q₀ ≈ 1.9 × 10⁻³ for atoms and Q₀ ≈ 1.7 × 10⁻² for molecules. Due to the upward shift of Q_a1, Q_a1 and Q_θ have opposite signs when 0 < cos θ_va < 0.28 for atoms and when 0 < cos θ_va < 1 for molecules. Thus, attractors arise at ξ = 0 for cos ψ_v between 0 and 0.28 (0 and 1) for atomic (molecular) outgoing particles. Since these attractors do not all satisfy the conditions on ω′ and τ_align for effective alignment, f_attract is less than 0.28 and 1 in these cases. A similar analysis applies when s_d = 0.3. Thus, it appears that subsonic mechanical torques can yield effective alignment even in the case of outgoing scenario (2) if the grain shape is such that |$\boldsymbol {Q}_{\Gamma , \mathrm{out}, (1)} {\cdot } {\hat{\boldsymbol a}}_1$| is not negligible, but that such shapes are rare. Of course, we are unable to draw a strong conclusion on this point since we have only examined 13 shapes.

Finally, consider the dynamics assuming specular reflection or outgoing scenario (2) in the subsonic limit. As shown in Appendix C, the rotationally averaged torque efficiency factors exhibit the same functional dependence on cos θ_va as for the torque associated with arriving atoms, except that |$\overline{\boldsymbol {Q}}_{\Gamma , i} \cdot {\hat{\boldsymbol a}}_1$| [i = spec or out(2)] can be non-zero when s_d = 0. Thus, just as with the torque associated with outgoing particles for grain 4 and outgoing scenario (1), the zero of Q_a1 shifts away from cos θ_va = 0, opening up a range of values of cos ψ_v for which attractors may occur at either ξ = 0 or π. If the simplifying assumptions of this discussion (e.g. neglect of complications in the drag torque and the possibility of attractors at values of cos ξ other than ±1) remain valid, then f_attract could reach values as high as

\begin{equation} f_{\mathrm{attract, max}} = \max \left[ \frac{|\boldsymbol {Q}_{\Gamma , \mathrm{mech}}(s_{\rm d}=0) \cdot {\hat{\boldsymbol a}}_1|}{s_{\rm d} |\overline{\boldsymbol {Q}}^{\prime }_{\Gamma , \mathrm{mech}} \cdot {\hat{\boldsymbol a}}_1|}, 1 \right], \end{equation}

(178)

where |$\boldsymbol {Q}_{\Gamma , \mathrm{mech}}$| includes contributions from both arriving atoms and reflected or outgoing particles (see equation 50) and the prime denotes the term linear in s_d (see Section 3.7).

The upper panel in Fig. 8 shows f_attract versus f_{attract, max} for s_d = 0.1 for all 13 grain shapes, considering specular reflection and both outgoing scenarios. In most cases, f_attract < f_{attract, max}, commonly because τ_align > 10⁶ yr for the attractors. In cases where f_attract > f_{attract, max}, the simplifying assumptions may be violated or there may be error due to insufficient numerical resolution in the torque evaluations.

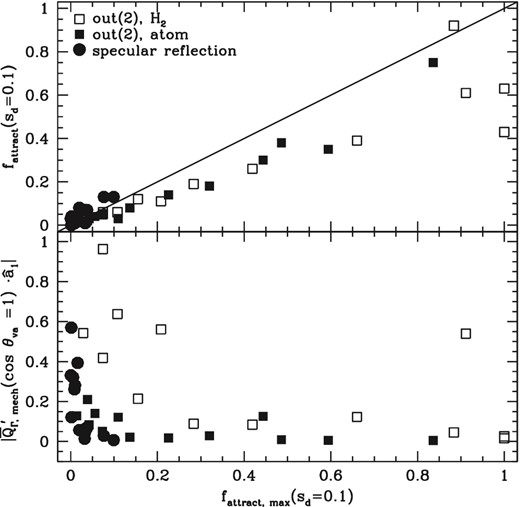
$fattract (upper panel) and $|\overline{\boldsymbol {Q}}^{ \prime }_{\Gamma , \mathrm{mech}}(\cos \theta _{va} =1) \cdot {\hat{\boldsymbol a}}_1|$ (lower panel) versus fattract, max for sd = 0.1$

Figure 8.

f_attract (upper panel) and |$|\overline{\boldsymbol {Q}}^{ \prime }_{\Gamma , \mathrm{mech}}(\cos \theta _{va} =1) \cdot {\hat{\boldsymbol a}}_1|$| (lower panel) versus f_{attract, max} for s_d = 0.1

Open in new tab Download slide

The lower panel in Fig. 8 shows |$|\overline{\boldsymbol {Q}}^{ \prime }_{\Gamma , \mathrm{mech}}(\cos \theta _{va} =1) \cdot {\hat{\boldsymbol a}}_1|$|⁠, a measure of the overall magnitude of the mechanical torque, again for s_d = 0.1. Note that, typically, the cases for which f_attract is substantial are characterized by low torque magnitudes. This is expected from the above analysis: the mechanical torque in the subsonic regime is the sum of a constant term that persists when s_d = 0 and a term proportional to s_d. The larger the former is in comparison to the latter, the larger the range of cos ψ_v for which attractors can occur. The one case for which both f_attract and the torque magnitude are large is for H₂ molecules departing in scenario (2) from grain 4. As with outgoing scenario (1), this grain happens to experience an unusually large torque even when not drifting relative to the gas.

As seen in Fig. 7, for some of the cases with relatively large f_attract when s_d = 0, f_attract is lower when s_d = 0.3; the term that persists when s_d = 0 is relatively less important when s_d = 0.3 than when s_d = 0.1. As discussed earlier, the increase in f_attract as s_d increases beyond 1 is due to the change in the shape of the torques; the torque that persists for zero drift is unimportant in these cases.

These results suggest that grain shapes which are most susceptible to alignment by mechanical torques in the subsonic regime may typically experience relatively weak mechanical torques, which therefore are more likely to be dominated by other types of torques (e.g. radiative torques). In future work, we will evaluate the radiative torques on the 13 grains considered here and examine the dynamics in full (rather than including only a subset of the torques) for a range of interstellar environments.

6.6 Comparison with Lazarian & Hoang (2007a)

In their study of radiative torques, Lazarian & Hoang (2007a, hereafter LH07a) found that the ratio |$R_{{\rm LH}} = Q_{e1}^{\mathrm{max}}/Q_{e2}^{\mathrm{max}}$| for a grain correlates well with the grain's alignment characteristics. Here Q_e1 is the component of the radiative torque efficiency factor along the direction |$\boldsymbol {S}$| of the radiation field anisotropy and Q_e2 is the component perpendicular to |$\boldsymbol {S}$| and in the plane spanned by |$\boldsymbol {S}$| and |${\hat{\boldsymbol a}}_1$|⁠. The superscript ‘max’ indicates the maximum absolute value as a function of the angle between |$\boldsymbol {S}$| and |${\hat{\boldsymbol a}}_1$|⁠. Their fig. 24 shows how the incidence of attractors with high angular momentum (i.e. the types that we examine here) varies with ψ (the angle between the magnetic field direction and |$\boldsymbol {S}$|⁠) as a function of R_LH. When 1 < R_LH < 2, no or very few high-J attractors are expected. As R_LH increases above 2, high-J attractors arise near ψ = 0 and extend to larger values of ψ as R_LH increases. Similarly, as R_LH decreases below 1, high-J attractors arise near ψ = 90° and extend to lower values of ψ as R_LH decreases.

It is of interest to check whether an analogous ratio describes the alignment by mechanical torques for the grains examined in this work. Thus, we define |$R_{{\rm LH}}^{\mathrm{mech}}$| in the same way as R_LH, considering the total mechanical torque efficiency (equation 50) and the components along |${\hat{\boldsymbol z}}_v$| and |${\hat{\boldsymbol x}}_v$| in place of Q_e1 and Q_e2, respectively (see Section 3.5).

Whereas LH07a considered values of R_LH from 0.1 to >20, |$R_{{\rm LH}}^{\mathrm{mech}}$| for the cases considered here ranges from ≈0.003 to ≈2.5 and is less than ≈1.4 for nearly all cases. Thus, we do not have the opportunity to compare the alignment behaviour for large values of the ratio.

Consider first outgoing scenario (1), for which only the torque associated with the arriving atoms is relevant (except for grain 4). For a given grain shape, |$R_{{\rm LH}}^{\mathrm{mech}}$| decreases as s_d increases, since |${\hat{\boldsymbol z}}_v$| is parallel to |${\hat{\boldsymbol s}}_{\rm d}$|⁠. When s_d = 0.1, |$R_{{\rm LH}}^{\mathrm{mech}} \approx 1.2$|–1.3 and there is a very low incidence of attractors (except for grain 4), consistent with the results in LH07a for alignment by radiative torques. As s_d increases (and |$R_{{\rm LH}}^{\mathrm{mech}}$| decreases), the incidence of attractors increases and are concentrated towards ψ_v = 90°, again as expected from fig. 24 in LH07a. However, the range of values of ψ_v for which attractors arise varies considerably among the grain shapes and is not correlated with |$R_{{\rm LH}}^{\mathrm{mech}}$|⁠.

For the other scenarios, the results diverge even further from those in LH07a. For example, for outgoing scenario (2) with outgoing H atoms, |$R_{{\rm LH}}^{\mathrm{mech}} \approx 1.3$|–1.4 for all grain shapes when s_d = 0.1. Whereas fig. 24 in LH07a indicates no high-J attractors (or perhaps only when ψ_v ≈ 90°) for this value of the ratio, we find attractors over a range of values of ψ_v. The extent of this range varies considerably with grain shape, with the maximum ψ_v at 90° and the minimum between 25° and 85°. For some other cases, the various grain shapes exhibit a larger range of values of |$R_{{\rm LH}}^{\mathrm{mech}}$|⁠. For these values of the ratio, it is expected from LH07a that the range of ψ_v for which high-J attractors arise should increase as |$R_{{\rm LH}}^{\mathrm{mech}}$| decreases. We do not find such a correlation.

Thus, it appears that the ratio |$R_{{\rm LH}}^{\mathrm{mech}}$| is not generally a reliable guide to the character of the alignment driven by mechanical torques. We will revisit this question in our upcoming work relaxing the assumption that the grain angular momentum always lies along |${\hat{\boldsymbol a}}_1$|⁠.

7 CONCLUSIONS

In this study, we have developed theoretical and computational tools for evaluating the mechanical torques experienced by irregularly shaped, drifting grains. We have examined various assumptions about how the colliding gas particles depart the grain (specular reflection, departure from an arbitrary location on the grain versus the location at which the incoming particle arrived, departure in atomic versus molecular form). We developed computer codes for all of these scenarios. Arbitrary values of the drift speed can be accommodated, as well as the extreme subsonic and supersonic limits. The codes were verified by comparing with known results (e.g. for spherical grains), by comparing the results for fairly high (low) values of s_d (the drift speed divided by the gas thermal speed) with the results for the supersonic (subsonic) limit, and by verifying that features of the torques common to all grain shapes were exhibited.

After evaluating the torques for 13 different grain shapes, we examined the rotational dynamics assuming steady rotation about the principal axis of greatest moment of inertia, |${\hat{\boldsymbol a}}_1$|⁠. We introduced the quantity f_attract to characterize the efficiency of alignment by mechanical torques (Section 6.4). For subsonic drift, f_attract varies considerably with grain shape and, for some shapes, with the assumptions regarding the departure of atoms/molecules from the grain. The efficiency of subsonic alignment is primarily determined by the magnitude of the torque on a non-drifting grain relative to the torque that increases in proportion to the drift speed. (More precisely, it is the component of the torque along |${\hat{\boldsymbol a}}_1$| that matters.) Thus, efficient alignment by mechanical torques in the subsonic regime may require that the torques be relatively weak, in which case they may be dominated by other types of torques.

As the drift speed increases from the subsonic to the supersonic regime, f_attract tends to increase, suggesting efficient alignment for all grains and most departure scenarios. Efficient alignment can result even for outgoing scenario (1), in which the location of a departing atom/molecule on the grain surface is not correlated with the location of arrival (cf. section 11.7 of LH07a). The increase in f_attract with s_d results from changes in the shape of the torques rather than from an increase in the torque magnitudes.

Future work will examine the dynamics without assuming rotation about |${\hat{\boldsymbol a}}_1$| and will consider the case that the outgoing molecules depart from special sites on the grain surface (Purcell 1979). We will also examine alignment by radiative torques for the 13 grains in this study. By examining the full dynamics under a range of interstellar conditions we hope to clarify the relative importance of the various candidate aligning processes and the environments in which they are operative.

REFERENCES

Andersson

B.-G.

2015

Lazarian

A.

de Gouveia Dal Pino

E. M.

Melioli

C.

Astrophysics and Space Science Library Vol. 407, Magnetic Fields in Diffuse Media

Springer-Verlag

Berlin

59

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Baines

M. J.

Williams

I. P.

1965

Nature

205

59

Crossref

Search ADS

Baines

M. J.

Williams

I. P.

Asebiomo

A. S.

1965

MNRAS

130

63

Crossref

Search ADS

Draine

B. T.

Weingartner

J. C.

1996

ApJ

470

551

Crossref

Search ADS

Draine

B. T.

Weingartner

J. C.

1997

ApJ

480

633

Crossref

Search ADS

Gold

T.

1952a

MNRAS

112

215

Crossref

Search ADS

Gold

T.

1952b

Nature

169

322

Crossref

Search ADS

Hoang

T.

Lazarian

A.

2008

MNRAS

388

117

Crossref

Search ADS

Lazarian

A.

2007

J. Quant. Spectrosc. Radiat. Transfer

106

225

Crossref

Search ADS

Lazarian

A.

Hoang

T.

2007a

MNRAS

378

910

(LH07a)

Crossref

Search ADS

Lazarian

A.

Hoang

T.

2007b

ApJ

669

L77

Crossref

Search ADS

Lee

H. M.

Draine

B. T.

1985

ApJ

290

211

Crossref

Search ADS

Muinonen

K.

Nousiainen

T.

Fast

P.

Lumme

K.

Peltoneimi

J.

1996

J. Quant. Spectrosc. Radiat. Transfer

55

577

Crossref

Search ADS

Press

W. H.

Teukolsky

S. A.

Vetterling

W. T.

Flannery

B. P.

1992

Numerical Recipes in FORTRAN; The Art of Scientific Computing

2nd edn

Cambridge Univ. Press

Cambridge, NY

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Purcell

E. M.

1979

ApJ

231

404

Crossref

Search ADS

Weingartner

J. C.

Draine

B. T.

2003

ApJ

589

289

Crossref

Search ADS

SUPPORTING INFORMATION

Additional Supporting Information may be found in the online version of this article:

Table 1. GRS expansion coefficients.

(Supplementary Data).

Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.

APPENDIX A: CALCULATION DETAILS

A1 Torque due to incoming atoms

Employing equations (21) and (22), the cross-products in the expression for |$\boldsymbol {Q}_{\Gamma , \mathrm{arr}}$| (equation 38) are

\begin{equation} {\hat{\boldsymbol r}} \times {\hat{\boldsymbol s}} = \sin \theta _{\mathrm{in}} \left[(\cos \theta \cos \phi \sin \phi _{\mathrm{in}} + \sin \phi \cos \phi _{\mathrm{in}}) {\hat{\boldsymbol x}} + (\cos \theta \sin \phi \sin \phi _{\mathrm{in}} - \cos \phi \cos \phi _{\mathrm{in}}) {\hat{\boldsymbol y}} - \sin \theta \sin \phi _{\mathrm{in}} \, {\hat{\boldsymbol z}} \right] \end{equation}

(A1)

and

\begin{equation} \frac{\boldsymbol {r}_{\mathrm{cm}}}{r_{\mathrm{sph}}} \times {\hat{\boldsymbol s}} = \frac{1}{r_{\mathrm{sph}}} [ (y_{\mathrm{cm}} s_{0z} - z_{\mathrm{cm}} s_{0y}) {\hat{\boldsymbol x}} + (z_{\mathrm{cm}} s_{0x} - x_{\mathrm{cm}} s_{0z}) {\hat{\boldsymbol y}} + (x_{\mathrm{cm}} s_{0y} - y_{\mathrm{cm}} s_{0x}) {\hat{\boldsymbol z}} ] \end{equation}

(A2)

with

\begin{equation} s_{0x} \equiv {\hat{\boldsymbol s}} {\cdot } {\hat{\boldsymbol x}} = {-} \cos \theta \cos \phi \sin \theta _{\mathrm{in}} \cos \phi _{\mathrm{in}} + \sin \phi \sin \theta _{\mathrm{in}} \sin \phi _{\mathrm{in}} - \sin \theta \cos \phi \cos \theta _{\mathrm{in}}, \end{equation}

(A3)

\begin{equation} s_{0y} \equiv {\hat{\boldsymbol s}} {\cdot } {\hat{\boldsymbol y}} = {-} \cos \theta \sin \phi \sin \theta _{\mathrm{in}} \cos \phi _{\mathrm{in}} - \cos \phi \sin \theta _{\mathrm{in}} \sin \phi _{\mathrm{in}} - \sin \theta \sin \phi \cos \theta _{\mathrm{in}}, \end{equation}

(A4)

\begin{equation} s_{0z} \equiv \hat{s} {\cdot } {\hat{\boldsymbol z}} = \sin \theta \sin \theta _{\mathrm{in}} \cos \phi _{\mathrm{in}} - \cos \theta \cos \theta _{\mathrm{in}}. \end{equation}

(A5)

Thus,

\begin{equation} \left( {\hat{\boldsymbol r}} - \frac{\boldsymbol {r}_{\mathrm{cm}}}{r_{\mathrm{sph}}} \right) \times {\hat{\boldsymbol s}} = A_x {\hat{\boldsymbol x}} + A_y {\hat{\boldsymbol y}} + A_z {\hat{\boldsymbol z}} \end{equation}

(A6)

with

\begin{equation} A_x = \sin \theta _{\mathrm{in}} (\cos \theta \cos \phi \sin \phi _{\mathrm{in}} + \sin \phi \cos \phi _{\mathrm{in}}) - \frac{y_{\mathrm{cm}} s_{0z} - z_{\mathrm{cm}} s_{0y}}{r_{\mathrm{sph}}} \end{equation}

(A7)

\begin{equation} A_y = \sin \theta _{\mathrm{in}} (\cos \theta \sin \phi \sin \phi _{\mathrm{in}} - \cos \phi \cos \phi _{\mathrm{in}}) - \frac{z_{\mathrm{cm}} s_{0x} - x_{\mathrm{cm}} s_{0z}}{r_{\mathrm{sph}}} \end{equation}

(A8)

\begin{equation} A_z = {-} \sin \theta _{\mathrm{in}} \sin \theta \sin \phi _{\mathrm{in}} - \frac{x_{\mathrm{cm}} s_{0y} - y_{\mathrm{cm}} s_{0x}}{r_{\mathrm{sph}}}. \end{equation}

(A9)

A2 Torque due to outgoing particles

In equation (46),

\begin{eqnarray} \eta _S \, \frac{\boldsymbol {r}_{\mathrm{surf}}}{a_{\mathrm{eff}}} \times {\hat{\boldsymbol N}} = \frac{r_{\mathrm{surf}}^3}{a_{\mathrm{eff}}} \, \nu _N \left\lbrace \left[ - w_2(\theta , \phi ) \sin \theta \sin \phi + w_3(\theta , \phi ) \cot \theta \cos \phi \right]{\hat{\boldsymbol x}} + \left[ w_2(\theta , \phi ) \sin \theta \cos \phi + w_3(\theta , \phi ) \cot \theta \sin \phi \right]{\hat{\boldsymbol y}} - w_3(\theta , \phi ) {\hat{\boldsymbol z}} \right\rbrace .\nonumber\\ \end{eqnarray}

(A10)

A3 Extreme subsonic limit

Equations (81) and (82) simplify to

\begin{equation} \boldsymbol {Q}_{\Gamma , \mathrm{arr}}(s_{\rm d} = 0) = \frac{1}{8 \pi } \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^3 \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2 \pi } \mathrm{d}\phi \int _0^{2 \pi } \mathrm{d}\phi _{\mathrm{in}} \left[ {\boldsymbol A}_1 \left(1 - u_{\rm c}^3\right) + {\boldsymbol A}_2 \left(1 - u_{\rm c}^2\right)^{3/2} \right] \end{equation}

(A11)

and

\begin{eqnarray} \boldsymbol {Q}^{\prime }_{\Gamma , \mathrm{arr}} &=& \pi ^{-3/2} \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^3 \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2 \pi } \mathrm{d}\phi \int _0^{2 \pi } \mathrm{d}\phi _{\mathrm{in}} \left\lbrace \frac{1}{2} \beta _1 {\boldsymbol A}_1 \left(1 - u_{\rm c}^4\right) + \frac{1}{2} \beta _2 {\boldsymbol A}_2 \left(1 - u_{\rm c}^2\right)^2 \right. \nonumber\\ && \left. +\,\frac{1}{4} \left( \beta _2 {\boldsymbol A}_1 + \beta _1 {\boldsymbol A}_2 \right) \left[ \cos ^{-1} u_{\rm c} + u_{\rm c} \left(1 - 2 u_{\rm c}^2\right) \sqrt{1 - u_{\rm c}^2} \right] \right\rbrace \end{eqnarray}

(A12)

where

\begin{equation} A_x = A_{1x} \cos \theta _{\mathrm{in}} + A_{2x} \sin \theta _{\mathrm{in}}, \end{equation}

(A13)

\begin{equation} s_{0x} = s_{0x, 1} \cos \theta _{\mathrm{in}} + s_{0x, 2} \sin \theta _{\mathrm{in}} \end{equation}

(A14)

(and likewise for y and z),

\begin{equation} s_{0x, 1} = {-} \sin \theta \cos \phi , \end{equation}

(A15)

\begin{equation} s_{0x, 2} = {-} \cos \theta \cos \phi \cos \phi _{\mathrm{in}} + \sin \phi \sin \phi _{\mathrm{in}}, \end{equation}

(A16)

\begin{equation} s_{0y, 1} = {-} \sin \theta \sin \phi , \end{equation}

(A17)

\begin{equation} s_{0y, 2} = {-} \cos \theta \sin \phi \cos \phi _{\mathrm{in}} - \cos \phi \sin \phi _{\mathrm{in}}, \end{equation}

(A18)

\begin{equation} s_{0z, 1} = {-} \cos \theta , \end{equation}

(A19)

\begin{equation} s_{0z, 2} = \sin \theta \cos \phi _{\mathrm{in}}, \end{equation}

(A20)

\begin{equation} A_{1x} = {-} \frac{y_{\mathrm{cm}} s_{0z, 1} - z_{\mathrm{cm}} s_{0y, 1}}{r_{\mathrm{sph}}}, \end{equation}

(A21)

\begin{equation} A_{2x} = \cos \theta \cos \phi \sin \phi _{\mathrm{in}} + \sin \phi \cos \phi _{\mathrm{in}} - \frac{y_{\mathrm{cm}} s_{0z, 2} - z_{\mathrm{cm}} s_{0y, 2}}{r_{\mathrm{sph}}}, \end{equation}

(A22)

\begin{equation} A_{1y} = {-} \frac{z_{\mathrm{cm}} s_{0x, 1} - x_{\mathrm{cm}} s_{0z, 1}}{r_{\mathrm{sph}}}, \end{equation}

(A23)

\begin{equation} A_{2y} = \cos \theta \sin \phi \sin \phi _{\mathrm{in}} - \cos \phi \cos \phi _{\mathrm{in}} - \frac{z_{\mathrm{cm}} s_{0x, 2} - x_{\mathrm{cm}} s_{0z, 2}}{r_{\mathrm{sph}}}, \end{equation}

(A24)

\begin{equation} A_{1z} = {-} \frac{x_{\mathrm{cm}} s_{0y, 1} - y_{\mathrm{cm}} s_{0x, 1}}{r_{\mathrm{sph}}}, \end{equation}

(A25)

\begin{equation} A_{2z} = {-} \sin \theta \sin \phi _{\mathrm{in}} - \frac{x_{\mathrm{cm}} s_{0y, 2} - y_{\mathrm{cm}} s_{0x, 2}}{r_{\mathrm{sph}}}. \end{equation}

(A26)

A4 Drag force in the extreme subsonic limit

Equations (107) and (108) simplify to

\begin{equation} \boldsymbol {Q}_{F, \mathrm{arr}}(s_{\rm d} = 0) = {-} \frac{1}{8 \pi } \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^2 \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2\pi } \mathrm{d}\phi \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \left[ \left(1-u_{\rm c}^3\right) {\hat{\boldsymbol r}} + \left(1-u_{\rm c}^2\right)^{3/2} \boldsymbol {M} \right] \end{equation}

(A27)

and

\begin{eqnarray} \boldsymbol {Q}^{\prime }_{F, \mathrm{arr}} &=& - \frac{\pi ^{-3/2}}{2} \left( \frac{r_{\mathrm{sph}}}{a_{\mathrm{eff}}} \right)^2 \int _{-1}^1 \mathrm{d}(\cos \theta ) \int _0^{2\pi } \mathrm{d}\phi \int _0^{2\pi } \mathrm{d}\phi _{\mathrm{in}} \biggl \lbrace \beta _1 \left(1 - u_{\rm c}^4\right) {\hat{\boldsymbol r}} + \beta _2 \left(1-u_{\rm c}^2\right)^2 \boldsymbol {M} \nonumber\\ &&+\,\frac{1}{2} \left[ u_{\rm c} \left(1-2 u_{\rm c}^2\right) \left(1- u_{\rm c}^2\right)^{1/2} + \cos ^{-1} u_{\rm c} \right] (\beta _2 {\hat{\boldsymbol r}} + \beta _1 \boldsymbol {M}) \biggr \rbrace \end{eqnarray}

(A28)

with

\begin{equation} \boldsymbol {M} = (\cos \phi _{\mathrm{in}} \cos \theta \cos \phi - \sin \phi _{\mathrm{in}} \sin \phi ) {\hat{\boldsymbol x}} + (\cos \phi _{\mathrm{in}} \cos \theta \sin \phi + \sin \phi _{\mathrm{in}} \cos \phi ) {\hat{\boldsymbol y}} - \cos \phi _{\mathrm{in}} \sin \theta \, {\hat{\boldsymbol z}}. \end{equation}

(A29)

APPENDIX B: SPECIAL RESULTS ASSOCIATED WITH ARRIVING ATOMS

Here we derive some general features of the arrival efficiency and arrival torque efficiency noted in Sections 3.7 and 5.1. First, note that when cos θ_va = 0, |${\hat{\boldsymbol \theta }}_v = {-} {\hat{\boldsymbol s}}_{\rm d}$|⁠. Since all of the incoming gas atoms have velocities along |$- {\hat{\boldsymbol s}}_{\rm d}$| in the limit s_d → ∞, |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}} {\cdot } {\hat{\boldsymbol \theta }}_v (\cos \theta _{va} = 0) \rightarrow 0$| as s_d → ∞. Similarly, since |${\hat{\boldsymbol a}}_1$| is parallel or antiparallel to |${\hat{\boldsymbol s}}_{\rm d}$| when cos θ_va = ±1, |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}} {\cdot } {\hat{\boldsymbol a}}_1 (\cos \theta _{va} = \pm 1) \rightarrow 0$| as s_d → ∞.

The remaining results are more readily apparent if we adopt an approach that dispenses with the enclosing sphere. For the remainder of this appendix, we will take the origin at the grain's centre of mass. For now, redefine the grain-body axes |$({\hat{\boldsymbol x}}, {\hat{\boldsymbol y}}, {\hat{\boldsymbol z}})$| such that θ_gr = 0 (i.e. the grain is moving along the |${\hat{\boldsymbol z}}$| direction). As usual, |${\hat{\boldsymbol z}}$| and |${\hat{\boldsymbol x}}$| are the reference axes for the polar angle θ and azimuthal angle ϕ, respectively. In this case, |$|{\boldsymbol s} + {\boldsymbol s}_{\rm d}|^2 = s^2 + s_{\rm d}^2 -2\,s s_{\rm d} \cos \theta$|⁠.

The rate at which gas atoms coming from within solid angle element dΩ about the direction (θ, ϕ), with reduced speeds between s and s + ds, strike an area element oriented perpendicular to the gas flow and with area dA_⊥ is

\begin{equation} {\rm d}R_{\mathrm{arr}} = n v_{\mathrm{th}} \, {\rm d}\Omega \, \pi ^{-3/2} \exp (-|{\boldsymbol s} + {\boldsymbol s}_{\rm d}|^2) \, s^3 \, {\rm d}s \, dA_{\perp }. \end{equation}

(B1)

The cross-sectional area A_⊥ that the grain presents to gas atoms coming from direction (θ, ϕ) can be expressed as

\begin{equation} A_{\perp }(\theta , \phi ) = \frac{1}{2} \int _0^{2\pi } {\rm d}\chi \, [b(\theta , \phi , \chi )]^2, \end{equation}

(B2)

where b(θ, ϕ, χ) is the largest impact parameter for which a gas atom collides with the grain as a function of a rotation angle χ about the direction (θ, ϕ). Since A_⊥ is the same for two directions on opposite sides of the sky, A_⊥(π − θ, ϕ + π) = A_⊥(θ, ϕ) and b(π − θ, ϕ + π, χ) = b(θ, ϕ, χ).

In the extreme subsonic limit (s_d ≪ 1) and with the grain-body axes oriented as noted above, |$\exp (-|{\boldsymbol s} + {\boldsymbol s}_{\rm d}|^2) \approx \exp (-s^2) \, (1+ 2\,s s_{\rm d} \cos \theta )$|⁠. Thus,

\begin{equation} R_{\mathrm{arr}} \approx n v_{\mathrm{th}} \pi ^{-3/2} \int _0^{\infty } {\rm d}s \, s^3 \exp ( -s^2 ) \int _0^{2\pi } {\rm d}\phi \int _0^1 {\rm d}(\cos \theta ) \left\lbrace 2 + 2\,s s_{\rm d} \left[ \cos \theta + \cos (\pi - \theta ) \right] \right\rbrace A_{\perp }(\theta , \phi ). \end{equation}

(B3)

Since cos θ + cos (π − θ) = 0, |$Q^{\prime }_{\mathrm{arr}}$| (i.e. the term proportional to s_d) vanishes.

For the remainder of this appendix, choose grain-body axes such that |$({\hat{\boldsymbol x}}, {\hat{\boldsymbol y}}, {\hat{\boldsymbol z}})$| lie along |$({\hat{\boldsymbol a}}_2, {\hat{\boldsymbol a}}_3, {\hat{\boldsymbol a}}_1)$|⁠. Taking χ = 0 along |${\hat{\boldsymbol \theta }}$| and increasing from there towards |${\hat{\boldsymbol \phi }}$| when 0 ≤ θ ≤ π/2, the angular momentum of an atom arriving with impact parameter r_⊥ is

\begin{equation} \Delta \boldsymbol {J}_{\mathrm{arr}}(\theta , \phi , \chi , r_{\perp }, s) = m v_{\mathrm{th}} s r_{\perp } \left[ - (\cos \chi \sin \phi + \sin \chi \cos \theta \cos \phi ) \, {\hat{\boldsymbol x}} + (\cos \chi \cos \phi - \sin \chi \cos \theta \sin \phi ) \, {\hat{\boldsymbol y}} + \sin \chi \sin \theta \, {\hat{\boldsymbol z}} \right] \end{equation}

(B4)

for 0 ≤ θ ≤ π/2. With the area element dA_⊥ = r_⊥dr_⊥dχ, the efficiency factor for the arrival torque is

\begin{equation} \boldsymbol {Q}_{\Gamma , \mathrm{arr}} = \pi ^{-3/2} \int _0^{2\pi } {\rm d}\phi \int _{-1}^1 {\rm d}(\cos \theta ) \int _0^{2\pi } {\rm d}\chi \int _0^{b(\theta , \phi , \chi )} {\rm d}r^{\prime }_{\perp } r^{\prime }_{\perp } \int _0^{\infty } {\rm d}s \, s^3\exp ( -|{\boldsymbol s} + {\boldsymbol s}_{\rm d}|^2 ) \frac{\Delta \boldsymbol {J}_{\mathrm{arr}}(\theta , \phi , \chi , r_{\perp }, s)}{m v_{\mathrm{th}} a_{\mathrm{eff}}}, \end{equation}

(B5)

where |$r^{\prime }_{\perp } = r_{\perp }/a_{\mathrm{eff}}$|⁠. Given direction (θ, ϕ) and the direction (θ_gr, ϕ_gr) of the grain's velocity,

\begin{equation} |{\boldsymbol s} + {\boldsymbol s}_{\rm d}|^2 = s_{\rm d}^2 + s^2 - 2 s_{\rm d} s [ \cos \theta _{\mathrm{gr}} \cos \theta + \sin \theta _{\mathrm{gr}} \sin \theta \cos (\phi - \phi _{\mathrm{gr}}) ]. \end{equation}

(B6)

Thus, for direction (π − θ, ϕ + π),

\begin{equation} |{\boldsymbol s} + {\boldsymbol s}_{\rm d}|^2 = s_{\rm d}^2 + s^2 + 2 s_{\rm d} s [ \cos \theta _{\mathrm{gr}} \cos \theta + \sin \theta _{\mathrm{gr}} \sin \theta \cos (\phi - \phi _{\mathrm{gr}}) ]. \end{equation}

(B7)

Since |$\Delta \boldsymbol {J}_{\mathrm{arr}}(\pi - \theta , \phi + \pi , \chi , r_{\perp }, s) = {-} \Delta \boldsymbol {J}_{\mathrm{arr}}(\theta , \phi , \chi , r_{\perp }, s)$|⁠, combining the terms for direction (θ, ϕ) and (π − θ, ϕ + π) in the expression for |$\boldsymbol {Q}_{\Gamma , \mathrm{arr}}$| yields

\begin{eqnarray} \boldsymbol {Q}_{\Gamma , \mathrm{arr}}(\theta _{\mathrm{gr}}, \phi _{\mathrm{gr}}) &=& \pi ^{-3/2} \int _0^{2\pi } {\rm d}\phi \int _0^1 {\rm d}(\cos \theta ) \int _0^{2\pi } {\rm d}\chi \int _0^{b(\theta , \phi , \chi )} {\rm d}r^{\prime }_{\perp } r^{\prime }_{\perp } \int _0^{\infty } {\rm d}s \, s^3 \exp \left[ - \left( s_{\rm d}^2 + s^2 \right) \right] \frac{\Delta \boldsymbol {J}_{\mathrm{arr}}(\theta , \phi , \chi , r_{\perp }, s)}{m v_{\mathrm{th}} a_{\mathrm{eff}}} \nonumber\\ &&\times\left( \exp \left\lbrace 2 s_{\rm d} s \left[ \cos \theta _{\mathrm{gr}} \cos \theta + \sin \theta _{\mathrm{gr}} \sin \theta \cos (\phi {-} \phi _{\mathrm{gr}}) \right] \right\rbrace {-} \exp \left\lbrace -2 s_{\rm d} s \left[ \cos \theta _{\mathrm{gr}} \cos \theta + \sin \theta _{\mathrm{gr}} \sin \theta \cos (\phi {-} \phi _{\mathrm{gr}}) \right] \right\rbrace \right). \end{eqnarray}

(B8)

Clearly, |$\boldsymbol {Q}_{\Gamma , \mathrm{arr}} = 0$| when s_d = 0. From equations (66)–(68) with |$({\hat{\boldsymbol x}}, {\hat{\boldsymbol y}}, {\hat{\boldsymbol z}}) = ({\hat{\boldsymbol a}}_2, {\hat{\boldsymbol a}}_3, {\hat{\boldsymbol a}}_1)$|⁠, θ_gr = θ_va and ϕ_gr = π/2 − Φ₂. Since Φ₂ is the grain's rotation angle about |${\hat{\boldsymbol a}}_1$|⁠,

\begin{equation} \overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}}(\theta _{va}) = \frac{1}{2\pi } \int _0^{2\pi } {\rm d}\phi _{\mathrm{gr}} \, \boldsymbol {Q}_{\Gamma , \mathrm{arr}}( \theta _{\mathrm{gr}} = \theta _{va}, \phi _{\mathrm{gr}}). \end{equation}

(B9)

Thus,

\begin{eqnarray} \overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}}(\theta _{va}) {\cdot } {\hat{\boldsymbol a}}_1 &=& \frac{\pi ^{-5/2}}{2} \int _0^{2\pi } {\rm d}\phi \int _0^1 {\rm d}(\cos \theta ) \sin \theta \int _0^{2\pi } {\rm d}\chi \sin \chi \int _0^{b(\theta , \phi , \chi )} {\rm d}r^{\prime }_{\perp } (r^{\prime }_{\perp })^2 \int _0^{\infty } {\rm d}s \, s^4 \exp \left[ - \left( s_{\rm d}^2 + s^2 \right) \right] \int _0^{2\pi } {\rm d}\phi _{\mathrm{gr}} \nonumber\\ &\times&\left( \exp \left\lbrace 2 s_{\rm d} s \left[ \cos \theta _{va} \cos \theta + \sin \theta _{va} \sin \theta \cos (\phi {-} \phi _{\mathrm{gr}}) \right] \right\rbrace {-} \exp \left\lbrace {-}2 s_{\rm d} s \left[ \cos \theta _{va} \cos \theta + \sin \theta _{va} \sin \theta \cos (\phi {-} \phi _{\mathrm{gr}}) \right] \right\rbrace \right). \end{eqnarray}

(B10)

Replacing the integration variable ϕ_gr with ϕ_gr + π in the second exponential,

\begin{eqnarray} \overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}}(\theta _{va}) {\cdot } {\hat{\boldsymbol a}}_1 &=& \pi ^{-5/2} \int _0^{2\pi } {\rm d}\phi \int _0^1 {\rm d}(\cos \theta ) \sin \theta \int _0^{2\pi } {\rm d}\chi \sin \chi \int _0^{b(\theta , \phi , \chi )} {\rm d}r^{\prime }_{\perp } (r^{\prime }_{\perp })^2 \int _0^{\infty } {\rm d}s \, s^4 \exp \left[ - \left( s_{\rm d}^2 + s^2 \right) \right] \int _0^{2\pi } {\rm d}\phi _{\mathrm{gr}} \nonumber\\ &&\times\exp \left[ 2 s_{\rm d} s \sin \theta _{va} \sin \theta \cos (\phi - \phi _{\mathrm{gr}}) \right] \sinh \left( 2 s_{\rm d} s \cos \theta _{va} \cos \theta \right). \end{eqnarray}

(B11)

Thus, |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}}(\theta _{va}) {\cdot } {\hat{\boldsymbol a}}_1$| is an odd function of cos θ_va. Retaining only the first-order term in sinh (2s_dscos θ_vacos θ) as s_d → 0, |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}}(\theta _{va}) {\cdot } {\hat{\boldsymbol a}}_1 \propto \cos \theta _{va}$| in the extreme subsonic limit.

Since |${\hat{\boldsymbol \theta }}_v = {\hat{\boldsymbol x}}_v \cos \theta _{va} - {\hat{\boldsymbol z}}_v \sin \theta _{va}$|⁠, equations (63), (65), and (71) yield

\begin{equation} \boldsymbol {Q}_{\Gamma , \mathrm{arr}} {\cdot } {\hat{\boldsymbol \theta }}_v = {-} \left( \boldsymbol {Q}_{\Gamma , \mathrm{arr}} {\cdot } {\hat{\boldsymbol x}} \, \sin \Phi _2 + \boldsymbol {Q}_{\Gamma , \mathrm{arr}} {\cdot } {\hat{\boldsymbol y}} \, \cos \Phi _2 \right) = {-} \left( \boldsymbol {Q}_{\Gamma , \mathrm{arr}} {\cdot } {\hat{\boldsymbol x}} \, \cos \phi _{\mathrm{gr}} + \boldsymbol {Q}_{\Gamma , \mathrm{arr}} {\cdot } {\hat{\boldsymbol y}} \, \sin \phi _{\mathrm{gr}} \right). \end{equation}

(B12)

From equations (B4) and (B12),

\begin{equation} \frac{\Delta \boldsymbol {J}_{\mathrm{arr}}(\theta , \phi , \chi , r_{\perp }, s)}{m v_{\mathrm{th}} s r_{\perp }} {\cdot } {\hat{\boldsymbol \theta }}_v = \cos \chi \sin (\phi - \phi _{\mathrm{gr}}) + \sin \chi \cos \theta \cos (\phi - \phi _{\mathrm{gr}}). \end{equation}

(B13)

From equations (B8) and (B13), |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}} {\cdot } {\hat{\boldsymbol \theta }}_v$| contains terms of the form sin (ϕ − ϕ_gr)exp [2s_dssin θ_vasin θcos (ϕ − ϕ_gr)] and cos (ϕ − ϕ_gr)exp [2s_dssin θ_vasin θcos (ϕ − ϕ_gr)]. When integrated over ϕ_gr (0 to 2π), the former yields zero and the latter yields 2πI₁(2s_dssin θ_vasin θ), where I₁(u) denotes the first-order modified Bessel function of the first kind. Since I₁(u) is an odd function of u,

\begin{eqnarray} \overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}}(\theta _{va}) {\cdot } {\hat{\boldsymbol \theta }}_v &=& 2 \pi ^{-3/2} \int _0^{2\pi } {\rm d}\phi \int _0^1 {\rm d}(\cos \theta ) \cos \theta \int _0^{2\pi } {\rm d}\chi \, \sin \chi \int _0^{b(\theta , \phi , \chi )} {\rm d}r^{\prime }_{\perp } (r^{\prime }_{\perp })^2 \int _0^{\infty } {\rm d}s \, s^4 \exp \left[- \left( s_{\rm d}^2 + s^2 \right) \right] \nonumber\\ &&\times I_1 (2 s_{\rm d} s \sin \theta _{va} \sin \theta ) \cosh (2 s_{\rm d} s \cos \theta _{va} \cos \theta ). \end{eqnarray}

(B14)

Thus, |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}}(\theta _{va}) {\cdot } {\hat{\boldsymbol \theta }}_v$| is an even function of cos θ_va. Retaining only the lowest order terms in cosh (2s_dscos θ_vacos θ) and I₁(2s_dssin θ_vasin θ) as s_d → 0, |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}}(\theta _{va}) {\cdot } {\hat{\boldsymbol \theta }}_v \propto \sin \theta _{va}$| in the extreme subsonic limit. Since I₁(0) = 0, |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}}(\theta _{va}) {\cdot } {\hat{\boldsymbol \theta }}_v (\cos \theta _{va} = \pm 1) =0$|⁠. The results derived here for the extreme subsonic limit can also be obtained from equation (82). Comparing equations (B11) and (B14), we see that |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}}(\theta _{va}) {\cdot } {\hat{\boldsymbol a}}_1$| and |$\overline{\boldsymbol {Q}}_{\Gamma , \mathrm{arr}}(\theta _{va}) {\cdot } {\hat{\boldsymbol \theta }}_v$| have the same sign when cos θ_va > 0.

APPENDIX C: SPECIAL RESULTS FOR THE EXTREME SUBSONIC LIMIT

Adopting the same approach used in the derivation of equation (B5), the rotationally averaged torque |$\overline{\boldsymbol {\Gamma }}(\theta _{va})$| associated with any process (except outgoing scenario 1) in the extreme subsonic limit is given by

\begin{eqnarray} \overline{\boldsymbol {\Gamma }}_i(\theta _{va}) &=& \frac{\pi ^{-5/2} n v_{\mathrm{th}} a_{\mathrm{eff}}^2}{2} \int _0^{2\pi } {\rm d}\phi _{\mathrm{gr}} \int _0^{2\pi } {\rm d}\phi \int _{-1}^1 {\rm d}(\cos \theta ) \int _0^{2\pi } {\rm d}\chi \int _0^{b(\theta , \phi , \chi )}\nonumber\\ &&\times\,{\rm d}r^{\prime }_{\perp } r^{\prime }_{\perp } \left\lbrace k_1 + k_2 s_{\rm d} \left[ \cos \theta _{va} \cos \theta + \sin \theta _{va} \sin \theta \cos (\phi - \phi _{\mathrm{gr}}) \right] \right\rbrace \Delta \boldsymbol {J}_i, \end{eqnarray}

(C1)

where |$\Delta \boldsymbol {J}_i$| is the angular momentum transferred during an event and the subscript i denotes the type of event (arrival of an atom, specular reflection, departure of a molecule or an atom following sticking). From equations (75) and (76), |$(k_1, k_2) = (3 \sqrt{\pi }/8, 2)$| for i = arr, spec and |$(k_1, k_2) = (1/2, 3 \sqrt{\pi }/4)$| for i = out(2). With grain-body axes chosen such that |$({\hat{\boldsymbol x}}, {\hat{\boldsymbol y}}, {\hat{\boldsymbol z}})$| lie along |$({\hat{\boldsymbol a}}_2, {\hat{\boldsymbol a}}_3, {\hat{\boldsymbol a}}_1)$|⁠, |$\Delta \boldsymbol {J} \cdot {\hat{\boldsymbol a}}_1 = \Delta J_z$| and |$\Delta \boldsymbol {J} \cdot {\hat{\boldsymbol \theta }}_v = {-}(\Delta J_x \cos \phi _{\mathrm{gr}} + \Delta J_y \sin \phi _{\mathrm{gr}})$| (equation B12). Since |$\Delta \boldsymbol {J}_i$| is independent of θ_va and ϕ_gr, equation (C1) reveals that (1) |$\overline{\boldsymbol {Q}}_{\Gamma , i} \cdot {\hat{\boldsymbol \theta }}_v = 0$| when s_d = 0, (2) |$\overline{\boldsymbol {Q}}_{\Gamma , i} \cdot {\hat{\boldsymbol a}}_1$| can be non-zero when s_d = 0 (though, as shown in Appendix B, this does not hold for the specific case of the torque associated with arriving atoms), (3) |$\overline{\boldsymbol {Q}}_{\Gamma , i}^{\prime } \cdot {\hat{\boldsymbol a}}_1 \propto \cos \theta _{va}$|⁠, 4. |$\overline{\boldsymbol {Q}}_{\Gamma , i}^{\prime } \cdot {\hat{\boldsymbol \theta }}_v \propto \sin \theta _{va}$|⁠.

Download all slides

Month:	Total Views:
November 2016	1
December 2016	1
February 2017	7
March 2017	6
April 2017	2
May 2017	3
June 2017	6
July 2017	1
October 2017	1
November 2017	2
February 2018	2
May 2018	2
July 2018	1
August 2018	2
October 2018	1
November 2018	1
February 2019	2
March 2019	2
April 2019	5
May 2019	4
June 2019	2
July 2019	7
August 2019	4
September 2019	3
October 2019	3
November 2019	11
December 2019	2
January 2020	8
February 2020	5
March 2020	5
April 2020	5
May 2020	4
June 2020	2
July 2020	6
August 2020	3
September 2020	16
October 2020	6
November 2020	3
December 2020	2
January 2021	4
February 2021	7
March 2021	10
April 2021	3
May 2021	4
June 2021	4
July 2021	15
August 2021	9
September 2021	5
October 2021	7
November 2021	10
December 2021	6
January 2022	2
February 2022	5
March 2022	6
April 2022	2
May 2022	4
June 2022	2
July 2022	9
August 2022	8
September 2022	9
October 2022	3
November 2022	2
December 2022	2
January 2023	2
February 2023	2
March 2023	5
April 2023	6
June 2023	7
July 2023	1
August 2023	3
September 2023	8
October 2023	4
November 2023	4
December 2023	7
January 2024	16
February 2024	12
March 2024	4
April 2024	15
May 2024	10
June 2024	16
July 2024	10
August 2024	6
September 2024	23
October 2024	16
November 2024	6
December 2024	2
January 2025	10
February 2025	3
March 2025	15
April 2025	9
May 2025	10

Article Contents

Alignment of interstellar grains by mechanical torques: suprathermally rotating Gaussian random spheres Free

Abstract

1 INTRODUCTION

2 GRAIN SHAPES

3 TORQUE CALCULATIONS: THEORY

3.1 Collisions of gas particles with the grain

3.2 Torque due to incoming and reflected atoms

3.3 Mechanical torque due to outgoing atoms or molecules

3.4 Total mechanical torque

3.5 Rotational averaging

3.6 Drag torque

3.7 Extreme subsonic limit

3.8 Extreme supersonic limit

3.9 Mechanical/drag force

4 TORQUE CALCULATIONS: COMPUTATIONAL APPROACH

4.1 Incoming trajectories

4.2 Arrival at the grain surface and reflection

4.3 Integrals over the reduced speed

4.4 Characterization of the grain surface

4.5 Torque evaluations

4.6 Code verification: spherical grains

5 TORQUE CALCULATIONS: COMPUTATIONAL RESULTS

5.1 Arrival rate and torques

5.2 Forces

6 DYNAMICS

6.1 Equations of motion

6.2 Stationary points

6.3 Crossover points

6.4 Results

6.5 Analysis

6.6 Comparison with Lazarian & Hoang (2007a)

7 CONCLUSIONS

REFERENCES

SUPPORTING INFORMATION

APPENDIX A: CALCULATION DETAILS

A1 Torque due to incoming atoms

A2 Torque due to outgoing particles

A3 Extreme subsonic limit

A4 Drag force in the extreme subsonic limit

APPENDIX B: SPECIAL RESULTS ASSOCIATED WITH ARRIVING ATOMS

APPENDIX C: SPECIAL RESULTS FOR THE EXTREME SUBSONIC LIMIT

Supplementary data

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Alignment of interstellar grains by mechanical torques: suprathermally rotating Gaussian random spheres