-
PDF
- Split View
-
Views
-
Cite
Cite
Adam B. Mantz, A Gibbs sampler for multivariate linear regression, Monthly Notices of the Royal Astronomical Society, Volume 457, Issue 2, 01 April 2016, Pages 1279–1288, https://doi.org/10.1093/mnras/stv3008
Close - Share Icon Share
Abstract
Kelly described an efficient algorithm, using Gibbs sampling, for performing linear regression in the fairly general case where non-zero measurement errors exist for both the covariates and response variables, where these measurements may be correlated (for the same data point), where the response variable is affected by intrinsic scatter in addition to measurement error, and where the prior distribution of covariates is modelled by a flexible mixture of Gaussians rather than assumed to be uniform. Here, I extend the Kelly algorithm in two ways. First, the procedure is generalized to the case of multiple response variables. Secondly, I describe how to model the prior distribution of covariates using a Dirichlet process, which can be thought of as a Gaussian mixture where the number of mixture components is learned from the data. I present an example of multivariate regression using the extended algorithm, namely fitting scaling relations of the gas mass, temperature, and luminosity of dynamically relaxed galaxy clusters as a function of their mass and redshift. An implementation of the Gibbs sampler in the r language, called lrgs, is provided.
1 INTRODUCTION
Linear regression is perhaps the most widely used example of parameter fitting throughout the sciences. Yet, the traditional ordinary least-squares (or weighted least-squares) approach to regression neglects some features that are practically ubiquitous in astrophysical data, namely the existence of measurement errors, often correlated with one another, on all quantities of interest, and the presence of residual, intrinsic scatter (i.e. physical scatter, not the result of measurement errors) about the best fit. Kelly (2007, hereafter K07) takes on this problem (see that work for a more extensive overview of the prior literature) by devising an efficient algorithm for simultaneously constraining the parameters of a linear model and the intrinsic scatter in the presence of such heteroscedastic and correlated measurement errors. In addition, the K07 approach corrects a bias that exists when the underlying distribution of covariates in a regression is assumed to be uniform, by modelling this distribution as a flexible mixture of Gaussian (normal) distributions and marginalizing over it.
The K07 model is considerably more complex, in terms of the number of free parameters, than traditional regression. Nevertheless, it can be efficiently constrained using a fully conjugate Gibbs sampler, as described in that work. Briefly, the approach takes advantage of the fact that, for a suitable model, the fully conditional posterior of certain parameters (or blocks of parameters)1 may be expressible as a known distribution which can be sampled from directly using standard numerical techniques. If all model parameters can be sampled this way, then a Gibbs sampler, which simply cycles through the list of parameters, updating or block-updating them in turn, can move efficiently through the parameter space. By repeatedly Gibbs sampling, a Markov chain that converges to the joint posterior distribution of all model parameters is generated (see e.g. Gelman et al. 2004 for theoretical background). The individual pieces (e.g. the model distributions of measurement error, intrinsic scatter, and the covariate prior distribution) of the K07 model are conjugate, making it suitable for this type of efficient Gibbs sampling. This is a key advantage in terms of making the resulting algorithm widely accessible to the community, since conjugate Gibbs samplers, unlike more general and powerful Markov Chain Monte Carlo samplers, require no a priori tuning by the user.
While K07 argue against the assumption of a uniform prior for covariates, it should be noted that the alternative of a Gaussian mixture model (or the Dirichlet process generalization introduced below) is not necessarily applicable in every situation either. When a well-motivated physical model of the distribution of covariates exists, it may well be preferable to use it, even at the expense of computational efficiency. In the general case, we can hope that a flexible parametrization like the Gaussian mixture is adequate, although it is always worth checking a posteriori that the model distribution of covariates provides a good description of the data. K07 and Sereno & Ettori (2015) discuss real applications in which a Gaussian distribution of covariates turns out to be adequate, despite the underlying physics being non-Gaussian.
This work describes two useful generalizations to the K07 algorithm. First, the number of response variables is allowed to be greater than one. Secondly, the prior distribution of covariates may be modelled using a Dirichlet process rather than as a mixture of Gaussians with a fixed number of components. A Dirichlet process describes a probability distribution over the space of probability distributions, and (in contrast to the many parameters required to specify a large mixing model) is described only by a concentration parameter and a base distribution. For the choice of a Gaussian base distribution, used here, the Dirichlet process can be thought of as a Gaussian mixture in which the number of mixture components is learned from the data and marginalized over as the fit progresses (see more discussion, in a different astrophysical context, by Schneider et al. 2015). This makes it a very general and powerful alternative to the standard fixed-size Gaussian mixture, as well as one that requires even less tuning by the user, since the number of mixture components need not be specified. Crucially, both of these generalizations preserve the conjugacy of the model, so that posterior samples can still be easily obtained by Gibbs sampling.
Of course, K07 (or this paper) does not provide the only implementation of conjugate Gibbs sampling, nor is that approach the only one possible for linear regression in the Bayesian context. Indeed, there exist more general statistical packages capable of identifying conjugate sampling strategies (where possible) based on an abstract model definition (e.g. bugs,2jags,3 and stan4). The use of more general Markov chain sampling techniques naturally allows for more general (non-conjugate) models and/or parametrizations (e.g. Maughan 2014; Robotham & Obreschkow 2015). Nevertheless, there is something appealing in the relative simplicity of implementation and use of the conjugate Gibbs approach, particularly as it applies so readily to the commonly used linear model with Gaussian scatter.
Section 2 describes the model employed in this work in more detail, and introduces notation. Section 3 outlines the changes to the K07 sampling algorithm needed to accommodate the generalizations above. Since this work is intended to extend that of K07, I confine this discussion only to steps which differ from that algorithm, and do not review the Gibbs sampling procedure in its entirety. However, the level of detail is intentionally high; between this document and K07, it should be straightforward for the interested reader to create his or her own implementation of the entire algorithm. Section 4 provides some example analyses, including one with real astrophysical data, and discusses some practical aspects of the approach.
The complete algorithm described here (with both Gaussian mixture and Dirichlet process models) has been implemented in the r language.5 The package is named Linear Regression by Gibbs Sampling (lrgs), the better to sow confusion among extragalactic astronomers. The code can be obtained from GitHub6 or the Comprehensive r Archive Network.7
2 MODEL AND NOTATION
Here, I review the model described by K07, introducing the generalization to multiple response variables (Section 2.1) and the use of the Dirichlet process to describe the prior distribution of the covariates (Section 2.2). The notation used here is summarized in Table 1; it differs slightly from that of K07, as noted. In this document, A ∼ B denotes a stochastic relationship in which a random variable A is drawn from the probability distribution B, and boldface distinguishes vector- or matrix-valued variables.
| . | Symbol . | Meaning . | K07 . |
|---|---|---|---|
| General | |$\mathcal {N}_\nu (\boldsymbol {\mu },\boldsymbol {\Sigma })$| | ν-dimensional normal distribution (mean |$\boldsymbol {\mu }$|, covariance |$\boldsymbol {\Sigma }$|) | |
| notation | |$\mathcal {W}(\bf{V},\nu )$| | Wishart distribution (scale matrix |$\bf{V}$|, ν degrees of freedom) | |
| Aij | Single element of matrix |$\bf{A}$| | ||
| |$\boldsymbol {A}_{j\cdot },\boldsymbol {A}_{\cdot j}$| | jth row or column of |$\bf{A}$| | ||
| |$\boldsymbol {A}_{\bar{j}\cdot },\boldsymbol {A}_{\cdot \bar{j}}$| | |$\bf{A}$| with the jth row or column removed | |$\boldsymbol {A}_{-j\cdot },\boldsymbol {A}_{\cdot -j}$| | |
| 1n | n × n identity matrix | ||
| Common | n | Number of data points | |
| parameters | p | Number of covariates | |
| m | Number of responses | 1 | |
| K | Number of Gaussian mixture components or clusters | ||
| |$\boldsymbol {x}_i,\boldsymbol {y}_i$| | Measured covariates and responses for data point i | ||
| |$\boldsymbol {M}_i$| | Measurement covariance matrix for data point i | |$\boldsymbol {\Sigma} _i$| | |
| |$\boldsymbol {\xi} _i,\boldsymbol {\eta} _i$| | True covariates and responses for data point i | ||
| |$\boldsymbol {\alpha }$| | Intercepts of the linear model | ||
| |$\boldsymbol {\beta }$| | Slopes of the linear model | ||
| |$\boldsymbol {\Sigma }$| | Intrinsic covariance about the linear model | σ2 | |
| |$\boldsymbol {G}$| | Mixture component/cluster identification for each data point | ||
| Gaussian | |$\boldsymbol {\pi }$| | Weight of the each mixture component | |
| mixture | |$\boldsymbol {\mu} _k$| | Mean of the kth component | |
| |$\boldsymbol {T}_k$| | Covariance of the kth component | ||
| |$\boldsymbol {\mu _0}$| | Mean of the prior distribution of each |$\boldsymbol {\mu} _k$| | ||
| |$\boldsymbol {U}$| | Covariance of the prior distribution of each |$\boldsymbol {\mu} _k$| | ||
| |$\boldsymbol {W}$| | Scale matrix of the prior distribution of each |$\boldsymbol {T}_k$| | ||
| Dirichlet | |$\boldsymbol {\mu }$| | Mean of the normal base distribution | |
| process | |$\boldsymbol {T}$| | Covariance of the normal base distribution | |
| κ | Concentration parameter of the process | ||
| a | Shape parameter of the prior of κ | ||
| b | Rate parameter of the prior of κ |
| . | Symbol . | Meaning . | K07 . |
|---|---|---|---|
| General | |$\mathcal {N}_\nu (\boldsymbol {\mu },\boldsymbol {\Sigma })$| | ν-dimensional normal distribution (mean |$\boldsymbol {\mu }$|, covariance |$\boldsymbol {\Sigma }$|) | |
| notation | |$\mathcal {W}(\bf{V},\nu )$| | Wishart distribution (scale matrix |$\bf{V}$|, ν degrees of freedom) | |
| Aij | Single element of matrix |$\bf{A}$| | ||
| |$\boldsymbol {A}_{j\cdot },\boldsymbol {A}_{\cdot j}$| | jth row or column of |$\bf{A}$| | ||
| |$\boldsymbol {A}_{\bar{j}\cdot },\boldsymbol {A}_{\cdot \bar{j}}$| | |$\bf{A}$| with the jth row or column removed | |$\boldsymbol {A}_{-j\cdot },\boldsymbol {A}_{\cdot -j}$| | |
| 1n | n × n identity matrix | ||
| Common | n | Number of data points | |
| parameters | p | Number of covariates | |
| m | Number of responses | 1 | |
| K | Number of Gaussian mixture components or clusters | ||
| |$\boldsymbol {x}_i,\boldsymbol {y}_i$| | Measured covariates and responses for data point i | ||
| |$\boldsymbol {M}_i$| | Measurement covariance matrix for data point i | |$\boldsymbol {\Sigma} _i$| | |
| |$\boldsymbol {\xi} _i,\boldsymbol {\eta} _i$| | True covariates and responses for data point i | ||
| |$\boldsymbol {\alpha }$| | Intercepts of the linear model | ||
| |$\boldsymbol {\beta }$| | Slopes of the linear model | ||
| |$\boldsymbol {\Sigma }$| | Intrinsic covariance about the linear model | σ2 | |
| |$\boldsymbol {G}$| | Mixture component/cluster identification for each data point | ||
| Gaussian | |$\boldsymbol {\pi }$| | Weight of the each mixture component | |
| mixture | |$\boldsymbol {\mu} _k$| | Mean of the kth component | |
| |$\boldsymbol {T}_k$| | Covariance of the kth component | ||
| |$\boldsymbol {\mu _0}$| | Mean of the prior distribution of each |$\boldsymbol {\mu} _k$| | ||
| |$\boldsymbol {U}$| | Covariance of the prior distribution of each |$\boldsymbol {\mu} _k$| | ||
| |$\boldsymbol {W}$| | Scale matrix of the prior distribution of each |$\boldsymbol {T}_k$| | ||
| Dirichlet | |$\boldsymbol {\mu }$| | Mean of the normal base distribution | |
| process | |$\boldsymbol {T}$| | Covariance of the normal base distribution | |
| κ | Concentration parameter of the process | ||
| a | Shape parameter of the prior of κ | ||
| b | Rate parameter of the prior of κ |
| . | Symbol . | Meaning . | K07 . |
|---|---|---|---|
| General | |$\mathcal {N}_\nu (\boldsymbol {\mu },\boldsymbol {\Sigma })$| | ν-dimensional normal distribution (mean |$\boldsymbol {\mu }$|, covariance |$\boldsymbol {\Sigma }$|) | |
| notation | |$\mathcal {W}(\bf{V},\nu )$| | Wishart distribution (scale matrix |$\bf{V}$|, ν degrees of freedom) | |
| Aij | Single element of matrix |$\bf{A}$| | ||
| |$\boldsymbol {A}_{j\cdot },\boldsymbol {A}_{\cdot j}$| | jth row or column of |$\bf{A}$| | ||
| |$\boldsymbol {A}_{\bar{j}\cdot },\boldsymbol {A}_{\cdot \bar{j}}$| | |$\bf{A}$| with the jth row or column removed | |$\boldsymbol {A}_{-j\cdot },\boldsymbol {A}_{\cdot -j}$| | |
| 1n | n × n identity matrix | ||
| Common | n | Number of data points | |
| parameters | p | Number of covariates | |
| m | Number of responses | 1 | |
| K | Number of Gaussian mixture components or clusters | ||
| |$\boldsymbol {x}_i,\boldsymbol {y}_i$| | Measured covariates and responses for data point i | ||
| |$\boldsymbol {M}_i$| | Measurement covariance matrix for data point i | |$\boldsymbol {\Sigma} _i$| | |
| |$\boldsymbol {\xi} _i,\boldsymbol {\eta} _i$| | True covariates and responses for data point i | ||
| |$\boldsymbol {\alpha }$| | Intercepts of the linear model | ||
| |$\boldsymbol {\beta }$| | Slopes of the linear model | ||
| |$\boldsymbol {\Sigma }$| | Intrinsic covariance about the linear model | σ2 | |
| |$\boldsymbol {G}$| | Mixture component/cluster identification for each data point | ||
| Gaussian | |$\boldsymbol {\pi }$| | Weight of the each mixture component | |
| mixture | |$\boldsymbol {\mu} _k$| | Mean of the kth component | |
| |$\boldsymbol {T}_k$| | Covariance of the kth component | ||
| |$\boldsymbol {\mu _0}$| | Mean of the prior distribution of each |$\boldsymbol {\mu} _k$| | ||
| |$\boldsymbol {U}$| | Covariance of the prior distribution of each |$\boldsymbol {\mu} _k$| | ||
| |$\boldsymbol {W}$| | Scale matrix of the prior distribution of each |$\boldsymbol {T}_k$| | ||
| Dirichlet | |$\boldsymbol {\mu }$| | Mean of the normal base distribution | |
| process | |$\boldsymbol {T}$| | Covariance of the normal base distribution | |
| κ | Concentration parameter of the process | ||
| a | Shape parameter of the prior of κ | ||
| b | Rate parameter of the prior of κ |
| . | Symbol . | Meaning . | K07 . |
|---|---|---|---|
| General | |$\mathcal {N}_\nu (\boldsymbol {\mu },\boldsymbol {\Sigma })$| | ν-dimensional normal distribution (mean |$\boldsymbol {\mu }$|, covariance |$\boldsymbol {\Sigma }$|) | |
| notation | |$\mathcal {W}(\bf{V},\nu )$| | Wishart distribution (scale matrix |$\bf{V}$|, ν degrees of freedom) | |
| Aij | Single element of matrix |$\bf{A}$| | ||
| |$\boldsymbol {A}_{j\cdot },\boldsymbol {A}_{\cdot j}$| | jth row or column of |$\bf{A}$| | ||
| |$\boldsymbol {A}_{\bar{j}\cdot },\boldsymbol {A}_{\cdot \bar{j}}$| | |$\bf{A}$| with the jth row or column removed | |$\boldsymbol {A}_{-j\cdot },\boldsymbol {A}_{\cdot -j}$| | |
| 1n | n × n identity matrix | ||
| Common | n | Number of data points | |
| parameters | p | Number of covariates | |
| m | Number of responses | 1 | |
| K | Number of Gaussian mixture components or clusters | ||
| |$\boldsymbol {x}_i,\boldsymbol {y}_i$| | Measured covariates and responses for data point i | ||
| |$\boldsymbol {M}_i$| | Measurement covariance matrix for data point i | |$\boldsymbol {\Sigma} _i$| | |
| |$\boldsymbol {\xi} _i,\boldsymbol {\eta} _i$| | True covariates and responses for data point i | ||
| |$\boldsymbol {\alpha }$| | Intercepts of the linear model | ||
| |$\boldsymbol {\beta }$| | Slopes of the linear model | ||
| |$\boldsymbol {\Sigma }$| | Intrinsic covariance about the linear model | σ2 | |
| |$\boldsymbol {G}$| | Mixture component/cluster identification for each data point | ||
| Gaussian | |$\boldsymbol {\pi }$| | Weight of the each mixture component | |
| mixture | |$\boldsymbol {\mu} _k$| | Mean of the kth component | |
| |$\boldsymbol {T}_k$| | Covariance of the kth component | ||
| |$\boldsymbol {\mu _0}$| | Mean of the prior distribution of each |$\boldsymbol {\mu} _k$| | ||
| |$\boldsymbol {U}$| | Covariance of the prior distribution of each |$\boldsymbol {\mu} _k$| | ||
| |$\boldsymbol {W}$| | Scale matrix of the prior distribution of each |$\boldsymbol {T}_k$| | ||
| Dirichlet | |$\boldsymbol {\mu }$| | Mean of the normal base distribution | |
| process | |$\boldsymbol {T}$| | Covariance of the normal base distribution | |
| κ | Concentration parameter of the process | ||
| a | Shape parameter of the prior of κ | ||
| b | Rate parameter of the prior of κ |
2.1 Gaussian mixture model
2.2 Dirichlet process model
In practice, for a given realization of the model parameters, the algorithm for realizing the Dirichlet process divides the data set into a finite number of clusters, with points in each cluster having identical values of |$\boldsymbol {\xi }$|.12 The vector of labels |$\boldsymbol {G}$| will identify which cluster each data point belongs to, similarly to its use in Section 2.1. A vector of cluster proportions, |$\boldsymbol {\pi }$|, could also be defined analogously. However, in practice, the procedure for Gibbs sampling the Dirichlet process model implicitly marginalizes over it, and so |$\boldsymbol {\pi }$| never explicitly appears in the calculations (Section 3.2).
3 THE GIBBS SAMPLER
Both of the models described above can be efficiently Gibbs sampled because they are fully conjugate. Recall that, in this situation, the sampling algorithm can be entirely specified as the set of conditional distributions used to sequentially update each parameter or block of parameters. Section 3.1 summarizes the changes to the K07 procedure needed to sample the Gaussian mixture model when there are multiple response variables, and Section 3.2 describes the procedure for sampling the Dirichlet process model.
In either case, an initial guess is needed for most of the free parameters, but this need not be very sophisticated. For example, it is generally acceptable to begin with the values of |$\lbrace \boldsymbol {\xi} _i\rbrace$| and |$\lbrace \boldsymbol {\eta} _i\rbrace$|, respectively, initialized to the measured values |$\lbrace \boldsymbol {x}_i\rbrace$| and |$\lbrace \boldsymbol {y}_i\rbrace$|, the intercepts |$\boldsymbol {\alpha }$| set to the average value of each column of |$\boldsymbol {Y}$|, and the slopes |$\boldsymbol {\beta }$| set to zero.13 Of course, more intelligent guesses will decrease the ‘burn-in’ time of the resulting Markov chain, but generally this is relatively short.
3.1 Sampling the Gaussian mixture model
The procedure for updating the parameters governing the distribution of covariates (|$\boldsymbol {G}$|, |$\boldsymbol {\pi }$|, |$\lbrace \boldsymbol {\mu} _k\rbrace$|, |$\lbrace \boldsymbol {T}_k\rbrace$|, |$\boldsymbol {\mu _0}$|, |$\boldsymbol {U}$| and |$\boldsymbol {W}$|, for which I adopt the same priors as K07) is not affected by the generalization to multiple responses, and the reader is referred to K07 for the details of those updates. Here, I review the procedure for Gibbs sampling the true values of the covariates and responses for each data point, |$\lbrace \boldsymbol {\xi} _i\rbrace$| and |$\lbrace \boldsymbol {\eta} _i\rbrace$|, the regression coefficients, |$\boldsymbol {\alpha }$| and |$\boldsymbol {\beta }$|, and the intrinsic covariance matrix, Σ.
3.1.1 Updating the covariates
3.1.2 Updating the responses
3.1.3 Updating the coefficients
Note that it is straightforward to sample from the product of equation (19) and a normal prior for |$\boldsymbol {\widetilde{B}}$|; this option is implemented in lrgs, although the default is a uniform prior.
3.1.4 Updating the intrinsic covariance
In practice, a sample can be generated by setting |$\boldsymbol {\Sigma }$| equal to |$(\boldsymbol {A}^{\mathrm{T}}\boldsymbol {A})^{-1}$|, where |$\boldsymbol {A}$| is (n − 1) × m and each row of |$\boldsymbol {A}$| is generated as |$\boldsymbol {A}_{i\cdot }\sim \mathcal {N}_m[\boldsymbol {0},(\boldsymbol {E}^{\mathrm{T}}\boldsymbol {E})^{-1}]$|.
3.2 Sampling the Dirichlet process model
If a Dirichlet process rather than a Gaussian mixture is used to describe the prior distribution of covariates, the procedure to update the |$\lbrace \boldsymbol {\xi} _i\rbrace$| differs from that given above. This step implicitly updates |$\boldsymbol {G}$|, which now identifies membership in one of a variable number of clusters (data points with identical values of |$\boldsymbol {\xi }$|). In addition, Gibbs updates to the hyperparameters of the Dirichlet process and its base distribution, κ, |$\boldsymbol {\mu }$| and |$\boldsymbol {T}$|, are possible. These are described below. Note that the updates to |$\boldsymbol {G}$|, |$\boldsymbol {\pi }$|, |$\lbrace \boldsymbol {\mu} _k\rbrace$|, |$\lbrace \boldsymbol {T}_k\rbrace$|, |$\boldsymbol {\mu _0}$|, |$\boldsymbol {U}$| and |$\boldsymbol {W}$| given in K07 are no longer applicable (of these, only |$\boldsymbol {G}$| and |$\boldsymbol {\pi }$| exist in the model).
3.2.1 Updating the covariates
Let K be the number of clusters (i.e. distinct labels in |$\boldsymbol {G}$|) at a given time. I follow the second algorithm given by Neal (2000), which first updates the cluster membership for each data point, and then draws new values of |$\boldsymbol {\xi }$| for each cluster.
3.2.2 Updating the Dirichlet process concentration
3.2.3 Updating the base distribution hyperparameters
4 EXAMPLES
This section provides two example applications of the methods discussed above, respectively, on a toy model and an astrophysical data set.
4.1 Toy model
Consider the case of a single covariate, generated by three distinct Gaussian components, and a single response variable. Table 2 shows the specific model parameters used to generate the data, and the toy data set is shown in the left-hand panel of Fig. 1. Because the Gaussians generating the covariates are not especially well separated compared to their widths, the presence of three populations is not striking, although a histogram of the measured covariates is suggestive of the underlying structure (centre panel of Fig. 1).
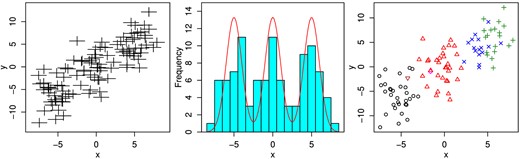
Left: the simulated data used to fit the toy model in Section 4.1. Centre: histogram of the simulated covariates, along with the three-Gaussian-mixture distribution from which they are drawn. Right: the simulated data, with colours/symbols reflecting the cluster assignments of the Dirichlet model at one step in the fit.
Model parameters used to generate the toy data set in Section 4.1. The distribution of covariates is taken to be a mixture of 3 Gaussians.
| Parameter . | Value . |
|---|---|
| n, p, m, K | 100, 1, 1, 3 |
| All |$\boldsymbol {M}_i$| | 12 |
| α | 0 |
| β | 1 |
| Σ | 9 |
| All πk | 1/3 |
| μk | 5(k − 2) |
| All Tk | 1 |
| Parameter . | Value . |
|---|---|
| n, p, m, K | 100, 1, 1, 3 |
| All |$\boldsymbol {M}_i$| | 12 |
| α | 0 |
| β | 1 |
| Σ | 9 |
| All πk | 1/3 |
| μk | 5(k − 2) |
| All Tk | 1 |
Model parameters used to generate the toy data set in Section 4.1. The distribution of covariates is taken to be a mixture of 3 Gaussians.
| Parameter . | Value . |
|---|---|
| n, p, m, K | 100, 1, 1, 3 |
| All |$\boldsymbol {M}_i$| | 12 |
| α | 0 |
| β | 1 |
| Σ | 9 |
| All πk | 1/3 |
| μk | 5(k − 2) |
| All Tk | 1 |
| Parameter . | Value . |
|---|---|
| n, p, m, K | 100, 1, 1, 3 |
| All |$\boldsymbol {M}_i$| | 12 |
| α | 0 |
| β | 1 |
| Σ | 9 |
| All πk | 1/3 |
| μk | 5(k − 2) |
| All Tk | 1 |
Suppose we had a physical basis for a three-component model (or suspected three components, by inspection), but wanted to allow for the possibility of more or less structure than a strict Gaussian mixture provides. The Dirichlet process supplies a way to do this. For a given κ and n, the distribution of K is known,15 so in principle a prior expectation for the number of clusters, say 3 ± 1, can be roughly translated into a Gamma prior on κ. Here, I instead adopt an uninformative prior on κ (Dorazio 2009), and compare the results to those of a Gaussian mixture model with K = 3.
Using the Dirichlet process model, results from a chain of 1000 Gibbs samples (discarding the first 10) are shown as shaded histograms in Fig. 1.16 The results are consistent with the input model values (vertical, dashed lines) for the parameters of interest (α, β, and Σ). The latent parameters describing the base distribution of the Dirichlet process are also consistent with the toy model, although they are poorly constrained. The right-hand panel of Fig. 1 shows the cluster assignments for a sample with K = 6 (the median of the chain); the clustered nature of the data is recognized, although the number of clusters tends to exceed the number of components in the input model.17 An equivalent analysis using a mixture of three Gaussians rather than a Dirichlet process model produces very similar constraints on the parameters of interest (hatched histograms in Fig. 2).
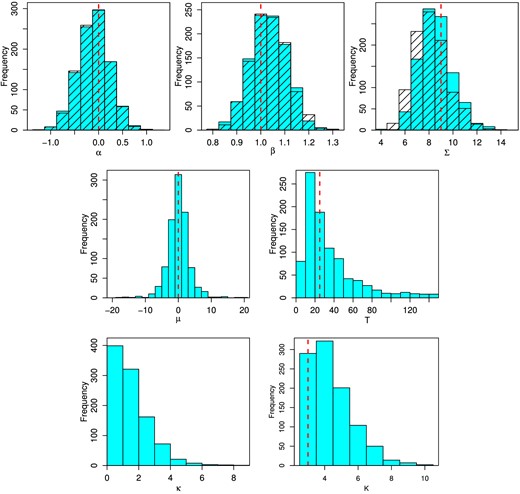
Histograms of parameter samples using a Dirichlet process (blue shaded) or three-Gaussian mixture (hatched) prior on the distribution of covariates, for the toy-model analysis of Section 4.1. Dashed vertical lines indicate the input values used to generate the data set. The hyperparameters of the Gaussian mixture model are not shown; these correctly converge to the mean and width of the three mixture components.
4.2 Scaling relations of relaxed galaxy clusters
As a real-life astrophysical example, I consider the scaling relations of dynamically relaxed galaxy clusters, using measurements presented by Mantz et al. (2015). Note that there are a number of subtleties in the interpretation of these results that will be discussed elsewhere; here the problem is considered only as an application of the method presented in this work.
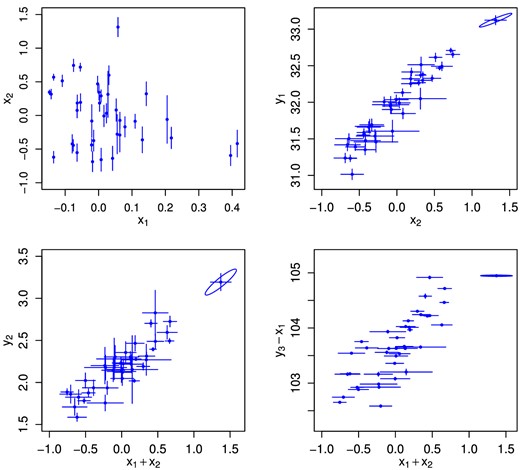
Scatter plots showing the distribution of measured covariates and responses for the p = 2, m = 3 problem of fitting galaxy cluster scaling relations described in Section 4.2. An ellipse illustrates the measurement covariance for the most massive (largest x2) cluster in each panel. The particular combinations of x and y plotted are conventional (cf. equation 34).
Because the redshifts are measured with very small uncertainties, this problem is not well suited to the Dirichlet process prior; intuitively, the number of clusters in the Dirichlet process must approach the number of data points because the data are strongly inconsistent with one another (i.e. are not exchangeable). Instead, I use a Gaussian mixture prior with K = 3, and verify that in practice the results are not sensitive to K (the parameters of interest differ negligibly from an analysis with K = 1).
Marginalized two-dimensional constraints on the power-law slopes of each scaling relation are shown in the top row of Fig. 4 (68.3 and 95.4 per cent confidence). On inspection, only the luminosity scaling relation appears to be in any tension with the expectation in equation (34), having a preference for a weaker dependence on E(z) and a stronger dependence on M. These conclusions are in good agreement with a variety of earlier work (e.g. Reiprich & Böhringer 2002; Zhang et al. 2007, 2008; Rykoff et al. 2008; Pratt et al. 2009; Vikhlinin et al. 2009; Leauthaud et al. 2010; Mantz et al. 2010; Reichert et al. 2011; Sereno & Ettori 2015; see also the review of Giodini et al. 2013).
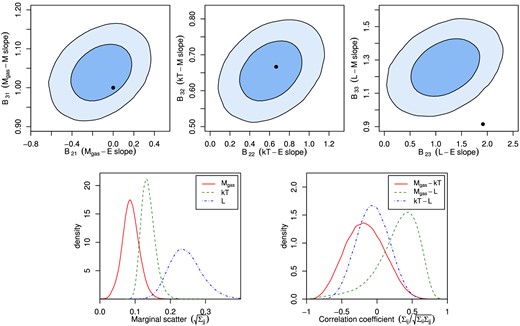
Top row: joint 68.3 and 95.4 per cent confidence regions on the slope parameters of each of the scaling relations in equation (34). Black circles indicate the self-similar expectation given in equation (34). Bottom left: posterior distributions for the marginal intrinsic scatter parameters of the model. Bottom right: posteriors for the off-diagonal intrinsic scatter terms, expressed as correlation coefficients.
The posterior distributions of the elements of the multidimensional intrinsic covariance matrix are shown in the bottom row of Fig. 4, after transforming to marginal scatter (square root of the diagonal) and correlation coefficients (for the off-diagonal elements). The intrinsic scatters of Mgas and kT at fixed M and z are in good agreement with other measurements in the literature (see Allen, Evrard & Mantz 2011; Giodini et al. 2013, and references therein); the scatter of L is lower than the ∼40 per cent typically found, likely because this analysis uses a special set of morphologically similar clusters rather than a more representative sample. The correlation coefficients are particularly challenging to measure, and the constraints are relatively poor. Nevertheless, the ability to efficiently place constraints on the full intrinsic covariance matrix is an important feature of this analysis. Within uncertainties, these results agree well with the few previous constraints on these correlation coefficients in the literature (Mantz et al. 2010; Maughan 2014). The best-fitting intrinsic covariance matrix is illustrated visually in Fig. 5, which compares it to the residuals of |$\boldsymbol {y}$| with respect to the best-fitting values of |$\boldsymbol {x}$| and the best-fitting scaling relations.
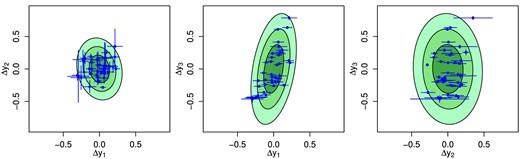
Residuals of |$\boldsymbol {y}$| with respect to the best-fitting values of |$\boldsymbol {x}$| and the best-fitting scaling relations. For clarity, measurement errors are shown as orthogonal bars, even though the measurement covariances are non-trivial. In particular, the ‘by-eye’ positive correlation in the left-hand panel is due to a positive correlation in the measurement uncertainties. Shaded ellipses correspond to 1σ, 2σ, and 3σ intrinsic scatter (in the two dimensions shown in each panel), according to the best-fitting intrinsic covariance matrix.
5 SUMMARY
I have generalized the Bayesian linear regression method described by K07 to the case of multiple response variables, and included a Dirichlet process model of the distribution of covariates (equivalent to a Gaussian mixture whose complexity is learned from the data). The algorithm described here is implemented independently of the linmix_erridl code of K07 as an r package called lrgs, which is publicly available. Two examples, respectively using a toy data set and real astrophysical data, are presented.
A number of further generalizations are possible. In principle, significant complexity can be added to the model of the intrinsic scatter in the form of a Gaussian mixture or Dirichlet process model (with a Gaussian base distribution) while maintaining conjugacy of the conditional posteriors, and thereby the efficiency of the Gibbs sampler. The case of censored data (upper limits on some measured responses) is discussed by K07. This situation, or, more generally, non-Gaussian measurement errors, can be handled by rejection sampling (at the expense of efficiency) but is not yet implemented in lrgs. Also of interest is the case of truncated data, where the selection of the data set depends on one of the response variables, and the data are consequently an incomplete and biased subset of a larger population. This case can in principle be handled by modelling the selection function and imputing the missing data (Gelman et al. 2004). lrgs is shared publicly on GitHub, and I hope that users who want more functionality will be interested in helping develop the code further.
The addition of Dirichlet process modelling to this work was inspired by extensive discussions with Michael Schneider and Phil Marshall. Anja von der Linden did some very helpful beta testing. I acknowledge support from the National Science Foundation under grant AST-1140019.
i.e. the posterior distribution for certain parameters conditional on the (fixed) values of all other parameters.
Note that in K07y preceded x as they correspond to rows and columns of M. The reverse convention is followed here.
In the notation used here, Gi is simply a label 1, 2, …, K, whereas K07 describe each Gi as a vector with all but one element zero. This distinction makes no practical difference.
While the inverse-Wishart distribution is conjugate in this context, and therefore computationally convenient, it has the generic disadvantage of imposing a particular structure on the marginal prior distributions of the variances and correlation coefficients that make up the resulting covariance matrix. In particular, large absolute values of the correlation coefficients preferentially correspond to large variances. This is sometimes undesirable, and from a practical standpoint it can occasionally result in the generation of computationally singular matrices. An alternative approach is to decompose a given covariance matrix, |$\boldsymbol {\Lambda }$|, as |$\bf{SRS}$|, where |$\bf{S}$| is diagonal and |$\bf{R}$| is a correlation matrix. This allows independent priors to be adopted for individual variances and correlation coefficients, which is usually more intuitive than using inverse-Wishart distribution, but at the expense that the resulting model is no longer conjugate. More extensive discussion of these options can be found in Barnard, McCulloch & Meng (2000), Gelman et al. (2004), and O'Malley & Zaslavsky (2008).
The conjugate prior for |$\boldsymbol {\mu _0}$| is normal, |$\mathcal {N}_p(\boldsymbol {u},\boldsymbol {V})$|, which is uniform in the limit |$\boldsymbol {V^{-1}}=\boldsymbol {0}$|. For |$\boldsymbol {W}$|, the conjugate prior is inverse-Wishart, |$\mathcal {W}^{-1}(\boldsymbol {\Psi }, \nu )$|, and the equivalent of the uniform distribution is realized by taking |$\boldsymbol {\Psi }=\boldsymbol {0}$| and ν = −(1 + d), where d is the size of |$\boldsymbol {\Psi }$| (in this case, d = p).
A pitfall of this approach occurs when few of the measured covariates are consistent with any others within their measurement errors. In that case, the number of clusters is necessarily similar in size to the number of data points, which is not generally the desired result.
Specifically, this simpleminded guess for the intercepts and slopes works reasonably well when the covariates have been approximately centred. More generally, estimates from an ordinary least-squares regression should provide a good starting point.
This expression assumes a Jeffreys (i.e. minimally informative) prior on Σ. More generally, one could use a prior |$\boldsymbol {\Sigma } \sim \mathcal {W}^{-1}(\boldsymbol {\Psi }, \nu _0)$|, in which case the conditional posterior becomes |$\boldsymbol {\Sigma } | \ldots \sim \mathcal {W}^{-1}\left(\boldsymbol {E}^{\mathrm{T}}\boldsymbol {E}+\boldsymbol {\Psi },\, n+\nu _0\right)$|. The Jeffreys prior corresponds to |$\boldsymbol {\Psi }=\boldsymbol {0}$| and ν0 = −1, while |$\boldsymbol {\Psi }=\boldsymbol {0}$| and ν0 = −(1 + m) corresponds to a prior that is uniform in |$\left|\boldsymbol {\Sigma }\right|$| (see e.g. Gelman et al. 2004). The K07 algorithm makes the latter assumption. The default in lrgs is the Jeffreys prior, but any inverse-Wishart prior can optionally be specified.
Specifically, K|n, κ ∼ s(n, K) κ Γ(κ)/Γ(κ + n), where s is an unsigned Stirling number of the first kind (Antoniak 1974).
For this particularly simple problem, the chain converges to the target distribution almost immediately. Comparing the first and second halves of the chain (or multiple independent chains) the Gelman–Rubin R statistic is <1.01 for every parameter. The autocorrelation length is also very short, ≲10 steps for every parameter.
We should generically expect this, since it is entirely possible for a mixture of many Gaussians to closely resemble a mixture with fewer components; e.g. in Fig. 2, we see that two of the six clusters are populated by single data points that are not outliers. The reverse is not true, and here it is interesting that the Dirichlet process cannot fit the data using fewer than K = 3 clusters (Fig. 2).
Galaxy clusters, not to be confused with the clusters of data points arising in the sampling of the Dirichlet process.
Here, I take L to be measured in a soft X-ray band, in practice 0.1–2.4 keV. Since the emissivity in this band is weakly dependent on temperature for hot clusters such as those in the data set, the resulting scaling relation has a shallower dependence on mass than the more familiar bolometric luminosity–mass relation, Lbol ∝ E(z)[E(z)M]4/3. The exponents in the L scaling of equation (34) are specific to the chosen energy band.
REFERENCES
SUPPORTING INFORMATION
Additional Supporting Information may be found in the online version of this article:
toy.dat
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.



