The inner knot of the Crab nebula

Lyutikov, Maxim; Komissarov, Serguei S.; Porth, Oliver

doi:10.1093/mnras/stv2570

Abstract

We model the inner knot of the Crab nebula as a synchrotron emission coming from the non-spherical MHD termination shock of relativistic pulsar wind. The post-shock flow is mildly relativistic; as a result the Doppler beaming has a strong impact on the shock appearance. The model can reproduce the knot location, size, elongation, brightness distribution, luminosity and polarization provided the effective magnetization of the section of the pulsar wind producing the knot is low, σ ≤ 1. In the striped wind model, this implies that the striped zone is rather wide, with the magnetic inclination angle of the Crab pulsar ≥45°; this agrees with the previous model-dependent estimate based on the gamma-ray emission of the pulsar. We conclude that the tiny knot is indeed a bright spot on the surface of a quasi-stationary magnetic relativistic shock and that this shock is a site of efficient particle acceleration. On the other hand, the deduced low magnetization of the knot plasma implies that this is an unlikely site for the Crab's gamma-ray flares, if they are related to the fast relativistic magnetic reconnection events.

MHD, radiation mechanisms: non-thermal, shock waves, pulsars: individual: Crab, ISM: supernova remnants

1 INTRODUCTION

The Crab pulsar and its pulsar wind nebula (PWN) remain prime targets for high-energy astrophysical research. In many ways, the current models of active galactic nuclei and gamma-ray bursts are based on what we have learned from the studies of the Crab. The recent detection of flares from the Crab nebula by AGILE and Fermi satellites (Abdo et al. 2011; Tavani et al. 2011) have brought this object into the ‘focal point’ once again. Their extreme properties seem impossible to explain within the standard theories of non-thermal particle acceleration and require their overhaul with important implications to high-energy astrophysics in general (e.g. Lyutikov 2010; Clausen-Brown & Lyutikov 2012; Cerutti, Uzdensky & Begelman 2012; Lyubarsky 2012; Bühler & Blandford 2014).

In the MHD models of the Crab nebula, the superfast magnetosonic relativistic wind of the Crab pulsar terminates at a reverse shock (Rees & Gunn 1974; Kennel & Coroniti 1984). However, finding the shock in the images of the Crab nebula has not been a straight-forward matter – there seem to be no sharp feature which can be undoubtedly identified with the shock surface. In their seminal paper, Kennel & Coroniti (1984) discuss the underluminous region hosting the Crab pulsar and surrounded by the optical wisps as an indicator of the shock presence. After the discovery of the inner X-ray ring by Chandra (Weisskopf et al. 2000; Hester et al. 2002), the ring is often referred to as the termination shock and yet this feature looks much more like a collection of knots than a smooth surface. A new twist in the story has come with the recent PIC simulations which show the shock particle acceleration is highly inefficient in even relatively weakly magnetized relativistic plasma (Sironi & Spitkovsky 2009, 2011a). These results make one doubt that the shock can be visible at all. On the other hand, the wind from an oblique rotator should have the so-called striped zone where the orientation of magnetic field alternated on the scale of the pulsar period. The magnetic energy associated with these stripes can be dissipated at the termination shock and converted into the energy of the wind particles (Lyubarsky 2003; Sironi & Spitkovsky 2011b; Amano & Kirk 2013; Pétri & Lyubarsky 2007).

Given the highly anisotropic nature of the wind, the termination shock is squashed along the polar direction and can be highly oblique with respect to the upstream flow (Lyubarsky 2002). Downstream of the shock, the flow can still be relativistic and its emission subject to strong Doppler beaming. The computer simulations of the Crab nebula and its radiation (Komissarov & Lyubarsky 2004) revealed the presence of a very bright compact feature in the synthetic synchrotron maps, highly reminiscent of the HST knot 1 of the Crab nebula located very close to the pulsar (also called the inner knot, Hester et al. 1995). (In these simulations, the termination shock was treated as source of synchrotron electrons with power-law energy spectrum, which then were carried out into the nebula by the shocked wind plasma.) This feature, confirmed in the later more advanced 2D (Camus et al. 2009) and 3D (Porth, Komissarov & Keppens 2014) simulations, is associated with the location at the termination shock where the shocked plasma flows in the direction of the fiducial observer and thus strongly Doppler-boosted. Komissarov & Lyutikov (2011) argued that given the short synchrotron lifetime of the high-energy electrons compared to the dynamical time-scale of the shock, the knot can be the main source of the gamma-ray emission from the nebula at 10–100 MeV.

Recently, a targeted multiwavelength study of the Crab's inner knot has been conducted by Rudy et al. (2015) in order to check if it shows any activity correlated with the gamma-ray flares. Although no such correlation has been found, the optical data reveal the structure and temporal evolution of the knot with unprecedented detail. In this paper, we investigate if the data are consistent with the MHD-shock model of the knot using simple analytical and semi-analytical tools. In particular, we combine the theoretical shape of the shock with the oblique shock jumps in order to obtain the Doppler beaming of the post shock emission and use this to determine the location, the shape and the brightness distribution of the knot.

2 GEOMETRY OF THE TERMINATION SHOCK

At the location of the termination shock, the magnetic field of the pulsar wind has the form of loops centred on the pulsar's rotational axis. The wind's termination shock is also symmetric with respect to the rotational axis and hence the magnetic field is parallel to the shock surface. The pulsar wind is not spherical – its luminosity per unit solid angle increases with the polar angle measured from the pulsar rotational axis. As a result, the termination shock is not spherical and the radial stream lines of the wind are generally not normal to the shock surface – locally the shock is oblique. In addition, the pulsar wind is ultrarelativistic and its thermal pressure is negligibly small. The corresponding shock equations have been analysed in Komissarov & Lyutikov (2011), Lyutikov, Balsara & Matthews (2012); see also Appendix A. Here we summarize their results using the notation introduced in Komissarov & Lyutikov (2011).

We differentiate the flow parameters upstream and downstream of the shock using indices ‘1’ and ‘2’, respectively. Denote as δ the angle between the velocity vector and the shock surface (the angle of attack). Then in the observer's frame

\begin{equation} \tan \delta _2= \chi \tan \delta _1 \end{equation}

(1)

and for the Lorentz factor of the flow

\begin{equation} \Gamma _2= \Gamma _1\left[1+\Gamma _1^2\sin ^2\delta _1(1-\chi ^2) \right]^{-1/2}\,, \end{equation}

(2)

where χ = v_n2/v_n1 is the ratio of the normal velocity components. For a strong shock, Γ₂ ≪ Γ₁ and the last equation reduces to

\begin{equation} \Gamma _2= (1-\chi ^2)^{-1/2}\csc \delta _1\,. \end{equation}

(3)

Assuming δ₁ ≫ 1/Γ₁ and using the ratio of specific heats γ = 4/3, Komissarov & Lyutikov (2011) obtained

\begin{equation} \chi = \frac{1+2\sigma _1 + \sqrt{16\sigma _1^2+16\sigma _1+1}}{6(1+\sigma _1)}\,, \end{equation}

(4)

where |$\sigma _1=B_1^{^{\prime }2}/\rho ^{\prime }_1$| is the magnetization parameter of the wind, B′ and ρ′ are the comoving values of the magnetic field and the rest-mass density of plasma, respectively. This is a monotonic function increasing from χ(0) = 1/3 to χ( + ∞) = 1. For σ₁ ≫ 1, one can use the approximation

\begin{equation} \chi \simeq 1 -\frac{1}{2\sigma _1}\,. \end{equation}

(5)

Using equation (3) we find that for σ₁ = 0

\begin{equation} \Gamma _2 = \frac{3}{2\sqrt{2}}\csc \delta _1\, \end{equation}

(6)

and for σ₁ ≫ 1

\begin{equation} \Gamma _2 \simeq \sqrt{\sigma _1}\csc \delta _1\,. \end{equation}

(7)

The deflection Δδ = δ₁ − δ₂ is given by

\begin{equation} \tan \Delta \delta = \frac{\tan \delta _1(1-\chi )}{1+\chi \tan ^2\delta _1}\,. \end{equation}

(8)

It reaches the maximum value of

\begin{equation} \tan (\Delta \delta _{\text{max}}) = \frac{1}{2}\frac{1-\chi }{\sqrt{\chi }} \quad \mbox{at}\quad \tan \delta _{1} = \chi ^{-1/2} \,. \end{equation}

(9)

For σ₁ = 0 this gives Δδ_max = π/6 at δ₁ = π/3, whereas for σ₁ ≫ 1 one has Δδ_max = 1/4σ₁ at δ₁ = π/4.

The total pressure |$\tilde{p}_{2} = p_2 +\frac{B_2^2}{2}$| downstream of the shock is

\begin{equation} \tilde{p}_2 = (1-\chi ) (F/c) \sin ^2\delta _1 \,, \end{equation}

(10)

where F is the upstream total energy flux density along the flow velocity (see Appendix A). For σ₁ = 0, this yields

\begin{equation} \tilde{p}_2 = \frac{2}{3}\frac{F}{c} \sin ^2\delta _1\, \end{equation}

(11)

whereas for σ₁ ≫ 1,

\begin{equation} \tilde{p}_2 = \frac{1}{2\sigma _1}\frac{F}{c} \sin ^2\delta _1\,. \end{equation}

(12)

One can see that for the same energy flux the post-shock pressure is significantly reduced compared to the purely hydro case.

Since the shock is driven into the wind by the pressure inside the nebula, p_n, which is approximately uniform in the nebula due to its slow expansion, we replace |$\tilde{p}_2$| with constant p_n, which makes our approach similar to the Kompaneets approximation (Kompaneets 1960). This approximation was already used by Lyubarsky (2002), to determine the shape of the termination shock for a weakly magnetized wind. It less clear if the approximation can hold well for the polar section of the shock where the magnetization and the Lorentz factor of the post-shock flow can be very high. This makes terms other than the total pressure potentially important in the transverse force balance. This is already seen in the numerical simulations with moderate wind magnetization, where the magnetic hoop stress leads to compression of the polar region (Porth et al. 2014). Moreover, these simulations show that the polar flow is highly variable. Keeping these in mind, we shell still shell proceed exploring the models based on the assumption |$\tilde{p}_2=p_n=$| const.

If the function R(θ) gives the spherical radius as a function of the polar angle on the shock surface then

\begin{equation} \tan \delta _1=\left(\frac{R}{R^{\prime }}\right)\,. \end{equation}

(13)

For an axisymmetric radial wind, its energy flux can be written as F = L₀f(θ)/4πR², where f(θ) describes the wind anisotropy. We will consider only f = sin ⁿθ, where n = 2 for the monopole model of the pulsar magnetosphere (Bogovalov 1999). Recently, Philippov, Spitkovsky & Cerutti (2015) argued for n = 4, based on their numerical simulations of pulsar magnetospheres. Substituting the expressions for sin δ₁ and F into equation (10), we obtain the shock-shape equation

\begin{equation} R^{\prime 2}+R^2 = \frac{L_0f(\theta )}{4\pi c p_n} (1-\chi ) \,. \end{equation}

(14)

Finally, we introduce the characteristic length-scale of the problem R₀ = L₀f(θ)/4πcp_n and arrive to the dimensionless equation

\begin{equation} X^{\prime 2}+X^2 = f(\theta )(1-\chi ) \,, \end{equation}

(15)

where X = R/R₀. (This is the modified version of our original equation 3.) The appropriate boundary condition is

\begin{equation} X(0)=0 \,. \end{equation}

(16)

When the shock terminates the striped part of the pulsar wind, the shock solution is modified due to the dissipation of the magnetic energy associated with the stripes. Lyubarsky (2003) have shown that the shock solution is actually the same as that for the unstriped flow where the energy of stripes is already converted into the bulk kinetic energy of the wind particles. Thus, as long as the shock solution is concerned it does not matter where the dissipation occurs, in the wind or at the shock. The magnetization of the wind that has lost its stripes can be found as

\begin{equation} \sigma _1=\sigma _0 \frac{\chi _\alpha (\theta )}{1+\sigma _0(1-\chi _\alpha (\theta ))}\,, \end{equation}

(17)

where

\begin{equation} \chi _\alpha (\theta ) = \left\lbrace \begin{array}{l{@}{\quad}l}(2\phi _\alpha (\theta )/\pi -1)^2, & \theta _m<\theta <\pi /2 \\ 1, & \theta \le \theta _m \end{array} \right., \end{equation}

(18)

and

\begin{equation*} \cos \phi _\alpha = \frac{\tan \theta _m}{\tan \theta }\, \end{equation*}

(Komissarov 2013). In these equations, θ_m = π/2 − α, where α is the pulsar's magnetic inclination angle, is the polar angle of the boundary separating the unstriped polar section of the pulsar wind from its equatorial striped zone and σ₀ is the original magnetization of the striped wind. Fig. 1 shows the wind magnetization after the dissipation of its stripes for σ₀ = 100 and α_m = 60° and 45°. The most interesting feature of these solutions is the rapid drop of σ at the boundary of the striped zone.

Figure 1.

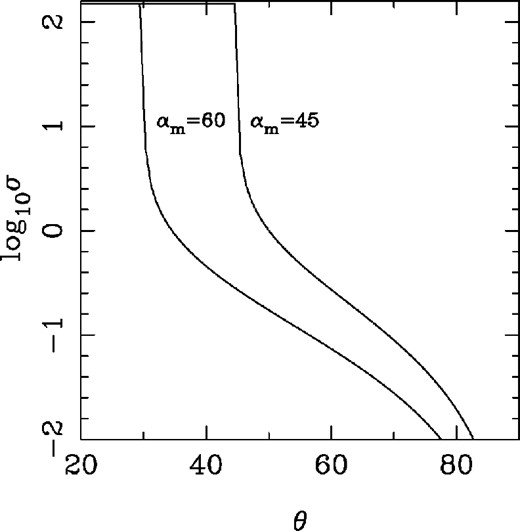
Magnetization of the striped wind zone after the dissipation of stripes for the magnetic inclination angles α_m = 60° and 45°.

Open in new tab Download slide

Equation (15) is integrated numerically. Due to its singularity at θ = 0, we use its asymptotic analytic solution

\begin{equation*} X=\frac{2(1-\chi (\sigma _0)) }{n+2} \theta ^{\frac{n}{2}+1} \end{equation*}

in order to move away from the origin.

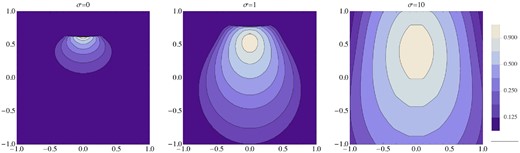
As a start, we consider the case of uniform σ₁, where it does not depend on the polar angle. This corresponds to the case of aligned rotator, α = 0, where σ₁ = σ₀ everywhere. The top panel of Fig. 2 shows the solutions for σ₁ = 0, 1 and 10. As one can see, for higher σ₁ the shock is located closer to the pulsar. This is in agreement with the earlier results by Kennel & Coroniti (1984). In fact, the curves differ only by the scaling factor |$\sqrt{1-\chi (\sigma _1)}$|⁠, as follows from equation (15).

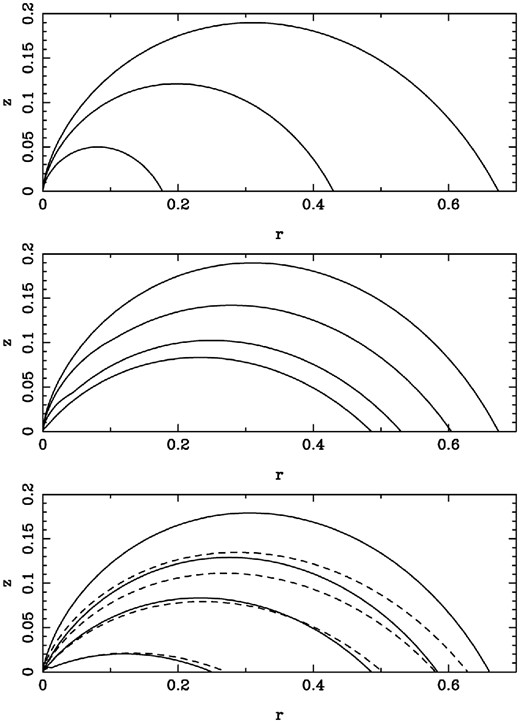
Top panel: shape of the termination shock for a uniform distribution of σ1. The curves correspond to σ1 = 0, 1 and 10, from top to bottom. Middle panel: shape of the termination shock for the non-uniform distribution of σ1 corresponding to a striped wind with α = π/4 and f(θ) = sin 2θ. The lines correspond to σ0 = 0, 1, 10 and 103, from top to bottom. Bottom panel: shape of the termination shock for the non-uniform distribution of σ1 corresponding to a striped wind σ0 = 103 and f(θ) = sin nθ. The lines correspond to α = 80°, 60°, 45° and 20°, from top to bottom. The solid lines correspond to n = 2 and the dashed lines to n = 4.

Figure 2.

Top panel: shape of the termination shock for a uniform distribution of σ₁. The curves correspond to σ₁ = 0, 1 and 10, from top to bottom. Middle panel: shape of the termination shock for the non-uniform distribution of σ₁ corresponding to a striped wind with α = π/4 and f(θ) = sin ²θ. The lines correspond to σ₀ = 0, 1, 10 and 10³, from top to bottom. Bottom panel: shape of the termination shock for the non-uniform distribution of σ₁ corresponding to a striped wind σ₀ = 10³ and f(θ) = sin ⁿθ. The lines correspond to α = 80°, 60°, 45° and 20°, from top to bottom. The solid lines correspond to n = 2 and the dashed lines to n = 4.

Open in new tab Download slide

When the variation of σ₁ due to the existence of the striped wind zone (see equation 17) is taken into account, the variation of the shock size is less dramatic. In the middle panel of Fig. 2, we show the solutions for α = π/4 and f(θ) = sin ²θ, corresponding to different values of the magnetization parameter σ₀. As σ₀ increases, the shock still becomes more compact, but as σ₀ → ∞ the dependence becomes very weak and the shock approaches some asymptotic shape. Such a turn is clearly connected with the existence of the striped wind section where σ₁(θ) becomes insensitive to σ₀:

\begin{equation} \sigma _1 \simeq \frac{\chi _\alpha (\theta )}{(1-\chi _\alpha (\theta ))}\,. \end{equation}

(19)

The bottom panel of Fig. 2 illustrates the dependence of the shock shape on the magnetic inclination angle α for σ₀ = 10³ and f(θ) = sin ⁿθ with n = 2, 4. As one can see, the shock becomes more compact as α decreases. This is expected, as for α = 0, the case of uniform magnetization with σ₁ = 10³ is recovered and in this case the shock size rapidly decreases with σ₀. However, even for α = 20° the equatorial radius of the shock is still much larger than that in the limiting case of α = 0. For n = 2, the total wind power is L_w = (10/15)L₀, whereas for n = 4 it is L_w = (8/15)L₀. Since it is more interesting to compare the results corresponding to the same wind power, we rescale the n = 4 solution of equation (15) by the factor |$\sqrt{5}/2$|⁠. In the bottom panel of Fig. 2 the n = 2 solutions are shown as solid lines and the n = 4 solutions as dashed lines. The difference between the two groups is not large, particularly for α ≤ 45°.

Fig. 3 zooms into the inner region of the middle panel of Fig. 2, where the shock exhibits a noticeable break. The origin of this break is easy to understand. At θ < θ_m, the magnetization σ₁ = σ₀ is constant. Hence, the shock curve is a miniature version of that of pure hydro shock (see equations 11 and 12). At θ = θ_m, σ₁(θ) rapidly drops leading to higher wind ‘ram’ pressure and the shock shoots out almost radially until the ‘ram’ pressure approaches that of the nebula. This interpretation suggests that for high σ₀, the shape of the equatorial part of the termination shock is independent on that in highly magnetized polar section.

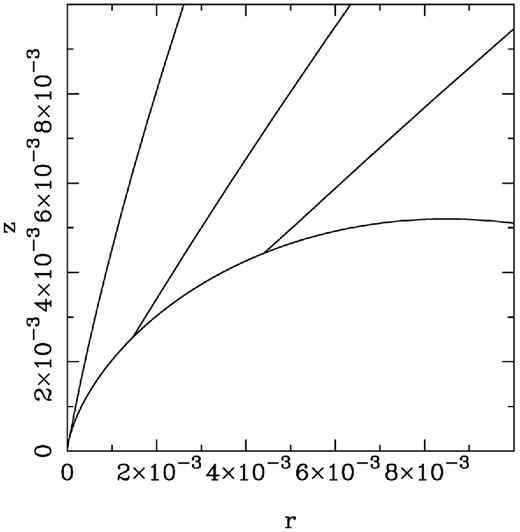
Shape of the termination shock near the origin. The solutions correspond to the model with σ0 = 103 and f(θ) = sin 2θ. As in the middle panel of Fig. 2, the magnetic inclination angle α = 80°, 60°, 45° and 20°, from top to bottom.

Figure 3.

Shape of the termination shock near the origin. The solutions correspond to the model with σ₀ = 10³ and f(θ) = sin ²θ. As in the middle panel of Fig. 2, the magnetic inclination angle α = 80°, 60°, 45° and 20°, from top to bottom.

Open in new tab Download slide

The low ram pressure of the termination shock in the high-σ polar region and the rapid drop of σ₁ around θ_m suggest that, as far as the equatorial part of the shock is concerned, one can ignore the presence of the polar section of the wind altogether. In this approximation, the appropriate boundary condition for equation (15) is

\begin{equation} X(\theta _m)=0\,. \end{equation}

(20)

Fig. 4 compares this approximate solution with the original one for α = 20°, the case in Fig. 2 with the largest unstriped sector. In this case, the difference between the solution is expected to be most profound. Yet, as one can see in this figure, it is still rather small. This result is particularly welcome as one expects to see significant deviation from the uniform pressure distribution of the shocked plasma in the polar region where the high-σ post-shock flow remains supersonic. The exact details of the flow in this region should not matter much.

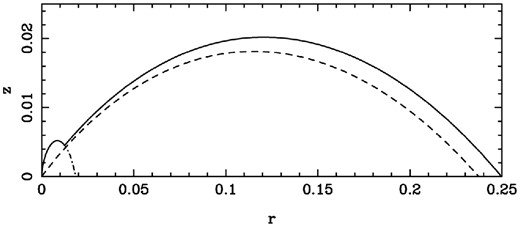
Shape of the termination shock for σ0 = 103 and f(θ) = sin 2θ and α = 20°. The solid line shows the original solution and the dashed one the approximate one for the truncated wind and the dash–dotted one the solution corresponding to σ1 = σ0.

Figure 4.

Shape of the termination shock for σ₀ = 10³ and f(θ) = sin ²θ and α = 20°. The solid line shows the original solution and the dashed one the approximate one for the truncated wind and the dash–dotted one the solution corresponding to σ₁ = σ₀.

Open in new tab Download slide

Strictly speaking, our analysis shows that there is no well defined unique shape of the termination shock which can be used to predict the emission properties of Crab's inner knot. On the other hand, the dependence on the wind parameters is not that strong. With the exception of very small magnetic inclination angle, the shock shape is approximately the same as found for the weakly-magnetized wind by Lyubarsky (2002). For this reason, we will use this shape for the rest of our paper. After small additional rescaling, the shock shape in this case is described by

\begin{equation} X^{\prime 2}+X^2 = f(\theta ) \,. \end{equation}

(21)

With f(θ) = sin ⁿθ, the asymptotic solutions of equation (21) are

\begin{equation} X\simeq \frac{\theta ^2}{2} \left( 1-\frac{7}{48}\theta ^2 \right)\,, \end{equation}

(22)

for n = 2 and

\begin{equation} X \simeq \frac{\theta ^3}{3} \left( 1-\frac{7}{90}\theta ^2 \right)\,, \end{equation}

(23)

for n = 4. The corresponding angles of attack are

\begin{equation} \delta _1 \simeq \theta /2 \end{equation}

(24)

and

\begin{equation} \delta _1 \simeq \theta /3 \end{equation}

(25)

respectively. Fig. 5 illustrates how the termination shock with n = 2 appears to a distant observer for the viewing angle of 60° to the symmetry axis.

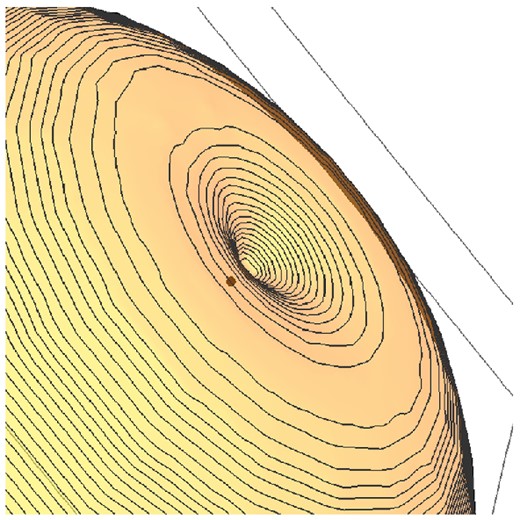
View of the polar region of the termination shock for f(θ) = sin 2θ and the viewing angle θob = 60°; the pulsar position is shown by the dot.

Figure 5.

View of the polar region of the termination shock for f(θ) = sin ²θ and the viewing angle θ_ob = 60°; the pulsar position is shown by the dot.

Open in new tab Download slide

3 ESTIMATES OF BASIC PARAMETERS

As the shocked plasma expands and slows down, its observed emissivity drops. Fig. 6, based the results of 3D RMHD simulations by Porth et al. (2014), illustrates this behaviour. One can see a relatively thin layer of enhanced emissivity just above the shock surface. Its thickness is approximately one-third of its distance from the line connecting the origin (pulsar) and the observer. The main reason for the drop of the emissivity with the distance from the shock is the reduction of the Doppler beaming.

Figure 6.

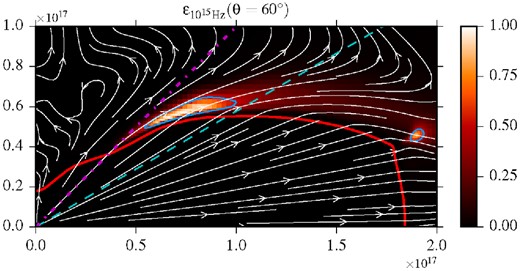
The observed optical emissivity of the post-shock flow in the 3D RMHD simulations of Porth et al. (2014). The arrowed lines are the instantaneous stream lines. The dashed line is the line of view and the blue curves show the regions of enhanced observed emissivity.

Open in new tab Download slide

Komissarov & Lyutikov (2011) estimated some of the the knot parameters in the shock model, assuming that they are determined by the Doppler boosting of the emission from the shocked plasma. In their calculations, they assumed that the velocity of the plasma is parallel to the shock surface. Here, we do a more careful and extended analysis.

Assuming a small size of the knot, we first ignore variations of the proper emissivity across the knot. In this case, the observed synchrotron emissivity is (e.g. Lyutikov, Pariev & Blandford 2003, see also Section 5)

\begin{equation} \epsilon _\nu \propto {\cal D}^{2+(p-1)/2} |B^{\prime }_\perp |^{(p+1)/2}\,, \end{equation}

(26)

where p is the spectral index of the electron energy spectrum, |$B^{\prime }_\perp$| is the normal to the line-of-sight component of magnetic field in the fluid frame and |${\cal D}=\Gamma ^{-1}(1-v \cos \alpha )^{-1}$| is the Doppler factor. Even if the magnetic field strength is constant over the knot, |$B^{\prime }_\perp$| may still vary significantly across the knot due to the relativistic aberration of light. However, along the symmetry axis in the plane of the sky |$B^{\prime }_\perp =B^{\prime }$|⁠, and it is only the Doppler factor that matters.

3.1 Low σ at the knot location

Based on equation (26) one can immediately rule out σ₁ ≥ 1 for the termination shock at the location of inner knot. The key observational data here is the clear separation of the knot from the pulsar (Rudy et al. 2015). This shows that that the beaming angle α_d is smaller compared to the deflection angle Δδ of streamlines at the shock. Defining α_d as the angle at which |${\cal D}^{2+(p-1)/2}$| reduces the factor of 2, we find that for the observed spectral index p ≈ 2.5

\begin{equation*} \alpha _d \approx \frac{1}{2\Gamma _2}. \end{equation*}

Using the maximum value for the deflection angle and Γ₂ for high σ₁ (equations 7 and 8) we find that

\begin{equation*} \frac{\alpha _d}{\Delta \delta } \approx 2\sqrt{\sigma _1}\sin \delta _1 = \sqrt{2\sigma _1}\,, \end{equation*}

where we used δ₁ = π/4 as the angle of attack with maximal deflection. For the case of δ₁ ≪ 1, we find that

\begin{equation*} \frac{\alpha _d}{\Delta \delta } \approx \sqrt{\sigma _1}\,. \end{equation*}

Both results show that for σ₁ ≥ 1 one has α_d > Δδ and hence the pulsar has to be embedded into the knot, in contradiction with the observations. Fig. 7 shows the ratio of angles as a function of σ₁ for δ₁ = π/4 and π/20. One can see, that the dependence of δ₁ is rather week. Using 7 and 8 one can show that for σ₁ ≪ 1

\begin{equation*} \frac{\alpha _d}{\Delta \delta } \approx 0.7\,, \end{equation*}

and thus the knot size is comparable with the separation from the pulsar. This conclusion does not depend on the shape of the termination shock and thus very robust.

Figure 7.

The ratio of the beaming and deflection angles.

Open in new tab Download slide

Since σ₁ is expected to be low only in the striped-wind zone, this allows us to conclude that the magnetic inclination angle α > 90° − θ_ob ≈ 30°, where θ_ob ≈ 60° the observed angle between the line of sight and the rotational axis of the Crab pulsar (Ng & Romani 2004). Based on this result we focus in the rest of the paper on the case of low σ₁.

3.2 Separation from the pulsar

The brightness peak of the knot corresponds to the point where the deflected streamline points directly towards the observer. The polar angle of this point θ_k = θ_ob − Δδ (see Fig. 8). Using equation (8) in the limit of small angles and equation (24), we find that

\begin{equation} \Delta \delta \approx (1-\chi )\delta _1 \approx (1-\chi )\frac{\theta }{2} \end{equation}

(27)

and

\begin{equation} \theta _{k}=\frac{2}{3-\chi }\theta _{\text{ob}} \,. \end{equation}

(28)

The angular separation between this point and the pulsar in the plane of the sky is

\begin{equation} \psi _{\rm k} \approx \frac{R_{\rm k}}{D} \Delta \delta \,, \end{equation}

(29)

where D is the distance to the pulsar. Denoting as R_ts and ψ_ts the linear equatorial radius of the termination shock and its angular size in the plane of the sky respectively,

\begin{equation} \frac{\psi _{\rm k}}{\psi _{\text{ts}}} = \frac{R_{\rm k}}{R_{\text{ts}}}\Delta \delta \,. \end{equation}

(30)

For σ ≪ 1, one has χ ≈ 1/3 and hence

\begin{equation} \Delta \delta \approx \frac{1}{4}\theta _{\text{ob}}\,, \quad \theta _{\rm k}=\frac{3}{4} \theta _{\text{ob}}\,. \end{equation}

(31)

Now R_k = 0.28 and ψ_ts = 11.4ψ_p ≈ 7.4 arcsec. This is approximately equal to the radius of the Crab's halo (Hester et al. 1995) and almost twice as small compared to the radius of its X-ray ring. For the shock shape function f(θ) = sin ⁴θ, one obtains R_k = R_s(θ_k) = 0.14R₀, R_ts = R_s(π/2) = 0.70R₀ and ψ_ts = 20ψ_p ≈ 13 arcsec. Thus, given the uncertainty of the shock shape, the theory and observations are quite consistent in the limit of low σ₁.

Figure 8.

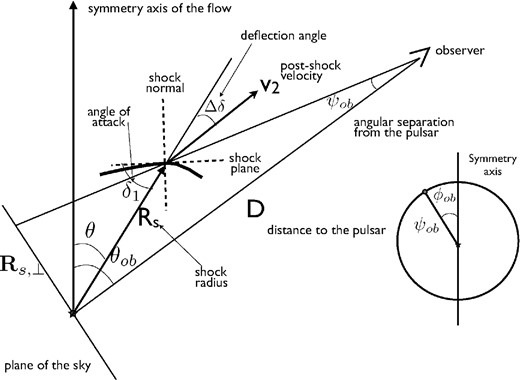
Geometry of the shock in the plane defined by the location of an observer, the pulsar and a point on the shock surface.

Open in new tab Download slide

3.3 Transverse size

The full half-brightness transverse size of the knot can be estimated as

\begin{equation} \Delta \psi _\perp = 2 \alpha _h \frac{R_{\rm k}}{D}\,, \end{equation}

(32)

where α_h is the angle between the line of sight and the velocity vector at the point on the shock, with the same position on the shock-defining curve as the centre of the knot, where the emissivity is reduced by the factor of two because of the Doppler effect and the relativistic aberration of light. Thus, we have

\begin{equation} \frac{\Delta \psi _\perp }{\psi _{\rm k}} = \frac{2\alpha _h}{\Delta \delta } \,. \end{equation}

(33)

The observed synchrotron emissivity is given by equation (26). Provided the knot size is small, one can assume that the magnetic field is uniform and write |$B^{\prime }_\perp =B^{\prime }\cos \alpha ^{\prime }$|⁠, where the α′ is the angle between the stream line and the line of sight in the fluid frame. The relativistic aberration of light gives

\begin{equation} \cos \alpha ^{\prime } =\frac{\cos \alpha -v}{1-v\cos \alpha }\,. \end{equation}

(34)

Substituting this into equation (26), we find that

\begin{equation} \epsilon _\nu \propto (1-v\cos \alpha )^{-(p+2)} (\cos \alpha -v)^{(p+1)/2}\,. \end{equation}

(35)

Approximating |$v\simeq 1-1/2\Gamma _2^2$| and cos α ≃ 1 − α²/2, this reads

\begin{equation} \epsilon _\nu \propto (1+x^2)^{-(p+2)} (1-x^2)^{(p+1)/2}\,, \end{equation}

(36)

where x = Γ₂α. For the observed p = 2.6, this equals to one half for x ≈ 0.33 and. Thus α_h ≈ 0.33/Γ₂ and equation (33) reads

\begin{equation} \frac{\Delta \psi _\perp }{\psi _{\rm k}} \approx \frac{0.66}{\Gamma _2\Delta \delta } \,. \end{equation}

(37)

Substituting into the last equation the expressions (3) and (8) in the approximation of small δ₁, we finally obtain

\begin{equation} \frac{\Delta \psi _\perp }{\psi _{\rm k}} \approx 0.66 \left(\frac{1+\chi }{1-\chi }\right)^{1/2} \,. \end{equation}

(38)

This is a monotonically increasing function of χ and has the absolute minimum value (Δψ_⊥/ψ_k)_min = 0.9 reached for σ₁ = 0 (χ = 1/3). For σ₁ = 10 this gives Δψ_⊥/ψ_k = 4.3. Observational measurements of the knot parameters are complicated by its small size and proximity to the bright Crab pulsar. Depending of the method used, the transverse size of the knot in HST images varies from Δψ_⊥ ≈ 0.3 arcsec to 0.56 arcsec, whereas ψ_k ≈ 0.65 arcsec (Rudy et al. 2015). This rules out high σ₁ and favors σ₁ ≪ 1 once more. The synthetic images of the knot presented in Section 4, give a somewhat smaller size compared to what follows from equation (38).

4 SYNTHETIC IMAGES

In this section we construct two-dimensional ‘images of the knot’. Obviously, in order to obtain the brightness distribution we need to integrate the emissivity along the line of sight. However, from the shock geometry, we can only conclude how it is distributed over the shock surface. Therefore, in this section we start by constructing images of this surface and later study the effects of finite thickness of the emitting layer. We expect a longer geometrical length of the emitting region along the line tangent to the shock surface. This factor would make the knot more compact along the symmetry axis in the image. On the other hand, the finite thickness of the emitting layer would tend to increase the knot size in this direction.

For all images presented in the paper we use θ_ob = π/3.

4.1 Emissivity maps

Given the shock shape and the ‘upstream’ magnetization parameter σ₁ one can determine the post-shock flow direction and its Lorentz factor, as well as the angle μ′ = π/2 − α′ between the line of sight and the magnetic field in the fluid frame. These allow us to compute the purely geometrical component of the synchrotron emissivity over the shock surface. Namely, equation 26 gives us that

\begin{equation} \epsilon _\nu \propto \epsilon _{\text{geom}}={\cal D}^{2+(p-1)/2} | \sin \mu ^{\prime }|^{(p+1)/2}\,. \end{equation}

(39)

Next, we project this distribution of ϵ_geom on the plane of the sky. The main contribution to the knot emission comes from the closest to the observer section of the shock surface. Due to the non-spherical shock geometry, the line of sight may intersect this section twice. In this case, we sum the contributions from both these points. Next, we rescale the image so that the maximum is located at 0.7 arcsec from the pulsar.

As an illustration, Fig. 9 shows the results for the shock shape described by equation (21) with n = 2 and constant magnetization parameter σ₁ = 0, 1, 10. One can see that only in the case σ₁ = 0 there is a clear separation between the knot and the pulsar, in full agreement with the results of Section 3. The plots also confirm the conclusion of Section 3, that high σ₁ models result in radially elongated elongated images, which is in conflict with the observations.

$Synthetic emission maps of the knot for σ1 = 0, 1, 10 (from left to right) and f(θ) = sin 2θ. In all cases, the distances are in arcsec, the pulsar is located at the origin and the emission peak is at 0.7 arcsec from the pulsar. The peak emissivity is normalized to unity and the third contour corresponds to one half of the peak value. For high σ ≥ 1 the inner knot is both very broad and elongated in radial direction, which is inconsistent with the observations. The contours start from 0.9 of the peak value and decrease by the factor of $\sqrt{2}$ thereafter.$

Figure 9.

Synthetic emission maps of the knot for σ₁ = 0, 1, 10 (from left to right) and f(θ) = sin ²θ. In all cases, the distances are in arcsec, the pulsar is located at the origin and the emission peak is at 0.7 arcsec from the pulsar. The peak emissivity is normalized to unity and the third contour corresponds to one half of the peak value. For high σ ≥ 1 the inner knot is both very broad and elongated in radial direction, which is inconsistent with the observations. The contours start from 0.9 of the peak value and decrease by the factor of |$\sqrt{2}$| thereafter.

Open in new tab Download slide

In Fig. 10, we compare the results for n = 2 and n = 4. One can see that the difference between the model is not dramatic – in the n = 4 model, the knot is a little bit more tangentially elongated. The proper shock emissivity may reduce with the distance from the pulsar reflecting the reduced wind power. To probe the importance of this factor, we also considered the model where the shock emissivity scales as R⁻²ϵ_geom – the results are shown in the right-hand panel of Fig. 10. One can see that the knot becomes significantly more compact and less elongated in the radial direction. This image is closer to those of the Crab's inner knot, which is approximately 2:1 in size (tangential over radial), while its separation from the pulsar, ∼0.65 arcsec is much larger than it's radial width (0.15 arcsec in the HST image and somewhat larger, 0.35 arcsec in the Keck image), (Rudy et al. 2015).

$Sensitivity of the synthetic images to the shock model. Left-hand panel: shock shape f(θ) = sin 2θ and uniform proper emissivity; center panel: shock shape f(θ) = sin 4θ and uniform proper emissivity; right-hand panel: shock shape f(θ) = sin 2θ and proper emissivity scaling with the spherical radius as ∝ R−2. In all the cases σ1 = 0. The contours start from 0.9 of the peak value and decrease by the factor of $\sqrt{2}$ thereafter.$

Figure 10.

Sensitivity of the synthetic images to the shock model. Left-hand panel: shock shape f(θ) = sin ²θ and uniform proper emissivity; center panel: shock shape f(θ) = sin ⁴θ and uniform proper emissivity; right-hand panel: shock shape f(θ) = sin ²θ and proper emissivity scaling with the spherical radius as ∝ R⁻². In all the cases σ₁ = 0. The contours start from 0.9 of the peak value and decrease by the factor of |$\sqrt{2}$| thereafter.

Open in new tab Download slide

Finally, we have also explored the case of the shock shape of striped wind described by equation (14), with σ₁ varying according to equation (17). In all models described here, the shock emissivity is ϵ = R⁻²ϵ_geom.

For large magnetic inclination angle α > θ_ob, the shock shape is very similar to the our ‘standard’ one. Moreover, σ₁ ≪ 1 and hence the images are not much different from those shown in Fig. 10. For small magnetic inclination angle α < θ_ob the knot emission comes from the inner lobe of the shock, where the shock shape is exactly the same as the standard one. However, σ₁ is very high now, leading to images which are in stark conflict with the observations (like the one in the left-hand panel of Fig. 9).

The most interesting is the case with α ≈ θ_ob, where the knot emission comes from the transitional section of the shock where σ₁ varies rapidly and the shock surface is closely aligned with the line of sight (see Fig. 11). In Fig. 12 we show the results for α = π/3 and π/4. One can see that for α = π/3, a the images can show a very high degree of elongation in the transverse direction. However, for α = π/4, this elongation is no longer seen. The results confirm our expectation that the differences between standard shock shape (equation 15) and that of the striped wind (21) are not dramatic and the conclusions based on the models with standard shape are quite robust.

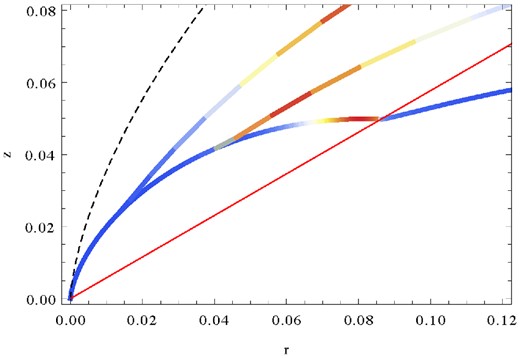
Shock contour for obliqueness of π/3, π/4, π/6 (top to bottom) for wind magnetization of σ0 = 10 and f(θ) = sin 2θ. The hydro shock solution is indicated dashed black. The shock-contours are colored with the Doppler factor cubed. Red contour describes the los to the Pulsar for the assumed inclination angle θob = 60°. Right-hand panel is a zoom-in. One can see the double-humped structure of the termination shock, leading to a emission closely aligned with the line of sight in the case of α = π/4.

Figure 11.

Shock contour for obliqueness of π/3, π/4, π/6 (top to bottom) for wind magnetization of σ₀ = 10 and f(θ) = sin ²θ. The hydro shock solution is indicated dashed black. The shock-contours are colored with the Doppler factor cubed. Red contour describes the los to the Pulsar for the assumed inclination angle θ_ob = 60°. Right-hand panel is a zoom-in. One can see the double-humped structure of the termination shock, leading to a emission closely aligned with the line of sight in the case of α = π/4.

Open in new tab Download slide

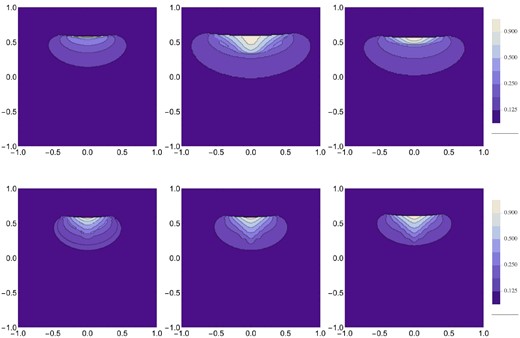
$Emissivity maps for the striped-wind shock shape. Top row: α = π/4. Bottom row: α = π/3. Left column: σ0 = 10, n = 2; riddle column: σ0 = 100, n = 2; right column: σ0 = 10, n = 4. The contours start from 0.9 of the peak value and decrease by the factor of $\sqrt{2}$ thereafter.$

Figure 12.

Emissivity maps for the striped-wind shock shape. Top row: α = π/4. Bottom row: α = π/3. Left column: σ₀ = 10, n = 2; riddle column: σ₀ = 100, n = 2; right column: σ₀ = 10, n = 4. The contours start from 0.9 of the peak value and decrease by the factor of |$\sqrt{2}$| thereafter.

Open in new tab Download slide

Rudy et al. (2015) also pointed out that the Crab's knot could be a bit convex away from the pulsar (the ‘smily face’). In the synthetic synchrotron maps presented in this section, the distant side of the knot has a sharp edge slightly convex the other way. This feature reflects the curvature of the folding edge of the shock surface projection on to the plane of the sky. However, in the images based on the RMHD numerical simulations of PWN the edge curvature is washed away (Porth et al. 2014). In these simulations, the emission comes from a layer of finite thickness downstream of the termination shock (see Fig. 6). As we show next, this can be an important factor in determining the detailed shape of the knot.

4.2 Brightness distribution

In order to probe the effect of finite thickness of the emitting layer, we need a model of volume emissivity away from the shock surface. Our starting point is the emissivity on the shock surface, which we assume to be

\begin{equation} \epsilon _0(R,\theta ,\phi ) \propto R^{-2}{\cal D}^{2+(p-1)/2} |\sin \mu ^{\prime }|^{(p+1)/2}. \end{equation}

(40)

The emissivity outside of the surface is then modelled as

\begin{equation} \epsilon (R,\theta )=\epsilon _0(R,\theta ,\phi )\delta _{\epsilon } (R,\theta )\,, \end{equation}

(41)

where the function δ_ϵ(R, θ) provides spreading about the surface. We choose it to be

\begin{equation} \delta _{\epsilon }(R,\theta )= \exp (- |R-R_{\rm s}(\theta )|/ (\epsilon _{\rm r} R_{\rm s}(\theta ))) \end{equation}

(42)

for R > R_s(θ) and

\begin{equation} \delta _{\epsilon }(R,\theta ) \tanh (-4|R-R_S(\theta )|/(\epsilon _{\rm r} R_{\rm s}(\theta ))) +1 \end{equation}

(43)

for R ≤ R_s(θ), where R = R_s(θ) is the shock radius. The parameter ϵ_r controls the relative thickness parameter. The factor of 4 in the argument of tanh provides much faster drop of emissivity in the direction towards the pulsar.

In Fig. 13 illustrates the results obtained for the shock shape parameter n = 2 with σ₁ = 0. As one can see, the ‘frown’ turns into a ‘smile’ already for ϵ_r = 0.1. At this point, the emissivity is still a sharp layer attached to the shock. Notwithstanding the ad hoc nature of this simple model, the results indicate that the shape of the knot is very sensitive to the downstream flow. We hence suggest that a modelling of the knot's shape must take into account the flow in the post-shock layer.

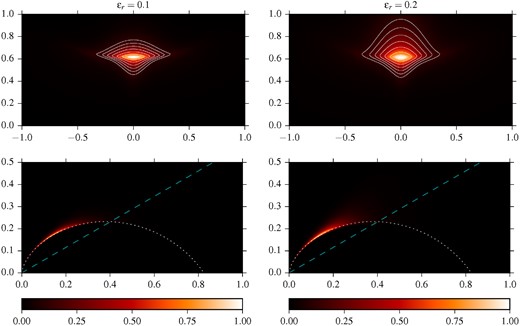
$Knot images resulting from emitting region of finite thickness (top) and corresponding emissivity distributions (bottom). The dashed line shows the line of sight and the white dotted line traces the assumed shape of the termination shock. The contours start from 0.9 of the peak brightness and decrease by the factor of $\sqrt{2}$ thereafter.$

Figure 13.

Knot images resulting from emitting region of finite thickness (top) and corresponding emissivity distributions (bottom). The dashed line shows the line of sight and the white dotted line traces the assumed shape of the termination shock. The contours start from 0.9 of the peak brightness and decrease by the factor of |$\sqrt{2}$| thereafter.

Open in new tab Download slide

5 POLARIZATION

Given the velocity field and the assumed magnetic structure of the flow (azimuthal) we can also calculate the polarization signature. In order to do this properly, the relativistic aberration of light has to be taken into account Lyutikov et al. (2003). In our case, the calculations are slightly different due to the different geometry of the problem. The details can be found in Appendix B.

We start with the case where emission come only from the shock surface. Fig. 14 shows the degree of polarization for the total flux coming from the shock with n = 2 and proper emissivity scaling as R⁻². (the results for n = 4θ look very similar.) One can see that for 0 < σ₁ < 1 the degree of polarization varies only slightly. For the observed value of p = 2.6, we obtain Π ≈ 50 per cent. For magnetization σ₁ ≥ 1, the polarization signal nearly coincides with that for a spherical shock (Lyutikov et al. 2003) – in this case the flow deflection angle Δδ is small and its speed is highly relativistic.

Figure 14.

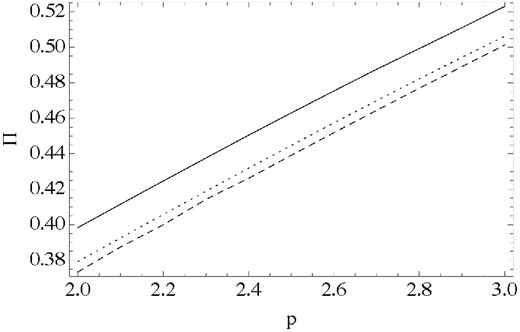
Polarization of the shock integral emission in the case of zero thickness as a function of the particle spectral index p. Solid curves correspond to the integration over the whole shock surface for models with σ₁ = 1, 0.1, 0 (top to bottom) and constant rest-frame emissivity. The dashed line shows the result for spherical surface obtained in Lyutikov et al. (2003).

Open in new tab Download slide

Thus, our model predicts high polarization of the knot emission in agreement the observations, but the predicted value is still somewhat lower than the observed one of Π ∼ 60 per cent (Moran et al. 2013). In order to understand the reason, we carried out additional polarization calculations.

To check if the finite thickness of the emitting layer can effect the polarization, we carried out calculations with the same volume emissivity model as in Section 4.2. The results are presented in Fig. 15, which shows that the degree of polarization remains largely unchanged – the changes are quite small – when the thickness is increased from 10 to 50 per cent of the local shock radius, the polarization increases by merely 2 per cent. This leads us to conclude that a finite extent of the emitting region alone is unlikely to explain the high observed degree of polarization.

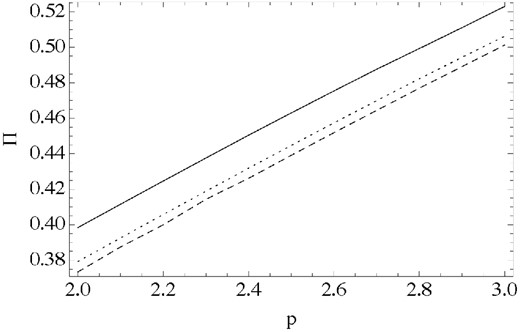
$Polarization fraction in the model with finite width of the emitting layer (σ1 = 0). The width is scaled with the local shock radius: 10 per cent – dashed, 20 per cent – dotted and 50 per cent solid. Even for a unrealistically wide emitting region of 50 per cent, the observed polarization degree of ∼60 per cent still cannot be reproduced.$

Figure 15.

Polarization fraction in the model with finite width of the emitting layer (σ₁ = 0). The width is scaled with the local shock radius: 10 per cent – dashed, 20 per cent – dotted and 50 per cent solid. Even for a unrealistically wide emitting region of 50 per cent, the observed polarization degree of ∼60 per cent still cannot be reproduced.

Open in new tab Download slide

In the observations of Moran et al. (2013), the knot polarization was measured in a very localized area with an aperture radius of 0.15 arcsec. However according to the data by Rudy et al. (2015), the transverse FWHM size of the knot is ≈0.32 arcsec and FWRMS size is ≈0.56 arcsec and hence the aperture used in Moran et al. (2013) captures only the bright inner part of the knot. This can be significant because the depolarization of total flux in our calculations is caused by the gradual rotation of the polarization vector across the knot, which is illustrated in Fig. 16. Thus, a smaller area of integration would give a higher polarization degree.

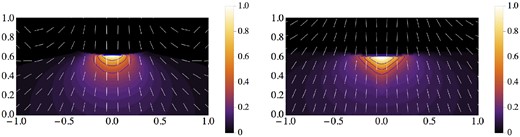
$Image of the knot (σ1 = 0) and its polarization vectors (E-field) for f(θ) = sin 2θ, (left) and f(θ) = sin 4θ, (right). At each location the polarization degree corresponds to the theoretical maximum for the synchrotron emission. The rotation of polarization vectors across the image results in depolarization of the integral emission. The contours start from 0.9 of the peak value and decrease by the factor of $\sqrt{2}$ thereafter.$

Figure 16.

Image of the knot (σ₁ = 0) and its polarization vectors (E-field) for f(θ) = sin ²θ, (left) and f(θ) = sin ⁴θ, (right). At each location the polarization degree corresponds to the theoretical maximum for the synchrotron emission. The rotation of polarization vectors across the image results in depolarization of the integral emission. The contours start from 0.9 of the peak value and decrease by the factor of |$\sqrt{2}$| thereafter.

Open in new tab Download slide

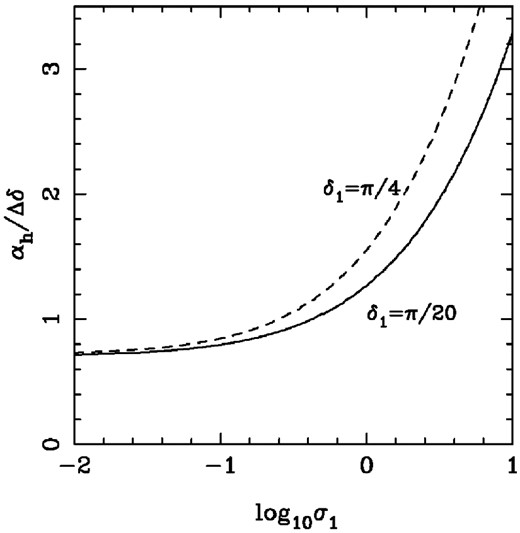
In order to investigate this effect we carried out additional calculations where the integration over the azimuthal angle was limited to the interval (−ϕ_b, +ϕ_b). To determine a reasonable range for ϕ_b, we recall that the knot emissivity decreases by the factor of two from its peak value for streamlines making angle α_h ≈ 0.33/Γ₂ ≈ 0.14 to the one leading to the peak (see Section 3.3).

In Fig. 17, we show the results of integration for ϕ_b = 0.1, 0.25 and 0.5. One can see that for all these value the polarization is significantly higher compared to what we obtained previously. In fact, for ϕ_b = 0.1 the flux polarization degree almost coincides with the theoretical maximum in uniform magnetic field. Deviations from the exact axial symmetry of our model will naturally reduce the polarization degree.

Figure 17.

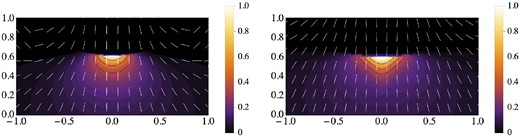
Polarization signal coming from the area of the shock limited by |ϕ| ≤ 0.1, 0.25, 0.5. (At the peak of emission the abscissa of 0.15 arcsec corresponds to ϕ ≈ 0.1.) The dashed line is the theoretical maximum for the synchrotron emission in uniform magnetic field.

Open in new tab Download slide

6 OTHER PROPERTIES

6.1 Energetics

Let us estimate the energy flux intercepted by the region producing the wind and compare it with the observed luminosity. To calculate the solid angle occupied by the knot, we recall that for σ₁ ≪ 1 the part of the flow which contributes to the knot emission occupies Δθ ≈ 0.3 with a Δϕ ≈ 0.66/Γ₂ ≈ 0.3 in the case σ₁ ≪ 1 (see Section 3). In the same limit, the deflection angle Δδ ≈ δ₁(1 − χ) ≈ θ_k/3, where θ_k is the coordinate of knot centre. This gives θ_k = θ_ob − Δδ ≈ 3θ_ob/4 ≈ π/4 and δ₁ ≈ π/8. The wind luminosity per unit solid angle |$L(\theta ) = {3 \over 8 \pi } L_{\rm w} \sin ^2 \theta$|⁠, where L_w is the total wind power. Thus, the energy passing through the knot is

\begin{equation} L_{\text{knot}} \approx 4 \times 10^{-3} L_{\rm w} = 2 \times 10^{36} {\rm erg\, s{^{-1}}} \,, \end{equation}

(44)

where L_w = 5 × 10³⁸ erg s⁻¹ is the current spin-down power of the Crab pulsar. Given the observed spectrum of the nebula, most of this energy is carried out by the electrons emitting in the optical band.

The observations give the isotropic optical-IR luminosity of the knot of 1.3 × 10³³ erg s⁻¹ (Rudy et al. 2015). Given the Doppler beaming angle of 1/Γ₂ with |$\Gamma _2\approx \delta _1^{-1} = 2.5$| the actual total knot luminosity is L_ob ≈ 1.6 × 10³¹ erg s⁻¹, implying the radiative efficiency of f_rad ≈ 10⁻⁵.

The synchrotron lifetime of optical electrons is

\begin{equation} t_{\text{syn}} \approx 2\times 10^5 B_{-3}^{-3/2}\, \mbox{days}\,, \end{equation}

(45)

where B₋₃ is the magnetic field in mGauss. Taking the knot size along streamlines of t_lc ≈ 10 light days as a reasonable estimate, the knot crossing time in the fluid frame will be t_lc ≈ 4 d. Hence, the theoretical radiative efficiency of the knot |$f_{\text{rad}} = t_{\text{lc}}/t_{\text{syn}} \approx 2\times 10^{-5} B_{-3}^{3/2}$|⁠, which is consistent with the observations.

For comparison, the total isotropic luminosity of bright wisps within 10 arcsec from the pulsar is about 10 times that of the inner knot, ≈10³⁴erg s⁻¹ (Hester et al. 1995).¹ Their proper motion indicates velocities v ≈ 0.6c. Hence the beaming angle in the θ direction is Δθ ≈ 0.6 and in the ϕ direction Δϕ ≈ 0.5, slightly smaller due to the anisotropy of the synchrotron emissivity in uniform magnetic field. The corresponding solid angle is about unity and hence the actual wisps luminosity is L_ob ≈ (1/4π) × 10³⁴erg s^{− 1}. The luminosity emitted in all directions will be higher on average by π/Δϕ, yielding L_wisps ≈ 5 × 10³³erg s⁻¹. According to the MHD theory, the wisps are arc-like structures of enhanced magnetic field advected in the equatorial direction (Camus et al. 2009; Porth et al. 2014). It is in this direction, where most of the pulsar wind power is transferred. Hence, the radiation efficiency of the wisp region

\begin{equation} f_{\text{rad}}=\frac{L_{\text{wisps}}}{L_{\text{w}}}\approx 10^{-5} \,, \end{equation}

(46)

which is similar to what we found for the knot.²

6.2 Variability

Moran et al. (2013) and Rudy et al. (2015) discuss the variability of the position, size and the luminosity of the inner knot – the position fluctuates relative to the mean by approximately 10 per cent on the time-scales of month(s). At the same time the overall size of knot correlates with the distance from the pulsar, while the luminosity anticorrelates with it.

The numerical simulations by Camus et al. (2009) and, Porth et al. (2014) show that inner region of PWN is highly dynamic and the shock surface is constantly changing as the result. When the external pressure drops the shock expands and when the pressure increases the shock recedes. The emission of wisps is one effect of this variability observed in the synthetic synchrotron images obtained in the simulations. The other one is the unsteady behaviour of the inner knot, whose position and brightness change in time. In fact, Porth et al. (2014) reported an anticorrelation of their synthetic knot luminosity with its projected distance from the pulsar.

In order to understand these results, let us consider the simplest model of the shock variability, where the shock shape is preserved but its length-scale R₀ fluctuates. In this case, the downstream emissivity is the same function of θ and ϕ up to a factor depending on R₀. This means that the ratio of the knot size to its separation from the pulsar remains unchanged (see Section 3), which is in good agreement with the HST observations, which give |$\psi _\perp \propto \psi _{\rm k}^{0.8\pm 0.13}$|⁠.

Regarding the total flux from the knot, we note the emissivity |$\epsilon _\nu \propto n^{\prime }_2 B_2^{^{\prime }(p+1)/2}$|⁠, where n′ the number density of emitting particles. The total flux of the knot F_ν ∝ ϵ_νA, where A is the knot area. Since, |$n^{\prime }_2\propto R_0^{-2}$|⁠, |$A\propto R_0^2$|⁠, |$B^{\prime }_2\propto R_0^{-1}$| and ψ_k ∝ R₀ we obtain

\begin{equation} F_\nu \propto \psi _{\rm k}^s \quad \mbox{where}\quad s= -(p+1)/2\,; \end{equation}

(47)

the same result as stated in Rudy et al. (2015). Thus, the shock model is consistent with the observed anticorrelation. For the observed spectral index p = 2.6, equation (47) gives s = 1.8, whereas the HST data suggest a somewhat larger value s = 2.39 ± 0.37 (Rudy et al. 2015). In reality, the shock variability may not be shape preserving, in which case the variability of its observed emissivity will be more complicated.

The results of computer simulations show that the shock variability is more complicated, with the shock shape changing as well in response to the external perturbations on the scale below R₀ (Porth et al. 2014). Thus, the predictions based on the model of uniform scaling should be considered as rather approximate.

Since in the MHD theory both the wisp production and the knot variability are related to the variations of the shock geometry, one would expect approximately the same time-scale for both these phenomena.³ Although the available observational data do not cover a sufficiently long period of time, they indicate that this may be the case (Hester et al. 2002; Moran et al. 2013; Rudy et al. 2015).

6.3 Connection to Crab's gamma-ray flares

The discovery of flares from the Crab nebula (Abdo et al. 2011; Tavani et al. 2011) challenges our understanding of particle acceleration in PWNe and possibly in other high-energy astrophysical sources.

The short lifetime of gamma-ray emitting electrons means that if they are accelerated at the termination shock then the gamma-ray emitting region is a thin layer above the shock where the flow Lorentz factor is still high and hence its emission is subject to the Doppler beaming. Komissarov & Lyutikov (2011) used this to argue that most of the observed gamma-ray emission of the Crab nebula may come from the inner knot. They and Lyutikov et al. (2012) also speculated that the gamma-ray flares of the Crab nebula may come from the knot as well and proposed to look for correlations between the knot's optical emission and the gamma-ray emission from the nebula. The relativistic post-shock flow may help to explain the peak frequency of flares exceeding the radiation reaction limit of ≈100 MeV (Lyutikov 2010; Komissarov & Lyutikov 2011). Moreover, a blob moving through the knot of ≈10 light days length would be observed for the time smaller by |$2 \Gamma _2^2$|⁠, which can explain the short time-scales of the Crab's flares.

The observed cut-off of the synchrotron spectrum of the Crab nebula at ∼100 MeV in the persistent Crab nebula emission and especially during the flares, when the cut-off energy approached even higher value of ∼400 MeV, is in conflict with slow stochastic acceleration mechanisms (Lyutikov 2010; Clausen-Brown & Lyutikov 2012). Alternatively, the flares may result from linear particle acceleration during explosive relativistic magnetic reconnection (e.g. Lyutikov & Uzdensky 2003; Lyubarsky 2005; Lyutikov 2010; Cerutti et al. 2014). Fast and efficient particle acceleration during the reconnection requires highly magnetized plasma, σ ≥ 1, in the flare-producing region (e.g. Lyubarsky 2012). However, our results show that the knot plasma cannot be that highly magnetized. Moreover, the magnetic field in this region is still expected to be very regular (after the dissipation of the small-scale magnetic stripes), namely azimuthal of the same orientation (Porth et al. 2014), and hence lacking current sheets required for the reconnection. Finally, the coordinated programs of optical observations did not reveal anything unusual about the inner knot emission during the gamma-ray flares (Weisskopf et al. 2013; Rudy et al. 2015). Thus, we have to admit that the Crab flares are unlikely to originate from its inner knot.

If flares do not come the termination shock then they are certainly not connected to the shock particle acceleration mechanism. An explosive magnetic reconnection seems to be the only realistic alternative. A favorable location for such reconnections would have high magnetization parameter σ = B²/w > 1, where w is the relativistic enthalpy, as this would ensure the relativistic Alfvén speed. In addition, its magnetic field should be somewhat disordered so that thin current sheets may develop. In PWNe, such plasma is expected to exist in the polar region downstream of the termination shock, which is fed by the unstriped section of the pulsar wind (Lyubarsky 2012; Komissarov 2013; Porth et al. 2014).

The current observations do not rule out yet that at energies below 100 MeV the synchrotron gamma-ray emission between flares is coming from the knot. If so, a slow variability of the persistent gamma-ray emission at these energies, on the time-scale of wisp production, is expected. Additional studies are required to clarify this issue.

7 COMPARISON WITH OTHER STUDIES

Almost simultaneously with our manuscript, the results of an independent study by Yuan & Blandford (2015) have become publicly available. (Some of their results have been outlined already in Rudy et al. 2015.) We agree in the conclusion that the observed knot parameters rule out high magnetization of the post-shock plasma. However, they could not reach a definitive conclusion on the acceptability of the shock model even in the low-magnetization regime, pointing to a number of difficulties. The main of them concern the transverse size of the knot, its shape and polarization.

For the transverse size, Yuan & Blandford (2015) claimed that in the basic shock model it exceeds the distance to the pulsar at least by the factor of 2.8, in conflict with the observations. However, this estimate is based on the assumption that the emissivity drops by the factor of 2 at an angle α_h = 1/Γ₂ to the velocity vector. In reality, the combination of the Doppler beaming with the anisotropy of the proper synchrotron emissivity in uniform magnetic field leads to a much smaller angle (see Section 3.3). Curiously, their synthetic image in Fig. 3b shows a much more compact knot, well in line with our results.

For the polarization of the integral shock emission, they obtained a value which is lower compared to that of the inner knot as obtained by Moran et al. (2013). In fact, this result agrees with our calculations, when the flux integration is carried out over the whole shock surface. However, in the observations, the polarization is measured only for the bright core of the knot (area with an aperture radius of 0.15 arcsec). We have demonstrated that smaller integration area leads to higher polarization degree, allowing a much better fit.

Finally, Yuan & Blandford (2015) pointed out that the shock model cannot reproduce the ‘smily’ shape of the knot, claimed in Rudy et al. (2015), but yields images more reminiscent of a ‘frown’. This conclusion is base on the model where the emission comes only from the shock surface, which also leads to a very sharp brightness drop at the distant (relative to the pulsar) edge of the knot. We have shown that in models with finite thickness of the emitting layer, these features do not survive and the frown can easily turn into a smile or even a pout. In fact, the experimentation with different geometries of streamlines in the emitting zone by Yuan & Blandford (2015) also show rather strong distortions of synthetic images. To address such details more advance models, based on computer simulations, are required.

8 CONCLUSION

In this paper, we have further explored the model of the Crab nebula inner knot as a Doppler-boosted emission from the termination shock of the pulsar wind. This model successfully explains a number of its observed properties.

Location. The knot is located on the same side of the pulsar as the Crab jet, along the symmetry axis of the inner nebula, and on the opposite side as the brighter section of the Crab torus. This is a direct consequence of the termination shock geometry and the Doppler-boosting.
Size. The knot size is comparable to its separation from the pulsar. This also follows from the shock geometry and the Doppler-beaming. The anisotropy of the proper synchrotron emissivity, which vanishes along the magnetic field direction in combination with the relativistic aberration of light is another significant factor. Only models with low magnetization of the post-shock flow, with the effective magnetization parameter of the wind σ₁ < 1 agree with the observations.
Elongation. The knot is elongated in the direction perpendicular to the symmetry axis. This is because the knot emission comes from the region where the shock surface is almost parallel to the line of sight.
Polarization. The knot polarization degree is high, and the electric vector is aligned with the symmetry axis. This come due to the fact that the post-shock magnetic field is highly ordered in the vicinity of the termination shock and azimuthal. In the model, the relativistic aberration of light leads to a noticeable rotation of the polarization vector along the knot and this prediction could be tested in future polarization observations. Accordingly, the polarization degree of the integral knot emission depends on the integration area – the bigger the area the smaller the degree is.
Luminosity. Taking into account Doppler-beaming, the observed radiative efficiency of the inner knot is consistent with efficient particle acceleration at the termination shock and the knot's magnetic field of one milli-Gauss strength, which is a reasonable value for the inner Crab nebula.
Variability. The knot flux is anticorrelated with its separation from the pulsar. In the numerical simulations, the termination shock is found to be highly unsteady, changing its size and shape. As the shock moves away from the pulsar, so does the knot region, which leads to lower magnetic field and hence lower emissivity. Another outcome of the shock variability in the MHD simulations is the emission of wisps and hence one expects both the processes to occur on the same time-scale, which is consistent with the observations.

In many cases, the agreement with the observed properties of the Crab's inner knot falls short of a perfect fit. Given the uncertainties in the shape of the termination shock, proper emissity of the shocked plasma and the post-shock flow which are present in the model it would be naive to expect more. Further investigations of the models, involving advanced numerical simulations, are needed to achieve this.

Our results may have a number of important implications to the astrophysics of relativistic plasma in general and that of PWN in particular. They show that the termination shock of the relativistic wind from the Crab pulsar is a reality and that this shock is a location of efficient particle acceleration. The strong Doppler-beaming of the emission from the shock explains why this shock has been so elusive. Only the emission from a small patch on the shock surface, the inner knot, is strongly Doppler-boosted and hence prominent. For most of the shock, its emission is beamed away from the Earth and hence difficult to observe.

The shock model of the inner knot allows us to constrain the parameters of the wind from the Crab pulsar. Taken directly, the model requires the wind to be particle-dominated, σ₁ < 1, at least at the polar latitudes of 40°–60°. However, in the case of a striped wind, its termination shock can mimic that of a low σ flow even when the actual wind magnetization is extremely high (Lyubarsky 2003). In this context, the magnetic inclination angle of the Crab pulsar should be above 45°, which means that most of the Poynting flux of the Crab wind is converted into particles, if not in the wind itself then at its termination shock (Komissarov 2013). This is in agreement with the results of numerical simulations, which can reproduce the observed properties of the inner Crab nebula extremely well in models with moderate wind magnetization (Porth et al. 2014). However, the polar region of a pulsar wind is free of stripes and can still inject highly magnetized plasma into its PWN.

The fact that during the gamma-ray flares of the Crab nebula the inner knot does not show any noticeable activity suggests that the flares occur somewhere else. This is consistent with the fact that any stochastic acceleration mechanism is too slow to compete with radiative losses and deliver electrons capable of emitting synchrotron photons of 100 MeV energy. Our conclusion that the inner-knot plasma is not highly magnetized also disfavours the knot as a site of explosive relativistic magnetic reconnection. To proceed really fast, the magnetic reconnection has to occur in magnetically dominated plasma (Lyutikov 2010; Clausen-Brown & Lyutikov 2012; Lyubarsky 2012; Cerutti et al. 2014; Sironi & Spitkovsky 2014). The inner polar region of the Crab nebula is the only location where such conditions can be met.

We would like to thank Roger Blandford for stimulating discussions of the issue. We also thank Paul Moran for information on the details of the polarization observations and Lorenzo Sironi for comments on the manuscript.

This work had been supported by NASA grant NNX12AF92G and NSF grant AST-1306672. SSK and OP are supported by STFC under the standard grant ST/I001816/1.

1

We used the wisp length of 3 arcsec, as stated in (Hester et al. 1995) for the ‘thin wisp’, to calculate the ratio of the isotropic wisps luminosity to that of the inner knot.

2

The maximal spectral power in the Crab nebula comes out in UV-soft X-rays, where the radiative times scales of leptons is roughly comparable to the age of the nebula. Most of this emission comes from the old volume-filling population of particles, and not from the freshly accelerated ones close to the termination shock.

3

Knot variability may occur on shorter scales (Lyutikov et al. 2012).

REFERENCES

Abdo

A. A.

et al.

Science

2011

331

739

Month:	Total Views:
January 2017	5
February 2017	1
March 2017	2
April 2017	1
May 2017	3
June 2017	7
July 2017	1
August 2017	1
September 2017	5
October 2017	1
November 2017	10
December 2017	6
January 2018	7
February 2018	1
April 2018	1
May 2018	8
June 2018	2
October 2018	3
November 2018	1
January 2019	2
February 2019	3
March 2019	17
April 2019	7
May 2019	5
June 2019	1
July 2019	12
August 2019	4
September 2019	4
October 2019	6
November 2019	18
December 2019	7
January 2020	10
February 2020	6
March 2020	7
April 2020	5
May 2020	4
June 2020	5
July 2020	4
August 2020	7
September 2020	4

Article Contents

The inner knot of the Crab nebula

Abstract

1 INTRODUCTION

2 GEOMETRY OF THE TERMINATION SHOCK

3 ESTIMATES OF BASIC PARAMETERS

3.1 Low σ at the knot location

3.2 Separation from the pulsar

3.3 Transverse size

4 SYNTHETIC IMAGES

4.1 Emissivity maps

4.2 Brightness distribution

5 POLARIZATION

6 OTHER PROPERTIES

6.1 Energetics

6.2 Variability

6.3 Connection to Crab's gamma-ray flares

7 COMPARISON WITH OTHER STUDIES

8 CONCLUSION

REFERENCES

APPENDIX A: OBLIQUE RELATIVISTIC MHD SHOCKS

APPENDIX B: EMISSIVITY CALCULATIONS

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only