-
PDF
- Split View
-
Views
-
Cite
Cite
K. Pavlovskii, N. Ivanova, Mass transfer and magnetic braking in Sco X-1, Monthly Notices of the Royal Astronomical Society, Volume 456, Issue 1, 11 February 2016, Pages 263–269, https://doi.org/10.1093/mnras/stv2685
Close - Share Icon Share
Abstract
Sco X-1 is a low-mass X-ray binary (LMXB) that has one of the most precisely determined set of binary parameters such as the mass accretion rate, companions mass ratio and the orbital period. For this system, as well as for a large fraction of other well-studied LMXBs, the observationally-inferred mass accretion rate is known to strongly exceed the theoretically expected mass transfer (MT) rate. We suggest that this discrepancy can be solved by applying a modified magnetic braking prescription, which accounts for increased wind mass-loss in evolved stars compared to main sequence stars. Using our MT framework based on mesa, we explore a large range of binaries at the onset of the MT. We identify the subset of binaries for which the MT tracks cross the Sco X-1 values for the mass ratio and the orbital period. We confirm that no solution can be found for which the standard magnetic braking can provide the observed accretion rates, while wind-boosted magnetic braking can provide the observed accretion rates for many progenitor binaries that evolve to the observed orbital period and mass ratio.
1 INTRODUCTION
Sco X-1 is the first extrasolar X-ray source discovered and is the brightest persistent X-ray source beside the Sun (Giacconi et al. 1962). The source has been extensively observed since its discovery in both radio and X-ray, and is classified as a low-mass X-ray binary (LMXB) for which a number of parameters have been obtained (see Section 2).
Evolution of a close binary after the compact object formation, and, specifically, the mass transfer (MT) rate during an LMXB phase, are governed by angular momentum loss. In a persistently accreting short-period binary with a giant or subgiant donor, the dominant angular momentum loss mechanism is magnetic braking (Rappaport, Joss & Webbink 1982). It is crucial that the first detailed numerical study of the population of short-period LMXBs has shown the unexpected strong mismatch between the MT rates in the theoretical population of LMXBs and the observationally-inferred mass accretion rates of known LMXBs (Podsiadlowski, Rappaport & Pfahl 2002). Most of the observed LMXBs, including Sco X-1, were found to have their mass accretion rates at least an order of magnitude higher than the theoretically expected MT rates for the same orbital periods (although it was unclear whether observational selection effects could cause this effect).
This alarming mismatch between theory and observations, albeit mainly noticed only by theorists doing detailed studies of the MT in LMXBs, have prompted several new ideas to explain how the magnetic braking operates in LMXBs. For example, Justham, Rappaport & Podsiadlowski (2006) suggested that Ap and Bp stars with radiative envelopes, due to their high magnetic fields and stellar winds could nevertheless experience a stronger than usual magnetic braking. Another idea, also related to the nature of the donor, was that a stronger magnetic braking could be achieved in short-period LMXBs if they have pre-main sequence donors (Ivanova 2006). How the transferred material can affect the orbital evolution also was explored. For example, Yungelson & Lasota (2008) resolved the magnetic braking problem by proposing that accretion discs in LMXBs are truncated, and Chen & Li (2006) explored the role of the circumbinary disc. At the moment, none of the ideas have become the mainstream method for producing LMXBs in population studies, despite inability of the standard magnetic braking theory to explain the LMXBs that are determined well. It is important to add that all the mentioned ideas were explored on the set of very short-period LMXBs, with the orbital periods less than about 10 h, and are not applicable to LMXBs with larger orbital period, like Sco X-1.
These facts led us to revisit the way magnetic braking is treated in LMXBs with subgiant and giant donors. We take the well-observed prototype LMXB – Sco X-1 – as an example for our simulations. We provide its observationally-derived properties in Section 2. In Section 3, we outline our revised prescription for magnetic braking. We provide detailed MT simulations for the case of Sco X-1 in Section 4.
2 OBSERVED PARAMETERS OF THE SYSTEM
From spectroscopic data, Steeghs & Casares (2002) infer the upper limit of mass ratio to be 0.46 (see the brief overview of the important observed parameters in Table 1). Assuming that the lowest-velocity emission lines originate at the inner Lagrangian point, using the radio inclination data from Fomalont, Geldzahler & Bradshaw (2001) and setting the accretor mass to 1.4 M⊙ gives a probable value of mass ratio 0.30 and donor mass 0.42 M⊙, in agreement with Mata Sánchez et al. (2015), who find the donor mass to be between 0.28 and 0.70 M⊙. The orbital period of the system is the best determined quantity, and is P = 0.787313 ± 0.000015d (Hynes & Britt 2012).
| Quantity . | Value . | Reference . |
|---|---|---|
| Mass ratio | ≈0.30 but ≲ 0.46 | S02 |
| Donor spectral class | later than K4 | M15 |
| Donor luminosity class | IV | M15 |
| Period, d | 0.787 313±0.000 015 | H12 |
| Distance, kpc | 2.8±0.3 | B99 |
| X-ray flux [2–20keV], erg s−1 cm−2 | 2.4 × 10−7 | B99 |
| Bolometric flux, erg s−1 cm−2 | 3.88 × 10−7 | W08 |
| Quantity . | Value . | Reference . |
|---|---|---|
| Mass ratio | ≈0.30 but ≲ 0.46 | S02 |
| Donor spectral class | later than K4 | M15 |
| Donor luminosity class | IV | M15 |
| Period, d | 0.787 313±0.000 015 | H12 |
| Distance, kpc | 2.8±0.3 | B99 |
| X-ray flux [2–20keV], erg s−1 cm−2 | 2.4 × 10−7 | B99 |
| Bolometric flux, erg s−1 cm−2 | 3.88 × 10−7 | W08 |
| Quantity . | Value . | Reference . |
|---|---|---|
| Mass ratio | ≈0.30 but ≲ 0.46 | S02 |
| Donor spectral class | later than K4 | M15 |
| Donor luminosity class | IV | M15 |
| Period, d | 0.787 313±0.000 015 | H12 |
| Distance, kpc | 2.8±0.3 | B99 |
| X-ray flux [2–20keV], erg s−1 cm−2 | 2.4 × 10−7 | B99 |
| Bolometric flux, erg s−1 cm−2 | 3.88 × 10−7 | W08 |
| Quantity . | Value . | Reference . |
|---|---|---|
| Mass ratio | ≈0.30 but ≲ 0.46 | S02 |
| Donor spectral class | later than K4 | M15 |
| Donor luminosity class | IV | M15 |
| Period, d | 0.787 313±0.000 015 | H12 |
| Distance, kpc | 2.8±0.3 | B99 |
| X-ray flux [2–20keV], erg s−1 cm−2 | 2.4 × 10−7 | B99 |
| Bolometric flux, erg s−1 cm−2 | 3.88 × 10−7 | W08 |
The donor has been identified to have spectral class K4 or later, and its luminosity class IV, subgiant (Mata Sánchez et al. 2015). The intrinsic effective temperature of the donor then should not be hotter than 4800 K. This upper limit includes uncertainties in the spectral class determination as discussed in Cox (2000), for a subgiant the intrinsic effective temperature is likely lower than this upper limit.
The X-ray luminosity of this system, as measured in 2–20 keV range, is 2.3 × 1038 erg s− 1 (Bradshaw, Fomalont & Geldzahler 1999). An estimate of its bolometric luminosity, from the bolometric flux and distance gives |$L_{\text{b}} = 3.6\pm 0.8 \times 10^{38}\,\rm {erg\,s^{-1}}$| (Watts et al. 2008). If the accreting star is 1.4 M⊙, the accreted material is 70 per cent hydrogen and opacities are provided by Thompson scattering, then the critical Eddington luminosity for this system is LEdd, TS = 2.1 × 1038 erg s− 1. This system is slightly above the Thompson scattering limited Eddington limit. The minimum MT rate that can support this bolometric luminosity for a non-rotating neutron star is |$\skew{3}\dot{M}_{\rm min} = 3.5\pm 0.8 \times 10^{-8}\,\rm {\mathrm{M}_{\odot }\ yr^{-1}}$| (for a 1.4 M⊙ neutron star with a radius of 11.5 km), and if one takes into account only X-ray output, then |$\skew{3}\dot{M}_{\rm min}^{X} \approx 2.2 \times 10^{-8}\,\rm {\mathrm{M}_{\odot }\ yr^{-1}}$|.
There is an evidence for the presence of a jet originating at the accretor, for details see Mirabel & Rodríguez (1999). We have not found any data on the possible circumbinary disc, which means that the non-conservative mode of MT, in which the specific angular momentum of the lost material is equal to that of the accretor is plausible. The possible transient nature of Sco X-1 has, to our knowledge, never been discussed, which implies that it is in a steady state, in which the relationship between accretion rate and X-ray luminosity stays roughly the same with time.
3 MAGNETIC BRAKING
It is widely accepted that magnetic braking – the removal of the angular momentum from a rotating star by the action of a magnetically coupled stellar wind – is crucial for studies of the formation and evolution of a number of classes of close binaries. It has been most deeply addressed for the case of cataclysmic variables (for details, see Knigge, Baraffe & Patterson 2011), but it also plays an important role for LMXBs.
It was Schatzman (1962) who recognized first that the slowing down of single stars can take place when the material lost from the stellar surface is kept in corotation with the star by the magnetic field. As a result, the specific angular momentum carried by the gas is significantly greater than in a spherically symmetric stellar wind. The corotation can be achieved if a star possesses a substantial magnetic field. The strength of the magnetic field has been linked to the generation of a magnetic field by dynamo action in a deep convective envelope.
Let us estimate what MT rate the Skumanich magnetic braking provides. For a binary system, assuming a conservative MT,
The mass ratio and donor mass in Sco X-1 are not very certain. The recent paper by Mata Sánchez et al. (2015) lists the intervals for the mass of the donor from 0.28 to 0.7 M⊙ and for the mass ratio from 0.28 to 0.51. We can test the effect of this uncertainty on our estimate. We considered the combinations of mass ratios 0.28, 0.5, 0.6, 0.7 and donor masses 0.28, 0.4, 0.51 M⊙. In all considered cases the mass accretion rate following from the Skumanich law doesn't exceed 2.7 × 10− 9 M⊙ yr− 1. This ensures that the uncertainties in the mass ratio and the donor mass are not likely to be the reason for the discrepancy between the observed mass accretion rate and the theoretical estimate.
We note, however, that Sco X-1 is an evolved star. In this case, it is important to realize that Skumanich magnetic braking law was scaled to match the observations of main sequence stars. This implicitly included two assumptions: (i) the wind mass-loss is as at the main sequence rate, and (ii) the magnetic field strength is only changing with the angular velocity.
If one assumes that the Bernoulli equation is legitimate, then the other two limiting cases are that velocity at the Alfvén surface can be reduced either to the local escape velocity, or is of order ∼ΩRA. These assumptions will lead to different powers of Ω and stellar wind mass-loss rate in the magnetic braking torque, thus there is no unique way to obtain |$\skew{3}\dot{J}_{\rm MB}$|. This uncertainty is also reflected in the existence of several prescriptions for the magnetic braking law, and the use of a free value for the parameter γ in the prescription of equation (1).
Compared to main sequence stars, subgiants are generally colder, and hence the assumption of isothermal wind velocity inside the Alfvén sphere may not hold – not even considering that the wind can be accelerated by the magnetic fields. Indeed, even for the Sun, we know that the temperature of the wind is substantially higher than the surface temperature, and also that the wind is both heated and accelerated via several mechanism (e.g. Cranmer, van Ballegooijen & Edgar 2007). Therefore, the generalized, albeit convenient, Bernoulli equation as in Mestel & Spruit (1987) is not valid.
A similar consideration of a dipole field can be done by supplanting B(r) with BS(R/r)3 in equation (6). Then equations (13) and (5) would produce an angular momentum loss rate that is proportional to |$\skew{3}\dot{M}_{\rm wind} \Omega B_{\rm S}^{4/3} R^{8/3}$|. As one can see, varying the geometry of the magnetic field changes the power law with which the magnetic field enters in the functional form. But it is the assumptions on reaching the Alfvén surface for the stars’ surface escape velocity and on the density profile that keep the functional form proportional to the wind mass-loss rate.
| log10(R/R⊙) . | |${\skew{3}\dot{M}}_{\rm Reim}/{\skew{3}\dot{\text{M}}}_{\odot }$| . | |$\tau _{\rm conv} / \tau ^{\odot }_{\rm conv}$| . |
|---|---|---|
| 0.27 | 4 | 3.7 |
| 0.95 | 260 | 9.2 |
| 1.23 | 1413 | 9.9 |
| 1.43 | 4500 | 11.0 |
| 1.57 | 10325 | 11.8 |
| log10(R/R⊙) . | |${\skew{3}\dot{M}}_{\rm Reim}/{\skew{3}\dot{\text{M}}}_{\odot }$| . | |$\tau _{\rm conv} / \tau ^{\odot }_{\rm conv}$| . |
|---|---|---|
| 0.27 | 4 | 3.7 |
| 0.95 | 260 | 9.2 |
| 1.23 | 1413 | 9.9 |
| 1.43 | 4500 | 11.0 |
| 1.57 | 10325 | 11.8 |
Notes. τconv – convective turnover time-scale in the mesa model. Wind is calculated as in Reimers (1975).
| log10(R/R⊙) . | |${\skew{3}\dot{M}}_{\rm Reim}/{\skew{3}\dot{\text{M}}}_{\odot }$| . | |$\tau _{\rm conv} / \tau ^{\odot }_{\rm conv}$| . |
|---|---|---|
| 0.27 | 4 | 3.7 |
| 0.95 | 260 | 9.2 |
| 1.23 | 1413 | 9.9 |
| 1.43 | 4500 | 11.0 |
| 1.57 | 10325 | 11.8 |
| log10(R/R⊙) . | |${\skew{3}\dot{M}}_{\rm Reim}/{\skew{3}\dot{\text{M}}}_{\odot }$| . | |$\tau _{\rm conv} / \tau ^{\odot }_{\rm conv}$| . |
|---|---|---|
| 0.27 | 4 | 3.7 |
| 0.95 | 260 | 9.2 |
| 1.23 | 1413 | 9.9 |
| 1.43 | 4500 | 11.0 |
| 1.57 | 10325 | 11.8 |
Notes. τconv – convective turnover time-scale in the mesa model. Wind is calculated as in Reimers (1975).
4 DETAILED EVOLUTION AND MASS TRANSFER
For the simulation of binary MT through the inner Lagrangian point (L1), we use our framework (Pavlovskii & Ivanova 2015) based on the mesa code.1mesa is a modern set of stellar libraries described in Paxton et al. (2011, 2013). We obtain the binary evolutionary tracks for systems with varying initial parameters. The donor mass at zero-age main sequence (ZAMS) was varied from 0.9 to 1.8 M⊙ and the initial neutron star mass was varied from 1.24 to 1.6 M⊙. For a fixed combination of masses from these ranges we adjust the initial period to find the tracks that pass as close as possible to the point of q = 0.30, P = 0.787, which corresponds to the observed parameters of Sco X-1. At the initial orbital period the donor is a ZAMS star orbiting a NS. We use solar metallicity for the donor.
We assume that the compact companion was already a neutron star when the initially less massive star overfilled its Roche lobe for the first time at the subgiant stage. We assume that the accretion rate is Thompson-scattering limited to |${\skew{3}\dot{M}}_{\rm Edd, TS} = 4 \pi c R / (0.2 (1 + X))$|, where R is neutron star radius, taken to be 11.5 km, X is the hydrogen abundance in the outer layers of the donor. The excess material above |${\skew{3}\dot{M}}_{\rm Edd, TS}$| is assumed to be taken away from the system carrying the specific angular momentum of the accretor.
We also assume that the components are circularized at all times, and that magnetic braking torque applied to the donor brakes the whole system via the tidal interaction. We utilize both the standard and wind-boosted prescription for the magnetic braking.
The results of these simulations for both wind-boosted (not τ-boosted) and regular magnetic braking are shown in Figs 1, 2 and 3. As can be seen in Fig. 1, in the wind-boosted model the accretion rate at the Sco X-1 point becomes closer to the observational estimate obtained in equation (2) as the donor's initial mass increases: the rates are respectively 1.4, 1.5, 1.5, 1.5, 1.8, 2.0 × 10− 8 M⊙ yr− 1, whereas the observed rate is 2.2 × 10− 8 M⊙ yr− 1. Note also that the obtained value of accretion rate is close to the estimate obtained in Section 3. For the models utilizing the regular magnetic braking prescription (Fig. 2), accretion rates vary from 0.1 to 0.2 × 10− 8 M⊙ yr− 1, which is more than an order of magnitude less than that observed.
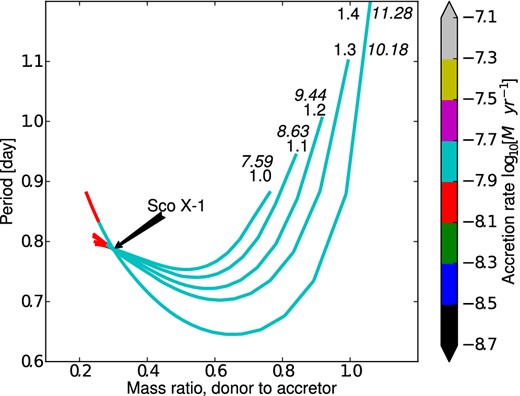
Models employing the ‘wind-boosted’ (not ‘τ-boosted’) magnetic braking law, given by equation (16). Each track corresponds to the evolution of a binary system that crosses the point corresponding to the observed parameters of Sco X-1, i.e. q = 0.30, P = 0.787. Tracks start when more than 0.01 M⊙ is accreted. Roman numbers denote initial donor mass in solar masses, italic numbers denote initial period in days. The initial NS (accretor) mass for all tracks is 1.3 M⊙. Colour denotes current mass accretion rate. Note that these simulated mass accretion rates agree with observations.
Varying the initial mass of the NS and taking more massive donors does change the shape of the tracks that pass through the Sco X-1 point, but the same feature remains unchanged: wind-boosted tracks have mass accretion rates at the Sco X-1 point comparable to the observations – for all tracks the mass accretion rate at Sco X-1 point is 2.0 × 10− 8 M⊙ yr− 1 and the unboosted tracks lack this agreement with the maximum accretion rate of 0.4 × 10− 8 M⊙ yr− 1 (see Figs 3 and 4).
Note that the shape of the tracks in Figs 3 and 4 is different from the ones in Figs 1 and 2. This is because in this case the donors overfill their Roche lobes before the deep enough convective envelope develops for the magnetic braking mechanism to start to operate. A convective envelope is established only after some mass is lost, this is when the magnetic braking switches on. These moments correspond to the turning points on the tracks. In attempt to verify if there are solutions resembling those in Fig. 1, without the turning point and with longer initial periods, we looked at the initial periods from 1.5 to 20 d for the 1.5 M⊙ donor and found no such solutions.
We find that systems with a more massive initial NS mass and donor mass experience non-conservative MT at the Sco X-1 point. For these systems, in the order of increasing donor ZAMS mass from 1.5 M⊙ to 1.9 M⊙, the MT rates are 2.3, 2.7, 3.3, 3.3, 2.5 × 10− 8 M⊙ yr− 1 (see Fig. 4). Among the tracks with initially 1.3 M⊙ accretor and 1.0 to 1.5 M⊙ donor ZAMS mass, only the one obtained with 1.5 M⊙ donor ZAMS mass is non-conservative with MT rate 2.2 × 10− 8 M⊙ yr− 1 (this track is not shown in Fig. 1). All tracks obtained with the classical magnetic braking prescription have conservative MT at the Sco X-1 point.
The effective temperature of the donor is 4661 K for 1.0 M⊙ donor and 1.3 M⊙ NS, and increases further with both initial donor mass and NS mass. For example, a 1.1 M⊙ donor with a 1.3 M⊙ NS would already have Teff = 4692 K and a 1.0 M⊙ donor with a 1.42 M⊙ NS has Teff = 4710 K. Because the maximum effective temperature of the donor is 4800 K, systems with donor ZAMS mass ≳ 1.6 M⊙ are unlikely to be the progenitors because in this case even for a 1.3 M⊙ neutron star the resulting effective temperature of the donor exceeds the 4800 K limit. If we fix the mass of the neutron star at 1.42 M⊙, then based on the observed accretion rate, the most likely ZAMS mass of the donor is between 1.4 and 1.5 M⊙.
Finally one can estimate to which degree the difference in convective turnover time-scale could affect these results. For this estimate one needs to know how the convective turnover time of the donor at the Sco X-1 point relates to the solar convective turnover time. In our models the ratio |$\tau _{\rm conv} / \tau ^{\odot }_{\rm conv}$| at the Sco X-1 point reaches 4. The magnetic braking torque could be additionally boosted by this factor, however this will not affect the mass accretion rates in those models, which already accrete at the Eddington rate, e.g. those shown in Fig. 4. We note that without any wind boost, and only considering the boost of the magnetic field due to convective turnover, the observed accretion rates can also be achieved, but we do not have detailed tracks for this case. We note that in the case when wind-boost is not taken into account, η should be taken as 2 in equation (16).
Using the wind-boosted magnetic braking law, for every considered combination of the initial masses of the donor and compact object we were able to find the initial period that led the binary system to the observed period and mass ratio of Sco X-1 and to the accretion rate comparable to that of Sco X-1. Similar to the results discussed in van der Sluys, Verbunt & Pols (2005), we see that the evolution of the orbital periods has a divergent manner, where both too short-orbital and too long-orbital period systems never arrive to Sco X-1 position. Indeed, none of the above combinations required us to set the initial orbital period of the binary to less than 1.15 d. In more details, we find two-mode behaviour that depends on whether the initial MT is conservative MT (with donors less massive than ∼1.5M⊙) or non-conservative MT (donor more massive than ∼1.5M⊙). If the donor is less massive than about 1.5 M⊙, the more massive a donor is, the weaker the dependence of period at q = 0.3 is on the initial period. For donors more massive than 1.5 M⊙ the tendency reverses: the higher is the donor mass, the stronger is the dependence of final period on the initial period. We therefore conclude that we have analysed the entire initial orbital period range that can produce binary systems at the orbital period as in Sco X-1.
5 CONCLUSION
We have conducted detailed simulations of the binary evolution of Sco X-1. Our simulations show that the commonly used prescription for magnetic braking, which is based on the observations of MS stars, is insufficient to explain the case of Sco X-1, where the donor is an evolved star (subgiant). Namely it provides a substantially lower mass accretion rate than observed, by at least an order of magnitude.
We suggest a different model of magnetic braking, which is suitable for stars with strong winds, such as the subgiant donor in Sco X-1. It turns out that this new model makes possible the formation of a binary system with the parameters that closely match Sco X-1 from a wide range of systems. In select models (see Fig. 4) with the observed period and mass ratio of Sco X-1 we obtain as little as ≈10 per cent discrepancy between the simulated and observed accretion rate and in all cases the accretion rate is comparable to the observations. The commonly used prescription gives approximately an order of magnitude lower accretion rate than observed.
Based solely on the known period, mass ratio and accretion rate, we couldn't constrain the parameters of the possible progenitor system. By varying the initial period we were able to obtain a binary with the observed period, mass ratio and comparable mass accretion rate from initial NS masses in the range of 1.24 to 1.6 M⊙ and donor ZAMS masses from 1.0 to 1.6 M⊙. However, based on the maximum effective temperature of the donor, which is 4800 K, the systems with donor ZAMS mass ≳ 1.6 M⊙ are unlikely to be the progenitors because in this case even for a 1.3 M⊙ neutron star the resulting effective temperature of the donor exceeds the 4800 K limit. We find that the effective temperature of the Sco X-1 donor rises with both the donor ZAMS mass and the initial NS mass. Under the standard assumption that the NS mass is 1.42 M⊙, the most likely ZAMS mass of the donor is from 1.4 to 1.5 M⊙, based on the observed accretion rate.
To make sure that the origin of a neutron star (e.g. whether it was formed via electron capture instead of core collapse) does not affect the theoretically anticipated mass accretion rate, we also tested initially less massive neutron stars, 1.24 M⊙. As can be expected from the estimates provided in Section 3, in the case of the standard magnetic braking, the accretion rates at which the binaries with low-mass neutron stars reach the Sco X-1 point (in terms of mass ratio and period) are much lower than observed in Sco X-1. At the same time, both initially less massive (1.24 M⊙) and more massive (1.42 M⊙) neutron stars have accretion rates comparable to the observations at the Sco X-1 point with wind-boosted magnetic braking prescription. Thus, although it is not possible to infer from our simulations whether or not Sco X-1 underwent accretion-induced collapse in the past, if it did, the regular magnetic braking scheme is still not sufficient to explain the observed accretion rate.
Without additional detailed simulations we can not rule out the possibility that a different mass ratio of the Sco X-1 could change the accretion rate anticipated from the standard magnetic braking scheme in a way that the difference between it and the observed value becomes smaller than an order of magnitude. However, based on the estimates conducted in Section 3 we consider that this is unlikely.
Keeping in mind the existing problems with binary simulations of the known LMXBs, we anticipate that this new magnetic braking model can (and should) be used in the simulations of other LMXBs with giant or subgiant donor and a compact accretor. For example, for the majority of LMXBs mentioned in Podsiadlowski et al. (2002), the observed mass accretion rate is approximately an order of magnitude higher than expected. There is also a major mismatch between the observed period decay in A0620-00 and the period decay expected for this system from the standard magnetic braking prescription. The observed decay is ∼ 0.6 ms yr− 1 (González Hernández, Rebolo & Casares 2014). An estimate that assumes conservative MT and the standard magnetic braking law with γ = 3 (equation 1) provides the period decay to be ∼ 0.05 ms yr− 1 (see also for discussion González Hernández et al. 2014). Applying the wind-boosted modified magnetic braking law we obtain the decay of 0.35 ms yr− 1, which is closer to the observed value; τ-boost that increases the surface magnetic field can explain remaining discrepancy. We note that this system is a candidate circumbinary disc systems (Wang & Wang 2014), and hence may have an additional mode for the angular momentum loss.
The LMXBs in elliptical galaxies, where they are thought to be the main source of X-ray radiation, can be observed with quite low detection limits of ∼ 1036erg s− 1. These data can be used in conjunction with population synthesis models to examine the formation scenarios of LMXBs. When an X-ray luminosity function (XLF) of an elliptical galaxy is simulated with population synthesis models, it turns out to be very sensitive to the magnetic braking prescription used (Fragos et al. 2008). Depending on the other free parameters of the population synthesis model, the discrepancy between XLFs obtained from different magnetic braking prescriptions reaches an order of magnitude. The probability that a simulated XLF is consistent with the observed one also differs drastically for different magnetic braking prescriptions, from practically zero to comparable to unity, and the majority of population synthesis models still gives results that are very unlikely to be consistent with the observations (Fragos et al. 2008). With the boosted model for magnetic braking, we also can foresee that not only mass accretion rates can be different, but also a class of LMXB systems, deemed to be transient with the standard magnetic braking, will become persistent. We anticipate that the new generation of population synthesis models made to simulate the XLF functions of elliptical galaxies, if switched to our modified model of magnetic braking, might give substantially different results.
KP was supported by Golden Bell Jar Scholarship. NI thanks NSERC Discovery and Canada Research Chairs Program. This research has been enabled by the use of computing resources provided by WestGrid and Compute/Calcul Canada.
Modules for Experiments in Stellar Astrophysics, http://mesa.sourceforge.net
REFERENCES






